|
| 1 | +--- |
| 2 | +title: MPC控制自行车模型沿轨迹运动 |
| 3 | +date: |
| 4 | + created: 2024-12-03 |
| 5 | + updated: 2024-12-03 |
| 6 | +categories: |
| 7 | + - 机器人 |
| 8 | +--- |
| 9 | + |
| 10 | +!!! quote |
| 11 | + |
| 12 | + 本文内容主要参考自 [深蓝学院-移动机器人运动规划](https://www.shenlanxueyuan.com/course/633) |
| 13 | + |
| 14 | +<!-- more --> |
| 15 | + |
| 16 | +## 1. 运动学自行车模型(Kinematic Bicycle Model) |
| 17 | + |
| 18 | +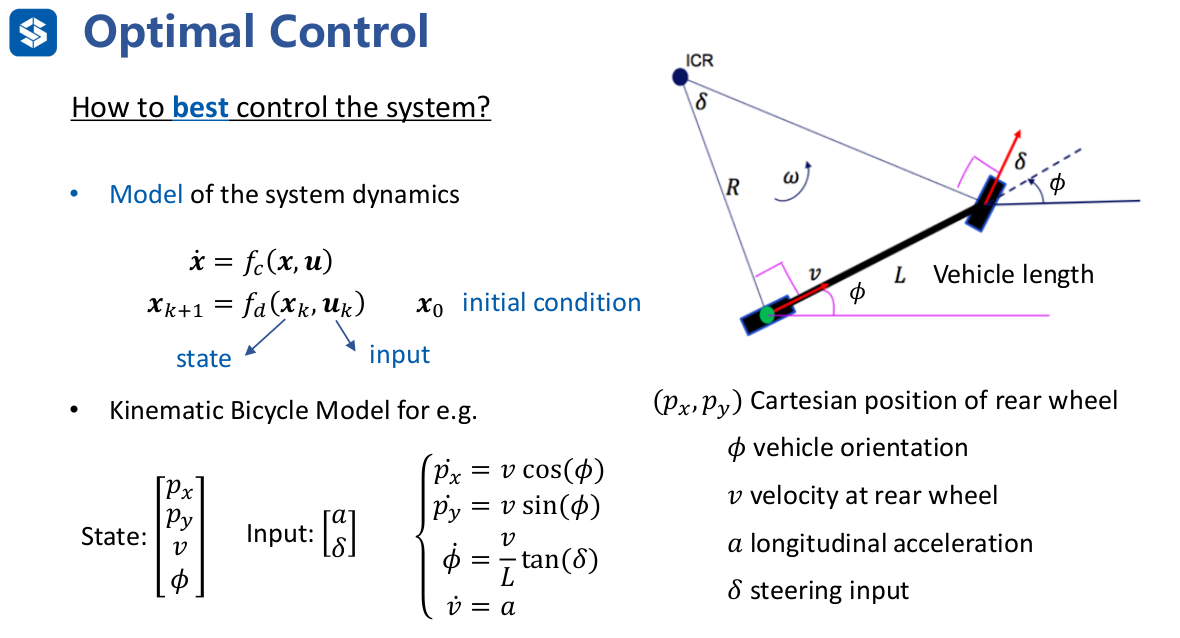 |
| 19 | + |
| 20 | +$$ |
| 21 | +\boldsymbol{\dot{x}} = \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\phi} \\ \dot{v} \end{bmatrix} = \begin{bmatrix} v \cos(\phi) \\ v \sin(\phi) \\ \frac{v}{L} \tan(\delta) \\ a \end{bmatrix} = f(\boldsymbol{x}, \boldsymbol{u}), \quad \boldsymbol{x} = \begin{bmatrix} x \\ y \\ \phi \\ v \end{bmatrix}, \quad \boldsymbol{u} = \begin{bmatrix} a \\ \delta \end{bmatrix} |
| 22 | +$$ |
| 23 | + |
| 24 | +## 2. 非线性时变模型线性化 |
| 25 | + |
| 26 | +如1所示,自行车模型是一个非线性时变模型,我们希望将其线性化,当系统的状态$x=\overline{\boldsymbol{x}}$,输入$u=\overline{\boldsymbol{u}}$时,有: |
| 27 | + |
| 28 | +$$ |
| 29 | +\boldsymbol{\dot{x}} = f(\overline{\boldsymbol{x}}, \overline{\boldsymbol{u}}) + \frac{\partial f}{\partial \boldsymbol{x}} (\boldsymbol{x} - \overline{\boldsymbol{x}}) + \frac{\partial f}{\partial \boldsymbol{u}} (\boldsymbol{u} - \overline{\boldsymbol{u}}) = A_c \boldsymbol{x} + B_c \boldsymbol{u} + g_c |
| 30 | +$$ |
| 31 | + |
| 32 | +根据线性化公式,我们可以得到线性化以后的自行车模型: |
| 33 | + |
| 34 | +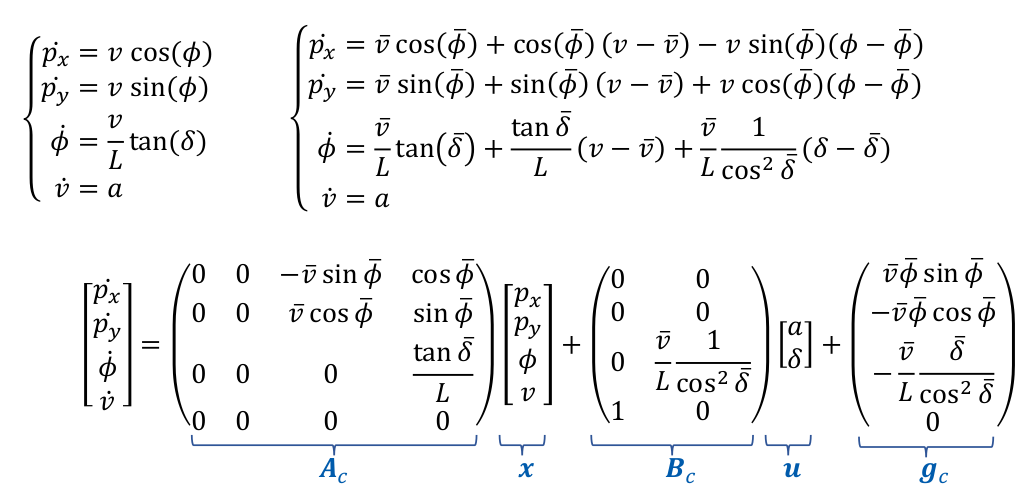 |
| 35 | + |
| 36 | +## 3. 线性时变模型离散化 |
| 37 | + |
| 38 | +$$ |
| 39 | +\begin{aligned} |
| 40 | +\boldsymbol{\dot{x}} &= A_c \boldsymbol{x} + B_c \boldsymbol{u} + g_c \\ |
| 41 | +\frac{\boldsymbol{x}_{k+1} - \boldsymbol{x}_k}{T_s} &= A_c \boldsymbol{x}_k + B_c \boldsymbol{u}_k + g_c \\ |
| 42 | +\boldsymbol{x}_{k+1} &= (\boldsymbol{I} + T_s A_c) \boldsymbol{x}_k + T_s B_c \boldsymbol{u}_k + T_s g_c \\ |
| 43 | +\boldsymbol{x}_{k+1} &= A_d \boldsymbol{x}_k + B_d \boldsymbol{u}_k + g_d |
| 44 | +\end{aligned} |
| 45 | +$$ |
| 46 | + |
| 47 | +$$ |
| 48 | +\boldsymbol{x}_{k+1} = A_d \boldsymbol{x}_k + B_d \boldsymbol{u}_k + g_d \\ |
| 49 | +其中:A_d = \boldsymbol{I} + T_s A_c, \quad B_d = T_s B_c, \quad g_d = T_s g_c |
| 50 | +$$ |
| 51 | + |
| 52 | +## 4. 成本函数(Cost Function) |
| 53 | + |
| 54 | +成本函数一般由状态转移成本和终端状态成本组成: |
| 55 | + |
| 56 | +$$ |
| 57 | +J = \sum_{k=0}^{N-1} q(\boldsymbol{x}_k, \boldsymbol{u}_k) + p(\boldsymbol{x}_N) |
| 58 | +$$ |
| 59 | + |
| 60 | +在本次任务中,我们希望自行车模型沿着轨迹运动,因此我们希望小车当前位置误差和朝向误差最小,即: |
| 61 | + |
| 62 | +$$ |
| 63 | +q(\boldsymbol{x}_k, \boldsymbol{u}_k) = (x_{k+1} - x_{k+1}^{ref})^2 + (y_{k+1} - y_{k+1}^{ref})^2 + \rho(\phi_{k+1} - \phi_{k+1}^{ref})^2 |
| 64 | +$$ |
| 65 | + |
| 66 | +同时,为了保持系统的稳定性,加上终端状态成本(**TODO:MPC stability and feasibility**): |
| 67 | + |
| 68 | +$$ |
| 69 | +p(\boldsymbol{x}_N) = \rho_N (x_N - x_N^{ref})^2 + \rho_N (y_N - y_N^{ref})^2 + (v_N - v_N^{ref})^2 + \rho*\rho_N (\phi_N - \phi_N^{ref})^2 |
| 70 | +$$ |
| 71 | + |
| 72 | +因此我们定义: |
| 73 | + |
| 74 | +$$ |
| 75 | +X = \begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_{N-1} \end{bmatrix}, |
| 76 | +X_{ref} = \begin{bmatrix} x_1^{ref} \\ x_2^{ref} \\ \cdots \\ x_{N-1}^{ref} \end{bmatrix}, |
| 77 | +U = \begin{bmatrix} u_0 \\ u_1 \\ \cdots \\ u_{N} \end{bmatrix} |
| 78 | +$$ |
| 79 | + |
| 80 | +$$ |
| 81 | +\boldsymbol{Q}=\quad |
| 82 | +\begin{pmatrix} |
| 83 | +\begin{bmatrix} |
| 84 | +1 & 0 & 0 & 0 \\ |
| 85 | +0 & 1 & 0 & 0 \\ |
| 86 | +0 & 0 & \rho & 0 \\ |
| 87 | +0 & 0 & 0 & 0 \\ |
| 88 | +\end{bmatrix} \\ |
| 89 | + & |
| 90 | +\begin{bmatrix} |
| 91 | +1 & 0 & 0 & 0 \\ |
| 92 | +0 & 1 & 0 & 0 \\ |
| 93 | +0 & 0 & \rho & 0 \\ |
| 94 | +0 & 0 & 0 & 0 |
| 95 | +\end{bmatrix} \\ |
| 96 | + & & \ddots \\ |
| 97 | + & & & |
| 98 | +\begin{bmatrix} |
| 99 | +\rho_N & 0 & 0 & 0 \\ |
| 100 | +0 & \rho_N & 0 & 0 \\ |
| 101 | +0 & 0 & \rho*\rho_N & 0 \\ |
| 102 | +0 & 0 & 0 & 1 |
| 103 | +\end{bmatrix} |
| 104 | +\end{pmatrix} |
| 105 | +$$ |
| 106 | + |
| 107 | +则有: |
| 108 | + |
| 109 | +$$ |
| 110 | +J = \frac{1}{2}(X - X_{ref})^T \boldsymbol{Q} (X - X_{ref}) |
| 111 | +$$ |
| 112 | + |
| 113 | +## 5. 约束条件(Constraints) |
| 114 | + |
| 115 | +$$ |
| 116 | +\begin{aligned} |
| 117 | +-v_{max} \leq &v_k \leq v_{max} \\ |
| 118 | +-a_{max} \leq &a_k \leq a_{max} \\ |
| 119 | +-\delta_{max} \leq &\delta_k \leq \delta_{max} \\ |
| 120 | +-\dot{\delta}_{max} \leq &\dot{\delta}_k \leq \dot{\delta}_{max} |
| 121 | +\end{aligned} |
| 122 | +$$ |
| 123 | + |
| 124 | +上述约束条件中$v_k$是状态变量,$a_k$、$\delta_k$是控制变量,而$\dot{\delta}_k$既不是状态变量也不是控制变量,因此需要进行转换 |
| 125 | + |
| 126 | +$$ |
| 127 | +\begin{aligned} |
| 128 | +&\dot{\delta}_k = \frac{\delta_{k} - \delta_{k-1}}{T_s} \\ |
| 129 | +=> - &\delta_{max}*T_s \leq \delta_{k} - \delta_{k-1} \leq \delta_{max}*T_s |
| 130 | +\end{aligned} |
| 131 | +$$ |
| 132 | + |
| 133 | +### 5.1 状态变量的线性约束 |
| 134 | + |
| 135 | +$$ |
| 136 | +\boldsymbol{l}_x \leq \boldsymbol{C}_x X \leq \boldsymbol{u}_x |
| 137 | +$$ |
| 138 | + |
| 139 | +其中 |
| 140 | + |
| 141 | +$$ |
| 142 | +\boldsymbol{l}_x = |
| 143 | +\begin{pmatrix} |
| 144 | +-v_{max} \\ |
| 145 | +-v_{max} \\ |
| 146 | +\vdots \\ |
| 147 | +-v_{max} |
| 148 | +\end{pmatrix} |
| 149 | +\boldsymbol{u}_x = |
| 150 | +\begin{pmatrix} |
| 151 | +v_{max} \\ |
| 152 | +v_{max} \\ |
| 153 | +\vdots \\ |
| 154 | +v_{max} |
| 155 | +\end{pmatrix} |
| 156 | +\boldsymbol{C}_x = |
| 157 | +\begin{pmatrix} |
| 158 | +\begin{bmatrix} |
| 159 | +0 & 0 & 0 & 1 |
| 160 | +\end{bmatrix} \\ |
| 161 | +& \ddots \\ |
| 162 | +& & \begin{bmatrix} |
| 163 | +0 & 0 & 0 & 1 |
| 164 | +\end{bmatrix} |
| 165 | +\end{pmatrix} |
| 166 | +$$ |
| 167 | + |
| 168 | +### 5.2 控制变量的线性约束 |
| 169 | + |
| 170 | +$$ |
| 171 | +\boldsymbol{l}_u \leq \boldsymbol{C}_u U \leq \boldsymbol{u}_u |
| 172 | +$$ |
| 173 | + |
| 174 | +其中 |
| 175 | + |
| 176 | +$$ |
| 177 | +\scriptsize |
| 178 | +\boldsymbol{l}_u = |
| 179 | +\begin{pmatrix} |
| 180 | +\begin{bmatrix} |
| 181 | +-a_{max} \\ -\delta_{max} \\ -\delta_{max}*T_s |
| 182 | +\end{bmatrix} \\ |
| 183 | +\begin{bmatrix} |
| 184 | +-a_{max} \\ -\delta_{max} \\ -\delta_{max}*T_s |
| 185 | +\end{bmatrix} \\ |
| 186 | +\vdots \\ |
| 187 | +\begin{bmatrix} |
| 188 | +-a_{max} \\ -\delta_{max} \\ -\delta_{max}*T_s |
| 189 | +\end{bmatrix} |
| 190 | +\end{pmatrix} |
| 191 | +\boldsymbol{u}_u = |
| 192 | +\begin{pmatrix} |
| 193 | +\begin{bmatrix} |
| 194 | +a_{max} \\ \delta_{max} \\ \delta_{max}*T_s |
| 195 | +\end{bmatrix} \\ |
| 196 | +\begin{bmatrix} |
| 197 | +a_{max} \\ \delta_{max} \\ \delta_{max}*T_s |
| 198 | +\end{bmatrix} \\ |
| 199 | +\vdots \\ |
| 200 | +\begin{bmatrix} |
| 201 | +a_{max} \\ \delta_{max} \\ \delta_{max}*T_s |
| 202 | +\end{bmatrix} |
| 203 | +\end{pmatrix} |
| 204 | +\boldsymbol{C}_u = |
| 205 | +\begin{pmatrix} |
| 206 | +\begin{bmatrix} |
| 207 | +1 & 0 \\ |
| 208 | +0 & 1 \\ |
| 209 | +0 & 1 |
| 210 | +\end{bmatrix} |
| 211 | +& & \\ |
| 212 | +\begin{bmatrix} |
| 213 | +0 & 0 \\ |
| 214 | +0 & 0 \\ |
| 215 | +0 & -1 |
| 216 | +\end{bmatrix} & |
| 217 | +\begin{bmatrix} |
| 218 | +1 & 0 \\ |
| 219 | +0 & 1 \\ |
| 220 | +0 & 1 |
| 221 | +\end{bmatrix} \\ |
| 222 | +& & \ddots \\ |
| 223 | +& & |
| 224 | +\begin{bmatrix} |
| 225 | +0 & 0 \\ |
| 226 | +0 & 0 \\ |
| 227 | +0 & -1 |
| 228 | +\end{bmatrix} & |
| 229 | +\begin{bmatrix} |
| 230 | +1 & 0 \\ |
| 231 | +0 & 1 \\ |
| 232 | +0 & 1 |
| 233 | +\end{bmatrix} |
| 234 | +\end{pmatrix} |
| 235 | +$$ |
| 236 | + |
| 237 | +## 6. 使用OSQP求解二次规划问题 |
| 238 | + |
| 239 | +!!! quote "OSQP文档: [OSQP](https://osqp.org/docs/index.html)" |
| 240 | + |
| 241 | +  |
| 242 | + |
| 243 | +由于我们需要求解的变量是$U$, 因此需要使用系统状态方程将$X$表示为$U$的函数: |
| 244 | + |
| 245 | +由3中的线性时变模型离散化公式,需要注意,将系统线性化的过程是基于当前状态的,即每个$x_{k+1}$对应的$A_d、B_d、g_d$都是不同的,以下分别记为$A_k、B_k、g_k$,则有: |
| 246 | + |
| 247 | +$$ |
| 248 | +\begin{aligned} |
| 249 | +\boldsymbol{x}_1 &= A_0 \boldsymbol{x}_0 + B_0 \boldsymbol{u}_0 + g_0 \\ |
| 250 | +\boldsymbol{x}_2 &= A_1 \boldsymbol{x}_1 + B_1 \boldsymbol{u}_1 + g_1 = A_1 A_0 \boldsymbol{x}_0 + A_1 B_0 \boldsymbol{u}_0 + A_1 g_0 + B_1 \boldsymbol{u}_1 + g_1 \\ |
| 251 | +\vdots \\ |
| 252 | +\boldsymbol{x}_N &= A_{N-1} \boldsymbol{x}_{N-1} + B_{N-1} \boldsymbol{u}_{N-1} + g_{N-1} |
| 253 | +\end{aligned} |
| 254 | +$$ |
| 255 | + |
| 256 | +由此可得 |
| 257 | + |
| 258 | +$$ |
| 259 | +X = A \boldsymbol{x}_0 + B U + G \\ |
| 260 | +$$ |
| 261 | + |
| 262 | +其中: |
| 263 | + |
| 264 | +$$ |
| 265 | +\small |
| 266 | +A = \begin{bmatrix} |
| 267 | +A_0 \\ |
| 268 | +A_1 A_0 \\ |
| 269 | +\vdots \\ |
| 270 | +\prod_{k=0}^{N-1} A_k |
| 271 | +\end{bmatrix} |
| 272 | +B = \begin{bmatrix} |
| 273 | +B_0 & 0 & \cdots & 0 & 0 \\ |
| 274 | +A_1 B_0 & B_1 & 0 & \cdots & 0 \\ |
| 275 | +\vdots & \vdots & \vdots & \vdots & \vdots \\ |
| 276 | +\prod_{k=1}^{N-1} A_k B_0 & \prod_{k=2}^{N-1} A_k B_1 & \cdots & A_{N-1} B_{N-2} & B_{N-1} |
| 277 | +\end{bmatrix} |
| 278 | +G = \begin{bmatrix} |
| 279 | +g_0 \\ |
| 280 | +A_1 g_0 + g_1 \\ |
| 281 | +\vdots \\ |
| 282 | +\sum_{k=0}^{N-2} (\prod_{i=k+1}^{N-1} A_i) g_k + g_{N-1} |
| 283 | +\end{bmatrix} |
| 284 | +$$ |
| 285 | + |
| 286 | +### 6.1 成本函数 |
| 287 | + |
| 288 | +由4中的成本函数,将上式带入,消去$X$,得到: |
| 289 | + |
| 290 | +$$ |
| 291 | +\begin{aligned} |
| 292 | +J &= \frac {1}{2} (A \boldsymbol{x}_0 + B U + G - X_{ref})^T \boldsymbol{Q} (A \boldsymbol{x}_0 + B U + G - X_{ref}) \\ |
| 293 | +&= \frac {1}{2} (B U + (A \boldsymbol{x}_0 + G - X_{ref}))^T \boldsymbol{Q} (B U + (A \boldsymbol{x}_0 + G - X_{ref})) \\ |
| 294 | +&= \frac {1}{2} U^T B^T \boldsymbol{Q} B U + (A \boldsymbol{x}_0 + G - X_{ref})^T \boldsymbol{Q} B U + \frac {1}{2} (A \boldsymbol{x}_0 + G - X_{ref})^T \boldsymbol{Q} (A \boldsymbol{x}_0 + G - X_{ref}). |
| 295 | +\end{aligned} |
| 296 | +$$ |
| 297 | + |
| 298 | +只保留和$U$相关的项,得到: |
| 299 | + |
| 300 | +$$ |
| 301 | +J = \frac {1}{2} U^T (B^T \boldsymbol{Q} B) U + (A \boldsymbol{x}_0 + G - X_{ref})^T \boldsymbol{Q} B U |
| 302 | +$$ |
| 303 | + |
| 304 | +### 6.2 约束条件 |
| 305 | + |
| 306 | +将系统状态方程带入5.1式,得到: |
| 307 | + |
| 308 | +$$ |
| 309 | +\begin{aligned} |
| 310 | +\boldsymbol{l}_x \leq &\boldsymbol{C}_x X \leq \boldsymbol{u}_x \\ |
| 311 | +\boldsymbol{l}_x \leq &\boldsymbol{C}_x (A \boldsymbol{x}_0 + B U + G) \leq \boldsymbol{u}_x \\ |
| 312 | +\boldsymbol{l}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G \leq &\boldsymbol{C}_x B U \leq \boldsymbol{u}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G |
| 313 | +\end{aligned} |
| 314 | +$$ |
| 315 | + |
| 316 | +由此可得: |
| 317 | + |
| 318 | +$$ |
| 319 | +\begin{bmatrix} |
| 320 | +\boldsymbol{l}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G \\ |
| 321 | +\boldsymbol{l}_u |
| 322 | +\end{bmatrix} |
| 323 | +\leq |
| 324 | +\begin{bmatrix} |
| 325 | +\boldsymbol{C}_x B \\ |
| 326 | +\boldsymbol{C}_u |
| 327 | +\end{bmatrix} |
| 328 | +U |
| 329 | +\leq |
| 330 | +\begin{bmatrix} |
| 331 | +\boldsymbol{u}_x - \boldsymbol{C}_x A \boldsymbol{x}_0 - \boldsymbol{C}_x G \\ |
| 332 | +\boldsymbol{u}_u |
| 333 | +\end{bmatrix} |
| 334 | +$$ |
| 335 | + |
| 336 | +## 7. 系统时延处理 |
| 337 | + |
| 338 | +假设系统时延为$\tau$, 则意味着当前时刻的控制量$u(t)$需要作用于$t+\tau$时刻的系统,如果我们把系统的初始状态$\hat{x}_0$定义成$\tau$时刻的状态,则同样可以利用之前所述内容进行求解。 |
| 339 | + |
| 340 | +对于一个系统$\dot{x} = f(x, u), x(0) = x_0$, 求解其$\tau$时刻的状态$x(\tau)$,可以使用Runge-Kutta方法进行数值求解,具体公式如下: |
| 341 | + |
| 342 | +$$ |
| 343 | +x_{n+1} = x_n + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4) |
| 344 | +$$ |
| 345 | + |
| 346 | +其中: |
| 347 | + |
| 348 | +$$ |
| 349 | +\begin{aligned} |
| 350 | +k_1 &= w(t_n, x_n) \\ |
| 351 | +k_2 &= w(t_n + \frac{h}{2}, x_n + \frac{h}{2}k_1) \\ |
| 352 | +k_3 &= w(t_n + \frac{h}{2}, x_n + \frac{h}{2}k_2) \\ |
| 353 | +k_4 &= w(t_n + h, x_n + hk_3) \\ |
| 354 | +\end{aligned} |
| 355 | +$$ |
0 commit comments