Skip to content

Latest commit

 

History

History
200 lines (172 loc) · 6.25 KB

README.md

File metadata and controls

200 lines (172 loc) · 6.25 KB
Raw

最小二乘法拟合曲线

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。 利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。 最小二乘法还可用于曲线拟合。

应用程序简介

如图为应用程序的主界面，通过导入数据按钮，可以导入需要拟合的数据：

数据的格式为txt，其内容如下：

1880	0.01
1890	0.02
1900	0.03
1910	0.04
1920	0.06
1930	0.08
1940	0.10
1950	0.13
1960	0.18
1970	0.24
1980	0.32

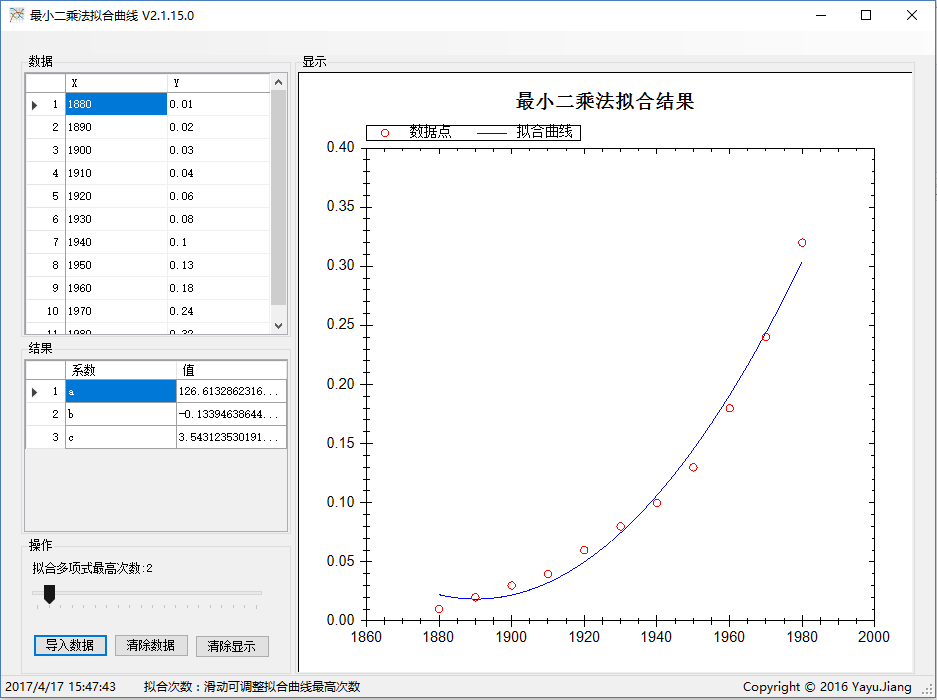
其中第一列表示横坐标x，第二列表示纵坐标y，一行表示一个点坐标，中间用制表符隔开。 导入数据后，显示导入数据，并自动计算拟合结果和生成图像。

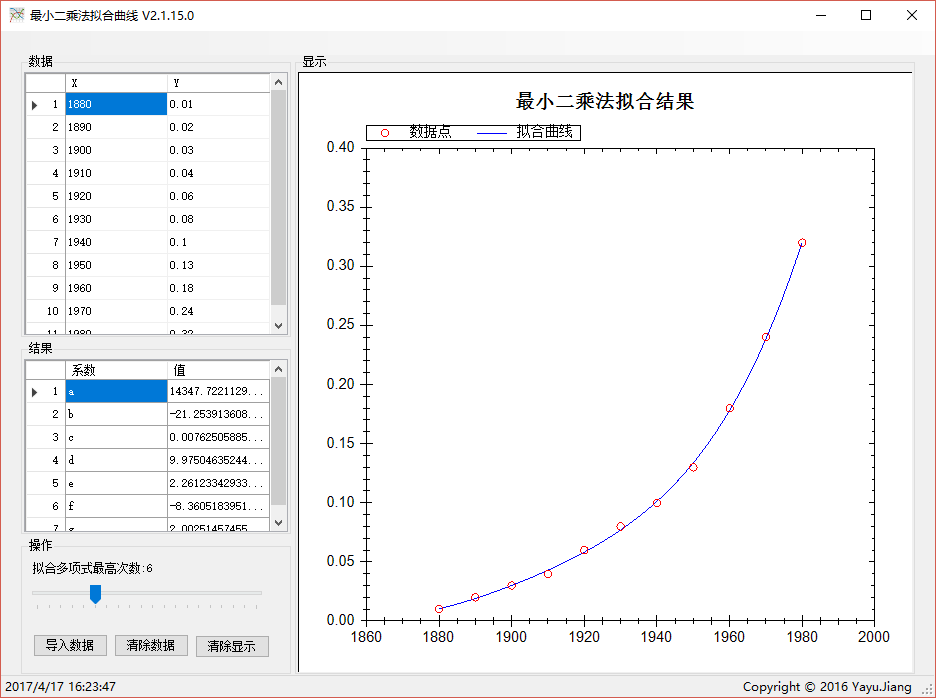
结果中将显示形如y=a+bx+cx^2+...拟合多项式的各项系数a,b,c...，滑动滑块可以调整拟合多项式的最高次数，拟合多项式结果和拟合曲线的图像会实时更新，如下为多项式最高次数为6的拟合结果：

核心代码

最小二乘拟合模块

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace 最小二乘法拟合曲线
{
    
    public static class LeastSquares
    {
        ///<summary>
        ///用最小二乘法拟合二元多次曲线
        ///例如y=ax+b
        ///其中MultiLine将返回a，b两个参数。
        ///a对应MultiLine[1]
        ///b对应MultiLine[0]
        ///</summary>
        ///<param name="arrX">已知点的x坐标集合</param>
        ///<param name="arrY">已知点的y坐标集合</param>
        ///<param name="length">已知点的个数</param>
        ///<param name="dimension">方程的最高次数</param>
        public static double[] MultiLine(double[] arrX, double[] arrY, int length, int dimension)//二元多次线性方程拟合曲线
        {
            int n = dimension + 1;                  //dimension次方程需要求 dimension+1个 系数
            double[,] Guass = new double[n, n + 1];      //高斯矩阵 例如：y=a0+a1*x+a2*x*x
            for (int i = 0; i < n; i++)
            {
                int j;
                for (j = 0; j < n; j++)
                {
                    Guass[i, j] = SumArr(arrX, j + i, length);
                }
                Guass[i, j] = SumArr(arrX, i, arrY, 1, length);
            }

            return ComputGauss(Guass, n);

        }
        private static double SumArr(double[] arr, int n, int length) //求数组的元素的n次方的和
        {
            double s = 0;
            for (int i = 0; i < length; i++)
            {
                if (arr[i] != 0 || n != 0)
                    s = s + Math.Pow(arr[i], n);
                else
                    s = s + 1;
            }
            return s;
        }
        private static double SumArr(double[] arr1, int n1, double[] arr2, int n2, int length)
        {
            double s = 0;
            for (int i = 0; i < length; i++)
            {
                if ((arr1[i] != 0 || n1 != 0) && (arr2[i] != 0 || n2 != 0))
                    s = s + Math.Pow(arr1[i], n1) * Math.Pow(arr2[i], n2);
                else
                    s = s + 1;
            }
            return s;

        }
        private static double[] ComputGauss(double[,] Guass, int n)
        {
            int i, j;
            int k, m;
            double temp;
            double max;
            double s;
            double[] x = new double[n];

            for (i = 0; i < n; i++) x[i] = 0.0;//初始化
            for (j = 0; j < n; j++)
            {
                max = 0;

                k = j;
                for (i = j; i < n; i++)
                {
                    if (Math.Abs(Guass[i, j]) > max)
                    {
                        max = Guass[i, j];
                        k = i;
                    }
                }
               if (k != j)
                {
                    for (m = j; m < n + 1; m++)
                    {
                        temp = Guass[j, m];
                        Guass[j, m] = Guass[k, m];
                        Guass[k, m] = temp;
                    }
                }
                if (0 == max)
                {
                    // "此线性方程为奇异线性方程" 
                   return x;
                }

                for (i = j + 1; i < n; i++)
                {
                    s = Guass[i, j];
                    for (m = j; m < n + 1; m++)
                    {
                        Guass[i, m] = Guass[i, m] - Guass[j, m] * s / (Guass[j, j]);
                    }
                }
            }

            for (i = n - 1; i >= 0; i--)
            {
                s = 0;
                for (j = i + 1; j < n; j++)
                {
                    s = s + Guass[i, j] * x[j];
                }
                x[i] = (Guass[i, n] - s) / Guass[i, i];
            }
            return x;
        }

    }
}

曲线绘制模块

  此处的函数图像的显示使用的是ZedGraph控件,其Sourceforge的下载地址为：https://sourceforge.net/projects/zedgraph/   绘图部分的实现如下：

zedGraph.GraphPane.CurveList.Clear();
zedGraph.IsShowPointValues = true;
zedGraph.GraphPane.Title = "最小二乘法拟合结果";
zedGraph.GraphPane.XAxis.Title = "";
zedGraph.GraphPane.YAxis.Title = "";

LineItem curve = zedGraph.GraphPane.AddCurve("数据点", X, Y, Color.Red, SymbolType.Circle);
curve.Line.IsVisible = false;

double[] Xs = new double[1000];
double[] Ys = new double[1000];
Xs[0] = X[0];
Ys[0] = getYvalue(Xs[0], args);
double step = (max(X) - min(X)) / 1000;
for (int i = 1; i < 1000; i++)
{
    Xs[i] = Xs[i - 1] + step;
    Ys[i] = getYvalue(Xs[i], args);
}

zedGraph.GraphPane.AddCurve("拟合曲线", Xs, Ys, Color.Blue, SymbolType.None);
zedGraph.AxisChange();
zedGraph.Invalidate();