appendix-misc-1.tex

%\title{
%	Miscellaneous Concepts
%}
\graphicspath{{/home/chaztikov/git/IBPINN/unc-dissertation/}}
%	{/home/chaztikov/git/IBPINN/unc-dissertation/notes/ref/Miscellaneous Concepts/images/}}

\section{Generalized Polynomial Chaos}

In this section, we briefly introduce the generalized Polynomial Chaos (gPC) expansion, an efficient method for assessing how the uncertainties in a model input manifest in its output. Later in Section gPC Based Surrogate Modeling Accelerated via Transfer Learning, we show how the gPC can be used as a surrogate for shape parameterization in both of the tessellated and constructive solid geometry modules.

The $p-t h$ degree $\mathrm{gPC}$ expansion for a $d$-dimensional input $\boldsymbol{\Xi}$ takes the following form

$$
u_{p}(\boldsymbol{\Xi})=\sum_{\mathbf{i} \in \Lambda_{p, d}} c_{\mathbf{i}} \psi_{\mathbf{i}}(\boldsymbol{\Xi})
$$

where $\mathbf{i}$ is a multi-index and $\Lambda_{p, d}$ is the set of multi-indices defined as

$$
\Lambda_{p, d}=\left\{\mathbf{i} \in \mathbb{N}_{0}^{d}:\|\mathbf{i}\|_{1} \leq p\right\},
$$

and the cardinality of $\Lambda_{d, p}$ is

$$
C=\left|\Lambda_{p, d}\right|=\frac{(p+d) !}{p ! d !}
$$

$\left\{c_{\mathbf{i}}\right\}_{\mathbf{i} \in \mathbb{N}_{0}^{d}}$ is the set of unknown coefficients of the expansion, and can be determined based on the methods of stochastic Galerkin, stochastic collocation, or least square ${ }^{2}$. For the example presented in this user guide, we will use the least square method. Although the number of required samples to solve this least square problem is $C$, it is recommended to use at least $2 C$ samples for a reasonable accuracy ${ }^{2} .\left\{\psi_{\mathbf{i}}\right\}_{\mathbf{i} \in \mathbb{N}_{0}^{d}}$ is the set of orthonormal basis functions that satisfy the following condition

$$
\int \psi_{\mathbf{m}}(\xi) \psi_{\mathbf{n}}(\xi) \rho(\xi) d \xi=\delta_{\mathbf{m n}}, \quad \mathbf{m}, \mathbf{n} \in \mathbb{N}_{0}^{d}
$$

For instance, for a uniformly and normally distributed $\psi$, the normalized Legendre and Hermite polynomials, respectively, satisfy the orthonormality condition in Equation (100). 

\section{Relative Function Spaces and Integral Identities}

In this section, we give some essential definitions of Relative function spaces, Sobolev spaces and some important equalities. All the integral in this section should be understood by Lebesgue integral.

$\underline{L^{p} \text { space }}$

Let $\Omega \subset \mathbb{R}^{d}$ is an open set. For any real number $1<p<\infty$, we define

$$
L^{p}(\Omega)=\left\{u: \Omega \mapsto \mathbb{R} \mid u \text { is measurable on } \Omega, \quad \int_{\Omega}|u|^{p} d x<\infty\right\},
$$

endowed with the norm

$$
\|u\|_{L^{p}(\Omega)}=\left(\int_{\Omega}|u|^{p} d x\right)^{\frac{1}{p}}
$$

For $p=\infty$, we have

$L^{\infty}(\Omega)=\{u: \Omega \mapsto \mathbb{R} \mid u$ is uniformly bounded in $\Omega$ except a zero measure setf,13) endowed with the norm

$$
\|u\|_{L^{\infty}(\Omega)}=\sup _{\Omega}|u| .
$$

Sometimes, for functions on unbounded domains, we consider their local integrability. To this end, we define the following local $L^{p}$ space

$$
L_{l o c}^{p}(\Omega)=\left\{u: \Omega \mapsto \mathbb{R} \mid u \in L^{p}(V), \forall V \subset \subset \Omega\right\}
$$

where $V \subset \subset \Omega$ means $V$ is a compact subset of $\Omega$.

$C^{k}$ space

Let $k \geq 0$ be an integer, and $\Omega \subset \mathbb{R}^{d}$ is an open set. The $C^{k}(\Omega)$ is the $k$-th differentiable function space given by

$$
C^{k}(\Omega)=\{u: \Omega \mapsto \mathbb{R} \mid u \text { is } k \text {-times continuously differentiable }\}
$$

Let $\alpha=\left(\alpha_{1}, \alpha_{2}, \cdots, \alpha_{d}\right)$ be a $d$-fold multi-index of order $|\alpha|=\alpha_{1}+\alpha_{2}+\cdots+\alpha_{n}=k$. The $k$-th order (classical) derivative of $u$ is denoted by

$$
D^{\alpha} u=\frac{\partial^{k}}{\partial x_{1}^{\alpha_{1}} \partial x_{2}^{\alpha_{2}} \cdots \partial x_{d}^{\alpha_{d}}} u
$$

For the closure of $\Omega$, denoted by $\bar{\Omega}$, we have

$C^{k}(\bar{\Omega})=\left\{u: \Omega \mapsto \mathbb{R} \mid D^{\alpha} u\right.$ is uniformly continuous on bounded subsets of $\left.\Omega(1 \emptyset \mid \&) \mid \leq k\right\}$

When $k=0$, we also write $C(\Omega)=C^{0}(\Omega)$ and $C(\bar{\Omega})=C^{0}(\bar{\Omega})$.

We also define the infinitely differentiable function space

$$
C^{\infty}(\Omega)=\{u: \Omega \mapsto \mathbb{R} \mid u \text { is infinitely differentiable }\}=\bigcap_{k=0}^{\infty} C^{k}(\Omega)
$$

and

$$
C^{\infty}(\bar{\Omega})=\bigcap_{k=0}^{\infty} C^{k}(\bar{\Omega})
$$

We use $C_{0}(\Omega)$ and $C_{0}^{k}(\Omega)$ denote these functions in $C(\Omega), C^{k}(\Omega)$ with compact support.

$W^{k, p}$ space

The weak derivative is given by the following definition ${ }^{1}$.

\section{Definition}

Suppose $u, v \in L_{l o c}^{1}(\Omega)$ and $\alpha$ is a multi-index. We say that $v$ is the $\alpha^{t h}$ weak derivative of $u$, written

$$
D^{\alpha} u=v
$$

provided

$$
\int_{\Omega} u D^{\alpha} \phi d x=(-1)^{|\alpha|} \int_{\Omega} v \phi d x
$$

for all test functions $\phi \in C_{0}^{\infty}(\Omega)$. As a typical example, let $u(x)=|x|$ and $\Omega=(-1,1)$. For calculus we know that $u$ is not (classical) differentiable at $x=0$. However, it has weak derivative

$$
(D u)(x)= \begin{cases}1 & x>0 \\ -1 & x \leq 0\end{cases}
$$

\section{Definition}

For an integer $k \geq 0$ and real number $p \geq 1$, the Sobolev space is defined by

$$
W^{k, p}(\Omega)=\left\{u \in L^{p}(\Omega)\left|D^{\alpha} u \in L^{p}(\Omega), \forall\right| \alpha \mid \leq k\right\}
$$

endowed with the norm

$$
\|u\|_{k, p}=\left(\int_{\Omega} \sum_{|\alpha| \leq k}\left|D^{\alpha} u\right|^{p}\right)^{\frac{1}{p}} .
$$

Obviously, when $k=0$, we have $W^{0, p}(\Omega)=L^{p}(\Omega)$.

When $p=2, W^{k, p}(\Omega)$ is a Hilbert space. And it also denoted by $H^{k}(\Omega)=W^{k, 2}(\Omega)$. The inner product in $H^{k}(\Omega)$ is given by

$$
\langle u, v\rangle=\int_{\Omega} \sum_{|\alpha| \leq k} D^{\alpha} u D^{\alpha} v d x
$$

A crucial subset of $W^{k, p}(\Omega)$, denoted by $W_{0}^{k, p}(\Omega)$, is

$$
W_{0}^{k, p}(\Omega)=\left\{u \in W^{k, p}(\Omega)\left|D^{\alpha} u\right|_{\partial \Omega}=0, \forall|\alpha| \leq k-1\right\}
$$

It is customary to write $H_{0}^{k}(\Omega)=W_{0}^{k, 2}(\Omega)$.

\section{Integral Identities}

In this subsection, we assume $\Omega \subset \mathbb{R}^{d}$ is a Lipschitz bounded domain (see ${ }^{3}$ for the definition of Lipschitz domain).

Theorem (Green's formulae)

Let $u, v \in C^{2}(\bar{\Omega})$. Then 1.

$$
\int_{\Omega} \Delta u d x=\int_{\partial \Omega} \frac{\partial u}{\partial n} d S
$$

2.

$$
\int_{\Omega} \nabla u \cdot \nabla v d x=-\int_{\Omega} u \Delta v d x+\int_{\partial \Omega} u \frac{\partial v}{\partial n} d S
$$

3.

$$
\int_{\Omega} u \Delta v-v \Delta u d x=\int_{\partial \Omega} u \frac{\partial v}{\partial n}-v \frac{\partial u}{\partial n} d S
$$

For curl operator we have some similar identities. To begin with, we define the 1D and 2D curl operators. For a scalar function $u\left(x_{1}, x_{2}\right) \in C^{1}(\bar{\Omega})$, we have

$$
\nabla \times u=\left(\frac{\partial u}{\partial x_{2}},-\frac{\partial u}{\partial x_{1}}\right)
$$

For a 2D vector function $\mathbf{v}=\left(v_{1}\left(x_{1}, x_{2}\right), v_{2}\left(x_{1}, x_{2}\right)\right) \in\left(C^{1}(\bar{\Omega})\right)^{2}$, we have

$$
\nabla \times \mathbf{v}=\frac{\partial v_{2}}{\partial x_{1}}-\frac{\partial v_{1}}{\partial x_{2}}
$$

Then we have the following integral identities for curl operators.

\section{Theorem}

1. Let $\Omega \subset \mathbb{R}^{3}$ and $\mathbf{u}, \mathbf{v} \in\left(C^{1}(\bar{\Omega})\right)^{3}$. Then

$$
\int_{\Omega} \nabla \times \mathbf{u} \cdot \mathbf{v} d x=\int_{\Omega} \mathbf{u} \cdot \nabla \times \mathbf{v} d x+\int_{\partial \Omega} \mathbf{n} \times \mathbf{u} \cdot \mathbf{v} d S
$$

where $\mathbf{n}$ is the unit outward normal.

2. Let $\Omega \subset \mathbb{R}^{2}$ and $\mathbf{u} \in\left(C^{1}(\bar{\Omega})\right)^{2}$ and $v \in C^{1}(\bar{\Omega})$. Then

$$
\int_{\Omega} \nabla \times \mathbf{u} v d x=\int_{\Omega} \mathbf{u} \cdot \nabla \times v d x+\int_{\partial \Omega} \tau \cdot \mathbf{u} v d S
$$

where $\tau$ is the unit tangent to $\partial \Omega$.

\section{Derivation of Variational Form Example}

Let $\Omega_{1}=(0,0.5) \times(0,1), \Omega_{2}=(0.5,1) \times(0,1), \Omega=(0,1)^{2}$. The interface is $\Gamma=\bar{\Omega}_{1} \cap \bar{\Omega}_{2}$, and the Dirichlet boundary is $\Gamma_{D}=\partial \Omega$. The domain for the problem can be visualized in Fig. 31. The problem was originally defined in 4 . 

\begin{figure}
	\centering
	\includegraphics[width=0.7\linewidth]{"notes/ref/Miscellaneous Concepts/images/2022_12_22_734b0f36e7e95935ae98g-6"}
	\caption{}
	%	\label{fig:20221222734b0f36e7e95935ae98g-7}
\end{figure}
%![](https://cdn.mathpix.com/cropped/2022_12_22_734b0f36e7e95935ae98g-6.jpg?height=410&width=986&top_left_y=92&top_left_x=576)
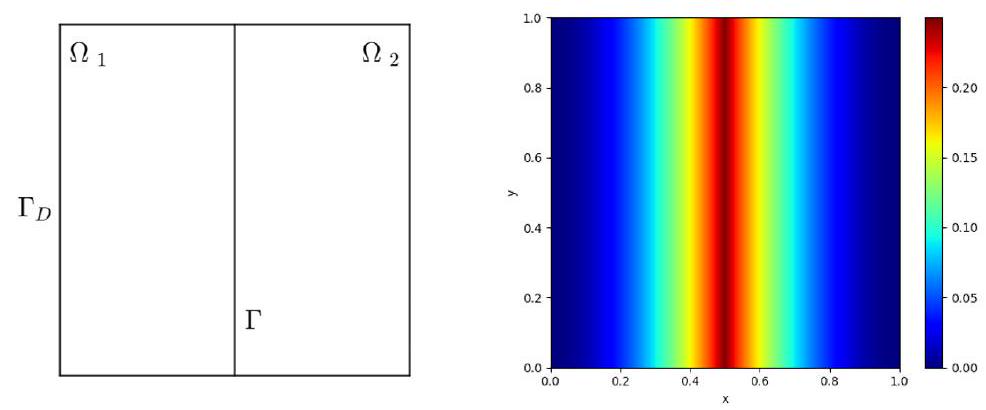
Fig. 31 Left: Domain of interface problem. Right: True Solution

The PDEs for the problem are defined as

$$
\begin{aligned}
	-u & =f & & \text { in } \Omega_{1} \cup \Omega_{2} \\
	u & =g_{D} & & \text { on } \Gamma_{D} \\
	\frac{\partial u}{\partial \mathbf{n}} & =g_{I} & & \text { on } \Gamma
\end{aligned}
$$

where $f=-2, g_{I}=2$ and

$$
g_{D}=\left\{\begin{array}{ll}
	x^{2} & 0 \leq x \leq \frac{1}{2} \\
	(x-1)^{2} & \frac{1}{2}<x \leq 1
\end{array} .\right.
$$

The $g_{D}$ is the exact solution of (125).

The jump $[\cdot]$ on the interface $\Gamma$ is defined by

$$
\left[\frac{\partial u}{\partial \mathbf{n}}\right]=\nabla u_{1} \cdot \mathbf{n}_{1}+\nabla u_{2} \cdot \mathbf{n}_{2}
$$

where $u_{i}$ is the solution in $\Omega_{i}$ and the $\mathbf{n}_{i}$ is the unit normal on $\partial \Omega_{i} \cap \Gamma$.

As suggested in the original reference, this problem does not accept a strong (classical) solution but only a unique weak solution $\left(g_{D}\right)$ which is shown in Fig. 31.

Note: It is noted that in the original paper ${ }^{4}$, the PDE is incorrect and (125) defines the corrected PDEs for the problem.

We now construct the variational form of (125). This is the first step to obtain its weak solution. Since the equation suggests that the solution's derivative is broken at interface $(\Gamma)$, we have to do the variational form on $\Omega_{1}$ and $\Omega_{2}$ separately. Specifically, let $v_{i}$ be a suitable test function on $\Omega_{i}$, and by integration by parts, we have for $i=1,2$, 

$$
\int_{\Omega_{i}}\left(\nabla u \cdot \nabla v_{i}-f v_{i}\right) d x-\int_{\partial \Omega_{i}} \frac{\partial u}{\partial \mathbf{n}} v_{i} d s=0
$$

If we are using one neural network and a test function defined on whole $\Omega$, then by adding these two equalities, we have

$$
\int_{\Omega}(\nabla u \cdot \nabla v-f v) d x-\int_{\partial} g_{I} v d s-\int_{\Gamma_{D}} \frac{\partial u}{\partial \mathbf{n}} v d s=0
$$

If we are using two neural networks, and the test functions are different on $\Omega_{1}$ and $\Omega_{2}$, then we may use the discontinuous Galerkin formulation ${ }^{5}$. To this end, we first define the jump and average of scalar and vector functions. Consider the two adjacent elements as shown in Fig. 32. $\mathbf{n}^{+}$and $\mathbf{n}^{-}$and unit normals for $T^{+}, T^{-}$on $F=T^{+} \cap T^{-}$, respectively. As we can observe, we have $\mathbf{n}^{+}=-\mathbf{n}^{-}$.

Let $u^{+}$and $u^{-}$be two scalar functions on $T^{+}$and $T^{-}$, and $\mathbf{v}^{+}$and $\mathbf{v}^{-}$are two vector fields on $T^{+}$and $T^{-}$, respectively. The jump and the average on $F$ is defined by

$$
\begin{array}{rr}
	\langle u\rangle=\frac{1}{2}\left(u^{+}+u^{-}\right) & \langle\mathbf{v}\rangle=\frac{1}{2}\left(\mathbf{v}^{+}+\mathbf{v}^{-}\right) \\
	\llbracket u \rrbracket=u^{+} \mathbf{n}^{+}+u^{-} \mathbf{n}^{-} & \llbracket \mathbf{v} \rrbracket=\mathbf{v}^{+} \cdot \mathbf{n}^{+}+\mathbf{v}^{-} \cdot \mathbf{n}^{-}
\end{array}
$$
\begin{figure}
	\centering
	\includegraphics[width=0.7\linewidth]{"notes/ref/Miscellaneous Concepts/images/2022_12_22_734b0f36e7e95935ae98g-7"}
	\caption{}
	%	\label{fig:20221222734b0f36e7e95935ae98g-7}
\end{figure}

%![](https://cdn.mathpix.com/cropped/2022_12_22_734b0f36e7e95935ae98g-7.jpg?height=428&width=739&top_left_y=1440&top_left_x=648)

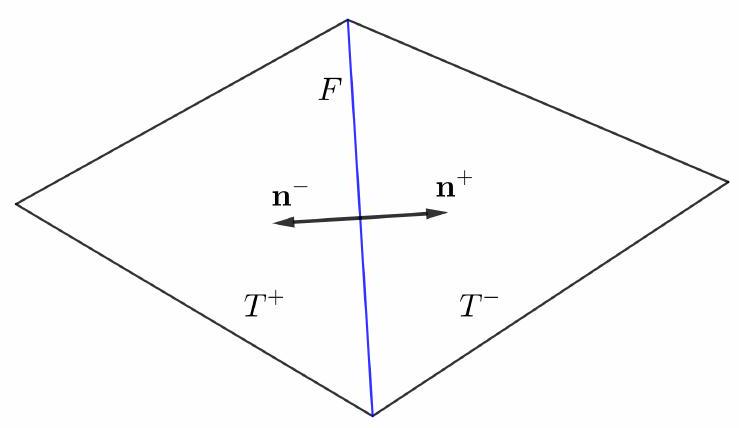
Fig. 32 Adjacent Elements.

Lemma

On $F$ of Fig. 32, we have

$$
\llbracket u \mathbf{v} \rrbracket=\llbracket u \rrbracket\langle\mathbf{v}\rangle+\llbracket \mathbf{v} \rrbracket\langle u\rangle .
$$

By using the above lemma, we have the following equality, which is an essential tool for discontinuous formulation.

Theorem Suppose $\Omega$ has been partitioned into a mesh. Let $\mathcal{T}$ be the set of all elements of the mesh, $\mathcal{F}_{I}$ be the set of all interior facets of the mesh, and $\mathcal{F}_{E}$ be the set of all exterior (boundary) facets of the mesh. Then we have

$$
\sum_{T \in \mathcal{T}} \int_{\partial T} \frac{\partial u}{\partial \mathbf{n}} v d s=\sum_{e \in \mathcal{F}_{I}} \int_{e}(\llbracket \nabla u \rrbracket\langle v\rangle+\langle\nabla u\rangle \llbracket v \rrbracket) d s+\sum_{e \in \mathcal{F}_{E}} \int_{e} \frac{\partial u}{\partial \mathbf{n}} v d s
$$

Using (127) and (132), we have the following variational form

$$
\sum_{i=1}^{2}\left(\nabla u_{i} \cdot v_{i}-f v_{i}\right) d x-\sum_{i=1}^{2} \int_{\Gamma_{D}} \frac{\partial u_{i}}{\partial \mathbf{n}} v_{i} d s-\int_{\partial}\left(g_{I}\langle v\rangle+\langle\nabla u\rangle \llbracket v \rrbracket d s=0\right.
$$

Details on how to use these forms can be found in tutorial Interface Problem by Variational Method.

\section{References}

[1] : $\quad$ Evans, Lawrence C. "Partial differential equations and Monge-Kantorovich mass transfer." Current developments in mathematics $1997.1$ (1997): 65-126.

[2] (1,2): Xiu, Dongbin. Numerical methods for stochastic computations. Princeton university press, 2010.

[3] : $\quad$ Monk, Peter. "A finite element method for approximating the time-harmonic Maxwell equations." Numerische mathematik $63.1$ (1992): 243-261.

[4] (1,2): Zang, Yaohua, et al. "Weak adversarial networks for high-dimensional partial differential equations." Journal of Computational Physics 411 (2020): 109409.

[5] : $\quad$ Cockburn, Bernardo, George E. Karniadakis, and Chi-Wang Shu, eds. Discontinuous Galerkin methods: theory, computation and applications. Vol. 11. Springer Science \& Business Media, 2012.