上一个暑假·写字
+
写这段话完全是因为,高考完的暑假我甚至闲得二刷了一遍甄嬛传。那天晚上正好看到皇帝假意让熹贵妃和亲,在剧里听到了这首词(诗?),顺手就写下来了。
+拍下来一直存着是因为,感觉字写的还行(?),一个暑假没怎么握笔的现在恐怕写不出来了。
+年底·寝室
+
年底的一个晚上,在寝室里给自己剪了头发。
+其实就是很暴力地拿剪刀把长发改短了,冬天披着很舒服也更好看。
+好!等到夏天过去了我还想再剪短一次!
+(其实手机里没删的图也有很多是心血来潮的自拍,还是不发了,笑死。
+元宵·闵大荒
+
2022 +年的元宵节那天,交大已经开学了,华子还没有。于是找了一位朋友带我混进去玩了一天。
+骑车从思源门晃到龙宾楼,又从宣怀大道步行回去。到电院附近转了转,恍惚想着如果当初没有拒交大 +IEEE,如今会过得怎么样呢,可能也不很满意,又或许会开心一些?月亮很圆,可惜没有拍到电院红色砖墙旁的满月,真的很漂亮。
+绿园好吃,菠萝包好吃。rua +了一把包图猫馆长,其实是我第一次摸猫猫,皮毛很温暖顺滑的感觉。过了两周听说猫猫失踪,不知道后来怎么样了。
+很快就是上海疫情,交大里面也很严重,人在北京差点被隔离。
+寒春·荷塘
+
春季学期在开学的前两天回了学校。开学前一天没啥事情,去逛了逛荷塘和近春园。怂怂地上了冰面,拍了张照片,还摔了一跤。
+但是南方人狂喜.jpg
+三月·成绩单
+
科协第一次部会之前在 C +楼开了成绩单,觉得很荒唐。也是春季学期摆烂的开始。
+第一学期其实为了 GPA 卷爆了,然而喜提体育 2.6,又被 C++ +选修课爆杀,但我仍然不认为 3.88 +有多低。打了排名之后感觉很奇怪,再一问同学才知道保护 GPA +的众多方式,比如学不会就退课一学期 20 +个学分,比如培养方案之外只选水课。
+我觉得这不值得。于是春季学期改变了下思路,自杀式瞎学占 5 +个学分但对我没什么大用的基物,2 学分的高代选讲当成 4 +学分的高代来学,甚至翘过 1-3 的工图课去旁听高代,听完课继续在 3300 +自习、画图。做了一些和培养方案没关系的事情,也有点伤害 +GPA,但是感觉很开心。
+不过幸好有两个 PF 的机会,用在了基物和工图上,导致 GPA 上了 +3.9,但排名纹丝不动。同时对微积分 A(2) 这门课的评价是啥也不是,喜提 B+ +但是没太当回事,感觉状态和文刀日肥的这篇文章有些像。
+期中·法图走廊
+
在图书馆吃东西是不好的行为,我自裁。
+当时期中周连考三门(微积分,基物,高代选)实在绷不住了,考试前夜就补觉,第二天不考试就复习到凌晨三点钟。记得有一天早晨起来实在难受,午饭前在六教的洗手间里吐了。
+这张图发生在某天的下午两点,没有什么食欲,然后躲在法图的一个没有灯的(好像和什么设备邻近的)走廊里吃了一个巧克力面包,喝了前一天买的饮料。
+生日·寝室阳台
+
生日正好是期中后一天,很有仪式感地点了布歌东京的蛋糕。好贵,但是好漂亮,味道也不错。
+从高一开始,自己过生日的时候就习惯半夜到暗一些的地方,去给自己点一下蜡烛。高一是在高中寝室的洗手间里,高二是在家,高三是躲在学校的化学实验室。这一次是在寝室的阳台上,还特地外卖买了打火机,不知道有没有违反寝室条例。
+认真地看了许久摇曳的火焰,吹灭之后感到很开心。出门的时候还没熄灯,开门回房间就已经全黑了,室友们在各自做自己的事情,完全没注意到我在做什么。感觉就像是在时间的缝隙里大喘气了一下,不打破原来的平静就是最好的。
+期末很丧的时候·消费主义陷阱们
+
有一段时间很丧,然后就喜欢晚上躲在被子里看一会美食视频再睡,主要是一人食的制作过程那种。然后想着以后也想有一个厨房,尝试着给自己做饭。
+不过从来都没怎么做过饭,感觉厨艺会很感人...叶公好龙吧。
+甚至还上淘宝找了找餐具,收藏了这套猫猫碗盘XD。
+另一个是一直想买的小包,设计很漂亮。虽然想了想使用场景只有偶尔出去玩的时候背,然后就搁置了没买。如果一段时间之后还是惦记着很想要,那就坚定地作为情绪价值买下来吧!XD
+周四晚上六点·声速实验
+
越是写请勿碰落,我越想去碰一下(猫猫行为
+这个温湿度仪一看就是小米出品,很有感觉,本来想买一个。然后某宝搜了一下价格就劝退了,况且真没必要。不买立省百分百!
+时间跨度很长·花
+
很喜欢鲜花。
+洋甘菊和水仙百合是今年的图,玫瑰是去年生日的,满天星当初偷偷养在高中教学楼的一个阶梯教室里,水杯上的杏花是在(高中的)食堂旁边的树上薅的。(破坏绿化,我自裁
+水仙百合(左上)和它们都不一样,凋谢的时候花瓣和花蕊会一点点脱落,然而茎叶还能保持翠绿很久。
+暑假·梗图
+
我 C +系语言的水平实在是不行,之前印象很深刻,刷书写了个链表,成功把我自己弄破防了。开学后的雷系数据结构恐怕要直接退课了...再过一学期吧。
+暑假学了一手 +Python,写了几个小任务,感觉很优雅。人生苦短,我使电锯(
+
制图实习有感:我只是一只小猫咪,你真的确定要给我 3.3 吗?
+但是感觉毫无疑问了,真的不是很会搞这个东西(悲
+
见者落泪(
+]]>上一个暑假·写字
-
写这段话完全是因为,高考完的暑假我甚至闲得二刷了一遍甄嬛传。那天晚上正好看到皇帝假意让熹贵妃和亲,在剧里听到了这首词(诗?),顺手就写下来了。
-拍下来一直存着是因为,感觉字写的还行(?),一个暑假没怎么握笔的现在恐怕写不出来了。
-年底·寝室
-
年底的一个晚上,在寝室里给自己剪了头发。
-其实就是很暴力地拿剪刀把长发改短了,冬天披着很舒服也更好看。
-好!等到夏天过去了我还想再剪短一次!
-(其实手机里没删的图也有很多是心血来潮的自拍,还是不发了,笑死。
-元宵·闵大荒
-
2022 -年的元宵节那天,交大已经开学了,华子还没有。于是找了一位朋友带我混进去玩了一天。
-骑车从思源门晃到龙宾楼,又从宣怀大道步行回去。到电院附近转了转,恍惚想着如果当初没有拒交大 -IEEE,如今会过得怎么样呢,可能也不很满意,又或许会开心一些?月亮很圆,可惜没有拍到电院红色砖墙旁的满月,真的很漂亮。
-绿园好吃,菠萝包好吃。rua -了一把包图猫馆长,其实是我第一次摸猫猫,皮毛很温暖顺滑的感觉。过了两周听说猫猫失踪,不知道后来怎么样了。
-很快就是上海疫情,交大里面也很严重,人在北京差点被隔离。
-寒春·荷塘
-
春季学期在开学的前两天回了学校。开学前一天没啥事情,去逛了逛荷塘和近春园。怂怂地上了冰面,拍了张照片,还摔了一跤。
-但是南方人狂喜.jpg
-三月·成绩单
-
科协第一次部会之前在 C -楼开了成绩单,觉得很荒唐。也是春季学期摆烂的开始。
-第一学期其实为了 GPA 卷爆了,然而喜提体育 2.6,又被 C++ -选修课爆杀,但我仍然不认为 3.88 -有多低。打了排名之后感觉很奇怪,再一问同学才知道保护 GPA -的众多方式,比如学不会就退课一学期 20 -个学分,比如培养方案之外只选水课。
-我觉得这不值得。于是春季学期改变了下思路,自杀式瞎学占 5 -个学分但对我没什么大用的基物,2 学分的高代选讲当成 4 -学分的高代来学,甚至翘过 1-3 的工图课去旁听高代,听完课继续在 3300 -自习、画图。做了一些和培养方案没关系的事情,也有点伤害 -GPA,但是感觉很开心。
-不过幸好有两个 PF 的机会,用在了基物和工图上,导致 GPA 上了 -3.9,但排名纹丝不动。同时对微积分 A(2) 这门课的评价是啥也不是,喜提 B+ -但是没太当回事,感觉状态和文刀日肥的这篇文章有些像。
-期中·法图走廊
-
在图书馆吃东西是不好的行为,我自裁。
-当时期中周连考三门(微积分,基物,高代选)实在绷不住了,考试前夜就补觉,第二天不考试就复习到凌晨三点钟。记得有一天早晨起来实在难受,午饭前在六教的洗手间里吐了。
-这张图发生在某天的下午两点,没有什么食欲,然后躲在法图的一个没有灯的(好像和什么设备邻近的)走廊里吃了一个巧克力面包,喝了前一天买的饮料。
-生日·寝室阳台
-
生日正好是期中后一天,很有仪式感地点了布歌东京的蛋糕。好贵,但是好漂亮,味道也不错。
-从高一开始,自己过生日的时候就习惯半夜到暗一些的地方,去给自己点一下蜡烛。高一是在高中寝室的洗手间里,高二是在家,高三是躲在学校的化学实验室。这一次是在寝室的阳台上,还特地外卖买了打火机,不知道有没有违反寝室条例。
-认真地看了许久摇曳的火焰,吹灭之后感到很开心。出门的时候还没熄灯,开门回房间就已经全黑了,室友们在各自做自己的事情,完全没注意到我在做什么。感觉就像是在时间的缝隙里大喘气了一下,不打破原来的平静就是最好的。
-期末很丧的时候·消费主义陷阱们
-
有一段时间很丧,然后就喜欢晚上躲在被子里看一会美食视频再睡,主要是一人食的制作过程那种。然后想着以后也想有一个厨房,尝试着给自己做饭。
-不过从来都没怎么做过饭,感觉厨艺会很感人...叶公好龙吧。
-甚至还上淘宝找了找餐具,收藏了这套猫猫碗盘XD。
-另一个是一直想买的小包,设计很漂亮。虽然想了想使用场景只有偶尔出去玩的时候背,然后就搁置了没买。如果一段时间之后还是惦记着很想要,那就坚定地作为情绪价值买下来吧!XD
-周四晚上六点·声速实验
-
越是写请勿碰落,我越想去碰一下(猫猫行为
-这个温湿度仪一看就是小米出品,很有感觉,本来想买一个。然后某宝搜了一下价格就劝退了,况且真没必要。不买立省百分百!
-时间跨度很长·花
-
很喜欢鲜花。
-洋甘菊和水仙百合是今年的图,玫瑰是去年生日的,满天星当初偷偷养在高中教学楼的一个阶梯教室里,水杯上的杏花是在(高中的)食堂旁边的树上薅的。(破坏绿化,我自裁
-水仙百合(左上)和它们都不一样,凋谢的时候花瓣和花蕊会一点点脱落,然而茎叶还能保持翠绿很久。
-暑假·梗图
-
我 C -系语言的水平实在是不行,之前印象很深刻,刷书写了个链表,成功把我自己弄破防了。开学后的雷系数据结构恐怕要直接退课了...再过一学期吧。
-暑假学了一手 -Python,写了几个小任务,感觉很优雅。人生苦短,我使电锯(
-
制图实习有感:我只是一只小猫咪,你真的确定要给我 3.3 吗?
-但是感觉毫无疑问了,真的不是很会搞这个东西(悲
-
见者落泪(
-]]>12月1日
+10月1日
-
-
十二月的第一天,又被封控了(。这次只封了宿舍楼三分之一的区域,居然还没躲过。
-抱着乐子人的心态起床洗漱,看到有封控区的人拉着箱子闯过楼里的警戒线,从别的单元门走了,大概是定好今天返乡的。与此同时,楼群里还有人在问订了今天下午的车票走不了了怎么办,笑死,你猜怎么办(
-偶然得到了一份早年数学系统计推断的期中题,看了一眼前半期确实在复习概率论(,涉及数理统计的就一点点 -statistic 的知识和 Delta -Method,这样的话在统计中心学好就没必要去重新上了。不过也有可能是早年卷子的原因,或许现在不一样了。
-然后发现 V1ncent19 写的统辅课程知识概要一直放在我的桌面上,昨天考前只顾着焦虑封楼去了,居然没看一眼。
-今天和室友说好了不去做核酸,解封的时候都晚上六点多了,这栋破楼现在本来就够危的了,实在不想去综体。
-让我看看几天不做核酸会有人找上门.jpg
-友人告诉我二附中有个
-升级人学妹选上了丘班,给我发了推送。打开看了一眼:
-
《并不算早》《小学二年级》
-可能,可能确实不算早吧(,我的童年很幸福,不知道市区的学校是怎么养蛊的 -x。但是这个属实给我一种,高中开始学竞赛已经半截入土了的感觉,很难形容(
+深切感受到了听力的衰退,七八年前在放学回家的公交车上听一格音量的耳机也能屏蔽噪音,现在要两格;昨天在抽代课上有个旁听的同学小声叫住我,问我要微信想要点课程资料,说了两遍我都没听清楚,凑近一点才听清楚他在说啥,感觉很抱歉。
+说起来那趟摇摇晃晃的宝山 8 +路,已经是七八年前的事了吗,我还记得很多细节。当时家住宝山这个小破郊区的边缘小镇,小破初中在宝山所谓的核心位置,其实说是核心也远不如城区繁华,只是靠近码头,发展得早一些。每天放学从友谊路挤上车,在牡丹江路上一路堵车,开到市三医院(现在叫市九北院了)门口才好一些。如果到了绕城高速上还堵,那这十公里恐怕就不是一个小时能走完的了。
+还记得遇到过几次意外的堵车,我还在绕城高速下过车,去旁边的铁力路站乘地铁去学校,那是 +3 +号线唯一一个地下站,据说是旁边的宝钢不让站台建在地上,出钱改到地下去的。现在已经记不清楚怎么从高速的一侧去往另一侧的地铁口了,想想当时为了上学还挺勇的,放在高中的话我就请个假打道回府了(什么啊
+人生会有几个七八年呢?(#每日悲观
+室友:你为啥要和刚高考完的小朋友卷离散啊?卷得过吗?
+我:我超,对啊,为什么呢(
+不过暑假上逻辑课之前大致看了一点离散(1)的内容,想来补完(x)一下;另外貌似会有图论,这玩意在我有关数竞的印象里非常恐怖,来看看.jpg
+看了一天初概,很破防,这课用英文讲不好吗(暴论)。连续型联合概率密度(Joint +PDF)还叫做联合密度,联合概率,明明直接拆成 Joint 和 PDF +就知道是什么了;Joint PMF,CDF 同理,Marginal +同理。什么边缘密度,边缘分布,离散型 +blahblah,甚至作业题题干上老师还把联合密度写成了联合分布,白浪费了很久和同学研究这是什么意思,中文太难了(
++
+John Von Neumann once said to Felix Smith, "Young man, in mathematics +you don't understand things. You just get used to them." This was a +response to Smith's fear about the method of characteristics.
+破防了,记之(
12月2日
+10月2日
-
-
今天没封楼,去了趟教室。不仅完整听完了一节课,不用课后返工,一天还做了之前三天的工作量(,感动死了。
-遇到了欧老师 -++,
坐在欧老师前面莫名有一种背后被班主任盯着的感觉然后抽代也做得比往常快很多(什么啊草
-晚上打算把几周没做的抽代 bonus -刷完,其实也没几道题。还是有点难的,主要问题是我现在感觉自己的基础摇摇欲坠(,扩域扩了好几天了还没太学会 -& -前学后忘,学环的后半部分的时候刚考完期中正好在摆,好像也没特别会(
-放一个友人的名言在这里:
+给同学讲题目,题面反正就是这张图,然后求这个种群灭亡的概率(
+感觉画得很好玩就放上来了。
+ +
+开学第三周就破防了,睡前喝了两大杯热豆浆。加蜂蜜还是没有直接加白砂糖甜,但是感觉健康一点(?
+这工程力学开始看不懂了,虽然必修但考虑中期给它退了,太闹心了。
+
10月3日
+-
+
梦到课咨委例会,我敲门进去发现里面的人都不认识,然后问了一句:
+“这里是告白实行委员会吗?”
+不是很懂你们这些二刺猿.jpg
+还梦到抽代期中一道题也不会做,何尝不是一种未卜先知(
+来到百京的第二年,还是学不会降温的时候怎么穿衣服。
+傍晚友人约了恰饭(其实是大倒苦水,大家过得都好惨),急着出门的时候实在不知道穿什么,扯了一件粉衬衫一件浅绿的风衣出来,草。还好颜色都偏浅,其实也没有难看,友人评价是像一颗草莓(
+到半路拍了张照片,其实拍的不是特别好,
+也不是很庵野,毕竟电线杆太远了。
+
学校东门对面的那个地方(叫东升乡八家村)真的挺庵野风的,有电线杆有护栏有
+电车地铁有路灯,高楼大厦之间一小片低矮的村庄。今天的天空也很有层次感,是我没抓住机会好好找个位置拍,残念。其实如果能再晚一点,在有地铁经过的时候骑车拍一段运动的录像就更好了,但是试过一次会非常抖,远远超过手持拍摄的那种抖动感。考虑买个手机支架(??
-
感觉从哪里开始一片混沌了的时候,就不要继续往后学了,从头看一遍,虽然很有可能再看一遍也只能学会之前已经会了的东西(
-
-希望周末两天还能出门,毕竟数值分析还没学呢,马原论文也没写(
+
黄昏是我一天中视力最差的时候,一眼望去满街都是美女,高楼和街道也变幻了通常的形状,像在电影里。你就站在楼梯的拐角,带着某种清香的味道,有点湿乎乎的,奇怪的气息。擦身而过的时候才知道你在哭,事情就在那时候发生了。
+——《恋爱的犀牛》
+ +据说这话原来是陈建斌说的,廖一梅(还是孟京辉?)曾经和陈建斌是同学,改了一下放到了剧本里。一到这种时候我就很想圣经吟唱(
12月3日
+10月4日
-
-
凌晨两点饿了吃了点东西,算不算吃早饭?(
-今天突然翻到了一些文章,是我高考之后的那个暑假,以及再往前的时间里写的东西。当时知道了一个可以印实体书的网站,只要自己排版就可以,于是兴致勃勃地把自己写过的青春疼痛文学(。)找出来排到了一起,还多写了很多篇。当然弄到一半就咕咕咕了,也幸亏没弄出来(
-今天拿出来看的时候让我自己都震撼,感觉现在贫瘠的表达和从前不可同日而语。是什么时候失去的?不知道。
-说都说了,放几张给大家当当乐子(
-
-
-
-
实际上和 ex -分手已经过去三年了(,现在看这个古早青春疼痛文学好羞耻啊,码掉的内容更羞耻,草(
-
-
这怎么比上一篇还羞耻?脑袋不清楚的时候写的东西是这样的
-
-
为什么配图是华子的录取通知书?我搞不懂(
-气氛都渲染到这儿了,想起来一件关于 ex -的事儿。大概是我高一寒假(2019 -年初)的时候,他比我高一级,要去参加华子举办的一个创新冬令营什么的项目,交几万块钱去美国游学。据说有升学优惠,
-但从结果上来看确是没有的。印象里临行前吵过一架,还见过这个活动华子给每个人发的一件长款羽绒服,以及他说中耳炎还要坐飞机之类的事情。有的时候我觉得记性好真不是一件好事,记得这些破事,又没有任何原因地就是忘不掉,真离谱。要说记性好似乎也不是特别好,昨天统推讲的东西现在就不记得了(x),我好像只对事件的记忆力稍好一些,除了翻黑历史之外完全没用的技能(
-找到了一份 -2020 -年的报名通知,但看这个日程感觉当年肯定因为突发的疫情没有成行,之后就再也没有过了。
-经过了这三年之后我现在想起来这件事,都觉得太遥远了。华子组织高中生出国游学,每个词听起来都似乎不太可能发生在我生活的这个星球上,但愿未来还能变回理所应当的范围。
-统推期中出了,和预期差不多。看了看班级成绩样本的次序统计量(草),感觉也挺符合预期,不知道到期末能不能混个 -A+(
-刚开课的时候老师说统推是基础五件里最难的,但我反正觉得是比初概简单,也有意思多了。初概里面初等的技巧让我抓狂,有一种回到高中竞赛的时候最讨厌概率计数题的感觉。想起来印象很深刻的一件事,高一的时候,学校的一试周常练习里有一个插板法的计数题,我当时想了半天自己找规律(草)糊出来了。结果老师讲评的时候轻飘飘地说“小学奥数都讲过插板法了,这个不用讲了吧”,给我的震撼是全方位的。
-后来就很不喜欢概率计数的题目,感觉联赛的这类题也和小奥没什么区别,一想到同龄人近十年前就掌握了我到当时也不知道的各种方法,就感觉太狡猾了。水平也菜,但高三联赛一试里的计数题是枚举法,倒也做对了,那次一试成绩很不错。这样的我现在居然打算去学统计了,令人感叹。
+看抽代看到凌晨,感觉每个地方对于置换群、对称群、对换群这三个概念的描述都不一样,真的很破防。我个人倾向于 +Undergraduate Algebra 的解释,把对称群认为是作用在 \(\lbrace 1,2,...,n \rbrace\) +上的置换的总集,把置换群认为是对称群的子群,比如说 \(A_n\) +也是一个置换群。然后对换群是比较广义的可以对于任意集合上的一一对应的一个说法。hx +给的解释是混淆置换群和对称群这个行为本身是为了避免混淆(??),我迷茫了。
+怀疑 hx 的进度现在已经是 zmx 的 1.5 倍了,
+难怪作业也是 1.5 +倍,已经 Sylow 了。很难想象这课不自学 or 预习的话怎么上。然后发现助教会在习题解答里面塞 bonus +题,我趣,好阴啊(不是),我一直都不看解答的来着。
+破防 +2.0:为什么要热衷于给每一个概念取名字,就按照符号叫不好吗(暴论
+破防 +3.0:我院另一个上抽代的人要退课跑路了,最开始还是她把我骗过来的,乐。
+破防 +4.0:听说好几个隔壁的高中同学都降转成功/目前有降转打算了,呜呜,我也想降转(暴论
+多读一年的话恐怕基础会好很多吧,不像现在一样畏畏缩缩,sigh。
+所以要不延毕吧(恶魔低语
+今晚课咨委和科协会议撞了,选了课咨委,20 +分钟搞定,听说科协开了一个钟头,
太棒了。
12月4日
+10月5日
-
-
一直想靠赖在学校里不回家、每天去教室自习什么的来保持一些秩序感。
-今晚去开完组会之后也刷完了最后一次阳光长跑,又看到所有考试都要求线上,似乎不回家的理由又减少了两个。然而给我妈打电话的时候还是借 -SRT -的实验需要在校做(笑死,虽然确实是这样没错,但是我根本还没开始)又拖延了一下,心里想的却是,考完试再回去罢。
-晚上饿了,突然想起来 2020 CGMO -的时候,在鹰潭一中食堂吃到的上清豆腐,好想念,但是从没在别的地方见到过,呜呜。
-跑到隔壁寝室问了当时也参赛了的同学一句,她说完全没印象了,怎么这样。
-突然在想要不要寒假报个什么去鹰潭的实践(有吗),然后去吃口豆腐,一瞬间一口上清豆腐的价值居然超越了克服社恐的困难,草。最近总有一种“想做的事情不赶快去做之后就没机会了”的感觉在脑袋里回荡,不知道是什么意思(
+睡前破防了,点开空间发现宗桑也在破防,万恶之源:
+
+
礼貌问候和开端:
+
+
对抗训练:
+
+
太艺术了,改天打印出来贴床头。笑了半个小时,快乐地睡着了。让我们说,谢谢宗桑!(
+何老板找我问统辅的问题,我才知道他想转 +quant,蛮意外的,以前以为他想去类似于经管那种不太技术的方向发展。胡言乱语了几句,其实就是提供了一下我知道的金融统计和金融数学的课和老师,quant +关于码的方面属实不是很了解,就不乱说了。
+然后他问我什么打算,我说我嘛,应该就是应数了,stat,bio-stat +都有可能。(注:生统和生物没啥关系,在会考之前我高中生物就垫底过 114514 +回
12月5日
+10月6日
-
-
下午打起精神写了个统推作业,结果写完交了被告知所有的分位数要查表 -/ 用 R 算出来,然而我全都写了符号就交了,还得返工,可恶啊(
-况且我还不怎么会用 R,更不爽了。
-吃完晚饭去七港九买了杯奶茶,感觉那边人好多,点了单之后对这个决定很后悔。想起来上次喝七港九是上个学期,在某门课上帮一个同学 -de 了个 -bug(虽然纯属期中考完闲得),后来他告诉我买了一杯奶茶放宿舍楼下作为感谢了,还挺开心的。
-之后还交流过几次作业,不过结课后就再也没说过话了。感觉人和人之间的关系真的很脆弱(这又是什么结论,不仅要看认识时的动机(,而且似乎如果没有见面 -/ 做同一件事 / -至少线上交流之类的事情连接在一起的话(好像这甚至只是必要条件),曾经有过的联系也会很快断开。越发觉得要珍惜当下的朋友啊(
-晚上回寝室,室友问我还记不记得紫四前几次封楼的时候,解封了之后楼下有好多情侣贴贴(确实还记得,11 -月 30 -日的日记里还写了)。结果今晚听说有人疑似发烧了(虽然不是我们楼层的),因为她男朋友住 -29 号楼((
-一边觉得相当不妙,一边又不想回去。不回家的理由要我说可以说出来很多,效率不高啊,好几个朋友也都还在校啊,在学校过年也没什么啦,之类的。但最本质的似乎还是没什么求生欲(,就像这段时间除了买了两管牙膏之外什么也没屯,很难为自己找到一个积极准备的动机。
+睡觉就是短暂地从世界上死掉。
+佛了,复习个初概期中搞的鸡飞狗跳,这样的话真到期中了的话怎么办,到期末了又该怎么办。
+感觉更多的是心态问题,有一种《这个东西最好是一直复习下去》的感觉就会搁置很多别的事情...
+看了一个 runzhi 给的抽代题,收获一张 runzhi 梗图:
+
+
最喜欢的一集.jpg
+他问我为什么不跟着茶园上抽代,理应平均水平比数学系低一点,还好卷一些吧?我超,为什么呢。
+不过茶园的数学水平和数学系相比,我还真不是很清楚,知道的数据就只有大一上微积分期中,茶园平均好像没到 +85,我好像 95 = =,所以感觉也不算很好?反过来如果让数学系考微 A +的话会咋样呢。
+罢了罢了,来都来了 XD。
+功成不必在我,我在必不成功。
+和 jdc 说了几句话,因为求真割据,现在数学系只有一个班 30 +个人,转入比例不能超过 15% 的话,今年只有 4 +个名额。现在有一个茶园人一个贵系人加入竞争,还有两位准备降转已经上了很多专业课的同学,这样就已经满了...实际上开放给物理系的互转名额每年都是浪费掉的,外面的又转不进来。
+大家都不容易啊。
12月6日
+10月7日
-
-
难得早起,难得在楼里有区域被封(虽然不包括我的寝室)之前润出了寝室,结果在三教逛了一圈,找不到一张平静的书桌(误),就回寝室了。
-之前周二下午这个时间是有体育课的,从来没去自习过,现在体育场馆关门不上课了,才知道实际上也没地方可去(
-于是今天可以预料地无事可记,就这样吧,卷抽代和数值去了。
+和室友聊天,发现一屋子人里就我没学过小学奥数 = =
+拥有一个快乐的、无所事事的童年也不错 +XD,虽然代价是高中竞赛的时候猛造各种轮子,尤其体现在概率计数里(
+初概期中考完了,明明小分值的难题都做得挺好,结果我飘了看错一个水题,当成无放回抽样了,三小问全寄掉,感觉很危。
+从竞赛做一试的时候就知道不能做快了,会寄,怎么总是记不住呢。sigh
+据说这课 50% 优秀率,所以如果出分之后在平均分上那就不记 +PF,不在的话就记了算了,之后再去摸一个概随。下学期还要上数学系的概率论 +(1),真就全都来一遍啊w
+然后发现没进综奖奖学金答辩,想了想确实是因为实践和志愿为零,虽然社工和学习拉的比较高,有自我感觉良好的嫌疑。麻烦给两个单项吧,真的缺钱(
+没做志愿是因为一直打算去答疑坊蹭工时,但又一直没去(x),实践的话单纯是不喜欢和一群不熟的人旅游,所以没参加过,罢了罢了。看了一圈认识的几个神也没进,又不破防了(?
+怎么全是坏消息啊!
+感觉最近是一个慢慢意识到自己也没有想象中那么厉害的状态,蛮消沉的。属于是难的不会,简单的又糊,中间的倒是会,又有啥用呢 +XD。
+于是晚上翘了一二九分声部的环节,叫上何老板去玉树吃了夜宵。没吃晚饭,然后夜宵一份烤冷面半份馄饨下肚感觉整个人都好起来了,食物治愈一切。辅导员也没来找我的茬,总感觉他早就放弃在类似的事情上说教我了,蛮好的x
12月7日
+10月8日
-
-
太魔幻了最近,从防疫到身边的各种事,唉不说了。
-在寝室里暴躁了一晚上,最后室友劝我算了算了,还是想想办法怎么期末考的时候不要发烧比较好,草,这就是华子人的务实罢(
-室友的电脑寄了,拿我的电脑码了一会,锐评要被我的 IDE -亮瞎了(,人类的悲欢并不相通。
-其实是我散光,dark mode -的话就看不清了。近视快十年了,度数几乎没涨,散光却越来越厉害,怪事(
-终于找到了三教小教室里最舒服的自习姿势,很难不想分享一下:
-
-
今天下午五小节网课,被迫带了充电线出门,到三教来仍然找不到一张平静的书桌(x),要么是情侣要么是结伴来自习的占着教室,都挺吵的。虽说有人推门进去的话可能就不会吵了,但说实话不太想尝试。看到旁边的小教室还有空的,虽然这个桌椅不舒服但也还是进去了。
-这个椅子是从讲台前面推过来的,腰不大好,习惯坐软的椅子,所以比较喜欢三教 -30 -人容量的教室。桌子拼起来也差不多够用,唯一不好的地方是中间拼起来的地方凹凸不平,不过书厚的话也问题不大。
-以上三条呈倒叙关系(
+开始赶一些落下的作业,尤其是抽代的 34 道题(
+张京华怎么塌房了...前段时间学 One Last Kiss +的时候才刷到过他的直播切片(
+很遗憾用这样的方式这么快又看到你一次.jpg
12月8日
+10月9日
-
-
最近一直在流水账,我自己都有点难以忍受。写日记的初衷之一是日省,之二是表达想法。实际上前者现在不需要写也可以做到,甚至有演变成内耗的趋势。而最近有关大环境的想法相必人人都有,我也就不多说了,另外的(主要是家里的)破事也根本不可能简短地写完,更不可能发出来,何况这是一个我一直在回避细说的话题。
-所以没话说就先把日记停了吧,应该不会很久。有兴趣蹲重新开更的话不用天天来看,不妨 -RSS 订阅一下(懒得研究的话直接点这个链接就行,虽然我还没来得及在 -follow.it -上确认作者身份;以及须知等我确认作者身份之后在后台能看到订阅者邮箱,介意的话可以换别的订阅平台 -/ -使用不常用邮箱)。本来一直不打算开这个功能的(可是为什么呢,好像也没什么理由),现在还是开了。
-我怎么看起来情绪不是很稳定的样子(,三次元里不是这样的,向赛博朋友们道个歉((
-
12月10日
-不是又开始写了,是因为交换申请的事情 emo 了(
---这两天在认真思考一个听起来很奇怪的问题:为了交换延毕一年是值得的吗?
-已知:
+仍然在赶作业,别的啥也没干,甚至又通宵了(
+不过顺便在 Math StackExchange +看了一些问题,学到许多;以及写完了之前的 Bonus 题,Wilson +定理什么的梦回高中竞赛,然后我查了一下这玩意怎么证,弹出来的第一条结果居然是 +OI Wiki(
-
-- -
不考虑保研,打算申请;
- -
我的培养方案太过稀烂 & -本科期间不能转专业,近两个学期加上政治课每个学期都选不到 10 -个学分的必限,全在修数学课准备跑路。交换的话又少一个学期,算了算无论是春季交换还是秋季交换,第八学期毕设都肯定开不了题;
- -
我自己的培养方案是双学位,这样下去哪怕不交换也有概率修不完。不过大四的时候全身长满肝 -& -多数没用的课都仅以通过为目标的话,应该还是能毕业,以及申请应该也不看到时候的成绩了;
- -
遗憾的是我很菜,GPA -绝对值看起来还可以,但在院系的排位比较抱歉,恐怕也申不到非常好的交换项目,不知道单纯为了提前护照到手(x)& -增加一段海外经历而交换值不值得; -(其实今天看表格的时候感觉,我院分到的项目要么我不配申请,要么配不上我(暴论
- -
延毕或许还可以带来一些别的好处,比如说我现在的数学基础像筛子一样就开始往后学了,再多学一年至少会好点。现在也还没开始嗑盐,多一年或许能多做一两段,etc;
- +
没钱,不考虑其他需要自主申请的不免学费的交换项目。
- 数竞正统在 OI!(
本来以为这是个博弈问题,以为不知道年级里有多少人想申请,不知道大家会怎么填志愿,甚至还想填个
-ETH,Cornell,南洋理工什么的口嗨一下。晚上室友告诉我其实大家的选择都在院系发的共享文档里,看了一眼
-ETH
-肯定是没戏了,感觉把目标定在曼大或者滑大是比较合适的,更倾向曼大,因为在春季。本来觉得莱斯也可以考虑,看了一眼在德州,算了(
其实如果有法国的项目是最好的,去法国学数学本来就是个很妙的决定,我甚至还会点法语(单指学了两学期二外,再学学可能勉强能过法语四级,现在记得多少也是另一回事)。可惜今年巴黎高师什么的都没有交换项目,不然就不用纠结了,我一定选这个。
-问了友人一句北大有没有交换项目,她说不知道,没关心。不知道为什么突然又 -emo 了。
-几个月前我还不太能懂“我将孤单而度过一生”,会想世界很大,一定有某个人在或远或近的地方等着告诉我“我等你很久了”,假设没有,也不是一件非常值得在意的事。如今我才知道这种不关心是因为,远方的爱人是虚无的,把视线落到身边的朋友身上才能体会到难过。最近我时不时会想站在上帝视角看到朋友们的安稳人生,这两年按部就班地完成培养方案,上课考试,跟着院系的大流磕盐,然后选一个导师轻轻松松地保研,再建设自己的家庭,人生就这么顺利地按照预设的也是令自己满意的轨道进行下去,是一件相当幸福的事情。后来猛地一惊,发现自己实在是沉溺在自己的世界里太久了,这种简单幸福的生活明明属于这个学校里的大多数人,我才是与我的朋友们不同的那一个。不过还算清醒的一点是我知道,任何人所拥有的这样的安稳都不值得为我而改变,我将孤独而度过一生——这是其中的一部分含义罢。
-话说回来我又有什么资格随便把人家的生活概括为“平静”,“幸福”,这不还是很傲慢吗。只是他人生命中的暗流不全为我所知,而我关注的又是他们觉得理所当然的部分。突然又想到以前写的这一段话:
---我想我也不是很绝望。楼下的女人和男人开始争吵了起来,这是意料之中的事情——我也会和我的母亲吵起来,因我在这里碌碌无为坐了这么久。如果人生沿途风景秀丽,那么死亡也并不可怕,然而现实给予的往往恰如其分,令人无话可说。把实践作为真理的理想也是很好的,乐观积极昂扬的一生。人生在适当的时候做出选择也是极好的,明智无悔。沉浸在日常的幸福里,睁大眼睛去看一切也是很好的,及时行乐,盲目无知但无可辩驳的一生。尼采说要高蹈着前行,我说伊卡洛斯飞不远。木心说艺术就是一切,我说它只是遮羞布。一切一切的理想在我来看都是欺骗,是仓皇人生面前的金碧辉煌的童话。这些意义和价值存在一天,人们就长醉不复醒一天,因为梦就是梦,而现实不为始终在做梦的人所知,他以为自己不该死亡,层见错出的痛苦也是不应当有的。
-
emo 完之后看看自己说的话,啧,不就出个国吗,矫情什么(
-UPD:最后一志愿填了 2024 春季的东大(实际是 4-7 -月),二志愿不知道填啥就填了墨尔本大学,也是春季。实际上如果东大申不上我可能就不去了,所以有点乱填的意思。虽然院系里只有一个人和我争东大的名额,还是有点虚的。
-虽然交换这个东西是铁没用的,尤其我选了东大,更没用了,反而一堆问题。包括并不限于短期考不出 -N1 -证书只能上研究生课(挑了半天没看到太多特别好的课),华子这边铁要延毕,影响春研暑研(但是都延毕了的话可能也不算很大的问题)。现在暂且想用出逃和延毕来逃避目前发生的事情,也想着还有很多个反悔的选项,毕竟没上飞机什么都还好说(
-不过选东大的话其实,真要去的话我自己差不多能用存款 cover -全程(从考托福一直到买机票回国)的费用(除去最近社工发的补贴,其余竟还是高考完家教的剩余),顺便 -push 一下自己赶快把语言成绩考出来,目前来看一切都还好..
-为什么朋友们都劝我快去东大然后帮他们代购专辑周边啊!
UPD 2:笑死,东大和墨大的名额都没拿到。
-其实我感觉凡是在这个院系里争取什么东西,哪怕觉得十拿九稳,也从来没顺利过。奖学金也是,交换申请也是,哪怕事实上自己的数值就是碾压别人,哪怕竞争者只有一个,也还是拿不到,真的有点奇怪呢。与我完全相反的是何老板,虽然我觉得他并不强(对不起但是我真的这么觉得,这是可以说的吗),但就是能在这些事情上一路顺利。性格决定命运(不是
-真说不在意也有点假,毕竟失去了一个延毕的好理由和平价旅游的机会,而春研暑研的目的地也不再可能是日本了。
-几天前 zcy -学长看完日记和我说不要去交换,看他评价自己说“我觉得这么久了,我已经是个完全不同的人了。先后两年心思已经收敛,很多东西以前觉得有意思,也许可以玩玩,后来发觉其实我有明确的主线,根本不想沾染”。
-我深深地觉得自己至今也没能明确主线,甚至怀疑我自己就是一个爱好 -wandering 的人。
-仅仅是确定方向,我就花了一年半的时间。从想润 CS -开始发现学不会,虽然现在想想绝对是入门的姿势有问题,郑莉的 C++ -我劝所有人都别上,不过我也自认为不是很有工程思维的人,早些放弃至少减少了沉没成本。然后逃避去了 -DS,但苦于 DS -找工的潜力实在有限(尤其国内),我又对金融非常排斥,纠结了很长一段时间。这时候发现了统计学科(当时指的是统计中心这种类似工科的应用型统计),虽然当时的认识不够准确,还被一位数学系的老学长批评过,但我现在深深感谢他没有让我一直当名词党,不然太可怕了。从这个时候开始发现自己不得不出国了,无论是隔壁数院还是华子数学系还是求真还是统计中心,跨保到合适的方向都十分困难,身为走过的省份还不如别人去过的国家多的小镇做题家又 -emo -了很久。不过真的开始准备追求学术之后又觉得出国是不错的选择,现在只会为 -settle down -遥不可及而感到可惜,没有以前那么痛苦了。后来按照学长的建议试着学习困难的数学,才意识到还有很多应数的分支。又因为初概出师不利,还在计算数学和统计之间举棋不定了一阵子,甚至还想过要不要再去了解一下运筹学和控制论。直到觉得数值分析寡淡无味,而统计推断更合我的审美(?),又名词党式地看了一些非参数检验和贝叶斯学派的东西,感觉很美妙,才在后半学期终于收敛到了统计,也有了一些认识上的更新。包括更倾向于统计理论,而不是生统这种偏应用型的方向了什么的。
-但事实上统计理论(其实计算数学理论也一样)的发展已经日趋成熟,搞不好未来还要继续变化,混不下去了折腾半天又回到应用(。除此之外这一年半没有做任何其他的准备,对磕盐仍然一片迷茫,连语言都没考没学(虽然准备一下也不费劲就是了(。
-当然可以说这是一种成长,但我想想只觉得太艰难太费时间了。一年半以来计划从来赶不上变化,修了一些没必要的课,做了很多和未来没关系的事,有的甚至因为开了个头,现在还不得不继续做下去(说的就是你我的破 -SRT,还有这个破离散还得期末考试,缓考算了)。每隔一阵子就会发现之前在做的事情失去了意义,斗志也因此磨灭了很多,会习惯性怀疑自己,这真的很可怕,也很令人难过。
-Just lose it(
-12月15日
+其实写完作业我也理解 hx 为什么从 Sylow 子群开始就加速冲了,从 Sylow +开始到有限生成 Abel +群(以及可解群)之间都是一个很连贯的逻辑,但是您有没有考虑过,就是没必要把所有课后题都布置成作业呢(
+我现在看到抽代就想吐,预习什么的还是留给睡一觉起来之后吧。
+目标是到周一晚上写完工程力学,抽代,离散和初概作业,然后抽代看到有限生成 +Abel 群。感觉很难。
+然后周二下午要 check +一下数值分析的进度,据说这周会有一个上机实验,但是要用 +MATLAB,我还不是很会。可恶啊可恶,为什么不能用 Python(
10月10日
-
-
本来没啥事,看到抽代助教把作业批出来了,文件比交的时候大了一丢丢,就好奇地点进去看了一眼。
-
-
其实那次写了以前遗留的一堆 bonus 题,遇到一个用理想引入 Zariski -Topology -的题,但背景不够写不出来后一问,所以就证了一半,然后写了句话掩饰做不出来的尴尬(
-我写的是“好酷!可惜我不懂 -Topology”,虽然现在都不太记得是什么东西了,但印象里写证明的时候确实觉得很酷。
-呜呜呜呜呜呜可惜助教可能都不知道我本科连转数的资格都没有(,更不知道各种原因导致以后要走统计,而这已经是我的倒数第二门代数课程了(
-课咨委说是按工作量发了调研补贴,我也不知道为什么我除了开例会喝奶茶一共就做过一个推送,还给我发了最高那一档,乐得我规划了一晚上期末考完去江西找我姐玩的行程(草
+你院综奖答辩前后怎么这么多瓜...听室友讲了两个,自己到处瞎看浪费时间的时候又不慎发现一个。
+其一大约是一个学年满绩的同学(其实他在 b +站有一个更为人熟知的称呼)没进综奖答辩发了一些牢骚,后来和好几个(?)辅导员闹起来了。我原以为他的重点在于质疑入围标准不够公开透明(不过标准是否应该公开透明又是另一个值得讨论的问题,在此略过),但实际不是;还有一个是听说有人出钱灌了篇环材类的 +SCI 然后拿出来吹什么的,盛名之下其实难副。
+有点意思。虽然一些了解到的信息让我觉得的确该骂,但到底还是有可取之处。我向来缺乏始终保持严谨的能力,上学期 +PF +了两门不擅长的专业课都没满绩,这学期刚开头初概就大翻车;又连开始了解一个课题该如何完成的勇气都尚且不足,空诩兴趣和热情有什么用呢。
+常怀谦卑之心。
+上周五 129 分声部咕咕了,今天辅导员才来找我,弧是否有些长。
+说是让我晚上去跟着行健重新分,我才不去呢。所以我有点笨比了,当天晚上虽然跑路了,但事后直接微信编个分数发给他不就好了嘛。现在想到倒也不算晚,至少少跑一趟蒙科楼。
+室友说她 233 但是没选上,据说这三个数字是音高音准音色,满分是 +5。想了想 111 不太符合美少女(??)的形象,那就 212 吧。
+昨天列的 to-do list +基本是搞定了,真不容易,但抽代只看了个大概。不管了,睡觉。
12月19日
+10月11日
-
-
我的环和域到底学了个什么玩意?这课真的能过吗?
-——观 PKU 抽代期末题有感
-——观自己写前几节的抽代作业有感
-——观 Galois 理论证明有感,定理证明我基本都写不出来的水平
-坏了,我认识的人和目前还留校的人取交集的话,只剩下我和室友这一对共轭健康责任人还没感染过了(
-室友锐评:有的时候都怀疑是因为我们俩的作息太阴间,醒着的时候奥密克戎要睡觉,感染不到。
-晚饭感觉吃得有点油腻,加上很长一段时间以来为了期末前都不要阳,我除了睡醒了去食堂提个盒饭回寝室、下楼拿外卖之外都没有实质上地出过门,于是今晚打算去散个步,顺便散到七港九买杯奶茶。还蛮有仪式感的,我还特地卷了个头发,挑了耳饰和发夹才出门。
-本来以为路上不会有什么人,可以在新民路中央横着走,没想到倒也没那么空旷,还是时不时有过路人的。我走位比较花,半路走着走着到了一个要么绕路,要么从苏世民旁边过去的境地。本来想心一横抄近道的,远远看到几个洋大人一边抽烟一边往我这边来了,遂放弃,赶紧跑。又不甘心绕路,就从路边的树林里钻进去了(
-路上顺便给我妈打了个电话,我说我在饭后散步,她说你吃饱了撑的。那倒也没错。
-提着奶茶回来的路上也不敢摘下口罩一边走一边喝,这次走了学堂路,工作日的晚上七点本来应该挤满了去上晚课的人,不禁想现在学校里人还少,还要为了期末考前的状态而躲人,下个学期会怎么度过呢?恢复正常了就躲不过,也没必要再这么躲下去了,甚至我就算这样自我隔离到期末,坐高铁回家的路上也十有八九要寄,就算不寄,寒假规划的几次近距离出游里也大概率会寄。
-又想起来一直觉得使用“正常”这个词的时候应该谨慎些,“normal”里面到底含有一个“norm”,可以理解为标准、规矩,意味着一些有话语权的人制定了一个规则。这个规则被人们或主动或被动地认同后,符合规矩的才会被称之为“正常”。所以正常到底是哪种正常,至少我认为的正常是已经再也回不来了。
-
12月20日
+约了 dwl 老师下周三的 +OOH,没想到这个东西真的没人约啊。点完预约之后又开始纠结,系统会不会给老师发通知说有学生约了 +OOH 呢?我要不要再给她发个邮件说一声...
+我想说的一些东西:
-
-
姑妄言之,姑妄听之。
-开始复习一学期都没听过课的中国工艺美术史(,虽然没听过课但我小测还一直分挺高的,毕竟是历史课(
-看讲义看到元代的章节,里面讲蒙古人的传说里他们的祖先是“苍狼白鹿”,就是苍青色的狼和惨白色的鹿,于是人们很崇拜这两种颜色,元代青花瓷的风靡也和这种颜色崇拜有关。后半句听起来有点扯,查了一下好像苍狼白鹿之说也是明代译者对蒙古文的误读,原文是讲蒙古人的祖先是两个人,他们的名字在蒙语里的意思分别是苍狼和白鹿。但是这个说法听起来就很酷,很野性的感觉,比原文还酷(,所以流传得广也是有道理的吧(
-(对不起我虽然自称文科生但我没文化,到现在才听说这个,轻喷 x
-写数值分析的时候突然意识到,这门课上真的学了很多 Newton -创造的数值方法。我现在一边学理论一边写代码来复现计算方法、和理论互证,看到它可以投入应用,而 -Newton 当初用的还真是纸和笔。
-之前想定要转数的时候思考过很久关于数学研究(尤其纯数,虽然我不去x)有什么意义的问题,迷糊了很久是做理论还是做应用更有价值(虽然我能力有限,做哪个可能不是价值决定的(。尽管这个问题非常老套,也有很多答案了,但我自己还是不可避免地会想。竞赛的时候我天真地认为数学的意义就是纯粹地攀登人类智力的巅峰,是一种艺术,听起来非常美好。但长大后脱离了竞赛这一套游戏规则,我觉得这个理由是站不住脚的。比如很容易就能推翻这个想法的问题是,为什么还要给为了满足自己而做研究的数学家大笔经费呢。
-另外一个中学时代听起来有点傻的困惑就是,怎么能创造出这么多数学理论的,你让我一个人在家憋着空想构造一个体系,哪怕是比较简单的,我也想不出来(当然我能力极其有限,Galois -就可以x)。甚至会因此而苦恼,觉得自己恐怕不是做理论的料(多少有点降智(。现实是不仅有暂时看起来没用的数学,其他许多理论的提出往往是一群人为了解决某一问题服务的,我还看不到意义,可能是因为在学习过时的(可能引起争议但我想不出来怎么形容 -XD)课程而没能走到前沿去(还得看磕盐啊x
-今天写 Newton-Cotes 公式笔记的时候,看到 Remark 里写到 \(n \geq 8\) 的时候稳定性失去保障,\(n\) 更高维的时候会发生 Runge -现象,因此在大规模计算中不会采用高阶 Newton-Cotes 公式进行数值积分。
-Runge 是二十世纪的人,去世的时候都还没有计算机,谈不上科学计算,而 -Runge 现象是 1901 年提出的;Newton -构造这个公式是为了纸笔计算某个积分的近似值的时候更加容易,服务于其他应用;教科书上紧随其后介绍的 -Gauss 求积作为一个性质巨好的优化,和 Newton-Cotes -公式本质的思想差别也不大,重在对余项的修正,不注意的话还以为是过了十天半个月(x)就拍脑袋想出来的,实际上比 -Newton 晚了一百年,但比 Runge -还是早一百多年。看起来很理所当然的一句性质,实际上是由很多后人整理起来的吧。突然意识到自己对数学细部的发展过程还是很缺乏认识,尽管这个例子也没有那么恰当。
-
-第一次觉得 Yau 让求真学数学史也不是那么没意义姑妄言之,姑妄听之(
-我不会计算,我只是在算术.jpg
-随手给博客改了个名,之前一直不知道叫什么,就直接拿 id -当了标题。
-『姑妄言之姑妄听之』,非常符合实际情况。不知道会不会因为太长而被迫换行,万一发生了我就把这一条删掉,当做无事发生(
-正好撑满,好耶!
+- 为初概翻车诚恳致歉并寻求一些建议( +
- 问问她对读研半路出家转数的一些想法,可行性分析(?),包括方向选择(数据科学?计算数学?统计?生统? +
- 求求她带我进组 or 推荐一些相关的组 or 做做 +SRT,我需要尝试一下知道自己能否有能力和兴趣做研究 +
- 关于数学系那边选哪些课(实复概全覆盖?点集拓扑泛函分析等偏向基础数学的内容?回头补数分??)来辅助统计学习这件事,以及我的现状(感觉抽代比初概好玩得多这正常吗)
12月21日
--
-
工艺美术史考完了期末,感觉良好,大部分靠 -cheatsheet,小部分靠小时候东看西看积累的历史小知识推断。想起来小的时候胡乱想以后要做什么的时候考虑过读历史、中文或者法律,总之是觉得读文科很不错,没考虑过理工科呢。
-下学期抢了一门人文课组的故宫学,我从大一开始就挺期待这门课,虽然听说讲得很无聊,但有个课上的时间读读书也不错。
-华子这个楼内疫情防控真有点一言难尽,紫荆六个单元分别有一个卫生间,原本是按照阳性的同学单独使用就近的卫生间。结果现在阳的太多,改成阳性统一最短路径用三单元的卫生间,就在我寝室门口(
-尝试在群里和一拍脑袋想出来这个主意的驻楼老师 -argue,为啥不能改成一三五单元给就近的阳性用,二四六给其他人,这路径岂不是更短(,也不至于某一个地方气溶胶浓度特别高,大家风险共担。然后被无视了(。不知道是不是还有什么别的考虑,打算等他们明天上班再面对面问一下。
-然后意识到实际上还是铁拳不砸到自己头上就不会刻意想着去反对的道理,虽然也人之常情,但多少还是有点莫名的愧疚,为曾经可能有过的事情。
-找了一些双厨狂喜的怪图,感觉很适合放在之后整理的讲义末尾整活(
-
-
我最喜欢的还是这张,是 FGO 某个亚种特异点章节通关之后的 CG。印象里 -1.0 的特异点通关就直接显示圣杯,2.0 空想树通关 CG -都是“空想切除”,只有几个 1.5 亚种特异点的章节的通关 CG 是不一样的。
-新宿章节是“证明完毕”,下总国章节是“一切完胜”,雅戈泰章节是“夜话团圆”,效果都很棒。可惜我玩的时候截的屏找不到了,就去 -b 站找剧情视频截了一下图。另外两个分别是这样的:
-
-
-
这年头谁还玩 FGO 啊,哦原来是我(
-写完了统推最后一讲的内容,感觉还有很多需要补充的东西,主要是实现和一些证明,还有一些我想要去了解的内容。导出了一下发现目前大概是 -80 页左右,排版排得密实一点,删一些图,可能也差不多会有这么多。
-预感最终会是一本不错的小册子,真期待啊。
+
希望不要临场丧失语言功能,另外伟清楼在哪里啊(
数值分析上机题允许 Python +了,然后看了一眼还是没啥思路(乐死),这好像是我的问题(
+总比从头学 MATLAB 好,总比从头学 MATLAB 好
老姐给我发了篇文章,我还以为标题党,点进去一看还蛮喜欢的,遂摘录。
++S:人总是会喜欢自己擅长的东西,我也不例外。那些在小学阶段能很快掌握鸡兔同笼,牛吃草问题和抽屉原理的小孩很容易对自己的智商感到自信。说实在的,自信是一个中国小孩能得到的最好祝福,尤其是在我们这片不会歧视书呆子的文化土壤上,你学好奥数的那几年会在同龄人中活得风生水起——你由此能从一众每天买干脆面开水浒卡的小学生中脱颖而出,进入一个好的中学,学会圆锥曲线和三角函数,由此能从一众每天去网吧抽中南海的中学生中脱颖而出,进入一个好的大学,学会拉格朗日中值定理和多重积分……
+B:等等,这一切的终点在哪儿?
+S:一个祝福,也是一个诅咒。
+B:那是?
+S:去华尔街当操盘手。
+B:我不明白。
+......
+S:(打断)我的一个同学炒币挣了200万;另一个同学在私募基金工作,已经快要拿到美国绿卡;还有一个同学去了高盛……
+B:呵,这就是精英的圈子吗?
+S:我知道你会生起一些朴素的嫉妒心,但就像我说的,他们是自信的数学天才,已经习惯了成功。
+B:我现在明白你刚才那句话的意思了。
+S:哪句话?
+B:一个祝福,也是一个诅咒。从鸡兔同笼走向在华尔街功成名就之路,你被这种幻觉困住了。
+S:甚至更早,珠脑速算。
+......
+S:你像是在面试我。
+B:并不是,说出你真实的看法就好。
+S:我真实的看法(停顿)…就是没什么看法。这就是现在我对大多数事情的看法,对,没什么看法。怎么看爆款?没什么看法。怎么看朝鲜?没什么看法。怎么看北京?没什么看法。怎么看大海?没什……哦,大海还不错。
+B:(痛心)你这样找起选题来会很困难的。
+......
+S:(打断)你还要说,派对上人与人的联结让你很感动。他们托举着彼此翻墙进入现场,总是会有陌生人问你是不是需要水,喝醉了会有人搀扶着你别摔下天台……这些我都看到了。
+
12月22日
+10月12日
-
-
室友原定后天回家,今早起来说喉咙不舒服,晚上就 38°C 了(
-我不知道我什么时候会开始发烧,只觉得抽代大概是复习不了或者考不了了,但明天的统推还是可以考罢。
-晚上摸鱼翻了翻 b -站收藏夹,发现有一段时间非常爱看一人食量的做饭视频,虽然几乎没有下过厨,肯定会是炸厨房选手,从前还是很期待有朝一日独自生活的时候自己做饭吃。
-又想了想虽然可以预料的是将来独自生活会成为常态,但好像从小到大还没有真正意义上独居过。要么住宿舍,要么走读,出省外培或者比赛也要么和家人一起,要么和同学拼房间,空间上自己一个人过夜就几乎没有过,还挺意外的。后天室友走后大概要住两周左右单人间,潜伏期长一些的话说不定跨年的时候会自己躺在床上发着烧跨(,第一次的独居生活怎么也没想到过会是这样的,令人感叹(
-与此同时我妈在上海也阳了,当初回不回家现在结果也都是一样的,令人感叹 -\(\times 2\)(
+- 今天又双叒叕做实验, +顺利苟过去了,很感谢暑假开头时候写了实验备忘录的我自己。 +
- 玉树的烤冷面不知怎的感觉不如上周好吃了,可能是太干了。下次试试馄饨。
12月25日
+10月13日
-
-
现在陷入了一个 dilemma——目前我还是没有症状,甚至我室友除了 22 -号晚上发了烧之外后来也没有症状了,但抗原确实是阳的。我也不好说后面几天会不会再有症状。如果现在复习抽代,31 -号不一定能正常考试,还耽误后面的科目;如果直接放弃抽代复习后面的,实际上又防护得好根本没有中招,就得缓考然后寒假继续学域论了,也好痛苦。实际上这两天光折腾搬寝室做清洁和根本没睡好觉,就耗了不少精力,没做什么事。
-更草的是昨晚终于回到自己床上睡觉之后,梦到抽代期末又考了一堆群论,而且全是稀奇古怪的初等技巧,既熟悉又不熟悉,好崩溃(
-给 wjd -老师写了封邮件想和她聊聊天,讲了一下自己打算整理一份讲义的计划(立 flag -防止咕咕),不过她一直未读,想了想也确实不该周末发邮件,等等吧。然后给统推讲义选了个封面(某些人期末周是真闲啊
-
-
是高一的时候在学校破坏绿化的产物,花瓣上的水珠拍出来很漂亮。再一次在相册里翻到它的时候第一反应是朱熹(?没记错吧)写的『山桃落乎,辛夷开未』,但其实山桃就是桃花,辛夷是玉兰花苞,和樱花都没关系。
-背后还有个小故事,和选这张图的原因(单纯觉得好看)没关系,讲出来给大家当乐子。高中的时候学校里有一大片樱花树,春天开花的时间大概有两周。高一那个春天我缠着 -ex -晚自习下课陪我去看(现在想想多少有点毛病),他不理我,然后我自己摘了一捧樱花放在水里拍照给他看,他还是不理我(所以说不只我有毛病,他更有毛病)。(怎么 -ex 小故事都听起来又惨又好笑
-所以这就是那张照片。下面垫的本子是草稿本,翻出来的时候才发现封面的法语我已经能读懂了;再下面垫的大概是化学试卷,高考拖我后腿没进新雅的元凶(。说起来我觉得新雅真不错,还可以分流去学数学(x),考上的话是做梦也能笑醒的程度。室友说新疆高考前几名一般都会选新雅,但新雅貌似每年在上海的录取分数线都是最低的,甚至经常因为没人要而顺延给分数更低的同学。高中时候的一个同学就高考压线,在新雅和复旦经管之间选择了后者,大概是被“理科实验班”这个名字唬住,以及不愿意离开家吧。我当初想的倒是如果进不了华子就去中科大,总之不是很想再留在上海,不过最后还是被家长老师逼着用交大兜了底。当然胶带也很好,我每年寒假都和同学约去交大玩一天,但现在想想真的去 -IEEE -或者致远的话恐怕也会很痛苦。但是本科可以转专业诶!可恶。不过想想我读过很多遍的《上海交通大学生存手册》和迟先生的《与恶龙斗,其乐无穷》,真进了世俗意义上非常成功的电院的话,还会有转出来的勇气吗?恐怕就在中游吊着,卷也不是躺也不是了。总之也很难说。
-扯远了。我还是很喜欢花的。高二的春天在上网课,五月才复学,没看到学校里的花;高三的春天我就自己又去看了几次,折了两枝插在水杯的挂绳上,那张照片在这一篇的倒数第二个一级标题里可以找到,花蕊偏绿色,应该不是樱花而是梨花。不过之后决然不会再回高中母校了,再也看不到了罢。大一的春天我在华子里薅了不少花瓣,夹成书签拼在一起,寄给了我姐,很有江南(?到底谁在江南)无所有,聊赠一枝春的感觉。
-发现 hx 下学期开了一门 2 -学分大水漫灌(说它水是因为看了一眼考卷,真的水)的初等数论,知道这个消息还是因为竞赛时候认识的几个来了华子的神下学期选了这门课水成绩。所以 -hx -两个学期上的本科生课程估计都是没人听的,他要是一直就教这两门课,恐怕也不会改善教学质量了罢,令人感叹(
-说到本科生教学的问题,今天给 wjd -老师发邮件的时候去统计中心官网确认她的邮箱,发现她的职称其实是讲师而不是助理教授,感觉在华子真的非常少见了。想起来她确实从来没说过自己搞科研或者带学生之类的事,倒是在课咨委听说过评教数据有效性判断的工作是她做的,大概还有为学校提供统计咨询之类的职责。dwl -老师也是讲师。
-难怪她俩上课上得比我见过的大多数老师都好,而且确实都是热爱教学,上课很有热情的类型。实际上感受下来统计中心已经是非常重视本科生教学的单位了,珍惜罢。
+躺床上听早八最多坚持半个小时...数值分析老师对不起,但是被窝真的太舒服了(
+然后就又还是肝一天,今天的 TODO 是写完 ODE +作业,抽代看完群论(太可怕了)然后修茴香豆,写前半周的抽代作业,可以的话工程力学作业也写了,实在没事干了就去搞本理力来补一下我看不懂的工程力学。
+SRT 看了半天,要么一看就好水,要么就是贵系立的项(
+丘数学中心就一个项目,统计中心没项目。梁鑫老师那个项目说是会线代和群论就行,
+那岂不是我上我也行。报了一下试试,邮件约了周六去唠嗑。资金 +500 块,是要拿来买演算纸和笔吗(和 lzy +聊了一下,他已经去过梁鑫老师那边了,大意就是这是个搞矩阵论的课题,属于比较冷门的方向,和未来方向不搭的话不建议去。
+-
+
- 可是我还能有啥选择呢?去吧。 +
12月26日
-Warning:今天是真的很碎又很长的碎碎念,有点 -biased,个人体验为主,谨慎阅读。要喷的话也请轻点(
-昨天说到《上海交通大学生存手册》,今天吃饭的时候又读了一遍。我第一次读这本小册子是大一的寒假,彼时九年义务教育时代从郊区卷到某个超级中学,和高三零基础速成高考的这十年时间给我留下了很强的做题家的肌肉记忆——高三的时候我还在知乎上自嘲力速双 -A -做题家。顺着这个惯性,第一学期做题的热情还很高涨,在微积分线代和法语这三门稍微重一些的课里随手卷出了三个 -A,让我产生了哪怕是华子的课业,也可以通过不断刷题练习轻松掌握,然后这四年就会这样在不断巩固基础之中过去,我学会了这一百多个学分的课程,就会摇身一变成为优秀的博士生预备役,这样的错觉。所以,当初这本小册子让我最震撼的是这一部分:
+10月14日
+-
+
随口问了一句何老板有没有看中的 +SRT,结果他想进的那个项目的立项人是我高中的一个学姐...这下内推了(bushi
+世界真小,让人喘不开气。
+hx 今天终于在讲完有限生成 Abel +群之后停下来讲了点低阶群结构,没继续冲可解群(
+Anyway,不影响他下周肯定能讲完群论。
+今天要稍微研究一下数学中心那个矩阵论 SRT 的内容:
-
-悲壮的学习方式
-古人刻苦学习的故事,直到现在还在我们的身边不断上演。据说每天在新、东上中下院和图书馆都有几千人在自习。学生趴在山一样高的习题集边上苦苦奋斗,绝对是我校作为国内一流大学的亮丽的风景线。挖空心思研究解题技巧的学生们,与同样挖空心思研究出题技巧的老师们,构成了一个完美的圆环。在二者日复一日的机械劳动中,我只看到纸张、电力,以及粮食不断被浪费,却看不到中华之崛起。
-我无意全盘否定同学们吃苦耐劳的精神,但这份精神充其量只能称为悲壮。我们耗费了大量的时间和精力掌握的那些考点、技巧,在真正的知识殿堂里根本登不上大雅之堂。哪怕我们特征值求得再熟练,积分积得再复杂,中国的载人飞船也不会因此而顺利上天。
-我手上一本1300页的数学手册,上面记录了人类文明从远古直到二十世纪后半叶的主要数学成果。而我校高等数学教材(上下册)所涵盖的内容,不超过其中的130页。一个真正有志于建造科学大厦的人,是不应抱着一块儿砖头精雕细琢的。
-学习最需要的,不是悲壮的毅力,而是对无限未知的渴求。
-最终来说,学习知识的目的是为后继的知识铺垫,以及培养创造性的思维。所谓有效率的学习,应当是以最高的效率获取知识,服务这两个目标。从现状来看,我们想要把什么都搞扎实的学习习惯,其效率是极端低下的,而在我们通过大量习题,最终扎实掌握的信息里,有效的“知识”却又是如此的少。
-今天,你学了多少?
+双随机矩阵与置换矩阵群凸包的谱集探索
+双随机矩阵是一类特殊矩阵,它的所有元素都是非负实数且每行每列元素之和都是1。这类矩阵在图论、概率论、矩阵论中都有广泛应用。确定一个复数是否可以作为某个矩阵的特征值,是特征值反问题研究的基础。例如,经典结果告诉我们,所有实对称矩阵的特征值的并集就是实数集,我们称之为实对称矩阵集的谱集是实数集;根据Schur-Horn定理就可以解出实对称矩阵的特征值反问题。类似地,为解决双随机矩阵的特征值反问题,首先就要考虑双随机矩阵集的谱集。1965年,Perfect和Mirsky提出猜想:n阶双随机矩阵集的谱集是所有内接于单位圆且一顶点位于实数1的正k +(k<=n)边形的并集。后人称之为Perfect-Mirsky猜想。当时二人就已证明该猜想在n=2,3的情形。n=4的情形在2015年被Levick、Pereira和Kribs证明。n=5的情形在2007年被 +Mashreghi和Rivard通过反例否定。其他情形至今仍无确定结论。Harlev、Johnson和Lim在2020年通过一系列数值实验侧面证实n=6,7,8,9,10,11应当是正确的。
+根据Birkhoff定理,所有双随机矩阵组成的集合就是所有同阶置换矩阵的凸包。因此双随机矩阵集的谱集就是对称群的凸包的谱集。2020年Jankowski、Johnson和Lim试图通过探索不同的置换矩阵组成的群的凸包的谱集来逐渐逼近Perfect-Mirsky猜想,他们考察了交换群、二面体群和四元数群。这些群都是比较简单的群,其结果与Perfect-Mirsky猜想相吻合。
+本项目试图沿着这一道路继续探索,利用矩阵分析、有限群论、群表示论等领域知识,逐步考察更复杂一些的群,例如两个或多个循环群的半直积、由两个或多个轮换复合出的置换生成的群等来进一步靠近Perfect-Mirsky猜想。
22 -年寒假偷渡进交大玩的时候,我还去东下院和包图朝圣了一下,观察了一下作者 -2008 -年记叙的这种悲壮的学习方式,到现在也还是一样的。当然这个观察毫无意义,毕竟华子里也是一样的,我现在每天也还是一样的。
-现在想想,其实仅有的没当传统做题家的两年,要么在摆烂,要么又被竞赛带进了另一个做题的怪圈,弱者是这样的。学到的东西有些是奇技淫巧,有些是高阶知识在初等平面上的投影,对现在也没有太大用处,偶尔会心一笑而已。这学期抽代里面用 -Eisenstein -判别法的时候,我只记得是高一看北大初等数论的时候看到过的一个判断多项式能否分解的定理,具体内容还得临时去查。其他东西也基本都忘得一干二净,只记得名词了。其他的获得大概就是认识了一些强度离谱的神,还有初步地完成了一些自我认识,这个是好事,虽然停留在比较浅薄的层面,但总比只学高考的话要好些。
-之前看到隔壁数院一个校友写的一篇文章,大概说学习珠脑运算、鸡兔同笼,带给一个中国小孩最宝贵的礼物是自信。我想了想竞赛被爆踩的两年好像也没自信过,更加焦虑、自卑,焦虑到高二的联赛喜提省三倒数(。后期逐渐变成了摆烂乐子人,退役前的愿望只是能完成最后一场比赛就好。我最自信的时候反而是高三退役变回做题家,因为这个我太熟了,我之前做了九年的题,相信再做一年的话绝不会差。哪怕高三第一次月考考了两百多名(注:我们年级一共 -350 -个人,所以真的很草)也还是非常自信,老师一度觉得我乐观得脑子有问题(。竞赛方面仅有的成绩都是退役前的最后一个月出的,不值一提,拿到奖牌奖状的时候我也不是很在意了。真正的高光时刻可能是几次 -ak,还有在场上切过几个得分率很低的题目,其实也没什么可说的,这些属于自己想起来的时候可以偷着乐(?)的范围。
-同学之前给我看过求真升级人的报道,大一爆杀丘赛,速通代数几何之类的神话,问我转数压力是不是很大。我说一点都没有啊,我又不和他们一起上课。实际上我上数学课甚至会尽量避开数学系的同学选课,打不过数学系和求真,但暗中欺负一些数辅统辅的同学还是可以的(不是x,其实就是没那么有压力)。反正也不是第一次被爆踩,而且我润应数了,来自神的压迫感根本追不上我。最重要的是,learn -at my own pace -才有可能学好。说实话这是逃避没错,但我真的不是很喜欢时时刻刻都要竞争,人和人之间何必在学习阶段就非要互相为难..(一厢情愿而已,因为资源不足啊。而且什么时候都不要互相为难才好吧 -= =)(开始暴论了
-Anyway,填强基志愿的时候没怎么纠结,就因为学过竞赛而随便填了数学,非常方便。填平行志愿时我一心想离开,本来填的一志愿是中科大,最后还是拗不过家长老师不断和我强调这样浪费了 -20 -分、虽然强基综评基本稳上但还是要保底什么的,改成了交大。科大数学放到了二志愿,人大统计放到了第三志愿。实际上有点好笑的是,我高三的时候真的很一心只读圣贤书,根本不知道 -CS -和金融很热门,直到出了分之后被按头报交大综评志愿,看往年的分段表才知道交大分数线最高的是 -IEEE 和 AI,然后就对着表格从上往下依次填了 -IEEE,AI,密院,理科试验班。
-综评面试之前一个自称 IEEE -的什么招生老师还给我打过电话,有一种钦定的感觉(?),还不断强调我报的前两个是他们的“王牌专业”,我听到这个词也不是非常感兴趣。其实理论上这些信息应该校友宣讲的时候就知道了,
-但交大那一场是 -ex 讲的,被我咕了。还有就是来华子之后实在学不会这个 b-物理,混不下去,思考转专业做研究转什么的时候有数学这个备选项,也很方便。不然我可能现在还在纠结以后要做什么。虽然一直都稀里糊涂的,时不时用脚投票,但总之最后发生的都是好事。现在在 Yau 的驱动下,高中生超前学习数学似乎分成了两条路径,一是传统的 -MO,二是基本以求真选拔为目标的、提前学习高等数学的升级途径。我记得上海取消初中数学竞赛之后,六年级(冷知识:上海的九年义务教育是五四制,六年级已经是初中了)的小朋友就不做初中竞赛题了,开始卷高中联赛,在不禁止初中生参加高中联赛的时代,被他们屠榜是很正常的现象,
-还好我高一的时候就禁了。所以现在最升级的六年级小朋友应该也是两条线一起准备的,令人感叹。与此同时,今年暑假回了一趟我的初中母校,它是宝山区最好的学校,是全市排第三名的公办学校,不需要交学费。但实际上在市里根本没人听说过。在我读初中的时候学校里还有课外讨论班,老师会讲一些轻微超越课堂难度的知识,
-我经常在课上稍微动下脑子就能表演薄纱所有人,很爽。那位开数学讨论班的老师从前和我关系很好,这次回去他告诉我双减之后对公办学校抓得最严,连课外讨论班这种东西都已经没有了,除了学习课本,就是在“素质教育”——听起来有点像日本曾经的“宽松教育”。没有资源、资本和信息,然而十几公里外市区的孩子们就享受着这一切,要我暴论一句的话,我觉得郊区做题家的处境和小镇做题家一样艰难。前阵子听说竞赛时耳熟能详的一个机构,假期要开分析系列讲座,为求真选拔做准备,突然有一种做题范围只是扩大了的感觉(。当然也还是不错的,能在中学阶段就被驱动着一窥前沿,至少知道 -MO 之外还有很广阔的天地,比天天搁那一边猜联赛四个大题的顺序一边学 -ACGN(x,指竞赛意义下的 Algebra / Combination / Geometry / Number -Theory)有用多了。虽然只要有升学优惠刺激就还是会收敛到做题,好在数学也不应该规避依靠做题提升技巧,至少做题掌握的知识对今后更有用了,这也是好的。每年牺牲两三个或许有那么一点希望的郊区做题家,换取集体升级,..大概还是很值得的吧。
-写完之后发现每两段话之间都没有衔接关系,毫无逻辑..随便看看吧
-12月27日
+看着好高深!(但是老师说群都不必学得多好就能做(在画饼
+TODO:
-
-
我感觉大概是终于理解域论了,从头到尾走了一遍逻辑到处都通了,有点狂喜。但并不代表会做题了,为了考试还得进行一个拟合。
-周六就考试了,这是否进度有点慢(
-半个多月来一直摸鱼和阴间作息,肉体还在东八区,睡眠已经到东三区了。昨晚(今天凌晨?)干脆直接没睡,实际上是躺下了睡不着,就起来了。
-已经很久没见过早上六点多是什么样子了,实际上天还没完全亮。看着外面黑乎乎的,上次冬天里起这么早大概还是高三,高中生真惨,还好我大二了(x
-所以今晚可以早点睡了,然后就调整回来了吧。
-喉咙很不舒服,感觉危。但是喝了一天热水吃了一板润喉糖就又好了,搞不清楚什么状况。
-后来大概理解了,住单人间之后我经常一边听歌一边跟着鬼哭狼嚎(别细问,要脸,不好听),加上附近的寝室都没人,更加肆无忌惮了,大概是有点劳损。
+- 了解一下双随机矩阵和谱集的结论 +
- Perfect-Mirsky 猜想,Levick、Pereira 和 Kribs 的证明,Mashreghi 和 +Rivard 的反例 +
- Jankowski、Johnson 和 Lim 对于交换群、二面体群和四元数群的考察 +
+搜了一圈感觉这个猜想下面就没几篇文章,全都列在这儿了,难怪说冷门(
+一开始没大明白什么叫复数集是一个什么 n 边形覆盖而成的凸包,看了 +Pereira(上文那位证明了 n=4 情形的教授)的讲座才明白这个猜想是在说啥。呃,然后讲着讲着就量子物理了,怎么会事呢,不看了(
+睡前读了谢惠连的《雪赋》。
++
未若兹雪,因时兴灭。
+
12月28日
+10月15日
-
-
学完了域又回头学习了一下环论,这下终于明白之前多项式里看起来莫名其妙的定义有什么用了,高情商说的话就是,教材和课程设计都还有可以优化的空间(。
-我又觉得我会了(
-刚看完域论再回去看环定义的时候,有一种“世界上怎么还有环不是含恒等元的交换环”的感觉(恼
-然后明天还得继续拟合近世代数 300 题,感觉 hx -很喜欢出一些不太抽象的题目,平时没怎么练习过。后天复习一下拟合过的题目,就要考试了。这本书买来一共做了两次,一次是期中之前找了几个题拟合,一次是期末之前再拟合一下。其余时间里连翻开看一眼的欲望都没有(难怪我做题这么菜 -qwq
-实际上细看觉得这书是对绿皮的一个挺好的辅助,一些绿皮上答案写得不好的练习题这本书上都有补充,另外也给了不少风格类似的题目。
-听说明天 CMO,于是去给 runzhi -加了个油(?),才知道他还真的在现场,去年是考生,今年已经是招生志愿者了。甘主任也太成功了(
+原来近春园西楼不是指理科楼啊...还以为要回到伤心地(x)了。19 +年金秋营的时候于品说物理系要搬到更好的地方去了,将来整个理科楼都是数学系的,到现在新物理馆好像也还没造好,xs。
+聊之前我还想着就算做不出东西来试试也好,结果老师劝我三学位课本来就多,还是珍惜时间打好基础为妙(
+很对,很对,跑路了。
+其他就没啥事了,今天要写完初概作业,然后复习数值分析第一章的内容,写上机作业。但愿能写出来(
+-
+
- 写出来了,开心,虽然中间破防了 114514 次( +
- 你猜我为什么不想转码了.jpg +
+头一回见到 ddl 延长(
+
12月29日
+10月16日
-
-
听说假期常和友人聚会去吃的一家烤肉店要关店了,在上海一共四个门店,暑假里关了一个,年底又关了一个,不知道还能不能撑得下去。北京有一家,不过也好久没去过了,不知道现在怎样。
-感觉到记忆的崩塌..
-网易云说我一年听歌听了 2516 小时 50 分钟,也就是平均每天 7 -个小时,真恐怖。特地打开朋友圈看了看,听得最多的人大概就是我的一半左右,其实也很多了,对听力不好。
-不过实际上真的听进去的没那么多吧。大多数情况下是当 -bgm,和白噪音没区别,习惯之后不听歌反而专注不了。平时走在路上也会戴耳机,虽然基本听不清在放什么,但是会有一种,虽然身在人流中,实际仍然蜷缩在自己的世界里的安全感呢。(注意交通安全啊 -kora
+今天就更没啥事了,继续把数值分析复习完呗,没事干了就预习抽代/看理力。写写数值分析的证明,虽然不知道这课最后考试有多看重证明,反正平时的纸笔作业又少又水,完全没有四学分的感觉。
+整理了一下昨天数值实验的内容,打算水一篇长期的博客,但是要等作业 +ddl +过了再发,不然万一被判协助抄袭,徒惹是非。还蛮有趣的,我是说如果这样轻量级地使用编程语言,debug +的痛苦还并不大于快乐。
+我越发觉得自己还是应该转数,并且意识到自己的 coding +能力在数学人里面还算可以,比较乐。
+暑假写的 Sharygin Geometry Olympic +题解终于成文了,指导老师还是写上了杨丕业老师,虽然他这次也没指导什么(x)。
+和他聊了一会,才知道他现在已经不在质心教竞赛了,而是去了长沙的一所高中教书。还记得 +19 +年金秋营(又是金秋营,那次金秋营确实对我意义蛮大的)考完第二天的试,我还去质心找他玩了,也帮忙完善了第二天的两个几何题解,似乎他们公众号上当时在题解里还写了“鸣谢外心姐姐”之类的话——因为质心的吉祥物是质心姐姐,于是我也随口编了个类似的名字。
+聊到最近在学什么,才知道 hx +是差不多和他同期的华子数学系学生。末了听他感叹同是丘赛优胜,走的路却完全不一样了。
12月30日
+10月17日
-
-
距离室友测出抗原阳已经过去七天了,我还没啥事,是否说明已经平安度过了(
-可能有在别人寝室坐椅子睡觉的那两晚上的功劳,毕竟我不想承认它是无用功(逃
-卷了一天抽代,但愿明天遇到的都是含幺交换环,睡了。
-hx -说期末的题目比期中容易一点,但我对他估计题目难度的能力表示悲观,所以还是很怂(
+今日仍然无事,早起感觉发烧了,休息了一天。
+还好不是第八周,还好不是第八周(
+CW:这一条是很暴躁的吐槽。(是时候去搞个折叠块的功能了(懒了,下次一定x
+这两天有高中同学又一次来邀请我参加情系母校,今年还是非常不想去。
+和母校并没有多少可以情系的,这似乎的确是我的问题。一个对竞赛(哪怕包括小学奥数)和高考都几乎没有了解的野鸡学校初中生在升上高中之后,先花两年多一点的时间学自以为的数学,摸了几个竞赛的破奖,又花八个月从零开始学习高考,最后摸了个相对高考生来说也还算不错的成绩,那当然是以一副做题家的姿态度过这三年的。任何“二附中人为之骄傲的高中快乐回忆”,中二一点讲就是“玫瑰色的青春”,对我来说既社恐地狱又真的是没时间。还有理科班夸张的 +9:1 +男女比下压抑的氛围,唯一一位关系好的女同学高二生病休学,无数竞赛和高考过程中的焦虑、自我怀疑,
+失败的恋爱经历,都无疑加重了自闭。或许也是一种好事,至少我现在自闭得挺快乐的(另一方面,我实在不认为这种活动有什么意义。举个例子来说,今年课咨委有一位二附中的学弟,物理竞赛拿了金牌,却跑到未央来读机械。原因是决赛现场被华子口头签约了钱学森力学班,于是强基报了行健,结果被华子以“二类生不报致理就是违约”调剂来了未央。天知道从第一届强基开始,你校有多少被华子口头签约的人(当然也包括本人)被毁约(当初华子给我的理由是求真分走了致理数学一个班,听起来还算合理吧),我这点破事当年还人尽皆知呢。当然,我这样的的确是没什么办法,没有过硬的成绩握在手里,被毁约也没话说,谁叫我无心间勾了那个“服从调剂”,不然现在岂不是在交大电院逍遥自在?但一个金牌,因为这种信息差毁掉四年(无意表示未央在价值上不如致理,我敬佩真正热爱这个学院里的学科的同学,只是对于他个人的期望来说,的确是毁了),尤其这还是曾经在零字班出现过的惨剧,我无法理解。
+校友二月办情系母校活动,四月又是校友导师交流会,五月随华子招生组去学校强基预面试和宣讲,六月招生干的离谱事情更多(比如今年某位学姐以假意承诺计金的伎俩,从北大信科挖了一个裸分线上分不是特别高的学生过来,最后扔进自动化。当然这是另一回事了),上下年级之间的交流不计其数,却连这种已经见多了、简单说几句话就可以避免的错误都改变不了,实在不知道在做些什么。须知在高三学生眼里,诸位是“可靠的有经验的学长学姐”乃至在招生季是“手握大权的朝廷命官”(尽管并不是)(这话并不恰当,但就那意思),但凡能负点责任呢?毁约自然是华子的不是,我已经骂不动了,但就任其发生吗?
+我的确在想我加入的话能不能至少改变点什么,这样直接逃跑只张着嘴数落别人的不是,也还是不负责任。然而我一向人微言轻,加入了情系母校和各种宣传也就是做边角杂活(校友导师活动的时候试过一次),哪里抵得过几位核心成员鼓吹华子幸福生活的安排呢?要说尽我所能,也就是真的对几个报强基的时候找我咨询的同学,说了所有的实话而已。
+还记得今年五月的时候在质心的公众号上看到了一位东北某校(记不清了)的同学,物理银牌却报了未央,把自己回归高考的心路投稿了出来。我托在质心认识的老师联系到了她,才知道她误以为报了未央可以任选工科专业,可以进她心仪的自动化,然而未央根本没这个专业;她的学校里不曾有过考进清华强基的前辈,本是寒门贵子,我最欣赏的类型;她更不知道这是一种华子眼里的毁约行为,在未央的分流排名也会垫底。可惜她的文章晚发了一步,我也晚来了一步,已经过了强基计划报名截止时间,今年也不再有六月确认志愿的环节。如今她在未央读生化环材之一,我拼尽全力,还是什么都没有做到。
+我痛恨信息差,痛恨“你不知道的东西正在伤害你”,而我如今混得还行,一部分还是托趁早认识到这一点的福。尽管在努力,也还是几乎没有帮助到任何人,落得只有在这里无能狂怒,真是 +loser 啊。
12月31日
+10月18日
-
-
最近几天卷抽代卷麻了,连日记都懒得同步,干脆到月底把最后五天的攒在一起发了,基本都不长。
-不是,这抽代早说考这么水,我也不至于一周全复习这玩意去了啊((
-考完第一门,晚上打算报复性看两部电影,然后写一下马原期末论文。
-一个是期待很久的《血观音》,一直很喜欢惠英红。说起来这里本来还有一段话,想想有点剧透,发出来的版本里就删掉了。其实如果是我自己的话完全不介意被剧透,甚至看电影之前一般会先去看看梗概,对情节有一个基本的想象之后再去看,能发现更多出色的地方。(推理剧剧透论外x
-说起来暑假里看的《不完美的她》就是周迅和惠英红主演的,她们两个我都很喜欢。但是这剧翻拍了日剧《母亲》还翻得完全变味了,卡司和原剧明明都这么棒,实在可惜。
-周迅近年来真的演了好多烂片二刷了《色,戒》,第二次看王佳芝给易先生唱《天涯歌女》的片段还是很难过啊(
--
-人生呀谁不
-惜呀惜青春
-想起来了
--
-人生が秒速で塗り変わる青春は風になる
-人生也在秒速中改变 青春将幻化为风
-(是花譜的《そして花になる》里的歌词(这不是一模一样嘛 x
-还想看《芳华》和《颐和园》(这个可以说吗),今年是来不及了,后面几天还得复习好几门课,考完数值分析(实际上就是考试周最后一天了)一定。
-考完试给抽代助教写了封邮件,这个学期收到了很多来自他的正反馈,夸张一点说,其实这些鼓励很能精准安抚一个基础像筛子一样甚至选课的时候有点战战兢兢的外系自卑菜狗(定语好长但都是实话),想表达一下感谢。写 -bonus 每次都有批复,在作业里提出的小问题也能得到解决什么的,感觉他很 -nice。
-然后被已读不回了(。上周给 wjd -老师写的邮件她也还未读,草,我以为我室友一周看一次邮箱就已经频率够低了的,怎么还有老师也一周不看邮箱的。有一种表白了之后还被人鸽了的感觉,还是两次((
-
-看微信头像的照片感觉助教很帅,但是一个学期以来根本没见到过真人啊 -kora!太遗憾了罢想起来一件事,大一的时候微积分 A -有位选课的时候总被抢爆的烫门老师(据说课讲得不错 & -调分力度大,别的老师基本都不调,我上 wxf -的课是一点调分都没有),一到期末学生就扎堆给她写感谢信,有的真的很肉麻。肯定有一些是出于真心,但只是为了在几百个人的大班上给她留下印象的,估计也不在少数。
-找了找和室友的聊天记录,甚至还有当时的两张图。反正我挺讨厌这样的,尤其是老师会把收到的话发朋友圈,自己也在助长这种风气。我实在不太相信写右边这段话的人多喜欢数学,这也太假了,看着好难受..
- -
-一年就要过去了呢。感谢陪伴!祝大家新年快乐,明年也继续来听我讲废话的话就更好啦!(x
+早晨起来还是低烧,于是摆烂翘了两节早课继续睡了,这下大概彻底是好了。下午室友发烧了,昨天下午何老板说也发烧了,草。明天要是华子搞出来三管阳性的话必有我们一份功劳(
+看北大猫协的推送在玩 EVA +梗,点进去一看是一只左眼瞎了的小猫起名叫明日香,我超,地狱笑话。
+结尾处这张照片怎么看抱着猫猫的人都像真嗣,不知道是巧合还是特意安排的(x
+
10月1日
+10月19日
-
-
深切感受到了听力的衰退,七八年前在放学回家的公交车上听一格音量的耳机也能屏蔽噪音,现在要两格;昨天在抽代课上有个旁听的同学小声叫住我,问我要微信想要点课程资料,说了两遍我都没听清楚,凑近一点才听清楚他在说啥,感觉很抱歉。
-说起来那趟摇摇晃晃的宝山 8 -路,已经是七八年前的事了吗,我还记得很多细节。当时家住宝山这个小破郊区的边缘小镇,小破初中在宝山所谓的核心位置,其实说是核心也远不如城区繁华,只是靠近码头,发展得早一些。每天放学从友谊路挤上车,在牡丹江路上一路堵车,开到市三医院(现在叫市九北院了)门口才好一些。如果到了绕城高速上还堵,那这十公里恐怕就不是一个小时能走完的了。
-还记得遇到过几次意外的堵车,我还在绕城高速下过车,去旁边的铁力路站乘地铁去学校,那是 -3 -号线唯一一个地下站,据说是旁边的宝钢不让站台建在地上,出钱改到地下去的。现在已经记不清楚怎么从高速的一侧去往另一侧的地铁口了,想想当时为了上学还挺勇的,放在高中的话我就请个假打道回府了(什么啊
-人生会有几个七八年呢?(#每日悲观
-室友:你为啥要和刚高考完的小朋友卷离散啊?卷得过吗?
-我:我超,对啊,为什么呢(
-不过暑假上逻辑课之前大致看了一点离散(1)的内容,想来补完(x)一下;另外貌似会有图论,这玩意在我有关数竞的印象里非常恐怖,来看看.jpg
-看了一天初概,很破防,这课用英文讲不好吗(暴论)。连续型联合概率密度(Joint -PDF)还叫做联合密度,联合概率,明明直接拆成 Joint 和 PDF -就知道是什么了;Joint PMF,CDF 同理,Marginal -同理。什么边缘密度,边缘分布,离散型 -blahblah,甚至作业题题干上老师还把联合密度写成了联合分布,白浪费了很久和同学研究这是什么意思,中文太难了(
--
-John Von Neumann once said to Felix Smith, "Young man, in mathematics -you don't understand things. You just get used to them." This was a -response to Smith's fear about the method of characteristics.
-破防了,记之(
-
10月2日
+今早去找 dwl 聊天,其实和 lx +聊完之后我对很多问题都大概是有数了,但这个 OOH +是早就约好的,不能鸽掉。正好统计中心这边的方向对我来说是退路一般的存在——基础数学搞不了可以搞应用,理论统计搞不了可以搞应统,总不至于饿死(
+wljj 好像不是很会画眉毛(什么啊和她聊天就盯着这个看去了吗
我认为数值分析应该改名高代(3)(逃
+第三周的时候我还在担心会不会根本讲不完,现在发现不用担心了,进度还蛮快,马上第三章又要讲完了(
+但也不是 hx 那种快,是这课内容本身不算太多。以及 bcl +的教学水平也是我见过的老师里相当不错的,起码是这学期听得最舒服的一节课,虽然好像他是第一次上这课?选课的时候我还为没选上 +hzy 而悲了很久,现在发现也不错。
SRT 报名一点也不顺利...退了 lx 老师的组之后打算找个水一点的 CS
+项目来加两学分
+4.0,结果分别给两个学生立项发了邮件,一个过了两天才回复说招满了,另一个到现在都没回复我,有点烦。为什么学长
+check 邮箱的频率还没我高啊!
于是换去工工系的一个组了,老师回的很快,过了俩小时就过审批了。感觉工工在各方面就是一种,下位替代一般的存在(...)
-
-
给同学讲题目,题面反正就是这张图,然后求这个种群灭亡的概率(
-感觉画得很好玩就放上来了。
- -
-开学第三周就破防了,睡前喝了两大杯热豆浆。加蜂蜜还是没有直接加白砂糖甜,但是感觉健康一点(?
-这工程力学开始看不懂了,虽然必修但考虑中期给它退了,太闹心了。
+- 我倒也不 care +到底是哪边,工工的话还可以靠一下统计中心的现代统计什么的,蛮好。 +
- 业余爱好,业余爱好(所以水平也业余x +
10月3日
+10月20日
-
-
梦到课咨委例会,我敲门进去发现里面的人都不认识,然后问了一句:
-“这里是告白实行委员会吗?”
-不是很懂你们这些二刺猿.jpg
-还梦到抽代期中一道题也不会做,何尝不是一种未卜先知(
-来到百京的第二年,还是学不会降温的时候怎么穿衣服。
-傍晚友人约了恰饭(其实是大倒苦水,大家过得都好惨),急着出门的时候实在不知道穿什么,扯了一件粉衬衫一件浅绿的风衣出来,草。还好颜色都偏浅,其实也没有难看,友人评价是像一颗草莓(
-到半路拍了张照片,其实拍的不是特别好,
-也不是很庵野,毕竟电线杆太远了。
-
学校东门对面的那个地方(叫东升乡八家村)真的挺庵野风的,有电线杆有护栏有
-电车地铁有路灯,高楼大厦之间一小片低矮的村庄。今天的天空也很有层次感,是我没抓住机会好好找个位置拍,残念。其实如果能再晚一点,在有地铁经过的时候骑车拍一段运动的录像就更好了,但是试过一次会非常抖,远远超过手持拍摄的那种抖动感。考虑买个手机支架(??
+怎么感觉要期中考试了?我超,如梦初醒(
+接下来两周时间基本都让给抽代就行了。期中考三门(然而期末要考 8 +门,很难想象到时候该怎么办),初概 PF +之后轻微摆烂并且后半期也不是很难,工程经济学第九周周末才考,有丰富的往年题,拟合一下就行。抽代反正也没有往年题,
+zmx +均分 50 的卷子就算能拿到又有什么用呢,可以去看看 PKU +的题,然后就注重把书和习题吃透。大致的计划是:
+-
+
复看一下茴香豆,很担心万一忘了什么东西(
+按章节重写当初不会做的课后题,有很多东西前后有联系,也有值得当做引理记录的
+我的群作用仍然一片混沌,困难的课后题主要指这个
+手推重要定理,第一遍看书的时候自己没推出来的定理例题什么的都可以再试试。不过主要是 +Sylow 及以后的一些东西,可解群,直积(这个简单点),有限生成 +Abel
+复习一些助教给的有点难度的 bonus 题,以及一些 Math StackExchange +上遇到的东西
+还有时间的话不妨看看近世 300 和 pku-lib +里的抽代题,感受一下隔壁是什么难度。虽然纯做怪题也没啥意思,考试所迫吧。
+
何宝你要是打算考到环论中段的话,能不能把题出简单点.jpg
+(为什么要叫何宝)(反正和同学平时就这么叫的)
+于是今天的进度是,浅看了一遍正规群列和可解群(bgm +是不是可以放花譜的不可解(x)),写了作业的前半部分,然后狼狈地带着我破碎的群论知识打开了环论章节。但愿能先看完环的定义那一节,写完课后题,再回头看一看上一节里 +hx 没布置的题目。有空的话把低阶有限群看了。
+越发觉得自己很多地方学的都有问题...
+何老板放弃了我的 Python 安利,转头用 R +写概随作业去了,某种意义来说也没问题,R +对统计方面的很多东西封装的更好。但他还在同步听机器学习的课,那为啥不善用 +Python 捏。据说他还上了微积分 C +和社科线代来复习和刷绩点,呃,每一件事我都不是很能理解(算了我估计也没人理解我在干什么
+总感觉他最近在问我很多 STFW +就能解决的问题,但是我觉得教会他怎么向搜索引擎描述问题比我自己去搜了发给他还费劲,稍微有点暴躁。想来他不知道我博客的存在,问题不大(好阴暗!x
+
10月21日
--黄昏是我一天中视力最差的时候,一眼望去满街都是美女,高楼和街道也变幻了通常的形状,像在电影里。你就站在楼梯的拐角,带着某种清香的味道,有点湿乎乎的,奇怪的气息。擦身而过的时候才知道你在哭,事情就在那时候发生了。
+贪婪,自私,残暴,冷酷,放荡,背叛,软弱,渺小
+贪婪,自私,残暴,冷酷,放荡,背叛,软弱,渺小
+渺小,渺小,渺小,渺小,渺小,渺小,渺小,渺小
——《恋爱的犀牛》
据说这话原来是陈建斌说的,廖一梅(还是孟京辉?)曾经和陈建斌是同学,改了一下放到了剧本里。一到这种时候我就很想圣经吟唱(
- -10月4日
+奖学金入账 0 元有感(x
+虽然但是,该干嘛干嘛,我又没有错。自有能兼顾迎合你院评价体系和自我发展的神,我恐怕不行,那还是自己混好比较重要。(草但是损失四到五位数人民币还是肉疼啊!
+10月22日
-
-
看抽代看到凌晨,感觉每个地方对于置换群、对称群、对换群这三个概念的描述都不一样,真的很破防。我个人倾向于 -Undergraduate Algebra 的解释,把对称群认为是作用在 \(\lbrace 1,2,...,n \rbrace\) -上的置换的总集,把置换群认为是对称群的子群,比如说 \(A_n\) -也是一个置换群。然后对换群是比较广义的可以对于任意集合上的一一对应的一个说法。hx -给的解释是混淆置换群和对称群这个行为本身是为了避免混淆(??),我迷茫了。
-怀疑 hx 的进度现在已经是 zmx 的 1.5 倍了,
-难怪作业也是 1.5 -倍,已经 Sylow 了。很难想象这课不自学 or 预习的话怎么上。然后发现助教会在习题解答里面塞 bonus -题,我趣,好阴啊(不是),我一直都不看解答的来着。
-破防 -2.0:为什么要热衷于给每一个概念取名字,就按照符号叫不好吗(暴论
-破防 -3.0:我院另一个上抽代的人要退课跑路了,最开始还是她把我骗过来的,乐。
-破防 -4.0:听说好几个隔壁的高中同学都降转成功/目前有降转打算了,呜呜,我也想降转(暴论
-多读一年的话恐怕基础会好很多吧,不像现在一样畏畏缩缩,sigh。
-所以要不延毕吧(恶魔低语
-今晚课咨委和科协会议撞了,选了课咨委,20 -分钟搞定,听说科协开了一个钟头,
太棒了。
+邮箱的垃圾箱里塞满了 Bridge Base Online +的广告邮件。上次打桥牌还是去年马杯之前,最后马杯我也没上,不过你院似乎成绩还不错,打过了求真,挺意外的。
+你院的桥牌队到现在还是只有 7 +个人,凑不出两桌,始终没有训练过(或许他们有练,没在群里说,我不知道);另外六个同学都是清华附中的,身为外人话说不到一块儿去。当然听说他们高中的桥牌队很强,我在二附中的时候从未听过有什么针对高中生的桥牌比赛,也就把学过的东西当做又一个不同于人的记忆,直接搁置掉了。于是我的水平还停留在初中,这也是初中学校留给我少数有意义的、较好的记忆之一。
+其实也有必要复健,桥牌是一项很有趣的棋牌运动,但暂时没心情。
+用北京健康宝拍的头像当参考生成了一张猫娘.jpg
+更新到 About 里了,我宣布我差不多就长这样(确信(确信
+
+
然后同样的咒语拿同学(男)的照片试了一下,生成了更多比这好看的猫娘,我不理解.jpg
+存档一下咒语和反咒(其实是在猫车老师发的咒语的基础上改的,反咒就没动),哪天闲了再玩玩(
++
+masterpiece, illustration, extremely detailed CG, comic style, +professional light, one girl, beautiful, white shirt with lace +collar,glasses with gray and thin frames, artistic, nekomimi, black +necklace ,small ear rings ,hair pin, long black hair, spread hair,shiny +hair, curvy hair, smile gently ,doll face ,closer interpupillary +distance,small nose, big gem brown eyes, bright eyes, necklace, +nekomimi, fringe,small pink lips,slightly flushed cheeks, classroom-like +background,
++
fat, lowres, bad legs, bad anatomy, text, error, extra digit, worst +quality, low quality, jpeg artifacts, blurry, forehead,
+
+今天 AK +了环理想那一节的习题(好多...),虽然写了一个下午,但是真挺爽的。
+以前觉得代数题依赖灵感,
+现在发现的确,但是摸清结构的话对于矫正思路还是比较有用的。然后去吃饭,在食堂遇到了上学期的高代选老师,远远看他和别人聊天,突然觉得他也是和何宝一样单纯可爱的人,总之很有数学中心青椒的气质。
+尽管他俩上课都是 +book reader女老师的话印象比较深的是 yh,尽管我也没怎么听过她上课,但看 handout +觉得思路应该很清楚,
就是字有点丑。但不知为何大家都说她教得不好,或许是有时会讲一些写在 +Remark 里面的内容,对工科的同学来说显得有些发散了吧。感觉 yh +很酷的样子,有事发邮件写公告不看微信群之类的举措我也觉得很棒,还有一次看她穿写着类似于 +Love is Love 句子的 T 恤来上课,这在华子是可以的吗(x)。
10月5日
+10月23日
-
-
睡前破防了,点开空间发现宗桑也在破防,万恶之源:
-
-
礼貌问候和开端:
-
-
对抗训练:
-
-
太艺术了,改天打印出来贴床头。笑了半个小时,快乐地睡着了。让我们说,谢谢宗桑!(
-何老板找我问统辅的问题,我才知道他想转 -quant,蛮意外的,以前以为他想去类似于经管那种不太技术的方向发展。胡言乱语了几句,其实就是提供了一下我知道的金融统计和金融数学的课和老师,quant -关于码的方面属实不是很了解,就不乱说了。
-然后他问我什么打算,我说我嘛,应该就是应数了,stat,bio-stat -都有可能。(注:生统和生物没啥关系,在会考之前我高中生物就垫底过 114514 -回
-
10月6日
--
-
睡觉就是短暂地从世界上死掉。
-佛了,复习个初概期中搞的鸡飞狗跳,这样的话真到期中了的话怎么办,到期末了又该怎么办。
-感觉更多的是心态问题,有一种《这个东西最好是一直复习下去》的感觉就会搁置很多别的事情...
-看了一个 runzhi 给的抽代题,收获一张 runzhi 梗图:
-
-
最喜欢的一集.jpg
-他问我为什么不跟着茶园上抽代,理应平均水平比数学系低一点,还好卷一些吧?我超,为什么呢。
-不过茶园的数学水平和数学系相比,我还真不是很清楚,知道的数据就只有大一上微积分期中,茶园平均好像没到 -85,我好像 95 = =,所以感觉也不算很好?反过来如果让数学系考微 A -的话会咋样呢。
-罢了罢了,来都来了 XD。
-功成不必在我,我在必不成功。
-和 jdc 说了几句话,因为求真割据,现在数学系只有一个班 30 -个人,转入比例不能超过 15% 的话,今年只有 4 -个名额。现在有一个茶园人一个贵系人加入竞争,还有两位准备降转已经上了很多专业课的同学,这样就已经满了...实际上开放给物理系的互转名额每年都是浪费掉的,外面的又转不进来。
-大家都不容易啊。
+写 ODE +作业写得无比暴躁,课讲得又水作业又麻烦,我还漏过几次签到,打算二阶段退课了。其实如果不是初概裂开用掉了 +PF 资格,本来就是打算给 ODE 一个 PF 的...
+往好处想,工科 ODE +不可能够用,迟早得学完整版;后期还有从零开始的统计推断,这个在统计中心上过就不打算去数学系再上了(据说数学系的统推也没啥意思,复习半个学期概率论),所以不能再像初概一样就云过去了。集中点精力吧,该抛弃就抛弃。
+体测完之后就变成了一滩史莱姆,今天基本没干啥事,肥宅瘫倒.jpg
+今晚发现了笛子姥爷以前画的小漫画《笛子的单恋史》,目测是实际事件改编。看得津津有味的时候突然发现没完结...已经好多年了,估计不打算继续画了。想来过去了这么多年,笛子姥爷早已组建家庭,大概也不把(现实中的)这事儿放心上了,弃坑情有可原。但是身为读者,草,好难受(
+最后碎碎念一条:看离散的 PPT 觉得右上角那个华子计算机系的 logo +蜜汁熟悉,再仔细一看最下面有个“1958”,大约是贵系成立的年份。这个要素让我感觉更熟悉了,然后想起来,二附中也是 +1958 年建校,校徽上也写了年份。四舍五入二附中 = +贵系(这个差距就像我今天体测仰卧起坐满分但 800 +米恐怕也就是刚及格,于是四舍五入我 = 鲤鱼姐(
+丢个图:(可以看出除此之外二者没有任何关系((
+
+
以及想明白了一个问题:我觉得转数比转码更好的一小部分原因是(最大的原因是学不会 += +=),如果让我一边上课一边磕盐一边实习,我恐怕会疯掉,至少会非常焦虑。我不清楚贵系的普通人是怎么生活的,至少我看到的神都三头六臂,白天上班晚上写作业还有空娱乐运动甚至保障睡眠,人脉也很广阔。另外转码其实就是一个相对功利的选择了,不见得走得太远。相比之下转数生活就单纯很多,沉下心来扎实基础,多看多思考,你甚至不需要(至少不必要,也不很主流)过早开始磕盐。
+如果能认识更多的转数人就好了。书院里自然极少,只认识两位,一位已经退学重考隔壁数院去了,我很钦佩,祝他成功。另一位还不知道是否确定要转,没有详聊。尽管有转数群,我还是和他们中的绝大多数人都不熟。其实我真的很羡慕本科就可以肉身到达数学系的同学,不说别的,主要是有机会降转甚至 +gap +一年的话,这个时间可以好好补一些基础,更自信些。或许现在不必多想,真需要了就赶快去补就好(
10月7日
+10月24日
-
-
和室友聊天,发现一屋子人里就我没学过小学奥数 = =
-拥有一个快乐的、无所事事的童年也不错 -XD,虽然代价是高中竞赛的时候猛造各种轮子,尤其体现在概率计数里(
-初概期中考完了,明明小分值的难题都做得挺好,结果我飘了看错一个水题,当成无放回抽样了,三小问全寄掉,感觉很危。
-从竞赛做一试的时候就知道不能做快了,会寄,怎么总是记不住呢。sigh
-据说这课 50% 优秀率,所以如果出分之后在平均分上那就不记 -PF,不在的话就记了算了,之后再去摸一个概随。下学期还要上数学系的概率论 -(1),真就全都来一遍啊w
-然后发现没进综奖奖学金答辩,想了想确实是因为实践和志愿为零,虽然社工和学习拉的比较高,有自我感觉良好的嫌疑。麻烦给两个单项吧,真的缺钱(
-没做志愿是因为一直打算去答疑坊蹭工时,但又一直没去(x),实践的话单纯是不喜欢和一群不熟的人旅游,所以没参加过,罢了罢了。看了一圈认识的几个神也没进,又不破防了(?
-怎么全是坏消息啊!
-感觉最近是一个慢慢意识到自己也没有想象中那么厉害的状态,蛮消沉的。属于是难的不会,简单的又糊,中间的倒是会,又有啥用呢 -XD。
-于是晚上翘了一二九分声部的环节,叫上何老板去玉树吃了夜宵。没吃晚饭,然后夜宵一份烤冷面半份馄饨下肚感觉整个人都好起来了,食物治愈一切。辅导员也没来找我的茬,总感觉他早就放弃在类似的事情上说教我了,蛮好的x
+体测完浑身疼,鼻子也难受,咸鱼。推抽代进度。
+抽代复习目前还在同态那里磨蹭,我到现在才终于明白了对应定理是干什么的,原来是一个类似于反演的操作,草。之后的置换群和循环群学的时候就没什么问题,感觉可以过得快一点。然后就是群作用,一些没见过的变换和几个式子的应用是难点,周四应该可以处理掉。此后的路径稍微平缓一些,精力放在 +check +重要定理的证明上即可,印象里没有非常困难的习题了,估计周日能搞完吧,吧。
+这周还有马原的读书报告,zad 今年任务量真大,不过 2000 +字好说。另外又要做实验了,稍微有点烦,实验报告 5000 +字起步还得卷拓展知识,比如说弦振动报告里还得给他写点 PDE +知识装一下,劲比马原大多了。
10月8日
+10月25日
-
-
开始赶一些落下的作业,尤其是抽代的 34 道题(
-张京华怎么塌房了...前段时间学 One Last Kiss -的时候才刷到过他的直播切片(
-很遗憾用这样的方式这么快又看到你一次.jpg
+我真的很怀疑有必要把工程力学退掉,或者期中之后抽一个周末集中把它学会了,不然要寄。
+能动系室友 4 学分的工程力学从牛顿力学讲起,我 2 +学分的工程力学实质是理论力学,草。受不了。
+最近经常会陷在思考抽代的难题里面,有的时候想得出来皆大欢喜,想不出来就又痛苦又浪费时间,甚至还想下次再抽时间继续想。何况有的时候我甚至没有答案可以去参考,感觉收获不大。唉。
+从小开始老母亲在学习上最爱和我说的一句话是“没有答案的题目不要做,做了也不知道对不对,浪费时间”,小时候为了考试做训练自然是对的,放到科研里自然又不对,所以现在这样的话究竟好不好呢(笑
+抽代期中才考 +1.5h(顺便吐槽下周五的下午,我要连考抽代期中和初概期末,中间相隔 15 +分钟。所以还好把初概 PF +了...),反正肯定是不适用在多个题目上停留很久的。范围到整环分式域。今天冲进度横跨三个小节,很震撼。不过昨晚刚复习完群同态,环同态就完全复读,洒洒水啦(错乱
+抽代助教可爱捏。
+看本人照片(微信头像)也感觉蛮可爱的
+
+
P1 是我刚发现有 bonus +的时候,那一周作业巨多,于是我交作业时备注了一下之后会慢慢写之前的题目,他还回了我一下;P2 +是后一周我把 bonus 补齐了交上去还给他纠正了几个地方之后,乐。
+剁手了一套世图的 GTM +风格笔记本,之前精装的那个摸鱼学导论和划水学导论 60 +一本,买不起,买了也不舍得写。这个平装的就亲民很多,四本六十多(虽然也不便宜)。
+说到这个,今天翻开 Pin +的一千零一页看了两眼(不要越到期中越爱干别的啊...),感觉没有想象中那么恐怖,至少不是全都那么恐怖。有希望但没信心寒假看到足够应对概率论(1)的位置。但我的优势可能在于上过初等概率论,在应用方面会好一些,尽管这对神们来说掌握起来并不困难。我发觉面对数学方面问题的时候就会心态平和很多,不在乎神能做到什么,只在乎自己是否竭尽全力。
+可能是没卷到那个程度,大家都有光明的未来我对数学分析的恐惧最早来自于高二,和 ycj +他们一起备考丘班(自然是失败了)的时候。当时看的是同济数分,现在看来和华子的微积分 +A +差不多难度,但对于高中的我(尤其上海高考不学导数,高中竞赛也不很需要导数)来说还是有些费劲。后来大一上了传说中的王晓峰老师的两个学期微积分,拼命下放各种高阶知识又不讲得很详细,让我感到非常难受,后期就没怎么听课了。lx +老师说得对,什么东西到最后,都会收敛靠到自己读书上去,而且只有靠自己。
+
+
(还没到货,在世图读者群里看到打样是长这样
+Introduction to that thing, but only for people who already known it. +—— Carol Firedman
+Whatever who wrote, none is understandable. —— Dave Firedman
+到时候自己留两本用,送 runzhi +一本,还有一本暂且留着,蹲个有缘人(什么
10月9日
+10月26日
-
-
仍然在赶作业,别的啥也没干,甚至又通宵了(
-不过顺便在 Math StackExchange -看了一些问题,学到许多;以及写完了之前的 Bonus 题,Wilson -定理什么的梦回高中竞赛,然后我查了一下这玩意怎么证,弹出来的第一条结果居然是 -OI Wiki(
+昨晚睡前想的是我这周就算不睡觉也做不完事情了,然后还是一觉睡了七个半小时,罪过。
+最近的 ddl 们:
-
-
- 数竞正统在 OI!( +
下周五交抽代作业,预计得有三四十道题,习惯了。
+当天还有这周的离散作业,周日晚上嗑着瓜子二倍速看回放然后写一下。
+下周四交数值分析纸笔题,四道题,但我好像还不大会,但也问题不大。
+下周三交实验报告,哈哈,五千字起步。
+当天还要交初概的两次作业,哈哈,哈哈。
+下周一交工程经济学作业,还没学,预计又是罚抄五到六页左右。我认为土木系每一门课脑子都有问题。
+本周日交马原读书报告,两千字,大概知道写什么了所以问题不大。
其实写完作业我也理解 hx 为什么从 Sylow 子群开始就加速冲了,从 Sylow -开始到有限生成 Abel -群(以及可解群)之间都是一个很连贯的逻辑,但是您有没有考虑过,就是没必要把所有课后题都布置成作业呢(
-我现在看到抽代就想吐,预习什么的还是留给睡一觉起来之后吧。
-目标是到周一晚上写完工程力学,抽代,离散和初概作业,然后抽代看到有限生成 -Abel 群。感觉很难。
-然后周二下午要 check -一下数值分析的进度,据说这周会有一个上机实验,但是要用 -MATLAB,我还不是很会。可恶啊可恶,为什么不能用 Python(
+于是保守估计这周末要通一宵,也可能要通两宵。
抽代也没复习完,初概虽然 PF +但还完全没复习,你怎么睡得着的.jpg
+10月10日
+10月27日
-
-
你院综奖答辩前后怎么这么多瓜...听室友讲了两个,自己到处瞎看浪费时间的时候又不慎发现一个。
-其一大约是一个学年满绩的同学(其实他在 b -站有一个更为人熟知的称呼)没进综奖答辩发了一些牢骚,后来和好几个(?)辅导员闹起来了。我原以为他的重点在于质疑入围标准不够公开透明(不过标准是否应该公开透明又是另一个值得讨论的问题,在此略过),但实际不是;还有一个是听说有人出钱灌了篇环材类的 -SCI 然后拿出来吹什么的,盛名之下其实难副。
-有点意思。虽然一些了解到的信息让我觉得的确该骂,但到底还是有可取之处。我向来缺乏始终保持严谨的能力,上学期 -PF -了两门不擅长的专业课都没满绩,这学期刚开头初概就大翻车;又连开始了解一个课题该如何完成的勇气都尚且不足,空诩兴趣和热情有什么用呢。
-常怀谦卑之心。
-上周五 129 分声部咕咕了,今天辅导员才来找我,弧是否有些长。
-说是让我晚上去跟着行健重新分,我才不去呢。所以我有点笨比了,当天晚上虽然跑路了,但事后直接微信编个分数发给他不就好了嘛。现在想到倒也不算晚,至少少跑一趟蒙科楼。
-室友说她 233 但是没选上,据说这三个数字是音高音准音色,满分是 -5。想了想 111 不太符合美少女(??)的形象,那就 212 吧。
-昨天列的 to-do list -基本是搞定了,真不容易,但抽代只看了个大概。不管了,睡觉。
+一边往前写抽代,一边往后看抽代。今天进度推的还行(
+暂时感觉环的一些东西有些不符合直觉。比如绿皮上整环分式域的第一个结论就让我摸不着头脑,刚拿到的时候自己独立证不出来,第一反应是困惑,在群论学习中倒是没有的。
+“我经常在想能回到那个时候就好了,但‘那个时候'究竟是什么时候呢,我也不知道。”
10月11日
--
-
约了 dwl 老师下周三的 -OOH,没想到这个东西真的没人约啊。点完预约之后又开始纠结,系统会不会给老师发通知说有学生约了 -OOH 呢?我要不要再给她发个邮件说一声...
-我想说的一些东西:
+10月28日
-
-
- 为初概翻车诚恳致歉并寻求一些建议( -
- 问问她对读研半路出家转数的一些想法,可行性分析(?),包括方向选择(数据科学?计算数学?统计?生统? -
- 求求她带我进组 or 推荐一些相关的组 or 做做 -SRT,我需要尝试一下知道自己能否有能力和兴趣做研究 -
- 关于数学系那边选哪些课(实复概全覆盖?点集拓扑泛函分析等偏向基础数学的内容?回头补数分??)来辅助统计学习这件事,以及我的现状(感觉抽代比初概好玩得多这正常吗) -
希望不要临场丧失语言功能,另外伟清楼在哪里啊(
-数值分析上机题允许 Python -了,然后看了一眼还是没啥思路(乐死),这好像是我的问题(
-总比从头学 MATLAB 好,总比从头学 MATLAB 好
-老姐给我发了篇文章,我还以为标题党,点进去一看还蛮喜欢的,遂摘录。
--
S:人总是会喜欢自己擅长的东西,我也不例外。那些在小学阶段能很快掌握鸡兔同笼,牛吃草问题和抽屉原理的小孩很容易对自己的智商感到自信。说实在的,自信是一个中国小孩能得到的最好祝福,尤其是在我们这片不会歧视书呆子的文化土壤上,你学好奥数的那几年会在同龄人中活得风生水起——你由此能从一众每天买干脆面开水浒卡的小学生中脱颖而出,进入一个好的中学,学会圆锥曲线和三角函数,由此能从一众每天去网吧抽中南海的中学生中脱颖而出,进入一个好的大学,学会拉格朗日中值定理和多重积分……
-B:等等,这一切的终点在哪儿?
-S:一个祝福,也是一个诅咒。
-B:那是?
-S:去华尔街当操盘手。
-B:我不明白。
-......
-S:(打断)我的一个同学炒币挣了200万;另一个同学在私募基金工作,已经快要拿到美国绿卡;还有一个同学去了高盛……
-B:呵,这就是精英的圈子吗?
-S:我知道你会生起一些朴素的嫉妒心,但就像我说的,他们是自信的数学天才,已经习惯了成功。
-B:我现在明白你刚才那句话的意思了。
-S:哪句话?
-B:一个祝福,也是一个诅咒。从鸡兔同笼走向在华尔街功成名就之路,你被这种幻觉困住了。
-S:甚至更早,珠脑速算。
-......
-S:你像是在面试我。
-B:并不是,说出你真实的看法就好。
-S:我真实的看法(停顿)…就是没什么看法。这就是现在我对大多数事情的看法,对,没什么看法。怎么看爆款?没什么看法。怎么看朝鲜?没什么看法。怎么看北京?没什么看法。怎么看大海?没什……哦,大海还不错。
-B:(痛心)你这样找起选题来会很困难的。
-......
-S:(打断)你还要说,派对上人与人的联结让你很感动。他们托举着彼此翻墙进入现场,总是会有陌生人问你是不是需要水,喝醉了会有人搀扶着你别摔下天台……这些我都看到了。
-
+充电台灯坏了,于是紧急翻出来了开学时候送的台灯,甚至还有当时的小卡片,谢谢李贤凯先生。
+月底了啊...今天凌晨解决完了群作用,重做课后题的时候发现除了 2 和 +4 +那两个相对重要的结论还是证不出来之外,别的题目都能速通了,感受良好。然后又通了半宵刷 +zmx 的抽代卷子,但没有计时,可能做了 2h +左右就困得不行了。最后两题还没看,前面做的应该能及格,貌似也没那么恐怖(貌似,但愿没有伪证,我真的很擅长伪证x
+先砸瓦鲁多一下,等我去把群论最后几节复习完回来再继续(
+初概最后一课了,下周两节课一节复习一节考期末。后半期我都没有很认真学,想想也挺遗憾的,上个学期一直对统辅的第一门课满怀期待来着。不过,后面还有多元和统计计算,这倒不是我最后一次见到婉璐姐姐,今后如果在统计中心做项目的话,想必会更经常见吧。
+大数定律 & 中心极限定理 & +收敛性,感觉倒是全学期最有意思的一节课。嗅到了很多分析的气息,但是这课凡是涉及到的都不要求,下学期概率论(1)再来。
+然而初概的笔记从期中之后就没有再写了,sigh。等下周五考完,在统计推断开始之前简单理一下,主要是自救。如果咕咕了的话就把那一篇撤掉吧。
+今晚包括明晚甚至后天晚上,都要刷夜做各种 dirty +work,白天要推抽代进度,还有复习 / +学习各种稍微有点用的东西,写作业。
10月12日
+10月29日
-
-
- 今天又双叒叕做实验, -顺利苟过去了,很感谢暑假开头时候写了实验备忘录的我自己。 -
- 玉树的烤冷面不知怎的感觉不如上周好吃了,可能是太干了。下次试试馄饨。 +
插播碎碎念笑话一则:
+我:先做 ddl 最晚的作业,然后往前慢慢推,就能正好在最早的 ddl +之前写完所有作业
+室友:那要是最早的 ddl 之前没完成怎么办
+我:不会的,闭区间套定理保证哪怕有无穷个 +ddl,也还可以有一个实数(时刻)在“做完所有作业”和“第一个 ddl +到来”这个区间里(开始伪证
+算工程经济学从一点算到四点,我靠,校园贷借了 10 万最后只还了 30 +万,这多吗,这不多
+华子搞那些防范诈骗的宣传还不如带大家都学学经济学x
+反正就是做了一天 dirty +work,凌晨算工程经济学,下午写读书笔记,晚上写实验报告,烦死。光栅衍射直到我缝合完报告都没理解到底是在干嘛,罢了罢了。
+能找到的公开的往年报告很少,貌似大物也不做这个,这给我造成了不小的麻烦。我放一份我的在这里:Click +Here,也更新到物理实验备忘录里去了,因为当初看不懂就没有写这个实验,现在这样当做补完了。
+本来今晚还想刷个夜,一鼓作气写完作业明天就开启复习,结果 hx 发链接说明早有致理的抽代讲座,还是去一下比较好。结果报名的人太多了,群里说非致理的人只能线上参加,这话说得,虽然也没什么毛病但是,好吧没有但是。
+也挺好的,线上的话九点半开始可以九点一刻起床,线下得八点多就起。
10月13日
--
-
躺床上听早八最多坚持半个小时...数值分析老师对不起,但是被窝真的太舒服了(
-然后就又还是肝一天,今天的 TODO 是写完 ODE -作业,抽代看完群论(太可怕了)然后修茴香豆,写前半周的抽代作业,可以的话工程力学作业也写了,实在没事干了就去搞本理力来补一下我看不懂的工程力学。
-SRT 看了半天,要么一看就好水,要么就是贵系立的项(
-丘数学中心就一个项目,统计中心没项目。梁鑫老师那个项目说是会线代和群论就行,
-那岂不是我上我也行。报了一下试试,邮件约了周六去唠嗑。资金 -500 块,是要拿来买演算纸和笔吗(和 lzy -聊了一下,他已经去过梁鑫老师那边了,大意就是这是个搞矩阵论的课题,属于比较冷门的方向,和未来方向不搭的话不建议去。
+10月30日
-
-
- 可是我还能有啥选择呢?去吧。 -
+我是 +five,我虽然早睡(指三点就上床了)了但还是没听抽代讲座,就早晨醒来坐在床上看着腾讯会议,觉得画质真不咋地,看着看着就迷糊过去了,醒来就开始白板讲题了,更拍不清楚了,直接退出会议摆烂。
+早晨起来感觉眼睛很不舒服,不能再熬了。今天处理完所有 +ddl,然后开始继续复习之前暂停掉的抽代,以及总要挤出点时间留给初概,总之其实压力还是很大。
+和何老板对了一下实验报告,发现我真是...只要不是所见即所得的写作,就能写出 +114514 个 typo,又改了一中午。给老板安利了我暑假里在 Overleaf +上投的物理实验报告模板,然后意识到那可能是我给科协学术部打的最后一份工了——这学期的活我都是能咕就咕,开了三次例会我找各种理由最后就去了一次,完全摆烂。等学期结束换岗的时候就走了,实在没有继续待下去的必要。
+晚上考完期中的友人来看我,去西门口和她聊了一会天,大倒苦水,吐槽我自己 +PF +了一门退了一门课还是忙不过来,回想了一下平时还是太摆了。然后从哼歌逐渐变成了一起戴着耳机唱歌(当然音量不是很大,周围没什么人,社恐.jpg),唱了告五人的《爱人错过》,还有 +EVA 的两首经典老歌,心情好起来了。
+说到这个,上次北大那只叫明日香的正在找领养的小猫,得猫瘟死掉了,唉。
+Can you give me one last kiss?
10月14日
+10月31日
-
-
随口问了一句何老板有没有看中的 -SRT,结果他想进的那个项目的立项人是我高中的一个学姐...这下内推了(bushi
-世界真小,让人喘不开气。
-hx 今天终于在讲完有限生成 Abel -群之后停下来讲了点低阶群结构,没继续冲可解群(
-Anyway,不影响他下周肯定能讲完群论。
-今天要稍微研究一下数学中心那个矩阵论 SRT 的内容:
+今天倒没啥别的事,刷了一天抽代,书差不多摸完了。这一遍感觉把之前模糊的内容都处理好了,此前不会的习题大多数也能速通,但是还是觉得有些题目真的是,奇技淫巧。
-
-双随机矩阵与置换矩阵群凸包的谱集探索
-双随机矩阵是一类特殊矩阵,它的所有元素都是非负实数且每行每列元素之和都是1。这类矩阵在图论、概率论、矩阵论中都有广泛应用。确定一个复数是否可以作为某个矩阵的特征值,是特征值反问题研究的基础。例如,经典结果告诉我们,所有实对称矩阵的特征值的并集就是实数集,我们称之为实对称矩阵集的谱集是实数集;根据Schur-Horn定理就可以解出实对称矩阵的特征值反问题。类似地,为解决双随机矩阵的特征值反问题,首先就要考虑双随机矩阵集的谱集。1965年,Perfect和Mirsky提出猜想:n阶双随机矩阵集的谱集是所有内接于单位圆且一顶点位于实数1的正k -(k<=n)边形的并集。后人称之为Perfect-Mirsky猜想。当时二人就已证明该猜想在n=2,3的情形。n=4的情形在2015年被Levick、Pereira和Kribs证明。n=5的情形在2007年被 -Mashreghi和Rivard通过反例否定。其他情形至今仍无确定结论。Harlev、Johnson和Lim在2020年通过一系列数值实验侧面证实n=6,7,8,9,10,11应当是正确的。
-根据Birkhoff定理,所有双随机矩阵组成的集合就是所有同阶置换矩阵的凸包。因此双随机矩阵集的谱集就是对称群的凸包的谱集。2020年Jankowski、Johnson和Lim试图通过探索不同的置换矩阵组成的群的凸包的谱集来逐渐逼近Perfect-Mirsky猜想,他们考察了交换群、二面体群和四元数群。这些群都是比较简单的群,其结果与Perfect-Mirsky猜想相吻合。
-本项目试图沿着这一道路继续探索,利用矩阵分析、有限群论、群表示论等领域知识,逐步考察更复杂一些的群,例如两个或多个循环群的半直积、由两个或多个轮换复合出的置换生成的群等来进一步靠近Perfect-Mirsky猜想。
+数学上不应该回避技巧的提升。——PIN
看着好高深!(但是老师说群都不必学得多好就能做(在画饼
-TODO:
--
-
- 了解一下双随机矩阵和谱集的结论 -
- Perfect-Mirsky 猜想,Levick、Pereira 和 Kribs 的证明,Mashreghi 和 -Rivard 的反例 -
- Jankowski、Johnson 和 Lim 对于交换群、二面体群和四元数群的考察 -
-搜了一圈感觉这个猜想下面就没几篇文章,全都列在这儿了,难怪说冷门(
-一开始没大明白什么叫复数集是一个什么 n 边形覆盖而成的凸包,看了 -Pereira(上文那位证明了 n=4 情形的教授)的讲座才明白这个猜想是在说啥。呃,然后讲着讲着就量子物理了,怎么会事呢,不看了(
-睡前读了谢惠连的《雪赋》。
+好吧,我谢罪(
+明天抽代课上写一下 PKU 题。
+晚上去吃了清芬一楼的羊肉泡馍,还蛮香的,汤的味道调得不错,北方人面食基因觉醒.jpg。热乎乎的一大碗,冬天破防时候的 +comfort food 又增加了(
+突然在想陕西人会不会觉得不好吃或者至少不正宗,就像我觉得清芬的生煎不是一般的难吃,但室友觉得还不错一样(
+十月的尾声,日记系列的第二篇也如期完结了。我以前以为这个系列至少会见证自己慢慢的改变,但这两个月中确实没有什么变化,除去学习的东西变了之外,生活还是那样,ddl +追着 ddl,摆烂,自学,摸鱼。
+不过,像我这样运气的人,一旦面临变化恐怕就是往不好的方向在改变,亲友离散(什么离散),生活不顺,诸如此类。因此没有承担可能发生的精神内耗,或许已经是一件很幸运的事了。
+昨天和友人在西门外轻声唱歌,唱《爱人错过》。这也是前几天偶然在你社看到,然后一听就觉得很喜欢,于是加入循环了的歌。其实歌词就那么几句话:
-
未若兹雪,因时兴灭。
-
+什么胡言乱语(
+好啦,下个月见!
我肯定 在几百年前 就说过爱你
+只是你忘了 我也没记起
+走过路过没遇过 回头转头还是错
+你我不曾感受过 相撞在街口 相撞在街口
+你妈没有告诉你 撞到人要说对不起
+本来今天好好的 爱人就错过 爱人就错过
+ +很奇怪吧 +XD,倒是和恋爱经历都没关系(x)。我想是因为听出了一种不安定的感觉而喜欢,尽管很担心这样的事情发生,但如果改变就在面前,还是要勇敢些。
+10月15日
--
-
原来近春园西楼不是指理科楼啊...还以为要回到伤心地(x)了。19 -年金秋营的时候于品说物理系要搬到更好的地方去了,将来整个理科楼都是数学系的,到现在新物理馆好像也还没造好,xs。
-聊之前我还想着就算做不出东西来试试也好,结果老师劝我三学位课本来就多,还是珍惜时间打好基础为妙(
-很对,很对,跑路了。
-其他就没啥事了,今天要写完初概作业,然后复习数值分析第一章的内容,写上机作业。但愿能写出来(
+]]>
11月1日
-
-
- 写出来了,开心,虽然中间破防了 114514 次( -
- 你猜我为什么不想转码了.jpg -
头一回见到 ddl 延长(
-
在 hx 课上看了 PKU +去年的抽代题,还好,还好,也就是最后一题有点懵。困得我降智。虽然这个 +110 +分钟真有点难绷,看来也是两节课加一个下课随堂考的,或许有参考意义呢?
+现在已经没人在乎何宝在讲的新课了,感觉大家课上都在复习(
焦虑地过抽代定理证明,毕竟何宝课上从来都只讲几个概念和证明,又说“考试和课堂内容相关”,很难不怀疑他要考定理。然后就麻了,这就是古老的神秘吗,我真的好菜(
看了看天气,下周要降温了,这周恐怕是最后一周穿衬衫的机会了罢。冬天(或者说秋季学期)的状态明显比春夏要好,一方面是春天我会过敏,总是昏昏沉沉的,然后就是怕热,夏天也过得很不舒服。
+倒是有点期待北京的雪,去年初雪的时候徒步从法图走回寝室,感到了来华子之后从未有过的宁静。然而上次在上海看到纷纷扬扬的雪,已经是四五年前的事情了。
10月16日
+11月2日
-
-
今天就更没啥事了,继续把数值分析复习完呗,没事干了就预习抽代/看理力。写写数值分析的证明,虽然不知道这课最后考试有多看重证明,反正平时的纸笔作业又少又水,完全没有四学分的感觉。
-整理了一下昨天数值实验的内容,打算水一篇长期的博客,但是要等作业 -ddl -过了再发,不然万一被判协助抄袭,徒惹是非。还蛮有趣的,我是说如果这样轻量级地使用编程语言,debug -的痛苦还并不大于快乐。
-我越发觉得自己还是应该转数,并且意识到自己的 coding -能力在数学人里面还算可以,比较乐。
-暑假写的 Sharygin Geometry Olympic -题解终于成文了,指导老师还是写上了杨丕业老师,虽然他这次也没指导什么(x)。
-和他聊了一会,才知道他现在已经不在质心教竞赛了,而是去了长沙的一所高中教书。还记得 -19 -年金秋营(又是金秋营,那次金秋营确实对我意义蛮大的)考完第二天的试,我还去质心找他玩了,也帮忙完善了第二天的两个几何题解,似乎他们公众号上当时在题解里还写了“鸣谢外心姐姐”之类的话——因为质心的吉祥物是质心姐姐,于是我也随口编了个类似的名字。
-聊到最近在学什么,才知道 hx -是差不多和他同期的华子数学系学生。末了听他感叹同是丘赛优胜,走的路却完全不一样了。
+好,一晚上学完初概后半学期内容!也不难嘛!(
+刷完样题之后就当做没初概期末这事儿了,摆烂。但心里到底还是有点难受。这课唯一的弊端就在于没有能很好地匹配的教材,MIT +的概率导论自然好,但是二者进度之间有太大差异,实在不方便。然而没有参考书对我来说就是毁灭性的,我现在越来越难以集中精力听谁说话,在听课里学到一些本来从书上就能得到的东西,或者在 +PPT 里学习什么的,真的不是很擅长。
+又开始焦虑自己后半期的统计推断能不能行,以及毫无分析基础,我这样真能寒假速通一下测度积分然后就去上概率论(1)吗,可是不上就来不及了,草,真想延毕一年。
+明天的时间还是让给抽代,虽然我觉得复习得差不多了,反正再复习该不会的也还是不会,何宝太 +book reader 导致我甚至不知道自己不会什么,草。
+听室友破防说来华子之前从没想过日子过成现在这样,还有她高中时对于华子的所有瑰丽幻想,实话说我有点无感(笑)。毕竟考进高中的时候就幻灭过一次了,而幻灭过一次就不会再有第二次,如果有,至少也不会那么严重。
+现在对华子幻灭,以后就不会再对另外的环境幻灭,一下子就降低了试错成本,好事(确信
+说到幻灭,为什么还有“如果有”这个选项呢,因为我对科协也幻灭过一次,只不过不太严重(
+我之前写过一篇文章表达过对你院科协的美好设想和一言难尽的现实,如今我已经不想改变它了,而是打算下学期直接跑路。你院对科协的定位就是主体在从游部,而学术部既边缘又臃肿,于是今年被丢了个举办科创日的任务,做其他部门懒得做了的杂活,(对我来说)很没意思。
+搭网站这个设想最后一次被提出是这学期的第一次例会,有一位新成员说可以给你院科协搭个网站写东西,把公众号的内容迁过去。部长说是那种用来宣传活动的网页吗,可以挂靠在书院的官网上。不了了之。我也没说什么,当时就觉得算了。
+看到 ex 之前的发言,虽然我一直在尽职地扮演一个合格的死去的 +ex,但也没必要向共同好友宣告我真的死掉了吧(笑
+
+
那你怀疑吧,你活该(错乱(好恶毒啊(啊不,其实已经很善良了 x
10月17日
+11月3日
-
-
今日仍然无事,早起感觉发烧了,休息了一天。
-还好不是第八周,还好不是第八周(
-CW:这一条是很暴躁的吐槽。(是时候去搞个折叠块的功能了(懒了,下次一定x
-这两天有高中同学又一次来邀请我参加情系母校,今年还是非常不想去。
-和母校并没有多少可以情系的,这似乎的确是我的问题。一个对竞赛(哪怕包括小学奥数)和高考都几乎没有了解的野鸡学校初中生在升上高中之后,先花两年多一点的时间学自以为的数学,摸了几个竞赛的破奖,又花八个月从零开始学习高考,最后摸了个相对高考生来说也还算不错的成绩,那当然是以一副做题家的姿态度过这三年的。任何“二附中人为之骄傲的高中快乐回忆”,中二一点讲就是“玫瑰色的青春”,对我来说既社恐地狱又真的是没时间。还有理科班夸张的 -9:1 -男女比下压抑的氛围,唯一一位关系好的女同学高二生病休学,无数竞赛和高考过程中的焦虑、自我怀疑,
-失败的恋爱经历,都无疑加重了自闭。或许也是一种好事,至少我现在自闭得挺快乐的(另一方面,我实在不认为这种活动有什么意义。举个例子来说,今年课咨委有一位二附中的学弟,物理竞赛拿了金牌,却跑到未央来读机械。原因是决赛现场被华子口头签约了钱学森力学班,于是强基报了行健,结果被华子以“二类生不报致理就是违约”调剂来了未央。天知道从第一届强基开始,你校有多少被华子口头签约的人(当然也包括本人)被毁约(当初华子给我的理由是求真分走了致理数学一个班,听起来还算合理吧),我这点破事当年还人尽皆知呢。当然,我这样的的确是没什么办法,没有过硬的成绩握在手里,被毁约也没话说,谁叫我无心间勾了那个“服从调剂”,不然现在岂不是在交大电院逍遥自在?但一个金牌,因为这种信息差毁掉四年(无意表示未央在价值上不如致理,我敬佩真正热爱这个学院里的学科的同学,只是对于他个人的期望来说,的确是毁了),尤其这还是曾经在零字班出现过的惨剧,我无法理解。
-校友二月办情系母校活动,四月又是校友导师交流会,五月随华子招生组去学校强基预面试和宣讲,六月招生干的离谱事情更多(比如今年某位学姐以假意承诺计金的伎俩,从北大信科挖了一个裸分线上分不是特别高的学生过来,最后扔进自动化。当然这是另一回事了),上下年级之间的交流不计其数,却连这种已经见多了、简单说几句话就可以避免的错误都改变不了,实在不知道在做些什么。须知在高三学生眼里,诸位是“可靠的有经验的学长学姐”乃至在招生季是“手握大权的朝廷命官”(尽管并不是)(这话并不恰当,但就那意思),但凡能负点责任呢?毁约自然是华子的不是,我已经骂不动了,但就任其发生吗?
-我的确在想我加入的话能不能至少改变点什么,这样直接逃跑只张着嘴数落别人的不是,也还是不负责任。然而我一向人微言轻,加入了情系母校和各种宣传也就是做边角杂活(校友导师活动的时候试过一次),哪里抵得过几位核心成员鼓吹华子幸福生活的安排呢?要说尽我所能,也就是真的对几个报强基的时候找我咨询的同学,说了所有的实话而已。
-还记得今年五月的时候在质心的公众号上看到了一位东北某校(记不清了)的同学,物理银牌却报了未央,把自己回归高考的心路投稿了出来。我托在质心认识的老师联系到了她,才知道她误以为报了未央可以任选工科专业,可以进她心仪的自动化,然而未央根本没这个专业;她的学校里不曾有过考进清华强基的前辈,本是寒门贵子,我最欣赏的类型;她更不知道这是一种华子眼里的毁约行为,在未央的分流排名也会垫底。可惜她的文章晚发了一步,我也晚来了一步,已经过了强基计划报名截止时间,今年也不再有六月确认志愿的环节。如今她在未央读生化环材之一,我拼尽全力,还是什么都没有做到。
-我痛恨信息差,痛恨“你不知道的东西正在伤害你”,而我如今混得还行,一部分还是托趁早认识到这一点的福。尽管在努力,也还是几乎没有帮助到任何人,落得只有在这里无能狂怒,真是 -loser 啊。
+吃到了社友的安利,于是今天一边听《万千花蕊慈母悲哀》一边写抽代,感觉要把自己超度了(
+和 illion 的《GASSHOW》很像诶,但是更偏向于悲伤了。
+然后又去听了源的 +Tokyo Dome +演唱会,以前很喜欢一边刷这场一边写作业,但是当初刷的那个视频下架了,只有缓存还在我的手机里。东蛋场每一首歌感觉都比专辑还好听...而且还有源的各种即兴演出 +> <
+草...明天不是连着两场考试吗,今天怎么净听歌去了。早点洗洗睡了,pray +for tomorrow
10月18日
+11月4日
-
-
早晨起来还是低烧,于是摆烂翘了两节早课继续睡了,这下大概彻底是好了。下午室友发烧了,昨天下午何老板说也发烧了,草。明天要是华子搞出来三管阳性的话必有我们一份功劳(
-看北大猫协的推送在玩 EVA -梗,点进去一看是一只左眼瞎了的小猫起名叫明日香,我超,地狱笑话。
-结尾处这张照片怎么看抱着猫猫的人都像真嗣,不知道是巧合还是特意安排的(x
- +
+抽代期中...题肯定是不难的,但相比之下我还是宁可考 zmx +的卷子,扎扎实实做三个小时。具体问题详见本篇篇末的“赛博猫猫敲键盘”。复盘越想越头痛,大概就是:
+第一题愣了一下不变因子组是什么来着,有惊无险。第三题没构造出来之后就直接做 +\(105\) +阶群去了,结果又手抖抖半天,慌得要死,浪费不少时间。然后是环同态,看完题大概五秒钟就想出来了,不夸张。我愿称之为最水的一题。回头写了一下循环群同构的第一问,手抖写错了 +114514 +遍,涂得乱七八糟。又看到最后一题第一问就作业原题,写完,第二题就一定义+归纳,结论对了但我过程也有点乱,不知道给几分。最后去做了循环群同构的后两问,用一下第一问结论感觉就那样。?问题是我第一问结论对了没有,至少我感觉是有问题的。然后又去想群运算构造,想不出来,但明明已经想到 +\((a+1)(b+1)=0\) +什么的了,就是没再往下想。交卷了。
+下午同时在物理上告别了初概,然而从现在开始我要复习初概了,因为过几天统计推断就开课了。
+emo 一下(
+大一的时候意气风发,大概是在我院这个舒适圈里躺着的缘故,觉得自己能做到很多事情,能去到很远的地方,又到底是怎么变成现在这么破防的呢x。这学期好像一直就没什么好消息,初概期中先裂了,不得已送了个 +PF,结果期末没复习都考得还不错,吗的。奖学金入账 0 +元,然后又是抽代期中,最近物理实验还崩。
+又想到上学期紫十二 remake +的同学,先但愿自己去数学系混的这两年不要有生命危险。绩点不知道能不能在申请之前苟住 +3.8,本来上学期期末还有 3.89,夏季学期土木系的烂课一出分直接给我送到 +3.83,容错率一下子无了,这学期体育 + +抽代又不知道要扣到哪去了。软弱的时候就很想往回退,什么申个 ms +算了,再想想花不起这个钱,又有哪家招我这种 five 当 +PhD,留国内容易点,吗的强基书院又各种限制,想往复旦退可能都没得退...
+一阶段 PF +了初概,二阶段要退常微分和基物实验。前者是没必要再上下去了,后者是上次光栅实验莫名其妙吃了个 +80 分,也没给出什么理由,我又不想在这种课上送一个 +3.6。问了一下老师,退实验课也几乎没有沉没成本,先前做过的实验明年想保留成绩的可以申请保留,不想保留的可以重做。
+实在不行的话跟现实低头一下,统辅为主,少上点 / 多 PF +一点数学系的课。真是弱者。
+后半期就,不得不转换一下重心,这下一定要苟住数值分析、统计推断和离散。工程力学也是,不能太拉胯,然后就,抽代尽力而为。
+我感觉我之后必须搞点水课来刷成绩了,真的是。
+还有些别的更令人难受的事情,但现在先不说了,暂且这样吧。
+
10月19日
--
-
今早去找 dwl 聊天,其实和 lx -聊完之后我对很多问题都大概是有数了,但这个 OOH -是早就约好的,不能鸽掉。正好统计中心这边的方向对我来说是退路一般的存在——基础数学搞不了可以搞应用,理论统计搞不了可以搞应统,总不至于饿死(
-wljj 好像不是很会画眉毛(什么啊和她聊天就盯着这个看去了吗
-我认为数值分析应该改名高代(3)(逃
-第三周的时候我还在担心会不会根本讲不完,现在发现不用担心了,进度还蛮快,马上第三章又要讲完了(
-但也不是 hx 那种快,是这课内容本身不算太多。以及 bcl -的教学水平也是我见过的老师里相当不错的,起码是这学期听得最舒服的一节课,虽然好像他是第一次上这课?选课的时候我还为没选上 -hzy 而悲了很久,现在发现也不错。
-SRT 报名一点也不顺利...退了 lx 老师的组之后打算找个水一点的 CS -项目
-来加两学分 -4.0,结果分别给两个学生立项发了邮件,一个过了两天才回复说招满了,另一个到现在都没回复我,有点烦。为什么学长 -check 邮箱的频率还没我高啊!于是换去工工系的一个组了,老师回的很快,过了俩小时就过审批了。感觉工工在各方面就是一种,下位替代一般的存在(...)
+11月5日
-
-
- 我倒也不 care -到底是哪边,工工的话还可以靠一下统计中心的现代统计什么的,蛮好。 -
- 业余爱好,业余爱好(所以水平也业余x -
+今天又是新的一天!(试图麻痹自己
+是不是全世界今天都在考物化,我下午一点起床的室友三点要考物化,偶然说了几句话的同学三点也考物化,来三教自习,坐我前面的人也在量子波动速读蓝皮的《简明物理化学》,两点半左右离开了。
+同学锐评我:本来桑海宁装的蛮好的,桑海话讲的也蛮好,最近看到桃李的大闸蟹就绕路,连胶东人都装不下去了吧(x
+的确家里一直没有吃水产的习惯,甚至还有点排斥,而我对某些范围不明的水产过敏,就连鱼虾都很少吃。之前偶然吃了一次桃李二层做的一种扁平的多宝鱼片,用辣椒和葱蒜点缀,再浇一勺鱼汤,感觉还不错。可惜现在似乎不做了,不知是不是也有丰产的时令,秋冬是吃不到的。
+在南方吃了 12 +年学校食堂,从来只有米饭,来到华子还是忍不住买面点做主食,母亲也叮嘱我寒假回家之前去牛街买些北方特产的面食带回家,那都是上海买不到的东西。小麦的香气还是刻在我和我的祖辈的记忆里。实际上我在记事后几乎从未踏足故乡,跟着父母几度辗转,在嘉兴度过童年,又来到上海。母亲对她家乡的县城、生长的环境颇有微词,于是我也迷茫,自己对几乎未曾谋面的故乡的依恋,大约只是经过了想象的粉饰吧。
+不说了,最近家里的事实在令人难受,在肉身还远在上千里之外的时候,先集中精力干点别的去..
+想起来三四月份的时候看过一部电影,情节还很清楚,但是电影名还有角色的名字一个也不记得了...最后还记得的一个特征是据说男女主拍完这一部电影之后真的出轨在一起了 += =,然后就搜到了...
+叫《夜以继日》。B 站评分不高,8.4,
(B +站评分有啥参考价值),查了一下 bangumi 是 7.4,远超我对 +bangumi 的预期,再一看是样本量太小了,才 24 个...
10月20日
--
-
怎么感觉要期中考试了?我超,如梦初醒(
-接下来两周时间基本都让给抽代就行了。期中考三门(然而期末要考 8 -门,很难想象到时候该怎么办),初概 PF -之后轻微摆烂并且后半期也不是很难,工程经济学第九周周末才考,有丰富的往年题,拟合一下就行。抽代反正也没有往年题,
-zmx -均分 50 的卷子就算能拿到又有什么用呢,可以去看看 PKU -的题,然后就注重把书和习题吃透。大致的计划是:
+11月6日
-
-
复看一下茴香豆,很担心万一忘了什么东西(
-按章节重写当初不会做的课后题,有很多东西前后有联系,也有值得当做引理记录的
-我的群作用仍然一片混沌,困难的课后题主要指这个
-手推重要定理,第一遍看书的时候自己没推出来的定理例题什么的都可以再试试。不过主要是 -Sylow 及以后的一些东西,可解群,直积(这个简单点),有限生成 -Abel
-复习一些助教给的有点难度的 bonus 题,以及一些 Math StackExchange -上遇到的东西
-还有时间的话不妨看看近世 300 和 pku-lib -里的抽代题,感受一下隔壁是什么难度。虽然纯做怪题也没啥意思,考试所迫吧。
-
何宝你要是打算考到环论中段的话,能不能把题出简单点.jpg
-(为什么要叫何宝)(反正和同学平时就这么叫的)
-于是今天的进度是,浅看了一遍正规群列和可解群(bgm -是不是可以放花譜的不可解(x)),写了作业的前半部分,然后狼狈地带着我破碎的群论知识打开了环论章节。但愿能先看完环的定义那一节,写完课后题,再回头看一看上一节里 -hx 没布置的题目。有空的话把低阶有限群看了。
-越发觉得自己很多地方学的都有问题...
-何老板放弃了我的 Python 安利,转头用 R -写概随作业去了,某种意义来说也没问题,R -对统计方面的很多东西封装的更好。但他还在同步听机器学习的课,那为啥不善用 -Python 捏。据说他还上了微积分 C -和社科线代来复习和刷绩点,呃,每一件事我都不是很能理解(算了我估计也没人理解我在干什么
-总感觉他最近在问我很多 STFW -就能解决的问题,但是我觉得教会他怎么向搜索引擎描述问题比我自己去搜了发给他还费劲,稍微有点暴躁。想来他不知道我博客的存在,问题不大(好阴暗!x
+今天开始速通之前放掉的数值分析。真的很想喷一下这教材的排版,标题和正文的字体几乎差不多大,节与节之间连点空隙都没有,但凡做成 +A4 大小的书,或者加到 400 +多页,也不至于阅读体验这么差。虽然它写的很详细,难得有证明全都在书上能找到的书,而且已经很厚了,但还是很难绷。
+这课只有期末,并且明确了不调分。但我感觉考试之外的 50 +分有手就行啊...数学系专业课还把出勤算 5 +分,作业也有手就行,真的蛮不可思议的。或许这是门专业课里的水课吗?我不知道。
+之前觉得老师长得很帅(甚至早八上课会觉得啊老师好帅还是别睡了(什么啊),就去搜了一下,包老师是中山大学的本科,在坡读的博。他的微信头像是他的一双儿女,眉眼都和他很像。
+其实我觉得去坡也是很不错的选择...
+和室友聊起来才知道你院(一字班)到现在还有 GPA 4.00 +的人,还不止一个。别的不说,我觉得体育能稳定拿 4.0 +就已经和我不是同一种生物了,根本没必要去了解人家的情况(
+说到这个,该刷月光长走了,我还差 21 +次呢。之前实验了一下,走路的配速略大于最低要求了,跑是不可能跑的,只能每天晚饭后走骑结合一下消消食这样子(
+老姐在南昌住院的复诊结果出来了,不是强直性脊柱炎,只是腰间盘膨出和炎症,(《只是》),值得庆祝。等她假期来上海请她吃饭。
10月21日
+11月7日
+-
+
今天马原课上读完了 PIN 多年前连载的 《Heroes in My +Heart》,很喜欢这个结尾:
-
-贪婪,自私,残暴,冷酷,放荡,背叛,软弱,渺小
-贪婪,自私,残暴,冷酷,放荡,背叛,软弱,渺小
-渺小,渺小,渺小,渺小,渺小,渺小,渺小,渺小
-——《恋爱的犀牛》
-奖学金入账 0 元有感(x
-虽然但是,该干嘛干嘛,我又没有错。自有能兼顾迎合你院评价体系和自我发展的神,我恐怕不行,那还是自己混好比较重要。(草但是损失四到五位数人民币还是肉疼啊!
-10月22日
--
-
邮箱的垃圾箱里塞满了 Bridge Base Online -的广告邮件。上次打桥牌还是去年马杯之前,最后马杯我也没上,不过你院似乎成绩还不错,打过了求真,挺意外的。
-你院的桥牌队到现在还是只有 7 -个人,凑不出两桌,始终没有训练过(或许他们有练,没在群里说,我不知道);另外六个同学都是清华附中的,身为外人话说不到一块儿去。当然听说他们高中的桥牌队很强,我在二附中的时候从未听过有什么针对高中生的桥牌比赛,也就把学过的东西当做又一个不同于人的记忆,直接搁置掉了。于是我的水平还停留在初中,这也是初中学校留给我少数有意义的、较好的记忆之一。
-其实也有必要复健,桥牌是一项很有趣的棋牌运动,但暂时没心情。
-用北京健康宝拍的头像当参考生成了一张猫娘.jpg
-更新到 About 里了,我宣布我差不多就长这样(确信(确信
-
-
然后同样的咒语拿同学(男)的照片试了一下,生成了更多比这好看的猫娘,我不理解.jpg
-存档一下咒语和反咒(其实是在猫车老师发的咒语的基础上改的,反咒就没动),哪天闲了再玩玩(
--
-masterpiece, illustration, extremely detailed CG, comic style, -professional light, one girl, beautiful, white shirt with lace -collar,glasses with gray and thin frames, artistic, nekomimi, black -necklace ,small ear rings ,hair pin, long black hair, spread hair,shiny -hair, curvy hair, smile gently ,doll face ,closer interpupillary -distance,small nose, big gem brown eyes, bright eyes, necklace, -nekomimi, fringe,small pink lips,slightly flushed cheeks, classroom-like -background,
--
fat, lowres, bad legs, bad anatomy, text, error, extra digit, worst -quality, low quality, jpeg artifacts, blurry, forehead,
+到这里就真的结束了吧,要毕业了。又想到了一个小故事是 Halmos +的,他写了一本著名的书叫做 Measure +Theory,当他完成此书的时候,心中喜悦难以抑制,向众人宣布:“我刚写完了 +Measure Theory 的最后一个字!”有人问:“最后一个字是什么?”Halmos +当时愣住了,连忙赶回办公室,再跑回来,告诉他们说是什么什么。
+我也写完了,最后一段话和本文无关,写给远在千里之外的一个女孩,每一天到 +bbs 上的时候,我总是假设你也上 +bbs,你也来看我的连载,希望你能喜欢这些故事哪怕只有一个,尽管你不喜欢数学也不喜欢我。
+--
+美丽有两种
+一是深刻又动人的方程
+一是你泛着倦意淡淡的笑容
-今天 AK -了环理想那一节的习题(好多...),虽然写了一个下午,但是真挺爽的。
-以前觉得代数题依赖灵感,
-现在发现的确,但是摸清结构的话对于矫正思路还是比较有用的。然后去吃饭,在食堂遇到了上学期的高代选老师,远远看他和别人聊天,突然觉得他也是和何宝一样单纯可爱的人,总之很有数学中心青椒的气质。
-尽管他俩上课都是 -book reader女老师的话印象比较深的是 yh,尽管我也没怎么听过她上课,但看 handout -觉得思路应该很清楚,
就是字有点丑。但不知为何大家都说她教得不好,或许是有时会讲一些写在 -Remark 里面的内容,对工科的同学来说显得有些发散了吧。感觉 yh -很酷的样子,有事发邮件写公告不看微信群之类的举措我也觉得很棒,还有一次看她穿写着类似于 -Love is Love 句子的 T 恤来上课,这在华子是可以的吗(x)。
-
10月23日
--
-
写 ODE -作业写得无比暴躁,课讲得又水作业又麻烦,我还漏过几次签到,打算二阶段退课了。其实如果不是初概裂开用掉了 -PF 资格,本来就是打算给 ODE 一个 PF 的...
-往好处想,工科 ODE -不可能够用,迟早得学完整版;后期还有从零开始的统计推断,这个在统计中心上过就不打算去数学系再上了(据说数学系的统推也没啥意思,复习半个学期概率论),所以不能再像初概一样就云过去了。集中点精力吧,该抛弃就抛弃。
-体测完之后就变成了一滩史莱姆,今天基本没干啥事,肥宅瘫倒.jpg
-今晚发现了笛子姥爷以前画的小漫画《笛子的单恋史》,目测是实际事件改编。看得津津有味的时候突然发现没完结...已经好多年了,估计不打算继续画了。想来过去了这么多年,笛子姥爷早已组建家庭,大概也不把(现实中的)这事儿放心上了,弃坑情有可原。但是身为读者,草,好难受(
-最后碎碎念一条:看离散的 PPT 觉得右上角那个华子计算机系的 logo -蜜汁熟悉,再仔细一看最下面有个“1958”,大约是贵系成立的年份。这个要素让我感觉更熟悉了,然后想起来,二附中也是 -1958 年建校,校徽上也写了年份。四舍五入二附中 = -贵系(这个差距就像我今天体测仰卧起坐满分但 800 -米恐怕也就是刚及格,于是四舍五入我 = 鲤鱼姐(
-丢个图:(可以看出除此之外二者没有任何关系((
-
-
以及想明白了一个问题:我觉得转数比转码更好的一小部分原因是(最大的原因是学不会 -= -=),如果让我一边上课一边磕盐一边实习,我恐怕会疯掉,至少会非常焦虑。我不清楚贵系的普通人是怎么生活的,至少我看到的神都三头六臂,白天上班晚上写作业还有空娱乐运动甚至保障睡眠,人脉也很广阔。另外转码其实就是一个相对功利的选择了,不见得走得太远。相比之下转数生活就单纯很多,沉下心来扎实基础,多看多思考,你甚至不需要(至少不必要,也不很主流)过早开始磕盐。
-如果能认识更多的转数人就好了。书院里自然极少,只认识两位,一位已经退学重考隔壁数院去了,我很钦佩,祝他成功。另一位还不知道是否确定要转,没有详聊。尽管有转数群,我还是和他们中的绝大多数人都不熟。其实我真的很羡慕本科就可以肉身到达数学系的同学,不说别的,主要是有机会降转甚至 -gap -一年的话,这个时间可以好好补一些基础,更自信些。或许现在不必多想,真需要了就赶快去补就好(
+一周以来的效率高峰发生在工程经济学课上,我没听,预习完了环的 3.7 +节还写完了课后题,搞定了之后居然又过了十几分钟才下课,第一次觉得时间慢得不可思议...
+恐怕也不是第一次,高三的时候我喜欢在数学课上写英语卷子,因为英语太烂了,要恶补。当时总觉得在数学课上伴着老师的安徽口音写作业,正确率比回家写的要高很多,甚至写得也快些。这是什么原理(
10月24日
+11月8日
-
-
体测完浑身疼,鼻子也难受,咸鱼。推抽代进度。
-抽代复习目前还在同态那里磨蹭,我到现在才终于明白了对应定理是干什么的,原来是一个类似于反演的操作,草。之后的置换群和循环群学的时候就没什么问题,感觉可以过得快一点。然后就是群作用,一些没见过的变换和几个式子的应用是难点,周四应该可以处理掉。此后的路径稍微平缓一些,精力放在 -check -重要定理的证明上即可,印象里没有非常困难的习题了,估计周日能搞完吧,吧。
-这周还有马原的读书报告,zad 今年任务量真大,不过 2000 -字好说。另外又要做实验了,稍微有点烦,实验报告 5000 -字起步还得卷拓展知识,比如说弦振动报告里还得给他写点 PDE -知识装一下,劲比马原大多了。
+昨天提到了我的高中数学老师,才想起他也是华子毕业的,大约是 2006 +年入职二附中,可能是最早一批来我校教书的清北人。现在学校里清北毕业的老师就很多了。据说他本硕读的是核工程,理应是工物系的。他既是班主任,也是数学老师,倒并不是竞赛教练,我们的数竞教练是隔壁班的唐立华老师,
+往往被叫做立华奏。前段日子看到他貌似升职了,简历上写着“培养出 +blahblah,blahblah,及女子数学奥林匹克金牌学生一名”(大意),恐怕指的是我。虽然我这个破铁牌和他没半毛钱关系,但人在他班里,功劳就归他了吧。当然除了名额是隔壁班唐老师给的之外,也和
+立华奏唐老师没什么关系。这么说好像很忘恩负义,但事实如此(不过其实我到现在也没理解的是,为什么高中三年他一直就当我不存在一样。同学当我不存在我可以理解,当时的男女比例比华子夸张多了,感觉大家甚至不好意思和女生说话,也没必要和我说话,我也自闭。毕业之后我就主动离开了高中同班同学的圈子,想来大多数人现在都已经不认识我了吧。
+扯远了,虽然班主任这个态度也很好,毕竟我即使不是什么刺头,倒也是热衷于自己默默搞事和钻空子的类型,只要不捅出篓子(事实上也没捅出过篓子,高中生在学校里能捅什么篓子x)他就懒得说我什么。于是我的日常就是轻微违反一些针对个人的规定,但能比较好地提高自己的生活质量和精神状态,比如带手机听个歌、不在气氛令人窒息的教室上晚自习、肥宅不出操,于是也没人管我,很爽。
+然而以前倒也有令我很难过的事情,比如我高三竞赛结束回头补高考,花了三个月就从年级 +50% +的地方冲到了一模区第二名(还是第三来着)什么的,还有中间大大小小的进步的时候,整个高三他在班上鼓励过几乎所有取得了进步的同学,却从来,从来没有一句话提到过我。到最后还是想开了,就把他当做一个给我批改作业和试卷的工具人就好,美中不足的是不交作业的话他会派人来催。
+虽然现在想想当时为这种事情难过有点傻,毕业之后我时常在友人面前喷他,尤其看到他简介上写我的铁牌是他教出来的之后,觉得这人,啧。但时至今日,我也还是对他当初的态度感到困惑,究竟为什么要这样呢?
+抽代出分了,还挺乐的,我一共就做了 85 分的题,得分效率竟超过了 +95%,就扣了群同态的一个没说明清楚的情况,我的很多担心都没有发生,说明运气不错,何宝相当温柔了。
+虽然他说“考试题目很难”,从成绩分布来看的确(大约是两个一伯分,六个 +90+,两个 80+(为什么这一段断档的这么厉害),在这之后还有 22 +人,具体忘了,其中有 10 个没及格)。恐怕是这边人均水平确实不如 zmx +的大班,想必她那里藏龙卧虎,而我们更不可能和求真比了。
+话说回来干嘛非要比,我(一部分原因)就是觉得数学中上水平的人也能有不错的出路(润应用),而且还能保持精神状态正常,才润来这里的。尽力学好自己的东西,享受乐趣,雨露均沾统计中心和数学系,差不多得了。
+另外何宝居然把答题纸发回来了,拿回去裱起来。我还从来没见过这种操作,一时不知道他是真傻白甜(错乱),信任大家不会搞出点查卷的幺蛾子,还是其实已经保留了电子版的原卷等碰瓷。想起我大一的线代老师,期中查卷时全副武装,要求预约排队不许携带纸笔并全程录像(听说的),笑死。
+一想到那个搞不出来的构造还是很蚌埠住,期末能不能多给点扎实的证明题...但至少做的基本都对了,对我来说也是大进步(
10月25日
+11月9日
-
-
我真的很怀疑有必要把工程力学退掉,或者期中之后抽一个周末集中把它学会了,不然要寄。
-能动系室友 4 学分的工程力学从牛顿力学讲起,我 2 -学分的工程力学实质是理论力学,草。受不了。
-最近经常会陷在思考抽代的难题里面,有的时候想得出来皆大欢喜,想不出来就又痛苦又浪费时间,甚至还想下次再抽时间继续想。何况有的时候我甚至没有答案可以去参考,感觉收获不大。唉。
-从小开始老母亲在学习上最爱和我说的一句话是“没有答案的题目不要做,做了也不知道对不对,浪费时间”,小时候为了考试做训练自然是对的,放到科研里自然又不对,所以现在这样的话究竟好不好呢(笑
-抽代期中才考 -1.5h(顺便吐槽下周五的下午,我要连考抽代期中和初概期末,中间相隔 15 -分钟。所以还好把初概 PF -了...),反正肯定是不适用在多个题目上停留很久的。范围到整环分式域。今天冲进度横跨三个小节,很震撼。不过昨晚刚复习完群同态,环同态就完全复读,洒洒水啦(错乱
-抽代助教可爱捏。
-看本人照片(微信头像)也感觉蛮可爱的
-
-
P1 是我刚发现有 bonus -的时候,那一周作业巨多,于是我交作业时备注了一下之后会慢慢写之前的题目,他还回了我一下;P2 -是后一周我把 bonus 补齐了交上去还给他纠正了几个地方之后,乐。
-剁手了一套世图的 GTM -风格笔记本,之前精装的那个摸鱼学导论和划水学导论 60 -一本,买不起,买了也不舍得写。这个平装的就亲民很多,四本六十多(虽然也不便宜)。
-说到这个,今天翻开 Pin -的一千零一页看了两眼(不要越到期中越爱干别的啊...),感觉没有想象中那么恐怖,至少不是全都那么恐怖。有希望但没信心寒假看到足够应对概率论(1)的位置。但我的优势可能在于上过初等概率论,在应用方面会好一些,尽管这对神们来说掌握起来并不困难。我发觉面对数学方面问题的时候就会心态平和很多,不在乎神能做到什么,只在乎自己是否竭尽全力。
-可能是没卷到那个程度,大家都有光明的未来我对数学分析的恐惧最早来自于高二,和 ycj -他们一起备考丘班(自然是失败了)的时候。当时看的是同济数分,现在看来和华子的微积分 -A -差不多难度,但对于高中的我(尤其上海高考不学导数,高中竞赛也不很需要导数)来说还是有些费劲。后来大一上了传说中的王晓峰老师的两个学期微积分,拼命下放各种高阶知识又不讲得很详细,让我感到非常难受,后期就没怎么听课了。lx -老师说得对,什么东西到最后,都会收敛靠到自己读书上去,而且只有靠自己。
-
-
(还没到货,在世图读者群里看到打样是长这样
-Introduction to that thing, but only for people who already known it. -—— Carol Firedman
-Whatever who wrote, none is understandable. —— Dave Firedman
-到时候自己留两本用,送 runzhi -一本,还有一本暂且留着,蹲个有缘人(什么
+统计推断开课了,会 follow +经典教材,这对我来说是个太好不过的消息了。数理课看电子教材有点难顶,这书又很贵,而且只用七周,于是我下课后速速去逸夫馆借到了最后一本书,乐到把手机忘在了书库里。回去找还迷路了,非常抓马。(为了几十块钱好卑鄙啊,这就是穷吧.jpg
+洗心革面,好好学习统计推断!(但愿不是 flag
+北馆和逸夫馆里好新哦,逸夫馆的绿色小台灯让我想起了高中图书馆里桌上的台灯,很温馨的感觉。可惜人实在太多了,有点社恐地狱,起码我觉得不是一个很适合(我)学习的地方,还是法图和三教比较好(悲
+月光长走的时候突发奇想打算去找找宁斋在哪里,何宝和上学期高代选老师的办公室都在宁斋,他俩都是近两年来华子的青椒,看来不仅是理科楼,近春园西楼也已经满了,
+为什么不是希尔伯特的旅馆呢在近春园西楼门口遇到了一只猫猫,旁边两个姐姐貌似在劝它“你就吃点吧,特地给你带的”,笑死。然后它真的低头开始吃了,说明猫猫爱世人,喵门。
+
+
从近春园西楼后面的小门进去,再走一段路就是宁斋,门外的院子是华子校园巴士的停车场。我以前路过这里多次,一直以为这个小楼是司机的休息室,没想到是宁斋啊。拍了两张对焦不同的照片,里面亮着灯的一间房间里似乎在开 +seminar,在寒风中远远望进去,很温馨的感觉(?
+
+
还看到了西楼社区,没想到都是那种很有北方特色的平房,有小院子和爬着植物的篱笆。我原以为会是楼房,原来华子的家属区也分为破的和豪华的,就像紫荆和南区 +/ 20-29 号楼一样(
+总的感觉西门附近的建筑都缺乏修缮,近春园西楼算是最好的了,后面的小院子也很破败,到处是杂草和碎石。
10月26日
--
-
昨晚睡前想的是我这周就算不睡觉也做不完事情了,然后还是一觉睡了七个半小时,罪过。
-最近的 ddl 们:
+11月10日
-
-
下周五交抽代作业,预计得有三四十道题,习惯了。
-当天还有这周的离散作业,周日晚上嗑着瓜子二倍速看回放然后写一下。
-下周四交数值分析纸笔题,四道题,但我好像还不大会,但也问题不大。
-下周三交实验报告,哈哈,五千字起步。
-当天还要交初概的两次作业,哈哈,哈哈。
-下周一交工程经济学作业,还没学,预计又是罚抄五到六页左右。我认为土木系每一门课脑子都有问题。
-本周日交马原读书报告,两千字,大概知道写什么了所以问题不大。
-
抽代也没复习完,初概虽然 PF -但还完全没复习,你怎么睡得着的.jpg
-于是保守估计这周末要通一宵,也可能要通两宵。
+查了一下下学期的课表,统计中心的课和数学系居然正交,太感动了。而且下学期放掉基物之后就没有必修的物理课了(如果不把数学物理方法当物理课的话),我去,太爽了,是打数学基础的好时候!
+分析基础非常悬,实复概三选二的话实分析暂时不打算上了,尽管它比复分析更有用,留给大三补好分析基础再来,改复分析 ++ 概率论(1);水一个概随,权当弥补这学期初概 PF +的绩点了;统辅的话是周在莹老师的线性回归分析和邓婉璐老师的多元统计分析,又能见到婉璐姐姐了,好耶!
+此外可以补一个统辅导论课,比如生物统计学导论或者统计学习导论(其实从 +workload +和对于进组细分方向的帮助来看,我可能还是更倾向于生统?),也了解一下应用场景,还能多认识一下统计中心其他的老师。没有意外的话(指确定不换方向的话)准备暑假进组。我真没想到统计中心还有 +NLP 的组(俞声老师),果然工工里面什么都有,但我是想走数理统计 or +Bio-Stat 的。
+数学物理方法是必修,还替代不了。我不是很清楚和 ODE+PDE +相比是不是弱化了数学强化了物理建模,那样的话有点恐怖,学不下去就退。土木系还有两门一看就很屑的必修课,测量学和工程地质,估计属于难度不高破事一堆给分还不好的那种,到时候再说。然后选一下基物实验,选一下政治课,选一下体育(或许可以再上一遍这学期的剑术?那不是爆杀吗 +x)再加个通识课。
+这样的话肯定是 30 +学分往上了,稍微有点恐怖,但考虑到概随约等于没有,可能也还好吧?反正学期中间要是觉得受不了了,就优先退掉必修课明年再来(草),没什么可顾虑的...。我每学期都嚷嚷着想选点水的通识课提绩点,但最后还是会 +all in 能学些东西的课,乐。
+最近想把之前看到的统辅课程测评重新排个版搬过来,我的博客读者中有几位统计学潜在选手,想卖个安利;另外原来的排版太糟糕了(x)。当时读到的时候给作者留了联系方式认识了一下,找他问问是否同意。
+UPD:搬过来啦。V1ncent19 学长还非常慷慨地表示欢迎以 CC BY-NC-SA 4.0 +继续传播。
+友:你大三下学期修不完必修课,不是不能保研吗?
+我:我不保研,我现在担心的是到大四春季还剩超过三门必修课的话毕设不能开题,别千辛万苦拿到 +offer 结果延毕了(
+想给我自己颁一个乐观抗压奖,真的,太乐观了
+聊到凸优化的时候想起来 xyx +上学期说在上包老师的凸优化,就去简单问了一句测评,确实是研究生课,40% +作业和 60% +两人一组大作业,和下学期求真那个应该会不太一样。他说他和包老师关系很好,我当即的感觉就是
现充好可怕,啊不是,擅长 +social 的人太厉害了。
10月27日
+11月11日
-
-
一边往前写抽代,一边往后看抽代。今天进度推的还行(
-暂时感觉环的一些东西有些不符合直觉。比如绿皮上整环分式域的第一个结论就让我摸不着头脑,刚拿到的时候自己独立证不出来,第一反应是困惑,在群论学习中倒是没有的。
-“我经常在想能回到那个时候就好了,但‘那个时候'究竟是什么时候呢,我也不知道。”
+学习数值分析的最好方法是抄书...梦回高中的时候看化学竞赛的同学抄各种砖头。抄了一遍就会了。
+抄到矩阵扰动了,还有线性迭代方法和非线性迭代要抄,我觉得我行了(确信
+开了一本 GTM 笔记本抄的,草,感觉很神圣(
+大雨天,中午出门的时候久违的闻到了湿润的空气的味道,一瞬间以为回到了南方。又想起来友人之前和我说“讲吴语的齐国人”的时候还说,有两个故乡是很幸福的事情吧,我说不是的,这样我根本没有故乡。
+晚上未央开推研会议,我懒得去,就让室友文字直播一下,然后去吃李先生了。李先生的牛肉烧饼真的好吃,塞得满满的,饼也很酥松,比牛肉面好吃,八块钱一个感觉不算太贵。吃完那边会也开完了,反正就是列了一个不允许跨保的黑名单(尚未公布),明确有金融和管理类,我觉得肯定也有计算机类,这样的话大家倒是沾了未央软件那十个人的光,软软怕是要被未央人卷了。然后据说大概率不能外推,出国不限制。其他消息还有只要能在未央毕业就能拿到推研资格,但是不自带名额。
+这已经比我想的要好一万倍了,我之前甚至想过,如果不能开出国成绩单的话,就先去做一年 +RA 再申请..
+所以这个会确实和我没关系,我想哪怕校内跨保他们也不会闲到限制去数学系和求真,而统计中心目前流落在外倒有可能被制裁。而我大概率是要出国的,就更没关系了。听完消息之后我第一个想起的还是大一的时候,看 +xyx +在小群里说想跨保去茶园要发多少顶会什么的,而我那个时候还在痛苦地纠结是转码还是转数,也还会因为码不出来而深夜破防,看到他的话更加焦虑了。不知道推研具体卡不卡茶园,他现在又在怎么想呢。
+吃完饭去做核酸,听涛的核酸队伍排得都要打结了,于是去了祖龙广场,才知道这个规模原来也算广场,和社友起名的“有鼎广场”差不多嘛x。人相比之下不算很多,而且没有灯,把脸埋在围巾里就没人看得出来我没戴口罩(
+抽代课上看转数环友吹水下学期的课哪个老师更好,我看了半天才意识到,我一没有必修志愿,二还得手动选课,哪个老师好和我有啥关系?
+概率论是王小群和梁宗霞,前者以前开概统,今年第一次开概率论,后者好像是定理原题默写大师,学不到东西,但我可能只能选他了。不过好像只要背诵得当给分就还好,也就算了,出卖灵魂就出卖吧。
+复分析是张广远和薛金鑫,虽然复分析不限数学系选课,但我没必修志愿可能也抢不到薛金鑫。环友评价张广远至少算是本手而不是俗手(而梁宗霞是断手x),那也还能接受。
10月28日
+11月12日
-
-
充电台灯坏了,于是紧急翻出来了开学时候送的台灯,甚至还有当时的小卡片,谢谢李贤凯先生。
-月底了啊...今天凌晨解决完了群作用,重做课后题的时候发现除了 2 和 -4 -那两个相对重要的结论还是证不出来之外,别的题目都能速通了,感受良好。然后又通了半宵刷 -zmx 的抽代卷子,但没有计时,可能做了 2h -左右就困得不行了。最后两题还没看,前面做的应该能及格,貌似也没那么恐怖(貌似,但愿没有伪证,我真的很擅长伪证x
-先砸瓦鲁多一下,等我去把群论最后几节复习完回来再继续(
-初概最后一课了,下周两节课一节复习一节考期末。后半期我都没有很认真学,想想也挺遗憾的,上个学期一直对统辅的第一门课满怀期待来着。不过,后面还有多元和统计计算,这倒不是我最后一次见到婉璐姐姐,今后如果在统计中心做项目的话,想必会更经常见吧。
-大数定律 & 中心极限定理 & -收敛性,感觉倒是全学期最有意思的一节课。嗅到了很多分析的气息,但是这课凡是涉及到的都不要求,下学期概率论(1)再来。
-然而初概的笔记从期中之后就没有再写了,sigh。等下周五考完,在统计推断开始之前简单理一下,主要是自救。如果咕咕了的话就把那一篇撤掉吧。
-今晚包括明晚甚至后天晚上,都要刷夜做各种 dirty -work,白天要推抽代进度,还有复习 / -学习各种稍微有点用的东西,写作业。
+熬大夜抄数值分析,抄完了 Jacobi,G-S 和 SOR +方法才睡觉,早晨起来又继续抄,太惨了。
+乐子一则:SOR 方法的迭代矩阵是 \(S_\omega=(D-\omega L)^{-1}((1-\omega)D+\omega +U)\),推导完之后觉得这怎么记得住啊,难道每次都要推一遍吗。结果自从把第一项幻视成 +dwl 之后就记住了:这个矩阵是 dwl 的逆再乘一个 \(D\) 和 \(U\) +的线性组合(对不起邓婉璐老师,真的对不起(
+这学期结束,我的代数学习可能就接近尾声了吧...线代,高代选,抽代,数值分析,遗憾的是高代全靠自己拼拼凑凑,没有很扎实地上完两学期,但暂时还是够用的。代数很有趣,我觉得初学的情况下远比分析有趣,毕竟还是具体一些,(但真让我做那种矩阵的怪题目我觉得也未必行),这几门课也很好地把我带进了转数的坑。之后看情况可能再去上个代数学前沿基础,或者上拓扑学,就真的要说再见了。听说下学期的代前基是 +zmx 讲,她这时候不应该在开高代 2 才对嘛。
+下午,翻开书,抄共轭梯度法。阅读定义的我:梯度是什么来着?(
+然后又想起来上学期各种暴躁,摆到最后喜提 B+ 还没记 PF 的微积分 +A2,果然是学得不行。但我在重读分析之前暂且先拒不承认自己有问题,一定是这课太破了((
++
+因为享受着它的灿烂
+因为忍受着它的腐烂
+你说别追啊 又依依不舍
+所以生命啊 它苦涩如歌
+歌单 ++(
10月29日
+11月13日
-
-
插播碎碎念笑话一则:
-我:先做 ddl 最晚的作业,然后往前慢慢推,就能正好在最早的 ddl -之前写完所有作业
-室友:那要是最早的 ddl 之前没完成怎么办
-我:不会的,闭区间套定理保证哪怕有无穷个 -ddl,也还可以有一个实数(时刻)在“做完所有作业”和“第一个 ddl -到来”这个区间里(开始伪证
-算工程经济学从一点算到四点,我靠,校园贷借了 10 万最后只还了 30 -万,这多吗,这不多
-华子搞那些防范诈骗的宣传还不如带大家都学学经济学x
-反正就是做了一天 dirty -work,凌晨算工程经济学,下午写读书笔记,晚上写实验报告,烦死。光栅衍射直到我缝合完报告都没理解到底是在干嘛,罢了罢了。
-能找到的公开的往年报告很少,貌似大物也不做这个,这给我造成了不小的麻烦。我放一份我的在这里:Click -Here,也更新到物理实验备忘录里去了,因为当初看不懂就没有写这个实验,现在这样当做补完了。
-本来今晚还想刷个夜,一鼓作气写完作业明天就开启复习,结果 hx 发链接说明早有致理的抽代讲座,还是去一下比较好。结果报名的人太多了,群里说非致理的人只能线上参加,这话说得,虽然也没什么毛病但是,好吧没有但是。
-也挺好的,线上的话九点半开始可以九点一刻起床,线下得八点多就起。
+抄完数值分析了,数了一下抄了 50 面 GTM +的本子...真麻了。不愧是古老的神秘(虽然相比之下不是很古老),idea +还是很多的。有一些东西我感觉还不是掌握得特别清楚,先搁置一下之后再来看。
+想起来友人和我说过的一句话,idea 远比调参重要,当然我对 AI 一窍不通啦 +:3
+昨天忘记发了,出寝室的时候看到楼下的叶子被扫成了一堆,非常漂亮:
+ +
+室友今天给我表演了一个在床上爬(
+其实看到各个高校爬行的视频的时候,我第一反应是想到了《春宵苦短,少女前进吧》里面女主跟着在玩行酒令(?是吗,忘了)的人们一起爬的情节..太阳底下无新事(??这是什么结论
+看到小学期工程计算机制图给 85 分的我一个 2.3 +的那个老师,成为了土木系“良师益友”提名教师,听我说谢谢你(。这学期在课咨委做完导论课的提案,下学期应该可以去改这门屑课了,当然应该不是我来带提案组,所以期末之前要和 +lyf +还有土木系那个学长再提一提这件事,不然还得拖一学期,还得伤害一批人的绩点(。
+摸鱼的时候排了一下下学期的课表,这已经 32 +学分了,还想加通识课,使不得。
+上学期选课的时候纠结无比,大改了 114514 +版才变成现在这样,而实际上也还是不完满,甚至数据结构还在我的课表里待过很长时间,开学后最终还是退掉了。这学期感觉不怎么需要纠结,难点在于顺利把这些课都选上
++
++ + ++ + + + + + + + + ++ Mon +Tue +Wed +Thu +Fri ++ +1 +工程地质 ++ + 概率论(1) ++ + +2 +概率论与数理统计 ++ + + 毛概 & 习概 ++ +3 ++ 剑术 +测量学(后八周) +基物实验 ++ + +4 +概率论(1) ++ + 基物实验 +数学物理方法 ++ +5 +复分析 ++ 复分析 ++ 数学物理方法 ++ + +6 ++ 线性回归分析 +生物统计学概论 +多元统计分析 ++ 这样来看的话没有多少用来大卷一场的下午和晚上了,所以下学期得努力早起,草,对我来说好难
10月30日
+11月14日
-
-
我是 -five,我虽然早睡(指三点就上床了)了但还是没听抽代讲座,就早晨醒来坐在床上看着腾讯会议,觉得画质真不咋地,看着看着就迷糊过去了,醒来就开始白板讲题了,更拍不清楚了,直接退出会议摆烂。
-早晨起来感觉眼睛很不舒服,不能再熬了。今天处理完所有 -ddl,然后开始继续复习之前暂停掉的抽代,以及总要挤出点时间留给初概,总之其实压力还是很大。
-和何老板对了一下实验报告,发现我真是...只要不是所见即所得的写作,就能写出 -114514 个 typo,又改了一中午。给老板安利了我暑假里在 Overleaf -上投的物理实验报告模板,然后意识到那可能是我给科协学术部打的最后一份工了——这学期的活我都是能咕就咕,开了三次例会我找各种理由最后就去了一次,完全摆烂。等学期结束换岗的时候就走了,实在没有继续待下去的必要。
-晚上考完期中的友人来看我,去西门口和她聊了一会天,大倒苦水,吐槽我自己 -PF -了一门退了一门课还是忙不过来,回想了一下平时还是太摆了。然后从哼歌逐渐变成了一起戴着耳机唱歌(当然音量不是很大,周围没什么人,社恐.jpg),唱了告五人的《爱人错过》,还有 -EVA 的两首经典老歌,心情好起来了。
-说到这个,上次北大那只叫明日香的正在找领养的小猫,得猫瘟死掉了,唉。
-Can you give me one last kiss?
+今日无事,记录一则和友人的扯皮:
++
友:我感觉你从放弃转码之后状态好多了
+友:说点你不爱听的,我觉得你就算当时去交大可能也会很痛苦,搞不好和 +xxx(指 ex)一样
+我:?倒也不至于,他这个单纯是因为实在不大聪明
+友:这是报复性发言吗(
+我:不是,我一直都这么觉得,反正感觉还不如我 +=。=,而我也不算什么聪明人
+我:我觉得他应该去读个文学硕士什么的,然后当翻译去,比较适合 XD
+友:小绿和小蓝吗
+我:嗯,感觉是一个本该成为小绿的人去做了小蓝的事情
+友:不是,我是想起来小绿要被小蓝开发的同声传译 AI 取代了
+友:(笑)说起来笛子已经很久不更新了,感觉是想不出来后面的剧情了
+我:所以现在有类似于同传的 AI 了吗
+友:有类似的产品吧,我用过 Otter.ai,遇到有口音的人就表现一般,还不如 +Chrome 字幕
+我:所以同传的场景会有人有口音吗
+友:不知道诶
+我:不知道诶
+友:不过你要是科班出身,有环境、资源还有 fellow +的话,可能也不会像在华子自己转码这么焦虑
+我:不知道,我的性格就很难有 fellow,也不擅长利用资源
+我:还是传统式的学习比较容易啊
+友:小镇做题家吗
+我:小镇做题家哦(笑)
+
+突然想起来还有门期中没考...周六的工程经济学,感觉可以周三再开始复习(
+就,过一遍 PPT,再拟合一遍往年题就行了。希望人没事。
+明天跑 1500,去年跑了 +8'20'',真的太强了,不知道怎么做到的。今年可能根本跑不进 +9'40'',但愿活着回来。
10月31日
+11月15日
-
-
今天倒没啥别的事,刷了一天抽代,书差不多摸完了。这一遍感觉把之前模糊的内容都处理好了,此前不会的习题大多数也能速通,但是还是觉得有些题目真的是,奇技淫巧。
--
-数学上不应该回避技巧的提升。——PIN
-好吧,我谢罪(
-明天抽代课上写一下 PKU 题。
-晚上去吃了清芬一楼的羊肉泡馍,还蛮香的,汤的味道调得不错,北方人面食基因觉醒.jpg。热乎乎的一大碗,冬天破防时候的 -comfort food 又增加了(
-突然在想陕西人会不会觉得不好吃或者至少不正宗,就像我觉得清芬的生煎不是一般的难吃,但室友觉得还不错一样(
-十月的尾声,日记系列的第二篇也如期完结了。我以前以为这个系列至少会见证自己慢慢的改变,但这两个月中确实没有什么变化,除去学习的东西变了之外,生活还是那样,ddl -追着 ddl,摆烂,自学,摸鱼。
-不过,像我这样运气的人,一旦面临变化恐怕就是往不好的方向在改变,亲友离散(什么离散),生活不顺,诸如此类。因此没有承担可能发生的精神内耗,或许已经是一件很幸运的事了。
-昨天和友人在西门外轻声唱歌,唱《爱人错过》。这也是前几天偶然在你社看到,然后一听就觉得很喜欢,于是加入循环了的歌。其实歌词就那么几句话:
--
-我肯定 在几百年前 就说过爱你
-只是你忘了 我也没记起
-走过路过没遇过 回头转头还是错
-你我不曾感受过 相撞在街口 相撞在街口
-你妈没有告诉你 撞到人要说对不起
-本来今天好好的 爱人就错过 爱人就错过
-很奇怪吧 -XD,倒是和恋爱经历都没关系(x)。我想是因为听出了一种不安定的感觉而喜欢,尽管很担心这样的事情发生,但如果改变就在面前,还是要勇敢些。
-什么胡言乱语(
-好啦,下个月见!
+- 活着跑完了 1500,正好 9'20'',比去年慢了 1 +分钟。其实我跑的时候还觉得自己挺快的(乐),以为能进 9 分钟。Anyway +这不重要,我这个羸弱的体质,跑完还活着 & 甚至能拿到 3 +分就很不错了。 +
- 今天也没啥别的事,只剩下跑完 1500 +之后腿还在疼,早点睡了,明后天还得预习工程经济学(悲
1月1日
+11月16日
-
-
这个系列居然存活到了 2023 年!
-
-表白成功了!收到抽代助教回复的邮件了!还加了好友,好哦!(-
-驰雨(x)同学:
-你好!非常抱歉现在才抽出时间来回复你,虽然已经向你发送了微信好友申请,但是还是认为同样给你回一封邮件比较有意义。
-其实我早就有留意到你不是数学系的学生,在和老师闲聊的时候曾有提到过这件事,大致意思是在本门课中给我留下最深刻印象的同学居然是学土木(hhhhhh当时我是猜测你是这个专业)的同学,许多我本以为他们并不会做出来的题目她也有认真去做。
--
-没猜错,只是我写邮件的时候还掩盖了一下,我说我一学位是物理,二学位是交通建管(确实也是实话
-实际上我和你的经历有许多的地方有一些相似,我本科入学的时候的专业并不是数学,而是某个工科专业,而且高中的时候数学学的一塌糊涂,对竞赛什么的也一窍不通。只是在大一的时候才觉得大学接触到的数学和高中完全不一样,更加有趣更加吸引人,于是才在大二转到了数学系,但不幸的是转专业的过程也不是一帆风顺,我被调剂到了计算数学专业。于是我在本科的后三年一边补大一落下来的课程,一边修基础数学高年级的课程,还不得不修计算数学的课程(听起来是非常狼狈)。
--
-其实我很难想象,在华子要是高中时没学过竞赛,甚至高考数学学得也不太好,大一再继续上那个锤的微积分 -A,真的能培养出兴趣甚至想转去数学系吗?那个微积分 A2 -直接给我上厌学了,真的烦死了...这是否说明隔壁的基础课教学质量已经远超世一大了(
-由于并不是科班出身,实际上我最初面对那些学基础数学的同学的时候还是有很大大大大一点自卑的(特别是自己本不属于这里却来旁听),总是不敢和他们去交流问题,或者是和他们交朋友,担心自己暴露出自己什么都不会的事实(x)所以我的本科时光过的并不快乐。一个转折点或许是自己成功跨保到了基础数学的直博,意识到自己或许也没有那么差劲,开始敢于和别人交流,敢于面对自己的不足。我感觉做数学有时候真诚非常的重要,自己不会就是不会,不会就要去搞清楚,和别人交流(hhhhhhhhh或许需要一大点厚脸皮吧x)这使得我之后的收获很大。
--
-太强了..要是我在隔壁成功转到计算数学的话可能只会想往统计挣扎一下,要么就既来之则安之,干脆不动了。在应用方向想往基础跑,真的相当有热情。
-不敢和原住民(?)们交流也真的很真实,我甚至都不太敢在转数环里说话,
-不过转数成功的同学平均水平好像远超原住民(?)。恐怕自己也是,等到有朝一日获得一点点小成就的时候,才能挺起腰杆来吧 -qwq另外一件事是,在学数学的时候你真的能碰到非常非常非常多厉害的人,比你厉害无数倍的人,这可能会击碎你的信心,可这又有什么关系呢?做好自己就好了!进一寸有一寸的欢喜,能比昨天的自己多会一些东西我认为就已经非常不错了。如果真的是想学数学,那就是一辈子的事情,早学一些晚学一些也没有什么大不了的。
+一些碎碎念:
+经常遇到一些需要找人合作完成的任务,有时是小组作业,有时单纯是想在课程群里随机抽样一个人对对作业答案。每当找到这么个组织的时候,如果其他成员是大腿,总是一件令人高兴的事情。我也比较喜欢预设其他成员是大腿,一般都会先发出来一个自己的解决方案请别人提提意见,尽管里面有很多我知道而且暂时解决不了的 +bug,总之是希望从别人那里得到一点启发。
+然而比较差的情况下别人根本发现不了 / 发现不全 bug +在哪里,欢欢喜喜地拿着我的破烂方案就跑了;比较好的情况也只是能把 bug +提出来,再反问我一句怎么办啊,能得到解决方案甚至只是能得到启发思路的情况极少。到最后总还是我自己吭哧吭哧把 +bug 修完,然后再让对方 check 一遍没有伪证。
+所以,难道到头来大腿竟是我自己(?有的时候又觉得有点好笑,
+希望以后读研的导师别是这样的。为什么突然这么想呢,因为最近统计推断的课上没有认识的人,于是抽样了一个经管 ++ 数辅的同学讨论作业。本以为数辅应该很强,没想到也只负责对我提 +issue(。刚刚上课的时候没听讲,自己把问题修完了,对方 check +了一下表示这下就不是伪证了,快乐地抄进了自己的作业里,而我课后还得补一下课堂内容x,感觉愣是给自己找了个甲方。SRT +也是,做工工 AI +的项目本以为能抱到大腿,看了另两个人的申请书才知道他们都没学过 +Python,这下大腿(暂时)真的是我自己了,感觉很艰难啊。
另一些碎碎念:
+首先要向阅读这一段的朋友道歉,我理解并尊重大家不同的卫生习惯,但我也确实洁癖,希望不要冒犯到(
+冬天手洗衣服会困难很多,冬衣一盆只能洗下一件,水也很冷,要戴橡胶手套,洗一次衣服要耗费不少心力。但我恐怕还是永远不会用楼里的公用洗衣机...今天洗了好几盆衣服,站在水池边上重复着搓洗的姿势,感觉像罚站一样。然后想起来了 +EVA TV 版里明日香的一段话(是的我还真的去找了,在 22 话):
-
-非常同意!x
-说起来我之前也一直这么想,后来被别人批评说不求上进(qwqqqq),难过了很久。不过人家是神,确实在他眼里我努力学习的东西都很 -trivial,所以并不是很能互相理解。那就不要互相理解了,坚持做自己就好。
-所以做自己最喜欢的事情就好啦,无论之后能不能做出来什么成果,无论这个领域已经聚集了多少大佬,但行好事,莫问前程。
-祝眉头舒展,顺问冬安。
+美里和笨蛋真嗣用过了的热水,谁会走进去啊? +被美里和笨蛋真嗣洗过内衣的洗衣机,谁会来用的啊? +美里和笨蛋真嗣用过的洗手间,谁会坐啊? +美里和笨蛋真嗣呼吸过的空气,谁会来呼吸啊? +讨厌美里,也讨厌真嗣,我更加讨厌第一适合者! +讨厌爸爸,也讨厌妈妈,但最讨厌的便是自己!
然后微信上还聊了很久,听他讲了一些大一没上数分高代还选了平转数学,一边补这两门,一边顶着计算数学的课还要学基础方向的小故事,在隔壁冲基础真的很强了,这又是怎么做到四年顺利毕业的qwq,我都想主动延毕了。我大概讲了讲自己遇到的一些小的困惑,一起吐槽了背书般痛苦的数值分析(,还闲聊了些别的,非常愉快。
-另外他给我看和 hx 的聊天记录,hx 的意思好像是要按比例调 -4.0,现在这个情况再按比例调的话岂不是要向下调分了,害怕,
-连我这种彩笔期末都能按题目顺序通畅地 -ak 甚至还给一个题加强了结论,感觉人均 90尴尬的是聊完我翻了翻他朋友圈才意识到,他本科好像是隔壁的,不是华子的。我虽然觉得“转到了计算数学”这个说法很奇怪,还以为四年前一个系里面专业都分得这么细,一直都给他预设成是在华子本研一起读的。更好笑的是我还跟他吐槽了半天诸如数分这样的几门本科生基础课稀碎的给分,和后续上课知识储备的问题,沃日,他还真的认真答了,反正对话里就感觉很奇怪又说不上哪里怪(
-找到了一张两年前的照片,其实昨天本来想发的,结果给忘了。
-
-
我的高中有年底最后一天开跨年晚会的活动,也是为期一个月的校园艺术节的尾声。大家说这是二附中最盛大的节日,但是说不清为什么我就是不喜欢这个活动。可能是因为当时不喜欢身边的人们,所以不愿意和谈笑中的大家坐在一起看演出,感觉尤其孤独,或许是天然抵触这种很有玫瑰色的青春氛围的节日,总之三年三次晚会我都没去过。晚会有一个高三大合唱的环节,高三的同学会一起拿着荧光棒唱排练了一个月的歌,然后被拍成视频(沃日,还真找到了),很情怀的样子。轮到我高三的时候我也没去,哪怕我的手完全是做题家的手。
-记得高三的那个跨年晚会之前刚考完一模,班主任买了蛋糕给大家分着吃。我太自闭了,一到这种时候就觉得真的好压抑,直接从教室里逃了出来。看到丢在垃圾桶旁边的蛋糕包装盒里有小的烟花棒,可能原来是要插在蛋糕上的,估计他们不会要了,就拿走了一支。晚上开晚会的时候大家去了体育馆,我也不是很想回家,就一个人坐在漆黑的楼道里看了会剧,突然摸到外套口袋里的烟花棒,忘了是去哪里找到了打火机,在楼道里点了一下,拍下了这张照片。看到四散的火花,一下子就雀跃了起来,现在还记得当时的心情呢。
-我和友人一直以来是非常好的朋友,突然意识到即使这样她也有不理解我的时候——比如上述的这个时刻,她正在体育馆举着荧光棒为大合唱泪目,并不理解我为什么不愿意投身这种气氛之中。高中的时候写过很矫情的话,叫做:
--
就像我们无法看到一生中全部的雪,也不能完全知道彼此叹息中的故事。
+我的洁癖倒还没有到精神崩坏的程度(,但感觉也是分两方面的。
+其一是对“卫生”的标准问题,还比较表象。我自觉自己对卫生的要求算是很高的,也是从小受母亲的影响,慢慢养成的各种习惯。就像进出洗手间会多带一张纸,用来包一下门把手和冲水的按钮,就像室友洗杯子就是在水龙头上冲一下,我要拿洗洁精洗,洗完再用饮水机的热水烫一下,就像在教室自习的时候坐下之前会拿张纸简单擦一下桌子,等等等等。以前有个朋友说我矫情,不过后来他就不是我的朋友了(笑)(倒不是因为他说了这句话,而是别的矛盾((
+其二是心理方面的。比如说,我在寝室里总是感觉很局促,最近越发这么觉得。身后的室友换衣服或者找东西的时候,喜欢把椅子推得很远,于是我和她之间的过道会变得很窄,甚至她搭在椅子背上的衣服会碰到我的椅子。这个时候我就很难受,会想到她的衣服在公共洗衣机里洗过又拿出来感觉不是很干净。另一个室友从前有一次晾衣服的时候,把拿不下的衣架放在了我桌上(因为我的位置离阳台很近),然后我就去买了两块桌帘把自己的桌子围了起来(其实也早就想这么干了,只是那也是一个这样做的契机)。因为感觉她的衣服在公共洗衣机里洗,又要挂在衣架上,好像也不是很干净...天啊怎么对公共洗衣机怨念这么大。
+而且这似乎也是一个亲疏的问题。我向来想要保持和世界保持距离的状态,不喜欢不熟悉的人碰到我,我的衣服,我的东西,我总感觉“不是很干净”,平时也尽量不会碰到别人的东西。但想了想友人在隔壁也一样把衣服放进洗衣机里洗,我和她见面也还是会亲亲热热地打闹,也会拉她的衣袖和手
+(首先,我不是女酮(,感觉矛盾起来了。但话说回来,和室友倒也不是特别疏远,对于寝室里和我关系最好的室友,我也还是不愿意和她、她的物品有物理上的接触。不过她也很尊重我的习惯,还蛮感谢的。但是想起来社聚的时候我也把自己的耳环(其实是耳夹啦,不敢打耳洞 += =)摘下来给好奇的社友把玩过,还分着吃了月饼(当然是掰着分的 = +=),却感觉很开心。是因为寝室对我来说是一个“更加私人,所以更需要保持洁净”的地方,还是因为和室友生活在一起,知道她们的生活习惯所以排斥?有点难说。
+这么听起来好像确实挺矫情的...草,感觉有概率会被喷。虽然这么说的话听起来很奇怪好像有点严重,但其实也还没到影响生活的程度(,一般遇到类似的情况都还是往自己身上找问题,会想“为什么我要把东西放在室友不小心会碰到的地方呢,下次要注意点”这样,稍微有点内耗,不过问题不大。
+
11月17日
+-
+
重新看了一眼昨晚的碎碎念,有点草,感觉这么形容之后自己看起来好像很难接近的样子,那倒也不是(
+仍然希望没有冒犯到大家,如果有的话,我还是再谢个罪吧(
+早上和朋友闲聊,才知道高中的时候很看好的一对情侣分手了,大概是异地的原因。当然,这件事已经过去一个月了,但我今天才知道,或者应该说才过去了一个月我就知道了,已经很快了。身边很多人都在不停地 +crush 和 break +up,吃瓜吃久了也多多少少会在某一对官宣之后就产生“他们会很长久”还是“不会很长久”的预感,虽然有这种预感似乎很罪恶,但还好我们都不是三体人。
+然而他们分开的消息还是让我小小的惊讶了一下,我不解的根源在于,算来都至少五年了,五年的情意分开也这么容易吗?或者我还想知道的是,五年的情意在分开之后会带来多大的惯性?
+我没什么可类比的,就反思了一下自己的人际关系。也就和老姐的关系最长久,大概认识了七年多了。顺带解释一句,虽然我这么叫她,但是没有血缘关系,只是 +15 +年的时候在网上认识的赛博朋友(草),她比我大一岁,也就这么叫了。一般来说和别人解释这个问题会很复杂,所以我会直接称呼她为姐姐,可以避免很多麻烦。其他线下也熟悉的朋友还没有超过五年的,友人还不到三年;认识 +runzhi +倒是已经四年多了,却也算不上非常熟,仅限于数学同好(?),有过很多长期断联的时间。
+虽然很不一样,但要我想象和老姐今后因为什么原因闹开,就不再联系了,我还是会认为不太可能。
+想起来之前友人向我抱怨自己感情方面的情况,我只想说,这都是很幸福的烦恼。人似浮萍,来体验一下我这种三年后地理位置在哪里都不知道的生活,再体验一下每天脚不沾地忙各种破事,就会只有迷茫,不会对这种事上心了。另一部分内容我本来想说又没说,毕竟每次和别人讲自己家里的事情,总是会让对方愧疚提起了这个话题,又一顿道歉。实际上从小的家庭环境确实让我对此无比悲观。悲观之后就会想开,怎么样都无所谓啦,有猫有狗就行。
+又想起来高考完之后,老姐给我的礼物里面夹的纸条,上面写,“驰雨小姐自由如风”,当然是祝愿。让我想到上一个叫我 +xx 小姐的还是 ex
这个 +b,当初还觉得很浪漫,乐死。然而如今想想,自由如风的另一层意思,恐怕是漂泊和无牵无挂。
+说到这里,打算周六考完试去把给老姐的礼物寄出去,倒也没什么大件,就是日常积攒的一些小东西,像之前去古北水镇买的兔儿爷泥塑,去故宫买的香膏和书签一类的东西,等等等等。把日常攒成一个小箱子之后,再写几张明信片附在里面寄给她,她也同样会这么做。小时候是互相写信,贴上邮票等邮政慢悠悠地走,虽然寄丢过一次。现在是用快递寄一些实体的东西,也很令人开心。
+箱子已经满了一阵子了,一直在我桌上放着。今天想到人似浮萍的说法,总觉得给她寄东西也寄不了几回,我就要离开这里去往不知道什么地方了,一阵凄凉。于是想着要赶快寄出去。
+
11月18日
+-
+
很有必要提醒一下自己,早晨睡醒 / +午睡睡醒反正总之刚睡醒的时候,千万别急着回消息别急着看社交媒体,不知道迷迷糊糊的时候会说出什么 +b 话,昨天也是今天也是,肠子悔青了
+更离谱的是,我已经连着咕了两节抽代了,本来觉得也无所谓,出勤率有 +30% 就不错了。咕了 5-3 的抽代之后来六教上 5-4,5-5 +的统计推断,先是在六教的斜坡上迎面遇到婉璐姐姐,想起来我摆烂的初概
+还有超松弛法矩阵,不过她至少没认出我来。结果往前走了走又遇到了刚下课出来的 +hx,我去,我觉得他至少脸熟我,还盯着我看了很久,真绷不住了。下周二去上课的时候还是换件衣服吧(
+无奖竞猜,这是哪里↓
+
+
这是晚上的华子招生办(
+其实我也不是很清楚这是不是招办,没做过招生工作。是从一教 104 +的后门走出来的时候拍的,拿去骗到了好多人。室友猜工字厅,何老板猜是网图,友人问是不是深山老林里的古寺(,看来是氛围到位了。
+右下角那个房间的屋顶看起来很独特,像日漫里的弓道场(?)不知道有没有机会进去看看是干什么的。
+明天考工程经济学期中怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办
+当然是先学一会统计推断,再看一会番(
+本来天气预报说是今晚下雨,于是吃完晚饭就回寝室了。把工程经济学的卷子拿出来,看了五秒钟,然后写了一会统计推断笔记,又打开了赛博朋克边缘行者(,其实已经很久没看过新番了,这部还挺戳我的。
+可是明天考工程经济学期中怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办(
++
-Data don't make any sense, we will have to resort to statistics.
尬死我了(,但确实大概就是这种感觉。不过又有什么关系呢。
-说起来原来想投给朱自清文学奖的稿今天基本上改完了(有些人期末周是真闲啊),但现在已经不想投了,自己留着就好。何必为了一个奖把自己的心剖出来给不相干的人看呢。虽然最后好像不会公示参赛作品,但一想到评审阶段我也还是觉得算了。(才不是觉得自己这水平根本没希望,才不是(
-今年(去年?)的跨年夜是观影马拉松!一个人在寝室连着看了《色,戒》、《血观音》和《牯岭街少年杀人事件》(这个实在太长,看了不到一半就睡了),翻到上面这张照片突然好想给自己点个烟花棒看,可惜买不到(。翻出来了生日买蛋糕时候送的蜡烛点了一下,烛光也很好看呢。(没有照片
+
统推讲完了数据简化原理,这句话戳到我了(如果有看我统计推断那篇文章,会知道此处 +statistics +指的是“统计量”而不是广泛的“统计”,所以其实是知识点哦(错乱
1月2日
+11月19日
-
-
这网络学堂真的有点乐,老师给了成绩之后可以选 -
-display:none,但只要会按 F12 就可以查到抽代成绩啦(还挺符合预期的,ak 了就是 ak -了,
简单的数理问题确定性很强,很给人安全感啊。想起来期中考完的时候破防了一晚上,觉得肯定是寄了,甚至梦到了 -4 学分的抽代喜提 2.6,只能带着日渐贫弱的 GPA在一个均绩 3.8+ -的院系里过一个相对失败的人生,在紫荆公寓的浅色床单上痛哭。没想到期中并没有想象得差,虽然没考过一个半小时的试,整场基本都在慌乱之中,浆糊一样的脑子根本写不出构造,但真的落笔写下的东西都写对了,学得还算扎实。而期末翻盘真的是存在的啊。(其实微积分 -A2 期中爆炸的时候也想期末翻盘,结果期末比期中更烂(
-虽然没有过生日的习惯,但是我还是会在生日前后借这个名义送自己一点小礼物,获得一个冲动消费的理由。去年生日的时候订了《恋爱的犀牛》的演出票,可惜四月底北京疫情,演出取消了。后来有点不开心,改成给自己买了一身看中了很久的裙子,也很喜欢。
-期末考之后打算在北京玩几天再回家。本来是想直奔江西,结果我姐说二月份要去上海实习,就约在了上海见。原来规划去故宫什么的地方走走,刚才突然想起来这件事,不抱希望地查了查《恋爱的犀牛》演出档期,居然 -1.4-1.15 之间真的在北京有场次,目测是空花组的演出。订了 1.10 -的票打算去看,非常幸运。
-本来是考虑订上海场的票的
-(才不是因为票价比北京场便宜一半),但上海场演出是 -2.14 开始,那天我就要回北京打 hpv -第二针了,恐怕是去不了的,就回家之前在北京看吧。现在不用再担心封校出不去,或者演出取消了呢。
-虽然不觉得会超过郝蕾段奕宏版的经典,而且真的已经在 b -站看过很多很多次了,但还是想去一次现场。
-和我妈打电话。她一如既往地劝我快去找对象,不存在的,乐。我也懒得和她讲自己的很多打算和考虑,就像现在告诉她我打算延毕一年她恐怕要应激,会争执很久,没有必要,暂且按自己的思考来生活就好,每次就糊弄过去。不过她今天问了我一个很有意思的问题:会喜欢学数学的男生吗?我很干脆地回答说大概率不会,把自己惊到了。
-想了想喜欢过的人们(不要细问,太羞耻了x)性格气质爱好甚至外貌特征都基本完全不一样,
-平等地在不同阶段同等水平地喜欢不同的人,不存在哪个人是白月光一直念念不忘甚至希望别人身上还带有他的影子之类的情况(什么啊。但确实有一个共同的特点是他们都不是很擅长或者至少不那么喜欢数学,读的专业五花八门但也都不是数学(啊其实基本后来都收敛到去搞 -CS 了,大家都好成功 qvq),大概是巧合吧。可能是竞赛的时候觉得数学组里很强但又有些怪的人(不好意思有点冒犯,或许叫做“比较独特的人”比较好,哪里独特我也说不出来但相信大家都有体会 -x)明显比别的组要多,相比之下化学组就很欢快随和,我经常被暴打完就去找他们玩,有几个曾经关系不错的同学,
-ex -也是化学组的(?。加上自己很菜,所以几乎从来不敢和神交流,导致有点刻板印象了。但是“学数学的人里面比较独特的比别的专业里要多”这件事貌似确实是真的,为什么呢。说到这里突然想起来,竞赛的时候一直非常自卑,以为我这么菜,组里的神应该都不认识我吧。最后一次联赛前我们在做模拟,彼时距离进 -IMO 国家队还有三四个月的 wyc -负责监考和发准考证,遇到不认识的人他会叫一下名字问座位在哪里,我还以为会叫到我,结果他最后是走到我面前把准考证递给了我。大一下学期上排球课,左爷爷正好和我同一个时段上课,我本以为他肯定不认识我,结果他还和我打了招呼,两次都挺意外的。
-不过想来大家认识我,根本不是因为我那羸弱的水平,甚至不是因为我菜得像个笑话(,而是因为我是组里非常少有的一直坚持到高三才退役的女生吧,混到了脸熟。高三那次联赛是省一里的唯一一个女生,同年拿了 -CGMO -Au,两件事叠在一起被沪上某个小有名气的升学公众号拿来大做文章蹭流量,从小学开始的经历都被扒了一遍。一想到这些还挺不高兴的,当时又要装作开心的样子被人祝贺(有什么好祝贺的,退一万步从功利角度来说这不就是纯纯竞赛落榜生),和现在被迫过女生节时接受礼物和祝福的感觉差不多。我之前提出来我能不能不要过女生节,我也不想给班里的男生过男生节,还被约喝茶了,不利于团结的话不要说((
-不要再写青春疼痛文学了,快去复习啊(
-看了一眼下学期的网络学堂,故宫学这门课的英译是 -Gugongology,Google 了一下这个词一共有 19 -条结果,草,什么冷门绝学(,很难想象交出国成绩单的时候国外学校会怎么想这玩意(
-看到了一个说法:
+工程经济学寄了,但好像相比别人也不算完全寄,不管了。
+去刷了一下 Mili 从 Iron Lotus +之后的作品,感觉风格都差不多,没有特别喜欢的...,收藏了一首 Dandelion +Girls, Dandelion Boys,但是之后可能也不太会再听。
+早期有很多(我认为的)神曲,印象最深的是幾年月,Nine Point +Eight,Vitamins,Cerebrite(入坑作x)和 world.execute(me) 这些。Mili +的歌词一贯都是在讲故事,几乎不会一句唱好几遍,但是早期的曲风相当多变,抓耳的也很多,这种感觉从 +Millennium Mother 这张专之后几乎就没有了。
+Iron Lotus 不错,开始进行一个单曲循环x
-
如前所述,故宫学于2003年正式提出,而敦煌学的出现要远远早于故宫学。学科名词出现的先后次序是衡量学科之间自觉性程度的标尺,即使是从英文拼写情况来看,两者的差异也十分明显——敦煌学已有一个国际公认的英文拼写,即Tunhuangology,而故宫学则有Gugongology、National -Palace Museum Studies和Studies of the Imperial -Palace等不同拼写形式,说明前者已是国际性学科,而后者的国际化程度还有待提升。
+Without you I could never be
+So sincerely thank you for everything
+It pains me to think
+我的学业导师(土水学院的)跟我聊了很久,中心思想就是——我这样全然不顾物理课,真的有可能延毕
+但是没办法,这学期进行到这里,我感到很焦虑。我唯一的愿望就是好好地完成每一门数学学习,无论是抽代还是统推还是数值分析,甚至回溯一下初概并往高等概率论过渡,或者着手做 +SRT,对我来说都比那个什么工程力学更有价值。工程力学从开学到现在,作业全靠抄何老板的先交上,只等着“某个周末有空了补一下”,可是没有一个周末能有空留给它。我深知如果拖着它这样下去必定什么都做不好,于是就退了。说起来这个 +SRT (对我来说)还是有点难度的,找了一下发现是把 Kaggle +上的一个题搬过来了。老师比较 nice,至少没有在学期中 push 大家。
+这样,这学期我落下了 8 学分专业课,包括 4 学分的基物,2 +学分的工程力学,还有意料之外的 2 +学分实验。实验倒不是问题,退课是遇到了给分巨烂的意外,且没有沉没成本,下学期或者明年这时候就可以补上。所以实际上有 +6 学分会堆到未来。下个学期我还会推掉 5 学分的基物,不知道会不会退 3 +学分的数学物理方法;大三上学期要把工程力学的 2 +学分补上,但有可能又要推掉 3 分流体力学或者 4 +分工程力学进阶,大四上学期还有 4 +分量子力学...真的太好笑了,土水专业居然要学量子力学。
+大三下学期会稍好一点,数学基础课除了实分析就都上完了,可能会去补一门基物。但无论怎么算,总是要有至少 +3 门物理课放在大四上学期完成,即使目标只是 +Pass,也依旧很困难——我真的很讨厌物理(如果有物理系的朋友读到,真的不好意思(。而且一旦 +Failure,我去,我不好说。当初如果不是为了读数学专业,我早就去学文科了,那样的话高考怕是真能上线,何苦被困在这里。(然而家里没钱读什么文科,还是会很挣扎罢x
+说实话,我自己真的觉得延毕没什么不好,这就和降转一样从容了。可惜我妈肯定会应激(,后面本来还有一段话,但被我删掉了。
1月3日
+11月20日
-
-
8 -号考数值分析,而我连着摆烂了两天,复习时间突然变得紧张了起来,考完之前更新大概会比较咕(
-虽然觉得对计算数学研究的问题不太感兴趣,不想往这个方向走了,但基本的数值方法毕竟是应数各个方向都会用到的,也是培养方案里(说得好像是我的培养方案一样)挺重要的必修课,不能摆过去啊 -qwq
-和甘主任唠嗑,他怎么大一上学期就已经在看 stein 了(
-虽然一直说别人学得多快有多升级都和我没关系,自己学扎实就足够了,但压迫感来自身边的朋友的时候果然还是有一点点难绷 -XD
-今天顿悟了最近作息混乱的原因——是光线的问题。拉上窗帘之后,台灯和白炽灯是寝室里仅有的光线来源,而且楼道里的灯坏了,从楼道那一侧也不往房间里面透光。如果一整天不出门也不看表,还独处一室的话,真的是感觉不出白天黑夜的区别的。从这个方面来说人和植物还挺像的,都很依赖自然光呢(
+写统推写到 +04:50,绷不住睡觉了。本来不打算同步昨天的日记了,刷牙的时候脑补了一下,是否会有朋友看我一天没更新以为我猝死了,草,还是更一下的好。
+建构定理解决问题的过程很有意思,但我现在是越来越讨厌做题。然而技巧的提升是必要的,所以还得做,唉。
+今天又一次自动审批从西门出去,在中关村北大街上呼吸了一会,回来就收到了封校通知,草。
+下周四我是真的有一趟就医,是八个月之前约的 HPV +九价疫苗,竟然八个月就排上了,感觉北京算很快了。要去顺义,祈祷那边不要封,以及祈祷院系的直男老师(非贬义x)们不要以为这是一件非必要的事情(,并已经做好了回来就被通知隔离的准备。
+去近春园或者紫光大厦住单间不比和室友住一起爽多了从西门回来的时候遇到一只小黑猫,本来想给它拍个照,结果窜出来一只狸花把它打了,有幸拍到了全过程。小黑猫需要法律援助的话可以联系我(不是(顺序是从右下角开始顺时针观看,手机自带的拼图愣是没有调换顺序的选项,我淦
+ +
+刚写完上一条,我室友就被隔离了。她为了 SRT +去李兆基做实验,结果李兆基封楼了,草(
+顺便吐槽一句,感觉她那个导师挺逆天的,开了好几个 SRT +招了几十个本科生进去给博士生打下手,还要求每周投入时间不得小于 +10h,进实验室要打卡计时什么的,这就是生化环材吗x。相比之下我导师真是仁慈,不停强调学业为主,每周啥也不干都行,大不了寒假再做。
1月4日
-数值分析一天看两个章节的话正好能看完,这个工作量水平基本上是肝一肝能保证完成的,还好。沃日,怎么感觉这课跟没学过似的,虽然我平时确实没怎么花时间,但这书我至少抄过一遍,PPT -课后也读过,这些内容都是学会过的啊(,怎么现在印象这么模糊。4 -个学分的课考试前一周学完,真有点刺激了,大家以后上这课的话千万不要学我。不过还好沾了这学期线上考试所以开卷的光,沃日,要是不开卷的话我更想象不出来这课要怎么考,感觉这玩意和别的理论还不一样,好多优化方法都像拍脑袋想出来的,只能嗯背。闭卷的话真要把公式全背下来吗,也没必要这样折磨人吧(
-6 -号的两个娱乐项目打算缓考了,寒假里复习的话加起来不会花超过三天时间,但这三天放在现在太宝贵了,匀不出来。
-这个破工程经济学,我一边上一边在心里骂,我将来既不做实体工程,又对经济不感兴趣,为什么非要我学。有时候入戏太深了,还真以为自己是数学系和统辅的了,每次想起来培养方案里的专业课是什么测量学,工程地质,工程力学,更好笑的是还得学量子力学,都觉得像个小丑(。没一个有用的,还难的要命,得花巨量时间处理,甚至可能要付出把更多一年的青春年华()用在在华子里坐牢的代价。都到这份上了,给分还给得巨烂,这院系真是有毛病。
-虽然天天骂华子,但还是终于明白了当初 SJTU IEEE -之类的选项是一个局部最优解,选华子仍然是不错的(陆本都差不多烂是吧x),中二一点讲,哪怕被折磨了这么久但总算是找到了真物(?啊?),尽管这个过程实在太漫长、太痛苦了,而且还远远没有结束。的确处处都取局部最优的话是到不了全局最优的,终值在取初值的时候就定下了。
-读过了许多算法和定理,仍然过不好这一生(点烟.jpg
-之前看学长写的“都是贵系的问题”那一部分,光是看都看得我焦虑不已,太累太绝望了,很难想象他那两天是怎么过的。后来一想其实华子大多院系的生态也就这个水平,拿我院出来一比,贵系好了不知道多少倍,又把我整破防了。不知道为什么想起 -ex 来(上次在博客里试着搜了一下 ex -这两个字母,出镜率过高了x),只记得他也是要润,正常情况的话最近大概也在套暑研?不知道会不会沾点 -UM-SJTU Joint Institution -的光,不了解。当然他看起来菜的离谱(,也或许并不会走 researcher -的路,我之前说觉得他去当翻译最好 -XD,现在也还是这么觉得。现在还偶尔会去翻翻他的各种社交媒体,我之前和朋友戏称,这也算我的人类观察活动之一。确实是这样的,和平时随手打开一个社交媒体的时候会试着搜搜看朋友的 -id -有什么区别呢?区别在于真的已经变成赛博幽灵,肉眼可见的将来不会再有多少联系了而已。这也很正常,举个例子来说就像我大概永远不会认识迟先生(,但是自从知道是校友之后就也时不时会去看看推。有时候看着看着 -ex -发的很多东西,会觉得真的也只是个再普通不过的一般路过肥宅罢了,和我从前写的青春疼痛文学里的那个带恶人似乎没什么重叠,才发现自己的心态也已经发生了挺大的转变。怎么说呢,祝大家都顺利吧。
-1月5日
--
-
又看了一遍,昨天这是在说啥?倒不是抽象,感觉早晨六七点写的东西未免有些,太随机了吧(
-数值分析,不过如此!学的时候觉得最困难,心理阴影最大的几个章节顺利过去了,后面是一些轻松愉快的多项式数值方法,感觉明天能速通完。
-无论如何它都算是数学系的养生课,分方向之前的那些基础课哪有考前速成能学得会的。
-不知道考试考多难,bcl -老师风格看起来比较友善,我也没题目可以拟合,就把课后题刷完了,感觉还好。
-今天发现只有概率统计方向不必修泛函分析 (1),有点震惊。
-wjd 老师在鸽了我的邮件 13 天之后终于回了,笑死(
-寒假的事好像实在有点多,先抽几天写完统推讲义和基物实验指南,今年基物实验 -3 -不能再退课了,我超,这课明年就停开了,因为二字班修订培养方案之后只需要做两个学期实验了,羡慕。然后还得速通数分到一个不至于原地去世的水平,以及 -learn R in 24 -hours,可以的话打算再浅看下统辅的两门理论课来着,毕竟下学期的难点在复和概还有统计学习导论这个码课,尽量得压缩下留给那俩半娱乐项目的精力。而且我还有期末缓了没考!草(
-我还想多整几次江浙一日游呢,到底是假期,抚平在华子造成的精神创伤最要紧。
-遛弯的时候不知怎么想起来,之前找一位学长问凸优化这门课的情况的时候,他简单介绍了下,然后说这课不卡优秀率只卡 -A+,“虽然我最后只有 A-”。我 mod -了一下,然后他说“数学人之间还是可以相互理解一下追求的嘛”。
+11月21日
-
-
- 我懂了,不是早上六七点钟写东西导致产物非常随机,而是我这个人就很随机,时不时“突然想起来”( -
我当时还蛮奇怪这个数学人是啥意思的,只知道他要转 AI -相关,难道转的是理论方向所以也自称数学人?还有点震惊他怎么知道我想转数的,我感觉我在现实世界的社交里一直还算低调,基本避开不提这些事。今天回来随手一搜才知道他以前也是 -MOer,原来是这个意思,不知道为啥我一直以为他是物竞的,报道上出了点儿偏差(
+昨天刚说周四要出校一趟,今天紫四就封了。本来封的这个点我应该在上课,结果早课被我翘了,就被封了,好似。
+昨晚失眠睡不着,翻来覆去到六点钟才睡,十点不到就被室友喊起来说封楼了,草。实际上我们都翘了课,所以正好在宿舍里被封;另一个室友昨晚就因为热爱科研住进了紫光,还有一位早晨上课去了,流落在外盘算了一天要不要跑路回家(是百京人
+今天解封之前也实在无心学习,一则睡得太少了,根本集中不了注意力,二则第一次封楼,又戒备又迷茫。于是和室友一起在宿舍里扯皮了半天,甚至久违地打开了朋友圈刷了刷其他被封同学的情况,不过看了一会觉得还是老样子,又光速关上了(
+十混一重新检都是阴性了,也解封了,仿佛除了给我带来生活失序外,没有对华子产生任何影响,渺小啊
+本来以为封楼会有上门核酸,结果并没有,解封了之后还得自己去做一天一检,华子从不让我失望。盘算了一下,今晚六点到十点的紫荆篮球场人流量可能类似于一个 +U-quadratic +distribution(x),于是八点左右去的,确实人不多。统计推断大胜利(不是
+看了一眼工程经济学出分了,瞄了一眼答案,上来 10 道判断题错了 4 +道,别的地方一分没扣,真的离谱,不愧是我。不过分数也还可以,期末只要不大寄就没事。
除非这老师也给 +85 分 2.3,90 分 3.3
1月7日
+11月22日
-
-
数学记号真是混乱...头大
-摸鱼的时候看了会 summary,发现统计计算的一大半内容好像就是数值分析的三个章节在统计问题里的应用,大概又要从头讲一遍数值方法,其余是一些统计里的特化(?)算法。眼前一黑,所以说我明年还得再学一遍这玩意是吗(,虽然会轻松很多就是了。
-点疯狂星期四经常拿咖啡凑单,正好还有券,最近把他家号称不同口味的咖啡都尝了一遍,没尝出区别,感觉都是刷锅水的味。虽然也没喝过刷锅水,但是我就觉得应该是刷锅水的味(
-最近不分白天黑夜地在复习数值分析,也努力让自己别再记忆随机游走了,没啥可记的,简单写个流水账。
+- 停滞不前
1月8日
--
-
早知道这数值分析考这么简单,我复习这些天干啥呢,还为它缓考了另外两门(x
-这话是不是考完抽代的时候也说过来着(
-一半都是没有布置成作业的课后习题,正好这两天刷完了,剩下的有手就行,我共轭梯度法呢我牛顿法解非线性方程组的几个变式呢我特征值方法呢怎么全都没有啊(x。不过学到了不少有用的东西,好耶(
+11月23日
-
-
说起来包老师的课真的讲得很好,虽然这门课是第一年开,他也是刚来华子不久的青椒(没有影射哪位老师的意思,没有 -x)。课堂上讲得很清楚,思想也很深刻,强推给之后也要修这门课的朋友。
-另外,这课的 PPT 简直仙品啊!我觉得不输 dwl,看着太享受了。
-讲课讲得好,内容充实,不在课后刷题量和奇技淫巧上为难人,考试顺利过,这不就是很理想的课程设计吗 -555,这几天备考卷昏了说出上面这些话才奇怪吧。可惜这种好处恐怕只有第一年能享受到,后来知道某个老师考得没那么难,可能就不会这么用心了。说到底好像还是学习态度有点问题(
-
-总算考完了,开摆!
-明天摆一天,看看电影写写统推讲义,去图书馆借几本书带回家看以及给下学期用,后天出去走一走,大后天打扫卫生收拾东西,12 -号回家。不过这周还得连夜卷一个工程经济学的加分论文,过两天再说吧,这破课还这么卷,好烦。
-总的来说,这学期虽然开局选了六门数学课,结果最后退了一门水的,又 -PF -了一门卷的,剩下的要么本来就不难要么碰巧选到了水一点的老师。所以似乎还是没体验到数学系的课劲有多大,在一个并没有做好心理建设的状态下,下学期就又选了六门,而且还要去碰瓷实复概里的复和概,感觉人肯定会出事的(悲
-
1月9日
-一天啥也没干,好不容易考完试,想摆烂却不知道怎么摆了,感觉是很空虚的疲惫。勉强补完了跨年观影马拉松时候没看完的《牯岭街少年杀人事件》,心情更沉重了。
-下午写了会统推讲义心情就好些了,参考着统计计算的讲义和刚刚考完还热乎的数值分析,给 -Newton 方法求解 MLE 的部分补充了一些变式和收敛条件,挺好玩的。
-晚上二刷了 BBC -神探夏洛克的第二季,我小时候不爱看巴斯克维尔的猎犬这一部,拍出来整体很昏暗,有很多丛林里穿梭的场景,稍微有点恐怖。所以其实不记得这一部的故事了,就二刷了一下。中间有一个猎犬来袭时,委托人把脸贴在家里的落地窗上往外张望的场景,玻璃里映出了他的脸,我就在想为什么要在家里装这么大一面玻璃幕墙,感觉很没有安全感。
-然后想起来(又开始 random walk -了是吗)高中在图书馆负一层自闭的时候,曾经随手翻开过书架底层的一本看起来有些奇怪的书,是阳版的《哈扎尔辞典》。前几页大概讲了这样一个故事:哈扎尔民族会因为在睡梦中被人叫醒而暴怒,因为他们认为人在睡觉的时候最脆弱,容易被恶人偷袭。阿捷赫公主为了在睡眠中保护自己,每晚命仆人在眼睑上写上毒咒字母,看到字母的人就会死去,早晨起床前由盲人婢女服侍自己梳洗,擦掉字母后才睁开眼睛。某天有人为她送来了一面快镜和一面慢镜,快镜可以映照出不久后的未来发生的事,慢镜映照出刚才已发生过的事,时间差是相等的。这两面镜子碰巧在她睡觉时送到面前,于是阿捷赫公主睁开眼睛时在慢镜中看到了自己眼睑上的字母,在快镜中看到了已经睁开眼睛的自己,危险的睡眠中安然无恙的她死于清醒的瞬间,镜子无法映照出的当下正是死亡时分。“她是在来自过去和未来的同时打击之下亡故的”(不知道会不会和原文出入很大,但我对这句话印象很深)。
-当时甚至还不知道这是真实存在过的民族的传说,还是完全的虚构,看完有点吓到了,没有把它借走,也一直没有再往下读。但这个关于镜子的隐喻一直记到现在,时不时会想起来,尤其是每次意识到想起它的时刻正是过去与未来的间隙,是阿捷赫脱离危险的梦醒时刻和死亡时分,总是会吓自己一跳。电影里的委托人满含恐惧地把脸贴在玻璃上,这既不是快镜也不是慢镜,因此玻璃里映照出一张一模一样的脸,而当下正是充满着死亡气息的恐怖时分呢。
-1月10日
-今天出门借书之前想起来昨天说到的《哈扎尔辞典》,搜了一下北馆也有馆藏,考虑要不要借一本来继续读,但是印象里很厚,带回去有些麻烦。然后在搜索结果里看到了一本《爱情故事的两个版本》,才知道《哈扎尔辞典》背后的小故事,太浪漫了:
+我为上周抽代作业里不会的题破防了整整一天一夜,无数次怀疑自己这个水平是不是后半学期要寄了,最后才知道是把差集 +\(R-P\) +当成了环上类似于环理想的加法的逆运算。我真的,我甚至还给它定义了半天这个运算是怎么一回事,怎么调整才良定义(没调出来),最后才意识到居然是差集,那写成 +\(R \backslash P\) 不好吗(
+看来是我离散水平不行,总之还是寄。
统计推断是后半期唯一一门我打算线下全勤的课,结果老师封小区里了(
+下午纠结了半天还是决定出门去三教找个教室上网课,常去的教室就 3203 和 +3303 空着。本来打算去 3203,走到门口看到里面只有一对情侣在聊天(,就去了 +3303。结果遇到了欧老师,很久没见了,蛮巧的。不过果然这种情况下基本上都是别人叫住我,不然我好像不会特地去看周围的人长啥样(x
+单人行动久了总会有和世界逐渐脱节的感觉,在线下遇到熟悉的朋友还是很令人开心的。
最近的破事感觉必须列个单子才能来得及做完且不遗漏了:
--题名:哈扎尔辞典 Dictionary of the Khazars
-作者:帕维奇, M [1929-2009]. (Pavic, Milorad)
-描述:这部类似“民族志”式的“辞典小说”写了一个幻想的古代民族“哈扎尔”人的历史以及有关这个民族的各种轶事。此书是《哈扎尔辞典》的阳本。阴本跟阳本并无多大差异,有人曾对照阅读,发现仅十一行文字有所不同。
-
--题名:爱情故事的两个版本 Ljubavni roman u dve price
-作者:米哈伊洛维奇, J. (Mihajlovic, Jasmina) ,帕维奇, M, 1929-2009, -(Pavic, Milorad)
-描述:本书是雅丝米娜·米哈伊洛维奇与米洛拉德·帕维奇共同创作的一部作品集。其中,“科托尔文具匣”收录夫妻二人围绕一个神秘的文具匣进行的同题创作,写作因此也成为作家夫妻间亲密而浪漫的约会方式;“爱情故事的两个版本”记录雅丝米娜向帕维奇“定制”故事的有趣经历,文学大师不同寻常的写作状态可见一斑;“迟到的情书”由帕维奇的小说碎片展开,引发出雅丝米娜对二人过往爱情生活的追忆和对丈夫深情的怀念;游记“哈扎尔海滨”记录雅丝米娜寻访《哈扎尔辞典》中那个“消失”的民族——“哈扎尔人”的见闻、体会和奇遇,也记录下二人对历史、时空、死亡等问题的思考和感悟。
-
其实高中的图书馆地下一层有很多大家都不知道的藏书,比如《中等数学》合订本(字面意思,真的是图书馆老师自己把月刊订在了一起),我还拿来刷过题,还有 -1940 -年代出版的李四光先生的《地质力学之基础与方法》(当时为了给地科社写科普推送,我甚至还读过这本书,是否预示了被调剂进土水学院的未来。这个故事也充分告诉我们,随意把普通爱好变成职业是行不通的啊!),村上春树的《刺杀骑士团长》,阿列克谢耶维奇的四件套《切尔诺贝利的悲鸣》,《锌皮娃娃兵》,《我还是想你,妈妈》,《我是女兵,也是女人》,还有《岛》也是在这里见到的,后来因此去读了维多利亚希斯洛普的其他作品,我更喜欢《线》。甚至新海诚三件套《秒速五厘米》《星之声》《言叶之庭》的轻小说都有。
-不过要说馆藏里最冷门的恐怕还是井上靖的作品《天平之甍》(甍读音通萌),是从日本视角讲唐代僧人东渡的故事,还有《孔子》。《天平之甍》里最后讲到,僧人淡海三船为敬谢来到日本时已经失明的鉴真,写下了“我是无明客,长迷有漏津。今朝蒙善诱,怀抱绝埃尘”的诗句,大意是称自己才是“无明客”,承蒙鉴真以佛法善诱,从而心怀脱俗。后两句分手的时候被我写下来送给了
-ex(开始青春疼痛文学了是吧),原本是想最后给他一点安慰(因为分手是我提的,我真善良)。但我后来想想觉得他一定永远不会关心这一句我从哪里见到、是什么意思,说到底他也一直都根本不太在乎这些,很难相互理解,罢了。并不是说我是文青(?)就要求他也得是的意思,只是说完全不在乎别人的心意的话会很令人失望,一向如此。
在半退役的苦闷高二,我在地下一层兜过无数圈,上述这些以及见到过的其他有趣的书几乎都借来看过一遍,它们是在这个学校里待了三年,真正影响我、改变了我的东西。只是一直都是崭新的,似乎不太有人会去地下一层的书库找书。一层也有一点比较有意思的书,印象里看到过一本全英文的烘焙书,放得很高,里面写了各种面包的做法,适合画饼充饥。但我想它在那里可能是因为书脊比较漂亮,被用来当装饰物的吧。但实际上一层书架不多,大多数放的是教辅和给竞赛的同学用的大学教材。桌椅很多,桌上还有台灯,基本是作为阅览室使用的,在里面卷自习的不少,我也曾经是其中的一员,后来遇到一些困扰(这个故事或许下次可以讲),就再也不去了。
-对了,想起《哈扎尔辞典》和《天平之甍》的时候是我难得的会为我的高中感到骄傲的瞬间,尽管我猜这两本书几乎不会有别人借来读过,但它至少存在于一个中学的图书馆里,这让我无比幸福。
-感觉在很没水平地掉书袋...实际上我确实喜欢阅读,但是并不算擅长写作。高中语文考试阅读从来都能随手拿高分,作文就不一定,太擅长写
-random thought
-和不停堆放读到过的东西,要么就是刹不住地表达情志,写不来议论文,经常被骂。虽然只是和同班同学相比的话,根本不需要作文写多好就能爆杀大家(?)。Anyway
-我写的东西实在没什么水平,感谢大家忍受我(,要我做读者的话还好一些,但坚持阅读,思考和写字,这才是我理想的生活啊。
好啦,碎碎念完之后,我要准备出门去看话剧啦~
-1月11日
-写个流水账。一边收拾东西一边摆烂,收完发现就一个行李箱,还有一个平时背的单肩包。单肩包里就放了贵重物品(其实除去电脑之外,我包里最贵重的东西是一支不算常用但一直带着的口红和一小瓶香水,草),证件,水杯和路上想读的《汴京残梦》,甚至没装满。说来惭愧,《汴京残梦》还是去年五月从毕业的社友那里收的二手,听说是黄仁宇(就是《万历十五年》的作者)的作品,就买了,到现在也没读,那位社友也很久没上线了。
-暑假来北京的时候带了行李箱,一个书包,一个单肩包,一个放在行李箱上的袋子,回去反而少带了很多。一想到明天在车上还要找个路人或者乘务员帮忙把行李箱抬到架子上,有点绷不住(。但是装了书之后我是真的拿不动,拿不动还要带这么沉的箱子回去,是不是我有点问题(#每日内疚 -#每日社恐
-晚上骑车出门兜了兜风,友人送了一张奈雪的券要过期了,就到东南门外的奈雪买了一杯。前两天趁最近闲着没事,还报了个今天的被试,赚点奶茶钱,其实就是在 -FIT 楼玩了会 VR,采集动捕数据。运动量超过一个月总和了(
-有道理,下次可以把打赏的提示改成 buy me a cup of bubble tea(奶茶用 -cup 吗(
-1月12日
-
-
今天在回家的路上,原本写了个长的,到家看看觉得不大适合发出来,就算了(
-我经常和朋友说我真的很焦虑,真的很焦虑,我和 Bowen L -(就是抽代助教啦,以后就这么称呼了)聊天的时候或者和 wjd -老师发邮件的时候也说过,焦虑已经成为了我生活的状态之一。然后大家都告诉我,不要焦虑啦,但不要焦虑的原因往往是因为焦虑也没用,只能消耗能量,所以不要焦虑。这话虽然没毛病,可是我听了之后更焦虑了——我在为因为自己的焦虑而消耗了做别的事的能量这件事而焦虑,为什么我这么辣鸡,每天要不停地破防和焦虑,别人不都克服了焦虑然后把时间花在有意义的事情上了吗,我怎么做不到呢?
-下次换个说法劝我吧,骗骗我也好啊(
-差点忘记了,1 月 11 日或者 12 日的话,要放一首歌在这里呢:《またねがあれば》by -當山みれい
-去年第一次遇到这首歌之后为旧事又破防了四个月之久,自闭太久了连破防都算是给自己找事做,有点傻。关于这两个日期就不细说了,总之还是青春疼痛文学(。其实除了第一段歌词和歌曲的封面之外也没有特别贴合的地方啦。
-很久没听过,才发现现在居然也要 vip 了(
+- √ 写完抽代上周作业 +
- √ 补上周课堂内容的 huixiangdou +
- √ 抽代本周进度 + 作业 +
- √ 统计推断上周作业有个题可能还要再改改 +
- 大数定律,中心极限之类的问题再回顾下,下周统推期中了 +
- 准备个微雕的统推期中 +cheatsheet,其实可以直接删改一下然后缩印博客文章( +
- √ 统计推断这周的内容 & 作业 +
- √ 把离散二倍速放完,作业随手写了 +
- √ 周四打九价 +hpv,据说很疼,但友人封着出不来只能自己去了,希望不要昏在半路 +
- √ 工程经济学小班课的作业 +
- √ 周五之前登选课系统把工程力学退了,这课必退无疑但是上周还在蹲 +PF,乐 +
- 周末数值分析抄书,写作业 +
- 工程经济学最后一次纸笔作业 +
- 工艺美术史期末的 cheatsheet,题目已发,可以准备了
1月13日
--
-
在北京苟了一个月没有感染,回家第一天就病倒了(
-虽然可能和不适应没有暖气的室内有关,应该只是感冒,总之是发烧了,躺平。
-工程经济学的加分论文到最后还是放弃了,实在是没兴趣做,算了吧。以前我还愿意为自己的专业课付出一点时间挣个好成绩,但自从找到兴趣点之后就越来越难以忍受这种被迫卷的工作,它们对我此后的人生毫无意义啊!
-但其实暑假里的工程计算机制图就是前车之鉴,因为没兴趣卷,被 curve -后吃了 2 学分的 -C。工程经济学据说给分正常,老师教这门课已经至少十年了,理应不会有太大的改变。我真的不想做额外的工作了,开学之后补考完期末拉倒。
-说实话,我真心钦佩院系里多数同学的吃苦耐劳。明明被这个专业恶心得不行,还兢兢业业地按计划完成培养方案里的每一门课,把加分论文卷成不写就等于减分的任务,在所剩无几的时间里塞几门 -CS 或者金融的课程,已经活成被华子 PUA -出的形状了。我从前还能做到,现在只生理性抗拒。当然可以说我是逃避,自己懒惰加上水平不行就赖学校和院系,但每个人展现出来的状态不也和环境有很大的关系吗(
-昨天在高铁上,半梦半醒中被一个同学拉着问软软和贵系还有工工几个组的差别(我也不是很懂啊!),听他谋划限制保研方向后还可以做的几个最优解,说软软某个导师门下几乎都是非清本,所以觉得自己可以去碰下瓷,以及“再不济软软总比土水强”(怎么乳软啊!),etc。
-华子从来不培养人,它只会 judge 人。你想接受这套逻辑,乖乖躺下给它 -judge,它还说你不配被 judge。
+
睡前听说何老板脱单了,他知道我不看朋友圈,特地在官宣前来告诉我了一声(??),以及明天是他的生日。蛮好的,虽然我这时只是想起他也是要出国的,不知道到底是已经确认了和对方能有未来,还是一时上头(。倘若是前者,那在概率上更是一件值得祝贺的事情。(虽然我很怀疑是后者(
然后想起来之前在紫四楼下遇到他在等人,封楼的时候他问我四层什么情况(而不是问我什么情况,屑同学 +x),甚至上学期问他实验报告写了没的时候他说正在写,结果我 10 min +后出门做核酸遇到他和一个女生走在一起,等等。诸如此类的事情总是有迹可循,感叹我自己虽然记性好,但到底还是不够敏锐,何尝不是一种缺点。
+草,怎么听起来像是败犬发言,其实就是普通朋友,甚至如果冷漠一点的话,应该叫做“同学”。
1月14日
-还在发烧,睡了一整天,所以没啥可写的。晚上好多了(
-1月15日
+11月24日
-
-
两天睡了至少 30 -h,总算缓过来了,感谢关心捏。做了三次抗原全都是阴性,烧了两天还没获得新冠抗体,真是有点亏。
-下午写了会统推讲义,差不多把统计量约定和性质写完了,
-发现以前的理解还有点不很对的地方,什么叫费曼学习法啊。打算发个邮件给老师,让她先检查一部分。说起来开个 -Repo -做这件事的话比较方便吧,不用时不时手动发邮件了,社恐狂喜,但不知道老师习不习惯。中学的时候似乎也学过样本方差的概念,当时就搞不懂为什么系数是 \(\frac{1}{n-1}\) 而不是 \(\frac{1}{n}\),不过这一部分高考和竞赛貌似都不考,也没讲过。现在才知道是作为统计量看待的话,修正系数之后才能作为无偏统计量来估计分布方差。
-上了大学才知道好多省份的高考还考线性回归,修统辅之前我连这是什么都没听说过,突然有些担心把这些东西写上去的话会不会太浅显了。不过上海高考连导数、动量这些东西都不学(听说现在要考导数了),还真的挺利好理科苦手(指我自己
-啊对了,暑假里写的几何题解终于发出来了。我之前和组长说我下次应该不会再写这个了,真的做不来难题,收几个水题跑路有点丢人,另一个是大龄玩家(?)好像也不应该再在高中生的游戏里浪费时间,该往前看了。
-不知道为什么,组长给冷老师发的邮件里说这是我们组最后一次写 Sharygin -了,卖了个情怀。别人也都是这个意见吗?
-但我对大学的数学竞赛似乎也没什么兴趣。觉得丘赛离自己太遥远,根本什么都还没学会,又觉得全国大学生数学竞赛那个报名非数组不大合适,数学组的话一样没学会。新生基础大赛的时候也是这样犹豫着,既没有报非数也没有报数学组,最后咕掉了。但当时到底是不是因为微积分 -A2 -学得太拉,怕在非数组里暴毙,我也记不得了,似乎有这个原因,那真是有点菜啊。麻了,快去学习(
-草,上面那个推送又把我名字写错了。虽然也不是第一次被写错名字,但找一下这个字很难吗(恼
-下雪了,但远远没到能积起来的程度,在半空中看雪是很大的,飘落到地面就没有了。
-本来想拍点什么,然而相比北方的大雪实在是寡淡。发现楼下有一只猫猫在打滚,橘白可爱捏。
-
-
晚上去盒马拿了我妈预定的两盒水果,看了眼价签,三斤小番茄 20 -块钱,六两草莓 30 -块。感觉自己真的是很没生活常识,常见的菜价我恐怕基本都说不出来,这种精细的水果自己一个人的时候也不怎么买,更不清楚了。想起来最近好多(?)up -主都在打丹东红颜草莓的广告,点开过一次链接才知道真挺贵的。又想起墨茶去世前几天说想吃草莓,大概也是现在这个时候。所以雪下得薄一些也没什么不好,在楼上看雪时埋怨雪不够大没有积起来,因为在楼上啊。
-#每日为赋新词强说愁 #每日不知道为什么但是感觉会被骂 -#每日叠甲
+去打了第一针九价,就,我姐之前恐吓我半天她打完之后的副作用,包括并不限于发烧头痛恶心 +blahblah,结果我打完除了胳膊有点酸(感觉是扎一针之后的正常现象)之外就没什么感觉了(
+我这个孱弱的身体素质,在(或许有必要的时候)倒还挺值得信赖的(
+ddl 要爆了,而我还在不紧不慢地摸鱼,这不对吧(
++
为什么会这样呢?我很难形容在肉眼可见的将来要失去一个好朋友的感觉,还阻止不了。
+
1月16日
-好像距离最后一门考完已经过了一个星期了,这一个星期没怎么玩但也没怎么学,到底干嘛去了呢(
-今天去了嘉兴,大概是规划过的江浙一日游的第一站,其实也只规划了第一站。来回火车票
-25 块,似乎比坐 16 号线去滴水湖还便宜。
嘉兴是我长大的地方,出生之后直到上小学之前都在这里度过。在南湖区逛了逛,除了父亲曾经供职的嘉兴学院和小时候住过的小区,就没看到什么和记忆相符的地点了,连幼儿园都搬走了,怎么会事呢(。本来是来治疗精神内耗的,结果光是迷路就给我走迷茫了。
-以前有一段时间对轨交线路比较感兴趣(倒不算车迷),玩过几次随机公交/地铁挑战,买一张一日票,不用动脑子,随机在换乘站下车搭另外的线路,还挺开心的。结果有次在复兴岛下车之后发现没地方去了,骑共享单车到五角场吃晚饭,草。后来虽然不怎么尝试了,但大多数换乘通道长什么样子我都有印象。也想过乘公交车省际来往,但是一直没有成行,这个肯定会更辛苦,不太有精力。
没拍什么照片,也没去乌镇和西塘,没买东西带回来。路上翻了翻包发现还带着学生证,随手打开一看,学籍注册栏的那两页一共有五个大框,可以贴十个学期的注册章,是否在暗示我延毕一年也贴得下(x
-所以为什么要跑这一趟呢?我也不是很清楚啊!
---就这样,他(波塞冬)几乎没有察看海洋,只是在匆匆攀登奥林匹斯山的途中,飞快地瞥上一眼,而且他的确从未在海洋里航行过。他常说,他以此等待世界末日的来临,到那时候,也许会出现一个安静的时刻,就在末日快要来临之前,在检查完最后一笔账目之后,他还来得及做一次快速而短暂的旅行。
-——卡夫卡《海神波塞冬》
-
1月17日
-
1月18日
+11月25日
-
-
昨天开 Learn Mathematical Analysis or Die -的时候其实根本没想好写什么,写好序言就直接传上来了,当时想的是就算不知道写啥,先给我一种“大家都知道我在学这个东西了所以不能再鸽下去了”的感觉也行,不然真的一天睡 -20 -个小时。后来发现我话挺多的,不愁没得说,以及真的开始看了之后觉得挺有意思的,不像以前一样恐惧了。
-可能是因为学过了抽代和数值,高代虽然没上课但除了多项式也基本学完了,所以再回头看数分觉得以前搞不懂的东西有些其实很好理解。总之确实,可以用很多种不同的顺序完成培养方案。
-不过明天要出门和友人小聚一下,就不 learn mathematical analysis -了,我选择 die(
-摘自 Learn Mathematical Analysis or Die:
--
-要开始构造实数了!用的是 Dedekind 分割。这个我也在 wxf 的微 A -课上听过,但他讲得并不认真,仅限念了一遍定义。后一节课课前有同学提问说,为什么一左一右两个集合就能代表一个实数呢?他不是很愿意理会的样子,反问说你是不是补退选进来的所以没听过第一节课啊,一只羊为什么代表 -\(1\) -呢,两个集合怎么不能代表一个数呢。
-他可能是觉得这个问题太 trivial -了吧,也或许只是当天心情不好而已,然而提问的同学看起来还是没理解的样子,还平白无故被敲打了一下,就茫然地坐下了。Anyway,在这之后我对这个课堂的印象就不是很好,后续也很少再去上课了。只是觉得,为什么不能好好讲清楚道理呢,就告诉同学理由是从几何直观的角度来看,把实数轴任意截断的一点都是实数,有这样的一个定义不就好了吗。当然,当然,应该是我吹毛求疵了,他可能真的只是当天心情不好,所以不太想解释,后来我也没怎么再听过他上课,不清楚还有没有类似的状况,可能属于是不小心碰到了一个极端情况。
-另外,单是讲过这个有什么意思呢,不说 Dedekind -分割满足序公理所以确实可以定义出实数,也不拿来用一下,就莫名其妙放一个定义在这里,课后又让做题目,感觉是在炫技。后来我也看过一部分他的讲义和回放,挺多莫名其妙的安排都有点像炫技,就彻底放弃跟进度,自己单开了。不过确实也没人逼你选他的微积分课,接受不了的话,换别的老师的课堂就好了,或许是个伪命题吧。
-虽然大多数同学都吹 wxf -讲课有多好,但我其实相当怀疑他们有一部分并没有听明白课堂内容,觉得老师讲的内容很高深,自己吹捧老师的话会显得很厉害而已。另外听说 -wxf -的答疑确实很认真,或许大家说他好是指这一部分吧,还是指他喜欢在课堂上和群里讲笑话?PPT -和讲义是准备得挺认真的,可惜我并不觉得设计得好,
-感觉白认真了。总之我是不太喜欢这种不彻底也不成体系的高阶知识下放,或许它自有意义,带大家了解一下也好。当然,和我相反的典型就是 -wl 他们,是真的学得很好,也喜欢 wxf -的课堂,所以我这些话很可能只是弱者的托词而已。也是啊,我觉得他讲得不好,大一的时候干嘛不自己去看一千零一页,而是单开去拟合微积分往年习题了呢,乐。弱者的牢骚暂且发到这里,下面继续说点正经的。
-画风其实是这样的,想到啥说啥。不过很奇怪吧,我觉得 wxf -的高级课堂没什么意思,几乎不怎么听课,也从没参与过课后的讨论班和群里的讨论。说到底我也不咋喜欢群里的氛围。前段时间那个课程群还在不停弹消息,大概是 -wxf -被推到校级的清韵烛光去了,大家又在膜,说到底这个也很正常,但不知道为什么我就觉得有点烦,直接退了群,第一次结课后退课程群。笑死,单从这些来看,我并不像是对数学很感兴趣的样子。
-wxf 爱好者(如果有的话)请轻点喷我(
-沃日,这个月评论区好热闹啊,
社恐震惊
+晚上 SRT 线上开周会:
+这周你做什么了?什么都没做。你做什么了?什么都没做。你做什么了?什么都没做。好,散会(
+我估计至少我自己持续到学期结束都会是这个状态了,哪有空管这些事啊((
+草,何宝不是说抽代课会有助教组织线下上课来着吗,我下午冲到教室,怎么就六个人,怎么助教都没来啊(。我才不会承认我是想看微信头像照片看起来很帅的助教才特地去教室的,所以他为什么不来啊(悲(好变态
+虽然但是,
蛞蝓扩域好抽象,一遍看不太懂了x
+貌似可以回家了,上学期我跃跃欲试,这学期我希望室友能不能早点走(草好阴暗
+北京的冬天更舒服一点,没必要回去,除了室内外温差有点大,刚进楼的时候很热之外,一切都还不错。想起来上海连绵的冬雨,总是有各种不太开心的回忆。印象很深的是高中时候的一次圣诞节,回家的路上雨水灌进了鞋子,好冷(。况且还没有看到北京的初雪啊,不急着回(
+给大家表演一个耳机线拧花(什么鬼
+
1月19日
+11月26日
-
-
前两天读完了一千零一页讲义的实数理论部分,又写了习题,给我乐死了。学完代数再来看这个也太爽了,完全解决了我秋季学期学抽代的时候想过的
-一个看起来很蠢的问题——实数域和普通的特征为 -\(0\) -的域到底有什么区别,特殊在哪里?明明它们在素域的层面上看起来还是一样的(实际上也不一样,没有序关系,但至少形式还是一样的),为什么素域之外的元素差别这么大?举个例子来说,普通的域在素域之外完全可以没有元素,为什么实数域却比有理数域多了那么多元素?何宝在课上时不时会指出,我们研究的域比较抽象,没有序关系。我虽然也觉得这个是重点,但并没有觉得是一种决定性的不同,以为是有什么别的更本质的不同,导致了在实数域上存在序关系,或者它只是“不同”之一。至于序是什么,不等号究竟是什么,序公理是什么,一概不知了。
+虽然现在是 26 号,11 月似乎还有好几天,但是看到下周五要交的作业的 +due 是 12 月 2 日的时候,还是比往常更深刻地感受到了时间的流逝(
+据说现在不回家就跑不了了,稍微有点动摇,但目前还是不打算走。不知道为什么我甚至已经做好了在学校过年的准备(只是一个心理预期),为什么会这样呢,夏天的时候明明很乐意回家的来着。
+月光长骑路过二教,旁边是周培源应用数学中心,停下来看了一眼。想起来之前还查过这个地方是干什么的,结果连个官网都没有,华子发的关于周培源中心的文章还是 +20 年前的,离谱。里面的老师似乎也很少,我知道的就雍稳安(下学期开 PDE +的老师)和章梅荣(好像是室友以前的微积分老师),有点怪。
+跟友人吐槽了一嘴,然后她问我怎么不直接冲进去问问里面是干啥的,我:?不社恐的人真恐怖,虽然也有一定道理
+室友今天突然让我去树洞自搜一下(名字首字母),总之好无语(
+补统推去了,最近的状态感觉就是快冬眠了
+
11月27日
--吾尝终日而思矣,不如须臾之所学也。
+因为享受着它的灿烂
+因为忍受着它的腐烂
+你说别追啊 又依依不舍
+所以生命啊 它苦涩如歌
感觉真的很丢人啊!怎么会有人这个时候才学这些东西
顺便把那一篇改成数分 I -速通日志了,感觉会写很长,就别合在一起了。
-后面和一元微积分重合比较多的部分大概可以快很多,毕竟这个我还是有胆量说自己学得不错的,感觉又有希望能学完了。
和友人来吃了暑假一起吃过的烤肉,当时也是在这里填了用餐人数 999 -人,点完单后收到了 4995 -元的餐位费账单,草。一个测试工程师走进烤肉店,烤肉店溢出了((
-一些今天的智慧发言,记之:
-++
11月28日
-
-- -
为什么只有 Elden Ring,没有 Elden Field,Elden Group,
Elden -Principal Ideal Domain,etc. ?- -
就像得证可以写作 Q.E.D.,或者直接画一个小方块(我 MO -时期甚至比较喜欢画完再涂黑,或者画上阴影)一样,我觉得良定义也可以有一个比较新的代词,叫 -happily ever after 就很好。中文的话 FGO 里翻译得不错,叫做夜话团圆。
-友:为什么不能叫做“你看看,我帮你把 bug -修完啦!”呢,我觉得这个也很合适(
连着通了两宵,其实今天凌晨熬夜做的事情本该放在周日的白天就做完,就是看一章数值分析然后写个作业罢了,时间上也绰绰有余。但很显然一天什么都没做,政治性抑郁的体验达到了最顶峰。昨天日记里一直在删删改改,到最后还是没更新出来,说过的话也全部删掉了。
+虽然不断地告诉自己这样不好,但果然还是很难克制住这种心情。好好地把精力放到自己的生活上罢。
看我这个作息,不知道的还以为我是负责半夜做核酸样本检验的。
今天刷了一下 QQ 和微信,发现 MO 时期同班的一个 MOer +删了我的好友,嘛。其实也可以理解,当时一起交流题解交换讲义的同学,现在已经是陌生人了啊。
+高中毕业之后(准确来说是收到录取通知书,回高中取到了档案,确认自己不会再回到这个地方之后),我就把绝大多数同学(包括上述这一位)迁移到了不常用的 +QQ 账号或者微信上,还退了班群。从此用自己的 QQ +发癫就感觉舒适了很多(,列表里还有友人,我姐,runzhi,竞赛时认识的赛博同好(??)们,和少数初高中阶段相处下来觉得还不错的同学。
+我也不清楚为什么要这样做,但就是很想脱离那个让人不舒服的环境,以至于用了有点极端的方式。但其实要让我说这个环境哪里让人不舒服,我也说不上来,明明从自己的角度来看过得自闭又自在,却还是平等地毫无理由地不喜欢身边不熟悉的人们,很难不怀疑是不是有什么心理问题。其实现在比从前还要自闭,倒没有类似的心理问题了。强行解释的话,就是高中时候班级的概念还很强,在人群里自闭的感觉就和被孤立了一样(什么中二日漫剧情(,而现在不是这样,多数人不都是独行的么。
我妈之前还数落我不懂得积攒人脉,不能总是这样在大多数人面前表演一个原地失踪,还和我讲把谁删了都不能把去学医了的同学给删了,万一以后有需要还得找人家(噗。可能再过若干年我会发现她说的也对吧,但是果然还是不愿意那样。
尽管凌晨爆了两管阳性,又封了一栋楼,时至今日我还是不太想回家,甚至抱有一丝大不了寒假在学校里推 +SRT,学学分析的想法。暑假在家待了三个月,躺得很爽,但确实啥也没干,倘若寒假回不去,至少在家时间的总和没有太大变化。
最近的想法又在改变了,主要是数值分析这课越到后来我越觉得学着很不爽,至少不太喜欢这个思维模式。又很难说清哪里出了问题,而统计推断渐入佳境,因此不是特别想考虑计算数学了。下学期看看能不能干脆删改一下,再挤一门统计学习导论进来(感觉要牺牲数物方法(
1月20日
+11月29日
-
-
突然觉得是不是下学期不该选复概而是应该选实概来着,它俩关系还大一点,读一千零一页还攒了点信心。
-现在选也来不及了,实分析只剩何凌冰,大概是听过他的数分之后接着上比较好,别折腾我了。至于取并集三门一起学,那要退统辅课才能活下去,我又不舍得,不要再动了。又要表演一个以任意顺序修培养方案。
-期末怎么只出了 8 -个学分的成绩,看来听说可以查成绩了就在大年二十九蹲点刷新 THUInfo -的我还是不够摆烂,还不如老师摆。数值分析和抽代都没有出,有点担忧是不是要看缓考的情况向下调分,我真的怀疑这两门课要调分就只能向下调(
-一学期没打开 THUInfo -的成绩单界面,于是时隔好几个月又看到小学期那门拿了 C -的工程计算机制图,麻了。
+马原再见,体育再见((PF 了
+看了眼考试周安排,抽代 16 周周六,其他三门都在 17 +周的周末,又要坚守到考试周的最后一天晚上。不过比较硬的几门课考试时间上还挺松散的,蛮好。
+怎么上海的同学基本都回家了,大家都好快,怎么就我还在这儿苟着(x
+明天统推期中,希望人没事,睡了。其实更要希望的是今天紫四别有人混管阳了,那恐怕只能在寝室里考了,真的很难想象(
1月21日
+11月30日
-
-
除夕啦。已经十多年不回老家过年了,说实话老家也没有给我们去的地方了,一直都是和我妈在家里过。过年的一天感觉和平时也没什么差别,除了上海外环以内全域禁燃烟花爆竹,我家正好在外环外面一点点,放得格外凶,傍晚开始爆竹声就没有停过。
-聊起来父亲那边的亲戚,说起堂哥(?是这么叫吗),是父亲的大哥的儿子,比我大六岁。上初中的时候听说他大学考得不好,最近又听说他考研考了三次,考上了一所二本,再读三年就要工作了。
-因为不怎么回老家的原因,我对堂哥的印象很模糊,但总感觉到亲近,印象里觉得他是个可爱、腼腆的人。大概只有两个记忆点,一个是五六岁的时候在父亲那边的农村老家过年,他把他的悠悠球拿给我玩儿,但我没玩过狭义上来说是男孩子的玩具,差点给他摔了,他好一顿大呼小叫。后来在院子里放鞭炮,大概是打了什么赌然后我赢了,他摘下毛线帽子,蹲下来让我弹他脑瓜崩。
-还有一次可能是刚上小学的寒假,大伯带他来上海,找姑姑一家和我家一起出去玩,也是最后一次和父亲那边的亲戚见面。姑父是生意人,很豪气,到陆家嘴请大家吃了披萨,然后还一起去了水族馆。大伯只买了堂哥的票,让他跟着大家进来玩,自己在外面等他出来。姑姑姑父带着堂妹玩得很欢,堂哥一路默默跟在我父亲身边,跟我们一起逛,也不怎么说话。最后到了纪念品店里,我挑了一串贝壳手链和一个小冰箱贴,冰箱贴是一个小瓶子,里面是水和油,界面处浮着一条塑料小鱼,无论怎么倾斜小鱼都会浮在界面上,不会沉下去。付了钱出来之后父亲在我身边轻声说,哥哥一个人来玩的,没人给他买东西,你把小鱼当做礼物送给他好不好。但我当时不愿意,父亲劝了两次之后还掉了眼泪,最后堂哥安慰我说他不想买东西,没关系的。
-长大了才懂得为什么大伯只买了哥哥一个人的票,懂得他为什么听话懂事,想起他的时候都会很难过,想着当初为什么没有把小鱼送给他。后来知道他在受教育的过程中一直在跟着大伯辗转,不停地转学,经常在一个省市读一学期,就要跟着大伯再去别的地方,来过上海,去过徐州,周口,也在山东的几个地方待过。分明各地学制教材都不一样,慢慢被折腾得成绩越来越差。即使我也经历过很长的贫乏的生活,但至少始终被母亲重视,安定地成长,还是幸运太多。现在也不知道他身在哪里,长成什么样子了,在学什么专业,将来打算做什么。最后的印象就是十多年前在纪念品商店里,他一个人站在货架前面看恐龙模型,后来仓皇地来安慰我,以及在水族馆里逛的时候他跟在父亲身后半步,怯生生的样子,父亲每每和他搭话,他都腼腆地笑。
-写完之后眼泪汪汪()地去找那个小鱼瓶子,一下子找不到,更加难过了,而贝壳手链带到北京去了,现在还放在学校里。住在上一个家里的时候小鱼瓶子还在呢,不知道是搬家搬丢了,还是搬来新家之后不知道放到哪儿去了,一定要好好找找。我想我一直为在事件上的记性好而烦恼,倒也没有必要,许多事情还是一定要记住,能记录下来的话会更可靠些。
-他的名字叫云飞。
-来点 TA 文学 #每日TA #终将成为TA(?
-今年的最后一天看到了 MashPlant -更新了学期总结,于是又去把之前的一些文字读了读。他的文章大概是所有我在线上能够 -reach -到的人的随记里面最喜欢的,每一篇都在不同的时期读过很多遍,甚至搭这个网站的时候没有多看,直接选了 -NexT 系列的主题大概也是因为看习惯了他的博客,随手就选了,实际上 NexT -很旧了吧。不过他不可能认识我就是了(
-我一直觉得我以前和 MashPlant -的心态很多都很像,无论是做题还是人际关系,当然他做题的水平比我强一万倍。像是之前他说在假期就开始做 -project,lab -一布置下来就要赶快做完,否则会很焦虑。我大一一开始也是这样的,网络学堂的剩余日期变成橙色的 -7 天就会很焦急,熬夜写 ddl -还有相当远的作业,结果非但没有减轻压力,反而疲于面对变化,甚至有几次不得不把提前完成的任务推倒重来。后来偶然看到了果壳的文章,感觉被戳到了痛处。因为知道作业是有确切答案的,才会这么积极去做,真正需要思考的事情反而不会想提前做完,像脑容量很小一样,慢慢就努力改掉了。
--
-高中积累作文素材时记过一句话,叔本华说:“人生实如钟摆,在痛苦与倦怠中徘徊”,应该从来没有真正在作文里用到过。但现在看好像挺有道理,至少对我是很贴切的,有作业的时候我会非常焦虑,完全不会考虑ddl,甚至是在作业还没发布的时候,我就是必须马上把它做出来,这里的痛苦是不少的。但是做完之后,我实在想不到我还能做什么。很多人对我说我这种性格应该去读PhD,我知道自己读不了,这种劲头仅限于有确定结果的事,也就是广义的做题,我害怕探索,不能接受失败。
-——《研一下总结》
-然而本科学习数学,确实还是做题为主。我后来焦虑的点就转移了,变成怎么能通过我这四年(五年?)擅长做题(实际上也不很擅长)这件事推出以后能够胜任研究。我和 -Bowen L -前段时间有很多次交流,有一次也谈到这个,他开玩笑说来读纯数吧,博士毕业都不硬性要求能发出来论文,导师觉得你有独立做研究的能力的话,就可以毕业了。
-说实话差点心动了。单纯用身边统计学的话的确大家从做题到研究的转换也没有什么大的困难,但我总是不知道自己能不能面对失败,或许该尽早去试试。另外,从高中开始,我总是希望通过复现他人的选择,来努力过好自己的人生。强基的时候我想利益最大化,研究和打听了学校里上一届几乎所有人的情况,也没有匹配到和自己相似的(= -=),最后也没有成功,于是把自己的失败也总结成了一个样本来告诫后人。现在也是一样,在恐惧的时候总是试图看看某几个前辈是怎么做的,来劝慰自己暂时不做额外的尝试也没有关系,好好读书。只是想起从前复现的失败,心里还是会持反对意见,复现是不可靠的,一定要自己去尝试,走不一样的路。就像 -MashPlant 说他在复现 -n+e,到底还是因为害怕失败,不敢去走前人没有尝试过确定可以成功的路,但我心里知道自己如果这样做,一定会失败的,可能是因为自己能力不足,但我更相信生活没有复现一说。
-人际关系嘛,更是很像了(。MashPlant -的文字读起来最大的感受就是孤寂。
--
-近期n+e写了他的研二上学期,全都是connection,与此完全相反,我的主题是“我将孤单度过一生”。我没学到他的精髓,甚至可能是学到了糟粕。这也没什么,他能力比我强,理应拥有更远大的未来。读的时候我就有感觉,数据也确实证实了,他的约八千字中有93个“我”,我的约一万字中有337个“我”,这还是我反复精简,删去很多主语之后的结果。我的文章,我的世界,唯一的核心永远只能是我自己。
-——《研一上总结》
-但是确实,往好处想,至少始终忠于自己。
-至少写到这里我还是发现,心态到底比从前好了很多。当然我不可能始终留在从前,一定会往前走。
-一大早数值分析出成绩了,很怪。我知道这个消息还是因为早上醒来,看到课程群里有人要求复核成绩。我是不需要复查,但我很好奇这课怎么评定谁是 -A 谁是 A+,每个人的表现似乎都一样,难道真的是看总评有没有拿到 98 -分及以上吗,那真有点无聊了(
-今天的怎么这么长(
-祝大家新年快乐! qwq
-
1月22日
--
-
按家里的习惯年初一要吃素,
还好可乐也算素食,感觉几乎没听说过别人家也有这样的习俗。据说是鲁东南和港台、广东部分地区都这样,你鲁省为什么会和南方有一样的习惯(
-今天发现个离谱的事情,成绩单上必修的工科概率论显示为被初概替代了,但是初概在期中之前就被我 -PF -了,应该不能替代才对,而且我也没交过替代申请表。问了一下才知道,那门工科概率论开课容量太少,所以院系里很多人都去上了初概来替代掉自己的必修;需要办课程替代的人太多,教务直接和开课的工工系对接,给所有修了这门课的人统一办了替代,不需要交申请;上学期碰巧可以给必修记 -PF,阴差阳错地就把我的也标记成已修了(
-我是想用概率论(1)替代的来着啊(恼,不过问题也不大,必限绩点对我来说没有意义。
-想着每天浪费时间都不知道浪费在什么上了,
还不如冤有头债有主,于是把明日方舟下载回来玩了一下,打算试试 -nano 的长草期插件。不过玩了一会就明白当初为什么退坑了(
+十一月的最后一天,被封控了(
+昨晚睡得早,早晨六点半左右不知怎么就醒了,嘴唇上感觉怪怪的,一摸裂了个小口子,问题不大。七点迷迷糊糊的时候楼道里广播响了,说楼里有人十混一阳,我超,我成预言家了。七点一刻左右广播说抗原阴性,于是想着大概问题不大,躺了一会直到八点左右才重新睡着,九点半再醒来的时候抗原已经阳了。
+然后还是在宿舍考了统推。晚上八点半吃上饭,八点三刻就解封了,大概华子的隔离床位也真的快顶不住了。出门刷了个月光长骑,给我妈打了电话,回来之后看到好几对情侣冲出单元门拥抱,我的第一反应居然是,晚上不冷吗,不能明天白天再说吗((
+这统推考两个半小时,然而我不到一个小时就写完了,后一个半小时全在找计算错误,还真的找出来一堆。本来想提前点交了,结果给老师发消息之前正好意识到一个题有问题,草,真的危。
+考的全是经典分布的性质,甚至矩法、MSE、多元 C-R Inequality +这些东西全都没考,所以没什么意思。不过也可以理解,太复杂的问题好像也不适合拿来考试,而且这课也没多少证明可做。
+室友跑路了俩了,我把书和电脑都搬到其中一位的桌上开卷(x)了,感觉很爽。效率低下难道是桌上太乱了的原因吗(
+首尾呼应一下(bushi),十一月北京没有下雪,印象里去年微积分期中的时候(大概 +11 月 8 +号左右?)就下了。然而看到南方都在飘雪了,南京上海武汉什么的,上海的第一场雪(虽然目测很小)很难得会这么早。是今年夏天大旱的原因罢?不是很懂,地理知识高考考完之后就全还给老师了 +x
+之前说留下来想看百京的初雪,结果不仅百京初雪遥遥无期,还错过了上海难得的雪,太亏了 +x
1月23日
-好像也没什么可写的(
-普通地读一千零一页,普通地做课后题但是没有答案,时不时怀疑自己伪证,要么就是最后一问不会做然后疯狂 -Google / Math -StackExchange(。期间还时不时切换到模拟器的界面去玩一下方舟,我完全理解什么叫凉性循环了。虽然年初二在读一千零一页这件事听起来很卷(,但是一直以来过年的状态都和正常的日子没什么区别,就是普通的寒假嘛。
-而且感觉读不完了,下学期要寄(
-1月24日
-今天好像也没发生什么有意思的事情(,修了半天博客的 LaTeX,发现不是 -NexT -的问题,松了一口气。过程在数分日志里简单写了一下,最后也没搬家到新版 -NexT -但是已经把新家装修好了,万一哪天旧房子真的塌掉了的话可以一键搬家(??
-相比之下感觉还是数分比较简单。
-
回坑之后第一次打新主题肉鸽,一遍通关,还是有点运气的。但一遍通关的代价是没想到会花 -40 分钟,接近三点才睡。舟已经不太能吸引我了,不玩了(
-平凡即是喜乐,还挺符合今天的心情(,旧版 NexT 没出问题的每一天也都是 -precious daily((
-1月25日
-推推数分,感觉那一篇已经根本不能叫速通了(悲
-1月30日
-我怎么感觉这一篇要烂尾(或者说已经烂尾了),在家摸数分实在没有什么可写的。
-昨晚和转数环里一个正在申请的学长聊了会天,备受打击,被锐评上课上得太慢了,申纯数基本没希望(但我也没这个打算啊
-kora),这也没办法。总之有点怀疑之前的估计恐怕是太乐观了些,延毕也成大概率的事情了,毕竟我根本没有先读个硕这个选项,在华子多读一年书单从花费上来看就便宜一万倍(倒也没有一万倍那么多(。不要花多少钱的硕又有点看不上(?),要花钱的又读不了/申不到,有申交换的时候那感觉了——把配不上我(?)的项目删掉,再把我不配的删掉,然后就啥也不剩了。
草,说到交换的事情,想起来之前在同学的年终总结里看到一句话:
---按照院系的标准,我似乎总是离一流差一点。
-但我好像从来没明白是差在哪里。
-
那我就不一样了,在院系的标准里我根本就不入流。或许他们是对的,我也不知道。
-我现在真在考虑退复分析然后去选 hlb -了,或者至少蹲一下能不能有机会选上另一个实分析的老师。之前想的是如果压力太大的话,大不了退掉 -statistical learning 换 bayesian -statistics,对我来说理论课总归比码课轻松很多。然而我现在只觉得悲观,大概早点学些应用也没什么不好的。
-1月31日
-写完昨天这些事之后觉得好烦。今天老姐来上海了,带她去天文馆玩了一下午。
-选天文馆也没什么特殊的意义,大概就听说是前两年新建的,还没有去过,以及它算是东南方向上地铁能够到达的最远的地方,我家在北面。
-

装置很炫酷,然而我物理太拉胯了,老姐读的文科,最后就变成了一起惊叹“好大!”“好漂亮!”“好闪!”,和来玩的小朋友没有区别。试了几个印纪念卡的机器,基本都是坏的,或者可能没墨/没纸了,总之就成功印出来两张,正面是天文馆的照片,背面印了(一些并不认识的)物理学家的生平。总之感觉其实比较适合中学生来玩,果然已经是过期 -jk 了(
-离滴水湖挺近的,出来之后租了个双人脚踏车绕着湖转了一圈,虽然天气不算好。或许是这边离海不远了,水汽多的原因吗,今天明明很热,坐地铁来的路上看市区也比较晴朗的样子。
-
找到一个前年暑假在这边车站拍到的广告,上面新兰下面柯哀,官方是懂端水的。
-
楼上往家里漏水,把天花板的墙皮泡起来了。上去问了一下他家房主在外地,还有个二房东在本地,租客今晚才从老家回来。要了二房东的联系方式,好像不是很愿意赔也不太想修,在嗯拖延,总感觉这个情况会很复杂,说不定还要找物业或者明天上楼吵架,麻了(
]]>2月1日
- - - - - - -- - - - - -- - - - - - -

2月2日
-今天去了苏州。实际上目的地也是乱选的,之前看到一个上海一小时高铁交通圈的文章,第一个就是苏州,所以就去了。然后也没什么目的地,除了去了普渡寺(离苏州北站很近)之外,其他都是漫无目的街头瞎逛了。
-在普渡寺看到的逆天祈福牌:
-
我也买了一块挂上去,付完钱也没想出来写些什么,最后写的是亲友平安健康。没有更大的愿望,也没有什么关于自己的愿望。
-晚上吃了苏州汤面,其实感觉和在上海吃到的差不多。在上海吃的最多的一家苏州面馆叫松鹤楼,最频繁去吃的一段时间是高三,自闭的时候就借走读的便利,出校吃了晚饭再回来上晚课。一般就是去离学校最近的商场吃松鹤楼的清汤面,非常香,借此短暂逃避学校里的氛围,是难得的很幸福的记忆。当时还不会骑车,走路太累了而且来不及,两公里的路还要坐地铁去,一碗面不到十块钱,来回地铁票六块,成本爆炸。
回程买了最慢的车次,只要十二块五,在车站附近买了一小袋热乎的板栗在火车上吃,属于是给自己找点事情做。平凡即是喜乐
2月3日
+12月1日
-
-
-
古廖夫一生积攒下的挫败感,在这一刻突然汹涌而至。他想起年轻时,有那么几年,毫不怀疑自己是个天才,他忘情地写着,稚拙的作品曾备受师友的夸赞;他沉醉在自己手造的光芒里,对未来满怀热望,相信自己能成为任何想成为的人物……他想起一个醉醺醺的夜晚,他坐在音乐学院的广场上,旁若无人地指挥着月光下飞驰的云影,澄鲜的乐句像从天外直灌入他的灵魂,他在黑暗中放声大笑……可到头来他又做成了什么呢?如今他跌坐在岁月的尽头,沮丧地认识到,这一生非但不是幸福的,甚至也不配称为不幸,因为整个的一生都用在了战战兢兢地回避着不幸,没有一天不是在提防,在忧虑,在克制,在沉默中庆幸,屈从于恐惧,隐藏着厌恶,躲进毫无意义的劳累中,期盼着不可言说的一切会过去,然后在忍受中习惯……
-古廖夫再也绷不住了。他捂着脸,在荒野中嚎啕起来。
+十二月的第一天,又被封控了(。这次只封了宿舍楼三分之一的区域,居然还没躲过。
+抱着乐子人的心态起床洗漱,看到有封控区的人拉着箱子闯过楼里的警戒线,从别的单元门走了,大概是定好今天返乡的。与此同时,楼群里还有人在问订了今天下午的车票走不了了怎么办,笑死,你猜怎么办(
偶然得到了一份早年数学系统计推断的期中题,看了一眼前半期确实在复习概率论(,涉及数理统计的就一点点 +statistic 的知识和 Delta +Method,这样的话在统计中心学好就没必要去重新上了。不过也有可能是早年卷子的原因,或许现在不一样了。
+然后发现 V1ncent19 写的统辅课程知识概要一直放在我的桌面上,昨天考前只顾着焦虑封楼去了,居然没看一眼。
今天和室友说好了不去做核酸,解封的时候都晚上六点多了,这栋破楼现在本来就够危的了,实在不想去综体。
+让我看看几天不做核酸会有人找上门.jpg
友人告诉我二附中有个
+升级人学妹选上了丘班,给我发了推送。打开看了一眼:
+
《并不算早》《小学二年级》
+可能,可能确实不算早吧(,我的童年很幸福,不知道市区的学校是怎么养蛊的 +x。但是这个属实给我一种,高中开始学竞赛已经半截入土了的感觉,很难形容(
12月2日
+-
+
今天没封楼,去了趟教室。不仅完整听完了一节课,不用课后返工,一天还做了之前三天的工作量(,感动死了。
+遇到了欧老师 +++,
坐在欧老师前面莫名有一种背后被班主任盯着的感觉然后抽代也做得比往常快很多(什么啊草
+晚上打算把几周没做的抽代 bonus +刷完,其实也没几道题。还是有点难的,主要问题是我现在感觉自己的基础摇摇欲坠(,扩域扩了好几天了还没太学会 +& +前学后忘,学环的后半部分的时候刚考完期中正好在摆,好像也没特别会(
+放一个友人的名言在这里:
++
感觉从哪里开始一片混沌了的时候,就不要继续往后学了,从头看一遍,虽然很有可能再看一遍也只能学会之前已经会了的东西(
-- 今天 b 站突然给我推了体育中考跳横箱的视频,突然想起来我当时还真的选了这个,每次跳着跟玩似的,最后拿了满分。打开视频一看,感觉这个项目好恐怖,不知道以前是怎么做到的,后来又是怎么变成现在的体育废物的( +
希望周末两天还能出门,毕竟数值分析还没学呢,马原论文也没写(
2月4日
-今天是友人的生日,实际上和往常一样,她是和家人以及其他朋友一起开趴度过的,我并不会参加这种活动,感觉参加了也会败大家的兴。中学的时候会等到寒假结束再把礼物当面送给她,今年我想了想早点拿到总比晚点拿到要好,况且我是那种只会送书的无聊人类,早点拿到的话寒假还来得及读完,开学就没空读了。所以就直接寄了个快递。
-我之前一直纠结应该怎么面对朋友的生日,代入自己的话就会纠结别人到底有没有过生日的习惯这件事,后来觉得就算不过生日的话收到祝福应该也会开心,所以要努力知道大家生日的时间然后至少要送一句祝福。不过经常觉得自己做得还不够,又担心会给别人心理压力(比如说要等价回报之类的负担),稍微有点想不清楚呢。
-上次给自己过生日还是上次,也不算过生日,就是馋蛋糕了所以找借口买了一个,点蜡烛也是觉得火苗摇曳的样子很好看。近几年来唯一一次生日许愿是 -18 -岁的时候,煞有介事地希望自己能尽快独当一面,当时所说的主要是想尽快经济独立。于是高考后的暑假还用华子的 -title -骗了些家教钱,尽管我不喜欢这样,但它支持我毫无心理负担地生活到现在,感谢所有当时找我上课的小朋友们,我想我也付出了等价或者超额的,真诚的劳动。
- - -2月6日
- -消失了几天没写什么东西,甚至有朋友发邮件问我的生命安全情况(,感谢关心(,看来等我年纪大了以后可以在博客或者别的什么媒介上立遗嘱,并且和人约定好,如果若干时间没有更新的话有可能是我出事了,要试着联系一下我。
-说起来前段时间和友人有一段关于遗嘱的对话,她的意见是说不定多感染几次新冠人就没了,最好提前准备个有法律效力的遗嘱。然后我就她告诉我的遗嘱注意事项提出了
-114514 个 corner
-case,发现都已经被安排好了,看来法师律师们就是现实世界的测试工程师。我当时想着这段话会聊得比较有意思,还(征得同意)录了个音,想把对话复刻到日记里,却一直没有做这件事。
其实我也不知道最近在干嘛,或者说可能是单纯不想把平庸的日子记下来,就没写什么。一直写不出来第二篇数分的前言,干脆就摆烂没有更新。说着
-everyday matters
-但是失去的日子就是找不回来,往前回忆的时候也想不出来除了在尝试怎么用
-Python 替代掉 R 之外做了什么,替代也不是很成功,难怪大家都用
-R(草这是什么结论
查了一下教学门户发现缓考的科目三月份才考(不是科目三,是科目/三月份),那还可以再摆几天。
-今日最佳:
-
然后发现我其实是练习时长零年半的数学练习生,2022 -年我的数学学习最大的收获是我终于开始学习数学了,听起来像绕口令。
-2月7日
-今天和一根扎进手指里的木刺搏斗了一下午,我为什么不去医院呢.jpg,传授一点自己处理的经验:
+12月3日
-
-
- 据(我妈)说可以把盐和醋 1:1 -兑热水,然后手指放进去泡几分钟就能掉了,我试了一下可能是因为扎的有点深,总之是没用的,而且已经有伤口的情况下泡盐水会痛啊!(我不会是个笨蛋吧.jpg) -
- wikihow -上还有别的稀奇古怪的方法,什么醋和苏打水兑热水之类的,原料不充足,没试。 -
- 但是直接泡热水还是有用的,让刺吸一下水变软一点就不那么痛了。 -
- 如果只是扎在表皮的话可以用消毒过的针把皮挑开然后把刺取出来,听起来很痛但应该是没什么感觉的。但我的扎的明显比较深,刺只露出来一个小头,直接用镊子夹不住,所以是用针伸到扎进去的地方把刺的角度调整了一下(这一步真的痛但是也真的有效),然后用镊子(掌握好力道的话指甲刀也可以)夹出来的。 -
- 注意消毒,处理完之后要消毒,工具用之前也都尽量消毒。 -
- 用胶布粘出来或许也是可以的,但我觉得不如用镊子能掌握好力度,万一断在里面就很麻烦。 -
- 扎得深的话不要试图把刺挤出来,一方面刺的边缘可能还有小的毛刺,另外试图挤出来的过程可能会越扎越深。我把刺拔出来之后手指还是明显肿了,应该是因为试着挤了很多次,发炎的地方就是用力挤的那一片。把刺拔出来之后可以轻轻挤一挤,大概可以防止感染。 +
凌晨两点饿了吃了点东西,算不算吃早饭?(
+今天突然翻到了一些文章,是我高考之后的那个暑假,以及再往前的时间里写的东西。当时知道了一个可以印实体书的网站,只要自己排版就可以,于是兴致勃勃地把自己写过的青春疼痛文学(。)找出来排到了一起,还多写了很多篇。当然弄到一半就咕咕咕了,也幸亏没弄出来(
+今天拿出来看的时候让我自己都震撼,感觉现在贫瘠的表达和从前不可同日而语。是什么时候失去的?不知道。
+说都说了,放几张给大家当当乐子(
+
+
+
+
实际上和 ex +分手已经过去三年了(,现在看这个古早青春疼痛文学好羞耻啊,码掉的内容更羞耻,草(
+
+
这怎么比上一篇还羞耻?脑袋不清楚的时候写的东西是这样的
+
+
为什么配图是华子的录取通知书?我搞不懂(
+气氛都渲染到这儿了,想起来一件关于 ex +的事儿。大概是我高一寒假(2019 +年初)的时候,他比我高一级,要去参加华子举办的一个创新冬令营什么的项目,交几万块钱去美国游学。据说有升学优惠,
+但从结果上来看确是没有的。印象里临行前吵过一架,还见过这个活动华子给每个人发的一件长款羽绒服,以及他说中耳炎还要坐飞机之类的事情。有的时候我觉得记性好真不是一件好事,记得这些破事,又没有任何原因地就是忘不掉,真离谱。要说记性好似乎也不是特别好,昨天统推讲的东西现在就不记得了(x),我好像只对事件的记忆力稍好一些,除了翻黑历史之外完全没用的技能(
+找到了一份 +2020 +年的报名通知,但看这个日程感觉当年肯定因为突发的疫情没有成行,之后就再也没有过了。
+经过了这三年之后我现在想起来这件事,都觉得太遥远了。华子组织高中生出国游学,每个词听起来都似乎不太可能发生在我生活的这个星球上,但愿未来还能变回理所应当的范围。
+统推期中出了,和预期差不多。看了看班级成绩样本的次序统计量(草),感觉也挺符合预期,不知道到期末能不能混个 +A+(
+刚开课的时候老师说统推是基础五件里最难的,但我反正觉得是比初概简单,也有意思多了。初概里面初等的技巧让我抓狂,有一种回到高中竞赛的时候最讨厌概率计数题的感觉。想起来印象很深刻的一件事,高一的时候,学校的一试周常练习里有一个插板法的计数题,我当时想了半天自己找规律(草)糊出来了。结果老师讲评的时候轻飘飘地说“小学奥数都讲过插板法了,这个不用讲了吧”,给我的震撼是全方位的。
+后来就很不喜欢概率计数的题目,感觉联赛的这类题也和小奥没什么区别,一想到同龄人近十年前就掌握了我到当时也不知道的各种方法,就感觉太狡猾了。水平也菜,但高三联赛一试里的计数题是枚举法,倒也做对了,那次一试成绩很不错。这样的我现在居然打算去学统计了,令人感叹。
当然,还是去医院比较好,用一次性筷子的时候要小心啊。附一个 wikikow -的链接,大概也是这些方法。
-2月8日
-想了一天也没想出来怎么写今天的日记。
-起因是突然想起初中时认识的一个学长。当时我对初升高还一无所知,不懂自主招生的规则,或者说觉得那和我这种郊区做题家根本没关系,我就该去争上中分给全区的唯一一个中考名额,更完全不懂竞赛。我妈机缘巧合认识了他妈妈,获得了一些当时来说很救命的信息,最后临时抱佛脚考到了不错的高中也该感谢他最初的帮助。
-高二上学期(2019 -年末)的时候看到了他的水滴筹信息,才知道他患了白血病,还有他化疗后拄着拐杖在开学典礼(或许是别的什么活动)上讲话的照片,他家已经变卖了所有家产,几次配型也不成功,当时在一个医疗团队里试用新药之类的信息。我妈试着联系他妈妈,发现微信被删掉了,就在水滴筹里捐了 -200 -块钱。后来再也没有音信,也逐渐淡忘了这件事,直到今天我突然想起他来,就问了我妈一句,才知道从那之后他的病情急转直下,似乎 -2020 年没到一半就去世了。
- -想了很多,写下来总觉得词不达意,干脆删掉了。最后上网尝试了很多搜索的组合,他的名字,初中和高中学校,入学年份,甚至我记得他在某个知名初中数学竞赛得过奖,这些信息都试着搜了搜,努力拼凑起来了一个形象,谢谢互联网的记忆。遗憾的是我只见过他一次(现在想想那时也已经算是他生命的末期,当初怎么会想到其实死神就在身后,令人感叹),不记得他长什么样子,只记得水滴筹上的照片很憔悴,没记住意气风发时的样子。虽然不了解他的亲朋好友如今的生活如何,但我想只要我每带着这一丝记忆多生活一天,就能保证他还没有被世上的所有人遗忘,所以要努力记得,要写下来。(这个格式听起来像在做证明题,我是不是不会说话了
-人世多为憾。今朝蒙善诱,怀抱绝埃尘。
-2月9日
-来点轻松的二次元相关。
-
其实第一版填了五个 EVA TV 或者剧场版,想想实在太多了,去翻了翻 -bangumi 换了几个也很合适的。
-入坑作本来想填守护甜心(,和柯南都是小时候同时看的,那个太子供向了,写出来恐怕大家都不认识。这么说来我已经是十多年的老二次元了,看的番好像还是不多,近两年基本就没看过新作。
-看最多次的是天气之子纯属意外,高二的时候我自己看了两遍,又和 ex
-去电影院看了一次(草(其实并不愉快,然后可能是因为这个所以疫情网课的时候(已经分手力)经常
-emo 就会拿出来看一看,也没什么别的原因。令人感叹。
最喜欢的我一直都选不出来(About 里面也提到过),硬要说的话还是 EVA TV -或者紫罗兰二选一,但是好像也都没到最喜欢的程度,就给一个最想安利和一个最佳画面。最佳配音是因为《春宵苦短,少女前进吧》里面的前辈是由星野源配音,我不太关注声优,掺点三次元爱好。C -& T 的配乐真的很不错但是被剧情拖得太惨,所以选它一下。
-友人评价说 Fate/Zero
-远远没到最虐的程度,但我觉得也很可以了,大概是因为我没看过魔法少女小圆。FZ
-也是我 fate 系列的入坑作,如果入坑第一部看的是 Fate/Stay Night
-的话可能根本就不会入 fate
-系列的坑,子世代比亲世代差远力!卫宫家今天的饭在 fate
-世界可以算是最轻松治愈的了,大家远离圣杯战争围在一起吃饭,印象挺深刻的。
然后是觉得四谎实在很单薄所以说它过誉,樱花庄的宠物女孩看了一半忍受不了就弃坑了,实在是不喜欢但是被身边的人安利过很多次,在心里直接拉黑成最讨厌了。离谱的那个是歌舞伎厅夏洛克,本土版的福尔摩斯改编,一开始觉得很新奇还追番了,前面看着也还行但剧情走向越来越离谱,我又比较喜欢原作(指小说),所以别看。这几个都挺主观的,因为也没看过太多离谱/不喜欢的番。
-2月10日
-今天可以用一句话总结:时隔四年还是五年,总之我二刷了一下秒速五厘米,发现自己终于看懂了,令人感叹。
- - - - - - - -2月11日
-最近躲着(?)没更新是因为这两天摸鱼读统计计算去了,PKU -的统计计算课是真不错,薄纱华子统辅的那个版本。
-我觉得我下学期干脆别上复分析了,去上个数分 2 -吧(,或者不上课但自己同步读实变函数论,总之现在就是非常不自信。
- - - -看了一眼 V1ncent 的申请结果,Biostat 的项目里 Umich MS/MPH 和 Emory -MSPH 都中了。不知怎的我也稍微缓解了一点失学焦虑,祝贺他。
- - -2月12日
--
-
今天发现 V1ncent -更新了统辅课程测评,于是也同步了一下最后的几门课,有兴趣可以去看一眼。
-通过另一个统计申请洞认识了 -Mariana,简单聊了聊。
-真惨,我一切学业学术相关的 connection 目前都还得靠树洞发展,包括认识 -LagrangeKMnO4 和 V1ncent19 也都是在树洞。
-好像真得改改选课。大概有几个 plan:
-Plan A:维持原状,但问题是数分 2 -我还没补完,原来多元微积分学得就很烂,直接上复分析是否有点送死。况且复分析除了留数之外对概统似乎都没有多大帮助,单纯是补课的话
-既然要延毕了那也不用现在就急着去学。Plan -B:把复分析退了,蹲一蹲林勇的实分析还能不能有课余量,或者能不能法外开恩手选上,可以的话就去上,没有就把时间空出来自己读实变函数教材,或者把时间用在多去和意向导师沟通上面也可以。
-Plan C:把复分析退了选数分 -2(说实话最好是行健那个班,保护绩点),但问题是它和概率论冲突了,让我放弃概率论是不太可能的,真麻烦啊。
-Plan -D:把复分析退了,选点自己培养方案里的课上谨防退学。我是不想选这个选项的,宁可自学实分析。
-Plan -E:把复分析退了,补一门统辅课。最好是能补到贝叶斯统计导论,不行的话实验设计分析也可以。
-我比较倾向 B 和 E,更倾向 -B。先前做的决定后来才发现问题很大,本来又是可以避免损失的,这种事情真的很讨厌。
-实际上今天是寒假在上海的最后一天,明天就要出发回学校了。今天要去上交见以前的同学,这个从去年开始就变成寒假的固定项目了。晚上会回来得比较晚,可能也来不及写日记,所以半夜更新一下,如果有想补充的东西的话可能明天会在高铁上补。
- - - - - - - - - - - -补点图:
-
-
思源湖边 up 主聚会.jpg
-
-
建议新民路吸取一些先进经验(
-
-
看着感觉穿越到了 efz 办公楼,不确定,再看一眼(
-其实是你交药学院(,路过的时候随手点了个位置。
-
-
以前一直以为对我来说是个最优解的电院,现在看来只是局部最优来着。
-不过在楼上直接写电院两个字是否有点太草率了(
-
2月13日
- -回北京了。昨晚这个时候我还坐在交大玉兰苑旁边的凉棚里,和同学一边喝奶茶一边吹风,听后面一桌打麻将的声音,附近都是各种小店,很有烟火气,甚至恍惚觉得总算感受到了现充式的大学生活。今晚我就在北京挨冻了,令人感叹(
-明天的计划是去打九价 hpv -第二针,本来友人说怕我打完副作用大晕在路上,要陪我一起去,结果她今天和我说私密马赛她明天要过情人节去了,哈哈.jpg
-2月14日
- - - -刚睡醒!
-今天去打九价,没想到第二针和第一针不能打在同一个胳膊上,要好几天抬不动右手了。这针不仅贵,还让我很有参与感,推药进去感觉每一下都巨疼。不过敲键盘和写字没什么问题,那这两天不得大卷一场?.jpg(不是
-下午回来在校门口听到有人一番论证之后得出结论“我们是 Bocchi the -cyclist!”,回头一看还真有四个人,草。
- - -2月15日
+12月4日
-
-
-
- -I’m always oscillating between “I’m crap” and “I have a vast, vast -soul”.
-
-到了北方的一些直观感受:洗完头之后头发又干又糙还起静电,洗完手之后手指轻微起皮按不开指纹锁。
-如果有和北京差不多冷但是又不这么干燥的地方就好了,最好水质也好一点。我一定是在做梦.jpg
-早晨又一次被楼上活动室装修砸醒,又一次以为这个破楼要塌了而狂喜,但它并没有塌,真遗憾。等了一会没声音了就又睡了个回笼觉。中午起床本来想出门,结果收拾东西的时候直接给平时用的单肩包的带子拉断了,真不愧是我。干脆以此为借口去处理了一些琐事,通过假装很忙来给自己一种今天没学也没关系吧的感觉,太罪恶了。
+一直想靠赖在学校里不回家、每天去教室自习什么的来保持一些秩序感。
+今晚去开完组会之后也刷完了最后一次阳光长跑,又看到所有考试都要求线上,似乎不回家的理由又减少了两个。然而给我妈打电话的时候还是借 +SRT +的实验需要在校做(笑死,虽然确实是这样没错,但是我根本还没开始)又拖延了一下,心里想的却是,考完试再回去罢。
+晚上饿了,突然想起来 2020 CGMO +的时候,在鹰潭一中食堂吃到的上清豆腐,好想念,但是从没在别的地方见到过,呜呜。
+跑到隔壁寝室问了当时也参赛了的同学一句,她说完全没印象了,怎么这样。
+突然在想要不要寒假报个什么去鹰潭的实践(有吗),然后去吃口豆腐,一瞬间一口上清豆腐的价值居然超越了克服社恐的困难,草。最近总有一种“想做的事情不赶快去做之后就没机会了”的感觉在脑袋里回荡,不知道是什么意思(
2月16日
+12月5日
-
-
- 今天要被友人拉出去看国家地理的展览,但其实这几天身体上就很疲倦很疲倦,包括昨天去买了下学期要用的 -Kai Lai Chung -的书之后原地开始非常焦虑,我什么都还没学会啊。不知道能不能打起精神来。 +
下午打起精神写了个统推作业,结果写完交了被告知所有的分位数要查表 +/ 用 R 算出来,然而我全都写了符号就交了,还得返工,可恶啊(
+况且我还不怎么会用 R,更不爽了。
+吃完晚饭去七港九买了杯奶茶,感觉那边人好多,点了单之后对这个决定很后悔。想起来上次喝七港九是上个学期,在某门课上帮一个同学 +de 了个 +bug(虽然纯属期中考完闲得),后来他告诉我买了一杯奶茶放宿舍楼下作为感谢了,还挺开心的。
+之后还交流过几次作业,不过结课后就再也没说过话了。感觉人和人之间的关系真的很脆弱(这又是什么结论,不仅要看认识时的动机(,而且似乎如果没有见面 +/ 做同一件事 / +至少线上交流之类的事情连接在一起的话(好像这甚至只是必要条件),曾经有过的联系也会很快断开。越发觉得要珍惜当下的朋友啊(
+晚上回寝室,室友问我还记不记得紫四前几次封楼的时候,解封了之后楼下有好多情侣贴贴(确实还记得,11 +月 30 +日的日记里还写了)。结果今晚听说有人疑似发烧了(虽然不是我们楼层的),因为她男朋友住 +29 号楼((
+一边觉得相当不妙,一边又不想回去。不回家的理由要我说可以说出来很多,效率不高啊,好几个朋友也都还在校啊,在学校过年也没什么啦,之类的。但最本质的似乎还是没什么求生欲(,就像这段时间除了买了两管牙膏之外什么也没屯,很难为自己找到一个积极准备的动机。
12月6日
-
-
来回的路上看完了柯南衍生 -TV《零的日常》,想想剧场版砸了那么多钱水平也就那样,我就不应该对这个小小的衍生剧抱有什么期待。也或许我该认清一个事实,就是现在的柯南和我小时候爱看的柯南已经根本不是一回事了,《零的日常》远远达不到《魔术快斗》的水平,现在的剧场版作画再精致也不会有 -M6,M12 那样的剧情了。到底是制作组变拉了,还是我长大了,或许都有吧(
-虽然这样我也还是每年都会看剧场版,哈哈(,情怀党最好骗了捏。
+难得早起,难得在楼里有区域被封(虽然不包括我的寝室)之前润出了寝室,结果在三教逛了一圈,找不到一张平静的书桌(误),就回寝室了。
+之前周二下午这个时间是有体育课的,从来没去自习过,现在体育场馆关门不上课了,才知道实际上也没地方可去(
+于是今天可以预料地无事可记,就这样吧,卷抽代和数值去了。
2月17日
+12月7日
-
-
为什么秋季选课的时候感觉想上的课都只有春季开,春季看选课的时候又反过来了(?
-今天攒够了蚂蚁森林的能量,种了一棵沙柳。今年大概是已经完成 KPI -了(?
-
-
查了一下,去年种了 4 棵不同种类的树,保护了 7 -平方米不同地区的土地,应该是能远超平均的:
-
-
-
当然经费不是我出,种树也不是我去现场挖坑(,说自己“种了树”“保护了土地”心里还是有些忐忑。据说云杉是最长寿的树,去年恰好攒了很久的能量种了一棵,它会在赤峰带着我的名牌比我多活很久很久,守护一小片土地,还是挺令人期待的。花棒和山桃是会开花的灌木/树,都种植在甘肃,有机会的话真想去看一看,
- -虽然理性上来说,我去一趟甘肃产生的碳排放比这几棵树能够转化的可能还多(,如果是山桃的话会有落英缤纷的场景吗?高中
-因为学不会生物而选考了地理,答过很多和保护生态相关的题目,也听老师讲了许多远方的故事。两年两位地理老师都是很有感染力的人,也都来自中西部,时不时谈起当地的生态情况。我不知道别的同学怎么想,但我大概是非常容易为这些事情难过的笨蛋,当时还挺揪心的。再往前可能要追溯到小时候看过的科普、《寂静的春天》之类的书籍,讲世界上的各种环境问题,每次看到都揪心不已,还会为自己没有力量帮助任何事情变好而难过。如今做的事情也微不足道,大概也尽力了。我大概从 -2019 年开始在蚂蚁森林种树和参与保护地项目,到现在为止种了 12 -棵树了,那有生之年好像还能再完成一些。正好昨天去看国家地理摄影展的时候,有一个放映纪录片的区域,讲的是国家地理杂志的发展过程,里面还讲到现在投入了很多经费用于环保事业、生物和生态研究工作。之前好像也有报道说中西部地区的水土流失正在因为植树而改善,还提到蚂蚁森林项目在其中起了很大作用。虽然单说前两天 -Ohio -的事故就让人揪心,但至少还有人在努力让世界变好,作为普通人大概也只能紧紧抓住这种微小的希望。
-向所有负责以上项目的基金会和奔赴现场完成工作的专业人士表示微不足道的感谢,也感谢支付宝公益。
+太魔幻了最近,从防疫到身边的各种事,唉不说了。
+在寝室里暴躁了一晚上,最后室友劝我算了算了,还是想想办法怎么期末考的时候不要发烧比较好,草,这就是华子人的务实罢(
+室友的电脑寄了,拿我的电脑码了一会,锐评要被我的 IDE +亮瞎了(,人类的悲欢并不相通。
+其实是我散光,dark mode +的话就看不清了。近视快十年了,度数几乎没涨,散光却越来越厉害,怪事(
+终于找到了三教小教室里最舒服的自习姿势,很难不想分享一下:
+
+
今天下午五小节网课,被迫带了充电线出门,到三教来仍然找不到一张平静的书桌(x),要么是情侣要么是结伴来自习的占着教室,都挺吵的。虽说有人推门进去的话可能就不会吵了,但说实话不太想尝试。看到旁边的小教室还有空的,虽然这个桌椅不舒服但也还是进去了。
+这个椅子是从讲台前面推过来的,腰不大好,习惯坐软的椅子,所以比较喜欢三教 +30 +人容量的教室。桌子拼起来也差不多够用,唯一不好的地方是中间拼起来的地方凹凸不平,不过书厚的话也问题不大。
+以上三条呈倒叙关系(
2月19日
+12月8日
-
-
数了一下培养方案里已经修完的和选了课的有 88 个学分,还有 76 -个学分没有选课。这个剩余数量对大二下学期来说大概确实是太多了,然而恐怖的是里面竟没有一门是我想上的了。
-晚饭饭点不是很饿就忘了去吃,但到了晚上又饿了,遂吃夜宵。去玉树看了一眼二楼夜宵还没恢复,灰溜溜爬回桃李,在最右边的窗口点了一份烤冷面,一串糖葫芦,又去点了一杯饮料,加起来不到十块。太棒了,下次还不吃晚饭(什
-室友返校看到我第一句话是“你胖了”,可恶,这种事情不是非得说出来罢(悲
-晚上本来在复习缓考,复习着复习着开始折纸(
-然后还翻相册找到了高中的时候折的东西,印象里挑战过非常多花球,但折完之后基本拍个照就送人了,大多数连照片都没拍。
-我其实是觉得只有折纸的过程比较有意思,折完了之后又没地方放,大多数作品还不能碰不能压,就很麻烦。正好同学觉得不需要自己研究就能获得成品简直太快乐了,这下各取所需了——以前折完之后就拍个照发空间,如果有人想要的话直接要走就好了。
-随便放几个,别的照片都找不着了,sigh。
-
-
其实我忘了这个是我折的还是存了别人折的照片了,当时在空间里看到另一个喜欢折纸的学长折了这个,就自己也去做了一个。看水印时间确实像当时做的,hmmm
-忘记是不是送给 ex 了,哈哈,如果是的话大概已经进垃圾处理场了((
-
-
这是个家里没纸了但还是想玩,所以做出来颜色很诡异的凡尔赛花球,我管它叫卷心菜。难得有手不能完全解决问题的情况,花芯好像是用镊子卷的,如果只是手工卷的话很容易散开,最后还挺牢固的。这个实在觉得有点脆弱,送出去的时候还找了个泡沫塑料的盒子当包装(
-可恶怎么只找到这两张啊(
-看起来还挺厉害(真的吗),不过我现在的水平仅限于下面这种立体贺卡难度的了(,今晚做了半个小时(
-
-
也没有合适的纸(,问室友要了粉色的格纹便签,努力假装是樱花(迫真
-Anyway,至少这个是可以收起来的,不太占地方。
-单纯是折的话就没什么难的,只是跟着别人做,耐心细致一点也就好了,集中精力的话很少有一遍不成功的情况。之前看过一些作品的设计过程,感觉我也就是能模仿一下成品罢了,啥也不是(
+最近一直在流水账,我自己都有点难以忍受。写日记的初衷之一是日省,之二是表达想法。实际上前者现在不需要写也可以做到,甚至有演变成内耗的趋势。而最近有关大环境的想法相必人人都有,我也就不多说了,另外的(主要是家里的)破事也根本不可能简短地写完,更不可能发出来,何况这是一个我一直在回避细说的话题。
+所以没话说就先把日记停了吧,应该不会很久。有兴趣蹲重新开更的话不用天天来看,不妨 +RSS 订阅一下(懒得研究的话直接点这个链接就行,虽然我还没来得及在 +follow.it +上确认作者身份;以及须知等我确认作者身份之后在后台能看到订阅者邮箱,介意的话可以换别的订阅平台 +/ +使用不常用邮箱)。本来一直不打算开这个功能的(可是为什么呢,好像也没什么理由),现在还是开了。
+我怎么看起来情绪不是很稳定的样子(,三次元里不是这样的,向赛博朋友们道个歉((
2月20日
+12月10日
+不是又开始写了,是因为交换申请的事情 emo 了(
+++这两天在认真思考一个听起来很奇怪的问题:为了交换延毕一年是值得的吗?
+已知:
-
- - - - - - -- -
体验了一下实复概连上,但是复分析上课的这个点我就已经饿了,遂退课。
-薛金鑫看起来很和善,大概是年轻老师的原因,一节课讲 114514 -个笑话。听起来这门课也比较轻松,不过最大的问题还是对概统都没太大帮助,以及我数分 -2 还没学完。所以补课完全可以明年再来。
-实分析感觉顶得住,谢谢 PIN 的讲义(狂喜
- +
今天才知道基物实验 2 -也是最后一次开课了,我还以为我们院系要倒闭了所以以后不开课了,知道是二字班又修订了一遍培养方案之后感到非常失落。上学期把它退了,所以这学期我得上 -4 学分实验课(恼),2 的时间还和别的课冲突了,破事真多啊这个书院。
-每学期必修课超过 10 -个学分我就会想似,所以一换一退了工程地质,不用上早八了。
- - -- +
不考虑保研,打算申请;
- +
我的培养方案太过稀烂 & +本科期间不能转专业,近两个学期加上政治课每个学期都选不到 10 +个学分的必限,全在修数学课准备跑路。交换的话又少一个学期,算了算无论是春季交换还是秋季交换,第八学期毕设都肯定开不了题;
- +
我自己的培养方案是双学位,这样下去哪怕不交换也有概率修不完。不过大四的时候全身长满肝 +& +多数没用的课都仅以通过为目标的话,应该还是能毕业,以及申请应该也不看到时候的成绩了;
- +
遗憾的是我很菜,GPA +绝对值看起来还可以,但在院系的排位比较抱歉,恐怕也申不到非常好的交换项目,不知道单纯为了提前护照到手(x)& +增加一段海外经历而交换值不值得; +(其实今天看表格的时候感觉,我院分到的项目要么我不配申请,要么配不上我(暴论
- +
延毕或许还可以带来一些别的好处,比如说我现在的数学基础像筛子一样就开始往后学了,再多学一年至少会好点。现在也还没开始嗑盐,多一年或许能多做一两段,etc;
没钱,不考虑其他需要自主申请的不免学费的交换项目。
2月21日
--
- -
杨不亚 (x) -老师今天找我拐弯抹角地问认不认识化工系的人,跟我扯了半天最后才说明来意:他想要一些华子的微积分和线代期末题,拿去给他现在带的小朋友准备丘班考试;他还在华子读书的时候(应该不止十年前了)只有化工系学生会会收集保存这些资料,所以以为现在还是这样,希望我找那边的同学委婉地要一点。
-大人,时代变了。
-我都高中毕业一年半了,退役也两年半
-(警觉)了,质心这个不知名竞赛机构(不过社友说很知名 -x)咋就还喜欢盯着我。到下午他们那个负责宣传企业文化的吉祥物(?)质心姐姐还来找我,说三月初要来华子玩,问我有没有空面基,可以给我带点新款质心周边小礼物来。我心里想的是咱们好像也不熟啊,以及你又是怎么能进学校的,新款质心周边不会还是氛围灯款加湿器吧,心理活动很丰富,最后只怂怂地回了一句没课的话一定来。问题是我也从来没在质心上过课,只参加过一次全国联考
结果因为参加的人太少喜提 -rank -1,另外就是以前给新星写题解的时候会让杨不亚老师帮忙翻译小语种题面,别的交集不保证没有但感觉应该零测。结果又是被邀请写软文,又是找我要题,现在还要面基,难道是看我比较好骗,非常恐怖.jpg- -
前三个学期都是把体育课放 -2-3,回来瘫倒然后洗个澡点个外卖洗洗衣服再打扫下卫生,就差不多磨蹭到晚课时间了,再出去上课。这学期终于意识到这样的话一天直接没了,实在划不来,于是
-冒着猝死的风险把体育课提到了 -2-2,顺便选了个不怎么累的项目。今天试了一下,下午两点多就能休息完然后出门进行一个卷,然而困难变成了这个时段教学楼没合适的地方可以卷,太乐了。晚课是线性回归,放 PPT -各种出事故。我还想发生甚么事了,一看老师的电脑是 -surface,那倒也正常。
- +
青春上海:今天是 neruko 老师的生日,但是今晚为 TA 庆生!(
--
本来以为这是个博弈问题,以为不知道年级里有多少人想申请,不知道大家会怎么填志愿,甚至还想填个
+ETH,Cornell,南洋理工什么的口嗨一下。晚上室友告诉我其实大家的选择都在院系发的共享文档里,看了一眼
+ETH
+肯定是没戏了,感觉把目标定在曼大或者滑大是比较合适的,更倾向曼大,因为在春季。本来觉得莱斯也可以考虑,看了一眼在德州,算了(
其实如果有法国的项目是最好的,去法国学数学本来就是个很妙的决定,我甚至还会点法语(单指学了两学期二外,再学学可能勉强能过法语四级,现在记得多少也是另一回事)。可惜今年巴黎高师什么的都没有交换项目,不然就不用纠结了,我一定选这个。
+问了友人一句北大有没有交换项目,她说不知道,没关心。不知道为什么突然又 +emo 了。
+几个月前我还不太能懂“我将孤单而度过一生”,会想世界很大,一定有某个人在或远或近的地方等着告诉我“我等你很久了”,假设没有,也不是一件非常值得在意的事。如今我才知道这种不关心是因为,远方的爱人是虚无的,把视线落到身边的朋友身上才能体会到难过。最近我时不时会想站在上帝视角看到朋友们的安稳人生,这两年按部就班地完成培养方案,上课考试,跟着院系的大流磕盐,然后选一个导师轻轻松松地保研,再建设自己的家庭,人生就这么顺利地按照预设的也是令自己满意的轨道进行下去,是一件相当幸福的事情。后来猛地一惊,发现自己实在是沉溺在自己的世界里太久了,这种简单幸福的生活明明属于这个学校里的大多数人,我才是与我的朋友们不同的那一个。不过还算清醒的一点是我知道,任何人所拥有的这样的安稳都不值得为我而改变,我将孤独而度过一生——这是其中的一部分含义罢。
+话说回来我又有什么资格随便把人家的生活概括为“平静”,“幸福”,这不还是很傲慢吗。只是他人生命中的暗流不全为我所知,而我关注的又是他们觉得理所当然的部分。突然又想到以前写的这一段话:
+++我想我也不是很绝望。楼下的女人和男人开始争吵了起来,这是意料之中的事情——我也会和我的母亲吵起来,因我在这里碌碌无为坐了这么久。如果人生沿途风景秀丽,那么死亡也并不可怕,然而现实给予的往往恰如其分,令人无话可说。把实践作为真理的理想也是很好的,乐观积极昂扬的一生。人生在适当的时候做出选择也是极好的,明智无悔。沉浸在日常的幸福里,睁大眼睛去看一切也是很好的,及时行乐,盲目无知但无可辩驳的一生。尼采说要高蹈着前行,我说伊卡洛斯飞不远。木心说艺术就是一切,我说它只是遮羞布。一切一切的理想在我来看都是欺骗,是仓皇人生面前的金碧辉煌的童话。这些意义和价值存在一天,人们就长醉不复醒一天,因为梦就是梦,而现实不为始终在做梦的人所知,他以为自己不该死亡,层见错出的痛苦也是不应当有的。
+
emo 完之后看看自己说的话,啧,不就出个国吗,矫情什么(
+UPD:最后一志愿填了 2024 春季的东大(实际是 4-7 +月),二志愿不知道填啥就填了墨尔本大学,也是春季。实际上如果东大申不上我可能就不去了,所以有点乱填的意思。虽然院系里只有一个人和我争东大的名额,还是有点虚的。
+虽然交换这个东西是铁没用的,尤其我选了东大,更没用了,反而一堆问题。包括并不限于短期考不出 +N1 +证书只能上研究生课(挑了半天没看到太多特别好的课),华子这边铁要延毕,影响春研暑研(但是都延毕了的话可能也不算很大的问题)。现在暂且想用出逃和延毕来逃避目前发生的事情,也想着还有很多个反悔的选项,毕竟没上飞机什么都还好说(
+不过选东大的话其实,真要去的话我自己差不多能用存款 cover +全程(从考托福一直到买机票回国)的费用(除去最近社工发的补贴,其余竟还是高考完家教的剩余),顺便 +push 一下自己赶快把语言成绩考出来,目前来看一切都还好..
+为什么朋友们都劝我快去东大然后帮他们代购专辑周边啊!
UPD 2:笑死,东大和墨大的名额都没拿到。
+其实我感觉凡是在这个院系里争取什么东西,哪怕觉得十拿九稳,也从来没顺利过。奖学金也是,交换申请也是,哪怕事实上自己的数值就是碾压别人,哪怕竞争者只有一个,也还是拿不到,真的有点奇怪呢。与我完全相反的是何老板,虽然我觉得他并不强(对不起但是我真的这么觉得,这是可以说的吗),但就是能在这些事情上一路顺利。性格决定命运(不是
+真说不在意也有点假,毕竟失去了一个延毕的好理由和平价旅游的机会,而春研暑研的目的地也不再可能是日本了。
+几天前 zcy +学长看完日记和我说不要去交换,看他评价自己说“我觉得这么久了,我已经是个完全不同的人了。先后两年心思已经收敛,很多东西以前觉得有意思,也许可以玩玩,后来发觉其实我有明确的主线,根本不想沾染”。
+我深深地觉得自己至今也没能明确主线,甚至怀疑我自己就是一个爱好 +wandering 的人。
+仅仅是确定方向,我就花了一年半的时间。从想润 CS +开始发现学不会,虽然现在想想绝对是入门的姿势有问题,郑莉的 C++ +我劝所有人都别上,不过我也自认为不是很有工程思维的人,早些放弃至少减少了沉没成本。然后逃避去了 +DS,但苦于 DS +找工的潜力实在有限(尤其国内),我又对金融非常排斥,纠结了很长一段时间。这时候发现了统计学科(当时指的是统计中心这种类似工科的应用型统计),虽然当时的认识不够准确,还被一位数学系的老学长批评过,但我现在深深感谢他没有让我一直当名词党,不然太可怕了。从这个时候开始发现自己不得不出国了,无论是隔壁数院还是华子数学系还是求真还是统计中心,跨保到合适的方向都十分困难,身为走过的省份还不如别人去过的国家多的小镇做题家又 +emo +了很久。不过真的开始准备追求学术之后又觉得出国是不错的选择,现在只会为 +settle down +遥不可及而感到可惜,没有以前那么痛苦了。后来按照学长的建议试着学习困难的数学,才意识到还有很多应数的分支。又因为初概出师不利,还在计算数学和统计之间举棋不定了一阵子,甚至还想过要不要再去了解一下运筹学和控制论。直到觉得数值分析寡淡无味,而统计推断更合我的审美(?),又名词党式地看了一些非参数检验和贝叶斯学派的东西,感觉很美妙,才在后半学期终于收敛到了统计,也有了一些认识上的更新。包括更倾向于统计理论,而不是生统这种偏应用型的方向了什么的。
+但事实上统计理论(其实计算数学理论也一样)的发展已经日趋成熟,搞不好未来还要继续变化,混不下去了折腾半天又回到应用(。除此之外这一年半没有做任何其他的准备,对磕盐仍然一片迷茫,连语言都没考没学(虽然准备一下也不费劲就是了(。
+当然可以说这是一种成长,但我想想只觉得太艰难太费时间了。一年半以来计划从来赶不上变化,修了一些没必要的课,做了很多和未来没关系的事,有的甚至因为开了个头,现在还不得不继续做下去(说的就是你我的破 +SRT,还有这个破离散还得期末考试,缓考算了)。每隔一阵子就会发现之前在做的事情失去了意义,斗志也因此磨灭了很多,会习惯性怀疑自己,这真的很可怕,也很令人难过。
+Just lose it(
+12月15日
+-
+
本来没啥事,看到抽代助教把作业批出来了,文件比交的时候大了一丢丢,就好奇地点进去看了一眼。
+
+
其实那次写了以前遗留的一堆 bonus 题,遇到一个用理想引入 Zariski +Topology +的题,但背景不够写不出来后一问,所以就证了一半,然后写了句话掩饰做不出来的尴尬(
+我写的是“好酷!可惜我不懂 +Topology”,虽然现在都不太记得是什么东西了,但印象里写证明的时候确实觉得很酷。
+呜呜呜呜呜呜可惜助教可能都不知道我本科连转数的资格都没有(,更不知道各种原因导致以后要走统计,而这已经是我的倒数第二门代数课程了(
+课咨委说是按工作量发了调研补贴,我也不知道为什么我除了开例会喝奶茶一共就做过一个推送,还给我发了最高那一档,乐得我规划了一晚上期末考完去江西找我姐玩的行程(草
2月22日
+12月19日
-
-
Statistical Learning,一门刚上了一节我就打算 PF 的课.jpg
-其实是 V1ncent19 说俞 sir -给分并没有其他统辅老师那么慷慨,我大概投入不了太多精力,水平不行花了时间也卷不出来,毕竟不是理论课,太弱小了。
- - - - - - - - - - - - -另外他还说俞 -sir 很帅,确实,不过 not my type(草还有就是这课紧跟在实分析早八之后上三个课时,今天一边听 linear models -for regression 一边觉得我也要 regress 了。
- -
-今天第一次在三次元遇到和我发型完全一样的人——王天颖老师!(
-虽然我一直觉得挺普通的,
放到二次元的话就更普通了,但是在生活里观察到的就是几乎没有人留普通的齐刘海和普通长度的头发,很怪。我妈的评价是太土了,草,我觉得还好吧(心虚
+我的环和域到底学了个什么玩意?这课真的能过吗?
+——观 PKU 抽代期末题有感
+——观自己写前几节的抽代作业有感
+——观 Galois 理论证明有感,定理证明我基本都写不出来的水平
+坏了,我认识的人和目前还留校的人取交集的话,只剩下我和室友这一对共轭健康责任人还没感染过了(
+室友锐评:有的时候都怀疑是因为我们俩的作息太阴间,醒着的时候奥密克戎要睡觉,感染不到。
+晚饭感觉吃得有点油腻,加上很长一段时间以来为了期末前都不要阳,我除了睡醒了去食堂提个盒饭回寝室、下楼拿外卖之外都没有实质上地出过门,于是今晚打算去散个步,顺便散到七港九买杯奶茶。还蛮有仪式感的,我还特地卷了个头发,挑了耳饰和发夹才出门。
+本来以为路上不会有什么人,可以在新民路中央横着走,没想到倒也没那么空旷,还是时不时有过路人的。我走位比较花,半路走着走着到了一个要么绕路,要么从苏世民旁边过去的境地。本来想心一横抄近道的,远远看到几个洋大人一边抽烟一边往我这边来了,遂放弃,赶紧跑。又不甘心绕路,就从路边的树林里钻进去了(
+路上顺便给我妈打了个电话,我说我在饭后散步,她说你吃饱了撑的。那倒也没错。
+提着奶茶回来的路上也不敢摘下口罩一边走一边喝,这次走了学堂路,工作日的晚上七点本来应该挤满了去上晚课的人,不禁想现在学校里人还少,还要为了期末考前的状态而躲人,下个学期会怎么度过呢?恢复正常了就躲不过,也没必要再这么躲下去了,甚至我就算这样自我隔离到期末,坐高铁回家的路上也十有八九要寄,就算不寄,寒假规划的几次近距离出游里也大概率会寄。
+又想起来一直觉得使用“正常”这个词的时候应该谨慎些,“normal”里面到底含有一个“norm”,可以理解为标准、规矩,意味着一些有话语权的人制定了一个规则。这个规则被人们或主动或被动地认同后,符合规矩的才会被称之为“正常”。所以正常到底是哪种正常,至少我认为的正常是已经再也回不来了。
2月23日
+12月20日
-
-
这学期开始晚上熄灯总是卡不准 12 点整,似乎一直都是在 12 点 02 -分,不知道是所有本科生楼都这样还是只有我们有偏差,看来至少我们宿舍楼已经平移到了东七又三十分之二十九区,马上就到九又四分之三站台了。
-
-
(草
-昨晚在四教上生统概论,出去打水才发现斜对角教室在上我们的专业课,这话听起来真荒谬啊。起因是认出了教室里坐着个同专业的认识的人,绕到前门一看 -PPT -上写的是一门我这学期没选的必修课的名字,往里面望了一下好像班里认识的几个人都在,怕被人发现就赶紧跑了。
-所以为什么要怕被人发现呢,我也不是很清楚,但我一直希望尽量降低自己在人群里尤其是班级里的存在感,希望被人暂时忘记,然后也尽可能不要唤醒别人的这一部分记忆。我做过很多这样的尝试,集体锻炼去其他班级的组,班会活动人间蒸发,以为只要不出现就自然地不会被想起来。糟糕的是大家会求补集,后来反而被班级同学津津乐道,因为只有几个女生却从来到不齐的情况实在太显眼了,大家纷纷猜测这个只有入学的时候见过几次的人是卷王还是什么神秘人。当然都不是,我可能只是社恐,可能也不止和社恐有关。其余情况不便详述,有些氛围我也不大喜欢。
-回去之后稍微有点感叹,家人一直不同意我延毕再申请,让我“过正常的生活”,觉得延毕“会被人在背后指点”,笑死,哪来的别人。夸张点说我的生活已经 -out of 3\(\sigma\) -了,怎么能用正常形容,既然这样就不可能被平庸的标准桎梏。
-
-今晚在转数环看到有二字班的茶园转数爷问 Atiyah -的交换代数书哪里找,我看着打出来的前面这句话陷入了沉思,感觉每一个字都在告诉我我一无是处(x
+姑妄言之,姑妄听之。
+开始复习一学期都没听过课的中国工艺美术史(,虽然没听过课但我小测还一直分挺高的,毕竟是历史课(
+看讲义看到元代的章节,里面讲蒙古人的传说里他们的祖先是“苍狼白鹿”,就是苍青色的狼和惨白色的鹿,于是人们很崇拜这两种颜色,元代青花瓷的风靡也和这种颜色崇拜有关。后半句听起来有点扯,查了一下好像苍狼白鹿之说也是明代译者对蒙古文的误读,原文是讲蒙古人的祖先是两个人,他们的名字在蒙语里的意思分别是苍狼和白鹿。但是这个说法听起来就很酷,很野性的感觉,比原文还酷(,所以流传得广也是有道理的吧(
+(对不起我虽然自称文科生但我没文化,到现在才听说这个,轻喷 x
+写数值分析的时候突然意识到,这门课上真的学了很多 Newton +创造的数值方法。我现在一边学理论一边写代码来复现计算方法、和理论互证,看到它可以投入应用,而 +Newton 当初用的还真是纸和笔。
+之前想定要转数的时候思考过很久关于数学研究(尤其纯数,虽然我不去x)有什么意义的问题,迷糊了很久是做理论还是做应用更有价值(虽然我能力有限,做哪个可能不是价值决定的(。尽管这个问题非常老套,也有很多答案了,但我自己还是不可避免地会想。竞赛的时候我天真地认为数学的意义就是纯粹地攀登人类智力的巅峰,是一种艺术,听起来非常美好。但长大后脱离了竞赛这一套游戏规则,我觉得这个理由是站不住脚的。比如很容易就能推翻这个想法的问题是,为什么还要给为了满足自己而做研究的数学家大笔经费呢。
+另外一个中学时代听起来有点傻的困惑就是,怎么能创造出这么多数学理论的,你让我一个人在家憋着空想构造一个体系,哪怕是比较简单的,我也想不出来(当然我能力极其有限,Galois +就可以x)。甚至会因此而苦恼,觉得自己恐怕不是做理论的料(多少有点降智(。现实是不仅有暂时看起来没用的数学,其他许多理论的提出往往是一群人为了解决某一问题服务的,我还看不到意义,可能是因为在学习过时的(可能引起争议但我想不出来怎么形容 +XD)课程而没能走到前沿去(还得看磕盐啊x
+今天写 Newton-Cotes 公式笔记的时候,看到 Remark 里写到 \(n \geq 8\) 的时候稳定性失去保障,\(n\) 更高维的时候会发生 Runge +现象,因此在大规模计算中不会采用高阶 Newton-Cotes 公式进行数值积分。
+Runge 是二十世纪的人,去世的时候都还没有计算机,谈不上科学计算,而 +Runge 现象是 1901 年提出的;Newton +构造这个公式是为了纸笔计算某个积分的近似值的时候更加容易,服务于其他应用;教科书上紧随其后介绍的 +Gauss 求积作为一个性质巨好的优化,和 Newton-Cotes +公式本质的思想差别也不大,重在对余项的修正,不注意的话还以为是过了十天半个月(x)就拍脑袋想出来的,实际上比 +Newton 晚了一百年,但比 Runge +还是早一百多年。看起来很理所当然的一句性质,实际上是由很多后人整理起来的吧。突然意识到自己对数学细部的发展过程还是很缺乏认识,尽管这个例子也没有那么恰当。
+
+第一次觉得 Yau 让求真学数学史也不是那么没意义姑妄言之,姑妄听之(
+我不会计算,我只是在算术.jpg
+随手给博客改了个名,之前一直不知道叫什么,就直接拿 id +当了标题。
+『姑妄言之姑妄听之』,非常符合实际情况。不知道会不会因为太长而被迫换行,万一发生了我就把这一条删掉,当做无事发生(
+正好撑满,好耶!
2月24日
+12月21日
-
-
睡前(指今天凌晨)磨蹭着写完了实分析作业,不仅胡说八道而且不停道歉(不),寒假写一千零一页的习题的时候总感觉自己在口胡但又没有证据(没有标答),搞得现在也不是很自信。结果做梦梦到实分析的特殊原因选课被拒绝了,这也能吃拒信?吓醒了(
-我现在课表上还只有 23 -个学分,这学期真是很轻松呢(迫真),这种要到开学第二周才能把课选满,第一次作业还得找助教交的日子啥时候才能结束啊(恼
-说起来实分析第一次课介绍助教的时候好像说了其中有一位上学期是抽代的助教(不确定,没听清),我还以为会是 -Bowen L,抬头一看是一位学姐,可能是 zmx -班上的,轻微失落。好想给他展示一下我糟糕的分析水平啊(什么啊草
-写完实分析作业之后刷了一下树洞,看到一个问能不能去隔壁数院做本科生科研的问题,于是又开始了我的数洞 -connection -环节,没想到(其实也有点想到了x)洞主是之前就认识的朋友,笑死了。
-我还真没想过这个,这下开阔思路了。2 月头上我焦虑地筛了一波 YMSC -的意向导师,发现把范围放宽到概统各个方向了也还是几乎没得选,还得回统计中心。顺便还摇到了一位隔壁数院本科然后来华子读研的学姐,下午简单聊了两句,她觉得我补课的进度尚可,可以考虑联系导师选方向了,推荐了几个北大的组。
- - - -然后她问了我一个一下子让我破了防的问题:概统是两个方向,总得选一个,你选哪个?
-我不到啊!
-简单概括一下,概率就又往基础跑了,当然是要基础扎实的,可能得上完实和概再说。统计的话生统也还行但是理论性太弱,先不要优先考虑,优先考虑就路走窄了,我之前倾向数理统计但是现在似乎版本已经有点落后了,目前的版本之子自然是 -learning,但真的能少写点代码就想少写点(悲)。最近另一个令我破防的事情是第一周上统辅课的体验简直不要太地狱,比实分析和概率论还地狱,这俩顶多就是纯粹的难(x)罢了,学不会是我的问题,而且目前还能学会,统辅课就一点也不难,但很玄学。万事万物跳过推导看结论,还有各种我理解不了的“我们凭感觉想想这个问题就是 -blahblah”,恐怖的是好像大家都是直感 -A,就我理解不能,血压很高,直觉真的是这么用的吗(悲)。不过也别找适不适合之类的借口了,理论的学不会,应用的理解不了,那必是我的问题。
-Anyway,好消息还是有的(这算哪门子好消息:
- -
-明天把作业写完,整理一下两门统辅课的笔记丢上来
盖住烂尾的数分,又该继续学缓考了。
+工艺美术史考完了期末,感觉良好,大部分靠 +cheatsheet,小部分靠小时候东看西看积累的历史小知识推断。想起来小的时候胡乱想以后要做什么的时候考虑过读历史、中文或者法律,总之是觉得读文科很不错,没考虑过理工科呢。
+下学期抢了一门人文课组的故宫学,我从大一开始就挺期待这门课,虽然听说讲得很无聊,但有个课上的时间读读书也不错。
+华子这个楼内疫情防控真有点一言难尽,紫荆六个单元分别有一个卫生间,原本是按照阳性的同学单独使用就近的卫生间。结果现在阳的太多,改成阳性统一最短路径用三单元的卫生间,就在我寝室门口(
+尝试在群里和一拍脑袋想出来这个主意的驻楼老师 +argue,为啥不能改成一三五单元给就近的阳性用,二四六给其他人,这路径岂不是更短(,也不至于某一个地方气溶胶浓度特别高,大家风险共担。然后被无视了(。不知道是不是还有什么别的考虑,打算等他们明天上班再面对面问一下。
+然后意识到实际上还是铁拳不砸到自己头上就不会刻意想着去反对的道理,虽然也人之常情,但多少还是有点莫名的愧疚,为曾经可能有过的事情。
+找了一些双厨狂喜的怪图,感觉很适合放在之后整理的讲义末尾整活(
+
+
我最喜欢的还是这张,是 FGO 某个亚种特异点章节通关之后的 CG。印象里 +1.0 的特异点通关就直接显示圣杯,2.0 空想树通关 CG +都是“空想切除”,只有几个 1.5 亚种特异点的章节的通关 CG 是不一样的。
+新宿章节是“证明完毕”,下总国章节是“一切完胜”,雅戈泰章节是“夜话团圆”,效果都很棒。可惜我玩的时候截的屏找不到了,就去 +b 站找剧情视频截了一下图。另外两个分别是这样的:
+
+
+
这年头谁还玩 FGO 啊,哦原来是我(
+写完了统推最后一讲的内容,感觉还有很多需要补充的东西,主要是实现和一些证明,还有一些我想要去了解的内容。导出了一下发现目前大概是 +80 页左右,排版排得密实一点,删一些图,可能也差不多会有这么多。
+预感最终会是一本不错的小册子,真期待啊。
2月25日
+12月22日
-
-
我真服了 lzx 了,一次作业布置三本书,记号还不太兼容(也可能我 4-1 -听数分去了没上课的原因罢),难怪环友说他是断手(
-昨晚写完 Kai Lai Chung -的习题美滋滋睡了,还想着就这吗,今天一看科大教材破防了。
-
-
“不管是好懂的地方难懂的地方,他讲完就通通听不懂”,笑死了。
-天气很好,中午去 C -楼的路上看到紫操上好多人,西南角还有人唱歌。回来写概率论作业,大周末的室友都出去玩了,我在寝室一边破防一边写了 -6 -页纸的作业。晚上去教室坐了会写统辅课笔记,回来看到室友带着四五个人在中厅聊天(
-属于是围观了一天现充生活,鼠鼠我好羡慕啊(x,为什么我啥也做不完啊(
+室友原定后天回家,今早起来说喉咙不舒服,晚上就 38°C 了(
+我不知道我什么时候会开始发烧,只觉得抽代大概是复习不了或者考不了了,但明天的统推还是可以考罢。
+晚上摸鱼翻了翻 b +站收藏夹,发现有一段时间非常爱看一人食量的做饭视频,虽然几乎没有下过厨,肯定会是炸厨房选手,从前还是很期待有朝一日独自生活的时候自己做饭吃。
+又想了想虽然可以预料的是将来独自生活会成为常态,但好像从小到大还没有真正意义上独居过。要么住宿舍,要么走读,出省外培或者比赛也要么和家人一起,要么和同学拼房间,空间上自己一个人过夜就几乎没有过,还挺意外的。后天室友走后大概要住两周左右单人间,潜伏期长一些的话说不定跨年的时候会自己躺在床上发着烧跨(,第一次的独居生活怎么也没想到过会是这样的,令人感叹(
+与此同时我妈在上海也阳了,当初回不回家现在结果也都是一样的,令人感叹 +\(\times 2\)(
2月26日
+12月25日
-
-
突然意识到这学期我有四个大作业(,统辅每门课各有一个,草,怎么会这样。
-那还有什么五一假期,两天写一个的话正好写完(悲
-今天好像又循环了。天气很好,紫操上很多人,两个室友分别带着自己外校的同学来逛华子,我一个人在寝室阴暗地爬行,外放甘き死よ、来たれ的时候一个室友带着她的朋友进来了,变成橙汁吧你们这些现充(无慈悲
-唯一不同的是我昨天写完了作业,于是今天就破防地去教室继续学缓考了。这工程经济学怎么就不进脑子啊,完全不想学不感兴趣的东西。问了没缓考的同学意思是这课好像就是严格按原始分给成绩,大概就是 -4.0 和 3.6 的差别,而且也就 2 -学分,似乎影响不大。但还是认真拟合一下吧,反正也没几天了,在刚递补上的实分析给我一个绩点震撼之前先攒一攒(
-群友给我发梗图:
-
-
我:哇这是一个 confidence coefficient 为 1 的 confidence -interval(昏过去
-啥也没学会,人先魔怔了(x
+现在陷入了一个 dilemma——目前我还是没有症状,甚至我室友除了 22 +号晚上发了烧之外后来也没有症状了,但抗原确实是阳的。我也不好说后面几天会不会再有症状。如果现在复习抽代,31 +号不一定能正常考试,还耽误后面的科目;如果直接放弃抽代复习后面的,实际上又防护得好根本没有中招,就得缓考然后寒假继续学域论了,也好痛苦。实际上这两天光折腾搬寝室做清洁和根本没睡好觉,就耗了不少精力,没做什么事。
+更草的是昨晚终于回到自己床上睡觉之后,梦到抽代期末又考了一堆群论,而且全是稀奇古怪的初等技巧,既熟悉又不熟悉,好崩溃(
+给 wjd +老师写了封邮件想和她聊聊天,讲了一下自己打算整理一份讲义的计划(立 flag +防止咕咕),不过她一直未读,想了想也确实不该周末发邮件,等等吧。然后给统推讲义选了个封面(某些人期末周是真闲啊
+
+
是高一的时候在学校破坏绿化的产物,花瓣上的水珠拍出来很漂亮。再一次在相册里翻到它的时候第一反应是朱熹(?没记错吧)写的『山桃落乎,辛夷开未』,但其实山桃就是桃花,辛夷是玉兰花苞,和樱花都没关系。
+背后还有个小故事,和选这张图的原因(单纯觉得好看)没关系,讲出来给大家当乐子。高中的时候学校里有一大片樱花树,春天开花的时间大概有两周。高一那个春天我缠着 +ex +晚自习下课陪我去看(现在想想多少有点毛病),他不理我,然后我自己摘了一捧樱花放在水里拍照给他看,他还是不理我(所以说不只我有毛病,他更有毛病)。(怎么 +ex 小故事都听起来又惨又好笑
+所以这就是那张照片。下面垫的本子是草稿本,翻出来的时候才发现封面的法语我已经能读懂了;再下面垫的大概是化学试卷,高考拖我后腿没进新雅的元凶(。说起来我觉得新雅真不错,还可以分流去学数学(x),考上的话是做梦也能笑醒的程度。室友说新疆高考前几名一般都会选新雅,但新雅貌似每年在上海的录取分数线都是最低的,甚至经常因为没人要而顺延给分数更低的同学。高中时候的一个同学就高考压线,在新雅和复旦经管之间选择了后者,大概是被“理科实验班”这个名字唬住,以及不愿意离开家吧。我当初想的倒是如果进不了华子就去中科大,总之不是很想再留在上海,不过最后还是被家长老师逼着用交大兜了底。当然胶带也很好,我每年寒假都和同学约去交大玩一天,但现在想想真的去 +IEEE +或者致远的话恐怕也会很痛苦。但是本科可以转专业诶!可恶。不过想想我读过很多遍的《上海交通大学生存手册》和迟先生的《与恶龙斗,其乐无穷》,真进了世俗意义上非常成功的电院的话,还会有转出来的勇气吗?恐怕就在中游吊着,卷也不是躺也不是了。总之也很难说。
+扯远了。我还是很喜欢花的。高二的春天在上网课,五月才复学,没看到学校里的花;高三的春天我就自己又去看了几次,折了两枝插在水杯的挂绳上,那张照片在这一篇的倒数第二个一级标题里可以找到,花蕊偏绿色,应该不是樱花而是梨花。不过之后决然不会再回高中母校了,再也看不到了罢。大一的春天我在华子里薅了不少花瓣,夹成书签拼在一起,寄给了我姐,很有江南(?到底谁在江南)无所有,聊赠一枝春的感觉。
+发现 hx 下学期开了一门 2 +学分大水漫灌(说它水是因为看了一眼考卷,真的水)的初等数论,知道这个消息还是因为竞赛时候认识的几个来了华子的神下学期选了这门课水成绩。所以 +hx +两个学期上的本科生课程估计都是没人听的,他要是一直就教这两门课,恐怕也不会改善教学质量了罢,令人感叹(
+说到本科生教学的问题,今天给 wjd +老师发邮件的时候去统计中心官网确认她的邮箱,发现她的职称其实是讲师而不是助理教授,感觉在华子真的非常少见了。想起来她确实从来没说过自己搞科研或者带学生之类的事,倒是在课咨委听说过评教数据有效性判断的工作是她做的,大概还有为学校提供统计咨询之类的职责。dwl +老师也是讲师。
+难怪她俩上课上得比我见过的大多数老师都好,而且确实都是热爱教学,上课很有热情的类型。实际上感受下来统计中心已经是非常重视本科生教学的单位了,珍惜罢。
2月27日
- +12月26日
+Warning:今天是真的很碎又很长的碎碎念,有点 +biased,个人体验为主,谨慎阅读。要喷的话也请轻点(
+昨天说到《上海交通大学生存手册》,今天吃饭的时候又读了一遍。我第一次读这本小册子是大一的寒假,彼时九年义务教育时代从郊区卷到某个超级中学,和高三零基础速成高考的这十年时间给我留下了很强的做题家的肌肉记忆——高三的时候我还在知乎上自嘲力速双 +A +做题家。顺着这个惯性,第一学期做题的热情还很高涨,在微积分线代和法语这三门稍微重一些的课里随手卷出了三个 +A,让我产生了哪怕是华子的课业,也可以通过不断刷题练习轻松掌握,然后这四年就会这样在不断巩固基础之中过去,我学会了这一百多个学分的课程,就会摇身一变成为优秀的博士生预备役,这样的错觉。所以,当初这本小册子让我最震撼的是这一部分:
- -- - - -
浪费了人生中宝贵的半个小时,获得了一个站在矿泉水瓶盖上的天使(真的能看出来吗,拜托超酷的诶(
-
别问我为什么是格纹的天使,又是问室友随便借的纸。背景是 Stein -的实分析,莫名很搭,下面发光的是我的一个圆形小夜灯(
-图纸附后:
-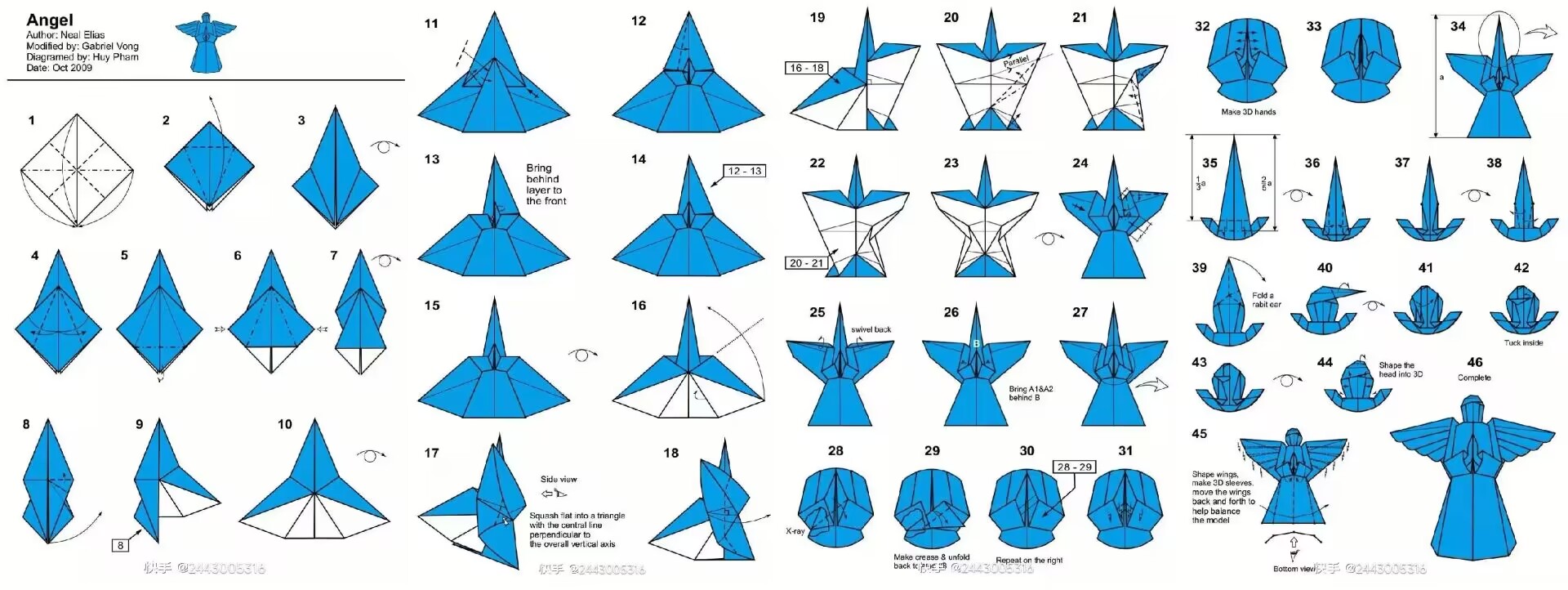
2月28日
-最高温度零下的时候我和室友都穿羽绒服,最高温不到十度的时候我穿开衫室友穿羽绒服,今天最高温 -17 度,我穿冲锋衣但室友还穿羽绒服,真有那么冷吗(
- -咋结尾呢(,请大家看个天吧。我以前一直觉得天黑就是单纯变黑,尤其上海阴雨天多,往往就是从灰白直接变黑,但也偶尔会有晚霞。总感觉先变成深蓝再变黑只有在北京见过。实际上感觉北京的天空饱和度很高,不是雾霾就是大晴天(怎么听起来是句废话),很少有阴云,是不怎么下雨的原因吗。
-
在线性回归课上一边敲这一段话一边思考这个月到底写了些什么,但好像没什么印象。实际上在公开连载之前我也一直有写日记的习惯,最开始的时候写的还是纸质版,写完了的日记只是存起来,基本也不会回来再看。唯一的用处是别人提到某一个时间点的时候如有需要可以回来查阅一下对应的时候我在做什么,尽管这也没有意义,只是我想让自己确信对生活是有把握的。
-咋这么沉重呢(,总之感谢你能读到这里。
- +悲壮的学习方式
+古人刻苦学习的故事,直到现在还在我们的身边不断上演。据说每天在新、东上中下院和图书馆都有几千人在自习。学生趴在山一样高的习题集边上苦苦奋斗,绝对是我校作为国内一流大学的亮丽的风景线。挖空心思研究解题技巧的学生们,与同样挖空心思研究出题技巧的老师们,构成了一个完美的圆环。在二者日复一日的机械劳动中,我只看到纸张、电力,以及粮食不断被浪费,却看不到中华之崛起。
+我无意全盘否定同学们吃苦耐劳的精神,但这份精神充其量只能称为悲壮。我们耗费了大量的时间和精力掌握的那些考点、技巧,在真正的知识殿堂里根本登不上大雅之堂。哪怕我们特征值求得再熟练,积分积得再复杂,中国的载人飞船也不会因此而顺利上天。
+我手上一本1300页的数学手册,上面记录了人类文明从远古直到二十世纪后半叶的主要数学成果。而我校高等数学教材(上下册)所涵盖的内容,不超过其中的130页。一个真正有志于建造科学大厦的人,是不应抱着一块儿砖头精雕细琢的。
+学习最需要的,不是悲壮的毅力,而是对无限未知的渴求。
+最终来说,学习知识的目的是为后继的知识铺垫,以及培养创造性的思维。所谓有效率的学习,应当是以最高的效率获取知识,服务这两个目标。从现状来看,我们想要把什么都搞扎实的学习习惯,其效率是极端低下的,而在我们通过大量习题,最终扎实掌握的信息里,有效的“知识”却又是如此的少。
+今天,你学了多少?
+ +22 +年寒假偷渡进交大玩的时候,我还去东下院和包图朝圣了一下,观察了一下作者 +2008 +年记叙的这种悲壮的学习方式,到现在也还是一样的。当然这个观察毫无意义,毕竟华子里也是一样的,我现在每天也还是一样的。
+现在想想,其实仅有的没当传统做题家的两年,要么在摆烂,要么又被竞赛带进了另一个做题的怪圈,弱者是这样的。学到的东西有些是奇技淫巧,有些是高阶知识在初等平面上的投影,对现在也没有太大用处,偶尔会心一笑而已。这学期抽代里面用 +Eisenstein +判别法的时候,我只记得是高一看北大初等数论的时候看到过的一个判断多项式能否分解的定理,具体内容还得临时去查。其他东西也基本都忘得一干二净,只记得名词了。其他的获得大概就是认识了一些强度离谱的神,还有初步地完成了一些自我认识,这个是好事,虽然停留在比较浅薄的层面,但总比只学高考的话要好些。
+之前看到隔壁数院一个校友写的一篇文章,大概说学习珠脑运算、鸡兔同笼,带给一个中国小孩最宝贵的礼物是自信。我想了想竞赛被爆踩的两年好像也没自信过,更加焦虑、自卑,焦虑到高二的联赛喜提省三倒数(。后期逐渐变成了摆烂乐子人,退役前的愿望只是能完成最后一场比赛就好。我最自信的时候反而是高三退役变回做题家,因为这个我太熟了,我之前做了九年的题,相信再做一年的话绝不会差。哪怕高三第一次月考考了两百多名(注:我们年级一共 +350 +个人,所以真的很草)也还是非常自信,老师一度觉得我乐观得脑子有问题(。竞赛方面仅有的成绩都是退役前的最后一个月出的,不值一提,拿到奖牌奖状的时候我也不是很在意了。真正的高光时刻可能是几次 +ak,还有在场上切过几个得分率很低的题目,其实也没什么可说的,这些属于自己想起来的时候可以偷着乐(?)的范围。
+同学之前给我看过求真升级人的报道,大一爆杀丘赛,速通代数几何之类的神话,问我转数压力是不是很大。我说一点都没有啊,我又不和他们一起上课。实际上我上数学课甚至会尽量避开数学系的同学选课,打不过数学系和求真,但暗中欺负一些数辅统辅的同学还是可以的(不是x,其实就是没那么有压力)。反正也不是第一次被爆踩,而且我润应数了,来自神的压迫感根本追不上我。最重要的是,learn +at my own pace +才有可能学好。说实话这是逃避没错,但我真的不是很喜欢时时刻刻都要竞争,人和人之间何必在学习阶段就非要互相为难..(一厢情愿而已,因为资源不足啊。而且什么时候都不要互相为难才好吧 += =)(开始暴论了
+Anyway,填强基志愿的时候没怎么纠结,就因为学过竞赛而随便填了数学,非常方便。填平行志愿时我一心想离开,本来填的一志愿是中科大,最后还是拗不过家长老师不断和我强调这样浪费了 +20 +分、虽然强基综评基本稳上但还是要保底什么的,改成了交大。科大数学放到了二志愿,人大统计放到了第三志愿。实际上有点好笑的是,我高三的时候真的很一心只读圣贤书,根本不知道 +CS +和金融很热门,直到出了分之后被按头报交大综评志愿,看往年的分段表才知道交大分数线最高的是 +IEEE 和 AI,然后就对着表格从上往下依次填了 +IEEE,AI,密院,理科试验班。
+综评面试之前一个自称 IEEE
+的什么招生老师还给我打过电话,有一种钦定的感觉(?),还不断强调我报的前两个是他们的“王牌专业”,我听到这个词也不是非常感兴趣。其实理论上这些信息应该校友宣讲的时候就知道了,但交大那一场是
+ex 讲的,被我咕了。还有就是来华子之后实在学不会这个 b
+物理,混不下去,思考转专业做研究转什么的时候有数学这个备选项,也很方便。不然我可能现在还在纠结以后要做什么。虽然一直都稀里糊涂的,时不时用脚投票,但总之最后发生的都是好事。
现在在 Yau 的驱动下,高中生超前学习数学似乎分成了两条路径,一是传统的
+MO,二是基本以求真选拔为目标的、提前学习高等数学的升级途径。我记得上海取消初中数学竞赛之后,六年级(冷知识:上海的九年义务教育是五四制,六年级已经是初中了)的小朋友就不做初中竞赛题了,开始卷高中联赛,在不禁止初中生参加高中联赛的时代,被他们屠榜是很正常的现象,还好我高一的时候就禁了。所以现在最升级的六年级小朋友应该也是两条线一起准备的,令人感叹。
与此同时,今年暑假回了一趟我的初中母校,它是宝山区最好的学校,是全市排第三名的公办学校,不需要交学费。但实际上在市里根本没人听说过。在我读初中的时候学校里还有课外讨论班,老师会讲一些轻微超越课堂难度的知识,我经常在课上稍微动下脑子就能表演薄纱所有人,很爽。那位开数学讨论班的老师从前和我关系很好,这次回去他告诉我双减之后对公办学校抓得最严,连课外讨论班这种东西都已经没有了,除了学习课本,就是在“素质教育”——听起来有点像日本曾经的“宽松教育”。没有资源、资本和信息,然而十几公里外市区的孩子们就享受着这一切,要我暴论一句的话,我觉得郊区做题家的处境和小镇做题家一样艰难。
前阵子听说竞赛时耳熟能详的一个机构,假期要开分析系列讲座,为求真选拔做准备,突然有一种做题范围只是扩大了的感觉(。当然也还是不错的,能在中学阶段就被驱动着一窥前沿,至少知道 +MO 之外还有很广阔的天地,比天天搁那一边猜联赛四个大题的顺序一边学 +ACGN(x,指竞赛意义下的 Algebra / Combination / Geometry / Number +Theory)有用多了。虽然只要有升学优惠刺激就还是会收敛到做题,好在数学也不应该规避依靠做题提升技巧,至少做题掌握的知识对今后更有用了,这也是好的。每年牺牲两三个或许有那么一点希望的郊区做题家,换取集体升级,..大概还是很值得的吧。
+写完之后发现每两段话之间都没有衔接关系,毫无逻辑..随便看看吧
+12月27日
+-
+
我感觉大概是终于理解域论了,从头到尾走了一遍逻辑到处都通了,有点狂喜。但并不代表会做题了,为了考试还得进行一个拟合。
+周六就考试了,这是否进度有点慢(
+半个多月来一直摸鱼和阴间作息,肉体还在东八区,睡眠已经到东三区了。昨晚(今天凌晨?)干脆直接没睡,实际上是躺下了睡不着,就起来了。
+已经很久没见过早上六点多是什么样子了,实际上天还没完全亮。看着外面黑乎乎的,上次冬天里起这么早大概还是高三,高中生真惨,还好我大二了(x
+所以今晚可以早点睡了,然后就调整回来了吧。
+喉咙很不舒服,感觉危。但是喝了一天热水吃了一板润喉糖就又好了,搞不清楚什么状况。
+后来大概理解了,住单人间之后我经常一边听歌一边跟着鬼哭狼嚎(别细问,要脸,不好听),加上附近的寝室都没人,更加肆无忌惮了,大概是有点劳损。
+
12月28日
+-
+
学完了域又回头学习了一下环论,这下终于明白之前多项式里看起来莫名其妙的定义有什么用了,高情商说的话就是,教材和课程设计都还有可以优化的空间(。
+我又觉得我会了(
+刚看完域论再回去看环定义的时候,有一种“世界上怎么还有环不是含恒等元的交换环”的感觉(恼
+然后明天还得继续拟合近世代数 300 题,感觉 hx +很喜欢出一些不太抽象的题目,平时没怎么练习过。后天复习一下拟合过的题目,就要考试了。这本书买来一共做了两次,一次是期中之前找了几个题拟合,一次是期末之前再拟合一下。其余时间里连翻开看一眼的欲望都没有(难怪我做题这么菜 +qwq
+实际上细看觉得这书是对绿皮的一个挺好的辅助,一些绿皮上答案写得不好的练习题这本书上都有补充,另外也给了不少风格类似的题目。
+听说明天 CMO,于是去给 runzhi +加了个油(?),才知道他还真的在现场,去年是考生,今年已经是招生志愿者了。甘主任也太成功了(
+
12月29日
+-
+
听说假期常和友人聚会去吃的一家烤肉店要关店了,在上海一共四个门店,暑假里关了一个,年底又关了一个,不知道还能不能撑得下去。北京有一家,不过也好久没去过了,不知道现在怎样。
+感觉到记忆的崩塌..
+网易云说我一年听歌听了 2516 小时 50 分钟,也就是平均每天 7 +个小时,真恐怖。特地打开朋友圈看了看,听得最多的人大概就是我的一半左右,其实也很多了,对听力不好。
+不过实际上真的听进去的没那么多吧。大多数情况下是当 +bgm,和白噪音没区别,习惯之后不听歌反而专注不了。平时走在路上也会戴耳机,虽然基本听不清在放什么,但是会有一种,虽然身在人流中,实际仍然蜷缩在自己的世界里的安全感呢。(注意交通安全啊 +kora
+
12月30日
+-
+
距离室友测出抗原阳已经过去七天了,我还没啥事,是否说明已经平安度过了(
+可能有在别人寝室坐椅子睡觉的那两晚上的功劳,毕竟我不想承认它是无用功(逃
+卷了一天抽代,但愿明天遇到的都是含幺交换环,睡了。
+hx +说期末的题目比期中容易一点,但我对他估计题目难度的能力表示悲观,所以还是很怂(
+
12月31日
+-
+
最近几天卷抽代卷麻了,连日记都懒得同步,干脆到月底把最后五天的攒在一起发了,基本都不长。
+不是,这抽代早说考这么水,我也不至于一周全复习这玩意去了啊((
+考完第一门,晚上打算报复性看两部电影,然后写一下马原期末论文。
+一个是期待很久的《血观音》,一直很喜欢惠英红。说起来这里本来还有一段话,想想有点剧透,发出来的版本里就删掉了。其实如果是我自己的话完全不介意被剧透,甚至看电影之前一般会先去看看梗概,对情节有一个基本的想象之后再去看,能发现更多出色的地方。(推理剧剧透论外x
+说起来暑假里看的《不完美的她》就是周迅和惠英红主演的,她们两个我都很喜欢。但是这剧翻拍了日剧《母亲》还翻得完全变味了,卡司和原剧明明都这么棒,实在可惜。
+周迅近年来真的演了好多烂片二刷了《色,戒》,第二次看王佳芝给易先生唱《天涯歌女》的片段还是很难过啊(
++
+人生呀谁不
+惜呀惜青春
+想起来了
++
+人生が秒速で塗り変わる青春は風になる
+人生也在秒速中改变 青春将幻化为风
+(是花譜的《そして花になる》里的歌词(这不是一模一样嘛 x
+还想看《芳华》和《颐和园》(这个可以说吗),今年是来不及了,后面几天还得复习好几门课,考完数值分析(实际上就是考试周最后一天了)一定。
+考完试给抽代助教写了封邮件,这个学期收到了很多来自他的正反馈,夸张一点说,其实这些鼓励很能精准安抚一个基础像筛子一样甚至选课的时候有点战战兢兢的外系自卑菜狗(定语好长但都是实话),想表达一下感谢。写 +bonus 每次都有批复,在作业里提出的小问题也能得到解决什么的,感觉他很 +nice。
+然后被已读不回了(。上周给 wjd +老师写的邮件她也还未读,草,我以为我室友一周看一次邮箱就已经频率够低了的,怎么还有老师也一周不看邮箱的。有一种表白了之后还被人鸽了的感觉,还是两次((
+
+看微信头像的照片感觉助教很帅,但是一个学期以来根本没见到过真人啊 +kora!太遗憾了罢想起来一件事,大一的时候微积分 A +有位选课的时候总被抢爆的烫门老师(据说课讲得不错 & +调分力度大,别的老师基本都不调,我上 wxf +的课是一点调分都没有),一到期末学生就扎堆给她写感谢信,有的真的很肉麻。肯定有一些是出于真心,但只是为了在几百个人的大班上给她留下印象的,估计也不在少数。
+找了找和室友的聊天记录,甚至还有当时的两张图。反正我挺讨厌这样的,尤其是老师会把收到的话发朋友圈,自己也在助长这种风气。我实在不太相信写右边这段话的人多喜欢数学,这也太假了,看着好难受..
+ +
+一年就要过去了呢。感谢陪伴!祝大家新年快乐,明年也继续来听我讲废话的话就更好啦!(x
+
11月1日
+1月1日
-
-
在 hx 课上看了 PKU -去年的抽代题,还好,还好,也就是最后一题有点懵。困得我降智。虽然这个 -110 -分钟真有点难绷,看来也是两节课加一个下课随堂考的,或许有参考意义呢?
-现在已经没人在乎何宝在讲的新课了,感觉大家课上都在复习(
-焦虑地过抽代定理证明,毕竟何宝课上从来都只讲几个概念和证明,又说“考试和课堂内容相关”,很难不怀疑他要考定理。然后就麻了,这就是古老的神秘吗,我真的好菜(
-看了看天气,下周要降温了,这周恐怕是最后一周穿衬衫的机会了罢。冬天(或者说秋季学期)的状态明显比春夏要好,一方面是春天我会过敏,总是昏昏沉沉的,然后就是怕热,夏天也过得很不舒服。
-倒是有点期待北京的雪,去年初雪的时候徒步从法图走回寝室,感到了来华子之后从未有过的宁静。然而上次在上海看到纷纷扬扬的雪,已经是四五年前的事情了。
+这个系列居然存活到了 2023 年!
+
+表白成功了!收到抽代助教回复的邮件了!还加了好友,好哦!(+
+驰雨(x)同学:
+你好!非常抱歉现在才抽出时间来回复你,虽然已经向你发送了微信好友申请,但是还是认为同样给你回一封邮件比较有意义。
+其实我早就有留意到你不是数学系的学生,在和老师闲聊的时候曾有提到过这件事,大致意思是在本门课中给我留下最深刻印象的同学居然是学土木(hhhhhh当时我是猜测你是这个专业)的同学,许多我本以为他们并不会做出来的题目她也有认真去做。
++
+没猜错,只是我写邮件的时候还掩盖了一下,我说我一学位是物理,二学位是交通建管(确实也是实话
+实际上我和你的经历有许多的地方有一些相似,我本科入学的时候的专业并不是数学,而是某个工科专业,而且高中的时候数学学的一塌糊涂,对竞赛什么的也一窍不通。只是在大一的时候才觉得大学接触到的数学和高中完全不一样,更加有趣更加吸引人,于是才在大二转到了数学系,但不幸的是转专业的过程也不是一帆风顺,我被调剂到了计算数学专业。于是我在本科的后三年一边补大一落下来的课程,一边修基础数学高年级的课程,还不得不修计算数学的课程(听起来是非常狼狈)。
++
+其实我很难想象,在华子要是高中时没学过竞赛,甚至高考数学学得也不太好,大一再继续上那个锤的微积分 +A,真的能培养出兴趣甚至想转去数学系吗?那个微积分 A2 +直接给我上厌学了,真的烦死了...这是否说明隔壁的基础课教学质量已经远超世一大了(
+由于并不是科班出身,实际上我最初面对那些学基础数学的同学的时候还是有很大大大大一点自卑的(特别是自己本不属于这里却来旁听),总是不敢和他们去交流问题,或者是和他们交朋友,担心自己暴露出自己什么都不会的事实(x)所以我的本科时光过的并不快乐。一个转折点或许是自己成功跨保到了基础数学的直博,意识到自己或许也没有那么差劲,开始敢于和别人交流,敢于面对自己的不足。我感觉做数学有时候真诚非常的重要,自己不会就是不会,不会就要去搞清楚,和别人交流(hhhhhhhhh或许需要一大点厚脸皮吧x)这使得我之后的收获很大。
++
+太强了..要是我在隔壁成功转到计算数学的话可能只会想往统计挣扎一下,要么就既来之则安之,干脆不动了。在应用方向想往基础跑,真的相当有热情。
+不敢和原住民(?)们交流也真的很真实,我甚至都不太敢在转数环里说话,
+不过转数成功的同学平均水平好像远超原住民(?)。恐怕自己也是,等到有朝一日获得一点点小成就的时候,才能挺起腰杆来吧 +qwq另外一件事是,在学数学的时候你真的能碰到非常非常非常多厉害的人,比你厉害无数倍的人,这可能会击碎你的信心,可这又有什么关系呢?做好自己就好了!进一寸有一寸的欢喜,能比昨天的自己多会一些东西我认为就已经非常不错了。如果真的是想学数学,那就是一辈子的事情,早学一些晚学一些也没有什么大不了的。
++
+非常同意!x
+说起来我之前也一直这么想,后来被别人批评说不求上进(qwqqqq),难过了很久。不过人家是神,确实在他眼里我努力学习的东西都很 +trivial,所以并不是很能互相理解。那就不要互相理解了,坚持做自己就好。
+所以做自己最喜欢的事情就好啦,无论之后能不能做出来什么成果,无论这个领域已经聚集了多少大佬,但行好事,莫问前程。
+祝眉头舒展,顺问冬安。
+然后微信上还聊了很久,听他讲了一些大一没上数分高代还选了平转数学,一边补这两门,一边顶着计算数学的课还要学基础方向的小故事,在隔壁冲基础真的很强了,这又是怎么做到四年顺利毕业的qwq,我都想主动延毕了。我大概讲了讲自己遇到的一些小的困惑,一起吐槽了背书般痛苦的数值分析(,还闲聊了些别的,非常愉快。
+另外他给我看和 hx 的聊天记录,hx 的意思好像是要按比例调 +4.0,现在这个情况再按比例调的话岂不是要向下调分了,害怕,
+连我这种彩笔期末都能按题目顺序通畅地 +ak 甚至还给一个题加强了结论,感觉人均 90尴尬的是聊完我翻了翻他朋友圈才意识到,他本科好像是隔壁的,不是华子的。我虽然觉得“转到了计算数学”这个说法很奇怪,还以为四年前一个系里面专业都分得这么细,一直都给他预设成是在华子本研一起读的。更好笑的是我还跟他吐槽了半天诸如数分这样的几门本科生基础课稀碎的给分,和后续上课知识储备的问题,沃日,他还真的认真答了,反正对话里就感觉很奇怪又说不上哪里怪(
+找到了一张两年前的照片,其实昨天本来想发的,结果给忘了。
+
+
我的高中有年底最后一天开跨年晚会的活动,也是为期一个月的校园艺术节的尾声。大家说这是二附中最盛大的节日,但是说不清为什么我就是不喜欢这个活动。可能是因为当时不喜欢身边的人们,所以不愿意和谈笑中的大家坐在一起看演出,感觉尤其孤独,或许是天然抵触这种很有玫瑰色的青春氛围的节日,总之三年三次晚会我都没去过。晚会有一个高三大合唱的环节,高三的同学会一起拿着荧光棒唱排练了一个月的歌,然后被拍成视频(沃日,还真找到了),很情怀的样子。轮到我高三的时候我也没去,哪怕我的手完全是做题家的手。
+记得高三的那个跨年晚会之前刚考完一模,班主任买了蛋糕给大家分着吃。我太自闭了,一到这种时候就觉得真的好压抑,直接从教室里逃了出来。看到丢在垃圾桶旁边的蛋糕包装盒里有小的烟花棒,可能原来是要插在蛋糕上的,估计他们不会要了,就拿走了一支。晚上开晚会的时候大家去了体育馆,我也不是很想回家,就一个人坐在漆黑的楼道里看了会剧,突然摸到外套口袋里的烟花棒,忘了是去哪里找到了打火机,在楼道里点了一下,拍下了这张照片。看到四散的火花,一下子就雀跃了起来,现在还记得当时的心情呢。
+我和友人一直以来是非常好的朋友,突然意识到即使这样她也有不理解我的时候——比如上述的这个时刻,她正在体育馆举着荧光棒为大合唱泪目,并不理解我为什么不愿意投身这种气氛之中。高中的时候写过很矫情的话,叫做:
++
+就像我们无法看到一生中全部的雪,也不能完全知道彼此叹息中的故事。
+尬死我了(,但确实大概就是这种感觉。不过又有什么关系呢。
+说起来原来想投给朱自清文学奖的稿今天基本上改完了(有些人期末周是真闲啊),但现在已经不想投了,自己留着就好。何必为了一个奖把自己的心剖出来给不相干的人看呢。虽然最后好像不会公示参赛作品,但一想到评审阶段我也还是觉得算了。(才不是觉得自己这水平根本没希望,才不是(
+今年(去年?)的跨年夜是观影马拉松!一个人在寝室连着看了《色,戒》、《血观音》和《牯岭街少年杀人事件》(这个实在太长,看了不到一半就睡了),翻到上面这张照片突然好想给自己点个烟花棒看,可惜买不到(。翻出来了生日买蛋糕时候送的蜡烛点了一下,烛光也很好看呢。(没有照片
11月2日
+1月2日
-
-
好,一晚上学完初概后半学期内容!也不难嘛!(
-刷完样题之后就当做没初概期末这事儿了,摆烂。但心里到底还是有点难受。这课唯一的弊端就在于没有能很好地匹配的教材,MIT -的概率导论自然好,但是二者进度之间有太大差异,实在不方便。然而没有参考书对我来说就是毁灭性的,我现在越来越难以集中精力听谁说话,在听课里学到一些本来从书上就能得到的东西,或者在 -PPT 里学习什么的,真的不是很擅长。
-又开始焦虑自己后半期的统计推断能不能行,以及毫无分析基础,我这样真能寒假速通一下测度积分然后就去上概率论(1)吗,可是不上就来不及了,草,真想延毕一年。
-明天的时间还是让给抽代,虽然我觉得复习得差不多了,反正再复习该不会的也还是不会,何宝太 -book reader 导致我甚至不知道自己不会什么,草。
-听室友破防说来华子之前从没想过日子过成现在这样,还有她高中时对于华子的所有瑰丽幻想,实话说我有点无感(笑)。毕竟考进高中的时候就幻灭过一次了,而幻灭过一次就不会再有第二次,如果有,至少也不会那么严重。
-现在对华子幻灭,以后就不会再对另外的环境幻灭,一下子就降低了试错成本,好事(确信
-说到幻灭,为什么还有“如果有”这个选项呢,因为我对科协也幻灭过一次,只不过不太严重(
-我之前写过一篇文章表达过对你院科协的美好设想和一言难尽的现实,如今我已经不想改变它了,而是打算下学期直接跑路。你院对科协的定位就是主体在从游部,而学术部既边缘又臃肿,于是今年被丢了个举办科创日的任务,做其他部门懒得做了的杂活,(对我来说)很没意思。
-搭网站这个设想最后一次被提出是这学期的第一次例会,有一位新成员说可以给你院科协搭个网站写东西,把公众号的内容迁过去。部长说是那种用来宣传活动的网页吗,可以挂靠在书院的官网上。不了了之。我也没说什么,当时就觉得算了。
-看到 ex 之前的发言,虽然我一直在尽职地扮演一个合格的死去的 -ex,但也没必要向共同好友宣告我真的死掉了吧(笑
-
-
那你怀疑吧,你活该(错乱(好恶毒啊(啊不,其实已经很善良了 x
+这网络学堂真的有点乐,老师给了成绩之后可以选 +
+display:none,但只要会按 F12 就可以查到抽代成绩啦(还挺符合预期的,ak 了就是 ak +了,
简单的数理问题确定性很强,很给人安全感啊。想起来期中考完的时候破防了一晚上,觉得肯定是寄了,甚至梦到了 +4 学分的抽代喜提 2.6,只能带着日渐贫弱的 GPA在一个均绩 3.8+ +的院系里过一个相对失败的人生,在紫荆公寓的浅色床单上痛哭。没想到期中并没有想象得差,虽然没考过一个半小时的试,整场基本都在慌乱之中,浆糊一样的脑子根本写不出构造,但真的落笔写下的东西都写对了,学得还算扎实。而期末翻盘真的是存在的啊。(其实微积分 +A2 期中爆炸的时候也想期末翻盘,结果期末比期中更烂(
+虽然没有过生日的习惯,但是我还是会在生日前后借这个名义送自己一点小礼物,获得一个冲动消费的理由。去年生日的时候订了《恋爱的犀牛》的演出票,可惜四月底北京疫情,演出取消了。后来有点不开心,改成给自己买了一身看中了很久的裙子,也很喜欢。
+期末考之后打算在北京玩几天再回家。本来是想直奔江西,结果我姐说二月份要去上海实习,就约在了上海见。原来规划去故宫什么的地方走走,刚才突然想起来这件事,不抱希望地查了查《恋爱的犀牛》演出档期,居然 +1.4-1.15 之间真的在北京有场次,目测是空花组的演出。订了 1.10 +的票打算去看,非常幸运。
+本来是考虑订上海场的票的
+(才不是因为票价比北京场便宜一半),但上海场演出是 +2.14 开始,那天我就要回北京打 hpv +第二针了,恐怕是去不了的,就回家之前在北京看吧。现在不用再担心封校出不去,或者演出取消了呢。
+虽然不觉得会超过郝蕾段奕宏版的经典,而且真的已经在 b +站看过很多很多次了,但还是想去一次现场。
+和我妈打电话。她一如既往地劝我快去找对象,不存在的,乐。我也懒得和她讲自己的很多打算和考虑,就像现在告诉她我打算延毕一年她恐怕要应激,会争执很久,没有必要,暂且按自己的思考来生活就好,每次就糊弄过去。不过她今天问了我一个很有意思的问题:会喜欢学数学的男生吗?我很干脆地回答说大概率不会,把自己惊到了。
+想了想喜欢过的人们(不要细问,太羞耻了x)性格气质爱好甚至外貌特征都基本完全不一样,
+平等地在不同阶段同等水平地喜欢不同的人,不存在哪个人是白月光一直念念不忘甚至希望别人身上还带有他的影子之类的情况(什么啊。但确实有一个共同的特点是他们都不是很擅长或者至少不那么喜欢数学,读的专业五花八门但也都不是数学(啊其实基本后来都收敛到去搞 +CS 了,大家都好成功 qvq),大概是巧合吧。可能是竞赛的时候觉得数学组里很强但又有些怪的人(不好意思有点冒犯,或许叫做“比较独特的人”比较好,哪里独特我也说不出来但相信大家都有体会 +x)明显比别的组要多,相比之下化学组就很欢快随和,我经常被暴打完就去找他们玩,有几个曾经关系不错的同学,
+ex +也是化学组的(?。加上自己很菜,所以几乎从来不敢和神交流,导致有点刻板印象了。但是“学数学的人里面比较独特的比别的专业里要多”这件事貌似确实是真的,为什么呢。说到这里突然想起来,竞赛的时候一直非常自卑,以为我这么菜,组里的神应该都不认识我吧。最后一次联赛前我们在做模拟,彼时距离进 +IMO 国家队还有三四个月的 wyc +负责监考和发准考证,遇到不认识的人他会叫一下名字问座位在哪里,我还以为会叫到我,结果他最后是走到我面前把准考证递给了我。大一下学期上排球课,左爷爷正好和我同一个时段上课,我本以为他肯定不认识我,结果他还和我打了招呼,两次都挺意外的。
+不过想来大家认识我,根本不是因为我那羸弱的水平,甚至不是因为我菜得像个笑话(,而是因为我是组里非常少有的一直坚持到高三才退役的女生吧,混到了脸熟。高三那次联赛是省一里的唯一一个女生,同年拿了 +CGMO +Au,两件事叠在一起被沪上某个小有名气的升学公众号拿来大做文章蹭流量,从小学开始的经历都被扒了一遍。一想到这些还挺不高兴的,当时又要装作开心的样子被人祝贺(有什么好祝贺的,退一万步从功利角度来说这不就是纯纯竞赛落榜生),和现在被迫过女生节时接受礼物和祝福的感觉差不多。我之前提出来我能不能不要过女生节,我也不想给班里的男生过男生节,还被约喝茶了,不利于团结的话不要说((
+不要再写青春疼痛文学了,快去复习啊(
+看了一眼下学期的网络学堂,故宫学这门课的英译是 +Gugongology,Google 了一下这个词一共有 19 +条结果,草,什么冷门绝学(,很难想象交出国成绩单的时候国外学校会怎么想这玩意(
+看到了一个说法:
++
如前所述,故宫学于2003年正式提出,而敦煌学的出现要远远早于故宫学。学科名词出现的先后次序是衡量学科之间自觉性程度的标尺,即使是从英文拼写情况来看,两者的差异也十分明显——敦煌学已有一个国际公认的英文拼写,即Tunhuangology,而故宫学则有Gugongology、National +Palace Museum Studies和Studies of the Imperial +Palace等不同拼写形式,说明前者已是国际性学科,而后者的国际化程度还有待提升。
+
11月3日
+1月3日
-
-
吃到了社友的安利,于是今天一边听《万千花蕊慈母悲哀》一边写抽代,感觉要把自己超度了(
-和 illion 的《GASSHOW》很像诶,但是更偏向于悲伤了。
-然后又去听了源的 -Tokyo Dome -演唱会,以前很喜欢一边刷这场一边写作业,但是当初刷的那个视频下架了,只有缓存还在我的手机里。东蛋场每一首歌感觉都比专辑还好听...而且还有源的各种即兴演出 -> <
-草...明天不是连着两场考试吗,今天怎么净听歌去了。早点洗洗睡了,pray -for tomorrow
+8 +号考数值分析,而我连着摆烂了两天,复习时间突然变得紧张了起来,考完之前更新大概会比较咕(
+虽然觉得对计算数学研究的问题不太感兴趣,不想往这个方向走了,但基本的数值方法毕竟是应数各个方向都会用到的,也是培养方案里(说得好像是我的培养方案一样)挺重要的必修课,不能摆过去啊 +qwq
+和甘主任唠嗑,他怎么大一上学期就已经在看 stein 了(
+虽然一直说别人学得多快有多升级都和我没关系,自己学扎实就足够了,但压迫感来自身边的朋友的时候果然还是有一点点难绷 +XD
+今天顿悟了最近作息混乱的原因——是光线的问题。拉上窗帘之后,台灯和白炽灯是寝室里仅有的光线来源,而且楼道里的灯坏了,从楼道那一侧也不往房间里面透光。如果一整天不出门也不看表,还独处一室的话,真的是感觉不出白天黑夜的区别的。从这个方面来说人和植物还挺像的,都很依赖自然光呢(
11月4日
+1月4日
+数值分析一天看两个章节的话正好能看完,这个工作量水平基本上是肝一肝能保证完成的,还好。沃日,怎么感觉这课跟没学过似的,虽然我平时确实没怎么花时间,但这书我至少抄过一遍,PPT +课后也读过,这些内容都是学会过的啊(,怎么现在印象这么模糊。4 +个学分的课考试前一周学完,真有点刺激了,大家以后上这课的话千万不要学我。不过还好沾了这学期线上考试所以开卷的光,沃日,要是不开卷的话我更想象不出来这课要怎么考,感觉这玩意和别的理论还不一样,好多优化方法都像拍脑袋想出来的,只能嗯背。闭卷的话真要把公式全背下来吗,也没必要这样折磨人吧(
+6 +号的两个娱乐项目打算缓考了,寒假里复习的话加起来不会花超过三天时间,但这三天放在现在太宝贵了,匀不出来。
+这个破工程经济学,我一边上一边在心里骂,我将来既不做实体工程,又对经济不感兴趣,为什么非要我学。有时候入戏太深了,还真以为自己是数学系和统辅的了,每次想起来培养方案里的专业课是什么测量学,工程地质,工程力学,更好笑的是还得学量子力学,都觉得像个小丑(。没一个有用的,还难的要命,得花巨量时间处理,甚至可能要付出把更多一年的青春年华()用在在华子里坐牢的代价。都到这份上了,给分还给得巨烂,这院系真是有毛病。
+虽然天天骂华子,但还是终于明白了当初 SJTU IEEE +之类的选项是一个局部最优解,选华子仍然是不错的(陆本都差不多烂是吧x),中二一点讲,哪怕被折磨了这么久但总算是找到了真物(?啊?),尽管这个过程实在太漫长、太痛苦了,而且还远远没有结束。的确处处都取局部最优的话是到不了全局最优的,终值在取初值的时候就定下了。
+读过了许多算法和定理,仍然过不好这一生(点烟.jpg
+之前看学长写的“都是贵系的问题”那一部分,光是看都看得我焦虑不已,太累太绝望了,很难想象他那两天是怎么过的。后来一想其实华子大多院系的生态也就这个水平,拿我院出来一比,贵系好了不知道多少倍,又把我整破防了。不知道为什么想起 +ex 来(上次在博客里试着搜了一下 ex +这两个字母,出镜率过高了x),只记得他也是要润,正常情况的话最近大概也在套暑研?不知道会不会沾点 +UM-SJTU Joint Institution +的光,不了解。当然他看起来菜的离谱(,也或许并不会走 researcher +的路,我之前说觉得他去当翻译最好 +XD,现在也还是这么觉得。现在还偶尔会去翻翻他的各种社交媒体,我之前和朋友戏称,这也算我的人类观察活动之一。确实是这样的,和平时随手打开一个社交媒体的时候会试着搜搜看朋友的 +id +有什么区别呢?区别在于真的已经变成赛博幽灵,肉眼可见的将来不会再有多少联系了而已。这也很正常,举个例子来说就像我大概永远不会认识迟先生(,但是自从知道是校友之后就也时不时会去看看推。有时候看着看着 +ex +发的很多东西,会觉得真的也只是个再普通不过的一般路过肥宅罢了,和我从前写的青春疼痛文学里的那个带恶人似乎没什么重叠,才发现自己的心态也已经发生了挺大的转变。怎么说呢,祝大家都顺利吧。
+1月5日
-
-
抽代期中...题肯定是不难的,但相比之下我还是宁可考 zmx -的卷子,扎扎实实做三个小时。具体问题详见本篇篇末的“赛博猫猫敲键盘”。复盘越想越头痛,大概就是:
-第一题愣了一下不变因子组是什么来着,有惊无险。第三题没构造出来之后就直接做 -\(105\) -阶群去了,结果又手抖抖半天,慌得要死,浪费不少时间。然后是环同态,看完题大概五秒钟就想出来了,不夸张。我愿称之为最水的一题。回头写了一下循环群同构的第一问,手抖写错了 -114514 -遍,涂得乱七八糟。又看到最后一题第一问就作业原题,写完,第二题就一定义+归纳,结论对了但我过程也有点乱,不知道给几分。最后去做了循环群同构的后两问,用一下第一问结论感觉就那样。?问题是我第一问结论对了没有,至少我感觉是有问题的。然后又去想群运算构造,想不出来,但明明已经想到 -\((a+1)(b+1)=0\) -什么的了,就是没再往下想。交卷了。
-下午同时在物理上告别了初概,然而从现在开始我要复习初概了,因为过几天统计推断就开课了。
-emo 一下(
-大一的时候意气风发,大概是在我院这个舒适圈里躺着的缘故,觉得自己能做到很多事情,能去到很远的地方,又到底是怎么变成现在这么破防的呢x。这学期好像一直就没什么好消息,初概期中先裂了,不得已送了个 -PF,结果期末没复习都考得还不错,吗的。奖学金入账 0 -元,然后又是抽代期中,最近物理实验还崩。
-又想到上学期紫十二 remake -的同学,先但愿自己去数学系混的这两年不要有生命危险。绩点不知道能不能在申请之前苟住 -3.8,本来上学期期末还有 3.89,夏季学期土木系的烂课一出分直接给我送到 -3.83,容错率一下子无了,这学期体育 + -抽代又不知道要扣到哪去了。软弱的时候就很想往回退,什么申个 ms -算了,再想想花不起这个钱,又有哪家招我这种 five 当 -PhD,留国内容易点,吗的强基书院又各种限制,想往复旦退可能都没得退...
-一阶段 PF -了初概,二阶段要退常微分和基物实验。前者是没必要再上下去了,后者是上次光栅实验莫名其妙吃了个 -80 分,也没给出什么理由,我又不想在这种课上送一个 -3.6。问了一下老师,退实验课也几乎没有沉没成本,先前做过的实验明年想保留成绩的可以申请保留,不想保留的可以重做。
-实在不行的话跟现实低头一下,统辅为主,少上点 / 多 PF -一点数学系的课。真是弱者。
-后半期就,不得不转换一下重心,这下一定要苟住数值分析、统计推断和离散。工程力学也是,不能太拉胯,然后就,抽代尽力而为。
-我感觉我之后必须搞点水课来刷成绩了,真的是。
-还有些别的更令人难受的事情,但现在先不说了,暂且这样吧。
- -
-
11月5日
+又看了一遍,昨天这是在说啥?倒不是抽象,感觉早晨六七点写的东西未免有些,太随机了吧(
数值分析,不过如此!学的时候觉得最困难,心理阴影最大的几个章节顺利过去了,后面是一些轻松愉快的多项式数值方法,感觉明天能速通完。
+无论如何它都算是数学系的养生课,分方向之前的那些基础课哪有考前速成能学得会的。
+不知道考试考多难,bcl +老师风格看起来比较友善,我也没题目可以拟合,就把课后题刷完了,感觉还好。
今天发现只有概率统计方向不必修泛函分析 (1),有点震惊。
wjd 老师在鸽了我的邮件 13 天之后终于回了,笑死(
+寒假的事好像实在有点多,先抽几天写完统推讲义和基物实验指南,今年基物实验 +3 +不能再退课了,我超,这课明年就停开了,因为二字班修订培养方案之后只需要做两个学期实验了,羡慕。然后还得速通数分到一个不至于原地去世的水平,以及 +learn R in 24 +hours,可以的话打算再浅看下统辅的两门理论课来着,毕竟下学期的难点在复和概还有统计学习导论这个码课,尽量得压缩下留给那俩半娱乐项目的精力。而且我还有期末缓了没考!草(
+我还想多整几次江浙一日游呢,到底是假期,抚平在华子造成的精神创伤最要紧。
遛弯的时候不知怎么想起来,之前找一位学长问凸优化这门课的情况的时候,他简单介绍了下,然后说这课不卡优秀率只卡 +A+,“虽然我最后只有 A-”。我 mod +了一下,然后他说“数学人之间还是可以相互理解一下追求的嘛”。
-
-
今天又是新的一天!(试图麻痹自己
-是不是全世界今天都在考物化,我下午一点起床的室友三点要考物化,偶然说了几句话的同学三点也考物化,来三教自习,坐我前面的人也在量子波动速读蓝皮的《简明物理化学》,两点半左右离开了。
-同学锐评我:本来桑海宁装的蛮好的,桑海话讲的也蛮好,最近看到桃李的大闸蟹就绕路,连胶东人都装不下去了吧(x
-的确家里一直没有吃水产的习惯,甚至还有点排斥,而我对某些范围不明的水产过敏,就连鱼虾都很少吃。之前偶然吃了一次桃李二层做的一种扁平的多宝鱼片,用辣椒和葱蒜点缀,再浇一勺鱼汤,感觉还不错。可惜现在似乎不做了,不知是不是也有丰产的时令,秋冬是吃不到的。
-在南方吃了 12 -年学校食堂,从来只有米饭,来到华子还是忍不住买面点做主食,母亲也叮嘱我寒假回家之前去牛街买些北方特产的面食带回家,那都是上海买不到的东西。小麦的香气还是刻在我和我的祖辈的记忆里。实际上我在记事后几乎从未踏足故乡,跟着父母几度辗转,在嘉兴度过童年,又来到上海。母亲对她家乡的县城、生长的环境颇有微词,于是我也迷茫,自己对几乎未曾谋面的故乡的依恋,大约只是经过了想象的粉饰吧。
-不说了,最近家里的事实在令人难受,在肉身还远在上千里之外的时候,先集中精力干点别的去..
-想起来三四月份的时候看过一部电影,情节还很清楚,但是电影名还有角色的名字一个也不记得了...最后还记得的一个特征是据说男女主拍完这一部电影之后真的出轨在一起了 -= =,然后就搜到了...
-叫《夜以继日》。B 站评分不高,8.4,
(B -站评分有啥参考价值),查了一下 bangumi 是 7.4,远超我对 -bangumi 的预期,再一看是样本量太小了,才 24 个...
+- 我懂了,不是早上六七点钟写东西导致产物非常随机,而是我这个人就很随机,时不时“突然想起来”(
11月6日
--
-
今天开始速通之前放掉的数值分析。真的很想喷一下这教材的排版,标题和正文的字体几乎差不多大,节与节之间连点空隙都没有,但凡做成 -A4 大小的书,或者加到 400 -多页,也不至于阅读体验这么差。虽然它写的很详细,难得有证明全都在书上能找到的书,而且已经很厚了,但还是很难绷。
-这课只有期末,并且明确了不调分。但我感觉考试之外的 50 -分有手就行啊...数学系专业课还把出勤算 5 -分,作业也有手就行,真的蛮不可思议的。或许这是门专业课里的水课吗?我不知道。
-之前觉得老师长得很帅(甚至早八上课会觉得啊老师好帅还是别睡了(什么啊),就去搜了一下,包老师是中山大学的本科,在坡读的博。他的微信头像是他的一双儿女,眉眼都和他很像。
-其实我觉得去坡也是很不错的选择...
-和室友聊起来才知道你院(一字班)到现在还有 GPA 4.00 -的人,还不止一个。别的不说,我觉得体育能稳定拿 4.0 -就已经和我不是同一种生物了,根本没必要去了解人家的情况(
-说到这个,该刷月光长走了,我还差 21 -次呢。之前实验了一下,走路的配速略大于最低要求了,跑是不可能跑的,只能每天晚饭后走骑结合一下消消食这样子(
-老姐在南昌住院的复诊结果出来了,不是强直性脊柱炎,只是腰间盘膨出和炎症,(《只是》),值得庆祝。等她假期来上海请她吃饭。
+
我当时还蛮奇怪这个数学人是啥意思的,只知道他要转 AI +相关,难道转的是理论方向所以也自称数学人?还有点震惊他怎么知道我想转数的,我感觉我在现实世界的社交里一直还算低调,基本避开不提这些事。今天回来随手一搜才知道他以前也是 +MOer,原来是这个意思,不知道为啥我一直以为他是物竞的,报道上出了点儿偏差(
11月7日
+1月7日
-
-
今天马原课上读完了 PIN 多年前连载的 《Heroes in My -Heart》,很喜欢这个结尾:
--
到这里就真的结束了吧,要毕业了。又想到了一个小故事是 Halmos -的,他写了一本著名的书叫做 Measure -Theory,当他完成此书的时候,心中喜悦难以抑制,向众人宣布:“我刚写完了 -Measure Theory 的最后一个字!”有人问:“最后一个字是什么?”Halmos -当时愣住了,连忙赶回办公室,再跑回来,告诉他们说是什么什么。
-我也写完了,最后一段话和本文无关,写给远在千里之外的一个女孩,每一天到 -bbs 上的时候,我总是假设你也上 -bbs,你也来看我的连载,希望你能喜欢这些故事哪怕只有一个,尽管你不喜欢数学也不喜欢我。
---
-美丽有两种
-一是深刻又动人的方程
-一是你泛着倦意淡淡的笑容
-
-一周以来的效率高峰发生在工程经济学课上,我没听,预习完了环的 3.7 -节还写完了课后题,搞定了之后居然又过了十几分钟才下课,第一次觉得时间慢得不可思议...
-恐怕也不是第一次,高三的时候我喜欢在数学课上写英语卷子,因为英语太烂了,要恶补。当时总觉得在数学课上伴着老师的安徽口音写作业,正确率比回家写的要高很多,甚至写得也快些。这是什么原理(
+数学记号真是混乱...头大
+摸鱼的时候看了会 summary,发现统计计算的一大半内容好像就是数值分析的三个章节在统计问题里的应用,大概又要从头讲一遍数值方法,其余是一些统计里的特化(?)算法。眼前一黑,所以说我明年还得再学一遍这玩意是吗(,虽然会轻松很多就是了。
+点疯狂星期四经常拿咖啡凑单,正好还有券,最近把他家号称不同口味的咖啡都尝了一遍,没尝出区别,感觉都是刷锅水的味。虽然也没喝过刷锅水,但是我就觉得应该是刷锅水的味(
+最近不分白天黑夜地在复习数值分析,也努力让自己别再记忆随机游走了,没啥可记的,简单写个流水账。
11月8日
+1月8日
-
-
昨天提到了我的高中数学老师,才想起他也是华子毕业的,大约是 2006 -年入职二附中,可能是最早一批来我校教书的清北人。现在学校里清北毕业的老师就很多了。据说他本硕读的是核工程,理应是工物系的。他既是班主任,也是数学老师,倒并不是竞赛教练,我们的数竞教练是隔壁班的唐立华老师,
-往往被叫做立华奏。前段日子看到他貌似升职了,简历上写着“培养出 -blahblah,blahblah,及女子数学奥林匹克金牌学生一名”(大意),恐怕指的是我。虽然我这个破铁牌和他没半毛钱关系,但人在他班里,功劳就归他了吧。当然除了名额是隔壁班唐老师给的之外,也和
-立华奏唐老师没什么关系。这么说好像很忘恩负义,但事实如此(不过其实我到现在也没理解的是,为什么高中三年他一直就当我不存在一样。同学当我不存在我可以理解,当时的男女比例比华子夸张多了,感觉大家甚至不好意思和女生说话,也没必要和我说话,我也自闭。毕业之后我就主动离开了高中同班同学的圈子,想来大多数人现在都已经不认识我了吧。
-扯远了,虽然班主任这个态度也很好,毕竟我即使不是什么刺头,倒也是热衷于自己默默搞事和钻空子的类型,只要不捅出篓子(事实上也没捅出过篓子,高中生在学校里能捅什么篓子x)他就懒得说我什么。于是我的日常就是轻微违反一些针对个人的规定,但能比较好地提高自己的生活质量和精神状态,比如带手机听个歌、不在气氛令人窒息的教室上晚自习、肥宅不出操,于是也没人管我,很爽。
-然而以前倒也有令我很难过的事情,比如我高三竞赛结束回头补高考,花了三个月就从年级 -50% -的地方冲到了一模区第二名(还是第三来着)什么的,还有中间大大小小的进步的时候,整个高三他在班上鼓励过几乎所有取得了进步的同学,却从来,从来没有一句话提到过我。到最后还是想开了,就把他当做一个给我批改作业和试卷的工具人就好,美中不足的是不交作业的话他会派人来催。
-虽然现在想想当时为这种事情难过有点傻,毕业之后我时常在友人面前喷他,尤其看到他简介上写我的铁牌是他教出来的之后,觉得这人,啧。但时至今日,我也还是对他当初的态度感到困惑,究竟为什么要这样呢?
-抽代出分了,还挺乐的,我一共就做了 85 分的题,得分效率竟超过了 -95%,就扣了群同态的一个没说明清楚的情况,我的很多担心都没有发生,说明运气不错,何宝相当温柔了。
-虽然他说“考试题目很难”,从成绩分布来看的确(大约是两个一伯分,六个 -90+,两个 80+(为什么这一段断档的这么厉害),在这之后还有 22 -人,具体忘了,其中有 10 个没及格)。恐怕是这边人均水平确实不如 zmx -的大班,想必她那里藏龙卧虎,而我们更不可能和求真比了。
-话说回来干嘛非要比,我(一部分原因)就是觉得数学中上水平的人也能有不错的出路(润应用),而且还能保持精神状态正常,才润来这里的。尽力学好自己的东西,享受乐趣,雨露均沾统计中心和数学系,差不多得了。
-另外何宝居然把答题纸发回来了,拿回去裱起来。我还从来没见过这种操作,一时不知道他是真傻白甜(错乱),信任大家不会搞出点查卷的幺蛾子,还是其实已经保留了电子版的原卷等碰瓷。想起我大一的线代老师,期中查卷时全副武装,要求预约排队不许携带纸笔并全程录像(听说的),笑死。
-一想到那个搞不出来的构造还是很蚌埠住,期末能不能多给点扎实的证明题...但至少做的基本都对了,对我来说也是大进步(
+早知道这数值分析考这么简单,我复习这些天干啥呢,还为它缓考了另外两门(x
+这话是不是考完抽代的时候也说过来着(
+一半都是没有布置成作业的课后习题,正好这两天刷完了,剩下的有手就行,我共轭梯度法呢我牛顿法解非线性方程组的几个变式呢我特征值方法呢怎么全都没有啊(x。不过学到了不少有用的东西,好耶(
+-
+
说起来包老师的课真的讲得很好,虽然这门课是第一年开,他也是刚来华子不久的青椒(没有影射哪位老师的意思,没有 +x)。课堂上讲得很清楚,思想也很深刻,强推给之后也要修这门课的朋友。
+另外,这课的 PPT 简直仙品啊!我觉得不输 dwl,看着太享受了。
+讲课讲得好,内容充实,不在课后刷题量和奇技淫巧上为难人,考试顺利过,这不就是很理想的课程设计吗 +555,这几天备考卷昏了说出上面这些话才奇怪吧。可惜这种好处恐怕只有第一年能享受到,后来知道某个老师考得没那么难,可能就不会这么用心了。说到底好像还是学习态度有点问题(
+
+总算考完了,开摆!
+明天摆一天,看看电影写写统推讲义,去图书馆借几本书带回家看以及给下学期用,后天出去走一走,大后天打扫卫生收拾东西,12 +号回家。不过这周还得连夜卷一个工程经济学的加分论文,过两天再说吧,这破课还这么卷,好烦。
+总的来说,这学期虽然开局选了六门数学课,结果最后退了一门水的,又 +PF +了一门卷的,剩下的要么本来就不难要么碰巧选到了水一点的老师。所以似乎还是没体验到数学系的课劲有多大,在一个并没有做好心理建设的状态下,下学期就又选了六门,而且还要去碰瓷实复概里的复和概,感觉人肯定会出事的(悲
11月9日
+1月9日
+一天啥也没干,好不容易考完试,想摆烂却不知道怎么摆了,感觉是很空虚的疲惫。勉强补完了跨年观影马拉松时候没看完的《牯岭街少年杀人事件》,心情更沉重了。
+下午写了会统推讲义心情就好些了,参考着统计计算的讲义和刚刚考完还热乎的数值分析,给 +Newton 方法求解 MLE 的部分补充了一些变式和收敛条件,挺好玩的。
+晚上二刷了 BBC +神探夏洛克的第二季,我小时候不爱看巴斯克维尔的猎犬这一部,拍出来整体很昏暗,有很多丛林里穿梭的场景,稍微有点恐怖。所以其实不记得这一部的故事了,就二刷了一下。中间有一个猎犬来袭时,委托人把脸贴在家里的落地窗上往外张望的场景,玻璃里映出了他的脸,我就在想为什么要在家里装这么大一面玻璃幕墙,感觉很没有安全感。
+然后想起来(又开始 random walk +了是吗)高中在图书馆负一层自闭的时候,曾经随手翻开过书架底层的一本看起来有些奇怪的书,是阳版的《哈扎尔辞典》。前几页大概讲了这样一个故事:哈扎尔民族会因为在睡梦中被人叫醒而暴怒,因为他们认为人在睡觉的时候最脆弱,容易被恶人偷袭。阿捷赫公主为了在睡眠中保护自己,每晚命仆人在眼睑上写上毒咒字母,看到字母的人就会死去,早晨起床前由盲人婢女服侍自己梳洗,擦掉字母后才睁开眼睛。某天有人为她送来了一面快镜和一面慢镜,快镜可以映照出不久后的未来发生的事,慢镜映照出刚才已发生过的事,时间差是相等的。这两面镜子碰巧在她睡觉时送到面前,于是阿捷赫公主睁开眼睛时在慢镜中看到了自己眼睑上的字母,在快镜中看到了已经睁开眼睛的自己,危险的睡眠中安然无恙的她死于清醒的瞬间,镜子无法映照出的当下正是死亡时分。“她是在来自过去和未来的同时打击之下亡故的”(不知道会不会和原文出入很大,但我对这句话印象很深)。
+当时甚至还不知道这是真实存在过的民族的传说,还是完全的虚构,看完有点吓到了,没有把它借走,也一直没有再往下读。但这个关于镜子的隐喻一直记到现在,时不时会想起来,尤其是每次意识到想起它的时刻正是过去与未来的间隙,是阿捷赫脱离危险的梦醒时刻和死亡时分,总是会吓自己一跳。电影里的委托人满含恐惧地把脸贴在玻璃上,这既不是快镜也不是慢镜,因此玻璃里映照出一张一模一样的脸,而当下正是充满着死亡气息的恐怖时分呢。
+1月10日
+今天出门借书之前想起来昨天说到的《哈扎尔辞典》,搜了一下北馆也有馆藏,考虑要不要借一本来继续读,但是印象里很厚,带回去有些麻烦。然后在搜索结果里看到了一本《爱情故事的两个版本》,才知道《哈扎尔辞典》背后的小故事,太浪漫了:
+++题名:哈扎尔辞典 Dictionary of the Khazars
+作者:帕维奇, M [1929-2009]. (Pavic, Milorad)
+描述:这部类似“民族志”式的“辞典小说”写了一个幻想的古代民族“哈扎尔”人的历史以及有关这个民族的各种轶事。此书是《哈扎尔辞典》的阳本。阴本跟阳本并无多大差异,有人曾对照阅读,发现仅十一行文字有所不同。
+
++题名:爱情故事的两个版本 Ljubavni roman u dve price
+作者:米哈伊洛维奇, J. (Mihajlovic, Jasmina) ,帕维奇, M, 1929-2009, +(Pavic, Milorad)
+描述:本书是雅丝米娜·米哈伊洛维奇与米洛拉德·帕维奇共同创作的一部作品集。其中,“科托尔文具匣”收录夫妻二人围绕一个神秘的文具匣进行的同题创作,写作因此也成为作家夫妻间亲密而浪漫的约会方式;“爱情故事的两个版本”记录雅丝米娜向帕维奇“定制”故事的有趣经历,文学大师不同寻常的写作状态可见一斑;“迟到的情书”由帕维奇的小说碎片展开,引发出雅丝米娜对二人过往爱情生活的追忆和对丈夫深情的怀念;游记“哈扎尔海滨”记录雅丝米娜寻访《哈扎尔辞典》中那个“消失”的民族——“哈扎尔人”的见闻、体会和奇遇,也记录下二人对历史、时空、死亡等问题的思考和感悟。
+
其实高中的图书馆地下一层有很多大家都不知道的藏书,比如《中等数学》合订本(字面意思,真的是图书馆老师自己把月刊订在了一起),我还拿来刷过题,还有 +1940 +年代出版的李四光先生的《地质力学之基础与方法》(当时为了给地科社写科普推送,我甚至还读过这本书,是否预示了被调剂进土水学院的未来。这个故事也充分告诉我们,随意把普通爱好变成职业是行不通的啊!),村上春树的《刺杀骑士团长》,阿列克谢耶维奇的四件套《切尔诺贝利的悲鸣》,《锌皮娃娃兵》,《我还是想你,妈妈》,《我是女兵,也是女人》,还有《岛》也是在这里见到的,后来因此去读了维多利亚希斯洛普的其他作品,我更喜欢《线》。甚至新海诚三件套《秒速五厘米》《星之声》《言叶之庭》的轻小说都有。
+不过要说馆藏里最冷门的恐怕还是井上靖的作品《天平之甍》(甍读音通萌),是从日本视角讲唐代僧人东渡的故事,还有《孔子》。《天平之甍》里最后讲到,僧人淡海三船为敬谢来到日本时已经失明的鉴真,写下了“我是无明客,长迷有漏津。今朝蒙善诱,怀抱绝埃尘”的诗句,大意是称自己才是“无明客”,承蒙鉴真以佛法善诱,从而心怀脱俗。后两句分手的时候被我写下来送给了
+ex(开始青春疼痛文学了是吧),原本是想最后给他一点安慰(因为分手是我提的,我真善良)。但我后来想想觉得他一定永远不会关心这一句我从哪里见到、是什么意思,说到底他也一直都根本不太在乎这些,很难相互理解,罢了。并不是说我是文青(?)就要求他也得是的意思,只是说完全不在乎别人的心意的话会很令人失望,一向如此。
在半退役的苦闷高二,我在地下一层兜过无数圈,上述这些以及见到过的其他有趣的书几乎都借来看过一遍,它们是在这个学校里待了三年,真正影响我、改变了我的东西。只是一直都是崭新的,似乎不太有人会去地下一层的书库找书。一层也有一点比较有意思的书,印象里看到过一本全英文的烘焙书,放得很高,里面写了各种面包的做法,适合画饼充饥。但我想它在那里可能是因为书脊比较漂亮,被用来当装饰物的吧。但实际上一层书架不多,大多数放的是教辅和给竞赛的同学用的大学教材。桌椅很多,桌上还有台灯,基本是作为阅览室使用的,在里面卷自习的不少,我也曾经是其中的一员,后来遇到一些困扰(这个故事或许下次可以讲),就再也不去了。
+对了,想起《哈扎尔辞典》和《天平之甍》的时候是我难得的会为我的高中感到骄傲的瞬间,尽管我猜这两本书几乎不会有别人借来读过,但它至少存在于一个中学的图书馆里,这让我无比幸福。
+感觉在很没水平地掉书袋...实际上我确实喜欢阅读,但是并不算擅长写作。高中语文考试阅读从来都能随手拿高分,作文就不一定,太擅长写
+random thought
+和不停堆放读到过的东西,要么就是刹不住地表达情志,写不来议论文,经常被骂。虽然只是和同班同学相比的话,根本不需要作文写多好就能爆杀大家(?)。Anyway
+我写的东西实在没什么水平,感谢大家忍受我(,要我做读者的话还好一些,但坚持阅读,思考和写字,这才是我理想的生活啊。
好啦,碎碎念完之后,我要准备出门去看话剧啦~
+1月11日
+写个流水账。一边收拾东西一边摆烂,收完发现就一个行李箱,还有一个平时背的单肩包。单肩包里就放了贵重物品(其实除去电脑之外,我包里最贵重的东西是一支不算常用但一直带着的口红和一小瓶香水,草),证件,水杯和路上想读的《汴京残梦》,甚至没装满。说来惭愧,《汴京残梦》还是去年五月从毕业的社友那里收的二手,听说是黄仁宇(就是《万历十五年》的作者)的作品,就买了,到现在也没读,那位社友也很久没上线了。
+暑假来北京的时候带了行李箱,一个书包,一个单肩包,一个放在行李箱上的袋子,回去反而少带了很多。一想到明天在车上还要找个路人或者乘务员帮忙把行李箱抬到架子上,有点绷不住(。但是装了书之后我是真的拿不动,拿不动还要带这么沉的箱子回去,是不是我有点问题(#每日内疚 +#每日社恐
+晚上骑车出门兜了兜风,友人送了一张奈雪的券要过期了,就到东南门外的奈雪买了一杯。前两天趁最近闲着没事,还报了个今天的被试,赚点奶茶钱,其实就是在 +FIT 楼玩了会 VR,采集动捕数据。运动量超过一个月总和了(
+有道理,下次可以把打赏的提示改成 buy me a cup of bubble tea(奶茶用 +cup 吗(
+1月12日
-
-
统计推断开课了,会 follow -经典教材,这对我来说是个太好不过的消息了。数理课看电子教材有点难顶,这书又很贵,而且只用七周,于是我下课后速速去逸夫馆借到了最后一本书,乐到把手机忘在了书库里。回去找还迷路了,非常抓马。(为了几十块钱好卑鄙啊,这就是穷吧.jpg
-洗心革面,好好学习统计推断!(但愿不是 flag
-北馆和逸夫馆里好新哦,逸夫馆的绿色小台灯让我想起了高中图书馆里桌上的台灯,很温馨的感觉。可惜人实在太多了,有点社恐地狱,起码我觉得不是一个很适合(我)学习的地方,还是法图和三教比较好(悲
-月光长走的时候突发奇想打算去找找宁斋在哪里,何宝和上学期高代选老师的办公室都在宁斋,他俩都是近两年来华子的青椒,看来不仅是理科楼,近春园西楼也已经满了,
-为什么不是希尔伯特的旅馆呢在近春园西楼门口遇到了一只猫猫,旁边两个姐姐貌似在劝它“你就吃点吧,特地给你带的”,笑死。然后它真的低头开始吃了,说明猫猫爱世人,喵门。
-
-
从近春园西楼后面的小门进去,再走一段路就是宁斋,门外的院子是华子校园巴士的停车场。我以前路过这里多次,一直以为这个小楼是司机的休息室,没想到是宁斋啊。拍了两张对焦不同的照片,里面亮着灯的一间房间里似乎在开 -seminar,在寒风中远远望进去,很温馨的感觉(?
-
-
还看到了西楼社区,没想到都是那种很有北方特色的平房,有小院子和爬着植物的篱笆。我原以为会是楼房,原来华子的家属区也分为破的和豪华的,就像紫荆和南区 -/ 20-29 号楼一样(
-总的感觉西门附近的建筑都缺乏修缮,近春园西楼算是最好的了,后面的小院子也很破败,到处是杂草和碎石。
+今天在回家的路上,原本写了个长的,到家看看觉得不大适合发出来,就算了(
+我经常和朋友说我真的很焦虑,真的很焦虑,我和 Bowen L +(就是抽代助教啦,以后就这么称呼了)聊天的时候或者和 wjd +老师发邮件的时候也说过,焦虑已经成为了我生活的状态之一。然后大家都告诉我,不要焦虑啦,但不要焦虑的原因往往是因为焦虑也没用,只能消耗能量,所以不要焦虑。这话虽然没毛病,可是我听了之后更焦虑了——我在为因为自己的焦虑而消耗了做别的事的能量这件事而焦虑,为什么我这么辣鸡,每天要不停地破防和焦虑,别人不都克服了焦虑然后把时间花在有意义的事情上了吗,我怎么做不到呢?
+下次换个说法劝我吧,骗骗我也好啊(
+差点忘记了,1 月 11 日或者 12 日的话,要放一首歌在这里呢:《またねがあれば》by +當山みれい
+去年第一次遇到这首歌之后为旧事又破防了四个月之久,自闭太久了连破防都算是给自己找事做,有点傻。关于这两个日期就不细说了,总之还是青春疼痛文学(。其实除了第一段歌词和歌曲的封面之外也没有特别贴合的地方啦。
+很久没听过,才发现现在居然也要 vip 了(
11月10日
+1月13日
-
-
查了一下下学期的课表,统计中心的课和数学系居然正交,太感动了。而且下学期放掉基物之后就没有必修的物理课了(如果不把数学物理方法当物理课的话),我去,太爽了,是打数学基础的好时候!
-分析基础非常悬,实复概三选二的话实分析暂时不打算上了,尽管它比复分析更有用,留给大三补好分析基础再来,改复分析 -+ 概率论(1);水一个概随,权当弥补这学期初概 PF -的绩点了;统辅的话是周在莹老师的线性回归分析和邓婉璐老师的多元统计分析,又能见到婉璐姐姐了,好耶!
-此外可以补一个统辅导论课,比如生物统计学导论或者统计学习导论(其实从 -workload -和对于进组细分方向的帮助来看,我可能还是更倾向于生统?),也了解一下应用场景,还能多认识一下统计中心其他的老师。没有意外的话(指确定不换方向的话)准备暑假进组。我真没想到统计中心还有 -NLP 的组(俞声老师),果然工工里面什么都有,但我是想走数理统计 or -Bio-Stat 的。
-数学物理方法是必修,还替代不了。我不是很清楚和 ODE+PDE -相比是不是弱化了数学强化了物理建模,那样的话有点恐怖,学不下去就退。土木系还有两门一看就很屑的必修课,测量学和工程地质,估计属于难度不高破事一堆给分还不好的那种,到时候再说。然后选一下基物实验,选一下政治课,选一下体育(或许可以再上一遍这学期的剑术?那不是爆杀吗 -x)再加个通识课。
-这样的话肯定是 30 -学分往上了,稍微有点恐怖,但考虑到概随约等于没有,可能也还好吧?反正学期中间要是觉得受不了了,就优先退掉必修课明年再来(草),没什么可顾虑的...。我每学期都嚷嚷着想选点水的通识课提绩点,但最后还是会 -all in 能学些东西的课,乐。
-最近想把之前看到的统辅课程测评重新排个版搬过来,我的博客读者中有几位统计学潜在选手,想卖个安利;另外原来的排版太糟糕了(x)。当时读到的时候给作者留了联系方式认识了一下,找他问问是否同意。
-UPD:搬过来啦。V1ncent19 学长还非常慷慨地表示欢迎以 CC BY-NC-SA 4.0 -继续传播。
-友:你大三下学期修不完必修课,不是不能保研吗?
-我:我不保研,我现在担心的是到大四春季还剩超过三门必修课的话毕设不能开题,别千辛万苦拿到 -offer 结果延毕了(
-想给我自己颁一个乐观抗压奖,真的,太乐观了
-聊到凸优化的时候想起来 xyx -上学期说在上包老师的凸优化,就去简单问了一句测评,确实是研究生课,40% -作业和 60% -两人一组大作业,和下学期求真那个应该会不太一样。他说他和包老师关系很好,我当即的感觉就是
现充好可怕,啊不是,擅长 -social 的人太厉害了。
+在北京苟了一个月没有感染,回家第一天就病倒了(
+虽然可能和不适应没有暖气的室内有关,应该只是感冒,总之是发烧了,躺平。
+工程经济学的加分论文到最后还是放弃了,实在是没兴趣做,算了吧。以前我还愿意为自己的专业课付出一点时间挣个好成绩,但自从找到兴趣点之后就越来越难以忍受这种被迫卷的工作,它们对我此后的人生毫无意义啊!
+但其实暑假里的工程计算机制图就是前车之鉴,因为没兴趣卷,被 curve +后吃了 2 学分的 +C。工程经济学据说给分正常,老师教这门课已经至少十年了,理应不会有太大的改变。我真的不想做额外的工作了,开学之后补考完期末拉倒。
+说实话,我真心钦佩院系里多数同学的吃苦耐劳。明明被这个专业恶心得不行,还兢兢业业地按计划完成培养方案里的每一门课,把加分论文卷成不写就等于减分的任务,在所剩无几的时间里塞几门 +CS 或者金融的课程,已经活成被华子 PUA +出的形状了。我从前还能做到,现在只生理性抗拒。当然可以说我是逃避,自己懒惰加上水平不行就赖学校和院系,但每个人展现出来的状态不也和环境有很大的关系吗(
+昨天在高铁上,半梦半醒中被一个同学拉着问软软和贵系还有工工几个组的差别(我也不是很懂啊!),听他谋划限制保研方向后还可以做的几个最优解,说软软某个导师门下几乎都是非清本,所以觉得自己可以去碰下瓷,以及“再不济软软总比土水强”(怎么乳软啊!),etc。
+华子从来不培养人,它只会 judge 人。你想接受这套逻辑,乖乖躺下给它 +judge,它还说你不配被 judge。
11月11日
+1月14日
+还在发烧,睡了一整天,所以没啥可写的。晚上好多了(
+1月15日
-
-
学习数值分析的最好方法是抄书...梦回高中的时候看化学竞赛的同学抄各种砖头。抄了一遍就会了。
-抄到矩阵扰动了,还有线性迭代方法和非线性迭代要抄,我觉得我行了(确信
-开了一本 GTM 笔记本抄的,草,感觉很神圣(
-大雨天,中午出门的时候久违的闻到了湿润的空气的味道,一瞬间以为回到了南方。又想起来友人之前和我说“讲吴语的齐国人”的时候还说,有两个故乡是很幸福的事情吧,我说不是的,这样我根本没有故乡。
-晚上未央开推研会议,我懒得去,就让室友文字直播一下,然后去吃李先生了。李先生的牛肉烧饼真的好吃,塞得满满的,饼也很酥松,比牛肉面好吃,八块钱一个感觉不算太贵。吃完那边会也开完了,反正就是列了一个不允许跨保的黑名单(尚未公布),明确有金融和管理类,我觉得肯定也有计算机类,这样的话大家倒是沾了未央软件那十个人的光,软软怕是要被未央人卷了。然后据说大概率不能外推,出国不限制。其他消息还有只要能在未央毕业就能拿到推研资格,但是不自带名额。
-这已经比我想的要好一万倍了,我之前甚至想过,如果不能开出国成绩单的话,就先去做一年 -RA 再申请..
-所以这个会确实和我没关系,我想哪怕校内跨保他们也不会闲到限制去数学系和求真,而统计中心目前流落在外倒有可能被制裁。而我大概率是要出国的,就更没关系了。听完消息之后我第一个想起的还是大一的时候,看 -xyx -在小群里说想跨保去茶园要发多少顶会什么的,而我那个时候还在痛苦地纠结是转码还是转数,也还会因为码不出来而深夜破防,看到他的话更加焦虑了。不知道推研具体卡不卡茶园,他现在又在怎么想呢。
-吃完饭去做核酸,听涛的核酸队伍排得都要打结了,于是去了祖龙广场,才知道这个规模原来也算广场,和社友起名的“有鼎广场”差不多嘛x。人相比之下不算很多,而且没有灯,把脸埋在围巾里就没人看得出来我没戴口罩(
-抽代课上看转数环友吹水下学期的课哪个老师更好,我看了半天才意识到,我一没有必修志愿,二还得手动选课,哪个老师好和我有啥关系?
-概率论是王小群和梁宗霞,前者以前开概统,今年第一次开概率论,后者好像是定理原题默写大师,学不到东西,但我可能只能选他了。不过好像只要背诵得当给分就还好,也就算了,出卖灵魂就出卖吧。
-复分析是张广远和薛金鑫,虽然复分析不限数学系选课,但我没必修志愿可能也抢不到薛金鑫。环友评价张广远至少算是本手而不是俗手(而梁宗霞是断手x),那也还能接受。
+两天睡了至少 30 +h,总算缓过来了,感谢关心捏。做了三次抗原全都是阴性,烧了两天还没获得新冠抗体,真是有点亏。
+下午写了会统推讲义,差不多把统计量约定和性质写完了,
+发现以前的理解还有点不很对的地方,什么叫费曼学习法啊。打算发个邮件给老师,让她先检查一部分。说起来开个 +Repo +做这件事的话比较方便吧,不用时不时手动发邮件了,社恐狂喜,但不知道老师习不习惯。中学的时候似乎也学过样本方差的概念,当时就搞不懂为什么系数是 \(\frac{1}{n-1}\) 而不是 \(\frac{1}{n}\),不过这一部分高考和竞赛貌似都不考,也没讲过。现在才知道是作为统计量看待的话,修正系数之后才能作为无偏统计量来估计分布方差。
+上了大学才知道好多省份的高考还考线性回归,修统辅之前我连这是什么都没听说过,突然有些担心把这些东西写上去的话会不会太浅显了。不过上海高考连导数、动量这些东西都不学(听说现在要考导数了),还真的挺利好理科苦手(指我自己
+啊对了,暑假里写的几何题解终于发出来了。我之前和组长说我下次应该不会再写这个了,真的做不来难题,收几个水题跑路有点丢人,另一个是大龄玩家(?)好像也不应该再在高中生的游戏里浪费时间,该往前看了。
+不知道为什么,组长给冷老师发的邮件里说这是我们组最后一次写 Sharygin +了,卖了个情怀。别人也都是这个意见吗?
+但我对大学的数学竞赛似乎也没什么兴趣。觉得丘赛离自己太遥远,根本什么都还没学会,又觉得全国大学生数学竞赛那个报名非数组不大合适,数学组的话一样没学会。新生基础大赛的时候也是这样犹豫着,既没有报非数也没有报数学组,最后咕掉了。但当时到底是不是因为微积分 +A2 +学得太拉,怕在非数组里暴毙,我也记不得了,似乎有这个原因,那真是有点菜啊。麻了,快去学习(
+草,上面那个推送又把我名字写错了。虽然也不是第一次被写错名字,但找一下这个字很难吗(恼
+下雪了,但远远没到能积起来的程度,在半空中看雪是很大的,飘落到地面就没有了。
+本来想拍点什么,然而相比北方的大雪实在是寡淡。发现楼下有一只猫猫在打滚,橘白可爱捏。
+
+
晚上去盒马拿了我妈预定的两盒水果,看了眼价签,三斤小番茄 20 +块钱,六两草莓 30 +块。感觉自己真的是很没生活常识,常见的菜价我恐怕基本都说不出来,这种精细的水果自己一个人的时候也不怎么买,更不清楚了。想起来最近好多(?)up +主都在打丹东红颜草莓的广告,点开过一次链接才知道真挺贵的。又想起墨茶去世前几天说想吃草莓,大概也是现在这个时候。所以雪下得薄一些也没什么不好,在楼上看雪时埋怨雪不够大没有积起来,因为在楼上啊。
+#每日为赋新词强说愁 #每日不知道为什么但是感觉会被骂 +#每日叠甲
11月12日
+1月16日
+好像距离最后一门考完已经过了一个星期了,这一个星期没怎么玩但也没怎么学,到底干嘛去了呢(
+今天去了嘉兴,大概是规划过的江浙一日游的第一站,其实也只规划了第一站。来回火车票
+25 块,似乎比坐 16 号线去滴水湖还便宜。
嘉兴是我长大的地方,出生之后直到上小学之前都在这里度过。在南湖区逛了逛,除了父亲曾经供职的嘉兴学院和小时候住过的小区,就没看到什么和记忆相符的地点了,连幼儿园都搬走了,怎么会事呢(。本来是来治疗精神内耗的,结果光是迷路就给我走迷茫了。
+以前有一段时间对轨交线路比较感兴趣(倒不算车迷),玩过几次随机公交/地铁挑战,买一张一日票,不用动脑子,随机在换乘站下车搭另外的线路,还挺开心的。结果有次在复兴岛下车之后发现没地方去了,骑共享单车到五角场吃晚饭,草。后来虽然不怎么尝试了,但大多数换乘通道长什么样子我都有印象。也想过乘公交车省际来往,但是一直没有成行,这个肯定会更辛苦,不太有精力。
没拍什么照片,也没去乌镇和西塘,没买东西带回来。路上翻了翻包发现还带着学生证,随手打开一看,学籍注册栏的那两页一共有五个大框,可以贴十个学期的注册章,是否在暗示我延毕一年也贴得下(x
+所以为什么要跑这一趟呢?我也不是很清楚啊!
+++就这样,他(波塞冬)几乎没有察看海洋,只是在匆匆攀登奥林匹斯山的途中,飞快地瞥上一眼,而且他的确从未在海洋里航行过。他常说,他以此等待世界末日的来临,到那时候,也许会出现一个安静的时刻,就在末日快要来临之前,在检查完最后一笔账目之后,他还来得及做一次快速而短暂的旅行。
+——卡夫卡《海神波塞冬》
+
1月17日
+
1月18日
-
-
熬大夜抄数值分析,抄完了 Jacobi,G-S 和 SOR -方法才睡觉,早晨起来又继续抄,太惨了。
-乐子一则:SOR 方法的迭代矩阵是 \(S_\omega=(D-\omega L)^{-1}((1-\omega)D+\omega -U)\),推导完之后觉得这怎么记得住啊,难道每次都要推一遍吗。结果自从把第一项幻视成 -dwl 之后就记住了:这个矩阵是 dwl 的逆再乘一个 \(D\) 和 \(U\) -的线性组合(对不起邓婉璐老师,真的对不起(
-这学期结束,我的代数学习可能就接近尾声了吧...线代,高代选,抽代,数值分析,遗憾的是高代全靠自己拼拼凑凑,没有很扎实地上完两学期,但暂时还是够用的。代数很有趣,我觉得初学的情况下远比分析有趣,毕竟还是具体一些,(但真让我做那种矩阵的怪题目我觉得也未必行),这几门课也很好地把我带进了转数的坑。之后看情况可能再去上个代数学前沿基础,或者上拓扑学,就真的要说再见了。听说下学期的代前基是 -zmx 讲,她这时候不应该在开高代 2 才对嘛。
-下午,翻开书,抄共轭梯度法。阅读定义的我:梯度是什么来着?(
-然后又想起来上学期各种暴躁,摆到最后喜提 B+ 还没记 PF 的微积分 -A2,果然是学得不行。但我在重读分析之前暂且先拒不承认自己有问题,一定是这课太破了((
--
因为享受着它的灿烂
-因为忍受着它的腐烂
-你说别追啊 又依依不舍
-所以生命啊 它苦涩如歌
+昨天开 Learn Mathematical Analysis or Die +的时候其实根本没想好写什么,写好序言就直接传上来了,当时想的是就算不知道写啥,先给我一种“大家都知道我在学这个东西了所以不能再鸽下去了”的感觉也行,不然真的一天睡 +20 +个小时。后来发现我话挺多的,不愁没得说,以及真的开始看了之后觉得挺有意思的,不像以前一样恐惧了。
+可能是因为学过了抽代和数值,高代虽然没上课但除了多项式也基本学完了,所以再回头看数分觉得以前搞不懂的东西有些其实很好理解。总之确实,可以用很多种不同的顺序完成培养方案。
+不过明天要出门和友人小聚一下,就不 learn mathematical analysis +了,我选择 die(
摘自 Learn Mathematical Analysis or Die:
++
-要开始构造实数了!用的是 Dedekind 分割。这个我也在 wxf 的微 A +课上听过,但他讲得并不认真,仅限念了一遍定义。后一节课课前有同学提问说,为什么一左一右两个集合就能代表一个实数呢?他不是很愿意理会的样子,反问说你是不是补退选进来的所以没听过第一节课啊,一只羊为什么代表 +\(1\) +呢,两个集合怎么不能代表一个数呢。
+他可能是觉得这个问题太 trivial +了吧,也或许只是当天心情不好而已,然而提问的同学看起来还是没理解的样子,还平白无故被敲打了一下,就茫然地坐下了。Anyway,在这之后我对这个课堂的印象就不是很好,后续也很少再去上课了。只是觉得,为什么不能好好讲清楚道理呢,就告诉同学理由是从几何直观的角度来看,把实数轴任意截断的一点都是实数,有这样的一个定义不就好了吗。当然,当然,应该是我吹毛求疵了,他可能真的只是当天心情不好,所以不太想解释,后来我也没怎么再听过他上课,不清楚还有没有类似的状况,可能属于是不小心碰到了一个极端情况。
+另外,单是讲过这个有什么意思呢,不说 Dedekind +分割满足序公理所以确实可以定义出实数,也不拿来用一下,就莫名其妙放一个定义在这里,课后又让做题目,感觉是在炫技。后来我也看过一部分他的讲义和回放,挺多莫名其妙的安排都有点像炫技,就彻底放弃跟进度,自己单开了。不过确实也没人逼你选他的微积分课,接受不了的话,换别的老师的课堂就好了,或许是个伪命题吧。
+虽然大多数同学都吹 wxf +讲课有多好,但我其实相当怀疑他们有一部分并没有听明白课堂内容,觉得老师讲的内容很高深,自己吹捧老师的话会显得很厉害而已。另外听说 +wxf +的答疑确实很认真,或许大家说他好是指这一部分吧,还是指他喜欢在课堂上和群里讲笑话?PPT +和讲义是准备得挺认真的,可惜我并不觉得设计得好,
+感觉白认真了。总之我是不太喜欢这种不彻底也不成体系的高阶知识下放,或许它自有意义,带大家了解一下也好。当然,和我相反的典型就是 +wl 他们,是真的学得很好,也喜欢 wxf +的课堂,所以我这些话很可能只是弱者的托词而已。也是啊,我觉得他讲得不好,大一的时候干嘛不自己去看一千零一页,而是单开去拟合微积分往年习题了呢,乐。弱者的牢骚暂且发到这里,下面继续说点正经的。
歌单 ++(
画风其实是这样的,想到啥说啥。不过很奇怪吧,我觉得 wxf +的高级课堂没什么意思,几乎不怎么听课,也从没参与过课后的讨论班和群里的讨论。说到底我也不咋喜欢群里的氛围。前段时间那个课程群还在不停弹消息,大概是 +wxf +被推到校级的清韵烛光去了,大家又在膜,说到底这个也很正常,但不知道为什么我就觉得有点烦,直接退了群,第一次结课后退课程群。笑死,单从这些来看,我并不像是对数学很感兴趣的样子。
+wxf 爱好者(如果有的话)请轻点喷我(
+沃日,这个月评论区好热闹啊,
社恐震惊
11月13日
+1月19日
-
-
抄完数值分析了,数了一下抄了 50 面 GTM -的本子...真麻了。不愧是古老的神秘(虽然相比之下不是很古老),idea -还是很多的。有一些东西我感觉还不是掌握得特别清楚,先搁置一下之后再来看。
-想起来友人和我说过的一句话,idea 远比调参重要,当然我对 AI 一窍不通啦 -:3
-昨天忘记发了,出寝室的时候看到楼下的叶子被扫成了一堆,非常漂亮:
- -
-室友今天给我表演了一个在床上爬(
-其实看到各个高校爬行的视频的时候,我第一反应是想到了《春宵苦短,少女前进吧》里面女主跟着在玩行酒令(?是吗,忘了)的人们一起爬的情节..太阳底下无新事(??这是什么结论
-看到小学期工程计算机制图给 85 分的我一个 2.3 -的那个老师,成为了土木系“良师益友”提名教师,听我说谢谢你(。这学期在课咨委做完导论课的提案,下学期应该可以去改这门屑课了,当然应该不是我来带提案组,所以期末之前要和 -lyf -还有土木系那个学长再提一提这件事,不然还得拖一学期,还得伤害一批人的绩点(。
-摸鱼的时候排了一下下学期的课表,这已经 32 -学分了,还想加通识课,使不得。
-上学期选课的时候纠结无比,大改了 114514 -版才变成现在这样,而实际上也还是不完满,甚至数据结构还在我的课表里待过很长时间,开学后最终还是退掉了。这学期感觉不怎么需要纠结,难点在于顺利把这些课都选上
--
-- - -- - - - - - - - - -- Mon -Tue -Wed -Thu -Fri -- -1 -工程地质 -- - 概率论(1) -- - -2 -概率论与数理统计 -- - - 毛概 & 习概 -- -3 -- 剑术 -测量学(后八周) -基物实验 -- - -4 -概率论(1) -- - 基物实验 -数学物理方法 -- -5 -复分析 -- 复分析 -- 数学物理方法 -- - -6 -- 线性回归分析 -生物统计学概论 -多元统计分析 -- 这样来看的话没有多少用来大卷一场的下午和晚上了,所以下学期得努力早起,草,对我来说好难
+前两天读完了一千零一页讲义的实数理论部分,又写了习题,给我乐死了。学完代数再来看这个也太爽了,完全解决了我秋季学期学抽代的时候想过的
+一个看起来很蠢的问题——实数域和普通的特征为 +\(0\) +的域到底有什么区别,特殊在哪里?明明它们在素域的层面上看起来还是一样的(实际上也不一样,没有序关系,但至少形式还是一样的),为什么素域之外的元素差别这么大?举个例子来说,普通的域在素域之外完全可以没有元素,为什么实数域却比有理数域多了那么多元素?何宝在课上时不时会指出,我们研究的域比较抽象,没有序关系。我虽然也觉得这个是重点,但并没有觉得是一种决定性的不同,以为是有什么别的更本质的不同,导致了在实数域上存在序关系,或者它只是“不同”之一。至于序是什么,不等号究竟是什么,序公理是什么,一概不知了。
++
+吾尝终日而思矣,不如须臾之所学也。
+感觉真的很丢人啊!怎么会有人这个时候才学这些东西
+顺便把那一篇改成数分 I +速通日志了,感觉会写很长,就别合在一起了。
+后面和一元微积分重合比较多的部分大概可以快很多,毕竟这个我还是有胆量说自己学得不错的,感觉又有希望能学完了。
+和友人来吃了暑假一起吃过的烤肉,当时也是在这里填了用餐人数 999 +人,点完单后收到了 4995 +元的餐位费账单,草。一个测试工程师走进烤肉店,烤肉店溢出了((
+一些今天的智慧发言,记之:
++
-
+
为什么只有 Elden Ring,没有 Elden Field,Elden Group,
Elden +Principal Ideal Domain,etc. ?
+就像得证可以写作 Q.E.D.,或者直接画一个小方块(我 MO +时期甚至比较喜欢画完再涂黑,或者画上阴影)一样,我觉得良定义也可以有一个比较新的代词,叫 +happily ever after 就很好。中文的话 FGO 里翻译得不错,叫做夜话团圆。
+友:为什么不能叫做“你看看,我帮你把 bug +修完啦!”呢,我觉得这个也很合适(
11月14日
+
+
1月20日
-
-
今日无事,记录一则和友人的扯皮:
--
友:我感觉你从放弃转码之后状态好多了
-友:说点你不爱听的,我觉得你就算当时去交大可能也会很痛苦,搞不好和 -xxx(指 ex)一样
-我:?倒也不至于,他这个单纯是因为实在不大聪明
-友:这是报复性发言吗(
-我:不是,我一直都这么觉得,反正感觉还不如我 -=。=,而我也不算什么聪明人
-我:我觉得他应该去读个文学硕士什么的,然后当翻译去,比较适合 XD
-友:小绿和小蓝吗
-我:嗯,感觉是一个本该成为小绿的人去做了小蓝的事情
-友:不是,我是想起来小绿要被小蓝开发的同声传译 AI 取代了
-友:(笑)说起来笛子已经很久不更新了,感觉是想不出来后面的剧情了
-我:所以现在有类似于同传的 AI 了吗
-友:有类似的产品吧,我用过 Otter.ai,遇到有口音的人就表现一般,还不如 -Chrome 字幕
-我:所以同传的场景会有人有口音吗
-友:不知道诶
-我:不知道诶
-友:不过你要是科班出身,有环境、资源还有 fellow -的话,可能也不会像在华子自己转码这么焦虑
-我:不知道,我的性格就很难有 fellow,也不擅长利用资源
-我:还是传统式的学习比较容易啊
-友:小镇做题家吗
-我:小镇做题家哦(笑)
-
-突然想起来还有门期中没考...周六的工程经济学,感觉可以周三再开始复习(
-就,过一遍 PPT,再拟合一遍往年题就行了。希望人没事。
-明天跑 1500,去年跑了 -8'20'',真的太强了,不知道怎么做到的。今年可能根本跑不进 -9'40'',但愿活着回来。
-
11月15日
--
-
- 活着跑完了 1500,正好 9'20'',比去年慢了 1 -分钟。其实我跑的时候还觉得自己挺快的(乐),以为能进 9 分钟。Anyway -这不重要,我这个羸弱的体质,跑完还活着 & 甚至能拿到 3 -分就很不错了。 -
- 今天也没啥别的事,只剩下跑完 1500 -之后腿还在疼,早点睡了,明后天还得预习工程经济学(悲 +
突然觉得是不是下学期不该选复概而是应该选实概来着,它俩关系还大一点,读一千零一页还攒了点信心。
+现在选也来不及了,实分析只剩何凌冰,大概是听过他的数分之后接着上比较好,别折腾我了。至于取并集三门一起学,那要退统辅课才能活下去,我又不舍得,不要再动了。又要表演一个以任意顺序修培养方案。
+期末怎么只出了 8 +个学分的成绩,看来听说可以查成绩了就在大年二十九蹲点刷新 THUInfo +的我还是不够摆烂,还不如老师摆。数值分析和抽代都没有出,有点担忧是不是要看缓考的情况向下调分,我真的怀疑这两门课要调分就只能向下调(
+一学期没打开 THUInfo +的成绩单界面,于是时隔好几个月又看到小学期那门拿了 C +的工程计算机制图,麻了。
11月16日
+1月21日
-
-
一些碎碎念:
-经常遇到一些需要找人合作完成的任务,有时是小组作业,有时单纯是想在课程群里随机抽样一个人对对作业答案。每当找到这么个组织的时候,如果其他成员是大腿,总是一件令人高兴的事情。我也比较喜欢预设其他成员是大腿,一般都会先发出来一个自己的解决方案请别人提提意见,尽管里面有很多我知道而且暂时解决不了的 -bug,总之是希望从别人那里得到一点启发。
-然而比较差的情况下别人根本发现不了 / 发现不全 bug -在哪里,欢欢喜喜地拿着我的破烂方案就跑了;比较好的情况也只是能把 bug -提出来,再反问我一句怎么办啊,能得到解决方案甚至只是能得到启发思路的情况极少。到最后总还是我自己吭哧吭哧把 -bug 修完,然后再让对方 check 一遍没有伪证。
-所以,难道到头来大腿竟是我自己(?有的时候又觉得有点好笑,
-希望以后读研的导师别是这样的。为什么突然这么想呢,因为最近统计推断的课上没有认识的人,于是抽样了一个经管 -+ 数辅的同学讨论作业。本以为数辅应该很强,没想到也只负责对我提 -issue(。刚刚上课的时候没听讲,自己把问题修完了,对方 check -了一下表示这下就不是伪证了,快乐地抄进了自己的作业里,而我课后还得补一下课堂内容x,感觉愣是给自己找了个甲方。SRT -也是,做工工 AI -的项目本以为能抱到大腿,看了另两个人的申请书才知道他们都没学过 -Python,这下大腿(暂时)真的是我自己了,感觉很艰难啊。
-另一些碎碎念:
-首先要向阅读这一段的朋友道歉,我理解并尊重大家不同的卫生习惯,但我也确实洁癖,希望不要冒犯到(
-冬天手洗衣服会困难很多,冬衣一盆只能洗下一件,水也很冷,要戴橡胶手套,洗一次衣服要耗费不少心力。但我恐怕还是永远不会用楼里的公用洗衣机...今天洗了好几盆衣服,站在水池边上重复着搓洗的姿势,感觉像罚站一样。然后想起来了 -EVA TV 版里明日香的一段话(是的我还真的去找了,在 22 话):
+除夕啦。已经十多年不回老家过年了,说实话老家也没有给我们去的地方了,一直都是和我妈在家里过。过年的一天感觉和平时也没什么差别,除了上海外环以内全域禁燃烟花爆竹,我家正好在外环外面一点点,放得格外凶,傍晚开始爆竹声就没有停过。
+聊起来父亲那边的亲戚,说起堂哥(?是这么叫吗),是父亲的大哥的儿子,比我大六岁。上初中的时候听说他大学考得不好,最近又听说他考研考了三次,考上了一所二本,再读三年就要工作了。
+因为不怎么回老家的原因,我对堂哥的印象很模糊,但总感觉到亲近,印象里觉得他是个可爱、腼腆的人。大概只有两个记忆点,一个是五六岁的时候在父亲那边的农村老家过年,他把他的悠悠球拿给我玩儿,但我没玩过狭义上来说是男孩子的玩具,差点给他摔了,他好一顿大呼小叫。后来在院子里放鞭炮,大概是打了什么赌然后我赢了,他摘下毛线帽子,蹲下来让我弹他脑瓜崩。
+还有一次可能是刚上小学的寒假,大伯带他来上海,找姑姑一家和我家一起出去玩,也是最后一次和父亲那边的亲戚见面。姑父是生意人,很豪气,到陆家嘴请大家吃了披萨,然后还一起去了水族馆。大伯只买了堂哥的票,让他跟着大家进来玩,自己在外面等他出来。姑姑姑父带着堂妹玩得很欢,堂哥一路默默跟在我父亲身边,跟我们一起逛,也不怎么说话。最后到了纪念品店里,我挑了一串贝壳手链和一个小冰箱贴,冰箱贴是一个小瓶子,里面是水和油,界面处浮着一条塑料小鱼,无论怎么倾斜小鱼都会浮在界面上,不会沉下去。付了钱出来之后父亲在我身边轻声说,哥哥一个人来玩的,没人给他买东西,你把小鱼当做礼物送给他好不好。但我当时不愿意,父亲劝了两次之后还掉了眼泪,最后堂哥安慰我说他不想买东西,没关系的。
+长大了才懂得为什么大伯只买了哥哥一个人的票,懂得他为什么听话懂事,想起他的时候都会很难过,想着当初为什么没有把小鱼送给他。后来知道他在受教育的过程中一直在跟着大伯辗转,不停地转学,经常在一个省市读一学期,就要跟着大伯再去别的地方,来过上海,去过徐州,周口,也在山东的几个地方待过。分明各地学制教材都不一样,慢慢被折腾得成绩越来越差。即使我也经历过很长的贫乏的生活,但至少始终被母亲重视,安定地成长,还是幸运太多。现在也不知道他身在哪里,长成什么样子了,在学什么专业,将来打算做什么。最后的印象就是十多年前在纪念品商店里,他一个人站在货架前面看恐龙模型,后来仓皇地来安慰我,以及在水族馆里逛的时候他跟在父亲身后半步,怯生生的样子,父亲每每和他搭话,他都腼腆地笑。
+写完之后眼泪汪汪()地去找那个小鱼瓶子,一下子找不到,更加难过了,而贝壳手链带到北京去了,现在还放在学校里。住在上一个家里的时候小鱼瓶子还在呢,不知道是搬家搬丢了,还是搬来新家之后不知道放到哪儿去了,一定要好好找找。我想我一直为在事件上的记性好而烦恼,倒也没有必要,许多事情还是一定要记住,能记录下来的话会更可靠些。
+他的名字叫云飞。
+来点 TA 文学 #每日TA #终将成为TA(?
+今年的最后一天看到了 MashPlant +更新了学期总结,于是又去把之前的一些文字读了读。他的文章大概是所有我在线上能够 +reach +到的人的随记里面最喜欢的,每一篇都在不同的时期读过很多遍,甚至搭这个网站的时候没有多看,直接选了 +NexT 系列的主题大概也是因为看习惯了他的博客,随手就选了,实际上 NexT +很旧了吧。不过他不可能认识我就是了(
+我一直觉得我以前和 MashPlant +的心态很多都很像,无论是做题还是人际关系,当然他做题的水平比我强一万倍。像是之前他说在假期就开始做 +project,lab +一布置下来就要赶快做完,否则会很焦虑。我大一一开始也是这样的,网络学堂的剩余日期变成橙色的 +7 天就会很焦急,熬夜写 ddl +还有相当远的作业,结果非但没有减轻压力,反而疲于面对变化,甚至有几次不得不把提前完成的任务推倒重来。后来偶然看到了果壳的文章,感觉被戳到了痛处。因为知道作业是有确切答案的,才会这么积极去做,真正需要思考的事情反而不会想提前做完,像脑容量很小一样,慢慢就努力改掉了。
-
-美里和笨蛋真嗣用过了的热水,谁会走进去啊? -被美里和笨蛋真嗣洗过内衣的洗衣机,谁会来用的啊? -美里和笨蛋真嗣用过的洗手间,谁会坐啊? -美里和笨蛋真嗣呼吸过的空气,谁会来呼吸啊? -讨厌美里,也讨厌真嗣,我更加讨厌第一适合者! -讨厌爸爸,也讨厌妈妈,但最讨厌的便是自己!
+高中积累作文素材时记过一句话,叔本华说:“人生实如钟摆,在痛苦与倦怠中徘徊”,应该从来没有真正在作文里用到过。但现在看好像挺有道理,至少对我是很贴切的,有作业的时候我会非常焦虑,完全不会考虑ddl,甚至是在作业还没发布的时候,我就是必须马上把它做出来,这里的痛苦是不少的。但是做完之后,我实在想不到我还能做什么。很多人对我说我这种性格应该去读PhD,我知道自己读不了,这种劲头仅限于有确定结果的事,也就是广义的做题,我害怕探索,不能接受失败。
+——《研一下总结》
我的洁癖倒还没有到精神崩坏的程度(,但感觉也是分两方面的。
-其一是对“卫生”的标准问题,还比较表象。我自觉自己对卫生的要求算是很高的,也是从小受母亲的影响,慢慢养成的各种习惯。就像进出洗手间会多带一张纸,用来包一下门把手和冲水的按钮,就像室友洗杯子就是在水龙头上冲一下,我要拿洗洁精洗,洗完再用饮水机的热水烫一下,就像在教室自习的时候坐下之前会拿张纸简单擦一下桌子,等等等等。以前有个朋友说我矫情,不过后来他就不是我的朋友了(笑)(倒不是因为他说了这句话,而是别的矛盾((
-其二是心理方面的。比如说,我在寝室里总是感觉很局促,最近越发这么觉得。身后的室友换衣服或者找东西的时候,喜欢把椅子推得很远,于是我和她之间的过道会变得很窄,甚至她搭在椅子背上的衣服会碰到我的椅子。这个时候我就很难受,会想到她的衣服在公共洗衣机里洗过又拿出来感觉不是很干净。另一个室友从前有一次晾衣服的时候,把拿不下的衣架放在了我桌上(因为我的位置离阳台很近),然后我就去买了两块桌帘把自己的桌子围了起来(其实也早就想这么干了,只是那也是一个这样做的契机)。因为感觉她的衣服在公共洗衣机里洗,又要挂在衣架上,好像也不是很干净...天啊怎么对公共洗衣机怨念这么大。
-而且这似乎也是一个亲疏的问题。我向来想要保持和世界保持距离的状态,不喜欢不熟悉的人碰到我,我的衣服,我的东西,我总感觉“不是很干净”,平时也尽量不会碰到别人的东西。但想了想友人在隔壁也一样把衣服放进洗衣机里洗,我和她见面也还是会亲亲热热地打闹,也会拉她的衣袖和手
-(首先,我不是女酮(,感觉矛盾起来了。但话说回来,和室友倒也不是特别疏远,对于寝室里和我关系最好的室友,我也还是不愿意和她、她的物品有物理上的接触。不过她也很尊重我的习惯,还蛮感谢的。但是想起来社聚的时候我也把自己的耳环(其实是耳夹啦,不敢打耳洞 -= =)摘下来给好奇的社友把玩过,还分着吃了月饼(当然是掰着分的 = -=),却感觉很开心。是因为寝室对我来说是一个“更加私人,所以更需要保持洁净”的地方,还是因为和室友生活在一起,知道她们的生活习惯所以排斥?有点难说。
-这么听起来好像确实挺矫情的...草,感觉有概率会被喷。虽然这么说的话听起来很奇怪好像有点严重,但其实也还没到影响生活的程度(,一般遇到类似的情况都还是往自己身上找问题,会想“为什么我要把东西放在室友不小心会碰到的地方呢,下次要注意点”这样,稍微有点内耗,不过问题不大。
+一大早数值分析出成绩了,很怪。我知道这个消息还是因为早上醒来,看到课程群里有人要求复核成绩。我是不需要复查,但我很好奇这课怎么评定谁是 +A 谁是 A+,每个人的表现似乎都一样,难道真的是看总评有没有拿到 98 +分及以上吗,那真有点无聊了(
+今天的怎么这么长(
+祝大家新年快乐! qwq
然而本科学习数学,确实还是做题为主。我后来焦虑的点就转移了,变成怎么能通过我这四年(五年?)擅长做题(实际上也不很擅长)这件事推出以后能够胜任研究。我和
+Bowen L
+前段时间有很多次交流,有一次也谈到这个,他开玩笑说来读纯数吧,博士毕业都不硬性要求能发出来论文,导师觉得你有独立做研究的能力的话,就可以毕业了。说实话差点心动了。单纯用身边统计学的话的确大家从做题到研究的转换也没有什么大的困难,但我总是不知道自己能不能面对失败,或许该尽早去试试。
另外,从高中开始,我总是希望通过复现他人的选择,来努力过好自己的人生。强基的时候我想利益最大化,研究和打听了学校里上一届几乎所有人的情况,也没有匹配到和自己相似的(= +=),最后也没有成功,于是把自己的失败也总结成了一个样本来告诫后人。现在也是一样,在恐惧的时候总是试图看看某几个前辈是怎么做的,来劝慰自己暂时不做额外的尝试也没有关系,好好读书。只是想起从前复现的失败,心里还是会持反对意见,复现是不可靠的,一定要自己去尝试,走不一样的路。就像 +MashPlant 说他在复现 +n+e,到底还是因为害怕失败,不敢去走前人没有尝试过确定可以成功的路,但我心里知道自己如果这样做,一定会失败的,可能是因为自己能力不足,但我更相信生活没有复现一说。
+人际关系嘛,更是很像了(。MashPlant +的文字读起来最大的感受就是孤寂。
+++近期n+e写了他的研二上学期,全都是connection,与此完全相反,我的主题是“我将孤单度过一生”。我没学到他的精髓,甚至可能是学到了糟粕。这也没什么,他能力比我强,理应拥有更远大的未来。读的时候我就有感觉,数据也确实证实了,他的约八千字中有93个“我”,我的约一万字中有337个“我”,这还是我反复精简,删去很多主语之后的结果。我的文章,我的世界,唯一的核心永远只能是我自己。
+——《研一上总结》
+
但是确实,往好处想,至少始终忠于自己。
+至少写到这里我还是发现,心态到底比从前好了很多。当然我不可能始终留在从前,一定会往前走。
+11月17日
+1月22日
-
-
重新看了一眼昨晚的碎碎念,有点草,感觉这么形容之后自己看起来好像很难接近的样子,那倒也不是(
-仍然希望没有冒犯到大家,如果有的话,我还是再谢个罪吧(
-早上和朋友闲聊,才知道高中的时候很看好的一对情侣分手了,大概是异地的原因。当然,这件事已经过去一个月了,但我今天才知道,或者应该说才过去了一个月我就知道了,已经很快了。身边很多人都在不停地 -crush 和 break -up,吃瓜吃久了也多多少少会在某一对官宣之后就产生“他们会很长久”还是“不会很长久”的预感,虽然有这种预感似乎很罪恶,但还好我们都不是三体人。
-然而他们分开的消息还是让我小小的惊讶了一下,我不解的根源在于,算来都至少五年了,五年的情意分开也这么容易吗?或者我还想知道的是,五年的情意在分开之后会带来多大的惯性?
-我没什么可类比的,就反思了一下自己的人际关系。也就和老姐的关系最长久,大概认识了七年多了。顺带解释一句,虽然我这么叫她,但是没有血缘关系,只是 -15 -年的时候在网上认识的赛博朋友(草),她比我大一岁,也就这么叫了。一般来说和别人解释这个问题会很复杂,所以我会直接称呼她为姐姐,可以避免很多麻烦。其他线下也熟悉的朋友还没有超过五年的,友人还不到三年;认识 -runzhi -倒是已经四年多了,却也算不上非常熟,仅限于数学同好(?),有过很多长期断联的时间。
-虽然很不一样,但要我想象和老姐今后因为什么原因闹开,就不再联系了,我还是会认为不太可能。
-想起来之前友人向我抱怨自己感情方面的情况,我只想说,这都是很幸福的烦恼。人似浮萍,来体验一下我这种三年后地理位置在哪里都不知道的生活,再体验一下每天脚不沾地忙各种破事,就会只有迷茫,不会对这种事上心了。另一部分内容我本来想说又没说,毕竟每次和别人讲自己家里的事情,总是会让对方愧疚提起了这个话题,又一顿道歉。实际上从小的家庭环境确实让我对此无比悲观。悲观之后就会想开,怎么样都无所谓啦,有猫有狗就行。
-又想起来高考完之后,老姐给我的礼物里面夹的纸条,上面写,“驰雨小姐自由如风”,当然是祝愿。让我想到上一个叫我 -xx 小姐的还是 ex
这个 -b,当初还觉得很浪漫,乐死。然而如今想想,自由如风的另一层意思,恐怕是漂泊和无牵无挂。
-说到这里,打算周六考完试去把给老姐的礼物寄出去,倒也没什么大件,就是日常积攒的一些小东西,像之前去古北水镇买的兔儿爷泥塑,去故宫买的香膏和书签一类的东西,等等等等。把日常攒成一个小箱子之后,再写几张明信片附在里面寄给她,她也同样会这么做。小时候是互相写信,贴上邮票等邮政慢悠悠地走,虽然寄丢过一次。现在是用快递寄一些实体的东西,也很令人开心。
-箱子已经满了一阵子了,一直在我桌上放着。今天想到人似浮萍的说法,总觉得给她寄东西也寄不了几回,我就要离开这里去往不知道什么地方了,一阵凄凉。于是想着要赶快寄出去。
+按家里的习惯年初一要吃素,
还好可乐也算素食,感觉几乎没听说过别人家也有这样的习俗。据说是鲁东南和港台、广东部分地区都这样,你鲁省为什么会和南方有一样的习惯(
+今天发现个离谱的事情,成绩单上必修的工科概率论显示为被初概替代了,但是初概在期中之前就被我 +PF +了,应该不能替代才对,而且我也没交过替代申请表。问了一下才知道,那门工科概率论开课容量太少,所以院系里很多人都去上了初概来替代掉自己的必修;需要办课程替代的人太多,教务直接和开课的工工系对接,给所有修了这门课的人统一办了替代,不需要交申请;上学期碰巧可以给必修记 +PF,阴差阳错地就把我的也标记成已修了(
+我是想用概率论(1)替代的来着啊(恼,不过问题也不大,必限绩点对我来说没有意义。
+想着每天浪费时间都不知道浪费在什么上了,
还不如冤有头债有主,于是把明日方舟下载回来玩了一下,打算试试 +nano 的长草期插件。不过玩了一会就明白当初为什么退坑了(
11月18日
--
-
很有必要提醒一下自己,早晨睡醒 / -午睡睡醒反正总之刚睡醒的时候,千万别急着回消息别急着看社交媒体,不知道迷迷糊糊的时候会说出什么 -b 话,昨天也是今天也是,肠子悔青了
-更离谱的是,我已经连着咕了两节抽代了,本来觉得也无所谓,出勤率有 -30% 就不错了。咕了 5-3 的抽代之后来六教上 5-4,5-5 -的统计推断,先是在六教的斜坡上迎面遇到婉璐姐姐,想起来我摆烂的初概
-还有超松弛法矩阵,不过她至少没认出我来。结果往前走了走又遇到了刚下课出来的 -hx,我去,我觉得他至少脸熟我,还盯着我看了很久,真绷不住了。下周二去上课的时候还是换件衣服吧(
-无奖竞猜,这是哪里↓
-
-
这是晚上的华子招生办(
-其实我也不是很清楚这是不是招办,没做过招生工作。是从一教 104 -的后门走出来的时候拍的,拿去骗到了好多人。室友猜工字厅,何老板猜是网图,友人问是不是深山老林里的古寺(,看来是氛围到位了。
-右下角那个房间的屋顶看起来很独特,像日漫里的弓道场(?)不知道有没有机会进去看看是干什么的。
-明天考工程经济学期中怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办
-当然是先学一会统计推断,再看一会番(
-本来天气预报说是今晚下雨,于是吃完晚饭就回寝室了。把工程经济学的卷子拿出来,看了五秒钟,然后写了一会统计推断笔记,又打开了赛博朋克边缘行者(,其实已经很久没看过新番了,这部还挺戳我的。
-可是明天考工程经济学期中怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办怎么办(
--
Data don't make any sense, we will have to resort to statistics.
+1月23日
+好像也没什么可写的(
+普通地读一千零一页,普通地做课后题但是没有答案,时不时怀疑自己伪证,要么就是最后一问不会做然后疯狂 +Google / Math +StackExchange(。期间还时不时切换到模拟器的界面去玩一下方舟,我完全理解什么叫凉性循环了。虽然年初二在读一千零一页这件事听起来很卷(,但是一直以来过年的状态都和正常的日子没什么区别,就是普通的寒假嘛。
+而且感觉读不完了,下学期要寄(
+1月24日
+今天好像也没发生什么有意思的事情(,修了半天博客的 LaTeX,发现不是 +NexT +的问题,松了一口气。过程在数分日志里简单写了一下,最后也没搬家到新版 +NexT +但是已经把新家装修好了,万一哪天旧房子真的塌掉了的话可以一键搬家(??
+相比之下感觉还是数分比较简单。
+
+
回坑之后第一次打新主题肉鸽,一遍通关,还是有点运气的。但一遍通关的代价是没想到会花 +40 分钟,接近三点才睡。舟已经不太能吸引我了,不玩了(
+平凡即是喜乐,还挺符合今天的心情(,旧版 NexT 没出问题的每一天也都是 +precious daily((
+1月25日
+推推数分,感觉那一篇已经根本不能叫速通了(悲
+1月30日
+我怎么感觉这一篇要烂尾(或者说已经烂尾了),在家摸数分实在没有什么可写的。
+昨晚和转数环里一个正在申请的学长聊了会天,
+备受打击,被锐评上课上得太慢了,申纯数基本没希望(但我也没这个打算啊 +kora),这也没办法。总之有点怀疑之前的估计恐怕是太乐观了些,延毕也成大概率的事情了,毕竟我根本没有先读个硕这个选项,在华子多读一年书单从花费上来看就便宜一万倍(倒也没有一万倍那么多(。不要花多少钱的硕又有点看不上(?),要花钱的又读不了/申不到,有申交换的时候那感觉了——把配不上我(?)的项目删掉,再把我不配的删掉,然后就啥也不剩了。草,说到交换的事情,想起来之前在同学的年终总结里看到一句话:
++
-按照院系的标准,我似乎总是离一流差一点。
+但我好像从来没明白是差在哪里。
统推讲完了数据简化原理,这句话戳到我了(如果有看我统计推断那篇文章,会知道此处 -statistics -指的是“统计量”而不是广泛的“统计”,所以其实是知识点哦(错乱
-
11月19日
--
-
工程经济学寄了,但好像相比别人也不算完全寄,不管了。
-去刷了一下 Mili 从 Iron Lotus -之后的作品,感觉风格都差不多,没有特别喜欢的...,收藏了一首 Dandelion -Girls, Dandelion Boys,但是之后可能也不太会再听。
-早期有很多(我认为的)神曲,印象最深的是幾年月,Nine Point -Eight,Vitamins,Cerebrite(入坑作x)和 world.execute(me) 这些。Mili -的歌词一贯都是在讲故事,几乎不会一句唱好几遍,但是早期的曲风相当多变,抓耳的也很多,这种感觉从 -Millennium Mother 这张专之后几乎就没有了。
-Iron Lotus 不错,开始进行一个单曲循环x
+那我就不一样了,在院系的标准里我根本就不入流。或许他们是对的,我也不知道。
+我现在真在考虑退复分析然后去选 hlb +了,或者至少蹲一下能不能有机会选上另一个实分析的老师。之前想的是如果压力太大的话,大不了退掉 +statistical learning 换 bayesian +statistics,对我来说理论课总归比码课轻松很多。然而我现在只觉得悲观,大概早点学些应用也没什么不好的。
+1月31日
+写完昨天这些事之后觉得好烦。今天老姐来上海了,带她去天文馆玩了一下午。
+选天文馆也没什么特殊的意义,大概就听说是前两年新建的,还没有去过,以及它算是东南方向上地铁能够到达的最远的地方,我家在北面。
+
+
+
装置很炫酷,然而我物理太拉胯了,老姐读的文科,最后就变成了一起惊叹“好大!”“好漂亮!”“好闪!”,和来玩的小朋友没有区别。试了几个印纪念卡的机器,基本都是坏的,或者可能没墨/没纸了,总之就成功印出来两张,正面是天文馆的照片,背面印了(一些并不认识的)物理学家的生平。总之感觉其实比较适合中学生来玩,果然已经是过期 +jk 了(
+离滴水湖挺近的,出来之后租了个双人脚踏车绕着湖转了一圈,虽然天气不算好。或许是这边离海不远了,水汽多的原因吗,今天明明很热,坐地铁来的路上看市区也比较晴朗的样子。
+
+
找到一个前年暑假在这边车站拍到的广告,上面新兰下面柯哀,官方是懂端水的。
+
+
楼上往家里漏水,把天花板的墙皮泡起来了。上去问了一下他家房主在外地,还有个二房东在本地,租客今晚才从老家回来。要了二房东的联系方式,好像不是很愿意赔也不太想修,在嗯拖延,总感觉这个情况会很复杂,说不定还要找物业或者明天上楼吵架,麻了(
+]]>
2月1日
+ + + + + +--Without you I could never be
-So sincerely thank you for everything
-It pains me to think
-
我的学业导师(土水学院的)跟我聊了很久,中心思想就是——我这样全然不顾物理课,真的有可能延毕
-但是没办法,这学期进行到这里,我感到很焦虑。我唯一的愿望就是好好地完成每一门数学学习,无论是抽代还是统推还是数值分析,甚至回溯一下初概并往高等概率论过渡,或者着手做 -SRT,对我来说都比那个什么工程力学更有价值。工程力学从开学到现在,作业全靠抄何老板的先交上,只等着“某个周末有空了补一下”,可是没有一个周末能有空留给它。我深知如果拖着它这样下去必定什么都做不好,于是就退了。说起来这个 -SRT (对我来说)还是有点难度的,找了一下发现是把 Kaggle -上的一个题搬过来了。老师比较 nice,至少没有在学期中 push 大家。
-这样,这学期我落下了 8 学分专业课,包括 4 学分的基物,2 -学分的工程力学,还有意料之外的 2 -学分实验。实验倒不是问题,退课是遇到了给分巨烂的意外,且没有沉没成本,下学期或者明年这时候就可以补上。所以实际上有 -6 学分会堆到未来。下个学期我还会推掉 5 学分的基物,不知道会不会退 3 -学分的数学物理方法;大三上学期要把工程力学的 2 -学分补上,但有可能又要推掉 3 分流体力学或者 4 -分工程力学进阶,大四上学期还有 4 -分量子力学...真的太好笑了,土水专业居然要学量子力学。
-大三下学期会稍好一点,数学基础课除了实分析就都上完了,可能会去补一门基物。但无论怎么算,总是要有至少 -3 门物理课放在大四上学期完成,即使目标只是 -Pass,也依旧很困难——我真的很讨厌物理(如果有物理系的朋友读到,真的不好意思(。而且一旦 -Failure,我去,我不好说。当初如果不是为了读数学专业,我早就去学文科了,那样的话高考怕是真能上线,何苦被困在这里。(然而家里没钱读什么文科,还是会很挣扎罢x
-说实话,我自己真的觉得延毕没什么不好,这就和降转一样从容了。可惜我妈肯定会应激(,后面本来还有一段话,但被我删掉了。

2月2日
+今天去了苏州。实际上目的地也是乱选的,之前看到一个上海一小时高铁交通圈的文章,第一个就是苏州,所以就去了。然后也没什么目的地,除了去了普渡寺(离苏州北站很近)之外,其他都是漫无目的街头瞎逛了。
+在普渡寺看到的逆天祈福牌:
+
我也买了一块挂上去,付完钱也没想出来写些什么,最后写的是亲友平安健康。没有更大的愿望,也没有什么关于自己的愿望。
+晚上吃了苏州汤面,其实感觉和在上海吃到的差不多。在上海吃的最多的一家苏州面馆叫松鹤楼,最频繁去吃的一段时间是高三,自闭的时候就借走读的便利,出校吃了晚饭再回来上晚课。一般就是去离学校最近的商场吃松鹤楼的清汤面,非常香,借此短暂逃避学校里的氛围,是难得的很幸福的记忆。当时还不会骑车,走路太累了而且来不及,两公里的路还要坐地铁去,一碗面不到十块钱,来回地铁票六块,成本爆炸。
回程买了最慢的车次,只要十二块五,在车站附近买了一小袋热乎的板栗在火车上吃,属于是给自己找点事情做。平凡即是喜乐
2月3日
+-
+
+
古廖夫一生积攒下的挫败感,在这一刻突然汹涌而至。他想起年轻时,有那么几年,毫不怀疑自己是个天才,他忘情地写着,稚拙的作品曾备受师友的夸赞;他沉醉在自己手造的光芒里,对未来满怀热望,相信自己能成为任何想成为的人物……他想起一个醉醺醺的夜晚,他坐在音乐学院的广场上,旁若无人地指挥着月光下飞驰的云影,澄鲜的乐句像从天外直灌入他的灵魂,他在黑暗中放声大笑……可到头来他又做成了什么呢?如今他跌坐在岁月的尽头,沮丧地认识到,这一生非但不是幸福的,甚至也不配称为不幸,因为整个的一生都用在了战战兢兢地回避着不幸,没有一天不是在提防,在忧虑,在克制,在沉默中庆幸,屈从于恐惧,隐藏着厌恶,躲进毫无意义的劳累中,期盼着不可言说的一切会过去,然后在忍受中习惯……
+古廖夫再也绷不住了。他捂着脸,在荒野中嚎啕起来。
+
+- 今天 b 站突然给我推了体育中考跳横箱的视频,突然想起来我当时还真的选了这个,每次跳着跟玩似的,最后拿了满分。打开视频一看,感觉这个项目好恐怖,不知道以前是怎么做到的,后来又是怎么变成现在的体育废物的(
11月20日
+2月4日
+今天是友人的生日,实际上和往常一样,她是和家人以及其他朋友一起开趴度过的,我并不会参加这种活动,感觉参加了也会败大家的兴。中学的时候会等到寒假结束再把礼物当面送给她,今年我想了想早点拿到总比晚点拿到要好,况且我是那种只会送书的无聊人类,早点拿到的话寒假还来得及读完,开学就没空读了。所以就直接寄了个快递。
+我之前一直纠结应该怎么面对朋友的生日,代入自己的话就会纠结别人到底有没有过生日的习惯这件事,后来觉得就算不过生日的话收到祝福应该也会开心,所以要努力知道大家生日的时间然后至少要送一句祝福。不过经常觉得自己做得还不够,又担心会给别人心理压力(比如说要等价回报之类的负担),稍微有点想不清楚呢。
+上次给自己过生日还是上次,也不算过生日,就是馋蛋糕了所以找借口买了一个,点蜡烛也是觉得火苗摇曳的样子很好看。近几年来唯一一次生日许愿是 +18 +岁的时候,煞有介事地希望自己能尽快独当一面,当时所说的主要是想尽快经济独立。于是高考后的暑假还用华子的 +title +骗了些家教钱,尽管我不喜欢这样,但它支持我毫无心理负担地生活到现在,感谢所有当时找我上课的小朋友们,我想我也付出了等价或者超额的,真诚的劳动。
+ + +2月6日
+ +消失了几天没写什么东西,甚至有朋友发邮件问我的生命安全情况(,感谢关心(,看来等我年纪大了以后可以在博客或者别的什么媒介上立遗嘱,并且和人约定好,如果若干时间没有更新的话有可能是我出事了,要试着联系一下我。
+说起来前段时间和友人有一段关于遗嘱的对话,她的意见是说不定多感染几次新冠人就没了,最好提前准备个有法律效力的遗嘱。然后我就她告诉我的遗嘱注意事项提出了
+114514 个 corner
+case,发现都已经被安排好了,看来法师律师们就是现实世界的测试工程师。我当时想着这段话会聊得比较有意思,还(征得同意)录了个音,想把对话复刻到日记里,却一直没有做这件事。
其实我也不知道最近在干嘛,或者说可能是单纯不想把平庸的日子记下来,就没写什么。一直写不出来第二篇数分的前言,干脆就摆烂没有更新。说着
+everyday matters
+但是失去的日子就是找不回来,往前回忆的时候也想不出来除了在尝试怎么用
+Python 替代掉 R 之外做了什么,替代也不是很成功,难怪大家都用
+R(草这是什么结论
查了一下教学门户发现缓考的科目三月份才考(不是科目三,是科目/三月份),那还可以再摆几天。
+今日最佳:
+
然后发现我其实是练习时长零年半的数学练习生,2022 +年我的数学学习最大的收获是我终于开始学习数学了,听起来像绕口令。
+2月7日
+今天和一根扎进手指里的木刺搏斗了一下午,我为什么不去医院呢.jpg,传授一点自己处理的经验:
-
-
写统推写到 -04:50,绷不住睡觉了。本来不打算同步昨天的日记了,刷牙的时候脑补了一下,是否会有朋友看我一天没更新以为我猝死了,草,还是更一下的好。
-建构定理解决问题的过程很有意思,但我现在是越来越讨厌做题。然而技巧的提升是必要的,所以还得做,唉。
-今天又一次自动审批从西门出去,在中关村北大街上呼吸了一会,回来就收到了封校通知,草。
-下周四我是真的有一趟就医,是八个月之前约的 HPV -九价疫苗,竟然八个月就排上了,感觉北京算很快了。要去顺义,祈祷那边不要封,以及祈祷院系的直男老师(非贬义x)们不要以为这是一件非必要的事情(,并已经做好了回来就被通知隔离的准备。
-去近春园或者紫光大厦住单间不比和室友住一起爽多了从西门回来的时候遇到一只小黑猫,本来想给它拍个照,结果窜出来一只狸花把它打了,有幸拍到了全过程。小黑猫需要法律援助的话可以联系我(不是(顺序是从右下角开始顺时针观看,手机自带的拼图愣是没有调换顺序的选项,我淦
- -
-刚写完上一条,我室友就被隔离了。她为了 SRT -去李兆基做实验,结果李兆基封楼了,草(
-顺便吐槽一句,感觉她那个导师挺逆天的,开了好几个 SRT -招了几十个本科生进去给博士生打下手,还要求每周投入时间不得小于 -10h,进实验室要打卡计时什么的,这就是生化环材吗x。相比之下我导师真是仁慈,不停强调学业为主,每周啥也不干都行,大不了寒假再做。
+- 据(我妈)说可以把盐和醋 1:1 +兑热水,然后手指放进去泡几分钟就能掉了,我试了一下可能是因为扎的有点深,总之是没用的,而且已经有伤口的情况下泡盐水会痛啊!(我不会是个笨蛋吧.jpg) +
- wikihow +上还有别的稀奇古怪的方法,什么醋和苏打水兑热水之类的,原料不充足,没试。 +
- 但是直接泡热水还是有用的,让刺吸一下水变软一点就不那么痛了。 +
- 如果只是扎在表皮的话可以用消毒过的针把皮挑开然后把刺取出来,听起来很痛但应该是没什么感觉的。但我的扎的明显比较深,刺只露出来一个小头,直接用镊子夹不住,所以是用针伸到扎进去的地方把刺的角度调整了一下(这一步真的痛但是也真的有效),然后用镊子(掌握好力道的话指甲刀也可以)夹出来的。 +
- 注意消毒,处理完之后要消毒,工具用之前也都尽量消毒。 +
- 用胶布粘出来或许也是可以的,但我觉得不如用镊子能掌握好力度,万一断在里面就很麻烦。 +
- 扎得深的话不要试图把刺挤出来,一方面刺的边缘可能还有小的毛刺,另外试图挤出来的过程可能会越扎越深。我把刺拔出来之后手指还是明显肿了,应该是因为试着挤了很多次,发炎的地方就是用力挤的那一片。把刺拔出来之后可以轻轻挤一挤,大概可以防止感染。
11月21日
+当然,还是去医院比较好,用一次性筷子的时候要小心啊。附一个 wikikow +的链接,大概也是这些方法。
+2月8日
+想了一天也没想出来怎么写今天的日记。
+起因是突然想起初中时认识的一个学长。当时我对初升高还一无所知,不懂自主招生的规则,或者说觉得那和我这种郊区做题家根本没关系,我就该去争上中分给全区的唯一一个中考名额,更完全不懂竞赛。我妈机缘巧合认识了他妈妈,获得了一些当时来说很救命的信息,最后临时抱佛脚考到了不错的高中也该感谢他最初的帮助。
+高二上学期(2019 +年末)的时候看到了他的水滴筹信息,才知道他患了白血病,还有他化疗后拄着拐杖在开学典礼(或许是别的什么活动)上讲话的照片,他家已经变卖了所有家产,几次配型也不成功,当时在一个医疗团队里试用新药之类的信息。我妈试着联系他妈妈,发现微信被删掉了,就在水滴筹里捐了 +200 +块钱。后来再也没有音信,也逐渐淡忘了这件事,直到今天我突然想起他来,就问了我妈一句,才知道从那之后他的病情急转直下,似乎 +2020 年没到一半就去世了。
+ +想了很多,写下来总觉得词不达意,干脆删掉了。最后上网尝试了很多搜索的组合,他的名字,初中和高中学校,入学年份,甚至我记得他在某个知名初中数学竞赛得过奖,这些信息都试着搜了搜,努力拼凑起来了一个形象,谢谢互联网的记忆。遗憾的是我只见过他一次(现在想想那时也已经算是他生命的末期,当初怎么会想到其实死神就在身后,令人感叹),不记得他长什么样子,只记得水滴筹上的照片很憔悴,没记住意气风发时的样子。虽然不了解他的亲朋好友如今的生活如何,但我想只要我每带着这一丝记忆多生活一天,就能保证他还没有被世上的所有人遗忘,所以要努力记得,要写下来。(这个格式听起来像在做证明题,我是不是不会说话了
+人世多为憾。今朝蒙善诱,怀抱绝埃尘。
+2月9日
+来点轻松的二次元相关。
+
其实第一版填了五个 EVA TV 或者剧场版,想想实在太多了,去翻了翻 +bangumi 换了几个也很合适的。
+入坑作本来想填守护甜心(,和柯南都是小时候同时看的,那个太子供向了,写出来恐怕大家都不认识。这么说来我已经是十多年的老二次元了,看的番好像还是不多,近两年基本就没看过新作。
+看最多次的是天气之子纯属意外,高二的时候我自己看了两遍,又和 ex
+去电影院看了一次(草(其实并不愉快,然后可能是因为这个所以疫情网课的时候(已经分手力)经常
+emo 就会拿出来看一看,也没什么别的原因。令人感叹。
最喜欢的我一直都选不出来(About 里面也提到过),硬要说的话还是 EVA TV +或者紫罗兰二选一,但是好像也都没到最喜欢的程度,就给一个最想安利和一个最佳画面。最佳配音是因为《春宵苦短,少女前进吧》里面的前辈是由星野源配音,我不太关注声优,掺点三次元爱好。C +& T 的配乐真的很不错但是被剧情拖得太惨,所以选它一下。
+友人评价说 Fate/Zero
+远远没到最虐的程度,但我觉得也很可以了,大概是因为我没看过魔法少女小圆。FZ
+也是我 fate 系列的入坑作,如果入坑第一部看的是 Fate/Stay Night
+的话可能根本就不会入 fate
+系列的坑,子世代比亲世代差远力!卫宫家今天的饭在 fate
+世界可以算是最轻松治愈的了,大家远离圣杯战争围在一起吃饭,印象挺深刻的。
然后是觉得四谎实在很单薄所以说它过誉,樱花庄的宠物女孩看了一半忍受不了就弃坑了,实在是不喜欢但是被身边的人安利过很多次,在心里直接拉黑成最讨厌了。离谱的那个是歌舞伎厅夏洛克,本土版的福尔摩斯改编,一开始觉得很新奇还追番了,前面看着也还行但剧情走向越来越离谱,我又比较喜欢原作(指小说),所以别看。这几个都挺主观的,因为也没看过太多离谱/不喜欢的番。
+2月10日
+今天可以用一句话总结:时隔四年还是五年,总之我二刷了一下秒速五厘米,发现自己终于看懂了,令人感叹。
+ + + + + + + +2月11日
+最近躲着(?)没更新是因为这两天摸鱼读统计计算去了,PKU +的统计计算课是真不错,薄纱华子统辅的那个版本。
+我觉得我下学期干脆别上复分析了,去上个数分 2 +吧(,或者不上课但自己同步读实变函数论,总之现在就是非常不自信。
+ + + +看了一眼 V1ncent 的申请结果,Biostat 的项目里 Umich MS/MPH 和 Emory +MSPH 都中了。不知怎的我也稍微缓解了一点失学焦虑,祝贺他。
+ + +2月12日
-
-
昨天刚说周四要出校一趟,今天紫四就封了。本来封的这个点我应该在上课,结果早课被我翘了,就被封了,好似。
-昨晚失眠睡不着,翻来覆去到六点钟才睡,十点不到就被室友喊起来说封楼了,草。实际上我们都翘了课,所以正好在宿舍里被封;另一个室友昨晚就因为热爱科研住进了紫光,还有一位早晨上课去了,流落在外盘算了一天要不要跑路回家(是百京人
-今天解封之前也实在无心学习,一则睡得太少了,根本集中不了注意力,二则第一次封楼,又戒备又迷茫。于是和室友一起在宿舍里扯皮了半天,甚至久违地打开了朋友圈刷了刷其他被封同学的情况,不过看了一会觉得还是老样子,又光速关上了(
-十混一重新检都是阴性了,也解封了,仿佛除了给我带来生活失序外,没有对华子产生任何影响,渺小啊
-本来以为封楼会有上门核酸,结果并没有,解封了之后还得自己去做一天一检,华子从不让我失望。盘算了一下,今晚六点到十点的紫荆篮球场人流量可能类似于一个 -U-quadratic -distribution(x),于是八点左右去的,确实人不多。统计推断大胜利(不是
-看了一眼工程经济学出分了,瞄了一眼答案,上来 10 道判断题错了 4 -道,别的地方一分没扣,真的离谱,不愧是我。不过分数也还可以,期末只要不大寄就没事。
除非这老师也给 -85 分 2.3,90 分 3.3
+今天发现 V1ncent +更新了统辅课程测评,于是也同步了一下最后的几门课,有兴趣可以去看一眼。
+通过另一个统计申请洞认识了 +Mariana,简单聊了聊。
+真惨,我一切学业学术相关的 connection 目前都还得靠树洞发展,包括认识 +LagrangeKMnO4 和 V1ncent19 也都是在树洞。
+好像真得改改选课。大概有几个 plan:
+Plan A:维持原状,但问题是数分 2 +我还没补完,原来多元微积分学得就很烂,直接上复分析是否有点送死。况且复分析除了留数之外对概统似乎都没有多大帮助,单纯是补课的话
+既然要延毕了那也不用现在就急着去学。Plan +B:把复分析退了,蹲一蹲林勇的实分析还能不能有课余量,或者能不能法外开恩手选上,可以的话就去上,没有就把时间空出来自己读实变函数教材,或者把时间用在多去和意向导师沟通上面也可以。
+Plan C:把复分析退了选数分 +2(说实话最好是行健那个班,保护绩点),但问题是它和概率论冲突了,让我放弃概率论是不太可能的,真麻烦啊。
+Plan +D:把复分析退了,选点自己培养方案里的课上谨防退学。我是不想选这个选项的,宁可自学实分析。
+Plan +E:把复分析退了,补一门统辅课。最好是能补到贝叶斯统计导论,不行的话实验设计分析也可以。
+我比较倾向 B 和 E,更倾向 +B。先前做的决定后来才发现问题很大,本来又是可以避免损失的,这种事情真的很讨厌。
+实际上今天是寒假在上海的最后一天,明天就要出发回学校了。今天要去上交见以前的同学,这个从去年开始就变成寒假的固定项目了。晚上会回来得比较晚,可能也来不及写日记,所以半夜更新一下,如果有想补充的东西的话可能明天会在高铁上补。
+ + + + + + + + + + + +补点图:
+
+
思源湖边 up 主聚会.jpg
+
+
建议新民路吸取一些先进经验(
+
+
看着感觉穿越到了 efz 办公楼,不确定,再看一眼(
+其实是你交药学院(,路过的时候随手点了个位置。
+
+
以前一直以为对我来说是个最优解的电院,现在看来只是局部最优来着。
+不过在楼上直接写电院两个字是否有点太草率了(
11月22日
+2月13日
+ +回北京了。昨晚这个时候我还坐在交大玉兰苑旁边的凉棚里,和同学一边喝奶茶一边吹风,听后面一桌打麻将的声音,附近都是各种小店,很有烟火气,甚至恍惚觉得总算感受到了现充式的大学生活。今晚我就在北京挨冻了,令人感叹(
+明天的计划是去打九价 hpv +第二针,本来友人说怕我打完副作用大晕在路上,要陪我一起去,结果她今天和我说私密马赛她明天要过情人节去了,哈哈.jpg
+2月14日
+ + + +刚睡醒!
+今天去打九价,没想到第二针和第一针不能打在同一个胳膊上,要好几天抬不动右手了。这针不仅贵,还让我很有参与感,推药进去感觉每一下都巨疼。不过敲键盘和写字没什么问题,那这两天不得大卷一场?.jpg(不是
+下午回来在校门口听到有人一番论证之后得出结论“我们是 Bocchi the +cyclist!”,回头一看还真有四个人,草。
+ + +2月15日
-
-
- 停滞不前 +
+
+ +I’m always oscillating between “I’m crap” and “I have a vast, vast +soul”.
+
+到了北方的一些直观感受:洗完头之后头发又干又糙还起静电,洗完手之后手指轻微起皮按不开指纹锁。
+如果有和北京差不多冷但是又不这么干燥的地方就好了,最好水质也好一点。我一定是在做梦.jpg
+早晨又一次被楼上活动室装修砸醒,又一次以为这个破楼要塌了而狂喜,但它并没有塌,真遗憾。等了一会没声音了就又睡了个回笼觉。中午起床本来想出门,结果收拾东西的时候直接给平时用的单肩包的带子拉断了,真不愧是我。干脆以此为借口去处理了一些琐事,通过假装很忙来给自己一种今天没学也没关系吧的感觉,太罪恶了。
11月23日
+2月16日
-
-
我为上周抽代作业里不会的题破防了整整一天一夜,无数次怀疑自己这个水平是不是后半学期要寄了,最后才知道是把差集 -\(R-P\) -当成了环上类似于环理想的加法的逆运算。我真的,我甚至还给它定义了半天这个运算是怎么一回事,怎么调整才良定义(没调出来),最后才意识到居然是差集,那写成 -\(R \backslash P\) 不好吗(
-看来是我离散水平不行,总之还是寄。
-统计推断是后半期唯一一门我打算线下全勤的课,结果老师封小区里了(
-下午纠结了半天还是决定出门去三教找个教室上网课,常去的教室就 3203 和 -3303 空着。本来打算去 3203,走到门口看到里面只有一对情侣在聊天(,就去了 -3303。结果遇到了欧老师,很久没见了,蛮巧的。不过果然这种情况下基本上都是别人叫住我,不然我好像不会特地去看周围的人长啥样(x
-单人行动久了总会有和世界逐渐脱节的感觉,在线下遇到熟悉的朋友还是很令人开心的。
-最近的破事感觉必须列个单子才能来得及做完且不遗漏了:
-+
- 今天要被友人拉出去看国家地理的展览,但其实这几天身体上就很疲倦很疲倦,包括昨天去买了下学期要用的 +Kai Lai Chung +的书之后原地开始非常焦虑,我什么都还没学会啊。不知道能不能打起精神来。
+
-
-
- √ 写完抽代上周作业 -
- √ 补上周课堂内容的 huixiangdou -
- √ 抽代本周进度 + 作业 -
- √ 统计推断上周作业有个题可能还要再改改 -
- 大数定律,中心极限之类的问题再回顾下,下周统推期中了 -
- 准备个微雕的统推期中 -cheatsheet,其实可以直接删改一下然后缩印博客文章( -
- √ 统计推断这周的内容 & 作业 -
- √ 把离散二倍速放完,作业随手写了 -
- √ 周四打九价 -hpv,据说很疼,但友人封着出不来只能自己去了,希望不要昏在半路 -
- √ 工程经济学小班课的作业 -
- √ 周五之前登选课系统把工程力学退了,这课必退无疑但是上周还在蹲 -PF,乐 -
- 周末数值分析抄书,写作业 -
- 工程经济学最后一次纸笔作业 -
- 工艺美术史期末的 cheatsheet,题目已发,可以准备了 +
来回的路上看完了柯南衍生 +TV《零的日常》,想想剧场版砸了那么多钱水平也就那样,我就不应该对这个小小的衍生剧抱有什么期待。也或许我该认清一个事实,就是现在的柯南和我小时候爱看的柯南已经根本不是一回事了,《零的日常》远远达不到《魔术快斗》的水平,现在的剧场版作画再精致也不会有 +M6,M12 那样的剧情了。到底是制作组变拉了,还是我长大了,或许都有吧(
+虽然这样我也还是每年都会看剧场版,哈哈(,情怀党最好骗了捏。
睡前听说何老板脱单了,他知道我不看朋友圈,特地在官宣前来告诉我了一声(??),以及明天是他的生日。蛮好的,虽然我这时只是想起他也是要出国的,不知道到底是已经确认了和对方能有未来,还是一时上头(。倘若是前者,那在概率上更是一件值得祝贺的事情。(虽然我很怀疑是后者(
然后想起来之前在紫四楼下遇到他在等人,封楼的时候他问我四层什么情况(而不是问我什么情况,屑同学 -x),甚至上学期问他实验报告写了没的时候他说正在写,结果我 10 min -后出门做核酸遇到他和一个女生走在一起,等等。诸如此类的事情总是有迹可循,感叹我自己虽然记性好,但到底还是不够敏锐,何尝不是一种缺点。
-草,怎么听起来像是败犬发言,其实就是普通朋友,甚至如果冷漠一点的话,应该叫做“同学”。
2月17日
+-
+
为什么秋季选课的时候感觉想上的课都只有春季开,春季看选课的时候又反过来了(?
+今天攒够了蚂蚁森林的能量,种了一棵沙柳。今年大概是已经完成 KPI +了(?
+
+
查了一下,去年种了 4 棵不同种类的树,保护了 7 +平方米不同地区的土地,应该是能远超平均的:
+
+
+
当然经费不是我出,种树也不是我去现场挖坑(,说自己“种了树”“保护了土地”心里还是有些忐忑。据说云杉是最长寿的树,去年恰好攒了很久的能量种了一棵,它会在赤峰带着我的名牌比我多活很久很久,守护一小片土地,还是挺令人期待的。花棒和山桃是会开花的灌木/树,都种植在甘肃,有机会的话真想去看一看,
+ +虽然理性上来说,我去一趟甘肃产生的碳排放比这几棵树能够转化的可能还多(,如果是山桃的话会有落英缤纷的场景吗?高中
+因为学不会生物而选考了地理,答过很多和保护生态相关的题目,也听老师讲了许多远方的故事。两年两位地理老师都是很有感染力的人,也都来自中西部,时不时谈起当地的生态情况。我不知道别的同学怎么想,但我大概是非常容易为这些事情难过的笨蛋,当时还挺揪心的。再往前可能要追溯到小时候看过的科普、《寂静的春天》之类的书籍,讲世界上的各种环境问题,每次看到都揪心不已,还会为自己没有力量帮助任何事情变好而难过。如今做的事情也微不足道,大概也尽力了。我大概从 +2019 年开始在蚂蚁森林种树和参与保护地项目,到现在为止种了 12 +棵树了,那有生之年好像还能再完成一些。正好昨天去看国家地理摄影展的时候,有一个放映纪录片的区域,讲的是国家地理杂志的发展过程,里面还讲到现在投入了很多经费用于环保事业、生物和生态研究工作。之前好像也有报道说中西部地区的水土流失正在因为植树而改善,还提到蚂蚁森林项目在其中起了很大作用。虽然单说前两天 +Ohio +的事故就让人揪心,但至少还有人在努力让世界变好,作为普通人大概也只能紧紧抓住这种微小的希望。
+向所有负责以上项目的基金会和奔赴现场完成工作的专业人士表示微不足道的感谢,也感谢支付宝公益。
11月24日
+ + + +2月19日
-
-
去打了第一针九价,就,我姐之前恐吓我半天她打完之后的副作用,包括并不限于发烧头痛恶心 -blahblah,结果我打完除了胳膊有点酸(感觉是扎一针之后的正常现象)之外就没什么感觉了(
-我这个孱弱的身体素质,在(或许有必要的时候)倒还挺值得信赖的(
-ddl 要爆了,而我还在不紧不慢地摸鱼,这不对吧(
--
为什么会这样呢?我很难形容在肉眼可见的将来要失去一个好朋友的感觉,还阻止不了。
-
+数了一下培养方案里已经修完的和选了课的有 88 个学分,还有 76 +个学分没有选课。这个剩余数量对大二下学期来说大概确实是太多了,然而恐怖的是里面竟没有一门是我想上的了。
+晚饭饭点不是很饿就忘了去吃,但到了晚上又饿了,遂吃夜宵。去玉树看了一眼二楼夜宵还没恢复,灰溜溜爬回桃李,在最右边的窗口点了一份烤冷面,一串糖葫芦,又去点了一杯饮料,加起来不到十块。太棒了,下次还不吃晚饭(什
+室友返校看到我第一句话是“你胖了”,可恶,这种事情不是非得说出来罢(悲
+晚上本来在复习缓考,复习着复习着开始折纸(
+然后还翻相册找到了高中的时候折的东西,印象里挑战过非常多花球,但折完之后基本拍个照就送人了,大多数连照片都没拍。
+我其实是觉得只有折纸的过程比较有意思,折完了之后又没地方放,大多数作品还不能碰不能压,就很麻烦。正好同学觉得不需要自己研究就能获得成品简直太快乐了,这下各取所需了——以前折完之后就拍个照发空间,如果有人想要的话直接要走就好了。
+随便放几个,别的照片都找不着了,sigh。
+
+
其实我忘了这个是我折的还是存了别人折的照片了,当时在空间里看到另一个喜欢折纸的学长折了这个,就自己也去做了一个。看水印时间确实像当时做的,hmmm
+忘记是不是送给 ex 了,哈哈,如果是的话大概已经进垃圾处理场了((
+
+
这是个家里没纸了但还是想玩,所以做出来颜色很诡异的凡尔赛花球,我管它叫卷心菜。难得有手不能完全解决问题的情况,花芯好像是用镊子卷的,如果只是手工卷的话很容易散开,最后还挺牢固的。这个实在觉得有点脆弱,送出去的时候还找了个泡沫塑料的盒子当包装(
+可恶怎么只找到这两张啊(
+看起来还挺厉害(真的吗),不过我现在的水平仅限于下面这种立体贺卡难度的了(,今晚做了半个小时(
+
+
也没有合适的纸(,问室友要了粉色的格纹便签,努力假装是樱花(迫真
+Anyway,至少这个是可以收起来的,不太占地方。
+单纯是折的话就没什么难的,只是跟着别人做,耐心细致一点也就好了,集中精力的话很少有一遍不成功的情况。之前看过一些作品的设计过程,感觉我也就是能模仿一下成品罢了,啥也不是(
11月25日
+2月20日
-
-
晚上 SRT 线上开周会:
-这周你做什么了?什么都没做。你做什么了?什么都没做。你做什么了?什么都没做。好,散会(
-我估计至少我自己持续到学期结束都会是这个状态了,哪有空管这些事啊((
-草,何宝不是说抽代课会有助教组织线下上课来着吗,我下午冲到教室,怎么就六个人,怎么助教都没来啊(。我才不会承认我是想看微信头像照片看起来很帅的助教才特地去教室的,所以他为什么不来啊(悲(好变态
-虽然但是,
蛞蝓扩域好抽象,一遍看不太懂了x
-貌似可以回家了,上学期我跃跃欲试,这学期我希望室友能不能早点走(草好阴暗
-北京的冬天更舒服一点,没必要回去,除了室内外温差有点大,刚进楼的时候很热之外,一切都还不错。想起来上海连绵的冬雨,总是有各种不太开心的回忆。印象很深的是高中时候的一次圣诞节,回家的路上雨水灌进了鞋子,好冷(。况且还没有看到北京的初雪啊,不急着回(
-给大家表演一个耳机线拧花(什么鬼
- +
+体验了一下实复概连上,但是复分析上课的这个点我就已经饿了,遂退课。
+薛金鑫看起来很和善,大概是年轻老师的原因,一节课讲 114514 +个笑话。听起来这门课也比较轻松,不过最大的问题还是对概统都没太大帮助,以及我数分 +2 还没学完。所以补课完全可以明年再来。
+实分析感觉顶得住,谢谢 PIN 的讲义(狂喜
+今天才知道基物实验 2 +也是最后一次开课了,我还以为我们院系要倒闭了所以以后不开课了,知道是二字班又修订了一遍培养方案之后感到非常失落。上学期把它退了,所以这学期我得上 +4 学分实验课(恼),2 的时间还和别的课冲突了,破事真多啊这个书院。
+每学期必修课超过 10 +个学分我就会想似,所以一换一退了工程地质,不用上早八了。
+ + +
11月26日
+ + + + + + +2月21日
-
-
虽然现在是 26 号,11 月似乎还有好几天,但是看到下周五要交的作业的 -due 是 12 月 2 日的时候,还是比往常更深刻地感受到了时间的流逝(
-据说现在不回家就跑不了了,稍微有点动摇,但目前还是不打算走。不知道为什么我甚至已经做好了在学校过年的准备(只是一个心理预期),为什么会这样呢,夏天的时候明明很乐意回家的来着。
-月光长骑路过二教,旁边是周培源应用数学中心,停下来看了一眼。想起来之前还查过这个地方是干什么的,结果连个官网都没有,华子发的关于周培源中心的文章还是 -20 年前的,离谱。里面的老师似乎也很少,我知道的就雍稳安(下学期开 PDE -的老师)和章梅荣(好像是室友以前的微积分老师),有点怪。
-跟友人吐槽了一嘴,然后她问我怎么不直接冲进去问问里面是干啥的,我:?不社恐的人真恐怖,虽然也有一定道理
-室友今天突然让我去树洞自搜一下(名字首字母),总之好无语(
-补统推去了,最近的状态感觉就是快冬眠了
+杨不亚 (x) +老师今天找我拐弯抹角地问认不认识化工系的人,跟我扯了半天最后才说明来意:他想要一些华子的微积分和线代期末题,拿去给他现在带的小朋友准备丘班考试;他还在华子读书的时候(应该不止十年前了)只有化工系学生会会收集保存这些资料,所以以为现在还是这样,希望我找那边的同学委婉地要一点。
+大人,时代变了。
+我都高中毕业一年半了,退役也两年半
+(警觉)了,质心这个不知名竞赛机构(不过社友说很知名 +x)咋就还喜欢盯着我。到下午他们那个负责宣传企业文化的吉祥物(?)质心姐姐还来找我,说三月初要来华子玩,问我有没有空面基,可以给我带点新款质心周边小礼物来。我心里想的是咱们好像也不熟啊,以及你又是怎么能进学校的,新款质心周边不会还是氛围灯款加湿器吧,心理活动很丰富,最后只怂怂地回了一句没课的话一定来。问题是我也从来没在质心上过课,只参加过一次全国联考
结果因为参加的人太少喜提 +rank +1,另外就是以前给新星写题解的时候会让杨不亚老师帮忙翻译小语种题面,别的交集不保证没有但感觉应该零测。结果又是被邀请写软文,又是找我要题,现在还要面基,难道是看我比较好骗,非常恐怖.jpg
+前三个学期都是把体育课放 +2-3,回来瘫倒然后洗个澡点个外卖洗洗衣服再打扫下卫生,就差不多磨蹭到晚课时间了,再出去上课。这学期终于意识到这样的话一天直接没了,实在划不来,于是
+冒着猝死的风险把体育课提到了 +2-2,顺便选了个不怎么累的项目。今天试了一下,下午两点多就能休息完然后出门进行一个卷,然而困难变成了这个时段教学楼没合适的地方可以卷,太乐了。晚课是线性回归,放 PPT +各种出事故。我还想发生甚么事了,一看老师的电脑是 +surface,那倒也正常。
+青春上海:今天是 neruko 老师的生日,但是今晚为 TA 庆生!(
+
+
11月27日
---因为享受着它的灿烂
-因为忍受着它的腐烂
-你说别追啊 又依依不舍
-所以生命啊 它苦涩如歌
-

11月28日
+2月22日
-
-
连着通了两宵,其实今天凌晨熬夜做的事情本该放在周日的白天就做完,就是看一章数值分析然后写个作业罢了,时间上也绰绰有余。但很显然一天什么都没做,政治性抑郁的体验达到了最顶峰。昨天日记里一直在删删改改,到最后还是没更新出来,说过的话也全部删掉了。
-虽然不断地告诉自己这样不好,但果然还是很难克制住这种心情。好好地把精力放到自己的生活上罢。
-看我这个作息,不知道的还以为我是负责半夜做核酸样本检验的。
-今天刷了一下 QQ 和微信,发现 MO 时期同班的一个 MOer -删了我的好友,嘛。其实也可以理解,当时一起交流题解交换讲义的同学,现在已经是陌生人了啊。
-高中毕业之后(准确来说是收到录取通知书,回高中取到了档案,确认自己不会再回到这个地方之后),我就把绝大多数同学(包括上述这一位)迁移到了不常用的 -QQ 账号或者微信上,还退了班群。从此用自己的 QQ -发癫就感觉舒适了很多(,列表里还有友人,我姐,runzhi,竞赛时认识的赛博同好(??)们,和少数初高中阶段相处下来觉得还不错的同学。
-我也不清楚为什么要这样做,但就是很想脱离那个让人不舒服的环境,以至于用了有点极端的方式。但其实要让我说这个环境哪里让人不舒服,我也说不上来,明明从自己的角度来看过得自闭又自在,却还是平等地毫无理由地不喜欢身边不熟悉的人们,
-很难不怀疑是不是有什么心理问题。其实现在比从前还要自闭,倒没有类似的心理问题了。强行解释的话,就是高中时候班级的概念还很强,在人群里自闭的感觉就和被孤立了一样(什么中二日漫剧情(,而现在不是这样,多数人不都是独行的么。我妈之前还数落我不懂得积攒人脉,不能总是这样在大多数人面前表演一个原地失踪,还和我讲把谁删了都不能把去学医了的同学给删了,万一以后有需要还得找人家(噗。可能再过若干年我会发现她说的也对吧,但是果然还是不愿意那样。
-尽管凌晨爆了两管阳性,又封了一栋楼,时至今日我还是不太想回家,甚至抱有一丝大不了寒假在学校里推 -SRT,学学分析的想法。暑假在家待了三个月,躺得很爽,但确实啥也没干,倘若寒假回不去,至少在家时间的总和没有太大变化。
-最近的想法又在改变了,主要是数值分析这课越到后来我越觉得学着很不爽,至少不太喜欢这个思维模式。又很难说清哪里出了问题,而统计推断渐入佳境,因此不是特别想考虑计算数学了。下学期看看能不能干脆删改一下,再挤一门统计学习导论进来(感觉要牺牲数物方法(
+Statistical Learning,一门刚上了一节我就打算 PF 的课.jpg
+其实是 V1ncent19 说俞 sir +给分并没有其他统辅老师那么慷慨,我大概投入不了太多精力,水平不行花了时间也卷不出来,毕竟不是理论课,太弱小了。
+ + + + + + + + + + + + +另外他还说俞 +sir 很帅,确实,不过 not my type(草还有就是这课紧跟在实分析早八之后上三个课时,今天一边听 linear models +for regression 一边觉得我也要 regress 了。
+ +
+今天第一次在三次元遇到和我发型完全一样的人——王天颖老师!(
+虽然我一直觉得挺普通的,
放到二次元的话就更普通了,但是在生活里观察到的就是几乎没有人留普通的齐刘海和普通长度的头发,很怪。我妈的评价是太土了,草,我觉得还好吧(心虚
11月29日
+2月23日
-
-
马原再见,体育再见((PF 了
-看了眼考试周安排,抽代 16 周周六,其他三门都在 17 -周的周末,又要坚守到考试周的最后一天晚上。不过比较硬的几门课考试时间上还挺松散的,蛮好。
-怎么上海的同学基本都回家了,大家都好快,怎么就我还在这儿苟着(x
-明天统推期中,希望人没事,睡了。其实更要希望的是今天紫四别有人混管阳了,那恐怕只能在寝室里考了,真的很难想象(
+这学期开始晚上熄灯总是卡不准 12 点整,似乎一直都是在 12 点 02 +分,不知道是所有本科生楼都这样还是只有我们有偏差,看来至少我们宿舍楼已经平移到了东七又三十分之二十九区,马上就到九又四分之三站台了。
+
+
(草
+昨晚在四教上生统概论,出去打水才发现斜对角教室在上我们的专业课,这话听起来真荒谬啊。起因是认出了教室里坐着个同专业的认识的人,绕到前门一看 +PPT +上写的是一门我这学期没选的必修课的名字,往里面望了一下好像班里认识的几个人都在,怕被人发现就赶紧跑了。
+所以为什么要怕被人发现呢,我也不是很清楚,但我一直希望尽量降低自己在人群里尤其是班级里的存在感,希望被人暂时忘记,然后也尽可能不要唤醒别人的这一部分记忆。我做过很多这样的尝试,集体锻炼去其他班级的组,班会活动人间蒸发,以为只要不出现就自然地不会被想起来。糟糕的是大家会求补集,后来反而被班级同学津津乐道,因为只有几个女生却从来到不齐的情况实在太显眼了,大家纷纷猜测这个只有入学的时候见过几次的人是卷王还是什么神秘人。当然都不是,我可能只是社恐,可能也不止和社恐有关。其余情况不便详述,有些氛围我也不大喜欢。
+回去之后稍微有点感叹,家人一直不同意我延毕再申请,让我“过正常的生活”,觉得延毕“会被人在背后指点”,笑死,哪来的别人。夸张点说我的生活已经 +out of 3\(\sigma\) +了,怎么能用正常形容,既然这样就不可能被平庸的标准桎梏。
+
+今晚在转数环看到有二字班的茶园转数爷问 Atiyah +的交换代数书哪里找,我看着打出来的前面这句话陷入了沉思,感觉每一个字都在告诉我我一无是处(x
11月30日
+2月24日
-
-
十一月的最后一天,被封控了(
-昨晚睡得早,早晨六点半左右不知怎么就醒了,嘴唇上感觉怪怪的,一摸裂了个小口子,问题不大。七点迷迷糊糊的时候楼道里广播响了,说楼里有人十混一阳,我超,我成预言家了。七点一刻左右广播说抗原阴性,于是想着大概问题不大,躺了一会直到八点左右才重新睡着,九点半再醒来的时候抗原已经阳了。
-然后还是在宿舍考了统推。晚上八点半吃上饭,八点三刻就解封了,大概华子的隔离床位也真的快顶不住了。出门刷了个月光长骑,给我妈打了电话,回来之后看到好几对情侣冲出单元门拥抱,我的第一反应居然是,晚上不冷吗,不能明天白天再说吗((
-这统推考两个半小时,然而我不到一个小时就写完了,后一个半小时全在找计算错误,还真的找出来一堆。本来想提前点交了,结果给老师发消息之前正好意识到一个题有问题,草,真的危。
-考的全是经典分布的性质,甚至矩法、MSE、多元 C-R Inequality -这些东西全都没考,所以没什么意思。不过也可以理解,太复杂的问题好像也不适合拿来考试,而且这课也没多少证明可做。
-室友跑路了俩了,我把书和电脑都搬到其中一位的桌上开卷(x)了,感觉很爽。效率低下难道是桌上太乱了的原因吗(
-首尾呼应一下(bushi),十一月北京没有下雪,印象里去年微积分期中的时候(大概 -11 月 8 -号左右?)就下了。然而看到南方都在飘雪了,南京上海武汉什么的,上海的第一场雪(虽然目测很小)很难得会这么早。是今年夏天大旱的原因罢?不是很懂,地理知识高考考完之后就全还给老师了 -x
-之前说留下来想看百京的初雪,结果不仅百京初雪遥遥无期,还错过了上海难得的雪,太亏了 -x
+睡前(指今天凌晨)磨蹭着写完了实分析作业,不仅胡说八道而且不停道歉(不),寒假写一千零一页的习题的时候总感觉自己在口胡但又没有证据(没有标答),搞得现在也不是很自信。结果做梦梦到实分析的特殊原因选课被拒绝了,这也能吃拒信?吓醒了(
+我现在课表上还只有 23 +个学分,这学期真是很轻松呢(迫真),这种要到开学第二周才能把课选满,第一次作业还得找助教交的日子啥时候才能结束啊(恼
+说起来实分析第一次课介绍助教的时候好像说了其中有一位上学期是抽代的助教(不确定,没听清),我还以为会是 +Bowen L,抬头一看是一位学姐,可能是 zmx +班上的,轻微失落。好想给他展示一下我糟糕的分析水平啊(什么啊草
+写完实分析作业之后刷了一下树洞,看到一个问能不能去隔壁数院做本科生科研的问题,于是又开始了我的数洞 +connection +环节,没想到(其实也有点想到了x)洞主是之前就认识的朋友,笑死了。
+我还真没想过这个,这下开阔思路了。2 月头上我焦虑地筛了一波 YMSC +的意向导师,发现把范围放宽到概统各个方向了也还是几乎没得选,还得回统计中心。顺便还摇到了一位隔壁数院本科然后来华子读研的学姐,下午简单聊了两句,她觉得我补课的进度尚可,可以考虑联系导师选方向了,推荐了几个北大的组。
+ + + +然后她问了我一个一下子让我破了防的问题:概统是两个方向,总得选一个,你选哪个?
+我不到啊!
+简单概括一下,概率就又往基础跑了,当然是要基础扎实的,可能得上完实和概再说。统计的话生统也还行但是理论性太弱,先不要优先考虑,优先考虑就路走窄了,我之前倾向数理统计但是现在似乎版本已经有点落后了,目前的版本之子自然是 +learning,但真的能少写点代码就想少写点(悲)。最近另一个令我破防的事情是第一周上统辅课的体验简直不要太地狱,比实分析和概率论还地狱,这俩顶多就是纯粹的难(x)罢了,学不会是我的问题,而且目前还能学会,统辅课就一点也不难,但很玄学。万事万物跳过推导看结论,还有各种我理解不了的“我们凭感觉想想这个问题就是 +blahblah”,恐怖的是好像大家都是直感 +A,就我理解不能,血压很高,直觉真的是这么用的吗(悲)。不过也别找适不适合之类的借口了,理论的学不会,应用的理解不了,那必是我的问题。
+Anyway,好消息还是有的(这算哪门子好消息:
+ +
+明天把作业写完,整理一下两门统辅课的笔记丢上来
盖住烂尾的数分,又该继续学缓考了。
4月1日
+2月25日
-
-
今天进行了一个 Montgomery’s method for ANOVA table construction +
我真服了 lzx 了,一次作业布置三本书,记号还不太兼容(也可能我 4-1 +听数分去了没上课的原因罢),难怪环友说他是断手(
+昨晚写完 Kai Lai Chung +的习题美滋滋睡了,还想着就这吗,今天一看科大教材破防了。
+
+
“不管是好懂的地方难懂的地方,他讲完就通通听不懂”,笑死了。
+天气很好,中午去 C +楼的路上看到紫操上好多人,西南角还有人唱歌。回来写概率论作业,大周末的室友都出去玩了,我在寝室一边破防一边写了 +6 +页纸的作业。晚上去教室坐了会写统辅课笔记,回来看到室友带着四五个人在中厅聊天(
+属于是围观了一天现充生活,鼠鼠我好羡慕啊(x,为什么我啥也做不完啊(
+
2月26日
+-
+
突然意识到这学期我有四个大作业(,统辅每门课各有一个,草,怎么会这样。
+那还有什么五一假期,两天写一个的话正好写完(悲
+今天好像又循环了。天气很好,紫操上很多人,两个室友分别带着自己外校的同学来逛华子,我一个人在寝室阴暗地爬行,外放甘き死よ、来たれ的时候一个室友带着她的朋友进来了,变成橙汁吧你们这些现充(无慈悲
+唯一不同的是我昨天写完了作业,于是今天就破防地去教室继续学缓考了。这工程经济学怎么就不进脑子啊,完全不想学不感兴趣的东西。问了没缓考的同学意思是这课好像就是严格按原始分给成绩,大概就是 +4.0 和 3.6 的差别,而且也就 2 +学分,似乎影响不大。但还是认真拟合一下吧,反正也没几天了,在刚递补上的实分析给我一个绩点震撼之前先攒一攒(
+群友给我发梗图:
+
+
我:哇这是一个 confidence coefficient 为 1 的 confidence +interval(昏过去
+啥也没学会,人先魔怔了(x
+
2月27日
+ ++ ++ + + +
浪费了人生中宝贵的半个小时,获得了一个站在矿泉水瓶盖上的天使(真的能看出来吗,拜托超酷的诶(
+
别问我为什么是格纹的天使,又是问室友随便借的纸。背景是 Stein +的实分析,莫名很搭,下面发光的是我的一个圆形小夜灯(
+图纸附后:
+
2月28日
+最高温度零下的时候我和室友都穿羽绒服,最高温不到十度的时候我穿开衫室友穿羽绒服,今天最高温 +17 度,我穿冲锋衣但室友还穿羽绒服,真有那么冷吗(
+ +咋结尾呢(,请大家看个天吧。我以前一直觉得天黑就是单纯变黑,尤其上海阴雨天多,往往就是从灰白直接变黑,但也偶尔会有晚霞。总感觉先变成深蓝再变黑只有在北京见过。实际上感觉北京的天空饱和度很高,不是雾霾就是大晴天(怎么听起来是句废话),很少有阴云,是不怎么下雨的原因吗。
+
在线性回归课上一边敲这一段话一边思考这个月到底写了些什么,但好像没什么印象。实际上在公开连载之前我也一直有写日记的习惯,最开始的时候写的还是纸质版,写完了的日记只是存起来,基本也不会回来再看。唯一的用处是别人提到某一个时间点的时候如有需要可以回来查阅一下对应的时候我在做什么,尽管这也没有意义,只是我想让自己确信对生活是有把握的。
+咋这么沉重呢(,总之感谢你能读到这里。
+ +]]>4月1日
+-
+
今天进行了一个 Montgomery’s method for ANOVA table construction 的学,大概是这学期统辅课上到现在我觉得
唯一最好玩的一个东西了。感觉三门课有意思的程度是生统概论 > 多元统计 > 线性回归,多元统计胜在理论推导多一点,虽然还是感觉有些地方有点虚浮,线性回归就真的好无聊(恼
@@ -7171,702 +7171,301 @@ CGMO
8月1日
- - - - -摆烂,本来想去看硬装的情况,合同上签的是七月底完工,但是到今天还没结束。然后学到了新知识:刮腻子要三遍,每一遍之后都要晾干,晾干之后刷墙漆之前还要磨平,所以真正刷漆要到明天了。
-在宜家下单了一部分家具,要说贵也不至于多贵,但是加起来就不便宜,怎么会是呢。在新家老破小里硬是装了个小吧台,放了两张高脚凳,越矮越喜欢爬高处的椅子。虽然也不知道有什么用,培养点喝酒的爱好吗(
突然想起来一个乐子,去年五月封校的时候时不时就一堆人去猫超排队屯食物和水。有一次和室友(点名 -wafarinliu -老师)一起去买东西,发现矿泉水又被搬得差不多了,开始思考我们要不要也做点什么准备,于是站在货架前面商量要不要提半打青啤回寝室(,怎么不算是水了呢。回去和另一个室友说这件事情,被锐评不愧是山东人和新疆人(
-之前不知道在哪里看到一个说法,国内软装家具质保最有保障的还是宜家,别的店不管做什么的都有可能家具还没坏就倒闭了,真到坏了也没地方修(
-8月2日
-验收了硬装,终于完事了。然而明天开始宜家就要送货和安装了,我也不知道是送一堆木板到家里还是拼好的送上门还是有人负责安装,说不定还要自己动手(狂喜(拼家具很好玩的(
中午起晚了出门之前没来得及吃午饭,就拿了片面包走,还在地铁上脑补要是去晚了就叼着面包冲进门装作很忙不是故意迟到的(。傍晚饿昏了冲进开封菜才意识到今天不是星期四,吃了点东西,路过麦麦又补了一个甜筒,再路过奈雪又补了一杯奶茶。胖什么胖,都是冰的,没有热量的(
晚上闲着没事又赛博占星了一次图一乐,为什么我的 N 也变成 S
-了,以前只有 J 和 P 会横跳的来着,快点变回来(
在家里的第 17
-天,感觉已经过了一年了一样漫长,各种原因地想回学校(
8月3日
-写点啥呢(
-是不是昨天甜食吃多了,今天开始爆痘,可能这是必要的牺牲吧(
-昨天说拼家具好玩,今天真就是直接送了零件来,还是稍微有点难绷。有点虚,不太确定需要多少工具,32
-头的螺丝刀和一套梅花扳手都放学校里了(所以为什么要放在学校里,是不是要寄希望于有手就行,或者买家具送工具(
说起来当初还是室友(仍然是 wafarinliu 老师)小学期参加硬件设计大赛(虽然但是这有什么必要加个链接呢()的时候多领了一盒
-32 头螺丝刀,结果还不回去了,然后给我的。但是真的很好用(
最近摆烂的时候时不时去看看物理系那个 3 学分的基础拓扑学的讲义,72
-页的小册子罢了,一个学期就只学点拓还能拿 3
-学分(不然难道让物理系的同学先学个抽代然后学代拓吗(,看起来好爽,我要不学完拓扑之后也去水个绩点。以前以为学点工科数学是洒洒水的事情,但是初概和微积分
-2
-接连给了我两拳,就不敢这么想了然后就只敢去上数学系的课了(什么。现在觉得可能只是我计算水平太差了,多少受不了这种水题看错一个条件算错一个数直接扣没的考试(有人又在为菜找借口,至少
-ywb 这个讲义看着好舒适啊(
8月4日
-闲着没事看了下 wty
-老师的主页(感觉可以说是闲着没事想欣赏下美女姐姐有没有发新照片((,发现她疑似(?这还有啥好疑似的呢)从华子跑路了,看了一眼今年六月才刚升了副教授,怎么会是呢。上学期居然上到了她在华子教的最后一门课,希望生统概论这课没事,有事也没关系,没啥可学的(
突然开始莫名其妙地慌了起来!沃日,ypk
-不会跑路吧,别过几个月我论文磕磕绊绊读完了结果他人不见了啊((。还有这课如果以后停开了或者由哪个老师转成中文授课,我今年上过的话还能不能计入外文课啊(
满地乱爬,今天又什么都没干,不会真要把工作量全留到八月底和实习期间吧,这段时间别的安排还挺多的,急((
-8月5日
- - - - - - -因为一些计划有变(两个橱柜的定制价太贵,打算直接在宜家买合适的成品),所以今天去新家拼家具的时候重新量了一些细部的尺寸,本来这一部分工作是想直接交给定制那边的。不量不拍照都不知道还存在很多问题。
-(我试着比划一下,但是感觉正常人听不懂(,其实有什么必要说出来呢((
--
-
其中一个橱柜下面直接是水泥地,上一位业主住在这里的时候一直都没有给这一块铺木地板,直接放了柜子。把旧的橱柜拆掉之后这里就是一个深 -7cm 的坑,买成品家具放进去的话很可能最下面的柜门被挡住打不开。
-之前一直没有管过这个问题是因为打算定制一个高脚/厚底的柜子严丝合缝地放进去,然而昨天拿到的报价实在逆天,宜家如果能挑到合适的成品可以省一半钱。
-解决方案是找包工头重新给这一块铺木地板,实际上也就一平方米,然后学到一个新(也不是很新,可能是复习)知识,木地板下面要先铺地龙(就是一个木架子),他们做出来不一定平,希望人没事(希望柜子没事
-量好另一个橱柜的尺寸,甚至都在宜家小程序初步挑了几个之后才发现柜子后面要走空调管道,扣掉这 -12cm 之后选择面就窄了很多,急。
-顶上有一个走水管的位置卡掉了很多层高,如果硬要保留层高就要卡掉宽度,为此多测了很多数据,趴地上画了个图感觉本质是个规划问题,如果考虑测量误差的话是不是个数值分析问题(
-旁边是不能动的承重墙(当然装修装到这个份上能动也不可能再动了),还要预留窗帘和门的位置,说到底房间隔断处是装个门还是厚窗帘本来都打算之后再想,然而为了买这个柜子就导致一定要提前决策,我还得先去挑窗帘(
-考虑所有限制以及最大化空间利用效率的话,最合适的几个柜子的分层高又有问题,很可能挂不下最长的衣服,还得回去量量衣服有多长,然后再跑一趟宜家量分层高(
-
逆天,翻新市区老破小的确比郊区新房装修困难(
在屋里烦躁地转来转去的时候又发现一些,截止主体验收的时候没处理完的问题:
--
-
- 刷漆的时候把踢脚线铲了还没装新的 -
- 木地板和瓷砖交界处还没做大理石的隔断(是这么叫吗)但是合同里有,怎么会是呢,这不得铲了重来吗 -
- 淋浴间还有一道挡水石没做 -
- 一些开关之类的安装杂项 -
反正工程款还没结,还能在包工头面前当一阵子大爷(,催着一个一个改就好了,小问题。只不过快要回百京了,还挺急的,远程监工也挺麻烦。
-量第二个橱柜的边边角角的尺寸,以及想这些问题的时候,很难不想起来一些测量学 -DNA:
---测量工作应遵循的原则是由整体到局部,由控制到碎部,步步检核
-
这么一说确实还挺对的,不过工程不应该都是这个步骤吗(我不懂啊我学不来工科,瞎说的((
8月6日
-挑窗帘,顺便把一直被催的灯具也挑了,周末估计宜家人很多所以没去,能吐槽的事情不多懒得写了,也可能是装修半个月我现在忍受能力已经大幅提升了,总之下略(
-晚饭吃麻辣香锅,点完单犹豫两秒把微辣改成了中辣,吃了个爽(。吃完还剩半盆辣椒,你们这儿辣椒不要钱的吗(
-想起来上学期在寝室一起点外卖的时候室友(还是 wafarinliu
-老师)被中辣背刺,还没尝过,等回百京了有空再一起比划比划(感觉最近日记里
-wafarinliu 老师含量过高,怎么会是呢((
8月7日
-翻到高中的照片发现来华子这两年头发其实变浓密了,真好((
-军训期间所有的 DNA -都早就洗掉了,只有某天在北体开演唱会的时候大家一起唱的《成都》洗不掉。其实在这之前我也没听过这歌,但是它一个月以来就是时不时地会在脑内开始放,今天干脆去循环了一会,怎么会是呢(
-进行一个发语音.amr
+7月1日
+ +上午晒了 3h 感觉真有点中暑,上次中暑还是 2019 CGMO
+的时候,当时好菜(。睡了一下午,今天训练结束之后寝室里每时每刻都有至少两个人在睡觉((
待会拉练,希望人没事。实在不想带自己的被子,找了个不用的被罩里面裹了个枕头蒙混过关,别散了啊(
+来点室友名言:你别去按照那个教程学是怎么打的,看一遍就行了,然后自己凭感觉打三横加两竖,肯定能打出来(
+她是对的(
+7月2日
+拉练,然后摆烂(,拉练出发之前和结束之后都有短暂的贴贴,满足了(
+从我高中军训的时候就在听我那位华子毕业的总之好像是什么状元的班主任满怀自豪地反复讲述他们当年背着被子走了 +20 km +的事迹,那个时候就已经开始为拉练这件事情烦躁。虽然也不是保证能考到华子但是反正上交也有拉练(,入学之后军训又推迟了两年,整整为此烦躁了五年。
+前一个小时还能和何老板以及班里那位 CCHO Au
+的哥们吹水,顺便听二位讲了讲投行实习做的事情以及他们的感情状况,学到很多,最后一个小时的时候开始逐渐和何老板掉队到后一排排尾,虽然还是在吹水但是频率和音量都低了很多(。毕竟是整个营的末端了,我在哪队尾就在哪,不妨碍后面的人行进,所以也没急着追。队尾的几个老哥大概也都是这个心态,一起摆烂了,还遇到了从上一个连掉队到我旁边的室友,蚌(
起来之后在楼道里听到有人打电话,说“哎呀人哪能要求十全十美呢,找对象看中对方身上的一些优点就可以忽略别的一些缺点了(大意)”。纯爱战士在心里默默点头正准备满意离场,结果听到她的下一句是“但是对我来说对方长得帅是最重要的,如果很帅的话哪怕有其他的一些问题我觉得也可以原谅(因为被震撼到了所以完整地记住了原文)”,草,怎么会是呢(
下午和晚上终于看完了 Munkres +上每本数学书都有的但我好像从来没学扎实过的集合论和逻辑(,跑步进入大家已经在数分里学完了(不太确定)的点集拓扑。给我的感觉就是贵校数学系在数分里面把什么都学完了,听说宗学的点拓只上七周,大概还是得自己赶一赶,没学过数分的我只能度过一个相对失败的人生(。在教学楼关门之前终于写出来第一节最后一个定理证明跑路了,虽然还是比预期的时间晚了 +20 min,但总之是好的(
+命运/好怪 很假 Fate/strange Fake -Whispers of
+Dawn-
+终于放送了,急急急,我已经迫不及待想看宝具对轰辣(
7月3日
+好困,感觉没啥可记的(
+两门上次没出成绩的课到现在也还是没出,真就拖到 ddl +再给我一拳是吧(
+ +下午贴了 1.5 h +回来之后发现三个室友都还在睡觉,明明是差不多时间上床的,草(。晚训完也贴到了,只不过能不能只贴不军训啊((
+ + +7月4日
+给老师发邮件之前单独列了个数学课的成绩单出来,虽然单算这些的话均绩远高于我自己的
+GPA
+但还是给我整绷不住了,怎么都是水课,然后才发现我好像是真的没怎么上过非常困难的课(。急了,怎么办,还要不要单列,单列了反而显得很菜(然而还是可以薄纱大部分去统计中心的人,所以先给那边的老师发了(
一杯茶一包烟一页 Munkres 看一天(,好绕。
+射击搞到晚上九点多,等了两个小时不到两分钟就打完了,麻了。我其实一直有点做不到闭左眼睁右眼,所以打靶的时候左手没扶枪,用来按眼睛了。还是打了 +90 +多环,虽然也没意义,毕竟不脱靶就有分,所以确实有(一只)手就行(。好像端枪的姿势不太对,后坐力震得锁骨疼(
+这个困扰其实物理实验的时候也有,感觉有的时候对焦或者读数看不清,只能左手按住左眼勉强看,不过军训射击怎么就不算一种物理实验了呢(。这里是不是该有个物理实验九宫格(
+懒得骂武装部了,累了。
+7月5日
+早训摆烂的时候我甚至躺在树荫下面睡着了,怎么会是呢。只记得有点无聊,然后就躺下了,哼了一会我贫瘠的华语歌歌单,班里一个同学问我在唱什么,我说是《南国的孩子》,给她发了一个我最喜欢的版本。然后迷迷糊糊地就闭上了眼睛,再次有意识就是醒来看到蓝天的时候吓了一跳,好像是第一次躺在地上睡着(
+后面又睡着了一次。咋说呢,后两天能不能也继续摆烂,最好还是有时间睡觉(
+体验了一天 wake up with no +email(。只不过这个暑假开始磕盐根本不现实,延毕的话确实是一点都不急,找两个老师留个印象,能有点别的指导(?)的话更好。
+急了,七月能把点集拓扑读完吗(
+ +所以到今天已经贴了两个月了(虽然今天并没有贴到,不知道为什么给我的感觉是,原来才两个月吗(,是不是每次想起来的时候脑内自动从三月就开始算了(
7月6日
+听说人在隔壁化院的高中同学已经跟着导师发 Nature
+了,而我昨天才刚收到和两个老师约时间聊天的邮件,怎么会是呢(大家都有光明的未来(x
到底要怎么样才能把这个 行列式 分列式的 bgm
+从脑子里赶出去,循环一天 One Last Kiss 和 Idol
+了,晚训还是又灌了回来,急急急(
室友锐评:你这个发型,是不是根本就没打算晚训,想贴到晚上的来着(
+还是室友锐评:急了,分列式和现男友以及前男友都站在同一列里,逆天(
+来点今晚东操的天空,但是玩闪耀!优骏少女玩得:
+
你还别说,左边阴影里这个云的分布真挺像的(
+7月7日
+这个 b 军训(,终于要结束了(
+没啥写的,今晚就打算开始把之前为了内务检查塞起来的东西摆回原位了。
+ +7月8日
+众所周知未央书院只有 14 +连(,但这个军训还是从我们被取消评优资格开始乐起来的,好事(
+拉练回来那天就觉得四教教室的地面不是很平坦,当时还以为是脚太痛了感受异常(,后面这几天在教室里走的时候感觉确实是不太平,不知道是我的幻觉还是设计师你在干什么啊设计师.jpg(
+今天突然看懂了 Munkres +上一个两天前卡住了的反例,然后被自己蠢到。下午课后题卡住想得脑袋疼,结果去吃饭的路上想明白了,再一次被蠢到。军训完第一天的阅读进度大约和之前一周的进度差不多吧(
+这书是女生节礼物额度报销的,当时还比较笨蛋,没直接影印电子版(版权意识薄弱.jpg),原版贵好几倍感觉不太值不如多报销两本书,就买了中译。现在感觉翻译质量也还可以,至少
+Hausdorff space 被翻译成了 Hausdorff 空间而不是豪斯多夫空间,点名批评
+Stein 中译本的博雷尔集(
最后一次去东操(?)的时候在路灯下面看到个这玩意,我直接一个测量学 +PTSD,想起来暑假里有测量实习和地质实习更崩溃了,那不就是军训 2.0 +吗。今早还在想防晒霜用不完了,急,现在也没必要急了,实习还得用(
+
(这个东西叫四等水准尺,确定地面高程用的((说不定测量实习的时候会在学校里用到它,绷不住了
+ +第一次大概也是最后一次用宿舍楼里的洗衣机是今天把军训的东西全部扔进去洗。本来还觉得问题有点大,这身衣服坐完东操坐北操,万一楼里有别的年级的人洗自己的衣服岂不是(,结果室友表示没啥问题,可以我先洗她再洗然后加消毒液空转一圈,让我不用有压力(。既然你们天天用洗衣机的人都这么说了那就 +ok fine(
+7月9日
+没有学期中间乱七八糟的作业,Munkres 的 solution manual +不如直接在手机上用 solverer 平替,解脱了,不用天天带电脑了。
+睡得很晚但醒得很早,早晨突然有个高中有一阵子聊得很多的群友给我发消息,说最近看了天之杯之后想入坑 +FGO,太恐怖了,我光速劝回(。Fate 系列的动画也好,FGO +也好,如果到现在完全没接触过的话还是别入坑了(只不过 FZ +还是值得一看的),但是如果都坚持看/玩到现在了的话就有一种必须要继续下去的感觉(。柯南剧场版好像也是这个道理,这些东西怎么都除了画质之外越做越烂(
+看了眼今天上海最高温 29 +度,本来觉得没啥,又看了一眼早晨下过雨之后空气湿度 100%,那体感不得 40 +度,草。下周回家估计就已经出梅了,一时不知道是湿热好还是干热好,虽然出梅了也肯定比北京湿,急了。
+中午骑车路过地质大学的时候看到一堆人扛着三脚架和全站仪往里面走,急了急了急了急了别提醒我暑假末尾还有个测量实习这回事了。旁边一条路的围墙上写了各种高中自然地理小知识,如果我还是个高中生的话会很感兴趣,但我现在在读这个 +b 专业所以看了只觉得好崩溃(,这下又过期 jk 了。
+荷清路比学堂路好走一万倍,没有意义不明的上下坡
+7月10日
+军训第一周在北操被不知名虫子(首先排除蚊子)在手臂上咬了几个包,后来不知道是过敏还是又多次被咬了,逐渐蔓延到了两条手臂上都有好多,抓起来的时候看着还挺吓人的。本来还觉得应该排除点别的原因,但是室友和她们班的一个同学都是和我一样的症状,大概就是军训的问题。要不要去校医院看一下呢,要么直接回家去华山医院看吧(
+认识硕哥还是四月底的那个推研转系讲座,当时就跟他说期末考完去找吴昊,他还劝我越早越好,五月的时候还给我推了吴昊组里一个学姐的微信。说起来这一通操作下来多少有点不去也得去了(,我清楚地记得是一节测量学的课,旧水的空调开了和没开一样,课也不想听,然后他突然来和我说吴昊组里有个想要学妹微信的学姐()的时候真有点社恐地狱。总之我一直把这事咕到军训之后,今天才去。
-- - -和我在成都的街头走一走
-直到所有的灯都熄灭了也不停留
-你会挽着我的衣袖 我会把手揣进裤兜
-走到玉林路的尽头 坐在小酒馆的门口
+数理基科是学物理的吗,你是致理书院的吗?
+哦哦,啊这,未央是什么(
+数分没学过问题不大吧,你概率论 1 +不也撑下来了,后面的课程里遇到不会的随时补就行。其实按这个来说你已经提前体验到科研的状态了!
虽然今天没出门搞装修,但在家用很暴力的方式修了一些坏掉的东西。淋浴的三角阀之前家人说一直转不动,调不了出水口但也勉强用着,报修的话光是上门费就要
-150,今天福至心灵双手用力一拧,立省
-150(。浴霸的灯罩是个嵌在天花板里的长方形盖子,之前掉下来两个角,掉的两个角装不回去,没掉的两个角又拆不下来,只好一直悬空着。今天找了片合适的
-流麻废材
-亚克力板卡在缝隙里固定住了,不确定在挤压下强度怎么样,但是又找不到其他密度低而且不锋利所以掉下来也没关系/不会被水汽影响的材料,不太放心又在天花板里面用绳子简单做了个支撑。
固定的时候突然想起来《牯岭街少年杀人事件》里小四的朋友在天花板上找到一把匕首的情节,在天花板里捣鼓半天不整点活属实和我气质不太符合,然而画不来镇宅符(,最后就在板子上写了个日期塑封了一下塞上去。
-还剩一个特定条件下会触发拧不紧的水龙头拆开发现不会修,又装回去了,至少学会拆水龙头了,可能是想说明有些钱还是要让别人赚。虽然不大贴切但还是想起来
-Disco Elysium 剧情里给我印象很深的一段,(我认为是在)暗示人的有限性的
-One More
-Door:
难绷(
+下个学期可能有必要把概率论 2 和 3 一并上完,据说是必要的基础(,而且
+3 只有秋季开课,错过等一年,2
+是两学期都开然后进度上有一个章节的区别。那就要退掉
+ODE
+和拓扑之一,感觉大概率是后者,宗学年年都有,而台湾腔不常见(,这样的话最近把
+Munkres 第二章看完当做补习数分,然后就可以停下来换回 Durrett
+了。今天顺便还偷跑到了吴昊概率论 1 和 2 的纸质版讲义,概率论 1
+的部分好像是她下学期要用的,虽然我翻了一下感觉就是 Durrett
+的精简换序版,然后把习题都换成了丘赛题,双厨狂喜(你都厨了些什么东西(。
下午到得比较早,在静斋转了两圈,看到二楼走廊尽头有一个开着门的巨大的办公室,里面还有小隔间,还以为是研讨间之类的,想着如果没人的话可以先进去坐一会。结果凑近一看门口的名牌是 +Shing-Tung Yau,绷不住了(
+顺便还看到了刁晗生的名牌,高中的时候就经常听教练念叨他,怎么不算师出同门了呢((别丢人了。之前环友发过李思门口的抽象画,今天看到了真迹,很生草,虽然但是到底为什么要贴在门上,我还是更能理解王浩然把《达拉崩吧》的歌词贴门口(
说到推研转系讲座就想起来,军训动员会的时候梁曦东说“大家入学的时候专业是限定的,大二结束选导师的院系/专业范围就会扩大很多,等到推研和做研究几乎全校范围内都可以选,范围是越来越广的(大意)”。我就不明白了,这个宽窄的顺序完全反了罢(
+开始玩 Disco +Elysium。暑假回家的一个月除了去拔智齿之外其实就三件事,监工家里的装修顺便跑几趟宜家搞软装,稍微学点数学,精神损伤的时候 +Disco Elysium 启动然后加重损伤(。本来是想 Death Stranding 和 Disco +Elysium 二选一的,后者比较便宜/夏促力度更大/更感兴趣就先买了。
+(Death Stranding 在愿望单里主要是有 Pop Virus
+的加成,是的我是来听歌的(
7月11日
+ + +吴昊讲义上的 P 和 E 全都是 mathbb,舒服了(
+Munkres 第二章结束了,把吴昊讲义的概率论 1
+部分走马观花复习了一下,好崩溃,这才过了不到一个月有些东西印象就有点模糊了。这个时候就要安慰自己,没事,抽代我更是忘完了,概率论
+2 也不是很分析,别管那么多接着往后看就是了(
晚上回寝室开答疑坊,给正在被小学期暴打的室友讲了会傅里叶变换和卷积。实际上傅里叶变换我真的已经忘完了,上次接触还是求特征函数,感觉也不太涉及什么分析性质,今晚一边看讲义一边现学现讲的(。看了看大作业要求给我整绷不住了,这真的是能用 +MATLAB 写出来的东西吗,希望人没事(
+开完答疑坊就开始开理发店:
--There is no way to open the supply depot door. Accept it. You cannot -open *all the doors*. You have to integrate this into your character. -Some doors will forever remain closed. Even if every single other door -will open at one time or another, maybe to a key, or maybe to some sort -of tool meant for opening doors... But this one will never accede to -such commands. A realization crucial to personal growth. Crucial.
+室友:哟你这个戒指挺好看的
+我:(中二发作)其实这是爱因兹贝伦家主的证明,圣杯战争就要来辣
+(室友也是月厨所以发癫也没问题室友:别中二了,这是个对戒吧
+我:(
人生是旷野,或者是 CRPG(
8月8日
-之前学鞅论的时候对 Durrett 上那个 Dubin's Inequality -的习题感到非常困惑,官方的 solution manual -上那个步骤我一眼完全没懂(应该主要是缺上下标,所以一遍看不懂它的设计),另一份两个韩国人写的答案直接把这题空过去了,然后我也跳了。
-今天(凌晨)又回来看的时候用最笨的办法把序列完整地写出来,才终于明白了归纳是个什么意思,然后也是直接在摘出的序列上动手做的又手动把每一段序列拼到一起证出来的,写完感觉真要长脑子了。结果看了眼 -MSE -上有人提问,原来完全用特征函数写然后很直观地用一下 switching -principle 的话就两行,这才是真 · -归纳,知道这个意思之后再回头看官方解答就明白上下标缺在哪里了,好崩溃(
-不过我还是觉得这个题目关于 \(Y_0\) -以及 \(N_0\) 和 \(0\) -的关系表达得也稍微有问题,之后想稍微在长脑子篇里讲一讲正确的做法,还是说其实是我英语太拉了所以误解了((
-顺带悟到了遇事不决可以把 \(X_{N_k \wedge -n}\) 这种逆天东西想成 \(X_{N_k(\omega) -\wedge n} (\omega)\) 的形式(可是为什么现在才悟到呢(,虽然很 -trivial -而且一般没必要,但是这种想问题想到神经损伤的时刻确实还是换一换比较清楚,本来就被答案绕进去,险些又因为 -stopping time 的概念开始怀疑自己这阵子都在学什么东西,真挺崩溃的((
-我平时会直接把 supermartingale 简写成 super-mart,submartingale
-同理。托这道题的福睡前满脑子就都是 super-mart,梦里也是
-super-mart,今天出门在外面进超市买水的时候还在想 mart
-不是商场来着吗,所以超市的英文是 super-mart
-吧,但为什么总觉得怪怪的呢(。走在路上还在想杜宾犬的英文难道是 Dubin
-吗,总觉得也怪怪的,想到方舟的杜宾教官才想起来是
-Dobermann(
说起来舟用的居然是 Dobermann 而不是 -Doberman,可能本意是作为姓氏,只不过教官本人确实是狗狗就是了(
-今天还去吃到了小杨生煎的 双肩包
-生煎包(是个沪语梗),虽然也没有非常喜欢,但还是比清芬生煎好太多了。想起来刚入学的时候
-wafarinliu
-老师激动地拉着我去清芬吃生煎说这个超好吃,但我觉得相比上海的真不咋地。后来有一次我激动地告诉她清芬的羊肉泡馍好吃,很适合当冬天的
-comfort
-food,她跟我说同生煎的理很可能比陕西的差远了,只是我吃不出来而已((
来点今天在外面拍的东西(
-
嘿,听好了,最近东部城市会举办一个超大的 -party,所有的风云人物都会参加,但你猜谁收不到邀请?
-(退后一步)(尬舞)
-是你!北京!
-
五角场的上海书城分店装修之后绝大部分区域都划给童书和教辅了,今天走累了进去摆烂的时候想找本书读,看到这个艺术生活读物的幕墙还以为终于有书看了,结果怎么会是呢((
-
所以最后跑去 MUJI 读随笔了,巴掌大的 150 -页的小书有一半是插图和语录,另一半是八篇散文,但是竖版书而且阅读顺序从右往左感觉不太习惯,读了大概 -2h -当做休息然后就回家了。感觉是那种很刻板印象的日本人写的(,读完右边这段话我的第一反应是,这个作者自己悟出了影子价格的概念((
-有的时候感觉读这个破双学位也算杂学旁收,如果不是工程经济学强制给我喂了一点经济学知识应该不会知道这个(
-装帧挺不错的,非常无印良品,只不过要 28
-块钱我还是觉得有点逆天,当然无印良品里绝大多数东西的要价我都觉得逆天(,白嫖下样书得了,下次还来(
8月9日
-因为啥都没干所以险些忘记写了,还好到现在还没收到类似于寒假时候“怎么没写日记你还活着吗”的邮件问候(
-还活着,而且
+7月12日
+猫超的老酸奶真好吃,请年轻酸奶在老酸奶陪同下观看(
今天去和 ypk +聊了个天,聊到饭点还一起去玉树吃了个饭(,稍微有点社恐地狱,不过算是个好的开局。然后被丢了一个 +linear regression 的问题和一篇 paper +读,可能是数学书看多了吧,我反正觉得 90 +页是一个,非常非常庞大的数字,不知道要读多久。下午简单翻了一下感觉 +notation 都不是很熟悉,不知道要额外多看多少 paper 才能看懂,急急急(
+虽然我感觉一上来聊天的环节里他像个留学中介一样(,还问我有无 dream +school,我随口说了个感觉 UMich +这样的就挺好的了,他问我为啥,我说因为我喜欢比较冷的地方,给他整不会了(
+来点乐子:
--INSULINDIAN PHASMID - I exist.
+吴昊我认识,她的方向好基础好难(
+既然要延毕的话可以再课业为主一个学期,下学期把随机过程和随机分析学了是好事,听吴昊的,不急(
+所以未央书院是学什么的(
+太经典了,每个老师都要问一遍那你们书院的同学是不是有好多想转 CS 的(
+我发现学数学的同学好多都不喜欢统辅课
+“找不到喜欢什么的话可以先排除不喜欢什么”“我不想写很多代码”“你们学数学的同学怎么都这么说”(
+那你当初为啥不去北大数院呢?(
+一到暑假清芬三楼停伙我就不知道该吃点啥了,你有什么推荐吗(
清芬战士喜加一

(?(什么发疯实录(
-8月10日
-又到了装修血压时刻,本来说了一大堆发出来之前还是删了,没必要以后回来看的时候再暴击一下本就脆弱的心血管(
-看到个这个,好乐,上海中学都能举办西部赛了,乌鲁木齐一中啥时候举办东南赛,中国啥时候举办欧洲杯((
8月11日
-继上学期在体育课上摔倒之后,今天又用同样的姿势在浴室里摔倒了,还好是在家里而不是在学校,眼前闪回的仍然是帝宝训练摔倒的演出,怎么会是呢(
-《What Remains of Edith Finch》终于降价了,光速进行一个买,据说 2h
-就能通,打算高铁上玩。试了下键鼠控制和视角很有双人成行那味,包括找不着路和不能手动存档也是(,但有点晕
-3D(
其实是看群友吹它是最强第九艺术,非常为 Disco Elysium
-感到不服遂打算玩一下试试
8月12日
-收行李,把 Durrett 装箱的时候想起来第四章的 examples -赶进度的时候跳过没看,翻出来以为摆烂间隙能速通,结果被一个没写清楚的 -Kakutani dichotomy -的证明整破防了。众所周知(?)这种美式教材讲究一个保姆级教学生怕读者看不懂,但是从进入第四章开始就逐渐透露出来一种“都看到这儿了不至于水平那么拉吧”的气息,会突发恶疾地在 -non-trivial -的地方敷衍,看不懂步骤的时候就会深刻怀疑自己是不是脑子有点问题,然后破大防(
-不太舒服所以间断地睡了好几觉,没干啥事,下略(
-8月13日
-后天回学校,今天把装修的事情交代了一下。之前有一个 to-do list
-专门记录没解决完的问题和指数增长的新问题,今天把宜家还需要买的东西/具体的步骤和各种想到想不到的注意事项写成了一个新的文档,两个一起留给家人(。虽然我相信我妈根本不会细看,到时候还是一个电话打给我问怎么办。不知道为什么总有一种离职跑路但跑不掉的感觉(
读其中一个橱柜的安装手册(来判断难度,到底是留到寒假回去我自己拼着玩还是干脆买个安装服务)的时候看到个抽象插图:
-
啥意思,一个人不能安装吗(,为什么只有右边的人有耳朵,多一个有耳朵和铅笔的人参与安装就可以了吗,那我为啥不能自己长出耳朵或者拿着铅笔(,还是说贴贴可以提高效率(,我也想贴贴((
仍然不舒服,下略(
-8月14日
-把三周的地质和测量实习改成了两周的纯测量,不知道工作量多大。想多留一周时间贴贴和学完全没学完的随机过程,而且一想到地质实习会遇到一堆同专业但又几乎可以说是不认识的同学(,自己没上过工程地质啥都不会,还有组队
-pre 写报告之类的烂事,完全 carry
-不了甚至还需要靠抱大腿的话还是算了吧。纯测量那边有两个军训期间比较聊得来的同学(是班里的两位
-CPHO/CCHO Au
-选手,多少有点同是天涯沦落人的喜剧感),组队体验可能稍好一点(啥
这样成绩单上会莫名其妙多出来两个 -W,明明是完全没开始上就退掉的课,挺逆天的,下学期去课咨委提一嘴(
-收完东西感觉箱子比来的时候重好多(,希望人没事。明天回百京了,现在还是好急(
-还是不舒服,下略((
-8月15日
+7月13日
+有个高中同学毕业之后把我 QQ +好友删了,后来又给我发了几次好友申请,每次我都直接无视,今天又来一次。不知道为什么这么执着,我又不欠他钱(,也不是很想加回来,但还是担心万一是有什么事情,就回了一句如果有事情可以加我微信说,然后给了微信号。结果他也没加,我不理解(
+后来一想应该是删好友的时候自动拉黑所以也收不到消息了,那太好了正好我其实也不大想加他微信(
中午雨正大的时候在双清路上被一个逆行的外卖骑手创了,没摔倒的代价是把车和伞扔了出去(?),人往另一边撤然后就顺利站住了,现在想想也有点想象不出来这个动作,不过没摔就好。然后发现右手大拇指指甲盖里在流血,也不太懂是为什么,不过也是小事。又骑上车之后觉得雨天单手打伞骑车还挺危险的,在学校里倒还好反正整条路都是自行车道(,在外面尤其是右手还一边扶车把一边拿着手机看路线,遇到突发情况刹车都很难,路又很滑。
+好像问题在于我不想用导航模式,每次都是自己看着地图走,不然其实可以直接听语音导航,也不用一直拿着手机还时不时要看两眼。说实话自己看地图还经常不慎走错和绕路,也没什么好的,但就是不想换(
+最近在大力 Disco Elysium,现在进度终于到 Day 3
+了,不知道啥时候才能完成一周目,但是感觉
+相比于刚开始玩的时候开个灯就能把自己整去世来说
+还算顺利。也有幸(?)在 Day 2 就看到了这一段名场面
+然后就昏了过去,吸引我入坑的 Dora's letter:
--从潮湿的地方来,到温暖干燥的你身边。
+Harry, I wanted to write you a letter, so you can read it when you +wake up. Maybe it will make you happy.
+Every morning when I step out and you're asleep behind me, I find a +little piece of sadness in me. I carry it in my chest down Voyager +Road... Every step I take, it grows. By the time I reach the fuel +station it has filled me entirely. I step on the light rail and look +back, sparks fall from the bow collector.
+I know it will be like this until late afternoon, when I get off the +42 -- and walk back to you... You, you... Every step I take will get +lighter. It almost makes me run! Sometimes I do.
+I can't believe I met you. I can't believe the happiness I feel with +you. You have a vast, vast soul and I will always, always, always come +back to it. Kisses, kisses, kisses.
印象里是沉迷方舟时候看过的一篇同人标题,说人话就是:回学校了,大贴特贴(
-残念,晕 3D 而且高铁上环境不太好没能打游戏,看了半天 Building reproducible analytical -pipelines with R -催眠,速睡。本来想在旁边小朋友的家长面前表演一个玩物丧志,希望没那个加深华子的刻板印象(
-8月16日
-一边贴一边看一些看不懂的东西,虽然还是看不懂但至少在看了,所以说贴贴真好(啥
-8月17日
-之前吴昊给我她的概率论讲义的时候跟我说 Markov Chain 和 Brownian -Motion 这几章《非常简单,工科生也要学的》,昨天被 Durrett -整破防之后带了她的讲义去教室看,感觉,感觉这两本书在讲的明明是同一个东西但根本不是同一个东西(,怎么会这样呢(
-总的来说我这两天真挺怀疑自己脑子是不是有点问题的,希望人没事(
-看到 hx -在一个啥的“青年教师教学能力进阶项目”拿了一等奖,给我整绷不住了,和他同组的是我当年的写沟老师(在生命学院本博,后来去了教研院),世界真小,不过这两个人怎么能做到在同一组的(
-吃饭刷北大猫协公众号,瞟到果壳发了个天气越热,数学成绩越差,我觉得合理,而且不只是数学成绩会受气温影响(。还好秋季学期要来了,秋天到初冬开暖气之前这段时间是最舒服的((
-晚上突发装修后遗症,盯了一会四教三楼一个嵌得角度挺刁钻的灯带,想的是这要是坏了会很难修吧(
-8月19日
-昨天难得太累了咕了日记,老姐来北京陪她出去玩,晚上回来贴贴了一下,回寝室和 -wafarinliu 老师扯皮,谢谢大家盘活我(啥
-远程验收了装修,也不知道还有没有什么问题但总之是交房了,可喜可贺,就算有也差不多得了。到最后了包工头还在跟我扯皮我买的柜子可能有什么问题总之不如定制,扯皮的时候把尺寸抄在草稿纸上打算问他到底哪里不合适,后来发现长宽高三个常数在乱七八糟全是符号的草稿纸上真的很格格不入,好久没见过这么多具体的数字了(
-吃饭的时候看到一个这玩意,以前看到竞赛生小作文都会默默划过去所以为什么不取关质心这个公众号,今天扫了一眼封面发现
-efz
-的录取通知书被拍进去了,内容和事情本身也挺逆天(,加上有一些熟悉的元素,还真的读完了。总的来说很符合我对你校竞赛生的刻板印象,以及华子还是一如既往地不当人(
不知道为什么(?)好困,感觉能早睡(
+7月14日
+早上双人成行,晚上去情人坡看星星,回寝室极乐迪斯科启动,如果不是中间在学概率论的话真有暑假那味了(
+越学概率论越急,之前一直看不太懂
+upcrossing,今天发现后面有个提示说看成和买股票一样,规定小于 \(a\) 金额时买入,大于 \(b\) 金额时卖出,只要存在 upcrossing
+就一定能赚到 \((b-a)\)
+的钱。联想到一些,高考完赚了点小钱之后买的已经砸在手里的基金(也不至于,总体还是赚的,全靠纳斯达克撑着(,完全理解了,是不是因为我一直犯懒只设定投然后就变成了现在这个样子(
观测到了夏季大三角,在 Stellarium 上看织女星的时候第一反应是 Admire +Vega,玩闪耀!优俊少女玩得(
+7月15日
+在寝室收拾行李和打扫卫生,明天就回家了。事实上今天快到中午才起床,一个室友比我还晚起来至少
+2h,怕收拾东西吵到她而且不能开灯,干脆极乐迪斯科启动(。之前大概看了一下游戏内容有
+10
+天,结果第四天下午到处跑着做任务突然被卷进帮派斗争,草,我的警枪都还没来得及找回来(,中弹后直到第六天上午才
+在 Kim 的照顾下
+醒过来。感觉明天高铁上再玩玩就真快要速通了(
刚把床上的东西收完就被另一个在接受小学期暴打的室友叫去帮忙,从教她装
+Pytorch 和 CUDA
+开始一直到把
+lab
+写完,就差不多到晚饭时间了,绷不住了,今天到底在干什么。不是自己的作业而且只有这一回,就觉得一边查一边写还挺好玩的,但如果这是我的小学期那肯定会觉得很烦(
填答疑坊工时的时候她说半天找不到我的名字,结果一看是在计算机类答疑里面找我(,绷不住了。才发现单次工时上限是
+150 min,还填了两次。感觉填个数学也不好 毕竟这又不是 learning
+theory,临时在答疑学科偏好里面加了一下 Python
+程设(?),填完工时赶紧撤销了,我不行。然后突然想到,为什么不直接去答疑坊找个真正的贵系志愿者帮忙呢((
这门课不是叫集成电路实验吗,为啥里面还会有个图像二分类的作业(。文档也非常逆天,感觉完全没接触过的话单看文档不可能理解是要做什么,比贵系暑培都差远了。页眉写的还是“2021
+小学期”,最逆天的是正文里面还出现了“使用命令 import pytorch
+和 pytorch.__version__ 检查安装结果”这种
+typo,绷不住了,万一真有人信了怎么办((
今天才发现网易云终于有 Life is PIANO 和 +R.I.P. +这两首我最喜欢的 G2R2018 +参赛曲了(虽然都不是冠军,顺带一提这一年的曲子还有 MARENOL,冠军是 Destr0yer),一开始都是在音游里听到的,以前都是在播客里面听,不沉迷音游之后没有听播客的习惯了所以也听得少了。R.I.P. +里那句“おはよう、朝だよ”也曾经被我用在了很多地方的个人简介里。
+喜欢看纸质书最大的弊端就是不方便搬运,颠了颠箱子稍微有点担忧。而且费老大劲搬回家要是没看多少又带回来就更蚌了(
7月16日
+在高铁上猝不及防地就把 Disco Elysium 通关了,一周目游戏时长 18.2
+h(能不能用这个时间去学学数学.jpg
虽然看起来大家都没玩过,但是这点吐槽大概也不会导致什么剧透(。其实如果是我的话看番或者打游戏一般都会先去看一眼剧透再开始,比较有掌控感(?)
--我一个数竞cmo银牌同学,综合成绩常年年级前五,综合营优秀评定,我校卓越毕业生,最后因为报的是热门的信计,也没有录取……校测只给到13分(招办说如果改成数学可以录取)
-
笑麻了,傻孩子们,快跑啊(
8月20日
-逛街的时候看到有个七夕写许愿牌的活动,一些真诚的祝福:
-
毕竟我偶尔想起来那些没上的物理课,会觉得五年毕业也很困难(。考公的考一开始还写错了,残念(
-被暴雨困在商场里走不了的时候去玩了一下自助拍照的机器,和老姐《初检合格》((
-
贴图的表情包还挺精髓的((x
-8月21日
-右手大拇指根好痛,有刚入坑音游的时候当拇指党结果玩太多玩出腱鞘炎那感觉了。怎么偏偏是这个手指,写题就讲究一个冥想,吃饭也好想把筷子扔掉(,下略(
8月22日
-早晨收到了玫瑰,去社聚还收到了 neruko -老师的小卡片,回来才发现卡背是透光的,好用心 qwq
-
以及
+-
+
直到破案和抓到犯人,游戏结束,我都没能找回自己的警枪,怎么会是呢(
+因为找枪需要晚上十点之后去和某个 NPC +对线,第四天中午接了这个任务,回来的路上就遇到了帮派斗争,被枪击之后第六天上午才醒,但是第六天下午就把案子破了(悲
+从和 Titus +对峙开始我就一共开了两个世界线,其中一个接任务比较早但是掷骰子运气不好导致很难玩,后续就没继续下去。而且貌似晚上九点之后 +Kim 会离队,我不敢一个人去找手里有把枪的 NPC +所以就搁置了这件事(挠头
+怎么突然就结束了,感觉这个结局多少有点烂尾,不过现实中被踢出制作团队的主创们已经给出了 +Disco Elysium 的最佳结局((
+我看到 Kim +开始总结说我是他见过最好的警督的时候就觉得不对劲,但是后面还提到要去拜访 +Lena、她就住在我家附近的时候还以为可以开新地图,去看看和前妻曾经生活过的房子。结果还是突然就结束了,然后开始放演职员表,甚至都没来得及截到 +Kim 的评价(
+金*真心*相信你。虽然我的对话选项都是在他面前发疯,但他真的好宽容((
+信息量太大了,只有任务提示没有对话回档和小地图确实有点困难,不停地迷路,不知道下一步要干什么所以只能胡乱和 +NPC 聊天,总的来说游戏性还是不太行,但这些问题之外也可以给 9 +分。
+可以给发行商扣大分吗(不是因为只想给 One Last Kiss 10 分才故意不给的
+如果按我的习惯
(xp?)来说开局人格会直接选 +Intellect,可惜体质太差很快就被嘲讽寄了。最后尝试的是给智力和精神平均匀了点数,Inland +Empire 发疯的体验非常好。如果有二周目(还玩?)我会选 +Psyche。
+用我破碎的法语读懂了
自己的名字 Du Bois 和+写在雪地上的那一句“UN JOUR JE SERAI DE RETOUR PRES DE +TOI”,总有一天我会回到你身边。
+
我爱它晦涩的文字和时常的疯狂,时而让我悲伤,时而让我充满希望。
--今天是乞巧节,希望织女赐我巧手,让我写证明少写点伪证,写代码少出点bug
+YOU: No, you're special. You had glowing lungs.
+DOLORES DEI: “My lungs do not *glow*, Harry. I am +just like all the others. None of us have glowing lungs—stop making me +into some kind of…”
+INLAND EMPIRE: [Legendary: Success] Then it's you. +*You* will make her lungs glow. Your pain is NOT meaningless.
8月23日
-十月终于要有赛马娘第三季看了,急急急急急(
-今天送老姐去北京西坐高铁,才知道这边不允许送站,买票进站的话最多提前大约六个小时,逆天。在这之前我还真以为所有的车站都是允许送站的,至少上海虹桥和北京南都是,然而以前也只有在这两个地方送站/被送站的经验(。等寒假回去测试一下上海站,上海西站和上海南站能不能送站,可以的话其实也想测测什么松江南金山北南翔北安亭西芦潮港站(开玩笑的,芦潮港站不办理客运,可以送就说明百京不行,不能送就买个从上海站到上海西站的票假装在运转好了((x
然后发现其实芦潮港站和清华园站(这个东西还挺冷知识的)这种早就已经停止办理客运的站点在 -12306 上也还可以选择,多少有点时代的眼泪了(x
-去年秋季学期在统计推断课上学 C-R Inequality 的时候老师还提了一句 C. -R. Rao 目前仍然在世,后来网上冲浪的时候还在统计之都读到了《C. -Radhakrishna Rao: A Century in Statistical Science》,R.I.P.
-对不起但如果不是去翻了一下的话我已经全然忘记 C-R Inequality
-的形式了((
8月24日
-晚饭和 Triang-jyed-driung -面了个基,虽然他看起来对欧老师更感兴趣,怎么会是呢((x
-新生好可怕(?,晚上听人在楼道里吹了半个多小时长笛,而且听起来好像不太会的样子((
测量实习组队好艰难,每到实践课组队都觉得和自己专业的同学大多都不是很熟还是挺麻烦的。找的第一组四缺一但是他们在何老板和我之间选择了何老板(,去问
-OscarZs
-一开始也是四缺一被拒,后来又可以了(,过了一阵第一组又润掉一个人,问我还能不能来,这次轮到我拒绝你们辣,总的来说好崩溃((
8月26日
-虽然昨天没写但其实是挺重要(?)的一天,但是没写(?
-从去年就在看《因果推断的统计方法》了,这两天终于在手机上看完了,学到许多但其实也没学到啥(。最开始看到统辅课里面有一门因果推断导论(不知道是不是叫这个名)的时候还在疑惑这也是统吗,一头雾水(x)地读完发现确实挺统的(
形式化定义真难,一开始疑惑 Casual Inference -到底是个什么东西的时候主要就觉得很难形式化定义,像 confounding -这样的东西在线性回归课上也只是举个例子说明,真看定义还是蛮绕的。
-后天要开始测量了,难绷。
-8月27日
-明天早八就要测量了,总感觉今天是十天内最后一次学数学,很崩溃,就郑重地往前给一些打星号的章节收了尾(,然后回去终于放心地把第四章的一整沓纸放进了影印书的那个壳儿里(。以前不知道是出于什么精神状态没看,如果看过的话读后面的东西应该会顺畅很多,#每日追悔莫及(
-然而测量的课前准备从申请 CASS 试用资格和现在 AutoCAD 都已经出到 2024
-版了但还是要求用 2014
-这一步开始我就觉得难绷了,上次感觉到相似的难绷应该还是上次领军训服装的时候。看这个测量实习的指导书感觉也挺军训的,尤其要穿两周长裤,本来想着如果只是规定穿的话那我就不穿顶多扣点分而已,后来看了看学长的工作日志感觉可能是外业测量的时候蚊子太多不得不穿(,工作环境好像还不如军训,好崩溃(
看到 ypk 今天给我发邮件说明早有个 talk
-可以来听一下的时候崩溃感达到了顶峰((有人需要吗在这里写一下好了
--8/28. 10-11am. 三教 1205
-Speaker 1: Yaqi Duan
-Title: Optimal policy evaluation using kernel-based -temporal difference methods
-Abstract: We study methods based on reproducing -kernel Hilbert spaces for estimating the value function of an -infinite-horizon discounted Markov reward process (MRP). We study a -regularized form of the kernel least-squares temporal difference (LSTD) -estimate. We analyze the error of this estimate in the L2(μ)-norm, where -μ denotes the stationary distribution of the underlying Markov chain. We -use empirical process theory techniques to derive a non-asymptotic upper -bound on the error with explicit dependence on the eigenvalues of the -associated kernel operator, as well as the instance-dependent variance -of the Bellman residual error. In addition, we prove minimax lower -bounds over sub-classes of MRPs, which shows that our rate is optimal in -terms of the sample size n and the effective horizon H=1/(1−γ). Whereas -existing worst-case theory predicts cubic scaling (H^3) in the effective -horizon, our theory reveals that there is in fact a much wider range of -scalings, depending on the kernel, the stationary distribution, and the -variance of the Bellman residual error. Notably, it is only parametric -and near-parametric problems that can ever achieve the worst-case cubic -scaling.
-Bio: Yaqi Duan is an Assistant Professor of -Technology, Operations and Statistics at New York University Stern -School of Business. Prior to joining NYU, she worked as a postdoctoral -researcher at Massachusetts Institute of Technology for one year. She -received her PhD from Princeton University and BS from Peking -University.
-Speaker 2: Kaizheng Wang
-Title: Pseudo-Labeling for Kernel Ridge Regression -under Covariate Shift
-Abstract: We develop and analyze a principled -approach to kernel ridge regression under covariate shift. The goal is -to learn a regression function with small mean squared error over a -target distribution, based on unlabeled data from there and labeled data -that may have a different feature distribution. We propose to split the -labeled data into two subsets and conduct kernel ridge regression on -them separately to obtain a collection of candidate models and an -imputation model. We use the latter to fill the missing labels and then -select the best candidate model accordingly. Our non-asymptotic excess -risk bounds show that in quite general scenarios, our estimator adapts -to the structure of the target distribution and the covariate shift. It -achieves the minimax optimal error rate up to a logarithmic factor. The -use of pseudo-labels in model selection does not have major negative -impacts.
-Short bio: Kaizheng Wang is an assistant professor -of Industrial Engineering and Operations Research, and a member of the -Data Science Institute at Columbia University. He works at the -intersection of machine learning, statistics, and optimization. He -received his PhD from Princeton University in 2020.
+Suggestion: [Medium: Success] "I know you still love +me."(Kiss her.)
+ARIST: No…
+DOLORES DEI: No answer. The arches of her brows +quiver as she looks you in the eye and backs away from you...
+EMPATHY [Medium: Success]: You won't do any of that. +You can barely make her cry.
+SHIVERS [Medium: Success]: All the roads will miss +her footsteps when she's gone from here.
+INLAND EMPIRE [Easy: Success]: A completely +different world.
+SUGGESTION [Medium: Success]: With your feet +trembling from the steps you took -- tepid and fearful -- you stand +against her; her body close to you, radiating warmth. With your eyes +closed, you move your lips on her mouth.
+DOLORES DEI: She is not kissing you back.
+YOU: I feel her breath...
+DOLORES DEI: Her chest rising like a pillow, warm +exhalations against the side of your mouth—her tender soul moving +through her lungs.
前段时间在家里闲着没事的时候整了一个计算闭合导线参数的小(不如说非常非常小)工具,看实习指导书上还有一个可选提交项目是使用的程序,确实可以卷交一下,前提是我最好对这个测量步骤没有什么理解性错误,闭合导线测量占比要是比支导线还少那就大寄特寄(。然而这一步难道是重点吗,重点难道不是我连全站仪都不是非常的会用、工程计算机制图或许就是
-2.3
-的水平所以也不会画图、然而测量学到现在都没有出分我甚至不知道它和工程计算机制图相比哪个更烂,而且这段时间看起来非常的缺少贴贴,吗(,那要不还是先希望队友没事吧((
不行,现在压力好大,又想起来组队的时候还是我主动去问能不能加组的,如果不是我的话他们本来明明有机会拥有一个啥都会的组员而不是我这样的
-five,别真坑队友了吧((
8月28日
-测量实习就是军训的一些证据:
--
-
都是 2 学分的小学期课程
-和同班/同专业的同学待在一起(
-(理论上来说是)早晨,下午和晚上干活,早晨起得很早,太热太晒的时间休息
-戴帽子,穿长袖长裤
-在学校里定向越野
-缺少贴贴
-
晚上回来疲惫地走进猫超买了盒酸奶,里面挤满了刚结束晚训的新生,对着楼梯口的镜子照了照自己,我的评价是穿得好奇怪一女的(。想起来下午在东主楼附近找合适的控制点的时候也是穿着这身奇奇怪怪的衣服,还遇到了 -TA,世界真小,不过我觉得 TA -新(?)发型还挺好看的,为啥上次社聚的时候大家都在乐((x
-白天实在不想听课,看了很久地理等级考之后就没再看过了的星球研究所,他们制图水平真的好高(
-8月29日
-早晨踏勘选点涂油漆之后其实就累了,中午爆睡俩小时。吃饭的时候看微信步数是
-7k 多一点,下午跑尺,晚上回来也就
-10k,然而地质实习的同学中午就人均破万了,好(
怎么能写的东西还不如工作日志多,下次要不直接把工作日志搬上来吧(谁要看啊
8月30日
-昨天跑尺的时候坐在马路牙子上思考 regular conditional expectation -和那个我有点看不懂的 transition probability 的 general definition -有啥关系,至少长得挺像的,某种程度上是把随机变量的定义修改成了映射到可测空间而不限制在 -\((R, \mathcal B^1 (R))\) -上,想到这里就感觉有点困了(。
-昨晚才发现之前看不懂主要是 notation -在前几章的角落里出现过但是又没有再提过多少有点你谁啊真不熟了,要是有索引就好了(。查 -MSE 看到一个关于为什么需要一个 general definition 的讨论,有个评论说
--"a random variable gives out a real number" Not necessarily, for -example, to model DNA sequences by Markov chains, one could choose -S={A,C,G,T}.
-
才想起来生统概论课上也举过类似的例子(单指用随机变量表示基因型)但我给忘了,老师当时还说了一句虽然随机变量定义上是取实数值但也可以换(大意),当时以为她在说废话于是记住了这件事,现在想想不知道是不是有别的深意(其实应该没有吧
昨晚查这玩意查上头了睡了还不到六个小时,最近实习有超长午休,本来以为今天可以先睡个觉然后学点数学来治疗精神损伤,结果剥蒜三小时闭合导线参数还没算出来,晚上继续剥蒜,还算了一些高程和支导线,早晨的角度闭合也是当场画图算的,计算器要按冒烟了,高考数学打计算器强度都没这么高(是的你沪高考数学是可以用计算器的,虽然不知道现在还能不能,至少以前会因此有很逆天的剥蒜。下午记水准测量读数的时候也一直在打计算器,数学壬不是这么用的,我最不会的就是剥蒜,但是还写错一个数,还好刚重测了存疑的两站就发现了,没返太多工(
明早四等水准测量,今晚看了几个例子大致知道是要干什么了。说起来今天得知水准测量的两把尺一定要是不同规格的时候 -CPU -都烧了,但实际操作也没那么难,还能预判读数在不在值域里,希望明天高程能闭合,再闭合不了/误报闭合失败我真要给队友谢罪了(。下午大概要测碎部,然而我对于怎么测碎部点甚至怎么记读数这件事尚且没有任何概念(
-下午看到老师说明天最好是六点到九点测四等水准,大家商量说往后推到七点半到十点半也不是不行,差点脱口而出“毕竟
-Lebesgue 测度有平移不变性”然后硬给憋回去了自己开始乐,并且默念这是
-surveying 不是 measure theory(
8月31日
-这两天我一直以为中午收工之后仪器是送到测量老师办公室保管的,今天才听清楚是送到其中一个队友的工位,碰巧也在新土木馆。连你院本科生都有工位,而某些系和某些书院到现在博士生工位都不够,博后工位还十人一间(
晚上看到个这个,光速克服拖延去下单了 -GTM274 的影印((这是可以说的吗((对不起但真买不起(。之前本来想读完 -Durrett 之后看 Markov Chains and Mixing -Times,但好像太专了,优先级不应该那么高(
-早上的四等水准太折磨了,作为一个对于最终成图没有任何帮助的支线任务,四个半小时测了整整 -28 -站还不得不用一些物理实验手段处理了一下(,好崩溃。最逆天的是这玩意的转点没法保存,只能一口气测完全程(
-测量实习中期要交的东西都做完了,下午站在东配楼门口测试了下碎部测量,然后聊了会天就收工了。聊天的时候无意中发现 -OscarZs -会把“什么什么东西看起来很糊”的“糊”读成四声,想起来之前欧老师也是,还以为是什么湖北特供口音,然后另一个家在河北的队友说他们那边也是这么读的(。稍微有点怀疑读成二声是什么江浙沪和山东莫名其妙统一起来了的口音了(
-]]>7月1日
- -上午晒了 3h 感觉真有点中暑,上次中暑还是 2019 CGMO
-的时候,当时好菜(。睡了一下午,今天训练结束之后寝室里每时每刻都有至少两个人在睡觉((
待会拉练,希望人没事。实在不想带自己的被子,找了个不用的被罩里面裹了个枕头蒙混过关,别散了啊(
-来点室友名言:你别去按照那个教程学是怎么打的,看一遍就行了,然后自己凭感觉打三横加两竖,肯定能打出来(
-她是对的(
-7月2日
-拉练,然后摆烂(,拉练出发之前和结束之后都有短暂的贴贴,满足了(
-从我高中军训的时候就在听我那位华子毕业的总之好像是什么状元的班主任满怀自豪地反复讲述他们当年背着被子走了 -20 km -的事迹,那个时候就已经开始为拉练这件事情烦躁。虽然也不是保证能考到华子但是反正上交也有拉练(,入学之后军训又推迟了两年,整整为此烦躁了五年。
-前一个小时还能和何老板以及班里那位 CCHO Au
-的哥们吹水,顺便听二位讲了讲投行实习做的事情以及他们的感情状况,学到很多,最后一个小时的时候开始逐渐和何老板掉队到后一排排尾,虽然还是在吹水但是频率和音量都低了很多(。毕竟是整个营的末端了,我在哪队尾就在哪,不妨碍后面的人行进,所以也没急着追。队尾的几个老哥大概也都是这个心态,一起摆烂了,还遇到了从上一个连掉队到我旁边的室友,蚌(
起来之后在楼道里听到有人打电话,说“哎呀人哪能要求十全十美呢,找对象看中对方身上的一些优点就可以忽略别的一些缺点了(大意)”。纯爱战士在心里默默点头正准备满意离场,结果听到她的下一句是“但是对我来说对方长得帅是最重要的,如果很帅的话哪怕有其他的一些问题我觉得也可以原谅(因为被震撼到了所以完整地记住了原文)”,草,怎么会是呢(
下午和晚上终于看完了 Munkres -上每本数学书都有的但我好像从来没学扎实过的集合论和逻辑(,跑步进入大家已经在数分里学完了(不太确定)的点集拓扑。给我的感觉就是贵校数学系在数分里面把什么都学完了,听说宗学的点拓只上七周,大概还是得自己赶一赶,没学过数分的我只能度过一个相对失败的人生(。在教学楼关门之前终于写出来第一节最后一个定理证明跑路了,虽然还是比预期的时间晚了 -20 min,但总之是好的(
-命运/好怪 很假 Fate/strange Fake -Whispers of
-Dawn-
-终于放送了,急急急,我已经迫不及待想看宝具对轰辣(
7月3日
-好困,感觉没啥可记的(
-两门上次没出成绩的课到现在也还是没出,真就拖到 ddl -再给我一拳是吧(
- -下午贴了 1.5 h -回来之后发现三个室友都还在睡觉,明明是差不多时间上床的,草(。晚训完也贴到了,只不过能不能只贴不军训啊((
- - -7月4日
-给老师发邮件之前单独列了个数学课的成绩单出来,虽然单算这些的话均绩远高于我自己的
-GPA
-但还是给我整绷不住了,怎么都是水课,然后才发现我好像是真的没怎么上过非常困难的课(。急了,怎么办,还要不要单列,单列了反而显得很菜(然而还是可以薄纱大部分去统计中心的人,所以先给那边的老师发了(
一杯茶一包烟一页 Munkres 看一天(,好绕。
-射击搞到晚上九点多,等了两个小时不到两分钟就打完了,麻了。我其实一直有点做不到闭左眼睁右眼,所以打靶的时候左手没扶枪,用来按眼睛了。还是打了 -90 -多环,虽然也没意义,毕竟不脱靶就有分,所以确实有(一只)手就行(。好像端枪的姿势不太对,后坐力震得锁骨疼(
-这个困扰其实物理实验的时候也有,感觉有的时候对焦或者读数看不清,只能左手按住左眼勉强看,不过军训射击怎么就不算一种物理实验了呢(。这里是不是该有个物理实验九宫格(
-懒得骂武装部了,累了。
-7月5日
-早训摆烂的时候我甚至躺在树荫下面睡着了,怎么会是呢。只记得有点无聊,然后就躺下了,哼了一会我贫瘠的华语歌歌单,班里一个同学问我在唱什么,我说是《南国的孩子》,给她发了一个我最喜欢的版本。然后迷迷糊糊地就闭上了眼睛,再次有意识就是醒来看到蓝天的时候吓了一跳,好像是第一次躺在地上睡着(
-后面又睡着了一次。咋说呢,后两天能不能也继续摆烂,最好还是有时间睡觉(
-体验了一天 wake up with no -email(。只不过这个暑假开始磕盐根本不现实,延毕的话确实是一点都不急,找两个老师留个印象,能有点别的指导(?)的话更好。
-急了,七月能把点集拓扑读完吗(
- -所以到今天已经贴了两个月了(虽然今天并没有贴到,不知道为什么给我的感觉是,原来才两个月吗(,是不是每次想起来的时候脑内自动从三月就开始算了(
7月6日
-听说人在隔壁化院的高中同学已经跟着导师发 Nature
-了,而我昨天才刚收到和两个老师约时间聊天的邮件,怎么会是呢(大家都有光明的未来(x
到底要怎么样才能把这个 行列式 分列式的 bgm
-从脑子里赶出去,循环一天 One Last Kiss 和 Idol
-了,晚训还是又灌了回来,急急急(
室友锐评:你这个发型,是不是根本就没打算晚训,想贴到晚上的来着(
-还是室友锐评:急了,分列式和现男友以及前男友都站在同一列里,逆天(
-来点今晚东操的天空,但是玩闪耀!优骏少女玩得:
-
你还别说,左边阴影里这个云的分布真挺像的(
-7月7日
-这个 b 军训(,终于要结束了(
-没啥写的,今晚就打算开始把之前为了内务检查塞起来的东西摆回原位了。
- -7月8日
-众所周知未央书院只有 14 -连(,但这个军训还是从我们被取消评优资格开始乐起来的,好事(
-拉练回来那天就觉得四教教室的地面不是很平坦,当时还以为是脚太痛了感受异常(,后面这几天在教室里走的时候感觉确实是不太平,不知道是我的幻觉还是设计师你在干什么啊设计师.jpg(
-今天突然看懂了 Munkres -上一个两天前卡住了的反例,然后被自己蠢到。下午课后题卡住想得脑袋疼,结果去吃饭的路上想明白了,再一次被蠢到。军训完第一天的阅读进度大约和之前一周的进度差不多吧(
-这书是女生节礼物额度报销的,当时还比较笨蛋,没直接影印电子版(版权意识薄弱.jpg),原版贵好几倍感觉不太值不如多报销两本书,就买了中译。现在感觉翻译质量也还可以,至少
-Hausdorff space 被翻译成了 Hausdorff 空间而不是豪斯多夫空间,点名批评
-Stein 中译本的博雷尔集(
最后一次去东操(?)的时候在路灯下面看到个这玩意,我直接一个测量学 -PTSD,想起来暑假里有测量实习和地质实习更崩溃了,那不就是军训 2.0 -吗。今早还在想防晒霜用不完了,急,现在也没必要急了,实习还得用(
-
(这个东西叫四等水准尺,确定地面高程用的((说不定测量实习的时候会在学校里用到它,绷不住了
- -第一次大概也是最后一次用宿舍楼里的洗衣机是今天把军训的东西全部扔进去洗。本来还觉得问题有点大,这身衣服坐完东操坐北操,万一楼里有别的年级的人洗自己的衣服岂不是(,结果室友表示没啥问题,可以我先洗她再洗然后加消毒液空转一圈,让我不用有压力(。既然你们天天用洗衣机的人都这么说了那就 -ok fine(
-7月9日
-没有学期中间乱七八糟的作业,Munkres 的 solution manual -不如直接在手机上用 solverer 平替,解脱了,不用天天带电脑了。
-睡得很晚但醒得很早,早晨突然有个高中有一阵子聊得很多的群友给我发消息,说最近看了天之杯之后想入坑 -FGO,太恐怖了,我光速劝回(。Fate 系列的动画也好,FGO -也好,如果到现在完全没接触过的话还是别入坑了(只不过 FZ -还是值得一看的),但是如果都坚持看/玩到现在了的话就有一种必须要继续下去的感觉(。柯南剧场版好像也是这个道理,这些东西怎么都除了画质之外越做越烂(
-看了眼今天上海最高温 29 -度,本来觉得没啥,又看了一眼早晨下过雨之后空气湿度 100%,那体感不得 40 -度,草。下周回家估计就已经出梅了,一时不知道是湿热好还是干热好,虽然出梅了也肯定比北京湿,急了。
-中午骑车路过地质大学的时候看到一堆人扛着三脚架和全站仪往里面走,急了急了急了急了别提醒我暑假末尾还有个测量实习这回事了。旁边一条路的围墙上写了各种高中自然地理小知识,如果我还是个高中生的话会很感兴趣,但我现在在读这个 -b 专业所以看了只觉得好崩溃(,这下又过期 jk 了。
-荷清路比学堂路好走一万倍,没有意义不明的上下坡
-7月10日
-军训第一周在北操被不知名虫子(首先排除蚊子)在手臂上咬了几个包,后来不知道是过敏还是又多次被咬了,逐渐蔓延到了两条手臂上都有好多,抓起来的时候看着还挺吓人的。本来还觉得应该排除点别的原因,但是室友和她们班的一个同学都是和我一样的症状,大概就是军训的问题。要不要去校医院看一下呢,要么直接回家去华山医院看吧(
-认识硕哥还是四月底的那个推研转系讲座,当时就跟他说期末考完去找吴昊,他还劝我越早越好,五月的时候还给我推了吴昊组里一个学姐的微信。说起来这一通操作下来多少有点不去也得去了(,我清楚地记得是一节测量学的课,旧水的空调开了和没开一样,课也不想听,然后他突然来和我说吴昊组里有个想要学妹微信的学姐()的时候真有点社恐地狱。总之我一直把这事咕到军训之后,今天才去。
---数理基科是学物理的吗,你是致理书院的吗?
-哦哦,啊这,未央是什么(
-数分没学过问题不大吧,你概率论 1 -不也撑下来了,后面的课程里遇到不会的随时补就行。其实按这个来说你已经提前体验到科研的状态了!
-
难绷(
-下个学期可能有必要把概率论 2 和 3 一并上完,据说是必要的基础(,而且
-3 只有秋季开课,错过等一年,2
-是两学期都开然后进度上有一个章节的区别。那就要退掉
-ODE
-和拓扑之一,感觉大概率是后者,宗学年年都有,而台湾腔不常见(,这样的话最近把
-Munkres 第二章看完当做补习数分,然后就可以停下来换回 Durrett
-了。今天顺便还偷跑到了吴昊概率论 1 和 2 的纸质版讲义,概率论 1
-的部分好像是她下学期要用的,虽然我翻了一下感觉就是 Durrett
-的精简换序版,然后把习题都换成了丘赛题,双厨狂喜(你都厨了些什么东西(。
下午到得比较早,在静斋转了两圈,看到二楼走廊尽头有一个开着门的巨大的办公室,里面还有小隔间,还以为是研讨间之类的,想着如果没人的话可以先进去坐一会。结果凑近一看门口的名牌是 -Shing-Tung Yau,绷不住了(
-顺便还看到了刁晗生的名牌,高中的时候就经常听教练念叨他,怎么不算师出同门了呢((别丢人了。之前环友发过李思门口的抽象画,今天看到了真迹,很生草,虽然但是到底为什么要贴在门上,我还是更能理解王浩然把《达拉崩吧》的歌词贴门口(
说到推研转系讲座就想起来,军训动员会的时候梁曦东说“大家入学的时候专业是限定的,大二结束选导师的院系/专业范围就会扩大很多,等到推研和做研究几乎全校范围内都可以选,范围是越来越广的(大意)”。我就不明白了,这个宽窄的顺序完全反了罢(
-开始玩 Disco -Elysium。暑假回家的一个月除了去拔智齿之外其实就三件事,监工家里的装修顺便跑几趟宜家搞软装,稍微学点数学,精神损伤的时候 -Disco Elysium 启动然后加重损伤(。本来是想 Death Stranding 和 Disco -Elysium 二选一的,后者比较便宜/夏促力度更大/更感兴趣就先买了。
-(Death Stranding 在愿望单里主要是有 Pop Virus
-的加成,是的我是来听歌的(
7月11日
- - -吴昊讲义上的 P 和 E 全都是 mathbb,舒服了(
-Munkres 第二章结束了,把吴昊讲义的概率论 1
-部分走马观花复习了一下,好崩溃,这才过了不到一个月有些东西印象就有点模糊了。这个时候就要安慰自己,没事,抽代我更是忘完了,概率论
-2 也不是很分析,别管那么多接着往后看就是了(
晚上回寝室开答疑坊,给正在被小学期暴打的室友讲了会傅里叶变换和卷积。实际上傅里叶变换我真的已经忘完了,上次接触还是求特征函数,感觉也不太涉及什么分析性质,今晚一边看讲义一边现学现讲的(。看了看大作业要求给我整绷不住了,这真的是能用 -MATLAB 写出来的东西吗,希望人没事(
-开完答疑坊就开始开理发店:
---室友:哟你这个戒指挺好看的
-我:(中二发作)其实这是爱因兹贝伦家主的证明,圣杯战争就要来辣
-(室友也是月厨所以发癫也没问题室友:别中二了,这是个对戒吧
-我:(
-
7月12日
-猫超的老酸奶真好吃,请年轻酸奶在老酸奶陪同下观看(
今天去和 ypk -聊了个天,聊到饭点还一起去玉树吃了个饭(,稍微有点社恐地狱,不过算是个好的开局。然后被丢了一个 -linear regression 的问题和一篇 paper -读,可能是数学书看多了吧,我反正觉得 90 -页是一个,非常非常庞大的数字,不知道要读多久。下午简单翻了一下感觉 -notation 都不是很熟悉,不知道要额外多看多少 paper 才能看懂,急急急(
-虽然我感觉一上来聊天的环节里他像个留学中介一样(,还问我有无 dream -school,我随口说了个感觉 UMich -这样的就挺好的了,他问我为啥,我说因为我喜欢比较冷的地方,给他整不会了(
-来点乐子:
---吴昊我认识,她的方向好基础好难(
-既然要延毕的话可以再课业为主一个学期,下学期把随机过程和随机分析学了是好事,听吴昊的,不急(
-所以未央书院是学什么的(
-太经典了,每个老师都要问一遍那你们书院的同学是不是有好多想转 CS 的(
-我发现学数学的同学好多都不喜欢统辅课
-“找不到喜欢什么的话可以先排除不喜欢什么”“我不想写很多代码”“你们学数学的同学怎么都这么说”(
-那你当初为啥不去北大数院呢?(
-一到暑假清芬三楼停伙我就不知道该吃点啥了,你有什么推荐吗(
-清芬战士喜加一
7月13日
-有个高中同学毕业之后把我 QQ -好友删了,后来又给我发了几次好友申请,每次我都直接无视,今天又来一次。不知道为什么这么执着,我又不欠他钱(,也不是很想加回来,但还是担心万一是有什么事情,就回了一句如果有事情可以加我微信说,然后给了微信号。结果他也没加,我不理解(
-后来一想应该是删好友的时候自动拉黑所以也收不到消息了,那太好了正好我其实也不大想加他微信(
中午雨正大的时候在双清路上被一个逆行的外卖骑手创了,没摔倒的代价是把车和伞扔了出去(?),人往另一边撤然后就顺利站住了,现在想想也有点想象不出来这个动作,不过没摔就好。然后发现右手大拇指指甲盖里在流血,也不太懂是为什么,不过也是小事。又骑上车之后觉得雨天单手打伞骑车还挺危险的,在学校里倒还好反正整条路都是自行车道(,在外面尤其是右手还一边扶车把一边拿着手机看路线,遇到突发情况刹车都很难,路又很滑。
-好像问题在于我不想用导航模式,每次都是自己看着地图走,不然其实可以直接听语音导航,也不用一直拿着手机还时不时要看两眼。说实话自己看地图还经常不慎走错和绕路,也没什么好的,但就是不想换(
-最近在大力 Disco Elysium,现在进度终于到 Day 3
-了,不知道啥时候才能完成一周目,但是感觉
-相比于刚开始玩的时候开个灯就能把自己整去世来说
-还算顺利。也有幸(?)在 Day 2 就看到了这一段名场面
-然后就昏了过去,吸引我入坑的 Dora's letter:
--Harry, I wanted to write you a letter, so you can read it when you -wake up. Maybe it will make you happy.
-Every morning when I step out and you're asleep behind me, I find a -little piece of sadness in me. I carry it in my chest down Voyager -Road... Every step I take, it grows. By the time I reach the fuel -station it has filled me entirely. I step on the light rail and look -back, sparks fall from the bow collector.
-I know it will be like this until late afternoon, when I get off the -42 -- and walk back to you... You, you... Every step I take will get -lighter. It almost makes me run! Sometimes I do.
-I can't believe I met you. I can't believe the happiness I feel with -you. You have a vast, vast soul and I will always, always, always come -back to it. Kisses, kisses, kisses.
-
不知道为什么(?)好困,感觉能早睡(
-7月14日
-早上双人成行,晚上去情人坡看星星,回寝室极乐迪斯科启动,如果不是中间在学概率论的话真有暑假那味了(
-越学概率论越急,之前一直看不太懂
-upcrossing,今天发现后面有个提示说看成和买股票一样,规定小于 \(a\) 金额时买入,大于 \(b\) 金额时卖出,只要存在 upcrossing
-就一定能赚到 \((b-a)\)
-的钱。联想到一些,高考完赚了点小钱之后买的已经砸在手里的基金(也不至于,总体还是赚的,全靠纳斯达克撑着(,完全理解了,是不是因为我一直犯懒只设定投然后就变成了现在这个样子(
观测到了夏季大三角,在 Stellarium 上看织女星的时候第一反应是 Admire -Vega,玩闪耀!优俊少女玩得(
-7月15日
-在寝室收拾行李和打扫卫生,明天就回家了。事实上今天快到中午才起床,一个室友比我还晚起来至少
-2h,怕收拾东西吵到她而且不能开灯,干脆极乐迪斯科启动(。之前大概看了一下游戏内容有
-10
-天,结果第四天下午到处跑着做任务突然被卷进帮派斗争,草,我的警枪都还没来得及找回来(,中弹后直到第六天上午才
-在 Kim 的照顾下
-醒过来。感觉明天高铁上再玩玩就真快要速通了(
刚把床上的东西收完就被另一个在接受小学期暴打的室友叫去帮忙,从教她装
-Pytorch 和 CUDA
-开始一直到把
-lab
-写完,就差不多到晚饭时间了,绷不住了,今天到底在干什么。不是自己的作业而且只有这一回,就觉得一边查一边写还挺好玩的,但如果这是我的小学期那肯定会觉得很烦(
填答疑坊工时的时候她说半天找不到我的名字,结果一看是在计算机类答疑里面找我(,绷不住了。才发现单次工时上限是
-150 min,还填了两次。感觉填个数学也不好 毕竟这又不是 learning
-theory,临时在答疑学科偏好里面加了一下 Python
-程设(?),填完工时赶紧撤销了,我不行。然后突然想到,为什么不直接去答疑坊找个真正的贵系志愿者帮忙呢((
这门课不是叫集成电路实验吗,为啥里面还会有个图像二分类的作业(。文档也非常逆天,感觉完全没接触过的话单看文档不可能理解是要做什么,比贵系暑培都差远了。页眉写的还是“2021
-小学期”,最逆天的是正文里面还出现了“使用命令 import pytorch
-和 pytorch.__version__ 检查安装结果”这种
-typo,绷不住了,万一真有人信了怎么办((
今天才发现网易云终于有 Life is PIANO 和 -R.I.P. -这两首我最喜欢的 G2R2018 -参赛曲了(虽然都不是冠军,顺带一提这一年的曲子还有 MARENOL,冠军是 Destr0yer),一开始都是在音游里听到的,以前都是在播客里面听,不沉迷音游之后没有听播客的习惯了所以也听得少了。R.I.P. -里那句“おはよう、朝だよ”也曾经被我用在了很多地方的个人简介里。
-喜欢看纸质书最大的弊端就是不方便搬运,颠了颠箱子稍微有点担忧。而且费老大劲搬回家要是没看多少又带回来就更蚌了(
7月16日
-在高铁上猝不及防地就把 Disco Elysium 通关了,一周目游戏时长 18.2
-h(能不能用这个时间去学学数学.jpg
虽然看起来大家都没玩过,但是这点吐槽大概也不会导致什么剧透(。其实如果是我的话看番或者打游戏一般都会先去看一眼剧透再开始,比较有掌控感(?)
---
-- -
直到破案和抓到犯人,游戏结束,我都没能找回自己的警枪,怎么会是呢(
-因为找枪需要晚上十点之后去和某个 NPC -对线,第四天中午接了这个任务,回来的路上就遇到了帮派斗争,被枪击之后第六天上午才醒,但是第六天下午就把案子破了(悲
-从和 Titus -对峙开始我就一共开了两个世界线,其中一个接任务比较早但是掷骰子运气不好导致很难玩,后续就没继续下去。而且貌似晚上九点之后 -Kim 会离队,我不敢一个人去找手里有把枪的 NPC -所以就搁置了这件事(挠头
- -
怎么突然就结束了,感觉这个结局多少有点烂尾,不过现实中被踢出制作团队的主创们已经给出了 -Disco Elysium 的最佳结局((
-我看到 Kim -开始总结说我是他见过最好的警督的时候就觉得不对劲,但是后面还提到要去拜访 -Lena、她就住在我家附近的时候还以为可以开新地图,去看看和前妻曾经生活过的房子。结果还是突然就结束了,然后开始放演职员表,甚至都没来得及截到 -Kim 的评价(
- -
金*真心*相信你。虽然我的对话选项都是在他面前发疯,但他真的好宽容((
- -
信息量太大了,只有任务提示没有对话回档和小地图确实有点困难,不停地迷路,不知道下一步要干什么所以只能胡乱和 -NPC 聊天,总的来说游戏性还是不太行,但这些问题之外也可以给 9 -分。
-可以给发行商扣大分吗(
不是因为只想给 One Last Kiss 10 分才故意不给的- -
如果按我的习惯
(xp?)来说开局人格会直接选 -Intellect,可惜体质太差很快就被嘲讽寄了。最后尝试的是给智力和精神平均匀了点数,Inland -Empire 发疯的体验非常好。如果有二周目(还玩?)我会选 -Psyche。- -
用我破碎的法语读懂了
自己的名字 Du Bois 和-写在雪地上的那一句“UN JOUR JE SERAI DE RETOUR PRES DE -TOI”,总有一天我会回到你身边。
我爱它晦涩的文字和时常的疯狂,时而让我悲伤,时而让我充满希望。
---YOU: No, you're special. You had glowing lungs.
-DOLORES DEI: “My lungs do not *glow*, Harry. I am -just like all the others. None of us have glowing lungs—stop making me -into some kind of…”
-INLAND EMPIRE: [Legendary: Success] Then it's you. -*You* will make her lungs glow. Your pain is NOT meaningless.
-
--Suggestion: [Medium: Success] "I know you still love -me."(Kiss her.)
-ARIST: No…
-DOLORES DEI: No answer. The arches of her brows -quiver as she looks you in the eye and backs away from you...
-EMPATHY [Medium: Success]: You won't do any of that. -You can barely make her cry.
-SHIVERS [Medium: Success]: All the roads will miss -her footsteps when she's gone from here.
-INLAND EMPIRE [Easy: Success]: A completely -different world.
-SUGGESTION [Medium: Success]: With your feet -trembling from the steps you took -- tepid and fearful -- you stand -against her; her body close to you, radiating warmth. With your eyes -closed, you move your lips on her mouth.
-DOLORES DEI: She is not kissing you back.
-YOU: I feel her breath...
-DOLORES DEI: Her chest rising like a pillow, warm -exhalations against the side of your mouth—her tender soul moving -through her lungs.
-
-DOLORES DEI: “Oh, yes. This is real darkness. It’s -not death, or war, or child molestation. Real darkness has love for a -face. The first death is in the heart, Harry.”
-DOLORES DEI: “See you tomorrow.”
+DOLORES DEI: “Oh, yes. This is real darkness. It’s +not death, or war, or child molestation. Real darkness has love for a +face. The first death is in the heart, Harry.”
+DOLORES DEI: “See you tomorrow.”
别的没干啥了,每次一到虹桥站感受到的最大不同都是南方潮湿的空气。今天上海在下暴雨,但是我一如既往地不记得带伞(,还好一直到下地铁都在室内,出地铁之后雨也停了。
@@ -8067,614 +7666,1015 @@ summary,听老师说多了刻进 DNA但还是啥也不会(
+9月1日
-感觉一年没学数学了,之前说感觉午休可以学,但是这两天要么午休也在忙着测算,要么太累直接大睡俩小时,一直没怎么看过。昨晚收工早倒是看了一下,之前没懂的地方稍微有进展了,但是不多(。今天继续往后看,有一种朦朦胧胧感觉要看懂了但又还差一点的感觉,解决的细节越来越多,仍然是稍微有进展,但是不多(,学得好慢。
-打开上个月的日记发现 8.1 在装修,8.31 -在测量,某种程度上来说整个八月都是在专业实践(,好崩溃。总觉得忙活装修已经是很久远的事情了,最近的进度因为太忙也没有再跟进,和宜家打电话沟通好像也是挺久之前了。
-前两天外业一直在做水准测量的记录,内业也做了不少计算,尤其四等水准测量是一边走一边记一边把计算器打到冒烟,到今天开始测碎部实在绷不住不想再记数据了,就选了画草图。脑子一抽打算把各个地方的草图画成边缘可以拼在一起的样式,到最后不仅有 -AutoCAD -的成图,各部分草图也可以拿透明胶粘在一起组成一张完整的手绘地图。除了强迫症发作之外这样或许对内业绘图的队友也更友好一点,于是就在大家面前夸下了海口(,结果今天画了两张 -A4 -纸,刚把美院周边测完就觉得实在太难了(,只能自我安慰图纸效果似乎还挺清楚的,对队友友好而且答辩也能吹一波(
-估计总共要画六到八张,希望人没事。这样的话之后几天草图就只能我来画了,轮不到换班跑尺或者读数养老了,寄(。还是原来那样,如果我还是原来那个喜欢地理的高中生的话应该会觉得画地图这种事情很有意思,但它现在是不得不上的专业课就觉得好痛苦,随便把一般的兴趣变成主业是完全行不通的事情,不过也可能只是 -jk 过期了(
-
虽然已经不负责读数和计算了,但是到晚上所有的数据表还是会莫名其妙都回到我手里,这是怎么会是呢(
-今天交中期的九样东西,这几天一直在劝诱(?)组长用 LaTeX
-写但成品还是 word 了,虽然很没必要但是好急(?
9月2日
-早晨出门正好看到大量研究生新生在往综体走,大概是开学典礼,一路上在心里默默锐评了一些院衫。
+8月1日
+ + + + +摆烂,本来想去看硬装的情况,合同上签的是七月底完工,但是到今天还没结束。然后学到了新知识:刮腻子要三遍,每一遍之后都要晾干,晾干之后刷墙漆之前还要磨平,所以真正刷漆要到明天了。
+在宜家下单了一部分家具,要说贵也不至于多贵,但是加起来就不便宜,怎么会是呢。在新家老破小里硬是装了个小吧台,放了两张高脚凳,越矮越喜欢爬高处的椅子。虽然也不知道有什么用,培养点喝酒的爱好吗(
突然想起来一个乐子,去年五月封校的时候时不时就一堆人去猫超排队屯食物和水。有一次和室友(点名 +wafarinliu +老师)一起去买东西,发现矿泉水又被搬得差不多了,开始思考我们要不要也做点什么准备,于是站在货架前面商量要不要提半打青啤回寝室(,怎么不算是水了呢。回去和另一个室友说这件事情,被锐评不愧是山东人和新疆人(
+之前不知道在哪里看到一个说法,国内软装家具质保最有保障的还是宜家,别的店不管做什么的都有可能家具还没坏就倒闭了,真到坏了也没地方修(
+8月2日
+验收了硬装,终于完事了。然而明天开始宜家就要送货和安装了,我也不知道是送一堆木板到家里还是拼好的送上门还是有人负责安装,说不定还要自己动手(狂喜(拼家具很好玩的(
中午起晚了出门之前没来得及吃午饭,就拿了片面包走,还在地铁上脑补要是去晚了就叼着面包冲进门装作很忙不是故意迟到的(。傍晚饿昏了冲进开封菜才意识到今天不是星期四,吃了点东西,路过麦麦又补了一个甜筒,再路过奈雪又补了一杯奶茶。胖什么胖,都是冰的,没有热量的(
晚上闲着没事又赛博占星了一次图一乐,为什么我的 N 也变成 S
+了,以前只有 J 和 P 会横跳的来着,快点变回来(
在家里的第 17
+天,感觉已经过了一年了一样漫长,各种原因地想回学校(
8月3日
+写点啥呢(
+是不是昨天甜食吃多了,今天开始爆痘,可能这是必要的牺牲吧(
+昨天说拼家具好玩,今天真就是直接送了零件来,还是稍微有点难绷。有点虚,不太确定需要多少工具,32
+头的螺丝刀和一套梅花扳手都放学校里了(所以为什么要放在学校里,是不是要寄希望于有手就行,或者买家具送工具(
说起来当初还是室友(仍然是 wafarinliu 老师)小学期参加硬件设计大赛(虽然但是这有什么必要加个链接呢()的时候多领了一盒
+32 头螺丝刀,结果还不回去了,然后给我的。但是真的很好用(
最近摆烂的时候时不时去看看物理系那个 3 学分的基础拓扑学的讲义,72
+页的小册子罢了,一个学期就只学点拓还能拿 3
+学分(不然难道让物理系的同学先学个抽代然后学代拓吗(,看起来好爽,我要不学完拓扑之后也去水个绩点。以前以为学点工科数学是洒洒水的事情,但是初概和微积分
+2
+接连给了我两拳,就不敢这么想了然后就只敢去上数学系的课了(什么。现在觉得可能只是我计算水平太差了,多少受不了这种水题看错一个条件算错一个数直接扣没的考试(有人又在为菜找借口,至少
+ywb 这个讲义看着好舒适啊(
8月4日
+闲着没事看了下 wty
+老师的主页(感觉可以说是闲着没事想欣赏下美女姐姐有没有发新照片((,发现她疑似(?这还有啥好疑似的呢)从华子跑路了,看了一眼今年六月才刚升了副教授,怎么会是呢。上学期居然上到了她在华子教的最后一门课,希望生统概论这课没事,有事也没关系,没啥可学的(
突然开始莫名其妙地慌了起来!沃日,ypk
+不会跑路吧,别过几个月我论文磕磕绊绊读完了结果他人不见了啊((。还有这课如果以后停开了或者由哪个老师转成中文授课,我今年上过的话还能不能计入外文课啊(
满地乱爬,今天又什么都没干,不会真要把工作量全留到八月底和实习期间吧,这段时间别的安排还挺多的,急((
+8月5日
+ + + + + + +因为一些计划有变(两个橱柜的定制价太贵,打算直接在宜家买合适的成品),所以今天去新家拼家具的时候重新量了一些细部的尺寸,本来这一部分工作是想直接交给定制那边的。不量不拍照都不知道还存在很多问题。
+(我试着比划一下,但是感觉正常人听不懂(,其实有什么必要说出来呢((
-
-
- 物理系是我看到唯一一个集合之后举着牌子排着队在学堂路上走的,其他院系大概都是自行前往( -
- 怎么有个院系的院衫就是一件印了字的大红色的纯色 polo -衫?原来是求真啊,那正常( -
- 核研院的 T 恤背面写着“缘起 200 号,逐梦核研人”,在路上想有没有“缘起 -600 号,宛平南路精神病人”( -
- 看了一路感觉材料学院的院衫是最好看的 -
看到水利系院衫,默默嫌弃地扭头骑车走了
-- 为什么分散地看到好几次网研院的但是一直没看到贵系的,
概率论不存在了
+ 其中一个橱柜下面直接是水泥地,上一位业主住在这里的时候一直都没有给这一块铺木地板,直接放了柜子。把旧的橱柜拆掉之后这里就是一个深 +7cm 的坑,买成品家具放进去的话很可能最下面的柜门被挡住打不开。
+之前一直没有管过这个问题是因为打算定制一个高脚/厚底的柜子严丝合缝地放进去,然而昨天拿到的报价实在逆天,宜家如果能挑到合适的成品可以省一半钱。
+解决方案是找包工头重新给这一块铺木地板,实际上也就一平方米,然后学到一个新(也不是很新,可能是复习)知识,木地板下面要先铺地龙(就是一个木架子),他们做出来不一定平,希望人没事(希望柜子没事
+量好另一个橱柜的尺寸,甚至都在宜家小程序初步挑了几个之后才发现柜子后面要走空调管道,扣掉这 +12cm 之后选择面就窄了很多,急。
+顶上有一个走水管的位置卡掉了很多层高,如果硬要保留层高就要卡掉宽度,为此多测了很多数据,趴地上画了个图感觉本质是个规划问题,如果考虑测量误差的话是不是个数值分析问题(
+旁边是不能动的承重墙(当然装修装到这个份上能动也不可能再动了),还要预留窗帘和门的位置,说到底房间隔断处是装个门还是厚窗帘本来都打算之后再想,然而为了买这个柜子就导致一定要提前决策,我还得先去挑窗帘(
+考虑所有限制以及最大化空间利用效率的话,最合适的几个柜子的分层高又有问题,很可能挂不下最长的衣服,还得回去量量衣服有多长,然后再跑一趟宜家量分层高(
终于把《相合之物》看完了(,是不是日常番集中补的话就会有点没意思,而且我是来看日式点心的,对主线也没啥兴趣。到最后已经是二倍速在看了,看完感觉终于解脱了(,怎么会这样呢。
-看到 bangumi 上第 12 话下面有一条评论:
+逆天,翻新市区老破小的确比郊区新房装修困难(
在屋里烦躁地转来转去的时候又发现一些,截止主体验收的时候没处理完的问题:
+-
+
- 刷漆的时候把踢脚线铲了还没装新的 +
- 木地板和瓷砖交界处还没做大理石的隔断(是这么叫吗)但是合同里有,怎么会是呢,这不得铲了重来吗 +
- 淋浴间还有一道挡水石没做 +
- 一些开关之类的安装杂项 +
反正工程款还没结,还能在包工头面前当一阵子大爷(,催着一个一个改就好了,小问题。只不过快要回百京了,还挺急的,远程监工也挺麻烦。
+量第二个橱柜的边边角角的尺寸,以及想这些问题的时候,很难不想起来一些测量学 +DNA:
--感谢在我备考的这段时间陪着我
+测量工作应遵循的原则是由整体到局部,由控制到碎部,步步检核
突然就有点理解日常番的精髓了(。想起来 20 年的时候在追《放学后海堤日记》,大约是高三最后一次联赛之前的一两天发烧了在家休息,迷迷糊糊睡醒看到钓鱼番更新了,本来赛前生病心情很不好很担忧状态,躺在床上看完最新一话还是开心了很多,然后爬起来洗了个澡。这番好像一直到确认退役的时候才完结,感觉考完联赛知道进队没戏,在家切换状态到高考和补作业的那两天似乎也看了最新一话,出上海赛区初步名单的那段时间也有看,所以说虽然现在完全不记得是在干啥了,说不定还不如《相合之物》好看,但印象还挺好的(
-今天主要在测建馆附近的楼,草图加了一张 A4 -纸,比例越发崩坏,这个建馆报告厅看起来和光华路一样宽。
-
早上测到建馆报告厅的时候感觉台阶设计得实在太抽象,就和组长商量了我中午先回去仔细想想怎么处理,下午带着画好的草图来测就会快很多。拍了一些靠近美院这一侧的照片就回去画大图了,下午也在下雨之前测完了东面和南面,本来应该 -flag -顺利回收快乐提前下班,结果绕到西面和北面一看才知道早晨把我整破防的东面和南面还算简单的,又回去画图,成品长得也挺抽象的。
-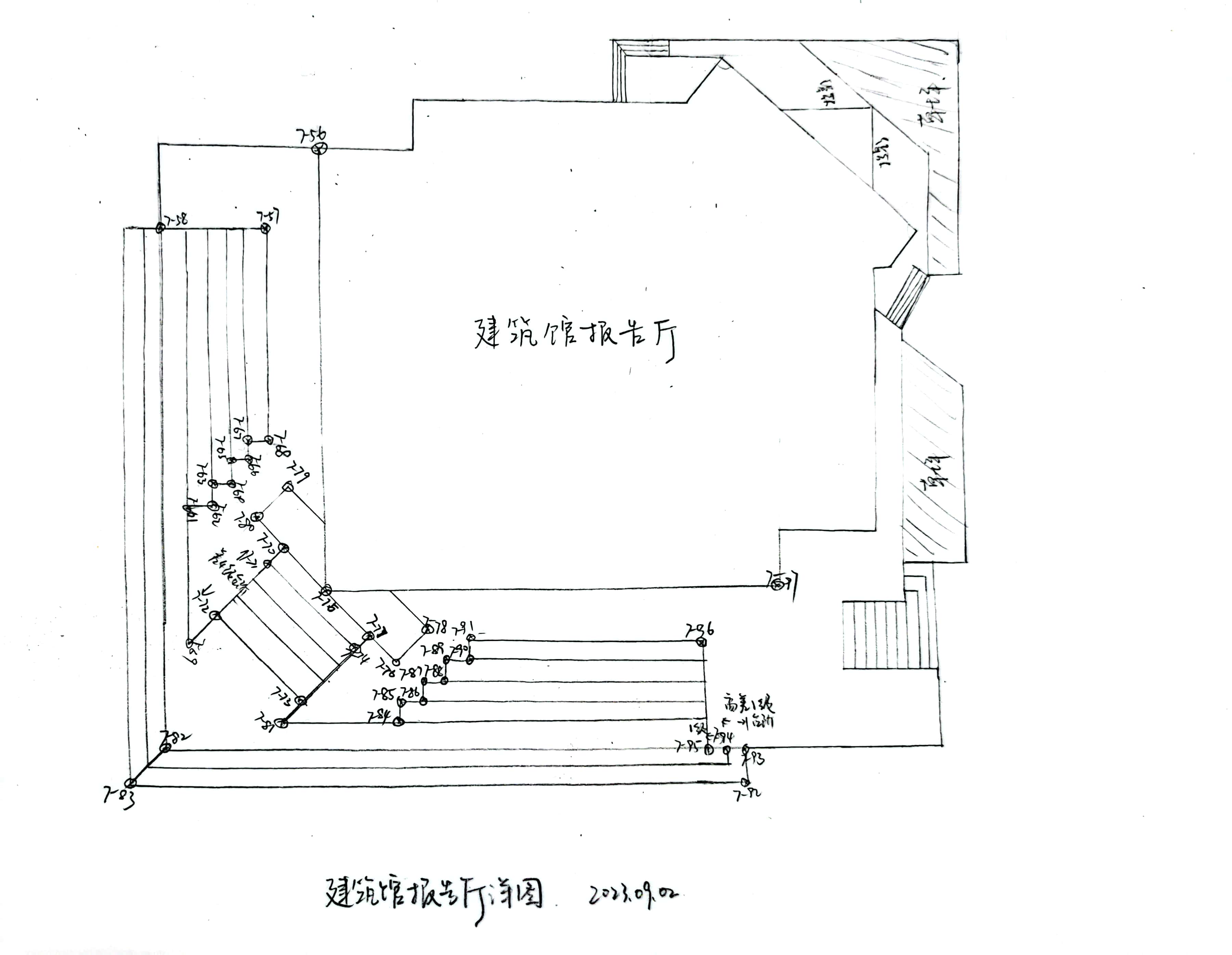
它还和继续教育学院有一座桥连在一起,往后绕了绕感觉继续教育学院和建馆咖啡厅也有点抽象,等测到这边的时候估计还要甚至要给这个详图再加纸再画大图,下次再说吧。
-上午只走了 5k 步,之前几天都是早上就快到 10k -了,但是感觉今天比以往都累。到教学楼放下东西之后几乎是跌跌撞撞走到四教三楼的神奇沙发(什么东西)上坐下开始休息,不知道是不是因为湿度大气压低所以即使气温不高也很不舒服,还是说这几天的疲惫其实在累积。晚上下班早,画完建馆报告厅的图之后应该可以看看数学的,但是总感觉很累甚至很焦躁也没看多少,就稍微多处理了一点点细节,一直没理解的问题到现在也还是不理解,有点麻烦了。
-9月3日
-早晨刷牙的时候想清楚之前 Durrett -上一直卡着的问题了,很乐,但是被自己蠢死(
-今天把草图基本画完了,南边勉强是测量的时候一边测一边画的,到建馆报告厅和门口的小树林就彻底现场画不出来了,中午照着地图画完下午对着草图选点测点,爽死。
-感觉明天能收工,后天肝图和 PPT,希望不是人生十大错觉(
-比例已经彻底崩坏了,这个清华路和光华路看起来都比建馆报告厅还宽,东配楼看着有建馆报告厅四倍大,但说实话主要是西南部分画太小了,东配楼和美院的比例还真就这样。
-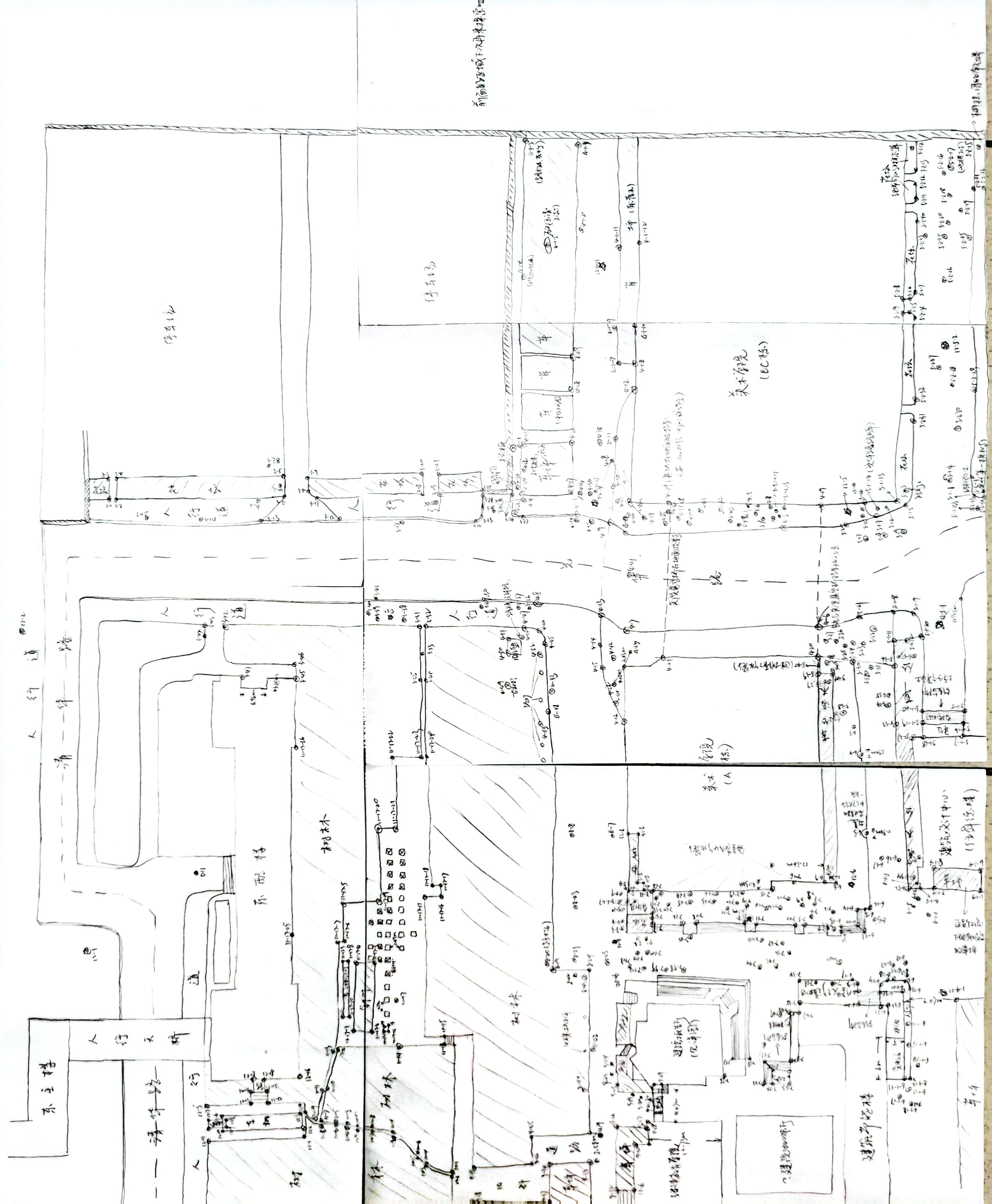
已经拍不清了(
-9月4日
-下午测东主楼的时候在路上遇到了一个疑似邱宝(坏了现在说到邱宝我第一反应为什么是
-Yau)的大叔,说疑似是因为这儿离工字厅有点远,而且他为啥会一个人在路上(x。过了一会有人来问路,问伟清楼怎么走,这我熟毕竟统计中心就在伟清楼,顺手指了一下。只不过他对我的称呼一直是“老师”,我们穿着工作服怎么看都更像修路工人而不是学校的老师(,稍微有点怀疑是不是遇到济南老乡了(x)。说起来确实快到
-全体济南人的节日 教师节了(
测东主楼东配楼之间的天桥的时候看到下面的路灯类似白玉兰的形状,一下子有点愣住,上海街头(或者可能只是我住的郊区是这样的 -x)有相当多这样形状的灯,因为上海市花是白玉兰。
-想回家了,可能也不是想回家,而是想回你沪了,我也不知道为什么(
-
今天是彻底收工了,晚上在做内业的工作,明天可能看成图的情况还要去补测(但愿不是大批量重测)一些东西,不好说。之前发现用发的卷尺量我的身高量出来一米七(,后来我们都管它叫自欺欺人尺了,但也还是在用这把尺测。今天发现棱镜高也会在戳地面的时候自己偷偷地变(,合着它也是自欺欺人棱镜,那这高程岂不是全是误差,看那个评图
-统计量
-标准里有一项还是高程和点位坐标的标准差,有点虚。最后大家讨论得到的结果是,总能及格的吧((
趴在地上把地图贴好了,画出来居然真的长宽近似相等,和正方形的测区基本符合,说明我瞎画的水平也还蛮高的嘛(。建馆报告厅的详图也画好了,打算后天拿到
-pre 现场展开 燕国地图 给大家一点小小的未央震撼((x
人家以为我很卷,实际上我只是怕拖队友后腿。
-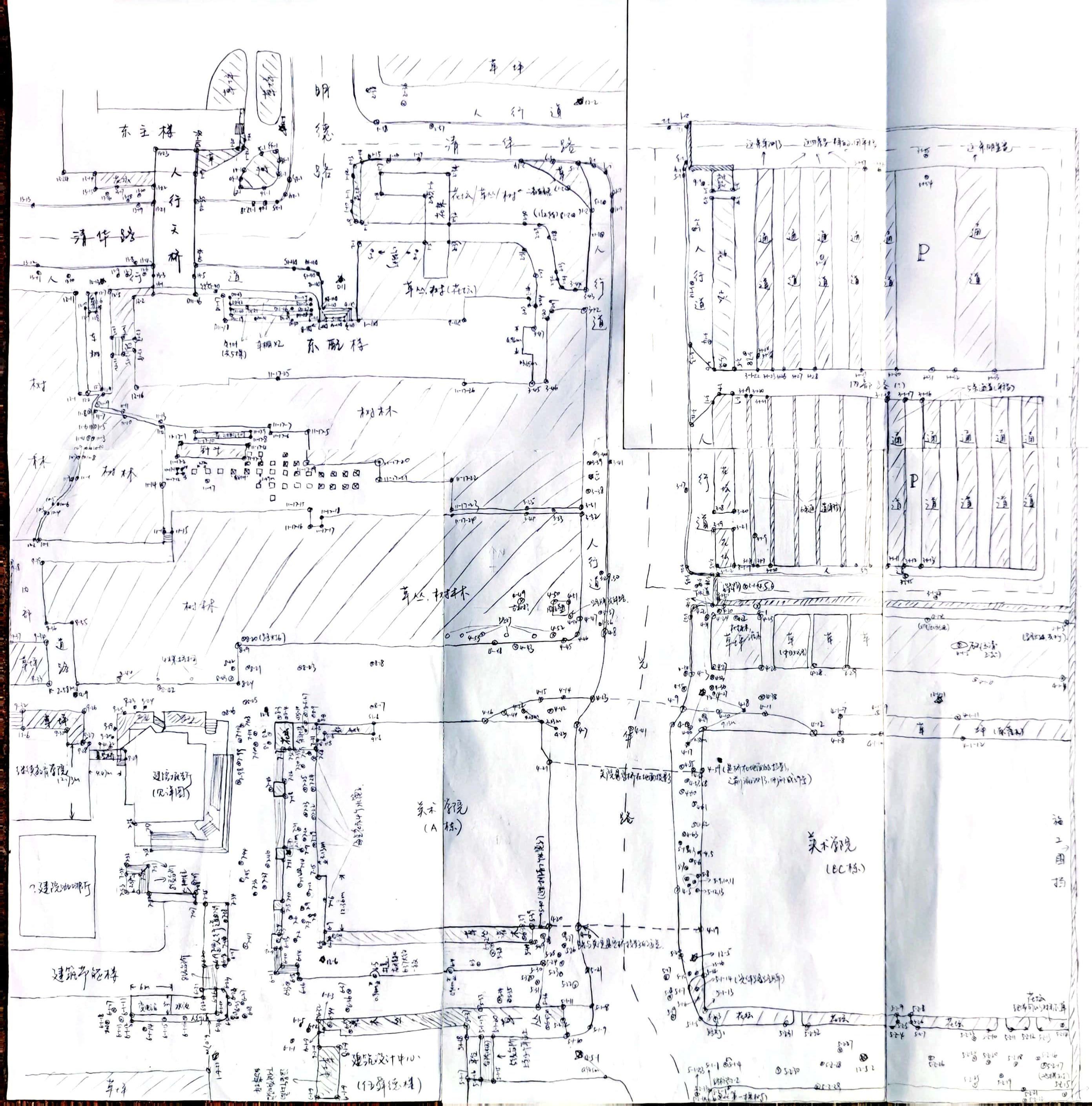
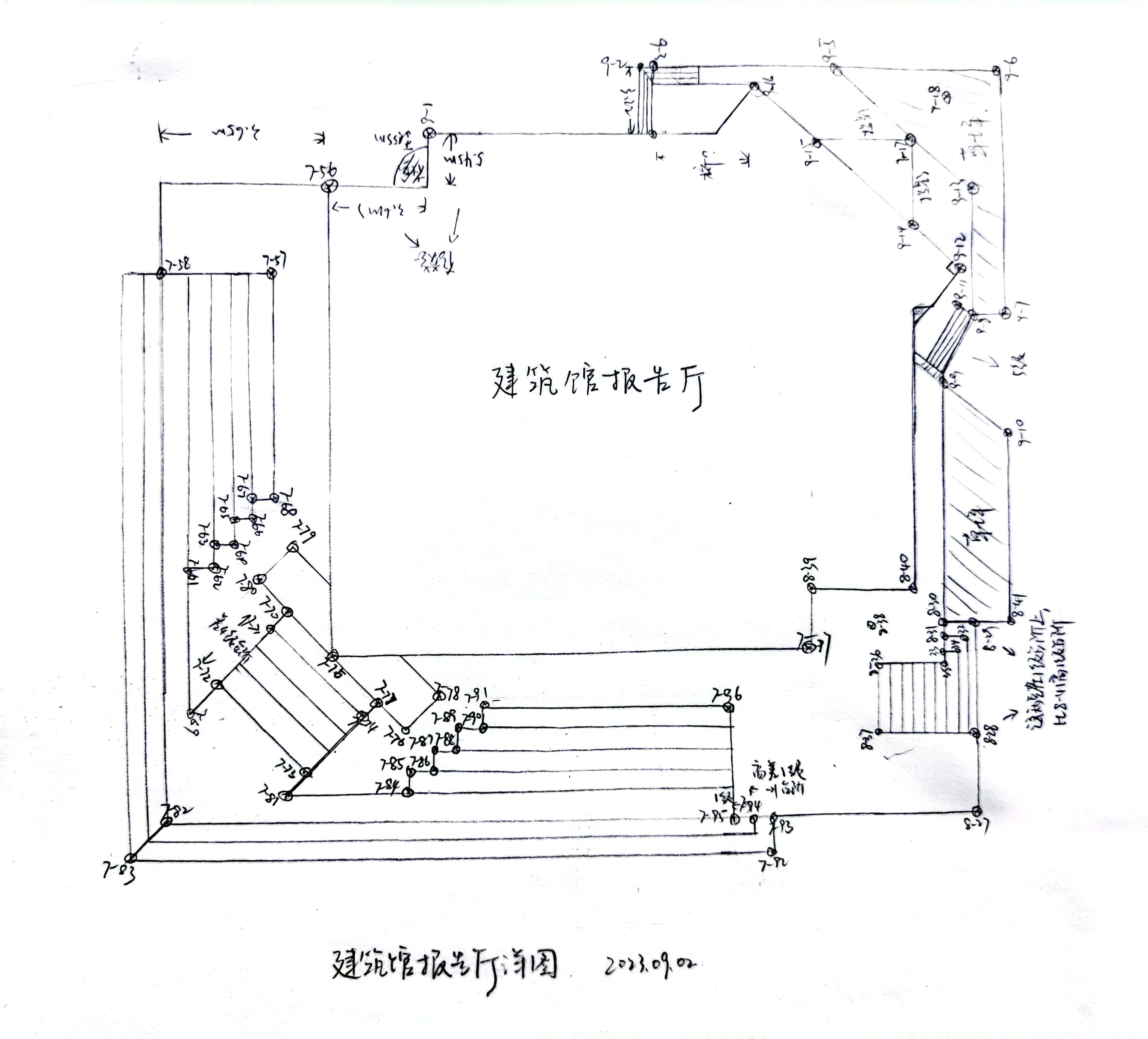
四等水准测量那天从早晨七点半开始,测到综体前面最后一站的时候已经是暴晒的正午,组长在旁边调平水准仪,我蹲在一边按计算器盘算着这一站大约测出多少高程才能闭合。第一遍测的读数出来之后我心算了一下感觉非常的不闭合,就告诉旁边的组长再看看读对了没有,但一直找不到问题。
-从 A 到 B 的测量非常完美,但是从 B 到 A -的过程中的确出了一点小问题。我们完全可以相信去程的数据,但是回程的问题在最后一站才会暴露出来,整个过程的转点都是自选的没有办法保存,连回去检查的机会都没有。为什么要用这种原始的方法测紫荆网球场的高程,这一定是既有的数据。当然后来的画地图更是没有意义的事情,没有哪个机构会采用我们的地图,是卫星地图不好用吗,我们是很业余地在用老旧过时的仪器重复做几十年前的人就已经做过的事情,精度可能还更低。
-于是我忍不住问旁边的组长,我们做这个事情有什么意义?他没有回答我,也可能只是没听清,说中午太晒了视野有点晃,然后又报了一组数据,让我再看看这下闭合了没有。
- - - - -9月5日
-上次看数学还是上次(,距离一点点推出所有的细节直到早晨刷牙的时候彻底想清楚 -Durrett -上卡住很久的那个问题已经有两天了,今早起来才抽出空自己重写又复盘了一遍,后面的进展就自然了很多。
-写完之后把它夹进 Durrett 里面准备出门去系馆,突然就想起来这个:
+这么一说确实还挺对的,不过工程不应该都是这个步骤吗(我不懂啊我学不来工科,瞎说的((
8月6日
+挑窗帘,顺便把一直被催的灯具也挑了,周末估计宜家人很多所以没去,能吐槽的事情不多懒得写了,也可能是装修半个月我现在忍受能力已经大幅提升了,总之下略(
+晚饭吃麻辣香锅,点完单犹豫两秒把微辣改成了中辣,吃了个爽(。吃完还剩半盆辣椒,你们这儿辣椒不要钱的吗(
+想起来上学期在寝室一起点外卖的时候室友(还是 wafarinliu
+老师)被中辣背刺,还没尝过,等回百京了有空再一起比划比划(感觉最近日记里
+wafarinliu 老师含量过高,怎么会是呢((
8月7日
+翻到高中的照片发现来华子这两年头发其实变浓密了,真好((
+军训期间所有的 DNA +都早就洗掉了,只有某天在北体开演唱会的时候大家一起唱的《成都》洗不掉。其实在这之前我也没听过这歌,但是它一个月以来就是时不时地会在脑内开始放,今天干脆去循环了一会,怎么会是呢(
+进行一个发语音.amr
--This is actually quite a triumph, even if it is hard to explain to -your friends and family members exactly what you have achieved.
-——《研一下总结》
+和我在成都的街头走一走
+直到所有的灯都熄灭了也不停留
+你会挽着我的衣袖 我会把手揣进裤兜
+走到玉林路的尽头 坐在小酒馆的门口
这两天没有来由的(真的吗?明明有很多来源)难过,想回家,也并不是想回家,想回上海了,然而秋季学期甚至还没有开始,这咋办。今天交了学费然后准备晚上回去的路上去注册,之前总觉得六千块钱是我的可支配财产里不小的一部分了,所以想一直捂到开学之前再交的(,只是再拖下去按我这个记性说不定开学就失学了。最重要的一点可能是从九月份开始每月多了一笔固定的入账(真的吗?说不定下个月就没有了吧),尽管并不多,它的来源让我有点难受,也不想在这里细讲,但当然要收下。
怎么听起来这么奇怪啊,可不是什么见不得人的事
才 5 -号就已经写了四千多字了,真能水,八月总共才写了一万字出头。测量实习可能是今年对我来说最后一次大规模(?)社交了,毕竟数学课又不用组队。
-9月6日
-测量实习,彻底下班!感觉比地质 +
-测量赚多了,就是不知道最后给的成绩赚不赚,不过总能及格吧(
早上买了瓶西柚味茶 \(\pi\) -带去教室就早饭吃,虽然身为糖水爱好者初二的时候就看到过同学从便利店买这个,但今天还真是第一次喝。感觉就是有一点点茶味儿和西柚味的比较清甜的糖水,说人话就是三到五分糖加香精,尤其这个茶味儿就像北京菜里面放的辣椒一样是摆着看的,但我确实比较喜欢喝糖水。
-高三的时候吃完饭时不时会拉上友人在零食窗口买奶茶回教室喝,看着像是学校自制的,质量很不稳定,时而齁甜时而这白开水怎么没味儿啊,小贵而且去晚了还买不到。感觉上好像就是需要一点糖刺激奖励机制,不然混不下去。我的体重会不会就是当时涨起来的呢(
-
没吃晚饭,本来想吃桃李夜宵的烤冷面再加串冰糖葫芦(前情提要:2023.02.19),最后买了碗小馄饨就饱了,最近口腔溃疡也吃不动冰糖葫芦,吃辣都得吸溜一阵,但是不能一天不吃带辣椒的菜。感觉整体不如玉树的夜宵但也确实便宜,而且不知道玉树夜宵暑假开没开,吃过最好吃的一顿玉树夜宵是一二九分声部那天晚上翘掉了活动和何老板去吃夜宵,两个人买了一份烤冷面一份馄饨拿小碗分着吃顺带吐槽院系这些没用的破事,可能是我没吃晚饭的原因,真贵但是真好吃啊,下次开学了去吃。下下次为了冰糖葫芦还不吃晚饭(
好喜欢汤带着鲜味的小馄饨(就是味精放的多),如果是小馄饨的话就是纯肉馅最好吃,饺子馅我最喜欢的是玉米猪肉,湾仔码头的煮着好吃但是有点贵,自己包的就不太好吃。而且我捏的饺子煮了之后一部分会破或者整个散开,买的速冻水饺看起来个个都有开口,煮了之后也只会漏油不会散开,很神奇。大概毕竟吃饭就是吃调料吧,我还是不太会配料,就只是能把东西做熟。不过众所周知上海宁过年不吃饺子吃汤圆,上个学期在桃李二楼吃饭的时候偶尔也买小碗汤圆当主食,好像十个四块钱而且还有一小碗汤,记不清了。汤圆馅就没有什么花头,都是黑芝麻,花生的我也不爱吃,但是都不如搬家之前在家附近超市里买的冷冻汤圆,煮熟之后咬一口糯米皮可以扯得很长。说到你沪特色碳水还得是
-双肩包
-生煎,小杨生煎那种纯肉馅最好吃,灵魂还是那口汤,大壶春的个头大就显得比较糙,我也吃不下。上次路过清芬的生煎窗口虽然不屑一顾但看到旁边有
-你好谢谢 小笼包
-再见,长得很像小时候在城隍庙吃到的那种,只不过我还是不太相信北方卖的小笼包,如果买了之后发现没有那口汤、皮很厚的话我会很难过。但还是想下次试试,就是不知道在清芬一楼单买一笼小笼包的话应该配点什么才能吃饱而且不碳水过量。主食的话米粉也很好吃啦,但我喜欢汤粉多于炒粉和拌粉,在上海火车站附近吃过一家据说很正宗的桂林米粉,高中学校旁边那个传奇广场有个店做的也很好吃但稍微咸了点,除了长泰广场松鹤楼的鸡汤面和某个炸鸡店的炸杏鲍菇之外,高三的时候我也会晚饭时间偷溜出去吃这家然后回来上课,就是太烫了每次要晾很久才能凉,时间充裕才能吃。两家店酸豆角都给得相当多而且好便宜,一碗肯定不到
-20
-块钱,米粉很滑很弹,前者的笋尖尤其好吃。后来再吃到这么好吃的笋是今年暑假在紫燕鸡挑卤味的时候一时兴起买了些拌笋,是用小米辣加别的调料拌的,和米粉里面的笋尖不是一个味道,但脆爽和鲜嫩多汁是一样的。
这是在干什么,用嘴炒菜吗(
- - -9月7日
- -早晨起来 wafarinliu -老师问我要不要一起点外卖,本来今天打算洗洗衣服再出门所以想答应的来着,结果查了一下上个月的账单给我整精神了,怎么明明是假期还一个月花了两个月的钱(,这个月当然更夸张毕竟刚交了学费。虽然都是正常的特殊开销(?)但还是立刻决定去桃李吃午饭了(。在猫超买东西的时候看到了之前一直想尝尝的三得利茉莉乌龙,虽然它写着无糖完全不符合我对糖水的期待,但毕竟是茶尝尝也不亏,当咖啡的平替喝也是我赚了。
-测量实习结束之后走在路上还是忍不住去看井盖上的字是正常现象吗(
-今天把芦毛灰姑娘看完(?)了,睡前看到有马纪念入场前会长和小栗帽的击掌就燃得不行但实在是困了(,早晨起来一口气看完了第二部就想打
-9
-分(不好说是不是冲动评分,可能是动画第二季的印象好导致对芦毛灰姑娘一上来就很有好感),晚上就看到目前连载的位置了。后面逐渐在变成
-Cygames 非常擅长的
-群像剧,小栗帽痛失主角位(,不知道啥时候才能画到有马纪念有终之美,急。
其实感觉应该标搁置才对,后面没打算追更,攒一阵子再看,那不就是搁置而不是看过(。也没必要分这么清(
-
急了,啥时候能看到芦毛灰姑娘动画化(。看第二季的时候最喜欢帝皇,但看了漫画感觉还是更喜欢小栗帽。要类比的话可以说从笠松到中央的经历是戳到我了,和好歌剧都不是血统优良的名马(9.8
-upd:是我记错了,这下乳好歌剧了,虽然也都说好歌剧血统一般但果然比起小栗帽还是强太多太多太多了)但也不是后者那样开挂的天才反而更加励志,还有“跑步是因为能跑,从站都站不住到能够跑起来已经很好了”总算是摆脱了两季动画的友情设定,第一季多少就有点因此走向废萌变得很无聊
-但其实也有人爱看废萌吧只是我不喜欢,帽门永存(
9月8日
-看到了《院友代表于品在北大数院2023年开学典礼上的发言》,里面每一句话都在骂我(,边读边再一次捶胸顿足为什么是去年上了抽代而不是今年上。晚上又看到《师说新语 | -“小米教授”薛金鑫:终结百年潘勒韦猜想,保持与学生共情的能力》,又一次捶胸顿足上个学期为什么只上了实分析(?)和概率论而没有上复分析(
-晚上看到一个
+ + +虽然今天没出门搞装修,但在家用很暴力的方式修了一些坏掉的东西。淋浴的三角阀之前家人说一直转不动,调不了出水口但也勉强用着,报修的话光是上门费就要
+150,今天福至心灵双手用力一拧,立省
+150(。浴霸的灯罩是个嵌在天花板里的长方形盖子,之前掉下来两个角,掉的两个角装不回去,没掉的两个角又拆不下来,只好一直悬空着。今天找了片合适的
+流麻废材
+亚克力板卡在缝隙里固定住了,不确定在挤压下强度怎么样,但是又找不到其他密度低而且不锋利所以掉下来也没关系/不会被水汽影响的材料,不太放心又在天花板里面用绳子简单做了个支撑。
固定的时候突然想起来《牯岭街少年杀人事件》里小四的朋友在天花板上找到一把匕首的情节,在天花板里捣鼓半天不整点活属实和我气质不太符合,然而画不来镇宅符(,最后就在板子上写了个日期塑封了一下塞上去。
+还剩一个特定条件下会触发拧不紧的水龙头拆开发现不会修,又装回去了,至少学会拆水龙头了,可能是想说明有些钱还是要让别人赚。虽然不大贴切但还是想起来
+Disco Elysium 剧情里给我印象很深的一段,(我认为是在)暗示人的有限性的
+One More
+Door:
--What doesn't kill you makes you stranger
+There is no way to open the supply depot door. Accept it. You cannot +open *all the doors*. You have to integrate this into your character. +Some doors will forever remain closed. Even if every single other door +will open at one time or another, maybe to a key, or maybe to some sort +of tool meant for opening doors... But this one will never accede to +such commands. A realization crucial to personal growth. Crucial.
笑晕(
-9月9日
-学会了一些用 Markov property 证明的结论之后逐渐不会用 Bayes' Theorem -了(
-横贯测量实习这些天到现在终于是看完 Recurrence and Transience -了,之前还是不熟悉长得奇形怪状的 -notation,熟悉了就好很多,但不会每一章都要这么痛苦一回吧(,感觉最近实在是有点迟钝。Hoil -Lee 的那份答案这一章到这里就没有了,下一道题就是 Ergodic -Theorems,只能去看 Durrett 自己写的老版本答案,和 5th edition -稍微有点对不上但也没再更新了,也问题不大。
-之前只能把 transient
-和暂态的意思对起来,今天随手查了下才知道还有候鸟的意思,感觉非常有道理,再一想这个好像高中的时候讲过(,对不起我高三的英语老师了。倒也没有非常对不起她,高三我真的有在努力学英语了,对不起的是高一高二的那位英语老师((。再想想其实有点没道理,单从字面上来看候鸟明明就是常返的,哪怕真的套
-Markov chain 的 recurrence 定义也能对得上,所以 Transient is
-Recurrent!(哲起来了(学数学学得
被没有口袋的女装 PUA -惯了,今天穿了条有口袋的裙子还是习惯性在没有手的时候把东西用胳膊夹住。说起来我本来以为下雨天会很冷所以穿了长裙的,结果中午去骑车拿了趟快递下摆就湿透了,崩溃。
-9月10日
-今天又是全体济南人的节日!(
-现在每天晚上去挑第二天喝什么茶已经成了一种固定的快乐了,甚至正在写一个
-茶饮料替代咖啡从口味价格和效果方面评价的可行性分析
-测评(,等我把所有猫超能买到的品牌和口味尝完就发((
昨天拿到了之前影印的书,翻了下感觉排版有点丑(。今天闲来无事打开 ESL
-看了一眼又舒服了,不过总不会这种七百多页看起来就一堆废话的书我都要打印出来看吧,差不多得了。读这个(相对来说)真轻松啊,跟看小说似的(
闲着没事的时候看到一份 lty 的讲义把 sub/supermartingale
-分别标成红色和绿色来代表看涨和看跌,笑麻了。正好今天做题 终于
-做到了 superharmonic function,才知道之前早就见到 harmonic function
-了只是不认识这种形式。回头看了下这个回答明白是在干啥了,只不过我还是更喜欢
-superman 的解释(
9月11日
-今晚回来难得还干了会活,把 Durrett 的 Markov chain
-章节通了,当然是把打星号的部分先跳了。以前还担心跳章节会有什么问题,结果每次看不懂下一章的时候就会回来把上一章跳过的部分读了,虽然对往下推进度也没有帮助,但是当时看起来很难的东西这时候反而成了舒适区,就有点草,然后竟然也都读完了。
往后翻了翻感觉读完 Ergodic Theorem 就可以换 GTM274 从 Brownian Motion -开始往下看了,但总觉得也没必要,现在 Durrett -这本成我的舒适区了,草。其实也不太清楚是不是把后面的东西留到概率论 2 -后半学期再学,现在先去读点高统甚至去挑着读点 PIN -比较好,更搞的是下学期数学系那两门课我是一门都不想上了,现在看着课表又陷入了沉思然后开始重新排课,某些人有(至少)两个培养方案是会哪个都修不完的(
-时不时会把 summing 看成 -summoning,颇有一种把求和项都召唤过来加在一起的感觉,好像也没错((
-突然想到以后是不是可以把 solution manual
-打印出来带去教室,就不用带电脑了(,所以相比用电脑来说哪个更环保呢
9月12日
-下学期课表又要变成不认识的样子了,已经连着三个学期了,补退选 II -要选的课比正选和补退选 I -加起来还多,后验上来看也都挺没效率的,只能说水平就这样知道吧.jpg
- -数学史的限选范围里居然有未央,好离谱(
-Durrett 单推人今天才发现他还有写《Essentials of
-Stochastic Process》,最新一版还是 2021
-年,虽然我不一定看、目测这本很入门、和 PTE(坏了以后不能把它简称为
-Durrett 了)有大量重合而且目测也不如 PTE 难,但它排版比 GTM274
-好多了,还是想印一份留着。有可能 continuous time Markov chain
-会用他的读,Poisson process 之前也只是在 Poisson convergence
-里简单读过可以顺带梳理一下,听说这一本的 Martingale 和 Markov chain
-顺序反过来有深意读起来很爽,最后一章那个 mathematical finance
-看着也挺好玩的,摸鱼的时候把模型当 examples
-看看。不过这书怎么这么多课后题(
晚上翻了翻发现《天浴》一直想看但是又一直没看,带着电脑躺到床上开摆,结果一个半小时的电影我看了两个半小时才看完,中间每次崩溃了就按暂停先缓一缓再说,看完又崩溃了半个小时(。这种东西我都会看一眼摘要甚至更细的剧评再看,本来以为没什么的,然而镜头表现出的冲击力还是远远超出预期。
-9月13日
-下午和友人吃到了 69
-折的海底捞,本来以为会想说的话也都没有说,吃饭要紧(帽门.jpg,眼泪最后还是从嘴角流出来的。第一次吃四宫格的火锅,虽然大多数东西还是都下了辣锅,但是猪肚鸡汤好香,煮出来的面条也好香(主要是味精加得多吧
逛了下那边的超市发现猫超的东方树叶种类还不是很齐,背了一瓶绿茶一瓶乌龙茶回来。
-是第一次骑车去上地那边,走着走着感觉不太对劲,这不就是拉练的时候走过的其中一段路吗,好崩溃。沿着自行车道一直走结果被高德提示偏航,按照它的路线拐过去发现厢白旗桥下面非机动车不能通行,好崩溃(二度),勉强从人行道上过的,问就是全地形共享单车。回来的时候探索了一下才发现我原来走的是对的,干脆直接把导航关了,结果本来想从北门进校,骑到西北门才发现怎么过了,好崩溃(三度(什么纵使三度迎来崩溃
最后在四教后面 30 分 28 秒极限锁车,以前以为只要超过 30 分钟就按 3
-块钱算,实际上是超过 30 分 30
-秒才算,赚死(。北京至少共享单车价格是比上海便宜一半的,在家的时候这种路程绝对不可能骑车,当然上海的公共交通建设其实就很少会让我骑这么老远,一般也就是解决下最后一公里的问题才会骑车(没有拉踩的意思(所以北京这个共享单车价格不会是在弥补稀碎的公交吧
9月14日
-试了试友人新提的公路车,差点把我腰撅断,座位往前调了调就变舒适了,差点忘记她比我高 -5cm -这件事了(悲),但还是稍微有点够不到刹车。骑起来确实快,就是全地形适应力不太行,要换车的话还是得换山地车。
-凌晨两点多看到新民路上有人在跑步,后面一群人骑着车一边追一边喊你这三千米不得跑个满分,其中一个还指着路边对同伴说我们每天早晨都是在这边集合然后带去东操训练,走这么远还不让骑车。原来是还在军训的新生,太猛了(
-身体不舒服,晚上去猫超发现有临期饭团买一送一,就着本来打算明天喝的茶吃掉感觉稍微好点了,这个搭配还挺日式校园午餐的,但是是夜宵(
-9月15日
-这个学是一定要上吗.jpg
-9月16日
-最近遇到很多很伤神的事情,今天身体又不舒服躺了一天,几乎已经一周没有学什么新东西了。这么多年了,就是在无数这样的时刻慢慢变得迟钝的吧。
-我也好想跑起来啊
-(玩闪耀优俊少女玩得(收收味
9月17日
-又到了该拿出这张图的时间:
-
不好说,说不定我过两周又放暑假了,上学主打一个体验(
-9月18日
-今天好闲啊(,早上去偷袭了一下吴昊(女)的概率论
-1,然后又去上了杨帆(男)的概率论
-2,总感觉求真书院的本科生课比研究生课难一点。概率论 2 教材是
-Durrett
-PTE,作业基本从上面出,讲的四章我已经看过两章多一点了,梦幻开局。然后听老师念了一遍又在黑板上抄了一遍
-conditional expectation
-那一节,像回到去年何翔的抽代了一样,啊不是至少这课教材和讲课用的都是英文(,就,感觉以后周日晚上可以晚点睡了((x
坐我旁边的是一个俄罗斯姐姐,似乎是求真的研究生新生,一开始没注意还想问她能不能加个微信把作业发给我一份,她转过头来我才开始切换语言系统(,有一种毫无防备突然开始 -TOEFL Speaking 的感觉,很难绷(
-发自我的手机
--
(草
-说起来下课还拿到了学生会发的开学加油小饼干,我寻思着恁大一个盒子不会是月饼吧,打开一看才知道是饼干。吃了才知道饼干里面居然是空心的还夹了字条(,很担心学生会的精神状态,不过居然拿了个数学相关,好评(。想起来上一个用优化问题类比的还是《求好人生的“优化问题” -| 毕业生代表吴清玉在北京大学2022年本科生毕业典礼上的发言》(
-
但是我一个三维空间里的碳基生物为什么要做矩阵,我不能做点不抽象的东西吗
又联想到一个 random walk in \(\mathbb -R^d\) 笑话:
+人生是旷野,或者是 CRPG(
8月8日
+之前学鞅论的时候对 Durrett 上那个 Dubin's Inequality +的习题感到非常困惑,官方的 solution manual +上那个步骤我一眼完全没懂(应该主要是缺上下标,所以一遍看不懂它的设计),另一份两个韩国人写的答案直接把这题空过去了,然后我也跳了。
+今天(凌晨)又回来看的时候用最笨的办法把序列完整地写出来,才终于明白了归纳是个什么意思,然后也是直接在摘出的序列上动手做的又手动把每一段序列拼到一起证出来的,写完感觉真要长脑子了。结果看了眼 +MSE +上有人提问,原来完全用特征函数写然后很直观地用一下 switching +principle 的话就两行,这才是真 · +归纳,知道这个意思之后再回头看官方解答就明白上下标缺在哪里了,好崩溃(
+不过我还是觉得这个题目关于 \(Y_0\) +以及 \(N_0\) 和 \(0\) +的关系表达得也稍微有问题,之后想稍微在长脑子篇里讲一讲正确的做法,还是说其实是我英语太拉了所以误解了((
+顺带悟到了遇事不决可以把 \(X_{N_k \wedge +n}\) 这种逆天东西想成 \(X_{N_k(\omega) +\wedge n} (\omega)\) 的形式(可是为什么现在才悟到呢(,虽然很 +trivial +而且一般没必要,但是这种想问题想到神经损伤的时刻确实还是换一换比较清楚,本来就被答案绕进去,险些又因为 +stopping time 的概念开始怀疑自己这阵子都在学什么东西,真挺崩溃的((
+我平时会直接把 supermartingale 简写成 super-mart,submartingale
+同理。托这道题的福睡前满脑子就都是 super-mart,梦里也是
+super-mart,今天出门在外面进超市买水的时候还在想 mart
+不是商场来着吗,所以超市的英文是 super-mart
+吧,但为什么总觉得怪怪的呢(。走在路上还在想杜宾犬的英文难道是 Dubin
+吗,总觉得也怪怪的,想到方舟的杜宾教官才想起来是
+Dobermann(
说起来舟用的居然是 Dobermann 而不是 +Doberman,可能本意是作为姓氏,只不过教官本人确实是狗狗就是了(
+今天还去吃到了小杨生煎的 双肩包
+生煎包(是个沪语梗),虽然也没有非常喜欢,但还是比清芬生煎好太多了。想起来刚入学的时候
+wafarinliu
+老师激动地拉着我去清芬吃生煎说这个超好吃,但我觉得相比上海的真不咋地。后来有一次我激动地告诉她清芬的羊肉泡馍好吃,很适合当冬天的
+comfort
+food,她跟我说同生煎的理很可能比陕西的差远了,只是我吃不出来而已((
来点今天在外面拍的东西(
+
嘿,听好了,最近东部城市会举办一个超大的 +party,所有的风云人物都会参加,但你猜谁收不到邀请?
+(退后一步)(尬舞)
+是你!北京!
+
五角场的上海书城分店装修之后绝大部分区域都划给童书和教辅了,今天走累了进去摆烂的时候想找本书读,看到这个艺术生活读物的幕墙还以为终于有书看了,结果怎么会是呢((
+
所以最后跑去 MUJI 读随笔了,巴掌大的 150 +页的小书有一半是插图和语录,另一半是八篇散文,但是竖版书而且阅读顺序从右往左感觉不太习惯,读了大概 +2h +当做休息然后就回家了。感觉是那种很刻板印象的日本人写的(,读完右边这段话我的第一反应是,这个作者自己悟出了影子价格的概念((
+有的时候感觉读这个破双学位也算杂学旁收,如果不是工程经济学强制给我喂了一点经济学知识应该不会知道这个(
+装帧挺不错的,非常无印良品,只不过要 28
+块钱我还是觉得有点逆天,当然无印良品里绝大多数东西的要价我都觉得逆天(,白嫖下样书得了,下次还来(
8月9日
+因为啥都没干所以险些忘记写了,还好到现在还没收到类似于寒假时候“怎么没写日记你还活着吗”的邮件问候(
+还活着,而且
--A drunk man will find his way home eventually, but a drunk bird may -get lost forever.
+INSULINDIAN PHASMID - I exist.
(大概就是说 \(\mathbb R^2\) 上的
-random walk 是常返的,但 \(\mathbb
-R^3\) 上的 random walk
-状态都是暂态,实在不知道要翻译成什么样
睡前还是没忍住去看了芦毛灰姑娘最新一话,甚至有幼年帝皇客串,awsl(
-
不准在中央面前无礼.jpg
有点难绷,然后特地翻到 20 话左右的地方去截了经典名场面(
-
帽门!
才发现这里帽的耳朵是往后翻的。最近赛马娘系列有新漫画了,看了第一卷感觉画风不如芦灰,又去看了看樱花桂冠的生平,有点子好奇大器晚成的故事要怎么做才能比较精彩。这个月到现在为止发了三张芦灰的漫画截图,并不是每张都有帽,但是居然每张都有皇帝。这个世界上哪有什么鲁铎黑,只有鲁铎厨和扭曲的鲁铎厨罢了((
9月19日
-选课的时候说想听台湾腔今天还真听到了,本来还以为会是英文授课的,这下如愿以偿了(
-上了两节数学课但还莫名挺休闲的,ODE -就是在扯闲篇,讲到最后成泛函了,怎么回事。期中考试似乎是随堂,不知道 -1.5h -能考点什么,这下真梦回何宝的抽代了。讲义印了但还没到,急急急。写完昨天概率论 -2 的作业发现 due 是 -10.2,就,我知道大三了还这样真不是很好但我就是停不下来地焦虑(
-掐指一算今天还真是从 jk 毕业之后第一次穿
-jk(,白丝真不耐脏啊。
9月20日
-今天最难的好像是现代生物学导论(,真不太会。高统在挂机以及听旁边两个哥们讲求真笑话(,运筹也挺休闲的。是不是我的选课有什么问题,现在总有一种学了概率论然后就可以到处嘎嘎乱杀应数课了的幻觉(暴论
-这运筹课好没意思,不过也是,建管系开的能有啥含金量,主人的任务罢了,不如下学期去上个数学规划
-贴贴 玩玩(
本来十一假期(如果还在北京的话)想去龙头牧场看看目白阿尔丹的墓碑,还想带束花带点胡萝卜(,今天一时兴起看了几个圣地巡礼视频又简单查了下,好像现在不开放了,牧场经营也出了点问题,残念。
-9月21日
-之前本来还想着如果压力太大的话就把优化理论换成非参导论水一下,今早做梦梦回上个学期在
-zzy
-课上坐大牢直接惊醒了,我脑子一定有问题才会想要再选她的课(叠甲:我不知道是她的问题还是我的问题,反正线性回归我坐大牢了,但也有同学说她讲得很好,所以可能只是我和她不合适)。退掉退掉,选优化理论
-去和 JasonL 老师面基((
昨晚本来不困,结果这个运筹课非要关着灯上,黑灯瞎火的给我整困了,就一边喝带的小瓶美式一边写高统作业。本来以为没什么问题结果晚上根本睡不着,好崩溃(,一边清醒着一边默念美式的美式的来安慰自己早八会没事的,最后还是有事了((
-感觉这学期的课程群几乎就没有,尤其数学课是真的一个都没有,哦原来是有 -10 -个学分的课我都还没选上啊(,哈哈,等我选上课网络学堂公告里的群二维码都过期了,怎么办呢((
-第一周就是在不停地发邮件问能不能冲选能不能手选,还有课后线下偷袭老师不停重复同一套话术:
+
(?(什么发疯实录(
+8月10日
+又到了装修血压时刻,本来说了一大堆发出来之前还是删了,没必要以后回来看的时候再暴击一下本就脆弱的心血管(
+看到个这个,好乐,上海中学都能举办西部赛了,乌鲁木齐一中啥时候举办东南赛,中国啥时候举办欧洲杯((
8月11日
+继上学期在体育课上摔倒之后,今天又用同样的姿势在浴室里摔倒了,还好是在家里而不是在学校,眼前闪回的仍然是帝宝训练摔倒的演出,怎么会是呢(
+《What Remains of Edith Finch》终于降价了,光速进行一个买,据说 2h
+就能通,打算高铁上玩。试了下键鼠控制和视角很有双人成行那味,包括找不着路和不能手动存档也是(,但有点晕
+3D(
其实是看群友吹它是最强第九艺术,非常为 Disco Elysium
+感到不服遂打算玩一下试试
8月12日
+收行李,把 Durrett 装箱的时候想起来第四章的 examples +赶进度的时候跳过没看,翻出来以为摆烂间隙能速通,结果被一个没写清楚的 +Kakutani dichotomy +的证明整破防了。众所周知(?)这种美式教材讲究一个保姆级教学生怕读者看不懂,但是从进入第四章开始就逐渐透露出来一种“都看到这儿了不至于水平那么拉吧”的气息,会突发恶疾地在 +non-trivial +的地方敷衍,看不懂步骤的时候就会深刻怀疑自己是不是脑子有点问题,然后破大防(
+不太舒服所以间断地睡了好几觉,没干啥事,下略(
+8月13日
+后天回学校,今天把装修的事情交代了一下。之前有一个 to-do list
+专门记录没解决完的问题和指数增长的新问题,今天把宜家还需要买的东西/具体的步骤和各种想到想不到的注意事项写成了一个新的文档,两个一起留给家人(。虽然我相信我妈根本不会细看,到时候还是一个电话打给我问怎么办。不知道为什么总有一种离职跑路但跑不掉的感觉(
读其中一个橱柜的安装手册(来判断难度,到底是留到寒假回去我自己拼着玩还是干脆买个安装服务)的时候看到个抽象插图:
+
啥意思,一个人不能安装吗(,为什么只有右边的人有耳朵,多一个有耳朵和铅笔的人参与安装就可以了吗,那我为啥不能自己长出耳朵或者拿着铅笔(,还是说贴贴可以提高效率(,我也想贴贴((
仍然不舒服,下略(
+8月14日
+把三周的地质和测量实习改成了两周的纯测量,不知道工作量多大。想多留一周时间贴贴和学完全没学完的随机过程,而且一想到地质实习会遇到一堆同专业但又几乎可以说是不认识的同学(,自己没上过工程地质啥都不会,还有组队
+pre 写报告之类的烂事,完全 carry
+不了甚至还需要靠抱大腿的话还是算了吧。纯测量那边有两个军训期间比较聊得来的同学(是班里的两位
+CPHO/CCHO Au
+选手,多少有点同是天涯沦落人的喜剧感),组队体验可能稍好一点(啥
这样成绩单上会莫名其妙多出来两个 +W,明明是完全没开始上就退掉的课,挺逆天的,下学期去课咨委提一嘴(
+收完东西感觉箱子比来的时候重好多(,希望人没事。明天回百京了,现在还是好急(
+还是不舒服,下略((
+8月15日
--老师好,我不是数学系的/我是本科生所以要特殊原因选这门课,现在还看不到网络学堂不知道第一周作业是哪些,能不能邮件发我一份,谢谢谢谢,谢谢老师。哦哦不用担心虽然我不是数学系的但我学过前置知识不会听不懂的,对我一直有在上数学课,也知道我选这课是在干什么。啊还有我要第二周周中才能选上课,能不能把第一次作业的 -ddl -延后一点或者给我个助教的邮箱我交过去,谢谢谢谢,谢谢老师,老师再见。
+从潮湿的地方来,到温暖干燥的你身边。
想想应该再问老师加个微信群的,抽代的时候我就是从何宝那里直接扫码加的群,现在居然给忘了,残念。遇到好奇心强的老师还要解释一下未央是什么东西(,我一个学物理和交通的同学怎么就来学数学了呢,还有为什么不转系难道是不想吗(,好崩溃。优化理论应该是最后一遍了(,但是下周可能还要给各个院系的教务发邮件打电话催手选审批,秦清的微信我上学期就加了,这学期真不想再找她了(
-说到抽代,又到秋季学期了,还能不能遇到像 Bowen L
-那么可爱的助教呢
9月22日
-第一周感觉就像体验上学,所有的课都像开盲盒
-而且也基本都不必修,还就那个充满期待(
这周最大的感想是原来不是每个老师英语口语都像 wty
-一样好,然而她已经润了,急
优化理论体感还挺良好,半听半摸的就过了,印象比较深的是讲 linear -programming 有人问为什么 cost function 里面有 \(|x_i|\) -也还算是线性函数,我当时想到的是把它拆成 \(x_i\) 正负部的和再多在 constraints -里面加两条不就变成线性的了嘛,结果老师说是把 \(|x_i|\) 换成 \(y_i\) 然后在 constraints 里加上 \(y_i \geq x_i ,y_i \geq - x_i\) -就可以,虽然也是等价的但是突然感觉有点不爽(,也觉得好像没学过分析就不太会从正负部考虑。后来翻了下教材发现上面这两种形式都给出来了,舒服(
-其实不算是严格的正负部,严格正负部的话 \(x_i ^+,x_i ^-\) 之中必有一个是 \(0\),在优化里就把两个直接都当成非负数也没关系,不要在意这些细节,警惕学魔怔了(
作业还没写完,但是在读 Durrett -ESP 的 continuous time Markov chains,写得比 PTE -友好而且入门一点,比如说这本上 Chapman-Kolmogorov Equation -的证明就直接用了 Bayesian Thm,PTE 当时用的是 Markov -property,初学直接给我干懵了(,但其实也是学到了很有用的技巧。然而令人悲伤的是 -PTE 的 Brownian motion 我也已经有点子看不懂了(。
-但其实 ESP -也还是有看不太懂的地方,虽然我有点怀疑可能是因为是直接从第四章开始看的,说不定有些东西在前面已经说过了但我没看到。之前打印凑页数满减的时候翻到了当年分系讲座的时候推荐的一份 -lecture -notes,这次正好拿出来对着看,就感觉稍好一点。
-另外之前觉得这书习题太多了,现在再看感觉其实有点少(,几十道题全都堆在章节最后看起来很恐怖,然而 -PTE 分散在每一部分的习题加起来可能比这个还多,不也都做下来了嘛。
-然而哥们也还是做不动了,挑着写点吧
-都在学概率论了,不如每次 random 一下选择做哪几道好了(x
9月23日
-周末睡大觉.jpg
-ODE
-作业看起来很水但想写严谨的话还真有点烦,这课不会就这样吧不会吧不会吧.jpg,算了就当
-预习
-复习数分了吧(。我的确时常感觉到没学数分有点头大,但是又没有那个心力再回去学了,选点这种课随便复习点(
这个学期竟然有 11 学分的必修,太辛苦了。本来有 13 -学分,但又担心万一剩的太少被按时结业就寄了,又退了一门。
-晚上在答疑坊值班甚至没来得及填完奖学金申请表,经过去年入账 0
-元之后我就知道我申自己院系的奖学金是自取其辱,但万一今年甩给我两千块钱来加倍羞辱我呢。去年必限/必限任在班级/年级里的排名这四个指标中的任何一个都可以拿来填学业奖学金,今年任何一个都到不了,甚至必限
-GPA 在班级里已经是后 50% 了,我说你们也太可怕了罢.jpg
然而就算这样去年也没有拿到一分钱,今年不更是纯纯的自取其辱,随便糊完然后看乐子.jpg
-9月24日
-今早去偷袭了下隔壁,想起来明天是 runzhi
-的生日就把他叫上一起吃饭了,出门之前翻了翻把我那本世图出版的 Functional
-Analysis by Stein 当礼物送了,写完 ODE
-作业之后把剩的一小摞作业纸也塞给他了,怎么会是呢。数学壬真方便,送纸质数学书当礼物就一定没问题(
本来没什么事,突然跑过去是因为听说理教四楼的椅子很舒服(,于是去坐了一下(#每日坐椅子(所以这个
-tag 到底是什么梗(。在那边半个小时写了三道 ODE
-作业,昨天在三教一下午写了两道,高下立判(不(当然是因为昨天下午先读了
-Walter 又写的作业,而且前两道更麻烦一点
非常好北大,爱来自隔壁,下周末还去(
-9月25日
-来点手选笑话:
-好消息是我下午一点多提交了所有的申请,三点就选上了优化理论;
-坏消息是到现在还没选上另三门;
-好消息是之前本来以为三门课要找三个不同院系的教务催审批,但现在来看不用了;
-坏消息是不需要找教务是因为审批目前还卡在老师那里,还没轮到教务批(
-报了个答疑坊小班辅导讲师的面试,其实招募是一周前的事了,不知道现在还缺不缺人。我也只能讲讲概/统/概统,不想再回去复习线代什么的,所以感觉就算面试也不是很需要准备,只是薪酬相比日常答疑来说还是比较可观的,有高中毕业之后带家教那味了(
-9月26日
-才第二周刚开始我就已经觉得这学期有点难顶了,现在最大的压力来源居然是,优化理论的作业必须 -LaTeX -不能交手写(,还以为这学期终于摆脱基物实验报告了,结果来了个每周一次的纯英文实验报告(。
-一下午一晚上没写完 -HW1,当然也有教材后面一小部分还没看完的原因。还是感觉如果手写的话晚上总还能干点别的,难怪 -zjz 在作业文件里写
---Please start early!
-
(
-晚上骑车的时候听到两个路人聊天:
---A: 那个算法导论的 ddl 是今晚吗
-B: 是的,但是我网络学堂上还没这门课呢
-
9月27日
-今早在路上遇到一位好歌剧(,骑车从我和旁边一辆车的缝隙里穿了过去,虽然吓我一跳但完全没发生事故,好强(
-(是在 neta 这个((
+印象里是沉迷方舟时候看过的一篇同人标题,说人话就是:回学校了,大贴特贴(
+残念,晕 3D 而且高铁上环境不太好没能打游戏,看了半天 Building reproducible analytical +pipelines with R +催眠,速睡。本来想在旁边小朋友的家长面前表演一个玩物丧志,希望没那个加深华子的刻板印象(
+8月16日
+一边贴一边看一些看不懂的东西,虽然还是看不懂但至少在看了,所以说贴贴真好(啥
+8月17日
+之前吴昊给我她的概率论讲义的时候跟我说 Markov Chain 和 Brownian +Motion 这几章《非常简单,工科生也要学的》,昨天被 Durrett +整破防之后带了她的讲义去教室看,感觉,感觉这两本书在讲的明明是同一个东西但根本不是同一个东西(,怎么会这样呢(
+总的来说我这两天真挺怀疑自己脑子是不是有点问题的,希望人没事(
+看到 hx +在一个啥的“青年教师教学能力进阶项目”拿了一等奖,给我整绷不住了,和他同组的是我当年的写沟老师(在生命学院本博,后来去了教研院),世界真小,不过这两个人怎么能做到在同一组的(
+吃饭刷北大猫协公众号,瞟到果壳发了个天气越热,数学成绩越差,我觉得合理,而且不只是数学成绩会受气温影响(。还好秋季学期要来了,秋天到初冬开暖气之前这段时间是最舒服的((
+晚上突发装修后遗症,盯了一会四教三楼一个嵌得角度挺刁钻的灯带,想的是这要是坏了会很难修吧(
+8月19日
+昨天难得太累了咕了日记,老姐来北京陪她出去玩,晚上回来贴贴了一下,回寝室和 +wafarinliu 老师扯皮,谢谢大家盘活我(啥
+远程验收了装修,也不知道还有没有什么问题但总之是交房了,可喜可贺,就算有也差不多得了。到最后了包工头还在跟我扯皮我买的柜子可能有什么问题总之不如定制,扯皮的时候把尺寸抄在草稿纸上打算问他到底哪里不合适,后来发现长宽高三个常数在乱七八糟全是符号的草稿纸上真的很格格不入,好久没见过这么多具体的数字了(
+吃饭的时候看到一个这玩意,以前看到竞赛生小作文都会默默划过去所以为什么不取关质心这个公众号,今天扫了一眼封面发现
+efz
+的录取通知书被拍进去了,内容和事情本身也挺逆天(,加上有一些熟悉的元素,还真的读完了。总的来说很符合我对你校竞赛生的刻板印象,以及华子还是一如既往地不当人(
--2000 -年有马纪念,在和田自己选位不佳、加上其他优秀赛马的紧盯之下,好歌剧从起跑起被其他马死死围在马群核心。和田龙二多次起身观察脱出路线未果,直到最后 -300 -米直道,由于名将怒涛冲刺、成田路失速的机缘巧合,马群让出了一闪即逝、仅可供一马通过的包围网缺口,好歌剧立即从这一缺口切出并凭借强劲的末脚一路冲刺,反超名将怒涛以鼻差夺冠。(这也是游戏中好歌剧固有技能发动条件要求被团团包围的由来)赛后和田龙二称,他当时已经对比赛绝望,路是好歌剧自己选的。(出处)
+我一个数竞cmo银牌同学,综合成绩常年年级前五,综合营优秀评定,我校卓越毕业生,最后因为报的是热门的信计,也没有录取……校测只给到13分(招办说如果改成数学可以录取)
玩闪耀优俊少女玩得(
这运筹学怎么天天关着灯上课,还在低速复读优化理论第一节课的一个零测度子集(,之前我问老师他还理直气壮地说这课不能替代,明明就是门水课。之前还想着下次带个台灯去上课,又感觉会被针对,麻了(
-9月28日
-在建筑材料课上困得睁不开眼睛,遂写现代生物学导论作业:
+笑麻了,傻孩子们,快跑啊(
8月20日
+逛街的时候看到有个七夕写许愿牌的活动,一些真诚的祝福:
+
毕竟我偶尔想起来那些没上的物理课,会觉得五年毕业也很困难(。考公的考一开始还写错了,残念(
+被暴雨困在商场里走不了的时候去玩了一下自助拍照的机器,和老姐《初检合格》((
+
贴图的表情包还挺精髓的((x
+8月21日
+右手大拇指根好痛,有刚入坑音游的时候当拇指党结果玩太多玩出腱鞘炎那感觉了。怎么偏偏是这个手指,写题就讲究一个冥想,吃饭也好想把筷子扔掉(,下略(
8月22日
+早晨收到了玫瑰,去社聚还收到了 neruko +老师的小卡片,回来才发现卡背是透光的,好用心 qwq
+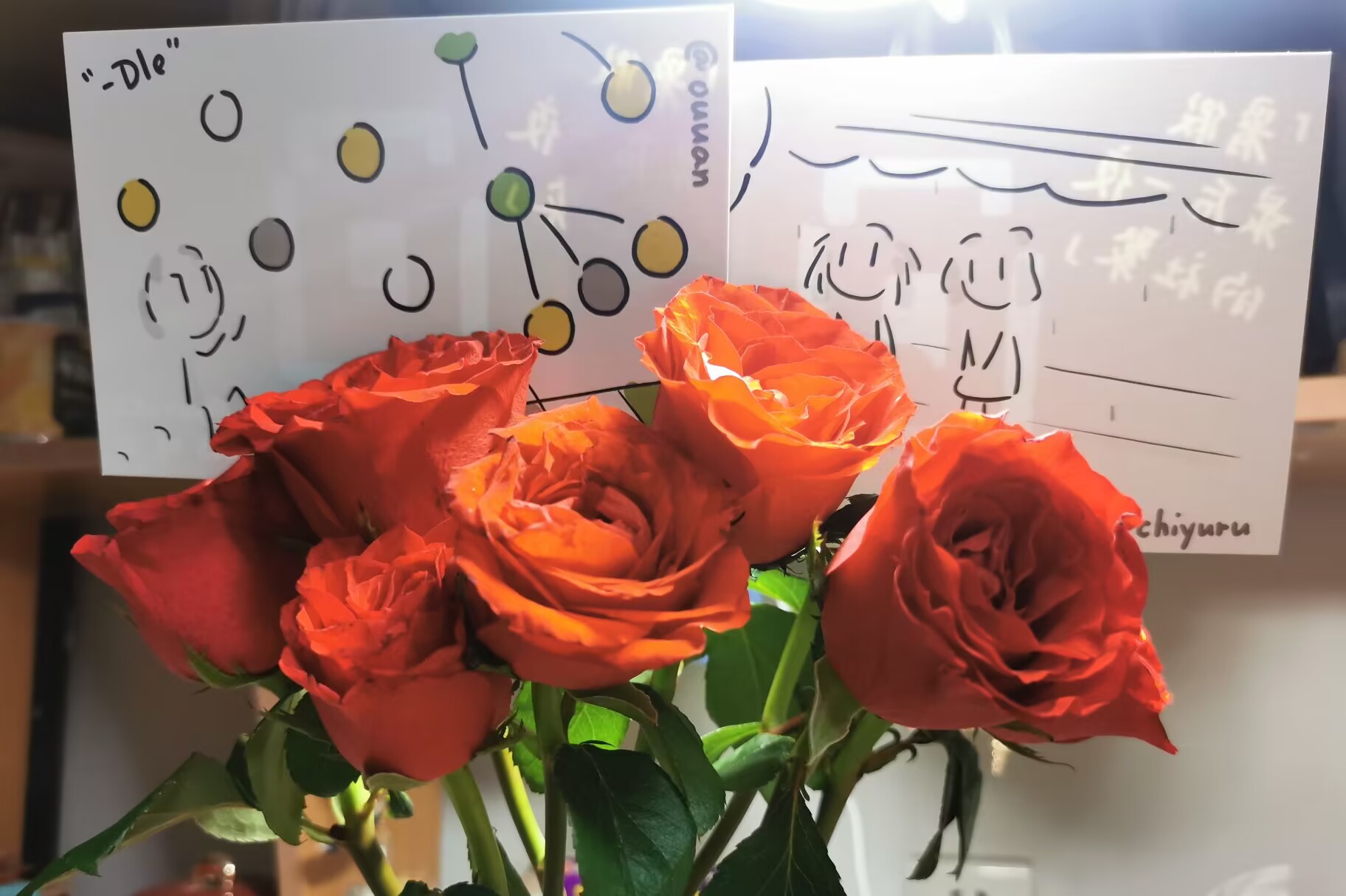
以及
--我:
-在建筑材料课上听老师讲化学
-与此同时在写生物作业
-这两门课我高中一门没考 一门 B+ 全班倒一
-一个都不会 好崩溃
-友:
-草
-远离数学寸步难行
-我:
-是的 但我现在数学也学得寸步难行
+今天是乞巧节,希望织女赐我巧手,让我写证明少写点伪证,写代码少出点bug
放假前一晚 4-6 的自带 PF -的通识水课课前说有小测把所有人骗去,结束的时候又说没有,素质极差(
-感觉这学期课也没有很多(挠头)但是为什么现在一天到晚都在学数学,不然连作业都写不完(
-再来段传世经典(x)对话:
+8月23日
+十月终于要有赛马娘第三季看了,急急急急急(
+今天送老姐去北京西坐高铁,才知道这边不允许送站,买票进站的话最多提前大约六个小时,逆天。在这之前我还真以为所有的车站都是允许送站的,至少上海虹桥和北京南都是,然而以前也只有在这两个地方送站/被送站的经验(。等寒假回去测试一下上海站,上海西站和上海南站能不能送站,可以的话其实也想测测什么松江南金山北南翔北安亭西芦潮港站(开玩笑的,芦潮港站不办理客运,可以送就说明百京不行,不能送就买个从上海站到上海西站的票假装在运转好了((x
然后发现其实芦潮港站和清华园站(这个东西还挺冷知识的)这种早就已经停止办理客运的站点在 +12306 上也还可以选择,多少有点时代的眼泪了(x
+去年秋季学期在统计推断课上学 C-R Inequality 的时候老师还提了一句 C. +R. Rao 目前仍然在世,后来网上冲浪的时候还在统计之都读到了《C. +Radhakrishna Rao: A Century in Statistical Science》,R.I.P.
+对不起但如果不是去翻了一下的话我已经全然忘记 C-R Inequality
+的形式了((
8月24日
+晚饭和 Triang-jyed-driung +面了个基,虽然他看起来对欧老师更感兴趣,怎么会是呢((x
+新生好可怕(?,晚上听人在楼道里吹了半个多小时长笛,而且听起来好像不太会的样子((
测量实习组队好艰难,每到实践课组队都觉得和自己专业的同学大多都不是很熟还是挺麻烦的。找的第一组四缺一但是他们在何老板和我之间选择了何老板(,去问
+OscarZs
+一开始也是四缺一被拒,后来又可以了(,过了一阵第一组又润掉一个人,问我还能不能来,这次轮到我拒绝你们辣,总的来说好崩溃((
8月26日
+虽然昨天没写但其实是挺重要(?)的一天,但是没写(?
+从去年就在看《因果推断的统计方法》了,这两天终于在手机上看完了,学到许多但其实也没学到啥(。最开始看到统辅课里面有一门因果推断导论(不知道是不是叫这个名)的时候还在疑惑这也是统吗,一头雾水(x)地读完发现确实挺统的(
形式化定义真难,一开始疑惑 Casual Inference +到底是个什么东西的时候主要就觉得很难形式化定义,像 confounding +这样的东西在线性回归课上也只是举个例子说明,真看定义还是蛮绕的。
+后天要开始测量了,难绷。
+8月27日
+明天早八就要测量了,总感觉今天是十天内最后一次学数学,很崩溃,就郑重地往前给一些打星号的章节收了尾(,然后回去终于放心地把第四章的一整沓纸放进了影印书的那个壳儿里(。以前不知道是出于什么精神状态没看,如果看过的话读后面的东西应该会顺畅很多,#每日追悔莫及(
+然而测量的课前准备从申请 CASS 试用资格和现在 AutoCAD 都已经出到 2024
+版了但还是要求用 2014
+这一步开始我就觉得难绷了,上次感觉到相似的难绷应该还是上次领军训服装的时候。看这个测量实习的指导书感觉也挺军训的,尤其要穿两周长裤,本来想着如果只是规定穿的话那我就不穿顶多扣点分而已,后来看了看学长的工作日志感觉可能是外业测量的时候蚊子太多不得不穿(,工作环境好像还不如军训,好崩溃(
看到 ypk 今天给我发邮件说明早有个 talk
+可以来听一下的时候崩溃感达到了顶峰((有人需要吗在这里写一下好了
--友:球队有个学弟大一就开始数分高代几何 励志转数
-我:要转的话不就该这样吗 我是失败例子
-友:也是 还有个学弟写了三周代码就想转码 还想卷 AI
-我:能理解 我写了三周的时候也想转 第四周好像讲到类了 -然后就不太想转了
+8/28. 10-11am. 三教 1205
+Speaker 1: Yaqi Duan
+Title: Optimal policy evaluation using kernel-based +temporal difference methods
+Abstract: We study methods based on reproducing +kernel Hilbert spaces for estimating the value function of an +infinite-horizon discounted Markov reward process (MRP). We study a +regularized form of the kernel least-squares temporal difference (LSTD) +estimate. We analyze the error of this estimate in the L2(μ)-norm, where +μ denotes the stationary distribution of the underlying Markov chain. We +use empirical process theory techniques to derive a non-asymptotic upper +bound on the error with explicit dependence on the eigenvalues of the +associated kernel operator, as well as the instance-dependent variance +of the Bellman residual error. In addition, we prove minimax lower +bounds over sub-classes of MRPs, which shows that our rate is optimal in +terms of the sample size n and the effective horizon H=1/(1−γ). Whereas +existing worst-case theory predicts cubic scaling (H^3) in the effective +horizon, our theory reveals that there is in fact a much wider range of +scalings, depending on the kernel, the stationary distribution, and the +variance of the Bellman residual error. Notably, it is only parametric +and near-parametric problems that can ever achieve the worst-case cubic +scaling.
+Bio: Yaqi Duan is an Assistant Professor of +Technology, Operations and Statistics at New York University Stern +School of Business. Prior to joining NYU, she worked as a postdoctoral +researcher at Massachusetts Institute of Technology for one year. She +received her PhD from Princeton University and BS from Peking +University.
+Speaker 2: Kaizheng Wang
+Title: Pseudo-Labeling for Kernel Ridge Regression +under Covariate Shift
+Abstract: We develop and analyze a principled +approach to kernel ridge regression under covariate shift. The goal is +to learn a regression function with small mean squared error over a +target distribution, based on unlabeled data from there and labeled data +that may have a different feature distribution. We propose to split the +labeled data into two subsets and conduct kernel ridge regression on +them separately to obtain a collection of candidate models and an +imputation model. We use the latter to fill the missing labels and then +select the best candidate model accordingly. Our non-asymptotic excess +risk bounds show that in quite general scenarios, our estimator adapts +to the structure of the target distribution and the covariate shift. It +achieves the minimax optimal error rate up to a logarithmic factor. The +use of pseudo-labels in model selection does not have major negative +impacts.
+Short bio: Kaizheng Wang is an assistant professor +of Industrial Engineering and Operations Research, and a member of the +Data Science Institute at Columbia University. He works at the +intersection of machine learning, statistics, and optimization. He +received his PhD from Princeton University in 2020.
9月29日
-为了报 seminar 写了个 CV,然后轻微破防,我怎么除了 GPA 和并不完整的 -core course 之外啥也没有(
-如果报上了是不是就可以两周出入北大一次了
-不知道能不能去北大,但那样的话这个 ODE 大概真是留不得了(
这学期选了几门研究生课,现在看到 8 和 9 -开头的近邻宝取件码都感觉有点像课程号,有点难绷。
-9月30日
-最近在听《她似了,又活了。她没似,他似了,所以她也似了。她又活了,可他们似了,所以她又似了。》,好美丽的精神状态,好喜欢(
-给 lq 的博士生发了报名 seminar 的邮件,然后:
+前段时间在家里闲着没事的时候整了一个计算闭合导线参数的小(不如说非常非常小)工具,看实习指导书上还有一个可选提交项目是使用的程序,确实可以卷交一下,前提是我最好对这个测量步骤没有什么理解性错误,闭合导线测量占比要是比支导线还少那就大寄特寄(。然而这一步难道是重点吗,重点难道不是我连全站仪都不是非常的会用、工程计算机制图或许就是
+2.3
+的水平所以也不会画图、然而测量学到现在都没有出分我甚至不知道它和工程计算机制图相比哪个更烂,而且这段时间看起来非常的缺少贴贴,吗(,那要不还是先希望队友没事吧((
不行,现在压力好大,又想起来组队的时候还是我主动去问能不能加组的,如果不是我的话他们本来明明有机会拥有一个啥都会的组员而不是我这样的
+five,别真坑队友了吧((
8月28日
+测量实习就是军训的一些证据:
+-
+
都是 2 学分的小学期课程
+和同班/同专业的同学待在一起(
+(理论上来说是)早晨,下午和晚上干活,早晨起得很早,太热太晒的时间休息
+戴帽子,穿长袖长裤
+在学校里定向越野
+缺少贴贴
+
晚上回来疲惫地走进猫超买了盒酸奶,里面挤满了刚结束晚训的新生,对着楼梯口的镜子照了照自己,我的评价是穿得好奇怪一女的(。想起来下午在东主楼附近找合适的控制点的时候也是穿着这身奇奇怪怪的衣服,还遇到了 +TA,世界真小,不过我觉得 TA +新(?)发型还挺好看的,为啥上次社聚的时候大家都在乐((x
+白天实在不想听课,看了很久地理等级考之后就没再看过了的星球研究所,他们制图水平真的好高(
+8月29日
+早晨踏勘选点涂油漆之后其实就累了,中午爆睡俩小时。吃饭的时候看微信步数是
+7k 多一点,下午跑尺,晚上回来也就
+10k,然而地质实习的同学中午就人均破万了,好(
怎么能写的东西还不如工作日志多,下次要不直接把工作日志搬上来吧(谁要看啊
8月30日
+昨天跑尺的时候坐在马路牙子上思考 regular conditional expectation +和那个我有点看不懂的 transition probability 的 general definition +有啥关系,至少长得挺像的,某种程度上是把随机变量的定义修改成了映射到可测空间而不限制在 +\((R, \mathcal B^1 (R))\) +上,想到这里就感觉有点困了(。
+昨晚才发现之前看不懂主要是 notation +在前几章的角落里出现过但是又没有再提过多少有点你谁啊真不熟了,要是有索引就好了(。查 +MSE 看到一个关于为什么需要一个 general definition 的讨论,有个评论说
--收到,后续会通知申请结果以及具体信息。
-祝好!
+"a random variable gives out a real number" Not necessarily, for +example, to model DNA sequences by Markov chains, one could choose +S={A,C,G,T}.
这个东西难道还有筛选还会过不了吗,你最好快点通知,要是过了第六周我就来不及退
-ODE 了((
假期为什么只开六教 A 区和清华学堂(,六教的蚊子太恐怖了,翻了翻 -2022.09.21 -的日记,一年过去了六教不知道第多少茬的新蚊子也还是和当时一样,只喜欢盯着我咬(。晚上鼓起勇气(?)探索了下清华学堂,在二楼看到数学学堂班专用的教室还是羡慕了(
-之前一直觉得头发太长了不太舒服,今早起来终于克服懒癌把理发剪刀找出来剪短了,结果克服得太过了给剪太短了(,现在显得脸好大肩也好宽,本来就稀疏的头发显得更没几根了。本来还在安慰自己过两个月到冬天需要头发来保暖的时候就又长出来了,然后想起来过两天有社聚,看了眼鸽鸽鸽还有之前没面基过的社友来,好崩溃((x
+才想起来生统概论课上也举过类似的例子(单指用随机变量表示基因型)但我给忘了,老师当时还说了一句虽然随机变量定义上是取实数值但也可以换(大意),当时以为她在说废话于是记住了这件事,现在想想不知道是不是有别的深意(其实应该没有吧
昨晚查这玩意查上头了睡了还不到六个小时,最近实习有超长午休,本来以为今天可以先睡个觉然后学点数学来治疗精神损伤,结果剥蒜三小时闭合导线参数还没算出来,晚上继续剥蒜,还算了一些高程和支导线,早晨的角度闭合也是当场画图算的,计算器要按冒烟了,高考数学打计算器强度都没这么高(是的你沪高考数学是可以用计算器的,虽然不知道现在还能不能,至少以前会因此有很逆天的剥蒜。下午记水准测量读数的时候也一直在打计算器,数学壬不是这么用的,我最不会的就是剥蒜,但是还写错一个数,还好刚重测了存疑的两站就发现了,没返太多工(
明早四等水准测量,今晚看了几个例子大致知道是要干什么了。说起来今天得知水准测量的两把尺一定要是不同规格的时候 +CPU +都烧了,但实际操作也没那么难,还能预判读数在不在值域里,希望明天高程能闭合,再闭合不了/误报闭合失败我真要给队友谢罪了(。下午大概要测碎部,然而我对于怎么测碎部点甚至怎么记读数这件事尚且没有任何概念(
+下午看到老师说明天最好是六点到九点测四等水准,大家商量说往后推到七点半到十点半也不是不行,差点脱口而出“毕竟
+Lebesgue 测度有平移不变性”然后硬给憋回去了自己开始乐,并且默念这是
+surveying 不是 measure theory(
8月31日
+这两天我一直以为中午收工之后仪器是送到测量老师办公室保管的,今天才听清楚是送到其中一个队友的工位,碰巧也在新土木馆。连你院本科生都有工位,而某些系和某些书院到现在博士生工位都不够,博后工位还十人一间(
晚上看到个这个,光速克服拖延去下单了 +GTM274 的影印((这是可以说的吗((对不起但真买不起(。之前本来想读完 +Durrett 之后看 Markov Chains and Mixing +Times,但好像太专了,优先级不应该那么高(
+早上的四等水准太折磨了,作为一个对于最终成图没有任何帮助的支线任务,四个半小时测了整整 +28 +站还不得不用一些物理实验手段处理了一下(,好崩溃。最逆天的是这玩意的转点没法保存,只能一口气测完全程(
+测量实习中期要交的东西都做完了,下午站在东配楼门口测试了下碎部测量,然后聊了会天就收工了。聊天的时候无意中发现 +OscarZs +会把“什么什么东西看起来很糊”的“糊”读成四声,想起来之前欧老师也是,还以为是什么湖北特供口音,然后另一个家在河北的队友说他们那边也是这么读的(。稍微有点怀疑读成二声是什么江浙沪和山东莫名其妙统一起来了的口音了(
]]>但还是啥也不会(
-虽然其实每年的十月好像都发生点惊吓,或者一些事后看来也不是什么好事的惊喜(
-10月1日
-北大一日游,顺了一盒茶叶几本书一个挂件回来,还有公路车一周体验卡,我到底是去干啥的((
-晚上骑公路车沿着周边的几条大路 描边
-飙车,不慎从路边一个下水口压过去的时候感觉车轮还没有下水道的缝隙宽,就挺危险的,全地形适应力实在是不太行。起步不太容易,速度太快了刹车也不好刹,需要提前好远就开始摁,有的时候最后还得脚刹,甚至我胳膊太短了如果不趴下去的话会有点够不到刹车。但是它快啊,骑着爽啊(
背单肩包实在不太适合飙这么远,中间累了的时候就不由自主地降低重心往车架上面趴,大概也能降低点风阻,而且这样好像很专业很帅的样子(。有点联想到小栗帽的跑步姿势了,离地面很近几乎会平行什么的(玩()玩得
10月2日
-昨晚飙了一个小时车,今天成功发烧了,国庆假期 -1(。
-但是下床吃饼干当晚饭的时候把还没布置的运筹学作业水完了,写完开始乐,顶点是什么松弛系数又是什么,这教材是一点看不懂,反正我是英文写的,总不会判错吧(x)。先观察下作业批改情况看看这课到底多逆天,实在不行第五周退了(
-躺在床上水群的时候看到有人问搞数学怎么样算 taste -好,我也不知道,但反正我的 taste -就停留在教材至少要满足是用英文写的和是用 LaTeX 排的这二者之一(
-10月3日
-这个烧退了吗,好像退过,但是又没退,如退(
-今天勉强往后看了点 LP,还以为可以把 ODE -写掉的。不是我说这个假期不会就要在生病中迷迷糊糊地过去了吧(
-10月4日
-清华学堂这个桌椅还挺舒服的,有很多可以踩的横杠,腿短人在椅子上也可以缩成一团(
看了一天 泛函分析 ODE(,还挺有意思的,只是把它用到 ODE
-里就没啥意思,这几个核心定理的条件看着就有点丑(。之前还在幻想一上来就概统了岂不是失去了在很多方向上探索下的体验,现在简单探索了两周觉得确实还是概统比较有意思(
说起来感觉至今都没有认识的做动力系统的数学壬,别的方向多多少少都知道几个,除了概统之外认识最多的应该是代数壬
-虽然都是赛博人,怎么会是呢。
晚上才知道大鸣大放居然也成为马娘了,之前还一直想着拿不到许可,第三季里怕是要直接删减
-看不到北黑吃瘪 或者是用路人马娘代替了,Cygames 太强力(
10月5日
-这赛马娘第三季一股浓浓的第一季的味儿(
大鸣大放好帅
--有特别篇珠玉在前,对跑步的演出有点无感。不过我跟巴普洛夫的狗一样,看到帝皇就开始头皮发麻,眼眶湿润,不知道怎么回事捏。
-
说起来感觉看到了很多 neta,但是字幕没标注所以也不确定是不是在
-neta(,看芦灰的尾注看得(
终于还是下了个闪耀优俊少女开始养马(,逃不过这一天(。能看到会动的小栗帽真好啊,帽门
10月6日
-简单给 Intro to LP 前三章收了个尾,看 zjz 主页上的课程大纲似乎讲完
-duality 之后就要开始 convex optimization
-了,但有本书我还没印,就非得印出来看吗,虽然不急但甚至有点急。说起来我每次说
-Jingzhao Zhang 的时候脑子里想的都是 Jingzhang Zhao,还有救吗(
本来今晚要去面试小班辅导讲师,结果嗯是到晚上六点左右才通知十点钟面试,这么晚而且看起来又很不靠谱(,干脆就咕掉了,进行了一个全程参加社聚。想买副塔罗牌遇事不决玩一玩了
这么一说我感觉最不靠谱的好像是我
明天开始练习在一些 不得不去又信息密度极低而且全是无效信息
-的土水学院的课上绣十字绣(
谋勇兼备退役了,之前还说是唯一一个在现役时代就进入赛马娘企划的马娘来着的。铁鸟翱天和杏目什么时候能来,急(
10月7日
-本来想打印下
-Boyd,翻了一下什么原来有七百多页啊,那用纸质感觉还不如看电子版了(。Jun
-Shao
-那本数理统计也是太厚了就没打出来看,不会真有人把查阅用的书打印出来看吧,高统的话感觉听课看
-PPT 也就差不多了,希望吧(
--@所有人 如果两位同学负责同一次 scribe -note,两位同学仅需要提交一份 note -即可,请两位同学私下自行沟通,并且相互检查最终提交的版本,谢谢!
-
好可怕,为什么不能一人交一份((
-同一个概率论问题我给室友写过一遍,国庆前就在小程序里答了两遍了,今天在志愿者群里又答了一遍,晚上值班又答了一遍,有三个是看不懂
-\(P_C(\cdot ) = P(\cdot | C)\)
-这个定义形式里面的点是什么意思(,一个是在纠结是不是要用概率的条件概率来算
-某种程度上来说水平很高,还有一个没说哪里不懂。绷不住了,你们这作业
-ddl 还挺长啊(
值班被问数值分析还给问挂黑板了,紧急临场打开教材 pdf
-开始回忆矩阵条件数是什么以及若干
-bound(,丢人((不丢人,我又不搞计算((x
今天是周一,明天是周五,后天是周一,再过几天又是周五,1!5!(
-10月8日
-今天是袁洋给张景昭代课,但是((
+9月1日
+感觉一年没学数学了,之前说感觉午休可以学,但是这两天要么午休也在忙着测算,要么太累直接大睡俩小时,一直没怎么看过。昨晚收工早倒是看了一下,之前没懂的地方稍微有进展了,但是不多(。今天继续往后看,有一种朦朦胧胧感觉要看懂了但又还差一点的感觉,解决的细节越来越多,仍然是稍微有进展,但是不多(,学得好慢。
+打开上个月的日记发现 8.1 在装修,8.31 +在测量,某种程度上来说整个八月都是在专业实践(,好崩溃。总觉得忙活装修已经是很久远的事情了,最近的进度因为太忙也没有再跟进,和宜家打电话沟通好像也是挺久之前了。
+前两天外业一直在做水准测量的记录,内业也做了不少计算,尤其四等水准测量是一边走一边记一边把计算器打到冒烟,到今天开始测碎部实在绷不住不想再记数据了,就选了画草图。脑子一抽打算把各个地方的草图画成边缘可以拼在一起的样式,到最后不仅有 +AutoCAD +的成图,各部分草图也可以拿透明胶粘在一起组成一张完整的手绘地图。除了强迫症发作之外这样或许对内业绘图的队友也更友好一点,于是就在大家面前夸下了海口(,结果今天画了两张 +A4 +纸,刚把美院周边测完就觉得实在太难了(,只能自我安慰图纸效果似乎还挺清楚的,对队友友好而且答辩也能吹一波(
+估计总共要画六到八张,希望人没事。这样的话之后几天草图就只能我来画了,轮不到换班跑尺或者读数养老了,寄(。还是原来那样,如果我还是原来那个喜欢地理的高中生的话应该会觉得画地图这种事情很有意思,但它现在是不得不上的专业课就觉得好痛苦,随便把一般的兴趣变成主业是完全行不通的事情,不过也可能只是 +jk 过期了(
+
虽然已经不负责读数和计算了,但是到晚上所有的数据表还是会莫名其妙都回到我手里,这是怎么会是呢(
+今天交中期的九样东西,这几天一直在劝诱(?)组长用 LaTeX
+写但成品还是 word 了,虽然很没必要但是好急(?
9月2日
+早晨出门正好看到大量研究生新生在往综体走,大概是开学典礼,一路上在心里默默锐评了一些院衫。
+-
+
- 物理系是我看到唯一一个集合之后举着牌子排着队在学堂路上走的,其他院系大概都是自行前往( +
- 怎么有个院系的院衫就是一件印了字的大红色的纯色 polo +衫?原来是求真啊,那正常( +
- 核研院的 T 恤背面写着“缘起 200 号,逐梦核研人”,在路上想有没有“缘起 +600 号,宛平南路精神病人”( +
- 看了一路感觉材料学院的院衫是最好看的 +
看到水利系院衫,默默嫌弃地扭头骑车走了
+- 为什么分散地看到好几次网研院的但是一直没看到贵系的,
概率论不存在了
+
终于把《相合之物》看完了(,是不是日常番集中补的话就会有点没意思,而且我是来看日式点心的,对主线也没啥兴趣。到最后已经是二倍速在看了,看完感觉终于解脱了(,怎么会这样呢。
+看到 bangumi 上第 12 话下面有一条评论:
--张老师出去玩了,我给大家代课(
-我虽然是搞优化的,但是这些我都没学过,simplex method -之前没怎么接触过(
-十年前在 Cornell -的时候在同学强烈建议下我去旁听了一门优化课,但是没参加考试所以还是不会(
-为了给大家上课我花了两个晚上学了这些,如果错了那是 zjz 的 PPT -有问题,不是我的错(
-Farka's lemma 是个很核心的定理,我在 Cornell -读书的时候老师讲了四五节课,但是我只能讲十分钟,因为我也不懂更深刻的东西(
+感谢在我备考的这段时间陪着我
我大震撼(x
-总的来说这节课槽点实在太多了,偏偏是(还不是自己选的吗)今天在做
-scribing,不过既然不是 zjz 本人讲的而且又有
-PPT(问题是也还没发诶(,那岂不是自由度还挺大(x
申请奖学金的时候就说感觉是在自取其辱,还真是(,今年综奖是差额答辩但也没进,我估计单项更没什么希望。放在去年我还百思不解,难过了一阵子,今年就变成了:
+突然就有点理解日常番的精髓了(。想起来 20 年的时候在追《放学后海堤日记》,大约是高三最后一次联赛之前的一两天发烧了在家休息,迷迷糊糊睡醒看到钓鱼番更新了,本来赛前生病心情很不好很担忧状态,躺在床上看完最新一话还是开心了很多,然后爬起来洗了个澡。这番好像一直到确认退役的时候才完结,感觉考完联赛知道进队没戏,在家切换状态到高考和补作业的那两天似乎也看了最新一话,出上海赛区初步名单的那段时间也有看,所以说虽然现在完全不记得是在干啥了,说不定还不如《相合之物》好看,但印象还挺好的(
+今天主要在测建馆附近的楼,草图加了一张 A4 +纸,比例越发崩坏,这个建馆报告厅看起来和光华路一样宽。
+
早上测到建馆报告厅的时候感觉台阶设计得实在太抽象,就和组长商量了我中午先回去仔细想想怎么处理,下午带着画好的草图来测就会快很多。拍了一些靠近美院这一侧的照片就回去画大图了,下午也在下雨之前测完了东面和南面,本来应该 +flag +顺利回收快乐提前下班,结果绕到西面和北面一看才知道早晨把我整破防的东面和南面还算简单的,又回去画图,成品长得也挺抽象的。
+
它还和继续教育学院有一座桥连在一起,往后绕了绕感觉继续教育学院和建馆咖啡厅也有点抽象,等测到这边的时候估计还要甚至要给这个详图再加纸再画大图,下次再说吧。
+上午只走了 5k 步,之前几天都是早上就快到 10k +了,但是感觉今天比以往都累。到教学楼放下东西之后几乎是跌跌撞撞走到四教三楼的神奇沙发(什么东西)上坐下开始休息,不知道是不是因为湿度大气压低所以即使气温不高也很不舒服,还是说这几天的疲惫其实在累积。晚上下班早,画完建馆报告厅的图之后应该可以看看数学的,但是总感觉很累甚至很焦躁也没看多少,就稍微多处理了一点点细节,一直没理解的问题到现在也还是不理解,有点麻烦了。
+9月3日
+早晨刷牙的时候想清楚之前 Durrett +上一直卡着的问题了,很乐,但是被自己蠢死(
+今天把草图基本画完了,南边勉强是测量的时候一边测一边画的,到建馆报告厅和门口的小树林就彻底现场画不出来了,中午照着地图画完下午对着草图选点测点,爽死。
+感觉明天能收工,后天肝图和 PPT,希望不是人生十大错觉(
+比例已经彻底崩坏了,这个清华路和光华路看起来都比建馆报告厅还宽,东配楼看着有建馆报告厅四倍大,但说实话主要是西南部分画太小了,东配楼和美院的比例还真就这样。
+
已经拍不清了(
+9月4日
+下午测东主楼的时候在路上遇到了一个疑似邱宝(坏了现在说到邱宝我第一反应为什么是
+Yau)的大叔,说疑似是因为这儿离工字厅有点远,而且他为啥会一个人在路上(x。过了一会有人来问路,问伟清楼怎么走,这我熟毕竟统计中心就在伟清楼,顺手指了一下。只不过他对我的称呼一直是“老师”,我们穿着工作服怎么看都更像修路工人而不是学校的老师(,稍微有点怀疑是不是遇到济南老乡了(x)。说起来确实快到
+全体济南人的节日 教师节了(
测东主楼东配楼之间的天桥的时候看到下面的路灯类似白玉兰的形状,一下子有点愣住,上海街头(或者可能只是我住的郊区是这样的 +x)有相当多这样形状的灯,因为上海市花是白玉兰。
+想回家了,可能也不是想回家,而是想回你沪了,我也不知道为什么(
+
今天是彻底收工了,晚上在做内业的工作,明天可能看成图的情况还要去补测(但愿不是大批量重测)一些东西,不好说。之前发现用发的卷尺量我的身高量出来一米七(,后来我们都管它叫自欺欺人尺了,但也还是在用这把尺测。今天发现棱镜高也会在戳地面的时候自己偷偷地变(,合着它也是自欺欺人棱镜,那这高程岂不是全是误差,看那个评图
+统计量
+标准里有一项还是高程和点位坐标的标准差,有点虚。最后大家讨论得到的结果是,总能及格的吧((
趴在地上把地图贴好了,画出来居然真的长宽近似相等,和正方形的测区基本符合,说明我瞎画的水平也还蛮高的嘛(。建馆报告厅的详图也画好了,打算后天拿到
+pre 现场展开 燕国地图 给大家一点小小的未央震撼((x
人家以为我很卷,实际上我只是怕拖队友后腿。
+

四等水准测量那天从早晨七点半开始,测到综体前面最后一站的时候已经是暴晒的正午,组长在旁边调平水准仪,我蹲在一边按计算器盘算着这一站大约测出多少高程才能闭合。第一遍测的读数出来之后我心算了一下感觉非常的不闭合,就告诉旁边的组长再看看读对了没有,但一直找不到问题。
+从 A 到 B 的测量非常完美,但是从 B 到 A +的过程中的确出了一点小问题。我们完全可以相信去程的数据,但是回程的问题在最后一站才会暴露出来,整个过程的转点都是自选的没有办法保存,连回去检查的机会都没有。为什么要用这种原始的方法测紫荆网球场的高程,这一定是既有的数据。当然后来的画地图更是没有意义的事情,没有哪个机构会采用我们的地图,是卫星地图不好用吗,我们是很业余地在用老旧过时的仪器重复做几十年前的人就已经做过的事情,精度可能还更低。
+于是我忍不住问旁边的组长,我们做这个事情有什么意义?他没有回答我,也可能只是没听清,说中午太晒了视野有点晃,然后又报了一组数据,让我再看看这下闭合了没有。
+ + + + +9月5日
+上次看数学还是上次(,距离一点点推出所有的细节直到早晨刷牙的时候彻底想清楚 +Durrett +上卡住很久的那个问题已经有两天了,今早起来才抽出空自己重写又复盘了一遍,后面的进展就自然了很多。
+写完之后把它夹进 Durrett 里面准备出门去系馆,突然就想起来这个:
--我好喜欢被未央书院羞辱啊!
+This is actually quite a triumph, even if it is hard to explain to +your friends and family members exactly what you have achieved.
+——《研一下总结》
无所谓,毕竟早就想到答疑坊志愿工时兑换成津贴所得的收入期望比拿去评奖学金更高了来着。室友给我看了几个综奖入围的公示材料,有的按我对一些事情的
-吃瓜 了解来说感觉挺虚浮的,换到我身上的话我觉得自己做的最
-concrete
-的事情还是学了几门数学,不过这放在评奖学金这件事里毕竟是扣分项。
某种程度上来说这个破地方也有优点,让我在一事无成的时候仍然充满自信,并且坚定相信是书院的问题(
既然要延毕那好像就有四次申奖学金的机会,这么说来可以又双叒叕被未央书院羞辱,好兴奋啊(
10月9日
-因为隔壁今天才开学的原因所以我的假期其实也跟着续了两天(,该好好学习了((
-虽然杨帆上课是 Durrett PTE -reader,但其实属于是听他念书也学到许多。今天发现上节课的其实都差不多忘完了(,但记住了一个挺有用的反例,就想起来还在学概率论 -1 -的时候甚至学完之后一段时间都时不时在几乎处处收敛和依概率收敛还有对应的期望上迷糊,每次都是仔细想想 -lzx 期末默写的那个刻进 DNA 里的反例就明白了。
-今天在讲 optional stopping theorem,有个定理觉得很熟悉,遍寻 Durrett -而不得,再一想是 lzx -当时的期末题。期末前最后一节课他就讲了半个小时鞅论,当时说要考这个的时候我还在心里吐槽是谁搞出来一个这么无聊的结论,从来没想到其实是在一个很重要的问题框架下的 -lemma,就挺深刻的。再看一眼其实两个月前做习题的时候就做到过,只是放在习题里的时候 -stopping time 的符号是 M 和 N 就没有认出来,今天课上用的是 S 和 T -才发现,绷不住了(
-来一句九月份我最喜欢的摘录(x
+这两天没有来由的(真的吗?明明有很多来源)难过,想回家,也并不是想回家,想回上海了,然而秋季学期甚至还没有开始,这咋办。今天交了学费然后准备晚上回去的路上去注册,之前总觉得六千块钱是我的可支配财产里不小的一部分了,所以想一直捂到开学之前再交的(,只是再拖下去按我这个记性说不定开学就失学了。最重要的一点可能是从九月份开始每月多了一笔固定的入账(真的吗?说不定下个月就没有了吧),尽管并不多,它的来源让我有点难受,也不想在这里细讲,但当然要收下。
怎么听起来这么奇怪啊,可不是什么见不得人的事
才 5 +号就已经写了四千多字了,真能水,八月总共才写了一万字出头。测量实习可能是今年对我来说最后一次大规模(?)社交了,毕竟数学课又不用组队。
+9月6日
+测量实习,彻底下班!感觉比地质 +
+测量赚多了,就是不知道最后给的成绩赚不赚,不过总能及格吧(
早上买了瓶西柚味茶 \(\pi\) +带去教室就早饭吃,虽然身为糖水爱好者初二的时候就看到过同学从便利店买这个,但今天还真是第一次喝。感觉就是有一点点茶味儿和西柚味的比较清甜的糖水,说人话就是三到五分糖加香精,尤其这个茶味儿就像北京菜里面放的辣椒一样是摆着看的,但我确实比较喜欢喝糖水。
+高三的时候吃完饭时不时会拉上友人在零食窗口买奶茶回教室喝,看着像是学校自制的,质量很不稳定,时而齁甜时而这白开水怎么没味儿啊,小贵而且去晚了还买不到。感觉上好像就是需要一点糖刺激奖励机制,不然混不下去。我的体重会不会就是当时涨起来的呢(
+
没吃晚饭,本来想吃桃李夜宵的烤冷面再加串冰糖葫芦(前情提要:2023.02.19),最后买了碗小馄饨就饱了,最近口腔溃疡也吃不动冰糖葫芦,吃辣都得吸溜一阵,但是不能一天不吃带辣椒的菜。感觉整体不如玉树的夜宵但也确实便宜,而且不知道玉树夜宵暑假开没开,吃过最好吃的一顿玉树夜宵是一二九分声部那天晚上翘掉了活动和何老板去吃夜宵,两个人买了一份烤冷面一份馄饨拿小碗分着吃顺带吐槽院系这些没用的破事,可能是我没吃晚饭的原因,真贵但是真好吃啊,下次开学了去吃。下下次为了冰糖葫芦还不吃晚饭(
好喜欢汤带着鲜味的小馄饨(就是味精放的多),如果是小馄饨的话就是纯肉馅最好吃,饺子馅我最喜欢的是玉米猪肉,湾仔码头的煮着好吃但是有点贵,自己包的就不太好吃。而且我捏的饺子煮了之后一部分会破或者整个散开,买的速冻水饺看起来个个都有开口,煮了之后也只会漏油不会散开,很神奇。大概毕竟吃饭就是吃调料吧,我还是不太会配料,就只是能把东西做熟。不过众所周知上海宁过年不吃饺子吃汤圆,上个学期在桃李二楼吃饭的时候偶尔也买小碗汤圆当主食,好像十个四块钱而且还有一小碗汤,记不清了。汤圆馅就没有什么花头,都是黑芝麻,花生的我也不爱吃,但是都不如搬家之前在家附近超市里买的冷冻汤圆,煮熟之后咬一口糯米皮可以扯得很长。说到你沪特色碳水还得是
+双肩包
+生煎,小杨生煎那种纯肉馅最好吃,灵魂还是那口汤,大壶春的个头大就显得比较糙,我也吃不下。上次路过清芬的生煎窗口虽然不屑一顾但看到旁边有
+你好谢谢 小笼包
+再见,长得很像小时候在城隍庙吃到的那种,只不过我还是不太相信北方卖的小笼包,如果买了之后发现没有那口汤、皮很厚的话我会很难过。但还是想下次试试,就是不知道在清芬一楼单买一笼小笼包的话应该配点什么才能吃饱而且不碳水过量。主食的话米粉也很好吃啦,但我喜欢汤粉多于炒粉和拌粉,在上海火车站附近吃过一家据说很正宗的桂林米粉,高中学校旁边那个传奇广场有个店做的也很好吃但稍微咸了点,除了长泰广场松鹤楼的鸡汤面和某个炸鸡店的炸杏鲍菇之外,高三的时候我也会晚饭时间偷溜出去吃这家然后回来上课,就是太烫了每次要晾很久才能凉,时间充裕才能吃。两家店酸豆角都给得相当多而且好便宜,一碗肯定不到
+20
+块钱,米粉很滑很弹,前者的笋尖尤其好吃。后来再吃到这么好吃的笋是今年暑假在紫燕鸡挑卤味的时候一时兴起买了些拌笋,是用小米辣加别的调料拌的,和米粉里面的笋尖不是一个味道,但脆爽和鲜嫩多汁是一样的。
这是在干什么,用嘴炒菜吗(
+ + +9月7日
+ +早晨起来 wafarinliu +老师问我要不要一起点外卖,本来今天打算洗洗衣服再出门所以想答应的来着,结果查了一下上个月的账单给我整精神了,怎么明明是假期还一个月花了两个月的钱(,这个月当然更夸张毕竟刚交了学费。虽然都是正常的特殊开销(?)但还是立刻决定去桃李吃午饭了(。在猫超买东西的时候看到了之前一直想尝尝的三得利茉莉乌龙,虽然它写着无糖完全不符合我对糖水的期待,但毕竟是茶尝尝也不亏,当咖啡的平替喝也是我赚了。
+测量实习结束之后走在路上还是忍不住去看井盖上的字是正常现象吗(
+今天把芦毛灰姑娘看完(?)了,睡前看到有马纪念入场前会长和小栗帽的击掌就燃得不行但实在是困了(,早晨起来一口气看完了第二部就想打
+9
+分(不好说是不是冲动评分,可能是动画第二季的印象好导致对芦毛灰姑娘一上来就很有好感),晚上就看到目前连载的位置了。后面逐渐在变成
+Cygames 非常擅长的
+群像剧,小栗帽痛失主角位(,不知道啥时候才能画到有马纪念有终之美,急。
其实感觉应该标搁置才对,后面没打算追更,攒一阵子再看,那不就是搁置而不是看过(。也没必要分这么清(
+
急了,啥时候能看到芦毛灰姑娘动画化(。看第二季的时候最喜欢帝皇,但看了漫画感觉还是更喜欢小栗帽。要类比的话可以说从笠松到中央的经历是戳到我了,和好歌剧都不是血统优良的名马(9.8
+upd:是我记错了,这下乳好歌剧了,虽然也都说好歌剧血统一般但果然比起小栗帽还是强太多太多太多了)但也不是后者那样开挂的天才反而更加励志,还有“跑步是因为能跑,从站都站不住到能够跑起来已经很好了”总算是摆脱了两季动画的友情设定,第一季多少就有点因此走向废萌变得很无聊
+但其实也有人爱看废萌吧只是我不喜欢,帽门永存(
9月8日
+看到了《院友代表于品在北大数院2023年开学典礼上的发言》,里面每一句话都在骂我(,边读边再一次捶胸顿足为什么是去年上了抽代而不是今年上。晚上又看到《师说新语 | +“小米教授”薛金鑫:终结百年潘勒韦猜想,保持与学生共情的能力》,又一次捶胸顿足上个学期为什么只上了实分析(?)和概率论而没有上复分析(
+晚上看到一个
--在华子通过上课来获取知识算是获取知识的鄙视链底端,但我必须要说数学这玩意自己学跟上课还是两码事(
+What doesn't kill you makes you stranger
如果不是统辅课的话( 统辅课算数学课吗
发自我的手机
--
你院又在配对学业导师,大三终于可以填不需要导师了,赢!这么说来军训期间我前两年水利系的那个学业导师那次约饭其实是和她的最后一顿了,但我没去,怎么还有点子残念(并没有
-去年秋季学期的第四周左右我约了一次 dwl 的 OOH,和她浅聊了 20
-min,我也不记得在说什么了,现在印象最深的是她好像不是很会画眉毛,手机壁纸是她一家四口的合影(对不起我不是故意看到的),以及她当时说自己在北大读本科的时候因为感觉女生不适合学基础数学所以选了统计,给我整不会了。倒也是我第一次去找老师聊天,后来还聊了好几个老师,干啥的都有。她讲的每门课我都学得很烂,初概直接绷不住
-PF
-了,在她那儿学的那些个初等高等夹心知识遗害无穷(,多元统计期中爆炸也就退了,打算下学期去上数学系那门同名研究生课。
为什么会想起来呢,因为今天听说有人想邀请她当自己的学业导师(。另外那个上学期评教结果里全校第一名的课是她这个多元统计,第二名是 -zzy 的线性回归,反正这两门课我都大坐牢,太难绷了,感觉不如 lzx(。
--
答疑坊小程序现在不仅新订单提醒消失了,连回复提醒都不好用了。有个单子以为早就结束了,没收到对方的追问回复提醒就给鸽了,然后查了下答疑订单统计里的平均分,哥们似乎被送了个一星差评,再接 -300 单就可以把它稀释回原来的水平了,虽然也没啥用但还是有点难绷((
-10月10日
-终于跳出了 -1!5!的循环,但是有没有一种可能其实只是在一个比较大的循环的中途(
-#闲的程度,今天发现优化理论一个助教在网络学堂填的邮箱是 -tsinghu.edu.cn(
-但其实一点都不闲吧,这课怎么作业这么多(,昨晚才刚把 scribing -交了,今天从吃完午饭开始写 HW2,卡着教室关门的点写完。印象里 HW1 -我周二断断续续写了一晚上,周三在高统课上继续写,到晚上运筹学还在写,实在不知道什么时候写完的,所以说相比之下 -HW2 还是很快的(错乱
-Geogebra + tikz
-画图真好看啊真好看(点头(如果把格线去掉的话
感觉学得不大扎实,也不是说不扎实,课上讲得好少把进度拉得好快,作业又似乎会布置一点 -reading -的部分。这书是写得又细又好,说到底也没啥本质难度,但信息密度太大了,三周上大几百页的内容哥们是真有点看不完(,您们茶园是这样的吗(
-今早躺在床上看到一个知乎回答,乐到垂死梦中惊坐起:
+笑晕(
+9月9日
+学会了一些用 Markov property 证明的结论之后逐渐不会用 Bayes' Theorem +了(
+横贯测量实习这些天到现在终于是看完 Recurrence and Transience +了,之前还是不熟悉长得奇形怪状的 +notation,熟悉了就好很多,但不会每一章都要这么痛苦一回吧(,感觉最近实在是有点迟钝。Hoil +Lee 的那份答案这一章到这里就没有了,下一道题就是 Ergodic +Theorems,只能去看 Durrett 自己写的老版本答案,和 5th edition +稍微有点对不上但也没再更新了,也问题不大。
+之前只能把 transient
+和暂态的意思对起来,今天随手查了下才知道还有候鸟的意思,感觉非常有道理,再一想这个好像高中的时候讲过(,对不起我高三的英语老师了。倒也没有非常对不起她,高三我真的有在努力学英语了,对不起的是高一高二的那位英语老师((。再想想其实有点没道理,单从字面上来看候鸟明明就是常返的,哪怕真的套
+Markov chain 的 recurrence 定义也能对得上,所以 Transient is
+Recurrent!(哲起来了(学数学学得
被没有口袋的女装 PUA +惯了,今天穿了条有口袋的裙子还是习惯性在没有手的时候把东西用胳膊夹住。说起来我本来以为下雨天会很冷所以穿了长裙的,结果中午去骑车拿了趟快递下摆就湿透了,崩溃。
+9月10日
+今天又是全体济南人的节日!(
+现在每天晚上去挑第二天喝什么茶已经成了一种固定的快乐了,甚至正在写一个
+茶饮料替代咖啡从口味价格和效果方面评价的可行性分析
+测评(,等我把所有猫超能买到的品牌和口味尝完就发((
昨天拿到了之前影印的书,翻了下感觉排版有点丑(。今天闲来无事打开 ESL
+看了一眼又舒服了,不过总不会这种七百多页看起来就一堆废话的书我都要打印出来看吧,差不多得了。读这个(相对来说)真轻松啊,跟看小说似的(
闲着没事的时候看到一份 lty 的讲义把 sub/supermartingale
+分别标成红色和绿色来代表看涨和看跌,笑麻了。正好今天做题 终于
+做到了 superharmonic function,才知道之前早就见到 harmonic function
+了只是不认识这种形式。回头看了下这个回答明白是在干啥了,只不过我还是更喜欢
+superman 的解释(
9月11日
+今晚回来难得还干了会活,把 Durrett 的 Markov chain
+章节通了,当然是把打星号的部分先跳了。以前还担心跳章节会有什么问题,结果每次看不懂下一章的时候就会回来把上一章跳过的部分读了,虽然对往下推进度也没有帮助,但是当时看起来很难的东西这时候反而成了舒适区,就有点草,然后竟然也都读完了。
往后翻了翻感觉读完 Ergodic Theorem 就可以换 GTM274 从 Brownian Motion +开始往下看了,但总觉得也没必要,现在 Durrett +这本成我的舒适区了,草。其实也不太清楚是不是把后面的东西留到概率论 2 +后半学期再学,现在先去读点高统甚至去挑着读点 PIN +比较好,更搞的是下学期数学系那两门课我是一门都不想上了,现在看着课表又陷入了沉思然后开始重新排课,某些人有(至少)两个培养方案是会哪个都修不完的(
+时不时会把 summing 看成 +summoning,颇有一种把求和项都召唤过来加在一起的感觉,好像也没错((
+突然想到以后是不是可以把 solution manual
+打印出来带去教室,就不用带电脑了(,所以相比用电脑来说哪个更环保呢
9月12日
+下学期课表又要变成不认识的样子了,已经连着三个学期了,补退选 II +要选的课比正选和补退选 I +加起来还多,后验上来看也都挺没效率的,只能说水平就这样知道吧.jpg
+ +数学史的限选范围里居然有未央,好离谱(
+Durrett 单推人今天才发现他还有写《Essentials of
+Stochastic Process》,最新一版还是 2021
+年,虽然我不一定看、目测这本很入门、和 PTE(坏了以后不能把它简称为
+Durrett 了)有大量重合而且目测也不如 PTE 难,但它排版比 GTM274
+好多了,还是想印一份留着。有可能 continuous time Markov chain
+会用他的读,Poisson process 之前也只是在 Poisson convergence
+里简单读过可以顺带梳理一下,听说这一本的 Martingale 和 Markov chain
+顺序反过来有深意读起来很爽,最后一章那个 mathematical finance
+看着也挺好玩的,摸鱼的时候把模型当 examples
+看看。不过这书怎么这么多课后题(
晚上翻了翻发现《天浴》一直想看但是又一直没看,带着电脑躺到床上开摆,结果一个半小时的电影我看了两个半小时才看完,中间每次崩溃了就按暂停先缓一缓再说,看完又崩溃了半个小时(。这种东西我都会看一眼摘要甚至更细的剧评再看,本来以为没什么的,然而镜头表现出的冲击力还是远远超出预期。
+9月13日
+下午和友人吃到了 69
+折的海底捞,本来以为会想说的话也都没有说,吃饭要紧(帽门.jpg,眼泪最后还是从嘴角流出来的。第一次吃四宫格的火锅,虽然大多数东西还是都下了辣锅,但是猪肚鸡汤好香,煮出来的面条也好香(主要是味精加得多吧
逛了下那边的超市发现猫超的东方树叶种类还不是很齐,背了一瓶绿茶一瓶乌龙茶回来。
+是第一次骑车去上地那边,走着走着感觉不太对劲,这不就是拉练的时候走过的其中一段路吗,好崩溃。沿着自行车道一直走结果被高德提示偏航,按照它的路线拐过去发现厢白旗桥下面非机动车不能通行,好崩溃(二度),勉强从人行道上过的,问就是全地形共享单车。回来的时候探索了一下才发现我原来走的是对的,干脆直接把导航关了,结果本来想从北门进校,骑到西北门才发现怎么过了,好崩溃(三度(什么纵使三度迎来崩溃
最后在四教后面 30 分 28 秒极限锁车,以前以为只要超过 30 分钟就按 3
+块钱算,实际上是超过 30 分 30
+秒才算,赚死(。北京至少共享单车价格是比上海便宜一半的,在家的时候这种路程绝对不可能骑车,当然上海的公共交通建设其实就很少会让我骑这么老远,一般也就是解决下最后一公里的问题才会骑车(没有拉踩的意思(所以北京这个共享单车价格不会是在弥补稀碎的公交吧
9月14日
+试了试友人新提的公路车,差点把我腰撅断,座位往前调了调就变舒适了,差点忘记她比我高 +5cm +这件事了(悲),但还是稍微有点够不到刹车。骑起来确实快,就是全地形适应力不太行,要换车的话还是得换山地车。
+凌晨两点多看到新民路上有人在跑步,后面一群人骑着车一边追一边喊你这三千米不得跑个满分,其中一个还指着路边对同伴说我们每天早晨都是在这边集合然后带去东操训练,走这么远还不让骑车。原来是还在军训的新生,太猛了(
+身体不舒服,晚上去猫超发现有临期饭团买一送一,就着本来打算明天喝的茶吃掉感觉稍微好点了,这个搭配还挺日式校园午餐的,但是是夜宵(
+9月15日
+这个学是一定要上吗.jpg
+9月16日
+最近遇到很多很伤神的事情,今天身体又不舒服躺了一天,几乎已经一周没有学什么新东西了。这么多年了,就是在无数这样的时刻慢慢变得迟钝的吧。
+我也好想跑起来啊
+(玩闪耀优俊少女玩得(收收味
9月17日
+又到了该拿出这张图的时间:
+
不好说,说不定我过两周又放暑假了,上学主打一个体验(
+9月18日
+今天好闲啊(,早上去偷袭了一下吴昊(女)的概率论
+1,然后又去上了杨帆(男)的概率论
+2,总感觉求真书院的本科生课比研究生课难一点。概率论 2 教材是
+Durrett
+PTE,作业基本从上面出,讲的四章我已经看过两章多一点了,梦幻开局。然后听老师念了一遍又在黑板上抄了一遍
+conditional expectation
+那一节,像回到去年何翔的抽代了一样,啊不是至少这课教材和讲课用的都是英文(,就,感觉以后周日晚上可以晚点睡了((x
坐我旁边的是一个俄罗斯姐姐,似乎是求真的研究生新生,一开始没注意还想问她能不能加个微信把作业发给我一份,她转过头来我才开始切换语言系统(,有一种毫无防备突然开始 +TOEFL Speaking 的感觉,很难绷(
+发自我的手机
++
(草
+说起来下课还拿到了学生会发的开学加油小饼干,我寻思着恁大一个盒子不会是月饼吧,打开一看才知道是饼干。吃了才知道饼干里面居然是空心的还夹了字条(,很担心学生会的精神状态,不过居然拿了个数学相关,好评(。想起来上一个用优化问题类比的还是《求好人生的“优化问题” +| 毕业生代表吴清玉在北京大学2022年本科生毕业典礼上的发言》(
+
但是我一个三维空间里的碳基生物为什么要做矩阵,我不能做点不抽象的东西吗
又联想到一个 random walk in \(\mathbb +R^d\) 笑话:
--他或许没有多么光彩的过去,但他可以埋葬许多光明的未来
-——写给我的班主任
+A drunk man will find his way home eventually, but a drunk bird may +get lost forever.
也写给我的高中班主任(
-10月11日
+(大概就是说 \(\mathbb R^2\) 上的
+random walk 是常返的,但 \(\mathbb
+R^3\) 上的 random walk
+状态都是暂态,实在不知道要翻译成什么样
睡前还是没忍住去看了芦毛灰姑娘最新一话,甚至有幼年帝皇客串,awsl(
+
不准在中央面前无礼.jpg
有点难绷,然后特地翻到 20 话左右的地方去截了经典名场面(
+
帽门!
才发现这里帽的耳朵是往后翻的。最近赛马娘系列有新漫画了,看了第一卷感觉画风不如芦灰,又去看了看樱花桂冠的生平,有点子好奇大器晚成的故事要怎么做才能比较精彩。这个月到现在为止发了三张芦灰的漫画截图,并不是每张都有帽,但是居然每张都有皇帝。这个世界上哪有什么鲁铎黑,只有鲁铎厨和扭曲的鲁铎厨罢了((
9月19日
+选课的时候说想听台湾腔今天还真听到了,本来还以为会是英文授课的,这下如愿以偿了(
+上了两节数学课但还莫名挺休闲的,ODE +就是在扯闲篇,讲到最后成泛函了,怎么回事。期中考试似乎是随堂,不知道 +1.5h +能考点什么,这下真梦回何宝的抽代了。讲义印了但还没到,急急急。写完昨天概率论 +2 的作业发现 due 是 +10.2,就,我知道大三了还这样真不是很好但我就是停不下来地焦虑(
+掐指一算今天还真是从 jk 毕业之后第一次穿
+jk(,白丝真不耐脏啊。
9月20日
+今天最难的好像是现代生物学导论(,真不太会。高统在挂机以及听旁边两个哥们讲求真笑话(,运筹也挺休闲的。是不是我的选课有什么问题,现在总有一种学了概率论然后就可以到处嘎嘎乱杀应数课了的幻觉(暴论
+这运筹课好没意思,不过也是,建管系开的能有啥含金量,主人的任务罢了,不如下学期去上个数学规划
+贴贴 玩玩(
本来十一假期(如果还在北京的话)想去龙头牧场看看目白阿尔丹的墓碑,还想带束花带点胡萝卜(,今天一时兴起看了几个圣地巡礼视频又简单查了下,好像现在不开放了,牧场经营也出了点问题,残念。
+9月21日
+之前本来还想着如果压力太大的话就把优化理论换成非参导论水一下,今早做梦梦回上个学期在
+zzy
+课上坐大牢直接惊醒了,我脑子一定有问题才会想要再选她的课(叠甲:我不知道是她的问题还是我的问题,反正线性回归我坐大牢了,但也有同学说她讲得很好,所以可能只是我和她不合适)。退掉退掉,选优化理论
+去和 JasonL 老师面基((
昨晚本来不困,结果这个运筹课非要关着灯上,黑灯瞎火的给我整困了,就一边喝带的小瓶美式一边写高统作业。本来以为没什么问题结果晚上根本睡不着,好崩溃(,一边清醒着一边默念美式的美式的来安慰自己早八会没事的,最后还是有事了((
+感觉这学期的课程群几乎就没有,尤其数学课是真的一个都没有,哦原来是有 +10 +个学分的课我都还没选上啊(,哈哈,等我选上课网络学堂公告里的群二维码都过期了,怎么办呢((
+第一周就是在不停地发邮件问能不能冲选能不能手选,还有课后线下偷袭老师不停重复同一套话术:
--你好,你的申请已通过,方便加一下我的微信,之后可能会拉微信群。且需要提供一下身份证号码和电话,用于申请北大的入校预约。
+老师好,我不是数学系的/我是本科生所以要特殊原因选这门课,现在还看不到网络学堂不知道第一周作业是哪些,能不能邮件发我一份,谢谢谢谢,谢谢老师。哦哦不用担心虽然我不是数学系的但我学过前置知识不会听不懂的,对我一直有在上数学课,也知道我选这课是在干什么。啊还有我要第二周周中才能选上课,能不能把第一次作业的 +ddl +延后一点或者给我个助教的邮箱我交过去,谢谢谢谢,谢谢老师,老师再见。
看来 CV 还是有点言过其实(x
+想想应该再问老师加个微信群的,抽代的时候我就是从何宝那里直接扫码加的群,现在居然给忘了,残念。遇到好奇心强的老师还要解释一下未央是什么东西(,我一个学物理和交通的同学怎么就来学数学了呢,还有为什么不转系难道是不想吗(,好崩溃。优化理论应该是最后一遍了(,但是下周可能还要给各个院系的教务发邮件打电话催手选审批,秦清的微信我上学期就加了,这学期真不想再找她了(
+说到抽代,又到秋季学期了,还能不能遇到像 Bowen L
+那么可爱的助教呢
9月22日
+第一周感觉就像体验上学,所有的课都像开盲盒
+而且也基本都不必修,还就那个充满期待(
这周最大的感想是原来不是每个老师英语口语都像 wty
+一样好,然而她已经润了,急
优化理论体感还挺良好,半听半摸的就过了,印象比较深的是讲 linear +programming 有人问为什么 cost function 里面有 \(|x_i|\) +也还算是线性函数,我当时想到的是把它拆成 \(x_i\) 正负部的和再多在 constraints +里面加两条不就变成线性的了嘛,结果老师说是把 \(|x_i|\) 换成 \(y_i\) 然后在 constraints 里加上 \(y_i \geq x_i ,y_i \geq - x_i\) +就可以,虽然也是等价的但是突然感觉有点不爽(,也觉得好像没学过分析就不太会从正负部考虑。后来翻了下教材发现上面这两种形式都给出来了,舒服(
+其实不算是严格的正负部,严格正负部的话 \(x_i ^+,x_i ^-\) 之中必有一个是 \(0\),在优化里就把两个直接都当成非负数也没关系,不要在意这些细节,警惕学魔怔了(
作业还没写完,但是在读 Durrett +ESP 的 continuous time Markov chains,写得比 PTE +友好而且入门一点,比如说这本上 Chapman-Kolmogorov Equation +的证明就直接用了 Bayesian Thm,PTE 当时用的是 Markov +property,初学直接给我干懵了(,但其实也是学到了很有用的技巧。然而令人悲伤的是 +PTE 的 Brownian motion 我也已经有点子看不懂了(。
+但其实 ESP +也还是有看不太懂的地方,虽然我有点怀疑可能是因为是直接从第四章开始看的,说不定有些东西在前面已经说过了但我没看到。之前打印凑页数满减的时候翻到了当年分系讲座的时候推荐的一份 +lecture +notes,这次正好拿出来对着看,就感觉稍好一点。
+另外之前觉得这书习题太多了,现在再看感觉其实有点少(,几十道题全都堆在章节最后看起来很恐怖,然而 +PTE 分散在每一部分的习题加起来可能比这个还多,不也都做下来了嘛。
+然而哥们也还是做不动了,挑着写点吧
+都在学概率论了,不如每次 random 一下选择做哪几道好了(x
9月23日
+周末睡大觉.jpg
+ODE
+作业看起来很水但想写严谨的话还真有点烦,这课不会就这样吧不会吧不会吧.jpg,算了就当
+预习
+复习数分了吧(。我的确时常感觉到没学数分有点头大,但是又没有那个心力再回去学了,选点这种课随便复习点(
这个学期竟然有 11 学分的必修,太辛苦了。本来有 13 +学分,但又担心万一剩的太少被按时结业就寄了,又退了一门。
+晚上在答疑坊值班甚至没来得及填完奖学金申请表,经过去年入账 0
+元之后我就知道我申自己院系的奖学金是自取其辱,但万一今年甩给我两千块钱来加倍羞辱我呢。去年必限/必限任在班级/年级里的排名这四个指标中的任何一个都可以拿来填学业奖学金,今年任何一个都到不了,甚至必限
+GPA 在班级里已经是后 50% 了,我说你们也太可怕了罢.jpg
然而就算这样去年也没有拿到一分钱,今年不更是纯纯的自取其辱,随便糊完然后看乐子.jpg
+9月24日
+今早去偷袭了下隔壁,想起来明天是 runzhi
+的生日就把他叫上一起吃饭了,出门之前翻了翻把我那本世图出版的 Functional
+Analysis by Stein 当礼物送了,写完 ODE
+作业之后把剩的一小摞作业纸也塞给他了,怎么会是呢。数学壬真方便,送纸质数学书当礼物就一定没问题(
本来没什么事,突然跑过去是因为听说理教四楼的椅子很舒服(,于是去坐了一下(#每日坐椅子(所以这个
+tag 到底是什么梗(。在那边半个小时写了三道 ODE
+作业,昨天在三教一下午写了两道,高下立判(不(当然是因为昨天下午先读了
+Walter 又写的作业,而且前两道更麻烦一点
非常好北大,爱来自隔壁,下周末还去(
+9月25日
+来点手选笑话:
+好消息是我下午一点多提交了所有的申请,三点就选上了优化理论;
+坏消息是到现在还没选上另三门;
+好消息是之前本来以为三门课要找三个不同院系的教务催审批,但现在来看不用了;
+坏消息是不需要找教务是因为审批目前还卡在老师那里,还没轮到教务批(
+报了个答疑坊小班辅导讲师的面试,其实招募是一周前的事了,不知道现在还缺不缺人。我也只能讲讲概/统/概统,不想再回去复习线代什么的,所以感觉就算面试也不是很需要准备,只是薪酬相比日常答疑来说还是比较可观的,有高中毕业之后带家教那味了(
+9月26日
+才第二周刚开始我就已经觉得这学期有点难顶了,现在最大的压力来源居然是,优化理论的作业必须 +LaTeX +不能交手写(,还以为这学期终于摆脱基物实验报告了,结果来了个每周一次的纯英文实验报告(。
+一下午一晚上没写完 +HW1,当然也有教材后面一小部分还没看完的原因。还是感觉如果手写的话晚上总还能干点别的,难怪 +zjz 在作业文件里写
--简历上的干货有一页吗?
+Please start early!
复习下 hx
-的(前)微信签名,看了一下现在已经是“不好!含猫量要超标了”,头像也换成猫猫而不是柴犬了(。可是我的
-CV 还不到一页,说明有用的东西确实严格小于一页(x
好好好(指下周六就可以去北大了(你这统计中心又没地方开讨论班,以后会不会全放在北大,看看人家数院新楼
太好了 ODE 不用太认真学了反正也不必修(速速 PF!
摸鱼玩赛马娘的时候感觉波旁跑步好让人放心,毕竟是跑逃的,从头开始就是前几名,不像某些跑差和追的(
-今天是 Yau
-发表如此成績如何招生讲话三周年!说起来周末我就要去求真招生考核现场当考务
-顺便一边感叹小朋友们的强度一边感叹怎么进了这么个大坑
-了,应该招生招得还蛮好的(
10月12日
-建筑材料课上讲化学,梦游中听到老师在夸一个在积极互动的同学“你提的问题全都是我这节课要讲的答案”,醒了,整不会了。这是什么,dual -的 dual 是 primal,function 的 function 是 functional 吗((
-看完赛马娘第二集感觉又好又怪,激情吐槽剧透一波(。
-内恰对话那段第二季的味上来了,小北黑和小光钻比赛疑似 neta
-血统(还是说是 neta 竞拍价呢
-x)差距也挺不错的,但演出还是好尬(。帝皇开始学老父亲装冷酷了,好不习惯
-但总感觉大概私下去安慰过大鸣大放了罢,也管管北黑啊,看到曾经的第一季主角特别周仅有的台词又是胡萝卜特饮感觉一如既往的胃疼(。在马路上看新闻放送的时候北黑的耳朵都快扭断了后面还要在和内恰的对话里再说一遍是因为感觉大鸣大放不参赛自己可能会赢而羞耻,勉强当做引出对话而不是这点事情都要掰开揉碎喂给观众的话还稍微好一点(是否有点婆罗门发言了。比赛做得就(,咋这么急啊,怎么不先表演个跑一次坂道三本再来比(
ED 的麦昆每一帧都好可爱,我开始非常理解帝皇(
-这都两话了,大鸣大放你说句话啊大鸣大放(,再不说话跑完宝冢纪念就要退役了
小北的爸爸是在 neta 马主吗,笑裂了
晚上水群的时候聊起来周末去求真招生考试当考务的事情,然后和 2019
-年华二复附丘班考核联合小队队长 ycj
-单独聊了几句,话题最后还是又拐到了赛马娘,啊不是,闪耀优俊少女的神奇翻译((
(
+晚上骑车的时候听到两个路人聊天:
-+我: 说起来日服的有马纪念是叫有马纪念吗 -国服我目测改成中山大奖赛了
-ycj:
-是的
-草 懂了 反正就是不能有马
-我:
-草 没马了(确信)
-ycj:
-还真是 怎么不叫有人纪念
-我:
-有优俊纪念
+A: 那个算法导论的 ddl 是今晚吗
+B: 是的,但是我网络学堂上还没这门课呢
+
9月27日
+今早在路上遇到一位好歌剧(,骑车从我和旁边一辆车的缝隙里穿了过去,虽然吓我一跳但完全没发生事故,好强(
+(是在 neta 这个((
+++2000 +年有马纪念,在和田自己选位不佳、加上其他优秀赛马的紧盯之下,好歌剧从起跑起被其他马死死围在马群核心。和田龙二多次起身观察脱出路线未果,直到最后 +300 +米直道,由于名将怒涛冲刺、成田路失速的机缘巧合,马群让出了一闪即逝、仅可供一马通过的包围网缺口,好歌剧立即从这一缺口切出并凭借强劲的末脚一路冲刺,反超名将怒涛以鼻差夺冠。(这也是游戏中好歌剧固有技能发动条件要求被团团包围的由来)赛后和田龙二称,他当时已经对比赛绝望,路是好歌剧自己选的。(出处)
+
玩闪耀优俊少女玩得(
这运筹学怎么天天关着灯上课,还在低速复读优化理论第一节课的一个零测度子集(,之前我问老师他还理直气壮地说这课不能替代,明明就是门水课。之前还想着下次带个台灯去上课,又感觉会被针对,麻了(
+9月28日
+在建筑材料课上困得睁不开眼睛,遂写现代生物学导论作业:
+++我:
+在建筑材料课上听老师讲化学
+与此同时在写生物作业
+这两门课我高中一门没考 一门 B+ 全班倒一
+一个都不会 好崩溃
+友:
+草
+远离数学寸步难行
+我:
+是的 但我现在数学也学得寸步难行
+
放假前一晚 4-6 的自带 PF +的通识水课课前说有小测把所有人骗去,结束的时候又说没有,素质极差(
+感觉这学期课也没有很多(挠头)但是为什么现在一天到晚都在学数学,不然连作业都写不完(
+再来段传世经典(x)对话:
+++友:球队有个学弟大一就开始数分高代几何 励志转数
+我:要转的话不就该这样吗 我是失败例子
+友:也是 还有个学弟写了三周代码就想转码 还想卷 AI
+我:能理解 我写了三周的时候也想转 第四周好像讲到类了 +然后就不太想转了
+
9月29日
+为了报 seminar 写了个 CV,然后轻微破防,我怎么除了 GPA 和并不完整的 +core course 之外啥也没有(
+如果报上了是不是就可以两周出入北大一次了
+不知道能不能去北大,但那样的话这个 ODE 大概真是留不得了(
这学期选了几门研究生课,现在看到 8 和 9 +开头的近邻宝取件码都感觉有点像课程号,有点难绷。
+9月30日
+最近在听《她似了,又活了。她没似,他似了,所以她也似了。她又活了,可他们似了,所以她又似了。》,好美丽的精神状态,好喜欢(
+给 lq 的博士生发了报名 seminar 的邮件,然后:
+++收到,后续会通知申请结果以及具体信息。
+祝好!
+
这个东西难道还有筛选还会过不了吗,你最好快点通知,要是过了第六周我就来不及退
+ODE 了((
假期为什么只开六教 A 区和清华学堂(,六教的蚊子太恐怖了,翻了翻 +2022.09.21 +的日记,一年过去了六教不知道第多少茬的新蚊子也还是和当时一样,只喜欢盯着我咬(。晚上鼓起勇气(?)探索了下清华学堂,在二楼看到数学学堂班专用的教室还是羡慕了(
+之前一直觉得头发太长了不太舒服,今早起来终于克服懒癌把理发剪刀找出来剪短了,结果克服得太过了给剪太短了(,现在显得脸好大肩也好宽,本来就稀疏的头发显得更没几根了。本来还在安慰自己过两个月到冬天需要头发来保暖的时候就又长出来了,然后想起来过两天有社聚,看了眼鸽鸽鸽还有之前没面基过的社友来,好崩溃((x
+]]>虽然其实每年的十月好像都发生点惊吓,或者一些事后看来也不是什么好事的惊喜(
+10月1日
+北大一日游,顺了一盒茶叶几本书一个挂件回来,还有公路车一周体验卡,我到底是去干啥的((
+晚上骑公路车沿着周边的几条大路 描边
+飙车,不慎从路边一个下水口压过去的时候感觉车轮还没有下水道的缝隙宽,就挺危险的,全地形适应力实在是不太行。起步不太容易,速度太快了刹车也不好刹,需要提前好远就开始摁,有的时候最后还得脚刹,甚至我胳膊太短了如果不趴下去的话会有点够不到刹车。但是它快啊,骑着爽啊(
背单肩包实在不太适合飙这么远,中间累了的时候就不由自主地降低重心往车架上面趴,大概也能降低点风阻,而且这样好像很专业很帅的样子(。有点联想到小栗帽的跑步姿势了,离地面很近几乎会平行什么的(玩()玩得
10月2日
+昨晚飙了一个小时车,今天成功发烧了,国庆假期 -1(。
+但是下床吃饼干当晚饭的时候把还没布置的运筹学作业水完了,写完开始乐,顶点是什么松弛系数又是什么,这教材是一点看不懂,反正我是英文写的,总不会判错吧(x)。先观察下作业批改情况看看这课到底多逆天,实在不行第五周退了(
+躺在床上水群的时候看到有人问搞数学怎么样算 taste +好,我也不知道,但反正我的 taste +就停留在教材至少要满足是用英文写的和是用 LaTeX 排的这二者之一(
+10月3日
+这个烧退了吗,好像退过,但是又没退,如退(
+今天勉强往后看了点 LP,还以为可以把 ODE +写掉的。不是我说这个假期不会就要在生病中迷迷糊糊地过去了吧(
+10月4日
+清华学堂这个桌椅还挺舒服的,有很多可以踩的横杠,腿短人在椅子上也可以缩成一团(
看了一天 泛函分析 ODE(,还挺有意思的,只是把它用到 ODE
+里就没啥意思,这几个核心定理的条件看着就有点丑(。之前还在幻想一上来就概统了岂不是失去了在很多方向上探索下的体验,现在简单探索了两周觉得确实还是概统比较有意思(
说起来感觉至今都没有认识的做动力系统的数学壬,别的方向多多少少都知道几个,除了概统之外认识最多的应该是代数壬
+虽然都是赛博人,怎么会是呢。
晚上才知道大鸣大放居然也成为马娘了,之前还一直想着拿不到许可,第三季里怕是要直接删减
+看不到北黑吃瘪 或者是用路人马娘代替了,Cygames 太强力(
10月5日
+这赛马娘第三季一股浓浓的第一季的味儿(
大鸣大放好帅
++有特别篇珠玉在前,对跑步的演出有点无感。不过我跟巴普洛夫的狗一样,看到帝皇就开始头皮发麻,眼眶湿润,不知道怎么回事捏。
+
说起来感觉看到了很多 neta,但是字幕没标注所以也不确定是不是在
+neta(,看芦灰的尾注看得(
终于还是下了个闪耀优俊少女开始养马(,逃不过这一天(。能看到会动的小栗帽真好啊,帽门
10月6日
+简单给 Intro to LP 前三章收了个尾,看 zjz 主页上的课程大纲似乎讲完
+duality 之后就要开始 convex optimization
+了,但有本书我还没印,就非得印出来看吗,虽然不急但甚至有点急。说起来我每次说
+Jingzhao Zhang 的时候脑子里想的都是 Jingzhang Zhao,还有救吗(
本来今晚要去面试小班辅导讲师,结果嗯是到晚上六点左右才通知十点钟面试,这么晚而且看起来又很不靠谱(,干脆就咕掉了,进行了一个全程参加社聚。想买副塔罗牌遇事不决玩一玩了
这么一说我感觉最不靠谱的好像是我
明天开始练习在一些 不得不去又信息密度极低而且全是无效信息
+的土水学院的课上绣十字绣(
谋勇兼备退役了,之前还说是唯一一个在现役时代就进入赛马娘企划的马娘来着的。铁鸟翱天和杏目什么时候能来,急(
10月7日
+本来想打印下
+Boyd,翻了一下什么原来有七百多页啊,那用纸质感觉还不如看电子版了(。Jun
+Shao
+那本数理统计也是太厚了就没打出来看,不会真有人把查阅用的书打印出来看吧,高统的话感觉听课看
+PPT 也就差不多了,希望吧(
++@所有人 如果两位同学负责同一次 scribe +note,两位同学仅需要提交一份 note +即可,请两位同学私下自行沟通,并且相互检查最终提交的版本,谢谢!
+
好可怕,为什么不能一人交一份((
+同一个概率论问题我给室友写过一遍,国庆前就在小程序里答了两遍了,今天在志愿者群里又答了一遍,晚上值班又答了一遍,有三个是看不懂
+\(P_C(\cdot ) = P(\cdot | C)\)
+这个定义形式里面的点是什么意思(,一个是在纠结是不是要用概率的条件概率来算
+某种程度上来说水平很高,还有一个没说哪里不懂。绷不住了,你们这作业
+ddl 还挺长啊(
值班被问数值分析还给问挂黑板了,紧急临场打开教材 pdf
+开始回忆矩阵条件数是什么以及若干
+bound(,丢人((不丢人,我又不搞计算((x
今天是周一,明天是周五,后天是周一,再过几天又是周五,1!5!(
+10月8日
+今天是袁洋给张景昭代课,但是((
+++张老师出去玩了,我给大家代课(
+我虽然是搞优化的,但是这些我都没学过,simplex method +之前没怎么接触过(
+十年前在 Cornell +的时候在同学强烈建议下我去旁听了一门优化课,但是没参加考试所以还是不会(
+为了给大家上课我花了两个晚上学了这些,如果错了那是 zjz 的 PPT +有问题,不是我的错(
+Farka's lemma 是个很核心的定理,我在 Cornell +读书的时候老师讲了四五节课,但是我只能讲十分钟,因为我也不懂更深刻的东西(
+
我大震撼(x
+总的来说这节课槽点实在太多了,偏偏是(还不是自己选的吗)今天在做
+scribing,不过既然不是 zjz 本人讲的而且又有
+PPT(问题是也还没发诶(,那岂不是自由度还挺大(x
申请奖学金的时候就说感觉是在自取其辱,还真是(,今年综奖是差额答辩但也没进,我估计单项更没什么希望。放在去年我还百思不解,难过了一阵子,今年就变成了:
+++我好喜欢被未央书院羞辱啊!
+
无所谓,毕竟早就想到答疑坊志愿工时兑换成津贴所得的收入期望比拿去评奖学金更高了来着。室友给我看了几个综奖入围的公示材料,有的按我对一些事情的
+吃瓜 了解来说感觉挺虚浮的,换到我身上的话我觉得自己做的最
+concrete
+的事情还是学了几门数学,不过这放在评奖学金这件事里毕竟是扣分项。
某种程度上来说这个破地方也有优点,让我在一事无成的时候仍然充满自信,并且坚定相信是书院的问题(
既然要延毕那好像就有四次申奖学金的机会,这么说来可以又双叒叕被未央书院羞辱,好兴奋啊(
10月9日
+因为隔壁今天才开学的原因所以我的假期其实也跟着续了两天(,该好好学习了((
+虽然杨帆上课是 Durrett PTE +reader,但其实属于是听他念书也学到许多。今天发现上节课的其实都差不多忘完了(,但记住了一个挺有用的反例,就想起来还在学概率论 +1 +的时候甚至学完之后一段时间都时不时在几乎处处收敛和依概率收敛还有对应的期望上迷糊,每次都是仔细想想 +lzx 期末默写的那个刻进 DNA 里的反例就明白了。
+今天在讲 optional stopping theorem,有个定理觉得很熟悉,遍寻 Durrett +而不得,再一想是 lzx +当时的期末题。期末前最后一节课他就讲了半个小时鞅论,当时说要考这个的时候我还在心里吐槽是谁搞出来一个这么无聊的结论,从来没想到其实是在一个很重要的问题框架下的 +lemma,就挺深刻的。再看一眼其实两个月前做习题的时候就做到过,只是放在习题里的时候 +stopping time 的符号是 M 和 N 就没有认出来,今天课上用的是 S 和 T +才发现,绷不住了(
+来一句九月份我最喜欢的摘录(x
+++在华子通过上课来获取知识算是获取知识的鄙视链底端,但我必须要说数学这玩意自己学跟上课还是两码事(
+
如果不是统辅课的话( 统辅课算数学课吗
发自我的手机
++
你院又在配对学业导师,大三终于可以填不需要导师了,赢!这么说来军训期间我前两年水利系的那个学业导师那次约饭其实是和她的最后一顿了,但我没去,怎么还有点子残念(并没有
+去年秋季学期的第四周左右我约了一次 dwl 的 OOH,和她浅聊了 20
+min,我也不记得在说什么了,现在印象最深的是她好像不是很会画眉毛,手机壁纸是她一家四口的合影(对不起我不是故意看到的),以及她当时说自己在北大读本科的时候因为感觉女生不适合学基础数学所以选了统计,给我整不会了。倒也是我第一次去找老师聊天,后来还聊了好几个老师,干啥的都有。她讲的每门课我都学得很烂,初概直接绷不住
+PF
+了,在她那儿学的那些个初等高等夹心知识遗害无穷(,多元统计期中爆炸也就退了,打算下学期去上数学系那门同名研究生课。
为什么会想起来呢,因为今天听说有人想邀请她当自己的学业导师(。另外那个上学期评教结果里全校第一名的课是她这个多元统计,第二名是 +zzy 的线性回归,反正这两门课我都大坐牢,太难绷了,感觉不如 lzx(。
++
答疑坊小程序现在不仅新订单提醒消失了,连回复提醒都不好用了。有个单子以为早就结束了,没收到对方的追问回复提醒就给鸽了,然后查了下答疑订单统计里的平均分,哥们似乎被送了个一星差评,再接 +300 单就可以把它稀释回原来的水平了,虽然也没啥用但还是有点难绷((
+10月10日
+终于跳出了 +1!5!的循环,但是有没有一种可能其实只是在一个比较大的循环的中途(
+#闲的程度,今天发现优化理论一个助教在网络学堂填的邮箱是 +tsinghu.edu.cn(
+但其实一点都不闲吧,这课怎么作业这么多(,昨晚才刚把 scribing +交了,今天从吃完午饭开始写 HW2,卡着教室关门的点写完。印象里 HW1 +我周二断断续续写了一晚上,周三在高统课上继续写,到晚上运筹学还在写,实在不知道什么时候写完的,所以说相比之下 +HW2 还是很快的(错乱
+Geogebra + tikz
+画图真好看啊真好看(点头(如果把格线去掉的话
感觉学得不大扎实,也不是说不扎实,课上讲得好少把进度拉得好快,作业又似乎会布置一点 +reading +的部分。这书是写得又细又好,说到底也没啥本质难度,但信息密度太大了,三周上大几百页的内容哥们是真有点看不完(,您们茶园是这样的吗(
+今早躺在床上看到一个知乎回答,乐到垂死梦中惊坐起:
+++他或许没有多么光彩的过去,但他可以埋葬许多光明的未来
+——写给我的班主任
+
也写给我的高中班主任(
+10月11日
+++你好,你的申请已通过,方便加一下我的微信,之后可能会拉微信群。且需要提供一下身份证号码和电话,用于申请北大的入校预约。
+
看来 CV 还是有点言过其实(x
+++简历上的干货有一页吗?
+
复习下 hx
+的(前)微信签名,看了一下现在已经是“不好!含猫量要超标了”,头像也换成猫猫而不是柴犬了(。可是我的
+CV 还不到一页,说明有用的东西确实严格小于一页(x
好好好(指下周六就可以去北大了(你这统计中心又没地方开讨论班,以后会不会全放在北大,看看人家数院新楼
太好了 ODE 不用太认真学了反正也不必修(速速 PF!
摸鱼玩赛马娘的时候感觉波旁跑步好让人放心,毕竟是跑逃的,从头开始就是前几名,不像某些跑差和追的(
+今天是 Yau
+发表如此成績如何招生讲话三周年!说起来周末我就要去求真招生考核现场当考务
+顺便一边感叹小朋友们的强度一边感叹怎么进了这么个大坑
+了,应该招生招得还蛮好的(
10月12日
+建筑材料课上讲化学,梦游中听到老师在夸一个在积极互动的同学“你提的问题全都是我这节课要讲的答案”,醒了,整不会了。这是什么,dual +的 dual 是 primal,function 的 function 是 functional 吗((
+看完赛马娘第二集感觉又好又怪,激情吐槽剧透一波(。
+内恰对话那段第二季的味上来了,小北黑和小光钻比赛疑似 neta
+血统(还是说是 neta 竞拍价呢
+x)差距也挺不错的,但演出还是好尬(。帝皇开始学老父亲装冷酷了,好不习惯
+但总感觉大概私下去安慰过大鸣大放了罢,也管管北黑啊,看到曾经的第一季主角特别周仅有的台词又是胡萝卜特饮感觉一如既往的胃疼(。在马路上看新闻放送的时候北黑的耳朵都快扭断了后面还要在和内恰的对话里再说一遍是因为感觉大鸣大放不参赛自己可能会赢而羞耻,勉强当做引出对话而不是这点事情都要掰开揉碎喂给观众的话还稍微好一点(是否有点婆罗门发言了。比赛做得就(,咋这么急啊,怎么不先表演个跑一次坂道三本再来比(
ED 的麦昆每一帧都好可爱,我开始非常理解帝皇(
+这都两话了,大鸣大放你说句话啊大鸣大放(,再不说话跑完宝冢纪念就要退役了
小北的爸爸是在 neta 马主吗,笑裂了
晚上水群的时候聊起来周末去求真招生考试当考务的事情,然后和 2019
+年华二复附丘班考核联合小队队长 ycj
+单独聊了几句,话题最后还是又拐到了赛马娘,啊不是,闪耀优俊少女的神奇翻译((
+我: 说起来日服的有马纪念是叫有马纪念吗 +国服我目测改成中山大奖赛了
+ycj:
+是的
+草 懂了 反正就是不能有马
+我:
+草 没马了(确信)
+ycj:
+还真是 怎么不叫有人纪念
+我:
+有优俊纪念
10月13日
虽然不管怎么样都不会这么选,但细细一想我确实已经完全失去大四在华子推研的可能性了(主要是因为前三学年必限差好多没修完(,甚至感觉到一丝淡淡的惆怅(x
@@ -9066,6115 +9066,4928 @@ WTA 的公众号,二十岁老猫过冬.jpg
-11月1日
-在通过双十一凑单练习优化(,这个月的答疑坊津贴还没到手但已经送出去了三分之一左右,好好好(
-选衣服的时候看到备注的春秋款直接幻视一个春秋分,你怎么知道春秋分刚刚天皇赏秋夺冠(看赛马娘看得
12月1日
+喉咙好点了,头还是嗡嗡的,急(
+做完非常后现代的建筑材料实验出来之后在文北楼旁边的垃圾桶看到个熟悉的东西,第一反应这不会是个混凝土块吧然后狠狠地嘲笑了自己做完实验看什么都像混凝土。走近一看怎么这个断面怎么这么标准的条状断裂(,怎么正面还有实验条件和批号的标注,还真是压碎的混凝土上岗再就业(
+
12月2日
+省流:今天修了一天电脑,好像学到许多(
+中午把配件从快递点取回来之后就开始动手拆电脑了,我寻思着不就是换个屏换个盖能有多难,结果直接那个错过了讨论班(。拆 +D +盖拔电源我轻车熟路,拆转轴拔屏线信号线重拳出击,拆转轴盖...诶怎么拆不下来,看了下发现是和 +B 盖连在一起的不用拆,学多(。正好摔的时候 A 盖和 B +盖已经有一条缝了还不用努力抠,只是这个 B +盖用双面胶粘在屏幕上实在有点费手(,拆的时候把旧屏又压碎了一点还把手划了,倒也都不是问题。然后是喜闻乐见的撕易拉胶,把屏幕拿下来一看,怎么和我想象的不太一样,A +盖后面两根线粘的死死的,其中一根焊在下面的结构上然后贴在后盖上,扒拉了一下撕不下来,草(
+仔细研究了下感觉不太清楚金属胶贴下面是只有胶还是有走线(但最后知道就只是胶,撕不下来的结构也不敢太大力,于是把四部分电脑收起来等晚上去科服问一下,打开旧 +surface 开始用 Overleaf +写作业强装淡定.jpg,然后很疑惑五六年前为什么会买这么难用的电脑(
+七点左右到 C +楼把四块电脑一块新屏一块新盖排成一排(,感觉对面的表情逐渐疑惑了起来(,就承认了是拆到一半感觉超过我能力了这样子(。最后是用热风枪把所有东西拆掉又贴到新盖上的,学到许多我也想买一个(不是
--考试的话除了 normal 和 Poisson -之外的分布我都会给在卷子上,抄就是了,毕竟别的很多分布的参数很混乱,我估计你们每个人说出来的 -Gamma 分布都不一样。
-另外如果连 normal 和 Poisson -都记不住的话我想你们也坐不到这个课堂上(
-搞应用的时候人家问你这个模型怎么不这样那样改,你就说 all models are -wrong but some are useful,我自己这个就是 useful 的;到搞 inference -的时候你又可以说自己的 model is exactly -correct,在什么场合就说什么话(
-——wwc
+A:我再研究一下你这个盖上的结构,旁边这块白的是啥啊
+我:这是我没撕干净的易拉胶(
但我上课在写上周作业,没仔细听还有没有别的暴论,急了(
-11月2日
-本来感觉学不完了,但这个 ODE 居然有点速通的意思,早知道不 PF
-了
-开玩笑的,我的练习量只有三次作业十五道题,速通只是能把讲义看完的程度(但这对我一个不搞
-ODE
-和动力系统只是学着玩顺便复习或者说预习分析的人来说已经足够了,可不敢碰瓷二字班小朋友(等等我不是马上就要变成二字班了吗
又到了虽然不用朋友圈但偶尔去看 Bowen L -最近在发啥如果间隔时间比较短就给他点个赞时间(,突然发现他的签名改成了
--以轻松愉快的心情面对就可以了
+A:你这拆的还挺好,要不要试试我们的招新面试
+我:我瞎拆的(,而且我还在答疑坊打着一份工呢(
+B:那算了,我们时薪没答疑坊高,还累(举热风枪
可爱捏 谢谢不焦虑了(并没有
- - - - - - -
-
下面是周常新鲜的赛马娘第三季第五话吐槽(
-确实是宝冢纪念,但没做完,下一话应该还是大鸣大放。yysy -最后做出来的这个大鸣大放的性格真和我想的一模一样,四舍五入是狂化的帝宝(,只是没猜到秋奈的声线。
-比赛演出还是不错的,大鸣大放骨折那一下确实给我整得心肺骤停了,第二季印象太深刻开始闪回帝宝的几次骨折。然而宝冢纪念还是在北黑视角下展开稍微有一小点失望,我以为会做出来大鸣大放骨折那一刻的心态,受伤的一瞬知道这是自己最后的末脚了,赛前对凯旋门赏的壮志已经化为泡影
-这下找到北黑参加凯旋门的执念源头了,于是忍住巨大的痛苦拼尽一切从外侧赶超错失的上届菊花赏冠军。或者至少有北黑知道这是最后一次和大鸣大放比赛的机会(虽然我知道赛前和赛中不可能做出来,毕竟北黑领放看不到身后的情况,她如果跑追的话倒是有机会,应该是会等到下一话知道大鸣大放失去竞赛能力之后表现。但如果赛中能有的话该多精彩啊),带着全部的心意去决战的描写。
本来还在期待能有大鸣大放的内心戏在好好看比赛演出,结果胜之石超过的时候北黑大喊一声你谁啊给我破功了,这活整得又好又烂的,真的不会得罪马主吗(
但现在给我的感觉是大鸣大放好像并不知道这次受伤就再也不能跑了,下一话会做成啥样呢。不管怎么样先期待一个上届骨折选手
-& 经典双冠马娘帝皇出面安慰大鸣大放(
大鸣大放的腿,斯哈斯哈( 嘟啦酱我的嘟啦酱
Eyecatch
-图的大鸣大放感觉有点小崩,头好大啊(琵琶晨光:?
这一话小北和光钻双双被史实杀,好好好(,不过光钻菊花赏就要赢了,感觉不会下一话塞到一起吧(
-胜之石你好惨胜之石(,明明赢了还被吐槽这谁啊完事在背景里一顿自嗨也太可怜了吧(虽然挺可爱的
高尚骏逸有戏份了(虽然只是举了几秒钟铁),决胜服总觉得很眼熟但就想不起来为什么,后来一想略像
-ISLAND 的女主(对不起凛音我想了半天也没想起来你叫啥)。观赛的两个看起来既路人又不太路人的
-有点像大拓太阳神的 马娘在 OP
-里也出现了,感觉可能是高尚骏逸的姐姐和妹妹。然而我都忘了这一场还有里见皇冠,其实发型真的蛮可爱的(。
说到 OP,ED 里面特别周腿上阴影的作画失误仍然没有改(
-但有一说一如果我是刚入坑的话看到这一话北黑被路人马娘莫名其妙史实杀,都不是被大鸣大放背刺,真的会气到吐血弃番的吧(
-11月3日
-昨晚在 MSE -上提了个遍寻不得但事后看来蠢得想把自己脑袋摘下来的问题,居然有 6 upvotes -还迅速收到了两个回答,reputation 涨了 -62,咋回事呢(。其实就是个突然在想又想不出来的反例,评论区还给多加了个条件,挺有意思的。
-上次在 MSE 提问是因为不会做 Bowen L -出的附加题但是又搜不到就问了,后来被识别成了 duplicated -但我说实话没觉得重复,本来有个 upvote -但是这个问题本身过了一年被删掉了,就又没有了。好好好,下次还问(
-凌晨的时候有环友问了个和 Durrett 上 recurrence -那一章的某几个习题长得十分甚至有九分相似的课后题,那几个题我本来就不会做而且答案上没有,也可能是处理收敛级数的水平不太行,但看到环友也都不会就放心了(
-说到环友,有个之前好像知道我要延毕的环友今天来问我是不是真的要延,我说是,他说别延毕一年最后来求真了就行(,正确的。然而说实话不去求真我就只能统计中心/出国了,总不能去投奔
-lzx
-吧,去统计中心这件事几乎零测(,强基不能转专业什么的我都已经看开了,实在是不能理解不允许外推的规定,否则能去北大
-能让我学数学的话大不了复旦也行(x)的话怎么不算兜底了呢。
我说如果不出意外(i.e. -学校不批准延毕之类的)肯定要延,他给了一些我意料之内的反应,比如说认为我能做出这个决定非常不容易什么的。其实并没有,我几乎毫不犹豫(,另外延毕这事儿我从大二上学期就开始口嗨了,属于是给自己做足了心理准备。
-周三运筹在讲整数规划,虽然不可能难但毕竟 zjz -没提过这个我也没学过,估计就是个 linear programming -的小的延伸(暴论,搜了份讲义考完前两门期中回来看((
-双十一买了个帽子,戴上之后有种莫名的既视感,想了想是后面的蝴蝶结有一丝丝像诗歌剧,那没事了,诗宝可爱(
11月4日
-本来还想着今天要去讨论班的,还想着上讨论班的时候可以写点 -ODE,结果起床之后想了想反正论文也没读过干脆别听了,直接变成那个去隔壁复习概率论(。哥们是真有点急了,现在拟合题目拟合得想吐了已经(
-Jianfa Lai 给了一个论文的 -list,从下次开始似乎也能提前知道要讲什么论文了,打算自己先读一下,不然纯听故事也没什么意思。
-紧赶慢赶把 optional stopping time 学完了。之前 variance of the
-gambler's ruin time
-那个题哪怕在作业里出了也一直不会,直接口胡了交上去的但也没扣我分,这课也不发作业答案,助教是个
-23 级的博士生,我其实稍微有点疑惑如果这课真是用来准备 脖子
-博资考的那他本人为什么不上(当然我不懂求真的脖子考具体规则所以不乱说了(,还是说他在自己
-TA 自己(。PTE 2nd edition solution manual 没这道题,Hoil Lee
-的答案感觉既看不懂又是错的,MSE
-上没仔细搜但是搜到的两个回答更是透着一股浓浓的 not worrying about the
-details(
今天福至心灵自己把它做出来了。然后心理压力瞬间减小了很多,optional
-stopping time
-那一章的习题也迅速过完了,想了想闲得不行的话可以把这个题在 MSE
-上写下来作为我的第一个回答,顺便发现了另一个之前不知道的定理用法,学到很多(这是学到吗,好像是自己教会自己许多((x
果然学数学就要去北大学(迫真,去了一趟感觉很缓解期中周精神状态(
-11月5日
-虽说昨天觉得不用慌了但果然考数学之前就是很难不慌(,希望能成功早睡(
-膝盖本来好很多了,结果上次又摔了脚踝,今天又被车蹬子打到了膝盖上还有淤青的地方,真好不了了,帝宝求你了放过我(。说起来上周体测
-800
-米测出了上高中之后就再也没见过的成绩,跑的时候甚至感觉还有余力,帝宝特有的受伤之后能变强是吧(
上次在 MSE -问的问题已经周榜第三了,好崩溃,这周会不会收到一封能在里面看到自己的 MSE -Weekly Newsletter(
-今天在教学楼洗手间里看到一个出水停不下来的水龙头,突然联想起大一的某个雨天骑车的时候一滴水打在我没锁屏的手机上然后连发了几十个表情包(,当时正好在旁边擦手,顺便拿纸擦了一下那个红外感应器(?我也不知道叫什么)上的水果然就不流了,学到许多(,而且日行一善(1/1)((
-这概率论 2 -颇有一种奶酪越多,奶酪孔越多,奶酪孔越多,奶酪越少,所以奶酪越多,奶酪越少的感觉(,学得越多不会的越多,题目拟合的越多之前会做的后来再看也不会了(,随便吧反正明早就考了((
-11月6日
-昨晚把时区猛往东调了六个(,果然入睡有点困难,吃了 1/3 -粒室友的安眠药然后光速睡着了。
-概率论大寄特寄,我是真没想到 yf -这么喜欢考计算,每道题都在算(还特别喜欢 random walk on graph,一个 -binary tree -一上来给我看傻了),我做计算本来就又慢又菜,这次干脆剩了个题没算完。考完之后在路上一边走一边想,算一个有 -\(n\) 种取值的 discrete random variable -的期望需要 \(2n-1\) -步,我也不知道算最后那个 triangular sequence -里每一个随机变量的期望花了多久,总觉得最后的 45min 转瞬即逝,看来确实 -\(O(n)\) 对我来说已经太难了((
-无所谓了,我现在越来越发现我考试发挥的水平就这样,之前已经复习挺好了,该掌握的也都熟练了,差不多得了。
-晚上看答疑坊群里说线代爆单了,想想我暂时没什么要紧的考试了就去秒了十几单,然后把生物作业写了,好闲啊(。明天考完 -ODE -要极限开始学整数规划然后写后天要交的作业,实在不行先把作业写了再学(
-这周大概还得赶赶高统的进度,虽然不期中考但落的有点多,然后就是没边没沿的优化了,真不知道咋复习,上周还休息了(
11月7日
-好崩溃,为什么要 PF -ODE,哥们就复习了两个下午,昨晚还在写生物作业,写完开始摸鱼抽卡摸到两点,躺床上看了一眼整理的笔记的照片一秒入睡(,早上六点半就醒了然后睡不着了。刚拿到卷子又开始流鼻血,怕时间来不及就一边捂着鼻子一边算,看起来还挺壮烈的。
-铺垫了这么多(,实际上我想说的是 70min 就 AK -了((,昨天概率论要是有这水平还愁啥(
-上来一看怎么第一题全是字儿,再一看这个 enumerate -写了六行居然是在解释什么叫唯一解无解和多解,我还以为善良到把判定法则给出来了(。说到底这课就没什么难的,除了一些计算细节(比如说 -(a) 的无穷多解几乎就和 Lecture 1 -讲过的那个一模一样)之外核心定理就两三个,像 (c) 这种除了套 -Picard-Lindelöf 之外也不太可能有什么别的办法,随便一放缩凑个 local -Lipshitz 就有了,问题是你这个 (b) 到底为什么压根不满足 initial value -condition 啊,我还给解出来了然后仔细一看逗哥们玩呢。
-中间两个就是只要学了微积分 A1 就会做的计算
-可能也不会毕竟其中有一个是 Jordan decomposition
-尽管我当初并不在乎唯一性乃至这么做的合理性之类的细节,最后一题本来还想着说不定有点小难,再仔细一看兄啊你这导数
-\(y^\prime = f\)
-怎么还是有界的,你这函数怎么还是在 \([-1,1]\) 上的,那不写个 Arzelà-Ascoli
-theorem 再用一下 LagrangeKMnO4 Lagrange mean value
-就直接带走了吗(悲

卷子可以带走,所以发出来也没啥吧(?
-我懂了,这学期主打一个学到就是赚到,别天天牵挂你那绩点了.jpg。下学期要去上
-PDE 替代培养方案里的数理方程,虽然不知道和 ODE 有多大关系
-而且重点应该是我那稀碎的多元微积分水平不太行,总之学一个先。
今天不知道是不是考完了的原因所有的课都开始哐哐布置作业,打开平时事不太多的高统发现布置了超过五个题,急死了,再打开优化作业一看真好啊竟然只有六道题(,再一看每道题平均三个小问,急死了((
-11月8日
-现在笔芯好难买啊,我平时只用
-0.38,本来就已经很难找了,这次缺的是蓝色笔芯,某宝都快翻烂了才找到以前一直用的那一款。不是墨蓝就是晶蓝,就想买支纯蓝色
-而且笔杆可爱一点不要纯透明的(草)的笔咋这么难呢。
优化期中就有两张正反面 cheatsheet,高统期末也有一张正反面 -cheatsheet,建筑材料直接那个开卷允许带书,感觉别说复习了光是塞 -cheatsheet 就够我喝一壶。
-今天突发恶疾看了一眼春季那个数学规划的大纲,这不就优化吗(。里面就非线性规划没学过,到明年去水一个工工的好了,考虑到数学系大三非泛函专业课的那个水平还是不去浪费时间了,好好学复分析吧((
-Shao Jun -这本数理统计越看越觉得也有点怪,感觉描述性的语言太多了,不能多列点公式吗(。像 -the conditional distribution of \(X\) -given \(T\) is known -这种话(我觉得)写在 remark 里就可以了,为什么会在定义里,去 example -里找式子感觉有点小抽象。
-喜提了第一个数学考试满分(,这是好事,但是 -ODE(,明早去看看分位数是多少。虽然考试其实 AK -过很多次但是基本上都有被小扣分,去年抽代期末还以为能满分结果笔误了两个被浅扣了一点,数值分析也 -AK 了但没公布成绩,看最后是 A 而不是 A+ 有点怀疑又笔误了(,说到底 ODE -可能也不是没有笔误只是批的松吧(
-11月9日
-睡大觉。
-本来觉得优化是下周五不用慌,今天仔细一算我这周连作业都写不完,急死了。
-今天写高统作业看到个好玩的:\(f_1f_2 -I_{A}+g_1g_2I_{A^c}=(f_1I_A + -g_1I_{A^c})(f_2I_A+g_2I_{A^c})\),实际上是在拆 exponential family -的题目里看到的,但那个题我看了一眼感觉不能拆就直接开始说 subset 的 -minimal sufficient 也是全集的 minimal sufficient 了(毕竟 subset 就是 -exponential family),似乎有点粗暴。
-赛马娘第六话钝评,端上来罢!
--
前天还是昨天看了预告其实就给我整不会了(
-上次宝冢纪念大鸣大放赛后明明骨折了还愣在北黑面前站起来了本来就有点给我整不会,我以为埋了个大瓜等这一话才知道再也不能跑了,开始掉小珍珠然后和北黑进行信念的传承,结果怎么是光钻?
-我超,总算有小林历奇了,光钻小林东商皇冠俊逸和北黑的修罗场人总算到齐了,而北黑还在和内恰贴(
-我有点评价不来这番的搞笑情节,感觉观感和第一季越来越像了,前半段真不是在水时长吗,后半段我其实看了预告就感觉应该会和麦昆谈心
-虽然里见家族和目白家族简直不是一个量级但反正目白牧场早就没了随便说呗
-但麦昆突然讲龟兔赛跑然后被打断还是给我气笑了,尴尬程度不亚于早已沦为胡萝卜特饮推销员的特别周在第一季
-OVA
-里面对着胜利奖券大声复述训练员怒斥早恋小情侣的那段话,及川启对自己不合时宜的插科打诨的强烈执着依然毫无反思甚至可能都没有认识,你不是马黑谁是马黑(
麦昆:比赛中落铁和斜行都是很常见的事(指天皇赏春落铁,天皇赏秋斜行被降十八着,真的很在行(
-总觉得这是麦昆第三季以来第一次说超过三句话(,太亚撒西了,我永远喜欢大西沙织
光钻这场菊花赏应该是目前为止做的最长的比赛,虽然最后冲刺全靠和观众一起吼还是给我整绷不住了,但不得不说里见家的姐姐们出场看比赛、光钻赛后掉小珍珠还真算是这一季里面截至目前情绪渲染的高峰了。
-现在魔咒破了,里见 魅魔
-皇冠后面能说点别的了吗,这么可爱的妹子没戏份的话真的好可惜(
下一话按照时间线应该是北黑光钻第一次有马纪念对决
-今天的小北不是我的对手,不知道北黑要怎么输。同场的又是万籁争鸣、高尚骏逸和胜之石(小北这次认识了吗?),但这三位都没能入着,其他马娘又是都没有版权(当然胜之石也没有),大鸣大放已经退役,很难想象这比赛会是什么抽象样子,大概只能搞女酮了(。估计是赛前
-修罗场,续上宝冢纪念的大鸣大放受伤和未能参加有马、凯旋门就退役的遗憾,或者能有个会动的
-winning live 和在 winning live 上和好贴贴的北黑光钻
-看看了。
啊所以真的还有人记得大鸣大放吗?还有人记得大鸣大放的凯旋门赏吗?
-如果说光钻个人回结束了才开始写大鸣大放这才知道自己不能再参赛了我还是会有点小小的难以接受但勉强接受也不是不行(,也不是非常不合理,但感觉接受不了也是有点因为和预期不符,宝冢纪念之后伤那么重早干啥去了。只能说或许要把“不能再参赛了”阐述成“未能参与有马纪念就遗憾地面临退役”,然而但凡把第六话前半段的抽象演出压一压然后讲大鸣大放的情况也比这好啊。
帝宝救一下啊,麦昆都开始当知心姐姐了,你救一下大鸣大放也行啊
11月10日
-昨晚把不考但是这周要交作业的三门课的作业写完了,心情好了很多没那么破防了,然后想了想我优化上周的内容还没仔细看呢,今天何必还要去教室,咕咕。
写运筹作业的时候还不知道昨晚讲的非线性优化是个啥东西,打开 PPT -一看哦原来就是凸优化的基本概念然后随便讲了几个数值算法,速通了。不过翻这 -PPT -的时候还是给我气笑了,不会写数学公式可以板书,别惦记着你那关着灯上课了.jpg
-好痛苦,选这么多数学课干啥。学新的东西掌握漂亮的技巧确实很开心,然而用选课来催促自己好好学的代价就是有一个在复习拟合中感到无比痛苦的超长考试月,在此期间就连去读一些写得很好的讲义和写作业都失去了应有的兴致,非考试科目的话甚至只想赶快掌握下表面的东西把作业写完然后就放下,省出时间复习,之后再来还债,好痛苦好痛苦。更痛的是哥们期末有八门课要考试,真能活下来吗(
-今天一边读 Boyd Chapter 4,5 -写作业(也没写完,急死了)一边辱骂优化这门课,要是按照上确界来准备的话就是五章 -Boyd 四章 Intro to LP 再加一章 Bubeck,然后读读课堂笔记再加一个上课讲的 -maxcut,两张双面 cheatsheet 我觉得少了,但是既然限定要 handwritten -我又觉得太多了(。这 Boyd Chapter 4 -到底在干啥呢,好像就罗列了一堆不同类型的 convex optimization -problems,我还以为会有什么稍微统一点的方法结果课后题仍然相当依赖人类智慧,甚至可以说只是依赖线性代数水平(
-想来想去只有一句锐评,这课比赛马娘第三季还能塞。
-11月11日
-写点啥呢(
-收获了一个 asuka 同款 朗枪帆布袋
-感觉有点地狱,找出处找了半天(
其实只是借用一周,骑车把之前用的帆布袋弄脏了((
晚上回来之后吃了个朗姆酒冰激凌,感觉头晕晕的,怎么会是呢,好菜(。
-11月12日
-双十一买了个咖啡杯,还买了一箱瓶装咖啡,结果就是到现在瓶装都没喝完
-作为一个懒狗
-更不可能自己泡了,想想新杯子一直放着也有点可惜,拿出来喝水了。300 ml
-的杯子有个奇效是走路的时候放在口袋里也不费劲,打一杯热水去吃饭来回路上当热水袋,回教室之后就正好可以喝了。
晚饭后饭困的频率越来越高,下次留一口咖啡吃完饭回来喝(...)或者饭后去骑会车好了。
-周五考试,两张正反面 cheatsheet -仍然没有开工,但是不紧不慢.jpg,怎么会是呢。今天把 Boyd Chapter 1,2,3 和 -Appendix -看了,总感觉线代水平似乎不太行,小急。为什么要在额外的纸上做笔记而不是直接抄在 -cheatsheet -上,我也不是很懂。不过还好,后面四天没有要写的作业(...)所以还挺有时间的。
-话说回来感觉与其微雕折磨自己不如随便找纸写大一点然后缩印到一张纸上(比划),明天去看看清芬打印水平行不行,实在不行去社友曾经推荐过的北馆(
-11月13日
-今天摸鱼的时候看到有个致理的同学在答疑坊小程序里问数分学不会怎么办要不要多刷题(,本来想话疗一下后来想想我也没学过数分还是另请高明吧,过了一会看这哥们又问了个离散,成分已经很明确了这还学数分学那么认真干什么.jpg(
在读优化的 scribe notes,读到 week 3 惊喜地发现还有人 LaTeX
-写得比我还丑,满意离场
自从找到可以把水果酸奶送楼下的店之后就有了晚饭之后骑车遛弯顺便回去取的动力,每次下单都在默念我一个月挣两千买点吃的怎么了总不至于真没钱考托福了吧.jpg
-晚上教室里另一个姐一直在乐,走的时候听到她 npy
-和她说我求你别笑了然后两个人开始一起乐(。除了当时在推一段推不出来的公式感觉有点小吵之外,羡慕和疑惑参半,好美丽的精神状态(,我怎么一天天的就完全乐不起来,反正每周离已经过去的周六越远整个人越乐不起来(
走在路上突然好想吃玉米肉馅的饺子,感觉是不可能存在于北方食堂的东西,晚上就在清芬多买了一个生煎当代餐,尽管也知道它比在上海随便找个店能吃到的差得太远太远了。晚上拿到的昨天买的青提上不知道为什么沾了好多泥,和上周末买了带去隔壁的完全不一样,费劲地洗了好久最后尝起来也不甜,你这白开水怎么没味儿。不过买到的芋泥厚乳很好喝,本来差点突发恶疾就冰着喝了,放暖气上热了一下留到洗完澡喝的,好香好香。
-乐不出来可能也是因为饭太难吃了,清芬一楼还就那个又贵又难吃。周六可以吃好点。
-11月14日
-昨天想吃玉米肉馅的饺子,在华子想必是不存在的,吃了个不好吃的生煎当代餐,完全和你沪的没得比。今天想吃汤圆,去桃李二楼的时候已经没有了,又没吃上。
-北京初冬这个天气不刮风的话真的很舒服,今天下午在一教摸鱼,出去交作业的时候顺便在后面的小土坡(?)上溜达了几圈,把围巾摊开当披肩披在卫衣外面就出去了。所以说感觉现在真没必要穿得特别厚,有一件抗风的外套就足够了。当然我没有,冲锋衣暑假带回家洗了之后忘记带回来了,那就骑车骑快点吧(
-晚上在教室看到前排一个男生在用香蕉空间看复微分形式的定义,大受震撼,又窥了下屏发现他旁边的女生在写复分析作业(,感觉求真爷实锤了,仔细一看哥们桌上的入党申请书写的求真 -2 党支部(。再右边的另一个男生在看 GTM,别的没看清就觉得一个图长得很像 -upcrossing inequality,看他翻了几页之后标题是 -martingale,不知道是哪本。浓度好高(
-这学期连期中周都还没活过去,看下学期的课表倒看得很乐呵,希望最后别变成在那嗯造两本
-Stein(其实我本来都不知道是造哪两本,但是看到下学期泛函是 xgy
-开课之后就确定了是实复(。春季的必修课我倒是上得差不多了,就几个很水的建管交通必修课随便摸摸就过去了。统计中心那边摸一个高统
-II 和高维概率 我觉得这两门总能命中 ypk,看到求真那里开了一门
-combinatorial
-optimization,简单查了查感觉和这学期优化理论接上了可以去学学,主要是既然同一个老师的
-deep learning theory
-没考试的话这课也不会有考试的对吧对吧对吧对吧哥们是真的考不动了((
下学期实分析是光叔和 lyx 但是看这个课容量我觉得我就是 lyx
-的份了(,本来不知道后面这哥们是谁,查了下以前学期都在开我不太关心的研究生课难怪不认识,但看了他在官网上的照片(右一)之后我觉得应该是个好人吧(迫真
PDE 没有 jhy,我只是想拿这课水
-看起来根本不可能学会因为不会转化物理模型的
-数理方程而已,那就不急着选了。
好想用上海话骂人哦,在华子没什么机会 gang 洋泾浜 sang hai
-ei wu 真是失去了很多乐趣(
11月15日
-早上突发恶疾看了会 Gaussian sequential -model,主要是周末讨论班讲这个,结果主讲人发的链接是一本 500 -页的书实在给我整不会了(,看一点是一点能听懂多少是多少吧(
--提醒各位同学,本周五是优化理论课程期中考试,时间和地点和日常上课一致。
-题目数量:6 道题目,包含证明题和解答题
-题目难度:TA 用时约 1.5h 完成
+A:所以为啥要单独买个屏买个壳呢,这样拆一遍壳很费劲的(
+我:对不起(
+B:所以咋不重买一个呢
+我:对不起(,但我都用惠普战 66 了不就说明没钱吗(
+C:别说人家啦,拆好带过来还没拆出啥问题挺好的了,不然还得拆一遍,费手
+我:对不起(
+A:他是在夸你
+我:对不起(
TA 好强(#每日TA
我寻思着 TA 用时约 1.5h
-完成到底是个什么难度(,开了下盒发现这哥们是前几年的丘赛概统银奖,那他怎么做了这么久,这考试是不是还挺难的(x
今天身体不舒服睡了好久,晚上感觉要小肝一下。怎么以前做出来的作业题第二遍看都觉得自己当初像会魔法一样
11月16日
-烦死了这优化快点考完吧,好想学点新的东西,ODE 和高统都是(
-不过今天看了不少 SDP,也算是学了。不知道后半学期讲不讲,反正当初讲 -max cut 的其中一个转换的时候 zjz 突然说了一句这就是个 -SDP(大意),然后在场的茶园爷看起来全都懂了,只有我愣住了,SDP -是啥,讲过吗(
-下午往 cheatsheet
-的最后一块空白上随便塞了点东西,晚上写了运筹作业,又看了点高统,感觉神清气爽(。希望明天没事,但我感觉
-bgm 都快换成 Komm süsser Tod 了(不如放欢乐颂怎么样
赛马娘,钝评,端!
--
又一次给我气笑了(
-真没绷住,我想着这次日本杯第三是表现高尚骏逸一生一次的末脚之前的高光之一了,再没有的话只能等明年春天皇赏的第二了。万籁争鸣是最后一次拿到第二名,此后再也没有进过前三。所以我还以为这次有马纪念可以像第二季的帝麦对决那样先铺垫个一集,结果又莫名其妙,比赛之前高尚骏逸又说一定要赢,然后又输了输完很不甘心,光钻日本杯的时候看着北黑赢了还就那个面无表情,有马纪念早上起来还想着给北黑留小纸条说自己先走了,到赛场上就甩脸子
-离婚
-不认人。要是说这就算描写了光钻比北黑对待竞技的心态更成熟的话我可要绷不住了,赢了之后也是北黑先向光钻搭话不然头也不回一个,那这场比赛光钻要是输了的话岂不是更要翻脸不认人了
-反正你这输赢也莫名其妙的除了按史实写之外啥也没有,性格还没有北黑成绩起起落落也没看到大的起伏、无论输赢都在笑来得讨喜。赛中莫名其妙地追上了超越了,两个人吼着吼着北黑不知道为什么就输了,我看了个啥(
跑步就跑步别吼了啊啊啊啊啊冲线那一段我直接把声音关了(黄金伶人/巨星俳优:那我呢?
-cy
-你还是搞女酮吧,之前的预期是第三季能和第一季差不多就行了,现在感觉好像还没第一季好看(
winning live
-冒了个尖我还想看北黑望着光钻的背影一边忍着不掉小珍珠一边跳舞(,之后直接转
-ED 也没绷住,想做搞笑番可以再单开一个四格别霍霍第三季
你还别说这 ED 相比正片来说还挺好看的,麦昆可爱捏
睡前想起来这回事躺床上拿手机直接在 b -站看的,看到标题把“我们的有马纪念”翻译成“我们的中山大奖赛”就已经开始绷不住了,第一季和第二季的时候不是还可以翻成有马纪念的吗,看了下吐槽似乎有些马名(大鸣大放?)都没按照香港竞马会的翻译来翻而是自己重新译了一个,乐(
-里见皇冠你怎么还惦记着你那魔咒(,不过和光钻的性格反差做的还不错,在没有破咒的时候皇冠是稍微相信魔咒每次失利都更加畏缩,光钻是始终不相信魔咒的存在一直在努力,光钻破咒了之后皇冠也受到鼓舞赢下了 -G1。只是香港瓶没版权做不了也有点小急(
-皇冠好涩,远景里高尚骏逸的小肉腿也好涩,怎么会是呢(
所以说真的没有人记得大鸣大放了是吗?cy -你要这版权有啥用啊,不就一背景板工具人吗,你看黄金伶人的替身(巨星俳优)不也演得好好的吗(
-帝皇谈心 怎么就这
-说了点啥啊(,还以为能类比一手帝麦对决,感觉在努力类比了又没类比,看在第三季这么塞的份上算了吧不吐槽了(
一集一比赛确实观感就不好人设也立不起来,不过看起来是要把北黑七冠至少菜名都报全,隔壁帝宝四个
-G1 还跳过了日本杯没提也是做了 13
-集,放平心态放平心态(。说难听点北黑和同世代马大多甚至都还没从种马退役,要端水照顾好
-马主的心情 也正常
-虽然除了把比赛塞完之外我也没看出来这是在激怒所有人还是在干啥,第二季播出的时候帝宝都竟走快十年了(,麦昆家目白牧场都寄了,随便魔改控制节奏也没啥,放平心态放平心态.jpg
11月17日
-昨晚睡不着吃了点安眠药,早上起来就感觉 dokidoki 的
-心悸,一直到下午才好一点,整个考试期间也挺不舒服的。我还想着周一考概率论之前也吃了药所以感觉考试状态不太好是错觉,是我太慌了所以不舒服,现在看来感觉确实和吃药有关系,下次
-直接把大晚上还搁那闹腾的室友打晕 不吃了(。
本来觉得没什么问题的,在医院开的药,禁忌症也没有高血压心脏病,但还是不舒服。
-这优化考试准备了真的有用吗(,斜前面一个哥们考着考着看起来嫌
-cheatsheet 碍事直接给扔旁边座位上了,笑死。zjz 怎么还一边考一边发
-hint,这是什么赛制,他要是不提醒 \(\log \det (X)\) 是 concave 的话我都快把
-duality 搓出来了,他一说这不约等于提示直接用 KKT
-了吗(。虽然造出来之后还因为不记得 Sherman-Morrison
-长啥样了小破防了一下,但再一想 hint
-里面甚至有逆矩阵的形式,乘起来不就好了,草。另外一个 hint
-发布(?)的时候是写在白板上的但我那个位置正好看不见,然后就出现了考试中途把其中一个助教叫住让他在我的草稿纸上写一下具体形式的梦幻场景(
当然这都不算什么,最重量级的还是今天在卷子上证明了一个 finite state
-Markov chain 一定有 recurrent state 因此它有 stationary
-measure,从而对于一个 stochastic matrix \(P\),\(p^TP=p^T\) 一定有非负解 \(p \succeq 0\)。这题让用 duality
-做,但我说实话连动手尝试一下怎么造一个奇形怪状的 primal-dual pair
-的兴趣都没有,而且它出个题还要在 remark 里提到 Markov chain,zjz
-也说不是非要用 duality
-可以用微积分线代知识,那我可就要表演一点小小的概统震撼了。希望能有分(
虽然本来还感觉了一下不知道能不能用 Brouwer fixed-point theorem
-但是又忍住了因为更不会证
一切都是虚张声势的线性代数,可惜我线代太菜了,只能徒手建造数学大厦了捏(
-但其实考试期间一直在 dokidoki
-心慌,搞得人很难受脑子也不清楚。同一个式子焦躁的时候写两三遍都写不对,椭圆不相交那个题的
-if 我明明拿 seperating hyperplane theorem 证完 only if
-之后一眼就出来了,还嗯是因为写不清楚正负号在那里多折腾了二十分钟,别的地方也不停地笔误,状态蛮糟糕的,几乎是到最后一刻才写完。但反正
-ak 了
-
晚上写了高统,好难,云了一点 Gaussian sequence model,看着像个
-toy model
-但是不会,不知道明天能听懂多少。暂且以坚持十分钟为目标(嗯?
又收到 BBO 的广告了,差不多考完了就好想打桥牌哦(
-11月18日
-今天 Gaussian sequence model -坚持了半个小时才掉线,感觉算大成功了(。后面一个小时就继续在看之前找到的讲义,没什么听了。不过 -slides -发群里了所以之后有心情的话感觉还能看看,这两天是不行了,期中耽误的 ddl -都赶不完(
-上午写了一会建筑材料实验报告,感觉这个报告的要义在于把 20 -张拍的照片全部塞进去(
-这张图我愿称之为《再见了,所有的混凝土块》(
-
右下角那个碎的那么厉害是我等实验的时候太无聊了把能手剥的碎屑都剥下来了((
-11月19日
-建筑材料实验周五做了一个半小时,周末写实验报告写了一天半最后写了 16 -页,导出来有 44 M(挠头
-它还有个文献调研的问题,今天被迫看了俩小时有关混凝土裂纹的论文(恼
-晚上去猫超买咖啡,发现纸盒装的 NEVER x COFFEE -回来了,虽然那个美式真的是我喝过最清醒的咖啡,但还是选了拿铁,那个味真的太(,只能说感觉是因为难喝所以清醒。
-路过果切的地方被八折吸引过去了,虽然事后想想只便宜了不到一块钱但是我出超市的时候手上还是多了一盒哈密瓜,怎么会是呢。昨晚在海底捞吃到了放在料台上的特别好吃的哈密瓜,今天自己买的反而都没那么好吃,难道说这就是
+顺便见到了人手一套的电动螺丝刀,寝室里 32
+头的那一套瞬间就不香了
12月3日
+这周的优化作业怎么这么抽象啊(,你谁(。其实我的意思是这周的优化作业怎么这么具体,虽然它一直都很具体但这周有两道题写起来好困难
牛顿法数值分析的时候已经学了个大全套了,看 zjz
+这个讲义感觉也太云了,这学期为什么要上这课呢。
今晚把周一晚上要交的作业写了,明天把周二下午要交的作业写了,后天把周三晚上要交的作业写了。我感觉我一天天的都挺忙的怎么还卡得这么紧呢(,原来是一直在看最近没布置作业的数理统计啊(
+12月4日
+初号机贴纸怎么还没到,急急急(。突然意识到之前的问题所在了,贴了二号机的电脑怎么能放在朗枪的包里(
+上周被喉咙痛折磨得不轻,这周感觉右半边腰特别疼,稍微一动就感觉像闪着了一样,活着真累。猫猫活到二十岁已经很不容易了,感觉快要不行了
下学期果然是林乾开高统
+2,杨朋昆开高维概率,但我寻思着统计中心就没几门博士生课你俩为什么要都放在
+4-2 开课,急了。再一看实分析也有一节
+4-2,感觉要冲突选课。再再一看发现复分析和组合优化也创了,感觉还要冲突选课,被冲突的当然是复分析就是了。往好处想下学期课表会显得比较空,因为都覆盖了
别的没有啥特别想上的课了,摸了个社科课组,再见了,所有的通识选修课(。体育打算选个壁球玩玩,这学期毽球没有上学期有意思,不想再踢了。必限就一两门,在考虑要不要上个基物
+2
+防止被退学,之后如果不每个学期浅浅学点物理的话我感觉我五年也毕不了业(
12月5日
+算了下感觉下学期必修就一门基物 2 +一门什么绿色交通系统就行,现在在考虑的是我大四春季有一些连着暑假一起春研暑研的宏伟计划(,所以为了不妨碍大五毕设开题,春季还是不能剩下太多课。大四上修量子力学和工程力学基础,大五上修工程力学 +CE,结构力学和流体力学然后随便它们烂成什么样(,最后一学期把工程地质和基物 +3 解决一下就行,还是能有条不紊地毕业捏(??
+我以前一直以为中厅是没有暖气的所以特别冷,今天发现就在饮水机旁边,摸了一下是冰凉的,有没有其他紫荆住户能告诉我这是不是正常现象((。说实话这真的合规吗,不是供暖室内低于
+18 度都不行吗(
本来想给核动力笔记本贴个电力充足,想了想还是没电的初号机更强一些,就给它再加强了一下(
+
12月6日
+今天穿北黑痛衣跑了 1500,英里距离适性 C +果然还是不够用,但立定跳远变强了非常多,感谢室友教我正确的姿势(
+下略。
+12月7日
+昨天跑了 +1500,今天就是一个人大困特困,腰背腿大痛特痛,于是大睡特睡,连高统 PPT +都没看完(
+12月8日
+北京的松鹤楼和上海的一样好吃,感觉稍微有点安慰(
+晚上在看运筹的决策分析,看了几页感觉定义有点像 decision +theory,还看到了简化版的 Bayes +rule,结果画风一转变成需要按固定格式写的小学数学应用题,我到底在期待什么(
+感觉有点小急,作业好多,但是又不是特别急,属于一个轻轻摸一下也能做完的情况(?
+12月9日
+处理了一些约等于在摸的作业(真的吗写高统作业不是次次都在痛苦嚎叫吗),然后对着优化不会做的那两道题继续阴暗爬行,然后
+yoasobi,然后睡觉(
听说 yyl +被非升即走了,这英文高代选这么有意思,我答疑还做了不少他们的作业题,以后就没了(悲
+晚上在紫荆吃了好吃的鸭腿饭,要不寒假回家试试复现(怎么这也能复现,拿到了前两天买的好喝的酸奶,室友的品位还是高(
12月10日
+学 Blumenthal's 0-1 law 的时候心里默念的是 +Duramente((,这听起来不是挺像的吗(
+好消息:十六周周三不用连考三门期末了!
+坏消息:因为高统提前到了前一天晚上考(
+感觉考完高统之后要回去紧急背生物,考完生物回寝室睡觉,然后下午稍微看一眼运筹就可以去考了,都不是问题,复习这些还不如早点开始写优化的 +cheatsheet(。但确实有个好消息是不用担心睡得不好影响考试了((
+晚上五分钟遇到了三只不同花色的猫猫,回去得稍晚了一点,骑车的时候感觉手比平时冷很多,然后就感觉到冷冷的冰粒子,啊不是,雪花拍在我脸上(
+一些和交大转数群友(?但确实是)的暴论:
--真的,一直到现在,我实在再没有吃到那夜似的好豆,——也不再看到那夜似的好戏了。
+H:
+你猜猜看我的数分助教是做什么的
+我:
+他既然觉得 Lebesgue 积分和 Riemann 积分不一样
+那先排除概率 再排除分析 我感觉统计也不至于(
+是代数吗 是不是本科不必修实变或者忘完了
+但我觉得这是个很基础很优美的结论 总应该知道的吧
+总觉得代数都是聪明人(刻板印象.jpg 是不是也不至于啊(x
+H:
+不是
+三个助教是同一个课题组的 做 PDE
+我:
+草 dbq 我想起来那句
+PDE 养活了不知道多少无能的数学家
+没有说他们的意思 只是无端联想(
+H:
+草
+礼拜五我问我那个助教是不是做分析的的时候
+感觉他稍微有点蚌埠住
11月20日
-今天和 ODE 作业搏斗了很久,到处搜了很多东西,算了 114514 -个级数,还挺有意思的。用解析函数逼近一个奇点邻域内的局部解,这种想法我甚至学微积分 -A1 -的时候就有,当时其实觉得自己什么都不会所以应该很不严谨吧,现在看到了完整的理论就很开心。不知道为什么 -ODE -感觉期中后突然上强度了,可能是期中前的东西确实学过一点的原因,也可能是我函数项级数很菜,或者合并同类项水平不行。感觉他前半学期在泛函,后半学期在泛函且复分析,而且是以本废物可以理解的简明易懂的方式在讲,学一门课赚了两门,好好好。
-周末听讨论班和看自己找的讲义的时候就感觉里面举的例子蛮熟悉的,哦这不就是数值分析的时候学过的那个
-Legendre
-基吗;昨天自闭搓衣服的时候一个在旁边洗漱的姐姐突然跟我搭话,说去年数值分析的时候就见过我,今年本来想上概率论
-2
-最后又没上但也看到我了(,我寻思着数值分析这课我也没去过几节才对怎么还就记住我了,还问我下学期要不要上
-bcl 的凸优化 可惜我已经在学了;今天看 ODE 讲义又开始 analytic
-function 了,乐死,一门课学完之后仅存的记忆用了一年半(
说到学微积分 A1 的时候,突然想起我大一也是和 OJ -搏斗了一整年,然而已经遥远得像在梦里发生的一样了,我现在就只记得大一好像啥也没学,然后微积分 -A2 -学得特别差,唯一有点意思的是学了一年法语。虽然现在也只学了不到一年半的数学,但感觉至少大二上学期学的东西现在还记得不少,甚至我第一次接触赋范空间什么的就是在数值分析,但你现在要是让我去写一点 -C/C++ 我只能说我根本都没这个勇气再动手了,还是写 R 吧(
-发现在和一个助教上同一门课,这算几代同堂(
+12月11日
+半夜两点跑到楼下在雪地里用一次性筷子默写了《雪赋》的最后一段,精神状态非常的好啊。
+
我相信这图上是看不清的但是说不定放上原文就能对起来了
--注:本次作业占分为平时2倍;3.6.24假设T是有界的随机变量;提交期限延长至12月4日,共14天。
+白羽虽白,质以轻兮,白玉虽白,空守贞兮。未若兹雪,因时兴灭。玄阴凝不昧其洁,太阳不固其节。节岂我名,洁岂我贞。凭云升降,从风飘零。值物赋象,任地班形。素因遇立,污随染成。纵心皓然,何虑何营?
既然占分是两倍,ddl -也是其他作业的两倍时间,那为什么不拆成两次作业来布置呢((
-为什么概率论 2 期末是 15 -周啊,这不是快了吗((。本来想这学期能在这课上学到一点 continuous time -Markov chain 就赢了,结果看现在这个进度根本不可能,把 Brownian motion -讲完就不错了。所以就是复习一些我学过的东西然后把基础打扎实一点,然后估计还要拿个不太好的成绩,乐不出来。
-上周作业有个 2017 年丘赛题(P2),反正我现在一看到 random walk on
-binary tree 就头疼,想起来期中做不出来的那道题也是个类似的设定有点
-PTSD。这一年的题也没公布答案,到处搜了半天也没有,可能等再动手试一试如果做不出来的话还是得自己在
-MSE 上问。前两天还有个数 21
-的哥们从环里加我问我这个题,我只能尴尬地说期中刚考完还没来得及做呢(的确如此),他说问了助教这题和
-Markov chain
-没关系就是硬算,我寻思着这助教原来会提前看我们的作业题啊,那他为什么从来不公布作业答案呢,是因为他自己会所以就怕我们也都学会吗(不是。昨晚翻了一下
-wh 暑假里给我的那本讲义,在第七章的习题里有,但也没答案啊(挠头
昨晚熄灯之后就对着 ODE -的讲义和这道题枯坐,很困很累了也学不进去什么东西,但反正还是能感觉到这周 -ODE -作业有点小难,然后丘赛题也没底,算了几项感觉找不到什么规律,就是很急。后来感觉很累了也没再继续动手做题,就开始枯坐,然后回忆期中的失败,别的课都好说没有特别离谱的,就概率论 -2 -开天窗一个大题还是给我整挺难受的,别的题加起来也扣了一点总之不是很好看,越想越难受了属于是。
-压力好大,周三考运筹我到现在还没开始复习,虽然知道很水,大多数都在优化里学过了,但要人肉算一堆东西的话还是有点难说。我想把 -Gaussian sequence model -在讨论班之前和之后读到学到的东西都整理出来,想去学一下相关的泛函基础,想动手写一写 -Frobenius method -的笔记,高统作业都写完了但说到底也不是很扎实,想回头再看一看,怎么就是做什么都没空呢,每天都在忙什么呢。
-11月21日
-复习运筹的时候一边看他这个 duality 一边乐,太简单粗暴了,连 -Lagrangian -都懒得提一下就把对偶形式怼出来,但说实话用影子价格解释还甚至有那么一点道理,又绷不住又乐。本来懒得多看了,然后刚刚一想不对啊优化是开卷,这课是闭卷,我甚至还得去仔细背一下 -LP duality -那个形式,不然我本来计算就很慢还容易错,什么都现推感觉来不及。可恶啊,优化有什么可开卷的,该开卷的是运筹(
-反正我明晚就要去运筹考场上使劲用英文写解答了,感觉助教批我作业的时候从来不看我写的啥,就直接找我划出来的答案看对不/对。如果全是计算的话这样似乎还挺危险的,算错一个全没了谁受得了啊(
-今天把以前写的作业又重新算了一遍,反正还是算不对,而且发现以前也有步骤不严谨的但是并没有批出来(
-看了下赛马娘下一话的预告,怎么又双叒叕是内恰,绷不住了,第三季的第三是内恰的第三(
11月22日
-下学期高统是林乾,似乎要大讲 decision theory 和
-minimax(
高统课上随便听了点然后在补看前几节课的 PPT
-写笔记(,听着听着怎么突然开始 loss function is convex,然后 take
-optimal parameter,还有 inadmissible
-了(。何必把概统优化运筹分开呢,不都是通的吗(不是
-换句话说其实感觉可能确实就得什么都会一点才行(
下午和室友聊天,我说我前两天读到了一些二三十年前的数学,特别感动,现在又退回一百年前了。结果她大受震撼,说她现在学的东西有很多二十年前都还不存在,还只是课上学的而不是磕盐做的,乐死了(
-运筹期中做了 40 min
-左右就水完了,本来想再浪费一会生命结果这教室实在太热了坐不下去了就跑了(,好好好,期中结束了,cheers(开始满意地吃刚洗好的今晚买的草莓.jpg(好怪哦
11月23日
-今天本来想补上上周至今没写的概率论作业,最后还是看了一天高统
-感觉既会了又没会,难道是在复刻区间套赶 ddl 法(
赛马娘,评,端(
--
这集好像没啥可说的,中段的文戏意外地还可以,帝宝的谈心反而让我越来越觉得第二季实在是强。原来制作组也知道北黑没目标啊。但不知道为什么评分非常低,比上一话还低(
说实话我看完几段谈心和商店街应援之后还感觉观感好多了,结果北黑大晚上跑下楼啊啊啊啊啊啊训练还是给我整崩溃了,包括一开屏又是上次比赛两个人啊啊啊啊啊啊真的是((
-谁说第三季没有 live 了,小北的爸爸不是开了两场 live
-了吗,虽然是兼用卡(
大鸣大放终于出现了,只不过开口第一句是突然问北黑你的目标是什么实在是有点生硬(,帝宝谈心也谈了,如果这些放在宝冢纪念之后就好了。该说 -better late than never 吗(
-高尚骏逸这描写怪怪的,不过刚刚连跪了好几场心情不好很正常,反而是极峰给我感觉看似安慰实则嘲讽(,私服也不是特别好看
-cy
-你的服装设计传统艺能呢。想想高尚骏逸出场加起来应该不超过五分钟就还是释然了(,人设立不起来是正常的,输了就在姐妹面前垮起个批脸也是正常的(,没看到在训练也是正常的,后面突然一生一次的末脚也是正常的((
-反正没有剧情也没关系,后面等角色在游戏里实装了再补个人剧情也行,第三季还就是那个宣传片,开摆!
11月24日
-下午在教室打开门看到门边坐的一个哥们在全屏玩原神,差点没绷住(
-去新土木馆 搅水泥
-建筑材料实验的时候那边正在消防演练,楼道里全是烟,我昨天刚洗的头,我的鼻子,这破专业怎么还折寿呢(
有时候有点怀疑是不是只有特定会触发任务的人能看到我(,搅水泥之前按组领表格的时候大家都在随便拿,我说前面有组号结果旁边的大哥还是没听到我的话就把我的拿走了(。直到他们发现不对在若干人之间传了很久之后另一个哥们把它放回去,我站他面前说能不能把第五组的给我,他还是没听到,绕过我放到讲台上就走了,草((
-然而今天搅水泥穿了一身白衣服,只蹭脏了一点已经是我赢了,晚饭吃香锅又快乐地往上面溅了三个油点((。虽然经常吃清芬但其实还是第一次吃香锅,你这中辣怎么没味啊(
-11月25日
-开始做双十一买的纸模了,似乎小栗帽比麦昆的简单一些,但裁下来几块头发之后人就已经晕了,希望能做完(
-今天写了一天概率论,主要就是在对着不会做的题发呆,还有睡大觉(,相对
-非常失败。这期中周的后劲怎么还没顶完,马上都十一周了,爆了(
太乐了,来点最喜欢的一集(这课显然不是我在上

11月26日
-最近答疑坊接的都是熟人的私活,值班也鸽了不知道多少了,干不动一点,津贴和
-最基本的别因为值班次数太少被踢出去了都
-有点寄。下周打算去补一次顺便写写这周的建筑材料实验报告,要是写不完就补两次反正我每次讨论班之后也都没心情去(,急急急。
晚上 yoasobi 的时候 突然感觉心口疼,20
-岁,一天到晚一副要寄了的样子,鉴定为老猫,喵喵
最近在校内找到了一家品控好价格正常送货上门的水果店,吃了很多在他家买的橘子
-主要是相比之下橘子是最方便吃的不怎么需要洗而且还不贵。想起来《我去世了,然后...》,感觉死前能吃够
-100 个,问题不大(
11月27日
-洗漱的时候听到两个致理数 0 的姐在聊天:
+今晚在作业里写了一个
+\[\{T_A \leq t\} = \cap_{n=1}^{\infty} +\cup _{s \in \mathbb Q \cap (0,t)} \cup_{i=1}^\infty \cup_{x \in \mathbb +Q^d \cap A_i} \{B(s) \in B_d(x,\frac{1}{n})\} \in \mathcal +F_t\]
+其实我只是在证 Brownian motion 中一个 \(F_\sigma\) set 的 hitting time 一定是 +stopping time(。能把 trivial +的东西写得这么丑陋和唬人,似乎觉醒了一点点灌水的天赋(
+12月12日
+明天暴雪橙色预警,但是我有四节课(疑惑
+下午写优化作业,因为认为 \(t(t+1)\) +在 \(t=0\) 时取值为 \(1\) +而疑惑了至少二十分钟。晚上在答疑坊值班教室友写概率论作业,五道剥蒜题给了我到现在都没有恢复的心理阴影(
+晚上回来又在赶之前在答疑坊接的一个这周要交的主人的任务,想了想这个月几乎就没多少津贴,还是干一下吧。
+12月13日
+下午在寝室和综体之间走了一个来回,晚上又在寝室和法图之间走了一个来回,还上了体育课,今天的运动量就到这了(。课好难,好冷,好困,好累,这学期怎么还不结束,这紫荆宿舍怎么还没塌掉,麻了(
+晚上在看高统的讲义,感到深深的疑惑,wwc +平时都在抄书这次怎么把书扬了整这么难,想了想好像之前也很难但好像学会了之后就会变简单(,希望吧。但是优化学起来完全不是这个感觉,学一点忘一点,也不知道是这课的问题还是我的问题。
+一到 asymptotic behavior
+就开始大力分析了,感觉自己好菜,以后谁再说统计简单我跟谁急
早上有点睡多了,晚上走回寝室的路上想了想在打烊之前拐去七港九买了杯奶茶,后来又来了几个人在纠结晚上再喝一杯会不会睡不着,要不要换成果茶。店员说已经没有奶茶了,我这杯是最后一杯,他们说太好了(。感觉我也赚了,大家都满意的世界达成了(
+12月14日
+今天研究了半个下午怎么配混凝土的各个组分(,感觉本质上是个有八个参数的非线性规划问题,虽然是有解的但是
+feasible set
+不是很大,解的可解释性()也都不太好。但如果想得到解释性好的解的话,可以稍微牺牲其中一个
+constraint,所以除了规划之外还可以整个 weighted cost function
+把它变成优化问题,乐死了(学数学学得
本来想参考下同学的(迫真,算着算着越来越不对劲,仔细一看他们公式代错了,草(
+因为没法解释其实也不太敢(?)和队友解释我这些迷思(,再加上这个活拆成六个人的份本来就不合理,就一个人把六个人的活给干了,至于干得怎么样还得看明天做出来的结果(,就图一乐吧。这玩意 +16 周有个 pre,到时候就心安理得地推掉给他们就好了,哥们 16 +周考四门课,真没时间陪你们玩泥巴了(
+今晚似乎是最后一个熄灯的晚上了,回去收拾一下直奔 C +楼把这个计算书敲完,这寝室真待不下去了,断电之后冻死(
+昨晚梦到在上讨论班(为什么,一个同学在台上讲他论文里证的一个不等式,另一个同学问他你的 +lower bound +既然可以达到那算什么不等式,不是可以相等的吗?还有一个同学问为什么常用的不等式里的符号都不是 +\(\neq\),这算什么不等式(。然后吓醒了,发现自己在床上而不是在讨论班坐牢,非常开心(
+所以这周六到底是考六级还是去讨论班呢,要不周六早上起床再说吧(
+12月15日
+探索了下 C 楼的刷夜,其实体感还挺好的,以后寝室太冷 / 太吵 / +太安静(?)可以经常来。但我这次居然是在刷夜写混凝土配合比计算书,乐(。一边写又一边抄文献,我知道做这个事情毫无意义,但昨天看到两个队友算错的数之后就稍微有点不舒服然后开始单干了(。其实我觉得我要求真的不高,能把公式都用对,满足所有的 +constraints,在此之上可解释性的要求也只有一两条,结果长得和大多数文献或者专利里差不多就行了,这不都是很合理和基本的想法(?
+然后今天做出来结果还挺好的,虽然是绝对的烂,但是相对的好,那就挺好的了(?
+看选课,发现下学期要选的其实没啥课,高统复分析组合优化
+还有基物 而已(。到处乱搜的时候看到求真有个计算概率,讲 MCMC
+之类的东西,用的书以 applied 开头(,稍微有点心动。再一看作业 50% 上机
+50%,更心动了,现在在我眼里写上机作业竟比考试更轻松(
茶园还有个因果推断前沿的 2 +学分的课,但感觉在方向上有点太细分了不好说有多大用处。
+早上起来看到 CoCo
+和恋与的联名,虽然早就不玩了但爷青结(,而且这好便宜,四舍五入一块亚克力两张拍立得两个杯套一个保温袋
+还送两杯糖水 才三十,遂点。不过前夫哥的那款 糖水
+奶茶不好喝,有一种玫瑰香精滞销于是捆了烫男人的谷子一起出售的感觉(
12月16日
+前几天一直走路,昨晚才又开始骑车。其实唯一的原因就是我只有一件羽绒服还是浅色的,万一真摔在泥水里就没衣服穿了((
+今天还是选了讨论班,第一次有我能全程听懂的,真不错。但说实话最后几个老师的锐评以及中间的提问和讨论才是很精髓,不管从找了乐子还是学到许多的角度来说都感觉在这个天来回骑了八公里挺值的((
+晚上回来去答疑坊值班,给室友讲概率论,算得我天昏地暗,结束之后换个教室爆睡,睡得正暖和的时候教室关门了,走到外面真冻麻了(。来点暴论,零下十几度本质上也还行啊,感觉冷的来源主要还是室内外温差大切换不过来,还有这个北京风真的太大了,没风的话也不至于(
+12月18日
+昨天一天都不太舒服,晚上好点了去刷了个夜,今天还去了早十,感觉睡眠不足一整天人都有点降智,包括但不限于在食堂掉了耳机,出门打水忘记把杯子带走,刮坏手机膜还又把手机掉地上一次(。今天早上洗脸洗着洗着感觉有股奇怪的味道手感也很怪,睁开眼睛一看流鼻血了还被我抹了半个脸,实在有点难绷(
+又该买手机膜了,然而上次凑单的时候怎么不买,虽然但是我还是觉得水凝膜是最好的,不接受任何反驳
看了下选课除了基物 2
+必掉之外其他都没事,应该考虑的是选了这么多乱七八糟的下学期开学之后退哪个。基物换个老师就行了
+然后就要换回我大一时的基物 1
+老师了,好但是又不太好,考试前要背好多题。上次上基物 1
+还是两年前,而下次上基物 3 应该是大五的春季,也就是两年后((
pad 到了,还就买前生产力买后 Arcaea,摸了一把 mili 的曲子,普通的 ftr +8 打了个 992,感觉又菜又不算太菜的。不能再摸了概率论真要寄了(
+12月19日
+有一说一这优化怎么还没赶上我上周二的进度(,这后半学期想学深一点的话算着还挺累的,不知道考试怎么考。
+Bubeck +好书,然而这课涉及的还是太少了,寒假能不能多看点。说起来寒假如果有心情把 +multi-dimensional Brownian motion 那一章看了的话就把 Durrett +从头到尾读完了,理论上来说这书看了半年多不应该变强吗可我怎么还这么菜呢(
+问题是光搁这看书,我的科研到底什么时候才能开始,急死了((。某种程度上来说就是换点没那么容易看的书啊不是 +paper 看(,但不知道为什么就是开始不了一点,考完试去跟 ypk 谢罪吧(
+今天才发现给 iPad 9 买了个二代 apple +pencil,也退不了了,笑晕。折了点价出掉,本来想拿这个钱再买个一代,想来想去还是买了支第三方的笔,一通优惠最后 +75 拿下,傻乐了半天,消费降级.jpg(
+快期末考试了还能学到新知识,好开心哦((
+12月20日
+在手写笔到货之前果然是不可能用板子干正事的,复健了一下 Arcaea 和 +Lanota(。今天下午去取了快递,在体育课见习的时候写了点作业。不过壳和贴膜还没到,还是不大方便带出门,今天带去体育课之前紧急付了 +apple care(
+ +用 EVA +终的海报定制了个壳儿,我理想中觉得会很好看,就是不知道到货会怎么样(,根据之前印手机壳儿和痛衣的经验来说应该会还好,但想了想既然是定制那不就说明不能退了吗,不好也得用吧(
+晚上发烧了,我说这一年到底生病多少次了,受不了一点(
+怎么算都是复习不完了,那怎么办呢,干脆好心态决定女人一生.jpg 吧(
+12月21日
+睡了一天,也不大有胃口吃东西,那么下周一的概率论期末怎么办呢,急急急急急急急急急急(
+晚上稍好一点了开始想吃东西,迅速点了杯奶茶,把冰箱里存的一盒龙眼吃掉了,不知道待会还会不会大睡特睡,不睡的话干脆就多学点吧(
+12月22日
+一学期下来发现还是高统最有意思,概率论不知道是不是因为学了两遍有点想吐了所以不好玩,优化也一般,探索了一年半最后还是收敛到了选择转数时懵懂地说打算做统计的起点。听起来也很合理,毕竟一个 +Brownian motion 会以概率 \(1\) +经过原点不可数多次((
+这学期选的其他数学课多少都有点(,下学期也不打算到处玩了(真的吗那你不妨说说都选了些什么课。ODE
+这课设计得是非常好但我不大用这玩意也没精力,给水过去了,唯一一次在别的地方见到
+ODE 还是 Brownian motion 里有个和 heat equation
+相关的结论(曾经在一个夜晚把在 C
+楼刷夜的我折磨的不轻,其实非常优美但也只用一个壳子罢了。
现在我也不知道科研会往哪个方向跑了,初期还是得贴着 ypk
+他让我看啥我看啥,沾着优化和统计的边跑
+前提是鸽了一个学期之后他别不理我了。优化这课上下来觉得没啥意思
+刚刚说什么来着,但感觉和数值分析一样思想和一些技术还是很泛用的,下学期去摸个求真的组合优化看看是不是茶园这课的问题罢(
虽然现在的下学期课表和真正的课表之间还差一个忒修斯之船,但可以预见到的形状是周二早八一节
+未必会去的 培养方案内水课后去上三课时 wwc
+的课,然后第三节午睡一会去体育课,回来洗澡洗衣服吃饭再去晚课,听起来就和这学期周三一模一样((
这概率论 2 前半学期的东西随便看看复习下定理和结论差不多得了,yf +说不太会再考很精细的证明了哥们也不想再学第三遍,如果考到不会干脆那个认栽。后半学期又觉得没讲啥,虽然 +Brownian motion 里面有很多涉及到 continuous time +的东西感觉思路还是挺不一样的但是这一章东西倒也并不多,还是不知道会考啥。麻了,学数学和学考试能一样吗,后面忘了,为什么要演奏春日影!然后把 +Ito's formula 学了,反正不考,学了我赚。
+这生物老师和助教怎么都这么喜欢空口鉴 ChatGPT,上课也经常说有人在用 AI +写作业,我唯一一次全程自己写的作业(只是一个思维导图整理)被她鉴成 +ChatGPT 写的了,有没有一种可能就是我自己完全没理解这课在学什么所以抄 PPT +抄出来看着没啥逻辑呢(。随便了,又没打回来让我重做,我就当没看到评语算了(
+今晚脑子一热把托福的 2100
+交了,约了春季学期初的考位,这下不想学的时候想想交的钱应该就能学了(,给寒假找了个摸鱼的
+upper
+bound。在真正的春季考英语、一场考试两个小时、考前只有大约三个月时间可以从头开始学、听说读写都要考、写作包括
+summary
+和作文,原来我时隔三年又要考英语春考辣(,你这上海英语春考怎么是在北京考啊(我也想约个上海的考位来着啊(
真正的原因是本来没有暑研计划的大三暑假现在被迫要找一个了,而我从大一下学期打算出国开始到现在连六级都一直拖着没考,唯一的语言成绩还是四级的分数,好丢人((,再不逼自己考一个怕要等到真申请之前滑铲了(
+12月23日
+之前不知道为什么有个印象是高统 I 作业期末 3:7,今天看了一眼 syllabus +才发现是五五开,给哥们高兴坏了毕竟这作业分都是白送(x
+之前读书上的定理的时候自然地形成了一个感觉,觉得 optional stopping +theorem 的题目要靠 uniformly integrable 拉 \(L^1\) 收敛,以及我觉得 \(E|X_N|<+\infty\) & \(X_n 1_{\{n<N\}}\) UI +这个条件是最好用的,因为前者非常好算,后者有的时候会 bounded by an +integrable r.v. \(Y\)。今天又摸了一手习题才意识到其实很多都能先把 +\(N\) 换成 \(n \wedge N\) 再用 MCT,DCT 和 Fatou's lemma +夹出可积,然后哪怕只能说明序列 a.s. 收敛也可以用 MCT 和 DCT +解决问题了,常看常新,但我果然毫无分析水平.jpg(
+虽然周四上午就退烧了,但到现在食欲都不行,前两天都没怎么吃东西,白人饭为主,带油的都没怎么吃,奶茶倒是喝了两杯。其实周三晚饭就觉得没啥胃口,过了一会就开始不舒服,也或许生病本身就是肠胃不舒服导致的所以一直恢复不过来。今天起来处理了一下冰箱里的吃的,周二买的小番茄在室外放了几个钟头才取回来,还好当时就记得把冻裂的挑出来丢掉了,没发生裂了之后又放了好几天的惨案(。之前的一瓶鲜牛奶本来计划是这两天喝掉,现在过期了,急。橘子一向是放在之前留下的一个纸箱里,不知道为什么压坏了一个,丢掉之后把剩下的转移了。洗了杯子和之前没来得及洗的衣服,多少有点仪式感,感觉是我家那边有生病痊愈之后要清洗用过的物品的习惯,一般把这叫做去病气。
Arcaea 收录 felys final remix +了,紧急摸了一下,结果梯子都爬不动,随便开一把都能掉 +980。难道是前两天小摸的几把 Lanota 导致的吗(
+感觉以前认识的音游人现在基本都以打 maimai +为主了,为什么呢(。骑车去五道口就挺远的,早起排队等机子,线下运动,可能需要和陌生人交流,感觉去不了一点((
+12月24日
+明天概率论怎么办,急,复习是早就复习完了晚上还看了会高统,但怎么感觉这课复习了也和考试没太大关系尤其是最后一章的习题也偏简单(
+早点睡了,考完这门后面 12 天内还有四门呢,乐(
+12月25日
+概率论拿到卷子:第一题名词解释怎么只有 8
+分了,第二题是个挺长的定理证明默写感觉还记得但最后中间还是糊了一点,好好好背刺我是吧,第三题就看楞了,为什么是一个群上的随机游走(虽然事后证明用到的群性质仅有有限群元素都有周期,方法仅有生成群元素的表示,但看到还是眼前一黑并花了很长时间细细思考我还记得的群性质(以及我为什么抽代有
+A(?。第四题比较常规一个定理甩上去就行,第五题常规但我好像用了不是很常规的方法(我觉得正常应该是
+Markov property
+放缩,但我写了一手归纳也没觉得有什么问题),但是正常的题占分太少了完全不够用!第六题为什么要手搓一些
+Laplace's equation 套着 heat equation
+的根(虽然事后也证明想到了就没啥),第七题又是一个课上从未讲过的树上随机游走,它甚至还有
+5 分 bonus
+但显然和我没什么关系,这次不同于期中的是当时还认真想了想,这次最后一题基本没来得及看,加时的
+15 分钟用 Galton's process 把第一问胡写一通但愿猜对答案骗到分了(乐
总之考这个试需要最多的可能是心态平和不要惊慌,还有就是感觉得自学一下树上随机游走的一些方法可惜我是一点不会,我也不想会(。为什么要学抽代这个问题现在不就解决了吗,不学抽代我哪知道那个题在说什么呢(乐
那要是有人没学过抽代怎么办
连我都学过抽代难道还有人没学过吗
其实期末分数应该和期中差不多甚至可能稍好点(在做梦,他就算一分不调也能有个 +B 吧(草。Anyway +反正这课就到这了,卷子又不是我改没必要多想,乐也乐完了,输也输麻了,PTE +差不多学完了。高统怎么办,优化怎么办,急(
+12月26日
+通宵干脏活,先写了点迫真数学作业然后这周有两个实验报告要交,这建筑材料实验怎么还要算数值积分,大半夜在那 +debug +给我梦回大一,我不想再过这样的日子了啊啊啊啊啊啊啊(?(那下学期为什么还在考虑选计算概率(
+今天看到社友发的梗图才明白昨天的树上随机游走是圣诞特供(x,这下圣诞有数学相伴了(
+
晚上摸音游随便开了一首新曲,初见接近 970 +感觉还行就保存了,二见休息段瞟到曲名 Sakura Fubuki 吓了一跳以为是 +Fubini,然后鲨了(指二见 980(
+12月27日
+这两天摸音游感觉到有个小问题是右手休息段接蛇的时候经常无意识地切换到无名指或者中指,然后需要继续打 +note 的话如果没换回来就容易爆 far。简而言之就是不仅有摸鱼癖还菜(
+晚上为了拿订的酸奶跑了一趟东北门,考虑到学校东边的乌鸦密度直接从东三门出校在荷清路飚了一段,路上没什么车的时候骑车兜风真的爽,尤其这两天也不大冷(我是这么觉得的)。这学期远超其他学期的强度下(至少我以前从来没有频繁去
+C
+楼刷夜过,没上过这么多研究生课)还能保持不崩溃的一大理由可能是找到了好吃的水果和酸奶,比如我敲这段话的时候就在吃很好吃的冰激凌酸奶,每周体育课后都能吃一小盒龙眼,基本每天都有橘子吃,偶尔还有葡萄青提草莓小番茄之类在北京算得上有点金贵的水果
+反正至少很难洗。
昨天才发现我这个月答疑坊志愿者升特级了,然后看了看表格悲伤地发现其实没几个人不是特级(,而我摸鱼摸了近一年才升上。涨工资好.jpg,至少买水果酸奶都不用眨眼然后也能被这个津贴轻松覆盖就是说。
+左手刹车线之前看着就不太对劲,至少它和另一边不对称,今天彻底掉下来了。不过反正还有右手刹能用,等我有时间研究这玩意怎么修了再说吧,感觉不难(大概
+12月28日
+原来 wwc 老师也是物转统(,等一下我为什么要说也,难道我也算吗((
+今天干了啥?早上写了建筑材料实验报告一直写到下午,中间去找建筑材料助教听了一下另一个实验的具体事项,然后睡了会,然后本来想学优化,结果优化还没学作业已经写完了,我寻思着你这作业需要用到任何课上学过的知识吗,这不都是微积分和线性代数的简单应用((。晚上回来写另一个迫真数学作业,现在在看优化 +Bubeck Chapter 4,待会上床之后把板子带上床争取看一两份生物 +ppt,急急急高统怎么办明天再说吧但明早还要早起(
+这周上了好多课,大多数都是考试前的最后一节所以也休息不了了(,好累(x
+早上感觉右手手腕疼,左手手指指根也有点疼,不知道是不是打音游打得,晚上回来爬梯子打了三遍骨折光三遍病女(都是 +prs,见笑了),感觉不疼了(?
--A:你毕设导师找好了吗
-B:找好了,是丘中心的 xx(没听清
-A:我还没找呢,现在数学系是不是已经没有有名额的老师了,那咋办
-B:丘中心和统计中心都可以,跨专业也可以,但是要申请
-A:我还在犹豫做运筹还是统计,我之前学运筹那几门课完全学不明白,感觉和运筹相比还是统计简单点
-B:丘中心做应数的老师就那几个,我怀疑现在可能已经没得选了(
+建筑材料老师:色谱光谱质谱这些里面的谱指的都是扫描
+我:啥?谱?
《还是统计简单点》,差点把这学期在上高统的我吓晕(,上周一直在补落下的进度,看
-Jun Shao 每次都离昏过去只差一点,虽然也确实很有意思就是了 抖 M
-就直说。哦她学的是数学系概统的那几门限选课啊,那确实还好(
但相比之下运筹难在哪了(不是
今天把上次那个二合一的高统作业写完了,进度也赶得差不多了(,binomial -distribution 的二三四阶矩加权和算得我天昏地暗还没有答案,最后 \(Var T\) 比 C-R lower bound -严格小而且完全看不出来哪儿错了(,希望期末没事((
-问题是 C-R lower bound 和 Delta method 算出来的 amse
-一样大,应该就没问题啊,那错的还是 \(VarT\)
-呗,问题是我没觉得错啊,助教看着想扣几分扣几分吧((
#每日学数学学得(
+12月29日
+本来今天打算的是学高统,结果写了一天优化的
+cheatsheet,又在闭区间套法学习(。本来很急优化这个云得不行的课要看多少东西,现在感恩
+Bubeck
+思路挺清楚的,感觉等下次发了最后一课的讲义之后再看一个晚上就能弄完了。那我在
+Boyd 那一块 Newton method 缺的营养谁给我补啊?
早晨起来顿悟,除了之前写的那个优化作业之后还要用 LaTeX
+誊写一遍,实验报告都写完了,那我还带着电脑干啥。所以对我来说电脑是一块必须竖着放但是可以写
+LaTeX (偶尔也可以写
+R)的屏幕兼搜索引擎,平板是一块可以平放在桌上当书看还可以写写画画的屏幕,而我
+95%
+以上的工作还是用纸笔完成的(虽然是相当原始的生活状态但感觉真的已经够了,甚至现在想想确实不需要
+Apple pencil,平替的笔就算写字不好用能拿来圈画一下重点或者标记一下 PPT
+上看过的部分就足够了(
那挺好的,后面一直到考试周结束非必要不带电脑出门了(草(#每日学数学学得(什么这也学数学学得(
+后面几天也没啥别的事了,什么那美好的仗我已经打过了,当行的路已经行尽了,所信的道也已经守住了,从此以后有公义的冠冕为我存留,希望高统没事。不知道两个半小时考五道题一道
+10 分直接计入总评是什么水平,那哥们至少得做个四道
+然后根据四舍五入没满分就是零分(草,希望真能没事。优化更不知道怎么考,至于生物其实
+PPT 已经当睡前读物溜了一圈了但啥都记不住啊(
12月30日
+很急。
+12月31日
+前天买的阳光玫瑰不好吃,皮很厚,不过这个季节还想吃到好吃的青提是否是我在做梦(
+今天早上八点多就起来了,打开很久没听的 One Last Kiss +开始复习高统,假装这一年我的生活都如此规律、尽在掌握,后来一想其实这个装模作样的过程才是精准概括了我的生活(
+发一张我本年度最喜欢的猫图,尽管这是前几天才看到的,最近只要有人和我说话我都会发一张过去。不过 +2021 年我最喜欢的一张自拍还是 12.31 +拍的,感觉非常正常(
+
--Brownian Motion -的定义看起来非常简单,但其实还需要验证是不是给出这三个条件就能确定唯一的一个过程,还有三个条件是不是冗余。我读博士的时候有个老师讲过一个故事,系里曾经有个搞代数的研究生做了一个很复杂的东西出来,答辩的时候委员会问了个很简单的问题,就是这个东西存不存在,他当时没回答出来,回去想了想确实不存在,就延毕重做了(
+在我国气象观测中,每天 20 +点是划分新旧两天气象数据的时间节点,所以对广大气象爱好者来说,气象意义上的 +2024 年此刻已经到来。
草(
-连一刻都没有为概率论 2 -写不完的作业和寄掉的期中哀悼,立刻赶到现场的是上周五的建筑材料实验报告,这周日要做的建筑材料课程实验,这周五要做的建筑材料实验,上周布置的生物作业,还有周四建筑材料研讨课要做的 -pre!
-晚上又遇到了两周前的周一在同一个位置上看 GTM -的男生,这次看到了封面,是 GTM 274,和我想的一样(
-感觉应该世界很小,很可能是吴昊的学生,但反正也不敢问(
-11月28日
-睡前躺着看了下今年的日本杯,不用想也是春秋分的散步大胜(。不说秋三冠怎么样了,求你了再跑一年吧别直接去当种马,我什么都会做的(
建筑材料研讨课的队友说 nature -上有一篇文章比较合适可以去看一下,我在心里默念:内恰上有一篇文章比较合适(
-越想越气,我放着讨论班的论文没看,搁这读建筑材料研讨课的论文,建筑材料实验报告还得随便引几篇,建筑材料的实验还有个这课的老师的论文没看要学一下怎么处理数据,生物作业也是文献调研题,看又看不懂,还就那个离谱(
-今天下午骑车的时候把电脑屏幕摔(?)碎了,在教室掏出来的时候大受震撼还以为寄没了,再仔细一看屏幕就碎了挺小一部分,看起来哈人只是因为顶盖变形比较严重。测了下主板键盘什么的都没啥问题,心情好了很多。修是不可能官方修的,只能自己买个盖买个屏幕换一换这样子,-300,本不富裕的家庭雪上加霜(
-
它正好裂在 已经战损的
-二号机贴纸这个地方,想想二号机的战损程度突然感觉好像就不应该贴这个(,遂下单初号机金属贴,只要驾驶员自闭就很耐造(
说实话这个 A 盖翘起来之后反而方便拆下来了,我赢(,B -盖边缘有一点轻微的变形,感觉拼装的时候或许会有小问题,暂且拿钳子掰了一下感觉应该还好,不至于再花几十块钱重新买一个。
-下单配件之后发现买屏幕的那家店在商品详情页写的是“不难,女学生,新手都能自己换好”,销量 -2 万 +,现在真的是 2023 -年吗?退货换了一家,点了个举报,虽然大概也没有什么用,除此之外能作为反抗的选项就是自证了吧,我拒绝。
-出于好奇查了下官修的价钱,感觉自己动手的话还是赚麻了又不觉得 300 -贵了((。后来想起来还可以带着配件去科服修,但也有点想自己拆着玩(?),到货再说吧。
-11月29日
-上午和中午认真听了会生物课
-然后四道雨课堂题错了三道,充分说明我是真的学不了这玩意,然后
-在队友完全失踪的状态下 把建筑材料 pre PPT
-做了,体育课前把建筑材料实验的实验报告写完了。今天是认真学专业课的一天(迫真
晚上本来想学一下今天的高统,然后想想作业也不是很急还是算了,更急的是概率论(,但不知道为什么不是很想学这个东西,期中裂开之后心态上有点摆了
-这不行吧。结果喉咙越来越痛直接睡了,原因不明但除了感冒了之外还能是什么呢,吃阿奇霉素.jpg
回寝室一看之前买的药都过期了,心态爆炸(
-11月30日
-喉咙还是好痛,现在是连带着头也好痛,人有事(。今天除了在睡就是在难受得睡不着,一天做了四道概率论,急死了(。这个月还只有 -30 天,更急了((
-吃西瓜霜的时候看了眼成分表,辅料是蔗糖,那你不标一下营养成分表告诉我每
-100g 有多少糖我哪知道要吃多少啊
马娘,评,端(
--
周一看了预告之后我还在想,看起来是日常贴贴回,这还能做烂了?
-看完:到底是我有问题还是 KAI -社有问题,感觉有点理解不了制作组的精神状态(
-早晨一起床突然说要去 随机公交挑战
-旅游,那光钻要是没被吵醒的话你就自己一个人去了呗,思考了一下和朋友之前出游的情况感觉到处晃悠还挺能理解的,这随机公交挑战还给我看出几分亲切感(。然后这个复刻光钻突发放狠话的二度离婚是怎么回事呢(,镜头一转就开始比赛了又是怎么回事呢,有一种比赛前的一回合选择了外出所以半个月都在摸回来突然比赛也能赢的错觉
上次北黑和光钻冲线的时候中间沉默而且没有特效的是黄金伶人(没版权)我还能理解,这次中间是高尚骏逸啊,怎么会是呢(。但是远景过弯的时候高尚骏逸的腿真的好可爱啊,好像觉醒
-xp 了
赛后为什么又是无视了第二名开始和第三的光钻贴呢,按理说第二名难道不是很重要吗,一边压制光钻一边逼迫北黑,换句话说光钻连高尚骏逸都跑不过还说没超过北黑什么的真的没问题吗。比赛中途也一直无视,很难想象之后要怎么刻画一生一次的末脚,要么就别写了,不然骏逸还要惨遭拥有一个单人回
居然有樱花桂冠,好评,但我总感觉突然插宣传片莫名其妙的,难道是对第三季的刻板印象导致的(
你看看第二季帝宝麦昆贴都是抱在一起互相鼓励,为什么小北和光钻贴就只有握手,真不熟(
其实我还是疑惑光钻冲线的时候这个闪回是什么意思呢,一直带着自己去看前方各种风景的是小北,ok -fine,但上次不是你赢了吗(。怎么不是想北黑这段时间以来相比自己进步了多少(然而我完全感觉不到!)而是在想这个(
-感觉蜜汁演出好多,不知道慢动作入闸是在干啥,小北比赛中间突然开领域(确信)我还以为给安排了点不存在的骨折戏份(,结果就这(。念叨凯旋门赏念叨到现在终于给了大鸣大放三个镜头,求你了下集别又把人家给忘了(。高尚骏逸冲刺的时候终于有台词了,所以下一话会是日本杯吗,那我大鸣大放呢((
-不过贴贴确实好看,特别好。
-这番真的还有必要继续追下去吗,真的有必要吗(
]]>二十岁老猫过冬.jpg
+12月1日
-喉咙好点了,头还是嗡嗡的,急(
-做完非常后现代的建筑材料实验出来之后在文北楼旁边的垃圾桶看到个熟悉的东西,第一反应这不会是个混凝土块吧然后狠狠地嘲笑了自己做完实验看什么都像混凝土。走近一看怎么这个断面怎么这么标准的条状断裂(,怎么正面还有实验条件和批号的标注,还真是压碎的混凝土上岗再就业(
-
12月2日
-省流:今天修了一天电脑,好像学到许多(
-中午把配件从快递点取回来之后就开始动手拆电脑了,我寻思着不就是换个屏换个盖能有多难,结果直接那个错过了讨论班(。拆 -D -盖拔电源我轻车熟路,拆转轴拔屏线信号线重拳出击,拆转轴盖...诶怎么拆不下来,看了下发现是和 -B 盖连在一起的不用拆,学多(。正好摔的时候 A 盖和 B -盖已经有一条缝了还不用努力抠,只是这个 B -盖用双面胶粘在屏幕上实在有点费手(,拆的时候把旧屏又压碎了一点还把手划了,倒也都不是问题。然后是喜闻乐见的撕易拉胶,把屏幕拿下来一看,怎么和我想象的不太一样,A -盖后面两根线粘的死死的,其中一根焊在下面的结构上然后贴在后盖上,扒拉了一下撕不下来,草(
-仔细研究了下感觉不太清楚金属胶贴下面是只有胶还是有走线(但最后知道就只是胶,撕不下来的结构也不敢太大力,于是把四部分电脑收起来等晚上去科服问一下,打开旧 -surface 开始用 Overleaf -写作业强装淡定.jpg,然后很疑惑五六年前为什么会买这么难用的电脑(
-七点左右到 C -楼把四块电脑一块新屏一块新盖排成一排(,感觉对面的表情逐渐疑惑了起来(,就承认了是拆到一半感觉超过我能力了这样子(。最后是用热风枪把所有东西拆掉又贴到新盖上的,学到许多我也想买一个(不是
---A:我再研究一下你这个盖上的结构,旁边这块白的是啥啊
-我:这是我没撕干净的易拉胶(
-
--A:你这拆的还挺好,要不要试试我们的招新面试
-我:我瞎拆的(,而且我还在答疑坊打着一份工呢(
-B:那算了,我们时薪没答疑坊高,还累(举热风枪
-
--A:所以为啥要单独买个屏买个壳呢,这样拆一遍壳很费劲的(
-我:对不起(
-B:所以咋不重买一个呢
-我:对不起(,但我都用惠普战 66 了不就说明没钱吗(
-C:别说人家啦,拆好带过来还没拆出啥问题挺好的了,不然还得拆一遍,费手
-我:对不起(
-A:他是在夸你
-我:对不起(
-
顺便见到了人手一套的电动螺丝刀,寝室里 32
-头的那一套瞬间就不香了
12月3日
-这周的优化作业怎么这么抽象啊(,你谁(。其实我的意思是这周的优化作业怎么这么具体,虽然它一直都很具体但这周有两道题写起来好困难
牛顿法数值分析的时候已经学了个大全套了,看 zjz
-这个讲义感觉也太云了,这学期为什么要上这课呢。
今晚把周一晚上要交的作业写了,明天把周二下午要交的作业写了,后天把周三晚上要交的作业写了。我感觉我一天天的都挺忙的怎么还卡得这么紧呢(,原来是一直在看最近没布置作业的数理统计啊(
-12月4日
-初号机贴纸怎么还没到,急急急(。突然意识到之前的问题所在了,贴了二号机的电脑怎么能放在朗枪的包里(
-上周被喉咙痛折磨得不轻,这周感觉右半边腰特别疼,稍微一动就感觉像闪着了一样,活着真累。猫猫活到二十岁已经很不容易了,感觉快要不行了
下学期果然是林乾开高统
-2,杨朋昆开高维概率,但我寻思着统计中心就没几门博士生课你俩为什么要都放在
-4-2 开课,急了。再一看实分析也有一节
-4-2,感觉要冲突选课。再再一看发现复分析和组合优化也创了,感觉还要冲突选课,被冲突的当然是复分析就是了。往好处想下学期课表会显得比较空,因为都覆盖了
别的没有啥特别想上的课了,摸了个社科课组,再见了,所有的通识选修课(。体育打算选个壁球玩玩,这学期毽球没有上学期有意思,不想再踢了。必限就一两门,在考虑要不要上个基物
-2
-防止被退学,之后如果不每个学期浅浅学点物理的话我感觉我五年也毕不了业(
12月5日
-算了下感觉下学期必修就一门基物 2 -一门什么绿色交通系统就行,现在在考虑的是我大四春季有一些连着暑假一起春研暑研的宏伟计划(,所以为了不妨碍大五毕设开题,春季还是不能剩下太多课。大四上修量子力学和工程力学基础,大五上修工程力学 -CE,结构力学和流体力学然后随便它们烂成什么样(,最后一学期把工程地质和基物 -3 解决一下就行,还是能有条不紊地毕业捏(??
-我以前一直以为中厅是没有暖气的所以特别冷,今天发现就在饮水机旁边,摸了一下是冰凉的,有没有其他紫荆住户能告诉我这是不是正常现象((。说实话这真的合规吗,不是供暖室内低于
-18 度都不行吗(
本来想给核动力笔记本贴个电力充足,想了想还是没电的初号机更强一些,就给它再加强了一下(
-
12月6日
-今天穿北黑痛衣跑了 1500,英里距离适性 C -果然还是不够用,但立定跳远变强了非常多,感谢室友教我正确的姿势(
-下略。
-12月7日
-昨天跑了 -1500,今天就是一个人大困特困,腰背腿大痛特痛,于是大睡特睡,连高统 PPT -都没看完(
-12月8日
-北京的松鹤楼和上海的一样好吃,感觉稍微有点安慰(
-晚上在看运筹的决策分析,看了几页感觉定义有点像 decision -theory,还看到了简化版的 Bayes -rule,结果画风一转变成需要按固定格式写的小学数学应用题,我到底在期待什么(
-感觉有点小急,作业好多,但是又不是特别急,属于一个轻轻摸一下也能做完的情况(?
-12月9日
-处理了一些约等于在摸的作业(真的吗写高统作业不是次次都在痛苦嚎叫吗),然后对着优化不会做的那两道题继续阴暗爬行,然后
-yoasobi,然后睡觉(
听说 yyl -被非升即走了,这英文高代选这么有意思,我答疑还做了不少他们的作业题,以后就没了(悲
-晚上在紫荆吃了好吃的鸭腿饭,要不寒假回家试试复现(怎么这也能复现,拿到了前两天买的好喝的酸奶,室友的品位还是高(
12月10日
-学 Blumenthal's 0-1 law 的时候心里默念的是 -Duramente((,这听起来不是挺像的吗(
-好消息:十六周周三不用连考三门期末了!
-坏消息:因为高统提前到了前一天晚上考(
-感觉考完高统之后要回去紧急背生物,考完生物回寝室睡觉,然后下午稍微看一眼运筹就可以去考了,都不是问题,复习这些还不如早点开始写优化的 -cheatsheet(。但确实有个好消息是不用担心睡得不好影响考试了((
-晚上五分钟遇到了三只不同花色的猫猫,回去得稍晚了一点,骑车的时候感觉手比平时冷很多,然后就感觉到冷冷的冰粒子,啊不是,雪花拍在我脸上(
-一些和交大转数群友(?但确实是)的暴论:
---H:
-你猜猜看我的数分助教是做什么的
-我:
-他既然觉得 Lebesgue 积分和 Riemann 积分不一样
-那先排除概率 再排除分析 我感觉统计也不至于(
-是代数吗 是不是本科不必修实变或者忘完了
-但我觉得这是个很基础很优美的结论 总应该知道的吧
-总觉得代数都是聪明人(刻板印象.jpg 是不是也不至于啊(x
-H:
-不是
-三个助教是同一个课题组的 做 PDE
-我:
-草 dbq 我想起来那句
-PDE 养活了不知道多少无能的数学家
-没有说他们的意思 只是无端联想(
-H:
-草
-礼拜五我问我那个助教是不是做分析的的时候
-感觉他稍微有点蚌埠住
-
12月11日
-半夜两点跑到楼下在雪地里用一次性筷子默写了《雪赋》的最后一段,精神状态非常的好啊。
-
我相信这图上是看不清的但是说不定放上原文就能对起来了
--白羽虽白,质以轻兮,白玉虽白,空守贞兮。未若兹雪,因时兴灭。玄阴凝不昧其洁,太阳不固其节。节岂我名,洁岂我贞。凭云升降,从风飘零。值物赋象,任地班形。素因遇立,污随染成。纵心皓然,何虑何营?
-
今晚在作业里写了一个
-\[\{T_A \leq t\} = \cap_{n=1}^{\infty} -\cup _{s \in \mathbb Q \cap (0,t)} \cup_{i=1}^\infty \cup_{x \in \mathbb -Q^d \cap A_i} \{B(s) \in B_d(x,\frac{1}{n})\} \in \mathcal -F_t\]
-其实我只是在证 Brownian motion 中一个 \(F_\sigma\) set 的 hitting time 一定是 -stopping time(。能把 trivial -的东西写得这么丑陋和唬人,似乎觉醒了一点点灌水的天赋(
-12月12日
-明天暴雪橙色预警,但是我有四节课(疑惑
-下午写优化作业,因为认为 \(t(t+1)\) -在 \(t=0\) 时取值为 \(1\) -而疑惑了至少二十分钟。晚上在答疑坊值班教室友写概率论作业,五道剥蒜题给了我到现在都没有恢复的心理阴影(
-晚上回来又在赶之前在答疑坊接的一个这周要交的主人的任务,想了想这个月几乎就没多少津贴,还是干一下吧。
-12月13日
-下午在寝室和综体之间走了一个来回,晚上又在寝室和法图之间走了一个来回,还上了体育课,今天的运动量就到这了(。课好难,好冷,好困,好累,这学期怎么还不结束,这紫荆宿舍怎么还没塌掉,麻了(
-晚上在看高统的讲义,感到深深的疑惑,wwc -平时都在抄书这次怎么把书扬了整这么难,想了想好像之前也很难但好像学会了之后就会变简单(,希望吧。但是优化学起来完全不是这个感觉,学一点忘一点,也不知道是这课的问题还是我的问题。
-一到 asymptotic behavior
-就开始大力分析了,感觉自己好菜,以后谁再说统计简单我跟谁急
早上有点睡多了,晚上走回寝室的路上想了想在打烊之前拐去七港九买了杯奶茶,后来又来了几个人在纠结晚上再喝一杯会不会睡不着,要不要换成果茶。店员说已经没有奶茶了,我这杯是最后一杯,他们说太好了(。感觉我也赚了,大家都满意的世界达成了(
-12月14日
-今天研究了半个下午怎么配混凝土的各个组分(,感觉本质上是个有八个参数的非线性规划问题,虽然是有解的但是
-feasible set
-不是很大,解的可解释性()也都不太好。但如果想得到解释性好的解的话,可以稍微牺牲其中一个
-constraint,所以除了规划之外还可以整个 weighted cost function
-把它变成优化问题,乐死了(学数学学得
本来想参考下同学的(迫真,算着算着越来越不对劲,仔细一看他们公式代错了,草(
-因为没法解释其实也不太敢(?)和队友解释我这些迷思(,再加上这个活拆成六个人的份本来就不合理,就一个人把六个人的活给干了,至于干得怎么样还得看明天做出来的结果(,就图一乐吧。这玩意 -16 周有个 pre,到时候就心安理得地推掉给他们就好了,哥们 16 -周考四门课,真没时间陪你们玩泥巴了(
-今晚似乎是最后一个熄灯的晚上了,回去收拾一下直奔 C -楼把这个计算书敲完,这寝室真待不下去了,断电之后冻死(
-昨晚梦到在上讨论班(为什么,一个同学在台上讲他论文里证的一个不等式,另一个同学问他你的 -lower bound -既然可以达到那算什么不等式,不是可以相等的吗?还有一个同学问为什么常用的不等式里的符号都不是 -\(\neq\),这算什么不等式(。然后吓醒了,发现自己在床上而不是在讨论班坐牢,非常开心(
-所以这周六到底是考六级还是去讨论班呢,要不周六早上起床再说吧(
-12月15日
-探索了下 C 楼的刷夜,其实体感还挺好的,以后寝室太冷 / 太吵 / -太安静(?)可以经常来。但我这次居然是在刷夜写混凝土配合比计算书,乐(。一边写又一边抄文献,我知道做这个事情毫无意义,但昨天看到两个队友算错的数之后就稍微有点不舒服然后开始单干了(。其实我觉得我要求真的不高,能把公式都用对,满足所有的 -constraints,在此之上可解释性的要求也只有一两条,结果长得和大多数文献或者专利里差不多就行了,这不都是很合理和基本的想法(?
-然后今天做出来结果还挺好的,虽然是绝对的烂,但是相对的好,那就挺好的了(?
-看选课,发现下学期要选的其实没啥课,高统复分析组合优化
-还有基物 而已(。到处乱搜的时候看到求真有个计算概率,讲 MCMC
-之类的东西,用的书以 applied 开头(,稍微有点心动。再一看作业 50% 上机
-50%,更心动了,现在在我眼里写上机作业竟比考试更轻松(
茶园还有个因果推断前沿的 2 -学分的课,但感觉在方向上有点太细分了不好说有多大用处。
-早上起来看到 CoCo
-和恋与的联名,虽然早就不玩了但爷青结(,而且这好便宜,四舍五入一块亚克力两张拍立得两个杯套一个保温袋
-还送两杯糖水 才三十,遂点。不过前夫哥的那款 糖水
-奶茶不好喝,有一种玫瑰香精滞销于是捆了烫男人的谷子一起出售的感觉(
12月16日
-前几天一直走路,昨晚才又开始骑车。其实唯一的原因就是我只有一件羽绒服还是浅色的,万一真摔在泥水里就没衣服穿了((
-今天还是选了讨论班,第一次有我能全程听懂的,真不错。但说实话最后几个老师的锐评以及中间的提问和讨论才是很精髓,不管从找了乐子还是学到许多的角度来说都感觉在这个天来回骑了八公里挺值的((
-晚上回来去答疑坊值班,给室友讲概率论,算得我天昏地暗,结束之后换个教室爆睡,睡得正暖和的时候教室关门了,走到外面真冻麻了(。来点暴论,零下十几度本质上也还行啊,感觉冷的来源主要还是室内外温差大切换不过来,还有这个北京风真的太大了,没风的话也不至于(
-12月18日
-昨天一天都不太舒服,晚上好点了去刷了个夜,今天还去了早十,感觉睡眠不足一整天人都有点降智,包括但不限于在食堂掉了耳机,出门打水忘记把杯子带走,刮坏手机膜还又把手机掉地上一次(。今天早上洗脸洗着洗着感觉有股奇怪的味道手感也很怪,睁开眼睛一看流鼻血了还被我抹了半个脸,实在有点难绷(
-又该买手机膜了,然而上次凑单的时候怎么不买,虽然但是我还是觉得水凝膜是最好的,不接受任何反驳
看了下选课除了基物 2
-必掉之外其他都没事,应该考虑的是选了这么多乱七八糟的下学期开学之后退哪个。基物换个老师就行了
-然后就要换回我大一时的基物 1
-老师了,好但是又不太好,考试前要背好多题。上次上基物 1
-还是两年前,而下次上基物 3 应该是大五的春季,也就是两年后((
pad 到了,还就买前生产力买后 Arcaea,摸了一把 mili 的曲子,普通的 ftr -8 打了个 992,感觉又菜又不算太菜的。不能再摸了概率论真要寄了(
-12月19日
-有一说一这优化怎么还没赶上我上周二的进度(,这后半学期想学深一点的话算着还挺累的,不知道考试怎么考。
-Bubeck -好书,然而这课涉及的还是太少了,寒假能不能多看点。说起来寒假如果有心情把 -multi-dimensional Brownian motion 那一章看了的话就把 Durrett -从头到尾读完了,理论上来说这书看了半年多不应该变强吗可我怎么还这么菜呢(
-问题是光搁这看书,我的科研到底什么时候才能开始,急死了((。某种程度上来说就是换点没那么容易看的书啊不是 -paper 看(,但不知道为什么就是开始不了一点,考完试去跟 ypk 谢罪吧(
-今天才发现给 iPad 9 买了个二代 apple -pencil,也退不了了,笑晕。折了点价出掉,本来想拿这个钱再买个一代,想来想去还是买了支第三方的笔,一通优惠最后 -75 拿下,傻乐了半天,消费降级.jpg(
-快期末考试了还能学到新知识,好开心哦((
-12月20日
-在手写笔到货之前果然是不可能用板子干正事的,复健了一下 Arcaea 和 -Lanota(。今天下午去取了快递,在体育课见习的时候写了点作业。不过壳和贴膜还没到,还是不大方便带出门,今天带去体育课之前紧急付了 -apple care(
- -用 EVA -终的海报定制了个壳儿,我理想中觉得会很好看,就是不知道到货会怎么样(,根据之前印手机壳儿和痛衣的经验来说应该会还好,但想了想既然是定制那不就说明不能退了吗,不好也得用吧(
-晚上发烧了,我说这一年到底生病多少次了,受不了一点(
-怎么算都是复习不完了,那怎么办呢,干脆好心态决定女人一生.jpg 吧(
-12月21日
-睡了一天,也不大有胃口吃东西,那么下周一的概率论期末怎么办呢,急急急急急急急急急急(
-晚上稍好一点了开始想吃东西,迅速点了杯奶茶,把冰箱里存的一盒龙眼吃掉了,不知道待会还会不会大睡特睡,不睡的话干脆就多学点吧(
-12月22日
-一学期下来发现还是高统最有意思,概率论不知道是不是因为学了两遍有点想吐了所以不好玩,优化也一般,探索了一年半最后还是收敛到了选择转数时懵懂地说打算做统计的起点。听起来也很合理,毕竟一个 -Brownian motion 会以概率 \(1\) -经过原点不可数多次((
-这学期选的其他数学课多少都有点(,下学期也不打算到处玩了(真的吗那你不妨说说都选了些什么课。ODE
-这课设计得是非常好但我不大用这玩意也没精力,给水过去了,唯一一次在别的地方见到
-ODE 还是 Brownian motion 里有个和 heat equation
-相关的结论(曾经在一个夜晚把在 C
-楼刷夜的我折磨的不轻,其实非常优美但也只用一个壳子罢了。
现在我也不知道科研会往哪个方向跑了,初期还是得贴着 ypk
-他让我看啥我看啥,沾着优化和统计的边跑
-前提是鸽了一个学期之后他别不理我了。优化这课上下来觉得没啥意思
-刚刚说什么来着,但感觉和数值分析一样思想和一些技术还是很泛用的,下学期去摸个求真的组合优化看看是不是茶园这课的问题罢(
虽然现在的下学期课表和真正的课表之间还差一个忒修斯之船,但可以预见到的形状是周二早八一节
-未必会去的 培养方案内水课后去上三课时 wwc
-的课,然后第三节午睡一会去体育课,回来洗澡洗衣服吃饭再去晚课,听起来就和这学期周三一模一样((
这概率论 2 前半学期的东西随便看看复习下定理和结论差不多得了,yf -说不太会再考很精细的证明了哥们也不想再学第三遍,如果考到不会干脆那个认栽。后半学期又觉得没讲啥,虽然 -Brownian motion 里面有很多涉及到 continuous time -的东西感觉思路还是挺不一样的但是这一章东西倒也并不多,还是不知道会考啥。麻了,学数学和学考试能一样吗,后面忘了,为什么要演奏春日影!然后把 -Ito's formula 学了,反正不考,学了我赚。
-这生物老师和助教怎么都这么喜欢空口鉴 ChatGPT,上课也经常说有人在用 AI -写作业,我唯一一次全程自己写的作业(只是一个思维导图整理)被她鉴成 -ChatGPT 写的了,有没有一种可能就是我自己完全没理解这课在学什么所以抄 PPT -抄出来看着没啥逻辑呢(。随便了,又没打回来让我重做,我就当没看到评语算了(
-今晚脑子一热把托福的 2100
-交了,约了春季学期初的考位,这下不想学的时候想想交的钱应该就能学了(,给寒假找了个摸鱼的
-upper
-bound。在真正的春季考英语、一场考试两个小时、考前只有大约三个月时间可以从头开始学、听说读写都要考、写作包括
-summary
-和作文,原来我时隔三年又要考英语春考辣(,你这上海英语春考怎么是在北京考啊(我也想约个上海的考位来着啊(
真正的原因是本来没有暑研计划的大三暑假现在被迫要找一个了,而我从大一下学期打算出国开始到现在连六级都一直拖着没考,唯一的语言成绩还是四级的分数,好丢人((,再不逼自己考一个怕要等到真申请之前滑铲了(
-12月23日
-之前不知道为什么有个印象是高统 I 作业期末 3:7,今天看了一眼 syllabus -才发现是五五开,给哥们高兴坏了毕竟这作业分都是白送(x
-之前读书上的定理的时候自然地形成了一个感觉,觉得 optional stopping -theorem 的题目要靠 uniformly integrable 拉 \(L^1\) 收敛,以及我觉得 \(E|X_N|<+\infty\) & \(X_n 1_{\{n<N\}}\) UI -这个条件是最好用的,因为前者非常好算,后者有的时候会 bounded by an -integrable r.v. \(Y\)。今天又摸了一手习题才意识到其实很多都能先把 -\(N\) 换成 \(n \wedge N\) 再用 MCT,DCT 和 Fatou's lemma -夹出可积,然后哪怕只能说明序列 a.s. 收敛也可以用 MCT 和 DCT -解决问题了,常看常新,但我果然毫无分析水平.jpg(
-虽然周四上午就退烧了,但到现在食欲都不行,前两天都没怎么吃东西,白人饭为主,带油的都没怎么吃,奶茶倒是喝了两杯。其实周三晚饭就觉得没啥胃口,过了一会就开始不舒服,也或许生病本身就是肠胃不舒服导致的所以一直恢复不过来。今天起来处理了一下冰箱里的吃的,周二买的小番茄在室外放了几个钟头才取回来,还好当时就记得把冻裂的挑出来丢掉了,没发生裂了之后又放了好几天的惨案(。之前的一瓶鲜牛奶本来计划是这两天喝掉,现在过期了,急。橘子一向是放在之前留下的一个纸箱里,不知道为什么压坏了一个,丢掉之后把剩下的转移了。洗了杯子和之前没来得及洗的衣服,多少有点仪式感,感觉是我家那边有生病痊愈之后要清洗用过的物品的习惯,一般把这叫做去病气。
Arcaea 收录 felys final remix -了,紧急摸了一下,结果梯子都爬不动,随便开一把都能掉 -980。难道是前两天小摸的几把 Lanota 导致的吗(
-感觉以前认识的音游人现在基本都以打 maimai -为主了,为什么呢(。骑车去五道口就挺远的,早起排队等机子,线下运动,可能需要和陌生人交流,感觉去不了一点((
-12月24日
-明天概率论怎么办,急,复习是早就复习完了晚上还看了会高统,但怎么感觉这课复习了也和考试没太大关系尤其是最后一章的习题也偏简单(
-早点睡了,考完这门后面 12 天内还有四门呢,乐(
-12月25日
-概率论拿到卷子:第一题名词解释怎么只有 8
-分了,第二题是个挺长的定理证明默写感觉还记得但最后中间还是糊了一点,好好好背刺我是吧,第三题就看楞了,为什么是一个群上的随机游走(虽然事后证明用到的群性质仅有有限群元素都有周期,方法仅有生成群元素的表示,但看到还是眼前一黑并花了很长时间细细思考我还记得的群性质(以及我为什么抽代有
-A(?。第四题比较常规一个定理甩上去就行,第五题常规但我好像用了不是很常规的方法(我觉得正常应该是
-Markov property
-放缩,但我写了一手归纳也没觉得有什么问题),但是正常的题占分太少了完全不够用!第六题为什么要手搓一些
-Laplace's equation 套着 heat equation
-的根(虽然事后也证明想到了就没啥),第七题又是一个课上从未讲过的树上随机游走,它甚至还有
-5 分 bonus
-但显然和我没什么关系,这次不同于期中的是当时还认真想了想,这次最后一题基本没来得及看,加时的
-15 分钟用 Galton's process 把第一问胡写一通但愿猜对答案骗到分了(乐
总之考这个试需要最多的可能是心态平和不要惊慌,还有就是感觉得自学一下树上随机游走的一些方法可惜我是一点不会,我也不想会(。为什么要学抽代这个问题现在不就解决了吗,不学抽代我哪知道那个题在说什么呢(乐
那要是有人没学过抽代怎么办
连我都学过抽代难道还有人没学过吗
其实期末分数应该和期中差不多甚至可能稍好点(在做梦,他就算一分不调也能有个 -B 吧(草。Anyway -反正这课就到这了,卷子又不是我改没必要多想,乐也乐完了,输也输麻了,PTE -差不多学完了。高统怎么办,优化怎么办,急(
-12月26日
-通宵干脏活,先写了点迫真数学作业然后这周有两个实验报告要交,这建筑材料实验怎么还要算数值积分,大半夜在那 -debug -给我梦回大一,我不想再过这样的日子了啊啊啊啊啊啊啊(?(那下学期为什么还在考虑选计算概率(
-今天看到社友发的梗图才明白昨天的树上随机游走是圣诞特供(x,这下圣诞有数学相伴了(
-
晚上摸音游随便开了一首新曲,初见接近 970 -感觉还行就保存了,二见休息段瞟到曲名 Sakura Fubuki 吓了一跳以为是 -Fubini,然后鲨了(指二见 980(
-12月27日
-这两天摸音游感觉到有个小问题是右手休息段接蛇的时候经常无意识地切换到无名指或者中指,然后需要继续打 -note 的话如果没换回来就容易爆 far。简而言之就是不仅有摸鱼癖还菜(
-晚上为了拿订的酸奶跑了一趟东北门,考虑到学校东边的乌鸦密度直接从东三门出校在荷清路飚了一段,路上没什么车的时候骑车兜风真的爽,尤其这两天也不大冷(我是这么觉得的)。这学期远超其他学期的强度下(至少我以前从来没有频繁去
-C
-楼刷夜过,没上过这么多研究生课)还能保持不崩溃的一大理由可能是找到了好吃的水果和酸奶,比如我敲这段话的时候就在吃很好吃的冰激凌酸奶,每周体育课后都能吃一小盒龙眼,基本每天都有橘子吃,偶尔还有葡萄青提草莓小番茄之类在北京算得上有点金贵的水果
-反正至少很难洗。
昨天才发现我这个月答疑坊志愿者升特级了,然后看了看表格悲伤地发现其实没几个人不是特级(,而我摸鱼摸了近一年才升上。涨工资好.jpg,至少买水果酸奶都不用眨眼然后也能被这个津贴轻松覆盖就是说。
-左手刹车线之前看着就不太对劲,至少它和另一边不对称,今天彻底掉下来了。不过反正还有右手刹能用,等我有时间研究这玩意怎么修了再说吧,感觉不难(大概
-12月28日
-原来 wwc 老师也是物转统(,等一下我为什么要说也,难道我也算吗((
-今天干了啥?早上写了建筑材料实验报告一直写到下午,中间去找建筑材料助教听了一下另一个实验的具体事项,然后睡了会,然后本来想学优化,结果优化还没学作业已经写完了,我寻思着你这作业需要用到任何课上学过的知识吗,这不都是微积分和线性代数的简单应用((。晚上回来写另一个迫真数学作业,现在在看优化 -Bubeck Chapter 4,待会上床之后把板子带上床争取看一两份生物 -ppt,急急急高统怎么办明天再说吧但明早还要早起(
-这周上了好多课,大多数都是考试前的最后一节所以也休息不了了(,好累(x
-早上感觉右手手腕疼,左手手指指根也有点疼,不知道是不是打音游打得,晚上回来爬梯子打了三遍骨折光三遍病女(都是 -prs,见笑了),感觉不疼了(?
---建筑材料老师:色谱光谱质谱这些里面的谱指的都是扫描
-我:啥?谱?
-
#每日学数学学得(
-12月29日
-本来今天打算的是学高统,结果写了一天优化的
-cheatsheet,又在闭区间套法学习(。本来很急优化这个云得不行的课要看多少东西,现在感恩
-Bubeck
-思路挺清楚的,感觉等下次发了最后一课的讲义之后再看一个晚上就能弄完了。那我在
-Boyd 那一块 Newton method 缺的营养谁给我补啊?
早晨起来顿悟,除了之前写的那个优化作业之后还要用 LaTeX
-誊写一遍,实验报告都写完了,那我还带着电脑干啥。所以对我来说电脑是一块必须竖着放但是可以写
-LaTeX (偶尔也可以写
-R)的屏幕兼搜索引擎,平板是一块可以平放在桌上当书看还可以写写画画的屏幕,而我
-95%
-以上的工作还是用纸笔完成的(虽然是相当原始的生活状态但感觉真的已经够了,甚至现在想想确实不需要
-Apple pencil,平替的笔就算写字不好用能拿来圈画一下重点或者标记一下 PPT
-上看过的部分就足够了(
那挺好的,后面一直到考试周结束非必要不带电脑出门了(草(#每日学数学学得(什么这也学数学学得(
-后面几天也没啥别的事了,什么那美好的仗我已经打过了,当行的路已经行尽了,所信的道也已经守住了,从此以后有公义的冠冕为我存留,希望高统没事。不知道两个半小时考五道题一道
-10 分直接计入总评是什么水平,那哥们至少得做个四道
-然后根据四舍五入没满分就是零分(草,希望真能没事。优化更不知道怎么考,至于生物其实
-PPT 已经当睡前读物溜了一圈了但啥都记不住啊(
12月30日
-很急。
-12月31日
-前天买的阳光玫瑰不好吃,皮很厚,不过这个季节还想吃到好吃的青提是否是我在做梦(
-今天早上八点多就起来了,打开很久没听的 One Last Kiss -开始复习高统,假装这一年我的生活都如此规律、尽在掌握,后来一想其实这个装模作样的过程才是精准概括了我的生活(
-发一张我本年度最喜欢的猫图,尽管这是前几天才看到的,最近只要有人和我说话我都会发一张过去。不过 -2021 年我最喜欢的一张自拍还是 12.31 -拍的,感觉非常正常(
-
--]]>在我国气象观测中,每天 20 -点是划分新旧两天气象数据的时间节点,所以对广大气象爱好者来说,气象意义上的 -2024 年此刻已经到来。
-
摘要来自《游焦山小记》,是高中时候读的,很喜欢,是那种读完不自觉会勾起嘴角的小记。但居然一直记到现在。
---予自丁酉来游,未遑穷讨。人事参商,忽忽数年,始一续至。又以羁绁俗缘,卒卒便去,如传舍然,不知此行定复何急,良可浩叹,自今以往,日月不居,一误难再,赋归之后,纵心独往,尚于兹山不能无情。当择春秋佳日,买小艇,被宿松寥阁上十日夕,以偿夙负,滔滔江水,实闻此言。
-
1月1日
-高统看完了,现在只要把 cheatsheet -抄完就好了(迫真,乐观一点的话明天还有机会能看看优化,我不好说,有机不会(
-奇怪的跨年方式增加了.jpg
-1月3日
-大学以来强度最大的一天结束了(,考了三门,期末一下子过半了(
-早上生导评价为还好没复习毕竟复习也没用,不过早晨七点多去考场在马路上骑车骑得很爽,自从换车之后骑行体验大幅增长,有的时候还在想华子有没有什么相关的社团之类的可以玩玩。这考试一半感觉小有把握,三分之一感觉能选一个出来但不大确定,剩下六分之一的判断题看不懂在说什么但你既然这么说了只要听起来不太离谱我就当你是对的好了.jpg
-然后一刻也没有为寄掉的生导而哀悼,立即赶到考场的是高统。拿到卷子半小时写了两道感觉稳了,再仔细一看怎么考 -U-estimable,非参数的东西不是特别熟有点小慌,我知道他那个 hint -大概是想让我说明 U-estimable with order \(m\) 会引出一个至多 \(m\) -阶的多项式,然后证明开个方就寄了,线性的部分只要想到对 population -做一个线性变换然后积分就好,脑子还算清楚想到了是类似于证明 \(\sigma^2\) 的 U-statistic -至少二阶那个定理的做法。但平方那里感觉写得不大行,似乎当时就已经很紧张了。还有个算 -amse 的题想了半天 sample variance 的渐进分布是什么(,还要讨论 \(\max \{0 , \bar X^2 - S^2 /n \}\) -的渐进分布,寄,没算出来,大致写了下我猜测的结论是 \(\mu \neq 0\) 时和 \(\bar X^2\) 以及 \(\bar X^2 - S^2/n\) 的 amse 一样,如果 \(\mu =0\) 的话这个怪东西会 asymptotically -more efficient,听起来蛮合理的因为这个题的目的是在 estimate \(\mu^2\),你要是让统计量都小于 \(0\) -了那还估个啥。这个时候都快十二点了,然后突然想出来前面那个 optimal -decision rule 的题怎么构造了,拿出最大算力算完手抖着交了。
-晚上就出分了,好快(,点进去发现好高还以为给我登错分了,看来我写的猜测的结论也给了点分,以及均分也没我想象的那么高,好好好特别好。前两天说感觉这课前十五周舒服得像在泡脚,课好作业好玩学到许多,第十六周写 -cheatsheet 就感觉像在喝整整 15 -周的洗脚水,今天考试发现之前喝的也没用(指 cheatsheet -几乎没用到,考前说要考定理证明哥们抄了满满两面结果完全没考,不讲武德)又被灌了一桶,但阅卷还是放过我了,真好。
-晚上运筹一个手解 \(3 \times 4\) -大小的线性规划没算完,评价为恶心人用的。不过这课期末占比 20% 所以考 50 -分就够用了。
-优化怎么办呢,感觉学的 Newton's method -已经是很久以前的事情了(,是不是应该感激他后半学期讲算法没讲梯度下降(
-1月4日
---是不是应该感激他后半学期讲算法没讲梯度下降(
-
我昨天在说什么(疑惑,其实我想说的是他没像数值分析那样讲梯度下降,毕竟这课的 -iteration \(x_{t+1} = x_t - \eta -\Delta_t\) 里面的 \(\eta\) -全都不用求直接说是 backtracking -得到的就糊过去了,数值分析那个讲法考前一天才看的话真的会死人的(
-今天凌晨试图在 C 楼刷夜,但我忽略了昨天早上是六点四十起的,把 scribe -notes 过了一遍直接倒在 C -楼隔间的懒人沙发上睡着了,睡得很暖和醒来之后又觉得好冷直接绝不调,看了会笔记然后回寝室一觉到中午。但是评价为睡沙发真挺舒服的,我还查了一下同款只要两百多,想买一个放家里(不
-一天速通优化,晚上离开教室的时候看到还有课友在抄 -cheatsheet,安心了一点(不
---我的 cheatsheet 除了 cheat 了我自己之外什么用都没有
-
更棘手的是明天考完优化还要紧急重做组员今晚交上来的建筑材料实验的 -pre,有一说一不想做可以早点告诉我让我有个心理准备自己解决,没必要到最后一刻交出来一个显然不是用手更别说带没带脑子做的东西然后确信有人会救场。
-1月5日
-这个 b -优化(,我被优化掉了((。反正我承认这课我学得不咋地,但考拉了也没什么值得自裁的,就是不会,期中后一节不落地去上课也没用,什么算法设计,不会.jpg。
-蹲个调分,不调也随便你(,以后还是只在数学系/求真/统计中心的范围内选课了(
-反正我真有点 PTSD -不想整优化了,更不太想碰完全不沾统计的算法(。还是统计好,高统考完两天了我还时不时会去想没做出来的那个题,今天竟突然明白了,而这个 -b 优化考完不到 12 小时后瞥到昨天的日记,backtracking -是怎么做的来着?
-下学期真的还要选组合优化吗(,求真课会不会好一点呢,要不干脆还是去上计算概率吧(
-中午基本没吃饭,感觉早饭午饭吃的面包加起来还不如喝的酸奶多(,考完试就去四教开始赶下午建材实验 -pre 的 PPT,成功在新土木馆讲了一些凸优化和 loss function -凑时长(,不管最后结果怎么样至少我觉得节目效果不错((。晚上大吃一斤香锅(?)结果吃太撑了,在猫超散步不知怎的看到买一送一就买了两瓶 -costa -的燕麦摩卡,付了款才想起来我超它买一送一肯定是因为不好喝啊。到教室就开始那个睡,一直睡到教室关门,还有一个实验报告没写,优化作业还没有打成 -LaTeX -结果还是在废纸堆里找到了上周写的纸质版,明天要赶一个五千字的结课论文,建筑材料一点没学下周二就考了,我急死(
-1月6日
-今天莫名其妙开始咳嗽了,晚上回来找上次咳嗽时候买的药找了好久,两个月里咳嗽两次发烧一次,20 -岁老猫.jpg。
-不过写了一天工程与法律(一个到了期末我才想起来它的存在的限选课)的大作业,搁那逆转裁判啊不是瞎判案子,好快乐(,给我整得寒假都有点想玩逆转裁判了(。我发现写这个东西和科研差不多,遇到一些不知道怎么判的情况加一个条件就会变得好判,那就编一个上去,看起来别太离谱就行(
-下面是一些整活欣赏(x
-
你们都是谁.jpg
-迟先生 驰先生,混入!

为了说明被告已知和原告签的是挂靠合同直接调一个吃饭时候的监控真的没问题吗((
-这些个被告怎么对一些对自己不利的证据全都无异议,高 风 亮 节(
-
任 人 唯 亲(
-1月7日
-又发烧了,新年第一烧(啊?,上次是十四周周三,这次是十六周周日,二十天内烧了两次,这个 -b 学校((
-但我不好说这次是什么情况,我觉得可能性最大的是室友为了缓考量统把自己冻感冒了,然后我这几天强度巨大又被她传染了,如果是的话真的难绷(
-还是咳嗽,但是没有昨天严重,喉咙不疼,又有了鼻塞之类的感冒常见症状。白天取了几个体温的样本感觉方差很小,upper -bound 是 37.5,lower bound 应该就是 37 -度,甚至有的时候按照标准来说不是发烧,但我体温一直有点偏低,而且感觉不舒服,就当做发烧好了。晚上感觉越来越不舒服,现在是到 -37.8 了,乐。
-看了一点建筑材料的 PPT,它周二就要考了,真的很急。
-1月8日
-昨晚开始往高了烧了,吃了退烧药之后感觉整个人烫烫烫完全睡不着,连带着喉咙痒咳嗽打喷嚏甚至右边智齿都在疼,很急,在床上把手机和 -pad 全玩没电了到五点钟才睡着,甚至还看了点 PPT(
-明天考建筑材料,很神奇的是我勉强算是复习完了。我的评价是随缘吧,然而这学期怎么有这么多考成啥样都随缘的课,感觉绩点危(。虽说出国壬
-3.7+ 管够 3.8 挺好,但 3.8
-在某个书院好像有点活不下去甚至都该紫菜了(。(x
1月9日
-昨晚一直挺好的,直到我去洗了个澡回来就开始不舒服了,一量 -37.5,哈哈.jpg。今天白天也降下去过,到晚上又 38 -度了,这绝望的轮回。为什么还在烧,我觉得这下大概率肺炎或者最近流行的什么甲流乙流了,寄。
-不管怎么样作为一个正常人断断续续烧了三天总是不太正常,而且都是白天还算舒服从傍晚开始烧,挺肺炎的,明天该去医院了。
-哦,今天还考建筑材料了啊,抄 PPT -水课,糊完跑了。附带我在后排全程咳嗽,咳到老师来问我要不要帮我打杯水,咳得我感觉脑浆都晃匀了反正现在头是震得挺疼的,对不起所有人.jpg
-1月10日
-昨晚又来了一轮 -38.5,人都快烧傻了,今天爬起来去了趟校医院,颇有一种被塞进猫包带去看病的错觉,事乙流(
-出门的时候都做好今晚彻夜在北医三院吊盐水的准备了,换洗的衣服都收拾了一个袋子只是没带上,还查了查车道沟附近有没有什么好点的酒店可以去休息的,结果在校医院开了盒奥司他韦被赶出来了,哈哈。事后想想可能再不去医院病都要好了(开玩笑的,不吃奥司他韦估计还是寄
-所以前两天为什么不自己买个试纸测一测呢(,被自己蠢到了。光搁那发烧吃退烧药退烧吃一些没啥用的药发烧吃退烧药了,这绝望的轮回(
-凌晨烫烫烫睡不着的时候看了点《繁花》,一个是因为我之前就特别喜欢辛芷蕾(虽然如懿传真的很难看吧但她真的很美),再一看似乎江浙一带练一练就能讲上海话的演员都到齐了
-甚至连 papi 酱都来了(,半夜点开测试了一下来沪 14
-年外地人的沪语水平,什么嘛不看字幕也是能听懂的嘛(x
不用看评论就知道肯定有吐槽演员洋泾浜的,我是听不太出来只觉得有一些语调比较怪,反正我讲起来更洋泾浜(
只不过这玩意怎么能拍出来 30 集的,二次元当久了有点看不动 13
-话以上的作品(
1月11日
- -昨晚又来了一轮 -38.5,哈哈,已经懒得写了,反正今晚的也已经开始了,就是没那么高(
-下学期一定摸一点不能这样上强度了我超,辛苦搞了一学期到期末歇了算什么事儿,崩溃((
-以前觉得能在床上躺着真是至福,现在一想到带着手机电脑 pad -温度计耳机水杯冷毛巾和药爬到床上,在漆黑一片里面烫烫烫然后等到退烧了才能睡着中间室友要是要睡了还得憋一阵子不能咳嗽,就觉得睡觉也好难受,要 -ptsd 了((
-今天临时发了两封要课程推的邮件,虽然都还没回但突然得知要推荐信之后我开始思考该问谁要的心理活动就差点没把我尴尬死(。问就是我压根都不敢去找 -lq/ypk,只能在统计中心找两个上过课成绩还好但除此之外完全不认得的老师要课推这样子((,要是去数学系要推的话我恐怕只能找 -lzx 了,其他重量级一点的老师的真数学课我都上得一塌糊涂,崩溃((
-1月12日
-病中在床上摸了摸光叔下学期的讲义,不得不说虽然我实分析当初学得一般,但还是在概率里一边做一边学常读常新很久了,感觉还行。组合优化不玩了的话干脆开学手选一个这玩意好了,反正说是还能少量扩容。
-为啥要个课推都这么难,闹麻了。如果 wty -还没走的话其实还可以找她问一下的,只不过她那个生统离我现在申的这玩意更是差得远了。目前手里只有一封,可以的话最好能找到 -zzy -要一封,毕竟这个项目看起来就没有理论,我能理解的部分就全是在搞数据,但想一想总比打灰有意思。zzy -下周要来录课感觉可以当面问一下,正好录的是之前上的那个线性回归,这两天就算是跑一趟伟清楼我也跑不动,今天在楼下一摸自行车座都积灰了。
-今天正好看到统计中心发了招聘通知,招一个 AP 一个讲师,毕竟 wjd -也要走了,要不要找她要个推荐信留作纪念呢,笑死。不知道她还会不会继续在高校,据我所知她是做咨询的。我看她下学期开了 -11 学分的课,不知道是不是以前也这样但有点哈人的。
-还是看看近处的 ODE 吧(
-1月13日
-病了一周把《繁花》看完了,还是不错的,就当回家之前做了 20 -个小时沪语听力,那托福怎么办(。
-突然发现这学期的笔记到最后都鸽掉了(心虚,高统后来转纸质了体验挺好,优化感觉不值得我每周花时间打字(。
-zzy
-答应给推荐信了,虽然她热情得让我有点怀疑到底谁是甲方(,姐姐真好谢谢姐姐。挺好的,现在就还有个
-PS 没写了,写不出来 但反正限定是固定字体大小的一页 A4
-纸那似乎也不多,感觉只能编一编统计和 IE
-之间的关系毕竟我校的统计中心还就那个在工工。考完 ODE 再说吧(。
还有两周回家,考完试除了去找 -ypk,摸实分析讲义和练托福之外还可以干点啥呢(还想干点啥呢(
-1月14日
-这一天天的就没有个身体舒服的时候.jpg,这下 ODE 有点小急了(
-1月15日
-这一天天的就没有个身体舒服的时候(复读
-1月16日
-考完了,这 ODE 不过如此,虽然谱性质我是一点不会放了个 15 -分的题,正经学分析的时候再来吧(
-推荐信还没交齐,急急急急急。PS -写不出来,这个倒是没那么急毕竟掌握在自己手里,这就打开 GPT -争取睡前写完.jpg
-1月17日
-开始学托福,但是上新东方 TPO
-做了两篇阅读就觉得有点无聊了(,感觉不如高中的时候考的校卷难((,啊不是,感觉随便看看了解下题型和流程就行了没必要做多少,还是练口语和写作吧。然而口语肯定是回家对着墙练或者等室友走了之后在寝室练,写作现在背了考前不会忘吗,那做听力吧,啊不是那还准备个啥闲着没事听听算了((
所以既然也不难为什么到现在都没考托福呢,需要语言成绩的时候啥也没有就挺崩溃的。
-最急的是到现在推荐信还没齐,马上 ddl 了,zzy
-答应给推的时候特别热情但为什么咕了(,老师都好忙啊(。邮件催了一下但还未读,感觉要么今天要去加她微信问一下要么得早点去蹲伟清楼了,哪个都是社恐地狱,能不能只交一封推荐信呢(。要不再约一下
-ypk 去一趟伟清楼全部解决好了(不是
说起来这个霸王茶姬和茶话弄有啥本质区别吗,之前一直听人说好喝所以特别火,去万柳的店看起来也不怎么需要排队。所以说茶颜悦色难道会比霸王茶姬和茶话弄好喝很多吗(质疑,感觉不能抱太高期待(?
-1月18日
-UTokyo ESEP 2024 申请结束了,催推荐信一直催到 ddl
-前半个小时,不仅急坏了而且催的时候实在忍不住脚趾抠地,但还好交上了,感觉申个没什么用的暑研身心都受到了不小的摧残
-所以说真的非润不可吗(。越发提醒我要开始贴
-ypk
-了不然找老师要个课推真的好困难(这和课推不课推有关系吗(。不过今天去了一趟才知道
-ypk
-已经不在伟清楼了,统计中心只有他搬去了焊接馆,难怪有一次讨论班是在那边开的,我不理解但总不会是他也要润了吧那我怎么办(,按理说
-wty 走了之后伟清楼不应该更加宽敞了才对吗(?
上个秋季学期我就在申 UTokyo
-的交换,院系二选一也没把名额给我,拿到名额的哥们也没真的去,麻。这学期又在申
-UTokyo,这次都不好说整个华子能不能有名额,感觉就图一乐吧,还得继续找保底。但我暑假真的好想去日本玩啊,我还在
-PS 里写 I'm a big fan of Japanese anime 什么的现在想想好丢人
下午一只手拿电脑一只手推车走回寝室的路上突然推不动了,一看路上有一根类似丝带
-实际上更像衣服拉链侧边的布条(?)的东西一头缠在了牙盘里,这是马路上该有的东西吗就算有它就应该缠在车上吗我真是摸不着头脑.jpg。进车棚把踏板轮胎牙盘裤子清理干净之后想想感觉得回去把它捡起来丢掉,在路上推着车走缠进来就算了也就是停在马路中央扯出来会尴尬一点,如果是骑车突然被缠感觉挺危险的。刚走回事故现场就发现了另一个正在和它左右互搏的路人,绷不住了((
好困好累好饿但是又不饿清华大学你把我害死了(
1月19日
-给导师发邮件,但已读不回了,我又急了,这是咕了一学期的代价吗(
-很摸地听了一些托福听力,但是只听了 lecture 没听
-conversation,这有什么练的必要吗(二度)。然而做的最烂的是一篇讲
-cat domestication 的,所以为什么要驯化猫猫,猫猫又没用((
1月20日
- -发现五道口开了家万圣书园,虽然二楼还没开放,急急急。上次去还是大概这学期前几周的时候去华子南门那家店,至福。逛了一圈,看到几本想看但是没看的书,还有几本感觉有点意思的,但好贵,没买,回来看电子版((
-回来路上第一次发现西郊宾馆藏在王庄路旁边的一条小巷子里,里面自行车似乎不让进,走着进去探索了一下。好破
所以说被取代的是哪家店呢,逛了一圈感觉没看到 也没听到
-之前那个机厅,不会是寄了吧,滴——蜡——熊——
今天闲着没事在翻华清大学课程攻略共享计划,开了点盒(。看了眼计量经济学的卷子怎么有且仅有线性回归,还一股
-zzy
-那个课的味儿,所以说数学万一学不下去的话可以转行的对吧((
Wake up with no email everyday(
-1月21日
-有什么能比熬了个大夜读完一本书然后发现这书好烂更令人难过吗,躺在床上气得睡不着(。好不容易睡着了结果做了个梦,梦到一天要在北京上海之间来回,到了下午一点想买回上海的票结果发现全卖完了连动车票都没剩,想了想京沪高铁票岂有卖完的时候,肯定是假的,然后就醒了(
-起床打扫卫生洗衣服,到晚饭把 窖藏两个月
-买来放了俩月没喝的奶啤拿出来,本来想去食堂一边吃饭一边喝,后来还是社恐了吃完饭回来在寝室阴暗地喝的。意外地很不错,平时酒仅限于浅尝
-我算什么沙东人,但这个除了闻起来有点酒味之外喝着更像益生菌饮料,还想着下学期一定多买点,带去上课喝(不是,结果过了一会劲上来了上床躺了两三个钟头,草((
Wake up with no email -everyday(
-1月22日
-每年一度的看《恋爱的犀牛》,去年是买了票去蜂巢剧场看蝴蝶组的演出,前年似乎是看了郝蕾段奕宏版,这次不知道为啥点了高中话剧社演出的版本,这男主还挺帅的我印象里好像当时知道他叫什么名字但现在忘记了
-现在再看还是觉得真的演得不错。当然这也是我第一次看这部话剧的版本,不过第一次也是在
-b 站看的,社恐没去现场。这剧本太伟大了好想背下来啊(。
但我读剧本好像是在看话剧之前,读了才想去看的。后来看到过带孟京辉廖一梅的采访的剧本版本,才知道“黄昏是我一天当中视力最差的时候
-blahblah”那句话是陈建斌说的,草,四大爷还是有点浪漫在身上的(
Wake up with no email everyday(,但我今天才知道 wwc
-组里目前没有本科生,有点惊讶。所以说万一真没人要我了其实去他那里也可以吧
-看起来还有机会跑路 econ 的样子(然而我最近为什么老在想跑路 econ
-呢,感觉也没有完全学不下去才对(,而且我是他两学期课程老粉了而且他认识我而且我还已经拿到过他的推荐信了((
1月23日
-出去玩了一天,但 wake up with an email
-today(。本来想今晚还收不到的话就去给 wwc
-发邮件了,这下(暂时)是错过了,也不好说之后会不会还是要跑过去((x
后面几天(不出意外的话)去天津玩,出发之前正好跟 ypk
-约了个午饭(,(不出意外的话应该算是)稍微有点极限,急急急。电脑就不带了,日记先咕个几天,26
-号再说。给因为乙流导致本来就很短的一月日记雪上加霜
上个月被何老板拉着报了个美赛,今天发现 2.1 -就要开始了,我还不知道我是去干啥的。看知识点只感觉理论嘎嘎清楚,Markov -chain 哥们能给你把 Durrett PTE -那一章空口讲一遍,但是咋用来解决问题呢,乐了。
-1月26日
-回北京了,收拾东西明天回家,累累累,急急急,明天高铁上慢慢补上前几天的(
-UTokyo ESEP
-项目的负责人发邮件跟我说不接受三月补交托福成绩单,寄。上次在 thos
-上填申请的时候未央教务就问我为什么能参加考试周期间开始的项目,这次
-UTokyo
-又说清华本科生按理是不能按时到的让我解释一下,反正我都说考试周没啥安排能赶得上,先把饼画了再说,危。
-但是用一下归纳法的话可以知道实复分析都是考试周一开始就考掉了,统计中心的课也都不进考试周,应该没啥问题吧。至少感觉比起能不能申请得到来说不算很大的问题(
1月24日(补
-主要是,去找导师的过程有点震撼我了,所以写一个(
-早晨醒来看到一个:
---“你会干什么啊?” “做证明。”
-“除了证明呢?” “算 cohomology。”
-“应用数学呢?统计?” “不会。那种东西有用么?”
-“那数学的以外你还会什么?编程?” “LaTeX。”
-“额。那你有没有什么爱好?” “看书呀。”
-“一般看什么书?” “Springer GTM。”
-
统计壬被骂了,但统计壬也别的什么都不会啊而且也不会算 -cohomology,又作为假数学壬被骂了一遍((
-在清芬三楼蹭了 ypk
-一顿饭,然后去参观(?)了他位于焊接馆的新办公室,没有电梯,楼里还一股味儿,听说焊接馆还发生过实验事故,具体来说就是炸了,才知道
-lq
-果然也搬过来了就在他隔壁,但统计中心官网上没更新,哥俩好。不知道伟清楼
-209 现在改成啥样了,但有独立的办公室是好事(
--ypk:具体来说你对什么样的问题比较感兴趣呢
-我:(疑惑)我不太会写代码,然后希望做更理论一点啊更准确来说是比较 -rigorous 的研究(比划)就反正我学统辅学得很痛苦最后 quit -了,在数学系学分析和代数那些基础课倒觉得不错,应数各个方向都可以考虑吧
-ypk:啊...再具体一点呢
-我:(疑惑)(我寻思着我也不知道什么问题好做啊)(试图转移话题)老师您最近有什么关注的问题吗
-ypk:我前两天和华为那帮人见了个面,讨论了一些 GPU -加速的问题,就比如怎么让矩阵乘法算的更快一点,要不你看看这个
-ypk:这是我前两天看到 Zipei Nie -发的随机优化的一个方法反正挺复杂的也不用写代码全是推公式,你看这些玩意这么复杂应该比较满足你对理论的要求了(。工程一点的做法的话 -Deepmind 用 AI -做了一个很不一样的,你回去顺着这两篇往前找找整个问题发展的脉络,开个 -overleaf project -写一写然后把链接给我吧,这是不是能起到一个监督的作用(
-ypk:你回去也可以读点 TCS -顶会别的文章看看还有没有感兴趣的话题,啊对就算是 TCS -也可以不写代码的(
-
我吓晕了怎么世界的尽头又是 CS(,现在投靠 wwc
-还来得及吗我反而觉得他做的时间序列和 M-estimation
-之类的东西变得靠谱起来了。先看一点试试吧,希望人没事(
看的时候就觉得 Zipei Nie
-这个名字有点熟悉,反正是上海某年的一个数学国家队,但不知道是华二的还是上中的。回去一查果然是上中的,确实,你华二数学什么水平还来碰瓷
从焊接馆出来头嗡嗡的只知道这事儿听起来和统计离得有点远(,但反正还是数学就问题不大(迫真,之后要是觉得不行再说吧,wwc -那里又没人。回寝室寄了个快递洗了点衣服,然后很极限地去天津了。
-1月27日
-回家了,好累啊(
-本来想在路上补一补前两天的日记,看了个电影就睡了,咕咕。今天把去年的柯南剧场版看了,虽然很烂就给了个 -6 -分但实在是乐得不行,很久没有看番笑得这么开心了((。顺便把柯南系列的作品都补标了,发现除了若干烂得这么多年来都一直有印象的剧场版之外别的都不记得了,也没怎么打分(
-1月28日
-白天在陪家人逛街,从 1.23 到现在每天都在外面
-还一天一杯奶茶,真有点摸了。晚上回来看美赛 O
-奖论文,没啥头猪啊不是没啥头绪,方法也不是很会,最后变成了在玩一些没啥用的小工具,但愿最后论文能看起来漂亮一点。
1月29日
-凌晨的时候在看美赛的论文,感觉 A -或许还是能做的但队友不一定爱看,去年的 A -似乎都不怎么需要数据直接编然后跑模拟就行了。BCD 我个人都不怎么想考虑,E -和 F -就很有一种老婆饼里没有老婆所以说数学建模和数学有什么关系的美感。看着看着给我都整婆罗门了,这简易的初等数学模型有什么学的必要吗,我知道它真的有用至少在这个比赛里比数分有用(,但我不大想仔细看。这比赛真值得我花四天时间打吗(
-看不下去了,发癫的时候上豆瓣标记已读了 PTE。
-一般来说到了寒假就需要重温一下明日方舟,简单看了眼最近的活动,怎么在种菜(。都不想下载了,机制这么复杂的游戏如同推导之前 -assumption 堆了三页纸的定理,总之是丑的(胡言乱语
-美赛也暂且不想看了,后天急了再说,开始读一点自己的论文。目前的进展是新建了一个 -overleaf project,但还没勇气把链接发出去(
-注册一亩三分地的时候发现我的 id 被用过了,没绷住((
-开学前大概要把托福口语和写作准备好,稍微读点论文,能排得上号的话在九院把智齿拔掉,投几所学校的暑研项目,还得打个美赛(。之前还想着感觉能学点别的,比如 -PTE -没看的几节,先学点复分析啥的,现在看来似乎没什么时间,把前面这些事做好就不错了(
-1月30日
- - -不知道为什么今天开始看时间序列了(绝对不是想跑路
-wwc,下学期 mld 休假没开课所以直接发了
-slides,看了看感觉这不就是随机过程吗这我熟,问题不大。翻着翻着我超怎么这么猛,他甚至还讲
-ergodic theorems,好喜欢啊不是 有点逆天。回头看了眼 V1ncent19
-的课程测评,我的评价是在统辅大讲理论的都是好课,比那个线性回归不知道高到哪里去了,看起来值得好评(x
然后又一想,wwc 那里没人是不是因为他去年休假了来着。
说起来我多元统计至今未修(去年春季退课了),虽说是统辅必修课但感觉也问题不大的样子。我又不需要统辅学位
1月31日
-累累累(
- - - -]]>2月1日
-过一会(?)就美赛了,我们仨(?)目前仍然是一个友谊第一比赛第二
-内恰第三 的氛围(,还能吃到他们俩的糖,挺好的。
今天还是在时间序列,感觉还挺有意思的,只不过 Time Series Analysis
-With Applications in R
-这本书看了一下感觉有点水,可能是作业题会从里面出,又不是上课现在就只看看讲义好了,似乎下学期金统也会用到的样子。怎么又变成在学而不是在磕盐了呢,急急急(,是不是等我把这个学了就可以换导师了
2月2日
-美赛受难记((
-好消息:上午我在负责详细看 E 题,讨论下来最后决定就是做 E 题
-坏消息:不大会做
-好消息:我觉得要用 ARIMA 做一部分,前段时间正好就在学时间序列
-坏消息:还没看到这里
-(
-下午洗数据的时候正好出成绩,这下我相信茶课调分的实力了(,然而概率论 -2 这个喜提 B+ 还是有点难受的。我知道他要是不调分的话我大概就是 B 或 B- -了而且期中爆炸确实是自己的问题但调得还是不够用力啊(x,求真课初体验大失败。
-其他的话,我生物甚至有 A(,另外这学期喜提了一个 -A+,坏消息是这门课叫建筑材料实验((
-2月3日
-美赛受难记,但是今天睡眠充足(,白天也没干啥。除了把论文里面不需要具体计算的部分写了之外,就是不停地在画图,流程图画了一个两个三个,其他 -introduction 性质的地图柱状图啥的也画了几个。原来美赛是美工大赛(
-虽然堆起来看着产出很多,但感觉还挺佛的,至少是没怎么动脑子,为后两天爆肝写论文打基础(迫真
-翻译:我就一臭写论文的,既不知道模型建得怎么样了,也不知道我能帮上点啥忙,那就睡觉吧。
-晚上感觉进度有点小慢,想了想也不是非要顺序推进毕竟最后一问和前面没啥关系,又找到了合适的论文,就先开始做了,减轻点压力。而且最后还要写个小作文,本来也算是我的活,那不如早点开始了。以此为理由把前面的模型的论文任务推回给了队友,让他们一边做一边写,听起来也蛮合理的,总比最后让我从头再开始学习模型
-还看不懂 然后压 ddl 写论文靠谱(
说实话我今天在一篇 heritage protection 相关的论文里终于明白了 -univariate, bivariate, multivariate analysis -的真正意义和对应的三种从来没想过要放一起看的方法,是不是我这个统人当得实在有点太抽象(字面义)了,就是说,太不应用了((
-2月4日
-美赛受难记,今天(我自己)刚磨蹭着做完最后一题,听起来非常光明,但是只做了这道题(
-一边做一边把这部分的论文写好了,现在就有 15 -页,也不知道后面要不要压字数。现在想帮忙做第二题但感觉也帮不上什么忙,又想到队友至多有一个会写 -LaTeX,毛骨悚然(x(
-肩颈都好痛,这破比赛打完之后得稍微休息一天,至少多在床上待一会(
-事已至此,先写 Report on Use of AI 和其他有的没的东西吧,比如说 model
-evaluation,sensitivity analysis,完全不存在的 assumption and
-justification,草怎么还有这么多事。这比赛没有 LLM
-的话怎么打啊,以前的选手太强了吧(
之前说觉得 Mili -现在的歌没有以前好听了,歌词也没那么戳我,但又稍微有点疑惑是不是我的偏见导致的,或者单纯就是 -Millennium Mother 这张专辑太强了。今天写论文的时候发现自己在哼 Extension of You -的旋律,又回去听了一下,还是像第一次看到歌词的时候一样要流泪了。
-2月5日
-美赛受难记,后面忘了,总之已经到最危难的时刻了,逸一时,误一世,啊啊啊啊啊啊(?
-2月6日
-美赛受难记,但结束了,不 disqualified 就是赢!
-万一今年有高于 S 的奖的话明年可以自己单刷一次,哦那样的话报名费要自付 -100 刀没人一起摊,好贵,算了(x)。而且感觉也很危,这次其实除了当 -regression monkey 之外就是在用嘴和 GPT 建模,不过 ICM -是不是就这样啊(。
-2月7日
-又活一天
-看了 #457994 之后又破防了(x
-2月8日
-摆了,详见最新一篇。
- - -2月9日
-年夜饭是巡湘记,好哦,不过它和望湘园的本质差别到底是啥呢,剁椒鱼头里面加的主食是面条而不是米线吗(
-提前一段时间订了座,今天去才知道全都订满了,坐得好挤,平时两个人还能坐四人桌,今天就被赶去角落的双人桌了。也挺合理,今晚还营业的餐厅本来就少,而且到底谁大过年的还想在家无偿做饭(。
- -晚上终于又开始推时间序列的进度了(
-2月10日
-今天在外环和中环之间搬东西,因为初一要吃素所以也没在外面吃东西,简单来说就是没吃啥,然后买了炸鸡回去等着零点之后当夜宵吃。我和我妈说等我润掉了年初一自己过的话就不吃素了,她说你别让我知道了就行。
-晚上一出顾村公园地铁站,这边放鞭炮放得空气已经五米之外看不到人了,吓晕。烟花爆竹哪怕在外环外也买不到,想放还要跑去江浙买,到底有啥可放的,好强的信念感。扫了单车之后看到有个在等公交的孕妇用手捂着口鼻,出于对孕妇的敬佩(真的主要是敬佩)我把包里多的口罩送给了她,听了一些吉祥话。搁平时我觉得我来不及听,因为这个共享单车 -16 -分钟就要计两块五了,但我现在有单车卡,半路感觉车骑起来不舒服还能当场停下换一辆,大概就这么阔气。
-不过还是不要这样就觉得我是什么好人(没人在乎这个,因为在路上骑车的时候我在想的是,这样的话昨天在巡湘记离店的时候多顺的一把薄荷糖就抵消了。顺带巡湘记的薄荷糖真的很好吃,比海底捞的好吃,而望湘园没有薄荷糖。
2月11日
-好想去淀山湖玩啊!坏了,这个假期不是在外环和中环之间搬东西就是在玩,盐是一点没磕,就看了一咪咪时间序列,开学真的,直接换导师算了,还能假装假期补习了前置知识。
今天在外面抽空看完了一个二医大(交医)的姐姐写的垃圾话公众号,真的,欲罢不能,看得我早上去宜家的时候直接坐过了站,本来想出站骑个车哪怕只有两公里也能过过瘾,结果为了再多看一会又往回坐了一站地铁。晚上在回家的路上看完了所有的文章,一边爽的不行并为我那些不能见人的垃圾话感到难过,它们就不配在阳光下暴晒并获得好几百阅读量,一边又惋惜乃至憎恨,这么刻薄又这么有才华还更新得这么慢,我要到什么时候才能再一次性吃上这么多这么好的饭。
-不行,我也要找个阴暗的角落大声说我的垃圾话,不是我和我姐天天讲的那种垃圾话,是我天天在心里大喊、晚上一大段一大段敲到电脑上又觉得万一发博客我的一切人际关系就都要毁掉了的那种垃圾话。
-顺带,上次不明不白地被宜家送货的师傅骂了,是一款常见的爱指手画脚觉得自己最牛逼的呀苏,一到楼下就讲怎么是个小姑娘在家里接货也没法帮忙搬,我说搬货上楼本来就是你们的服务范围,伊刚上海人都蛮客气的呀你怎么这样子,我今天跑了多少单人家家里男主人都会得搭把手额呀。我让他小心点不要碰花了刚刷过的墙不要乱踩我家里的地板,他嫌我女小囡事体多,我问如果这个换过的床架还有问题的话能不能再换,他跟我讲阿姨啊哪能可能再出问题,跟你们女人家真是怎么讲道理也没用,我说我在复旦念数学(是的我感觉这话在这里听起来甚至比说在华子念数学更有底气一些,还好伊嘟囔了一句高材生也这么没素质就走了,也没问我要学生证,是我懂概率还是你懂概率(抱歉其实我心里知道我懂的那些概率也没什么用。后来跟客服投诉了服务态度差,获得了一张一百块的代金券,很想和客服说我的乳腺结节不止这些钱,又怕对面长结节,算了。今天用它买了一些没啥用的东西回来,本来想买个狗狗甚至大鲨鱼玩偶,但我妈让我买衣架和鞋刷子(叹气。
晚上吃了贵州菜,本着都没吃过但是哪家店排队最长应该就最好吃的心态去吃了山石榴,好吃,能把我辣得嘶溜嘶溜,就是歌单不太行。我也鉴不出来预制菜,只要端上来有热乎气我就当锅气了,但反正确实就挺好吃的,管它呢。
-2月12日
-累累累,摆摆摆,先别说科研和学习了,暑研怎么办托福怎么办(乐
-2月13日
-前面忘了,后面也忘了,总之今天要看二月十三(
-用了四五年的 我妈的同事随手送她于是她又随手送给我的
-星巴克联名款卡包裂开了,然而感觉在淘宝怎么挑都挑不到这么合适的,不是没有挂绳就是卡册类型的要么就超过二十块已经不在我的财力范围内了。搜了一下才知道原来这个七八十,难怪好用,感觉是我不配((
2月14日
-早晨起来洗完脸发现脸颊上红红的,还觉得要么是睡得太暖和了要么是气色好(,结果到晚上都没退下去还越来越肿,才发现久违地过敏了,吃氯雷他定然后昏睡.jpg
-大冬天的到底是在对什么过敏啊,情人节吗,还是说今天 22 -度所以我的身体以为这是上海的春天了然后就过敏了(
-2月15日
- -时间序列好难,急,还有个暑研项目一周后截止但我什么都还没填,托福是什么,怎么能这么摆(乐
-2月16日
-前两天右边嘴角起了个痘,现在差不多好了,今天左边嘴角又起了一个,记之(
- -2月17日
-昨晚登了一下高中的智学网账号,今天卸载之前又看了一眼当时的一些原卷,鄙人高考前英语作文甚至能有 -22/25 -这样的伟业,又和我这两天写的托福练习作文对比了一下,我恨不得回去让我高三的英语老师重造一个月。
-于是今天又开始对着阅读划词组背句子了,背一点算一点,我总能把它们塞到毫不相干的作文主题的合适位置里的。然后不知道为什么就去补巨人了,后面忘了,心脏撒撒给哟(
-2月18日
-感觉托福听力的最大障碍是没法集中精力听完五段,听三个我就累了。之前一直以为 -lecture 会比 conversation 难,结果现在发现还是 conversation -比较困难,急急急,语速太快了没跟上就寄了。不过应该换个思路,conversation -就别记笔记了,听懂了也没太多可记的,没听懂记了也没用。
-省流:今天做了一些听力和写作,然而在家也没法练口语,就又去补巨人了。来点锐评:
---我:
-这番里面的马真的都画的好好啊
--
俺の愛馬が!
-要不要搞个自由之翼的披风穿 jk 外面
-好便宜 才四五十 就是太中二了
-只恨我初中的时候没看这个
-友:
-沃日 初中哪有这么多钱 (?)
-我:
-确实
-但是如果初中的时候看这个 现在就不会想买了
-还可以早点和谏山创和解
-友:
-那也不一定
-我:
-没事 我都能和市川春子和解
-谏山创算什么
-友:
-创创
-全部创了
-我:
-你看过宝石之国漫画吗 和解了吗
-友:
-没看漫画
-我:
-fine 那你可以去和解一下
-友:
-笑死 听说小绿最后变成人了
-感觉难绷
-我:
-不是 这个结局我觉得可以预料到
-但是它的过程实在是令人震撼
-就看到动漫魂肉骨那个说法的时候我感觉就差不多了
-但是后面这个过程我接受不了
-不过我也和解了
-友:
-好好好 无所谓
-都这个年纪了什么和解不了啊
-我:
-确实 又不是女高了
-看这玩意看到现在我还是只关心马
--
这个体型真就是速度竞马,但好像比一般的赛马小一点(
--
蹄铁背景没绷住
-但是时速 75~80 km 还是太恐怖了吧
-赛马一般 1km 跑 60 秒左右吧
-查了下世界纪录是 53.7 s,所以是时速 67 km
-怎么人全死了啊 就爱看这种
-但撤退的时候根本没人关心他们的马怎么样了 急
-我:
-太典了
-把 Ayanami 还回来 啊不是 把 Eren 还回来
-我说这不就是换皮 EVA 吗 不话疗的那种 所以评分会比 EVA 低一点
-友:
-确实 但是三笠是面瘫
-我:
-不错啊 那就是 Ayanami 加强了 能要求把真嗣还回来了
-可惜我最喜欢 Asuka 巨人没有这号角色
-友:
-是 傲娇在这个世界活不了一点
-我:
-别骂了 但 Asuka 强啊
-所以 Misato 桑可以代兵长吗
-不太能代 他太强了 而且不够涩
-友:
-兵长多色啊 战损了更色
-Misato 至始至终都是完整的 (不是)
-我:
-我靠 你别引诱我的 xp
-
(?
-2月19日
-进巨第一季看完了,真的,EVA 和 FZ 之后好久没吃到这么好的饭了(
-那为什么打 8 分而不是 9 分呢(因为不够 EVA 或 FZ(x
明天去交大,摸一天,感觉也属于定番(
-凌晨练了个口语比练别的加起来都精彩:
---题目:Talk about a famous person that you admire. Explain why you -respect this person.
-我:Ummm(思考)(十五秒快过去了还想不出来能说什么)(急急急)
-One of the famous person I admire is Shing-Tung Yau, a famous -mathematician who enjoys high reputation in the whole world (
-
2月20日
-今天去交大了,蛮累的,之后再写。前年这时候在后悔当初为什么拒了电院那个 -IEEE -班(,去年这时候觉得没去交也没什么反正去了也学不会,今年发现去交或者去旦学数学其实都很爽,唉(x
-和初中同学聊了聊天,她告诉我她考前三天才开始学口语和写作最后 -102,小分也都够用,ok(,感觉确实每天要练但也不是非得特别紧张((
-因为路程比较远所以昨晚下好了进巨第二季还带了充电宝,在地铁上看完了,第三季也开了个头。虽然槽点也不少,但还是好久没吃到这么好的饭了(二度,看了这么多有的没的才发现,我果然还是喜欢这种啊((
-2月21日
-进巨第三季前半看完了,王政篇给了 9 -分。往后看看发现这玩意真的好长啊,最终季还分上下部分,还有若干 -OVA,稍微有点看不动了,寒假能看到看海就差不多得了。不过我属于是不往后看剧透又不一口气补完就抓耳挠腮坐立不安,不同于第二季我和艾伦一样疑惑,王政篇之后看剧透和设定终于看得懂了。何况这个体量的作品如果不提前知道一些思路又不二刷的话真的会漏掉很多细节,失去的震撼感在丰富的内容面前是可以让位的。
-晚上卡 ddl
-交了一个暑研申请,主要是我太拖了,推荐信倒是今早我还在大睡的时候就收到了(。其实寒假除了几个校级的项目之外就压根没找,咋办呢,总不能真去实习吧,实在不行能以
-2025 年不毕业为理由直接不选课吗(
想了想倒还是和小时候一样,我妈前脚出门上班我后脚打开电脑开始看动漫,然后在她回家之前加速补作业(交申请,给 -wwc -写邮件),晚上在她眼皮子底下随便干点有的没的(练托福写作)。快要回学校了。
-明天本来是想去滨江道骑车,陆家嘴签证拿到了,下暴雨的话恐怕就不行了,大不了明年冬天再说。总之要从静安寺换乘买
-Lilian by the
-way,不能骑车的话就去世纪大道走走好了,然后早点回家收拾东西。
2月22日
-又该选课了(,课表再次变成了不认识的样子。好消息是一周三休了,坏消息是周二好像有五节课(((
-2月23日
-最近光是安装的家具送来的时候工具包里多余的材料就攒下了这么多,轻轻地崩溃了:
-
如果还有下次(?)的话我选全屋定制(
-明天回学校了,希望高铁不要晚点太多((
-2月24日
-喝到茶颜悦色了,虽然我的评价是,就这(x)。感觉还是得现买现喝,下次一定(
-带回寝室拍了个照,怎么不算是一种谷子了呢:
-
在高铁上补了进巨最终季 part 1,看到第 15
-话后半段的时候到站了,急急急急急(。马莱篇感觉确实没那么有趣,但单凭莎夏那几话都也还是
-8 分的水平。其实到第三季结束发现 104
-期配角三人组还是完整的的时候我就感觉要刀莎夏了(主要是莎夏太单纯了,刀另两个人效果就没那么好(,完全是死于谏山创的刀法(。很难评价谏山创和虚渊玄谁更爱的战士,单看
-Fate/Zero 似乎还是谏山创更疯,感觉得去补一下魔圆再说(
题外话,感觉我最看重的还是单回质量,像 Fate/Extra Last Encore
-即使作为粉丝向作品来看大约就是 7 分(对路人来说还不到 6
-分,实在绷不住,然而因为童谣那两话我就愿意给个
-8。后来聊了聊设定和一些问题(简称我要求被剧透(,感觉全系列除了完结篇有待考察之外应该能稳定在至少
-8 分,但后面应该既有争议又很难像第三季一样有趣又震撼,给不出 9 了。
虽然但是,三笠你的脸到后期怎么画成这样了啊,我看得睡不着觉。就感觉,诶,很空虚,没有什么永垂不朽。
-感觉最近实在是赛马和进巨都看太多了,加上下午还在吐槽既然想要保留王血何必安排希斯托莉娅怀孕,还不如让吉克在生命的最后一年猛猛当种马效率高(。结果傍晚睡觉梦到进巨的设定集里有九大巨人的配种费表,进巨和始祖最高要一亿日元左右,平均水平是四五千万,只有车力最低是两千万,实在没绷住(
-其实北黑和春秋分今年的配种费都是两千万,已经是种马的最高价格了(
2月25日
-前段时间在上海疑似因为天气太暖和,时隔好几年犯鼻炎了。昨天还好一点,今天收拾东西可能吃灰吃多了又开始打喷嚏了(
-完全不想上学,于是今晚把进巨最终季 part 1 看了,待会上床写托福(
-2月26日
-难受的春季学期开始了,前半段气温还可以但暖气难受,后半段气温难受(
-最终还是打算在课表里加可靠性数据与生存分析了,虽然是很细的生统方向跟我几乎就没关系,但其实完全出于我的一厢情愿(?),因为 -wjd -这学期结束就要离开华子了。如果不算高统的话,她当年那门统推是让我印象最好的一门统辅课,可惜几乎全是线上上的。而且说实话和我完全没关系的课我也上了不少了(,大不了水水过,而且很可能没有期末考,另外很多东西生统概论的时候也学过了。
-第一次点了瑞幸(其实只是需要它的纸袋子,发现券还蛮多的,后面可以多点几次。果然好多冰,这个不额外加糖的丝绒生椰拿铁怎么也这么甜(
来个很烂的谐音梗:
---室友:下午没课,我打算把冬天的衣服都拿去干洗店洗
-我:今天是你大洗的日子啊!
-
于是晚上我就把菜汤弄到衣服上回去洗了,寄(
-2月27日
-早八之前买了杯瑞幸,是 064 -号,进店的时候看到咖啡师在赶早七,一排一排地做咖啡(,感觉很惨。早十课上坐我斜前面的同学的瑞幸是 -429 号,感觉更惨了((
-有点子上瘾,这玩意比瓶装好喝多了啊((
-2月28日
-现在总感觉喝咖啡能维持清醒的时间越来越短了,虽然一个寒假都几乎没喝但还是不行,一会就困。喝了两天瑞幸获得了两个袋子,其实是想折纸了(x
-
今天把进巨看完了,晚课坐在中间排用电脑看了完结篇后篇(,现在想想开始感到尴尬了(。不钝评了,虽然不喜欢未来视的设定(相比之下“这是由你亲手开始的故事啊!”这句真是我全系列最喜欢的台词)但好歹圆回来给了结局已经很好了,出彩的部分基本集中在前三季,表现力也一直很强,补完还是很值的。
-刚在六教再见了所有的巨人(,下课出来就被树吓了一跳,好难绷((
-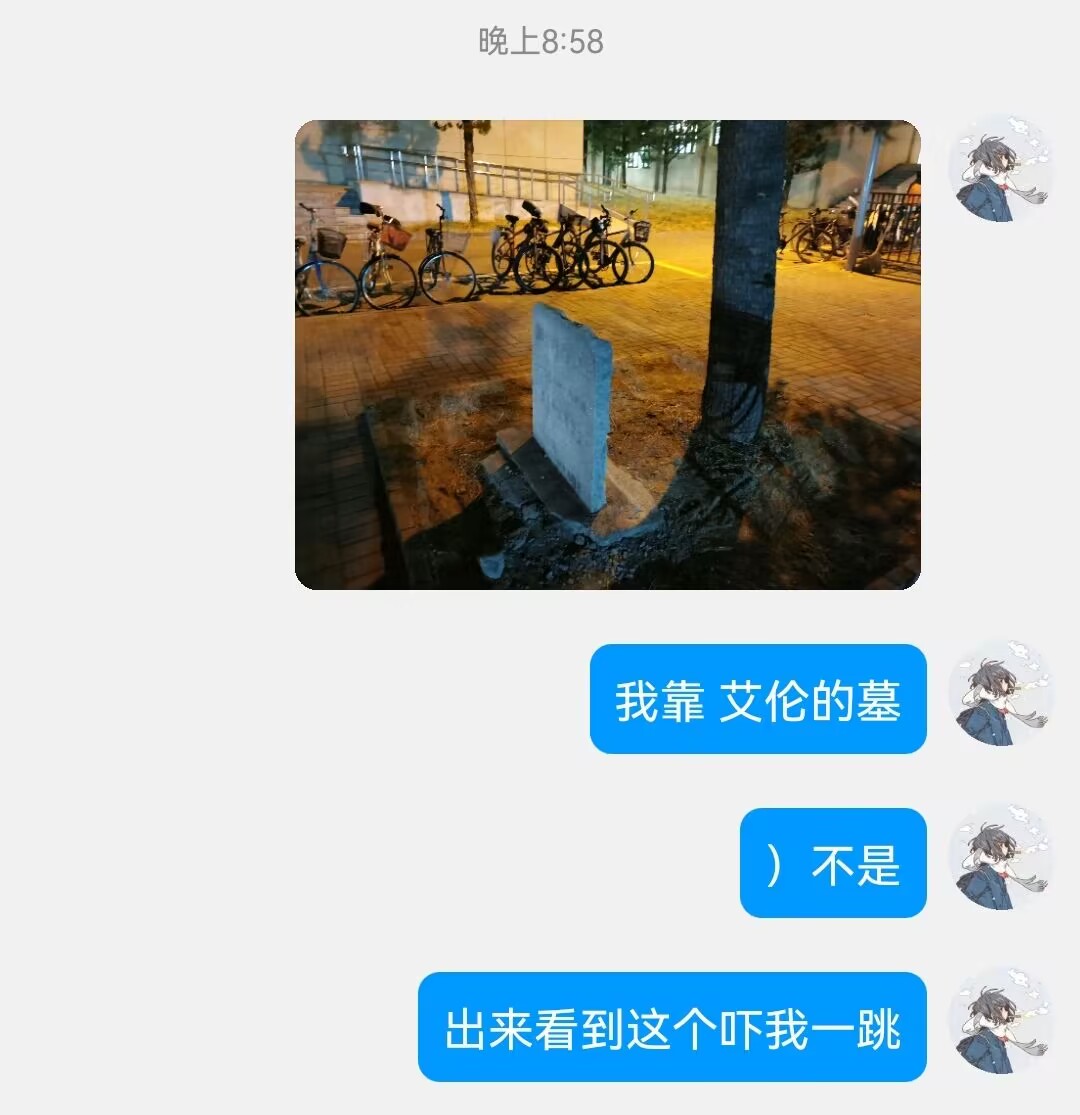
2月29日
-高统 II 讲 -Bayesian、其他的一些估计方法和非参数统计,之前我还一直犹豫要不要去上 dwl -开的那门贝叶斯,感觉不上又不踏实,上了既然是她的课那我必吃 -3.6(,又找不到明显的上位替代,这下没事了。不过毕竟是第二学期了,不像上学期开始的时候我还以为是个很摸的课(,一上来就在上强度,急。
-lq
-讲课还挺好的,奶一口,单看第一节课我感觉他恐怕是统计中心最会讲课的老师了,甚至比
-wwc 和 wjd
-都好(,这俩在我心里已经是讲得最好的了,别人更是((。有 slides
-和板书,除了读 PPT
-之外还讲一些直观理解之类的东西,不然一上来还挺头大的,感觉 4-2 以后
-起得来床的话 还是值得一去。
托福终于摆脱听力阅读越做越菜了。今晚突然意识到阅读是不是不应该先通读文章再做题,而是要直接对着题目一段一段读,但试了一下感觉也并没有省时间,还错得更多了,还是按自己的节奏来吧(
-]]>3月1日
-昨天喝了瑞幸的珞珈樱花拿铁,为什么不是顾村公园樱花拿铁,是樱花节名气还不够大吗(确实是。感觉第一次吃到和樱花沾边但是味道意外地不错的食物,可能主要是也没什么樱花味吧(。今天又来一杯,明天打算点个美式(
好像后面又有线条小狗和瑞幸的联名了,点两杯才能有周边怎么办
-太好了这回我堂堂正正喝两杯(
这个计算概率,我不好说,后半部分是一些 SDE
-数值解法但哥们完全没学过这玩意,但好像会提一下背景知识,这课上也好多没上过概率论
-3
-的,希望人没事。老师下个学期就要离开华子了,又收集到一门绝版课程,但愿这样的话给分能好点(。第一次作业在课上就写完了,体验绝佳(不
3月2日
-昨天早上九点二十起床,在去自取了一杯瑞幸的情况下在上课前顺利走进了六教二楼的教室,现在是越来越强了。今早就暴毙了,直接一个补觉(
-你说得对,现在是第一周,但我已经急了,怎么实分析和基物 2 -作业都这么多。实分析作业我寒假没写是我的问题我自裁,但基物 2 -是从衍射学起哥们连干涉都压根没学(,现在处在一个回头看基础设定的状态,书上明明都是数学公式但我怎么看不懂一点捏(。学了一晚上,我痛死(
-早知道当初报第一周周末的托福,乐了。
-但唯一的好消息是我今天下午在 C -楼研讨间练口语的时候发现这玩意其实不是很难,至少我 independent speaking -不会没话说,果然瞎扯我还是有一手。但是后面三道题有概率说不完,还是得学习一个高速神言(
-瑞幸冰美式可以加双份奶,有券于是五块钱到手了。我现在理解为什么说减脂期喝美式了,这玩意是真有点抑制食欲,不是那种通过饱腹感来抑制,而是通过在嘴里残留一些苦味来让人不想吃饭(
-3月3日
-今天的瑞幸可能是定位有问题,不知道为什么下单下到清华科技园店去了。我还寻思着清芬这边一直都没有茶咖系列,今天怎么突然有了,提示取餐的时候才发现。从四教过去其实也不远,感觉和从寝室到四教差不多,甚至还要近一些,而且清华路以南是家属区所以路修的比较好,比北边好走很多。
-但是这玩意真的好难喝啊,我下单的时候就想,茉莉花香拿铁,这六个字没有一个听起来是难喝的,于是带着幻想乐颠颠地骑了好远的路。但是就是很难喝,不像营销说的是茶叶泡出来的,味道像茶粉。也是,十块钱难道还想喝真茶叶和真咖啡豆吗,醒醒。
-所以清芬店没有茶咖是因为这玩意太难喝了所以让大家不要喝吗,它真的我哭死
天气不错,所以下错单出去骑车也没什么怨言,反而很开心。等考完托福找时间出去骑车吧——开玩笑的。
-我突然理解了,学基物我还看它那个证明干啥,鉴定为数学学魔怔了。反正也看不懂,拟合一下题目拉倒(
-写了一下午一晚上实分析作业还没写完,倒也不怎么难,但主要是在看讲义,反正都是这个妹妹我见过的那种感觉(。明天应该能写完了吧,我草,为什么第一周这么累,难道真是因为物理和实分析都布置了两周的作业的原因吗。
-猛猛约下周早上的研讨间练口语,但愿作息能顺带变得健康点(。现在我也不知道问题到底会在哪一部分了,是口语自我感觉良好实际很菜还是别的不行,难不成会是阅读不行吗(,这样的话好像不是很老中((
3月4日
-开学到现在光是把菜汤弄到身上跑回寝室洗都已经两次了,感觉开学那天我对着室友说出“今天是你大洗的日子”这么烂的梗之后命运的齿轮就开始旋转了,寄。
线条小狗和瑞幸的联名太可爱力,虽然今天起得稍微有点晚了,早晨赶着去练口语就没来得及买,但单杯的袋子也挺好的。明天从早八上到晚十,感觉可以整两杯
-来获得一张贴纸。
下午上生存分析的时候发现从四教四楼可以看到 W -楼,视野是这样的。从远处看感觉这个层高很逼仄(在说什么废话
-
3月5日
- - -明天下午要和 wwc -聊,现在很急,首先我要跟他讲一遍我是未央的然后我要延毕 -etc,现在我不知道为什么很担心他到底带不带本科生尤其是之后打算润的本科生了(虽然但是会有人不带吗(,希望人没事。
- - -晚上回来吃了三个(中等大小的)番茄,尝了一个今天买的芒果。室友大受震撼问我不是减脂期吗我说对啊晚饭没吃饱而且这个加餐不是挺减脂的吗((
-唉,我说我减脂是因为 BMI -超了,而且总感觉精力不济,室友说你就是服美役。那我就要开始跟她暴论了,明明很多说别人在服美役的人要么是自己也在偷偷服,要么就是天生一副符合主流审美的好皮囊轮不到你来服啊!随时随地吃任何东西都不胖的人不许说别人为了健康减肥是服美役,就像我夏天都不打防晒冬天只擦保湿和素颜霜而你尽力护肤也只能达到一个亚健康的状态一样。最后这句话把她搞破防了,现在我在算热量她在拍脸,嘿嘿(
-然后她小红书十分钟之后回来问我一杯瑞幸拿铁二百大卡怎么下得去嘴的,我破防了,明天喝美式(x
-3月6日
-今天和 wwc -聊了,回来一看我昨天在担心些什么(。今年他招的博士生正好是未央零字班的,不仅省略解释一堆这书院是什么玩意,他还先我一步锐评“你们这个培养方案真是不可理喻”,感觉来对地方了(。虽然预想的是搞时间序列,但他给我的问题是 -network model & graphon estimation -说是最近在看这个,而且概率会用得多一点,也挺好,先看吧。
-喝了一圈意外地发现还是厚乳拿铁最好喝,奶味很浓郁,也不怎么甜,热量也还行。其实瑞幸招牌的生椰拿铁我完全没喝出来哪里好喝了(,感觉还不如贝纳颂那一款,也不如丝绒生椰和冰吸生椰。下周开始有柚
-C 美式了,好好好。
早上出门之前称了下体重,怎么现在 BMI -就已经正常了,好怪哦。感觉也不是最近有意识地减脂的结果毕竟也没几天(,而是寒假在家要自己做饭所以就瘦了(草(。晚上开心地吃了顿米粉(别骂了,辣汤又溅到了风衣上(,烂梗的惩罚没完没了。
-然而这个清芬它有什么低热量的主食吗,每天这个米饭都吃得我相当纠结,人家桃李还有杂粮饭可以选(
-3月7日
-看了一下午论文,感觉头很大(,吃晚饭的时候在考虑能不能本科毕业直接去当高中老师((x
-虽然我感觉正文其实真没有什么非常困难的数学,很多地方为了贴合真实的处理甚至都没那么严谨了(挠头,但这个思路真的是看得我一愣一愣的(,顺着思路倒是结果都能随手推,但好累(。
-yysy 这个 supplementary materials 需要读吗,我之前看 wwc -发给我的两篇都是 biometrika -上的文章,感觉都不长,还很乐,还觉得可能下周就可以汇报了,但这才发现证明全在 -supplementary data 里面(,要读的话得到什么时候啊(x
-今天把咖啡撒到身上了,我错了我以后真的不再玩烂梗了,饶了我吧((
-诶,我发现减肥能给自己带来一种错觉,就是别人给我拍的照片看起来也没那么魁梧了(。
- - - -3月8日
-早上起来看了一眼,今天计算概率复习简单的概率论,虽然看 logistic
-感觉老师可能会讲一些求真笑话(like
-数学家至少要精通两个方向(我猜的)但还是又躺下了(,有一种求真招生反诈宣传片的美感。
诶,昨天才和群友说起来还好高三春季的时候连去考一下求真的念头都没动,毕竟当时是第一届,风评还没有这么差,虽然我觉得既然要考物理的话我是考不上的,但万一考上了就太可怕了。然后我想了想为什么没考呢,好像单纯就是懒得准备了(,毕竟到当时高考也准备得还可以,春考看得过去,大概还有感觉高三的英语老师很可爱,不如多和她贴贴(并不(谢谢她救我(
躺了一会起来练了下 TOEFL test ready 上剩的三篇写作,一个 integrated -和两个 independent 都给我判了 -5/5,很怪,总不能真是字数多就行了吧(。其中有一个 independent writing -是讨论除了电子产品之外二百年内最伟大的科技成就,我:statistical -models!(
-打了两遍 integrated writing 才把模板背下来,希望后天早上还记得(
-它那个估分区间除了告诉我口语很烂之外就没啥用了,口语是 B2,听读写都是 -C1,我本来觉得 advanced 听起来就挺好的了,后来才知道最高是 C2 -proficiency(。就不练了,睡大觉(
-3月10日
-今天 参加了一场贵族运动 考完托福了。早上进汇佳考点之后在
-ETS
-考试中心大楼里等,听到一楼会议室里在吵架讨薪,有个领导一样的人说,我们不是没给发工资,是吧,工资的三个部分,blahblah
-都结过了,blahblah
-本来就已经降了,并不是拖欠,blahblah,然后被大家骂了(
考前是说台面上的两支笔只能带走一支,结果我走的时候监考老师让我都带上,好怪哦,她不会是在搞我吧(x
-
坐在我左边的是一个出生日期 2010.12.30
-的小朋友,考试期间我感觉她不仅在不停乱动还时不时余光瞟我,可能是嫌我太老了,但愿不是要带我一起
-HOLD。右边的小朋友是 2009.07 忘了几号出生的,没什么存在感。
总之考前就很有压力。我默默感叹,什么叫托福从娃娃抓起啊,感觉很上流,很京爷。所以左边的小朋友先我一步开始用
-Chinglish
-和很尖锐的娃娃音开始说口语的时候我就没绷住,一下子就很幻灭。我像她这么大的时候刚从上海的一所乡镇小学毕业进入一所乡镇初中,别说拿出两千块给我考试了,全家一个月都不一定吃这么多钱,然而那时的我都没这么
-Chinglish。而且,我高中进入某个只刷题啥也不干的精英学校之后就基本没有开口说过英语了,我现在不算很
-Chinglish 真得归功于我小学初中的乡村教师们,唉,果然不是我有
-privilege,而是北京就是不行。(我素质好差
但我乐了这一下之后听力最后一篇就开始掉线了,当然本来也有点听不懂,一下子没绷住之后更是开始豁边了,六个题目最后都有点乱选,活该。
-客观题考完就立刻出分了,阅读 28 听力
-26,虽然听力很豁边但是考虑到我最后一篇都是猜的,所以真的,给分不错(。阅读也没啥可说的,感觉比
-TPO
-难一点,两篇各有一道题不大确定(说实话我觉得都是烂题,完全没在考逻辑,在考和出题人是不是同一个脑回路),就当一篇错一个,28
-也不亏。虽然考完刷刷小红书看到大家都 29
-30(不是我今天这场,而是在小红书发分数的不是这个水平就是拉胯的不行求安慰,没有什么普通人),感觉还得拼一把写作和口语的运气,先不奶了。
写作一篇写了 300 字一篇写了 180 -字,我也觉得很吓人,怎么会写这么多,平时似乎打字打不了这么快。独立写作是问 -work 和 relationship -哪个更重要,看了三十秒题目就开始瞎掰了。口语的话,第二篇口语有一句话没说完,别的应该都还好。但愿没有高估自己(
-诶,但是我考前就一直很担心一个问题,就是两个小时不能喝水的话怎么办,半个小时不让喝我都会有点头晕,不是真的因为干渴而头晕,而是不让我喝我就很有心理压力,就更快地失水。到现场发现问题比我想的更严重,不到八点钟就把柜子锁起来上楼了,三个多小时都没能喝到水,更糟糕的是我忘记带润唇膏了,都没法厚涂一下。还算聪明的是把水锁进柜子之前我把卫衣袖口整个打湿了,中间用它贴贴嘴唇或者碰一下脸降降温,权当一个心理安慰,勉强有效。
-但是考完发现我没经验又社恐没问监考老师被摆了一道,水是可以带上二楼的,只是要放在考场外面的休息区,开考后就不能喝了。之前我就这个问题问过我认识的仅有的两个考过托福的人,只可惜二位都是八个小时不喝水也没关系的奇人,一个说不知道,另一个一开始说不知道后来又说不能带,而且我搜小红书也没搜到过类似的问题,就很奇怪,往往什么奇怪的问题都能在小红书找到同类,这个反而没有,大家都这么耐渴的吗,我可能还是不适合在地球生存。
-唉,作业写不完了,paper 啥时候才能读完呢。
-3月11日
-实分析进入测度之后明显就有了一种这我熟(赞赏)的感觉(,毕竟概率论用了这么久,看来还是点拓水平不行。你还别说,ly -和 lxg -两个版本都学过一遍感觉挺好的,有很具体的例子和构造可以用来理解抽象的问题。只不过这课到底上到哪了,我好像到现在为止就去了一次,明天得去看看这周到底要交多少作业((
-高统不知道为什么刚开学就掉线了,感觉是很晚才选上课一直看不到课件的问题,急了,明天进行一个 -Lec 2 -和作业的补。他这个作业不仅有书后题还有自己出的习题,急急急,Bayesian -一点都没学过(
-辅导员又发了个发展意向调查,为什么没有延毕的选项也不能自己填一个,为什么就连出国用的语言成绩都没有考完了还没出分这个选项,几个月之前我填的导师还是 -ypk 这次就改成了 -wwc(,蚌埠住了。最后两个问题是现在在跟哪个导师做什么课题,目前有哪些成果,我真觉得没必要告诉这哥们(,差点填了不方便透露/ -I've signed an NDA((x
-昨晚回来还就那个摸,按照之前在小红书看到的教程改了瑞幸的单杯纸袋,今天我逢人就掏出来炫耀:
-
(其实是立体的但不知道为什么看起来不是很立体(可能堆高度用的是纳米胶而不是泡棉胶的问题(
-今天拿到第二波联动的物料了,感觉之后还可以玩几次(别摸了(
-3月12日
-托福 checked in 了,不会真得等到周五吧(,急急急(
-植树节在蚂蚁森林搞了个大的,发现三年前领的山杏还没种下去,蚌埠住了。
-今天去听了下实分析,感觉很休闲,去年学的是实变函数与泛函分析,今年好像是真在学测度与积分(
-3月13日
-开学仅仅两周多三天就发烧了,这学校绝对有问题(
-月初立了一个这个月不喝奶茶的
-flag(其实是我糖前了,令人感叹(别笑话我啊,很多人去查查也都有只是不知道罢了啊!,饭点的时候烧的很高没吃晚饭,刚刚感觉饿了就点了点吃的,还是忍不住点了一杯茶话弄,我有罪((
明晚有一个高统作业要交但我就写了一半,后天有个基物作业要交但是还没学,下午我跟可能会点名的 -sb -必修课(它叫做绿色交通系统)的助教说我发烧了能不能开个雨课堂,他跟老师商量一通决定不开线上,并要求我过两天去校医院补个证明交给他,我蚌埠住了呀。又想起来它还有个据说很恶心的大作业,并且何老板这学期也没上这课所以就没人能帮忙一起水过去,我打算过一阵把这课退了。
-急了呀,就有一种很想指着天空说这上面绝对有个人在搞我的感觉(
-3月14日
-昨晚写了高统作业,哪怕洗了个澡一直到睡前体温也是正常的(。今早是被自己热醒的,一量
-37.5,我感觉我像一个在散发蒸汽的超大巨,不知道阿尔敏每次变身超大巨之后难不难受,是不是也像发烧一样(
今天上半场在发烧,中间退烧之后稍微缓了一阵子,晚上痛经了(。所以就又是啥也没干的一天,莫名其妙放了两天假,很难想象这个周末要还多少债,科研到底怎么办急急急(。先别想这个了,明早能好好地活着就挺好的了((
-周五似乎是托福出分的 ddl -了,首考所以好像要等到下午,很急,想起我的两千一百块钱就睡不着了,但它至少不是早晨就出所以又睡得着了(?
-3月15日
-早上果然还是不行,生完病虚得很,躺了。从周三到今天我就上了一节课,还是个体育课,说是上课其实就是在边上坐着咳嗽了一个半小时,太寄了,周末要还多少债(
-但好消息是基物作业是下周五交而不是这周五,我又舒服了。
-托福果然首考出分慢,刷了半天小红书看到非首考的都是上午就出了,我一直到下午快六点才出。口语 -22 写作 -27,充分证明确实还是老中(。感觉这个口语小分应该是不太行,查了一下似乎 -JHU 和 UCLA 的线都没过,印象里其他学校也有一些做 TA -需要口语小分更高的要求,恐怕之后还得考,虽然我也不知道这个东西到底有啥技巧。
-但总之轻轻地过百了(103
-倒也完全算不上高),一段时间内至少暑研可以放心用这个成绩,之后再刷一两次就好
-毕竟理论上来说这个成绩只有两年有效期挺不到我入学所以不管怎么样都要再考的(
隔壁寝室的姐比我早一周在天津考了托福,今天我出分之后她勒着我的脖子喊果然上海宁就是基础好,我说停停有没有一种可能我小学初中都是念的乡镇学校,高中就竞赛结束后学了三个月英语,结果随机破防了隔壁另一位竞赛落榜生(x
-哈哈,大三了,我终于也是有语言成绩的人了(
-3月16日
-早上本来打算去习题课交作业,醒来感受到了比昨晚强烈不知道多少倍的喉咙痛,一量又发烧了。求你了放过我吧,我感觉在某个地方绝对有个人在一边乐一边搞我啊(
-先不说别的,我已经四天没喝咖啡了,不仅每天困色特了,瑞幸优惠券都过期好几张了((
-记得之前在转数环看到过有环友说刚发现自己几年来一直没拼对 -continuous,结果我今天看 Cramer's theorem for large deviation -的时候突然意识到学统计学了快两年我好像一直把 standard deviation 写成 -standard derivative(,当然其实也没怎么写过,一般都在公式里直接表示成 -\(s^2\) 或者 sd -而已,但就是,我有的时候自己在颅内读出来就是 standard -derivative,狠狠破防了(
-下午不烧了,晚上从教室回来又烧了,我受不了了。
-3月17日
-头发好长,再留一留就能发动地鸣了。虽然很热但我暂时还不想剪,想搞一个很久之前就梦寐以求(?)的危险的发型,虽然也未必好看吧(
-后感冒症状是不停地流鼻涕还鼻塞,有一种高中的时候过敏性鼻炎的感觉,擤鼻涕擤得我鼻子周围的皮都快破了。然后发现,诶,来北京之后哪怕所谓很严重的花粉季我也没再过敏了,不如上海的春天一根毛。
-现在晚上回寝室纸笔都懒得往外掏了,以后争取每周用晚上的时间把计算概率和生存分析的作业写掉,然后平时就彻底不用带电脑了,某种程度上来说
-以防在路上平地摔把电脑摔坏(。感觉平板没有那么多容易战损的点,而且我买
-Apple Care 了,随便造(
前几天忘记在哪看到协和 4+4 -那个培养计划今年的招生方案了,简单来说就是理工科读四年本科然后转去念医学,再过四年毕业也是医学博士,能考执业医师证。诶,我想起来很丢脸的一件事是高三的时候我妈讲如果裸分擦线的话干脆不要零志愿报协和了,不如直接走强基,我当时正苦于竞赛 -PTSD 导致我不想学这个 b -数学了,我觉得这玩意既学不会又真的很没用(草,于是这时我感觉突然找到了一个我可以学的东西,我说我不,我就要学医,哪怕裸分过线好几分我也要填协和!然后和我妈关于裸分正好擦线这个八字没一撇的事情居然还吵架吵了很久,我还赌气去看了半天这个 -4+4 是怎么回事,感觉哪怕真的强基了也还是有机会转进去的嘛!
-直到后来群友问我这个化学和生物水平怎么学医,然后有一个正好比我大一届的群友对我谆谆教诲在华子要补习 -35 -学分的生物课代表着什么,fine,我就放下了这件事(,还把探微从强基那个志愿表上第三志愿的地方删掉了(。当时如果把服从调剂那个框也顺便反选掉,我现在就在 -SJTU 不知道在干啥了,多是一件美事啊(悲
-把这件事完整地回忆了一遍之后我比较震惊的是,我高三的时候就觉得学这个
-b 数学没啥用(主要是竞赛 PTSD
-感觉自己学不会,但也确实在质疑学这玩意干啥),感觉还不如学医有用,真的很超前,比我现在还超前,令人感叹。后来怎么把这个想法给忘了呢(可能还是因为发现别的都学不会吧
3月18日
-早上起来我又一次在寝室大喊大叫陷入崩溃,我问室友,我要怎么样才能让 -wwc -相信我真的病了一周,我不是不想科研我是真的没时间,我作业都要写不完了。室友说,你现在这个鼻音的严重程度,去和他说句话他应该就能理解了。
-我现在在我不想努力了我明天早十不去了要不干脆把金统也给退了吧,和,逃げちゃ駄目だ逃げちゃ駄目だ逃げちゃ駄目だ,之间反复纠结(
-晚上回来我又开始跟室友嚷嚷,我说我之前想买平板就是觉得带个电脑只为了看 -pdf -很麻烦,但现在又觉得哪怕只是为了水群打字快一点也最好买个配平板的键盘,还有就是我看论文要到处搜东西的,似乎又是电脑好一点,那不就又回去了吗。室友说,你白天不写代码吗?我说我不写啊,我写的代码都是 -trivial 的,帮 GPT -润色一下就能用的,这种事情就不要白天做了,晚上回来摆烂的时候顺便搞搞好了,我写作业都是纸笔的。
-室友扑哧一笑,说了一句很伤害我的话:哦哟,二十多岁了还在打数理基础啊。
-她想了想又说了一句:你数理基础只打了一半,现在数学基础行了,总算开始学基物了,后面还要打两年物理基础。
-我蚌埠住了(
-晚上看邮件发现早已忘记这回事的 ESEP 出结果了,果然是:
---We regret to inform you
-
搞得我又焦虑了(倒也没有,我真的已经身心俱疲,没有力气应付土木系诸如实习和上课这些破事了。所以我明早桥梁工程要休息了(
3月19日
-在实分析课上读 已经两周没去的 金统 PPT,一边听 Hausdorff
-测度一边感叹 ARMA
-这个东西真简单啊(。还记得我前几天吐槽为什么要把进击的巨人给格里沙而不是黛娜被锐评别合成大西瓜了,我寻思着
-ARMA,ARIMA,ARCH 和 GARCH 不更是合成大西瓜吗(
我怎么感觉这个高统 II 比高统 I 劲大了这么多,早晨起来看助教给我批了个 -80 分的作业直接宕机了,我错了我下次一定好好算最终答案(。上周的 slides -到现在还没发,急急急,那我周四去上个啥(。
-写实分析作业,又遇到去年在 Stein 见过的
-感觉只能称之为是数学题也不知道具体是什么的
-题了,还是不会,我蚌埠住了 习惯就好。
晚上回来继续写生存分析的作业,我实在不明白这个助教为什么非要把作业布置在 -word 里,就算真的喜欢 word 胜过 LaTeX(不理解但尊重祝福),也好歹把 -Excel 的数据复制过来而不是截个图放里面吧(
-定番之沙尘暴前一天洗了头,因为不想再洗一次所以戴了个帽子,晚上还是感觉头油油的,难道是戴帽子闷得(
-今天在路上普通地走,一辆自行车倒在我面前,听到前面的路人说,纯爱战车应声倒地,我绷不住了(
-3月20日
-今天想打开桥梁工程作业附的 .dwg,想起来我早就把 AutoCAD
-卸载了,哑然失笑。转 pdf
-打开一看乐了,我有点看不懂他在画一个,呃,是什么情况的一个不知道什么地方。又想了想还是
-逃避 先写基物比较着急,打开 PPT 就困了,我受不了了。
是的,清华大学土水学院(强调)以及未央书院(强调)就联合培养出了我这个水平的人(
-凌晨手写了一个 life table
-estimation,写得我火气色色桑就上来了,如果不是他让我 repeat the solution
-with R 我直接把 Excel
-做的截图放上去了(抱歉但我其实是做不到的,我的强迫症实在不允许我模仿助教(。我寻思着我那么大一堆
-R package 怎么就找不到一个 censorship at the end of interval
-的处理能调包一秒轻松解决问题,但确实是找不到,只有
-biostat3::lifetab 是 middle of the interval
-的做法,是否说明实际上没人会纠结这种问题但这个真空中的球形鸡一般的作业就是把这个当做考点(
这周生存分析的作业写了三个摸鱼的晚上,总算是交上了。今晚开始写基物,明天加急写基物,后天晚上开始写计算概率,周末加急催何老板写一下桥梁工程(,只要这些能在周一晚上之前写完,我就闭环了,以后白天就只要操心高统实分析和科研(草这也太多了吧)顺带还得听课和写写笔记就行了(。上学期何老板跟我说他白天上班晚上学习,我还觉得怎么这么猛,现在也(隔几天)体验一手(
下午读了一篇论文,读得我吱哇乱叫,大受震撼,总算读完(其实定理证明还没看,R -code 写日记之前才刚刚打开)之后打开另一篇,感觉好了很多(,果然 -Biometrika 还是短,太温柔了。
-骑车回去的路上想了想,后面要系统地学的数学课其实只有泛函,复分析和概率论
-3 了(PDE
-这种为了替代数理方程而不得不上的除外,其余就是随便选选课听个乐。别人实复概只学一个学期,我每年一门搞到最后学了三年(其实复分析我真也没有很想上,只是感觉此前没学过工科的复变函数又不去上个复分析的话,很难说自己是学数学的(。但这个进度完全是用这两年来在主修专业作为一具保持最低生命体征的尸体(i.e.
-每学期只选 6
-学分培养方案课程)换来的,一想到后面还得还这个债,有点崩溃了。
3月21日
-wwc -把这个题目给我的时候还说可能会用到一些概率图模型和随机矩阵,还殷切关照我有没有把 -Durrett -学完,结果看下来我感觉这个只和线性代数关系比较大,而我的掌握只能说是烂。
-这个高统作业,它怎么就这么麻烦,我以为今天可以下午把 PPT -看完作业写完然后晚上把基物写掉,结果一直到教室关门都没把高统作业写完,fine,fine。
-我昨天只是看了篇 -paper,上周只是生病了,我没有杀人放火吧,怎么现在什么作业都交不上啊(
--- -室友:好多 1 啊
-我:哪里哪里哪里哪里
-室友:网络学堂的课程作业
-
3月22日
-受不了了,昨晚熬夜写基物作业,今天通知基物第七周周三或者周六就要考期中,虽然这玩意能早点考掉也算一件好事,但我是真的学不会,除了把作业题全背下来,真的,别无他法(
---室友:你早点睡吧,明天的作业交得上今晚就别熬了
-我:我每天晚上都在努力把一个网络学堂的 1 掰成 0 然后才能睡觉(
-
从开学到现在掉了七八斤了,于是今天上完体育课点了杯茶话弄去教室一边崩溃一边赶作业,在奶茶里面算是热量不怎么高的了所以放过我吧,今天又没喝咖啡,喝杯奶茶怎么了(。感觉现在是一个不喝点什么就没法好好学习的状态,怎么会是呢(
为什么这个咳嗽和鼻塞还是不好,急了。
-3月23日
-今天读了另一篇 graphon -estimation,就,每个操作都在意料之外但又情理之中(,很难说。后天争取把总结写完,周二就有脸去上课了。但我觉得很悬,光是把我批注的问题搞清楚都不知道还需要查多少东西。
-我只是又读了一个下午论文,晚上去答疑坊值班的时候我甚至在看基物 PPT -写物理作业,但我现在为什么有五个作业没交呢,就是说,这是一个什么原理呢。
-我现在感觉可能计算概率得退掉了,一个只有作业没有考试的课记 PF -总觉得有点亏,但我真的扛不起生活的重担了。
-3月24日
-上次还在骂生存分析的代码作业,结果金统的 R code -写麻了,又写了三个晚上,我转不起来了,真要退计算概率了。
---我:绷不住了呀 作业拿 ARMA 预测后两周的上证指数
-友:是桑海宁就给我直接写 5000
-能预测准吗
-我:哎呀 反正就是三千点多一点 也差不太多的
-
下午满怀疑惑地把桥梁工程的作业做了,就,我要是第四周就已经会设计桥了,那我还上你这课是要干什么呢(
-这个高统 II 怎么比 I -难这么多呢,明明只是换了个老师讲同一本书的后半部分。可能难度主要来自换了个助教(,他会认真出一些找不到答案的问题,还批的很严格,急急急(
-感觉得纠结一下明天是学实分析还是开始写总结,不出意外的话周二还是没脸去上课,然而一切的前提是今晚真能把高统搞完(。想起来上学期上建筑材料的时候听到有个哥们在抱怨,说,我现在就觉得像不会游泳但是掉进河里了一样,时间一周一周地过去,就像一个一个浪打过来,我就只能勉强浮在水面上不沉下去,上岸是不可能的(
-似乎还有点过敏了,本来昨天觉得咳嗽要好了,今天又重了很多,严重的时候感觉喘不上气来(
-3月25日
-之前听说厚乳拿铁里面也还是有白砂糖(主要是厚乳里面有),但毕竟很少,不过还是换澳白喝了几天。现实是喝了三次睡了两次(,口感也水水的,还是换回厚乳拿铁了,所以你这厚乳里面到底是加了什么(。听说澳白如果点热的味道会浓一点(或者说原教旨主义澳白就不能做冰的,但我实在不喜欢喝热饮,自己泡咖啡坚持不下来也主要是因为没条件冻冰块,再说就算有能冷冻的冰箱也远远比不上店里用制冰机做的冰,感觉不如买瓶装或者直接就瑞幸了。
-熬夜把高统作业磨蹭完了,有个实在不会做的题到网上到处乱找,最后又是在
-lty 的主页上找到的答案,PKUnb(。一看上来先把 prior 取成
-inverse Gamma,这什么东西(,我还搁那用指数分布族一个个试,拿头做(
开始写(只有两篇 paper -的)总结了,发现之前还有理解错的地方,没懂的地方也在一个一个看。写了四页,刚把 -background 和一些用到的背景知识(比如说我以前真的不知道什么是 spectral -clustering)记好(毕竟这个我也要看的所以记一下也不丢人罢(,graphon -linear estimation 还没有开始写 oracle-based analysis -的程度,已经四页了,什么时候是个头(
-我感觉这学期非常不妙(各种意义上(
-早上起来重新修了一下昨天造的桥,我抽象锐评,怎么看都总有一种艾伦的始祖巨人的既视感(,就是,把上拱当成肋骨,左边是垂下来的头,右边是腿((
-
诶,这个桥,缩小一点看感觉还不错的样子。
-下午上生存分析的时候不知道为什么突然又焦虑延毕之后能不能顺利毕业了,于是重新排了一下后面两年的必修课课表,大概是秋季每学期要上五六门专业课的程度。春季倒是没什么课(如果明年春季要春研也能勉强安排得过来),要学的数学课也没剩多少了,主要就是多花时间磕盐。我感觉我像是 -gap 了两年,马上要回去正经上学了。
- -- - - - - - --
3月26日
-现在就是一个,诶,非常的疲倦。
-把 graphon estimation 那一篇写了,还剩另一个 clustering -的,目前的进度是还在研究 k-means clustering 和 spectral clustering -各自是个什么情况的状态。有的时候真挺想打个电话问问作者,你们这样子做 -approximation -真的没问题吗真的不害怕吗?我看着都害怕。还就真的没问题,bias 和 variance -都控住了,data analysis 结果也挺好(
-3月27日
-报了下丘赛,虽然未必去考(,不能带 cheatsheet 的话我是一个背 Delta -Method 都费劲的状态,大概就这个水平,也没空(
-今天歇了一天,写实分析作业和基物作业,然后两个都没写完,麻了。
-3月28日
-又歇了一天,还是没写完。基物这个作业对着书倒也确实可以勉强做出来,但是考试没书也没 -cheatsheet 怎么办呢((
-3月29日
-又活了一周,真不错,这周末要是还写不完我那个总结的话感觉就很难活到下周了(
-为什么这学期写了这么多码啊,虽然也挺好毕竟确实该练练了(。但这周开始的时候好像刚把金统的写完,写金统之前才刚写完上次生存分析的,今天上课把上周计算概率的写了(感觉强度并不大,大概还是不退课了),课上就一直在写,体育课上课之前在写,上完课回来又在狠狠调一个正负号,晚上写完实分析回来又写了计算概率这周的一道题,写了一半这次生存分析的作业。之前看论文感觉有必要去看一下他那个 -Rmd 来看看我到底理解对了没有,看的时候感觉好疑惑,又开始调((
-从生病之后鸽了两次计算概率,今天一去:
---:今天是第五周,是单周,那按惯例辟谣一个小道消息,关于本科生申国自然的 -blahblah
-:我们早点下课,因为我下午就要去曲阜了,我现在是本科生事务主管所以得跟着(
-:中央音乐学院还为这个活动贡献了一首歌,我们待会课间放一下!哦对了,我感觉下周应该可以给大家放一个现场的视频!
-
今天看到一段对话:
---A: 求问基物 3 pyk 期中期末考的内容是和教材关系大还是和 ppt -关系大,感觉这俩差别好大
-B:ppt 和作业
-C:作业
-D:其实跟往年题关系最大
-B:还真是
-C:确实
-
我第一反应:有的人还在对着相关性找 dependent variable -和考虑要不要把它们放进模型做回归的阶段,有的人已经直接上 auto regression -了,感觉受到了启发!(指对于我的基物期中(虽然我是基物 2
-晚上回来开幕雷击,东京工业大学暑研的邮件是 Congratulations -开头的(。本来这两天还在苦恼要怎么无痛延掉施工实习,都差点想去交钱申暑期短课了,好好好。不知道为什么我这次申暑研毫无动力,主要还是并不是真·暑研吧,就按华子的官方项目申了俩,录取率 -50%(喜
-3月30日
-你还别说,我上次说觉得好像看论文看半天没理解对一个比较基本的问题,昨晚看了会 -Rmd -感觉更不对了,今天又仔细读了读文章发现真不对,草。不过这样一来我终于理解他说的那个 -strong consistency 是什么意思了,我之前一直百思不解的是,这和 statistic -sequence 的那个 consistency 到底能有什么关系,把自己蠢笑了(
-明天一定把总结写完,再写不完真来不及了,真的,不知道为什么考了一个托福生了一个病,然后看了两篇论文了解了一个问题的框架之后就要期中考试了,我是大废物(
-第七周周三基物期中,第八周周一生存分析,实分析不知道什么时候,但我感觉这玩意强度远低于去年,或者说习题和习题课强度远低于讲义正文,我在讲义看得晕头转向忍无可忍跳过证明的情况下还能随手鲨习题,就,不太好评价。
-总之我受不了了(强装平静
-3月31日
-月底了,来欣赏一下这个月喝了点啥(去医院看糖尿病的时候记得带上你那破本子.jpg
-这个本子是美赛的时候数学系发的纪念品,还一次给每个人发了四本 2024 -年的计划本,摸不着头脑了。不过我发现贴咖啡标签正好,不如拿出来用一下。
-
基本全勤了,3.13 到 3.16 -在生病没喝咖啡,喝了三杯茶话弄当感冒药(,芊芊绿雪和云过处后来又回购了两次,便宜好喝,不加糖不是很好喝但比较有安慰感。周五一般都会有一杯茶话弄是因为体育课真的累,而且如果早课咕掉了的话也没必要再喝咖啡,不如整一杯奶茶。瑞幸的话,我一般不喝美式折磨自己,对生椰系列也没什么兴趣,就还是厚乳拿铁和澳白喝得最多,厚乳是很困的时候喝,澳白在不是很忙可以歇会或者睡得比较多的时候喝,不过理论上来说还是澳白更健康一点。
-可以看出来撕瑞幸标签越来越娴熟了,一开始每次都撕坏,后来掌握了一个技巧是喝完之后把冰块倒掉,稍微用热水从里面浇一下杯壁,很容易就能撕下来。
-我职业病犯了,统计了一下取餐号,还有点单时间,就是不知道怎么把这两个结合起来分析比较好。随便用 -R 跑了一下,目前还没有重复的取餐号,但是有一对只相差 2,是 \((485,487)\),还有两对都只相差 4,是 \((613,617)\) 和 \((485,481)\)。虽然 \((481,485,487)\) -非常接近,但点单时间可以说是毫无关系,只不过都是厚乳拿铁。考虑数字重新排列的话还有 -\((617,167,761)\) 和 \((841,481)\),到现在为止 481 和 617 -出现频率谜一样的高。没有买到过取餐号是 3 开头的咖啡。
-别搁这玩了,总结还差一个 statistical lower bound -的东西仍然存疑,周一上午总要用定时邮件发过去的,快去写罢(。明早还要去办护照,还得早起一点画个淡妆然后处理一下刘海和披发的问题。之前查了一下虽然申领流程可以在校内办,但校内没有邮寄的选项,之后还是要跑到阜成路取,受不了了。
-]]>4月1日
-终于把总结交了,凌晨两点钟已经是一个半梦半醒的状态了,越看越觉得我验证出来有点问题的一个矩阵计算真的有问题,于是把它写进了总结里面,白天也没想着再看一眼就给
-wwc
-发邮件了,想起来这件事的时候蚌埠住了。我现在都没有勇气再打开那篇文章和我写的总结研究一下到底是不是真的有问题,但其实问题不大,我只是觉得每个
-extended covariate 前面那个系数并不是完全相同的,但改一下总之还是能做出
-Cholesky 分解的形式 而且还能体现 node
-heterogeneity!,就无所谓了((
话是这么说,但是邮件被已读不回了,虽然这很正常毕竟它真的很长,但我现在真的是很难不害怕(x)。我明天又有点不敢去上课了,但又不敢不去(,大概就是这样的一个状态。
-早上去办护照,照澜院的派出所倒是对发型很宽容,允许披发和刘海拍照(当然也没到盖住眉毛的程度。就是不知道为什么我早上起来化妆半小时,拍出来还像通缉犯捏(
-悲报:清芬瑞幸关门了,我今天是骑车去清华科技园那家瑞幸取的咖啡,就是不知道有早课的话要怎么办比较好。现在是真的有点喝不得瓶装了,既没有冰又含很多糖还不是现做的价格也差不多,这怎么喝嘛((
-4月2日
-昨天问教务才知道施工实习需要用学校官方的暑研项目(只有这种才有批件)申请延后,我歪打正着因为懒得自己找也没什么办法找暑研,就只投了两个官方项目,正好中了一个,暑假就可以歇了。
-但现在的问题是,明年还有这么好的运气吗,那我是不是最好今年寒假去把它解决掉。但如果寒假补实习据说给分会比较糟糕,也不知道过年期间能不能给放假,虽然这些事情找零字班问问就好但我问的那个学长怎么不回我(。何老板在用暑期课程申请替代,倒也可以看看他的情况,如果成功了的话明年学一下就行,不成功的话,我真的不知道是今年暑假去实习好还是寒假补实习然后顶四学分低绩点好,比较缺乏信息的一个状态。
-好累,好累,好累好累好累。科研感觉得暂时咕一下而且最近也没什么活(如果我不去自己找活的话,下周三就基物期中了,我还是一个你问我波长是啥我只能干两碗饭的程度(
尤其是昨天今天加起来写了 23
-道实分析,梦回抽代(但难度其实也差不多就梦回抽代,我尸体真有点不舒服了。诶,但我周三近似于没课,所以说清明假期已经开始了,嘿嘿。
4月3日
-感觉,打开一个搁置了三天以上的 overleaf project -需要非常大的勇气((
-节前把目前所有的作业写完了,每个难缠的 1 终于都乖乖变成了
-0。我现在明白为什么周三效率最低了,因为这一天要写基物作业,一边呜啊呜啊一边写,写完之后都得缓好久。今晚在预习(x)基物,努力理解了一下偏振到底是在干什么,所以说,波长到底是什么来着((x
晚上洗澡的时候旁边两个人在说:
---A: 我今天终于去做实验了,这是我第一次杀小鼠,我一次杀了八只!
-B: 是不是你的师兄师姐杀不动了
-
路人害怕.jpg
-4月4日
-学习偏振,在我完全理解一切和我啥也没明白之间反复横跳,感觉是学物理的一个正常状态(
-我跟群友说学这玩意真的好痛苦,哪怕只是背答案,群友锐评基物 2 -和实分析其实都是 4 学分,你看着办吧.jpg,好崩溃((
-4月5日
---A: zgy 会点名的你们也不去?
-B: 哥 早八
-别说点名
-叫我起床出门捡人民币我都起不来啊
-
分享一则环友发言(
-4月6日
-这清明莫名其妙就过完了,急急急,实分析怎么办基物怎么办(
-今天 28 -度,去清华科技园买咖啡突然就变得痛苦了起来,想起去年端午每天都要死在路上一样的状态,求求清芬瑞幸早日开业(
-4月7日
-最近越来越容易失眠了,是不是睡前最好还是别写题,写码和物理作业倒是经常写着写着就困了,写完数学不缓个一个小时感觉都有点睡不着,哪怕只是光叔实分析作业这个水平(?(。于是今早就没去计算概率,非常遗憾没看到求真祭孔现场视频,只不过运气不错的是今天讲
-Markov chain 的理论,耳熟能详,而且还没讲到 MCMC,下次一定。
虽然实分析也耳熟能详了,而且光叔到现在还没到当年林勇大约第三周的进度,但我还是认真复习了一下他这个讲义
-但跳过了一些证明。现在就是一点轻微的混乱,有的时候会稍微怀疑他俩是不是相容的而不敢乱写(。他这个期中到底会是个什么情况啊,感觉每周狠狠写一堆作业然后狠狠写一份习题课卷子,实际却也算是没怎么学,有点小急。
来点 锐评 批注((


4月8日
-基物终于看完一遍,然而看完变换光学忘衍射,看完衍射忘偏振,看完偏振之后,屏函数是什么来着?希望
-csm 守序善良一点,我都两学期老粉了说不定基物 3
-还要见面能不能捞捞(
唯一的好事是找到了失踪半学期的计算器,然后 csm -在群里说这次用不着,全都是简单计算。我疑惑了呀,所以说不涉及乱七八糟的波长甚至不涉及 -\(n_o, n_e\) -之类的吗,那还能考什么(,难不成考证明或者直接用符号计算吗,我训练集里没这些啊(
-4月9日
-基物怎么办啊,算了,很快就会结束的(
-原来托福成绩单还会邮寄一份,两千块钱听个响,啊不是,已经听了好几个响了(。出分的时候看到成绩单上有当天早上考前给拍的蓝底照片的时候已经崩溃了,结果还给我寄一份,受不了了((
-期中考完不知道有多少作业要补,还得讲组会
-的同构异形体。为什么不开组会而是让大家一起听单人报告,太可怕了吧(
4月10日
-基物期中不知道为什么这么多画图题,不会,差不多得了(。这个班成分还挺复杂的,但理论上这学期是给物理系开课,所以出现几个一小时就交卷的人应该也很正常吧,是吧((
-本来以为考完基物解决心腹大患之后可以狠狠学一天,但还是摆了,又困又累,明明晚上睡了七个半小时,午后又睡了将近一个小时,还灌了一杯拿铁,怎么会是呢。不知道实分析期中考到哪里,但考前总得把讲义再翻一遍吧。生存分析就随缘了,最后一年开课了,也没几个人,而且毕竟是 -wjd,应该会比较善良,平时记的笔记删减一下打印出来当做 cheatsheet -就行了。
-明早要去取护照,通缉犯.jpg。但凡拍照的时候稍微笑一下也好啊,相比之下我现在看身份证照片都觉得挺好看的了。
-4月11日
-高统不知道为什么又掉线了,上周放假,这周这个时间我正好要去取护照,已经没印象这课半个月前在干啥了。护照上打印出来的照片看起来比我当时照的还要白,不知道是不是又 -p -过了,还是覆膜之后反光看起来就确实更白一点(?),于是黑眼圈也更深了,像一个潜逃期间三天没有合眼的通缉犯(
-清芬瑞幸无了之后我就一直去清华科技园买,可能清明期间科技园的员工都真的放假了而我还在坚持点单(,导致我订单数进了他们门店前 -20,然而清芬还在的时候似乎全勤都进不了((。今天回来的路上在万柳吃的饭顺带点了咖啡带回来,于是现在就已经掉出榜了,加上明天是茶话弄日(?,感觉要无了(但是为什么要在榜上呢,为什么呢((x
-基物成绩很快的出,比我估的 baseline -还是高很多,虽然也就那样吧但挺好的挺好的,感觉比我高中时候强多了((
-感觉这周莫名其妙的就要过完了,上了六天课但也没觉得很漫长什么的,说明中间基物期中带来的压力已经超过了一切,于是它解脱了以后的幸福感能够抵消其余所有的痛苦(。剩下就写写作业,还有 -all in 实分析了(生存分析:那我呢
-4月12日
-我麻了,痛苦的一天从看了匪夷所思的桥梁工程作业开始,我一直以为这是个水课,结果怎么还要求先修工程力学的?我是一个一学位物理二学位土水大类、在某书院中游 -GPA -的大三(下学期)学生,你就默认我知道什么是弹性模量、截面应力和挠度,这合理吗(
-稍微缓了一下,早上起来看到计算概率已经掉线了的讲义,我又麻了。不过这个好说,首先这周还是没布置作业,而且它无论如何都比桥梁工程好说,学一下就好了(
-生存分析 cheatsheet -还没开始,倒也不是很急,而且一想到它没有期末就很开心,期中考完之后就等于不存在了。虽然期中之前也不太存在,就偶尔晚上要写写码。早上起来,上完体育课以及晚上回来写了写金统作业,倒是很平复焦虑,谢谢你 -wwc,但如果能选一本在网上找得到答案的书布置作业就更好了(
-最近买了两盒棉条想尝试一下,今晚突然想起来去认真查了一下 -TSS,好可怕(。但我最担心的是,我感觉我在学校里感冒发烧真的非常频繁,发生在经期前后也很常见,TSS -的症状和流感也没啥区别,那怎么办,以后每次生病都要直奔医院吗(。我其实都有点怀疑跑去校医院跟医生说因为用了棉条然后最近生病了怀疑 -TSS 人家会不会注意我在说啥((
-下午回来看到在布置校马设施,一阵头痛(,不知道明早要怎么闯出紫荆区去习题课交作业。去年校马的时候正好是实分析期中考试,还是在明理楼,就没绷住,今年怎么还在实分析(
-4月13日
-晚上本来就不太舒服,吃饭也晚,结果吃完饭收盘子的阿姨打翻一个面碗,被泼了一身油汤。只能说幸好除了外套之外都是今晚本来就要洗的衣服,食堂经理赔了干洗的费用,但有没有一种可能哪怕外衣我都是手洗,贴身的衣服更是不想干洗(除非真的洗不掉(衬衫上的油真有点洗不掉,再努力一下,实在不行真得干洗毕竟这衣服好贵((,唉(
-上次打算等到周日去问一下同学桥梁工程作业要怎么写,结果今晚他先发制人来问我怎么做,我绷不住了,哥你不是学过工程力学吗(。可能确实是这课逆天吧,我也不知道啊(
-唉,生存分析,这就开始看(
-4月14日
-生存分析咋办(?
-4月15日
-生存分析赢麻了,昨晚 cheatsheet 上还有一块空的,就把 log rank 和 -score test for cox model -等价的那个证明打印出来贴上去了。结果今天问这两个有什么区别,可以通过理论证明,或者用给定数据验证两个统计量相等的方式来说明,我寻思着让我算两个贼复杂的东西还要让它们相等,那我大概率算出来就不相等,就直接抄证明了。昨晚写桥梁工程作业,写的时候不知道里面有两个东西是相等的,算出来才发现真的相等,说明 -priori 是非常重要的(什么
-唉,wjd -的卷子一如既往出得真好,讲课也好,华子就是一个没有能力留住教学好的老师的状态,当然它可能也没啥兴趣留住。
-考完之后 wjd 锐评:
---怎么大家考完试第一反应都是掏出手机来刷一会,然后露出满意的笑容
-看来是考了两个半小时的试,中途一直摸不到手机,上面就发生了很多有意思的事情
-
4月16日
-这个 b 实分析(,真看不完了,现在又说 5.4 -节也要考,但又来不及讲,虽然讲不讲也都无所谓但是,唉(x
-4月17日
-急急急,急中又夹杂着一丝不急,反正就是晚上回来先洗了个澡然后吃了一个小时水果(?
-4月18日
-天气热起来了,这种熟悉的黏腻的感觉又回来了,好烦(
-继清芬瑞幸看起来彻底要无了之后,今天清华科技园店也没了。昨天没喝不知道什么情况,但今天下午一点打开点单发现店里除了点心之外全部缺货的时候,悬着的心真的死了(
-想了想旁边还有个库迪,听说这两家打架打得厉害,还有人嫌瑞幸贵就拿库迪当平替,就去探索了一下,结论是替不了一点。我寻思着既然都当平替了那总得便宜点吧,我在美团买瑞幸券是每天九块九,库迪虽然全场九块九那不也还是九块九吗(。店面小很多,生椰拿铁都抄了瑞幸的怎么不顺手抄一下厚乳(,澳白只有热的(倒也正常,思来想去选了一个流云拿铁,主要是我没看出来这个是什么东西,于是我想总之是拿铁吧还能错到哪里去!结果提回去尝了一口怎么比奶茶还甜,冰也化得很快。之前还看大家吐槽瑞幸的冰太多化得太慢,然而在 -30 -度的天气下我真的就希望它多一点化得慢一点,既不要融到咖啡里面影响味道,还能在我热得很烦躁的时候贴贴脸安慰一下(
-那怎么办,清华科技园这个是突发情况还是寄了啊(,难道以后去北大科技园买吗,下次干脆进北大买算了(
-好累啊,怎么就这么累啊,这实分析快点考完吧(。学这个 b -数学平时就像泡脚一样细细欣赏优美的经典理论,到考试之前就得狠狠地喝洗脚水,管你每个结论怎么证明的,先把它记住再说((
-4月19日
-累了,已经开始畅想考完去孚王府玩,吃必胜客 EVA 联名(
-4月20日
-终于考完了!休息!
-下午拿到实分析卷子之后我有点,啊主要是,有很多的疑惑,这真是实分析?这不是数分,不是微积分吗,因为太水了所以我都怀疑到底有没有伪证的程度,只有附加题稍微有一丢丢难度,虽然这个怎么看都不可能正着证出来所以反证一枪秒了也没啥吧。不知道是出于想装个逼,还是最近复习得太痛苦了想赶快结束这一切(,还是晚上原定有出去吃饭的计划,写完附加题就跟在一个人后面提前 -45 min 左右交了。
-跟在别人后面交其实是因为,考完要在台上领后半学期讲义,他那个实在是太贵了(,而且我学期初就自己在某宝印好了(好孩子不要学),我又怕一个人上去被叫住,就只能挑个有人一起交卷的时机混过去。不过一出来走了两步就想起来第二题那个方体覆盖好像写拉了,边界上没完全盖住,虽然他真不一定仔细看或者心慈手软的话就当我笔误了放过或者扣不了几分,但是严格起来的话全扣也不是没道理。无所谓了,我附加题都写了,怎么样也不会出大问题。
-只是感觉,早知这样的话何必痛苦地复习一周呢(。什么新的东西都没有学到,就单纯是在大口喝洗脚水,挺没意思的。不过也没什么可早知道的,somehow -这就是在不知道之后会发生什么的情况下做的无悔的选择了(看巨人看得(
-所以 lxg -之后能不能开个泛函啊,我真的好想在他这里水过去,甚至他如果在我毕业之前还开下一轮数分的话我真的想去水一个,分析基础还是不咋地(
-晚上去吃了 EVA -联名,本来想要明日香的吧唧,但店员说吧唧只剩三款的时候我就感觉有点不妙,领完的两款怎么想都是大烫门明日香和渚薰才对,果然一盒还剩下一个绫波丽,一群真希波和一大群真嗣(。想了想我那边有一个渚薰的吧唧,就拿了个真嗣凑了一对贴贴,看起来也还好嘛!只是左边像 -mappa 的进巨画风右边像 WIT 而且还有个必胜客联名的标注罢了!
-
所以为什么都不要真嗣,他不可爱吗(?
-明天去世图读者开放日,不知道会冲动消费点啥,总不至于支持一手影印本 -PTE 吧(?
-4月21日
-不知道为什么还是很累,而且这澳白我喝一次睡一次,网络学堂还有七个猛 1 -在等我(,第九周要讲论文,急。
-今晚回来把头发剪了,天气太热不地鸣了,love & peace(。
-4月22日
-累麻了,论文证明看不动一点,我感觉它看起来就是单纯地算了 20 页(
-今天的瑞幸取餐号是 001,但昨天是 032,前天是 031(
-遇到了一个剪头发之后的常见问题,显得肩很宽,穿泡泡袖尤其灾难。算了凉快就好(
-4月23日
-实分析这期中成绩下来好令人幸福(,今天扫了眼写拉了的那个题(但其实助教放过了,谢谢助教)的答案,恍然大悟我为什么要重新给方体写一个 -2 -进方体的覆盖,它那个条件不就是个针对方体的不等式来着吗(。有一说一我能想到的解释只有,平时写作业写到 -2 -进方体的时候我都不知道怎么翻译才好,用到的时候就在英文里夹杂中文的这几个字,期中脑子一抽想用中文写答卷,一上来不知道为什么满脑子就都是 -2 进方体 2 进方体 2 进方体了(
-感觉比起做别的事情,现在更需要的是狠狠补充几天睡眠,尽快让这个疲惫的感觉消失,不然真的除了写作业啥都干不下去,效率蛮低的(
-打算把讲论文挪到五一之后了,很累,看不太动,也确实还再需要点时间,另外又搞了篇新的。
-高统 II 好难啊,虽然每个 slide 都比 wwc -当时短不少,但定理看起来复杂多了,抄笔记的时候总是很疑惑学这个东西干什么它真能有用吗,顺带稍微考虑一下是不是可以乱用这些估计方法做手里的问题,但也没有什么头绪。作业也写得很麻,wwc -之前布置的作业至少都是课后题也大多数都有答案,lq -搞一堆自己出的题目,磨蹭很久才能写完,这考试要怎么考(
-4月24日
-写了一天高统,还是没写完,蛮崩溃的。
-晚上在户外停了五分钟,腿上被蚊子叮了三个包(
-想起来前天和室友的一段对话:
---室友:你腿上的疤是被蚊子叮了吗(指)
-我:应该是去年的,今年还没被叮过这么多
-室友:啊这
-室友:ok,我没有别的意思,很健康的两条腿(指)
-我:所以对于健康的定义其实是,正常地遭受生活的磋磨的结果是吗?
-室友:啊这
-室友:你还别说
-
4月25日
-晚上在路上又被人撞了,令人感叹(,是非常常见的前车的哥们刷着手机就唐突左拐了,我一个急刹加按铃既没能拦住他也没能阻止后面的人撞我,唉((
-我说这学校的新生入学教育能不能整点实在的,至少拿半个小时讲讲骑行规范,比如说转向要减速,回头看或者至少打个手势(说实话我也不知道这两个到底哪个难,但回头看比打手势安全多了),车多的时候不要乱变道,etc(
-唉,抱怨也没用,不如复读一些神腿们的教诲:有竞技的入门水平,平时就更应该有在路上调停事故的能力,自己不要不自觉地狠拉速度,至少还要能预判一些常见的问题,比别人更快地做出反应避免事故发生((
别骂了别骂了((
复盘一下,我被撞的时候刹住站稳了没摔,我感觉没摔这件事还算是给后车的哥们支撑了一下至少他人还狠狠扶了我一下(,只是衣服又脏了(。车应该没啥事,顺便狠狠教育了几句前车,我感觉已经赢了至少尽力了((
-我真的,我开学就是玩了个烂梗,结果衣服就不停地脏,以后真的不敢了饶了我吧((
-4月26日
-我写量子力学 -belike:叉乘是什么东西来着(。有的时候真觉得很丢人,都不太好意思说学过数学(这之间有关系吗
-晚上勉强把高统作业交了,实在写不出来了,算了(。怎么就这么阴间啊,每个题长得都像 -open problem -一样,用的定理也奇形怪状的,实在搞不定。然而从第一次的批改来看他这个作业给分还挺严格的,唉。我上得比较烂的课都是名字里带 -2 的,比如概率论 2 和微积分 2(,感觉基物 2 也差不多可以算上了,高统 II -比高统 I 难巨多可能也是正常现象吧(
-总之暂时下班了,感谢 wjd -送来的九天长假(指下周一的课她有事就放掉了。总之明天先去闪现一下郑州,后天回。
-昨晚在答疑坊值班,想起来过两天有一个要交的期中论文可能只能在高铁上写了,在一晚上一单都没接到的情况下还花 -120 购入了一个 ipad -键盘(。晚上回去何老板找我问问题,才终于又有了一点在答疑坊干活的实感,毕竟 -5~8 周津贴统计里甚至没有我的名字,这是怎么一回事呢((
-今天取快递回来之后室友锐评:你确定这玩意 120 吗,我觉得把罗技的 logo -遮掉的话看起来顶多 -30。可能是粉色就会显得廉价(,但选粉色绝对不是我自愿的,是粉色款比别的便宜 -20 -块,否则就买灰色或者卡其色了,我还真是第一次见到不仅不收粉红税还粉红免税的东西((,大概是因为卖不出去或者确实是看着很廉价导致的吧((
-晚上回来试了一下,除了键位距离有点小一下子不习惯之外没什么毛病,稍微熟悉一下也就好了,我手比较小反而挺友好的。现在的问题是它和平板加起来都快和电脑一样重了(但如果把平板保护套拿掉就会轻很多),这一套还不能码代码,那为什么呢(。只能理解成上次电脑屏幕碎掉之后还是觉得带着 -apple care 期限内的平板乱跑比较有安全感,以及平板看 PPT -确实比电脑爽很多这样子,键盘只是救急,只是救急(默念(
-4月27日
-现在这个发型虽然穿衣服要注意下不要显得肩太宽,但很适合戴耳环,以前头发很长的时候戴了也看不到,还会担心掉了都不知道(虽然我的耳夹均价不超过十块而且都是淘宝常见款式,但也还是不想掉(。不过我没有耳洞,也不打算打,一般都是戴耳夹,鉴于我不想承认是因为怕痛而不敢打,所以我一般都说是因为要防止改变自己的拓扑结构(
4月28日
-闪现郑州,在街边吃碳水大餐(,这边好像真的很喜欢在路边放桌椅吃饭,虽然感觉胡辣汤和烩面都没有特别合胃口,有点太咸了。下午去郑州博物院,每到这个时候都感叹当初学工艺美术史的时候多么幸福。买回来一堆文创,多到我现在根本没有勇气去看这一趟花了多少钱(
-高铁开出北京之后我皮都展开了,虽然去的时候坐和谐号没有插座是怎么一回事呢(,回来一开进北京就不舒服了(
-在高铁上写完了合同法期中作业,还写了点别的,现在开始急计算概率作业了(
-4月29日
-尝了下瑞幸新品青提味拿铁,蚌埠住了(,一边喝一边思考我到底为什么会对这个东西有期待,是为什么呢(
-看了一天计算概率,补了一个月的内容(。晚上一直在研究 KFC 啊不是 KMC -和他之前说的那个加速方法到底要怎么样才能拼起来,最后才明白是证明里面要用到那个加速方法的结论,绷不住了。
-现在处于一个刚搞明白要干啥的状态(也不好说是不是真的明白了),还没开始码,急急急((
-4月30日
-
5.5 update: 总不会现在还有人想看这个吧?
-总结:库迪好难喝,不要买。
-]]>五月的失败从 Yau contest 直接弃赛开始!
- -5月4日
-突然闪现!前几天一直没写是五一华子游客太多了,也没有合适的教学楼可以去,更没有工位和实验室,于是躲去乡下(不是)瘫了四天,作业还越写越多,也没搞科研。
二月份打的美赛出奖项了,本来都做好拿蓝色证书的准备了,结果竟然是 -honorable mention,今年 ICM -获奖率比以前高一些,运气还不错。开了下盒感觉华子 S -还是挺多的(,那我还蛮强的嘛!而且整体上看 ICM 这边 E 题选题比例高达 -52%,华子倒是有 38 支队伍狠狠选 D,获奖情况并不如 E 的 12 个队伍,我们 E -人真是太厉害啦((
-最近还有很多事情搞不清头绪,比如暑期实习延期的问题似乎该去和教务沟通下了,再不沟通都该选课了,我也还是不知道要不要延期,可能还得和别的前辈聊聊。科研毫无进度,不是在期中考试就是写作业就是摆烂,你要是问我为什么四月论文阅读笔记消失了,我只能干两碗饭。瘫了四天回来上秤直接给我搞沉默了,晚上出去紧急骑车补救了一下。
-事已至此,那怎么办,先睡觉吧((
-5月5日
-看了一丢丢论文的证明,结果它真的就是狠狠地用泰勒展开和 OLS 算了 20 -页,通篇难度不超过数分 1 高代 1 和概率论 1,我叹为观止。
-还有一篇证明没看,之前自己找的一篇文章就看了个梗概,后天要见阔别两周的导,害怕(
-5月6日
-前两天在乡下(?)住的时候我发现证明看不下去的时候可以躺下看,缺点是整个人的状态比较的被动接受,另外因为没法用纸笔算所以一些细节只能随便脑一下,或者多攒几个等有精神了再坐起来验证,也可能会直接睡过去(。搞得我现在一看证明就想找个地方躺着。等暑假回家想买个 -Luckysac -那样的懒人沙发,但家里又不是没有床(,寝室也不能放,更不能天天背着去教室(。所以最佳的论文阅读地点其实是 -C 楼的双人研讨间(?(但不知道装修之后它还在吗
-昨天看了好多泰勒展开,今天又看了十余个泰勒展开。说真的,它在证明上真没有本质的难度,但就算每个定理给到我面前让我去证,所有的技术(除了条件概率)在大一就都已经学会了,我怀疑我缺乏的还是一种在尖叫“这 -tm 也能继续算吗”的情况下真的继续算下去并算出来的能力(
-晚上一觉醒来看证明,看到这一句 \(\frac{2n}{n+1} - (u+v) >0\) -的时候我的小脑真的萎缩了。虽然后来反应过来他的意思是只要证这个条件下成立否则显然,但是,唉((
-
5月7日
-很久没有腰疼了,怎么最近突然又不行了(
-又双叒叕身体不太舒服,本来想继续读论文,结果只好写了点作业,生存分析考完试之后只有两次作业了,难度骤降,速通了。金统这个大作业的要求和没要求有啥区别(,晚上上课的时候大概查了查,又去看了眼自己的
-portfolio(,想起来之前一直说可以买点黄金但一直没买(好像是在观望,问题是这是在观望什么,单纯是忘了吧),就搁那狠狠地投纳指和狠狠地捞一个亏了好多的医疗,最近金价暴涨只能看着易方达黄金总资产
-0.67
-元捶胸顿足。干脆做个金价的分析好了,多上几个时间序列模型拟合一手,然后做个资产配置,最后再因子分析这样子(yysy
-我很好奇因子分析真能做吗,感觉只能宏观解释,要么就是找一点比较有
-confounding
-意味的因子来回归一下这样),后半学期他如果还讲点啥有意思的我就再给他缝上去(,反正这个大作业目的只是要把这学期讲过的内容串起来罢了((将要面对的现实:对着收集来的数据完全不会写码
之前订了一件 PKU SMS
-的文化衫,是拓扑咖啡馆那款,周末就可以取了。下学期泛函看老师可能还是不太能上(我也不到啊),实在不行就去把拓扑和微分流形一锅端了,假装是基础人(主要是数学系这概统和计算方向的课都实在没啥可上的啊
5月8日
-好热,这教室里怎么还不开空调,完全那个没心情学,这下真看论文看得汗流浃背了((
5月9日
-教室终于开空调了,但是开空调之前好热没去买咖啡,于是今天睡得很死((
-这基物到底是在干什么呢,不是很理解,PPT -也不说人话,感觉浪费大半天看这玩意也没用,还得去看教材。虽然好像是会算的,但是换个皮可能又不会了这样子。我要求也不高,就希望它能 -3.6 平安落地(
-晚上直接摆了,想起来前段时间看的宫崎骏访谈,于是把痞子制作 EVA -终期间的纪录片看了(?,又补完了(
-5月10日
-今天看到求真夏令营的题,先疑惑了一下这是在招博士生还是本科生,想起来去年秋季已经招过本科生了,于是开始思考现在去考这个卷子的人是几字班,好像是一字班,诶等一下,那我是?(
-体育课测仰卧起坐和 50 米,仰卧起坐定番先花 50 秒做 50 个然后躺下休息 -10 秒(,躺完被老师拉起来示范怎么一秒一个,没绷住(。50 -米这辈子第一次见到进 9 -秒甚至及格了,减脂之后确实各种意义上来讲变强了一些(
-不想刷乐动力了,感觉能及格((
-5月11日
-今天填推研意向统计,又有点没绷住,虽然我还要延毕,但怎么已经轮到我这一届推研了?我毫无心理准备。我科研还是现在这个 -beyonds,和啥都没有也妹区别。填了推迟推研之后又绷住了,反正我不推研,真推研的话去统计中心不太是问题,就算是求真看昨天那个卷子复习一下我上我也行,最大的问题其实是拿推研资格(,也即前三年课程中未完成的不超过三门,我觉得我明年也做不到。然后又没绷住,有没有一种可能我不推研是因为我要出国啊,那对科研的要求不是更高吗,真破防了(
-但我感觉我室友也都和我一个状态,除了一个室友要去教研院读硕或者直接工作之外,另两位都完全没科研在等着强基
-100%
-推研给分配一个去处(,又不特别焦虑了((。虽然我不知道数学系是什么情况,但真有未来一年里能发出来
-paper
-的吗,这种事情总感觉该发生在隔壁(。想了想得出结论还是别想了,去看了个证明,然后规划了一手暑假头上去江西和两湖找我姐
-同居 玩一周多点,期间可能在她家潜心读论文两三天((
之前看到过一篇推送说相比首都机场和大兴机场,天津滨海的机票会便宜一些。今天被北京到南昌七百多块的高铁票价吓晕了,又不想卧铺,除了夏天没办法洗澡以及洁癖地狱之外,16 -个小时实在太长了,12 -个小时的卧铺还要三百多接近四百,实在没啥必要。查了下大兴飞南昌的机票感觉早点买的话可以接受,又查了下天津飞南昌的机票感觉非常可以接受(,是一个从北京去天津待一天哪怕住一晚再飞南昌,加起来也比高铁便宜点的情况,还少坐三个多小时(。另外南昌回上海的高铁不算贵,中三省(对不起我其实也是今晚才知道有这么个称呼)转一圈加起来还没上次去郑州贵,冲了。
-比起微分流形,今天看矩阵运算看麻了,下学年有点想去补票一个完整的高代了。我说真的,比起在读研之前就把研究生课全部上完(e.g. -我之前想去学概率论 3,现在觉得会一点实用的随机分析和 SDE -暂且够了)到时候还得再学一遍,这种越拖越不好意思甚至再也没办法补票的课去上一个会心里更踏实吧(
-5月12日
-看证明,越看越疑惑,我怎么感觉他这个里面这么多问题(,typo
-不计其数就算了,第一页上来不等号就是反的吓我一跳(。最主要的是我真觉得算错了很多东西,有个
-log-normal distribution 的期望就真的不对,虽然改改系数勉强可以 bound
-住,但看他算出来那个值就很迷惑,真不是故意写错的吗。后面还有类似于“因为
-\(a + b > 2c\) 所以 \(a > 2c\) 和 \(b > 2c\)
-至少其中之一成立”的怪事,我猜他想说的是 \(a
-> c\) 和 \(b > c\)
-至少其中之一成立,虽然就差个系数改改也不是什么问题但是(。虽然还是有看了证明也没懂的点,但想了想先去重新验了一下正文里之前怀疑他搞错了的一个
-Cholesky 分解,还是觉得不对,需要给每个点加
-weight,这下更有信心觉得是他错了而不是我错了(
但有一说一,如果是真的需要加 -weight,证明就有点出小问题,我没看出来怎么继续按这个看起来还算合理的全局假设来控误差(。如果要给假设改个大的的话,他后面那一堆 -show that the signals under blahblah are strong enough to satisfy the -conditions in Theorems 1 and 2 -怎么办(。所以,这时候我是该怀疑一下我自己吗(,感觉得整理一下然后问问导这样子。
-先去看了看另一篇 graphon estimation 的文章,上次那个 local linear
-regression
-是真的算得很厉害,就是一种,假设并不复杂但结果挺好的,其他线性模型看起来也还有很多可以挖掘的点,还得学习一个。五一在乡下休息的时候我其实还想了想怎么把
-GLM 往上面塞,毕竟它也真有 covariates(sry
5月13日
-今天把生存分析的论文看了,怎么不算是一种搞科研了?(
-晚上重新算了昨天那一坨,又找了下发现 supplementary material
-里面有一处改过来了,正文的确错了,但另一个地方没改,这啥意思(。给导发个邮件实话实说了,belike
-现在出了点小问题,然后描述了一下这个小问题,如果真要尽快讲 pre
-的话也可以先讲 graphon estimation,反正我也读了几篇别的可以说说
-而且我觉得这个问题会比较分析一点,就是说还稍微能算一点,不急的话再等我算算另一个看能怎么救。另外我得狠狠写作业了所以这周不知道还有多少时间算,先别急
-急的话要么您自己来算,或者教教我量子力学罢((
5月14日
-最近睡眠实在是不行,感觉也体现在每天都在混沌做梦上,主打一个醒不过来或者睡了很久还是累。大概也和莫名其妙压力很大有关,一眼望到头的本科生活板上钉钉要续费一年,续费完了也没有留在国内读研的可能性,也完全看不到申请之前多这一年能搞出什么东西来,如果说大一大二好歹是探索了很多终于定下了方向,那大三这一年到底干了啥呢。昨晚睡前焦虑得不行,狠狠地查了一些我知道的人的
-pub,最后把知乎下载回来给 24 Fall
-下面每个数学相关的点了个赞,然后沉沉睡去(
今天写了一天作业,补了补笔记,感觉稍好一点了,可能做这些不怎么费劲的事情到底可以麻痹一下。明后两天要把基物和高统仔细学一下,这俩都掉线挺久了。期末周结束得很早,虽然比较阴间的是
-19 号早上基物晚上实分析,21 号桥梁工程,但到底就这三门课 虽然 16
-周生存分析要
-pre,还有金统和高统的期末,什么某个通识课要考期末这难道还得复习吗(
时隔一周多终于拿到因公出国的批件了,明后天尽量去找土木系教务审批延期,总之要在夏季学期选课之前搞完。其实我也没什么别的考量,最重要的是夏天到乡下上工地实在太热了,我受不了,冠冕堂皇地讲就是会影响暑假的科研计划,所以我想延到寒假实习。
-说到选课,今天看了下秋季学期的本科生课程,索然无味(,选个拓扑选个高代走人,统计计算也不太想上(我真不是很想再上
-zzy
-的课了,虽然这个或许也是复习高代?我对算法的了解仅限于数值分析介绍的那些和计算概率讲的一点点,统计特化的计算完全不懂,也许学一下是有好处,但不是非得上课),毕竟还有量子力学(想开点,这个也是复习线代)和工程力学基础这两门不得不品鉴的必修课,和大约三门比较水的必修,该把重心放到科研上了。
5月15日
-状态真不太行,怎么每个学期到后八周都过成这个 beyonds(
-5月16日
-草这实分析作业怎么这么多啊,前两天没意识到问题的严重性完全没看
-其实是物理更危急导致的,今天边看边写搞了一天还没搞完,明天又没空写,真寄了。高统到现在还没开始,堆了三个没看的
-slides 了。
算了无所谓(,周六早上反正我去中科院数学所公众科学日
-追星,也不去交作业了,线上交还可以再迟一点,顺便也去那边看看世图新书展销。从寝室骑车两公里多就到了,压力不大,跟晨练似的,这总不至于再咕了(。前两天报了六月初的清北统计论坛
-去吃茶歇和追星,总不至于过不了审不让我去吧((
悲观一点说目测到期末之前没什么时间磕盐了,这学期绩点别爆炸就不错了,从下学期开始一定少选课。
-5月17日
-本来还在急这周实分析的作业,明天肯定交不上了,得找个理由交网络学堂,晚上在答疑坊小程序里看到一个问上周作业题的,什么叫松弛感啊(,这下不急了(
-今晚在教室看到有人在看 Fate(目测是 HF 线),爷青回(
-5月18日
-今早去数学所了,虽然八点钟就开始了但我十点才到,听了三个报告,了解的话题再加上科普向就听得很乐,来晚了于是没听到院士报告(。中间摸鱼的时候顺便看了眼今年数学所的博士招生考试题,看在我没学复变不会做求真那个级数题的份上承认求真的题比数学所难,但数学所题量好大计算好多啊,感觉这么一说也有点难(。
但强基就算保研也不能离开华子,北大都去不了更不可能去数学所,又有什么关系呢(
-中午结束之前和世图的一个编辑姐姐(群友)面基了一下,本来想买世图的新笔记本(前情提要:在摸鱼学导论和划水学原理之后又出了新系列的本子,详见这里),但是去太晚了,那个数学家用的量子理论笔记本没了,下次网上买吧(。没仔细逛展销,来晚了就光急着去计算实验室了,反正
-GTM 也没上新,浅浅瞥的几眼里没看到
-Durrett,不支持了(看到应该也不会支持的(。进校门了才想起来结束之前忘记回世图的摊位盖章了,枉费我还带了集章本,算了反正世图的活动挺多的,而且就那几个章(
现场中学生好多啊,羡慕,搁我高中的时候学校旁边只有个上海硅酸盐研究所,完全没这个条件(。遇到了一些认识的人,主要是隔壁
-SMS
-的几个,不过完全没被认出来,标准结局了属于是。遗憾的是今天没穿隔壁
-SMS
-那件院衫,正好还有个拓扑相关的报告,不过还好没穿毕竟我完全是云的,下学期一定学(

5月19日
-退一万步讲,这学期变成这个 beyonds,这门高统 2 -就没有任何责任吗(。它讲贝叶斯,一些深入的 MLE -和非参,我不知道怎么形容但我真的完全看不出来这些东西会在哪里有用,也可能比较 -advanced -就是这样子的,每节课几个不知所云的主定理和看了也白看的证明,反复嘲笑我是大废物。作业也很逆天,五一前和 -MLE asymptotic properties -那几个主定理搏斗还啥都没证出来犹在眼前,今天本来想补补笔记结果算了一天 -one-step -MLE,他这个作业哥们连算都算不清桑,我实在很难想象考试要怎么考。
-说实话从来没有上个课上得这么悲观过(?),它和高统 1 -已经没啥关系了,倒是和搞科研看不懂论文的感觉比较像,可能研究生课就是这样的,问题是我好像过不了多久也要变成研究生了啊(大叫
-5月20日
-前天没买到的笔记本今天到货了,我是自愿学习量子力学的(
左边这本这学期基物量子部分稍微写写,下学期还有一门量子力学用来写写笔记。右边那个可能下学期写高代,拓扑懒得写了反正有现成的。好久没用笔记本写东西了,近一年来都是直接写纸上然后收集起来。

总之下学期就这两门数学课了,高代 1 -大概比较挂机,我想补的东西应该大部分都在 2 -吧。看了下研究生课果然还是索然无味,不多选了,学概率论 3 -的意义可能并不如多花点时间读论文大,还得学量子力学,以及另外四门不得不品鉴的什么东西(,实在不行再找一两门课刷 -GPA,虽然暂时感觉不太需要吧。
-今天看到这个,差点一个激动就买了明日香款,后来仔细一看不是两张卡
-69,是一张卡正面明日香背面真希波卖
-69。我倒也不是不喜欢真希波,更不是没钱,我只是想要一个完整的明日香,所以我不买了(。另外第三新上海市的
-EVA 联名是真不少,不急着买这一个(
另,今天在生存分析课上更新了平板上的 Arcaea,不知道是否构成
-playing video games during lecture,记个 * 真书院的小过(
5月21日
-困困困,摆摆摆,我感觉我的睡眠问题也逐渐变得显著了,睡不着是真的难绷。
-现在有六个作业和一个也不算很大的大作业要写,该用闭区间套法了(。日子一天一天过去,实在看不到什么希望(
-今天收到了一个幻方猎头的好友申请,假如我这个本科要读六年的话,我可能暑假真的会去实习刮点钱,可惜它只有五年(
-5月22日
-星野源似乎塌房了,哥们上次在国内出名可能还是和新垣结衣结婚,上上次可能还是和新垣结衣搭戏(x)。不过自从我姐追 -kinki kids -塌房以及见证过很多类似的事之后,我就觉得当日本男艺人的粉丝之前得做好这么个准备(?),所以倒觉得没啥(??),而且毕竟没花过钱就更无所谓了(?)。话说回来 -Tokyo Dome 的那场演出是真的很棒啊,唉(
-相比之下今天更糟心的是买的水果和酸奶被偷了,可能是在这家消费过很多了的原因,店家还问我明早要不要送一份新的过来。明天还找不到的话就查监控去了,不是因为我正义感强,而是十来块钱对我来说就挺多的了所以我真的很需要让偷外卖的人赔钱(来个
-* 真书院的小过
晚上去开隔壁书院的年级大会(,正好看到唯一一个在华子的初中同学在斜后面,线上癫了一会,学了一天量子之后精神状态奇妙地变得好多了(但也不太好,进度还是慢一章(
-5月23日
-到底为什么要让我学量子力学啊!除了去求真可以少上一门课之外想不出来还有什么别的用处(
-早上帮刚换了新寝室的室友搬了点东西,以后晚上回寝室就没人陪我说话了。我只是想永远身边能有人陪我闹着玩,三天之后就要失去一个,两年后要离开几乎所有人,想想还是有点难受的。一般到这种时候就要想,按我现在这个情况其实也不好说能不能有学上,就不分离焦虑了,就申请焦虑了(
七点一刻到六教楼下才想起来下午待的教室晚上有课,但我忘了这回事,走之前扔了一堆东西在那里,又冲回四教拿。进门看到一楼在一年一度课间音乐会,扫了一眼没有 -neruko 就跑了(?),结果冲上楼梯看到 neruko -就站在上面,在整个人卡住的状态下匆忙打了个招呼,事后一想怎么不算一种社长线下交接仪式了呢((
-这作业啥时候能写完啊,急着急着都不太急了。好几门课已经严重落后于进度了,真的,这是最后一个选这么多课的学期了,以后再也不敢了。
-5月24日
-好累啊,周五感觉一般就是混一天过去,上体育课导致的。
-喉咙有点痛,开始紧急多喝水吃草珊瑚和西瓜霜含片了,希望明天能好。印象里小时候觉得草珊瑚含片很好吃,后来不知道为什么一直吃的是西瓜霜,上次感冒的时候两种都买了一些,发现西瓜霜显著比草珊瑚好吃,就纯甜,不像草珊瑚一样微甜中带着一股药味,不知道以前咋想的。大概是草珊瑚含片不含蔗糖的原因吧,所以虽然味道很怪但以后大概还是吃这个(?)
-5月25日
-金统大作业启动,然后突然想起来华子还欠着我一笔钱(,急了,周一问问(。钱难挣狗难当,这学期从答疑坊得到的收入越来越少,逐渐变成偶尔去看一眼小程序然后看眼缘答题
-简称不怎么干活也做题 PTSD
-了,到现在值班次数都不够,我觉得暂且也别申请焦虑了,先申请费焦虑吧(,怎么一天到晚的这么多事要操心。
室友搬完寝室了,虽然刚刚还在微信上和她讲垃圾话,但我真的希望能一直这样。那种事不要啊!室友找了别的室友什么的……!我希望她一辈子都会想着我,我死了之后也暂时……至少持续十年吧!
5月26日
-这个学期变成这个 beyonds,除了高统 2 -需要承担责任之外,这个桥梁工程难道就是清白的吗((
-5月27日
-鼻炎犯了,一直到早上七点都没睡着,九点多又被室友吵醒,然后又被楼长吵醒,过了一会又被上课回来的室友吵醒,兄弟非常恐怖(。下午实在撑不住就补觉了,两点才起来,错过了我能上到的 -wjd 讲的最后一节课,有点小难受。
-今天下午听了统计中心的两个报告,第一个是生统的听个乐呵,申请 UNC
-能不能给点好处啊哥(x。另一个是 signed
-network,把我认识的模型和聚类方法都捏到一起了,看到前段时间大折磨的正交矩阵乘逼近还是有点没绷住(。不过之前确实没从生成网络的这个角度考虑过为什么
-graphon 和一系列的 model 能够 make sense,看到 one step estimation
-想起不知道怎么办好的高统 2,背后一凉。
查了下 Weijing Tang
-竟是华子数学系校友,难怪会来统计中心作报告,这地方分明已经烂完了(暴论
5月28日
-累累累困困困,下午走进六教感觉教室太热了,遂转身离开把课翘了(
-睡眠质量真的不行,再这样下去真能活得过我那棵空气凤梨吗(。那 618
-要不要买个手环(啥(或者直接买个 apple watch 呢(我没事吧
5月29日
-背了一本物理书一本笔记本去教室,一天都没拿出来,搁那嗯算高统,明天还得背着(
-急急急,急急急,急急急。
-5月30日
-昨晚通了个宵,通完宵之后躺在床上想,后面 20
-天要考六门课,还要交一个大作业,不知道还有多少小作业,就蚌埠住了,更睡不着了(。但是今天白天起来把基物第四章学会了,还赶上了进度,习题久违地会做,心情稍微好了一点。感觉别搁那儿看讲义和课本了,不如看雨课堂的视频总结挑不会的听,然后在讲稿里搜索“考”查看会考的原题(
下学期真要上量子力学吗,我不会数理方程诶。虽然大多数东西也不能说真不会,但我不想算(,要不上个流体力学吧,听说这个东西蛮水的(真 -· 蛮水的)。但我现在 cx 的量子力学排在队列 -1/51,感觉很有可能补选上,蚌埠住了(
-这周实分析要交啥啊,怎么突然不发公告了,怪事。我都把 7.1
-写完了,看习题课似乎才到 Fourier,他啥时候这么慢了(
5月31日
-不是,你这实分析怎么一下把我写完的全交了(,现在已经变成周五上午布置作业,周五晚上/周六早上交了吗,有点恐怖(。好消息是今晚把前两周的习题课卷子都看完了,坏消息是明天的只能明天再说(
-爆肝了两天之后感觉压力稍微轻一点了,周末一天往后写实分析,一天整理下基物,晚上回寝室继续赶金统的大作业,再准备下生存分析的 -pre 就差不多了,还有多出来的时间的话(不太可能的样子)该开始准备 -cheatsheet 了。
-然后是定番:
-
这个月已经出现了两次重复的数字,一个是 776(可惜 5.5 -那天的标签我忘记撕了),另一个是 819,第一次出现 819 -是三月份,正好是我第一次去清华科技园店买咖啡的时候。奶茶喝得越来越多了,感觉说明真的压力很大(
-虽然五月份有读了一点文章,但 work log 是纸质版的(,下次再说吧。
-]]>6月1日
-如题(
-原汤化原食,开始用去年实分析作业的背面打草稿做今年的实分析作业(
-晚上回来围观室友改简历,原来把课上做的项目写简历上是正常现象的吗(,想了想又觉得我好像连课上做的项目都没有(难不成金统这个能算?),这是怎么会是呢((
---室友:我后来想了想还是把系里夏令营的报名撤了 因为我确实不想读博
-首先我没什么学术追求,我的水平也没资格谈这个,其次钱对我来说真的很重要
-我:我也是!
-室友:是吧!我目前的烦恼都是钱不够导致的,暂时还没有什么用钱解决不了的问题
-所以我去搞卓越工程师咯!
-
6月2日
-想来想去,期末这日子过成这样,基物可能需要负主要责任(。
-6月3日
-生存分析 pre,把高统 2 -的东西搬过来狠狠装了一下,掩饰我根本没多读任何相关工作这件事((
-开始写金统 -cheatsheet,有一种很快就能搞定然后去搞高统的感觉,又觉得现在不应该这么闲吧,难道不应该先开始复习实分析,至少往后写点作业吗(
-6月4日
-不是你这实分析这周要把第七章课后题写完是什么意思(。虽然说第八章不考(但我总觉得完全不排除
-lxg
-第十六周心血来潮把它讲了然后考的可能性(,但第八章本来就只有十来页啊(
金统 cheatsheet 写完了,这课又简单又难的,原理都水得很,但要全考实
-证
-分析的话恐怕有点(。下一个是高统,本来以为合同法是闭卷随便看两眼 PPT
-差不多得了,结果这下可以带法条,蚌埠住了,又多一个 cheatsheet
-要做((。最需要 cheatsheet 的难道不是基物吗,凭什么就它没有(
感觉稍微可以喘口气了,但也完全不能摆,总之再熬两周就放假了(什么原来后两周要干这么多破事啊((
-昨天今天都没来得及在下午第一节课之前去买瑞幸,昨天在售货机上随手拿了一瓶星巴克美式,结果那个味儿实在是给我恶心到了(,为什么要演奏春日影,啊不是,为什么要在 -0 -蔗糖美式里面加赤藓糖醇?我真的一直郁闷到晚上,心情太差了就点了杯奶茶,惯性定律果然今晚又点了杯奶茶(。
-最近每天晚上洗完澡一边吃东西一边看两话巨人然后才想干活,最速二刷了属于是。感觉可能是第一遍看的时候被唬到了,我承认第三季 -part 2 很强,但 part 1 就这(,也就是个 -8。反而之前以为单纯是个过渡回的第二季单看不屈的誓言就值得给个 9(
-6月5日
-真的要熬穿了,其实还是有点干不完,想到基物光学也要考心里就有点发毛,何况量子学得也不咋地。但如果只是背诵 -PPT 的话应该就还好(?),或者说恐怕最后会变成只来得及背诵 PPT -上划的重点了吧。昨晚熬夜写实分析作业和金统 cheatsheet,白天又在写高统 -cheatsheet,明明睡得不少还困得不行,看到以前会做的题目现在莫名其妙不会了,感觉到前所未有的疲惫。
-我倒不会说是之前太摆了导致现在变成这个样子,我确实没觉得这学期什么时候真的很摆过,如果读论文不算在摆的话,可是论文也就读了三四篇。那么答案显而易见,大约并不是选了太多课导致的,而是能力不足。所以说如果这学期 -GPA 没有很难看的话,下学期就不选高代 1 刷分了(
-还好金统大作业延到 22 号了,等我 21 号晚上考完还能写 15 -个小时(。代码基本上已经跑通了,感觉单纯是把剩下的废话说完的话这点时间能写得完,还就那个比美赛不知道轻松到哪里去了。或者说考完 -19 号那两门之后其实也就可以开始搞了,无论如何现在压力稍微小了点。
-6月6日
-实在想不出来高统 2 -要怎么考,是一个他要是考按定义计算和通过计算证明的话可能还好,但 MLE -那一坨东西我连模仿证明都做不出来的情况,学第二遍也不会。
-有点小破防,然后摆起来了,这样不行吧((
-今晚摸鱼把进巨第三季 part 1
-最后一话看了,王政篇除了政变之外的内容确实都是 8~9 分水平(,平均一下 8
-分差不多。明晚开始玛利亚之墙夺回战,看看有没有可能真给 part 2(连同 EVA
-TV,真心为你和猫鼠一起)调到 10 分去((搓手(#每日调分
-这下 10 分要变水了,不如把赛马娘第二季也抬上去吧(x
6月7日
-这高统 2 -复习得我感觉自己还就那个好没能力,应该去读个硕然后直接找工作,就,学了两年数学还没这么崩溃过(,从来没有因为学数学半夜哭出来,上次这样可能还是大一搁那儿深夜和 -OJ -左右互搏(。真不能再这么上课了,但又很难说集中精力科研会不会更崩溃,是否更应该少走弯路了(
-好黑暗的日子,我真觉得我精神状态有点要出问题了,然而这个期末还有两周才熬完。后两个学期的学分都不算多,算了一下哪怕这学期爆炸 -GPA 也还算 -robust,只是不知道延期施工实习会不会导致给分出问题,还得留余地。最糟糕的情况下基物靠背题目混过去拿个低一点的成绩,尽力保护住数学课这样。
-查了下网络学堂,上学期除去几门课公布成绩,一共交了 48 -个作业,这学期到现在已经 64 个了,还活着就挺好的。
-6月8日
-我好没能力.jpg,不过看看实分析又觉得比较有能力了(?
-很累,但晚上完全睡不着,在床上挣扎到五点钟起来把桥梁工程作业写了,写了两三道基物,然后倒头就睡(。天气也直白地热起来了,不过完全不如去年端午,痛苦回忆.jpg。中午出门感觉好虚,一热就更难受了,还是没自己去买咖啡,瑞幸外卖点不起,库迪 -app -外卖竟能用美团到店券,好文明,虽然配送高了点但也还能接受,最近大概要依赖下咖啡外卖了。
-我好像下雨的时候从来不记得带伞,但是太阳一晒就能记得带遮阳伞了(
-6月9日
-想来想去感觉下学期真得搬走了,反正延毕会导致至少要搬一次家,不如下学期就直接搬走,在这儿继续住我是真的天天都睡不着。当然,从大一上学期期末开始我就想换宿舍了,一直没动多半是懒且意志不坚定,所以为了坚定决心,我晚上回来跟隔壁寝室的一个姐在中厅里嚷嚷了半天,四舍五入大家已经都知道了,那就是必须得走了(。
-一会感觉能复习完,一会又觉得不能,还是先看看周二考的两门课吧。金统的 -cheatsheet 是周二做完的,周日的我:这课是干啥的来着(
-6月10日
-摆了(
-6月11日
-我是真的会因为夜里睡了半个小时醒来就睡不着了而哭出来(,好崩溃(
-这金统在考啥(,我做 cheatsheet
-的时候就在想把东西都塞上去是想考试的时候现学吗,结果真的现学了,希望高统
-2
-也能来得及现学。虽然怪没底的但反正也就这样了(,他但凡拿出上学期高统
-1 薄纱大家的那个状态呢(x
合同法挺摆的,它到底是不是一个 PF -的课啊,怎么到结课了也不是很清楚这个问题(
-你说得对,但是我高统 cheatsheet 还没弄完,怎么会是呢((
-6月12日
-急,摆(
-6月13日
-现在是 6 月 13 号(
-这高统折磨了一学期,期末竟是抄写和计算大赛(。虽然平时比较 push -能学到很多东西,加上考试不为难人确实是非常非常好的,但还是整得我又气又乐的,大概最近真的太焦虑了(
-昨晚是一个月以来睡得最好的一晚,记之。不过下午还是因为早上抄写太累了睡了会,晚上没忍住在早晨喝过咖啡的情况下又点了个奶茶,唉((
-基物怎么办,急(
-6月14日
-好困,怎么会这样,这能复习完吗(
-6月15日
-一整天只学基物的话效率好低,但实分析其实也不是很想学(。它看起来一副只考期中后的样子,虽然考前提示里那个默证我一上来就没绷住(
-唉,其实还有个大作业没写完,怎么会是呢(
-6月16日
-最近感觉整个腿脚都是水肿的,实在很难受。一个是休息得不好的体现,另外也真好久没怎么锻炼了,体力差了很多。没在减脂甚至也努力多吃饭了,体重还是一直掉,期末考完是否该去绕绕圈了(但这个天气真别在户外锻炼吧
唉,我妈今天问我为什么没考阿赛(,还把入围名单里一些上海的年级相差不大的竞赛生都找出来了(。我不好说,但我确实对阿赛丘赛啥的都没太大兴趣,说好听点是精力有限,很多东西学完考完期末就不想二刷准备比赛了,投入大量时间学不到很新的东西,感觉不如读点文章有用,但可能本质上还是竞赛 -PTSD 导致的(
-6月17日
-我现在感觉进巨最终季 part 1 也挺好的,马莱篇文戏是真那个有 9
-分水平,至少比第二季和第三季 part 1 强(。但它评分只有 7.7,我理解是
-MAPPA
-画面相比霸权社实在不行,以及放送的时候漫画快出到结局了,这一季里还有谏山创手刃莎夏(,所以说这下更不得不打
-9 了(
到底要不要调一波分呢,急(。说实话现在我打 9 -的里面有几个如果再看一遍很可能就不会给 9 -了,所以我打算不去二刷(,的这么一个情况(,另外也有再看一遍大约也不会动评分的。这样的话把其他真的很喜欢的拉到 -10 区分出来大概也挺好的(
-今天把光学看了,又拟合了一下原子物理的几个题。唉,这基物赶紧考了吧,多给一天也学不进去啥(
-6月18日
-如果我现在大一,明天要考两门四学分的课,大概已经昏过去了。但我现在大三下了,所以我今天玩了一整天,这怎么不算一种成熟呢(
-6月19日
-基物至少连着看了五天,喜提四学分 -3.3,实分析就看了两个下午,一个小时做完了,唉(
-想了想一年前还在选没人选的课选课法,主打一个不和数学系一起上课而是混在数辅里面,否则感觉考不过,现在已经如果我不是数学壬的话那这里大多数人也都不是.jpg -了(
-虽然后半学期学得依托,Fourier -变换的题也不一定做得出来,好像也没有几个提前交卷的,但感觉考试的时候但凡把空调打开,也不至于做完六道题扔下附加题直接闭眼开睡(。可以交卷之后速速拎包跑路,还把水杯落在桌上了((
-6月20日
-桥梁工程看了一天就差不多看完了,反正对我来说也就是复习一下之前看懂了的部分,不懂的也不太可能懂了(,随便考吧。这样的话有望提前一点把大作业写完,然后这学期就下班了,真是个漫长的噩梦。
-这两天晚上稍微轻松点了,二刷进巨的速度变成了一晚上三话(。第一次看的时候觉得不咋地,现在感觉马莱篇质量是真的高,突然有点想不通为什么第三季
-part 1 比最终季分数高(
6月21日
-结束了,不用再战斗了(
-昨晚熬了一下把金统大作业差不多写完了,待会稍微再改改就交,下班了。
-6月22日
-啥也没干,收拾了下寝室,晚上教(前)室友速通了一手假设检验和线性回归,本来以为会搞到很晚,结果离教室关门还留了 -2h,遂开始手机 b -站看魔圆(。虽然比较担心看到了正版番剧(,但是急,而且也没啥事干,算了(
-我评价:这玩意是 EVA,进巨和 FZ 三合一吗(
-6月23日
-一离开北京,整个人就好多了(喜
-6月24日
-14 周的时候虽然这个期末已经乱成一锅粥只能趁热喝了,但抽空听了一下 -Weijing Tang 的报告,感觉这个 signed network model -看起来还蛮有意思的(。今天读了一些她引用的文章(
-这么说来下次可以找机会把 14 周我咕掉的那节生存分析的课听一下(。
-二刷了娜娜家,虽然还是很不错但总感觉没上次好吃了(?),难道这就是相见不如怀念(。上次的柠檬鸡和这次的烤翅味道都一般般,但咖喱很好吃,薯条分量很大,下次(如果还有下次的话)把肉换成土豆泥之类的小食或者干脆去楼下鲜芋仙吃个甜点吧(。
-6月25日
-到今天为止已经三天没喝咖啡了,每天都睡得很香,日均睡眠九小时以上,我觉得可能自然状态下就应该睡这么多(
-大概也不是没喝咖啡的问题,昨晚晚饭后喝了杯奶茶一样睡得很香,主要还是没在寝室住了吧。
-西塔老太太好吃,但最好吃的是免费的土豆泥(。虽然在天津一顿吃出了上海的人均稍微有点不满,但毕竟连锁店,口味也是熟悉的偏甜口,沪人狂喜。
-6月26日
-去了下天津博物馆,本来还想着心情好的话顺便去下旁边自然博物馆,结果一个是起得太晚来不及了,另外虽然没法苛责什么但天博确实是我去过最不行的省博(。)了。
-而且旁边万象城那家九龙冰室,怎么能把菠萝咕咾肉做得那么难吃,不如文通冰室一根。那个双皮奶端上来尝了一口我就觉得有点不妙,这家店不像是很会做饭的样子(,果然是在天津踩到的唯一一个大雷。难道去吃粤菜就只能点烧鸭饭或者叉烧吗(
-6月27日
-回北京了,在城际铁路上就已经感觉到悲伤了((
-回寝室打扫卫生,收拾东西,看了点番(?),准备后天飞南昌了。
-已经连续五天没喝咖啡但精神饱满了,原来日均九小时睡眠是最好的咖啡因(乐
-6月28日
-现在是 6 月 28 号晚上十一点十二分,航班不到 3/4 -天之后就要起飞了,但我的行李箱目前还是空着的,更别提下楼试称重了,这是怎么一回事呢,我啥时候变成 -P 人了((x
-6月29日
-是的我是第一次坐飞机,某种程度上也是不想第一次坐飞机是在暑研的时候(为什么)所以这次飞了,当然北京到南昌的高铁本来就贵得离谱所以飞机确实省钱。
-然而这个雨下得(,真的疲惫了,早上起来收到了延误 3 小时 20 -分钟的通知,到机场之后首都机场这里开始雷阵雨,预定起飞时间的时候广播说飞不了先别排队了,过了十分钟开始登机(。登机之后又是漫长的飞不了,十点钟的时候广播说暂时飞不了先别急,于是我给我姐发了条消息说别出来接我了,我啥时候到了自己来就行,两分钟后突然起飞,等我反应过来的时候机头已经抬起来了,早已飞行模式但也不敢再打开流量了(
-昨天还在想为什么要提前预定特殊飞机餐,订的还是低脂餐,就这么喜欢鸡胸肉吗。结果毫无胃口的晚上十一点拿到柠檬味的鸡胸肉,没什么味道的全麦包,以及沙拉和水果的时候,我还是感觉比旁边半夜吃宫保鸡丁饭的人要幸福一点(
-一点钟到昌北机场,惴惴不安地打了个网约车,司机先让我从平台取消订单,我寻思着我平台打车不就是图个有监管吗,遂拒绝,同意把平台的抽成额外打给他;然后一看车牌号和高德上显示的也不一样,汗流浃背了,拍了发给我姐。行李放进后备箱之后司机突然说这一单要拼车,和一位提公文包的中年男子,我立即跳脚破口大骂,说要拼的话你拉他一个人走,我把行李拿下来,虽然骂完有点后悔怕挨打(,但可能我距离比较长能多赚点,司机真听我的了,就开走了。到我姐家之后还是觉得蛮汗流浃背的,就是,但愿以后别再遇到这种半夜打车的情况了(
-6月30日
-睡到中午,起来去了省博,布展真不太行,全混在一起没啥记忆点。下楼去文创店看了一圈,这都啥(。现在越来越觉得在河南省博钱花的还蛮值的(。
-在江西省博转了一下午,感觉把今年能看到的小孩都看完了,反正你赣的生育率不怎么是问题(迫真
-]]>7月1日
-本来今天要早晨六点多起来去海昏侯博物馆,但起来一看外面下暴雨,遂在家补觉,摆烂,读论文(。说是读论文,我感觉和抄书甚至做手账差不多水平,就是平时在纸面上不会这样干,用平板反而比较(,但毕竟这儿也没桌子(
-长沙感觉去不了了,现在还在不停下雨,到处淹着,遂退票。在考虑是早两天回家还是在这边多读两天论文((
-7月2日
-下暴雨,仍然在读论文,然后就是晚上雨停之后出去吃吃饭,很摸的一个状态。
-仍然在读一些 signed network -相关的文章,离我导一开始让我看的东西越来越远了(。这两天读的几篇主要是一些不那么统的会议的文章,有点水(,算了能看进去点也行吧。
-之前听 hst 说 hd 在和 ypk 一起做概率图模型,最近发了篇 -ICML,我还想着这又是什么方向,今天搜了一下发现哈哈不就是我这玩意吗!只不过我和我导一直管它叫网络数据或者 -social network,好吧以后不这么叫了,听着有点不像统(
-下午六点被告知明早七点去武汉的高铁被取消了,看了下这车也不往湖南开,可能是路过九江导致的。紧急改了后天的票,改订的酒店倒是还便宜了点,就明天去海昏侯博物馆看看金子这样子。感觉以后还是不要在七月初在南方玩这样,当然北京也在下暴雨(吧),反正变数很大。当然也没有几个以后了,寒假要补实习,暑假就暑研了,除了延毕那一年可能会松弛一点之外,就只可能学期中间出去摸一摸这样子。
-7月3日
-还是下雨,海昏侯又咕了,这下得等到从武汉回来再说了(
-上午看了 TCL model -的那篇文章,看到它的初衷是想把朋友的朋友(很大概率)还是朋友这种传递关系的概率表示出来,最后证明了还是符合 -FCL 的,感觉听起来很可以推广到另一种类型的 balanced triangle,在 random -insertion / wedge closing -的步骤里多加一步控制正负号,再多估计一个参数就好。然后随手一查发现这件事六年前(在这篇发表的六年后)就有人做过了,文章和这篇长得不能说完全一样只能说也没差太多,遗憾离场(x
-下午傍晚出去逛了逛,这南昌已经待了四天了,回来还得待两天,每天都在愁吃点什么((x
-7月4日
-二刷完进巨最终季 part 2,抬到了 9 -分,比第一遍的观感更好。之前一直没注意到,最后一话在帐篷里喝酒的时候艾伦看着三笠和阿尔敏那个眷恋的眼神,抛开二刷注意到文戏改编得很优秀,也真的理解了人物动机之后,哪怕只看这一段都感觉已经有 -9 的理由了(。
-前两天在谷子店没忍住买了一对艾笠的色纸,虽然 MAPPA -出品真有点丑,但看完最终季我已经和画风和解了(。但是回来的路上我姐问我这是一对男酮 -cp 吗的时候真的还是有点没绷住((
-7月7日
-回南昌了,前面几天的在写了在写了(
-7月8日
-昨天说在写了之后就真的开始写了,狠狠吐了一万字,虽然我今晚就想发出来让所有人嫉妒我的才华(嫉妒我的手腕力量),但还是过几天再发吧。写完其中几个在高铁上就在构思的段落之后,我感觉自己文思泉涌无所不能,但把它补完成一篇有逻辑字句通顺的文章的过程中,我只能反复默念:完成比完美更重要。
-7月9日
-一整天了,没有人来找我偷跑我的一万字,封笔了(不是
-明天回上海,现在已经是看到上海地铁屏蔽门会觉得很陌生的状态(
-7月10日
-回家了,终于可以开包看一眼就能从安检员身边大摇大摆走过去,抱歉但是各个方面来说第一次觉得上海这么好((
-早上去南昌西站的时候,虽然我拖了个箱子还背了两个包,但显然安检员对我箱子里有什么毫无兴趣,她只让我打开帆布袋把水拿出来喝一口(
-另,今天在高铁上成功自己把箱子举起来放到了行李架上,还得继续练。
-7月11日
-在我姐家里的时候就没有网,三台设备全靠手机开热点,现在回家还是没网,好崩溃((
-我妈对茶颜悦色小零食大加赞赏,又买了一堆(。我蹭免邮又买了点茶包,上次那个比普通冷萃茶贵五块钱多一个票据收纳盒的茶礼盒里面还送了个纸徽章,茶包的包装也特别有意思,真的值了。感觉下次想喝茶颜悦色可以去南京或者无锡,至少我对南京的印象还是很好的,可以坐京沪高铁回家/去学校的路上在南京南站中途下个车这样子(
-五一的时候我在一边写高统作业一边骂,顺便在口嗨怎么把 GLM -塞到当时在看的论文里,后来高统 II 奇迹般地摸到一个 A-,打破了每门课的 2 -都会很拉胯的魔咒(微积分,基物和概率论,但数学课 A- -确实好像也算有点拉胯(啥)。现在我好像真遇到了一个塞 GLM -的机会(,啥时候和 wwc 约着聊一下(
-之前觉得看论文看麻了之后读一下光叔的数分讲义还挺好的,现在觉得其实某些论文比数分讲义简单不少((x
-7月12日
-179 的 EVA
-展早鸟特典票我说买就买(,哈哈,但它是国内首展诶,特典看起来确实很值。感觉总不至于八月份没空去看吧,冲了,可免税代购周边(啥
最近都好能睡啊,这样不行吧(
-7月13日
-不太舒服,几乎就是躺了一天,中间起来狂暴做家务(
-什么科研,啥都整不出来,急急急(x
-7月14日
-读论文,睡觉,睡醒做饭,做完饭洗碗洗锅,洗完就累了,睡觉(
-洗锅的时候感觉我的生活差不多就和做饭一样,不知道在忙些什么东西,但是就是一天到晚都很忙,还糊了满脸油烟这样子。刚坐下来打开平板开始回忆我平时是干什么的来着哦好像是学数学的,我妈神神秘秘跑到我身边说我给你买了两个小礼物,打开淘宝一看是两盆花。我感觉她已经在想象家里鸟语(指我每天不知道在说什么鸟话)花香生机勃勃的这样一个场景,但我只觉得眼前一黑,我一地鸡毛的生活里,真的,再塞不进两个需要我照顾的东西了(
-今天在厨房里发现了九个插座。不是,它到底是想起到一个什么样的作用啊(挠头
-7月15日
-摸了(,终于把这个 tutorial 看完了((
-7月16日
-今天看一个 signed Laplacian,完全没看懂,一上来开始说可以用振子理解 -eigenvalue(可能我也没理解对)blahblah,遗憾退场(
-这 Umich 好喜欢研究 signed network 啊,搞物理的也在发 signed
-network,是因为 Harary 是 Umich 的吗,怎么不算是歪打正着地离
-dream school 近了一点捏(并没有
不是,这情况怎么急转直下,变成了我现在就已经有点想回学校了,但是我 -EVA 展的票要 8.2 之后才能去看所以回不去啊我超(
-7月17日
-睡前在想为啥没有人在 adjacent matrix 里放 \(\pm -i\)(暴论),思考了一下这得有多少种三角形然后就迅速睡着了(
-这九院口外挂号挂了一周了还没挂上,想了想感觉还是下学期或者暑假末尾直接北医三院吧,体验下公费医疗(。上次拔左边的智齿前前后后拔出了一次托福的价钱,虽然确实弄得挺好的但还是(
-7月18日
-开始 读 Stein(多大的人了还在读 Stein( 补石头门,看
-bangumi
-评价好像前期节奏很慢,大概正好每天一边吃饭一边看。初中的时候好像就想看了,但是在游戏和动画之间犹豫不决,结果
-neither 了(
今天想把蒸锅拿出来洗一洗,结果在橱柜里找到了厨房的第十个插座(,它到底是想起到一个什么样的作用啊(二度
-7月19日
-今天外出,回了一趟宝山,顺路去宜家 零元购
-把积分兑成了一个靠垫和一堆小垃圾(。气温 38
-度我在户外健步如飞,感觉比(声称)36 度的南昌和武汉舒服多了((
所以我(看完 EVA -展之后)到底啥时候回学校(,之前担心的一些事情现在好像都不需要我了(?),现在都有点疑惑为啥这个暑假没去施工实习,真的就单纯因为怕热吗(。现在每天就是在家里不务正业地乱看文章(但我的正业到底是啥),已经从 -signed network 看着看着不知道顺着哪条线被带到 matrix estimation -去了。正好下周一统计中心(现在改口叫统计系我都还不大适应)有个报告讲这个,顺便听一下。为什么要在日记里写这个捏,因为我怕我忘了(。
-导针对我想跟他聊聊 signed network -的邮件向我提问:上学期让你看的那两篇怎么样了,啥时候讲一下?我哈哈大笑,什么 -stochastic block -model,它真的太丑了所以定义都忘记了捏!这就再去看一眼(。
-而且我的智齿好痛,今年已经肿了无数次了,虽然北医三院挂号看起来也很难,但想回去拔牙(。
-7月20日
-回去看学期中间看的那篇 adjusted
-covariates,发现它和我前段时间看的一个 signed network 都引了同一篇 2020
-年的文章,考虑到 balanced theory,出现 co-citation
-就不得不去读一下了(x
但说实话这样一读我完全理解之前那个 signed network 了,就是给 2020
-年那篇套上了一个选择符号的步骤,这和六年后在 TCL
-里加正负号不就是一样的思路捏(,不过他多做了一个优化所以多推了若干
-bound,用了一些 花里胡哨的
-MLE。但是这篇把故事讲得很好,我的理解是造了一个也比较符合直觉的
-population level balance 的概念,然后成功从这里引过去了。本质上是 inner
-product model 在 signed network 里的推广,但故事讲的是 balance
-这样子,也顺利吸引到了我这种因为对 balance 和 signed network
-感兴趣而来的人结果最后怎么吃了一大口 ERGM(x
来都来了,不如去看下 Terry Tao 那篇 matrix completion
-吧!反正之前 low-rank method for signed network 也用到了来着!
-那我的汇报到底要说点啥捏(
很久没追番了,最近竟然在以追番的状态看 7
-月那部擅长逃跑的殿下(,我也不想的,但是很久没有这么命中我好球区的男主了
-但是作画转场真的顶级,单纯欣赏画面也值了(
7月21日
-这石头门好几天没看现在有点不大想看了(,前期节奏好慢,但也还是再坚持一下罢(。然后今天去把辉夜姬物语看了,我之前一直以为这是宫崎骏的作品,但我不太喜欢宫崎骏(这是可以说的吗?)所以一直没看,今天才发现不是,遂补(
-最终还是去把 bangumi 评分调了,给进巨第三季 part 2 和 EVA
-TV、真心喂你 真心为你拉到了 10 分,大概确实 9 和 10
-之间还是有一些必须区分开的差距,别的 9
-看了半天感觉实在动不了了,只有想往下打到 8
-的(。但也没往下调,毕竟当时打 9 也一定有我的道理(?
看了一天 error bound,晚上盯着不等式里的 \(e^{M_1}\) 陷入困惑,k-th iteration 的 error -metric 是 \(e_k\),个么 \(e\) 是啥?再一想,\(e\) 就是 \(e\) 啊((
-一直担心(并没有)的事情终于发生了。很久没说过话的高中校友唐突开聊,我对他的了解止于他大一的时候从 -FDU 数院转出了,然后:
---友:你现在在搞啥科研吗?数学哪个方向捏?
-(我内心:直接说统计是不是有点太宽泛了,social network -听起来像人文社科的,要说 random graph -也不是不行,但我当时听到概率图模型这个名字的时候都没意识到就是我在搞的这个东西,说英文会比较容易理解吗?但是已经犹豫很久了还没回是不是会显得有点没礼貌啊,就 -network model 吧!)
-我:network model
-友:哦哦
-友:那你是本科学数学,研究生转码?
-友:是看开了吗
-
(挠头
-]]>先前把统辅当做很有趣的数学分支,被转数环的学长泼了冷水说“统计中心的风格可能会不大适应”,另一位学长也说“统辅不是你期待的样子”,目前看中心开课的意思也好像有点当工科的辅助来学。我到底多大程度上能接受严谨的数学推导?又能走多远?统辅还是数辅还是我全都要,这是一个问题。
初概这玩意儿前八周上完,约等于梦回高中月考,我定义呢我证明呢啊怎么直接拿来用了?在考虑下学期去数学系重新上概(1),甚至考虑跟实复分析,但是数分的空缺真的没问题吗。当然,没有退初概还是为了跟上统辅的进度,毕竟后八周还有统计推断,我也没完全放弃统辅,目前或许是我目光短浅了。
-这门课和教材也没什么映射关系(而且看老师的意思是也没有教材,草),直接按照 -Lecture n -的顺序写吧。本来想放进茴香豆篇,但概率论这边举例比较多,放在一起又很冗长,还是算了。
-Lecture 1
--
-
- 概率模型:概率模型由样本空间和概率构成。每一个概率模型都关联着一个试验。
-
-
-
- 样本空间是一个集合,概率模型对应的试验产生的所有可能结果形成样本空间,记作 -\(\Omega\)。比如说,概率模型为抛硬币,样本空间即为 -\(\lbrace head,tail -\rbrace\)。样本空间可以是离散的,也可以是连续的。 -
- 事件 \(A\) -是样本空间的子集,也就是某些试验结果的集合。概率 \(P(A)\) 分配到事件 \(A\) 上。 -
- - 概率公理:非负性,归一化,可加性。 -
- 概率的性质:两个技巧,归纳法和取补集。 -
Lecture 2
--
-
事件域(或称为 \(\sigma-\)域,\(\sigma-\)代数):对于样本空间 \(\Omega\),\(F\) 表示 \(\Omega\) 的某些子集构成的集合,如果 \(F\) 满足以下三个条件:
--
-
- \(\Omega \in F\) ; -
- 对于任意的 \(A\in F\),有 \(A^c \in F\); -
- 如果 \(A_n \in F\),\(n=1,2,...\),则 \(\cup_{n=1}^\infty A_n \in F\)。 -
那么称 \(F\) 为 \(\Omega\) 上的事件域,称 \(F\) 中的元素为事件,称 \((\Omega,F)\) 为可测空间。
-从而,有且只有 \(F\) -中的每个事件都能分配概率,这就圈定了我们所关心的事件的范围。
-事件域的一些性质如下:
--
-
- 两个事件域的并集不一定是事件域,但交集一定是。(Trivial) -
- 事件域对集合的任何计算都是封闭的,包括事件列的极限运算。 -
-概率,也称为概率测度:设 \((\Omega,F)\) -为可测空间,\(P\) -是定义在 \(F\) 上的函数,如果 \(P\) 满足以下三个条件:
--
-
- 非负性,完全性(Trivial) -
- 可列可加性(\(\sigma-additivity\)):对于 \(F\) 中互不相交的事件 \(A_1,A_2,...\) ,有 \(P(\cup _{n=1} ^\infty A_n) = \Sigma _{n=1} ^\infty -P(A_n)\)。 -
那么称 \(P\) 为 \(F\) 上的概率测度,简称概率。
-对于上述定义的样本空间,事件域和概率测度,我们称 \((\Omega,F,P)\) 为概率空间。
-简单举个例子,在掷硬币的概率模型中,样本空间是 \(\lbrace Head,Tail \rbrace\),事件域是 \(\lbrace \lbrace Head,Tail \rbrace, \lbrace Head -\rbrace, \lbrace Tail \rbrace, \emptyset -\rbrace\),此时样本空间和事件域构成可测空间。事件域中的每一个元素都是事件,概率测度为 -\(P(\lbrace Head \rbrace) = p\), \(P(\lbrace Tail \rbrace)=1-p\)。(这是考虑了 -\(biased\) \(coin\) 的情况)
-概率测度的一些性质:
--
-
- 对于单调增序列,有 \(\lim_{n \to \infty} -A_n = \cup_{i=1} ^\infty A_i\), \(P(\lim_{n \to \infty}A_n) = \lim_{x \to -\infty}P(A_n)\)。 -
- 单调减序列同理。 -
-条件概率(定义略)的若干性质:
--
-
对互不相容的事件列 $B_i $,有 \(P(\cup -_{i=1}^\infty B_i|A) = \Sigma _{i=1} ^\infty P(B_i -|A)\)。
-用 \(P_A(·)=P(·|A)\) 表示在事件 -\(A\) -发生条件下的条件概率,这仍然是一个概率测度,\((\Omega,F,P_A)\) 仍然是一个概率空间。
-当然,此时我们可以把 \(A\) -之外的结果排除掉,记作 \((A,A\cap -F,P_A)\)。
-
-乘法公式:设 \((\Omega, F,P)\) -是概率空间,\(A_i \in F\),\(i = 1,2,...,n\),且 \(P(A_1 \cap A_2 \cap ... \cap -A_{n-1})>0\),于是有\(P(\cap_{i=1}^n -A_i) = P(A_1) \Pi_{i=2}^n P(A_i|A_1\cap A_2 \cap ... \cap -A_{i-1})\)。
-举个例子:某人写了 \(n\) -封信,将其装入 \(n\) -个写有地址的信封,全部装错的概率 \(q_0\) 为?恰有 \(r\) 个信封装对的概率 \(q_r\) 为?
--
-
- 在第一个问题下面,我们考虑记事件 \(A_i\) 为第 \(i\) -个信封装对的事件,利用容斥原理即可。 -
- 在第二个问题下面,其实问题主要在于怎么考虑是哪 \(r\) 个信封放对了的问题。“指定的某 \(r\) 个信封放对了”这一事件的概率等于“从 -\(n\) 个信封里无放回地取出 \(r\) 个正好是前 \(r\) 号”的概率。又因为从 \(n\) 个信封里指定 \(r\) 个有 \(C_n -^r\) 种方式,于是这一部分的概率为 \(\frac{1}{r!}\)。 -
-全概率公式:将 \(\Omega\) -分割成事件 \(A_1,A_2,...,A_n\) -的并,另有其中的事件 \(B\),可以对每个 -\(i\) 得到 \(P(B|A_i)\),于是 \(P(B) = \Sigma_{i=1}^n P(A_i)P(B|Ai) = -\Sigma_{i=1}^n P(B \cap A_i)\)。
-这个时候,我们称 \(\lbrace A_i -\rbrace\) 是 \(\Omega\) -的一个分割。同时,式中的 \(n\) 可以用 -\(\infty\) 代替。
-举个例子:一个袋子里有 \(n\) -个白球和 \(m\) 个黑球,从中无放回地取出 -\(k\) 个球,求第 \(k\) 次取得黑球的概率。
--
-
- 递归:第一次取黑球的概率影响第二次,第二次影响第三次...简单列个数列可以看出来取黑球的概率是定值,即为 -\(\frac{m}{m+n}\)。 -
- 排队:把 \(m+n\) 个球排成一列,算第 -\(k\) 个恰为黑球的概率即可。 -
-\(Bayes\) 准则:设 \((\Omega,F,P)\) 是概率空间,\(B,A_i \in F\),\(i=1,2,...,n\),\(\lbrace A_i \rbrace\) 是 \(\Omega\) 的一个分割。我们要用 \(P(B|A_i)\) 算 \(P(A_i|B)\),就可以使用 \(Bayes\) 准则:\(P(A_i|B)=\frac{P(A_i)P(B|A_i)}{\Sigma_{j=1}^n -P(A_j)P(B|A_j)}\) 。
-
Lecture 3
--
-
(两两)独立性,条件独立性和一组事件的相互独立性
--
-
对于概率空间 \((\Omega,F,P)\),\(A,B,C \in F\),独立性指的是 \(P(A\cap B) = P(A)P(B)\),条件独立性指的是 -\(P(A\cap B|C)=P(A|C)P(B|C)\)。
-那么这二者有什么关系呢?答案是没有关系(
-简单举个反例:抛掷两次均匀的硬币,令 \(H_1=\lbrace\)第一枚正面朝上\(\rbrace\),\(H_2=\lbrace\)第二枚正面朝上\(\rbrace\),\(D=\lbrace\)两枚硬币结果相反\(\rbrace\)。于是有 \(P(H_1 \cap H_2) = P(H_1)P(H_2)\),但是 -\(P(H_1 \cap H_2 |D) = 0,P(H_1|D) = -\frac{1}{2},P(H_2|D) = -\frac{1}{2}\)。也就是说,独立性不能推出条件独立性。
-一组事件的相互独立性涉及到概率空间 \((\Omega,F,P)\) 中的一组事件 \(A_1,A_2,...,A_n\),如果对于任意非空子集 -\(S\subset \lbrace 1,2,...,n -\rbrace\),都有\(P(\cap_{i \in S} -A_i)=\Pi_{i\in S} P(A_i)\),那么称这一组事件是相互独立的。
-根据 \(S\) -的完备性可以知道,两两独立性也不能推出一组事件的相互独立性。
-TODO:记得复习一下赌徒破产模型。
-
-随机变量何种情况下是良定义的?
--
-
- 设 \((\Omega,F)\) 为可测空间,如果 -\(\Omega\) 上的函数 \(X(\omega)\) 满足:对 \(\forall x \in R\),\(\lbrace \omega | X(\omega) \leq x\rbrace \in -F\),则称 \(X(\omega)\) 为 \((\Omega,F)\) 上的随机变量。 -
-
Lecture 4
--
-
对于离散型随机变量 \(X\),称 -\(P(X=x_k) = p_k\) 为 \(X\) 的概率分布,称 \(\lbrace p_k \rbrace\) 为概率分布列,简称为 -\(PMF\)。当其规律不够明显时可以写成表格形式。
--
-
两点(\(Bernoulli\))分布:掷硬币或正或反,\(P(X=0)=p,P(X=1)=1-p\)。
-二项(\(Binomial\))分布:试验成功的概率为 \(p\),重复 \(n\) 次试验成功 \(k\) 次的概率,\(P(X=k) = C_n ^k p^k -(1-p)^{n-k}\)。它是二项式展开的其中一项,故名二项分布。
-二项分布的最大可能值(即中心项)的推断:考虑二项式展开。
-......这里空间不够大,别的写不下了(其实是不需要记忆离散型分布的名字,会讲故事就行。
-泊松(\(Poission\))分布:\(P(X=k)=\frac{\lambda ^k}{k!} -e^{-\lambda}\)。一般来说,记随机变量 \(Y\sim P(\lambda)\) 表示 \(Y\) 服从参数为 \(\lambda\) 的泊松分布。
-放射粒子模型揭示了二项分布可以用泊松分布近似的事实。
-TODO:复习粒子模型,做书上习题 \(2.2\)。
-
-对于连续型随机变量的定义如下:设随机变量 \(X\),如果存在非负函数 \(f(x)\) 满足对任意的 \(a<b\),\(P(a<X\leq b)=\int _a ^b f(x) dx\),则称 -\(X\) 为连续型随机变量。称 \(f(x)\) 为 \(X\) -的概率密度函数,简称概率密度或者密度(\(PDF\))。
-这并不意味着 \(X(\omega)\) -是连续函数,因为样本空间可能没有任何的拓扑结构,谈不上连续性。
--
-
均匀(\(Uniform\))分布:\(f(x) = \frac{1}{b-a},x \in (a,b)\),此时记 -\(X \sim U(a,b)\)。
-指数(\(Exponential\))分布:\(f(x) = \lambda e^{-\lambda x},x\geq -0\),此时记 \(X\sim -\epsilon(\lambda)\)。
-如果 \(X\) 是连续型非负随机变量,则 -\(X\) 服从指数分布的充要条件是 \(X\) 没有记忆性,也就是说 \(P(X>s+t|X>s) = -P(X>t)\)。(可以由条件概率公式证出,Trivial.)
-\(X\) -的失效率就是单位长度时间内失效的概率,可推知即为 \(\lambda\)。也称其为尺度参数(rate -parameter)。
-TODO:再推一遍 \(X\sim -\epsilon(\lambda)\) 时,\(Y=\lambda -X\),则 \(Y\sim \epsilon -(1)\)。
-正态分布(\(Normal\) \(Distribution\)):\(f(x)=\frac{1}{\sigma \sqrt{2 \pi}} -exp(-\frac{(x-\mu)^2}{2\sigma ^2}),x \in R\),此时记 \(X\sim N(\mu ,\sigma^2)\)。
-正态分布的函数图像关于 \(x=\mu\) -对称,在此处取最大值 \(f(\mu) = (\sigma -\sqrt{2\pi})^{-1}\)。关于 \(x=\mu \pm -\sigma\) 处有拐点。
-
-
Lecture 5
--
-
概率分布函数(\(CDF\)):对随机变量 \(X\),称 \(x\) 的函数 \(F(x) -= P(X\leq x),x \in R\) 为 \(X\) -的概率分布函数,也称为累积分布函数,分布函数。
--
-
对一个 \(PMF\) 书写 \(CDF\),它一般是一个分段函数。
-对一个 \(PDF\) 书写 \(CDF\),记随机变量 \(X\) 的概率密度为 \(f(x)\),则其分布函数为 \(F(x) = \int_{-\infty}^x f(t) dt,x \in R\)。 -对于一个已知的 \(F(x)\),只能确定连续点 -\(x\) 处的概率密度为 \(f(x) = -F'(x)\),显然在不连续点处是无法确定的。
--
-
- 注:连续型随机变量的概率密度不必为连续函数,允许可列个单点断开。那它为什么叫连续型呢?这与 -\(F(x)\) -的形式有关。同时离散型这一形容也与 \(F(x)\) 有关。 -
-举个例子:标准正态分布的概率密度为 \(\phi(x)=\frac{1}{\sqrt{2 \pi}} -exp(-\frac{x^2}{2}),x \in R\)。其分布函数记为 \(\Phi(x)\),其值需要查表,当然也可以丢进 -MATLAB 算,但是不要求(
-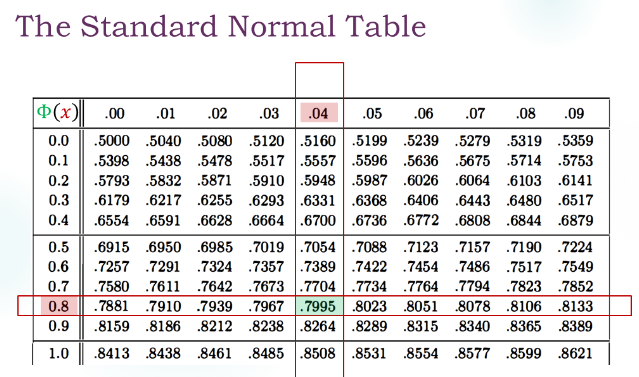 -
-再举个例子:正态分布函数的概率密度计算中,可以对 \(\frac{x-\mu}{\sigma}\) -进行换元,从而变为标准正态分布的情况。
-再再举个例子:指数分布的分布函数要注意分段,考虑 \(x<0\) 的情况。
-TODO:去看一下几何随机变量和指数随机变量的分布函数的逼近,这是利用 -\(CDF\) 寻找 \(PMF,PDF\) 之间关系的例子。
-分布函数对一切随机变量都适用,这是它相对 \(PMF,PDF\) 的优势。
-
-对于一个随机变量 \(X\) 的函数 -\(g(X)\),怎么去寻找 \(g(X)\) -的概率分布?(这一部分其实是做题方法)
--
-
最简单的情形:\(X\) -是离散型随机变量,对每一个 \(X\) 的取值 -\(x\),确定 \(Y=g(x)\) -时的概率分布列即可。有需要的话还可以化成 \(CDF\)。
-曲线救国:考察 \(Y=g(X)\) -的分布,若 \(g(x)\) -是连续函数,那么可以先得到 \(Y\) 的 \(CDF\) 为 \(F_Y(y)=P(Y\leq y)\),再求导得到 \(f_Y(y)=F_Y'(y)\)。
-特殊情况 1:线性的 \(g(X)\) -可以直接从 \(f_X(x)\) 得到 \(f_Y(y)\) 而无需计算 \(CDF\)。
-形如 \(Y=aX+b\) ,有 \(f_Y(y)=\frac{1}{|a|} -f_X(\frac{y-b}{a})\)。(其实还是用 \(CDF\) 证明的)
-特殊情况 2:对于严格单调的 \(g(x)\),考虑 \(Y=g(X)\)。记 \(h(y)\) 是 \(g(x)\) 的逆映射,于是 \(f_Y(y)=f_X(h(y))|h'(y)|\),这可以通过考虑事件 -\(\lbrace x<X<x+\delta \rbrace\) -来证明。
-特殊情况 -3:像正态分布这样的特殊分布,遇到的时候建议先考虑能不能在 \(\Phi(x)\) -的尺度先行利用对称性化简。
-
-
Lecture 6
--
-
\(n\) 维随机向量:如果 \(X_1,X_2,...,X_n\) 都是概率空间 \((\Omega,F,P)\) 上的随机变量,那么称 \(X=(X_1,X_2,...,X_n)\) 为概率空间 \((\Omega,F,P)\) 上的 \(n\) 维随机向量。
-那么怎么从随机变量上迁移来诸多的概念呢?
--
-
联合概率分布函数:设 \(X=(X_1,X_2,...,X_n)\) 为随机向量,称 \(R^n\) 上的 \(n\) 元函数 \(F(x_1,x_2,...,x_n)=P(X_1<x_1,...,X_n<x_n)\) -为 \(X=(X_1,X_2,...,X_n)\) -的联合概率分布函数,简称为联合分布或者分布函数。
-有关离散型随机向量:如果 \(X_1,X_2,...,X_n\) 都是离散型随机变量,则称 -\(X=(X_1,X_2,...,X_n)\) -为离散型随机向量。如果所有 \(X_i\) -的不同取值为 \(x(j_1,j_2,...,j_n)=(x_1(j_1),x_2(j_2),...,x_n(j_n))\),则称 -\(p_{j_1 j_2 ... -j_n}=P(X=x(j_1,j_2,...,j_n))\) 是 \(X\) 的联合分布列。
--
-
举个例子:设 \(F(x,y)\) 是 \((X,Y)\) 的联合分布,则 \(X,Y\) 有概率分布:
-\(F_X(x) = P(X \leq x,Y \leq \infty) = -F(x,\infty)\),
-\(F_Y(y) = P(X \leq \infty,Y \leq y) = -F(\infty ,y)\)。
-于是,对于矩形 \(D=\lbrace a<X \leq b,c -< Y \leq d \rbrace\),有 \(P((X,Y)\in D) = -F(b,d)-F(b,c)-F(a,d)+F(a,c)\)。
-
-有关连续型随机向量:简单来说,考虑二维的情形,如果 \((X,Y)\) 有联合密度 \(f(x,y)\),则 \(X\) 和 \(Y\) 分别有概率密度 \(f_X(x)=\int_{-\infty} ^{\infty} -f(x,y)dy\),\(f_Y(y)=\int_{-\infty}^{\infty} -f(x,y)dx\)。
-延拓到 \(n\) 维的情况,被积函数 -\(f_k(x_1,x_2,...,x_k)=\int_{R^{n-k}} -f(x_1,x_2,...,x_k) dx_{k+1}...dx_n\) 是为 \((X_1,...,X_n)\) -的联合密度,称之为边缘密度(Marginal PDF)。
-连续型随机向量的独立性:对每个 \(i(1\leq i \leq n)\),随机变量 \(X_i\) 有概率密度 \(f_i(x_i)\),则 \(X_1,X_2,...,X_n\) -相互独立的充分必要条件为随机向量 \(X=(X_1,X_2,...,X_n)\) 有联合密度 \(f_1(x_1)f_2(x_2)...f_n(x_n),(x_1,x_2,...,x_n)\in -R^n\)。
-经典连续型随机向量例:二元正态分布
-设 \(\mu_1,\mu_2\) 为常数,\(\sigma_1,\sigma_2\) 为正常数,\(\rho \in (-1,1)\) 中的常数。如果随机向量 -\((X,Y)\) 有概率密度
-\(f(x,y)=\frac{1}{2\pi \sigma_1 \sigma_2 -\sqrt{1-\rho^2}}exp(-\frac{1} {2(1-\rho^2)} [\frac{(x-\mu_1)^2}{\sigma_1 -^2} + \frac{(y-\mu_2)^2}{\sigma_2 ^2} - \frac{2\rho -(x-\mu_1)(y-\mu_2)}{\sigma_1 \sigma_2}])\),
-那么称 \((X,Y)\) -服从二元正态分布,记为 \((X,Y)\sim -N(\mu_1,\mu_2,\sigma_1^2, \sigma_2^2, \rho)\)。
--
-
- 一些性质:\(X,Y\) 独立的充要条件是 -\(\rho=0\)。(Trivial) -
-联合分布(Joint CDF)与联合密度(Joint PDF):已知联合密度 \(f(x,y)\),于是有联合分布 \(F(x,y) = \int _{-\infty} ^x \int _{-\infty} ^y -f(u,v)dudv\)。
-当 \(f(x,y)\) 连续时,有 \(f(x,y) = \frac{\partial^2 F(x,y)}{\partial x -\partial y}\)。更一般地,如果该混合偏导数不存在,那么 \(f(x,y)=0\)。
-连续型条件概率分布:设随机向量 \((X,Y)\) 有联合密度 \(f(x,y)\),\(Y\) 有边缘密度 \(f_Y(y)\)。若在确定的 \(y_0\) 处 \(f_Y(y_0)>0\),则称 \(P(X \leq x | Y=y_0) = \frac{\int_{-\infty} ^x -f(s,y_0) ds}{f_Y(y_0)}\) 为给定条件 \(Y=y_0\) 下,\(X\) 的条件分布函数(conditional CDF),记为 -\(F_{X|Y}(x|y_0)\)。
-于是条件分布密度为 \(f_{X|Y}(x|y_0) = -\frac{f(x,y_0)}{f_Y(y_0)}\)。(conditional PDF)
--
-
一些性质:
-$F_{X|Y}(x|y)=P(Xx|Y=y)={-} ^x f{X|Y}(s|y)ds, x R $。
-如果 \(F_{X|Y}(x|y)\) 关于 \(x\) -连续,且除去至少可列个点后有连续的导数,则在偏导数存在时,\(f_{X|Y}(x|y_0)=\frac{\partial -F_{X|Y}(x|y)}{\partial x}\),否则为 \(0\)。
-
-
-
期中插播提示
--
-
关于连续型概率分布之前的误解:连续型的随机变量不能随便取单点的概率,因为单点处的概率就是 -\(0\),这就是为什么要定义一个概率密度的原因。概率密度的大小可以是任意的,不一定要小于 -\(1\),只要它的积分能够表示某一段(区域)的概率即可,这个在联合分布中有比较多的体现。
-总之,虽然 \(F(x,y) = \int_{-\infty}^x -\int_{-\infty}^y f(u,v)dudv\),但是 \(f(u,v)\) 不等同于 \(P(X=u,Y=v)\)。同理,如果要算条件概率的话,可以用 -\(F_{X|Y}(x|y)=P(x_1\leq X\leq -x_2|Y=y)=\int_{x_1}^{x_2} f_{X|Y} (s|y)ds\),也就是对 cond PDF -来积分求解。
-(但是,出于记忆公式的方便考虑,我还是会把它当成单点处的概率来列写公式(
-关于随机变量的独立性,定义如下:设 \(X_1,X_2,...,X_n\) 是 \((\Omega,F)\) 上的随机变量,如果对任意的实数 -\(x_1,x_2,...,x_n\) 有 \(P(X_1\leq x_1,X_2 \leq x_2,...,X_n \leq -x_n)=P(X_1\leq x_1)...P(X_n\leq x_n)\) 成立,则称随机变量 \(X_1,X_2,...,X_n\) 相互独立。
-同时,设随机变量 \(X_1,X_2,...,X_n\) -相互独立,\(g_1(x),g_2(x),...,g_n(x)\) -是一元实可测函数,\(\phi(x_1,x_2,...,x_k)\) 是 \(k\) 元实可测函数,则:
--
-
- 随机变量 \(g_1(X_1),...,g_n(X_n)\) -相互独立; -
- 随机变量 \(\phi(X_1,...,X_k),X_{k+1},...,X_n\) -相互独立。 -
这在样题的某个判断题中,以离散型随机变量的形式出现了,于是我自己证明了一下。实际上是一个更一般的结论。
-单调事件列的概率极限问题:以单调增序列 \(\lbrace A_i\rbrace\) 为例,有结论 \(lim_{n\to \infty} A_n=\cup _{i=1}^{\infty} -A_i\),于是极限概率为:
-\(P(\cup _{i=1}^{\infty} A_i) = P( lim -_{n\to \infty} A_n) = lim _{n \to \infty} P(A_n)\)。
-对于一些不单调的事件序列,可以用交并补构造一个单调序列,使得可以使用上述规律。
-事件列的上下极限的通俗说法:设 \(\lbrace A_i \rbrace\) 是 \(\Omega\) -中的一个事件列,定义上下极限为:
-\(lim_{n\to \infty} sup A _n = \cap -_{n=1}^{\infty} \cup _{k=n}^{\infty} A_k =\lbrace \omega \in \Omega: -\omega\) 属于无穷多个 \(A_i\rbrace\)。
-\(lim_{n\to \infty} inf A _n = \cup -_{n=1}^{\infty} \cap _{k=n}^{\infty} A_k =\lbrace \omega \in \Omega: -\omega\) 属于所有的 \(A_i\) -除去有限个\(\rbrace\)。
-当上下极限相等时称 \(\lbrace A_i -\rbrace\) 的极限存在。
-条件概率中会忘记的常识:对互不相容的事件列 \(\lbrace B_i \rbrace\),有 \(P(\cup _{i=1}^{\infty} B_i | A) = \Sigma -_{i=1}^{\infty} P(B_i | A)\)。
-一个 insight:求条件概率时我们可以把 \(A\) 之外的结果排除掉,记作 \((A,A\cap -F,P_A)\),这个事件域上完全可以有概率分布,因此不必为折棒太郎题惊讶。
-注意一组事件“相互独立”所要求的完备性。
-复习指南:
--
-
以上全部 TODO
-去看一下习题课中《一个有助于理解独立性的题目》和 Polya -坛子问题第二问。
-Poisoner's Dilemma
-A family has two girls while at least one names Lilia
-记一下几个重要分布,以及二元正态
-过一遍离散型、连续型随机向量的独立性证明,二元正态分布的独立性证明。
-折棒太郎折木棍问题的随机向量表述,Buffon 问题
-
-最后是一个我比较个人向的整理,根据考试重点和过往习题。Click -Here
-记得多用归纳!
-
Lecture 7
-又是全新的一门课辣(自我洗脑)
-]]>于是最后在作业期中期末占比约各三分之一、期中考了 94、wjd -老师海底捞调分的情况下考了个 A-(,就挺耻辱的。
-时隔一年学了 statistical decision theory 之后我逐渐理解一切(
- -非常短的一集,我随便喵两句。
-12.8 upd: 我超,我给学杂了,pivot rule 是 linear programming -里的,这玩意叫 pivot statistic,翻译过来叫枢轴量(
-Statistical Decision Theory
-多快好省的 decision theory 复习。
-Nonrandomized Decision
--
-
Let \(X\) be a sample from a -population \(P \in \mathcal P\). A -statistical decision theory is an action that we take after observing -\(X\), for example, a conclusion about -\(P\) or a characteristic about \(P\) according to the observation. We use -\(\mathbb A\) to denote the set of -allowable actions, and let \(\mathcal -F_{\mathbb A}\) be a \(\sigma\)-field on \(\mathbb A\). Then the measurable space -\((\mathbb A, \mathcal F_{\mathbb A})\) -is called the action space.
-Let \(\mathcal X\) be the range -of \(X\) and \(\mathcal F_{\mathcal X}\) be a \(\sigma\)-field on \(\mathcal X\). A decision rule is a -measurable function (actually a statistic) \(T\) from \((\mathcal X, \mathcal F_{\mathcal X})\) to -\((\mathbb A, \mathcal F_{\mathbb -A})\). If a decision rule \(T\) -is chosen, then we take the action \(T(X)\) whence \(X\) is observed. That's where the name -"decision rule" comes from.
-In statistical decision theory, we set a criterion using a loss -function \(L\), which is a function -from \(\mathcal P \times \mathbb A\) to -\([0, +\infty)\), and is Borel on \((\mathbb A, \mathcal F_{\mathbb A})\) for -each fixed \(P \in \mathcal P\). If -\(X=x\) is observed and our decision -rule is \(T(X)\), then our "loss" in -making the decision \(T(X)\) is \(L(P, T(x))\), which is still random -according to \(P\).
-The average loss for the decision rule \(T\), which is called the risk of \(T\), is defined to be
-\[R_T(P) = E[L(P,T(X))] = \int_{\mathcal -X} L(P, T(x)) dP_X(x).\]
-If the family \(\mathcal P\) is a -parameter family then the loss function and the risk can also be denoted -as \(L(\theta, T(X))\) and \(R_T(\theta)\).
-
Randomized Decision
--
-
Sometimes it is more useful to consider the randomized decision -rules. A randomized decision rule is a function \(\delta\) on \(\mathcal X \times \mathcal F_{\mathbb A}\) -such that, for every \(A \in \mathcal -F_{\mathbb A}\), \(\delta(\cdot, -A)\) is a Borel function and, for every \(x \in \mathcal X\), \(\delta(x, \cdot)\) is a probability measure -on \((\mathbb A, \mathcal F_{\mathbb -A})\).
-The nonrandomized decision rule \(T\) previously discussed can be viewed as a -special randomized decision rule with \(\delta -(x, \{a\}) = I_{\{a\}}(T(x)), a \in \mathbb A, x \in \mathcal -X\).
-The loss function for a randomized rule \(\delta\) is defined as \(L(P,\delta,x) = \int_{\mathbb A} L(P,a) d\delta -(x,a)\), and the risk is then
-\[R_\delta(P) = E[L(P,\delta,X)] = -\int_{\mathcal X} \int_{\mathbb A} L(P,a) d\delta (x,a) -dP_X(x).\]
-
Test Evaluation
--
-
A rule \(T_1(X)\) is as good as -\(T_2(X)\) if and only if \(R_{T_1}(P) \leq R_{T_2}(P)\) for any \(P \in \mathcal P\).
-A rule \(T_1(X)\) is better than -\(T_2(X)\) if and only if \(R_{T_2}(P)\) if and only if \(R_{T_1}(P) \leq R_{T_2}(P)\) for any \(P \in \mathcal P\), and there exists at -least one \(P \in \mathcal P\) s.t. -\(R_{T_1} (P) < R_{T_2}(P)\).
-Two decision rules are equivalent if and only if \(R_{T_1}(P) = R_{T_2}(P)\) holds for any -\(P\in \mathcal P\).
-If there is a decision rule \(T^*\) -that is as good as any other rule in \(\mathfrak F\), a class of allowable -decision rules, then \(T^*\) is said to -be \(\mathfrak F\)-optimal (or optimal -if \(\mathfrak F\) contains all -possible rules).
-
Hypothesis Testing
-Fundamental -Settings of Nonrandomized Testing
-都见过但陌生又熟悉.jpg
-Hypothesis Testing Problem
--
-
Let \(\mathcal P\) be a family -of distributions, \(\mathcal P_0 \subset -P\) and \(\mathcal P_1 = \mathcal P -\setminus \mathcal P_0\). A hypothesis testing problem can be -formulated as that of deciding which of the following two statements are -true:
-\[H_0 : P \in \mathcal P_1 \quad -\text{versus} \quad H_1 : P \in \mathcal P_1\]
-The action space for this problem contains only two elements, -i.e., \(\mathbb A = \{0,1\}\), where -\(0\) is the action of accepting \(H_0\) and \(1\) is the action of accepting \(H_1\). A decision rule is called a test, -and must has the form \(T(X) = -I_C(X)\), in which \(C \in \mathcal -F_{\mathcal X}\) is called the rejection region (because if \(X\in C\) we take \(T(X) = 1\), i.e. reject \(H_0\)).
-
Loss and Risk
--
-
A simple loss function for the problem is the \(0-1\) loss: \(L(P,a)=0\) if a correct decision is made -and \(L(P,a)=1\) otherwise. Under this -loss, the risk is
-\[R_T(P) = \begin{cases} P(T(X)=1) = -P(X\in C)& \quad P \in \mathcal P_0 \\ P(T(X)=0) = P(X \in C^c) -&\quad P \in \mathcal P_1 \end{cases} = P(X \in C) I_{\mathcal -P_0}(P) + P(X \notin C)I_{\mathcal P_1}(P).\]
-There are two types of statistical errors we may commit: -rejecting \(H_0\) when \(H_0\) is true (called the type I error) and -accepting \(H_0\) when \(H_0\) is wrong (called the type II -error).
-In statistical inference, a test \(T\), which is a statistic from \(\mathcal X\) to \(\{0,1\}\), is assessed by the probabilities -of making two types of errors (w.r.t. the \(0-1\) loss function):
-\[\alpha_T(P) = P(T(X)=1) = P(X\in C) -\quad P\in P_0\]
-\[1-\alpha_T(P) = P(T(X)=0) = P(X \notin -C) \quad P \in \mathcal P_1\]
-These two error probabilities cannot be minimized or even bounded by -a fixed \(\alpha \in (0,1)\) -simultaneouly when we have a fixed sample size.
-
How to Reach the Optimal -Test
--
-
A common approach to finding an optimal test is to assign a small -bound \(\alpha\) to one of the error -probabilities (which will also leads to a small rejection region/), say, -\(\alpha_T(P), P \in \mathcal P_0\), -and then attempt to minimize the other one subject to
-\[\sup_{P \in \mathcal P_0} \alpha_T(P) -\leq \alpha.\]
-The small bound \(\alpha\) is called -the level of significance, and the left side is called the size of the -test \(T\).
-Actually we're using the minimax rule w.r.t. the type II error, i.e. -to minimize \(\sup_{P \in \mathcal P_1} 1- -\alpha_T(P)\) under the constraint \(\sup_{P\in \mathcal P_0} \alpha_T(P) \leq -\alpha\), which will give a minimax rule \(T_\alpha^*(X)\) as the test at level of -significance \(\alpha\).
-
The Famous P-value
--
-
It's a good practice to assess the smallest possible level of -significance at which \(H_0\) would be -rejected for the computed \(T_\alpha^*(x)\) after observing \(x\), i.e. \(\hat -\alpha(x) = \inf \{\alpha \in (0,1) : T_\alpha^*(x)=1 \}\). Such -\(\hat \alpha (x)\) is also a statistic -depending on observed \(x\), and is -called the p-value for the test \(T_\alpha -^*\).
-The test can also be interpreted as \(T_\alpha^* (x) = I_{(0,\alpha)} (\hat -\alpha(x))\), thus we can find the p-value here.
-
Example of -Nonrandomized Parameter Test
-举个例子来结束这些神神叨叨。
-Example 1: Let \(X_1,X_2, -\cdots, X_n\) be i.i.d. from the \(N(\mu,\sigma^2)\) distribution with an -unknown \(\mu \in \mathbb R\) and a -known \(\sigma^2 >0\). Consider the -hypothesis \(H_0 : \mu \leq \mu_0 \quad -\text{versus} \quad H_1 : \mu > \mu_0\), where \(\mu_0\) is a fixed constant. Since the -sample mean \(\bar X\) is sufficient -for \(\mu \in \mathbb R\), it is -reasonable to consider the following class of tests: \(T_c(X) = I_{(c,\infty)}(\bar X)\).
-By the property of normal distributions, \(\alpha_{T_c}(\mu) = P(T_c(X)=1) = 1-\Phi -\left(\frac{\sqrt n (c - \mu)}{\sigma} \right)\), and for some -level of significance \(\alpha\) we -consider the type I error constraint \(\sup -_{\mu \leq \mu_0} \alpha_{T_c}(\mu) = 1-\Phi \left(\frac{\sqrt n -(c-\mu_0)}{\sigma} \right) \leq \alpha\), then the optimal test -should satisfy \(c_\alpha \geq \sigma -z_{1-\alpha} / \sqrt n + \mu_0\).
-The next step is to minimize \(1-\alpha_{T_c}(\mu)=\Phi \left(\frac{\sqrt n (c - -\mu)}{\sigma} \right)\) under the constraints \(c_\alpha \geq \sigma z_{1-\alpha} / \sqrt n + -\mu_0\) and \(\mu > \mu_0\), -the optimal test is \(c_\alpha ^*= \sigma -z_{1-\alpha} / \sqrt n + \mu_0\), and \(T_{c_\alpha ^*} (X) = I_{(c_\alpha ^*, -\infty)}(\bar X)\).
-According to the definition of p-value \(\hat \alpha(x) = \inf\{\alpha \in (0,1): -T_{c_\alpha ^*} (x) =1\}\), we can obtain \(\sigma z_{1-\hat \alpha(x)} / \sqrt n + \mu_0= -\bar x\) for any observed \(x\). -Thus \(\hat \alpha(x) =1-\Phi(\frac{\sqrt -n}{\sigma} \left(\bar x - \mu_0 \right))\) as a function of the -observed data.
-Randomized Test
-In Example 1, the equality in \(\sup_{P \in -\mathcal P_0} \alpha_T(P) \leq \alpha\) can always be achieved by -a suitable choice of \(c\). This is not -true in general. In such cases where the equality can't be attained, we -may consider randomized tests.
--
-
A randomized decision rule is a probability measure \(\delta(x,\cdot)\) on the action space for -any fixed \(x\). Since the action space -\((\mathbb A, \mathcal F_{\mathbb A} -)\) contains only two points \(\mathbb -A = \{0,1 \}\), then any randomized test of a hypothesis testing -problem is equivalent to a statistic \(T(X) -\in [0,1]\), with \(T(x) = -\delta(x,\{1\})\) and \(1-T(x) = \delta -(x,\{0\})\). In other words the expectation of \(T(X)I_{(0,1)}\) must be \(0\).
-In contrast, a nonrandomized test is a special case of randomized -test, where \(T(X)\) doesn't take value -in \((0,1)\).
-For any randomized test \(T(X)\), we define the type I error -probability to be \(\alpha_T(P) = ET(X), P \in -\mathcal P_0\), and the type II error probability to be \(1-\alpha_T(P) = 1-ET(X), P \in \mathcal -P_1\). The optimization rules are the same as the nonrandomized -case.
-
Example 2: Assume that the sample \(X\) from a binomial distribution \(B(\theta,n)\) with an unknown \(\theta \in (0,1)\) and a fixed integer -\(n >1\). Consider the hypothesis -\(H_0 : \theta \in (0, \theta_0] \quad -\text{versus} \quad H_1 : \theta \in (\theta_0 ,1)\) and the -following class of randomized tests:
-\[T_{j,q}(X) = \begin{cases} 1 \quad & -X>j \\ q \quad & X=j \\ 0 \quad & X <j -\end{cases}\]
-where \(j=0,1,\cdots,n-1\) and \(q \in [0,1]\). Then
-\[\alpha_{T_{j,q}}(\theta) = P(X>j) + -qP(X=j), \; 0 < \theta \leq \theta_0.\]
-For any \(\alpha \in (0,1)\) there -exists an integer \(j\) and \(q \in (0,1)\) such that the size of \(T_{j,q}\) is exactly \(\alpha\), i.e. the upper bound is attained -through randomized test.
-Confidence Sets
-Let \(\theta\) be a \(k\)-vector of unknown parameters related to -the unknown population \(P \in \mathcal -P\), \(C(X)\) in the range of -\(\theta\) and only depends on the -sample \(X\). If \(\inf_{P \in \mathcal P} P(\theta \in C(X)) \geq -1-\alpha\), then \(C(X)\) is -called a confidence set for \(\theta\) -with level of significance \(1-\alpha\).
-Actually if the constraint above holds, the coverage probability of -\(C(X)\) is at least \(1-\alpha\), though \(C(x)\) either covers or doesn't cover \(\theta\) whence we observe \(X=x\). To be more , the coverage -probability implies that when we make \(n\) random observations of \(X=x\) from the population and \(n\) confidence regions correspondingly, -then there are about \(n (1-\alpha)\) -among them covers \(\theta\).
-Comments
-一些不负责任的暴论/吐槽(
--
-
上统推的时候 wjd 说“一般情况下倾向于拒绝 \(H_0\)”的时候就给我整震撼了,那我把 \(H_0\) 和 \(H_1\) 换一下不行吗(。你早说 decision rule -就是个示性函数,\(0\) 对应 \(H_0\),\(1\) 对应 \(H_1\) 的话我还至于一年来都没记清楚 type I -error 和 type II error 分别是什么吗(x
-另一个不能理解的点是 randomized -test,看她举的例子还以为这个东西就是用来做 \(H_0: \theta = \theta _0 \; \text{versus} \; H_1 : -\theta \neq \theta_0\) 这种检验的,然后给 \(\theta = \theta_0\) 一个 \(q \in (0,1)\) -的值。感觉没怎么说过是因为达不到 upper bound -有点浪费所以用单点处来补足的这个想法,
-可能也不排除当时已经是网课了所以是我听课不认真(但也不可能先把 randomized rule 讲一遍,再把 minimax rule -讲一下说明为什么是缩小 \(\sup -\alpha_T(P)\),在这之前总得把 measure -是啥说清楚,我说实话很怀疑很多人修统辅到最后连概率空间和 \(\sigma\)-field -都没完全搞清楚,
一直在安慰大家这个不考那个不考的 dwl -全责。但有的时候也很佩服统辅这些课能把故事完全限制在初等上还能讲明白(大概吧,我经常是听不明白,但看起来大家都很明白)的功力(
-感觉就是之前一直没学本质,当时前四周的 statistics -看起来有点难但学会了 exponential family -的算法之后就薄纱一切了,反正大家也不会条件期望
dwl 全责-不可能真拿定义算 sufficient statistics 和 -UMVUE;后半学期我就在疑惑这统计真的和数学有关系吗(,讲完基本概念之后就开始讲那些个 -normal distribution family -上假设检验的例子,最后还要像八股文一样地考,可能确实是限制在初等上的话实在没什么可学的(
-总之虽然吐槽了很多,我还是很认可去年统计推断这门课的,但只能说真想学点数学 -
-而不只是薄纱大家来愉悦身心(有的时候可能只会被反杀罢)-的话还是别修统辅课了,调性不合(。
-所以说去年这时候确实是对自己很没信心啊(今年也没有啊(
-
这什么破标题(
-参考了《Applied -Mathematical Programming》Chapter 9,10 和一份相应的 notes。
- -为什么要做 integer programming?一般来说 linear programming -也可以得到一个答案,把它 round -一下不就好了?但其实有一些很实际的理由导致 integer programming -是必须的,就像线性回归中 dummy variable 也是必须的一样(啥
-一般来说把 integer programming 的 integer condition 移除后的 linear -programming problem 称为其相应的 relaxed problem,integer programming 的 -feasible set 一定是其 relax problem feasible set 的子集,其 optimal cost -也不会超过 relaxed problem 的 optimal -cost。这很好理解,就是取了个限定更强的形式。
--
-
round 得到的结果未必还是最优的。比如:
-\[\begin{aligned}\textbf{maximize} \quad -& 8x_1+11x_2+ 6x_3 +4x_4 \\ \textbf{subject to} \quad -& 5x_1+7x_2+4x_3+3x_4 \leq 14 \\ \quad &x_j \in \{0,1\}, \quad -j=1,2,3,4 \end{aligned}\]
-如果用 linear programming 会得到 optimal solution 是 \((1,1,0.5,0)^T\),round 一下得到 \((1,1,1,0)\) 并不在 feasible set -中。与此同时实际上的 optimal solution 是 \((0,1,1,1)^T\),哪怕反向 round -也得不到精确的结果。
-但是每个通过 round 得到的结果都比真正的 integer programming 的 -optimal cost 要小,某种程度上来说给出了一个估计。
-integer programming -可以反映许多很难描述的条件。例如两个条件至多成立一个,用某个 integer -variable 表示选择与否,等等。
-哪怕真的可以用 round 的方法得到解,也不知道反向/正向 round -的结果是不是最好的,而在一些实际问题里哪怕只是相差 \(1\) 也会造成成本/效益的巨大差异。
-
另外 integer programming 的困难在于 optimal solution -不再一定在顶点处取到,而且 feasible set -是离散的点集,其数量远大于顶点数量,不太可能用枚举得到答案。
-Standard Settings
-Interger programming 的标准形式一般来说相对简单,但和 linear -programming 稍有不同:
-\[\begin{aligned} \textbf{maximize} \quad -& c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & -x_j \in \mathbb N \end{aligned}\]
-其中要求 \(c \geq 0, A \geq 0, b \geq
-0\)(指的是 \(A\) 的每个分量
-\(a_{ij}\) 都要是非负的
-而不是正定什么的要求)。
这样写相对粗糙。事实上,如果 \(A\) -只表示一个一维的 constraint 则称为 knapsack problem,否则是 -multidimensional knapsack problem;如果所有的 \(x_j\) 均在 \(0,1\) 上取值则称为 pure integer -programming,否则是 mixed linear programming。
-对应的 pure integer programming 的标准形式是:
-\[\begin{aligned} \textbf{maximize} \quad -& c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & -x_j \in \{0,1\} \end{aligned}\]
-同样要求 \(c \geq 0, A \geq 0, b \geq -0\)。
-Standardize to 0-1 Knapsack -Problem
-最明显的一些要求是 \(c\geq 0,A\geq -0\),至于 \(b\) -谋事在人成事在天(。
-对于 1-dimension 来说一般来说如果有看到 \(c_i \geq 0, a_i \leq 0\) 的话直接把 \(x_i\) 取为 \(1\),因为这变相的扩容了 constraint -的上限;如果 \(c_i \leq 0 ,a_i \geq 0\) -则置为 \(0\),显然它的存在既会占用资源又减小上限。如果 -\(c_i ,a_i \leq 0\) 同时成立就用 \(y_i = 1-x_i\) -代替原变量即可,从而得到标准形式。
-Multidimension 咋办,他也没说啊(挠头(
感觉可能就不用动了,反正后面的求解里面都还是考虑 relaxed LP -问题,直接按照 LP 的 standardized form 来化简就可以。当然如果有一溜 -\(\{a_{ij}\}_{i=1}^m \leq 0, c_i \geq -0\) 这种情况的话直接把 \(x_{i}\) -置 \(1\) -即可,少一个变量是一个。或者也可能是用 \(x_1\) 和 \(1-x_i\) 替换来保证所有的 \(c_i\) 为正。
-Solutions to Integer -Programming
-Relaxed Linear Programming
-比较符合直觉的一种方案就是把它和对应的 linear programming problem -结合起来看,它们之间的确存在一定的关系,甚至在某一些情况下可以得到对于 -integer programming 的估计(未必是精确值)。
-\[\begin{aligned} \textbf{maximize} \quad -& c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & -x_j \in \mathbb N \end{aligned} \quad \quad \quad \begin{aligned} -\textbf{maximize} \quad & c^Tx \\ \textbf{subject to} \quad & Ax -\leq b \\ \quad & x_j \geq 0 \end{aligned}\]
-(暂且先不考虑 0-1 knapsack)
-注意在实际计算中想要解出(比如用 simplex method)relaxed problem -还需要再做一步 standardize,此处略去。
-此时有:
--
-
- 如果 LP 的 optimal solution 恰好是个 integer solution 那么也一定是 -IP 的 optimal solution; -
- LP 的 optimal cost 一定比 IP 的 optimal cost 更大; -
- 如果 \(c\) 的所有分量也是整数,则将 -LP 的 optimal solution 向下取整得到的解也在 feasible set 里,而且至少比 -IP 的 optimal cost 更大(因为 round 之后的结果未必是 \(0,1\) 取值的,不一定是 IP 的解)。 -
Bound and Branch
-Pure Integer Programming
-本质上就是,利用 relaxed linear programming 来寻找一组 optimal -solution(一般用 simplex method)\(x= -(x_1,x_2,\cdots,x_n)\),其中会有若干个是非整数解,记为 \(x_{m1},x_{m2},\cdots,x_{mk}\)。此时可以对每个 -\(x_{mi}\) 是向上 round 还是向下 round -做一个分割,就回到了 seperating hyperplane theorem。这样就得到了一个 -tree,它的每一组分叉都多加了一个条件,解出所有分叉上点的解即可。
-来个示意图,我也不知道为什么这个图在书上就是颈椎病图,凑合看吧(
-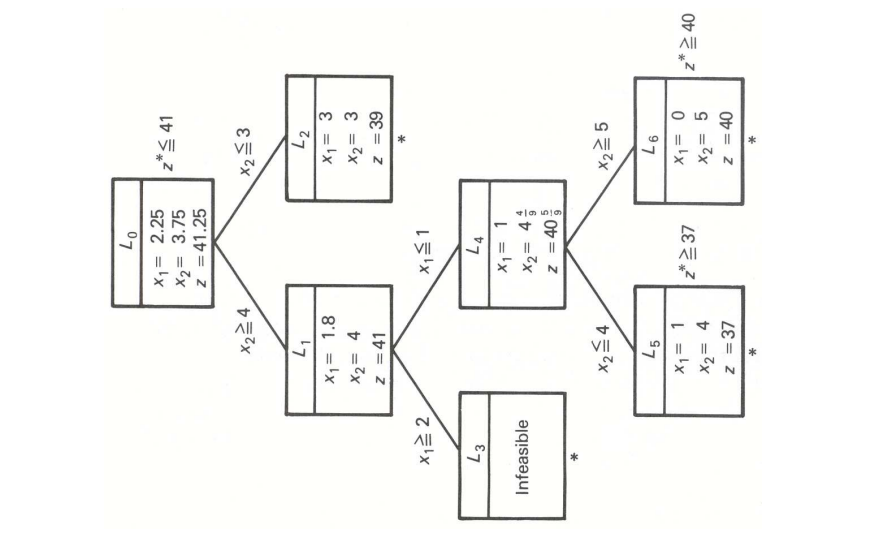
某种程度上来说和 ellipsoid method -非常相似,都是在原条件的基础上继续用 cutting plane -加条件然后继续往下解。所以说需要考虑的问题也是相似的,也即算法何时终止、time -usage 如何、这棵树上的 optimal solution 是否就是真正的 optimal -solution(只是在对每个非整数变量做 -round,听起来不是特别靠谱)。特别地,还有树上所有的分支应该以什么样的顺序求解才最优、能否中途去掉一些 -inactive 的分支来保证计算量最小。
--
-
首先观察到所有的 \(c_i\) -都是正的(如果不是正的请把 \(x_i\) 换成 -\((1-y_i)\)),所以可以用 dual problem -来解
但总觉得没啥必要
-计算得到的最初的 \(L_0\) 的 -optimal cost 记为 \(\bar -z\),这样这棵树上的每一个 optimal cost 都不会大于 \(\bar z\)。
-在计算的过程中,如果已经有某个 subproblem 得到了 integer solution -和相应的 optimal cost \(z^*\),则如果在其他 active subproblem with -fractional solution 中得到了更小的 optimal cost \(z \leq z^*\),则说明无论如何分划,这一 -active subproblem 所对应的平面区域上都不可能找到 optimal -cost,直接将其置为 inactive 即可。
-换言之,在找到一个 optimal cost 为 \(z^*\) 之后,只需要再寻找一个 optimal cost -为 \(z\),满足 \(z^* \leq z \leq \bar z\) 的整数解。这就是 -bound and branch 中 bound 的来源。
-Infeasible subproblem 也不需要再分划下去。
-
最后得到的 algorithm 大致是:
--
-
- Solve the linear relaxation of the problem. If the solution is -integer, then we are done. Otherwise create two new subproblems by -branching on a fractional variable. -
- A subproblem is not active when any of the following occurs:
-
-
-
- You used the subproblem to branch on -
- All variables in the solution are integer -
- The subproblem is infeasible -
- You can fathom the subproblem by a bounding argument -
- - Choose an active subproblem and branch on a fractional variable. -Repeat until there are no active subproblems. -
Mixed Integer Programming
-Mixed integer programming 的 bound and branch -方法和上述几乎并无不同,只是每一次加条件做分枝的时候只对 integer -variable 加条件,计算量会隐性地小一点。
-Cutting Plane Method
-我个人认为课件上说这个条件在二维条件下用比 bound and branch
-简单这件事非常逆天,就,我用 bound and branch 来解 integer programming
-的时候也是用画图来做的啊,谁真的拿 simplex method 解 \(2^k\) 个 linear programming
-啊((
用一个例子来解释:
-\[\begin{aligned}\textbf{maximize} -&\quad 7x_1+ 9x_2 \\ \textbf{subject to}& \quad -x_1+3x_2 \leq 6 -\\ & \quad 7x_1+x_2 \leq 35 \\ & \quad x_1,x_2 \in \mathbb -N \end{aligned}\]
-类似于化成 linear programming 的方法,但是相应的 slack variable -也是正整数:
-\[\begin{aligned}\textbf{minimize} -&\quad -7x_1- 9x_2 \\ \textbf{subject to}& \quad -x_1+3x_2+s_1=6 -\\ & \quad 7x_1+x_2 +s_2= 35 \\ & \quad x_1,x_2,s_1,s_2 \in -\mathbb N \end{aligned}\]
-用 simplex method 得到一个最终的 full tableau(也就是无视掉上述 -linear programming 的整数条件进行一个优化的做,得到 LP 对应的 optimal -solution),此时的 tableau 如下所示:
-| - | - | \(x_1\) | -\(x_2\) | -\(s_1\) | -\(s_2\) | -
|---|---|---|---|---|---|
| - | \(63\) | -\(0\) | -\(0\) | -\(28/11\) | -\(15/11\) | -
| \(x_2\) | -\(7/2\) | -\(0\) | -\(1\) | -\(7/22\) | -\(1/22\) | -
| \(x_1\) | -\(9/2\) | -\(1\) | -\(0\) | -\(-1/22\) | -\(3/22\) | -
也就是说在计算中最后得到的 constraints 为:
-\[\begin{aligned} & x_2+7/22 s_1+ -1/22s_2=7/2 \\ & x_1 - 1/22 s_1+ 3/22 s_2= 9/2 -\end{aligned}\]
-把所有的整数部分放在左边,分数 round 到最小放在右边(注意要让右边所有 -variable 的系数为负,且绝对值小于 \(1\),这样才能往后加 constraints):
-\[\begin{aligned} & x_2-3 = -1/2-7/22s_1-1/22s_2 \\ &x_1 - s_1-4 =1/2-21/22s_1-3/22s_2 -\end{aligned}\]
-这给出了新的 constraints :
-\[\begin{aligned}& 1/2-7/22s_1-1/22s_2 -\leq 0 \\ & 1/2 - 21/22s_1-3/22s_2 \leq 0 -\end{aligned}\]
-Solution to 0-1 Knapsack -Problem
-这 PPT 上怎么说是一个一个试啊(挠头
-举个例子先:
-\[\begin{aligned} \textbf{maximize} \quad -& z=3x_1-2x_2+5x_3 \\ \textbf{subject to} \quad & x_1+2x_2-x_3 -\leq 2 \\ & x_2+4x_2+x_3 \leq 4 \\& x_2+x_3 \leq 3 \\ -&4x_2+x_3 \leq 6 \\ & x_1,x_2,x_3 \in \{0,1\} -\end{aligned}\]
-当然可以把 \((x_1,x_2,x_3)\) 按照 -\(000,001,010,011,100,101,110,111\) -来逐个尝试,稍微简化一下的话可以考虑
-\[\begin{aligned} \textbf{maximize} \quad -& z=5x_3 +3x_1-2x_2\\ \textbf{subject to} \quad & x_1+2x_2-x_3 -\leq 2 \\ & x_2+4x_2+x_3 \leq 4 \\& x_2+x_3 \leq 3 \\ -&4x_2+x_3 \leq 6 \\ & x_1,x_2,x_3 \in -\{0,1\} \end{aligned}\]
-把 cost function 中系数最大的 \(5x_3\) 提到最前面,如果能够达到最大则 \(x_3=1\) 的情况较为有利。我们发现 \((x_1,x_2,x_3) = (0,0,1)\) 能够符合 -constraints 而且 cost 为 \(5\),因此其后讨论其他取值时 cost 小于 \(5\) 的可以无需带入检查 -constraints,直接舍去。
-]]>选课的时候我还侥幸以为生统概论可以放松心情,来随便听听简单了解一下那种。可能是前置没学完的原因,倒也没那么水,ANOVA -还是花了不少时间看的。
-wty 老师的英语口语真不错,可惜我听力一般,一走神就寄了。还是要感谢 V1ncent19
-的统辅笔记救我,不过他看起来是前置都学完了来上的这个,写的有点抽象,我想写个废话多一点具体点的。
Analysis of Variance
-示例——Treatment of -Lead-Exposed Children Trial
-100 名被试被分成两组分别使用安慰剂和药剂,在实验开始前、实验第 1, 4, -6 周分别检验了血液铅含量水平。第 i 名被试的实验开始前水平为 \(y_{i1}\),实验结束后水平为 \(y_{i2}\),变化水平为 \(d_i = -y_{i2}-y_{i1}\),希望利用这些数据观察药剂的有效程度。
-假设线性回归模型为 \(d_i = \beta_0 + -\beta_1 x_i +e_i\),注意此处的 \(x_i\) -是一个分类统计量,也就是说被试使用安慰剂时取 \(x_i = 0\),被试使用试验药剂时 \(x_i =1\)。做一些假设检验:
--
-
- \(H_0: \beta_0 =0\) -检验了安慰剂组的平均变化是否为 \(0\) -
- \(H_0:\beta_1 = 0\) -检验了安慰剂组和药剂组之间的平均差异是否为 \(0\),也即药剂是否对治疗有作用 -
这一模型也可以写作 \(y_{i2} = y_{i1} + -\beta_0 +\beta_1 x_i + e_i\),但实际上 \(y_{i1}\) 对于 \(y_{i2}\) 的影响也有待商榷,未必在 \(y_{i1}\) 变化一个单位时,\(y_{i2}\) -也随之变化一个单位,所以模型可以修正为 \(y_{i2} = \beta_0 + \beta_1 x_i +\beta_2 y_{i1} -+e_i\)。这样又多出来一个假设检验:
--
-
- \(H_0 :\beta _2 = 0\) -检验了初始状态对末态是否有影响 -
不同的检验模型会得到一些不同的结果。类似的场景是我们的出发点。
-One Factor ANOVA
-首先给出一个希望做检验的场景:\(n_T\) 个实验对象被分成 \(r\) 组,每组有 \(n_i\) 个实验对象,有 \(n_T = \Sigma_{i=1} ^r n_i\)。由此我们得到 -\(n_T\) 个数据 \(Y_{ij}\),\(i\) 表示组别,\(1\leq i \leq r\),\(j\) 表示在某一组内的编号,\(1 \leq j \leq n_i\)。
-Cell means model
-模型假设是 \(Y_{ij} = \mu_i + -\varepsilon_{ij}\)。
-其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim -N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。考虑一些统计量作为参数的估计量:
-\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 -}^{n_i} Y_{ij} = \hat \mu _i\]
-\[\bar{Y}_{..} = \frac{1}{n_T} -\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r -n_i \bar{Y}_{i.}\]
-\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 -/ (n_i -1) \]
-\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r -(n_i -1) s_i ^2 = \hat \sigma^2\]
-在这一模型中,我们关注的假设检验是 \(i\) 组实验之间是否存在差异,假设检验表示为 -\(H_0 : \mu_1= \mu_2 = ... = \mu_r = -\mu\),对应的备择假设即为 \(\{ \mu_i -\}_{i=1} ^r\) 中存在不同的项。检验最经典的方法即为 -ANOVA,analysis of variance。核心是以下的分解:
-\[\begin{aligned} SSTO = \Sigma_i -\Sigma_j(Y_{ij} - \bar Y_{..})^2 &= \Sigma_i \Sigma_j (Y_{ij} - \bar -Y_{i.} +\bar Y_{i.} - \bar Y_{..})^2 \\& = \Sigma_i n_i (\bar Y_{i.} -- \bar Y_{..})^2 + \Sigma_i \Sigma_j (Y_{ij} - \bar Y_{i.})^2 \\ -&=SSTR + SSE \end{aligned}\]
-可以观察到,\(SSTR\) -是组间差距,体现了不同组别之间的差别,\(SSE\) -是组内差距,体现了同一组内各数据的偏差。注意 \(SSTR\) 的自由度是 \(r-1\),\(SSE\) 的自由度是 \(n_T - r\),\(SSTO\) 的自由度是 \(n_T - 1\)。由此可以求出 \(MSE= \frac{SSE}{n_T -r}\),\(MSTR = -\frac{SSTR}{r-1}\)。作业里证明了两个统计量的期望,\(\mathbb E(MSE) = \sigma^2\),\(\mathbb E(MSTR) = \sigma^2 +\frac{\Sigma_i n_i -(\mu _i -\mu_.)^2}{r-1}\),其中 \(\mu_. -= \frac{\Sigma_i n_i \mu_i}{n_T}\)。
-在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 _{n_T - -r}\),\(\frac{SSTR}{\sigma^2} \sim -\chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,n_T -r}\) -作为最终的检验统计量。
-当 \(F^* > F(1-\alpha , r-1 , n_T --r)\) 时拒绝原假设,否则接受;\(Power = -P(F^* > F(1-\alpha , r-1,n_T -r)| \delta)\),其中 \(\delta\) 是一个非中心偏移量,\(\delta = \frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i -n_i (\mu_i - \mu_.)^2}\)。
-Factor Effects Model
-Factor Effects Model 是 Cell Means Model -的一个重新参数化的结果。模型假设是 \(Y_{ij} = -\mu + \tau_i + \varepsilon_{ij}\)。
-其中,\(\mu_i\) -是整体的理论均值,\(\varepsilon _{ij} i.i.d. -\sim N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 -\(\mu , \tau_1 , ..., \tau_r , -\sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = -0\),如果没有这个约束会导致存在多组解。考虑一些统计量作为参数的估计量:
-\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 -}^{n_i} Y_{ij} = \hat \tau _i + \hat \mu\]
-\[\bar{Y}_{..} = \frac{1}{n_T} -\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r -n_i \bar{Y}_{i.} = \hat{\mu}\]
-\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 -/ (n_i -1) \]
-\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r -(n_i -1) s_i ^2 = \hat \sigma^2\]
-在这一模型中,我们关注的假设检验仍然是 \(i\) 组实验之间是否存在差异,假设检验表示为 -\(H_0 : \tau_1= \tau_2 = ... = \tau_r = -0\),对应的备择假设即为 \(\{ \mu_i -\}_{i=1} ^r\) 中存在不同的项。factor effects model -在参数的含义上比 cell mean model 更清晰。
-Two Factors ANOVA
-首先给出一个希望做检验的场景:\(nab\) 个实验对象被分成 \(a\times b\) 组,每组有 \(n\) 个实验对象。第 \(ij\) 组的实验条件是 \(A\) 因素的等级为 \(i\),\(B\) -因素的等级为 \(j\),其中有 \(1 \leq i \leq a, 1\leq j \leq -b\)。由此我们得到 \(nab\) 个数据 -\(Y_{ijk}\),\(i\) 表示以 \(A\) 因素分类的组别,\(j\) 表示以 \(B\) 因素分类的组别,\(k\) 表示在某一组内的编号,\(1 \leq k \leq n\)。
-每一组都是 \(n\) 个人,这是一个 -balanced design。
-Factor Effects Model
-模型假设是 \(Y_{ijk} = \mu +\alpha_i + -\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
-其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) -表示和两个因素同时相关的变化,相当于一个交叉项。
-这里面有 \((a+1)(b+1)\) -个参数,对其也有一定的约束:\(\Sigma_i -\alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j -(\alpha \beta)_{ij} -=0\)。做一些其他的参数假设,让参数含义更清晰:
-\[\mu_{i.} = \alpha_i -+\mu_{..}\]
-\[\mu_{.j} = \beta _j + -\mu_{..}\]
-\[\mu_{ij} = \mu_{..} +\alpha_i + \beta_j -+(\alpha \beta)_{ij}\]
-如果 \((\alpha \beta)_{ij}=0\) -则说明因素 \(A,B\) -之间不存在相互作用的关系,这样的模型称为 additive model。
-考虑一些统计量作为参数的估计量:
-\[\bar{Y}_{ij.} = \frac{1}{n} \Sigma_{k=1 -}^{n} Y_{ijk} = \hat \mu_{ij} = \hat \mu + \hat \alpha _i + \hat -\beta_j + \hat{(\alpha \beta)}_{ij}\]
-\[\bar{Y}_{i..} = \frac{1}{bn} -\Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \alpha_i = -\hat \mu_{i.}\]
-\[\bar{Y}_{.j.} = \frac{1}{an} -\Sigma_{i=1}^a \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \beta_j = -\hat \mu_{.j}\]
-\[\bar{Y}_{...} = -\frac{1}{abn}\Sigma_{i=1}^a \Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = -\hat{\mu} \]
-Two factors ANOVA 的方差分解更复杂一些:
-\[\begin{aligned} SSTO &= \Sigma_i -\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{...})^2 \\ &= \Sigma_i -\Sigma_j \Sigma_k ((\bar Y_{i..} - \bar Y_{...})+(\bar{Y}_{.j.} - \bar -Y_{...}) +(\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...}) -+(Y_{ijk} - \bar Y_{ij.}))^2 \\&=bn\Sigma_i (\bar Y_{i..} - \bar -Y_{...})^2+an\Sigma_j (\bar{Y}_{.j.} - \bar Y_{...})^2+n\Sigma_i -\Sigma_j (\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...})^2+ -\Sigma_{i}\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{ij.})^2 \\&=SSA -+SSB+SSAB+SSE \end{aligned}\]
-其中,\(SSA\) 的自由度是 \(a-1\),\(SSB\) 的自由度是 \(b-1\),\(SSAB\) 的自由度是 \((a-1)(b-1)\),\(SSE\) 的自由度是 \(ab(n-1)\)。在这一个复杂问题中我们关心不同的问题,可以做出三种不同的假设检验,有对应的检验统计量。
--
-
- \(A\) 因素是否会导致差异?\(H_0: \alpha_1 =\alpha_2=...=\alpha_a\),在 -\(H_0\) 下有 \(F^* = \frac{SSA/(a-1)}{SSE/(ab(n-1))} \sim -F_{a-1,ab(n-1)}\) -
- \(B\) 因素是否会导致差异?\(H_0: \beta_1 =\beta_2=...=\beta_b\),在 -\(H_0\) 下有 \(F^* = \frac{SSB/(b-1)}{SSE/(ab(n-1))} \sim -F_{b-1,ab(n-1)}\) -
- \(A,B\) 是否联合作用?\(H_0:(\alpha \beta)_{ij}=0, \forall 1 \leq i \leq -a,1\leq j \leq b\),在 \(H_0\) -下有 \(F^*=\frac{SSAB/(a-1)(b-1)}{SSE/(ab(n-1))} \sim -F_{(a-1)(b-1),ab(n-1)}\) -
Random Effect Test
-Why random effects?
-事实上,有的时候对于一个 cell means model 或者 factor effects -model,我们并不是很关心每个 \(\mu_i\) -的检验,而是关心整体的 \(\mu_.\) -的情况;这种情况下一般 level of factor -也是随机从一个总体里取出的。所以需要改变一些模型假设,进行 random effect -的检验。
-Cell means model for random -effect
-回顾一下 cell means model:
---模型假设是 \(Y_{ij} = \mu_i + -\varepsilon_{ij}\)。
-其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim -N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。
-
对于 cell means model for random effect,需要把 \(\mu_i\) 视作一组随机变量而非参数:
---模型假设是 \(Y_{ij} = \mu_i + -\varepsilon_{ij}\)。其中有 \(i = -1,2,...,r\),\(j -=1,2,...,n\),暂时设定为一个 balanced test。
-其中,\(\mu_i \sim N(\mu_., \sigma_\mu -^2)\) 不要求相互独立,\(\varepsilon_{ij}\) i.i.d. \(\sim N(0,\sigma^2)\),且 \(\mu_i\) 和 \(\varepsilon_{ij}\) 之间是相互独立的。 -因此,这一模型中共有 \(3\) -个参数,分别是 \(\mu_., \sigma_\mu, -\sigma\),而且 \(Y_{ij}\) -不相互独立。
-事实上,我们不要求关于特定的 \(\mu_i\) 的结论,而是关心在 population \(\lbrace \mu_i \rbrace_{i=1} ^r\) -上的推断,以推断 \(\mu\) 和 \(\sigma_\mu^2\) 为主。
-
简单推导可以得到以下结论:
--
-
- \(\mathbb E(Y_{ij}) = \mu_.\) -
- \(Var(Y_{ij}) = \sigma^2 +\sigma_\mu -^2\) -
- \(Cov(Y_{ij} , Y_{ij'}) = \sigma_\mu -^2, j \neq j'\) -
- \(Cov(Y_{ij},Y_{i'j'}) = 0, i \neq -i', j \neq j'\) -
- \(\mathbb E(MSE) = \sigma^2\) -
- \(\mathbb E(MSTR) = \sigma^2 + n\sigma_\mu -^2\) -
记 \(\sigma_Y^2 = \sigma_\mu^2 + -\sigma^2\),有一个在推断中有意义的参数是 \(\frac{\sigma_\mu ^2}{\sigma_Y ^2} = -\frac{\sigma_\mu ^2}{\sigma_\mu ^2 + -\sigma^2}\)。这表征了在整体方差中,由 \(Y_{ij}\) 的随机性产生的比例。
-对此我们常做的一个检验是 \(H_0 :\sigma_\mu -^2 = 0; H_a: \sigma_\mu ^2 >0\),原假设的含义在于说明 \(\mu_i\) 是相等的,事实上这和 fixed effect -下的 cell means model 所做的检验是相同的。在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 -_{r(n-1)}\),\(\frac{SSTR}{\sigma^2} -\sim \chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,r(n-1)}\) -作为最终的检验统计量。
-当 \(F^* > F(1-\alpha , r-1 , -r(n-1))\) 时拒绝原假设,否则接受;\(Power = P(F^* > F(1-\alpha , r-1,r(n-1))| -\delta)\),其中 \(\delta\) -是一个非中心偏移量,\(\delta = -\frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i n_i (\mu_i - -\mu_.)^2}\)。这里是暂时认为做的是 balanced test。
-如果实验并不是一个 balanced test,每一组的数据量为 \(n_1,n_2,...,n_r\) 且有 \(n_T = \Sigma_{i=1} ^r n_i\),于是有:
-\[\mathbb E(MSTR) = \sigma^2 + n' -\sigma_\mu ^2, \quad n' = \frac{1}{r-1} [n_T - \frac{\Sigma_{i=1}^r -n_i ^2}{n_T}]\]
-对这一模型的参数做一些估计,上文中提到 cell means model for random -effect 有三个参数 $_., ^2 $ 和 \(\sigma_\mu -^2\),事实上对于后两个参数我们也关心 \(\frac{\sigma_\mu ^2}{\sigma_\mu ^2 + -\sigma^2}\) 的估计,以下还是在 balanced test -的前提下分点来阐述技术细节:
--
-
\(\mu_.\) 的一个无偏估计即为 -\(Y_{..} = \frac{\Sigma_{i=1}^r \Sigma_{j=1}^n -Y_{ij} }{rn}\),它的方差是 \(Var(Y_{..}) = \frac{\sigma^2}{rn} + -\frac{\sigma_\mu ^2}{r}\)。
-因此 \(s^2(\bar{Y}_{..}) = -\frac{MSTR}{rn}\) 是 \(Y_{..}\) -的方差的无偏估计,\(\mu_.\) -的置信区间是 \(\bar{Y}_{..} \pm -t(1-\alpha/2;r-1)s(\bar{Y}_{.. } )\)。
-由于 \(\frac{MSTR/(n\sigma_\mu ^2 + -\sigma^2)}{MSE/ \sigma^2} \sim F_{r-1,r(n-1)}\),因此有:
-\[L = \frac 1n [\frac{MSTR}{MSE} -(\frac{1}{F[1-\alpha/2;r-1;r(n-1)]})-1]\]
-\[R = \frac 1n [\frac{MSTR}{MSE} -(\frac{1}{F[\alpha/2; r-1,r(n-1)]})-1]\]
-此时 \(\frac{\sigma_\mu ^2}{\sigma_\mu ^2 + -\sigma^2}\) 的 \(100(1-\alpha) -\%\) 置信区间是 \([\frac{L}{1+L} , -\frac{R}{1+R}]\)。
-\(\sigma^2\) 的无偏估计是 \(MSE = \frac{\Sigma_{i=1} ^r \Sigma_{j=1}^n (Y_{ij} -- \bar Y_{i.})}{r(n-1)}\),置信区间的估计可以建立在 \(\frac{r(n-1)MSE}{\sigma^2} \sim -\chi^2[r(n-1)]\) 的基础上,于是有 \(\sigma^2\) 的 \(100(1-\alpha) \%\) 置信区间是 \([\frac{r(n-1)MSE}{\chi^2[1-\alpha /2; r(n-1)]}, -\frac{r(n-1)MSE}{\chi^2 [\alpha/2;r(n-1)]}]\)
-\(\sigma_\mu^2\) 的无偏估计是 -\(s_\mu ^2 = \frac{MSTR - -MSE}{n}\),但有时数据点决定此处点估计值是负的,此时就用 \(0\) 来代替 \(\sigma_\mu ^2\) 的估计值。
-
Random factor effects model
-相应地可以对 cell means model for random effect 做一些改进。回顾一下 -factor effects model:
---Factor Effects Model 是 Cell Means Model -的一个重新参数化的结果。模型假设是 \(Y_{ij} = -\mu + \tau_i + \varepsilon_{ij}\)。
-其中,\(\mu_i\) -是整体的理论均值,\(\varepsilon _{ij}\) -i.i.d. \(\sim -N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 \(\mu , \tau_1 , ..., \tau_r , -\sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = -0\),如果没有这个约束会导致存在多组解。
-
Random factor effects model 也是 cell means model for random effects -的一个重新参数化的结果。
---模型假设是 \(Y_{ij} = \mu + \tau_i -+\varepsilon_{ij}\),其中 \(i = -1,2,...,a,j=1,2,...,n_i\)。相对于 cell means model for random -effect,这里将 \(\tau_i\) -都视作随机变量,满足 \(\tau_i \sim -N(0,\sigma_\tau ^2)\) 不要求相互独立,\(\varepsilon_{ij}\) i.i.d. \(\sim N(0,\sigma^2)\),且 \(\tau_i\) 和 \(\varepsilon_{ij}\) -之间是相互独立的。这一模型中也是三个参数,分别是 \(\mu_., \sigma_\mu, \sigma\),而且 \(Y_{ij}\) 不相互独立。
-由于是随机变量,自然不再要求满足 \(\Sigma_{i=1}^a \tau_i =0\) 的限制。
-
实际上可以看到,在 random effect 意义下,factor effects model 和 cell -means model -的关系更紧密了,只是相差一个常数。因此所有的检验和推断可以类似的进行。
-Mixed factors effects model
-回顾一下 two factors effects model:
---模型假设是 \(Y_{ijk} = \mu +\alpha_i + -\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
-其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) -表示和两个因素同时相关的变化,相当于一个交叉项。
-这里面有 \((a+1)(b+1)\) -个参数,对其也有一定的约束:\(\Sigma_i -\alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j -(\alpha \beta)_{ij} =0\)。
-
类似地,mixed factors effects model 也是把模型假设进行了一些修改,将 -\(\alpha_i\) 从参数改成了随机变量。注意 -\(\alpha_i , \beta_j\) 中只要有一个改为 -random effect,其联合作用 \((\alpha -\beta)_{ij}\) 也变为随机变量而非参数。
---模型假设是 \(Y_{ijk} = \mu +\alpha_i + -\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
-其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) -表示和两个因素同时相关的变化,相当于一个交叉项。
-需要满足一定的约束:
--
-- \(\Sigma_{i=1} ^ a \alpha _i -=0\)
-- \(\beta_j \sim N(0,\sigma_\beta -^2)\)
-- \((\alpha \beta)_{ij} \sim -N(0,\sigma_{\alpha \beta}^2)\)
-
检验方式和统计量见 ANOVA table construction 环节。
-ANOVA table construction
-e.g: three factors model
-\[Y_{ijkl} = \mu + \alpha_i + \beta_j + -\gamma _k +(\alpha \beta)_{ij} + (\alpha \gamma)_{ik} + (\beta -\gamma)_{jk} + (\alpha \beta \gamma)_{ijk} + -\varepsilon_{ijkl}\]
-\[i = 1,2,...,a\]
-\[j = 1,2,...,b\]
-\[k = 1,2,...,c\]
-\[l = 1,2,...,n\]
-其中 \(a\) 是 fixed effect,而 \(b,c\) 是 random effect。于是模型参数是 -\(\theta = \lbrace \mu , -\alpha_i^{i=1,2,...,a} , \sigma_\beta^2 , \sigma_\gamma ^2 , -\sigma_{\alpha \beta}^2 , \sigma_{\beta \gamma }^2 , -\sigma_{\alpha,\gamma}^2, \sigma_{\alpha,\beta,\gamma}^2,\sigma^2 -\rbrace\)
-ANOVA table construction 的过程详见 Statistics Note by -V1ncent19,P212-215,这里仅给出结果:
-| Random/Fix | -F | -R | -R | -R | -- |
|---|---|---|---|---|---|
| # level | -a | -b | -c | -n | -- |
| Index | -i | -j | -k | -l | -\(\mathbb E(MS)\) | -
| \(\alpha_i\) | -0 | -b | -c | -n | -\(\sigma^2 + cn \sigma_{\alpha \beta}^2 + -bn \sigma_{\alpha \gamma}^2 + n \sigma_{\alpha \beta \gamma}^2 + bcn -\frac{\Sigma \alpha_i ^2}{a-1}\) | -
| \(\beta_j\) | -a | -1 | -c | -n | -\(\sigma^2 + an \sigma_{\beta \gamma}^2 + -acn \sigma_{\beta}^2\) | -
| \(\gamma_k\) | -a | -b | -1 | -n | -\(\sigma^2 + an \sigma_{\beta \gamma}^2 + -abn \sigma_{\gamma}^2\) | -
| \((\alpha \beta)_{ij}\) | -0 | -1 | -c | -n | -\(\sigma^2 + cn \sigma_{\alpha \beta}^2 + -n \sigma_{\alpha \beta \gamma}^2\) | -
| \((\alpha \gamma)_{ik}\) | -0 | -b | -1 | -n | -\(\sigma ^2 + bn \sigma_{\alpha \gamma}^2 -+ n \sigma_{\alpha \beta \gamma}^2\) | -
| \((\beta \gamma)_{jk}\) | -a | -1 | -1 | -n | -\(\sigma^2 + an\sigma_{\beta -\gamma}^2\) | -
| \((\alpha \beta -\gamma)_{ijk}\) | -0 | -1 | -1 | -n | -\(\sigma^2 + n \sigma_{\alpha \beta -\gamma}^2\) | -
| \(\varepsilon_{ijkl}\) | -1 | -1 | -1 | -1 | -\(\sigma^2\) | -
于是可以利用上述期望进行检验:
--
-
- \(H_0 : \alpha_1 = \alpha_2 = -...=\alpha_a\),检验 \(F_{\alpha_i} ^* -= \frac{MS_\alpha + MS_{\alpha ]beta \gamma}}{MS_{\alpha \beta} + -MS_{\alpha \gamma}} \sim ^{H_0} F_{(a-1)+(a-1)(b-1)(c-1), -(a-1)(b-1)+(a-1)(c-1)}\) -
- \(H_0 : \sigma^2 =0\) -
- \(H_0 : \sigma_{\beta}^2 =0\) -
- ...... -
R code for ANOVA
-详见 Mixed -ANOVA in R,和课上讲的是同一个东西但是更精细一点(
-期末考前又去看我第二次作业的那个 -project,绷不住了,我怎么做了个不合理的 mixed effect model -还拿了满分(
-实验设计方法
-不如说是实验设计小知识(
-Designed experiment 的主要目标是研究若干 explanatory factor 和 -response variable 之间的因果关系。在实验中变量控制情况(也就是所谓的 -treatments)和被试者的匹配之间是完全随机的,例如在试药时安慰剂和特效药是随机分发的,甚至会将实验条件对被试者保密。
-Observational & -Experimental Study
--
-
Observational study: The investigator use the data observed in -the population to make inference on the relationship between the -variables
-Experimental study: The investigator intervene in the natural -history by actively alternating one of the variables and then making -inference on the relationship between the variables based on the -outcomes
-
简单来说,直接研究通过观察收集来的数据就是 observational -study,数据只来自于自然的观察,收集者对事物发生不作任何干涉;experimental -study 则需要实验者自行控制变量,在所需条件下收集数据,再进行研究。
-Crossed and Nested Factors
-这是多因素分析中的一个概念。
--
-
Crossed factors: all combinations of the levels of the two -factors are included in the study. e.g.
-- -
- - - -Factor Combination -Temperature -Solvent Concentration -Outcome -- -1 -Low -Low -/ -- -2 -Low -High -/ -- -3 -High -Low -/ -- - -4 -High -High -/ -
-Nested factors: the level of one factor are unique to a -particular level of another factor. e.g.
-- -
- - - -Factor Combination -Temperature -Solvent Concentration -Outcome -- -1 -Low -Low -/ -- - -2 -High -High -/ -
-
Completely randomized design
--
-
对于一个有三个因素的 designed -experiment,建立的模型包括三个部分:
-\(Y=\) overall constant + treatment -effect + experimental error
-如果采用线性回归模型,以三个因素为例,全体被试者被分为 \(8\) 组,使得
-\[Y_{ij} = \beta_0 + \beta_1 X_{ij1} + -\beta_2 X_{ij2} + \beta_3 X_{ij3} + \varepsilon_{ij}\]
-可以轻松地将其和上述的三个模型组成部分对应起来。其中 \(X_1,X_2,X_3\) 类似于示性函数,此处是一种 -categorical variable,$X_i = 1 $ if treatment \(i\),otherwise \(0\)。
-也可以用因子效应模型来考虑这个问题,表示起来会比较容易;另外要注意的是,regression -model 关心平均响应的预测,但 factor effect model -更关心平均响应的差别。
-仍然以上一部分中的 Treatment of Lead-Exposed Children Trial -为例。
-\(100\) -名被试被分成两组分别使用安慰剂和药剂,在实验开始前、实验第 \(1, 4, 6\) 周分别检验了血液铅含量水平。第 i -名被试的实验开始前水平为 \(y_{i1}\),实验结束后水平为 \(y_{i2}\),变化水平为 \(d_i = -y_{i2}-y_{i1}\),希望利用这些数据观察药剂的有效程度。
-我们在这一实验中设定三个不同的 explanatory factor,分别是 treatment -type (succimer or placebo),children's ID (from \(1\) to \(100\),用于展示个体间的差别),time point -(week \(0,1,4,6\))。其中,treatment -type 和 time point 可能会协同作用。Outcome,也即 response variable -设定为血铅浓度 \(Y\)。
-模型为:
-\[Y_{ijt} = \mu + \alpha_i + \beta_{j(i)} -+ \gamma_t + (\alpha \gamma)_{it} + \varepsilon_{ijt}\]
-参数假设为:
-\[\beta_{j(i)} \sim N(0,\sigma_\beta -^2)\]
-\[\varepsilon_{ijk} \sim -N(0,\sigma^2)\]
-自由度和方差分解为:
-\[Y_{ijt} - Y_{...} = (\bar Y_{i..} - \bar -Y_{...}) +(\bar Y_{..t} - \bar Y_{...}) +(\bar Y_{i.t} - \bar Y_{i..} - -\bar Y_{..t} + \bar Y_{...}) + (\bar Y_{ij.} - \bar Y_{i..}) + (Y_{ijt} -- \bar Y_{ij.} - \bar Y_{i.t} + \bar Y_{i..})\]
-\[df: Nn-1 = -(a-1)+(n-1)+(a-1)(n-1)+(N-a)+(N-a)(n-1)\]
-可以提出并进行检验的问题有:
--
-
安慰剂和药剂之间有无明显的区别?在第 \(0,1,4,6\) -周时,两组之间的血铅值是否有明显差异?
-\(H_0: \mu_t(S) = \mu_t(P), \forall t= -1,2,3,4\),其中 \(\mu_t = \mu + -\gamma_t + (\alpha -\gamma)_{it}\),也即取出全体和时间有关的项。
-也可以换一种表示方法:安慰剂和药剂是否在降低血铅方面有同等的效果?
-\(H_0 : \mu_t(S) - \mu_1 (S) = \mu_t(P) - -\mu_1(P),\forall t =2,3,4\)
-可以推出这等价于 \(H_0: (\alpha -\gamma)_{it} = 0,\forall i = 1,2, -t=1,2,3,4\),这是因为参数假设中认为 \(\Sigma (\alpha \gamma)_{it}=0\)。
-
-
Clinical Trials
-临床试验最准确的定义是 the evaluation of intervention (treatment) on -disease in a controlled experimental -setting(绷不住了,感觉看原文比翻译过来要靠谱的多),有不同的类型。
-Randomized clinical trial
-RCT -的目的一般是在不存在因素的互相干扰情况下做对比,目的往往有找出最好的治疗方案,测试药剂相对于安慰剂的效果,等等。因此,实验组必须在各个方面和初始量化指标上都是一致的,在此基础上接受不同的治疗方案,才能控制变量找出方案对于效果的影响。
-RCT -是最有力的临床试验方案,因为是对几乎相同的组别随机分配治疗方案,得到的结果是普适性的。
-Non-randomized clinical -trial
-不随机的点有很多,比如被试者可以自行选择想参加实验的组,自由选择使用的是药剂还是安慰剂,或者这一分组是被实验组织者人为设定而不是随机分配的。
-Contingency Table in -Clinical Trials
-Clinical trial 里面也会用到一些 contingency table -和相应的检验。在这里先给出我们关注的问题和一些相应的定义。
-此处我们主要关心的情境是,两组被试者分别使用 medicine 和 -placebo,可能会出现 adverse reaction -也可能不会出现,统计全体被试者的反应得到以下表格:
-| - | Adverse Reaction (\(D\)) | -No Adverse Reaction (\(D^C\)) | -Total | -
|---|---|---|---|
| Medicine (\(E\)) | -\(n_{11}\) | -\(n_{12}\) | -\(n_{1+}\) | -
| Placebo (\(E^C\)) | -\(n_{21}\) | -\(n_{22}\) | -\(n_{2+}\) | -
| Total | -\(n_{+1}\) | -\(n_{+2}\) | -\(n_{++}\) | -
相应地定义 \(p_1\) 是 medicine -组发生不良反应的概率,\(p_2\) 是 -placebo 组发生不良反应的概率。于是有:
-\[p_1 = \mathbb P(D | E) , p_2 = \mathbb -P(D |E^C)\]
-\[\text{Risk Difference} = \Delta = p_1 - -p_2\]
-\[\text{Relative Risk} = \phi = -\frac{p_1}{p_2}\]
-\[\text{Odds Ratio} = \theta = \frac{p_1 / -(1-p_1)}{p_2 / (1-p_2)}\]
-在这样的情境下我们希望做的检验即为 \(H_0 : -p_1 = p_2\),也即观察 medicine 相对 placebo -来说是否发生不良反应的可能性是相同的。事实上由于上述条件概率的定义,也就是希望检验 -adverse reaction 和 medicine/placebo 的选择是独立的。这就归结为了 -contingency table 的 independence inference,详见下一部分的 Pearson Test -和 Likelihood Ratio Test。
-另外,我们希望使用观察到的数据 \(n_{ij}\) -对上述参数做一些估计。但具体的估计与 clinical trial -的类型有关,此处分别考虑两种类型的 clinical trial,分别是 prospective -clinical trial 和 retrospective clinical trial。
-虽然 contingency table 从理论上来说对于随机变量 \(Y,Z\) -是完全对称的,但是在实验设计中我们需要先确定 \(Y\) 或者 \(Z\),进行优先级的选择后再收集数据。这可能会导致条件概率不同。
-Prospective clinical trial
-招募了许多患有某一疾病的被试者进行试药,\(Y -= E / E^C\) 是 medicine 或者 placebo -组在实验开始之前就对全体被试者划分好了,于是 \(Z = D / D^C\) -是是否出现不良反应的量度,是我们在实验中需要关注的。
-在这一实验中由于是预先招募了被试者,所以 \(n_{1+},n_{2+},n_{++}\) 是确定的数值。
-Prospective clinical trial -显然更可控一些,但是也会遇到一些生存分析的问题。另外,如果是关于罕见病的实验,这一方式可能会比较低效。
-此时有参数估计:
-\[\hat p_1 = \frac{n_{11}}{n_{1+}}, \hat -p_2 = \frac{n_{21}}{n_{2+}}\]
-\[\hat \phi = \frac{n_{11}/ -n_{1+}}{n_{21}/ n_{2+}}\]
-\[\hat \theta = -\frac{n_{11}n_{22}}{n_{21}n_{12}}\]
-\[\hat{Var} ( \log \hat \theta) = -\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + -\frac{1}{n_{22}}\]
-注意一些参数含义:\(\phi\) 和 \(\theta\) -都表示了组间差距,如果这两个参数比较大就说明 \(Y\) 对 \(Z\) 和 \(Z^C\) 的影响不同。
-Retrospective clinical trial
-招募了许多产生了不良反应和未产生不良反应的患者,\(Z = D/D^C\) -是是否有不良反应的组在实验开始之前就对被试者划分好了。再对他们发放问卷或者进行采访,了解出现不良反应之前的用药历史。
-在这一实验中对被试者进行的划分是关于 \(Z\) 的,因此 \(n_{+1},n_{+2},n_{++}\) 是确定的数值。
-Retrospective clinical trial 显然是没有那么精准的,我们难以精准控制 -\(Y\),但是数据的收集更快更方便。
-此时有参数估计:
-\[\hat p_1 = \frac{\rho -\frac{n_{11}}{n_{+1}}}{\rho \frac{n_{11}}{n_{+1}}+(1-\rho) -\frac{n_{12}}{n_{+2}}},\hat p_2 = \frac{\rho \frac{n_{21}}{n_{+1}}}{\rho -\frac{n_{21}}{n_{+1}}+(1-\rho) \frac{n_{22}}{n_{+2}}} \]
-其中 \(\rho\) 是人群中的发病率。
-\[\hat \phi = \frac{\hat p_1}{\hat -p_2}\]
-\[\hat \theta = -\frac{n_{11}n_{22}}{n_{21}n_{12}}\]
-\[\hat{Var} ( \log \hat \theta) = -\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + -\frac{1}{n_{22}}\]
-可以发现 odds ratio 在两种 clinical trial -里是一致的,因此这一参数更佳。
-Gehan's Two-Stage Design
-如果某一实验看起来完全达不到我们的最低期望,那我们希望能够尽早在临床试验的早期抛弃这一选择。比如说,对于 -\(n\) -位患者,我们能够接受的最低治疗成功率是 \(20\%\),那么在治疗有效的患者数小于 \(m\) -时就可以认为这一治疗方案是无效的,然后尽早放弃继续的探索。Gehan's -two-stage design 展示了选取 \(m\) -的方式。
-实际上这个过程类似于寻找算法的终止条件。在最初的状态下选择 \(n_0\) -名患者参与治疗,如果这些人里面没有治疗有效的,那么直接停止这一实验过程;否则继续做实验,并且每次加入新的被试者,希望能够达到期望的最低治疗成功率。
-比如说,我们认为当有 \(\pi _0 = -20\%\) -的患者症状缓解时,可以认为这一治疗方案是有效的,这也就是可以接受的最低治疗成功率。在 -Gehan's two-stage design 里设定 level 是 \(\alpha_0 = 5 -\%\),在此基础下考虑第一次实验的被试数量 \(n_0\) 的取值。
-事实上治疗有效果的患者数是一个服从伯努利分布的随机变量 \(X \sim B(\pi)\),那么 \(P(X_0 = 0) = (1-\pi)^{n_0}\leq \alpha_0\) -对于任意的 \(\pi \geq \pi_0\) -是成立的,那么 \(n_0 \geq \frac{\log -(0.05)}{\log (1-0.20)}=14\) 即为第一次实验的最少被试数量。
-也可以通过置信区间的方法来确定。我们希望能够有 \(95 \%\) -的信度认为这一实验可以继续下去,允许 \(\pi_0\) 有 \(\pm -15 \%\) 的浮动,则最少的被试参与数满足 \(1.96(\frac{(1-\pi_0)\pi_0}{n})^{\frac 1 2} = -0.15\),解得 \(n=28\)。
-Inference on Contingency -Table
-简单来说,孟德尔种豌豆那个表格就是一个 contingency -table,到底为什么呈现出 \(9:3:3:1\) -的规律也可以用 goodness of fit test 进行检验。Contingency table analysis -本质上是对 categorical data 的检验。
-Motivation Example
-我们希望知道吸烟和肺癌之间有无确切的联系,采集了一些数据:吸烟且肺癌的有 -\(688\) 人,吸烟但没有得肺癌的有 \(650\) 人;不吸烟且肺癌的有 \(21\) 人,不吸烟且没有得肺癌的有 \(59\) 人。样本量共计 \(1418\) 人,列表如下:
-| - | Lung Cancer | -Healthy | -Total | -
|---|---|---|---|
| Smoke | -688 | -650 | -1338 | -
| Not Smoke | -21 | -59 | -80 | -
| Total | -709 | -709 | -1418 | -
“看起来”吸烟和肺癌是有关系的,因为吸烟者得肺癌的频率看似更高。但是如何从频率得到概率,仍然需要一些检验的逻辑。
-Contingency Table
-抽象出来的 contingency table 的逻辑是这样的:
-| - | \(Z=1\) | -\(Z=2\) | -Total | -
|---|---|---|---|
| \(Y=1\) | -\(n_{11}\) | -\(n_{12}\) | -\(n_{1+}\) | -
| \(Y=2\) | -\(n_{21}\) | -\(n_{22}\) | -\(n_{2+}\) | -
| Total | -\(n_{+1}\) | -\(n_{+2}\) | -\(n_{++}\) | -
当然,\(Y\) 和 \(Z\) -都可以有更多的指标,这不影响我们的构造。比如说它可以长成下面这种通用的形式:
-| - | 1 | -... | -J | -total | -
|---|---|---|---|---|
| 1 | -\(n_{11}\) | -... | -\(n_{1J}\) | -\(n_{1+}\) | -
| ... | -... | -... | -... | -... | -
| I | -\(n_{I1}\) | -... | -\(n_{IJ}\) | -\(n_{I+}\) | -
| total | -\(n_{+1}\) | -... | -\(n_{+J}\) | -\(n_{++}\) | -
与此同时,\(Y\) 和 \(Z\) -的位置是完全对称的,可以交换二者在行和列里的顺序。
-在 \(n_{++},n_{1+},n_{2+},n_{+1},n_{+2}\) -都已知的情况下,完全可以把 \(n_{11}\) -视作一个随机变量,当然表格中的 \(n_{ij}\) -都可以被视为随机变量,但四者中有其一被确定后整个表格就完全被确定,因此只需要讨论 -\(n_{11}\) 的数值。
-事实上,\(n_{11}\) -服从的是超几何分布。\(P(n_{11} = k) = -\frac{C_{n_{1+}}^k C_{n_{2+}}^{n_{+1}-k}}{C_{n_{++}}^{n_{+1}}}\) -对于 \(\max(0,n_{1+} + n_{+1}-n) \leq k \leq -\min(n_{1+},n_{+1})\) 都成立。
-P-value Calculation -Example: 女士品茶
-对于一个如下所示的表格,希望判断品茶的女士是否真的有品尝先加奶还是先加茶的能力——尽管看起来是有的,\(4\) -次尝试里她只失误了一次,但是我们希望通过一些更严谨的推断方法来证明。
-| Actually poured first | -- | Lady says poured first | -
|---|---|---|
| - | tea | -milk | -
| tea | -3 | -1 | -
| milk | -1 | -3 | -
由于 \(P(n_{11} = 3) = \frac{C_4 ^3 C_4 -^1}{C_8 ^4} = \frac{16}{70}\),\(P(n_{11}=4) = \frac{C_4 ^4 C_4 ^0}{C_8 ^4} = -\frac{1}{70}\),回顾 p-value -的定义是“比所得数据更加极端的情形所出现的概率”,事实上也就是 \(P(n_{11} \geq 3) = \frac{16}{70} + \frac{1}{70} = -\frac{17}{70} = -0.243\),无法给出充足的证据证明这位女士能够品出添加的顺序。
-Inference on Independence
-Contingency table 的通用形式如下所示:
-| - | 1 | -... | -J | -total | -
|---|---|---|---|---|
| 1 | -\(n_{11}\) | -... | -\(n_{1J}\) | -\(n_{1+}\) | -
| ... | -... | -... | -... | -... | -
| I | -\(n_{I1}\) | -... | -\(n_{IJ}\) | -\(n_{I+}\) | -
| total | -\(n_{+1}\) | -... | -\(n_{+J}\) | -\(n_{++}\) | -
另一个检验的重点在于 \(Y\) 和 \(Z\) 联合作用于 \(\{ n_{ij} \}\) -的取值时,我们希望了解二者的作用是否独立。
-如果二者的作用独立,就有 \(\pi_{ij} = -P(Y=i,Z=j) = P(Y=i)P(Z=j) = \pi_{i+} -\pi_{+j}\)。因此我们只要检查实际的 contingency table -和理想中符合二者独立时的 contingency table 有何区别,此处用到 Goodness -of Fit Test。
-Hypothesis
-\(H_0:\) The independence model is -true, i.e. \(\pi_{ij}= \pi_{i+} -\pi_{+j}\) for all pairs of \((i,j)\).
-\(H_1 :\) The saturated model is -true, i.e. \(\pi_{ij}\neq \pi_{i+} -\pi_{+j}\) for at least one pair of \((i,j)\).
-Test Statistic
--
-
The standard Pearson Chi-Square statistic:
-\[X^2 = \Sigma_i \Sigma_j \frac{(O_{ij} - -E_{ij})^2}{E_{ij}} \sim ^{approx} \chi^2 _{(I-1)(J-1)}\]
-Likelihood Ratio Test statistic:
-$G^2 = -2 () = 2 i j O{ij} {E{ij} } ^{approx} ^2 -_{(I-1)(J-1)} $
-
注意 \(X^2\) 和 \(G^2\) -的分布都是近似分布,二者并不是等价的检验统计量,计算值时常不同,但检验结果往往是类似的。
-Survival Analysis
-Basic Concepts
-首先要明确一些概念,给我的感觉是像黑话一样(
-Concept
-Event -是指生存分析所研究的事件,大多数情况下是指某种治疗过程中患者死亡这样的事件发生,但其实生存分析的应用很广泛,甚至不只是在生医领域都有这些概念的使用。患者治疗后恢复/犯人被释放后再次犯罪/确诊新冠都可以作为研究所感兴趣的事件,这些事件发生就称为 -event。
-At risk 是指尚未发生 event 的个体。事实上大多数情况下研究的 event
-都是患者去世之类的负面事件,因此尚未发生 event
-的个体会被先入为主地定义成 at risk,即为暴露在即将发生 event
-的风险下。什么达摩克斯之剑
Function
-一些常用的函数:
--
-
- survival function:\(S(t) = P(T > t) = -1-P(T \leq t) = 1-F(t)\) -
- mean survival time:\(E(T) = \int_{0} -^{\infty} 1-F(t) dt = \int_{0} ^{\infty} S(t ) dt\) -
- hazard function:\(\lambda (t) = \lim_{t -\downarrow 0} \frac{P(t \leq T < t+\Delta t | T \geq t)}{\Delta t} = -\frac{f(t)}{S(t)} = \frac{-S'(t)}{S(t)} = -\frac{d}{dt} \log -S(t)\) -
- cumulative hazard function:\(\Lambda (t) -= \int_0 ^{t} \lambda(s) ds = - \log S(t)\) -
事实上都是对 \(T\) 的分布函数 \(F(t)\) 的变形。
-Data
-生存分析中有两种不同的数据,censored data 和 uncensored data。
-Censored data 是指在研究过程中未能记录到 event 发生(未能记录到 -failure)的数据,往往是因为直到研究结束 event -都尚未发生,或者研究对象中途退出研究,也可能是没有及时发现跟进从而未能记录准确的时间,等等。Censored -data 又分为三种情况,right-censored,left-censored 和 interval-censored -的情况。
--
-
- right-censored data 往往是生存期比所记录的时间要长的情况,censor -time 在 event time 之前。例如临床试验持续了一段时间,将 event -设定为观察到患者死亡。某一位患者在第一周加入试验,试验持续十周结束,他直到试验结束都保持健康,没有发生 -event,则他的生存期是 10+ weeks,这是一个 right-censored data。 -
- left-censored data 的一个例子是认为 event -是感染新冠,一位患者在试验第七天发现抗原阳性,但在这之前没有做过检测,不清楚是从什么时候开始感染新冠的,只知道 -censor time 在 event time 之后。因此这是一个 left-censored data。 -
- interval-censored data 的一个例子仍然是认为 event -是感染新冠,一位患者在试验第三天抗原阴性,第七天发现抗原阳性,但在这两次检测之间没有做过检测,也还是不清楚从什么时候开始感染新冠,只知道 -event time 在两个 censor time 之间。称为一个 interval-censored -data。 -
此处简化情况,只研究 right-censored data,尝试对它进行标记。记 -survival time 为 \(T\),censor time 为 -\(C\),记 right-censored data 为 \((X,\delta)\),其中 \(X = \min(T,C)\)。\(\delta\) 是一个示性变量,如果 \(X = C\) 则 \(\delta=0\),也就是 event 未发生;否则 \(\delta=1\),\(X = -T\),也就是观察到了 event 发生。
-每一组数据贡献的 likelihood 是 \(\lambda -(x)^\delta S(x)\),整体的 likelihood function 即为 $ L = _{i=1} -^n (x_i )^{_i} S(x_i)$。
-Kaplan & Meier Estimation
-Theory
-一个估计 survival function 的方法。原理上来说是把 \(S(t) = P(T >t)\) -分解成了一列条件概率的积:
-\[S(t) = P(T>t) = P(T>t_1) P(T>t -| T>t_1) = P(T>t_1) \{\Pi_{j=2} ^k P(T>t_j | T>t_{j-1}) \} -P(T>t|T>t_k)\]
-与此同时重新组织数据,计算每个时刻的 items at risk 和 count of -events,列表如下:
-| Distinct Event Times | -\(t_0\) | -\(t_1\) | -... | -\(t_k\) | -
|---|---|---|---|---|
| # of events at \(t_j\) | -\(0\) | -\(d_1\) | -... | -\(d_k\) | -
| # at risk at \(t_j\) | -\(n\) | -\(n_1\) | -... | -\(n_k\) | -
此时认为条件概率的估计量为 \(\hat P (T> -t_j | T> t_{j-1}) = \frac{n_j - d_j}{n_j}\),因此 survival -function 的估计是:
-\[\hat S(t) = \Pi_{j=1}^k \frac{n_j - -d_j}{n_j} = \Pi_{j=1} ^n (1- \frac{d_j}{n_j})\]
-Example
-对于一组生存数据:\(4 \quad 5+ \quad 6 -\quad 10+ \quad 6 \quad 2 \quad 6\)
-重新排序得到:\(2 \quad 4 \quad 5+ \quad 6 -\quad 6 \quad 6 \quad 10+\)
-按照 event time 重新组织数据,并计算 Kaplan-Meier Estimator:
-| Distinct Event Times | -0 | -2 | -4 | -6 | -
|---|---|---|---|---|
| # of events at \(t_j\) | -0 | -1 | -1 | -3 | -
| # at risk at \(t_j\) | -7 | -7 | -6 | -4 | -
| \(\hat S(t)\) | -1 | -\(\frac{6}{7}\) | -\(\frac{5}{7}\) | -\(\frac{5}{28}\) | -
Cox Proportional Hazard -Model
-Theory
-在生存分析中数据往往是 skewed -的情况,希望分析变量(比如,患者的年龄,所用的药物,实验组别)对于生存期的影响时,一般对 -hazard function 采用 \(\lambda(t) = \lambda_0 -(t) e^{X^T\beta}\) 模型,类似于一个 transformed linear -regression。
-其中,\(\lambda_0(t)\) -作为一个调整参数,只和时间有关,和 explanatory variable \(X\) 无关。
-以一元的 explanatory variable \(X\) -为例,不同数据之间的 hazard ratio 是:
-\[\frac{\lambda_i(t)}{\lambda_j (t)} = -\frac{\lambda_0(t)}{\lambda_0(t)} \frac{exp(\beta_0 + \beta_1 -X_i)}{exp(\beta_0 + \beta_1 X_j)} = e^{(X_i - X_j)\beta_1}\]
-模型假设是 \((T_i ,C_i)\) 在 \(X_i\) -给定的条件下是条件独立的,这是一个针对 censored data 的假设。
-另外一个结论是在时间 \(t\) -处,uncensored 对象 \(i\) 发生 event -的概率是 \(P_i(t) = \frac{ exp(x_i -\beta)}{\Sigma_j I(T_j \geq t) exp(x_j -\beta)}\)。由此可知,用于估计 \(\beta\) 的 likelihood function 是:
-\[L(\beta) = \Pi_{j=1}^ k \frac{ exp(x_i -\beta)}{\Sigma_j I(T_j \geq t) exp(x_j \beta)} = \Pi_{j=1} ^n (\frac{ -exp(x_i \beta)}{\Sigma_j I(T_j \geq t) exp(x_j \beta)})^{\delta -_i}\]
-仍然是以一元的 explanatory variable \(X\) 为例,hazard ratio 是 \(HR = \frac{\lambda(t | -\text{exposure})}{\lambda(t| \text{not exposure})} = \frac{\lambda_0 (t) -exp(\beta_1)}{\lambda_0(t)} = exp(\beta_1)\)
-Example
-分别有五位患者参与两种试药,生存数据如下所示,希望通过 Cox Model -来比较不同种类的药物效果。
-Drug A: \(8+ \quad 132 \quad 52 \quad 220 -\quad 75+\)
-Drug B: \(45 \quad 80 \quad 90+ \quad 20 + -\quad 120\)
-此处的唯一一个 explanatory variable 即为用药种类,认为 \(X_i = \begin{cases} 1 \quad \text{i use drug A}\\ -0 \quad \text{i use drug B} \end{cases}\);
-对数据重新排序,得到:\(8+ \quad 20+ \quad -45 \quad 52 \quad 75+ \quad 80 \quad 90+ \quad 120 \quad 132 \quad -220\),对应的 \(X_i\) 是 \(1,0,0,1,1,0,0,0,1,1\)。
-Cox model 设定为 \(\lambda_i (t) = -\lambda_0 (t) e^{X ^T\beta} = \lambda_0 (t) \exp(\beta_0 +\beta_1 -X_i)\),\(i=1,2,...,10\)。
-此时的 partial likelihood function 是 \(PL(\beta) = \Pi_{i=1}^n (\frac{\exp(\beta^T -X_i)}{\Sigma_{j: t_j \geq t_i} \exp(\beta^T -X_j)})\),代入数据有:
-\[PL(\beta) = \Pi_{i=1}^{10} -\frac{\exp(\beta_0 + \beta_1 X_i)}{\Sigma_{j: t_j \geq t_i} \exp(\beta_0 -+ \beta_1 X_i)} = \frac{exp(2\beta_1)}{360(1+\exp (\beta_1))^3 -(5+4\exp(\beta_1)) (3+4\exp(\beta_1)) (2+3\exp(\beta_1)) -(1+3\exp(\beta_1))}\]
-对其进行 maximum likelihood 处理即可得到 \(\beta_1\) 的估计值。至于 \(\beta_0\) -的估计其实没什么意义,上下直接消掉了。
-Why Cox Model
--
-
- 体现了 explanatory variable 带来的影响 -
- baseline hazard \(\lambda_0 (t)\) -事实上并不重要,一般也用不到 -
- 得到 proportional hazard function -就可以作图比较是否有一个时间点处发生明显的差异 -
- 单独对不同组别的 event 发生情况使用 p-value -(见下一部分)并不够,需要精确到每个个体的生存时间 -
Comparison of Survival -Curves
-Log Rank Test
-想要比较两组数据的生存期情况,比如说,试药组和安慰剂组之间有无生存周期上的差别,来判断药物是否有效或者有副作用。这里涉及到的问题都属于比较简单的情况,一般用一个 -log rank test 就可以了。
-| - | Distinct Event Times | -\(t_1\) | -... | -\(t_i\) | -... | -\(t_k\) | -
|---|---|---|---|---|---|---|
| Pooled sample | -# of Events | -\(d_1\) | -... | -\(d_i\) | -... | -\(d_k\) | -
| - | # at Risk at \(t_i\) | -\(n_1\) | -... | -\(n_i\) | -... | -\(n_k\) | -
| Sample 1 | -# of Events | -\(d_{11}\) | -... | -\(d_{1i}\) | -... | -\(d_{1k}\) | -
| - | # at Risk at \(t_i\) | -\(n_{11}\) | -... | -\(n_{1i}\) | -... | -\(n_{1k}\) | -
| Sample 2 | -# of Events | -\(d_{21}\) | -... | -\(d_{2i}\) | -... | -\(d_{2k}\) | -
| - | # at Risk at \(t_i\) | -\(n_{21}\) | -... | -\(n_{2i}\) | -... | -\(n_{2k}\) | -
有以下的近似分布关系,对近似正态分布做检验即可:
-\[ U = \Sigma_{i=1} ^k (d_{1i} - \frac{d_i -n_{1i}}{n_i})\]
-\[\hat{Var} (U) = \Sigma_{i=1} ^k -(\frac{d_i n_{1i} (n_i - d_i)(n_i - n_{1i})}{n_i ^2 (n_i --1)})\]
-\[\frac{U}{\hat{Var} (U)^{\frac 1 2}} \sim -^{H_0,asy} N(0,1)\]
-P-value mode
-对于组织成 contingency table 形式的数据,按照逻辑回归部分的 p-value -方法检验即可。一个数据的例子如下所示:
-| - | Drug A | -Drug B | -
|---|---|---|
| Alive | -10 | -16 | -
| Dead | -8 | -4 | -
完结撒花
-在这之后讲的东西都不考了,我不想做生统,也不是很感兴趣,不想写了。说到底高中的时候连生物都没选考,怎么会想到来尝试生统概论的(。希望大作业没事。
-昨天才在路上遇到了 wty
-老师和她男朋友/爱人,相比之下(草)她好娇小好可爱,呜呜呜(虽然感觉她也瞟了我好几眼,不会也认识我吧,不会是这个发型太有辨识度了我又每次都苟在最后一排就被记住了吧(
传统艺能一下(不会现在还有人是 FGO 厨吧,不会吧不会吧(
-
后记:莫名其妙拿了个
-A,实际上期末考大寄特寄好几问没做完,我还在想这课能不挂就挺好的了,不知道是老师太善良还是毕业班同学太多帮忙抬上来的((只不过之前看
-V1ncent19 说他这课是 A+,羡慕(x
3月1日
+昨天喝了瑞幸的珞珈樱花拿铁,为什么不是顾村公园樱花拿铁,是樱花节名气还不够大吗(确实是。感觉第一次吃到和樱花沾边但是味道意外地不错的食物,可能主要是也没什么樱花味吧(。今天又来一杯,明天打算点个美式(
好像后面又有线条小狗和瑞幸的联名了,点两杯才能有周边怎么办
+太好了这回我堂堂正正喝两杯(
这个计算概率,我不好说,后半部分是一些 SDE
+数值解法但哥们完全没学过这玩意,但好像会提一下背景知识,这课上也好多没上过概率论
+3
+的,希望人没事。老师下个学期就要离开华子了,又收集到一门绝版课程,但愿这样的话给分能好点(。第一次作业在课上就写完了,体验绝佳(不
3月2日
+昨天早上九点二十起床,在去自取了一杯瑞幸的情况下在上课前顺利走进了六教二楼的教室,现在是越来越强了。今早就暴毙了,直接一个补觉(
+你说得对,现在是第一周,但我已经急了,怎么实分析和基物 2 +作业都这么多。实分析作业我寒假没写是我的问题我自裁,但基物 2 +是从衍射学起哥们连干涉都压根没学(,现在处在一个回头看基础设定的状态,书上明明都是数学公式但我怎么看不懂一点捏(。学了一晚上,我痛死(
+早知道当初报第一周周末的托福,乐了。
+但唯一的好消息是我今天下午在 C +楼研讨间练口语的时候发现这玩意其实不是很难,至少我 independent speaking +不会没话说,果然瞎扯我还是有一手。但是后面三道题有概率说不完,还是得学习一个高速神言(
+瑞幸冰美式可以加双份奶,有券于是五块钱到手了。我现在理解为什么说减脂期喝美式了,这玩意是真有点抑制食欲,不是那种通过饱腹感来抑制,而是通过在嘴里残留一些苦味来让人不想吃饭(
+3月3日
+今天的瑞幸可能是定位有问题,不知道为什么下单下到清华科技园店去了。我还寻思着清芬这边一直都没有茶咖系列,今天怎么突然有了,提示取餐的时候才发现。从四教过去其实也不远,感觉和从寝室到四教差不多,甚至还要近一些,而且清华路以南是家属区所以路修的比较好,比北边好走很多。
+但是这玩意真的好难喝啊,我下单的时候就想,茉莉花香拿铁,这六个字没有一个听起来是难喝的,于是带着幻想乐颠颠地骑了好远的路。但是就是很难喝,不像营销说的是茶叶泡出来的,味道像茶粉。也是,十块钱难道还想喝真茶叶和真咖啡豆吗,醒醒。
+所以清芬店没有茶咖是因为这玩意太难喝了所以让大家不要喝吗,它真的我哭死
天气不错,所以下错单出去骑车也没什么怨言,反而很开心。等考完托福找时间出去骑车吧——开玩笑的。
+我突然理解了,学基物我还看它那个证明干啥,鉴定为数学学魔怔了。反正也看不懂,拟合一下题目拉倒(
+写了一下午一晚上实分析作业还没写完,倒也不怎么难,但主要是在看讲义,反正都是这个妹妹我见过的那种感觉(。明天应该能写完了吧,我草,为什么第一周这么累,难道真是因为物理和实分析都布置了两周的作业的原因吗。
+猛猛约下周早上的研讨间练口语,但愿作息能顺带变得健康点(。现在我也不知道问题到底会在哪一部分了,是口语自我感觉良好实际很菜还是别的不行,难不成会是阅读不行吗(,这样的话好像不是很老中((
3月4日
+开学到现在光是把菜汤弄到身上跑回寝室洗都已经两次了,感觉开学那天我对着室友说出“今天是你大洗的日子”这么烂的梗之后命运的齿轮就开始旋转了,寄。
线条小狗和瑞幸的联名太可爱力,虽然今天起得稍微有点晚了,早晨赶着去练口语就没来得及买,但单杯的袋子也挺好的。明天从早八上到晚十,感觉可以整两杯
+来获得一张贴纸。
下午上生存分析的时候发现从四教四楼可以看到 W +楼,视野是这样的。从远处看感觉这个层高很逼仄(在说什么废话
+
3月5日
+ + +明天下午要和 wwc +聊,现在很急,首先我要跟他讲一遍我是未央的然后我要延毕 +etc,现在我不知道为什么很担心他到底带不带本科生尤其是之后打算润的本科生了(虽然但是会有人不带吗(,希望人没事。
+ + +晚上回来吃了三个(中等大小的)番茄,尝了一个今天买的芒果。室友大受震撼问我不是减脂期吗我说对啊晚饭没吃饱而且这个加餐不是挺减脂的吗((
+唉,我说我减脂是因为 BMI +超了,而且总感觉精力不济,室友说你就是服美役。那我就要开始跟她暴论了,明明很多说别人在服美役的人要么是自己也在偷偷服,要么就是天生一副符合主流审美的好皮囊轮不到你来服啊!随时随地吃任何东西都不胖的人不许说别人为了健康减肥是服美役,就像我夏天都不打防晒冬天只擦保湿和素颜霜而你尽力护肤也只能达到一个亚健康的状态一样。最后这句话把她搞破防了,现在我在算热量她在拍脸,嘿嘿(
+然后她小红书十分钟之后回来问我一杯瑞幸拿铁二百大卡怎么下得去嘴的,我破防了,明天喝美式(x
+3月6日
+今天和 wwc +聊了,回来一看我昨天在担心些什么(。今年他招的博士生正好是未央零字班的,不仅省略解释一堆这书院是什么玩意,他还先我一步锐评“你们这个培养方案真是不可理喻”,感觉来对地方了(。虽然预想的是搞时间序列,但他给我的问题是 +network model & graphon estimation +说是最近在看这个,而且概率会用得多一点,也挺好,先看吧。
+喝了一圈意外地发现还是厚乳拿铁最好喝,奶味很浓郁,也不怎么甜,热量也还行。其实瑞幸招牌的生椰拿铁我完全没喝出来哪里好喝了(,感觉还不如贝纳颂那一款,也不如丝绒生椰和冰吸生椰。下周开始有柚
+C 美式了,好好好。
早上出门之前称了下体重,怎么现在 BMI +就已经正常了,好怪哦。感觉也不是最近有意识地减脂的结果毕竟也没几天(,而是寒假在家要自己做饭所以就瘦了(草(。晚上开心地吃了顿米粉(别骂了,辣汤又溅到了风衣上(,烂梗的惩罚没完没了。
+然而这个清芬它有什么低热量的主食吗,每天这个米饭都吃得我相当纠结,人家桃李还有杂粮饭可以选(
+3月7日
+看了一下午论文,感觉头很大(,吃晚饭的时候在考虑能不能本科毕业直接去当高中老师((x
+虽然我感觉正文其实真没有什么非常困难的数学,很多地方为了贴合真实的处理甚至都没那么严谨了(挠头,但这个思路真的是看得我一愣一愣的(,顺着思路倒是结果都能随手推,但好累(。
+yysy 这个 supplementary materials 需要读吗,我之前看 wwc +发给我的两篇都是 biometrika +上的文章,感觉都不长,还很乐,还觉得可能下周就可以汇报了,但这才发现证明全在 +supplementary data 里面(,要读的话得到什么时候啊(x
+今天把咖啡撒到身上了,我错了我以后真的不再玩烂梗了,饶了我吧((
+诶,我发现减肥能给自己带来一种错觉,就是别人给我拍的照片看起来也没那么魁梧了(。
+ + + +3月8日
+早上起来看了一眼,今天计算概率复习简单的概率论,虽然看 logistic
+感觉老师可能会讲一些求真笑话(like
+数学家至少要精通两个方向(我猜的)但还是又躺下了(,有一种求真招生反诈宣传片的美感。
诶,昨天才和群友说起来还好高三春季的时候连去考一下求真的念头都没动,毕竟当时是第一届,风评还没有这么差,虽然我觉得既然要考物理的话我是考不上的,但万一考上了就太可怕了。然后我想了想为什么没考呢,好像单纯就是懒得准备了(,毕竟到当时高考也准备得还可以,春考看得过去,大概还有感觉高三的英语老师很可爱,不如多和她贴贴(并不(谢谢她救我(
躺了一会起来练了下 TOEFL test ready 上剩的三篇写作,一个 integrated +和两个 independent 都给我判了 +5/5,很怪,总不能真是字数多就行了吧(。其中有一个 independent writing +是讨论除了电子产品之外二百年内最伟大的科技成就,我:statistical +models!(
+打了两遍 integrated writing 才把模板背下来,希望后天早上还记得(
+它那个估分区间除了告诉我口语很烂之外就没啥用了,口语是 B2,听读写都是 +C1,我本来觉得 advanced 听起来就挺好的了,后来才知道最高是 C2 +proficiency(。就不练了,睡大觉(
+3月10日
+今天 参加了一场贵族运动 考完托福了。早上进汇佳考点之后在
+ETS
+考试中心大楼里等,听到一楼会议室里在吵架讨薪,有个领导一样的人说,我们不是没给发工资,是吧,工资的三个部分,blahblah
+都结过了,blahblah
+本来就已经降了,并不是拖欠,blahblah,然后被大家骂了(
考前是说台面上的两支笔只能带走一支,结果我走的时候监考老师让我都带上,好怪哦,她不会是在搞我吧(x
+
坐在我左边的是一个出生日期 2010.12.30
+的小朋友,考试期间我感觉她不仅在不停乱动还时不时余光瞟我,可能是嫌我太老了,但愿不是要带我一起
+HOLD。右边的小朋友是 2009.07 忘了几号出生的,没什么存在感。
总之考前就很有压力。我默默感叹,什么叫托福从娃娃抓起啊,感觉很上流,很京爷。所以左边的小朋友先我一步开始用
+Chinglish
+和很尖锐的娃娃音开始说口语的时候我就没绷住,一下子就很幻灭。我像她这么大的时候刚从上海的一所乡镇小学毕业进入一所乡镇初中,别说拿出两千块给我考试了,全家一个月都不一定吃这么多钱,然而那时的我都没这么
+Chinglish。而且,我高中进入某个只刷题啥也不干的精英学校之后就基本没有开口说过英语了,我现在不算很
+Chinglish 真得归功于我小学初中的乡村教师们,唉,果然不是我有
+privilege,而是北京就是不行。(我素质好差
但我乐了这一下之后听力最后一篇就开始掉线了,当然本来也有点听不懂,一下子没绷住之后更是开始豁边了,六个题目最后都有点乱选,活该。
+客观题考完就立刻出分了,阅读 28 听力
+26,虽然听力很豁边但是考虑到我最后一篇都是猜的,所以真的,给分不错(。阅读也没啥可说的,感觉比
+TPO
+难一点,两篇各有一道题不大确定(说实话我觉得都是烂题,完全没在考逻辑,在考和出题人是不是同一个脑回路),就当一篇错一个,28
+也不亏。虽然考完刷刷小红书看到大家都 29
+30(不是我今天这场,而是在小红书发分数的不是这个水平就是拉胯的不行求安慰,没有什么普通人),感觉还得拼一把写作和口语的运气,先不奶了。
写作一篇写了 300 字一篇写了 180 +字,我也觉得很吓人,怎么会写这么多,平时似乎打字打不了这么快。独立写作是问 +work 和 relationship +哪个更重要,看了三十秒题目就开始瞎掰了。口语的话,第二篇口语有一句话没说完,别的应该都还好。但愿没有高估自己(
+诶,但是我考前就一直很担心一个问题,就是两个小时不能喝水的话怎么办,半个小时不让喝我都会有点头晕,不是真的因为干渴而头晕,而是不让我喝我就很有心理压力,就更快地失水。到现场发现问题比我想的更严重,不到八点钟就把柜子锁起来上楼了,三个多小时都没能喝到水,更糟糕的是我忘记带润唇膏了,都没法厚涂一下。还算聪明的是把水锁进柜子之前我把卫衣袖口整个打湿了,中间用它贴贴嘴唇或者碰一下脸降降温,权当一个心理安慰,勉强有效。
+但是考完发现我没经验又社恐没问监考老师被摆了一道,水是可以带上二楼的,只是要放在考场外面的休息区,开考后就不能喝了。之前我就这个问题问过我认识的仅有的两个考过托福的人,只可惜二位都是八个小时不喝水也没关系的奇人,一个说不知道,另一个一开始说不知道后来又说不能带,而且我搜小红书也没搜到过类似的问题,就很奇怪,往往什么奇怪的问题都能在小红书找到同类,这个反而没有,大家都这么耐渴的吗,我可能还是不适合在地球生存。
+唉,作业写不完了,paper 啥时候才能读完呢。
+3月11日
+实分析进入测度之后明显就有了一种这我熟(赞赏)的感觉(,毕竟概率论用了这么久,看来还是点拓水平不行。你还别说,ly +和 lxg +两个版本都学过一遍感觉挺好的,有很具体的例子和构造可以用来理解抽象的问题。只不过这课到底上到哪了,我好像到现在为止就去了一次,明天得去看看这周到底要交多少作业((
+高统不知道为什么刚开学就掉线了,感觉是很晚才选上课一直看不到课件的问题,急了,明天进行一个 +Lec 2 +和作业的补。他这个作业不仅有书后题还有自己出的习题,急急急,Bayesian +一点都没学过(
+辅导员又发了个发展意向调查,为什么没有延毕的选项也不能自己填一个,为什么就连出国用的语言成绩都没有考完了还没出分这个选项,几个月之前我填的导师还是 +ypk 这次就改成了 +wwc(,蚌埠住了。最后两个问题是现在在跟哪个导师做什么课题,目前有哪些成果,我真觉得没必要告诉这哥们(,差点填了不方便透露/ +I've signed an NDA((x
+昨晚回来还就那个摸,按照之前在小红书看到的教程改了瑞幸的单杯纸袋,今天我逢人就掏出来炫耀:
+
(其实是立体的但不知道为什么看起来不是很立体(可能堆高度用的是纳米胶而不是泡棉胶的问题(
+今天拿到第二波联动的物料了,感觉之后还可以玩几次(别摸了(
+3月12日
+托福 checked in 了,不会真得等到周五吧(,急急急(
+植树节在蚂蚁森林搞了个大的,发现三年前领的山杏还没种下去,蚌埠住了。
+今天去听了下实分析,感觉很休闲,去年学的是实变函数与泛函分析,今年好像是真在学测度与积分(
+3月13日
+开学仅仅两周多三天就发烧了,这学校绝对有问题(
+月初立了一个这个月不喝奶茶的
+flag(其实是我糖前了,令人感叹(别笑话我啊,很多人去查查也都有只是不知道罢了啊!,饭点的时候烧的很高没吃晚饭,刚刚感觉饿了就点了点吃的,还是忍不住点了一杯茶话弄,我有罪((
明晚有一个高统作业要交但我就写了一半,后天有个基物作业要交但是还没学,下午我跟可能会点名的 +sb +必修课(它叫做绿色交通系统)的助教说我发烧了能不能开个雨课堂,他跟老师商量一通决定不开线上,并要求我过两天去校医院补个证明交给他,我蚌埠住了呀。又想起来它还有个据说很恶心的大作业,并且何老板这学期也没上这课所以就没人能帮忙一起水过去,我打算过一阵把这课退了。
+急了呀,就有一种很想指着天空说这上面绝对有个人在搞我的感觉(
+3月14日
+昨晚写了高统作业,哪怕洗了个澡一直到睡前体温也是正常的(。今早是被自己热醒的,一量
+37.5,我感觉我像一个在散发蒸汽的超大巨,不知道阿尔敏每次变身超大巨之后难不难受,是不是也像发烧一样(
今天上半场在发烧,中间退烧之后稍微缓了一阵子,晚上痛经了(。所以就又是啥也没干的一天,莫名其妙放了两天假,很难想象这个周末要还多少债,科研到底怎么办急急急(。先别想这个了,明早能好好地活着就挺好的了((
+周五似乎是托福出分的 ddl +了,首考所以好像要等到下午,很急,想起我的两千一百块钱就睡不着了,但它至少不是早晨就出所以又睡得着了(?
+3月15日
+早上果然还是不行,生完病虚得很,躺了。从周三到今天我就上了一节课,还是个体育课,说是上课其实就是在边上坐着咳嗽了一个半小时,太寄了,周末要还多少债(
+但好消息是基物作业是下周五交而不是这周五,我又舒服了。
+托福果然首考出分慢,刷了半天小红书看到非首考的都是上午就出了,我一直到下午快六点才出。口语 +22 写作 +27,充分证明确实还是老中(。感觉这个口语小分应该是不太行,查了一下似乎 +JHU 和 UCLA 的线都没过,印象里其他学校也有一些做 TA +需要口语小分更高的要求,恐怕之后还得考,虽然我也不知道这个东西到底有啥技巧。
+但总之轻轻地过百了(103
+倒也完全算不上高),一段时间内至少暑研可以放心用这个成绩,之后再刷一两次就好
+毕竟理论上来说这个成绩只有两年有效期挺不到我入学所以不管怎么样都要再考的(
隔壁寝室的姐比我早一周在天津考了托福,今天我出分之后她勒着我的脖子喊果然上海宁就是基础好,我说停停有没有一种可能我小学初中都是念的乡镇学校,高中就竞赛结束后学了三个月英语,结果随机破防了隔壁另一位竞赛落榜生(x
+哈哈,大三了,我终于也是有语言成绩的人了(
+3月16日
+早上本来打算去习题课交作业,醒来感受到了比昨晚强烈不知道多少倍的喉咙痛,一量又发烧了。求你了放过我吧,我感觉在某个地方绝对有个人在一边乐一边搞我啊(
+先不说别的,我已经四天没喝咖啡了,不仅每天困色特了,瑞幸优惠券都过期好几张了((
+记得之前在转数环看到过有环友说刚发现自己几年来一直没拼对 +continuous,结果我今天看 Cramer's theorem for large deviation +的时候突然意识到学统计学了快两年我好像一直把 standard deviation 写成 +standard derivative(,当然其实也没怎么写过,一般都在公式里直接表示成 +\(s^2\) 或者 sd +而已,但就是,我有的时候自己在颅内读出来就是 standard +derivative,狠狠破防了(
+下午不烧了,晚上从教室回来又烧了,我受不了了。
+3月17日
+头发好长,再留一留就能发动地鸣了。虽然很热但我暂时还不想剪,想搞一个很久之前就梦寐以求(?)的危险的发型,虽然也未必好看吧(
+后感冒症状是不停地流鼻涕还鼻塞,有一种高中的时候过敏性鼻炎的感觉,擤鼻涕擤得我鼻子周围的皮都快破了。然后发现,诶,来北京之后哪怕所谓很严重的花粉季我也没再过敏了,不如上海的春天一根毛。
+现在晚上回寝室纸笔都懒得往外掏了,以后争取每周用晚上的时间把计算概率和生存分析的作业写掉,然后平时就彻底不用带电脑了,某种程度上来说
+以防在路上平地摔把电脑摔坏(。感觉平板没有那么多容易战损的点,而且我买
+Apple Care 了,随便造(
前几天忘记在哪看到协和 4+4 +那个培养计划今年的招生方案了,简单来说就是理工科读四年本科然后转去念医学,再过四年毕业也是医学博士,能考执业医师证。诶,我想起来很丢脸的一件事是高三的时候我妈讲如果裸分擦线的话干脆不要零志愿报协和了,不如直接走强基,我当时正苦于竞赛 +PTSD 导致我不想学这个 b +数学了,我觉得这玩意既学不会又真的很没用(草,于是这时我感觉突然找到了一个我可以学的东西,我说我不,我就要学医,哪怕裸分过线好几分我也要填协和!然后和我妈关于裸分正好擦线这个八字没一撇的事情居然还吵架吵了很久,我还赌气去看了半天这个 +4+4 是怎么回事,感觉哪怕真的强基了也还是有机会转进去的嘛!
+直到后来群友问我这个化学和生物水平怎么学医,然后有一个正好比我大一届的群友对我谆谆教诲在华子要补习 +35 +学分的生物课代表着什么,fine,我就放下了这件事(,还把探微从强基那个志愿表上第三志愿的地方删掉了(。当时如果把服从调剂那个框也顺便反选掉,我现在就在 +SJTU 不知道在干啥了,多是一件美事啊(悲
+把这件事完整地回忆了一遍之后我比较震惊的是,我高三的时候就觉得学这个
+b 数学没啥用(主要是竞赛 PTSD
+感觉自己学不会,但也确实在质疑学这玩意干啥),感觉还不如学医有用,真的很超前,比我现在还超前,令人感叹。后来怎么把这个想法给忘了呢(可能还是因为发现别的都学不会吧
3月18日
+早上起来我又一次在寝室大喊大叫陷入崩溃,我问室友,我要怎么样才能让 +wwc +相信我真的病了一周,我不是不想科研我是真的没时间,我作业都要写不完了。室友说,你现在这个鼻音的严重程度,去和他说句话他应该就能理解了。
+我现在在我不想努力了我明天早十不去了要不干脆把金统也给退了吧,和,逃げちゃ駄目だ逃げちゃ駄目だ逃げちゃ駄目だ,之间反复纠结(
+晚上回来我又开始跟室友嚷嚷,我说我之前想买平板就是觉得带个电脑只为了看 +pdf +很麻烦,但现在又觉得哪怕只是为了水群打字快一点也最好买个配平板的键盘,还有就是我看论文要到处搜东西的,似乎又是电脑好一点,那不就又回去了吗。室友说,你白天不写代码吗?我说我不写啊,我写的代码都是 +trivial 的,帮 GPT +润色一下就能用的,这种事情就不要白天做了,晚上回来摆烂的时候顺便搞搞好了,我写作业都是纸笔的。
+室友扑哧一笑,说了一句很伤害我的话:哦哟,二十多岁了还在打数理基础啊。
+她想了想又说了一句:你数理基础只打了一半,现在数学基础行了,总算开始学基物了,后面还要打两年物理基础。
+我蚌埠住了(
+晚上看邮件发现早已忘记这回事的 ESEP 出结果了,果然是:
+++We regret to inform you
+
搞得我又焦虑了(倒也没有,我真的已经身心俱疲,没有力气应付土木系诸如实习和上课这些破事了。所以我明早桥梁工程要休息了(
3月19日
+在实分析课上读 已经两周没去的 金统 PPT,一边听 Hausdorff
+测度一边感叹 ARMA
+这个东西真简单啊(。还记得我前几天吐槽为什么要把进击的巨人给格里沙而不是黛娜被锐评别合成大西瓜了,我寻思着
+ARMA,ARIMA,ARCH 和 GARCH 不更是合成大西瓜吗(
我怎么感觉这个高统 II 比高统 I 劲大了这么多,早晨起来看助教给我批了个 +80 分的作业直接宕机了,我错了我下次一定好好算最终答案(。上周的 slides +到现在还没发,急急急,那我周四去上个啥(。
+写实分析作业,又遇到去年在 Stein 见过的
+感觉只能称之为是数学题也不知道具体是什么的
+题了,还是不会,我蚌埠住了 习惯就好。
晚上回来继续写生存分析的作业,我实在不明白这个助教为什么非要把作业布置在 +word 里,就算真的喜欢 word 胜过 LaTeX(不理解但尊重祝福),也好歹把 +Excel 的数据复制过来而不是截个图放里面吧(
+定番之沙尘暴前一天洗了头,因为不想再洗一次所以戴了个帽子,晚上还是感觉头油油的,难道是戴帽子闷得(
+今天在路上普通地走,一辆自行车倒在我面前,听到前面的路人说,纯爱战车应声倒地,我绷不住了(
+3月20日
+今天想打开桥梁工程作业附的 .dwg,想起来我早就把 AutoCAD
+卸载了,哑然失笑。转 pdf
+打开一看乐了,我有点看不懂他在画一个,呃,是什么情况的一个不知道什么地方。又想了想还是
+逃避 先写基物比较着急,打开 PPT 就困了,我受不了了。
是的,清华大学土水学院(强调)以及未央书院(强调)就联合培养出了我这个水平的人(
+凌晨手写了一个 life table
+estimation,写得我火气色色桑就上来了,如果不是他让我 repeat the solution
+with R 我直接把 Excel
+做的截图放上去了(抱歉但我其实是做不到的,我的强迫症实在不允许我模仿助教(。我寻思着我那么大一堆
+R package 怎么就找不到一个 censorship at the end of interval
+的处理能调包一秒轻松解决问题,但确实是找不到,只有
+biostat3::lifetab 是 middle of the interval
+的做法,是否说明实际上没人会纠结这种问题但这个真空中的球形鸡一般的作业就是把这个当做考点(
这周生存分析的作业写了三个摸鱼的晚上,总算是交上了。今晚开始写基物,明天加急写基物,后天晚上开始写计算概率,周末加急催何老板写一下桥梁工程(,只要这些能在周一晚上之前写完,我就闭环了,以后白天就只要操心高统实分析和科研(草这也太多了吧)顺带还得听课和写写笔记就行了(。上学期何老板跟我说他白天上班晚上学习,我还觉得怎么这么猛,现在也(隔几天)体验一手(
下午读了一篇论文,读得我吱哇乱叫,大受震撼,总算读完(其实定理证明还没看,R +code 写日记之前才刚刚打开)之后打开另一篇,感觉好了很多(,果然 +Biometrika 还是短,太温柔了。
+骑车回去的路上想了想,后面要系统地学的数学课其实只有泛函,复分析和概率论
+3 了(PDE
+这种为了替代数理方程而不得不上的除外,其余就是随便选选课听个乐。别人实复概只学一个学期,我每年一门搞到最后学了三年(其实复分析我真也没有很想上,只是感觉此前没学过工科的复变函数又不去上个复分析的话,很难说自己是学数学的(。但这个进度完全是用这两年来在主修专业作为一具保持最低生命体征的尸体(i.e.
+每学期只选 6
+学分培养方案课程)换来的,一想到后面还得还这个债,有点崩溃了。
3月21日
+wwc +把这个题目给我的时候还说可能会用到一些概率图模型和随机矩阵,还殷切关照我有没有把 +Durrett +学完,结果看下来我感觉这个只和线性代数关系比较大,而我的掌握只能说是烂。
+这个高统作业,它怎么就这么麻烦,我以为今天可以下午把 PPT +看完作业写完然后晚上把基物写掉,结果一直到教室关门都没把高统作业写完,fine,fine。
+我昨天只是看了篇 +paper,上周只是生病了,我没有杀人放火吧,怎么现在什么作业都交不上啊(
+++ +室友:好多 1 啊
+我:哪里哪里哪里哪里
+室友:网络学堂的课程作业
+
3月22日
+受不了了,昨晚熬夜写基物作业,今天通知基物第七周周三或者周六就要考期中,虽然这玩意能早点考掉也算一件好事,但我是真的学不会,除了把作业题全背下来,真的,别无他法(
+++室友:你早点睡吧,明天的作业交得上今晚就别熬了
+我:我每天晚上都在努力把一个网络学堂的 1 掰成 0 然后才能睡觉(
+
从开学到现在掉了七八斤了,于是今天上完体育课点了杯茶话弄去教室一边崩溃一边赶作业,在奶茶里面算是热量不怎么高的了所以放过我吧,今天又没喝咖啡,喝杯奶茶怎么了(。感觉现在是一个不喝点什么就没法好好学习的状态,怎么会是呢(
为什么这个咳嗽和鼻塞还是不好,急了。
+3月23日
+今天读了另一篇 graphon +estimation,就,每个操作都在意料之外但又情理之中(,很难说。后天争取把总结写完,周二就有脸去上课了。但我觉得很悬,光是把我批注的问题搞清楚都不知道还需要查多少东西。
+我只是又读了一个下午论文,晚上去答疑坊值班的时候我甚至在看基物 PPT +写物理作业,但我现在为什么有五个作业没交呢,就是说,这是一个什么原理呢。
+我现在感觉可能计算概率得退掉了,一个只有作业没有考试的课记 PF +总觉得有点亏,但我真的扛不起生活的重担了。
+3月24日
+上次还在骂生存分析的代码作业,结果金统的 R code +写麻了,又写了三个晚上,我转不起来了,真要退计算概率了。
+++我:绷不住了呀 作业拿 ARMA 预测后两周的上证指数
+友:是桑海宁就给我直接写 5000
+能预测准吗
+我:哎呀 反正就是三千点多一点 也差不太多的
+
下午满怀疑惑地把桥梁工程的作业做了,就,我要是第四周就已经会设计桥了,那我还上你这课是要干什么呢(
+这个高统 II 怎么比 I +难这么多呢,明明只是换了个老师讲同一本书的后半部分。可能难度主要来自换了个助教(,他会认真出一些找不到答案的问题,还批的很严格,急急急(
+感觉得纠结一下明天是学实分析还是开始写总结,不出意外的话周二还是没脸去上课,然而一切的前提是今晚真能把高统搞完(。想起来上学期上建筑材料的时候听到有个哥们在抱怨,说,我现在就觉得像不会游泳但是掉进河里了一样,时间一周一周地过去,就像一个一个浪打过来,我就只能勉强浮在水面上不沉下去,上岸是不可能的(
+似乎还有点过敏了,本来昨天觉得咳嗽要好了,今天又重了很多,严重的时候感觉喘不上气来(
+3月25日
+之前听说厚乳拿铁里面也还是有白砂糖(主要是厚乳里面有),但毕竟很少,不过还是换澳白喝了几天。现实是喝了三次睡了两次(,口感也水水的,还是换回厚乳拿铁了,所以你这厚乳里面到底是加了什么(。听说澳白如果点热的味道会浓一点(或者说原教旨主义澳白就不能做冰的,但我实在不喜欢喝热饮,自己泡咖啡坚持不下来也主要是因为没条件冻冰块,再说就算有能冷冻的冰箱也远远比不上店里用制冰机做的冰,感觉不如买瓶装或者直接就瑞幸了。
+熬夜把高统作业磨蹭完了,有个实在不会做的题到网上到处乱找,最后又是在
+lty 的主页上找到的答案,PKUnb(。一看上来先把 prior 取成
+inverse Gamma,这什么东西(,我还搁那用指数分布族一个个试,拿头做(
开始写(只有两篇 paper +的)总结了,发现之前还有理解错的地方,没懂的地方也在一个一个看。写了四页,刚把 +background 和一些用到的背景知识(比如说我以前真的不知道什么是 spectral +clustering)记好(毕竟这个我也要看的所以记一下也不丢人罢(,graphon +linear estimation 还没有开始写 oracle-based analysis +的程度,已经四页了,什么时候是个头(
+我感觉这学期非常不妙(各种意义上(
+早上起来重新修了一下昨天造的桥,我抽象锐评,怎么看都总有一种艾伦的始祖巨人的既视感(,就是,把上拱当成肋骨,左边是垂下来的头,右边是腿((
+
诶,这个桥,缩小一点看感觉还不错的样子。
+下午上生存分析的时候不知道为什么突然又焦虑延毕之后能不能顺利毕业了,于是重新排了一下后面两年的必修课课表,大概是秋季每学期要上五六门专业课的程度。春季倒是没什么课(如果明年春季要春研也能勉强安排得过来),要学的数学课也没剩多少了,主要就是多花时间磕盐。我感觉我像是 +gap 了两年,马上要回去正经上学了。
+ ++ + + + + + ++
3月26日
+现在就是一个,诶,非常的疲倦。
+把 graphon estimation 那一篇写了,还剩另一个 clustering +的,目前的进度是还在研究 k-means clustering 和 spectral clustering +各自是个什么情况的状态。有的时候真挺想打个电话问问作者,你们这样子做 +approximation +真的没问题吗真的不害怕吗?我看着都害怕。还就真的没问题,bias 和 variance +都控住了,data analysis 结果也挺好(
+3月27日
+报了下丘赛,虽然未必去考(,不能带 cheatsheet 的话我是一个背 Delta +Method 都费劲的状态,大概就这个水平,也没空(
+今天歇了一天,写实分析作业和基物作业,然后两个都没写完,麻了。
+3月28日
+又歇了一天,还是没写完。基物这个作业对着书倒也确实可以勉强做出来,但是考试没书也没 +cheatsheet 怎么办呢((
+3月29日
+又活了一周,真不错,这周末要是还写不完我那个总结的话感觉就很难活到下周了(
+为什么这学期写了这么多码啊,虽然也挺好毕竟确实该练练了(。但这周开始的时候好像刚把金统的写完,写金统之前才刚写完上次生存分析的,今天上课把上周计算概率的写了(感觉强度并不大,大概还是不退课了),课上就一直在写,体育课上课之前在写,上完课回来又在狠狠调一个正负号,晚上写完实分析回来又写了计算概率这周的一道题,写了一半这次生存分析的作业。之前看论文感觉有必要去看一下他那个 +Rmd 来看看我到底理解对了没有,看的时候感觉好疑惑,又开始调((
+从生病之后鸽了两次计算概率,今天一去:
+++:今天是第五周,是单周,那按惯例辟谣一个小道消息,关于本科生申国自然的 +blahblah
+:我们早点下课,因为我下午就要去曲阜了,我现在是本科生事务主管所以得跟着(
+:中央音乐学院还为这个活动贡献了一首歌,我们待会课间放一下!哦对了,我感觉下周应该可以给大家放一个现场的视频!
+
今天看到一段对话:
+++A: 求问基物 3 pyk 期中期末考的内容是和教材关系大还是和 ppt +关系大,感觉这俩差别好大
+B:ppt 和作业
+C:作业
+D:其实跟往年题关系最大
+B:还真是
+C:确实
+
我第一反应:有的人还在对着相关性找 dependent variable +和考虑要不要把它们放进模型做回归的阶段,有的人已经直接上 auto regression +了,感觉受到了启发!(指对于我的基物期中(虽然我是基物 2
+晚上回来开幕雷击,东京工业大学暑研的邮件是 Congratulations +开头的(。本来这两天还在苦恼要怎么无痛延掉施工实习,都差点想去交钱申暑期短课了,好好好。不知道为什么我这次申暑研毫无动力,主要还是并不是真·暑研吧,就按华子的官方项目申了俩,录取率 +50%(喜
+3月30日
+你还别说,我上次说觉得好像看论文看半天没理解对一个比较基本的问题,昨晚看了会 +Rmd +感觉更不对了,今天又仔细读了读文章发现真不对,草。不过这样一来我终于理解他说的那个 +strong consistency 是什么意思了,我之前一直百思不解的是,这和 statistic +sequence 的那个 consistency 到底能有什么关系,把自己蠢笑了(
+明天一定把总结写完,再写不完真来不及了,真的,不知道为什么考了一个托福生了一个病,然后看了两篇论文了解了一个问题的框架之后就要期中考试了,我是大废物(
+第七周周三基物期中,第八周周一生存分析,实分析不知道什么时候,但我感觉这玩意强度远低于去年,或者说习题和习题课强度远低于讲义正文,我在讲义看得晕头转向忍无可忍跳过证明的情况下还能随手鲨习题,就,不太好评价。
+总之我受不了了(强装平静
+3月31日
+月底了,来欣赏一下这个月喝了点啥(去医院看糖尿病的时候记得带上你那破本子.jpg
+这个本子是美赛的时候数学系发的纪念品,还一次给每个人发了四本 2024 +年的计划本,摸不着头脑了。不过我发现贴咖啡标签正好,不如拿出来用一下。
+
基本全勤了,3.13 到 3.16 +在生病没喝咖啡,喝了三杯茶话弄当感冒药(,芊芊绿雪和云过处后来又回购了两次,便宜好喝,不加糖不是很好喝但比较有安慰感。周五一般都会有一杯茶话弄是因为体育课真的累,而且如果早课咕掉了的话也没必要再喝咖啡,不如整一杯奶茶。瑞幸的话,我一般不喝美式折磨自己,对生椰系列也没什么兴趣,就还是厚乳拿铁和澳白喝得最多,厚乳是很困的时候喝,澳白在不是很忙可以歇会或者睡得比较多的时候喝,不过理论上来说还是澳白更健康一点。
+可以看出来撕瑞幸标签越来越娴熟了,一开始每次都撕坏,后来掌握了一个技巧是喝完之后把冰块倒掉,稍微用热水从里面浇一下杯壁,很容易就能撕下来。
+我职业病犯了,统计了一下取餐号,还有点单时间,就是不知道怎么把这两个结合起来分析比较好。随便用 +R 跑了一下,目前还没有重复的取餐号,但是有一对只相差 2,是 \((485,487)\),还有两对都只相差 4,是 \((613,617)\) 和 \((485,481)\)。虽然 \((481,485,487)\) +非常接近,但点单时间可以说是毫无关系,只不过都是厚乳拿铁。考虑数字重新排列的话还有 +\((617,167,761)\) 和 \((841,481)\),到现在为止 481 和 617 +出现频率谜一样的高。没有买到过取餐号是 3 开头的咖啡。
+别搁这玩了,总结还差一个 statistical lower bound +的东西仍然存疑,周一上午总要用定时邮件发过去的,快去写罢(。明早还要去办护照,还得早起一点画个淡妆然后处理一下刘海和披发的问题。之前查了一下虽然申领流程可以在校内办,但校内没有邮寄的选项,之后还是要跑到阜成路取,受不了了。
+]]>11月1日
+在通过双十一凑单练习优化(,这个月的答疑坊津贴还没到手但已经送出去了三分之一左右,好好好(
+选衣服的时候看到备注的春秋款直接幻视一个春秋分,你怎么知道春秋分刚刚天皇赏秋夺冠(看赛马娘看得
++考试的话除了 normal 和 Poisson +之外的分布我都会给在卷子上,抄就是了,毕竟别的很多分布的参数很混乱,我估计你们每个人说出来的 +Gamma 分布都不一样。
+另外如果连 normal 和 Poisson +都记不住的话我想你们也坐不到这个课堂上(
+搞应用的时候人家问你这个模型怎么不这样那样改,你就说 all models are +wrong but some are useful,我自己这个就是 useful 的;到搞 inference +的时候你又可以说自己的 model is exactly +correct,在什么场合就说什么话(
+——wwc
+
但我上课在写上周作业,没仔细听还有没有别的暴论,急了(
+11月2日
+本来感觉学不完了,但这个 ODE 居然有点速通的意思,早知道不 PF
+了
+开玩笑的,我的练习量只有三次作业十五道题,速通只是能把讲义看完的程度(但这对我一个不搞
+ODE
+和动力系统只是学着玩顺便复习或者说预习分析的人来说已经足够了,可不敢碰瓷二字班小朋友(等等我不是马上就要变成二字班了吗
又到了虽然不用朋友圈但偶尔去看 Bowen L +最近在发啥如果间隔时间比较短就给他点个赞时间(,突然发现他的签名改成了
+++以轻松愉快的心情面对就可以了
+
可爱捏 谢谢不焦虑了(并没有
+ + + + + + +
+
下面是周常新鲜的赛马娘第三季第五话吐槽(
+确实是宝冢纪念,但没做完,下一话应该还是大鸣大放。yysy +最后做出来的这个大鸣大放的性格真和我想的一模一样,四舍五入是狂化的帝宝(,只是没猜到秋奈的声线。
+比赛演出还是不错的,大鸣大放骨折那一下确实给我整得心肺骤停了,第二季印象太深刻开始闪回帝宝的几次骨折。然而宝冢纪念还是在北黑视角下展开稍微有一小点失望,我以为会做出来大鸣大放骨折那一刻的心态,受伤的一瞬知道这是自己最后的末脚了,赛前对凯旋门赏的壮志已经化为泡影
+这下找到北黑参加凯旋门的执念源头了,于是忍住巨大的痛苦拼尽一切从外侧赶超错失的上届菊花赏冠军。或者至少有北黑知道这是最后一次和大鸣大放比赛的机会(虽然我知道赛前和赛中不可能做出来,毕竟北黑领放看不到身后的情况,她如果跑追的话倒是有机会,应该是会等到下一话知道大鸣大放失去竞赛能力之后表现。但如果赛中能有的话该多精彩啊),带着全部的心意去决战的描写。
本来还在期待能有大鸣大放的内心戏在好好看比赛演出,结果胜之石超过的时候北黑大喊一声你谁啊给我破功了,这活整得又好又烂的,真的不会得罪马主吗(
但现在给我的感觉是大鸣大放好像并不知道这次受伤就再也不能跑了,下一话会做成啥样呢。不管怎么样先期待一个上届骨折选手
+& 经典双冠马娘帝皇出面安慰大鸣大放(
大鸣大放的腿,斯哈斯哈( 嘟啦酱我的嘟啦酱
Eyecatch
+图的大鸣大放感觉有点小崩,头好大啊(琵琶晨光:?
这一话小北和光钻双双被史实杀,好好好(,不过光钻菊花赏就要赢了,感觉不会下一话塞到一起吧(
+胜之石你好惨胜之石(,明明赢了还被吐槽这谁啊完事在背景里一顿自嗨也太可怜了吧(虽然挺可爱的
高尚骏逸有戏份了(虽然只是举了几秒钟铁),决胜服总觉得很眼熟但就想不起来为什么,后来一想略像
+ISLAND 的女主(对不起凛音我想了半天也没想起来你叫啥)。观赛的两个看起来既路人又不太路人的
+有点像大拓太阳神的 马娘在 OP
+里也出现了,感觉可能是高尚骏逸的姐姐和妹妹。然而我都忘了这一场还有里见皇冠,其实发型真的蛮可爱的(。
说到 OP,ED 里面特别周腿上阴影的作画失误仍然没有改(
+但有一说一如果我是刚入坑的话看到这一话北黑被路人马娘莫名其妙史实杀,都不是被大鸣大放背刺,真的会气到吐血弃番的吧(
+11月3日
+昨晚在 MSE +上提了个遍寻不得但事后看来蠢得想把自己脑袋摘下来的问题,居然有 6 upvotes +还迅速收到了两个回答,reputation 涨了 +62,咋回事呢(。其实就是个突然在想又想不出来的反例,评论区还给多加了个条件,挺有意思的。
+上次在 MSE 提问是因为不会做 Bowen L +出的附加题但是又搜不到就问了,后来被识别成了 duplicated +但我说实话没觉得重复,本来有个 upvote +但是这个问题本身过了一年被删掉了,就又没有了。好好好,下次还问(
+凌晨的时候有环友问了个和 Durrett 上 recurrence +那一章的某几个习题长得十分甚至有九分相似的课后题,那几个题我本来就不会做而且答案上没有,也可能是处理收敛级数的水平不太行,但看到环友也都不会就放心了(
+说到环友,有个之前好像知道我要延毕的环友今天来问我是不是真的要延,我说是,他说别延毕一年最后来求真了就行(,正确的。然而说实话不去求真我就只能统计中心/出国了,总不能去投奔
+lzx
+吧,去统计中心这件事几乎零测(,强基不能转专业什么的我都已经看开了,实在是不能理解不允许外推的规定,否则能去北大
+能让我学数学的话大不了复旦也行(x)的话怎么不算兜底了呢。
我说如果不出意外(i.e. +学校不批准延毕之类的)肯定要延,他给了一些我意料之内的反应,比如说认为我能做出这个决定非常不容易什么的。其实并没有,我几乎毫不犹豫(,另外延毕这事儿我从大二上学期就开始口嗨了,属于是给自己做足了心理准备。
+周三运筹在讲整数规划,虽然不可能难但毕竟 zjz +没提过这个我也没学过,估计就是个 linear programming +的小的延伸(暴论,搜了份讲义考完前两门期中回来看((
+双十一买了个帽子,戴上之后有种莫名的既视感,想了想是后面的蝴蝶结有一丝丝像诗歌剧,那没事了,诗宝可爱(
11月4日
+本来还想着今天要去讨论班的,还想着上讨论班的时候可以写点 +ODE,结果起床之后想了想反正论文也没读过干脆别听了,直接变成那个去隔壁复习概率论(。哥们是真有点急了,现在拟合题目拟合得想吐了已经(
+Jianfa Lai 给了一个论文的 +list,从下次开始似乎也能提前知道要讲什么论文了,打算自己先读一下,不然纯听故事也没什么意思。
+紧赶慢赶把 optional stopping time 学完了。之前 variance of the
+gambler's ruin time
+那个题哪怕在作业里出了也一直不会,直接口胡了交上去的但也没扣我分,这课也不发作业答案,助教是个
+23 级的博士生,我其实稍微有点疑惑如果这课真是用来准备 脖子
+博资考的那他本人为什么不上(当然我不懂求真的脖子考具体规则所以不乱说了(,还是说他在自己
+TA 自己(。PTE 2nd edition solution manual 没这道题,Hoil Lee
+的答案感觉既看不懂又是错的,MSE
+上没仔细搜但是搜到的两个回答更是透着一股浓浓的 not worrying about the
+details(
今天福至心灵自己把它做出来了。然后心理压力瞬间减小了很多,optional
+stopping time
+那一章的习题也迅速过完了,想了想闲得不行的话可以把这个题在 MSE
+上写下来作为我的第一个回答,顺便发现了另一个之前不知道的定理用法,学到很多(这是学到吗,好像是自己教会自己许多((x
果然学数学就要去北大学(迫真,去了一趟感觉很缓解期中周精神状态(
+11月5日
+虽说昨天觉得不用慌了但果然考数学之前就是很难不慌(,希望能成功早睡(
+膝盖本来好很多了,结果上次又摔了脚踝,今天又被车蹬子打到了膝盖上还有淤青的地方,真好不了了,帝宝求你了放过我(。说起来上周体测
+800
+米测出了上高中之后就再也没见过的成绩,跑的时候甚至感觉还有余力,帝宝特有的受伤之后能变强是吧(
上次在 MSE +问的问题已经周榜第三了,好崩溃,这周会不会收到一封能在里面看到自己的 MSE +Weekly Newsletter(
+今天在教学楼洗手间里看到一个出水停不下来的水龙头,突然联想起大一的某个雨天骑车的时候一滴水打在我没锁屏的手机上然后连发了几十个表情包(,当时正好在旁边擦手,顺便拿纸擦了一下那个红外感应器(?我也不知道叫什么)上的水果然就不流了,学到许多(,而且日行一善(1/1)((
+这概率论 2 +颇有一种奶酪越多,奶酪孔越多,奶酪孔越多,奶酪越少,所以奶酪越多,奶酪越少的感觉(,学得越多不会的越多,题目拟合的越多之前会做的后来再看也不会了(,随便吧反正明早就考了((
+11月6日
+昨晚把时区猛往东调了六个(,果然入睡有点困难,吃了 1/3 +粒室友的安眠药然后光速睡着了。
+概率论大寄特寄,我是真没想到 yf +这么喜欢考计算,每道题都在算(还特别喜欢 random walk on graph,一个 +binary tree +一上来给我看傻了),我做计算本来就又慢又菜,这次干脆剩了个题没算完。考完之后在路上一边走一边想,算一个有 +\(n\) 种取值的 discrete random variable +的期望需要 \(2n-1\) +步,我也不知道算最后那个 triangular sequence +里每一个随机变量的期望花了多久,总觉得最后的 45min 转瞬即逝,看来确实 +\(O(n)\) 对我来说已经太难了((
+无所谓了,我现在越来越发现我考试发挥的水平就这样,之前已经复习挺好了,该掌握的也都熟练了,差不多得了。
+晚上看答疑坊群里说线代爆单了,想想我暂时没什么要紧的考试了就去秒了十几单,然后把生物作业写了,好闲啊(。明天考完 +ODE +要极限开始学整数规划然后写后天要交的作业,实在不行先把作业写了再学(
+这周大概还得赶赶高统的进度,虽然不期中考但落的有点多,然后就是没边没沿的优化了,真不知道咋复习,上周还休息了(
11月7日
+好崩溃,为什么要 PF +ODE,哥们就复习了两个下午,昨晚还在写生物作业,写完开始摸鱼抽卡摸到两点,躺床上看了一眼整理的笔记的照片一秒入睡(,早上六点半就醒了然后睡不着了。刚拿到卷子又开始流鼻血,怕时间来不及就一边捂着鼻子一边算,看起来还挺壮烈的。
+铺垫了这么多(,实际上我想说的是 70min 就 AK +了((,昨天概率论要是有这水平还愁啥(
+上来一看怎么第一题全是字儿,再一看这个 enumerate +写了六行居然是在解释什么叫唯一解无解和多解,我还以为善良到把判定法则给出来了(。说到底这课就没什么难的,除了一些计算细节(比如说 +(a) 的无穷多解几乎就和 Lecture 1 +讲过的那个一模一样)之外核心定理就两三个,像 (c) 这种除了套 +Picard-Lindelöf 之外也不太可能有什么别的办法,随便一放缩凑个 local +Lipshitz 就有了,问题是你这个 (b) 到底为什么压根不满足 initial value +condition 啊,我还给解出来了然后仔细一看逗哥们玩呢。
+中间两个就是只要学了微积分 A1 就会做的计算
+可能也不会毕竟其中有一个是 Jordan decomposition
+尽管我当初并不在乎唯一性乃至这么做的合理性之类的细节,最后一题本来还想着说不定有点小难,再仔细一看兄啊你这导数
+\(y^\prime = f\)
+怎么还是有界的,你这函数怎么还是在 \([-1,1]\) 上的,那不写个 Arzelà-Ascoli
+theorem 再用一下 LagrangeKMnO4 Lagrange mean value
+就直接带走了吗(悲

卷子可以带走,所以发出来也没啥吧(?
+我懂了,这学期主打一个学到就是赚到,别天天牵挂你那绩点了.jpg。下学期要去上
+PDE 替代培养方案里的数理方程,虽然不知道和 ODE 有多大关系
+而且重点应该是我那稀碎的多元微积分水平不太行,总之学一个先。
今天不知道是不是考完了的原因所有的课都开始哐哐布置作业,打开平时事不太多的高统发现布置了超过五个题,急死了,再打开优化作业一看真好啊竟然只有六道题(,再一看每道题平均三个小问,急死了((
+11月8日
+现在笔芯好难买啊,我平时只用
+0.38,本来就已经很难找了,这次缺的是蓝色笔芯,某宝都快翻烂了才找到以前一直用的那一款。不是墨蓝就是晶蓝,就想买支纯蓝色
+而且笔杆可爱一点不要纯透明的(草)的笔咋这么难呢。
优化期中就有两张正反面 cheatsheet,高统期末也有一张正反面 +cheatsheet,建筑材料直接那个开卷允许带书,感觉别说复习了光是塞 +cheatsheet 就够我喝一壶。
+今天突发恶疾看了一眼春季那个数学规划的大纲,这不就优化吗(。里面就非线性规划没学过,到明年去水一个工工的好了,考虑到数学系大三非泛函专业课的那个水平还是不去浪费时间了,好好学复分析吧((
+Shao Jun +这本数理统计越看越觉得也有点怪,感觉描述性的语言太多了,不能多列点公式吗(。像 +the conditional distribution of \(X\) +given \(T\) is known +这种话(我觉得)写在 remark 里就可以了,为什么会在定义里,去 example +里找式子感觉有点小抽象。
+喜提了第一个数学考试满分(,这是好事,但是 +ODE(,明早去看看分位数是多少。虽然考试其实 AK +过很多次但是基本上都有被小扣分,去年抽代期末还以为能满分结果笔误了两个被浅扣了一点,数值分析也 +AK 了但没公布成绩,看最后是 A 而不是 A+ 有点怀疑又笔误了(,说到底 ODE +可能也不是没有笔误只是批的松吧(
+11月9日
+睡大觉。
+本来觉得优化是下周五不用慌,今天仔细一算我这周连作业都写不完,急死了。
+今天写高统作业看到个好玩的:\(f_1f_2 +I_{A}+g_1g_2I_{A^c}=(f_1I_A + +g_1I_{A^c})(f_2I_A+g_2I_{A^c})\),实际上是在拆 exponential family +的题目里看到的,但那个题我看了一眼感觉不能拆就直接开始说 subset 的 +minimal sufficient 也是全集的 minimal sufficient 了(毕竟 subset 就是 +exponential family),似乎有点粗暴。
+赛马娘第六话钝评,端上来罢!
++
前天还是昨天看了预告其实就给我整不会了(
+上次宝冢纪念大鸣大放赛后明明骨折了还愣在北黑面前站起来了本来就有点给我整不会,我以为埋了个大瓜等这一话才知道再也不能跑了,开始掉小珍珠然后和北黑进行信念的传承,结果怎么是光钻?
+我超,总算有小林历奇了,光钻小林东商皇冠俊逸和北黑的修罗场人总算到齐了,而北黑还在和内恰贴(
+我有点评价不来这番的搞笑情节,感觉观感和第一季越来越像了,前半段真不是在水时长吗,后半段我其实看了预告就感觉应该会和麦昆谈心
+虽然里见家族和目白家族简直不是一个量级但反正目白牧场早就没了随便说呗
+但麦昆突然讲龟兔赛跑然后被打断还是给我气笑了,尴尬程度不亚于早已沦为胡萝卜特饮推销员的特别周在第一季
+OVA
+里面对着胜利奖券大声复述训练员怒斥早恋小情侣的那段话,及川启对自己不合时宜的插科打诨的强烈执着依然毫无反思甚至可能都没有认识,你不是马黑谁是马黑(
麦昆:比赛中落铁和斜行都是很常见的事(指天皇赏春落铁,天皇赏秋斜行被降十八着,真的很在行(
+总觉得这是麦昆第三季以来第一次说超过三句话(,太亚撒西了,我永远喜欢大西沙织
光钻这场菊花赏应该是目前为止做的最长的比赛,虽然最后冲刺全靠和观众一起吼还是给我整绷不住了,但不得不说里见家的姐姐们出场看比赛、光钻赛后掉小珍珠还真算是这一季里面截至目前情绪渲染的高峰了。
+现在魔咒破了,里见 魅魔
+皇冠后面能说点别的了吗,这么可爱的妹子没戏份的话真的好可惜(
下一话按照时间线应该是北黑光钻第一次有马纪念对决
+今天的小北不是我的对手,不知道北黑要怎么输。同场的又是万籁争鸣、高尚骏逸和胜之石(小北这次认识了吗?),但这三位都没能入着,其他马娘又是都没有版权(当然胜之石也没有),大鸣大放已经退役,很难想象这比赛会是什么抽象样子,大概只能搞女酮了(。估计是赛前
+修罗场,续上宝冢纪念的大鸣大放受伤和未能参加有马、凯旋门就退役的遗憾,或者能有个会动的
+winning live 和在 winning live 上和好贴贴的北黑光钻
+看看了。
啊所以真的还有人记得大鸣大放吗?还有人记得大鸣大放的凯旋门赏吗?
+如果说光钻个人回结束了才开始写大鸣大放这才知道自己不能再参赛了我还是会有点小小的难以接受但勉强接受也不是不行(,也不是非常不合理,但感觉接受不了也是有点因为和预期不符,宝冢纪念之后伤那么重早干啥去了。只能说或许要把“不能再参赛了”阐述成“未能参与有马纪念就遗憾地面临退役”,然而但凡把第六话前半段的抽象演出压一压然后讲大鸣大放的情况也比这好啊。
帝宝救一下啊,麦昆都开始当知心姐姐了,你救一下大鸣大放也行啊
11月10日
+昨晚把不考但是这周要交作业的三门课的作业写完了,心情好了很多没那么破防了,然后想了想我优化上周的内容还没仔细看呢,今天何必还要去教室,咕咕。
写运筹作业的时候还不知道昨晚讲的非线性优化是个啥东西,打开 PPT +一看哦原来就是凸优化的基本概念然后随便讲了几个数值算法,速通了。不过翻这 +PPT +的时候还是给我气笑了,不会写数学公式可以板书,别惦记着你那关着灯上课了.jpg
+好痛苦,选这么多数学课干啥。学新的东西掌握漂亮的技巧确实很开心,然而用选课来催促自己好好学的代价就是有一个在复习拟合中感到无比痛苦的超长考试月,在此期间就连去读一些写得很好的讲义和写作业都失去了应有的兴致,非考试科目的话甚至只想赶快掌握下表面的东西把作业写完然后就放下,省出时间复习,之后再来还债,好痛苦好痛苦。更痛的是哥们期末有八门课要考试,真能活下来吗(
+今天一边读 Boyd Chapter 4,5 +写作业(也没写完,急死了)一边辱骂优化这门课,要是按照上确界来准备的话就是五章 +Boyd 四章 Intro to LP 再加一章 Bubeck,然后读读课堂笔记再加一个上课讲的 +maxcut,两张双面 cheatsheet 我觉得少了,但是既然限定要 handwritten +我又觉得太多了(。这 Boyd Chapter 4 +到底在干啥呢,好像就罗列了一堆不同类型的 convex optimization +problems,我还以为会有什么稍微统一点的方法结果课后题仍然相当依赖人类智慧,甚至可以说只是依赖线性代数水平(
+想来想去只有一句锐评,这课比赛马娘第三季还能塞。
+11月11日
+写点啥呢(
+收获了一个 asuka 同款 朗枪帆布袋
+感觉有点地狱,找出处找了半天(
其实只是借用一周,骑车把之前用的帆布袋弄脏了((
晚上回来之后吃了个朗姆酒冰激凌,感觉头晕晕的,怎么会是呢,好菜(。
+11月12日
+双十一买了个咖啡杯,还买了一箱瓶装咖啡,结果就是到现在瓶装都没喝完
+作为一个懒狗
+更不可能自己泡了,想想新杯子一直放着也有点可惜,拿出来喝水了。300 ml
+的杯子有个奇效是走路的时候放在口袋里也不费劲,打一杯热水去吃饭来回路上当热水袋,回教室之后就正好可以喝了。
晚饭后饭困的频率越来越高,下次留一口咖啡吃完饭回来喝(...)或者饭后去骑会车好了。
+周五考试,两张正反面 cheatsheet +仍然没有开工,但是不紧不慢.jpg,怎么会是呢。今天把 Boyd Chapter 1,2,3 和 +Appendix +看了,总感觉线代水平似乎不太行,小急。为什么要在额外的纸上做笔记而不是直接抄在 +cheatsheet +上,我也不是很懂。不过还好,后面四天没有要写的作业(...)所以还挺有时间的。
+话说回来感觉与其微雕折磨自己不如随便找纸写大一点然后缩印到一张纸上(比划),明天去看看清芬打印水平行不行,实在不行去社友曾经推荐过的北馆(
+11月13日
+今天摸鱼的时候看到有个致理的同学在答疑坊小程序里问数分学不会怎么办要不要多刷题(,本来想话疗一下后来想想我也没学过数分还是另请高明吧,过了一会看这哥们又问了个离散,成分已经很明确了这还学数分学那么认真干什么.jpg(
在读优化的 scribe notes,读到 week 3 惊喜地发现还有人 LaTeX
+写得比我还丑,满意离场
自从找到可以把水果酸奶送楼下的店之后就有了晚饭之后骑车遛弯顺便回去取的动力,每次下单都在默念我一个月挣两千买点吃的怎么了总不至于真没钱考托福了吧.jpg
+晚上教室里另一个姐一直在乐,走的时候听到她 npy
+和她说我求你别笑了然后两个人开始一起乐(。除了当时在推一段推不出来的公式感觉有点小吵之外,羡慕和疑惑参半,好美丽的精神状态(,我怎么一天天的就完全乐不起来,反正每周离已经过去的周六越远整个人越乐不起来(
走在路上突然好想吃玉米肉馅的饺子,感觉是不可能存在于北方食堂的东西,晚上就在清芬多买了一个生煎当代餐,尽管也知道它比在上海随便找个店能吃到的差得太远太远了。晚上拿到的昨天买的青提上不知道为什么沾了好多泥,和上周末买了带去隔壁的完全不一样,费劲地洗了好久最后尝起来也不甜,你这白开水怎么没味儿。不过买到的芋泥厚乳很好喝,本来差点突发恶疾就冰着喝了,放暖气上热了一下留到洗完澡喝的,好香好香。
+乐不出来可能也是因为饭太难吃了,清芬一楼还就那个又贵又难吃。周六可以吃好点。
+11月14日
+昨天想吃玉米肉馅的饺子,在华子想必是不存在的,吃了个不好吃的生煎当代餐,完全和你沪的没得比。今天想吃汤圆,去桃李二楼的时候已经没有了,又没吃上。
+北京初冬这个天气不刮风的话真的很舒服,今天下午在一教摸鱼,出去交作业的时候顺便在后面的小土坡(?)上溜达了几圈,把围巾摊开当披肩披在卫衣外面就出去了。所以说感觉现在真没必要穿得特别厚,有一件抗风的外套就足够了。当然我没有,冲锋衣暑假带回家洗了之后忘记带回来了,那就骑车骑快点吧(
+晚上在教室看到前排一个男生在用香蕉空间看复微分形式的定义,大受震撼,又窥了下屏发现他旁边的女生在写复分析作业(,感觉求真爷实锤了,仔细一看哥们桌上的入党申请书写的求真 +2 党支部(。再右边的另一个男生在看 GTM,别的没看清就觉得一个图长得很像 +upcrossing inequality,看他翻了几页之后标题是 +martingale,不知道是哪本。浓度好高(
+这学期连期中周都还没活过去,看下学期的课表倒看得很乐呵,希望最后别变成在那嗯造两本
+Stein(其实我本来都不知道是造哪两本,但是看到下学期泛函是 xgy
+开课之后就确定了是实复(。春季的必修课我倒是上得差不多了,就几个很水的建管交通必修课随便摸摸就过去了。统计中心那边摸一个高统
+II 和高维概率 我觉得这两门总能命中 ypk,看到求真那里开了一门
+combinatorial
+optimization,简单查了查感觉和这学期优化理论接上了可以去学学,主要是既然同一个老师的
+deep learning theory
+没考试的话这课也不会有考试的对吧对吧对吧对吧哥们是真的考不动了((
下学期实分析是光叔和 lyx 但是看这个课容量我觉得我就是 lyx
+的份了(,本来不知道后面这哥们是谁,查了下以前学期都在开我不太关心的研究生课难怪不认识,但看了他在官网上的照片(右一)之后我觉得应该是个好人吧(迫真
PDE 没有 jhy,我只是想拿这课水
+看起来根本不可能学会因为不会转化物理模型的
+数理方程而已,那就不急着选了。
好想用上海话骂人哦,在华子没什么机会 gang 洋泾浜 sang hai
+ei wu 真是失去了很多乐趣(
11月15日
+早上突发恶疾看了会 Gaussian sequential +model,主要是周末讨论班讲这个,结果主讲人发的链接是一本 500 +页的书实在给我整不会了(,看一点是一点能听懂多少是多少吧(
+++提醒各位同学,本周五是优化理论课程期中考试,时间和地点和日常上课一致。
+题目数量:6 道题目,包含证明题和解答题
+题目难度:TA 用时约 1.5h 完成
+
TA 好强(#每日TA
我寻思着 TA 用时约 1.5h
+完成到底是个什么难度(,开了下盒发现这哥们是前几年的丘赛概统银奖,那他怎么做了这么久,这考试是不是还挺难的(x
今天身体不舒服睡了好久,晚上感觉要小肝一下。怎么以前做出来的作业题第二遍看都觉得自己当初像会魔法一样
11月16日
+烦死了这优化快点考完吧,好想学点新的东西,ODE 和高统都是(
+不过今天看了不少 SDP,也算是学了。不知道后半学期讲不讲,反正当初讲 +max cut 的其中一个转换的时候 zjz 突然说了一句这就是个 +SDP(大意),然后在场的茶园爷看起来全都懂了,只有我愣住了,SDP +是啥,讲过吗(
+下午往 cheatsheet
+的最后一块空白上随便塞了点东西,晚上写了运筹作业,又看了点高统,感觉神清气爽(。希望明天没事,但我感觉
+bgm 都快换成 Komm süsser Tod 了(不如放欢乐颂怎么样
赛马娘,钝评,端!
++
又一次给我气笑了(
+真没绷住,我想着这次日本杯第三是表现高尚骏逸一生一次的末脚之前的高光之一了,再没有的话只能等明年春天皇赏的第二了。万籁争鸣是最后一次拿到第二名,此后再也没有进过前三。所以我还以为这次有马纪念可以像第二季的帝麦对决那样先铺垫个一集,结果又莫名其妙,比赛之前高尚骏逸又说一定要赢,然后又输了输完很不甘心,光钻日本杯的时候看着北黑赢了还就那个面无表情,有马纪念早上起来还想着给北黑留小纸条说自己先走了,到赛场上就甩脸子
+离婚
+不认人。要是说这就算描写了光钻比北黑对待竞技的心态更成熟的话我可要绷不住了,赢了之后也是北黑先向光钻搭话不然头也不回一个,那这场比赛光钻要是输了的话岂不是更要翻脸不认人了
+反正你这输赢也莫名其妙的除了按史实写之外啥也没有,性格还没有北黑成绩起起落落也没看到大的起伏、无论输赢都在笑来得讨喜。赛中莫名其妙地追上了超越了,两个人吼着吼着北黑不知道为什么就输了,我看了个啥(
跑步就跑步别吼了啊啊啊啊啊冲线那一段我直接把声音关了(黄金伶人/巨星俳优:那我呢?
+cy
+你还是搞女酮吧,之前的预期是第三季能和第一季差不多就行了,现在感觉好像还没第一季好看(
winning live
+冒了个尖我还想看北黑望着光钻的背影一边忍着不掉小珍珠一边跳舞(,之后直接转
+ED 也没绷住,想做搞笑番可以再单开一个四格别霍霍第三季
你还别说这 ED 相比正片来说还挺好看的,麦昆可爱捏
睡前想起来这回事躺床上拿手机直接在 b +站看的,看到标题把“我们的有马纪念”翻译成“我们的中山大奖赛”就已经开始绷不住了,第一季和第二季的时候不是还可以翻成有马纪念的吗,看了下吐槽似乎有些马名(大鸣大放?)都没按照香港竞马会的翻译来翻而是自己重新译了一个,乐(
+里见皇冠你怎么还惦记着你那魔咒(,不过和光钻的性格反差做的还不错,在没有破咒的时候皇冠是稍微相信魔咒每次失利都更加畏缩,光钻是始终不相信魔咒的存在一直在努力,光钻破咒了之后皇冠也受到鼓舞赢下了 +G1。只是香港瓶没版权做不了也有点小急(
+皇冠好涩,远景里高尚骏逸的小肉腿也好涩,怎么会是呢(
所以说真的没有人记得大鸣大放了是吗?cy +你要这版权有啥用啊,不就一背景板工具人吗,你看黄金伶人的替身(巨星俳优)不也演得好好的吗(
+帝皇谈心 怎么就这
+说了点啥啊(,还以为能类比一手帝麦对决,感觉在努力类比了又没类比,看在第三季这么塞的份上算了吧不吐槽了(
一集一比赛确实观感就不好人设也立不起来,不过看起来是要把北黑七冠至少菜名都报全,隔壁帝宝四个
+G1 还跳过了日本杯没提也是做了 13
+集,放平心态放平心态(。说难听点北黑和同世代马大多甚至都还没从种马退役,要端水照顾好
+马主的心情 也正常
+虽然除了把比赛塞完之外我也没看出来这是在激怒所有人还是在干啥,第二季播出的时候帝宝都竟走快十年了(,麦昆家目白牧场都寄了,随便魔改控制节奏也没啥,放平心态放平心态.jpg
11月17日
+昨晚睡不着吃了点安眠药,早上起来就感觉 dokidoki 的
+心悸,一直到下午才好一点,整个考试期间也挺不舒服的。我还想着周一考概率论之前也吃了药所以感觉考试状态不太好是错觉,是我太慌了所以不舒服,现在看来感觉确实和吃药有关系,下次
+直接把大晚上还搁那闹腾的室友打晕 不吃了(。
本来觉得没什么问题的,在医院开的药,禁忌症也没有高血压心脏病,但还是不舒服。
+这优化考试准备了真的有用吗(,斜前面一个哥们考着考着看起来嫌
+cheatsheet 碍事直接给扔旁边座位上了,笑死。zjz 怎么还一边考一边发
+hint,这是什么赛制,他要是不提醒 \(\log \det (X)\) 是 concave 的话我都快把
+duality 搓出来了,他一说这不约等于提示直接用 KKT
+了吗(。虽然造出来之后还因为不记得 Sherman-Morrison
+长啥样了小破防了一下,但再一想 hint
+里面甚至有逆矩阵的形式,乘起来不就好了,草。另外一个 hint
+发布(?)的时候是写在白板上的但我那个位置正好看不见,然后就出现了考试中途把其中一个助教叫住让他在我的草稿纸上写一下具体形式的梦幻场景(
当然这都不算什么,最重量级的还是今天在卷子上证明了一个 finite state
+Markov chain 一定有 recurrent state 因此它有 stationary
+measure,从而对于一个 stochastic matrix \(P\),\(p^TP=p^T\) 一定有非负解 \(p \succeq 0\)。这题让用 duality
+做,但我说实话连动手尝试一下怎么造一个奇形怪状的 primal-dual pair
+的兴趣都没有,而且它出个题还要在 remark 里提到 Markov chain,zjz
+也说不是非要用 duality
+可以用微积分线代知识,那我可就要表演一点小小的概统震撼了。希望能有分(
虽然本来还感觉了一下不知道能不能用 Brouwer fixed-point theorem
+但是又忍住了因为更不会证
一切都是虚张声势的线性代数,可惜我线代太菜了,只能徒手建造数学大厦了捏(
+但其实考试期间一直在 dokidoki
+心慌,搞得人很难受脑子也不清楚。同一个式子焦躁的时候写两三遍都写不对,椭圆不相交那个题的
+if 我明明拿 seperating hyperplane theorem 证完 only if
+之后一眼就出来了,还嗯是因为写不清楚正负号在那里多折腾了二十分钟,别的地方也不停地笔误,状态蛮糟糕的,几乎是到最后一刻才写完。但反正
+ak 了
+
晚上写了高统,好难,云了一点 Gaussian sequence model,看着像个
+toy model
+但是不会,不知道明天能听懂多少。暂且以坚持十分钟为目标(嗯?
又收到 BBO 的广告了,差不多考完了就好想打桥牌哦(
+11月18日
+今天 Gaussian sequence model +坚持了半个小时才掉线,感觉算大成功了(。后面一个小时就继续在看之前找到的讲义,没什么听了。不过 +slides +发群里了所以之后有心情的话感觉还能看看,这两天是不行了,期中耽误的 ddl +都赶不完(
+上午写了一会建筑材料实验报告,感觉这个报告的要义在于把 20 +张拍的照片全部塞进去(
+这张图我愿称之为《再见了,所有的混凝土块》(
+
右下角那个碎的那么厉害是我等实验的时候太无聊了把能手剥的碎屑都剥下来了((
+11月19日
+建筑材料实验周五做了一个半小时,周末写实验报告写了一天半最后写了 16 +页,导出来有 44 M(挠头
+它还有个文献调研的问题,今天被迫看了俩小时有关混凝土裂纹的论文(恼
+晚上去猫超买咖啡,发现纸盒装的 NEVER x COFFEE +回来了,虽然那个美式真的是我喝过最清醒的咖啡,但还是选了拿铁,那个味真的太(,只能说感觉是因为难喝所以清醒。
+路过果切的地方被八折吸引过去了,虽然事后想想只便宜了不到一块钱但是我出超市的时候手上还是多了一盒哈密瓜,怎么会是呢。昨晚在海底捞吃到了放在料台上的特别好吃的哈密瓜,今天自己买的反而都没那么好吃,难道说这就是
+++真的,一直到现在,我实在再没有吃到那夜似的好豆,——也不再看到那夜似的好戏了。
+
11月20日
+今天和 ODE 作业搏斗了很久,到处搜了很多东西,算了 114514 +个级数,还挺有意思的。用解析函数逼近一个奇点邻域内的局部解,这种想法我甚至学微积分 +A1 +的时候就有,当时其实觉得自己什么都不会所以应该很不严谨吧,现在看到了完整的理论就很开心。不知道为什么 +ODE +感觉期中后突然上强度了,可能是期中前的东西确实学过一点的原因,也可能是我函数项级数很菜,或者合并同类项水平不行。感觉他前半学期在泛函,后半学期在泛函且复分析,而且是以本废物可以理解的简明易懂的方式在讲,学一门课赚了两门,好好好。
+周末听讨论班和看自己找的讲义的时候就感觉里面举的例子蛮熟悉的,哦这不就是数值分析的时候学过的那个
+Legendre
+基吗;昨天自闭搓衣服的时候一个在旁边洗漱的姐姐突然跟我搭话,说去年数值分析的时候就见过我,今年本来想上概率论
+2
+最后又没上但也看到我了(,我寻思着数值分析这课我也没去过几节才对怎么还就记住我了,还问我下学期要不要上
+bcl 的凸优化 可惜我已经在学了;今天看 ODE 讲义又开始 analytic
+function 了,乐死,一门课学完之后仅存的记忆用了一年半(
说到学微积分 A1 的时候,突然想起我大一也是和 OJ +搏斗了一整年,然而已经遥远得像在梦里发生的一样了,我现在就只记得大一好像啥也没学,然后微积分 +A2 +学得特别差,唯一有点意思的是学了一年法语。虽然现在也只学了不到一年半的数学,但感觉至少大二上学期学的东西现在还记得不少,甚至我第一次接触赋范空间什么的就是在数值分析,但你现在要是让我去写一点 +C/C++ 我只能说我根本都没这个勇气再动手了,还是写 R 吧(
+发现在和一个助教上同一门课,这算几代同堂(
+++注:本次作业占分为平时2倍;3.6.24假设T是有界的随机变量;提交期限延长至12月4日,共14天。
+
既然占分是两倍,ddl +也是其他作业的两倍时间,那为什么不拆成两次作业来布置呢((
+为什么概率论 2 期末是 15 +周啊,这不是快了吗((。本来想这学期能在这课上学到一点 continuous time +Markov chain 就赢了,结果看现在这个进度根本不可能,把 Brownian motion +讲完就不错了。所以就是复习一些我学过的东西然后把基础打扎实一点,然后估计还要拿个不太好的成绩,乐不出来。
+上周作业有个 2017 年丘赛题(P2),反正我现在一看到 random walk on
+binary tree 就头疼,想起来期中做不出来的那道题也是个类似的设定有点
+PTSD。这一年的题也没公布答案,到处搜了半天也没有,可能等再动手试一试如果做不出来的话还是得自己在
+MSE 上问。前两天还有个数 21
+的哥们从环里加我问我这个题,我只能尴尬地说期中刚考完还没来得及做呢(的确如此),他说问了助教这题和
+Markov chain
+没关系就是硬算,我寻思着这助教原来会提前看我们的作业题啊,那他为什么从来不公布作业答案呢,是因为他自己会所以就怕我们也都学会吗(不是。昨晚翻了一下
+wh 暑假里给我的那本讲义,在第七章的习题里有,但也没答案啊(挠头
昨晚熄灯之后就对着 ODE +的讲义和这道题枯坐,很困很累了也学不进去什么东西,但反正还是能感觉到这周 +ODE +作业有点小难,然后丘赛题也没底,算了几项感觉找不到什么规律,就是很急。后来感觉很累了也没再继续动手做题,就开始枯坐,然后回忆期中的失败,别的课都好说没有特别离谱的,就概率论 +2 +开天窗一个大题还是给我整挺难受的,别的题加起来也扣了一点总之不是很好看,越想越难受了属于是。
+压力好大,周三考运筹我到现在还没开始复习,虽然知道很水,大多数都在优化里学过了,但要人肉算一堆东西的话还是有点难说。我想把 +Gaussian sequence model +在讨论班之前和之后读到学到的东西都整理出来,想去学一下相关的泛函基础,想动手写一写 +Frobenius method +的笔记,高统作业都写完了但说到底也不是很扎实,想回头再看一看,怎么就是做什么都没空呢,每天都在忙什么呢。
+11月21日
+复习运筹的时候一边看他这个 duality 一边乐,太简单粗暴了,连 +Lagrangian +都懒得提一下就把对偶形式怼出来,但说实话用影子价格解释还甚至有那么一点道理,又绷不住又乐。本来懒得多看了,然后刚刚一想不对啊优化是开卷,这课是闭卷,我甚至还得去仔细背一下 +LP duality +那个形式,不然我本来计算就很慢还容易错,什么都现推感觉来不及。可恶啊,优化有什么可开卷的,该开卷的是运筹(
+反正我明晚就要去运筹考场上使劲用英文写解答了,感觉助教批我作业的时候从来不看我写的啥,就直接找我划出来的答案看对不/对。如果全是计算的话这样似乎还挺危险的,算错一个全没了谁受得了啊(
+今天把以前写的作业又重新算了一遍,反正还是算不对,而且发现以前也有步骤不严谨的但是并没有批出来(
+看了下赛马娘下一话的预告,怎么又双叒叕是内恰,绷不住了,第三季的第三是内恰的第三(
11月22日
+下学期高统是林乾,似乎要大讲 decision theory 和
+minimax(
高统课上随便听了点然后在补看前几节课的 PPT
+写笔记(,听着听着怎么突然开始 loss function is convex,然后 take
+optimal parameter,还有 inadmissible
+了(。何必把概统优化运筹分开呢,不都是通的吗(不是
+换句话说其实感觉可能确实就得什么都会一点才行(
下午和室友聊天,我说我前两天读到了一些二三十年前的数学,特别感动,现在又退回一百年前了。结果她大受震撼,说她现在学的东西有很多二十年前都还不存在,还只是课上学的而不是磕盐做的,乐死了(
+运筹期中做了 40 min
+左右就水完了,本来想再浪费一会生命结果这教室实在太热了坐不下去了就跑了(,好好好,期中结束了,cheers(开始满意地吃刚洗好的今晚买的草莓.jpg(好怪哦
11月23日
+今天本来想补上上周至今没写的概率论作业,最后还是看了一天高统
+感觉既会了又没会,难道是在复刻区间套赶 ddl 法(
赛马娘,评,端(
++
这集好像没啥可说的,中段的文戏意外地还可以,帝宝的谈心反而让我越来越觉得第二季实在是强。原来制作组也知道北黑没目标啊。但不知道为什么评分非常低,比上一话还低(
说实话我看完几段谈心和商店街应援之后还感觉观感好多了,结果北黑大晚上跑下楼啊啊啊啊啊啊训练还是给我整崩溃了,包括一开屏又是上次比赛两个人啊啊啊啊啊啊真的是((
+谁说第三季没有 live 了,小北的爸爸不是开了两场 live
+了吗,虽然是兼用卡(
大鸣大放终于出现了,只不过开口第一句是突然问北黑你的目标是什么实在是有点生硬(,帝宝谈心也谈了,如果这些放在宝冢纪念之后就好了。该说 +better late than never 吗(
+高尚骏逸这描写怪怪的,不过刚刚连跪了好几场心情不好很正常,反而是极峰给我感觉看似安慰实则嘲讽(,私服也不是特别好看
+cy
+你的服装设计传统艺能呢。想想高尚骏逸出场加起来应该不超过五分钟就还是释然了(,人设立不起来是正常的,输了就在姐妹面前垮起个批脸也是正常的(,没看到在训练也是正常的,后面突然一生一次的末脚也是正常的((
+反正没有剧情也没关系,后面等角色在游戏里实装了再补个人剧情也行,第三季还就是那个宣传片,开摆!
11月24日
+下午在教室打开门看到门边坐的一个哥们在全屏玩原神,差点没绷住(
+去新土木馆 搅水泥
+建筑材料实验的时候那边正在消防演练,楼道里全是烟,我昨天刚洗的头,我的鼻子,这破专业怎么还折寿呢(
有时候有点怀疑是不是只有特定会触发任务的人能看到我(,搅水泥之前按组领表格的时候大家都在随便拿,我说前面有组号结果旁边的大哥还是没听到我的话就把我的拿走了(。直到他们发现不对在若干人之间传了很久之后另一个哥们把它放回去,我站他面前说能不能把第五组的给我,他还是没听到,绕过我放到讲台上就走了,草((
+然而今天搅水泥穿了一身白衣服,只蹭脏了一点已经是我赢了,晚饭吃香锅又快乐地往上面溅了三个油点((。虽然经常吃清芬但其实还是第一次吃香锅,你这中辣怎么没味啊(
+11月25日
+开始做双十一买的纸模了,似乎小栗帽比麦昆的简单一些,但裁下来几块头发之后人就已经晕了,希望能做完(
+今天写了一天概率论,主要就是在对着不会做的题发呆,还有睡大觉(,相对
+非常失败。这期中周的后劲怎么还没顶完,马上都十一周了,爆了(
太乐了,来点最喜欢的一集(这课显然不是我在上

11月26日
+最近答疑坊接的都是熟人的私活,值班也鸽了不知道多少了,干不动一点,津贴和
+最基本的别因为值班次数太少被踢出去了都
+有点寄。下周打算去补一次顺便写写这周的建筑材料实验报告,要是写不完就补两次反正我每次讨论班之后也都没心情去(,急急急。
晚上 yoasobi 的时候 突然感觉心口疼,20
+岁,一天到晚一副要寄了的样子,鉴定为老猫,喵喵
最近在校内找到了一家品控好价格正常送货上门的水果店,吃了很多在他家买的橘子
+主要是相比之下橘子是最方便吃的不怎么需要洗而且还不贵。想起来《我去世了,然后...》,感觉死前能吃够
+100 个,问题不大(
11月27日
+洗漱的时候听到两个致理数 0 的姐在聊天:
+++A:你毕设导师找好了吗
+B:找好了,是丘中心的 xx(没听清
+A:我还没找呢,现在数学系是不是已经没有有名额的老师了,那咋办
+B:丘中心和统计中心都可以,跨专业也可以,但是要申请
+A:我还在犹豫做运筹还是统计,我之前学运筹那几门课完全学不明白,感觉和运筹相比还是统计简单点
+B:丘中心做应数的老师就那几个,我怀疑现在可能已经没得选了(
+
《还是统计简单点》,差点把这学期在上高统的我吓晕(,上周一直在补落下的进度,看
+Jun Shao 每次都离昏过去只差一点,虽然也确实很有意思就是了 抖 M
+就直说。哦她学的是数学系概统的那几门限选课啊,那确实还好(
但相比之下运筹难在哪了(不是
今天把上次那个二合一的高统作业写完了,进度也赶得差不多了(,binomial +distribution 的二三四阶矩加权和算得我天昏地暗还没有答案,最后 \(Var T\) 比 C-R lower bound +严格小而且完全看不出来哪儿错了(,希望期末没事((
+问题是 C-R lower bound 和 Delta method 算出来的 amse
+一样大,应该就没问题啊,那错的还是 \(VarT\)
+呗,问题是我没觉得错啊,助教看着想扣几分扣几分吧((
++Brownian Motion +的定义看起来非常简单,但其实还需要验证是不是给出这三个条件就能确定唯一的一个过程,还有三个条件是不是冗余。我读博士的时候有个老师讲过一个故事,系里曾经有个搞代数的研究生做了一个很复杂的东西出来,答辩的时候委员会问了个很简单的问题,就是这个东西存不存在,他当时没回答出来,回去想了想确实不存在,就延毕重做了(
+
草(
+连一刻都没有为概率论 2 +写不完的作业和寄掉的期中哀悼,立刻赶到现场的是上周五的建筑材料实验报告,这周日要做的建筑材料课程实验,这周五要做的建筑材料实验,上周布置的生物作业,还有周四建筑材料研讨课要做的 +pre!
+晚上又遇到了两周前的周一在同一个位置上看 GTM +的男生,这次看到了封面,是 GTM 274,和我想的一样(
+感觉应该世界很小,很可能是吴昊的学生,但反正也不敢问(
+11月28日
+睡前躺着看了下今年的日本杯,不用想也是春秋分的散步大胜(。不说秋三冠怎么样了,求你了再跑一年吧别直接去当种马,我什么都会做的(
建筑材料研讨课的队友说 nature +上有一篇文章比较合适可以去看一下,我在心里默念:内恰上有一篇文章比较合适(
+越想越气,我放着讨论班的论文没看,搁这读建筑材料研讨课的论文,建筑材料实验报告还得随便引几篇,建筑材料的实验还有个这课的老师的论文没看要学一下怎么处理数据,生物作业也是文献调研题,看又看不懂,还就那个离谱(
+今天下午骑车的时候把电脑屏幕摔(?)碎了,在教室掏出来的时候大受震撼还以为寄没了,再仔细一看屏幕就碎了挺小一部分,看起来哈人只是因为顶盖变形比较严重。测了下主板键盘什么的都没啥问题,心情好了很多。修是不可能官方修的,只能自己买个盖买个屏幕换一换这样子,-300,本不富裕的家庭雪上加霜(
+
它正好裂在 已经战损的
+二号机贴纸这个地方,想想二号机的战损程度突然感觉好像就不应该贴这个(,遂下单初号机金属贴,只要驾驶员自闭就很耐造(
说实话这个 A 盖翘起来之后反而方便拆下来了,我赢(,B +盖边缘有一点轻微的变形,感觉拼装的时候或许会有小问题,暂且拿钳子掰了一下感觉应该还好,不至于再花几十块钱重新买一个。
+下单配件之后发现买屏幕的那家店在商品详情页写的是“不难,女学生,新手都能自己换好”,销量 +2 万 +,现在真的是 2023 +年吗?退货换了一家,点了个举报,虽然大概也没有什么用,除此之外能作为反抗的选项就是自证了吧,我拒绝。
+出于好奇查了下官修的价钱,感觉自己动手的话还是赚麻了又不觉得 300 +贵了((。后来想起来还可以带着配件去科服修,但也有点想自己拆着玩(?),到货再说吧。
+11月29日
+上午和中午认真听了会生物课
+然后四道雨课堂题错了三道,充分说明我是真的学不了这玩意,然后
+在队友完全失踪的状态下 把建筑材料 pre PPT
+做了,体育课前把建筑材料实验的实验报告写完了。今天是认真学专业课的一天(迫真
晚上本来想学一下今天的高统,然后想想作业也不是很急还是算了,更急的是概率论(,但不知道为什么不是很想学这个东西,期中裂开之后心态上有点摆了
+这不行吧。结果喉咙越来越痛直接睡了,原因不明但除了感冒了之外还能是什么呢,吃阿奇霉素.jpg
回寝室一看之前买的药都过期了,心态爆炸(
+11月30日
+喉咙还是好痛,现在是连带着头也好痛,人有事(。今天除了在睡就是在难受得睡不着,一天做了四道概率论,急死了(。这个月还只有 +30 天,更急了((
+吃西瓜霜的时候看了眼成分表,辅料是蔗糖,那你不标一下营养成分表告诉我每
+100g 有多少糖我哪知道要吃多少啊
马娘,评,端(
++
周一看了预告之后我还在想,看起来是日常贴贴回,这还能做烂了?
+看完:到底是我有问题还是 KAI +社有问题,感觉有点理解不了制作组的精神状态(
+早晨一起床突然说要去 随机公交挑战
+旅游,那光钻要是没被吵醒的话你就自己一个人去了呗,思考了一下和朋友之前出游的情况感觉到处晃悠还挺能理解的,这随机公交挑战还给我看出几分亲切感(。然后这个复刻光钻突发放狠话的二度离婚是怎么回事呢(,镜头一转就开始比赛了又是怎么回事呢,有一种比赛前的一回合选择了外出所以半个月都在摸回来突然比赛也能赢的错觉
上次北黑和光钻冲线的时候中间沉默而且没有特效的是黄金伶人(没版权)我还能理解,这次中间是高尚骏逸啊,怎么会是呢(。但是远景过弯的时候高尚骏逸的腿真的好可爱啊,好像觉醒
+xp 了
赛后为什么又是无视了第二名开始和第三的光钻贴呢,按理说第二名难道不是很重要吗,一边压制光钻一边逼迫北黑,换句话说光钻连高尚骏逸都跑不过还说没超过北黑什么的真的没问题吗。比赛中途也一直无视,很难想象之后要怎么刻画一生一次的末脚,要么就别写了,不然骏逸还要惨遭拥有一个单人回
居然有樱花桂冠,好评,但我总感觉突然插宣传片莫名其妙的,难道是对第三季的刻板印象导致的(
你看看第二季帝宝麦昆贴都是抱在一起互相鼓励,为什么小北和光钻贴就只有握手,真不熟(
其实我还是疑惑光钻冲线的时候这个闪回是什么意思呢,一直带着自己去看前方各种风景的是小北,ok +fine,但上次不是你赢了吗(。怎么不是想北黑这段时间以来相比自己进步了多少(然而我完全感觉不到!)而是在想这个(
+感觉蜜汁演出好多,不知道慢动作入闸是在干啥,小北比赛中间突然开领域(确信)我还以为给安排了点不存在的骨折戏份(,结果就这(。念叨凯旋门赏念叨到现在终于给了大鸣大放三个镜头,求你了下集别又把人家给忘了(。高尚骏逸冲刺的时候终于有台词了,所以下一话会是日本杯吗,那我大鸣大放呢((
+不过贴贴确实好看,特别好。
+这番真的还有必要继续追下去吗,真的有必要吗(
+]]>摘要来自《游焦山小记》,是高中时候读的,很喜欢,是那种读完不自觉会勾起嘴角的小记。但居然一直记到现在。
+++予自丁酉来游,未遑穷讨。人事参商,忽忽数年,始一续至。又以羁绁俗缘,卒卒便去,如传舍然,不知此行定复何急,良可浩叹,自今以往,日月不居,一误难再,赋归之后,纵心独往,尚于兹山不能无情。当择春秋佳日,买小艇,被宿松寥阁上十日夕,以偿夙负,滔滔江水,实闻此言。
+
1月1日
+高统看完了,现在只要把 cheatsheet +抄完就好了(迫真,乐观一点的话明天还有机会能看看优化,我不好说,有机不会(
+奇怪的跨年方式增加了.jpg
+1月3日
+大学以来强度最大的一天结束了(,考了三门,期末一下子过半了(
+早上生导评价为还好没复习毕竟复习也没用,不过早晨七点多去考场在马路上骑车骑得很爽,自从换车之后骑行体验大幅增长,有的时候还在想华子有没有什么相关的社团之类的可以玩玩。这考试一半感觉小有把握,三分之一感觉能选一个出来但不大确定,剩下六分之一的判断题看不懂在说什么但你既然这么说了只要听起来不太离谱我就当你是对的好了.jpg
+然后一刻也没有为寄掉的生导而哀悼,立即赶到考场的是高统。拿到卷子半小时写了两道感觉稳了,再仔细一看怎么考 +U-estimable,非参数的东西不是特别熟有点小慌,我知道他那个 hint +大概是想让我说明 U-estimable with order \(m\) 会引出一个至多 \(m\) +阶的多项式,然后证明开个方就寄了,线性的部分只要想到对 population +做一个线性变换然后积分就好,脑子还算清楚想到了是类似于证明 \(\sigma^2\) 的 U-statistic +至少二阶那个定理的做法。但平方那里感觉写得不大行,似乎当时就已经很紧张了。还有个算 +amse 的题想了半天 sample variance 的渐进分布是什么(,还要讨论 \(\max \{0 , \bar X^2 - S^2 /n \}\) +的渐进分布,寄,没算出来,大致写了下我猜测的结论是 \(\mu \neq 0\) 时和 \(\bar X^2\) 以及 \(\bar X^2 - S^2/n\) 的 amse 一样,如果 \(\mu =0\) 的话这个怪东西会 asymptotically +more efficient,听起来蛮合理的因为这个题的目的是在 estimate \(\mu^2\),你要是让统计量都小于 \(0\) +了那还估个啥。这个时候都快十二点了,然后突然想出来前面那个 optimal +decision rule 的题怎么构造了,拿出最大算力算完手抖着交了。
+晚上就出分了,好快(,点进去发现好高还以为给我登错分了,看来我写的猜测的结论也给了点分,以及均分也没我想象的那么高,好好好特别好。前两天说感觉这课前十五周舒服得像在泡脚,课好作业好玩学到许多,第十六周写 +cheatsheet 就感觉像在喝整整 15 +周的洗脚水,今天考试发现之前喝的也没用(指 cheatsheet +几乎没用到,考前说要考定理证明哥们抄了满满两面结果完全没考,不讲武德)又被灌了一桶,但阅卷还是放过我了,真好。
+晚上运筹一个手解 \(3 \times 4\) +大小的线性规划没算完,评价为恶心人用的。不过这课期末占比 20% 所以考 50 +分就够用了。
+优化怎么办呢,感觉学的 Newton's method +已经是很久以前的事情了(,是不是应该感激他后半学期讲算法没讲梯度下降(
+1月4日
+++是不是应该感激他后半学期讲算法没讲梯度下降(
+
我昨天在说什么(疑惑,其实我想说的是他没像数值分析那样讲梯度下降,毕竟这课的 +iteration \(x_{t+1} = x_t - \eta +\Delta_t\) 里面的 \(\eta\) +全都不用求直接说是 backtracking +得到的就糊过去了,数值分析那个讲法考前一天才看的话真的会死人的(
+今天凌晨试图在 C 楼刷夜,但我忽略了昨天早上是六点四十起的,把 scribe +notes 过了一遍直接倒在 C +楼隔间的懒人沙发上睡着了,睡得很暖和醒来之后又觉得好冷直接绝不调,看了会笔记然后回寝室一觉到中午。但是评价为睡沙发真挺舒服的,我还查了一下同款只要两百多,想买一个放家里(不
+一天速通优化,晚上离开教室的时候看到还有课友在抄 +cheatsheet,安心了一点(不
+++我的 cheatsheet 除了 cheat 了我自己之外什么用都没有
+
更棘手的是明天考完优化还要紧急重做组员今晚交上来的建筑材料实验的 +pre,有一说一不想做可以早点告诉我让我有个心理准备自己解决,没必要到最后一刻交出来一个显然不是用手更别说带没带脑子做的东西然后确信有人会救场。
+1月5日
+这个 b +优化(,我被优化掉了((。反正我承认这课我学得不咋地,但考拉了也没什么值得自裁的,就是不会,期中后一节不落地去上课也没用,什么算法设计,不会.jpg。
+蹲个调分,不调也随便你(,以后还是只在数学系/求真/统计中心的范围内选课了(
+反正我真有点 PTSD +不想整优化了,更不太想碰完全不沾统计的算法(。还是统计好,高统考完两天了我还时不时会去想没做出来的那个题,今天竟突然明白了,而这个 +b 优化考完不到 12 小时后瞥到昨天的日记,backtracking +是怎么做的来着?
+下学期真的还要选组合优化吗(,求真课会不会好一点呢,要不干脆还是去上计算概率吧(
+中午基本没吃饭,感觉早饭午饭吃的面包加起来还不如喝的酸奶多(,考完试就去四教开始赶下午建材实验 +pre 的 PPT,成功在新土木馆讲了一些凸优化和 loss function +凑时长(,不管最后结果怎么样至少我觉得节目效果不错((。晚上大吃一斤香锅(?)结果吃太撑了,在猫超散步不知怎的看到买一送一就买了两瓶 +costa +的燕麦摩卡,付了款才想起来我超它买一送一肯定是因为不好喝啊。到教室就开始那个睡,一直睡到教室关门,还有一个实验报告没写,优化作业还没有打成 +LaTeX +结果还是在废纸堆里找到了上周写的纸质版,明天要赶一个五千字的结课论文,建筑材料一点没学下周二就考了,我急死(
+1月6日
+今天莫名其妙开始咳嗽了,晚上回来找上次咳嗽时候买的药找了好久,两个月里咳嗽两次发烧一次,20 +岁老猫.jpg。
+不过写了一天工程与法律(一个到了期末我才想起来它的存在的限选课)的大作业,搁那逆转裁判啊不是瞎判案子,好快乐(,给我整得寒假都有点想玩逆转裁判了(。我发现写这个东西和科研差不多,遇到一些不知道怎么判的情况加一个条件就会变得好判,那就编一个上去,看起来别太离谱就行(
+下面是一些整活欣赏(x
+
你们都是谁.jpg
+迟先生 驰先生,混入!

为了说明被告已知和原告签的是挂靠合同直接调一个吃饭时候的监控真的没问题吗((
+这些个被告怎么对一些对自己不利的证据全都无异议,高 风 亮 节(
+
任 人 唯 亲(
+1月7日
+又发烧了,新年第一烧(啊?,上次是十四周周三,这次是十六周周日,二十天内烧了两次,这个 +b 学校((
+但我不好说这次是什么情况,我觉得可能性最大的是室友为了缓考量统把自己冻感冒了,然后我这几天强度巨大又被她传染了,如果是的话真的难绷(
+还是咳嗽,但是没有昨天严重,喉咙不疼,又有了鼻塞之类的感冒常见症状。白天取了几个体温的样本感觉方差很小,upper +bound 是 37.5,lower bound 应该就是 37 +度,甚至有的时候按照标准来说不是发烧,但我体温一直有点偏低,而且感觉不舒服,就当做发烧好了。晚上感觉越来越不舒服,现在是到 +37.8 了,乐。
+看了一点建筑材料的 PPT,它周二就要考了,真的很急。
+1月8日
+昨晚开始往高了烧了,吃了退烧药之后感觉整个人烫烫烫完全睡不着,连带着喉咙痒咳嗽打喷嚏甚至右边智齿都在疼,很急,在床上把手机和 +pad 全玩没电了到五点钟才睡着,甚至还看了点 PPT(
+明天考建筑材料,很神奇的是我勉强算是复习完了。我的评价是随缘吧,然而这学期怎么有这么多考成啥样都随缘的课,感觉绩点危(。虽说出国壬
+3.7+ 管够 3.8 挺好,但 3.8
+在某个书院好像有点活不下去甚至都该紫菜了(。(x
1月9日
+昨晚一直挺好的,直到我去洗了个澡回来就开始不舒服了,一量 +37.5,哈哈.jpg。今天白天也降下去过,到晚上又 38 +度了,这绝望的轮回。为什么还在烧,我觉得这下大概率肺炎或者最近流行的什么甲流乙流了,寄。
+不管怎么样作为一个正常人断断续续烧了三天总是不太正常,而且都是白天还算舒服从傍晚开始烧,挺肺炎的,明天该去医院了。
+哦,今天还考建筑材料了啊,抄 PPT +水课,糊完跑了。附带我在后排全程咳嗽,咳到老师来问我要不要帮我打杯水,咳得我感觉脑浆都晃匀了反正现在头是震得挺疼的,对不起所有人.jpg
+1月10日
+昨晚又来了一轮 +38.5,人都快烧傻了,今天爬起来去了趟校医院,颇有一种被塞进猫包带去看病的错觉,事乙流(
+出门的时候都做好今晚彻夜在北医三院吊盐水的准备了,换洗的衣服都收拾了一个袋子只是没带上,还查了查车道沟附近有没有什么好点的酒店可以去休息的,结果在校医院开了盒奥司他韦被赶出来了,哈哈。事后想想可能再不去医院病都要好了(开玩笑的,不吃奥司他韦估计还是寄
+所以前两天为什么不自己买个试纸测一测呢(,被自己蠢到了。光搁那发烧吃退烧药退烧吃一些没啥用的药发烧吃退烧药了,这绝望的轮回(
+凌晨烫烫烫睡不着的时候看了点《繁花》,一个是因为我之前就特别喜欢辛芷蕾(虽然如懿传真的很难看吧但她真的很美),再一看似乎江浙一带练一练就能讲上海话的演员都到齐了
+甚至连 papi 酱都来了(,半夜点开测试了一下来沪 14
+年外地人的沪语水平,什么嘛不看字幕也是能听懂的嘛(x
不用看评论就知道肯定有吐槽演员洋泾浜的,我是听不太出来只觉得有一些语调比较怪,反正我讲起来更洋泾浜(
只不过这玩意怎么能拍出来 30 集的,二次元当久了有点看不动 13
+话以上的作品(
1月11日
+ +昨晚又来了一轮 +38.5,哈哈,已经懒得写了,反正今晚的也已经开始了,就是没那么高(
+下学期一定摸一点不能这样上强度了我超,辛苦搞了一学期到期末歇了算什么事儿,崩溃((
+以前觉得能在床上躺着真是至福,现在一想到带着手机电脑 pad +温度计耳机水杯冷毛巾和药爬到床上,在漆黑一片里面烫烫烫然后等到退烧了才能睡着中间室友要是要睡了还得憋一阵子不能咳嗽,就觉得睡觉也好难受,要 +ptsd 了((
+今天临时发了两封要课程推的邮件,虽然都还没回但突然得知要推荐信之后我开始思考该问谁要的心理活动就差点没把我尴尬死(。问就是我压根都不敢去找 +lq/ypk,只能在统计中心找两个上过课成绩还好但除此之外完全不认得的老师要课推这样子((,要是去数学系要推的话我恐怕只能找 +lzx 了,其他重量级一点的老师的真数学课我都上得一塌糊涂,崩溃((
+1月12日
+病中在床上摸了摸光叔下学期的讲义,不得不说虽然我实分析当初学得一般,但还是在概率里一边做一边学常读常新很久了,感觉还行。组合优化不玩了的话干脆开学手选一个这玩意好了,反正说是还能少量扩容。
+为啥要个课推都这么难,闹麻了。如果 wty +还没走的话其实还可以找她问一下的,只不过她那个生统离我现在申的这玩意更是差得远了。目前手里只有一封,可以的话最好能找到 +zzy +要一封,毕竟这个项目看起来就没有理论,我能理解的部分就全是在搞数据,但想一想总比打灰有意思。zzy +下周要来录课感觉可以当面问一下,正好录的是之前上的那个线性回归,这两天就算是跑一趟伟清楼我也跑不动,今天在楼下一摸自行车座都积灰了。
+今天正好看到统计中心发了招聘通知,招一个 AP 一个讲师,毕竟 wjd +也要走了,要不要找她要个推荐信留作纪念呢,笑死。不知道她还会不会继续在高校,据我所知她是做咨询的。我看她下学期开了 +11 学分的课,不知道是不是以前也这样但有点哈人的。
+还是看看近处的 ODE 吧(
+1月13日
+病了一周把《繁花》看完了,还是不错的,就当回家之前做了 20 +个小时沪语听力,那托福怎么办(。
+突然发现这学期的笔记到最后都鸽掉了(心虚,高统后来转纸质了体验挺好,优化感觉不值得我每周花时间打字(。
+zzy
+答应给推荐信了,虽然她热情得让我有点怀疑到底谁是甲方(,姐姐真好谢谢姐姐。挺好的,现在就还有个
+PS 没写了,写不出来 但反正限定是固定字体大小的一页 A4
+纸那似乎也不多,感觉只能编一编统计和 IE
+之间的关系毕竟我校的统计中心还就那个在工工。考完 ODE 再说吧(。
还有两周回家,考完试除了去找 +ypk,摸实分析讲义和练托福之外还可以干点啥呢(还想干点啥呢(
+1月14日
+这一天天的就没有个身体舒服的时候.jpg,这下 ODE 有点小急了(
+1月15日
+这一天天的就没有个身体舒服的时候(复读
+1月16日
+考完了,这 ODE 不过如此,虽然谱性质我是一点不会放了个 15 +分的题,正经学分析的时候再来吧(
+推荐信还没交齐,急急急急急。PS +写不出来,这个倒是没那么急毕竟掌握在自己手里,这就打开 GPT +争取睡前写完.jpg
+1月17日
+开始学托福,但是上新东方 TPO
+做了两篇阅读就觉得有点无聊了(,感觉不如高中的时候考的校卷难((,啊不是,感觉随便看看了解下题型和流程就行了没必要做多少,还是练口语和写作吧。然而口语肯定是回家对着墙练或者等室友走了之后在寝室练,写作现在背了考前不会忘吗,那做听力吧,啊不是那还准备个啥闲着没事听听算了((
所以既然也不难为什么到现在都没考托福呢,需要语言成绩的时候啥也没有就挺崩溃的。
+最急的是到现在推荐信还没齐,马上 ddl 了,zzy
+答应给推的时候特别热情但为什么咕了(,老师都好忙啊(。邮件催了一下但还未读,感觉要么今天要去加她微信问一下要么得早点去蹲伟清楼了,哪个都是社恐地狱,能不能只交一封推荐信呢(。要不再约一下
+ypk 去一趟伟清楼全部解决好了(不是
说起来这个霸王茶姬和茶话弄有啥本质区别吗,之前一直听人说好喝所以特别火,去万柳的店看起来也不怎么需要排队。所以说茶颜悦色难道会比霸王茶姬和茶话弄好喝很多吗(质疑,感觉不能抱太高期待(?
+1月18日
+UTokyo ESEP 2024 申请结束了,催推荐信一直催到 ddl
+前半个小时,不仅急坏了而且催的时候实在忍不住脚趾抠地,但还好交上了,感觉申个没什么用的暑研身心都受到了不小的摧残
+所以说真的非润不可吗(。越发提醒我要开始贴
+ypk
+了不然找老师要个课推真的好困难(这和课推不课推有关系吗(。不过今天去了一趟才知道
+ypk
+已经不在伟清楼了,统计中心只有他搬去了焊接馆,难怪有一次讨论班是在那边开的,我不理解但总不会是他也要润了吧那我怎么办(,按理说
+wty 走了之后伟清楼不应该更加宽敞了才对吗(?
上个秋季学期我就在申 UTokyo
+的交换,院系二选一也没把名额给我,拿到名额的哥们也没真的去,麻。这学期又在申
+UTokyo,这次都不好说整个华子能不能有名额,感觉就图一乐吧,还得继续找保底。但我暑假真的好想去日本玩啊,我还在
+PS 里写 I'm a big fan of Japanese anime 什么的现在想想好丢人
下午一只手拿电脑一只手推车走回寝室的路上突然推不动了,一看路上有一根类似丝带
+实际上更像衣服拉链侧边的布条(?)的东西一头缠在了牙盘里,这是马路上该有的东西吗就算有它就应该缠在车上吗我真是摸不着头脑.jpg。进车棚把踏板轮胎牙盘裤子清理干净之后想想感觉得回去把它捡起来丢掉,在路上推着车走缠进来就算了也就是停在马路中央扯出来会尴尬一点,如果是骑车突然被缠感觉挺危险的。刚走回事故现场就发现了另一个正在和它左右互搏的路人,绷不住了((
好困好累好饿但是又不饿清华大学你把我害死了(
1月19日
+给导师发邮件,但已读不回了,我又急了,这是咕了一学期的代价吗(
+很摸地听了一些托福听力,但是只听了 lecture 没听
+conversation,这有什么练的必要吗(二度)。然而做的最烂的是一篇讲
+cat domestication 的,所以为什么要驯化猫猫,猫猫又没用((
1月20日
+ +发现五道口开了家万圣书园,虽然二楼还没开放,急急急。上次去还是大概这学期前几周的时候去华子南门那家店,至福。逛了一圈,看到几本想看但是没看的书,还有几本感觉有点意思的,但好贵,没买,回来看电子版((
+回来路上第一次发现西郊宾馆藏在王庄路旁边的一条小巷子里,里面自行车似乎不让进,走着进去探索了一下。好破
所以说被取代的是哪家店呢,逛了一圈感觉没看到 也没听到
+之前那个机厅,不会是寄了吧,滴——蜡——熊——
今天闲着没事在翻华清大学课程攻略共享计划,开了点盒(。看了眼计量经济学的卷子怎么有且仅有线性回归,还一股
+zzy
+那个课的味儿,所以说数学万一学不下去的话可以转行的对吧((
Wake up with no email everyday(
+1月21日
+有什么能比熬了个大夜读完一本书然后发现这书好烂更令人难过吗,躺在床上气得睡不着(。好不容易睡着了结果做了个梦,梦到一天要在北京上海之间来回,到了下午一点想买回上海的票结果发现全卖完了连动车票都没剩,想了想京沪高铁票岂有卖完的时候,肯定是假的,然后就醒了(
+起床打扫卫生洗衣服,到晚饭把 窖藏两个月
+买来放了俩月没喝的奶啤拿出来,本来想去食堂一边吃饭一边喝,后来还是社恐了吃完饭回来在寝室阴暗地喝的。意外地很不错,平时酒仅限于浅尝
+我算什么沙东人,但这个除了闻起来有点酒味之外喝着更像益生菌饮料,还想着下学期一定多买点,带去上课喝(不是,结果过了一会劲上来了上床躺了两三个钟头,草((
Wake up with no email +everyday(
+1月22日
+每年一度的看《恋爱的犀牛》,去年是买了票去蜂巢剧场看蝴蝶组的演出,前年似乎是看了郝蕾段奕宏版,这次不知道为啥点了高中话剧社演出的版本,这男主还挺帅的我印象里好像当时知道他叫什么名字但现在忘记了
+现在再看还是觉得真的演得不错。当然这也是我第一次看这部话剧的版本,不过第一次也是在
+b 站看的,社恐没去现场。这剧本太伟大了好想背下来啊(。
但我读剧本好像是在看话剧之前,读了才想去看的。后来看到过带孟京辉廖一梅的采访的剧本版本,才知道“黄昏是我一天当中视力最差的时候
+blahblah”那句话是陈建斌说的,草,四大爷还是有点浪漫在身上的(
Wake up with no email everyday(,但我今天才知道 wwc
+组里目前没有本科生,有点惊讶。所以说万一真没人要我了其实去他那里也可以吧
+看起来还有机会跑路 econ 的样子(然而我最近为什么老在想跑路 econ
+呢,感觉也没有完全学不下去才对(,而且我是他两学期课程老粉了而且他认识我而且我还已经拿到过他的推荐信了((
1月23日
+出去玩了一天,但 wake up with an email
+today(。本来想今晚还收不到的话就去给 wwc
+发邮件了,这下(暂时)是错过了,也不好说之后会不会还是要跑过去((x
后面几天(不出意外的话)去天津玩,出发之前正好跟 ypk
+约了个午饭(,(不出意外的话应该算是)稍微有点极限,急急急。电脑就不带了,日记先咕个几天,26
+号再说。给因为乙流导致本来就很短的一月日记雪上加霜
上个月被何老板拉着报了个美赛,今天发现 2.1 +就要开始了,我还不知道我是去干啥的。看知识点只感觉理论嘎嘎清楚,Markov +chain 哥们能给你把 Durrett PTE +那一章空口讲一遍,但是咋用来解决问题呢,乐了。
+1月26日
+回北京了,收拾东西明天回家,累累累,急急急,明天高铁上慢慢补上前几天的(
+UTokyo ESEP
+项目的负责人发邮件跟我说不接受三月补交托福成绩单,寄。上次在 thos
+上填申请的时候未央教务就问我为什么能参加考试周期间开始的项目,这次
+UTokyo
+又说清华本科生按理是不能按时到的让我解释一下,反正我都说考试周没啥安排能赶得上,先把饼画了再说,危。
+但是用一下归纳法的话可以知道实复分析都是考试周一开始就考掉了,统计中心的课也都不进考试周,应该没啥问题吧。至少感觉比起能不能申请得到来说不算很大的问题(
1月24日(补
+主要是,去找导师的过程有点震撼我了,所以写一个(
+早晨醒来看到一个:
+++“你会干什么啊?” “做证明。”
+“除了证明呢?” “算 cohomology。”
+“应用数学呢?统计?” “不会。那种东西有用么?”
+“那数学的以外你还会什么?编程?” “LaTeX。”
+“额。那你有没有什么爱好?” “看书呀。”
+“一般看什么书?” “Springer GTM。”
+
统计壬被骂了,但统计壬也别的什么都不会啊而且也不会算 +cohomology,又作为假数学壬被骂了一遍((
+在清芬三楼蹭了 ypk
+一顿饭,然后去参观(?)了他位于焊接馆的新办公室,没有电梯,楼里还一股味儿,听说焊接馆还发生过实验事故,具体来说就是炸了,才知道
+lq
+果然也搬过来了就在他隔壁,但统计中心官网上没更新,哥俩好。不知道伟清楼
+209 现在改成啥样了,但有独立的办公室是好事(
++ypk:具体来说你对什么样的问题比较感兴趣呢
+我:(疑惑)我不太会写代码,然后希望做更理论一点啊更准确来说是比较 +rigorous 的研究(比划)就反正我学统辅学得很痛苦最后 quit +了,在数学系学分析和代数那些基础课倒觉得不错,应数各个方向都可以考虑吧
+ypk:啊...再具体一点呢
+我:(疑惑)(我寻思着我也不知道什么问题好做啊)(试图转移话题)老师您最近有什么关注的问题吗
+ypk:我前两天和华为那帮人见了个面,讨论了一些 GPU +加速的问题,就比如怎么让矩阵乘法算的更快一点,要不你看看这个
+ypk:这是我前两天看到 Zipei Nie +发的随机优化的一个方法反正挺复杂的也不用写代码全是推公式,你看这些玩意这么复杂应该比较满足你对理论的要求了(。工程一点的做法的话 +Deepmind 用 AI +做了一个很不一样的,你回去顺着这两篇往前找找整个问题发展的脉络,开个 +overleaf project +写一写然后把链接给我吧,这是不是能起到一个监督的作用(
+ypk:你回去也可以读点 TCS +顶会别的文章看看还有没有感兴趣的话题,啊对就算是 TCS +也可以不写代码的(
+
我吓晕了怎么世界的尽头又是 CS(,现在投靠 wwc
+还来得及吗我反而觉得他做的时间序列和 M-estimation
+之类的东西变得靠谱起来了。先看一点试试吧,希望人没事(
看的时候就觉得 Zipei Nie
+这个名字有点熟悉,反正是上海某年的一个数学国家队,但不知道是华二的还是上中的。回去一查果然是上中的,确实,你华二数学什么水平还来碰瓷
从焊接馆出来头嗡嗡的只知道这事儿听起来和统计离得有点远(,但反正还是数学就问题不大(迫真,之后要是觉得不行再说吧,wwc +那里又没人。回寝室寄了个快递洗了点衣服,然后很极限地去天津了。
+1月27日
+回家了,好累啊(
+本来想在路上补一补前两天的日记,看了个电影就睡了,咕咕。今天把去年的柯南剧场版看了,虽然很烂就给了个 +6 +分但实在是乐得不行,很久没有看番笑得这么开心了((。顺便把柯南系列的作品都补标了,发现除了若干烂得这么多年来都一直有印象的剧场版之外别的都不记得了,也没怎么打分(
+1月28日
+白天在陪家人逛街,从 1.23 到现在每天都在外面
+还一天一杯奶茶,真有点摸了。晚上回来看美赛 O
+奖论文,没啥头猪啊不是没啥头绪,方法也不是很会,最后变成了在玩一些没啥用的小工具,但愿最后论文能看起来漂亮一点。
1月29日
+凌晨的时候在看美赛的论文,感觉 A +或许还是能做的但队友不一定爱看,去年的 A +似乎都不怎么需要数据直接编然后跑模拟就行了。BCD 我个人都不怎么想考虑,E +和 F +就很有一种老婆饼里没有老婆所以说数学建模和数学有什么关系的美感。看着看着给我都整婆罗门了,这简易的初等数学模型有什么学的必要吗,我知道它真的有用至少在这个比赛里比数分有用(,但我不大想仔细看。这比赛真值得我花四天时间打吗(
+看不下去了,发癫的时候上豆瓣标记已读了 PTE。
+一般来说到了寒假就需要重温一下明日方舟,简单看了眼最近的活动,怎么在种菜(。都不想下载了,机制这么复杂的游戏如同推导之前 +assumption 堆了三页纸的定理,总之是丑的(胡言乱语
+美赛也暂且不想看了,后天急了再说,开始读一点自己的论文。目前的进展是新建了一个 +overleaf project,但还没勇气把链接发出去(
+注册一亩三分地的时候发现我的 id 被用过了,没绷住((
+开学前大概要把托福口语和写作准备好,稍微读点论文,能排得上号的话在九院把智齿拔掉,投几所学校的暑研项目,还得打个美赛(。之前还想着感觉能学点别的,比如 +PTE +没看的几节,先学点复分析啥的,现在看来似乎没什么时间,把前面这些事做好就不错了(
+1月30日
+ + +不知道为什么今天开始看时间序列了(绝对不是想跑路
+wwc,下学期 mld 休假没开课所以直接发了
+slides,看了看感觉这不就是随机过程吗这我熟,问题不大。翻着翻着我超怎么这么猛,他甚至还讲
+ergodic theorems,好喜欢啊不是 有点逆天。回头看了眼 V1ncent19
+的课程测评,我的评价是在统辅大讲理论的都是好课,比那个线性回归不知道高到哪里去了,看起来值得好评(x
然后又一想,wwc 那里没人是不是因为他去年休假了来着。
说起来我多元统计至今未修(去年春季退课了),虽说是统辅必修课但感觉也问题不大的样子。我又不需要统辅学位
1月31日
+累累累(
+ + + +]]>4月1日
+终于把总结交了,凌晨两点钟已经是一个半梦半醒的状态了,越看越觉得我验证出来有点问题的一个矩阵计算真的有问题,于是把它写进了总结里面,白天也没想着再看一眼就给
+wwc
+发邮件了,想起来这件事的时候蚌埠住了。我现在都没有勇气再打开那篇文章和我写的总结研究一下到底是不是真的有问题,但其实问题不大,我只是觉得每个
+extended covariate 前面那个系数并不是完全相同的,但改一下总之还是能做出
+Cholesky 分解的形式 而且还能体现 node
+heterogeneity!,就无所谓了((
话是这么说,但是邮件被已读不回了,虽然这很正常毕竟它真的很长,但我现在真的是很难不害怕(x)。我明天又有点不敢去上课了,但又不敢不去(,大概就是这样的一个状态。
+早上去办护照,照澜院的派出所倒是对发型很宽容,允许披发和刘海拍照(当然也没到盖住眉毛的程度。就是不知道为什么我早上起来化妆半小时,拍出来还像通缉犯捏(
+悲报:清芬瑞幸关门了,我今天是骑车去清华科技园那家瑞幸取的咖啡,就是不知道有早课的话要怎么办比较好。现在是真的有点喝不得瓶装了,既没有冰又含很多糖还不是现做的价格也差不多,这怎么喝嘛((
+4月2日
+昨天问教务才知道施工实习需要用学校官方的暑研项目(只有这种才有批件)申请延后,我歪打正着因为懒得自己找也没什么办法找暑研,就只投了两个官方项目,正好中了一个,暑假就可以歇了。
+但现在的问题是,明年还有这么好的运气吗,那我是不是最好今年寒假去把它解决掉。但如果寒假补实习据说给分会比较糟糕,也不知道过年期间能不能给放假,虽然这些事情找零字班问问就好但我问的那个学长怎么不回我(。何老板在用暑期课程申请替代,倒也可以看看他的情况,如果成功了的话明年学一下就行,不成功的话,我真的不知道是今年暑假去实习好还是寒假补实习然后顶四学分低绩点好,比较缺乏信息的一个状态。
+好累,好累,好累好累好累。科研感觉得暂时咕一下而且最近也没什么活(如果我不去自己找活的话,下周三就基物期中了,我还是一个你问我波长是啥我只能干两碗饭的程度(
尤其是昨天今天加起来写了 23
+道实分析,梦回抽代(但难度其实也差不多就梦回抽代,我尸体真有点不舒服了。诶,但我周三近似于没课,所以说清明假期已经开始了,嘿嘿。
4月3日
+感觉,打开一个搁置了三天以上的 overleaf project +需要非常大的勇气((
+节前把目前所有的作业写完了,每个难缠的 1 终于都乖乖变成了
+0。我现在明白为什么周三效率最低了,因为这一天要写基物作业,一边呜啊呜啊一边写,写完之后都得缓好久。今晚在预习(x)基物,努力理解了一下偏振到底是在干什么,所以说,波长到底是什么来着((x
晚上洗澡的时候旁边两个人在说:
+++A: 我今天终于去做实验了,这是我第一次杀小鼠,我一次杀了八只!
+B: 是不是你的师兄师姐杀不动了
+
路人害怕.jpg
+4月4日
+学习偏振,在我完全理解一切和我啥也没明白之间反复横跳,感觉是学物理的一个正常状态(
+我跟群友说学这玩意真的好痛苦,哪怕只是背答案,群友锐评基物 2 +和实分析其实都是 4 学分,你看着办吧.jpg,好崩溃((
+4月5日
+++A: zgy 会点名的你们也不去?
+B: 哥 早八
+别说点名
+叫我起床出门捡人民币我都起不来啊
+
分享一则环友发言(
+4月6日
+这清明莫名其妙就过完了,急急急,实分析怎么办基物怎么办(
+今天 28 +度,去清华科技园买咖啡突然就变得痛苦了起来,想起去年端午每天都要死在路上一样的状态,求求清芬瑞幸早日开业(
+4月7日
+最近越来越容易失眠了,是不是睡前最好还是别写题,写码和物理作业倒是经常写着写着就困了,写完数学不缓个一个小时感觉都有点睡不着,哪怕只是光叔实分析作业这个水平(?(。于是今早就没去计算概率,非常遗憾没看到求真祭孔现场视频,只不过运气不错的是今天讲
+Markov chain 的理论,耳熟能详,而且还没讲到 MCMC,下次一定。
虽然实分析也耳熟能详了,而且光叔到现在还没到当年林勇大约第三周的进度,但我还是认真复习了一下他这个讲义
+但跳过了一些证明。现在就是一点轻微的混乱,有的时候会稍微怀疑他俩是不是相容的而不敢乱写(。他这个期中到底会是个什么情况啊,感觉每周狠狠写一堆作业然后狠狠写一份习题课卷子,实际却也算是没怎么学,有点小急。
来点 锐评 批注((


4月8日
+基物终于看完一遍,然而看完变换光学忘衍射,看完衍射忘偏振,看完偏振之后,屏函数是什么来着?希望
+csm 守序善良一点,我都两学期老粉了说不定基物 3
+还要见面能不能捞捞(
唯一的好事是找到了失踪半学期的计算器,然后 csm +在群里说这次用不着,全都是简单计算。我疑惑了呀,所以说不涉及乱七八糟的波长甚至不涉及 +\(n_o, n_e\) +之类的吗,那还能考什么(,难不成考证明或者直接用符号计算吗,我训练集里没这些啊(
+4月9日
+基物怎么办啊,算了,很快就会结束的(
+原来托福成绩单还会邮寄一份,两千块钱听个响,啊不是,已经听了好几个响了(。出分的时候看到成绩单上有当天早上考前给拍的蓝底照片的时候已经崩溃了,结果还给我寄一份,受不了了((
+期中考完不知道有多少作业要补,还得讲组会
+的同构异形体。为什么不开组会而是让大家一起听单人报告,太可怕了吧(
4月10日
+基物期中不知道为什么这么多画图题,不会,差不多得了(。这个班成分还挺复杂的,但理论上这学期是给物理系开课,所以出现几个一小时就交卷的人应该也很正常吧,是吧((
+本来以为考完基物解决心腹大患之后可以狠狠学一天,但还是摆了,又困又累,明明晚上睡了七个半小时,午后又睡了将近一个小时,还灌了一杯拿铁,怎么会是呢。不知道实分析期中考到哪里,但考前总得把讲义再翻一遍吧。生存分析就随缘了,最后一年开课了,也没几个人,而且毕竟是 +wjd,应该会比较善良,平时记的笔记删减一下打印出来当做 cheatsheet +就行了。
+明早要去取护照,通缉犯.jpg。但凡拍照的时候稍微笑一下也好啊,相比之下我现在看身份证照片都觉得挺好看的了。
+4月11日
+高统不知道为什么又掉线了,上周放假,这周这个时间我正好要去取护照,已经没印象这课半个月前在干啥了。护照上打印出来的照片看起来比我当时照的还要白,不知道是不是又 +p +过了,还是覆膜之后反光看起来就确实更白一点(?),于是黑眼圈也更深了,像一个潜逃期间三天没有合眼的通缉犯(
+清芬瑞幸无了之后我就一直去清华科技园买,可能清明期间科技园的员工都真的放假了而我还在坚持点单(,导致我订单数进了他们门店前 +20,然而清芬还在的时候似乎全勤都进不了((。今天回来的路上在万柳吃的饭顺带点了咖啡带回来,于是现在就已经掉出榜了,加上明天是茶话弄日(?,感觉要无了(但是为什么要在榜上呢,为什么呢((x
+基物成绩很快的出,比我估的 baseline +还是高很多,虽然也就那样吧但挺好的挺好的,感觉比我高中时候强多了((
+感觉这周莫名其妙的就要过完了,上了六天课但也没觉得很漫长什么的,说明中间基物期中带来的压力已经超过了一切,于是它解脱了以后的幸福感能够抵消其余所有的痛苦(。剩下就写写作业,还有 +all in 实分析了(生存分析:那我呢
+4月12日
+我麻了,痛苦的一天从看了匪夷所思的桥梁工程作业开始,我一直以为这是个水课,结果怎么还要求先修工程力学的?我是一个一学位物理二学位土水大类、在某书院中游 +GPA +的大三(下学期)学生,你就默认我知道什么是弹性模量、截面应力和挠度,这合理吗(
+稍微缓了一下,早上起来看到计算概率已经掉线了的讲义,我又麻了。不过这个好说,首先这周还是没布置作业,而且它无论如何都比桥梁工程好说,学一下就好了(
+生存分析 cheatsheet +还没开始,倒也不是很急,而且一想到它没有期末就很开心,期中考完之后就等于不存在了。虽然期中之前也不太存在,就偶尔晚上要写写码。早上起来,上完体育课以及晚上回来写了写金统作业,倒是很平复焦虑,谢谢你 +wwc,但如果能选一本在网上找得到答案的书布置作业就更好了(
+最近买了两盒棉条想尝试一下,今晚突然想起来去认真查了一下 +TSS,好可怕(。但我最担心的是,我感觉我在学校里感冒发烧真的非常频繁,发生在经期前后也很常见,TSS +的症状和流感也没啥区别,那怎么办,以后每次生病都要直奔医院吗(。我其实都有点怀疑跑去校医院跟医生说因为用了棉条然后最近生病了怀疑 +TSS 人家会不会注意我在说啥((
+下午回来看到在布置校马设施,一阵头痛(,不知道明早要怎么闯出紫荆区去习题课交作业。去年校马的时候正好是实分析期中考试,还是在明理楼,就没绷住,今年怎么还在实分析(
+4月13日
+晚上本来就不太舒服,吃饭也晚,结果吃完饭收盘子的阿姨打翻一个面碗,被泼了一身油汤。只能说幸好除了外套之外都是今晚本来就要洗的衣服,食堂经理赔了干洗的费用,但有没有一种可能哪怕外衣我都是手洗,贴身的衣服更是不想干洗(除非真的洗不掉(衬衫上的油真有点洗不掉,再努力一下,实在不行真得干洗毕竟这衣服好贵((,唉(
+上次打算等到周日去问一下同学桥梁工程作业要怎么写,结果今晚他先发制人来问我怎么做,我绷不住了,哥你不是学过工程力学吗(。可能确实是这课逆天吧,我也不知道啊(
+唉,生存分析,这就开始看(
+4月14日
+生存分析咋办(?
+4月15日
+生存分析赢麻了,昨晚 cheatsheet 上还有一块空的,就把 log rank 和 +score test for cox model +等价的那个证明打印出来贴上去了。结果今天问这两个有什么区别,可以通过理论证明,或者用给定数据验证两个统计量相等的方式来说明,我寻思着让我算两个贼复杂的东西还要让它们相等,那我大概率算出来就不相等,就直接抄证明了。昨晚写桥梁工程作业,写的时候不知道里面有两个东西是相等的,算出来才发现真的相等,说明 +priori 是非常重要的(什么
+唉,wjd +的卷子一如既往出得真好,讲课也好,华子就是一个没有能力留住教学好的老师的状态,当然它可能也没啥兴趣留住。
+考完之后 wjd 锐评:
+++怎么大家考完试第一反应都是掏出手机来刷一会,然后露出满意的笑容
+看来是考了两个半小时的试,中途一直摸不到手机,上面就发生了很多有意思的事情
+
4月16日
+这个 b 实分析(,真看不完了,现在又说 5.4 +节也要考,但又来不及讲,虽然讲不讲也都无所谓但是,唉(x
+4月17日
+急急急,急中又夹杂着一丝不急,反正就是晚上回来先洗了个澡然后吃了一个小时水果(?
+4月18日
+天气热起来了,这种熟悉的黏腻的感觉又回来了,好烦(
+继清芬瑞幸看起来彻底要无了之后,今天清华科技园店也没了。昨天没喝不知道什么情况,但今天下午一点打开点单发现店里除了点心之外全部缺货的时候,悬着的心真的死了(
+想了想旁边还有个库迪,听说这两家打架打得厉害,还有人嫌瑞幸贵就拿库迪当平替,就去探索了一下,结论是替不了一点。我寻思着既然都当平替了那总得便宜点吧,我在美团买瑞幸券是每天九块九,库迪虽然全场九块九那不也还是九块九吗(。店面小很多,生椰拿铁都抄了瑞幸的怎么不顺手抄一下厚乳(,澳白只有热的(倒也正常,思来想去选了一个流云拿铁,主要是我没看出来这个是什么东西,于是我想总之是拿铁吧还能错到哪里去!结果提回去尝了一口怎么比奶茶还甜,冰也化得很快。之前还看大家吐槽瑞幸的冰太多化得太慢,然而在 +30 +度的天气下我真的就希望它多一点化得慢一点,既不要融到咖啡里面影响味道,还能在我热得很烦躁的时候贴贴脸安慰一下(
+那怎么办,清华科技园这个是突发情况还是寄了啊(,难道以后去北大科技园买吗,下次干脆进北大买算了(
+好累啊,怎么就这么累啊,这实分析快点考完吧(。学这个 b +数学平时就像泡脚一样细细欣赏优美的经典理论,到考试之前就得狠狠地喝洗脚水,管你每个结论怎么证明的,先把它记住再说((
+4月19日
+累了,已经开始畅想考完去孚王府玩,吃必胜客 EVA 联名(
+4月20日
+终于考完了!休息!
+下午拿到实分析卷子之后我有点,啊主要是,有很多的疑惑,这真是实分析?这不是数分,不是微积分吗,因为太水了所以我都怀疑到底有没有伪证的程度,只有附加题稍微有一丢丢难度,虽然这个怎么看都不可能正着证出来所以反证一枪秒了也没啥吧。不知道是出于想装个逼,还是最近复习得太痛苦了想赶快结束这一切(,还是晚上原定有出去吃饭的计划,写完附加题就跟在一个人后面提前 +45 min 左右交了。
+跟在别人后面交其实是因为,考完要在台上领后半学期讲义,他那个实在是太贵了(,而且我学期初就自己在某宝印好了(好孩子不要学),我又怕一个人上去被叫住,就只能挑个有人一起交卷的时机混过去。不过一出来走了两步就想起来第二题那个方体覆盖好像写拉了,边界上没完全盖住,虽然他真不一定仔细看或者心慈手软的话就当我笔误了放过或者扣不了几分,但是严格起来的话全扣也不是没道理。无所谓了,我附加题都写了,怎么样也不会出大问题。
+只是感觉,早知这样的话何必痛苦地复习一周呢(。什么新的东西都没有学到,就单纯是在大口喝洗脚水,挺没意思的。不过也没什么可早知道的,somehow +这就是在不知道之后会发生什么的情况下做的无悔的选择了(看巨人看得(
+所以 lxg +之后能不能开个泛函啊,我真的好想在他这里水过去,甚至他如果在我毕业之前还开下一轮数分的话我真的想去水一个,分析基础还是不咋地(
+晚上去吃了 EVA +联名,本来想要明日香的吧唧,但店员说吧唧只剩三款的时候我就感觉有点不妙,领完的两款怎么想都是大烫门明日香和渚薰才对,果然一盒还剩下一个绫波丽,一群真希波和一大群真嗣(。想了想我那边有一个渚薰的吧唧,就拿了个真嗣凑了一对贴贴,看起来也还好嘛!只是左边像 +mappa 的进巨画风右边像 WIT 而且还有个必胜客联名的标注罢了!
+
所以为什么都不要真嗣,他不可爱吗(?
+明天去世图读者开放日,不知道会冲动消费点啥,总不至于支持一手影印本 +PTE 吧(?
+4月21日
+不知道为什么还是很累,而且这澳白我喝一次睡一次,网络学堂还有七个猛 1 +在等我(,第九周要讲论文,急。
+今晚回来把头发剪了,天气太热不地鸣了,love & peace(。
+4月22日
+累麻了,论文证明看不动一点,我感觉它看起来就是单纯地算了 20 页(
+今天的瑞幸取餐号是 001,但昨天是 032,前天是 031(
+遇到了一个剪头发之后的常见问题,显得肩很宽,穿泡泡袖尤其灾难。算了凉快就好(
+4月23日
+实分析这期中成绩下来好令人幸福(,今天扫了眼写拉了的那个题(但其实助教放过了,谢谢助教)的答案,恍然大悟我为什么要重新给方体写一个 +2 +进方体的覆盖,它那个条件不就是个针对方体的不等式来着吗(。有一说一我能想到的解释只有,平时写作业写到 +2 +进方体的时候我都不知道怎么翻译才好,用到的时候就在英文里夹杂中文的这几个字,期中脑子一抽想用中文写答卷,一上来不知道为什么满脑子就都是 +2 进方体 2 进方体 2 进方体了(
+感觉比起做别的事情,现在更需要的是狠狠补充几天睡眠,尽快让这个疲惫的感觉消失,不然真的除了写作业啥都干不下去,效率蛮低的(
+打算把讲论文挪到五一之后了,很累,看不太动,也确实还再需要点时间,另外又搞了篇新的。
+高统 II 好难啊,虽然每个 slide 都比 wwc +当时短不少,但定理看起来复杂多了,抄笔记的时候总是很疑惑学这个东西干什么它真能有用吗,顺带稍微考虑一下是不是可以乱用这些估计方法做手里的问题,但也没有什么头绪。作业也写得很麻,wwc +之前布置的作业至少都是课后题也大多数都有答案,lq +搞一堆自己出的题目,磨蹭很久才能写完,这考试要怎么考(
+4月24日
+写了一天高统,还是没写完,蛮崩溃的。
+晚上在户外停了五分钟,腿上被蚊子叮了三个包(
+想起来前天和室友的一段对话:
+++室友:你腿上的疤是被蚊子叮了吗(指)
+我:应该是去年的,今年还没被叮过这么多
+室友:啊这
+室友:ok,我没有别的意思,很健康的两条腿(指)
+我:所以对于健康的定义其实是,正常地遭受生活的磋磨的结果是吗?
+室友:啊这
+室友:你还别说
+
4月25日
+晚上在路上又被人撞了,令人感叹(,是非常常见的前车的哥们刷着手机就唐突左拐了,我一个急刹加按铃既没能拦住他也没能阻止后面的人撞我,唉((
+我说这学校的新生入学教育能不能整点实在的,至少拿半个小时讲讲骑行规范,比如说转向要减速,回头看或者至少打个手势(说实话我也不知道这两个到底哪个难,但回头看比打手势安全多了),车多的时候不要乱变道,etc(
+唉,抱怨也没用,不如复读一些神腿们的教诲:有竞技的入门水平,平时就更应该有在路上调停事故的能力,自己不要不自觉地狠拉速度,至少还要能预判一些常见的问题,比别人更快地做出反应避免事故发生((
别骂了别骂了((
复盘一下,我被撞的时候刹住站稳了没摔,我感觉没摔这件事还算是给后车的哥们支撑了一下至少他人还狠狠扶了我一下(,只是衣服又脏了(。车应该没啥事,顺便狠狠教育了几句前车,我感觉已经赢了至少尽力了((
+我真的,我开学就是玩了个烂梗,结果衣服就不停地脏,以后真的不敢了饶了我吧((
+4月26日
+我写量子力学 +belike:叉乘是什么东西来着(。有的时候真觉得很丢人,都不太好意思说学过数学(这之间有关系吗
+晚上勉强把高统作业交了,实在写不出来了,算了(。怎么就这么阴间啊,每个题长得都像 +open problem +一样,用的定理也奇形怪状的,实在搞不定。然而从第一次的批改来看他这个作业给分还挺严格的,唉。我上得比较烂的课都是名字里带 +2 的,比如概率论 2 和微积分 2(,感觉基物 2 也差不多可以算上了,高统 II +比高统 I 难巨多可能也是正常现象吧(
+总之暂时下班了,感谢 wjd +送来的九天长假(指下周一的课她有事就放掉了。总之明天先去闪现一下郑州,后天回。
+昨晚在答疑坊值班,想起来过两天有一个要交的期中论文可能只能在高铁上写了,在一晚上一单都没接到的情况下还花 +120 购入了一个 ipad +键盘(。晚上回去何老板找我问问题,才终于又有了一点在答疑坊干活的实感,毕竟 +5~8 周津贴统计里甚至没有我的名字,这是怎么一回事呢((
+今天取快递回来之后室友锐评:你确定这玩意 120 吗,我觉得把罗技的 logo +遮掉的话看起来顶多 +30。可能是粉色就会显得廉价(,但选粉色绝对不是我自愿的,是粉色款比别的便宜 +20 +块,否则就买灰色或者卡其色了,我还真是第一次见到不仅不收粉红税还粉红免税的东西((,大概是因为卖不出去或者确实是看着很廉价导致的吧((
+晚上回来试了一下,除了键位距离有点小一下子不习惯之外没什么毛病,稍微熟悉一下也就好了,我手比较小反而挺友好的。现在的问题是它和平板加起来都快和电脑一样重了(但如果把平板保护套拿掉就会轻很多),这一套还不能码代码,那为什么呢(。只能理解成上次电脑屏幕碎掉之后还是觉得带着 +apple care 期限内的平板乱跑比较有安全感,以及平板看 PPT +确实比电脑爽很多这样子,键盘只是救急,只是救急(默念(
+4月27日
+现在这个发型虽然穿衣服要注意下不要显得肩太宽,但很适合戴耳环,以前头发很长的时候戴了也看不到,还会担心掉了都不知道(虽然我的耳夹均价不超过十块而且都是淘宝常见款式,但也还是不想掉(。不过我没有耳洞,也不打算打,一般都是戴耳夹,鉴于我不想承认是因为怕痛而不敢打,所以我一般都说是因为要防止改变自己的拓扑结构(
4月28日
+闪现郑州,在街边吃碳水大餐(,这边好像真的很喜欢在路边放桌椅吃饭,虽然感觉胡辣汤和烩面都没有特别合胃口,有点太咸了。下午去郑州博物院,每到这个时候都感叹当初学工艺美术史的时候多么幸福。买回来一堆文创,多到我现在根本没有勇气去看这一趟花了多少钱(
+高铁开出北京之后我皮都展开了,虽然去的时候坐和谐号没有插座是怎么一回事呢(,回来一开进北京就不舒服了(
+在高铁上写完了合同法期中作业,还写了点别的,现在开始急计算概率作业了(
+4月29日
+尝了下瑞幸新品青提味拿铁,蚌埠住了(,一边喝一边思考我到底为什么会对这个东西有期待,是为什么呢(
+看了一天计算概率,补了一个月的内容(。晚上一直在研究 KFC 啊不是 KMC +和他之前说的那个加速方法到底要怎么样才能拼起来,最后才明白是证明里面要用到那个加速方法的结论,绷不住了。
+现在处于一个刚搞明白要干啥的状态(也不好说是不是真的明白了),还没开始码,急急急((
+4月30日
+
5.5 update: 总不会现在还有人想看这个吧?
+总结:库迪好难喝,不要买。
+]]>五月的失败从 Yau contest 直接弃赛开始!
+ +5月4日
+突然闪现!前几天一直没写是五一华子游客太多了,也没有合适的教学楼可以去,更没有工位和实验室,于是躲去乡下(不是)瘫了四天,作业还越写越多,也没搞科研。
二月份打的美赛出奖项了,本来都做好拿蓝色证书的准备了,结果竟然是 +honorable mention,今年 ICM +获奖率比以前高一些,运气还不错。开了下盒感觉华子 S +还是挺多的(,那我还蛮强的嘛!而且整体上看 ICM 这边 E 题选题比例高达 +52%,华子倒是有 38 支队伍狠狠选 D,获奖情况并不如 E 的 12 个队伍,我们 E +人真是太厉害啦((
+最近还有很多事情搞不清头绪,比如暑期实习延期的问题似乎该去和教务沟通下了,再不沟通都该选课了,我也还是不知道要不要延期,可能还得和别的前辈聊聊。科研毫无进度,不是在期中考试就是写作业就是摆烂,你要是问我为什么四月论文阅读笔记消失了,我只能干两碗饭。瘫了四天回来上秤直接给我搞沉默了,晚上出去紧急骑车补救了一下。
+事已至此,那怎么办,先睡觉吧((
+5月5日
+看了一丢丢论文的证明,结果它真的就是狠狠地用泰勒展开和 OLS 算了 20 +页,通篇难度不超过数分 1 高代 1 和概率论 1,我叹为观止。
+还有一篇证明没看,之前自己找的一篇文章就看了个梗概,后天要见阔别两周的导,害怕(
+5月6日
+前两天在乡下(?)住的时候我发现证明看不下去的时候可以躺下看,缺点是整个人的状态比较的被动接受,另外因为没法用纸笔算所以一些细节只能随便脑一下,或者多攒几个等有精神了再坐起来验证,也可能会直接睡过去(。搞得我现在一看证明就想找个地方躺着。等暑假回家想买个 +Luckysac +那样的懒人沙发,但家里又不是没有床(,寝室也不能放,更不能天天背着去教室(。所以最佳的论文阅读地点其实是 +C 楼的双人研讨间(?(但不知道装修之后它还在吗
+昨天看了好多泰勒展开,今天又看了十余个泰勒展开。说真的,它在证明上真没有本质的难度,但就算每个定理给到我面前让我去证,所有的技术(除了条件概率)在大一就都已经学会了,我怀疑我缺乏的还是一种在尖叫“这 +tm 也能继续算吗”的情况下真的继续算下去并算出来的能力(
+晚上一觉醒来看证明,看到这一句 \(\frac{2n}{n+1} - (u+v) >0\) +的时候我的小脑真的萎缩了。虽然后来反应过来他的意思是只要证这个条件下成立否则显然,但是,唉((
+
5月7日
+很久没有腰疼了,怎么最近突然又不行了(
+又双叒叕身体不太舒服,本来想继续读论文,结果只好写了点作业,生存分析考完试之后只有两次作业了,难度骤降,速通了。金统这个大作业的要求和没要求有啥区别(,晚上上课的时候大概查了查,又去看了眼自己的
+portfolio(,想起来之前一直说可以买点黄金但一直没买(好像是在观望,问题是这是在观望什么,单纯是忘了吧),就搁那狠狠地投纳指和狠狠地捞一个亏了好多的医疗,最近金价暴涨只能看着易方达黄金总资产
+0.67
+元捶胸顿足。干脆做个金价的分析好了,多上几个时间序列模型拟合一手,然后做个资产配置,最后再因子分析这样子(yysy
+我很好奇因子分析真能做吗,感觉只能宏观解释,要么就是找一点比较有
+confounding
+意味的因子来回归一下这样),后半学期他如果还讲点啥有意思的我就再给他缝上去(,反正这个大作业目的只是要把这学期讲过的内容串起来罢了((将要面对的现实:对着收集来的数据完全不会写码
之前订了一件 PKU SMS
+的文化衫,是拓扑咖啡馆那款,周末就可以取了。下学期泛函看老师可能还是不太能上(我也不到啊),实在不行就去把拓扑和微分流形一锅端了,假装是基础人(主要是数学系这概统和计算方向的课都实在没啥可上的啊
5月8日
+好热,这教室里怎么还不开空调,完全那个没心情学,这下真看论文看得汗流浃背了((
5月9日
+教室终于开空调了,但是开空调之前好热没去买咖啡,于是今天睡得很死((
+这基物到底是在干什么呢,不是很理解,PPT +也不说人话,感觉浪费大半天看这玩意也没用,还得去看教材。虽然好像是会算的,但是换个皮可能又不会了这样子。我要求也不高,就希望它能 +3.6 平安落地(
+晚上直接摆了,想起来前段时间看的宫崎骏访谈,于是把痞子制作 EVA +终期间的纪录片看了(?,又补完了(
+5月10日
+今天看到求真夏令营的题,先疑惑了一下这是在招博士生还是本科生,想起来去年秋季已经招过本科生了,于是开始思考现在去考这个卷子的人是几字班,好像是一字班,诶等一下,那我是?(
+体育课测仰卧起坐和 50 米,仰卧起坐定番先花 50 秒做 50 个然后躺下休息 +10 秒(,躺完被老师拉起来示范怎么一秒一个,没绷住(。50 +米这辈子第一次见到进 9 +秒甚至及格了,减脂之后确实各种意义上来讲变强了一些(
+不想刷乐动力了,感觉能及格((
+5月11日
+今天填推研意向统计,又有点没绷住,虽然我还要延毕,但怎么已经轮到我这一届推研了?我毫无心理准备。我科研还是现在这个 +beyonds,和啥都没有也妹区别。填了推迟推研之后又绷住了,反正我不推研,真推研的话去统计中心不太是问题,就算是求真看昨天那个卷子复习一下我上我也行,最大的问题其实是拿推研资格(,也即前三年课程中未完成的不超过三门,我觉得我明年也做不到。然后又没绷住,有没有一种可能我不推研是因为我要出国啊,那对科研的要求不是更高吗,真破防了(
+但我感觉我室友也都和我一个状态,除了一个室友要去教研院读硕或者直接工作之外,另两位都完全没科研在等着强基
+100%
+推研给分配一个去处(,又不特别焦虑了((。虽然我不知道数学系是什么情况,但真有未来一年里能发出来
+paper
+的吗,这种事情总感觉该发生在隔壁(。想了想得出结论还是别想了,去看了个证明,然后规划了一手暑假头上去江西和两湖找我姐
+同居 玩一周多点,期间可能在她家潜心读论文两三天((
之前看到过一篇推送说相比首都机场和大兴机场,天津滨海的机票会便宜一些。今天被北京到南昌七百多块的高铁票价吓晕了,又不想卧铺,除了夏天没办法洗澡以及洁癖地狱之外,16 +个小时实在太长了,12 +个小时的卧铺还要三百多接近四百,实在没啥必要。查了下大兴飞南昌的机票感觉早点买的话可以接受,又查了下天津飞南昌的机票感觉非常可以接受(,是一个从北京去天津待一天哪怕住一晚再飞南昌,加起来也比高铁便宜点的情况,还少坐三个多小时(。另外南昌回上海的高铁不算贵,中三省(对不起我其实也是今晚才知道有这么个称呼)转一圈加起来还没上次去郑州贵,冲了。
+比起微分流形,今天看矩阵运算看麻了,下学年有点想去补票一个完整的高代了。我说真的,比起在读研之前就把研究生课全部上完(e.g. +我之前想去学概率论 3,现在觉得会一点实用的随机分析和 SDE +暂且够了)到时候还得再学一遍,这种越拖越不好意思甚至再也没办法补票的课去上一个会心里更踏实吧(
+5月12日
+看证明,越看越疑惑,我怎么感觉他这个里面这么多问题(,typo
+不计其数就算了,第一页上来不等号就是反的吓我一跳(。最主要的是我真觉得算错了很多东西,有个
+log-normal distribution 的期望就真的不对,虽然改改系数勉强可以 bound
+住,但看他算出来那个值就很迷惑,真不是故意写错的吗。后面还有类似于“因为
+\(a + b > 2c\) 所以 \(a > 2c\) 和 \(b > 2c\)
+至少其中之一成立”的怪事,我猜他想说的是 \(a
+> c\) 和 \(b > c\)
+至少其中之一成立,虽然就差个系数改改也不是什么问题但是(。虽然还是有看了证明也没懂的点,但想了想先去重新验了一下正文里之前怀疑他搞错了的一个
+Cholesky 分解,还是觉得不对,需要给每个点加
+weight,这下更有信心觉得是他错了而不是我错了(
但有一说一,如果是真的需要加 +weight,证明就有点出小问题,我没看出来怎么继续按这个看起来还算合理的全局假设来控误差(。如果要给假设改个大的的话,他后面那一堆 +show that the signals under blahblah are strong enough to satisfy the +conditions in Theorems 1 and 2 +怎么办(。所以,这时候我是该怀疑一下我自己吗(,感觉得整理一下然后问问导这样子。
+先去看了看另一篇 graphon estimation 的文章,上次那个 local linear
+regression
+是真的算得很厉害,就是一种,假设并不复杂但结果挺好的,其他线性模型看起来也还有很多可以挖掘的点,还得学习一个。五一在乡下休息的时候我其实还想了想怎么把
+GLM 往上面塞,毕竟它也真有 covariates(sry
5月13日
+今天把生存分析的论文看了,怎么不算是一种搞科研了?(
+晚上重新算了昨天那一坨,又找了下发现 supplementary material
+里面有一处改过来了,正文的确错了,但另一个地方没改,这啥意思(。给导发个邮件实话实说了,belike
+现在出了点小问题,然后描述了一下这个小问题,如果真要尽快讲 pre
+的话也可以先讲 graphon estimation,反正我也读了几篇别的可以说说
+而且我觉得这个问题会比较分析一点,就是说还稍微能算一点,不急的话再等我算算另一个看能怎么救。另外我得狠狠写作业了所以这周不知道还有多少时间算,先别急
+急的话要么您自己来算,或者教教我量子力学罢((
5月14日
+最近睡眠实在是不行,感觉也体现在每天都在混沌做梦上,主打一个醒不过来或者睡了很久还是累。大概也和莫名其妙压力很大有关,一眼望到头的本科生活板上钉钉要续费一年,续费完了也没有留在国内读研的可能性,也完全看不到申请之前多这一年能搞出什么东西来,如果说大一大二好歹是探索了很多终于定下了方向,那大三这一年到底干了啥呢。昨晚睡前焦虑得不行,狠狠地查了一些我知道的人的
+pub,最后把知乎下载回来给 24 Fall
+下面每个数学相关的点了个赞,然后沉沉睡去(
今天写了一天作业,补了补笔记,感觉稍好一点了,可能做这些不怎么费劲的事情到底可以麻痹一下。明后两天要把基物和高统仔细学一下,这俩都掉线挺久了。期末周结束得很早,虽然比较阴间的是
+19 号早上基物晚上实分析,21 号桥梁工程,但到底就这三门课 虽然 16
+周生存分析要
+pre,还有金统和高统的期末,什么某个通识课要考期末这难道还得复习吗(
时隔一周多终于拿到因公出国的批件了,明后天尽量去找土木系教务审批延期,总之要在夏季学期选课之前搞完。其实我也没什么别的考量,最重要的是夏天到乡下上工地实在太热了,我受不了,冠冕堂皇地讲就是会影响暑假的科研计划,所以我想延到寒假实习。
+说到选课,今天看了下秋季学期的本科生课程,索然无味(,选个拓扑选个高代走人,统计计算也不太想上(我真不是很想再上
+zzy
+的课了,虽然这个或许也是复习高代?我对算法的了解仅限于数值分析介绍的那些和计算概率讲的一点点,统计特化的计算完全不懂,也许学一下是有好处,但不是非得上课),毕竟还有量子力学(想开点,这个也是复习线代)和工程力学基础这两门不得不品鉴的必修课,和大约三门比较水的必修,该把重心放到科研上了。
5月15日
+状态真不太行,怎么每个学期到后八周都过成这个 beyonds(
+5月16日
+草这实分析作业怎么这么多啊,前两天没意识到问题的严重性完全没看
+其实是物理更危急导致的,今天边看边写搞了一天还没搞完,明天又没空写,真寄了。高统到现在还没开始,堆了三个没看的
+slides 了。
算了无所谓(,周六早上反正我去中科院数学所公众科学日
+追星,也不去交作业了,线上交还可以再迟一点,顺便也去那边看看世图新书展销。从寝室骑车两公里多就到了,压力不大,跟晨练似的,这总不至于再咕了(。前两天报了六月初的清北统计论坛
+去吃茶歇和追星,总不至于过不了审不让我去吧((
悲观一点说目测到期末之前没什么时间磕盐了,这学期绩点别爆炸就不错了,从下学期开始一定少选课。
+5月17日
+本来还在急这周实分析的作业,明天肯定交不上了,得找个理由交网络学堂,晚上在答疑坊小程序里看到一个问上周作业题的,什么叫松弛感啊(,这下不急了(
+今晚在教室看到有人在看 Fate(目测是 HF 线),爷青回(
+5月18日
+今早去数学所了,虽然八点钟就开始了但我十点才到,听了三个报告,了解的话题再加上科普向就听得很乐,来晚了于是没听到院士报告(。中间摸鱼的时候顺便看了眼今年数学所的博士招生考试题,看在我没学复变不会做求真那个级数题的份上承认求真的题比数学所难,但数学所题量好大计算好多啊,感觉这么一说也有点难(。
但强基就算保研也不能离开华子,北大都去不了更不可能去数学所,又有什么关系呢(
+中午结束之前和世图的一个编辑姐姐(群友)面基了一下,本来想买世图的新笔记本(前情提要:在摸鱼学导论和划水学原理之后又出了新系列的本子,详见这里),但是去太晚了,那个数学家用的量子理论笔记本没了,下次网上买吧(。没仔细逛展销,来晚了就光急着去计算实验室了,反正
+GTM 也没上新,浅浅瞥的几眼里没看到
+Durrett,不支持了(看到应该也不会支持的(。进校门了才想起来结束之前忘记回世图的摊位盖章了,枉费我还带了集章本,算了反正世图的活动挺多的,而且就那几个章(
现场中学生好多啊,羡慕,搁我高中的时候学校旁边只有个上海硅酸盐研究所,完全没这个条件(。遇到了一些认识的人,主要是隔壁
+SMS
+的几个,不过完全没被认出来,标准结局了属于是。遗憾的是今天没穿隔壁
+SMS
+那件院衫,正好还有个拓扑相关的报告,不过还好没穿毕竟我完全是云的,下学期一定学(

5月19日
+退一万步讲,这学期变成这个 beyonds,这门高统 2 +就没有任何责任吗(。它讲贝叶斯,一些深入的 MLE +和非参,我不知道怎么形容但我真的完全看不出来这些东西会在哪里有用,也可能比较 +advanced +就是这样子的,每节课几个不知所云的主定理和看了也白看的证明,反复嘲笑我是大废物。作业也很逆天,五一前和 +MLE asymptotic properties +那几个主定理搏斗还啥都没证出来犹在眼前,今天本来想补补笔记结果算了一天 +one-step +MLE,他这个作业哥们连算都算不清桑,我实在很难想象考试要怎么考。
+说实话从来没有上个课上得这么悲观过(?),它和高统 1 +已经没啥关系了,倒是和搞科研看不懂论文的感觉比较像,可能研究生课就是这样的,问题是我好像过不了多久也要变成研究生了啊(大叫
+5月20日
+前天没买到的笔记本今天到货了,我是自愿学习量子力学的(
左边这本这学期基物量子部分稍微写写,下学期还有一门量子力学用来写写笔记。右边那个可能下学期写高代,拓扑懒得写了反正有现成的。好久没用笔记本写东西了,近一年来都是直接写纸上然后收集起来。

总之下学期就这两门数学课了,高代 1 +大概比较挂机,我想补的东西应该大部分都在 2 +吧。看了下研究生课果然还是索然无味,不多选了,学概率论 3 +的意义可能并不如多花点时间读论文大,还得学量子力学,以及另外四门不得不品鉴的什么东西(,实在不行再找一两门课刷 +GPA,虽然暂时感觉不太需要吧。
+今天看到这个,差点一个激动就买了明日香款,后来仔细一看不是两张卡
+69,是一张卡正面明日香背面真希波卖
+69。我倒也不是不喜欢真希波,更不是没钱,我只是想要一个完整的明日香,所以我不买了(。另外第三新上海市的
+EVA 联名是真不少,不急着买这一个(
另,今天在生存分析课上更新了平板上的 Arcaea,不知道是否构成
+playing video games during lecture,记个 * 真书院的小过(
5月21日
+困困困,摆摆摆,我感觉我的睡眠问题也逐渐变得显著了,睡不着是真的难绷。
+现在有六个作业和一个也不算很大的大作业要写,该用闭区间套法了(。日子一天一天过去,实在看不到什么希望(
+今天收到了一个幻方猎头的好友申请,假如我这个本科要读六年的话,我可能暑假真的会去实习刮点钱,可惜它只有五年(
+5月22日
+星野源似乎塌房了,哥们上次在国内出名可能还是和新垣结衣结婚,上上次可能还是和新垣结衣搭戏(x)。不过自从我姐追 +kinki kids +塌房以及见证过很多类似的事之后,我就觉得当日本男艺人的粉丝之前得做好这么个准备(?),所以倒觉得没啥(??),而且毕竟没花过钱就更无所谓了(?)。话说回来 +Tokyo Dome 的那场演出是真的很棒啊,唉(
+相比之下今天更糟心的是买的水果和酸奶被偷了,可能是在这家消费过很多了的原因,店家还问我明早要不要送一份新的过来。明天还找不到的话就查监控去了,不是因为我正义感强,而是十来块钱对我来说就挺多的了所以我真的很需要让偷外卖的人赔钱(来个
+* 真书院的小过
晚上去开隔壁书院的年级大会(,正好看到唯一一个在华子的初中同学在斜后面,线上癫了一会,学了一天量子之后精神状态奇妙地变得好多了(但也不太好,进度还是慢一章(
+5月23日
+到底为什么要让我学量子力学啊!除了去求真可以少上一门课之外想不出来还有什么别的用处(
+早上帮刚换了新寝室的室友搬了点东西,以后晚上回寝室就没人陪我说话了。我只是想永远身边能有人陪我闹着玩,三天之后就要失去一个,两年后要离开几乎所有人,想想还是有点难受的。一般到这种时候就要想,按我现在这个情况其实也不好说能不能有学上,就不分离焦虑了,就申请焦虑了(
七点一刻到六教楼下才想起来下午待的教室晚上有课,但我忘了这回事,走之前扔了一堆东西在那里,又冲回四教拿。进门看到一楼在一年一度课间音乐会,扫了一眼没有 +neruko 就跑了(?),结果冲上楼梯看到 neruko +就站在上面,在整个人卡住的状态下匆忙打了个招呼,事后一想怎么不算一种社长线下交接仪式了呢((
+这作业啥时候能写完啊,急着急着都不太急了。好几门课已经严重落后于进度了,真的,这是最后一个选这么多课的学期了,以后再也不敢了。
+5月24日
+好累啊,周五感觉一般就是混一天过去,上体育课导致的。
+喉咙有点痛,开始紧急多喝水吃草珊瑚和西瓜霜含片了,希望明天能好。印象里小时候觉得草珊瑚含片很好吃,后来不知道为什么一直吃的是西瓜霜,上次感冒的时候两种都买了一些,发现西瓜霜显著比草珊瑚好吃,就纯甜,不像草珊瑚一样微甜中带着一股药味,不知道以前咋想的。大概是草珊瑚含片不含蔗糖的原因吧,所以虽然味道很怪但以后大概还是吃这个(?)
+5月25日
+金统大作业启动,然后突然想起来华子还欠着我一笔钱(,急了,周一问问(。钱难挣狗难当,这学期从答疑坊得到的收入越来越少,逐渐变成偶尔去看一眼小程序然后看眼缘答题
+简称不怎么干活也做题 PTSD
+了,到现在值班次数都不够,我觉得暂且也别申请焦虑了,先申请费焦虑吧(,怎么一天到晚的这么多事要操心。
室友搬完寝室了,虽然刚刚还在微信上和她讲垃圾话,但我真的希望能一直这样。那种事不要啊!室友找了别的室友什么的……!我希望她一辈子都会想着我,我死了之后也暂时……至少持续十年吧!
5月26日
+这个学期变成这个 beyonds,除了高统 2 +需要承担责任之外,这个桥梁工程难道就是清白的吗((
+5月27日
+鼻炎犯了,一直到早上七点都没睡着,九点多又被室友吵醒,然后又被楼长吵醒,过了一会又被上课回来的室友吵醒,兄弟非常恐怖(。下午实在撑不住就补觉了,两点才起来,错过了我能上到的 +wjd 讲的最后一节课,有点小难受。
+今天下午听了统计中心的两个报告,第一个是生统的听个乐呵,申请 UNC
+能不能给点好处啊哥(x。另一个是 signed
+network,把我认识的模型和聚类方法都捏到一起了,看到前段时间大折磨的正交矩阵乘逼近还是有点没绷住(。不过之前确实没从生成网络的这个角度考虑过为什么
+graphon 和一系列的 model 能够 make sense,看到 one step estimation
+想起不知道怎么办好的高统 2,背后一凉。
查了下 Weijing Tang
+竟是华子数学系校友,难怪会来统计中心作报告,这地方分明已经烂完了(暴论
5月28日
+累累累困困困,下午走进六教感觉教室太热了,遂转身离开把课翘了(
+睡眠质量真的不行,再这样下去真能活得过我那棵空气凤梨吗(。那 618
+要不要买个手环(啥(或者直接买个 apple watch 呢(我没事吧
5月29日
+背了一本物理书一本笔记本去教室,一天都没拿出来,搁那嗯算高统,明天还得背着(
+急急急,急急急,急急急。
+5月30日
+昨晚通了个宵,通完宵之后躺在床上想,后面 20
+天要考六门课,还要交一个大作业,不知道还有多少小作业,就蚌埠住了,更睡不着了(。但是今天白天起来把基物第四章学会了,还赶上了进度,习题久违地会做,心情稍微好了一点。感觉别搁那儿看讲义和课本了,不如看雨课堂的视频总结挑不会的听,然后在讲稿里搜索“考”查看会考的原题(
下学期真要上量子力学吗,我不会数理方程诶。虽然大多数东西也不能说真不会,但我不想算(,要不上个流体力学吧,听说这个东西蛮水的(真 +· 蛮水的)。但我现在 cx 的量子力学排在队列 +1/51,感觉很有可能补选上,蚌埠住了(
+这周实分析要交啥啊,怎么突然不发公告了,怪事。我都把 7.1
+写完了,看习题课似乎才到 Fourier,他啥时候这么慢了(
5月31日
+不是,你这实分析怎么一下把我写完的全交了(,现在已经变成周五上午布置作业,周五晚上/周六早上交了吗,有点恐怖(。好消息是今晚把前两周的习题课卷子都看完了,坏消息是明天的只能明天再说(
+爆肝了两天之后感觉压力稍微轻一点了,周末一天往后写实分析,一天整理下基物,晚上回寝室继续赶金统的大作业,再准备下生存分析的 +pre 就差不多了,还有多出来的时间的话(不太可能的样子)该开始准备 +cheatsheet 了。
+然后是定番:
+
这个月已经出现了两次重复的数字,一个是 776(可惜 5.5 +那天的标签我忘记撕了),另一个是 819,第一次出现 819 +是三月份,正好是我第一次去清华科技园店买咖啡的时候。奶茶喝得越来越多了,感觉说明真的压力很大(
+虽然五月份有读了一点文章,但 work log 是纸质版的(,下次再说吧。
+]]>2月1日
+过一会(?)就美赛了,我们仨(?)目前仍然是一个友谊第一比赛第二
+内恰第三 的氛围(,还能吃到他们俩的糖,挺好的。
今天还是在时间序列,感觉还挺有意思的,只不过 Time Series Analysis
+With Applications in R
+这本书看了一下感觉有点水,可能是作业题会从里面出,又不是上课现在就只看看讲义好了,似乎下学期金统也会用到的样子。怎么又变成在学而不是在磕盐了呢,急急急(,是不是等我把这个学了就可以换导师了
2月2日
+美赛受难记((
+好消息:上午我在负责详细看 E 题,讨论下来最后决定就是做 E 题
+坏消息:不大会做
+好消息:我觉得要用 ARIMA 做一部分,前段时间正好就在学时间序列
+坏消息:还没看到这里
+(
+下午洗数据的时候正好出成绩,这下我相信茶课调分的实力了(,然而概率论 +2 这个喜提 B+ 还是有点难受的。我知道他要是不调分的话我大概就是 B 或 B- +了而且期中爆炸确实是自己的问题但调得还是不够用力啊(x,求真课初体验大失败。
+其他的话,我生物甚至有 A(,另外这学期喜提了一个 +A+,坏消息是这门课叫建筑材料实验((
+2月3日
+美赛受难记,但是今天睡眠充足(,白天也没干啥。除了把论文里面不需要具体计算的部分写了之外,就是不停地在画图,流程图画了一个两个三个,其他 +introduction 性质的地图柱状图啥的也画了几个。原来美赛是美工大赛(
+虽然堆起来看着产出很多,但感觉还挺佛的,至少是没怎么动脑子,为后两天爆肝写论文打基础(迫真
+翻译:我就一臭写论文的,既不知道模型建得怎么样了,也不知道我能帮上点啥忙,那就睡觉吧。
+晚上感觉进度有点小慢,想了想也不是非要顺序推进毕竟最后一问和前面没啥关系,又找到了合适的论文,就先开始做了,减轻点压力。而且最后还要写个小作文,本来也算是我的活,那不如早点开始了。以此为理由把前面的模型的论文任务推回给了队友,让他们一边做一边写,听起来也蛮合理的,总比最后让我从头再开始学习模型
+还看不懂 然后压 ddl 写论文靠谱(
说实话我今天在一篇 heritage protection 相关的论文里终于明白了 +univariate, bivariate, multivariate analysis +的真正意义和对应的三种从来没想过要放一起看的方法,是不是我这个统人当得实在有点太抽象(字面义)了,就是说,太不应用了((
+2月4日
+美赛受难记,今天(我自己)刚磨蹭着做完最后一题,听起来非常光明,但是只做了这道题(
+一边做一边把这部分的论文写好了,现在就有 15 +页,也不知道后面要不要压字数。现在想帮忙做第二题但感觉也帮不上什么忙,又想到队友至多有一个会写 +LaTeX,毛骨悚然(x(
+肩颈都好痛,这破比赛打完之后得稍微休息一天,至少多在床上待一会(
+事已至此,先写 Report on Use of AI 和其他有的没的东西吧,比如说 model
+evaluation,sensitivity analysis,完全不存在的 assumption and
+justification,草怎么还有这么多事。这比赛没有 LLM
+的话怎么打啊,以前的选手太强了吧(
之前说觉得 Mili +现在的歌没有以前好听了,歌词也没那么戳我,但又稍微有点疑惑是不是我的偏见导致的,或者单纯就是 +Millennium Mother 这张专辑太强了。今天写论文的时候发现自己在哼 Extension of You +的旋律,又回去听了一下,还是像第一次看到歌词的时候一样要流泪了。
+2月5日
+美赛受难记,后面忘了,总之已经到最危难的时刻了,逸一时,误一世,啊啊啊啊啊啊(?
+2月6日
+美赛受难记,但结束了,不 disqualified 就是赢!
+万一今年有高于 S 的奖的话明年可以自己单刷一次,哦那样的话报名费要自付 +100 刀没人一起摊,好贵,算了(x)。而且感觉也很危,这次其实除了当 +regression monkey 之外就是在用嘴和 GPT 建模,不过 ICM +是不是就这样啊(。
+2月7日
+又活一天
+看了 #457994 之后又破防了(x
+2月8日
+摆了,详见最新一篇。
+ + +2月9日
+年夜饭是巡湘记,好哦,不过它和望湘园的本质差别到底是啥呢,剁椒鱼头里面加的主食是面条而不是米线吗(
+提前一段时间订了座,今天去才知道全都订满了,坐得好挤,平时两个人还能坐四人桌,今天就被赶去角落的双人桌了。也挺合理,今晚还营业的餐厅本来就少,而且到底谁大过年的还想在家无偿做饭(。
+ +晚上终于又开始推时间序列的进度了(
+2月10日
+今天在外环和中环之间搬东西,因为初一要吃素所以也没在外面吃东西,简单来说就是没吃啥,然后买了炸鸡回去等着零点之后当夜宵吃。我和我妈说等我润掉了年初一自己过的话就不吃素了,她说你别让我知道了就行。
+晚上一出顾村公园地铁站,这边放鞭炮放得空气已经五米之外看不到人了,吓晕。烟花爆竹哪怕在外环外也买不到,想放还要跑去江浙买,到底有啥可放的,好强的信念感。扫了单车之后看到有个在等公交的孕妇用手捂着口鼻,出于对孕妇的敬佩(真的主要是敬佩)我把包里多的口罩送给了她,听了一些吉祥话。搁平时我觉得我来不及听,因为这个共享单车 +16 +分钟就要计两块五了,但我现在有单车卡,半路感觉车骑起来不舒服还能当场停下换一辆,大概就这么阔气。
+不过还是不要这样就觉得我是什么好人(没人在乎这个,因为在路上骑车的时候我在想的是,这样的话昨天在巡湘记离店的时候多顺的一把薄荷糖就抵消了。顺带巡湘记的薄荷糖真的很好吃,比海底捞的好吃,而望湘园没有薄荷糖。
2月11日
+好想去淀山湖玩啊!坏了,这个假期不是在外环和中环之间搬东西就是在玩,盐是一点没磕,就看了一咪咪时间序列,开学真的,直接换导师算了,还能假装假期补习了前置知识。
今天在外面抽空看完了一个二医大(交医)的姐姐写的垃圾话公众号,真的,欲罢不能,看得我早上去宜家的时候直接坐过了站,本来想出站骑个车哪怕只有两公里也能过过瘾,结果为了再多看一会又往回坐了一站地铁。晚上在回家的路上看完了所有的文章,一边爽的不行并为我那些不能见人的垃圾话感到难过,它们就不配在阳光下暴晒并获得好几百阅读量,一边又惋惜乃至憎恨,这么刻薄又这么有才华还更新得这么慢,我要到什么时候才能再一次性吃上这么多这么好的饭。
+不行,我也要找个阴暗的角落大声说我的垃圾话,不是我和我姐天天讲的那种垃圾话,是我天天在心里大喊、晚上一大段一大段敲到电脑上又觉得万一发博客我的一切人际关系就都要毁掉了的那种垃圾话。
+顺带,上次不明不白地被宜家送货的师傅骂了,是一款常见的爱指手画脚觉得自己最牛逼的呀苏,一到楼下就讲怎么是个小姑娘在家里接货也没法帮忙搬,我说搬货上楼本来就是你们的服务范围,伊刚上海人都蛮客气的呀你怎么这样子,我今天跑了多少单人家家里男主人都会得搭把手额呀。我让他小心点不要碰花了刚刷过的墙不要乱踩我家里的地板,他嫌我女小囡事体多,我问如果这个换过的床架还有问题的话能不能再换,他跟我讲阿姨啊哪能可能再出问题,跟你们女人家真是怎么讲道理也没用,我说我在复旦念数学(是的我感觉这话在这里听起来甚至比说在华子念数学更有底气一些,还好伊嘟囔了一句高材生也这么没素质就走了,也没问我要学生证,是我懂概率还是你懂概率(抱歉其实我心里知道我懂的那些概率也没什么用。后来跟客服投诉了服务态度差,获得了一张一百块的代金券,很想和客服说我的乳腺结节不止这些钱,又怕对面长结节,算了。今天用它买了一些没啥用的东西回来,本来想买个狗狗甚至大鲨鱼玩偶,但我妈让我买衣架和鞋刷子(叹气。
晚上吃了贵州菜,本着都没吃过但是哪家店排队最长应该就最好吃的心态去吃了山石榴,好吃,能把我辣得嘶溜嘶溜,就是歌单不太行。我也鉴不出来预制菜,只要端上来有热乎气我就当锅气了,但反正确实就挺好吃的,管它呢。
+2月12日
+累累累,摆摆摆,先别说科研和学习了,暑研怎么办托福怎么办(乐
+2月13日
+前面忘了,后面也忘了,总之今天要看二月十三(
+用了四五年的 我妈的同事随手送她于是她又随手送给我的
+星巴克联名款卡包裂开了,然而感觉在淘宝怎么挑都挑不到这么合适的,不是没有挂绳就是卡册类型的要么就超过二十块已经不在我的财力范围内了。搜了一下才知道原来这个七八十,难怪好用,感觉是我不配((
2月14日
+早晨起来洗完脸发现脸颊上红红的,还觉得要么是睡得太暖和了要么是气色好(,结果到晚上都没退下去还越来越肿,才发现久违地过敏了,吃氯雷他定然后昏睡.jpg
+大冬天的到底是在对什么过敏啊,情人节吗,还是说今天 22 +度所以我的身体以为这是上海的春天了然后就过敏了(
+2月15日
+ +时间序列好难,急,还有个暑研项目一周后截止但我什么都还没填,托福是什么,怎么能这么摆(乐
+2月16日
+前两天右边嘴角起了个痘,现在差不多好了,今天左边嘴角又起了一个,记之(
+ +2月17日
+昨晚登了一下高中的智学网账号,今天卸载之前又看了一眼当时的一些原卷,鄙人高考前英语作文甚至能有 +22/25 +这样的伟业,又和我这两天写的托福练习作文对比了一下,我恨不得回去让我高三的英语老师重造一个月。
+于是今天又开始对着阅读划词组背句子了,背一点算一点,我总能把它们塞到毫不相干的作文主题的合适位置里的。然后不知道为什么就去补巨人了,后面忘了,心脏撒撒给哟(
+2月18日
+感觉托福听力的最大障碍是没法集中精力听完五段,听三个我就累了。之前一直以为 +lecture 会比 conversation 难,结果现在发现还是 conversation +比较困难,急急急,语速太快了没跟上就寄了。不过应该换个思路,conversation +就别记笔记了,听懂了也没太多可记的,没听懂记了也没用。
+省流:今天做了一些听力和写作,然而在家也没法练口语,就又去补巨人了。来点锐评:
+++我:
+这番里面的马真的都画的好好啊
++
俺の愛馬が!
+要不要搞个自由之翼的披风穿 jk 外面
+好便宜 才四五十 就是太中二了
+只恨我初中的时候没看这个
+友:
+沃日 初中哪有这么多钱 (?)
+我:
+确实
+但是如果初中的时候看这个 现在就不会想买了
+还可以早点和谏山创和解
+友:
+那也不一定
+我:
+没事 我都能和市川春子和解
+谏山创算什么
+友:
+创创
+全部创了
+我:
+你看过宝石之国漫画吗 和解了吗
+友:
+没看漫画
+我:
+fine 那你可以去和解一下
+友:
+笑死 听说小绿最后变成人了
+感觉难绷
+我:
+不是 这个结局我觉得可以预料到
+但是它的过程实在是令人震撼
+就看到动漫魂肉骨那个说法的时候我感觉就差不多了
+但是后面这个过程我接受不了
+不过我也和解了
+友:
+好好好 无所谓
+都这个年纪了什么和解不了啊
+我:
+确实 又不是女高了
+看这玩意看到现在我还是只关心马
++
这个体型真就是速度竞马,但好像比一般的赛马小一点(
++
蹄铁背景没绷住
+但是时速 75~80 km 还是太恐怖了吧
+赛马一般 1km 跑 60 秒左右吧
+查了下世界纪录是 53.7 s,所以是时速 67 km
+怎么人全死了啊 就爱看这种
+但撤退的时候根本没人关心他们的马怎么样了 急
+我:
+太典了
+把 Ayanami 还回来 啊不是 把 Eren 还回来
+我说这不就是换皮 EVA 吗 不话疗的那种 所以评分会比 EVA 低一点
+友:
+确实 但是三笠是面瘫
+我:
+不错啊 那就是 Ayanami 加强了 能要求把真嗣还回来了
+可惜我最喜欢 Asuka 巨人没有这号角色
+友:
+是 傲娇在这个世界活不了一点
+我:
+别骂了 但 Asuka 强啊
+所以 Misato 桑可以代兵长吗
+不太能代 他太强了 而且不够涩
+友:
+兵长多色啊 战损了更色
+Misato 至始至终都是完整的 (不是)
+我:
+我靠 你别引诱我的 xp
+
(?
+2月19日
+进巨第一季看完了,真的,EVA 和 FZ 之后好久没吃到这么好的饭了(
+那为什么打 8 分而不是 9 分呢(因为不够 EVA 或 FZ(x
明天去交大,摸一天,感觉也属于定番(
+凌晨练了个口语比练别的加起来都精彩:
+++题目:Talk about a famous person that you admire. Explain why you +respect this person.
+我:Ummm(思考)(十五秒快过去了还想不出来能说什么)(急急急)
+One of the famous person I admire is Shing-Tung Yau, a famous +mathematician who enjoys high reputation in the whole world (
+
2月20日
+今天去交大了,蛮累的,之后再写。前年这时候在后悔当初为什么拒了电院那个 +IEEE +班(,去年这时候觉得没去交也没什么反正去了也学不会,今年发现去交或者去旦学数学其实都很爽,唉(x
+和初中同学聊了聊天,她告诉我她考前三天才开始学口语和写作最后 +102,小分也都够用,ok(,感觉确实每天要练但也不是非得特别紧张((
+因为路程比较远所以昨晚下好了进巨第二季还带了充电宝,在地铁上看完了,第三季也开了个头。虽然槽点也不少,但还是好久没吃到这么好的饭了(二度,看了这么多有的没的才发现,我果然还是喜欢这种啊((
+2月21日
+进巨第三季前半看完了,王政篇给了 9 +分。往后看看发现这玩意真的好长啊,最终季还分上下部分,还有若干 +OVA,稍微有点看不动了,寒假能看到看海就差不多得了。不过我属于是不往后看剧透又不一口气补完就抓耳挠腮坐立不安,不同于第二季我和艾伦一样疑惑,王政篇之后看剧透和设定终于看得懂了。何况这个体量的作品如果不提前知道一些思路又不二刷的话真的会漏掉很多细节,失去的震撼感在丰富的内容面前是可以让位的。
+晚上卡 ddl
+交了一个暑研申请,主要是我太拖了,推荐信倒是今早我还在大睡的时候就收到了(。其实寒假除了几个校级的项目之外就压根没找,咋办呢,总不能真去实习吧,实在不行能以
+2025 年不毕业为理由直接不选课吗(
想了想倒还是和小时候一样,我妈前脚出门上班我后脚打开电脑开始看动漫,然后在她回家之前加速补作业(交申请,给 +wwc +写邮件),晚上在她眼皮子底下随便干点有的没的(练托福写作)。快要回学校了。
+明天本来是想去滨江道骑车,陆家嘴签证拿到了,下暴雨的话恐怕就不行了,大不了明年冬天再说。总之要从静安寺换乘买
+Lilian by the
+way,不能骑车的话就去世纪大道走走好了,然后早点回家收拾东西。
2月22日
+又该选课了(,课表再次变成了不认识的样子。好消息是一周三休了,坏消息是周二好像有五节课(((
+2月23日
+最近光是安装的家具送来的时候工具包里多余的材料就攒下了这么多,轻轻地崩溃了:
+
如果还有下次(?)的话我选全屋定制(
+明天回学校了,希望高铁不要晚点太多((
+2月24日
+喝到茶颜悦色了,虽然我的评价是,就这(x)。感觉还是得现买现喝,下次一定(
+带回寝室拍了个照,怎么不算是一种谷子了呢:
+
在高铁上补了进巨最终季 part 1,看到第 15
+话后半段的时候到站了,急急急急急(。马莱篇感觉确实没那么有趣,但单凭莎夏那几话都也还是
+8 分的水平。其实到第三季结束发现 104
+期配角三人组还是完整的的时候我就感觉要刀莎夏了(主要是莎夏太单纯了,刀另两个人效果就没那么好(,完全是死于谏山创的刀法(。很难评价谏山创和虚渊玄谁更爱的战士,单看
+Fate/Zero 似乎还是谏山创更疯,感觉得去补一下魔圆再说(
题外话,感觉我最看重的还是单回质量,像 Fate/Extra Last Encore
+即使作为粉丝向作品来看大约就是 7 分(对路人来说还不到 6
+分,实在绷不住,然而因为童谣那两话我就愿意给个
+8。后来聊了聊设定和一些问题(简称我要求被剧透(,感觉全系列除了完结篇有待考察之外应该能稳定在至少
+8 分,但后面应该既有争议又很难像第三季一样有趣又震撼,给不出 9 了。
虽然但是,三笠你的脸到后期怎么画成这样了啊,我看得睡不着觉。就感觉,诶,很空虚,没有什么永垂不朽。
+感觉最近实在是赛马和进巨都看太多了,加上下午还在吐槽既然想要保留王血何必安排希斯托莉娅怀孕,还不如让吉克在生命的最后一年猛猛当种马效率高(。结果傍晚睡觉梦到进巨的设定集里有九大巨人的配种费表,进巨和始祖最高要一亿日元左右,平均水平是四五千万,只有车力最低是两千万,实在没绷住(
+其实北黑和春秋分今年的配种费都是两千万,已经是种马的最高价格了(
2月25日
+前段时间在上海疑似因为天气太暖和,时隔好几年犯鼻炎了。昨天还好一点,今天收拾东西可能吃灰吃多了又开始打喷嚏了(
+完全不想上学,于是今晚把进巨最终季 part 1 看了,待会上床写托福(
+2月26日
+难受的春季学期开始了,前半段气温还可以但暖气难受,后半段气温难受(
+最终还是打算在课表里加可靠性数据与生存分析了,虽然是很细的生统方向跟我几乎就没关系,但其实完全出于我的一厢情愿(?),因为 +wjd +这学期结束就要离开华子了。如果不算高统的话,她当年那门统推是让我印象最好的一门统辅课,可惜几乎全是线上上的。而且说实话和我完全没关系的课我也上了不少了(,大不了水水过,而且很可能没有期末考,另外很多东西生统概论的时候也学过了。
+第一次点了瑞幸(其实只是需要它的纸袋子,发现券还蛮多的,后面可以多点几次。果然好多冰,这个不额外加糖的丝绒生椰拿铁怎么也这么甜(
来个很烂的谐音梗:
+++室友:下午没课,我打算把冬天的衣服都拿去干洗店洗
+我:今天是你大洗的日子啊!
+
于是晚上我就把菜汤弄到衣服上回去洗了,寄(
+2月27日
+早八之前买了杯瑞幸,是 064 +号,进店的时候看到咖啡师在赶早七,一排一排地做咖啡(,感觉很惨。早十课上坐我斜前面的同学的瑞幸是 +429 号,感觉更惨了((
+有点子上瘾,这玩意比瓶装好喝多了啊((
+2月28日
+现在总感觉喝咖啡能维持清醒的时间越来越短了,虽然一个寒假都几乎没喝但还是不行,一会就困。喝了两天瑞幸获得了两个袋子,其实是想折纸了(x
+
今天把进巨看完了,晚课坐在中间排用电脑看了完结篇后篇(,现在想想开始感到尴尬了(。不钝评了,虽然不喜欢未来视的设定(相比之下“这是由你亲手开始的故事啊!”这句真是我全系列最喜欢的台词)但好歹圆回来给了结局已经很好了,出彩的部分基本集中在前三季,表现力也一直很强,补完还是很值的。
+刚在六教再见了所有的巨人(,下课出来就被树吓了一跳,好难绷((
+
2月29日
+高统 II 讲 +Bayesian、其他的一些估计方法和非参数统计,之前我还一直犹豫要不要去上 dwl +开的那门贝叶斯,感觉不上又不踏实,上了既然是她的课那我必吃 +3.6(,又找不到明显的上位替代,这下没事了。不过毕竟是第二学期了,不像上学期开始的时候我还以为是个很摸的课(,一上来就在上强度,急。
+lq
+讲课还挺好的,奶一口,单看第一节课我感觉他恐怕是统计中心最会讲课的老师了,甚至比
+wwc 和 wjd
+都好(,这俩在我心里已经是讲得最好的了,别人更是((。有 slides
+和板书,除了读 PPT
+之外还讲一些直观理解之类的东西,不然一上来还挺头大的,感觉 4-2 以后
+起得来床的话 还是值得一去。
托福终于摆脱听力阅读越做越菜了。今晚突然意识到阅读是不是不应该先通读文章再做题,而是要直接对着题目一段一段读,但试了一下感觉也并没有省时间,还错得更多了,还是按自己的节奏来吧(
+]]>6月1日
+如题(
+原汤化原食,开始用去年实分析作业的背面打草稿做今年的实分析作业(
+晚上回来围观室友改简历,原来把课上做的项目写简历上是正常现象的吗(,想了想又觉得我好像连课上做的项目都没有(难不成金统这个能算?),这是怎么会是呢((
+++室友:我后来想了想还是把系里夏令营的报名撤了 因为我确实不想读博
+首先我没什么学术追求,我的水平也没资格谈这个,其次钱对我来说真的很重要
+我:我也是!
+室友:是吧!我目前的烦恼都是钱不够导致的,暂时还没有什么用钱解决不了的问题
+所以我去搞卓越工程师咯!
+
6月2日
+想来想去,期末这日子过成这样,基物可能需要负主要责任(。
+6月3日
+生存分析 pre,把高统 2 +的东西搬过来狠狠装了一下,掩饰我根本没多读任何相关工作这件事((
+开始写金统 +cheatsheet,有一种很快就能搞定然后去搞高统的感觉,又觉得现在不应该这么闲吧,难道不应该先开始复习实分析,至少往后写点作业吗(
+6月4日
+不是你这实分析这周要把第七章课后题写完是什么意思(。虽然说第八章不考(但我总觉得完全不排除
+lxg
+第十六周心血来潮把它讲了然后考的可能性(,但第八章本来就只有十来页啊(
金统 cheatsheet 写完了,这课又简单又难的,原理都水得很,但要全考实
+证
+分析的话恐怕有点(。下一个是高统,本来以为合同法是闭卷随便看两眼 PPT
+差不多得了,结果这下可以带法条,蚌埠住了,又多一个 cheatsheet
+要做((。最需要 cheatsheet 的难道不是基物吗,凭什么就它没有(
感觉稍微可以喘口气了,但也完全不能摆,总之再熬两周就放假了(什么原来后两周要干这么多破事啊((
+昨天今天都没来得及在下午第一节课之前去买瑞幸,昨天在售货机上随手拿了一瓶星巴克美式,结果那个味儿实在是给我恶心到了(,为什么要演奏春日影,啊不是,为什么要在 +0 +蔗糖美式里面加赤藓糖醇?我真的一直郁闷到晚上,心情太差了就点了杯奶茶,惯性定律果然今晚又点了杯奶茶(。
+最近每天晚上洗完澡一边吃东西一边看两话巨人然后才想干活,最速二刷了属于是。感觉可能是第一遍看的时候被唬到了,我承认第三季 +part 2 很强,但 part 1 就这(,也就是个 +8。反而之前以为单纯是个过渡回的第二季单看不屈的誓言就值得给个 9(
+6月5日
+真的要熬穿了,其实还是有点干不完,想到基物光学也要考心里就有点发毛,何况量子学得也不咋地。但如果只是背诵 +PPT 的话应该就还好(?),或者说恐怕最后会变成只来得及背诵 PPT +上划的重点了吧。昨晚熬夜写实分析作业和金统 cheatsheet,白天又在写高统 +cheatsheet,明明睡得不少还困得不行,看到以前会做的题目现在莫名其妙不会了,感觉到前所未有的疲惫。
+我倒不会说是之前太摆了导致现在变成这个样子,我确实没觉得这学期什么时候真的很摆过,如果读论文不算在摆的话,可是论文也就读了三四篇。那么答案显而易见,大约并不是选了太多课导致的,而是能力不足。所以说如果这学期 +GPA 没有很难看的话,下学期就不选高代 1 刷分了(
+还好金统大作业延到 22 号了,等我 21 号晚上考完还能写 15 +个小时(。代码基本上已经跑通了,感觉单纯是把剩下的废话说完的话这点时间能写得完,还就那个比美赛不知道轻松到哪里去了。或者说考完 +19 号那两门之后其实也就可以开始搞了,无论如何现在压力稍微小了点。
+6月6日
+实在想不出来高统 2 +要怎么考,是一个他要是考按定义计算和通过计算证明的话可能还好,但 MLE +那一坨东西我连模仿证明都做不出来的情况,学第二遍也不会。
+有点小破防,然后摆起来了,这样不行吧((
+今晚摸鱼把进巨第三季 part 1
+最后一话看了,王政篇除了政变之外的内容确实都是 8~9 分水平(,平均一下 8
+分差不多。明晚开始玛利亚之墙夺回战,看看有没有可能真给 part 2(连同 EVA
+TV,真心为你和猫鼠一起)调到 10 分去((搓手(#每日调分
+这下 10 分要变水了,不如把赛马娘第二季也抬上去吧(x
6月7日
+这高统 2 +复习得我感觉自己还就那个好没能力,应该去读个硕然后直接找工作,就,学了两年数学还没这么崩溃过(,从来没有因为学数学半夜哭出来,上次这样可能还是大一搁那儿深夜和 +OJ +左右互搏(。真不能再这么上课了,但又很难说集中精力科研会不会更崩溃,是否更应该少走弯路了(
+好黑暗的日子,我真觉得我精神状态有点要出问题了,然而这个期末还有两周才熬完。后两个学期的学分都不算多,算了一下哪怕这学期爆炸 +GPA 也还算 +robust,只是不知道延期施工实习会不会导致给分出问题,还得留余地。最糟糕的情况下基物靠背题目混过去拿个低一点的成绩,尽力保护住数学课这样。
+查了下网络学堂,上学期除去几门课公布成绩,一共交了 48 +个作业,这学期到现在已经 64 个了,还活着就挺好的。
+6月8日
+我好没能力.jpg,不过看看实分析又觉得比较有能力了(?
+很累,但晚上完全睡不着,在床上挣扎到五点钟起来把桥梁工程作业写了,写了两三道基物,然后倒头就睡(。天气也直白地热起来了,不过完全不如去年端午,痛苦回忆.jpg。中午出门感觉好虚,一热就更难受了,还是没自己去买咖啡,瑞幸外卖点不起,库迪 +app +外卖竟能用美团到店券,好文明,虽然配送高了点但也还能接受,最近大概要依赖下咖啡外卖了。
+我好像下雨的时候从来不记得带伞,但是太阳一晒就能记得带遮阳伞了(
+6月9日
+想来想去感觉下学期真得搬走了,反正延毕会导致至少要搬一次家,不如下学期就直接搬走,在这儿继续住我是真的天天都睡不着。当然,从大一上学期期末开始我就想换宿舍了,一直没动多半是懒且意志不坚定,所以为了坚定决心,我晚上回来跟隔壁寝室的一个姐在中厅里嚷嚷了半天,四舍五入大家已经都知道了,那就是必须得走了(。
+一会感觉能复习完,一会又觉得不能,还是先看看周二考的两门课吧。金统的 +cheatsheet 是周二做完的,周日的我:这课是干啥的来着(
+6月10日
+摆了(
+6月11日
+我是真的会因为夜里睡了半个小时醒来就睡不着了而哭出来(,好崩溃(
+这金统在考啥(,我做 cheatsheet
+的时候就在想把东西都塞上去是想考试的时候现学吗,结果真的现学了,希望高统
+2
+也能来得及现学。虽然怪没底的但反正也就这样了(,他但凡拿出上学期高统
+1 薄纱大家的那个状态呢(x
合同法挺摆的,它到底是不是一个 PF +的课啊,怎么到结课了也不是很清楚这个问题(
+你说得对,但是我高统 cheatsheet 还没弄完,怎么会是呢((
+6月12日
+急,摆(
+6月13日
+现在是 6 月 13 号(
+这高统折磨了一学期,期末竟是抄写和计算大赛(。虽然平时比较 push +能学到很多东西,加上考试不为难人确实是非常非常好的,但还是整得我又气又乐的,大概最近真的太焦虑了(
+昨晚是一个月以来睡得最好的一晚,记之。不过下午还是因为早上抄写太累了睡了会,晚上没忍住在早晨喝过咖啡的情况下又点了个奶茶,唉((
+基物怎么办,急(
+6月14日
+好困,怎么会这样,这能复习完吗(
+6月15日
+一整天只学基物的话效率好低,但实分析其实也不是很想学(。它看起来一副只考期中后的样子,虽然考前提示里那个默证我一上来就没绷住(
+唉,其实还有个大作业没写完,怎么会是呢(
+6月16日
+最近感觉整个腿脚都是水肿的,实在很难受。一个是休息得不好的体现,另外也真好久没怎么锻炼了,体力差了很多。没在减脂甚至也努力多吃饭了,体重还是一直掉,期末考完是否该去绕绕圈了(但这个天气真别在户外锻炼吧
唉,我妈今天问我为什么没考阿赛(,还把入围名单里一些上海的年级相差不大的竞赛生都找出来了(。我不好说,但我确实对阿赛丘赛啥的都没太大兴趣,说好听点是精力有限,很多东西学完考完期末就不想二刷准备比赛了,投入大量时间学不到很新的东西,感觉不如读点文章有用,但可能本质上还是竞赛 +PTSD 导致的(
+6月17日
+我现在感觉进巨最终季 part 1 也挺好的,马莱篇文戏是真那个有 9
+分水平,至少比第二季和第三季 part 1 强(。但它评分只有 7.7,我理解是
+MAPPA
+画面相比霸权社实在不行,以及放送的时候漫画快出到结局了,这一季里还有谏山创手刃莎夏(,所以说这下更不得不打
+9 了(
到底要不要调一波分呢,急(。说实话现在我打 9 +的里面有几个如果再看一遍很可能就不会给 9 +了,所以我打算不去二刷(,的这么一个情况(,另外也有再看一遍大约也不会动评分的。这样的话把其他真的很喜欢的拉到 +10 区分出来大概也挺好的(
+今天把光学看了,又拟合了一下原子物理的几个题。唉,这基物赶紧考了吧,多给一天也学不进去啥(
+6月18日
+如果我现在大一,明天要考两门四学分的课,大概已经昏过去了。但我现在大三下了,所以我今天玩了一整天,这怎么不算一种成熟呢(
+6月19日
+基物至少连着看了五天,喜提四学分 +3.3,实分析就看了两个下午,一个小时做完了,唉(
+想了想一年前还在选没人选的课选课法,主打一个不和数学系一起上课而是混在数辅里面,否则感觉考不过,现在已经如果我不是数学壬的话那这里大多数人也都不是.jpg +了(
+虽然后半学期学得依托,Fourier +变换的题也不一定做得出来,好像也没有几个提前交卷的,但感觉考试的时候但凡把空调打开,也不至于做完六道题扔下附加题直接闭眼开睡(。可以交卷之后速速拎包跑路,还把水杯落在桌上了((
+6月20日
+桥梁工程看了一天就差不多看完了,反正对我来说也就是复习一下之前看懂了的部分,不懂的也不太可能懂了(,随便考吧。这样的话有望提前一点把大作业写完,然后这学期就下班了,真是个漫长的噩梦。
+这两天晚上稍微轻松点了,二刷进巨的速度变成了一晚上三话(。第一次看的时候觉得不咋地,现在感觉马莱篇质量是真的高,突然有点想不通为什么第三季
+part 1 比最终季分数高(
6月21日
+结束了,不用再战斗了(
+昨晚熬了一下把金统大作业差不多写完了,待会稍微再改改就交,下班了。
+6月22日
+啥也没干,收拾了下寝室,晚上教(前)室友速通了一手假设检验和线性回归,本来以为会搞到很晚,结果离教室关门还留了 +2h,遂开始手机 b +站看魔圆(。虽然比较担心看到了正版番剧(,但是急,而且也没啥事干,算了(
+我评价:这玩意是 EVA,进巨和 FZ 三合一吗(
+6月23日
+一离开北京,整个人就好多了(喜
+6月24日
+14 周的时候虽然这个期末已经乱成一锅粥只能趁热喝了,但抽空听了一下 +Weijing Tang 的报告,感觉这个 signed network model +看起来还蛮有意思的(。今天读了一些她引用的文章(
+这么说来下次可以找机会把 14 周我咕掉的那节生存分析的课听一下(。
+二刷了娜娜家,虽然还是很不错但总感觉没上次好吃了(?),难道这就是相见不如怀念(。上次的柠檬鸡和这次的烤翅味道都一般般,但咖喱很好吃,薯条分量很大,下次(如果还有下次的话)把肉换成土豆泥之类的小食或者干脆去楼下鲜芋仙吃个甜点吧(。
+6月25日
+到今天为止已经三天没喝咖啡了,每天都睡得很香,日均睡眠九小时以上,我觉得可能自然状态下就应该睡这么多(
+大概也不是没喝咖啡的问题,昨晚晚饭后喝了杯奶茶一样睡得很香,主要还是没在寝室住了吧。
+西塔老太太好吃,但最好吃的是免费的土豆泥(。虽然在天津一顿吃出了上海的人均稍微有点不满,但毕竟连锁店,口味也是熟悉的偏甜口,沪人狂喜。
+6月26日
+去了下天津博物馆,本来还想着心情好的话顺便去下旁边自然博物馆,结果一个是起得太晚来不及了,另外虽然没法苛责什么但天博确实是我去过最不行的省博(。)了。
+而且旁边万象城那家九龙冰室,怎么能把菠萝咕咾肉做得那么难吃,不如文通冰室一根。那个双皮奶端上来尝了一口我就觉得有点不妙,这家店不像是很会做饭的样子(,果然是在天津踩到的唯一一个大雷。难道去吃粤菜就只能点烧鸭饭或者叉烧吗(
+6月27日
+回北京了,在城际铁路上就已经感觉到悲伤了((
+回寝室打扫卫生,收拾东西,看了点番(?),准备后天飞南昌了。
+已经连续五天没喝咖啡但精神饱满了,原来日均九小时睡眠是最好的咖啡因(乐
+6月28日
+现在是 6 月 28 号晚上十一点十二分,航班不到 3/4 +天之后就要起飞了,但我的行李箱目前还是空着的,更别提下楼试称重了,这是怎么一回事呢,我啥时候变成 +P 人了((x
+6月29日
+是的我是第一次坐飞机,某种程度上也是不想第一次坐飞机是在暑研的时候(为什么)所以这次飞了,当然北京到南昌的高铁本来就贵得离谱所以飞机确实省钱。
+然而这个雨下得(,真的疲惫了,早上起来收到了延误 3 小时 20 +分钟的通知,到机场之后首都机场这里开始雷阵雨,预定起飞时间的时候广播说飞不了先别排队了,过了十分钟开始登机(。登机之后又是漫长的飞不了,十点钟的时候广播说暂时飞不了先别急,于是我给我姐发了条消息说别出来接我了,我啥时候到了自己来就行,两分钟后突然起飞,等我反应过来的时候机头已经抬起来了,早已飞行模式但也不敢再打开流量了(
+昨天还在想为什么要提前预定特殊飞机餐,订的还是低脂餐,就这么喜欢鸡胸肉吗。结果毫无胃口的晚上十一点拿到柠檬味的鸡胸肉,没什么味道的全麦包,以及沙拉和水果的时候,我还是感觉比旁边半夜吃宫保鸡丁饭的人要幸福一点(
+一点钟到昌北机场,惴惴不安地打了个网约车,司机先让我从平台取消订单,我寻思着我平台打车不就是图个有监管吗,遂拒绝,同意把平台的抽成额外打给他;然后一看车牌号和高德上显示的也不一样,汗流浃背了,拍了发给我姐。行李放进后备箱之后司机突然说这一单要拼车,和一位提公文包的中年男子,我立即跳脚破口大骂,说要拼的话你拉他一个人走,我把行李拿下来,虽然骂完有点后悔怕挨打(,但可能我距离比较长能多赚点,司机真听我的了,就开走了。到我姐家之后还是觉得蛮汗流浃背的,就是,但愿以后别再遇到这种半夜打车的情况了(
+6月30日
+睡到中午,起来去了省博,布展真不太行,全混在一起没啥记忆点。下楼去文创店看了一圈,这都啥(。现在越来越觉得在河南省博钱花的还蛮值的(。
+在江西省博转了一下午,感觉把今年能看到的小孩都看完了,反正你赣的生育率不怎么是问题(迫真
+]]>7月1日
+本来今天要早晨六点多起来去海昏侯博物馆,但起来一看外面下暴雨,遂在家补觉,摆烂,读论文(。说是读论文,我感觉和抄书甚至做手账差不多水平,就是平时在纸面上不会这样干,用平板反而比较(,但毕竟这儿也没桌子(
+长沙感觉去不了了,现在还在不停下雨,到处淹着,遂退票。在考虑是早两天回家还是在这边多读两天论文((
+7月2日
+下暴雨,仍然在读论文,然后就是晚上雨停之后出去吃吃饭,很摸的一个状态。
+仍然在读一些 signed network +相关的文章,离我导一开始让我看的东西越来越远了(。这两天读的几篇主要是一些不那么统的会议的文章,有点水(,算了能看进去点也行吧。
+之前听 hst 说 hd 在和 ypk 一起做概率图模型,最近发了篇 +ICML,我还想着这又是什么方向,今天搜了一下发现哈哈不就是我这玩意吗!只不过我和我导一直管它叫网络数据或者 +social network,好吧以后不这么叫了,听着有点不像统(
+下午六点被告知明早七点去武汉的高铁被取消了,看了下这车也不往湖南开,可能是路过九江导致的。紧急改了后天的票,改订的酒店倒是还便宜了点,就明天去海昏侯博物馆看看金子这样子。感觉以后还是不要在七月初在南方玩这样,当然北京也在下暴雨(吧),反正变数很大。当然也没有几个以后了,寒假要补实习,暑假就暑研了,除了延毕那一年可能会松弛一点之外,就只可能学期中间出去摸一摸这样子。
+7月3日
+还是下雨,海昏侯又咕了,这下得等到从武汉回来再说了(
+上午看了 TCL model +的那篇文章,看到它的初衷是想把朋友的朋友(很大概率)还是朋友这种传递关系的概率表示出来,最后证明了还是符合 +FCL 的,感觉听起来很可以推广到另一种类型的 balanced triangle,在 random +insertion / wedge closing +的步骤里多加一步控制正负号,再多估计一个参数就好。然后随手一查发现这件事六年前(在这篇发表的六年后)就有人做过了,文章和这篇长得不能说完全一样只能说也没差太多,遗憾离场(x
+下午傍晚出去逛了逛,这南昌已经待了四天了,回来还得待两天,每天都在愁吃点什么((x
+7月4日
+二刷完进巨最终季 part 2,抬到了 9 +分,比第一遍的观感更好。之前一直没注意到,最后一话在帐篷里喝酒的时候艾伦看着三笠和阿尔敏那个眷恋的眼神,抛开二刷注意到文戏改编得很优秀,也真的理解了人物动机之后,哪怕只看这一段都感觉已经有 +9 的理由了(。
+前两天在谷子店没忍住买了一对艾笠的色纸,虽然 MAPPA +出品真有点丑,但看完最终季我已经和画风和解了(。但是回来的路上我姐问我这是一对男酮 +cp 吗的时候真的还是有点没绷住((
+7月7日
+回南昌了,前面几天的在写了在写了(
+7月8日
+昨天说在写了之后就真的开始写了,狠狠吐了一万字,虽然我今晚就想发出来让所有人嫉妒我的才华(嫉妒我的手腕力量),但还是过几天再发吧。写完其中几个在高铁上就在构思的段落之后,我感觉自己文思泉涌无所不能,但把它补完成一篇有逻辑字句通顺的文章的过程中,我只能反复默念:完成比完美更重要。
+7月9日
+一整天了,没有人来找我偷跑我的一万字,封笔了(不是
+明天回上海,现在已经是看到上海地铁屏蔽门会觉得很陌生的状态(
+7月10日
+回家了,终于可以开包看一眼就能从安检员身边大摇大摆走过去,抱歉但是各个方面来说第一次觉得上海这么好((
+早上去南昌西站的时候,虽然我拖了个箱子还背了两个包,但显然安检员对我箱子里有什么毫无兴趣,她只让我打开帆布袋把水拿出来喝一口(
+另,今天在高铁上成功自己把箱子举起来放到了行李架上,还得继续练。
+7月11日
+在我姐家里的时候就没有网,三台设备全靠手机开热点,现在回家还是没网,好崩溃((
+我妈对茶颜悦色小零食大加赞赏,又买了一堆(。我蹭免邮又买了点茶包,上次那个比普通冷萃茶贵五块钱多一个票据收纳盒的茶礼盒里面还送了个纸徽章,茶包的包装也特别有意思,真的值了。感觉下次想喝茶颜悦色可以去南京或者无锡,至少我对南京的印象还是很好的,可以坐京沪高铁回家/去学校的路上在南京南站中途下个车这样子(
+五一的时候我在一边写高统作业一边骂,顺便在口嗨怎么把 GLM +塞到当时在看的论文里,后来高统 II 奇迹般地摸到一个 A-,打破了每门课的 2 +都会很拉胯的魔咒(微积分,基物和概率论,但数学课 A- +确实好像也算有点拉胯(啥)。现在我好像真遇到了一个塞 GLM +的机会(,啥时候和 wwc 约着聊一下(
+之前觉得看论文看麻了之后读一下光叔的数分讲义还挺好的,现在觉得其实某些论文比数分讲义简单不少((x
+7月12日
+179 的 EVA
+展早鸟特典票我说买就买(,哈哈,但它是国内首展诶,特典看起来确实很值。感觉总不至于八月份没空去看吧,冲了,可免税代购周边(啥
最近都好能睡啊,这样不行吧(
+7月13日
+不太舒服,几乎就是躺了一天,中间起来狂暴做家务(
+什么科研,啥都整不出来,急急急(x
+7月14日
+读论文,睡觉,睡醒做饭,做完饭洗碗洗锅,洗完就累了,睡觉(
+洗锅的时候感觉我的生活差不多就和做饭一样,不知道在忙些什么东西,但是就是一天到晚都很忙,还糊了满脸油烟这样子。刚坐下来打开平板开始回忆我平时是干什么的来着哦好像是学数学的,我妈神神秘秘跑到我身边说我给你买了两个小礼物,打开淘宝一看是两盆花。我感觉她已经在想象家里鸟语(指我每天不知道在说什么鸟话)花香生机勃勃的这样一个场景,但我只觉得眼前一黑,我一地鸡毛的生活里,真的,再塞不进两个需要我照顾的东西了(
+今天在厨房里发现了九个插座。不是,它到底是想起到一个什么样的作用啊(挠头
+7月15日
+摸了(,终于把这个 tutorial 看完了((
+7月16日
+今天看一个 signed Laplacian,完全没看懂,一上来开始说可以用振子理解 +eigenvalue(可能我也没理解对)blahblah,遗憾退场(
+这 Umich 好喜欢研究 signed network 啊,搞物理的也在发 signed
+network,是因为 Harary 是 Umich 的吗,怎么不算是歪打正着地离
+dream school 近了一点捏(并没有
不是,这情况怎么急转直下,变成了我现在就已经有点想回学校了,但是我 +EVA 展的票要 8.2 之后才能去看所以回不去啊我超(
+7月17日
+睡前在想为啥没有人在 adjacent matrix 里放 \(\pm +i\)(暴论),思考了一下这得有多少种三角形然后就迅速睡着了(
+这九院口外挂号挂了一周了还没挂上,想了想感觉还是下学期或者暑假末尾直接北医三院吧,体验下公费医疗(。上次拔左边的智齿前前后后拔出了一次托福的价钱,虽然确实弄得挺好的但还是(
+7月18日
+开始 读 Stein(多大的人了还在读 Stein( 补石头门,看
+bangumi
+评价好像前期节奏很慢,大概正好每天一边吃饭一边看。初中的时候好像就想看了,但是在游戏和动画之间犹豫不决,结果
+neither 了(
今天想把蒸锅拿出来洗一洗,结果在橱柜里找到了厨房的第十个插座(,它到底是想起到一个什么样的作用啊(二度
+7月19日
+今天外出,回了一趟宝山,顺路去宜家 零元购
+把积分兑成了一个靠垫和一堆小垃圾(。气温 38
+度我在户外健步如飞,感觉比(声称)36 度的南昌和武汉舒服多了((
所以我(看完 EVA +展之后)到底啥时候回学校(,之前担心的一些事情现在好像都不需要我了(?),现在都有点疑惑为啥这个暑假没去施工实习,真的就单纯因为怕热吗(。现在每天就是在家里不务正业地乱看文章(但我的正业到底是啥),已经从 +signed network 看着看着不知道顺着哪条线被带到 matrix estimation +去了。正好下周一统计中心(现在改口叫统计系我都还不大适应)有个报告讲这个,顺便听一下。为什么要在日记里写这个捏,因为我怕我忘了(。
+导针对我想跟他聊聊 signed network +的邮件向我提问:上学期让你看的那两篇怎么样了,啥时候讲一下?我哈哈大笑,什么 +stochastic block +model,它真的太丑了所以定义都忘记了捏!这就再去看一眼(。
+而且我的智齿好痛,今年已经肿了无数次了,虽然北医三院挂号看起来也很难,但想回去拔牙(。
+7月20日
+回去看学期中间看的那篇 adjusted
+covariates,发现它和我前段时间看的一个 signed network 都引了同一篇 2020
+年的文章,考虑到 balanced theory,出现 co-citation
+就不得不去读一下了(x
但说实话这样一读我完全理解之前那个 signed network 了,就是给 2020
+年那篇套上了一个选择符号的步骤,这和六年后在 TCL
+里加正负号不就是一样的思路捏(,不过他多做了一个优化所以多推了若干
+bound,用了一些 花里胡哨的
+MLE。但是这篇把故事讲得很好,我的理解是造了一个也比较符合直觉的
+population level balance 的概念,然后成功从这里引过去了。本质上是 inner
+product model 在 signed network 里的推广,但故事讲的是 balance
+这样子,也顺利吸引到了我这种因为对 balance 和 signed network
+感兴趣而来的人结果最后怎么吃了一大口 ERGM(x
来都来了,不如去看下 Terry Tao 那篇 matrix completion
+吧!反正之前 low-rank method for signed network 也用到了来着!
+那我的汇报到底要说点啥捏(
很久没追番了,最近竟然在以追番的状态看 7
+月那部擅长逃跑的殿下(,我也不想的,但是很久没有这么命中我好球区的男主了
+但是作画转场真的顶级,单纯欣赏画面也值了(
7月21日
+这石头门好几天没看现在有点不大想看了(,前期节奏好慢,但也还是再坚持一下罢(。然后今天去把辉夜姬物语看了,我之前一直以为这是宫崎骏的作品,但我不太喜欢宫崎骏(这是可以说的吗?)所以一直没看,今天才发现不是,遂补(
+最终还是去把 bangumi 评分调了,给进巨第三季 part 2 和 EVA
+TV、真心喂你 真心为你拉到了 10 分,大概确实 9 和 10
+之间还是有一些必须区分开的差距,别的 9
+看了半天感觉实在动不了了,只有想往下打到 8
+的(。但也没往下调,毕竟当时打 9 也一定有我的道理(?
看了一天 error bound,晚上盯着不等式里的 \(e^{M_1}\) 陷入困惑,k-th iteration 的 error +metric 是 \(e_k\),个么 \(e\) 是啥?再一想,\(e\) 就是 \(e\) 啊((
+一直担心(并没有)的事情终于发生了。很久没说过话的高中校友唐突开聊,我对他的了解止于他大一的时候从 +FDU 数院转出了,然后:
+++友:你现在在搞啥科研吗?数学哪个方向捏?
+(我内心:直接说统计是不是有点太宽泛了,social network +听起来像人文社科的,要说 random graph +也不是不行,但我当时听到概率图模型这个名字的时候都没意识到就是我在搞的这个东西,说英文会比较容易理解吗?但是已经犹豫很久了还没回是不是会显得有点没礼貌啊,就 +network model 吧!)
+我:network model
+友:哦哦
+友:那你是本科学数学,研究生转码?
+友:是看开了吗
+
(挠头
+7月22日
+成功听到了报告,甚至下午三点半就打开了腾讯会议(但前面这第一个报告是在说啥),对我来说很厉害了(?
+之前只看过一篇关于 Kronecker product 的文章,讲的是怎么用一个 \(2 \times 2\) 的矩阵反复做 Kronecker product +得到一个 \(2^N\) 的矩阵作为 adjacent +matrix,然后它和 Chung-Lu model +在一定条件下是等价的。今天听的这个我一开始以为也是差不多的目的,结果怎么唐突推广到 +time series(,但作为 SVD 的推广,把维数也加进 penalty +还是蛮有意思的。
+有的时候觉得我不会是个废物吧?一时兴起开始学 +RKHS,找了个讲义结果从早看到晚,一天啥都没干刚看明白(。
]]>茶园老师和教务手都太快了,俩小时速通特殊原因选课,下次还来。
+先前把统辅当做很有趣的数学分支,被转数环的学长泼了冷水说“统计中心的风格可能会不大适应”,另一位学长也说“统辅不是你期待的样子”,目前看中心开课的意思也好像有点当工科的辅助来学。我到底多大程度上能接受严谨的数学推导?又能走多远?统辅还是数辅还是我全都要,这是一个问题。
初概这玩意儿前八周上完,约等于梦回高中月考,我定义呢我证明呢啊怎么直接拿来用了?在考虑下学期去数学系重新上概(1),甚至考虑跟实复分析,但是数分的空缺真的没问题吗。当然,没有退初概还是为了跟上统辅的进度,毕竟后八周还有统计推断,我也没完全放弃统辅,目前或许是我目光短浅了。
+这门课和教材也没什么映射关系(而且看老师的意思是也没有教材,草),直接按照 +Lecture n +的顺序写吧。本来想放进茴香豆篇,但概率论这边举例比较多,放在一起又很冗长,还是算了。
Lecture 1
-打开 Introduction to Linear Optimization,看到第一章标题是 linear -programming,差点 PTSD 到当场退课(
-实际上就是线性规划,和(我害怕的那个)programming 没什么关系(
-Standardized Linear -Programming
-Reduce to Standardized -Format
-
-
线性优化众所周知应该是线性的(草),最朴素的想法下它可以转换为以下形式:
-\[\text{minimize} \quad c^Tx\]
-\[\text{subject to} \quad \begin{aligned} -& a_i^Tx \geq b_i \quad i \in M_1 \\ & a_i^Tx \leq b_i \quad i -\in M_2 \\ & a_i^Tx = b_i \quad i \in M_3 \\ & x_j \geq 0 \quad -\quad j \in N_1 \\ & x_j \leq 0 \quad \quad j \in N_2 -\end{aligned}\]
-主要是通过取 \(-c\) 把 maximize -问题变为 minimize,以及将不同的 constraints 分类。
-想要改成更为统一、方便处理的形式,可以通过取负将所有的 -constraints 改为 \(a_i ^T x \geq -b_i\),但还是全取等最好。
-\[\text{minimize} \quad c^Tx\]
-\[\text{subject to} \quad \begin{aligned} -& A^Tx =b \\ & x_j \geq 0 \end{aligned}\]
-具体来说只需要再经历以下两步化简:
+- 概率模型:概率模型由样本空间和概率构成。每一个概率模型都关联着一个试验。
-
-
- 将不受限制的 free variable 拆解为 \(x_i = -x_i ^+ - x_i ^-\),则有 \(x_i^+ \geq 0, -x_i ^- \geq 0\); -
- 将 \(\sum_{j=1} ^n a_{ij} x_j \leq -b_i\) 改为 \(\sum_{j=1} ^n a_{ij} x_j + -y_i = b_i, \text{with} \; y_i \geq 0\) +
- 样本空间是一个集合,概率模型对应的试验产生的所有可能结果形成样本空间,记作 +\(\Omega\)。比如说,概率模型为抛硬币,样本空间即为 +\(\lbrace head,tail +\rbrace\)。样本空间可以是离散的,也可以是连续的。 +
- 事件 \(A\) +是样本空间的子集,也就是某些试验结果的集合。概率 \(P(A)\) 分配到事件 \(A\) 上。 +
+ - 概率公理:非负性,归一化,可加性。 +
- 概率的性质:两个技巧,归纳法和取补集。
注意到 \(x_j \geq 0\) -是对所有变量成立的,我还是第二次看才发现这个问题。
+Lecture 2
+-
+
事件域(或称为 \(\sigma-\)域,\(\sigma-\)代数):对于样本空间 \(\Omega\),\(F\) 表示 \(\Omega\) 的某些子集构成的集合,如果 \(F\) 满足以下三个条件:
+-
+
- \(\Omega \in F\) ; +
- 对于任意的 \(A\in F\),有 \(A^c \in F\); +
- 如果 \(A_n \in F\),\(n=1,2,...\),则 \(\cup_{n=1}^\infty A_n \in F\)。
Other Optimization Problems
-也会遇到一些其他形式的优化问题,在 cost function -之类的地方有些许改动,处理思想仍然是一样的。
+那么称 \(F\) 为 \(\Omega\) 上的事件域,称 \(F\) 中的元素为事件,称 \((\Omega,F)\) 为可测空间。
+从而,有且只有 \(F\) +中的每个事件都能分配概率,这就圈定了我们所关心的事件的范围。
+事件域的一些性质如下:
-
-
\[\text{minimize} \quad -\max_{i=1,2,...,m} (c_i^Tx+d_i)\]
-\[\text{subject to} \quad Ax \geq -b\]
-只需要把 cost function 变成 \(m\) 个 -constraints 就可以了:
-\[\text{minimize} \quad z\]
-\[\text{subject to} \begin{aligned} \quad -& Ax \geq b \\ & z \geq c_i^Tx + d_i \quad \text{for} \; i = -1,2,...,m\end{aligned}\]
-\[\text{minimize} \quad \sum_{i=1}^n -c_i | x_i|\]
-\[\text{subject to} \quad Ax \geq -b\]
-这个在日记里吐槽过了,我个人认为更符合直觉的是拆正负部,只是需要保证二者之一是 -\(0\),还是不方便,学实分析学得。也可以改成:
-\[\text{minimize} \quad \sum_{i=1}^n c_i -y_i\]
-\[\text{subject to} \begin{aligned} \quad -& Ax \geq b \\ & x_i \leq y_i, -x_i \leq y_i \quad \text{for} \; -i=1,2,...,n \\ & y_i \geq 0 \quad \quad \quad \ \ \ \qquad -\text{for} \; i =1,2,...,n \end{aligned}\]
+- 两个事件域的并集不一定是事件域,但交集一定是。(Trivial) +
- 事件域对集合的任何计算都是封闭的,包括事件列的极限运算。 +
+概率,也称为概率测度:设 \((\Omega,F)\) +为可测空间,\(P\) +是定义在 \(F\) 上的函数,如果 \(P\) 满足以下三个条件:
+-
+
- 非负性,完全性(Trivial) +
- 可列可加性(\(\sigma-additivity\)):对于 \(F\) 中互不相交的事件 \(A_1,A_2,...\) ,有 \(P(\cup _{n=1} ^\infty A_n) = \Sigma _{n=1} ^\infty +P(A_n)\)。
都很 trivial,初等变换一下就好了。
-Solutions to LP Problems
-首先 LP problem 有四种可能性,学着学着都要忘了。
+那么称 \(P\) 为 \(F\) 上的概率测度,简称概率。
+对于上述定义的样本空间,事件域和概率测度,我们称 \((\Omega,F,P)\) 为概率空间。
+简单举个例子,在掷硬币的概率模型中,样本空间是 \(\lbrace Head,Tail \rbrace\),事件域是 \(\lbrace \lbrace Head,Tail \rbrace, \lbrace Head +\rbrace, \lbrace Tail \rbrace, \emptyset +\rbrace\),此时样本空间和事件域构成可测空间。事件域中的每一个元素都是事件,概率测度为 +\(P(\lbrace Head \rbrace) = p\), \(P(\lbrace Tail \rbrace)=1-p\)。(这是考虑了 +\(biased\) \(coin\) 的情况)
+概率测度的一些性质:
+-
+
- 对于单调增序列,有 \(\lim_{n \to \infty} +A_n = \cup_{i=1} ^\infty A_i\), \(P(\lim_{n \to \infty}A_n) = \lim_{x \to +\infty}P(A_n)\)。 +
- 单调减序列同理。 +
+条件概率(定义略)的若干性质:
+-
+
对互不相容的事件列 $B_i $,有 \(P(\cup +_{i=1}^\infty B_i|A) = \Sigma _{i=1} ^\infty P(B_i +|A)\)。
+用 \(P_A(·)=P(·|A)\) 表示在事件 +\(A\) +发生条件下的条件概率,这仍然是一个概率测度,\((\Omega,F,P_A)\) 仍然是一个概率空间。
+当然,此时我们可以把 \(A\) +之外的结果排除掉,记作 \((A,A\cap +F,P_A)\)。
+
+乘法公式:设 \((\Omega, F,P)\) +是概率空间,\(A_i \in F\),\(i = 1,2,...,n\),且 \(P(A_1 \cap A_2 \cap ... \cap +A_{n-1})>0\),于是有\(P(\cap_{i=1}^n +A_i) = P(A_1) \Pi_{i=2}^n P(A_i|A_1\cap A_2 \cap ... \cap +A_{i-1})\)。
+举个例子:某人写了 \(n\) +封信,将其装入 \(n\) +个写有地址的信封,全部装错的概率 \(q_0\) 为?恰有 \(r\) 个信封装对的概率 \(q_r\) 为?
+-
+
- 在第一个问题下面,我们考虑记事件 \(A_i\) 为第 \(i\) +个信封装对的事件,利用容斥原理即可。 +
- 在第二个问题下面,其实问题主要在于怎么考虑是哪 \(r\) 个信封放对了的问题。“指定的某 \(r\) 个信封放对了”这一事件的概率等于“从 +\(n\) 个信封里无放回地取出 \(r\) 个正好是前 \(r\) 号”的概率。又因为从 \(n\) 个信封里指定 \(r\) 个有 \(C_n +^r\) 种方式,于是这一部分的概率为 \(\frac{1}{r!}\)。 +
+全概率公式:将 \(\Omega\) +分割成事件 \(A_1,A_2,...,A_n\) +的并,另有其中的事件 \(B\),可以对每个 +\(i\) 得到 \(P(B|A_i)\),于是 \(P(B) = \Sigma_{i=1}^n P(A_i)P(B|Ai) = +\Sigma_{i=1}^n P(B \cap A_i)\)。
+这个时候,我们称 \(\lbrace A_i +\rbrace\) 是 \(\Omega\) +的一个分割。同时,式中的 \(n\) 可以用 +\(\infty\) 代替。
+举个例子:一个袋子里有 \(n\) +个白球和 \(m\) 个黑球,从中无放回地取出 +\(k\) 个球,求第 \(k\) 次取得黑球的概率。
-
-
- There exists a unique optimal solution. -
- There exist multiple optimal solutions; in that case, the set of -optimal solutions can be either bounded or unbounded. -
- The optimal cost is \(-\infty\), -and no feasible solution is optimal. -
- The feasible set is empty. (The LP problem is infeasible.) +
- 递归:第一次取黑球的概率影响第二次,第二次影响第三次...简单列个数列可以看出来取黑球的概率是定值,即为 +\(\frac{m}{m+n}\)。 +
- 排队:把 \(m+n\) 个球排成一列,算第 +\(k\) 个恰为黑球的概率即可。 +
+\(Bayes\) 准则:设 \((\Omega,F,P)\) 是概率空间,\(B,A_i \in F\),\(i=1,2,...,n\),\(\lbrace A_i \rbrace\) 是 \(\Omega\) 的一个分割。我们要用 \(P(B|A_i)\) 算 \(P(A_i|B)\),就可以使用 \(Bayes\) 准则:\(P(A_i|B)=\frac{P(A_i)P(B|A_i)}{\Sigma_{j=1}^n +P(A_j)P(B|A_j)}\) 。
Notations
-一些拼不对的单词了属于是。
-突然发现其实可以在笔记里多放点迷言迷语:
-
Lecture 3
-
-
A polyhedron is a set that can be described as -\(\{x \in \mathbb R^n | Ax \geq b \}\), -where \(A\) is an \(m\times n\) matrix and \(b \in \mathbb R^m\).
-A set \(S \subset \mathbb R^n\) -is bounded if there exists a constant \(K\) such that the absolute value of every -component of every element of \(S\) is -less than or equal to \(K\).
-Let \(a\) be a non-zero vector -on \(\mathbb R^n\) and let \(b\) be a scalar, thus:
+(两两)独立性,条件独立性和一组事件的相互独立性
-
-
- The set \(\{x \in \mathbb R^n | a^Tx =b -\}\) is called a hyperplane. -
- The set \(\{x \in \mathbb R^n | a^Tx \geq -b \}\) is called a half-space. +
对于概率空间 \((\Omega,F,P)\),\(A,B,C \in F\),独立性指的是 \(P(A\cap B) = P(A)P(B)\),条件独立性指的是 +\(P(A\cap B|C)=P(A|C)P(B|C)\)。
+那么这二者有什么关系呢?答案是没有关系(
+简单举个反例:抛掷两次均匀的硬币,令 \(H_1=\lbrace\)第一枚正面朝上\(\rbrace\),\(H_2=\lbrace\)第二枚正面朝上\(\rbrace\),\(D=\lbrace\)两枚硬币结果相反\(\rbrace\)。于是有 \(P(H_1 \cap H_2) = P(H_1)P(H_2)\),但是 +\(P(H_1 \cap H_2 |D) = 0,P(H_1|D) = +\frac{1}{2},P(H_2|D) = +\frac{1}{2}\)。也就是说,独立性不能推出条件独立性。
+一组事件的相互独立性涉及到概率空间 \((\Omega,F,P)\) 中的一组事件 \(A_1,A_2,...,A_n\),如果对于任意非空子集 +\(S\subset \lbrace 1,2,...,n +\rbrace\),都有\(P(\cap_{i \in S} +A_i)=\Pi_{i\in S} P(A_i)\),那么称这一组事件是相互独立的。
+根据 \(S\) +的完备性可以知道,两两独立性也不能推出一组事件的相互独立性。
+TODO:记得复习一下赌徒破产模型。
-A set \(S \subset \mathbb R^n\) -is convex if for any \(x , y -\in S\) and any \(\lambda \in -[0,1]\), we have \(\lambda x + -(1-\lambda) y \in S\).
-Let \(x_1 ,x_2,...,x_n\) be -vectors in \(\mathbb R^k\) and let -\(\lambda_1, \lambda_2,...,\lambda_n\) -be non-negative scalars whose sum is unity.
-The convex hull of \(x_1, -x_2,...,x_n\) is the set of all convex combinations of these -vectors, i.e.,
-\[\{\sum_{i=1}^n \lambda_i x_i | -\sum_{i=1}^n \lambda_i =1 \; \text{and} \; \lambda_i \in [0,1] -\}\]
-
有一些很 trivial 的结论,看起来既重要又不重要的,希望有脑子就行。
-
随机变量何种情况下是良定义的?
-
-
- One writes \(f(x) = O(g(x))\) if -there exists a positive real number \(M\) and a real number \(x_0\) s.t. \(f(x) -\leq Mg(x)\) for any \(x \geq -x_0\). -
- One writes \(f(x) = \Omega (g(x))\) -if there exists a positive real number \(M\) and a real number \(x_0\) s.t. \(f(x) -\geq M g(x)\) for any \(x\geq -x_0\). -
- One writes \(f(x) = \Theta (g(x))\) -if \(f(x)= O(g(x))\) and \(f(x) = \Omega(g(x))\). +
- 设 \((\Omega,F)\) 为可测空间,如果 +\(\Omega\) 上的函数 \(X(\omega)\) 满足:对 \(\forall x \in R\),\(\lbrace \omega | X(\omega) \leq x\rbrace \in +F\),则称 \(X(\omega)\) 为 \((\Omega,F)\) 上的随机变量。 +
这门课上为什么有人没学过算法不知道这些是什么啊.jpg
-How to Describe Optimal -Solutions
-有三种刻画 corner point 的方法,我们稍后证明它们在 polyhedron -里是等价的。
+Lecture 4
-
-
Let \(P\) be a polyhedron. A -vector \(x\in P\) is an extreme -point of \(P\) if we cannot -find two vectors \(y,z \in P\), both -different from \(x\), and a scalar -\(\lambda \in [0,1]\) such that \(x = \lambda y + (1-\lambda) z\).
-Let \(P\) be a polyhedron. A -vector \(x\in P\) is an -vertex of \(P\) if -there exists a vector \(c \in \mathbb -R^n\) such that \(c^T x < c^T -y\) for all \(y \in P\) and -\(y\neq x\). (Also holds for > by -taking \(-c\))
-Let \(P\) be a polyhedron. A -vector \(x\in P\) is an basic -solution of \(P\) if:
+对于离散型随机变量 \(X\),称 +\(P(X=x_k) = p_k\) 为 \(X\) 的概率分布,称 \(\lbrace p_k \rbrace\) 为概率分布列,简称为 +\(PMF\)。当其规律不够明显时可以写成表格形式。
-
-
- All equality constraints holds. -
- Out of the constraints that are active at \(x\), there are \(n\) of them that are linearly -independent. -
Moreover, if \(x\) is a basic -solution that satisfies all the constraints, we say it's a basic -feasible solution.
-
所以说只要 constraints 的个数是有限的,那么其中选择 \(n\) 个 linearly independent -的方法是有限的,basic (feasible) solution 的个数就是有限的。
-注意到定义 basic solution 的时候事实上 equality constraints 和 -inequality constraints -的地位不等,然而作为一个线性优化问题是可以在这方面有很多等价形式的,事实上 -basic solution 会受到 polyhedron 定义形式的影响,具体的例子详见 P49 -的平面规划问题。另外,basic feasible solution 不会受到 polyhedron -形式的影响。
-最后是有关这三个定义等价性的定理:
-Let \(P\) be a nonempty polyhedron -and let \(x \in P\), then the following -are equivalent:
+两点(\(Bernoulli\))分布:掷硬币或正或反,\(P(X=0)=p,P(X=1)=1-p\)。
二项(\(Binomial\))分布:试验成功的概率为 \(p\),重复 \(n\) 次试验成功 \(k\) 次的概率,\(P(X=k) = C_n ^k p^k +(1-p)^{n-k}\)。它是二项式展开的其中一项,故名二项分布。
+二项分布的最大可能值(即中心项)的推断:考虑二项式展开。
......这里空间不够大,别的写不下了(其实是不需要记忆离散型分布的名字,会讲故事就行。
泊松(\(Poission\))分布:\(P(X=k)=\frac{\lambda ^k}{k!} +e^{-\lambda}\)。一般来说,记随机变量 \(Y\sim P(\lambda)\) 表示 \(Y\) 服从参数为 \(\lambda\) 的泊松分布。
+放射粒子模型揭示了二项分布可以用泊松分布近似的事实。
+TODO:复习粒子模型,做书上习题 \(2.2\)。
对于连续型随机变量的定义如下:设随机变量 \(X\),如果存在非负函数 \(f(x)\) 满足对任意的 \(a<b\),\(P(a<X\leq b)=\int _a ^b f(x) dx\),则称 +\(X\) 为连续型随机变量。称 \(f(x)\) 为 \(X\) +的概率密度函数,简称概率密度或者密度(\(PDF\))。
+这并不意味着 \(X(\omega)\) +是连续函数,因为样本空间可能没有任何的拓扑结构,谈不上连续性。
-
-
- \(x\) is an extreme point. -
- \(x\) is a vertex. -
- \(x\) is a basic feasible -solution. +
均匀(\(Uniform\))分布:\(f(x) = \frac{1}{b-a},x \in (a,b)\),此时记 +\(X \sim U(a,b)\)。
+指数(\(Exponential\))分布:\(f(x) = \lambda e^{-\lambda x},x\geq +0\),此时记 \(X\sim +\epsilon(\lambda)\)。
+如果 \(X\) 是连续型非负随机变量,则 +\(X\) 服从指数分布的充要条件是 \(X\) 没有记忆性,也就是说 \(P(X>s+t|X>s) = +P(X>t)\)。(可以由条件概率公式证出,Trivial.)
+\(X\) +的失效率就是单位长度时间内失效的概率,可推知即为 \(\lambda\)。也称其为尺度参数(rate +parameter)。
+TODO:再推一遍 \(X\sim +\epsilon(\lambda)\) 时,\(Y=\lambda +X\),则 \(Y\sim \epsilon +(1)\)。
+正态分布(\(Normal\) \(Distribution\)):\(f(x)=\frac{1}{\sigma \sqrt{2 \pi}} +exp(-\frac{(x-\mu)^2}{2\sigma ^2}),x \in R\),此时记 \(X\sim N(\mu ,\sigma^2)\)。
+正态分布的函数图像关于 \(x=\mu\) +对称,在此处取最大值 \(f(\mu) = (\sigma +\sqrt{2\pi})^{-1}\)。关于 \(x=\mu \pm +\sigma\) 处有拐点。
+
证明太长了,这里写不下( 但说实话从 extreme point 推 basic
-feasible solution 还不是很显然,要用一点点分析智慧(
Algebraic Approach to -Optimal Solutions
-说了这么多,也把 basic feasible solution -用三种方式刻画出来了,但是对于具体例子的计算还是借助矩阵工具。
-有一个 applicable procedure:
-For constructing basic solutions for a polyhedron \(P= \{x \in \mathbb R^n | Ax = b , x \geq 0 -\}\), use the three-step procedures below:
+Lecture 5
-
-
Choose \(m\) linearly -independent columns \(A_{B(1)}, A_{B(2)}, -\cdots , A_{B(m)}\) and solve
-\[\begin{bmatrix} | & | & \cdots -&| \\ A_{B(1)} & A_{B(2)} & \cdots & A_{B(m)} \\ \cdots -& \cdots &\cdots & \cdots \\ | & | & \cdots & | -\end{bmatrix} \begin{bmatrix} x_{B(1)} \\ x_{B(2)} \\ \cdots \\ -x_{B(m)} \end{bmatrix} = \begin{bmatrix}b_1 \\ b_2 \\ \cdots \\ b_m -\end{bmatrix}\]
-Take \(x_i =0\) for \(i \neq B(1),B(2), \cdots, B(m)\)
-Combine all the components of \(x\) and get the basic solution of the base -\((A_{B(1)}, A_{B(2)}, \cdots , -A_{B(m)})\).
-
不同的 base 可以得到不同的 basic solution,也可能会得到相同的。
-在解 basic solution 的时候本质上只用到了 \(m\) 个 constraint equalities 作为 -base,以及 \(n-m\) 个 non-negative -constraints,实际上 \(x\) 可能不仅在这 -\(n\) 个 constraints 处 -active,如果有多于 \(n\) 个 constraints -在 \(x\) 处 active 则称它是一个 -degenerate basic solution。
-很明显的一点是在 polyhedron 里如果一个 basic solution 有多于 \(n-m\) 个分量是 \(0\),那么它一定 -degenerate。由矩阵解的唯一性,这也是 degenerate basic solution -的唯一情形。
-Existence of Vertex
-非常口胡地说,要有 basic feasible solution -至少区域的边界上要先有个角吧(比划
+概率分布函数(\(CDF\)):对随机变量 \(X\),称 \(x\) 的函数 \(F(x) += P(X\leq x),x \in R\) 为 \(X\) +的概率分布函数,也称为累积分布函数,分布函数。
-
-
- A polyhedron \(P \subset \Re^n\) -\(\textbf{contains a line}\) if there -exists a vector \(x \in P\) and a -nonzero vector \(d \in \Re^n\) such -that \(x + \lambda d \in P\) holds for -all scalar \(\lambda\). +
对一个 \(PMF\) 书写 \(CDF\),它一般是一个分段函数。
+对一个 \(PDF\) 书写 \(CDF\),记随机变量 \(X\) 的概率密度为 \(f(x)\),则其分布函数为 \(F(x) = \int_{-\infty}^x f(t) dt,x \in R\)。 +对于一个已知的 \(F(x)\),只能确定连续点 +\(x\) 处的概率密度为 \(f(x) = +F'(x)\),显然在不连续点处是无法确定的。
+-
+
- 注:连续型随机变量的概率密度不必为连续函数,允许可列个单点断开。那它为什么叫连续型呢?这与 +\(F(x)\) +的形式有关。同时离散型这一形容也与 \(F(x)\) 有关。 +
+举个例子:标准正态分布的概率密度为 \(\phi(x)=\frac{1}{\sqrt{2 \pi}} +exp(-\frac{x^2}{2}),x \in R\)。其分布函数记为 \(\Phi(x)\),其值需要查表,当然也可以丢进 +MATLAB 算,但是不要求(
+ +
+再举个例子:正态分布函数的概率密度计算中,可以对 \(\frac{x-\mu}{\sigma}\) +进行换元,从而变为标准正态分布的情况。
+再再举个例子:指数分布的分布函数要注意分段,考虑 \(x<0\) 的情况。
+TODO:去看一下几何随机变量和指数随机变量的分布函数的逼近,这是利用 +\(CDF\) 寻找 \(PMF,PDF\) 之间关系的例子。
+分布函数对一切随机变量都适用,这是它相对 \(PMF,PDF\) 的优势。
+
对于一个随机变量 \(X\) 的函数 +\(g(X)\),怎么去寻找 \(g(X)\) +的概率分布?(这一部分其实是做题方法)
+-
+
最简单的情形:\(X\) +是离散型随机变量,对每一个 \(X\) 的取值 +\(x\),确定 \(Y=g(x)\) +时的概率分布列即可。有需要的话还可以化成 \(CDF\)。
+曲线救国:考察 \(Y=g(X)\) +的分布,若 \(g(x)\) +是连续函数,那么可以先得到 \(Y\) 的 \(CDF\) 为 \(F_Y(y)=P(Y\leq y)\),再求导得到 \(f_Y(y)=F_Y'(y)\)。
+特殊情况 1:线性的 \(g(X)\) +可以直接从 \(f_X(x)\) 得到 \(f_Y(y)\) 而无需计算 \(CDF\)。
+形如 \(Y=aX+b\) ,有 \(f_Y(y)=\frac{1}{|a|} +f_X(\frac{y-b}{a})\)。(其实还是用 \(CDF\) 证明的)
+特殊情况 2:对于严格单调的 \(g(x)\),考虑 \(Y=g(X)\)。记 \(h(y)\) 是 \(g(x)\) 的逆映射,于是 \(f_Y(y)=f_X(h(y))|h'(y)|\),这可以通过考虑事件 +\(\lbrace x<X<x+\delta \rbrace\) +来证明。
+特殊情况 +3:像正态分布这样的特殊分布,遇到的时候建议先考虑能不能在 \(\Phi(x)\) +的尺度先行利用对称性化简。
+
也就是说范围里面不能有直线才能有 vertex。
+Lecture 6
-
-
Suppose that the polyhedron \(P = \{x -\in \Re^n \mid \textbf{a}_i^T x \geqslant b_i , i=1,2, \cdots, m -\}\) is nonempty. Then the following is equivalent:
+\(n\) 维随机向量:如果 \(X_1,X_2,...,X_n\) 都是概率空间 \((\Omega,F,P)\) 上的随机变量,那么称 \(X=(X_1,X_2,...,X_n)\) 为概率空间 \((\Omega,F,P)\) 上的 \(n\) 维随机向量。
+那么怎么从随机变量上迁移来诸多的概念呢?
-
-
The polyhedron \(P\) has at -least one extreme point.
-The polyhedron does not contain a line.
-There exist \(n\) vectors out of -the family \(\textbf{a}_1, \textbf{a}_2, -\cdots, \textbf{a}_m\), which are linearly independent.
+联合概率分布函数:设 \(X=(X_1,X_2,...,X_n)\) 为随机向量,称 \(R^n\) 上的 \(n\) 元函数 \(F(x_1,x_2,...,x_n)=P(X_1<x_1,...,X_n<x_n)\) +为 \(X=(X_1,X_2,...,X_n)\) +的联合概率分布函数,简称为联合分布或者分布函数。
+有关离散型随机向量:如果 \(X_1,X_2,...,X_n\) 都是离散型随机变量,则称 +\(X=(X_1,X_2,...,X_n)\) +为离散型随机向量。如果所有 \(X_i\) +的不同取值为 \(x(j_1,j_2,...,j_n)=(x_1(j_1),x_2(j_2),...,x_n(j_n))\),则称 +\(p_{j_1 j_2 ... +j_n}=P(X=x(j_1,j_2,...,j_n))\) 是 \(X\) 的联合分布列。
+-
+
举个例子:设 \(F(x,y)\) 是 \((X,Y)\) 的联合分布,则 \(X,Y\) 有概率分布:
+\(F_X(x) = P(X \leq x,Y \leq \infty) = +F(x,\infty)\),
+\(F_Y(y) = P(X \leq \infty,Y \leq y) = +F(\infty ,y)\)。
+于是,对于矩形 \(D=\lbrace a<X \leq b,c +< Y \leq d \rbrace\),有 \(P((X,Y)\in D) = +F(b,d)-F(b,c)-F(a,d)+F(a,c)\)。
+
+有关连续型随机向量:简单来说,考虑二维的情形,如果 \((X,Y)\) 有联合密度 \(f(x,y)\),则 \(X\) 和 \(Y\) 分别有概率密度 \(f_X(x)=\int_{-\infty} ^{\infty} +f(x,y)dy\),\(f_Y(y)=\int_{-\infty}^{\infty} +f(x,y)dx\)。
+延拓到 \(n\) 维的情况,被积函数 +\(f_k(x_1,x_2,...,x_k)=\int_{R^{n-k}} +f(x_1,x_2,...,x_k) dx_{k+1}...dx_n\) 是为 \((X_1,...,X_n)\) +的联合密度,称之为边缘密度(Marginal PDF)。
+连续型随机向量的独立性:对每个 \(i(1\leq i \leq n)\),随机变量 \(X_i\) 有概率密度 \(f_i(x_i)\),则 \(X_1,X_2,...,X_n\) +相互独立的充分必要条件为随机向量 \(X=(X_1,X_2,...,X_n)\) 有联合密度 \(f_1(x_1)f_2(x_2)...f_n(x_n),(x_1,x_2,...,x_n)\in +R^n\)。
+经典连续型随机向量例:二元正态分布
+设 \(\mu_1,\mu_2\) 为常数,\(\sigma_1,\sigma_2\) 为正常数,\(\rho \in (-1,1)\) 中的常数。如果随机向量 +\((X,Y)\) 有概率密度
+\(f(x,y)=\frac{1}{2\pi \sigma_1 \sigma_2 +\sqrt{1-\rho^2}}exp(-\frac{1} {2(1-\rho^2)} [\frac{(x-\mu_1)^2}{\sigma_1 +^2} + \frac{(y-\mu_2)^2}{\sigma_2 ^2} - \frac{2\rho +(x-\mu_1)(y-\mu_2)}{\sigma_1 \sigma_2}])\),
+那么称 \((X,Y)\) +服从二元正态分布,记为 \((X,Y)\sim +N(\mu_1,\mu_2,\sigma_1^2, \sigma_2^2, \rho)\)。
+-
+
- 一些性质:\(X,Y\) 独立的充要条件是 +\(\rho=0\)。(Trivial) +
+联合分布(Joint CDF)与联合密度(Joint PDF):已知联合密度 \(f(x,y)\),于是有联合分布 \(F(x,y) = \int _{-\infty} ^x \int _{-\infty} ^y +f(u,v)dudv\)。
+当 \(f(x,y)\) 连续时,有 \(f(x,y) = \frac{\partial^2 F(x,y)}{\partial x +\partial y}\)。更一般地,如果该混合偏导数不存在,那么 \(f(x,y)=0\)。
+连续型条件概率分布:设随机向量 \((X,Y)\) 有联合密度 \(f(x,y)\),\(Y\) 有边缘密度 \(f_Y(y)\)。若在确定的 \(y_0\) 处 \(f_Y(y_0)>0\),则称 \(P(X \leq x | Y=y_0) = \frac{\int_{-\infty} ^x +f(s,y_0) ds}{f_Y(y_0)}\) 为给定条件 \(Y=y_0\) 下,\(X\) 的条件分布函数(conditional CDF),记为 +\(F_{X|Y}(x|y_0)\)。
+于是条件分布密度为 \(f_{X|Y}(x|y_0) = +\frac{f(x,y_0)}{f_Y(y_0)}\)。(conditional PDF)
+-
+
一些性质:
+$F_{X|Y}(x|y)=P(Xx|Y=y)={-} ^x f{X|Y}(s|y)ds, x R $。
+如果 \(F_{X|Y}(x|y)\) 关于 \(x\) +连续,且除去至少可列个点后有连续的导数,则在偏导数存在时,\(f_{X|Y}(x|y_0)=\frac{\partial +F_{X|Y}(x|y)}{\partial x}\),否则为 \(0\)。
+
一个更重要的定理是关于 bounded polyhedron 和 standardized problem -的:
+期中插播提示
-
-
- Every nonempty bounded polyhedron and every nonempty polyhedron in -standard form has at least one basic feasible solution. +
关于连续型概率分布之前的误解:连续型的随机变量不能随便取单点的概率,因为单点处的概率就是 +\(0\),这就是为什么要定义一个概率密度的原因。概率密度的大小可以是任意的,不一定要小于 +\(1\),只要它的积分能够表示某一段(区域)的概率即可,这个在联合分布中有比较多的体现。
+总之,虽然 \(F(x,y) = \int_{-\infty}^x +\int_{-\infty}^y f(u,v)dudv\),但是 \(f(u,v)\) 不等同于 \(P(X=u,Y=v)\)。同理,如果要算条件概率的话,可以用 +\(F_{X|Y}(x|y)=P(x_1\leq X\leq +x_2|Y=y)=\int_{x_1}^{x_2} f_{X|Y} (s|y)ds\),也就是对 cond PDF +来积分求解。
+(但是,出于记忆公式的方便考虑,我还是会把它当成单点处的概率来列写公式(
+关于随机变量的独立性,定义如下:设 \(X_1,X_2,...,X_n\) 是 \((\Omega,F)\) 上的随机变量,如果对任意的实数 +\(x_1,x_2,...,x_n\) 有 \(P(X_1\leq x_1,X_2 \leq x_2,...,X_n \leq +x_n)=P(X_1\leq x_1)...P(X_n\leq x_n)\) 成立,则称随机变量 \(X_1,X_2,...,X_n\) 相互独立。
+同时,设随机变量 \(X_1,X_2,...,X_n\) +相互独立,\(g_1(x),g_2(x),...,g_n(x)\) +是一元实可测函数,\(\phi(x_1,x_2,...,x_k)\) 是 \(k\) 元实可测函数,则:
+-
+
- 随机变量 \(g_1(X_1),...,g_n(X_n)\) +相互独立; +
- 随机变量 \(\phi(X_1,...,X_k),X_{k+1},...,X_n\) +相互独立。
这是因为前者显然不含直线,后者定义在 \(\{x -\geq 0\}\) 的区域里也不含直线。注意到所有的 LP problem -其实都可以转化为后者的形式,所以说实际上都是有 basic feasible solution -的。这话比较模糊,意思是对于新的 standardized problem 一定会有 basic -feasible solution,然而把这个解限制到原来问题的维度中得到的解未必会是 -basic feasible solution。
-不过没有关系,我们会在后面看到实际上这已经够用了,因为目的不是解 -basic feasible solution,而是找出 optimal cost。在 standardized problem -下的 optimal cost 可以用 basic feasible solution 得到,而它和原问题的 -optimal cost 一致。
-Why is Vertex Important?
-说了这么多,为啥要解 basic feasible solution,对做 optimal cost -有什么好处吗?事实上,optimal cost 要么 unbounded,要么是在 basic -feasible solution 处取到,所以说只要 optimal cost 不是 \(-\infty\) 就就把所有的 basic feasible -solution 找出来溜一遍就好了。
-严肃一点用定理来说明的话是以下几条,对应书上 Section 2.6:
+这在样题的某个判断题中,以离散型随机变量的形式出现了,于是我自己证明了一下。实际上是一个更一般的结论。
+单调事件列的概率极限问题:以单调增序列 \(\lbrace A_i\rbrace\) 为例,有结论 \(lim_{n\to \infty} A_n=\cup _{i=1}^{\infty} +A_i\),于是极限概率为:
+\(P(\cup _{i=1}^{\infty} A_i) = P( lim +_{n\to \infty} A_n) = lim _{n \to \infty} P(A_n)\)。
+对于一些不单调的事件序列,可以用交并补构造一个单调序列,使得可以使用上述规律。
+事件列的上下极限的通俗说法:设 \(\lbrace A_i \rbrace\) 是 \(\Omega\) +中的一个事件列,定义上下极限为:
+\(lim_{n\to \infty} sup A _n = \cap +_{n=1}^{\infty} \cup _{k=n}^{\infty} A_k =\lbrace \omega \in \Omega: +\omega\) 属于无穷多个 \(A_i\rbrace\)。
+\(lim_{n\to \infty} inf A _n = \cup +_{n=1}^{\infty} \cap _{k=n}^{\infty} A_k =\lbrace \omega \in \Omega: +\omega\) 属于所有的 \(A_i\) +除去有限个\(\rbrace\)。
+当上下极限相等时称 \(\lbrace A_i +\rbrace\) 的极限存在。
+条件概率中会忘记的常识:对互不相容的事件列 \(\lbrace B_i \rbrace\),有 \(P(\cup _{i=1}^{\infty} B_i | A) = \Sigma +_{i=1}^{\infty} P(B_i | A)\)。
+一个 insight:求条件概率时我们可以把 \(A\) 之外的结果排除掉,记作 \((A,A\cap +F,P_A)\),这个事件域上完全可以有概率分布,因此不必为折棒太郎题惊讶。
+注意一组事件“相互独立”所要求的完备性。
+复习指南:
-
-
- Suppose the linear programming problem \(P\) has at least one extreme point, and -there exists at least one optimal solution. Then there exist one optimal -solution and is the extreme point of \(P\). -
- Suppose the linear programming problem \(P\) has at least one extreme point. Then, -either the optimal cost is \(-\infty\) -or there exist one extreme point, and it's also one of the optimal -solution. +
以上全部 TODO
+去看一下习题课中《一个有助于理解独立性的题目》和 Polya +坛子问题第二问。
+Poisoner's Dilemma
+A family has two girls while at least one names Lilia
+记一下几个重要分布,以及二元正态
+过一遍离散型、连续型随机向量的独立性证明,二元正态分布的独立性证明。
+折棒太郎折木棍问题的随机向量表述,Buffon 问题
+
+最后是一个我比较个人向的整理,根据考试重点和过往习题。Click +Here
+记得多用归纳!
注意到任意一个 LP problem 都可以转化为标准形式并保持 cost -不变,每个标准形式都有 extreme point,所以说上一条定理实际上是对任意 LP -problem 成立的。
-另外,第一个定理并不能推出第二个,因为并非 optimal cost 不是 \(-\infty\) 就能推出有 optimal -solution,比如说在 \(x >0\) 上找 -\(\frac 1x\) 的最小值,既不是 \(-\infty\) 也不存在 optimal solution。zjz 的 -PPT 还有 yy 讲课的时候都说 -trivial,实际上是不能这么推的。但可以通过沿特定方向移动到下一个 basic -feasible solution 的方法证明这种情况在 LP problem -里不会出现,这也就是第二个定理的证明。
-Lecture 2
-这节课和 Ruizhe Shi 合作的 scribing 见 -https://www.overleaf.com/read/hwpxppmfnjbk。
-说实话我觉得 scribing 是写给队友和老师看的罢了,所以当然还要有个
-从里面复制然后暴论的 废话版本写给自己看。
Simplex Method
-简单来说 simplex method 是从一个 basic feasible solution -出发,用最简单的计算方法寻找下一个 basic feasible solution -的方法。从几何的角度来说从多边形的一个顶点出发到另一个顶点,当然是沿着中间连接的边走过去最方便,所以也就是在寻找 -adjacent basic feasible solution。
---Recap: Two basic solutions are said adjacent iff -there are \(n-1\) linearly independent -constraints that are active at both of them. We also say that two bases -are adjacent if they share all but one column.
-
也就是说,修改 solution vector 中的一对 component 即可。
-Find the Initial Solution
-想开始一个循环的算法得先有个 initial solution -才能开始罢(,为了计算复杂性不如选个最简单的。
-在 LP 问题的标准化中经常会有加入一些 artificial variable -来把不等号改成等号的行为,比如说 \(a^T x \geq -b\) 完全可以写成 \(a_1 x_1 + \cdots + -a_n x_n + y_1 = b\),里面这个 \(y_1\) 就是一个 artificial -variable。它的系数是 \(1\),放在整个矩阵里其实可以作为最简单的 -linearly independent column 选出来计算 basic feasible solution。
-即使是在标准形式下也可以用这个思路来找一个简单的 initial -solution,考虑:
-\[\begin{aligned} - \text{minimize} \quad & \textbf{c}^T x \\ - \text{subject to} \quad & \textbf{Ax} = \textbf{b} \\ - & \textbf{x} \geqslant \textbf{0} -\end{aligned}\]
-By multiplying some rows of \(\textbf{A}\) by \(-1\), we can assume without loss of -generality that \(\textbf{b} \geqslant -\textbf{0}\). We now introduce a vector of artificial variables -\(\textbf{y}\) and consider the -auxiliary problem:
-\[\begin{aligned} - \text{minimize} \quad & y_1 + y_2 + \cdots + y_m \\ - \text{subject to} \quad & \textbf{Ax} + \textbf{y} = b \\ - & \textbf{x} \geqslant 0 \\ - & \textbf{y} \geqslant 0 -\end{aligned}\]
-这个 auxiliary problem 的初始化很容易,让 \(\textbf {x} =0\) 且 \(\textbf {y} = b\) 就是 basic feasible -solution,对应 basis 为 \(\textbf {I}_{m -\times m}\)。 某种程度上 auxiliary problem 等同于 original -problem。首先,如果 \(\textbf {x}\) 是 -original problem 的 basic feasible solution,则将 \(\textbf {x}\) 和 \(\textbf {y} =0\) 结合起来会产生 auxiliary -problem 的 optimal solution。另一方面,如果能获得 auxiliary problem 的 -optimal solution,则根据约束 \(\textbf {y} -\geqslant 0\),它必须满足 \(\textbf -{y}=0\)。于是 \(\textbf {x}\) 是 -original problem 的 basic feasible solution。
-另外如果auxiliary problem 的 optimal cost 不是零,那么 original -problem 是 infeasible 的。所以我们可以直接考虑下面的 auxiliary problem -来解 original problem 的 optimal solution,用它简单形式下的 initial -solution 开始 simplex method。
-Develop Feasible Direction
-所谓的 feasible direction 其实就是我们希望“沿着边来移动 solution -point”的那个边。当然移动的时候未必会沿着边来移动,可能就直接按照两个顶点的连线移动,但是怎么说呢,就是个形象点的说法(
+Lecture 7
+又是全新的一门课辣(自我洗脑)
+]]>于是最后在作业期中期末占比约各三分之一、期中考了 94、wjd +老师海底捞调分的情况下考了个 A-(,就挺耻辱的。
+时隔一年学了 statistical decision theory 之后我逐渐理解一切(
+ +非常短的一集,我随便喵两句。
+12.8 upd: 我超,我给学杂了,pivot rule 是 linear programming +里的,这玩意叫 pivot statistic,翻译过来叫枢轴量(
+Statistical Decision Theory
+多快好省的 decision theory 复习。
+Nonrandomized Decision
-
-
- Let \(\textbf{x}\) be an element of -a polyhedron \(P\). A vector \(\textbf{d} \in \Re^n\) is said to be a -feasible direction at \(x\), if there exists a positive scalar -\(\theta\) for which \(\textbf{x}+\theta \textbf{d} \in P\). +
Let \(X\) be a sample from a +population \(P \in \mathcal P\). A +statistical decision theory is an action that we take after observing +\(X\), for example, a conclusion about +\(P\) or a characteristic about \(P\) according to the observation. We use +\(\mathbb A\) to denote the set of +allowable actions, and let \(\mathcal +F_{\mathbb A}\) be a \(\sigma\)-field on \(\mathbb A\). Then the measurable space +\((\mathbb A, \mathcal F_{\mathbb A})\) +is called the action space.
+Let \(\mathcal X\) be the range +of \(X\) and \(\mathcal F_{\mathcal X}\) be a \(\sigma\)-field on \(\mathcal X\). A decision rule is a +measurable function (actually a statistic) \(T\) from \((\mathcal X, \mathcal F_{\mathcal X})\) to +\((\mathbb A, \mathcal F_{\mathbb +A})\). If a decision rule \(T\) +is chosen, then we take the action \(T(X)\) whence \(X\) is observed. That's where the name +"decision rule" comes from.
+In statistical decision theory, we set a criterion using a loss +function \(L\), which is a function +from \(\mathcal P \times \mathbb A\) to +\([0, +\infty)\), and is Borel on \((\mathbb A, \mathcal F_{\mathbb A})\) for +each fixed \(P \in \mathcal P\). If +\(X=x\) is observed and our decision +rule is \(T(X)\), then our "loss" in +making the decision \(T(X)\) is \(L(P, T(x))\), which is still random +according to \(P\).
+The average loss for the decision rule \(T\), which is called the risk of \(T\), is defined to be
+\[R_T(P) = E[L(P,T(X))] = \int_{\mathcal +X} L(P, T(x)) dP_X(x).\]
+If the family \(\mathcal P\) is a +parameter family then the loss function and the risk can also be denoted +as \(L(\theta, T(X))\) and \(R_T(\theta)\).
在上一次得到的 basic feasible solution 里假设 basis \(B\) 的下标是 \(B(1),B(2),\cdots, B(m)\),记 \(I = \{B(1) , B(2), \cdots , -B(m)\}\)。本质上每一次希望的移动就是在 \(I^c\) 里面挑选一个新的下标 \(j\) 然后将 \(x_j\) 变为 \(1\),为了保证 basic feasible solution 的 -\(n\) 个 active constraints -的条件,还需要再在 \(I\) -里面挑选一个下标 \(B(i)\) 然后将 \(x_{B(i)}\) 变为 \(0\)。
-从 applicable 的角度来说,具体的计算步骤是:
+Randomized Decision
-
-
- 选择一个 \(I^c\) 中的 \(j\) 作为新的下标,计算 \(B^{-1}A_j\) 作为 \(d_{B(1)}, d_{B(2)}, \cdots, d_{B(m)}\) -的值,记 \(d_j=1\),其余的分量保持 -\(0\)。 -
- 寻找一个合适的 \(\theta\) 使得 -\(x +\theta d\) 是一个最合适的 basic -feasible solution +
Sometimes it is more useful to consider the randomized decision +rules. A randomized decision rule is a function \(\delta\) on \(\mathcal X \times \mathcal F_{\mathbb A}\) +such that, for every \(A \in \mathcal +F_{\mathbb A}\), \(\delta(\cdot, +A)\) is a Borel function and, for every \(x \in \mathcal X\), \(\delta(x, \cdot)\) is a probability measure +on \((\mathbb A, \mathcal F_{\mathbb +A})\).
+The nonrandomized decision rule \(T\) previously discussed can be viewed as a +special randomized decision rule with \(\delta +(x, \{a\}) = I_{\{a\}}(T(x)), a \in \mathbb A, x \in \mathcal +X\).
+The loss function for a randomized rule \(\delta\) is defined as \(L(P,\delta,x) = \int_{\mathbb A} L(P,a) d\delta +(x,a)\), and the risk is then
+\[R_\delta(P) = E[L(P,\delta,X)] = +\int_{\mathcal X} \int_{\mathbb A} L(P,a) d\delta (x,a) +dP_X(x).\]
实际上如果确定了 \(j\),这里的 \(\theta\) -的选择范围就是有限的了,只有对于小于 \(0\) 的 \(d_{B(i)}\) 才能作为移动到 \(0\) 的方向。
-\[\begin{aligned} - \theta =\left(-\frac{x_{B(i)}}{d_{B(i)}}\right), \; -\{i=1,\ldots,m,d_{B(i)}<0\} - \end{aligned}\]
-然而其实连 \(j\) -都没确定呢,一开始是随便取的,嘿嘿。所以下面要考虑怎么选择 \(j\),其后怎么选择 \(\theta\),或者两个其实也可以一起选就是了,但是计算复杂度可能又会提高。
-Choice of Adjacent -Basic Feasible Solution
-Feasible direction -确认了之后就要考虑到底按照哪个下标来移动,最朴素的想法是突然想起来这是个优化问题(,然后按照单次移动的 -cost 相关的问题来考虑。
+Test Evaluation
-
-
Let \(\textbf{x}\) be a basic -solution, let \(\textbf{B}\) be an -associated basis matrix, and let \(\textbf{c}_B\) be the vector of costs of -the basic variables. For each \(j\), we -define the reduced cost \(\bar c_j\) of the variables \(x_j\) according to the formula
-\[\begin{aligned} - \bar c_j=c_j-\textbf{c}_B \textbf{B}^{-1}\textbf{A}_j. - \end{aligned}\]
+A rule \(T_1(X)\) is as good as +\(T_2(X)\) if and only if \(R_{T_1}(P) \leq R_{T_2}(P)\) for any \(P \in \mathcal P\).
+A rule \(T_1(X)\) is better than +\(T_2(X)\) if and only if \(R_{T_2}(P)\) if and only if \(R_{T_1}(P) \leq R_{T_2}(P)\) for any \(P \in \mathcal P\), and there exists at +least one \(P \in \mathcal P\) s.t. +\(R_{T_1} (P) < R_{T_2}(P)\).
+Two decision rules are equivalent if and only if \(R_{T_1}(P) = R_{T_2}(P)\) holds for any +\(P\in \mathcal P\).
+If there is a decision rule \(T^*\) +that is as good as any other rule in \(\mathfrak F\), a class of allowable +decision rules, then \(T^*\) is said to +be \(\mathfrak F\)-optimal (or optimal +if \(\mathfrak F\) contains all +possible rules).
这样定义了一个关于各个 \(j\) -对应的单位 reduced cost,也就是 \(x_j\) -每增加 \(1\) 会导致 cost -减少的量,当然是减得越多越好。另外 \(\bar -c_j\) 在 \(j\) 取 \(I\) 中的下标时等于 \(0\),这其实很能 make sense,毕竟不能再按照 -\(B(i)\) 来作为加入 basis -的下标了,会导致的 cost 变化也只能是 \(0\)。所以 reduced cost 是一个 general -definition,可以再用它们来定义一个向量 \(\bar -c\),其各个分量就是 reduced cost。
-寻找下一个 basic feasible solution -的最好的选择就是找一个绝对值最大(实际上最小)的 \(\bar c_j\),沿着这个方向移动最大的一个 -\(\theta^*>0\),然后 cost 就减少了 -\(\theta^* \bar c_j\)。这样选择 \(\bar c_j\) 和对应的下标 \(j\) 从直觉上来说可以经历更少的步数到达 -optimal solution,降低算法复杂度。
-另外,也可以从某个点处的 reduced cost vector \(\bar c\) -看出一些东西,主要有关这个点有没有达到 optimal cost,等等。
--
-
- Consider a basic feasible solution \(x\) associated with a basis matrix \(B\), and let \(\bar c\) be the corresponding vector of
-reduced costs.
-
-
-
- If \(\bar c \geq 0\), then \(x\) is optimal. -
- If \(x\) is optimal and -nondegenerate, then \(\bar c \geq -0\). -
- - A basis matrix \(B\) is optimal iff
+
Hypothesis Testing
+Fundamental +Settings of Nonrandomized Testing
+都见过但陌生又熟悉.jpg
+Hypothesis Testing Problem
-
-
- \(B^{-1}b \geq 0\) -
- \(\bar c^T = c^T - c^T _B B^{-1} A \geq -0^T\) -
+ Let \(\mathcal P\) be a family +of distributions, \(\mathcal P_0 \subset +P\) and \(\mathcal P_1 = \mathcal P +\setminus \mathcal P_0\). A hypothesis testing problem can be +formulated as that of deciding which of the following two statements are +true:
+\[H_0 : P \in \mathcal P_1 \quad +\text{versus} \quad H_1 : P \in \mathcal P_1\]
+The action space for this problem contains only two elements, +i.e., \(\mathbb A = \{0,1\}\), where +\(0\) is the action of accepting \(H_0\) and \(1\) is the action of accepting \(H_1\). A decision rule is called a test, +and must has the form \(T(X) = +I_C(X)\), in which \(C \in \mathcal +F_{\mathcal X}\) is called the rejection region (because if \(X\in C\) we take \(T(X) = 1\), i.e. reject \(H_0\)).
Termination
-最后两个问题是:算法会不会进入循环?会不会找不到 optimal solution -就停下来?答案是都不会。
-因为只有有限个 basic feasible -solution,所以只要不经过同一个点两遍,就可以遍历所有的可能性。不经过同一个点两遍这件事通过 -lexicographic pivoting rule -来决定,保证从字典序上来说所有的解是递增的,就不会出现循环。
-另外既然 optimal solution 要么是 \(-\infty\) 要么是在某个 basic feasible -solution 处取到,那么既然遍历(注意并不是真正的遍历,并不会走到 cost -比较大的一些 basic feasible solution,比如说比 initial solution 的 cost -更大的解就不可能取到,这能提高效率且不遗漏)了 basic feasible solution -就一定能找到 optimal solution,所以说 simplex method -是个非常完满的算法。
-Summary
-最后总结一下 simplex method 的步骤。
--
-
- 通过解 auxiliary problem 找到一个本质 trivial 的 initial -solution;它可能不存在,此时原问题 infeasible; -
- 通过做 \(\bar c^T = c^T - c^T_B
-B^{-1}A\) 得到在此处的 reduced cost vector,
-
-
-
- 如果 \(\bar c \geq -0\),说明目前的解就是 optimal solution -
- 否则找出绝对值最大的 \(\bar -c_j\),确定下标 \(j\),再找出对应的 feasible direction 是 -\(d_B = -B^{-1}A, d_j=1\). -
- - 通过找 \(\theta^* = \max \{\theta \geq 0
-\mid x +\theta d \in P \}\) 来更新 basic feasible solution 为
-\(y = x+\theta d\),可能遇到:
+
Loss and Risk
-
-
- 如果 \(\theta\) unbounded,则 -optimal cost 也是 \(-\infty\); -
- 否则可以更新 optimal cost 和对应的 basic feasible -solution,然后重复以上步骤直到找到 optimal solution。 -
+ A simple loss function for the problem is the \(0-1\) loss: \(L(P,a)=0\) if a correct decision is made +and \(L(P,a)=1\) otherwise. Under this +loss, the risk is
+\[R_T(P) = \begin{cases} P(T(X)=1) = +P(X\in C)& \quad P \in \mathcal P_0 \\ P(T(X)=0) = P(X \in C^c) +&\quad P \in \mathcal P_1 \end{cases} = P(X \in C) I_{\mathcal +P_0}(P) + P(X \notin C)I_{\mathcal P_1}(P).\]
+There are two types of statistical errors we may commit: +rejecting \(H_0\) when \(H_0\) is true (called the type I error) and +accepting \(H_0\) when \(H_0\) is wrong (called the type II +error).
+In statistical inference, a test \(T\), which is a statistic from \(\mathcal X\) to \(\{0,1\}\), is assessed by the probabilities +of making two types of errors (w.r.t. the \(0-1\) loss function):
+\[\alpha_T(P) = P(T(X)=1) = P(X\in C) +\quad P\in P_0\]
+\[1-\alpha_T(P) = P(T(X)=0) = P(X \notin +C) \quad P \in \mathcal P_1\]
+These two error probabilities cannot be minimized or even bounded by +a fixed \(\alpha \in (0,1)\) +simultaneouly when we have a fixed sample size.
Introduction to Duality
-把 LP problem 变成它的 dual problem 的 motivation -其实来自拉格朗日乘子法,本质上是对 cost function 的形式 penalize -一个条件,如果不满足条件的话 cost function -就会变大,从而找到最小值。
-想必这个过程推起来很简单吧我就不写了
简单来说,primal problem 和 dual problem 的对应关系是这样的:
-\[\begin{aligned} \text{minimize} -\quad & c^T x \\ \text{subject to} \quad & a_i ^T x \geq b -\quad i \in M_1 \\ & a_i ^T x \leq b_i \quad i \in M_2 \\ & -a_i ^T x = b_i \quad i \in M_3 \\ & x_j \geq 0 \quad j \in -N_1 \\ & x_j \leq 0 \quad j \in N_2 \\ & x_j \; \text{free} -\quad j \in N_3 \end{aligned} \quad \quad \quad \begin{aligned} -\text{maximize} \quad & p^T b \\ \text{subject to} \quad & -p_i \geq 0 \quad i \in M_1 \\ & p_i \leq 0 \quad i \in M_2 \\ -& p_i \; \text{free} \quad i \in M_3 \\ & p^TA_j \leq c_j -\quad j \in N_1 \\ & p^TA_j \geq c_j \quad j \in N_2 \\ & -p^TA_j = c_j \quad j \in N_3 \end{aligned}\]
-可以看出来 dual 的 dual 就是 primal。
-除此之外还需要一些定理来说明 dual 和 primal 的 cost 之间的关系。
-Duality Theorems
--
-
(Weak Duality) If \(x\) is a -feasible solution to the primal problem and \(p\) is a feasible solution to the dual -problem, then \(p^Tb\leqslant -c^Tx\).
-Proof: Set \(u_i = p_i -(a_i^Tx - b_i), v_j = (c_j - p^TA_j) x_j\), then by feasibility -\(u_i \geq 0, v_i \geq 0\).
-Therefore \(\sum_{i,j}u_i +v_j = p^T(Ax-b) -+ (c^T- p^TA)x = c^Tx - p^Tb \geq 0\).
+How to Reach the Optimal +Test
-
-
- If the optimal cost in the primal is \(-\infty\), then the dual one must be -infeasible. -
- If the optimal cost in the dual is \(+\infty\), then the primal one must be -infeasible. -
- Let \(x\) and \(p\) be feasible solutions to the primal and -the dual problem respectively, and suppose that \(p^T b = c^Tx\) holds. Then \(x\) and \(p\) are optimal solutions to the primal and -the dual respectively. -
+A common approach to finding an optimal test is to assign a small +bound \(\alpha\) to one of the error +probabilities (which will also leads to a small rejection region/), say, +\(\alpha_T(P), P \in \mathcal P_0\), +and then attempt to minimize the other one subject to
+\[\sup_{P \in \mathcal P_0} \alpha_T(P) +\leq \alpha.\]
+The small bound \(\alpha\) is called +the level of significance, and the left side is called the size of the +test \(T\).
+Actually we're using the minimax rule w.r.t. the type II error, i.e. +to minimize \(\sup_{P \in \mathcal P_1} 1- +\alpha_T(P)\) under the constraint \(\sup_{P\in \mathcal P_0} \alpha_T(P) \leq +\alpha\), which will give a minimax rule \(T_\alpha^*(X)\) as the test at level of +significance \(\alpha\).
Weak duality 引出的第三条最重要,如果 \(x\) 不是 optimal solution 则对任意的 -feasible solution \(x'\) 都有 \(c^Tx' \geq p^Tb = -c^Tx\),导致矛盾,\(p\) 的 -optimality 同理。这说明了 \(c^Tx = -p^Tb\) 可以导出二者分别在此处取到 optimal -cost,这引出了更重要的一条 strong duality,保证其一有 optimal solution -的时候另一个也有。
+The Famous P-value
-
-
(Strong Duality) If a linear programming problem has an optimal -solution, so does its dual, and the respective optimal costs are -equal.
-Proof: Consider the problem in standard form. The -simplex method (with lexicographic pivoting rule) terminates with an -optimal solution \(x^*\) and an optimal -basis \(B\), then \[\begin{aligned} - \bar c^T=c^T-c_B^TB^{-1}A\geqslant0. -\end{aligned}\]
-Let \(p^*=(c_B^T B^{-1})^T\) as the -corresponding optimal solution \(p\), -then \[\begin{aligned} - (p^*)^TA=c_B^T B^{-1}A\leqslant c^T, -\end{aligned}\] and \[\begin{aligned} -(p^*)^Tb=c_B^TB^{-1}b=c_B^Tx_B=c^Tx^*. -\end{aligned}\] So the strong duality holds.
+It's a good practice to assess the smallest possible level of +significance at which \(H_0\) would be +rejected for the computed \(T_\alpha^*(x)\) after observing \(x\), i.e. \(\hat +\alpha(x) = \inf \{\alpha \in (0,1) : T_\alpha^*(x)=1 \}\). Such +\(\hat \alpha (x)\) is also a statistic +depending on observed \(x\), and is +called the p-value for the test \(T_\alpha +^*\).
+The test can also be interpreted as \(T_\alpha^* (x) = I_{(0,\alpha)} (\hat +\alpha(x))\), thus we can find the p-value here.
最后来个 Farka's lemma,把 constraints -作为一个矩阵从原来的优化问题里面抽出来看:
--
-
- (Farka's lemma) Let \(A\) be a
-matrix of dimensions \(m\times n\) and
-let \(b\) be a vector in \(\Re ^m\). Then exactly one of the following
-two alternative holds:
+
Example of +Nonrandomized Parameter Test
+举个例子来结束这些神神叨叨。
+Example 1: Let \(X_1,X_2, +\cdots, X_n\) be i.i.d. from the \(N(\mu,\sigma^2)\) distribution with an +unknown \(\mu \in \mathbb R\) and a +known \(\sigma^2 >0\). Consider the +hypothesis \(H_0 : \mu \leq \mu_0 \quad +\text{versus} \quad H_1 : \mu > \mu_0\), where \(\mu_0\) is a fixed constant. Since the +sample mean \(\bar X\) is sufficient +for \(\mu \in \mathbb R\), it is +reasonable to consider the following class of tests: \(T_c(X) = I_{(c,\infty)}(\bar X)\).
+By the property of normal distributions, \(\alpha_{T_c}(\mu) = P(T_c(X)=1) = 1-\Phi +\left(\frac{\sqrt n (c - \mu)}{\sigma} \right)\), and for some +level of significance \(\alpha\) we +consider the type I error constraint \(\sup +_{\mu \leq \mu_0} \alpha_{T_c}(\mu) = 1-\Phi \left(\frac{\sqrt n +(c-\mu_0)}{\sigma} \right) \leq \alpha\), then the optimal test +should satisfy \(c_\alpha \geq \sigma +z_{1-\alpha} / \sqrt n + \mu_0\).
+The next step is to minimize \(1-\alpha_{T_c}(\mu)=\Phi \left(\frac{\sqrt n (c - +\mu)}{\sigma} \right)\) under the constraints \(c_\alpha \geq \sigma z_{1-\alpha} / \sqrt n + +\mu_0\) and \(\mu > \mu_0\), +the optimal test is \(c_\alpha ^*= \sigma +z_{1-\alpha} / \sqrt n + \mu_0\), and \(T_{c_\alpha ^*} (X) = I_{(c_\alpha ^*, +\infty)}(\bar X)\).
+According to the definition of p-value \(\hat \alpha(x) = \inf\{\alpha \in (0,1): +T_{c_\alpha ^*} (x) =1\}\), we can obtain \(\sigma z_{1-\hat \alpha(x)} / \sqrt n + \mu_0= +\bar x\) for any observed \(x\). +Thus \(\hat \alpha(x) =1-\Phi(\frac{\sqrt +n}{\sigma} \left(\bar x - \mu_0 \right))\) as a function of the +observed data.
+Randomized Test
+In Example 1, the equality in \(\sup_{P \in +\mathcal P_0} \alpha_T(P) \leq \alpha\) can always be achieved by +a suitable choice of \(c\). This is not +true in general. In such cases where the equality can't be attained, we +may consider randomized tests.
-
-
- There exists some \(x\geqslant 0\) -such that \(Ax=b\). -
- There exists some vector \(p\) such -that \(p^TA\geqslant 0\) and \(p^Tb<0\). -
- - (Farka's corollary) Let \(A_1,\ldots,A_n\) and \(b\) be given vectors and suppose that any -vector \(p\) that satisfies \(p^TA_i\geqslant 0\), \(i=1,\ldots,n\), must also satisfy \(p^Tb\geqslant 0\). Then \(b\) can be expressed as a nonnegative -linear combination of the vectors \(A_1,\ldots, A_n\). +
A randomized decision rule is a probability measure \(\delta(x,\cdot)\) on the action space for +any fixed \(x\). Since the action space +\((\mathbb A, \mathcal F_{\mathbb A} +)\) contains only two points \(\mathbb +A = \{0,1 \}\), then any randomized test of a hypothesis testing +problem is equivalent to a statistic \(T(X) +\in [0,1]\), with \(T(x) = +\delta(x,\{1\})\) and \(1-T(x) = \delta +(x,\{0\})\). In other words the expectation of \(T(X)I_{(0,1)}\) must be \(0\).
+In contrast, a nonrandomized test is a special case of randomized +test, where \(T(X)\) doesn't take value +in \((0,1)\).
+For any randomized test \(T(X)\), we define the type I error +probability to be \(\alpha_T(P) = ET(X), P \in +\mathcal P_0\), and the type II error probability to be \(1-\alpha_T(P) = 1-ET(X), P \in \mathcal +P_1\). The optimization rules are the same as the nonrandomized +case.
就变成了很普通但是又看着有点奇怪的矩阵变换问题,谁知道背后还有个优化问题.jpg。事实上对于不同形式的 -primal 和 dual problem -我们都可以写出来一对相反的条件,让它们二者成立其一。
-Lecture 3
-在上这节课之前我把 HW2 写完了,相应地其实就把 Nash equilibrium -那道题做了。是周二晚上吃饭之前写完的,吃饭之前多花了五分钟写成 LaTeX -然后超级开心地离开四教,吃完回来又读了一遍感觉证得很好,真的很喜欢这个方法还有这整个问题。
-所以我还是忍不住在 acknowledge 里面写了 MashPlant 日记里那段话:
---All exercises but Ex 4.29 are finished on my own. Among them I -appreciate the solution of Ex 4.10 most (though trivial), as this is -actually quite a triumph, even if it's hard to explain to your friends -or family members.
-
好了现在大家都知道我不会做 Ex 4.29 了
然后 Lecture 3 -上又把这个问题拿出来讲了,顺便把这个作业题也证明了,有点不爽((x
-Nash Equilibrium
-先把 theorem 丢出来,然后写一个我的证明:
-Theory
-Ex 4.10
-Consider the standard form problem of minimizing \(c^Tx\) subject to \(Ax = b, x \geq 0\). We define the -Lagrangean by
-\[L(x,p) = c^Tx + p^T(b-Ax)\]
-Consider the following game: player 1 chooses some \(x \geq 0\), and player 2 chooses some \(p\); then, player 1 pays to player 2 the -amount \(L(x,p)\). Player 1 would like -to minimize \(L(x,p)\), while player 2 -would like to maximize it.
-A pair \((x^*,p^*)\) with \(x^* \geq 0\), is called an equilibrium -point if \(L(x^*,p) \leq L(x^*,p^*) \leq -L(x,p^*), \; \forall x \geq 0, \forall p\).
-(Thus, we have an equilibrium if no player is able to prove her -performance by unilaterally modifying her choice.)
-Show that a pair (\(x^*,p^*\)) is an -equilibrium if and only if \(x^*\) and -\(p^*\) are optimal solutions to the -standard form problem under consideration and its dual respectively.
-Proof:
-Consider the primal problem and the dual problem in the following -form:
-\[\begin{aligned} - \textbf{minimize} \quad & c^Tx \\ - \textbf{subject to} \quad & Ax = b \\ - & x \geq 0 -\end{aligned} \quad \quad \quad -\begin{aligned} - \textbf{maximize} \quad & p^Tb \\ - \textbf{subject to} \quad & A^T b \leq c \\ - \\ -\end{aligned}\]
--
-
- If \(x^*\) and \(p^*\) are optimal solutions to the primal -problem and the dual problem respectively, then there is: -
\[L(x^*, p) = c^Tx^* + p^T(b -Ax^*) = -c^Tx^* = L(x^*, p^*)\]
-\[L(x,p^*) = c^Tx + p^{*T} (b-Ax) = (c^T - -p^{*T} A)x + p^{*T} b \geq p^{*T} b = c^Tx^*\]
-according to the strong duality theorem.
-Therefore \(L(x^*,p) \leq L(x^*,p^*) \leq -L(x,p^*)\) holds, and \((x^*,p^*)\) is an equilibrium.
--
-
- If \((x^*,p^*)\) is an equilibrium, -first to prove that \(x^*\) is a -feasible solution to the primal problem. Consider the first inequality -\(L(x^*, p ) \leq L(x^*, p^*)\) which -holds for any \(p\). If \(b - Ax^* \neq 0\), by taking \(p = b - Ax^* +p^*\), we can obtain -
\[L(x^*,p) - L(x^*, p^*) = (p- -p^*)^T(b-Ax^*) = (b-Ax^*)(b-Ax^*) >0,\]
-which leads to contradiction. Therefore \(Ax^* = b\) holds, \(x^*\) is a feasible solution to the primal -problem and \(L(x^*, p^*) = c^T -x^*\).
-Next step we prove that \(p^*\) is a -feasible solution to the dual problem. Consider the second inequality -\(c^T x^* = L(x^*,p^*) \leq L(x, p^*)\) -which holds for any \(x \geq 0\). By -taking \(x =0\) we can obtain that -\(c^T x^* \leq L(0,p^*) = p^{*T}b\) -holds.
-Moreover, if there exists \(i\) s.t. -\(c_i - p^T A_i <0\), we can take -\(x_i = -\frac{p^{*T}b - c^Tx^*}{c_i - p^{*T} -A_i} +1\) and \(x_j =0\) for all -\(j \neq i\), then \(x \geq 0\). Take such \(x\) to the inequality and there is:
-\[c^Tx^* = L(x^*,p^*) \leq L(x,p^*) = -p^{*T} b + (c_i - p^{*T} A_i) x_i < p^{*T} b - (p^{*T}b - c^Tx^*) = -c^Tx^* ,\]
-which leads to contradiction. Thus \(c_i - -p^{*T} A_i \geq 0\) holds for any subscript \(i\), i.e. \(c - -p^{*T}A \geq 0\). Therefore \(p^*\) is a feasible solution to the dual -problem.
-According to the inequality \(c^T x^* \leq -p^{*T}b\) we obtained before and the weak duality theorem, there -is \(c^T x^* = p^{*T} b\), and -therefore \(x^*, p^*\) are optimal -solutions to the primal problem and the dual problem respectively.
-Application
-其实已经挺清楚的了,就是说 \(\max_p \min_x -L(x,p) = \min_x \max_p L(x,p)\) 这样子,所以说 dual 和 primal -得到的结果是一致的。
-Application of Farka's Lemma
-先回顾下 Farka's lemma:
-(Farka's lemma) Let \(A\) be a -matrix of dimensions \(m\times n\) and -let \(b\) be a vector in \(\Re ^m\). Then exactly one of the following -two alternative holds:
+Example 2: Assume that the sample \(X\) from a binomial distribution \(B(\theta,n)\) with an unknown \(\theta \in (0,1)\) and a fixed integer +\(n >1\). Consider the hypothesis +\(H_0 : \theta \in (0, \theta_0] \quad +\text{versus} \quad H_1 : \theta \in (\theta_0 ,1)\) and the +following class of randomized tests:
+\[T_{j,q}(X) = \begin{cases} 1 \quad & +X>j \\ q \quad & X=j \\ 0 \quad & X <j +\end{cases}\]
+where \(j=0,1,\cdots,n-1\) and \(q \in [0,1]\). Then
+\[\alpha_{T_{j,q}}(\theta) = P(X>j) + +qP(X=j), \; 0 < \theta \leq \theta_0.\]
+For any \(\alpha \in (0,1)\) there +exists an integer \(j\) and \(q \in (0,1)\) such that the size of \(T_{j,q}\) is exactly \(\alpha\), i.e. the upper bound is attained +through randomized test.
+Confidence Sets
+Let \(\theta\) be a \(k\)-vector of unknown parameters related to +the unknown population \(P \in \mathcal +P\), \(C(X)\) in the range of +\(\theta\) and only depends on the +sample \(X\). If \(\inf_{P \in \mathcal P} P(\theta \in C(X)) \geq +1-\alpha\), then \(C(X)\) is +called a confidence set for \(\theta\) +with level of significance \(1-\alpha\).
+Actually if the constraint above holds, the coverage probability of +\(C(X)\) is at least \(1-\alpha\), though \(C(x)\) either covers or doesn't cover \(\theta\) whence we observe \(X=x\). To be more , the coverage +probability implies that when we make \(n\) random observations of \(X=x\) from the population and \(n\) confidence regions correspondingly, +then there are about \(n (1-\alpha)\) +among them covers \(\theta\).
+Comments
+一些不负责任的暴论/吐槽(
+-
+
上统推的时候 wjd 说“一般情况下倾向于拒绝 \(H_0\)”的时候就给我整震撼了,那我把 \(H_0\) 和 \(H_1\) 换一下不行吗(。你早说 decision rule +就是个示性函数,\(0\) 对应 \(H_0\),\(1\) 对应 \(H_1\) 的话我还至于一年来都没记清楚 type I +error 和 type II error 分别是什么吗(x
+另一个不能理解的点是 randomized +test,看她举的例子还以为这个东西就是用来做 \(H_0: \theta = \theta _0 \; \text{versus} \; H_1 : +\theta \neq \theta_0\) 这种检验的,然后给 \(\theta = \theta_0\) 一个 \(q \in (0,1)\) +的值。感觉没怎么说过是因为达不到 upper bound +有点浪费所以用单点处来补足的这个想法,
+可能也不排除当时已经是网课了所以是我听课不认真(但也不可能先把 randomized rule 讲一遍,再把 minimax rule +讲一下说明为什么是缩小 \(\sup +\alpha_T(P)\),在这之前总得把 measure +是啥说清楚,我说实话很怀疑很多人修统辅到最后连概率空间和 \(\sigma\)-field +都没完全搞清楚,
一直在安慰大家这个不考那个不考的 dwl +全责。但有的时候也很佩服统辅这些课能把故事完全限制在初等上还能讲明白(大概吧,我经常是听不明白,但看起来大家都很明白)的功力(
+感觉就是之前一直没学本质,当时前四周的 statistics +看起来有点难但学会了 exponential family +的算法之后就薄纱一切了,反正大家也不会条件期望
dwl 全责+不可能真拿定义算 sufficient statistics 和 +UMVUE;后半学期我就在疑惑这统计真的和数学有关系吗(,讲完基本概念之后就开始讲那些个 +normal distribution family +上假设检验的例子,最后还要像八股文一样地考,可能确实是限制在初等上的话实在没什么可学的(
+总之虽然吐槽了很多,我还是很认可去年统计推断这门课的,但只能说真想学点数学 +
+而不只是薄纱大家来愉悦身心(有的时候可能只会被反杀罢)+的话还是别修统辅课了,调性不合(。
+所以说去年这时候确实是对自己很没信心啊(今年也没有啊(
+
这什么破标题(
+参考了《Applied +Mathematical Programming》Chapter 9,10 和一份相应的 notes。
+ +为什么要做 integer programming?一般来说 linear programming +也可以得到一个答案,把它 round +一下不就好了?但其实有一些很实际的理由导致 integer programming +是必须的,就像线性回归中 dummy variable 也是必须的一样(啥
+一般来说把 integer programming 的 integer condition 移除后的 linear +programming problem 称为其相应的 relaxed problem,integer programming 的 +feasible set 一定是其 relax problem feasible set 的子集,其 optimal cost +也不会超过 relaxed problem 的 optimal +cost。这很好理解,就是取了个限定更强的形式。
-
-
- There exists some \(x\geqslant 0\) -such that \(Ax=b\). -
- There exists some vector \(p\) such -that \(p^TA\geqslant 0\) and \(p^Tb<0\). +
round 得到的结果未必还是最优的。比如:
+\[\begin{aligned}\textbf{maximize} \quad +& 8x_1+11x_2+ 6x_3 +4x_4 \\ \textbf{subject to} \quad +& 5x_1+7x_2+4x_3+3x_4 \leq 14 \\ \quad &x_j \in \{0,1\}, \quad +j=1,2,3,4 \end{aligned}\]
+如果用 linear programming 会得到 optimal solution 是 \((1,1,0.5,0)^T\),round 一下得到 \((1,1,1,0)\) 并不在 feasible set +中。与此同时实际上的 optimal solution 是 \((0,1,1,1)^T\),哪怕反向 round +也得不到精确的结果。
+但是每个通过 round 得到的结果都比真正的 integer programming 的 +optimal cost 要小,某种程度上来说给出了一个估计。
+integer programming +可以反映许多很难描述的条件。例如两个条件至多成立一个,用某个 integer +variable 表示选择与否,等等。
+哪怕真的可以用 round 的方法得到解,也不知道反向/正向 round +的结果是不是最好的,而在一些实际问题里哪怕只是相差 \(1\) 也会造成成本/效益的巨大差异。
除了用一对 primal problem 和 dual problem -记这个结论之外,还可以用一个图来直观地理解:
-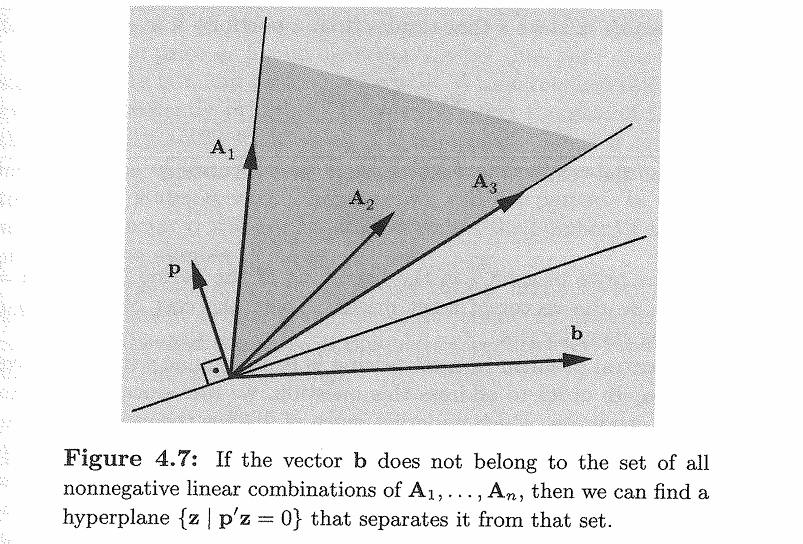
当 \(b\) 不落在 \(A_i\) 和 \(x \geq -0\) -构造出的阴影范围内,也就是说第一个条件不满足的时候,就一定存在 \(p\) 使得 \(p\) 和 \(b\) 的夹角是“钝角”,而且 \(p\) 和每个 \(A_i\) 的夹角是“锐角”。
-考虑一个有 \(n\) -种商品的贸易过程,每次购买的份额是一个 asset vector \(x = -(x_1,x_2,...,x_n)\),初始状态下的价格是一个 price vector \(p = -(p_1,p_2,...,p_n)\),因此初始状态下投入的资金是 \(p^Tx\)。一段时间后会呈现出 \(m\) 种状态之一,第 \(i\) 种状态下这 \(n\) 种商品的售价是一个 payoff vector \((r_{i1},r_{i2},...,r_{in})\)。由此构造一个 -payoff matrix:
-\[R= \begin{bmatrix} r_{11} & r_{12} -& \cdots & r_{1n} \\ \cdots & \cdots & \cdots & -\cdots \\\cdots & \cdots & \cdots & \cdots \\ r_{m1} & -r_{m2} & \cdots & r_{mn} \end{bmatrix}\]
-取 \(w = Rx = (w_1,w_2,\cdots,w_m)\) -作为购买份额为 \(x\) 时,最终在 \(m\) 个状态下分别得到的收入。有一个 absence -of arbitrage -condition,大概就是说不可能在负投资的状态下得到正收益,也就是说 \(Rx \geq 0\) 可以推出 \(p^Tx \geq 0\)。
-由 Farka's lemma 可知此时第二条不成立,一定存在 \(q \geq 0\) 使得 \(R ^T q = p\)。
-The Center of Gravity Method
-实际上就是一个不断切割已有的 polyhedron 来找到 optimal solution -的过程。简单来说从初始状态开始,每个状态下手里有一个多边形 \(S_t\)(feasible set 的 subset)和它的质心 -\(x_t\),然后把使得取值大于 \(c^Tx_t\) 的部分切掉,也就是取 \(S_t\) 和 hyperapce \(\{x \in \mathbb R^n \mid c^T(x-x^T) > 0 -\}\) 的交这一部分作为不可能取到 optimal cost -的区域,余下的部分是下一状态的多边形 \(S_{t+1}\) 和相应的质心 \(x_{t+1}\),由此按照所需的精度来逼近 optimal -cost。
-写成算法的步骤来说也非常简单,实际上每次就操作两步。先取整个 feasible -set 作为 \(S_1\),然后:
--
-
- Take \(x_t = \frac{1}{Vol(S_t)} \int_{x -\in S_t} x \; dx\) as the center of gravity of the polyhedron -\(S_t\); -
- Take \(S_{t+1} = S_t \cap \{x \mid -c^T(x-x_t) \leq 0 \}\) as the new polyhedron. -
一直重复直到 \(S_t\) 足够小,此时 -\(c^T x_t\) 和 optimal cost \(c^Tx^*\) -的误差也会足够小。这由一些定理保证。
+另外 integer programming 的困难在于 optimal solution +不再一定在顶点处取到,而且 feasible set +是离散的点集,其数量远大于顶点数量,不太可能用枚举得到答案。
+Standard Settings
+Interger programming 的标准形式一般来说相对简单,但和 linear +programming 稍有不同:
+\[\begin{aligned} \textbf{maximize} \quad +& c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & +x_j \in \mathbb N \end{aligned}\]
+其中要求 \(c \geq 0, A \geq 0, b \geq
+0\)(指的是 \(A\) 的每个分量
+\(a_{ij}\) 都要是非负的
+而不是正定什么的要求)。
这样写相对粗糙。事实上,如果 \(A\) +只表示一个一维的 constraint 则称为 knapsack problem,否则是 +multidimensional knapsack problem;如果所有的 \(x_j\) 均在 \(0,1\) 上取值则称为 pure integer +programming,否则是 mixed linear programming。
+对应的 pure integer programming 的标准形式是:
+\[\begin{aligned} \textbf{maximize} \quad +& c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & +x_j \in \{0,1\} \end{aligned}\]
+同样要求 \(c \geq 0, A \geq 0, b \geq +0\)。
+Standardize to 0-1 Knapsack +Problem
+最明显的一些要求是 \(c\geq 0,A\geq +0\),至于 \(b\) +谋事在人成事在天(。
+对于 1-dimension 来说一般来说如果有看到 \(c_i \geq 0, a_i \leq 0\) 的话直接把 \(x_i\) 取为 \(1\),因为这变相的扩容了 constraint +的上限;如果 \(c_i \leq 0 ,a_i \geq 0\) +则置为 \(0\),显然它的存在既会占用资源又减小上限。如果 +\(c_i ,a_i \leq 0\) 同时成立就用 \(y_i = 1-x_i\) +代替原变量即可,从而得到标准形式。
+Multidimension 咋办,他也没说啊(挠头(
感觉可能就不用动了,反正后面的求解里面都还是考虑 relaxed LP +问题,直接按照 LP 的 standardized form 来化简就可以。当然如果有一溜 +\(\{a_{ij}\}_{i=1}^m \leq 0, c_i \geq +0\) 这种情况的话直接把 \(x_{i}\) +置 \(1\) +即可,少一个变量是一个。或者也可能是用 \(x_1\) 和 \(1-x_i\) 替换来保证所有的 \(c_i\) 为正。
+Solutions to Integer +Programming
+Relaxed Linear Programming
+比较符合直觉的一种方案就是把它和对应的 linear programming problem +结合起来看,它们之间的确存在一定的关系,甚至在某一些情况下可以得到对于 +integer programming 的估计(未必是精确值)。
+\[\begin{aligned} \textbf{maximize} \quad +& c^Tx \\ \textbf{subject to} \quad & Ax \leq b \\ \quad & +x_j \in \mathbb N \end{aligned} \quad \quad \quad \begin{aligned} +\textbf{maximize} \quad & c^Tx \\ \textbf{subject to} \quad & Ax +\leq b \\ \quad & x_j \geq 0 \end{aligned}\]
+(暂且先不考虑 0-1 knapsack)
+注意在实际计算中想要解出(比如用 simplex method)relaxed problem +还需要再做一步 standardize,此处略去。
+此时有:
-
-
Let \(K\) be a centered convex -set (i.e. \(\int_{x \in K} xdx=0\)), -then for any \(w \in \mathbb R^n\), -\(w \neq 0\), one has
-\[Vol(\mathcal K \cap \{x \in \mathbb R^n -: x^T w \geq 0\}) \geq \frac 1 e Vol(\mathcal K)\]
+- 如果 LP 的 optimal solution 恰好是个 integer solution 那么也一定是 +IP 的 optimal solution; +
- LP 的 optimal cost 一定比 IP 的 optimal cost 更大; +
- 如果 \(c\) 的所有分量也是整数,则将 +LP 的 optimal solution 向下取整得到的解也在 feasible set 里,而且至少比 +IP 的 optimal cost 更大(因为 round 之后的结果未必是 \(0,1\) 取值的,不一定是 IP 的解)。
这告诉我们每个新的多边形和原多边形之间有一个体积关系是 \(Vol(S_{t+1}) \leq (1-\frac 1 e) Vol(S_t) \leq -\cdots \leq (1-\frac 1 e)^t Vol(S_1)\),再对于 \(\varepsilon = (1-\frac 1 e)^{t/n}\) 取 -\(\mathcal S_\varepsilon = \{(1-\varepsilon -)x^* + \varepsilon x, \forall x \in S_1\}\),实际上是对 \(S_1\) 做了一个仿射变换。此时有 \(Vol(S_\varepsilon)=\varepsilon^n Vol(S_1) = -(1-\frac 1 e)^tVol(S_1) \geq Vol(S_{t+1})\),于是可以找到一个 -\(x_\varepsilon \in S_\varepsilon\) -使其在 \(t\) 时刻时仍在 \(S_t\) 中,而 \(t+1\) 时刻就被“裁剪”了出去。
-所以有
-\[c^Tx_{t+1} < c^Tx_\varepsilon = -c^T((1-\varepsilon)x^*+ \varepsilon x) \leq c^Tx^* + 2B\varepsilon -=c^Tx^*+2B(1-\frac 1 e)^{t/n}\]
-也就是说 \(c^Tx_{t+1} - c^Tx^* < -2B(1-\frac 1 e)^{t/n}\) 作为 \(t+1\) 时刻下取值距离 optimal cost -的误差可以被控制,并且我们可以在 \(O(n -\log(\frac{1}{\varepsilon}))\) 时间下得到误差为 \(\varepsilon\) 的 cost 和 solution。这比 -simplex method 误差大一些,但是 polynomial time algorithm。
-The Ellipsoid Method
-讲这个的时候我太困了,上楼找了个教室睡觉,没听。我估计我困成那样听也听不懂,他这个手稿太抽象了也看不大懂,貌似书上也没这一部分,哥们有点子崩溃(。等
-scribing 了。
我都学会了 scribing 还没出来,自己写一个吧。
-Notations
-首先是一些记号:
-
Bound and Branch
+Pure Integer Programming
+本质上就是,利用 relaxed linear programming 来寻找一组 optimal +solution(一般用 simplex method)\(x= +(x_1,x_2,\cdots,x_n)\),其中会有若干个是非整数解,记为 \(x_{m1},x_{m2},\cdots,x_{mk}\)。此时可以对每个 +\(x_{mi}\) 是向上 round 还是向下 round +做一个分割,就回到了 seperating hyperplane theorem。这样就得到了一个 +tree,它的每一组分叉都多加了一个条件,解出所有分叉上点的解即可。
+来个示意图,我也不知道为什么这个图在书上就是颈椎病图,凑合看吧(
+
某种程度上来说和 ellipsoid method +非常相似,都是在原条件的基础上继续用 cutting plane +加条件然后继续往下解。所以说需要考虑的问题也是相似的,也即算法何时终止、time +usage 如何、这棵树上的 optimal solution 是否就是真正的 optimal +solution(只是在对每个非整数变量做 +round,听起来不是特别靠谱)。特别地,还有树上所有的分支应该以什么样的顺序求解才最优、能否中途去掉一些 +inactive 的分支来保证计算量最小。
-
-
A set \(E\) of vectors in \(\mathbb R^N\) of the form \(E = E(z,D) = \{x \in \mathbb R^n \mid (x- z)^T -D^{-1} (x-z) \leq1 \}\), where \(D\) is an \(n -\times n\) positive definite symmetric matrix, is called an -ellipsoid with center \(z \in \mathbb -R^n\).
-If \(D\) is a \(n \times n\) nonsingular matrix and \(b \in \mathbb R^n\), then the mapping \(S: \mathbb R^n \to \mathbb R^n\) defined by -\(S(x) = Dx + b\), is called an affine -transformation.
+首先观察到所有的 \(c_i\) +都是正的(如果不是正的请把 \(x_i\) 换成 +\((1-y_i)\)),所以可以用 dual problem +来解
但总觉得没啥必要
+计算得到的最初的 \(L_0\) 的 +optimal cost 记为 \(\bar +z\),这样这棵树上的每一个 optimal cost 都不会大于 \(\bar z\)。
+在计算的过程中,如果已经有某个 subproblem 得到了 integer solution +和相应的 optimal cost \(z^*\),则如果在其他 active subproblem with +fractional solution 中得到了更小的 optimal cost \(z \leq z^*\),则说明无论如何分划,这一 +active subproblem 所对应的平面区域上都不可能找到 optimal +cost,直接将其置为 inactive 即可。
+换言之,在找到一个 optimal cost 为 \(z^*\) 之后,只需要再寻找一个 optimal cost +为 \(z\),满足 \(z^* \leq z \leq \bar z\) 的整数解。这就是 +bound and branch 中 bound 的来源。
+Infeasible subproblem 也不需要再分划下去。
注意到仿射变换都是可逆的,所以可以把仿射变换的像定义成
+最后得到的 algorithm 大致是:
+-
+
- Solve the linear relaxation of the problem. If the solution is +integer, then we are done. Otherwise create two new subproblems by +branching on a fractional variable. +
- A subproblem is not active when any of the following occurs:
+
-
+
- You used the subproblem to branch on +
- All variables in the solution are integer +
- The subproblem is infeasible +
- You can fathom the subproblem by a bounding argument +
+ - Choose an active subproblem and branch on a fractional variable. +Repeat until there are no active subproblems. +
Mixed Integer Programming
+Mixed integer programming 的 bound and branch +方法和上述几乎并无不同,只是每一次加条件做分枝的时候只对 integer +variable 加条件,计算量会隐性地小一点。
+Cutting Plane Method
+我个人认为课件上说这个条件在二维条件下用比 bound and branch
+简单这件事非常逆天,就,我用 bound and branch 来解 integer programming
+的时候也是用画图来做的啊,谁真的拿 simplex method 解 \(2^k\) 个 linear programming
+啊((
用一个例子来解释:
+\[\begin{aligned}\textbf{maximize} +&\quad 7x_1+ 9x_2 \\ \textbf{subject to}& \quad -x_1+3x_2 \leq 6 +\\ & \quad 7x_1+x_2 \leq 35 \\ & \quad x_1,x_2 \in \mathbb +N \end{aligned}\]
+类似于化成 linear programming 的方法,但是相应的 slack variable +也是正整数:
+\[\begin{aligned}\textbf{minimize} +&\quad -7x_1- 9x_2 \\ \textbf{subject to}& \quad -x_1+3x_2+s_1=6 +\\ & \quad 7x_1+x_2 +s_2= 35 \\ & \quad x_1,x_2,s_1,s_2 \in +\mathbb N \end{aligned}\]
+用 simplex method 得到一个最终的 full tableau(也就是无视掉上述 +linear programming 的整数条件进行一个优化的做,得到 LP 对应的 optimal +solution),此时的 tableau 如下所示:
+| + | + | \(x_1\) | +\(x_2\) | +\(s_1\) | +\(s_2\) | +
|---|---|---|---|---|---|
| + | \(63\) | +\(0\) | +\(0\) | +\(28/11\) | +\(15/11\) | +
| \(x_2\) | +\(7/2\) | +\(0\) | +\(1\) | +\(7/22\) | +\(1/22\) | +
| \(x_1\) | +\(9/2\) | +\(1\) | +\(0\) | +\(-1/22\) | +\(3/22\) | +
也就是说在计算中最后得到的 constraints 为:
+\[\begin{aligned} & x_2+7/22 s_1+ +1/22s_2=7/2 \\ & x_1 - 1/22 s_1+ 3/22 s_2= 9/2 +\end{aligned}\]
+把所有的整数部分放在左边,分数 round 到最小放在右边(注意要让右边所有 +variable 的系数为负,且绝对值小于 \(1\),这样才能往后加 constraints):
+\[\begin{aligned} & x_2-3 = +1/2-7/22s_1-1/22s_2 \\ &x_1 - s_1-4 =1/2-21/22s_1-3/22s_2 +\end{aligned}\]
+这给出了新的 constraints :
+\[\begin{aligned}& 1/2-7/22s_1-1/22s_2 +\leq 0 \\ & 1/2 - 21/22s_1-3/22s_2 \leq 0 +\end{aligned}\]
+Solution to 0-1 Knapsack +Problem
+这 PPT 上怎么说是一个一个试啊(挠头
+举个例子先:
+\[\begin{aligned} \textbf{maximize} \quad +& z=3x_1-2x_2+5x_3 \\ \textbf{subject to} \quad & x_1+2x_2-x_3 +\leq 2 \\ & x_2+4x_2+x_3 \leq 4 \\& x_2+x_3 \leq 3 \\ +&4x_2+x_3 \leq 6 \\ & x_1,x_2,x_3 \in \{0,1\} +\end{aligned}\]
+当然可以把 \((x_1,x_2,x_3)\) 按照 +\(000,001,010,011,100,101,110,111\) +来逐个尝试,稍微简化一下的话可以考虑
+\[\begin{aligned} \textbf{maximize} \quad +& z=5x_3 +3x_1-2x_2\\ \textbf{subject to} \quad & x_1+2x_2-x_3 +\leq 2 \\ & x_2+4x_2+x_3 \leq 4 \\& x_2+x_3 \leq 3 \\ +&4x_2+x_3 \leq 6 \\ & x_1,x_2,x_3 \in +\{0,1\} \end{aligned}\]
+把 cost function 中系数最大的 \(5x_3\) 提到最前面,如果能够达到最大则 \(x_3=1\) 的情况较为有利。我们发现 \((x_1,x_2,x_3) = (0,0,1)\) 能够符合 +constraints 而且 cost 为 \(5\),因此其后讨论其他取值时 cost 小于 \(5\) 的可以无需带入检查 +constraints,直接舍去。
+]]>选课的时候我还侥幸以为生统概论可以放松心情,来随便听听简单了解一下那种。可能是前置没学完的原因,倒也没那么水,ANOVA +还是花了不少时间看的。
+wty 老师的英语口语真不错,可惜我听力一般,一走神就寄了。还是要感谢 V1ncent19
+的统辅笔记救我,不过他看起来是前置都学完了来上的这个,写的有点抽象,我想写个废话多一点具体点的。
Analysis of Variance
+示例——Treatment of +Lead-Exposed Children Trial
+100 名被试被分成两组分别使用安慰剂和药剂,在实验开始前、实验第 1, 4, +6 周分别检验了血液铅含量水平。第 i 名被试的实验开始前水平为 \(y_{i1}\),实验结束后水平为 \(y_{i2}\),变化水平为 \(d_i = +y_{i2}-y_{i1}\),希望利用这些数据观察药剂的有效程度。
+假设线性回归模型为 \(d_i = \beta_0 + +\beta_1 x_i +e_i\),注意此处的 \(x_i\) +是一个分类统计量,也就是说被试使用安慰剂时取 \(x_i = 0\),被试使用试验药剂时 \(x_i =1\)。做一些假设检验:
-
-
- \(S(L) = \{y \in \mathbb R^n \mid y = Dx -+b, \text{for some } x\in L \}\) -
- The volume of a set \(L \in \mathbb -R^n\), which is denoted by \(Vol(L)\), is defined as \(Vol(L) = \int_{x \in L}dx\) +
- \(H_0: \beta_0 =0\) +检验了安慰剂组的平均变化是否为 \(0\) +
- \(H_0:\beta_1 = 0\) +检验了安慰剂组和药剂组之间的平均差异是否为 \(0\),也即药剂是否对治疗有作用
然后就可以得到仿射变换后的体积是
+这一模型也可以写作 \(y_{i2} = y_{i1} + +\beta_0 +\beta_1 x_i + e_i\),但实际上 \(y_{i1}\) 对于 \(y_{i2}\) 的影响也有待商榷,未必在 \(y_{i1}\) 变化一个单位时,\(y_{i2}\) +也随之变化一个单位,所以模型可以修正为 \(y_{i2} = \beta_0 + \beta_1 x_i +\beta_2 y_{i1} ++e_i\)。这样又多出来一个假设检验:
-
-
If \(S(x) = Dx + b\) then \(Vol(S(L)) = |det(D)| Vol(L)\)
-Proof: \(Vol(S(L)) = -\int_{y \in S(L)} dy = \int_{x \in L} |det(D)| dx = |det(D)| -Vol(L)\)
+- \(H_0 :\beta _2 = 0\) +检验了初始状态对末态是否有影响
Algorithm
-目标是考虑一个 \(Ax \geq b\) -形式的优化问题的 feasible set,也就是一个 polyhedron \(P\) 是否是空集的问题,可以用一个 Ellipsoid -Algorithm -来解决。既然是用迭代算法解决,其实就不能太苛求精细程度,我们约定最后得到的覆盖椭圆的面积小于 -\(\varepsilon\) 时就认为 \(P\) 是一个空集。
-首先考虑一个覆盖所求 polyhedron \(P\) 的椭圆 \(E_t\),如果其中心 \(x_t \in P\) 则找到了一个 \(P\) 中的解,可以得出 \(P\) 是非空的;如果 \(x_t \notin P\) 那么 \(x_t\) 一定违反了其中的某个 constraint \(a_i ^Tx \geq b_i\),\(P\) 一定在 halfspace \(\{x \in \mathbb R^n \mid a_i^T x \geq a_i^Tx_t -\}\) 和 \(E_t\) -的交集里,这样我们再做一个新的更小的椭圆 \(E_{t+1}\) -来覆盖这一部分,就可以继续这一算法。
-来个我非常喜欢的图!
-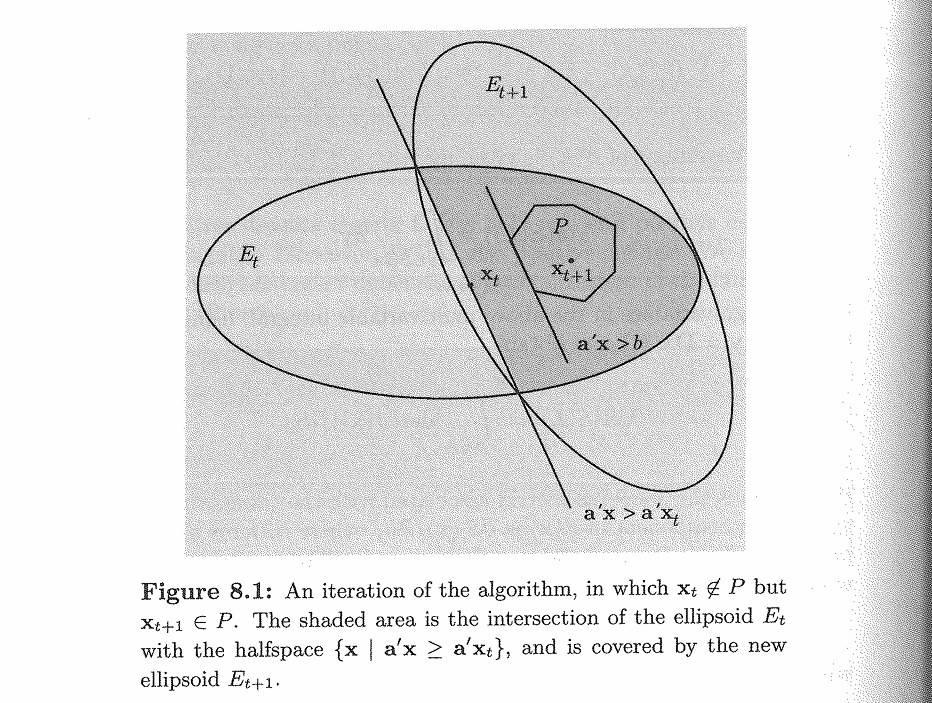
现在需要解决的问题仍然是 termination 问题,也就是是否 \(E_{t+1}\) 的体积一定比 \(E_t\) -更小。以下定理保证了它们的体积之间一定有一个指数级的减少:
--
-
Let \(E = E(z,D)\) be an -ellipsoid in \(\mathbb R^n\), and let -\(a\) be a nonzero vector. Consider the -halfspace \(H = \{x \in \mathbb R ^n \mid a^Tx -\geq a^T z \}\) and let
-\[\bar z = z + -\frac{1}{n+1} \frac{Da}{\sqrt{a^TDa}}\]
-\[\bar D = \frac{n^2}{n^2-1} (D - -\frac{2}{n+1} \frac{Daa^TD}{a^TDa})\]
-Then \(\bar D\) is positive definite -and the new ellipsoid \(\bar E = E(\bar z, -\bar D)\) satisfies the following properties:
+不同的检验模型会得到一些不同的结果。类似的场景是我们的出发点。
+One Factor ANOVA
+首先给出一个希望做检验的场景:\(n_T\) 个实验对象被分成 \(r\) 组,每组有 \(n_i\) 个实验对象,有 \(n_T = \Sigma_{i=1} ^r n_i\)。由此我们得到 +\(n_T\) 个数据 \(Y_{ij}\),\(i\) 表示组别,\(1\leq i \leq r\),\(j\) 表示在某一组内的编号,\(1 \leq j \leq n_i\)。
+Cell means model
+模型假设是 \(Y_{ij} = \mu_i + +\varepsilon_{ij}\)。
+其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim +N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。考虑一些统计量作为参数的估计量:
+\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 +}^{n_i} Y_{ij} = \hat \mu _i\]
+\[\bar{Y}_{..} = \frac{1}{n_T} +\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r +n_i \bar{Y}_{i.}\]
+\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 +/ (n_i -1) \]
+\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r +(n_i -1) s_i ^2 = \hat \sigma^2\]
+在这一模型中,我们关注的假设检验是 \(i\) 组实验之间是否存在差异,假设检验表示为 +\(H_0 : \mu_1= \mu_2 = ... = \mu_r = +\mu\),对应的备择假设即为 \(\{ \mu_i +\}_{i=1} ^r\) 中存在不同的项。检验最经典的方法即为 +ANOVA,analysis of variance。核心是以下的分解:
+\[\begin{aligned} SSTO = \Sigma_i +\Sigma_j(Y_{ij} - \bar Y_{..})^2 &= \Sigma_i \Sigma_j (Y_{ij} - \bar +Y_{i.} +\bar Y_{i.} - \bar Y_{..})^2 \\& = \Sigma_i n_i (\bar Y_{i.} +- \bar Y_{..})^2 + \Sigma_i \Sigma_j (Y_{ij} - \bar Y_{i.})^2 \\ +&=SSTR + SSE \end{aligned}\]
+可以观察到,\(SSTR\) +是组间差距,体现了不同组别之间的差别,\(SSE\) +是组内差距,体现了同一组内各数据的偏差。注意 \(SSTR\) 的自由度是 \(r-1\),\(SSE\) 的自由度是 \(n_T - r\),\(SSTO\) 的自由度是 \(n_T - 1\)。由此可以求出 \(MSE= \frac{SSE}{n_T -r}\),\(MSTR = +\frac{SSTR}{r-1}\)。作业里证明了两个统计量的期望,\(\mathbb E(MSE) = \sigma^2\),\(\mathbb E(MSTR) = \sigma^2 +\frac{\Sigma_i n_i +(\mu _i -\mu_.)^2}{r-1}\),其中 \(\mu_. += \frac{\Sigma_i n_i \mu_i}{n_T}\)。
+在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 _{n_T - +r}\),\(\frac{SSTR}{\sigma^2} \sim +\chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,n_T -r}\) +作为最终的检验统计量。
+当 \(F^* > F(1-\alpha , r-1 , n_T +-r)\) 时拒绝原假设,否则接受;\(Power = +P(F^* > F(1-\alpha , r-1,n_T -r)| \delta)\),其中 \(\delta\) 是一个非中心偏移量,\(\delta = \frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i +n_i (\mu_i - \mu_.)^2}\)。
+Factor Effects Model
+Factor Effects Model 是 Cell Means Model +的一个重新参数化的结果。模型假设是 \(Y_{ij} = +\mu + \tau_i + \varepsilon_{ij}\)。
+其中,\(\mu_i\) +是整体的理论均值,\(\varepsilon _{ij} i.i.d. +\sim N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 +\(\mu , \tau_1 , ..., \tau_r , +\sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = +0\),如果没有这个约束会导致存在多组解。考虑一些统计量作为参数的估计量:
+\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 +}^{n_i} Y_{ij} = \hat \tau _i + \hat \mu\]
+\[\bar{Y}_{..} = \frac{1}{n_T} +\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r +n_i \bar{Y}_{i.} = \hat{\mu}\]
+\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 +/ (n_i -1) \]
+\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r +(n_i -1) s_i ^2 = \hat \sigma^2\]
+在这一模型中,我们关注的假设检验仍然是 \(i\) 组实验之间是否存在差异,假设检验表示为 +\(H_0 : \tau_1= \tau_2 = ... = \tau_r = +0\),对应的备择假设即为 \(\{ \mu_i +\}_{i=1} ^r\) 中存在不同的项。factor effects model +在参数的含义上比 cell mean model 更清晰。
+Two Factors ANOVA
+首先给出一个希望做检验的场景:\(nab\) 个实验对象被分成 \(a\times b\) 组,每组有 \(n\) 个实验对象。第 \(ij\) 组的实验条件是 \(A\) 因素的等级为 \(i\),\(B\) +因素的等级为 \(j\),其中有 \(1 \leq i \leq a, 1\leq j \leq +b\)。由此我们得到 \(nab\) 个数据 +\(Y_{ijk}\),\(i\) 表示以 \(A\) 因素分类的组别,\(j\) 表示以 \(B\) 因素分类的组别,\(k\) 表示在某一组内的编号,\(1 \leq k \leq n\)。
+每一组都是 \(n\) 个人,这是一个 +balanced design。
+Factor Effects Model
+模型假设是 \(Y_{ijk} = \mu +\alpha_i + +\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
+其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) +表示和两个因素同时相关的变化,相当于一个交叉项。
+这里面有 \((a+1)(b+1)\) +个参数,对其也有一定的约束:\(\Sigma_i +\alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j +(\alpha \beta)_{ij} +=0\)。做一些其他的参数假设,让参数含义更清晰:
+\[\mu_{i.} = \alpha_i ++\mu_{..}\]
+\[\mu_{.j} = \beta _j + +\mu_{..}\]
+\[\mu_{ij} = \mu_{..} +\alpha_i + \beta_j ++(\alpha \beta)_{ij}\]
+如果 \((\alpha \beta)_{ij}=0\) +则说明因素 \(A,B\) +之间不存在相互作用的关系,这样的模型称为 additive model。
+考虑一些统计量作为参数的估计量:
+\[\bar{Y}_{ij.} = \frac{1}{n} \Sigma_{k=1 +}^{n} Y_{ijk} = \hat \mu_{ij} = \hat \mu + \hat \alpha _i + \hat +\beta_j + \hat{(\alpha \beta)}_{ij}\]
+\[\bar{Y}_{i..} = \frac{1}{bn} +\Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \alpha_i = +\hat \mu_{i.}\]
+\[\bar{Y}_{.j.} = \frac{1}{an} +\Sigma_{i=1}^a \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \beta_j = +\hat \mu_{.j}\]
+\[\bar{Y}_{...} = +\frac{1}{abn}\Sigma_{i=1}^a \Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = +\hat{\mu} \]
+Two factors ANOVA 的方差分解更复杂一些:
+\[\begin{aligned} SSTO &= \Sigma_i +\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{...})^2 \\ &= \Sigma_i +\Sigma_j \Sigma_k ((\bar Y_{i..} - \bar Y_{...})+(\bar{Y}_{.j.} - \bar +Y_{...}) +(\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...}) ++(Y_{ijk} - \bar Y_{ij.}))^2 \\&=bn\Sigma_i (\bar Y_{i..} - \bar +Y_{...})^2+an\Sigma_j (\bar{Y}_{.j.} - \bar Y_{...})^2+n\Sigma_i +\Sigma_j (\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...})^2+ +\Sigma_{i}\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{ij.})^2 \\&=SSA ++SSB+SSAB+SSE \end{aligned}\]
+其中,\(SSA\) 的自由度是 \(a-1\),\(SSB\) 的自由度是 \(b-1\),\(SSAB\) 的自由度是 \((a-1)(b-1)\),\(SSE\) 的自由度是 \(ab(n-1)\)。在这一个复杂问题中我们关心不同的问题,可以做出三种不同的假设检验,有对应的检验统计量。
-
-
- \(E \cap H \subset \bar E\) -
- \(Vol(\bar E) < e^{-1/(2(n+1))} -Vol(E)\) -
Proof: First consider \(a -= e_1. D = I_{n \times n}\) and the center of \(E_0\) as \(z = -0\). It's trivial to see that the first property holds. In this -case the positive definite matrix of \(\bar -E_0\) is \(D = diag((\frac{n}{n+1})^2, -\frac{n^2}{n^2-1}, \cdots,\frac{n^2}{n^2-1})\), and the center is -\(a = -(\frac{1}{n+1},0,\cdots,0)^T\).
-Now by constructing an affine transformation we can consider the -general case. The transformation T should let \(T(E) = E_0, T(H) = H_0\) and \(T(\bar E) = \bar E_0\). By some elementary -observations we can obtain that affine transformations preserve set -inclusion, i.e. if \(E_0 \cap H_0 \subset \bar -E_0\), then there is \(T(E_0) \cap -T(H_0) \subset T(\bar E_0)\), therefore the first property holds -naturally.
-Let \(R\) be the rotation matrix -corresponding to the vector \(u = D^{\frac 1 -2} a\), i.e.,
-\[R^TR = I, \quad RD^{\frac 1 2}a_i = -\|D^{\frac 1 2} a_i \| e_1\]
-Consider the following affine transformation:
-\[T(x) = R(D^{-\frac 1 -2}(x-z))\]
-Therefore,
-\(\begin{aligned} x \in E & \iff -(x-z)^TD^{-1}(x-z)\leq 1 \\ & \iff (x-z)^TD^{-\frac 1 -2}R^TRD^{-\frac 1 2}(x-z)\leq 1 \\ & \iff T(x)^T T(x) \leq 1 \\ -& \iff T(x) \in E_0, \end{aligned}\)
-which implies that \(T(E) = -E_0\).
-Similarly,
-\[\begin{aligned} x \in H & \iff -a_i^T(x-z )\geq 0 \\ & \iff \|D^{-\frac 1 2}a_i \| e_1 ^T RD^{-\frac -1 2} (x-z) \geq 0 \\ & \iff e_1 ^T T(x) \geq 0 \\ & \iff T(x) -\in H_0, \end{aligned}\]
-which implies \(T(H) = H_0\).
-Moreover there is also \(T(\bar E) = \bar -E_0\) and we omit the complicated algebraic manipulations. -Therefore \(E \cap H \subset \bar E\) -holds according to the properties of affine transformation. Next we -prove the conclusion about the volume.
-\(\frac{Vol(\bar E)}{Vol(E)} = -\frac{Vol(T(\bar E))}{Vol(T(E))} = \frac{Vol(\bar E_0)}{Vol(E_0)} = -det(D_0 ^{\frac 1 2}) = -(\frac{n}{\sqrt{n^2-1}})^{n-1}(\frac{n}{n+1})\)
-Consider
-\[(\frac{n^2}{n^2-1})^{\frac{n-1}{2}}(\frac{n}{n+1}) -= (1+\frac{1}{n^2-1})^{\frac{n-1}{2}}(1-\frac{1}{n+1}) \leq -(e^{\frac{1}{n^2-1}})^{\frac{n-1}{2}} e^{-\frac{1}{n+1}} -= e^{-\frac{1}{2(n+1)}},\]
-and the desired result follows.
+- \(A\) 因素是否会导致差异?\(H_0: \alpha_1 =\alpha_2=...=\alpha_a\),在 +\(H_0\) 下有 \(F^* = \frac{SSA/(a-1)}{SSE/(ab(n-1))} \sim +F_{a-1,ab(n-1)}\) +
- \(B\) 因素是否会导致差异?\(H_0: \beta_1 =\beta_2=...=\beta_b\),在 +\(H_0\) 下有 \(F^* = \frac{SSB/(b-1)}{SSE/(ab(n-1))} \sim +F_{b-1,ab(n-1)}\) +
- \(A,B\) 是否联合作用?\(H_0:(\alpha \beta)_{ij}=0, \forall 1 \leq i \leq +a,1\leq j \leq b\),在 \(H_0\) +下有 \(F^*=\frac{SSAB/(a-1)(b-1)}{SSE/(ab(n-1))} \sim +F_{(a-1)(b-1),ab(n-1)}\)
另外如果估计得再精细一点的话下界其实是 \(\exp(-\frac{1}{2n})\)(详见 -Bubeck),可以对函数求导做。
-所以只要初始状态的 ellipsoid -体积有限,算法一定会在有限时间内终止,可以用来解决 feasiblility -的问题,这是一个可以在 \(O(n \log -\varepsilon)\) 时间内结束的算法,实际上对于找 feasible solution -来说还是很快的。但 feasible solution -一个单点对于优化问题来说其实没什么用,我们的目标仍然是寻找 optimal -cost,为此需要一些类似于 center of gravity method 的方法。
-另外 ellipsoid method 也可以用来解决 optimal cost -的逼近,有这样一个体积关系了之后原理和 center of gravity method -类似:
-每个新的 ellipsoid 和上一时刻 ellipsoid 之间有一个体积关系是
-\(Vol(S_{t+1}) \leq \exp(-\frac{1}{2n})
-Vol(S_t) \leq \cdots \leq \exp(-\frac{t}{2n}) Vol(S_1)\),再对于
-\(\varepsilon = \exp(-\frac{t}{2n^2})\)
-取 \(\mathcal S_\varepsilon = \{(1-\varepsilon
-)x^* + \varepsilon x, \forall x \in S_1\}\),实际上是对 \(S_1\) 做了一个仿射变换。此时有 \(Vol(S_\varepsilon)=\varepsilon^n Vol(S_1) =
-\exp(-\frac{t}{2n}) Vol(S_1) \geq
-Vol(S_{t+1})\),于是可以找到一个 \(x_\varepsilon \in S_\varepsilon\) 使其在
-\(t\) 时刻时仍在 \(S_t\) 中,而 \(t+1\) 时刻就被“裁剪”了出去。
所以有:
\[c^Tx_{t+1} < c^Tx_\varepsilon =
-c^T((1-\varepsilon)x^*+ \varepsilon x) \leq c^Tx^* + 2B\varepsilon
-=c^Tx^*+2B \exp(-\frac{t}{2n^2}),\]
也就是说 \(c^Tx_{t+1} - c^Tx^* < 2B
-\exp(-\frac{t}{2n^2})\) 作为 \(t+1\) 时刻下取值距离 optimal cost
-的误差可以被控制,并且我们可以在 \(O(n^2
-\log(\frac{1}{\varepsilon}))\) 时间下得到误差为 \(\varepsilon\) 的 cost 和
-solution。同样是得到的 cost 比 simplex method 误差大一些并非精确值,但是
-polynomial time algorithm,虽然比起 center of gravity method
-来说消耗更大,但也有它的优势。
之前的想法一直有大问题,我当时也没怎么看懂 Bubeck -那本书的内容,更是完全不理解为什么 time usage 里面还有 \(R/r\) -的项。今晚做出来优化作业第一题之后醍醐灌顶,直接复制到这里来就很清楚了。
-Problem: Consider the following convex optimization -problem (\(f,g_i\) are convex):
-\[\text{minimize} \quad f(x)\]
-\[\text{subject to} \quad g_i(x) \leq 0, -i=1,2,\cdots,m.\]
-Let \(\mathcal K = \{x \mid g_i(x) \leq 0, -i=1,2,\cdots,m\}\). Assume that there exists \(x_,x_0^\prime\) s.t. \(\mathcal K\) is between balls of radius -\(r,R\),
-\[B(x_0,r) \subseteq \mathcal K \subseteq -B(x_0^\prime,R)\]
-Further assume that \(\sup_{x \in \mathcal -K} |f(x)| \leq B\). Given any \(x \in -\mathbb R^n\) one can evaluate \(f(x),g_i(x), \nabla f(x) , \nabla g_i(x)\). -Propose an efficient implementation of the Ellipsoid's method. Prove -that the algorithm converges in \(\mathcal -O(n^2 \log(\frac{BR}{r \varepsilon}))\) iterations to find an -\(\varepsilon\) optimal solution.
-Solution: To begin the algorithm, we set \(\mathcal E_0 = B(x_0^\prime, R)\) and \(c_0 = x_0^\prime\) as its center. At time -\(t\) we divide the possible results -into two situations as follows.
+Random Effect Test
+Why random effects?
+事实上,有的时候对于一个 cell means model 或者 factor effects +model,我们并不是很关心每个 \(\mu_i\) +的检验,而是关心整体的 \(\mu_.\) +的情况;这种情况下一般 level of factor +也是随机从一个总体里取出的。所以需要改变一些模型假设,进行 random effect +的检验。
+Cell means model for random +effect
+回顾一下 cell means model:
+++模型假设是 \(Y_{ij} = \mu_i + +\varepsilon_{ij}\)。
+其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim +N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。
+
对于 cell means model for random effect,需要把 \(\mu_i\) 视作一组随机变量而非参数:
+++模型假设是 \(Y_{ij} = \mu_i + +\varepsilon_{ij}\)。其中有 \(i = +1,2,...,r\),\(j +=1,2,...,n\),暂时设定为一个 balanced test。
+其中,\(\mu_i \sim N(\mu_., \sigma_\mu +^2)\) 不要求相互独立,\(\varepsilon_{ij}\) i.i.d. \(\sim N(0,\sigma^2)\),且 \(\mu_i\) 和 \(\varepsilon_{ij}\) 之间是相互独立的。 +因此,这一模型中共有 \(3\) +个参数,分别是 \(\mu_., \sigma_\mu, +\sigma\),而且 \(Y_{ij}\) +不相互独立。
+事实上,我们不要求关于特定的 \(\mu_i\) 的结论,而是关心在 population \(\lbrace \mu_i \rbrace_{i=1} ^r\) +上的推断,以推断 \(\mu\) 和 \(\sigma_\mu^2\) 为主。
+
简单推导可以得到以下结论:
-
-
If \(c_t \notin \mathcal K\), -then there is some constraints \(g_i(x) \leq -0\) violated so that \(c_t\) -does not lie in the feasible set. We find the violated constraints by -calling the zeroth order oracle \(g_i(c_t)\) and compare their value with -\(0\). To save the computational source -we just pick the violated constraint \(g_i(c_t) >0\) with the smallest -subscript, and number it as \(g_i^{(t)}\).
-Thus the feasible set \(\mathcal K\) -lies in \(\mathcal E _t \cap \{x \mid g_i -^{(t)} (x) \leq g_i ^{(t)} (c_t)\} \subseteq \mathcal E _t \cap \{x \mid -\nabla g_i^{(t)}(c_t)^T (x-c_t) \leq 0\}\) according to the -definition of subgradient. And the exact value of subgradient \(\nabla g_i^{(t)}(c_t)\) can be obtained by -calling the first order oracle \(\nabla -g_i^{(t)}\).
-Then we can just construct the \((t+1)\)-th ellipsoid by covering the set -shown above, i.e. \(\mathcal E_{t+1} \supseteq -\mathcal E _t \cap \{x \mid \nabla g_i^{(t)}(c_t)^T (x-c_t) \leq -0\}\).
-The second case is much easier. If we found \(c_t \in \mathcal K\), by considering the -subset \(\mathcal E_t \cap \{ x \mid f(x) < -f(c_t)\} \subseteq \mathcal E_t\), we can either find \(c_t\) is optimal by observing that the set -is empty or found a better solution through iteration.
-According to the definition of subgradient, there is \(\mathcal E_t \cap \{x \mid f(x) < f(c_t)\} -\subseteq \mathcal E_t \cap \{ x \mid \nabla f(c_t)^T (x-c_t) \leq -0\}\). Then we can just construct the \((t+1)\)-th ellipsoid by covering the set -shown above, i.e. \(\mathcal E_{t+1} \supseteq -\mathcal E _t \cap \{ x \mid \nabla f(c_t)^T (x-c_t) \leq 0\}\), -in which the value of subgradient \(\nabla -f(c_t)\) can be obtained by calling the first order oracle \(\nabla f\).
+- \(\mathbb E(Y_{ij}) = \mu_.\) +
- \(Var(Y_{ij}) = \sigma^2 +\sigma_\mu +^2\) +
- \(Cov(Y_{ij} , Y_{ij'}) = \sigma_\mu +^2, j \neq j'\) +
- \(Cov(Y_{ij},Y_{i'j'}) = 0, i \neq +i', j \neq j'\) +
- \(\mathbb E(MSE) = \sigma^2\) +
- \(\mathbb E(MSTR) = \sigma^2 + n\sigma_\mu +^2\)
For both situations, we can obtain \(\mathcal E_{t+1}\) with the least volume -such that \(Vol(\mathcal E_{t+1} ) \leq -\exp(-\frac{1}{2n}) Vol(\mathcal E_t)\) according to the theorem -we proved in class (and we can construct the exact form of \(\mathcal E_{t+1}\) through the complex -equation, which won't be shown again in this solution).
-Therefore, if \(t \geq 2n^2 -\log(\frac{R}{r})\) there is \(Vol(\mathcal E_t) \leq Vol(B(x_0,r))\) and -\(\{c_1,c_2,\cdots,c_t\} \cap \mathcal K \neq -\varnothing\). From now on we only consider the time that ensures -\(\{c_1,c_2,\cdots,c_t\} \cap \mathcal K \neq -\varnothing\).
-For fixed \(\varepsilon >0\), we -take \(\mathcal K_\varepsilon = -\{(1-\varepsilon)x^* + \varepsilon x \mid \forall x \in -B(x_0,r)\}\) as an affine transformation, in which \(x^*\) is the optimal solution of this -problem. Moreover we denote \(x_t \triangleq -\arg \min_{c_s \in \{c_0,c_1,\cdots, c_t\} \cap \mathcal K} -f(c_s)\).
-When we take \(\varepsilon = \frac{R}{r} -\exp(-\frac{t}{2n^2})\) there is \[Vol(\mathcal K_\varepsilon ) = \varepsilon^n -Vol(B(x_0,r)) = \varepsilon^n (\frac{r}{R})^n Vol(B(x_0^\prime ,R)) = -\exp(-\frac{t}{2n^2}) Vol(B(x_0^\prime, R)) > Vol(\mathcal -E_t)\]
-This inequality implies that there exists one time \(r \in \{1,2,\cdots,t\}\) s.t. there exists -\(x_\varepsilon \in \mathcal -K_\varepsilon\), \(x_\varepsilon \in -\mathcal E_{r-1}\), but \(x_\varepsilon -\notin \mathcal E_r\), therefore \(x_\varepsilon\) is not optimal. According -to the convexity of \(f(x)\), there is -\[f(x_t) < f(c_r) -\leq f(x_\varepsilon) = f((1-\varepsilon)x^* + \varepsilon x_r) \leq -(1-\varepsilon) f(x^*) + \varepsilon f(x_r) \leq f(x^*) + -2B\varepsilon,\] which implies that \[f(x_t) - f(x^*) \leq 2B\varepsilon = -\frac{2BR}{r} \exp(-\frac{t}{2n^2}).\]
-Then we can conclude that the algorithm converges in \(\mathcal O(n^2 \log(\frac{BR}{\varepsilon -r}))\) iterations to find an \(\varepsilon\) optimal solution, and the -desired result follows.
-Lecture 4
-睡了(,等个笔记((
-10.23 UPD:今天布置了个优化 HW3 -但又迅速删掉了,我也不知道为什么要同时把讲义也删掉,当时正好在贴所以也没来得及下(。这助教是否也是一个优化算法控制的,要传就把所有的东西都传上来要删就全部删掉,来保证要么所有人都满意要么所有人都不满意(。
-Convex Optimization
-Notations
-#每日迷神
-
记 \(\sigma_Y^2 = \sigma_\mu^2 + +\sigma^2\),有一个在推断中有意义的参数是 \(\frac{\sigma_\mu ^2}{\sigma_Y ^2} = +\frac{\sigma_\mu ^2}{\sigma_\mu ^2 + +\sigma^2}\)。这表征了在整体方差中,由 \(Y_{ij}\) 的随机性产生的比例。
+对此我们常做的一个检验是 \(H_0 :\sigma_\mu +^2 = 0; H_a: \sigma_\mu ^2 >0\),原假设的含义在于说明 \(\mu_i\) 是相等的,事实上这和 fixed effect +下的 cell means model 所做的检验是相同的。在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 +_{r(n-1)}\),\(\frac{SSTR}{\sigma^2} +\sim \chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,r(n-1)}\) +作为最终的检验统计量。
+当 \(F^* > F(1-\alpha , r-1 , +r(n-1))\) 时拒绝原假设,否则接受;\(Power = P(F^* > F(1-\alpha , r-1,r(n-1))| +\delta)\),其中 \(\delta\) +是一个非中心偏移量,\(\delta = +\frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i n_i (\mu_i - +\mu_.)^2}\)。这里是暂时认为做的是 balanced test。
+如果实验并不是一个 balanced test,每一组的数据量为 \(n_1,n_2,...,n_r\) 且有 \(n_T = \Sigma_{i=1} ^r n_i\),于是有:
+\[\mathbb E(MSTR) = \sigma^2 + n' +\sigma_\mu ^2, \quad n' = \frac{1}{r-1} [n_T - \frac{\Sigma_{i=1}^r +n_i ^2}{n_T}]\]
+对这一模型的参数做一些估计,上文中提到 cell means model for random +effect 有三个参数 $_., ^2 $ 和 \(\sigma_\mu +^2\),事实上对于后两个参数我们也关心 \(\frac{\sigma_\mu ^2}{\sigma_\mu ^2 + +\sigma^2}\) 的估计,以下还是在 balanced test +的前提下分点来阐述技术细节:
-
-
- A set \(C \in \mathbb R^n\) is -affine iff for any \(x,y \in C\) and -any \(\theta \in \mathbb R\), there is -\(\theta x + (1-\theta) y \in C\), -therefore the whole line lies in \(C\). +
\(\mu_.\) 的一个无偏估计即为 +\(Y_{..} = \frac{\Sigma_{i=1}^r \Sigma_{j=1}^n +Y_{ij} }{rn}\),它的方差是 \(Var(Y_{..}) = \frac{\sigma^2}{rn} + +\frac{\sigma_\mu ^2}{r}\)。
+因此 \(s^2(\bar{Y}_{..}) = +\frac{MSTR}{rn}\) 是 \(Y_{..}\) +的方差的无偏估计,\(\mu_.\) +的置信区间是 \(\bar{Y}_{..} \pm +t(1-\alpha/2;r-1)s(\bar{Y}_{.. } )\)。
+由于 \(\frac{MSTR/(n\sigma_\mu ^2 + +\sigma^2)}{MSE/ \sigma^2} \sim F_{r-1,r(n-1)}\),因此有:
+\[L = \frac 1n [\frac{MSTR}{MSE} +(\frac{1}{F[1-\alpha/2;r-1;r(n-1)]})-1]\]
+\[R = \frac 1n [\frac{MSTR}{MSE} +(\frac{1}{F[\alpha/2; r-1,r(n-1)]})-1]\]
+此时 \(\frac{\sigma_\mu ^2}{\sigma_\mu ^2 + +\sigma^2}\) 的 \(100(1-\alpha) +\%\) 置信区间是 \([\frac{L}{1+L} , +\frac{R}{1+R}]\)。
+\(\sigma^2\) 的无偏估计是 \(MSE = \frac{\Sigma_{i=1} ^r \Sigma_{j=1}^n (Y_{ij} +- \bar Y_{i.})}{r(n-1)}\),置信区间的估计可以建立在 \(\frac{r(n-1)MSE}{\sigma^2} \sim +\chi^2[r(n-1)]\) 的基础上,于是有 \(\sigma^2\) 的 \(100(1-\alpha) \%\) 置信区间是 \([\frac{r(n-1)MSE}{\chi^2[1-\alpha /2; r(n-1)]}, +\frac{r(n-1)MSE}{\chi^2 [\alpha/2;r(n-1)]}]\)
+\(\sigma_\mu^2\) 的无偏估计是 +\(s_\mu ^2 = \frac{MSTR - +MSE}{n}\),但有时数据点决定此处点估计值是负的,此时就用 \(0\) 来代替 \(\sigma_\mu ^2\) 的估计值。
+
Random factor effects model
+相应地可以对 cell means model for random effect 做一些改进。回顾一下 +factor effects model:
+++Factor Effects Model 是 Cell Means Model +的一个重新参数化的结果。模型假设是 \(Y_{ij} = +\mu + \tau_i + \varepsilon_{ij}\)。
+其中,\(\mu_i\) +是整体的理论均值,\(\varepsilon _{ij}\) +i.i.d. \(\sim +N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 \(\mu , \tau_1 , ..., \tau_r , +\sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = +0\),如果没有这个约束会导致存在多组解。
+
Random factor effects model 也是 cell means model for random effects +的一个重新参数化的结果。
+++模型假设是 \(Y_{ij} = \mu + \tau_i ++\varepsilon_{ij}\),其中 \(i = +1,2,...,a,j=1,2,...,n_i\)。相对于 cell means model for random +effect,这里将 \(\tau_i\) +都视作随机变量,满足 \(\tau_i \sim +N(0,\sigma_\tau ^2)\) 不要求相互独立,\(\varepsilon_{ij}\) i.i.d. \(\sim N(0,\sigma^2)\),且 \(\tau_i\) 和 \(\varepsilon_{ij}\) +之间是相互独立的。这一模型中也是三个参数,分别是 \(\mu_., \sigma_\mu, \sigma\),而且 \(Y_{ij}\) 不相互独立。
+由于是随机变量,自然不再要求满足 \(\Sigma_{i=1}^a \tau_i =0\) 的限制。
+
实际上可以看到,在 random effect 意义下,factor effects model 和 cell +means model +的关系更紧密了,只是相差一个常数。因此所有的检验和推断可以类似的进行。
+Mixed factors effects model
+回顾一下 two factors effects model:
+++模型假设是 \(Y_{ijk} = \mu +\alpha_i + +\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
+其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) +表示和两个因素同时相关的变化,相当于一个交叉项。
+这里面有 \((a+1)(b+1)\) +个参数,对其也有一定的约束:\(\Sigma_i +\alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j +(\alpha \beta)_{ij} =0\)。
+
类似地,mixed factors effects model 也是把模型假设进行了一些修改,将 +\(\alpha_i\) 从参数改成了随机变量。注意 +\(\alpha_i , \beta_j\) 中只要有一个改为 +random effect,其联合作用 \((\alpha +\beta)_{ij}\) 也变为随机变量而非参数。
+++模型假设是 \(Y_{ijk} = \mu +\alpha_i + +\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
+其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) +表示和两个因素同时相关的变化,相当于一个交叉项。
+需要满足一定的约束:
-
-- Therefore, if \(C\) is an affine -set and \(x_0 \in C\), then the set -\(V = \{x-x_0 \mid \forall x \in C\}\) -is a subspace.
-An affine hull of \(C\) is denoted -as \(aff(C) = \{\theta_1 x_1+ \theta_2 -x_2+\cdots+ \theta_k x_k \mid \forall k \in \mathbb Z_+, x_i \in C, -\theta_i \in \mathbb R \}\) -The relative interior \(relint(C) = \{x\in -C \mid \exist r >0 , \text{s.t. } B(x,r) \cap aff(C) \subseteq C -\}\) +\(\Sigma_{i=1} ^ a \alpha _i +=0\) +\(\beta_j \sim N(0,\sigma_\beta +^2)\) +\((\alpha \beta)_{ij} \sim +N(0,\sigma_{\alpha \beta}^2)\) + +
检验方式和统计量见 ANOVA table construction 环节。
+ANOVA table construction
+e.g: three factors model
+\[Y_{ijkl} = \mu + \alpha_i + \beta_j + +\gamma _k +(\alpha \beta)_{ij} + (\alpha \gamma)_{ik} + (\beta +\gamma)_{jk} + (\alpha \beta \gamma)_{ijk} + +\varepsilon_{ijkl}\]
+\[i = 1,2,...,a\]
+\[j = 1,2,...,b\]
+\[k = 1,2,...,c\]
+\[l = 1,2,...,n\]
+其中 \(a\) 是 fixed effect,而 \(b,c\) 是 random effect。于是模型参数是 +\(\theta = \lbrace \mu , +\alpha_i^{i=1,2,...,a} , \sigma_\beta^2 , \sigma_\gamma ^2 , +\sigma_{\alpha \beta}^2 , \sigma_{\beta \gamma }^2 , +\sigma_{\alpha,\gamma}^2, \sigma_{\alpha,\beta,\gamma}^2,\sigma^2 +\rbrace\)
+ANOVA table construction 的过程详见 Statistics Note by +V1ncent19,P212-215,这里仅给出结果:
+| Random/Fix | +F | +R | +R | +R | ++ |
|---|---|---|---|---|---|
| # level | +a | +b | +c | +n | ++ |
| Index | +i | +j | +k | +l | +\(\mathbb E(MS)\) | +
| \(\alpha_i\) | +0 | +b | +c | +n | +\(\sigma^2 + cn \sigma_{\alpha \beta}^2 + +bn \sigma_{\alpha \gamma}^2 + n \sigma_{\alpha \beta \gamma}^2 + bcn +\frac{\Sigma \alpha_i ^2}{a-1}\) | +
| \(\beta_j\) | +a | +1 | +c | +n | +\(\sigma^2 + an \sigma_{\beta \gamma}^2 + +acn \sigma_{\beta}^2\) | +
| \(\gamma_k\) | +a | +b | +1 | +n | +\(\sigma^2 + an \sigma_{\beta \gamma}^2 + +abn \sigma_{\gamma}^2\) | +
| \((\alpha \beta)_{ij}\) | +0 | +1 | +c | +n | +\(\sigma^2 + cn \sigma_{\alpha \beta}^2 + +n \sigma_{\alpha \beta \gamma}^2\) | +
| \((\alpha \gamma)_{ik}\) | +0 | +b | +1 | +n | +\(\sigma ^2 + bn \sigma_{\alpha \gamma}^2 ++ n \sigma_{\alpha \beta \gamma}^2\) | +
| \((\beta \gamma)_{jk}\) | +a | +1 | +1 | +n | +\(\sigma^2 + an\sigma_{\beta +\gamma}^2\) | +
| \((\alpha \beta +\gamma)_{ijk}\) | +0 | +1 | +1 | +n | +\(\sigma^2 + n \sigma_{\alpha \beta +\gamma}^2\) | +
| \(\varepsilon_{ijkl}\) | +1 | +1 | +1 | +1 | +\(\sigma^2\) | +
于是可以利用上述期望进行检验:
+-
+
- \(H_0 : \alpha_1 = \alpha_2 = +...=\alpha_a\),检验 \(F_{\alpha_i} ^* += \frac{MS_\alpha + MS_{\alpha ]beta \gamma}}{MS_{\alpha \beta} + +MS_{\alpha \gamma}} \sim ^{H_0} F_{(a-1)+(a-1)(b-1)(c-1), +(a-1)(b-1)+(a-1)(c-1)}\) +
- \(H_0 : \sigma^2 =0\) +
- \(H_0 : \sigma_{\beta}^2 =0\) +
- ......
简单来说,affine set/affine hull 和 convex -版本的唯一区别就是参数不需要取在 \([0,1]\) 之间,所以它一般是个平面。
+R code for ANOVA
+详见 Mixed +ANOVA in R,和课上讲的是同一个东西但是更精细一点(
+期末考前又去看我第二次作业的那个 +project,绷不住了,我怎么做了个不合理的 mixed effect model +还拿了满分(
+实验设计方法
+不如说是实验设计小知识(
+Designed experiment 的主要目标是研究若干 explanatory factor 和 +response variable 之间的因果关系。在实验中变量控制情况(也就是所谓的 +treatments)和被试者的匹配之间是完全随机的,例如在试药时安慰剂和特效药是随机分发的,甚至会将实验条件对被试者保密。
+Observational & +Experimental Study
-
-
A set \(C\) is called a cone iff -\(\forall x \in C\) and for any \(\theta > 0\), there is \(\theta x \in C\).
-(Extended convex function) A function \(f : \mathbb R^n \to \mathbb R\) is convex, -we can extend its domain \(dom(f)\) to -\(\mathbb R^n\) by taking \(f(x) = \infty\) for any \(x \notin dom(f)\).
-(Epigraph of a function) \(epi(f) = -\{(x,t) \mid t \geq f(x)\}\)
-Therefore \(f\) is a convex function -if and only if \(epi(f)\) is a convex -set.
+Observational study: The investigator use the data observed in +the population to make inference on the relationship between the +variables
+Experimental study: The investigator intervene in the natural +history by actively alternating one of the variables and then making +inference on the relationship between the variables based on the +outcomes
Basic Theorems
+简单来说,直接研究通过观察收集来的数据就是 observational +study,数据只来自于自然的观察,收集者对事物发生不作任何干涉;experimental +study 则需要实验者自行控制变量,在所需条件下收集数据,再进行研究。
+Crossed and Nested Factors
+这是多因素分析中的一个概念。
-
-
(Seperating Hyperplane Theorem) Suppose \(C,D\) are nonempty disjoint convex sets, -then there exists \(a \neq 0\), \(a,b \in \mathbb R^n\) s.t. \(C \subseteq \{x \in \mathbb R^n \mid a^Tx \leq -b\}\) and \(D \subseteq \{x \in \mathbb -R^n \mid a^Tx \geq b\}\).
-Proof: We only consider the case when \(C,D\) are both closed and bounded.
-Define \(dist(C,D) = \inf\{\|u-v\|_2 \mid u -\in C,v \in D \}\) as the distance between \(C,D\), then by closed and boundness we can -find \(c \in C, d \in D\) s.t. \(dist(C,D) = \|c-d\|_2\). Take \(a = d-c\), \(b = -\frac 1 2 (\|d\|_2^2 - \|c\|_2^2)\).
-Then the affine transformation \(f(x) = -a^Tx - b\) will let \(f(x) -<0\) for any \(x \in D\), and -\(f(x) >0\) for any \(x \in C\).
-(Supporting Hyperplane Theorem) Suppose \(C\) is convex, then for any \(x \in bd(C)\) here exists a supporting -vector \(a \neq 0, a \in \mathbb R^n\), -s.t. \(\forall x \in C\), \(a^Tx_0 \leq a^Tx\). (\(bd(C)\) is the boundary of \(C\))
+Crossed factors: all combinations of the levels of the two +factors are included in the study. e.g.
++ +
+ + + +Factor Combination +Temperature +Solvent Concentration +Outcome ++ +1 +Low +Low +/ ++ +2 +Low +High +/ ++ +3 +High +Low +/ ++ + +4 +High +High +/ +
+Nested factors: the level of one factor are unique to a +particular level of another factor. e.g.
++ +
+ + + +Factor Combination +Temperature +Solvent Concentration +Outcome ++ +1 +Low +Low +/ ++ + +2 +High +High +/ +
别的没什么了,convex function -的性质什么的真没必要再写一遍了,他又不讲 subgradient。
-Lecture 5
-才隔了两周,今天怎么又是哥们在做 scribing 啊(。read-only 的链接在这里。
-今天讲一些 convex optimization 里的例子,给哥们整的一愣一愣的。
-Examples in Convex -Optimization
-Notations
-#每日迷神
-
你还别说现在还真不一定书上都有了,那个 max cut 给哥们整不会了,Boyd -上面没写,Bubeck 就写了一点而且还把课上的内容跳过去了。而且 Bubeck -本来就简略,看了个寂寞。
+Completely randomized design
-
-
The following optimization problem is called a convex -optimization problem if \(x_0, f_i\) -are convex, and \(h_i\) are linear:
-\[\begin{aligned} -\textbf{minimize} \quad & f_0(x) \\ -\textbf{subject to} \quad & f_i(x) \leq 0 \\ -& h_i (x) =0 -\end{aligned}\]
-\(x\) is a \(\varepsilon\)-suboptimal if \(f_0(x) \leq p^* + \varepsilon\), in which -\(p^*\) is the optimal value of the -convex optimization problem.
-\(x_0\) is locally optimal if -there exists \(R >0\) s.t. \(x_0\) is the optimal solution to:
+对于一个有三个因素的 designed +experiment,建立的模型包括三个部分:
+\(Y=\) overall constant + treatment +effect + experimental error
+如果采用线性回归模型,以三个因素为例,全体被试者被分为 \(8\) 组,使得
+\[Y_{ij} = \beta_0 + \beta_1 X_{ij1} + +\beta_2 X_{ij2} + \beta_3 X_{ij3} + \varepsilon_{ij}\]
+可以轻松地将其和上述的三个模型组成部分对应起来。其中 \(X_1,X_2,X_3\) 类似于示性函数,此处是一种 +categorical variable,$X_i = 1 $ if treatment \(i\),otherwise \(0\)。
+也可以用因子效应模型来考虑这个问题,表示起来会比较容易;另外要注意的是,regression +model 关心平均响应的预测,但 factor effect model +更关心平均响应的差别。
+仍然以上一部分中的 Treatment of Lead-Exposed Children Trial +为例。
+\(100\) +名被试被分成两组分别使用安慰剂和药剂,在实验开始前、实验第 \(1, 4, 6\) 周分别检验了血液铅含量水平。第 i +名被试的实验开始前水平为 \(y_{i1}\),实验结束后水平为 \(y_{i2}\),变化水平为 \(d_i = +y_{i2}-y_{i1}\),希望利用这些数据观察药剂的有效程度。
+我们在这一实验中设定三个不同的 explanatory factor,分别是 treatment +type (succimer or placebo),children's ID (from \(1\) to \(100\),用于展示个体间的差别),time point +(week \(0,1,4,6\))。其中,treatment +type 和 time point 可能会协同作用。Outcome,也即 response variable +设定为血铅浓度 \(Y\)。
+模型为:
+\[Y_{ijt} = \mu + \alpha_i + \beta_{j(i)} ++ \gamma_t + (\alpha \gamma)_{it} + \varepsilon_{ijt}\]
+参数假设为:
+\[\beta_{j(i)} \sim N(0,\sigma_\beta +^2)\]
+\[\varepsilon_{ijk} \sim +N(0,\sigma^2)\]
+自由度和方差分解为:
+\[Y_{ijt} - Y_{...} = (\bar Y_{i..} - \bar +Y_{...}) +(\bar Y_{..t} - \bar Y_{...}) +(\bar Y_{i.t} - \bar Y_{i..} - +\bar Y_{..t} + \bar Y_{...}) + (\bar Y_{ij.} - \bar Y_{i..}) + (Y_{ijt} +- \bar Y_{ij.} - \bar Y_{i.t} + \bar Y_{i..})\]
+\[df: Nn-1 = +(a-1)+(n-1)+(a-1)(n-1)+(N-a)+(N-a)(n-1)\]
+可以提出并进行检验的问题有:
+-
+
安慰剂和药剂之间有无明显的区别?在第 \(0,1,4,6\) +周时,两组之间的血铅值是否有明显差异?
+\(H_0: \mu_t(S) = \mu_t(P), \forall t= +1,2,3,4\),其中 \(\mu_t = \mu + +\gamma_t + (\alpha +\gamma)_{it}\),也即取出全体和时间有关的项。
+也可以换一种表示方法:安慰剂和药剂是否在降低血铅方面有同等的效果?
+\(H_0 : \mu_t(S) - \mu_1 (S) = \mu_t(P) - +\mu_1(P),\forall t =2,3,4\)
+可以推出这等价于 \(H_0: (\alpha +\gamma)_{it} = 0,\forall i = 1,2, +t=1,2,3,4\),这是因为参数假设中认为 \(\Sigma (\alpha \gamma)_{it}=0\)。
+
\[\begin{aligned} - \textbf{minimize} \quad & f_0(x) \\ - \textbf{subject to} \quad & f_i(x) \leq 0 \\ - & h_i (x) =0 \\ - & \|x-x_0\| \leq R \end{aligned}\]
-Why Convex Optimization?
-为什么研究凸优化?一个是 linear programming problem -有它的局限性,许多问题只能往凸优化的方向转化。另外凸性质实际上是非常美妙的。下面是一个很 -trivial 的例子,我们对 convex optimization -的转化问题的探究远不止于此。
-Why is convex optimization important? That's because some non-convex -problems have underlying convexity. For example, we consider the -following optimization problem:
-\[\begin{aligned} -\textbf{minimize} \quad & f_0(x)=x_1^2+x_2^2 \\ -\textbf{subject to} \quad & f_1(x) = \frac{x_1}{1+x_2^2} \leq 0 \\ -& h_i (x) = (x_1+x_2)^2 =0 -\end{aligned}\]
-which can easily be transformed into a standard convex optimization -problem.
-Example: Max Cut Problem
-别 TCS 了求你了求你了求你了(
-通过一个 max cut problem 来体现从 nonconvex optimization 向 convex -optimization 的转化,从方法论的层面上来说是两步。
-Why are convex optimization problems important? That's because many -non-convex optimization problems can be transformed into convex ones, -and we can solve convex optimization problems through mature -technologies. Generally speaking, the process contains two steps:
--
-
- First, transform the non-convex problem into convex ones through -relaxation. -
- Next recover a solution from the convex problem to the non-convex -one through random rounding. -
Notations
+Clinical Trials
+临床试验最准确的定义是 the evaluation of intervention (treatment) on +disease in a controlled experimental +setting(绷不住了,感觉看原文比翻译过来要靠谱的多),有不同的类型。
+Randomized clinical trial
+RCT +的目的一般是在不存在因素的互相干扰情况下做对比,目的往往有找出最好的治疗方案,测试药剂相对于安慰剂的效果,等等。因此,实验组必须在各个方面和初始量化指标上都是一致的,在此基础上接受不同的治疗方案,才能控制变量找出方案对于效果的影响。
+RCT +是最有力的临床试验方案,因为是对几乎相同的组别随机分配治疗方案,得到的结果是普适性的。
+Non-randomized clinical +trial
+不随机的点有很多,比如被试者可以自行选择想参加实验的组,自由选择使用的是药剂还是安慰剂,或者这一分组是被实验组织者人为设定而不是随机分配的。
+Contingency Table in +Clinical Trials
+Clinical trial 里面也会用到一些 contingency table +和相应的检验。在这里先给出我们关注的问题和一些相应的定义。
+此处我们主要关心的情境是,两组被试者分别使用 medicine 和 +placebo,可能会出现 adverse reaction +也可能不会出现,统计全体被试者的反应得到以下表格:
+| + | Adverse Reaction (\(D\)) | +No Adverse Reaction (\(D^C\)) | +Total | +
|---|---|---|---|
| Medicine (\(E\)) | +\(n_{11}\) | +\(n_{12}\) | +\(n_{1+}\) | +
| Placebo (\(E^C\)) | +\(n_{21}\) | +\(n_{22}\) | +\(n_{2+}\) | +
| Total | +\(n_{+1}\) | +\(n_{+2}\) | +\(n_{++}\) | +
相应地定义 \(p_1\) 是 medicine +组发生不良反应的概率,\(p_2\) 是 +placebo 组发生不良反应的概率。于是有:
+\[p_1 = \mathbb P(D | E) , p_2 = \mathbb +P(D |E^C)\]
+\[\text{Risk Difference} = \Delta = p_1 - +p_2\]
+\[\text{Relative Risk} = \phi = +\frac{p_1}{p_2}\]
+\[\text{Odds Ratio} = \theta = \frac{p_1 / +(1-p_1)}{p_2 / (1-p_2)}\]
+在这样的情境下我们希望做的检验即为 \(H_0 : +p_1 = p_2\),也即观察 medicine 相对 placebo +来说是否发生不良反应的可能性是相同的。事实上由于上述条件概率的定义,也就是希望检验 +adverse reaction 和 medicine/placebo 的选择是独立的。这就归结为了 +contingency table 的 independence inference,详见下一部分的 Pearson Test +和 Likelihood Ratio Test。
+另外,我们希望使用观察到的数据 \(n_{ij}\) +对上述参数做一些估计。但具体的估计与 clinical trial +的类型有关,此处分别考虑两种类型的 clinical trial,分别是 prospective +clinical trial 和 retrospective clinical trial。
+虽然 contingency table 从理论上来说对于随机变量 \(Y,Z\) +是完全对称的,但是在实验设计中我们需要先确定 \(Y\) 或者 \(Z\),进行优先级的选择后再收集数据。这可能会导致条件概率不同。
+Prospective clinical trial
+招募了许多患有某一疾病的被试者进行试药,\(Y += E / E^C\) 是 medicine 或者 placebo +组在实验开始之前就对全体被试者划分好了,于是 \(Z = D / D^C\) +是是否出现不良反应的量度,是我们在实验中需要关注的。
+在这一实验中由于是预先招募了被试者,所以 \(n_{1+},n_{2+},n_{++}\) 是确定的数值。
+Prospective clinical trial +显然更可控一些,但是也会遇到一些生存分析的问题。另外,如果是关于罕见病的实验,这一方式可能会比较低效。
+此时有参数估计:
+\[\hat p_1 = \frac{n_{11}}{n_{1+}}, \hat +p_2 = \frac{n_{21}}{n_{2+}}\]
+\[\hat \phi = \frac{n_{11}/ +n_{1+}}{n_{21}/ n_{2+}}\]
+\[\hat \theta = +\frac{n_{11}n_{22}}{n_{21}n_{12}}\]
+\[\hat{Var} ( \log \hat \theta) = +\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + +\frac{1}{n_{22}}\]
+注意一些参数含义:\(\phi\) 和 \(\theta\) +都表示了组间差距,如果这两个参数比较大就说明 \(Y\) 对 \(Z\) 和 \(Z^C\) 的影响不同。
+Retrospective clinical trial
+招募了许多产生了不良反应和未产生不良反应的患者,\(Z = D/D^C\) +是是否有不良反应的组在实验开始之前就对被试者划分好了。再对他们发放问卷或者进行采访,了解出现不良反应之前的用药历史。
+在这一实验中对被试者进行的划分是关于 \(Z\) 的,因此 \(n_{+1},n_{+2},n_{++}\) 是确定的数值。
+Retrospective clinical trial 显然是没有那么精准的,我们难以精准控制 +\(Y\),但是数据的收集更快更方便。
+此时有参数估计:
+\[\hat p_1 = \frac{\rho +\frac{n_{11}}{n_{+1}}}{\rho \frac{n_{11}}{n_{+1}}+(1-\rho) +\frac{n_{12}}{n_{+2}}},\hat p_2 = \frac{\rho \frac{n_{21}}{n_{+1}}}{\rho +\frac{n_{21}}{n_{+1}}+(1-\rho) \frac{n_{22}}{n_{+2}}} \]
+其中 \(\rho\) 是人群中的发病率。
+\[\hat \phi = \frac{\hat p_1}{\hat +p_2}\]
+\[\hat \theta = +\frac{n_{11}n_{22}}{n_{21}n_{12}}\]
+\[\hat{Var} ( \log \hat \theta) = +\frac{1}{n_{11}} + \frac{1}{n_{12}} + \frac{1}{n_{21}} + +\frac{1}{n_{22}}\]
+可以发现 odds ratio 在两种 clinical trial +里是一致的,因此这一参数更佳。
+Gehan's Two-Stage Design
+如果某一实验看起来完全达不到我们的最低期望,那我们希望能够尽早在临床试验的早期抛弃这一选择。比如说,对于 +\(n\) +位患者,我们能够接受的最低治疗成功率是 \(20\%\),那么在治疗有效的患者数小于 \(m\) +时就可以认为这一治疗方案是无效的,然后尽早放弃继续的探索。Gehan's +two-stage design 展示了选取 \(m\) +的方式。
+实际上这个过程类似于寻找算法的终止条件。在最初的状态下选择 \(n_0\) +名患者参与治疗,如果这些人里面没有治疗有效的,那么直接停止这一实验过程;否则继续做实验,并且每次加入新的被试者,希望能够达到期望的最低治疗成功率。
+比如说,我们认为当有 \(\pi _0 = +20\%\) +的患者症状缓解时,可以认为这一治疗方案是有效的,这也就是可以接受的最低治疗成功率。在 +Gehan's two-stage design 里设定 level 是 \(\alpha_0 = 5 +\%\),在此基础下考虑第一次实验的被试数量 \(n_0\) 的取值。
+事实上治疗有效果的患者数是一个服从伯努利分布的随机变量 \(X \sim B(\pi)\),那么 \(P(X_0 = 0) = (1-\pi)^{n_0}\leq \alpha_0\) +对于任意的 \(\pi \geq \pi_0\) +是成立的,那么 \(n_0 \geq \frac{\log +(0.05)}{\log (1-0.20)}=14\) 即为第一次实验的最少被试数量。
+也可以通过置信区间的方法来确定。我们希望能够有 \(95 \%\) +的信度认为这一实验可以继续下去,允许 \(\pi_0\) 有 \(\pm +15 \%\) 的浮动,则最少的被试参与数满足 \(1.96(\frac{(1-\pi_0)\pi_0}{n})^{\frac 1 2} = +0.15\),解得 \(n=28\)。
+Inference on Contingency +Table
+简单来说,孟德尔种豌豆那个表格就是一个 contingency +table,到底为什么呈现出 \(9:3:3:1\) +的规律也可以用 goodness of fit test 进行检验。Contingency table analysis +本质上是对 categorical data 的检验。
+Motivation Example
+我们希望知道吸烟和肺癌之间有无确切的联系,采集了一些数据:吸烟且肺癌的有 +\(688\) 人,吸烟但没有得肺癌的有 \(650\) 人;不吸烟且肺癌的有 \(21\) 人,不吸烟且没有得肺癌的有 \(59\) 人。样本量共计 \(1418\) 人,列表如下:
+| + | Lung Cancer | +Healthy | +Total | +
|---|---|---|---|
| Smoke | +688 | +650 | +1338 | +
| Not Smoke | +21 | +59 | +80 | +
| Total | +709 | +709 | +1418 | +
“看起来”吸烟和肺癌是有关系的,因为吸烟者得肺癌的频率看似更高。但是如何从频率得到概率,仍然需要一些检验的逻辑。
+Contingency Table
+抽象出来的 contingency table 的逻辑是这样的:
+| + | \(Z=1\) | +\(Z=2\) | +Total | +
|---|---|---|---|
| \(Y=1\) | +\(n_{11}\) | +\(n_{12}\) | +\(n_{1+}\) | +
| \(Y=2\) | +\(n_{21}\) | +\(n_{22}\) | +\(n_{2+}\) | +
| Total | +\(n_{+1}\) | +\(n_{+2}\) | +\(n_{++}\) | +
当然,\(Y\) 和 \(Z\) +都可以有更多的指标,这不影响我们的构造。比如说它可以长成下面这种通用的形式:
+| + | 1 | +... | +J | +total | +
|---|---|---|---|---|
| 1 | +\(n_{11}\) | +... | +\(n_{1J}\) | +\(n_{1+}\) | +
| ... | +... | +... | +... | +... | +
| I | +\(n_{I1}\) | +... | +\(n_{IJ}\) | +\(n_{I+}\) | +
| total | +\(n_{+1}\) | +... | +\(n_{+J}\) | +\(n_{++}\) | +
与此同时,\(Y\) 和 \(Z\) +的位置是完全对称的,可以交换二者在行和列里的顺序。
+在 \(n_{++},n_{1+},n_{2+},n_{+1},n_{+2}\) +都已知的情况下,完全可以把 \(n_{11}\) +视作一个随机变量,当然表格中的 \(n_{ij}\) +都可以被视为随机变量,但四者中有其一被确定后整个表格就完全被确定,因此只需要讨论 +\(n_{11}\) 的数值。
+事实上,\(n_{11}\) +服从的是超几何分布。\(P(n_{11} = k) = +\frac{C_{n_{1+}}^k C_{n_{2+}}^{n_{+1}-k}}{C_{n_{++}}^{n_{+1}}}\) +对于 \(\max(0,n_{1+} + n_{+1}-n) \leq k \leq +\min(n_{1+},n_{+1})\) 都成立。
+P-value Calculation +Example: 女士品茶
+对于一个如下所示的表格,希望判断品茶的女士是否真的有品尝先加奶还是先加茶的能力——尽管看起来是有的,\(4\) +次尝试里她只失误了一次,但是我们希望通过一些更严谨的推断方法来证明。
+| Actually poured first | ++ | Lady says poured first | +
|---|---|---|
| + | tea | +milk | +
| tea | +3 | +1 | +
| milk | +1 | +3 | +
由于 \(P(n_{11} = 3) = \frac{C_4 ^3 C_4 +^1}{C_8 ^4} = \frac{16}{70}\),\(P(n_{11}=4) = \frac{C_4 ^4 C_4 ^0}{C_8 ^4} = +\frac{1}{70}\),回顾 p-value +的定义是“比所得数据更加极端的情形所出现的概率”,事实上也就是 \(P(n_{11} \geq 3) = \frac{16}{70} + \frac{1}{70} = +\frac{17}{70} = +0.243\),无法给出充足的证据证明这位女士能够品出添加的顺序。
+Inference on Independence
+Contingency table 的通用形式如下所示:
+| + | 1 | +... | +J | +total | +
|---|---|---|---|---|
| 1 | +\(n_{11}\) | +... | +\(n_{1J}\) | +\(n_{1+}\) | +
| ... | +... | +... | +... | +... | +
| I | +\(n_{I1}\) | +... | +\(n_{IJ}\) | +\(n_{I+}\) | +
| total | +\(n_{+1}\) | +... | +\(n_{+J}\) | +\(n_{++}\) | +
另一个检验的重点在于 \(Y\) 和 \(Z\) 联合作用于 \(\{ n_{ij} \}\) +的取值时,我们希望了解二者的作用是否独立。
+如果二者的作用独立,就有 \(\pi_{ij} = +P(Y=i,Z=j) = P(Y=i)P(Z=j) = \pi_{i+} +\pi_{+j}\)。因此我们只要检查实际的 contingency table +和理想中符合二者独立时的 contingency table 有何区别,此处用到 Goodness +of Fit Test。
+Hypothesis
+\(H_0:\) The independence model is +true, i.e. \(\pi_{ij}= \pi_{i+} +\pi_{+j}\) for all pairs of \((i,j)\).
+\(H_1 :\) The saturated model is +true, i.e. \(\pi_{ij}\neq \pi_{i+} +\pi_{+j}\) for at least one pair of \((i,j)\).
+Test Statistic
-
-
- A cut in an undirected graph \(G = (V, -\mathcal E)\) is defined as \(A -\subseteq V\).The capacity of a cut \(A\) is defined as \(c(A) = | \{(u,v)\in \mathcal E \mid u \in A, u \in -A^c\}|\). +
The standard Pearson Chi-Square statistic:
+\[X^2 = \Sigma_i \Sigma_j \frac{(O_{ij} - +E_{ij})^2}{E_{ij}} \sim ^{approx} \chi^2 _{(I-1)(J-1)}\]
+Likelihood Ratio Test statistic:
+$G^2 = -2 () = 2 i j O{ij} {E{ij} } ^{approx} ^2 +_{(I-1)(J-1)} $
而 max cut 问题就是寻找最大的 \(c(A)\),尽管我不知道这样做有什么意义,但它是 -NP-hard 的。所以我们只需要找到一个 polynomial time -的算法就可以证明...(逃
+注意 \(X^2\) 和 \(G^2\) +的分布都是近似分布,二者并不是等价的检验统计量,计算值时常不同,但检验结果往往是类似的。
+Survival Analysis
+Basic Concepts
+首先要明确一些概念,给我的感觉是像黑话一样(
+Concept
+Event +是指生存分析所研究的事件,大多数情况下是指某种治疗过程中患者死亡这样的事件发生,但其实生存分析的应用很广泛,甚至不只是在生医领域都有这些概念的使用。患者治疗后恢复/犯人被释放后再次犯罪/确诊新冠都可以作为研究所感兴趣的事件,这些事件发生就称为 +event。
+At risk 是指尚未发生 event 的个体。事实上大多数情况下研究的 event
+都是患者去世之类的负面事件,因此尚未发生 event
+的个体会被先入为主地定义成 at risk,即为暴露在即将发生 event
+的风险下。什么达摩克斯之剑
Function
+一些常用的函数:
-
-
- An \(\alpha\)-approximate max cut -is a cut \(A\) s.t. \(c(A) \geq \alpha \max_{U \subseteq V} -c(U)\). +
- survival function:\(S(t) = P(T > t) = +1-P(T \leq t) = 1-F(t)\) +
- mean survival time:\(E(T) = \int_{0} +^{\infty} 1-F(t) dt = \int_{0} ^{\infty} S(t ) dt\) +
- hazard function:\(\lambda (t) = \lim_{t +\downarrow 0} \frac{P(t \leq T < t+\Delta t | T \geq t)}{\Delta t} = +\frac{f(t)}{S(t)} = \frac{-S'(t)}{S(t)} = -\frac{d}{dt} \log +S(t)\) +
- cumulative hazard function:\(\Lambda (t) += \int_0 ^{t} \lambda(s) ds = - \log S(t)\)
\(\frac -1 2\)-Approximate Approach
-怎么是概率做法,真稀奇。
-To be more specific, we can give a \(\frac{1}{2}\)-approximate max cut by -randomly adding each point \(v\) in -\(V\) to the cut \(A\) with probability \(\frac{1}{2}\). Consider the expectation of -\(c(A)\) here and we can get:
-\[\mathbb E_A(c(A)) = \mathbb E_A -\sum_{(u,v)\in \mathcal E} 1_{(u \in A,v \in A^c)} = \sum_{(u,v) \in -\mathcal E} P(u \in A, v \in A^c) = \sum_{(u,v) \in \mathcal E} -\frac{1}{2} = \frac{|\mathcal E|}{2}.\]
-然而这还是很粗糙。
-Linear Approach
-如果没有 convex optimization 的话就是考虑一些 linear programming -的近似,举两个失败的 approach 说明这很困难:
+事实上都是对 \(T\) 的分布函数 \(F(t)\) 的变形。
+Data
+生存分析中有两种不同的数据,censored data 和 uncensored data。
+Censored data 是指在研究过程中未能记录到 event 发生(未能记录到 +failure)的数据,往往是因为直到研究结束 event +都尚未发生,或者研究对象中途退出研究,也可能是没有及时发现跟进从而未能记录准确的时间,等等。Censored +data 又分为三种情况,right-censored,left-censored 和 interval-censored +的情况。
-
-
Consider the following formulation of the problem:
-\[\begin{aligned} - \textbf{maximize}_{x\in \mathbb R^n} \quad & \sum_{(u,v)\in -\mathcal E} \frac{1}{2}(1-x_ux_v) \\ - \textbf{subject to} \quad & x_v \in \{-1,1\} -\end{aligned}\]
-This is not a linear programming problem, and we can transform it -by denoting \(z_e = x_ux_v, e=(u,v) \in -\mathcal{E}\):
-\[\begin{aligned} - \textbf{maximize}_{x,z} \quad & \sum_{e \in E} \frac{1}{2 } -(1-z_e) \\ - \textbf{subject to} \quad & z_{(u,v)} \geq -x_u -x_v -1 \\ - & z_{(u,v)} \geq x_u +x_v -1 \\ - & x_v \in [-1,1] -\end{aligned}\]
+- right-censored data 往往是生存期比所记录的时间要长的情况,censor +time 在 event time 之前。例如临床试验持续了一段时间,将 event +设定为观察到患者死亡。某一位患者在第一周加入试验,试验持续十周结束,他直到试验结束都保持健康,没有发生 +event,则他的生存期是 10+ weeks,这是一个 right-censored data。 +
- left-censored data 的一个例子是认为 event +是感染新冠,一位患者在试验第七天发现抗原阳性,但在这之前没有做过检测,不清楚是从什么时候开始感染新冠的,只知道 +censor time 在 event time 之后。因此这是一个 left-censored data。 +
- interval-censored data 的一个例子仍然是认为 event +是感染新冠,一位患者在试验第三天抗原阴性,第七天发现抗原阳性,但在这两次检测之间没有做过检测,也还是不清楚从什么时候开始感染新冠,只知道 +event time 在两个 censor time 之间。称为一个 interval-censored +data。
However, this still fails for we can choose \(x_v =x_u=0\) and \(z_{(u,v)} =-1\) in the feasible set, which -means the approach will only give a randomized choice of \(A\). Now turn to convex optimization for -help.
-Convex Transformation
+此处简化情况,只研究 right-censored data,尝试对它进行标记。记 +survival time 为 \(T\),censor time 为 +\(C\),记 right-censored data 为 \((X,\delta)\),其中 \(X = \min(T,C)\)。\(\delta\) 是一个示性变量,如果 \(X = C\) 则 \(\delta=0\),也就是 event 未发生;否则 \(\delta=1\),\(X = +T\),也就是观察到了 event 发生。
+每一组数据贡献的 likelihood 是 \(\lambda +(x)^\delta S(x)\),整体的 likelihood function 即为 $ L = _{i=1} +^n (x_i )^{_i} S(x_i)$。
+Kaplan & Meier Estimation
+Theory
+一个估计 survival function 的方法。原理上来说是把 \(S(t) = P(T >t)\) +分解成了一列条件概率的积:
+\[S(t) = P(T>t) = P(T>t_1) P(T>t +| T>t_1) = P(T>t_1) \{\Pi_{j=2} ^k P(T>t_j | T>t_{j-1}) \} +P(T>t|T>t_k)\]
+与此同时重新组织数据,计算每个时刻的 items at risk 和 count of +events,列表如下:
+| Distinct Event Times | +\(t_0\) | +\(t_1\) | +... | +\(t_k\) | +
|---|---|---|---|---|
| # of events at \(t_j\) | +\(0\) | +\(d_1\) | +... | +\(d_k\) | +
| # at risk at \(t_j\) | +\(n\) | +\(n_1\) | +... | +\(n_k\) | +
此时认为条件概率的估计量为 \(\hat P (T> +t_j | T> t_{j-1}) = \frac{n_j - d_j}{n_j}\),因此 survival +function 的估计是:
+\[\hat S(t) = \Pi_{j=1}^k \frac{n_j - +d_j}{n_j} = \Pi_{j=1} ^n (1- \frac{d_j}{n_j})\]
+Example
+对于一组生存数据:\(4 \quad 5+ \quad 6 +\quad 10+ \quad 6 \quad 2 \quad 6\)
+重新排序得到:\(2 \quad 4 \quad 5+ \quad 6 +\quad 6 \quad 6 \quad 10+\)
+按照 event time 重新组织数据,并计算 Kaplan-Meier Estimator:
+| Distinct Event Times | +0 | +2 | +4 | +6 | +
|---|---|---|---|---|
| # of events at \(t_j\) | +0 | +1 | +1 | +3 | +
| # at risk at \(t_j\) | +7 | +7 | +6 | +4 | +
| \(\hat S(t)\) | +1 | +\(\frac{6}{7}\) | +\(\frac{5}{7}\) | +\(\frac{5}{28}\) | +
Cox Proportional Hazard +Model
+Theory
+在生存分析中数据往往是 skewed +的情况,希望分析变量(比如,患者的年龄,所用的药物,实验组别)对于生存期的影响时,一般对 +hazard function 采用 \(\lambda(t) = \lambda_0 +(t) e^{X^T\beta}\) 模型,类似于一个 transformed linear +regression。
+其中,\(\lambda_0(t)\) +作为一个调整参数,只和时间有关,和 explanatory variable \(X\) 无关。
+以一元的 explanatory variable \(X\) +为例,不同数据之间的 hazard ratio 是:
+\[\frac{\lambda_i(t)}{\lambda_j (t)} = +\frac{\lambda_0(t)}{\lambda_0(t)} \frac{exp(\beta_0 + \beta_1 +X_i)}{exp(\beta_0 + \beta_1 X_j)} = e^{(X_i - X_j)\beta_1}\]
+模型假设是 \((T_i ,C_i)\) 在 \(X_i\) +给定的条件下是条件独立的,这是一个针对 censored data 的假设。
+另外一个结论是在时间 \(t\) +处,uncensored 对象 \(i\) 发生 event +的概率是 \(P_i(t) = \frac{ exp(x_i +\beta)}{\Sigma_j I(T_j \geq t) exp(x_j +\beta)}\)。由此可知,用于估计 \(\beta\) 的 likelihood function 是:
+\[L(\beta) = \Pi_{j=1}^ k \frac{ exp(x_i +\beta)}{\Sigma_j I(T_j \geq t) exp(x_j \beta)} = \Pi_{j=1} ^n (\frac{ +exp(x_i \beta)}{\Sigma_j I(T_j \geq t) exp(x_j \beta)})^{\delta +_i}\]
+仍然是以一元的 explanatory variable \(X\) 为例,hazard ratio 是 \(HR = \frac{\lambda(t | +\text{exposure})}{\lambda(t| \text{not exposure})} = \frac{\lambda_0 (t) +exp(\beta_1)}{\lambda_0(t)} = exp(\beta_1)\)
+Example
+分别有五位患者参与两种试药,生存数据如下所示,希望通过 Cox Model +来比较不同种类的药物效果。
+Drug A: \(8+ \quad 132 \quad 52 \quad 220 +\quad 75+\)
+Drug B: \(45 \quad 80 \quad 90+ \quad 20 + +\quad 120\)
+此处的唯一一个 explanatory variable 即为用药种类,认为 \(X_i = \begin{cases} 1 \quad \text{i use drug A}\\ +0 \quad \text{i use drug B} \end{cases}\);
+对数据重新排序,得到:\(8+ \quad 20+ \quad +45 \quad 52 \quad 75+ \quad 80 \quad 90+ \quad 120 \quad 132 \quad +220\),对应的 \(X_i\) 是 \(1,0,0,1,1,0,0,0,1,1\)。
+Cox model 设定为 \(\lambda_i (t) = +\lambda_0 (t) e^{X ^T\beta} = \lambda_0 (t) \exp(\beta_0 +\beta_1 +X_i)\),\(i=1,2,...,10\)。
+此时的 partial likelihood function 是 \(PL(\beta) = \Pi_{i=1}^n (\frac{\exp(\beta^T +X_i)}{\Sigma_{j: t_j \geq t_i} \exp(\beta^T +X_j)})\),代入数据有:
+\[PL(\beta) = \Pi_{i=1}^{10} +\frac{\exp(\beta_0 + \beta_1 X_i)}{\Sigma_{j: t_j \geq t_i} \exp(\beta_0 ++ \beta_1 X_i)} = \frac{exp(2\beta_1)}{360(1+\exp (\beta_1))^3 +(5+4\exp(\beta_1)) (3+4\exp(\beta_1)) (2+3\exp(\beta_1)) +(1+3\exp(\beta_1))}\]
+对其进行 maximum likelihood 处理即可得到 \(\beta_1\) 的估计值。至于 \(\beta_0\) +的估计其实没什么意义,上下直接消掉了。
+Why Cox Model
-
-
The basic idea is to replace \(x_u.x_v\) with \(n-1\) dimensional vectors and construct an -auxiliary problem, which is called semi-definite relaxation:
-\[\begin{aligned} - \textbf{maximize} \quad & \sum_{(u,v) \in \mathcal E} -\frac{1}{2} (1-x_u^Tx_v) \\ - \textbf{subject to} \quad & x_u \in S^{n-1} \text{ for any -}u=1,2,\cdots,n -\end{aligned}\]
-in which \(S^{n-1}\) is the unit -sphere in \(\mathbb R^{n-1}\). Observe -that \(\frac{1}{4}\|x_u-x_v\|^2 =\frac{1}{4} -(x_u -x_v)^T(x_u-x_v) = \frac{1}{2} (1-x_ux_v)\), and \(\frac{1}{2} \sum_{e \in \mathcal E} (1-z_e) = -\frac{1}{4} \sum_{(u,v)\in \mathcal E} \|x_u - x_v\|^2\).
-Now we take \(\text{Maxcut}^\circ -(C)\) as the optimal cost of the auxiliary problem and denote -\(\text{Maxcut} (C)\) as the optimal -cost of the original problem. Then there is \(\text{Maxcut} (C) \leq \text{Maxcut}^\circ -(C)\) because any optimal solution of the original problem can be -transformed into a feasible solution in the auxiliary one.
-To be more precise, if \(\{x_u\}\) -is an optimal solution to the original problem, then for any \(x_u = 1\) there is \(x_v = -1\) for each \(v \in \{v \mid (u,v) \in \mathcal E\}\). -Therefore we can take \(x_u = e_1\), -\(x_v = -e_1\) for any \(v \in \{v \mid (u,v) \in \mathcal E\}\) as -a feasible solution to the auxiliary problem, and the cost is equal to -the optimal cost of the original one.
-However the auxiliary problem is still non-convex, we'd like to -consider another optimization problem as follows:
-\[\begin{aligned} - \textbf{minimize} \quad & X \cdot A = \sum_{i,j \in V} X_{ij} -A_{ij} \\ - \textbf{subject to} \quad & X \geq 0 \; \\ - & X_{ii}=1 -\end{aligned}\]
-in which \(X \geq 0\) means \(X\) is semi-definite, i.e. \(X \in S_+^n, X \in \mathbb R^{n \times -n}\).
-We set \(A_{ij}=1\) if \((i,j) \in \mathcal E\), else \(A_{ij}=0\). Now we prove that the two -problems above are equivalent.
-The following two max-cut optimization problems are -equivalent:
+- 体现了 explanatory variable 带来的影响 +
- baseline hazard \(\lambda_0 (t)\) +事实上并不重要,一般也用不到 +
- 得到 proportional hazard function +就可以作图比较是否有一个时间点处发生明显的差异 +
- 单独对不同组别的 event 发生情况使用 p-value +(见下一部分)并不够,需要精确到每个个体的生存时间
\[\begin{aligned} - \textbf{maximize} \quad & \sum_{(u,v) \in \mathcal E} -\frac{1}{2} (1-x_u^Tx_v) \\ - \textbf{subject to} \quad & x_u \in S^{n-1} \\ - \\ - \end{aligned} \quad \quad \quad - \begin{aligned} - \textbf{minimize} \quad & X \cdot A = \sum_{i,j \in V} -X_{ij} A_{ij} \\ - \textbf{subject to} \quad & X \geq 0 \; \\ - & X_{ii}=1 - \end{aligned}\]
-Proof: Note that \(X_{ij} -= x_i^T x_j\) (and sometimes \(X\) is called the gram matrix), -therefore
-\[\begin{aligned} - X \in S_+^n \text{ is feasible } & \iff X_{ij}=1 \text{ -for any } i \in V \\ - & \iff \|x_u \|=1 \text{ for any } u \in V \\ - & \iff x_u \in S^{n-1} \text{ for any } u \in V - \end{aligned}\]
-and the desired result follows.
+Comparison of Survival +Curves
+Log Rank Test
+想要比较两组数据的生存期情况,比如说,试药组和安慰剂组之间有无生存周期上的差别,来判断药物是否有效或者有副作用。这里涉及到的问题都属于比较简单的情况,一般用一个 +log rank test 就可以了。
+| + | Distinct Event Times | +\(t_1\) | +... | +\(t_i\) | +... | +\(t_k\) | +
|---|---|---|---|---|---|---|
| Pooled sample | +# of Events | +\(d_1\) | +... | +\(d_i\) | +... | +\(d_k\) | +
| + | # at Risk at \(t_i\) | +\(n_1\) | +... | +\(n_i\) | +... | +\(n_k\) | +
| Sample 1 | +# of Events | +\(d_{11}\) | +... | +\(d_{1i}\) | +... | +\(d_{1k}\) | +
| + | # at Risk at \(t_i\) | +\(n_{11}\) | +... | +\(n_{1i}\) | +... | +\(n_{1k}\) | +
| Sample 2 | +# of Events | +\(d_{21}\) | +... | +\(d_{2i}\) | +... | +\(d_{2k}\) | +
| + | # at Risk at \(t_i\) | +\(n_{21}\) | +... | +\(n_{2i}\) | +... | +\(n_{2k}\) | +
有以下的近似分布关系,对近似正态分布做检验即可:
+\[ U = \Sigma_{i=1} ^k (d_{1i} - \frac{d_i +n_{1i}}{n_i})\]
+\[\hat{Var} (U) = \Sigma_{i=1} ^k +(\frac{d_i n_{1i} (n_i - d_i)(n_i - n_{1i})}{n_i ^2 (n_i +-1)})\]
+\[\frac{U}{\hat{Var} (U)^{\frac 1 2}} \sim +^{H_0,asy} N(0,1)\]
+P-value mode
+对于组织成 contingency table 形式的数据,按照逻辑回归部分的 p-value +方法检验即可。一个数据的例子如下所示:
+| + | Drug A | +Drug B | +
|---|---|---|
| Alive | +10 | +16 | +
| Dead | +8 | +4 | +
完结撒花
+在这之后讲的东西都不考了,我不想做生统,也不是很感兴趣,不想写了。说到底高中的时候连生物都没选考,怎么会想到来尝试生统概论的(。希望大作业没事。
+昨天才在路上遇到了 wty
+老师和她男朋友/爱人,相比之下(草)她好娇小好可爱,呜呜呜(虽然感觉她也瞟了我好几眼,不会也认识我吧,不会是这个发型太有辨识度了我又每次都苟在最后一排就被记住了吧(
传统艺能一下(不会现在还有人是 FGO 厨吧,不会吧不会吧(
+
后记:莫名其妙拿了个
+A,实际上期末考大寄特寄好几问没做完,我还在想这课能不挂就挺好的了,不知道是老师太善良还是毕业班同学太多帮忙抬上来的((只不过之前看
+V1ncent19 说他这课是 A+,羡慕(x
*高木贞治函数(学不完了,咕了
-我们先在 \([0,1]\) 区间上定义 \(\psi(x)=\begin{cases}x, \ \ \ \ 0\leqslant x -<\dfrac{1}{2};\\1-x, \ \ \dfrac{1}{2}\leqslant x \leqslant -1.\end{cases}\)
-接下来,以 \(1\) 为周期,我们可以将 -\(\psi\) 延拓成 \(\mathbb R\) -上的周期函数(连续)并且仍然将它记作 \(\psi\),它的函数图像好像是锯齿一般。
-我们定义Takagi函数 \(T\colon \mathbb -R\rightarrow \mathbb R\) 如下:\(T(x)=\sum_{k=0}^\infty \frac{1}{2^k}\psi(2^k -x)\)
-我们实际上可以考虑部分和 \(\displaystyle -T_n(x)=\sum_{k=0}^n \frac{1}{2^k}\psi(2^k x)\)。当 \(n\) -越来越大的时候,它们的图像看起来逐渐地收敛。这个习题的目标是粗略地研究Takagi函数的性质。
+*高木贞治函数(学不完了,咕了
+我们先在 \([0,1]\) 区间上定义 \(\psi(x)=\begin{cases}x, \ \ \ \ 0\leqslant x +<\dfrac{1}{2};\\1-x, \ \ \dfrac{1}{2}\leqslant x \leqslant +1.\end{cases}\)
+接下来,以 \(1\) 为周期,我们可以将 +\(\psi\) 延拓成 \(\mathbb R\) +上的周期函数(连续)并且仍然将它记作 \(\psi\),它的函数图像好像是锯齿一般。
+我们定义Takagi函数 \(T\colon \mathbb +R\rightarrow \mathbb R\) 如下:\(T(x)=\sum_{k=0}^\infty \frac{1}{2^k}\psi(2^k +x)\)
+我们实际上可以考虑部分和 \(\displaystyle +T_n(x)=\sum_{k=0}^n \frac{1}{2^k}\psi(2^k x)\)。当 \(n\) +越来越大的时候,它们的图像看起来逐渐地收敛。这个习题的目标是粗略地研究Takagi函数的性质。
+-
+
证明,\(T(x)\) 是 \(\mathbb R\) 上良好定义的有界连续函数。
+良好定义:\(T(x) \leq \sum_{k=0}^\infty +\frac{1}{2^k} = 2\),一定是收敛级数,所以是良好定义的。
+有界:如上所述。
+连续函数:它是连续函数的级数和,也是连续函数。
+对于 \(x\in [0,1]\),假设 \(x=\displaystyle\sum_{n=1}^\infty +\frac{a_n}{2^n}\) 是 \(x\) 的 +\(2\)-进制展开,其中 \(a_n=0\) 或者 \(1\)。我们令 \(v_n=\displaystyle\sum_{k=1}^n +a_k\)。我们定义函数 \(\sigma_n(y)=a_n+(1-2a_n)y\),其中 \(y=0\) 或者 \(1\)。证明,\(\psi(2^m +x)=\sum_{n=1}^\infty\frac{\sigma_{m+1}(a_{m+n})}{2^n}\)
+Trivial.
+对于 \(x\in [0,1]\),假设 \(x=\displaystyle\sum_{n=1}^\infty +\frac{a_n}{2^n}\) 是 \(x\) 的 +\(2\)-进制展开。证明,\(T(x)=\sum_{n=1}^\infty\frac{(1-a_n)v_n+a_n(n-v_n)}{2^n}\)
+假设 \(x_0=\dfrac{k_0}{2^{m_0}}\in(0.1]\),其中 +\(k_0\in\mathbb{Z}_{\geqslant 1}\) +是奇数,\(m_0\in \mathbb{Z}_{\geqslant +0}\)。令 \(h_n=\dfrac{1}{2^n}\),其中 \(n\in \mathbb{Z}_{\geqslant +m_0}\)。证明,数列 \(\bigl\{\dfrac{T(x+h_n)-T(x)}{h_n}\bigr\}_{n\geqslant +m_0}\) 不收敛。
+\(f\) 是定义在非空的开区间 \(I\) 上实数值函数。如果 \(f\) 在 \(a\) 处可导,
+证明,\(\lim_{(h,h')\rightarrow (0,0), +\atop \\ +h>0,h'>0}\frac{f(a+h)-f(a-h')}{h+h'}=f'(a)\),
+这里极限 \(\displaystyle +\lim_{(h,h')\rightarrow (0,0), \atop \\ h>0,h'>0}\) +的意义指的是任意的序列 \((h_n,h'_n)\rightarrow (0,0), +h_n>0,h'_n>0\) 所对应的序列都收敛。
+\(f\) 是定义在非空的开区间 \(I\) 上实数值函数。假设 \(f\in C^1(I)\)(连续可微),\(a\in I\),
+
证明,\(\lim_{(h,h')\rightarrow (0,0), +\atop h+h'\neq +0}\frac{f(a+h)-f(a-h')}{h+h'}=f'(a)\)
+-
+
假设 \(x\in +[0,1]\),使得对任意的正整数 \(n\),\(2^n +x\) 都不是整数。对于每个正整数 \(n\),我们用下面的公式定义序列 \(\{h_n\}_{n \geqslant 1}\) 和 \(\{h'_n\}_{n \geqslant 1}\):\(\floor{2^n x}=2^n(x-h'_n), \ \ \floor{2^n +x}+1=2^n(x+h_n)\)
+其中函数 \(\floor{y}\) +按照定义是不超过 \(y\) 的最大的整数(即 +\(y\) 的整数部分(如果 \(y\geqslant 0\)))。证明,对每个给定的 +\(n\),\(h_n+h'_n=2^{-n}\) 并且对每个整数 \(1\leqslant \ell \leqslant n-1\),开区间 +\(\bigl(2^\ell(x-h'_n),2^\ell(x+h_n)\bigr)\) +中不包含任何的整数和半整数。
+假设 \(x\in +[0,1]\),使得对任意的正整数 \(n\),\(2^n +x\) 都不是整数,我们沿用~E7)中的符号,
+证明,数列 \(\Bigl\{\dfrac{T(x+h_n)-T(x-h'_n)}{h_n+h'_n}\Bigr\}_{n\geqslant +1}\) 不收敛。
+证明,\(T(x)\) 是 \(\mathbb R\) +上处处连续处处不可微的函数。
+证明,我们有如下的函数方程:
+\(T(x)=\begin{cases}2x+\dfrac{T(4x)}{4},\ \ +0\leqslant x <\dfrac{1}{4};\\\dfrac{1}{2}+\dfrac{T(4x-1)}{4},\ \ +\dfrac{1}{4}\leqslant x +<\dfrac{1}{2};\\\dfrac{1}{2}+\dfrac{T(4x-2)}{4},\ \ +\dfrac{1}{2}\leqslant x <\dfrac{3}{4};\\2-2x+\dfrac{T(4x-3)}{4},\ \ +\dfrac{3}{4}\leqslant x \leqslant 1.\end{cases}\)
+(Takagi函数图像的自相似性)令 \(\Gamma=\bigl\{(x,T(x))\mid 0\leqslant x\leqslant +1\bigr\}\subset \mathbb R^2\) 是 \(T\) 在区间 \([0,1]\) +上的函数图像。我们定义如下四个仿射变换 \(\Phi_i\colon \mathbb R^2\rightarrow \mathbb +R^2\):
+-
+
\(\Phi_0 \left(\begin{array}{ccc}x \\y +\end{array} \right)&= \left(\begin{array}{ccc}\frac{1}{4} & 0 +\\\frac{1}{2} & \frac{1}{4} \end{array} +\right)\left(\begin{array}{ccc}x \\y \end{array} +\right)\)
+\(\Phi_1 \left(\begin{array}{ccc}x \\y +\end{array} \right)= \left(\begin{array}{ccc}\frac{1}{4} & 0 \\0 +& \frac{1}{4} \end{array} \right)\left(\begin{array}{ccc}x \\y +\end{array} \right)+\left(\begin{array}{ccc}\frac{1}{4} +\\\frac{1}{2}\end{array}\right)\)
+\(\Phi_2 \left(\begin{array}{ccc}x \\y +\end{array} \right)&= \left(\begin{array}{ccc}\frac{1}{4} & 0 +\\0 & \frac{1}{4} \end{array} \right)\left(\begin{array}{ccc}x \\y +\end{array} \right)+\left(\begin{array}{ccc}\frac{1}{2} +\\\frac{1}{2}\end{array}\right)\)
+\(\Phi_3 \left(\begin{array}{ccc}x \\y +\end{array} \right)= \left(\begin{array}{ccc}\frac{1}{4} & 0 +\\-\frac{1}{2} & \frac{1}{4} \end{array} +\right)\left(\begin{array}{ccc}x \\y \end{array} +\right)+\left(\begin{array}{ccc}\frac{3}{4} +\\\frac{1}{2}\end{array}\right)\)
+证明,\(\Phi_i\) 恰好把 \(\Gamma\) 变成 \(T\) 在区间 \([\dfrac{i}{4},\dfrac{i+1}{4}]\) +上的图像,其中 \(i=0,1,2,3\)。
+
+令 \(S_0=\{(x,y)\in \mathbb R^2 \mid +0\leqslant x\leqslant 1, 0\leqslant y \leqslant 1\}\) 是 \(\mathbb R^2\) 上的闭方块。对每个 \(n\geqslant 0\),我们定义 \(\displaystyle +S_{n+1}=\bigcup_{k=0}^3\Phi_k(S_n)\)。证明,\(S_n\) 是平面上一列单调下降的紧集并且 \(\displaystyle \Gamma=\bigcap_{n\geqslant +0}S_n\)。我们有 \(S_1\) 和 \(S_2\) 的示意图:
+证明,\(\displaystyle\sup_{x\in \mathbb +R}T(x) \leqslant \dfrac{2}{3}\)。
+找一个 \(c\in [0,1]\),使得 +\(T(c)=\dfrac{2}{3}\)。
+(\(T^{-1}(\dfrac{2}{3})\) +的Cantor集的结构)对于 \(x\in +[0,1]\),假设 \(x=\displaystyle\sum_{n=1}^\infty +\frac{b_n}{4^n}\) 是 \(x\) 的 +\(4\)-进制展开,其中 \(b_n=0,1,2,3\)。
+证明,\(\Bigl\{x\in [0,1]\bigm| +T(x)=\dfrac{2}{3}\Bigr\}=\Bigl\{x\in [0,1]\bigm| x=\sum_{n=1}^\infty +\frac{b_n}{4^n}, b_n\in \{1,2\}\Bigr\}\)
+仿照 11,研究 \(\Phi_1\) 和 +\(\Phi_2\) 在集合 \(\bigl\{(x,T(x))\bigm| x\in +[0,1],T(x)=\dfrac{2}{3}\bigr\}\) +上自相似的作用。(这是一个Hausdorff维数为 \(\dfrac{1}{2}\) 的集合)。
+
梦话 2.0:这作业怎么这么多啊
+中值定理和Taylor展开
+如果不额外说明,\(f\) 总代表一个区间 +\(I\) 上定义的函数。
+-
+
设 \(f\) 在点 \(x\) +处有二阶导数。证明,下面的极限给出了二阶导数:$ f''(x) = _{h } $
+可以用定义,也可以直接洛。
+(Taylor 展开式的唯一性,Peano余项)。假设 \(f\) 在 \(x_0\) 附近的函数,并且当 \(x\rightarrow x_0\) 是,满足
+$ f(x) &= a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + + a_n (x-x_0)^n + +o(|x-x_0|^n)\ &= b_0 + b_1 (x-x_0) + b_2 (x-x_0)^2 + + b_n (x-x_0)^n ++ o(|x-x_0|^n)$
+其中 \(a_i, b_i, i=0,\cdots,n\) +是实数,那么,对任意的 \(i\),我们都有 +\(a_i=b_i\)。
+有 \(\lim _{x \to x_0} +\frac{A(x)-B(x)}{(x-x_0)^n} =0\),于是有 \(a_0 = b_0,...,a_{n-1}= +b_{n-1}\),最后可以推出 \(a_n = +b_n\)。
+假设 \(f\) 在 \(0\) 处有 \(n\) 阶导数。证明,如果 \(f(x)\) 是偶函数(奇函数), \(f\) 在 \(0\) 处的Taylor展开式(Peano余项)中只有 +\(x\) 的偶次项(奇数项)。
+Trivial.
+(Rolle定理的简单推广)设函数在有限或无穷的区间 \((a,b)\) 上可微并且 \(\displaystyle\lim_{x \to a^+} f(x) = \lim_{x \to +b^-} f(x)\)。证明,存在 \(x_0 \in +(a,b)\),使得 \(f'(x_0) = +0\)。
+如果不存在,那么 \(f'(x)\) 在 +\((a,b)\) 上恒正或恒负,\(f(x)\) 在 \((a,b)\) 上是严格单调函数,矛盾。
+设函数 \(f \in C^0([a,b])\) +并且在 \((a,b)\) 上可微。证明,\(f\) 在 \([a,b]\) 上严格递增的充分必要条件是对任意 +\(x\in (a,b)\),\(f'(x) \geqslant 0\) 并且在任意子区间 +\((c,d) \subset (a,b)\) 上,\(f'(x)\) 不恒等于 \(0\)。
+如果 \(f(x)\) 在 \([a,b]\) +上严格单调递增,那么这两个结论很好推。
+如果满足这两个条件,那么至少有 \(f(x)\) 在 \([a,b]\) 上非严格单调递增,可能存在 \(f(x_1) =f(x_2)\) 的情况,\(x_1 \neq x_2\)。此时对任意 \(s \in (x_1,x_2)\) 都有 \(f(s)=f(x_1)\),于是在这一子区间上 \(f'(x) =0\),矛盾。
+\(g\in C(\mathbb R)\) 在 \(\mathbb{R}\) 上可微。假设存在常数 \(M\),使得 \(\displaystyle\sup_{x \in \mathbb{R}}|g'(x)| +\leqslant M\)。 对任意的 \(\varepsilon +> 0\),我们定义 \(f_\varepsilon(x) = +x + \varepsilon g(x)\),证明,存在仅依赖于 \(M\) 的常数 \(\delta = \delta(M) > 0\),使得当 \(\varepsilon < \delta\) 时,\(f\colon \mathbb{R} \rightarrow \mathbb{R}\) +是双射。
+取 \(\delta = \frac{1}{2M}\) +即可。
+设函数 \(f\) 在 \([a,b]\) 上有两阶导数并且 \(f'(a) = f'(b) = 0\)。证明,存在 +\(c \in (a,b)\) 使得 \(|f''(c)| \geqslant \frac{4}{(b-a)^2}|f(b) +- f(a)|\)
+存在 \(s \in (a,b)\) 使得 \(f'(s) = \frac{f(b)-f(a)}{b-a}\),存在 +\(t \in (a,s)\) 满足 \(f''(t) = \frac{f'(s)}{s-a} = +\frac{f(b)-f(a)}{(b-a)(s-a)}\)。
+于是 \(t\) 就是满足题意的 \(c\)。
+假设 \(f\) 在 \(\mathbb{R}\) 上二次可导,对 \(k=0,1,2\),我们假设 \(M_k = \displaystyle\sup_{x \in \mathbb{R}} +|f^{(k)}(x)|\) 都是有限的。 证明,\(M_1^2 \leq 2 M_0 M_2\)。
+随便写个 Lagrange 余项的泰勒展开:$f(x+h)= f(x)+f'(x)h+ 2 f''(t)h^2 +\(,\)t (x,x+h)$。
+然后推一个不等式就行了。
+假设 \(f\) 在 \((0,+\infty)\) 上二次可导,\(f''\) 在 \((0,+\infty)\) 上有界并且 \(\displaystyle\lim_{x \rightarrow +\infty} f(x) = +0\)。证明,\(\displaystyle\lim_{x \to ++\infty} f'(x) = 0\)。
+随便写个 Lagrange 余项的泰勒展开:$f(x+h)= f(x)+f'(x)h+ 2 f''(t)h^2 +\(,\)t (x,x+h)$。
+取 \(x \to + \infty\),于是此时 +\(f'(x) =- \frac 1 2 f''(t) h ++\frac{f(x+h)-f(x)}{h}\)。对任意的 \(\varepsilon >0\),只要取 \(|f(x+h)-f(x)|<\varepsilon ^2\)(Cauchy +收敛准则),取 \(h < +\varepsilon\),就有 \(|f'(x)|<\frac{M\varepsilon}{2}\),说明它也会收敛到 +\(0\)。
+
极大值的判定
+\(f\) 在 \((a,b)\) 上可微。假设对于 \(x_0 \in (a,b)\),我们有 \(f'(x_0) = 0\)。
+-
+
证明,\(f\) 在 \(x_0\) +处取局部极大值的一个充分条件是:存在某一邻域 \((x_0 - \delta, x_0 + \delta) \subset +(a,b)\),使得
+\(f'(x)= \begin{cases}< 0, \ +\text{对所有的}~x \in (x_0-\delta, x_0);\\\\> 0, \ \text{对所有的}~ x +\in (x_0, x_0+\delta).\end{cases}\)
+Trivial.
+(最重要的判别方法,有很多应用)证明,如果 \(f''(x_0)\) 存在并且 \(f''(x_0) < 0\),那么 \(f\) 在 \(x_0\) 处取局部极大值。
+说明在某个邻域 \((x_0 - \delta, x_0 + +\delta) \subset (a,b)\) 有 $f''(x) $,也就是 \(f'(x)\) +在邻域上递减,也就是上题的情况。
+假定 \(f\) 在 \(x_0\) 处有 \(n\) 阶导数,\(f'(x_0) = \cdots = f^{(n-1)}(x_0) = 0\) +并且 \(f^{(n)}(x_0) \neq 0\),试讨论 +\(f\) 在 \(x_0\) 处取局部极大值的条件(对 \(n\) 分奇偶讨论)。
+\(f(x)-f(x_0) = \frac{1}{n!} f^{(n)} (x_0) +(x-x_0)^n + o(|x-x_0|^n)\),所以 \(n\) 是奇数则不是局部最值,\(n\) 是偶数且 \(f^{(n)}(x_0) < 0\) +局部极大,否则局部极小。
+
多项式的根
+(提示:利用中值定理和 \(n\)-次多项式的至多(恰好)有 \(n\) 个根)
+-
+
证明,如果实系数多项式 \(P_n(x) = a_n +x^n + a_{n-1} x^{n-1} + \cdots + a_0\) 的根都是实数(不妨设 \(a_n\neq 0\)),那么它的逐次导函数 \(P_n'(x)\),\(P_n''(x)\) ,\(\cdots\), \(P_n^{(n-1)}(x)\) 的根也都是实数。
+只考虑一阶导数的根。\(P_n(x)\) 有 +\(n\) 个实数根(计入重根),Rolle +定理保证 \(P_n ' (x)\) 有 \(n-1\) +个实数根(也可能计入了重根,这个并不重要),归纳即证。
+证明,Legendre 多项式 \(P_n(x) = +\dfrac{1}{2^n n!} \dfrac{d^n}{dx^n}(x^2 - 1)^n\) +的根都是实数并且包含于区间 \((-1,1)\) +中。
+\(P(x) = (x^2-1)^n\) +的根都是实数,这是一个 \(2n\) +阶多项式,它的 \(n\) +次导函数的根也一定都是实数。Rolle 定理保证这些根全部落在 \(P(x)\) 的根包围的区间里。
+还要证明 \(P_n(x)\) 的根不是 \(1,-1\)。这个可以通过 \(n\) 次求导之后的形式确定。
+证明,\(L_n(x) = \dfrac{e^x}{n!} +\dfrac{d^n}{dx^n}(e^{-x}x^n)\) +是多项式并且它所有的根都是正实数。
+因为这是 Laguerre 多项式!(暴论
+类似的考虑,也很 trivial.
+证明,\(H_n(x) = (-1)^n e^{x^2} +\dfrac{d^n}{dx^n}(e^{-x^2})\) +是多项式并且它所有的根都是实数。
+因为这是 Hermite 多项式!(什么嘛,我的数值分析学得也没那么差嘛
+写一个递推:\(H_{n+1} (x)=2xH_n(x) - +H_n' (x)\),所以是多项式。归纳地证明 \(H_n\) 的所有根都是实数时,\(H_{n+1}\) 的所有根都是实数。
+
Emile Borel 引理
+第一部分:截断函数的构造
-
-
证明,\(T(x)\) 是 \(\mathbb R\) 上良好定义的有界连续函数。
-良好定义:\(T(x) \leq \sum_{k=0}^\infty -\frac{1}{2^k} = 2\),一定是收敛级数,所以是良好定义的。
-有界:如上所述。
-连续函数:它是连续函数的级数和,也是连续函数。
-对于 \(x\in [0,1]\),假设 \(x=\displaystyle\sum_{n=1}^\infty -\frac{a_n}{2^n}\) 是 \(x\) 的 -\(2\)-进制展开,其中 \(a_n=0\) 或者 \(1\)。我们令 \(v_n=\displaystyle\sum_{k=1}^n -a_k\)。我们定义函数 \(\sigma_n(y)=a_n+(1-2a_n)y\),其中 \(y=0\) 或者 \(1\)。证明,\(\psi(2^m -x)=\sum_{n=1}^\infty\frac{\sigma_{m+1}(a_{m+n})}{2^n}\)
-Trivial.
-对于 \(x\in [0,1]\),假设 \(x=\displaystyle\sum_{n=1}^\infty -\frac{a_n}{2^n}\) 是 \(x\) 的 -\(2\)-进制展开。证明,\(T(x)=\sum_{n=1}^\infty\frac{(1-a_n)v_n+a_n(n-v_n)}{2^n}\)
-假设 \(x_0=\dfrac{k_0}{2^{m_0}}\in(0.1]\),其中 -\(k_0\in\mathbb{Z}_{\geqslant 1}\) -是奇数,\(m_0\in \mathbb{Z}_{\geqslant -0}\)。令 \(h_n=\dfrac{1}{2^n}\),其中 \(n\in \mathbb{Z}_{\geqslant -m_0}\)。证明,数列 \(\bigl\{\dfrac{T(x+h_n)-T(x)}{h_n}\bigr\}_{n\geqslant -m_0}\) 不收敛。
-\(f\) 是定义在非空的开区间 \(I\) 上实数值函数。如果 \(f\) 在 \(a\) 处可导,
-证明,\(\lim_{(h,h')\rightarrow (0,0), -\atop \\ -h>0,h'>0}\frac{f(a+h)-f(a-h')}{h+h'}=f'(a)\),
-这里极限 \(\displaystyle -\lim_{(h,h')\rightarrow (0,0), \atop \\ h>0,h'>0}\) -的意义指的是任意的序列 \((h_n,h'_n)\rightarrow (0,0), -h_n>0,h'_n>0\) 所对应的序列都收敛。
-\(f\) 是定义在非空的开区间 \(I\) 上实数值函数。假设 \(f\in C^1(I)\)(连续可微),\(a\in I\),
+定义函数 \(\phi\colon \mathbb +R\rightarrow \mathbb R\):
+\(\phi(x)=\begin{cases}e^{-\frac{1}{x^2}}, +\ \ x>0;\\0, \ \ \ \ x\leqslant 0.\end{cases}\)
+证明,\(\phi\in C^\infty(\mathbb +R)\)。
+只要证明在 \(x=0\) +处无限可微。实际上一阶导数是 \(0\),二阶及以上可以归纳地证明都是 \(0\)。
+定义函数 \(\chi\colon \mathbb +R\rightarrow \mathbb R\):\(\chi(x)=\frac{\phi(2-|x|)}{\phi(2-|x|)+\phi(|x|-1)}\),证明,\(\chi(x)\in C^\infty(\mathbb R)\) 并且 \(\chi\big|_{[-1,1]}\equiv 1\),\(\chi\big|_{(-\infty,-2]\cup [2,\infty)}\equiv +0\),\(0\leqslant \chi(x)\leqslant +1\) 并且是偶函数。
+\(\chi\big|_{[-1,1]}\equiv +1\),\(\chi\big|_{(-\infty,-2]\cup +[2,\infty)}\equiv 0\) +这两个结论是显然的,所以在这几个区间上都是无限维可导。在 \([1,2]\) 上显然也无限维可导,所以只要证明在 +\(1\) 和 \(2\) +两点处无限维可导。(因为是偶函数,所以很容易可以看出负数区间上是一样的)。这两个也很好证明,一阶导数都是 +\(0\)。
+证明,对任意的 \(0<a<b\),存在光滑偶函数 \(\rho(x)\in C^\infty(\mathbb R)\),使得 +\(\rho\big|_{[-a,a]}\equiv 1\),\(\rho\big|_{(-\infty,-b]\cup [b,\infty)}\equiv +0\),\(0\leqslant \rho(x)\leqslant +1\)。
+构造 \(\rho (x) = +\frac{\phi(b-|x|)}{\phi(b-|x|)+\phi(|x|-a)}\)。
+证明,存在偶函数 \(\psi \in +C^\infty(\mathbb R^n)\),使得 \(\psi\big|_{\{x\mid|x|\leqslant 1\}}\equiv +1\),\(\psi\big|_{\{x\mid|x|\geqslant +2\}}\equiv 0\),\(0\leqslant \psi(x +)\leqslant 1\)。
+构造 \(\psi (x) = +\chi(|x|)\)。
证明,\(\lim_{(h,h')\rightarrow (0,0), -\atop h+h'\neq -0}\frac{f(a+h)-f(a-h')}{h+h'}=f'(a)\)
+第二部分:逐项求导定理
+\(I=[a,b]\) 是闭区间,\(\{f_k\}_{k\geqslant 0}\) 是 \(C^1(I)\) 的一列函数,我们假设 \(\displaystyle \sum_{k=0}^\infty f_k\) 在 +\(I\) 上逐点收敛,即对任意的 \(x\in I\),\(\displaystyle \sum_{k=0}^\infty f_k(x)\) +收敛,我们记 \(f(x)=\displaystyle +\sum_{k=0}^\infty f_k(x)\)。
-
-
假设 \(x\in -[0,1]\),使得对任意的正整数 \(n\),\(2^n -x\) 都不是整数。对于每个正整数 \(n\),我们用下面的公式定义序列 \(\{h_n\}_{n \geqslant 1}\) 和 \(\{h'_n\}_{n \geqslant 1}\):\(\floor{2^n x}=2^n(x-h'_n), \ \ \floor{2^n -x}+1=2^n(x+h_n)\)
-其中函数 \(\floor{y}\) -按照定义是不超过 \(y\) 的最大的整数(即 -\(y\) 的整数部分(如果 \(y\geqslant 0\)))。证明,对每个给定的 -\(n\),\(h_n+h'_n=2^{-n}\) 并且对每个整数 \(1\leqslant \ell \leqslant n-1\),开区间 -\(\bigl(2^\ell(x-h'_n),2^\ell(x+h_n)\bigr)\) -中不包含任何的整数和半整数。
-假设 \(x\in -[0,1]\),使得对任意的正整数 \(n\),\(2^n -x\) 都不是整数,我们沿用~E7)中的符号,
-证明,数列 \(\Bigl\{\dfrac{T(x+h_n)-T(x-h'_n)}{h_n+h'_n}\Bigr\}_{n\geqslant -1}\) 不收敛。
-证明,\(T(x)\) 是 \(\mathbb R\) -上处处连续处处不可微的函数。
-证明,我们有如下的函数方程:
-\(T(x)=\begin{cases}2x+\dfrac{T(4x)}{4},\ \ -0\leqslant x <\dfrac{1}{4};\\\dfrac{1}{2}+\dfrac{T(4x-1)}{4},\ \ -\dfrac{1}{4}\leqslant x -<\dfrac{1}{2};\\\dfrac{1}{2}+\dfrac{T(4x-2)}{4},\ \ -\dfrac{1}{2}\leqslant x <\dfrac{3}{4};\\2-2x+\dfrac{T(4x-3)}{4},\ \ -\dfrac{3}{4}\leqslant x \leqslant 1.\end{cases}\)
-(Takagi函数图像的自相似性)令 \(\Gamma=\bigl\{(x,T(x))\mid 0\leqslant x\leqslant -1\bigr\}\subset \mathbb R^2\) 是 \(T\) 在区间 \([0,1]\) -上的函数图像。我们定义如下四个仿射变换 \(\Phi_i\colon \mathbb R^2\rightarrow \mathbb -R^2\):
+我们假设函数级数 \(\displaystyle +\sum_{k=0}^\infty f'_k(x)\) 在 \(I\) 上绝对收敛,即数项的级数 \(\displaystyle \sum_{k=0}^\infty +\|f'_k\|_\infty\) 收敛,其中 \(\displaystyle \|f\|_\infty=\sup_{x\in +I}|f(x)|\)。证明,\(f\) +是可导的并且 \(f'(x)=\displaystyle +\sum_{k=0}^\infty f'_k(x)\)。(提示:设法将求和拆 \(\displaystyle \sum_{k=0}^\infty = +\sum_{k=0}^N+\displaystyle \sum_{k=N+1}^\infty\))
+\(\displaystyle \sum_{k=0}^\infty +f'_k(x)\) 在 \(I\) +上绝对收敛,所以 \(\displaystyle +\sum_{k=0}^\infty f'_k(x)\) 在 \(I\) +上逐点都是收敛的,上式右端一定收敛。所以只要证明这个等号成立。
+对任意的 \(\varepsilon +>0\),找一个合适的 \(|x-x_0| < +\delta\) 和一个合适的 \(N \in \mathbb +Z+\),满足:
+\(|\frac{f_k(x)-f_k(x_0)}{x-x_0} - f_k +'(x_0) | <\varepsilon\) 对 \(k=0,1,2,...,N\) 都成立(导数的定义),而且 +\(|\displaystyle \sum_{k=N+1}^\infty +\|f'_k\|_\infty|<\varepsilon\)(收敛列的 Cauchy +性质)。
+于是 $|{k=0}^- {k=0}f'k(x)| |{k=0}N - +{k=0}^N f'k(x)|+|{k=N+1}^- {k=N+1}^f'_k(x)| $。
+右边第一项的上界是 \(N\varepsilon\),第二项用一下 Lagrange +中值定理处理前一个级数和,可以知道上界是 \(2\varepsilon\)。
+因此 \(\lim _{x \to x_0} \displaystyle +\sum_{k=0}^\infty \frac{f_k(x)-f_k(x_0)}{x-x_0}- \displaystyle +\sum_{k=0}^\infty f'_k(x) =0\),也就是 \(f'(x)=\displaystyle \sum_{k=0}^\infty +f'_k(x)\),得证。
+(逐项求导定理)\(I=[a,b]\) +是闭区间,\(\{f_k\}_{k\geqslant 0}\) 是 +\(C^1(I)\) 的一列函数,我们假设 \(\displaystyle \sum_{k=0}^\infty f_k\) 在 +\(I\) 上逐点收敛。如果函数级数 \(\displaystyle \sum_{k=0}^\infty +f'_k(x)\) 在 \(I\) +上一致收敛,那么 \(f\) 是可导的并且 +\(f'(x)=\displaystyle \sum_{k=0}^\infty +f'_k(x)\)。
+证明 \(f\) +是可导的只需要证明导函数的这个式子成立。
+\(\displaystyle \sum_{k=0}^\infty +f'_k(x)\) 在 \(I\) +上一致收敛也可以推出,对 \(\varepsilon +>0\),存在某个合适的 \(N\) +使得 \(|\displaystyle \sum_{k=N+1}^\infty +f'_k(x)| < \varepsilon\) 对任意的 \(x\in I\) +都成立,所以前一题不等式里的第二项仍然被 \(2\varepsilon\) +控制,不等式仍然可以成立。
+同时,\(f'(x)=\displaystyle +\sum_{k=0}^\infty f'_k(x)\) 右端也对任意的 \(x \in I\) +都是收敛级数,是良定义的。
+试利用逐项求导定理计算 \(e^x\) +的导数。
+Trivial,无穷级数求导之后形式仍然相同。
+
第三部分:Borel引理的证明
+我们现在任意给定一个数列 \(\{a_k\}_{k\geqslant 0}\)。
-
-
\(\Phi_0 \left(\begin{array}{ccc}x \\y -\end{array} \right)&= \left(\begin{array}{ccc}\frac{1}{4} & 0 -\\\frac{1}{2} & \frac{1}{4} \end{array} -\right)\left(\begin{array}{ccc}x \\y \end{array} -\right)\)
-\(\Phi_1 \left(\begin{array}{ccc}x \\y -\end{array} \right)= \left(\begin{array}{ccc}\frac{1}{4} & 0 \\0 -& \frac{1}{4} \end{array} \right)\left(\begin{array}{ccc}x \\y -\end{array} \right)+\left(\begin{array}{ccc}\frac{1}{4} -\\\frac{1}{2}\end{array}\right)\)
-\(\Phi_2 \left(\begin{array}{ccc}x \\y -\end{array} \right)&= \left(\begin{array}{ccc}\frac{1}{4} & 0 -\\0 & \frac{1}{4} \end{array} \right)\left(\begin{array}{ccc}x \\y -\end{array} \right)+\left(\begin{array}{ccc}\frac{1}{2} -\\\frac{1}{2}\end{array}\right)\)
-\(\Phi_3 \left(\begin{array}{ccc}x \\y -\end{array} \right)= \left(\begin{array}{ccc}\frac{1}{4} & 0 -\\-\frac{1}{2} & \frac{1}{4} \end{array} -\right)\left(\begin{array}{ccc}x \\y \end{array} -\right)+\left(\begin{array}{ccc}\frac{3}{4} -\\\frac{1}{2}\end{array}\right)\)
-证明,\(\Phi_i\) 恰好把 \(\Gamma\) 变成 \(T\) 在区间 \([\dfrac{i}{4},\dfrac{i+1}{4}]\) -上的图像,其中 \(i=0,1,2,3\)。
-
令 \(S_0=\{(x,y)\in \mathbb R^2 \mid -0\leqslant x\leqslant 1, 0\leqslant y \leqslant 1\}\) 是 \(\mathbb R^2\) 上的闭方块。对每个 \(n\geqslant 0\),我们定义 \(\displaystyle -S_{n+1}=\bigcup_{k=0}^3\Phi_k(S_n)\)。证明,\(S_n\) 是平面上一列单调下降的紧集并且 \(\displaystyle \Gamma=\bigcap_{n\geqslant -0}S_n\)。我们有 \(S_1\) 和 \(S_2\) 的示意图:
证明,\(\displaystyle\sup_{x\in \mathbb -R}T(x) \leqslant \dfrac{2}{3}\)。
找一个 \(c\in [0,1]\),使得 -\(T(c)=\dfrac{2}{3}\)。
(\(T^{-1}(\dfrac{2}{3})\) -的Cantor集的结构)对于 \(x\in -[0,1]\),假设 \(x=\displaystyle\sum_{n=1}^\infty -\frac{b_n}{4^n}\) 是 \(x\) 的 -\(4\)-进制展开,其中 \(b_n=0,1,2,3\)。
-证明,\(\Bigl\{x\in [0,1]\bigm| -T(x)=\dfrac{2}{3}\Bigr\}=\Bigl\{x\in [0,1]\bigm| x=\sum_{n=1}^\infty -\frac{b_n}{4^n}, b_n\in \{1,2\}\Bigr\}\)
仿照 11,研究 \(\Phi_1\) 和 -\(\Phi_2\) 在集合 \(\bigl\{(x,T(x))\bigm| x\in -[0,1],T(x)=\dfrac{2}{3}\bigr\}\) -上自相似的作用。(这是一个Hausdorff维数为 \(\dfrac{1}{2}\) 的集合)。
对任意给定的正数 \(\lambda_k>0\),试计算函数 \(f_k(x)=\dfrac{a_k}{k!}x^k\chi(t_k x)\) 在 +\(x=0\) +处的任意阶导数(包括零阶)。
+\(n\) 阶导数:$n k $ 时是 \(0\),\(n=k\) 时是 \(a_k\)。
证明,当 \(k\geqslant 2n\) +时,我们有 \(f_k^{(n)}(x)=a_k\sum_{\ell=0}^n{n +\choose \ell}\frac{t_k^{n-\ell}}{(k-\ell)!}x^{k-\ell}\chi^{(n-\ell)}(t_k +x)\)
+归纳就好了。
(Borel引理)任意给定一个数列 \(\{a_k\}_{k\geqslant 0}\),证明,存在 \(\mathbb R\) 上的光滑函数 \(f\),使得对任意的 \(k\geqslant 0\),\(f^{(k)}(0)=a_k\)。(提示:略难。)
+取 \(f(x) = \displaystyle \sum_{k=0}^\infty +f_k(x)\),如果它可以逐项求导,那么是能够满足后一个条件的,所以只要证明 +\(f(x)\) 在 \(0\) +处的导数可以通过级数的逐项求导得到。另外想证明它是光滑函数的话,要归纳证明每一阶导函数都可以继续逐项求导。
+注意这里还有个未知的数列 \(t_k\) +可以用来取值并控制这一函数,所以只要证明对任意的 \(n \in \mathbb Z +\),有 \(\displaystyle \sum_{k=0}^\infty +f^{(n)}_k(x)\) 是在 \(I=[-a,a]\) +上一致收敛的。
+\(k\geq 2n\) 时,\(\| f^{(n)}_k \| _\infty \leq a_k A +\sum_{\ell=0}^n{n \choose \ell}\frac{t_k^{n-\ell}}{(k-\ell)!}x^{k-\ell} +\leq a_kA \sum_{\ell=0}^n{n \choose \ell}t_k^{n-\ell}a^{k-\ell}= a_kAa^k +(\frac 1 a + t_k)^n\)。其中我们取 \(a = +\frac{1}{t_k}\),于是右边可以继续放缩成 \(A2^n t_k^n (a_k \frac{1}{t_k ^k})\),只要取 +\(t_k = 2|a_k| +1\) 就能保证 \(\displaystyle \sum_{k=2n}^\infty \| a_k +\frac{1}{t_k ^k} \|\) 是收敛的。
+于是 $_{k=0}^| f{(n)}k(x) | = {k=0}{2n-1} | +f{(n)}k(x) | + {k=2n}| f^{(n)}_k(x) | $ +右边两项一个有限,一个一致收敛,因此总体也是一致收敛的。于是有 \(\displaystyle \sum_{k=0}^\infty +f^{(n)}_k(x)\) 是在 \(I=[-a,a]\) +上一致收敛的。
第四部分:Peano对Borel引理的证明(选做部分,不交作业)
+-
+
\(\{c_k\}_{k\geqslant 0}\) 和 +\(\{b_k\}_{k\geqslant 0}\) +是两个序列,其中 \(b_k\) +都是正数。证明,
+\(\Bigl(\frac{c_k x^k}{1+b_k +x^2}\Bigr)^{(n)}(0)=\begin{cases}n!(-1)^jc_{n-2j}b_{n-2j}^j, \ +\text{若}~k=n-2j, j\in \mathbb{Z}_{\geqslant 0};\\0, \ \ \ +\text{其它情形}.\end{cases}\)
+Trivial.
+证明,存在常数 \(C\),对任意的 +\(k\geqslant n+2\),对任意的 \(x\),我们有
+\(\Big|\Bigl(\frac{c_k x^k}{1+b_k +x^2}\Bigr)^{(n)}(x)\Big|\leqslant +C(n+1)!\frac{|c_k|k!}{b_k}|x|^{k-n-2}\)
+李在赣神魔.jpg
+证明,当 \(\{c_k\}_{k\geqslant +0}\) 给定的时候,我们可以选取 \(b_k\),使得 \(b_k\) 仅依赖于 \(c_k\) 的选取,并且函数级数 \(\displaystyle f(x)=\sum_{k=0}^\infty \frac{c_k +x^k}{1+b_k x^2}\) 是无限次可微分的。
+如果我们只要求 \(I=(-1,1)\) +的区间应该是可以做到的,让 \(b_k = \frac{|c_k| +k!}{(n+1)!}\) 就可以保证 \(\displaystyle \sum_{k=n+2}^\infty \frac{c_k +x^k}{1+b_k x^2}\) 的 \(n\) +阶微分是收敛列,对于任意取的 \(n \in \mathbb +Z+\) 可以知道 \(\displaystyle +\sum_{k=0}^{n+1} \frac{c_k x^k}{1+b_k x^2}\) 的 \(n\) 阶微分是有限的。所以 \(f^{(n)}(x)\) 存在。
+证明,\(f(0)=c_0\),\(f'(0)=c_1\),并且当 \(n\geqslant 2\) 时,我们有
+\(\frac{f^{(n)}(0)}{n!}=d_n+\sum_{j=1}^{[\frac{n}{2}]}(-1)^jc_{n-2j}b_{n-2j}^j\)
+第一问给出了,trivial.
+这里这个 \(d_n\) 或许就是 \(c_n\)?
+证明,我们可以通过恰当的选取 \(\{c_k\}_{k\geqslant 0}\) 和 \(\{b_k\}_{k\geqslant 0}\) +来证明Borel引理。
+李在赣神魔.jpg
+\(f\) +是光滑函数已经证明了,在第三问里面我们要求 \(b_k\) 是依赖于 \(c_k\) 的数列,因此只要求出所有的 \(c_k\) 就可以了。
+对简单的情形,取 \(c_0 = +a_0\),\(c_1 = a_1\),\(n=2\) 时可以推出 \(a_2 = 2(c_2 - c_0 b_0)\),其中 \(c_0,b_0\) 都已知,可以推出 \(c_2\)。找规律就知道每个 \(\frac{f^{(n)}(0)}{n!}=d_n+\sum_{j=1}^{[\frac{n}{2}]}(-1)^jc_{n-2j}b_{n-2j}^j\) +式中都可以推出新的 \(c_n\),依靠的是已知的 \(c_0,c_1,...,c_n\) 的信息。此时 \(f\) 满足 Borel 引理,得证。
梦话 2.0:这作业怎么这么多啊
-中值定理和Taylor展开
-如果不额外说明,\(f\) 总代表一个区间 -\(I\) 上定义的函数。
+梦话 +3.0:为什么积分章节的习题看起来还是导数
+如果不另加说明,\(f\) 总代表某区间 +\(I\) 上实值函数。
+如果对任意的 \(x,y \in I\) 和 \(t \in (0,1)\),都有 \(f(tx + (1-t)y) < tf(x) + +(1-t)f(y)\),我们就称 \(f\) +为严格凸的。仿照课堂上凹函数的定义,我们可以类似地定义严格凹的函数(即 +\(-f\) 是严格凸的)。
+凸函数的基本性质
-
-
设 \(f\) 在点 \(x\) -处有二阶导数。证明,下面的极限给出了二阶导数:$ f''(x) = _{h } $
-可以用定义,也可以直接洛。
-(Taylor 展开式的唯一性,Peano余项)。假设 \(f\) 在 \(x_0\) 附近的函数,并且当 \(x\rightarrow x_0\) 是,满足
-$ f(x) &= a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + + a_n (x-x_0)^n + -o(|x-x_0|^n)\ &= b_0 + b_1 (x-x_0) + b_2 (x-x_0)^2 + + b_n (x-x_0)^n -+ o(|x-x_0|^n)$
-其中 \(a_i, b_i, i=0,\cdots,n\) -是实数,那么,对任意的 \(i\),我们都有 -\(a_i=b_i\)。
-有 \(\lim _{x \to x_0} -\frac{A(x)-B(x)}{(x-x_0)^n} =0\),于是有 \(a_0 = b_0,...,a_{n-1}= -b_{n-1}\),最后可以推出 \(a_n = -b_n\)。
-假设 \(f\) 在 \(0\) 处有 \(n\) 阶导数。证明,如果 \(f(x)\) 是偶函数(奇函数), \(f\) 在 \(0\) 处的Taylor展开式(Peano余项)中只有 -\(x\) 的偶次项(奇数项)。
+试证明凸函数的如下基本性质:
+-
+
如果 \(f,g\) 是区间 \(I\) 上的凸函数,那么 \(f+g\) 也是凸函数。
Trivial.
-(Rolle定理的简单推广)设函数在有限或无穷的区间 \((a,b)\) 上可微并且 \(\displaystyle\lim_{x \to a^+} f(x) = \lim_{x \to -b^-} f(x)\)。证明,存在 \(x_0 \in -(a,b)\),使得 \(f'(x_0) = -0\)。
-如果不存在,那么 \(f'(x)\) 在 -\((a,b)\) 上恒正或恒负,\(f(x)\) 在 \((a,b)\) 上是严格单调函数,矛盾。
-设函数 \(f \in C^0([a,b])\) -并且在 \((a,b)\) 上可微。证明,\(f\) 在 \([a,b]\) 上严格递增的充分必要条件是对任意 -\(x\in (a,b)\),\(f'(x) \geqslant 0\) 并且在任意子区间 -\((c,d) \subset (a,b)\) 上,\(f'(x)\) 不恒等于 \(0\)。
-如果 \(f(x)\) 在 \([a,b]\) -上严格单调递增,那么这两个结论很好推。
-如果满足这两个条件,那么至少有 \(f(x)\) 在 \([a,b]\) 上非严格单调递增,可能存在 \(f(x_1) =f(x_2)\) 的情况,\(x_1 \neq x_2\)。此时对任意 \(s \in (x_1,x_2)\) 都有 \(f(s)=f(x_1)\),于是在这一子区间上 \(f'(x) =0\),矛盾。
-\(g\in C(\mathbb R)\) 在 \(\mathbb{R}\) 上可微。假设存在常数 \(M\),使得 \(\displaystyle\sup_{x \in \mathbb{R}}|g'(x)| -\leqslant M\)。 对任意的 \(\varepsilon -> 0\),我们定义 \(f_\varepsilon(x) = -x + \varepsilon g(x)\),证明,存在仅依赖于 \(M\) 的常数 \(\delta = \delta(M) > 0\),使得当 \(\varepsilon < \delta\) 时,\(f\colon \mathbb{R} \rightarrow \mathbb{R}\) -是双射。
-取 \(\delta = \frac{1}{2M}\) -即可。
-设函数 \(f\) 在 \([a,b]\) 上有两阶导数并且 \(f'(a) = f'(b) = 0\)。证明,存在 -\(c \in (a,b)\) 使得 \(|f''(c)| \geqslant \frac{4}{(b-a)^2}|f(b) -- f(a)|\)
-存在 \(s \in (a,b)\) 使得 \(f'(s) = \frac{f(b)-f(a)}{b-a}\),存在 -\(t \in (a,s)\) 满足 \(f''(t) = \frac{f'(s)}{s-a} = -\frac{f(b)-f(a)}{(b-a)(s-a)}\)。
-于是 \(t\) 就是满足题意的 \(c\)。
-假设 \(f\) 在 \(\mathbb{R}\) 上二次可导,对 \(k=0,1,2\),我们假设 \(M_k = \displaystyle\sup_{x \in \mathbb{R}} -|f^{(k)}(x)|\) 都是有限的。 证明,\(M_1^2 \leq 2 M_0 M_2\)。
-随便写个 Lagrange 余项的泰勒展开:$f(x+h)= f(x)+f'(x)h+ 2 f''(t)h^2 -\(,\)t (x,x+h)$。
-然后推一个不等式就行了。
-假设 \(f\) 在 \((0,+\infty)\) 上二次可导,\(f''\) 在 \((0,+\infty)\) 上有界并且 \(\displaystyle\lim_{x \rightarrow +\infty} f(x) = -0\)。证明,\(\displaystyle\lim_{x \to -+\infty} f'(x) = 0\)。
-随便写个 Lagrange 余项的泰勒展开:$f(x+h)= f(x)+f'(x)h+ 2 f''(t)h^2 -\(,\)t (x,x+h)$。
-取 \(x \to + \infty\),于是此时 -\(f'(x) =- \frac 1 2 f''(t) h -+\frac{f(x+h)-f(x)}{h}\)。对任意的 \(\varepsilon >0\),只要取 \(|f(x+h)-f(x)|<\varepsilon ^2\)(Cauchy -收敛准则),取 \(h < -\varepsilon\),就有 \(|f'(x)|<\frac{M\varepsilon}{2}\),说明它也会收敛到 -\(0\)。
+如果 \(f,g\) 是 区间 \(I\) 上的单调递增的非负的凸函数, 那么 \(fg\) 是凸函数。
+Trivial.
+如果 \(f\) 是 区间 \(I\) 上的凸函数,\(g\) 是 区间 \(J +\supset f(I)\) 上的单调递增凸函数, 那么 \(g \circ f\) 是凸函数。
+Trivial.
+如果 \(f,g\) 是 区间 \(I\) 上的凸函数, 那么 \(h(x) = \max\{f(x),g(x)\}\) 是凸函数。
+Trivial.
+
+假设 \(f\in +C\bigl((a,b)\bigr)\)。如果对任意的 \(x,y \in (a,b)\),都有 \(\displaystyle f\left(\frac{x+y}{2}\right) +\leqslant \frac{f(x) + f(y)}{2}\),证明,\(f\) 是凸函数。
+对任意的有理数可以用二进制,无理数点可以用有理数的稠密性逼近。
+\(f\) 是 \([a,b]\) 上的凸函数。如果存在 \(c \in (a,b)\),使得 \(f(c) \geqslant +\max\{f(a),f(b)\}\)。试证明,\(f\) 是常值函数。
+Trivial.
+\(f\) 是 \(\mathbb{R}\) 上的凸函数。如果 \(f\) 在 \(\mathbb{R}\) 上有界,证明,\(f\) 是常值函数。
+如果不是常值函数,也就是存在 \(f(a) = +f(b)\),那对于第三个点 \(c \to +\infty\) 一起比较斜率就知道 \(f(c)\) 无界了。
+设 \(f\) 是区间 \(I\) 上的严格凸函数。假设 \(f(x_0) \in I\) 是 \(f\) 的局部极小值,证明,\(x_0\) 是 \(f\) 唯一的整体极小值点,即对任意的 \(x \in I-\{x_0\}\),我们有 \(f(x_0) < f(x)\)。
+局部极小值的意思是存在一个邻域 \(J \subset +I\) 使得 \(f(x_0)\) +在其中最小。取 \(x_1 \in (x_0,x_0 ++\delta)\),\(x_2 \notin J\) 且 +\(f(x_2) \leq +f(x_0)\),比较三者的斜率知道不符合严格凸条件。
+\(I\) 是开区间。证明,\(f\) 是凸函数等价于对任意点 \(x_0 \in I\),存在实数 \(a \in \mathbb{R}\),使得对任意的 \(x \in I\),我们都有 \(f(x) \geqslant a(x - x_0) + f(x_0)\)。
+正推取 \(a = f'(x_0)\),反推考虑 +\(x_0\) +和左右两点组成的三点的斜率关系。
极大值的判定
-\(f\) 在 \((a,b)\) 上可微。假设对于 \(x_0 \in (a,b)\),我们有 \(f'(x_0) = 0\)。
+凸函数与不等式
-
-
证明,\(f\) 在 \(x_0\) -处取局部极大值的一个充分条件是:存在某一邻域 \((x_0 - \delta, x_0 + \delta) \subset -(a,b)\),使得
-\(f'(x)= \begin{cases}< 0, \ -\text{对所有的}~x \in (x_0-\delta, x_0);\\\\> 0, \ \text{对所有的}~ x -\in (x_0, x_0+\delta).\end{cases}\)
-Trivial.
-(最重要的判别方法,有很多应用)证明,如果 \(f''(x_0)\) 存在并且 \(f''(x_0) < 0\),那么 \(f\) 在 \(x_0\) 处取局部极大值。
-说明在某个邻域 \((x_0 - \delta, x_0 + -\delta) \subset (a,b)\) 有 $f''(x) $,也就是 \(f'(x)\) -在邻域上递减,也就是上题的情况。
-假定 \(f\) 在 \(x_0\) 处有 \(n\) 阶导数,\(f'(x_0) = \cdots = f^{(n-1)}(x_0) = 0\) -并且 \(f^{(n)}(x_0) \neq 0\),试讨论 -\(f\) 在 \(x_0\) 处取局部极大值的条件(对 \(n\) 分奇偶讨论)。
-\(f(x)-f(x_0) = \frac{1}{n!} f^{(n)} (x_0) -(x-x_0)^n + o(|x-x_0|^n)\),所以 \(n\) 是奇数则不是局部最值,\(n\) 是偶数且 \(f^{(n)}(x_0) < 0\) -局部极大,否则局部极小。
+试求所有的正数 \(a\),使得不等式 +\(a^x \geqslant x^a\) 对任意的 \(x > 0\) 都成立。
+\(x=a\) 是函数 \(f(x) = a^x - x^a\) +的一个零点,于是它也是一个极小值点,此处导数值为 \(0\) 且二阶导数为正。
+于是 \(a=e\)。
+证明如下不等式并给出等号成立的条件:对任意正数 $x_i $ 和 $t_i +\((\)i=1,,n\(),\)_{i=1}^n t_i = 1$,都有
+$( {i=1}^n t_i x_i )^{ {i=1}^n t_i x_i} _{i=1}^n x_i^{t_i +x_i} $
+两边取对数然后用 Jensen 不等式。
+证明Young不等式并给出等号成立的条件:对于任意正数 \(a,b\),任意的实数 \(p,q\),其中 \(\dfrac{1}{p} + \dfrac{1}{q} = 1\)(我们要求 +\(p\) 和 \(q\) 不是 \(0\) 或者 \(1\)),我们有
+\(ab \leqslant \frac{a^p}{p} + +\frac{b^q}{q}, \ \ \text{如果}~p > 1; \ \ ab \geqslant \frac{a^p}{p} ++ \frac{b^q}{q}, \ \ \text{如果}~p < 1\)
+这个高中竞赛的时候就证明过,咕了。
+证明 Holder 不等式并给出等号成立的条件:设 \(x_i,y_i \geqslant 0\),其中 \(i = 1,\cdots,n\),\(p,q \neq 0,1\),其中 $ + = 1$,我们有
+\(\sum_{i=1}^{n} x_i y_i \leqslant +\left(\sum_{i=1}^{n}x_i^p\right)^{1/p}\left(\sum_{i=1}^{n}y_i^q\right)^{1/q}, +\ \text{如果}~p > 1; ~\sum_{i=1}^{n} x_i y_i \geqslant +\left(\sum_{i=1}^{n}x_i^p\right)^{1/p}\left(\sum_{i=1}^{n}y_i^q\right)^{1/q},\ +\text{如果}~p < 1\)
+在上述不等式中,如果 \(p < +0\),我们假设 \(x_i > +0\)。(这个不等式的结论比证明重要得多,同学们可以参考其它资料来写下证明)
+高中竞赛的时候也证明过,咕了。
多项式的根
-(提示:利用中值定理和 \(n\)-次多项式的至多(恰好)有 \(n\) 个根)
+利用(高阶)导数的信息刻画函数(低阶导数)
+在本习题中,我们把函数 \(f\) 也记为 +\(f^{(0)}\)。
-
-
证明,如果实系数多项式 \(P_n(x) = a_n -x^n + a_{n-1} x^{n-1} + \cdots + a_0\) 的根都是实数(不妨设 \(a_n\neq 0\)),那么它的逐次导函数 \(P_n'(x)\),\(P_n''(x)\) ,\(\cdots\), \(P_n^{(n-1)}(x)\) 的根也都是实数。
-只考虑一阶导数的根。\(P_n(x)\) 有 -\(n\) 个实数根(计入重根),Rolle -定理保证 \(P_n ' (x)\) 有 \(n-1\) -个实数根(也可能计入了重根,这个并不重要),归纳即证。
-证明,Legendre 多项式 \(P_n(x) = -\dfrac{1}{2^n n!} \dfrac{d^n}{dx^n}(x^2 - 1)^n\) -的根都是实数并且包含于区间 \((-1,1)\) -中。
-\(P(x) = (x^2-1)^n\) -的根都是实数,这是一个 \(2n\) -阶多项式,它的 \(n\) -次导函数的根也一定都是实数。Rolle 定理保证这些根全部落在 \(P(x)\) 的根包围的区间里。
-还要证明 \(P_n(x)\) 的根不是 \(1,-1\)。这个可以通过 \(n\) 次求导之后的形式确定。
-证明,\(L_n(x) = \dfrac{e^x}{n!} -\dfrac{d^n}{dx^n}(e^{-x}x^n)\) -是多项式并且它所有的根都是正实数。
-因为这是 Laguerre 多项式!(暴论
-类似的考虑,也很 trivial.
-证明,\(H_n(x) = (-1)^n e^{x^2} -\dfrac{d^n}{dx^n}(e^{-x^2})\) -是多项式并且它所有的根都是实数。
-因为这是 Hermite 多项式!(什么嘛,我的数值分析学得也没那么差嘛
-写一个递推:\(H_{n+1} (x)=2xH_n(x) - -H_n' (x)\),所以是多项式。归纳地证明 \(H_n\) 的所有根都是实数时,\(H_{n+1}\) 的所有根都是实数。
+我们假设 \(f\in +C\bigl([0,1]\bigr)\),\(g\) 在 +\([0,1]\) 上可导且 \(g(0) = 0\)。如果存在常数 \(\lambda \neq 0\),使得对任意的 \(x\in [0,1]\),都有 \(|g(x)f(x) + \lambda g'(x)| \leqslant +|g(x)|\), 证明,\(g(x) \equiv +0\)。
+\(f\) 在 \((-1,1)\) 上二阶可导,\(f(0) = f'(0) = 0\)。如果对任意的 \(x\in (-1,1)\),都有 \(|f''(x)| \leqslant +|f(x)|+|f'(x)|\),证明,\(f(x) +\equiv 0\)。
+设 \(f\) 在 \(\mathbb R\) 上二阶可导,满足 \(f(0) = f'(0) = 0\), 且存在正实数 \(C\) 使得, 对所有的 \(x\in \mathbb R\), 有 \(|f''(x)| \le +C|f(x)f'(x)|\)。证明,\(f(x) \equiv +0\), \(\forall x \in \mathbb +R\)。
+\(n\) 是正整数,\(f\) 在 \(\mathbb +R\) 上 \(n\) 阶可导,\(f(0) = f'(0) = \cdots = f^{(n-1)}(0) = +0\)。如果 \(C\in\mathbb{R}_{>0}\) 和 \(\ell \in \mathbb{Z}_{\geqslant +0}\),使得对任意 \(x\in \mathbb +R\) 都有 \(|f^{(n)}(x)| \leqslant +C|f^{(\ell)}(x)|\),证明,\(f(x) \equiv +0\)。
+\(n\) 是正整数,证明,多项式 +\(\displaystyle P(x) = \sum_{k=0}^{n+1} +C_{n+1}^k (-1)^k (x-k)^n\) 是 \(0\)。
+考虑 \(x^i\) 的系数,全都是 \(0\)。(好怪
+\(f\in C^\infty(\mathbb +R)\)。假设存在正实数 \(C\),使得对任意 \(n \in \mathbb{Z}_{\geqslant 0}\) 和任意的 +\(x \in \mathbb R\),我们都有 \(|f^{(n)}(x)| \leqslant C\)。
+-
+
证明,给定任意的 \(x_0 \in \mathbb +R\),我们可以(以 \(x_0\) +为中心)将 \(f(x)\) 在 \(\mathbb R\) 上展开为无穷Taylor级数,即\(f(x) = \sum_{k=0}^\infty +\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k, \qquad \forall x \in \mathbb +R\)
+只要证明这个级数是逐点收敛的,实际上 \(|f(x) |\leq C \exp(x-x_0)\)。
+\(E\subset \mathbb R\) +是一个无穷集并且有界。证明,如果 \(f\) +在 \(E\) 上的取值都是零,那么 \(f\equiv 0\)。
+
+假设 \(f\in +C^2\bigl((0,1)\bigr)\),\(\displaystyle\lim_{x\to 1^-}f(x) = +0\)。如果存在 \(C>0\),使得对任意 \(x\in (0,1)\),我们都有不等式 \((1-x)^2|f''(x)| \leqslant +C\)。证明,\(\displaystyle\lim_{x\to +1^-} (1-x)f'(x) = 0\).
Emile Borel 引理
-第一部分:截断函数的构造
+函数的重根
+上传者注:本题题设条件下可以举出很多反例,建议读者将可微条件全部改为足够高阶连续可微,或者光滑。
+如果 \(f\) 在 \(x_0\) 的一个邻域内满足 \(f(x) = (x-x_0)^r g(x)\),其中 \(r \in \mathbb{Z}_{\geqslant 0}\),\(g\) 在 \(x_0\) 处连续并且 \(g(x_0) \neq 0\),那么我们就称 \(x_0\) 为 \(f\) 的 \(r\)-重根。我们注意到,\(0\)-重根并非根。
-
-
定义函数 \(\phi\colon \mathbb -R\rightarrow \mathbb R\):
-\(\phi(x)=\begin{cases}e^{-\frac{1}{x^2}}, -\ \ x>0;\\0, \ \ \ \ x\leqslant 0.\end{cases}\)
-证明,\(\phi\in C^\infty(\mathbb -R)\)。
-只要证明在 \(x=0\) -处无限可微。实际上一阶导数是 \(0\),二阶及以上可以归纳地证明都是 \(0\)。
-定义函数 \(\chi\colon \mathbb -R\rightarrow \mathbb R\):\(\chi(x)=\frac{\phi(2-|x|)}{\phi(2-|x|)+\phi(|x|-1)}\),证明,\(\chi(x)\in C^\infty(\mathbb R)\) 并且 \(\chi\big|_{[-1,1]}\equiv 1\),\(\chi\big|_{(-\infty,-2]\cup [2,\infty)}\equiv -0\),\(0\leqslant \chi(x)\leqslant -1\) 并且是偶函数。
-\(\chi\big|_{[-1,1]}\equiv -1\),\(\chi\big|_{(-\infty,-2]\cup -[2,\infty)}\equiv 0\) -这两个结论是显然的,所以在这几个区间上都是无限维可导。在 \([1,2]\) 上显然也无限维可导,所以只要证明在 -\(1\) 和 \(2\) -两点处无限维可导。(因为是偶函数,所以很容易可以看出负数区间上是一样的)。这两个也很好证明,一阶导数都是 -\(0\)。
-证明,对任意的 \(0<a<b\),存在光滑偶函数 \(\rho(x)\in C^\infty(\mathbb R)\),使得 -\(\rho\big|_{[-a,a]}\equiv 1\),\(\rho\big|_{(-\infty,-b]\cup [b,\infty)}\equiv -0\),\(0\leqslant \rho(x)\leqslant -1\)。
-构造 \(\rho (x) = -\frac{\phi(b-|x|)}{\phi(b-|x|)+\phi(|x|-a)}\)。
-证明,存在偶函数 \(\psi \in -C^\infty(\mathbb R^n)\),使得 \(\psi\big|_{\{x\mid|x|\leqslant 1\}}\equiv -1\),\(\psi\big|_{\{x\mid|x|\geqslant -2\}}\equiv 0\),\(0\leqslant \psi(x -)\leqslant 1\)。
-构造 \(\psi (x) = -\chi(|x|)\)。
+假设 \(x_0\) 是 \(f\) 的 \(r\)-重根,其中 \(r\geqslant 1\)。证明,如果 \(g(x) = \dfrac{f(x)}{(x-x_0)^r}\) 可微,那么 +\(x_0\) 是 \(f'\) 的 \((r-1)\)-重根。
+\(f'(x) = (x-x_0)^r g'(x) - rg(x) +(x-x_0)^{r-1}\)。
+假设 \(f\) 为 \(\mathbb R\) 上 \(n\) 阶的可微函数。证明,如果 \(f(x) = 0\) 有 \(n+1\) 个不同的实根,那么 \(f^{(n)}(x) = 0\) 至少有一个实根。
+不停用 Lagrange 中值定理。
+\(f\) 为 \(\mathbb R\) 上的可微函数。假设 \(f(x) = 0\) 按重数计算恰有 \(r\) 个实根,也就是说,\(f(x) = 0\) 有 \(s\) 个相异的实根 \(x_1, x_2, \cdots, x_s\),它们的重数分别为 +\(r_1, r_2, \cdots, r_s\) 并且 \(r_1+r_2 + \cdots + r_s = r\)。证明,\(f'(x) = 0\) 按重数计至少有 \(r-1\) 个根。
+\(f'(x)\) 对于相异的实根 \(x_1, x_2, \cdots, x_s\),它们的重数分别为 +\(r_1-1, r_2-1, \cdots, r_s-1\) +,并且在 \(x_1, x_2, \cdots, x_s\) +之间用 Lagrange 中值定理还有 \(s-1\) +个根,于是共有 \(r-1\) 个根。
+假设 \(f\) 为 \(\mathbb R\) 上 \(n\) 阶的可微函数。证明,如果 \(f(x) = 0\) 按重数计恰有 \(n+1\) 个实根,那么 \(f^{(n)}(x) = 0\) 至少有一个实根。
+归纳。
第二部分:逐项求导定理
-\(I=[a,b]\) 是闭区间,\(\{f_k\}_{k\geqslant 0}\) 是 \(C^1(I)\) 的一列函数,我们假设 \(\displaystyle \sum_{k=0}^\infty f_k\) 在 -\(I\) 上逐点收敛,即对任意的 \(x\in I\),\(\displaystyle \sum_{k=0}^\infty f_k(x)\) -收敛,我们记 \(f(x)=\displaystyle -\sum_{k=0}^\infty f_k(x)\)。
+积分
+2023 年 2 月 8 +日,星期三,学了半天积分结果配套的作业题还是导数题,摸不着头脑.jpg
+Riemann 积分
-
-
我们假设函数级数 \(\displaystyle -\sum_{k=0}^\infty f'_k(x)\) 在 \(I\) 上绝对收敛,即数项的级数 \(\displaystyle \sum_{k=0}^\infty -\|f'_k\|_\infty\) 收敛,其中 \(\displaystyle \|f\|_\infty=\sup_{x\in -I}|f(x)|\)。证明,\(f\) -是可导的并且 \(f'(x)=\displaystyle -\sum_{k=0}^\infty f'_k(x)\)。(提示:设法将求和拆 \(\displaystyle \sum_{k=0}^\infty = -\sum_{k=0}^N+\displaystyle \sum_{k=N+1}^\infty\))
-\(\displaystyle \sum_{k=0}^\infty -f'_k(x)\) 在 \(I\) -上绝对收敛,所以 \(\displaystyle -\sum_{k=0}^\infty f'_k(x)\) 在 \(I\) -上逐点都是收敛的,上式右端一定收敛。所以只要证明这个等号成立。
-对任意的 \(\varepsilon ->0\),找一个合适的 \(|x-x_0| < -\delta\) 和一个合适的 \(N \in \mathbb -Z+\),满足:
-\(|\frac{f_k(x)-f_k(x_0)}{x-x_0} - f_k -'(x_0) | <\varepsilon\) 对 \(k=0,1,2,...,N\) 都成立(导数的定义),而且 -\(|\displaystyle \sum_{k=N+1}^\infty -\|f'_k\|_\infty|<\varepsilon\)(收敛列的 Cauchy -性质)。
-于是 $|{k=0}^- {k=0}f'k(x)| |{k=0}N - -{k=0}^N f'k(x)|+|{k=N+1}^- {k=N+1}^f'_k(x)| $。
-右边第一项的上界是 \(N\varepsilon\),第二项用一下 Lagrange -中值定理处理前一个级数和,可以知道上界是 \(2\varepsilon\)。
-因此 \(\lim _{x \to x_0} \displaystyle -\sum_{k=0}^\infty \frac{f_k(x)-f_k(x_0)}{x-x_0}- \displaystyle -\sum_{k=0}^\infty f'_k(x) =0\),也就是 \(f'(x)=\displaystyle \sum_{k=0}^\infty -f'_k(x)\),得证。
-(逐项求导定理)\(I=[a,b]\) -是闭区间,\(\{f_k\}_{k\geqslant 0}\) 是 -\(C^1(I)\) 的一列函数,我们假设 \(\displaystyle \sum_{k=0}^\infty f_k\) 在 -\(I\) 上逐点收敛。如果函数级数 \(\displaystyle \sum_{k=0}^\infty -f'_k(x)\) 在 \(I\) -上一致收敛,那么 \(f\) 是可导的并且 -\(f'(x)=\displaystyle \sum_{k=0}^\infty -f'_k(x)\)。
-证明 \(f\) -是可导的只需要证明导函数的这个式子成立。
-\(\displaystyle \sum_{k=0}^\infty -f'_k(x)\) 在 \(I\) -上一致收敛也可以推出,对 \(\varepsilon ->0\),存在某个合适的 \(N\) -使得 \(|\displaystyle \sum_{k=N+1}^\infty -f'_k(x)| < \varepsilon\) 对任意的 \(x\in I\) -都成立,所以前一题不等式里的第二项仍然被 \(2\varepsilon\) -控制,不等式仍然可以成立。
-同时,\(f'(x)=\displaystyle -\sum_{k=0}^\infty f'_k(x)\) 右端也对任意的 \(x \in I\) -都是收敛级数,是良定义的。
-试利用逐项求导定理计算 \(e^x\) -的导数。
-Trivial,无穷级数求导之后形式仍然相同。
+阶梯函数是最简单的一类积分函数,它的积分值对于任意相容的分划都是相等的。这是一个很美妙的证明,用到了一个简单的逻辑:$$ +和 \(\sigma '\) 的并 \(\sigma \cup \sigma '\) +是二者的一个加细;如果 \(\sigma_1\) 是 +\(\sigma _2\) +的一个加细且它们都是相容的分割,那么二者的积分值相等;因此 \(\sigma\) 和 \(\sigma '\) 的积分都和 \(\sigma \cup \sigma '\) +的积分相等,由任意性可知任意划分的积分都相等。
+阶梯函数的积分是满足线性性的,它还满足一些看起来很显然但其实证明也不是很难的性质,略了。
+为了扩大可以“积分”的函数的种类(目前只有阶梯函数积分),试一下用阶梯函数积分逼近一般的连续函数。
+一个技术性的引理(定义),实际上类似于极限的 \(\delta - \varepsilon\) +描述和点列描述法:
++
+\(I=[a,b]\) 是有界闭区间,\(f\colon I\rightarrow \mathbb R\) +是函数,如下命题是等价的:
+-
+
对任意的 \(\varepsilon>0\),存在两个阶梯函数 \(F_\varepsilon\colon I \rightarrow \mathbb +R\) 和 \(\Psi_\varepsilon\colon I +\rightarrow \mathbb R\),使得对任意的 \(x\in I\),都有
+\(\big|f(x)-F_\varepsilon(x)\big|<\Psi_\varepsilon(x)\) +并且 \(\int_I \Psi_\varepsilon +<\varepsilon\)
+存在两个阶梯函数的序列 \(\{f_n\}_{n\geqslant 1} \subset +\mathcal{E}(I)\) 和 \(\{\psi_n\}_{n\geqslant 1} \subset +\mathcal{E}(I)\),使得对任意的 \(x\in +I\),都有
+\(\big|f(x)-f_n(x)\big|<\psi_n(x)\) 并且 $ +_{n}_I _n =0$
第三部分:Borel引理的证明
-我们现在任意给定一个数列 \(\{a_k\}_{k\geqslant 0}\)。
+满足二者之一时,称 \(f\) +可以被阶梯函数逼近,是区间 \(I\) 上 +Riemann 可积的函数。\(\mathcal R (I)\) +表示全体 \(I\) 上 Riemann +可积的函数。此时可以定义 \(f\) 的 +Riemann 积分:\(\int_{I}=\int_{a}^b\colon +\mathcal{R}(I)\rightarrow V, \ \ f\mapsto \lim_{n\rightarrow \infty} +\int_a^b f_n\)。
+关于这个定义为什么是良定义的问题,首先要证明上述极限存在,再证明 +\(f\) 的积分定义不依赖于具体的 \(\lbrace f_n \rbrace\) 和 \(\lbrace \psi_n +\rbrace\),实际上它们都是简单的阶梯函数,所以由定义都是容易证明的。
+研究一下 \(I\) 上的 Riemann +可积空间 \(\mathcal R (I)\) +的性质,由于我之前根本没学会这个,还是写细一点。
+比较容易证明的几个性质是:\(\mathcal R +(I)\) 是实数域上的线性空间,\(\mathcal +R(I)\) 上的函数都有界(注意 \(I\) +还是一个闭区间的情况,这里还没有研究到广义积分),阶梯函数都在 \(\mathcal R (I)\) 中,Riemann +可积函数取绝对值也还是 Riemann 可积的,乘积也是 Riemann 可积的。
+其他的性质有:\(\mathcal R (I)\) +包含所有的 \(C(I)\) +上函数(利用一致连续性手动切出逼近的阶梯函数),有限维的情况。
++
\(C(I)\subset \mathcal{R}(I)\)。
+假设 \(f\in C(I)\),根据 \(f\) 的一致连续性,对任意的 \(\varepsilon>0\),存在 \(n\in\mathbb{Z}_{\geqslant +1}\),使得对任意的 \(x,y\in +I\),当 \(|x-y|<\dfrac{1}{n}\) 时,我们有 \(|f(x)-f(y)|<\frac{\varepsilon}{b-a}\)。此时,我们令
+\(F(x)=\sum_{k=1}^n +f\bigl(a+k\frac{b-a}{n}\bigr)\mathbf{1}_{[a+(k-1)\frac{b-a}{n},a+k\frac{b-a}{n}]}(x)\),
+其中,\(\mathbf{1}_{[a+(k-1)\frac{b-a}{n},a+k\frac{b-a}{n}]}\) +是示性函数。这个 \(F(x)\) +显然是阶梯函数。由一致连续性,我们知道
+\(\big|f(x)-F(x)\big|<\Psi_\varepsilon(x)\equiv +\frac{\varepsilon}{b-a}\),所以,\(\int_a^b \Psi_\varepsilon(x) +=\varepsilon\)。从而,\(f\) +是Riemann可积的函数。
+
+
Darboux 上下和
+这是一个刻画 Riemann 可积的实数值函数的方法。
+当然,刻画 Riemann +可积函数的方式一共有四种,彼此等价,具体就不说了,可见:Read +More
+梦话:终于找到积分的作业在哪了但是还没写
+积分定义的补充与扩展
+我们总假设 \(I=[a,b]\subset \mathbb +R\) 是一个有界闭区间,\(V\) +是一个赋范线性空间。
-
-
对任意给定的正数 \(\lambda_k>0\),试计算函数 \(f_k(x)=\dfrac{a_k}{k!}x^k\chi(t_k x)\) 在 -\(x=0\) -处的任意阶导数(包括零阶)。
-\(n\) 阶导数:$n k $ 时是 \(0\),\(n=k\) 时是 \(a_k\)。
-证明,当 \(k\geqslant 2n\) -时,我们有 \(f_k^{(n)}(x)=a_k\sum_{\ell=0}^n{n -\choose \ell}\frac{t_k^{n-\ell}}{(k-\ell)!}x^{k-\ell}\chi^{(n-\ell)}(t_k -x)\)
-归纳就好了。
-(Borel引理)任意给定一个数列 \(\{a_k\}_{k\geqslant 0}\),证明,存在 \(\mathbb R\) 上的光滑函数 \(f\),使得对任意的 \(k\geqslant 0\),\(f^{(k)}(0)=a_k\)。(提示:略难。)
-取 \(f(x) = \displaystyle \sum_{k=0}^\infty -f_k(x)\),如果它可以逐项求导,那么是能够满足后一个条件的,所以只要证明 -\(f(x)\) 在 \(0\) -处的导数可以通过级数的逐项求导得到。另外想证明它是光滑函数的话,要归纳证明每一阶导函数都可以继续逐项求导。
-注意这里还有个未知的数列 \(t_k\) -可以用来取值并控制这一函数,所以只要证明对任意的 \(n \in \mathbb Z +\),有 \(\displaystyle \sum_{k=0}^\infty -f^{(n)}_k(x)\) 是在 \(I=[-a,a]\) -上一致收敛的。
-\(k\geq 2n\) 时,\(\| f^{(n)}_k \| _\infty \leq a_k A -\sum_{\ell=0}^n{n \choose \ell}\frac{t_k^{n-\ell}}{(k-\ell)!}x^{k-\ell} -\leq a_kA \sum_{\ell=0}^n{n \choose \ell}t_k^{n-\ell}a^{k-\ell}= a_kAa^k -(\frac 1 a + t_k)^n\)。其中我们取 \(a = -\frac{1}{t_k}\),于是右边可以继续放缩成 \(A2^n t_k^n (a_k \frac{1}{t_k ^k})\),只要取 -\(t_k = 2|a_k| +1\) 就能保证 \(\displaystyle \sum_{k=2n}^\infty \| a_k -\frac{1}{t_k ^k} \|\) 是收敛的。
-于是 $_{k=0}^| f{(n)}k(x) | = {k=0}{2n-1} | -f{(n)}k(x) | + {k=2n}| f^{(n)}_k(x) | $ -右边两项一个有限,一个一致收敛,因此总体也是一致收敛的。于是有 \(\displaystyle \sum_{k=0}^\infty -f^{(n)}_k(x)\) 是在 \(I=[-a,a]\) -上一致收敛的。
+\(\sigma_1,\sigma_2\in +\mathcal{S}\) 是两个分划。证明,对任意的 \(\varepsilon>0\),总存在分划 \(\sigma\),使得 \(\sigma\prec \sigma_1\),\(\sigma\prec \sigma_2\) 并且它的步长 \(|\sigma|<\varepsilon\)。
+对 \(\sigma_1 \cup \sigma_2\) +再加细就可以了。
+考虑在 \(V\) +中取值的阶梯/简单函数的空间 \(\mathcal{E}(I)\),证明,这是 \(\mathbb R\)-线性空间并且积分算子 \(\displaystyle\int_{a}^b\colon +\mathcal{E}(I)\rightarrow V\) +是良好定义的(不依赖于分划的选取)并且是线性映射,其中积分的定义方式与函数在 +\(\mathbb R\) +中取值时的方式一致。据此,用阶梯函数逼近的方式定义在 \(V\) +中取值的Riemann可积的函数。你不需要写下细节但是你应该对照笔记研究原来证明的每一步。
+假设 \(f\colon I\rightarrow +\mathbb{R}^n\),其中 \(f_i\) 是 +\(f\) 的每个分量。那么 \(f\in \mathcal{R}(I)\) 当且仅当对每个分量 +\(f_i\) 我们都有 \(f_i\in \mathcal{R}(I)\)。特别地,当 \(f\colon \mathbb R\rightarrow \mathbb{C}\) +时,我们有 \(\displaystyle \int_a^b f = +\int_a^b \mathbb Re f+i\int_{a}^b \Im f\),其中 \(\mathbb Re f\) 和 \(\Im f\) 分别为 \(f\) 的实部和虚部。
+试证明积分的区间可加性:假设 \(a<c<b\),那么对于任意的 \(f\in \mathcal{R}(I)\),我们有 \(f\) 在 \([a,c]\) 和 \([c,b]\) 上的限制都是阶梯函数,并且 \(\int_{a}^b f =\int_{a}^c f+\int_c^b +f\)。
+证明,对于任意两个分划 \(\sigma\) 和 \(\sigma'\),它们所对应的Darboux上下和满足
+\(\underline{S}(f;\sigma)\leqslant +\overline{S}(f;\sigma')\)
+据此证明,如果 \(f\in +\mathcal{R}(I)\),就有 \(\displaystyle\lim_{|\sigma|\rightarrow +0}|\underline{S}(f;\sigma)-\overline{S}(f;\sigma)|=0\),即对任意的 +\(\varepsilon>0\),一定存在 \(\delta>0\),对任意的分划 \(\sigma\),只要 \(|\sigma|<\delta\),我们就有 \(|\underline{S}(f;\sigma)-\overline{S}(f;\sigma)|<\varepsilon\)
+\(f\in +\mathcal{R}(I)\)。证明,改变 \(f\) +在有限个点上的取值所得到的函数仍是Riemann可积的并且积分与 \(f\) 的相同。
+\(f\in C([a,b])\)。假设对任意的 +\(x\in I\),我们都有 \(f(x)\geqslant 0\) 并且存在点 \(x_0 \in I\) 使得 \(f(x_0) > 0\)。 证明,\(\displaystyle\int_a^b f > 0\)。
+(不定积分的分部积分公式:对计算不定积分有用)假设 \(f,g\in C^1(I)\),那么,我们有
+\(\int f'\cdot g=f\cdot g-\int f\cdot +g'\)
+(不定积分的变量替换公式:对计算不定积分有用)假设 \(\Phi\colon \mathbb R\rightarrow \mathbb R\) +可微,\(f\) 是连续函数,那么
+\(\int (f\circ \Phi)\Phi'=\int +f\)
+
思考题:多项式逼近和Weierstrass--Stone定理
+我们要证明如下著名的定理:任意给定有界闭区间 \(I=[a,b]\) +上的连续函数,我们总是可以用一个多项式来足够好地逼近它。更精确地说,给定 +\(f\in C([a,b])\),对任意的 \(\varepsilon>0\),存在多项式 \(P_\varepsilon\),使得 \(\displaystyle \sup_{x\in +[a,b]}|f(x)-P_\varepsilon(x)|<\varepsilon\),即若用 \(P([a,b])\) 表示 \([a,b]\) 上多项式函数组成的空间,则 \(P([a,b])\) 在度量空间 \(C([a,b])\) 中稠密(\(C([a,b])\) 上用的范数是 \(\|f\|_\infty=\displaystyle \sup_{x\in +[a,b]}|f(x)|\))。
+Dini定理及应用
+-
+
(Dini定理)假设 \(K\subset \mathbb +R^n\) 是紧子集,\(f_n\colon +K\rightarrow \mathbb R\) 是一列连续函数,它们逐点地收敛到连续函数 +\(f\colon K\rightarrow \mathbb +R\),即对每个 \(x\in +K\),我们都有 \(\displaystyle +\lim_{n\rightarrow \infty}f_n(x)=f(x)\)。证明,如果 \(\{f_n\}_{n\geqslant 1}\) +是上升的函数列(即对任意 \(x\in K\) 和 +\(n\),我们都有 \(f_n(x)\leqslant f_{n+1}(x)\)),那么 \(f_n\) 一致收敛到 \(f\)。(参考荆公子的某次习题课)
+考虑区间 \(I=[-1,1]\)。我们通过归纳的方式定义一族多项式函数:
+\(P_0(x)=0, \ \ +P_{n+1}(x)=P_n(x)+\frac{1}{2}(x^2-P_n^2(x))\)
+证明,对任意的 \(n\) 和 \(x\),我们都有 \(0\leqslant P_n(x)\leqslant P_{n+1}(x)\leqslant +|x|\)。
+证明,绝对值函数 \(|x|\) 在 +\(I=[-1,1]\) +上可以被多项式一致地逼近,即对任意的 \(\varepsilon>0\),存在某个多项式函数 +\(P_\varepsilon(x)\),使得 \(\displaystyle \sup_{x\in +[-1,1]}\big||x|-P_\varepsilon(x)\big|<\varepsilon\)。
第四部分:Peano对Borel引理的证明(选做部分,不交作业)
+区间上的情形
+这一部分中,我们假设 \(I=[0,1]\),\(n\) 是正整数。
-
-
\(\{c_k\}_{k\geqslant 0}\) 和 -\(\{b_k\}_{k\geqslant 0}\) -是两个序列,其中 \(b_k\) -都是正数。证明,
-\(\Bigl(\frac{c_k x^k}{1+b_k -x^2}\Bigr)^{(n)}(0)=\begin{cases}n!(-1)^jc_{n-2j}b_{n-2j}^j, \ -\text{若}~k=n-2j, j\in \mathbb{Z}_{\geqslant 0};\\0, \ \ \ -\text{其它情形}.\end{cases}\)
-Trivial.
-证明,存在常数 \(C\),对任意的 -\(k\geqslant n+2\),对任意的 \(x\),我们有
-\(\Big|\Bigl(\frac{c_k x^k}{1+b_k -x^2}\Bigr)^{(n)}(x)\Big|\leqslant -C(n+1)!\frac{|c_k|k!}{b_k}|x|^{k-n-2}\)
-李在赣神魔.jpg
-证明,当 \(\{c_k\}_{k\geqslant -0}\) 给定的时候,我们可以选取 \(b_k\),使得 \(b_k\) 仅依赖于 \(c_k\) 的选取,并且函数级数 \(\displaystyle f(x)=\sum_{k=0}^\infty \frac{c_k -x^k}{1+b_k x^2}\) 是无限次可微分的。
-如果我们只要求 \(I=(-1,1)\) -的区间应该是可以做到的,让 \(b_k = \frac{|c_k| -k!}{(n+1)!}\) 就可以保证 \(\displaystyle \sum_{k=n+2}^\infty \frac{c_k -x^k}{1+b_k x^2}\) 的 \(n\) -阶微分是收敛列,对于任意取的 \(n \in \mathbb -Z+\) 可以知道 \(\displaystyle -\sum_{k=0}^{n+1} \frac{c_k x^k}{1+b_k x^2}\) 的 \(n\) 阶微分是有限的。所以 \(f^{(n)}(x)\) 存在。
-证明,\(f(0)=c_0\),\(f'(0)=c_1\),并且当 \(n\geqslant 2\) 时,我们有
-\(\frac{f^{(n)}(0)}{n!}=d_n+\sum_{j=1}^{[\frac{n}{2}]}(-1)^jc_{n-2j}b_{n-2j}^j\)
-第一问给出了,trivial.
-这里这个 \(d_n\) 或许就是 \(c_n\)?
-证明,我们可以通过恰当的选取 \(\{c_k\}_{k\geqslant 0}\) 和 \(\{b_k\}_{k\geqslant 0}\) -来证明Borel引理。
-李在赣神魔.jpg
-\(f\) -是光滑函数已经证明了,在第三问里面我们要求 \(b_k\) 是依赖于 \(c_k\) 的数列,因此只要求出所有的 \(c_k\) 就可以了。
-对简单的情形,取 \(c_0 = -a_0\),\(c_1 = a_1\),\(n=2\) 时可以推出 \(a_2 = 2(c_2 - c_0 b_0)\),其中 \(c_0,b_0\) 都已知,可以推出 \(c_2\)。找规律就知道每个 \(\frac{f^{(n)}(0)}{n!}=d_n+\sum_{j=1}^{[\frac{n}{2}]}(-1)^jc_{n-2j}b_{n-2j}^j\) -式中都可以推出新的 \(c_n\),依靠的是已知的 \(c_0,c_1,...,c_n\) 的信息。此时 \(f\) 满足 Borel 引理,得证。
+对任意的 \(0\leqslant k\leqslant +n\),我们定义 \(p_{n,k}(x)=\displaystyle{n \choose +k}x^k(1-x)^{n-k}\)。证明,\(\displaystyle \sum_{0\leqslant k \leqslant +n}p_{n,k}(x-\frac{k}{n})^2=\frac{x(1-x)}{n}\)。
+任意给定 \(f\in +C([0,1])\),我们定义 \(B_{f,n}(x)= +\displaystyle\sum_{0\leqslant k \leqslant n}f\bigl(\frac{k}{n}\bigr){n +\choose k}x^k(1-x)^{n-k}\)。对 \(x\in +[0,1]\),证明,
+\(|f(x)-B_{f,n}(x)|\leqslant \sum_{k=0}^n +\bigl|f(x)-f\bigl(\frac{k}{n}\bigr)\bigr|p_{n,k}(x)\)
+(用Bernstein多项式逼近连续函数)任意给定 \(f\in C([0,1])\),证明,对任意 \(\varepsilon>0\),总存在 \(n\),使得 \(\|f-B_{f,n}\|_\infty +<\varepsilon\)。
梦话 -3.0:为什么积分章节的习题看起来还是导数
-如果不另加说明,\(f\) 总代表某区间 -\(I\) 上实值函数。
-如果对任意的 \(x,y \in I\) 和 \(t \in (0,1)\),都有 \(f(tx + (1-t)y) < tf(x) + -(1-t)f(y)\),我们就称 \(f\) -为严格凸的。仿照课堂上凹函数的定义,我们可以类似地定义严格凹的函数(即 -\(-f\) 是严格凸的)。
-凸函数的基本性质
+++Remark:用概率论的观点,\(x\in +[0,1]\) 给定,Bernstein多项式逼近的的方法讲的是概率测度
+\(\mu_x=\displaystyle\sum_{k=0}^n {n +\choose j}x^k(1-x)^{n-k}\delta_{\frac{k}{n}}\) 的极限是Dirac测度 +\(\delta_x\)。
+
紧集上的情形
+从此往后,我们假设 \(K\subset \mathbb +R^n\) 是紧集,\(C(K)\) 是 \(K\) 上的实数值连续函数所构成的线性空间,用 +\(P(K)\) 表示 \(K\) 上多项式函数组成的空间(即形如 \(\displaystyle \sum_{|\alpha|\leqslant m} c_\alpha +x^\alpha\) 的函数,其中 \(m\) +是正整数,\(\alpha\) +是多重指标,请参见关于多重偏导数的课堂笔记)。
-
-
试证明凸函数的如下基本性质:
+假设 \(\mathcal{A}\subset C(K)\) +是非零的线性子空间。如果对任意的 \(f,g\in +\mathcal{A}\),它们的乘积 \(f\cdot g +\in \mathcal{A}\),我们就把 \(\mathcal{A}\) 称作是 \(C(K)\) 的一个子代数。证明,\(P(K)\) 是 \(C(K)\) 的子代数。
+非零的线性子空间 \(\mathcal{A}\subset +C(K)\) 是闭子代数,也就是说如果 \(\{f_k\}_{k \geqslant 1}\subset +\mathcal{A}\),\(f_k\) +一致收敛到 \(f\),那么 \(f\in \mathcal{A}\)。假设常值函数 \(1\in \mathcal{A}\),证明,如果 \(f\in \mathcal{A}\),那么 \(|f|\in \mathcal{A}\)。(提示: 利用 +W3)
+假设 \(\mathcal{A}\subset C(K)\) +是子集,如果对任意的 \(x,x'\in +K\),\(x\neq x'\),都存在 +\(f\in \mathcal{A}\),使得 \(f(x)\neq f(x')\),我们就称 \(\mathcal{A}\) 是能够区分点的。证明,\(P(K)\) 是能够区分点的。
+假设 \(f,g\in C(K)\)。证明,函数 +\(f\wedge g (x)=\min\{f(x),g(x)\}\) 和 +\(f\vee g (x)=\max\{f(x),g(x)\}\) +都是连续的。
+假设 \(\mathcal{A}\subset C(K)\) +是子集,如果对任意的 \(f,g\in +\mathcal{A}\),\(f\wedge g, f\vee g \in +\mathcal{A}\),我们就称 \(\mathcal{A}\) 是 \(\wedge\vee\)-封闭的。证明,\(\overline{P(K)}\) 是 \(\wedge\vee\)-封闭的,其中 \(\overline{P(K)}=\bigl\{f\in +C(K)\bigm|\text{存在}\{f_k\}_{k\geqslant1}\subset P(K), +f_k\text{一致收敛到}f\bigr\}\) 为 \(P(K)\) 在 \(C(K)\) 中的闭包。
+我们现在假设 \(\mathcal{A}\subset +C(K)\) 是 \(\wedge\vee\)-封闭的,并且对任意的 \(\alpha,\beta \in \mathbb R\),任意的 \(x,y \in K\),\(x\neq y\)(我们此时假设 \(K\) 至少含有两个点)都存在函数 \(\varphi\in A\),使得 \(\varphi(x)=\alpha\),\(\varphi(y)=\beta\)。
+我们通过下面的步骤来证明 \(\mathcal{A}\subset C(K)\) +是稠密的(即对任意给定的连续函数 \(f\in +C(K)\),对任意的 \(\varepsilon>0\),总存在 \(\varphi \in \mathcal{A}\),使得 \(\|\varphi-f\|_{\infty}<\varepsilon\)):
-
-
如果 \(f,g\) 是区间 \(I\) 上的凸函数,那么 \(f+g\) 也是凸函数。
-Trivial.
-如果 \(f,g\) 是 区间 \(I\) 上的单调递增的非负的凸函数, 那么 \(fg\) 是凸函数。
-Trivial.
-如果 \(f\) 是 区间 \(I\) 上的凸函数,\(g\) 是 区间 \(J -\supset f(I)\) 上的单调递增凸函数, 那么 \(g \circ f\) 是凸函数。
-Trivial.
-如果 \(f,g\) 是 区间 \(I\) 上的凸函数, 那么 \(h(x) = \max\{f(x),g(x)\}\) 是凸函数。
-Trivial.
+- 固定 \(x_0\in X\),对任意的 \(y\in K\),我们选取 \(\varphi_y\in \mathcal{A}\),使得 \(\varphi_y(x_0)=f(x_0)\) 并且 \(\varphi_y(y)=f(y)\),这样我们得到一族 \(\{f_y\in \mathcal{A}\mid y\in +K\}\),据此,对每个 \(y\in +K\),可以定义 \(U_y=\{z\in K\mid +\varphi_y(z)>f(z)-\varepsilon\}\)。证明,存在有限个 \(y_1,\cdots,y_m\in K\),使得 \(K\subset U_{y_1}\cup \cdots \cup +U_{y_m}\)。 +
- 证明,\(\varphi_{x_0}=\displaystyle\sup_{x\in +K}\{\varphi_{y_1}(x),\cdots, \varphi_{y_m}(x)\}\in \mathcal{A}\) +并且对任意的 \(x\in K\),我们都有 \(\varphi_{x_0}(x)-f(x)>-\varepsilon\)。 +
- 证明,存在 \(\varphi \in +\mathcal{A}\),使得对任意的 \(x\in +K\),都有 \(|\varphi(x)-f(x)|<\varepsilon\)。
-假设 \(f\in -C\bigl((a,b)\bigr)\)。如果对任意的 \(x,y \in (a,b)\),都有 \(\displaystyle f\left(\frac{x+y}{2}\right) -\leqslant \frac{f(x) + f(y)}{2}\),证明,\(f\) 是凸函数。
-对任意的有理数可以用二进制,无理数点可以用有理数的稠密性逼近。
-\(f\) 是 \([a,b]\) 上的凸函数。如果存在 \(c \in (a,b)\),使得 \(f(c) \geqslant -\max\{f(a),f(b)\}\)。试证明,\(f\) 是常值函数。
-Trivial.
-\(f\) 是 \(\mathbb{R}\) 上的凸函数。如果 \(f\) 在 \(\mathbb{R}\) 上有界,证明,\(f\) 是常值函数。
-如果不是常值函数,也就是存在 \(f(a) = -f(b)\),那对于第三个点 \(c \to -\infty\) 一起比较斜率就知道 \(f(c)\) 无界了。
-设 \(f\) 是区间 \(I\) 上的严格凸函数。假设 \(f(x_0) \in I\) 是 \(f\) 的局部极小值,证明,\(x_0\) 是 \(f\) 唯一的整体极小值点,即对任意的 \(x \in I-\{x_0\}\),我们有 \(f(x_0) < f(x)\)。
-局部极小值的意思是存在一个邻域 \(J \subset -I\) 使得 \(f(x_0)\) -在其中最小。取 \(x_1 \in (x_0,x_0 -+\delta)\),\(x_2 \notin J\) 且 -\(f(x_2) \leq -f(x_0)\),比较三者的斜率知道不符合严格凸条件。
-\(I\) 是开区间。证明,\(f\) 是凸函数等价于对任意点 \(x_0 \in I\),存在实数 \(a \in \mathbb{R}\),使得对任意的 \(x \in I\),我们都有 \(f(x) \geqslant a(x - x_0) + f(x_0)\)。
-正推取 \(a = f'(x_0)\),反推考虑 -\(x_0\) -和左右两点组成的三点的斜率关系。
+证明,如果子代数 \(\mathcal{A}\subset +C(K)\) 是能够区分点的,\(\wedge\vee\)-封闭的并且包含所有的常数值函数,那么 +\(\mathcal{A}\subset C(K)\) +是稠密的。
+(Weierstrass--Stone定理)如果 \(\mathcal{A}\subset C(K)\) +是一个能区分点的子代数并且包含常值函数 \(1\),那么 \(\mathcal{A}\subset C(K)\) +是稠密的。
+
++Remark:我们还有一种复值函数的Weierstrass--Stone定理,在很多的场合有着重要的应用,有兴趣的同学可以自己查阅。
+
-
+
多项式函数 \(P(K)\) +在连续函数空间 \(C(K)\) +中是稠密的。
+给定以 \(2\pi\) 为周期的连续函数 +\(f\in C(\mathbb R)\)。证明,任给 \(\varepsilon>0\),总存在一个有限的三角级数
+\(T(x)=\sum_{-N\leqslant k \leqslant N} a_k +\cos(kx)+\sum_{-N\leqslant k \leqslant N} b_k \sin(kx)\)
+其中 \(N\) 是正整数,\(a_k,b_k\) 是实数,使得对任意的 \(x\in \mathbb R\),我们都有 \(|f(x)-T(x)|<\varepsilon\)。(提示:考虑 +\(C([0,2\pi])\) +和它的某个子代数)
+
转数环环友:你可以以任意顺序完成培养方案(
+ +虽然已经学过一遍初级版,这次速通是作为观点的补充和复习,但还是很虚的。
+说到这个任意顺序完成培养方案,摘一个 PIN 的前言(逃
+++事实上,我们所接触的大多国内优秀同学都直接或者间接地默认数学学习一定顺序,须得按部就班,层层递进,才能扎实地进步。这种想法本身没有错,但是数学的发展绝对不是线性的,知识也不存在先天的顺序。一个普遍被提及的例证就是从 +Newton 引入积分 (反流数术) 到 Cauchy +的极限理论被广泛接受中间至少有半个世纪的光景, +那个优秀的数学家层出不穷,利用还没有被严格化的积分理论作出了很多享誉后世的工作。
+数学学习不应该被课程设置 (甚至被其名称) +切割。比如说,所谓的曲线或者曲面的几何学、数学物理方程都可以称为 (多元) +微积分学习的好例题,很多微积分知识就是为了解决这样的问题应运而生的。微积分课程就应该学习和研究这样的例子,不能简单地将它们归结为是微分几何或者微分方程的内容而忽略。仅仅为了教学而刻意构造的各种例题长远来看有目光短浅之嫌。这种做法通常还会从心理上折射出胆怯的影子,以至于有同学误以为课程的顺序和难度有关联,“后面” +的课程比 “前面” 的课程困难。唯有正视,方能前行。
+
高二的时候我曾经备考过一阵子丘班 +(prototype),不过因为当年联赛翻车省三的原因(,连初审都没有通过。组队备考的五个人里只有我们的队长 +ycj +顺利去了北京,又通过了笔试,最终在面试中被刷掉了,他现在在上海理工大学,真的很可惜。cy +后来放弃了,安心备考 +CMO,拿了银牌,现在在华子读数学,太成功了!不过虽然秋季学期一同上了数值分析,我至今也没和他面基成功。xzx +和 wry +似乎分别去了西安交大和上海财大,和他们没有很熟,后来也没再联系了。
+同时,这一段自学给我留下了对数分深刻的心理阴影,和不知道怎么手选又问不明白并列成为了大一没有学数分,而是选了微积分 +A 的两大原因,也成为了我本科很可能延毕一年的众多原因之二(
+使用的教材是常庚哲、史济怀《数学分析教程》,速通讲义是北京大学数学分析讲义和一千零一页,前者是后者的子集,的确更友善一些,用于提点重点,感谢甘主任对速通事业的支持!习题册是谢惠民《数学分析习题课讲义》,不过我觉得应该来不及做太多。
+并不是打算写知识点,没什么必要,只是想在这里哔哔赖赖一下,或许会试着虚空使用 +Feynman +学习法?毕竟是速通,要快一些,不然下学期就寄了。发这一篇的主要目的是虚空被监督进度,毕竟我的效率实在是低下。
+按照欧老师的年终(粗略)统计,数分二和三课后加起来花了 210 +h,我打算速通到数分二为止,也就是整个寒假每天都在学的话,日均也要学 7 +h(。这显然是不可能的,毕竟我同时还有一些其他事务要做,比如点 R +的技能树、编写统推讲义、推 +SRT、以及准备缓考科目。最重要的是,我还得摸鱼和出去玩啊!但还是尽量试试看,学到哪算哪,够用就行(了吗?
+实数的构造
+从抽代出发,事情变得简单了很多
+2023 年 1 月 17 日,星期二,很冷还没有暖气。
+大一的时候报了 wxf 老师的微积分 +A,这一块他其实也讲了一些,但是并不够严谨,我听着有点痛苦。说实在的我就不喜欢他这个授课的方式,下放知识又不彻底,等于炫技,不如不要下放。
+结果因为他不查考勤,微积分 A2 还是选了他的,最后大翻车。
+这一次会更加严谨、耐心,并保持好奇。
+-
+
用域公理、序公理和 Achimedes +公理定义了实数域;整数和有理数可以用映射嵌入实数域,这个嵌入映射对于整数是单射。
+这个学过抽代之后倒是很好理解了,构造出域之后就有了最基本的三个元素 +\(0,1,-1\),把 \(n\) 个 \(1\) 加起来就是正整数 \(n\),考虑整数的分式域就是有理数域。实数域是一个特征为 +\(0\) +的域,这样构造出来的有理数域是它的最小子域,也即素域。
+为有理数定义了序关系 \(\frac{m}{n}>\frac{p}{q} \iff mq>np\) +之后, 就可以把序关系也嵌入到实数域里了,是成立的。
+\(\mathbb{Q} \subseteq +\mathbb{R}\),但是还没有从域的角度定义出 \(\mathbb{R} - \mathbb{Q}\) +里的元素,也就是无理数。仅仅是如上定义的话,一个所谓的实数域里完全可以只有有理数,也能满足序公理、域公理和 +Achimedes 公理,而我们想要一些其他的元素。比如说,\(\sqrt{2}\) 怎么定义?
+当然可以对 \(\mathbb{Q}\) +做关于多项式 \(x^2-2\) 的 Galois +扩域(暴论,我不是很清楚这两个理论体系到底谁先谁后,还是别这么干比较好),但是这样可以做出很多形式上不相同的域,比如熟知的 +\(\mathbb{Q} (\sqrt{2})\) 和 \(\mathbb{Q}[x] / +(x^2-2)\),虽然它们本质上是同构的,但序关系无从保障。所以还是换个方法,也就是后面的 +Dedekind 分割。
+确界原理的证明非常炫酷,我每次写完一遍都觉得非常牛逼,可惜后来只记得是用每次缩小一半的区间套证明,具体细节还是自己写不出来。
+但是这样得到的 \(sup X\) +是一个闭区间套的极限,并不好用。更加好用的定义是对于任意 \(\varepsilon >0\),存在 \(x \in X\),使得 \(x>sup X - +\varepsilon\)。通俗一些说,上确界再小一点点都不可以。
+如果反过来假设确界定理成立,闭区间套公理可以很容易地被证明,只要分别取 +\(\lbrace a_n \rbrace\) 的上确界和 +\(\lbrace b_n \rbrace\) +的下确界,夹出的区间就恰好是所有区间的交集。在已有序公理、域公理和 +Achimedes 公理的情况下二者是等价的。
+度量空间在数值分析课堂的引论里学过,当时在讲矩阵的范数如何定义,是从最普通的 +\(\mathbb{R} +^n\)讲起的,赞美包老师。虽然他这样根本不像在给数学系讲课,感觉有点照顾非数学系选课学生的意思。我的数分真是吃百家饭,这样也很好,多少消除一些曾经的心理阴影。
+对于度量空间 \((X,d)\),\(Y \subset X\) 是子集,如果对任意的 \(x \in X\) 和任意的 \(\varepsilon >0\) 都存在 \(y \in Y\),使得 \(d(y,x)< \varepsilon\),那么称 \(Y\) 在 \(X\) 上是稠密的。直观上来说,就是 \(X\) 上任意一个点都有 \(Y\) +上的一个点和它离得要多近有多近。举个例子的话,有理数和无理数在实数上都是稠密的,证明起来很简单,反复二分就可以了。
+然后就是线性空间的定义,印象里线性代数的最后一章就是学这个,当时不知道数域是什么,给我愁的,以为真的要把八条运算法则都背下来来证明一个东西是某个域上的线性空间,
+当时要是会抽代就好了。总之,\(F\) 是一个数域,\(V\) +是某一集合,满足一些运算法则的时候,三元组 \((V,+,\times )\) 是一个 \(F-\) 线性空间。
凸函数与不等式
+今天的数分就学到这里 +.jpg,内容大约是一周的量,还是有点少。明天再来.jpg
+2023 年 1 月 18 日,星期三,还是很冷但是稍微升温了一些。
-
-
试求所有的正数 \(a\),使得不等式 -\(a^x \geqslant x^a\) 对任意的 \(x > 0\) 都成立。
-\(x=a\) 是函数 \(f(x) = a^x - x^a\) -的一个零点,于是它也是一个极小值点,此处导数值为 \(0\) 且二阶导数为正。
-于是 \(a=e\)。
-证明如下不等式并给出等号成立的条件:对任意正数 $x_i $ 和 $t_i -\((\)i=1,,n\(),\)_{i=1}^n t_i = 1$,都有
-$( {i=1}^n t_i x_i )^{ {i=1}^n t_i x_i} _{i=1}^n x_i^{t_i -x_i} $
-两边取对数然后用 Jensen 不等式。
-证明Young不等式并给出等号成立的条件:对于任意正数 \(a,b\),任意的实数 \(p,q\),其中 \(\dfrac{1}{p} + \dfrac{1}{q} = 1\)(我们要求 -\(p\) 和 \(q\) 不是 \(0\) 或者 \(1\)),我们有
-\(ab \leqslant \frac{a^p}{p} + -\frac{b^q}{q}, \ \ \text{如果}~p > 1; \ \ ab \geqslant \frac{a^p}{p} -+ \frac{b^q}{q}, \ \ \text{如果}~p < 1\)
-这个高中竞赛的时候就证明过,咕了。
-证明 Holder 不等式并给出等号成立的条件:设 \(x_i,y_i \geqslant 0\),其中 \(i = 1,\cdots,n\),\(p,q \neq 0,1\),其中 $ + = 1$,我们有
-\(\sum_{i=1}^{n} x_i y_i \leqslant -\left(\sum_{i=1}^{n}x_i^p\right)^{1/p}\left(\sum_{i=1}^{n}y_i^q\right)^{1/q}, -\ \text{如果}~p > 1; ~\sum_{i=1}^{n} x_i y_i \geqslant -\left(\sum_{i=1}^{n}x_i^p\right)^{1/p}\left(\sum_{i=1}^{n}y_i^q\right)^{1/q},\ -\text{如果}~p < 1\)
-在上述不等式中,如果 \(p < -0\),我们假设 \(x_i > -0\)。(这个不等式的结论比证明重要得多,同学们可以参考其它资料来写下证明)
-高中竞赛的时候也证明过,咕了。
+要开始构造实数了!用的是 Dedekind 分割。这个我也在 wxf 的微 A +课上听过,但他讲得并不认真,仅限念了一遍定义。后一节课课前有同学提问说,为什么一左一右两个集合就能代表一个实数呢?他不是很愿意理会的样子,反问说你是不是补退选进来的所以没听过第一节课啊,一只羊为什么代表 +\(1\) +呢,两个集合怎么不能代表一个数呢。
+他可能是觉得这个问题太 trivial +了吧,也或许只是当天心情不好而已,然而提问的同学看起来还是没理解的样子,还平白无故被敲打了一下,就茫然地坐下了。Anyway,在这之后我对这个课堂的印象就不是很好,后续也很少再去上课了。只是觉得,为什么不能好好讲清楚道理呢,就告诉同学理由是从几何直观的角度来看,把实数轴任意截断的一点都是实数,有这样的一个定义不就好了吗。当然,当然,应该是我吹毛求疵了,他可能真的只是当天心情不好,所以不太想解释,后来我也没怎么再听过他上课,不清楚还有没有类似的状况,可能属于是不小心碰到了一个极端情况。
+另外,单是讲过这个有什么意思呢,不说 Dedekind +分割满足序公理所以确实可以定义出实数,也不拿来用一下,就莫名其妙放一个定义在这里,课后又让做题目,感觉是在炫技。后来我也看过一部分他的讲义和回放,挺多莫名其妙的安排都有点像炫技,就彻底放弃跟进度,自己单开了。不过确实也没人逼你选他的微积分课,接受不了的话,换别的老师的课堂就好了,或许是个伪命题吧。
+虽然大多数同学都吹 wxf +讲课有多好,但我其实相当怀疑他们有一部分并没有听明白课堂内容,觉得老师讲的内容很高深,自己吹捧老师的话会显得很厉害而已。另外听说 +wxf +的答疑确实很认真,或许大家说他好是指这一部分吧,还是指他喜欢在课堂上和群里讲笑话?PPT +和讲义是准备得挺认真的,可惜我并不觉得设计得好,
+感觉白认真了。总之我是不太喜欢这种不彻底也不成体系的高阶知识下放,或许它自有意义,带大家了解一下也好。当然,和我相反的典型就是 +wl 他们,是真的学得很好,也喜欢 wxf +的课堂,所以我这些话很可能只是弱者的托词而已。也是啊,我觉得他讲得不好,大一的时候干嘛不自己去看一千零一页,而是单开去拟合微积分往年习题了呢,乐。弱者的牢骚暂且发到这里,下面继续说点正经的。
+这下三纸无驴了。注意 Dedekind +分割的断点是有理数时,会把它归到右侧区间里,这是为了保证左侧无最大元。一般把左侧的区间记为 +\(X\),也称这个分割代表的实数是 \(X\)。
+Dedekind +分割是满足序公理的,在这里需要先定义这一分割的序关系。对于实数 \(X,Y\),如果 \(X +\subsetneq Y\),则有 \(X<Y\)。这个很好理解,\(X\) 比 \(Y\) 短一些,也就是 \(X\) 的端点在 \(Y\) 左侧,即 \(X<Y\)。再证明这个序关系满足序公理的五条要求即可。
+有了这样一个对实数的描述,就可以写出确界定理的第二种证明,也很炫酷。
+现在我们有了一个叫做实数的东西(Dedekind +分割),它离组成实数域还差很远,因为域上的两种运算,加法和乘法,尚未被定义。我们来定义一下,然后先证明它是良好定义的,不会出 +bug。这指的是,对于两个实数的运算结果也是 Dedekind +分割,且满足若干加法公理,并且是加法良定义的。
+加法定义:\(X+Y=\lbrace x+y | x \in X,y \in +Y \rbrace\),零元素为 \(\bar{0} = X_0 = +\lbrace x \in \mathbb{Q} | x<0 \rbrace\)。
+乘法定义:恒等元为 \(\bar{1}= X_1 = \lbrace +x \in \mathbb{Q} | x <1 +\rbrace\),需要根据正负性来分类定义。这个是 PIN +的作业,我写作业去了。
利用(高阶)导数的信息刻画函数(低阶导数)
-在本习题中,我们把函数 \(f\) 也记为 -\(f^{(0)}\)。
+Summary
+总之,在第一章里面,于我而言实际上是在抽代的基础上,为一个特征为 +\(0\) +的域在其素域的基础上添置了一些多余元素,让它也满足序公理和 Achimedes +公理,这就符合实数域的定义了。为了使用的方便起见,又用 Dedekind +分割确定了实数域元素的具体形式,把它和日常使用的实数域对应起来。这一过程中为了磨合一些 +bug,完成了不计其数的良定义确认,我愿称之为夜话团圆。
+素域就是熟知的 \(\mathbb{Q}\),由恒等元和零元素造出的整数环与其分式域构成。在此基础上,对素域元素做了一个序关系的定义,并嵌入实数域中,证明了它是符合序公理和 +Achimedes +公理的。这说明这一做法可行,下一个任务就是具象化实数域的元素,也即实数。
+第二个创举是用 Dedekind +分割构造所谓的实数的确切形式,这里用了一个几何的观点,就是把实数轴折断,把左半边的集合 +\(X\) +称为一个实数,通俗意义上来说,它代表的实际上是断点处的那个真正的实数。我们对创造出的这个实数进行了集合意义上的序、加法和乘法的定义。于是全体 +Dedekind 分割真正意义上构成了一个满足序公理和 Achimedes +公理的域,这便和我们日常使用的实数没有差别了。
+此外,还有一个很有趣的东西叫做确界原理,它描述的是一个有上/下界的集合必有上/下确界。围绕它有三个证明,前两个是证明确界原理和区间套公理等价,第三个是用 +Dedekind +分割作出的确切的实数来证明确界原理的确成立。用区间套公理推确界原理的证明最酷炫,希望我以后还能记得怎么做,以及它的细节。
+抽代真好用,赞美。我建议大家都和我一样,先学代数再学分析(什么啊
+学到这里,学过的几门数学课已经被充分利用过了。微积分自不必说,抽代上面说过了,高代的线性空间定义也出现过了,赋范空间和度量空间在数值分析的引论课上听过,甚至写习题写到可数理论,给了我一点小小的离散数学震撼,我以前一直以为这课没用,白学了。往后云端漫步了一点,在数分 +II 里找到了上学期在初概里了解过的 \(\sigma +-\)代数,其实属于是测度知识了,但把它当成高等概率论知识也未尝不可嘛(。另外我的初概学得稀烂,可以近似认为是在统计推断里学会的,也算是做了贡献(,不然就它还没出镜啦。
+什么叫做可以以任意顺序修完培养方案啊。我现在也理解为什么说数分难了,大一入学第一节课就学这玩意的话,反正我一下子受不了,会很想退学。不过这以前是 +Yau 班讲义来着,难怪我不配(
+梦话:可数集与不可数集
+2023 年 1 月 19 日,星期四,v 我 50,谢谢。
+在第一章继续逗留了一会,想补充一些可数(或者说可列)的东西。
+刚拿到习题的时候以为是离散数学,后来发现还是不太一样。这一部分先由 +PIN +的习题展开,顺便理一下我在离散数学里学到的东西,发现两边在用不太类似的定义逻辑,接合在一起之后也有些 +happily ever after 了。
+终于在香蕉空间找到了开源的页面,省了很多打字的心力,赞美!以及发现原来最初编写这份讲义的是曾经访问了我博客的 +zrc 学长,由可爱的 _rqy +完成了香蕉空间上的工作,世界真小,qwq,感谢前辈做出的贡献。
+课后习题:可数集与不可数集
+令 \(\mathbb{N}\) +表示自然数的集合(包括 \(0\))。\(X\) 是一个集合,如果存在单射 \(f\colon X\rightarrow \mathbb{N}\),我们就称 +\(X\) 是可数的。如果 \(X\) 不是可数的,我们就称它是不可数的。
-
-
我们假设 \(f\in -C\bigl([0,1]\bigr)\),\(g\) 在 -\([0,1]\) 上可导且 \(g(0) = 0\)。如果存在常数 \(\lambda \neq 0\),使得对任意的 \(x\in [0,1]\),都有 \(|g(x)f(x) + \lambda g'(x)| \leqslant -|g(x)|\), 证明,\(g(x) \equiv -0\)。
-\(f\) 在 \((-1,1)\) 上二阶可导,\(f(0) = f'(0) = 0\)。如果对任意的 \(x\in (-1,1)\),都有 \(|f''(x)| \leqslant -|f(x)|+|f'(x)|\),证明,\(f(x) -\equiv 0\)。
-设 \(f\) 在 \(\mathbb R\) 上二阶可导,满足 \(f(0) = f'(0) = 0\), 且存在正实数 \(C\) 使得, 对所有的 \(x\in \mathbb R\), 有 \(|f''(x)| \le -C|f(x)f'(x)|\)。证明,\(f(x) \equiv -0\), \(\forall x \in \mathbb -R\)。
-\(n\) 是正整数,\(f\) 在 \(\mathbb -R\) 上 \(n\) 阶可导,\(f(0) = f'(0) = \cdots = f^{(n-1)}(0) = -0\)。如果 \(C\in\mathbb{R}_{>0}\) 和 \(\ell \in \mathbb{Z}_{\geqslant -0}\),使得对任意 \(x\in \mathbb -R\) 都有 \(|f^{(n)}(x)| \leqslant -C|f^{(\ell)}(x)|\),证明,\(f(x) \equiv -0\)。
-\(n\) 是正整数,证明,多项式 -\(\displaystyle P(x) = \sum_{k=0}^{n+1} -C_{n+1}^k (-1)^k (x-k)^n\) 是 \(0\)。
-考虑 \(x^i\) 的系数,全都是 \(0\)。(好怪
-\(f\in C^\infty(\mathbb -R)\)。假设存在正实数 \(C\),使得对任意 \(n \in \mathbb{Z}_{\geqslant 0}\) 和任意的 -\(x \in \mathbb R\),我们都有 \(|f^{(n)}(x)| \leqslant C\)。
+证明,有限集是可数的。
+Trivial.
+证明,可数集合的子集是可数的。
+Trivial,原映射的“一部分”,也就是它的导出映射对于剩余的元素仍然为单射。
+证明,如果 \(X\) +是可数集,那么我们总可以将 \(X\) 写成 +\(X=\{x_1,x_2, x_3, +\cdots\}\)(即可以把 \(X\) +中的元素用自然数来标号)。(我们可以从一个开始一个一个的数下去把这些元素都罗列出来,所以叫做可数集)
+存在单射 \(f\colon X\rightarrow +\mathbb{N}\),考虑 \(Im f\) +是一个自然数集合,由其一般性知可以表示为 \(\{ +1,2,3,... \}\)。
+证明,有理数 \(\mathbb{Q}\) +是可数集。
+可以按分子分母绝对值之和写个大三角,不过我在知乎上看到过一个很酷的证明,摘录如下:
++
不难证明 \(\mathbb {N}\times \mathbb +{N}\) 是可数集(考虑双射 $(n,m)^n(2m+1)-1 $),从而 \(\mathbb Z\times(\mathbb Z\backslash +\{0\})\) 可数。
+由 Cantor-Schröder–Bernstein 定理即得证。
+
+证明,可数个可数集合的并集也是可数集,也就是说,如果 \(X_1,X_2, \cdots, X_n, \cdots\) +都是可数集合,那么它们的并集 \(\displaystyle +\bigcup_{n\geqslant 1} X_n\) +也是可数集合。(提示:这是一个需要记住的经典证明,请查阅参考书或者网络)
+排矩阵,列大三角。
+\(X\) 是可数的,映射 \(f\colon X\rightarrow Y\) +是满射。证明,\(Y\) 是可数的。
+存在单射 \(g \colon Y \to X\) 和 +\(h \colon X \to \mathbb N\),其复合 +\(g \cdot h \colon Y \to \mathbb N\) +也是单射。
+按照以下步骤证明 \(\mathbb R\) +是不可数的(同学们可以查阅一个用所谓对角线法则的经典证明,我们的证明基于区间套原理):
-
-
证明,给定任意的 \(x_0 \in \mathbb -R\),我们可以(以 \(x_0\) -为中心)将 \(f(x)\) 在 \(\mathbb R\) 上展开为无穷Taylor级数,即\(f(x) = \sum_{k=0}^\infty -\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k, \qquad \forall x \in \mathbb -R\)
-只要证明这个级数是逐点收敛的,实际上 \(|f(x) |\leq C \exp(x-x_0)\)。
-\(E\subset \mathbb R\) -是一个无穷集并且有界。证明,如果 \(f\) -在 \(E\) 上的取值都是零,那么 \(f\equiv 0\)。
+若 \(J\subset \mathbb R\) +是闭区间并且它的长度 \(|J|>0\)。证明,对任意的 \(x\in \mathbb R\),总存在闭区间 \(I\),使得 \(I\subset J\),\(|I|>0\) 且 \(x\notin I\)。
+用实数 \(x\) 的 Dedekind +分割定义,取 $ I = J X^ $,只要证明它的长度非 \(0\),trivial.
+证明,如果 \(\{x_1,x_2,\cdots\}\) 是 \(\mathbb R\) +的一个可数子集,那么存在闭区间套 \(I_1\supset +I_2 \supset \cdots\),使得对任意的 \(n\),\(x_n \notin +I_{n}\)。
+取 \(I_1\) 为 \(X_1 ^\prime\) 的长度大于 \(0\) 的闭区间,按上一问的方法构造闭区间 +\(I_2\),使得 \(I_2 \subset I_1\),\(|I_2|>0\) 且 \(x_2\notin I_2\)。类似地构造 \(I_3,I_4,...\) 即可。
+证明,\(\mathbb R\) 不可数。
+反证法,设 \(\mathbb R\) 可数,也即 +\(\mathbb R\) 可以表示成 \(\mathbb R =\lbrace x_1,x_2,... \rbrace\) +的形式。因此存在上述的闭区间套,使得闭区间的交集里不含有 \(\mathbb R\) +的任何一个元素,是一个空集。这和区间套公理是矛盾的。
+嗯?这就证明完了?好美妙!
-假设 \(f\in -C^2\bigl((0,1)\bigr)\),\(\displaystyle\lim_{x\to 1^-}f(x) = -0\)。如果存在 \(C>0\),使得对任意 \(x\in (0,1)\),我们都有不等式 \((1-x)^2|f''(x)| \leqslant -C\)。证明,\(\displaystyle\lim_{x\to -1^-} (1-x)f'(x) = 0\).
-
函数的重根
-上传者注:本题题设条件下可以举出很多反例,建议读者将可微条件全部改为足够高阶连续可微,或者光滑。
-如果 \(f\) 在 \(x_0\) 的一个邻域内满足 \(f(x) = (x-x_0)^r g(x)\),其中 \(r \in \mathbb{Z}_{\geqslant 0}\),\(g\) 在 \(x_0\) 处连续并且 \(g(x_0) \neq 0\),那么我们就称 \(x_0\) 为 \(f\) 的 \(r\)-重根。我们注意到,\(0\)-重根并非根。
--
-
假设 \(x_0\) 是 \(f\) 的 \(r\)-重根,其中 \(r\geqslant 1\)。证明,如果 \(g(x) = \dfrac{f(x)}{(x-x_0)^r}\) 可微,那么 -\(x_0\) 是 \(f'\) 的 \((r-1)\)-重根。
-\(f'(x) = (x-x_0)^r g'(x) - rg(x) -(x-x_0)^{r-1}\)。
-假设 \(f\) 为 \(\mathbb R\) 上 \(n\) 阶的可微函数。证明,如果 \(f(x) = 0\) 有 \(n+1\) 个不同的实根,那么 \(f^{(n)}(x) = 0\) 至少有一个实根。
-不停用 Lagrange 中值定理。
-\(f\) 为 \(\mathbb R\) 上的可微函数。假设 \(f(x) = 0\) 按重数计算恰有 \(r\) 个实根,也就是说,\(f(x) = 0\) 有 \(s\) 个相异的实根 \(x_1, x_2, \cdots, x_s\),它们的重数分别为 -\(r_1, r_2, \cdots, r_s\) 并且 \(r_1+r_2 + \cdots + r_s = r\)。证明,\(f'(x) = 0\) 按重数计至少有 \(r-1\) 个根。
-\(f'(x)\) 对于相异的实根 \(x_1, x_2, \cdots, x_s\),它们的重数分别为 -\(r_1-1, r_2-1, \cdots, r_s-1\) -,并且在 \(x_1, x_2, \cdots, x_s\) -之间用 Lagrange 中值定理还有 \(s-1\) -个根,于是共有 \(r-1\) 个根。
-假设 \(f\) 为 \(\mathbb R\) 上 \(n\) 阶的可微函数。证明,如果 \(f(x) = 0\) 按重数计恰有 \(n+1\) 个实根,那么 \(f^{(n)}(x) = 0\) 至少有一个实根。
-归纳。
+证明,如果 \(X\) +是不可数集,\(A\) 是 \(X\) 的可数子集,那么 \(X-A\) 是不可数的。
+反证法,trivial.
+证明,任意的长度不为 \(0\) +的区间(无论开或闭)都是不可数的。
+反证法,否则它是可数的,可以表示成 $X= x_1,x_2,... $ +的形式。于是也可以按前述方法构造出其上的一个区间套 \(X \supset X_1 \supset X_2 \supset +...\),满足除了 \(X\) +之外的区间都是闭区间,且闭区间的交集是空集,这是矛盾的。
+证明,复数 \(\mathbb{C}\) +是不可数的。
+反证法,如果复数集是可数的,它的子集 \(\mathbb R\) 也一定可数,矛盾。
+假设 \(\mathcal{I}\) 是 \(\mathbb R\) +上的某些开区间组成的集合,它满足如下性质:对任意的 \(I,J \in \mathcal{I}\),\(I\neq J\),那么它们的交集是空集,即 \(I\cap J=\emptyset\)。证明,\(\mathcal{I}\) 是可数集。
+习题没有答案,于是我只能做一些不负责任的暴论:
+回到定义,想找一个从 \(\mathcal I\) +到 \(\mathbb N\) 的单射 \(f\)。只要考虑在 \(R_ +\) 上的全体集合,对任意的 \(I \in \mathcal I\),取 \(f(I)\) 为区间 \(I\) +覆盖的最小整数,这些整数一定两两不同,也就构成了一个到 \(\mathbb N\) 的单射。
+但是不一定每个区间都覆盖一个整数,所以我想做个不负责任的操作:如果 +\(I = (a,b)\) +不覆盖整数,则将所有区间的端点关于 \(a\) 的距离放大,直到放大后的区间 \(I ^ \prime =(a,b ^ \prime)\) +能覆盖住某一个整数,从左至右对每一个区间都这样操作。
积分
-2023 年 2 月 8 -日,星期三,学了半天积分结果配套的作业题还是导数题,摸不着头脑.jpg
-Riemann 积分
--
-
阶梯函数是最简单的一类积分函数,它的积分值对于任意相容的分划都是相等的。这是一个很美妙的证明,用到了一个简单的逻辑:$$ -和 \(\sigma '\) 的并 \(\sigma \cup \sigma '\) -是二者的一个加细;如果 \(\sigma_1\) 是 -\(\sigma _2\) -的一个加细且它们都是相容的分割,那么二者的积分值相等;因此 \(\sigma\) 和 \(\sigma '\) 的积分都和 \(\sigma \cup \sigma '\) -的积分相等,由任意性可知任意划分的积分都相等。
-阶梯函数的积分是满足线性性的,它还满足一些看起来很显然但其实证明也不是很难的性质,略了。
-为了扩大可以“积分”的函数的种类(目前只有阶梯函数积分),试一下用阶梯函数积分逼近一般的连续函数。
-一个技术性的引理(定义),实际上类似于极限的 \(\delta - \varepsilon\) -描述和点列描述法:
--
-\(I=[a,b]\) 是有界闭区间,\(f\colon I\rightarrow \mathbb R\) -是函数,如下命题是等价的:
+找到了作者在源代码注释里留下的彩蛋:
-
-
对任意的 \(\varepsilon>0\),存在两个阶梯函数 \(F_\varepsilon\colon I \rightarrow \mathbb -R\) 和 \(\Psi_\varepsilon\colon I -\rightarrow \mathbb R\),使得对任意的 \(x\in I\),都有
-\(\big|f(x)-F_\varepsilon(x)\big|<\Psi_\varepsilon(x)\) -并且 \(\int_I \Psi_\varepsilon -<\varepsilon\)
-存在两个阶梯函数的序列 \(\{f_n\}_{n\geqslant 1} \subset -\mathcal{E}(I)\) 和 \(\{\psi_n\}_{n\geqslant 1} \subset -\mathcal{E}(I)\),使得对任意的 \(x\in -I\),都有
-\(\big|f(x)-f_n(x)\big|<\psi_n(x)\) 并且 $ -_{n}_I _n =0$
+证明,不能用可数条直线覆盖平面,即如果 \(\ell_1,\ell_2,\cdots\) 是平面 \(\mathbb{R}^2\) 上可数条直线,那么 \(\displaystyle \bigcup_{k\geqslant 1}\ell_k\neq +\mathbb R^2\)。
+一个圆心在 \((x_0,y_0)\) +处,半径为 \(r>0\) 的闭圆盘 \(\overline{B_r(x_0,y_0)}\),指的是:
+\(\overline{B_r(x_0,y_0)}=\{(x,y)\mid +(x-x_0)^2+(y-y_0)^2\leqslant r^2\}\);
+证明,不能用(无论可数个还是不可数个)两两不相交的闭圆盘(半径大于零)(圆心和半径可以变化)覆盖 +\(\mathbb +R^2\),使得两个不同的圆盘至多有一个点是重合的。
+纯属娱乐,对后面学习分析并无帮助。
满足二者之一时,称 \(f\) -可以被阶梯函数逼近,是区间 \(I\) 上 -Riemann 可积的函数。\(\mathcal R (I)\) -表示全体 \(I\) 上 Riemann -可积的函数。此时可以定义 \(f\) 的 -Riemann 积分:\(\int_{I}=\int_{a}^b\colon -\mathcal{R}(I)\rightarrow V, \ \ f\mapsto \lim_{n\rightarrow \infty} -\int_a^b f_n\)。
-关于这个定义为什么是良定义的问题,首先要证明上述极限存在,再证明 -\(f\) 的积分定义不依赖于具体的 \(\lbrace f_n \rbrace\) 和 \(\lbrace \psi_n -\rbrace\),实际上它们都是简单的阶梯函数,所以由定义都是容易证明的。
-研究一下 \(I\) 上的 Riemann -可积空间 \(\mathcal R (I)\) -的性质,由于我之前根本没学会这个,还是写细一点。
-比较容易证明的几个性质是:\(\mathcal R -(I)\) 是实数域上的线性空间,\(\mathcal -R(I)\) 上的函数都有界(注意 \(I\) -还是一个闭区间的情况,这里还没有研究到广义积分),阶梯函数都在 \(\mathcal R (I)\) 中,Riemann -可积函数取绝对值也还是 Riemann 可积的,乘积也是 Riemann 可积的。
-其他的性质有:\(\mathcal R (I)\) -包含所有的 \(C(I)\) -上函数(利用一致连续性手动切出逼近的阶梯函数),有限维的情况。
--
\(C(I)\subset \mathcal{R}(I)\)。
-假设 \(f\in C(I)\),根据 \(f\) 的一致连续性,对任意的 \(\varepsilon>0\),存在 \(n\in\mathbb{Z}_{\geqslant -1}\),使得对任意的 \(x,y\in -I\),当 \(|x-y|<\dfrac{1}{n}\) 时,我们有 \(|f(x)-f(y)|<\frac{\varepsilon}{b-a}\)。此时,我们令
-\(F(x)=\sum_{k=1}^n -f\bigl(a+k\frac{b-a}{n}\bigr)\mathbf{1}_{[a+(k-1)\frac{b-a}{n},a+k\frac{b-a}{n}]}(x)\),
-其中,\(\mathbf{1}_{[a+(k-1)\frac{b-a}{n},a+k\frac{b-a}{n}]}\) -是示性函数。这个 \(F(x)\) -显然是阶梯函数。由一致连续性,我们知道
-\(\big|f(x)-F(x)\big|<\Psi_\varepsilon(x)\equiv -\frac{\varepsilon}{b-a}\),所以,\(\int_a^b \Psi_\varepsilon(x) -=\varepsilon\)。从而,\(f\) -是Riemann可积的函数。
-
+如果 \(X\) 是有限集,证明,存在 +\(\varphi\colon X\rightarrow Y\),使得 +\(\varphi\) 是双射。
+如果 \(X\) 是可数集,证明,存在 +\(\varphi\colon X\rightarrow Y\),使得 +\(\varphi\) 是双射。
\(\sigma_1,\sigma_2\in -\mathcal{S}\) 是两个分划。证明,对任意的 \(\varepsilon>0\),总存在分划 \(\sigma\),使得 \(\sigma\prec \sigma_1\),\(\sigma\prec \sigma_2\) 并且它的步长 \(|\sigma|<\varepsilon\)。
-对 \(\sigma_1 \cup \sigma_2\) -再加细就可以了。
-考虑在 \(V\) -中取值的阶梯/简单函数的空间 \(\mathcal{E}(I)\),证明,这是 \(\mathbb R\)-线性空间并且积分算子 \(\displaystyle\int_{a}^b\colon -\mathcal{E}(I)\rightarrow V\) -是良好定义的(不依赖于分划的选取)并且是线性映射,其中积分的定义方式与函数在 -\(\mathbb R\) -中取值时的方式一致。据此,用阶梯函数逼近的方式定义在 \(V\) -中取值的Riemann可积的函数。你不需要写下细节但是你应该对照笔记研究原来证明的每一步。
-假设 \(f\colon I\rightarrow -\mathbb{R}^n\),其中 \(f_i\) 是 -\(f\) 的每个分量。那么 \(f\in \mathcal{R}(I)\) 当且仅当对每个分量 -\(f_i\) 我们都有 \(f_i\in \mathcal{R}(I)\)。特别地,当 \(f\colon \mathbb R\rightarrow \mathbb{C}\) -时,我们有 \(\displaystyle \int_a^b f = -\int_a^b \mathbb Re f+i\int_{a}^b \Im f\),其中 \(\mathbb Re f\) 和 \(\Im f\) 分别为 \(f\) 的实部和虚部。
-试证明积分的区间可加性:假设 \(a<c<b\),那么对于任意的 \(f\in \mathcal{R}(I)\),我们有 \(f\) 在 \([a,c]\) 和 \([c,b]\) 上的限制都是阶梯函数,并且 \(\int_{a}^b f =\int_{a}^c f+\int_c^b -f\)。
-证明,对于任意两个分划 \(\sigma\) 和 \(\sigma'\),它们所对应的Darboux上下和满足
-\(\underline{S}(f;\sigma)\leqslant -\overline{S}(f;\sigma')\)
-据此证明,如果 \(f\in -\mathcal{R}(I)\),就有 \(\displaystyle\lim_{|\sigma|\rightarrow -0}|\underline{S}(f;\sigma)-\overline{S}(f;\sigma)|=0\),即对任意的 -\(\varepsilon>0\),一定存在 \(\delta>0\),对任意的分划 \(\sigma\),只要 \(|\sigma|<\delta\),我们就有 \(|\underline{S}(f;\sigma)-\overline{S}(f;\sigma)|<\varepsilon\)
-\(f\in -\mathcal{R}(I)\)。证明,改变 \(f\) -在有限个点上的取值所得到的函数仍是Riemann可积的并且积分与 \(f\) 的相同。
-\(f\in C([a,b])\)。假设对任意的 -\(x\in I\),我们都有 \(f(x)\geqslant 0\) 并且存在点 \(x_0 \in I\) 使得 \(f(x_0) > 0\)。 证明,\(\displaystyle\int_a^b f > 0\)。
-(不定积分的分部积分公式:对计算不定积分有用)假设 \(f,g\in C^1(I)\),那么,我们有
-\(\int f'\cdot g=f\cdot g-\int f\cdot -g'\)
-(不定积分的变量替换公式:对计算不定积分有用)假设 \(\Phi\colon \mathbb R\rightarrow \mathbb R\) -可微,\(f\) 是连续函数,那么
-\(\int (f\circ \Phi)\Phi'=\int -f\)
+考虑 \(X\) 的子集的集合 \(\mathcal{F}=\{A \subset X\mid X'\cup +h(A)\subset A \}\)。证明,\(\mathcal{F}\) 非空。
+证明,如果 \(A\in +\mathcal{F}\),那么 \(X'\cup +h(A)\in \mathcal{F}\)。
(Dini定理)假设 \(K\subset \mathbb -R^n\) 是紧子集,\(f_n\colon -K\rightarrow \mathbb R\) 是一列连续函数,它们逐点地收敛到连续函数 -\(f\colon K\rightarrow \mathbb -R\),即对每个 \(x\in -K\),我们都有 \(\displaystyle -\lim_{n\rightarrow \infty}f_n(x)=f(x)\)。证明,如果 \(\{f_n\}_{n\geqslant 1}\) -是上升的函数列(即对任意 \(x\in K\) 和 -\(n\),我们都有 \(f_n(x)\leqslant f_{n+1}(x)\)),那么 \(f_n\) 一致收敛到 \(f\)。(参考荆公子的某次习题课)
-考虑区间 \(I=[-1,1]\)。我们通过归纳的方式定义一族多项式函数:
-\(P_0(x)=0, \ \ -P_{n+1}(x)=P_n(x)+\frac{1}{2}(x^2-P_n^2(x))\)
-证明,对任意的 \(n\) 和 \(x\),我们都有 \(0\leqslant P_n(x)\leqslant P_{n+1}(x)\leqslant -|x|\)。
-证明,绝对值函数 \(|x|\) 在 -\(I=[-1,1]\) -上可以被多项式一致地逼近,即对任意的 \(\varepsilon>0\),存在某个多项式函数 -\(P_\varepsilon(x)\),使得 \(\displaystyle \sup_{x\in -[-1,1]}\big||x|-P_\varepsilon(x)\big|<\varepsilon\)。
+证明,\(A_0\in\mathcal{F}\)。
+证明,\(X'\cup +h(A_0)=A_0\)。
+令 \(B_0=X-A_0\)。证明,\(f(A_0)\cap g^{-1}(B_0)=\emptyset\) 并且 +\(f(A_0)\cup g^{-1}(B_0)=Y\)。
+我们定义映射 \(\varphi\colon +X\rightarrow Y\):对于 \(x\in +X\),我们要求 \(\varphi(x)=\begin{cases}f(x), \ &\text{如果} +x\in A_0;\\g^{-1}(x), \ &\text{如果} x\in +B_0.\end{cases}\)
+证明,这是双射。
对任意的 \(0\leqslant k\leqslant -n\),我们定义 \(p_{n,k}(x)=\displaystyle{n \choose -k}x^k(1-x)^{n-k}\)。证明,\(\displaystyle \sum_{0\leqslant k \leqslant -n}p_{n,k}(x-\frac{k}{n})^2=\frac{x(1-x)}{n}\)。
-任意给定 \(f\in -C([0,1])\),我们定义 \(B_{f,n}(x)= -\displaystyle\sum_{0\leqslant k \leqslant n}f\bigl(\frac{k}{n}\bigr){n -\choose k}x^k(1-x)^{n-k}\)。对 \(x\in -[0,1]\),证明,
-\(|f(x)-B_{f,n}(x)|\leqslant \sum_{k=0}^n -\bigl|f(x)-f\bigl(\frac{k}{n}\bigr)\bigr|p_{n,k}(x)\)
-(用Bernstein多项式逼近连续函数)任意给定 \(f\in C([0,1])\),证明,对任意 \(\varepsilon>0\),总存在 \(n\),使得 \(\|f-B_{f,n}\|_\infty -<\varepsilon\)。
+在离散数学里,更确切一点讲,在集合论里,介绍了一种关系,叫做等势。这一概念由 +Cantor +提出,用来解决这样的一个困惑:为什么完全平方数貌似比正整数少很多,但是它们却可以一一对应?如何比较两个无穷集合谁的元素多,谁的元素少,谁更“无穷”?
+等势被定义为:如果集合 \(X\) 和 +\(Y\) +之间如果存在双射,那么称二者等势,利用 Schroeder-Bernstein +定理可知如果有单射 \(f\colon X\rightarrow +Y\) 和单射 \(g\colon Y\rightarrow +X\),那么 \(X\) 和 \(Y\) 等势,写作 \(X \approx Y\)。实际上有 \(\mathbb N \approx \mathbb Q \approx \mathbb +Z\),等等。
+另外一个定义是集合的基数,记为 \(card(X)\),精确地测量集合的某些性质。我们定义 +\(card(X) \leq card(Y)\) 等价于有单射 +\(f\colon X\rightarrow +Y\),因此由等势的结论,有 \(card(X)=card(Y)\) 等价于 \(X \approx +Y\)。与此同时,我们希望对这个虚无缥缈的概念做一些基本的规定,比如说把某些特殊的集合的基数作为标尺,来衡量其他集合的基数大小。我们选取了 +\(card(\mathbb N) = \aleph _0\),\(card(\mathbb R) = \aleph _1\) +作为这样的尺度。
+当然,对于有穷的集合,它的基数就是它的元素个数,此时称为有限基数,否则称为无限基数,我们不对有限基数多做讨论。上述的“尺度”中,\(\aleph _0\) +是最小的无限基数,它也大于所有的有限基数。
+基数理论的一个用处在于,可以用来衡量无穷集合的可数性。一个集合 +\(X\) 满足 \(card(X) \leq \aleph _0\) +等价于它是可数的,也就是说,可数集 \(X\) 要么是有限集合,要么基数是 \(\aleph _0\),可以和 \(\mathbb N\) +一一对应,也就是习题里面提到的,可数集可以表示成 \(X = \lbrace x_1,x_2,... \rbrace\) +的形式。
假设 \(\mathcal{A}\subset C(K)\) -是非零的线性子空间。如果对任意的 \(f,g\in -\mathcal{A}\),它们的乘积 \(f\cdot g -\in \mathcal{A}\),我们就把 \(\mathcal{A}\) 称作是 \(C(K)\) 的一个子代数。证明,\(P(K)\) 是 \(C(K)\) 的子代数。
-非零的线性子空间 \(\mathcal{A}\subset -C(K)\) 是闭子代数,也就是说如果 \(\{f_k\}_{k \geqslant 1}\subset -\mathcal{A}\),\(f_k\) -一致收敛到 \(f\),那么 \(f\in \mathcal{A}\)。假设常值函数 \(1\in \mathcal{A}\),证明,如果 \(f\in \mathcal{A}\),那么 \(|f|\in \mathcal{A}\)。(提示: 利用 -W3)
-假设 \(\mathcal{A}\subset C(K)\) -是子集,如果对任意的 \(x,x'\in -K\),\(x\neq x'\),都存在 -\(f\in \mathcal{A}\),使得 \(f(x)\neq f(x')\),我们就称 \(\mathcal{A}\) 是能够区分点的。证明,\(P(K)\) 是能够区分点的。
-假设 \(f,g\in C(K)\)。证明,函数 -\(f\wedge g (x)=\min\{f(x),g(x)\}\) 和 -\(f\vee g (x)=\max\{f(x),g(x)\}\) -都是连续的。
-假设 \(\mathcal{A}\subset C(K)\) -是子集,如果对任意的 \(f,g\in -\mathcal{A}\),\(f\wedge g, f\vee g \in -\mathcal{A}\),我们就称 \(\mathcal{A}\) 是 \(\wedge\vee\)-封闭的。证明,\(\overline{P(K)}\) 是 \(\wedge\vee\)-封闭的,其中 \(\overline{P(K)}=\bigl\{f\in -C(K)\bigm|\text{存在}\{f_k\}_{k\geqslant1}\subset P(K), -f_k\text{一致收敛到}f\bigr\}\) 为 \(P(K)\) 在 \(C(K)\) 中的闭包。
-我们现在假设 \(\mathcal{A}\subset -C(K)\) 是 \(\wedge\vee\)-封闭的,并且对任意的 \(\alpha,\beta \in \mathbb R\),任意的 \(x,y \in K\),\(x\neq y\)(我们此时假设 \(K\) 至少含有两个点)都存在函数 \(\varphi\in A\),使得 \(\varphi(x)=\alpha\),\(\varphi(y)=\beta\)。
-我们通过下面的步骤来证明 \(\mathcal{A}\subset C(K)\) -是稠密的(即对任意给定的连续函数 \(f\in -C(K)\),对任意的 \(\varepsilon>0\),总存在 \(\varphi \in \mathcal{A}\),使得 \(\|\varphi-f\|_{\infty}<\varepsilon\)):
+- 实际上,对于集合 \(X,Y\),序关系 +\(card(X) \leq card(Y)\) +成立等价于有单射 \(f\colon X\rightarrow +Y\)。由此就可以验证这个关系满足序公理了。 +
- 固定 \(x_0\in X\),对任意的 \(y\in K\),我们选取 \(\varphi_y\in \mathcal{A}\),使得 \(\varphi_y(x_0)=f(x_0)\) 并且 \(\varphi_y(y)=f(y)\),这样我们得到一族 \(\{f_y\in \mathcal{A}\mid y\in -K\}\),据此,对每个 \(y\in -K\),可以定义 \(U_y=\{z\in K\mid -\varphi_y(z)>f(z)-\varepsilon\}\)。证明,存在有限个 \(y_1,\cdots,y_m\in K\),使得 \(K\subset U_{y_1}\cup \cdots \cup -U_{y_m}\)。 -
- 证明,\(\varphi_{x_0}=\displaystyle\sup_{x\in -K}\{\varphi_{y_1}(x),\cdots, \varphi_{y_m}(x)\}\in \mathcal{A}\) -并且对任意的 \(x\in K\),我们都有 \(\varphi_{x_0}(x)-f(x)>-\varepsilon\)。 -
- 证明,存在 \(\varphi \in -\mathcal{A}\),使得对任意的 \(x\in -K\),都有 \(|\varphi(x)-f(x)|<\varepsilon\)。 -
证明,如果子代数 \(\mathcal{A}\subset -C(K)\) 是能够区分点的,\(\wedge\vee\)-封闭的并且包含所有的常数值函数,那么 -\(\mathcal{A}\subset C(K)\) -是稠密的。
-(Weierstrass--Stone定理)如果 \(\mathcal{A}\subset C(K)\) -是一个能区分点的子代数并且包含常值函数 \(1\),那么 \(\mathcal{A}\subset C(K)\) -是稠密的。
+- 答案是可以的,但还是到实分析里再学吧(
课后习题: +Schroeder-Bernstein 定理
+实际上,PIN 还有一道习题 Schroeder-Bernstein +定理。这道题就不打算写了,学不完了 +.jpg,我把它轻轻放在这里,作为后面补充的引子:
+假设 \(X\) 和 \(Y\) 是两个集合,映射 \(f\colon X\rightarrow Y\) 和 \(g\colon Y\rightarrow X\) 都是单射。我们令 +\(X'=X-g(Y)\)。
+-
+
Darboux 上下和
-这是一个刻画 Riemann 可积的实数值函数的方法。
-当然,刻画 Riemann -可积函数的方式一共有四种,彼此等价,具体就不说了,可见:Read -More
-梦话:终于找到积分的作业在哪了但是还没写
-积分定义的补充与扩展
-我们总假设 \(I=[a,b]\subset \mathbb -R\) 是一个有界闭区间,\(V\) -是一个赋范线性空间。
+从现在开始,对 \(X\) +不加任何的限制。 我们令 \(h\colon X\rightarrow +X\) 是复合映射 \(h=g\circ +f\)。
-
-
思考题:多项式逼近和Weierstrass--Stone定理
-我们要证明如下著名的定理:任意给定有界闭区间 \(I=[a,b]\) -上的连续函数,我们总是可以用一个多项式来足够好地逼近它。更精确地说,给定 -\(f\in C([a,b])\),对任意的 \(\varepsilon>0\),存在多项式 \(P_\varepsilon\),使得 \(\displaystyle \sup_{x\in -[a,b]}|f(x)-P_\varepsilon(x)|<\varepsilon\),即若用 \(P([a,b])\) 表示 \([a,b]\) 上多项式函数组成的空间,则 \(P([a,b])\) 在度量空间 \(C([a,b])\) 中稠密(\(C([a,b])\) 上用的范数是 \(\|f\|_\infty=\displaystyle \sup_{x\in -[a,b]}|f(x)|\))。
-Dini定理及应用
+我们定义\(A_0=\bigcap_{A\in +\mathcal{F}}A=\{x\in X\mid\)对任意的\(A\in \mathcal{F},\)都有\(x\in A\}\)。
-
-
区间上的情形
-这一部分中,我们假设 \(I=[0,1]\),\(n\) 是正整数。
+根据上述,我们证明了 Schroeder-Bernstein 定理:如果有单射 \(f\colon X\rightarrow Y\) 和单射 \(g\colon Y\rightarrow +X\),那么存在着两个集合之间的双射 \(\varphi\colon X\rightarrow Y\)。
+离散数学复习:等势与基数
-
-
--Remark:用概率论的观点,\(x\in -[0,1]\) 给定,Bernstein多项式逼近的的方法讲的是概率测度
-\(\mu_x=\displaystyle\sum_{k=0}^n {n -\choose j}x^k(1-x)^{n-k}\delta_{\frac{k}{n}}\) 的极限是Dirac测度 -\(\delta_x\)。
-
紧集上的情形
-从此往后,我们假设 \(K\subset \mathbb -R^n\) 是紧集,\(C(K)\) 是 \(K\) 上的实数值连续函数所构成的线性空间,用 -\(P(K)\) 表示 \(K\) 上多项式函数组成的空间(即形如 \(\displaystyle \sum_{|\alpha|\leqslant m} c_\alpha -x^\alpha\) 的函数,其中 \(m\) -是正整数,\(\alpha\) -是多重指标,请参见关于多重偏导数的课堂笔记)。
+但是,离散数学没有解答的是,为什么基数可以比较大小?我们可以看到 +\(\aleph _0\),$_1 $ +的出现,就代表了基数的取值未必是实数域上的子集。那么它的取值集合上的序关系是怎么定义的,是否满足序公理?
-
-
但是为什么任意两个基数都可以比较大小呢?在 \(\mathbb R\) +之外还有更多稀奇古怪的集合,以前可能想象不出来,学了抽代之后一想这些真的毛骨悚然,它们都可以互相将基数拿来比较大小吗?
-
-
-+Remark:我们还有一种复值函数的Weierstrass--Stone定理,在很多的场合有着重要的应用,有兴趣的同学可以自己查阅。
-
这样再看 Cantor 定理,也就是实数集 \(\mathbb R\) +不可数这一条定理,写成基数的形式就等价于,\(\aleph _1 = card(\mathbb R) > \aleph +_0\)。
-
-
多项式函数 \(P(K)\) -在连续函数空间 \(C(K)\) -中是稠密的。
-给定以 \(2\pi\) 为周期的连续函数 -\(f\in C(\mathbb R)\)。证明,任给 \(\varepsilon>0\),总存在一个有限的三角级数
-\(T(x)=\sum_{-N\leqslant k \leqslant N} a_k -\cos(kx)+\sum_{-N\leqslant k \leqslant N} b_k \sin(kx)\)
-其中 \(N\) 是正整数,\(a_k,b_k\) 是实数,使得对任意的 \(x\in \mathbb R\),我们都有 \(|f(x)-T(x)|<\varepsilon\)。(提示:考虑 -\(C([0,2\pi])\) -和它的某个子代数)
+我们在离散数学里定义了 \(card(\mathbb +N) = \aleph _0\) +是最小的无限基数,却没有说明为什么最小。也就是没有说明,为什么可数的无限集是无限集里面最小的。所以,暂时只能从已经证明出的 +\(\mathbb R\) 不可数,来证明 \(\aleph _1 > \aleph _0\) +这两个特殊的无限基数之间的大小关系。
+Cantor 给出了另外一个证明。记 \(\mathcal P(X)\) 为 \(X\) 的幂集合,也即 \(X\) +的全体子集(包括空集和自身)构成的集合。
+引理:如果 \(X\) 非空,那么 \(card(\mathcal P (X)) > +card(X)\)。使用反证法证明,否则二者相等,存在 \(\mathcal P (X)\) 和 \(X\) 之间的一一对应 \(f \colon X \to \mathcal P (X)\)。记 \(A = \lbrace x \colon x \notin f(x) +\rbrace\),证明 \(f^{-1} (A)\) +和 $ A$ 不等即可。
+而 \([0,1]\) +上的实数用二进制表示后,\(0\) +的位置构成了自然数集的子集;自然数的任意一个子集都对应一个实数。因此 +\(R \supset \mathcal P (\mathbb +N)\),有 \(card([0,1]) = card (\mathbb +R) \geq card(\mathcal P (\mathbb N)) > card(\mathbb N) = \aleph +_0\),实数集不可数。
最后,虽然看起来有些夜话团圆了,但基数还是很抽象。希尔伯特 23 +问的第一问连续统假设即是关于基数的一个看似很基本的问题,问 \(\aleph _0\) 和 \(\aleph _1\) +之间是否还有别的基数。这一问题被证明和 ZFC +公理体系互相独立,目前仍不知真伪。
+极限
+极限,数列和级数
+2023 年 1 月 20 +日,星期五,睡前本来想看极限结果去写了可数集的补充内容,字数翻了个倍。
+这样下去的话,大概要每一个章节开一篇文章写比较合适了。昨天改标题的时候差点把文件名改了,想了想那样的话原有的两条评论显示不出来,不是很妙。或许有迁移 +issue +之类的方法,没有试过也没有研究,不清楚能不能做到,多一事不如少一事。
+好像没什么可写的,这一部分都和微积分 A +学的内容差不多。不过讲义里的一些观点很有意思,我把原文摘录下来:
--【上海市出入境管理局】感谢您申请陆家嘴签证。非常遗憾的通知您,由于您过去三个月没内有 -City Walk, Gap Hour 及 Camping 记录,我们在 Salomon, Lululemon, Tesla, -Omakase 及 Apple Store -均未查询到您的消费记录并且查到您在蜜雪冰城消费过多杯柠檬水,故本次签证被拒。
+然而,根据极限的定义,如果有极限,我们要先验地知道极限是什么才可以利用定义来证明。事实上,要想猜到这个极限的值是很困难的。通过这个例子,我们发现极限的定义对于判断极限是否存并没有太大的帮助。
+从概念上而言,极限的定义在哲学意义上有一个先天的缺陷:判断数列收敛与否,应该由数列本身所决定而不需要依赖于外在的信息,比如说事先知道极限是什么。换句话说,我们想要内蕴地来考虑极限问题。这种看法和思考方式对数学的学习是大有裨益的。
再来点申请文学:
-2024 Spring 申请选手,background 不强,身份证不是 310 -开头的,目前住在浦西比较远的地方,主要的几个指标都消费不起。唯一的优势是高中有过张江高科的三年学签,虽然偏了些但到底在浦东,还和陆家嘴都在二号线上,就是不知道过了几年了还有没有用,求问证明材料还需要提交当时的成绩单吗?最近是三个月内正好买了 -iPad 所以在 Apple Store 买过 Lanota -曲包,数额不大,其他消费记录无。打算趁这个寒假抽几个 Gap Day 刷一些 City -Walk/Ride 记录,年后申请陆家嘴签证,方便开学前去滨江骑行道骑车(
-说人话:摆烂一天,出去骑车玩儿了(
- -2024.02.08
-我以前没有在上海市区骑过车。一方面是高考之后才学会骑车,后来在上海的时间就少了,另一方面你沪的共享单车比北京贵一倍,我感觉都很难有慢下来看风景的想法(,自己家里没自行车,有车也不方便带去市区,不过搬到普陀之后可以考虑,而且我毕业之后还挺想把现在的车送回家的。还有就是一直听说市区骑行管得很严交警很多,路况也不是很好,更不可能像在北京一样还能随便逆行(好孩子不要学。
-但内环以内适合逛的就那点地方,如果想去好几个地方玩的话地铁三块钱三块钱地刷也不是很值。何况这是冬天,现在还不骑车的话难道夏天骑吗,夏天我可是会买一张一日票无论多近多绕都坐地铁的(x
-哪里可以骑车
-在我高中还不会骑车的时候就听说过高中同学骑车逆行惨遭被交警拦下罚款 50 -的惨案,后来也知道淮海中路自行车禁行的名梗,所以今天去市区骑车还是有那么一点点小紧张,主要还是担心在毫不知情的情况下被罚款。当然最后没有,但十字路口交警的密度还是让我大开眼界,在他们身边停下的时候还听到对讲机里在说有电瓶车沿着某条路逆行了帮忙拦一下什么的,搞得我远远看到穿黄绿马甲的人就害怕。
-所以怎么判断哪里不能骑车?
+想起来数值分析学过的一些方法,比如对牛顿法失败的方程,也即有重根的方程重做某种牛顿法的时候,需要先知道重根是几次才能做出来,笑死。不过按照这个思路还是做出了很多改进方法,像魔法 +qwq
+此处“内蕴地”考虑极限问题,指的就是后面的 Cauchy +收敛原则:一个数列收敛等价于它是柯西列。
+++在数学中, 对于每一个数学对象 (例如极限) , +我们会例行公事般地考虑它的一些常见的性质. 比如说, +这个对象最基本的例子是什么, 这种对象是否存在, +如果存在的话它是否具有唯一性, 它的子对象和商对象 (如果有的话) +都具有什么性质 (比如说遗传了原来的对象的什么性质) , +这个对象的可计算性以及在特定映射下的行为等等. 作为例子, +我们刚刚见到一个点列的子对象 (即子列) 遗传了点列的收敛性 (和有界性) . +尽管这是一种八股文一般的讨论方式 (Bourbaki 学派是这种方式最忠实的实践者) +, 但是是非常有效率的一种学习和记忆方式, +我们在课程上会尽量的按照这种习惯来学习. 特别要强调的是, +每一个定义大家都应该搞清楚最基本的例子是什么。
+
你知道那个叫概念的东西是什么嘛.jpg
+然后是学微积分的时候讲过就过了,不会再用的一个定理:
-
-
如果能记住哪些路段禁行就没有问题啦!上海有 -124 条道路禁止骑行,也不是很多嘛(迫真
-我今天 random
walkride -的过程中经过了长宁、静安、黄浦、普陀、徐汇,反正我是分不清哪个区有哪些的(
-禁行路段路口都会有标识,但其实整得我很紧张,一个是远远看到交警就有点慌,也担心看漏了。而且因为眼神不太好今天还看混了下面这两个,一开始以为右边的也是自行车禁行所以多绕了些路,实际上只是禁三轮车和摩托车(尴尬挠头
-但是警用摩托车似乎可以走诶。(
- -
-骑行导航能通行的地方一般是可以骑车的,一般也是准确的毕竟禁行的路就那几条。但我更喜欢 -random walk -而非提前确定好去哪里以及查路线,另外需要看导航也很麻烦。
-有自行车道的地方可以骑自行车(大概吧?
-但市区很多年岁比较久远的窄马路(点名梧桐区)分不出自行车道来,骑行体验也不是很好(下详)。没必要用一个必要条件做判断来限制自己(
-最后也是最粗暴的方法,如果前面有车(不是共享单车的话就很稳了)跟着骑就行了(
+(Bolzano–Weierstrass 的列紧性定理) 任意有界的实数序列 \(\{x_n\}_{n\geq 1}\) +必有单调收敛的子列。
+Cauchy 判别法(略)
+注意 Cauchy +判别法仅能在实数列中使用,因为其证明需要关于有界的论述。
总的来说不是很难,我今天唯一路过的禁行路段就是大名鼎鼎的淮海中路,这个连我都本来就知道(。
-骑行体验
-除了第一次在这边骑车担心上错路,看到交警会有点紧张之外,其实路况也不算很好。一个是很多地方没有自行车道,只能在机动车道上和车挤一挤,另外老马路凹凸不平的很多,即使看起来稍微平整的也可能很颠,共享单车没有减震器本身也不行。今天在江苏路买了两盒鲍师傅然后去骑车玩,一路上颠得我感觉在徐汇的时候海苔肉松小贝已经变成了肉松小贝海苔,到长宁恐怕已经是小贝肉松海苔了。
-但梧桐区确实很漂亮,有很多又安静风景又好的小路。像武康路本身就是建筑保护区,愚园路这种网红景点路上人和车都很多,但不远处的余庆路和天平社区也都有非常漂亮的小洋楼,路上几乎就没人。但我好像有点改不掉一不留神就开始快骑的习惯,一条小路五六百米很快就到头了,才发现错过了一些,又不愿意掉头了。
-另外开个骑行卡会从容很多,不用寸止停车也不担心骑慢了倾家荡产。说到底我今天突然开始骑车玩就是因为发现投放了一批青桔新车,车筐里有一块钱开七天骑行卡的活动广告。
-
青桔活动这四个字看起来怎么这么像青结活动(
-风景
-不完全是骑车的时候看到的,总之我都很喜欢。
-
走不出的万航渡路,而且前两天美赛的一个具体案例分析我们就选了 -Indonesia,现在看到就想吐(对不起
-
我做了一个违背祖宗的决定:我去看武康大楼了(
-楼对面拍照的人很多,位于武康路和淮海中路(自行车禁行)路口,但我其实没觉得这个楼多好看诶,像火车头(我自裁。但是这张的天空颜色很漂亮,紫色柔柔地晕染开来的感觉,我也梦想融入这永恒。

这张看起来快到天平社区了,我超级喜欢这个小灯笼,远看像小柿子一样,还会在风里轻轻地
-匀速
-转动,喜庆又不土气(说的就是你啊某些路上挂的超大灯笼。后面的树枝上面缠了红色的彩灯,像红梅一样(逆风如解意容易莫摧残.mp3),特别漂亮。
这就不得不提天津站附近某些树上的彩灯了(鞭尸,不是缠上去的而是披上去的,敷衍就算了,之前看到这个的时候真没绷住(
-
晚上去吃饭在旁边店里看到的小玩意,古灵精怪的,好有意思哦。
-就是贵。
-路线
-
太混沌了,我回来之后按照感觉上走过的地方标了一下,至少它在存在路线重复的情况下是一个连通图,吧?
-比如说华山路的一些路段我就在不同的行程里骑了好几遍,尤其是交通大学站附近的那一小段,精神 -SJTU -人实锤(但这是徐汇校区而已.jpg)。今天还验证了二维随机游走是常返的,怎么也走不出万航渡路,江苏路和华山路,虽然后两条本质上是一条路(
-美观起见我把地图横过来了,右下角是指北针。
-2024.02.10
-今天沿着铜川路骑了一趟,从岚皋路下地铁然后一路骑到了定边路地铁站,没有再往嘉怡路走,就回家了。
-一开始扫了一辆旧车,大约是到真光公园的时候觉得骑着费劲,停下来换了一辆新的。除了新之外,座椅的确比以前的要软一些。这么阔气的原因还是七天单车卡没有用完,快到期了,急急急。
-路线
-可能是居民区加上在外环和中环之间的原因,这边交警密度没有市区那么恐怖,心情挺好的(?
-铜川路就是铜川路嘛,还要什么路线图(
-
2024.02.11
-今天还是沿着铜川路骑车,果然还是跟我妈一起骑车更有那个成就感,因为共享单车也可以拉她好远(x。去环宇城吃山石榴,然后在地下二层逛了山姆会员店。我才知道这个店它只有会员才能进去,而会员甚至每年要交 -60 -块钱,还是我妈这位尊贵的会员紧急送我一个亲友卡才把我带进去,然后我进去看每个人都像在看六十块钱。
-严谨一点来说,我看两个人一起逛的就像每个人三十块钱,三个人每个人二十块钱,四个人十五,五个人十二,六个人十块,不是葫芦娃一家出来逛街的话也不太会更多了,看来这个会费设置是很有道理的。
-感觉线下逛过山姆之后申请签证的成功率又高了一些(x
-线路图和昨天的一样,不再放一个了(
-]]>我不会 MATLAB,又懒得学,就选了 Python。反正作业就是造轮子,也不能用 -MATLAB 的函数,那 Python 不亏。
- -声明:本文更新时间均在数值实验作业截止日期后,详情可查询 commits -记录,不存在任何抄袭或协助抄袭现象。
-线性方程组直接解法
-一开始还是有点虚的,NumPy 和 Pandas -都是前学后忘,于是第一次作业拖到周末才写,意外地顺利。
-反正就是不停地写循环,略烦。
-\(LDL^T\) 法
+另外,把级数的部分和视为一个数列的话,也可以用数列的性质来判断无穷级数是否收敛。也即,对于无穷级数 +\(x_1 + x_2 + ...+x_n +...\),考虑 +\(X_i = x_1 + x_2 + ... + +x_i\),于是有无穷级数收敛等价于实数序列 \(\{x_n\}_{n\geq 1}\) 收敛,可以使用 Cauchy +判别法或定义判别的方式进行判断。考虑一种特殊的级数:
+-
+
\(\{a_n\}_{n\geqslant 1}\) +是递减的正实数的数列并且 \(\displaystyle\lim_{n\rightarrow +\infty}a_n=0\)。假设级数 \(\sum_{k=1}^\infty\) \(a_k\) 发散。那么,对任意 \(x\in \mathbb R\),我们可以选取一组正负号 +\(\iota_k\in \{\pm 1\}\),使得级数 +\(\sum_{k=1}^\infty \iota_k a_k\) +收敛并且 \(\Sigma_{k=1}^\infty \iota_k +a_k=x\)。
+或许算是后面习题里的 Riemann +重排定理的一个变式,总之证明是一样的。
+
实际上,学级数的时候讲了很多判别法,无外乎绝对收敛和比较收敛。原理上都是 +Cauchy 收敛的变式。
+指数函数和三角函数的级数定义
+2023 年 1 月 22 日,星期日,吃着素感觉脑子转不起来了(x
+我们假装自己只会用整数和有理数,然后用级数和极限分别定义了 \(e\),不仅在级数角度有熟知的 \(\displaystyle\lim_{n\rightarrow \infty}(1+ +\frac{1}{n})^n=e\),级数的表示是 \(\sum +_{k=0} ^{+\infty} \frac{1}{k!} = +e\)。同样的,我们也想假装只会用多项式,来定义指数函数和三角函数。
-
-
算法就是 \(LDL^T\) -法。书上啥都有。
-比较痛的一点是,这个方法为了提高效率把 \(L\) 和 \(D\) 直接存储在 \(A\) -里了,但是最后计算误差的时候需要调用原值 \(A\),所以做分解之前应该先备份一个原矩阵。向量 -\(b\) 的备份同理。
-实现如下:
--# 任务一:改进的平方根法求解线性方程组
import numpy as np
from numpy.linalg import norm
n = 32
H = 1./(np.arange(1, n + 1)+np.arange(0, n)[:,np.newaxis]) #构造n阶Hilbert矩阵
xtrue = np.ones((n, 1))
x = np.ones((n, 1))
b = H.dot(xtrue)
#待定系数法计算LDL^t分解
K = H.copy()
c = b.copy()
for j in range(0, n):
for k in range(0, j):
K[j, j] = K[j, j] - K[j, k] * K[j, k] * K[k, k]
for i in range(j + 1, n):
for k in range(0, j):
K[i, j] = K[i, j] - K[i, k] * K[j, k] * K[k, k]
K[i,j] = K[i, j] / K[j, j]
#写出L和D的具体形式
L = np.zeros((n, n))
D = np.zeros((n, n))
for i in range(0, n):
L[i, i] = 1
for j in range(0, i):
L[i, j] = K[i, j]
D[i, i] = K[i, i]
#解方程Ly=b
y = np.zeros((n, 1))
y[0] = c[0]
for i in range(1, n):
for j in range(0, i):
c[i] = c[i] - K[i, j] * y[j]
y[i] = c[i]
#解方程DL^tx=y
x = np.zeros((n, 1))
x[n-1] = c[n-1] / K[n-1,n-1]
for i in range(n-2, -1, -1):
x[i] = y[i] / K[i,i]
for j in range(i+1, n):
x[i] = x[i] - K[j,i] * x[j]
#输出结果
print('相对残量为: %.4f'%(norm(b - np.matmul(H, x)) / norm(b)))
print('相对误差为: %.4f'%(norm(x - xtrue) / norm(xtrue)))输出结果:
--相对残量为: 0.0000
相对误差为: 111.3149残量为 \(0\) 说明分解正确。考虑到 -\(Hilbert\) -矩阵是个病态矩阵,这个值还算可以接受。虽然真值是一个分量全为 \(1\) 的 \(32\) 阶向量,而数值解从第 \(7\) -个分量开始就大量出现绝对值是两位数的情况了。
-\(LDL^T\) 分解从结果来看仍然是 \(LU\) 分解的一种变形,但在本实验中,利用 -\(LU\) -分解得到的数值解各分量量级偏小,甚至达到 \(10^{-5}\) 级别。输出结果为:
--相对残量为: 0.0000
相对误差为: 73385.0585相对误差大了两个量级,说明对于对称矩阵来说 \(LDL^T\) 分解是更好的选择。
-我在做数值实验的过程中先解决了 \(LU\) 分解,回头又做了 \(LDL^T\) -分解,因此二者的结果不能很好地匹配也造成了不小的困难..
+定义指数函数 \(\exp\colon \mathbb R +\rightarrow \mathbb R\) 如下:\(x\mapsto \exp(x)=e^x=\sum_{k=0}^\infty +\frac{x^k}{k!}\)。可以看到这个形式和 \(e\) 的定义是很相似的。
+首先需要验证这是良定义的,也就是对于任意的 \(x \in \mathbb R\),有 \(\exp(x)=\sum_{k=0}^\infty \frac{x^k}{k!}\) +是一个收敛的无穷级数。证明的话,实际上是从某一位处截断,对后面的无穷项进行一个放缩控制。
+虽然我们熟知对任意的 \(x,y\in \mathbb +R\) 有 \(e^{x+y}=e^x\cdot +e^y\),但是这在级数层面是不那么明显的。
+上述性质对于复数 \(x\) +也成立,从而引出对三角函数的定义。
+利用指数映射 \(\exp(z)\) +可以定义正弦和余弦函数:
+\(\cos z =\frac{e^{iz}+e^{-iz}}{2} = +\sum_{k=0}^\infty \frac{(-1)^k x^{2k}}{(2k)!}\),
+$ z ={e{iz}-e{-iz} 2i} = _{k=0}^$。
+换句话说,目前 \(\sin(z)\) 和 \(\cos(z)\) +使用级数来定义的。至于其余三角函数,是根据 \(\cos z ,\sin z\) +的和差积商定义的。特别地,有 Euler公式:\(e^{iz}=\cos z + i \sin z\)。
+所以,三角函数完全可以被代数地定义,只用无穷项的多项式,不需要用到三角形。级数实际是沟通代数和几何的重要工具。我们可以用上述两个公式和已知的指数函数性质,证明出三角函数的众多性质,例如平方和为 +\(1\),等等。
\(LU\) 法
+Summary
+这一部分最大的贡献是定义出了 \(e\),指数函数和三角函数。不同于之前的视角,一千零一页中介绍了一个内蕴的判别角度,即从数列本身的性质出发推出其自身是否收敛,得出了重要的 +Cauchy 判别法。当然,Cauchy +判别法的使用场景限于实数,在其他的距离空间上未必成立。当然,极限还有其他的求法,例如夹逼方法,上下极限,定义法。
+与此同时,回忆了一些级数的内容,而级数本质上还是数列。级数这一部分在微积分里是放在微积分 +A(2) +的最后一章介绍的,感觉很不合理,实际上完全可以在极限的地方就讲,不过没有必要,另外可能也是为了引出 +Fourier +变换。总之,有了两组级数函数之后,对于中学里已知的内容的使用就可以更加大胆一些了。
+梦话:既然习题没有答案那我就胡说八道了
+2023 年 1 月 23 +日,星期一,其实我不喜欢在初学(?)的时候做没有答案的习题,anyway +还是写一写。
+Riemann 重排定理
+证明下面有趣的定理:如果实数项级数 \(\displaystyle\sum_{n=1}^\infty a_n\) +收敛但不绝对收敛,那么可以将级数重新排列,使得重排后的级数可以收敛到任意事先指定的 +\(\alpha\in \mathbb +R\cup\{-\infty,+\infty\}\)。假设 \(\varphi\colon \mathbb{Z}_{\geqslant 1}\rightarrow +\mathbb{Z}_{\geqslant 1}\) 是正整数到自身的双射,令 \(b_k = a_{\varphi(k)}\),序列 \(\{b_k\}_{k\geqslant 1}\) 被称为是 \(\{a_n\}_{n\geqslant 1}\) 的一个重排,级数 +\(\displaystyle\sum_{k=1}^\infty b_k\) +被称为是级数 \(\displaystyle\sum_{n=1}^\infty +a_n\) 的一个重排。
+我们将 \(\{a_n\}_{n\geqslant 1}\) +中的非负项(\(\geqslant +0\))的全体按照它们在 \(\{a_n\}_{n +\geqslant 1}\) 中的先后次序排列得到序列 \(c_1,c_2,c_3,...\);类似地,将 \(\{a_n\}_{n \geqslant 1}\) 中的负项(\(<0\))按原顺序排列得到序列 \(d_1,d_2,d_3,\cdots\)。
-
-
我感觉最难的是从
-.mat文件里载入矩阵...\(LU\) -法,学过线代就能做,我大一上学期的 C++ 大作业里还写这个了..
-实现如下:
+证明,\(\displaystyle\lim_{n\to \infty} +c_n = 0\),\(\displaystyle\lim_{n\to +\infty} d_n = 0\)。
+Trivial,它们分别是原序列 \(\{a_n\}_{n\geqslant 1}\) +的两个子列,收敛结果和原序列相同。
+证明,\(\displaystyle\sum_{n=1}^\infty +c_n = +\infty\),\(\displaystyle\sum_{n=1}^\infty d_n = +-\infty\)。
+Trivial,反证法假设否则有 \(\displaystyle\sum_{n=1}^\infty c_n = +C\),且有 \(\displaystyle\sum_{n=1}^\infty +a_n=A\),\(A,C \in \mathbb +R\),那么有 \(\displaystyle\sum_{n=1}^\infty d_n = A-C \in +\mathbb R\),级数绝对收敛。矛盾。
+证明: 对任意 \(\alpha \in \mathbb +R\),存在级数 \(\displaystyle\sum_{n=1}^\infty a_n\) +的一个重排 \(\displaystyle\sum_{k=1}^\infty +b_k\),使得 \(\displaystyle +\sum_{k=1}^\infty b_k = \alpha\)。
+不妨设 \(\alpha +>0\)。正项是发散的,于是存在一个 \(n_1\) 使得 $ c_1 + c_2 +...+ c_{ {n_1} } +< c_1 + c_2 +...+ c_{ {n_1} }+c_{ {n _1} + 1}$。
+取 \(\delta _1 = c_1 + c_2 +...+ c _{n_1}+c +_{n _1 + 1} - \alpha >0\),由负项是发散的,于是存在一个 \(m_1\) 使得:
+$d_1 + d_2 + ... +d _{ {m _1} } > -_1 d 1 + d_2 + ... +d +{ {m _1} +1 } $。再取 \(0 < \delta _2 += d_1 + d_2 + ... +d _{m _1 } + \delta _1 < \delta +_1\),此为一次操作。
+每做一次操作,\(\delta\) +都会相应地减小,始终非负。于是有 \((c_1+...+c +_ {n_1 +1 }) + (d_1+...+d _{m _1})+...\) 是一个收敛到 \(\alpha\) 的重排级数。
+证明: 存在级数 \(\displaystyle\sum_{n=1}^\infty a_n\) +的一个重排 \(\displaystyle\sum_{k=1}^\infty +x_k\),使得 \(\displaystyle +\sum_{k=1}^\infty x_k = +\infty\)。
+我不是很确定啊,但是我打算徒手捏一个:取一个固定的实数 \(M>0\),每一次操作分别从正的部分和负的部分,取一段 +\(c_i + ... + c_{i+k}\) 和 \(d_j + ... + d _{j+l}\) 使得其和大于等于 +\(M\)。于是每一次操作得到的小段和都大于等于 +\(M\),最后的级数和是发散的。
# 任务二:实现按列存储的JKI型LU分解 |
类似地,注意算法虽然是在 \(A\)
-上进行的,但在程序中需要保留 \(A\)
-的原值来计算相对误差,因此在函数中使用的应该是 \(A\) 的复制,也就有了
-A=B.copy() 这一步。
输出结果:
-relerr = 0.0000 |
相对误差接近于 \(0\),说明实验是成功的。
-后记
-不是,这玩意不是我后来咕咕了没再写,而是布置过一次作业之后就再也没有了(
-本来说是基本每一讲后面都有数值实验的,结果不知道是老师咕咕还是助教咕咕,总之是并没有再布置过实验,少了很多乐趣。之前看过贵系数值分析的资料 -Repo,两边的风格还是很不一样的。
-就这么草率地结束了..
-]]>其实是在课上同步写笔记体验很不错,dwl -老师的风格一如既往的稳健,课堂节奏正好。在课上敲笔记总比摸鱼好。
- -Lecture 1
-吹水,然后讲了点基本概念。
-多元数据的组织
-对于多元数据,常见的形式是一个 population 中的样本个体(称为 -item)有不同的项,每个 item 呈现出 p 个 variable 的取值。我们每次在 -population 中抽样会取出 \(n\) 个 -item,实际上获得了 \(np\) 个数据。
-一般用矩阵组织二元数据,以随机变量作为列元素,把 population 中的 item -作为横行。也就是说 \(n\) 个 item 各自有 -p 个随机变量项目的情况下,可以把它组织成 \(n -\times p\) 尺寸的表格:
-| - | Variable 1 | -Variable 2 | -... | -Variable i | -... | -Variable p | -
|---|---|---|---|---|---|---|
| Item 1 | -\(x_{11}\) | -\(x_{12}\) | -... | -\(x_{1i}\) | -... | -\(x_{1p}\) | -
| Item 2 | -\(x_{21}\) | -\(x_{22}\) | -... | -\(x_{2i}\) | -... | -\(x_{2p}\) | -
| ... | -... | -... | -... | -... | -... | -... | -
| Item j | -\(x_{j1}\) | -\(x_{j2}\) | -... | -\(x_{ji}\) | -... | -\(x_{jp}\) | -
| ... | -... | -... | -... | -... | -... | -... | -
| Item n | -\(x_{n1}\) | -\(x_{n2}\) | -... | -\(x_{ni}\) | -... | -\(x_{np}\) | -
实际上就是一个 \(n \times p\) -大小的矩阵,每个 \(X_{ji}\) -都可以视作随机变量。因此,每一次从 population 中随机抽样出 \(n\) 个 -item,都能得到一个不同的多元数据矩阵作为 observed data,在 multivariate -statistics 中,observed data 一般是矩阵。
-更本质地,可以把一个随机矩阵视为 \(n\) 个随机向量,每个随机向量代表了一个 item -的具体分量数据。并且可以认为这 \(n\) 个 -items 是彼此独立的(\(n\) -次独立的取样),于是可以认为 joint distribution 是 \(n\) 个 PDF 之积。
-描述性统计量
-老生常谈了捏。对于上述的 observed data,可以纵向观察各个 variable -的性质。
+Cesaro 求和极限
+设 \(\{a_n\}_{n\geqslant 1}\) +为实数序列,我们定义算数平均值序列 \(\displaystyle\sigma_n = \frac{a_1 + a_2 + \cdots + +a_n}{n}\),其中 \(n=1,2,3,\cdots\)。
+-
+
假设 \(\displaystyle\lim_{n\to \infty} +a_n = a\)。证明,\(\displaystyle\lim_{n\to \infty} \sigma_n = +a\)。
+Trivial.
+构造一个不收敛的序列 \(\{a_n\}_{n\geqslant 1}\),使得 \(\displaystyle\lim_{n \to \infty} \sigma_n = +0\)。
+\(a_ i = (-1) ^i\)。
+是否存在序列 \(\{a_n\}_{n\geqslant +1}\),使得对任意 \(n\geqslant +1\),都有 \(a_n > 0\) 并且 +\(\displaystyle\limsup_{n\to \infty} a_n = +\infty\) 然而 \(\displaystyle\lim_{n\to +\infty} \sigma_n = 0\)?
+\(a_{i^2}=\sqrt{i},\) 其余为 \(1 \over i^2\)。(感谢 neruko +的勘误!qwq
+对 \(k \geqslant 1\), 记 \(b_k = a_{k+1} - a_k\)。证明,对任意的 \(n\geqslant 2\),都有 \(\displaystyle a_n - \sigma_n = \frac{1}{n} +\sum_{k=1}^{n-1} k b_k\)。
+Trivial.
+设 \(\displaystyle\lim_{k\to \infty} k +b_k = 0\) 并且 \(\{\sigma_n\}_{n\geqslant 1}\) +收敛。证明,\(\{a_n\}\) 也收敛。
+注意,这是 (1) 在条件 \(n|a_{n+1}-a_n| \to +0\) 这一额外条件下的逆命题。
+Trivial,上一题左右对 \(n\) +取极限,利用极限的可加性。至于右边的极限为什么是 \(0\),用 \(\varepsilon - N\) 写一下。
+把 (5) 的条件减弱为: \(\{ k +b_k\}_{k\geqslant 1}\) 是有界的并且 \(\displaystyle\lim_{n \to \infty} \sigma_n = +\sigma\)。证明,\(\displaystyle\lim_{n\to \infty} a_n = +\sigma\)。
+?不会.jpg
+
根式和指数的定义
+这个问题的目的是在 \(\mathbb R\) +上定义初等函数 \(\sqrt[n]{x}\) 和 \(b^x\),比如说我们自然希望定义 \(\sqrt[n]{x}\) 为满足 \(y^n = x\) 唯一的正实数。
-
-
列均值/sample mean :\(\bar{x_k} = -\frac{1}{n} \Sigma_{i=1}^{n} x_{ik}\),\(k=1,2,...,p\)
-直观来说体现了分布的位置。
-列方差/sample variance :\(s_k ^2 = -s_{kk} = \frac{1}{n} \Sigma_{i=1}^n (x_{ik}-\bar{x_k})^2\),\(k=1,2,...,p\)
-直观来说体现了分布的分散程度。
-实际上,可以看到此处列方差的系数是 \(\frac{1}{n}\) 而不是传统的 \(\frac{1}{n-1}\),这是由使用场景决定的。在统计推断中,如果需要无偏统计量则使用 -\(\frac{1}{n-1}\),如果需要极大似然估计(MLE)则使用 -\(\frac{1}{n}\)。尤其是样本量 \(n\) -很大的情况下,二者的差别并不大,可以不做严格的区分。
-协方差,相关系数:直观上来说体现了线性相关性,相关系数为正则正相关,否则负相关,为 -\(0\) 不相关。
-协方差定义为 \(s_{ik} = \frac 1 n -\Sigma_{j=1}^n (x_{ji} - \bar{x_i}) (x_{ji} - -\bar{x_k})\),可以看到实际上 \(s_{ik} = -s_{ki}\),于是协方差矩阵有
-\[ \begin{bmatrix} s_{11} & s_{12} -& ...& s_{1p}\\ s_{21} & s_{22} & ...& s_{2p} \\ ... -& ...&...&... \\ s_{p1} & s_{p2} &...&s_{pp} -\end{bmatrix}\]
-的形式,这是一个对角元为正的对称矩阵。
-类似地,相关系数定义为 $_{ik} = { } $ -的形式,也有对应的协方差矩阵,是一个对角元均为 \(1\) 的对称矩阵。
+给定正整数 \(n\) 和实数 \(x>0\),证明:如果正实数 \(y_1\) 和 \(y_2\) 满足 \(y_1^n = x=y_2^n\),那么 \(y_1=y_2\)。
+Trivial.
+证明,如果 \(x>0\),那么集合 +\(E(x) = \{t \in \mathbb R \mid t^n < +x\}\) 是非空的并且有上界。
+Trivial,首先 \(0 \in E(x)\),再对 +\(x\) 讨论。当 \(0<x<1\) 时有 \(\forall t \in E(x), t<1\),当 $1 x $ +时有 \(\forall t \in E(x),t \leq +x\)。
+证明,\(y = \sup E(x)\) 满足 +\(y^n = x\) 并且 \(y>0\)。
+首先有 \(0 \in E(x)\),于是 \(sup E(x) \geq 0\)。如果 \(supE(x) = 0\) 则不存在 \(\varepsilon >0,\varepsilon ^n +<x\)。取 \(\varepsilon ^n = +\frac{x}{2}\) 则矛盾。于是 \(y>0\)。再证明 \(y^n =x\)。显然对于 \(\forall y \in \mathbb R, y^n \geq x\) 都有 +$y $ 是 \(E(x)\) 的上界,而对于 \(\forall z \in \mathbb R,z^n < x\),存在 +\((z ^\prime) ^n = z_n +x\) 使得 \(z^ \prime \in E(x)\) 且 \(z^\prime >z\),于是这样的 \(z\) 都不是上界。因此 \(supE(x) = min \lbrace y \in \mathbb R, y^n \geq x +\rbrace\),也即题中定义。
+证明, 映射 \(\sqrt[n]{\cdot}\colon +\mathbb R_{>0}\to \mathbb R_{>0}, \ \ x \mapsto +\sqrt[n]{x}=y\) 是良好定义的。我们也记 \(\sqrt[n]{x}\) 为 \(x^{\frac1n}\)。
+良好定义的意思是,对于任意的 \(x = +x^\prime\),有 \(y=y^ +\prime\)。否则 \(y \neq y^ +\prime\),但由上题定义,上确界是唯一的。
+证明,\(\sqrt[n]{\cdot}\colon \mathbb +R_{>0}\to \mathbb R_{>0}\) 是双射。
+有以上铺垫后是显然的。
+\(a,b\) 是正实数,\(n\) 为正整数。证明,\((ab)^{\frac1n} = +a^{\frac1n}b^{\frac1n}\)
+定义 \(A(x) = \lbrace t \in \mathbb R \mid +t^n <a \rbrace\),\(B(x) = \lbrace t +\in \mathbb R \mid t^n <b \rbrace\),\(C(x) = \lbrace t \in \mathbb R \mid t^n <a +b\rbrace\),只要证明 \(A(x)B(x)=C(x)\),(集合相等的证明是左右互相包含),然后考虑两个集合的上确界则得证。
也可以由随机向量矩阵得到相应的 sample mean 向量和 sample variance -向量。
-Mahalanobis Distance
-用来判断不同 item 的 的“距离”,从来衡量两组数据的相似性。实际上不同的 -variance 有不同的量纲,我们想比较不同 item 的差异,需要把 variance -的量纲“统一”来计算二者的差异。使用 Mahalanobis distance 来计算。
-假设两个 item 的数据值分别是 \(P = -(x_1,x_2,...,x_p),Q= (y_1,y_2,...,y_p)\),记整体 sample mean -向量为 \(\mu = -(\mu_1,\mu_2,...,\mu_p)\),协方差矩阵为 \(\Sigma\)。在不同的使用场景下,Mahalanobis -distance 有不同的形式,主要在以下方面处理了差异:
+在接下来的问题里,我们给定实数 \(b>1\) 来定义以 \(b\) 为底的指数函数 \(x \mapsto b^x\)。
-
-
通过给差值除掉此维度数据的协方差,来规范尺度差异。本质上是个仿射变换。
-\(d(P,Q) = \sqrt{\frac{(x_1 - -y_1)^2}{s_{11} } + \frac{(x_2 - y_2)^2}{s_{22} } + ... +\frac{(x_p - -y_p)^2}{s_{pp} } }\)
-希望能够用二次型的形式直观表述 \(P\) 和 \(Q\),或者 \(P\) 和 \(\mu\) 之间的差异。
-\(d(P,\mu) = \sqrt{(x-\mu) ^T \Sigma ^{-1} -(x-\mu)}\)
-\(d(P,Q) = \sqrt{(x-y)^T \Sigma^{-1} -(x-y)}\)
+设 \(m,n,p,q \in +\mathbb{Z}\),其中 \(n>0\),\(q>0\)。令 \(r += \dfrac{m}{n} = \dfrac{p}{q}\) 为有理数 \(r\) 的两种表示。证明 \((b^m)^{\frac1n} = (b^p)^{\frac1q}\)
+Trivial.
+证明,对任意的有理数 \(r\),函数 +\(r\mapsto b^r\) 是良好定义的。
+Trivial.
+证明,对任意的有理数 \(r,s\),我们有 \(b^{r+s} = b^rb^s\)。
+记 \(r = \frac mn ,s= \frac +pq\),于是 \(b^{r+s} = +b^{\frac{mq+np}{nq} }=(b^{mq} b^{np} ) ^{\frac{1}{nq} }= b ^{\frac mn} +b^{\frac pq} = b^r b^s\)。
+对于 \(x \in \mathbb R\),令 +\(B(x)=\{b^t \mid t \in \mathbb{Q}, t +\leqslant x\}\)。证明,\(B(x)\) +非空且有上界。我们定义 \(b^x = \sup +B(x)\), 这就定义了映射 \(x \mapsto +b^x\)。
+其实和之前那个也差不多,不写了。
+证明,如果 \(r\) 是有理数,那么 +\(b^r = \sup B(r),\forall r \in +\mathbb{Q}\)。我们定义的指数映射在 \(r\in \mathbb{Q}\) 时和之前是一致的。
+和上一题一样。
+证明,上题中定义的映射满足, 对任意的 \(x,y \in \mathbb R\),都有 \(b^{x+y} = b^x b^y\)。
+证明 \(X(r)Y(r)=Z(r)\),于是上确界相等。
+证明,当 \(b=e\) +时,这样定义的函数和课程中定义的 \(e^x\) 是一致的。
+嗯?
+\(\exp(x)=\sum_{k=0}^\infty +\frac{x^k}{k!}\)。上述定义的 \(e^x = +sup B(x) = sup \{e^t \mid t \in \mathbb{Q}, t \leqslant +x\}\)。
+我不到啊,或许他想让我证明的是 \((\sum_{k=0}^\infty \frac{1}{k!}) ^x = +\sum_{k=0}^\infty \frac{x^k}{k!}\) +吗?这个课上好像证过。
此外还有两个结论:
+根式的逼近
+给定正实数 \(\alpha\) 和初始值 \(x_1 > +\sqrt{\alpha}\),我们归纳地定义序列 \(\{x_n\}_{n\geqslant 1}\):\(x_{n+1} = \frac{1}{2}\left(x_n + +\frac{\alpha}{x_n}\right), n = 1,2,\cdots\)
-
-
设 \(Z\) -是一个随机向量,记它的均值向量为 \(\mu -_Z\),协方差矩阵为 \(\Sigma -_Z\),二者均有限。\(A\) -是任意的对称矩阵。于是有 \(E[Z^T AZ] = -trace(A\Sigma_Z) + \mu_Z ^T A \mu_Z\)。
-Proof:考虑迹的性质。\(E[Z^T AZ] = tr(E[Z^T AZ]) = E[tr(Z^TAZ)] = -E[tr(AZZ^T)] = tr(E[AZZ^T]) = tr(AE[ZZ^T])\),由\(Z\) 是随机向量,\(E[ZZ^T] = (\Sigma_Z + \mu_Z ^T \mu_Z)\),故 -\(tr(AE[ZZ^T]) = tr(A\Sigma_Z) + tr(A\mu_Z -\mu_Z^T) = trace(A\Sigma_Z) + \mu_Z ^T A \mu_Z\)。
-2-范数的期望:\(p\) 阶随机向量 -\(X\) 有有限的均值向量 \(\mu\) 和协方差矩阵 \(\Sigma\),于是 \(E[|| X - \mu ||_2 ^2] = \Sigma_{i=1} ^p -\sigma_{ii}\)。
-Proof: 在上一个结论中取 \(A=I\),于是 \(E[|| X - \mu ||_2 ^2] = E[(X-\mu )^T I (X-\mu)] = -tr(I\Sigma) = \Sigma_{i=1} ^p \sigma_{ii}\)。
-Remark: 对于独立同分布的 \(X\) 和 \(Y\),有相同的均值向量和协方差矩阵,于是 -\(E[||X-Y||_2^2] = 2 \Sigma _{i=1} ^p \sigma -_{ii}\)。
+证明,\(\{x_n\}_{n\geqslant 1}\) +是递减的并且 \(\displaystyle\lim_{n\to \infty} +x_n = \sqrt{\alpha}\)(在问题E中已经定义)。这表明,从任意大于 +\(\sqrt{\alpha}\) +的初值出发,可用上述迭代公式近似地计算(逼近)\(\sqrt{\alpha}\)。
+Trivial,因为这就是 Newton 法(狗头
+定义逼近的误差项 \(\varepsilon_n = x_n +- \sqrt{\alpha}\)。证明,\(\displaystyle\varepsilon_{n+1} = +\frac{\varepsilon_n^2}{2x_n} < +\frac{\varepsilon_n^2}{2\sqrt{\alpha}}\)。
+Trivial,这是 Newton 法的二阶收敛性质(逃
+证明,如果 \(\beta = +2\sqrt{\alpha}\),那么 \(\displaystyle\varepsilon_{n+1} < \beta +\left(\frac{\varepsilon_1}{\beta}\right)^{2^n}\)。这表明它的收敛速度非常快。
+Trivial.
+设 \(\alpha = 3\),\(x_1 = 2\),验证 \(\dfrac{\varepsilon_1}{\beta} < +0.1\),继而 \(\varepsilon_5 < 4\cdot +10^{-16}\),\(\varepsilon_6 < 4 +\cdot 10^{-32}\)。
+略(
+试用纸和笔,计算 \(\sqrt{3}\) +的精确到小数点5位的近似值。
+略(
最后来考虑 Mahalanobis distance 的期望。\(p\) 阶随机向量 \(X\) 有有限的均值向量 \(\mu\) 和协方差矩阵 \(\Sigma\),其 Mahalanobis distance 定义为 -\(||X- \mu ||_\Sigma = d(X,\mu) = -\sqrt{(X-\mu)^T \Sigma^{-1} (X-\mu)}\),利用上述结论则 \(E[||X- \mu ||_\Sigma ^2] = p\)。
-同理,对于独立同分布的 \(X\) 和 -\(Y\),有 \(E[||X-Y||_\Sigma ^2] = 2p\)。
-Exploratory Data Analysis -(EDA)
-这个其实在线性回归课上也学过,主要讲的是数据清洗的原则和方法,也没有什么很实际的内容,感觉在扯皮。wljj -的课上比较注重解释一些看起来很炫酷的图是怎么画的,真的很应用。
-这个能用 RMarkdown 写的话就好了,Typora 什么时候能支持 -RMarkdown(暴论
-Boxplot
-data = matrix(0,nrow=12,ncol=2) |
(假装在用 Rmd(
-boxplot 包含了很多信息。盒子的上边表示数据中的 75% 分位数,下边表示 -25% 分位数,盒子中间的线表示中位数。我们将 75% 分位数和 25% -分位数的差记作 IQR,则盒子上边距离最上方的“触角”的距离是 1.5 -IQR,下边同理。
-对于正态分布来说,两个触角之间的距离表示了所有正常数据的范围,离开这个范围的数据基本上是 -out of 3\(\sigma\) 的,可以直观地去除 -outlier。
-在 R 的绘图中会将上“触角”的值定为 75% quantile + 1.5 IQR -和最大数据之间的较大值,下“触角”同理,因此在上面的这个例子里,两组数据的 -25% quantile 和 75% quantile 都是相同的,绘图结果有差别。
-Histogram
-柱状图的宽度还是有讲究的,适当的宽度可以看出分布的形状。通用的是 -\(h =( \frac{24\sqrt{\pi} } {n})^{\frac{1}{3} -}\)。
-hist(mpg$hwy,main = "Histogram of highway miles per gallon",breaks = round(max(mpg$hwy)-min(mpg$hwy)/(24*sqrt(pi)/length(mpg$hwy))^(1/3))) |
Scatter Plot
-散点图有很 fancy 的版本,这里展示一些实现:
+接下来,我们换另外一个迭代公式。固定 \(\alpha > 1\) 和 \(y_1 > \sqrt{\alpha}\),定义 \(y_{n+1} = {\alpha + {y_n} \over 1 + {y_n}} = y_n + +{\alpha - {y_n}^2 \over 1+{y_n} }\),$ n = 1,2,... $
+-
+
证明,\(\{y_{2k-1}\}_{k\geqslant +1}\) 为递减序列。
+这是一个大于 \(\sqrt{\alpha }\) +的序列,有 \(y_3 = \frac{\alpha + y_2}{1+y_2} += \frac{(\alpha +1 )y_1 + 2 \alpha}{2y_1 + \alpha +1} < +y_1\),可以推广到每一项。
+证明,\(\{y_{2k}\}_{k\geqslant +1}\) 为递增序列。
+Trivial,基本同上。
+证明,\(\displaystyle\lim_{n\to \infty} +y_n = \sqrt{\alpha}\)。
+上述的两个序列分别单调有界,各自收敛。由递推式可知都收敛到 \(\sqrt{\alpha }\),于是整体收敛。
+试讨论逼近 \(\sqrt{\alpha}\) +的收敛速度并与之前的比较。
+肯定是不如 Newton 方法收敛得快的。
+记逼近的误差项 \(\varepsilon_n = x_n - +\sqrt{\alpha}\),于是 \(\displaystyle\lim_{n\to \infty} \frac{\varepsilon +_{n+1} } {\varepsilon _n } = \frac{1-\sqrt{\alpha} }{1+\sqrt{\alpha} +}\),这个序列线性收敛,而 Newton 方法二阶收敛。
+
给我一点小小的数值分析震撼,但我感觉比前面的题都简单(
+梦话 2.0:乘积级数
+其实乘积级数完全可以用对数函数拆成求和级数,可惜的是我们现在还没有对数函数,所以都是靠各种技巧来证明。
+-
+
乘积级数的收敛以及 Cauchy 判别法:\(\{a_n\}_{n\geqslant 1}\) +是复数的数列,我们假设对任意的 \(n\),\(a_n\neq +0\)。令 \(P_n=a_1\cdot a_2\cdot \cdots +\cdot a_n\),如果数列 \(\{P_n\}_{n\geqslant 1}\) 的极限存在且不是 +\(\mathbf{0}\),称无限乘积 \(\displaystyle\prod_{n\geqslant 1}a_n\) +收敛且记 \(\displaystyle\prod_{n\geqslant +1}a_n=\lim_{n\rightarrow \infty}P_n\)。
+我们有这种情况下的 Cauchy 判别准则:\(\displaystyle\prod_{n\geqslant 1}a_n\) +收敛当且仅当对任意的 \(\varepsilon>0\),存在 \(N\),使得对任意的 \(n\geqslant N\),任意的 \(p\geqslant 0\),我们都有 \(\big|a_n\cdot a_{n+1}\cdot \cdots \cdot +a_{n+p}-1\big|<\varepsilon\)。
+除此之外还有一个特殊情况:对于正数列 \(\{a_n\}_{n\geqslant 1}\),乘积 \(\displaystyle\prod_{n=1}^{\infty}(1+a_n)\) +收敛(极限必然不是零)等价于 \(\displaystyle\sum_{n =1}^{\infty} a_n\) +收敛。当然,有对数的话可以近似成 \(ln(1+a_n) +\approx a_n\),直观上二者就相等。严格的证明也不困难。
+实际上,如果数列介于区间 \((0,1)\) +之间,二者也等价于乘积 \(\displaystyle\prod_{n=1}^{\infty}(1-a_n)\) +收敛。从对数的直观上来说也是明显的,但证明稍有不同。
+这样的话限制还是比较多的,只对正实数有效。如果想要推广到复数,就需要更强的条件。\(\{a_n\}_{n\geqslant 1}\) 是复数的数列,如果 +\(\displaystyle\prod_{n=1}^{\infty}(1+|a_n|)\) +收敛(等价地说,就是 \(\displaystyle\sum_{n +=1}^{\infty} a_n\) 绝对收敛),则 \(\displaystyle\prod_{n=1}^{\infty}(1+a_n)\) +收敛(极限不是零)。
+
2023 年 1 月 24 日,星期二,修了半天 LaTeX 然后摸了半天鱼(
+顺便解决了一些历史问题,比如把博客搬到(去年八月换的)新电脑上来了,说来真的有点蠢,感觉搬家好麻烦就同时用着两个电脑了(。旧电脑是 +surface,换掉之后一直仍然承担着晚上回寝室之后负责 deploy +博客和时不时需要一块手写屏的功能。
+其实后来检查了半天,发现除了 NexT +之外都是最新版本,不清楚究竟是哪里有问题,就换了个 +renderer,然后就好了(其实去看了下最新版 NexT +的文档,它的意思好像也是最好不要用 hexo-renderer-marked,就换了 +hexo-renderer-pandoc,虽然还有少量问题但基本还是在人工排查没那么费劲的范围里,先这样吧)。倒是也把新版本的 +NexT 设置好了,但是当时搞的彩色标签暂时没找到好的替代 = +=,原来的办法不太好用了,就还是暂时再用用旧的,哪天确定是它出了问题的话也可以一键搬家到新版(,以及有问题就可以自己在新版上测了,这次还要谢谢 +JasonL 老师的帮助,谢谢华子音游群让我半夜加到了老师的好友((
+到底是什么原因呢,是换了新电脑的原因还是魔改的原因,总之仓库里原来 +200 多条 commits +没有了。本来想着内容都还在也没什么问题,但是今天无聊翻邮件的时候突然想起来,有一条在 +commits +里的评论也跟着消失了。怪我没什么经验还不咋仔细,要是想到开个新的分支的话就好了。或许有什么恢复的方法吗,感觉没有(
+凌晨的时候本来在等备份,随手开了局舟,没想到一次通关,大概是什么回坑 +buff(。不过感觉不咋好玩,逐渐失去兴趣了,打算把活动打完就卸载掉。
+(这不是数分日志来着吗)(问题在这里发现的就在这儿解决一下好了)
+
2023 年 1 月 25 日,星期三,= =
-
-
Scatter Plot
-放一个我线性回归作业里的图罢。
--men <- c(72.5,71.5,70.5,69.5,68.5,67.5,66.5,65.5,64.5)
brothers <- c(71.1,70.2,69.6,69.5,68.7,67.7,67.0,66.5,65.6)
p = plot.default(men,brothers,xlim = c(63,73),ylim=c(65,72),main = 'Heights of men and their brothers',xlab = 'medium heights of the men',ylab = 'medium heights of the brothers',col = "blue")
abline(lm(brothers~men))
-
lm(brothers~men)
-Scatter Plot Matrix
--library(GGally)
lizard<-read.csv('t1-3.dat',sep='',header=F)
names(lizard)<-c('mass','svl','hls')
ggpairs(lizard,title = 'scatter plot matrix of lizard') -
-3D Scatter Plot
--library(scatterplot3d)
data(iris)
head(iris)-scatterplot3d(iris[,1:3])
-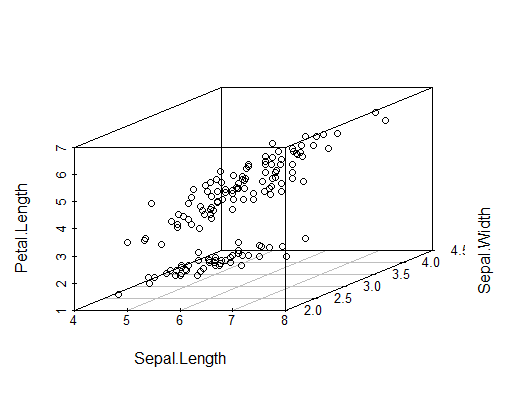
colors <- c("#999999","#E69F00","#56B4E9")
colors <- colors[as.numeric(iris$Species)]
scatterplot3d(iris[,1:3],pch=16,color=colors,main='3D scatter plot of iris flower', grid=TRUE, box=TRUE, type="h")
+定义了一个很新的函数,叫做欧拉乘积公式,也可以就叫 \(\zeta\)- 函数。
+假设 \(\mathcal{P}\) +是所有的素数组成的集合,我们可以将它们从小到大排列为 \(2=p_1<p_2<p_3<\cdots\)。对于 \(s>1\),\(\zeta\)- 函数
+\(\zeta(s)=\sum_{n=1}^\infty +\frac{1}{n^s}\) 是良好定义的。那么, 我们有 \(\zeta(s)=\prod_{p\in +\mathcal{P}}\frac{1}{1-p^{-s}}\),
+其中上面的乘积是收敛的(我们可以假定是按照素数从小到大的顺序来做乘积的)。
+又到了高中竞赛的噩梦环节,Abel +求和公式。形式很简单,证明也很简单,但是应用和技巧多得离谱(
+\(\{a_k\}_{k\geqslant 1}\) 和 \(\{b_k\}_{k\geqslant 1}\) +是复数(矩阵)的序列,那么 \(\sum_{k=1}^n{a_kb_k}=S_nb_n+\sum_{k=1}^{n-1}S_k(b_k-b_{k+1})\),其中我们用 +\(S_n=a_1+a_2+\cdots+a_n\) 表示数列 +\(\{a_k\}_{k\geqslant 1}\) +的部分和。
+Abel 公式其实就是离散形式的分部积分公式,而且 Abel +和的部分截断和的形式也很不错:
+\(\sum_{n+1\leqslant k \leqslant m} a_k b_k += S_mb_m-S_nb_n+\sum_{k=n}^{m-1}S_k(b_k-b_{k+1})\)
+于是有一个针对它的 Dirichlet +收敛判别法,证明即是对上面的部分截断和放缩,做 Cauchy 判别法:如果\(\{b_k\}_{k\geqslant 1}\) 是单调数列并且 +\(\displaystyle\lim_{k\rightarrow +\infty}b_k=0\),而且存在 \(M\),使得对任意的 \(n\geqslant 1\),\(|S_n|\leqslant M\),那么无穷级数 \(\displaystyle\sum_{k=1}^\infty{a_kb_k}\) +收敛。
+相应地还有 Abel 收敛判别法:\(\{b_k\}_{k\geqslant 1}\) +是单调有界数列,级数 \(a_1+a_2+a_3+\cdots\) 收敛,则级数 \(\displaystyle\sum_{k=1}^\infty{a_kb_k}\) +收敛。同样使用截断和的 Cauchy 判别即可。
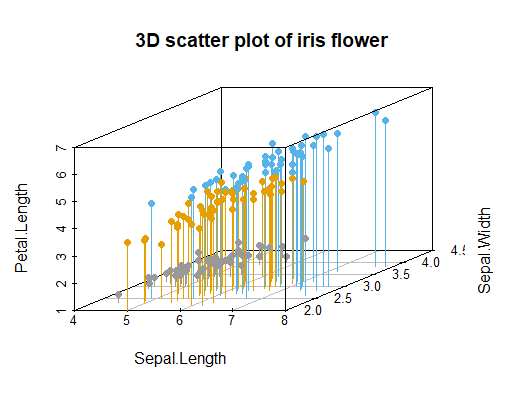
Lecture 2
-介绍了一些矩阵方法,以及复习线性代数。
-Linear Algebra
-什么嘛,我线代学得还可以嘛(喜
-矩阵分解的复习就跳过了,也就那点东西,主要是谱分解和奇异值分解。
-Matrix -Interpretation of Mahalanobis-distance
-注意一些左乘矩阵代表的意义,比如在 Mahalanobis -距离中常用的处理方式是旋转和伸缩,二者分别可以左乘一个正交矩阵/对角矩阵来完成。
-因此,回忆一下 Mahalanobis 距离的表达式 \(d(P,Q) = \sqrt{(x-y)^T \Sigma^{-1} -(x-y)}\),其中要求 \(\Sigma\) -是一个对称正定矩阵,可以分解为 \(\Sigma = P -AP^T\) 的形式,其中 \(P\) -是正交矩阵,\(A\) -是特征值对角矩阵。
-Matrix Inequality
-Extended Cauchy-Schwartz Inequality:对于两个 \(p \times 1\) 大小的向量 \(b,d\),任意的 \(B\) 满足是对称正定矩阵,于是有
-\[(b^T d)^2 \leq (b^T Bb)(d B^{-1} -d)\],
-等号成立当且仅当 \(b=cB^{-1} -d\),\(c\) 是常数。
-Proof(证明摘自 Vica's -Blog):注意到
-\[\boldsymbol{b}^\intercal\boldsymbol{d}=\boldsymbol{b}^\intercal\boldsymbol{I}\boldsymbol{d}=\boldsymbol{b}^\intercal\boldsymbol{B}^{1/2}\boldsymbol{B}^{-1/2}\boldsymbol{d}=(\boldsymbol{B}^{1/2}\boldsymbol{b})^\intercal(\boldsymbol{B}^{-1/2}\boldsymbol{d})\]
-然后套用柯西不等式即得证。
-Maximization Lemma:\(B\) 是对称正定矩阵,\(d\) 是给定的向量,于是对于任意不为零的向量 -\(x\),有
-\[\max _{x\neq 0} \frac{(x^T d)^2}{x^T Bx} -= d^T B^{-1} d\],
-取到最大值时有 \(x = c B^{-1} -d\),\(c\) 是常数。
-Proof:即为 Extended Cauchy-Schwartz Inequality -的变形。
-描述性统计量的矩阵表示
-上次说到把二维数据组织成 \(n \times -p\) 尺寸的表格:
-| - | Variable 1 | -Variable 2 | -... | -Variable i | -... | -Variable p | -
|---|---|---|---|---|---|---|
| Item 1 | -\(x_{11}\) | -\(x_{12}\) | -... | -\(x_{1i}\) | -... | -\(x_{1p}\) | -
| Item 2 | -\(x_{21}\) | -\(x_{22}\) | -... | -\(x_{2i}\) | -... | -\(x_{2p}\) | -
| ... | -... | -... | -... | -... | -... | -... | -
| Item j | -\(x_{j1}\) | -\(x_{j2}\) | -... | -\(x_{ji}\) | -... | -\(x_{jp}\) | -
| ... | -... | -... | -... | -... | -... | -... | -
| Item n | -\(x_{n1}\) | -\(x_{n2}\) | -... | -\(x_{ni}\) | -... | -\(x_{np}\) | -
实际上就是一个 \(n \times p\) -大小的矩阵,记为 \(A = -[y_1,y_2,...,y_p]\)。
-sample mean vector 也可以写成矩阵变换的表示:$ {X} = A^T _n$,其中 -\(\mathbb 1_p\) 表示 \(p\) 个分量都是 \(1\) 的向量。
-covariance matrix 也可以写成矩阵表达:$ n S_p = A^T (I_n - _n _n^T) -A$,事实上 \(\mathbb 1_n \mathbb 1_n -^T=\mathbb 1_{n\times n}\) 是一个分量都为 \(1\) 的矩阵。
-correlation matrix 在 covariance matrix 的基础上继续做变换即可。记 -$D^{ 2} = diag(,..., ) $,于是 correlation matrix 可以记为 \(R_p= D^{-\frac 1 2} S_p D^{-\frac 1 -2}\)
-在此基础上再定义一个 generalized sample variance,事实上是 covariance -matrix -的行列式值的绝对值,也就是这个对称矩阵的全体特征值的积的绝对值。由行列式的形式可以知道它是一个和各个 -covariance coefficient -相关的式子,一定程度上可以反映数据的离散程度(但因为是标量,缺乏各个方向上的数据的离散情况)。例如对于二维数据(\(p=2\)),可以知道 \(|S|=s_{11} s_{22} (1- r_{12}^2)\)。
-另一个常用的表示是 covariance matrix -的迹,也即这个对称矩阵的全体特征值的和。
-Lecture 3
-今天介绍多元正态分布。
-多元正态分布
+梦话 +3.0:距离空间与赋范线性空间
+赋范线性空间这我也熟啊,也是数值分析里学的(学的时候有点痛苦就是了,而且有点惶恐,因为感觉附近都是数学系的人,他们好像都会了 +qwq(而且都是大三的同学,天哪当时选课的时候真有勇气
-
-
多元正态分布的概率密度形式和一元是完全类似的:
-\[f(x) = \frac{1}{(2\pi) ^{p/2} |\Sigma -|^{1/2}} exp(-\frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2})\]
-其中,\(\mu\) 是 \(x\) 的均值,\(\Sigma\) 是 \(x\) -的协方差矩阵,这是一个正定矩阵。
-先把二元的情况拿出来观察,\(p=2\),于是有 \(f(x) = \frac{1}{2\pi |\Sigma|^{1/2}} -exp(-\frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2})\)。其中有
-\[\mu = \begin{bmatrix} \mu_1 \\ \mu_2 -\end{bmatrix} = \begin{bmatrix} E(X_1) \\ E(X_2) \end{bmatrix}, \Sigma = -\begin{bmatrix} Var{X_1} & Cov(X_1,X_2) \\ Cov(X_1,X_2) & -Var(X_2)\end{bmatrix}\]
-我们想对 \(\mu\) 和 \(\Sigma\) 做一些估计,回顾一下统计推断里的 -MLE 估计,矩估计等等方法。
+距离空间是一个不够强的定义,只对空间上的两个点的距离做了定义,要求它们满足三角不等式。比如说,以绝对值为距离的距离空间 +\(\mathbb Q\) 上有 \(x_n=\displaystyle \sum_{k=0}^n +\frac{1}{k!}\) 是 Cauchy 列但不收敛(因为收敛到 \(e\),是无理数)。因此,定义完备的距离空间 +\((X,d)\),如果其上每个 Cauchy +列都收敛。比如 \(X=\mathbb R\),\(d(x,y)=|x-y|\) +就是完备的距离空间。
+然后讲义上讲了一个压缩映射定理(或者 Banach +不动点定理更好听),嗨呀这个我也熟,是数值分析里非线性方程的迭代解法那一章里面的最初条件,某种意义上来说也是做迭代能找到不动点的前提。不过这次把它放到完备距离空间里了。
+数值分析里用的是更完备的空间,也就是赋范线性空间,实际上就是让距离空间的距离定义又满足了范数的条件,也就是数乘的线性性质而已。另外要求空间是线性空间,这个也没什么难的。
++
+这三种范数都是上面线性空间情况直接搬过来的. 实际上, 利用矩阵的知识, +我们还可以定义其他更有几何意义的范数, +比如说我们可以利用矩阵的特征值来定义一些范数, 限于知识范围, +我们不再展开.
+嘿嘿,这个我会(这不是应该的吗到底在自豪什么.jpg
+最后在完备的赋范线性空间(也就是
+BananaBanach +空间)上证明了一些极限的相容性,其实我的感受就是把绝对值推广成了范数,证明某些对于实数的操作,在赋范线性空间上对向量 +/ 矩阵也是能成立的。比如说定义一个 \(e^A\),但 \(A\) 是一个 \(n +\times n\) +大小的复系数矩阵。听起来很抽象,不知道会得到一个什么怪物结果,但是回顾 +\(e^x\) 的级数定义就可以知道,\(e^A = \sum_{k=0} ^\infty {A^k \over +k!}\),也就是说 exp 函数在矩阵上是一个 \(M_n (\mathbb R) \to M_n (\mathbb R)\) +的映射,得到的结果还是一个 \(n \times +n\) 大小的复系数矩阵。
+要做的任务就是证明 \(e^A\) +的良定义性质,也就是级数的收敛性。在这里用一个赋范空间上的绝对收敛概念,原本实数空间上的绝对收敛是对于绝对值而言,在赋范空间上改成对范数而言即可,这样还是能够通过绝对收敛推出收敛(因为范数和绝对值同样有三角不等式性质)。关于 +\(e^A = \sum_{k=0} ^\infty {A^k \over +k!}\) +的绝对收敛性质也很好证明,可以使用矩阵范数的等价性。当然,如果这个矩阵范数是一个向量相容范数,就更简单了。
+不过,在这样的定义里,\(e^{A+B} = e^A +e^B\) 是不一定成立的,因为两个矩阵未必交换。但是 \(e^{sA} e^{tA} = e^{(s+t)A}\) +仍然成立。
补充:矩阵向量求导、期望
+梦话 +4.0:既然习题没有答案那我就继续胡说八道了
+怎么作业这么多啊!
+说到习题没有答案这个问题,今天在知乎搜了一下居然有民间版本流传,作者是 +MO 和 OI 双修的高中生,太升级了。
+习题还在做,做完了再来碎碎念,然后就终于可以离开极限去学连续性了(
+2023 年 1 月 26 日,星期四,今天没有 die +只是作业写起来真的有点慢(,这一章的习题全都做了哦。
+连续函数的定义和基本性质
-
-
向量求导很熟悉了,就是 Jacobian matrix -那一套。但在多元统计里使用的求导矩阵是 Jacobian matrix -的转置。有一些看起来轻微抽象的结论:
-\[\frac{\partial}{\partial x} Ax = -A^T\]
-\[\frac{\partial}{\partial x} x^TA = -A\]
-\[\frac{\partial}{\partial x} x^Tx = -2x\]
-\[\frac{\partial}{\partial x} x^TAx = -Ax+A^Tx\]
-实际上都非常容易推导,把 \(Ax\) 视为 -\(x\) -的线性变换,再对分量求导即可。
-对矩阵的求导暂时只考虑对称正定的情况。
-\[\frac{\partial |A|}{\partial A} = |A| -A^{-1}\]
-\[\frac{\partial tr(AB)}{\partial A} -=B^T\]
-\[\frac{\partial tr(A^{-1}B)}{\partial A} -= -A^{-1}B^TA^{-1}\]
-有点抽象(
-对于某一个 population \(c^T X = -\begin{bmatrix} c_1 & c_2 & ... &c_p \end{bmatrix} -\begin{bmatrix} X_1 \\ X_2 \\...\\X_p \end{bmatrix}\), 其期望变为 -\(c^T \mu\),方差变为 \(c^T \Sigma c\);
-如果 \(c^TX\) 是一个 -sample,同理样本均值变为 \(c^T -\mu\),样本方差变为 \(c^T -Sc\)。
-对于两个 population \(b^TX\) 和 -\(c^TX\),有 \(Cov(b^T X,c^TX) = b^TXc\)。
-注意这里是对一个随机向量的 \(p\) -个分量在做线性组合,而不是对若干个随机向量的组合,期望和方差都是标量而不是向量!
+(函数极限的Cauchy判别准则)给定函数 \(f\colon (a,x_0)\cup (x_0,b)\rightarrow +\mathbb{R}\)。那么,\(f\) 在 +\(x_0\) 处有极限当且仅当对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x_1,x_2\in (x_0-\delta,x_0+\delta)\),都有 +\(|f(x_1)-f(x_2)|<\varepsilon\)。
+如果有极限,这是定义,trivial.
+如果对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x_1,x_2\in (x_0-\delta,x_0+\delta)\),都有 +\(|f(x_1)-f(x_2)|<\varepsilon\),那么取某一个固定的 +\(\varepsilon\),找到这样的区间 \(X=(x_0-\delta,x_0+\delta)\),任意取一组 +\(X\) 上收敛到 \(x_0\) 的点列 \(y_0,y_1,...,y_n,...\),它们的函数值序列 +\(\lbrace f(y_n) \rbrace _{n \geq 1}\) +是 Cauchy 列,一定收敛。
+至于为什么会收敛到 \(f(x_0)\) +这一点,这是因为 \(\lbrace y_n \rbrace _{n +\geq 1}\) 的极限是 \(x_0\)。
+假设 \(I\) 是一个非空的区间并且 +\(I\) 不是一个点,证明,\(I\) 上的连续函数 \(C(I)\) 所构成的 \(\mathbb R\)-线性空间是无限维的。
+这题我会!数值分析里学过!多项式的基 \(\lbrace 1,x,x^2,... \rbrace\) +是无限维的,因为它们彼此线性无关。
+假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) 是映射。假设 \(x_0\in X\),如果对任意 \(X\) 中的点列 \(\{x_n\}_{n\geqslant 1}\),\(x_n\stackrel{d_X}{\longrightarrow}x_0\),我们都有 +\(f(x_n)\stackrel{d_Y}{\longrightarrow}f(x_0)\),我们就称 +\(f\) 在 \(x_0\) 处是连续的。如果 \(f\) 在一切 \(x\in +X\) 处均连续,那么我们就称 \(f\) +是距离空间之间的连续映射。
+假设 \((X,d_X)\),\((Y,d_Y)\) 和 \((Z,d_Z)\) 是三个距离空间,\(f\colon X\rightarrow Y\),\(g\colon Y\rightarrow Z\) +均为连续映射。证明,它们的复合 \(g\circ +f\colon X\rightarrow Z\) 也是连续映射。
+一句话题意:连续映射的复合还是连续映射(
+Trivial.
+假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) 是连续映射。如果 +\(d'_X\) 是与 \(d_X\) 等价的距离,\(d'_Y\) 是与 \(d_Y\) 等价的距离,那么,对于 \((X,d'_X)\) 和 \((Y,d'_Y)\) 而言,\(f\) 也是连续映射。
+等价的距离意思是对任意的 \(x_1 , x_2 \in +X\),存在固定的参数 \(c,C \in +R\),使得 \(c d^{\prime} _X (x_1,x_2) +\leq d _X (x_1,x_2) \leq C d^{\prime} _X +(x_1,x_2)\),代入一下连续的定义,取一个小一点的 \(\varepsilon\) 就可以了。
+在 \(\mathbb R^n\) +上我们配有常见的距离,比如说 \(d_2\)(请参考之前的讲义);\((X,d_X)\) 是距离空间。我们将映射 \(f\colon X\rightarrow \mathbb R^n\) +写成分量的形式:\(f\colon X\rightarrow \mathbb +R^n, \ \ x\mapsto f(x)=(f_1(x),f_2(x),\cdots,f_n(x))\)
+其中 \(f_i\colon X\rightarrow \mathbb +R\) 是函数。证明,\(f\) +是连续映射当且仅当对所有的 \(i=1,\cdots,n\),\(f_i\) 是连续函数。
+如果每个 \(f_i (x)\) +都是连续函数,那么对于收敛到 \(x_0\) +的点列 \(\lbrace x_i \rbrace _{i \geq +1}\),对任意的 \(\varepsilon +>0\),存在一个最小的 \(\delta\) 和最大的 \(N\),使得对任意分量函数,都有 \(n >N\) 时,\(| +f_i(x_n)-f_i(x_0) | <\varepsilon\)。于是此时也有 \(| f(x_n) - f(x_0) | <\sqrt{n} +\varepsilon\),连续。(追求美观的话可以在第一步把 \(\varepsilon\) 改成 \(\varepsilon \over \sqrt{n}\))
+如果 \(f(x)\) +是连续函数,那么分量的误差小于整体误差,每个分量都收敛。
+(这个我在数值分析也学过!耶!
+假设 \((X,d_X)\) +是距离空间,\((V,\|\cdot\|)\) +是赋范线性空间,\(f\colon X\rightarrow +V\) 和 \(g\colon X\rightarrow +V\) 是连续映射。证明,它们的和与差(自然的定义)\(f\pm g\colon X\rightarrow V\) +也是连续映射。
+如果 \(V=\mathbb{C}\)(或者 \(n\times n\) +的矩阵构成的赋范线性空间),那么 \(f\cdot +g\colon X\rightarrow \mathbb{C}\) 是连续映射。
+如果 \(V=\mathbb{C}\) 并且对任意的 +\(x\in X\),\(g(x)\neq 0\),那么 \(\dfrac{f}{g}\colon X\rightarrow +\mathbb{C}\) 是连续映射。
+你可以选择上面的一个情况来证明。
+PIN 你真的有点无聊(哭),其实都挺 trivial 的。
+试找出 \(\mathbb R\) +上定义的函数
+\(f(x)=\begin{cases}\frac{1}{q}, \ +&\text{如果 $x=\dfrac{p}{q}$ 是有理数,其中 $p\in \mathbb{Z}$,$q\in +\mathbb{Z}_{\geqslant 1}$ 且 $p$ 和 $q$ 互素};\\ 0, \ &\text{如果 +$x$ 是无理数}\end{cases}\)
+的所有不连续点。
+回顾一下:连续点的含义是 \(f\) 在 +\(x_0\) +处有(唯一的,左右相等的)极限,当且仅当对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x_1,x_2\in (x_0-\delta,x_0+\delta)\),都有 +\(|f(x_1)-f(x_2)|<\varepsilon\)。
+对于有理数点,其实很容易就能找到一个趋近于它的无理数点列。取一个它左侧的无理数点 +\(k\),二者一起不停找二分点,就可以取出一个趋近于这个有理数点的无理数点列。它的函数值是收敛不到 +\(\frac 1 q\) +的,于是所有的有理数点都是不连续点。
+但是 \(0\) +的函数值是咋定义的呢?如果函数值就是 \(0\),那它是唯一一个有理数连续点。
+对于无理数点 \(t\),对任意的 \(\varepsilon >0\),总能够取 \(\delta\) 满足 \(t\) 的去心邻域 \(T = (t-\delta,t) \cup (t,t+\delta)\) +里面没有形如 \(p \over q\) +的有理数,使得分子分母互素,而且 \(q < +\frac{1}{\varepsilon}\),因此对任意 $ x_1 ,x_2 T$,有 \(| f(x_1 ) - f(x_2) | < +\varepsilon\),总是收敛的。
+至于为什么可以做到这一点,这是因为记把 \(t\) 附近 \(q < +{1 \over \varepsilon }\) 的有理数点中离它最近的距离记为 \(d\),取 \(\delta += \frac d 2\) 即可,而这样的有理数点是有穷个,一定可以找到对应的 +\(d>0\)。
+总之,所有的不连续点的集合是 \(\mathbb +Q\),视情况可能 \(0\) +会是连续的,这里定义的好像不是很好。
多元正态分布参数估计
-极大似然估计
-这个我在课上自己推出来了(喜),还喜提了 dwl 老师在我身边叫我名字 + -纠正书写,她居然还记得我,但想起来我开摆的初概,真是又开心又尴尬(。结论是:
-对于 \(X_1,X_2,...,X_n\) i.i.d. -\(\sim N_p (\mu,\Sigma)\),参数 \(\mu\) 和 \(\Sigma\) 的极大似然估计是:
-\[ \hat{\mu}_{MLE} = \bar{X}\]
-\[\hat{\Sigma}_{MLE} = \frac{1}{n} -\Sigma_{i=1} ^n (X_j - \bar{X})(X_j - \bar{X})^T\]
-无偏估计
-首先考虑样本方差为 \(S = \frac{1}{n-1} -\Sigma_{i=1} ^n (X_j - \bar{X})(X_j - \bar{X})^T = \frac{n}{n-1} -\hat{\Sigma}_{MLE}\),它是 \(\Sigma\) 的无偏估计;\(\mu\) 的无偏估计显然是 \(\bar{X}\)。
-事实上还有性质:\(Cov(\bar{X}) = \frac 1 n -\Sigma\);\(S\) 和 \(\bar{X}\) -互相独立,且是一组充分统计量(用因子分解定理简单看一下)。
-多元正态分布的性质
+级数收敛性
+眼前一黑,我直接一个梦回微积分 A2(,这一部分就比较水字数了。
-
-
\(X \sim N_p(\mu , \Sigma) \iff a^TX -\sim N(a^T\mu,a^T\Sigma a)\) 对任意的 \(a \in \mathbb R^p\) 成立。
-\(X\sim N_p(\mu ,\Sigma) \iff AX+d \sim -N_p(A\mu +d , A\Sigma A^T)\) 对任意的 \(d\in \mathbb R^p\) 成立。
-对于特定的 \(N_p(\mu , -\Sigma)\),我们可以用 \(p\) -个标准正态分布捏出来。对于任意的 \(Z_1,Z_2,...,Z_p\) i.i.d. \(\sim N(0,1)\),记 \(Z=(Z_1,Z_2,...,Z_p)^T\)。对任意的对称正定矩阵 -\(\Sigma\) 和实向量 \(\mu \in \mathbb R^p\),有 \(X = \mu + \Sigma^{\frac 1 2} Z \sim -N_p(\mu,\Sigma)\)。
-对于满足多元正态分布的 \(X = -(X_1,X_2,...,X_p)^T \sim N_p(\mu ,\Sigma)\),我们可以根据 \(\mu\),\(\Sigma\) 的信息找到任意一组 \((X_{i1},X_{i2},...,X_{ij})\) -的期望和方差,也可以通过协方差矩阵得到任意一对 \((X_i,X_j)\) -之间的独立性关系(注意对于正态分布,独立和不相关是等价的,对于其他分布不能这样推理)。
-然而对于相关的随机向量,例如 \(\begin{bmatrix} X_1 \\ X_2\end{bmatrix}\sim -N_{q_1+q_2} (\begin{bmatrix}\mu_1 \\ \mu_2 \end{bmatrix},\begin{bmatrix} -\Sigma_{11} &\Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} -\end{bmatrix})\),其中 \(| -\Sigma_{22}|>0\),可以看到 \(X_1,X_2\) -之间并不独立。此时我们有另一种结果: $(X_1 | X_2 = x_2) N(1 + -{12} {22}^{-1} (x_2 - 2),{11} - {12 } -{22}^{-1} {21}) $
-Proof:(这是我写在作业里的一个方法,写个作业用蹩脚英文,现在看看绷不住了)
-According to the resolution:
-\[\Sigma = \begin{bmatrix} \Sigma_{11} -& \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix} -= \begin{bmatrix}\Sigma_{11} - \Sigma_{12 } \Sigma_{22}^{-1} -\Sigma_{21} & \Sigma _{12} \\ 0 & -\Sigma_{22}\end{bmatrix} \begin{bmatrix}I &0 \\ -\Sigma_{22} ^{-1} -\Sigma_{21} & I\end{bmatrix}^{-1}\]
-Note that:
-\((x-\mu)^T \Sigma ^{-1} (x-\mu) = -\begin{bmatrix}x_1^T - \mu_1^T & x_2^T - \mu_2^T\end{bmatrix} -\begin{bmatrix} I & 0 \\ -\Sigma_{22}^{-1} \Sigma_{21} & -I\end{bmatrix} \begin{bmatrix}(\Sigma_{11} - \Sigma_{12 } -\Sigma_{22}^{-1} \Sigma_{21})^{-1} & 0 \\ 0 & \Sigma_{22}^{-1} -\end{bmatrix} \begin{bmatrix}I & -\Sigma_{12} \Sigma_{22} ^{-1} \\ 0 -&I\end{bmatrix} \begin{bmatrix}x_1 - \mu_1 \\ x_2- -\mu_2\end{bmatrix}\)
-We can know that \((x_1^T -\mu_1^T) - -(x_2^T - \mu_2^T ) \Sigma_{22}^{-1} \Sigma_{21} \sim N(0,\Sigma_{11} - -\Sigma_{12 } \Sigma_{22}^{-1} \Sigma_{21})\),
-so that \(X_1 \sim N(\mu_1 +\Sigma_{21} -\Sigma_{22}^{-1} (x_2 - \mu_2)\),${11} - {12 } -{22}^{-1} {21}) $, the conditional distribution can be derived -from the distribution.
-因此可以看到,即使随机向量的两部分之间有相关性,也可以进行分离。
-\(X \sim -N_p(\mu,\Sigma)\),于是有 \((X-\mu) ^T -\Sigma^{-1}(X-\mu) \sim \chi_p ^2\)。
-Proof:取 \(Z=\Sigma^{\frac 1 2} \sim N_p -(0,I_p)\)。
-于是 \((X-\mu) ^T \Sigma^{-1} (X-\mu) = -[(X-\mu)^T \Sigma^{-\frac 1 2}] [\Sigma^{-\frac 1 2} (X-\mu)] = Z^TZ -=\Sigma_{i=1} ^p Z_i ^2 \sim \chi_p ^2\)。
-\(X_1,X_2,..,X_n\) -是相互独立的多元正态分布,\(X_j \sim N_p(\mu_j -, \Sigma)\),记 \(V_1 = -c_1X_1+c_2X_2+...+c_nX_n = c^TX\)。
+- 试判断下列级数的收敛性。
-
-
- \(V_1 \sim N_p(c^T \mu , c^Tc -\Sigma)\); -
- 对于 \(V_2 = -b_1X_1+b_2X_2+...+b_nX_n\),有 \(V_1,V_2\) 的协方差矩阵为 \(\begin{bmatrix} c^Tc\Sigma & b^Tc\Sigma \\ -b^Tc\Sigma & b^Tb\Sigma \end{bmatrix}\)。 -
- \(V_1,V_2\) 相互独立 \(\iff b^Tc = 0\)(由上一结论直接得出) -
尤其要注意此处与上一部分最后一段的关系,\(V_1,V_2\) -是在对若干随机向量做线性组合,上一部分最后一段是在对一个随机向量的全体分量做线性组合。也可以从所得结果的维数来判断。
-
Lecture 4
-单正态分布总体的推断。
-Wishart Distribution
+\(\sum_{n=1}^\infty +(\sqrt{n+1}-\sqrt{n})\)
+发散,trivial.
\(\sum_{n=1}^\infty +\frac{\sqrt{n+1}-\sqrt{n}}{n}\)
+收敛,trivial.
$_{n=2}(-1)n $
+收敛,因为数列 \(n^{1 \over n}\) +单调减并趋近 \(1\),对于某个被 \(\varepsilon\) 控制的 \(n >N\),有 \(\sum_{n=N+1}^\infty (\sqrt[n]{n}-1)^n < +\sum_{n=N+1}^\infty \varepsilon ^n\)。
$_{n=1}^ (x) $
+\(|x|<1\) 或 \(x=1\) 时单项收敛不到 \(0\),级数发散;否则收敛。
$_{n=1}^ $
+收敛,trivial.
$_{n=1}()n $
+收敛,单项放缩。
$_{n=1}^ $
+发散,验一下不符合 Cauchy 列。
\(\sum_{n=2}^\infty \frac{1}{(\log +n)^{\log n}}\)
+感觉可以用积分法判断收敛(,但是还没学过积分(,怎么办呢。
+也可以放缩,\(n > N\) 时有 \(\frac{1}{(\log n)^{\log n}} < +\frac{1}{n^M}\)。收敛。
$_{n=1}^ $
+单项可以写成更好的形式:${(n^{1 n} / (n+ {1 n} ) ^{1 } )}^{n ^2 +1} $ +(天哪这个能渲染出来吗,好担心)
+发散。
$_{n=1}(-1){n-1} $
+收敛,Dirichlet 判别。
$_{n=1}^ $
+发散,trivial.
\(\sum_{n=1}^\infty +\left(1+\frac{1}{2}+\cdots + \frac1n\right)\frac{\sin +nx}{n}\)
+收敛。拆分 \(b_n = \frac{1}{n} (1 + \frac 1 +2 +...+ \frac 1 n)\),\(a_n = \sin +nx\),用 Dirichlet 判别法,其中 \(b_n +< \frac{log _2 n}{n}\)。
+需要注意的是要讨论一下 \(x = 2k +\pi\) 的情况。
-
-
$S = _{i=1} ^n (X_j - {X})(X_j - {X})^T $,有 \((n-1)S =\Sigma_{i=1} ^{n-1} Z_i Z_i^T \sim -W_p(n-1,\Sigma)\),其中 \(Z_i \sim N_p -(0,\Sigma)\)。
-类似于一个 \(\chi^2\) -分布在多元分布上的推广。
-对于 \(A_1 \sim -W_p(m_1,\Sigma)\),\(A_2 \sim -W_p(m_2,\Sigma)\) 且 \(A_1,A_2\) -相互独立,则有 \(A_1 +A_2 \sim W_p -(m_1+m_2,\Sigma)\)。
-对于 \(A \sim -W_p(m,\Sigma)\),$C $ 是一个 \(p\times -p\) 大小的可逆矩阵,则 \(C^TAC \sim -W_p(m,C^T\Sigma C)\)。
-注意 \(C\) 可以是 $k p $ -大小的矩阵,此时也有 \(C^TAC \sim W_k(m, -C^T\Sigma C)\)。这是因为 \(A = -\Sigma_{i=1}^m Z_iZ_i ^T\),其中 \(Z -\sim N_p(0,\Sigma)\),于是有 \(C^TAC -=\Sigma_{i=1} ^m C^TZ_i Z_i ^TC\) 且 \(C^TZ_i \sim N_k ( 0, C^T\Sigma C)\),因此 -\(C^TAC \sim W_k(m,C^T\Sigma -C)\)。此处尤其需要注意随机向量的维数改变为 \(k\) 维。
-以上两个性质都可以轻松地通过 Wishart distribution -的构造推出。
+$_{n=2}(-1)n $
+不绝对收敛,感觉也可以用积分判别,懒得多想了(
+收敛,trivial.
+$_{n=2}^ $
+不绝对收敛,求一下 \(\sin +\frac{n\pi}{4}\) 的值就知道了。
+收敛,trivial.
+$_{n=1}(-1)n $
+不绝对收敛,分离常数之后发现一部分收敛一部分不收敛。
+收敛,仍然是分离常数,trivial.
+\(\sum_{n=1}^\infty +(-1)^{\frac{n(n-1)}{2}} \frac{n^{10}}{a^n} \qquad (a>1)\)
+绝对收敛,trivial.
+
One Sample T-test
+递减正项级数的凝聚检验法
+假设正整数 \(b\geqslant 2\),\(f\colon (1,\infty)\rightarrow +\mathbb{R}_{>0}\) 是递减(未必严格递减)函数。
-
-
在一元情况下有 \(\frac{\sqrt{n}(\bar{X} -- \mu_0)}{\sigma} \sim N(0,1)\) 和 \(\frac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1} -^2\),以及 \(\frac{\bar{X} - -\mu_0}{S/\sqrt n} \sim t_{n-1}\) 和 \((\frac{\bar{X} - \mu_0}{S/\sqrt n})^2 \sim -F_{1,n-1}\),这些都是假设检验中常用的检验统计量。我们希望能够推广到多元的情况。
-对于一族 \(X_1,X_2,...,X_n \sim N_p(\mu , -\Sigma)\),假设 \(H_0 :\mu = \mu_0 ; -H_1 :\mu \neq \mu_0\)。
-在 \(H_0\) 下有
-\[\frac{T^2}{n-1} = \sqrt n (\bar{X} - -\mu_0)^T (\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1} \sqrt n (\bar{X} - -\mu_0) = Z_1 (\Sigma_{i=1} ^n Z_iZ_i^T)^{-1}Z_i^T \sim \frac{p}{n-p} -F_{p,n-p}\]
-也就是说 \(\frac{n-p}{p(n-1)} T^2 \sim -F_{p,n-p}\),当 \(T_0 ^2 > T^2 -(\alpha) = \frac{p(n-1)}{n-p} F_{p,n-p}(\alpha)\) -时拒绝原假设。这被称为 Hotelling distribution。
-对于 \(X_i \sim -N_p(\mu,\Sigma)\),考虑 \(Y_i = -CX_i+d\),其中 $C $ 是 \(p \times -p\) 的矩阵,\(d\) 是 \(p \times 1\) -的向量。这是一族多元正态分布的线性变换。
-于是有 \(\bar{Y} = C -\bar{X}+d\),\(S_Y = -\frac{1}{n-1}\Sigma_{i=1}^n (Y_i - \bar{Y_i})(Y_i-\bar Y_i)^T = -CS_XC^T\),考虑其期望有 \(\mu _Y = C -\mu +d\),在假设 \(H_0\) 下有 -\(\mu_{Y,0} = C \mu_0 +d\)。于是对应的 -Hotelling Statistic 是
-\(\begin{aligned} T^2 _Y &= \sqrt n -(\bar Y - \mu_{Y,0})^T (\Sigma (Y_i - \bar{Y})(Y_i - \bar Y)^T)^{-1} -\sqrt n (\bar{Y} - \mu_{Y,0}) \\& =\sqrt n (\bar{X} - \mu_0)^T C^T -C^{-T}(\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1}C^{-1}C \sqrt n -(\bar{X} - \mu_0) \\& =\sqrt n (\bar{X} - \mu_0)^T (\Sigma (X_j - -\bar X)(X_j - \bar X)^T)^{-1} \sqrt n (\bar{X} - \mu_0) \\& =T^2_X -\end{aligned}\)
-可以看到与做线性变换之前是相同的,也即对于 \(Y_i = CX_i +d\),可以使用相同的 test -statistic 进行检验。
-实际上,Hotelling test 和 likelihood ratio test -是完全等价的,这个可以在一元的情况下看到,也可以推广到多元。多元情况下的 -likelihood ratio 是:
-\[\Lambda = (\frac{|\hat \Sigma|}{|\hat -\Sigma_0|}) ^{\frac n 2}= (\frac{|\Sigma_{j=1} ^n (x_j - \bar x)(x_j - -\bar x)^T|}{|\Sigma_{j=1} ^ n (x_j - \mu_0)(x_j-\mu_0)^T|})^{\frac n -2}\]
-由此得到 test statistic 的另一表示,不需要对矩阵 \(S\) 求逆:
-\[T^2 = (n-1) \frac{|\Sigma_{j=1} ^n (x_j -- \mu_0)(x_j - \mu_0)^T|}{|\Sigma_{j=1} ^ n (x_j - \bar x)(x_j-\bar -x)^T|} - (n-1)\]
+证明下面的不等式:\((b-1)b^{k-1}f(b^{k})\leqslant +\sum_{j=b^{k-1}}^{b^k-1} f(j) \leqslant +(b-1)b^{k-1}f(b^{k-1})\)
+什么茶歇题。Trivial.
+证明:级数 ${n=1}^f(n) $ 和 $ {n=1}bn f(b^n)$ +同时收敛或者同时发散。
+我们称通过后者的收敛来判断前者收敛的方法为凝聚检验法。
+根据上一问求和,trivial.
+证明,\(\displaystyle \sum_{n=2}^\infty +\frac{1}{n\log n}\) 是发散的。
+不如试试积分收敛法(被捂嘴拖走
+取 \(b=2\) +知道它和调和级数是同收敛同发散的。
+证明,\(\displaystyle\sum_{n=100}^\infty \frac{1}{(n\log +n) (\log (\log n))}\) 是发散的。
+它和上一问的级数是同收敛同发散的。
+证明,如果 \(s>1\),那么 +\(\displaystyle\sum_{n=1}^\infty +\frac{1}{n^s}\) 是收敛的;如果 \(0<s<1\),那么 \(\displaystyle\sum_{n=1}^\infty +\frac{1}{n^s}\) 是发散的。
+取 \(b=2\) +知它和一个等比数列同收敛同发散。
+假设 \(s>1\)。证明,\(\displaystyle\sum_{n=2}^\infty \frac{1}{n(\log +n)^s}\) 和 \(\displaystyle\sum_{n=10}^\infty \frac{1}{(n\log +n)(\log(\log n))^s}\) 都收敛。
+前一个和上一问同收敛同发散。后一个和 \(\displaystyle\sum_{n=10}^\infty \frac{1}{n {\log^s +n} }\) 同收敛同发散。
Confidence Interval of -\(\mu_{p \times 1}\)
-Confidence Region of the -Mean
-已知 \(Z_1,Z_2,...,Z_n i.i.d \sim -N_p(\mu,\Sigma)\),对于已有的数据 \(z_1,z_2,...,z_n\) 希望求得 \(\mu\) 的置信区间,其中 \(\mu ,\Sigma\) 均未知。在一元的情况下 (\(p=1\)) 可以使用 \(\frac{\bar Z - \mu}{s / \sqrt n} \sim -t_{n-1}\) 进行估计。\(\mu\) 的 -\(100(1-\alpha)\%\) 置信区间是 \((\bar Z - t_{n-1,\alpha /2} \frac{s}{\sqrt n},\bar -Z +t_{n-1,\alpha /2} \frac{s}{\sqrt n})\)。
-在多元情况下,有 $ T^2 F_{p,n-p}$,其中 \(T^2 = n (\bar Z - \mu)^T S^{-1} (\bar Z - -\mu)\)。于是 \(\mu\) 的 \(100(1-\alpha)\%\) -置信域是满足以下条件的区域:
-\[R(x) = \{\mu: n(\bar Z - \mu )^T S^{-1} -(\bar Z -\mu) \leq c^2 , c^2 = T^2(\alpha) = -\frac{p(n-1)}{n-p}F_{p,n-p}(\alpha) \}\]
-这是一个椭圆。
-Individual Coverage -Intervals
-接下来考虑 \(Z_1,Z_2,...,Z_n\) -的线性组合 \(a^T Z = a_1 Z_1 + ... +a_n -Z_n\),我们希望估计它的均值 \(a^T -\mu\),这是一个标量。
-由于 \(a^T Z \sim N(a^T \mu, a^T \Sigma -a)\),因此 \(a^T \mu\) 的 \(100 \% (1-\beta)\) 置信区间是 \((a^T \bar Z - t_{n-1}(\beta/2) \sqrt{a^T \frac S n -a},a^T \bar Z + t_{n-1}(\beta/2) \sqrt{a^T \frac S n a})\)
-以下继续考虑 \(Z_1,Z_2,...,Z_n\) -的一族共 \(m\) 个线性组合 \(a_1 ^T Z,a_2 ^T Z,...,a_m ^TZ\) -的置信区间推断。
-Bonferroni's Method
-对于 \(m\) 个不同的线性组合 \(a_1^TZ,a_2^TZ,...,a_m^TZ\),分别对其做置信系数为 -\(\frac \alpha m\) 的置信区间,则这 -\(m\) -个区间拼在一起得到的矩体就至少能够包含住真正的置信域。
-也就是说,对每个 \(a_i^T\mu\) -做置信区间:\((a_i ^T\bar{X} - -t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_i ^T \frac S n a_i},a_i ^T\bar{X} + -t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_i ^T \frac S n a_i} )\)
-拼在一起得到的矩体
-\[(a_1 ^T\bar{X} - -t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_1 ^T \frac S n a_1},a_1 ^T\bar{X} + -t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_1 ^T \frac S n a_1} ) \times \cdots -\times(a_m ^T\bar{X} - t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_m ^T \frac S n -a_m},a_m ^T\bar{X} + t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_m ^T \frac S n -a_m} )\]
-即为一个符合条件的置信域。实际上这一置信域的置信系数比 \(\alpha\) 更大,只是一个粗略的估计。
-\(T^2\) -interval
-事实上,对任意的线性变换 \(a^TZ\) -都存在一个统一的 simultaneous coverage interval,也称作 \(T^2\) interval,是
-\((a^T \bar{X} - c\sqrt{a^T \frac S n -a},a^T \bar{X} + c\sqrt{a^T \frac S n a})\),其中 \(c^2 = T^2(\alpha) = \frac{p(n-1)}{n-p} -F_{p,n-p}(\alpha)\)。
-这个置信域比 Bonferroni's Method 得到的置信域更大。
-注意当 \(a\) 在 \(S^{-1}\bar X\) 方向上时以上区间正好是一个 -\(100\%(1-\alpha)\) -的置信区间,也即这个时候区间取到最大。但这一方向会随着样本的变化而变化。
-Real World(?
-对 \(Z_i\) -做线性变换得到的椭圆会在形状和方向上有所变化,但与 \(T^2\) interval -得到的矩形相切。不同置信区间的覆盖面积如图所示。
-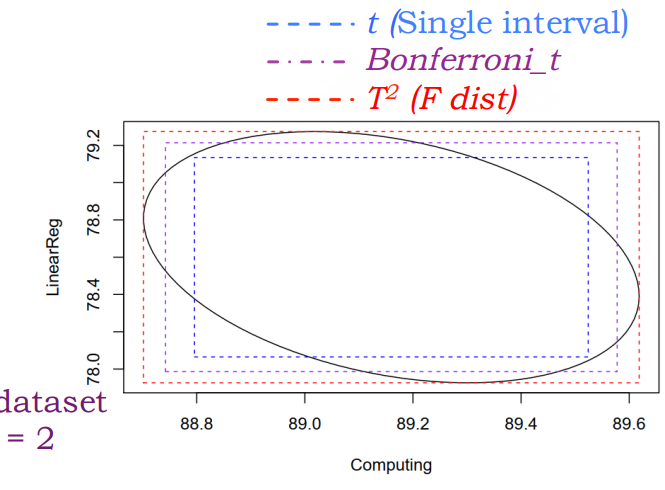
Lecture 5
-Two Population Test
-双正态同方差总体的均值比较
+++Remark:上述的几个收敛的结论是标准并且重要的,记住这几个结论对于收敛以及函数大小的理解很有帮助。这里的证明尽管巧妙,但是等我们接触到积分的时候,我们就可以用统一的、简单的、更本质的也更容易记忆的方法来证明这些结论。
+
实数列的上下极限的刻画
+设 \(\{a_n\}_{n \geqslant 1}\) +是一个实数列。先补充几个定义:
+\(\alpha \in \mathbb R\),如果对任意 +\(\varepsilon>0\), 存在无穷多 \(n\),使得 \(a_n +\in (\alpha-\varepsilon,\alpha+\varepsilon)\),我们称 \(\alpha\) 为 \(\{a_n\}_{n\geqslant 1}\) 的一个极限点;
+如果对任意 \(M>0\),存在无穷多个 +\(n\),使得 \(a_n \in (M,\infty)\),我们就称 \(+\infty\) 为 \(\{a_n\}_{n\geqslant 1}\) 的一个极限点;
+如果对任意 \(M>0\),存在无穷多个 +\(n\),使得 \(a_n \in (-\infty,-M)\),我们就称 \(-\infty\) 为 \(\{a_n\}_{n\geqslant 1}\) 的一个极限点。
-
-
两个总体中随机抽样得到的样本和相关统计量分别表示如下:
--
- - -- - - - - - -Sample -\(X_{11},X_{12},...,X_{1n_1}\) -\(X_{21},X_{22},...,X_{2n_2}\) -- -Sample Mean -\(\bar X_1 = \frac{1}{n_1} \Sigma_{j=1} -^{n_1} X_{1j}\) -\(\bar X_2= \frac{1}{n_2} \Sigma_{j=1} -^{n_2} X_{2j}\) -- - -Sample Covariance Matrix -\(S_1 = \frac{1}{n_1 -1 }\Sigma_{j=1} -^{n_1} (X_{1j} - \bar X_1)(X_{1j} - \bar X_1)^T\) -\(S_2= \frac{1}{n_2 -1 }\Sigma_{j=1} -^{n_2} (X_{2j} - \bar X_2)(X_{2j} - \bar X_2)^T\) -
-检验前对于两个总体的假设:
+证明,\(\alpha\in \mathbb R\) 是 +\(\{a_n\}_{n\geqslant 1}\) +的极限点当且仅当该数列有子序列 \(\{a_{n_k}\}_{k\geqslant 1}\) 收敛于 \(\alpha\)。
+对于 \(\varepsilon _1 = 1\),取 +\(a_1 \in +(\alpha-\varepsilon_1,\alpha+\varepsilon_1)\);再取 \(\varepsilon _2 = |\alpha - a_1|\),继续取 +\(a_2\),依次操作就得到了收敛子序列。
+反过来是显然的。
+证明,\(+\infty\) 是 \(\{a_n\}_{n\geqslant 1}\) +的极限点当且仅当该数列有子序列 \(\{a_{n_k}\}_{k\geqslant 1}\) 使得 \(\displaystyle\lim_{k\to \infty} a_{n_k} = ++\infty\)。
+Trivial.
+令 \(E = \bigl\{\alpha \in \mathbb R +\cup \{\pm \infty\} \,\rvert\, \alpha \text{ 是 } \{a_n\}_{n\geqslant 1} +\text{ 的极限点}\bigr\}\) 为 \(\{a_n\}_{n\geqslant1}\) +的所有极限点所组成的集合(它是 \(\mathbb R +\cup \{\pm \infty\}\) 的子集)。证明,\(E \ne \emptyset\)。
+考察 $sup {a_n}_{n} = + $ 或者 \(inf +\{a_n\}_{n\geqslant1} = -\infty\),如果有二者之一则有 \(+\infty \in E\) 或者 \(-\infty \in E\)。
+否则,\(\{a_n\}_{n\geqslant1}\) +是有界的。如果它收敛于一点,则这一点是极限点,\(E\) 非空。
+否则,\(\{a_n\}_{n\geqslant1}\) +有界且不收敛,它也有收敛的子列,子列收敛的极限是极限点。(救命,差点忘了这个
+证明:\(E \subset \mathbb R\) +当且仅当数列 \(\{a_n\}_{n\geqslant 1}\) +有界。
+Trivial.
+假设 \(\{a_n\}_{n\geqslant 1}\) +有界。试证明,\(\displaystyle \sup E = +\limsup_{n\to \infty} a_n\),\(\displaystyle\inf E = \liminf_{n\to \infty} +a_n\)。
+是我困迷糊了吗?我不是很理解诶,比如说数列 \(1,1,100000,1,1,1,1,1,...\),真的符合第一条吗?
+假设 \(\{a_n\}_{n\geqslant 1}\) +有界。令 \(a^*= \displaystyle\limsup_{n\to +\infty} a_n\),证明如下两个命题:
-
-
- \(X_{11},X_{12},...,X_{1n_1}\) -i.i.d. \(\sim -N_p(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim N_p(\mu_2,\Sigma_2)\) -
- 两组样本之间相互独立 -
- 在 \(n_1,n_2\) 较小的情况下,假设 -\(\Sigma = \Sigma_1 = \Sigma_2\) +
\(a^* \in E\)(所以 \(\sup E\in E\));
+对任意 \(x > a^*\),存在 +\(N \in \mathbb{Z}_{\geqslant +1}\),使得对任意 \(n>N\),都有 \(a_n < x\)。
-Hypothesis: \(H_0 : \mu_1 - \mu_2 = -\delta_0\),\(H_1 : \mu_1 - \mu_2 \neq -\delta_0\)
-检验统计量的构造:
-由于 \(S_{pooled} = \frac{n_1 -1 -}{n_1+n_2-2}S_1 + \frac{n_2 -1}{n_1 + n_2 -2}S_2 \sim \frac{W_p(n_1 +n_2 --2,\Sigma)}{n_1+n_2-2}\),可以以此构造 Test statistic:
-\[(\frac{1}{n_1} + \frac{1}{n_2})^{-1} -(\bar X_1 - \bar X_2 - \delta_0)^T S_{pooled}^{-1} (\bar X_1 - \bar X_2 -- \delta_0) \sim \frac{p(n_1+n_2-2)}{n_1+n_2-p-1} -F_{p,n_1+n_2-p-1}\]
-当 \(T_0 ^2 > -\frac{p(n_1+n_2-2)}{n_1+n_2-p-1} F_{p,n_1+n_2-p-1} (\alpha)\) -时拒绝原假设。
-置信区间的构造:
-对于任意的线性变换 \(a^T(\mu_1 - -\mu_2)\),simultaneous confidence interval 是
-\[(a^T(\bar X_1 - \bar X_2) - c \sqrt{a^T -(\frac{1}{n_1} + \frac{1}{n_2}) S_{pooled} a},a^T(\bar X_1 - \bar X_2) + -c \sqrt{a^T (\frac{1}{n_1} + \frac{1}{n_2}) S_{pooled} a})\]
-其中 \(c^2 = \frac{p(n_1+n_2 --2)}{n_1+n_2-p-1}\)。
-注意到 \(a\) 的任意性,可以通过取 -\(a_i=e_i\) 的方式来求得 \(\mu_1 - \mu_2\) 的各个分量的置信区间;当 -\(a\) 与 \(S_{pooled}^{-1} (\bar X_1 - \bar X_2)\) -时上述置信区间的 confidence level 恰为 \(100 -\% (1-\alpha)\)。
+试举一个数列 \(\{a_n\}_{n\geqslant +1}\) 作为例子,使得 \(E\cap \mathbb R +\ne \emptyset\) 且 \(E\not\subseteq +\mathbb R\)。
+这题我会!
+\(1,2,1,3,1,4,...,1,n,1,n+1,...\),于是 \(E=\lbrace 1 , +\infty \rbrace\)。
+试举一个数列 \(\{a_n\}_{n\geqslant +1}\) 作为例子,使得 \(E\) +为无穷集。
+这题我也会!
+\(1,1,2,1,2,3,1,2,3,4,1,2,3,4,5,...\),于是 +\(E=\mathbb Z ^{+} \cup \lbrace + \infty +\rbrace\)。
+有可数集那味了!
Large Sample Test
-Large Sample Behavior
-在大样本场景下,类似于一元的中心极限定理,我们不需要正态性也可以推出一些关于 -\(\bar X,S\) 在此时的近似分布。
-$X_1 , X_2 ,...,X_n $ i.i.d. 来自某一总体,其均值为 \(\mu\),协方差矩阵为 \(\Sigma\),不必要求正态分布。于是有:
+*素数的倒数和
+根据第七次课的内容,对于 \(s>1\),我们可以定义 \(\zeta\)-函数 \(\zeta(s)=\sum_{n=1}^\infty +\frac{1}{n^s}\),
+并且证明了Euler乘积公式:\(\zeta(s)=\prod_{p\in +\mathcal{P}}\frac{1}{1-p^{-s}}\),其中 \(\mathcal{P}\) 是全体素数的集合。
+据此证明,级数 \(\sum_{p\in +\mathcal{P}}\frac{1}{p^s}\) 对于 \(s>1\) 是收敛的;对于 \(0<s\leqslant 1\) +是发散的(这给出了有无穷多个素数的另一个证明)。
+胡说八道:
+我觉得吧,\(\zeta(s)=\prod_{p\in +\mathcal{P}}\frac{1}{1-p^{-s}} = \prod_{p\in +\mathcal{P}}(1+\frac{1}{p^{s} - 1})\) 收敛等价于 \(\sum_{p\in \mathcal{P}} \frac{1}{p^{s} - +1}\) 收敛,那么 \(s >1\) +时素数的倒数和也收敛。
+(毫无必要啊!直接小于调和级数和就可以了 T_T)
+其实我想胡说八道的是,\(\zeta(s)=\prod_{p\in +\mathcal{P}}\frac{1}{1-p^{-s}}\) 收敛能不能等价于 \(\zeta(s)=\prod_{p\in +\mathcal{P}}(1-p^{-s})\) 收敛,再等价于 \(\sum_{p \in \mathcal P} p^{-s}\) 收敛?
+*Basel问题的Euler“证明”
+对任意的 \(\theta\in \mathbb R\) 和 +\(n\in \mathbb{Z}_{\geqslant +1}\),试证明恒等式 \(\frac{\sin\bigl((2n+1)\theta\bigr)}{(2n+1)\sin\theta}=\prod_{k=1}^n +\left(1-\frac{\sin^2(\theta)}{\sin^2\left(\frac{k\pi}{2n+1}\right)}\right)\)
+据此证明,对任意的 \(x\in \mathbb +R\),我们都有 \(\frac{\sin(\pi x)}{\pi +x}=\prod_{n=1}^\infty\left(1-\frac{x^2}{n^2}\right)\)
+(如果 \(x=0\),我们将左边定义为极限 +\(\displaystyle \lim_{x\rightarrow +0}\frac{\sin(\pi x)}{\pi x}\))
+胡说八道:
+这题还真的不是胡说八道,第一问是数值分析里学过的,第二类 Chebyshev +多项式代入化简((
+后一问大概只要取 \(\theta = \frac{\pi +x}{2n+1}\),然后让 \(n \to +\infty\)。
+++Remark:
+根据上面的公式,形式上,我们就有 \(sin(\pi +x)=\pi x\prod_{n=1}^\infty\left(1-\frac{x^2}{n^2}\right)=\pi +x\left(1-\left(\sum_{n=1}^\infty\frac{1}{n^2}\right)x^2+(\cdots)x^4+(\cdots)x^6+\cdots +\right)\)
+所以,右边 \(x^3\) 的系数就是 \(\displaystyle-\pi\sum_{n=1}^\infty\frac{1}{n^2}\)。根据我们对于 +\(\sin\) 的定义
+\(\sin z =\frac{e^{iz}-e^{-iz}}{2i} = +\sum_{k=0}^\infty \frac{(-1)^k z^{2k+1}}{(2k+1)!}\)
+所以,\(\sin(\pi x)\) 中展开式的 +\(x^3\) 项的系数是 \(-\dfrac{\pi^3}{6}\)。比较系数,我们得到所谓的Basel问题的解:
+\(\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}\)
+这是 Euler 原始的想法,他就是利用了上面的乘积公式来猜测最终的极限是 +\(\dfrac{\pi^2}{6}\)。有趣的是,他观察到 +\(\dfrac{\sin(\pi x)}{\pi x}\) +的零点恰好是 \(x=\pm n\),所以如果 +\(\dfrac{\sin(\pi x)}{\pi x}\) +的行为与多项式类似的话,那么这个函数应该是单项式的乘积,所以 Euler +认为
+\(\frac{\sin(\pi x)}{\pi x}=c\prod_{n\in +\mathbb{Z}-\{0\}}\left(1-\frac{x}{n}\right)=c\prod_{n=1}^\infty\left(1-\frac{x^2}{n^2}\right)\)。
+其中 \(c\) 是一个待定的常数,通过取 +\(x\rightarrow 0\) 的极限,他计算出 +\(c=1\)。
+
连续性
+进入新的章节啦!qwq
+2023 年 1 月 27 日,星期五,我要先去睡个觉((
+函数的连续性
-
-
- \(\sqrt n (\bar X - \mu) \sim -N_p(0,\Sigma)\) -
- \(n (\bar X - \mu) S^{-1} (\bar X - \mu) -\sim \chi^2 _p\) +
函数值在单点处的收敛有两种定义方式,一个是任意收敛点列,一个是 +\(\varepsilon - \delta\) +语言。关于在单点处的连续性,Heine 定理保证二者是等价的。
+证明中可以灵活选用两种定义方式,很可能一种比另一种叙述起来简单很多。
+单点连续,局部连续和全局连续是完全不一样的概念。最基础的定义是关于函数值的单点连续性的,全局连续往往由开覆盖的全体局部连续推出。
+*所以说,函数的连续性本质上是一个局部的性质。很重要的一个例子是,假设函数 +\(f\colon I_1\cup I_2\rightarrow \mathbb +R\) 定义在两个不相交的开区间的并集上,按照定义,如果 \(f\) 在每个点上都连续,\(f\) 就是在 \(I_1\cup I_2\) 上连续的。尽管函数图像在 +\(I_1\cup I_2\) +是“断开的”,这个函数仍然是连续的(因为连续性本质上是个局部性质,在 \(I_1\) 和 \(I_2\) 上分别连续即可)。
+用 \(C(I)\) 表示区间 \(I\) 上的连续函数的全体所构成的集合,\((C(I),+,⋅)\) 是一个环。
++
+不夸张的说,我们在数学中遇到(几乎)一切连续函数都是通过两种手段构造的:第一,通过连续函数的复合和四则运算;第二,通过逼近的方式,特别是级数的方式来定义,比如说 +\(\exp\) +的构造。这种逼近的方式是最值得我们注意的,我们很快会发现,\(C(I)\) 这个空间和实数 \(\mathbb R\) +很相似,构造无理数就是通过有理数逼近的方式。
+更具体一点,我们会在 \(C(I)\) +上面给定一个范数 \(\|\cdot +\|_{\infty}\) 并且证明这样得到的赋范线性空间是完备的。此时,任给 +\(f\in +C(I)\),我们可以仿照实数的情况定义 \(e^f : =\sum_{n=0}^\infty +\frac{f^k}{n!}\)。
+在完备的赋范线性空间中,我们只要全盘照抄实数的情况就可以证明上面的(函数)级数收敛,从而 +\(e^f\) +是良好定义的并且是连续函数。特别地,我们可以通过这种方式定义 \(e^x\)(把 \(x\) 看成是函数 \(f\))而且说明这和我们最初定义的 \(\exp(x)\) 是一码事。
+在这种类比下,我们就可以利用对实数的直观来研究函数空间,从而得到很多关于函数的深刻结果。在课程后面的学习中,我们会遇到很具体的例子,比方说存在处处连续但是处处都不能微分的函数,我们就是通过构造函数的级数来实现的。
+总之,从用具体的级数和定义 \(e\),再定义出 \(e^x\),然后介绍了赋范线性空间以及为矩阵定义了 +\(e^A\),现在又为函数定义了 \(e^f\)。每当不知道怎么理解 \(e\) +的时候,试着代入级数就懂了。期待一些函数级数收敛构造出的连续函数。
注意其中 \(S = \frac{1}{n-1} \Sigma_{i=1} -^n (X_i - \bar X)(X_i - \bar X)^T\),上述两式为近似分布,在 \(n\) 远大于 \(p\) 的条件下成立。
-这是我们进行后续推断的基础。
-大样本单总体均值推断
-$X_1 , X_2 ,...,X_n $ i.i.d. 来自某一总体,其均值为 \(\mu\),协方差矩阵为 \(\Sigma\),不必要求正态分布。
-假设 \(H_0 : \mu = \mu_0; H_1 : \mu \neq -\mu_0\),于是 test statistic 是 \(n(\bar x - \mu_0)^T S^{-1} (\bar x - \mu_0 ) \sim -\chi^2 _p\),当 \(T_0^2 > \chi_p ^2 -(\alpha)\) 时拒绝原假设。
-对于任意的线性变换 \(a^TX\),\(a^T \mu\) 的 simultaneous CI 是 \((a^T \bar X - \sqrt{\chi^2 _p (\alpha)} -\sqrt{\frac{a^TSa}{n} },a^T \bar X + \sqrt{\chi^2 _p (\alpha)} -\sqrt{\frac{a^TSa}{n} })\)
-大样本双异方差总体均值推断
+连续映射
-
-
检验前对于两个总体的假设:
+连续函数是一个局限比较强的定义,把 $C $ +映射到它自身而已。所以要定义一个连续映射的概念;
+假设 \((X,d)\) 和 \((Y,d_Y)\) 是两个距离空间,\(f\colon X\rightarrow Y\) +是这两个距离空间之间的映射。假设 \(x_0\in +X\),\(y_0=f(x_0)\in +Y\)。如果对任意 \(\varepsilon>0\),总存在 \(\delta>0\),使得对任意满足 \(d(x,x_0)<\delta\) 的 \(x \in X\),都有 \(d_Y\bigl(f(x),f(x_0)\bigr)<\varepsilon\),我们就称 +\(f\) 在 \(x_0\) 处连续。如果 \(f\) 在 \(X\) 的每个点处都连续,那么我们就称 \(f\) 是连续映射。
+我们可以看到,连续映射的自由度很大,两个距离空间的元素,各自的范数定义都很自由。
+考虑一个 \(\exp : M_n(\mathbb C) \to +M_n(\mathbb C)\) +的映射,它的定义我们用级数写过也证明收敛了,下面来证明它是连续映射。记 +\(M_n(\mathbb C)\) 上的范数是 Frobenius +范数,它是一个相容范数,放缩起来会比较容易(我不是很懂为什么讲义上说这是 +\(2-\)范数,矩阵的 \(2-\)范数不是特征值相关的那个嘛?),\(\exp(A) = \sum_{k=0} ^{+\infty} {A^k \over +k!}\)。
+\(\exp : \mathbb R \to \mathbb R\) +的证明用 \(\varepsilon - \delta\) +语言就能轻松地写完。把它迁移到矩阵空间上,证明会复杂一些,用了相容范数的性质。
+
连续函数的性质
-
-
- \(X_{11},X_{12},...,X_{1n_1}\) -i.i.d. \(\sim -Population(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim Population(\mu_2,\Sigma_2)\) -
- 两组样本之间相互独立 -
- 在 \(n_1,n_2\) 较大(均远大于 \(p\))的情况下,我们允许 \(\Sigma_1 \neq \Sigma_2\) -
Hypothesis: \(H_0 :\mu_1 - \mu_2 = -\delta_0; H_1 : \mu_1 - \mu_2 \neq \delta_0\)
Test statistic: \((\bar X_1 - \bar X_2 -- \delta_0 )^T (\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2 )^{-1} (\bar X_1 - -\bar X_2 - \delta_0) \sim ^{H_0} \chi^2 _p\),当 \(T_0 ^2 > \chi^2_p(\alpha)\) -时拒绝原假设。
标准的 \(\mu_1 - \mu_2\) 的 -\(100\% (1-\alpha)\) -置信域是一个椭圆,由区域
-\[\{\mu_1 -\mu_2 : ( \bar X_1 - \bar X_2 - -(\mu_1 - \mu_2))^T(\frac{1}{n_1}S_1 +\frac{1}{n_2}S_2)^{-1}(\bar X_1 - -\bar X_2 - (\mu_1 - \mu_2)) \leq \chi^2_p(\alpha)=c^2 \}\]
-表示。
-类似地考虑 \(X_1,X_2\) -的线性变换,\(a^T(\mu_1 - \mu_2)\) 的 -simultaneous CI 是
-\[(a^T(\bar X_1 - \bar X_2) - c -\sqrt{a^T(\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2)a},a^T(\bar X_1 - \bar -X_2) + c \sqrt{a^T(\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2)a} ),c^2 = -\chi^2_p(\alpha)\]
一个关于单调函数的性质,感觉还挺有必要记一下:
+\(I\) 是区间(可开可闭),\(f\colon I \rightarrow \mathbb R\) 是 \(I\) 上的单调函数,那么
+-
+
对任意 \(x_0\in I\),\(f\) 在 \(x_0\) 处的左极限 \(\displaystyle\lim_{x\rightarrow +x_0^-}f(x)\) 和右极限 \(\displaystyle\lim_{x\rightarrow +x_0^+}f(x)\) 都存在(原文如此。但是如果 \(I\) 是闭区间而 \(x_0\) 是其端点,那么 \(f\) 在 \(x_0\) 处的左/右极限可能为无穷)
+\(f\) 在 \(I\) +上的不连续点的集合是可数的。(这表明单调函数 \(f\) 在“大部分”点处都是连续的)
+
第一问的证明其实也是取 \(x_0\) +点左侧的无穷点列,它们的函数值构成有上界的无穷点列,一定有极限。不妨设 +\(f\) +是一个单调增函数,则这个极限可以表示为 \(\sup +f(x) , x \in (x_0 , x_0 - +\delta)\)。再验证这个极限是左极限,用上确界的性质。
+第二问的话,放一个证明在这里:
++考虑 \(f\) 的不连续点的集合 \(Y=\bigl\{y\in I\bigm| \text{$f$ 在 $y$ +处不连续}\bigr\}\)。
+对于任意 \(y\in Y\),按照定义,\(\displaystyle \lim_{x\rightarrow x_0^-}f(x)\neq +\lim_{x\rightarrow +x_0^+}f(x)\)。再利用上面推论中的结论,我们知道,对任意 \(y\in Y\),我们有 \(\lim_{x\rightarrow y^-}f(x) < +\lim_{x\rightarrow y^+}f(x)\)。
+据此,对于任意 \(y\in +Y\),都唯一地确定了一个非空的开区间 \(I_y=(\lim_{x\rightarrow +y^-}f(x),\lim_{x\rightarrow y^+}f(x))\),即我们构造了映射 \(Y\rightarrow \bigl\{\text{$\mathbb R$ +上的全体非空开区间}\bigr\}, \ \ y\mapsto I_y\)
+利用单调性,我们首先说明对任意的 \(y_1,y_2\in Y\),\(y_1\neq y_2\),\(I_{y_1}\cap I_{y_2}=\emptyset\):
+不妨假设 \(y_1<y_2\),根据上面的推论的结论,我们可以选取单调下降的数列 +\(\{x_k\}_{k\geqslant 1}\),使得 \(x_k \downarrow y_1\)(从右边逼近)并且 +\(\displaystyle\lim_{k\rightarrow \infty} +f(x_k)\) 为 \(I_{y_1}\) +的右端点;类似地,我们选取单调上升的数列 \(\{z_k\}_{k\geqslant 1}\),\(z_k\uparrow y_2\)(从左边逼近),使得 \(\displaystyle\lim_{k\rightarrow \infty} +f(z_k)\) 为 \(I_{y_2}\) +的左端点。由于 \(y_1<y_2\),我们可以假设对任意 \(k\) 都有 \(x_k<z_k\),所以 \(\displaystyle\lim_{k\rightarrow \infty} +f(x_k)\leqslant \displaystyle\lim_{k\rightarrow \infty} +f(z_k)\),也就是说 \(I_{y_1}\) +的右端点要么在 \(I_{y_2}\) +的左端点的左边要么重合,由于这两个区间都是开区间,所以它们的交集是空集。
+这样,我们就得到了一组 \(\mathbb R\) +上两两不相交的非空开区间 \(\bigl\{I_y\bigm| +y\in Y\bigr\}\),我们在每个开区间 \(I_y\) 里选定一个有理数 \(q_y\),由于这些开区间互不相交,这些有理数 +\(q_y\) +也决定了这些开区间。从而,我们得到了单射
+\(Y\rightarrow \mathbb{Q}, \ \ y\mapsto +q_y\)。
+由于有理数是可数的,所以 \(Y\) +可数。
+
介值定理。
+又到了我最爱的闭区间套定理时间!.jpg。为什么说是我最爱的闭区间套定理呢,因为:
+++我:先做 ddl 最晚的作业,然后往前慢慢推,就能正好在最早的 ddl +之前写完所有作业
+室友:那要是最早的 ddl 之前没完成怎么办
+我:不会的,闭区间套定理保证哪怕有无穷个 +ddl,也还可以有一个时刻在“做完所有作业”和“第一个 ddl +到来”这个区间里(
+
我们要求介值定理的区间一定是一个“连通的”区间,也即所谓的 \([a,b]\),否则会举出反例。毕竟,函数的连续性并不要求定义域也是连续的,在若干个区间上分别定义出的连续函数接在一起,就是一个全局连续的函数,但是不能满足介值定理。
+介值定理有很多奇技淫巧的题目,我在学微积分 A +的时候也写过一些,虽然挺好玩,但是感觉并没有什么意义。它比较有意义的一个点在于,第一次成功通过给定的一个任意函数值找到它的原像,也就是说可以用来得到一些“逆映射”的结论。对于闭区间上的单调函数,直观上来说它的逆是比较好找的,这是一个可以通过介值定理得到的结论。
+\(f\colon [a,b]\rightarrow \mathbb +R\) 是严格递增(或者递减)的连续函数,那么 \(f\) 是从 \([a,b]\) 到 \([f(a),f(b)]\) 的双射,并且其逆映射 \(f^{-1}\colon [f(a),f(b)]\rightarrow [a,b]\) +是连续的。
+++Remark:这是 \(1\)-元函数的特殊性质,究其根本,是因为 +\(1\) 维空间上面 \(\mathbb R\) 有序关系 \(\leqslant\) 而在 \(\mathbb R^n\) 上是没有的。
+
由此,我们可以为一些单调的初等函数构造它们的逆,也终于可以得到 \(\sqrt{x},\log x\) 这样的函数了。
+一般的对数函数和幂函数只要改变一些系数就能得到,比如 \(x^ \alpha = e^ {\alpha \log{x} }\),\(\log_\alpha (x)= {\log x \over \log +\alpha}\)。实际上,这二者既分别关于 \(x\) 和 \(\alpha\) 连续,也关于 \((x,\alpha)\) +连续。(这是两个不同的概念)
++Remark:中学我们对 \(e\) +的了解很少,所以和 \(e\) +相关的对象反而变得容易理解,因为我们只需要验证关于 \(e\) +的很少的几个已经知道的性质即可;然而,对于 \(\pi\) 以及相关的 \(\sin x\) +等三角函数,我们了解很多它们的性质,这反而给我们新发展的函数理论带来了很大的挑战:我们在定义这些对象的同时要能够证明它们满足所知的所有性质。实际上,我们必须建立了整个微积分的理论之后才能够做到这一点。
+日本京都大学的数学家望月新一在他的宇宙际Teichmuller理论的论文(他在这一系列论文中声称他证明了abc猜想,目前还没有得到承认)里说:Unlike +many mathematical papers, which are devoted to verifying properties of +mathematical objects that are either well-known or easily constructed +from well-known mathematical objects, in the present series of papers, +most of our efforts will be devoted to constructing new mathematical +objects. 我们这里构造的幂函数就是他所说的“well-known or easily +constructed from well-known mathematical objects”。
+
假设 \(\mathbb R\) 上定义函数 +\(f(x)\) 是连续的,如果我们知道 \(f\) 在有理数上的取值,那么对任意的无理数 +\(x\),我们任取一列有理数 \(r_i\),使得 \(r_i\rightarrow x\),连续性保证了 \(\displaystyle f(x)=f(\lim_{i\rightarrow \infty} +r_i)=\lim_{i\rightarrow \infty } f(r_i)\),所以 \(f(x)\) 可以确定。注意到 \(\mathbb{Q}\) 是 \(\mathbb R\) +中“很小”的子集,由连续性,它已经可以确定 \(f\) +了!这是分析学最重要的精神之一:如何从“局部”到整体。
+如果这个局部是对于整体稠密的,那么它完全可以决定整体。严格的表述是:
+\((X,d)\) 和 \((Y,d_Y)\) 是距离空间,\(X' \subset X\) +是一个稠密的子集,我们仍然用 \(d\) 表示 +\(X'\) 上的距离。对任意的连续映射 +\(F_1\colon X\rightarrow Y\) 和 \(F_2\colon X\rightarrow Y\),\(F_1\big|_{X'}=F_2\big|_{X'}\),那么,\(F_1=F_2\),换而言之,连续映射被它在一个稠密子集上的限制所决定。
+假设 \(x\in X\),我们任意选取 \(\{x'_n\}_{n\geqslant 1}\subset +X'\),使得 \(x'_n\rightarrow +x\)。因为 \(F_1\) 和 \(F_2\) 在 \(X\) 上连续,所以
+\(F_1(x)=\lim_{n\rightarrow +\infty}F_1(x'_n)=\lim_{n\rightarrow +\infty}F_2(x'_n)=F_2(x)\),命题得证。
大样本双总体方差推断
+连续函数的拓扑刻画
+不是,怎么唐突开始升级了啊!
+2023 年 1 月 28 +日,星期六,我妈开始上班了所以我终于可以白天学这个东西了.jpg
+++在开始介绍拓扑的概念之前, 我们引用 John von Neumann 的一段话:
+Young man, in mathematics you don’t understand things. You just get +used to them.
+
稍微有点难(
+大概也没什么可写的,因为全都没见过所以大概只能抄概念,那还不如直接看原文,而且我已经纸质抄过一遍了 +qwq
+而且实际上所有的东西又在习题里以距离空间的加强版出现了。实数轴上唯一不同的是,开集可以表示为可数个开区间的并,这是特有的性质。
+Summary
+之前讨论极限某种意义上来说都是关于点,性质也都是离散的。这一节考虑了函数的性质,涉及到连续变化的集合的函数值的性质。但令人欣慰的是,至少关于函数连续性的讨论还是可以通过点列、\(\varepsilon - \delta\) +语言来进行,这是已经熟悉的内容。
+其次,我们在这一部分之前对于函数的定义,只有基本的多项式函数、一些收敛的级数和 +\(e^x\)。一方面,通过介值定理我们基于单调函数的逆映射得到了 +\(x^{1 \over n}\),\(\log _{\alpha} x\) +函数的定义,并确认它们也是连续函数;另一方面,我们继续拓展了 \(e\) 相关函数的定义丰富性,从原始的 \(e\) 到 \(e^x\),再到赋范线性空间上的 \(e^A\)(尽管它不能满足一些 \(e^x\) 有的性质),这一次又添加了 \(e^f\) +的定义。即使都是在级数的意义下进行定义,看起来大同小异,但是分别验证收敛性是必要的,这次还额外验证了 +\(e^A\) 在 Frobenius +范数下的连续性。
+然后学了一点拓扑内容,大概讲了讲开集闭集的概念,引出了连续函数的第三种刻画:等价于任意开集的逆映集还是开集。
+梦话:胡说八道一些证明题
+计算对于做题家来说太 trivial +了,所以胡说八道一些证明题。我想我也没有非常胡说八道,毕竟不会做的题你让我胡说八道,我也说不出来什么,sigh。
+距离空间上的拓扑与连续性
-
-
检验前对于两个总体的假设:
+(距离空间上的Heine定理)假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) +是映射。我们有两种方式来定义连续映射(参见第3次作业题的A3)和第9次课)
-
-
- \(X_{11},X_{12},...,X_{1n_1}\) -i.i.d. \(\sim -Population(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim Population(\mu_2,\Sigma_2)\) -
- 两组样本之间相互独立 -
-Hypothesis: \(H_0 : \Sigma_1 = -\Sigma_2; H_1 : \Sigma_1 \neq \Sigma_2\)
-Test statistic:考虑 likelihood ratio \(\Lambda = \frac{max_{\theta \in \Theta_0} -L(\theta)}{max_{\theta \in \Theta} L(\theta)} = \frac{|S_1|^{n_1 /2} -|S_2|^{n_2/2}}{|S_{pooled}|^{n_1+n_2-2/2}}\),自由度之差为 \(v-v_0 = df(\Theta) - df(\Theta_0)\),于是在 -\(H_0\) 假设下有 \(-2 \ln \Lambda \sim \chi^2_{v-v_0}\) -是为检验统计量。
-George Box 对其进行了修改,使得可以对 \(g\) 个总体进行方差推断,具体略去。
+假设 \(x_0\in X\),如果对任意 +\(X\) 中的点列 \(\{x_n\}_{n\geqslant 1}\),\(x_n\stackrel{d_X}{\longrightarrow}x_0\),我们都有 +\(f(x_n)\stackrel{d_Y}{\longrightarrow}f(x_0)\),我们就称 +\(f\) 在 \(x_0\) 处是连续的。如果 \(f\) 在一切 \(x\in +X\) 处均连续,那么我们就称 \(f\) +是距离空间之间的连续映射。
+假设 \(x_0\in X\),\(y_0=f(x_0)\in Y\)。如果对任意的 \(\varepsilon>0\),总存在 \(\delta>0\),使得对任意满足 \(d_X(x,x_0)<\delta\) 的 \(x \in X\),都有 \(d_Y\bigl(f(x),f(x_0)\bigr)<\varepsilon\),我们就称 +\(f\) 在 \(x_0\) 处连续。如果 \(f\) 在 \(X\) 的每个点处都连续,那么我们就称 \(f\) 是连续映射。
+证明,上面两个对连续映射的定义是等价的。
Assumption Check
-类似于线性回归中所讲的内容,此处略去。
-Lecture 6
-关于主成分分析(Principal Component Analysis)在 population -上的理论和在 sample -上的应用。希望通过对一系列随机变量的线性变换和组合,分析维度更小的数据来达到同样的结果。
-For Population
-PCA 方法的具体操作
-面对的问题模型可以视作:随机向量 \(X^T = -[X_1 , X_2,...,X_p]\) 有 \(p \times -p\) 维的协方差矩阵 \(\Sigma\) -和对应的 \(p\) 个非负特征值 \(\lambda _1 \geq \lambda_2 \geq ... \geq \lambda_p -\geq 0\),分别对应单位特征向量 \(e_1,e_2,...,e_p\),这是一组正交基。
-我们希望能够找出 \(Y_1, -Y_2,...,Y_p\) 满足 \(Y_i = a_i ^T -X\),使得 \(a_i ^T a_i -=1\),\(Var(Y_i)\) 最大,且 -\(Cov(Y_i, Y_j)=a_i ^T \Sigma -a_j=0\)。事实上由 Rayleigh 商可以知道,只要取 \(a_i = e_i\) 就可以三个愿望一次满足(,且有 -\(Var(Y_i) = \lambda_i\),证明是 -trivial 的。
-这个变换有一些性质:
+Trivial.
+\((X,d)\) 是距离空间。对任意的点 +\(x\in X\),\(r>0\),我们称 \(B(x,r)=\bigl\{y\in X\mid +d(y,x)<r\bigr\}\) 为以 \(x\) +为中心以 \(r\) +为半径的开球。证明,对任意的点 \(x\in +X\),\(r>0\),如果 \(x'\in B(x,r)\),那么存在 \(r'>0\),使得 \(B(x',r')\subset B(x,r)\)。
+如果 \(U\subset X\) +是若干开球的并,即 \(U=\displaystyle +\bigcup_{\alpha \in \mathcal{A}} B(x_\alpha,r_\alpha)\)(指标集 +\(\mathcal{A}\) 是任意的),就称 \(X\) 是距离空间 \((X,d)\) 中的开集。证明,\(U\subset X\) 是开集当且仅当对任意的 \(x\in U\),存在 \(\delta_x>0\),使得 \(B(x,\delta_x)\subset U\)。
+前一问按照定义写一下就可以了;后一问用前一问的结论。Trivial.
+直观上来看就是,取开球内部的一个点,有一个这个点决定的小球在开球内。其实就是开区间的推广。
(距离空间上的标准拓扑)我们用 \(\mathcal{T}\) 表示距离空间 \((X,d)\) 上的开集的全体,其中,我们规定 +\(\emptyset\) 和 \(X\) 都是开集。证明,它们满足:
-
-
\(\Sigma_{i=1}^p Var(X_i) = -\Sigma_{i=1}^p \sigma_{ii} = trace(\Sigma) = \Sigma_{i=1}^p \lambda_i = -\Sigma_{i=1}^p Var(Y_i)\)
-说明 PCA 前后的信息没有损失。
-可以通过 \(Var(Y_i)\) 在 \(\Sigma_{i=1} ^p Var(Y_i)\) -中的占比判断这一信息的重要程度,这一数值为 \(\frac{\lambda_i}{\lambda_1 + ... -\lambda_p}\)
-\(Cov(Y_i , X_j) = Cov(e_i ^T X, I_j ^T -X) = e_i ^T \Sigma I_j = \lambda_i e_i^T I_j = \lambda_i -e_{ij}\)
-因此二者之间的相关系数为 \(\rho_{Y_i , X_j} -= \frac{Cov(Y_i,X_j)}{\sqrt{Var(Y_i) Var(X_j)}} = \frac{e_{ij} \sqrt -\lambda_i}{\sqrt \sigma_{ii}}, i,j = 1,2,...,p\)。
-对于固定的 \(j\) 有 \(\Sigma_{i=1}^p \rho_{Y_i,X_j}^2 = -1\)。这一相关系数显示了 \(X_j\) -的方差可以被 \(Y_i\) -解释的比例。
+- \(\emptyset \in \mathcal{T}\), +\(X \in \mathcal{T}\)。 +
- 对任意开集的集合 \(\{U_{\alpha}\}_{\alpha +\in \mathcal{A}}\),其中 \(\mathcal{A}\) 为指标集合,我们有 \(\displaystyle\bigcup_{\alpha \in +\mathcal{A}}U_\alpha \in \mathcal{T}\)。 +
- 对任意有限个开集 \(U_1,U_2,\cdots, U_m \in +\mathcal{T}\),我们有 \(\displaystyle\bigcap_{1\leqslant i\leqslant m}U_i +\in \mathcal{T}\)。
事实上,有的时候直观显示出来 \(Y_i = -e_i^TX\) 中 \(X_j\) -前系数较小,这并不说明 \(X_j\) -的影响较小,计算 \(\rho_{Y_i,X_j}\) -可能会体现出较大的相关系数,显示二者之间有较大的相关性。
-正规化随机变量下的 PCA
-实际使用中可能存在一些单位的变化、尺度变化导致 PCA -的系数出现不同的情况。我们讨论 standardized variable \(Z_k= \frac{(X_k - \mu_k)}{\sqrt \sigma_{kk}}, k -=1,2,...,p\) 下的 PCA 变换。
-事实上有 \(Z = diag(\sqrt{\sigma_{11}^{-1} -},\sqrt{\sigma_{22}^{-1} },...,\sqrt{\sigma_{pp}^{-1} } ) -(X-\mu)\),于是 \(Cov(Z) = -diag(\sigma_{11},\sigma_{22},...,\sigma_{pp})\)。 -由此即得正规化情况下的 PCA 变化的参数细节,不再赘述。
-多元正态分布下的 PCA
-当 \(X\sim N_p(\mu ,\Sigma)\) -时,好像下节课再讲(
-For Sample
-回顾一下多元情况下的样本方差:
+第一个是定义,第二个也是定义。
+第三个的话,取 \(x \in +\displaystyle\bigcap_{1\leqslant i\leqslant m}U_i\),有小球 \(B(x,\delta _i) \in +U_i\),则最小的一个开球在全体开集的交集中。由 \(x\) +的任意性,用一下上一题的结论即证。
\((X,d)\) 是距离空间。如果 \(F\subset X\) 的补集是开集,我们就称 \(F\) 是闭集。证明,\(F\) 是闭集当且仅当对任意点列 \(\{x_n\}_{n\geqslant 1}\in F\),如果 \(\displaystyle \lim_{n\rightarrow \infty}x_n = +x\),那么 \(x \in F\)。
+如果 \(F\) +是闭集,且对于这样的序列有 \(x \notin +F\),则 \(x \in X-F\),也就是说 +\(x\) 在一个开集中,有一个包裹 \(x\) +的小球也在开集中,所有这个序列里的点都和 \(x\) 隔着小球半径的距离,不可能收敛到 \(x\),矛盾。
+如果对任意的序列都有这样的结论,而且 \(F\) 不是闭集,\(X-F\) 不是开集,那么存在一个 \(x \in X-F\) 使得对任意 \(\delta >0\),都有 \(B(x,\delta)\) 不完全在 \(X-F\) 中。也就是说,对任意的 \(\delta >0\),总存在 \(y \in F\) 使得 \(d(x,y)<\delta\)。也就是说,存在一个 +\(F\) 中的收敛到 \(x\) 的序列,使得 \(x \notin F\),这和前提矛盾。
--协方差定义为 \(s_{ik} = \frac 1 n -\Sigma_{j=1}^n (x_{ji} - \bar{x_i}) (x_{ji} - -\bar{x_k})\),可以看到实际上 \(s_{ik} = -s_{ki}\),于是协方差矩阵有
-\[ \begin{bmatrix} s_{11} & s_{12} -& ...& s_{1p}\\ s_{21} & s_{22} & ...& s_{2p} \\ ... -& ...&...&... \\ s_{p1} & s_{p2} &...&s_{pp} -\end{bmatrix}\]
-的形式,这是一个对角元为正的对称矩阵。
-
事实上,对于已知的 \(x = -[x_1,x_2,...,x_p]\),希望取 \(\hat{y_i} -= \hat{e_i} ^T x = \hat e_{i1}x_1 + \hat e_{i2} x_2 + ... +\hat e_{ip} -x_p\) 满足 \(\hat e_i ^T \hat e_i = -1\),$Cov(y_i , y_j) = 0 $ 对不相等的 \(i ,j\) 都成立,且 \(Var(\hat y_i) = \hat \lambda_i, i = -1,2,...,p\)。\(\hat y_i\) 称为 -\(i\)-th sample principal component -(score),即 sample PCs。
-类似于 population 情况下的 PCA,sample PCs 有以下性质:
+写逆命题也是一种技术,比如我差点以为一个集合不是开集就是闭集,这是不对的。
+比如说在实数集上,有 \((1,2) \cup +(3,5]\) 既不是开集也不是闭集。
+证明,距离空间 \((X,d)\) +上的闭集,
-
-
- \(\Sigma_{i=1} ^p Var(\hat y_i) = -\Sigma_{i=1}^p s_{ii} = \Sigma_{i=1}^p \hat \lambda_i\) -
- \(\rho_{\hat{y_i} ,x_k} = -\frac{\hat{e}_{ik} \sqrt {\hat{\lambda}_k} }{\sqrt s_{kk} -}\) +
- \(\emptyset\) 和 \(X\) 都是闭集。 +
- 任意多闭集的交集还是闭集。 +
- 有限个闭集的并集还是闭集。
Practical Issues
-在实践中求得了 PC -的表达式,还需要进行一定的取舍和判断,从而选出需要使用的值。
-理论很巧妙,但我真的不想写代码实现(
-How many principal -components to retain
-可以画一个 scree plot,值在底端且明显小的需要排除。对于 sample -principal component score 且是 standardized sample 的情况下,可以选取 -cutoff point 是 \(1\),舍弃所有使得 -\(Var(Y_i) <1\) 的 -PCs,留下的即是真正的主成分。
-Check normality -assumption & detect outliers
+这都是上上题的逆否,自然是成立的。
假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) +是映射。那么,如下三个叙述是等价的:
-
-
- 检验正态性可以用最大的几个 PCs -
- 检验离群值可以用最小的几个 PCs +
- \(f\) 是连续映射。 +
- 对任意 \(Y\) 中的开集 \(U\),其逆像 \(f^{-1}(U)\) 为 \(X\) 中的开集。 +
- 对任意 \(Y\) 中的闭集 \(F\),其逆像 \(f^{-1}(F)\) 为 \(X\) 中的闭集。
Limitations
--
-
- PCA -只使用了协方差矩阵里的值,实际上没有把数据包含的信息利用完全 -
- 只进行线性变换 -
- 很难反映变量之间的线性关系 -
- 对离群值敏感 +
我不想证明 \((1)\) 和 \((3)\) 之间的关系,所以验证 \((1) \to (2)\),\((2) \to (1)\),\((2) \iff (3)\)。
+\((1) \to (2)\):如果 \(f\) 是连续映射,\(U\) 是开集,我们想证明对于任意的 \(x \in f^{-1}(U)\),有 \(x\) 为中心的一个开球也在 \(f^{-1}(U)\) 中。令 \(y=f(x)\),而 \(f\) 是连续映射,所以在 \(x\) 点也连续。于是对任意的 \(\varepsilon >0\),存在 \(\delta\) 使得对任意的 \(x'\in B(x,\delta)\),有 \(d(f(x),f(x'))<\varepsilon\),也即 +\(f(x') \in B(f(x),\varepsilon +)=B(y,\varepsilon)\)。因此,只要取满足 \(B(y,\varepsilon) \subset U\) 的 \(\varepsilon\),就能得到 \(B(x,\delta) \subset f^{-1}(U)\)。于是 \(f^{-1}(U)\) 也是开集,得证。
+\((2) \iff (3)\):只要证明 \(f^{-1}(F) \subset X-f^{-1}(X-F)\),还有 +\(f^{-1}(U) \subset +X-f^{-1}(X-U)\),trivial.
+\((2) \to +(1)\):现在假设对任意的开集 \(U\),\(f^{-1}(U)\) 是开集,我们来证明 \(f\) 是连续的:给定 \(x_0\in \mathbb R\),令 \(y_0=f(x_0)\),考虑 \(y_0\) 处的开集 \(B(y_0,\delta)\)。由于 \(f^{-1}\bigl(B(y_0,\delta)\bigr)\) 为开集且 +\(x_0\in +f^{-1}\bigl(B(y_0,\delta)\bigr)\),所以存在 \(\varepsilon >0\),使得 \(B(x_0,\varepsilon)\subset +f^{-1}\bigl(B(y_0,\delta)\bigr)\),从而,\(f\bigl(B(x_0,\varepsilon)\bigr)\subset +B(y_0,\delta)\),这说明对任意的 \(\delta\),存在 \(\varepsilon\),使得当 $ d(x,x_0)<$ +时,我们有 \(d(f(x),f(x_0))<\delta\),从而 \(f\) 在 \(x_0\) 处连续。
\((X,d)\) 是距离空间,\(A\subset X\) 是子集,我们将包含 \(A\) 的所有闭集交 \(\overline{A}\) 为 \(A\) 的闭包,根据上题,这是闭集,所以是包含 +\(A\) 的最小闭集。
+对于 \(x\in X\),如果存在点列 \(\{a_k\}_{k\geqslant 1}\subset A\),使得 +\(\displaystyle \lim_{k\rightarrow \infty}a_k += x\),并且其中 \(a_k\neq +x\),我们就称 \(x\) 是 \(A\) 的一个聚点。
+\(A\) 的聚点不一定都在 \(A\) 中,\(A\) 中的点也不一定都是 \(A\) 的聚点。\(A\) 中不是 \(A\) 的聚点的点被称为 \(A\) 的孤立点。\(A\) 的聚点组成的集合被称为 \(A\) 的导集,记作 \(A'\)。如果 \(X=X'\),我们称 \(X\) 为完美集。
+证明,\(\overline{A}=A'\cup +A\)。特别地,\(F\) +是闭集当且仅当 \(F\) 的聚点都在 \(F\) 中,即 \(F=F'\cup F=\overline{F}\)。
+首先证明闭包里包含所有聚点(包含 \(A\) 是显然的)。如果有一个序列和它们的极限 +\(x\) 使得 \(x \neq x_n\),且 \(x \notin \bar{A}\),这和 \(\bar{A}\) 是闭集矛盾。因此 \(\overline{A} \supset A'\cup +A\)(看起来好别扭
+再证明闭包里所有的点要么在 \(A\) +中,要么是聚点。如果有 \(x \in +\bar{A}\) 且 \(x \notin +A\),我们要证明它是一个聚点,只要构造出一个收敛到 \(x\) 的 \(A\) 中序列。实际上,对任意的 \(\varepsilon >0\) 都存在 \(x' \in A\) 使得 \(d(x',x)<\varepsilon\),也就是说 +\(B(x,\varepsilon)\) 始终和 \(A\) 有交。否则存在某个 \(\varepsilon\) 使得 \(A \cap B(x,\varepsilon) = +\emptyset\),那么一定有一个包含 \(A\) 的闭集 \(S=X-B(x,\varepsilon)\),\(x \notin S\),这和 \(x \in \bar{A}\) 矛盾。所以 \(x\) 一定是一个聚点。
+如果 \(A\) 是闭集,那么 \(A=\bar{A}\),所以聚点一定都在 \(A\) 中。
(距离空间的乘积与连续映射)假设 \((Y,d_Y)\) 和 \((Z,d_Z)\) 是距离空间,我们定义 \(Y\times Z\) 上的距离函数
+\(d_{Y\times Z}\colon \bigl(Y\times +Z\bigr){ \times} \bigl(Y\times Z\bigr) \rightarrow \mathbb R_{\geqslant +0}, \ \ \bigl((y_1,z_1),(y_2,z_2)\bigr)\mapsto +\sqrt{d(y_1,y_2)^2+d(z_1,z_2)^2}\)
+证明,\(d_{Y\times Z}\) 是 \(Y\times Z\) +上的距离函数。证明,两个自然的投影映射是连续的:
+\(\pi_Y\colon Y\times Z \rightarrow Y, \ +(y,z)\mapsto y; \ \pi_Z\colon Y\times Z \rightarrow Z, \ (y,z)\mapsto +z\)
+证明,给定距离空间 \((X,d)\) 和 +\((Y\times Z,d_{Y\times Z})\) +之间的映射 \(F\colon X\rightarrow Y\times +Z\),那么,\(F\) +连续当且仅当两个复合映射 \(\pi_Y \circ F\colon +X\rightarrow Y\) 和 \(\pi_Z \circ +F\colon X\rightarrow Z\) 都连续。
+其实都挺 trivial 的。
证明,加法映射 \(+\) 和乘法映射 +\(\times\) 都是连续映射,其中
+\(+\colon \mathbb R^2\rightarrow \mathbb R, +\ \ (x,y)\mapsto x+y; \ \ \ \ \times \colon \mathbb R^2\rightarrow +\mathbb R, \ \ (x,y)\mapsto x\cdot y\)
+Trivial.
证明,矩阵上的加法映射 \(+\) +和乘法映射 \(\bullet\) +都是连续映射,其中
+\(+\colon \mathbf{M}_n(\mathbb R)\times +\mathbf{M}_n(\mathbb R)\rightarrow \mathbf{M}_n(\mathbb R), \ \ +(A,B)\mapsto A+B;\ \ \ \ \bullet\colon \mathbf{M}_n(\mathbb R)\times +\mathbf{M}_n(\mathbb R)\rightarrow \mathbf{M}_n(\mathbb R), \ \ +(A,B)\mapsto A\cdot B\)
+定义距离为 \(d(A,B) = +||A-B||_F\)(Frobenius +范数),然后就可以用相容性的不等式了,trivial.
证明,\(\mathbf{M}_n(\mathbb +R)\) 上的可逆矩阵的全体 \(\mathbf{GL}_n(\mathbb R)\) 是 \(\mathbf{M}_n(\mathbb R)\) +中的开集。(提示:构造一个连续映射使得该集合是连续映射的逆像)
+做连续映射(行列式)\(det: \mathbb R^{n +\times n} \to \mathbb R\),\(A \to +det(A)\),于是 \(det^{-1} ((-\infty,0) +\cup (0,\infty)) = GL_n(\mathbb R)\) 是开集。
+至于行列式运算为什么是连续的,因为它本质上是关于 \(n^2\) +个变量的多项式(,所以关于各个分量连续。
+我胡说八道的啊,我觉得我好像有必要补一补高代(
证明,取逆映射 \({\rm Inv}\colon +\mathbf{GL}_n(\mathbb R)\rightarrow \mathbf{GL}_n(\mathbb R), \ \ +A\mapsto A^{-1}\) 是连续映射。
+记任意可逆矩阵集 \(U\) 的原像为 +\(Inv^{-1} U\),它是 \(GL_n (\mathbb R)\) +的子集,也是一个开集。所以 \(Inv\) +是连续映射。
+看到这个 \(Inv\) 我还以为要联动 +Galois 理论了,吓一跳。
后记
-期中考完就退课了,于是这一篇写到 lecture 6 就烂尾了,乐(
-多元问题确实太难了,我到现在绩点最低的一门数学课是微积分
-A(2),意思是别的都 4.0 就它 3.6
-还是五个学分(这是可以说的吗)。当时就觉得多元微积分真的好麻烦。然而多元统计难度不在多元而在统计,这属实是我没想到的。
之前在 Vincent19 主页上看到过这样一句话:
---A key difference between mathematics and statistics is that the -former is full of lemmas while the latter is full of dilemmas.
-
事实上,统计对我来说最大的困难还是面对 dilemma -应该怎么做这样的问题。半个学期下来我始终觉得如今学到的处理统计问题的方法都是原始而 -trivial -的,你能想到的最容易的方法就是最好的解决方案。线性回归课堂上没有任何需要动脑超过五分钟的推导,周老师时不时说我们这个不是数学课,数学不好也不要害怕,这让我无比难受,我自己是否也有点阴暗了。然而无论是看图用眼睛做模型诊断,还是写无穷无尽却又几乎一成不变的 -R code 然后在 ANOVA table -里分析数据和模型参数的细微差别,都几乎让我崩溃。多元统计时不时出现的 CI -选择和“几何直观”也一样困扰我。我想我真的不擅长处理这么具体的场景,我宁愿去读晦涩的 -lemma,像解谜游戏一样,我还是只喜欢做游戏。
-所以,统计中心的应统课果然还是不适合我,或许数学系的统计课会稍有不同,或许不会这么纠结现实的应用问题,但我还是厌倦了。另外,我发觉自己的分析水平也没那么差。如果不是再退线性回归的话这学期要没课上了,其实是想一起丢掉的。只能说我还是太弱了,从数学转去搞统计的同学不在少数,好像只有我这样困扰。
-当时写统推笔记的时候在开头写下了“实在不行的话,(方向)该换还得换啊”这样的话,然而统推很顺利地上完了,还以为方向就这么定下来了,不用再继续颠沛流离。现在却是又一次要换掉了,再一次抛弃一切。开玩笑的,统计转概率也不算是放弃一切,不然怎么会合称“概统”呢。
-我之前写“感觉自己 20th -的主题是出走”,后来觉得不是,出走会是我一生的主题,cause I have a vast, -vast soul.
-希望自己在概率这条路上走得远一点吧,暂时先和统计说再见了...等等还有两门课还在上呢(
-]]>这个操作是合理的。我和物理本来就不合适,结合上学期的经验可以发现,无论有没有学过原理,我唯一的解决方案就是按计划一帧一帧地做实验,才不至于大脑空白。加之我秋季学期就没选理论课,理论水平也就是现在这样了,倘若现在不写,将来更写不出来。上学期因为仓促,只在讲义上手写了一些要点,有的时候记不清了就会不知所措,所以这次码个字可以详细一点。
这样的话,物理实验就变成了大猩猩也能做的体力活罢了。我不否认这个想法,也无意论辩这门课是否有意义,将本文视作作者的救命手册即可。
注:未经授权禁止转载,本人不希望在院系里受到关注;所有提到的引用,包括图片,文字,数据信息等,著作权归原作者所有;一概不提供文中提到的自用实验表格,请自行阅读实验讲义,勿直接伸手。
-完整报告篇
-用单色仪测定介质的吸收曲线
-原理简述
-一束光入射到有一定厚度的介质上时,有一部分光被反射,另一部分被吸收,其余被透射——也即进入有厚度\(d\)的介质。根据各部分的光强,可以定义出介质板的光谱外透射率\(T=\frac{I_T}{I_0}\)和光谱透射率\(T_{i}=\frac{I_2}{I_1}\)。
-(此处应该有图,但是没有图。)
-光谱透射率同时与介质的性质和入射光的波长\(\lambda\)相关。为什么这么说呢?因为忽略介质内散射的情况下\(T_{i}=e^{-\alpha d}\),\(\alpha\)称为介质的线性吸收系数,与介质的性质和入射光波长有关。
-经过若干次透射后,透射光的光强为一个等比数列的和,即为\(I_T=\frac{I_0(1-R)^2e^{-\alpha -d}}{1-R^2e^{-2\alpha d}}\)。其中,\(I_{0}\)为入射光强,\(R\)为单一界面上的反射率。由此可以计算光谱外透射率\(T=\frac{I_T}{I_0}\)。
-在实际实验中,使用了两块仅厚度不同的试样,计算后近似得出光谱外透射率的比值,我们不加证明地给出吸收系数的近似:\(\alpha=\frac{lnT_{1}-lnT_{2}}{d_{2}-d_{1}}\) -。实际实验中,用微电流放大器的显示值\(V_{1}\),\(V_{2}\)分别替换上式的\(T_{1}\),\(T_{2}\)。
-应该做什么?在纸上记什么?
-你不懂仪器的构造,但是没关系,跟着做就行了。
-校对单色仪的波长示值
-单色仪长这个样子:
- -第一步,通过两个鼓轮调入射狭缝 S1 和出射狭缝 S2 -的宽度,分别约为 1mm 和 2mm(目测即可)。
-第二步,把汞灯放在 S1 前面,打开汞灯,把手轮转到 -577.0~579.1nm 之间的某一位置(通过波长示数器观察)。
-显微镜目镜和物镜拧紧放在 S2 前面,调一调高度和与 S2 -的距离,观察到像这样的图像。黄的叫谱线,黑的叫狭缝刃口。
- ---关小入射狭缝 S1 -使两条谱线分开,在谱线沿缝方向宽度基本均匀、亮度好的前提下, -使狭缝尽量窄,谱线尽量细。再关小出射狭缝 -S2,同时微动手轮,使其中一条谱线始终在狭缝中央,直至狭缝宽度与谱线同宽(此时微动手轮,谱线即被遮挡,谱线消失)。
-
纸上谈兵来说,如上操作可以得到单条谱线的波长示值(显示在波长计数器上)。按这个办法慢慢调波长,在标准值附近分别找两条黄线,一条紫线和一条绿线的示值,把它们记在第一个表里,差值的平均值就是单色仪波长示值的系统误差,之后要修约。
-标准值是黄线 579.1nm, 黄线 577.0nm,绿线 546.1nm,紫线 435.8nm。
-用汞灯调狭缝宽度
-第一步,将单色仪的波长读数装置转到示值在 -577.0~579.1nm 之间的某一位置。将出射缝 S2 的宽度暂时调至约 -2mm。用显微镜观察汞的两条黄谱线(577.0nm 和 -579.1nm)。如果看不到谱线,增加 S2 缝宽或改变波长示值。
-第二步,缓慢增加入射狭缝 S1 -的宽度,使谱线变宽,直到两条黄谱线刚好碰上且不重叠为止,此时入射狭缝宽约0.8mm。再调节出射狭缝 -S2 -的宽度,同时微调手轮,使出缝宽度与其中一条谱线宽度大致相同,此时出缝与入缝同宽,约 -0.8mm。
-此后不要再动单色仪,光强就能满足吸收系数测量的要求。此部分不需要记录数据。
-溴钨灯/光路调节,而不是溴钨灯光/路调节
-第一步,溴钨灯按讲义上写的接三路输出电源,调整设置。
-然后,讲义上是这样写的:
---为了减少单色仪的光能损失,提高透光效率(充分利用单色仪的全孔径和相对孔径 -D/f),根据图 12 光路图,计算聚光镜和光源的位置。
-聚光(透)镜的参数见前面。单色仪焦距 f=300mm (即图 12 的 -b=300mm),单色仪球面镜(准直镜)的光栏宽度 -D=50mm。成像规律符合 Gauss 公式。
-使球面镜的孔径 D -充分照明,两个相似三角形应有下列关系:d/D=a/b。
-
翻译成人话:聚光镜摆在狭缝前面 18cm 处,溴钨灯摆在聚光镜前面 -9cm -处,注意共轴。当然,得在表格上画个图,装模作样算一下这两个数据。
-第二步,手轮调到 -610.0nm,调整各种位置。用眼睛靠近出射狭缝 S2 观察红色谱线。
-具体怎么调?先粗调后细调。
-粗调:溴钨灯电流建议用 -2.0A。微调光源的位置,用眼睛观察溴钨灯在入射狭缝 S1 -处所成的清晰实像,粗略调节等高同轴。
-细调:溴钨灯电流建议用 1.50A。用眼睛靠近出射狭缝 S2 -观察光谱,左右(共轴)调节聚光镜至合适位置,不管条纹亮度均匀否,只关注条纹上、下边缘的圆弧左右对称否,调至对称。
-再前后、左右微调溴钨灯,眼睛能看到亮度均匀的光谱(条纹),差不多这样。
- -调节好透镜和溴钨灯位置后,固定好它们。
-最后的仪器安装
-第一步,把样品装在 S2 -上,先薄再厚,具体操作摘录如下:
---将装有钕玻璃吸收片的样品反面的红点对准S2 -上红点,顺时针旋转样品,听到咔的声音,样品已锁定,往外拉一下,确认已安装好。
-取样品时侧面小螺钉往里轻推,逆时针旋转即可取下。
-
第二步,装硅光电二极管探头。
---将探头插入样品正面的圆柱孔内(插到底),确认电缆接头处于拧紧状态。
-
如果还是手笨接不好仪器,就求助一下旁边同学吧,没救了。
测量环节
-对每一个样品,观察对各色光的吸收情况。
-从 610.0nm 到 550.0nm -转动手轮测定两个最大的吸收峰(光电探测器上的电压示值最小)的波长位置并记录。要求每隔 -2nm 测一次示值,在吸收峰左右 4nm 范围内测量点更密,取整数每隔 0.5nm -测量一次,记录在最后一个表里。
-注意:测量要消空程,即只向一个方向转动手轮, 一次完成。
-测完数据要分析计算什么?画哪些图?
+函数的零点
+其实一共有八道题,但另外七个都很 +trivial,这个没有一眼看出来,所以还是写一写。
-
-
- 根据\(\alpha=\frac{lnV_{1}-lnV_{2}}{d_{2}-d_{1}}\),列表计算每个波长对应的\(\alpha\) -
- 画一个\(\lambda-\alpha\)图,是为吸收曲线。从中读出两个峰值的数值,然后按波长修正规则修一下。 -
- 误差分析讨论和回答思考题,可参考祖传实验报告。 +
\(f\colon \mathbb R\rightarrow \mathbb +R\) 是函数,对 \(c\in \mathbb +R\),我们定义 \(f^{-1}(c)=\{x\in +\mathbb R\mid f(x)=c\}\)。证明,如果对任意 \(c\in \mathbb R\),我们都有 \(|f^{-1}(c)|=2\),那么 \(f\) 不是连续函数。
+说明任意取一个开集 \(U \subset +R\),都有 \(f^{-1}(U) = \lbrace 2 +\rbrace\) 或 \(\lbrace -2 +\rbrace\) 或 \(\lbrace 2,-2 +\rbrace\),都不是开集,所以 \(f\) 不连续。
+给我一点小小的拓扑震撼(
+貌似也可以用介值定理,就随便讨论一下,夹几个区间出来就行,但是没必要。
本文写作中用到的参考
+*思考题
-
-
单色仪实验操作视频:
-https://www.bilibili.com/video/BV17A411L7mg?spm_id_from=333.337.search-card.all.click&vd_source=6ae5c31a80120436d23cf7b7c7ceb3ba
-清华大学2021秋基础物理实验(2)讲义
+假设 \(A\subset \mathbb R\) +是一个可数集。证明,存在单调函数 \(f\colon +\mathbb R\rightarrow \mathbb R\),使得 \(f\) 的不连续点的集合恰好是 \(A\)。
+大概可以分段构造 \(f(x)=x+T_i,x \in +(x_i,x_{i+1})\),来保证是单调增函数且不连续。
+函数 \(f\colon [0,1]\rightarrow +[0,1]\) 是递增的函数,证明,\(f\) 有不动点。
+考虑 \(F(x)=f(x)-x\),一定有不动点。
+考虑 \([0,1]\) +到自身的自同胚,即 \({\rm +Homeo}([0,1])=\bigl\{f\colon [0,1]\rightarrow [0,1]\bigm| \text{$f$ +为连续的双射}\bigr\}\)
+我们知道对于任意的 \(f\in {\rm +Homeo}([0,1])\),\(f^{-1}\in {\rm +Homeo}([0,1])\)。假设 \(f\in {\rm +Homeo}([0,1])\) 并且 \(0\) 和 +\(1\) 是它仅有的不动点,\(g\in {\rm Homeo}([0,1])\) 并且 \(0\) 和 \(1\) 也是它仅有的不动点,证明,存在 \(h\in {\rm Homeo}([0,1])\),使得 \(h^{-1}\circ f\circ h =g\)。
偏振光学系列实验
-原理简述
+一致连续性
+2023 年 1 月 29 +日,星期日,我觉得凡是带有“一致”的东西都蛮恐怖的,比如 UMVUE(
+惭愧地说,一致连续性其实我以前没有学会过,因为考试不考(。再来一遍.jpg
+草,我之前把数分分成 I 和 II +都觉得挺奇怪的,但目前已经三万多字了,Typora +开始有点卡了(。所以这次又分别分了上下,暂且以期中考试为界吧。
+紧性与开覆盖
+是没接触过的很新的东西(,我怀疑这也不是数分内容,全在抄。好像也没抄会。
+一致连续性
-
-
- 什么是偏振光?
这不重要
+ 假设 \(f\colon X\rightarrow \mathbb +R\) 是连续函数,如果对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x,y\in X\),只要 \(d(x,y)<\delta\),就有 \(|f(x)-f(y)|<\varepsilon\),就称 \(f\) 在 \(X\) 上一致连续。
+看起来很像 Lipschitz 条件,不过 Lipschitz +条件其实是特化版的,是一致连续的充分条件,用来解决一些不动点问题。
+有界闭区间上的连续函数一定一致连续。
+一致收敛和逐点收敛的区别实际上是关于点 \(x\) 的差别,对 \(N\) 的依赖进行区分即可。对于一个函数序列 +\(\lbrace f_n : X \to R \rbrace\) +和函数 \(f: X \to R\),有:
+逐点收敛是指,对任意的 \(x \in +X\),任意 \(\varepsilon +>0\),存在 \(N=N(\varepsilon , +x)\) 使得当 \(n >N\) +时,\(| f_n(x) - f(x) | < +\varepsilon\)。
+一致收敛是指,对任意的 \(\varepsilon +>0\),存在 \(N=N(\varepsilon)\) 使得对任意的 \(x \in X\),有 \(|f_n(x) - f(x) | <\varepsilon\),也就是 +\(\sup_{x \in X} | f_n(x) - f(x) | +<\varepsilon\)。
+这样来看的话,显然有一致收敛能够推出逐点收敛,逐点收敛能推出一致收敛的要求是固定 +\(\varepsilon\) 时存在 \(N\) 的上确界 \(\sup _{x \in X}N(\varepsilon , +x)\),这个上确界不能是无穷。但 \(X\) 的形式不能在任意条件下保证这一点。
+从计算的角度来看,逐点收敛到的函数相当于固定 \(x\),取 \(n \to +\infty\),可以由此继续判断是否一致收敛到逐点收敛的函数。
一个单色偏振光可以分解为两个互相垂直的线偏振光的叠加。表示如下:
-\[ \begin{cases}{} \ E_x = a_1\cos -\omega t \\\\ E_y = a_2\cos (\omega t+\delta) \\ \end{cases} -\]
-其中的\(\delta\)被称为\(x\)方向偏振分量相对于\(y\)方向偏振分量的位相延迟量。显然,偏振光的“形状”由式中参数决定,主要探讨椭圆、圆和线偏振光的情况。引入偏振方向的概念: -\(\alpha=arctan(\frac{a_2}{a_1} -cos\delta)\)
-我们不加证明地给出关于椭圆偏振光的参数求解式。其中定义\(\psi\)为椭圆的长轴方位角,我也不知道这个是什么意思。
\[ \begin{equation} -\begin{cases} \psi &= \frac{1}{2}arctan(tan2\beta cos\delta) -\\\\ \frac{b^2}{a^2} &= \frac{2}{1+\sqrt{1-(sin2\beta -sin\delta)^2}}-1 \\\\ \beta -&=arctan(\frac{a_2}{a_1}) \\ \end{cases} \end{equation} -\]
+级数收敛构造连续函数
+本质上是把绝对值推广成函数的无穷范数,用来证明收敛。
+梦话:证明题,但胡说八道
+连续,一致连续和一致收敛
+-
+
证明,函数 \(e^x\) 在 \(\mathbb R\) 上不是一致连续的而在 \((-\infty,0]\) 上是一致连续的。
+Trivial.
+证明,幂函数映射 \(\mathbb +R_{>0}\times \mathbb R, \ \ (x,\alpha)\mapsto x^\alpha\) 是 +\(\mathbb R_{>0}\times \mathbb R\) +上的连续函数。
+因为 \(x^\alpha = e^{\alpha \ln +x}\),且 \(\mathbb R_{>0}\times +\mathbb R \to \mathbb R\),\((x,\alpha) +\to \alpha \ln x\) 连续,\(\mathbb R +\to \mathbb R\),\(x \to e^x\) +也连续。
+二者的叠加(??这个叫什么来着啊)也是连续函数,而且是 \(\mathbb R_{>0}\times \mathbb R \to \mathbb +R\) 的连续函数。
+证明,第九次课中定义的幂函数满足如下的性质:对任意 \(x,y>0\) 和 \(\alpha, \beta\),我们有 \((xy)^\alpha=x^\alpha y^\alpha\),\((x^\alpha)^\beta=x^{\alpha \beta}\); \(a^{\log_a x} =x\);如果 \(x>0\),\(y>0\),那么 \(a^{x+y}=a^x a^y\),\(\log_a(x\cdot +y)=\log_a(x)+\log_a(y)\)。
+\((xy) ^\alpha = e^{\alpha \ln xy} = +e^{\alpha (\ln x+\ln y)} = e^{\alpha \ln x}e^{\alpha \ln y} = x^\alpha +y^\alpha\)。
+类似地证明其他几个式子,总之一些 trivial 的性质对于 \(e^x\) 和 \(\ln +x\) 成立,只要努力代入就可以了。
+在 \([0,1)\) +区间上考虑连续函数的序列 \(\{f_n(x)\}_{n\geqslant 1}\),其中 \(f_n(x)=x^n\)。证明,对任意的 \(a<1\),\(\{f_n(x)\}_{n\geqslant 1}\) 在 \([0,a]\) 上一致收敛到 \(0\) 这个函数;但是 \(\{f_n(x)\}_{n\geqslant 1}\) 在 \([0,1)\) 上不一致收敛。
+连续函数列在闭区间上有一致控制:\(\sup_{x +\in X} | f_n(x) - f(x) | = a^n <\varepsilon\),只要取 \(N > \log _a \varepsilon\) +即可,于是一致收敛。
+在 \([0,1)\) 上也还是逐点收敛到 +\(f=0\) 的,只要证明不一致收敛到 \(f=0\) 即可。实际上有 \(\sup_{x \in X} | f_n(x) - f(x) | = +1\)。
+在 \(\mathbb R\) +上考虑连续函数的序列 \(\{f_n(x)\}_{n\geqslant +1}\),其中 \(f_n(x)=\dfrac{nx}{1+n^2x^2}\)。证明,\(\{f_n(x)\}_{n\geqslant 1}\) 在 \(\mathbb R\) 上逐点收敛到 \(0\) 这个函数但是 \(\{f_n(x)\}_{n\geqslant 1}\) 在 \(\mathbb R\) 上不一致收敛。
+逐点收敛只要对 \(n \to \infty\) +即可,是收敛到 \(f=0\) 的。
+考虑一致收敛的问题,${x X} | f_n(x) - f(x) | = {x X} | { nx ++{ 1 nx}}| = 2 $,并不会一致收敛。
+在 \(\mathbb R\) +上考虑连续函数的序列 \(\{f_n(x)\}_{n\geqslant +1}\),其中 \(f_n(x)=\begin{cases}\dfrac{nx^2}{1+nx}, \ +&x>0;\\& \\\dfrac{nx^3}{1+nx^2}, \ &x\leqslant +0\end{cases}\).
+试研究 \(\{f_n(x)\}_{n\geqslant 1}\) +在 \(\mathbb R\) +上逐点收敛性和一致收敛性。
+逐点收敛到 \(f=x\),有手就行(,以下考虑一致收敛性。
+对于 \(x >0\),有 \(\sup_{x \in X} | f_n(x) - f(x) | = \sup_{x \in X} +|\frac{x}{1+nx}|<\frac 1 n < \varepsilon\) 可以在 \(N >\frac 1 \varepsilon\) 时做到。
+对于 \(x \leq 0\),有 \(\sup_{x \in X} | f_n(x) - f(x) | = \sup_{x \in X} +|\frac{x}{1+nx^2 }|<\frac{1}{2 \sqrt{n} } < +\varepsilon\),可以在 \(N> +\frac{1}{4\varepsilon^2}\) 时做到。
+所以取 \(N =[ \max \lbrace \frac 1 +\varepsilon , \frac{1}{4\varepsilon^2} \rbrace ] +1\) +即有一致收敛。
+给定连续函数 \(\varphi\colon \mathbb +R_{\geqslant 0}\rightarrow \mathbb R\),满足 \(\varphi(0)=0\),\(\displaystyle \lim_{x\rightarrow +\infty}\varphi(x)=0\) 并且 \(\varphi\) 不恒为零。证明,\(\mathbb R_{\geqslant 0}\) +上的连续函数的序列 \(\{f_n(x)\}_{n\geqslant +1}\) 和 \(\{g_n(x)\}_{n\geqslant +1}\) 逐点收敛到 \(0\) +这个函数但是不一致收敛,其中 \(f_n(x)=\varphi(nx)\),\(g_n(x)=\varphi\left(\dfrac{x}{n}\right)\)。
+Trivial.
+(一致连续性的应用:积分的定义)\([a,b]\) 是有限闭区间,\(f\in C\bigl([a,b]\bigr)\) +是实数值的函数。给定 \(n\geqslant +1\),我们将 \([a,b]\) 均分为 +\(n\) 份:\([[a,b]=[a_1,b_1]\cup [a_2,b_2]\cup \cdots \cup +[a_n,b_n], \ \ a_1=a, b_k=a_{k+1}~(k=1,\cdots, n-1), +b_n=b\),
+其中对于 \(k=1,2,\cdots,n\),\(a_k=a+\dfrac{k-1}{n}(b-a)\)。我们定义 \(S_n=\sum_{k=1}^n \frac{b-a}{n}f(a_k)\)
+证明,\(\{S_n\}_{n\geqslant 1}\) +收敛,我们用 $_{a}^b f $ 这个符号来记极限 \(\displaystyle \lim_{n\rightarrow +\infty}S_n\)。进一步证明,映射
+${a}^bC([a,b])R, f{a}^b f $ 是线性映射,并且如果我们在 +\(C\bigl([a,b]\bigr)\) 用距离函数 \(d_\infty\) 来考虑,那么这是连续映射。
+(提示:为了证明 \(\{S_n\}_{n\geqslant +1}\) 是Cauchy列,我们可以将 \(S_{n}\) 和 \(S_m\) 都与 \(S_{nm}\) 做比较)
+考虑部分和序列收敛。是因为 \(f\) +在闭区间 \([a,b]\) +上有最大值和最小值,于是 \((b-a)s \leq S_n +\leq (b-a)S\)。比较 \(S_m\) 和 +\(S_{nm}\) +能比出来什么呢...?作差用中值定理的话,二者的差可以控制在 \([\frac{n-1}{2mn} s,\frac{n-1}{2mn} S]\) +之间,确实可以控制在 \(\varepsilon\) +之内。但是只用 \(S_m\) 和 \(S_{mn}\) 做比较就可以得到是 Cauchy +列的结论吗?
+线性映射是因为 \(f + g \to \int_{a}^b +f+g\),有 \(\int_{a}^b f+g +=\displaystyle \lim_{n\rightarrow \infty}(S_n+T_n)= \displaystyle +\lim_{n\rightarrow \infty}S_n + \displaystyle \lim_{n\rightarrow +\infty}T_n = \int_{a}^b f +\int_{a}^b g\)。
+回顾一下距离函数是 \(d_\infty (f,g) = +\sup_{x \in X} |f(x)-g(x)|\),想证明映射 \(\int_{a}^b\colon C\bigl([a,b]\bigr)\rightarrow +\mathbb R\) 是连续映射,只要证明对任意的 \(\varepsilon >0\),存在 \(\delta\) 使得 \(d_\infty (f,g) < \delta\) 时有 \(|\int_{a}^b f - \int_{a}^b +g|<\varepsilon\)。
+由于这个映射是线性的,我们知道 \(|\int_{a}^b f - \int_{a}^b g| = |\int_{a}^b (f-g)| +< |\int_{a}^b d_{\infty}(f,g) | = +(b-a)d_{\infty}(f,g)\),因此只要取 \(\delta = \frac {\varepsilon} {(b-a)}\) +就能够满足要求。因此这个映射是连续的。
+证明Cauchy的一个定理: 任给函数 \(f\colon [a,+\infty) \to +\mathbb{R}\),我们假设 \(f\) +任意闭子区间 \([a,b]\) 上有界 +(上界可能依赖于 \(b\)), +那么下面两个式子当等号右边极限存在时成立:
+\(\lim_{x \to +\infty} \frac{f(x)}{x} = +\lim_{x \to + \infty} [f(x+1) - f(x)],\\\lim_{x \to + \infty} +[f(x)]^{1/x} = \lim_{x \to + \infty} \frac{f(x+1)}{f(x)}, \ \ +\text{进一步假设对任意的 $x \in [a,\infty)$,$f(x) \geqslant c > +0$}\)
+首先,给下面的式子取个对数就能得到上面的式子,所以只要证明上面的式子。
+记 \(A = \lim_{x \to + \infty} [f(x+1) - +f(x)]\),于是对任意 \(\varepsilon +>0\),存在 \(N \in \mathbb +Z^+\) 使得 \(x >N\) +时都有:
+\(A-\varepsilon < f(x+1) - f(x) < +A+\varepsilon\) 成立。
+因此 \(f(y) = (f(y)-f(y-1)) + +(f(y-1)-f(y-2))+ ... +( f(n+1)-f(n)) +f(n)\),其中 \(n = N\),再做 \(\frac{f(y)}{y}\) +取极限即得到结论。
+
和一致连续性相关的问题
+-
+
如果连续函数 \(f\) +在开区间(有限或无限)\(I \subset +\mathbb{R}\) 上是单调并且有界的,那么 \(f\) 在 \(I\) 上一致连续。
+Trivial.
+\(I\) +是长度有限的区间(不一定是闭的)。 证明,\(I\) 上的实值函数 \(f\) 一致连续的充分必要条件是 \(f\) 把Cauchy列映成Cauchy列(即如果 \(\{x_n\}_{n \geqslant 1} \subset I\) +是Cauchy列,那么 \(\{f(x_n) \}_{n \geqslant +1}\) 也是Cauchy列)。
+如果 \(f\) 一致连续,由 Cauchy +列和一致连续的定义知道 \(\{f(x_n) \}_{n +\geqslant 1}\) 也是 Cauchy 列。
+如果映射到的点列也是 Cauchy 列,且 \(f\) 不一致连续。那么存在一个 \(\varepsilon >0\),使得对任意的 \(\delta\),都存在 \(x,y \in I\) 满足 \(|x-y|<\delta\) 且 +$|f(x)-f(y)|>$。取一个和 \(\lbrace x_n +\rbrace\) 相近的数列 \(\lbrace y_n +\rbrace\),满足 \(|x_n - y_n |< +\frac 1 n\) 而且 \(|f(x_n) - f(y_n)| +>\varepsilon\),而且一定满足 \(\lbrace y_n \rbrace \subset I\)。那么 \(\lbrace x_n \rbrace\) 是收敛的 Cauchy +列,\(\lbrace y_n \rbrace\) +也是收敛到同一点的 Cauchy 列。
+取序列 \(x_1,y_1,x_2,y_2,...,\) +也是一个 Cauchy 列,但它的映射并不是 Cauchy 列,矛盾。
+不会做于是 MSE 了半天 qwq
+\(f\) 在 \(\mathbb{R}\) 上一致连续。证明,存在 \(a, b \in \mathbb{R}_{>0}\),使得对任意的 +\(x\in \mathbb R\),我们都有 \(|f(x)| \leqslant a |x| + b\)
+取 \(b = |f(0)|\),对 \(\varepsilon = 1\),取一致连续定义中对应的 +\(\delta\),于是 \(|x - 0| <\delta\) 时一定有 $ |f(x) - +f(0)|<1$,可以得到 \(|f(x)| < |f(0)| +1 += b+1\)。
+因此,对于任意的 \(x \in \mathbb +R_+\),有 \(|f(x) - f(x-\delta)| < +1\),可以推出 \(|f(x) - f(0)| < +([\frac{1}{\delta}]+1) |x|\)。对于 \(x +\in R_-\) 也可以得到类似的结论,于是只要取 \(b=|f(0)|\),\(a = +[\frac 1 \delta] +1\),原式成立。
+假设函数 \(f\) 在 \([0,\infty)\) 上一致连续并且对任意的 \(x \in [0,1]\),我们都有 \(\displaystyle \lim_{n \rightarrow +\infty}f(x+n) = +0\)(这里 \(n\) 是整数)。 +证明,\(\lim_{x \to +\infty}f(x) = +0\)。如果我们将条件减弱为 \(f\) +在 \([0,\infty)\) 连续, +结论是否依然成立? 证明或举出反例。
+如果有一致连续条件:
+先取一个固定的 \(x\in [0,1]\) +和一个固定的 \(\varepsilon +>0\),存在一个 \(\delta = +\delta(\varepsilon)\) 使得对任意的 \(|x-y|<\delta\),有 \(|f(x)-f(y)|<\varepsilon\)。存在一个 +\(N=N(x,\varepsilon)\),使得对任意的 +\(n>N\),有 \(|f(x+n)|<\varepsilon\)。我们先固定这个 +\(n\)。
+对任意的 \(t \in [x+n,x+n+1]\),有 +\(|x+n-t|<p\delta\),于是 \(|f(t)-f(x+n)|<p\varepsilon\),\(p = \frac{1}{\delta}\)。于是有 \(|f(t)|<(p+1)\varepsilon\)。
+把上述中的 \(n\) 改成 \(n+1,n+2,...\),都有 \(|f(t)|<(p+1)\varepsilon\)。于是对任意的 +\(y \in [x+n,+\infty)\),有 \(|f(y)|<(p+1)\varepsilon\),也就是说 +\(\lim_{x \to +\infty}f(x) = 0\)。
+如果没有一致连续条件,结论是不成立的。取 \(f(x) = \frac{xsin \pi x}{1+x^2 \sin^2 \pi +x}\),它没有极限吧?
+假设 \(X\) 是区间,\(f\colon X \rightarrow \mathbb{R}\) +是连续函数。如果存在正常数 \(L\),使得对任意的 \(x, y \in X\),都有 \(|f(x) - f(y)| \leqslant L|x-y|\),我们就称 +\(f\) 在 \(X\) 上满足Lipschitz条件。
-
-
- 偏振片是干什么的?好像是用来产生线偏振光的。 +
证明,\(f\) 在 \(X\) 上满足Lipschitz条件是 \(f\) 在 \(X\) 一致连续的充分条件。
+Trivial.
+判断上述条件是否是必要条件? 证明或举出反例。
+不是必要的,比如取 \(f(x) = +\sqrt{x}\),\(x \in [0,1]\) +即有一致连续,但不满足 Lipschitz 条件。
+假设 \(f\) 在 \([a,+\infty)\) 上满足Lipschitz条件,其中 +\(a > 0\),试证明 \(\dfrac{f(x)}{x}\) 在 \([a,+\infty)\) 一致连续。
+取任意的 \(\delta \in \mathbb +R+\),考虑 \(x,y \in +[a,+\infty)\) 且 \(|x-y|=\delta\) 的情况。此时有 \(|f(x) - f(y)|\leq L\delta\),且 \(f(x)\) 一致连续。于是 \(|\frac{f(x)}{x} - \frac{f(y)}{y}| < |\frac{f(y) +\delta}{xy} |+|\frac{L\delta}{x}| < (\frac{L+t}{a}+ \frac{b}{a^2}) +\delta\),也满足 Lipschitz 条件,也一致连续。
+上述的 \(t\) 和 \(b\) 是使得 \(|f(x)| \leq t|x| + b\) 成立的值。
+我超,好难(
+
首先,在这张图中,透射轴是偏振片上的那条轴,我们简称为\(x\)轴;消光轴是垂直于偏振片的轴,简称为\(y\)轴。沿\(x\)轴振动光波的光强透射率为\(T_1\),它接近\(1\);沿\(y\)轴振动光波的光强透射率为\(T_2\),它接近\(0\)。二者小比大得到一个很小的值\(e\),即为消光比。
-马吕斯定律:振动方向和\(x\)轴方向成\(\theta\)角的线偏振光,经过偏振片后的透射率为 -\[T_\theta=(T_1-T_2)cos^2\theta+T_2\] -提出这个定律有什么意义?
-实验中两个偏振片的组合(一个称为起偏器,一个称为检偏器)成为一组仪器。起偏器产生的线偏振光经过检偏器。因此,由马吕斯定律,二者的\(x\)轴夹角即为\(\theta\)。从结论来看,二者的\(x\)轴垂直(\(\cos -\theta=0\))则发生消光现象,二者的\(x\)轴平行(\(\cos -\theta=1\))则透射光强最大。
+*思考题
-
-
- 反射和折射时的起偏现象 -
电矢量形式的菲涅耳公式我看不懂,也不知道是干嘛的(直球)。
-和实验相关的东西翻译成人话来说就是,偏振器的透射轴方向可以由布儒斯特角确定。具体如下:
- -预置光束在三棱镜上的入射角\(\theta_i\)为\(arctan\text n\),其中\(\text -n\)为玻璃的反射率,也即初入射角约为56°。旋转偏振片到某个角度可以发现白纸屏上的光点很暗。微调二者,使得光点达到最暗时的入射角为布儒斯特角\(\theta_B\),且此时偏振片的透射轴(\(x\)轴)方向平行于三棱镜上的入射面。
-以下与实验无关,可在实验前阅读中跳过。讲义上还有一段关于S分量反射率的叙述,目测是菲涅尔定律的推导:
---此时, S 分量的反射率为\(R_{SB}=\frac{(n^2-1)^2}{(n^2+1)^2}\)。
-
关于反应堆玻片堆:
-+上式表示的反射率\(R_{SB}\) -一般较小,反射光较弱。光束以\(\theta_B\)射入多块平行玻璃板以获得只有 -P 分量的线偏振透射光,经过 N 块玻璃片的 2N -个表面后,S 分量的总透射率为\[(1-R_{SB})^{2N}=[1+(n-1)^2/2n]^{-4N}\]在\(N\)较大时,其值接近于\(0\)。这种起偏装置就叫做玻片堆。
-
连续函数 \(f\colon \mathbb R\rightarrow +\mathbb R\) 满足如下性质:对任意的 \(\delta>0\),我们都有 \(\displaystyle \lim_{n\rightarrow \infty} +f(n\delta)=0\),证明,\(\displaystyle +\lim_{x\rightarrow +\infty} f(x)=0\)。
+对任意的 \(\delta >0\),\(\varepsilon >0\),存在 \(N=N(\delta,\varepsilon)\) 满足对任意的 +\(n >N\),有 \(|f(n \delta)| <\varepsilon\)。于是只要取 +\(X= \sup \{\delta N(\delta , +\varepsilon)\}\),就有 \(\forall x > +X\),\(|f(x)|<\varepsilon\)。问题在于这个 \(X\) 是否存在。
+我们规定 \(\delta \in (0,1]\),于是 +\(X < \sup +\{N(\delta,\varepsilon)\}\),其中 \(\delta \in (0,1]\) 且 \(\varepsilon\) 固定。
连续函数 \(\varphi\colon \mathbb +R\rightarrow \mathbb R\) 满足如下两个性质:
-
-
- 延迟器和波片 +
它在无穷远的行为如下:\(\displaystyle +\lim_{x\rightarrow +\infty}\bigl( +\varphi(x)-x\bigr)=+\infty\)。
+\(\varphi\) 的不动点集 \(\bigl\{x\in \mathbb R\bigm| +\varphi(x)=x\bigr\}\) 是非空的有限集。
一般来说,线偏振光入射延迟器后出射为椭圆偏振光。其他的我就一句都没看懂了...不过没关系,一样可以做实验。
-实验中需要操作的是判断波片快慢轴,定出方向,做一些测量。我们直接在下一部分说明。
-应该做什么?在附的实验表上记什么?
-组装仪器
- -这是一个分光计改装的实验仪。
-打开激光器,粗调2,3的轴线,小平台基本水平且与分光计主轴垂直。激光光斑不要太靠近偏振片区域的边缘。
-电阻箱阻值100Ω,使得毫伏表示数大于1毫伏。
-观测布儒斯特角和偏振器的特性
-玻璃片放在平台上,反射面过平台中心点。以下的此为“x”指实验表中的部分填写。
-第一步,确定光束正入射棱镜表面时平台方位角\(\alpha_{i=0}\)。用小纸片扎一个小孔,放在激光器出射光束处,调整棱镜表面的反射光在纸屏上的亮点和小孔重合,记下此时的平台方位角即为\(\alpha_{i=0}\)。能不能搞点正常的下标啊
第二步,旋转棱镜使得光束的入射角\(\theta_i\)约为55°。旋转2到某个角度可以发现白纸屏上的光点很暗。微调入射角和起偏器,使得光点达到最暗时的平台方位角为\(\alpha_B\)。起偏器2的方向角为\(P_{\leftrightarrow}\)。能不能搞点正常的下标啊
第二步要连做三次,得到一个平台方位角的平均值\(\alpha_B\),然后布儒斯特角测量值就是\(\alpha_{i=0}-\alpha_B\),然后折射率就是布儒斯特角取一个正切值。此为“4”。
-第三步,如上得到一个起偏器方向角的平均值\(P_{\leftrightarrow}\),把2置于平均值位置。拿走玻璃片,转动3使得光强探测器上电压值最小,此时即为正交消光。在表格里记下3上度盘的度数为\(a_\uparrow\),可以看一下\(a_\uparrow\)是否和\(P_{\leftrightarrow}\)大约相差\(90°\)作为验证,此为“5”。能不能搞点正常的下标啊
第四步,保持偏振器2不动,将3的轮盘角多加\(90\)度,从而恢复到二者\(x\)轴平行的情况。在此基础上每次加上\(0,15,30,45,60,75,80,84,87,90\)度,得到二者\(x\)轴的夹角为以上数据。记下对应的电压值,注意夹角为\(90\)度时可以视作已经消光,示数为环境光光强。此为“6”。
-波片的特性研究
-第一步,把3的轮盘角调回\(a_\uparrow\),安装波片\(C_0\)到2盘的度盘上,使得\(C_0\)上白点处对应的直径大致竖直。微调\(C_0\)使得电压示数最小,记录下此时内圈的游标盘示数为\(C_0\),此时有\(C_0\)的快轴竖直。此为“7”。
-第二步,\(C_0\)不动,在小平台上放上\(C_x\)使得光束可以垂直透过。旋转\(C_x\)使得电压示数最小,此时\(C_x\)的某个轴已经垂直于2的透射轴,达到竖直方向。记下此时\(C_x\)的度盘数值,记为\(C_x\)。此为“8”。
-第三步,此时二者都不要再动,就有\(C_0\)的快轴和\(C_x\)的某一个轴平行。保证偏振器2的轮盘角为\(P_{\leftrightarrow}\),偏振器3的轮盘角为\(a_\uparrow\)。然后在此基础上给\(P_{\leftrightarrow}\)加上\(15°\),转动3的轮盘角使得二者消光(表现为电压示数最小),记下此时的3度盘角度和转动的差值角度。每次测量结束后,将偏振器3的轮盘角归回\(a_\uparrow\)。
-还要再做两次,分别给\(P_{\leftrightarrow}\)加上\(30°\)和\(45°\),调节3的轮盘角。可以发现3的转动差值和给\(P_{\leftrightarrow}\)加上的角度差不多,作为验证。因为这组成了一个半波片。此为“9”。
-第四步,转动\(C_0\),给\(C_0\)加上90°使得\(C_0\)的快轴处于水平位置,和\(C_x\)的某一个轴垂直。与第三步类似地求出3的轮盘角增加差值。可以发现3的转动差值约等于给\(P_{\leftrightarrow}\)加上的角度取负,作为验证。因为这组成了一个全波片。此为“10”。
-这几步操作证明了\(C_x\)竖直的“某一个轴”其实是快轴。
-单个\(\frac{1}{4}\)波片的特性研究
-第一步,取下\(C_x\),把2归回\(P_{\leftrightarrow}\),把3归回\(a_\uparrow\)。将2的轮盘角多加\(22.5°\),于是记录下\(P=P_{\leftrightarrow}+22.5°\)。调节3使得偏振器3的透射轴与偏振器2的透射轴平行,记下此时的轮盘角\(a_i\)。然后转动\(C_0\),分别记录最大的电压值和最小的电压值。
-然后,重复第一步,仅把其中的“\(22.5°\)”分别改为\(45°,67.5°\)实验两次即可。把此过程中的数据都记在表格里,下面的计算暂时先不用管。
-第二步,把光源挡住,记一个系统误差电压值\(I_0\),填在表格边上那个空里面。此为“11”。
-测完数据要分析计算什么?画哪些图?
--
-
- 计算实验元件玻璃的布儒斯特角和折射率。前文已体现。 -
- 绘图验证马吕斯定律 +
证明,如果 \(f\colon \mathbb R\rightarrow +\mathbb R\) 是连续函数并且满足 \(f\circ +\varphi =f\),那么 \(f\) +一定是常值函数。
+对于 \(\forall M>0\),存在 \(N >0\),满足 \(x > N\) 时一定有 \(\varphi(x) - x >M\)。
+?.jpg
连续函数 \(f\colon \mathbb R_{\geqslant +0}\rightarrow \mathbb R\) 满足 \(\displaystyle \lim_{x\rightarrow +\infty} +\frac{f(x)}{x}=0\)。假设 \(\{a_n\}_{n\geqslant 1}\) +是一列非负实数的数列并且数列 \(\{\dfrac{a_n}{n}\}_{n\geqslant 1}\) +是有界的,证明,\(\displaystyle +\lim_{n\rightarrow \infty} \frac{f(a_n)}{n}=0\)
+对任意 \(\varepsilon >0\),存在 +\(M\) 使得 \(x>M\) 时总有 \(|f(x)|<\varepsilon x\)。
+如果数列 \(\lbrace a_n \rbrace\) +无界,则取 \(N = \sup \lbrace |\frac{a_n}{n}| +\rbrace\),\(|\frac{f(a_n)}{n}| = +|\frac{f(a_n)}{a_n}| |\frac{a_n}{n}|\leq N |\frac{f(a_n)}{a_n}| \leq +N\varepsilon\),或有 \(|\frac{f(a_n)}{n}| <|\frac{\sup |f([0,K])|}{n}| +\to 0\)。
+如果数列 \(\lbrace a_n \rbrace\) +有界,则显然有 \(|\frac{f(a_n)}{n}| +<|\frac{\sup |f([\inf a_n,\sup a_n])|}{n}| \to 0\)。
用表6的数据分析\(\frac{I_m-I_{min}}{I_{max}-I_{min}}\)和\((\cos -x)^2\)之间的线性关系(即二者相等),并绘制一个以\(\theta\)为自变量的图,体现\(\frac{I_m-I_{min}}{I_{max}-I_{min}}\)和\((\cos x)^2\)两条曲线的变化。其中\(I_{min}\)和\(I_{max}\)分别代表\(\theta\)为\(90°\)和\(0°\)时的光强测量值。
+*娱乐问题:素数是无限多的拓扑证明 +(Furstenberg, 1955)
+\(X\) 是集合,\(\mathcal{T}=\{U\mid U\subset X\}\) 是 \(X\) +的某些子集所组成的集合。如果下面三个条件成立
-
-
- 观测偏振光通过半波片和全波片的现象。前文已体现。 -
- 线偏振光通过\(\frac{1}{4}\)波片 +
\(\emptyset \in \mathcal{T}\), +\(X \in \mathcal{T}\)。
+对任意的 \(\{U_{\alpha}\}_{\alpha \in +\mathcal{A}}\subset \mathcal{T}\),其中 \(\mathcal{A}\) 为指标集合,我们有 \(\displaystyle\bigcup_{\alpha \in +\mathcal{A}}U_\alpha \in \mathcal{T}\)。
+对任意有限个 \(U_1,U_2,\cdots, U_m \in +\mathcal{T}\),我们有 \(\displaystyle\bigcap_{1\leqslant i\leqslant m}U_i +\in \mathcal{T}\)。
其实就是把表格补满的过程。
-其中,计算波片相延可以使用\(|sin\delta_r|=\frac{2\sqrt{(I_{min}/I_{max})}}{sin(2\beta)(1+I_{min}/I_{max})}\)来计算。三个值都略小于\(90°\)。理论值均为\(90°\)。
-用\(\alpha\)计算长轴方位角则有\(\psi\)和\(\alpha\)相差\(90°\),但要把\(\psi\)调到\([-90°,90°]\)的范围内。三个理论值分别为\(0°,45°,90°\)。
-用公式计算长轴方位角,则把\(\psi=\frac{1}{2}arctan(tan2\beta -cos\delta)\)代入算一下即可。理论值罗列同上,应该差距不大。
-其余分析参考祖传实验报告即可。
-本文写作中用到的参考
+我们就称 \(\mathcal{T}\) 是 \(X\) 上的一个拓扑,每个 \(U\in \mathcal{T}\) 都被称作是(拓扑 \(\mathcal{T}\) 下的)开集。我们把二元组 +\((X,\mathcal{T})\) +称作是一个拓扑空间。
+假设 \((X',\mathcal{T}')\) +是拓扑空间,\(f\colon X\rightarrow +X'\),如果对每个 \(U'\in +\mathcal{T}'\),我们有 \(f^{-1}(U')\in \mathcal{T}\),我们就称 +\(f\) 是连续映射。
+给定拓扑空间 \((X,\mathcal{T})\),考虑子集 \(F\subset X\),如果其补集 \(X-F\) 是开集(即 \(X-F\in \mathcal{T}\)),我们就称 \(F\) 是在拓扑 \(\mathcal{T}\) +下的)闭集。对于闭集,我们有如下的性质:
-
-
清华大学2021秋基础物理实验(2)讲义
-清华大学2011级尚恩垚学长的大物实验报告《偏振光学实验》
+\(\emptyset\) 和 \(X\) 都是闭集。
+任意多闭集的交集是闭集。
+有限个闭集的并集是闭集。
(说来惭愧,我一个学基物的,看了别人的大物实验祖传报告,才学会了这个实验x)
-塞曼效应实验
-待填坑。
-光栅衍射实验
-笔者直到实验结束也没明白这是在做什么。
-放一个我自己的实验报告在这里,希望将来的社恐同学们不要再被困扰到了,到期末我会把信息脱敏后上传 -GitHub 和课程资源共享计划。Click -Here
-简要报告篇
-摩擦系数实验
-为什么这学期会有这么个实验...
-是新出的题目,暑假期间没有拿到讲义,可能不会写了。
-弗兰克-赫兹实验
-原理简述
-完全看不懂,拉倒吧。总感觉也不影响实验
应该做什么?
-第一次实验的接线
- -实验仪“放大倍数”档位选择“\(×1\)”档,“扫描选择”档位置于“手动”档。打开一体机电脑。参考讲义上的\(10(a)\)给实验管箱接线(或者照抄上图),检查无误后准备通电。
通电时先打开实验仪背后红色按钮,再按下实验仪前面的“灯丝电流开关”(若不按下此按钮,灯丝电流输出为 -0A)。然后在实验仪上调整灯丝电流在\(0.8A\)附近,拒斥场电压在\(7.5V\)附近,控制栅电压在\(1.5V\)左右。
-寻找实验条件
-缓慢在实验仪上增加扫描电压\(U_a\),观察板极电流\(I_p\)的变化情况。 -当看到其起伏变化时,分别改变实验仪上的三个参数,定性观察每个参量对\(I_p\)的影响。如果随着\(U_a\)的增加在 \(0 -∼ 85V\) 内能大致观察到\(I_p\)有 -\(6\) -个峰,峰与谷的差别相对比较明显,则达到最佳测试条件。此时把实验仪上的档位切成自动扫描,启动自动采集软件绘制曲线,获取峰值电压。
-太抽象了,所以我找了一份实验数据,来自刘丁菡学长,大概这样:
- -注意以下要点:
+娱乐问题:素数是无限多的拓扑证明(Furstenberg,1955)
+考虑 \(X=\mathbb{Z}\) +为全体整数的集合,对于 \(a,b \in +\mathbb{Z}\),其中 \(a\geqslant +1\),我们定义 \(U_{a,b}=\{ka+b\mid k +\in \mathbb{Z}\}\)(就是以 \(b\) +为某一项的双边的等差数列)。我们定义 \(X\) 的子集的集合 \(\mathcal{T}\):如果 \(U\in \mathcal{T}\),要么 \(U=\emptyset\),要么 \(U\) 是某些 \(U_{a,b}\) 的并集。
-
-
- 实验仪上的灯丝电流不能一次改变很大,大概在\(0.01∼0.02A\)左右;调整灯丝电流后要等两三分钟再观察\(I_p\)的变化,有一个滞后。 -
- 扫描电压\(U_a\)较大时尽量使用自动挡位测量,用完之后尽快调零。如果出现电流表指针打表,要尽快调小扫描电压,关闭灯丝电流的开关。 +
\(U\in +\mathcal{T}\)。证明,\(x\in U\) +当且仅当存在 \(a\geqslant 1\),使得 +\(U_{a,x}\in \mathcal{T}\)。
+对于 \(x\in U\),一定有 \(x \in U_{s,t}\),于是 \(x=ks+t\),那么 \(U_{s,x}=U_{s,t} \in \mathcal T\)。
+证明,\(\mathbb{Z}\in +\mathcal{T}\)。
+\(\mathbb Z = U_{1,0} \in \mathcal +T\)。
+证明,对于任意的 \(\{U_i\}_{i \in +I}\subset \mathcal{T}\),那么 \(\bigcup +U_i\in \mathcal{T}\)。
+Trivial.
+证明, 如果 \(U,V\in +\mathcal{T}\),那么 \(U\cap V\in +\mathcal{T}\)。
+Trivial.
+证明,任何有限集合都不是开集;任何补集是有限的集合都不是闭集。
+Trivial.
+证明,\(U_{a,b}\) +即时开集也是闭集。
+它是开集,它的补集是 \(\cup_{c\in [1,a],c +\neq b} U_{a,c}\),也是开集,所以它自己也是闭集。
+证明,\(\displaystyle\mathbb{Z}-\{-1,1\}=\bigcup_{p~\text{是素数}}U_{p,0}\)。
+因为整数环去掉 \(0\) 之后是一个 +UFD。(草
+用反证法证明,有无限多个素数.
+如果只有有限个素数。\(U_{p,0}\) +是闭集,\(\bigcup_{p~\text{是素数}}U_{p,0}\) +是有限个闭集的并,还是闭集。那么 \(\lbrace +-1,1 \rbrace\) 在 \(\mathbb Z\) +上的补集是一个闭集,它是开集,而且是有限集,矛盾。
+我超,好强。
跟着FH软件教程操作
-按照教程一直做到第三步,第四步校准仪器的时候输入自动扫描电压\(U_a\)的最大值为\(90V\),扫描出完整的\(6\)个峰和谷。第五步数据采集模块中选择数据个数为\(200\),点间延时为\(100ms\)为最佳。此后一直根据教程行动即可,得到第一份数据。
-定性研究的操作
-保持灯丝电流和拒斥电压不动,改变控制栅电压在\(1.0V,1.5V,2.0V,2.5V,3.0V\)这些值上变化,扫出曲线。
-保持灯丝电流和控制栅电压不动,改变拒斥电压在\(5.0V,6.0V,7.0V,8.0V,9.0V\)这些值上变化,扫出曲线。
-氩原子更高激发态的情况
-这一次是两人一组,等待大佬救我
类似的操作,把亚克力板接进电路,设定最佳实验条件。在软件上调整扫描电压最大值为\(30V\)。在实验仪上调整灯丝电流在\(0.78A\)附近,控制栅电压在\(1.5V\)左右。拒斥场电压分别调整为\(2.0V,2.5V,3.0V\)。类似扫描出\(I_p-U_a\)的归一化和非归一化曲线。
-注意以下的要点:
+期中考试
+考试时间为 2 小时 25 +分钟。两道大题之间是相互独立的。考试中后面的问题可以使用前面问题的结论(无论答题人是否已经得到正确的证明或者答案)。
+基本概念和技巧的考察
-
-
- 只需要图上有两个峰。第二个峰大约出现在\(25V\)左右,因此最大扫描电压只需要\(30V\)。而且\(I_p\)的最大峰值对应不超过\(50\mu A\)。 -
- 祖传报告中指出这一步实验仪上的另两个参数保持不变即可,和讲义不是很一样。我倾向于相信祖传报告。 +
试用 \(\varepsilon-N\) +语言证明:\(\displaystyle \lim_{n\rightarrow +\infty}\dfrac{n}{n^2+1}=0\)。
+Trivial.
+试用 \(\varepsilon-\delta\) +语言说明函数 \(\mathbb R\) 上的函数 +\(f(x)=\begin{cases} \sin(\frac{1}{x}), &\ +\ x\neq 0;\\0,&\ \ x=0\end{cases}\) 在 \(x=0\) 处不连续。
+Trivial.
+计算极限:\(\displaystyle +\lim_{n\rightarrow +\infty}\left(1^2+2^2+3^2+\cdots+n^2\right)^\frac{1}{n}\)。
+\(1\)。
+证明,级数 \(\displaystyle +\sum_{n=1}^\infty \frac{2n+1}{n^2(n+100)^2}\) 收敛。
+小于二阶调和级数,trivial.
+给定实数的序列 \(\{a_n\}_{n\geqslant +1}\),假设级数 \(\displaystyle +\sum_{n=1}^\infty a_n\) 收敛。证明,对任意的实数 \(x\in (-1,1)\),级数 \(\displaystyle \sum_{n=1}^\infty a_n x^n\) +也收敛。(提示:利用Abel判别法)
+PIN 真的,我哭死,他期中考试还在基础题上给提示(
+Trivial.
+假设 \(f\) 是非空开区间 \((a,b)\) 上的连续函数,证明,对任意的 \(x_1,x_2\in (a,b)\),存在 \(x_0 \in (a,b)\),使得
+\(f(x_0)=\frac{1}{2}\bigl(f(x_1)+f(x_2)\bigr)\)
+介值定理,trivial.
+假设函数 \(f:\mathbb R\rightarrow +\mathbb R\) 是以 \(1\) +为周期的连续函数,即对任意的 \(x\in \mathbb +R\),我们有 \(f(x+1)=f(x)\)。证明,\(f\) 有界并且能取到其最大值,即存在 \(x_0\in \mathbb R\),使得 \(f(x_0)=\displaystyle \sup_{x\in \mathbb +R}f(x)\)。
+Trivial.
+证明,\(f(x)=\sqrt{x+1}\) 作为 +\(\mathbb R_{\geqslant 0}\) +上的函数是一致连续的。
+因为满足 Lipschitz 条件,\(L=\frac 1 +2\)。
实验结束后可以断开其他元件的连接,整理仪器,处理自己的数据。
-测完数据要分析计算什么?
-测试\(I_p-U_a\)曲线,得到氩原子第一激发电位
-找到第一部分数据的 Excel 表格 Data -页,取六个峰值的电压数据和测量次数(注意舍去一看就不对的值),到 Origin -里拟合数据。由于曲线上相邻两峰值之间的电位差就是氩原子的第一激发电\(U_g\),因此处理得到的斜率就是第一激发电位。
-太抽象了,这是一张示例处理表格,来自刘丁菡学长,其中的 \(Slope-Value\) 就是所需要的值。
- -关于不确定度的计算,公式都在下面了:
-\[\Delta_A=S_b=b\sqrt{\frac{2(1-R^2)}{n-2}}\]
-\[\Delta_B=0.001×b+0.01\]
-\[U_g=(b±\Delta_{U_g})\]
-其中\(b\)是斜率,\(R^2\)是拟合的最后一列方差,\(n\)是实验次数(即为\(6\)),\(\Delta_{U_g}\)是两个系差平方和的开方。
-氩原子受击后回到基态辐射出的光波波长
-套下面两个公式:
-\[\lambda=\frac{hc}{eU_g}\]
-\[\Delta_\lambda=\lambda\frac{\Delta_{U_g}}{U_g}\]
-实验中观测不到发光是因为这是紫外波段而不是可见光波段,也因此用壳罩住了管子防止对人体造成伤害。
-定性研究栅极电压和拒斥电压对\(I_p\)的影响
-控制栅电压的影响:由图可知,从峰值对应的扫描电压上看,随着 \(U_G\) 值的增大,曲线中峰 -值所对应的扫描电压值稍向左偏移;从峰值的相对大小来看,随着 \(U_G\) 值的增大,峰值先增大后减小,在 \(U_G≈ 2.0V\) -附近能观测到峰值最大,说明此时单位时间到达极板的电子最多。 -理论解释见祖传报告,反正我也写不出来。例图如下,来自刘丁菡学长:
- -拒斥电压的影响:由图可知,随着 \(U_R\) -值的增大,曲线绝对值下移、峰谷值之间的差距变 -大、曲线中峰值所对应的扫描电压值稍向右偏移。理论解释见祖传报告,反正我也写不出来。例图如下,来自刘丁菡学长:
- -更高激发态的研究
-例图如下,来自刘丁菡学长。\(U_R\) -整体对曲线的影响与第一激发态是类似的,即随着 \(U_R\) -的增大,曲线整体下移,峰谷差值增大,峰值向右移动。但差别在于曲线的形状有所不同,即没有出现很明显的一个峰值,而是峰值附近有一个小平台。理论解释见祖传报告,反正我也写不出来。
- -解答思考题
-见祖传报告。
-本文写作中用到的参考
+级数
+首先回忆一下二项式展开:\(\displaystyle +(1+z)^n=\sum_{k=0}^n {n \choose k} z^k\)。特别地, 当 \(z=1\) 时,我们有 \(\displaystyle 2^n=\sum_{k=0}^n {n \choose +k}\)。
+给定一个复数的数列 \(\{a_k\}_{k\geqslant +0}\),我们定义新的数列 \(\{a_n^*\}_{n\geqslant 0}\),其中 \(a_n^*=\frac{1}{2^n}\sum_{k=0}^n {n \choose +k}a_k\)
+等比数列
+这一部分中,我们假设对任意的 \(k\geqslant +0\),\(a_k=z^k\),其中 \(z\) 为复数。
-
-
- 清华大学2020级刘丁菡学长的基物实验报告《弗兰克-赫兹实验》 +
证明,如果 \(|z|<1\),那么级数 \(\displaystyle \sum_{k=0}^\infty a_k\) +收敛。我们用 \(A(z)\) +表示这个极限。
+Trivial,\(A(z) = +\frac{1}{1-z}\)。
+证明,如果 \(|z|<1\),那么级数 \(\displaystyle \sum_{k=0}^\infty a^*_k\) +收敛。我们用 \(A^*(z)\) +表示这个极限。
+Trivial 但差点被骗了,总之 \(a_k ^* = +\frac{z+1}{2}\),\(A^*(z) = +\frac{2}{1-z}\)。
+证明,如果 \(|z|\geqslant +1\),那么级数 \(\displaystyle +\sum_{k=0}^\infty a_k\) 不收敛。
+Trivial.
+试找出一个 \(z\in +\mathbb{C}\),\(|z|>1\),级数 +\(\displaystyle \sum_{k=0}^\infty +a^*_k\) 收敛。
+级数部分和是 \(\frac{2}{1-z} +(1-(\frac{z+1}{2})^{k+1})\),取 \(z = +-2\) 即可。
+证明,如果 \(|z|=1\) 并且 \(z\neq\pm 1\),那么级数 \(\displaystyle \sum_{k=0}^\infty a^*_k\) +收敛。
+Trivial.
感谢学长的图救我老命,不然这个实验真的看不懂在干嘛...
-几何光学系列实验
-不喜欢系列实验,真的好麻烦。
-原理简述
-会算相似三角形就行
收敛性比较
+这一部分中,我们假设 \(\{a_k\}_{k\geqslant +0}\) 为实数的序列。
-
-
- 薄透镜的成像规律 +
证明,当 \(k\in \mathbb{Z}_{\geqslant +0}\) 固定的时候,我们有:
+-
+
- \(\lim_{n\rightarrow \infty} {n \choose +k}/{\frac{n^k}{k!}}=1\) +
- \(\lim_{n\rightarrow \infty} {n \choose +k}/{2^n}=0\)
经典公式:\(\frac{1}{f}=\frac{1}{p}+\frac{1}{q}\),其中 -\(p\),\(q\) 分别代表物距和像距;\(\beta=-\frac{q}{p}\)称为线放大率。
-它们有很多正负性质的要求:前三者实物/实像/凸透镜为正,虚物/虚像/凹透镜为负,\(\beta\)在实像时为负,虚像时为正。
+Trivial.
+任意给定非负整数 \(n>q\),我们定义 \(a_{n,q}^*=\frac{1}{2^n}\sum_{k=0}^q {n \choose +k}a_k\),对每个固定的 \(q\),计算 \(\displaystyle \lim_{n\rightarrow \infty} +a_{n,q}^*\)。
+\(0\)。
+如果 \(\displaystyle \lim_{n\rightarrow +\infty} a_{n}=0\),证明,\(\displaystyle \lim_{n\rightarrow \infty} +a_{n}^*=0\)。
+定义证明。
+如果 \(\displaystyle \lim_{n\rightarrow +\infty} a_{n}\) 存在,证明,\(\displaystyle \lim_{n\rightarrow \infty} +a_{n}^*\) 存在并且恰好等于 \(\displaystyle \lim_{n\rightarrow \infty} +a_{n}\)。
+定义证明。
+如果 \(\displaystyle \lim_{n\rightarrow +\infty} a^*_{n}\) 存在,\(\displaystyle +\lim_{n\rightarrow \infty} a_{n}\) 是否一定存在?
+不一定,取 \(a_n = +(-1)^n\)。
+
在后面的问题中,对任意的 \(n\geqslant +0\),我们定义部分和 \(S_n=\sum_{k=0}^n +a_k, \ \ S^*_n=\sum_{k=0}^n a^*_k, \ \ U_n=2^n S_n^*\)
-
-
- 内调焦望远镜 +
证明,对任意的 \(n\geqslant +0\),\(U_n\) 都可以写成 \(S_0,S_1,\cdots,S_n\) +的整系数线性组合:\(U_n=\sum_{k=0}^n {n+1 +\choose k+1} S_k\)
+Trivial.
+证明,如果级数 \(\displaystyle +\sum_{k=0}^\infty a_k\) 收敛,那么 \(\displaystyle \sum_{k=0}^\infty a^*_k\) +也收敛。
+Trivial.
望远镜是由一个物镜一个目镜组成的。当我们用一组物镜组替代物镜时,不必移动物镜和目镜间的距离\(l\),而是直接改变物镜组的焦距即可达到整体调焦的效果。这就叫做内调焦望远镜。
-实验中用到的物镜组是一个凸透镜\(L_1\)和一个凹透镜\(L_2\)组成的。这是一个最简单的变焦物竞组物镜组。原理是\(L_2\)的物方焦点在\(L_1\)的像方焦点右侧时,改变两个透镜的间距\(d\)就能达到内部调焦的效果。此时取二者的“正焦距”(我不太会描述)为\(f_1'\)和\(f_2\),物镜的组合焦距即为\(f_o'=\frac{f_1'f_2}{d+f_2-f_1'}\)。要求满足\(f_1'-f_2<d<f_1'\)才能如上调节。
我们把目镜的焦距记作\(f_e\)。望远镜的视放大率即为\(\Gamma_T=-\frac{f_o}{f_e}\)。这个数值的绝对值越大,观察到的像越大。比如说,观察远物的时候可以通过调小\(d\)来放大\(f_o\),观察近物的时候不想改变物镜组和目镜组之间的距离,直接放大\(d\)即可。
-应该做什么?
-A0.薄透镜成像规律
-为了满足近轴光线条件,要进行共轴调节。
-粗调的时候,先把光源,物,透镜靠拢,调节到中心大约在一条平行于导轨的直线上。总之怎么看着舒服就怎么调。
-细调的原理是大象追小象大像追小像。当物与像的距离大于 \(4f\)
-时,凸透镜从物移到像的过程中会成两次清晰的像,一大一小。要做的就是移动像和透镜的位置,使得\(B_1\)追上\(B_2\),也即两个像差不多大,这可以通过像屏上的坐标贴纸判断。此时像在透镜的主光轴上。
不要动平行光管,就是那个挺长的不认识的东西。此处无记录要求。
B1.物像距法测量薄凸透镜焦距
-这很明示了,读个数据套公式就行。
-B2.共轭法测量薄凸透镜焦距
-读个数据套另一个公式:\(f=\frac{b^2-a^2}{4b}\),其中 \(a\) 指两次透镜位置间距离。
-B3.焦距仪法测薄凸透镜焦距
-读六组数据写在表格上,比较麻烦的是算不确定度。这一部分已经在讲义和实验表上详细手写了,照做即可,不再打一遍了。
-C1.主面间距测量
- -5中的C.2应为B.3。不过我不太懂怎么通过这几个参数算主面间距,好怪。此处留坑。
-C2.修正共轭法系差
-again,算就对了。
-D.用焦距仪测凸透镜的焦距的附加透镜法
-这个讲义上也说的挺清楚的。注意先给玻罗板取某一线对记录下来,第一步和第二步要用一样的线对(废话)。
最后的凹透镜焦距是\(f_2=-\frac{f_1 -y_0}{y''}\),由于是凹透镜的原因,焦距记为负的。
-E.内调焦望远镜的物镜组研究
-第一步,分别对物镜组中的凹凸透镜进行共轴调节,用焦距仪法测此组光具焦距值\(f_o'\)作为物镜焦距。反推得到此时凹凸透镜的距离\(d=\frac{f_2f_1'}{f_o'}+f_1'-f_2\)。其中,由于凹凸透镜的焦距已经在B和D实验中测出,直接取用其值即可。
-第二步,改变凹凸透镜距离使得长焦透镜\(L_1\)距离测微目镜约\(10cm\)。得到第二个测量值。
-第三步,分别假设凹凸透镜的焦距,然后画一个类似下图的图。
- -这张图的逻辑是:以纵轴表示自变量\(d\),横轴表示四个因变量。其计算公式分别为:
-\[l_{L_1H}=-\frac{f_1'd}{d+f_2-f_1'}\]
-\[l_{L_1H'}=-\frac{d(d-f_1')}{d+f_2-f_1'}\]
-\[F'=l_{L_1H'}+f_o'\]
-\[F=l_{L_1H}-f_o'\]
-其中,凸透镜\(f_1'=0.3m\),凹透镜\(f_2=0.2m\)。所以这个图是不是实验之前就能画出来
本文写作中用到的参考
+连续函数环的极大理想
+假设 \(a<b\) +是实数,我们研究有界闭区间上的实数值连续函数的空间 \(C\bigl([a,b]\bigr)\)。对于子集 \(I\subset +C\bigl([a,b]\bigr)\),如果它满足如下三个条件:
-
-
- 透镜焦距实验-仪器详解 +
\(I\neq \emptyset\),\(I \neq C\bigl([a,b]\bigr)\);
+对任意的 \(\varphi \in +I\),\(\psi \in I\),我们有 +\(\varphi+\psi \in I\);
+对任意的 \(\varphi \in +I\),\(f \in +C\bigl([a,b]\bigr)\),我们有 \(\varphi\cdot f \in I\).
https://www.bilibili.com/video/BV163411q7NP?spm_id_from=333.999.0.0&vd_source=6ae5c31a80120436d23cf7b7c7ceb3ba
+我们就称 \(I\) 是 \(C\bigl([a,b]\bigr)\) 的一个理想。假设 \(\mathfrak{m}\) 是 \(C\bigl([a,b]\bigr)\) +的理想并且不存在其它的包含 \(\mathfrak{m}\) 的理想,我们就称 \(\mathfrak{m}\) 是 \(C\bigl([a,b]\bigr)\) +的一个极大理想(即若理想 \(I\supset +\mathfrak{m}\),那么 \(I +=\mathfrak{m}\))。
-
-
- 清华大学2011级耿强学长的大物实验报告《透镜焦距的测定》P181 +
对任意的子集 \(A\subset +[a,b]\),令 \(I(A)=\left\{f\in +C\bigl([a,b]\bigr)\big| \text{对任意的 $x\in +A$,$f(x)=0$}\right\}\)。证明,\(I(A)\) 是 \(C\bigl([a,b]\bigr)\) 的理想。\(I([a,b])\) 是什么?证明,如果有两个子集 +\(A\subset B\subset [a,b]\),那么 \(I(A)\supset I(B)\)。是否存在 \(A\subset [a,b]\) 为真子集,使得 \(I(A)=\{0\}\)?
+前几问都是有手就行。最后一问取 \(A = +(a,b)\)。
+证明,如果 \(I \subset +C\bigl([a,b]\bigr)\) 是理想,那么常值函数 \(1\notin I\)。进一步证明,如果 \(I \subset C\bigl([a,b]\bigr)\) +是理想,那么对任意的 \(f\in I\),\(f\) 在 \([a,b]\) 上一定有零点(即 \(f(x)=0\) 在 \([a,b]\) 上有解)。
+如果是理想且恒等元在理想中,那么所有元素都在理想中,矛盾。
+如果 \(f \in I\) 且在 \([a,b]\) 上没有零点,那么它是可逆的,\(f^{-1} \in C([a,b])\),于是 \(1 = f \cdot f^{-1} \in I\),矛盾。
+对于 \(f \in +C\bigl([a,b]\bigr)\),证明,集合 \(V(f)=\bigl\{x\in [a,b]\big| f(x)=0\bigr\}\) +是闭集。进一步证明,对于理想 \(I \subset +C\bigl([a,b]\bigr)\),集合 \(V(I)=\bigl\{x\in [a,b]\big| \text{对任意的 $f\in +I$},~ f(x)=0\bigr\}\) 是闭集。如果理想 \(I \subset C\bigl([a,b]\bigr)\) 使得 \(V(I)\) 为全空间 \([a,b]\),你是否能够确定 \(I\)?
+记 \(T = \lbrace 0 \rbrace\),而 +\(f^{-1} (T) = V(f)\) +保持闭集性质。
+\(V(I) = \cap _{f\in I} +V(f)\),闭集的交集还是闭集。
+如果 \(V(I) = [a,b]\),那么对任意的 +\(f \in I\) 都有 \(V(f) = [a,b]\),也就是说 \(f=0\),\(I\) 是平凡理想。
+对任意的点 \(x\in +[a,b]\),我们令 \(A=\{x\}\) 并记 +\(\mathfrak{m}_x +=I(A)=I\bigl(\{x\}\bigr)\),即 \(\mathfrak{m}_x=\left\{f\in C\bigl([a,b]\bigr)\big| +f(x)=0\right\}\)。
+证明,\(\mathfrak{m}_x\) +是极大理想。
+我差点想直接证明 \(C([a,b])\) 是一个 +PID,仔细一想里面的不可逆元全是零因子,根本不是整环。
+不介意我用点抽代知识吧?
+作环同态 \(t: C([a,b]) \to \mathbb +R\),\(f \to +f(x)\)。如果存在极大理想 \(\mathfrak{m} +\supset \mathfrak{m}_x\),且使得存在 \(g\in \mathfrak m\),\(g(x) \neq 0\)。
+于是 \(\ker t = \mathfrak +m_x\),\(C([a,b]) / \mathfrak m _x +\cong \mathbb R\) 是一个域,也即 \(\mathfrak m _x\) 是一个极大理想。
+证明,如果 \(\mathfrak{m}\) 是 +\(C\bigl([a,b]\bigr)\) +的极大理想,那么存在 \(x\in [a,b]\) +使得 \(\mathfrak{m}=\mathfrak{m}_x\)。(提示:利用 +\([a,b]\) 是紧的)
+如果 \(\mathfrak m\) +是一个极大理想,而且不存在一个使得 \(\mathfrak +m = \mathfrak m _x\) 的 \(x\in +[a,b]\)。
+于是对任意 \(x \in [a,b]\),存在 +\(f_x\) 使得 \(f_x(x) \neq 0\)。由 \([a,b]\) 是紧的可知存在一列函数 \(f_1,f_2,...,f_n\),满足对任意 \(x \in [a,b]\),存在 \(i \in \lbrace 1,2,...,n \rbrace\),使得 +\(f_i (x) \neq 0\)。于是 \(F=f_1 ^2 + ... + f_n ^2 \in \mathfrak m\) +且是单位,矛盾。
+是否存在理想 \(I \subset +C\bigl([a,b]\bigr)\) 使得 \(V(I)=\emptyset\)?
+任意一个理想都被包含在某个极大理想中,\(V(I) \neq \emptyset\)。
+假设 \(A\) 是闭集,证明,\(V(I(A))=A\)。
+\(I(A)=\left\{f\in C\bigl([a,b]\bigr)\big| +\text{对任意的 $x\in A$,$f(x)=0$}\right\}\),
+\(V(f)=\bigl\{x\in [a,b]\big| +f(x)=0\bigr\}\)。
+在努力回忆 Galois +对应(?)是什么东西,但是忘了(,不知道有没有关系。
+胡说八道:首先 \(A \in +V(I(A))\),然后证明对任意的 \(x \in +V(I(A))\) 有 \(x \in +A\)。否则存在 \(s \notin +A\),且对任意的 \(f \in I(A)\) +都有 \(f(s)=0\)。我们只要构造出一个不符合此条件的 +\(g \in I(A)\) 即可,而 \(g\in I(A)\) 在 \([a,b]\) 上有可数个零点,且 \(g(s)\neq 0\),逐段构造使其连续,且在 \(A\) 上取值均为 \(0\) 即可。
写在最后
-我一向把物理实验当成“可以摆弄仪器的好玩的课”,高中学竞赛的时候就羡慕物化生竞赛的同学可以做实验,我们只能一直待在教室里写题。但是哪怕基物实验
-1 拿了
-A-,对于实验的原理仍然不甚了解。到最后每学期六次做实验三次写报告成为了生活中的调剂,不用太动脑子就能写出一大片东西,好像自己很努力一样。
在 Overleaf 上无意间找到了清华大学近代物理实验报告模板。朱老师的要求和这个还是很不一样。发现也没有用于普通实验的模板,于是改了改我的自用模板,还行。
-GitHub -地址:https://github.com/Chiyuru/THU-Fundamental-Physics-Report
-但是用 LaTeX 写实验报告的人哪个没有自己的模板啊
您又在假装干活了是吗
++Remark:
+上面的结论可以推广到紧的距离空间的情形:假设 \((X,d)\) 是紧的距离空间,\(C(X)\) 是 \(X\) +上复数值的连续函数的全体,那么我们有如下的一一对应:\(X \longrightarrow \bigl\{\text{$C(X)$ +的极大理想}\bigr\}, \ \ x\mapsto \mathfrak{m}_x\)
+其中 \(\mathfrak{m}_x=\left\{f\in +C\bigl(X\bigr)\big| f(x)=0\right\}\)。据此,我们把可以把环 \(C(X)\) 中的极大理想想象成空间的点,从而通过 +\(C(X)\) 中的代数对象来研究 \(X\) 上的几何,这是代数几何的开端。
+
休整
+导数异常地轻松,半摸半写一天就写得差不多了,作为一个休息,之后会随第二篇直接发上来,作为二月的开端。
+我觉得可能还是学不完,2.13 +就要回北京了,后面要复习一下缓考的一门(水)课,大概还有两周时间给数分。学到这里也花了差不多两周,第一周一边学一边摆,第二周其他任务几乎全部停滞,就一直在读这本书。其实大多数精力都放在做习题上面了,原来的计划是习题跳着看一看就好,但还是改变了主意,想扎实一点。
+说到底我也在怀疑选这本书到底对不对了,感觉 PIN +在讲一种很新的数分(,很怀疑和正常的版本是不是有差别,但应该是闭包才对吧(。实际上在我开始速通的后几天,转数环里就发了光叔的前两学期讲义,但是当时也没有换,就一直到这里了。PIN +确实讲得深,但是似乎还是缺少技巧的训练。算了,我又不是现在要考丘赛,那些之后再说吧。
+还是在害怕。要用四周积累来的知识和已经学了一年半分析的同学一起上新学期的课程,我觉得真的好难。虽然微不足道的成功经验告诉我最重要的是不要害怕,但是果然,连做到不害怕都好难(
+
转数环环友:你可以以任意顺序完成培养方案(
+有参考 Vica Yang +的统辅笔记,JhZhang +的课堂笔记和 V1ncent19 +的统辅笔记,如有引用均会在文中注明,在此向前辈表示感谢。
-虽然已经学过一遍初级版,这次速通是作为观点的补充和复习,但还是很虚的。
-说到这个任意顺序完成培养方案,摘一个 PIN 的前言(逃
---事实上,我们所接触的大多国内优秀同学都直接或者间接地默认数学学习一定顺序,须得按部就班,层层递进,才能扎实地进步。这种想法本身没有错,但是数学的发展绝对不是线性的,知识也不存在先天的顺序。一个普遍被提及的例证就是从 -Newton 引入积分 (反流数术) 到 Cauchy -的极限理论被广泛接受中间至少有半个世纪的光景, -那个优秀的数学家层出不穷,利用还没有被严格化的积分理论作出了很多享誉后世的工作。
-数学学习不应该被课程设置 (甚至被其名称) -切割。比如说,所谓的曲线或者曲面的几何学、数学物理方程都可以称为 (多元) -微积分学习的好例题,很多微积分知识就是为了解决这样的问题应运而生的。微积分课程就应该学习和研究这样的例子,不能简单地将它们归结为是微分几何或者微分方程的内容而忽略。仅仅为了教学而刻意构造的各种例题长远来看有目光短浅之嫌。这种做法通常还会从心理上折射出胆怯的影子,以至于有同学误以为课程的顺序和难度有关联,“后面” -的课程比 “前面” 的课程困难。唯有正视,方能前行。
-
高二的时候我曾经备考过一阵子丘班 -(prototype),不过因为当年联赛翻车省三的原因(,连初审都没有通过。组队备考的五个人里只有我们的队长 -ycj -顺利去了北京,又通过了笔试,最终在面试中被刷掉了,他现在在上海理工大学,真的很可惜。cy -后来放弃了,安心备考 -CMO,拿了银牌,现在在华子读数学,太成功了!不过虽然秋季学期一同上了数值分析,我至今也没和他面基成功。xzx -和 wry -似乎分别去了西安交大和上海财大,和他们没有很熟,后来也没再联系了。
-同时,这一段自学给我留下了对数分深刻的心理阴影,和不知道怎么手选又问不明白并列成为了大一没有学数分,而是选了微积分 -A 的两大原因,也成为了我本科很可能延毕一年的众多原因之二(
-使用的教材是常庚哲、史济怀《数学分析教程》,速通讲义是北京大学数学分析讲义和一千零一页,前者是后者的子集,的确更友善一些,用于提点重点,感谢甘主任对速通事业的支持!习题册是谢惠民《数学分析习题课讲义》,不过我觉得应该来不及做太多。
-并不是打算写知识点,没什么必要,只是想在这里哔哔赖赖一下,或许会试着虚空使用 -Feynman -学习法?毕竟是速通,要快一些,不然下学期就寄了。发这一篇的主要目的是虚空被监督进度,毕竟我的效率实在是低下。
-按照欧老师的年终(粗略)统计,数分二和三课后加起来花了 210 -h,我打算速通到数分二为止,也就是整个寒假每天都在学的话,日均也要学 7 -h(。这显然是不可能的,毕竟我同时还有一些其他事务要做,比如点 R -的技能树、编写统推讲义、推 -SRT、以及准备缓考科目。最重要的是,我还得摸鱼和出去玩啊!但还是尽量试试看,学到哪算哪,够用就行(了吗?
-实数的构造
-从抽代出发,事情变得简单了很多
-2023 年 1 月 17 日,星期二,很冷还没有暖气。
-大一的时候报了 wxf 老师的微积分 -A,这一块他其实也讲了一些,但是并不够严谨,我听着有点痛苦。说实在的我就不喜欢他这个授课的方式,下放知识又不彻底,等于炫技,不如不要下放。
-结果因为他不查考勤,微积分 A2 还是选了他的,最后大翻车。
-这一次会更加严谨、耐心,并保持好奇。
--
-
用域公理、序公理和 Achimedes -公理定义了实数域;整数和有理数可以用映射嵌入实数域,这个嵌入映射对于整数是单射。
-这个学过抽代之后倒是很好理解了,构造出域之后就有了最基本的三个元素 -\(0,1,-1\),把 \(n\) 个 \(1\) 加起来就是正整数 \(n\),考虑整数的分式域就是有理数域。实数域是一个特征为 -\(0\) -的域,这样构造出来的有理数域是它的最小子域,也即素域。
-为有理数定义了序关系 \(\frac{m}{n}>\frac{p}{q} \iff mq>np\) -之后, 就可以把序关系也嵌入到实数域里了,是成立的。
-\(\mathbb{Q} \subseteq -\mathbb{R}\),但是还没有从域的角度定义出 \(\mathbb{R} - \mathbb{Q}\) -里的元素,也就是无理数。仅仅是如上定义的话,一个所谓的实数域里完全可以只有有理数,也能满足序公理、域公理和 -Achimedes 公理,而我们想要一些其他的元素。比如说,\(\sqrt{2}\) 怎么定义?
-当然可以对 \(\mathbb{Q}\) -做关于多项式 \(x^2-2\) 的 Galois -扩域(暴论,我不是很清楚这两个理论体系到底谁先谁后,还是别这么干比较好),但是这样可以做出很多形式上不相同的域,比如熟知的 -\(\mathbb{Q} (\sqrt{2})\) 和 \(\mathbb{Q}[x] / -(x^2-2)\),虽然它们本质上是同构的,但序关系无从保障。所以还是换个方法,也就是后面的 -Dedekind 分割。
-确界原理的证明非常炫酷,我每次写完一遍都觉得非常牛逼,可惜后来只记得是用每次缩小一半的区间套证明,具体细节还是自己写不出来。
-但是这样得到的 \(sup X\) -是一个闭区间套的极限,并不好用。更加好用的定义是对于任意 \(\varepsilon >0\),存在 \(x \in X\),使得 \(x>sup X - -\varepsilon\)。通俗一些说,上确界再小一点点都不可以。
-如果反过来假设确界定理成立,闭区间套公理可以很容易地被证明,只要分别取 -\(\lbrace a_n \rbrace\) 的上确界和 -\(\lbrace b_n \rbrace\) -的下确界,夹出的区间就恰好是所有区间的交集。在已有序公理、域公理和 -Achimedes 公理的情况下二者是等价的。
-度量空间在数值分析课堂的引论里学过,当时在讲矩阵的范数如何定义,是从最普通的 -\(\mathbb{R} -^n\)讲起的,赞美包老师。虽然他这样根本不像在给数学系讲课,感觉有点照顾非数学系选课学生的意思。我的数分真是吃百家饭,这样也很好,多少消除一些曾经的心理阴影。
-对于度量空间 \((X,d)\),\(Y \subset X\) 是子集,如果对任意的 \(x \in X\) 和任意的 \(\varepsilon >0\) 都存在 \(y \in Y\),使得 \(d(y,x)< \varepsilon\),那么称 \(Y\) 在 \(X\) 上是稠密的。直观上来说,就是 \(X\) 上任意一个点都有 \(Y\) -上的一个点和它离得要多近有多近。举个例子的话,有理数和无理数在实数上都是稠密的,证明起来很简单,反复二分就可以了。
-然后就是线性空间的定义,印象里线性代数的最后一章就是学这个,当时不知道数域是什么,给我愁的,以为真的要把八条运算法则都背下来来证明一个东西是某个域上的线性空间,
-当时要是会抽代就好了。总之,\(F\) 是一个数域,\(V\) -是某一集合,满足一些运算法则的时候,三元组 \((V,+,\times )\) 是一个 \(F-\) 线性空间。
-
今天的数分就学到这里 -.jpg,内容大约是一周的量,还是有点少。明天再来.jpg
-2023 年 1 月 18 日,星期三,还是很冷但是稍微升温了一些。
+Lecture 1
+主要是在吹水,开玩笑以及活跃气氛。正经的内容大概就一个古老的回归现象,我还没有听得很懂,麻了。
+Galton's Experiment
+以下全是胡说八道,不能保证完全对。
+介绍正态分布的时候会有一个很经典的小球过钉板的演示实验,最后落在底部的球似乎呈现出一个正态分布。但实际上球和钉子的每次碰撞都是一个 +Bernoulli 过程,过了 n 层钉板就是 n 次 Bernoulli +过程加和,可以近似为正态分布。实际上只要 n +够大,由中心极限定理任何分布的加和都可以被近似为正态分布。
+但我觉得实际上小球的情况并不是独立的,毕竟过程中会有相互的碰撞,真的没问题吗(
+回归现象的起源是 Galton +对于父代和子代的身高做了一个统计,发现身高远离均值的父母的后代往往身高会比他们更接近平均水平,也就是某一身高水平的父母的孩子的身高中位数作为因变量,父母身高作为自变量时,拟合出的直线的斜率小于 +\(1\)。
+假设不发生回归现象,则和钉板现象一样,后代的性状会逐渐分散,这被认为是一个种群稳定性状的方式。听起来很玄学,似乎也有一个稍微合理的生物学解释了,但我们希望从统计学的角度分析这件事,背后是存在数学规律的。
+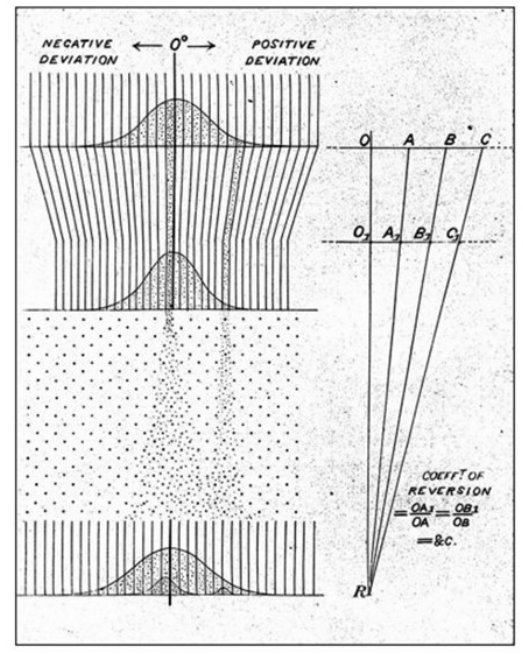
上图是课程中反复出现的一张图,对此做了很多解释。最上面的正态分布是父代的身高情况(实际上是父母身高的加权和),通过一个“倾斜槽”之后的第二个正态分布展示了子代的身高情况,比父代更加靠近中心。下方也有一个类似于钉板的装置,n +层钉板指的就是 n +代繁衍的过程,或者也可以指代一代繁衍中的其他影响身高的非基因因素,它们被视作独立同分布的,因此加和由中心极限定理可以被近似为正态分布。
+图中还呈现出了父代中的一个小组“过钉板”后的结果,是一个小的正态分布。实际上子代的数据就是由一个一个小的正态分布叠加起来的,而正态分布可以线性相加,所以最后呈现出的还是正态分布。
+好玄学,我也不知道我在说什么,甚至不是很确定自己理解对了没有。
+Anyway,还是 think mathematically,记 \(X_i\) 为第 \(i\) 代的种群身高变化量,\(\lbrace X_i \rbrace\) +是独立同分布的。则记父代种群的随机变量为 \(F= +\Sigma _{i=1} ^n X_i\),子代种群的随机变量为 \(S= +\Sigma_{i=1}^nX_i\),考虑二者的相关系数:
+\(\rho(F,S) = +\frac{cov(F,S)}{\sqrt{Var(F)Var(S)} } = \frac{Var(F) + Cov +(F,X_n)}{\sqrt{Var(F)Var(S)} } +=1+\frac{cov(F,X_n)}{Var(F)}<1\),因此 \(\rho(F,X_n)<0\) 也即二者呈负相关。
+一些术语
-
-
要开始构造实数了!用的是 Dedekind 分割。这个我也在 wxf 的微 A -课上听过,但他讲得并不认真,仅限念了一遍定义。后一节课课前有同学提问说,为什么一左一右两个集合就能代表一个实数呢?他不是很愿意理会的样子,反问说你是不是补退选进来的所以没听过第一节课啊,一只羊为什么代表 -\(1\) -呢,两个集合怎么不能代表一个数呢。
-他可能是觉得这个问题太 trivial -了吧,也或许只是当天心情不好而已,然而提问的同学看起来还是没理解的样子,还平白无故被敲打了一下,就茫然地坐下了。Anyway,在这之后我对这个课堂的印象就不是很好,后续也很少再去上课了。只是觉得,为什么不能好好讲清楚道理呢,就告诉同学理由是从几何直观的角度来看,把实数轴任意截断的一点都是实数,有这样的一个定义不就好了吗。当然,当然,应该是我吹毛求疵了,他可能真的只是当天心情不好,所以不太想解释,后来我也没怎么再听过他上课,不清楚还有没有类似的状况,可能属于是不小心碰到了一个极端情况。
-另外,单是讲过这个有什么意思呢,不说 Dedekind -分割满足序公理所以确实可以定义出实数,也不拿来用一下,就莫名其妙放一个定义在这里,课后又让做题目,感觉是在炫技。后来我也看过一部分他的讲义和回放,挺多莫名其妙的安排都有点像炫技,就彻底放弃跟进度,自己单开了。不过确实也没人逼你选他的微积分课,接受不了的话,换别的老师的课堂就好了,或许是个伪命题吧。
-虽然大多数同学都吹 wxf -讲课有多好,但我其实相当怀疑他们有一部分并没有听明白课堂内容,觉得老师讲的内容很高深,自己吹捧老师的话会显得很厉害而已。另外听说 -wxf -的答疑确实很认真,或许大家说他好是指这一部分吧,还是指他喜欢在课堂上和群里讲笑话?PPT -和讲义是准备得挺认真的,可惜我并不觉得设计得好,
-感觉白认真了。总之我是不太喜欢这种不彻底也不成体系的高阶知识下放,或许它自有意义,带大家了解一下也好。当然,和我相反的典型就是 -wl 他们,是真的学得很好,也喜欢 wxf -的课堂,所以我这些话很可能只是弱者的托词而已。也是啊,我觉得他讲得不好,大一的时候干嘛不自己去看一千零一页,而是单开去拟合微积分往年习题了呢,乐。弱者的牢骚暂且发到这里,下面继续说点正经的。
-这下三纸无驴了。注意 Dedekind -分割的断点是有理数时,会把它归到右侧区间里,这是为了保证左侧无最大元。一般把左侧的区间记为 -\(X\),也称这个分割代表的实数是 \(X\)。
-Dedekind -分割是满足序公理的,在这里需要先定义这一分割的序关系。对于实数 \(X,Y\),如果 \(X -\subsetneq Y\),则有 \(X<Y\)。这个很好理解,\(X\) 比 \(Y\) 短一些,也就是 \(X\) 的端点在 \(Y\) 左侧,即 \(X<Y\)。再证明这个序关系满足序公理的五条要求即可。
-有了这样一个对实数的描述,就可以写出确界定理的第二种证明,也很炫酷。
-现在我们有了一个叫做实数的东西(Dedekind -分割),它离组成实数域还差很远,因为域上的两种运算,加法和乘法,尚未被定义。我们来定义一下,然后先证明它是良好定义的,不会出 -bug。这指的是,对于两个实数的运算结果也是 Dedekind -分割,且满足若干加法公理,并且是加法良定义的。
-加法定义:\(X+Y=\lbrace x+y | x \in X,y \in -Y \rbrace\),零元素为 \(\bar{0} = X_0 = -\lbrace x \in \mathbb{Q} | x<0 \rbrace\)。
-乘法定义:恒等元为 \(\bar{1}= X_1 = \lbrace -x \in \mathbb{Q} | x <1 -\rbrace\),需要根据正负性来分类定义。这个是 PIN -的作业,我写作业去了。
-
Summary
-总之,在第一章里面,于我而言实际上是在抽代的基础上,为一个特征为 -\(0\) -的域在其素域的基础上添置了一些多余元素,让它也满足序公理和 Achimedes -公理,这就符合实数域的定义了。为了使用的方便起见,又用 Dedekind -分割确定了实数域元素的具体形式,把它和日常使用的实数域对应起来。这一过程中为了磨合一些 -bug,完成了不计其数的良定义确认,我愿称之为夜话团圆。
-素域就是熟知的 \(\mathbb{Q}\),由恒等元和零元素造出的整数环与其分式域构成。在此基础上,对素域元素做了一个序关系的定义,并嵌入实数域中,证明了它是符合序公理和 -Achimedes -公理的。这说明这一做法可行,下一个任务就是具象化实数域的元素,也即实数。
-第二个创举是用 Dedekind -分割构造所谓的实数的确切形式,这里用了一个几何的观点,就是把实数轴折断,把左半边的集合 -\(X\) -称为一个实数,通俗意义上来说,它代表的实际上是断点处的那个真正的实数。我们对创造出的这个实数进行了集合意义上的序、加法和乘法的定义。于是全体 -Dedekind 分割真正意义上构成了一个满足序公理和 Achimedes -公理的域,这便和我们日常使用的实数没有差别了。
-此外,还有一个很有趣的东西叫做确界原理,它描述的是一个有上/下界的集合必有上/下确界。围绕它有三个证明,前两个是证明确界原理和区间套公理等价,第三个是用 -Dedekind -分割作出的确切的实数来证明确界原理的确成立。用区间套公理推确界原理的证明最酷炫,希望我以后还能记得怎么做,以及它的细节。
-抽代真好用,赞美。我建议大家都和我一样,先学代数再学分析(什么啊
-学到这里,学过的几门数学课已经被充分利用过了。微积分自不必说,抽代上面说过了,高代的线性空间定义也出现过了,赋范空间和度量空间在数值分析的引论课上听过,甚至写习题写到可数理论,给了我一点小小的离散数学震撼,我以前一直以为这课没用,白学了。往后云端漫步了一点,在数分 -II 里找到了上学期在初概里了解过的 \(\sigma --\)代数,其实属于是测度知识了,但把它当成高等概率论知识也未尝不可嘛(。另外我的初概学得稀烂,可以近似认为是在统计推断里学会的,也算是做了贡献(,不然就它还没出镜啦。
-什么叫做可以以任意顺序修完培养方案啊。我现在也理解为什么说数分难了,大一入学第一节课就学这玩意的话,反正我一下子受不了,会很想退学。不过这以前是 -Yau 班讲义来着,难怪我不配(
-梦话:可数集与不可数集
-2023 年 1 月 19 日,星期四,v 我 50,谢谢。
-在第一章继续逗留了一会,想补充一些可数(或者说可列)的东西。
-刚拿到习题的时候以为是离散数学,后来发现还是不太一样。这一部分先由 -PIN -的习题展开,顺便理一下我在离散数学里学到的东西,发现两边在用不太类似的定义逻辑,接合在一起之后也有些 -happily ever after 了。
-终于在香蕉空间找到了开源的页面,省了很多打字的心力,赞美!以及发现原来最初编写这份讲义的是曾经访问了我博客的 -zrc 学长,由可爱的 _rqy -完成了香蕉空间上的工作,世界真小,qwq,感谢前辈做出的贡献。
-课后习题:可数集与不可数集
-令 \(\mathbb{N}\) -表示自然数的集合(包括 \(0\))。\(X\) 是一个集合,如果存在单射 \(f\colon X\rightarrow \mathbb{N}\),我们就称 -\(X\) 是可数的。如果 \(X\) 不是可数的,我们就称它是不可数的。
+一般来说,我们把 \(X\) 作为 +predictor/input/explanatory variable,把 \(Y\) 作为 response/output/dependent +variable。
\(Y \sim X\) 被称为 simple +regression,一元总归是简单的。
+\(Y \sim X_1,X_2,...,X_p\) 称为 +multiple/multivariate regression,实际上这两者是不一样的。
+如果每个回归式中有超过一个 \(X\) +就称为 multiple regression,如果有多个 \(Y\) 就称为 multivariate +regression,并且每个式子里只能有一个不同的 dependent variable。
+还有叫做 multivariate multiple regression 的回归方法,也就是用多个 +\(X\) 来预测多个 \(Y\) 的情况,每个 \(Y\) 出现在不同的式子里。
一般来说 \(Y\) +是连续型随机变量,\(X\) +可以是连续型、离散型或者分类型随机变量。有一些名词,不抄了,简单列一下:
+
Lecture 2
+Simple Linear Regression
+数据的组织和表示
+Simple linear regression 的数据一般是二元数据对 \((X_i , Y_i)\),每一对数据称为一个 +case。数据集记作 \((X_1,Y_1),...,(X_n,Y_n)\),其中 \(X_i\) 是 i-th observed explanatory +variable,\(Y_i\) 是 i-th observed +response variable。
+模型的表示
+\(Y_i = \beta_0 + \beta_1 X_i + \varepsilon +_i\),\(\varepsilon _i\) 被称为 +random error term,其中 \(\beta_0,\beta_1\) +是参数。为了简化模型便于操作,需要对 random error term 做一些假设:
-
-
证明,有限集是可数的。
-Trivial.
-证明,可数集合的子集是可数的。
-Trivial,原映射的“一部分”,也就是它的导出映射对于剩余的元素仍然为单射。
-证明,如果 \(X\) -是可数集,那么我们总可以将 \(X\) 写成 -\(X=\{x_1,x_2, x_3, -\cdots\}\)(即可以把 \(X\) -中的元素用自然数来标号)。(我们可以从一个开始一个一个的数下去把这些元素都罗列出来,所以叫做可数集)
-存在单射 \(f\colon X\rightarrow -\mathbb{N}\),考虑 \(Im f\) -是一个自然数集合,由其一般性知可以表示为 \(\{ -1,2,3,... \}\)。
-证明,有理数 \(\mathbb{Q}\) -是可数集。
-可以按分子分母绝对值之和写个大三角,不过我在知乎上看到过一个很酷的证明,摘录如下:
--
不难证明 \(\mathbb {N}\times \mathbb -{N}\) 是可数集(考虑双射 $(n,m)^n(2m+1)-1 $),从而 \(\mathbb Z\times(\mathbb Z\backslash -\{0\})\) 可数。
-由 Cantor-Schröder–Bernstein 定理即得证。
-
-证明,可数个可数集合的并集也是可数集,也就是说,如果 \(X_1,X_2, \cdots, X_n, \cdots\) -都是可数集合,那么它们的并集 \(\displaystyle -\bigcup_{n\geqslant 1} X_n\) -也是可数集合。(提示:这是一个需要记住的经典证明,请查阅参考书或者网络)
-排矩阵,列大三角。
-\(X\) 是可数的,映射 \(f\colon X\rightarrow Y\) -是满射。证明,\(Y\) 是可数的。
-存在单射 \(g \colon Y \to X\) 和 -\(h \colon X \to \mathbb N\),其复合 -\(g \cdot h \colon Y \to \mathbb N\) -也是单射。
-按照以下步骤证明 \(\mathbb R\) -是不可数的(同学们可以查阅一个用所谓对角线法则的经典证明,我们的证明基于区间套原理):
+- 均值为 \(E(\varepsilon_i) = +0\),方差为 \(Var(\varepsilon _i) = +\sigma ^2\),注意 \(\sigma\) +是一个未知常数,也视作参数; +
- 不同的 \(\varepsilon _i\) 和 \(\varepsilon _j\) +是不相关的。注意此处不需要不独立。 +
对于更强的模型,例如 simple linear regression model with normal +error,我们直接要求 \(\varepsilon_1,...,\varepsilon_n i.i.d. \sim +N(0,\sigma^2)\)(因为正态分布的不相关性和独立性等价)。这是一个很广泛的假设,但有时正态假设是明显有问题的,需要修正。
+事实上,在 linear regression model 中,\(X_i\) 和 \(Y_i\) 的地位是不对等的。\(X_i\) 被视为不带随机性的常数,而 \(Y_i\) 因为 \(\varepsilon_i\) 的存在是一个随机变量,有 +\(E(Y_i) = \beta_0 + \beta_1 +X_i\),\(Var(Y_i)=Var(\varepsilon_i) = +\sigma^2\)。因此,回归线可以视作 \((X_i, E(Y_i))\) 连成的直线,而数据点 \((X_i,Y_i)\) 分布在回归线附近。
+特别地,在正态假设下, 有 \(Y_i \sim +N(\beta_0 + \beta_1 X_i,\sigma^2)\),\(i=1,2,...,n\)。
+参数的意义和求算
+斜率 \(\beta_1\) 的意义为 \(X_i\) 增加 1 单位时 \(Y_i\) 的变化量;截距 \(\beta_0\) 的意义分两种情况解释,当 \(X_i\) 取值范围中有 \(0\) 时即为 \(X_i=0\) 时的平均响应 \(E(Y_i)\),否则截距没有意义。
+Least Sum of Square 方法
+求算最佳参数实际上就是求使得 sum of squared diff 最小的 \(\hat{\beta_0},\hat{\beta_1}\),从而得到 +\(Y_i\) 的估计值 $= + X_i $。于是有 +\(\hat{\beta_0},\hat{\beta_1} = \arg \min +_{\beta_0,\beta_1} \Sigma(Y_i - \beta_0 - \beta_1X_i)^2=\arg \min +_{\beta_0,\beta_1} \Sigma_{i=1 } ^n e_i +^2\)。求导即可简单地得出:
+\[b_1 = \hat{\beta_1} = \frac{\Sigma_i +(X_i - \bar{X})(Y_i - \bar{Y})}{\Sigma _i (X_i-\bar{X})^2}\]
+\[b_0 = \hat{\beta_0} = \bar{Y} - b_1 +\bar{X}\]
+记残差为 \(e_i = Y_i - \hat{Y_i}= Y_i - +\hat{\beta_0} - \hat{\beta_1} X_i=\beta_0 + \beta_1X_i +\varepsilon _i - +\hat{\beta_0} - \hat{\beta_1}X_i \approx \varepsilon _i\) ,也即 +\(e_i\) 为某一组 observed data \(Y_1,Y_2,...,Y_n\) 之下得到的残差,但绝非 +\(\varepsilon _i\) +本身。残差是观测到的确定值,而 \(\varepsilon +_i\) 是随机变量。
+事实上求导的过程蕴含以下结论:
+\[\Sigma _{i=1} ^n e_i=0\]
+\[\Sigma _{i=1} ^{n} X_i e_i = +0\]
+以上二式可以看做对 \(e_i\) +的线性约束,\(\lbrace e_i \rbrace\) +的自由度是 \(n-2\),互相之间不是独立的,这也是和 \(\lbrace \varepsilon _i \rbrace\) +的差别之一。由此还可以得到一些其他性质,例如回归线必过 \((\bar{X},\bar{Y})\),不在此一一列举。
+以上即为参数 \(\beta_0,\beta_1\) +的估计方法。下面再考虑参数 \(\sigma\) +的估计,使用残差 \(e_1,...,e_n\) +来考虑。
+取 \(\hat{\sigma ^2} = \frac{\Sigma _{i=1} +^n e_i ^2}{n-2}\)。这是因为 \(e_1,e_2,...,e_n\) 的自由度为 \(df_E = n-2\),由此考虑 sum of square \(SSE= \Sigma_{i=1} ^n (Y_i - \hat{Y_i})^2=\Sigma +_{i=1} ^n e_i ^2\),定义 mean of squared errors \(MSE= \frac{SSE}{df_E} = \frac{\Sigma_{i=1}^n e_i +^2}{n-2}\) 为 \(\hat{\sigma +^2}\)。
+MLE 方法
+也可以用推断课上的 MLE 方法。实际上,我们想找到一个 \(\beta_0,\beta_1\) 的最佳估计,还可以使用 +MLE 方法进行估计。
+在正态假设下,我们可以将 \(n\) +组数据视作 \(n\) +个互相独立的随机变量,取使得其likelihood function 最大的一组 \(\beta_0,\beta_1,\sigma^2\) +作为估计量。likelihood function 即为 \(f(y_1,y_2,...,y_n) = +f_1(y_1)...f_n(y_n)\),得到的 estimator 中 \(\hat{\beta_0},\hat{\beta_1}\) 与 least sum +of square 中得出的估计量相同,但 \(\hat{\sigma +^2} = \frac{\Sigma _{i=1} ^n e_i +^2}{n}\)。注意这是一个有偏的估计量,而 least sum of square +得到的估计量是无偏的。
+推断复习
+咕了。什么嘛,我推断学得还是可以的嘛(x
+Lecture 3
+线性回归中的推断
+回顾一下,无论是 OLS 方法还是 MLE 方法,我们得到的参数估计 \(b_0\),\(b_1\) 都是相同的:
+\[b_1 = \hat{\beta_1} = \frac{\Sigma_i +(X_i - \bar{X})(Y_i - \bar{Y})}{\Sigma _i (X_i-\bar{X})^2}\]
+\[b_0 = \hat{\beta_0} = \bar{Y} - b_1 +\bar{X}\]
+通过简单的计算可以知道:
+\[E(b_1) = \beta_1,Var(b_1) ={\sigma^2 +\over S_{XX}},s^2(b_1) = \frac{s^2}{S_{XX}}\],
+其中 \(S_{XX} = \Sigma_{i=1} ^n (X_i - +\bar{X})^2\), \(s^2 = \hat{\sigma}^2 = +\frac{\Sigma_{i=1}^n e_i^2}{n-2}\)。
+而且有 \(Cov(b_1, \bar Y)=0\)。
+参数推断
-
-
若 \(J\subset \mathbb R\) -是闭区间并且它的长度 \(|J|>0\)。证明,对任意的 \(x\in \mathbb R\),总存在闭区间 \(I\),使得 \(I\subset J\),\(|I|>0\) 且 \(x\notin I\)。
-用实数 \(x\) 的 Dedekind -分割定义,取 $ I = J X^ $,只要证明它的长度非 \(0\),trivial.
-证明,如果 \(\{x_1,x_2,\cdots\}\) 是 \(\mathbb R\) -的一个可数子集,那么存在闭区间套 \(I_1\supset -I_2 \supset \cdots\),使得对任意的 \(n\),\(x_n \notin -I_{n}\)。
-取 \(I_1\) 为 \(X_1 ^\prime\) 的长度大于 \(0\) 的闭区间,按上一问的方法构造闭区间 -\(I_2\),使得 \(I_2 \subset I_1\),\(|I_2|>0\) 且 \(x_2\notin I_2\)。类似地构造 \(I_3,I_4,...\) 即可。
-证明,\(\mathbb R\) 不可数。
-反证法,设 \(\mathbb R\) 可数,也即 -\(\mathbb R\) 可以表示成 \(\mathbb R =\lbrace x_1,x_2,... \rbrace\) -的形式。因此存在上述的闭区间套,使得闭区间的交集里不含有 \(\mathbb R\) -的任何一个元素,是一个空集。这和区间套公理是矛盾的。
-嗯?这就证明完了?好美妙!
+对 \(\beta_1\) 进行推断:null +hypothesis 为 \(H_0: \beta_1 +=0\),这样设置是因为关心两个变量之间是否存在线性关系。
+在假设 \(H_0\) 下可以考虑 test +statistic 为 \(T= \frac{b_1 -0}{s(b_1)} \sim +t_{n-2}\),这是因为 \(H_0\) +假设下 \(b_1-0 \sim +N(0,\frac{\sigma}{\sqrt{Sxx}})\),我们一般用 \(\sigma\) 的无偏估计 \(\hat{\sigma} = \sqrt{\frac{\Sigma_{i=1}^n e_i +^2}{n-2}}\) 来处理。
+level of significance 为 \(\alpha\),于是当 observed data \(t_0\) 满足 \(|t_0| > t_{n-2,1-\alpha /2}\) 时 reject +\(H_0\)。
+如果没有拒绝 \(H_0\),通常的可能有以下三种:
+-
+
- 发生了 Type II Error,没有成功拒绝掉 \(H_0\) 而事实相反; +
- \(X\) 和 \(Y\) 之间确实没有什么线性关系; +
- \(X\) 和 \(Y\) 之间有关系,但是非线性。(这句话原来的 +typo 是“有线性关系,但是非线性”,绷不住了,中午被 Photon +指出来了,非常感谢他)
-证明,如果 \(X\) -是不可数集,\(A\) 是 \(X\) 的可数子集,那么 \(X-A\) 是不可数的。
-反证法,trivial.
-证明,任意的长度不为 \(0\) -的区间(无论开或闭)都是不可数的。
-反证法,否则它是可数的,可以表示成 $X= x_1,x_2,... $ -的形式。于是也可以按前述方法构造出其上的一个区间套 \(X \supset X_1 \supset X_2 \supset -...\),满足除了 \(X\) -之外的区间都是闭区间,且闭区间的交集是空集,这是矛盾的。
-证明,复数 \(\mathbb{C}\) -是不可数的。
-反证法,如果复数集是可数的,它的子集 \(\mathbb R\) 也一定可数,矛盾。
-假设 \(\mathcal{I}\) 是 \(\mathbb R\) -上的某些开区间组成的集合,它满足如下性质:对任意的 \(I,J \in \mathcal{I}\),\(I\neq J\),那么它们的交集是空集,即 \(I\cap J=\emptyset\)。证明,\(\mathcal{I}\) 是可数集。
-习题没有答案,于是我只能做一些不负责任的暴论:
-回到定义,想找一个从 \(\mathcal I\) -到 \(\mathbb N\) 的单射 \(f\)。只要考虑在 \(R_ +\) 上的全体集合,对任意的 \(I \in \mathcal I\),取 \(f(I)\) 为区间 \(I\) -覆盖的最小整数,这些整数一定两两不同,也就构成了一个到 \(\mathbb N\) 的单射。
-但是不一定每个区间都覆盖一个整数,所以我想做个不负责任的操作:如果 -\(I = (a,b)\) -不覆盖整数,则将所有区间的端点关于 \(a\) 的距离放大,直到放大后的区间 \(I ^ \prime =(a,b ^ \prime)\) -能覆盖住某一个整数,从左至右对每一个区间都这样操作。
+对 \(\beta_1\) 做 confidence +interval:由于在 \(\beta_1\) +代表斜率的情况下,有 \(\frac{b_1 - +\beta_1}{s(b_1)} \sim^{H_0} t_{n-2}\)。
+于是 \(P(\frac{|b_1-\beta_1|}{s(b_1)} < +t_{n-2,1-\alpha /2}) = 1-\alpha\),\(\beta_1\) 的 100%\((1-\alpha)\) confidence interval 是
+\[(b_1 - t_{n-2,1-\alpha /2} s(b_1),b_1 + +t_{n-2,1-\alpha /2} s(b_1))\]
+类似地可以对 \(\beta_0\) +做推断,有 \(\frac{b_0 -\beta_0}{s(b_0)} \sim +t_{n-2}\),因此如果 null hypothesis 为 \(H_0: \beta_0 =0\),rejection region +即为满足条件 $ > t_{n-2,1-/2} $ 的数据。对于偏移的 null hypothesis +\(H_0 : \beta_0 =c\),也只要相应地移动 +rejection region 即可。
+100%\((1-\alpha)\) confidence +interval 为 \((b_0 - t_{n-2,1-\alpha /2} +s(b_0),b_0 + t_{n-2,1-\alpha /2} s(b_0))\)。
+实际上我们一般对 \(\beta_0\) +的推断不感兴趣,因为这个参数未必有意义,依赖于 \(X\) 的取值范围。
+以上都是对单个参数进行推断,实际上我们也可以进行 joint +inference:
+同时推断两个参数 \((\beta_0,\beta_1)\),这时候得到的就是 +confidence region,使得 \(P((\beta_0,\beta_1) +\in S \subset \mathbb R^2) = 100(1-\alpha) \%\)。实际上因为 \((b_0 , b_1) ^T \sim N((\beta_0,\beta_1)^T , +\sigma^2 \Sigma_{2\times 2})\),所以最小的 confidence region +是一个椭圆。
+实际上我们也可以考虑做一个矩形的 confidence +region,也即对两个参数分别作 confidence interval,confidence coefficient +分别为 \(\sqrt{1-\alpha} \approx +1-\frac{\alpha}{2}\)。因此 confidence region 为:
+\[ (b_1 - t_{n-2,1-\alpha /4} s(b_1),b_1 + +t_{n-2,1-\alpha /4} s(b_1)) \times (b_0 - t_{n-2,1-\alpha /4} s(b_0),b_0 ++ t_{n-2,1-\alpha /4} s(b_0))\]
找到了作者在源代码注释里留下的彩蛋:
+参数推断的角度来说 \(\beta_1\) +的推断远比 \(\beta_0\) +重要,它表征线性关系,而且从预测的角度来说,\(\beta_1\) 的推断如果不够精细,会导致远离 +\(\bar X\) 处的 \(X_h\) 对应的估计量误差很大。
+Power Function
+一个 significance test 的 power 指的是 reject \(H_0\) 时 \(H_1\) 是正确的的概率,也就是 \(1-P(\)Type II Error\()\)。实际上一个推断是好的的情况下需要既不 +over-powered 也不 under powered,这和 Type I Error 与 Type II Error +此消彼长的性质有关。
+Power function 一般是一个关于参数的函数。以推断 \(\beta_1\) 的过程为例,计算这一推断的 power +function。
-
-
证明,不能用可数条直线覆盖平面,即如果 \(\ell_1,\ell_2,\cdots\) 是平面 \(\mathbb{R}^2\) 上可数条直线,那么 \(\displaystyle \bigcup_{k\geqslant 1}\ell_k\neq -\mathbb R^2\)。
-一个圆心在 \((x_0,y_0)\) -处,半径为 \(r>0\) 的闭圆盘 \(\overline{B_r(x_0,y_0)}\),指的是:
-\(\overline{B_r(x_0,y_0)}=\{(x,y)\mid -(x-x_0)^2+(y-y_0)^2\leqslant r^2\}\);
-证明,不能用(无论可数个还是不可数个)两两不相交的闭圆盘(半径大于零)(圆心和半径可以变化)覆盖 -\(\mathbb -R^2\),使得两个不同的圆盘至多有一个点是重合的。
-纯属娱乐,对后面学习分析并无帮助。
+我们在线性回归参数推断里会用到一种非中心化 t-分布。普通的 +t-分布是关于 \(x=0\) 对称的,非中心化 +t-分布有一定的偏差。注意并不是整体在坐标轴方向上的移动,其形状也发生了变化。表达式为 +\(t(df, \delta ) = \frac{N(0,1) + +\delta}{\sqrt{\chi_{df} / df}}\)。
+对 \(\beta_1\) 进行推断:null +hypothesis 为 \(H_0: \beta_1 +=0\),这样设置是因为关心两个变量之间是否存在线性关系。
+在假设 \(H_0\) 下可以考虑 test +statistic 为 \(T= \frac{b_1 -0}{s(b_1)} \sim +t_{n-2}\),然而在 \(H_1\) +下,
+\[T=\frac{b_1}{s(b_1)} = \frac{b_1 - +\beta_1 + \beta_1}{s(b_1)} = \frac{b_1-\beta_1}{s(b_1)} + \frac{\beta_1 +/ \sigma(b_1)}{s(b_1)/\sigma(b_1)} = \frac{N(0,1) + +\delta}{\sqrt{\chi_{df} / df}} \sim +t(n-2,\beta_1/\sigma(b_1))\]
+于是 \(Power(\beta_1) = P(Reject H_0 | H_1 +holds) = P(|T| > t_{n-2,1-\alpha /2} | \beta_1 \neq 0) = +P(T<t_{n-2,\alpha /2}) +1-P(T<t_{n-2,1-\alpha +/2})\),其中在 \(\beta_1 \neq +0\) 的条件下,\(T\sim t(n-2,\beta_1 / +\sigma(b_1))\)。
课后习题: -Schroeder-Bernstein 定理
-实际上,PIN 还有一道习题 Schroeder-Bernstein -定理。这道题就不打算写了,学不完了 -.jpg,我把它轻轻放在这里,作为后面补充的引子:
-假设 \(X\) 和 \(Y\) 是两个集合,映射 \(f\colon X\rightarrow Y\) 和 \(g\colon Y\rightarrow X\) 都是单射。我们令 -\(X'=X-g(Y)\)。
+BLUE
+ +简单来说,OLS Estimators 是 the best linear unbiased estimator,简称 +OLS estimators 是 BLUE。best 的意思是方差最小,这是不难证明的。
+BLUE 是非常好的性质,也希望我以后能 go blue(逃
+Lecture 4
+Prediction & ANOVA,感谢 zzy 救我的生统概论(
+Estimation & Prediction
+平均响应的推断
+有了线性回归模型之后当然是要用来做预测,通过已有数据拟合出一个线性模型,再用来估计未知点的值。对于需要估计的点 +\(X_h\),一般来说估计值都是考虑平均响应 +(mean response) \(\mu_h = E(Y_h) = \beta_0 ++\beta_1 X_h\),把 \(\hat{\mu_h} = b_0 ++ b_1 X_h\) 作为 \(\mu_h\) +的估计。这是一个 +estimator,既然如此就要考虑它的性质,也要先考虑平均响应的置信区间。
-
-
如果 \(X\) 是有限集,证明,存在 -\(\varphi\colon X\rightarrow Y\),使得 -\(\varphi\) 是双射。
-如果 \(X\) 是可数集,证明,存在 -\(\varphi\colon X\rightarrow Y\),使得 -\(\varphi\) 是双射。
+\(E(\hat{\mu_h}) = E(b_0) + E(b_1)X_h = +\beta_0 + \beta_1 X_h = \mu_h\) ,是 unbiased estimator
+\(Var(\hat{\mu_h}) = Var(\bar{Y}+ +b_1(X_h - \bar{X})) = \sigma^2 [\frac{1}{n} + \frac{(X_h - +\bar{X})^2}{\Sigma (X_i -\bar{X})^2}]\) ,是 minimum +variance
+\(\hat{\mu_h} = \bar{Y} + (X_h - +\bar{X}) b_1\),由于 \(\bar{Y}\) +和 \(b_1\) 都有正态假设,因此 \(\hat{\mu_h}\) 也服从正态分布,\(\hat{\mu_h} \sim N(\mu_h , +Var(\hat{\mu_h}))\)。
+\(Var(\hat{\mu_h})\) 的估计量是 +\(s^2(\hat{\mu_h}) = s^2[\frac 1 n + +\frac{(X_h-\bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\),于是有 \(\frac{\hat{\mu_h} - \mu_h}{s(\hat{\mu_h})} \sim +t_{n-2}\)。
+因此,\(\mu_h\) 的 \(100 \% (1-\alpha)\) confidence interval 是 +\((\hat{\mu_h} - t_{n-2, 1-\alpha /2} +s(\hat{\mu_h}),\hat{\mu_h} + t_{n-2, 1-\alpha /2} +s(\hat{\mu_h}))\)。confidence interval 的长度为 $2t_{n-2, 1-/2} +s() = 2t_{n-2, 1-/2} s $,其中 \(s = +\sqrt{[\frac{\Sigma_{i=1}^n +e_i^2}{n-2}]}\)。因此置信区间的长度是近似于随 \(X_h - \bar{X}\) +递增而递增的。也就是说,\(X_h\) +距离 \(\bar{X}\) +越远,置信区间的长度越大,准确性越难保证。
+综上,我们成功找到了这个对于 \(\mu_h\) 的估计的置信区间。
从现在开始,对 \(X\) -不加任何的限制。 我们令 \(h\colon X\rightarrow -X\) 是复合映射 \(h=g\circ -f\)。
+预测值的推断
+上述估计的是预测值的平均响应,对于新观测点的值需要改成:\(Y_{h(new)} = \beta_0 + \beta_1 X_h ++\varepsilon\) 且有 \(E(\varepsilon) = +0,Var(\varepsilon) = \sigma^2\)。注意这里 \(\varepsilon\) 是随机变量,\(\beta_0,\beta_1\) 是未知值的参数,\(X_h\) 是已知的常数。
+对它做估计 \(\hat{Y}_{h(new)} = \hat{\mu_h} += b_0+b_1 X_h\) 仍然是和平均响应相同,考虑这个估计的性质。
-
-
考虑 \(X\) 的子集的集合 \(\mathcal{F}=\{A \subset X\mid X'\cup -h(A)\subset A \}\)。证明,\(\mathcal{F}\) 非空。
-证明,如果 \(A\in -\mathcal{F}\),那么 \(X'\cup -h(A)\in \mathcal{F}\)。
+\(E(\hat{Y}_{h(new)}) = E(b_0 + b_1 +X_h) = \beta_0 + \beta_1 X_h\)
+从简单的情形开始,如果 \(\beta_0,\beta_1,\sigma\) +都是已知的参数,则在正态假设下 \(\frac{Y_{h(new)} -E(Y_h)}{\sigma}\sim +N(0,1)\)(非正态假设情况下服从未知分布),\(Y_{h(new)}\) 的 confidence interval 是 +\((E(Y_h) - z_{1-\alpha /2} \sigma,E(Y_h) + +z_{1-\alpha /2} \sigma)\)。
+一般情况下,设 \(d_h = Y_{h(new)} - +\hat{Y}_{h(new)} = Y_{h(new)} - \hat{\mu_h}\),于是有 \(E(d_h) = 0\)。
+计算可知方差 \(Var(d_h) = Var(Y_{h(new)} - +\hat{\mu} _h) = Var(Y_{h(new)})+Var(\hat{\mu_h}) = \sigma^2[1+\frac 1 n ++\frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\);
+standard error 为 \(s^2(d_h) = s^2 [1+\frac +1 n +\frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\);
+于是有 \(\frac{d_h - E(d_h)}{s(d_h)} = +\frac{d_h}{s(d_h)} = \frac{Y_{h(new)} - \hat{\mu}_h}{s(d_h)} \sim +t_{n-2}\),\(Y_{h(new)}\) +的置信区间是 \((\hat{\mu}_h - s(d_h) +t_{n-2,1-\alpha/2},\hat{\mu}_h + s(d_h) +t_{n-2,1-\alpha/2})\),这个区间一般叫做 prediction +interval,长度是 \(2 t_{n-2,1-\alpha/2} +s(d_h)\),其中 \(s^2(d_h) = s^2 + +s^2(\hat{\mu}_h +^2)\),因此预测区间比平均响应的置信区间略宽。
我们定义\(A_0=\bigcap_{A\in -\mathcal{F}}A=\{x\in X\mid\)对任意的\(A\in \mathcal{F},\)都有\(x\in A\}\)。
+预测值的平均的推断
+考虑在新值 \(X_h\) 处的 \(m\) 个观测值的平均值,为 ${Y_h} = m +{i=1} ^m Y{h(new) i} = _0 +1 X_h+ 1m {i=1}^m _i +$,预测值的平均仍然是 \(\hat{Y_h}=b_0 + b_1 +X_h\)。有 \(\varepsilon _i \sim +N(0,\sigma^2)\) 为正态假设。于是 \(Var(\bar{Y}_h - \hat{Y_h}) = \sigma^2 [\frac 1m + +\frac 1 n + \frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}] \leq +Var(d_h)\)。
+它的宽度小于 prediction interval,但也大于平均响应的 confidence +interval。
+Confidence Band for +Entire Regression Line
+怎么翻译都没那味,就写原文吧。
+希望找到一个 confidence band:\(\lbrace +(x,y): L(x)<y<U(x), x\in \mathbb R \rbrace\),对于任意点 +\(x\) 有 \(P[l(x) < \beta_0 +\beta_1 x <u(x)] = +1-\alpha\)。对于固定的点 \(x\),\(100 \% +(1-\alpha)\) 置信区间为 \((\hat{\mu_x} +- t_{n-2, 1-\alpha /2} s(\hat{\mu_x}),\hat{\mu_x} + t_{n-2, 1-\alpha /2} +s(\hat{\mu_x}))\)。
+所以只要取 \(W=max\{(\hat{\mu}_x - +\mu_x)/s(\hat{\mu}_x) \}\),即有置信区间为 \((\hat{\mu}_x - W s(\hat{\mu_x}),\hat{\mu}_x + W +s(\hat{\mu_x}))\),其中 \(W = +\sqrt{2F_{1-\alpha,2,n-2}}\)。实际上 \(W > t_{n-2,1-\alpha /2}\),也就是说 +confidence band 处处比 confidence interval 更宽,level of confidence +\(\alpha'\) 也更小。
+Summary
+一个显示 confidence interval of mean response,prediction interval 和 +confidence band 宽度关系的图:
+
Analysis of Variance (ANOVA)
+Variance Estimator
+先上点概念:
-
-
证明,\(A_0\in\mathcal{F}\)。
-证明,\(X'\cup -h(A_0)=A_0\)。
-令 \(B_0=X-A_0\)。证明,\(f(A_0)\cap g^{-1}(B_0)=\emptyset\) 并且 -\(f(A_0)\cup g^{-1}(B_0)=Y\)。
-我们定义映射 \(\varphi\colon -X\rightarrow Y\):对于 \(x\in -X\),我们要求 \(\varphi(x)=\begin{cases}f(x), \ &\text{如果} -x\in A_0;\\g^{-1}(x), \ &\text{如果} x\in -B_0.\end{cases}\)
-证明,这是双射。
+Total Sum of Squares: \(SST= \Sigma(Y_i +- \bar{Y})^2\),\(df_{SST} = +n-1\)
+Sample Variance: \(S_n ^2 = +\frac{SST}{n-1}\),是非常熟悉的统计量。
+Variation due to Error: \(SSE = +\Sigma(Y_i -\hat{Y}_i)^2= \Sigma e_i ^2\), \(df_{SSE} = n-2\)
+Mean Square Error: \(MSE = \frac{SSE}{df} = +\frac{\Sigma_{i=1} ^n e_i ^2}{n-2}\),可以作为 \(\sigma^2 = Var(\varepsilon)\) +的一个估计。
+\(E(MSE) = \sigma^2\)
+Variation due to Regression: \(SSR = +\Sigma(\hat{Y}_i - \bar{Y})^2 = b_1 ^2 \Sigma (X_i-\bar{X})^2\), +\(df_{SSR} = 1\)
+Mean Squares of Regression: \(MSR = +\frac{SSR}{df} = SSR\)
+$E(MSR) = E(SSR) = E(b_1 ^2) ((X_i - {X})^2)= ^2 + _1^2 (X_i - {X})^2 +$;
根据上述,我们证明了 Schroeder-Bernstein 定理:如果有单射 \(f\colon X\rightarrow Y\) 和单射 \(g\colon Y\rightarrow -X\),那么存在着两个集合之间的双射 \(\varphi\colon X\rightarrow Y\)。
-离散数学复习:等势与基数
+可以计算得到 \(SST=SSE+SSR\),自由度方面也是 \(df_{SST} = df_{SSE}+df_{SSR}\)。
+事实上在 Lecture 2 中我们考虑过是选取 sample variance 还是选取 MSE +作为 \(\hat{\sigma}^2\),这里的定义给出了更清晰的答案:\(SSE\) 更加注重原值和模型之间的联系,把 +\(\hat{Y_i}\) 作为 \(Y_i\) 的估计值,在 sample variance 中是把 +\(\bar{Y}\) 作为 \(Y_i\) 的估计值,前者更好地体现了 \(\varepsilon\) 的场景。
+F-检验
+我们希望通过以上统计量检验 \(X,Y\) +之间是否存在线性关系。考虑假设 \(H_0: \beta_1 += 0 ; H_1 : \beta_1 \neq 0\)。
+在正态假设和 \(H_0\) 成立条件下,取 +test statistic 为 \(F= \frac{MSR}{MSE} = +\frac{SSR / df_R}{SSE / df_E} = \frac{\chi_{dfR}/df_R}{\chi_{dfE}/df_E} +\sim F_{df_R,df_E} = F_{1,n-2}\)。考虑拒绝 \(H_0\) 的情况,我们要求 \(F_0 > F_{1-\alpha,df_R,df_E} = F_{1-\alpha, +1,n-2}\),满足此条件的 \((X,Y)\) +构成 rejection region。或者从 P-value 的角度来看,满足不等式 \(P(F>F_0 | F_{1,n-2}) < \alpha\) +的全体 \((X,Y)\) 落在 rejection region +中。
+考虑检验的 power function。在 \(H_1: +\beta_1 \neq 0\) 条件下,Power(\(\beta_1\)) = \(P(F> F_{1-\alpha , 1,n-2} | non-central +F)\)。
+General Linear Test
+另一种检验上述假设的方式。考虑假设 \(H_0: +\beta_1 = 0 ; H_1 : \beta_1 \neq +0\),我们来比较两种不同的模型:
+full model: \(Y_i = \beta_0+\beta_1 X_i ++\varepsilon _i\),reduced model: \(Y_i += \beta_0 + \varepsilon_i\),在 \(H_0\) +假设成立时两个模型是等价的。考虑方差统计量:
-
-
在离散数学里,更确切一点讲,在集合论里,介绍了一种关系,叫做等势。这一概念由 -Cantor -提出,用来解决这样的一个困惑:为什么完全平方数貌似比正整数少很多,但是它们却可以一一对应?如何比较两个无穷集合谁的元素多,谁的元素少,谁更“无穷”?
-等势被定义为:如果集合 \(X\) 和 -\(Y\) -之间如果存在双射,那么称二者等势,利用 Schroeder-Bernstein -定理可知如果有单射 \(f\colon X\rightarrow -Y\) 和单射 \(g\colon Y\rightarrow -X\),那么 \(X\) 和 \(Y\) 等势,写作 \(X \approx Y\)。实际上有 \(\mathbb N \approx \mathbb Q \approx \mathbb -Z\),等等。
-另外一个定义是集合的基数,记为 \(card(X)\),精确地测量集合的某些性质。我们定义 -\(card(X) \leq card(Y)\) 等价于有单射 -\(f\colon X\rightarrow -Y\),因此由等势的结论,有 \(card(X)=card(Y)\) 等价于 \(X \approx -Y\)。与此同时,我们希望对这个虚无缥缈的概念做一些基本的规定,比如说把某些特殊的集合的基数作为标尺,来衡量其他集合的基数大小。我们选取了 -\(card(\mathbb N) = \aleph _0\),\(card(\mathbb R) = \aleph _1\) -作为这样的尺度。
-当然,对于有穷的集合,它的基数就是它的元素个数,此时称为有限基数,否则称为无限基数,我们不对有限基数多做讨论。上述的“尺度”中,\(\aleph _0\) -是最小的无限基数,它也大于所有的有限基数。
-基数理论的一个用处在于,可以用来衡量无穷集合的可数性。一个集合 -\(X\) 满足 \(card(X) \leq \aleph _0\) -等价于它是可数的,也就是说,可数集 \(X\) 要么是有限集合,要么基数是 \(\aleph _0\),可以和 \(\mathbb N\) -一一对应,也就是习题里面提到的,可数集可以表示成 \(X = \lbrace x_1,x_2,... \rbrace\) -的形式。
+- \(SSE(F) = SSE\) for full model +with \(df_{EF}\),在 simple linear +regression 下 \(df_{EF}=n-2\),\(SSE(F) = SSE\) +
- \(SSE(R) = SSE\) for reduced model +with \(df_{ER}\),在 simple linear +regression 下 \(df_{ER}=n-1\),\(SSE(R) = SST\)
但是,离散数学没有解答的是,为什么基数可以比较大小?我们可以看到 -\(\aleph _0\),$_1 $ -的出现,就代表了基数的取值未必是实数域上的子集。那么它的取值集合上的序关系是怎么定义的,是否满足序公理?
+在 \(H_0\) 假设下,$F = +F_{(df_{ER}-df_{EF}),df_{EF}} $。实际上,在 simple linear regression +下和 F-检验是一致的。但是 general linear test +是一个更广泛的方法,可以用于任何形式的线性检验。
+Pearson Correlation r
+\(r = \frac{\Sigma (X_i - \bar{X})(Y_i - +\bar{Y})}{\sqrt{\Sigma(X_i - \bar{X})^2} \sqrt{\Sigma(Y_i - +\bar{Y})^2}}\) 被称为相关系数,反映了一组数据 \((X,Y)\) 之间的线性关系程度。
+\(R^2 = \frac{SSR}{SST}\) +被称为决定系数,事实上在 simple linear regression 下有 \(r^2=R^2\),因为 \(r = b_1 \frac{\sigma_X}{\sigma_Y}\)。
+
Lecture 5
+回顾一下简单线性回归的模型假设:\(Y_i = +\beta_1 X_i + \beta_0 +\varepsilon _i\)
-
-
- 实际上,对于集合 \(X,Y\),序关系 -\(card(X) \leq card(Y)\) -成立等价于有单射 \(f\colon X\rightarrow -Y\)。由此就可以验证这个关系满足序公理了。 +
- \(\varepsilon _1, \varepsilon _2 ,..., +\varepsilon_n\) 相互独立 +
- \(\varepsilon_i\) 服从正态分布 +
- \(\mathbb E(\varepsilon _i) = +0\),\(Var(\varepsilon_i) = +\sigma^2\)
但是为什么任意两个基数都可以比较大小呢?在 \(\mathbb R\) -之外还有更多稀奇古怪的集合,以前可能想象不出来,学了抽代之后一想这些真的毛骨悚然,它们都可以互相将基数拿来比较大小吗?
+可以总结成 LINE: linearity, independence, normality, equal +variance
+Diagnostics of X
+诊断的方式粗暴一点来说就是肉眼诊断,用一些可视化工具(主要是画图)和其他方式来检验模型的假设是否符合。如果违反了模型假设,结果很有可能不可靠。此时需要用一些弥补的方式来处理。
+Why +diagnose——Distribution and Confounding
+诊断过程需要关注的是 \(X\) 而非 +\(Y\),因为 \(Y\) 之间是独立异分布的。\(Y_i \sim N(\beta_0 +\beta_1 X_i , +\sigma^2)\)。
+\(X\) 完全是常数,所谓的 \(X\) 的分布指的仅仅是 \(X_1,X_2,...,X_n\) +在数轴上的排布,不是概率分布。但 \(X_i\) +的分布会影响到模型的效果,直观上举个例子来说,\(X_i\) 的位置至少会影响到 \(Var(b_1) = \frac{1}{\Sigma_i (X_i - \bar X)^2} +\sigma^2\) 也就是 \(b_1\) +的分散程度,这是会影响到推断显著性的因素,所以即使是常数也还是要对 \(X\) 进行一些诊断。
+我们一般希望 \(X\) +是类似于正态的分布,这样的数据比较有代表性。可以使用 qq-plot +进行检查。
+除此之外诊断 \(X\) 的另一意义在于 +\(X\) +本身可能也是和其他因素有混杂的。举个例子来说,如果高温既会导致冰激凌销量增加又会导致鲨鱼攻击人的次数增加,很可能会发现冰激凌销量和鲨鱼攻击行为次数之间有线性的关系,事实上这就是一个没有选对合适的 +explanatory variable \(X\) +却得到了看似合理的模型的例子,但这样的结论是有问题的,\(X\) 本身和气温这一因素混杂。
+此时如果分别对冰激凌销量-气温和鲨鱼攻击行为-气温作一个 sequence +plot,会发现二者都分别和气温有关系,那就有必要把气温作为一个 explanatory +variable 加入模型的考虑,这是一种针对 confounding 的诊断方法。
+四参数
+有一些可以关心的量(甚至不能说是统计量,毕竟 \(X\) 也不是随机变量),除了 range +之外实际上就是一阶到四阶矩:
-
-
- 答案是可以的,但还是到实分析里再学吧( +
- sample mean 展现了 \(X\) +的主要位置 +
- standard deviation 展现了数据的分散程度 +
- 偏度 skewness \(g_1 = \frac{m_3}{m_2 +^\frac 3 2} = \frac{\frac 1 n \Sigma_{i=1}^n (x_i - \bar x)^3}{(\frac 1 +n \Sigma_{i=1}^n (x_i -\bar x)^2)^\frac 3 2}\) +展现了数据的对称性 +
- 峰度 kurtosis \(g_2 = \frac{m_4}{m_2 ^2} +-3 = \frac{\frac 1 n \Sigma_{i=1}^n (x_i - \bar x )^4}{(\frac 1 n +\Sigma_{i=1} ^n (x_i -\bar x)^2)^2} - 3\) +展现了数据相对于正态分布的尾迹 +
- range 展现了 \(X\) 的分布范围
这样再看 Cantor 定理,也就是实数集 \(\mathbb R\) -不可数这一条定理,写成基数的形式就等价于,\(\aleph _1 = card(\mathbb R) > \aleph -_0\)。
+其中值得关注的是偏度和峰度两个统计量,因为之前没有提过。想起来一个乐子,Pearson
+在《Lady Tasting
+Tea》里曾经认为一个分布只要有一阶到四阶矩的参数就可以完全确定,但实际上
+Poisson 分布的四个参数都是 \(\lambda\),是不行的。
-
-
我们在离散数学里定义了 \(card(\mathbb -N) = \aleph _0\) -是最小的无限基数,却没有说明为什么最小。也就是没有说明,为什么可数的无限集是无限集里面最小的。所以,暂时只能从已经证明出的 -\(\mathbb R\) 不可数,来证明 \(\aleph _1 > \aleph _0\) -这两个特殊的无限基数之间的大小关系。
-Cantor 给出了另外一个证明。记 \(\mathcal P(X)\) 为 \(X\) 的幂集合,也即 \(X\) -的全体子集(包括空集和自身)构成的集合。
-引理:如果 \(X\) 非空,那么 \(card(\mathcal P (X)) > -card(X)\)。使用反证法证明,否则二者相等,存在 \(\mathcal P (X)\) 和 \(X\) 之间的一一对应 \(f \colon X \to \mathcal P (X)\)。记 \(A = \lbrace x \colon x \notin f(x) -\rbrace\),证明 \(f^{-1} (A)\) -和 $ A$ 不等即可。
-而 \([0,1]\) -上的实数用二进制表示后,\(0\) -的位置构成了自然数集的子集;自然数的任意一个子集都对应一个实数。因此 -\(R \supset \mathcal P (\mathbb -N)\),有 \(card([0,1]) = card (\mathbb -R) \geq card(\mathcal P (\mathbb N)) > card(\mathbb N) = \aleph -_0\),实数集不可数。
-
最后,虽然看起来有些夜话团圆了,但基数还是很抽象。希尔伯特 23 -问的第一问连续统假设即是关于基数的一个看似很基本的问题,问 \(\aleph _0\) 和 \(\aleph _1\) -之间是否还有别的基数。这一问题被证明和 ZFC -公理体系互相独立,目前仍不知真伪。
-极限
-极限,数列和级数
-2023 年 1 月 20 -日,星期五,睡前本来想看极限结果去写了可数集的补充内容,字数翻了个倍。
-这样下去的话,大概要每一个章节开一篇文章写比较合适了。昨天改标题的时候差点把文件名改了,想了想那样的话原有的两条评论显示不出来,不是很妙。或许有迁移 -issue -之类的方法,没有试过也没有研究,不清楚能不能做到,多一事不如少一事。
-好像没什么可写的,这一部分都和微积分 A -学的内容差不多。不过讲义里的一些观点很有意思,我把原文摘录下来:
---然而,根据极限的定义,如果有极限,我们要先验地知道极限是什么才可以利用定义来证明。事实上,要想猜到这个极限的值是很困难的。通过这个例子,我们发现极限的定义对于判断极限是否存并没有太大的帮助。
-从概念上而言,极限的定义在哲学意义上有一个先天的缺陷:判断数列收敛与否,应该由数列本身所决定而不需要依赖于外在的信息,比如说事先知道极限是什么。换句话说,我们想要内蕴地来考虑极限问题。这种看法和思考方式对数学的学习是大有裨益的。
-
想起来数值分析学过的一些方法,比如对牛顿法失败的方程,也即有重根的方程重做某种牛顿法的时候,需要先知道重根是几次才能做出来,笑死。不过按照这个思路还是做出了很多改进方法,像魔法 -qwq
-此处“内蕴地”考虑极限问题,指的就是后面的 Cauchy -收敛原则:一个数列收敛等价于它是柯西列。
---在数学中, 对于每一个数学对象 (例如极限) , -我们会例行公事般地考虑它的一些常见的性质. 比如说, -这个对象最基本的例子是什么, 这种对象是否存在, -如果存在的话它是否具有唯一性, 它的子对象和商对象 (如果有的话) -都具有什么性质 (比如说遗传了原来的对象的什么性质) , -这个对象的可计算性以及在特定映射下的行为等等. 作为例子, -我们刚刚见到一个点列的子对象 (即子列) 遗传了点列的收敛性 (和有界性) . -尽管这是一种八股文一般的讨论方式 (Bourbaki 学派是这种方式最忠实的实践者) -, 但是是非常有效率的一种学习和记忆方式, -我们在课程上会尽量的按照这种习惯来学习. 特别要强调的是, -每一个定义大家都应该搞清楚最基本的例子是什么。
-
你知道那个叫概念的东西是什么嘛.jpg
-然后是学微积分的时候讲过就过了,不会再用的一个定理:
+关于偏度:
-
-
(Bolzano–Weierstrass 的列紧性定理) 任意有界的实数序列 \(\{x_n\}_{n\geq 1}\) -必有单调收敛的子列。
-Cauchy 判别法(略)
-注意 Cauchy -判别法仅能在实数列中使用,因为其证明需要关于有界的论述。
+- \(g_1 <0\) 时称为 negatively +skewed,左尾比较长,所以也会称为 skewed left +
- \(g_1 >0\) 时称为 positively +skewed,右尾比较长,所以也会称为 skewed right
另外,把级数的部分和视为一个数列的话,也可以用数列的性质来判断无穷级数是否收敛。也即,对于无穷级数 -\(x_1 + x_2 + ...+x_n +...\),考虑 -\(X_i = x_1 + x_2 + ... + -x_i\),于是有无穷级数收敛等价于实数序列 \(\{x_n\}_{n\geq 1}\) 收敛,可以使用 Cauchy -判别法或定义判别的方式进行判断。考虑一种特殊的级数:
+由图可见偏度是能够体现数据的对称程度的。实际上对称程度是相对正态分布而言的。
+一般来说对于一个左偏的分布,会有 mean < median < +mode(众数),如果右偏则会是 mode < median < mean。当然 mean 和 +median 的顺序不一定准确,以及对于完全对称的分布会有三者相等。
+注意如果分布有多个峰值,此时 skewness 不一定还适用。
关于峰度:
-
-
\(\{a_n\}_{n\geqslant 1}\) -是递减的正实数的数列并且 \(\displaystyle\lim_{n\rightarrow -\infty}a_n=0\)。假设级数 \(\sum_{k=1}^\infty\) \(a_k\) 发散。那么,对任意 \(x\in \mathbb R\),我们可以选取一组正负号 -\(\iota_k\in \{\pm 1\}\),使得级数 -\(\sum_{k=1}^\infty \iota_k a_k\) -收敛并且 \(\Sigma_{k=1}^\infty \iota_k -a_k=x\)。
-或许算是后面习题里的 Riemann -重排定理的一个变式,总之证明是一样的。
+- \(g_2>0\) 时称为 +leptokurtic,尖峰态下双尾较长。 +
- \(g_2 <0\) 时称为 +platykurtic,低峰态下双尾较短。
实际上,学级数的时候讲了很多判别法,无外乎绝对收敛和比较收敛。原理上都是 -Cauchy 收敛的变式。
-指数函数和三角函数的级数定义
-2023 年 1 月 22 日,星期日,吃着素感觉脑子转不起来了(x
-我们假装自己只会用整数和有理数,然后用级数和极限分别定义了 \(e\),不仅在级数角度有熟知的 \(\displaystyle\lim_{n\rightarrow \infty}(1+ -\frac{1}{n})^n=e\),级数的表示是 \(\sum -_{k=0} ^{+\infty} \frac{1}{k!} = -e\)。同样的,我们也想假装只会用多项式,来定义指数函数和三角函数。
+注意峰度的所谓尖峰态低峰态和尾部数据性质也都是相对正态分布而言的。正态分布的峰度就是 +\(3\),因此峰度的公式里有一个减去 \(3\) 的操作,作为和正态分布的比对。
+有的时候会把不减去 \(3\) 的称为 +kurtosis,减去 \(3\) 则称为 excess +kurtosis,使用的时候要注意。
+实际上峰度带来的度量信息包括峰和尾两部分,单独出现尖峰的条件不能作为判断 +\(g_2\) 正负性的依据,只是表征了 \(\bar X\) +附近的情况,和尾部情况综合起来看才可以;峰度的正负性和方差的大小无关。
+尾部的情况可以通过 Q-Q plot 查看:
+
诊断 assumptions
+最常用的 assumption +诊断方法是使用残差图进行诊断,一元线性回归中我们可以直接使用 \(e_i \sim X\) 图,也可以使用 \(e_i \sim \hat Y\) +图进行诊断,二者本质上只相差横轴的尺度和位置。在多元线性回归中就直接使用 +\(e_i \sim \hat Y\) 图进行诊断。
+除此之外也有很多理论检验的方法,虽然听起来更 +concrete,但其实实际应用中还是肉眼检查最有效。
+模型诊断可能发现的一些问题:
-
-
定义指数函数 \(\exp\colon \mathbb R -\rightarrow \mathbb R\) 如下:\(x\mapsto \exp(x)=e^x=\sum_{k=0}^\infty -\frac{x^k}{k!}\)。可以看到这个形式和 \(e\) 的定义是很相似的。
-首先需要验证这是良定义的,也就是对于任意的 \(x \in \mathbb R\),有 \(\exp(x)=\sum_{k=0}^\infty \frac{x^k}{k!}\) -是一个收敛的无穷级数。证明的话,实际上是从某一位处截断,对后面的无穷项进行一个放缩控制。
-虽然我们熟知对任意的 \(x,y\in \mathbb -R\) 有 \(e^{x+y}=e^x\cdot -e^y\),但是这在级数层面是不那么明显的。
-上述性质对于复数 \(x\) -也成立,从而引出对三角函数的定义。
-利用指数映射 \(\exp(z)\) -可以定义正弦和余弦函数:
-\(\cos z =\frac{e^{iz}+e^{-iz}}{2} = -\sum_{k=0}^\infty \frac{(-1)^k x^{2k}}{(2k)!}\),
-$ z ={e{iz}-e{-iz} 2i} = _{k=0}^$。
-换句话说,目前 \(\sin(z)\) 和 \(\cos(z)\) -使用级数来定义的。至于其余三角函数,是根据 \(\cos z ,\sin z\) -的和差积商定义的。特别地,有 Euler公式:\(e^{iz}=\cos z + i \sin z\)。
-所以,三角函数完全可以被代数地定义,只用无穷项的多项式,不需要用到三角形。级数实际是沟通代数和几何的重要工具。我们可以用上述两个公式和已知的指数函数性质,证明出三角函数的众多性质,例如平方和为 -\(1\),等等。
+- \(Y\) 和 \(X\) 之间没有线性关系但是硬拟合了一个 +
- \(\sigma ^2\) +不能视作常数,也即异方差 +
- \(\varepsilon _i\) +不服从正态分布 +
- \(\varepsilon _i\) +之间彼此不独立 +
- 模型可以拟合,但数据中有 outlier
Summary
-这一部分最大的贡献是定义出了 \(e\),指数函数和三角函数。不同于之前的视角,一千零一页中介绍了一个内蕴的判别角度,即从数列本身的性质出发推出其自身是否收敛,得出了重要的 -Cauchy 判别法。当然,Cauchy -判别法的使用场景限于实数,在其他的距离空间上未必成立。当然,极限还有其他的求法,例如夹逼方法,上下极限,定义法。
-与此同时,回忆了一些级数的内容,而级数本质上还是数列。级数这一部分在微积分里是放在微积分 -A(2) -的最后一章介绍的,感觉很不合理,实际上完全可以在极限的地方就讲,不过没有必要,另外可能也是为了引出 -Fourier -变换。总之,有了两组级数函数之后,对于中学里已知的内容的使用就可以更加大胆一些了。
-梦话:既然习题没有答案那我就胡说八道了
-2023 年 1 月 23 -日,星期一,其实我不喜欢在初学(?)的时候做没有答案的习题,anyway -还是写一写。
-Riemann 重排定理
-证明下面有趣的定理:如果实数项级数 \(\displaystyle\sum_{n=1}^\infty a_n\) -收敛但不绝对收敛,那么可以将级数重新排列,使得重排后的级数可以收敛到任意事先指定的 -\(\alpha\in \mathbb -R\cup\{-\infty,+\infty\}\)。假设 \(\varphi\colon \mathbb{Z}_{\geqslant 1}\rightarrow -\mathbb{Z}_{\geqslant 1}\) 是正整数到自身的双射,令 \(b_k = a_{\varphi(k)}\),序列 \(\{b_k\}_{k\geqslant 1}\) 被称为是 \(\{a_n\}_{n\geqslant 1}\) 的一个重排,级数 -\(\displaystyle\sum_{k=1}^\infty b_k\) -被称为是级数 \(\displaystyle\sum_{n=1}^\infty -a_n\) 的一个重排。
-我们将 \(\{a_n\}_{n\geqslant 1}\) -中的非负项(\(\geqslant -0\))的全体按照它们在 \(\{a_n\}_{n -\geqslant 1}\) 中的先后次序排列得到序列 \(c_1,c_2,c_3,...\);类似地,将 \(\{a_n\}_{n \geqslant 1}\) 中的负项(\(<0\))按原顺序排列得到序列 \(d_1,d_2,d_3,\cdots\)。
+以下给出一些发现问题的方法:
+非线性关系
+简而言之,\(Y\) 和 \(X\) +之间可能并不是一个线性关系,但是我们采用了线性模型进行拟合。
+找出问题的手段是使用 \(e_i \sim
+X_i\) 图诊断 \(Y\) 和 \(X\) 的线性关系是否过拟合。具体来说,给
+\(e_i \sim X_i\) 再做一个拟合图线
+scatter.smooth,观察和 \(h=0\) 是否偏离较大。虽然通过 \(Y \sim X\) 也可以看出来,但是 \(e_i \sim X\) 图更加明显。
即使线性关系是显著的(R 中得到 \(R^2\) 较大、斜率 \(\beta_1\) +显著),也不说明线性模型是最好的拟合模型。
+异方差问题
+-
+
实际上的残差并不符合方差相等的假设,则称为异方差问题。即使发生这样的情况也未必会影响到 +\(\beta_1,\beta_0\) +的估计值,因为计算过程和这一假设实际上是无关的。但是,异方差问题会导致 +\(b_0,b_1\) +不再是使得方差最小的估计,失去了 BLUE +性质,但仍然是无偏的估计。问题会反映在关于 \(\beta_1,\beta_0\) +的推断中,导致推断或者置信区间不是效率最高的。
+举个例子,比如说 \(Y_i = 30 +100X_i + 10X_i +\varepsilon_i\),实际上是有 \(\varepsilon_i \sim N(0,10X_i +\sigma^2)\),方差并不相同。
+画图检查最典型的异方差情况是画出 \(e_i \sim +X\) 图后发现 \(X\) 越大,\(e_i\) +越分散,呈现出一个扇形的分布形态。
+模型的诊断也可以使用一些理论方法,异方差检验中常用的几种检验如下所示:
-
-
证明,\(\displaystyle\lim_{n\to \infty} -c_n = 0\),\(\displaystyle\lim_{n\to -\infty} d_n = 0\)。
-Trivial,它们分别是原序列 \(\{a_n\}_{n\geqslant 1}\) -的两个子列,收敛结果和原序列相同。
-证明,\(\displaystyle\sum_{n=1}^\infty -c_n = +\infty\),\(\displaystyle\sum_{n=1}^\infty d_n = --\infty\)。
-Trivial,反证法假设否则有 \(\displaystyle\sum_{n=1}^\infty c_n = -C\),且有 \(\displaystyle\sum_{n=1}^\infty -a_n=A\),\(A,C \in \mathbb -R\),那么有 \(\displaystyle\sum_{n=1}^\infty d_n = A-C \in -\mathbb R\),级数绝对收敛。矛盾。
-证明: 对任意 \(\alpha \in \mathbb -R\),存在级数 \(\displaystyle\sum_{n=1}^\infty a_n\) -的一个重排 \(\displaystyle\sum_{k=1}^\infty -b_k\),使得 \(\displaystyle -\sum_{k=1}^\infty b_k = \alpha\)。
-不妨设 \(\alpha ->0\)。正项是发散的,于是存在一个 \(n_1\) 使得 $ c_1 + c_2 +...+ c_{ {n_1} } -< c_1 + c_2 +...+ c_{ {n_1} }+c_{ {n _1} + 1}$。
-取 \(\delta _1 = c_1 + c_2 +...+ c _{n_1}+c -_{n _1 + 1} - \alpha >0\),由负项是发散的,于是存在一个 \(m_1\) 使得:
-$d_1 + d_2 + ... +d _{ {m _1} } > -_1 d 1 + d_2 + ... +d -{ {m _1} +1 } $。再取 \(0 < \delta _2 -= d_1 + d_2 + ... +d _{m _1 } + \delta _1 < \delta -_1\),此为一次操作。
-每做一次操作,\(\delta\) -都会相应地减小,始终非负。于是有 \((c_1+...+c -_ {n_1 +1 }) + (d_1+...+d _{m _1})+...\) 是一个收敛到 \(\alpha\) 的重排级数。
-证明: 存在级数 \(\displaystyle\sum_{n=1}^\infty a_n\) -的一个重排 \(\displaystyle\sum_{k=1}^\infty -x_k\),使得 \(\displaystyle -\sum_{k=1}^\infty x_k = +\infty\)。
-我不是很确定啊,但是我打算徒手捏一个:取一个固定的实数 \(M>0\),每一次操作分别从正的部分和负的部分,取一段 -\(c_i + ... + c_{i+k}\) 和 \(d_j + ... + d _{j+l}\) 使得其和大于等于 -\(M\)。于是每一次操作得到的小段和都大于等于 -\(M\),最后的级数和是发散的。
+Bartlett 方法,本质上是 likelihood ratio +test,但非常依赖残差的正态假设。也即,如果检验结果是拒绝原假设,未必是真的发生了异方差现象,也可能是因为残差不服从正态分布造成了干扰。
+Levene & modified Levene (B.F.) 方法,非常常见。
+对于可能影响方差导致异方差的因素 \(Z\),将 \(e_i +^2\) 相对于 \(Z\) +再做一次线性回归,得到的 SSR 记为 \(SSR^*\)。
+此时 \(LM = \frac{SSR^*/2}{(SSE/n)^2} \sim +\chi_1 ^2\) 再进行检验。
+
Cesaro 求和极限
-设 \(\{a_n\}_{n\geqslant 1}\) -为实数序列,我们定义算数平均值序列 \(\displaystyle\sigma_n = \frac{a_1 + a_2 + \cdots + -a_n}{n}\),其中 \(n=1,2,3,\cdots\)。
+正态性假设
+\(\varepsilon _i\) +并不服从正态分布,这可以通过 QQ-plot 观察是否有 \(\varepsilon_{(i)} = \mu + \sigma +Z_i\),或者直接画 histogram 检查是否有正态的形状。
+
理论方法之中 Shapiro-Wilk 方法是最佳的,有最大的 +power,但是对于样本量是敏感的。也就是说,如果检验结果是 \(\varepsilon_i\) +不服从正态分布,也可能是因为样本量太大导致了错误判断。
+注意正态性检验是完全可以把 \(\{\varepsilon +_i \}\) 作为一组数据放在一起观察整体的分布的,但是对 \(\{Y_i \}\) +不可以这样做,它们彼此之间服从的是不同的条件分布。
+相关性
+\(\varepsilon_i\) +之间可能并不独立,有可能都受到 \(t_i\) +的影响,等等。如果有类似可能考虑的因素可以对其做 sequence plot。
+理论方法中最常用的是 Durbin-Watson 方法。
+Outlier
+模型的数据里有 outlier,不同性质的 outlier +对回归线的影响不尽相同,具体的在 Lecture 6 +中再细说。简单来说就是,outlier 的 \(X_i\) 越接近 \(\bar{X}\),对于回归线的斜率影响越小,但如果距离 +\(\bar{X}\) +比较远,则会产生比较强的杠杆效应。
+即使模型中存在 outlier,参数的估计也可以是比较准确的。做 \(e_i \sim X\) 图可以查看是否存在 +outlier,也可以使用 \(Y_i \sim X_i\) +的图来观察是否有距离回归线很远的点,这是最明显的一类 +outlier。然后可以尝试剔除这样的点再重新做回归,检查各系数。
+关于 \(R^2\)
+如果在某一线性模型中得到 \(R^2 = +0.69\),能否说明这一线性模型是显著的?
-
-
假设 \(\displaystyle\lim_{n\to \infty} -a_n = a\)。证明,\(\displaystyle\lim_{n\to \infty} \sigma_n = -a\)。
-Trivial.
-构造一个不收敛的序列 \(\{a_n\}_{n\geqslant 1}\),使得 \(\displaystyle\lim_{n \to \infty} \sigma_n = -0\)。
-\(a_ i = (-1) ^i\)。
-是否存在序列 \(\{a_n\}_{n\geqslant -1}\),使得对任意 \(n\geqslant -1\),都有 \(a_n > 0\) 并且 -\(\displaystyle\limsup_{n\to \infty} a_n = -\infty\) 然而 \(\displaystyle\lim_{n\to -\infty} \sigma_n = 0\)?
-\(a_{i^2}=\sqrt{i},\) 其余为 \(1 \over i^2\)。(感谢 neruko -的勘误!qwq
-对 \(k \geqslant 1\), 记 \(b_k = a_{k+1} - a_k\)。证明,对任意的 \(n\geqslant 2\),都有 \(\displaystyle a_n - \sigma_n = \frac{1}{n} -\sum_{k=1}^{n-1} k b_k\)。
-Trivial.
-设 \(\displaystyle\lim_{k\to \infty} k -b_k = 0\) 并且 \(\{\sigma_n\}_{n\geqslant 1}\) -收敛。证明,\(\{a_n\}\) 也收敛。
-注意,这是 (1) 在条件 \(n|a_{n+1}-a_n| \to -0\) 这一额外条件下的逆命题。
-Trivial,上一题左右对 \(n\) -取极限,利用极限的可加性。至于右边的极限为什么是 \(0\),用 \(\varepsilon - N\) 写一下。
-把 (5) 的条件减弱为: \(\{ k -b_k\}_{k\geqslant 1}\) 是有界的并且 \(\displaystyle\lim_{n \to \infty} \sigma_n = -\sigma\)。证明,\(\displaystyle\lim_{n\to \infty} a_n = -\sigma\)。
-?不会.jpg
+- 事实上可以。\(R^2 = 0.69\) +已经是相对大的数值了,说明模型对于方差的解释能力是相对好的;另一方面考虑 +\(r = \sqrt{R^2} > +0.8\),相关系数其实是比较大的,可以认为这一模型是合适的。 +
- 但是,这并不能说明线性模型是这一问题下最好的模型。\(R^2\) +想要多大就可以多大,例如给模型加入新的多项式型变量,总能更多地解释一些方差,不能单纯地追求 +\(R^2\) 的大小。 +
- 另外,如果在不同的模型比较中对 \(\{Y_i +\}\) 做了变换,比如进行了标准化或者 Box-Cox +transform,此时是不能和原始的模型再进行 \(R^2\) 的比较的,只能检查单个 \(R^2\) 的值能否接受。这是因为 \(SST\) 已经随着 \(\{Y_i \}\) +的变化而变化了,模型的方差解释能力 \(\frac{SSR}{SST}\) 无法比较。
根式和指数的定义
-这个问题的目的是在 \(\mathbb R\) -上定义初等函数 \(\sqrt[n]{x}\) 和 \(b^x\),比如说我们自然希望定义 \(\sqrt[n]{x}\) 为满足 \(y^n = x\) 唯一的正实数。
+Lecture 6
+Built-in Diagnostic Plots in +R
+R 内置的四个诊断图是 \(e_i \sim \hat +Y\),Q-Q plot,\(\sqrt{|\text{Standardized Residuals}|} \sim \hat +Y\),Cook's distance +图。前两个都比较简单,一个是万能的残差图,另一个是残差的正态性检验,主要说一下后两个图。
+Scale-Location Plot
+\(\sqrt{|\text{Standardized Residuals}|} +\sim \hat Y\) 作图体现了 residuals +随拟合值的分布情况,主要用来检验异方差。实际上在上一讲里面是直接用 \(e_i \sim X\) +来检验异方差的,这里用了标准化的残差开方,有一些考虑:
-
-
给定正整数 \(n\) 和实数 \(x>0\),证明:如果正实数 \(y_1\) 和 \(y_2\) 满足 \(y_1^n = x=y_2^n\),那么 \(y_1=y_2\)。
-Trivial.
-证明,如果 \(x>0\),那么集合 -\(E(x) = \{t \in \mathbb R \mid t^n < -x\}\) 是非空的并且有上界。
-Trivial,首先 \(0 \in E(x)\),再对 -\(x\) 讨论。当 \(0<x<1\) 时有 \(\forall t \in E(x), t<1\),当 $1 x $ -时有 \(\forall t \in E(x),t \leq -x\)。
-证明,\(y = \sup E(x)\) 满足 -\(y^n = x\) 并且 \(y>0\)。
-首先有 \(0 \in E(x)\),于是 \(sup E(x) \geq 0\)。如果 \(supE(x) = 0\) 则不存在 \(\varepsilon >0,\varepsilon ^n -<x\)。取 \(\varepsilon ^n = -\frac{x}{2}\) 则矛盾。于是 \(y>0\)。再证明 \(y^n =x\)。显然对于 \(\forall y \in \mathbb R, y^n \geq x\) 都有 -$y $ 是 \(E(x)\) 的上界,而对于 \(\forall z \in \mathbb R,z^n < x\),存在 -\((z ^\prime) ^n = z_n +x\) 使得 \(z^ \prime \in E(x)\) 且 \(z^\prime >z\),于是这样的 \(z\) 都不是上界。因此 \(supE(x) = min \lbrace y \in \mathbb R, y^n \geq x -\rbrace\),也即题中定义。
-证明, 映射 \(\sqrt[n]{\cdot}\colon -\mathbb R_{>0}\to \mathbb R_{>0}, \ \ x \mapsto -\sqrt[n]{x}=y\) 是良好定义的。我们也记 \(\sqrt[n]{x}\) 为 \(x^{\frac1n}\)。
-良好定义的意思是,对于任意的 \(x = -x^\prime\),有 \(y=y^ -\prime\)。否则 \(y \neq y^ -\prime\),但由上题定义,上确界是唯一的。
-证明,\(\sqrt[n]{\cdot}\colon \mathbb -R_{>0}\to \mathbb R_{>0}\) 是双射。
-有以上铺垫后是显然的。
-\(a,b\) 是正实数,\(n\) 为正整数。证明,\((ab)^{\frac1n} = -a^{\frac1n}b^{\frac1n}\)
-定义 \(A(x) = \lbrace t \in \mathbb R \mid -t^n <a \rbrace\),\(B(x) = \lbrace t -\in \mathbb R \mid t^n <b \rbrace\),\(C(x) = \lbrace t \in \mathbb R \mid t^n <a -b\rbrace\),只要证明 \(A(x)B(x)=C(x)\),(集合相等的证明是左右互相包含),然后考虑两个集合的上确界则得证。
+关注 magnitude 所以需要一个正值,选择了先取绝对值
+取绝对值之后的数据往往人为造成了右偏,开方可以缓解一些
+standardize 之后绝大多数 \(e_i\) +都收入了 \([-2,2]\) +这一范围内(正态分布的主要区间),更清晰,有可比性
+虽然理论上的 \(\varepsilon_i\) +是独立分布的,但是残差之间是有约束关系的,\(Var(e_i) = (1-h_{ii})\sigma^2\),也就是说 +\(e_i\) 的变动范围本身就和其在 \(x\) 轴上的位置(也即 \(X_i\) 的大小)相关。较大的 \(X_i\) 会对应 \(e_i\) +的更大方差,导致可能会看起来像异方差。
+标准化并开方能够一定程度缓解这样的问题。
在接下来的问题里,我们给定实数 \(b>1\) 来定义以 \(b\) 为底的指数函数 \(x \mapsto b^x\)。
+如果此图上的残差点分布看起来比较随机,拟合线也相对平行于 \(x\) 轴,基本可以认为是异方差。
+Cook's Distance
+图中被标出数字的点/靠近右上角和右下角/红线之外的点需要重视一下,是 +high leverage point 或者 outlier,可以进一步检验。
+Residuals & Leverage
+Leverage
+定义每一点的杠杆值为 \(h_{ii} = +\frac{\partial \hat Y_i}{\partial Y_i} \in [0,1]\),表征了某一个 +\(X_i\) 对应的 \(Y_i\) +变动一个单位时,会导致回归线上的响应值变动的大小,也就是说,这一点的变化对于整个回归模型的影响。
+事实上,\(X_i\) 对应的点的 leverage +是 \(h_{ii} = \frac 1 n + \frac{(X_i - \bar +X)^2}{\Sigma_j (X_i - \bar X)^2}\),\(h_{ii}\) 越大会导致 \(Var(e_i) = (1- h_{ii})\sigma^2\) 越小,因此 +\(e_i\) 的变动范围变小,\(\hat Y_i\) +能够变动的范围也较小,会导致回归线受较大的影响;从 leverage +的表达式可以看出来,\(|X_i -\bar X|\) +越大会导致杠杆值越大,也就是说远离中心的点对回归线造成的影响较大。
+我们对 extreme values 做一些分类:
-
-
设 \(m,n,p,q \in -\mathbb{Z}\),其中 \(n>0\),\(q>0\)。令 \(r -= \dfrac{m}{n} = \dfrac{p}{q}\) 为有理数 \(r\) 的两种表示。证明 \((b^m)^{\frac1n} = (b^p)^{\frac1q}\)
-Trivial.
-证明,对任意的有理数 \(r\),函数 -\(r\mapsto b^r\) 是良好定义的。
-Trivial.
-证明,对任意的有理数 \(r,s\),我们有 \(b^{r+s} = b^rb^s\)。
-记 \(r = \frac mn ,s= \frac -pq\),于是 \(b^{r+s} = -b^{\frac{mq+np}{nq} }=(b^{mq} b^{np} ) ^{\frac{1}{nq} }= b ^{\frac mn} -b^{\frac pq} = b^r b^s\)。
-对于 \(x \in \mathbb R\),令 -\(B(x)=\{b^t \mid t \in \mathbb{Q}, t -\leqslant x\}\)。证明,\(B(x)\) -非空且有上界。我们定义 \(b^x = \sup -B(x)\), 这就定义了映射 \(x \mapsto -b^x\)。
-其实和之前那个也差不多,不写了。
-证明,如果 \(r\) 是有理数,那么 -\(b^r = \sup B(r),\forall r \in -\mathbb{Q}\)。我们定义的指数映射在 \(r\in \mathbb{Q}\) 时和之前是一致的。
-和上一题一样。
-证明,上题中定义的映射满足, 对任意的 \(x,y \in \mathbb R\),都有 \(b^{x+y} = b^x b^y\)。
-证明 \(X(r)Y(r)=Z(r)\),于是上确界相等。
-证明,当 \(b=e\) -时,这样定义的函数和课程中定义的 \(e^x\) 是一致的。
-嗯?
-\(\exp(x)=\sum_{k=0}^\infty -\frac{x^k}{k!}\)。上述定义的 \(e^x = -sup B(x) = sup \{e^t \mid t \in \mathbb{Q}, t \leqslant -x\}\)。
-我不到啊,或许他想让我证明的是 \((\sum_{k=0}^\infty \frac{1}{k!}) ^x = -\sum_{k=0}^\infty \frac{x^k}{k!}\) -吗?这个课上好像证过。
+Outlier: 离群值是对于其 \(Y\) +值而言的,\(Y_i\) +的实际取值远离通常该有的范围,则这一点会被认为是 outlier。
+High Leverage Point: 高杠杆值点是对于其 \(X_i\) 的取值而言的,由上述分析可以得到 +\(h_{ii}\) 较大的主要条件。
+Influential Point: +强影响力点指的是移除此点后,回归线会发生较大的变化的点。
+如果一个点既是 outlier 又是 high leverage point,那它一定是 +influential point,直觉上来看是因为它的 \(X\) 和 \(Y\) +都具有一定的特征,会对回归线造成较大的影响。
+
如果 \(h_{ii} > 2p/n\) +一般就称为高杠杆值点。
+Studentized Residual
+一个 influential point +造成回归线的巨大改变无法在残差图上体现出来,因此我们希望有一种手段能够体现出它和其他正常点的巨大差异。一个自然的想法是先移除它再做回归线,然后在这一模型上体现残差,即为 +studentized residual。
+这么说还是太抽象了,放个图好了:
+
具体来说,studentized residual 和 standardized residual +有一些差别:
+-
+
standardized residual: \(\frac{e_i}{s(e_i)}\),由于 \(Var(e_i) = (1-h_{ii})\sigma^2\),则 \(s^2 (e_i) = +(1-h_{ii})MSE\),代入即可。
+deleted residual: \(d_i = Y_i - \hat +Y_{i(-i)}\),其中 \(\hat +Y_{i(-i)}\) 是 \(X_i\) +在去除这一点的模型中所对应的响应。
+studentized residual: \(\frac{d_i}{s(d_i)}\),同理有 \(s^2(d_i) = (1-h_{ii})MSE_i\),\(MSE_i\) 是去除第 \(i\) 点的模型对应的 MSE。
+事实上 \(e_i^* = \frac{d_i}{s(d_i)} = +\frac{e_i}{\sqrt{MSE(1-h_{ii})}}\) 是 internal studentized +residual,当 \(|e_i ^*| >2\) +时认为是一个 outlier。
+studentized deleted residual 如下所示:
+
根式的逼近
-给定正实数 \(\alpha\) 和初始值 \(x_1 > -\sqrt{\alpha}\),我们归纳地定义序列 \(\{x_n\}_{n\geqslant 1}\):\(x_{n+1} = \frac{1}{2}\left(x_n + -\frac{\alpha}{x_n}\right), n = 1,2,\cdots\)
+Cook's Distance
+考虑 \(D_i = \frac{\Sigma_j (\hat Y_j - +\hat Y_{j(-i)})^2}{ps^2}= \frac{e_i^2}{p\cdot MSE} +\frac{h_{ii}}{(1-h_{ii})^2}\),其中 \(\hat Y_{j(-i)}\) 指的是 \(X_j\) 在去除第 \(i\) 点的模型中对应的平均响应值。第 \(i\) 点的 Cook's distance \(D_i\) 表征的是第 \(i\) +点的值对全体预测值(也就是回归线)的影响力。\(D_i\) 越大越说明这是个 high influential +point,一般吧 threshold 作为 \(0.5\) +或者 \(\frac 4 n\)。
+Lack of fit test
+怀疑某个模型并不符合线性,且其某一 \(X_i\) 点处有多个对应的 \(Y\),也即这一点处存在 replicates 或者说 +repeated observation 的时候,可以进行失拟检验。具体来说,可以进一步细分 +SSE 为 sum of pure error 和 sum of lack of fit +error,前者由数据的随机性导致,后者由线性模型的失拟性造成。
+事实上也是 general linear test 的一种,这里的 full model 就是 cell +mean model \(Y_{ij} = \mu_i + +\varepsilon_{ij}\),reduced model 是线性模型 \(Y_{ij}=\beta_0 +\beta_1 X_i + +\varepsilon_{ij}\)。也就是说,实际上的 \(H_0: \mu_i = \beta_0 + \beta_1 X_i\),拒绝 +\(H_0\) 时说明 reduced model 失拟。
+对 SSE 进行进一步的拆分,将其改变为 \(SSE = +SSPE +SSLF\),具体表达式和自由度如下所示:
+\[\Sigma_{i=1} ^c +\Sigma_{j=1}^{n_i}(Y_{ij} - \hat Y_{ij})^2 = \Sigma_{i=1} ^c +\Sigma_{j=1}^{n_i}(Y_{ij} - \bar Y_{i.})^2+ \Sigma_{i=1} ^c +\Sigma_{j=1}^{n_i}(\bar Y_{i.} - \hat Y_{ij})^2\]
+\[SSE = SSPE + SSLF\]
+\[(n-2) = (n-c)+(c-2)\]
+因此,对应地有 \(E(MSPE) = \sigma^2,E(MSLF) += \sigma^2 + \frac{\Sigma_i n_i (\mu_i - (\beta_0 + \beta_1 +X_i))^2}{c-2}\),test statistic 是 \(F^* = \frac{MSLF}{MSPE} \sim ^{H_0} +F(n-c,c-2)\)。
+这也就说明了为什么失拟检验只有在存在 replicates +的时候才能做,因为这时才会有 \(n > +c\),使得模型不至于退化。
+Remedy Methods
+补救非线性
+通过 \(e_i \sim X\) +观察到模型并不是完全线性的时候,如果不想再改变 +assumptions,可以转而选择非线性的模型。
+R 中可以调用函数 nls。
补救异方差
+可以使用 weighted analysis,具体参见 Lecture 12 的内容。
+补救非正态
+如果残差体现出非正态分布的性质,可以对 \(Y\)
+做变换继续使用线性模型,也可以使用其他的模型来允许残差不同分布。在 R
+中可以调用函数 glm。
Transformation
+有以下任一需求的时候都可以考虑对 \(Y_i\) 做变换:
-
-
证明,\(\{x_n\}_{n\geqslant 1}\) -是递减的并且 \(\displaystyle\lim_{n\to \infty} -x_n = \sqrt{\alpha}\)(在问题E中已经定义)。这表明,从任意大于 -\(\sqrt{\alpha}\) -的初值出发,可用上述迭代公式近似地计算(逼近)\(\sqrt{\alpha}\)。
-Trivial,因为这就是 Newton 法(狗头
-定义逼近的误差项 \(\varepsilon_n = x_n -- \sqrt{\alpha}\)。证明,\(\displaystyle\varepsilon_{n+1} = -\frac{\varepsilon_n^2}{2x_n} < -\frac{\varepsilon_n^2}{2\sqrt{\alpha}}\)。
-Trivial,这是 Newton 法的二阶收敛性质(逃
-证明,如果 \(\beta = -2\sqrt{\alpha}\),那么 \(\displaystyle\varepsilon_{n+1} < \beta -\left(\frac{\varepsilon_1}{\beta}\right)^{2^n}\)。这表明它的收敛速度非常快。
-Trivial.
-设 \(\alpha = 3\),\(x_1 = 2\),验证 \(\dfrac{\varepsilon_1}{\beta} < -0.1\),继而 \(\varepsilon_5 < 4\cdot -10^{-16}\),\(\varepsilon_6 < 4 -\cdot 10^{-32}\)。
-略(
-试用纸和笔,计算 \(\sqrt{3}\) -的精确到小数点5位的近似值。
-略(
+- 稳定方差:观察到 \(\varepsilon_i\) +似乎是异方差的 +
- 提高正态性 +
- 简化模型,提高解释性
接下来,我们换另外一个迭代公式。固定 \(\alpha > 1\) 和 \(y_1 > \sqrt{\alpha}\),定义 \(y_{n+1} = {\alpha + {y_n} \over 1 + {y_n}} = y_n + -{\alpha - {y_n}^2 \over 1+{y_n} }\),$ n = 1,2,... $
+最普遍的方法是 Box-Cox Transformation,取 \(Y^* = +(Y^\lambda-1)/\lambda\),首要任务是找到最合适的 \(\lambda\) +做变换。事实上所谓的“最合适”包含两层意义,其一是希望模型拟合程度较高,其二是希望 +\(\lambda\) 使得 \(Y^*\) +的形式尽量简洁明了,解释性强,也就是取所谓的 convenient lambda。例如取 +\(\lambda=0\) 时有 \(Y^* = \log Y\),取 \(\lambda\) +为整数时即为多项式回归,等等。
+另外不同的 \(\lambda\) +值会对数据的右偏有不同程度的改善,右尾压缩最明显的是开根和取对数;也可以取负值来压缩左尾。
+在实际使用中往往是直接对 \(\lambda\) +取一个 sequence,找到近似取到 maximum likelihood 或者使得 SSE 最小的 +\(\lambda\) +的一个置信区间,再在其中寻找合适的 convenient lambda。
+一些典型的数据分布和变换方法:
+
Miscellaneous Topics
+一些杂谈,关于 simple linear regression 的最后内容。
+Regression Through the +Origin
+非常坏回归,爱来自自由度(
+强迫过原点回归的时候斜率的估计是 \(\hat +\beta_1 = \frac{\Sigma X_iY_i}{\Sigma +X_i^2}\),这会导致一些很严重的后果:
-
-
证明,\(\{y_{2k-1}\}_{k\geqslant -1}\) 为递减序列。
-这是一个大于 \(\sqrt{\alpha }\) -的序列,有 \(y_3 = \frac{\alpha + y_2}{1+y_2} -= \frac{(\alpha +1 )y_1 + 2 \alpha}{2y_1 + \alpha +1} < -y_1\),可以推广到每一项。
-证明,\(\{y_{2k}\}_{k\geqslant -1}\) 为递增序列。
-Trivial,基本同上。
-证明,\(\displaystyle\lim_{n\to \infty} -y_n = \sqrt{\alpha}\)。
-上述的两个序列分别单调有界,各自收敛。由递推式可知都收敛到 \(\sqrt{\alpha }\),于是整体收敛。
-试讨论逼近 \(\sqrt{\alpha}\) -的收敛速度并与之前的比较。
-肯定是不如 Newton 方法收敛得快的。
-记逼近的误差项 \(\varepsilon_n = x_n - -\sqrt{\alpha}\),于是 \(\displaystyle\lim_{n\to \infty} \frac{\varepsilon -_{n+1} } {\varepsilon _n } = \frac{1-\sqrt{\alpha} }{1+\sqrt{\alpha} -}\),这个序列线性收敛,而 Newton 方法二阶收敛。
+- 残差的和 \(\Sigma e_i \neq +0\),这导致 \((Y_i - \bar Y)^2 = (Y_i - +\hat Y_i)^2 + (\hat Y_i - \bar Y)^2 + 2(Y_i - \hat Y_i)(\hat Y_i - \bar +Y)\) 的交互项无法消去,于是也不能再对 SST 做分解成为 SSE 和 SSR +之和。 +
- SSE 此时的自由度是 \(n-1\),SST +的自由度也不再是 SSE 和 SSR 的自由度之和。
给我一点小小的数值分析震撼,但我感觉比前面的题都简单(
-梦话 2.0:乘积级数
-其实乘积级数完全可以用对数函数拆成求和级数,可惜的是我们现在还没有对数函数,所以都是靠各种技巧来证明。
+Inverse Predictions
+对 \(Y \sim X\) 做回归得到 \(y = b_0 + b_1 x\) 和对 \(X \sim Y\) 做回归得到 \(x = a_0 + a_1 y\) +中,实际上在绝大多数情况下都有 \(a_1 b_1 \neq +1\)。也就是说,两种回归的结果不能简单地用线性求反函数得到,这听起来有点反直觉但确实是合理的,做 +\(Y \sim X\) 回归的目标是取得关于 \(Y\) 的最小残差平方和,做 \(X\sim Y\) 回归的目标是取得关于 \(X\) +的最小残差平方和,目标不一致得到的结果自然不同。
+用理论来解释的话,取相关系数 \(r = +\frac{\sum (X_i - \bar X)(Y_i - \bar Y)}{\sqrt{\sum (X_i - \bar X)^2} +\sqrt{\sum (Y_i - \bar Y)^2}}\),记 \(S_Y = \sqrt{\sum (Y_i - \bar Y)^2},S_X = +\sqrt{\sum (X_i - \bar X)^2}\),于是有:
+\(b_1 = r \frac{S_Y}{S_X},a_1 = r +\frac{S_X}{S_Y}\),因此 \(b_1a_1 = +r^2\)。两条回归线之间的夹角是 \(\tan +\theta = \frac{1-r^2}{r(\frac{S_X}{S_Y} + +\frac{S_Y}{S_X})}\)。
+如果对于某个响应值 \(Y_i\) +需要反向预测输入变量 \(X_i\),应该选择 +\(\hat X_h = \frac{Y_h - b_0}{b_1}\) +而不是反过来做 \(X\) 关于 \(Y\) 的回归。
+Limitations of \(R^2\)
+使用 \(R^2\) +作为判断依据的时候要注意以下问题:
-
-
乘积级数的收敛以及 Cauchy 判别法:\(\{a_n\}_{n\geqslant 1}\) -是复数的数列,我们假设对任意的 \(n\),\(a_n\neq -0\)。令 \(P_n=a_1\cdot a_2\cdot \cdots -\cdot a_n\),如果数列 \(\{P_n\}_{n\geqslant 1}\) 的极限存在且不是 -\(\mathbf{0}\),称无限乘积 \(\displaystyle\prod_{n\geqslant 1}a_n\) -收敛且记 \(\displaystyle\prod_{n\geqslant -1}a_n=\lim_{n\rightarrow \infty}P_n\)。
-我们有这种情况下的 Cauchy 判别准则:\(\displaystyle\prod_{n\geqslant 1}a_n\) -收敛当且仅当对任意的 \(\varepsilon>0\),存在 \(N\),使得对任意的 \(n\geqslant N\),任意的 \(p\geqslant 0\),我们都有 \(\big|a_n\cdot a_{n+1}\cdot \cdots \cdot -a_{n+p}-1\big|<\varepsilon\)。
-除此之外还有一个特殊情况:对于正数列 \(\{a_n\}_{n\geqslant 1}\),乘积 \(\displaystyle\prod_{n=1}^{\infty}(1+a_n)\) -收敛(极限必然不是零)等价于 \(\displaystyle\sum_{n =1}^{\infty} a_n\) -收敛。当然,有对数的话可以近似成 \(ln(1+a_n) -\approx a_n\),直观上二者就相等。严格的证明也不困难。
-实际上,如果数列介于区间 \((0,1)\) -之间,二者也等价于乘积 \(\displaystyle\prod_{n=1}^{\infty}(1-a_n)\) -收敛。从对数的直观上来说也是明显的,但证明稍有不同。
-这样的话限制还是比较多的,只对正实数有效。如果想要推广到复数,就需要更强的条件。\(\{a_n\}_{n\geqslant 1}\) 是复数的数列,如果 -\(\displaystyle\prod_{n=1}^{\infty}(1+|a_n|)\) -收敛(等价地说,就是 \(\displaystyle\sum_{n -=1}^{\infty} a_n\) 绝对收敛),则 \(\displaystyle\prod_{n=1}^{\infty}(1+a_n)\) -收敛(极限不是零)。
+\(R^2\) +不能作为拟合程度的度量。\(R^2 = \frac{b_1 ^2 +\sum (X_i - \bar X)^2}{\sum (Y_i - \bar Y)^2}\) +的形式显示了,实际上如果把 \(X\) +的取值变得足够分散,\(R^2\) +的取值想要多大就能有多大。
+不同的散点分布情况可以得到几乎相同的 \(R^2\),一定要画图检查线性模型是不是最合理的。
+ +
+不能对于不同的模型比较 \(R^2\),归根结底 \(R^2\) 反映的是模型对于 SST 的解释能力,SST +一旦改变就不能交叉对比。因此上述 transformation 中对于系数 \(\lambda\) 的比选标准是 maximum +likelihood。
+\(R^2\) 不能显示 \(X\) 和 \(Y\) 之间的因果关系,因为 \(Y\sim X\) 和 \(X +\sim Y\) 这两种回归得到的 \(R^2\) 是相等的。
+
Lecture 7
+从一元线性回归过渡到多元回归的部分,介绍回归方程的矩阵表达。
+矩阵表达
+把 \(n\) 个回归方程的形式改成:
+\[\begin{bmatrix}Y_1 \\ Y_2 \\ ... \\ Y_n +\end{bmatrix} = \begin{bmatrix}1 & X_{1,1} & X_{2,1} &... +& X_{p-1,1} \\ 1 & X_{1,2} & X_{2,2} & ... & +X_{p-1,2} \\ ... & ... & ... &... & ... \\ 1 & +X_{1,n} & X_{2,n} & ... & X_{p-1,n} \end{bmatrix} +\begin{bmatrix}\beta_0 \\ \beta_1 \\ ... \\ \beta_{p-1} \end{bmatrix} + +\begin{bmatrix}\varepsilon_1 \\ \varepsilon_2 \\ ... \\ \varepsilon_n +\end{bmatrix}\]
+\[Y = X \beta + \varepsilon\]
+假设 \(\varepsilon \sim N_n(0, \sigma^2 +I_{n \times n})\),则有 \(Y \sim N_n(X +\beta , \sigma^2 I_{n \times n})\),以下考虑参数矩阵 \(\beta\) 的估计:
+\[b = \hat \beta = (X^TX)^{-1} X^T Y \sim +N_p(\beta , (X^TX)^{-1} \sigma^2)\]
+和 simple linear regression 相同,\(b\) 也有 BLUE 的性质。
+因此有 \(Y\) 的平均响应为 \(\hat Y = X \hat \beta = X(X^TX)^{-1} +X^TY\),其中记 \(H = X(X^TX)^{-1} +X^T\),这就是著名的 hat +matrix,围绕它有很多性质,后面再说;由于残差 \(e = Y - \hat Y = (I - X(X^TX)^{-1} +X^T)Y\),因此 simple linear regression 中对于 \(e\) 的限制在此处相应地修改为 \(e^T \hat Y = Y^T(I - X(X^TX)^{-1} X^T) +(X(X^TX)^{-1} X^T)Y = 0\)。
+相应地,\(\sigma\) 的估计量可以改成 +\(s^2 = \frac{e^Te}{n-p} = +\frac{Y^T(I-H)Y}{n-p}\),这就是 MSE,是 \(\sigma^2\) 的无偏估计;又因为 \(Var(b) = (X^TX)^{-1} \sigma^2\),因此有 +\(\hat Var(b) = (X^TX)^{-1} \hat \sigma^2 = +s^2 (X^TX)^{-1}\) 是 \(Var(b)\) +的估计。
+ANOVA 中的方差和自由度拆分在这里仍然适用:
+\[SST = (Y - \bar Y \mathbb 1_n)^T (Y - +\bar Y \mathbb 1_n), \quad df = n-1\]
+\[SSM = (\hat Y - \bar Y \mathbb +1_n)^T(\hat Y - \bar Y \mathbb 1_n), \quad df = p-1\]
+\[SSE = (Y - \hat Y)^T(Y- \hat Y), \quad +df=n-p\]
+\(F-\)test 的检验统计量是 \(F^* = \frac{MSM}{MSE} \sim^{H_0} +F_{p-1,n-p}\),其中假设是 \(H_0 +:\beta_1 = \beta_2 = ... =\beta_{p-1}=0\);决定系数 \(R^2 = \frac{SSM}{SST}\) +仍然保持不变,显示了线性模型解释方差的能力;adjusted \(R^2\) 定义为 \(1- +\frac{MSE}{MST} = 1- \frac{n-1}{n-p} \frac{SSE}{SST}\),相对于 +\(R^2\) 的优势在于,\(R^2\) +在有任意的变量进入模型时都会增大,但如果新变量的显著性不足会导致 +adjusted \(R^2\) +下降,是一个更有力的参数。
+Hat Matrix
+Hat Matrix 有丰富的性质,在这里列举一些和统计关联比较大的。
+\[Cov(e) = Cov((I-H)Y) = (I-H)^T \sigma^2 +(I-H) = \sigma^2 (I-H)\]
+\[Cov(e_i , e_j) = -\sigma^2 +h_{ij}\]
+\[Var(e_i) = \sigma^2 +(1-h_{ii})\]
+其中 \(h_{ij}\) 是矩阵 \(I -H\) 的分量。
+事实上,第 \(i\) 点的杠杆值就是 +\(h_{ii}\)。可以通过 \(H = H^2\) 这一性质简单地证明出 \(h_{ii} \leq +1\),这也和杠杆值的定义是符合的。
+Multiple Linear Regression
+-
+
关于多元回归的系数 \(\beta_1,\beta_2,...,\beta_{p-1}\)(也称为偏回归系数),我们仍然可以按照 +SLR 时的方式解释它们:\(\beta_i\) 是在 +\(X_1,X_2,...,X_{i-1},X_{i+1},...,X_{p-1}\) +不变时,\(X_i\) 变化一个单位导致 \(E(Y)\) 的变化量。
+实际上这就引出了多元回归的一个巨大隐患:并不是所有的变量都完全不相关,一旦 +\(X_1,X_2\) 之间有相关性存在,改变 +\(X_1\) 的时候很难保证 \(X_2\) +不变,多元回归的系数解释性因此变差。
+虽然理论上确实可能存在完全不相关的变量,但是对应的数据也很难不相关。
+\(Var(e_i) = \sigma^2 +(1-h_{ii})\),因此在线性回归中,位于中间(靠近 \(\bar X\))的 \(X\) +拟合能力较弱(杠杆值低,对回归线的影响较弱)但是预测能力较好(\(Var(e_i)\) 较小,\(\hat Y\) +能够变动的范围小)。相反地,位于两端的 \(X\) 拟合能力较强但是预测能力较弱。
+事实上我们是不能轻易预测已有数据范围之外的 \(x\) +的响应的,理由如上所述,此时的预测能力很弱。
2023 年 1 月 24 日,星期二,修了半天 LaTeX 然后摸了半天鱼(
-顺便解决了一些历史问题,比如把博客搬到(去年八月换的)新电脑上来了,说来真的有点蠢,感觉搬家好麻烦就同时用着两个电脑了(。旧电脑是 -surface,换掉之后一直仍然承担着晚上回寝室之后负责 deploy -博客和时不时需要一块手写屏的功能。
-其实后来检查了半天,发现除了 NexT -之外都是最新版本,不清楚究竟是哪里有问题,就换了个 -renderer,然后就好了(其实去看了下最新版 NexT -的文档,它的意思好像也是最好不要用 hexo-renderer-marked,就换了 -hexo-renderer-pandoc,虽然还有少量问题但基本还是在人工排查没那么费劲的范围里,先这样吧)。倒是也把新版本的 -NexT 设置好了,但是当时搞的彩色标签暂时没找到好的替代 = -=,原来的办法不太好用了,就还是暂时再用用旧的,哪天确定是它出了问题的话也可以一键搬家到新版(,以及有问题就可以自己在新版上测了,这次还要谢谢 -JasonL 老师的帮助,谢谢华子音游群让我半夜加到了老师的好友((
-到底是什么原因呢,是换了新电脑的原因还是魔改的原因,总之仓库里原来 -200 多条 commits -没有了。本来想着内容都还在也没什么问题,但是今天无聊翻邮件的时候突然想起来,有一条在 -commits -里的评论也跟着消失了。怪我没什么经验还不咋仔细,要是想到开个新的分支的话就好了。或许有什么恢复的方法吗,感觉没有(
-凌晨的时候本来在等备份,随手开了局舟,没想到一次通关,大概是什么回坑 -buff(。不过感觉不咋好玩,逐渐失去兴趣了,打算把活动打完就卸载掉。
-(这不是数分日志来着吗)(问题在这里发现的就在这儿解决一下好了)
-
2023 年 1 月 25 日,星期三,= =
+Lecture 8
+Explanatory Data +Analysis——Transformation
+Why look at Y
+一般来说 \(Y\) +的分布我们是不用太在意的,毕竟不是同分布,但其实考虑到做变换的话还是要稍微看一下它的分布。
+如果分布是高度有偏的,做变换把长尾的部分往中央收一收可以得到的效果有:
-
-
定义了一个很新的函数,叫做欧拉乘积公式,也可以就叫 \(\zeta\)- 函数。
-假设 \(\mathcal{P}\) -是所有的素数组成的集合,我们可以将它们从小到大排列为 \(2=p_1<p_2<p_3<\cdots\)。对于 \(s>1\),\(\zeta\)- 函数
-\(\zeta(s)=\sum_{n=1}^\infty -\frac{1}{n^s}\) 是良好定义的。那么, 我们有 \(\zeta(s)=\prod_{p\in -\mathcal{P}}\frac{1}{1-p^{-s}}\),
-其中上面的乘积是收敛的(我们可以假定是按照素数从小到大的顺序来做乘积的)。
-又到了高中竞赛的噩梦环节,Abel -求和公式。形式很简单,证明也很简单,但是应用和技巧多得离谱(
-\(\{a_k\}_{k\geqslant 1}\) 和 \(\{b_k\}_{k\geqslant 1}\) -是复数(矩阵)的序列,那么 \(\sum_{k=1}^n{a_kb_k}=S_nb_n+\sum_{k=1}^{n-1}S_k(b_k-b_{k+1})\),其中我们用 -\(S_n=a_1+a_2+\cdots+a_n\) 表示数列 -\(\{a_k\}_{k\geqslant 1}\) -的部分和。
-Abel 公式其实就是离散形式的分部积分公式,而且 Abel -和的部分截断和的形式也很不错:
-\(\sum_{n+1\leqslant k \leqslant m} a_k b_k -= S_mb_m-S_nb_n+\sum_{k=n}^{m-1}S_k(b_k-b_{k+1})\)
-于是有一个针对它的 Dirichlet -收敛判别法,证明即是对上面的部分截断和放缩,做 Cauchy 判别法:如果\(\{b_k\}_{k\geqslant 1}\) 是单调数列并且 -\(\displaystyle\lim_{k\rightarrow -\infty}b_k=0\),而且存在 \(M\),使得对任意的 \(n\geqslant 1\),\(|S_n|\leqslant M\),那么无穷级数 \(\displaystyle\sum_{k=1}^\infty{a_kb_k}\) -收敛。
-相应地还有 Abel 收敛判别法:\(\{b_k\}_{k\geqslant 1}\) -是单调有界数列,级数 \(a_1+a_2+a_3+\cdots\) 收敛,则级数 \(\displaystyle\sum_{k=1}^\infty{a_kb_k}\) -收敛。同样使用截断和的 Cauchy 判别即可。
+减小 SST,修正模型的显著性;
+把拖尾方向可能的 outlier +向内收,有可能可以变成正常的数据来使用;另一侧原来数据比较集中,做变换如果可以将分布拉长的话便于观察其中的一些特征;
+实际上 outlier +并不能随意的扔掉,做变换的想法是能够保留就尽量保留。有些时候很多现象就隐藏在出现了 +outlier +这件事情上面,比如臭氧层空洞没有被尽早发现就是因为相关的数据被当成 +outlier 扔掉了。
+方差对于 skewed data 和 outlier 都比较敏感;
+对于 skewed data,均值并不是中心位置很好的显示。
梦话 -3.0:距离空间与赋范线性空间
-赋范线性空间这我也熟啊,也是数值分析里学的(学的时候有点痛苦就是了,而且有点惶恐,因为感觉附近都是数学系的人,他们好像都会了 -qwq(而且都是大三的同学,天哪当时选课的时候真有勇气
+但通常来说做变换之前都需要三思:
-
-
距离空间是一个不够强的定义,只对空间上的两个点的距离做了定义,要求它们满足三角不等式。比如说,以绝对值为距离的距离空间 -\(\mathbb Q\) 上有 \(x_n=\displaystyle \sum_{k=0}^n -\frac{1}{k!}\) 是 Cauchy 列但不收敛(因为收敛到 \(e\),是无理数)。因此,定义完备的距离空间 -\((X,d)\),如果其上每个 Cauchy -列都收敛。比如 \(X=\mathbb R\),\(d(x,y)=|x-y|\) -就是完备的距离空间。
-然后讲义上讲了一个压缩映射定理(或者 Banach -不动点定理更好听),嗨呀这个我也熟,是数值分析里非线性方程的迭代解法那一章里面的最初条件,某种意义上来说也是做迭代能找到不动点的前提。不过这次把它放到完备距离空间里了。
-数值分析里用的是更完备的空间,也就是赋范线性空间,实际上就是让距离空间的距离定义又满足了范数的条件,也就是数乘的线性性质而已。另外要求空间是线性空间,这个也没什么难的。
--
-这三种范数都是上面线性空间情况直接搬过来的. 实际上, 利用矩阵的知识, -我们还可以定义其他更有几何意义的范数, -比如说我们可以利用矩阵的特征值来定义一些范数, 限于知识范围, -我们不再展开.
-嘿嘿,这个我会(这不是应该的吗到底在自豪什么.jpg
-最后在完备的赋范线性空间(也就是
-BananaBanach -空间)上证明了一些极限的相容性,其实我的感受就是把绝对值推广成了范数,证明某些对于实数的操作,在赋范线性空间上对向量 -/ 矩阵也是能成立的。比如说定义一个 \(e^A\),但 \(A\) 是一个 \(n -\times n\) -大小的复系数矩阵。听起来很抽象,不知道会得到一个什么怪物结果,但是回顾 -\(e^x\) 的级数定义就可以知道,\(e^A = \sum_{k=0} ^\infty {A^k \over -k!}\),也就是说 exp 函数在矩阵上是一个 \(M_n (\mathbb R) \to M_n (\mathbb R)\) -的映射,得到的结果还是一个 \(n \times -n\) 大小的复系数矩阵。
-要做的任务就是证明 \(e^A\) -的良定义性质,也就是级数的收敛性。在这里用一个赋范空间上的绝对收敛概念,原本实数空间上的绝对收敛是对于绝对值而言,在赋范空间上改成对范数而言即可,这样还是能够通过绝对收敛推出收敛(因为范数和绝对值同样有三角不等式性质)。关于 -\(e^A = \sum_{k=0} ^\infty {A^k \over -k!}\) -的绝对收敛性质也很好证明,可以使用矩阵范数的等价性。当然,如果这个矩阵范数是一个向量相容范数,就更简单了。
-不过,在这样的定义里,\(e^{A+B} = e^A -e^B\) 是不一定成立的,因为两个矩阵未必交换。但是 \(e^{sA} e^{tA} = e^{(s+t)A}\) -仍然成立。
+- 做变换后可解释性会有问题,比如 Box-Cox Transformation 中奇怪的 \(\lambda\) +取值会导致可解释性变差,实验数据有的时候需要保留单位,做变换之后会失去意义; +
- 会导致 \(H_0\) 改变; +
- 不一定能够改进正态性,做变换未必有好的效果; +
- 做了变换得到结果之后,变回原始数据很可能破坏无偏性; +
- 破坏了残差的分布。
梦话 -4.0:既然习题没有答案那我就继续胡说八道了
-怎么作业这么多啊!
-说到习题没有答案这个问题,今天在知乎搜了一下居然有民间版本流传,作者是 -MO 和 OI 双修的高中生,太升级了。
-习题还在做,做完了再来碎碎念,然后就终于可以离开极限去学连续性了(
-2023 年 1 月 26 日,星期四,今天没有 die -只是作业写起来真的有点慢(,这一章的习题全都做了哦。
-连续函数的定义和基本性质
+有一些平替方案:GLM, resampling methods, non-parametric methods
+另外我们一般不会对 \(X\) +做变换,除非做变换之后和 \(Y\) +有非常明确的关系,另一个原因是做变换可能会导致共线性。
+Why log Transformation
+对 right-skewed data 做 log transformation +的好处是显著多于其他类型的变换的:
-
-
(函数极限的Cauchy判别准则)给定函数 \(f\colon (a,x_0)\cup (x_0,b)\rightarrow -\mathbb{R}\)。那么,\(f\) 在 -\(x_0\) 处有极限当且仅当对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x_1,x_2\in (x_0-\delta,x_0+\delta)\),都有 -\(|f(x_1)-f(x_2)|<\varepsilon\)。
-如果有极限,这是定义,trivial.
-如果对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x_1,x_2\in (x_0-\delta,x_0+\delta)\),都有 -\(|f(x_1)-f(x_2)|<\varepsilon\),那么取某一个固定的 -\(\varepsilon\),找到这样的区间 \(X=(x_0-\delta,x_0+\delta)\),任意取一组 -\(X\) 上收敛到 \(x_0\) 的点列 \(y_0,y_1,...,y_n,...\),它们的函数值序列 -\(\lbrace f(y_n) \rbrace _{n \geq 1}\) -是 Cauchy 列,一定收敛。
-至于为什么会收敛到 \(f(x_0)\) -这一点,这是因为 \(\lbrace y_n \rbrace _{n -\geq 1}\) 的极限是 \(x_0\)。
-假设 \(I\) 是一个非空的区间并且 -\(I\) 不是一个点,证明,\(I\) 上的连续函数 \(C(I)\) 所构成的 \(\mathbb R\)-线性空间是无限维的。
-这题我会!数值分析里学过!多项式的基 \(\lbrace 1,x,x^2,... \rbrace\) -是无限维的,因为它们彼此线性无关。
-假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) 是映射。假设 \(x_0\in X\),如果对任意 \(X\) 中的点列 \(\{x_n\}_{n\geqslant 1}\),\(x_n\stackrel{d_X}{\longrightarrow}x_0\),我们都有 -\(f(x_n)\stackrel{d_Y}{\longrightarrow}f(x_0)\),我们就称 -\(f\) 在 \(x_0\) 处是连续的。如果 \(f\) 在一切 \(x\in -X\) 处均连续,那么我们就称 \(f\) -是距离空间之间的连续映射。
-假设 \((X,d_X)\),\((Y,d_Y)\) 和 \((Z,d_Z)\) 是三个距离空间,\(f\colon X\rightarrow Y\),\(g\colon Y\rightarrow Z\) -均为连续映射。证明,它们的复合 \(g\circ -f\colon X\rightarrow Z\) 也是连续映射。
-一句话题意:连续映射的复合还是连续映射(
-Trivial.
-假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) 是连续映射。如果 -\(d'_X\) 是与 \(d_X\) 等价的距离,\(d'_Y\) 是与 \(d_Y\) 等价的距离,那么,对于 \((X,d'_X)\) 和 \((Y,d'_Y)\) 而言,\(f\) 也是连续映射。
-等价的距离意思是对任意的 \(x_1 , x_2 \in -X\),存在固定的参数 \(c,C \in -R\),使得 \(c d^{\prime} _X (x_1,x_2) -\leq d _X (x_1,x_2) \leq C d^{\prime} _X -(x_1,x_2)\),代入一下连续的定义,取一个小一点的 \(\varepsilon\) 就可以了。
-在 \(\mathbb R^n\) -上我们配有常见的距离,比如说 \(d_2\)(请参考之前的讲义);\((X,d_X)\) 是距离空间。我们将映射 \(f\colon X\rightarrow \mathbb R^n\) -写成分量的形式:\(f\colon X\rightarrow \mathbb -R^n, \ \ x\mapsto f(x)=(f_1(x),f_2(x),\cdots,f_n(x))\)
-其中 \(f_i\colon X\rightarrow \mathbb -R\) 是函数。证明,\(f\) -是连续映射当且仅当对所有的 \(i=1,\cdots,n\),\(f_i\) 是连续函数。
-如果每个 \(f_i (x)\) -都是连续函数,那么对于收敛到 \(x_0\) -的点列 \(\lbrace x_i \rbrace _{i \geq -1}\),对任意的 \(\varepsilon ->0\),存在一个最小的 \(\delta\) 和最大的 \(N\),使得对任意分量函数,都有 \(n >N\) 时,\(| -f_i(x_n)-f_i(x_0) | <\varepsilon\)。于是此时也有 \(| f(x_n) - f(x_0) | <\sqrt{n} -\varepsilon\),连续。(追求美观的话可以在第一步把 \(\varepsilon\) 改成 \(\varepsilon \over \sqrt{n}\))
-如果 \(f(x)\) -是连续函数,那么分量的误差小于整体误差,每个分量都收敛。
-(这个我在数值分析也学过!耶!
-假设 \((X,d_X)\) -是距离空间,\((V,\|\cdot\|)\) -是赋范线性空间,\(f\colon X\rightarrow -V\) 和 \(g\colon X\rightarrow -V\) 是连续映射。证明,它们的和与差(自然的定义)\(f\pm g\colon X\rightarrow V\) -也是连续映射。
-如果 \(V=\mathbb{C}\)(或者 \(n\times n\) -的矩阵构成的赋范线性空间),那么 \(f\cdot -g\colon X\rightarrow \mathbb{C}\) 是连续映射。
-如果 \(V=\mathbb{C}\) 并且对任意的 -\(x\in X\),\(g(x)\neq 0\),那么 \(\dfrac{f}{g}\colon X\rightarrow -\mathbb{C}\) 是连续映射。
-你可以选择上面的一个情况来证明。
-PIN 你真的有点无聊(哭),其实都挺 trivial 的。
-试找出 \(\mathbb R\) -上定义的函数
-\(f(x)=\begin{cases}\frac{1}{q}, \ -&\text{如果 $x=\dfrac{p}{q}$ 是有理数,其中 $p\in \mathbb{Z}$,$q\in -\mathbb{Z}_{\geqslant 1}$ 且 $p$ 和 $q$ 互素};\\ 0, \ &\text{如果 -$x$ 是无理数}\end{cases}\)
-的所有不连续点。
-回顾一下:连续点的含义是 \(f\) 在 -\(x_0\) -处有(唯一的,左右相等的)极限,当且仅当对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x_1,x_2\in (x_0-\delta,x_0+\delta)\),都有 -\(|f(x_1)-f(x_2)|<\varepsilon\)。
-对于有理数点,其实很容易就能找到一个趋近于它的无理数点列。取一个它左侧的无理数点 -\(k\),二者一起不停找二分点,就可以取出一个趋近于这个有理数点的无理数点列。它的函数值是收敛不到 -\(\frac 1 q\) -的,于是所有的有理数点都是不连续点。
-但是 \(0\) -的函数值是咋定义的呢?如果函数值就是 \(0\),那它是唯一一个有理数连续点。
-对于无理数点 \(t\),对任意的 \(\varepsilon >0\),总能够取 \(\delta\) 满足 \(t\) 的去心邻域 \(T = (t-\delta,t) \cup (t,t+\delta)\) -里面没有形如 \(p \over q\) -的有理数,使得分子分母互素,而且 \(q < -\frac{1}{\varepsilon}\),因此对任意 $ x_1 ,x_2 T$,有 \(| f(x_1 ) - f(x_2) | < -\varepsilon\),总是收敛的。
-至于为什么可以做到这一点,这是因为记把 \(t\) 附近 \(q < -{1 \over \varepsilon }\) 的有理数点中离它最近的距离记为 \(d\),取 \(\delta -= \frac d 2\) 即可,而这样的有理数点是有穷个,一定可以找到对应的 -\(d>0\)。
-总之,所有的不连续点的集合是 \(\mathbb -Q\),视情况可能 \(0\) -会是连续的,这里定义的好像不是很好。
+- \(\log Y_1 - \log Y_2 = \log (1+ \frac{Y_1 +- Y_2}{Y_2}) \approx \frac{Y_1 - +Y_2}{Y_2}\),可以把绝对误差变为相对误差来讨论; +
- \(\log Y\) +可以让数据的分布更对称,出于计算的考虑 +
- 如果 \(Y\) 全部都是正数,但 \(Y = X \beta + \varepsilon \sim N(X \beta, \sigma^2 +I)\),一个多元正态分布的数据全部是正数的概率非常小,假设不合理。 +
但是最大的问题就是可解释性。对于参数 \(\beta\) 的解释是在 \(X\) 增长一个单位时 \(Y\) +的平均响应的对应变化,在这里我们选择的是报告平均响应变化的百分比,也即 +\(\frac{e^{(X+1)b} - e^{Xb}}{e^{Xb}} = e^b +\times 100 \%\),作为一个补救措施。
+MLR vs SLR
+相比于 simple linear regression,MLR +的变量增多了之后需要考虑的问题也增加了,复杂度也变大了。
+变量选择
+破事很多:
+-
+
- 单独一个 \(X_i\) +在模型里不显著也不能直接扔掉,它可能是 suppressor +variable,会让别的变量显著 +
- 多个变量的模型显著不能推出单个变量显著 +
- 单变量模型中,变量显著性 \(t\) +检验和模型显著性 \(F\) 检验的 p-value +相等,因为 \(F_{1,n} = t_n ^2\) +
- 其余变量是否需要进入模型,可以先考虑残差对于其余各个变量的回归显著性,先测试最显著的变量进入模型
级数收敛性
-眼前一黑,我直接一个梦回微积分 A2(,这一部分就比较水字数了。
+有的时候我们认为模型里变量越多越好,有的时候越少越好,这取决于做回归的目的:
-
-
- 试判断下列级数的收敛性。 +
- 回归模型是为了预测:变量越多或者说 adjusted \(R^2\) +越大,解释的方差越多,预测水平越好 +
- 回归模型是为了解释:变量越少,explanatory variable 和 response +之间的关系越明确,解释性越好 +
总之,会随着模型中进入的变量而改变的参数有:
-
-
\(\sum_{n=1}^\infty -(\sqrt{n+1}-\sqrt{n})\)
-发散,trivial.
-\(\sum_{n=1}^\infty -\frac{\sqrt{n+1}-\sqrt{n}}{n}\)
-收敛,trivial.
-$_{n=2}(-1)n $
-收敛,因为数列 \(n^{1 \over n}\) -单调减并趋近 \(1\),对于某个被 \(\varepsilon\) 控制的 \(n >N\),有 \(\sum_{n=N+1}^\infty (\sqrt[n]{n}-1)^n < -\sum_{n=N+1}^\infty \varepsilon ^n\)。
-$_{n=1}^ (x) $
-\(|x|<1\) 或 \(x=1\) 时单项收敛不到 \(0\),级数发散;否则收敛。
-$_{n=1}^ $
-收敛,trivial.
-$_{n=1}()n $
-收敛,单项放缩。
-$_{n=1}^ $
-发散,验一下不符合 Cauchy 列。
-\(\sum_{n=2}^\infty \frac{1}{(\log -n)^{\log n}}\)
-感觉可以用积分法判断收敛(,但是还没学过积分(,怎么办呢。
-也可以放缩,\(n > N\) 时有 \(\frac{1}{(\log n)^{\log n}} < -\frac{1}{n^M}\)。收敛。
-$_{n=1}^ $
-单项可以写成更好的形式:${(n^{1 n} / (n+ {1 n} ) ^{1 } )}^{n ^2 +1} $ -(天哪这个能渲染出来吗,好担心)
-发散。
-$_{n=1}(-1){n-1} $
-收敛,Dirichlet 判别。
-$_{n=1}^ $
-发散,trivial.
-\(\sum_{n=1}^\infty -\left(1+\frac{1}{2}+\cdots + \frac1n\right)\frac{\sin -nx}{n}\)
-收敛。拆分 \(b_n = \frac{1}{n} (1 + \frac 1 -2 +...+ \frac 1 n)\),\(a_n = \sin -nx\),用 Dirichlet 判别法,其中 \(b_n -< \frac{log _2 n}{n}\)。
-需要注意的是要讨论一下 \(x = 2k -\pi\) 的情况。
-
诡异的现象
+有的时候会遇到 Significance & low \(R^2\) +同时出现的情况,也就是某个变量看起来是显著的,但是 \(R^2\) +很低,解释方差的能力并不好。这是正常的现象。
-
-
$_{n=2}(-1)n $
-不绝对收敛,感觉也可以用积分判别,懒得多想了(
-收敛,trivial.
-$_{n=2}^ $
-不绝对收敛,求一下 \(\sin -\frac{n\pi}{4}\) 的值就知道了。
-收敛,trivial.
-$_{n=1}(-1)n $
-不绝对收敛,分离常数之后发现一部分收敛一部分不收敛。
-收敛,仍然是分离常数,trivial.
-\(\sum_{n=1}^\infty -(-1)^{\frac{n(n-1)}{2}} \frac{n^{10}}{a^n} \qquad (a>1)\)
-绝对收敛,trivial.
-
回到 \(R^2\) 的定义和 F +检验的本质可以发现,\(R^2 = \frac{SSR}{SST}, +F^* = \frac{MSR}{MSE} = \frac{R^2}{1-R^2} \frac{n-p}{p-1}\),如果 +\(n\) 非常大,即使 \(R^2\) 很小也和 \(F^*\) 很大之间并不矛盾。
\(R^2\) 的分母 \(SST\) +实际上表征了数据的分散程度,数据非常分散的时候是可能导致 \(R^2\) +减小的。但是数据分散和存在线性并不矛盾,图中的两个线性关系当然都显著,但是 +\(R^2\) 有巨大的差距。
+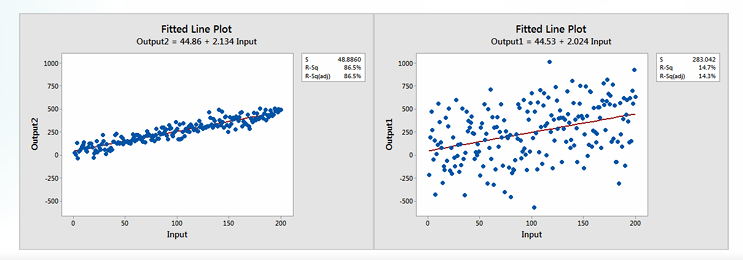
递减正项级数的凝聚检验法
-假设正整数 \(b\geqslant 2\),\(f\colon (1,\infty)\rightarrow -\mathbb{R}_{>0}\) 是递减(未必严格递减)函数。
+Inference
+-
+
多重线性回归的推断里面也有一个著名定理:\(Y \sim N_n(X \beta , \sigma^2 I)\),于是有 +\(b \sim N_p(\beta , \sigma^2 +(X^TX)^{-1})\),以及:
+-
+
- \(\frac{e^Te}{\sigma^2} = +\frac{SSE}{\sigma^2} \sim \chi^2_{n-p}\) +
- \(b\) 和 \(SSE\) 相互独立 +
由此得到很多推断方法。
+关于 \(b_k\) 的推断和 +CI,主要关注 \(b_k \sim N(\beta_k, +\sigma^2((X^TX)^{-1})_{k,k})\),希望检验 \(H_0 : \beta_k =0; H_1 : \beta_k \neq +0\)。
+检验统计量是 \(t^* = \frac{b_k}{s(b_k)} = +\frac{b_k}{\sqrt{MSE ((X^TX)^{-1})_{k,k}}}\sim ^{H_0} +t_{n-p}\),由此可以检查单个变量的显著性。注意此处所谓的显著性,指的是第 +\(k\) +个变量最后一个进入模型时的显著性,无论它在 R table 里排列在哪里。和 +general linear test 的结果一致。如果这一检验体现出来变量 \(X_k\) +不显著,绝大多数情况下是可以不保留的。
+\(100(1-\alpha) \%\) 置信区间是 +\((b_k \pm t_{1-\alpha /2,n-p} +s(b_k))\),注意 \(s(b_k)\) +的含义在上述已经提到。
+关于 \(E(Y_h)\) 的推断和 +CI,考虑 \(\mu_h = E(Y_h) = X_{h} +\beta\)。
+其估计量是 \(\hat \mu_h = X_h b = X_h +(X^TX)^{-1} X^TY \sim N(\mu_h , \sigma^2 X_h (X^TX)^{-1} +X_h^T)\),于是 \(s^2(\hat \mu_h) = MSE +\cdot X_h (X^TX)^{-1} X_h^T\)。因此 \(\mu_h\) 的 \(100 +(1-\alpha) \%\) 置信区间是 \((\hat +\mu_h \pm t_{1-\alpha /2 , n-p} s(\hat \mu_h))\)
+考虑 \(Y_h = X_h \beta + +\varepsilon\),有 \(\hat Y_h - Y_h \sim +N(0,\sigma^2 + \sigma^2 X_h (X^TX)^{-1} X_h^T)\), \(s^2(\hat Y_h - Y_h) = MSE \cdot (1+X_h (X^TX)^{-1} +X_h ^T)\),因此 \(Y_h\) 的 \(100 (1-\alpha) \%\) 置信区间是 \((\hat Y_h \pm t_{\alpha /2 , n-p} s(\hat Y_h - +Y_h))\)
+
Lecture 9
+Extra Sum of Squares
+想法很简单,定义就是把一个新的变量加入模型后可以额外解释的方差,例如模型中本来存在 +\(X_2\) 时,加入 \(X_1\) 后可以额外解释的方差是 \(SSR(X_1 | X_2) = SSR(X_1 ,X_2) - SSR(X_2) = +SSE(X_2) - SSE(X_1,X_2)\)。
+在多重回归中分解 sum of squares 的方式最常见的是 Type I method:
+\(SSR(X_1,X_2,X_3,X_4) = SSR(X_1) + SSR(X_2 +|X_1) + SSR(X_3 |X_1,X_2)+SSR(X_4 |X_1,X_2,X_3)\)
+也就是所谓的 sequential sum of squares 的方法,在
+anova() 中的列表就是这样的分解方式,分掉了所有的 SSR。
SAS 中的 sum of square 分解有三种模式,以考虑 A,B,AB 三种因子(2-way +ANOVA)的情况如下排列:
+
可以看到 type I 就是按照 sequential +的模式进入模型,认为不同的变量有重要性的排序,先进入理论上来说最有必要进入模型的 +A,再进入 B,最后进入 AB,分别计算 extra sum of squares;type II +忽略了交互效应 AB,对于 A 和 B 的单变量分解是与 type I 相同的;type III +和之前提到的 t 检验类似,每个模型的 extra sum of square +分解都是考虑它最后一个进入模型时带来的方差解释能力,但这里实际上存在一个问题,按照 +hierarchy 的原则来说如果主效应 A,B +之一不显著/没有进入模型,是不能允许交互项 AB 进入模型的。
+General Linear Test
+Test Reduced Model
+一种检验 full model 和 reduced model +之间关系的检验方法,例如对于存在五个变量 \(X_1,X_2,X_3,X_4,X_5\) 的 full model +和存在三个变量 \(X_1,X_2,X_3\) 的 +reduced model 来说,假设 \(H_0: \beta_4 = +\beta_5 = 0; H_1:\beta_4,\beta_5\) 中至少有一个不是 \(0\)。
+检验统计量是 \(F^* = \frac{(SSE(R) - +SSE(F))/(df_E(R) - df_E(F)}{SSE(F)/df_E(F)}\sim ^{H_0} +F_{df_E(R)-df_E(F),df_E(F)}\),注意第一个自由度实际上是两个模型相差的变量个数,分母中的 +\(SSE(R) - SSE(F) = SSR(F) - SSE(R) = +SSR(X_4,X_5|X_1,X_2,X_3)\) 实际上是 extra sum of squares。
+事实上我们是 prefer 接受 \(H_0\) +的,就相当于可以使用变量更少的模型,解释性更强;但是有的时候检验做出来接受 +\(H_0\),也需要考虑一下是不是数据量太小导致 +power 不够,如果数据量够大就可以放心地使用 reduced model 了。
+Test Linear Hypothesis
+实际上只要是关于回归系数的线性检验就都可以用 general linear test +来进行,比如 \(H_0 : \beta_1 + 3 \beta_2 +=12\),等等。
+\(H_0 : C \beta =t\),\(C\) 是有关 \(\beta\) 的约束条件的矩阵,检验统计量是 +\(F = \frac{(C \hat \beta - t)^T (C(X^TX)^{-1} +C^T)^{-1} (C \hat \beta - t)}{qs^2} \sim^{H_0} F_{q,n-p}\),其中 +\(q=rank(C)\)。
+偏决定系数 & 偏相关系数
+\(R^2_{Yk|1,2,...,k-1,k+1,...,q} = +\frac{SSR(X_k | +X_1,..,X_{k-1},X_{k+1},...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)} = +1- +\frac{SSE(X_1,X_2,...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)}\)
+本质上说的是,模型中新进入的 \(X_k\) +带来的 extra sum of squares 解释了 SSE +的比例,也即解释了没有由原来的变量解释掉的方差比率。
+实际上另一种表现形式可以是,我们认为 \(R^2_{Yk|1,2,...,k-1,k+1,...,q} = +\frac{SSE(R)-SSE(F)}{SSE(R)} = \frac{SSR(X_k |X_{-k})}{SST(Y|X_{-k})} = +R^2(Y|X_{-k}, X_k|X_{-k})\)
+也就是说,实际上是对于 \(Y|X_{-k} \sim +X_k|X_{-k}\) 这两组残差做线性回归,得到的决定系数正好是 \(X_k\) 的偏决定系数。
+实际上偏相关系数 \(r_{k|1,2,...,k-1,k+1,...,q} = sign(\hat +\beta_k)\sqrt{R^2_{Yk|1,2,...,k-1,k+1,...,q}}\) +表征的就是这两组残差之间的相关系数,如果有 \(0 +< r_{3|12} < r_{12}\) 就说明变量 \(X_3\) 可以部分解释 \(X_1,X_2\) 之间的相关性。
+标准回归
+Motivation
+-
+
- 如果 \(X_1,X_2\) +之间的尺度差距过大会导致 \(\beta_1,\beta_2\) +的尺度也有差距,无法直接比较,也可能会影响变量显著性。 +
- 会导致 designed matrix 接近不满秩,计算逆矩阵出现问题。 +
Method——Correlation +Transformation
+考虑 \(s_Y = \sqrt{\frac{\sum_i (Y_i - \bar +Y)^2}{n-1}}, s_{X_k} = \sqrt{\frac{\sum_i (X_{ik}-\bar +X_k)^2}{n-1}}\),对变量和响应值分别做标准化:
+\[\begin{aligned} \frac{1}{\sqrt{n-1}} +\frac{Y_i - \bar Y}{s_Y}& = \frac{1}{\sqrt{n-1}} \frac{(\beta_0 + +\beta_1 X_{i1} + \beta_2 X_{i2} + \varepsilon_i)-(\beta_0 + \beta_1 \bar +X_1 + \beta_2 \bar X_2 + \bar +\varepsilon)}{s_Y}\\&=\frac{1}{\sqrt{n-1}}\frac{\beta_1(X_{i1} - +\bar X_1) + \beta_2 (X_{i2}-\bar X_2) + (\varepsilon_i - \bar +\varepsilon)}{s_Y}\\&=\frac{\beta_1 s_{X1}}{s_Y} \frac{(X_{i1}-\bar +X_1)}{\sqrt{n-1} s_{X1}} + \frac{\beta_2 s_{X2}}{s_Y} \frac{(X_{i2}-\bar +X_2)}{\sqrt{n-1} s_{X2}} + \frac{\varepsilon_i - \bar +\varepsilon}{\sqrt{n-1}s_Y} \end{aligned}\]
+\[Y_i^* = 0 + \beta_1^* X_{i1}^* + +\beta_2^* X_{i2}^* + ... +\beta_{p-1}^* X_{i,p-1}^* + +\varepsilon_i\]
+其中 \(\beta_k ^* = \frac{s_{X_k}}{S_Y} +\beta_k\) 是新的回归系数。
+-
+
注意这个方法是有一些问题的,比如说破坏了残差的假设,以及强迫过原点。
+标准回归的系数估计和 ANOVA table 都发生了改变,这是因为 SST +变成了 \(1\),ANOVA table +自然会变化。但是偏决定系数都是由偏相关系数直接决定的,所以没有变化。
+类似地,如果只对 \(X\) +做变换而不改变 \(Y\),会有系数发生改变,但是 ANOVA table +和偏决定系数都不变。
+
Suppressor Variable
+如果有 \(SSR(X_2 |X_1) > +SSR(X_2)\),也就是 \(X_1\) +在模型里的时候会让 \(X_2\) 更显著,则称 +\(X_1\) 是一个 suppressor +variable。原理是 \(X_1\) +可以帮助解释一部分 \(X_2\) +中的噪音,使得 \(X_2\) 更显著。
+\(X_1\) +本身未必是显著的,这也就说明了如果单一变量不显著的话也不能贸然扔掉,它可能会是一个抑制变量。更极端的情况下,假设 +\(X_1\) 和 \(Y\) 完全无关,有 \(X_2\) 在模型中不会改变 \(X_1\) 的系数估计,但是会导致 \(R^2_{Y2|1} \neq R^2_{Y2}\)。
+一般来说脑补一下这种类似韦恩图的直观解释就好。
+
Lecture 10
+Multicollinearity
+关于多重共线性的一些研究,先考虑一些极端情况,然后观察多重共线性会导致什么后果。
+Zero Collinearity
+在几个解释变量完全没有共线性的情况称为正交设计,也就是说设计矩阵的各列之间是正交的。这是一个很好的情况,互相之间并不会干扰,有 +\(X^TX = diag(||X_0||^2 , +||X_1||^2,...,||X_{p-1}||^2)\),且有 \(b_j = \frac{X_j ^TY}{||X_j||^2}\),\(Var(b_j) = +\frac{\sigma^2}{||X_j||^2}\)。
+结果就是无论进多少变量都不会影响单个 \(b_j\) 的估计,但是会影响到 \(MSE\) 导致 p-value 的变化。与此同时 type I, +II, III ANOVA table 的结果是一样的,这是因为 extra sum of squares +就是单个变量能解释的方差。
+
Linearly Dependent
+一个比较极端的例子是完全线性相关,比如变量之间有 \(c_1 X_1 + ... +c_{p-1}X_{p-1}=c\) +这样的关系,会导致设计阵不满秩无法求逆。从数学上来说只要去掉其中一个变量即可,但是在统计上未必合适的。
+Multicollinearity
+正常一些的情况就是普通的多重共线性,从回归结果来看多重共线性的一大特征就是模型整体显著,但是没有一个变量是显著的。回归结果的显著性是代表每个变量最后一个进入模型时的显著性,也就是说明每个变量几乎都是可以被前面进入模型的变量表示出来的。多重共线性有以下危害:
-
-
证明下面的不等式:\((b-1)b^{k-1}f(b^{k})\leqslant -\sum_{j=b^{k-1}}^{b^k-1} f(j) \leqslant -(b-1)b^{k-1}f(b^{k-1})\)
-什么茶歇题。Trivial.
-证明:级数 ${n=1}^f(n) $ 和 $ {n=1}bn f(b^n)$ -同时收敛或者同时发散。
-我们称通过后者的收敛来判断前者收敛的方法为凝聚检验法。
-根据上一问求和,trivial.
-证明,\(\displaystyle \sum_{n=2}^\infty -\frac{1}{n\log n}\) 是发散的。
-不如试试积分收敛法(被捂嘴拖走
-取 \(b=2\) -知道它和调和级数是同收敛同发散的。
-证明,\(\displaystyle\sum_{n=100}^\infty \frac{1}{(n\log -n) (\log (\log n))}\) 是发散的。
-它和上一问的级数是同收敛同发散的。
-证明,如果 \(s>1\),那么 -\(\displaystyle\sum_{n=1}^\infty -\frac{1}{n^s}\) 是收敛的;如果 \(0<s<1\),那么 \(\displaystyle\sum_{n=1}^\infty -\frac{1}{n^s}\) 是发散的。
-取 \(b=2\) -知它和一个等比数列同收敛同发散。
-假设 \(s>1\)。证明,\(\displaystyle\sum_{n=2}^\infty \frac{1}{n(\log -n)^s}\) 和 \(\displaystyle\sum_{n=10}^\infty \frac{1}{(n\log -n)(\log(\log n))^s}\) 都收敛。
-前一个和上一问同收敛同发散。后一个和 \(\displaystyle\sum_{n=10}^\infty \frac{1}{n {\log^s -n} }\) 同收敛同发散。
+- \(X_1,X_2\) +之间较大的多重共线性会导致对于单个变量的 \(Var(b_i)\) +增大,但是仍然是无偏估计。这也就说明了,出现多重共线性时 \(b_i\) 的方差很大,会导致 \(b_i\) +的估计值并不准确。举个例子来说,有的时候理论上 \(X_i\) 和 \(Y\) +之间是正相关,但是得到的系数估计是负的,就有可能是因为 \(Var(b_i)\) +过大导致一组数据得到的结果距离“真实值”有很大的偏差,甚至从正相关变成了负相关。 +
- Type I SS 和 Type II SS +的结果可能是不同的,因为变量之间对方差解释有竞争,也可能有 suppressor +variable,进入模型的顺序在此时变得重要了起来,二者不同的结果可能导致判断上的问题。 +
- 两部分解释变量解释了同一部分的方差,导致模型解释能力下降。模型整体显著但每一个变量都不显著,很有可能是过拟合了。 +
- 从数学上来说 \(X^TX\) +接近退化,求逆时导致数值误差增大。
--Remark:上述的几个收敛的结论是标准并且重要的,记住这几个结论对于收敛以及函数大小的理解很有帮助。这里的证明尽管巧妙,但是等我们接触到积分的时候,我们就可以用统一的、简单的、更本质的也更容易记忆的方法来证明这些结论。
-
实数列的上下极限的刻画
-设 \(\{a_n\}_{n \geqslant 1}\) -是一个实数列。先补充几个定义:
-\(\alpha \in \mathbb R\),如果对任意 -\(\varepsilon>0\), 存在无穷多 \(n\),使得 \(a_n -\in (\alpha-\varepsilon,\alpha+\varepsilon)\),我们称 \(\alpha\) 为 \(\{a_n\}_{n\geqslant 1}\) 的一个极限点;
-如果对任意 \(M>0\),存在无穷多个 -\(n\),使得 \(a_n \in (M,\infty)\),我们就称 \(+\infty\) 为 \(\{a_n\}_{n\geqslant 1}\) 的一个极限点;
-如果对任意 \(M>0\),存在无穷多个 -\(n\),使得 \(a_n \in (-\infty,-M)\),我们就称 \(-\infty\) 为 \(\{a_n\}_{n\geqslant 1}\) 的一个极限点。
+
有一些弥补的方案,但是要视建立模型的目的而定:
-
-
证明,\(\alpha\in \mathbb R\) 是 -\(\{a_n\}_{n\geqslant 1}\) -的极限点当且仅当该数列有子序列 \(\{a_{n_k}\}_{k\geqslant 1}\) 收敛于 \(\alpha\)。
-对于 \(\varepsilon _1 = 1\),取 -\(a_1 \in -(\alpha-\varepsilon_1,\alpha+\varepsilon_1)\);再取 \(\varepsilon _2 = |\alpha - a_1|\),继续取 -\(a_2\),依次操作就得到了收敛子序列。
-反过来是显然的。
-证明,\(+\infty\) 是 \(\{a_n\}_{n\geqslant 1}\) -的极限点当且仅当该数列有子序列 \(\{a_{n_k}\}_{k\geqslant 1}\) 使得 \(\displaystyle\lim_{k\to \infty} a_{n_k} = -+\infty\)。
-Trivial.
-令 \(E = \bigl\{\alpha \in \mathbb R -\cup \{\pm \infty\} \,\rvert\, \alpha \text{ 是 } \{a_n\}_{n\geqslant 1} -\text{ 的极限点}\bigr\}\) 为 \(\{a_n\}_{n\geqslant1}\) -的所有极限点所组成的集合(它是 \(\mathbb R -\cup \{\pm \infty\}\) 的子集)。证明,\(E \ne \emptyset\)。
-考察 $sup {a_n}_{n} = + $ 或者 \(inf -\{a_n\}_{n\geqslant1} = -\infty\),如果有二者之一则有 \(+\infty \in E\) 或者 \(-\infty \in E\)。
-否则,\(\{a_n\}_{n\geqslant1}\) -是有界的。如果它收敛于一点,则这一点是极限点,\(E\) 非空。
-否则,\(\{a_n\}_{n\geqslant1}\) -有界且不收敛,它也有收敛的子列,子列收敛的极限是极限点。(救命,差点忘了这个
-证明:\(E \subset \mathbb R\) -当且仅当数列 \(\{a_n\}_{n\geqslant 1}\) -有界。
-Trivial.
-假设 \(\{a_n\}_{n\geqslant 1}\) -有界。试证明,\(\displaystyle \sup E = -\limsup_{n\to \infty} a_n\),\(\displaystyle\inf E = \liminf_{n\to \infty} -a_n\)。
-是我困迷糊了吗?我不是很理解诶,比如说数列 \(1,1,100000,1,1,1,1,1,...\),真的符合第一条吗?
-假设 \(\{a_n\}_{n\geqslant 1}\) -有界。令 \(a^*= \displaystyle\limsup_{n\to -\infty} a_n\),证明如下两个命题:
+如果单纯是为了预测,其实增大模型的 sample size +是可以解决问题的
+如果是为了解释性,需要做很多其他的努力,比如移除一些变量,对变量做变换,PCA +方法等等。
+仍然存在很多问题,比如移除变量时万一移除了某个重要的类别型变量,可能会导致 +Simpson's Paradox 出现,移除变量也会导致系数估计的方差减小,可能减小 MSE +但是会导致 bias 增大,但如果移除了一个重要的解释变量会导致它进入 error +term,进而导致 \(\sigma^2\) +的估计增大,需要 trade-off;
+做变换不一定能成功降低共线性还会造成解释上的困难,PCA +的解释性更差,等等。
+
Multicollinearity 可能有以下来源:
-
-
\(a^* \in E\)(所以 \(\sup E\in E\));
-对任意 \(x > a^*\),存在 -\(N \in \mathbb{Z}_{\geqslant -1}\),使得对任意 \(n>N\),都有 \(a_n < x\)。
-
试举一个数列 \(\{a_n\}_{n\geqslant -1}\) 作为例子,使得 \(E\cap \mathbb R -\ne \emptyset\) 且 \(E\not\subseteq -\mathbb R\)。
-这题我会!
-\(1,2,1,3,1,4,...,1,n,1,n+1,...\),于是 \(E=\lbrace 1 , +\infty \rbrace\)。
试举一个数列 \(\{a_n\}_{n\geqslant -1}\) 作为例子,使得 \(E\) -为无穷集。
-这题我也会!
-\(1,1,2,1,2,3,1,2,3,4,1,2,3,4,5,...\),于是 -\(E=\mathbb Z ^{+} \cup \lbrace + \infty -\rbrace\)。
-有可数集那味了!
*素数的倒数和
-根据第七次课的内容,对于 \(s>1\),我们可以定义 \(\zeta\)-函数 \(\zeta(s)=\sum_{n=1}^\infty -\frac{1}{n^s}\),
-并且证明了Euler乘积公式:\(\zeta(s)=\prod_{p\in -\mathcal{P}}\frac{1}{1-p^{-s}}\),其中 \(\mathcal{P}\) 是全体素数的集合。
-据此证明,级数 \(\sum_{p\in -\mathcal{P}}\frac{1}{p^s}\) 对于 \(s>1\) 是收敛的;对于 \(0<s\leqslant 1\) -是发散的(这给出了有无穷多个素数的另一个证明)。
-胡说八道:
-我觉得吧,\(\zeta(s)=\prod_{p\in -\mathcal{P}}\frac{1}{1-p^{-s}} = \prod_{p\in -\mathcal{P}}(1+\frac{1}{p^{s} - 1})\) 收敛等价于 \(\sum_{p\in \mathcal{P}} \frac{1}{p^{s} - -1}\) 收敛,那么 \(s >1\) -时素数的倒数和也收敛。
-(毫无必要啊!直接小于调和级数和就可以了 T_T)
-其实我想胡说八道的是,\(\zeta(s)=\prod_{p\in -\mathcal{P}}\frac{1}{1-p^{-s}}\) 收敛能不能等价于 \(\zeta(s)=\prod_{p\in -\mathcal{P}}(1-p^{-s})\) 收敛,再等价于 \(\sum_{p \in \mathcal P} p^{-s}\) 收敛?
-*Basel问题的Euler“证明”
-对任意的 \(\theta\in \mathbb R\) 和 -\(n\in \mathbb{Z}_{\geqslant -1}\),试证明恒等式 \(\frac{\sin\bigl((2n+1)\theta\bigr)}{(2n+1)\sin\theta}=\prod_{k=1}^n -\left(1-\frac{\sin^2(\theta)}{\sin^2\left(\frac{k\pi}{2n+1}\right)}\right)\)
-据此证明,对任意的 \(x\in \mathbb -R\),我们都有 \(\frac{\sin(\pi x)}{\pi -x}=\prod_{n=1}^\infty\left(1-\frac{x^2}{n^2}\right)\)
-(如果 \(x=0\),我们将左边定义为极限 -\(\displaystyle \lim_{x\rightarrow -0}\frac{\sin(\pi x)}{\pi x}\))
-胡说八道:
-这题还真的不是胡说八道,第一问是数值分析里学过的,第二类 Chebyshev -多项式代入化简((
-后一问大概只要取 \(\theta = \frac{\pi -x}{2n+1}\),然后让 \(n \to -\infty\)。
---Remark:
-根据上面的公式,形式上,我们就有 \(sin(\pi -x)=\pi x\prod_{n=1}^\infty\left(1-\frac{x^2}{n^2}\right)=\pi -x\left(1-\left(\sum_{n=1}^\infty\frac{1}{n^2}\right)x^2+(\cdots)x^4+(\cdots)x^6+\cdots -\right)\)
-所以,右边 \(x^3\) 的系数就是 \(\displaystyle-\pi\sum_{n=1}^\infty\frac{1}{n^2}\)。根据我们对于 -\(\sin\) 的定义
-\(\sin z =\frac{e^{iz}-e^{-iz}}{2i} = -\sum_{k=0}^\infty \frac{(-1)^k z^{2k+1}}{(2k+1)!}\)
-所以,\(\sin(\pi x)\) 中展开式的 -\(x^3\) 项的系数是 \(-\dfrac{\pi^3}{6}\)。比较系数,我们得到所谓的Basel问题的解:
-\(\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}\)
-这是 Euler 原始的想法,他就是利用了上面的乘积公式来猜测最终的极限是 -\(\dfrac{\pi^2}{6}\)。有趣的是,他观察到 -\(\dfrac{\sin(\pi x)}{\pi x}\) -的零点恰好是 \(x=\pm n\),所以如果 -\(\dfrac{\sin(\pi x)}{\pi x}\) -的行为与多项式类似的话,那么这个函数应该是单项式的乘积,所以 Euler -认为
-\(\frac{\sin(\pi x)}{\pi x}=c\prod_{n\in -\mathbb{Z}-\{0\}}\left(1-\frac{x}{n}\right)=c\prod_{n=1}^\infty\left(1-\frac{x^2}{n^2}\right)\)。
-其中 \(c\) 是一个待定的常数,通过取 -\(x\rightarrow 0\) 的极限,他计算出 -\(c=1\)。
-
连续性
-进入新的章节啦!qwq
-2023 年 1 月 27 日,星期五,我要先去睡个觉((
-函数的连续性
+Polynomial Regression
+多项式回归可能会导致很强的共线性,比如一个只取 \(0\) 和 \(1\) 的类别型变量取 \(x\) 和 \(x^2\)进入模型就完全共线。
+有一个弥补的方案就是使用 centered +data,为每一个变量减去一个均值,导致数值有正有负,再做非负的平方项就得到共线性不那么强的两个解释变量。实际上再进一步对数据做尺度上的标准化也可以,但是对系数估计没有任何影响。
+对数据做中心化不会导致高阶项的系数改变,但有可能会导致低阶项的系数和 +extra sum of squares +变化。另外如果显著性不随之变化的话也有可能是出现了正交设计的情况,需要按照结果分析。
+交互项
+模型中存在交互项的本质就是 \(X_i\) +对于 \(Y\) 的效应和回归系数估计都会受到 +\(X_j\) 的影响。
-
-
函数值在单点处的收敛有两种定义方式,一个是任意收敛点列,一个是 -\(\varepsilon - \delta\) -语言。关于在单点处的连续性,Heine 定理保证二者是等价的。
-证明中可以灵活选用两种定义方式,很可能一种比另一种叙述起来简单很多。
-单点连续,局部连续和全局连续是完全不一样的概念。最基础的定义是关于函数值的单点连续性的,全局连续往往由开覆盖的全体局部连续推出。
-*所以说,函数的连续性本质上是一个局部的性质。很重要的一个例子是,假设函数 -\(f\colon I_1\cup I_2\rightarrow \mathbb -R\) 定义在两个不相交的开区间的并集上,按照定义,如果 \(f\) 在每个点上都连续,\(f\) 就是在 \(I_1\cup I_2\) 上连续的。尽管函数图像在 -\(I_1\cup I_2\) -是“断开的”,这个函数仍然是连续的(因为连续性本质上是个局部性质,在 \(I_1\) 和 \(I_2\) 上分别连续即可)。
-用 \(C(I)\) 表示区间 \(I\) 上的连续函数的全体所构成的集合,\((C(I),+,⋅)\) 是一个环。
--
-不夸张的说,我们在数学中遇到(几乎)一切连续函数都是通过两种手段构造的:第一,通过连续函数的复合和四则运算;第二,通过逼近的方式,特别是级数的方式来定义,比如说 -\(\exp\) -的构造。这种逼近的方式是最值得我们注意的,我们很快会发现,\(C(I)\) 这个空间和实数 \(\mathbb R\) -很相似,构造无理数就是通过有理数逼近的方式。
-更具体一点,我们会在 \(C(I)\) -上面给定一个范数 \(\|\cdot -\|_{\infty}\) 并且证明这样得到的赋范线性空间是完备的。此时,任给 -\(f\in -C(I)\),我们可以仿照实数的情况定义 \(e^f : =\sum_{n=0}^\infty -\frac{f^k}{n!}\)。
-在完备的赋范线性空间中,我们只要全盘照抄实数的情况就可以证明上面的(函数)级数收敛,从而 -\(e^f\) -是良好定义的并且是连续函数。特别地,我们可以通过这种方式定义 \(e^x\)(把 \(x\) 看成是函数 \(f\))而且说明这和我们最初定义的 \(\exp(x)\) 是一码事。
-在这种类比下,我们就可以利用对实数的直观来研究函数空间,从而得到很多关于函数的深刻结果。在课程后面的学习中,我们会遇到很具体的例子,比方说存在处处连续但是处处都不能微分的函数,我们就是通过构造函数的级数来实现的。
-总之,从用具体的级数和定义 \(e\),再定义出 \(e^x\),然后介绍了赋范线性空间以及为矩阵定义了 -\(e^A\),现在又为函数定义了 \(e^f\)。每当不知道怎么理解 \(e\) -的时候,试着代入级数就懂了。期待一些函数级数收敛构造出的连续函数。
+如果 \(X_2\) 是连续型变量而 +\(X_1\) +是类别型变量,回归模型中包含二者的交互项,例如:
+\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 ++ \beta_3 X_1X_2+\varepsilon\]
+这就说明对于 group 1,也就是 \(X_1 = +0\) 时模型是 \(Y = \beta_0+ \beta_2 X_2 ++ \varepsilon\),对于 group 2 也就是 \(X_1 = 1\) 时模型是 \(Y = (\beta_0 + \beta_1 )+(\beta_2 + \beta_3)X_2 + +\varepsilon\)。希望检验的问题是 \(\beta_1,\beta_3\) 是否为 \(0\) +来查看两组回归线的斜率、截距之间是否存在差异。
+如果二者都是连续型变量也是类似的情况,相比之下类别型变量和连续型变量的交互效应有显著的分组意义。
连续映射
+Lecture 11
+模型选择方法
+一些没那么数学的
-
-
连续函数是一个局限比较强的定义,把 $C $ -映射到它自身而已。所以要定义一个连续映射的概念;
-假设 \((X,d)\) 和 \((Y,d_Y)\) 是两个距离空间,\(f\colon X\rightarrow Y\) -是这两个距离空间之间的映射。假设 \(x_0\in -X\),\(y_0=f(x_0)\in -Y\)。如果对任意 \(\varepsilon>0\),总存在 \(\delta>0\),使得对任意满足 \(d(x,x_0)<\delta\) 的 \(x \in X\),都有 \(d_Y\bigl(f(x),f(x_0)\bigr)<\varepsilon\),我们就称 -\(f\) 在 \(x_0\) 处连续。如果 \(f\) 在 \(X\) 的每个点处都连续,那么我们就称 \(f\) 是连续映射。
-我们可以看到,连续映射的自由度很大,两个距离空间的元素,各自的范数定义都很自由。
-考虑一个 \(\exp : M_n(\mathbb C) \to -M_n(\mathbb C)\) -的映射,它的定义我们用级数写过也证明收敛了,下面来证明它是连续映射。记 -\(M_n(\mathbb C)\) 上的范数是 Frobenius -范数,它是一个相容范数,放缩起来会比较容易(我不是很懂为什么讲义上说这是 -\(2-\)范数,矩阵的 \(2-\)范数不是特征值相关的那个嘛?),\(\exp(A) = \sum_{k=0} ^{+\infty} {A^k \over -k!}\)。
-\(\exp : \mathbb R \to \mathbb R\) -的证明用 \(\varepsilon - \delta\) -语言就能轻松地写完。把它迁移到矩阵空间上,证明会复杂一些,用了相容范数的性质。
+- 喜闻乐见的穷举,可惜只能处理不超过 \(n=40\) 个变量的情况 +
- stepwise greedy method,不喜闻乐见的要写代码,理解 idea +就好(心虚
连续函数的性质
+一些准则
+假设可供选择的 explanatory variable 有 \(P-1\) 个,从中选择 \(p-1\) 个并进行判断。
-
-
一个关于单调函数的性质,感觉还挺有必要记一下:
-\(I\) 是区间(可开可闭),\(f\colon I \rightarrow \mathbb R\) 是 \(I\) 上的单调函数,那么
+观察 \(R^2\) 和 adjusted \(R^2\),取后者较大的模型
+观察 mallow's \(C_p\),\(\Gamma_p = \frac{E(SSE(p))}{\sigma^2} - (n-2p) +\geq p\),实际上在操作中只能取 \(\hat +\Gamma_p = \frac{SSE(p)}{MSE(P)}-(n-2p)\)。
-
-
对任意 \(x_0\in I\),\(f\) 在 \(x_0\) 处的左极限 \(\displaystyle\lim_{x\rightarrow -x_0^-}f(x)\) 和右极限 \(\displaystyle\lim_{x\rightarrow -x_0^+}f(x)\) 都存在(原文如此。但是如果 \(I\) 是闭区间而 \(x_0\) 是其端点,那么 \(f\) 在 \(x_0\) 处的左/右极限可能为无穷)
-\(f\) 在 \(I\) -上的不连续点的集合是可数的。(这表明单调函数 \(f\) 在“大部分”点处都是连续的)
+- 如果 \(\hat \Gamma_p \gg p\) +说明存在显著的误差,可能遗漏了重要的变量没有进入模型 +
- 如果 \(\hat \Gamma_p \ll p\) +说明过拟合了,导致 \(SSE(p) \ll +MSE(P)\) +
- 如果 \(\hat \Gamma_p \approx p\) +说明是 unbiased,取接近于 \(p\) 的 +mallow's \(C_p\) +中最小的一个对应的模型。
第一问的证明其实也是取 \(x_0\) -点左侧的无穷点列,它们的函数值构成有上界的无穷点列,一定有极限。不妨设 -\(f\) -是一个单调增函数,则这个极限可以表示为 \(\sup -f(x) , x \in (x_0 , x_0 - -\delta)\)。再验证这个极限是左极限,用上确界的性质。
-第二问的话,放一个证明在这里:
--
考虑 \(f\) 的不连续点的集合 \(Y=\bigl\{y\in I\bigm| \text{$f$ 在 $y$ -处不连续}\bigr\}\)。
-对于任意 \(y\in Y\),按照定义,\(\displaystyle \lim_{x\rightarrow x_0^-}f(x)\neq -\lim_{x\rightarrow -x_0^+}f(x)\)。再利用上面推论中的结论,我们知道,对任意 \(y\in Y\),我们有 \(\lim_{x\rightarrow y^-}f(x) < -\lim_{x\rightarrow y^+}f(x)\)。
-据此,对于任意 \(y\in -Y\),都唯一地确定了一个非空的开区间 \(I_y=(\lim_{x\rightarrow -y^-}f(x),\lim_{x\rightarrow y^+}f(x))\),即我们构造了映射 \(Y\rightarrow \bigl\{\text{$\mathbb R$ -上的全体非空开区间}\bigr\}, \ \ y\mapsto I_y\)
-利用单调性,我们首先说明对任意的 \(y_1,y_2\in Y\),\(y_1\neq y_2\),\(I_{y_1}\cap I_{y_2}=\emptyset\):
-不妨假设 \(y_1<y_2\),根据上面的推论的结论,我们可以选取单调下降的数列 -\(\{x_k\}_{k\geqslant 1}\),使得 \(x_k \downarrow y_1\)(从右边逼近)并且 -\(\displaystyle\lim_{k\rightarrow \infty} -f(x_k)\) 为 \(I_{y_1}\) -的右端点;类似地,我们选取单调上升的数列 \(\{z_k\}_{k\geqslant 1}\),\(z_k\uparrow y_2\)(从左边逼近),使得 \(\displaystyle\lim_{k\rightarrow \infty} -f(z_k)\) 为 \(I_{y_2}\) -的左端点。由于 \(y_1<y_2\),我们可以假设对任意 \(k\) 都有 \(x_k<z_k\),所以 \(\displaystyle\lim_{k\rightarrow \infty} -f(x_k)\leqslant \displaystyle\lim_{k\rightarrow \infty} -f(z_k)\),也就是说 \(I_{y_1}\) -的右端点要么在 \(I_{y_2}\) -的左端点的左边要么重合,由于这两个区间都是开区间,所以它们的交集是空集。
-这样,我们就得到了一组 \(\mathbb R\) -上两两不相交的非空开区间 \(\bigl\{I_y\bigm| -y\in Y\bigr\}\),我们在每个开区间 \(I_y\) 里选定一个有理数 \(q_y\),由于这些开区间互不相交,这些有理数 -\(q_y\) -也决定了这些开区间。从而,我们得到了单射
-\(Y\rightarrow \mathbb{Q}, \ \ y\mapsto -q_y\)。
-由于有理数是可数的,所以 \(Y\) -可数。
-
-介值定理。
-又到了我最爱的闭区间套定理时间!.jpg。为什么说是我最爱的闭区间套定理呢,因为:
--
-我:先做 ddl 最晚的作业,然后往前慢慢推,就能正好在最早的 ddl -之前写完所有作业
-室友:那要是最早的 ddl 之前没完成怎么办
-我:不会的,闭区间套定理保证哪怕有无穷个 -ddl,也还可以有一个时刻在“做完所有作业”和“第一个 ddl -到来”这个区间里(
-我们要求介值定理的区间一定是一个“连通的”区间,也即所谓的 \([a,b]\),否则会举出反例。毕竟,函数的连续性并不要求定义域也是连续的,在若干个区间上分别定义出的连续函数接在一起,就是一个全局连续的函数,但是不能满足介值定理。
-介值定理有很多奇技淫巧的题目,我在学微积分 A -的时候也写过一些,虽然挺好玩,但是感觉并没有什么意义。它比较有意义的一个点在于,第一次成功通过给定的一个任意函数值找到它的原像,也就是说可以用来得到一些“逆映射”的结论。对于闭区间上的单调函数,直观上来说它的逆是比较好找的,这是一个可以通过介值定理得到的结论。
-\(f\colon [a,b]\rightarrow \mathbb -R\) 是严格递增(或者递减)的连续函数,那么 \(f\) 是从 \([a,b]\) 到 \([f(a),f(b)]\) 的双射,并且其逆映射 \(f^{-1}\colon [f(a),f(b)]\rightarrow [a,b]\) -是连续的。
--
-Remark:这是 \(1\)-元函数的特殊性质,究其根本,是因为 -\(1\) 维空间上面 \(\mathbb R\) 有序关系 \(\leqslant\) 而在 \(\mathbb R^n\) 上是没有的。
-由此,我们可以为一些单调的初等函数构造它们的逆,也终于可以得到 \(\sqrt{x},\log x\) 这样的函数了。
-一般的对数函数和幂函数只要改变一些系数就能得到,比如 \(x^ \alpha = e^ {\alpha \log{x} }\),\(\log_\alpha (x)= {\log x \over \log -\alpha}\)。实际上,这二者既分别关于 \(x\) 和 \(\alpha\) 连续,也关于 \((x,\alpha)\) -连续。(这是两个不同的概念)
--
Remark:中学我们对 \(e\) -的了解很少,所以和 \(e\) -相关的对象反而变得容易理解,因为我们只需要验证关于 \(e\) -的很少的几个已经知道的性质即可;然而,对于 \(\pi\) 以及相关的 \(\sin x\) -等三角函数,我们了解很多它们的性质,这反而给我们新发展的函数理论带来了很大的挑战:我们在定义这些对象的同时要能够证明它们满足所知的所有性质。实际上,我们必须建立了整个微积分的理论之后才能够做到这一点。
-日本京都大学的数学家望月新一在他的宇宙际Teichmuller理论的论文(他在这一系列论文中声称他证明了abc猜想,目前还没有得到承认)里说:Unlike -many mathematical papers, which are devoted to verifying properties of -mathematical objects that are either well-known or easily constructed -from well-known mathematical objects, in the present series of papers, -most of our efforts will be devoted to constructing new mathematical -objects. 我们这里构造的幂函数就是他所说的“well-known or easily -constructed from well-known mathematical objects”。
-
-假设 \(\mathbb R\) 上定义函数 -\(f(x)\) 是连续的,如果我们知道 \(f\) 在有理数上的取值,那么对任意的无理数 -\(x\),我们任取一列有理数 \(r_i\),使得 \(r_i\rightarrow x\),连续性保证了 \(\displaystyle f(x)=f(\lim_{i\rightarrow \infty} -r_i)=\lim_{i\rightarrow \infty } f(r_i)\),所以 \(f(x)\) 可以确定。注意到 \(\mathbb{Q}\) 是 \(\mathbb R\) -中“很小”的子集,由连续性,它已经可以确定 \(f\) -了!这是分析学最重要的精神之一:如何从“局部”到整体。
-如果这个局部是对于整体稠密的,那么它完全可以决定整体。严格的表述是:
-\((X,d)\) 和 \((Y,d_Y)\) 是距离空间,\(X' \subset X\) -是一个稠密的子集,我们仍然用 \(d\) 表示 -\(X'\) 上的距离。对任意的连续映射 -\(F_1\colon X\rightarrow Y\) 和 \(F_2\colon X\rightarrow Y\),\(F_1\big|_{X'}=F_2\big|_{X'}\),那么,\(F_1=F_2\),换而言之,连续映射被它在一个稠密子集上的限制所决定。
-假设 \(x\in X\),我们任意选取 \(\{x'_n\}_{n\geqslant 1}\subset -X'\),使得 \(x'_n\rightarrow -x\)。因为 \(F_1\) 和 \(F_2\) 在 \(X\) 上连续,所以
-\(F_1(x)=\lim_{n\rightarrow -\infty}F_1(x'_n)=\lim_{n\rightarrow -\infty}F_2(x'_n)=F_2(x)\),命题得证。
+\(AIC = n \log (\frac{SSE(p)}{n}) + +2p\),\(BIC = n \log (\frac{SSE(p)}{n}) ++ (\log n)p\),二者都是最小值对应的模型最合适。
+注意 BIC 实际上相比 AIC +加了一个更大的惩罚在模型的变量数上,更注重解释性;一般来说有 \(BIC>AIC\)。
+Predicted Residual Error Sum of Squares:\(PRESS(p) = \sum_{i=1}^n (Y_i - \hat +Y_{i(-i)})^2\),实际上有 \(Y_i - \hat +Y_{i(-i)} = \frac{e_i}{1-h_{ii}}\)。
+取使得 \(PRESS(p)\) +最小的模型。用来观察过拟合与否。
+Prediction \(R_p^2\):\(R_p^2 = +1-\frac{PRESS}{SST}\),如果模型里噪音过大,则有 \(PRESS >SST\),此时 \(R_p^2<0\) 也是可以取负值的。如果有 \(R_p^2 \ll R^2\) +则也可能是过拟合了,即使有些独立变量是显著的。
实际上理论的形式对于 \(P\) 有 \(\Gamma_P =P\)。
+连续函数的拓扑刻画
-不是,怎么唐突开始升级了啊!
-2023 年 1 月 28 -日,星期六,我妈开始上班了所以我终于可以白天学这个东西了.jpg
---在开始介绍拓扑的概念之前, 我们引用 John von Neumann 的一段话:
-Young man, in mathematics you don’t understand things. You just get -used to them.
-
稍微有点难(
-大概也没什么可写的,因为全都没见过所以大概只能抄概念,那还不如直接看原文,而且我已经纸质抄过一遍了 -qwq
-而且实际上所有的东西又在习题里以距离空间的加强版出现了。实数轴上唯一不同的是,开集可以表示为可数个开区间的并,这是特有的性质。
-Summary
-之前讨论极限某种意义上来说都是关于点,性质也都是离散的。这一节考虑了函数的性质,涉及到连续变化的集合的函数值的性质。但令人欣慰的是,至少关于函数连续性的讨论还是可以通过点列、\(\varepsilon - \delta\) -语言来进行,这是已经熟悉的内容。
-其次,我们在这一部分之前对于函数的定义,只有基本的多项式函数、一些收敛的级数和 -\(e^x\)。一方面,通过介值定理我们基于单调函数的逆映射得到了 -\(x^{1 \over n}\),\(\log _{\alpha} x\) -函数的定义,并确认它们也是连续函数;另一方面,我们继续拓展了 \(e\) 相关函数的定义丰富性,从原始的 \(e\) 到 \(e^x\),再到赋范线性空间上的 \(e^A\)(尽管它不能满足一些 \(e^x\) 有的性质),这一次又添加了 \(e^f\) -的定义。即使都是在级数的意义下进行定义,看起来大同小异,但是分别验证收敛性是必要的,这次还额外验证了 -\(e^A\) 在 Frobenius -范数下的连续性。
-然后学了一点拓扑内容,大概讲了讲开集闭集的概念,引出了连续函数的第三种刻画:等价于任意开集的逆映集还是开集。
-梦话:胡说八道一些证明题
-计算对于做题家来说太 trivial -了,所以胡说八道一些证明题。我想我也没有非常胡说八道,毕竟不会做的题你让我胡说八道,我也说不出来什么,sigh。
-距离空间上的拓扑与连续性
--
-
(距离空间上的Heine定理)假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) -是映射。我们有两种方式来定义连续映射(参见第3次作业题的A3)和第9次课)
+我们选择模型一般会考虑 adjusted \(R^2\),AIC 或者 mallow's \(C_p\)。
+模型诊断
+Partial Regression Plots
+每个 \(X_i\) 都可以做出一张 partial +regression plot,也即所谓的 AV-plot,实际上就是对 \(Y|X_{-i} \sim X_i|X_{-i}\) +这两部分残差互相做回归得到的图,展示了完整模型中 \(Y \sim X_i\) +之间的边际关系。也可以用来检测非线性关系、异方差问题和 outliers。
+Studentized Residuals
+补充在 Lecture 6 里了。
+Assessing Outliers
+有以下指标可以考虑:
-
-
假设 \(x_0\in X\),如果对任意 -\(X\) 中的点列 \(\{x_n\}_{n\geqslant 1}\),\(x_n\stackrel{d_X}{\longrightarrow}x_0\),我们都有 -\(f(x_n)\stackrel{d_Y}{\longrightarrow}f(x_0)\),我们就称 -\(f\) 在 \(x_0\) 处是连续的。如果 \(f\) 在一切 \(x\in -X\) 处均连续,那么我们就称 \(f\) -是距离空间之间的连续映射。
-假设 \(x_0\in X\),\(y_0=f(x_0)\in Y\)。如果对任意的 \(\varepsilon>0\),总存在 \(\delta>0\),使得对任意满足 \(d_X(x,x_0)<\delta\) 的 \(x \in X\),都有 \(d_Y\bigl(f(x),f(x_0)\bigr)<\varepsilon\),我们就称 -\(f\) 在 \(x_0\) 处连续。如果 \(f\) 在 \(X\) 的每个点处都连续,那么我们就称 \(f\) 是连续映射。
-证明,上面两个对连续映射的定义是等价的。
+Difference caused to fitted values:\((DFFIT)_i = \hat Y_i - \hat Y_{i(-i)} = +\frac{h_{ii}}{1-h_{ii}} e_i\)
+Studentized DFFIT:\((DFFITS)_i = +\frac{\hat Y_i - \hat Y_{i(-i)}}{\sqrt{MSE_{-i} h_{ii}}} = t_i +\sqrt{\frac{h_{ii}}{1-h_{ii}}}\)。
+对于不太大的数据量,如果 \(|DFFITS|>1\) +则认为是强影响力点,大数据量时认为 \(|DFFITS|>2\frac{\sqrt p}{\sqrt n}\) +是强影响力点。
+Cook's Distance:\(D_i = \frac{e_i^2}{p +\cdot MSE} \frac{h_{ii}}{(1-h_{ii})^2}\),在 R +中认为某个点有强影响力的 threshold 是 \(0.5\),事实上如果一个点的 Cook's distance +分布距离其他点较远,就可以认为是强影响力点了。
+Difference in Beta Estimates:\((DFBETAS)_{k(-i)} = \frac{b_k - +b_{k(-i)}}{\sqrt{MSE_{(-i)} c_{kk}}}\),其中 \(c_{kk}\) 是 \((X^TX)^{-1}\) 的第 \(k \times k\) 个分量。
+对于大的数据量,如果 \(|DFFITS|>1\) +则认为是对于回归系数估计值的强影响力点,不太大的数据量时认为 \(|DFFITS|>\frac{2}{\sqrt n}\) +是对于回归系数估计值的强影响力点。
Trivial.
-\((X,d)\) 是距离空间。对任意的点 -\(x\in X\),\(r>0\),我们称 \(B(x,r)=\bigl\{y\in X\mid -d(y,x)<r\bigr\}\) 为以 \(x\) -为中心以 \(r\) -为半径的开球。证明,对任意的点 \(x\in -X\),\(r>0\),如果 \(x'\in B(x,r)\),那么存在 \(r'>0\),使得 \(B(x',r')\subset B(x,r)\)。
-如果 \(U\subset X\) -是若干开球的并,即 \(U=\displaystyle -\bigcup_{\alpha \in \mathcal{A}} B(x_\alpha,r_\alpha)\)(指标集 -\(\mathcal{A}\) 是任意的),就称 \(X\) 是距离空间 \((X,d)\) 中的开集。证明,\(U\subset X\) 是开集当且仅当对任意的 \(x\in U\),存在 \(\delta_x>0\),使得 \(B(x,\delta_x)\subset U\)。
-前一问按照定义写一下就可以了;后一问用前一问的结论。Trivial.
-直观上来看就是,取开球内部的一个点,有一个这个点决定的小球在开球内。其实就是开区间的推广。
-(距离空间上的标准拓扑)我们用 \(\mathcal{T}\) 表示距离空间 \((X,d)\) 上的开集的全体,其中,我们规定 -\(\emptyset\) 和 \(X\) 都是开集。证明,它们满足:
+Multicollinearity Diagnose
+有以下两个指标:
-
-
- \(\emptyset \in \mathcal{T}\), -\(X \in \mathcal{T}\)。 -
- 对任意开集的集合 \(\{U_{\alpha}\}_{\alpha -\in \mathcal{A}}\),其中 \(\mathcal{A}\) 为指标集合,我们有 \(\displaystyle\bigcup_{\alpha \in -\mathcal{A}}U_\alpha \in \mathcal{T}\)。 -
- 对任意有限个开集 \(U_1,U_2,\cdots, U_m \in -\mathcal{T}\),我们有 \(\displaystyle\bigcap_{1\leqslant i\leqslant m}U_i -\in \mathcal{T}\)。 +
- Variance Inflation +Factor:多重共线性经常导致方差膨胀,这是一个表征的指标,\((VIF)_k = (1- R_k^2)^{-1}\),其中 \(R_k^2\) 指的是将 \(X_k\) 相对于其他 \(p-2\) 个 explanatory variable +做回归得到的决定系数。如果 \((VIF)_k \gg +1\) 则认为第 \(k\) 个变量 \(X_k\) 是会发生多重共线性的变量。 +
- Tolerance:\(TOL = +1/VIF\),判断准则类似上述。
第一个是定义,第二个也是定义。
-第三个的话,取 \(x \in -\displaystyle\bigcap_{1\leqslant i\leqslant m}U_i\),有小球 \(B(x,\delta _i) \in -U_i\),则最小的一个开球在全体开集的交集中。由 \(x\) -的任意性,用一下上一题的结论即证。
-\((X,d)\) 是距离空间。如果 \(F\subset X\) 的补集是开集,我们就称 \(F\) 是闭集。证明,\(F\) 是闭集当且仅当对任意点列 \(\{x_n\}_{n\geqslant 1}\in F\),如果 \(\displaystyle \lim_{n\rightarrow \infty}x_n = -x\),那么 \(x \in F\)。
-如果 \(F\) -是闭集,且对于这样的序列有 \(x \notin -F\),则 \(x \in X-F\),也就是说 -\(x\) 在一个开集中,有一个包裹 \(x\) -的小球也在开集中,所有这个序列里的点都和 \(x\) 隔着小球半径的距离,不可能收敛到 \(x\),矛盾。
-如果对任意的序列都有这样的结论,而且 \(F\) 不是闭集,\(X-F\) 不是开集,那么存在一个 \(x \in X-F\) 使得对任意 \(\delta >0\),都有 \(B(x,\delta)\) 不完全在 \(X-F\) 中。也就是说,对任意的 \(\delta >0\),总存在 \(y \in F\) 使得 \(d(x,y)<\delta\)。也就是说,存在一个 -\(F\) 中的收敛到 \(x\) 的序列,使得 \(x \notin F\),这和前提矛盾。
--
写逆命题也是一种技术,比如我差点以为一个集合不是开集就是闭集,这是不对的。
-比如说在实数集上,有 \((1,2) \cup -(3,5]\) 既不是开集也不是闭集。
-
-证明,距离空间 \((X,d)\) -上的闭集,
+Lecture 12
+本节探讨 remedies for multiple linear +regression,主要是异方差情况和多重共线性。
+Equal Variance Remedy
+这一部分主要处理模型发生异方差问题的情况。
+也就是说,实际上有 \(\varepsilon_1, +\varepsilon_2, ..., \varepsilon_n\) 的方差不全为 \(\sigma^2\),记方差为 \(\sigma_1 ^2,\sigma_2 ^2 , ..., \sigma_n +^2\)。此时的 likelihood function 是:
+\[L(\beta_1,\beta_2) = \Pi_{i=1} ^n +f_i(\beta_1, \beta_2 |X_i,Y_i) = \Pi_{i=1}^n (\frac{1}{\sqrt{2\pi} +\sigma_i} exp(-\frac 1 2 (\frac{Y_i - \beta_0 -\beta_1 +X_i}{\sigma_i})^2)) \]
+可以看到 ordinary least square 条件得到的 \(b_0 = \hat \beta_0,b_1 = \hat \beta_1\) +不再满足 MLE 的条件。但如果是在不知异方差的情况下仍然使用 OLS 或者 MLE +条件得到的参数估计,仍然是可以满足无偏性的,但不满足最小方差性质。
+Weighted Regression
+简单来说,通过选取 \(\{ w_i = +\frac{1}{\sigma_i ^2} \}_{i=1} ^n\) 作为权重,考虑 \(\Sigma_{i=1} ^n w_i e_i^2 = \Sigma_{i=1} ^n +(\frac{Y_i - \beta_0 - \beta_1 X_{i,1} - ... - \beta_{p-1} +X_{i,p-1}}{\sigma_i})^2\) 的最小性问题。
-
-
- \(\emptyset\) 和 \(X\) 都是闭集。 -
- 任意多闭集的交集还是闭集。 -
- 有限个闭集的并集还是闭集。 +
最简单的情况,\(\sigma_1,...,\sigma_n\) 均已知,则有 \(w_i = \frac{1}{\sigma_i ^2}\),
+取 \(W = \begin{bmatrix} \frac{1}{\sigma_1 +^2} & & & \\ &...& & \\ & & & +\frac{1}{\sigma_n^2} \end{bmatrix}\) 使得回归问题变为 \(W^{\frac 1 2} Y = W^{\frac 1 2} X \beta + W^{\frac +1 2} \varepsilon\),记 \(Y^* = W^{\frac +1 2} Y, X^* = W^{\frac 1 2} X, \varepsilon^* = W^{\frac 1 2} +\varepsilon\),由于 \(Var(\varepsilon^*) = I_{n\times n}\) +满足同方差条件,因此新的回归问题是符合条件的。
+注意新的回归问题 \(Y^* = X^* \beta + +\varepsilon^*\) 事实上没有改变系数 \(\beta\),但系数估计 \(b_w = (X^TWX)^{-1} (X^TWY)\) +是改变了的,这是正常现象,因为对这一问题做 remedy +的主要原因就是假设不满足,导致按照 OLS 做出的系数估计不准确,因此 +weighted regression 做出的修正也是相对于原系数 \(\beta\) 的。
+\(b_w\) 仍然是无偏估计,也保证 \(Var(b_w) = (X^TWX)^{-1}\) +是最小方差。
+稍微复杂一点的情况,虽然 \(\sigma_i^2\) 未知但 \(\sigma^2_i / \sigma_j ^2\) 均已知,取 \(w_i = \frac{\sigma_1 ^2}{\sigma_i^2 }\) +即可。于是有:
+取 \(W = \sigma_1 ^2 \begin{bmatrix} +\frac{1}{\sigma_1 ^2} & & & \\ &...& & \\ & +& & \frac{1}{\sigma_n^2} \end{bmatrix}\) 使得回归问题变为 +\(W^{\frac 1 2} Y = W^{\frac 1 2} X \beta + +W^{\frac 1 2} \varepsilon\),记 \(Y^* = +W^{\frac 1 2} Y, X^* = W^{\frac 1 2} X, \varepsilon^* = W^{\frac 1 2} +\varepsilon\),由于 \(Var(\varepsilon^*) = \sigma_1 ^2 I_{n\times +n}\) 满足同方差条件,因此新的回归问题是符合条件的。
+新的回归系数估计是 \(b_w = +(X^TWX)^{-1}(X^TWY)\),\(Var(b_w) = +\sigma_1^2(X^TWX)^{-1}\),由此还可以做出对 \(\sigma_1\) 的参数估计,\(\hat \sigma_1 ^2 = MSE_{wls} = \frac{\Sigma(Y^*_i +- \hat Y^*_i)^2}{n-p}= \frac{\Sigma w_i(Y_i - \hat Y_i)^2}{n-p} = +\frac{\Sigma w_i e_i ^2}{n-p}\),其中 \(w_i = +\frac{\sigma_1^2}{\sigma_i^2}\)。
+一般情况下 \(\{ \sigma_i \}\) +是完全未知的,我们是在模型诊断中发现异方差的现象,因此不可能直接通过方差值推权重系数。这个时候一般有两种选择:
+-
+
重复试验取 \(Y_i\) 的方差估计 +\(s_i^2\),于是权重系数为 \(w_i = \frac{1}{s_i ^2}\)。
+先对 \(Y\sim X\) 进行 OLS +回归,取出此时的 residual \(\{e_i \}\) +作为 \(\{ \sigma _i \}\) 的估计,取 +\(w_i = \frac{1}{e_i ^2}\) +作为权重即可。
+效果不明显时多迭代几次。
+
这都是上上题的逆否,自然是成立的。
-假设 \((X,d_X)\) 和 \((Y,d_Y)\) 是距离空间,\(f\colon X\rightarrow Y\) -是映射。那么,如下三个叙述是等价的:
+在观察 weighted least square 和 ordinary least square +模型差别时,注意:
-
-
- \(f\) 是连续映射。 -
- 对任意 \(Y\) 中的开集 \(U\),其逆像 \(f^{-1}(U)\) 为 \(X\) 中的开集。 -
- 对任意 \(Y\) 中的闭集 \(F\),其逆像 \(f^{-1}(F)\) 为 \(X\) 中的闭集。 +
- \(R^2\) 以及 adjusted \(R^2\) 的数值差别没有很强的意义,WLS +情况下原始数据 \(\{ Y_i \}\) +已经发生了变化,实际上 SST 也已经变了,没有什么比较的意义。 +
- 需要关注的点是 residual standard error,越接近 \(1\) 越说明异方差的调整是成功的。 +
- 有时会观察到 WLS 情况下 \(\hat +\sigma^2\) 在减小,似乎数据的分散程度在减小,这是因为 MSE +在减小。但是 WLS 和 OLS 情况下的 MSE 和 MST 都没有比较的意义,因此 \(\hat \sigma\) +的变化也没有研究的价值。唯一确定的是它会接近于 \(1\),这一点可以证明异方差的调整效果是成功的。
我不想证明 \((1)\) 和 \((3)\) 之间的关系,所以验证 \((1) \to (2)\),\((2) \to (1)\),\((2) \iff (3)\)。
-\((1) \to (2)\):如果 \(f\) 是连续映射,\(U\) 是开集,我们想证明对于任意的 \(x \in f^{-1}(U)\),有 \(x\) 为中心的一个开球也在 \(f^{-1}(U)\) 中。令 \(y=f(x)\),而 \(f\) 是连续映射,所以在 \(x\) 点也连续。于是对任意的 \(\varepsilon >0\),存在 \(\delta\) 使得对任意的 \(x'\in B(x,\delta)\),有 \(d(f(x),f(x'))<\varepsilon\),也即 -\(f(x') \in B(f(x),\varepsilon -)=B(y,\varepsilon)\)。因此,只要取满足 \(B(y,\varepsilon) \subset U\) 的 \(\varepsilon\),就能得到 \(B(x,\delta) \subset f^{-1}(U)\)。于是 \(f^{-1}(U)\) 也是开集,得证。
-\((2) \iff (3)\):只要证明 \(f^{-1}(F) \subset X-f^{-1}(X-F)\),还有 -\(f^{-1}(U) \subset -X-f^{-1}(X-U)\),trivial.
-\((2) \to -(1)\):现在假设对任意的开集 \(U\),\(f^{-1}(U)\) 是开集,我们来证明 \(f\) 是连续的:给定 \(x_0\in \mathbb R\),令 \(y_0=f(x_0)\),考虑 \(y_0\) 处的开集 \(B(y_0,\delta)\)。由于 \(f^{-1}\bigl(B(y_0,\delta)\bigr)\) 为开集且 -\(x_0\in -f^{-1}\bigl(B(y_0,\delta)\bigr)\),所以存在 \(\varepsilon >0\),使得 \(B(x_0,\varepsilon)\subset -f^{-1}\bigl(B(y_0,\delta)\bigr)\),从而,\(f\bigl(B(x_0,\varepsilon)\bigr)\subset -B(y_0,\delta)\),这说明对任意的 \(\delta\),存在 \(\varepsilon\),使得当 $ d(x,x_0)<$ -时,我们有 \(d(f(x),f(x_0))<\delta\),从而 \(f\) 在 \(x_0\) 处连续。
-\((X,d)\) 是距离空间,\(A\subset X\) 是子集,我们将包含 \(A\) 的所有闭集交 \(\overline{A}\) 为 \(A\) 的闭包,根据上题,这是闭集,所以是包含 -\(A\) 的最小闭集。
-对于 \(x\in X\),如果存在点列 \(\{a_k\}_{k\geqslant 1}\subset A\),使得 -\(\displaystyle \lim_{k\rightarrow \infty}a_k -= x\),并且其中 \(a_k\neq -x\),我们就称 \(x\) 是 \(A\) 的一个聚点。
-\(A\) 的聚点不一定都在 \(A\) 中,\(A\) 中的点也不一定都是 \(A\) 的聚点。\(A\) 中不是 \(A\) 的聚点的点被称为 \(A\) 的孤立点。\(A\) 的聚点组成的集合被称为 \(A\) 的导集,记作 \(A'\)。如果 \(X=X'\),我们称 \(X\) 为完美集。
-证明,\(\overline{A}=A'\cup -A\)。特别地,\(F\) -是闭集当且仅当 \(F\) 的聚点都在 \(F\) 中,即 \(F=F'\cup F=\overline{F}\)。
-首先证明闭包里包含所有聚点(包含 \(A\) 是显然的)。如果有一个序列和它们的极限 -\(x\) 使得 \(x \neq x_n\),且 \(x \notin \bar{A}\),这和 \(\bar{A}\) 是闭集矛盾。因此 \(\overline{A} \supset A'\cup -A\)(看起来好别扭
-再证明闭包里所有的点要么在 \(A\) -中,要么是聚点。如果有 \(x \in -\bar{A}\) 且 \(x \notin -A\),我们要证明它是一个聚点,只要构造出一个收敛到 \(x\) 的 \(A\) 中序列。实际上,对任意的 \(\varepsilon >0\) 都存在 \(x' \in A\) 使得 \(d(x',x)<\varepsilon\),也就是说 -\(B(x,\varepsilon)\) 始终和 \(A\) 有交。否则存在某个 \(\varepsilon\) 使得 \(A \cap B(x,\varepsilon) = -\emptyset\),那么一定有一个包含 \(A\) 的闭集 \(S=X-B(x,\varepsilon)\),\(x \notin S\),这和 \(x \in \bar{A}\) 矛盾。所以 \(x\) 一定是一个聚点。
-如果 \(A\) 是闭集,那么 \(A=\bar{A}\),所以聚点一定都在 \(A\) 中。
-(距离空间的乘积与连续映射)假设 \((Y,d_Y)\) 和 \((Z,d_Z)\) 是距离空间,我们定义 \(Y\times Z\) 上的距离函数
-\(d_{Y\times Z}\colon \bigl(Y\times -Z\bigr){ \times} \bigl(Y\times Z\bigr) \rightarrow \mathbb R_{\geqslant -0}, \ \ \bigl((y_1,z_1),(y_2,z_2)\bigr)\mapsto -\sqrt{d(y_1,y_2)^2+d(z_1,z_2)^2}\)
-证明,\(d_{Y\times Z}\) 是 \(Y\times Z\) -上的距离函数。证明,两个自然的投影映射是连续的:
-\(\pi_Y\colon Y\times Z \rightarrow Y, \ -(y,z)\mapsto y; \ \pi_Z\colon Y\times Z \rightarrow Z, \ (y,z)\mapsto -z\)
-证明,给定距离空间 \((X,d)\) 和 -\((Y\times Z,d_{Y\times Z})\) -之间的映射 \(F\colon X\rightarrow Y\times -Z\),那么,\(F\) -连续当且仅当两个复合映射 \(\pi_Y \circ F\colon -X\rightarrow Y\) 和 \(\pi_Z \circ -F\colon X\rightarrow Z\) 都连续。
-其实都挺 trivial 的。
-证明,加法映射 \(+\) 和乘法映射 -\(\times\) 都是连续映射,其中
-\(+\colon \mathbb R^2\rightarrow \mathbb R, -\ \ (x,y)\mapsto x+y; \ \ \ \ \times \colon \mathbb R^2\rightarrow -\mathbb R, \ \ (x,y)\mapsto x\cdot y\)
-Trivial.
-证明,矩阵上的加法映射 \(+\) -和乘法映射 \(\bullet\) -都是连续映射,其中
-\(+\colon \mathbf{M}_n(\mathbb R)\times -\mathbf{M}_n(\mathbb R)\rightarrow \mathbf{M}_n(\mathbb R), \ \ -(A,B)\mapsto A+B;\ \ \ \ \bullet\colon \mathbf{M}_n(\mathbb R)\times -\mathbf{M}_n(\mathbb R)\rightarrow \mathbf{M}_n(\mathbb R), \ \ -(A,B)\mapsto A\cdot B\)
-定义距离为 \(d(A,B) = -||A-B||_F\)(Frobenius -范数),然后就可以用相容性的不等式了,trivial.
-证明,\(\mathbf{M}_n(\mathbb -R)\) 上的可逆矩阵的全体 \(\mathbf{GL}_n(\mathbb R)\) 是 \(\mathbf{M}_n(\mathbb R)\) -中的开集。(提示:构造一个连续映射使得该集合是连续映射的逆像)
-做连续映射(行列式)\(det: \mathbb R^{n -\times n} \to \mathbb R\),\(A \to -det(A)\),于是 \(det^{-1} ((-\infty,0) -\cup (0,\infty)) = GL_n(\mathbb R)\) 是开集。
-至于行列式运算为什么是连续的,因为它本质上是关于 \(n^2\) -个变量的多项式(,所以关于各个分量连续。
-我胡说八道的啊,我觉得我好像有必要补一补高代(
-证明,取逆映射 \({\rm Inv}\colon -\mathbf{GL}_n(\mathbb R)\rightarrow \mathbf{GL}_n(\mathbb R), \ \ -A\mapsto A^{-1}\) 是连续映射。
-记任意可逆矩阵集 \(U\) 的原像为 -\(Inv^{-1} U\),它是 \(GL_n (\mathbb R)\) -的子集,也是一个开集。所以 \(Inv\) -是连续映射。
-看到这个 \(Inv\) 我还以为要联动 -Galois 理论了,吓一跳。
+模型假设是 \(Y_{ij} = \mu_i + +\varepsilon_{ij}\)。
+其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim +N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。考虑一些统计量作为参数的估计量:
+\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 +}^{n_i} Y_{ij} = \hat \mu _i\]
+\[\bar{Y}_{..} = \frac{1}{n_T} +\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r +n_i \bar{Y}_{i.}\]
+\[s_i ^2 = \Sigma_{j=1} ^{n_i} (Y_{ij} - +\bar Y_{i.})^2 / (n_i -1) \]
+\[s^2 =\Sigma_{i=1} ^r \Sigma_{j=1} ^{n_i} +(Y_{ij} - \bar Y_{i.})^2 =\frac{1}{n_T- r} \Sigma_{i=1}^r (n_i -1) s_i +^2 = \hat \sigma^2\]
+在这一模型中,我们关注的假设检验是 \(i\) 组实验之间是否存在差异,假设检验表示为 +\(H_0 : \mu_1= \mu_2 = ... = \mu_r = +\mu\),对应的备择假设即为 \(\{ \mu_i +\}_{i=1} ^r\) 中存在不同的项。检验最经典的方法即为 +ANOVA,analysis of variance。核心是以下的分解:
+\[\begin{aligned} SSTO = \Sigma_i +\Sigma_j(Y_{ij} - \bar Y_{..})^2 &= \Sigma_i \Sigma_j (Y_{ij} - \bar +Y_{i.} +\bar Y_{i.} - \bar Y_{..})^2 \\& = \Sigma_i n_i (\bar Y_{i.} +- \bar Y_{..})^2 + \Sigma_i \Sigma_j (Y_{ij} - \bar Y_{i.})^2 \\ +&=SSTR + SSE \end{aligned}\]
+可以观察到,\(SSTR\) +是组间差距,体现了不同组别之间的差别,\(SSE\) +是组内差距,体现了同一组内各数据的偏差。注意 \(SSTR\) 的自由度是 \(r-1\),\(SSE\) 的自由度是 \(n_T - r\),\(SSTO\) 的自由度是 \(n_T - 1\)。
+两个统计量的期望是 \(\mathbb E(MSE) = +\sigma^2\),\(\mathbb E(MSTR) = +\sigma^2 +\frac{\Sigma_i n_i (\mu _i -\mu_.)^2}{r-1}\),其中 +\(\mu_. = \frac{\Sigma_i n_i +\mu_i}{n_T}\)。
+在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 _{n_T - +r}\),\(\frac{SSTR}{\sigma^2} \sim +\chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,n_T -r}\) +作为最终的检验统计量。
+当 \(F^* > F(1-\alpha , r-1 , n_T +-r)\) 时拒绝原假设,否则接受;\(Power = +P(F^* > F(1-\alpha , r-1,n_T -r)| \delta)\),其中 \(\delta\) 是一个非中心偏移量,\(\delta = \frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i +n_i (\mu_i - \mu_.)^2}\)。
+也可以作为一个线性回归的问题来看待,design matrix 是 $ X =
+\[\begin{bmatrix} 1 & 0 & 0 & +... & 0 \\ 0 & 1 & 0 & ... & 0 \\ ... +&...&...&...&... \\ 0 & 0 & 0 & ... & 1 +\end{bmatrix}\] +$,系数向量是 \(\mu = \begin{bmatrix} \mu_1 +\\ \mu_2 \\ ... \\ \mu_r \end{bmatrix}\),因此整体的回归方程是 $ +Y = X + $,注意这个回归问题是强迫过原点的。
\(f\colon \mathbb R\rightarrow \mathbb -R\) 是函数,对 \(c\in \mathbb -R\),我们定义 \(f^{-1}(c)=\{x\in -\mathbb R\mid f(x)=c\}\)。证明,如果对任意 \(c\in \mathbb R\),我们都有 \(|f^{-1}(c)|=2\),那么 \(f\) 不是连续函数。
-说明任意取一个开集 \(U \subset -R\),都有 \(f^{-1}(U) = \lbrace 2 -\rbrace\) 或 \(\lbrace -2 -\rbrace\) 或 \(\lbrace 2,-2 -\rbrace\),都不是开集,所以 \(f\) 不连续。
-给我一点小小的拓扑震撼(
-貌似也可以用介值定理,就随便讨论一下,夹几个区间出来就行,但是没必要。
+Factor Effects Model 是 Cell Means Model +的一个重新参数化的结果。模型假设是 \(Y_{ij} = +\mu + \tau_i + \varepsilon_{ij}\)。
+其中,\(\mu_i\) +是整体的理论均值,\(\varepsilon _{ij} i.i.d. +\sim N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 +\(\mu , \tau_1 , ..., \tau_r , +\sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = +0\),如果没有这个约束会导致存在多组解。考虑一些统计量作为参数的估计量:
+\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 +}^{n_i} Y_{ij} = \hat \tau _i + \hat \mu\]
+\[\bar{Y}_{..} = \frac{1}{n_T} +\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r +n_i \bar{Y}_{i.} = \hat{\mu}\]
+\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 +/ (n_i -1) \]
+\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r +(n_i -1) s_i ^2 = \hat \sigma^2\]
+在这一模型中,我们关注的假设检验仍然是 \(i\) 组实验之间是否存在差异,假设检验表示为 +\(H_0 : \tau_1= \tau_2 = ... = \tau_r = +0\),对应的备择假设即为 \(\{ \mu_i +\}_{i=1} ^r\) 中存在不同的项。factor effects model +在参数的含义上比 cell mean model 更清晰。
+可以作为一个线性回归的问题来看待,design matrix 是 $ X =
+\[\begin{bmatrix} 1 & 1 & 0 & +... & 0 \\ 1 & 0 & 1 & ... & 0 \\ ... +&...&...&...&... \\ 1 & -1 & -1 & ... & +-1 \end{bmatrix}\] +$,系数向量是 \(\mu = \begin{bmatrix} \mu +\\ \tau_1 \\ \tau_2 \\ ... \\ \tau_{r-1} +\end{bmatrix}\),因此整体的回归方程是 $ Y = X + +$,注意这个回归问题的截距就是 \(\mu\),不强迫过原点,相比 cell mean model +算是做了一点点优化。
假设 \(A\subset \mathbb R\) -是一个可数集。证明,存在单调函数 \(f\colon -\mathbb R\rightarrow \mathbb R\),使得 \(f\) 的不连续点的集合恰好是 \(A\)。
-大概可以分段构造 \(f(x)=x+T_i,x \in -(x_i,x_{i+1})\),来保证是单调增函数且不连续。
-函数 \(f\colon [0,1]\rightarrow -[0,1]\) 是递增的函数,证明,\(f\) 有不动点。
-考虑 \(F(x)=f(x)-x\),一定有不动点。
-考虑 \([0,1]\) -到自身的自同胚,即 \({\rm -Homeo}([0,1])=\bigl\{f\colon [0,1]\rightarrow [0,1]\bigm| \text{$f$ -为连续的双射}\bigr\}\)
-我们知道对于任意的 \(f\in {\rm -Homeo}([0,1])\),\(f^{-1}\in {\rm -Homeo}([0,1])\)。假设 \(f\in {\rm -Homeo}([0,1])\) 并且 \(0\) 和 -\(1\) 是它仅有的不动点,\(g\in {\rm Homeo}([0,1])\) 并且 \(0\) 和 \(1\) 也是它仅有的不动点,证明,存在 \(h\in {\rm Homeo}([0,1])\),使得 \(h^{-1}\circ f\circ h =g\)。
+在做回归之前要注明哪些变量是 factor:
+> data$design = factor(data$design)
> fit = lm(cases ~ design, data = data)
> summary(fit)
+方便查看 \(\hat \mu_i\) +的命令是过原点回归,但查看 MSR 的方式是不过原点回归。
+\(Std.Error_i ^2 = Var(\hat \mu_i) = +Var(\frac{\Sigma_{j=1}^{n_i} Y_{ij}}{n_i}) = \frac{\hat \sigma^2}{n_i}= +\frac{s^2}{n_i}\)
+\(sd_i ^2 = s_i ^2\),由此计算出 +\(s^2\) 后再得到每个 \(Std.Error\) 的值是 \(\frac{s}{\sqrt n_i}\)。
- Tukey's HSD Method: 使用 q-test,取 \(t_c += \frac{\bar y _{max} - \bar y_{min}}{\sqrt 2 s /\sqrt +n}\);适用于两两检验。 +
- Scheffe's Method: 使用 F-test,取 \(t_c = +\sqrt{(r-1)F(1-\alpha, r-1, n_T +-r)}\),适用于线性组合的对照(contrast,见下)。实际上也过于保守了,导致 +power 比较低。 +
假设 \(f\colon X\rightarrow \mathbb -R\) 是连续函数,如果对任意的 \(\varepsilon>0\),存在 \(\delta>0\),使得对任意的 \(x,y\in X\),只要 \(d(x,y)<\delta\),就有 \(|f(x)-f(y)|<\varepsilon\),就称 \(f\) 在 \(X\) 上一致连续。
-看起来很像 Lipschitz 条件,不过 Lipschitz -条件其实是特化版的,是一致连续的充分条件,用来解决一些不动点问题。
-有界闭区间上的连续函数一定一致连续。
-一致收敛和逐点收敛的区别实际上是关于点 \(x\) 的差别,对 \(N\) 的依赖进行区分即可。对于一个函数序列 -\(\lbrace f_n : X \to R \rbrace\) -和函数 \(f: X \to R\),有:
-逐点收敛是指,对任意的 \(x \in -X\),任意 \(\varepsilon ->0\),存在 \(N=N(\varepsilon , -x)\) 使得当 \(n >N\) -时,\(| f_n(x) - f(x) | < -\varepsilon\)。
-一致收敛是指,对任意的 \(\varepsilon ->0\),存在 \(N=N(\varepsilon)\) 使得对任意的 \(x \in X\),有 \(|f_n(x) - f(x) | <\varepsilon\),也就是 -\(\sup_{x \in X} | f_n(x) - f(x) | -<\varepsilon\)。
-这样来看的话,显然有一致收敛能够推出逐点收敛,逐点收敛能推出一致收敛的要求是固定 -\(\varepsilon\) 时存在 \(N\) 的上确界 \(\sup _{x \in X}N(\varepsilon , -x)\),这个上确界不能是无穷。但 \(X\) 的形式不能在任意条件下保证这一点。
-从计算的角度来看,逐点收敛到的函数相当于固定 \(x\),取 \(n \to -\infty\),可以由此继续判断是否一致收敛到逐点收敛的函数。
+- \(A\) 因素是否会导致差异?\(H_0: \alpha_1 =\alpha_2=...=\alpha_a\),在 +\(H_0\) 下有 \(F^* = \frac{SSA/(a-1)}{SSE/(ab(n-1))} \sim +F_{a-1,ab(n-1)}\) +
- \(B\) 因素是否会导致差异?\(H_0: \beta_1 =\beta_2=...=\beta_b\),在 +\(H_0\) 下有 \(F^* = \frac{SSB/(b-1)}{SSE/(ab(n-1))} \sim +F_{b-1,ab(n-1)}\) +
- \(A,B\) 是否联合作用?\(H_0:(\alpha \beta)_{ij}=0, \forall 1 \leq i \leq +a,1\leq j \leq b\),在 \(H_0\) +下有 \(F^*=\frac{SSAB/(a-1)(b-1)}{SSE/(ab(n-1))} \sim +F_{(a-1)(b-1),ab(n-1)}\)
证明,函数 \(e^x\) 在 \(\mathbb R\) 上不是一致连续的而在 \((-\infty,0]\) 上是一致连续的。
-Trivial.
-证明,幂函数映射 \(\mathbb -R_{>0}\times \mathbb R, \ \ (x,\alpha)\mapsto x^\alpha\) 是 -\(\mathbb R_{>0}\times \mathbb R\) -上的连续函数。
-因为 \(x^\alpha = e^{\alpha \ln -x}\),且 \(\mathbb R_{>0}\times -\mathbb R \to \mathbb R\),\((x,\alpha) -\to \alpha \ln x\) 连续,\(\mathbb R -\to \mathbb R\),\(x \to e^x\) -也连续。
-二者的叠加(??这个叫什么来着啊)也是连续函数,而且是 \(\mathbb R_{>0}\times \mathbb R \to \mathbb -R\) 的连续函数。
-证明,第九次课中定义的幂函数满足如下的性质:对任意 \(x,y>0\) 和 \(\alpha, \beta\),我们有 \((xy)^\alpha=x^\alpha y^\alpha\),\((x^\alpha)^\beta=x^{\alpha \beta}\); \(a^{\log_a x} =x\);如果 \(x>0\),\(y>0\),那么 \(a^{x+y}=a^x a^y\),\(\log_a(x\cdot -y)=\log_a(x)+\log_a(y)\)。
-\((xy) ^\alpha = e^{\alpha \ln xy} = -e^{\alpha (\ln x+\ln y)} = e^{\alpha \ln x}e^{\alpha \ln y} = x^\alpha -y^\alpha\)。
-类似地证明其他几个式子,总之一些 trivial 的性质对于 \(e^x\) 和 \(\ln -x\) 成立,只要努力代入就可以了。
-在 \([0,1)\) -区间上考虑连续函数的序列 \(\{f_n(x)\}_{n\geqslant 1}\),其中 \(f_n(x)=x^n\)。证明,对任意的 \(a<1\),\(\{f_n(x)\}_{n\geqslant 1}\) 在 \([0,a]\) 上一致收敛到 \(0\) 这个函数;但是 \(\{f_n(x)\}_{n\geqslant 1}\) 在 \([0,1)\) 上不一致收敛。
-连续函数列在闭区间上有一致控制:\(\sup_{x -\in X} | f_n(x) - f(x) | = a^n <\varepsilon\),只要取 \(N > \log _a \varepsilon\) -即可,于是一致收敛。
-在 \([0,1)\) 上也还是逐点收敛到 -\(f=0\) 的,只要证明不一致收敛到 \(f=0\) 即可。实际上有 \(\sup_{x \in X} | f_n(x) - f(x) | = -1\)。
-在 \(\mathbb R\) -上考虑连续函数的序列 \(\{f_n(x)\}_{n\geqslant -1}\),其中 \(f_n(x)=\dfrac{nx}{1+n^2x^2}\)。证明,\(\{f_n(x)\}_{n\geqslant 1}\) 在 \(\mathbb R\) 上逐点收敛到 \(0\) 这个函数但是 \(\{f_n(x)\}_{n\geqslant 1}\) 在 \(\mathbb R\) 上不一致收敛。
-逐点收敛只要对 \(n \to \infty\) -即可,是收敛到 \(f=0\) 的。
-考虑一致收敛的问题,${x X} | f_n(x) - f(x) | = {x X} | { nx -+{ 1 nx}}| = 2 $,并不会一致收敛。
-在 \(\mathbb R\) -上考虑连续函数的序列 \(\{f_n(x)\}_{n\geqslant -1}\),其中 \(f_n(x)=\begin{cases}\dfrac{nx^2}{1+nx}, \ -&x>0;\\& \\\dfrac{nx^3}{1+nx^2}, \ &x\leqslant -0\end{cases}\).
-试研究 \(\{f_n(x)\}_{n\geqslant 1}\) -在 \(\mathbb R\) -上逐点收敛性和一致收敛性。
-逐点收敛到 \(f=x\),有手就行(,以下考虑一致收敛性。
-对于 \(x >0\),有 \(\sup_{x \in X} | f_n(x) - f(x) | = \sup_{x \in X} -|\frac{x}{1+nx}|<\frac 1 n < \varepsilon\) 可以在 \(N >\frac 1 \varepsilon\) 时做到。
-对于 \(x \leq 0\),有 \(\sup_{x \in X} | f_n(x) - f(x) | = \sup_{x \in X} -|\frac{x}{1+nx^2 }|<\frac{1}{2 \sqrt{n} } < -\varepsilon\),可以在 \(N> -\frac{1}{4\varepsilon^2}\) 时做到。
-所以取 \(N =[ \max \lbrace \frac 1 -\varepsilon , \frac{1}{4\varepsilon^2} \rbrace ] +1\) -即有一致收敛。
-给定连续函数 \(\varphi\colon \mathbb -R_{\geqslant 0}\rightarrow \mathbb R\),满足 \(\varphi(0)=0\),\(\displaystyle \lim_{x\rightarrow -\infty}\varphi(x)=0\) 并且 \(\varphi\) 不恒为零。证明,\(\mathbb R_{\geqslant 0}\) -上的连续函数的序列 \(\{f_n(x)\}_{n\geqslant -1}\) 和 \(\{g_n(x)\}_{n\geqslant -1}\) 逐点收敛到 \(0\) -这个函数但是不一致收敛,其中 \(f_n(x)=\varphi(nx)\),\(g_n(x)=\varphi\left(\dfrac{x}{n}\right)\)。
-Trivial.
-(一致连续性的应用:积分的定义)\([a,b]\) 是有限闭区间,\(f\in C\bigl([a,b]\bigr)\) -是实数值的函数。给定 \(n\geqslant -1\),我们将 \([a,b]\) 均分为 -\(n\) 份:\([[a,b]=[a_1,b_1]\cup [a_2,b_2]\cup \cdots \cup -[a_n,b_n], \ \ a_1=a, b_k=a_{k+1}~(k=1,\cdots, n-1), -b_n=b\),
-其中对于 \(k=1,2,\cdots,n\),\(a_k=a+\dfrac{k-1}{n}(b-a)\)。我们定义 \(S_n=\sum_{k=1}^n \frac{b-a}{n}f(a_k)\)
-证明,\(\{S_n\}_{n\geqslant 1}\) -收敛,我们用 $_{a}^b f $ 这个符号来记极限 \(\displaystyle \lim_{n\rightarrow -\infty}S_n\)。进一步证明,映射
-${a}^bC([a,b])R, f{a}^b f $ 是线性映射,并且如果我们在 -\(C\bigl([a,b]\bigr)\) 用距离函数 \(d_\infty\) 来考虑,那么这是连续映射。
-(提示:为了证明 \(\{S_n\}_{n\geqslant -1}\) 是Cauchy列,我们可以将 \(S_{n}\) 和 \(S_m\) 都与 \(S_{nm}\) 做比较)
-考虑部分和序列收敛。是因为 \(f\) -在闭区间 \([a,b]\) -上有最大值和最小值,于是 \((b-a)s \leq S_n -\leq (b-a)S\)。比较 \(S_m\) 和 -\(S_{nm}\) -能比出来什么呢...?作差用中值定理的话,二者的差可以控制在 \([\frac{n-1}{2mn} s,\frac{n-1}{2mn} S]\) -之间,确实可以控制在 \(\varepsilon\) -之内。但是只用 \(S_m\) 和 \(S_{mn}\) 做比较就可以得到是 Cauchy -列的结论吗?
-线性映射是因为 \(f + g \to \int_{a}^b -f+g\),有 \(\int_{a}^b f+g -=\displaystyle \lim_{n\rightarrow \infty}(S_n+T_n)= \displaystyle -\lim_{n\rightarrow \infty}S_n + \displaystyle \lim_{n\rightarrow -\infty}T_n = \int_{a}^b f +\int_{a}^b g\)。
-回顾一下距离函数是 \(d_\infty (f,g) = -\sup_{x \in X} |f(x)-g(x)|\),想证明映射 \(\int_{a}^b\colon C\bigl([a,b]\bigr)\rightarrow -\mathbb R\) 是连续映射,只要证明对任意的 \(\varepsilon >0\),存在 \(\delta\) 使得 \(d_\infty (f,g) < \delta\) 时有 \(|\int_{a}^b f - \int_{a}^b -g|<\varepsilon\)。
-由于这个映射是线性的,我们知道 \(|\int_{a}^b f - \int_{a}^b g| = |\int_{a}^b (f-g)| -< |\int_{a}^b d_{\infty}(f,g) | = -(b-a)d_{\infty}(f,g)\),因此只要取 \(\delta = \frac {\varepsilon} {(b-a)}\) -就能够满足要求。因此这个映射是连续的。
-证明Cauchy的一个定理: 任给函数 \(f\colon [a,+\infty) \to -\mathbb{R}\),我们假设 \(f\) -任意闭子区间 \([a,b]\) 上有界 -(上界可能依赖于 \(b\)), -那么下面两个式子当等号右边极限存在时成立:
-\(\lim_{x \to +\infty} \frac{f(x)}{x} = -\lim_{x \to + \infty} [f(x+1) - f(x)],\\\lim_{x \to + \infty} -[f(x)]^{1/x} = \lim_{x \to + \infty} \frac{f(x+1)}{f(x)}, \ \ -\text{进一步假设对任意的 $x \in [a,\infty)$,$f(x) \geqslant c > -0$}\)
-首先,给下面的式子取个对数就能得到上面的式子,所以只要证明上面的式子。
-记 \(A = \lim_{x \to + \infty} [f(x+1) - -f(x)]\),于是对任意 \(\varepsilon ->0\),存在 \(N \in \mathbb -Z^+\) 使得 \(x >N\) -时都有:
-\(A-\varepsilon < f(x+1) - f(x) < -A+\varepsilon\) 成立。
-因此 \(f(y) = (f(y)-f(y-1)) + -(f(y-1)-f(y-2))+ ... +( f(n+1)-f(n)) +f(n)\),其中 \(n = N\),再做 \(\frac{f(y)}{y}\) -取极限即得到结论。
+\(t\) Distribution:
+\(t\) distribution with degree of +freedom \(n\):$ T==t_n$
+Upper \(\alpha\)-fractile of \(t_\nu\), satisfies \(\mathbb{P}(T\geq +c)=\alpha\),$t_{,}={c}(Tc)=,Tt$
+\(F\) Distribution:
+\(F\) distribution with degree of +freedom \(m\) and \(n\):$ F=F_{m,n}$
+-
+
- If \(Z\sim F_{m,n}\), then \(\dfrac{1}{Z}\sim F_{n,m}\); +
- If \(T\sim t_n\), then \(T^2\sim F_{1,n}\); +
- \(F_{m,n,1-\alpha}=\dfrac{1}{F_{n,m,\alpha}}\) +。 +
如果连续函数 \(f\) -在开区间(有限或无限)\(I \subset -\mathbb{R}\) 上是单调并且有界的,那么 \(f\) 在 \(I\) 上一致连续。
-Trivial.
-\(I\) -是长度有限的区间(不一定是闭的)。 证明,\(I\) 上的实值函数 \(f\) 一致连续的充分必要条件是 \(f\) 把Cauchy列映成Cauchy列(即如果 \(\{x_n\}_{n \geqslant 1} \subset I\) -是Cauchy列,那么 \(\{f(x_n) \}_{n \geqslant -1}\) 也是Cauchy列)。
-如果 \(f\) 一致连续,由 Cauchy -列和一致连续的定义知道 \(\{f(x_n) \}_{n -\geqslant 1}\) 也是 Cauchy 列。
-如果映射到的点列也是 Cauchy 列,且 \(f\) 不一致连续。那么存在一个 \(\varepsilon >0\),使得对任意的 \(\delta\),都存在 \(x,y \in I\) 满足 \(|x-y|<\delta\) 且 -$|f(x)-f(y)|>$。取一个和 \(\lbrace x_n -\rbrace\) 相近的数列 \(\lbrace y_n -\rbrace\),满足 \(|x_n - y_n |< -\frac 1 n\) 而且 \(|f(x_n) - f(y_n)| ->\varepsilon\),而且一定满足 \(\lbrace y_n \rbrace \subset I\)。那么 \(\lbrace x_n \rbrace\) 是收敛的 Cauchy -列,\(\lbrace y_n \rbrace\) -也是收敛到同一点的 Cauchy 列。
-取序列 \(x_1,y_1,x_2,y_2,...,\) -也是一个 Cauchy 列,但它的映射并不是 Cauchy 列,矛盾。
-不会做于是 MSE 了半天 qwq
-\(f\) 在 \(\mathbb{R}\) 上一致连续。证明,存在 \(a, b \in \mathbb{R}_{>0}\),使得对任意的 -\(x\in \mathbb R\),我们都有 \(|f(x)| \leqslant a |x| + b\)
-取 \(b = |f(0)|\),对 \(\varepsilon = 1\),取一致连续定义中对应的 -\(\delta\),于是 \(|x - 0| <\delta\) 时一定有 $ |f(x) - -f(0)|<1$,可以得到 \(|f(x)| < |f(0)| +1 -= b+1\)。
-因此,对于任意的 \(x \in \mathbb -R_+\),有 \(|f(x) - f(x-\delta)| < -1\),可以推出 \(|f(x) - f(0)| < -([\frac{1}{\delta}]+1) |x|\)。对于 \(x -\in R_-\) 也可以得到类似的结论,于是只要取 \(b=|f(0)|\),\(a = -[\frac 1 \delta] +1\),原式成立。
-假设函数 \(f\) 在 \([0,\infty)\) 上一致连续并且对任意的 \(x \in [0,1]\),我们都有 \(\displaystyle \lim_{n \rightarrow +\infty}f(x+n) = -0\)(这里 \(n\) 是整数)。 -证明,\(\lim_{x \to +\infty}f(x) = -0\)。如果我们将条件减弱为 \(f\) -在 \([0,\infty)\) 连续, -结论是否依然成立? 证明或举出反例。
-如果有一致连续条件:
-先取一个固定的 \(x\in [0,1]\) -和一个固定的 \(\varepsilon ->0\),存在一个 \(\delta = -\delta(\varepsilon)\) 使得对任意的 \(|x-y|<\delta\),有 \(|f(x)-f(y)|<\varepsilon\)。存在一个 -\(N=N(x,\varepsilon)\),使得对任意的 -\(n>N\),有 \(|f(x+n)|<\varepsilon\)。我们先固定这个 -\(n\)。
-对任意的 \(t \in [x+n,x+n+1]\),有 -\(|x+n-t|<p\delta\),于是 \(|f(t)-f(x+n)|<p\varepsilon\),\(p = \frac{1}{\delta}\)。于是有 \(|f(t)|<(p+1)\varepsilon\)。
-把上述中的 \(n\) 改成 \(n+1,n+2,...\),都有 \(|f(t)|<(p+1)\varepsilon\)。于是对任意的 -\(y \in [x+n,+\infty)\),有 \(|f(y)|<(p+1)\varepsilon\),也就是说 -\(\lim_{x \to +\infty}f(x) = 0\)。
-如果没有一致连续条件,结论是不成立的。取 \(f(x) = \frac{xsin \pi x}{1+x^2 \sin^2 \pi -x}\),它没有极限吧?
-假设 \(X\) 是区间,\(f\colon X \rightarrow \mathbb{R}\) -是连续函数。如果存在正常数 \(L\),使得对任意的 \(x, y \in X\),都有 \(|f(x) - f(y)| \leqslant L|x-y|\),我们就称 -\(f\) 在 \(X\) 上满足Lipschitz条件。
+For \(X_1,X_2,\ldots,X_n\) +independent with \(X_i\sim +N(\mu_i,\sigma^2_i)\), then \(\sum_{i=1}^n\left(\frac{X_i-\mu_i}{\sigma_i}\right)^2\sim +\chi^2_n\)
+For \(X_1,X_2,\ldots,X_n\) +i.i.d.\(\sim N(\mu,\sigma^2)\), then $ +T=t_{n-1} $
+For \(X_1,X_2,\ldots,X_m\) +i.i.d.\(\sim N(\mu_1,\sigma^2)\), \(Y_1,Y_2,\ldots,Y_n\) i.i.d.\(\sim N(\mu_2,\sigma^2)\),d enote sample +pooled variance \(S_{\omega}^2=\dfrac{(m-1)S^2_1+(n-1)S^2_2}{m+n-2}\), +then \(T=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{S_{\omega}}\cdot +\sqrt{\frac{mn}{m+n}}\sim t_{m+n-2}\)
+For \(X_1,X_2,\ldots,X_m\) +i.i.d.\(\sim N(\mu,\sigma^2)\), \(Y_1,Y_2,\ldots,Y_n\) i.i.d.\(\sim N(\mu_2,\sigma^2)\), then +$T=F_{m-1,n-1} $
+For \(X_1,X_2,\ldots,X_n\) +i.i.d. \(\sim \varepsilon(\lambda)\), +then $ 2n{X}=2{i=1}^nX_i ^2{2n} $
+Remark:for \(X_i\sim\varepsilon(\lambda)=\Gamma(1,\lambda)\),\(2\lambda\sum_{i=1}^nX_i\sim\Gamma(n,1/2)=\chi^2_{2n}\).
+
Multicollinearity Remedy
+如果存在多重共线性,主要发生的问题是 \(X^TX\) +求逆是一个病态的数值问题,误差很大。实际上极端来说如果存在完全共线性,\(X^TX\) 会退化为不满秩的情况。
+可以用 ridge regression 对多重共线性进行弥补。
+Ridge Regression
+主要的 idea 是如果 \((X^TX)\) +接近于不满秩,则在参数估计中将其改变为 \((X^TX ++\lambda I)\),\(\lambda\) +是待取的参数。对于矩阵的对角元进行改变如同突起的山脊,因此得名岭回归。
+Ridge regression 的本质是对优化问题进行了修改。OLS +中的优化问题是求使得 \((Y-X\beta)^T +(Y-X\beta)\) 最小的 \(\beta\),ridge regression 中将 \(|| \beta ||_2 ^2 = \Sigma_{i=0} ^{p-1} +\beta_i^2\) 加入了优化,对 \(\beta\) 的长度(事实上应该称之为 2- +范数)做惩罚。因此,实际上是求使得 \((Y-X +\beta )^T (Y-X \beta) + \lambda \Sigma_{i=0} ^{p-1}\beta_i ^2\) +最小的 \(\hat \beta = (X^TX + \lambda I)^{-1} +X^TY\),这使得参数估计 \(b = \hat +\beta\) 呈现出比 OLS 下长度和方差都更小的特征。
+在实际应用中,需要通过确定最佳的 \(\lambda\) 从而得到合适的参数估计,一般是对 +\(\lambda\) 取一个 sequence +进行尝试。如果发现某个 explanatory variable 的系数在 \(\lambda\) 增大时很快下降到 \(0\),实际上它很有可能是不需要进入模型的。
+应用岭回归来弥补模型的多重共线性的时候,既是为了消除共线性,也是在牺牲一些 +\(\hat \beta\) +的无偏性来换取更小的方差。
+LASSO & Elastic Net
+LASSO 中把惩罚的 \(\beta\) +长度替换为了 \(\beta\) 的 1- +范数,弹性网络则是对 LASSO 和 ridge regression 进行了结合。
+本质上都是 Bayesian modes。
+Influencial Cases Remedy
+更改一些更 robust 的优化模型,例如 least absolute deviation 和 least +median of squares,缺点是算起来会比较困难。
+或者考虑非参数模型。
+Nonlinearity Remedy
+考虑局部多项式回归/局部回归,总之是对数据进行分块,所谓的 +lowess。
+Lecture 13
+One Factor ANOVA
+(从生统笔记复制来的)
+首先给出一个希望做检验的场景:\(n_T\) 个实验对象被分成 \(r\) 组,每组有 \(n_i\) 个实验对象,有 \(n_T = \Sigma_{i=1} ^r n_i\)。由此我们得到 +\(n_T\) 个数据 \(Y_{ij}\),\(i\) 表示组别,\(1\leq i \leq r\),\(j\) 表示在某一组内的编号,\(1 \leq j \leq n_i\)。
+Cell means model
+-
+
函数的零点
-其实一共有八道题,但另外七个都很 -trivial,这个没有一眼看出来,所以还是写一写。
+Factor Effects Model
-
-
*思考题
+Example
-
-
一致连续性
-2023 年 1 月 29 -日,星期日,我觉得凡是带有“一致”的东西都蛮恐怖的,比如 UMVUE(
-惭愧地说,一致连续性其实我以前没有学会过,因为考试不考(。再来一遍.jpg
-草,我之前把数分分成 I 和 II -都觉得挺奇怪的,但目前已经三万多字了,Typora -开始有点卡了(。所以这次又分别分了上下,暂且以期中考试为界吧。
-紧性与开覆盖
-是没接触过的很新的东西(,我怀疑这也不是数分内容,全在抄。好像也没抄会。
-一致连续性
+Inference on One-Way ANOVA
+Confidence Interval for \(\mu_i\)
+事实上这只是个理论上可做的问题而已,现实中不会对 \(\mu_i\) 做推断,我们关注的是 \(\mu_i\) 之间的差异。
+由于 \(\bar Y_{i.} \sim N(\mu_i , \sigma^2 +/ n_i)\),因此 \(\mu_i\) 的 +pooled confidence interval 是 \((\bar Y_{i.} - +t_c \frac{s}{\sqrt n_i} , \bar Y_{i.} + t_c \frac{s}{\sqrt +n_i})\),其中 \(t_c = +t(1-\frac{\alpha}{2}, n_T -r)\)。注意其中的 \(s^2\) 在上面已经有定义,实际上就是 +SSE。
+当然也可以认为是 \((\bar Y_{i.} - t_c s_i , +\bar Y_{i.} + t_c s_i)\),\(s_i\) 是每个 \(\mu_i\) 对应的 \(sd_i\)。但是这样得到的置信区间一般来说较宽,准确性不如 +pooled confidence interval,我们不太会采用。
+实际上这样做 t-test 的话 family-wise error rate +很大,即使做出显著的效果也很有可能是发生了 Type I Error。
+Bonferroni Confidence +Intervals for \(\mu_i\)
+想要同时估计所有的 \(\mu_i\) +的时候可以采用 Bonferroni method,但是也有明显的缺点是一旦 factor level +\(r\) 较大,就会导致每个 \(\mu_i\) 都不显著,置信区间的 level of +significance 只有 \(\alpha / +2r\),几乎是无效的。
+同样是 t-test,但过于保守了。对于较小的 \(r\) 可以进行尝试。
+Test Difference in Means
+由于 \(\bar Y_{i.} - \bar Y_{j.} \sim +N(\mu_i - \mu_k , \frac{\sigma^2}{n_i} + \frac{\sigma +^2}{n_j})\),\(\mu_i - \mu_k\) +的 confidence interval 是 \((\bar Y_{i.} - +\bar Y_{j.}-t_c s(\bar Y_{i.} - \bar Y_{k.}), \bar Y_{i.} - \bar +Y_{j.}+t_c s(\bar Y_{i.} - \bar Y_{k.}))\),其中 \(s(\bar Y_i. - \bar Y_k.) = \sqrt{\frac{\hat +\sigma^2}{n_i} + \frac{\hat \sigma^2}{n_j}} = s \sqrt{\frac{1}{n_i} + +\frac{1}{n_j}}\),\(t_c\) +是和检验方法有关的常数。
+由于一共有 \(r\) 个 mean \(\mu_i\),所以一共要做 \(\frac{r(r-1)}{2}\) +次检验来确定两两之间有无差异。
+-
+
Contrast
+Concept
+关于对照的具体定义是,取一组均值为 \(0\) 的常数作为权重,即为 \(\Sigma_{i=1} ^r c_i =0\),此时研究 \(L = \Sigma_{i=1} ^r c_i \mu_i\) +的推断。
+注意到 \(\hat L = \Sigma c_i \bar Y_i . +\sim N(L, Var(\hat L))\),其中 \(Var(\hat L) = \Sigma c_i ^2 Var(\bar Y_i +.)\),\(\hat Var (\hat L) = MSE \Sigma( +c^2_i / n_i)\)。
+test statistic 是 \(T= \frac{\hat L - +L_0}{\sqrt{\hat Var(\hat L)}} \sim t(n_T-r)\)。例如在 \(H_0 : L =0\) 下有 \(T = \frac{\Sigma c_i \bar Y_i .}{\sqrt{MSE \Sigma +c^2_i / n_i}} \sim t(n_T -r)\),于是 \(T^2 = \frac{(\Sigma c_i \bar Y_i.)^2}{MSE \Sigma +c_i^2 /n_i} = \frac{SSC/1}{MSE} \sim F(1,n_T-r)\),其中定义 \(SSC = (\Sigma c_i \bar Y_i.)^2 / \Sigma +(c_i^2/n_i)\),称为 sum of contrast。
+Multiple Contrasts
+可以利用 R 同时检验若干组 contrast,比如同时检验 \(\mu_1 = \mu_2, \mu_3 = \mu_2 , \mu_1 =( \mu_1 + +\mu_2+\mu_3 )/ 3\)
+实际上 linear hypothesis test 和 multiple comparison +的主要差别在于自由度,比如说对于 \(\mu_1 = +\mu_2 = \mu_3\) 做检验,前者会将其拆成两个两两检验,自由度是 +\(2\),后者会作为一个整体的 +contrast,自由度是 \(1\)。
+Lecture 14
+依旧来自生统概论的笔记。
+Two-Way ANOVA
+首先给出一个希望做检验的场景:\(nab\) 个实验对象被分成 \(a\times b\) 组,每组有 \(n\) 个实验对象。第 \(ij\) 组的实验条件是 \(A\) 因素的等级为 \(i\),\(B\) +因素的等级为 \(j\),其中有 \(1 \leq i \leq a, 1\leq j \leq +b\)。由此我们得到 \(nab\) 个数据 +\(Y_{ijk}\),\(i\) 表示以 \(A\) 因素分类的组别,\(j\) 表示以 \(B\) 因素分类的组别,\(k\) 表示在某一组内的编号,\(1 \leq k \leq n\)。
+每一组都是 \(n\) 个人,这是一个 +balanced design。
+Cell Mean Model
+模型假设是 \(Y_{ijk} = \mu_{ij} + +\varepsilon_{ijk}\)。
+其中,\(\mu_{ij}\) 是第 \({i \times j}\) 水平的均值,\(\varepsilon_{ijk}\) i.i.d. \(\sim N(0,\sigma^2)\),模型中实际上有 \(ab+1\) 个未知参数需要估计。
+\(\mu_{ij}\) 的估计量是 \(\bar Y_{ij.} = \sum_k Y_{ijk} /n\),对于 +\(i \times j\) 水平的方差估计是 \(s_{ij}^2 = \sum_k (Y_{ijk} - \bar Y_{ij.})^2 / +(n-1)\)。但是想要估计 \(\sigma^2\) 时必须要将所有的数值加权 pool +起来做估计,是 \(s^2 = \sum_{ij} (n_{ij}-1) +s_{ij} ^2 / \sum_{ij} (n_{ij}-1)\),注意到如果是 balanced test +的情况实际上就是 \(s^2 = \sum_{ij} s^2_{ij} / +ab\) 直接做平均的结果。更倾向于 pooled \(s^2\) +是因为自由度更大,数据利用更充分。
+直接通过看图来观察两个因子之间是否存在交互效应、单因子是否显著这件事的时候,比较经典的情况就是以下两种:
+
上面第一张图中可以发现两条回归线之间存在斜率的差异,说明 B 因子对于 A +因子的效果存在影响,也就是存在交互效应;在 \(b_2\) level 上 A 因子是不显著的,但在 \(b_1\) level 上 A 因子显著;同理在 \(a_1\) level 上 B 因子不显著,但在 \(a_2\) level 上 B +因子显著。实际上在这个情况下交互效应显著,主效应虽然显著但也没有太大意义了,不过想要解释也是可以的,可以认为 +A 因子带来的效应至少不是负效应。
+第二张图里更有两条回归线交叉,存在斜率的差异,交互效应显著;但主效应此时可能无法解释,尤其是如果两条回归线完全交叉成 +\(\times\) 形状,A 因子会在不同的 B +因子条件下起到相反的作用。所以一般是认为交互效应显著时主效应显著,但没有解释意义。显著性和解释性之间无关。
+在读 R code 的时候直接把所有的 estimation 读作 factor effect model +的系数,再代回就可以理解系数的来源了。这一部分在 factor effects model +里详述。
+Factor Effects Model
+模型假设是 \(Y_{ijk} = \mu +\alpha_i + +\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
+其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) +表示和两个因素同时相关的变化,相当于一个交叉项。
+这里面有 \((a+1)(b+1)\) +个参数,对其也有一定的约束:\(\Sigma_i +\alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j +(\alpha \beta)_{ij} =0\),事实上有 \(a+b-1\) 个关于交互效应的约束,有 \(2\) 个关于单因子效应的约束,实际上包含 +\(\sigma^2\) 后仍然是有 \(ab+1\) +个参数。做一些其他的参数假设,让参数含义更清晰:
+\[\mu_{i.} = \alpha_i ++\mu_{..}\]
+\[\mu_{.j} = \beta _j + +\mu_{..}\]
+\[\mu_{ij} = \mu_{..} +\alpha_i + \beta_j ++(\alpha \beta)_{ij}\]
+如果 \((\alpha \beta)_{ij}=0\) +则说明因素 \(A,B\) +之间不存在相互作用的关系,这样的模型称为 additive model。
+考虑一些统计量作为参数的估计量:
+\[\bar{Y}_{ij.} = \frac{1}{n} \Sigma_{k=1 +}^{n} Y_{ijk} = \hat \mu_{ij} = \hat \mu + \hat \alpha _i + \hat +\beta_j + \hat{(\alpha \beta)}_{ij}\]
+\[\bar{Y}_{i..} = \frac{1}{bn} +\Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \alpha_i = +\hat \mu_{i.}\]
+\[\bar{Y}_{.j.} = \frac{1}{an} +\Sigma_{i=1}^a \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \beta_j = +\hat \mu_{.j}\]
+\[\bar{Y}_{...} = +\frac{1}{abn}\Sigma_{i=1}^a \Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = +\hat{\mu} \]
+Two factors ANOVA 的方差分解更复杂一些:
+\[\begin{aligned} SSTO &= \Sigma_i +\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{...})^2 \\ &= \Sigma_i +\Sigma_j \Sigma_k ((\bar Y_{i..} - \bar Y_{...})+(\bar{Y}_{.j.} - \bar +Y_{...}) +(\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...}) ++(Y_{ijk} - \bar Y_{ij.}))^2 \\&=bn\Sigma_i (\bar Y_{i..} - \bar +Y_{...})^2+an\Sigma_j (\bar{Y}_{.j.} - \bar Y_{...})^2+n\Sigma_i +\Sigma_j (\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...})^2+ +\Sigma_{i}\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{ij.})^2 \\&=SSA ++SSB+SSAB+SSE \end{aligned}\]
+其中,\(SSA\) 的自由度是 \(a-1\),\(SSB\) 的自由度是 \(b-1\),\(SSAB\) 的自由度是 \((a-1)(b-1)\),\(SSE\) 的自由度是 \(ab(n-1)\),\(SSTO\) 的自由度是 \(abn-1\)。在这一个复杂问题中我们关心不同的问题,可以做出三种不同的假设检验,有对应的检验统计量。
-
-
级数收敛构造连续函数
-本质上是把绝对值推广成函数的无穷范数,用来证明收敛。
-梦话:证明题,但胡说八道
-连续,一致连续和一致收敛
--
-
不能直接用 chi-square 统计量作为检验统计量的原因是实际上 \(MSE,MSA\) 等统计量中都带有未知的 \(\sigma^2\) 参数项。
+注意 \(n_{ij}\) +是相等的也就是平衡设计,所以 Type I 和 Type III ANOVA +的结果是一样的。
+Two-Way ANOVA in R
+模型假设是 \(Y_{ijk} = \mu +\alpha_i + +\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
+其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) +表示和两个因素同时相关的变化,相当于一个交叉项。
+这里面有 \((a+1)(b+1)\) +个参数,对其也有一定的约束。R code 中的约束是和上述理论不同的,因此 +estimator 的读取也并不相同,认为 \(\alpha_1 = +\beta_1 = (\alpha \beta)_{1j} = (\alpha +\beta)_{i1}=0\),事实上也还是 \(a+b+1\) 个约束条件,可以估计出 \(ab+1\) 个不同参数。
+相应地,对应的 design matrix 也不尽相同。这里以 \(a=3,b=2,n=2\) 为例,coefficient table +如下所示:
+
Coefficient table 里的 Intercept 代表的实际上是 \(\mu\),预设了 \(\beta_1=0\),height2 即为 \(\beta_2\),height3 即为 \(\beta_3\);预设了 \(\alpha_1=0\),width2 即为 \(\alpha_2\);关于交互效应项,由于预设了 +\((\alpha \beta)_{11} = (\alpha \beta)_{12} = +(\alpha \beta)_{13} =(\alpha +\beta)_{21}=0\),不为零的交互效应项只有两个,分别由 +height2:weight2 对应 \((\alpha +\beta)_{22}\),height2:weight3 对应 \((\alpha \beta)_{23}\)。
+由此我们可以依次按照 \(\mu_{ij} = \mu + +\alpha_i + \beta_j +(\alpha \beta)_{ij}\) 算出所有的 \(\mu_{ij}\) 的估计量。
+在这之后我们希望得到一个关于 \(12\) +个数据的设计阵,实际上就是把数据和上述分析对应起来:
+
Least Square Means
+遇到非平衡设计,或者 covariates +的情况(连续型变量和类别性变量产生交互效应的情况),需要考虑 least +square means 而不是 pooled means。简单来说 least square means +是均值的均值,达到了最小的方差,而 pooled means +就是全体数据的均值,在非平衡设计的情况下很可能引入偏差。
+
Balanced Test
+对于一个平衡设计来说,它本质上是一个正交设计,模型中进一个因子还是两个因子都不会改变彼此的系数估计,只有自由度会有改变。least +square mean 就是普通的 pooled mean,one-way ANOVA 和 two-way ANOVA +的结果一致。
+Unbalanced Test
+非平衡设计的时候 one-way ANOVA 的结果仍然是一样的,least square mean +和 pooled mean 得到的都是这一组内所有的观测值的平均。在这里就是认为 A +因子的 height1 level 的估计值是 \(\hat \mu_{1} += \frac 1 3(X_{11} +X_{12} +X_{13}) = 43\)。
+但是新加入一个因子做 two-way ANOVA 就会导致 least square mean +下的系数估计发生变化,从 coefficient table 可以看出 \(\mu_{i1}\) 和 \(\mu_{i2}\) +都改变了(绷不住了,虽然并不知道是怎么变的,但是会从系数表读出每一个 +\(\mu_{ij}\) 就可以了),仍然使用 \(\frac 1 2(\mu_{i1}+\mu_{i2})\) 作为 \(\mu_{i.}\) +的估计,就也会相应地发生变化。
+事实上 least square mean 还可以称作 predicted mean 的原因就是,此处的 +\(\mu_{11}\) 和 \(\mu_{12}\) 分别作为 \(1\times 1,1\times 2\) +这两格的预测值出现,它们的平均就作为 \(\mu_{1.}\) 这一个 A 因子的 height1 level +对应的预测值出现。在具体的例子里,此处因为得到的估计是 \(\hat \mu_{11} = 41, \hat \mu_{12} = +44\),于是认为 \(\hat \mu_{1.} = \frac +1 2 (\hat \mu_{11} + \hat \mu_{12}) = 42.5\)。
+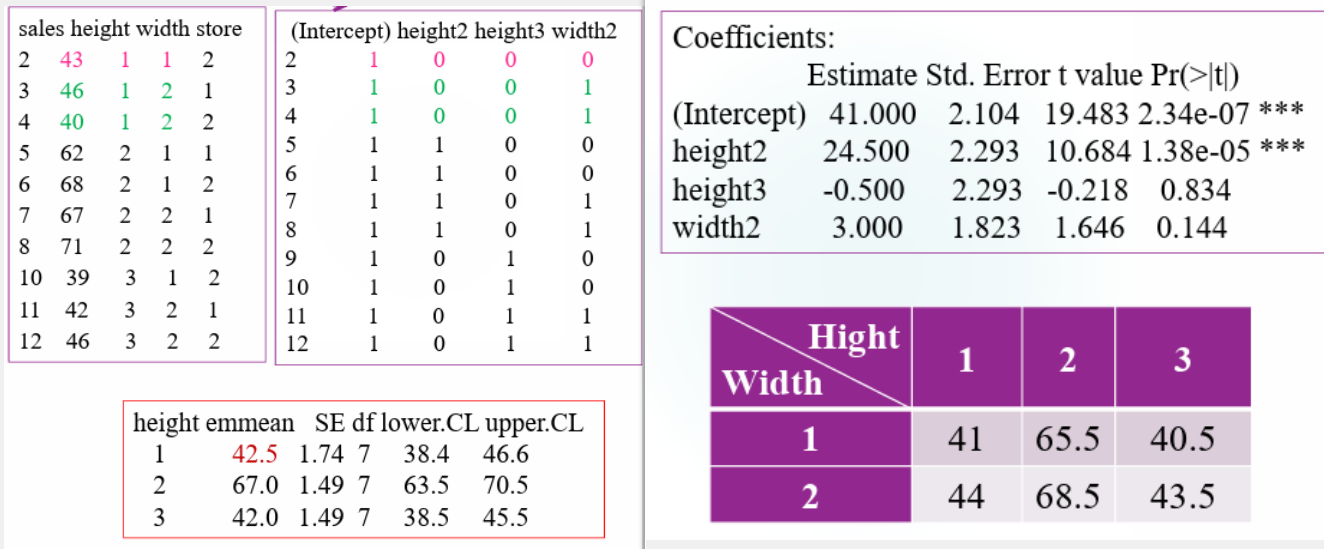
总之可以看到,unbalance test 会导致实验设计并不是正交的,B +因子的加入会对 A 因子的均值估计产生影响,这也是我们一般希望使用 balanced +test 的理由。
+Model Diagnose & Remedy
+马上要告别应统了,于是不考也就不想学了,摆烂。
+附录
+常见重要分布
+From Statistic +Note P10, by V1ncent19
+| \(X\) | +\(p_X(k)\big/f_X(x)\) | +\(\mathbb{E}\) | +\(var\) | +PGF | +MGF | +
|---|---|---|---|---|---|
| \(\mathrm{Bern} (p)\) | ++ | \(p\) | +\(pq\) | ++ | \(q+pe^s\) | +
| \(B (n,p)\) | +\(C_n^k p^k(1-p)^{n-k}\) | +\(np\) | +\(npq\) | +\((q+ps)^n\) | +\((q+pe^s)^n\) | +
| \(\mathrm{Geo} (p)\) | +\((1-p)^{k-1}p\) | +\(\dfrac{1}{p}\) | +\(\dfrac{q}{p^2}\) | +\(\dfrac{ps}{1-qs}\) | +\(\dfrac{pe^s}{1-qe^s}\) | +
| \(H(n,M,N)\) | +\(\dfrac{C_M^kC_{N-M}^{n-k}}{C_N^n}\) | +\(n\dfrac{M}{N}\) | +\(\dfrac{nM(N-n)(N-M)}{N^2(n-1)}\) | ++ | + |
| \(P(\lambda)\) | +\(\dfrac{\lambda^k}{k!}e^{-\lambda}\) | +\(\lambda\) | +\(\lambda\) | +\(e^{\lambda(s-1)}\) | +\(e^{\lambda(e^s-1)}\) | +
| \(U(a,b)\) | +\(\dfrac{1}{b-a}\) | +\(\dfrac{a+b}{2}\) | +\(\dfrac{(b-a)^2}{12}\) | ++ | \(\dfrac{e^{sb}-e^{sa}}{(b-a)^s}\) | +
| \(N(\mu,\sigma^2)\) | +\(\dfrac{1}{\sigma +\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\) | +\(\mu\) | +\(\sigma^2\) | ++ | \(e^{\frac{\sigma^2s^2}{2}+\mu +s}\) | +
| \(\epsilon(\lambda)\) | +\(\lambda e^{-\lambda x}\) | +\(\dfrac{1}{\lambda}\) | +\(\dfrac{1}{\lambda^2}\) | ++ | \(\frac{\lambda}{\lambda-s}\) | +
| \(\Gamma(\alpha,\lambda)\) | +\(\dfrac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda +x}\) | +\(\dfrac{\alpha}{\lambda}\) | +\(\dfrac{\alpha}{\lambda^2}\) | ++ | \(\left(\frac{\lambda}{\lambda-s}\right)^\alpha\) | +
| \(B(\alpha,\beta)\) | +\(\dfrac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\) | +\(\dfrac{\alpha}{\alpha+\beta}\) | +\(\dfrac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\) | ++ | + |
| \(\chi^2_n\) | +\(\dfrac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}\) | +\(n\) | +\(2n\) | ++ | $ (1-2s)^{-n/2} $ | +
| \(t_\nu\) | +\(\dfrac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\Gamma(\frac{\nu}{2})}(1+\frac{x^2}{\nu})^{-\frac{\nu+1}{2}}\) | +\(0\) | +\(\dfrac{\nu}{\nu-2}\) | ++ | + |
| \(F_{m,n}\) | +\(\dfrac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{m}{2})\Gamma(\frac{n}{2})}\dfrac{m^\frac{m}{2}n^\frac{n}{2}x^{\frac{m}{2}-1}}{(mx+n)^{\frac{m+n}{2}}}\) | +\(\dfrac{n}{n-2}\) | +\(\dfrac{2n^2(m+n-2)}{m(n-2)^2(n-4)}\) | ++ | + |
Consider \(X_1,X_2,\ldots,X_n\) +i.i.d. \(\sim N(0,1)\); \(Y,Y_1,Y_2,\ldots,Y_m\) i.i.d. \(\sim N(0,1)\) - \(\chi^2\) Distribution:
+\(\chi^2\) distribution with degree +of freedom \(n\):$ =_{i=1}^n +X_i22_n$。 For independent \(\xi_i\sim\chi^2_{n_i},\, +i=1,2,\ldots,k\):\(x_{i_0}=\sum_{i=1}^k\xi_i\sim\chi^2_{n_1+\ldots+n_k}\)
+-
+
和一致连续性相关的问题
+Some useful lemmas in statistical inference:
-
-
分位数速查
+来自 Package stats, version 4.2.1。
+其实都可以直接查文档啦(,R 的文档还是很保姆式的。
+t-分布模拟
+t-distribution 下有四个函数,分别是 density, CDF, quantile +function(\(CDF^{-1}\)),还有一个是随机生成一个模拟数组。
+dt(x, df, ncp, log = FALSE) 用来计算 PDF 的函数值 \(f(x)\),df 是自由度,ncp 表示非中心化参数
+\(\delta\);
pt(x, df, ncp, lower.tail = TRUE, log.p = FALSE)
+用来计算 CDF 的函数值 \(F(x)\),注意
+lower.tail = TRUE 时计算的是左边值 \(F(x)\),否则实际计算了 \(1-F(x)\)。
qt(p, df, ncp, lower.tail = TRUE, log.p = TRUE)
+用来计算分位数,也即 \(F^{-1}(p)\),其他参数意义同上。
一些我的作业里的函数参考:
+> qt(1 - 0.025, df = 8) |
这里计算的是 \(t_{8,0.975}\) +的下分位数,实际上是一个 level of significance 为 \(0.05\) 的双尾检验中用到的分位数。
+> 2 * pt(-8.529, df = 8) |
这里是在计算一个 P-value,计算的是比 observed data \(-8.529\) 更极端的数据的出现概率,单边是 +\(F (-8.529)\),注意此处的“极端”包含比 +\(-8.529\) 更小和比 \(8.529\) 更大这两种情况,实际上是 \(F(-8.529) + 1- F(8.529)\)。
+由于 t-distribution 是对称的,可以简化为 \(2 \times F(-8.529)\)。
+> ncp <- 2.0/0.50 |
这是一个非中心的 t 检验,实际上是在计算 Power Function。
+正态分布模拟
+常用的三个函数是
+dnorm,pnorm,qnorm,含义与
+t-分布中的 dt,pt,qt 相似。
dnorm(x, mean = 0, sd = 1, log = FALSE) |
注意一般正态检验中都是使用标准正态分布,也就是不需要去改变
+mean 和 sd 的默认值。
> pnorm(0) |
F-分布模拟
+df(x, df1, df2, ncp, log = FALSE) |
注意 \(F\)
+分布的两个自由度都可以取到无穷,写作 df1 = Inf。
Chi-square 分布模拟
+dchisq(x, df, ncp = 0, log = FALSE) |
其他常用 R 命令
+持续更新中,基本都是作业里扒出来的。
+confidence interval
+confint(object, parm, level = 0.95, ...) |
注意 confidence coefficient 的默认值是 \(0.95\),confint
+函数是用于拟合模型参数的置信区间估计,例如:
model <- lm(data) |
2.5 % 97.5 % |
这个附录怎么全咕了啊,不过无所谓了,这课我本来就是在摆烂(
+完结撒花
+一点都不 happily ever +after,说是找到了新的方向,谁知道概率又会不会很艰难呢。
+这课明显东西比统计推断多,但是导出成 PDF +一看比统推笔记少了二十多页。
+总之都结束了,笑一个吧(
+
++【上海市出入境管理局】感谢您申请陆家嘴签证。非常遗憾的通知您,由于您过去三个月没内有 +City Walk, Gap Hour 及 Camping 记录,我们在 Salomon, Lululemon, Tesla, +Omakase 及 Apple Store +均未查询到您的消费记录并且查到您在蜜雪冰城消费过多杯柠檬水,故本次签证被拒。
+
再来点申请文学:
+2024 Spring 申请选手,background 不强,身份证不是 310 +开头的,目前住在浦西比较远的地方,主要的几个指标都消费不起。唯一的优势是高中有过张江高科的三年学签,虽然偏了些但到底在浦东,还和陆家嘴都在二号线上,就是不知道过了几年了还有没有用,求问证明材料还需要提交当时的成绩单吗?最近是三个月内正好买了 +iPad 所以在 Apple Store 买过 Lanota +曲包,数额不大,其他消费记录无。打算趁这个寒假抽几个 Gap Day 刷一些 City +Walk/Ride 记录,年后申请陆家嘴签证,方便开学前去滨江骑行道骑车(
+说人话:摆烂一天,出去骑车玩儿了(
+ +2024.02.08
+我以前没有在上海市区骑过车。一方面是高考之后才学会骑车,后来在上海的时间就少了,另一方面你沪的共享单车比北京贵一倍,我感觉都很难有慢下来看风景的想法(,自己家里没自行车,有车也不方便带去市区,不过搬到普陀之后可以考虑,而且我毕业之后还挺想把现在的车送回家的。还有就是一直听说市区骑行管得很严交警很多,路况也不是很好,更不可能像在北京一样还能随便逆行(好孩子不要学。
+但内环以内适合逛的就那点地方,如果想去好几个地方玩的话地铁三块钱三块钱地刷也不是很值。何况这是冬天,现在还不骑车的话难道夏天骑吗,夏天我可是会买一张一日票无论多近多绕都坐地铁的(x
+哪里可以骑车
+在我高中还不会骑车的时候就听说过高中同学骑车逆行惨遭被交警拦下罚款 50 +的惨案,后来也知道淮海中路自行车禁行的名梗,所以今天去市区骑车还是有那么一点点小紧张,主要还是担心在毫不知情的情况下被罚款。当然最后没有,但十字路口交警的密度还是让我大开眼界,在他们身边停下的时候还听到对讲机里在说有电瓶车沿着某条路逆行了帮忙拦一下什么的,搞得我远远看到穿黄绿马甲的人就害怕。
+所以怎么判断哪里不能骑车?
-
-
证明,\(f\) 在 \(X\) 上满足Lipschitz条件是 \(f\) 在 \(X\) 一致连续的充分条件。
-Trivial.
-判断上述条件是否是必要条件? 证明或举出反例。
-不是必要的,比如取 \(f(x) = -\sqrt{x}\),\(x \in [0,1]\) -即有一致连续,但不满足 Lipschitz 条件。
-假设 \(f\) 在 \([a,+\infty)\) 上满足Lipschitz条件,其中 -\(a > 0\),试证明 \(\dfrac{f(x)}{x}\) 在 \([a,+\infty)\) 一致连续。
-取任意的 \(\delta \in \mathbb -R+\),考虑 \(x,y \in -[a,+\infty)\) 且 \(|x-y|=\delta\) 的情况。此时有 \(|f(x) - f(y)|\leq L\delta\),且 \(f(x)\) 一致连续。于是 \(|\frac{f(x)}{x} - \frac{f(y)}{y}| < |\frac{f(y) -\delta}{xy} |+|\frac{L\delta}{x}| < (\frac{L+t}{a}+ \frac{b}{a^2}) -\delta\),也满足 Lipschitz 条件,也一致连续。
-上述的 \(t\) 和 \(b\) 是使得 \(|f(x)| \leq t|x| + b\) 成立的值。
-我超,好难(
-
如果能记住哪些路段禁行就没有问题啦!上海有 +124 条道路禁止骑行,也不是很多嘛(迫真
+我今天 random walk ride
+的过程中经过了长宁、静安、黄浦、普陀、徐汇,反正我是分不清哪个区有哪些的(
禁行路段路口都会有标识,但其实整得我很紧张,一个是远远看到交警就有点慌,也担心看漏了。而且因为眼神不太好今天还看混了下面这两个,一开始以为右边的也是自行车禁行所以多绕了些路,实际上只是禁三轮车和摩托车(尴尬挠头
+但是警用摩托车似乎可以走诶。(
+
骑行导航能通行的地方一般是可以骑车的,一般也是准确的毕竟禁行的路就那几条。但我更喜欢 +random walk +而非提前确定好去哪里以及查路线,另外需要看导航也很麻烦。
有自行车道的地方可以骑自行车(大概吧?
+但市区很多年岁比较久远的窄马路(点名梧桐区)分不出自行车道来,骑行体验也不是很好(下详)。没必要用一个必要条件做判断来限制自己(
最后也是最粗暴的方法,如果前面有车(不是共享单车的话就很稳了)跟着骑就行了(
*思考题
+总的来说不是很难,我今天唯一路过的禁行路段就是大名鼎鼎的淮海中路,这个连我都本来就知道(。
+骑行体验
+除了第一次在这边骑车担心上错路,看到交警会有点紧张之外,其实路况也不算很好。一个是很多地方没有自行车道,只能在机动车道上和车挤一挤,另外老马路凹凸不平的很多,即使看起来稍微平整的也可能很颠,共享单车没有减震器本身也不行。今天在江苏路买了两盒鲍师傅然后去骑车玩,一路上颠得我感觉在徐汇的时候海苔肉松小贝已经变成了肉松小贝海苔,到长宁恐怕已经是小贝肉松海苔了。
+但梧桐区确实很漂亮,有很多又安静风景又好的小路。像武康路本身就是建筑保护区,愚园路这种网红景点路上人和车都很多,但不远处的余庆路和天平社区也都有非常漂亮的小洋楼,路上几乎就没人。但我好像有点改不掉一不留神就开始快骑的习惯,一条小路五六百米很快就到头了,才发现错过了一些,又不愿意掉头了。
+另外开个骑行卡会从容很多,不用寸止停车也不担心骑慢了倾家荡产。说到底我今天突然开始骑车玩就是因为发现投放了一批青桔新车,车筐里有一块钱开七天骑行卡的活动广告。
+
青桔活动这四个字看起来怎么这么像青结活动(
+风景
+不完全是骑车的时候看到的,总之我都很喜欢。
+
走不出的万航渡路,而且前两天美赛的一个具体案例分析我们就选了 +Indonesia,现在看到就想吐(对不起
+
我做了一个违背祖宗的决定:我去看武康大楼了(
+楼对面拍照的人很多,位于武康路和淮海中路(自行车禁行)路口,但我其实没觉得这个楼多好看诶,像火车头(我自裁。但是这张的天空颜色很漂亮,紫色柔柔地晕染开来的感觉,我也梦想融入这永恒。

这张看起来快到天平社区了,我超级喜欢这个小灯笼,远看像小柿子一样,还会在风里轻轻地
+匀速
+转动,喜庆又不土气(说的就是你啊某些路上挂的超大灯笼。后面的树枝上面缠了红色的彩灯,像红梅一样(逆风如解意容易莫摧残.mp3),特别漂亮。
这就不得不提天津站附近某些树上的彩灯了(鞭尸,不是缠上去的而是披上去的,敷衍就算了,之前看到这个的时候真没绷住(
+
晚上去吃饭在旁边店里看到的小玩意,古灵精怪的,好有意思哦。
+就是贵。
+路线
+
太混沌了,我回来之后按照感觉上走过的地方标了一下,至少它在存在路线重复的情况下是一个连通图,吧?
+比如说华山路的一些路段我就在不同的行程里骑了好几遍,尤其是交通大学站附近的那一小段,精神 +SJTU +人实锤(但这是徐汇校区而已.jpg)。今天还验证了二维随机游走是常返的,怎么也走不出万航渡路,江苏路和华山路,虽然后两条本质上是一条路(
+美观起见我把地图横过来了,右下角是指北针。
+2024.02.10
+今天沿着铜川路骑了一趟,从岚皋路下地铁然后一路骑到了定边路地铁站,没有再往嘉怡路走,就回家了。
+一开始扫了一辆旧车,大约是到真光公园的时候觉得骑着费劲,停下来换了一辆新的。除了新之外,座椅的确比以前的要软一些。这么阔气的原因还是七天单车卡没有用完,快到期了,急急急。
+路线
+可能是居民区加上在外环和中环之间的原因,这边交警密度没有市区那么恐怖,心情挺好的(?
+铜川路就是铜川路嘛,还要什么路线图(
+
2024.02.11
+今天还是沿着铜川路骑车,果然还是跟我妈一起骑车更有那个成就感,因为共享单车也可以拉她好远(x。去环宇城吃山石榴,然后在地下二层逛了山姆会员店。我才知道这个店它只有会员才能进去,而会员甚至每年要交 +60 +块钱,还是我妈这位尊贵的会员紧急送我一个亲友卡才把我带进去,然后我进去看每个人都像在看六十块钱。
+严谨一点来说,我看两个人一起逛的就像每个人三十块钱,三个人每个人二十块钱,四个人十五,五个人十二,六个人十块,不是葫芦娃一家出来逛街的话也不太会更多了,看来这个会费设置是很有道理的。
+感觉线下逛过山姆之后申请签证的成功率又高了一些(x
+线路图和昨天的一样,不再放一个了(
+]]>我不会 MATLAB,又懒得学,就选了 Python。反正作业就是造轮子,也不能用 +MATLAB 的函数,那 Python 不亏。
+ +声明:本文更新时间均在数值实验作业截止日期后,详情可查询 commits +记录,不存在任何抄袭或协助抄袭现象。
+线性方程组直接解法
+一开始还是有点虚的,NumPy 和 Pandas +都是前学后忘,于是第一次作业拖到周末才写,意外地顺利。
+反正就是不停地写循环,略烦。
+\(LDL^T\) 法
-
-
连续函数 \(f\colon \mathbb R\rightarrow -\mathbb R\) 满足如下性质:对任意的 \(\delta>0\),我们都有 \(\displaystyle \lim_{n\rightarrow \infty} -f(n\delta)=0\),证明,\(\displaystyle -\lim_{x\rightarrow +\infty} f(x)=0\)。
-对任意的 \(\delta >0\),\(\varepsilon >0\),存在 \(N=N(\delta,\varepsilon)\) 满足对任意的 -\(n >N\),有 \(|f(n \delta)| <\varepsilon\)。于是只要取 -\(X= \sup \{\delta N(\delta , -\varepsilon)\}\),就有 \(\forall x > -X\),\(|f(x)|<\varepsilon\)。问题在于这个 \(X\) 是否存在。
-我们规定 \(\delta \in (0,1]\),于是 -\(X < \sup -\{N(\delta,\varepsilon)\}\),其中 \(\delta \in (0,1]\) 且 \(\varepsilon\) 固定。
-连续函数 \(\varphi\colon \mathbb -R\rightarrow \mathbb R\) 满足如下两个性质:
+算法就是 \(LDL^T\) +法。书上啥都有。
+比较痛的一点是,这个方法为了提高效率把 \(L\) 和 \(D\) 直接存储在 \(A\) +里了,但是最后计算误差的时候需要调用原值 \(A\),所以做分解之前应该先备份一个原矩阵。向量 +\(b\) 的备份同理。
+实现如下:
++# 任务一:改进的平方根法求解线性方程组
import numpy as np
from numpy.linalg import norm
n = 32
H = 1./(np.arange(1, n + 1)+np.arange(0, n)[:,np.newaxis]) #构造n阶Hilbert矩阵
xtrue = np.ones((n, 1))
x = np.ones((n, 1))
b = H.dot(xtrue)
#待定系数法计算LDL^t分解
K = H.copy()
c = b.copy()
for j in range(0, n):
for k in range(0, j):
K[j, j] = K[j, j] - K[j, k] * K[j, k] * K[k, k]
for i in range(j + 1, n):
for k in range(0, j):
K[i, j] = K[i, j] - K[i, k] * K[j, k] * K[k, k]
K[i,j] = K[i, j] / K[j, j]
#写出L和D的具体形式
L = np.zeros((n, n))
D = np.zeros((n, n))
for i in range(0, n):
L[i, i] = 1
for j in range(0, i):
L[i, j] = K[i, j]
D[i, i] = K[i, i]
#解方程Ly=b
y = np.zeros((n, 1))
y[0] = c[0]
for i in range(1, n):
for j in range(0, i):
c[i] = c[i] - K[i, j] * y[j]
y[i] = c[i]
#解方程DL^tx=y
x = np.zeros((n, 1))
x[n-1] = c[n-1] / K[n-1,n-1]
for i in range(n-2, -1, -1):
x[i] = y[i] / K[i,i]
for j in range(i+1, n):
x[i] = x[i] - K[j,i] * x[j]
#输出结果
print('相对残量为: %.4f'%(norm(b - np.matmul(H, x)) / norm(b)))
print('相对误差为: %.4f'%(norm(x - xtrue) / norm(xtrue)))输出结果:
++相对残量为: 0.0000
相对误差为: 111.3149残量为 \(0\) 说明分解正确。考虑到 +\(Hilbert\) +矩阵是个病态矩阵,这个值还算可以接受。虽然真值是一个分量全为 \(1\) 的 \(32\) 阶向量,而数值解从第 \(7\) +个分量开始就大量出现绝对值是两位数的情况了。
+\(LDL^T\) 分解从结果来看仍然是 \(LU\) 分解的一种变形,但在本实验中,利用 +\(LU\) +分解得到的数值解各分量量级偏小,甚至达到 \(10^{-5}\) 级别。输出结果为:
++相对残量为: 0.0000
相对误差为: 73385.0585相对误差大了两个量级,说明对于对称矩阵来说 \(LDL^T\) 分解是更好的选择。
+我在做数值实验的过程中先解决了 \(LU\) 分解,回头又做了 \(LDL^T\) +分解,因此二者的结果不能很好地匹配也造成了不小的困难..
+
\(LU\) 法
+-
+
我感觉最难的是从
+.mat文件里载入矩阵...\(LU\) +法,学过线代就能做,我大一上学期的 C++ 大作业里还写这个了..
+实现如下:
+
# 任务二:实现按列存储的JKI型LU分解 |
类似地,注意算法虽然是在 \(A\)
+上进行的,但在程序中需要保留 \(A\)
+的原值来计算相对误差,因此在函数中使用的应该是 \(A\) 的复制,也就有了
+A=B.copy() 这一步。
输出结果:
+relerr = 0.0000 |
相对误差接近于 \(0\),说明实验是成功的。
+后记
+不是,这玩意不是我后来咕咕了没再写,而是布置过一次作业之后就再也没有了(
+本来说是基本每一讲后面都有数值实验的,结果不知道是老师咕咕还是助教咕咕,总之是并没有再布置过实验,少了很多乐趣。之前看过贵系数值分析的资料 +Repo,两边的风格还是很不一样的。
+就这么草率地结束了..
+]]>其实是在课上同步写笔记体验很不错,dwl +老师的风格一如既往的稳健,课堂节奏正好。在课上敲笔记总比摸鱼好。
+ +Lecture 1
+吹水,然后讲了点基本概念。
+多元数据的组织
+对于多元数据,常见的形式是一个 population 中的样本个体(称为 +item)有不同的项,每个 item 呈现出 p 个 variable 的取值。我们每次在 +population 中抽样会取出 \(n\) 个 +item,实际上获得了 \(np\) 个数据。
+一般用矩阵组织二元数据,以随机变量作为列元素,把 population 中的 item +作为横行。也就是说 \(n\) 个 item 各自有 +p 个随机变量项目的情况下,可以把它组织成 \(n +\times p\) 尺寸的表格:
+| + | Variable 1 | +Variable 2 | +... | +Variable i | +... | +Variable p | +
|---|---|---|---|---|---|---|
| Item 1 | +\(x_{11}\) | +\(x_{12}\) | +... | +\(x_{1i}\) | +... | +\(x_{1p}\) | +
| Item 2 | +\(x_{21}\) | +\(x_{22}\) | +... | +\(x_{2i}\) | +... | +\(x_{2p}\) | +
| ... | +... | +... | +... | +... | +... | +... | +
| Item j | +\(x_{j1}\) | +\(x_{j2}\) | +... | +\(x_{ji}\) | +... | +\(x_{jp}\) | +
| ... | +... | +... | +... | +... | +... | +... | +
| Item n | +\(x_{n1}\) | +\(x_{n2}\) | +... | +\(x_{ni}\) | +... | +\(x_{np}\) | +
实际上就是一个 \(n \times p\) +大小的矩阵,每个 \(X_{ji}\) +都可以视作随机变量。因此,每一次从 population 中随机抽样出 \(n\) 个 +item,都能得到一个不同的多元数据矩阵作为 observed data,在 multivariate +statistics 中,observed data 一般是矩阵。
+更本质地,可以把一个随机矩阵视为 \(n\) 个随机向量,每个随机向量代表了一个 item +的具体分量数据。并且可以认为这 \(n\) 个 +items 是彼此独立的(\(n\) +次独立的取样),于是可以认为 joint distribution 是 \(n\) 个 PDF 之积。
+描述性统计量
+老生常谈了捏。对于上述的 observed data,可以纵向观察各个 variable +的性质。
-
-
它在无穷远的行为如下:\(\displaystyle -\lim_{x\rightarrow +\infty}\bigl( -\varphi(x)-x\bigr)=+\infty\)。
-\(\varphi\) 的不动点集 \(\bigl\{x\in \mathbb R\bigm| -\varphi(x)=x\bigr\}\) 是非空的有限集。
-
证明,如果 \(f\colon \mathbb R\rightarrow -\mathbb R\) 是连续函数并且满足 \(f\circ -\varphi =f\),那么 \(f\) -一定是常值函数。
-对于 \(\forall M>0\),存在 \(N >0\),满足 \(x > N\) 时一定有 \(\varphi(x) - x >M\)。
-?.jpg
-连续函数 \(f\colon \mathbb R_{\geqslant -0}\rightarrow \mathbb R\) 满足 \(\displaystyle \lim_{x\rightarrow +\infty} -\frac{f(x)}{x}=0\)。假设 \(\{a_n\}_{n\geqslant 1}\) -是一列非负实数的数列并且数列 \(\{\dfrac{a_n}{n}\}_{n\geqslant 1}\) -是有界的,证明,\(\displaystyle -\lim_{n\rightarrow \infty} \frac{f(a_n)}{n}=0\)
-对任意 \(\varepsilon >0\),存在 -\(M\) 使得 \(x>M\) 时总有 \(|f(x)|<\varepsilon x\)。
-如果数列 \(\lbrace a_n \rbrace\) -无界,则取 \(N = \sup \lbrace |\frac{a_n}{n}| -\rbrace\),\(|\frac{f(a_n)}{n}| = -|\frac{f(a_n)}{a_n}| |\frac{a_n}{n}|\leq N |\frac{f(a_n)}{a_n}| \leq -N\varepsilon\),或有 \(|\frac{f(a_n)}{n}| <|\frac{\sup |f([0,K])|}{n}| -\to 0\)。
-如果数列 \(\lbrace a_n \rbrace\) -有界,则显然有 \(|\frac{f(a_n)}{n}| -<|\frac{\sup |f([\inf a_n,\sup a_n])|}{n}| \to 0\)。
列均值/sample mean :\(\bar{x_k} = +\frac{1}{n} \Sigma_{i=1}^{n} x_{ik}\),\(k=1,2,...,p\)
+直观来说体现了分布的位置。
列方差/sample variance :\(s_k ^2 = +s_{kk} = \frac{1}{n} \Sigma_{i=1}^n (x_{ik}-\bar{x_k})^2\),\(k=1,2,...,p\)
+直观来说体现了分布的分散程度。
+实际上,可以看到此处列方差的系数是 \(\frac{1}{n}\) 而不是传统的 \(\frac{1}{n-1}\),这是由使用场景决定的。在统计推断中,如果需要无偏统计量则使用 +\(\frac{1}{n-1}\),如果需要极大似然估计(MLE)则使用 +\(\frac{1}{n}\)。尤其是样本量 \(n\) +很大的情况下,二者的差别并不大,可以不做严格的区分。
协方差,相关系数:直观上来说体现了线性相关性,相关系数为正则正相关,否则负相关,为 +\(0\) 不相关。
+协方差定义为 \(s_{ik} = \frac 1 n +\Sigma_{j=1}^n (x_{ji} - \bar{x_i}) (x_{ji} - +\bar{x_k})\),可以看到实际上 \(s_{ik} = +s_{ki}\),于是协方差矩阵有
+\[ \begin{bmatrix} s_{11} & s_{12} +& ...& s_{1p}\\ s_{21} & s_{22} & ...& s_{2p} \\ ... +& ...&...&... \\ s_{p1} & s_{p2} &...&s_{pp} +\end{bmatrix}\]
+的形式,这是一个对角元为正的对称矩阵。
+类似地,相关系数定义为 $_{ik} = { } $ +的形式,也有对应的协方差矩阵,是一个对角元均为 \(1\) 的对称矩阵。
*娱乐问题:素数是无限多的拓扑证明 -(Furstenberg, 1955)
-\(X\) 是集合,\(\mathcal{T}=\{U\mid U\subset X\}\) 是 \(X\) -的某些子集所组成的集合。如果下面三个条件成立
+也可以由随机向量矩阵得到相应的 sample mean 向量和 sample variance +向量。
+Mahalanobis Distance
+用来判断不同 item 的 的“距离”,从来衡量两组数据的相似性。实际上不同的 +variance 有不同的量纲,我们想比较不同 item 的差异,需要把 variance +的量纲“统一”来计算二者的差异。使用 Mahalanobis distance 来计算。
+假设两个 item 的数据值分别是 \(P = +(x_1,x_2,...,x_p),Q= (y_1,y_2,...,y_p)\),记整体 sample mean +向量为 \(\mu = +(\mu_1,\mu_2,...,\mu_p)\),协方差矩阵为 \(\Sigma\)。在不同的使用场景下,Mahalanobis +distance 有不同的形式,主要在以下方面处理了差异:
-
-
\(\emptyset \in \mathcal{T}\), -\(X \in \mathcal{T}\)。
-对任意的 \(\{U_{\alpha}\}_{\alpha \in -\mathcal{A}}\subset \mathcal{T}\),其中 \(\mathcal{A}\) 为指标集合,我们有 \(\displaystyle\bigcup_{\alpha \in -\mathcal{A}}U_\alpha \in \mathcal{T}\)。
-对任意有限个 \(U_1,U_2,\cdots, U_m \in -\mathcal{T}\),我们有 \(\displaystyle\bigcap_{1\leqslant i\leqslant m}U_i -\in \mathcal{T}\)。
+通过给差值除掉此维度数据的协方差,来规范尺度差异。本质上是个仿射变换。
+\(d(P,Q) = \sqrt{\frac{(x_1 - +y_1)^2}{s_{11} } + \frac{(x_2 - y_2)^2}{s_{22} } + ... +\frac{(x_p - +y_p)^2}{s_{pp} } }\)
+希望能够用二次型的形式直观表述 \(P\) 和 \(Q\),或者 \(P\) 和 \(\mu\) 之间的差异。
+\(d(P,\mu) = \sqrt{(x-\mu) ^T \Sigma ^{-1} +(x-\mu)}\)
+\(d(P,Q) = \sqrt{(x-y)^T \Sigma^{-1} +(x-y)}\)
我们就称 \(\mathcal{T}\) 是 \(X\) 上的一个拓扑,每个 \(U\in \mathcal{T}\) 都被称作是(拓扑 \(\mathcal{T}\) 下的)开集。我们把二元组 -\((X,\mathcal{T})\) -称作是一个拓扑空间。
-假设 \((X',\mathcal{T}')\) -是拓扑空间,\(f\colon X\rightarrow -X'\),如果对每个 \(U'\in -\mathcal{T}'\),我们有 \(f^{-1}(U')\in \mathcal{T}\),我们就称 -\(f\) 是连续映射。
-给定拓扑空间 \((X,\mathcal{T})\),考虑子集 \(F\subset X\),如果其补集 \(X-F\) 是开集(即 \(X-F\in \mathcal{T}\)),我们就称 \(F\) 是在拓扑 \(\mathcal{T}\) -下的)闭集。对于闭集,我们有如下的性质:
+此外还有两个结论:
-
-
\(\emptyset\) 和 \(X\) 都是闭集。
-任意多闭集的交集是闭集。
-有限个闭集的并集是闭集。
+设 \(Z\) +是一个随机向量,记它的均值向量为 \(\mu +_Z\),协方差矩阵为 \(\Sigma +_Z\),二者均有限。\(A\) +是任意的对称矩阵。于是有 \(E[Z^T AZ] = +trace(A\Sigma_Z) + \mu_Z ^T A \mu_Z\)。
+Proof:考虑迹的性质。\(E[Z^T AZ] = tr(E[Z^T AZ]) = E[tr(Z^TAZ)] = +E[tr(AZZ^T)] = tr(E[AZZ^T]) = tr(AE[ZZ^T])\),由\(Z\) 是随机向量,\(E[ZZ^T] = (\Sigma_Z + \mu_Z ^T \mu_Z)\),故 +\(tr(AE[ZZ^T]) = tr(A\Sigma_Z) + tr(A\mu_Z +\mu_Z^T) = trace(A\Sigma_Z) + \mu_Z ^T A \mu_Z\)。
+2-范数的期望:\(p\) 阶随机向量 +\(X\) 有有限的均值向量 \(\mu\) 和协方差矩阵 \(\Sigma\),于是 \(E[|| X - \mu ||_2 ^2] = \Sigma_{i=1} ^p +\sigma_{ii}\)。
+Proof: 在上一个结论中取 \(A=I\),于是 \(E[|| X - \mu ||_2 ^2] = E[(X-\mu )^T I (X-\mu)] = +tr(I\Sigma) = \Sigma_{i=1} ^p \sigma_{ii}\)。
+Remark: 对于独立同分布的 \(X\) 和 \(Y\),有相同的均值向量和协方差矩阵,于是 +\(E[||X-Y||_2^2] = 2 \Sigma _{i=1} ^p \sigma +_{ii}\)。
娱乐问题:素数是无限多的拓扑证明(Furstenberg,1955)
-考虑 \(X=\mathbb{Z}\) -为全体整数的集合,对于 \(a,b \in -\mathbb{Z}\),其中 \(a\geqslant -1\),我们定义 \(U_{a,b}=\{ka+b\mid k -\in \mathbb{Z}\}\)(就是以 \(b\) -为某一项的双边的等差数列)。我们定义 \(X\) 的子集的集合 \(\mathcal{T}\):如果 \(U\in \mathcal{T}\),要么 \(U=\emptyset\),要么 \(U\) 是某些 \(U_{a,b}\) 的并集。
+最后来考虑 Mahalanobis distance 的期望。\(p\) 阶随机向量 \(X\) 有有限的均值向量 \(\mu\) 和协方差矩阵 \(\Sigma\),其 Mahalanobis distance 定义为 +\(||X- \mu ||_\Sigma = d(X,\mu) = +\sqrt{(X-\mu)^T \Sigma^{-1} (X-\mu)}\),利用上述结论则 \(E[||X- \mu ||_\Sigma ^2] = p\)。
+同理,对于独立同分布的 \(X\) 和 +\(Y\),有 \(E[||X-Y||_\Sigma ^2] = 2p\)。
+Exploratory Data Analysis +(EDA)
+这个其实在线性回归课上也学过,主要讲的是数据清洗的原则和方法,也没有什么很实际的内容,感觉在扯皮。wljj +的课上比较注重解释一些看起来很炫酷的图是怎么画的,真的很应用。
+这个能用 RMarkdown 写的话就好了,Typora 什么时候能支持 +RMarkdown(暴论
+Boxplot
+data = matrix(0,nrow=12,ncol=2) |

(假装在用 Rmd(
+boxplot 包含了很多信息。盒子的上边表示数据中的 75% 分位数,下边表示 +25% 分位数,盒子中间的线表示中位数。我们将 75% 分位数和 25% +分位数的差记作 IQR,则盒子上边距离最上方的“触角”的距离是 1.5 +IQR,下边同理。
+对于正态分布来说,两个触角之间的距离表示了所有正常数据的范围,离开这个范围的数据基本上是 +out of 3\(\sigma\) 的,可以直观地去除 +outlier。
+在 R 的绘图中会将上“触角”的值定为 75% quantile + 1.5 IQR +和最大数据之间的较大值,下“触角”同理,因此在上面的这个例子里,两组数据的 +25% quantile 和 75% quantile 都是相同的,绘图结果有差别。
+Histogram
+柱状图的宽度还是有讲究的,适当的宽度可以看出分布的形状。通用的是 +\(h =( \frac{24\sqrt{\pi} } {n})^{\frac{1}{3} +}\)。
+hist(mpg$hwy,main = "Histogram of highway miles per gallon",breaks = round(max(mpg$hwy)-min(mpg$hwy)/(24*sqrt(pi)/length(mpg$hwy))^(1/3))) |

Scatter Plot
+散点图有很 fancy 的版本,这里展示一些实现:
-
-
\(U\in -\mathcal{T}\)。证明,\(x\in U\) -当且仅当存在 \(a\geqslant 1\),使得 -\(U_{a,x}\in \mathcal{T}\)。
-对于 \(x\in U\),一定有 \(x \in U_{s,t}\),于是 \(x=ks+t\),那么 \(U_{s,x}=U_{s,t} \in \mathcal T\)。
-证明,\(\mathbb{Z}\in -\mathcal{T}\)。
-\(\mathbb Z = U_{1,0} \in \mathcal -T\)。
-证明,对于任意的 \(\{U_i\}_{i \in -I}\subset \mathcal{T}\),那么 \(\bigcup -U_i\in \mathcal{T}\)。
-Trivial.
-证明, 如果 \(U,V\in -\mathcal{T}\),那么 \(U\cap V\in -\mathcal{T}\)。
-Trivial.
-证明,任何有限集合都不是开集;任何补集是有限的集合都不是闭集。
-Trivial.
-证明,\(U_{a,b}\) -即时开集也是闭集。
-它是开集,它的补集是 \(\cup_{c\in [1,a],c -\neq b} U_{a,c}\),也是开集,所以它自己也是闭集。
-证明,\(\displaystyle\mathbb{Z}-\{-1,1\}=\bigcup_{p~\text{是素数}}U_{p,0}\)。
-因为整数环去掉 \(0\) 之后是一个 -UFD。(草
-用反证法证明,有无限多个素数.
-如果只有有限个素数。\(U_{p,0}\) -是闭集,\(\bigcup_{p~\text{是素数}}U_{p,0}\) -是有限个闭集的并,还是闭集。那么 \(\lbrace --1,1 \rbrace\) 在 \(\mathbb Z\) -上的补集是一个闭集,它是开集,而且是有限集,矛盾。
-我超,好强。
+Scatter Plot
+放一个我线性回归作业里的图罢。
++men <- c(72.5,71.5,70.5,69.5,68.5,67.5,66.5,65.5,64.5)
brothers <- c(71.1,70.2,69.6,69.5,68.7,67.7,67.0,66.5,65.6)
p = plot.default(men,brothers,xlim = c(63,73),ylim=c(65,72),main = 'Heights of men and their brothers',xlab = 'medium heights of the men',ylab = 'medium heights of the brothers',col = "blue")
abline(lm(brothers~men))
+
lm(brothers~men)
+Scatter Plot Matrix
++library(GGally)
lizard<-read.csv('t1-3.dat',sep='',header=F)
names(lizard)<-c('mass','svl','hls')
ggpairs(lizard,title = 'scatter plot matrix of lizard') +
+3D Scatter Plot
++library(scatterplot3d)
data(iris)
head(iris)+scatterplot3d(iris[,1:3])
+
colors <- c("#999999","#E69F00","#56B4E9")
colors <- colors[as.numeric(iris$Species)]
scatterplot3d(iris[,1:3],pch=16,color=colors,main='3D scatter plot of iris flower', grid=TRUE, box=TRUE, type="h")
期中考试
-考试时间为 2 小时 25 -分钟。两道大题之间是相互独立的。考试中后面的问题可以使用前面问题的结论(无论答题人是否已经得到正确的证明或者答案)。
-基本概念和技巧的考察
+
Lecture 2
+介绍了一些矩阵方法,以及复习线性代数。
+Linear Algebra
+什么嘛,我线代学得还可以嘛(喜
+矩阵分解的复习就跳过了,也就那点东西,主要是谱分解和奇异值分解。
+Matrix +Interpretation of Mahalanobis-distance
+注意一些左乘矩阵代表的意义,比如在 Mahalanobis +距离中常用的处理方式是旋转和伸缩,二者分别可以左乘一个正交矩阵/对角矩阵来完成。
+因此,回忆一下 Mahalanobis 距离的表达式 \(d(P,Q) = \sqrt{(x-y)^T \Sigma^{-1} +(x-y)}\),其中要求 \(\Sigma\) +是一个对称正定矩阵,可以分解为 \(\Sigma = P +AP^T\) 的形式,其中 \(P\) +是正交矩阵,\(A\) +是特征值对角矩阵。
+Matrix Inequality
+Extended Cauchy-Schwartz Inequality:对于两个 \(p \times 1\) 大小的向量 \(b,d\),任意的 \(B\) 满足是对称正定矩阵,于是有
+\[(b^T d)^2 \leq (b^T Bb)(d B^{-1} +d)\],
+等号成立当且仅当 \(b=cB^{-1} +d\),\(c\) 是常数。
+Proof(证明摘自 Vica's +Blog):注意到
+\[\boldsymbol{b}^\intercal\boldsymbol{d}=\boldsymbol{b}^\intercal\boldsymbol{I}\boldsymbol{d}=\boldsymbol{b}^\intercal\boldsymbol{B}^{1/2}\boldsymbol{B}^{-1/2}\boldsymbol{d}=(\boldsymbol{B}^{1/2}\boldsymbol{b})^\intercal(\boldsymbol{B}^{-1/2}\boldsymbol{d})\]
+然后套用柯西不等式即得证。
+Maximization Lemma:\(B\) 是对称正定矩阵,\(d\) 是给定的向量,于是对于任意不为零的向量 +\(x\),有
+\[\max _{x\neq 0} \frac{(x^T d)^2}{x^T Bx} += d^T B^{-1} d\],
+取到最大值时有 \(x = c B^{-1} +d\),\(c\) 是常数。
+Proof:即为 Extended Cauchy-Schwartz Inequality +的变形。
+描述性统计量的矩阵表示
+上次说到把二维数据组织成 \(n \times +p\) 尺寸的表格:
+| + | Variable 1 | +Variable 2 | +... | +Variable i | +... | +Variable p | +
|---|---|---|---|---|---|---|
| Item 1 | +\(x_{11}\) | +\(x_{12}\) | +... | +\(x_{1i}\) | +... | +\(x_{1p}\) | +
| Item 2 | +\(x_{21}\) | +\(x_{22}\) | +... | +\(x_{2i}\) | +... | +\(x_{2p}\) | +
| ... | +... | +... | +... | +... | +... | +... | +
| Item j | +\(x_{j1}\) | +\(x_{j2}\) | +... | +\(x_{ji}\) | +... | +\(x_{jp}\) | +
| ... | +... | +... | +... | +... | +... | +... | +
| Item n | +\(x_{n1}\) | +\(x_{n2}\) | +... | +\(x_{ni}\) | +... | +\(x_{np}\) | +
实际上就是一个 \(n \times p\) +大小的矩阵,记为 \(A = +[y_1,y_2,...,y_p]\)。
+sample mean vector 也可以写成矩阵变换的表示:$ {X} = A^T _n$,其中 +\(\mathbb 1_p\) 表示 \(p\) 个分量都是 \(1\) 的向量。
+covariance matrix 也可以写成矩阵表达:$ n S_p = A^T (I_n - _n _n^T) +A$,事实上 \(\mathbb 1_n \mathbb 1_n +^T=\mathbb 1_{n\times n}\) 是一个分量都为 \(1\) 的矩阵。
+correlation matrix 在 covariance matrix 的基础上继续做变换即可。记 +$D^{ 2} = diag(,..., ) $,于是 correlation matrix 可以记为 \(R_p= D^{-\frac 1 2} S_p D^{-\frac 1 +2}\)
+在此基础上再定义一个 generalized sample variance,事实上是 covariance +matrix +的行列式值的绝对值,也就是这个对称矩阵的全体特征值的积的绝对值。由行列式的形式可以知道它是一个和各个 +covariance coefficient +相关的式子,一定程度上可以反映数据的离散程度(但因为是标量,缺乏各个方向上的数据的离散情况)。例如对于二维数据(\(p=2\)),可以知道 \(|S|=s_{11} s_{22} (1- r_{12}^2)\)。
+另一个常用的表示是 covariance matrix +的迹,也即这个对称矩阵的全体特征值的和。
+Lecture 3
+今天介绍多元正态分布。
+多元正态分布
-
-
试用 \(\varepsilon-N\) -语言证明:\(\displaystyle \lim_{n\rightarrow -\infty}\dfrac{n}{n^2+1}=0\)。
-Trivial.
-试用 \(\varepsilon-\delta\) -语言说明函数 \(\mathbb R\) 上的函数 -\(f(x)=\begin{cases} \sin(\frac{1}{x}), &\ -\ x\neq 0;\\0,&\ \ x=0\end{cases}\) 在 \(x=0\) 处不连续。
-Trivial.
-计算极限:\(\displaystyle -\lim_{n\rightarrow -\infty}\left(1^2+2^2+3^2+\cdots+n^2\right)^\frac{1}{n}\)。
-\(1\)。
-证明,级数 \(\displaystyle -\sum_{n=1}^\infty \frac{2n+1}{n^2(n+100)^2}\) 收敛。
-小于二阶调和级数,trivial.
-给定实数的序列 \(\{a_n\}_{n\geqslant -1}\),假设级数 \(\displaystyle -\sum_{n=1}^\infty a_n\) 收敛。证明,对任意的实数 \(x\in (-1,1)\),级数 \(\displaystyle \sum_{n=1}^\infty a_n x^n\) -也收敛。(提示:利用Abel判别法)
-PIN 真的,我哭死,他期中考试还在基础题上给提示(
-Trivial.
-假设 \(f\) 是非空开区间 \((a,b)\) 上的连续函数,证明,对任意的 \(x_1,x_2\in (a,b)\),存在 \(x_0 \in (a,b)\),使得
-\(f(x_0)=\frac{1}{2}\bigl(f(x_1)+f(x_2)\bigr)\)
-介值定理,trivial.
-假设函数 \(f:\mathbb R\rightarrow -\mathbb R\) 是以 \(1\) -为周期的连续函数,即对任意的 \(x\in \mathbb -R\),我们有 \(f(x+1)=f(x)\)。证明,\(f\) 有界并且能取到其最大值,即存在 \(x_0\in \mathbb R\),使得 \(f(x_0)=\displaystyle \sup_{x\in \mathbb -R}f(x)\)。
-Trivial.
-证明,\(f(x)=\sqrt{x+1}\) 作为 -\(\mathbb R_{\geqslant 0}\) -上的函数是一致连续的。
-因为满足 Lipschitz 条件,\(L=\frac 1 -2\)。
+多元正态分布的概率密度形式和一元是完全类似的:
+\[f(x) = \frac{1}{(2\pi) ^{p/2} |\Sigma +|^{1/2}} exp(-\frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2})\]
+其中,\(\mu\) 是 \(x\) 的均值,\(\Sigma\) 是 \(x\) +的协方差矩阵,这是一个正定矩阵。
+先把二元的情况拿出来观察,\(p=2\),于是有 \(f(x) = \frac{1}{2\pi |\Sigma|^{1/2}} +exp(-\frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2})\)。其中有
+\[\mu = \begin{bmatrix} \mu_1 \\ \mu_2 +\end{bmatrix} = \begin{bmatrix} E(X_1) \\ E(X_2) \end{bmatrix}, \Sigma = +\begin{bmatrix} Var{X_1} & Cov(X_1,X_2) \\ Cov(X_1,X_2) & +Var(X_2)\end{bmatrix}\]
+我们想对 \(\mu\) 和 \(\Sigma\) 做一些估计,回顾一下统计推断里的 +MLE 估计,矩估计等等方法。
级数
-首先回忆一下二项式展开:\(\displaystyle -(1+z)^n=\sum_{k=0}^n {n \choose k} z^k\)。特别地, 当 \(z=1\) 时,我们有 \(\displaystyle 2^n=\sum_{k=0}^n {n \choose -k}\)。
-给定一个复数的数列 \(\{a_k\}_{k\geqslant -0}\),我们定义新的数列 \(\{a_n^*\}_{n\geqslant 0}\),其中 \(a_n^*=\frac{1}{2^n}\sum_{k=0}^n {n \choose -k}a_k\)
-等比数列
-这一部分中,我们假设对任意的 \(k\geqslant -0\),\(a_k=z^k\),其中 \(z\) 为复数。
+补充:矩阵向量求导、期望
-
-
证明,如果 \(|z|<1\),那么级数 \(\displaystyle \sum_{k=0}^\infty a_k\) -收敛。我们用 \(A(z)\) -表示这个极限。
-Trivial,\(A(z) = -\frac{1}{1-z}\)。
-证明,如果 \(|z|<1\),那么级数 \(\displaystyle \sum_{k=0}^\infty a^*_k\) -收敛。我们用 \(A^*(z)\) -表示这个极限。
-Trivial 但差点被骗了,总之 \(a_k ^* = -\frac{z+1}{2}\),\(A^*(z) = -\frac{2}{1-z}\)。
-证明,如果 \(|z|\geqslant -1\),那么级数 \(\displaystyle -\sum_{k=0}^\infty a_k\) 不收敛。
-Trivial.
-试找出一个 \(z\in -\mathbb{C}\),\(|z|>1\),级数 -\(\displaystyle \sum_{k=0}^\infty -a^*_k\) 收敛。
-级数部分和是 \(\frac{2}{1-z} -(1-(\frac{z+1}{2})^{k+1})\),取 \(z = --2\) 即可。
-证明,如果 \(|z|=1\) 并且 \(z\neq\pm 1\),那么级数 \(\displaystyle \sum_{k=0}^\infty a^*_k\) -收敛。
-Trivial.
+向量求导很熟悉了,就是 Jacobian matrix +那一套。但在多元统计里使用的求导矩阵是 Jacobian matrix +的转置。有一些看起来轻微抽象的结论:
+\[\frac{\partial}{\partial x} Ax = +A^T\]
+\[\frac{\partial}{\partial x} x^TA = +A\]
+\[\frac{\partial}{\partial x} x^Tx = +2x\]
+\[\frac{\partial}{\partial x} x^TAx = +Ax+A^Tx\]
+实际上都非常容易推导,把 \(Ax\) 视为 +\(x\) +的线性变换,再对分量求导即可。
+对矩阵的求导暂时只考虑对称正定的情况。
+\[\frac{\partial |A|}{\partial A} = |A| +A^{-1}\]
+\[\frac{\partial tr(AB)}{\partial A} +=B^T\]
+\[\frac{\partial tr(A^{-1}B)}{\partial A} += -A^{-1}B^TA^{-1}\]
+有点抽象(
+对于某一个 population \(c^T X = +\begin{bmatrix} c_1 & c_2 & ... &c_p \end{bmatrix} +\begin{bmatrix} X_1 \\ X_2 \\...\\X_p \end{bmatrix}\), 其期望变为 +\(c^T \mu\),方差变为 \(c^T \Sigma c\);
+如果 \(c^TX\) 是一个 +sample,同理样本均值变为 \(c^T +\mu\),样本方差变为 \(c^T +Sc\)。
+对于两个 population \(b^TX\) 和 +\(c^TX\),有 \(Cov(b^T X,c^TX) = b^TXc\)。
+注意这里是对一个随机向量的 \(p\) +个分量在做线性组合,而不是对若干个随机向量的组合,期望和方差都是标量而不是向量!
收敛性比较
-这一部分中,我们假设 \(\{a_k\}_{k\geqslant -0}\) 为实数的序列。
+多元正态分布参数估计
+极大似然估计
+这个我在课上自己推出来了(喜),还喜提了 dwl 老师在我身边叫我名字 + +纠正书写,她居然还记得我,但想起来我开摆的初概,真是又开心又尴尬(。结论是:
+对于 \(X_1,X_2,...,X_n\) i.i.d. +\(\sim N_p (\mu,\Sigma)\),参数 \(\mu\) 和 \(\Sigma\) 的极大似然估计是:
+\[ \hat{\mu}_{MLE} = \bar{X}\]
+\[\hat{\Sigma}_{MLE} = \frac{1}{n} +\Sigma_{i=1} ^n (X_j - \bar{X})(X_j - \bar{X})^T\]
+无偏估计
+首先考虑样本方差为 \(S = \frac{1}{n-1} +\Sigma_{i=1} ^n (X_j - \bar{X})(X_j - \bar{X})^T = \frac{n}{n-1} +\hat{\Sigma}_{MLE}\),它是 \(\Sigma\) 的无偏估计;\(\mu\) 的无偏估计显然是 \(\bar{X}\)。
+事实上还有性质:\(Cov(\bar{X}) = \frac 1 n +\Sigma\);\(S\) 和 \(\bar{X}\) +互相独立,且是一组充分统计量(用因子分解定理简单看一下)。
+多元正态分布的性质
-
-
证明,当 \(k\in \mathbb{Z}_{\geqslant -0}\) 固定的时候,我们有:
+\(X \sim N_p(\mu , \Sigma) \iff a^TX +\sim N(a^T\mu,a^T\Sigma a)\) 对任意的 \(a \in \mathbb R^p\) 成立。
+\(X\sim N_p(\mu ,\Sigma) \iff AX+d \sim +N_p(A\mu +d , A\Sigma A^T)\) 对任意的 \(d\in \mathbb R^p\) 成立。
+对于特定的 \(N_p(\mu , +\Sigma)\),我们可以用 \(p\) +个标准正态分布捏出来。对于任意的 \(Z_1,Z_2,...,Z_p\) i.i.d. \(\sim N(0,1)\),记 \(Z=(Z_1,Z_2,...,Z_p)^T\)。对任意的对称正定矩阵 +\(\Sigma\) 和实向量 \(\mu \in \mathbb R^p\),有 \(X = \mu + \Sigma^{\frac 1 2} Z \sim +N_p(\mu,\Sigma)\)。
+对于满足多元正态分布的 \(X = +(X_1,X_2,...,X_p)^T \sim N_p(\mu ,\Sigma)\),我们可以根据 \(\mu\),\(\Sigma\) 的信息找到任意一组 \((X_{i1},X_{i2},...,X_{ij})\) +的期望和方差,也可以通过协方差矩阵得到任意一对 \((X_i,X_j)\) +之间的独立性关系(注意对于正态分布,独立和不相关是等价的,对于其他分布不能这样推理)。
+然而对于相关的随机向量,例如 \(\begin{bmatrix} X_1 \\ X_2\end{bmatrix}\sim +N_{q_1+q_2} (\begin{bmatrix}\mu_1 \\ \mu_2 \end{bmatrix},\begin{bmatrix} +\Sigma_{11} &\Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} +\end{bmatrix})\),其中 \(| +\Sigma_{22}|>0\),可以看到 \(X_1,X_2\) +之间并不独立。此时我们有另一种结果: $(X_1 | X_2 = x_2) N(1 + +{12} {22}^{-1} (x_2 - 2),{11} - {12 } +{22}^{-1} {21}) $
+Proof:(这是我写在作业里的一个方法,写个作业用蹩脚英文,现在看看绷不住了)
+According to the resolution:
+\[\Sigma = \begin{bmatrix} \Sigma_{11} +& \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{bmatrix} += \begin{bmatrix}\Sigma_{11} - \Sigma_{12 } \Sigma_{22}^{-1} +\Sigma_{21} & \Sigma _{12} \\ 0 & +\Sigma_{22}\end{bmatrix} \begin{bmatrix}I &0 \\ -\Sigma_{22} ^{-1} +\Sigma_{21} & I\end{bmatrix}^{-1}\]
+Note that:
+\((x-\mu)^T \Sigma ^{-1} (x-\mu) = +\begin{bmatrix}x_1^T - \mu_1^T & x_2^T - \mu_2^T\end{bmatrix} +\begin{bmatrix} I & 0 \\ -\Sigma_{22}^{-1} \Sigma_{21} & +I\end{bmatrix} \begin{bmatrix}(\Sigma_{11} - \Sigma_{12 } +\Sigma_{22}^{-1} \Sigma_{21})^{-1} & 0 \\ 0 & \Sigma_{22}^{-1} +\end{bmatrix} \begin{bmatrix}I & -\Sigma_{12} \Sigma_{22} ^{-1} \\ 0 +&I\end{bmatrix} \begin{bmatrix}x_1 - \mu_1 \\ x_2- +\mu_2\end{bmatrix}\)
+We can know that \((x_1^T -\mu_1^T) - +(x_2^T - \mu_2^T ) \Sigma_{22}^{-1} \Sigma_{21} \sim N(0,\Sigma_{11} - +\Sigma_{12 } \Sigma_{22}^{-1} \Sigma_{21})\),
+so that \(X_1 \sim N(\mu_1 +\Sigma_{21} +\Sigma_{22}^{-1} (x_2 - \mu_2)\),${11} - {12 } +{22}^{-1} {21}) $, the conditional distribution can be derived +from the distribution.
+因此可以看到,即使随机向量的两部分之间有相关性,也可以进行分离。
+\(X \sim +N_p(\mu,\Sigma)\),于是有 \((X-\mu) ^T +\Sigma^{-1}(X-\mu) \sim \chi_p ^2\)。
+Proof:取 \(Z=\Sigma^{\frac 1 2} \sim N_p +(0,I_p)\)。
+于是 \((X-\mu) ^T \Sigma^{-1} (X-\mu) = +[(X-\mu)^T \Sigma^{-\frac 1 2}] [\Sigma^{-\frac 1 2} (X-\mu)] = Z^TZ +=\Sigma_{i=1} ^p Z_i ^2 \sim \chi_p ^2\)。
+\(X_1,X_2,..,X_n\) +是相互独立的多元正态分布,\(X_j \sim N_p(\mu_j +, \Sigma)\),记 \(V_1 = +c_1X_1+c_2X_2+...+c_nX_n = c^TX\)。
-
-
- \(\lim_{n\rightarrow \infty} {n \choose -k}/{\frac{n^k}{k!}}=1\) -
- \(\lim_{n\rightarrow \infty} {n \choose -k}/{2^n}=0\) +
- \(V_1 \sim N_p(c^T \mu , c^Tc +\Sigma)\); +
- 对于 \(V_2 = +b_1X_1+b_2X_2+...+b_nX_n\),有 \(V_1,V_2\) 的协方差矩阵为 \(\begin{bmatrix} c^Tc\Sigma & b^Tc\Sigma \\ +b^Tc\Sigma & b^Tb\Sigma \end{bmatrix}\)。 +
- \(V_1,V_2\) 相互独立 \(\iff b^Tc = 0\)(由上一结论直接得出)
Trivial.
-任意给定非负整数 \(n>q\),我们定义 \(a_{n,q}^*=\frac{1}{2^n}\sum_{k=0}^q {n \choose -k}a_k\),对每个固定的 \(q\),计算 \(\displaystyle \lim_{n\rightarrow \infty} -a_{n,q}^*\)。
-\(0\)。
-如果 \(\displaystyle \lim_{n\rightarrow -\infty} a_{n}=0\),证明,\(\displaystyle \lim_{n\rightarrow \infty} -a_{n}^*=0\)。
-定义证明。
-如果 \(\displaystyle \lim_{n\rightarrow -\infty} a_{n}\) 存在,证明,\(\displaystyle \lim_{n\rightarrow \infty} -a_{n}^*\) 存在并且恰好等于 \(\displaystyle \lim_{n\rightarrow \infty} -a_{n}\)。
-定义证明。
-如果 \(\displaystyle \lim_{n\rightarrow -\infty} a^*_{n}\) 存在,\(\displaystyle -\lim_{n\rightarrow \infty} a_{n}\) 是否一定存在?
-不一定,取 \(a_n = -(-1)^n\)。
+
尤其要注意此处与上一部分最后一段的关系,\(V_1,V_2\) +是在对若干随机向量做线性组合,上一部分最后一段是在对一个随机向量的全体分量做线性组合。也可以从所得结果的维数来判断。
在后面的问题中,对任意的 \(n\geqslant -0\),我们定义部分和 \(S_n=\sum_{k=0}^n -a_k, \ \ S^*_n=\sum_{k=0}^n a^*_k, \ \ U_n=2^n S_n^*\)
+Lecture 4
+单正态分布总体的推断。
+Wishart Distribution
-
-
证明,对任意的 \(n\geqslant -0\),\(U_n\) 都可以写成 \(S_0,S_1,\cdots,S_n\) -的整系数线性组合:\(U_n=\sum_{k=0}^n {n+1 -\choose k+1} S_k\)
-Trivial.
-证明,如果级数 \(\displaystyle -\sum_{k=0}^\infty a_k\) 收敛,那么 \(\displaystyle \sum_{k=0}^\infty a^*_k\) -也收敛。
-Trivial.
+$S = _{i=1} ^n (X_j - {X})(X_j - {X})^T $,有 \((n-1)S =\Sigma_{i=1} ^{n-1} Z_i Z_i^T \sim +W_p(n-1,\Sigma)\),其中 \(Z_i \sim N_p +(0,\Sigma)\)。
+类似于一个 \(\chi^2\) +分布在多元分布上的推广。
+对于 \(A_1 \sim +W_p(m_1,\Sigma)\),\(A_2 \sim +W_p(m_2,\Sigma)\) 且 \(A_1,A_2\) +相互独立,则有 \(A_1 +A_2 \sim W_p +(m_1+m_2,\Sigma)\)。
+对于 \(A \sim +W_p(m,\Sigma)\),$C $ 是一个 \(p\times +p\) 大小的可逆矩阵,则 \(C^TAC \sim +W_p(m,C^T\Sigma C)\)。
+注意 \(C\) 可以是 $k p $ +大小的矩阵,此时也有 \(C^TAC \sim W_k(m, +C^T\Sigma C)\)。这是因为 \(A = +\Sigma_{i=1}^m Z_iZ_i ^T\),其中 \(Z +\sim N_p(0,\Sigma)\),于是有 \(C^TAC +=\Sigma_{i=1} ^m C^TZ_i Z_i ^TC\) 且 \(C^TZ_i \sim N_k ( 0, C^T\Sigma C)\),因此 +\(C^TAC \sim W_k(m,C^T\Sigma +C)\)。此处尤其需要注意随机向量的维数改变为 \(k\) 维。
+以上两个性质都可以轻松地通过 Wishart distribution +的构造推出。
连续函数环的极大理想
-假设 \(a<b\) -是实数,我们研究有界闭区间上的实数值连续函数的空间 \(C\bigl([a,b]\bigr)\)。对于子集 \(I\subset -C\bigl([a,b]\bigr)\),如果它满足如下三个条件:
+One Sample T-test
-
-
\(I\neq \emptyset\),\(I \neq C\bigl([a,b]\bigr)\);
-对任意的 \(\varphi \in -I\),\(\psi \in I\),我们有 -\(\varphi+\psi \in I\);
-对任意的 \(\varphi \in -I\),\(f \in -C\bigl([a,b]\bigr)\),我们有 \(\varphi\cdot f \in I\).
+在一元情况下有 \(\frac{\sqrt{n}(\bar{X} +- \mu_0)}{\sigma} \sim N(0,1)\) 和 \(\frac{(n-1)S^2}{\sigma^2} \sim \chi_{n-1} +^2\),以及 \(\frac{\bar{X} - +\mu_0}{S/\sqrt n} \sim t_{n-1}\) 和 \((\frac{\bar{X} - \mu_0}{S/\sqrt n})^2 \sim +F_{1,n-1}\),这些都是假设检验中常用的检验统计量。我们希望能够推广到多元的情况。
+对于一族 \(X_1,X_2,...,X_n \sim N_p(\mu , +\Sigma)\),假设 \(H_0 :\mu = \mu_0 ; +H_1 :\mu \neq \mu_0\)。
+在 \(H_0\) 下有
+\[\frac{T^2}{n-1} = \sqrt n (\bar{X} - +\mu_0)^T (\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1} \sqrt n (\bar{X} - +\mu_0) = Z_1 (\Sigma_{i=1} ^n Z_iZ_i^T)^{-1}Z_i^T \sim \frac{p}{n-p} +F_{p,n-p}\]
+也就是说 \(\frac{n-p}{p(n-1)} T^2 \sim +F_{p,n-p}\),当 \(T_0 ^2 > T^2 +(\alpha) = \frac{p(n-1)}{n-p} F_{p,n-p}(\alpha)\) +时拒绝原假设。这被称为 Hotelling distribution。
+对于 \(X_i \sim +N_p(\mu,\Sigma)\),考虑 \(Y_i = +CX_i+d\),其中 $C $ 是 \(p \times +p\) 的矩阵,\(d\) 是 \(p \times 1\) +的向量。这是一族多元正态分布的线性变换。
+于是有 \(\bar{Y} = C +\bar{X}+d\),\(S_Y = +\frac{1}{n-1}\Sigma_{i=1}^n (Y_i - \bar{Y_i})(Y_i-\bar Y_i)^T = +CS_XC^T\),考虑其期望有 \(\mu _Y = C +\mu +d\),在假设 \(H_0\) 下有 +\(\mu_{Y,0} = C \mu_0 +d\)。于是对应的 +Hotelling Statistic 是
+\(\begin{aligned} T^2 _Y &= \sqrt n +(\bar Y - \mu_{Y,0})^T (\Sigma (Y_i - \bar{Y})(Y_i - \bar Y)^T)^{-1} +\sqrt n (\bar{Y} - \mu_{Y,0}) \\& =\sqrt n (\bar{X} - \mu_0)^T C^T +C^{-T}(\Sigma (X_j - \bar X)(X_j - \bar X)^T)^{-1}C^{-1}C \sqrt n +(\bar{X} - \mu_0) \\& =\sqrt n (\bar{X} - \mu_0)^T (\Sigma (X_j - +\bar X)(X_j - \bar X)^T)^{-1} \sqrt n (\bar{X} - \mu_0) \\& =T^2_X +\end{aligned}\)
+可以看到与做线性变换之前是相同的,也即对于 \(Y_i = CX_i +d\),可以使用相同的 test +statistic 进行检验。
+实际上,Hotelling test 和 likelihood ratio test +是完全等价的,这个可以在一元的情况下看到,也可以推广到多元。多元情况下的 +likelihood ratio 是:
+\[\Lambda = (\frac{|\hat \Sigma|}{|\hat +\Sigma_0|}) ^{\frac n 2}= (\frac{|\Sigma_{j=1} ^n (x_j - \bar x)(x_j - +\bar x)^T|}{|\Sigma_{j=1} ^ n (x_j - \mu_0)(x_j-\mu_0)^T|})^{\frac n +2}\]
+由此得到 test statistic 的另一表示,不需要对矩阵 \(S\) 求逆:
+\[T^2 = (n-1) \frac{|\Sigma_{j=1} ^n (x_j +- \mu_0)(x_j - \mu_0)^T|}{|\Sigma_{j=1} ^ n (x_j - \bar x)(x_j-\bar +x)^T|} - (n-1)\]
我们就称 \(I\) 是 \(C\bigl([a,b]\bigr)\) 的一个理想。假设 \(\mathfrak{m}\) 是 \(C\bigl([a,b]\bigr)\) -的理想并且不存在其它的包含 \(\mathfrak{m}\) 的理想,我们就称 \(\mathfrak{m}\) 是 \(C\bigl([a,b]\bigr)\) -的一个极大理想(即若理想 \(I\supset -\mathfrak{m}\),那么 \(I -=\mathfrak{m}\))。
+Confidence Interval of +\(\mu_{p \times 1}\)
+Confidence Region of the +Mean
+已知 \(Z_1,Z_2,...,Z_n i.i.d \sim +N_p(\mu,\Sigma)\),对于已有的数据 \(z_1,z_2,...,z_n\) 希望求得 \(\mu\) 的置信区间,其中 \(\mu ,\Sigma\) 均未知。在一元的情况下 (\(p=1\)) 可以使用 \(\frac{\bar Z - \mu}{s / \sqrt n} \sim +t_{n-1}\) 进行估计。\(\mu\) 的 +\(100(1-\alpha)\%\) 置信区间是 \((\bar Z - t_{n-1,\alpha /2} \frac{s}{\sqrt n},\bar +Z +t_{n-1,\alpha /2} \frac{s}{\sqrt n})\)。
+在多元情况下,有 $ T^2 F_{p,n-p}$,其中 \(T^2 = n (\bar Z - \mu)^T S^{-1} (\bar Z - +\mu)\)。于是 \(\mu\) 的 \(100(1-\alpha)\%\) +置信域是满足以下条件的区域:
+\[R(x) = \{\mu: n(\bar Z - \mu )^T S^{-1} +(\bar Z -\mu) \leq c^2 , c^2 = T^2(\alpha) = +\frac{p(n-1)}{n-p}F_{p,n-p}(\alpha) \}\]
+这是一个椭圆。
+Individual Coverage +Intervals
+接下来考虑 \(Z_1,Z_2,...,Z_n\) +的线性组合 \(a^T Z = a_1 Z_1 + ... +a_n +Z_n\),我们希望估计它的均值 \(a^T +\mu\),这是一个标量。
+由于 \(a^T Z \sim N(a^T \mu, a^T \Sigma +a)\),因此 \(a^T \mu\) 的 \(100 \% (1-\beta)\) 置信区间是 \((a^T \bar Z - t_{n-1}(\beta/2) \sqrt{a^T \frac S n +a},a^T \bar Z + t_{n-1}(\beta/2) \sqrt{a^T \frac S n a})\)
+以下继续考虑 \(Z_1,Z_2,...,Z_n\) +的一族共 \(m\) 个线性组合 \(a_1 ^T Z,a_2 ^T Z,...,a_m ^TZ\) +的置信区间推断。
+Bonferroni's Method
+对于 \(m\) 个不同的线性组合 \(a_1^TZ,a_2^TZ,...,a_m^TZ\),分别对其做置信系数为 +\(\frac \alpha m\) 的置信区间,则这 +\(m\) +个区间拼在一起得到的矩体就至少能够包含住真正的置信域。
+也就是说,对每个 \(a_i^T\mu\) +做置信区间:\((a_i ^T\bar{X} - +t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_i ^T \frac S n a_i},a_i ^T\bar{X} + +t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_i ^T \frac S n a_i} )\)
+拼在一起得到的矩体
+\[(a_1 ^T\bar{X} - +t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_1 ^T \frac S n a_1},a_1 ^T\bar{X} + +t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_1 ^T \frac S n a_1} ) \times \cdots +\times(a_m ^T\bar{X} - t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_m ^T \frac S n +a_m},a_m ^T\bar{X} + t_{n-1}(\frac{\alpha}{2m}) \sqrt{a_m ^T \frac S n +a_m} )\]
+即为一个符合条件的置信域。实际上这一置信域的置信系数比 \(\alpha\) 更大,只是一个粗略的估计。
+\(T^2\) +interval
+事实上,对任意的线性变换 \(a^TZ\) +都存在一个统一的 simultaneous coverage interval,也称作 \(T^2\) interval,是
+\((a^T \bar{X} - c\sqrt{a^T \frac S n +a},a^T \bar{X} + c\sqrt{a^T \frac S n a})\),其中 \(c^2 = T^2(\alpha) = \frac{p(n-1)}{n-p} +F_{p,n-p}(\alpha)\)。
+这个置信域比 Bonferroni's Method 得到的置信域更大。
+注意当 \(a\) 在 \(S^{-1}\bar X\) 方向上时以上区间正好是一个 +\(100\%(1-\alpha)\) +的置信区间,也即这个时候区间取到最大。但这一方向会随着样本的变化而变化。
+Real World(?
+对 \(Z_i\) +做线性变换得到的椭圆会在形状和方向上有所变化,但与 \(T^2\) interval +得到的矩形相切。不同置信区间的覆盖面积如图所示。
+
Lecture 5
+Two Population Test
+双正态同方差总体的均值比较
-
-
对任意的子集 \(A\subset -[a,b]\),令 \(I(A)=\left\{f\in -C\bigl([a,b]\bigr)\big| \text{对任意的 $x\in -A$,$f(x)=0$}\right\}\)。证明,\(I(A)\) 是 \(C\bigl([a,b]\bigr)\) 的理想。\(I([a,b])\) 是什么?证明,如果有两个子集 -\(A\subset B\subset [a,b]\),那么 \(I(A)\supset I(B)\)。是否存在 \(A\subset [a,b]\) 为真子集,使得 \(I(A)=\{0\}\)?
-前几问都是有手就行。最后一问取 \(A = -(a,b)\)。
-证明,如果 \(I \subset -C\bigl([a,b]\bigr)\) 是理想,那么常值函数 \(1\notin I\)。进一步证明,如果 \(I \subset C\bigl([a,b]\bigr)\) -是理想,那么对任意的 \(f\in I\),\(f\) 在 \([a,b]\) 上一定有零点(即 \(f(x)=0\) 在 \([a,b]\) 上有解)。
-如果是理想且恒等元在理想中,那么所有元素都在理想中,矛盾。
-如果 \(f \in I\) 且在 \([a,b]\) 上没有零点,那么它是可逆的,\(f^{-1} \in C([a,b])\),于是 \(1 = f \cdot f^{-1} \in I\),矛盾。
-对于 \(f \in -C\bigl([a,b]\bigr)\),证明,集合 \(V(f)=\bigl\{x\in [a,b]\big| f(x)=0\bigr\}\) -是闭集。进一步证明,对于理想 \(I \subset -C\bigl([a,b]\bigr)\),集合 \(V(I)=\bigl\{x\in [a,b]\big| \text{对任意的 $f\in -I$},~ f(x)=0\bigr\}\) 是闭集。如果理想 \(I \subset C\bigl([a,b]\bigr)\) 使得 \(V(I)\) 为全空间 \([a,b]\),你是否能够确定 \(I\)?
-记 \(T = \lbrace 0 \rbrace\),而 -\(f^{-1} (T) = V(f)\) -保持闭集性质。
-\(V(I) = \cap _{f\in I} -V(f)\),闭集的交集还是闭集。
-如果 \(V(I) = [a,b]\),那么对任意的 -\(f \in I\) 都有 \(V(f) = [a,b]\),也就是说 \(f=0\),\(I\) 是平凡理想。
-对任意的点 \(x\in -[a,b]\),我们令 \(A=\{x\}\) 并记 -\(\mathfrak{m}_x -=I(A)=I\bigl(\{x\}\bigr)\),即 \(\mathfrak{m}_x=\left\{f\in C\bigl([a,b]\bigr)\big| -f(x)=0\right\}\)。
-证明,\(\mathfrak{m}_x\) -是极大理想。
-我差点想直接证明 \(C([a,b])\) 是一个 -PID,仔细一想里面的不可逆元全是零因子,根本不是整环。
-不介意我用点抽代知识吧?
-作环同态 \(t: C([a,b]) \to \mathbb -R\),\(f \to -f(x)\)。如果存在极大理想 \(\mathfrak{m} -\supset \mathfrak{m}_x\),且使得存在 \(g\in \mathfrak m\),\(g(x) \neq 0\)。
-于是 \(\ker t = \mathfrak -m_x\),\(C([a,b]) / \mathfrak m _x -\cong \mathbb R\) 是一个域,也即 \(\mathfrak m _x\) 是一个极大理想。
-证明,如果 \(\mathfrak{m}\) 是 -\(C\bigl([a,b]\bigr)\) -的极大理想,那么存在 \(x\in [a,b]\) -使得 \(\mathfrak{m}=\mathfrak{m}_x\)。(提示:利用 -\([a,b]\) 是紧的)
-如果 \(\mathfrak m\) -是一个极大理想,而且不存在一个使得 \(\mathfrak -m = \mathfrak m _x\) 的 \(x\in -[a,b]\)。
-于是对任意 \(x \in [a,b]\),存在 -\(f_x\) 使得 \(f_x(x) \neq 0\)。由 \([a,b]\) 是紧的可知存在一列函数 \(f_1,f_2,...,f_n\),满足对任意 \(x \in [a,b]\),存在 \(i \in \lbrace 1,2,...,n \rbrace\),使得 -\(f_i (x) \neq 0\)。于是 \(F=f_1 ^2 + ... + f_n ^2 \in \mathfrak m\) -且是单位,矛盾。
-是否存在理想 \(I \subset -C\bigl([a,b]\bigr)\) 使得 \(V(I)=\emptyset\)?
-任意一个理想都被包含在某个极大理想中,\(V(I) \neq \emptyset\)。
-假设 \(A\) 是闭集,证明,\(V(I(A))=A\)。
-\(I(A)=\left\{f\in C\bigl([a,b]\bigr)\big| -\text{对任意的 $x\in A$,$f(x)=0$}\right\}\),
-\(V(f)=\bigl\{x\in [a,b]\big| -f(x)=0\bigr\}\)。
-在努力回忆 Galois -对应(?)是什么东西,但是忘了(,不知道有没有关系。
-胡说八道:首先 \(A \in -V(I(A))\),然后证明对任意的 \(x \in -V(I(A))\) 有 \(x \in -A\)。否则存在 \(s \notin -A\),且对任意的 \(f \in I(A)\) -都有 \(f(s)=0\)。我们只要构造出一个不符合此条件的 -\(g \in I(A)\) 即可,而 \(g\in I(A)\) 在 \([a,b]\) 上有可数个零点,且 \(g(s)\neq 0\),逐段构造使其连续,且在 \(A\) 上取值均为 \(0\) 即可。
+两个总体中随机抽样得到的样本和相关统计量分别表示如下:
++
+ + ++ + + + + + +Sample +\(X_{11},X_{12},...,X_{1n_1}\) +\(X_{21},X_{22},...,X_{2n_2}\) ++ +Sample Mean +\(\bar X_1 = \frac{1}{n_1} \Sigma_{j=1} +^{n_1} X_{1j}\) +\(\bar X_2= \frac{1}{n_2} \Sigma_{j=1} +^{n_2} X_{2j}\) ++ + +Sample Covariance Matrix +\(S_1 = \frac{1}{n_1 -1 }\Sigma_{j=1} +^{n_1} (X_{1j} - \bar X_1)(X_{1j} - \bar X_1)^T\) +\(S_2= \frac{1}{n_2 -1 }\Sigma_{j=1} +^{n_2} (X_{2j} - \bar X_2)(X_{2j} - \bar X_2)^T\) +
+检验前对于两个总体的假设:
+-
+
- \(X_{11},X_{12},...,X_{1n_1}\) +i.i.d. \(\sim +N_p(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim N_p(\mu_2,\Sigma_2)\) +
- 两组样本之间相互独立 +
- 在 \(n_1,n_2\) 较小的情况下,假设 +\(\Sigma = \Sigma_1 = \Sigma_2\) +
+Hypothesis: \(H_0 : \mu_1 - \mu_2 = +\delta_0\),\(H_1 : \mu_1 - \mu_2 \neq +\delta_0\)
+检验统计量的构造:
+由于 \(S_{pooled} = \frac{n_1 -1 +}{n_1+n_2-2}S_1 + \frac{n_2 -1}{n_1 + n_2 -2}S_2 \sim \frac{W_p(n_1 +n_2 +-2,\Sigma)}{n_1+n_2-2}\),可以以此构造 Test statistic:
+\[(\frac{1}{n_1} + \frac{1}{n_2})^{-1} +(\bar X_1 - \bar X_2 - \delta_0)^T S_{pooled}^{-1} (\bar X_1 - \bar X_2 +- \delta_0) \sim \frac{p(n_1+n_2-2)}{n_1+n_2-p-1} +F_{p,n_1+n_2-p-1}\]
+当 \(T_0 ^2 > +\frac{p(n_1+n_2-2)}{n_1+n_2-p-1} F_{p,n_1+n_2-p-1} (\alpha)\) +时拒绝原假设。
+置信区间的构造:
+对于任意的线性变换 \(a^T(\mu_1 - +\mu_2)\),simultaneous confidence interval 是
+\[(a^T(\bar X_1 - \bar X_2) - c \sqrt{a^T +(\frac{1}{n_1} + \frac{1}{n_2}) S_{pooled} a},a^T(\bar X_1 - \bar X_2) + +c \sqrt{a^T (\frac{1}{n_1} + \frac{1}{n_2}) S_{pooled} a})\]
+其中 \(c^2 = \frac{p(n_1+n_2 +-2)}{n_1+n_2-p-1}\)。
+注意到 \(a\) 的任意性,可以通过取 +\(a_i=e_i\) 的方式来求得 \(\mu_1 - \mu_2\) 的各个分量的置信区间;当 +\(a\) 与 \(S_{pooled}^{-1} (\bar X_1 - \bar X_2)\) +时上述置信区间的 confidence level 恰为 \(100 +\% (1-\alpha)\)。
--Remark:
-上面的结论可以推广到紧的距离空间的情形:假设 \((X,d)\) 是紧的距离空间,\(C(X)\) 是 \(X\) -上复数值的连续函数的全体,那么我们有如下的一一对应:\(X \longrightarrow \bigl\{\text{$C(X)$ -的极大理想}\bigr\}, \ \ x\mapsto \mathfrak{m}_x\)
-其中 \(\mathfrak{m}_x=\left\{f\in -C\bigl(X\bigr)\big| f(x)=0\right\}\)。据此,我们把可以把环 \(C(X)\) 中的极大理想想象成空间的点,从而通过 -\(C(X)\) 中的代数对象来研究 \(X\) 上的几何,这是代数几何的开端。
-
休整
-导数异常地轻松,半摸半写一天就写得差不多了,作为一个休息,之后会随第二篇直接发上来,作为二月的开端。
-我觉得可能还是学不完,2.13 -就要回北京了,后面要复习一下缓考的一门(水)课,大概还有两周时间给数分。学到这里也花了差不多两周,第一周一边学一边摆,第二周其他任务几乎全部停滞,就一直在读这本书。其实大多数精力都放在做习题上面了,原来的计划是习题跳着看一看就好,但还是改变了主意,想扎实一点。
-说到底我也在怀疑选这本书到底对不对了,感觉 PIN -在讲一种很新的数分(,很怀疑和正常的版本是不是有差别,但应该是闭包才对吧(。实际上在我开始速通的后几天,转数环里就发了光叔的前两学期讲义,但是当时也没有换,就一直到这里了。PIN -确实讲得深,但是似乎还是缺少技巧的训练。算了,我又不是现在要考丘赛,那些之后再说吧。
-还是在害怕。要用四周积累来的知识和已经学了一年半分析的同学一起上新学期的课程,我觉得真的好难。虽然微不足道的成功经验告诉我最重要的是不要害怕,但是果然,连做到不害怕都好难(
-
有参考 Vica Yang -的统辅笔记,JhZhang -的课堂笔记和 V1ncent19 -的统辅笔记,如有引用均会在文中注明,在此向前辈表示感谢。
- -Lecture 1
-主要是在吹水,开玩笑以及活跃气氛。正经的内容大概就一个古老的回归现象,我还没有听得很懂,麻了。
-Galton's Experiment
-以下全是胡说八道,不能保证完全对。
-介绍正态分布的时候会有一个很经典的小球过钉板的演示实验,最后落在底部的球似乎呈现出一个正态分布。但实际上球和钉子的每次碰撞都是一个 -Bernoulli 过程,过了 n 层钉板就是 n 次 Bernoulli -过程加和,可以近似为正态分布。实际上只要 n -够大,由中心极限定理任何分布的加和都可以被近似为正态分布。
-但我觉得实际上小球的情况并不是独立的,毕竟过程中会有相互的碰撞,真的没问题吗(
-回归现象的起源是 Galton -对于父代和子代的身高做了一个统计,发现身高远离均值的父母的后代往往身高会比他们更接近平均水平,也就是某一身高水平的父母的孩子的身高中位数作为因变量,父母身高作为自变量时,拟合出的直线的斜率小于 -\(1\)。
-假设不发生回归现象,则和钉板现象一样,后代的性状会逐渐分散,这被认为是一个种群稳定性状的方式。听起来很玄学,似乎也有一个稍微合理的生物学解释了,但我们希望从统计学的角度分析这件事,背后是存在数学规律的。
-
上图是课程中反复出现的一张图,对此做了很多解释。最上面的正态分布是父代的身高情况(实际上是父母身高的加权和),通过一个“倾斜槽”之后的第二个正态分布展示了子代的身高情况,比父代更加靠近中心。下方也有一个类似于钉板的装置,n -层钉板指的就是 n -代繁衍的过程,或者也可以指代一代繁衍中的其他影响身高的非基因因素,它们被视作独立同分布的,因此加和由中心极限定理可以被近似为正态分布。
-图中还呈现出了父代中的一个小组“过钉板”后的结果,是一个小的正态分布。实际上子代的数据就是由一个一个小的正态分布叠加起来的,而正态分布可以线性相加,所以最后呈现出的还是正态分布。
-好玄学,我也不知道我在说什么,甚至不是很确定自己理解对了没有。
-Anyway,还是 think mathematically,记 \(X_i\) 为第 \(i\) 代的种群身高变化量,\(\lbrace X_i \rbrace\) -是独立同分布的。则记父代种群的随机变量为 \(F= -\Sigma _{i=1} ^n X_i\),子代种群的随机变量为 \(S= -\Sigma_{i=1}^nX_i\),考虑二者的相关系数:
-\(\rho(F,S) = -\frac{cov(F,S)}{\sqrt{Var(F)Var(S)} } = \frac{Var(F) + Cov -(F,X_n)}{\sqrt{Var(F)Var(S)} } -=1+\frac{cov(F,X_n)}{Var(F)}<1\),因此 \(\rho(F,X_n)<0\) 也即二者呈负相关。
-一些术语
+Large Sample Test
+Large Sample Behavior
+在大样本场景下,类似于一元的中心极限定理,我们不需要正态性也可以推出一些关于 +\(\bar X,S\) 在此时的近似分布。
+$X_1 , X_2 ,...,X_n $ i.i.d. 来自某一总体,其均值为 \(\mu\),协方差矩阵为 \(\Sigma\),不必要求正态分布。于是有:
-
-
一般来说,我们把 \(X\) 作为 -predictor/input/explanatory variable,把 \(Y\) 作为 response/output/dependent -variable。
-\(Y \sim X\) 被称为 simple -regression,一元总归是简单的。
-\(Y \sim X_1,X_2,...,X_p\) 称为 -multiple/multivariate regression,实际上这两者是不一样的。
-如果每个回归式中有超过一个 \(X\) -就称为 multiple regression,如果有多个 \(Y\) 就称为 multivariate -regression,并且每个式子里只能有一个不同的 dependent variable。
-还有叫做 multivariate multiple regression 的回归方法,也就是用多个 -\(X\) 来预测多个 \(Y\) 的情况,每个 \(Y\) 出现在不同的式子里。
-一般来说 \(Y\) -是连续型随机变量,\(X\) -可以是连续型、离散型或者分类型随机变量。有一些名词,不抄了,简单列一下:
- +
+- \(\sqrt n (\bar X - \mu) \sim +N_p(0,\Sigma)\) +
- \(n (\bar X - \mu) S^{-1} (\bar X - \mu) +\sim \chi^2 _p\)
Lecture 2
-Simple Linear Regression
-数据的组织和表示
-Simple linear regression 的数据一般是二元数据对 \((X_i , Y_i)\),每一对数据称为一个 -case。数据集记作 \((X_1,Y_1),...,(X_n,Y_n)\),其中 \(X_i\) 是 i-th observed explanatory -variable,\(Y_i\) 是 i-th observed -response variable。
-模型的表示
-\(Y_i = \beta_0 + \beta_1 X_i + \varepsilon -_i\),\(\varepsilon _i\) 被称为 -random error term,其中 \(\beta_0,\beta_1\) -是参数。为了简化模型便于操作,需要对 random error term 做一些假设:
+注意其中 \(S = \frac{1}{n-1} \Sigma_{i=1} +^n (X_i - \bar X)(X_i - \bar X)^T\),上述两式为近似分布,在 \(n\) 远大于 \(p\) 的条件下成立。
+这是我们进行后续推断的基础。
+大样本单总体均值推断
+$X_1 , X_2 ,...,X_n $ i.i.d. 来自某一总体,其均值为 \(\mu\),协方差矩阵为 \(\Sigma\),不必要求正态分布。
+假设 \(H_0 : \mu = \mu_0; H_1 : \mu \neq +\mu_0\),于是 test statistic 是 \(n(\bar x - \mu_0)^T S^{-1} (\bar x - \mu_0 ) \sim +\chi^2 _p\),当 \(T_0^2 > \chi_p ^2 +(\alpha)\) 时拒绝原假设。
+对于任意的线性变换 \(a^TX\),\(a^T \mu\) 的 simultaneous CI 是 \((a^T \bar X - \sqrt{\chi^2 _p (\alpha)} +\sqrt{\frac{a^TSa}{n} },a^T \bar X + \sqrt{\chi^2 _p (\alpha)} +\sqrt{\frac{a^TSa}{n} })\)
+大样本双异方差总体均值推断
-
-
- 均值为 \(E(\varepsilon_i) = -0\),方差为 \(Var(\varepsilon _i) = -\sigma ^2\),注意 \(\sigma\) -是一个未知常数,也视作参数; -
- 不同的 \(\varepsilon _i\) 和 \(\varepsilon _j\) -是不相关的。注意此处不需要不独立。 +
检验前对于两个总体的假设:
+-
+
- \(X_{11},X_{12},...,X_{1n_1}\) +i.i.d. \(\sim +Population(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim Population(\mu_2,\Sigma_2)\) +
- 两组样本之间相互独立 +
- 在 \(n_1,n_2\) 较大(均远大于 \(p\))的情况下,我们允许 \(\Sigma_1 \neq \Sigma_2\) +
+Hypothesis: \(H_0 :\mu_1 - \mu_2 = +\delta_0; H_1 : \mu_1 - \mu_2 \neq \delta_0\)
+Test statistic: \((\bar X_1 - \bar X_2 +- \delta_0 )^T (\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2 )^{-1} (\bar X_1 - +\bar X_2 - \delta_0) \sim ^{H_0} \chi^2 _p\),当 \(T_0 ^2 > \chi^2_p(\alpha)\) +时拒绝原假设。
+标准的 \(\mu_1 - \mu_2\) 的 +\(100\% (1-\alpha)\) +置信域是一个椭圆,由区域
+\[\{\mu_1 -\mu_2 : ( \bar X_1 - \bar X_2 - +(\mu_1 - \mu_2))^T(\frac{1}{n_1}S_1 +\frac{1}{n_2}S_2)^{-1}(\bar X_1 - +\bar X_2 - (\mu_1 - \mu_2)) \leq \chi^2_p(\alpha)=c^2 \}\]
+表示。
+类似地考虑 \(X_1,X_2\) +的线性变换,\(a^T(\mu_1 - \mu_2)\) 的 +simultaneous CI 是
+\[(a^T(\bar X_1 - \bar X_2) - c +\sqrt{a^T(\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2)a},a^T(\bar X_1 - \bar +X_2) + c \sqrt{a^T(\frac{1}{n_1} S_1 + \frac{1}{n_2} S_2)a} ),c^2 = +\chi^2_p(\alpha)\]
对于更强的模型,例如 simple linear regression model with normal -error,我们直接要求 \(\varepsilon_1,...,\varepsilon_n i.i.d. \sim -N(0,\sigma^2)\)(因为正态分布的不相关性和独立性等价)。这是一个很广泛的假设,但有时正态假设是明显有问题的,需要修正。
-事实上,在 linear regression model 中,\(X_i\) 和 \(Y_i\) 的地位是不对等的。\(X_i\) 被视为不带随机性的常数,而 \(Y_i\) 因为 \(\varepsilon_i\) 的存在是一个随机变量,有 -\(E(Y_i) = \beta_0 + \beta_1 -X_i\),\(Var(Y_i)=Var(\varepsilon_i) = -\sigma^2\)。因此,回归线可以视作 \((X_i, E(Y_i))\) 连成的直线,而数据点 \((X_i,Y_i)\) 分布在回归线附近。
-特别地,在正态假设下, 有 \(Y_i \sim -N(\beta_0 + \beta_1 X_i,\sigma^2)\),\(i=1,2,...,n\)。
-参数的意义和求算
-斜率 \(\beta_1\) 的意义为 \(X_i\) 增加 1 单位时 \(Y_i\) 的变化量;截距 \(\beta_0\) 的意义分两种情况解释,当 \(X_i\) 取值范围中有 \(0\) 时即为 \(X_i=0\) 时的平均响应 \(E(Y_i)\),否则截距没有意义。
-Least Sum of Square 方法
-求算最佳参数实际上就是求使得 sum of squared diff 最小的 \(\hat{\beta_0},\hat{\beta_1}\),从而得到 -\(Y_i\) 的估计值 $= + X_i $。于是有 -\(\hat{\beta_0},\hat{\beta_1} = \arg \min -_{\beta_0,\beta_1} \Sigma(Y_i - \beta_0 - \beta_1X_i)^2=\arg \min -_{\beta_0,\beta_1} \Sigma_{i=1 } ^n e_i -^2\)。求导即可简单地得出:
-\[b_1 = \hat{\beta_1} = \frac{\Sigma_i -(X_i - \bar{X})(Y_i - \bar{Y})}{\Sigma _i (X_i-\bar{X})^2}\]
-\[b_0 = \hat{\beta_0} = \bar{Y} - b_1 -\bar{X}\]
-记残差为 \(e_i = Y_i - \hat{Y_i}= Y_i - -\hat{\beta_0} - \hat{\beta_1} X_i=\beta_0 + \beta_1X_i +\varepsilon _i - -\hat{\beta_0} - \hat{\beta_1}X_i \approx \varepsilon _i\) ,也即 -\(e_i\) 为某一组 observed data \(Y_1,Y_2,...,Y_n\) 之下得到的残差,但绝非 -\(\varepsilon _i\) -本身。残差是观测到的确定值,而 \(\varepsilon -_i\) 是随机变量。
-事实上求导的过程蕴含以下结论:
-\[\Sigma _{i=1} ^n e_i=0\]
-\[\Sigma _{i=1} ^{n} X_i e_i = -0\]
-以上二式可以看做对 \(e_i\) -的线性约束,\(\lbrace e_i \rbrace\) -的自由度是 \(n-2\),互相之间不是独立的,这也是和 \(\lbrace \varepsilon _i \rbrace\) -的差别之一。由此还可以得到一些其他性质,例如回归线必过 \((\bar{X},\bar{Y})\),不在此一一列举。
-以上即为参数 \(\beta_0,\beta_1\) -的估计方法。下面再考虑参数 \(\sigma\) -的估计,使用残差 \(e_1,...,e_n\) -来考虑。
-取 \(\hat{\sigma ^2} = \frac{\Sigma _{i=1} -^n e_i ^2}{n-2}\)。这是因为 \(e_1,e_2,...,e_n\) 的自由度为 \(df_E = n-2\),由此考虑 sum of square \(SSE= \Sigma_{i=1} ^n (Y_i - \hat{Y_i})^2=\Sigma -_{i=1} ^n e_i ^2\),定义 mean of squared errors \(MSE= \frac{SSE}{df_E} = \frac{\Sigma_{i=1}^n e_i -^2}{n-2}\) 为 \(\hat{\sigma -^2}\)。
-MLE 方法
-也可以用推断课上的 MLE 方法。实际上,我们想找到一个 \(\beta_0,\beta_1\) 的最佳估计,还可以使用 -MLE 方法进行估计。
-在正态假设下,我们可以将 \(n\) -组数据视作 \(n\) -个互相独立的随机变量,取使得其likelihood function 最大的一组 \(\beta_0,\beta_1,\sigma^2\) -作为估计量。likelihood function 即为 \(f(y_1,y_2,...,y_n) = -f_1(y_1)...f_n(y_n)\),得到的 estimator 中 \(\hat{\beta_0},\hat{\beta_1}\) 与 least sum -of square 中得出的估计量相同,但 \(\hat{\sigma -^2} = \frac{\Sigma _{i=1} ^n e_i -^2}{n}\)。注意这是一个有偏的估计量,而 least sum of square -得到的估计量是无偏的。
-推断复习
-咕了。什么嘛,我推断学得还是可以的嘛(x
-Lecture 3
-线性回归中的推断
-回顾一下,无论是 OLS 方法还是 MLE 方法,我们得到的参数估计 \(b_0\),\(b_1\) 都是相同的:
-\[b_1 = \hat{\beta_1} = \frac{\Sigma_i -(X_i - \bar{X})(Y_i - \bar{Y})}{\Sigma _i (X_i-\bar{X})^2}\]
-\[b_0 = \hat{\beta_0} = \bar{Y} - b_1 -\bar{X}\]
-通过简单的计算可以知道:
-\[E(b_1) = \beta_1,Var(b_1) ={\sigma^2 -\over S_{XX}},s^2(b_1) = \frac{s^2}{S_{XX}}\],
-其中 \(S_{XX} = \Sigma_{i=1} ^n (X_i - -\bar{X})^2\), \(s^2 = \hat{\sigma}^2 = -\frac{\Sigma_{i=1}^n e_i^2}{n-2}\)。
-而且有 \(Cov(b_1, \bar Y)=0\)。
-参数推断
+大样本双总体方差推断
-
-
对 \(\beta_1\) 进行推断:null -hypothesis 为 \(H_0: \beta_1 -=0\),这样设置是因为关心两个变量之间是否存在线性关系。
-在假设 \(H_0\) 下可以考虑 test -statistic 为 \(T= \frac{b_1 -0}{s(b_1)} \sim -t_{n-2}\),这是因为 \(H_0\) -假设下 \(b_1-0 \sim -N(0,\frac{\sigma}{\sqrt{Sxx}})\),我们一般用 \(\sigma\) 的无偏估计 \(\hat{\sigma} = \sqrt{\frac{\Sigma_{i=1}^n e_i -^2}{n-2}}\) 来处理。
-level of significance 为 \(\alpha\),于是当 observed data \(t_0\) 满足 \(|t_0| > t_{n-2,1-\alpha /2}\) 时 reject -\(H_0\)。
-如果没有拒绝 \(H_0\),通常的可能有以下三种:
+检验前对于两个总体的假设:
-
-
- 发生了 Type II Error,没有成功拒绝掉 \(H_0\) 而事实相反; -
- \(X\) 和 \(Y\) 之间确实没有什么线性关系; -
- \(X\) 和 \(Y\) 之间有关系,但是非线性。(这句话原来的 -typo 是“有线性关系,但是非线性”,绷不住了,中午被 Photon -指出来了,非常感谢他) +
- \(X_{11},X_{12},...,X_{1n_1}\) +i.i.d. \(\sim +Population(\mu_1,\Sigma_1)\),\(X_{21},X_{22},...,X_{2 n_2}\) i.i.d. \(\sim Population(\mu_2,\Sigma_2)\) +
- 两组样本之间相互独立
-对 \(\beta_1\) 做 confidence -interval:由于在 \(\beta_1\) -代表斜率的情况下,有 \(\frac{b_1 - -\beta_1}{s(b_1)} \sim^{H_0} t_{n-2}\)。
-于是 \(P(\frac{|b_1-\beta_1|}{s(b_1)} < -t_{n-2,1-\alpha /2}) = 1-\alpha\),\(\beta_1\) 的 100%\((1-\alpha)\) confidence interval 是
-\[(b_1 - t_{n-2,1-\alpha /2} s(b_1),b_1 + -t_{n-2,1-\alpha /2} s(b_1))\]
-类似地可以对 \(\beta_0\) -做推断,有 \(\frac{b_0 -\beta_0}{s(b_0)} \sim -t_{n-2}\),因此如果 null hypothesis 为 \(H_0: \beta_0 =0\),rejection region -即为满足条件 $ > t_{n-2,1-/2} $ 的数据。对于偏移的 null hypothesis -\(H_0 : \beta_0 =c\),也只要相应地移动 -rejection region 即可。
-100%\((1-\alpha)\) confidence -interval 为 \((b_0 - t_{n-2,1-\alpha /2} -s(b_0),b_0 + t_{n-2,1-\alpha /2} s(b_0))\)。
-实际上我们一般对 \(\beta_0\) -的推断不感兴趣,因为这个参数未必有意义,依赖于 \(X\) 的取值范围。
-以上都是对单个参数进行推断,实际上我们也可以进行 joint -inference:
-同时推断两个参数 \((\beta_0,\beta_1)\),这时候得到的就是 -confidence region,使得 \(P((\beta_0,\beta_1) -\in S \subset \mathbb R^2) = 100(1-\alpha) \%\)。实际上因为 \((b_0 , b_1) ^T \sim N((\beta_0,\beta_1)^T , -\sigma^2 \Sigma_{2\times 2})\),所以最小的 confidence region -是一个椭圆。
-实际上我们也可以考虑做一个矩形的 confidence -region,也即对两个参数分别作 confidence interval,confidence coefficient -分别为 \(\sqrt{1-\alpha} \approx -1-\frac{\alpha}{2}\)。因此 confidence region 为:
-\[ (b_1 - t_{n-2,1-\alpha /4} s(b_1),b_1 + -t_{n-2,1-\alpha /4} s(b_1)) \times (b_0 - t_{n-2,1-\alpha /4} s(b_0),b_0 -+ t_{n-2,1-\alpha /4} s(b_0))\]
+Hypothesis: \(H_0 : \Sigma_1 = +\Sigma_2; H_1 : \Sigma_1 \neq \Sigma_2\)
+Test statistic:考虑 likelihood ratio \(\Lambda = \frac{max_{\theta \in \Theta_0} +L(\theta)}{max_{\theta \in \Theta} L(\theta)} = \frac{|S_1|^{n_1 /2} +|S_2|^{n_2/2}}{|S_{pooled}|^{n_1+n_2-2/2}}\),自由度之差为 \(v-v_0 = df(\Theta) - df(\Theta_0)\),于是在 +\(H_0\) 假设下有 \(-2 \ln \Lambda \sim \chi^2_{v-v_0}\) +是为检验统计量。
+George Box 对其进行了修改,使得可以对 \(g\) 个总体进行方差推断,具体略去。
参数推断的角度来说 \(\beta_1\) -的推断远比 \(\beta_0\) -重要,它表征线性关系,而且从预测的角度来说,\(\beta_1\) 的推断如果不够精细,会导致远离 -\(\bar X\) 处的 \(X_h\) 对应的估计量误差很大。
-Power Function
-一个 significance test 的 power 指的是 reject \(H_0\) 时 \(H_1\) 是正确的的概率,也就是 \(1-P(\)Type II Error\()\)。实际上一个推断是好的的情况下需要既不 -over-powered 也不 under powered,这和 Type I Error 与 Type II Error -此消彼长的性质有关。
-Power function 一般是一个关于参数的函数。以推断 \(\beta_1\) 的过程为例,计算这一推断的 power -function。
+Assumption Check
+类似于线性回归中所讲的内容,此处略去。
+Lecture 6
+关于主成分分析(Principal Component Analysis)在 population +上的理论和在 sample +上的应用。希望通过对一系列随机变量的线性变换和组合,分析维度更小的数据来达到同样的结果。
+For Population
+PCA 方法的具体操作
+面对的问题模型可以视作:随机向量 \(X^T = +[X_1 , X_2,...,X_p]\) 有 \(p \times +p\) 维的协方差矩阵 \(\Sigma\) +和对应的 \(p\) 个非负特征值 \(\lambda _1 \geq \lambda_2 \geq ... \geq \lambda_p +\geq 0\),分别对应单位特征向量 \(e_1,e_2,...,e_p\),这是一组正交基。
+我们希望能够找出 \(Y_1, +Y_2,...,Y_p\) 满足 \(Y_i = a_i ^T +X\),使得 \(a_i ^T a_i +=1\),\(Var(Y_i)\) 最大,且 +\(Cov(Y_i, Y_j)=a_i ^T \Sigma +a_j=0\)。事实上由 Rayleigh 商可以知道,只要取 \(a_i = e_i\) 就可以三个愿望一次满足(,且有 +\(Var(Y_i) = \lambda_i\),证明是 +trivial 的。
+这个变换有一些性质:
+-
+
\(\Sigma_{i=1}^p Var(X_i) = +\Sigma_{i=1}^p \sigma_{ii} = trace(\Sigma) = \Sigma_{i=1}^p \lambda_i = +\Sigma_{i=1}^p Var(Y_i)\)
+说明 PCA 前后的信息没有损失。
+可以通过 \(Var(Y_i)\) 在 \(\Sigma_{i=1} ^p Var(Y_i)\) +中的占比判断这一信息的重要程度,这一数值为 \(\frac{\lambda_i}{\lambda_1 + ... +\lambda_p}\)
+\(Cov(Y_i , X_j) = Cov(e_i ^T X, I_j ^T +X) = e_i ^T \Sigma I_j = \lambda_i e_i^T I_j = \lambda_i +e_{ij}\)
+因此二者之间的相关系数为 \(\rho_{Y_i , X_j} += \frac{Cov(Y_i,X_j)}{\sqrt{Var(Y_i) Var(X_j)}} = \frac{e_{ij} \sqrt +\lambda_i}{\sqrt \sigma_{ii}}, i,j = 1,2,...,p\)。
+对于固定的 \(j\) 有 \(\Sigma_{i=1}^p \rho_{Y_i,X_j}^2 = +1\)。这一相关系数显示了 \(X_j\) +的方差可以被 \(Y_i\) +解释的比例。
+
事实上,有的时候直观显示出来 \(Y_i = +e_i^TX\) 中 \(X_j\) +前系数较小,这并不说明 \(X_j\) +的影响较小,计算 \(\rho_{Y_i,X_j}\) +可能会体现出较大的相关系数,显示二者之间有较大的相关性。
+正规化随机变量下的 PCA
+实际使用中可能存在一些单位的变化、尺度变化导致 PCA +的系数出现不同的情况。我们讨论 standardized variable \(Z_k= \frac{(X_k - \mu_k)}{\sqrt \sigma_{kk}}, k +=1,2,...,p\) 下的 PCA 变换。
+事实上有 \(Z = diag(\sqrt{\sigma_{11}^{-1} +},\sqrt{\sigma_{22}^{-1} },...,\sqrt{\sigma_{pp}^{-1} } ) +(X-\mu)\),于是 \(Cov(Z) = +diag(\sigma_{11},\sigma_{22},...,\sigma_{pp})\)。 +由此即得正规化情况下的 PCA 变化的参数细节,不再赘述。
+多元正态分布下的 PCA
+当 \(X\sim N_p(\mu ,\Sigma)\) +时,好像下节课再讲(
+For Sample
+回顾一下多元情况下的样本方差:
+++协方差定义为 \(s_{ik} = \frac 1 n +\Sigma_{j=1}^n (x_{ji} - \bar{x_i}) (x_{ji} - +\bar{x_k})\),可以看到实际上 \(s_{ik} = +s_{ki}\),于是协方差矩阵有
+\[ \begin{bmatrix} s_{11} & s_{12} +& ...& s_{1p}\\ s_{21} & s_{22} & ...& s_{2p} \\ ... +& ...&...&... \\ s_{p1} & s_{p2} &...&s_{pp} +\end{bmatrix}\]
+的形式,这是一个对角元为正的对称矩阵。
+
事实上,对于已知的 \(x = +[x_1,x_2,...,x_p]\),希望取 \(\hat{y_i} += \hat{e_i} ^T x = \hat e_{i1}x_1 + \hat e_{i2} x_2 + ... +\hat e_{ip} +x_p\) 满足 \(\hat e_i ^T \hat e_i = +1\),$Cov(y_i , y_j) = 0 $ 对不相等的 \(i ,j\) 都成立,且 \(Var(\hat y_i) = \hat \lambda_i, i = +1,2,...,p\)。\(\hat y_i\) 称为 +\(i\)-th sample principal component +(score),即 sample PCs。
+类似于 population 情况下的 PCA,sample PCs 有以下性质:
-
-
我们在线性回归参数推断里会用到一种非中心化 t-分布。普通的 -t-分布是关于 \(x=0\) 对称的,非中心化 -t-分布有一定的偏差。注意并不是整体在坐标轴方向上的移动,其形状也发生了变化。表达式为 -\(t(df, \delta ) = \frac{N(0,1) + -\delta}{\sqrt{\chi_{df} / df}}\)。
-对 \(\beta_1\) 进行推断:null -hypothesis 为 \(H_0: \beta_1 -=0\),这样设置是因为关心两个变量之间是否存在线性关系。
-在假设 \(H_0\) 下可以考虑 test -statistic 为 \(T= \frac{b_1 -0}{s(b_1)} \sim -t_{n-2}\),然而在 \(H_1\) -下,
-\[T=\frac{b_1}{s(b_1)} = \frac{b_1 - -\beta_1 + \beta_1}{s(b_1)} = \frac{b_1-\beta_1}{s(b_1)} + \frac{\beta_1 -/ \sigma(b_1)}{s(b_1)/\sigma(b_1)} = \frac{N(0,1) + -\delta}{\sqrt{\chi_{df} / df}} \sim -t(n-2,\beta_1/\sigma(b_1))\]
-于是 \(Power(\beta_1) = P(Reject H_0 | H_1 -holds) = P(|T| > t_{n-2,1-\alpha /2} | \beta_1 \neq 0) = -P(T<t_{n-2,\alpha /2}) +1-P(T<t_{n-2,1-\alpha -/2})\),其中在 \(\beta_1 \neq -0\) 的条件下,\(T\sim t(n-2,\beta_1 / -\sigma(b_1))\)。
+- \(\Sigma_{i=1} ^p Var(\hat y_i) = +\Sigma_{i=1}^p s_{ii} = \Sigma_{i=1}^p \hat \lambda_i\) +
- \(\rho_{\hat{y_i} ,x_k} = +\frac{\hat{e}_{ik} \sqrt {\hat{\lambda}_k} }{\sqrt s_{kk} +}\)
BLUE
- -简单来说,OLS Estimators 是 the best linear unbiased estimator,简称 -OLS estimators 是 BLUE。best 的意思是方差最小,这是不难证明的。
-BLUE 是非常好的性质,也希望我以后能 go blue(逃
-Lecture 4
-Prediction & ANOVA,感谢 zzy 救我的生统概论(
-Estimation & Prediction
-平均响应的推断
-有了线性回归模型之后当然是要用来做预测,通过已有数据拟合出一个线性模型,再用来估计未知点的值。对于需要估计的点 -\(X_h\),一般来说估计值都是考虑平均响应 -(mean response) \(\mu_h = E(Y_h) = \beta_0 -+\beta_1 X_h\),把 \(\hat{\mu_h} = b_0 -+ b_1 X_h\) 作为 \(\mu_h\) -的估计。这是一个 -estimator,既然如此就要考虑它的性质,也要先考虑平均响应的置信区间。
+Practical Issues
+在实践中求得了 PC +的表达式,还需要进行一定的取舍和判断,从而选出需要使用的值。
+理论很巧妙,但我真的不想写代码实现(
+How many principal +components to retain
+可以画一个 scree plot,值在底端且明显小的需要排除。对于 sample +principal component score 且是 standardized sample 的情况下,可以选取 +cutoff point 是 \(1\),舍弃所有使得 +\(Var(Y_i) <1\) 的 +PCs,留下的即是真正的主成分。
+Check normality +assumption & detect outliers
-
-
\(E(\hat{\mu_h}) = E(b_0) + E(b_1)X_h = -\beta_0 + \beta_1 X_h = \mu_h\) ,是 unbiased estimator
-\(Var(\hat{\mu_h}) = Var(\bar{Y}+ -b_1(X_h - \bar{X})) = \sigma^2 [\frac{1}{n} + \frac{(X_h - -\bar{X})^2}{\Sigma (X_i -\bar{X})^2}]\) ,是 minimum -variance
-\(\hat{\mu_h} = \bar{Y} + (X_h - -\bar{X}) b_1\),由于 \(\bar{Y}\) -和 \(b_1\) 都有正态假设,因此 \(\hat{\mu_h}\) 也服从正态分布,\(\hat{\mu_h} \sim N(\mu_h , -Var(\hat{\mu_h}))\)。
-\(Var(\hat{\mu_h})\) 的估计量是 -\(s^2(\hat{\mu_h}) = s^2[\frac 1 n + -\frac{(X_h-\bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\),于是有 \(\frac{\hat{\mu_h} - \mu_h}{s(\hat{\mu_h})} \sim -t_{n-2}\)。
-因此,\(\mu_h\) 的 \(100 \% (1-\alpha)\) confidence interval 是 -\((\hat{\mu_h} - t_{n-2, 1-\alpha /2} -s(\hat{\mu_h}),\hat{\mu_h} + t_{n-2, 1-\alpha /2} -s(\hat{\mu_h}))\)。confidence interval 的长度为 $2t_{n-2, 1-/2} -s() = 2t_{n-2, 1-/2} s $,其中 \(s = -\sqrt{[\frac{\Sigma_{i=1}^n -e_i^2}{n-2}]}\)。因此置信区间的长度是近似于随 \(X_h - \bar{X}\) -递增而递增的。也就是说,\(X_h\) -距离 \(\bar{X}\) -越远,置信区间的长度越大,准确性越难保证。
-综上,我们成功找到了这个对于 \(\mu_h\) 的估计的置信区间。
+- 检验正态性可以用最大的几个 PCs +
- 检验离群值可以用最小的几个 PCs
预测值的推断
-上述估计的是预测值的平均响应,对于新观测点的值需要改成:\(Y_{h(new)} = \beta_0 + \beta_1 X_h -+\varepsilon\) 且有 \(E(\varepsilon) = -0,Var(\varepsilon) = \sigma^2\)。注意这里 \(\varepsilon\) 是随机变量,\(\beta_0,\beta_1\) 是未知值的参数,\(X_h\) 是已知的常数。
-对它做估计 \(\hat{Y}_{h(new)} = \hat{\mu_h} -= b_0+b_1 X_h\) 仍然是和平均响应相同,考虑这个估计的性质。
+Limitations
-
-
\(E(\hat{Y}_{h(new)}) = E(b_0 + b_1 -X_h) = \beta_0 + \beta_1 X_h\)
-从简单的情形开始,如果 \(\beta_0,\beta_1,\sigma\) -都是已知的参数,则在正态假设下 \(\frac{Y_{h(new)} -E(Y_h)}{\sigma}\sim -N(0,1)\)(非正态假设情况下服从未知分布),\(Y_{h(new)}\) 的 confidence interval 是 -\((E(Y_h) - z_{1-\alpha /2} \sigma,E(Y_h) + -z_{1-\alpha /2} \sigma)\)。
-一般情况下,设 \(d_h = Y_{h(new)} - -\hat{Y}_{h(new)} = Y_{h(new)} - \hat{\mu_h}\),于是有 \(E(d_h) = 0\)。
-计算可知方差 \(Var(d_h) = Var(Y_{h(new)} - -\hat{\mu} _h) = Var(Y_{h(new)})+Var(\hat{\mu_h}) = \sigma^2[1+\frac 1 n -+\frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\);
-standard error 为 \(s^2(d_h) = s^2 [1+\frac -1 n +\frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}]\);
-于是有 \(\frac{d_h - E(d_h)}{s(d_h)} = -\frac{d_h}{s(d_h)} = \frac{Y_{h(new)} - \hat{\mu}_h}{s(d_h)} \sim -t_{n-2}\),\(Y_{h(new)}\) -的置信区间是 \((\hat{\mu}_h - s(d_h) -t_{n-2,1-\alpha/2},\hat{\mu}_h + s(d_h) -t_{n-2,1-\alpha/2})\),这个区间一般叫做 prediction -interval,长度是 \(2 t_{n-2,1-\alpha/2} -s(d_h)\),其中 \(s^2(d_h) = s^2 + -s^2(\hat{\mu}_h -^2)\),因此预测区间比平均响应的置信区间略宽。
+- PCA +只使用了协方差矩阵里的值,实际上没有把数据包含的信息利用完全 +
- 只进行线性变换 +
- 很难反映变量之间的线性关系 +
- 对离群值敏感
预测值的平均的推断
-考虑在新值 \(X_h\) 处的 \(m\) 个观测值的平均值,为 ${Y_h} = m -{i=1} ^m Y{h(new) i} = _0 +1 X_h+ 1m {i=1}^m _i -$,预测值的平均仍然是 \(\hat{Y_h}=b_0 + b_1 -X_h\)。有 \(\varepsilon _i \sim -N(0,\sigma^2)\) 为正态假设。于是 \(Var(\bar{Y}_h - \hat{Y_h}) = \sigma^2 [\frac 1m + -\frac 1 n + \frac{(X_h - \bar{X})^2}{\Sigma(X_i - \bar{X})^2}] \leq -Var(d_h)\)。
-它的宽度小于 prediction interval,但也大于平均响应的 confidence -interval。
-Confidence Band for -Entire Regression Line
-怎么翻译都没那味,就写原文吧。
-希望找到一个 confidence band:\(\lbrace -(x,y): L(x)<y<U(x), x\in \mathbb R \rbrace\),对于任意点 -\(x\) 有 \(P[l(x) < \beta_0 +\beta_1 x <u(x)] = -1-\alpha\)。对于固定的点 \(x\),\(100 \% -(1-\alpha)\) 置信区间为 \((\hat{\mu_x} -- t_{n-2, 1-\alpha /2} s(\hat{\mu_x}),\hat{\mu_x} + t_{n-2, 1-\alpha /2} -s(\hat{\mu_x}))\)。
-所以只要取 \(W=max\{(\hat{\mu}_x - -\mu_x)/s(\hat{\mu}_x) \}\),即有置信区间为 \((\hat{\mu}_x - W s(\hat{\mu_x}),\hat{\mu}_x + W -s(\hat{\mu_x}))\),其中 \(W = -\sqrt{2F_{1-\alpha,2,n-2}}\)。实际上 \(W > t_{n-2,1-\alpha /2}\),也就是说 -confidence band 处处比 confidence interval 更宽,level of confidence -\(\alpha'\) 也更小。
-Summary
-一个显示 confidence interval of mean response,prediction interval 和 -confidence band 宽度关系的图:
-
Analysis of Variance (ANOVA)
-Variance Estimator
-先上点概念:
+后记
+期中考完就退课了,于是这一篇写到 lecture 6 就烂尾了,乐(
+多元问题确实太难了,我到现在绩点最低的一门数学课是微积分
+A(2),意思是别的都 4.0 就它 3.6
+还是五个学分(这是可以说的吗)。当时就觉得多元微积分真的好麻烦。然而多元统计难度不在多元而在统计,这属实是我没想到的。
之前在 Vincent19 主页上看到过这样一句话:
+++A key difference between mathematics and statistics is that the +former is full of lemmas while the latter is full of dilemmas.
+
事实上,统计对我来说最大的困难还是面对 dilemma +应该怎么做这样的问题。半个学期下来我始终觉得如今学到的处理统计问题的方法都是原始而 +trivial +的,你能想到的最容易的方法就是最好的解决方案。线性回归课堂上没有任何需要动脑超过五分钟的推导,周老师时不时说我们这个不是数学课,数学不好也不要害怕,这让我无比难受,我自己是否也有点阴暗了。然而无论是看图用眼睛做模型诊断,还是写无穷无尽却又几乎一成不变的 +R code 然后在 ANOVA table +里分析数据和模型参数的细微差别,都几乎让我崩溃。多元统计时不时出现的 CI +选择和“几何直观”也一样困扰我。我想我真的不擅长处理这么具体的场景,我宁愿去读晦涩的 +lemma,像解谜游戏一样,我还是只喜欢做游戏。
+所以,统计中心的应统课果然还是不适合我,或许数学系的统计课会稍有不同,或许不会这么纠结现实的应用问题,但我还是厌倦了。另外,我发觉自己的分析水平也没那么差。如果不是再退线性回归的话这学期要没课上了,其实是想一起丢掉的。只能说我还是太弱了,从数学转去搞统计的同学不在少数,好像只有我这样困扰。
+当时写统推笔记的时候在开头写下了“实在不行的话,(方向)该换还得换啊”这样的话,然而统推很顺利地上完了,还以为方向就这么定下来了,不用再继续颠沛流离。现在却是又一次要换掉了,再一次抛弃一切。开玩笑的,统计转概率也不算是放弃一切,不然怎么会合称“概统”呢。
+我之前写“感觉自己 20th +的主题是出走”,后来觉得不是,出走会是我一生的主题,cause I have a vast, +vast soul.
+希望自己在概率这条路上走得远一点吧,暂时先和统计说再见了...等等还有两门课还在上呢(
+]]>这个操作是合理的。我和物理本来就不合适,结合上学期的经验可以发现,无论有没有学过原理,我唯一的解决方案就是按计划一帧一帧地做实验,才不至于大脑空白。加之我秋季学期就没选理论课,理论水平也就是现在这样了,倘若现在不写,将来更写不出来。上学期因为仓促,只在讲义上手写了一些要点,有的时候记不清了就会不知所措,所以这次码个字可以详细一点。
这样的话,物理实验就变成了大猩猩也能做的体力活罢了。我不否认这个想法,也无意论辩这门课是否有意义,将本文视作作者的救命手册即可。
注:未经授权禁止转载,本人不希望在院系里受到关注;所有提到的引用,包括图片,文字,数据信息等,著作权归原作者所有;一概不提供文中提到的自用实验表格,请自行阅读实验讲义,勿直接伸手。
+完整报告篇
+用单色仪测定介质的吸收曲线
+原理简述
+一束光入射到有一定厚度的介质上时,有一部分光被反射,另一部分被吸收,其余被透射——也即进入有厚度\(d\)的介质。根据各部分的光强,可以定义出介质板的光谱外透射率\(T=\frac{I_T}{I_0}\)和光谱透射率\(T_{i}=\frac{I_2}{I_1}\)。
+(此处应该有图,但是没有图。)
+光谱透射率同时与介质的性质和入射光的波长\(\lambda\)相关。为什么这么说呢?因为忽略介质内散射的情况下\(T_{i}=e^{-\alpha d}\),\(\alpha\)称为介质的线性吸收系数,与介质的性质和入射光波长有关。
+经过若干次透射后,透射光的光强为一个等比数列的和,即为\(I_T=\frac{I_0(1-R)^2e^{-\alpha +d}}{1-R^2e^{-2\alpha d}}\)。其中,\(I_{0}\)为入射光强,\(R\)为单一界面上的反射率。由此可以计算光谱外透射率\(T=\frac{I_T}{I_0}\)。
+在实际实验中,使用了两块仅厚度不同的试样,计算后近似得出光谱外透射率的比值,我们不加证明地给出吸收系数的近似:\(\alpha=\frac{lnT_{1}-lnT_{2}}{d_{2}-d_{1}}\) +。实际实验中,用微电流放大器的显示值\(V_{1}\),\(V_{2}\)分别替换上式的\(T_{1}\),\(T_{2}\)。
+应该做什么?在纸上记什么?
+你不懂仪器的构造,但是没关系,跟着做就行了。
+校对单色仪的波长示值
+单色仪长这个样子:
+ +第一步,通过两个鼓轮调入射狭缝 S1 和出射狭缝 S2 +的宽度,分别约为 1mm 和 2mm(目测即可)。
+第二步,把汞灯放在 S1 前面,打开汞灯,把手轮转到 +577.0~579.1nm 之间的某一位置(通过波长示数器观察)。
+显微镜目镜和物镜拧紧放在 S2 前面,调一调高度和与 S2 +的距离,观察到像这样的图像。黄的叫谱线,黑的叫狭缝刃口。
+ +++关小入射狭缝 S1 +使两条谱线分开,在谱线沿缝方向宽度基本均匀、亮度好的前提下, +使狭缝尽量窄,谱线尽量细。再关小出射狭缝 +S2,同时微动手轮,使其中一条谱线始终在狭缝中央,直至狭缝宽度与谱线同宽(此时微动手轮,谱线即被遮挡,谱线消失)。
+
纸上谈兵来说,如上操作可以得到单条谱线的波长示值(显示在波长计数器上)。按这个办法慢慢调波长,在标准值附近分别找两条黄线,一条紫线和一条绿线的示值,把它们记在第一个表里,差值的平均值就是单色仪波长示值的系统误差,之后要修约。
+标准值是黄线 579.1nm, 黄线 577.0nm,绿线 546.1nm,紫线 435.8nm。
+用汞灯调狭缝宽度
+第一步,将单色仪的波长读数装置转到示值在 +577.0~579.1nm 之间的某一位置。将出射缝 S2 的宽度暂时调至约 +2mm。用显微镜观察汞的两条黄谱线(577.0nm 和 +579.1nm)。如果看不到谱线,增加 S2 缝宽或改变波长示值。
+第二步,缓慢增加入射狭缝 S1 +的宽度,使谱线变宽,直到两条黄谱线刚好碰上且不重叠为止,此时入射狭缝宽约0.8mm。再调节出射狭缝 +S2 +的宽度,同时微调手轮,使出缝宽度与其中一条谱线宽度大致相同,此时出缝与入缝同宽,约 +0.8mm。
+此后不要再动单色仪,光强就能满足吸收系数测量的要求。此部分不需要记录数据。
+溴钨灯/光路调节,而不是溴钨灯光/路调节
+第一步,溴钨灯按讲义上写的接三路输出电源,调整设置。
+然后,讲义上是这样写的:
+++为了减少单色仪的光能损失,提高透光效率(充分利用单色仪的全孔径和相对孔径 +D/f),根据图 12 光路图,计算聚光镜和光源的位置。
+聚光(透)镜的参数见前面。单色仪焦距 f=300mm (即图 12 的 +b=300mm),单色仪球面镜(准直镜)的光栏宽度 +D=50mm。成像规律符合 Gauss 公式。
+使球面镜的孔径 D +充分照明,两个相似三角形应有下列关系:d/D=a/b。
+
翻译成人话:聚光镜摆在狭缝前面 18cm 处,溴钨灯摆在聚光镜前面 +9cm +处,注意共轴。当然,得在表格上画个图,装模作样算一下这两个数据。
+第二步,手轮调到 +610.0nm,调整各种位置。用眼睛靠近出射狭缝 S2 观察红色谱线。
+具体怎么调?先粗调后细调。
+粗调:溴钨灯电流建议用 +2.0A。微调光源的位置,用眼睛观察溴钨灯在入射狭缝 S1 +处所成的清晰实像,粗略调节等高同轴。
+细调:溴钨灯电流建议用 1.50A。用眼睛靠近出射狭缝 S2 +观察光谱,左右(共轴)调节聚光镜至合适位置,不管条纹亮度均匀否,只关注条纹上、下边缘的圆弧左右对称否,调至对称。
+再前后、左右微调溴钨灯,眼睛能看到亮度均匀的光谱(条纹),差不多这样。
+ +调节好透镜和溴钨灯位置后,固定好它们。
+最后的仪器安装
+第一步,把样品装在 S2 +上,先薄再厚,具体操作摘录如下:
+++将装有钕玻璃吸收片的样品反面的红点对准S2 +上红点,顺时针旋转样品,听到咔的声音,样品已锁定,往外拉一下,确认已安装好。
+取样品时侧面小螺钉往里轻推,逆时针旋转即可取下。
+
第二步,装硅光电二极管探头。
+++将探头插入样品正面的圆柱孔内(插到底),确认电缆接头处于拧紧状态。
+
如果还是手笨接不好仪器,就求助一下旁边同学吧,没救了。
测量环节
+对每一个样品,观察对各色光的吸收情况。
+从 610.0nm 到 550.0nm +转动手轮测定两个最大的吸收峰(光电探测器上的电压示值最小)的波长位置并记录。要求每隔 +2nm 测一次示值,在吸收峰左右 4nm 范围内测量点更密,取整数每隔 0.5nm +测量一次,记录在最后一个表里。
+注意:测量要消空程,即只向一个方向转动手轮, 一次完成。
+测完数据要分析计算什么?画哪些图?
-
-
Total Sum of Squares: \(SST= \Sigma(Y_i -- \bar{Y})^2\),\(df_{SST} = -n-1\)
-Sample Variance: \(S_n ^2 = -\frac{SST}{n-1}\),是非常熟悉的统计量。
-Variation due to Error: \(SSE = -\Sigma(Y_i -\hat{Y}_i)^2= \Sigma e_i ^2\), \(df_{SSE} = n-2\)
-Mean Square Error: \(MSE = \frac{SSE}{df} = -\frac{\Sigma_{i=1} ^n e_i ^2}{n-2}\),可以作为 \(\sigma^2 = Var(\varepsilon)\) -的一个估计。
-\(E(MSE) = \sigma^2\)
-Variation due to Regression: \(SSR = -\Sigma(\hat{Y}_i - \bar{Y})^2 = b_1 ^2 \Sigma (X_i-\bar{X})^2\), -\(df_{SSR} = 1\)
-Mean Squares of Regression: \(MSR = -\frac{SSR}{df} = SSR\)
-$E(MSR) = E(SSR) = E(b_1 ^2) ((X_i - {X})^2)= ^2 + _1^2 (X_i - {X})^2 -$;
+- 根据\(\alpha=\frac{lnV_{1}-lnV_{2}}{d_{2}-d_{1}}\),列表计算每个波长对应的\(\alpha\) +
- 画一个\(\lambda-\alpha\)图,是为吸收曲线。从中读出两个峰值的数值,然后按波长修正规则修一下。 +
- 误差分析讨论和回答思考题,可参考祖传实验报告。
可以计算得到 \(SST=SSE+SSR\),自由度方面也是 \(df_{SST} = df_{SSE}+df_{SSR}\)。
-事实上在 Lecture 2 中我们考虑过是选取 sample variance 还是选取 MSE -作为 \(\hat{\sigma}^2\),这里的定义给出了更清晰的答案:\(SSE\) 更加注重原值和模型之间的联系,把 -\(\hat{Y_i}\) 作为 \(Y_i\) 的估计值,在 sample variance 中是把 -\(\bar{Y}\) 作为 \(Y_i\) 的估计值,前者更好地体现了 \(\varepsilon\) 的场景。
-F-检验
-我们希望通过以上统计量检验 \(X,Y\) -之间是否存在线性关系。考虑假设 \(H_0: \beta_1 -= 0 ; H_1 : \beta_1 \neq 0\)。
-在正态假设和 \(H_0\) 成立条件下,取 -test statistic 为 \(F= \frac{MSR}{MSE} = -\frac{SSR / df_R}{SSE / df_E} = \frac{\chi_{dfR}/df_R}{\chi_{dfE}/df_E} -\sim F_{df_R,df_E} = F_{1,n-2}\)。考虑拒绝 \(H_0\) 的情况,我们要求 \(F_0 > F_{1-\alpha,df_R,df_E} = F_{1-\alpha, -1,n-2}\),满足此条件的 \((X,Y)\) -构成 rejection region。或者从 P-value 的角度来看,满足不等式 \(P(F>F_0 | F_{1,n-2}) < \alpha\) -的全体 \((X,Y)\) 落在 rejection region -中。
-考虑检验的 power function。在 \(H_1: -\beta_1 \neq 0\) 条件下,Power(\(\beta_1\)) = \(P(F> F_{1-\alpha , 1,n-2} | non-central -F)\)。
-General Linear Test
-另一种检验上述假设的方式。考虑假设 \(H_0: -\beta_1 = 0 ; H_1 : \beta_1 \neq -0\),我们来比较两种不同的模型:
-full model: \(Y_i = \beta_0+\beta_1 X_i -+\varepsilon _i\),reduced model: \(Y_i -= \beta_0 + \varepsilon_i\),在 \(H_0\) -假设成立时两个模型是等价的。考虑方差统计量:
+本文写作中用到的参考
-
-
- \(SSE(F) = SSE\) for full model -with \(df_{EF}\),在 simple linear -regression 下 \(df_{EF}=n-2\),\(SSE(F) = SSE\) -
- \(SSE(R) = SSE\) for reduced model -with \(df_{ER}\),在 simple linear -regression 下 \(df_{ER}=n-1\),\(SSE(R) = SST\) +
单色仪实验操作视频:
+https://www.bilibili.com/video/BV17A411L7mg?spm_id_from=333.337.search-card.all.click&vd_source=6ae5c31a80120436d23cf7b7c7ceb3ba
+清华大学2021秋基础物理实验(2)讲义
在 \(H_0\) 假设下,$F = -F_{(df_{ER}-df_{EF}),df_{EF}} $。实际上,在 simple linear regression -下和 F-检验是一致的。但是 general linear test -是一个更广泛的方法,可以用于任何形式的线性检验。
-Pearson Correlation r
-\(r = \frac{\Sigma (X_i - \bar{X})(Y_i - -\bar{Y})}{\sqrt{\Sigma(X_i - \bar{X})^2} \sqrt{\Sigma(Y_i - -\bar{Y})^2}}\) 被称为相关系数,反映了一组数据 \((X,Y)\) 之间的线性关系程度。
-\(R^2 = \frac{SSR}{SST}\) -被称为决定系数,事实上在 simple linear regression 下有 \(r^2=R^2\),因为 \(r = b_1 \frac{\sigma_X}{\sigma_Y}\)。
-
Lecture 5
-回顾一下简单线性回归的模型假设:\(Y_i = -\beta_1 X_i + \beta_0 +\varepsilon _i\)
+偏振光学系列实验
+原理简述
-
-
- \(\varepsilon _1, \varepsilon _2 ,..., -\varepsilon_n\) 相互独立 -
- \(\varepsilon_i\) 服从正态分布 -
- \(\mathbb E(\varepsilon _i) = -0\),\(Var(\varepsilon_i) = -\sigma^2\) +
- 什么是偏振光?
这不重要
可以总结成 LINE: linearity, independence, normality, equal -variance
-Diagnostics of X
-诊断的方式粗暴一点来说就是肉眼诊断,用一些可视化工具(主要是画图)和其他方式来检验模型的假设是否符合。如果违反了模型假设,结果很有可能不可靠。此时需要用一些弥补的方式来处理。
-Why -diagnose——Distribution and Confounding
-诊断过程需要关注的是 \(X\) 而非 -\(Y\),因为 \(Y\) 之间是独立异分布的。\(Y_i \sim N(\beta_0 +\beta_1 X_i , -\sigma^2)\)。
-\(X\) 完全是常数,所谓的 \(X\) 的分布指的仅仅是 \(X_1,X_2,...,X_n\) -在数轴上的排布,不是概率分布。但 \(X_i\) -的分布会影响到模型的效果,直观上举个例子来说,\(X_i\) 的位置至少会影响到 \(Var(b_1) = \frac{1}{\Sigma_i (X_i - \bar X)^2} -\sigma^2\) 也就是 \(b_1\) -的分散程度,这是会影响到推断显著性的因素,所以即使是常数也还是要对 \(X\) 进行一些诊断。
-我们一般希望 \(X\) -是类似于正态的分布,这样的数据比较有代表性。可以使用 qq-plot -进行检查。
-除此之外诊断 \(X\) 的另一意义在于 -\(X\) -本身可能也是和其他因素有混杂的。举个例子来说,如果高温既会导致冰激凌销量增加又会导致鲨鱼攻击人的次数增加,很可能会发现冰激凌销量和鲨鱼攻击行为次数之间有线性的关系,事实上这就是一个没有选对合适的 -explanatory variable \(X\) -却得到了看似合理的模型的例子,但这样的结论是有问题的,\(X\) 本身和气温这一因素混杂。
-此时如果分别对冰激凌销量-气温和鲨鱼攻击行为-气温作一个 sequence -plot,会发现二者都分别和气温有关系,那就有必要把气温作为一个 explanatory -variable 加入模型的考虑,这是一种针对 confounding 的诊断方法。
-四参数
-有一些可以关心的量(甚至不能说是统计量,毕竟 \(X\) 也不是随机变量),除了 range -之外实际上就是一阶到四阶矩:
+一个单色偏振光可以分解为两个互相垂直的线偏振光的叠加。表示如下:
+\[ \begin{cases}{} \ E_x = a_1\cos +\omega t \\\\ E_y = a_2\cos (\omega t+\delta) \\ \end{cases} +\]
+其中的\(\delta\)被称为\(x\)方向偏振分量相对于\(y\)方向偏振分量的位相延迟量。显然,偏振光的“形状”由式中参数决定,主要探讨椭圆、圆和线偏振光的情况。引入偏振方向的概念: +\(\alpha=arctan(\frac{a_2}{a_1} +cos\delta)\)
+我们不加证明地给出关于椭圆偏振光的参数求解式。其中定义\(\psi\)为椭圆的长轴方位角,我也不知道这个是什么意思。
\[ \begin{equation} +\begin{cases} \psi &= \frac{1}{2}arctan(tan2\beta cos\delta) +\\\\ \frac{b^2}{a^2} &= \frac{2}{1+\sqrt{1-(sin2\beta +sin\delta)^2}}-1 \\\\ \beta +&=arctan(\frac{a_2}{a_1}) \\ \end{cases} \end{equation} +\]
-
-
- sample mean 展现了 \(X\) -的主要位置 -
- standard deviation 展现了数据的分散程度 -
- 偏度 skewness \(g_1 = \frac{m_3}{m_2 -^\frac 3 2} = \frac{\frac 1 n \Sigma_{i=1}^n (x_i - \bar x)^3}{(\frac 1 -n \Sigma_{i=1}^n (x_i -\bar x)^2)^\frac 3 2}\) -展现了数据的对称性 -
- 峰度 kurtosis \(g_2 = \frac{m_4}{m_2 ^2} --3 = \frac{\frac 1 n \Sigma_{i=1}^n (x_i - \bar x )^4}{(\frac 1 n -\Sigma_{i=1} ^n (x_i -\bar x)^2)^2} - 3\) -展现了数据相对于正态分布的尾迹 -
- range 展现了 \(X\) 的分布范围 +
- 偏振片是干什么的?好像是用来产生线偏振光的。
其中值得关注的是偏度和峰度两个统计量,因为之前没有提过。想起来一个乐子,Pearson
-在《Lady Tasting
-Tea》里曾经认为一个分布只要有一阶到四阶矩的参数就可以完全确定,但实际上
-Poisson 分布的四个参数都是 \(\lambda\),是不行的。
-
-
关于偏度:
+ +首先,在这张图中,透射轴是偏振片上的那条轴,我们简称为\(x\)轴;消光轴是垂直于偏振片的轴,简称为\(y\)轴。沿\(x\)轴振动光波的光强透射率为\(T_1\),它接近\(1\);沿\(y\)轴振动光波的光强透射率为\(T_2\),它接近\(0\)。二者小比大得到一个很小的值\(e\),即为消光比。
+马吕斯定律:振动方向和\(x\)轴方向成\(\theta\)角的线偏振光,经过偏振片后的透射率为 +\[T_\theta=(T_1-T_2)cos^2\theta+T_2\] +提出这个定律有什么意义?
+实验中两个偏振片的组合(一个称为起偏器,一个称为检偏器)成为一组仪器。起偏器产生的线偏振光经过检偏器。因此,由马吕斯定律,二者的\(x\)轴夹角即为\(\theta\)。从结论来看,二者的\(x\)轴垂直(\(\cos +\theta=0\))则发生消光现象,二者的\(x\)轴平行(\(\cos +\theta=1\))则透射光强最大。
-
-
- \(g_1 <0\) 时称为 negatively -skewed,左尾比较长,所以也会称为 skewed left -
- \(g_1 >0\) 时称为 positively -skewed,右尾比较长,所以也会称为 skewed right +
- 反射和折射时的起偏现象
由图可见偏度是能够体现数据的对称程度的。实际上对称程度是相对正态分布而言的。
-一般来说对于一个左偏的分布,会有 mean < median < -mode(众数),如果右偏则会是 mode < median < mean。当然 mean 和 -median 的顺序不一定准确,以及对于完全对称的分布会有三者相等。
-注意如果分布有多个峰值,此时 skewness 不一定还适用。
-关于峰度:
+电矢量形式的菲涅耳公式我看不懂,也不知道是干嘛的(直球)。
+和实验相关的东西翻译成人话来说就是,偏振器的透射轴方向可以由布儒斯特角确定。具体如下:
+ +预置光束在三棱镜上的入射角\(\theta_i\)为\(arctan\text n\),其中\(\text +n\)为玻璃的反射率,也即初入射角约为56°。旋转偏振片到某个角度可以发现白纸屏上的光点很暗。微调二者,使得光点达到最暗时的入射角为布儒斯特角\(\theta_B\),且此时偏振片的透射轴(\(x\)轴)方向平行于三棱镜上的入射面。
+以下与实验无关,可在实验前阅读中跳过。讲义上还有一段关于S分量反射率的叙述,目测是菲涅尔定律的推导:
++
+此时, S 分量的反射率为\(R_{SB}=\frac{(n^2-1)^2}{(n^2+1)^2}\)。
+关于
+反应堆玻片堆:+
上式表示的反射率\(R_{SB}\) +一般较小,反射光较弱。光束以\(\theta_B\)射入多块平行玻璃板以获得只有 +P 分量的线偏振透射光,经过 N 块玻璃片的 2N +个表面后,S 分量的总透射率为\[(1-R_{SB})^{2N}=[1+(n-1)^2/2n]^{-4N}\]在\(N\)较大时,其值接近于\(0\)。这种起偏装置就叫做玻片堆。
+-
-
- \(g_2>0\) 时称为 -leptokurtic,尖峰态下双尾较长。 -
- \(g_2 <0\) 时称为 -platykurtic,低峰态下双尾较短。 -
注意峰度的所谓尖峰态低峰态和尾部数据性质也都是相对正态分布而言的。正态分布的峰度就是 -\(3\),因此峰度的公式里有一个减去 \(3\) 的操作,作为和正态分布的比对。
-有的时候会把不减去 \(3\) 的称为 -kurtosis,减去 \(3\) 则称为 excess -kurtosis,使用的时候要注意。
-实际上峰度带来的度量信息包括峰和尾两部分,单独出现尖峰的条件不能作为判断 -\(g_2\) 正负性的依据,只是表征了 \(\bar X\) -附近的情况,和尾部情况综合起来看才可以;峰度的正负性和方差的大小无关。
-尾部的情况可以通过 Q-Q plot 查看:
- +
+- 延迟器和波片
诊断 assumptions
-最常用的 assumption -诊断方法是使用残差图进行诊断,一元线性回归中我们可以直接使用 \(e_i \sim X\) 图,也可以使用 \(e_i \sim \hat Y\) -图进行诊断,二者本质上只相差横轴的尺度和位置。在多元线性回归中就直接使用 -\(e_i \sim \hat Y\) 图进行诊断。
-除此之外也有很多理论检验的方法,虽然听起来更 -concrete,但其实实际应用中还是肉眼检查最有效。
-模型诊断可能发现的一些问题:
+一般来说,线偏振光入射延迟器后出射为椭圆偏振光。其他的我就一句都没看懂了...不过没关系,一样可以做实验。
+实验中需要操作的是判断波片快慢轴,定出方向,做一些测量。我们直接在下一部分说明。
+应该做什么?在附的实验表上记什么?
+组装仪器
+ +这是一个分光计改装的实验仪。
+打开激光器,粗调2,3的轴线,小平台基本水平且与分光计主轴垂直。激光光斑不要太靠近偏振片区域的边缘。
+电阻箱阻值100Ω,使得毫伏表示数大于1毫伏。
+观测布儒斯特角和偏振器的特性
+玻璃片放在平台上,反射面过平台中心点。以下的此为“x”指实验表中的部分填写。
+第一步,确定光束正入射棱镜表面时平台方位角\(\alpha_{i=0}\)。用小纸片扎一个小孔,放在激光器出射光束处,调整棱镜表面的反射光在纸屏上的亮点和小孔重合,记下此时的平台方位角即为\(\alpha_{i=0}\)。能不能搞点正常的下标啊
第二步,旋转棱镜使得光束的入射角\(\theta_i\)约为55°。旋转2到某个角度可以发现白纸屏上的光点很暗。微调入射角和起偏器,使得光点达到最暗时的平台方位角为\(\alpha_B\)。起偏器2的方向角为\(P_{\leftrightarrow}\)。能不能搞点正常的下标啊
第二步要连做三次,得到一个平台方位角的平均值\(\alpha_B\),然后布儒斯特角测量值就是\(\alpha_{i=0}-\alpha_B\),然后折射率就是布儒斯特角取一个正切值。此为“4”。
+第三步,如上得到一个起偏器方向角的平均值\(P_{\leftrightarrow}\),把2置于平均值位置。拿走玻璃片,转动3使得光强探测器上电压值最小,此时即为正交消光。在表格里记下3上度盘的度数为\(a_\uparrow\),可以看一下\(a_\uparrow\)是否和\(P_{\leftrightarrow}\)大约相差\(90°\)作为验证,此为“5”。能不能搞点正常的下标啊
第四步,保持偏振器2不动,将3的轮盘角多加\(90\)度,从而恢复到二者\(x\)轴平行的情况。在此基础上每次加上\(0,15,30,45,60,75,80,84,87,90\)度,得到二者\(x\)轴的夹角为以上数据。记下对应的电压值,注意夹角为\(90\)度时可以视作已经消光,示数为环境光光强。此为“6”。
+波片的特性研究
+第一步,把3的轮盘角调回\(a_\uparrow\),安装波片\(C_0\)到2盘的度盘上,使得\(C_0\)上白点处对应的直径大致竖直。微调\(C_0\)使得电压示数最小,记录下此时内圈的游标盘示数为\(C_0\),此时有\(C_0\)的快轴竖直。此为“7”。
+第二步,\(C_0\)不动,在小平台上放上\(C_x\)使得光束可以垂直透过。旋转\(C_x\)使得电压示数最小,此时\(C_x\)的某个轴已经垂直于2的透射轴,达到竖直方向。记下此时\(C_x\)的度盘数值,记为\(C_x\)。此为“8”。
+第三步,此时二者都不要再动,就有\(C_0\)的快轴和\(C_x\)的某一个轴平行。保证偏振器2的轮盘角为\(P_{\leftrightarrow}\),偏振器3的轮盘角为\(a_\uparrow\)。然后在此基础上给\(P_{\leftrightarrow}\)加上\(15°\),转动3的轮盘角使得二者消光(表现为电压示数最小),记下此时的3度盘角度和转动的差值角度。每次测量结束后,将偏振器3的轮盘角归回\(a_\uparrow\)。
+还要再做两次,分别给\(P_{\leftrightarrow}\)加上\(30°\)和\(45°\),调节3的轮盘角。可以发现3的转动差值和给\(P_{\leftrightarrow}\)加上的角度差不多,作为验证。因为这组成了一个半波片。此为“9”。
+第四步,转动\(C_0\),给\(C_0\)加上90°使得\(C_0\)的快轴处于水平位置,和\(C_x\)的某一个轴垂直。与第三步类似地求出3的轮盘角增加差值。可以发现3的转动差值约等于给\(P_{\leftrightarrow}\)加上的角度取负,作为验证。因为这组成了一个全波片。此为“10”。
+这几步操作证明了\(C_x\)竖直的“某一个轴”其实是快轴。
+单个\(\frac{1}{4}\)波片的特性研究
+第一步,取下\(C_x\),把2归回\(P_{\leftrightarrow}\),把3归回\(a_\uparrow\)。将2的轮盘角多加\(22.5°\),于是记录下\(P=P_{\leftrightarrow}+22.5°\)。调节3使得偏振器3的透射轴与偏振器2的透射轴平行,记下此时的轮盘角\(a_i\)。然后转动\(C_0\),分别记录最大的电压值和最小的电压值。
+然后,重复第一步,仅把其中的“\(22.5°\)”分别改为\(45°,67.5°\)实验两次即可。把此过程中的数据都记在表格里,下面的计算暂时先不用管。
+第二步,把光源挡住,记一个系统误差电压值\(I_0\),填在表格边上那个空里面。此为“11”。
+测完数据要分析计算什么?画哪些图?
-
-
- \(Y\) 和 \(X\) 之间没有线性关系但是硬拟合了一个 -
- \(\sigma ^2\) -不能视作常数,也即异方差 -
- \(\varepsilon _i\) -不服从正态分布 -
- \(\varepsilon _i\) -之间彼此不独立 -
- 模型可以拟合,但数据中有 outlier +
- 计算实验元件玻璃的布儒斯特角和折射率。前文已体现。 +
- 绘图验证马吕斯定律
以下给出一些发现问题的方法:
-非线性关系
-简而言之,\(Y\) 和 \(X\) -之间可能并不是一个线性关系,但是我们采用了线性模型进行拟合。
-找出问题的手段是使用 \(e_i \sim
-X_i\) 图诊断 \(Y\) 和 \(X\) 的线性关系是否过拟合。具体来说,给
-\(e_i \sim X_i\) 再做一个拟合图线
-scatter.smooth,观察和 \(h=0\) 是否偏离较大。虽然通过 \(Y \sim X\) 也可以看出来,但是 \(e_i \sim X\) 图更加明显。
即使线性关系是显著的(R 中得到 \(R^2\) 较大、斜率 \(\beta_1\) -显著),也不说明线性模型是最好的拟合模型。
-异方差问题
--
-
实际上的残差并不符合方差相等的假设,则称为异方差问题。即使发生这样的情况也未必会影响到 -\(\beta_1,\beta_0\) -的估计值,因为计算过程和这一假设实际上是无关的。但是,异方差问题会导致 -\(b_0,b_1\) -不再是使得方差最小的估计,失去了 BLUE -性质,但仍然是无偏的估计。问题会反映在关于 \(\beta_1,\beta_0\) -的推断中,导致推断或者置信区间不是效率最高的。
-举个例子,比如说 \(Y_i = 30 +100X_i + 10X_i -\varepsilon_i\),实际上是有 \(\varepsilon_i \sim N(0,10X_i -\sigma^2)\),方差并不相同。
-画图检查最典型的异方差情况是画出 \(e_i \sim -X\) 图后发现 \(X\) 越大,\(e_i\) -越分散,呈现出一个扇形的分布形态。
-模型的诊断也可以使用一些理论方法,异方差检验中常用的几种检验如下所示:
+用表6的数据分析\(\frac{I_m-I_{min}}{I_{max}-I_{min}}\)和\((\cos +x)^2\)之间的线性关系(即二者相等),并绘制一个以\(\theta\)为自变量的图,体现\(\frac{I_m-I_{min}}{I_{max}-I_{min}}\)和\((\cos x)^2\)两条曲线的变化。其中\(I_{min}\)和\(I_{max}\)分别代表\(\theta\)为\(90°\)和\(0°\)时的光强测量值。
-
-
Bartlett 方法,本质上是 likelihood ratio -test,但非常依赖残差的正态假设。也即,如果检验结果是拒绝原假设,未必是真的发生了异方差现象,也可能是因为残差不服从正态分布造成了干扰。
-Levene & modified Levene (B.F.) 方法,非常常见。
-对于可能影响方差导致异方差的因素 \(Z\),将 \(e_i -^2\) 相对于 \(Z\) -再做一次线性回归,得到的 SSR 记为 \(SSR^*\)。
-此时 \(LM = \frac{SSR^*/2}{(SSE/n)^2} \sim -\chi_1 ^2\) 再进行检验。
-
+- 观测偏振光通过半波片和全波片的现象。前文已体现。 +
- 线偏振光通过\(\frac{1}{4}\)波片
正态性假设
-\(\varepsilon _i\) -并不服从正态分布,这可以通过 QQ-plot 观察是否有 \(\varepsilon_{(i)} = \mu + \sigma -Z_i\),或者直接画 histogram 检查是否有正态的形状。
-
理论方法之中 Shapiro-Wilk 方法是最佳的,有最大的 -power,但是对于样本量是敏感的。也就是说,如果检验结果是 \(\varepsilon_i\) -不服从正态分布,也可能是因为样本量太大导致了错误判断。
-注意正态性检验是完全可以把 \(\{\varepsilon -_i \}\) 作为一组数据放在一起观察整体的分布的,但是对 \(\{Y_i \}\) -不可以这样做,它们彼此之间服从的是不同的条件分布。
-相关性
-\(\varepsilon_i\) -之间可能并不独立,有可能都受到 \(t_i\) -的影响,等等。如果有类似可能考虑的因素可以对其做 sequence plot。
-理论方法中最常用的是 Durbin-Watson 方法。
-Outlier
-模型的数据里有 outlier,不同性质的 outlier -对回归线的影响不尽相同,具体的在 Lecture 6 -中再细说。简单来说就是,outlier 的 \(X_i\) 越接近 \(\bar{X}\),对于回归线的斜率影响越小,但如果距离 -\(\bar{X}\) -比较远,则会产生比较强的杠杆效应。
-即使模型中存在 outlier,参数的估计也可以是比较准确的。做 \(e_i \sim X\) 图可以查看是否存在 -outlier,也可以使用 \(Y_i \sim X_i\) -的图来观察是否有距离回归线很远的点,这是最明显的一类 -outlier。然后可以尝试剔除这样的点再重新做回归,检查各系数。
-关于 \(R^2\)
-如果在某一线性模型中得到 \(R^2 = -0.69\),能否说明这一线性模型是显著的?
+其实就是把表格补满的过程。
+其中,计算波片相延可以使用\(|sin\delta_r|=\frac{2\sqrt{(I_{min}/I_{max})}}{sin(2\beta)(1+I_{min}/I_{max})}\)来计算。三个值都略小于\(90°\)。理论值均为\(90°\)。
+用\(\alpha\)计算长轴方位角则有\(\psi\)和\(\alpha\)相差\(90°\),但要把\(\psi\)调到\([-90°,90°]\)的范围内。三个理论值分别为\(0°,45°,90°\)。
+用公式计算长轴方位角,则把\(\psi=\frac{1}{2}arctan(tan2\beta +cos\delta)\)代入算一下即可。理论值罗列同上,应该差距不大。
+其余分析参考祖传实验报告即可。
+本文写作中用到的参考
-
-
- 事实上可以。\(R^2 = 0.69\) -已经是相对大的数值了,说明模型对于方差的解释能力是相对好的;另一方面考虑 -\(r = \sqrt{R^2} > -0.8\),相关系数其实是比较大的,可以认为这一模型是合适的。 -
- 但是,这并不能说明线性模型是这一问题下最好的模型。\(R^2\) -想要多大就可以多大,例如给模型加入新的多项式型变量,总能更多地解释一些方差,不能单纯地追求 -\(R^2\) 的大小。 -
- 另外,如果在不同的模型比较中对 \(\{Y_i -\}\) 做了变换,比如进行了标准化或者 Box-Cox -transform,此时是不能和原始的模型再进行 \(R^2\) 的比较的,只能检查单个 \(R^2\) 的值能否接受。这是因为 \(SST\) 已经随着 \(\{Y_i \}\) -的变化而变化了,模型的方差解释能力 \(\frac{SSR}{SST}\) 无法比较。 +
清华大学2021秋基础物理实验(2)讲义
+清华大学2011级尚恩垚学长的大物实验报告《偏振光学实验》
Lecture 6
-Built-in Diagnostic Plots in -R
-R 内置的四个诊断图是 \(e_i \sim \hat -Y\),Q-Q plot,\(\sqrt{|\text{Standardized Residuals}|} \sim \hat -Y\),Cook's distance -图。前两个都比较简单,一个是万能的残差图,另一个是残差的正态性检验,主要说一下后两个图。
-Scale-Location Plot
-\(\sqrt{|\text{Standardized Residuals}|} -\sim \hat Y\) 作图体现了 residuals -随拟合值的分布情况,主要用来检验异方差。实际上在上一讲里面是直接用 \(e_i \sim X\) -来检验异方差的,这里用了标准化的残差开方,有一些考虑:
+(说来惭愧,我一个学基物的,看了别人的大物实验祖传报告,才学会了这个实验x)
+塞曼效应实验
+待填坑。
+光栅衍射实验
+笔者直到实验结束也没明白这是在做什么。
+放一个我自己的实验报告在这里,希望将来的社恐同学们不要再被困扰到了,到期末我会把信息脱敏后上传 +GitHub 和课程资源共享计划。Click +Here
+简要报告篇
+摩擦系数实验
+为什么这学期会有这么个实验...
+是新出的题目,暑假期间没有拿到讲义,可能不会写了。
+弗兰克-赫兹实验
+原理简述
+完全看不懂,拉倒吧。总感觉也不影响实验
应该做什么?
+第一次实验的接线
+ +实验仪“放大倍数”档位选择“\(×1\)”档,“扫描选择”档位置于“手动”档。打开一体机电脑。参考讲义上的\(10(a)\)给实验管箱接线(或者照抄上图),检查无误后准备通电。
通电时先打开实验仪背后红色按钮,再按下实验仪前面的“灯丝电流开关”(若不按下此按钮,灯丝电流输出为 +0A)。然后在实验仪上调整灯丝电流在\(0.8A\)附近,拒斥场电压在\(7.5V\)附近,控制栅电压在\(1.5V\)左右。
+寻找实验条件
+缓慢在实验仪上增加扫描电压\(U_a\),观察板极电流\(I_p\)的变化情况。 +当看到其起伏变化时,分别改变实验仪上的三个参数,定性观察每个参量对\(I_p\)的影响。如果随着\(U_a\)的增加在 \(0 +∼ 85V\) 内能大致观察到\(I_p\)有 +\(6\) +个峰,峰与谷的差别相对比较明显,则达到最佳测试条件。此时把实验仪上的档位切成自动扫描,启动自动采集软件绘制曲线,获取峰值电压。
+太抽象了,所以我找了一份实验数据,来自刘丁菡学长,大概这样:
+ +注意以下要点:
-
-
关注 magnitude 所以需要一个正值,选择了先取绝对值
-取绝对值之后的数据往往人为造成了右偏,开方可以缓解一些
-standardize 之后绝大多数 \(e_i\) -都收入了 \([-2,2]\) -这一范围内(正态分布的主要区间),更清晰,有可比性
-虽然理论上的 \(\varepsilon_i\) -是独立分布的,但是残差之间是有约束关系的,\(Var(e_i) = (1-h_{ii})\sigma^2\),也就是说 -\(e_i\) 的变动范围本身就和其在 \(x\) 轴上的位置(也即 \(X_i\) 的大小)相关。较大的 \(X_i\) 会对应 \(e_i\) -的更大方差,导致可能会看起来像异方差。
-标准化并开方能够一定程度缓解这样的问题。
+- 实验仪上的灯丝电流不能一次改变很大,大概在\(0.01∼0.02A\)左右;调整灯丝电流后要等两三分钟再观察\(I_p\)的变化,有一个滞后。 +
- 扫描电压\(U_a\)较大时尽量使用自动挡位测量,用完之后尽快调零。如果出现电流表指针打表,要尽快调小扫描电压,关闭灯丝电流的开关。
如果此图上的残差点分布看起来比较随机,拟合线也相对平行于 \(x\) 轴,基本可以认为是异方差。
-Cook's Distance
-图中被标出数字的点/靠近右上角和右下角/红线之外的点需要重视一下,是 -high leverage point 或者 outlier,可以进一步检验。
-Residuals & Leverage
-Leverage
-定义每一点的杠杆值为 \(h_{ii} = -\frac{\partial \hat Y_i}{\partial Y_i} \in [0,1]\),表征了某一个 -\(X_i\) 对应的 \(Y_i\) -变动一个单位时,会导致回归线上的响应值变动的大小,也就是说,这一点的变化对于整个回归模型的影响。
-事实上,\(X_i\) 对应的点的 leverage -是 \(h_{ii} = \frac 1 n + \frac{(X_i - \bar -X)^2}{\Sigma_j (X_i - \bar X)^2}\),\(h_{ii}\) 越大会导致 \(Var(e_i) = (1- h_{ii})\sigma^2\) 越小,因此 -\(e_i\) 的变动范围变小,\(\hat Y_i\) -能够变动的范围也较小,会导致回归线受较大的影响;从 leverage -的表达式可以看出来,\(|X_i -\bar X|\) -越大会导致杠杆值越大,也就是说远离中心的点对回归线造成的影响较大。
-我们对 extreme values 做一些分类:
+跟着FH软件教程操作
+按照教程一直做到第三步,第四步校准仪器的时候输入自动扫描电压\(U_a\)的最大值为\(90V\),扫描出完整的\(6\)个峰和谷。第五步数据采集模块中选择数据个数为\(200\),点间延时为\(100ms\)为最佳。此后一直根据教程行动即可,得到第一份数据。
+定性研究的操作
+保持灯丝电流和拒斥电压不动,改变控制栅电压在\(1.0V,1.5V,2.0V,2.5V,3.0V\)这些值上变化,扫出曲线。
+保持灯丝电流和控制栅电压不动,改变拒斥电压在\(5.0V,6.0V,7.0V,8.0V,9.0V\)这些值上变化,扫出曲线。
+氩原子更高激发态的情况
+这一次是两人一组,等待大佬救我
类似的操作,把亚克力板接进电路,设定最佳实验条件。在软件上调整扫描电压最大值为\(30V\)。在实验仪上调整灯丝电流在\(0.78A\)附近,控制栅电压在\(1.5V\)左右。拒斥场电压分别调整为\(2.0V,2.5V,3.0V\)。类似扫描出\(I_p-U_a\)的归一化和非归一化曲线。
+注意以下的要点:
-
-
Outlier: 离群值是对于其 \(Y\) -值而言的,\(Y_i\) -的实际取值远离通常该有的范围,则这一点会被认为是 outlier。
-High Leverage Point: 高杠杆值点是对于其 \(X_i\) 的取值而言的,由上述分析可以得到 -\(h_{ii}\) 较大的主要条件。
-Influential Point: -强影响力点指的是移除此点后,回归线会发生较大的变化的点。
-如果一个点既是 outlier 又是 high leverage point,那它一定是 -influential point,直觉上来看是因为它的 \(X\) 和 \(Y\) -都具有一定的特征,会对回归线造成较大的影响。
+- 只需要图上有两个峰。第二个峰大约出现在\(25V\)左右,因此最大扫描电压只需要\(30V\)。而且\(I_p\)的最大峰值对应不超过\(50\mu A\)。 +
- 祖传报告中指出这一步实验仪上的另两个参数保持不变即可,和讲义不是很一样。我倾向于相信祖传报告。
如果 \(h_{ii} > 2p/n\) -一般就称为高杠杆值点。
-Studentized Residual
-一个 influential point -造成回归线的巨大改变无法在残差图上体现出来,因此我们希望有一种手段能够体现出它和其他正常点的巨大差异。一个自然的想法是先移除它再做回归线,然后在这一模型上体现残差,即为 -studentized residual。
-这么说还是太抽象了,放个图好了:
-
具体来说,studentized residual 和 standardized residual -有一些差别:
+实验结束后可以断开其他元件的连接,整理仪器,处理自己的数据。
+测完数据要分析计算什么?
+测试\(I_p-U_a\)曲线,得到氩原子第一激发电位
+找到第一部分数据的 Excel 表格 Data +页,取六个峰值的电压数据和测量次数(注意舍去一看就不对的值),到 Origin +里拟合数据。由于曲线上相邻两峰值之间的电位差就是氩原子的第一激发电\(U_g\),因此处理得到的斜率就是第一激发电位。
+太抽象了,这是一张示例处理表格,来自刘丁菡学长,其中的 \(Slope-Value\) 就是所需要的值。
+ +关于不确定度的计算,公式都在下面了:
+\[\Delta_A=S_b=b\sqrt{\frac{2(1-R^2)}{n-2}}\]
+\[\Delta_B=0.001×b+0.01\]
+\[U_g=(b±\Delta_{U_g})\]
+其中\(b\)是斜率,\(R^2\)是拟合的最后一列方差,\(n\)是实验次数(即为\(6\)),\(\Delta_{U_g}\)是两个系差平方和的开方。
+氩原子受击后回到基态辐射出的光波波长
+套下面两个公式:
+\[\lambda=\frac{hc}{eU_g}\]
+\[\Delta_\lambda=\lambda\frac{\Delta_{U_g}}{U_g}\]
+实验中观测不到发光是因为这是紫外波段而不是可见光波段,也因此用壳罩住了管子防止对人体造成伤害。
+定性研究栅极电压和拒斥电压对\(I_p\)的影响
+控制栅电压的影响:由图可知,从峰值对应的扫描电压上看,随着 \(U_G\) 值的增大,曲线中峰 +值所对应的扫描电压值稍向左偏移;从峰值的相对大小来看,随着 \(U_G\) 值的增大,峰值先增大后减小,在 \(U_G≈ 2.0V\) +附近能观测到峰值最大,说明此时单位时间到达极板的电子最多。 +理论解释见祖传报告,反正我也写不出来。例图如下,来自刘丁菡学长:
+ +拒斥电压的影响:由图可知,随着 \(U_R\) +值的增大,曲线绝对值下移、峰谷值之间的差距变 +大、曲线中峰值所对应的扫描电压值稍向右偏移。理论解释见祖传报告,反正我也写不出来。例图如下,来自刘丁菡学长:
+ +更高激发态的研究
+例图如下,来自刘丁菡学长。\(U_R\) +整体对曲线的影响与第一激发态是类似的,即随着 \(U_R\) +的增大,曲线整体下移,峰谷差值增大,峰值向右移动。但差别在于曲线的形状有所不同,即没有出现很明显的一个峰值,而是峰值附近有一个小平台。理论解释见祖传报告,反正我也写不出来。
+ +解答思考题
+见祖传报告。
+本文写作中用到的参考
-
-
standardized residual: \(\frac{e_i}{s(e_i)}\),由于 \(Var(e_i) = (1-h_{ii})\sigma^2\),则 \(s^2 (e_i) = -(1-h_{ii})MSE\),代入即可。
-deleted residual: \(d_i = Y_i - \hat -Y_{i(-i)}\),其中 \(\hat -Y_{i(-i)}\) 是 \(X_i\) -在去除这一点的模型中所对应的响应。
-studentized residual: \(\frac{d_i}{s(d_i)}\),同理有 \(s^2(d_i) = (1-h_{ii})MSE_i\),\(MSE_i\) 是去除第 \(i\) 点的模型对应的 MSE。
-事实上 \(e_i^* = \frac{d_i}{s(d_i)} = -\frac{e_i}{\sqrt{MSE(1-h_{ii})}}\) 是 internal studentized -residual,当 \(|e_i ^*| >2\) -时认为是一个 outlier。
-studentized deleted residual 如下所示:
- +
+- 清华大学2020级刘丁菡学长的基物实验报告《弗兰克-赫兹实验》
Cook's Distance
-考虑 \(D_i = \frac{\Sigma_j (\hat Y_j - -\hat Y_{j(-i)})^2}{ps^2}= \frac{e_i^2}{p\cdot MSE} -\frac{h_{ii}}{(1-h_{ii})^2}\),其中 \(\hat Y_{j(-i)}\) 指的是 \(X_j\) 在去除第 \(i\) 点的模型中对应的平均响应值。第 \(i\) 点的 Cook's distance \(D_i\) 表征的是第 \(i\) -点的值对全体预测值(也就是回归线)的影响力。\(D_i\) 越大越说明这是个 high influential -point,一般吧 threshold 作为 \(0.5\) -或者 \(\frac 4 n\)。
-Lack of fit test
-怀疑某个模型并不符合线性,且其某一 \(X_i\) 点处有多个对应的 \(Y\),也即这一点处存在 replicates 或者说 -repeated observation 的时候,可以进行失拟检验。具体来说,可以进一步细分 -SSE 为 sum of pure error 和 sum of lack of fit -error,前者由数据的随机性导致,后者由线性模型的失拟性造成。
-事实上也是 general linear test 的一种,这里的 full model 就是 cell -mean model \(Y_{ij} = \mu_i + -\varepsilon_{ij}\),reduced model 是线性模型 \(Y_{ij}=\beta_0 +\beta_1 X_i + -\varepsilon_{ij}\)。也就是说,实际上的 \(H_0: \mu_i = \beta_0 + \beta_1 X_i\),拒绝 -\(H_0\) 时说明 reduced model 失拟。
-对 SSE 进行进一步的拆分,将其改变为 \(SSE = -SSPE +SSLF\),具体表达式和自由度如下所示:
-\[\Sigma_{i=1} ^c -\Sigma_{j=1}^{n_i}(Y_{ij} - \hat Y_{ij})^2 = \Sigma_{i=1} ^c -\Sigma_{j=1}^{n_i}(Y_{ij} - \bar Y_{i.})^2+ \Sigma_{i=1} ^c -\Sigma_{j=1}^{n_i}(\bar Y_{i.} - \hat Y_{ij})^2\]
-\[SSE = SSPE + SSLF\]
-\[(n-2) = (n-c)+(c-2)\]
-因此,对应地有 \(E(MSPE) = \sigma^2,E(MSLF) -= \sigma^2 + \frac{\Sigma_i n_i (\mu_i - (\beta_0 + \beta_1 -X_i))^2}{c-2}\),test statistic 是 \(F^* = \frac{MSLF}{MSPE} \sim ^{H_0} -F(n-c,c-2)\)。
-这也就说明了为什么失拟检验只有在存在 replicates -的时候才能做,因为这时才会有 \(n > -c\),使得模型不至于退化。
-Remedy Methods
-补救非线性
-通过 \(e_i \sim X\) -观察到模型并不是完全线性的时候,如果不想再改变 -assumptions,可以转而选择非线性的模型。
-R 中可以调用函数 nls。
补救异方差
-可以使用 weighted analysis,具体参见 Lecture 12 的内容。
-补救非正态
-如果残差体现出非正态分布的性质,可以对 \(Y\)
-做变换继续使用线性模型,也可以使用其他的模型来允许残差不同分布。在 R
-中可以调用函数 glm。
Transformation
-有以下任一需求的时候都可以考虑对 \(Y_i\) 做变换:
+感谢学长的图救我老命,不然这个实验真的看不懂在干嘛...
+几何光学系列实验
+不喜欢系列实验,真的好麻烦。
+原理简述
+会算相似三角形就行
-
-
- 稳定方差:观察到 \(\varepsilon_i\) -似乎是异方差的 -
- 提高正态性 -
- 简化模型,提高解释性 +
- 薄透镜的成像规律
最普遍的方法是 Box-Cox Transformation,取 \(Y^* = -(Y^\lambda-1)/\lambda\),首要任务是找到最合适的 \(\lambda\) -做变换。事实上所谓的“最合适”包含两层意义,其一是希望模型拟合程度较高,其二是希望 -\(\lambda\) 使得 \(Y^*\) -的形式尽量简洁明了,解释性强,也就是取所谓的 convenient lambda。例如取 -\(\lambda=0\) 时有 \(Y^* = \log Y\),取 \(\lambda\) -为整数时即为多项式回归,等等。
-另外不同的 \(\lambda\) -值会对数据的右偏有不同程度的改善,右尾压缩最明显的是开根和取对数;也可以取负值来压缩左尾。
-在实际使用中往往是直接对 \(\lambda\) -取一个 sequence,找到近似取到 maximum likelihood 或者使得 SSE 最小的 -\(\lambda\) -的一个置信区间,再在其中寻找合适的 convenient lambda。
-一些典型的数据分布和变换方法:
-
Miscellaneous Topics
-一些杂谈,关于 simple linear regression 的最后内容。
-Regression Through the -Origin
-非常坏回归,爱来自自由度(
-强迫过原点回归的时候斜率的估计是 \(\hat -\beta_1 = \frac{\Sigma X_iY_i}{\Sigma -X_i^2}\),这会导致一些很严重的后果:
+经典公式:\(\frac{1}{f}=\frac{1}{p}+\frac{1}{q}\),其中 +\(p\),\(q\) 分别代表物距和像距;\(\beta=-\frac{q}{p}\)称为线放大率。
+它们有很多正负性质的要求:前三者实物/实像/凸透镜为正,虚物/虚像/凹透镜为负,\(\beta\)在实像时为负,虚像时为正。
-
-
- 残差的和 \(\Sigma e_i \neq -0\),这导致 \((Y_i - \bar Y)^2 = (Y_i - -\hat Y_i)^2 + (\hat Y_i - \bar Y)^2 + 2(Y_i - \hat Y_i)(\hat Y_i - \bar -Y)\) 的交互项无法消去,于是也不能再对 SST 做分解成为 SSE 和 SSR -之和。 -
- SSE 此时的自由度是 \(n-1\),SST -的自由度也不再是 SSE 和 SSR 的自由度之和。 +
- 内调焦望远镜
Inverse Predictions
-对 \(Y \sim X\) 做回归得到 \(y = b_0 + b_1 x\) 和对 \(X \sim Y\) 做回归得到 \(x = a_0 + a_1 y\) -中,实际上在绝大多数情况下都有 \(a_1 b_1 \neq -1\)。也就是说,两种回归的结果不能简单地用线性求反函数得到,这听起来有点反直觉但确实是合理的,做 -\(Y \sim X\) 回归的目标是取得关于 \(Y\) 的最小残差平方和,做 \(X\sim Y\) 回归的目标是取得关于 \(X\) -的最小残差平方和,目标不一致得到的结果自然不同。
-用理论来解释的话,取相关系数 \(r = -\frac{\sum (X_i - \bar X)(Y_i - \bar Y)}{\sqrt{\sum (X_i - \bar X)^2} -\sqrt{\sum (Y_i - \bar Y)^2}}\),记 \(S_Y = \sqrt{\sum (Y_i - \bar Y)^2},S_X = -\sqrt{\sum (X_i - \bar X)^2}\),于是有:
-\(b_1 = r \frac{S_Y}{S_X},a_1 = r -\frac{S_X}{S_Y}\),因此 \(b_1a_1 = -r^2\)。两条回归线之间的夹角是 \(\tan -\theta = \frac{1-r^2}{r(\frac{S_X}{S_Y} + -\frac{S_Y}{S_X})}\)。
-如果对于某个响应值 \(Y_i\) -需要反向预测输入变量 \(X_i\),应该选择 -\(\hat X_h = \frac{Y_h - b_0}{b_1}\) -而不是反过来做 \(X\) 关于 \(Y\) 的回归。
-Limitations of \(R^2\)
-使用 \(R^2\) -作为判断依据的时候要注意以下问题:
+望远镜是由一个物镜一个目镜组成的。当我们用一组物镜组替代物镜时,不必移动物镜和目镜间的距离\(l\),而是直接改变物镜组的焦距即可达到整体调焦的效果。这就叫做内调焦望远镜。
+实验中用到的物镜组是一个凸透镜\(L_1\)和一个凹透镜\(L_2\)组成的。这是一个最简单的变焦物竞组物镜组。原理是\(L_2\)的物方焦点在\(L_1\)的像方焦点右侧时,改变两个透镜的间距\(d\)就能达到内部调焦的效果。此时取二者的“正焦距”(我不太会描述)为\(f_1'\)和\(f_2\),物镜的组合焦距即为\(f_o'=\frac{f_1'f_2}{d+f_2-f_1'}\)。要求满足\(f_1'-f_2<d<f_1'\)才能如上调节。
我们把目镜的焦距记作\(f_e\)。望远镜的视放大率即为\(\Gamma_T=-\frac{f_o}{f_e}\)。这个数值的绝对值越大,观察到的像越大。比如说,观察远物的时候可以通过调小\(d\)来放大\(f_o\),观察近物的时候不想改变物镜组和目镜组之间的距离,直接放大\(d\)即可。
+应该做什么?
+A0.薄透镜成像规律
+为了满足近轴光线条件,要进行共轴调节。
+粗调的时候,先把光源,物,透镜靠拢,调节到中心大约在一条平行于导轨的直线上。总之怎么看着舒服就怎么调。
+细调的原理是大象追小象大像追小像。当物与像的距离大于 \(4f\)
+时,凸透镜从物移到像的过程中会成两次清晰的像,一大一小。要做的就是移动像和透镜的位置,使得\(B_1\)追上\(B_2\),也即两个像差不多大,这可以通过像屏上的坐标贴纸判断。此时像在透镜的主光轴上。
不要动平行光管,就是那个挺长的不认识的东西。此处无记录要求。
B1.物像距法测量薄凸透镜焦距
+这很明示了,读个数据套公式就行。
+B2.共轭法测量薄凸透镜焦距
+读个数据套另一个公式:\(f=\frac{b^2-a^2}{4b}\),其中 \(a\) 指两次透镜位置间距离。
+B3.焦距仪法测薄凸透镜焦距
+读六组数据写在表格上,比较麻烦的是算不确定度。这一部分已经在讲义和实验表上详细手写了,照做即可,不再打一遍了。
+C1.主面间距测量
+ +5中的C.2应为B.3。不过我不太懂怎么通过这几个参数算主面间距,好怪。此处留坑。
+C2.修正共轭法系差
+again,算就对了。
+D.用焦距仪测凸透镜的焦距的附加透镜法
+这个讲义上也说的挺清楚的。注意先给玻罗板取某一线对记录下来,第一步和第二步要用一样的线对(废话)。
最后的凹透镜焦距是\(f_2=-\frac{f_1 +y_0}{y''}\),由于是凹透镜的原因,焦距记为负的。
+E.内调焦望远镜的物镜组研究
+第一步,分别对物镜组中的凹凸透镜进行共轴调节,用焦距仪法测此组光具焦距值\(f_o'\)作为物镜焦距。反推得到此时凹凸透镜的距离\(d=\frac{f_2f_1'}{f_o'}+f_1'-f_2\)。其中,由于凹凸透镜的焦距已经在B和D实验中测出,直接取用其值即可。
+第二步,改变凹凸透镜距离使得长焦透镜\(L_1\)距离测微目镜约\(10cm\)。得到第二个测量值。
+第三步,分别假设凹凸透镜的焦距,然后画一个类似下图的图。
+ +这张图的逻辑是:以纵轴表示自变量\(d\),横轴表示四个因变量。其计算公式分别为:
+\[l_{L_1H}=-\frac{f_1'd}{d+f_2-f_1'}\]
+\[l_{L_1H'}=-\frac{d(d-f_1')}{d+f_2-f_1'}\]
+\[F'=l_{L_1H'}+f_o'\]
+\[F=l_{L_1H}-f_o'\]
+其中,凸透镜\(f_1'=0.3m\),凹透镜\(f_2=0.2m\)。所以这个图是不是实验之前就能画出来
本文写作中用到的参考
-
-
\(R^2\) -不能作为拟合程度的度量。\(R^2 = \frac{b_1 ^2 -\sum (X_i - \bar X)^2}{\sum (Y_i - \bar Y)^2}\) -的形式显示了,实际上如果把 \(X\) -的取值变得足够分散,\(R^2\) -的取值想要多大就能有多大。
-不同的散点分布情况可以得到几乎相同的 \(R^2\),一定要画图检查线性模型是不是最合理的。
- -
-不能对于不同的模型比较 \(R^2\),归根结底 \(R^2\) 反映的是模型对于 SST 的解释能力,SST -一旦改变就不能交叉对比。因此上述 transformation 中对于系数 \(\lambda\) 的比选标准是 maximum -likelihood。
-\(R^2\) 不能显示 \(X\) 和 \(Y\) 之间的因果关系,因为 \(Y\sim X\) 和 \(X -\sim Y\) 这两种回归得到的 \(R^2\) 是相等的。
+- 透镜焦距实验-仪器详解
Lecture 7
-从一元线性回归过渡到多元回归的部分,介绍回归方程的矩阵表达。
-矩阵表达
-把 \(n\) 个回归方程的形式改成:
-\[\begin{bmatrix}Y_1 \\ Y_2 \\ ... \\ Y_n -\end{bmatrix} = \begin{bmatrix}1 & X_{1,1} & X_{2,1} &... -& X_{p-1,1} \\ 1 & X_{1,2} & X_{2,2} & ... & -X_{p-1,2} \\ ... & ... & ... &... & ... \\ 1 & -X_{1,n} & X_{2,n} & ... & X_{p-1,n} \end{bmatrix} -\begin{bmatrix}\beta_0 \\ \beta_1 \\ ... \\ \beta_{p-1} \end{bmatrix} + -\begin{bmatrix}\varepsilon_1 \\ \varepsilon_2 \\ ... \\ \varepsilon_n -\end{bmatrix}\]
-\[Y = X \beta + \varepsilon\]
-假设 \(\varepsilon \sim N_n(0, \sigma^2 -I_{n \times n})\),则有 \(Y \sim N_n(X -\beta , \sigma^2 I_{n \times n})\),以下考虑参数矩阵 \(\beta\) 的估计:
-\[b = \hat \beta = (X^TX)^{-1} X^T Y \sim -N_p(\beta , (X^TX)^{-1} \sigma^2)\]
-和 simple linear regression 相同,\(b\) 也有 BLUE 的性质。
-因此有 \(Y\) 的平均响应为 \(\hat Y = X \hat \beta = X(X^TX)^{-1} -X^TY\),其中记 \(H = X(X^TX)^{-1} -X^T\),这就是著名的 hat -matrix,围绕它有很多性质,后面再说;由于残差 \(e = Y - \hat Y = (I - X(X^TX)^{-1} -X^T)Y\),因此 simple linear regression 中对于 \(e\) 的限制在此处相应地修改为 \(e^T \hat Y = Y^T(I - X(X^TX)^{-1} X^T) -(X(X^TX)^{-1} X^T)Y = 0\)。
-相应地,\(\sigma\) 的估计量可以改成 -\(s^2 = \frac{e^Te}{n-p} = -\frac{Y^T(I-H)Y}{n-p}\),这就是 MSE,是 \(\sigma^2\) 的无偏估计;又因为 \(Var(b) = (X^TX)^{-1} \sigma^2\),因此有 -\(\hat Var(b) = (X^TX)^{-1} \hat \sigma^2 = -s^2 (X^TX)^{-1}\) 是 \(Var(b)\) -的估计。
-ANOVA 中的方差和自由度拆分在这里仍然适用:
-\[SST = (Y - \bar Y \mathbb 1_n)^T (Y - -\bar Y \mathbb 1_n), \quad df = n-1\]
-\[SSM = (\hat Y - \bar Y \mathbb -1_n)^T(\hat Y - \bar Y \mathbb 1_n), \quad df = p-1\]
-\[SSE = (Y - \hat Y)^T(Y- \hat Y), \quad -df=n-p\]
-\(F-\)test 的检验统计量是 \(F^* = \frac{MSM}{MSE} \sim^{H_0} -F_{p-1,n-p}\),其中假设是 \(H_0 -:\beta_1 = \beta_2 = ... =\beta_{p-1}=0\);决定系数 \(R^2 = \frac{SSM}{SST}\) -仍然保持不变,显示了线性模型解释方差的能力;adjusted \(R^2\) 定义为 \(1- -\frac{MSE}{MST} = 1- \frac{n-1}{n-p} \frac{SSE}{SST}\),相对于 -\(R^2\) 的优势在于,\(R^2\) -在有任意的变量进入模型时都会增大,但如果新变量的显著性不足会导致 -adjusted \(R^2\) -下降,是一个更有力的参数。
-Hat Matrix
-Hat Matrix 有丰富的性质,在这里列举一些和统计关联比较大的。
-\[Cov(e) = Cov((I-H)Y) = (I-H)^T \sigma^2 -(I-H) = \sigma^2 (I-H)\]
-\[Cov(e_i , e_j) = -\sigma^2 -h_{ij}\]
-\[Var(e_i) = \sigma^2 -(1-h_{ii})\]
-其中 \(h_{ij}\) 是矩阵 \(I -H\) 的分量。
-事实上,第 \(i\) 点的杠杆值就是 -\(h_{ii}\)。可以通过 \(H = H^2\) 这一性质简单地证明出 \(h_{ii} \leq -1\),这也和杠杆值的定义是符合的。
-Multiple Linear Regression
+https://www.bilibili.com/video/BV163411q7NP?spm_id_from=333.999.0.0&vd_source=6ae5c31a80120436d23cf7b7c7ceb3ba
+-
+
- 清华大学2011级耿强学长的大物实验报告《透镜焦距的测定》P181 +
写在最后
+我一向把物理实验当成“可以摆弄仪器的好玩的课”,高中学竞赛的时候就羡慕物化生竞赛的同学可以做实验,我们只能一直待在教室里写题。但是哪怕基物实验
+1 拿了
+A-,对于实验的原理仍然不甚了解。到最后每学期六次做实验三次写报告成为了生活中的调剂,不用太动脑子就能写出一大片东西,好像自己很努力一样。
在 Overleaf 上无意间找到了清华大学近代物理实验报告模板。朱老师的要求和这个还是很不一样。发现也没有用于普通实验的模板,于是改了改我的自用模板,还行。
+GitHub +地址:https://github.com/Chiyuru/THU-Fundamental-Physics-Report
+但是用 LaTeX 写实验报告的人哪个没有自己的模板啊
您又在假装干活了是吗
茶园老师和教务手都太快了,俩小时速通特殊原因选课,下次还来。
+ +Lecture 1
+打开 Introduction to Linear Optimization,看到第一章标题是 linear +programming,差点 PTSD 到当场退课(
+实际上就是线性规划,和(我害怕的那个)programming 没什么关系(
+Standardized Linear +Programming
+Reduce to Standardized +Format
-
-
关于多元回归的系数 \(\beta_1,\beta_2,...,\beta_{p-1}\)(也称为偏回归系数),我们仍然可以按照 -SLR 时的方式解释它们:\(\beta_i\) 是在 -\(X_1,X_2,...,X_{i-1},X_{i+1},...,X_{p-1}\) -不变时,\(X_i\) 变化一个单位导致 \(E(Y)\) 的变化量。
-实际上这就引出了多元回归的一个巨大隐患:并不是所有的变量都完全不相关,一旦 -\(X_1,X_2\) 之间有相关性存在,改变 -\(X_1\) 的时候很难保证 \(X_2\) -不变,多元回归的系数解释性因此变差。
-虽然理论上确实可能存在完全不相关的变量,但是对应的数据也很难不相关。
-\(Var(e_i) = \sigma^2 -(1-h_{ii})\),因此在线性回归中,位于中间(靠近 \(\bar X\))的 \(X\) -拟合能力较弱(杠杆值低,对回归线的影响较弱)但是预测能力较好(\(Var(e_i)\) 较小,\(\hat Y\) -能够变动的范围小)。相反地,位于两端的 \(X\) 拟合能力较强但是预测能力较弱。
-事实上我们是不能轻易预测已有数据范围之外的 \(x\) -的响应的,理由如上所述,此时的预测能力很弱。
+线性优化众所周知应该是线性的(草),最朴素的想法下它可以转换为以下形式:
+\[\text{minimize} \quad c^Tx\]
+\[\text{subject to} \quad \begin{aligned} +& a_i^Tx \geq b_i \quad i \in M_1 \\ & a_i^Tx \leq b_i \quad i +\in M_2 \\ & a_i^Tx = b_i \quad i \in M_3 \\ & x_j \geq 0 \quad +\quad j \in N_1 \\ & x_j \leq 0 \quad \quad j \in N_2 +\end{aligned}\]
+主要是通过取 \(-c\) 把 maximize +问题变为 minimize,以及将不同的 constraints 分类。
+想要改成更为统一、方便处理的形式,可以通过取负将所有的 +constraints 改为 \(a_i ^T x \geq +b_i\),但还是全取等最好。
+\[\text{minimize} \quad c^Tx\]
+\[\text{subject to} \quad \begin{aligned} +& A^Tx =b \\ & x_j \geq 0 \end{aligned}\]
+具体来说只需要再经历以下两步化简:
+-
+
- 将不受限制的 free variable 拆解为 \(x_i = +x_i ^+ - x_i ^-\),则有 \(x_i^+ \geq 0, +x_i ^- \geq 0\); +
- 将 \(\sum_{j=1} ^n a_{ij} x_j \leq +b_i\) 改为 \(\sum_{j=1} ^n a_{ij} x_j + +y_i = b_i, \text{with} \; y_i \geq 0\)
Lecture 8
-Explanatory Data -Analysis——Transformation
-Why look at Y
-一般来说 \(Y\) -的分布我们是不用太在意的,毕竟不是同分布,但其实考虑到做变换的话还是要稍微看一下它的分布。
-如果分布是高度有偏的,做变换把长尾的部分往中央收一收可以得到的效果有:
+注意到 \(x_j \geq 0\) +是对所有变量成立的,我还是第二次看才发现这个问题。
+
Other Optimization Problems
+也会遇到一些其他形式的优化问题,在 cost function +之类的地方有些许改动,处理思想仍然是一样的。
-
-
减小 SST,修正模型的显著性;
-把拖尾方向可能的 outlier -向内收,有可能可以变成正常的数据来使用;另一侧原来数据比较集中,做变换如果可以将分布拉长的话便于观察其中的一些特征;
-实际上 outlier -并不能随意的扔掉,做变换的想法是能够保留就尽量保留。有些时候很多现象就隐藏在出现了 -outlier -这件事情上面,比如臭氧层空洞没有被尽早发现就是因为相关的数据被当成 -outlier 扔掉了。
-方差对于 skewed data 和 outlier 都比较敏感;
-对于 skewed data,均值并不是中心位置很好的显示。
+\[\text{minimize} \quad +\max_{i=1,2,...,m} (c_i^Tx+d_i)\]
+\[\text{subject to} \quad Ax \geq +b\]
+只需要把 cost function 变成 \(m\) 个 +constraints 就可以了:
+\[\text{minimize} \quad z\]
+\[\text{subject to} \begin{aligned} \quad +& Ax \geq b \\ & z \geq c_i^Tx + d_i \quad \text{for} \; i = +1,2,...,m\end{aligned}\]
+\[\text{minimize} \quad \sum_{i=1}^n +c_i | x_i|\]
+\[\text{subject to} \quad Ax \geq +b\]
+这个在日记里吐槽过了,我个人认为更符合直觉的是拆正负部,只是需要保证二者之一是 +\(0\),还是不方便,学实分析学得。也可以改成:
+\[\text{minimize} \quad \sum_{i=1}^n c_i +y_i\]
+\[\text{subject to} \begin{aligned} \quad +& Ax \geq b \\ & x_i \leq y_i, -x_i \leq y_i \quad \text{for} \; +i=1,2,...,n \\ & y_i \geq 0 \quad \quad \quad \ \ \ \qquad +\text{for} \; i =1,2,...,n \end{aligned}\]
但通常来说做变换之前都需要三思:
+都很 trivial,初等变换一下就好了。
+Solutions to LP Problems
+首先 LP problem 有四种可能性,学着学着都要忘了。
-
-
- 做变换后可解释性会有问题,比如 Box-Cox Transformation 中奇怪的 \(\lambda\) -取值会导致可解释性变差,实验数据有的时候需要保留单位,做变换之后会失去意义; -
- 会导致 \(H_0\) 改变; -
- 不一定能够改进正态性,做变换未必有好的效果; -
- 做了变换得到结果之后,变回原始数据很可能破坏无偏性; -
- 破坏了残差的分布。 +
- There exists a unique optimal solution. +
- There exist multiple optimal solutions; in that case, the set of +optimal solutions can be either bounded or unbounded. +
- The optimal cost is \(-\infty\), +and no feasible solution is optimal. +
- The feasible set is empty. (The LP problem is infeasible.)
有一些平替方案:GLM, resampling methods, non-parametric methods
-另外我们一般不会对 \(X\) -做变换,除非做变换之后和 \(Y\) -有非常明确的关系,另一个原因是做变换可能会导致共线性。
-Why log Transformation
-对 right-skewed data 做 log transformation -的好处是显著多于其他类型的变换的:
+Notations
+一些拼不对的单词了属于是。
+突然发现其实可以在笔记里多放点迷言迷语:
+
-
-
- \(\log Y_1 - \log Y_2 = \log (1+ \frac{Y_1 -- Y_2}{Y_2}) \approx \frac{Y_1 - -Y_2}{Y_2}\),可以把绝对误差变为相对误差来讨论; -
- \(\log Y\) -可以让数据的分布更对称,出于计算的考虑 -
- 如果 \(Y\) 全部都是正数,但 \(Y = X \beta + \varepsilon \sim N(X \beta, \sigma^2 -I)\),一个多元正态分布的数据全部是正数的概率非常小,假设不合理。 +
A polyhedron is a set that can be described as +\(\{x \in \mathbb R^n | Ax \geq b \}\), +where \(A\) is an \(m\times n\) matrix and \(b \in \mathbb R^m\).
+A set \(S \subset \mathbb R^n\) +is bounded if there exists a constant \(K\) such that the absolute value of every +component of every element of \(S\) is +less than or equal to \(K\).
+Let \(a\) be a non-zero vector +on \(\mathbb R^n\) and let \(b\) be a scalar, thus:
+-
+
- The set \(\{x \in \mathbb R^n | a^Tx =b +\}\) is called a hyperplane. +
- The set \(\{x \in \mathbb R^n | a^Tx \geq +b \}\) is called a half-space. +
+A set \(S \subset \mathbb R^n\) +is convex if for any \(x , y +\in S\) and any \(\lambda \in +[0,1]\), we have \(\lambda x + +(1-\lambda) y \in S\).
+Let \(x_1 ,x_2,...,x_n\) be +vectors in \(\mathbb R^k\) and let +\(\lambda_1, \lambda_2,...,\lambda_n\) +be non-negative scalars whose sum is unity.
+The convex hull of \(x_1, +x_2,...,x_n\) is the set of all convex combinations of these +vectors, i.e.,
+\[\{\sum_{i=1}^n \lambda_i x_i | +\sum_{i=1}^n \lambda_i =1 \; \text{and} \; \lambda_i \in [0,1] +\}\]
但是最大的问题就是可解释性。对于参数 \(\beta\) 的解释是在 \(X\) 增长一个单位时 \(Y\) -的平均响应的对应变化,在这里我们选择的是报告平均响应变化的百分比,也即 -\(\frac{e^{(X+1)b} - e^{Xb}}{e^{Xb}} = e^b -\times 100 \%\),作为一个补救措施。
-MLR vs SLR
-相比于 simple linear regression,MLR -的变量增多了之后需要考虑的问题也增加了,复杂度也变大了。
-变量选择
-破事很多:
+有一些很 trivial 的结论,看起来既重要又不重要的,希望有脑子就行。
+
-
-
- 单独一个 \(X_i\) -在模型里不显著也不能直接扔掉,它可能是 suppressor -variable,会让别的变量显著 -
- 多个变量的模型显著不能推出单个变量显著 -
- 单变量模型中,变量显著性 \(t\) -检验和模型显著性 \(F\) 检验的 p-value -相等,因为 \(F_{1,n} = t_n ^2\) -
- 其余变量是否需要进入模型,可以先考虑残差对于其余各个变量的回归显著性,先测试最显著的变量进入模型 +
- One writes \(f(x) = O(g(x))\) if +there exists a positive real number \(M\) and a real number \(x_0\) s.t. \(f(x) +\leq Mg(x)\) for any \(x \geq +x_0\). +
- One writes \(f(x) = \Omega (g(x))\) +if there exists a positive real number \(M\) and a real number \(x_0\) s.t. \(f(x) +\geq M g(x)\) for any \(x\geq +x_0\). +
- One writes \(f(x) = \Theta (g(x))\) +if \(f(x)= O(g(x))\) and \(f(x) = \Omega(g(x))\).
有的时候我们认为模型里变量越多越好,有的时候越少越好,这取决于做回归的目的:
+这门课上为什么有人没学过算法不知道这些是什么啊.jpg
+How to Describe Optimal +Solutions
+有三种刻画 corner point 的方法,我们稍后证明它们在 polyhedron +里是等价的。
-
-
- 回归模型是为了预测:变量越多或者说 adjusted \(R^2\) -越大,解释的方差越多,预测水平越好 -
- 回归模型是为了解释:变量越少,explanatory variable 和 response -之间的关系越明确,解释性越好 +
Let \(P\) be a polyhedron. A +vector \(x\in P\) is an extreme +point of \(P\) if we cannot +find two vectors \(y,z \in P\), both +different from \(x\), and a scalar +\(\lambda \in [0,1]\) such that \(x = \lambda y + (1-\lambda) z\).
+Let \(P\) be a polyhedron. A +vector \(x\in P\) is an +vertex of \(P\) if +there exists a vector \(c \in \mathbb +R^n\) such that \(c^T x < c^T +y\) for all \(y \in P\) and +\(y\neq x\). (Also holds for > by +taking \(-c\))
+Let \(P\) be a polyhedron. A +vector \(x\in P\) is an basic +solution of \(P\) if:
+-
+
- All equality constraints holds. +
- Out of the constraints that are active at \(x\), there are \(n\) of them that are linearly +independent.
总之,会随着模型中进入的变量而改变的参数有:
+Moreover, if \(x\) is a basic +solution that satisfies all the constraints, we say it's a basic +feasible solution.
+
所以说只要 constraints 的个数是有限的,那么其中选择 \(n\) 个 linearly independent +的方法是有限的,basic (feasible) solution 的个数就是有限的。
+注意到定义 basic solution 的时候事实上 equality constraints 和 +inequality constraints +的地位不等,然而作为一个线性优化问题是可以在这方面有很多等价形式的,事实上 +basic solution 会受到 polyhedron 定义形式的影响,具体的例子详见 P49 +的平面规划问题。另外,basic feasible solution 不会受到 polyhedron +形式的影响。
+最后是有关这三个定义等价性的定理:
+Let \(P\) be a nonempty polyhedron +and let \(x \in P\), then the following +are equivalent:
-
-
- 回归系数(\(\hat \beta_i\)) -
- standard error -
- 模型显著性 +
- \(x\) is an extreme point. +
- \(x\) is a vertex. +
- \(x\) is a basic feasible +solution. +
证明太长了,这里写不下( 但说实话从 extreme point 推 basic
+feasible solution 还不是很显然,要用一点点分析智慧(
Algebraic Approach to +Optimal Solutions
+说了这么多,也把 basic feasible solution +用三种方式刻画出来了,但是对于具体例子的计算还是借助矩阵工具。
+有一个 applicable procedure:
+For constructing basic solutions for a polyhedron \(P= \{x \in \mathbb R^n | Ax = b , x \geq 0 +\}\), use the three-step procedures below:
+-
+
Choose \(m\) linearly +independent columns \(A_{B(1)}, A_{B(2)}, +\cdots , A_{B(m)}\) and solve
+\[\begin{bmatrix} | & | & \cdots +&| \\ A_{B(1)} & A_{B(2)} & \cdots & A_{B(m)} \\ \cdots +& \cdots &\cdots & \cdots \\ | & | & \cdots & | +\end{bmatrix} \begin{bmatrix} x_{B(1)} \\ x_{B(2)} \\ \cdots \\ +x_{B(m)} \end{bmatrix} = \begin{bmatrix}b_1 \\ b_2 \\ \cdots \\ b_m +\end{bmatrix}\]
+Take \(x_i =0\) for \(i \neq B(1),B(2), \cdots, B(m)\)
+Combine all the components of \(x\) and get the basic solution of the base +\((A_{B(1)}, A_{B(2)}, \cdots , +A_{B(m)})\).
诡异的现象
-有的时候会遇到 Significance & low \(R^2\) -同时出现的情况,也就是某个变量看起来是显著的,但是 \(R^2\) -很低,解释方差的能力并不好。这是正常的现象。
+不同的 base 可以得到不同的 basic solution,也可能会得到相同的。
+在解 basic solution 的时候本质上只用到了 \(m\) 个 constraint equalities 作为 +base,以及 \(n-m\) 个 non-negative +constraints,实际上 \(x\) 可能不仅在这 +\(n\) 个 constraints 处 +active,如果有多于 \(n\) 个 constraints +在 \(x\) 处 active 则称它是一个 +degenerate basic solution。
+很明显的一点是在 polyhedron 里如果一个 basic solution 有多于 \(n-m\) 个分量是 \(0\),那么它一定 +degenerate。由矩阵解的唯一性,这也是 degenerate basic solution +的唯一情形。
+Existence of Vertex
+非常口胡地说,要有 basic feasible solution +至少区域的边界上要先有个角吧(比划
-
-
回到 \(R^2\) 的定义和 F -检验的本质可以发现,\(R^2 = \frac{SSR}{SST}, -F^* = \frac{MSR}{MSE} = \frac{R^2}{1-R^2} \frac{n-p}{p-1}\),如果 -\(n\) 非常大,即使 \(R^2\) 很小也和 \(F^*\) 很大之间并不矛盾。
-\(R^2\) 的分母 \(SST\) -实际上表征了数据的分散程度,数据非常分散的时候是可能导致 \(R^2\) -减小的。但是数据分散和存在线性并不矛盾,图中的两个线性关系当然都显著,但是 -\(R^2\) 有巨大的差距。
- +
+- A polyhedron \(P \subset \Re^n\) +\(\textbf{contains a line}\) if there +exists a vector \(x \in P\) and a +nonzero vector \(d \in \Re^n\) such +that \(x + \lambda d \in P\) holds for +all scalar \(\lambda\).
Inference
+也就是说范围里面不能有直线才能有 vertex。
-
-
多重线性回归的推断里面也有一个著名定理:\(Y \sim N_n(X \beta , \sigma^2 I)\),于是有 -\(b \sim N_p(\beta , \sigma^2 -(X^TX)^{-1})\),以及:
+Suppose that the polyhedron \(P = \{x +\in \Re^n \mid \textbf{a}_i^T x \geqslant b_i , i=1,2, \cdots, m +\}\) is nonempty. Then the following is equivalent:
-
-
- \(\frac{e^Te}{\sigma^2} = -\frac{SSE}{\sigma^2} \sim \chi^2_{n-p}\) -
- \(b\) 和 \(SSE\) 相互独立 +
The polyhedron \(P\) has at +least one extreme point.
+The polyhedron does not contain a line.
+There exist \(n\) vectors out of +the family \(\textbf{a}_1, \textbf{a}_2, +\cdots, \textbf{a}_m\), which are linearly independent.
+
由此得到很多推断方法。
-关于 \(b_k\) 的推断和 -CI,主要关注 \(b_k \sim N(\beta_k, -\sigma^2((X^TX)^{-1})_{k,k})\),希望检验 \(H_0 : \beta_k =0; H_1 : \beta_k \neq -0\)。
-检验统计量是 \(t^* = \frac{b_k}{s(b_k)} = -\frac{b_k}{\sqrt{MSE ((X^TX)^{-1})_{k,k}}}\sim ^{H_0} -t_{n-p}\),由此可以检查单个变量的显著性。注意此处所谓的显著性,指的是第 -\(k\) -个变量最后一个进入模型时的显著性,无论它在 R table 里排列在哪里。和 -general linear test 的结果一致。如果这一检验体现出来变量 \(X_k\) -不显著,绝大多数情况下是可以不保留的。
-\(100(1-\alpha) \%\) 置信区间是 -\((b_k \pm t_{1-\alpha /2,n-p} -s(b_k))\),注意 \(s(b_k)\) -的含义在上述已经提到。
关于 \(E(Y_h)\) 的推断和 -CI,考虑 \(\mu_h = E(Y_h) = X_{h} -\beta\)。
-其估计量是 \(\hat \mu_h = X_h b = X_h -(X^TX)^{-1} X^TY \sim N(\mu_h , \sigma^2 X_h (X^TX)^{-1} -X_h^T)\),于是 \(s^2(\hat \mu_h) = MSE -\cdot X_h (X^TX)^{-1} X_h^T\)。因此 \(\mu_h\) 的 \(100 -(1-\alpha) \%\) 置信区间是 \((\hat -\mu_h \pm t_{1-\alpha /2 , n-p} s(\hat \mu_h))\)
-考虑 \(Y_h = X_h \beta + -\varepsilon\),有 \(\hat Y_h - Y_h \sim -N(0,\sigma^2 + \sigma^2 X_h (X^TX)^{-1} X_h^T)\), \(s^2(\hat Y_h - Y_h) = MSE \cdot (1+X_h (X^TX)^{-1} -X_h ^T)\),因此 \(Y_h\) 的 \(100 (1-\alpha) \%\) 置信区间是 \((\hat Y_h \pm t_{\alpha /2 , n-p} s(\hat Y_h - -Y_h))\)
一个更重要的定理是关于 bounded polyhedron 和 standardized problem +的:
+-
+
- Every nonempty bounded polyhedron and every nonempty polyhedron in +standard form has at least one basic feasible solution.
Lecture 9
-Extra Sum of Squares
-想法很简单,定义就是把一个新的变量加入模型后可以额外解释的方差,例如模型中本来存在 -\(X_2\) 时,加入 \(X_1\) 后可以额外解释的方差是 \(SSR(X_1 | X_2) = SSR(X_1 ,X_2) - SSR(X_2) = -SSE(X_2) - SSE(X_1,X_2)\)。
-在多重回归中分解 sum of squares 的方式最常见的是 Type I method:
-\(SSR(X_1,X_2,X_3,X_4) = SSR(X_1) + SSR(X_2 -|X_1) + SSR(X_3 |X_1,X_2)+SSR(X_4 |X_1,X_2,X_3)\)
-也就是所谓的 sequential sum of squares 的方法,在
-anova() 中的列表就是这样的分解方式,分掉了所有的 SSR。
SAS 中的 sum of square 分解有三种模式,以考虑 A,B,AB 三种因子(2-way -ANOVA)的情况如下排列:
-
可以看到 type I 就是按照 sequential -的模式进入模型,认为不同的变量有重要性的排序,先进入理论上来说最有必要进入模型的 -A,再进入 B,最后进入 AB,分别计算 extra sum of squares;type II -忽略了交互效应 AB,对于 A 和 B 的单变量分解是与 type I 相同的;type III -和之前提到的 t 检验类似,每个模型的 extra sum of square -分解都是考虑它最后一个进入模型时带来的方差解释能力,但这里实际上存在一个问题,按照 -hierarchy 的原则来说如果主效应 A,B -之一不显著/没有进入模型,是不能允许交互项 AB 进入模型的。
-General Linear Test
-Test Reduced Model
-一种检验 full model 和 reduced model -之间关系的检验方法,例如对于存在五个变量 \(X_1,X_2,X_3,X_4,X_5\) 的 full model -和存在三个变量 \(X_1,X_2,X_3\) 的 -reduced model 来说,假设 \(H_0: \beta_4 = -\beta_5 = 0; H_1:\beta_4,\beta_5\) 中至少有一个不是 \(0\)。
-检验统计量是 \(F^* = \frac{(SSE(R) - -SSE(F))/(df_E(R) - df_E(F)}{SSE(F)/df_E(F)}\sim ^{H_0} -F_{df_E(R)-df_E(F),df_E(F)}\),注意第一个自由度实际上是两个模型相差的变量个数,分母中的 -\(SSE(R) - SSE(F) = SSR(F) - SSE(R) = -SSR(X_4,X_5|X_1,X_2,X_3)\) 实际上是 extra sum of squares。
-事实上我们是 prefer 接受 \(H_0\) -的,就相当于可以使用变量更少的模型,解释性更强;但是有的时候检验做出来接受 -\(H_0\),也需要考虑一下是不是数据量太小导致 -power 不够,如果数据量够大就可以放心地使用 reduced model 了。
-Test Linear Hypothesis
-实际上只要是关于回归系数的线性检验就都可以用 general linear test -来进行,比如 \(H_0 : \beta_1 + 3 \beta_2 -=12\),等等。
-\(H_0 : C \beta =t\),\(C\) 是有关 \(\beta\) 的约束条件的矩阵,检验统计量是 -\(F = \frac{(C \hat \beta - t)^T (C(X^TX)^{-1} -C^T)^{-1} (C \hat \beta - t)}{qs^2} \sim^{H_0} F_{q,n-p}\),其中 -\(q=rank(C)\)。
-偏决定系数 & 偏相关系数
-\(R^2_{Yk|1,2,...,k-1,k+1,...,q} = -\frac{SSR(X_k | -X_1,..,X_{k-1},X_{k+1},...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)} = -1- -\frac{SSE(X_1,X_2,...,X_q)}{SSE(X_1,...,X_{k-1},X_{k+1},...,X_q)}\)
-本质上说的是,模型中新进入的 \(X_k\) -带来的 extra sum of squares 解释了 SSE -的比例,也即解释了没有由原来的变量解释掉的方差比率。
-实际上另一种表现形式可以是,我们认为 \(R^2_{Yk|1,2,...,k-1,k+1,...,q} = -\frac{SSE(R)-SSE(F)}{SSE(R)} = \frac{SSR(X_k |X_{-k})}{SST(Y|X_{-k})} = -R^2(Y|X_{-k}, X_k|X_{-k})\)
-也就是说,实际上是对于 \(Y|X_{-k} \sim -X_k|X_{-k}\) 这两组残差做线性回归,得到的决定系数正好是 \(X_k\) 的偏决定系数。
-实际上偏相关系数 \(r_{k|1,2,...,k-1,k+1,...,q} = sign(\hat -\beta_k)\sqrt{R^2_{Yk|1,2,...,k-1,k+1,...,q}}\) -表征的就是这两组残差之间的相关系数,如果有 \(0 -< r_{3|12} < r_{12}\) 就说明变量 \(X_3\) 可以部分解释 \(X_1,X_2\) 之间的相关性。
-标准回归
-Motivation
+这是因为前者显然不含直线,后者定义在 \(\{x +\geq 0\}\) 的区域里也不含直线。注意到所有的 LP problem +其实都可以转化为后者的形式,所以说实际上都是有 basic feasible solution +的。这话比较模糊,意思是对于新的 standardized problem 一定会有 basic +feasible solution,然而把这个解限制到原来问题的维度中得到的解未必会是 +basic feasible solution。
+不过没有关系,我们会在后面看到实际上这已经够用了,因为目的不是解 +basic feasible solution,而是找出 optimal cost。在 standardized problem +下的 optimal cost 可以用 basic feasible solution 得到,而它和原问题的 +optimal cost 一致。
+Why is Vertex Important?
+说了这么多,为啥要解 basic feasible solution,对做 optimal cost +有什么好处吗?事实上,optimal cost 要么 unbounded,要么是在 basic +feasible solution 处取到,所以说只要 optimal cost 不是 \(-\infty\) 就就把所有的 basic feasible +solution 找出来溜一遍就好了。
+严肃一点用定理来说明的话是以下几条,对应书上 Section 2.6:
-
-
- 如果 \(X_1,X_2\) -之间的尺度差距过大会导致 \(\beta_1,\beta_2\) -的尺度也有差距,无法直接比较,也可能会影响变量显著性。 -
- 会导致 designed matrix 接近不满秩,计算逆矩阵出现问题。 +
- Suppose the linear programming problem \(P\) has at least one extreme point, and +there exists at least one optimal solution. Then there exist one optimal +solution and is the extreme point of \(P\). +
- Suppose the linear programming problem \(P\) has at least one extreme point. Then, +either the optimal cost is \(-\infty\) +or there exist one extreme point, and it's also one of the optimal +solution.
Method——Correlation -Transformation
-考虑 \(s_Y = \sqrt{\frac{\sum_i (Y_i - \bar -Y)^2}{n-1}}, s_{X_k} = \sqrt{\frac{\sum_i (X_{ik}-\bar -X_k)^2}{n-1}}\),对变量和响应值分别做标准化:
-\[\begin{aligned} \frac{1}{\sqrt{n-1}} -\frac{Y_i - \bar Y}{s_Y}& = \frac{1}{\sqrt{n-1}} \frac{(\beta_0 + -\beta_1 X_{i1} + \beta_2 X_{i2} + \varepsilon_i)-(\beta_0 + \beta_1 \bar -X_1 + \beta_2 \bar X_2 + \bar -\varepsilon)}{s_Y}\\&=\frac{1}{\sqrt{n-1}}\frac{\beta_1(X_{i1} - -\bar X_1) + \beta_2 (X_{i2}-\bar X_2) + (\varepsilon_i - \bar -\varepsilon)}{s_Y}\\&=\frac{\beta_1 s_{X1}}{s_Y} \frac{(X_{i1}-\bar -X_1)}{\sqrt{n-1} s_{X1}} + \frac{\beta_2 s_{X2}}{s_Y} \frac{(X_{i2}-\bar -X_2)}{\sqrt{n-1} s_{X2}} + \frac{\varepsilon_i - \bar -\varepsilon}{\sqrt{n-1}s_Y} \end{aligned}\]
-\[Y_i^* = 0 + \beta_1^* X_{i1}^* + -\beta_2^* X_{i2}^* + ... +\beta_{p-1}^* X_{i,p-1}^* + -\varepsilon_i\]
-其中 \(\beta_k ^* = \frac{s_{X_k}}{S_Y} -\beta_k\) 是新的回归系数。
+注意到任意一个 LP problem 都可以转化为标准形式并保持 cost +不变,每个标准形式都有 extreme point,所以说上一条定理实际上是对任意 LP +problem 成立的。
+另外,第一个定理并不能推出第二个,因为并非 optimal cost 不是 \(-\infty\) 就能推出有 optimal +solution,比如说在 \(x >0\) 上找 +\(\frac 1x\) 的最小值,既不是 \(-\infty\) 也不存在 optimal solution。zjz 的 +PPT 还有 yy 讲课的时候都说 +trivial,实际上是不能这么推的。但可以通过沿特定方向移动到下一个 basic +feasible solution 的方法证明这种情况在 LP problem +里不会出现,这也就是第二个定理的证明。
+Lecture 2
+这节课和 Ruizhe Shi 合作的 scribing 见 +https://www.overleaf.com/read/hwpxppmfnjbk。
+说实话我觉得 scribing 是写给队友和老师看的罢了,所以当然还要有个
+从里面复制然后暴论的 废话版本写给自己看。
Simplex Method
+简单来说 simplex method 是从一个 basic feasible solution +出发,用最简单的计算方法寻找下一个 basic feasible solution +的方法。从几何的角度来说从多边形的一个顶点出发到另一个顶点,当然是沿着中间连接的边走过去最方便,所以也就是在寻找 +adjacent basic feasible solution。
+++Recap: Two basic solutions are said adjacent iff +there are \(n-1\) linearly independent +constraints that are active at both of them. We also say that two bases +are adjacent if they share all but one column.
+
也就是说,修改 solution vector 中的一对 component 即可。
+Find the Initial Solution
+想开始一个循环的算法得先有个 initial solution +才能开始罢(,为了计算复杂性不如选个最简单的。
+在 LP 问题的标准化中经常会有加入一些 artificial variable +来把不等号改成等号的行为,比如说 \(a^T x \geq +b\) 完全可以写成 \(a_1 x_1 + \cdots + +a_n x_n + y_1 = b\),里面这个 \(y_1\) 就是一个 artificial +variable。它的系数是 \(1\),放在整个矩阵里其实可以作为最简单的 +linearly independent column 选出来计算 basic feasible solution。
+即使是在标准形式下也可以用这个思路来找一个简单的 initial +solution,考虑:
+\[\begin{aligned} + \text{minimize} \quad & \textbf{c}^T x \\ + \text{subject to} \quad & \textbf{Ax} = \textbf{b} \\ + & \textbf{x} \geqslant \textbf{0} +\end{aligned}\]
+By multiplying some rows of \(\textbf{A}\) by \(-1\), we can assume without loss of +generality that \(\textbf{b} \geqslant +\textbf{0}\). We now introduce a vector of artificial variables +\(\textbf{y}\) and consider the +auxiliary problem:
+\[\begin{aligned} + \text{minimize} \quad & y_1 + y_2 + \cdots + y_m \\ + \text{subject to} \quad & \textbf{Ax} + \textbf{y} = b \\ + & \textbf{x} \geqslant 0 \\ + & \textbf{y} \geqslant 0 +\end{aligned}\]
+这个 auxiliary problem 的初始化很容易,让 \(\textbf {x} =0\) 且 \(\textbf {y} = b\) 就是 basic feasible +solution,对应 basis 为 \(\textbf {I}_{m +\times m}\)。 某种程度上 auxiliary problem 等同于 original +problem。首先,如果 \(\textbf {x}\) 是 +original problem 的 basic feasible solution,则将 \(\textbf {x}\) 和 \(\textbf {y} =0\) 结合起来会产生 auxiliary +problem 的 optimal solution。另一方面,如果能获得 auxiliary problem 的 +optimal solution,则根据约束 \(\textbf {y} +\geqslant 0\),它必须满足 \(\textbf +{y}=0\)。于是 \(\textbf {x}\) 是 +original problem 的 basic feasible solution。
+另外如果auxiliary problem 的 optimal cost 不是零,那么 original +problem 是 infeasible 的。所以我们可以直接考虑下面的 auxiliary problem +来解 original problem 的 optimal solution,用它简单形式下的 initial +solution 开始 simplex method。
+Develop Feasible Direction
+所谓的 feasible direction 其实就是我们希望“沿着边来移动 solution +point”的那个边。当然移动的时候未必会沿着边来移动,可能就直接按照两个顶点的连线移动,但是怎么说呢,就是个形象点的说法(
-
-
注意这个方法是有一些问题的,比如说破坏了残差的假设,以及强迫过原点。
-标准回归的系数估计和 ANOVA table 都发生了改变,这是因为 SST -变成了 \(1\),ANOVA table -自然会变化。但是偏决定系数都是由偏相关系数直接决定的,所以没有变化。
-类似地,如果只对 \(X\) -做变换而不改变 \(Y\),会有系数发生改变,但是 ANOVA table -和偏决定系数都不变。
+- Let \(\textbf{x}\) be an element of +a polyhedron \(P\). A vector \(\textbf{d} \in \Re^n\) is said to be a +feasible direction at \(x\), if there exists a positive scalar +\(\theta\) for which \(\textbf{x}+\theta \textbf{d} \in P\).
Suppressor Variable
-如果有 \(SSR(X_2 |X_1) > -SSR(X_2)\),也就是 \(X_1\) -在模型里的时候会让 \(X_2\) 更显著,则称 -\(X_1\) 是一个 suppressor -variable。原理是 \(X_1\) -可以帮助解释一部分 \(X_2\) -中的噪音,使得 \(X_2\) 更显著。
-\(X_1\) -本身未必是显著的,这也就说明了如果单一变量不显著的话也不能贸然扔掉,它可能会是一个抑制变量。更极端的情况下,假设 -\(X_1\) 和 \(Y\) 完全无关,有 \(X_2\) 在模型中不会改变 \(X_1\) 的系数估计,但是会导致 \(R^2_{Y2|1} \neq R^2_{Y2}\)。
-一般来说脑补一下这种类似韦恩图的直观解释就好。
-
Lecture 10
-Multicollinearity
-关于多重共线性的一些研究,先考虑一些极端情况,然后观察多重共线性会导致什么后果。
-Zero Collinearity
-在几个解释变量完全没有共线性的情况称为正交设计,也就是说设计矩阵的各列之间是正交的。这是一个很好的情况,互相之间并不会干扰,有 -\(X^TX = diag(||X_0||^2 , -||X_1||^2,...,||X_{p-1}||^2)\),且有 \(b_j = \frac{X_j ^TY}{||X_j||^2}\),\(Var(b_j) = -\frac{\sigma^2}{||X_j||^2}\)。
-结果就是无论进多少变量都不会影响单个 \(b_j\) 的估计,但是会影响到 \(MSE\) 导致 p-value 的变化。与此同时 type I, -II, III ANOVA table 的结果是一样的,这是因为 extra sum of squares -就是单个变量能解释的方差。
-
Linearly Dependent
-一个比较极端的例子是完全线性相关,比如变量之间有 \(c_1 X_1 + ... +c_{p-1}X_{p-1}=c\) -这样的关系,会导致设计阵不满秩无法求逆。从数学上来说只要去掉其中一个变量即可,但是在统计上未必合适的。
-Multicollinearity
-正常一些的情况就是普通的多重共线性,从回归结果来看多重共线性的一大特征就是模型整体显著,但是没有一个变量是显著的。回归结果的显著性是代表每个变量最后一个进入模型时的显著性,也就是说明每个变量几乎都是可以被前面进入模型的变量表示出来的。多重共线性有以下危害:
+在上一次得到的 basic feasible solution 里假设 basis \(B\) 的下标是 \(B(1),B(2),\cdots, B(m)\),记 \(I = \{B(1) , B(2), \cdots , +B(m)\}\)。本质上每一次希望的移动就是在 \(I^c\) 里面挑选一个新的下标 \(j\) 然后将 \(x_j\) 变为 \(1\),为了保证 basic feasible solution 的 +\(n\) 个 active constraints +的条件,还需要再在 \(I\) +里面挑选一个下标 \(B(i)\) 然后将 \(x_{B(i)}\) 变为 \(0\)。
+从 applicable 的角度来说,具体的计算步骤是:
-
-
- \(X_1,X_2\) -之间较大的多重共线性会导致对于单个变量的 \(Var(b_i)\) -增大,但是仍然是无偏估计。这也就说明了,出现多重共线性时 \(b_i\) 的方差很大,会导致 \(b_i\) -的估计值并不准确。举个例子来说,有的时候理论上 \(X_i\) 和 \(Y\) -之间是正相关,但是得到的系数估计是负的,就有可能是因为 \(Var(b_i)\) -过大导致一组数据得到的结果距离“真实值”有很大的偏差,甚至从正相关变成了负相关。 -
- Type I SS 和 Type II SS -的结果可能是不同的,因为变量之间对方差解释有竞争,也可能有 suppressor -variable,进入模型的顺序在此时变得重要了起来,二者不同的结果可能导致判断上的问题。 -
- 两部分解释变量解释了同一部分的方差,导致模型解释能力下降。模型整体显著但每一个变量都不显著,很有可能是过拟合了。 -
- 从数学上来说 \(X^TX\) -接近退化,求逆时导致数值误差增大。 +
- 选择一个 \(I^c\) 中的 \(j\) 作为新的下标,计算 \(B^{-1}A_j\) 作为 \(d_{B(1)}, d_{B(2)}, \cdots, d_{B(m)}\) +的值,记 \(d_j=1\),其余的分量保持 +\(0\)。 +
- 寻找一个合适的 \(\theta\) 使得 +\(x +\theta d\) 是一个最合适的 basic +feasible solution

有一些弥补的方案,但是要视建立模型的目的而定:
+实际上如果确定了 \(j\),这里的 \(\theta\) +的选择范围就是有限的了,只有对于小于 \(0\) 的 \(d_{B(i)}\) 才能作为移动到 \(0\) 的方向。
+\[\begin{aligned} + \theta =\left(-\frac{x_{B(i)}}{d_{B(i)}}\right), \; +\{i=1,\ldots,m,d_{B(i)}<0\} + \end{aligned}\]
+然而其实连 \(j\) +都没确定呢,一开始是随便取的,嘿嘿。所以下面要考虑怎么选择 \(j\),其后怎么选择 \(\theta\),或者两个其实也可以一起选就是了,但是计算复杂度可能又会提高。
+Choice of Adjacent +Basic Feasible Solution
+Feasible direction +确认了之后就要考虑到底按照哪个下标来移动,最朴素的想法是突然想起来这是个优化问题(,然后按照单次移动的 +cost 相关的问题来考虑。
-
-
如果单纯是为了预测,其实增大模型的 sample size -是可以解决问题的
-如果是为了解释性,需要做很多其他的努力,比如移除一些变量,对变量做变换,PCA -方法等等。
-仍然存在很多问题,比如移除变量时万一移除了某个重要的类别型变量,可能会导致 -Simpson's Paradox 出现,移除变量也会导致系数估计的方差减小,可能减小 MSE -但是会导致 bias 增大,但如果移除了一个重要的解释变量会导致它进入 error -term,进而导致 \(\sigma^2\) -的估计增大,需要 trade-off;
-做变换不一定能成功降低共线性还会造成解释上的困难,PCA -的解释性更差,等等。
+Let \(\textbf{x}\) be a basic +solution, let \(\textbf{B}\) be an +associated basis matrix, and let \(\textbf{c}_B\) be the vector of costs of +the basic variables. For each \(j\), we +define the reduced cost \(\bar c_j\) of the variables \(x_j\) according to the formula
+\[\begin{aligned} + \bar c_j=c_j-\textbf{c}_B \textbf{B}^{-1}\textbf{A}_j. + \end{aligned}\]
Multicollinearity 可能有以下来源:
+这样定义了一个关于各个 \(j\) +对应的单位 reduced cost,也就是 \(x_j\) +每增加 \(1\) 会导致 cost +减少的量,当然是减得越多越好。另外 \(\bar +c_j\) 在 \(j\) 取 \(I\) 中的下标时等于 \(0\),这其实很能 make sense,毕竟不能再按照 +\(B(i)\) 来作为加入 basis +的下标了,会导致的 cost 变化也只能是 \(0\)。所以 reduced cost 是一个 general +definition,可以再用它们来定义一个向量 \(\bar +c\),其各个分量就是 reduced cost。
+寻找下一个 basic feasible solution +的最好的选择就是找一个绝对值最大(实际上最小)的 \(\bar c_j\),沿着这个方向移动最大的一个 +\(\theta^*>0\),然后 cost 就减少了 +\(\theta^* \bar c_j\)。这样选择 \(\bar c_j\) 和对应的下标 \(j\) 从直觉上来说可以经历更少的步数到达 +optimal solution,降低算法复杂度。
+另外,也可以从某个点处的 reduced cost vector \(\bar c\) +看出一些东西,主要有关这个点有没有达到 optimal cost,等等。
-
-
- 抽样时 \(X\) 的区域太小 -
- 理论上两个变量就是相关的却一起放进了模型,比如家庭收入和房屋面积 -
- 使用多项式回归 -
- \(p>n\) -
- 某些变量彼此是受同一隐含的因素影响的,比如一些 time series data -
Polynomial Regression
-多项式回归可能会导致很强的共线性,比如一个只取 \(0\) 和 \(1\) 的类别型变量取 \(x\) 和 \(x^2\)进入模型就完全共线。
-有一个弥补的方案就是使用 centered -data,为每一个变量减去一个均值,导致数值有正有负,再做非负的平方项就得到共线性不那么强的两个解释变量。实际上再进一步对数据做尺度上的标准化也可以,但是对系数估计没有任何影响。
-对数据做中心化不会导致高阶项的系数改变,但有可能会导致低阶项的系数和 -extra sum of squares -变化。另外如果显著性不随之变化的话也有可能是出现了正交设计的情况,需要按照结果分析。
-交互项
-模型中存在交互项的本质就是 \(X_i\) -对于 \(Y\) 的效应和回归系数估计都会受到 -\(X_j\) 的影响。
+-
-
如果 \(X_2\) 是连续型变量而 -\(X_1\) -是类别型变量,回归模型中包含二者的交互项,例如:
-\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 -+ \beta_3 X_1X_2+\varepsilon\]
-这就说明对于 group 1,也就是 \(X_1 = -0\) 时模型是 \(Y = \beta_0+ \beta_2 X_2 -+ \varepsilon\),对于 group 2 也就是 \(X_1 = 1\) 时模型是 \(Y = (\beta_0 + \beta_1 )+(\beta_2 + \beta_3)X_2 + -\varepsilon\)。希望检验的问题是 \(\beta_1,\beta_3\) 是否为 \(0\) -来查看两组回归线的斜率、截距之间是否存在差异。
-如果二者都是连续型变量也是类似的情况,相比之下类别型变量和连续型变量的交互效应有显著的分组意义。
-
Lecture 11
-模型选择方法
-一些没那么数学的
+-
-
- 喜闻乐见的穷举,可惜只能处理不超过 \(n=40\) 个变量的情况 -
- stepwise greedy method,不喜闻乐见的要写代码,理解 idea -就好(心虚 +
- \(B^{-1}b \geq 0\) +
- \(\bar c^T = c^T - c^T _B B^{-1} A \geq +0^T\) +
一些准则
-假设可供选择的 explanatory variable 有 \(P-1\) 个,从中选择 \(p-1\) 个并进行判断。
+Termination
+最后两个问题是:算法会不会进入循环?会不会找不到 optimal solution +就停下来?答案是都不会。
+因为只有有限个 basic feasible +solution,所以只要不经过同一个点两遍,就可以遍历所有的可能性。不经过同一个点两遍这件事通过 +lexicographic pivoting rule +来决定,保证从字典序上来说所有的解是递增的,就不会出现循环。
+另外既然 optimal solution 要么是 \(-\infty\) 要么是在某个 basic feasible +solution 处取到,那么既然遍历(注意并不是真正的遍历,并不会走到 cost +比较大的一些 basic feasible solution,比如说比 initial solution 的 cost +更大的解就不可能取到,这能提高效率且不遗漏)了 basic feasible solution +就一定能找到 optimal solution,所以说 simplex method +是个非常完满的算法。
+Summary
+最后总结一下 simplex method 的步骤。
-
-
观察 \(R^2\) 和 adjusted \(R^2\),取后者较大的模型
-观察 mallow's \(C_p\),\(\Gamma_p = \frac{E(SSE(p))}{\sigma^2} - (n-2p) -\geq p\),实际上在操作中只能取 \(\hat -\Gamma_p = \frac{SSE(p)}{MSE(P)}-(n-2p)\)。
+- 通过解 auxiliary problem 找到一个本质 trivial 的 initial +solution;它可能不存在,此时原问题 infeasible; +
- 通过做 \(\bar c^T = c^T - c^T_B
+B^{-1}A\) 得到在此处的 reduced cost vector,
-
-
- 如果 \(\hat \Gamma_p \gg p\) -说明存在显著的误差,可能遗漏了重要的变量没有进入模型 -
- 如果 \(\hat \Gamma_p \ll p\) -说明过拟合了,导致 \(SSE(p) \ll -MSE(P)\) -
- 如果 \(\hat \Gamma_p \approx p\) -说明是 unbiased,取接近于 \(p\) 的 -mallow's \(C_p\) -中最小的一个对应的模型。 -
实际上理论的形式对于 \(P\) 有 \(\Gamma_P =P\)。
- \(AIC = n \log (\frac{SSE(p)}{n}) + -2p\),\(BIC = n \log (\frac{SSE(p)}{n}) -+ (\log n)p\),二者都是最小值对应的模型最合适。
-注意 BIC 实际上相比 AIC -加了一个更大的惩罚在模型的变量数上,更注重解释性;一般来说有 \(BIC>AIC\)。
-Predicted Residual Error Sum of Squares:\(PRESS(p) = \sum_{i=1}^n (Y_i - \hat -Y_{i(-i)})^2\),实际上有 \(Y_i - \hat -Y_{i(-i)} = \frac{e_i}{1-h_{ii}}\)。
-取使得 \(PRESS(p)\) -最小的模型。用来观察过拟合与否。
-Prediction \(R_p^2\):\(R_p^2 = -1-\frac{PRESS}{SST}\),如果模型里噪音过大,则有 \(PRESS >SST\),此时 \(R_p^2<0\) 也是可以取负值的。如果有 \(R_p^2 \ll R^2\) -则也可能是过拟合了,即使有些独立变量是显著的。
+- 如果 \(\bar c \geq +0\),说明目前的解就是 optimal solution +
- 否则找出绝对值最大的 \(\bar +c_j\),确定下标 \(j\),再找出对应的 feasible direction 是 +\(d_B = -B^{-1}A, d_j=1\). +
-
+
- 如果 \(\theta\) unbounded,则 +optimal cost 也是 \(-\infty\); +
- 否则可以更新 optimal cost 和对应的 basic feasible +solution,然后重复以上步骤直到找到 optimal solution。 +
我们选择模型一般会考虑 adjusted \(R^2\),AIC 或者 mallow's \(C_p\)。
-模型诊断
-Partial Regression Plots
-每个 \(X_i\) 都可以做出一张 partial -regression plot,也即所谓的 AV-plot,实际上就是对 \(Y|X_{-i} \sim X_i|X_{-i}\) -这两部分残差互相做回归得到的图,展示了完整模型中 \(Y \sim X_i\) -之间的边际关系。也可以用来检测非线性关系、异方差问题和 outliers。
-Studentized Residuals
-补充在 Lecture 6 里了。
-Assessing Outliers
-有以下指标可以考虑:
+Introduction to Duality
+把 LP problem 变成它的 dual problem 的 motivation +其实来自拉格朗日乘子法,本质上是对 cost function 的形式 penalize +一个条件,如果不满足条件的话 cost function +就会变大,从而找到最小值。
+想必这个过程推起来很简单吧我就不写了
简单来说,primal problem 和 dual problem 的对应关系是这样的:
+\[\begin{aligned} \text{minimize} +\quad & c^T x \\ \text{subject to} \quad & a_i ^T x \geq b +\quad i \in M_1 \\ & a_i ^T x \leq b_i \quad i \in M_2 \\ & +a_i ^T x = b_i \quad i \in M_3 \\ & x_j \geq 0 \quad j \in +N_1 \\ & x_j \leq 0 \quad j \in N_2 \\ & x_j \; \text{free} +\quad j \in N_3 \end{aligned} \quad \quad \quad \begin{aligned} +\text{maximize} \quad & p^T b \\ \text{subject to} \quad & +p_i \geq 0 \quad i \in M_1 \\ & p_i \leq 0 \quad i \in M_2 \\ +& p_i \; \text{free} \quad i \in M_3 \\ & p^TA_j \leq c_j +\quad j \in N_1 \\ & p^TA_j \geq c_j \quad j \in N_2 \\ & +p^TA_j = c_j \quad j \in N_3 \end{aligned}\]
+可以看出来 dual 的 dual 就是 primal。
+除此之外还需要一些定理来说明 dual 和 primal 的 cost 之间的关系。
+Duality Theorems
-
-
Difference caused to fitted values:\((DFFIT)_i = \hat Y_i - \hat Y_{i(-i)} = -\frac{h_{ii}}{1-h_{ii}} e_i\)
-Studentized DFFIT:\((DFFITS)_i = -\frac{\hat Y_i - \hat Y_{i(-i)}}{\sqrt{MSE_{-i} h_{ii}}} = t_i -\sqrt{\frac{h_{ii}}{1-h_{ii}}}\)。
-对于不太大的数据量,如果 \(|DFFITS|>1\) -则认为是强影响力点,大数据量时认为 \(|DFFITS|>2\frac{\sqrt p}{\sqrt n}\) -是强影响力点。
-Cook's Distance:\(D_i = \frac{e_i^2}{p -\cdot MSE} \frac{h_{ii}}{(1-h_{ii})^2}\),在 R -中认为某个点有强影响力的 threshold 是 \(0.5\),事实上如果一个点的 Cook's distance -分布距离其他点较远,就可以认为是强影响力点了。
-Difference in Beta Estimates:\((DFBETAS)_{k(-i)} = \frac{b_k - -b_{k(-i)}}{\sqrt{MSE_{(-i)} c_{kk}}}\),其中 \(c_{kk}\) 是 \((X^TX)^{-1}\) 的第 \(k \times k\) 个分量。
-对于大的数据量,如果 \(|DFFITS|>1\) -则认为是对于回归系数估计值的强影响力点,不太大的数据量时认为 \(|DFFITS|>\frac{2}{\sqrt n}\) -是对于回归系数估计值的强影响力点。
+(Weak Duality) If \(x\) is a +feasible solution to the primal problem and \(p\) is a feasible solution to the dual +problem, then \(p^Tb\leqslant +c^Tx\).
+Proof: Set \(u_i = p_i +(a_i^Tx - b_i), v_j = (c_j - p^TA_j) x_j\), then by feasibility +\(u_i \geq 0, v_i \geq 0\).
+Therefore \(\sum_{i,j}u_i +v_j = p^T(Ax-b) ++ (c^T- p^TA)x = c^Tx - p^Tb \geq 0\).
+-
+
- If the optimal cost in the primal is \(-\infty\), then the dual one must be +infeasible. +
- If the optimal cost in the dual is \(+\infty\), then the primal one must be +infeasible. +
- Let \(x\) and \(p\) be feasible solutions to the primal and +the dual problem respectively, and suppose that \(p^T b = c^Tx\) holds. Then \(x\) and \(p\) are optimal solutions to the primal and +the dual respectively. +
Multicollinearity Diagnose
-有以下两个指标:
+Weak duality 引出的第三条最重要,如果 \(x\) 不是 optimal solution 则对任意的 +feasible solution \(x'\) 都有 \(c^Tx' \geq p^Tb = +c^Tx\),导致矛盾,\(p\) 的 +optimality 同理。这说明了 \(c^Tx = +p^Tb\) 可以导出二者分别在此处取到 optimal +cost,这引出了更重要的一条 strong duality,保证其一有 optimal solution +的时候另一个也有。
-
-
- Variance Inflation -Factor:多重共线性经常导致方差膨胀,这是一个表征的指标,\((VIF)_k = (1- R_k^2)^{-1}\),其中 \(R_k^2\) 指的是将 \(X_k\) 相对于其他 \(p-2\) 个 explanatory variable -做回归得到的决定系数。如果 \((VIF)_k \gg -1\) 则认为第 \(k\) 个变量 \(X_k\) 是会发生多重共线性的变量。 -
- Tolerance:\(TOL = -1/VIF\),判断准则类似上述。 +
(Strong Duality) If a linear programming problem has an optimal +solution, so does its dual, and the respective optimal costs are +equal.
+Proof: Consider the problem in standard form. The +simplex method (with lexicographic pivoting rule) terminates with an +optimal solution \(x^*\) and an optimal +basis \(B\), then \[\begin{aligned} + \bar c^T=c^T-c_B^TB^{-1}A\geqslant0. +\end{aligned}\]
+Let \(p^*=(c_B^T B^{-1})^T\) as the +corresponding optimal solution \(p\), +then \[\begin{aligned} + (p^*)^TA=c_B^T B^{-1}A\leqslant c^T, +\end{aligned}\] and \[\begin{aligned} +(p^*)^Tb=c_B^TB^{-1}b=c_B^Tx_B=c^Tx^*. +\end{aligned}\] So the strong duality holds.
Lecture 12
-本节探讨 remedies for multiple linear -regression,主要是异方差情况和多重共线性。
-Equal Variance Remedy
-这一部分主要处理模型发生异方差问题的情况。
-也就是说,实际上有 \(\varepsilon_1, -\varepsilon_2, ..., \varepsilon_n\) 的方差不全为 \(\sigma^2\),记方差为 \(\sigma_1 ^2,\sigma_2 ^2 , ..., \sigma_n -^2\)。此时的 likelihood function 是:
-\[L(\beta_1,\beta_2) = \Pi_{i=1} ^n -f_i(\beta_1, \beta_2 |X_i,Y_i) = \Pi_{i=1}^n (\frac{1}{\sqrt{2\pi} -\sigma_i} exp(-\frac 1 2 (\frac{Y_i - \beta_0 -\beta_1 -X_i}{\sigma_i})^2)) \]
-可以看到 ordinary least square 条件得到的 \(b_0 = \hat \beta_0,b_1 = \hat \beta_1\) -不再满足 MLE 的条件。但如果是在不知异方差的情况下仍然使用 OLS 或者 MLE -条件得到的参数估计,仍然是可以满足无偏性的,但不满足最小方差性质。
-Weighted Regression
-简单来说,通过选取 \(\{ w_i = -\frac{1}{\sigma_i ^2} \}_{i=1} ^n\) 作为权重,考虑 \(\Sigma_{i=1} ^n w_i e_i^2 = \Sigma_{i=1} ^n -(\frac{Y_i - \beta_0 - \beta_1 X_{i,1} - ... - \beta_{p-1} -X_{i,p-1}}{\sigma_i})^2\) 的最小性问题。
+最后来个 Farka's lemma,把 constraints +作为一个矩阵从原来的优化问题里面抽出来看:
-
-
最简单的情况,\(\sigma_1,...,\sigma_n\) 均已知,则有 \(w_i = \frac{1}{\sigma_i ^2}\),
-取 \(W = \begin{bmatrix} \frac{1}{\sigma_1 -^2} & & & \\ &...& & \\ & & & -\frac{1}{\sigma_n^2} \end{bmatrix}\) 使得回归问题变为 \(W^{\frac 1 2} Y = W^{\frac 1 2} X \beta + W^{\frac -1 2} \varepsilon\),记 \(Y^* = W^{\frac -1 2} Y, X^* = W^{\frac 1 2} X, \varepsilon^* = W^{\frac 1 2} -\varepsilon\),由于 \(Var(\varepsilon^*) = I_{n\times n}\) -满足同方差条件,因此新的回归问题是符合条件的。
-注意新的回归问题 \(Y^* = X^* \beta + -\varepsilon^*\) 事实上没有改变系数 \(\beta\),但系数估计 \(b_w = (X^TWX)^{-1} (X^TWY)\) -是改变了的,这是正常现象,因为对这一问题做 remedy -的主要原因就是假设不满足,导致按照 OLS 做出的系数估计不准确,因此 -weighted regression 做出的修正也是相对于原系数 \(\beta\) 的。
-\(b_w\) 仍然是无偏估计,也保证 \(Var(b_w) = (X^TWX)^{-1}\) -是最小方差。
-稍微复杂一点的情况,虽然 \(\sigma_i^2\) 未知但 \(\sigma^2_i / \sigma_j ^2\) 均已知,取 \(w_i = \frac{\sigma_1 ^2}{\sigma_i^2 }\) -即可。于是有:
-取 \(W = \sigma_1 ^2 \begin{bmatrix} -\frac{1}{\sigma_1 ^2} & & & \\ &...& & \\ & -& & \frac{1}{\sigma_n^2} \end{bmatrix}\) 使得回归问题变为 -\(W^{\frac 1 2} Y = W^{\frac 1 2} X \beta + -W^{\frac 1 2} \varepsilon\),记 \(Y^* = -W^{\frac 1 2} Y, X^* = W^{\frac 1 2} X, \varepsilon^* = W^{\frac 1 2} -\varepsilon\),由于 \(Var(\varepsilon^*) = \sigma_1 ^2 I_{n\times -n}\) 满足同方差条件,因此新的回归问题是符合条件的。
-新的回归系数估计是 \(b_w = -(X^TWX)^{-1}(X^TWY)\),\(Var(b_w) = -\sigma_1^2(X^TWX)^{-1}\),由此还可以做出对 \(\sigma_1\) 的参数估计,\(\hat \sigma_1 ^2 = MSE_{wls} = \frac{\Sigma(Y^*_i -- \hat Y^*_i)^2}{n-p}= \frac{\Sigma w_i(Y_i - \hat Y_i)^2}{n-p} = -\frac{\Sigma w_i e_i ^2}{n-p}\),其中 \(w_i = -\frac{\sigma_1^2}{\sigma_i^2}\)。
-一般情况下 \(\{ \sigma_i \}\) -是完全未知的,我们是在模型诊断中发现异方差的现象,因此不可能直接通过方差值推权重系数。这个时候一般有两种选择:
+- (Farka's lemma) Let \(A\) be a
+matrix of dimensions \(m\times n\) and
+let \(b\) be a vector in \(\Re ^m\). Then exactly one of the following
+two alternative holds:
+
-
+
- There exists some \(x\geqslant 0\) +such that \(Ax=b\). +
- There exists some vector \(p\) such +that \(p^TA\geqslant 0\) and \(p^Tb<0\). +
+ - (Farka's corollary) Let \(A_1,\ldots,A_n\) and \(b\) be given vectors and suppose that any +vector \(p\) that satisfies \(p^TA_i\geqslant 0\), \(i=1,\ldots,n\), must also satisfy \(p^Tb\geqslant 0\). Then \(b\) can be expressed as a nonnegative +linear combination of the vectors \(A_1,\ldots, A_n\). +
就变成了很普通但是又看着有点奇怪的矩阵变换问题,谁知道背后还有个优化问题.jpg。事实上对于不同形式的 +primal 和 dual problem +我们都可以写出来一对相反的条件,让它们二者成立其一。
+Lecture 3
+在上这节课之前我把 HW2 写完了,相应地其实就把 Nash equilibrium +那道题做了。是周二晚上吃饭之前写完的,吃饭之前多花了五分钟写成 LaTeX +然后超级开心地离开四教,吃完回来又读了一遍感觉证得很好,真的很喜欢这个方法还有这整个问题。
+所以我还是忍不住在 acknowledge 里面写了 MashPlant 日记里那段话:
+++All exercises but Ex 4.29 are finished on my own. Among them I +appreciate the solution of Ex 4.10 most (though trivial), as this is +actually quite a triumph, even if it's hard to explain to your friends +or family members.
+
好了现在大家都知道我不会做 Ex 4.29 了
然后 Lecture 3 +上又把这个问题拿出来讲了,顺便把这个作业题也证明了,有点不爽((x
+Nash Equilibrium
+先把 theorem 丢出来,然后写一个我的证明:
+Theory
+Ex 4.10
+Consider the standard form problem of minimizing \(c^Tx\) subject to \(Ax = b, x \geq 0\). We define the +Lagrangean by
+\[L(x,p) = c^Tx + p^T(b-Ax)\]
+Consider the following game: player 1 chooses some \(x \geq 0\), and player 2 chooses some \(p\); then, player 1 pays to player 2 the +amount \(L(x,p)\). Player 1 would like +to minimize \(L(x,p)\), while player 2 +would like to maximize it.
+A pair \((x^*,p^*)\) with \(x^* \geq 0\), is called an equilibrium +point if \(L(x^*,p) \leq L(x^*,p^*) \leq +L(x,p^*), \; \forall x \geq 0, \forall p\).
+(Thus, we have an equilibrium if no player is able to prove her +performance by unilaterally modifying her choice.)
+Show that a pair (\(x^*,p^*\)) is an +equilibrium if and only if \(x^*\) and +\(p^*\) are optimal solutions to the +standard form problem under consideration and its dual respectively.
+Proof:
+Consider the primal problem and the dual problem in the following +form:
+\[\begin{aligned} + \textbf{minimize} \quad & c^Tx \\ + \textbf{subject to} \quad & Ax = b \\ + & x \geq 0 +\end{aligned} \quad \quad \quad +\begin{aligned} + \textbf{maximize} \quad & p^Tb \\ + \textbf{subject to} \quad & A^T b \leq c \\ + \\ +\end{aligned}\]
+-
+
- If \(x^*\) and \(p^*\) are optimal solutions to the primal +problem and the dual problem respectively, then there is: +
\[L(x^*, p) = c^Tx^* + p^T(b -Ax^*) = +c^Tx^* = L(x^*, p^*)\]
+\[L(x,p^*) = c^Tx + p^{*T} (b-Ax) = (c^T - +p^{*T} A)x + p^{*T} b \geq p^{*T} b = c^Tx^*\]
+according to the strong duality theorem.
+Therefore \(L(x^*,p) \leq L(x^*,p^*) \leq +L(x,p^*)\) holds, and \((x^*,p^*)\) is an equilibrium.
+-
+
- If \((x^*,p^*)\) is an equilibrium, +first to prove that \(x^*\) is a +feasible solution to the primal problem. Consider the first inequality +\(L(x^*, p ) \leq L(x^*, p^*)\) which +holds for any \(p\). If \(b - Ax^* \neq 0\), by taking \(p = b - Ax^* +p^*\), we can obtain +
\[L(x^*,p) - L(x^*, p^*) = (p- +p^*)^T(b-Ax^*) = (b-Ax^*)(b-Ax^*) >0,\]
+which leads to contradiction. Therefore \(Ax^* = b\) holds, \(x^*\) is a feasible solution to the primal +problem and \(L(x^*, p^*) = c^T +x^*\).
+Next step we prove that \(p^*\) is a +feasible solution to the dual problem. Consider the second inequality +\(c^T x^* = L(x^*,p^*) \leq L(x, p^*)\) +which holds for any \(x \geq 0\). By +taking \(x =0\) we can obtain that +\(c^T x^* \leq L(0,p^*) = p^{*T}b\) +holds.
+Moreover, if there exists \(i\) s.t. +\(c_i - p^T A_i <0\), we can take +\(x_i = -\frac{p^{*T}b - c^Tx^*}{c_i - p^{*T} +A_i} +1\) and \(x_j =0\) for all +\(j \neq i\), then \(x \geq 0\). Take such \(x\) to the inequality and there is:
+\[c^Tx^* = L(x^*,p^*) \leq L(x,p^*) = +p^{*T} b + (c_i - p^{*T} A_i) x_i < p^{*T} b - (p^{*T}b - c^Tx^*) = +c^Tx^* ,\]
+which leads to contradiction. Thus \(c_i - +p^{*T} A_i \geq 0\) holds for any subscript \(i\), i.e. \(c - +p^{*T}A \geq 0\). Therefore \(p^*\) is a feasible solution to the dual +problem.
+According to the inequality \(c^T x^* \leq +p^{*T}b\) we obtained before and the weak duality theorem, there +is \(c^T x^* = p^{*T} b\), and +therefore \(x^*, p^*\) are optimal +solutions to the primal problem and the dual problem respectively.
+Application
+其实已经挺清楚的了,就是说 \(\max_p \min_x +L(x,p) = \min_x \max_p L(x,p)\) 这样子,所以说 dual 和 primal +得到的结果是一致的。
+Application of Farka's Lemma
+先回顾下 Farka's lemma:
+(Farka's lemma) Let \(A\) be a +matrix of dimensions \(m\times n\) and +let \(b\) be a vector in \(\Re ^m\). Then exactly one of the following +two alternative holds:
-
-
重复试验取 \(Y_i\) 的方差估计 -\(s_i^2\),于是权重系数为 \(w_i = \frac{1}{s_i ^2}\)。
-先对 \(Y\sim X\) 进行 OLS -回归,取出此时的 residual \(\{e_i \}\) -作为 \(\{ \sigma _i \}\) 的估计,取 -\(w_i = \frac{1}{e_i ^2}\) -作为权重即可。
-效果不明显时多迭代几次。
-
在观察 weighted least square 和 ordinary least square -模型差别时,注意:
+除了用一对 primal problem 和 dual problem +记这个结论之外,还可以用一个图来直观地理解:
+
当 \(b\) 不落在 \(A_i\) 和 \(x \geq +0\) +构造出的阴影范围内,也就是说第一个条件不满足的时候,就一定存在 \(p\) 使得 \(p\) 和 \(b\) 的夹角是“钝角”,而且 \(p\) 和每个 \(A_i\) 的夹角是“锐角”。
+考虑一个有 \(n\) +种商品的贸易过程,每次购买的份额是一个 asset vector \(x = +(x_1,x_2,...,x_n)\),初始状态下的价格是一个 price vector \(p = +(p_1,p_2,...,p_n)\),因此初始状态下投入的资金是 \(p^Tx\)。一段时间后会呈现出 \(m\) 种状态之一,第 \(i\) 种状态下这 \(n\) 种商品的售价是一个 payoff vector \((r_{i1},r_{i2},...,r_{in})\)。由此构造一个 +payoff matrix:
+\[R= \begin{bmatrix} r_{11} & r_{12} +& \cdots & r_{1n} \\ \cdots & \cdots & \cdots & +\cdots \\\cdots & \cdots & \cdots & \cdots \\ r_{m1} & +r_{m2} & \cdots & r_{mn} \end{bmatrix}\]
+取 \(w = Rx = (w_1,w_2,\cdots,w_m)\) +作为购买份额为 \(x\) 时,最终在 \(m\) 个状态下分别得到的收入。有一个 absence +of arbitrage +condition,大概就是说不可能在负投资的状态下得到正收益,也就是说 \(Rx \geq 0\) 可以推出 \(p^Tx \geq 0\)。
+由 Farka's lemma 可知此时第二条不成立,一定存在 \(q \geq 0\) 使得 \(R ^T q = p\)。
+The Center of Gravity Method
+实际上就是一个不断切割已有的 polyhedron 来找到 optimal solution +的过程。简单来说从初始状态开始,每个状态下手里有一个多边形 \(S_t\)(feasible set 的 subset)和它的质心 +\(x_t\),然后把使得取值大于 \(c^Tx_t\) 的部分切掉,也就是取 \(S_t\) 和 hyperapce \(\{x \in \mathbb R^n \mid c^T(x-x^T) > 0 +\}\) 的交这一部分作为不可能取到 optimal cost +的区域,余下的部分是下一状态的多边形 \(S_{t+1}\) 和相应的质心 \(x_{t+1}\),由此按照所需的精度来逼近 optimal +cost。
+写成算法的步骤来说也非常简单,实际上每次就操作两步。先取整个 feasible +set 作为 \(S_1\),然后:
+-
+
- Take \(x_t = \frac{1}{Vol(S_t)} \int_{x +\in S_t} x \; dx\) as the center of gravity of the polyhedron +\(S_t\); +
- Take \(S_{t+1} = S_t \cap \{x \mid +c^T(x-x_t) \leq 0 \}\) as the new polyhedron. +
一直重复直到 \(S_t\) 足够小,此时 +\(c^T x_t\) 和 optimal cost \(c^Tx^*\) +的误差也会足够小。这由一些定理保证。
-
-
- \(R^2\) 以及 adjusted \(R^2\) 的数值差别没有很强的意义,WLS -情况下原始数据 \(\{ Y_i \}\) -已经发生了变化,实际上 SST 也已经变了,没有什么比较的意义。 -
- 需要关注的点是 residual standard error,越接近 \(1\) 越说明异方差的调整是成功的。 -
- 有时会观察到 WLS 情况下 \(\hat -\sigma^2\) 在减小,似乎数据的分散程度在减小,这是因为 MSE -在减小。但是 WLS 和 OLS 情况下的 MSE 和 MST 都没有比较的意义,因此 \(\hat \sigma\) -的变化也没有研究的价值。唯一确定的是它会接近于 \(1\),这一点可以证明异方差的调整效果是成功的。 +
Let \(K\) be a centered convex +set (i.e. \(\int_{x \in K} xdx=0\)), +then for any \(w \in \mathbb R^n\), +\(w \neq 0\), one has
+\[Vol(\mathcal K \cap \{x \in \mathbb R^n +: x^T w \geq 0\}) \geq \frac 1 e Vol(\mathcal K)\]
Multicollinearity Remedy
-如果存在多重共线性,主要发生的问题是 \(X^TX\) -求逆是一个病态的数值问题,误差很大。实际上极端来说如果存在完全共线性,\(X^TX\) 会退化为不满秩的情况。
-可以用 ridge regression 对多重共线性进行弥补。
-Ridge Regression
-主要的 idea 是如果 \((X^TX)\) -接近于不满秩,则在参数估计中将其改变为 \((X^TX -+\lambda I)\),\(\lambda\) -是待取的参数。对于矩阵的对角元进行改变如同突起的山脊,因此得名岭回归。
-Ridge regression 的本质是对优化问题进行了修改。OLS -中的优化问题是求使得 \((Y-X\beta)^T -(Y-X\beta)\) 最小的 \(\beta\),ridge regression 中将 \(|| \beta ||_2 ^2 = \Sigma_{i=0} ^{p-1} -\beta_i^2\) 加入了优化,对 \(\beta\) 的长度(事实上应该称之为 2- -范数)做惩罚。因此,实际上是求使得 \((Y-X -\beta )^T (Y-X \beta) + \lambda \Sigma_{i=0} ^{p-1}\beta_i ^2\) -最小的 \(\hat \beta = (X^TX + \lambda I)^{-1} -X^TY\),这使得参数估计 \(b = \hat -\beta\) 呈现出比 OLS 下长度和方差都更小的特征。
-在实际应用中,需要通过确定最佳的 \(\lambda\) 从而得到合适的参数估计,一般是对 -\(\lambda\) 取一个 sequence -进行尝试。如果发现某个 explanatory variable 的系数在 \(\lambda\) 增大时很快下降到 \(0\),实际上它很有可能是不需要进入模型的。
-应用岭回归来弥补模型的多重共线性的时候,既是为了消除共线性,也是在牺牲一些 -\(\hat \beta\) -的无偏性来换取更小的方差。
-LASSO & Elastic Net
-LASSO 中把惩罚的 \(\beta\) -长度替换为了 \(\beta\) 的 1- -范数,弹性网络则是对 LASSO 和 ridge regression 进行了结合。
-本质上都是 Bayesian modes。
-Influencial Cases Remedy
-更改一些更 robust 的优化模型,例如 least absolute deviation 和 least -median of squares,缺点是算起来会比较困难。
-或者考虑非参数模型。
-Nonlinearity Remedy
-考虑局部多项式回归/局部回归,总之是对数据进行分块,所谓的 -lowess。
-Lecture 13
-One Factor ANOVA
-(从生统笔记复制来的)
-首先给出一个希望做检验的场景:\(n_T\) 个实验对象被分成 \(r\) 组,每组有 \(n_i\) 个实验对象,有 \(n_T = \Sigma_{i=1} ^r n_i\)。由此我们得到 -\(n_T\) 个数据 \(Y_{ij}\),\(i\) 表示组别,\(1\leq i \leq r\),\(j\) 表示在某一组内的编号,\(1 \leq j \leq n_i\)。
-Cell means model
+这告诉我们每个新的多边形和原多边形之间有一个体积关系是 \(Vol(S_{t+1}) \leq (1-\frac 1 e) Vol(S_t) \leq +\cdots \leq (1-\frac 1 e)^t Vol(S_1)\),再对于 \(\varepsilon = (1-\frac 1 e)^{t/n}\) 取 +\(\mathcal S_\varepsilon = \{(1-\varepsilon +)x^* + \varepsilon x, \forall x \in S_1\}\),实际上是对 \(S_1\) 做了一个仿射变换。此时有 \(Vol(S_\varepsilon)=\varepsilon^n Vol(S_1) = +(1-\frac 1 e)^tVol(S_1) \geq Vol(S_{t+1})\),于是可以找到一个 +\(x_\varepsilon \in S_\varepsilon\) +使其在 \(t\) 时刻时仍在 \(S_t\) 中,而 \(t+1\) 时刻就被“裁剪”了出去。
+所以有
+\[c^Tx_{t+1} < c^Tx_\varepsilon = +c^T((1-\varepsilon)x^*+ \varepsilon x) \leq c^Tx^* + 2B\varepsilon +=c^Tx^*+2B(1-\frac 1 e)^{t/n}\]
+也就是说 \(c^Tx_{t+1} - c^Tx^* < +2B(1-\frac 1 e)^{t/n}\) 作为 \(t+1\) 时刻下取值距离 optimal cost +的误差可以被控制,并且我们可以在 \(O(n +\log(\frac{1}{\varepsilon}))\) 时间下得到误差为 \(\varepsilon\) 的 cost 和 solution。这比 +simplex method 误差大一些,但是 polynomial time algorithm。
+The Ellipsoid Method
+讲这个的时候我太困了,上楼找了个教室睡觉,没听。我估计我困成那样听也听不懂,他这个手稿太抽象了也看不大懂,貌似书上也没这一部分,哥们有点子崩溃(。等
+scribing 了。
我都学会了 scribing 还没出来,自己写一个吧。
+Notations
+首先是一些记号:
+
-
-
模型假设是 \(Y_{ij} = \mu_i + -\varepsilon_{ij}\)。
-其中,\(\mu_i\) 是第 \(i\) 组的理论均值,\(\varepsilon _{ij}\) i.i.d. \(\sim -N(0,\sigma^2)\)。注意到在这一模型假设中有 \(r+1\) 个参数,分别是 \(\mu_1,\mu_2,...,\mu_r,\sigma^2\),我们需要用得到的数据来对这些未知参数进行估计。考虑一些统计量作为参数的估计量:
-\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 -}^{n_i} Y_{ij} = \hat \mu _i\]
-\[\bar{Y}_{..} = \frac{1}{n_T} -\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r -n_i \bar{Y}_{i.}\]
-\[s_i ^2 = \Sigma_{j=1} ^{n_i} (Y_{ij} - -\bar Y_{i.})^2 / (n_i -1) \]
-\[s^2 =\Sigma_{i=1} ^r \Sigma_{j=1} ^{n_i} -(Y_{ij} - \bar Y_{i.})^2 =\frac{1}{n_T- r} \Sigma_{i=1}^r (n_i -1) s_i -^2 = \hat \sigma^2\]
-在这一模型中,我们关注的假设检验是 \(i\) 组实验之间是否存在差异,假设检验表示为 -\(H_0 : \mu_1= \mu_2 = ... = \mu_r = -\mu\),对应的备择假设即为 \(\{ \mu_i -\}_{i=1} ^r\) 中存在不同的项。检验最经典的方法即为 -ANOVA,analysis of variance。核心是以下的分解:
-\[\begin{aligned} SSTO = \Sigma_i -\Sigma_j(Y_{ij} - \bar Y_{..})^2 &= \Sigma_i \Sigma_j (Y_{ij} - \bar -Y_{i.} +\bar Y_{i.} - \bar Y_{..})^2 \\& = \Sigma_i n_i (\bar Y_{i.} -- \bar Y_{..})^2 + \Sigma_i \Sigma_j (Y_{ij} - \bar Y_{i.})^2 \\ -&=SSTR + SSE \end{aligned}\]
-可以观察到,\(SSTR\) -是组间差距,体现了不同组别之间的差别,\(SSE\) -是组内差距,体现了同一组内各数据的偏差。注意 \(SSTR\) 的自由度是 \(r-1\),\(SSE\) 的自由度是 \(n_T - r\),\(SSTO\) 的自由度是 \(n_T - 1\)。
-两个统计量的期望是 \(\mathbb E(MSE) = -\sigma^2\),\(\mathbb E(MSTR) = -\sigma^2 +\frac{\Sigma_i n_i (\mu _i -\mu_.)^2}{r-1}\),其中 -\(\mu_. = \frac{\Sigma_i n_i -\mu_i}{n_T}\)。
-在 \(H_0\) 成立时,\(\frac{SSE}{\sigma^2} \sim \chi^2 _{n_T - -r}\),\(\frac{SSTR}{\sigma^2} \sim -\chi^2_{r-1}\)。因此 \(F=\frac{MSTR}{MSE} \sim F_{r-1,n_T -r}\) -作为最终的检验统计量。
-当 \(F^* > F(1-\alpha , r-1 , n_T --r)\) 时拒绝原假设,否则接受;\(Power = -P(F^* > F(1-\alpha , r-1,n_T -r)| \delta)\),其中 \(\delta\) 是一个非中心偏移量,\(\delta = \frac{1}{\sigma} \sqrt{\frac 1 r \Sigma_i -n_i (\mu_i - \mu_.)^2}\)。
-也可以作为一个线性回归的问题来看待,design matrix 是 $ X =
-\[\begin{bmatrix} 1 & 0 & 0 & -... & 0 \\ 0 & 1 & 0 & ... & 0 \\ ... -&...&...&...&... \\ 0 & 0 & 0 & ... & 1 -\end{bmatrix}\] -$,系数向量是 \(\mu = \begin{bmatrix} \mu_1 -\\ \mu_2 \\ ... \\ \mu_r \end{bmatrix}\),因此整体的回归方程是 $ -Y = X + $,注意这个回归问题是强迫过原点的。
+A set \(E\) of vectors in \(\mathbb R^N\) of the form \(E = E(z,D) = \{x \in \mathbb R^n \mid (x- z)^T +D^{-1} (x-z) \leq1 \}\), where \(D\) is an \(n +\times n\) positive definite symmetric matrix, is called an +ellipsoid with center \(z \in \mathbb +R^n\).
+If \(D\) is a \(n \times n\) nonsingular matrix and \(b \in \mathbb R^n\), then the mapping \(S: \mathbb R^n \to \mathbb R^n\) defined by +\(S(x) = Dx + b\), is called an affine +transformation.
Factor Effects Model
+注意到仿射变换都是可逆的,所以可以把仿射变换的像定义成
-
-
Factor Effects Model 是 Cell Means Model -的一个重新参数化的结果。模型假设是 \(Y_{ij} = -\mu + \tau_i + \varepsilon_{ij}\)。
-其中,\(\mu_i\) -是整体的理论均值,\(\varepsilon _{ij} i.i.d. -\sim N(0,\sigma^2)\)。它的参数比 cell mean model 多一个,分别是 -\(\mu , \tau_1 , ..., \tau_r , -\sigma^2\),但是自由度是相同的,因为 \(\{ \tau _i \}_{i=1}^r\) 存在一个约束 \(\Sigma_{i=1}^r \tau_i = -0\),如果没有这个约束会导致存在多组解。考虑一些统计量作为参数的估计量:
-\[\bar{Y}_{i.} = \frac{1}{n_i} \Sigma_{j=1 -}^{n_i} Y_{ij} = \hat \tau _i + \hat \mu\]
-\[\bar{Y}_{..} = \frac{1}{n_T} -\Sigma_{i=1}^r \Sigma_{j=1} ^{n_i} Y_{ij} = \frac{1}{n_T} \Sigma_{i=1}^r -n_i \bar{Y}_{i.} = \hat{\mu}\]
-\[s_i ^2 = \Sigma(Y_{ij} - \bar Y_{i.})^2 -/ (n_i -1) \]
-\[s^2 = \frac{1}{n_T- r} \Sigma_{i=1}^r -(n_i -1) s_i ^2 = \hat \sigma^2\]
-在这一模型中,我们关注的假设检验仍然是 \(i\) 组实验之间是否存在差异,假设检验表示为 -\(H_0 : \tau_1= \tau_2 = ... = \tau_r = -0\),对应的备择假设即为 \(\{ \mu_i -\}_{i=1} ^r\) 中存在不同的项。factor effects model -在参数的含义上比 cell mean model 更清晰。
-可以作为一个线性回归的问题来看待,design matrix 是 $ X =
-\[\begin{bmatrix} 1 & 1 & 0 & -... & 0 \\ 1 & 0 & 1 & ... & 0 \\ ... -&...&...&...&... \\ 1 & -1 & -1 & ... & --1 \end{bmatrix}\] -$,系数向量是 \(\mu = \begin{bmatrix} \mu -\\ \tau_1 \\ \tau_2 \\ ... \\ \tau_{r-1} -\end{bmatrix}\),因此整体的回归方程是 $ Y = X + -$,注意这个回归问题的截距就是 \(\mu\),不强迫过原点,相比 cell mean model -算是做了一点点优化。
+- \(S(L) = \{y \in \mathbb R^n \mid y = Dx ++b, \text{for some } x\in L \}\) +
- The volume of a set \(L \in \mathbb +R^n\), which is denoted by \(Vol(L)\), is defined as \(Vol(L) = \int_{x \in L}dx\)
Example
+然后就可以得到仿射变换后的体积是
+-
+
If \(S(x) = Dx + b\) then \(Vol(S(L)) = |det(D)| Vol(L)\)
+Proof: \(Vol(S(L)) = +\int_{y \in S(L)} dy = \int_{x \in L} |det(D)| dx = |det(D)| +Vol(L)\)
+
Algorithm
+目标是考虑一个 \(Ax \geq b\) +形式的优化问题的 feasible set,也就是一个 polyhedron \(P\) 是否是空集的问题,可以用一个 Ellipsoid +Algorithm +来解决。既然是用迭代算法解决,其实就不能太苛求精细程度,我们约定最后得到的覆盖椭圆的面积小于 +\(\varepsilon\) 时就认为 \(P\) 是一个空集。
+首先考虑一个覆盖所求 polyhedron \(P\) 的椭圆 \(E_t\),如果其中心 \(x_t \in P\) 则找到了一个 \(P\) 中的解,可以得出 \(P\) 是非空的;如果 \(x_t \notin P\) 那么 \(x_t\) 一定违反了其中的某个 constraint \(a_i ^Tx \geq b_i\),\(P\) 一定在 halfspace \(\{x \in \mathbb R^n \mid a_i^T x \geq a_i^Tx_t +\}\) 和 \(E_t\) +的交集里,这样我们再做一个新的更小的椭圆 \(E_{t+1}\) +来覆盖这一部分,就可以继续这一算法。
+来个我非常喜欢的图!
+
现在需要解决的问题仍然是 termination 问题,也就是是否 \(E_{t+1}\) 的体积一定比 \(E_t\) +更小。以下定理保证了它们的体积之间一定有一个指数级的减少:
+-
+
Let \(E = E(z,D)\) be an +ellipsoid in \(\mathbb R^n\), and let +\(a\) be a nonzero vector. Consider the +halfspace \(H = \{x \in \mathbb R ^n \mid a^Tx +\geq a^T z \}\) and let
+\[\bar z = z + +\frac{1}{n+1} \frac{Da}{\sqrt{a^TDa}}\]
+\[\bar D = \frac{n^2}{n^2-1} (D - +\frac{2}{n+1} \frac{Daa^TD}{a^TDa})\]
+Then \(\bar D\) is positive definite +and the new ellipsoid \(\bar E = E(\bar z, +\bar D)\) satisfies the following properties:
-
-
在做回归之前要注明哪些变量是 factor:
-> data$design = factor(data$design)
> fit = lm(cases ~ design, data = data)
> summary(fit)
-方便查看 \(\hat \mu_i\) -的命令是过原点回归,但查看 MSR 的方式是不过原点回归。
-\(Std.Error_i ^2 = Var(\hat \mu_i) = -Var(\frac{\Sigma_{j=1}^{n_i} Y_{ij}}{n_i}) = \frac{\hat \sigma^2}{n_i}= -\frac{s^2}{n_i}\)
-\(sd_i ^2 = s_i ^2\),由此计算出 -\(s^2\) 后再得到每个 \(Std.Error\) 的值是 \(\frac{s}{\sqrt n_i}\)。
+- \(E \cap H \subset \bar E\) +
- \(Vol(\bar E) < e^{-1/(2(n+1))} +Vol(E)\)
Inference on One-Way ANOVA
-Confidence Interval for \(\mu_i\)
-事实上这只是个理论上可做的问题而已,现实中不会对 \(\mu_i\) 做推断,我们关注的是 \(\mu_i\) 之间的差异。
-由于 \(\bar Y_{i.} \sim N(\mu_i , \sigma^2 -/ n_i)\),因此 \(\mu_i\) 的 -pooled confidence interval 是 \((\bar Y_{i.} - -t_c \frac{s}{\sqrt n_i} , \bar Y_{i.} + t_c \frac{s}{\sqrt -n_i})\),其中 \(t_c = -t(1-\frac{\alpha}{2}, n_T -r)\)。注意其中的 \(s^2\) 在上面已经有定义,实际上就是 -SSE。
-当然也可以认为是 \((\bar Y_{i.} - t_c s_i , -\bar Y_{i.} + t_c s_i)\),\(s_i\) 是每个 \(\mu_i\) 对应的 \(sd_i\)。但是这样得到的置信区间一般来说较宽,准确性不如 -pooled confidence interval,我们不太会采用。
-实际上这样做 t-test 的话 family-wise error rate -很大,即使做出显著的效果也很有可能是发生了 Type I Error。
-Bonferroni Confidence -Intervals for \(\mu_i\)
-想要同时估计所有的 \(\mu_i\) -的时候可以采用 Bonferroni method,但是也有明显的缺点是一旦 factor level -\(r\) 较大,就会导致每个 \(\mu_i\) 都不显著,置信区间的 level of -significance 只有 \(\alpha / -2r\),几乎是无效的。
-同样是 t-test,但过于保守了。对于较小的 \(r\) 可以进行尝试。
-Test Difference in Means
-由于 \(\bar Y_{i.} - \bar Y_{j.} \sim -N(\mu_i - \mu_k , \frac{\sigma^2}{n_i} + \frac{\sigma -^2}{n_j})\),\(\mu_i - \mu_k\) -的 confidence interval 是 \((\bar Y_{i.} - -\bar Y_{j.}-t_c s(\bar Y_{i.} - \bar Y_{k.}), \bar Y_{i.} - \bar -Y_{j.}+t_c s(\bar Y_{i.} - \bar Y_{k.}))\),其中 \(s(\bar Y_i. - \bar Y_k.) = \sqrt{\frac{\hat -\sigma^2}{n_i} + \frac{\hat \sigma^2}{n_j}} = s \sqrt{\frac{1}{n_i} + -\frac{1}{n_j}}\),\(t_c\) -是和检验方法有关的常数。
-由于一共有 \(r\) 个 mean \(\mu_i\),所以一共要做 \(\frac{r(r-1)}{2}\) -次检验来确定两两之间有无差异。
--
-
- Tukey's HSD Method: 使用 q-test,取 \(t_c -= \frac{\bar y _{max} - \bar y_{min}}{\sqrt 2 s /\sqrt -n}\);适用于两两检验。 -
- Scheffe's Method: 使用 F-test,取 \(t_c = -\sqrt{(r-1)F(1-\alpha, r-1, n_T --r)}\),适用于线性组合的对照(contrast,见下)。实际上也过于保守了,导致 -power 比较低。 +
Proof: First consider \(a += e_1. D = I_{n \times n}\) and the center of \(E_0\) as \(z = +0\). It's trivial to see that the first property holds. In this +case the positive definite matrix of \(\bar +E_0\) is \(D = diag((\frac{n}{n+1})^2, +\frac{n^2}{n^2-1}, \cdots,\frac{n^2}{n^2-1})\), and the center is +\(a = +(\frac{1}{n+1},0,\cdots,0)^T\).
+Now by constructing an affine transformation we can consider the +general case. The transformation T should let \(T(E) = E_0, T(H) = H_0\) and \(T(\bar E) = \bar E_0\). By some elementary +observations we can obtain that affine transformations preserve set +inclusion, i.e. if \(E_0 \cap H_0 \subset \bar +E_0\), then there is \(T(E_0) \cap +T(H_0) \subset T(\bar E_0)\), therefore the first property holds +naturally.
+Let \(R\) be the rotation matrix +corresponding to the vector \(u = D^{\frac 1 +2} a\), i.e.,
+\[R^TR = I, \quad RD^{\frac 1 2}a_i = +\|D^{\frac 1 2} a_i \| e_1\]
+Consider the following affine transformation:
+\[T(x) = R(D^{-\frac 1 +2}(x-z))\]
+Therefore,
+\(\begin{aligned} x \in E & \iff +(x-z)^TD^{-1}(x-z)\leq 1 \\ & \iff (x-z)^TD^{-\frac 1 +2}R^TRD^{-\frac 1 2}(x-z)\leq 1 \\ & \iff T(x)^T T(x) \leq 1 \\ +& \iff T(x) \in E_0, \end{aligned}\)
+which implies that \(T(E) = +E_0\).
+Similarly,
+\[\begin{aligned} x \in H & \iff +a_i^T(x-z )\geq 0 \\ & \iff \|D^{-\frac 1 2}a_i \| e_1 ^T RD^{-\frac +1 2} (x-z) \geq 0 \\ & \iff e_1 ^T T(x) \geq 0 \\ & \iff T(x) +\in H_0, \end{aligned}\]
+which implies \(T(H) = H_0\).
+Moreover there is also \(T(\bar E) = \bar +E_0\) and we omit the complicated algebraic manipulations. +Therefore \(E \cap H \subset \bar E\) +holds according to the properties of affine transformation. Next we +prove the conclusion about the volume.
+\(\frac{Vol(\bar E)}{Vol(E)} = +\frac{Vol(T(\bar E))}{Vol(T(E))} = \frac{Vol(\bar E_0)}{Vol(E_0)} = +det(D_0 ^{\frac 1 2}) = +(\frac{n}{\sqrt{n^2-1}})^{n-1}(\frac{n}{n+1})\)
+Consider
+\[(\frac{n^2}{n^2-1})^{\frac{n-1}{2}}(\frac{n}{n+1}) += (1+\frac{1}{n^2-1})^{\frac{n-1}{2}}(1-\frac{1}{n+1}) \leq +(e^{\frac{1}{n^2-1}})^{\frac{n-1}{2}} e^{-\frac{1}{n+1}} += e^{-\frac{1}{2(n+1)}},\]
+and the desired result follows.
Contrast
-Concept
-关于对照的具体定义是,取一组均值为 \(0\) 的常数作为权重,即为 \(\Sigma_{i=1} ^r c_i =0\),此时研究 \(L = \Sigma_{i=1} ^r c_i \mu_i\) -的推断。
-注意到 \(\hat L = \Sigma c_i \bar Y_i . -\sim N(L, Var(\hat L))\),其中 \(Var(\hat L) = \Sigma c_i ^2 Var(\bar Y_i -.)\),\(\hat Var (\hat L) = MSE \Sigma( -c^2_i / n_i)\)。
-test statistic 是 \(T= \frac{\hat L - -L_0}{\sqrt{\hat Var(\hat L)}} \sim t(n_T-r)\)。例如在 \(H_0 : L =0\) 下有 \(T = \frac{\Sigma c_i \bar Y_i .}{\sqrt{MSE \Sigma -c^2_i / n_i}} \sim t(n_T -r)\),于是 \(T^2 = \frac{(\Sigma c_i \bar Y_i.)^2}{MSE \Sigma -c_i^2 /n_i} = \frac{SSC/1}{MSE} \sim F(1,n_T-r)\),其中定义 \(SSC = (\Sigma c_i \bar Y_i.)^2 / \Sigma -(c_i^2/n_i)\),称为 sum of contrast。
-Multiple Contrasts
-可以利用 R 同时检验若干组 contrast,比如同时检验 \(\mu_1 = \mu_2, \mu_3 = \mu_2 , \mu_1 =( \mu_1 + -\mu_2+\mu_3 )/ 3\)
-实际上 linear hypothesis test 和 multiple comparison -的主要差别在于自由度,比如说对于 \(\mu_1 = -\mu_2 = \mu_3\) 做检验,前者会将其拆成两个两两检验,自由度是 -\(2\),后者会作为一个整体的 -contrast,自由度是 \(1\)。
-Lecture 14
-依旧来自生统概论的笔记。
-Two-Way ANOVA
-首先给出一个希望做检验的场景:\(nab\) 个实验对象被分成 \(a\times b\) 组,每组有 \(n\) 个实验对象。第 \(ij\) 组的实验条件是 \(A\) 因素的等级为 \(i\),\(B\) -因素的等级为 \(j\),其中有 \(1 \leq i \leq a, 1\leq j \leq -b\)。由此我们得到 \(nab\) 个数据 -\(Y_{ijk}\),\(i\) 表示以 \(A\) 因素分类的组别,\(j\) 表示以 \(B\) 因素分类的组别,\(k\) 表示在某一组内的编号,\(1 \leq k \leq n\)。
-每一组都是 \(n\) 个人,这是一个 -balanced design。
-Cell Mean Model
-模型假设是 \(Y_{ijk} = \mu_{ij} + -\varepsilon_{ijk}\)。
-其中,\(\mu_{ij}\) 是第 \({i \times j}\) 水平的均值,\(\varepsilon_{ijk}\) i.i.d. \(\sim N(0,\sigma^2)\),模型中实际上有 \(ab+1\) 个未知参数需要估计。
-\(\mu_{ij}\) 的估计量是 \(\bar Y_{ij.} = \sum_k Y_{ijk} /n\),对于 -\(i \times j\) 水平的方差估计是 \(s_{ij}^2 = \sum_k (Y_{ijk} - \bar Y_{ij.})^2 / -(n-1)\)。但是想要估计 \(\sigma^2\) 时必须要将所有的数值加权 pool -起来做估计,是 \(s^2 = \sum_{ij} (n_{ij}-1) -s_{ij} ^2 / \sum_{ij} (n_{ij}-1)\),注意到如果是 balanced test -的情况实际上就是 \(s^2 = \sum_{ij} s^2_{ij} / -ab\) 直接做平均的结果。更倾向于 pooled \(s^2\) -是因为自由度更大,数据利用更充分。
-直接通过看图来观察两个因子之间是否存在交互效应、单因子是否显著这件事的时候,比较经典的情况就是以下两种:
-
上面第一张图中可以发现两条回归线之间存在斜率的差异,说明 B 因子对于 A -因子的效果存在影响,也就是存在交互效应;在 \(b_2\) level 上 A 因子是不显著的,但在 \(b_1\) level 上 A 因子显著;同理在 \(a_1\) level 上 B 因子不显著,但在 \(a_2\) level 上 B -因子显著。实际上在这个情况下交互效应显著,主效应虽然显著但也没有太大意义了,不过想要解释也是可以的,可以认为 -A 因子带来的效应至少不是负效应。
-第二张图里更有两条回归线交叉,存在斜率的差异,交互效应显著;但主效应此时可能无法解释,尤其是如果两条回归线完全交叉成 -\(\times\) 形状,A 因子会在不同的 B -因子条件下起到相反的作用。所以一般是认为交互效应显著时主效应显著,但没有解释意义。显著性和解释性之间无关。
-在读 R code 的时候直接把所有的 estimation 读作 factor effect model -的系数,再代回就可以理解系数的来源了。这一部分在 factor effects model -里详述。
-Factor Effects Model
-模型假设是 \(Y_{ijk} = \mu +\alpha_i + -\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
-其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) -表示和两个因素同时相关的变化,相当于一个交叉项。
-这里面有 \((a+1)(b+1)\) -个参数,对其也有一定的约束:\(\Sigma_i -\alpha_i = \Sigma_j \beta_j = \Sigma_i (\alpha \beta)_{ij} = \Sigma_j -(\alpha \beta)_{ij} =0\),事实上有 \(a+b-1\) 个关于交互效应的约束,有 \(2\) 个关于单因子效应的约束,实际上包含 -\(\sigma^2\) 后仍然是有 \(ab+1\) -个参数。做一些其他的参数假设,让参数含义更清晰:
-\[\mu_{i.} = \alpha_i -+\mu_{..}\]
-\[\mu_{.j} = \beta _j + -\mu_{..}\]
-\[\mu_{ij} = \mu_{..} +\alpha_i + \beta_j -+(\alpha \beta)_{ij}\]
-如果 \((\alpha \beta)_{ij}=0\) -则说明因素 \(A,B\) -之间不存在相互作用的关系,这样的模型称为 additive model。
-考虑一些统计量作为参数的估计量:
-\[\bar{Y}_{ij.} = \frac{1}{n} \Sigma_{k=1 -}^{n} Y_{ijk} = \hat \mu_{ij} = \hat \mu + \hat \alpha _i + \hat -\beta_j + \hat{(\alpha \beta)}_{ij}\]
-\[\bar{Y}_{i..} = \frac{1}{bn} -\Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \alpha_i = -\hat \mu_{i.}\]
-\[\bar{Y}_{.j.} = \frac{1}{an} -\Sigma_{i=1}^a \Sigma_{k=1} ^{n} Y_{ijk} = \hat{\mu} +\hat \beta_j = -\hat \mu_{.j}\]
-\[\bar{Y}_{...} = -\frac{1}{abn}\Sigma_{i=1}^a \Sigma_{j=1}^b \Sigma_{k=1} ^{n} Y_{ijk} = -\hat{\mu} \]
-Two factors ANOVA 的方差分解更复杂一些:
-\[\begin{aligned} SSTO &= \Sigma_i -\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{...})^2 \\ &= \Sigma_i -\Sigma_j \Sigma_k ((\bar Y_{i..} - \bar Y_{...})+(\bar{Y}_{.j.} - \bar -Y_{...}) +(\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...}) -+(Y_{ijk} - \bar Y_{ij.}))^2 \\&=bn\Sigma_i (\bar Y_{i..} - \bar -Y_{...})^2+an\Sigma_j (\bar{Y}_{.j.} - \bar Y_{...})^2+n\Sigma_i -\Sigma_j (\bar{Y}_{ij.} - \bar Y_{i..} -\bar Y_{.j.} +\bar Y_{...})^2+ -\Sigma_{i}\Sigma_j \Sigma_k (Y_{ijk} - \bar Y_{ij.})^2 \\&=SSA -+SSB+SSAB+SSE \end{aligned}\]
-其中,\(SSA\) 的自由度是 \(a-1\),\(SSB\) 的自由度是 \(b-1\),\(SSAB\) 的自由度是 \((a-1)(b-1)\),\(SSE\) 的自由度是 \(ab(n-1)\),\(SSTO\) 的自由度是 \(abn-1\)。在这一个复杂问题中我们关心不同的问题,可以做出三种不同的假设检验,有对应的检验统计量。
+另外如果估计得再精细一点的话下界其实是 \(\exp(-\frac{1}{2n})\)(详见 +Bubeck),可以对函数求导做。
+所以只要初始状态的 ellipsoid +体积有限,算法一定会在有限时间内终止,可以用来解决 feasiblility +的问题,这是一个可以在 \(O(n \log +\varepsilon)\) 时间内结束的算法,实际上对于找 feasible solution +来说还是很快的。但 feasible solution +一个单点对于优化问题来说其实没什么用,我们的目标仍然是寻找 optimal +cost,为此需要一些类似于 center of gravity method 的方法。
+另外 ellipsoid method 也可以用来解决 optimal cost +的逼近,有这样一个体积关系了之后原理和 center of gravity method +类似:
+每个新的 ellipsoid 和上一时刻 ellipsoid 之间有一个体积关系是
+\(Vol(S_{t+1}) \leq \exp(-\frac{1}{2n})
+Vol(S_t) \leq \cdots \leq \exp(-\frac{t}{2n}) Vol(S_1)\),再对于
+\(\varepsilon = \exp(-\frac{t}{2n^2})\)
+取 \(\mathcal S_\varepsilon = \{(1-\varepsilon
+)x^* + \varepsilon x, \forall x \in S_1\}\),实际上是对 \(S_1\) 做了一个仿射变换。此时有 \(Vol(S_\varepsilon)=\varepsilon^n Vol(S_1) =
+\exp(-\frac{t}{2n}) Vol(S_1) \geq
+Vol(S_{t+1})\),于是可以找到一个 \(x_\varepsilon \in S_\varepsilon\) 使其在
+\(t\) 时刻时仍在 \(S_t\) 中,而 \(t+1\) 时刻就被“裁剪”了出去。
所以有:
\[c^Tx_{t+1} < c^Tx_\varepsilon =
+c^T((1-\varepsilon)x^*+ \varepsilon x) \leq c^Tx^* + 2B\varepsilon
+=c^Tx^*+2B \exp(-\frac{t}{2n^2}),\]
也就是说 \(c^Tx_{t+1} - c^Tx^* < 2B
+\exp(-\frac{t}{2n^2})\) 作为 \(t+1\) 时刻下取值距离 optimal cost
+的误差可以被控制,并且我们可以在 \(O(n^2
+\log(\frac{1}{\varepsilon}))\) 时间下得到误差为 \(\varepsilon\) 的 cost 和
+solution。同样是得到的 cost 比 simplex method 误差大一些并非精确值,但是
+polynomial time algorithm,虽然比起 center of gravity method
+来说消耗更大,但也有它的优势。
之前的想法一直有大问题,我当时也没怎么看懂 Bubeck +那本书的内容,更是完全不理解为什么 time usage 里面还有 \(R/r\) +的项。今晚做出来优化作业第一题之后醍醐灌顶,直接复制到这里来就很清楚了。
+Problem: Consider the following convex optimization +problem (\(f,g_i\) are convex):
+\[\text{minimize} \quad f(x)\]
+\[\text{subject to} \quad g_i(x) \leq 0, +i=1,2,\cdots,m.\]
+Let \(\mathcal K = \{x \mid g_i(x) \leq 0, +i=1,2,\cdots,m\}\). Assume that there exists \(x_,x_0^\prime\) s.t. \(\mathcal K\) is between balls of radius +\(r,R\),
+\[B(x_0,r) \subseteq \mathcal K \subseteq +B(x_0^\prime,R)\]
+Further assume that \(\sup_{x \in \mathcal +K} |f(x)| \leq B\). Given any \(x \in +\mathbb R^n\) one can evaluate \(f(x),g_i(x), \nabla f(x) , \nabla g_i(x)\). +Propose an efficient implementation of the Ellipsoid's method. Prove +that the algorithm converges in \(\mathcal +O(n^2 \log(\frac{BR}{r \varepsilon}))\) iterations to find an +\(\varepsilon\) optimal solution.
+Solution: To begin the algorithm, we set \(\mathcal E_0 = B(x_0^\prime, R)\) and \(c_0 = x_0^\prime\) as its center. At time +\(t\) we divide the possible results +into two situations as follows.
-
-
- \(A\) 因素是否会导致差异?\(H_0: \alpha_1 =\alpha_2=...=\alpha_a\),在 -\(H_0\) 下有 \(F^* = \frac{SSA/(a-1)}{SSE/(ab(n-1))} \sim -F_{a-1,ab(n-1)}\) -
- \(B\) 因素是否会导致差异?\(H_0: \beta_1 =\beta_2=...=\beta_b\),在 -\(H_0\) 下有 \(F^* = \frac{SSB/(b-1)}{SSE/(ab(n-1))} \sim -F_{b-1,ab(n-1)}\) -
- \(A,B\) 是否联合作用?\(H_0:(\alpha \beta)_{ij}=0, \forall 1 \leq i \leq -a,1\leq j \leq b\),在 \(H_0\) -下有 \(F^*=\frac{SSAB/(a-1)(b-1)}{SSE/(ab(n-1))} \sim -F_{(a-1)(b-1),ab(n-1)}\) +
If \(c_t \notin \mathcal K\), +then there is some constraints \(g_i(x) \leq +0\) violated so that \(c_t\) +does not lie in the feasible set. We find the violated constraints by +calling the zeroth order oracle \(g_i(c_t)\) and compare their value with +\(0\). To save the computational source +we just pick the violated constraint \(g_i(c_t) >0\) with the smallest +subscript, and number it as \(g_i^{(t)}\).
+Thus the feasible set \(\mathcal K\) +lies in \(\mathcal E _t \cap \{x \mid g_i +^{(t)} (x) \leq g_i ^{(t)} (c_t)\} \subseteq \mathcal E _t \cap \{x \mid +\nabla g_i^{(t)}(c_t)^T (x-c_t) \leq 0\}\) according to the +definition of subgradient. And the exact value of subgradient \(\nabla g_i^{(t)}(c_t)\) can be obtained by +calling the first order oracle \(\nabla +g_i^{(t)}\).
+Then we can just construct the \((t+1)\)-th ellipsoid by covering the set +shown above, i.e. \(\mathcal E_{t+1} \supseteq +\mathcal E _t \cap \{x \mid \nabla g_i^{(t)}(c_t)^T (x-c_t) \leq +0\}\).
+The second case is much easier. If we found \(c_t \in \mathcal K\), by considering the +subset \(\mathcal E_t \cap \{ x \mid f(x) < +f(c_t)\} \subseteq \mathcal E_t\), we can either find \(c_t\) is optimal by observing that the set +is empty or found a better solution through iteration.
+According to the definition of subgradient, there is \(\mathcal E_t \cap \{x \mid f(x) < f(c_t)\} +\subseteq \mathcal E_t \cap \{ x \mid \nabla f(c_t)^T (x-c_t) \leq +0\}\). Then we can just construct the \((t+1)\)-th ellipsoid by covering the set +shown above, i.e. \(\mathcal E_{t+1} \supseteq +\mathcal E _t \cap \{ x \mid \nabla f(c_t)^T (x-c_t) \leq 0\}\), +in which the value of subgradient \(\nabla +f(c_t)\) can be obtained by calling the first order oracle \(\nabla f\).
不能直接用 chi-square 统计量作为检验统计量的原因是实际上 \(MSE,MSA\) 等统计量中都带有未知的 \(\sigma^2\) 参数项。
-注意 \(n_{ij}\) -是相等的也就是平衡设计,所以 Type I 和 Type III ANOVA -的结果是一样的。
-Two-Way ANOVA in R
-模型假设是 \(Y_{ijk} = \mu +\alpha_i + -\beta_j +(\alpha \beta)_{ij} + \varepsilon_{ijk}\)。
-其中,\(\mu\) 是整体的均值,\(\alpha_i\) 代表只和等级为 \(i\) 的因素 \(A\) 有关的变化,\(\beta_j\) 表示只和等级为 \(j\) 的因素 \(B\) 有关的变化,\((\alpha \beta)_{ij}\) -表示和两个因素同时相关的变化,相当于一个交叉项。
-这里面有 \((a+1)(b+1)\) -个参数,对其也有一定的约束。R code 中的约束是和上述理论不同的,因此 -estimator 的读取也并不相同,认为 \(\alpha_1 = -\beta_1 = (\alpha \beta)_{1j} = (\alpha -\beta)_{i1}=0\),事实上也还是 \(a+b+1\) 个约束条件,可以估计出 \(ab+1\) 个不同参数。
-相应地,对应的 design matrix 也不尽相同。这里以 \(a=3,b=2,n=2\) 为例,coefficient table -如下所示:
-
Coefficient table 里的 Intercept 代表的实际上是 \(\mu\),预设了 \(\beta_1=0\),height2 即为 \(\beta_2\),height3 即为 \(\beta_3\);预设了 \(\alpha_1=0\),width2 即为 \(\alpha_2\);关于交互效应项,由于预设了 -\((\alpha \beta)_{11} = (\alpha \beta)_{12} = -(\alpha \beta)_{13} =(\alpha -\beta)_{21}=0\),不为零的交互效应项只有两个,分别由 -height2:weight2 对应 \((\alpha -\beta)_{22}\),height2:weight3 对应 \((\alpha \beta)_{23}\)。
-由此我们可以依次按照 \(\mu_{ij} = \mu + -\alpha_i + \beta_j +(\alpha \beta)_{ij}\) 算出所有的 \(\mu_{ij}\) 的估计量。
-在这之后我们希望得到一个关于 \(12\) -个数据的设计阵,实际上就是把数据和上述分析对应起来:
-
Least Square Means
-遇到非平衡设计,或者 covariates -的情况(连续型变量和类别性变量产生交互效应的情况),需要考虑 least -square means 而不是 pooled means。简单来说 least square means -是均值的均值,达到了最小的方差,而 pooled means -就是全体数据的均值,在非平衡设计的情况下很可能引入偏差。
-
Balanced Test
-对于一个平衡设计来说,它本质上是一个正交设计,模型中进一个因子还是两个因子都不会改变彼此的系数估计,只有自由度会有改变。least -square mean 就是普通的 pooled mean,one-way ANOVA 和 two-way ANOVA -的结果一致。
-Unbalanced Test
-非平衡设计的时候 one-way ANOVA 的结果仍然是一样的,least square mean -和 pooled mean 得到的都是这一组内所有的观测值的平均。在这里就是认为 A -因子的 height1 level 的估计值是 \(\hat \mu_{1} -= \frac 1 3(X_{11} +X_{12} +X_{13}) = 43\)。
-但是新加入一个因子做 two-way ANOVA 就会导致 least square mean -下的系数估计发生变化,从 coefficient table 可以看出 \(\mu_{i1}\) 和 \(\mu_{i2}\) -都改变了(绷不住了,虽然并不知道是怎么变的,但是会从系数表读出每一个 -\(\mu_{ij}\) 就可以了),仍然使用 \(\frac 1 2(\mu_{i1}+\mu_{i2})\) 作为 \(\mu_{i.}\) -的估计,就也会相应地发生变化。
-事实上 least square mean 还可以称作 predicted mean 的原因就是,此处的 -\(\mu_{11}\) 和 \(\mu_{12}\) 分别作为 \(1\times 1,1\times 2\) -这两格的预测值出现,它们的平均就作为 \(\mu_{1.}\) 这一个 A 因子的 height1 level -对应的预测值出现。在具体的例子里,此处因为得到的估计是 \(\hat \mu_{11} = 41, \hat \mu_{12} = -44\),于是认为 \(\hat \mu_{1.} = \frac -1 2 (\hat \mu_{11} + \hat \mu_{12}) = 42.5\)。
-
总之可以看到,unbalance test 会导致实验设计并不是正交的,B -因子的加入会对 A 因子的均值估计产生影响,这也是我们一般希望使用 balanced -test 的理由。
-Model Diagnose & Remedy
-马上要告别应统了,于是不考也就不想学了,摆烂。
-附录
-常见重要分布
-From Statistic -Note P10, by V1ncent19
-| \(X\) | -\(p_X(k)\big/f_X(x)\) | -\(\mathbb{E}\) | -\(var\) | -PGF | -MGF | -
|---|---|---|---|---|---|
| \(\mathrm{Bern} (p)\) | -- | \(p\) | -\(pq\) | -- | \(q+pe^s\) | -
| \(B (n,p)\) | -\(C_n^k p^k(1-p)^{n-k}\) | -\(np\) | -\(npq\) | -\((q+ps)^n\) | -\((q+pe^s)^n\) | -
| \(\mathrm{Geo} (p)\) | -\((1-p)^{k-1}p\) | -\(\dfrac{1}{p}\) | -\(\dfrac{q}{p^2}\) | -\(\dfrac{ps}{1-qs}\) | -\(\dfrac{pe^s}{1-qe^s}\) | -
| \(H(n,M,N)\) | -\(\dfrac{C_M^kC_{N-M}^{n-k}}{C_N^n}\) | -\(n\dfrac{M}{N}\) | -\(\dfrac{nM(N-n)(N-M)}{N^2(n-1)}\) | -- | - |
| \(P(\lambda)\) | -\(\dfrac{\lambda^k}{k!}e^{-\lambda}\) | -\(\lambda\) | -\(\lambda\) | -\(e^{\lambda(s-1)}\) | -\(e^{\lambda(e^s-1)}\) | -
| \(U(a,b)\) | -\(\dfrac{1}{b-a}\) | -\(\dfrac{a+b}{2}\) | -\(\dfrac{(b-a)^2}{12}\) | -- | \(\dfrac{e^{sb}-e^{sa}}{(b-a)^s}\) | -
| \(N(\mu,\sigma^2)\) | -\(\dfrac{1}{\sigma -\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\) | -\(\mu\) | -\(\sigma^2\) | -- | \(e^{\frac{\sigma^2s^2}{2}+\mu -s}\) | -
| \(\epsilon(\lambda)\) | -\(\lambda e^{-\lambda x}\) | -\(\dfrac{1}{\lambda}\) | -\(\dfrac{1}{\lambda^2}\) | -- | \(\frac{\lambda}{\lambda-s}\) | -
| \(\Gamma(\alpha,\lambda)\) | -\(\dfrac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda -x}\) | -\(\dfrac{\alpha}{\lambda}\) | -\(\dfrac{\alpha}{\lambda^2}\) | -- | \(\left(\frac{\lambda}{\lambda-s}\right)^\alpha\) | -
| \(B(\alpha,\beta)\) | -\(\dfrac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\) | -\(\dfrac{\alpha}{\alpha+\beta}\) | -\(\dfrac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\) | -- | - |
| \(\chi^2_n\) | -\(\dfrac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}\) | -\(n\) | -\(2n\) | -- | $ (1-2s)^{-n/2} $ | -
| \(t_\nu\) | -\(\dfrac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\Gamma(\frac{\nu}{2})}(1+\frac{x^2}{\nu})^{-\frac{\nu+1}{2}}\) | -\(0\) | -\(\dfrac{\nu}{\nu-2}\) | -- | - |
| \(F_{m,n}\) | -\(\dfrac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{m}{2})\Gamma(\frac{n}{2})}\dfrac{m^\frac{m}{2}n^\frac{n}{2}x^{\frac{m}{2}-1}}{(mx+n)^{\frac{m+n}{2}}}\) | -\(\dfrac{n}{n-2}\) | -\(\dfrac{2n^2(m+n-2)}{m(n-2)^2(n-4)}\) | -- | - |
Consider \(X_1,X_2,\ldots,X_n\) -i.i.d. \(\sim N(0,1)\); \(Y,Y_1,Y_2,\ldots,Y_m\) i.i.d. \(\sim N(0,1)\) - \(\chi^2\) Distribution:
-\(\chi^2\) distribution with degree -of freedom \(n\):$ =_{i=1}^n -X_i22_n$。 For independent \(\xi_i\sim\chi^2_{n_i},\, -i=1,2,\ldots,k\):\(x_{i_0}=\sum_{i=1}^k\xi_i\sim\chi^2_{n_1+\ldots+n_k}\)
+For both situations, we can obtain \(\mathcal E_{t+1}\) with the least volume +such that \(Vol(\mathcal E_{t+1} ) \leq +\exp(-\frac{1}{2n}) Vol(\mathcal E_t)\) according to the theorem +we proved in class (and we can construct the exact form of \(\mathcal E_{t+1}\) through the complex +equation, which won't be shown again in this solution).
+Therefore, if \(t \geq 2n^2 +\log(\frac{R}{r})\) there is \(Vol(\mathcal E_t) \leq Vol(B(x_0,r))\) and +\(\{c_1,c_2,\cdots,c_t\} \cap \mathcal K \neq +\varnothing\). From now on we only consider the time that ensures +\(\{c_1,c_2,\cdots,c_t\} \cap \mathcal K \neq +\varnothing\).
+For fixed \(\varepsilon >0\), we +take \(\mathcal K_\varepsilon = +\{(1-\varepsilon)x^* + \varepsilon x \mid \forall x \in +B(x_0,r)\}\) as an affine transformation, in which \(x^*\) is the optimal solution of this +problem. Moreover we denote \(x_t \triangleq +\arg \min_{c_s \in \{c_0,c_1,\cdots, c_t\} \cap \mathcal K} +f(c_s)\).
+When we take \(\varepsilon = \frac{R}{r} +\exp(-\frac{t}{2n^2})\) there is \[Vol(\mathcal K_\varepsilon ) = \varepsilon^n +Vol(B(x_0,r)) = \varepsilon^n (\frac{r}{R})^n Vol(B(x_0^\prime ,R)) = +\exp(-\frac{t}{2n^2}) Vol(B(x_0^\prime, R)) > Vol(\mathcal +E_t)\]
+This inequality implies that there exists one time \(r \in \{1,2,\cdots,t\}\) s.t. there exists +\(x_\varepsilon \in \mathcal +K_\varepsilon\), \(x_\varepsilon \in +\mathcal E_{r-1}\), but \(x_\varepsilon +\notin \mathcal E_r\), therefore \(x_\varepsilon\) is not optimal. According +to the convexity of \(f(x)\), there is +\[f(x_t) < f(c_r) +\leq f(x_\varepsilon) = f((1-\varepsilon)x^* + \varepsilon x_r) \leq +(1-\varepsilon) f(x^*) + \varepsilon f(x_r) \leq f(x^*) + +2B\varepsilon,\] which implies that \[f(x_t) - f(x^*) \leq 2B\varepsilon = +\frac{2BR}{r} \exp(-\frac{t}{2n^2}).\]
+Then we can conclude that the algorithm converges in \(\mathcal O(n^2 \log(\frac{BR}{\varepsilon +r}))\) iterations to find an \(\varepsilon\) optimal solution, and the +desired result follows.
+Lecture 4
+睡了(,等个笔记((
+10.23 UPD:今天布置了个优化 HW3 +但又迅速删掉了,我也不知道为什么要同时把讲义也删掉,当时正好在贴所以也没来得及下(。这助教是否也是一个优化算法控制的,要传就把所有的东西都传上来要删就全部删掉,来保证要么所有人都满意要么所有人都不满意(。
+Convex Optimization
+Notations
+#每日迷神
+
-
-
\(t\) Distribution:
-\(t\) distribution with degree of -freedom \(n\):$ T==t_n$
-Upper \(\alpha\)-fractile of \(t_\nu\), satisfies \(\mathbb{P}(T\geq -c)=\alpha\),$t_{,}={c}(Tc)=,Tt$
-\(F\) Distribution:
-\(F\) distribution with degree of -freedom \(m\) and \(n\):$ F=F_{m,n}$
+- A set \(C \in \mathbb R^n\) is
+affine iff for any \(x,y \in C\) and
+any \(\theta \in \mathbb R\), there is
+\(\theta x + (1-\theta) y \in C\),
+therefore the whole line lies in \(C\).
-
-
- If \(Z\sim F_{m,n}\), then \(\dfrac{1}{Z}\sim F_{n,m}\); -
- If \(T\sim t_n\), then \(T^2\sim F_{1,n}\); -
- \(F_{m,n,1-\alpha}=\dfrac{1}{F_{n,m,\alpha}}\) -。 +
- Therefore, if \(C\) is an affine +set and \(x_0 \in C\), then the set +\(V = \{x-x_0 \mid \forall x \in C\}\) +is a subspace.
+ - An affine hull of \(C\) is denoted +as \(aff(C) = \{\theta_1 x_1+ \theta_2 +x_2+\cdots+ \theta_k x_k \mid \forall k \in \mathbb Z_+, x_i \in C, +\theta_i \in \mathbb R \}\) +
- The relative interior \(relint(C) = \{x\in +C \mid \exist r >0 , \text{s.t. } B(x,r) \cap aff(C) \subseteq C +\}\)
Some useful lemmas in statistical inference:
+简单来说,affine set/affine hull 和 convex +版本的唯一区别就是参数不需要取在 \([0,1]\) 之间,所以它一般是个平面。
-
-
For \(X_1,X_2,\ldots,X_n\) -independent with \(X_i\sim -N(\mu_i,\sigma^2_i)\), then \(\sum_{i=1}^n\left(\frac{X_i-\mu_i}{\sigma_i}\right)^2\sim -\chi^2_n\)
-For \(X_1,X_2,\ldots,X_n\) -i.i.d.\(\sim N(\mu,\sigma^2)\), then $ -T=t_{n-1} $
-For \(X_1,X_2,\ldots,X_m\) -i.i.d.\(\sim N(\mu_1,\sigma^2)\), \(Y_1,Y_2,\ldots,Y_n\) i.i.d.\(\sim N(\mu_2,\sigma^2)\),d enote sample -pooled variance \(S_{\omega}^2=\dfrac{(m-1)S^2_1+(n-1)S^2_2}{m+n-2}\), -then \(T=\frac{(\bar{X}-\bar{Y})-(\mu_1-\mu_2)}{S_{\omega}}\cdot -\sqrt{\frac{mn}{m+n}}\sim t_{m+n-2}\)
-For \(X_1,X_2,\ldots,X_m\) -i.i.d.\(\sim N(\mu,\sigma^2)\), \(Y_1,Y_2,\ldots,Y_n\) i.i.d.\(\sim N(\mu_2,\sigma^2)\), then -$T=F_{m-1,n-1} $
-For \(X_1,X_2,\ldots,X_n\) -i.i.d. \(\sim \varepsilon(\lambda)\), -then $ 2n{X}=2{i=1}^nX_i ^2{2n} $
-Remark:for \(X_i\sim\varepsilon(\lambda)=\Gamma(1,\lambda)\),\(2\lambda\sum_{i=1}^nX_i\sim\Gamma(n,1/2)=\chi^2_{2n}\).
+A set \(C\) is called a cone iff +\(\forall x \in C\) and for any \(\theta > 0\), there is \(\theta x \in C\).
+(Extended convex function) A function \(f : \mathbb R^n \to \mathbb R\) is convex, +we can extend its domain \(dom(f)\) to +\(\mathbb R^n\) by taking \(f(x) = \infty\) for any \(x \notin dom(f)\).
+(Epigraph of a function) \(epi(f) = +\{(x,t) \mid t \geq f(x)\}\)
+Therefore \(f\) is a convex function +if and only if \(epi(f)\) is a convex +set.
+
Basic Theorems
+-
+
(Seperating Hyperplane Theorem) Suppose \(C,D\) are nonempty disjoint convex sets, +then there exists \(a \neq 0\), \(a,b \in \mathbb R^n\) s.t. \(C \subseteq \{x \in \mathbb R^n \mid a^Tx \leq +b\}\) and \(D \subseteq \{x \in \mathbb +R^n \mid a^Tx \geq b\}\).
+Proof: We only consider the case when \(C,D\) are both closed and bounded.
+Define \(dist(C,D) = \inf\{\|u-v\|_2 \mid u +\in C,v \in D \}\) as the distance between \(C,D\), then by closed and boundness we can +find \(c \in C, d \in D\) s.t. \(dist(C,D) = \|c-d\|_2\). Take \(a = d-c\), \(b = +\frac 1 2 (\|d\|_2^2 - \|c\|_2^2)\).
+Then the affine transformation \(f(x) = +a^Tx - b\) will let \(f(x) +<0\) for any \(x \in D\), and +\(f(x) >0\) for any \(x \in C\).
+(Supporting Hyperplane Theorem) Suppose \(C\) is convex, then for any \(x \in bd(C)\) here exists a supporting +vector \(a \neq 0, a \in \mathbb R^n\), +s.t. \(\forall x \in C\), \(a^Tx_0 \leq a^Tx\). (\(bd(C)\) is the boundary of \(C\))
+
别的没什么了,convex function +的性质什么的真没必要再写一遍了,他又不讲 subgradient。
+Lecture 5
+才隔了两周,今天怎么又是哥们在做 scribing 啊(。read-only 的链接在这里。
+今天讲一些 convex optimization 里的例子,给哥们整的一愣一愣的。
+Examples in Convex +Optimization
+Notations
+#每日迷神
+
你还别说现在还真不一定书上都有了,那个 max cut 给哥们整不会了,Boyd +上面没写,Bubeck 就写了一点而且还把课上的内容跳过去了。而且 Bubeck +本来就简略,看了个寂寞。
+-
+
The following optimization problem is called a convex +optimization problem if \(x_0, f_i\) +are convex, and \(h_i\) are linear:
+\[\begin{aligned} +\textbf{minimize} \quad & f_0(x) \\ +\textbf{subject to} \quad & f_i(x) \leq 0 \\ +& h_i (x) =0 +\end{aligned}\]
+\(x\) is a \(\varepsilon\)-suboptimal if \(f_0(x) \leq p^* + \varepsilon\), in which +\(p^*\) is the optimal value of the +convex optimization problem.
+\(x_0\) is locally optimal if +there exists \(R >0\) s.t. \(x_0\) is the optimal solution to:
+
\[\begin{aligned} + \textbf{minimize} \quad & f_0(x) \\ + \textbf{subject to} \quad & f_i(x) \leq 0 \\ + & h_i (x) =0 \\ + & \|x-x_0\| \leq R \end{aligned}\]
+Why Convex Optimization?
+为什么研究凸优化?一个是 linear programming problem +有它的局限性,许多问题只能往凸优化的方向转化。另外凸性质实际上是非常美妙的。下面是一个很 +trivial 的例子,我们对 convex optimization +的转化问题的探究远不止于此。
+Why is convex optimization important? That's because some non-convex +problems have underlying convexity. For example, we consider the +following optimization problem:
+\[\begin{aligned} +\textbf{minimize} \quad & f_0(x)=x_1^2+x_2^2 \\ +\textbf{subject to} \quad & f_1(x) = \frac{x_1}{1+x_2^2} \leq 0 \\ +& h_i (x) = (x_1+x_2)^2 =0 +\end{aligned}\]
+which can easily be transformed into a standard convex optimization +problem.
+Example: Max Cut Problem
+别 TCS 了求你了求你了求你了(
+通过一个 max cut problem 来体现从 nonconvex optimization 向 convex +optimization 的转化,从方法论的层面上来说是两步。
+Why are convex optimization problems important? That's because many +non-convex optimization problems can be transformed into convex ones, +and we can solve convex optimization problems through mature +technologies. Generally speaking, the process contains two steps:
+-
+
- First, transform the non-convex problem into convex ones through +relaxation. +
- Next recover a solution from the convex problem to the non-convex +one through random rounding. +
Notations
+-
+
- A cut in an undirected graph \(G = (V, +\mathcal E)\) is defined as \(A +\subseteq V\).The capacity of a cut \(A\) is defined as \(c(A) = | \{(u,v)\in \mathcal E \mid u \in A, u \in +A^c\}|\). +
而 max cut 问题就是寻找最大的 \(c(A)\),尽管我不知道这样做有什么意义,但它是 +NP-hard 的。所以我们只需要找到一个 polynomial time +的算法就可以证明...(逃
+-
+
- An \(\alpha\)-approximate max cut +is a cut \(A\) s.t. \(c(A) \geq \alpha \max_{U \subseteq V} +c(U)\). +
\(\frac +1 2\)-Approximate Approach
+怎么是概率做法,真稀奇。
+To be more specific, we can give a \(\frac{1}{2}\)-approximate max cut by +randomly adding each point \(v\) in +\(V\) to the cut \(A\) with probability \(\frac{1}{2}\). Consider the expectation of +\(c(A)\) here and we can get:
+\[\mathbb E_A(c(A)) = \mathbb E_A +\sum_{(u,v)\in \mathcal E} 1_{(u \in A,v \in A^c)} = \sum_{(u,v) \in +\mathcal E} P(u \in A, v \in A^c) = \sum_{(u,v) \in \mathcal E} +\frac{1}{2} = \frac{|\mathcal E|}{2}.\]
+然而这还是很粗糙。
+Linear Approach
+如果没有 convex optimization 的话就是考虑一些 linear programming +的近似,举两个失败的 approach 说明这很困难:
+-
+
Consider the following formulation of the problem:
+\[\begin{aligned} + \textbf{maximize}_{x\in \mathbb R^n} \quad & \sum_{(u,v)\in +\mathcal E} \frac{1}{2}(1-x_ux_v) \\ + \textbf{subject to} \quad & x_v \in \{-1,1\} +\end{aligned}\]
+This is not a linear programming problem, and we can transform it +by denoting \(z_e = x_ux_v, e=(u,v) \in +\mathcal{E}\):
+\[\begin{aligned} + \textbf{maximize}_{x,z} \quad & \sum_{e \in E} \frac{1}{2 } +(1-z_e) \\ + \textbf{subject to} \quad & z_{(u,v)} \geq -x_u -x_v -1 \\ + & z_{(u,v)} \geq x_u +x_v -1 \\ + & x_v \in [-1,1] +\end{aligned}\]
+
However, this still fails for we can choose \(x_v =x_u=0\) and \(z_{(u,v)} =-1\) in the feasible set, which +means the approach will only give a randomized choice of \(A\). Now turn to convex optimization for +help.
+Convex Transformation
+-
+
The basic idea is to replace \(x_u.x_v\) with \(n-1\) dimensional vectors and construct an +auxiliary problem, which is called semi-definite relaxation:
+\[\begin{aligned} + \textbf{maximize} \quad & \sum_{(u,v) \in \mathcal E} +\frac{1}{2} (1-x_u^Tx_v) \\ + \textbf{subject to} \quad & x_u \in S^{n-1} \text{ for any +}u=1,2,\cdots,n +\end{aligned}\]
+in which \(S^{n-1}\) is the unit +sphere in \(\mathbb R^{n-1}\). Observe +that \(\frac{1}{4}\|x_u-x_v\|^2 =\frac{1}{4} +(x_u -x_v)^T(x_u-x_v) = \frac{1}{2} (1-x_ux_v)\), and \(\frac{1}{2} \sum_{e \in \mathcal E} (1-z_e) = +\frac{1}{4} \sum_{(u,v)\in \mathcal E} \|x_u - x_v\|^2\).
+Now we take \(\text{Maxcut}^\circ +(C)\) as the optimal cost of the auxiliary problem and denote +\(\text{Maxcut} (C)\) as the optimal +cost of the original problem. Then there is \(\text{Maxcut} (C) \leq \text{Maxcut}^\circ +(C)\) because any optimal solution of the original problem can be +transformed into a feasible solution in the auxiliary one.
+To be more precise, if \(\{x_u\}\) +is an optimal solution to the original problem, then for any \(x_u = 1\) there is \(x_v = -1\) for each \(v \in \{v \mid (u,v) \in \mathcal E\}\). +Therefore we can take \(x_u = e_1\), +\(x_v = -e_1\) for any \(v \in \{v \mid (u,v) \in \mathcal E\}\) as +a feasible solution to the auxiliary problem, and the cost is equal to +the optimal cost of the original one.
+However the auxiliary problem is still non-convex, we'd like to +consider another optimization problem as follows:
+\[\begin{aligned} + \textbf{minimize} \quad & X \cdot A = \sum_{i,j \in V} X_{ij} +A_{ij} \\ + \textbf{subject to} \quad & X \geq 0 \; \\ + & X_{ii}=1 +\end{aligned}\]
+in which \(X \geq 0\) means \(X\) is semi-definite, i.e. \(X \in S_+^n, X \in \mathbb R^{n \times +n}\).
+We set \(A_{ij}=1\) if \((i,j) \in \mathcal E\), else \(A_{ij}=0\). Now we prove that the two +problems above are equivalent.
+The following two max-cut optimization problems are +equivalent:
分位数速查
-来自 Package stats, version 4.2.1。
-其实都可以直接查文档啦(,R 的文档还是很保姆式的。
-t-分布模拟
-t-distribution 下有四个函数,分别是 density, CDF, quantile -function(\(CDF^{-1}\)),还有一个是随机生成一个模拟数组。
-dt(x, df, ncp, log = FALSE) 用来计算 PDF 的函数值 \(f(x)\),df 是自由度,ncp 表示非中心化参数
-\(\delta\);
pt(x, df, ncp, lower.tail = TRUE, log.p = FALSE)
-用来计算 CDF 的函数值 \(F(x)\),注意
-lower.tail = TRUE 时计算的是左边值 \(F(x)\),否则实际计算了 \(1-F(x)\)。
qt(p, df, ncp, lower.tail = TRUE, log.p = TRUE)
-用来计算分位数,也即 \(F^{-1}(p)\),其他参数意义同上。
一些我的作业里的函数参考:
-> qt(1 - 0.025, df = 8) |
这里计算的是 \(t_{8,0.975}\) -的下分位数,实际上是一个 level of significance 为 \(0.05\) 的双尾检验中用到的分位数。
-> 2 * pt(-8.529, df = 8) |
这里是在计算一个 P-value,计算的是比 observed data \(-8.529\) 更极端的数据的出现概率,单边是 -\(F (-8.529)\),注意此处的“极端”包含比 -\(-8.529\) 更小和比 \(8.529\) 更大这两种情况,实际上是 \(F(-8.529) + 1- F(8.529)\)。
-由于 t-distribution 是对称的,可以简化为 \(2 \times F(-8.529)\)。
-> ncp <- 2.0/0.50 |
这是一个非中心的 t 检验,实际上是在计算 Power Function。
-正态分布模拟
-常用的三个函数是
-dnorm,pnorm,qnorm,含义与
-t-分布中的 dt,pt,qt 相似。
dnorm(x, mean = 0, sd = 1, log = FALSE) |
注意一般正态检验中都是使用标准正态分布,也就是不需要去改变
-mean 和 sd 的默认值。
> pnorm(0) |
F-分布模拟
-df(x, df1, df2, ncp, log = FALSE) |
注意 \(F\)
-分布的两个自由度都可以取到无穷,写作 df1 = Inf。
Chi-square 分布模拟
-dchisq(x, df, ncp = 0, log = FALSE) |
其他常用 R 命令
-持续更新中,基本都是作业里扒出来的。
-confidence interval
-confint(object, parm, level = 0.95, ...) |
注意 confidence coefficient 的默认值是 \(0.95\),confint
-函数是用于拟合模型参数的置信区间估计,例如:
model <- lm(data) |
2.5 % 97.5 % |
这个附录怎么全咕了啊,不过无所谓了,这课我本来就是在摆烂(
-完结撒花
-一点都不 happily ever -after,说是找到了新的方向,谁知道概率又会不会很艰难呢。
-这课明显东西比统计推断多,但是导出成 PDF -一看比统推笔记少了二十多页。
-总之都结束了,笑一个吧(
-
\[\begin{aligned} + \textbf{maximize} \quad & \sum_{(u,v) \in \mathcal E} +\frac{1}{2} (1-x_u^Tx_v) \\ + \textbf{subject to} \quad & x_u \in S^{n-1} \\ + \\ + \end{aligned} \quad \quad \quad + \begin{aligned} + \textbf{minimize} \quad & X \cdot A = \sum_{i,j \in V} +X_{ij} A_{ij} \\ + \textbf{subject to} \quad & X \geq 0 \; \\ + & X_{ii}=1 + \end{aligned}\]
+Proof: Note that \(X_{ij} += x_i^T x_j\) (and sometimes \(X\) is called the gram matrix), +therefore
+\[\begin{aligned} + X \in S_+^n \text{ is feasible } & \iff X_{ij}=1 \text{ +for any } i \in V \\ + & \iff \|x_u \|=1 \text{ for any } u \in V \\ + & \iff x_u \in S^{n-1} \text{ for any } u \in V + \end{aligned}\]
+and the desired result follows.
]]>process_data 函数中:(20 p.t.s)
-
-
- 构建
image_dir与 -label_dir(pathlib.Path)
- - 构建
-
filename_list(os.listdir,对字符串切片取消后缀名)
- - 将处理后的字符串写入
{working_dir}/file.txt-(写入文件)
-
calc_label 函数中:(20 p.t.s)
--
-
- 按照函数注释中的内容完成函数 -
- 正确的做法预处理
train数据集中的数据应该在 10 min -以内完成
- - 提示:将
label视为传统的二维数组进行遍历需要至少 1024 -\(\times\) 768 次计算,而这在 8000 -张图片上运行会导致处理效率的降低
- - 提示:能否借助 NumPy 中的工具进行高效并行计算? -
- 提示:
np.isin,np.sum
-
打开 train/labels,哇塞都好黑啊。
打开 datasets/dataset_landscape_generator.py
-研究了亿下,总之就是填四个函数,注释给得已经很清楚了。一个是利用 NumPy
-打标签,写了半天循环才想起来可以直接使用表达式的值。然后没理解错的话就是写个路径,存所有图片的文件名,然后把标签结果的
-.txt 输出到 data/imgs里去。
大概看懂了思路是什么,不需要自己写的地方的具体实现有的还是不太明白。不过程序跑出来的时候还是有点又惊讶又激动的,原来我也可以做到的吗XD。(站在巨人的肩膀上XD(这还只是个开始
-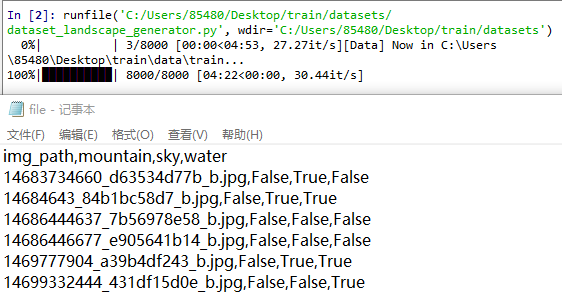
Subtask 2 及以后
-Repo -上的最新代码是已经填好大部分的版本,部分地方微调了一下。然后就是疯狂读文档试图理解他在干什么,虽然也没全懂...。
-但是因为显卡的问题,所以都是在友人的电脑上完成的,也不写啥了。
-提交结果
-
唔...因为很怂所以甚至没有用自己的学号提交...本来想用 2021114514 -的,但是怎么偏偏 ban 了这个啊!
-
交上去之后一想,好像确实也有用这个学号的人,再一查正好是同一个院系里的,啊这。那就让你赚点暑培奖励吧
虽然是满分(因为平均过 0.80 了),但因为 Mountain 实在偏低所以没过 -Strong -Baseline。自己的设备不合适也没什么机会再调了,要么下次再把友人骗出来一次 -= =。
-后记
-在考虑再试一次,然后用自己的学号提交...为什么总是在这些事情上这么自卑呢 -= =
-虽然理论水平不行,但是能跑出个结果倒是还挺好玩。
-显卡要熟了
反正不是我自己的
后记再后记
-又修了一天电脑,然后把 Anaconda 卸了,皈依 VSCode -神教。怀疑之前怎么换源都装不上 PyTorch 是因为 Anaconda -污染路径,其实类似问题还蛮多的,感觉很难解决,没必要。
-大概就是拎包入住的公寓和需要自己装修的房子的区别吧。
-今天又试着调了参,分数怎么比原来更低了(乐
-还是没能以自己的名义交上去,做不到。
-最后的后记
-仓促之中调整的还是不够,所以想试着在自己的电脑上用 A 卡跑出来。
-所以巧合之下发现原来的 main.py
-还写错了一个地方,是不是觉得没有人会真的用 A 卡或者 Mac
-跑这个x。
# main.py |
然后真的是结结实实地跑了十轮,十个小时。从早晨跑到晚上。这一天就当做给自己放假了,坐在电脑旁边读了一直想读的两本书,一本是毛姆的《面纱》,一本是钱穆的《中国历代政治得失》。
-不插电源的话一张图跑 5~6s,插电只要 3.5s -左右。一开始没插电源,电量下去之后一度飙到了 6.5s,有点吓到。
-最后还是没能过 Strong
-Baseline,数据其实也没有之前那一次的好,但是用自己的学号提交了。人类是有极限的
-A 卡是有极限的,一轮一小时的话实在是跑不动,所以就先这样了。
一些奇怪的散热方式:
-
下面垫的是数值分析和抽代的书(
-
鸠占鹊巢,于是我坐在了地上(
-刚在原仓库下提交了
-Issue,总感觉对方好像没意识到问题其实只是在于,这个值应该是
-int 而不是str而已(。不过也不太会有人用 CPU
-硬跑了,就这样吧。
总之完结撒花!
-]]> -退役两年人员写几何题快裂开了,从来没觉得做题这么难过。但是蛮好玩的,什么叫思维体操啊(
-只做了一点微小的贡献,谢谢大家。
- -


显然,本人不善几何。尤其是自己的通讯地址变成华子之后水平骤降,每次都是替大家扫水题,然后排最后一个。其实这次论数量论质量都应该是排第四的,但是为了给新成员让路所以还是排最后了...啊就这样吧
-XD,也不重要。还是看看远处的 SRT 吧家人们
在新星发文章的最高记录是二作,大概是 2020 Vietnam Mathmatics -Olympic。成员们来来去去,最年轻的也马上高三了,或许是最后一次合作,起码我应该不会再参加了。
-第一次在电脑上用 Geogebra,之前都是在手机上用,电脑上用 -Sketchpad。Geogebra 上手莫名很快,手感也很熟悉,再一想发现快捷键和 -AutoCAD 一模一样,这下职业病了。然后也是第一次尝试用 tikz 在 LaTeX -文档里插图,感觉还挺好用,赞美。
-另外,谁能想到我五个几何题做了一天呢(思维体操,思维体操.jpg
-8-1
-非常水,我甚至能 15 分钟解决(
-Sharygin2022.pdf(策划不给源代码,可恶(?
-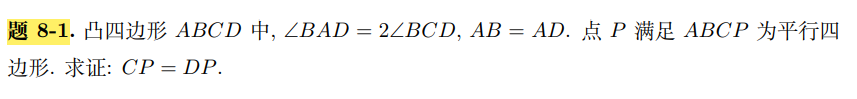
Sharygin-by-Chiyuru.tex
-\textbf{8-1 证明:}取$\triangle BCD$的外心为$O$.于是有$OB=OD,AB=AD$,由于 |
8-1.ggb(tikz 看起来丑丑的?
-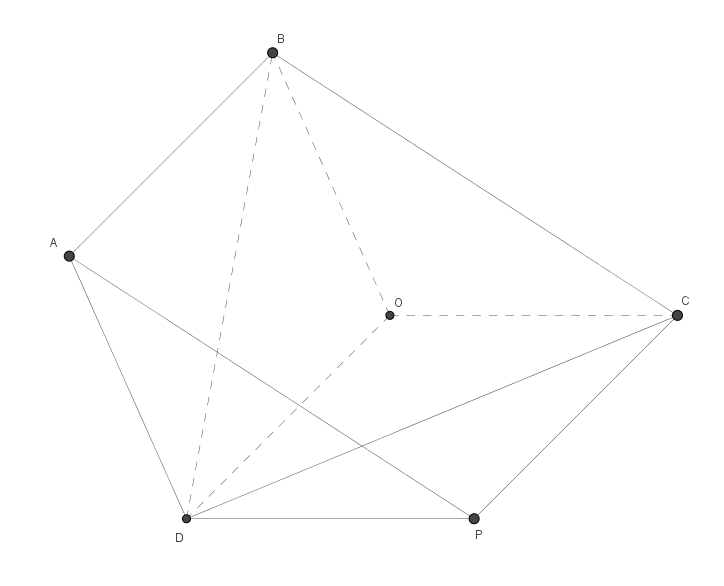
8-2
-稍微有点痛,但是也还好,还是水题。
-Sharygin2022.pdf
-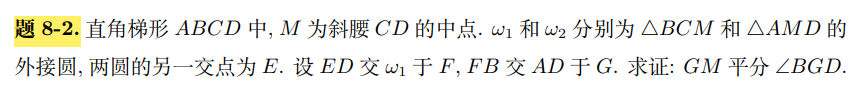
Sharygin-by-Chiyuru.tex
-\textbf{8-2 证明:}取$\omega_1$与$AB$的交点为$E'$. |
8-2.ggb
-
策划说他写了个脚本批量修改 tikz 的格式,我们只要交个 .ggb -就好了。所以我前两张图的线粗细都不一样,测试一下(
-8-4
-这个题太痛了,我想了有一个多小时,然后发现自己好傻。
-Sharygin2022.pdf
-
Sharygin-by-Chiyuru.tex
-\textbf{8-4 证明:}取$\astrosun (OPN)$ 和$CD$的另一交点为$S$,$\astrosun (OPM)$和$AB$的另一交点为$T$. |
《迎 刃 而 解》
-8-4.ggb
-
8-7
-这个最痛。组合几何,尤其是答案都出乎意料的组合几何,太痛了(
-Sharygin2022.pdf
-
Sharygin-by-Chiyuru.tex
-\textbf{8-7 解:}否。证明如下: |
8-7.ggb
-
9-1
-这不比前面的都简单太多了?.jpg
-Sharygin2022.pdf
-
Sharygin-by-Chiyuru.tex
-\textbf{9-1 证明:} |
9-1.ggb
-
后记与碎碎念
-等到发表了(可能会拖到十月、十一月?)再来补个后记。其实就是丢个链接和文档,权当记录了。
-看到行在清华公众号发的推文,才知道北京已经凉快些了,是初秋。上海还是每天都 -40°C 左右,热得好难受。
-这么说来,快要回去了。
-后后记:Update 8-6
-这个锅甩来甩去又回到了我手上,不会做,晚上把它翻译好了。
-摸到了倒数第二作x。
-Sharygin2022.pdf
-
Sharygin-8-6-by-Chiyuru.tex
-\textbf{8-6 解:}我们首先给出作图方式: |
8-6.ggb
-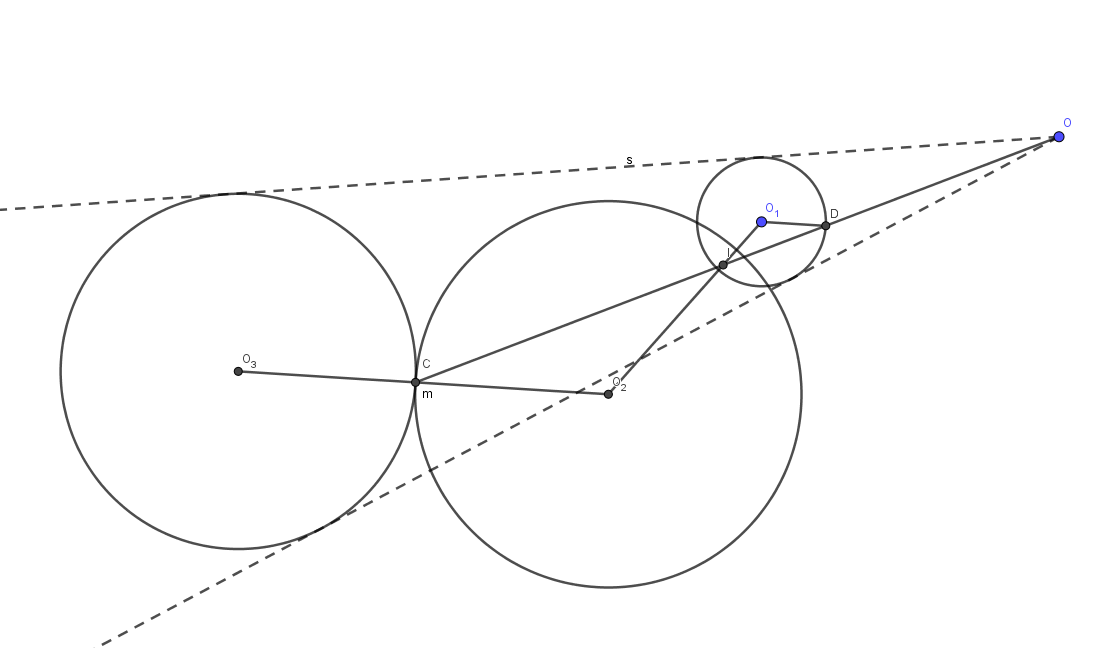
image_dir 与
+label_dir(pathlib.Path)filename_list(os.listdir,对字符串切片取消后缀名){working_dir}/file.txt
+(写入文件)calc_label 函数中:(20 p.t.s)
+-
+
- 按照函数注释中的内容完成函数 +
- 正确的做法预处理
train数据集中的数据应该在 10 min +以内完成
+ - 提示:将
label视为传统的二维数组进行遍历需要至少 1024 +\(\times\) 768 次计算,而这在 8000 +张图片上运行会导致处理效率的降低
+ - 提示:能否借助 NumPy 中的工具进行高效并行计算? +
- 提示:
np.isin,np.sum
+
打开 train/labels,哇塞都好黑啊。
打开 datasets/dataset_landscape_generator.py
+研究了亿下,总之就是填四个函数,注释给得已经很清楚了。一个是利用 NumPy
+打标签,写了半天循环才想起来可以直接使用表达式的值。然后没理解错的话就是写个路径,存所有图片的文件名,然后把标签结果的
+.txt 输出到 data/imgs里去。
大概看懂了思路是什么,不需要自己写的地方的具体实现有的还是不太明白。不过程序跑出来的时候还是有点又惊讶又激动的,原来我也可以做到的吗XD。(站在巨人的肩膀上XD(这还只是个开始
+
Subtask 2 及以后
+Repo +上的最新代码是已经填好大部分的版本,部分地方微调了一下。然后就是疯狂读文档试图理解他在干什么,虽然也没全懂...。
+但是因为显卡的问题,所以都是在友人的电脑上完成的,也不写啥了。
+提交结果
+
唔...因为很怂所以甚至没有用自己的学号提交...本来想用 2021114514 +的,但是怎么偏偏 ban 了这个啊!
+
交上去之后一想,好像确实也有用这个学号的人,再一查正好是同一个院系里的,啊这。那就让你赚点暑培奖励吧
虽然是满分(因为平均过 0.80 了),但因为 Mountain 实在偏低所以没过 +Strong +Baseline。自己的设备不合适也没什么机会再调了,要么下次再把友人骗出来一次 += =。
+后记
+在考虑再试一次,然后用自己的学号提交...为什么总是在这些事情上这么自卑呢 += =
+虽然理论水平不行,但是能跑出个结果倒是还挺好玩。
+显卡要熟了
反正不是我自己的
后记再后记
+又修了一天电脑,然后把 Anaconda 卸了,皈依 VSCode +神教。怀疑之前怎么换源都装不上 PyTorch 是因为 Anaconda +污染路径,其实类似问题还蛮多的,感觉很难解决,没必要。
+大概就是拎包入住的公寓和需要自己装修的房子的区别吧。
+今天又试着调了参,分数怎么比原来更低了(乐
+还是没能以自己的名义交上去,做不到。
+最后的后记
+仓促之中调整的还是不够,所以想试着在自己的电脑上用 A 卡跑出来。
+所以巧合之下发现原来的 main.py
+还写错了一个地方,是不是觉得没有人会真的用 A 卡或者 Mac
+跑这个x。
# main.py |
然后真的是结结实实地跑了十轮,十个小时。从早晨跑到晚上。这一天就当做给自己放假了,坐在电脑旁边读了一直想读的两本书,一本是毛姆的《面纱》,一本是钱穆的《中国历代政治得失》。
+不插电源的话一张图跑 5~6s,插电只要 3.5s +左右。一开始没插电源,电量下去之后一度飙到了 6.5s,有点吓到。
+最后还是没能过 Strong
+Baseline,数据其实也没有之前那一次的好,但是用自己的学号提交了。人类是有极限的
+A 卡是有极限的,一轮一小时的话实在是跑不动,所以就先这样了。
一些奇怪的散热方式:
+
下面垫的是数值分析和抽代的书(
+
鸠占鹊巢,于是我坐在了地上(
+刚在原仓库下提交了
+Issue,总感觉对方好像没意识到问题其实只是在于,这个值应该是
+int 而不是str而已(。不过也不太会有人用 CPU
+硬跑了,就这样吧。

总之完结撒花!
]]>退役两年人员写几何题快裂开了,从来没觉得做题这么难过。但是蛮好玩的,什么叫思维体操啊(
+只做了一点微小的贡献,谢谢大家。
+ +


显然,本人不善几何。尤其是自己的通讯地址变成华子之后水平骤降,每次都是替大家扫水题,然后排最后一个。其实这次论数量论质量都应该是排第四的,但是为了给新成员让路所以还是排最后了...啊就这样吧
+XD,也不重要。还是看看远处的 SRT 吧家人们
在新星发文章的最高记录是二作,大概是 2020 Vietnam Mathmatics +Olympic。成员们来来去去,最年轻的也马上高三了,或许是最后一次合作,起码我应该不会再参加了。
+第一次在电脑上用 Geogebra,之前都是在手机上用,电脑上用 +Sketchpad。Geogebra 上手莫名很快,手感也很熟悉,再一想发现快捷键和 +AutoCAD 一模一样,这下职业病了。然后也是第一次尝试用 tikz 在 LaTeX +文档里插图,感觉还挺好用,赞美。
+另外,谁能想到我五个几何题做了一天呢(思维体操,思维体操.jpg
+8-1
+非常水,我甚至能 15 分钟解决(
+Sharygin2022.pdf(策划不给源代码,可恶(?
+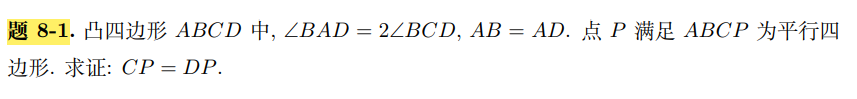
Sharygin-by-Chiyuru.tex
+\textbf{8-1 证明:}取$\triangle BCD$的外心为$O$.于是有$OB=OD,AB=AD$,由于 |
8-1.ggb(tikz 看起来丑丑的?
+
8-2
+稍微有点痛,但是也还好,还是水题。
+Sharygin2022.pdf
+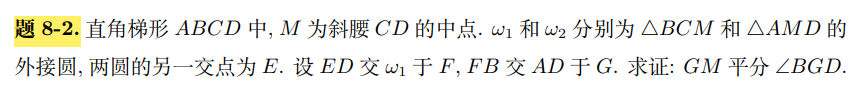
Sharygin-by-Chiyuru.tex
+\textbf{8-2 证明:}取$\omega_1$与$AB$的交点为$E'$. |
8-2.ggb
+
策划说他写了个脚本批量修改 tikz 的格式,我们只要交个 .ggb +就好了。所以我前两张图的线粗细都不一样,测试一下(
+8-4
+这个题太痛了,我想了有一个多小时,然后发现自己好傻。
+Sharygin2022.pdf
+
Sharygin-by-Chiyuru.tex
+\textbf{8-4 证明:}取$\astrosun (OPN)$ 和$CD$的另一交点为$S$,$\astrosun (OPM)$和$AB$的另一交点为$T$. |
《迎 刃 而 解》
+8-4.ggb
+
8-7
+这个最痛。组合几何,尤其是答案都出乎意料的组合几何,太痛了(
+Sharygin2022.pdf
+
Sharygin-by-Chiyuru.tex
+\textbf{8-7 解:}否。证明如下: |
8-7.ggb
+
9-1
+这不比前面的都简单太多了?.jpg
+Sharygin2022.pdf
+
Sharygin-by-Chiyuru.tex
+\textbf{9-1 证明:} |
9-1.ggb
+
后记与碎碎念
+等到发表了(可能会拖到十月、十一月?)再来补个后记。其实就是丢个链接和文档,权当记录了。
+看到行在清华公众号发的推文,才知道北京已经凉快些了,是初秋。上海还是每天都 +40°C 左右,热得好难受。
+这么说来,快要回去了。
+后后记:Update 8-6
+这个锅甩来甩去又回到了我手上,不会做,晚上把它翻译好了。
+摸到了倒数第二作x。
+Sharygin2022.pdf
+
Sharygin-8-6-by-Chiyuru.tex
+\textbf{8-6 解:}我们首先给出作图方式: |
8-6.ggb
+
在 Hello
+World!和 About
+里就提到过,我有很多游戏的坑。音游有
+Lanota、Arcaea,抽卡类塔防有明日方舟,其实也玩过若干国产乙女游戏,若干
+GalGame,棋牌类有雀魂,还有不知道该怎么分类的 Fate/Grand
+Order(FGO)。每次玩着玩着就会回到 FGO
+去,可能是别的游戏都有或挺大或不小的圈子,而半死不活的 FGO
+没有。即使有,想要无视也很容易,因为身边没有玩 FGO 的朋友了。
五月初的时候方舟周年庆,于是一年一度回了坑,兴趣高涨。体验了一下这一年来漏掉的活动,新的肉鸽系统和保全派驻,还毕业了尘影余音这个不大不小的活动。只不过因为同学在七月新活动更新的时候,发消息讲了几句他已经打完第一波关卡看完剧情了,我就突然感觉无趣,草草卸载开始冬眠。就是一瞬间,开始对这个“需要"每天上线刷材料、和友人互动讨论玩梗、肝新剧情的系统感到疲倦。下次再来,可能就是明年五月了,也可能更晚。
+然后很快就是 Arcaea 4.0
+更新,更新之后的早晨大家惊呼对立被光反杀,我才知道两年后的今天终于有新剧情和突破既有定数的新歌了。然后今天上推偶然知道刺球(@SkisK刺球)抢到了
+Testify BYD 全球首 PM(-33)和收到官方恭喜,更新后的几天内没有其他
+PM,更是离理论值很远。看了一眼手元,感觉真的非常科幻,我一辈子可能也不会碰到这张谱了吧。另外,官方的意思是全球范围内有PM就复活对立吗
很久不玩 Arcaea +了主要是因为条件不允许。在学校的话不想日常在寝室里表演爆敲手机屏,感觉会很吵。只是假期玩的话水平也上不去,所以偶尔想打歌了的话下回来敲一敲就好。“身边”玩音游的大多是以前的高中同学,不过我已经主动在母校毕业生中隐藏自己了,屏蔽和退出了一些群,不太像以前一样和他们互动,也就渐渐被忘记了;还有你清的一些音游人,都比我强很多,一般就是偶尔聊起来,或者碰巧刷到他们的视频。尽管你清音游相关社团印象里在我高中时就听说和憧憬过,但现如今也没有加入的打算。事实上,到现在为止我没有加入过任何社团,可能以后也不会。
+乙女游戏更容易厌倦,我也不是去体验恋爱的,单纯是欣赏一下美工;剧情也还算有点意思。不过国乙的通病还得是不氪金就当狗和任务繁琐,回坑很快就觉得像上班一样,没意思了。GalGame +因为太挑剔,很难遇到喜欢的作品,朋友的推荐大多数也不合胃口,试错试多了就麻了。
+雀魂的话, +惭愧地说我不是很会打。寒假的时候三人场刷到雀士然后发现还会掉回去,觉得好累,就没再上线过了。身边打雀的朋友人均很强,也没人注意到本菜狗的悄悄跑路。
+总之到最后就是会跑回 FGO。从前一起玩 FGO +的朋友现在无一例外都弃坑了,而且都再也没回去过,缺乏社交性反而很惬意;活动关卡打不打也很无所谓,许多活动都是复刻,四五年前就体验过了;老玩家的原因,材料资源很充足,不需要肝,一段时间不登录也不会天塌下来;型月世界的设定很复杂,游戏和不同线路的番剧会相互呼应,刷着番打游戏体验很好(指路型月我最喜欢的一条线《Fate/EXTRA Last +Encore》);另外,因为是手游的原因,很轻量。
+其中最要紧的还是“缺乏社交性”这一项。本来就不是很擅长社交,也不太想为了跟上朋友们讨论的梗而去打活动,不想再听到“你怎么跳过剧情啊,方舟的精髓就是剧情”这种评论。有的时候很疲惫了来玩游戏,就是只想暴力打打关卡而已。为了维持社交而每日登录、互动、活动肝到毕业这样的烦恼更是没有了。关卡也没有特别难的,要么蓝卡队总能苟过去,不能的话就不打了,反正也没有什么很特别的奖励。感兴趣的话可以看看 +B 站的花式打法,只是不知道这几年过去还有多少 up 在做这方面的视频。
+还记得初三的暑假在地铁上打 +FGO,有个上海大学的路人小哥激动地叫住我想看看我的 +box,只可惜我是小米渠道服,没有加到他的好友。或许当时这个游戏就已经不是那么热门了。
+说了这么多,一句话总结的话,就是:
+++我又社恐自闭了。
+
如果再要加一句,那就是:
+++]]>我觉得“连打游戏都在摆烂”其实是一件很正常的事情。
+
在 Hello
-World!和 About
-里就提到过,我有很多游戏的坑。音游有
-Lanota、Arcaea,抽卡类塔防有明日方舟,其实也玩过若干国产乙女游戏,若干
-GalGame,棋牌类有雀魂,还有不知道该怎么分类的 Fate/Grand
-Order(FGO)。每次玩着玩着就会回到 FGO
-去,可能是别的游戏都有或挺大或不小的圈子,而半死不活的 FGO
-没有。即使有,想要无视也很容易,因为身边没有玩 FGO 的朋友了。
五月初的时候方舟周年庆,于是一年一度回了坑,兴趣高涨。体验了一下这一年来漏掉的活动,新的肉鸽系统和保全派驻,还毕业了尘影余音这个不大不小的活动。只不过因为同学在七月新活动更新的时候,发消息讲了几句他已经打完第一波关卡看完剧情了,我就突然感觉无趣,草草卸载开始冬眠。就是一瞬间,开始对这个“需要"每天上线刷材料、和友人互动讨论玩梗、肝新剧情的系统感到疲倦。下次再来,可能就是明年五月了,也可能更晚。
-然后很快就是 Arcaea 4.0
-更新,更新之后的早晨大家惊呼对立被光反杀,我才知道两年后的今天终于有新剧情和突破既有定数的新歌了。然后今天上推偶然知道刺球(@SkisK刺球)抢到了
-Testify BYD 全球首 PM(-33)和收到官方恭喜,更新后的几天内没有其他
-PM,更是离理论值很远。看了一眼手元,感觉真的非常科幻,我一辈子可能也不会碰到这张谱了吧。另外,官方的意思是全球范围内有PM就复活对立吗
很久不玩 Arcaea -了主要是因为条件不允许。在学校的话不想日常在寝室里表演爆敲手机屏,感觉会很吵。只是假期玩的话水平也上不去,所以偶尔想打歌了的话下回来敲一敲就好。“身边”玩音游的大多是以前的高中同学,不过我已经主动在母校毕业生中隐藏自己了,屏蔽和退出了一些群,不太像以前一样和他们互动,也就渐渐被忘记了;还有你清的一些音游人,都比我强很多,一般就是偶尔聊起来,或者碰巧刷到他们的视频。尽管你清音游相关社团印象里在我高中时就听说和憧憬过,但现如今也没有加入的打算。事实上,到现在为止我没有加入过任何社团,可能以后也不会。
-乙女游戏更容易厌倦,我也不是去体验恋爱的,单纯是欣赏一下美工;剧情也还算有点意思。不过国乙的通病还得是不氪金就当狗和任务繁琐,回坑很快就觉得像上班一样,没意思了。GalGame -因为太挑剔,很难遇到喜欢的作品,朋友的推荐大多数也不合胃口,试错试多了就麻了。
-雀魂的话, -惭愧地说我不是很会打。寒假的时候三人场刷到雀士然后发现还会掉回去,觉得好累,就没再上线过了。身边打雀的朋友人均很强,也没人注意到本菜狗的悄悄跑路。
-总之到最后就是会跑回 FGO。从前一起玩 FGO -的朋友现在无一例外都弃坑了,而且都再也没回去过,缺乏社交性反而很惬意;活动关卡打不打也很无所谓,许多活动都是复刻,四五年前就体验过了;老玩家的原因,材料资源很充足,不需要肝,一段时间不登录也不会天塌下来;型月世界的设定很复杂,游戏和不同线路的番剧会相互呼应,刷着番打游戏体验很好(指路型月我最喜欢的一条线《Fate/EXTRA Last -Encore》);另外,因为是手游的原因,很轻量。
-其中最要紧的还是“缺乏社交性”这一项。本来就不是很擅长社交,也不太想为了跟上朋友们讨论的梗而去打活动,不想再听到“你怎么跳过剧情啊,方舟的精髓就是剧情”这种评论。有的时候很疲惫了来玩游戏,就是只想暴力打打关卡而已。为了维持社交而每日登录、互动、活动肝到毕业这样的烦恼更是没有了。关卡也没有特别难的,要么蓝卡队总能苟过去,不能的话就不打了,反正也没有什么很特别的奖励。感兴趣的话可以看看 -B 站的花式打法,只是不知道这几年过去还有多少 up 在做这方面的视频。
-还记得初三的暑假在地铁上打 -FGO,有个上海大学的路人小哥激动地叫住我想看看我的 -box,只可惜我是小米渠道服,没有加到他的好友。或许当时这个游戏就已经不是那么热门了。
-说了这么多,一句话总结的话,就是:
---我又社恐自闭了。
-
如果再要加一句,那就是:
---]]>我觉得“连打游戏都在摆烂”其实是一件很正常的事情。
-