| 03 | Fundamental Data Structures |
Using Arrays:
Linked Lists:
|
| 04 | Algorithm Analysis |
Functions:

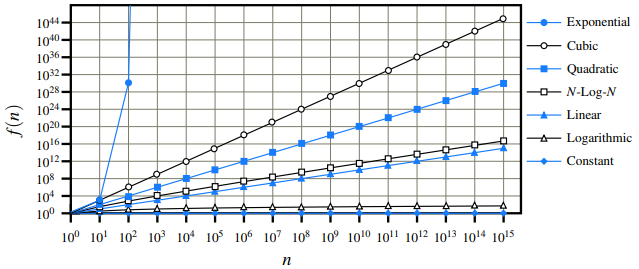
Seven functions commonly used in the analysis of algorithms. Note, logn = log2n. Also, we denote with a a constant greater than 1.
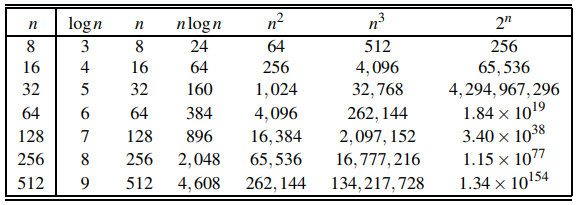
Example growth rates to show order of asymptotically betters algorithms.
- A constant function is a function whose (output) value is the same for every input value.
f(n) = c
Example code
- The logarithm function is the inverse function to exponentiation (power).
x = logbn if and only if bx = n.
The value b is known as the base of the logarithm. The most common base for the logarithm function in computer science is 2 as computers store integers in binary. In fact, this base is so common that we will typically omit it from the notation when it is 2:
logn = log2n
Example code
- The linear function:
f(n) = n
Given an input value n, the linear function f assigns the value n itself.
This function arises in algorithm analysis any time we have to do a single basic operation for each of n elements. For example, comparing a number x to each element of an array of size n will require n comparisons. The linear function also represents the best running time we can hope to achieve for any algorithm that processes each of n objects that are not already in the computer’s memory, because reading in the n objects already requires n operations.
Example code
- The N-Log-N function
f(n) = nlogn
Assigns to an input n the value of n times the logarithm base-two of n. This function grows a little more rapidly than the linear function and a lot less rapidly than the quadratic function; therefore, we would greatly prefer an algorithm with a running time that is proportional to nlogn, than one with quadratic running time.
Example code
- Quadratic function
f(n) = n2
Given an input value n, the function f assigns the product of n with itself (i.e., n squared).
There are many algorithms that have nested loops, where the inner loop performs a linear number of operations and the outer loop is performed a linear number of times. Thus, in such cases, the algorithm performs n * n = n2 operations
- The cubic function
f(n) = n3
Assigns an input value n the product of n with itself three times. The cubic function appears less frequently in the context of algorithm analysis than the constant, linear, and quadratic functions, but it does appear from time to time.
- The linear, quadratic and cubic functions can each be viewed as being part of a larger class of functions, the polynomials. A polynomial function has the form:
f(n) = a0 + a1n + a2n2 + a3n3 +···+ adnd
where a0,a1,...,ad are constants, called the coefficients of the polynomial, and ad ≠ 0. Integer d, which indicates the highest power in the polynomial, is called the degree of the polynomial.
Example code
- Summations (denoted with an enlarged capital Greek sigma symbol) gives us a shorthand way of expressing sums of increasing terms that have a regular structure
Examples: For a sequence of consecutive integers:
b∑i=a f(i) = f(a) + f(a+1) + f(a+2) +···+ f(b)
If the the integers in question were 1 to 100, using a summation, we can rewrite the formula:
100∑i=1 i
The value of this summation is 5050. It can be found without performing 99 additions, since it can be shown (for instance by mathematical induction) that
n∑i=1 i = n(n+1) / 2
- The Exponential function
f(n) = bn
where b is a positive constant, called the base, and the argument n is the exponent. That is, function f(n) assigns to the input argument n the value obtained by multiplying the base b by itself n times.
Example code
- Geometric series is a series with a constant ratio between successive terms. E.g.: 1/2 + 1/4 + 1/8 + 1/16 + ... is geometric, because each successive term can be obtained by multiplying the previous term by 1/2.
Asymptotic Analysis:
-
primitive operations such as the following:
- Assigning a value to a variable
- Following an object reference
- Performing an arithmetic operation (for example, adding two numbers)
- Comparing two numbers
- Accessing a single element of an array by index
- Calling a method
- Returning from a method
- “Big-Oh” Notation is used to describe the performance or complexity of an algorithm. Big O specifically describes the worst-case scenario, and can be used to describe the execution time required or the space used (e.g. in memory or on disk).
Let f(n) and g(n) be functions mapping positive integers to positive real numbers. We say that f(n) is O(g(n)) (or f(n) is big-Oh of g(n)) if there is a real constant c > 0 and an integer constant n0 ≥ 1 such that:
f(n) ≤ cg(n), for n ≥ n0
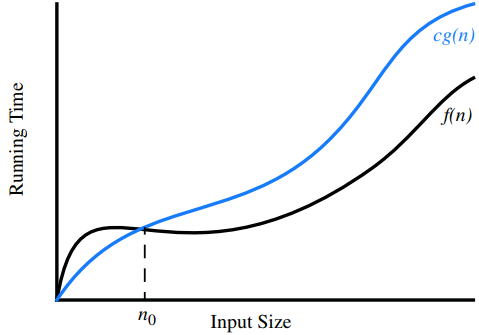
It is considered poor taste to include constant factors and lower-order terms in the big-Oh notation. The seven functions are the most common.
- Big-Omega (Ω) provides an asymptotic way of saying that a function grows at a rate that is “greater than or equal to” (rather tha big-Oh's “less than or equal to”)
We say that f(n) is Ω(g(n)), pronounced “f(n) is big-Omega of g(n),” if g(n) is O(f(n)), that is, there is a real constant c > 0 and an integer constant n0 ≥ 1 such that:
f(n) ≥ cg(n), for n ≥ n0
- Big-Theta (Θ) allows us to say that two functions grow at the same rate, up to constant factors.
f(n) is Θ(g(n)), pronounced “f(n) is big-Theta of g(n),” if f(n) is O(g(n)) and f(n) is Ω(g(n)), that is, there are real constants c′ > 0 and c′′ > 0, and an integer constant n0 ≥ 1 such that c′g(n) ≤ f(n) ≤ c′′g(n), for n ≥ n0
Simple Justification Techniques:
- A counterexample is a special kind of example that disproves a statement or proposition.
- Example: The proposition "all students are lazy". Because this statement makes the claim that a certain property (laziness) holds for all students, even a single example of a diligent student will prove it false. Thus, any hard-working student is a counterexample to "all students are lazy".
- Contraposition is an inference that says that a conditional statement is logically equivalent to its contrapositive. The contrapositive of the statement has its antecedent and consequent inverted and flipped: the contrapositive of
P == Q is thus !P == !Q.
- Example: The proposition "All cats are mammals" can be restated as the conditional "If something is a cat, then it is a mammal". Now, the law says that statement is identical to the contrapositive "If something is not a mammal, then it is not a cat."
- De Morgan's laws - justification by contradiction; Regardless of whether applying to sets, propositions, or logic gates, the structure is always the same:
Not (A and B) is the same as Not A or Not B.
Not (A or B) is the same as Not A and Not B.
- Mathematical induction is a mathematical proof technique. It is essentially used to prove that a property P(n) holds for every natural number n, i.e. for n = 0, 1, 2, 3, and so on. The method of induction requires two cases to be proved. The first case, called the base case (or, sometimes, the basis), proves that the property holds for the number 0. The second case, called the induction step, proves that, if the property holds for one natural number n, then it holds for the next natural number n + 1. These two steps establish the property P(n) for every natural number n = 0, 1, 2, 3, ... The base step need not begin with zero. Often it begins with the number one, and it can begin with any natural number, establishing the truth of the property for all natural numbers greater than or equal to the starting number.
- A loop invarient is a property of a program loop that is true before (and after) each iteration.
|
| 05 | Recursion |
Examples:
- The factorial function, n!
n! =
{ 1 if n = 0
{ n * (n−1) if n ≥ 1
Example code
Recursion tree: 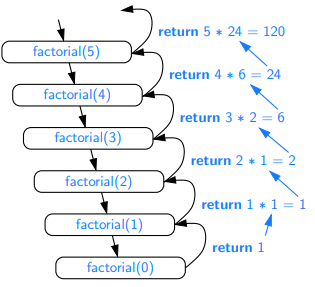
In Java, each time a method (recursive or otherwise) is called, a structure known as an activation record or activation frame is created to store information about the progress of that invocation of the method. This frame stores the parameters and local variables specific to a given call of the method, and information about which command in the body of the method is currently executing.
- Fibonacci numbers
F0 = 0
F1 = 1
Fn = Fn−2 +Fn−1 for n > 1.
Example code (good and bad examples)
- An English ruler has a recursive pattern that is a simple example of a fractal structure. Below is an example of a 2 inch ruler with major tick length of 3:
--- 0
-
--
-
--- 1
-
--
-
--- 2
We denote the length of the tick designating a whole inch as the major tick length. Between the marks for whole inches, the ruler contains a series of minor ticks, placed at intervals of 1/2 inch, 1/4 inch, and so on. As the size of the interval decreases by half, the tick length decreases by one. In general, an interval with a central tick length L ≥ 1 is composed of:
- An interval with a central tick length L−1
- A single tick of length L
- An interval with a central tick length L−1
Example code
Example code recursion trace: 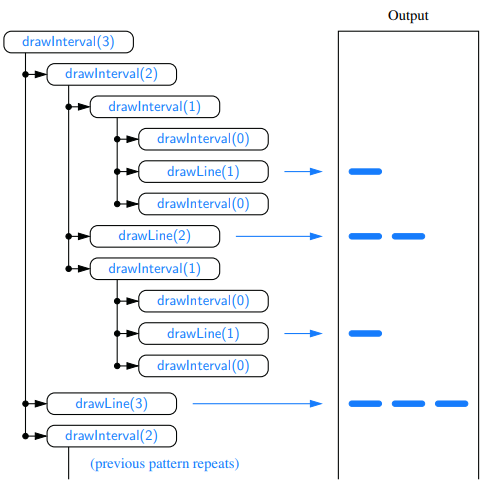
- The binary search algorithm is used to efficiently locate a target value within a sorted (indexable) sequence of n elements stored in an array.
Complexity: O(log n)
Example code
Note, when the sequence is unsorted, the standard approach to search for a target value is to use a loop to examine every element, until either finding the target or exhausting the data set. This algorithm is known as linear or sequential search, and it runs in O(n) time (i.e., linear time) since every element is inspected in the worst case.
Terms:
- Candidate: an element of the sequence which at the current stage of the search, may match the target
- Low: candidate element has the index of at least low; Initially set to 0
- High: candidate element has the index of at most high; Initially set to n-1 or
n.length - 1
- Median candidate: mid = (low + high)/2 - Initially set as the median of the array
Three cases considered:
- If the target equals the median candidate, then we have found the item we are looking for, and the search terminates successfully.
- If the target is less than the median candidate, then we recur on the first half of the sequence, that is, on the interval of indices from low to mid−1.
- If the target is greater than the median candidate, then we recur on the second half of the sequence, that is, on the interval of indices from mid+1 to high
Binary search example where target value 22 on a sorted array with 16 elements:
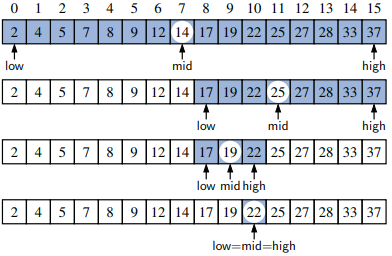
- File systems - Recursively inspect a tree structure, in this instance a file system of an arbitrary depth to discover the cumulative disk size.
Example code
Types of recursion:
- If a recursive call starts at most one other, we call this a linear recursion - Example code
- If a recursive call may start two others, we call this a binary recursion - Example code
- If a recursive call may start three or more others, this is multiple recursion
|
| 06 | Stacks, Queues, and Deques |
Stacks:
- A collection of objects that are inserted and removed via last-in, first-out (LIFO)
- Java 8 Stack class API:
boolean empty() - Tests if this stack is empty.E peek() - Looks at the object at the top of this stack without removing it from the stack.E pop() - Removes the object at the top of this stack and returns that object as the value of this function.E push(E item) - Pushes an item onto the top of this stack.
- Current documentation for the Stack class recommends that it not be used, as LIFO functionality (and more) is provided by a more general data structure known as a double-ended queue (deque) - ArrayDeque documentation: This class is likely to be faster than Stack when used as a stack, and faster than LinkedList when used as a queue.
- Example code:
Queues and Double-Ended Queues (Deques):
- A collection of objects that are inserted and removed via first-in, first-out (FIFO)
- Java 8 Queue interface API
| Throws exception | Returns special value |
|---|
| Insert | add(e) | offer(e) |
| Remove | remove() | poll() |
| Examine | element() | peek() |
- Example code:
|
| 07 | List and Iterator Abstract Data Types (ADTs) |
The List ADT:
- Simple ArrayList class with bounded capacity: Array List
- A dynamically sized ArrayList, utilizing a resize method which doubles the array size once limit reached: Dynamic Array List
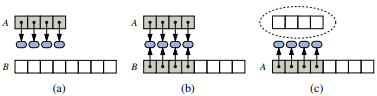
Resize logic: (a) Create new array B; (b) Store elements of A in B; (c) Reassign reference A to the new array
- Amortized Analysis of dynamic arrays shows that performing a sequence of push operations on a dynamic array is actually quite efficient as over time the resize method is only called when the array is size of 2, 4, 8, 16 etc. So, every time the resize method is not called, we gain 'credit' for the later call.
- For dyanamic arrays, a arithmetic progression strategy is significantly worse for overall performance.
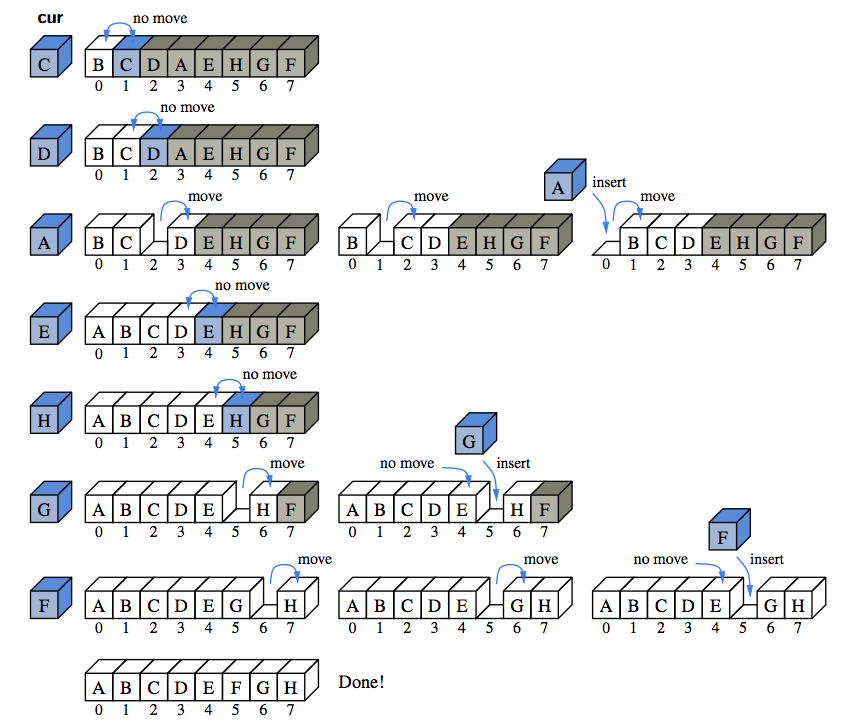
- Positional Lists: Indices are not a good abstraction for describing a more local view of a position in a sequence, because the index of an entry changes over time, e.g. a persons position in a queue waiting for tickets. Example code: Positional List
- Sorting of a positional list example using a marker to indicate at what (right most) point elements have been sorted, the position after the marker as the pivot, and walk, to move leftward from the marker, as long as there remains a preceding element with value larger than the pivot’s.
- Move-to-Front Heuristic - In many real-life access sequences (e.g., Web pages visited by a user), once an element is accessed it is more likely to be accessed again in the near future. Such scenarios are said to possess locality of reference. A heuristic, or rule of thumb, that attempts to take advantage of the locality of reference that is present in an access sequence is the move-to-front heuristic. To apply this heuristic, each time we access an element we move it all the way to the front of the list
Iterators:
- A software design pattern that abstracts the process of scanning through a sequence of elements, one element at a time. It plays a fundamental role in support of the “for-each” loop syntax
- See example code in Array List, inner class
ArrayIterator
- Java 8 docs
The Java Collections Framework
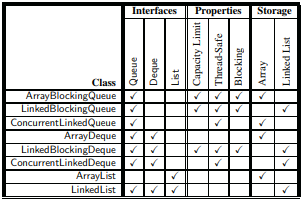
|
| 08 | Trees |
Trees:
- A tree is an abstract data type that stores elements hierarchically with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
- Two nodes that are children of the same parent are siblings. A node v is external if v has no children. A node v is internal if it has one or more children. External nodes are also known as leaves.
- A node u subtree of T rooted at a node v is the tree consisting of all the descendants of v in T (including v itself)
- An edge of tree T is a pair of nodes (u,v) such that u is the parent of v, or vice versa. A path of T is a sequence of nodes such that any two consecutive nodes in the sequence form an edge.
The Tree Abstract Data Type:
|