字典树又称单词查找数、前缀树、Trie [trai] 树,是一种哈希树的变种,常用于统计、排序和保存大量的字符串(也不限于字符串),所以经常被搜索引擎用于文本词频统计,很直观的用处就在我们在百度和google搜索某个词汇时往往会有“联想提示”。字典树可以利用字符串的公共前缀减少查询时间,最大限度地减小无用的字符串比较,所以查询效率比哈希树高。
基本操作有:查找、插入和删除(比较少)
Trie 是一颗非典型的多叉树模型,多叉就是每个结点的分支数量可以为多个,为什么说非典型呢?因为它和一般的多叉树不一样,尤其在结点的数据结构设计上,比如一般的多叉树的结点是这样的
struct TreeNode {
char value; // 结点值
TreeNode* children[num]; // 指向孩子结点
}Trie 的结点为
struct TrieNode {
bool isEnd; // 该结点是否是一个串的结束
TrieNode* next[26]; // 字母映射表
}其中 字符映射表next 的用处在于TrieNode结点中不用直接保存字符值,通过包含 a-z 26个字符的字母映射表标识当前结点下一个可能出现的所有字符的链接,因此我们可以通过一个父节点来预知它所有子结点的值
for (int i = 0; i < 26; i++) {
char ch = 'a' + i;
if (parentNode->next[i] == NULL) {
说明父结点的后一个字母不可为 ch
} else {
说明父结点的后一个字母可以是 ch
}
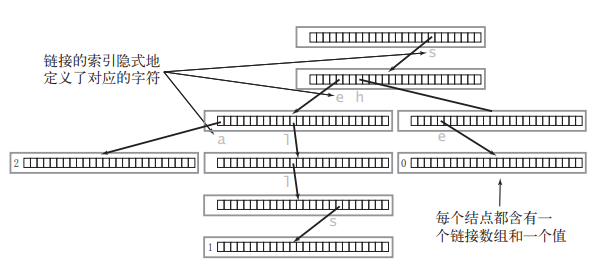
}我们来看一个例子:对于包含三个单词 "sea","sells","she" 的字典树可以是如下的结构:
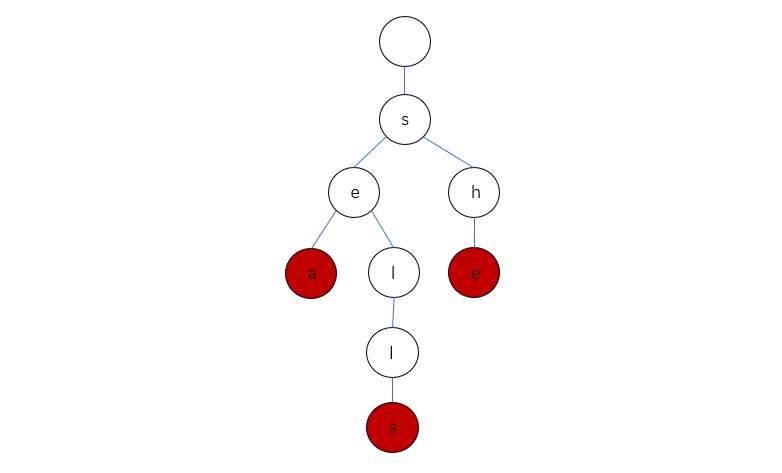
字典树中一般还有大量的空链接,因此在绘制一颗单词查找树时一般会忽略空链接,同时为了方便理解我们通常将字典树简化如下:
定义类
class Trie {
private:
vector<TrieNode*> next;
bool isEnd;
Trie() : isEnd(false), next(26, nullptr) {
}
// 手动释放内存
~Trie() {
for (auto& n : next)
delete n;
}
public:
// 插入和查询操作
}插入
目的:向 Trie 中插入一个单词 word
实现:和链表类似,首先从根结点的子结点开始与 word 第一个字符进行匹配,一直匹配到前缀链上没有对应的字符,此时开始不断开辟新的结点,直到插入完 word 的最后一个字符,同时还要 将最后一个结点 isEnd = true,表示它是一个单词的末尾
void insert(string word) {
Trie* node = this;
for (char c: word) {
if (node->next[c-'a'] == nullptr) {
node->next[c-'a'] = new Trie();
}
node = node->next[c-'a'];
}
node->isEnd = true;
}查找
目的:在 Trie 中查找某个单词 word
实现:从根结点的子结点开始,一直向下匹配即可,如果没有匹配完就出现结点值为空,返回 false;如果匹配到最后一个字符,直接判断结点 node->isEnd
bool search (string word) {
Trie* node = this;
for (char c: word) {
node = node->next[c-'a'];
if (node == nullptr) {
return false;
}
}
return node->isEnd;
}前缀匹配
目的:判断 Trie 中是否有以 prefix 为前缀的单词
实现:和 search 操作类似,只是不需要判断最后一个字符结点的 isEnd,因为既然能匹配到最后一个字符,那后面一定有单词是以它为前缀的
bool startsWith(string prefix) {
Trie* node = this;
for (char c : prefix) {
node = node->next[c-'a'];
if (node == nullptr) {
return false;
}
}
return true;
}总结
Trie树 的宗旨是 一次建树,多次查询,具有如下特点
- 形状唯一: Trie 的形状和单词的插入或删除顺序无关,也就说对于任意给定的一组单词,Trie 的形状都是唯一的
-
查询次数与单词长度相关:查找或插入一个长度为
L的单词,访问 next 数组的次数最多为L+1,和 Trie 中包含多少单词无关 -
空间复杂度高:Trie 的每个结点中都保留一个字母表,这是很耗费空间的。如果 Trie 的高度为 n,字母表大小为 m,最坏的情况是 Trie 中还不存在前缀相同的单词,那么空间复杂度就位
$O(m^n)$
前面说到使用字典树空间复杂度较高,因为用到了 next 数组,每个数组包含 m 个字母 (一般 m=26),另外 m 很大时复杂度就更大。因此可以使用哈希表来存储元素,使用哈希表代替数组进行基本操作时就需要判断是否存在对应的 key,一个很典型的题目如下:
// 648.单词替换
class Trie
{
private:
unordered_map<char, Trie *> children;
public:
Trie() {}
// 插入单词建立前缀树
void insert(string word)
{
Trie *cur = this;
for (char &c : word)
{
if (!cur->children.count(c))
{
cur->children[c] = new Trie();
}
cur = cur->children[c];
}
cur->children['#'] = new Trie(); // 设置结束标志
}
// 查询前缀树
string findRoot(string &word)
{
string root;
Trie *cur = this;
for (char &c : word)
{
if (cur->children.count('#'))
{
return root;
}
if (!cur->children.count(c))
{
return word;
}
root.push_back(c);
cur = cur->children[c];
}
return root;
}
};
class Solution
{
public:
string replaceWords(vector<string> &dictionary, string sentence)
{
Trie *trie = new Trie();
// 建立前缀树
for (auto &word : dictionary)
{
trie->insert(word);
}
vector<string> words = split(sentence, ' ');
string ans;
// 对于 sentence 中的每个单词查询前缀
for (auto &word : words)
{
ans += trie->findRoot(word);
ans += "";
}
return ans.substr(0, ans.size() - 1);
}
// C++ split 函数
vector<string> split(string &str, char ch)
{
int pos = 0;
int start = 0;
vector<string> ret;
while (pos < str.size()) {
while (pos < str.size() && str[pos] == ch) {
pos++;
}
start = pos;
while (pos < str.size() && str[pos] != ch) {
pos++;
}
if (start < str.size()) {
ret.emplace_back(str.substr(start, pos - start));
}
}
return ret;
}
};参考:单词替换官方题解
另外为了方便管理内存,可以只用 智能指针 加以优化,例如 211.添加与搜索单词
| 题目 | 说明 | 题解 |
|---|---|---|
| 208. 实现 Trie (前缀树) | 最基础的构建前缀树题目:通过插入建树,查询操作 | 解 |
| 211. 添加与搜索单词 - 数据结构设计 | 注意对于通配符.的判断最好使用递归回溯 |
解 |
| 648. 单词替换 | 暴力法可以,C++需要自己写split函数,通过dictionary建树,对每个单词使用查询前缀操作 | 解 |
| 677. 键值映射 | 前缀树叶子结点增加 val 属性记录,其实暴力哈希表更简单 | 解 |
| 676. 实现一个魔法字典 | 暴力法,前缀树在查询必须修改一个字母时很绕 | 解 |
| 745. 前缀和后缀搜索 | 注意题目是返回具有前缀和后缀的单词在字典中的最大下标 | 解 |
| 1032. 字符流 | 比较常规的字典树,为了查找后缀,需要逆序插入字符串建树 | ylb |
| 1803. 统计异或值在范围内的数对有多少 | 比较难理解,JS暴力可过,C++优化(很强),哈希表枚举也可以,字典树是经典,参考图 | 0x3F Trie |
说明:
- 『211.添加与搜索单词』这题如果考虑“优化内存”时,可以手动写析构函数,注释如果使用智能指针需要独占的智能指针
unique_ptr,而不能使用共享内存的智能指针shared_ptr,另外 注意,一般传参的时候用裸指针,尤其是只读情况下,很少直接传智能指针。但也非绝对,也有传智能指针的场景。 传裸指针比智能指针耗时少,参考:LeetCode-Feedback/LeetCode-Feedback#8693 - 对于『745.前缀和后缀搜索』需要构建一个前缀树和一个后缀树,然后另外需要维护一个下标数组用户标识具有指定前缀和后缀的单词下标,具体可以参考:C++ 前缀后缀树