Given a query
$q$ (context) and a set of documents$D$ (items), the goal is to order elements of$D$ such that the resulting ranked list maximizes a user satisfaction metric$Q$ (criteria).
Except the subjective criteria, we can take advantage of NLP to unserstand the query and documnets and apply big data technology to process so many documents.
- https://culpepper.io/publications/gcbc19-wsdm.pdf
- Learning to Efficiently Rank with Cascades
- https://www.nsf.gov/awardsearch/showAward?AWD_ID=1144034
- https://www1.cs.columbia.edu/~gravano/Qual/Papers/singhal.pdf
- https://github.com/frutik/awesome-search
- https://booking.ai/publications/home
This document set is often retrieved from the collection using a simple unsupervised bag-of-words method, e.g. BM25. This can potentially lead to learning a suboptimal ranking, since many relevant documents may be excluded from the initially retrieved set.
- https://blog.csdn.net/u013510838/article/details/123023259
- https://www.khoury.northeastern.edu/home/vip/teach/IRcourse/IR_surveys/
Our aim in matching stage is to exclude the irrelevant documents with the query
From another perspective, it is to choose
where
- Probabilistic n-Choose-k Models for Classification and Ranking
- Finding the Best of Both Worlds: Faster and More Robust Top-k Document Retrieval
- Top-k learning to rank: labeling, ranking and evaluation
- Why Not Yet: Fixing a Top-k Ranking that is Not Fair to Individuals
- FA*IR: A Fair Top-k Ranking Algorithm
- https://haystackconf.com/
- https://www.mices.co/
- Search @ Nextdoor: What are our Neighbors Searching For?
- Ranking Relevance in Yahoo Search
- Search Relevance Methodology
- https://opensourceconnections.com/blog/2023/03/20/beyond-search-relevance-search-result-quality/
- https://www.sigir.org/sigir2007/tutorial2d.html
- https://haystackconf.com/us2023/talk-2/
- https://www.elastic.co/what-is/search-relevance
The assumptions about relevance are as follows:
- Relevance is assumed to be a property of the document given information need only, assessable without reference to other documents; and
- The relevance property is assumed to be binary.
Either of these assumptions is at the least arguable.
- The Probabilistic Relevance Framework: BM25 and Beyond
- https://www.khoury.northeastern.edu/home/vip/teach/IRcourse/IR_surveys/robertson_foundations.pdf
There are fundamental differences between semantic matching and relevance matching:
Semantic matching emphasizes “meaning” correspondences by exploiting
lexicalinformation (e.g., words, phrases, entities) andcompositional structures(e.g., dependency trees), while relevance matching focuses onkeyword matching.
- Relevance under the Iceberg: Reasonable Prediction for Extreme Multi-label Classification
- Extreme Multi-label Classification from Aggregated Labels
- Build Faster with Less: A Journey to Accelerate Sparse Model Building for Semantic Matching in Product Search
- https://www.khoury.northeastern.edu/home/vip/teach/IRcourse/IR_surveys/ml_for_match-step2.pdf
- https://www.elastic.co/guide/en/elasticsearch/reference/current/semantic-search.html
- COIL: Revisit Exact Lexical Match in Information Retrieval with Contextualized Inverted List
- NAIL: Lexical Retrieval Indices with Efficient Non-Autoregressive Decoders
- A Dense Representation Framework for Lexical and Semantic Matching
- SPLADE v2: Sparse Lexical and Expansion Model for Information Retrieval
- https://arxiv.org/abs/2107.05720
DSSM stands for Deep Structured Semantic Model, or more general, Deep Semantic Similarity Model.
DSSM can be used to develop latent semantic models that project entities of different types (e.g., queries and documents) into a common low-dimensional semantic space for a variety of machine learning tasks such as ranking and classification.
For example, in web search ranking, the relevance of a document given a query can be readily computed as the distance between them in that space.
DSSM is extended as the two tower model, where the query and document are represented as vectors via different neural networks.
- https://eng.snap.com/embedding-based-retrieval
- https://haystack.deepset.ai/
- Embedding-based Retrieval in Facebook Search
- Embedding-based Product Retrieval in Taobao Search
- Que2Engage: Embedding-based Retrieval for Relevant and Engaging Products at Facebook Marketplace
- From Distillation to Hard Negative Sampling: Making Sparse Neural IR Models More Effective
- Embedding-based Query Language Models
- https://www.elastic.co/cn/blog/may-2023-launch-information-retrieval-elasticsearch-ai-model
- Beyond the known: exploratory and diversity search with vector embeddings
- Using Vector Databases to Scale Multimodal Embeddings, Retrieval and Generation
- Search Engines: Combining Inverted and ANN Indexes for Scale
- Evaluating embedding based retrieval beyond historical search results
- https://www.elastic.co/cn/blog/improving-information-retrieval-elastic-stack-hybrid
- Mastering Hybrid Search: Blending Classic Ranking Functions with Vector Search for Superior Search Relevance
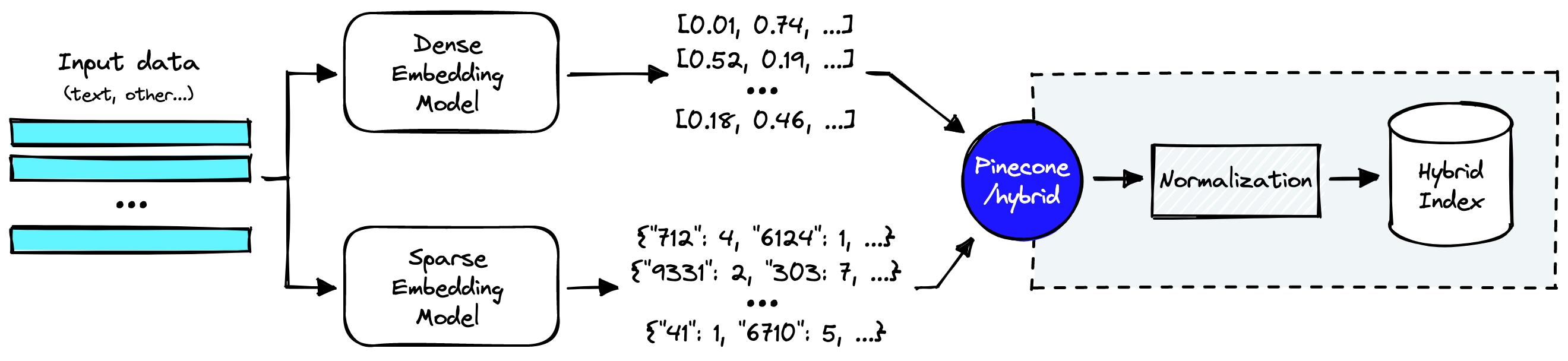
- https://www.pinecone.io/learn/hybrid-search-intro/
- An Analysis of Fusion Functions for Hybrid Retrieval
- https://learn.microsoft.com/zh-CN/azure/search/hybrid-search-ranking
- https://opensearch.org/blog/hybrid-search/
- https://qdrant.tech/articles/hybrid-search/
- https://www.pinecone.io/learn/hybrid-search-intro/
- https://milvus.io/docs/hybridsearch.md
When there is just a single criterion (or "judge") for ranking, the task is relatively easy,
and is simply a reaction of the judge's opinions and biases.
In contrast, this paper addresses the problem of computing a "consensus" ranking of the alternatives,
given the individual ranking preferences of several judges. We call this the rank aggregation problem.
The goal of pre-rank is to select some documents(items) efficiently.
- COLD: Towards the Next Generation of Pre-Ranking System
- Towards a Better Trade-off between Effectiveness and Efficiency in Pre-Ranking: A Learnable Feature Selection based Approach
- Rethinking Large-scale Pre-ranking System: Entire-chain Cross-domain Models
- Rethinking the Role of Pre-ranking in Large-scale E-Commerce Searching System
- IntTower: The Next Generation of Two-Tower Model for Pre-Ranking System
Given a query
$q$ (context) and a set of documents$D$ (items), the goal is to order elements of$D$ such that the resulting ranked list maximizes a user satisfaction metric$Q$ (criteria).
In cascaded ranking architecture, the set
- http://ltr-tutorial-sigir19.isti.cnr.it/program-overview/
- Efficient and Effective Tree-based and Neural Learning to Rank
- https://aclanthology.org/2023.acl-long.771/
Learning to rank is usually formalized as a supervised learning task, while unsupervised learning and semi-supervised learning formulations are also possible. In learning, training data consisting of sets of objects as well as the total or partial orders of the objects in each set is given, and a ranking model is learned using the data. In prediction, a new set of objects is given, and a ranking list of the objects is created using the ranking model.
- A Systematic Study of Feature Selection Methods for Learning to Rank Algorithms
- FSMRank: feature selection algorithm for learning to rank
- Neural Feature Selection for Learning to Rank
LambdaRank introduced the
You can think of these gradients as little arrows attached to each document in the ranked list, indicating which direction we’d like those documents to move. LambdaRank simply took the RankNet gradients, which we knew worked well, and scaled them by the change in NDCG found by swapping each pair of documents. We found that this training generated models with significantly improved relevance (as measured by NDCG) and had an added bonus of uncovering a further trick that improved overall training speed (for both RankNet and LambdaRank). Furthermore, surprisingly, we found empirical evidence (see also this paper) that the training procedure does actually optimize NDCG, even though the method, although intuitive and sensible, has no such guarantee.
We compute the gradients of RankNet by: $$ \frac{\partial L}{\partial w} = \sum_{(i, j)}\frac{\partial L_{i, j}}{\partial w}=\sum_{(i, j)}[\frac{\partial L_{i, j}}{\partial s_i}+\frac{\partial L_{i,j}}{\partial s_j}]. $$
Observe that
$$ {\lambda}{i,j}=\frac{\partial L{i, j}}{\partial s_i} = -\frac{\partial L_{i, j}}{\partial s_j} = -\frac{\sigma}{1 + \exp(\sigma(s_i - s_j))}. $$
What is more, we can extend it to
$$
{\lambda}_{i,j}= -\frac{\sigma}{1+\exp(\sigma( s_i -s_j))}|\Delta Z|,
$$
where
And
- http://blog.camlcity.org/blog/lambdarank.html
- LambdaFM: Learning Optimal Ranking with Factorization Machines Using Lambda Surrogates
- Practical Lessons from Predicting Clicks on Ads at Facebook
LambdaMART is the boosted tree version of LambdaRank, which is based on RankNet. It takes the ranking problem as classification problem.
MART stands for Multiple Additive Regression Tree. In LambdaRank, we compute the gradient. And we can use this gradient to make up the GBRT.
LambdaMART had an added advantage: the training of tree ensemble models can be very significantly sped up over the neural net equivalent (this work, led by O. Dekel, is not yet published). This allows us to train with much larger data sets, which again gives improved ranking accuracy. From RankNet: A ranking retrospective.
To implement LambdaMART we just use MART, specifying appropriate gradients
and the Newton step.
The key point is the gradient of the ${\lambda}i$:
$$ w_i = \frac{\partial y_i}{\partial F{k-1}(\vec{x}_i)} $$
where
- LambdaMART 不太简短之介绍
- Learning To Rank之LambdaMART的前世今生s
- LambdaMart Slides
- From RankNet to LambdaRank to LambdaMART: An Overview
- Ranknet a ranking retrospective
- LambdaMart Demystified
- Unbiased LambdaMART: An Unbiased Pairwise Learning-to-Rank Algorithm
GBRT+LR can also used to predict the CTR ratio. On short but incomplete word, it is GBRT + LR - gradient boosting regression tree and logistic regression. GBRT is introduced at the Boosting section. LR is to measure the cost as the same in RankNet.
- Learning From Weights: A Cost-Sensitive Approach For Ad Retrieval
- https://www.jianshu.com/p/96173f2c2fb4
- Boosted Ranking Models: A Unifying Framework for Ranking Predictions
- https://www.cnblogs.com/genyuan/p/9788294.html
- https://ml-compiled.readthedocs.io/en/latest/ranking.html
- The LambdaLoss Framework for Ranking Metric Optimization
- Revisiting Approximate Metric Optimization in the Age of Deep Neural Networks
- On Optimizing Top-𝐾 Metrics for Neural Ranking Models
- LambdaRank Gradients are Incoherent
- https://arxiv.org/abs/1810.11921
- https://arxiv.org/abs/2102.07619
- https://arxiv.org/abs/2105.05563
- https://arxiv.org/abs/2304.13643
Beyond user satisfaction metric, the system can re-rank the candidates to consider additional criteria or constraints.
- https://github.com/LibRerank-Community/LibRerank/
- https://librerank-community.github.io/slides-recsys22-tutorial-neuralreranking.pdf
- https://librerank-community.github.io/
- https://arxiv.org/pdf/2202.06602.pdf
- Personalized Re-ranking for Recommendation
- Diversity in Ranking using Negative Reinforcement
- Matching Search Result Diversity with User Diversity Acceptance in Web Search Sessions
- https://ujwalgadiraju.com/Publications/Bias2020.pdf
- https://www.ashudeepsingh.com/
- Fairness in Ranking: A Survey
- Fair ranking: a critical review, challenges, and future directions
- Fairness in Ranking, Part I: Score-Based Ranking
- Fairness in Ranking, Part II: Learning-to-Rank and Recommender Systems
- Fairness of Exposure in Rankings
- Fairness in Recommendation Ranking through Pairwise Comparisons
- https://arxiv.org/abs/2002.11293
- https://www.microsoft.com/en-us/research/publication/adversarial-ranking-language-generation/
- Cascading Bandits: Learning to Rank in the Cascade Model
- Pre-training Methods in Information Retrieval
Given a user query, the top matching layer is responsible for providing semantically relevant ad candidates to the next layer, while the ranking layer at the bottom concerns more about business indicators (e.g., CPM, ROI, etc.) of those ads. The clear separation between the matching and ranking objectives results in a lower commercial return.
The Mobius project has been established to address this serious issue.
- MOBIUS: Towards the Next Generation of Query-Ad Matching in Baidu’s Sponsored Search
- RankFlow: Joint Optimization of Multi-Stage Cascade Ranking Systems as Flows
- Joint Optimization of Cascade Ranking Models
- After initial retrieval results are presented, allow the user to provide feedback on the relevance of one or more of the retrieved documents.
- Use this feedback information to reformulate the query.
- Produce new results based on reformulated query.
- Allows more interactive, multi-pass process.