Skip to content

Latest commit

 

History

History
1056 lines (780 loc) · 69 KB

Graph Algorithms.md

File metadata and controls

1056 lines (780 loc) · 69 KB
Raw

Graph and Networks

The world is driven by connections—from financial and communication systems to social and biological processes. Revealing the meaning behind these connections drives breakthroughs across industries in areas such as identifying fraud rings and optimizing recommendations to evaluating the strength of a group and predicting cascading failures. Graph and networks are the language to describe the connected entities. They focus on the connections and consider the crowd as a network. They are close with topology.

Graph is mathematical abstract or generalization of the connection between entities. It is an important part of discrete mathematics -- graph theory. And graph processing is widely applied in industry and science such as the network analysis, graph convolutional network (GCN), probabilistic graph model(PGM) and knowledge graph, which are introduced in other chapters.

Resource On Graph Processing

Toolkits

Graph as Data Structure

A graph ${G=(V,E)}$ consists of a finite set of vertices $V(G)$ and a set of edges $E(G)$ consisting of distinct, unordered pairs of vertices, where nodes stand for entities and edges stand for their connections. It is the foundation of network science. It is the fact that the feature is nothing except the connection that makes different from the common data.

Graphs provide a powerful way to represent and exploit these connections. Graphs can be used to model such diverse areas as computer vision, natural language processing, and recommender systems. [^12]

The connections can be directed, weighted even probabilistic. It can be studied from the perspectives of matrix analysis and discrete mathematics.

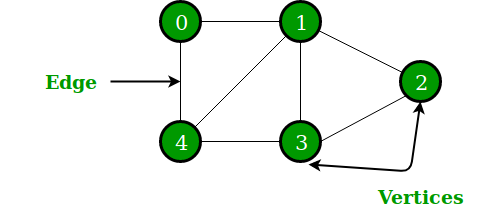
All data in computer machine is digitalized bits. The primitive goal is to represent graph in computer as one data structure.

The adjacency matrix

Definition: Let $G$ be a graph with $V(G) = {1,\dots,n}$ and $E(G) = {e_1,\dots, e_m}$.The adjacency matrix of $G$, denoted by $A(G)$, is the $n\times n$ matrix defined as follows. The rows and the columns of $A(G)$ are indexed by $V(G)$. If $i \not= j$ then the $(i, j)$-entry of $A(G)$ is $0$ for vertices $i$ and $j$ nonadjacent, and the $(i, j)$-entry is $\color{red}{\text{1}}$ for $i$ and $j$ adjacent. The $(i,i)$-entry of $A(G)$ is 0 for $i = 1,\dots,n.$ We often denote $A(G)$ simply by $A$.

Adjacency Matrix is also used to represent weighted graphs. If the $(i, j)$-entry of $A(G)$ is $w_{i, j}$, i.e. $A[i][j] = w_{i, j}$, then there is an edge from vertex $i$ to vertex $j$ with weight $w$. The Adjacency Matrix of weighted graphs $G$ is also called weight matrix of $G$, denoted by $W(G)$ or simply by $W$.

Definition: Let $G=(V, E)$ be a graph with $V(G) = {1,\dots,n}$ and $E(G) = {e_1,\dots, e_m}$. Suppose each edge of $G$ is assigned an orientation, which is arbitrary but fixed. The (vertex-edge) incidence matrix of $G$, denoted by $Q(G)$, is the $n \times m$ matrix defined as follows. The rows and the columns of $Q(G)$ are indexed by $V(G)$ and $E(G)$, respectively. The $(i, j)$-entry of $Q(G)$ is 0 if vertex $i$ and edge $e_j$ are not incident, and otherwise it is $\color{red}{\text{1 or −1}}$ according as $e_j$ originates or terminates at $i$, respectively. We often denote $Q(G)$ simply by $Q$. Whenever we mention $Q(G)$ it is assumed that the edges of $G$ are oriented. See Graph representations using set and hash at https://www.geeksforgeeks.org/graph-representations-using-set-hash/.

Definition: In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. From the wikipedia page at https://www.wikiwand.com/en/Degree_(graph_theory). The degree of a vertex $v$ is denoted $\deg(v)$ or $\deg v$. Degree matrix $D$ is a diagonal matrix such that $D_{i,i}=\sum_{j} w_{i,j}$ for the weighted graph with $W=(w_{i,j})$.

Definition: A directed graph (or digraph) is a set of vertices and a collection of directed edges that each connects an ordered pair of vertices. We say that a directed edge points from the first vertex in the pair and points to the second vertex in the pair. We use the names 0 through V-1 for the vertices in a V-vertex graph. Via https://algs4.cs.princeton.edu/42digraph/.

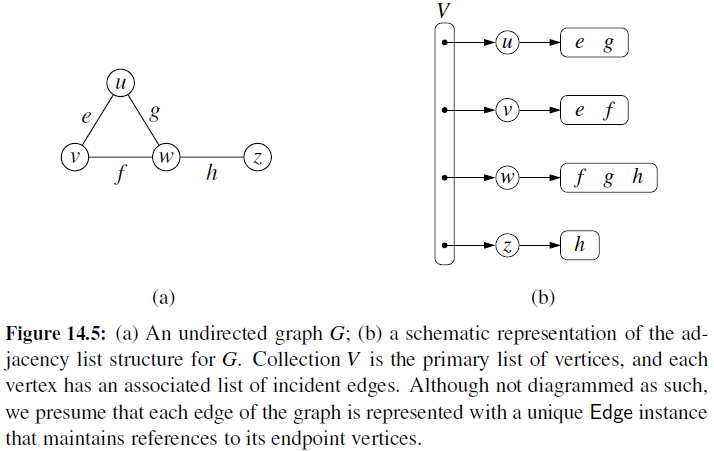
Adjacency List is an array of lists. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs. See more representation of graph in computer in https://www.geeksforgeeks.org/graph-data-structure-and-algorithms/. Although the adjacency-list representation is asymptotically at least as efficient as the adjacency-matrix representation, the simplicity of an adjacency matrix may make it preferable when graphs are reasonably small. Moreover, if the graph is unweighted, there is an additional advantage in storage for the adjacency-matrix representation.

Cayley graph of F2 in Wikimedia Moreno Sociogram 1st Grade

Graph Theory and Linear Algebra

It seems that graph theory is partially the application of nonnegative matrix theory. Graph Algorithms in the Language of Linear Algebra shows how to leverage existing parallel matrix computation techniques and the large amount of software infrastructure that exists for these computations to implement efficient and scalable parallel graph algorithms. The benefits of this approach are reduced algorithmic complexity, ease of implementation, and improved performance.

Definition A walk in a digraph is an alternating sequence of vertices and edges that begins with a vertex, ends with a vertex, and such that for every edge $\left<u\to v\right>$ in the walk, vertex $u$ is the element just before the edge, and vertex $v$ is the next element after the edge.

A payoff of this representation is that we can use matrix powers to count numbers of walks between vertices. The adjacent matrix ${A(G)}^k$ provides a count of the number of length $k$ walks between vertices in any digraph $G$.

Definition The length-k walk counting matrix for an n-vertex graph $G$ is the $n \times n$ matrix $C^{k}$ such that: $$ C_{uv}^{k} ::= \text{the number of length-k walks from $u$ to $v$}. $$

The length-k counting matrix of a digraph $G$ is ${A(G)}^k$, for all $k\in\mathbb{N}$.

Definition A walk in an undirected graph is a sequence of vertices, where each successive pair of vertices are adjacent; informally, we can also think of a walk as a sequence of edges. A walk is called a path if it visits each vertex at most once. For any two vertices $u$ and $v$ in a graph $G$, we say that $v$ is reachable from $u$ if $G$ contains a walk (and therefore a path) between $u$ and $v$. An undirected graph is connected if every vertex is reachable from every other vertex. A cycle is a path that starts and ends at the same vertex and has at least one edge.

Operators on Graph

Like linear algebra, we define the graph and then we would like to know their properties, their transformation and their invariants.

We will limit our attention to undirected graphs and view them as a discrete analog of manifolds. We define the vertex set $V={1,\dots,n}$ (it can be any set containing n objects, which we canonically map to the above set of natural numbers from 1 to n); the edge set and the edge set $E\subset V\times V$. An undirected graph has $(i,j)\in E⇔(j,i)\in E$. We further define the vertex weights as the function $a:V\to (0,\infty)$ and the edge weights as $w:E\to \mathbb R_+$ (in fact, w can be defined on the entire $V×V$ with $w_{ij}=0$ meaning $(i,j)\not\in E$). We refer to the tuple $G=(V,E,a,w)$ as to a weighted undirected graph.

If $G(V, E)$ is undirected graph. $V$ are vertices, $E$ are edges, T are triangles/3-cliques, i.e., if $(i, j, k)\in T\iff {i , j}, {j , k}, {k, i}\in E.$

  • Function on vertices(vertex field): $s : V \to \mathbb R$. Such a function assigns a real number to each graph node.
  • Edge flows(edge field ): $X:V\times V\to \mathbb R$, where $X(i, j)=0,$ if $(i, j)\not\in E$ and $X(i, j)=-X(j,i)$ for all $(i, j)$.
  • Triangular flows: $\Phi: V\times V\times V\to\mathbb R$ where $\Phi(i, j ,k)=0$ if $(i, j, k)\not\in T$ and $\Phi(i, j, k)=\Phi(k, i, j)=\Phi(j, k, i)=-\Phi(j, i, k)=-\Phi(i, k, j)=-\Phi(k,j,i)$ for all $i, j, k$.

Some operators on Graph

Operators Definition
Graph combinatorial gradient: grad $\text{(grad s)(i, j)}=s_j - s_i$
Graph combinatorial curl: curl $\text{(curl X)(i, j, k)}=X_{ij}+X_{jk}+X_{ik}$
Graph combinatorial divergence: div $\text{(div X)(i)}= \sum_{j}w_{ij}X_{ij}$
Graph Laplacian $\Delta_0=div\circ grad$
Graph Helmholtzian $\Delta_1=curl^{\ast}\circ curl-grad\circ div$
Co-boundary Mapping

We consider real-valued functions on the set of the graph’s vertices, $f : V \to \mathbb R$. Such a function assigns a real number to each graph node. $f$ is a vector indexed by the graph’s vertices, hence $f\in\mathbb{R}^{n}$. Notation: $f = (f(v_1), \cdots , f(v_n)) = (f(1), . . . , f(n))$.

The adjacency matrix can be viewed as an operator: $$g=Af;g(i)=\sum_{i\sim j}f(j)$$ which is the extension of degree function.

Let each edge in the graph have an arbitrary but fixed orientation.

The incidence matrix of a graph $G$ is a $|V|\times |E|$ matrix defined as follows: $$Q(G)=\triangledown= \begin{cases} \triangledown_{ev}=-1, &\text{if $v$ is the initial vertex of edge $e$}\ \triangledown_{ev}=1, &\text{if $v$ is the terminal vertex of edge $e$}\ \triangledown_{ev}=0, &\text{if $v$ is not in the edge $e$} \end{cases} $$

$\color{red}{Note}$ that the column sums of $Q(G)$ are 0s so the rows of $Q(G)$ is linearly dependent.

  • If the graph $G$ is connected on $n$ vertices, the rank of incidence matrix $\triangledown$ is $n-1$, i.e. $rank(\triangledown)=n-1$.
  • If $G$ is a graph on $n$ vertices and has $k$ connected components, then $rank(\triangledown)=n-k$.

The mapping $f \to \nabla f$ is known as the co-boundary mapping of the graph defined by $$(\nabla f)(e_{ij})=f(v_j)-f(v_i)$$

where $e_{ij}$ is the edge and $v_i$($v_j$) is the initial(terminal) node of the edge $e_{ij}$.

And $\nabla f$ is the product of the incidence matrix $\triangledown$ and the function $f$.

Graph Curl
Graph Divergence
Graph Laplacians

Definition: Let $G$ be a graph with $V(G) = {1,\dots,n}$ and $E(G) = {e_1,\dots, e_m}$.The Laplacian matrix of $G$, denoted by $L(G)$, is the $n\times n$ matrix defined as follows. The rows and the columns of $L(G)$ are indexed by $V(G)$. If $i \not= j$ then the $(i, j)$-entry of $L(G)$ is $0$ for vertices $i$ and $j$ nonadjacent, and the $(i, j)$-entry is $\color{red}{\text{ −1}}$ for $i$ and $j$ adjacent. The $(i,i)$-entry of $L(G)$ is $\color{red}{d_i}$, the degree of the vertex $i$, for $i = 1,\dots,n.$ In other words, the $(i,i)$-entry of $L(G)$, ${L(G)}{i,j}$, is defined by $${L(G)}{i,j} = D - A = \begin{cases} \deg(V_i) & \text{if $i=j$,}\ -1 & \text{if $i\not= j$ and $V_i$ and $V_j$ is adjacent,} \ 0 & \text{otherwise.}\end{cases}$$ Laplacian matrix of a graph $G$ with weighted matrix $W$ is ${L^{W}=D-W}$, where $D$ is the degree matrix of $G$. We often denote $L(G)$ simply by $L$ or $\triangle$.

If $\triangledown$ is the incidence matrix of the graph, the Laplacians are defined as $$L=\triangle =\triangledown^T\triangledown.$$ So $(Lf)(v_i)=\sum_{i\sim j}f(v_i)-f(v_j)$.

We consider undirected weighted graphs: Each edge $e_{ij}$ is weighted by $w_{ij} > 0$. The Laplacian as an operator: $$(\triangle f)(v_i)=\sum_{v_j\sim v_i}w_{ij}(f(v_i)-f(v_j)).$$

As a quadratic form: $$f^T\triangle f=\sum_{v_j\sim v_i}w_{ij}(f(v_i)-f(v_j))^2$$

The Laplacian of the graph $L=\triangle$ is symmetric and positive semi-definite.

Therefore, a graph with one connected component has the constant vector $u_1 = 1_n$ as the only eigenvector with eigenvalue 0.

Each connected component has an associated Laplacian. Therefore, we can write matrix $L$ as a block diagonal matrix: $$L=\begin{pmatrix} L_1\quad \quad \quad\quad\ \ \quad\ddots \ \ \quad \quad \quad\quad\quad L_k \end{pmatrix}.$$

  • Each block corresponds to a connected component, hence each matrix $L_i$ has an eigenvalue 0 with multiplicity 1.
  • The spectrum of $L$ is given by the union of the spectra of $L_i$.
  • The eigenspace corresponding to $\lambda_1 = \cdots = \lambda_k = 0$ is spanned by the k mutually orthogonal vectors:
  • These vectors are the indicator vectors of the graph’s connected components.

It is also called as Kirchhoff matrix or information matrix.

Kirchhoff matrix tree theorem If $G$ is a connected graph, then the cofactor of the Laplacian matrix are all equal and the common value is the number of spanning tree of the graph $G$.

Graph Helmholtzian

(Helmholtz decomposition)：$G = (V; E)$ is undirected, unweighted graph. $\Delta_1$ is its Helmholtzian. The space of edge flows admits orthogonal decomposition: $$L^2(E)=im(grad)\oplus ker(\Delta_1)\oplus im(curl^{\ast}).$$ Furthermore, $ker(\Delta_1) = ker(curl) \cap ker(div)$.

Graph Convolution
Graph Fourier Transform
Transform Name Transform Representation Transform Description
Karhunen-Loeve Transform (KLT) “Sparsest” signal representation given available statistical model Can be expensive (if poorly structured)
Discrete Cosine Transform (DCT) non-sparse signal representation across sharp boundaries little (fixed transform)
Graph Fourier Transform (GFT) minimizes the total rate of signal’s transform representation & transform description
Matrix Theory Graph Theory ----- ---
Matrix Addition ? Spectral Theory ?
Matrix Power ? Jordan Form ?
Matrix Multiplication ? Rank ?
Basis ? Spectra ?

Spectral Graph Theory

As the title suggests, Spectral Graph Theory is about the eigenvalues and eigenvectors of matrices associated with graphs, and their applications. ---|--- ---|--- Adjacency matrix| ${A}$ Degree matrix | ${D}$ Laplacian matrix| ${L}$

For the symmetric matrix $L = D - A$, we can obtain that $x^T Lx=\sum_{(u,v)\in E}(x_u-x_v)^2$. If the graph ${G}$ is directed, then $x^T Lx=\sum_{(u,v)\in E}w(u,v) (x_u-x_v)^2$.

Let $G = (V;E)$ be a graph, and let $\lambda=(\lambda_1, \cdots, \lambda_n)^T$ be the eigenvalues of its Laplacian matrix. Then, $\lambda_2>0$ if and only if G is connected.

There are many iterative computational methods to approximate the eigenvalues of the graph-related matrices.

Spectral Clustering Algorithm

Spectral method is the kernel tricks applied to locality preserving projections as to reduce the dimension, which is as the data preprocessing for clustering.

In multivariate statistics and the clustering of data, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the data set.

Similarity matrix is to measure the similarity between the input features ${\mathbf{x}i}{i=1}^{n}\subset\mathbb{R}^{p}$. For example, we can use Gaussian kernel function $$ f(\mathbf{x_i},\mathbf{x}j)=exp(-\frac{{|\mathbf{x_i}-\mathbf{x}j|}2^2}{2\sigma^2}) $$ to measure the similarity of inputs. The element of similarity matrix $S$ is $S{i, j} = exp(-\frac{{| \mathbf{x_i} -\mathbf{x}j|}2^2}{2\sigma^2})$. Thus $S$ is symmetrical, i.e. $S{i, j}=S{j, i}$ for $i,j\in{1,2,\dots, n}$. If the sample size $n\gg p$, the storage of similarity matrix is much larger than the original input ${\mathbf{x}i }{i=1}^{n}$, when we would only preserve the entries above some values. The Laplacian matrix is defined by $L=D-S$ where $D = Diag{D_1, D_2, \dots, D_n}$ and $D{i} = \sum{j=1}^{n} S_{i,j} = \sum_{j=1}^{n} exp(-\frac{{|\mathbf{x_i} - \mathbf{x}_j|}_2^2}{2\sigma^2})$.

Then we can apply principal component analysis to the Laplacian matrix $L$ to reduce the data dimension. After that we can perform $K-means$ or other clustering.

PageRank

Raluca Tanase and Remus Radu, in The Mathematics of Web Search, asserted that

The usefulness of a search engine depends on the relevance of the result set it gives back. There may of course be millions of web pages that include a particular word or phrase; however some of them will be more relevant, popular, or authoritative than others. A user does not have the ability or patience to scan through all pages that contain the given query words. One expects the relevant pages to be displayed within the top 20-30 pages returned by the search engine.

Modern search engines employ methods of ranking the results to provide the "best" results first that are more elaborate than just plain text ranking. One of the most known and influential algorithms for computing the relevance of web pages is the Page Rank algorithm used by the Google search engine. It was invented by Larry Page and Sergey Brin while they were graduate students at Stanford, and it became a Google trademark in 1998. The idea that Page Rank brought up was that, the importance of any web page can be judged by looking at the pages that link to it. If we create a web page i and include a hyperlink to the web page j, this means that we consider j important and relevant for our topic. If there are a lot of pages that link to j, this means that the common belief is that page j is important. If on the other hand, j has only one backlink, but that comes from an authoritative site k, (like www.google.com, www.cnn.com, www.cornell.edu) we say that k transfers its authority to j; in other words, k asserts that j is important. Whether we talk about popularity or authority, we can iteratively assign a rank to each web page, based on the ranks of the pages that point to it.

PageRank is the first importance measure of webpage in large scale application. And this is content-free so that it does not take the relevance of webpages into consideration.

Here's how the PageRank is determined. Suppose that page $P_j$ has $l_j$ links. If one of those links is to page $P_i$, then $P_j$ will pass on $1/l_j$ of its importance to $P_i$. The importance ranking of $P_i$ is then the sum of all the contributions made by pages linking to it. That is, if we denote the set of pages linking to $P_i$ by $B_i$, then $$I(P_i)=\sum_{P_j\in B_i}\frac{I(P_j)}{l_j}.$$

Note that the importance ranking of $P_i$ is the finite sum of 2 factors: the importance of its neighbors' importance $I(P_j)$ and the number of links $l_j$ when $P_j\in B_i$ thus it can be rewritten as $$I(P_i)=\sum_{j} [I(P_j)\cdot \frac{1}{l_j}] \mathbb{I}(ij)$$ where the indicator function $\mathbb{I}(ij)$ is equal to 1 if the page $P_i$ is linked with the page $P_j$. If we define a matrix, called the hyper-link matrix, $\mathbf{H}=[\mathbf{H}{ij}]$ in which the entry in the $i^{th}$ row and $j^{th}$ column is $$ [\mathbf{H}{ij}]= \begin{cases} \frac{1}{l_j}\quad &\text{if $P_j\in B_i$},\ 0 \quad & \text{otherwise}. \end{cases} $$

The condition above defining the PageRank $I$ may be expressed as

$$ I = {\bf H}I $$ In other words, the vector I is an eigenvector of the matrix H with eigenvalue 1. We also call this a stationary vector of H.

It is not very simple and easy to compute the eigenvalue vectors of large scale matrix. If we denote by $\bf 1$the $n\times n$ matrix whose entries are all one, we obtain the Google matrix:

$$ {\bf G}=\alpha{\bf S}+ (1-\alpha)\frac{1}{n}{\bf 1} $$ Notice now that G is stochastic as it is a combination of stochastic matrices. Furthermore, all the entries of G are positive, which implies that G is both primitive and irreducible. Therefore, G has a unique stationary vector I that may be found using the power method.

TrustRank

Shortest Paths

In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) in a graph such that the sum of the weights of its constituent edges is minimized.

Given the start node and end node, it is supposed to identify whether there is a path and find the shortest path(s) among all these possible paths.

The distance between the node $u$ and $v$ is the minimal number $k$ that makes $A^{k}_{uv}>0$. Given two nodes $E_1, E_2$ in graph $\mathrm{G}$, if we would like begin from the node $E_1$ to the end node $E_2$, we must judege that if there is a path from $E_1$ to $E_2$ before finding the shortest way. In the perspective of optimization, the feasible domain is finite in the shortest path problem.

Depth-first Search and Breadth-First

Because it is unknown whether there is a path between the given nodes, it is necessary to take the first brave walk into a neighbor of the start node $E_1$.

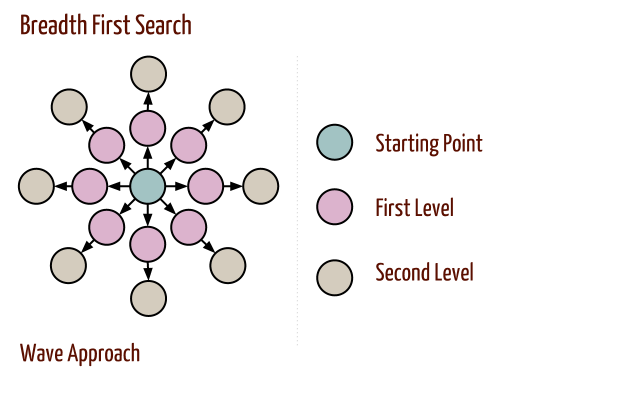
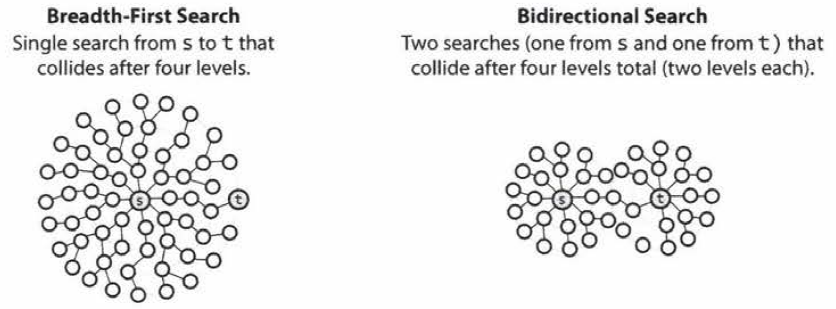
Breadth first search explores the space level by level only when there are no more states to be explored at a given level does the algorithm move on to the next level. We implement BFS using lists open and closed to keep track of progress through the state space. In the order list, the elements will be those who have been generated but whose children have not been examined. The closed list records the states that have been examined and whose children have been generated. The order of removing the states from the open list will be the order of searching. The open is maintained as a queue on the first in first out data structure. States are added to the right of the list and removed from the left.

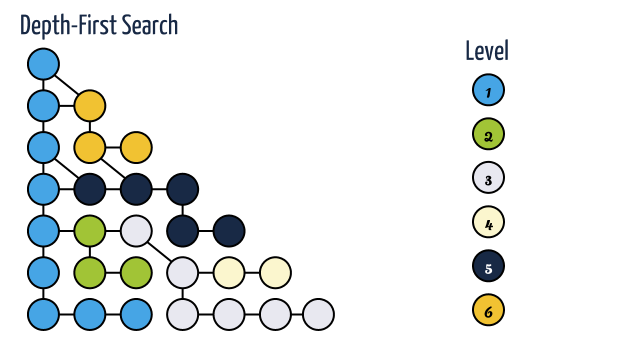
After initialization, each vertex is enqueued at most once and hence dequeued at most once. The operations of enqueuing and dequeuing take $O (1)$ time, so the total time devoted to queue operations is $O (v)$. Because the adjacency list of each vertex is scanned only when the vertex is dequeued, the adjacency list of each vertex is scanned at most once. Since the sum of the lengths of all the adjacency lists is the $ta(E)$, at most $O(E)$ time is spent in total scanning adjacency lists. The overhead for the initialization is $O(v)$, and thus the total running time of BFS is $O(v+E)$. Thus, breadth first search runs in time linear in the size of the adjacency list representation.

In depth first search, when a state is examined all of its children and their descendants are examined before any of its siblings. Depth first search goes deeper into the search space whenever this is possible, only when no further descendants of a state can be found, are its siblings considered.

A depth first traversal takes O(N*E) time for adjacency list representation and $O(N^2)$ for matrix representation.

$A^{\ast}$ Algorithm

As introduced in wikipedia, $A^{\ast}$ algorithm has its advantages and disadvantages:

In computer science, $A^{\ast}$ (pronounced "A star") is a computer algorithm that is widely used in path finding and graph traversal, which is the process of finding a path between multiple points, called "nodes". It enjoys widespread use due to its performance and accuracy. However, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance, although other work has found $A^{\ast}$ to be superior to other approaches.

First we learn the Dijkstra's algorithm. Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.

For example, we want to find the shortest path between a and b in the following graph. The distance of every pair is given.

  1. the distance to its neighbors is computed:
a(0) 2 3 6
0 7 9 14
  1. as the first step, compute the distance to all neighbors:
2 3 4 3 4 6
0 10 15 0 11 2

Now we have 2 choices from 1 to 3: (1) $1\to3\mid 9$;(2) $1\to 2\to3\mid (7+10=17 >9)$. And we find all paths from 1 to 3 and the shortest path from 1 to 3 is $1\to3$ with distance 9.

From 1 to 4: (1) $1\to2\to4\mid 7+15=22$; (2) $1\to3\to4\mid 9+11=20<22$. the shortest path from 1 to 6 is $1\to3\to4$ with distance 20.

From 1 to 6: (1) $1\to6\mid 14$; (2) $1\to3\to6\mid 9+2=11<14$. the shortest path from 1 to 6 is $1\to3\to6$ with distance 11.

  1. distance to neighbor:
4 b 6 b
0 6 0 9

$1\to3\to4\to b\mid 9+11+6=26$ and $1\to3\to6\to b\mid 9+2+9=20<26$ is the shortest.

Dijkstra algorithm

See the page at Wikipedia $A^{\ast}$ search algorithm

Graph adjacency matrix duality

Perhaps even more important is the duality that exists with the fundamental operation of linear algebra (vector matrix multiply) and a breadth-first search (BFS) step performed on G from a starting vertex s: $$ BFS(G, s) \iff A^T v, v(s)=1. $$

This duality allows graph algorithms to be simply recast as a sequence of linear algebraic operations. Many additional relations exist between fundamental linear algebraic operations and fundamental graph operations

Directed Acyclic Graph

Directed acyclic graph (DAG) is the directed graph without any cycles. It is used widely in scheduling, distributed computation.

Definition The acyclic graph is called forest. A connected acyclic graph is called a tree.

A graph $G$ is a tree if and only if $G$ is a forest and $|V(G)|=|E(G)| + 1$.

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge ${uv}$, vertex ${u}$ comes before ${v}$ in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.

Chemical Graph Theory

Graph theory applied in the study of molecular structures represents an interdisciplinary science, called chemical graph theory or molecular topology.

A chemical graph is a model of a chemical system, used to characterize the interactions among its components: atoms, bonds, groups of atoms or molecules. A structural formula of a chemical compound can be represented by a molecular graph, its vertices being atoms and edges corresponding to covalent bonds. Usually hydrogen atoms are not depicted in which case we speak of hydrogen depleted molecular graphs.

In a multigraph two points may be joined by more than one line. If multibonds are taken into account, a variant of adjacency matrix $A(G)$ , denoted $C(G)$, (the connectivity matrix) can be written: $$ {[C]}{ij}=\begin{cases} b{ij} &\text{if $i\not=j$ and $(i, j)\in E(G)$},\ 0 &\text{otherwise} \end{cases} $$ where $b_{ij}$ is the conventional bond order: 1; 2; 3; 1.5 for simple, double, triple and aromatic bonds, respectively.

Distance Matrix $D(G)$, is a square symmetric table, of size $n\times n$, similar to adjacency matrix by replacing the entity of topological distance: $$ {[D]}{ij}=\begin{cases} d{ij} &\text{if $i\not=j$},\ 0 &\text{otherwise} \end{cases} $$ where $d_{ij}$, the topological distance between $i$ and $j$.

M. V. Diudea, I. Gutman and L. Jantschi in Molecular Topology claims that

A single number, representing a chemical structure, in graph-theoretical terms, is called a topological descriptor. Being a structural invariant it does not depend on the labeling or the pictorial representation of a graph. Despite the considerable loss of information by the projection in a single number of a structure, such descriptors found broad applications in the correlation and prediction of several molecular properties1,2 and also in tests of similarity and isomorphism.

The simplest TI is the half sum of entries in the adjacency matrix $A$: $$A=\frac{1}{2}\sum_{ij}{[A]}_{ij}.$$

The Indices of Platt, F, Gordon-Scantlebury, N2, and Bertz, B1： $$F={\sum}{i}\sum{j}{[EA]}{ij}=2\sum{i}C_{2}^{\delta_i}=2 N2=2 B1$$ where $EA$ is the Edge Adjacency matrix. This index is twice the Gordon - Scantlebury index, N2 , defined as the number of modes in which the acyclic fragment C-C-C may be superposed on a molecular graph $$N2=\sum_{i}{(P_2)}_i.$$ This index equals the number of all paths of length 2, P2 , in graph. The last one can be calculated combinatorially from the vertex degree, $\delta_i$ .

First TIs based on adjacency matrix (i.e., based on connectivity) were introduced by the Group from Zagreb: $$ M_1=\sum_{i}\delta_i^2, \ M_2=\sum_{(i,j)\in E(G)}\delta_i\delta_j $$ where $\delta_i, \delta_j$ are the vertex degrees for any two adjacent vertices.

The Randic Index, $\chi$ $$\chi=\sum_{(i,j)\in E(G)}(\delta_i\delta_j)^{-\frac{1}{2}} $$ $\chi$ - called the connectivity index, is calculated on edge, by using the vertex degrees of its endpoints. The $\chi$ values decrease as the branching increases within a set of alkane isomers. They increase by the number of atoms in the molecular graph.

It can extended the summation over all paths of length $e$: $$\chi^{e}=\sum_{p_e}(\delta_i\delta_j\cdots \delta_{e+1})^{-\frac{1}{2}} $$ where $(\delta_i, \delta_j, \cdots, \delta_{e+1}$ are the vertex degrees along the path $p_e$.

Wiener-Type Indices In acyclic structures, the Wiener index, W and its extension, the hyper-Wiener index, WW can be defined as $$ W=W(G)={\sum}e N{i,e}N_{e,j} \ WW=WW(G)={\sum}e N{i,p}N_{p, j} $$

where $N_i$ and $N_j$ denote the number of vertices lying on the two sides of the edge $e$ or path $p$, respectively, having the endpoints $i$ and $j$. Other main definitions38,39 of the Wiener-type indices are based on the distance matrices, $$ W=\frac{1}{2}\sum_{i}\sum_{j}{[D_e]}{ij},\ WW=\frac{1}{2}\sum{i}\sum_{j}{[D_p]}_{ij}. $$

INDICES BASED ON RECIPROCAL MATRICES

INDICES BASED ON COMBINATION OF MATRICES

INDICES BASED ON EIGENVALUES AND EIGENVECTORS

Topological descriptors Topological index

Graph Partitioning

Definition: Separators A subsect of vertices ${C}$ of a graph ${G}$ with ${n}$ vertices is an $f(n)$-separator that $\delta$-splits if $|C|<f(n)$ and vertices $G-C$ can be partitioned into two sets ${A}$ and ${B}$ such that $|A|, |B|<\delta n$ and there is no edge between ${A}$ and ${B}$, where $f$ is a positive function and $0<\delta < 1$.

The fundamental problem that is trying to solve is that of splitting a large irregular graphs into ${k}$ parts. This problem has applications in many different areas including, parallel/distributed computing (load balancing of computations), scientific computing (fill-reducing matrix re-orderings), EDA algorithms for VLSI CAD (placement), data mining (clustering), social network analysis (community discovery), pattern recognition, relationship network analysis, etc. The partitioning is usually done so that it satisfies certain constraints and optimizes certain objectives. The most common constraint is that of producing equal-size partitions, whereas the most common objective is that of minimizing the number of cut edges (i.e., the edges that straddle partition boundaries). However, in many cases, different application areas tend to require their own type of constraints and objectives; thus, making the problem all that more interesting and challenging!

The research in the lab is focusing on a class of algorithms that have come to be known as multilevel graph partitioning algorithms. These algorithms solve the problem by following an approximate-and-solve paradigm, which is very effective for this as well as other (combinatorial) optimization problems.

Over the years we focused and produced good solutions for a number of graph-partitioning related problems. This includes partitioning algorithms for graphs corresponding to finite element meshes, multilevel nested dissection, parallel graph/mesh partitioning, dynamic/adaptive graph repartitioning, multi-constraint and multi-objective partitioning, and circuit and hypergraph partitioning.

Let $P = {p_i, \cdots, p_n }$ be a set of ${n}$ points in $\mathbb{R}^d$. For each $p_i\in P$, let $N(p_i)$ be a closest neighbor of ${p}$ in ${P}$, where ties are broken arbitrarily. Similarly, for any integer ${k}$, let $N_k(p_i)$ be the set of ${k}$ nearest neighbors of ${p}$ in ${P}$, where the ties too are broken arbitrarily.

Definition A ${k}$-nearest neighborhood graph of $P = {p_i, \cdots, p_n }$ in $\mathbb{R}^d$ , is a graph with vertices $V = {1, \cdots,n}$, and edges ${E}$,

$$ E = { (i, j) \mid p_i\in N_k(p_j)\quad \text{or}\quad p_j \in N_k(p_i) }. $$

A Spectral Analysis of Moore Graphs

Graph Kernel

Like kernels in kernel methods, graph kernel is used as functions measuring the similarity of pairs of graphs. They allow kernelized learning algorithms such as support vector machines to work directly on graphs, without having to do feature extraction to transform them to fixed-length, real-valued feature vectors.

Definition : Find a mapping $f$ of the vertices of $G_1$ to the vertices of $G_2$ such that $G_1$ and $G_2$ are identical; i.e. $(x, y)$ is an edge of $G_1$ if and only if $(f(x),f(y))$ is an edge of $G_2$. Then ${f}$ is an isomorphism, and $G_1$ and $G_2$ are called isomorphic.

No polynomial-time algorithm is known for graph isomorphism. Graph kernel are convolution kernels on pairs of graphs. A graph kernel makes the whole family kernel methods applicable to graphs.

Von Neumann diffusion is defined as $$K_{VND}=\sum_{k=0}^{\infty}{\alpha}^{k}{A}^{k}=(I-\alpha A)^{-1}, \alpha\in[0,1].$$

Exponential diffusion is defined as $K_{ED}=\sum_{k=0}^{\infty}\frac{1}{k!}{\alpha}^{k}{A}^{k}=\exp(\alpha A)$. Katz method is defined as the truncation of Von Neumann diffusion $$S_K=\sum_{k=0}^{K}{\alpha}^{k}{A}^{k}=(I-\alpha A)^{-1}(\alpha A-{\alpha}^K {A}^K).$$

Semi-supervised Learning based Graph

Dirichlet energy functional is defined as $$\mathbb{E}(f)=\frac{1}{2}\int_{U}{|\nabla f|}^2\mathrm d x$$ $$\mathbb{E}(f)=\frac{1}{2}\sum_{i, j}w_{i,j}{|f_i -f_j|}^2\implies f(h)=\frac{\sum_{i}w_{i,h}f(i)}{\sum_i w_{i,h}}$$

Link Prediction

The above algorithms are unsupervised algorithms so what is the supervised algorithms in graph data sets? Do prediction algorithms such as classification and regression matter?

Probability on Graph

It is to answer the question how to characterize a network in the term of some summary statistic. The following distribution may be the key:

  • the distribution of the degree;
  • the distribution of the eigenvalue of the Laplacian matrix;
  • random matrix and dynamical network.

A particle moves around the vertex-set ${V}$. Having arrived at the vertex $S_n$ at time n, its next position Sn+1 is chosen uniformly at random from the set of neighbours of $S_n$. The trajectory of the particle is called a symmetric random walk (SRW) on ${G}$. Two of the basic questions concerning symmetric random walk are:

  1. Under what conditions is the walk recurrent, in that it returns (almost surely) to its starting point?
  2. How does the distance between S0 and Sn behave as $n\to\infty$?

Graph Learning

Graph Learning is to learn from the graph data: Simply said, it’s the application of machine learning techniques on graph-like data. Deep learning techniques (neural networks) can, in particular, be applied and yield new opportunities which classic algorithms cannot deliver.

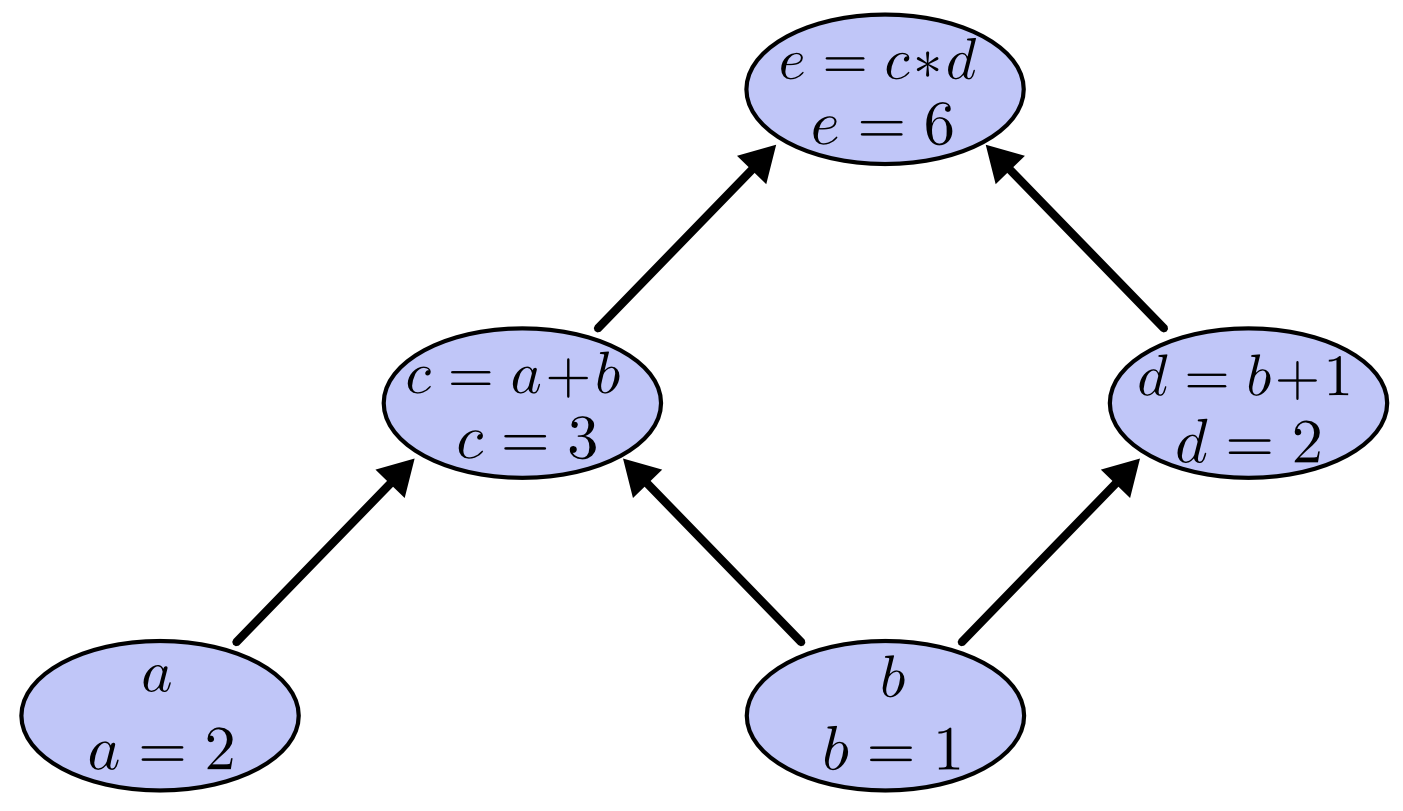
Computational Graph

Computational graphs are a nice way to think about mathematical expressions, where the mathematical expression will be in the decomposed form and in topological order.

A computational graph is defined as a directed graph where the nodes correspond to mathematical operations. Computational graphs are a way of expressing and evaluating a mathematical expression.

To create a computational graph, we make each of these operations, along with the input variables, into nodes. When one node’s value is the input to another node, an arrow goes from one to another. These sorts of graphs come up all the time in computer science, especially in talking about functional programs. They are very closely related to the notions of dependency graphs and call graphs. They’re also the core abstraction behind the popular deep learning framework TensorFlow. Computational graph is an convenient representation of the work flow or process pipeline, which describes the dependence/composite relationship of every variable. Additionally, each composite relationship is specified.

A computational graph is a directed graph where the nodes correspond to operations or variables. Variables can feed their value into operations, and operations can feed their output into other operations.

The basic idea in a computational graph is to express some model—for example a feedforward neural network—as a directed graph expressing a sequence of computational steps. Each step in the sequence corresponds to a vertex in the computational graph; each step corresponds to a simple operation that takes some inputs and produces some output as a function of its inputs. Directed edges in the graph are used to specify the inputs to each vertex.

Computational Graph of Decision Tree

Decision tree looks like a simple graph without loops, where only the leaf nodes specify the output values and the middle nodes specify their test or computation. Computational graph is regarded as an extension of deep neural network. The computational graph of deep neural network focus on two parts: the operation of each node and automatic differentiation.

In deep neural network, the operation of middle node is a smooth activation function such as $\sigma(x)=\frac{1}{1+\exp(-x)}$ or ReLU and it maps every input in the element-wise sense. All input of the deep neural network share the same depth and activation function in computational graph. More complex architecture can include some feedback structure.

In decision tree, the operation of middle node is a test function such as typical statistical test and it determines the input next state - for example terminated or not. Different inputs have different depth and test function in computational graph. The test function depends on the splitting criteria when building a decision tree. In vanilla decision tree, the test function does not change the inputs and the final outputs of a leaf depend its instances labels.

We select a feature and find the optimal splitting point recursively and then the outputs are as some summary of the instances of the leaf nodes.

QuickScorer establishes tree traversal by applying bitwise AND to boolean representations of FALSE nodes, i.e., nodemask. Bitvector representation of the tree nodes makes it possible express the building procedure of decision tree in the language of computational graph.

Suppose $X\in\mathbb{R}^p$ is the input of the decision tree, categorical feature will consider later. The first thing is to rewrite the test as one function, i.e., transforming the if-then sentence to number/bit computation. The second thing is to represent a decision tree as some tabular data frame.

There are 4 steps of tree traversal of QuickScorer:

  • build the nodemasks of each middle node in decision tree with the length equal to the number of leaf nodes $B=(B_1,B_2,\cdots, B_{|T|})$;
  • find the FALSE nodes with respect to an input $x$;
  • apply bitwise AND to boolean representations of FALSE nodes and return the results $v_h$;
  • the leftmost bit equal to 1 in $v_h$ corresponds to the exit leaf $e_h$.

See more details of this procedure in the following links.

The following is to translate the procedure to the language of computational graph. We suppose that the decision tree is built by a greedy way.

Different from building the tree, prediction of decision tree is a tree traversal in nature. Inspired by QuickScorer, we split such prediction to the following stages.

The first stage is to find the false nodes in the decision tree with respect to the input $x$: $$h=\frac{-(Sign[Sx-t])+1}{2}$$ where so-called selection matrix $S\in\mathbb{R}^{n_L\times p}$ consists of one-hot row vector in $\mathbb{R}^p$ representing which feature is tested in a node; the bias vector $t\in\mathbb{R}^{n_L}$ is the optimal point of each node associated with one feature; $Sign(\cdot)$ is the element-wise sign function. Here $n_L$ is the number of the middle nodes. If the feature of $x$ is greater than the splitting point, the corresponding node is a true node. Otherwise, the node is False node.

The second stage is to apply bitwise AND to false nodes $$H=(B , ,\operatorname{Diag}(h))^{\otimes}$$

where the notation ${\otimes}$ is a element-wise multiplication of the non-zeros columns of a matrix; $Diag(x)$ maps a vector to a diagonal matrix; $B\in\mathbb{B}^{L\times n_L}$ is the bitvector matrix of the decision tree. Every columns of $B$ is a bit-vector of node; $B , ,\operatorname{Diag}(h)$ is the matrix multiplication of matrix $B$ and $\operatorname{Diag}(h)$. Here $L$ is the number of exit leaf nodes.

The final stage is to determine the output $$v[i]\ i=min(HP)^+ $$ where $P=(1,2, \cdots, L)^T\in\mathbb{R}^L$ and $L$ is the number of the exist leaves; $v[i]$ are the $i$th elements of vector $v$; $(HP)^+$ are the positive elements of vector $HP$; $min(v)$ outputs the minimum values in the vector $v$.

In a compact form, a decision tree is expressed as follows:

$$T(x)=v[\min((B,,\operatorname{Diag}[\frac{-(Sign[Sx-t])+1}{2}] )^{\oplus} P)^+]$$ where the notation ${\otimes}$ is a element-wise multiplication of the non-zeros columns of a matrix; $Diag(x)$ maps a vector to a matrix; $B$ is the bitvector matrix of the decision tree.

The hierarchical structure of decision tree is clear: $$x\to h\to H\to v[i]\ \mathbb{R}^p \to\mathbb{B}^{n_L}\to\mathbb{B}^{L}\to\mathbb{R} $$

It is really a shallow model. And its hidden layers are sparse binary.

Now there is nothing rather than expressing the decision tree in the language of computational graph. It looks far from a step function. However, note that

  • the $Sign$ function is a step function.
  • the matrix $S$ and $B$ are binary, i.e., their elements are 0 or 1.
  • $min()$ only select one element.

All if-then tests transform to numerical computation.

From mathematical consideration, can we replace the $Sign$ function with some smooth function? Can we generalize the $S, B$ to real matrices? Can we apply gradient-based methods to train a decision tree?

In the language of computational graph, how can we describe the (gradient) boosting decision tree? The structure information of the decision tree transforms to the bitvector matrix $B$. The splitting points information transforms to the pair $(S, t)$. Given triple(tuple) $(S, t, B)$, we can traverse a tree to each leaf. The question is if it is a ono-one mapping from a decision tree to $(S, t, B, v)$?

Dynamic Computational Graphs

A Dynamic Computational Graph is a mutable system represented as a directed graph of data flow between operations. It can be visualized as shapes containing text connected by arrows, whereby the vertices (shapes) represent operations on the data flowing along the edges (arrows).

The main difference between frameworks that uses static computation graph like Tensor Flow, CNTK and frameworks that uses dynamic computation graph like Pytorch and DyNet is that the latter works as follows, a different computation graph is constructed from scratch for each training sample, forward and backward propagation are then take place so in another words the user is free to use different networks for each input sample but this of course will cost you a little overhead but don’t worry frameworks like DyNet has an optimized C++ backend and lightweight graph representation. Experiments show that DyNet’s speeds are faster than or comparable with static declaration toolkits while the static graph frameworks the graph is defined once and then the optimization graph compiler then produced optimization graph and all the training samples are then feed to this graph .On the one hand, once compiled, large graphs can be run efficiently on either the CPU or a GPU, making it ideal for large graphs with a fixed structure, where only the inputs change between instances. However, the compilation step itself can be costly, and it makes the interface more cumbersome to work with.

Dynamic Graphs

In many applications of graph algorithms, including communication networks, graphics, assembly planning, and VLSI design, graphs are subject to discrete changes, such as additions or deletions of edges or vertices. In the last decades there has been a growing interest in such dynamically changing graphs, and a whole body of algorithms and data structures for dynamic graphs has been discovered. In a typical dynamic graph problem one would like to answer queries on graphs that are undergoing a sequence of updates, for instance, insertions and deletions of edges and vertices. The goal of a dynamic graph algorithm is to update efficiently the solution of a problem after dynamic changes, rather than having to recompute it from scratch each time. Given their powerful versatility, it is not surprising that dynamic algorithms and dynamic data structures are often more difficult to design and analyze than their static counterparts.