算法设计
English | 中文
量化过程将宽范围的数值表示为小范围的近似值,从而达到有损压缩的目的。例如:16位的JPG文件转换成4色的GIF文件,就是把RGB颜色空间的颜色量化成4种颜色的过程。还有,把身高为161、164、178、184的4名学生表示成“160-169阶段的2名,170-179阶段的1名、180以上阶段的1名”的方式也是量化。 现要把小于1000的自然数组成的序列量化成s个自然数组成的序列。量化的方法其实很多,例如,只用两个数表示序列{1 2 3 4 5 6 7 8 9 10},就可以表示成{3 3 3 3 3 7 7 7 7 7}。或还可以用{1 1 1 1 1 10 10 10 10 10}的形式表示。那么,各数值误差平方之和最小的量化结果是多少呢?
比如,把序列{1 2 3 4 5}量化成{2 2 3 3 3},各数值量化后的误差是-1、0、0、1、2。那么,误差平方之和是1+0+0+1+4=6。但是,如果量化成{2 2 4 4 4},那么误差平方之和是1+0+1+0+1=3。接下来请编写程序,求用s个数值量化给定序列后,误差平方之和的最小值。
第一行输入测试用例的个数C(1<=C<=50)。各测试用例的第一行输入序列的长度n(1<=n<=100),以及可使用的数值个数s(1<=s<=10)。第二行输入序列的n个整数,且序列的所有数值是1000以下的自然数。
每个测试用例将在1行内输出用s个数值量化给定序列时产生的最小误差平方之和。
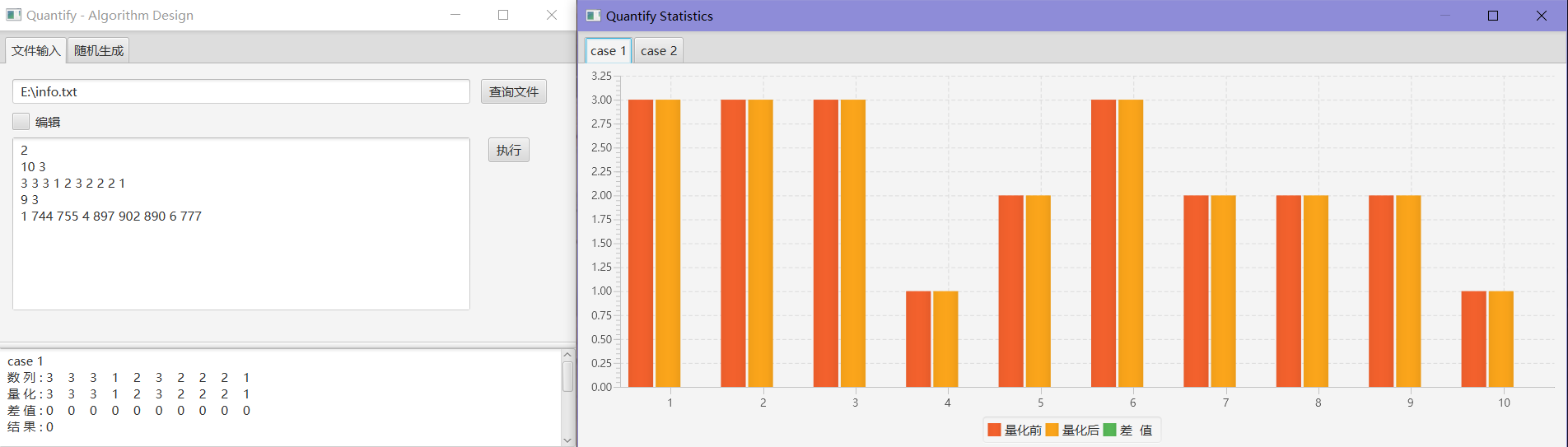
2
10 3
3 3 3 1 2 3 2 2 2 1
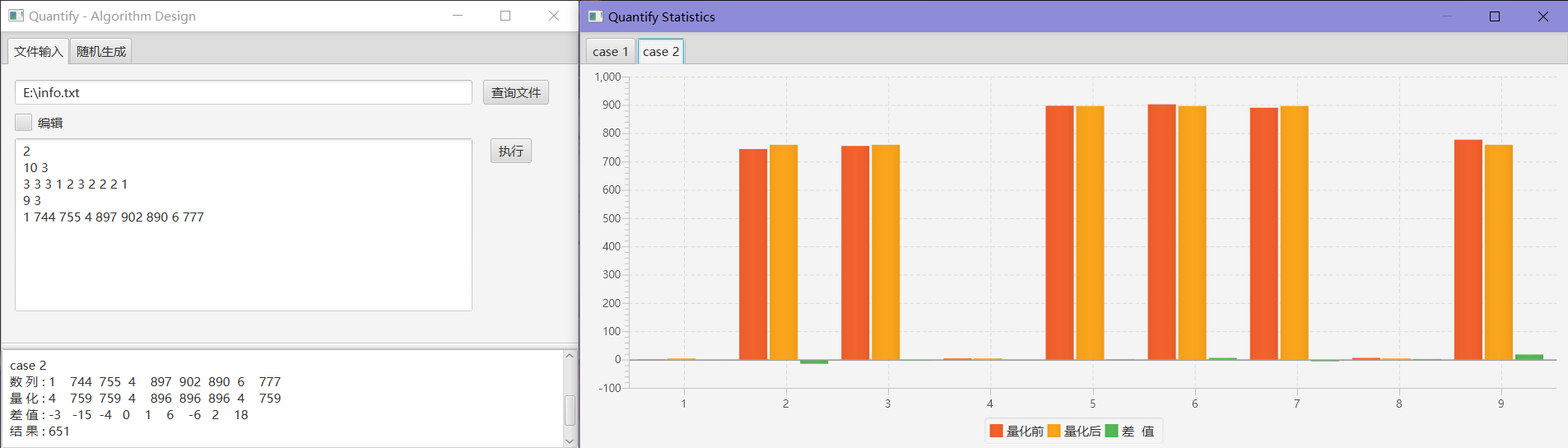
9 3
1 744 755 4 897 902 890 6 777
0
651