All spherical calculations are based on 3D-vectors, their dot, cross, triple products, and positions relative to planes.
A vector must implement ICartesian interface:
public interface ICartesian
{
double X { get; }
double Y { get; }
double Z { get; }
void SetCartesian(double x, double y, double z);
}
Some extension methods for the ICartesian interface are generic and can return a result of any type implementing ICartesian. Interface method SetCartesian is used there for result initialization with X,Y,Z values. Classes implementing ICartesian may have some other properties depending on X,Y,Z. SetCartesian is a place where to maintain consistency of these properties with X,Y,Z. aleprojects.spherical namespace provides Cartesian class representing a basic vector.
A location on a sphere must implement the IGeoCoordinate interface:
public interface IGeoCoordinate
{
double Latitude { get; } // Latitude in degrees.
double Longitude { get; } // Longitude in degrees.
}
The SphericalExtension static class provides extension methods for the ICartesian and IGeoCoordinate interfaces. Examples:
Cartesian vectorI = new Cartesian(1.0, 0.0, 0.0, false);
Cartesian vectorJ = new Cartesian(0.0, 1.0, 0.0, false);
Cartesian N = vectorI.CrossProduct<Cartesian>(vectorJ);
GeoCoordinate L = vectorJ.CrossProduct<GeoCoordinate>(vectorI);
double angle = vectorI.Angle(vectorJ);
I'll not focus on such methods like DotProduct, CrossProduct, Angle, etc, because their use and purpose are obvious. But some methods for typical geospatial tasks are worth mentioning and explaining.
public static bool InsideTriangle<T, U>(this T cartesian, U V1, U V2, U V3)
where T : ICartesian
where U : ICartesian
This method checks if the vector cartesian is inside the spherical triangle with the V1, V2, V3 vertices. The method calculates triple products of the cartesian with each pair of vectors. The first criterion is that all results are of one sign. If the vector is inside, an opposite vector will produce triple products of one sign too. So, the second criterion is an angle between cartesian and sum of triangle vertices, it must be greater than π/2. This method is a cornerstone of the sphere triangular grid.
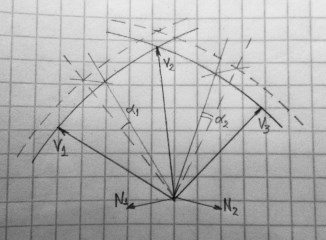
This method inflates or deflates a convex polygon.
public static List<T> InflateConvex<T, U>(IEnumerable<U> polygon, IReadOnlyList<double> angles)
where T : ICartesian, new()
where U : ICartesian
The idea behind calculations is to rotate planes formed by vertices vectors to an angle which is a distance on a sphere divided by sphere radius. InflateConvex rotates normal vectors N1 = V1 x V2, N2 = V2 x V3, etc. that represent planes. Next step is to find new vertices of the inflated convex. They are cross products of the rotated normal vectors N1 x N2, etc.
angles parameter must contain at least 1 element. InflateConvex takes the next value in angles for the next plane and uses the last value for the rest planes if the length of angles is less than the number of the convex vertices.
public static int SectionsIntersect<T, U>(T V1S1, T V2S1, U V1S2, U V2S2)
where T : ICartesian
where U : ICartesian
public static int SectionsIntersect<T, U>(T V1S1, T V2S1, U V1S2, U V2S2, double tolerance)
where T : ICartesian
where U : ICartesian
This method checks that two sections (geodesical lines) on a sphere intersect. First, this method takes a plane formed by vertices V1S1 and V2S1 and checks positions of vertices V1S2 and V2S2 relative to the plane. Then the same with the plane formed by V1S2 and V2S2 and the positions of V1S1 and V2S1. The method returns a negative number if the sections don't intersect, positive if intersect, zero if some section end belongs to another section. Overloaded method with tolerance parameter tests if the sections are close enough to each other to consider them intersecting. Tolerance is an angle in radians at the coordinates origin, real distance on the surface is tolerance*sphere_radius.
public static bool InsidePolygon<T, U>(this T cartesian, IEnumerable<U> polygon, U polygonCenter = default)
where T : ICartesian
where U : ICartesian
This method checks if a vector cartesian is inside a polygon including its borders using winding number algorithm. The polygon can be of any shape. If the polygon is a convex, it is better to use InsideConvex method.
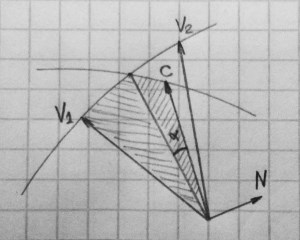
public static double TestSection<T, U>(this T cartesian, U V1, U V2)
where T : ICartesian
where U : ICartesian
This method checks if a vector cartesian is between two vectors V1 and V2. First, it builds a plane using V1 and V2. Then it takes an angle between the vector cartesian and this plane and corrects it with π/2 angle. The method returns this angle, its positive value indicates that cartesian is between the vectors, negative if not. The next step is to build another plane containing cartesian and perpendicular to the plane obtained in the first step. Finally, it checks positions of V1 and V2 relative to this plane. If they are on the opposite sides, the result is positive.
This drawing demonstrates TestSection method. If to call C.TestSection(V1,V2) with C,V1,V2 as they drawn, it will return positive alpha angle indicating success. Alpha*sphere_radius is a distance from the point C to the arc on the sphere. If C is out of the arc V1V2, method will return negative value of the angle.
public static int TestPolyline(this ICartesian cartesian, IEnumerable<ICartesian> polyline, double tolerance, bool reverse, PolylineSectionTest userTest, out double angleFromPolyline)
public static PolylineTestResult TestPolyline(this ICartesian cartesian, IEnumerable<ICartesian> polyline, double tolerance, bool reverse, PolylineSectionTest userTest, PolylineTestResult result)
This method works in a similar way as TestSection. It applies TestSection to all sections of the polyline with some additional checks. First additional check is how far from the polyline the point can stand. The tolerance parameter is an angle in radians at the coordinates origin, it represents maximum distance as tolerance*sphere_radius. Second optional check is the userTest delegate, if it is not null. If the task is only to check the position of a point relative to a polyline, no need to use delegate. If the task is to guide moving point along directional route polyline, then the delegate is required.
Example:
List<Cartesian> polyline = SphericalExtension.DecodeGooglePolyline<Cartesian>("mk~F`c~uOOuCCqCEiCSkD_@gC");
Cartesian location = new Cartesian(41.84524, -87.64902);
double heading = 85.0 * Math.PI / 180.0; // 85 degrees, almost to the East
double speed = 40; // units don't matter in this example, let it be mph.
double tolerance = 30; // 30 meters
PolylineSectionTest geometryTest = (v0, v1, v2, angle, azimuth) =>
{
// the higher speed, the less fluctuations of a heading calculated from GPS data.
double diff = speed < 10.0 ? Math.PI / 4.0 : Math.PI / 10.0;
double azimuth2;
return Math.Abs(heading.BearingsDiff(azimuth)) < diff ||
(v0 != null &&
(Math.Abs(heading.BearingsDiff(azimuth2 = v0.BearingTo(v1))) < diff ||
heading.BearingInRange(azimuth, azimuth2)));
};
PolylineTestResult testResult = location.TestPolyline(
polyline,
tolerance / SphericalExtension.EARTH_MEAN_RADIUS,
false,
geometryTest,
null);
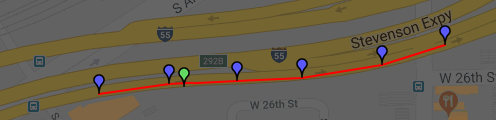
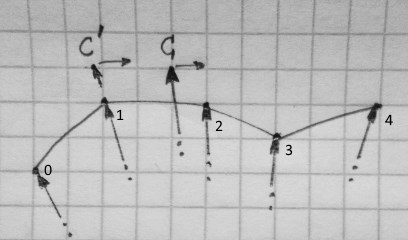
In most cases the geometryTest delegate is called with v0 = null and v1, v2 corresponding to the section of the polyline most closest to the point. This is the case of point C on the drawing below. In this case it is enough to compare current heading with the azimuth from v1 to v2. The azumuth parameter of the delegate holds this azimuth. HeadingsDiff is the extension method of the SphericalExtesion static class. The angle parameter if multiplied by SphericalExtension.EARTH_MEAN_RADIUS represents a distance to the section.
Sometimes it is possible that the point is close enough to some vertex of polyline, but failed the TestSection for both sections. Point C' on the drawing demonstrates this situation. When such a thing happens, v0 parameter is not null. In this case we need to make additional test for the heading. First, we compare the heading with the azimuth of v0,v1 (points marked 0, 1 on the drawing). If this test fails, we check if the heading is within range of the azimuths of neighbour sections. BearingInRange is the standard extension method.
Finally, if the polyline test succeeds, it return non-null object of PolylineTestResult type. SectionIndex property contains index of the section found, the same as the index of the first vertex of the section. There is useful method DistanceToEnd returning a distance along the polyline from the point to the end.
If we apply TestPolyline to the next received point with the same polyline and with the result for the previous point, new test will begin from SectionIndex vertex of the polyline.
testResult = nextLocation.TestPolyline(
polyline,
tolerance / SphericalExtension.EARTH_MEAN_RADIUS,
false,
geometryTest,
testResult); // <----
If the new test succeeds, testResult will be updated with new values. If the test fails, Fails property will be incremented by 1. How to handle non-zero Fails is up to developer. This may happen if bad GPS data is received, but desired behavior is not to leave a route immediately.
public static DateTime Sunrise<T>(this T location, DateTimeOffset date)
where T : ICartesian
This method calculates a time of sunrise for a given location and date. The method uses only date.Year, date.Month, date.Day, and date.Offset components of the date. date.Offset is important for the calculation and considered as the time zone. The method returns DateTime.MaxValue if the Sun never rises at this location, DateTime.MinValue if never sets. In other cases, it returns local sunrise time.
public static DateTime Sunset<T>(this T location, DateTimeOffset date)
where T : ICartesian
This method calculates a time of sunset for a given location and date. The method uses only date.Year, date.Month, date.Day, and date.Offset components of the date. date.Offset is important for the calculation and considered as a time zone. The method returns DateTime.MaxValue if the Sun never rises at this location, DateTime.MinValue if never sets. In other cases, it returns local sunset time.
public static (DateTime sunrise, DateTime sunset) NearestSunriseSunset<T>(this T location, DateTimeOffset date)
where T : ICartesian
Returns times of nearest past and future events. If specified time is after sunset for this date, the method returns time of sunrise for the next day. If specified time is before sunrise for this date, the method returns time of sunset for the previous day. Otherwise, it returns time of sunrise and sunset for the specified date. This makes easy to check if the current time is dark or not, and to switch your app to the dark theme. Example:
var time = DateTimeOffset.Now;
var (sunrise, sunset) = location.NearestSunriseSunset(time);
if (time.DateTime > sunrise && time.DateTime < sunset)
{
// Day time
}
else
{
// Dark time
}
if the Sun never rises, the method returns (DateTime.MaxValue, DateTime.MinValue). If the Sun never sets, it returns (DateTime.MinValue, DateTime.MaxValue).
Extension method DayTime does the same as the example above.
public static bool DayTime<T>(this T location, DateTimeOffset date)
where T : ICartesian