3241_Time_Taken_to_Mark_All_Nodes.md

3241. Time Taken to Mark All Nodes

Difficulty: hard

Link: https://leetcode.com/problems/time-taken-to-mark-all-nodes/

Contains PNG: Yes

PNG Links:

• https://assets.leetcode.com/uploads/2024/06/01/screenshot-2024-06-02-122236.png
• https://assets.leetcode.com/uploads/2024/06/01/screenshot-2024-06-02-122249.png
• https://assets.leetcode.com/uploads/2024/06/03/screenshot-2024-06-03-210550.png

Problem Statement

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree.

Initially, all nodes are unmarked. For each node i:

• If i is odd, the node will get marked at time x if there is at least one node adjacent to it which was marked at time x - 1.
• If i is even, the node will get marked at time x if there is at least one node adjacent to it which was marked at time x - 2.

Return an array times where times[i] is the time when all nodes get marked in the tree, if you mark node i at time t = 0.

Note that the answer for each times[i] is independent, i.e. when you mark node i all other nodes are unmarked.

Example 1:

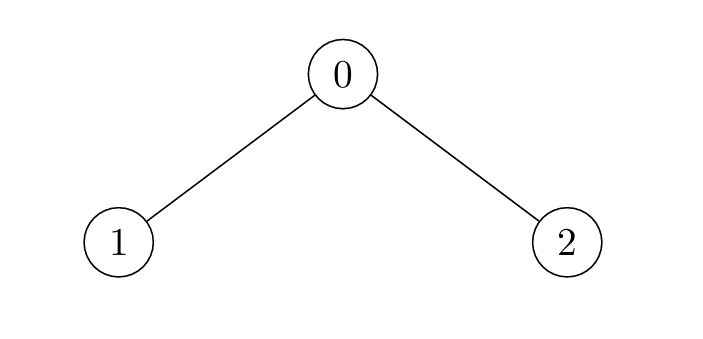
Input: edges = [[0,1],[0,2]]

Output: [2,4,3]

Explanation:

• For i = 0:
  • Node 1 is marked at t = 1, and Node 2 at t = 2.
• For i = 1:
  • Node 0 is marked at t = 2, and Node 2 at t = 4.
• For i = 2:
  • Node 0 is marked at t = 2, and Node 1 at t = 3.

Example 2:

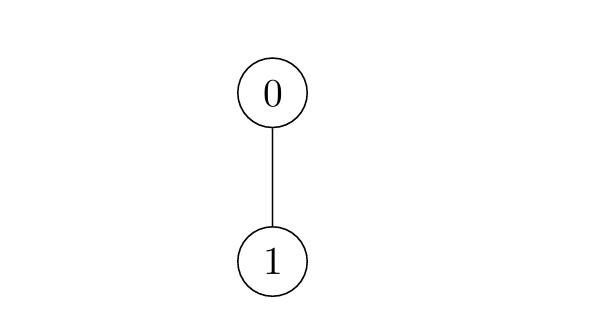
Input: edges = [[0,1]]

Output: [1,2]

Explanation:

• For i = 0:
  • Node 1 is marked at t = 1.
• For i = 1:
  • Node 0 is marked at t = 2.

Example 3:

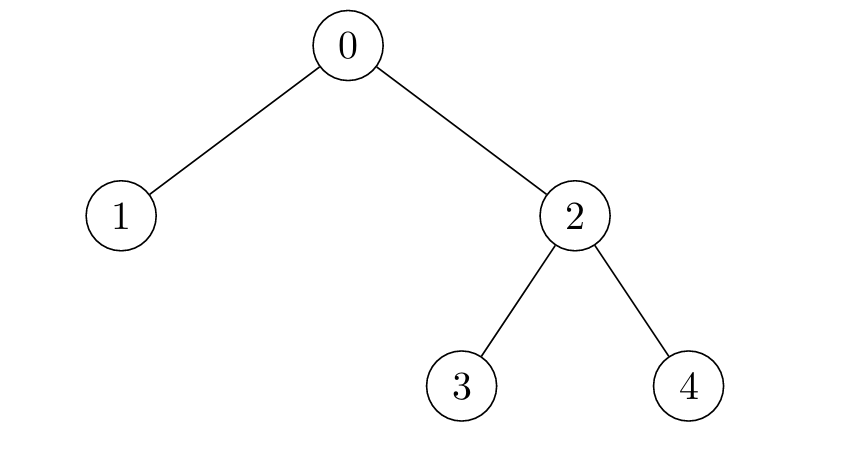
Input: edges = [[2,4],[0,1],[2,3],[0,2]]

Output: [4,6,3,5,5]

Explanation:

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= edges[i][0], edges[i][1] <= n - 1
• The input is generated such that edges represents a valid tree.

Hints

• 1. Can we use dp on trees?
• 2. Store the two most distant children for each node.
• 3. When re-rooting the tree, keep a variable for distance to the root node.

Code Templates

Cpp

class Solution {
public:
    vector<int> timeTaken(vector<vector<int>>& edges) {
        
    }
};

Java

class Solution {
    public int[] timeTaken(int[][] edges) {
        
    }
}

Python

class Solution:
    def timeTaken(self, edges: List[List[int]]) -> List[int]: