红黑树和2-3书有着等价的关系。我们了解了红黑树之前,必须先了解2-3这种数据结构。
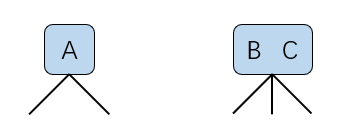
2-3 树也满足树的基本结构。但是一个节点可以存储一个或者两个元素。每一个节点可以有两个或者三个孩子。
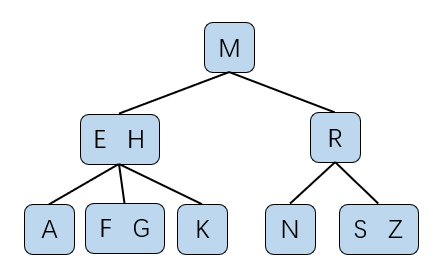
下面是一种2-3树的结构。排序的方式是根据字符的大小。
我们可以根据上面的结构来验证2-3树是否满足树的基本结构。
A->E->F->G->H->K->M->N->R->S->Z
可以对树结构进行中序遍历来查看该结构是否具有顺序性。我们可以得出一个结论就是:
可以看得出来任意节点的孩子节点的高度是相同的。下面就开始介绍这种数据结构是如何维持平衡性的。
通过介绍如何添加元素来介绍这种树结构是如何维持平衡性的。
下面以实例进行讲解,这个地方主要还是靠大家的看。
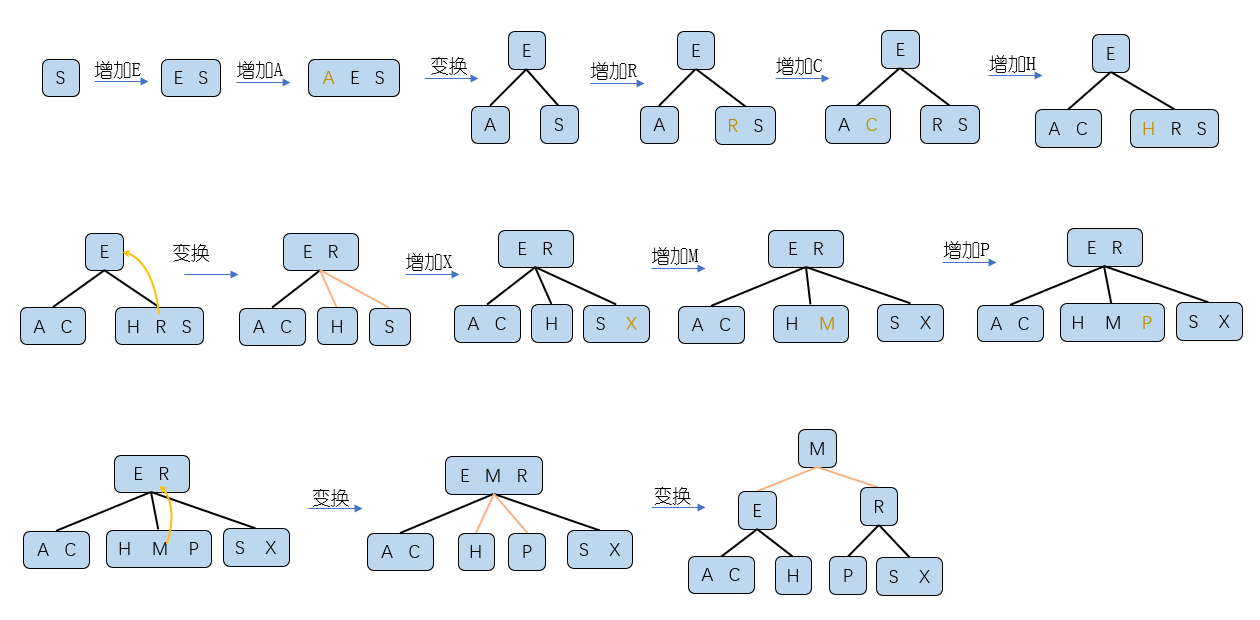
添加的顺序是:S->E->A->R->C->H->X->M->P
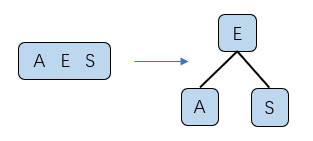
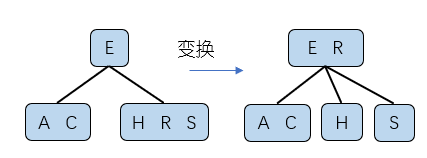
最关键的还是在于变换的操作。 由于2-3树的节点最多只能存放2个元素,当有三个元素(四节点)的时候就需要进行变换。
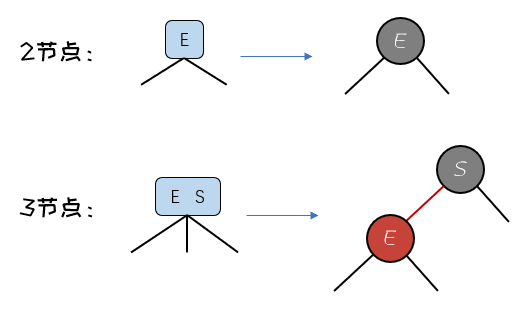
对于这种分裂并不会破坏树结构的绝对平衡的性质,仍是一个绝对平衡的树结构。对于新提出来的元素需要和父亲节点进行融合。红黑树和2-3之间可以进行等价转换。
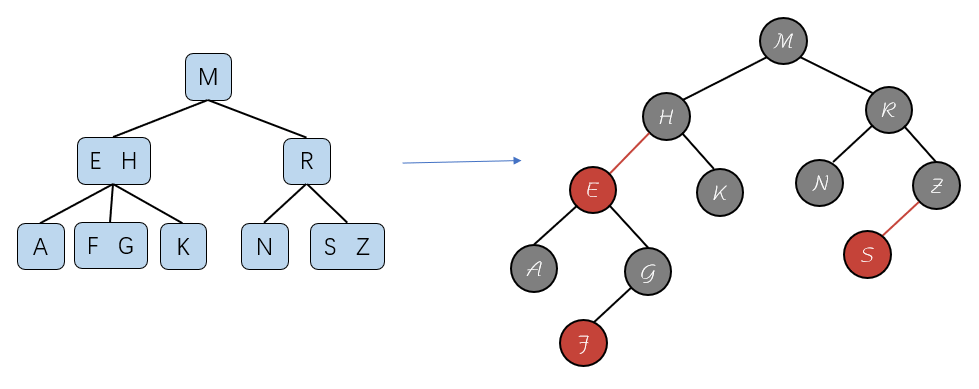
通过上面的等价转换可以看出来,定义红色节点都是向左倾斜。用过表示节点的颜色来识别该节点是否是红色节点。 对于我们上面的2-3树我们可以对其进行转换,如下图:
根据上面的图例,我们可以得出下面几点结论:
- 每一个节点是要么是红色的,要么是黑色的
- 每一个叶子节点(最后的空节点)均为黑色的
- 根节点为黑色节点
- 如果一个节点为红色的,那么他的孩子节点均为黑色的(否则触发变换)
- 从任意一个节点到达叶子节点,经过的黑色节点数是相同的(绝对平衡性)
解读性质:
- 对于性质一比较好理解,一个节点的颜色只有两种状态。
- 对于性质二这里的叶子节点并不是指左右子树均为空的节点,这个性质应该叫做定义,红黑树中定义空节点的颜色就是黑色,这里和性质三相吻合
- 对于性质三,和性质二是吻合的,对于一个空树,它也是一种红黑树,那么它既是叶子节点也是根节点,所以他的节点颜色也是黑色。
- 对于性质四,可以从2-3树中得出结论,红色节点的产生于3节点,红色节点连接的子节点来自于下一个2节点或者3节点,对于2节点来说,它本身的颜色就是黑色的,对于3节点而言,拆分成红黑结构的时候,是黑色的节点连接父亲节点。所以可以得出性质四
- 对于性质五,可以通过红黑树的绝对平衡性得出,因此也可以拓展出一个结论,红黑树是一种保持黑平衡的的二叉树
由于红黑树和2-3具有等价的关系,所以添加元素主要分为向2节点和三节点进行元素的添加,两者对应不同的情况。
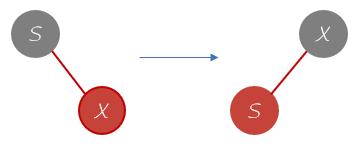
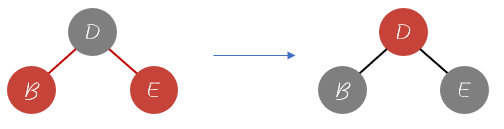
由于我们添加的节点都是红色的节点,并且红色节点一直保持左倾,对于下面这种情况,就需要进行一次旋转操作。如果添加元素本身就是再左边则无需变换。变换的操作就是和AVL树一样进行一次左旋转操作,并且将颜色进行互换。如果新加入的节点本身就在左变则不需要进行变换。对应的函数为 leftRotate()
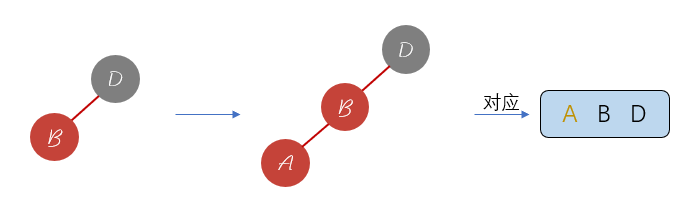
我们知道3节点添加位置主要包含三种,左边、中间和右边,下面逐一进行分析。 对于添加至右边的情况:
对于这种情况,只需要将左右孩子节点的颜色全部变成黑色即可,我们在前面说过,新生成的父亲节点要去和上面的节点继续去融合,融合就意味着该节点的颜色为红色,也是一种类似的颜色互换的形式。对应的函数称之为颜色反转,对应的函数为flipColor()
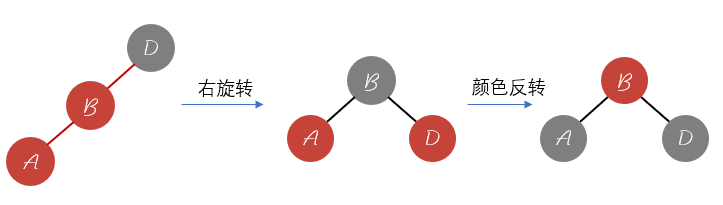
对于添加至左边的情况:
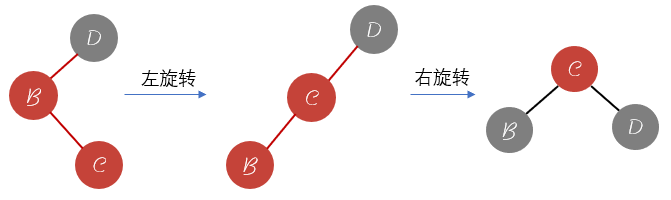
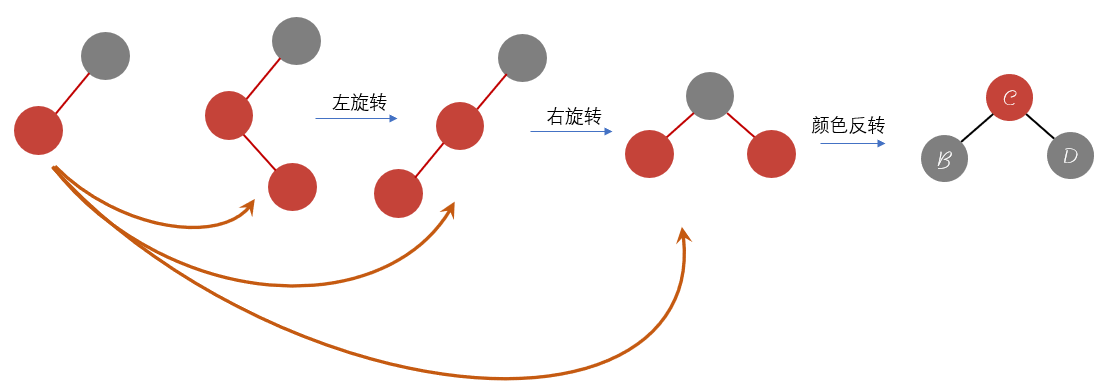
这种情况就是对应的右旋转过程,而且注意颜色的反转变换。右旋转过程和左旋转类似,颜色也是进行互换。最后在进行一次颜色反转操作。对于添加至中间的情况: 添加至中间的过程是一个组合的过程,可以先看成2节点的左旋转过程和3节点的右旋转过程。
具体的添加元素操作可以直接使用下面这张图,便于理解。
红黑树和二分搜索树的节点函数大致相同,只不过增加了对节点颜色的标识。 节点内部类的实现:
private class Node{ //内部类
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){ // 节点信息的初始化
this.key = key;
this.value = value;
left = null;
right = null;
color = RED; // 新建的节点永远是融合节点,红色节点
}
}红黑树的基本架构程序实现:
public class RBTree<K extends Comparable<K>, V extends Comparable<V>>{
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
//内部类 省略
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
}对于红黑树这种结构,我们增加了对颜色的判断,所有我们引入isRed函数来判断这个节点是否是红色的。 程序实现:
private boolean isRed(Node node) {
if (node == null)
return BLACK;
return node.color;
}基本辅助函数的实现,主要是对成员变量的一个get操作以及判断红黑树是否为空。 程序实现:
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}我们根据上面的性质可以得到,根节点的颜色必须为黑色,所以添加完元素后的根节点我们需要手动指定为黑色,因为我们新增的节点永远是红色的,所以我们需要手动将root变为黑色,调用方式仍然是调用私有递归函数。
public void add(K key, V value) {
root = add(root, key, value);
root.color = BLACK; //手动将根节点变为黑色
}在2节点中添加元素,并且在节点右边添加元素会触发左旋转,进而保证红色节点的左倾性。 左旋转程序实现:
private Node leftRotate(Node node) {
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
//颜色互换
x.color = node.color;
node.color = RED;
return x;
}在3节点中添加元素涉及左中右三种情况,上面讲过,在右边添加元素触发颜色反装。 颜色反转程序实现:
private void flipColors(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}在向三节点中最左边添加元素,触发右旋转过程。右旋转过程中还要进行一次颜色反转。 右旋转程序实现:
private Node rightRotate(Node node) {
Node x = node.left;
//右旋转
node.left = x.right;
x.right = node;
//颜色互换
x.color = node.color;
node.color = RED;
return x;
}其他的添加元素的变换都是基于颜色变换,左右旋转组合而来的。
具体的调用方法和AVL树相同,在增加完元素的时候,对元素进行判断,是一个在回朔的过程中进行操作。 增加函数的程序实现:
private Node add(Node node, K key, V value) {
if (node == null){
size++;
return new Node(key, value);
}
//首先进行元素的添加
if (key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if (key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else
node.key = key;
//添加完成后,维护平衡性
//左节点为黑,右节点为红
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
//左节点为红,左节点的左节点也为红
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
//左右节点均为红
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}从严格意义上讲,红黑树并不是一种严格的平衡二叉树。在最差的情况下,红黑树的高度为2log(n),这是因为在最差的情况下,每一个黑节点都有一个红色节点,但是由于时间复杂度不考虑红黑树的时间复杂度也是O(log(n))级别的。
适应场景: 红黑树适应于添加删除元素频繁的场景。而对于查询元素来说,红黑树并不是严格意义上的平衡树,在最坏的情况树的高度可以达到2log(n),所以说不同的场景适应于不同的算法。但是综合性能来说的话,红黑树的性能任然高于一些其他的树结构。
更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
或者关注我的微信公众号:TeaUrn
或者扫描下方二维码进行关注。里面有惊喜等你哦。
源码地址:可在公众号内回复 数据结构与算法源码 即可获得。