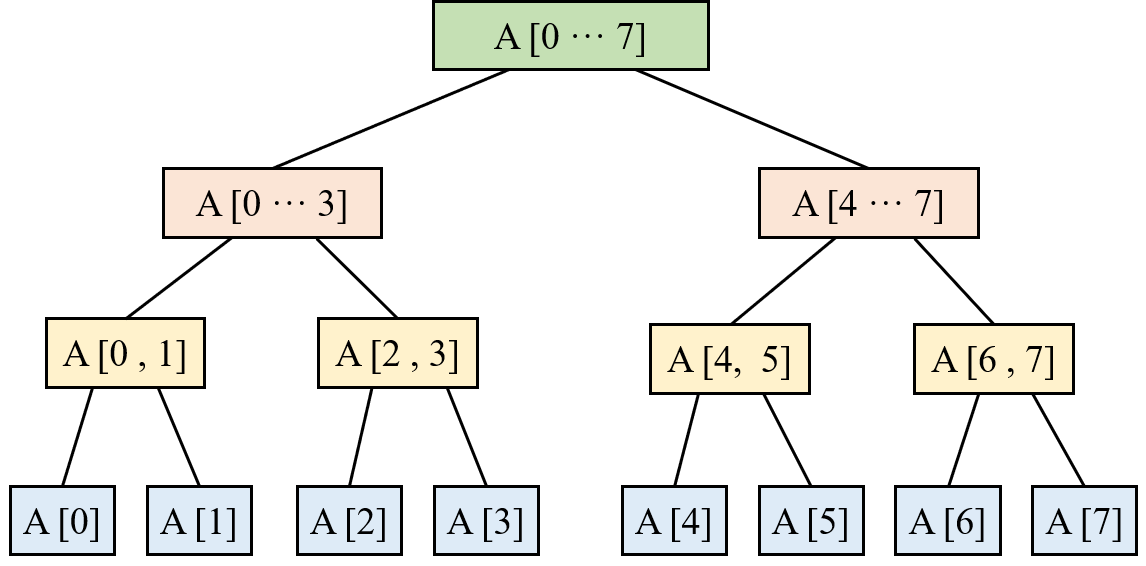
相信大家都见过一个经典的比赛题目(区间染色):在一个数组结构当中,对某一端区间不断的进行染色。在m次操作后,在这个数组中包含了多少种颜色。以及在m次操作后我们在某一区间可以看见多少种颜色。
其中主要包含两种操作,染色操作(更新区间)以及查询操作(查询区间)。我们发现我们主要是针对区间进行操作,而且我们只关心区间的颜色种类的个数,并不关心它的颜色是什么。
如果我们采用最基本的数组遍历的操作。使用数组实现,两种操作的时间复杂度均为O(N)级别的操作。这样我们的线段树显得就尤为重要。
还有一种经典问题就是区间查询:例如我们在一段数组内查询某一个区间的最大值、最小值或者区间数字和。针对区间进行操作的我们都要想要线段树这种数据结构。由于我们线段树采用的树结构,所以时间复杂度就会很低。
时间复杂度:
| 数组实现 | 线段树实现 | |
|---|---|---|
| 更新操作 | O(N) | O(log(N)) |
| 查询操作 | O(N) | O(log(N)) |
在线段树中我们并不考虑增加元素和删除元素,我们只考虑在已有的数组结构中构建线段树这种数据结构。
我们可以看出,一个数组分成了很多区间,基本上都是对半劈开,小伙伴可能会问了,结构变得更加复杂了。在这里正是运用了计算机领域的一句话 :
用空间换取时间
注意: 每一个区间并不是存储一个区间,而是一个值。例如我们以求和为例,==A[0 ··· 3]== 节点存储的是这个区间的和。如果是最大值,那么存储的就是这一个区间的最大值。
例子: 当我们查询A[2-5]区间的和,那我们只需要知道A[2-3]和A[4-5]的和就可以啦,我们并不需要遍历2-5的所有数据。
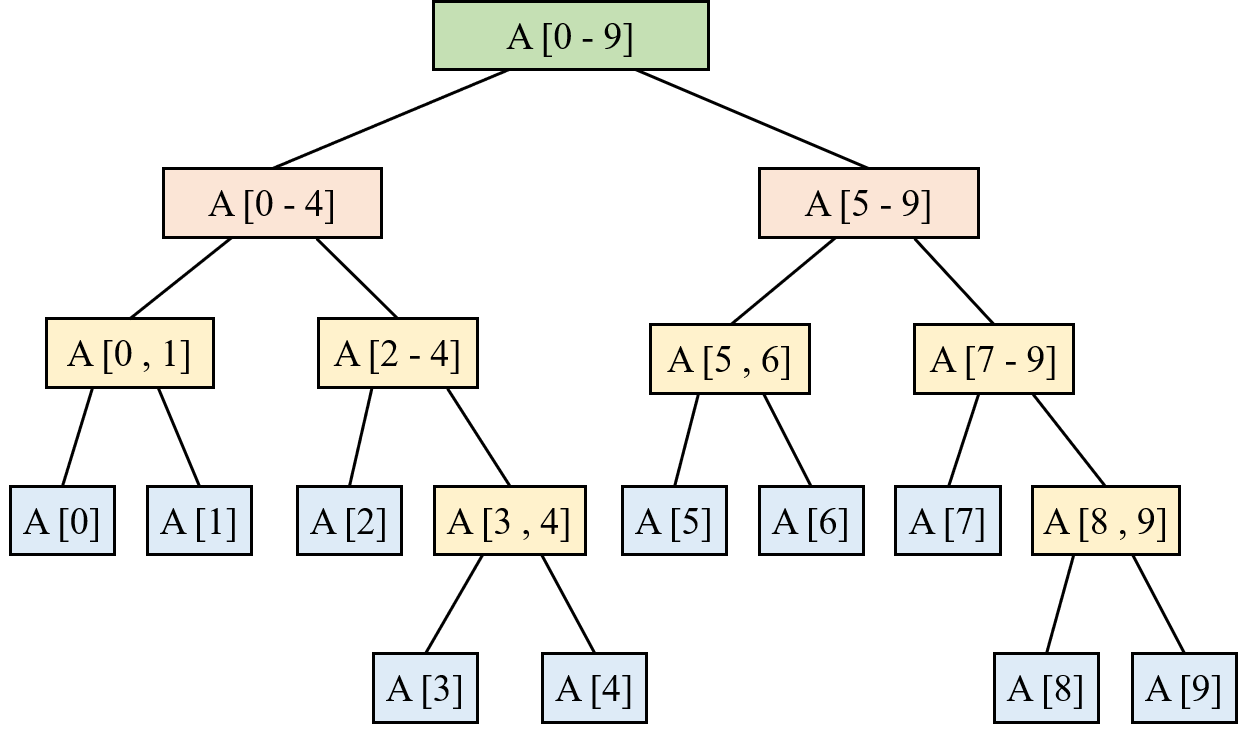
上面的例子当中,正好数组大小正好是 满二叉树,其实不是。我们看下面的图:
看得出来,这并不是一个满的二叉树,也不是一个完全二叉树。但是这是一个平衡二叉树。
平衡二叉树: 最大深度和最小深度之间的差值为 1 。
我们知道线段树是我们损失空间来减小时间的,那我们实际过程中,需要多少空间呢。下面我们就来推导一下。
| 层数 | 节点个数 |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| ··· | ··· |
| h - 1 |
对于满的二叉树来说,$h$ 层一共有$2^h-1$个节点。所以大约等于
最后一层的节点数大致等于(差1)前面所有层数节点之和。
假设我们的数组有 n 个元素,按照满的二叉树的形式来看,最底下一层元素的个数为 n。那么他上面的所有节点和也为n,所以对应的总个数为==2 * n==。这只是还在满二叉树的情况下。如果我们的元素不是2的整数次幂,那么它就构成了平衡二叉树,所以需要向下扩充一层,这一层的个数等于我们上面所有节点的和也就是 2 * n。加起来就是 4 * n。我们可以得出结论:
对于存储 n 个元素的线段树,我们需要开辟 4 倍的空间大小。
虽然我们浪费了大量的空间来存储,但是我们在时间复杂度上有着巨大的提升。随着社会的发展,存储已经变得不再是问题,问题变成了时间速度问题,所以说牺牲空间提升时间是一件非常有意义的事情。
在实际过程中底层并不确定用户对线段树执行什么操作,求和,最大值还是最小值操作,所以这里我们引入merge函数,用户来指定他们需要对线段树执行什么操作。 Merge接口函数:
public interface Merger<E> {
E merge(E a, E b);
}在构造函数里面需要用户传入用户设定的Merge实例对象,以对线段树进行用户想要类型的操作。 构造函数实现:
public SegmentTree(E[] arr, Merger<E> merger) {
this.merger = merger; // 指定merge实例
data = (E[])new Object[arr.length]; //拷贝数组
System.arraycopy(arr, 0, data, 0, arr.length);
tree = (E[])new Object[4 * arr.length]; //开启4倍的空间
buildSegmentTree(0, 0, data.length - 1);
}主要包含数据的接口操作,例如getSize和get操作。
public int getSize() {
return data.length;
}
public E get(int index) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal");
return data[index];
}这里我们线段树的底层依然是数组,所以我们依然可以按照我们之前的 MaxHeap 最大堆 那种结构来实现。
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
}我们需要在treeIndex索引的位置创建数组区间。这里我们采用递归方式进行构建树结构。为什么采用递归的形式呢,因为我们需要慢慢回朔到顶层,而且在构建的时候我们需要采用后序遍历的形式,这样才能保证节点最后合并孩子节点。
private void buildSegmentTree(int treeIndex, int l, int r) {
if (l == r) {
tree[treeIndex] = data[l];
return;
}
int mid = l + (r - l) / 2; //中间值
buildSegmentTree(leftChild(treeIndex), l, mid);
buildSegmentTree(rightChild(treeIndex), mid + 1, r);
tree[treeIndex] = merger.merge(tree[leftChild(treeIndex)], tree[rightChild(treeIndex)]);
}查询操作主要涉及的问题就是区间查找匹配的问题,所以在递归的问题匹配主要分为三种情况:
- 查询区间完全在右孩子区间上
- 查询区间完全在左孩子区间上
- 查询区间部分在左孩子区间上,部分在右孩子区间上
public E query(int queryL, int queryR) {
if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length)
throw new IllegalArgumentException("index is illegal");
return query(0,0,data.length - 1, queryL, queryR);
}
private E query(int treeIndex, int l, int r, int queryL, int queryR) {
if (l == queryL && r == queryR)
return tree[treeIndex];
int mid = l + (r - l) / 2; //中间值
int leftTreeIndex = leftChild(treeIndex); //左索引
int rightTreeIndex = rightChild(treeIndex); //右索引
if (queryL >= mid + 1) //去右子树查找
return query(rightTreeIndex, mid + 1, r, queryL, queryR);
else if (queryR <= mid) // 去左子树查找
return query(leftTreeIndex, l, mid, queryL, queryR);
E left = query(leftTreeIndex, l, mid, queryL, mid); // 分开查询
E right = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
return merger.merge(left, right); //将分开的元素合并
}当我们对数组的某一个索引位置进行修改,我们需要先找到这个树结构的索引位置,然后不断回朔,重新合并。
程序实现:
public void set(int index, E e) {
if (index < 0 || index >= data.length)
throw new IllegalArgumentException("Index is illegal");
data[index] = e;
set(0, 0, data.length - 1, index, e);
}
private void set(int treeIndex, int l, int r, int index, E e) {
if (l == r){
tree[treeIndex] = e;
return;
}
int mid = l + (l - r) / 2;
if (index > mid)
set(rightChild(treeIndex), mid + 1, r, index, e);
else
set(leftChild(treeIndex), l, mid, index, e);
tree[treeIndex] = merger.merge(tree[leftChild(treeIndex)], tree[rightChild(treeIndex)]);
}更多精彩内容,大家可以转到我的主页:曲怪曲怪的主页
或者关注我的微信公众号:TeaUrn
或者扫描下方二维码进行关注。里面有惊喜等你哦。
源码地址:可在公众号内回复 数据结构与算法源码 即可获得。