|
10 | 10 | " <td align=\"center\"><a target=\"_blank\" href=\"http://introtodeeplearning.com\">\n", |
11 | 11 | " <img src=\"https://i.ibb.co/Jr88sn2/mit.png\" style=\"padding-bottom:5px;\" />\n", |
12 | 12 | " Visit MIT Deep Learning</a></td>\n", |
13 | | - " <td align=\"center\"><a target=\"_blank\" href=\"https://colab.research.google.com/github/aamini/introtodeeplearning/blob/master/lab1/solutions/PT_Part1_Intro_Solution.ipynb\">\n", |
| 13 | + " <td align=\"center\"><a target=\"_blank\" href=\"https://colab.research.google.com/github/MITDeepLearning/introtodeeplearning/blob/master/lab1/solutions/PT_Part1_Intro_Solution.ipynb\">\n", |
14 | 14 | " <img src=\"https://i.ibb.co/2P3SLwK/colab.png\" style=\"padding-bottom:5px;\" />Run in Google Colab</a></td>\n", |
15 | | - " <td align=\"center\"><a target=\"_blank\" href=\"https://github.com/aamini/introtodeeplearning/blob/master/lab1/solutions/PT_Part1_Intro_Solution.ipynb\">\n", |
| 15 | + " <td align=\"center\"><a target=\"_blank\" href=\"https://github.com/MITDeepLearning/introtodeeplearning/blob/master/lab1/solutions/PT_Part1_Intro_Solution.ipynb\">\n", |
16 | 16 | " <img src=\"https://i.ibb.co/xfJbPmL/github.png\" height=\"70px\" style=\"padding-bottom:5px;\" />View Source on GitHub</a></td>\n", |
17 | 17 | "</table>\n", |
18 | 18 | "\n", |
|
241 | 241 | "\n", |
242 | 242 | "A convenient way to think about and visualize computations in a machine learning framework like PyTorch is in terms of graphs. We can define this graph in terms of tensors, which hold data, and the mathematical operations that act on these tensors in some order. Let's look at a simple example, and define this computation using PyTorch:\n", |
243 | 243 | "\n", |
244 | | - "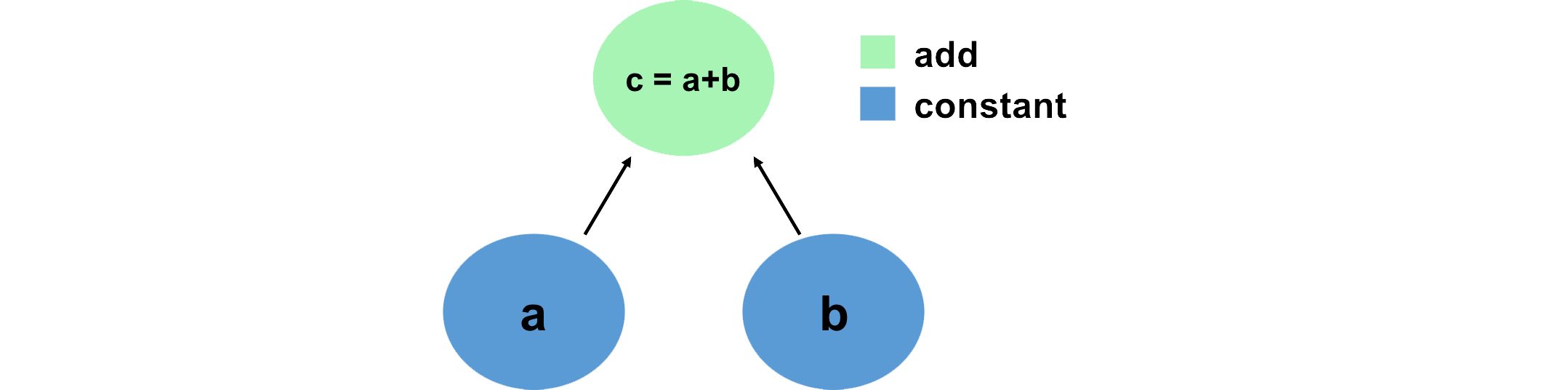" |
| 244 | + "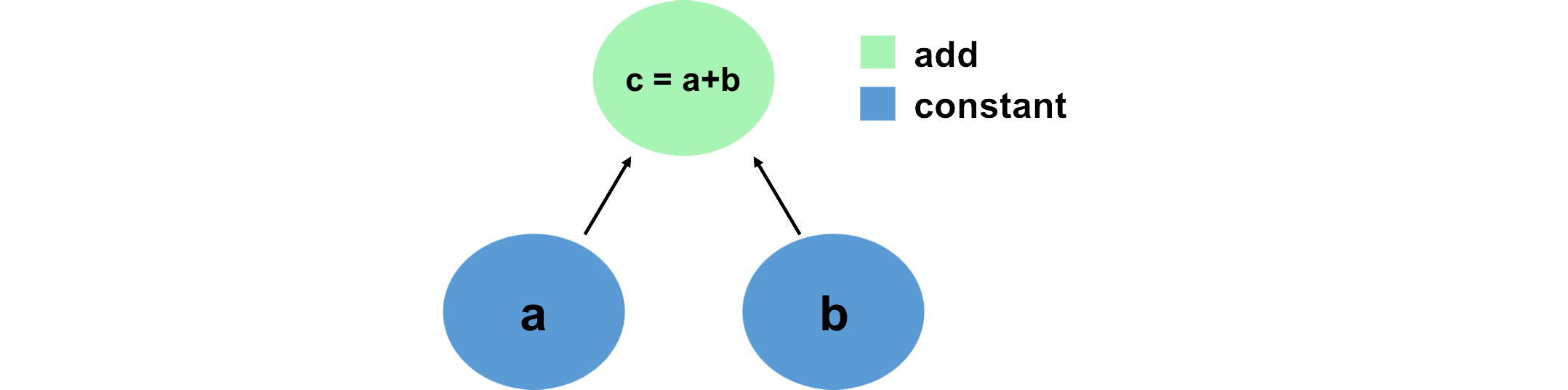" |
245 | 245 | ] |
246 | 246 | }, |
247 | 247 | { |
|
282 | 282 | "\n", |
283 | 283 | "Now let's consider a slightly more complicated example:\n", |
284 | 284 | "\n", |
285 | | - "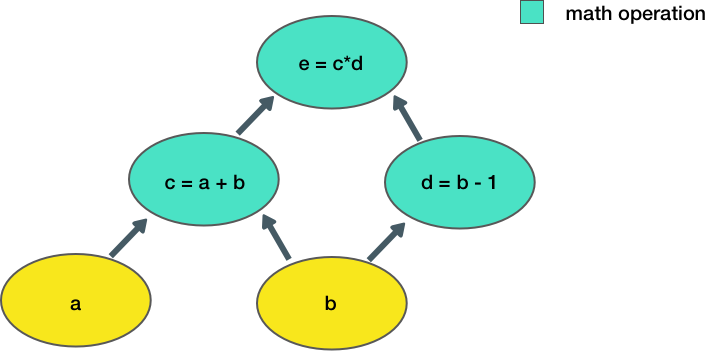\n", |
| 285 | + "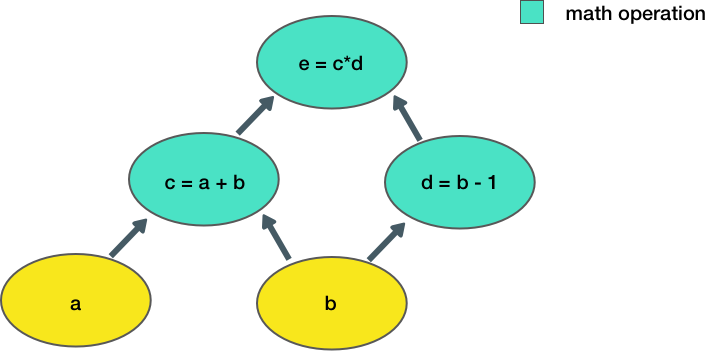\n", |
286 | 286 | "\n", |
287 | 287 | "Here, we take two inputs, `a, b`, and compute an output `e`. Each node in the graph represents an operation that takes some input, does some computation, and passes its output to another node.\n", |
288 | 288 | "\n", |
|
364 | 364 | "\n", |
365 | 365 | "Let's consider the example of a simple perceptron defined by just one dense (aka fully-connected or linear) layer: $ y = \\sigma(Wx + b) $, where $W$ represents a matrix of weights, $b$ is a bias, $x$ is the input, $\\sigma$ is the sigmoid activation function, and $y$ is the output.\n", |
366 | 366 | "\n", |
367 | | - "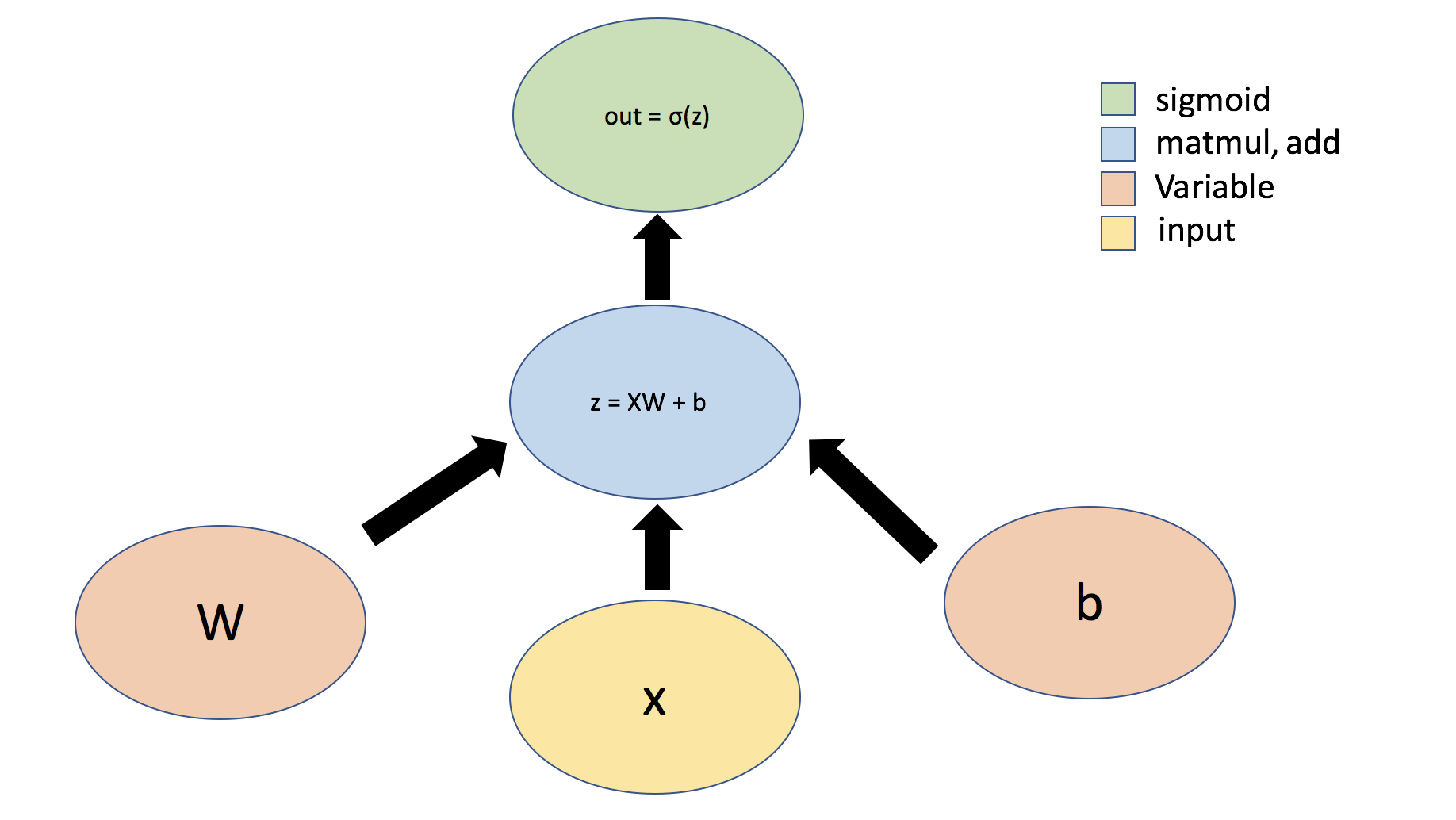\n", |
| 367 | + "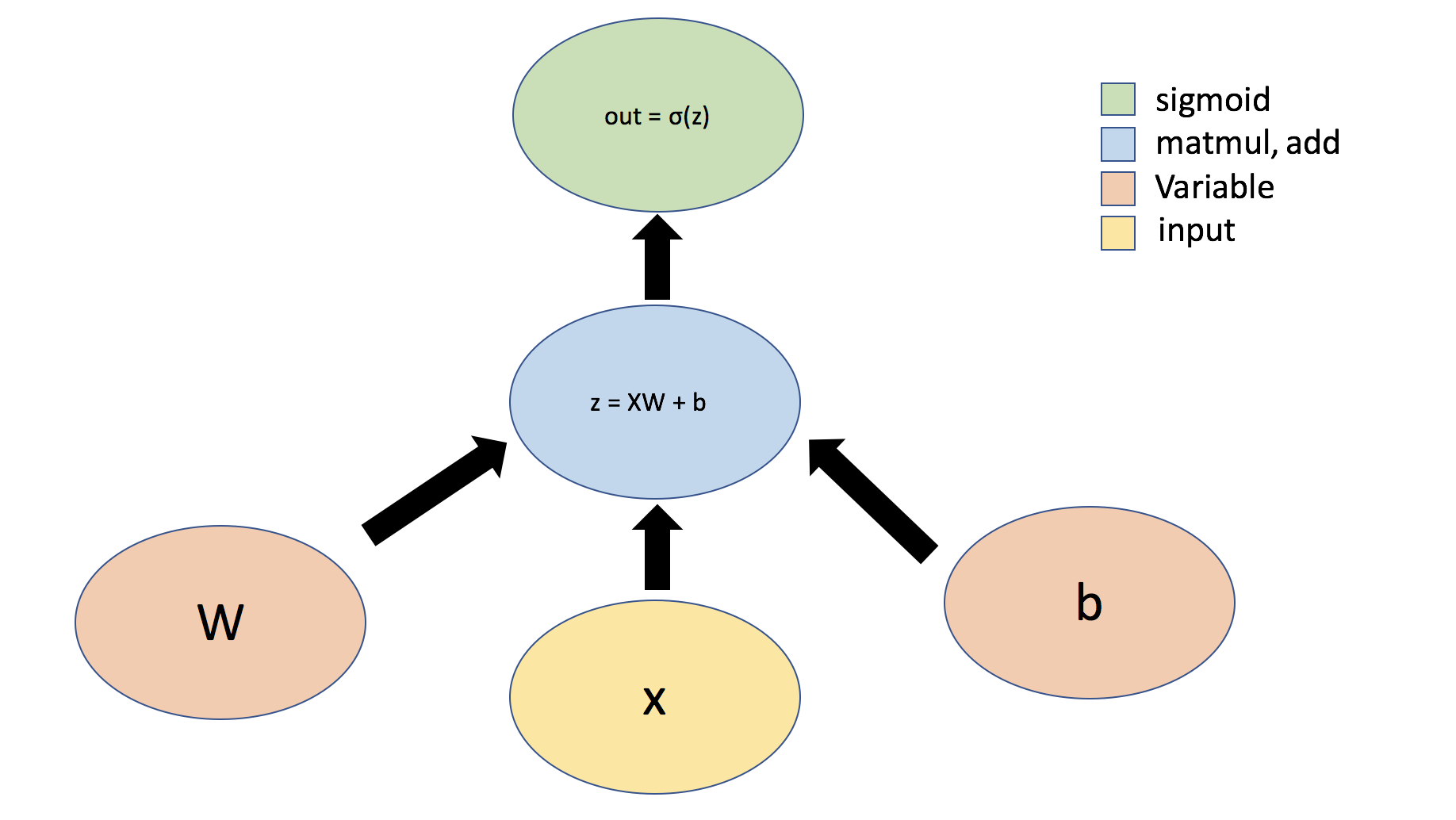\n", |
368 | 368 | "\n", |
369 | 369 | "We will use `torch.nn.Module` to define layers -- the building blocks of neural networks. Layers implement common neural networks operations. In PyTorch, when we implement a layer, we subclass `nn.Module` and define the parameters of the layer as attributes of our new class. We also define and override a function [``forward``](https://pytorch.org/docs/stable/generated/torch.nn.Module.html#torch.nn.Module.forward), which will define the forward pass computation that is performed at every step. All classes subclassing `nn.Module` should override the `forward` function.\n", |
370 | 370 | "\n", |
|
0 commit comments