14.FIR数字滤波器的基本结构.md

[TOC]

FIR数字滤波器的基本结构

FIR数字滤波器的特点

系统函数： $$ H(z)=\sum_{n=0}^{N-1} h(n) z^{-n} $$

有 $N-1$ 个零点分布于 $z$ 平面

$z=0$ 处是 $N-1$ 阶极点

1. 系统的单位抽样响应 $h(n)$ 有限长, 设 $N$ 点

2. 系统函数 $H(z)$ 在 $|z|>0$ 处收敛, 有限 $z$ 平面只有零点, 全部极点在 $z=0$ 处 (因果系统)

3. 无输出到输入的反馈, 一般为非递归型结构

$$ H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^{M} b_{k} z^{-k}}{1-\sum_{k=1}^{N} a_{k} z^{-k}} \\ H(z)=\sum_{n=0}^{N-1} h(n) z^{-n}\\ y(n)=\sum_{k=1}^{N} a_{k} y(n-k)+\sum_{k=0}^{M} b_{k} x(n-k)\\ y(n)=\sum_{m=0}^{N-1} h(m) x(n-m) $$

直接型 (横截型、卷积型)

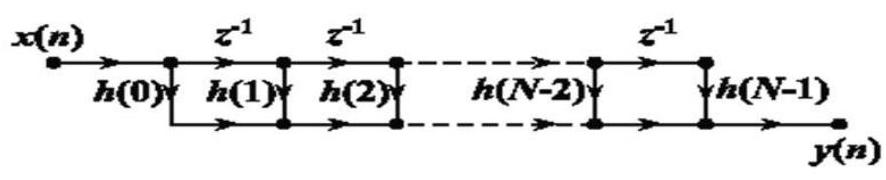
差分方程 $$ \quad y(n)=\sum_{m=0}^{N-1} h(m) x(n-m) $$ FIR滤波器的横截型结构

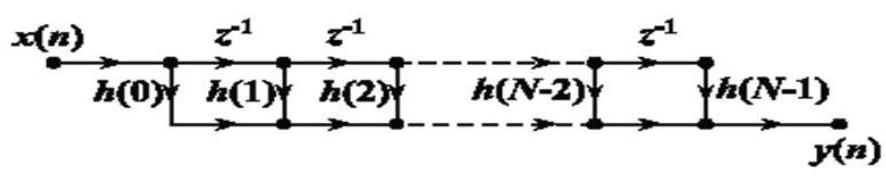
FIR滤波器的转置结构

级联型

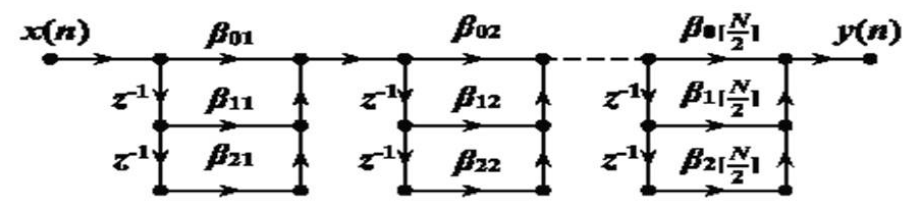
将 $H(z)$ 分解成实系数二阶因式的乘积形式:

$$ &H(z)=\sum_{n=0}^{N-1} h(n) z^{-n}=\prod_{k=1}^{[N / 2]}\left(\beta_{0 k}+\beta_{1 k} z^{-1}+\beta_{2 k} z^{-2}\right) \\ $$

FIR滤波器的级联型浯枃(N为奇数)

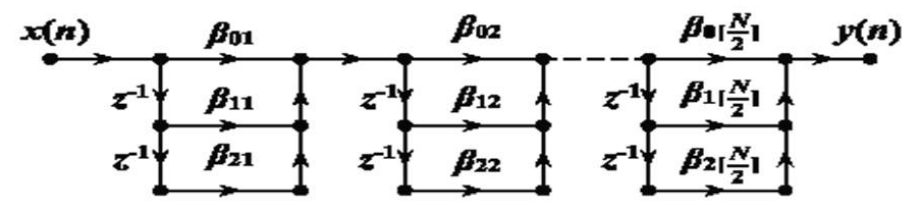
$N$ 为偶数时, 其中有一个 $\beta_{2 k}=0 \quad(N-1$ 个零点 $)$

级联型的特点

• 每个基本节控制一对零点,，便于控制滤波器的传输零点

• 系数比直接型多，所需的乘法运算多

频率抽样型

$N$ 个频率抽样 $H(k)$ 恢复 $H(z)$ 的内插公式:

$$ \begin{aligned} H(z) &=\left(1-z^{-N}\right) \frac{1}{N} \sum_{k=0}^{N-1} \frac{H(k)}{1-W_{N}^{-k} z^{-1}} \\ &=\frac{1}{N} H_{c}(z) \sum_{k=0}^{N-1} H_{k}^{\prime}(z) \end{aligned} $$

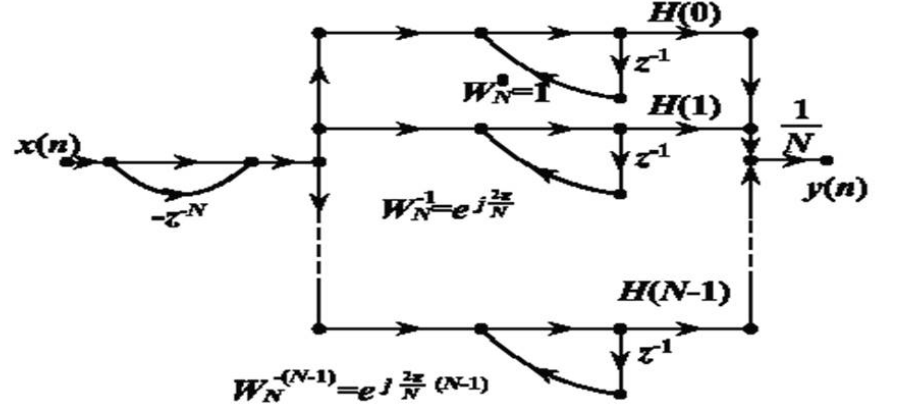
又名梳状滤波器，示意图如下

子系统

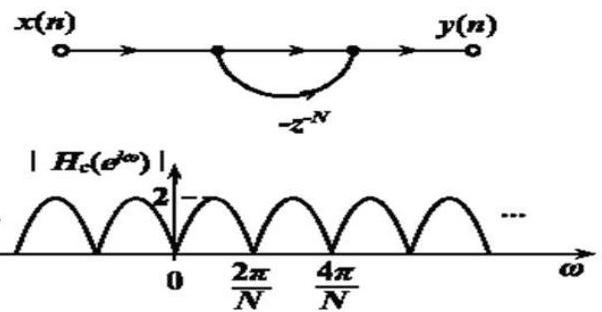
$$ H_{c}(z)=1-z^{-N} $$

是 $N$ 节延时单元的梳状滤波器

在单位圆上有 $N$ 个等间隔角度的零点:

$$ z_{k}=e^{j \frac{2 \pi}{N} k} \quad k=0,1, \ldots, N-1 $$

• 频率响应 :

$$ \begin{aligned} H_{c}\left(e^{j \omega}\right)&=1-e^{-j \omega N} \\ &=e^{-j \frac{\omega N}{2}}\left(e^{j \frac{\omega N}{2}}-e^{-j \frac{\omega N}{2}}\right) \\ &=2 j e^{-j \frac{\omega N}{2}} \sin \frac{\omega N}{2} \end{aligned} $$

子系统

$$ H_{k}^{\prime}(z)=\frac{H(k)}{1-W_{N}^{-k} z^{-1}} $$

谐振器

单位圆上有一个极点 $$ z_{k}=W_{N}^{-k}=e^{j \frac{2 \pi}{N} k} $$

与第 $k$ 个零点相抵消, 使该频率 $\omega=\frac{2 \pi}{N} k$ 处的频率响应等于 $H(k)$

$$ H(z)=\left(1-z^{-N}\right) \frac{1}{N} \sum_{k=0}^{N-1} \frac{H(k)}{1-W_{N}^{-k} z^{-1}} $$

FIR滤波器的频率抽样型结构

频率抽样型结构的优缺点

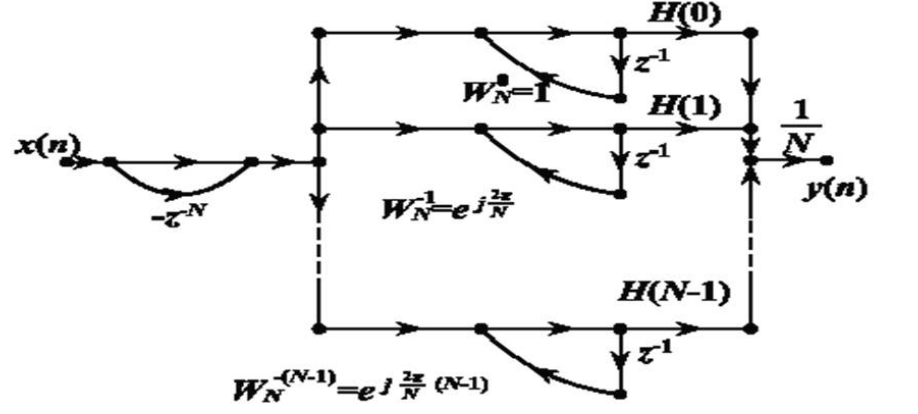
调整 $H(k)$ 就可以有效地调整频响特性

• 若 $h(n)$ 长度相同, 则网络结构完全相同, 除了各支路增益 $H(k)$, 便于标准化、模块化

• 有限字长效应可能导致零极点不能完全对消, 导致系统不稳定

• 系数多为复数, 增加了复数乘法和存储量

快速卷积结构

FIR滤波器的快速卷积结构

线性相位FIR滤波器的结构

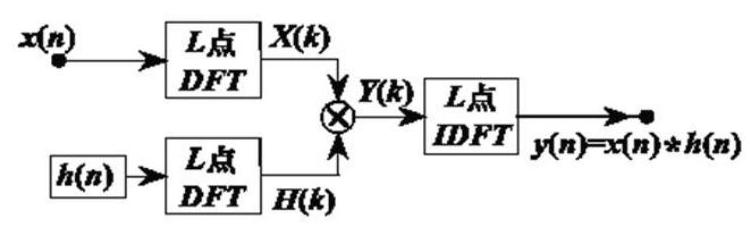
$\mathrm{FIR}$ 滤波器单位抽样响应 $h(n)$ 为实数, $0 \leq n \leq N-1$ 且满足:

偶对称：

$$ h(n)=h(N-1-n) $$

或奇对称: $$ h(n)=-h(N-1-n) $$ 即对称中心在 $(N-1) / 2$ 处

则这种FIR滤波器具有严格线性相位。

• $N$ 为奇数

$$ \begin{aligned} H(z) &=\sum_{n=0}^{N-1} h(n) z^{-n} \\ &=\sum_{n=0}^{\frac{N-1}{2}-1} h(n) z^{-n}+h\left(\frac{N-1}{2}\right) z^{-\frac{N-1}{2}}+\sum_{n=\frac{N-1}{2}+1}^{N-1} h(n) z^{-n} \\ \end{aligned} $$

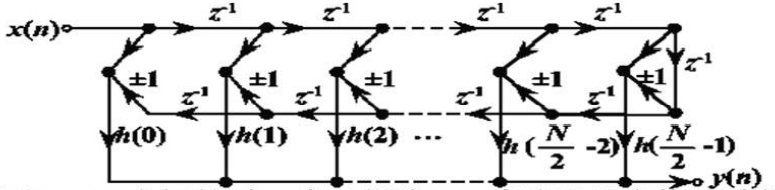
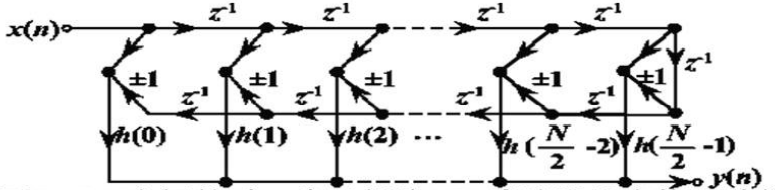
令 $n=N-1-m$ $$ H(z)=\sum_{n=0}^{\frac{N-1}{2}-1} h(n)\left[z^{-n} \pm z^{-(N-1-n)}\right]+h\left(\frac{N-1}{2}\right) z^{-\frac{N-1}{2}} $$ N为奇数时线性相位FIR滤波器的直接型结构

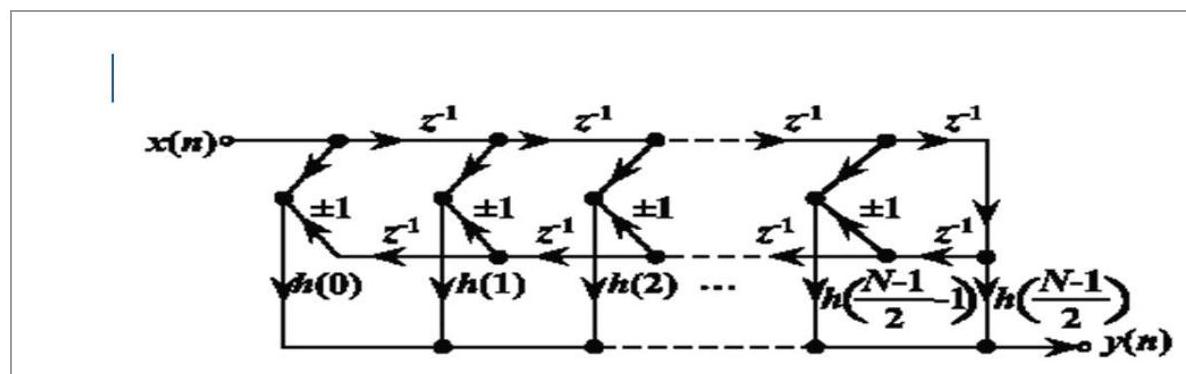
$h(n)$ 偶对称，取 “+”

$h(n)$ 奇对称, 取“ -", 且 $h\left(\frac{N-1}{2}\right)=0$

• $N$ 为偶数

$$ \begin{aligned} H(z) &=\sum_{n=0}^{N-1} h(n) z^{-n}=\sum_{n=0}^{\frac{N}{2}-1} h(n) z^{-n}+\sum_{n=\frac{N}{2}}^{N-1} h(n) z^{-n} \\ &=\sum_{n=0}^{\frac{N}{2}-1} h(n)\left[z^{-n} \pm z^{-(N-1-n)}\right] \end{aligned} $$

N为偶数时，线性相位FIR滤波器的直接型结构

$h(n)$ 偶对称时，$\pm 1$ 取 $+1$ ，$h(n)$ 奇对称时 $\pm 1$ 取 $-1$