4.2 DIT.md

[TOC]

4.2 按时间抽取(DIT)的基-2 FFT算法

库利——图基算法

算法原理

设序列点数 $N=2^L, L$ 为整数。 若不满足, 则补零。

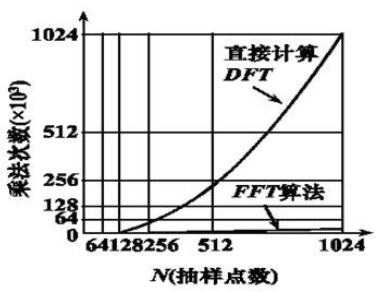
$N$ 为2的整数幂的FFT算法称基-2FFT算法。

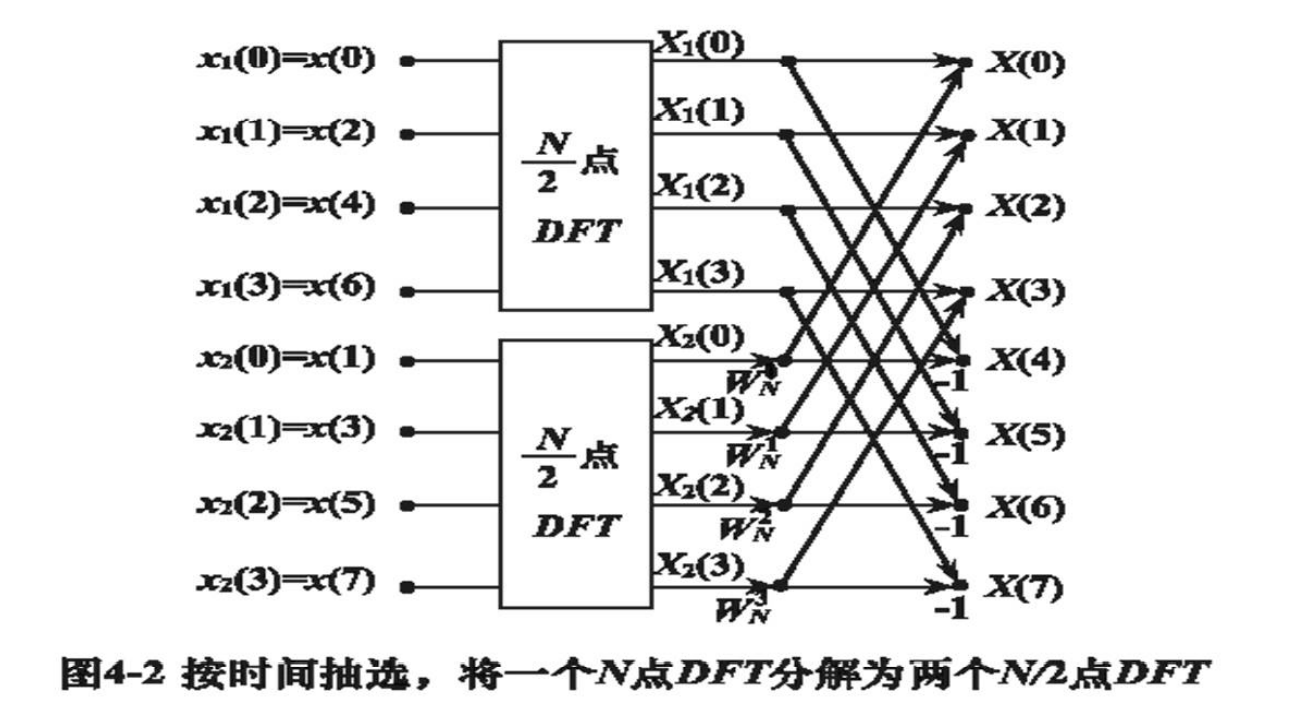
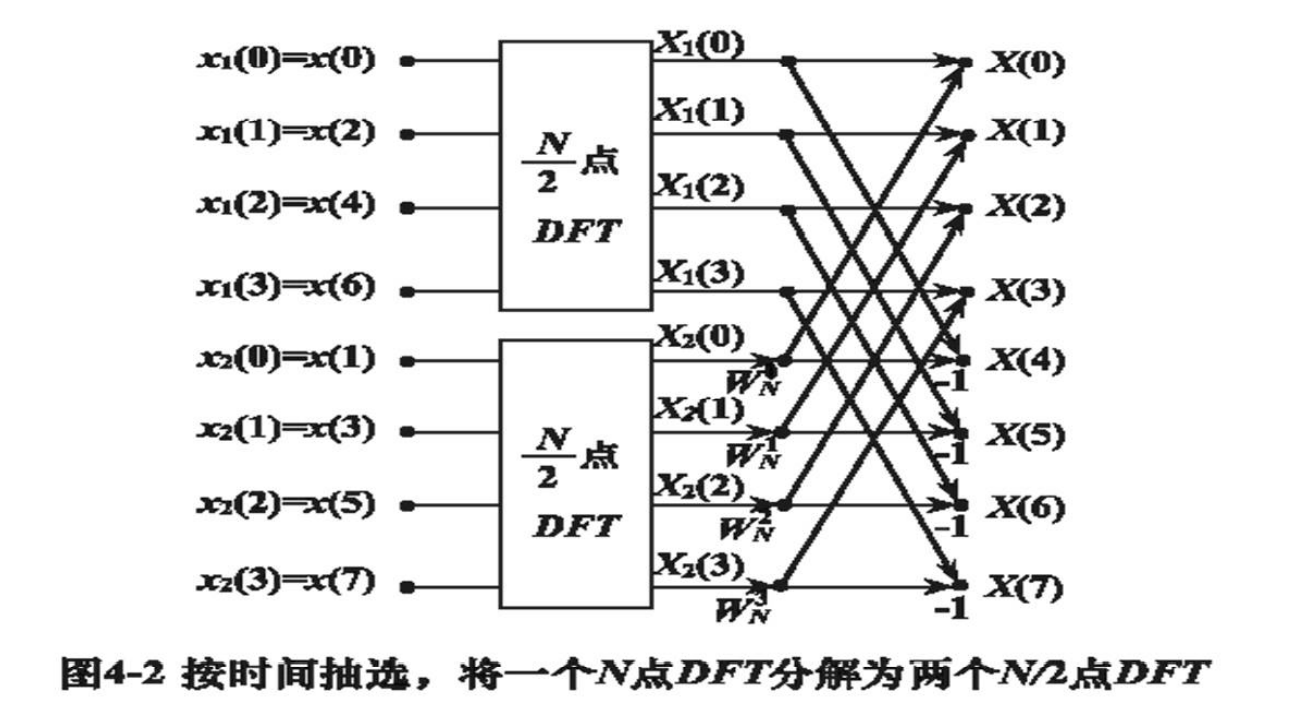
将序列 $x(n)$ 按 $n$ 的奇偶分成两组： $$ x(2 r)=x_1(r) \ x(2 r+1)=x_2(r)\ r=0,1, \ldots, N / 2-1 $$ 则$x(n)$的DFT $$ \begin{aligned} X(k)&=\sum_{n=0}^{N-1} x(n) W_N^{n k}\ &=\sum_{r=0}^{N / 2-1} x(2 r) W_N^{2 r k}+\sum_{r=0}^{N / 2-1} x(2 r+1) W_N^{(2 r+1) k}\ &=\sum_{r=0}^{N / 2-1} x_1(r)\left(W_N^2\right)^{r k}+W_N^k \sum_{r=0}^{N / 2-1} x_2(r)\left(W_N^2\right)^{r k}\ &=\sum_{r=0}^{N / 2-1} x_1(r) W_{N / 2}^{r k}+W_N^{k} \sum_{r=0}^{N / 2-1} x_2(r) W_{N / 2}^{r k} \ &=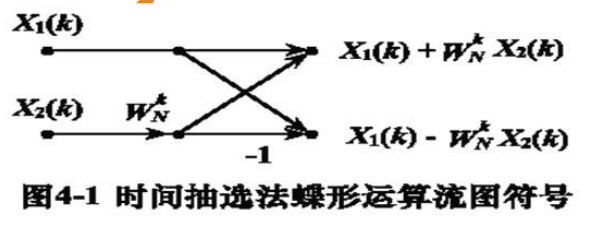X_1(k)+W_N^k X_2(k) \ \ &r, k=0,1, \ldots N / 2-1 \end{aligned} $$ 这是前半部分

再利用周期性求 $X(k)$ 的后半部分

$\because X_1(k), X_2(k)$ 是以 $N / 2$ 为周期 的 $$ \therefore X_1\left(k+\frac{N}{2}\right)=X_1(k) \quad X_2\left(k+\frac{N}{2}\right)=X_2(k) $$ 又因为 $$ W_N^{k+\frac{N}{2}}=W_N^{N / 2} W_N^k=-W_N^k $$ 故 $$ \left{\begin{array}{c} X(k)=X_1(k)+W_N^k X_2(k) \ X\left(k+\frac{N}{n}\right)=X_1(k)-W_N^k X_2(k) \end{array}\right.\ \ k=0,1, \ldots, N / 2-1 $$

分解后的运算量

	复数乘法	复数加法
一个 $N / 2$ 点DFT	$(N / 2)^2$	$N / 2(N / 2-1)$
两个 $N / 2$ 点DFT	$N^{2 }/2$	$N(N / 2-1)$
一个蝶形	1	2
$N / 2$ 个蝶形	$N/2$	$N$
总计	$N^2 / 2+N / 2\approx N^2 / 2$	$N(N / 2-1)+N\approx N^2 / 2$

运算量少了近一半

继续分解

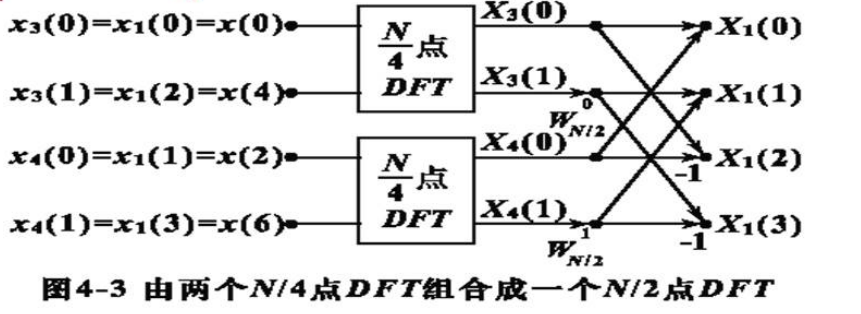
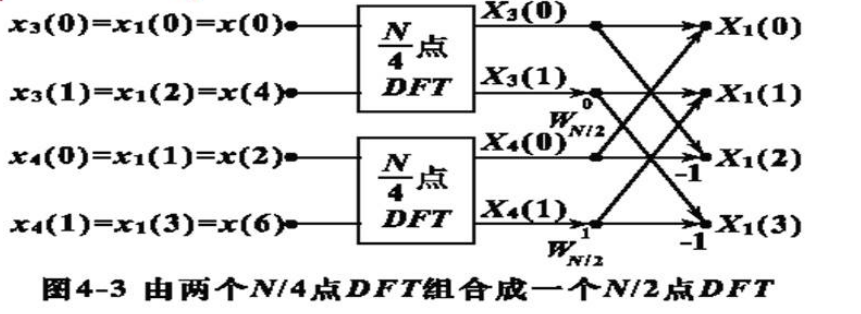
$N /$ 2仍为偶数，进一步分解 $$ N / 2 \rightarrow N / 4 $$

$$ \left{\begin{array}{c} x_1(2 l)=x_3(l) \\ x_1(2 l+1)=x_4(l) \end{array}\right.\\ \\ l=0,1, \ldots, N / 4-1 $$

$$ \left{\begin{array}{c} X_1(k)=X_3(k)+W_{N / 2}^k X_4(k) \\ X_1\left(k+\frac{N}{4}\right)=X_3(k)-W_{N / 2}^k X_4(k) \end{array}\right.\\ \\ k=0,1, \ldots, \frac{N}{4}-1 $$

同理 $$ \left{\begin{array}{c} X_2(k)=X_5(k)+W_{N / 2}^k X_6(k) \ X_2\left(k+\frac{N}{4}\right)=X_5(k)-W_{N / 2}^k X_6(k) \end{array}\right.\ \ k=0,1, \ldots, \frac{N}{4}-1 $$ 其中 $$ X_5(k)=\operatorname{DFT}\left[x_5(l)\right]=\operatorname{DFT}\left[x_2(2 l)\right] \ X_6(k)=\operatorname{DFT}\left[x_6(l)\right]=\operatorname{DFT}\left[x_2(2 l+1)\right] \ \ l=0,1, \ldots, N / 4-1 $$

直到分解的尽头

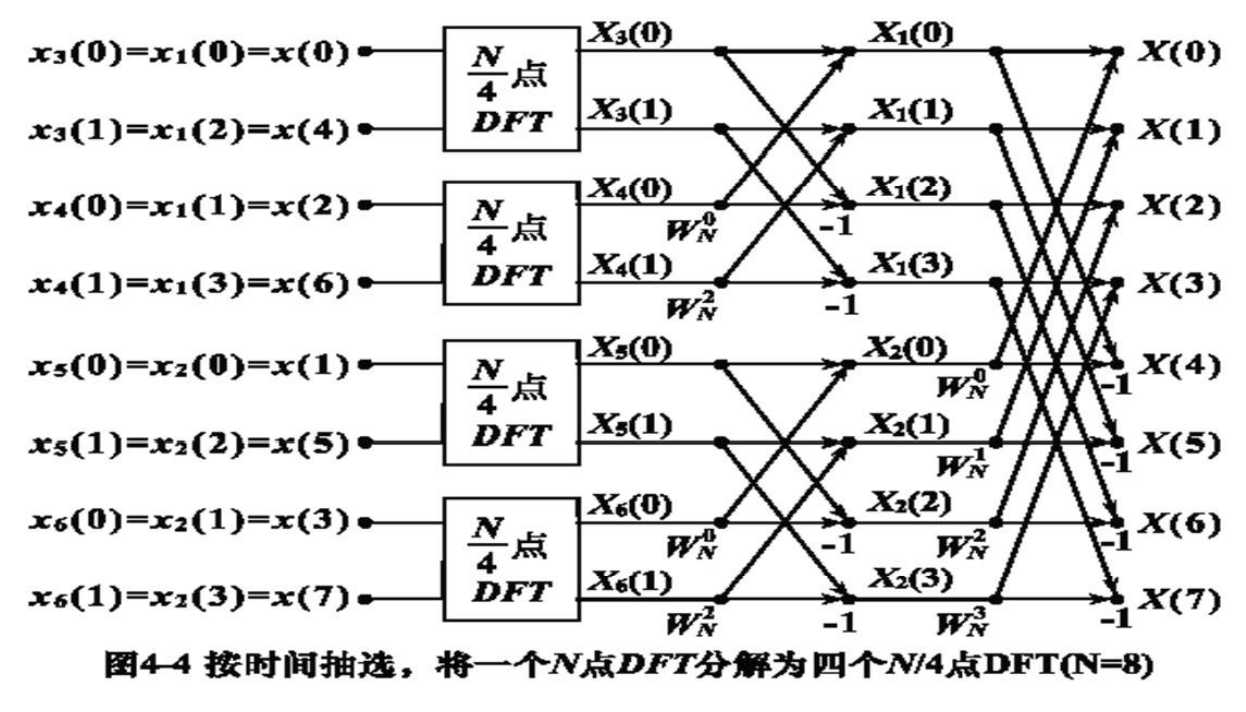
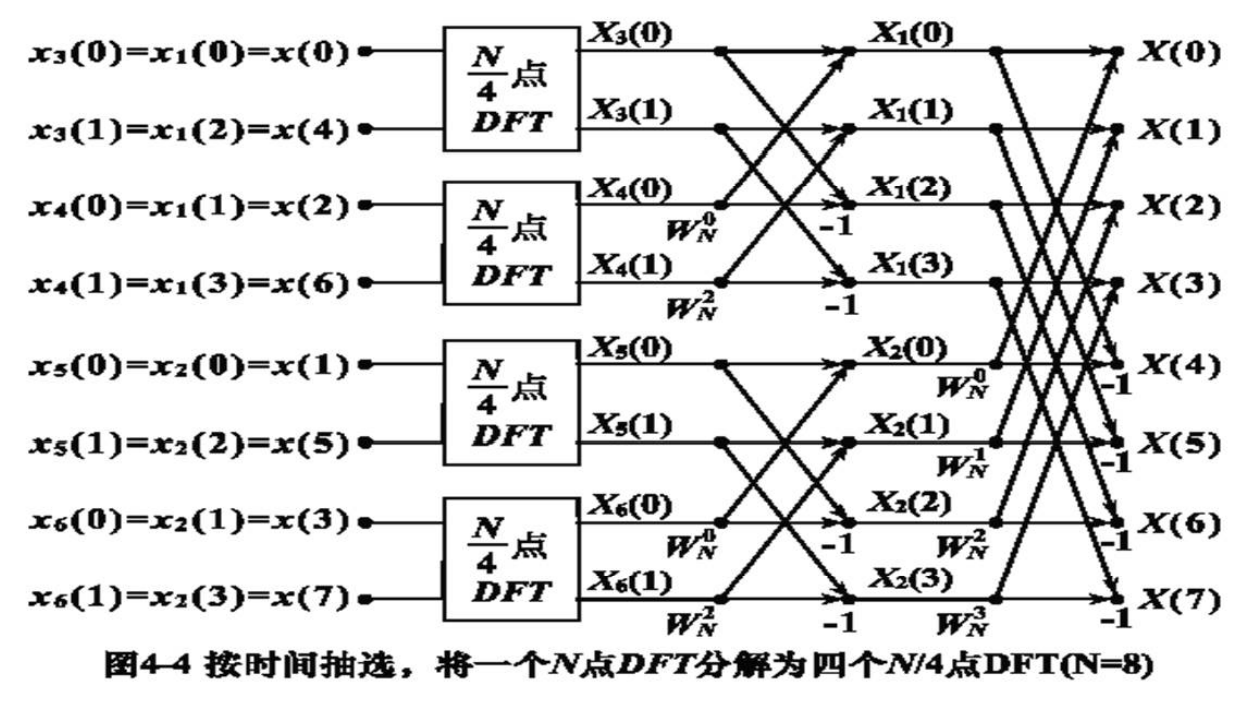
这样逐级分解，直到2点DFT

当 $N=8$ 时，即分解到 $X_3(k) ， X_4(k) ， X_5(k) ， X_6(k) ， k=0,1$ $$ \left{\begin{aligned} X_3(0) &=x_3(0) W_2^0+W_2^0 x_3(1)=x(0)+W_N^0 x(4) \ X_3(1) &=x_3(0) W_2^0+W_2^1 x_3(1)=x(0)-W_N^0 x(4) \end{aligned}\right.\ X_4(k)=\sum_{l=0}^{N / 4-1} x_4(l) W_{N / 4}^{l k}=\sum_{l=0}^1 x_4(l) W_{N / 4}^{l k} \quad k=0,1\ \left{\begin{array}{r} X_4(0)=x_4(0) W_2^0+W_2^0 x_4(1)=x(2)+W_N^0 x(6) \ X_4(1)=x_4(0) W_2^0+W_2^1 x_4(1)=x(2)-W_N^0 x(6) \end{array}\right. $$

运算量

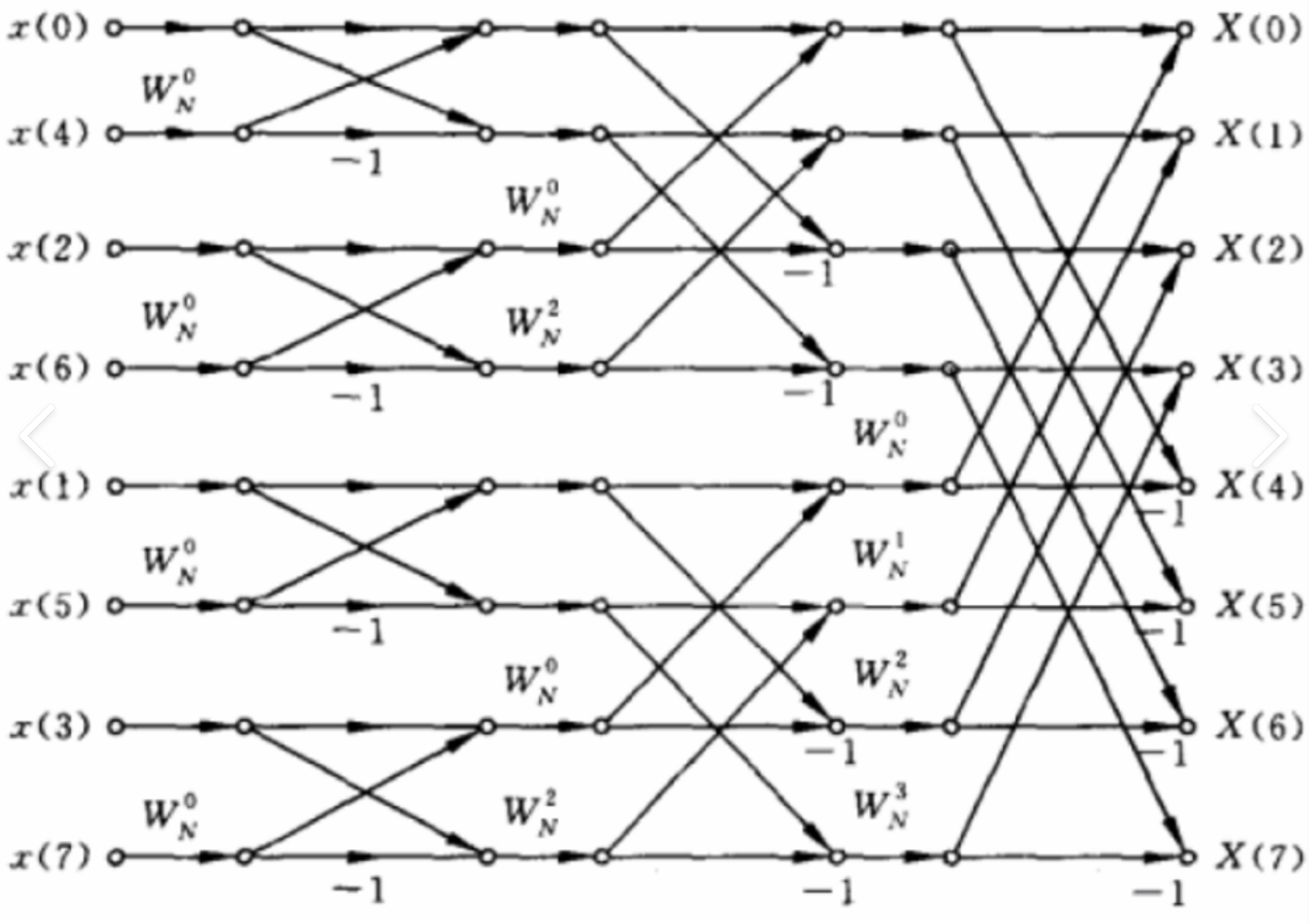
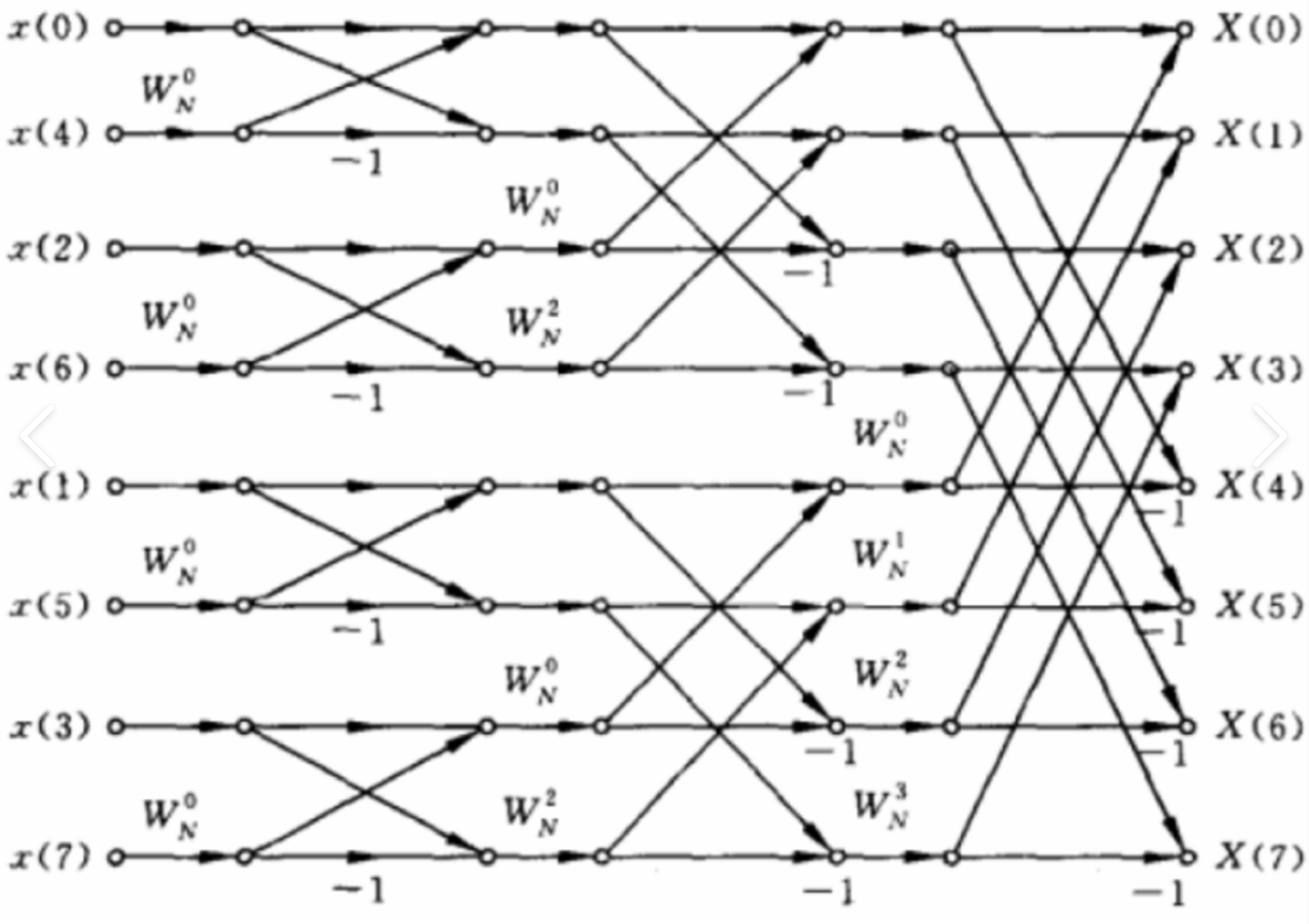
当 $N=2^L$ 时，共有 $L$ 级蝶形，每级 $N / 2$ 个蝶形，每个蝶形有 1 次复数 乘法2次复数加法。

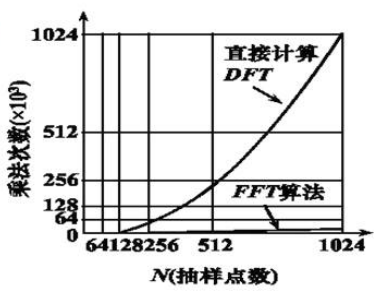
复数乘法 $$ m_F=\frac{N}{2} L=\frac{N}{2} \log _2 N $$ 复数加法 $$ a_F=N L=N \log _2 N $$ 比较DFT $$ \frac{m_F(D F T)}{m_F(F F T)}=\frac{N^2}{\frac{N}{2} \log _2 N}=\frac{2 N}{\log _2 N} $$

算法特点

原位计算

$$ \left{\begin{array}{l} X_m(k)=X_{m-1}(k)+X_{m-1}(j) W_N^r \\ X_m(j)=X_{m-1}(k)-X_{m-1}(j) W_N^r \end{array}\right. $$

$m$ 表示第 $m$ 级迭代, $k, j$ 表示数据所在的行数

所谓原位计算, 就是当数据输入到存储器后, 每一级运算的结果仍然则存在这同一组存储器中, 直到最后输出, 中间无需其它存储器。

倒位序

$$ n=\left(n_2 n_1 n_0\right)_2\\ \hat{n}=\left(n_0 n_1 n_2\right)_2 $$

倒位序的实现

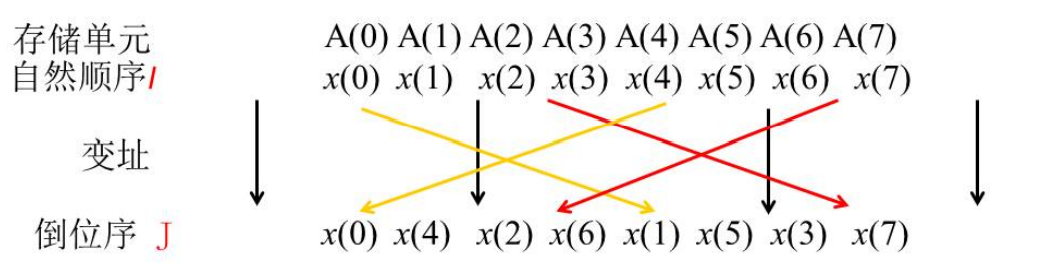
在实际运算时, 先按自然顺序将输入序列存入存储单元, 再通过变址运算将自 然顺序变换成按DIT-FFT算法要求的顺序。变址过程可用程序实现-称为“整序”或 "重排"

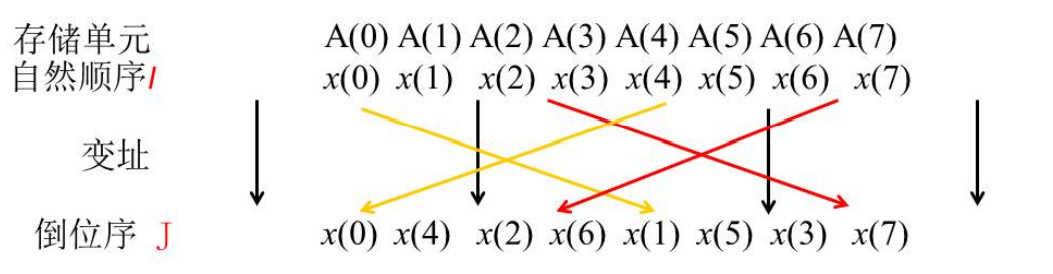
(1) 当 I=J时, 数据不必调换; (2) 当 $I \neq J$ 时, 必须将原来存放数据 $x$ (I) 送入暂存器 $R$, 再将 $x(J)$ 送入 $x(I), R$ 中内容送 $\mathrm{x}(\mathrm{J})$, 进行数据对调; (3)为了避免再次调换已调换过的数据, 保证调换只进行一次, 否则又变回原状, 只在 $\mathrm{I}<\mathrm{J}$ 时, 调换。

算法实现（补充）

采用雷德算法：已知数i的倒位序是j，求下一个数的倒位序

int i,j,k;
int temp;
for(j=0,i=0;i
{
if(i<j)
{
temp = x[j];
x[j] = x[i];
x[i] = temp;
}
k = N/2; //求j的下一个倒位序
while(j >= k) //如果k<=j,表示j的最高位为1
{
j = j-k; //把最高位变成0
k = k/2; //k/2，比较次高位，依次类推，逐个比较，直到某个位为0
}
j = j+k; //把0改为
}