[TOC]
理由:
- 压缩用于通讯
- 加密,保证安全性
[TOC]
虽然表示图像需要大量的数据, 但图像数据是高度相关的, 或者说存在冗余 (Redundancy) 信息, 去掉这些冗余信息后可以有效压缩图像, 同时又不会损害图像的有效信息。数字图像的写余主要表现为以下几种形式: 空间几余、时间冗余、视觉杂、 信息熵咒余、结构冗余和知识冗余。
-
空间冗余:图像内部相邻像素之间存在较强的相关性所造成的咒余。
-
时间写余: 视频图像序列中的不同帧之间的相关性所造成的写余。
-
视觉冗余: 是指人眼不能感知或不敏感的那部分图像信息。
-
信息熵冗余: 也称编码冗余,如果图像中平均每个像素使用的比特数大于该图像的信息熵, 则图像中存在咒余, 这种冗余称为信息熵冗余。
-
结构冗余:是指图像中存在很强的纹理结构或自相似性。
-
知识冗余: 是指在有些图像中还包含与某些先验知识有关的信息。
图像数据的这些冗余信息为图像压缩编码提供了依据。如, 利用人眼对蓝光不敏感的视觉特性, 在对彩色图像编码时, 就可以用较低的精度对蓝色分量进行编码。图像编码的目的就是充分利用图像中存在的各种呪余信息, 特别是空间几余、时间冗余以及视觉冗余, 以尽量少的比特数来表示图像。利用各种冗余信息, 压缩编码技术能够很好地解决在将模拟信号转换为数字信号后所产生的带宽需求增加的问题, 它是使数字信号走上实用化的关键技术之一, 表3-1中列出了几种常见应用的码率。 $$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \text { 应用场合 } & \text { 比特/像素 } & \text { 像索数/行 } & \text { 行数/帧 } & \text { 帧数/秒 } & \text { 亮色比 } & \text { 比特/秒(压缩前) } & \text { 比特/秒(压缩后) } \ \hline \text { 高清晰电视 } & 8 & 1920 & 1080 & 30 & 4: 1: 1 & 1.18 ~Gb / s & 20 \sim 25 Mb / s \ \hline \text { 普通电视 } & 8 & 720 & 480 & 30 & 4: 1: 1 & 167 Mb / s & 4 \sim 8 Mb / s \ \hline \text { 会议电视 } & 8 & 352 & 288 & 30 & 4: 1: 1 & 36.5 Mb / s & 1.5 \sim 2 Mb / s \ \hline \text { 桌上电视 } & 8 & 176 & 144 & 30 & 4: 1: 1 & 9.1 Mb / s & 128 ~Kb / s \ \hline \text { 电视电话 } & 8 & 128 & 112 & 30 & 4: 1: 1 & 5.2 Mb / s & 56 ~Kb / s \ \hline \end{array} $$ 表3-1 几种常见应用的码率
根据编码过程中是否存在信息损耗可将图像编码分为有损压缩和无损压缩。
-
无损压缩: 无信息损失, 解压缩时能够从压缩数据精确地恢复原始图像;
-
有损压缩:不能精确重建原始图像, 存在一定程度的失真。
图像冗余有损压缩的原理 $$ \begin{array}{|l|l|l|l|l|} \hline 36 & 35 & 34 & 34 & 34 \ \hline 34 & 34 & 32 & 34 & 34 \ \hline 33 & 37 & 30 & 34 & 34 \ \hline 34 & 34 & 34 & 34 & 34 \ \hline 34 & 35 & 34 & 34 & 31 \ \hline \end{array} \Rightarrow \begin{array}{|l|l|l|l|l|} \hline 34 & 34 & 34 & 34 & 34 \ \hline 34 & 34 & 34 & 34 & 34 \ \hline 34 & 34 & 34 & 34 & 34 \ \hline 34 & 34 & 34 & 34 & 34 \ \hline 34 & 34 & 34 & 34 & 34 \ \hline \end{array} \Rightarrow \begin{array}{|l|l|} \hline 25 &34\ \hline \end{array} $$ 图像冗余无损压缩的原理 $$ \begin{array}{|l|l|l|l|} \hline\quad & \quad&\quad &\quad\ \hline & & &\ \hline & & &\ \hline & & &\ \hline \end{array} \Rightarrow \begin{array}{|l|l|l|l|} \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \ \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \ \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \ \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \ \hline \end{array} \Rightarrow \begin{array}{|c|c|} \hline 16 & RGB \ \hline \end{array} $$
- 第一代压缩编码
八十年代以前, 主要是根据传统的信源编码方法。
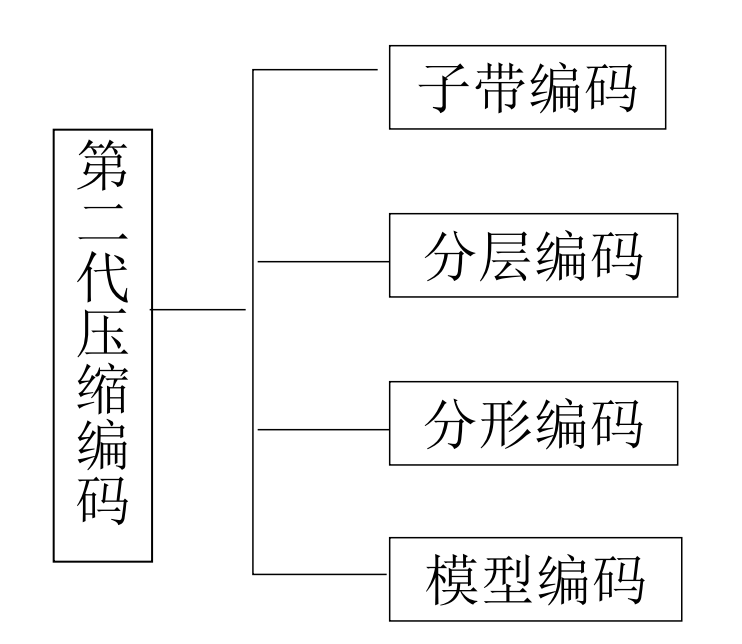
- 第二代压缩编码
八十年代以后, 突破信源编码理论, 结合分形、 模型基、神经网络、小波变换等数学工具, 充分利用视觉系统生理心理特性和图像信源的各种特性。
根据编码原理可以将图像编码分为熵编码、预测编码、变换编码和混合编码等。
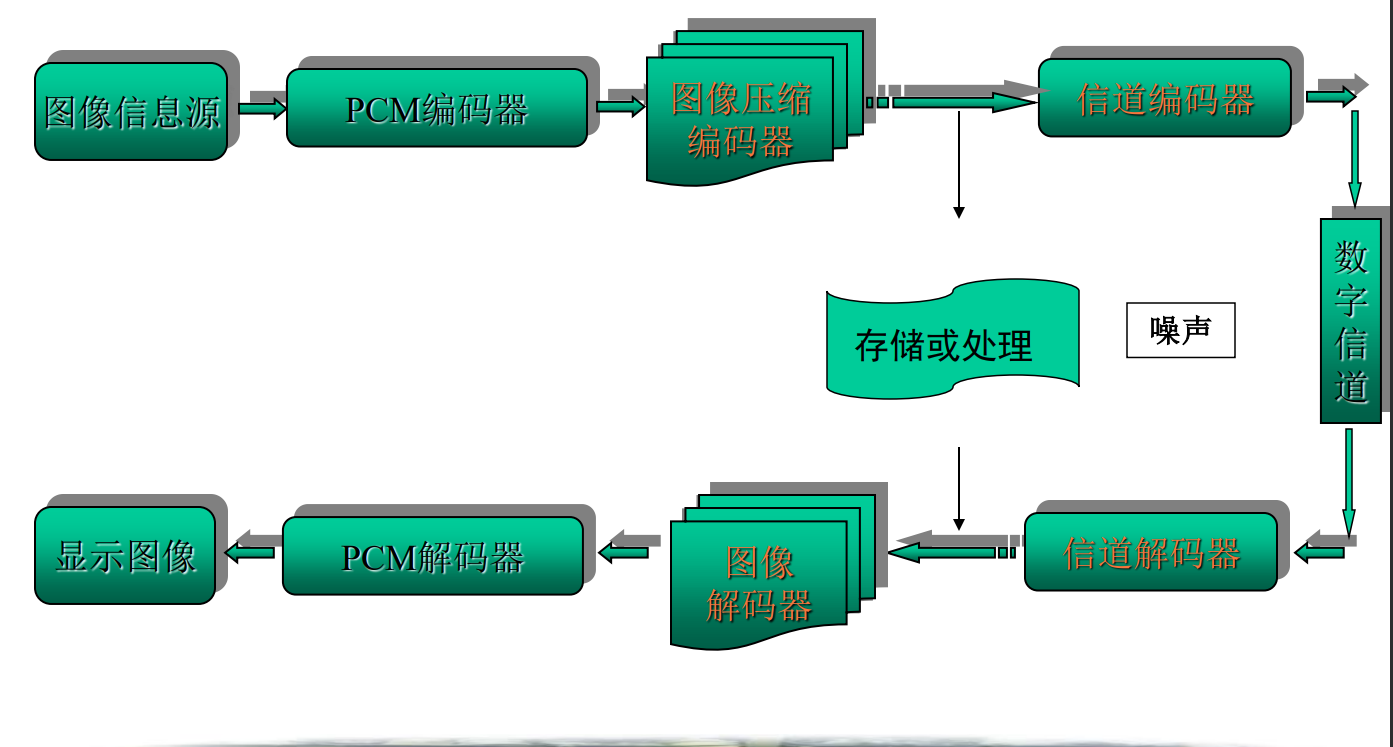
图像压缩编码系统原理框图
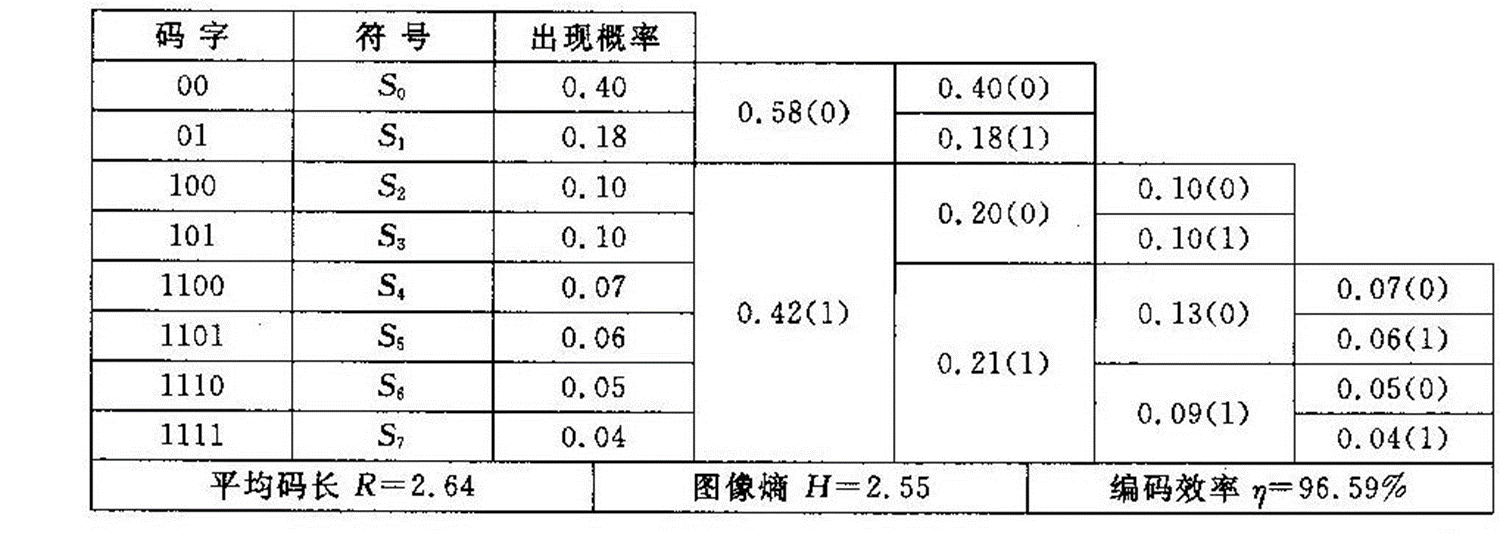
(1) 熵编码。熵编码是纯粹基于信号统计特性的编码技术, 是一种无损编码。熵编码的基本原理是给出现概率较大的符号赋予一个短码字, 而给出现概率较小的符号赋予一个长码字, 从而使得最终的平均码长很小。 常见的熵编码方法有行程编码 (Run Length Encoding)、哈夫曼编码和算术编码。
(2)预测编码。预测编码是基于图像数据的空间或时间冗余特性, 用相邻的已知像素(或像素块)来预测当前像素(或像素块)的取值, 然后再对预测误差进行量化和编码。预测编码可分为帧内预测和帧间预测, 常用的预测编码有差分脉码调制(Differential Pulse Code Modulation,DPCM)和运动补偿法。
(3)变换编码。变换编码通常是将空间域上的图像经过正交变换映射到另一变换域上, 使变换后的系数之间的相关性降低。 图像变换本身并不能压缩数据, 但变换后图像的大部分能量只集中到少数几个变换系数上, 采用适当的量化和熵编码就可以有效地压缩图像。
(4) 混合编码。混合编码是指综合了熵编码、变换编码或预测编码的编码方法, 如JPEG标准和MPEG标准。
根据对压缩编码后的图像进行重建的准确程度, 可将常用的图像编码方法分为三类:
(1)信息保持编码: 也称无失真编码, 它要求在编解码过程中保证图像信息不丢失, 从而可以完整地重建图像。信息保持编码的压缩比较低, 一般不超过3: 1, 主要应用在图像的数字存储方面, 常用于医学图像编码中。
(2)保真度编码: 主要利用人眼的视觉特性, 在允许的失真 (Lossy) 条件下或一定的保真度准则下, 最大限度地压缩图像。保真度编码可以实现较大的压缩比, 主要用于数字电视技术、静止图像通信、娱乐等方面。对于这些图像,过高的空间分辨率和过多的灰度层次, 不仅增加了数据量, 而且人眼也接收不到。因此在编码过程中, 可以丢掉一些人眼不敏感的信息, 在保证一定的视觉效果条件下提高压缩比。
(3) 特征提取: 在图像识别、分析和分类等技术中, 往往并不需要全部图像信息, 而只要对感兴趣的部分特征信息进行编码即可压缩数据。例如, 对遥感图像进行农作物分类时,就只需对用于区别农作物与非农作物, 以及农作物类别之间的特征进行编码, 而可以忽略道路、河流、建筑物等其他背景信息。
图像编码已经发展了几十年, 人们不断提出新的压缩方法。如, 利用人工神经网络 (Artificial Neural Network, ANN) 的压缩编码、分形编码(Fractal Coding)、小波编码(Wavelet Coding)、基于对象的压缩编码(Object Based Coding)和基于模型的压缩编码(Model Based Coding)等等。
1)分形编码
分形编码是在波兰美籍数学家B.B.Mandelbrot建立的分形几何理论的基础上发展起来的一种编码方法。分形编码最大限度地利用了图像在空间域上的自相似性(即局部与整体之间存在某种相似性),通过消除图像的几何几穴余来压缩数据。 M.Barnsley将迭代函数系统 (Iterate Function System,IFS) 用于描述图像的自相似性, 并将其用于图像编码, 对某些特定图像获得了10 000: 1的压缩比。分形编码过程十分复杂, 而解码过程却很简单, 故通常用于对图像编码一次, 而需译码多次的信息传播应用中。
2)小波编码
1989年, S.G.Mallat首次将小波变换用于图像编码。经过小波变换后的图像, 具有良好的空间方向选择性, 而且是多分辨率的, 能够保持原图像在各种分辨率下的精细结构, 与人的视觉特性十分吻合。
3)模型编码
模型编码是近几年发展起来的一种很有前途的低比特率编码方法, 其基本出发点是在编、解码两端分别建立起相同的模型,编码时利用先验模型抽取图像中的主要信息并用模型参数的形式表示,解码时则利用所接收的模型参数重建图像。
随着众多图像压缩算法的出现, 如何评价图像压缩算法就成为重要的课题。一般说来, 评价图像压缩算法的优劣主要有以下4个参数。
1)算法的编码效率
算法的编码效率通常有几种表现形式: 平均码字长度(R), 图像的压缩比 (rate,
图像大小为
由此可见, 图像熵
对于一种图像编码方法, 设第
于是,可定义编码效率
每秒钟所需的传输比特数bps为
压缩比
2)编码图像的质量
图像质量评价可分为客观质量评价和主观质量评价。最常用
的客观质量评价指标是均方误差 (MSE) 和峰值信噪比
(PSNR),其定义如下:
主观质量评价是指由一批观察者对编码图像进行观察并打分, 然后综合所有人的评判结果, 给出图像的质量评价。客观质量评价能够快速有效地评价编码图像的质量, 但符合客观质量评价指标的图像不一定具有较好的主观质量。主观质量评价能够与人的视觉效果相匹配, 但其评判过程缓慢费时。
3)算法的适用范围
特定的图像编码算法具有其相应的适用范围, 并不对所有图像都有效。一般说来, 大多数基于图像信息统计特性的压缩算法具有较广的适用范围, 而一些特定的编码算法的适用范围较窄, 如分形编码主要用于自相似性高的图像。
4)算法的复杂度
算法的复杂度即指完成图像压缩和解压缩所需的运算量和硬件实现该算法的难易程度。优秀的压缩算法要求有较高的压缩比, 压缩和解压缩快, 算法简单, 易于硬件实现, 还要求解压缩后的图像质量较好。选用编码方法时一定要考虑图像信源本身的统计特性、多媒体系统(硬件和软件产品)的适应能力、应用环境以及技术标准。
图象熵:
图像灰度集合为
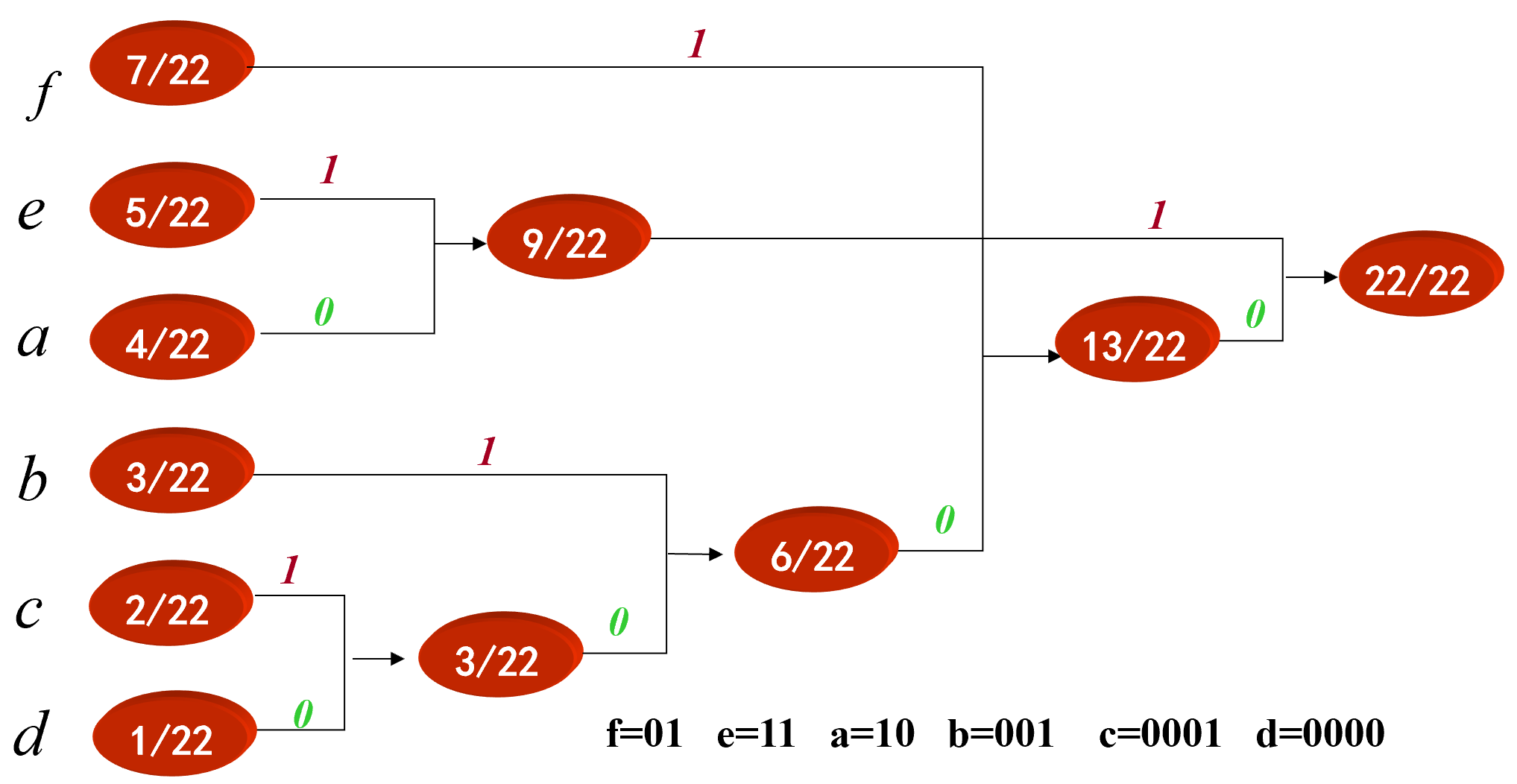
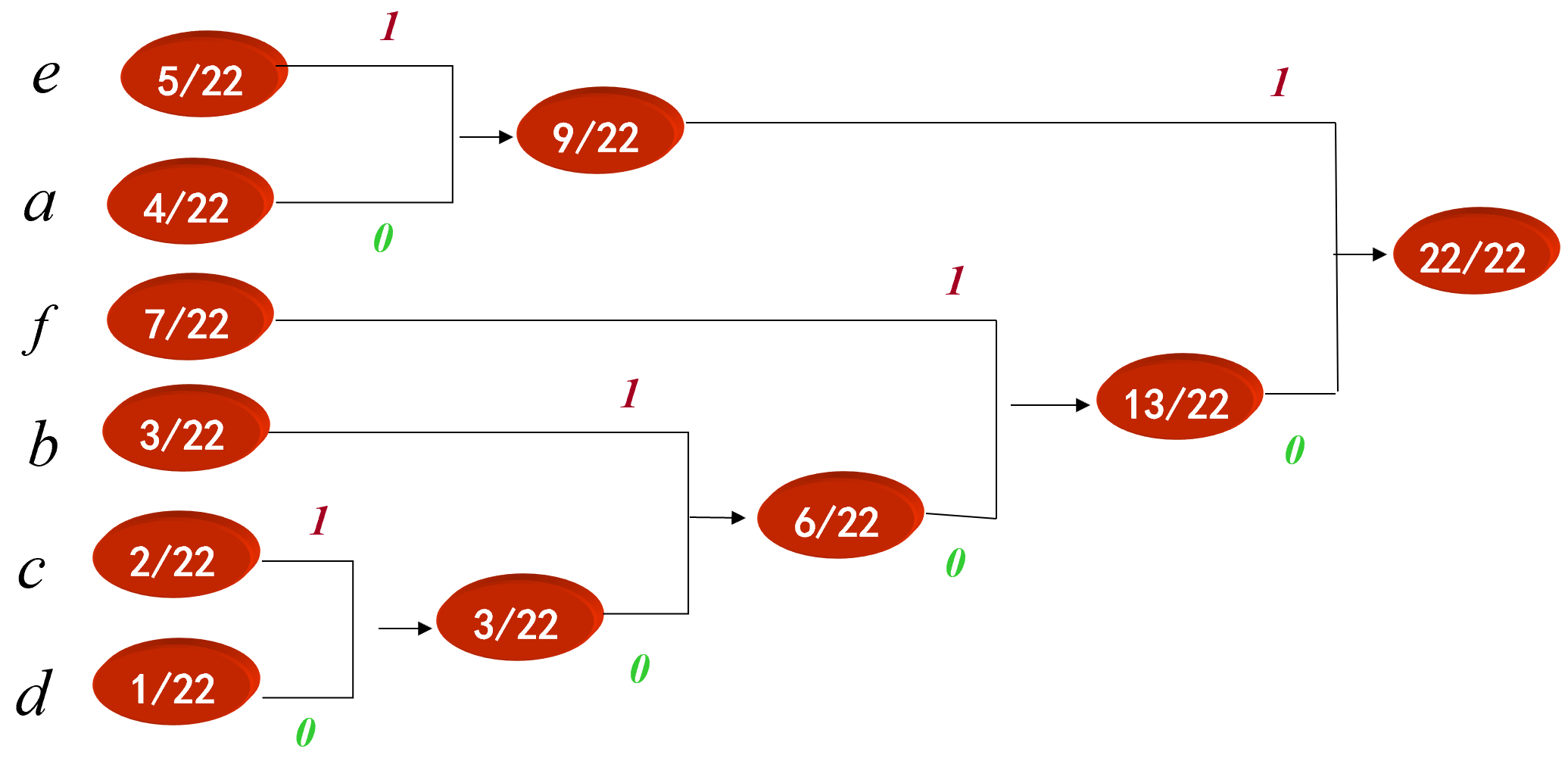
举例:
$$
\frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
$$
编码:
11011011011011111111111111100111001110110101010100000000
(共
Huffman 编码步骤: 1、先将图象灰度级按出现的概率由大到小顺序排列; 2、将最小两个概率相加, 形成一个新的概率集合, 再按第 (1) 步方法重排, 如此重复进行直到只有两个概率为止; 3、分配码长。码长分配从最后一步开始反向进行, 对最后两个概率一个赋予“0”, 一个赋予“1”
整理:
f=01 e=11 a=10 b=001 c=0001 d=0000 $$ \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) } $$ 经过Huffman编码之后的数据为:
1010101010001001001000100010000111111111101010101010101
(共
Huffman编码在图像压缩中的实现 我们知道, 对一幅图像进行编码时, 如果图像的大小大于 256 时, 这幅图像的不同的码字就有可能是很大, 例如极限为 256 个不同的码字。 对整幅图直接进行Huffman编码时, 小分布的灰度值, 就有可能具有很长的编码。 如: 100位以上, 这样不但达不到压缩的效果反而会使数据量加大, 应该如何处理?
常用的且有效的方法是: 将图像分割成若干的小块, 对每块进行独立的Huffman编码。例如: 分成$8\times 8$的子块, 就可以大大降低不同灰度值的个数(最多是64而不是256)。
香农-范诺 (Shannon-Fannon) 编码也是一种常见的可变字长编码。与哈夫曼编码相似, 当信源符号出现的概率正好为
香农-范诺编码的步骤如下:
(1)将信源符号按其出现概率从大到小排序;
(2)按照式 (3-8) 计算出各概率对应的码字长度
为便于比较, 仍以例4-1中图像为对象, 对其进行香农-范诺编码, 结果如表3-3所示。由于在此采用二进制对码字赋值, 故在利用式 (3-9) 计算码字长度
表3-3 香农-范诺编码
$$ 平均码长 R=3.17 \quad图像熵 H=2.55 \quad \text { 编㐷效率 } \eta=80.4 %\ \begin{array}{|c|c|c|c|c|c|} \hline \text { 信源符号 } & \text { 出现概率 } P_i & \text { 码字长度 } N_i & \text { 蔂加概率 } A_i & \text { 转换为二进制 } & \text { 分配码字 } B_i \ \hline S_0 & 0.40 & 2 & 0 & 0 & 00 \ \hline S_1 & 0.18 & 3 & 0.40 & 01100 & 011 \ \hline S_2 & 0.10 & 4 & 0.58 & 10010 & 1001 \ \hline S_3 & 0.10 & 4 & 0.68 & 10100 & 1010 \ \hline S_4 & 0.07 & 4 & 0.78 & 11000 & 1100 \ \hline S_5 & 0.06 & 5 & 0.85 & 1101100 & 11011 \ \hline S_6 & 0.05 & 5 & 0.91 & 1110100 & 11101 \ \hline S_7 & 0.04 & 5 & 0.96 & 1111010 & 11110 \ \hline \end{array}\
$$ 除此之外, 还有二分法香农-范诺编码方法。其步骤如下: (1) 首先统计出每个符号出现的概率; (2) 从左到右对上述概率从大到小排序; (3) 从这个概率集合中的某个位置将其分为两个子集合,并尽量使两个子集合的概率和近似相等,给前面一个子集合赋值为0, 后面一个子集合赋值为1; (4) 重复步骤3,直到各个子集合中只有一个元素为止; (5) 将每个元素所属的子集合的值依次串起来,即可得到各个元素的香农-范诺编码。
表3-4 二分法香农-范诺编码
行程编码又称行程长度编码(Run Length Encoding, RLE), 是一种熵编码,其编码原理相当简单,即将具有相同值的连续串用其串长和一个代表值来代替, 该连续串就称为行程,串长称为行程长度。例如,有一字符串“aabbbcddddd”, 则经行程长度编码后, 该字符串可以只用“2a3b1c5d”来表示。 行程编码分为定长和不定长编码两种。定长编码是指编码的行程长度所用的二进制位数固定,而变长行程编码是指对不同范围的行程长度使用不同位数的二进制位数进行编码。使用变长行程编码需要增加标志位来表明所使用的二进制位数。
行程编码比较适合于二值图像的编码,一般用于量化后出现大量零系数连续的场合,用行程来表示连零码。如果图像是由很多块颜色或灰度相同的大面积区域组成的,那么采用行程编码可以达到很高的压缩比。如果图像中的数据非常分散,则行程编码不但不能压缩数据,反而会增加图像文件的大小。为了达到较好的压缩效果,一般不单独采用行程编码, 而是和其他编码方法结合使用。例如, 在JPEG中, 就综合使用了行程编码、DCT、量化编码以及哈夫曼编码, 先对图像作分块处理, 再对这些分块图像进行离散余弦变换(DCT), 对变换后的频域数据进行量化并作Z字形扫描,接着对扫描结果作行程编码, 对行程编码后的结果再作哈夫曼编码。
PCX文件分为文件头和图像压缩数据两个部分。如果是256色图像,则还有一个256色调色板存于文件尾部。文件头全长128字节,包含了图像的大小和颜色以及PCX文件的版本标识等信息,图像压缩数据紧跟在文件头之后。如果没有使用调色板, 那么图像压缩数据存储的是实际像素值;否则,存储的是调色板的索引值。当压缩数据是实际的像素值时,它们按颜色平面和扫描行存储,即每行先存储所有R分量,再存储所有G分量, 最后存储所有B分量,一行数据存储完后,接着存储下一行数据。如果使用了调色板,则不会分解为单独的颜色平面存储。读者可以查阅图像文件格式的相关书籍了解PCX文件的详细格式。下面以256色PCX文件为例, 说明PCX文件中的行程编码。
在256色PCX文件中,每个像素占一字节, 压缩数据以字节为单位逐行进行编码,每行填充到偶数字节。PCX文件规定编码时的最大行程长度为63,如果行程长度大于63,则必须分多次存储。对于长度大于1的行程,编码时先存入其行程长度(长度L加上192即0xC0),再存入该行程的代表值,行程长度和行程的代表值分别占一字节。对于长度为1的行程,即单个像素, 如果该像素的值小于或等于0xC0, 则编码时直接存入该像素值, 而不存储长度信息;否则,先存入0xC1,再存入该像素值,这样做的目的是为了避免该像素值被误认为长度信息。例如,连续100个灰度值为0x80的像素, 其编码(以十六进制表示)应为FF 80 25 80。上面的编码中出现FF的长度信息是由63与0xC0相加所得。
对256色PCX文件解码时,首先从压缩数据部分读取一个字节,判断该值是否大于0xC0,如果是,则表明该字节是行程长度信息, 取其低六位(相当于减去0xC0)作为行程长度L,读取下一个字节作为像素值并重复L次存入图像数据缓冲区;否则, 直接将该字节存入图像数据缓冲区。
虽然几乎所有的图像应用软件都支持PCX文件格式,但由于它的压缩比不高, 因而现在用得不是很多。
LZW(Lempel-Ziv&Welch)编码又称字串表编码,属于一种无损编码,是Welch将Lempel和Ziv所提出的无损压缩技术改进后的压缩方法。LZW编码与行程编码类似,也是对字符串进行编码从而实现压缩,但它在编码的同时还生成了特定字符串以及与之对应的索引字符串表。
LZW编码的基本思想是:在编码过程中,将所遇到的字符串建立一个字符串表,表中的每个字符串都对应一个索引,编码时用该字符串在字串表中的索引来代替原始的数据串。例如,一幅8位的灰度图像,我们可以采用12位来表示每个字符串的索引,前256个索引用于对应可能出现的256种灰度,由此可建立一个初始的字符串表,而剩余的3840个索引就可分配给在压缩过程中出现的新字符串,这样就生成了一个完整的字符串表,压缩数据就可以只保存它在字符串表中的索引,从而达到压缩数据的目的。字符串表是在压缩过程中动态生成的,不必将它保存在压缩文件里,因为解压缩时字符串表可以由压缩文件中的信息重新生成。
GIF(GraphicsInterchangeFormat)最初是由美国CompuServe于1987年开发的一种压缩位图格式。它可支持多达256种的颜色,具有极佳的压缩效率,已成为Internet上一种流行的文件格式。GIF图像文件采用的是一种改良的LZW压缩算法,通常称为GIF-LZW压缩算法。GIF图像文件以块(又称为区域结构)的方式来存储图像相关的信息,具体的文件格式可参考图像文件格式的相关书籍。下面简要介绍GIF-LZW的编码方法。
设S1、S2为两个存放字符串的临时变量,LZW_CLEAR和LZW_EOI分别为字符表初始化标志和编码结束标志,GIF-LZW的编码步骤如下:
(1)根据图像中使用的颜色数初始化一个字串表,字串表中的每个颜色对应一个索引。在初始字串表的末尾再添加两个符号(LZW_CLEAR和LZW_EOI)的索引。设置字符串变量S1、S2并初始化为空。
(2)接着输出LZW_CLEAR在字串表中的索引。
(3)从图像数据流中第一个字符(假设数据以字符串表示)开始,每次读取一个字符,将其赋给字符串变量S2。
(4)判断“S1+S2”是否已存在于字串表中。如果字串表中存在“S1+S2”,则S1=S1+S2;否则,输出S1在字串表中的索引,并在字串表末尾为“S1+S2”添加索引,同时,S1=S2。
(5)重复第3和第4步,直到所有字符读完为止。
(6)输出S1中的字符串在字串表中的索引,然后输出结束标志LZW_EOI的索引,编码完毕。
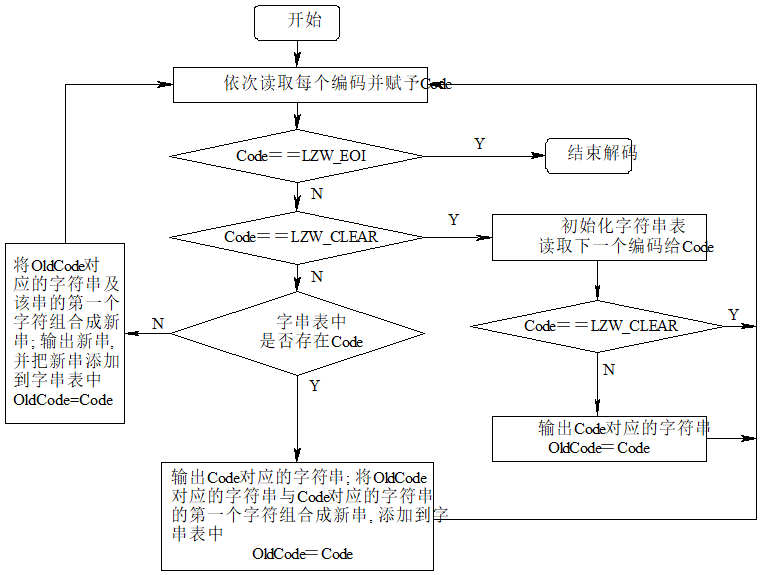
GIF-LZW的解码过程比较复杂,它和编码过程正好相反,即将编码后的码字转换成对应的字符串,重新生成字串表,然后依次输出对应的字符串即可。GIF-LZW的解码流程如图3-2所示,表中的Code和OldCode是两个存放索引的临时变量。
图3-2GIF-LZW解码流程
设有一来源于4色(以a、b、c、d表示)图像的数据流aabcabbbbd,现对其进行LZW编码。编码过程如下: 编码前,首先需要初始化一个字符串表。由于图像中只有四种颜色,因而我们可以只用4比特表示字符串表中每个字符串的索引,表中的前4项代表4种颜色,后两项分别表示初始化和图像结束标志,建立的初始化字符串表如表3-5所示。接着把S1和S2初始化为空(即NULL),输出LZW_CLEAR的在字符串表中的索引值4H,接下来是对图像数据的编码。
表3-5初始化字符串表 $$ \begin{array}{|c|c|} \hline \text{字符串}&\text{索引}\ \hline a&0H\ \hline b&1H\ \hline c&2H\ \hline d&3H\ \hline \text{LZW_CLEAR}&4H\ \hline \text{LZW_EOI}&5H\ \hline \end{array} $$
读取图像数据流的第一个字符“a”,赋给S2,因S1+S2=“a”已存在字串表中,所以S1=S1+S2=“a”。 接着读入下一个字符“a”赋给S2,因S1+S2=“aa”不存在于字串表中,所以输出S1=“a”的索引0H,同时在字符串表末尾添加新字符串“aa”的索引6H,并使S1=S2=“a”。 依次读取数据流中的每个字符,如果S1+S2没有出现在字符串表中,则输出S1中的字符串的索引,并在字符串表末尾为新字符串S1+S2添加索引,并使S1=S2;否则,不输出任何结果,只是使S1=S1+S2。所有字符处理完毕后,输出S1中的字符串的索引,最后输出结束标志LZW_EOI的索引。至此,编码完毕,完整的编码过程如表3-6所示,最后的编码结果为“4001271B35”(以十六进制表示)。
表3-6GIF-LZW编码过程 $$ \begin{array}{|c|c|c|c|c|} \hline \text { 输入数据 S2 } & \text { S1+S2 } & \text { 输出结果 } & \text { S1 } & \text { 生成的新字符串及索引 } \ \hline \text { NULL } & \text { NULL } & 4 H & \text { NULL } & \ \hline a & a & & a & \ \hline a & aa & 0 H & a & aa<6 H> \ \hline b & ab & 0 H & a & ab<7 H> \ \hline c & bc & 1 H & c & ca<9 H> \ \hline a & ca & 2 H & a & \ \hline b & ab & & ab & abb \ \hline b & abb & 7 H & b & bb \ \hline b & bb & 1 H & b & \ \hline b & bb & & bb & bbd \ \hline d & bbd & BH & d & \ \hline & & 3 H & & \ \hline & & 5 H & & \ \hline \end{array} $$ 下面对上述编码结果“4001271B35”进行解码。按图3-2的解码流程,首先读取第一个编码Code=4H,由于它为LZW_CLEAR,因此需初始化字符串表,结果如表3-5所示(在实际应用中,可根据文件头中给定的信息建立初始字符串表)。
读入下一个编码Code=0H,由于它不等于LZW_CLEAR,因此输出字串表中0H对应的字符串“a”,同时使OldCode=Code=0H。
读入下一个编码Code=0H,由于字串表中存在该索引,因此输出0H所对应的字符串“a”,然后将OldCode=0H所对应的字符串“a”加上Code=0H所对应的字符串的第一个字符“a”,即“aa”添加到字串表中,其索引为6H,同时使ldCode=Code=0H。
读入下一个编码Code=1H,由于字串表中存在该索引,因此输出1H所对应的字符串“b”,然后将OldCode=0H所对应的字符串“a”加上Code=1H所对应的字符串的第一个字符“b”,即“ab”添加到字串表中,其索引为7H,同时使OldCode=Code=1H。
读入下一个编码Code=2H,由于字串表中存在该索引,因此输出2H所对应的字符串“c”,然后将OldCode=1H所对应的字符串“b”加上Code=2H所对应的字符串的第一个字符“c”,即“bc”添加到字串表中,其索引为8H,同时使OldCode=Code=2H。
读入下一个编码Code=7H,由于字串表中存在该索引,因此输出7H所对应的字符串“ab”,然后将OldCode=2H所对应的字符串“c”加上Code=7H所对应的字符串的第一个字符“a”,即“ca”添加到字串表中,其索引为9H,同时使OldCode=Code=7H。
读入下一个编码Code=1H,由于字串表中存在该索引,因此输出1H所对应的字符串“b”,然后将OldCode=7H所对应的字符串“ab”加上Code=1H所对应的字符串的第一个字符“b”,即“abb”添加到字串表中,其索引为AH,同时使OldCode=Code=1H。
读入下一个编码Code=BH,由于字串表中不存在该索引,因此输出OldCode=1H所对应的字符串“b”加上该字符串的第一个字符“b”,即“bb”,同时将“aa”添加到字串表中,其索引为BH,同时使OldCode=Code=BH。
读入下一个编码Code=3H,由于字串表中存在该索引,因此输出其对应的字符串“d”,然后将OldCode=BH所对应的字符串“bb”加上Code=3H所对应的字符串的第一个字符“d”,即“bbd”添加到字串表中,其索引为CH,同时使OldCode=Code=3H。读入下一个编码Code=5H,它等于LZW_EOI,数据解码完毕,最后的解码结果为aabcabbbbd。为清晰起见,完整的解码过程如表3-7所示。
表3-7GIF-LZW解码过程 $$ \begin{array}{|c|c|c|c|c|} \hline \text { 输入数据 Code } & \text { 新字符串的来源 } & \text { 输出结果 } & \text { OldCode } & \text { 生成的新串及索引 } \ \hline 4 H & & & & \ \hline 0 H & & a & 0 H & \ \hline 0 H & \text { Str(OldCode)+FirstStr(Code) }=aa & a & 0 H & aa<6 H> \ \hline 1 H & \text { Str(OldCode)+FirstStr(Code) }=ab & b & 1 H & ab<7 H> \ \hline 2 H & \text { Str(OldCode)+FirstStr(Code) }=bc & c & 2 H & bc<8 H> \ \hline 7 H & \text { Str(OldCode)+FirstStr(Code) }=ca & ab & 7 H & ca<9 H> \ \hline 1 H & \text { Str(OldCode)+FirstStr(Code) }=abb & b & 1 H & abb \ \hline BH & \text { Str(OldCode)+FirstStr(OldCode) }=bb & bb & BH & bb \ \hline 3 H & \text { Str(OldCode)+FirstStr(Code) }=bbd & d & 3 H & bbd \ \hline 5 H & & & & \ \hline \end{array} $$
算术编码有两种模式:一种是基于信源概率统计特性的固定编码模式,另一种是针对未知信源概率模型的自适应模式。自适应模式中各个符号的概率初始值都相同, 它们依据出现的符号而相应地改变。只要编码器和解码器都使用相同的初始值和相同的改变值的方法,那么它们的概率模型将保持一致。上述两种形式的算术编码均可用硬件实现,其中自适应模式适用于不进行概率统计的场合。有关实验数据表明,在未知信源概率分布的情况下, 算术编码一般要优于Huffman编码。在JPEG扩展系统中,就用算术编码取代了哈夫曼编码。
下面结合一个实例来阐述固定模式的算术编码的具体方法。 设一待编码的数据序列 (即信源) 为 “ dacab", 信源中各符号出现的概率依次为
第三个被压缩的符号为 “
从这个区间可以看出,0.1101101位于这个区间内并且其编码最短, 故把其作为数据序列“dacab”的编码输出。考虑到算术编码中任一数据序列的编码都含有“0.”,所以在编码时,可以不考虑“0.”,于是把1101101作为本例中的数据序列的算术编码。由此可见, 数据序列“dacab”用7比特的二进制代码就可以表示, 平均码长为1.4比特/字符。
解码是编码的逆过程,根据编码时的概率分配表和压缩后数据代码所在的范围,确定代码所对应的每一个数据符号。由此可见,算术编码的实现方法要比哈夫曼编码复杂一些。
注意 作DCT变换时,一般不是对整个图象作一次变换,而是将图象划为88或1616的子图象,然后对各个子图象作DCT变换.
采用快速DCT变换
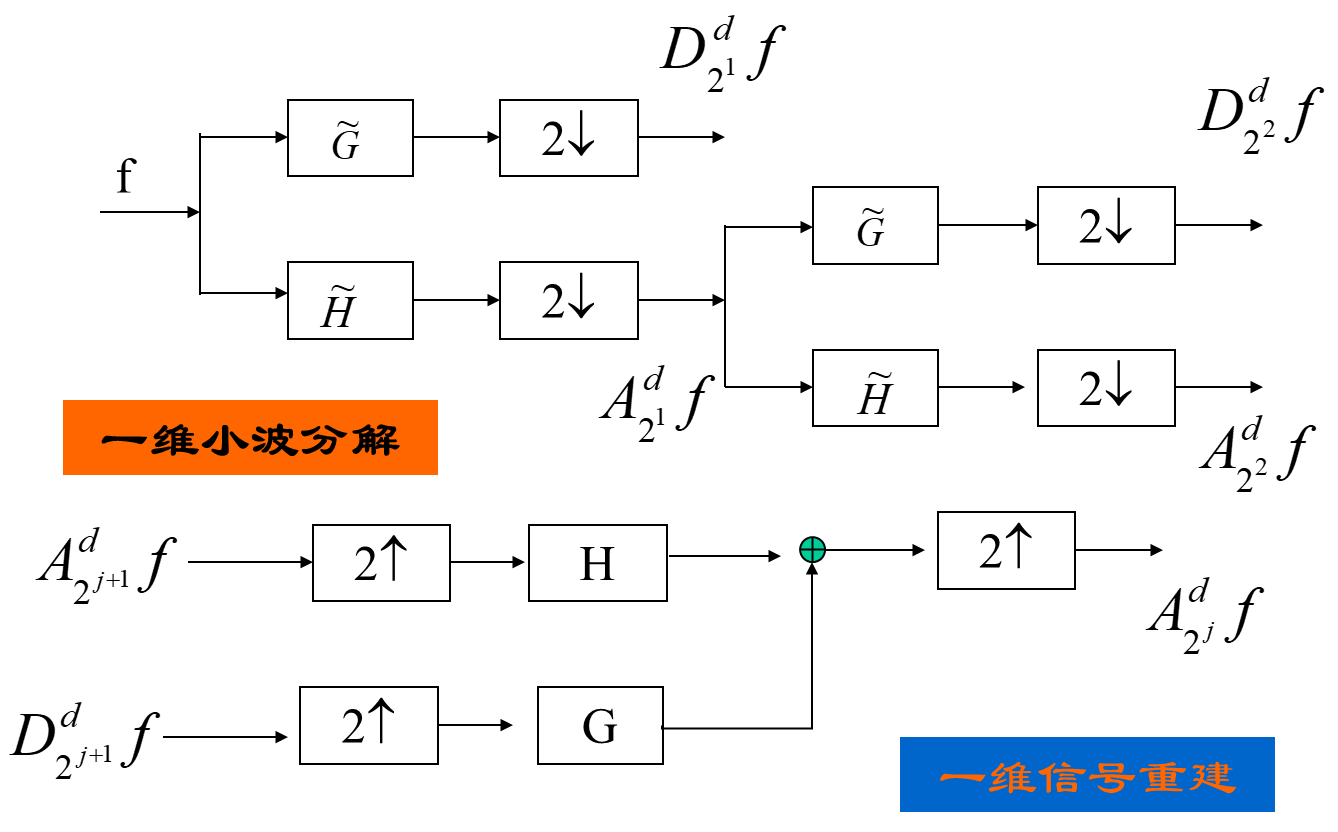
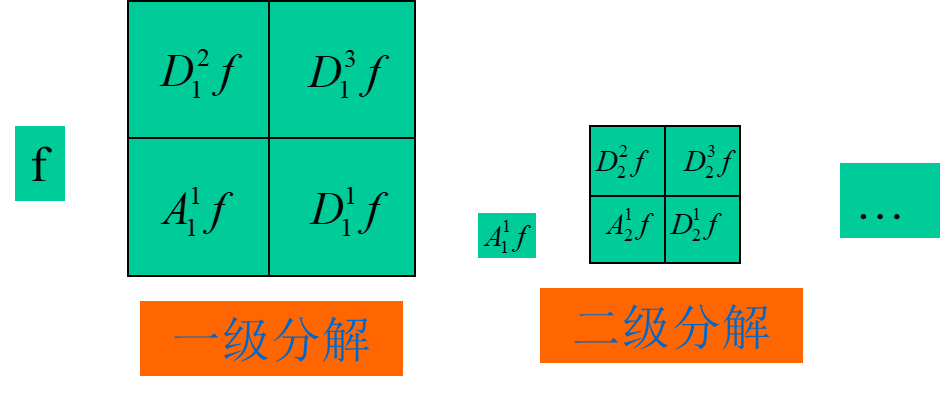
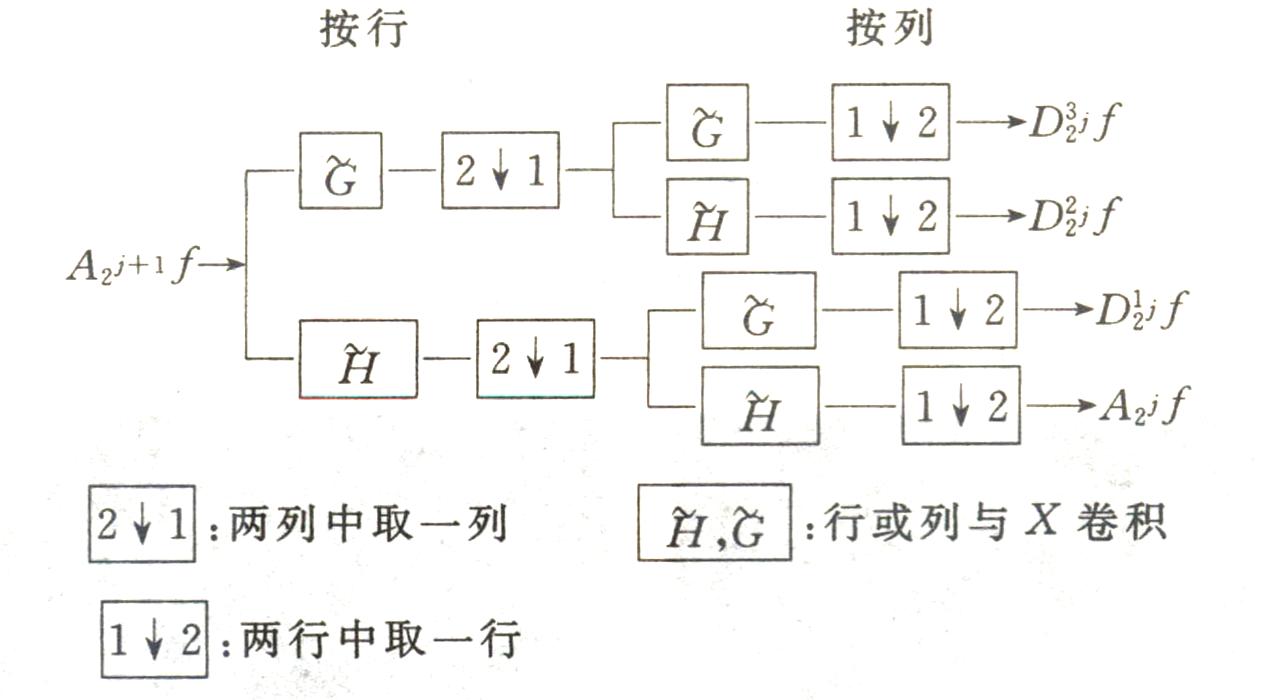
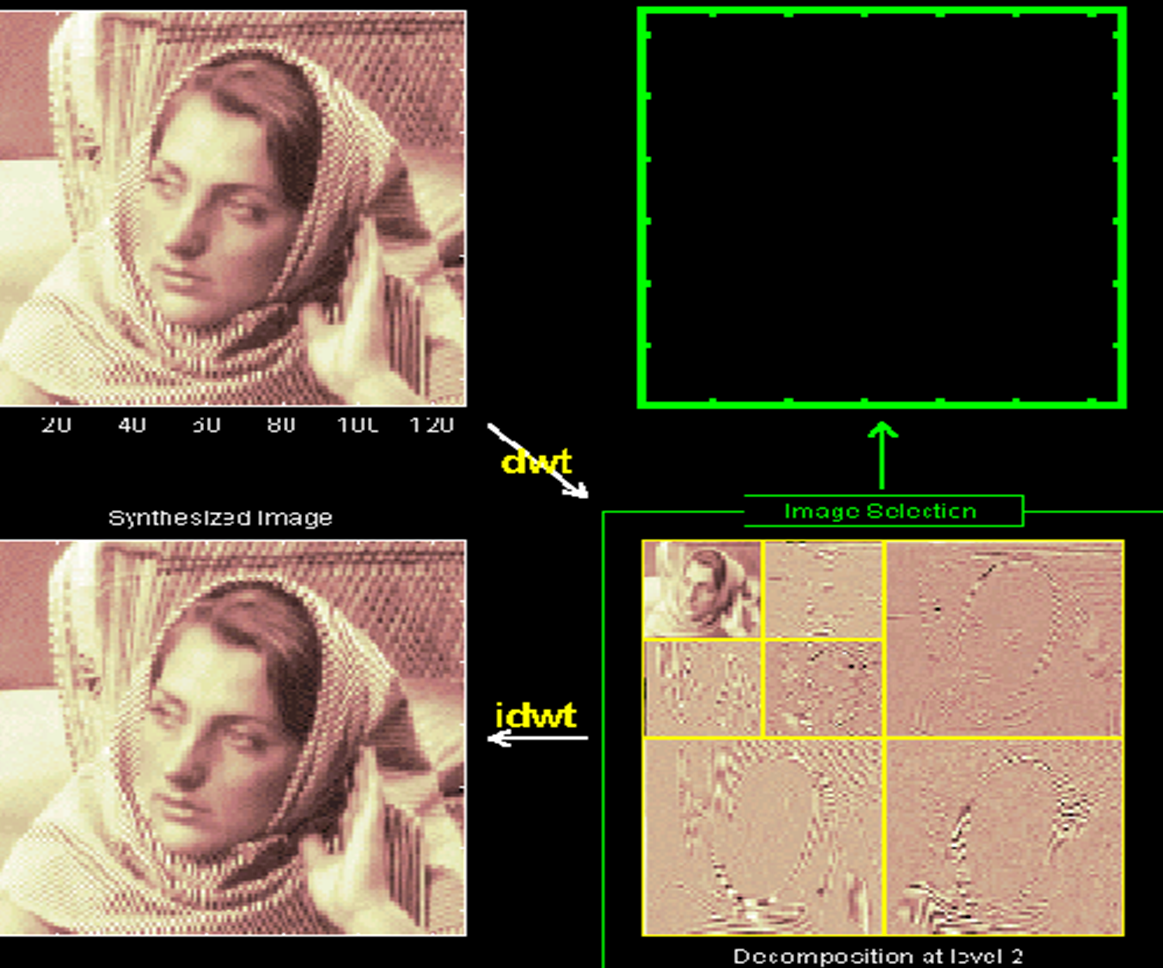
二维小波变换
一愊图象经小波变换成
二维小波分解
二维小波重建
基于小波变换编码原理
图象的最终目的是让人看, 而人的视觉系统对高频分量不敏感, 因此高频分量可以粗略编码, 而对图象的质量影响不大,并且高频部分有很高的相似性。由于细节部分对应于图象的高频分量, 考虎视觉特点, 它可以用较高的厓缩比编码, 而
混合编码实现的可能性及有效性:
回顾一下讲过的几个内容的特点
- 行程编码:擅长于重复数字的压缩。
- Huffman编码:擅长于像素个数的不同编码。
- DCT变换:擅长将高频部分分离出来。
例: $$ \frac{aaaa}{4}\frac{bbb}{3}\frac{cc}{2}\frac{d}{1}\frac{eeeee}{5}\frac{fffffff}{7} $$ 行程编码: $$ 4a3b2c1d5e7f \ $$ 共$6\times(8+3)= 66Bits$
Huffman编码: $$ f=01\quad e=11 \quad a=10 \quad b=001\quad c=0001\quad d=0000\
$$ 编码为 $$ 1010101010001001001000100010000111111111101010101010101 $$ 共$7\times2+5\times2+4\times2+3\times3+2\times4+1\times4=53 bits$
Hufman与行程编码混合: $$ 41030012000110000511701 $$ 共:$3+2+3+3+3+4+3+4+3+2+3+2=35 bits$
一:
一次小波变换+DCT变换.行程编码+Huffman编码
二:
一次小波变换+差值编码+变字长行程编码+Huffman编码
| 原图 | 复原图 |
|---|---|
 |
 |
信噪比:66.02
压缩比:11.83:1
| 原图 | 复原图 |
|---|---|
 |
 |
信噪比:64.55
压缩比:26.50:1
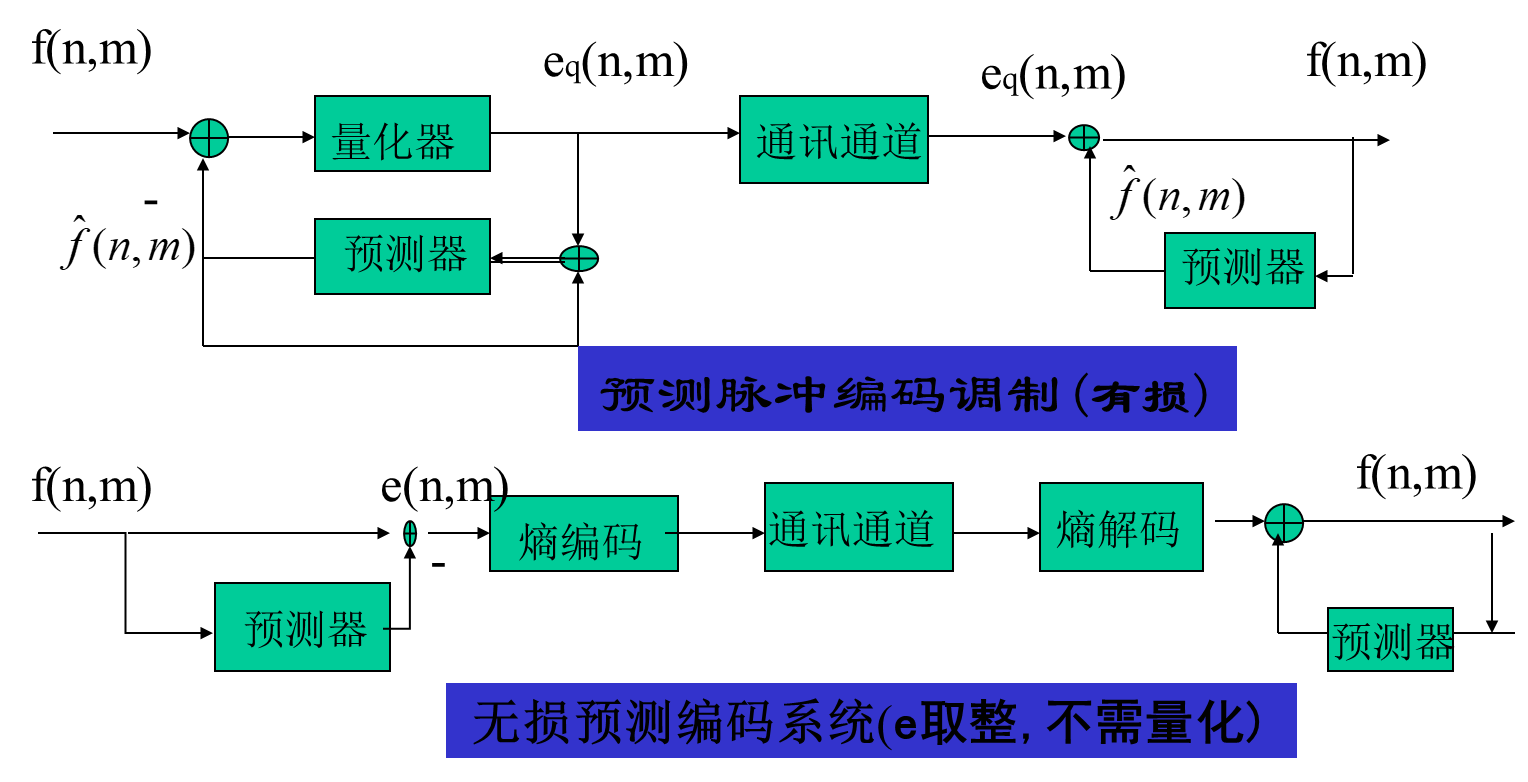
利用图象局部邻域象素的可预测性来进行圧缩.
设:
为了重建图象,需要传输预测系数和误差编码,这种编码方式称为预测脉冲编码调制(DPCM),如图:
假设图象的某一行
预测系数通过下式求解 $$ \left[\begin{array}{cccc} R(0) & R(1) & \cdots & R(P-1) \ R(1) & R(2) & \cdots & R(P-2) \ \vdots & \vdots & \vdots & \vdots \ R(P-1) & R(P-2) & \cdots & R(0) \end{array}\right]\left[\begin{array}{c} a(1) \ a(2) \ \vdots \ a(P) \end{array}\right]=\left[\begin{array}{c} R(1) \ R(2) \ \vdots \ R(P) \end{array}\right] $$
二维模型:
$$
\hat{f}(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}r(n-i, m-j)
$$
通过求解E最小:
$$
\left.\left.E\left[\mid f(n, m)-\sum \sum{(i, j) \in A} a(i, j) f(n-i), m-j\right)\right|^2\right]
$$
得:
JPEG是面向静态图像编码的国际标准。在相同图像质量条件下, JPEG文件拥有比其他图像文件格式更高的压缩比。JPEG目前被广泛应用于多媒体和网络程序中,是现今万维网中使用最广泛的两种图像文件格式之一。JPEG是一种有损压缩, 即在压缩过程中会丢失数据,每次编辑JPEG图像后,图像就会被重复压缩一次, 损失就会有所增加。
JPEG允许四种编码模式:
(1) 顺序式(Sequential)DCT方式:从左到右、从上到下对图像顺序进行基于离散余弦变换(DCT)的编码。DCT理论上是可逆的,但在计算时存在误差,因而基于DCT的编码模式是一种有损编码。
(2) 渐进式(Progressive)DCT方式:基于DCT,对图像分层次进行处理,从模糊到清晰地传输图像(与GIF文件的交错方式类似)。有两种实现方法,一种是频谱选择法,即按Z形扫描的序号将DCT量化序数分成几个频段,每个频段对应一次扫描, 每块均先传送低频扫描数据,得到原图概貌,再依次传送高频扫描数据,使图像逐渐清晰;另一种是逐次逼近法,即每次扫描全部DCT量化序数,但每次的表示精度逐渐提高。
(3) 无失真(Lossless)方式: 使用线性预测器,如DPCM, 而不是基于DCT。
(4) 分层(Hierarchical)方式: 在空间域将源图像以不同的分辨率表示,每个分辨率对应一次扫描, 处理时可以基于DCT或预测编码,可以是渐进式,也可以是顺序式。
JPEG定义了三种系统:基本系统(Baseline System)、扩展系统(Extended System)和无失真压缩系统(Lossless System)。一个符合JPEG标准的编解码器至少要满足基本系统的技术指标。
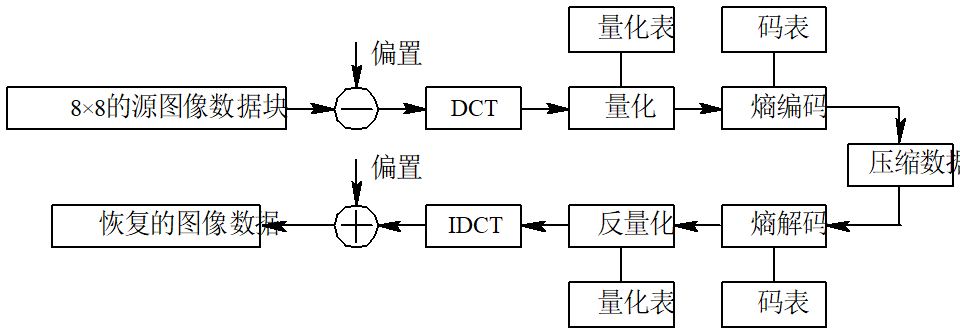
基本的JPEG算法属于变换类编码,下面针对基于DCT的顺序式基本系统编码来说明JPEG的编码方法。
图3-3 JPEG 编码流程图
- 数据分块
对图像进行编码前, 将每个分量图像分割成不重叠的
$8 \times 8$ 像素块, 每一个$8 \times 8$ 像素块称为一个数据单元 (DU)。在彩色图像中, JPEG分别压缩图像的每个彩色分量。虽然JPEG可以压缩通常的红绿蓝分量, 但在$Y_{b} C_{r}$ 空间的压缩效果会更好。 这是因为人眼对色彩的变化不如对亮度的变化敏感, 因而对色彩的编码可以比对亮度的编码粗糙些, 这主要体现在不同的采样频率和量化精度上。因此, 编码前一般先将图像从RGB空间转换到$YC_{b} C_{i}$ 空间,再把各分量图像分割成$8 \times 8$ 数据块。
在对图像采样时, 可以采用不同的采样频率, 这种技术称为二次采样。由于亮度比色彩更重要, 因而对
-
DCT处理 图像数据块分割后, 即以 MCU为单位顺序将DU进行二维离散余弦变换。对以无符号数表示的具有
$P$ 位精度的输入数据, 在DCT前要减去$2^{P-1}$ , 转换成有符号数, 而在IDCT后, 应加上$2^{P-1}$ , 转换成无符号数。对每个$8 \times 8$ 的数据块$DU$ 进行$DCT$ 后, 得到的64个系数代表了该图像块的频率成分,其中低频分量集中在左上角, 高频分量分布在右下角。系数矩阵左上角的叫做直流(DC)系数,它代表了该数据块的平均值, 其余 63 个叫交流(AC)系数。3) 系数量化 在DCT处理中得到的64个系数中,低频分量包含了图像亮度等主要信息。在从空间域到频域的变换中,图像中的缓慢变化比快速变化更易引起人眼的注意, 所以在重建图像时,低频分量的重要性高于高频分量。因而在编码时可以忽略高频分量, 从而达到压缩的目的,这也是量化的根据和目的。
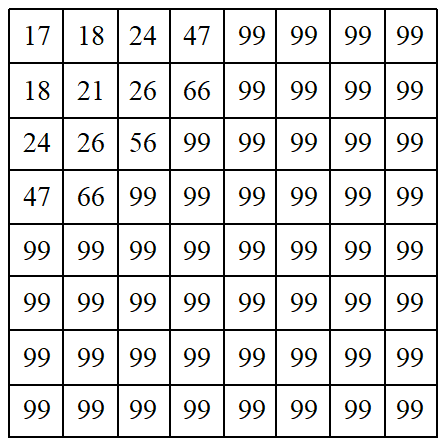
在JPEG标准中,用具有64个独立元素的量化表来规定DCT域中相应的64个系数的量化精度,使得对某个系数的具体量化阶取决于人眼对该频率分量的视觉敏感程度。理论上,对不同的空间分辨率、数据精度等情况,应该有不同的量化表。不过,一般采用图3-4和图3-5所示的量化表,可取得较好的视觉效果。之所以用两张量化表,是因为Y分量比Cb和Cr更重要些,因而对Y采用细量化,而对Cb和Cr采用粗量化。量化就是用DCT变换后的系数除以量化表中相对应的量化阶后四舍五入取整。由于量化表中左上角的值较小,而右下角的值较大, 因而起到了保持低频分量、 抑制高频分量的作用。
图3-4 亮度量化表
图3-5 色度量化表
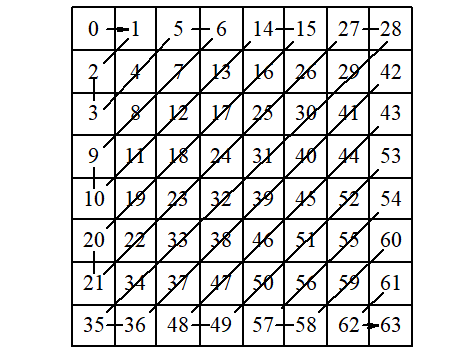
4) Z形扫描
DCT系数量化后,构成一个稀疏矩阵,用Z(Zigzag)形扫描将其变成一维数列,将有利于熵编码。Z形扫描的顺序如图3-6所示。
图3-6 DCT系数的Z形扫描顺序
5) DC系数编码
DC系数反映了一个8×8数据块的平均亮度,一般与相邻块有较大的相关性。JPEG对DC系数作差分编码,即用前一数据块的同一分量的DC系数作为当前块的预测值,再对当前块的实际值与预测值的差值作哈夫曼编码。
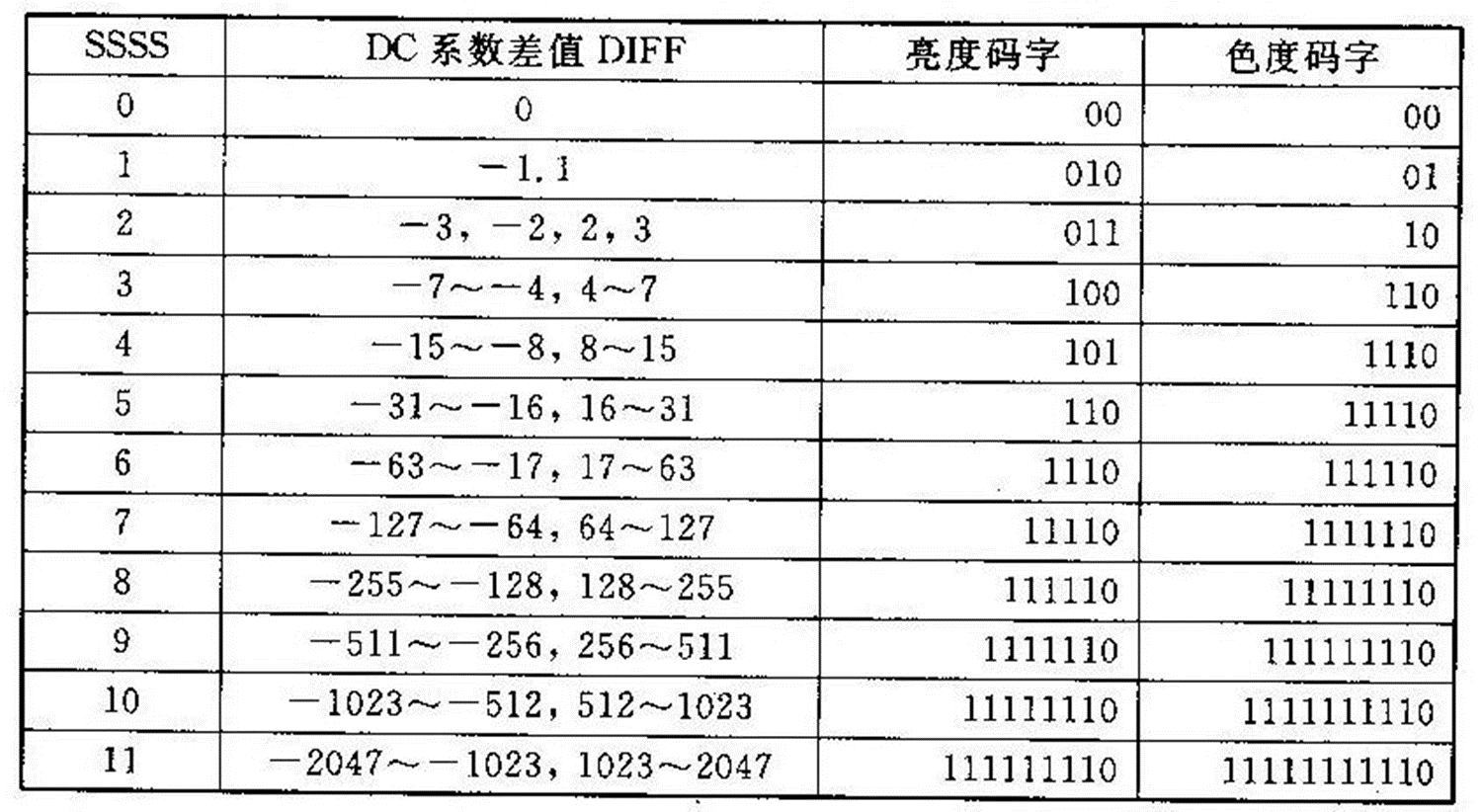
若DC系数的动态范围为-1024~+1024,则差值的动态范围为-2047~+2047。如果为每个差值赋予一个码字, 则码表过于庞大。因此,JPEG对码表进行了简化,采用“前缀码(SSSS)+尾码”来表示。前缀码指明了尾码的有效位数B, 可以根据DIFF从表3-8中查出前缀码对应的哈夫曼编码。尾码的取值取决于DC系数的差值和前缀码。如果DC系数的差值DIFF大于等于0,则尾码的码字为DIFF的B位原码;否则,取DIFF的B位反码。
表3-8 图像分量为8位时DC系数差值的典型哈夫曼编码表
6) AC系数编码
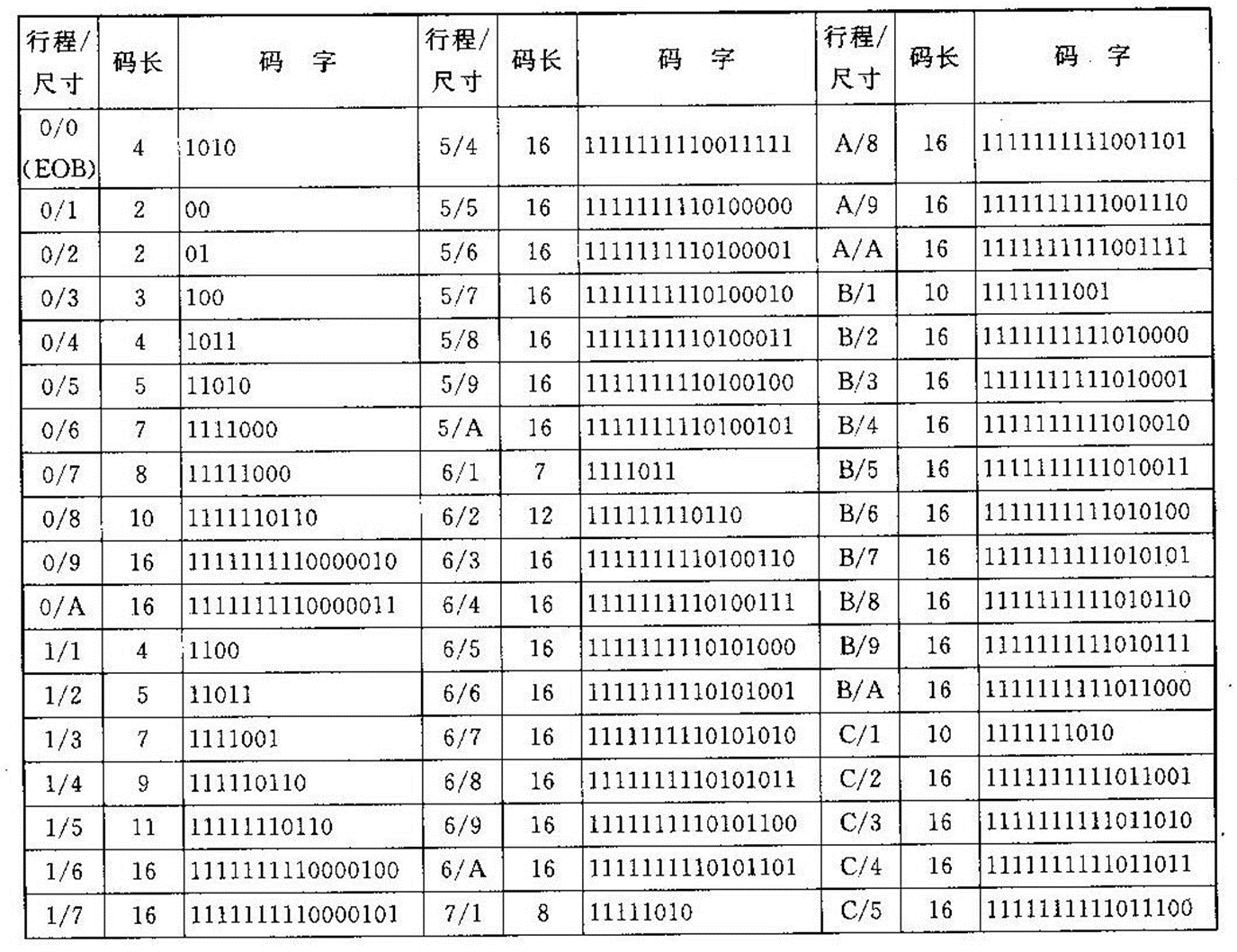
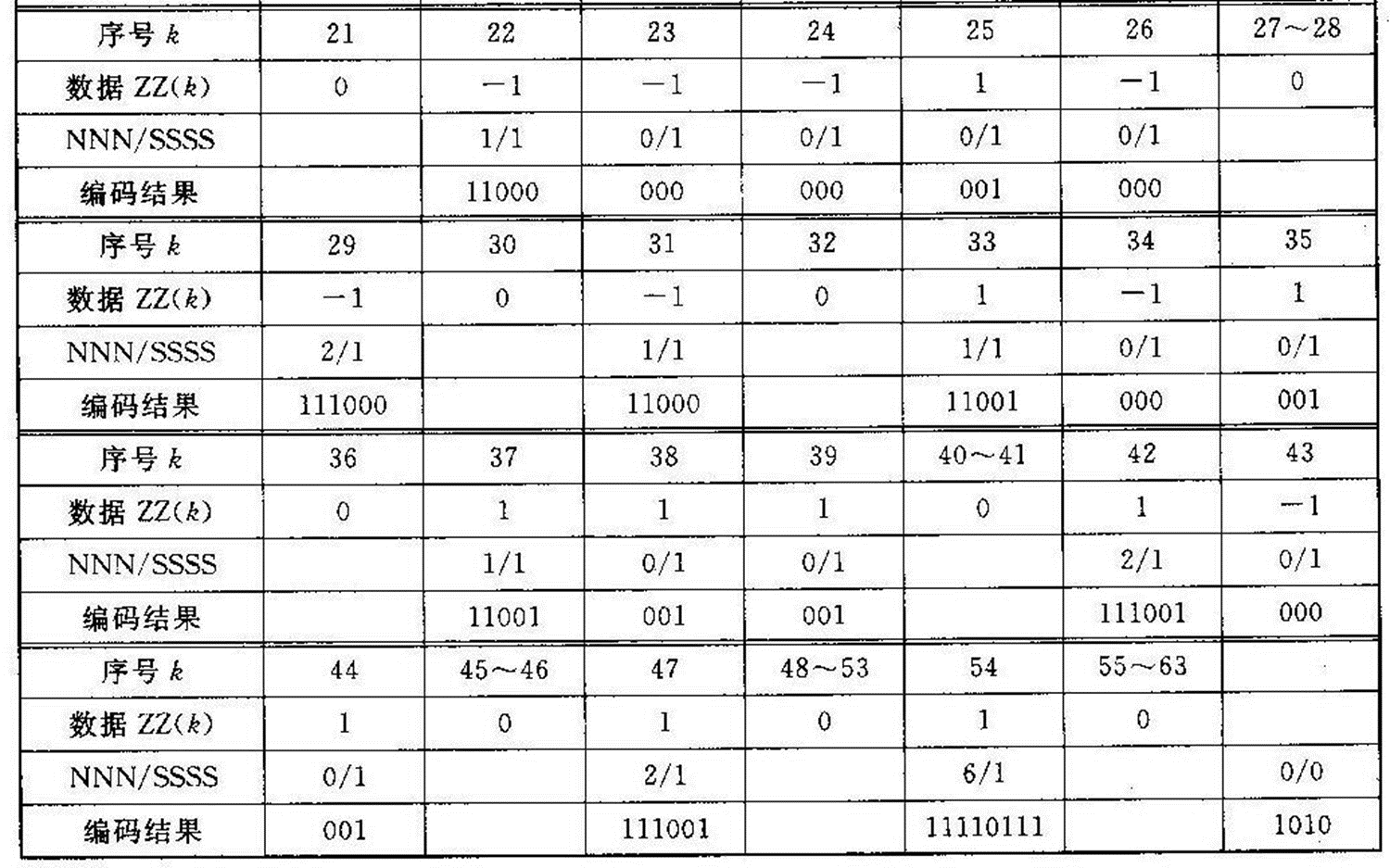
经Z形排列后的AC系数,更有可能出现连续0组成的字符串, 从而对其进行行程编码将有利于压缩数据。JPEG将一个非零DC系数及其前面的0行程长度(连续0的个数)的组合称为一个事件。将每个事件编码表示为“NNNN/SSSS+尾码”, 其中, NNNN为0行程的长度,SSSS表示尾码的有效位数B(即当前非0系数所占的比特数),如果非零AC系数大于等于0, 则尾码的码字为该系数的B位原码, 否则, 取该系数的B位反码。
由于只用4位表示0行程的长度,故在JPEG编码中,最大0行程只能等于15。当0行程长度大于16时,需要将其分开多次编码, 即对前面的每16个0以“F/0”表示,对剩余的继续编码。
表3-9 AC系数的尾码位数表
| SSSS | AC系数的尾码位数表 |
|---|---|
| 0 | 0 |
| 1 | -1,1 |
| 2 | -3, -2, 2, 3 |
| 3 | -7~-4, 4~7 |
| 4 | -15~-8, 8~15 |
| 5 | -31~-16, 16~31 |
| 6 | -63~-17, 17~63 |
| 7 | -127~-64, 64~127 |
| 8 | -255~-128, 128~255 |
| 9 | -511 |
| 10 | -1023~-512, 512~1023 |
表3-10 亮度AC系数码表
表3-11 色差AC系数编码
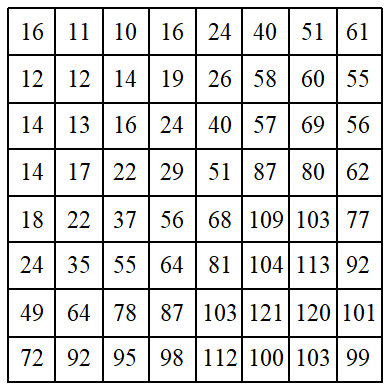
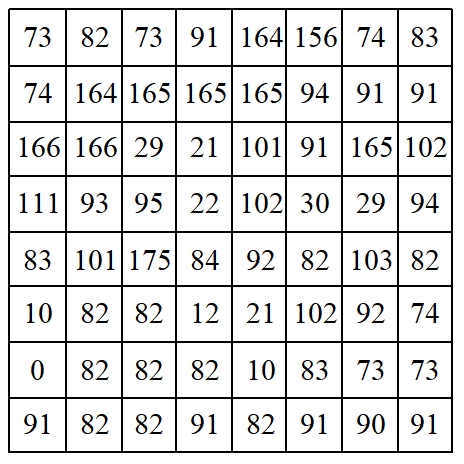
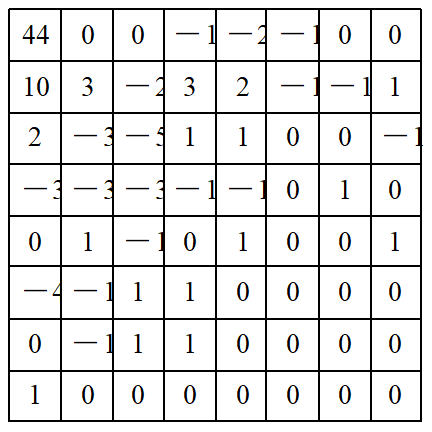
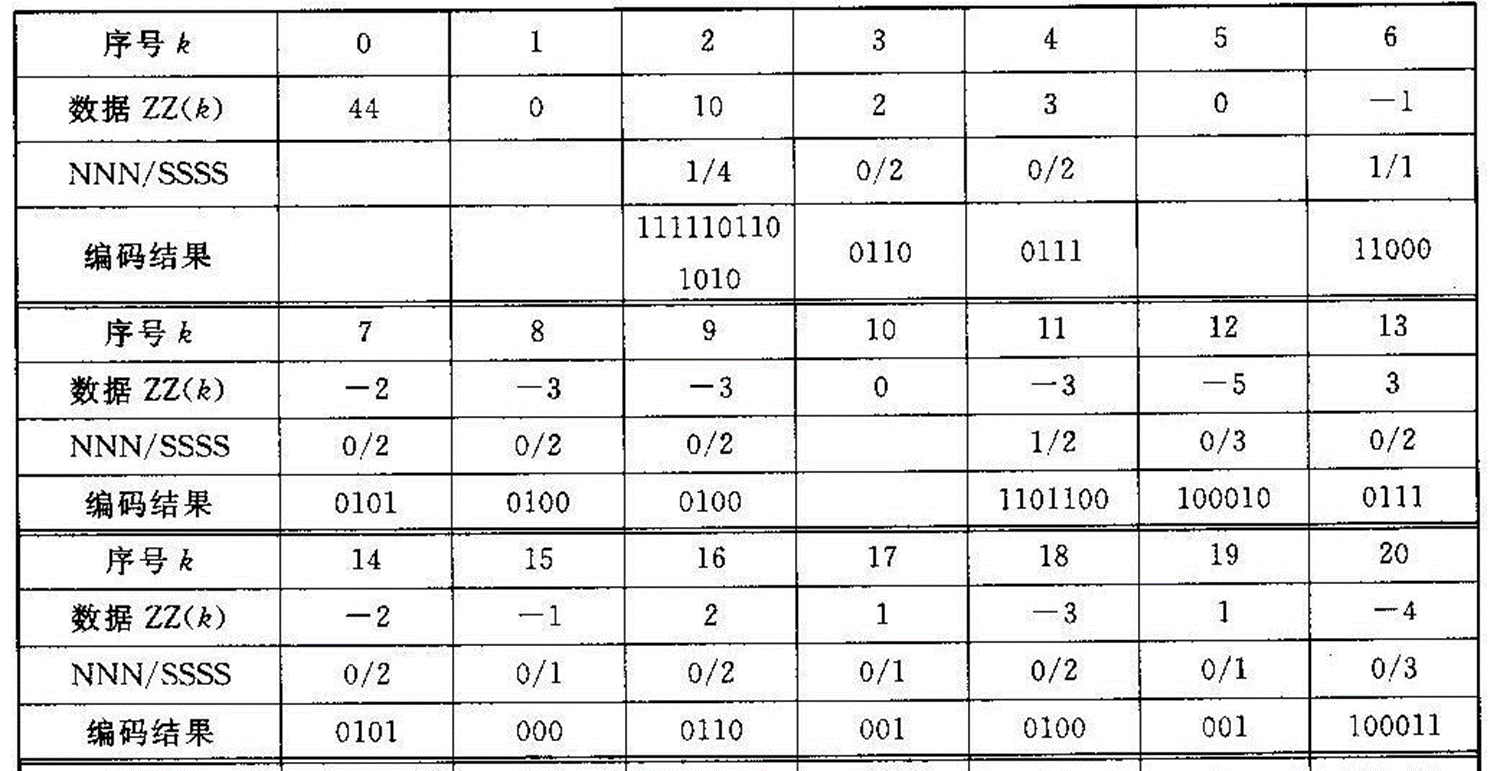
3.11.2 JPEG编码实例 下面结合一个实例来讲述JPEG基本系统的编码过程。设有一图像亮度数据块如图3-7所示,对其进行离散余弦变换后, 用图3-4所示的亮度量化表对系数矩阵量化后的结果如图3-8所示。对量化结果按图3-6所示的顺序进行Z形扫描, 并对扫描结果的DC及AC系数进行编码的结果见表3-12。由于数据较多, 为简便起见, 这里只对几个系数的编码加以说明。
图3-7 源图像亮度数据块
图3-8 量化结果
表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
1) DC系数的编码
在量化系数矩阵的Z形扫描结果中,第一个系数为DC系数。假设前一亮度数据块的DC系数为40, 则差值DIFF=44-40=4, 因4在(-7~-4, 4~7)范围内, 由表3-8查得SSSS=3,其前缀码字为“100”, 3位尾码即为4的二进制原码“100”, 从而DC系数的编码为“100100”。如果前一数据块的DC系数为48, 则DIFF=-4, 由表10-8查得SSSS及前缀码字同上,其3位尾码即-4的反码“011”, 因此DC系数的编码为“100011”。解码时, 由前缀码“100”可知尾码有3位,若前缀码字是“100”, 因其最高位为1,故可得DC系数的差值为4; 若前缀码字为“011”,因最高位为0,知其为负, 故取反后可得差值为-4。
2) AC系数的编码
在Z形扫描结果中,第一个非零AC系数为10。在它前面的连零个数为1, 即NNNN=1。根据AC系数10从表3-9查得SSSS=4, 由NNNN/SSSS=1/4从表3-10查得其哈夫曼码字为“111110110”, 而10的二进制码为“1010”, 因此该AC系数的编码为“1111101101010”。由于篇幅所限,其他AC系数的编码就不再赘述, 结果见表10-12。在Z形扫描结果中的末尾,除第54个系数非零外, 其他系数全为零, 故直接用一个结束块“EOB(0/0)”结束本块,由表3-10查得其码字为“1010”。于是,最后该亮度块的编码为(其中,假定差值为4)100100111110110101001100111110000101010001001101100100010011101010000110001010000110001111000000000001000111000110001100100000111001001001111001000001111001111101111010,共用了168位,而原始图像块需8×8×8=512位,因此压缩比为3.048。
JPEG压缩编码示例
实现哈夫曼编码的过程实际是构造一个哈夫曼二叉树, 它可分为两大部分:构造哈夫曼树和在哈夫曼树上求叶节点的编码。在构造哈夫曼树时,可设置一个结构数组HuffmanNode保存哈夫曼树中各节点的信息。结构数组元素定义如下:
typedef struct
{
int Weight; //保存哈夫曼树节点的权值, 在此是指频数
int Flag; //当Flag=0时, 表示该节点未加入树中, 为1时表示已加入树中
int Parent; //存放节点的父节点在节点数组中的序号
int LChild; //存放节点的左子节点在节点数组中的序号
int RChild; //存放节点的右子节点在节点数组中的序号
} HuffmanNode;
对于一幅BMP图像,调用CpointPro类下的GetHistogram()成员函数可获得图像的直方图数据m_fFreq,这些数据即各灰度出现的频数。利用这些数据可直接进行哈夫曼编码。哈夫曼编码的代码如下:
void CDlgHuffman::Huffman()
{
CString str;
int i, j, x1, x2, c, p;
int m1, m2;
LV_ITEM lvitem; // ListCtrl的ITEM
int iActualItem; //中间变量, 用于保存ListCtrl中添加的ITEM编号
HuffmanNode *huffNode; //存放哈夫曼树的节点
CString *strCode; //指向各字符的哈夫曼编码的指针
int *iMap; //位置映射指针
int iNumNode = 0; //频数不为零的节点数(或灰度数)
//统计直方图数据中频数不为零的灰度数, 并只对不为零的节点编码
for(i = 0; i < m_iLeafNum; i++)
{
if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
iNumNode++;
}
//对于具有iNumNode个叶节点的哈夫曼树, 它具有2 iNumNode -1个节点
huffNode = new HuffmanNode[iNumNode * 2 - 1];
strCode = new CString[iNumNode]
iMap = new int[iNumNode];
//初始化huffNode中的各节点
for(i = 0; i < iNumNode * 2 - 1; i++)
{
huffNode[i].Weight = 0;
huffNode[i].Parent = 0;
huffNode[i].Flag = 0;
huffNode[i].LChild = -1;
huffNode[i].RChild = -1;
}
//输入iNumNode个叶节点的权值即频数, iMap存放的是频数不为零的灰度值
j = 0;
for(i = 0; i < m_iLeafNum; i++)
{
if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
{
huffNode[j].Weight = m_fFreq[i + m_ChannelSel * m_iLeafNum];
iMap[j] = i;
j++;
}
}
//构造哈夫曼树, 对iNumNode个叶节点, 需构造iNumNode-1次
for(i = 0; i < iNumNode - 1; i++)
{
//对Flag为0的节点比较排序, 选出两个权值最小的子树, x1和x2用于确定
//两子树在数组中的序号, m1和m2用于存放最小两子树的权值
m1 = m2 = m_iSizeImage;
x1 = x2 = 0;
for (j = 0; j < iNumNode + i; j++)
{
if (huffNode[j].Weight < m1 && huffNode[j].Flag = = 0)
{
m2 = m1;
x2 = x1;
m1 = huffNode[j].Weight;
x1 = j;
}
else if (huffNode[j].Weight < m2 && huffNode[j].Flag = = 0)
{
m2 = huffNode[j].Weight;
x2 = j;
}
}
//将找出的两棵最小子树合并为一棵子树
huffNode[x1].Parent = iNumNode + i;
huffNode[x2].Parent = iNumNode + i;
// Flag为1, 说明该节点已经成为其他节点的子节点
huffNode[x1].Flag = 1;
huffNode[x2].Flag = 1;
huffNode[iNumNode + i].Weight = huffNode[x1].Weight + huffNode[x2].Weight;
//权值较小的子树作为右子树
huffNode[iNumNode + i].LChild = x2;
huffNode[iNumNode + i].RChild = x1;
}
//求每个叶节点的哈夫曼编码
for(i = 0; i < iNumNode; i++)
{
c = i;
p = huffNode[c].Parent;
//由叶节点上溯到树根
while (p != 0)
{
//如果是左子树, 则代码的高一位添加0, 否则添加1
if (huffNode[p].LChild = = c)
strCode[i] = "0" + strCode[i];
else
strCode[i] = "1" + strCode[i];
c = p;
p = huffNode[c].Parent;
}
}
//计算平均码字长度和图像熵
int CodeLen = 0;
m_fEntropy = 0.0;
for(i = 0; i < iNumNode; i ++
{
CodeLen += huffNode[i].Weight * strCode[i].GetLength();
m_fEntropy -= ((double)huffNode[i].Weight / m_iSizeImage) *
log((double)huffNode[i].Weight / m_iSizeImage) / log(2.0);
}
//计算平均码字长度
m_fAvCodeLen = (double)CodeLen/m_iSizeImage;
// 计算编码效率
m_fCodeEfficiency = m_fEntropy / m_fAvCodeLen;
//更新对话框上的文本框中的内容
UpdateData(FALSE);
lvitem.mask = LVIF_TEXT;
//输出哈夫曼编码结果
for (i = 0; i < iNumNode; i ++)
{
if (huffNode[i].Weight > 0)
{
// 添加一项
lvitem.iItem = m_lstTable.GetItemCount();
str.Format("%u", iMap[i]);
lvitem.iSubItem = 0;
lvitem.pszText = (LPTSTR)(LPCTSTR)str;
iActualItem = m_lstTable.InsertItem(&lvitem);
// 添加其他列
lvitem.iItem = iActualItem;
// 添加灰度值出现的频率
lvitem.iSubItem = 1;
str.Format("%f", (float)huffNode[i].Weight / m_iSizeImage);
lvitem.pszText = (LPTSTR)(LPCTSTR)str;
m_lstTable.SetItem(&lvitem);
// 添加哈夫曼编码
lvitem.iSubItem = 2;
lvitem.pszText = (LPTSTR)(LPCTSTR)strCode[i];
m_lstTable.SetItem(&lvitem);
// 添加码字长度
lvitem.iSubItem = 3;
str.Format("%u", strCode[i].GetLength());
lvitem.pszText = (LPTSTR)(LPCTSTR)str;
m_lstTable.SetItem(&lvitem);
}
}
delete[] huffNode;
delete[] strCode;
delete[] iMap;
}