[TOC]
由6.3节分析可知:
$$
\mathrm{ISI}=\sum_{n \neq k} a_n h\left[(k-n) T_B+t_0\right]
$$
若能使:
$$
\mathrm \sum_{n \neq k} a_n h\left[(k-n) T_B+t_0\right] = 0
$$
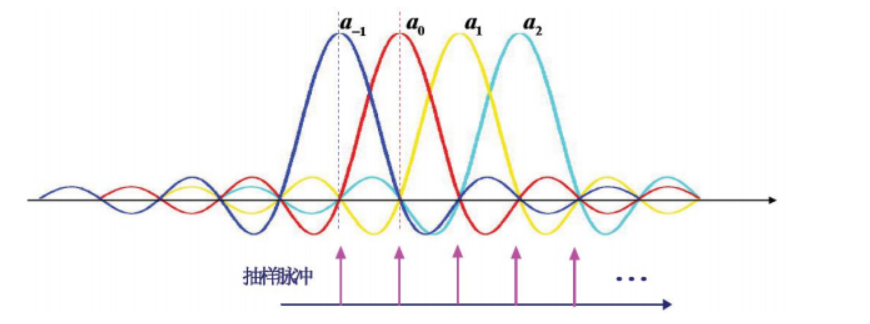
则无ISI;
怎么做? P145
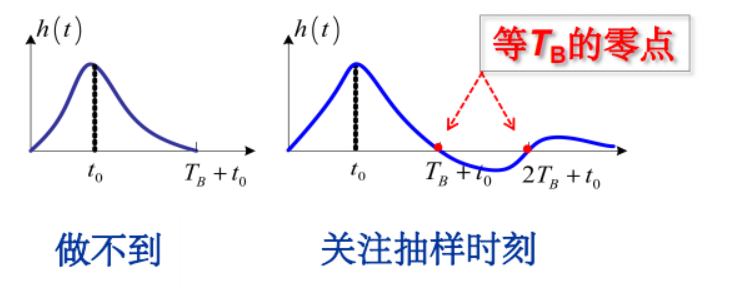
使码元抽样判决时刻上正好为0,就不会对后面的码元的判决造成干扰,即消除了ISI,如下图所示:
$$
h\left(k T_B\right)=\left{\begin{array}{l}
1, \quad k=0 \\
0, \quad k \text { 为其他整数 }
\end{array}\right.
$$
含义:本码元抽样时刻有值,其他码元抽样时刻均为0
$$
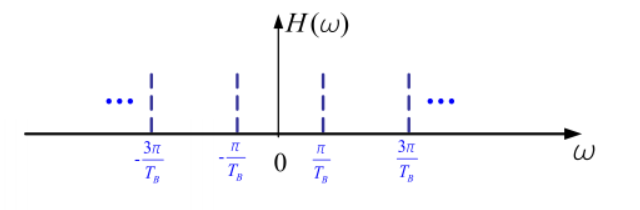
\sum_i H\left(\omega+\frac{2 \pi i}{T_B}\right)=T_B, \quad|\omega| \leq \frac{\pi}{T_B}
$$
——检验或设计$H(\omega)$能否消除码间串扰的理论依据。
含义:
“切割、平移/对折、叠加” $\rightarrow$ 理想LPF
则以$R_B = 1/T_B$的速率传输时,无码间串扰
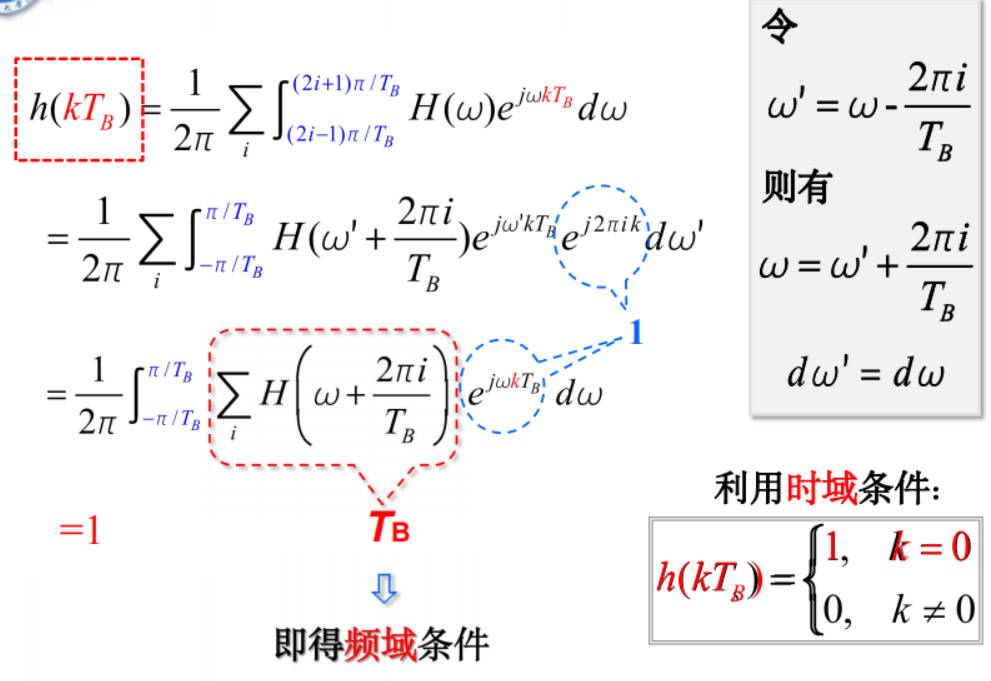
根据 $H(\omega) \Leftrightarrow h(t)$, 并利用时域条件:
分段积分求和:
$$
\begin{aligned}
h\left(k T_B\right) & =\frac{1}{2 \pi} \int_{-\infty}^{\infty} H(\omega) e^{j \omega k T_B} d \omega \
& =\frac{1}{2 \pi} \sum_i \int_{(2 i-1) \pi / T_B}^{(2 i+1) \pi / T_B} H(\omega) e^{j \omega k T_B} d \omega
\end{aligned}
$$
示例:
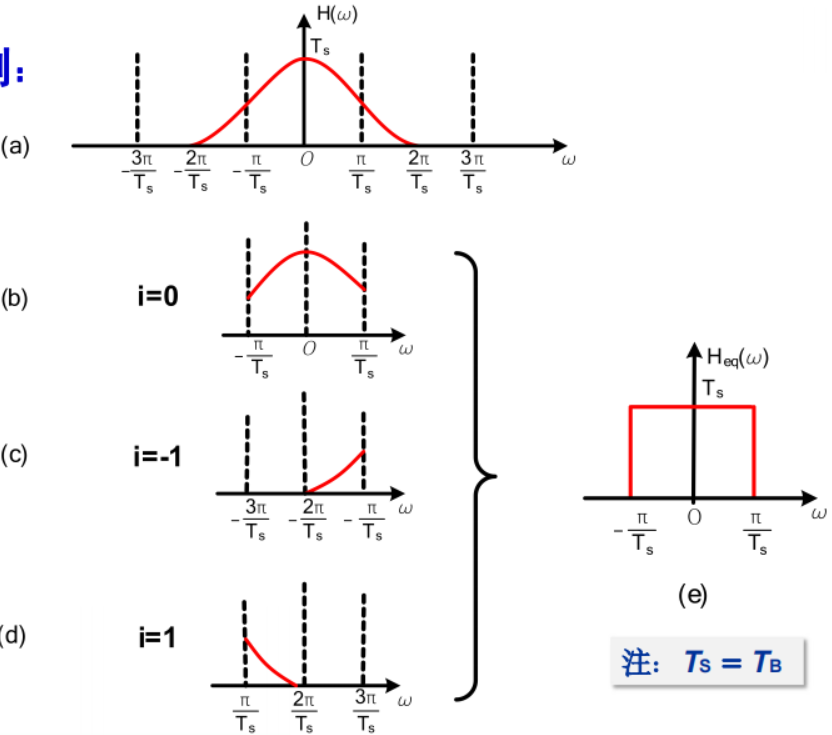
$$
H(\omega)= \begin{cases}T_B, & |\omega| \leq \frac{\pi}{T_B} \ 0, & |\omega|>\frac{\pi}{T_B}\end{cases}
$$
$$\Downarrow$$
$$
h(t)=S a\left(\frac{\pi}{T_B} t\right)
$$
传输特性:
冲激响应:
奈奎斯特带宽(最窄带宽)$B$:
$$
B=\frac{1}{2 T_B}=f_N
$$
奈奎斯特速率(无ISI的最高波特率)$R_B$:
$$
R_B=\frac{1}{T_B}=2 f_N
$$
即对于带宽为$B$的低通理想传输特性,若输入数据以$R_B$波特的速率进行传输,则不会产生ISI。
无码间串扰的基带系统最高频带利用率$\eta$
$$
\eta=R_B / B=2(\mathrm{Baud} / \mathrm{Hz})
$$
$$
\eta_b=R_b / B=2 \log _2 \mathrm{M}(\mathrm{bps} / \mathrm{Hz})
$$
存在的问题:
- 特性陡峭, 不易实现
- 响应曲线尾部收敛慢,摆幅大,对定时要求严格。
解决方案:
- 对$H(\omega)$在$f_N$处按“奇对称条件”进行“圆滑/滚降”
$$\downarrow\downarrow\downarrow\downarrow$$
滚降:为了解决理想低通特性存在的问题,可以使理想低通滤波器特性的边沿缓慢下降
如图:只要$H(\omega)$在滚降段中心频率处呈奇对称的振幅特性,就满足消除码间串扰的条件。
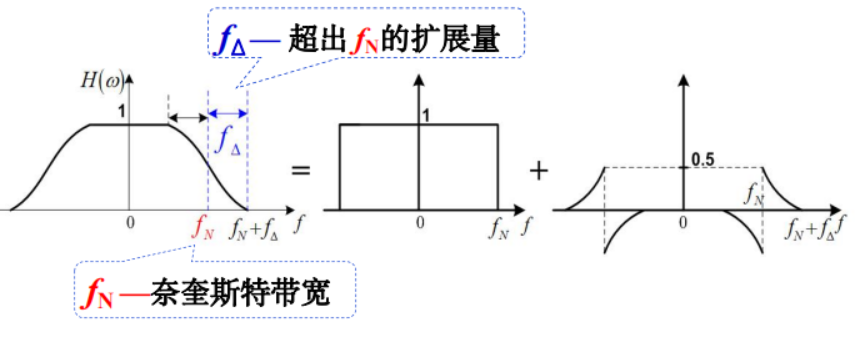
引入滚降系数,描述滚降程度:
$$
\alpha=\frac{f_{\Delta}}{f_N} \quad(0 \sim 1)
$$
$$
\begin{aligned}
&R_B=1/T_B = 2f_N\\
&B=f_N+f_{\Delta}=(1+a) f_N\\
&\eta=\frac{R_B}{B}=\frac{2}{1+\alpha}(\text { Baud } / \mathrm{Hz})\\
&\eta_{\mathrm{b}}=\frac{R_b}{B}=\frac{2}{1+\alpha} \log _2 \mathrm{M}(\mathrm{bps} / \mathrm{Hz})
\end{aligned}
$$
频域与时域对应:
$$
\begin{aligned}
& H(\omega)=\left{\begin{array}{cc}
T_B, & 0 \leq|\omega|<\frac{(1-\alpha) \pi}{T_B} \\
\frac{T_B}{2}\left[1+\sin \frac{T_B}{2 \alpha}\left(\frac{\pi}{T_B}-\omega\right)\right], & \frac{(1-\alpha) \pi}{T_B} \leq|\omega|<\frac{(1+\alpha) \pi}{T_B} \\
0, & |\omega| \geq \frac{(1+\alpha) \pi}{T_B}
\end{array}\right. \\
& h(t)=\frac{\sin \pi t / T_B}{\pi t / T_B} \cdot \frac{\cos \alpha \pi t / T_B}{1-4 \alpha^2 t^2 / T_B^2}
\end{aligned}
$$
余弦滚降滤波器的特点:
- 特性易实现
- 响应曲线尾部收敛快,摆幅小,对定时要求严格
代价:
$\alpha=0$, 理想低通 $\eta=2(B / H z)$ —— 最高
缺点:
$\alpha=1$, 升余弦 $\eta=1(B / H z)$ —— 降低
优点:
能否把这两种系统的优点集于一身呢?
部分响应技术:
$>\eta=2$ Baud $/ \mathrm{Hz}$;
$>\mathrm{H}(\omega)$ 易实现;
$>\mathrm{h}(\mathrm{t})$ 尾部收敛快





