diff --git a/Machine Learning/Liner Regression/README.md b/Machine Learning/1. Liner Regression/README.md
similarity index 100%
rename from Machine Learning/Liner Regression/README.md
rename to Machine Learning/1. Liner Regression/README.md
diff --git a/Machine Learning/Liner Regression/demo/README.md b/Machine Learning/1. Liner Regression/demo/README.md
similarity index 100%
rename from Machine Learning/Liner Regression/demo/README.md
rename to Machine Learning/1. Liner Regression/demo/README.md
diff --git a/Machine Learning/Liner Regression/demo/housing_price.py b/Machine Learning/1. Liner Regression/demo/housing_price.py
similarity index 100%
rename from Machine Learning/Liner Regression/demo/housing_price.py
rename to Machine Learning/1. Liner Regression/demo/housing_price.py
diff --git a/Machine Learning/Liner Regression/demo/kc_test.txt b/Machine Learning/1. Liner Regression/demo/kc_test.txt
similarity index 100%
rename from Machine Learning/Liner Regression/demo/kc_test.txt
rename to Machine Learning/1. Liner Regression/demo/kc_test.txt
diff --git a/Machine Learning/Liner Regression/demo/kc_train.txt b/Machine Learning/1. Liner Regression/demo/kc_train.txt
similarity index 100%
rename from Machine Learning/Liner Regression/demo/kc_train.txt
rename to Machine Learning/1. Liner Regression/demo/kc_train.txt
diff --git a/Machine Learning/2.Logistics Regression/README.md b/Machine Learning/2. Logistics Regression/README.md
similarity index 100%
rename from Machine Learning/2.Logistics Regression/README.md
rename to Machine Learning/2. Logistics Regression/README.md
diff --git a/Machine Learning/2.Logistics Regression/demo/CreditScoring.ipynb b/Machine Learning/2. Logistics Regression/demo/CreditScoring.ipynb
similarity index 100%
rename from Machine Learning/2.Logistics Regression/demo/CreditScoring.ipynb
rename to Machine Learning/2. Logistics Regression/demo/CreditScoring.ipynb
diff --git a/Machine Learning/2.Logistics Regression/demo/KaggleCredit2.csv.zip b/Machine Learning/2. Logistics Regression/demo/KaggleCredit2.csv.zip
similarity index 100%
rename from Machine Learning/2.Logistics Regression/demo/KaggleCredit2.csv.zip
rename to Machine Learning/2. Logistics Regression/demo/KaggleCredit2.csv.zip
diff --git a/Machine Learning/2.Logistics Regression/demo/README.md b/Machine Learning/2. Logistics Regression/demo/README.md
similarity index 100%
rename from Machine Learning/2.Logistics Regression/demo/README.md
rename to Machine Learning/2. Logistics Regression/demo/README.md
diff --git a/Machine Learning/2.Logistics Regression/2.Logistics Regression.md b/Machine Learning/2.Logistics Regression/2.Logistics Regression.md
deleted file mode 100644
index f960ba3..0000000
--- a/Machine Learning/2.Logistics Regression/2.Logistics Regression.md
+++ /dev/null
@@ -1,114 +0,0 @@
-## 目录
-- [1. 什么是逻辑回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#1-什么是逻辑回归)
-- [2. 什么是Sigmoid函数](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#2-什么是sigmoid函数)
-- [3. 损失函数是什么](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#3-损失函数是什么)
-- [4.可以进行多分类吗?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#4可以进行多分类吗)
-- [5.逻辑回归有什么优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#5逻辑回归有什么优点)
-- [6. 逻辑回归有哪些应用](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#6-逻辑回归有哪些应用)
-- [7. 逻辑回归常用的优化方法有哪些](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#7-逻辑回归常用的优化方法有哪些)
- - [7.1 一阶方法](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#71-一阶方法)
- - [7.2 二阶方法:牛顿法、拟牛顿法:](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#72-二阶方法牛顿法拟牛顿法)
-- [8. 逻辑斯特回归为什么要对特征进行离散化。](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#8-逻辑斯特回归为什么要对特征进行离散化)
-- [9. 逻辑回归的目标函数中增大L1正则化会是什么结果。](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/2.Logistics%20Regression#9-逻辑回归的目标函数中增大l1正则化会是什么结果)
-- [10. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/demo/CreditScoring.ipynb)
-
-## 1. 什么是逻辑回归
-
-逻辑回归是用来做分类算法的,大家都熟悉线性回归,一般形式是Y=aX+b,y的取值范围是[-∞, +∞],有这么多取值,怎么进行分类呢?不用担心,伟大的数学家已经为我们找到了一个方法。
-
-也就是把Y的结果带入一个非线性变换的**Sigmoid函数**中,即可得到[0,1]之间取值范围的数S,S可以把它看成是一个概率值,如果我们设置概率阈值为0.5,那么S大于0.5可以看成是正样本,小于0.5看成是负样本,就可以进行分类了。
-
-## 2. 什么是Sigmoid函数
-
-函数公式如下:
-
-
-
-函数中t无论取什么值,其结果都在[0,-1]的区间内,回想一下,一个分类问题就有两种答案,一种是“是”,一种是“否”,那0对应着“否”,1对应着“是”,那又有人问了,你这不是[0,1]的区间吗,怎么会只有0和1呢?这个问题问得好,我们假设分类的**阈值**是0.5,那么超过0.5的归为1分类,低于0.5的归为0分类,阈值是可以自己设定的。
-
-好了,接下来我们把aX+b带入t中就得到了我们的逻辑回归的一般模型方程:
-
-=\frac{1}{1+e^{(aX+b)}})
-
-结果P也可以理解为概率,换句话说概率大于0.5的属于1分类,概率小于0.5的属于0分类,这就达到了分类的目的。
-
-## 3. 损失函数是什么
-
-逻辑回归的损失函数是 **log loss**,也就是**对数似然函数**,函数公式如下:
-
-
-
-公式中的 y=1 表示的是真实值为1时用第一个公式,真实 y=0 用第二个公式计算损失。为什么要加上log函数呢?可以试想一下,当真实样本为1是,但h=0概率,那么log0=∞,这就对模型最大的惩罚力度;当h=1时,那么log1=0,相当于没有惩罚,也就是没有损失,达到最优结果。所以数学家就想出了用log函数来表示损失函数。
-
-最后按照梯度下降法一样,求解极小值点,得到想要的模型效果。
-
-## 4.可以进行多分类吗?
-
-可以的,其实我们可以从二分类问题过度到多分类问题(one vs rest),思路步骤如下:
-
-1.将类型class1看作正样本,其他类型全部看作负样本,然后我们就可以得到样本标记类型为该类型的概率p1。
-
-2.然后再将另外类型class2看作正样本,其他类型全部看作负样本,同理得到p2。
-
-3.以此循环,我们可以得到该待预测样本的标记类型分别为类型class i时的概率pi,最后我们取pi中最大的那个概率对应的样本标记类型作为我们的待预测样本类型。
-
-
-
-总之还是以二分类来依次划分,并求出最大概率结果。
-
-## 5.逻辑回归有什么优点
-
-- LR能以概率的形式输出结果,而非只是0,1判定。
-- LR的可解释性强,可控度高(你要给老板讲的嘛…)。
-- 训练快,feature engineering之后效果赞。
-- 因为结果是概率,可以做ranking model。
-
-## 6. 逻辑回归有哪些应用
-
-- CTR预估/推荐系统的learning to rank/各种分类场景。
-- 某搜索引擎厂的广告CTR预估基线版是LR。
-- 某电商搜索排序/广告CTR预估基线版是LR。
-- 某电商的购物搭配推荐用了大量LR。
-- 某现在一天广告赚1000w+的新闻app排序基线是LR。
-
-## 7. 逻辑回归常用的优化方法有哪些
-
-### 7.1 一阶方法
-
-梯度下降、随机梯度下降、mini 随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
-
-### 7.2 二阶方法:牛顿法、拟牛顿法:
-
-这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。
-
-缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
-
-拟牛顿法: 不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩阵)、 L-BFGS(可以减少BFGS所需的存储空间)。
-
-## 8. 逻辑斯特回归为什么要对特征进行离散化。
-
-1. 非线性!非线性!非线性!逻辑回归属于广义线性模型,表达能力受限;单变量离散化为N个后,每个变量有单独的权重,相当于为模型引入了非线性,能够提升模型表达能力,加大拟合; 离散特征的增加和减少都很容易,易于模型的快速迭代;
-2. 速度快!速度快!速度快!稀疏向量内积乘法运算速度快,计算结果方便存储,容易扩展;
-3. 鲁棒性!鲁棒性!鲁棒性!离散化后的特征对异常数据有很强的鲁棒性:比如一个特征是年龄>30是1,否则0。如果特征没有离散化,一个异常数据“年龄300岁”会给模型造成很大的干扰;
-4. 方便交叉与特征组合:离散化后可以进行特征交叉,由M+N个变量变为M*N个变量,进一步引入非线性,提升表达能力;
-5. 稳定性:特征离散化后,模型会更稳定,比如如果对用户年龄离散化,20-30作为一个区间,不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反,所以怎么划分区间是门学问;
-6. 简化模型:特征离散化以后,起到了简化了逻辑回归模型的作用,降低了模型过拟合的风险。
-
-## 9. 逻辑回归的目标函数中增大L1正则化会是什么结果。
-
-所有的参数w都会变成0。
-
-## 10. 代码实现
-
-GitHub:[https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/demo/CreditScoring.ipynb](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/demo/CreditScoring.ipynb)
-
-------
-
-
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 -
diff --git a/Machine Learning/3.Desition Tree/DecisionTree.csv b/Machine Learning/3. Desition Tree/DecisionTree.csv
similarity index 100%
rename from Machine Learning/3.Desition Tree/DecisionTree.csv
rename to Machine Learning/3. Desition Tree/DecisionTree.csv
diff --git a/Machine Learning/3.Desition Tree/DecisionTree.ipynb b/Machine Learning/3. Desition Tree/DecisionTree.ipynb
similarity index 100%
rename from Machine Learning/3.Desition Tree/DecisionTree.ipynb
rename to Machine Learning/3. Desition Tree/DecisionTree.ipynb
diff --git a/Machine Learning/3.Desition Tree/Desition Tree.md b/Machine Learning/3. Desition Tree/Desition Tree.md
similarity index 100%
rename from Machine Learning/3.Desition Tree/Desition Tree.md
rename to Machine Learning/3. Desition Tree/Desition Tree.md
diff --git a/Machine Learning/3.Desition Tree/README.md b/Machine Learning/3. Desition Tree/README.md
similarity index 100%
rename from Machine Learning/3.Desition Tree/README.md
rename to Machine Learning/3. Desition Tree/README.md
diff --git a/Machine Learning/3.1 Random Forest/3.1 Random Forest.md b/Machine Learning/3.1 Random Forest/3.1 Random Forest.md
deleted file mode 100644
index ad0c974..0000000
--- a/Machine Learning/3.1 Random Forest/3.1 Random Forest.md
+++ /dev/null
@@ -1,104 +0,0 @@
-## 目录
-- [1.什么是随机森林](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#1什么是随机森林)
- - [1.1 Bagging思想](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#11-bagging思想)
- - [1.2 随机森林](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#12-随机森林)
-- [2. 随机森林分类效果的影响因素](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#2-随机森林分类效果的影响因素)
-- [3. 随机森林有什么优缺点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#3-随机森林有什么优缺点)
-- [4. 随机森林如何处理缺失值?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#4-随机森林如何处理缺失值)
-- [5. 什么是OOB?随机森林中OOB是如何计算的,它有什么优缺点?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#5-什么是oob随机森林中oob是如何计算的它有什么优缺点)
-- [6. 随机森林的过拟合问题](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#6-随机森林的过拟合问题)
-- [7. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest/RandomForestRegression.ipynb)
-
-## 1.什么是随机森林
-
-### 1.1 Bagging思想
-
-Bagging是bootstrap aggregating。思想就是从总体样本当中随机取一部分样本进行训练,通过多次这样的结果,进行投票获取平均值作为结果输出,这就极大可能的避免了不好的样本数据,从而提高准确度。因为有些是不好的样本,相当于噪声,模型学入噪声后会使准确度不高。
-
-**举个例子**:
-
-假设有1000个样本,如果按照以前的思维,是直接把这1000个样本拿来训练,但现在不一样,先抽取800个样本来进行训练,假如噪声点是这800个样本以外的样本点,就很有效的避开了。重复以上操作,提高模型输出的平均值。
-
-### 1.2 随机森林
-
-Random Forest(随机森林)是一种基于树模型的Bagging的优化版本,一棵树的生成肯定还是不如多棵树,因此就有了随机森林,解决决策树泛化能力弱的特点。(可以理解成三个臭皮匠顶过诸葛亮)
-
-而同一批数据,用同样的算法只能产生一棵树,这时Bagging策略可以帮助我们产生不同的数据集。**Bagging**策略来源于bootstrap aggregation:从样本集(假设样本集N个数据点)中重采样选出Nb个样本(有放回的采样,样本数据点个数仍然不变为N),在所有样本上,对这n个样本建立分类器(ID3\C4.5\CART\SVM\LOGISTIC),重复以上两步m次,获得m个分类器,最后根据这m个分类器的投票结果,决定数据属于哪一类。
-
-**每棵树的按照如下规则生成:**
-
-1. 如果训练集大小为N,对于每棵树而言,**随机**且有放回地从训练集中的抽取N个训练样本,作为该树的训练集;
-2. 如果每个样本的特征维度为M,指定一个常数m< 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!qq群号:【541954936】
-
diff --git a/Machine Learning/3.Desition Tree/DecisionTree.csv b/Machine Learning/3. Desition Tree/DecisionTree.csv
similarity index 100%
rename from Machine Learning/3.Desition Tree/DecisionTree.csv
rename to Machine Learning/3. Desition Tree/DecisionTree.csv
diff --git a/Machine Learning/3.Desition Tree/DecisionTree.ipynb b/Machine Learning/3. Desition Tree/DecisionTree.ipynb
similarity index 100%
rename from Machine Learning/3.Desition Tree/DecisionTree.ipynb
rename to Machine Learning/3. Desition Tree/DecisionTree.ipynb
diff --git a/Machine Learning/3.Desition Tree/Desition Tree.md b/Machine Learning/3. Desition Tree/Desition Tree.md
similarity index 100%
rename from Machine Learning/3.Desition Tree/Desition Tree.md
rename to Machine Learning/3. Desition Tree/Desition Tree.md
diff --git a/Machine Learning/3.Desition Tree/README.md b/Machine Learning/3. Desition Tree/README.md
similarity index 100%
rename from Machine Learning/3.Desition Tree/README.md
rename to Machine Learning/3. Desition Tree/README.md
diff --git a/Machine Learning/3.1 Random Forest/3.1 Random Forest.md b/Machine Learning/3.1 Random Forest/3.1 Random Forest.md
deleted file mode 100644
index ad0c974..0000000
--- a/Machine Learning/3.1 Random Forest/3.1 Random Forest.md
+++ /dev/null
@@ -1,104 +0,0 @@
-## 目录
-- [1.什么是随机森林](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#1什么是随机森林)
- - [1.1 Bagging思想](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#11-bagging思想)
- - [1.2 随机森林](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#12-随机森林)
-- [2. 随机森林分类效果的影响因素](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#2-随机森林分类效果的影响因素)
-- [3. 随机森林有什么优缺点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#3-随机森林有什么优缺点)
-- [4. 随机森林如何处理缺失值?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#4-随机森林如何处理缺失值)
-- [5. 什么是OOB?随机森林中OOB是如何计算的,它有什么优缺点?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#5-什么是oob随机森林中oob是如何计算的它有什么优缺点)
-- [6. 随机森林的过拟合问题](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.1%20Random%20Forest#6-随机森林的过拟合问题)
-- [7. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest/RandomForestRegression.ipynb)
-
-## 1.什么是随机森林
-
-### 1.1 Bagging思想
-
-Bagging是bootstrap aggregating。思想就是从总体样本当中随机取一部分样本进行训练,通过多次这样的结果,进行投票获取平均值作为结果输出,这就极大可能的避免了不好的样本数据,从而提高准确度。因为有些是不好的样本,相当于噪声,模型学入噪声后会使准确度不高。
-
-**举个例子**:
-
-假设有1000个样本,如果按照以前的思维,是直接把这1000个样本拿来训练,但现在不一样,先抽取800个样本来进行训练,假如噪声点是这800个样本以外的样本点,就很有效的避开了。重复以上操作,提高模型输出的平均值。
-
-### 1.2 随机森林
-
-Random Forest(随机森林)是一种基于树模型的Bagging的优化版本,一棵树的生成肯定还是不如多棵树,因此就有了随机森林,解决决策树泛化能力弱的特点。(可以理解成三个臭皮匠顶过诸葛亮)
-
-而同一批数据,用同样的算法只能产生一棵树,这时Bagging策略可以帮助我们产生不同的数据集。**Bagging**策略来源于bootstrap aggregation:从样本集(假设样本集N个数据点)中重采样选出Nb个样本(有放回的采样,样本数据点个数仍然不变为N),在所有样本上,对这n个样本建立分类器(ID3\C4.5\CART\SVM\LOGISTIC),重复以上两步m次,获得m个分类器,最后根据这m个分类器的投票结果,决定数据属于哪一类。
-
-**每棵树的按照如下规则生成:**
-
-1. 如果训练集大小为N,对于每棵树而言,**随机**且有放回地从训练集中的抽取N个训练样本,作为该树的训练集;
-2. 如果每个样本的特征维度为M,指定一个常数m< 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!qq群号:【541954936】 diff --git a/Machine Learning/3.2 GBDT/3.2 GBDT.md b/Machine Learning/3.2 GBDT/3.2 GBDT.md
deleted file mode 100644
index 41d75f5..0000000
--- a/Machine Learning/3.2 GBDT/3.2 GBDT.md
+++ /dev/null
@@ -1,118 +0,0 @@
-## 目录
-- [1. 解释一下GBDT算法的过程](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#1-解释一下gbdt算法的过程)
- - [1.1 Boosting思想](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#11-boosting思想)
- - [1.2 GBDT原来是这么回事](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#12-gbdt原来是这么回事)
-- [2. 梯度提升和梯度下降的区别和联系是什么?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#2-梯度提升和梯度下降的区别和联系是什么)
-- [3. GBDT的优点和局限性有哪些?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#3-gbdt的优点和局限性有哪些)
- - [3.1 优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#31-优点)
- - [3.2 局限性](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#32-局限性)
-- [4. RF(随机森林)与GBDT之间的区别与联系](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#4-rf随机森林与gbdt之间的区别与联系)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-## 1. 解释一下GBDT算法的过程
-
-GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,使用的是**Boosting**的思想。
-
-### 1.1 Boosting思想
-
-Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
-
-Bagging与Boosting的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
-
-### 1.2 GBDT原来是这么回事
-
-GBDT的原理很简单,就是所有弱分类器的结果相加等于预测值,然后下一个弱分类器去拟合误差函数对预测值的残差(这个残差就是预测值与真实值之间的误差)。当然了,它里面的弱分类器的表现形式就是各棵树。
-
-举一个非常简单的例子,比如我今年30岁了,但计算机或者模型GBDT并不知道我今年多少岁,那GBDT咋办呢?
-
-- 它会在第一个弱分类器(或第一棵树中)随便用一个年龄比如20岁来拟合,然后发现误差有10岁;
-- 接下来在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
-- 接着在第三棵树中用3岁拟合剩下的差距,发现差距只有1岁了;
-- 最后在第四课树中用1岁拟合剩下的残差,完美。
-- 最终,四棵树的结论加起来,就是真实年龄30岁(实际工程中,gbdt是计算负梯度,用负梯度近似残差)。
-
-**为何gbdt可以用用负梯度近似残差呢?**
-
-回归任务下,GBDT 在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数,
-
-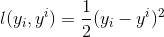
-
-那此时的负梯度是这样计算的
-
-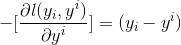
-
-所以,当损失函数选用均方损失函数是时,每一次拟合的值就是(真实值 - 当前模型预测的值),即残差。此时的变量是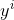,即“当前预测模型的值”,也就是对它求负梯度。
-
-**训练过程**
-
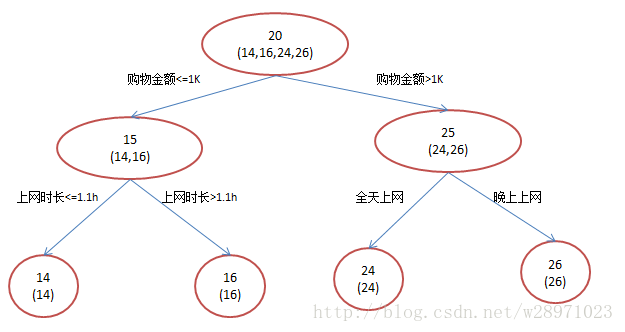
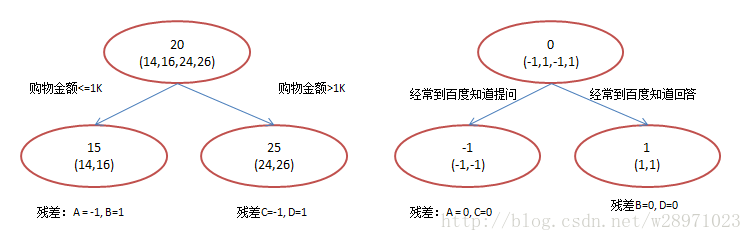
-简单起见,假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练,会得到如下图所示结果:
-
-
-
-现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点做多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图所示结果:
-
-
-
-在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两拨,每拨用平均年龄作为预测值。
-
-- 此时计算残差(残差的意思就是:A的实际值 - A的预测值 = A的残差),所以A的残差就是实际值14 - 预测值15 = 残差值-1。
-- 注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值。
-
-然后拿它们的残差-1、1、-1、1代替A B C D的原值,到第二棵树去学习,第二棵树只有两个值1和-1,直接分成两个节点,即A和C分在左边,B和D分在右边,经过计算(比如A,实际值-1 - 预测值-1 = 残差0,比如C,实际值-1 - 预测值-1 = 0),此时所有人的残差都是0。残差值都为0,相当于第二棵树的预测值和它们的实际值相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了,即每个人都得到了真实的预测值。
-
-换句话说,现在A,B,C,D的预测值都和真实年龄一致了。Perfect!
-
-- A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
-- B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
-- C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
-- D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
-
-所以,GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
-
-## 2. 梯度提升和梯度下降的区别和联系是什么?
-
-下表是梯度提升算法和梯度下降算法的对比情况。可以发现,两者都是在每 一轮迭代中,利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更 新,只不过在梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参 数的更新。而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函 数空间中,从而大大扩展了可以使用的模型种类。
-
-
-
-## 3. **GBDT**的优点和局限性有哪些?
-
-### 3.1 优点
-
-1. 预测阶段的计算速度快,树与树之间可并行化计算。
-2. 在分布稠密的数据集上,泛化能力和表达能力都很好,这使得GBDT在Kaggle的众多竞赛中,经常名列榜首。
-3. 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性,能够自动发现特征间的高阶关系。
-
-### 3.2 局限性
-
-1. GBDT在高维稀疏的数据集上,表现不如支持向量机或者神经网络。
-2. GBDT在处理文本分类特征问题上,相对其他模型的优势不如它在处理数值特征时明显。
-3. 训练过程需要串行训练,只能在决策树内部采用一些局部并行的手段提高训练速度。
-
-## 4. RF(随机森林)与GBDT之间的区别与联系
-
-**相同点**:
-
-- 都是由多棵树组成,最终的结果都是由多棵树一起决定。
-- RF和GBDT在使用CART树时,可以是分类树或者回归树。
-
-**不同点**:
-
-- 组成随机森林的树可以并行生成,而GBDT是串行生成
-- 随机森林的结果是多数表决表决的,而GBDT则是多棵树累加之和
-- 随机森林对异常值不敏感,而GBDT对异常值比较敏感
-- 随机森林是减少模型的方差,而GBDT是减少模型的偏差
-- 随机森林不需要进行特征归一化。而GBDT则需要进行特征归一化
-
-## 5. 代码实现
-
-GitHub:[https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!qq群号:【541954936】
diff --git a/Machine Learning/3.2 GBDT/3.2 GBDT.md b/Machine Learning/3.2 GBDT/3.2 GBDT.md
deleted file mode 100644
index 41d75f5..0000000
--- a/Machine Learning/3.2 GBDT/3.2 GBDT.md
+++ /dev/null
@@ -1,118 +0,0 @@
-## 目录
-- [1. 解释一下GBDT算法的过程](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#1-解释一下gbdt算法的过程)
- - [1.1 Boosting思想](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#11-boosting思想)
- - [1.2 GBDT原来是这么回事](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#12-gbdt原来是这么回事)
-- [2. 梯度提升和梯度下降的区别和联系是什么?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#2-梯度提升和梯度下降的区别和联系是什么)
-- [3. GBDT的优点和局限性有哪些?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#3-gbdt的优点和局限性有哪些)
- - [3.1 优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#31-优点)
- - [3.2 局限性](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#32-局限性)
-- [4. RF(随机森林)与GBDT之间的区别与联系](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#4-rf随机森林与gbdt之间的区别与联系)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-## 1. 解释一下GBDT算法的过程
-
-GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,使用的是**Boosting**的思想。
-
-### 1.1 Boosting思想
-
-Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
-
-Bagging与Boosting的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
-
-### 1.2 GBDT原来是这么回事
-
-GBDT的原理很简单,就是所有弱分类器的结果相加等于预测值,然后下一个弱分类器去拟合误差函数对预测值的残差(这个残差就是预测值与真实值之间的误差)。当然了,它里面的弱分类器的表现形式就是各棵树。
-
-举一个非常简单的例子,比如我今年30岁了,但计算机或者模型GBDT并不知道我今年多少岁,那GBDT咋办呢?
-
-- 它会在第一个弱分类器(或第一棵树中)随便用一个年龄比如20岁来拟合,然后发现误差有10岁;
-- 接下来在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
-- 接着在第三棵树中用3岁拟合剩下的差距,发现差距只有1岁了;
-- 最后在第四课树中用1岁拟合剩下的残差,完美。
-- 最终,四棵树的结论加起来,就是真实年龄30岁(实际工程中,gbdt是计算负梯度,用负梯度近似残差)。
-
-**为何gbdt可以用用负梯度近似残差呢?**
-
-回归任务下,GBDT 在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数,
-
-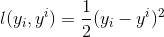
-
-那此时的负梯度是这样计算的
-
-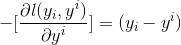
-
-所以,当损失函数选用均方损失函数是时,每一次拟合的值就是(真实值 - 当前模型预测的值),即残差。此时的变量是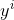,即“当前预测模型的值”,也就是对它求负梯度。
-
-**训练过程**
-
-简单起见,假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练,会得到如下图所示结果:
-
-
-
-现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点做多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图所示结果:
-
-
-
-在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两拨,每拨用平均年龄作为预测值。
-
-- 此时计算残差(残差的意思就是:A的实际值 - A的预测值 = A的残差),所以A的残差就是实际值14 - 预测值15 = 残差值-1。
-- 注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值。
-
-然后拿它们的残差-1、1、-1、1代替A B C D的原值,到第二棵树去学习,第二棵树只有两个值1和-1,直接分成两个节点,即A和C分在左边,B和D分在右边,经过计算(比如A,实际值-1 - 预测值-1 = 残差0,比如C,实际值-1 - 预测值-1 = 0),此时所有人的残差都是0。残差值都为0,相当于第二棵树的预测值和它们的实际值相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了,即每个人都得到了真实的预测值。
-
-换句话说,现在A,B,C,D的预测值都和真实年龄一致了。Perfect!
-
-- A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
-- B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
-- C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
-- D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
-
-所以,GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
-
-## 2. 梯度提升和梯度下降的区别和联系是什么?
-
-下表是梯度提升算法和梯度下降算法的对比情况。可以发现,两者都是在每 一轮迭代中,利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更 新,只不过在梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参 数的更新。而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函 数空间中,从而大大扩展了可以使用的模型种类。
-
-
-
-## 3. **GBDT**的优点和局限性有哪些?
-
-### 3.1 优点
-
-1. 预测阶段的计算速度快,树与树之间可并行化计算。
-2. 在分布稠密的数据集上,泛化能力和表达能力都很好,这使得GBDT在Kaggle的众多竞赛中,经常名列榜首。
-3. 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性,能够自动发现特征间的高阶关系。
-
-### 3.2 局限性
-
-1. GBDT在高维稀疏的数据集上,表现不如支持向量机或者神经网络。
-2. GBDT在处理文本分类特征问题上,相对其他模型的优势不如它在处理数值特征时明显。
-3. 训练过程需要串行训练,只能在决策树内部采用一些局部并行的手段提高训练速度。
-
-## 4. RF(随机森林)与GBDT之间的区别与联系
-
-**相同点**:
-
-- 都是由多棵树组成,最终的结果都是由多棵树一起决定。
-- RF和GBDT在使用CART树时,可以是分类树或者回归树。
-
-**不同点**:
-
-- 组成随机森林的树可以并行生成,而GBDT是串行生成
-- 随机森林的结果是多数表决表决的,而GBDT则是多棵树累加之和
-- 随机森林对异常值不敏感,而GBDT对异常值比较敏感
-- 随机森林是减少模型的方差,而GBDT是减少模型的偏差
-- 随机森林不需要进行特征归一化。而GBDT则需要进行特征归一化
-
-## 5. 代码实现
-
-GitHub:[https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!qq群号:【541954936】 -
-
-
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md b/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
deleted file mode 100644
index 99cc3fb..0000000
--- a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
+++ /dev/null
@@ -1,119 +0,0 @@
-## 目录
-- [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
- - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
- - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
- - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
- - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
-- [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
-- [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
-- [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-- [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
-
-## 1. 什么是XGBoost
-
-XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
-
-说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
-
-关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
-
-### 1.1 XGBoost树的定义
-
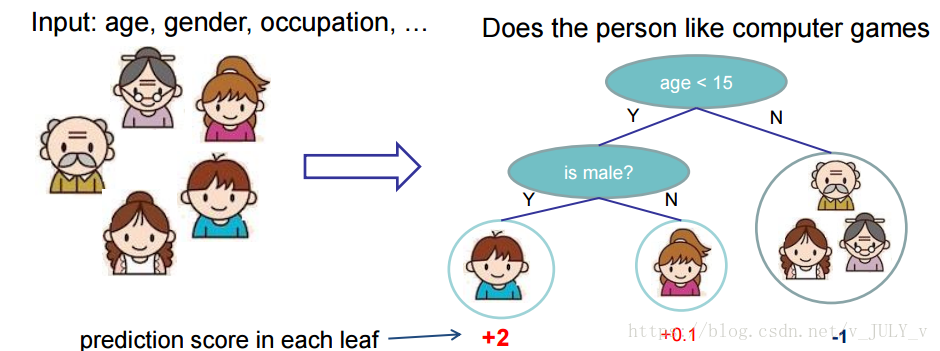
-先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
-
-
-
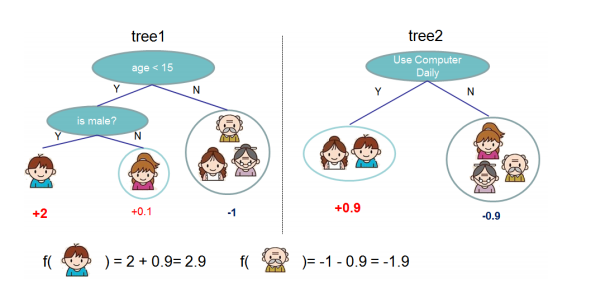
-就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
-
-
-
-恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
-
-事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
-
-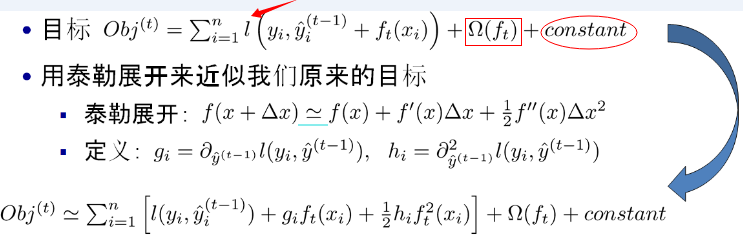
-
-其中:
-
-- 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
-- 红色方框所框起来的是正则项(包括L1正则、L2正则)
-- 红色圆圈所圈起来的为常数项
-- 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
-
-看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-XGBoost的**核心算法思想**不难,基本就是:
-
-1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
-2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
-3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
-
-显然,我们的目标是要使得树群的预测值尽量接近真实值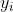,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
-
-
-
-那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
-
-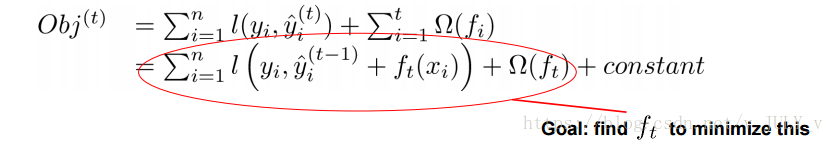
-
-实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
-
-### 1.2 正则项:树的复杂度
-
-XGBoost对树的复杂度包含了两个部分:
-
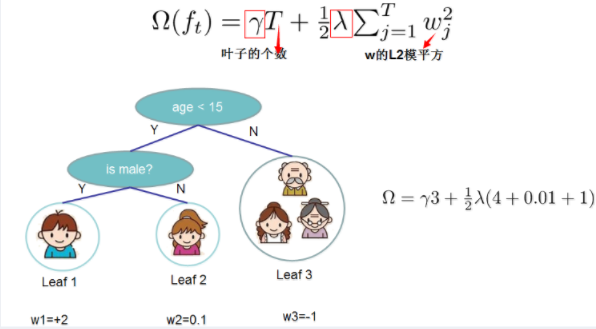
-- 一个是树里面叶子节点的个数T
-- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
-
-
-
-我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
-
-=\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
-
-正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
-
-### 1.3 树该怎么长
-
-很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
-
-不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
-
-总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
-
-### 1.4 如何停止树的循环生成
-
-凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
-
-1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
-2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
-3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
-
-## 2. XGBoost与GBDT有什么不同
-
-除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
-
-1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
-2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
-3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
-4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
-5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
-6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
-
-## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
-
-XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
-
-## 4. 代码实现
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-
-## 5. 参考文献
-
-[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
-
-
-
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md b/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
deleted file mode 100644
index 99cc3fb..0000000
--- a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
+++ /dev/null
@@ -1,119 +0,0 @@
-## 目录
-- [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
- - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
- - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
- - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
- - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
-- [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
-- [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
-- [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-- [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
-
-## 1. 什么是XGBoost
-
-XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
-
-说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
-
-关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
-
-### 1.1 XGBoost树的定义
-
-先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
-
-
-
-就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
-
-
-
-恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
-
-事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
-
-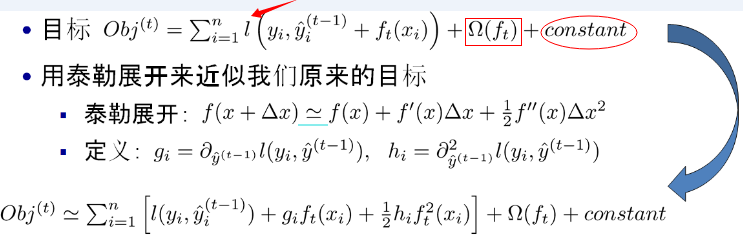
-
-其中:
-
-- 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
-- 红色方框所框起来的是正则项(包括L1正则、L2正则)
-- 红色圆圈所圈起来的为常数项
-- 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
-
-看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-XGBoost的**核心算法思想**不难,基本就是:
-
-1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
-2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
-3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
-
-显然,我们的目标是要使得树群的预测值尽量接近真实值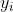,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
-
-
-
-那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
-
-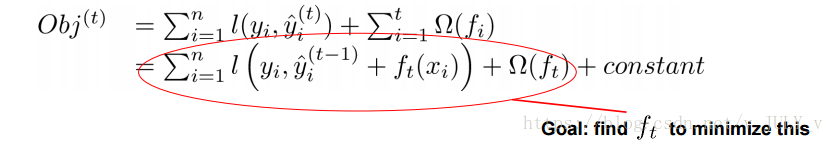
-
-实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
-
-### 1.2 正则项:树的复杂度
-
-XGBoost对树的复杂度包含了两个部分:
-
-- 一个是树里面叶子节点的个数T
-- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
-
-
-
-我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
-
-=\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
-
-正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
-
-### 1.3 树该怎么长
-
-很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
-
-不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
-
-总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
-
-### 1.4 如何停止树的循环生成
-
-凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
-
-1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
-2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
-3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
-
-## 2. XGBoost与GBDT有什么不同
-
-除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
-
-1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
-2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
-3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
-4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
-5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
-6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
-
-## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
-
-XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
-
-## 4. 代码实现
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-
-## 5. 参考文献
-
-[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 diff --git a/Machine Learning/3.3 XGBoost/README.md b/Machine Learning/3.3 XGBoost/README.md
index 99cc3fb..045129f 100644
--- a/Machine Learning/3.3 XGBoost/README.md
+++ b/Machine Learning/3.3 XGBoost/README.md
@@ -106,7 +106,7 @@ XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更
## 4. 代码实现
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/XGBoost.ipynb)
## 5. 参考文献
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb b/Machine Learning/3.3 XGBoost/XGBoost.ipynb
similarity index 100%
rename from Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb
rename to Machine Learning/3.3 XGBoost/XGBoost.ipynb
diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md b/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
deleted file mode 100644
index 2413005..0000000
--- a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
+++ /dev/null
@@ -1,86 +0,0 @@
-## 目录
-- [1. LightGBM是什么东东](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#1-lightgbm是什么东东)
- - [1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#11-lightgbm在哪些地方进行了优化----区别xgboost)
- - [1.2 Histogram算法](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#12-histogram算法)
- - [1.3 带深度限制的Leaf-wise的叶子生长策略](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#13-带深度限制的leaf-wise的叶子生长策略)
- - [1.4 直方图差加速](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#14-直方图差加速)
- - [1.5 直接支持类别特征](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#15-直接支持类别特征)
-- [2. LightGBM优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#2-lightgbm优点)
-- [3. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-## 1. LightGBM是什么东东
-
-不久前微软DMTK(分布式机器学习工具包)团队在GitHub上开源了性能超越其他boosting工具的LightGBM,在三天之内GitHub上被star了1000次,fork了200次。知乎上有近千人关注“如何看待微软开源的LightGBM?”问题,被评价为“速度惊人”,“非常有启发”,“支持分布式”,“代码清晰易懂”,“占用内存小”等。
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练。
-
-LightGBM在Higgs数据集上LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6,并且准确率也有提升。GBDT在每一次迭代的时候,都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据,普通的GBDT算法是不能满足其需求的。
-
-LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。
-
-### 1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?
-
-- 基于Histogram的决策树算法
-- 带深度限制的Leaf-wise的叶子生长策略
-- 直方图做差加速直接
-- 支持类别特征(Categorical Feature)
-- Cache命中率优化
-- 基于直方图的稀疏特征优化多线程优化。
-
-
-
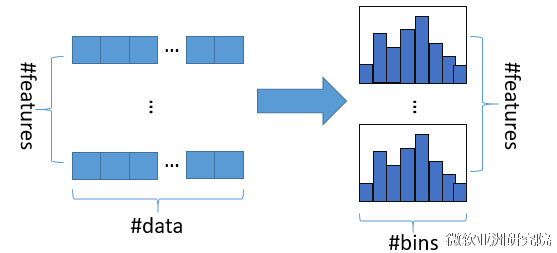
-### 1.2 Histogram算法
-
-直方图算法的基本思想是先把连续的浮点特征值离散化成k个整数(其实又是分桶的思想,而这些桶称为bin,比如[0,0.1)→0, [0.1,0.3)→1),同时构造一个宽度为k的直方图。
-
-在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
-
-
-
-使用直方图算法有很多优点。首先,最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果,而且可以只保存特征离散化后的值,而这个值一般用8位整型存储就足够了,内存消耗可以降低为原来的1/8。然后在计算上的代价也大幅降低,预排序算法每遍历一个特征值就需要计算一次分裂的增益,而直方图算法只需要计算k次(k可以认为是常数),时间复杂度从O(#data*#feature)优化到O(k*#features)。
-
-### 1.3 带深度限制的Leaf-wise的叶子生长策略
-
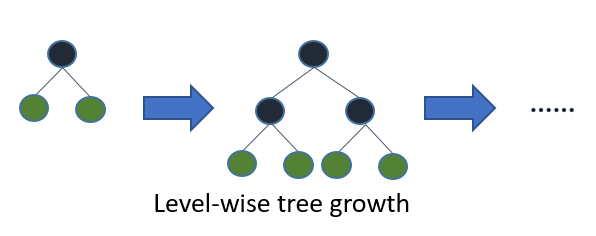
-在XGBoost中,树是按层生长的,称为Level-wise tree growth,同一层的所有节点都做分裂,最后剪枝,如下图所示:
-
-
-
-Level-wise过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
-
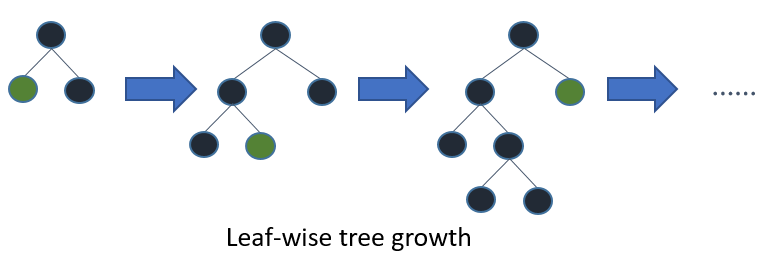
-在Histogram算法之上,LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise)
-的决策树生长策略,而使用了带有深度限制的按叶子生长 (leaf-wise)算法。
-
-
-
-Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
-
-### 1.4 直方图差加速
-
-LightGBM另一个优化是Histogram(直方图)做差加速。一个容易观察到的现象:一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
-
-利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
-
-### 1.5 直接支持类别特征
-
-实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。据我们所知,LightGBM是第一个直接支持类别特征的GBDT工具。
-
-## 2. LightGBM优点
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有以下优点:
-
-- 更快的训练速度
-- 更低的内存消耗
-- 更好的准确率
-- 分布式支持,可以快速处理海量数据
-
-## 3. 代码实现
-
-为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
diff --git a/Machine Learning/3.3 XGBoost/README.md b/Machine Learning/3.3 XGBoost/README.md
index 99cc3fb..045129f 100644
--- a/Machine Learning/3.3 XGBoost/README.md
+++ b/Machine Learning/3.3 XGBoost/README.md
@@ -106,7 +106,7 @@ XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更
## 4. 代码实现
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/XGBoost.ipynb)
## 5. 参考文献
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb b/Machine Learning/3.3 XGBoost/XGBoost.ipynb
similarity index 100%
rename from Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb
rename to Machine Learning/3.3 XGBoost/XGBoost.ipynb
diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md b/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
deleted file mode 100644
index 2413005..0000000
--- a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
+++ /dev/null
@@ -1,86 +0,0 @@
-## 目录
-- [1. LightGBM是什么东东](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#1-lightgbm是什么东东)
- - [1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#11-lightgbm在哪些地方进行了优化----区别xgboost)
- - [1.2 Histogram算法](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#12-histogram算法)
- - [1.3 带深度限制的Leaf-wise的叶子生长策略](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#13-带深度限制的leaf-wise的叶子生长策略)
- - [1.4 直方图差加速](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#14-直方图差加速)
- - [1.5 直接支持类别特征](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#15-直接支持类别特征)
-- [2. LightGBM优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#2-lightgbm优点)
-- [3. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-## 1. LightGBM是什么东东
-
-不久前微软DMTK(分布式机器学习工具包)团队在GitHub上开源了性能超越其他boosting工具的LightGBM,在三天之内GitHub上被star了1000次,fork了200次。知乎上有近千人关注“如何看待微软开源的LightGBM?”问题,被评价为“速度惊人”,“非常有启发”,“支持分布式”,“代码清晰易懂”,“占用内存小”等。
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练。
-
-LightGBM在Higgs数据集上LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6,并且准确率也有提升。GBDT在每一次迭代的时候,都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据,普通的GBDT算法是不能满足其需求的。
-
-LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。
-
-### 1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?
-
-- 基于Histogram的决策树算法
-- 带深度限制的Leaf-wise的叶子生长策略
-- 直方图做差加速直接
-- 支持类别特征(Categorical Feature)
-- Cache命中率优化
-- 基于直方图的稀疏特征优化多线程优化。
-
-
-
-### 1.2 Histogram算法
-
-直方图算法的基本思想是先把连续的浮点特征值离散化成k个整数(其实又是分桶的思想,而这些桶称为bin,比如[0,0.1)→0, [0.1,0.3)→1),同时构造一个宽度为k的直方图。
-
-在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
-
-
-
-使用直方图算法有很多优点。首先,最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果,而且可以只保存特征离散化后的值,而这个值一般用8位整型存储就足够了,内存消耗可以降低为原来的1/8。然后在计算上的代价也大幅降低,预排序算法每遍历一个特征值就需要计算一次分裂的增益,而直方图算法只需要计算k次(k可以认为是常数),时间复杂度从O(#data*#feature)优化到O(k*#features)。
-
-### 1.3 带深度限制的Leaf-wise的叶子生长策略
-
-在XGBoost中,树是按层生长的,称为Level-wise tree growth,同一层的所有节点都做分裂,最后剪枝,如下图所示:
-
-
-
-Level-wise过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
-
-在Histogram算法之上,LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise)
-的决策树生长策略,而使用了带有深度限制的按叶子生长 (leaf-wise)算法。
-
-
-
-Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
-
-### 1.4 直方图差加速
-
-LightGBM另一个优化是Histogram(直方图)做差加速。一个容易观察到的现象:一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
-
-利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
-
-### 1.5 直接支持类别特征
-
-实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。据我们所知,LightGBM是第一个直接支持类别特征的GBDT工具。
-
-## 2. LightGBM优点
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有以下优点:
-
-- 更快的训练速度
-- 更低的内存消耗
-- 更好的准确率
-- 分布式支持,可以快速处理海量数据
-
-## 3. 代码实现
-
-为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb b/Machine Learning/3.4 LightGBM/LightGBM.ipynb
similarity index 100%
rename from Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb
rename to Machine Learning/3.4 LightGBM/LightGBM.ipynb
diff --git a/Machine Learning/3.4 LightGBM/README.md b/Machine Learning/3.4 LightGBM/README.md
index 2413005..f468a5e 100644
--- a/Machine Learning/3.4 LightGBM/README.md
+++ b/Machine Learning/3.4 LightGBM/README.md
@@ -77,7 +77,7 @@ LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Micr
为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/LightGBM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/4. SVM/4. SVM.md b/Machine Learning/4. SVM/4. SVM.md
deleted file mode 100644
index 3b4faae..0000000
--- a/Machine Learning/4. SVM/4. SVM.md
+++ /dev/null
@@ -1,225 +0,0 @@
-## 目录
-- [1. 讲讲SVM](#1-讲讲svm)
- - [1.1 一个关于SVM的童话故事](#11-一个关于svm的童话故事)
- - [1.2 理解SVM:第一层](#12-理解svm第一层)
- - [1.3 深入SVM:第二层](#13-深入svm第二层)
- - [1.4 SVM的应用](#14-svm的应用)
-- [2. SVM的一些问题](#2-svm的一些问题)
-- [3. LR和SVM的联系与区别](#3-lr和svm的联系与区别)
-- [4. 线性分类器与非线性分类器的区别以及优劣](#4-线性分类器与非线性分类器的区别以及优劣)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 讲讲SVM
-
-### 1.1 一个关于SVM的童话故事
-
-支持向量机(Support Vector Machine,SVM)是众多监督学习方法中十分出色的一种,几乎所有讲述经典机器学习方法的教材都会介绍。关于SVM,流传着一个关于天使与魔鬼的故事。
-
-传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务。魔鬼又加入了更多的球。随着球的增多,似乎有的球不能再被原来的木棍正确分开,如下图所示。
-
-
-
-SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开。
-
-看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使一个新的挑战,如下图所示。
-
-
-
-
-
-按照这种球的摆法,世界上貌似没有一根木棒可以将它们 完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借 念力抓起一张纸片,插在了两类球的中间。从魔鬼的角度看这些 球,则像是被一条曲线完美的切开了。
-
-
-
-后来,“无聊”的科学家们把这些球称为“数据”,把木棍称为“分类面”,找到最 大间隔的木棒位置的过程称为“优化”,拍桌子让球飞到空中的念力叫“核映射”,在 空中分隔球的纸片称为“分类超平面”。这便是SVM的童话故事。
-
-### 1.2 理解SVM:第一层
-
-支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
-
-**线性分类器:**给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者0,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( wT中的T代表转置):
-
-
-
-这里可以查看我之前的逻辑回归章节回顾:[点击打开](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md)
-
-这个超平面可以用分类函数 =w^Tx+b)表示,当f(x) 等于0的时候,x便是位于超平面上的点,而f(x)大于0的点对应 y=1 的数据点,f(x)小于0的点对应y=-1的点,如下图所示:
-
-
-
-#### 1.2.1 函数间隔与几何间隔
-
-在超平面w*x+b=0确定的情况下,|w*x+b|能够表示点x到距离超平面的远近,而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了**函数间隔**(functional margin)的概念。
-
-函数间隔公式: =yf(x))
-
-而超平面(w,b)关于数据集T中所有样本点(xi,yi)的函数间隔最小值(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
-
-)
-
-但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),所以只有函数间隔还远远不够。
-
-**几何间隔**
-
-事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔(geometrical margin)的概念。假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x0 ,w 是垂直于超平面的一个向量,$\gamma$为样本x到超平面的距离,如下图所示:
-
-
-
-这里我直接给出几何间隔的公式,详细推到请查看博文:[点击进入](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-几何间隔: 
-
-从上述函数间隔和几何间隔的定义可以看出:几何间隔就是**函数间隔除以||w||**,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
-
-#### 1.2.2 最大间隔分类器的定义
-
-对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
-
-
-
-通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 =w^Tx+b)的值任意大,亦即函数间隔可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上了,使得在缩放w和b的时候几何间隔的值是不会改变的,它只随着超平面的变动而变动,因此,这是更加合适的一个间隔。换言之,这里要找的最大间隔分类超平面中的**“间隔”指的是几何间隔。**
-
-如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔,两条虚线间隔边界之间的距离等于2倍几何间隔,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足 =1),对于所有不是支持向量的点,则显然有 >1)。
-
-
-
-OK,到此为止,算是了解到了SVM的第一层,对于那些只关心怎么用SVM的朋友便已足够,不必再更进一层深究其更深的原理。
-
-#### 1.2.3 最大间隔损失函数Hinge loss
-
-SVM 求解使通过建立二次规划原始问题,引入拉格朗日乘子法,然后转换成对偶的形式去求解,这是一种理论非常充实的解法。这里换一种角度来思考,在机器学习领域,一般的做法是经验风险最小化 (empirical risk minimization,ERM),即构建假设函数(Hypothesis)为输入输出间的映射,然后采用损失函数来衡量模型的优劣。求得使损失最小化的模型即为最优的假设函数,采用不同的损失函数也会得到不同的机器学习算法。SVM采用的就是Hinge Loss,用于“最大间隔(max-margin)”分类。
-
-_j-(f(x_i,W)_{y_i}-\bigtriangleup)))
-
-- 对于训练集中的第i个数据xi
-- 在W下会有一个得分结果向量f(xi,W)
-- 第j类的得分为我们记作f(xi,W)j
-
-要理解这个公式,首先先看下面这张图片:
-
-
-
-1. 在生活中我们都会认为没有威胁的才是最好的,比如拿成绩来说,自己考了第一名99分,而第二名紧随其后98分,那么就会有不安全的感觉,就会认为那家伙随时都有可能超过我。如果第二名是85分,那就会感觉安全多了,第二名需要花费很大的力气才能赶上自己。拿这个例子套到上面这幅图也是一样的。
-2. 上面这幅图delta左边的红点是一个**安全警戒线**,什么意思呢?也就是说**预测错误得分**超过这个安全警戒线就会得到一个惩罚权重,让这个预测错误值退回到安全警戒线以外,这样才能够保证预测正确的结果具有唯一性。
-3. 对应到公式中, _j)就是错误分类的得分。后面一项就是 **正确得分 - delta = 安全警戒线值**,两项的差代表的就是惩罚权重,越接近正确得分,权重越大。当错误得分在警戒线以外时,两项相减得到负数,那么损失函数的最大值是0,也就是没有损失。
-4. 一直往复循环训练数据,直到最小化损失函数为止,也就找到了分类超平面。
-
-### 1.3 深入SVM:第二层
-
-#### 1.3.1 从线性可分到线性不可分
-
-接着考虑之前得到的目标函数(令函数间隔=1):
-
-\ge1,i=1,...,n)
-
-**转换为对偶问题**,解释一下什么是对偶问题,对偶问题是实质相同但从不同角度提出不同提法的一对问题。
-
-由于求 的最大值相当于求 的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,很明显,两者问题等价):
-
-\ge1,i=1,...,n)
-
-因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
-
-此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:**一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。**
-
-详细过程请参考文章末尾给出的参考链接。
-
-#### 1.3.2 核函数Kernel
-
-事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
-
-具体来说,**在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。**如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
-
-
-
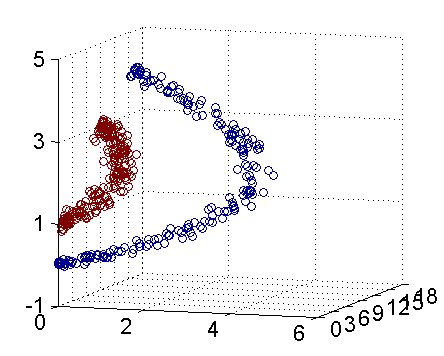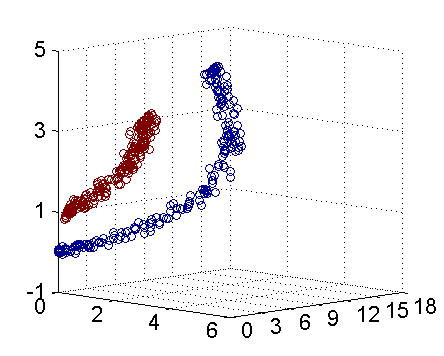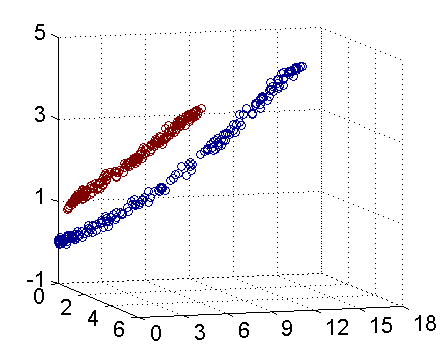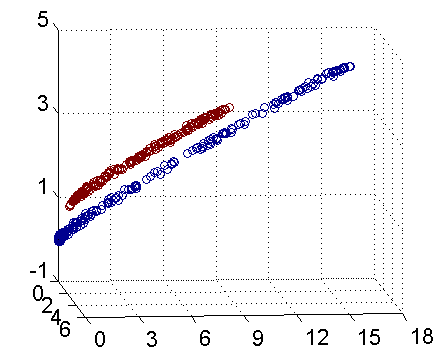
-
-
-通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:**多项式核、高斯核、线性核。**
-
-读者可能还是没明白核函数到底是个什么东西?我再简要概括下,即以下三点:
-
-1. 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
-2. 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的。那咋办呢?
-3. 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,避免了直接在高维空间中的复杂计算。
-
-**如果数据中出现了离群点outliers,那么就可以使用松弛变量来解决。**
-
-#### 1.3.3 总结
-
-不准确的说,SVM它本质上即是一个分类方法,用 w^T+b 定义分类函数,于是求w、b,为寻最大间隔,引出1/2||w||^2,继而引入拉格朗日因子,化为对拉格朗日乘子a的求解(求解过程中会涉及到一系列最优化或凸二次规划等问题),如此,求w.b与求a等价,而a的求解可以用一种快速学习算法SMO,至于核函数,是为处理非线性情况,若直接映射到高维计算恐维度爆炸,故在低维计算,等效高维表现。
-
-OK,理解到这第二层,已经能满足绝大部分人一窥SVM原理的好奇心,针对于面试来说已经足够了。
-
-### 1.4 SVM的应用
-
-SVM在很多诸如**文本分类,图像分类,生物序列分析和生物数据挖掘,手写字符识别等领域有很多的应用**,但或许你并没强烈的意识到,SVM可以成功应用的领域远远超出现在已经在开发应用了的领域。
-
-## 2. SVM的一些问题
-
-1. 是否存在一组参数使SVM训练误差为0?
-
- 答:存在
-
-2. 训练误差为0的SVM分类器一定存在吗?
-
- 答:一定存在
-
-3. 加入松弛变量的SVM的训练误差可以为0吗?
-
- 答:使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由 于我们的优化目标改变了,并不再是使训练误差最小。
-
-4. **带核的SVM为什么能分类非线性问题?**
-
- 答:核函数的本质是两个函数的內积,通过核函数将其隐射到高维空间,在高维空间非线性问题转化为线性问题, SVM得到超平面是高维空间的线性分类平面。其分类结果也视为低维空间的非线性分类结果, 因而带核的SVM就能分类非线性问题。
-
-5. **如何选择核函数?**
-
- - 如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
- - 如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
- - 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。
-
-## 3. LR和SVM的联系与区别
-
-### 3.1 相同点
-
-- 都是线性分类器。本质上都是求一个最佳分类超平面。
-- 都是监督学习算法。
-- 都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有:KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
-
-### 3.2 不同点
-
-- LR是参数模型,svm是非参数模型,linear和rbf则是针对数据线性可分和不可分的区别;
-- 从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
-- SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
-- 逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
-- logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
-
-## 4. 线性分类器与非线性分类器的区别以及优劣
-
-线性和非线性是针对模型参数和输入特征来讲的;比如输入x,模型y=ax+ax^2 那么就是非线性模型,如果输入是x和X^2则模型是线性的。
-
-- 线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
-
- LR,贝叶斯分类,单层感知机、线性回归
-
-- 非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
-
- 决策树、RF、GBDT、多层感知机
-
-**SVM两种都有(看线性核还是高斯核)**
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-
-## 6. 参考文献
-
-[支持向量机通俗导论(理解SVM的三层境界)](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb b/Machine Learning/3.4 LightGBM/LightGBM.ipynb
similarity index 100%
rename from Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb
rename to Machine Learning/3.4 LightGBM/LightGBM.ipynb
diff --git a/Machine Learning/3.4 LightGBM/README.md b/Machine Learning/3.4 LightGBM/README.md
index 2413005..f468a5e 100644
--- a/Machine Learning/3.4 LightGBM/README.md
+++ b/Machine Learning/3.4 LightGBM/README.md
@@ -77,7 +77,7 @@ LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Micr
为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/LightGBM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/4. SVM/4. SVM.md b/Machine Learning/4. SVM/4. SVM.md
deleted file mode 100644
index 3b4faae..0000000
--- a/Machine Learning/4. SVM/4. SVM.md
+++ /dev/null
@@ -1,225 +0,0 @@
-## 目录
-- [1. 讲讲SVM](#1-讲讲svm)
- - [1.1 一个关于SVM的童话故事](#11-一个关于svm的童话故事)
- - [1.2 理解SVM:第一层](#12-理解svm第一层)
- - [1.3 深入SVM:第二层](#13-深入svm第二层)
- - [1.4 SVM的应用](#14-svm的应用)
-- [2. SVM的一些问题](#2-svm的一些问题)
-- [3. LR和SVM的联系与区别](#3-lr和svm的联系与区别)
-- [4. 线性分类器与非线性分类器的区别以及优劣](#4-线性分类器与非线性分类器的区别以及优劣)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 讲讲SVM
-
-### 1.1 一个关于SVM的童话故事
-
-支持向量机(Support Vector Machine,SVM)是众多监督学习方法中十分出色的一种,几乎所有讲述经典机器学习方法的教材都会介绍。关于SVM,流传着一个关于天使与魔鬼的故事。
-
-传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务。魔鬼又加入了更多的球。随着球的增多,似乎有的球不能再被原来的木棍正确分开,如下图所示。
-
-
-
-SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开。
-
-看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使一个新的挑战,如下图所示。
-
-
-
-
-
-按照这种球的摆法,世界上貌似没有一根木棒可以将它们 完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借 念力抓起一张纸片,插在了两类球的中间。从魔鬼的角度看这些 球,则像是被一条曲线完美的切开了。
-
-
-
-后来,“无聊”的科学家们把这些球称为“数据”,把木棍称为“分类面”,找到最 大间隔的木棒位置的过程称为“优化”,拍桌子让球飞到空中的念力叫“核映射”,在 空中分隔球的纸片称为“分类超平面”。这便是SVM的童话故事。
-
-### 1.2 理解SVM:第一层
-
-支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
-
-**线性分类器:**给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者0,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( wT中的T代表转置):
-
-
-
-这里可以查看我之前的逻辑回归章节回顾:[点击打开](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md)
-
-这个超平面可以用分类函数 =w^Tx+b)表示,当f(x) 等于0的时候,x便是位于超平面上的点,而f(x)大于0的点对应 y=1 的数据点,f(x)小于0的点对应y=-1的点,如下图所示:
-
-
-
-#### 1.2.1 函数间隔与几何间隔
-
-在超平面w*x+b=0确定的情况下,|w*x+b|能够表示点x到距离超平面的远近,而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了**函数间隔**(functional margin)的概念。
-
-函数间隔公式: =yf(x))
-
-而超平面(w,b)关于数据集T中所有样本点(xi,yi)的函数间隔最小值(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
-
-)
-
-但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),所以只有函数间隔还远远不够。
-
-**几何间隔**
-
-事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔(geometrical margin)的概念。假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x0 ,w 是垂直于超平面的一个向量,$\gamma$为样本x到超平面的距离,如下图所示:
-
-
-
-这里我直接给出几何间隔的公式,详细推到请查看博文:[点击进入](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-几何间隔: 
-
-从上述函数间隔和几何间隔的定义可以看出:几何间隔就是**函数间隔除以||w||**,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
-
-#### 1.2.2 最大间隔分类器的定义
-
-对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
-
-
-
-通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 =w^Tx+b)的值任意大,亦即函数间隔可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上了,使得在缩放w和b的时候几何间隔的值是不会改变的,它只随着超平面的变动而变动,因此,这是更加合适的一个间隔。换言之,这里要找的最大间隔分类超平面中的**“间隔”指的是几何间隔。**
-
-如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔,两条虚线间隔边界之间的距离等于2倍几何间隔,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足 =1),对于所有不是支持向量的点,则显然有 >1)。
-
-
-
-OK,到此为止,算是了解到了SVM的第一层,对于那些只关心怎么用SVM的朋友便已足够,不必再更进一层深究其更深的原理。
-
-#### 1.2.3 最大间隔损失函数Hinge loss
-
-SVM 求解使通过建立二次规划原始问题,引入拉格朗日乘子法,然后转换成对偶的形式去求解,这是一种理论非常充实的解法。这里换一种角度来思考,在机器学习领域,一般的做法是经验风险最小化 (empirical risk minimization,ERM),即构建假设函数(Hypothesis)为输入输出间的映射,然后采用损失函数来衡量模型的优劣。求得使损失最小化的模型即为最优的假设函数,采用不同的损失函数也会得到不同的机器学习算法。SVM采用的就是Hinge Loss,用于“最大间隔(max-margin)”分类。
-
-_j-(f(x_i,W)_{y_i}-\bigtriangleup)))
-
-- 对于训练集中的第i个数据xi
-- 在W下会有一个得分结果向量f(xi,W)
-- 第j类的得分为我们记作f(xi,W)j
-
-要理解这个公式,首先先看下面这张图片:
-
-
-
-1. 在生活中我们都会认为没有威胁的才是最好的,比如拿成绩来说,自己考了第一名99分,而第二名紧随其后98分,那么就会有不安全的感觉,就会认为那家伙随时都有可能超过我。如果第二名是85分,那就会感觉安全多了,第二名需要花费很大的力气才能赶上自己。拿这个例子套到上面这幅图也是一样的。
-2. 上面这幅图delta左边的红点是一个**安全警戒线**,什么意思呢?也就是说**预测错误得分**超过这个安全警戒线就会得到一个惩罚权重,让这个预测错误值退回到安全警戒线以外,这样才能够保证预测正确的结果具有唯一性。
-3. 对应到公式中, _j)就是错误分类的得分。后面一项就是 **正确得分 - delta = 安全警戒线值**,两项的差代表的就是惩罚权重,越接近正确得分,权重越大。当错误得分在警戒线以外时,两项相减得到负数,那么损失函数的最大值是0,也就是没有损失。
-4. 一直往复循环训练数据,直到最小化损失函数为止,也就找到了分类超平面。
-
-### 1.3 深入SVM:第二层
-
-#### 1.3.1 从线性可分到线性不可分
-
-接着考虑之前得到的目标函数(令函数间隔=1):
-
-\ge1,i=1,...,n)
-
-**转换为对偶问题**,解释一下什么是对偶问题,对偶问题是实质相同但从不同角度提出不同提法的一对问题。
-
-由于求 的最大值相当于求 的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,很明显,两者问题等价):
-
-\ge1,i=1,...,n)
-
-因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
-
-此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:**一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。**
-
-详细过程请参考文章末尾给出的参考链接。
-
-#### 1.3.2 核函数Kernel
-
-事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
-
-具体来说,**在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。**如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
-
-
-
-
-
-通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:**多项式核、高斯核、线性核。**
-
-读者可能还是没明白核函数到底是个什么东西?我再简要概括下,即以下三点:
-
-1. 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
-2. 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的。那咋办呢?
-3. 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,避免了直接在高维空间中的复杂计算。
-
-**如果数据中出现了离群点outliers,那么就可以使用松弛变量来解决。**
-
-#### 1.3.3 总结
-
-不准确的说,SVM它本质上即是一个分类方法,用 w^T+b 定义分类函数,于是求w、b,为寻最大间隔,引出1/2||w||^2,继而引入拉格朗日因子,化为对拉格朗日乘子a的求解(求解过程中会涉及到一系列最优化或凸二次规划等问题),如此,求w.b与求a等价,而a的求解可以用一种快速学习算法SMO,至于核函数,是为处理非线性情况,若直接映射到高维计算恐维度爆炸,故在低维计算,等效高维表现。
-
-OK,理解到这第二层,已经能满足绝大部分人一窥SVM原理的好奇心,针对于面试来说已经足够了。
-
-### 1.4 SVM的应用
-
-SVM在很多诸如**文本分类,图像分类,生物序列分析和生物数据挖掘,手写字符识别等领域有很多的应用**,但或许你并没强烈的意识到,SVM可以成功应用的领域远远超出现在已经在开发应用了的领域。
-
-## 2. SVM的一些问题
-
-1. 是否存在一组参数使SVM训练误差为0?
-
- 答:存在
-
-2. 训练误差为0的SVM分类器一定存在吗?
-
- 答:一定存在
-
-3. 加入松弛变量的SVM的训练误差可以为0吗?
-
- 答:使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由 于我们的优化目标改变了,并不再是使训练误差最小。
-
-4. **带核的SVM为什么能分类非线性问题?**
-
- 答:核函数的本质是两个函数的內积,通过核函数将其隐射到高维空间,在高维空间非线性问题转化为线性问题, SVM得到超平面是高维空间的线性分类平面。其分类结果也视为低维空间的非线性分类结果, 因而带核的SVM就能分类非线性问题。
-
-5. **如何选择核函数?**
-
- - 如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
- - 如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
- - 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。
-
-## 3. LR和SVM的联系与区别
-
-### 3.1 相同点
-
-- 都是线性分类器。本质上都是求一个最佳分类超平面。
-- 都是监督学习算法。
-- 都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有:KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
-
-### 3.2 不同点
-
-- LR是参数模型,svm是非参数模型,linear和rbf则是针对数据线性可分和不可分的区别;
-- 从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
-- SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
-- 逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
-- logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
-
-## 4. 线性分类器与非线性分类器的区别以及优劣
-
-线性和非线性是针对模型参数和输入特征来讲的;比如输入x,模型y=ax+ax^2 那么就是非线性模型,如果输入是x和X^2则模型是线性的。
-
-- 线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
-
- LR,贝叶斯分类,单层感知机、线性回归
-
-- 非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
-
- 决策树、RF、GBDT、多层感知机
-
-**SVM两种都有(看线性核还是高斯核)**
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-
-## 6. 参考文献
-
-[支持向量机通俗导论(理解SVM的三层境界)](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 -
diff --git a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md b/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
deleted file mode 100644
index 8d97b78..0000000
--- a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
+++ /dev/null
@@ -1,223 +0,0 @@
-## 目录
-- [1. 对概率图模型的理解](#1-对概率图模型的理解)
-- [2. 细数贝叶斯网络](#2-细数贝叶斯网络)
- - [2.1 频率派观点](#21-频率派观点)
- - [2.2 贝叶斯学派](#22-贝叶斯学派)
- - [2.3 贝叶斯定理](#23-贝叶斯定理)
- - [2.4 贝叶斯网络](#24-贝叶斯网络)
- - [2.5 朴素贝叶斯](#25-朴素贝叶斯)
-- [3. 基于贝叶斯的一些问题](#3-基于贝叶斯的一些问题)
-- [4. 生成式模型和判别式模型的区别](#4-生成式模型和判别式模型的区别)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 对概率图模型的理解
-
-概率图模型是用图来表示变量概率依赖关系的理论,结合概率论与图论的知识,利用图来表示与模型有关的变量的联合概率分布。由图灵奖获得者Pearl开发出来。
-
-如果用一个词来形容概率图模型(Probabilistic Graphical Model)的话,那就是“优雅”。对于一个实际问题,我们希望能够挖掘隐含在数据中的知识。概率图模型构建了这样一幅图,用观测结点表示观测到的数据,用隐含结点表示潜在的知识,用边来描述知识与数据的相互关系,**最后基于这样的关系图获得一个概率分布**,非常“优雅”地解决了问题。
-
-概率图中的节点分为隐含节点和观测节点,边分为有向边和无向边。从概率论的角度,节点对应于随机变量,边对应于随机变量的依赖或相关关系,其中**有向边表示单向的依赖,无向边表示相互依赖关系**。
-
-概率图模型分为**贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)**两大类。贝叶斯网络可以用一个有向图结构表示,马尔可夫网络可以表 示成一个无向图的网络结构。更详细地说,概率图模型包括了朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等,在机器学习的诸多场景中都有着广泛的应用。
-
-## 2. 细数贝叶斯网络
-
-### 2.1 频率派观点
-
-长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。而且概率虽然未知,但最起码是一个确定的值。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,而且不论你取了多少次,取得白球的**概率θ始终都是1/2**,即不随观察结果X 的变化而变化。
-
-这种**频率派**的观点长期统治着人们的观念,直到后来一个名叫Thomas Bayes的人物出现。
-
-### 2.2 贝叶斯学派
-
-托马斯·贝叶斯Thomas Bayes(1702-1763)在世时,并不为当时的人们所熟知,很少发表论文或出版著作,与当时学术界的人沟通交流也很少,用现在的话来说,贝叶斯就是活生生一民间学术“屌丝”,可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”,翻译过来则是:机遇理论中一个问题的解。你可能觉得我要说:这篇论文的发表随机产生轰动效应,从而奠定贝叶斯在学术史上的地位。
-
-
-
-这篇论文可以用上面的例子来说明,“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率θ是多少?”贝叶斯认为取得白球的概率是个不确定的值,因为其中含有机遇的成分。比如,一个朋友创业,你明明知道创业的结果就两种,即要么成功要么失败,但你依然会忍不住去估计他创业成功的几率有多大?你如果对他为人比较了解,而且有方法、思路清晰、有毅力、且能团结周围的人,你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式,便是**贝叶斯式的思考方式。**
-
-**先简单总结下频率派与贝叶斯派各自不同的思考方式:**
-
-- 频率派把需要推断的参数θ看做是固定的未知常数,即概率虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
-- 而贝叶斯派的观点则截然相反,他们认为参数是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数的分布。
-
-贝叶斯派既然把看做是一个随机变量,所以要计算的分布,便得事先知道的无条件分布,即在有样本之前(或观察到X之前),有着怎样的分布呢?
-
-比如往台球桌上扔一个球,这个球落会落在何处呢?如果是不偏不倚的把球抛出去,那么此球落在台球桌上的任一位置都有着相同的机会,即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为**先验分布,或着无条件分布**。
-
-其中,先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决,解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如,某工厂每天都要对产品进行质检,以评估产品的不合格率θ,经过一段时间后便会积累大量的历史资料,这些历史资料便是先验知识,有了这些先验知识,便在决定对一个产品是否需要每天质检时便有了依据,如果以往的历史资料显示,某产品的不合格率只有0.01%,便可视为信得过产品或免检产品,只每月抽检一两次,从而省去大量的人力物力。
-
-而**后验分布**π(θ|X)一般也认为是在给定样本X的情况下的θ条件分布,而使π(θ|X)达到最大的值θMD称为**最大后验估计**,类似于经典统计学中的**极大似然估计**。
-
-综合起来看,则好比是人类刚开始时对大自然只有少得可怜的先验知识,但随着不断观察、实验获得更多的样本、结果,使得人们对自然界的规律摸得越来越透彻。所以,贝叶斯方法既符合人们日常生活的思考方式,也符合人们认识自然的规律,经过不断的发展,最终占据统计学领域的半壁江山,与经典统计学分庭抗礼。
-
-### 2.3 贝叶斯定理
-
-**条件概率**(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
-
-
-
-比如上图,在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率:
-
-=\frac{P(A\cap_{.}B)}{P(B)})
-
-联合概率: 或者P(A,B))
-
-边缘概率(先验概率):P(A)或者P(B)
-
-### 2.4 贝叶斯网络
-
-贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model),是一种概率图模型,于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓朴结构是一个有向无环图(DAG)。
-
-
-
-贝叶斯网络的有向无环图中的节点表示随机变量 
-
-它们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。
-
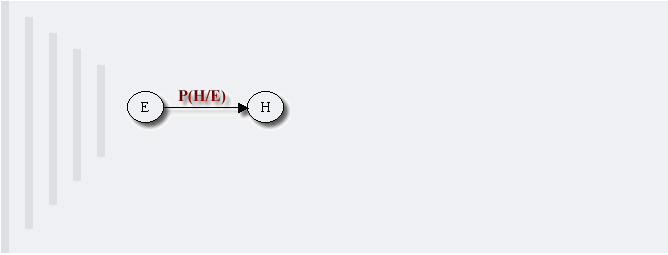
-例如,假设节点E直接影响到节点H,即E→H,则用从E指向H的箭头建立结点E到结点H的有向弧(E,H),权值(即连接强度)用条件概率P(H|E)来表示,如下图所示:
-
-
-
-简言之,把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖,用圈表示随机变量(random variables),用箭头表示条件依赖(conditional dependencies)。
-
-此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
-
-=P(x_k|x_1,...,x_{k-1})...P(x_2|x_1)P(x_1))
-
-#### 2.4.1 贝叶斯网络的结构形式
-
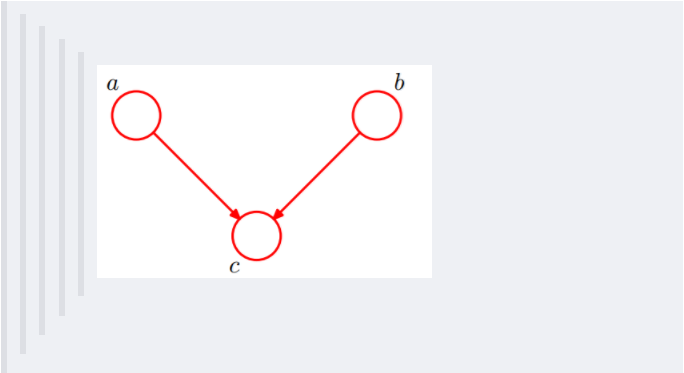
-**1. head-to-head**
-
-
-
-依上图,所以有:P(a,b,c) = P(a)*P(b)*P(c|a,b)成立,即在c未知的条件下,a、b被阻断(blocked),是独立的,称之为head-to-head条件独立。
-
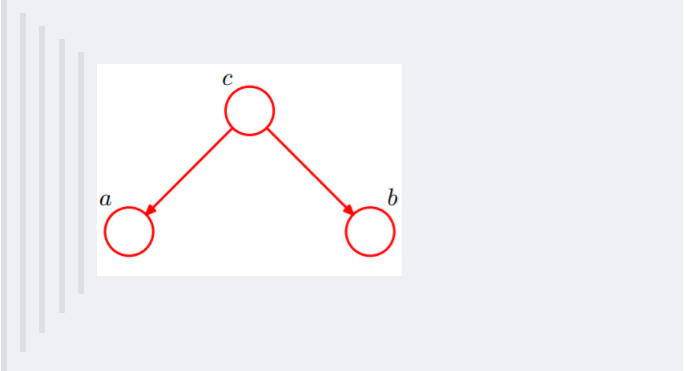
-**2. tail-to-tail**
-
-
-
-考虑c未知,跟c已知这两种情况:
-
-1. 在c未知的时候,有:P(a,b,c)=P(c)*P(a|c)*P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-2. 在c已知的时候,有:P(a,b|c)=P(a,b,c)/P(c),然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中,得到:P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c),即c已知时,a、b独立。
-
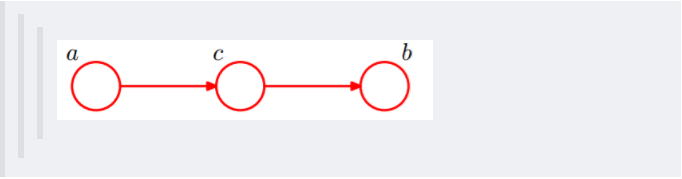
-**3. head-to-tail**
-
-
-
-还是分c未知跟c已知这两种情况:
-
-1. c未知时,有:P(a,b,c)=P(a)*P(c|a)*P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-
-2. c已知时,有:P(a,b|c)=P(a,b,c)/P(c),且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c),可化简得到:
-
- 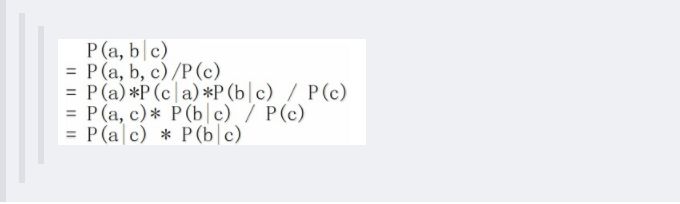
-
- 所以,在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
-
- 这个head-to-tail其实就是一个链式网络,如下图所示:
-
- 
-
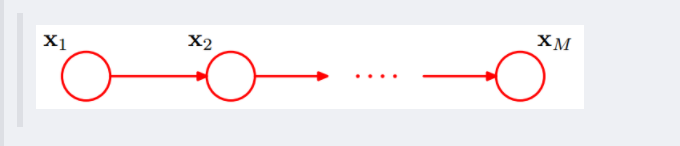
- 根据之前对head-to-tail的讲解,我们已经知道,在xi给定的条件下,xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢?意味着:xi+1的分布状态只和xi有关,和其他变量条件独立。通俗点说,当前状态只跟上一状态有关,跟上上或上上之前的状态无关。这种顺次演变的随机过程,就叫做**马尔科夫链**(Markov chain)。对于马尔科夫链我们下一节再细讲。
-
-#### 2.4.2 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
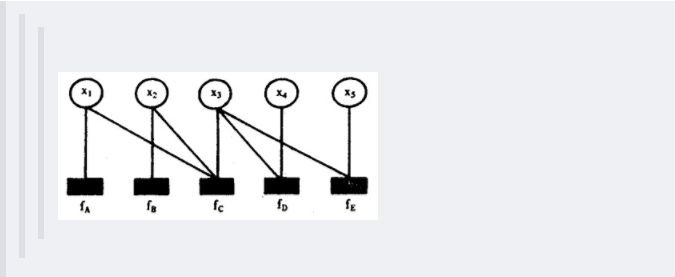
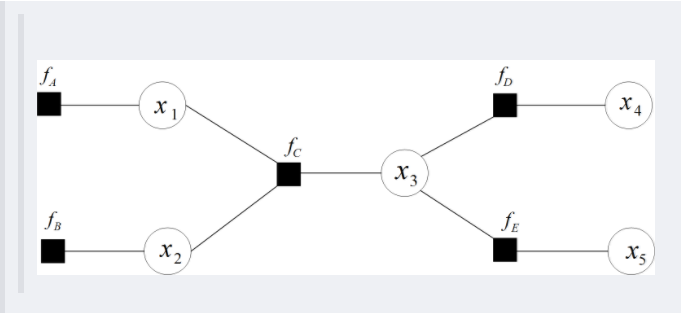
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔科夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-### 2.5 朴素贝叶斯
-
-朴素贝叶斯(Naive Bayesian)是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯原理简单,也很容易实现,多用于文本分类,比如垃圾邮件过滤。**朴素贝叶斯可以看做是贝叶斯网络的特殊情况:即该网络中无边,各个节点都是独立的。 **
-
-朴素贝叶斯朴素在哪里呢? —— **两个假设**:
-
-- 一个特征出现的概率与其他特征(条件)独立;
-- 每个特征同等重要。
-
-贝叶斯公式如下:
-
-
-
-下面以一个例子来解释朴素贝叶斯,给定数据如下:
-
-
-
-现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
-
-这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!这里我们联系到朴素贝叶斯公式:
-
-
-
-我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,这三个变量都能通过统计的方法求得。
-
-等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
-
-**但是为什么需要假设特征之间相互独立呢?**
-
-1. 我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
-
- 36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
-
-2. 假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
-
-根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
-
-**朴素贝叶斯优点**:
-
-- 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
-- 分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
-
-**朴素贝叶斯缺点**:
-
-理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
-
-朴素贝叶斯模型(Naive Bayesian Model)的**朴素(Naive)的含义是"很简单很天真"**地假设样本特征彼此独立. 这个假设现实中基本上不存在, 但特征相关性很小的实际情况还是很多的, 所以这个模型仍然能够工作得很好。
-
-## 3. 基于贝叶斯的一些问题
-
-1. 解释朴素贝叶斯算法里面的先验概率、似然估计和边际似然估计?
- - **先验概率:**就是因变量(二分法)在数据集中的比例。这是在你没有任何进一步的信息的时候,是对分类能做出的最接近的猜测。
- - **似然估计:**似然估计是在其他一些变量的给定的情况下,一个观测值被分类为1的概率。例如,“FREE”这个词在以前的垃圾邮件使用的概率就是似然估计。
- - **边际似然估计:**边际似然估计就是,“FREE”这个词在任何消息中使用的概率。
-
-## 4. 生成式模型和判别式模型的区别
-
-- **判别模型**(discriminative model)通过求解条件概率分布P(y|x)或者直接计算y的值来预测y。
-
- 线性回归(Linear Regression),逻辑回归(Logistic Regression),支持向量机(SVM), 传统神经网络(Traditional Neural Networks),线性判别分析(Linear Discriminative Analysis),条件随机场(Conditional Random Field)
-
-- **生成模型**(generative model)通过对观测值和标注数据计算联合概率分布P(x,y)来达到判定估算y的目的。
-
- 朴素贝叶斯(Naive Bayes), 隐马尔科夫模型(HMM),贝叶斯网络(Bayesian Networks)和隐含狄利克雷分布(Latent Dirichlet Allocation)、混合高斯模型
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-
-## 6. 参考文献
-
-[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
-
diff --git a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md b/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
deleted file mode 100644
index 8d97b78..0000000
--- a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
+++ /dev/null
@@ -1,223 +0,0 @@
-## 目录
-- [1. 对概率图模型的理解](#1-对概率图模型的理解)
-- [2. 细数贝叶斯网络](#2-细数贝叶斯网络)
- - [2.1 频率派观点](#21-频率派观点)
- - [2.2 贝叶斯学派](#22-贝叶斯学派)
- - [2.3 贝叶斯定理](#23-贝叶斯定理)
- - [2.4 贝叶斯网络](#24-贝叶斯网络)
- - [2.5 朴素贝叶斯](#25-朴素贝叶斯)
-- [3. 基于贝叶斯的一些问题](#3-基于贝叶斯的一些问题)
-- [4. 生成式模型和判别式模型的区别](#4-生成式模型和判别式模型的区别)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 对概率图模型的理解
-
-概率图模型是用图来表示变量概率依赖关系的理论,结合概率论与图论的知识,利用图来表示与模型有关的变量的联合概率分布。由图灵奖获得者Pearl开发出来。
-
-如果用一个词来形容概率图模型(Probabilistic Graphical Model)的话,那就是“优雅”。对于一个实际问题,我们希望能够挖掘隐含在数据中的知识。概率图模型构建了这样一幅图,用观测结点表示观测到的数据,用隐含结点表示潜在的知识,用边来描述知识与数据的相互关系,**最后基于这样的关系图获得一个概率分布**,非常“优雅”地解决了问题。
-
-概率图中的节点分为隐含节点和观测节点,边分为有向边和无向边。从概率论的角度,节点对应于随机变量,边对应于随机变量的依赖或相关关系,其中**有向边表示单向的依赖,无向边表示相互依赖关系**。
-
-概率图模型分为**贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)**两大类。贝叶斯网络可以用一个有向图结构表示,马尔可夫网络可以表 示成一个无向图的网络结构。更详细地说,概率图模型包括了朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等,在机器学习的诸多场景中都有着广泛的应用。
-
-## 2. 细数贝叶斯网络
-
-### 2.1 频率派观点
-
-长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。而且概率虽然未知,但最起码是一个确定的值。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,而且不论你取了多少次,取得白球的**概率θ始终都是1/2**,即不随观察结果X 的变化而变化。
-
-这种**频率派**的观点长期统治着人们的观念,直到后来一个名叫Thomas Bayes的人物出现。
-
-### 2.2 贝叶斯学派
-
-托马斯·贝叶斯Thomas Bayes(1702-1763)在世时,并不为当时的人们所熟知,很少发表论文或出版著作,与当时学术界的人沟通交流也很少,用现在的话来说,贝叶斯就是活生生一民间学术“屌丝”,可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”,翻译过来则是:机遇理论中一个问题的解。你可能觉得我要说:这篇论文的发表随机产生轰动效应,从而奠定贝叶斯在学术史上的地位。
-
-
-
-这篇论文可以用上面的例子来说明,“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率θ是多少?”贝叶斯认为取得白球的概率是个不确定的值,因为其中含有机遇的成分。比如,一个朋友创业,你明明知道创业的结果就两种,即要么成功要么失败,但你依然会忍不住去估计他创业成功的几率有多大?你如果对他为人比较了解,而且有方法、思路清晰、有毅力、且能团结周围的人,你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式,便是**贝叶斯式的思考方式。**
-
-**先简单总结下频率派与贝叶斯派各自不同的思考方式:**
-
-- 频率派把需要推断的参数θ看做是固定的未知常数,即概率虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
-- 而贝叶斯派的观点则截然相反,他们认为参数是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数的分布。
-
-贝叶斯派既然把看做是一个随机变量,所以要计算的分布,便得事先知道的无条件分布,即在有样本之前(或观察到X之前),有着怎样的分布呢?
-
-比如往台球桌上扔一个球,这个球落会落在何处呢?如果是不偏不倚的把球抛出去,那么此球落在台球桌上的任一位置都有着相同的机会,即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为**先验分布,或着无条件分布**。
-
-其中,先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决,解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如,某工厂每天都要对产品进行质检,以评估产品的不合格率θ,经过一段时间后便会积累大量的历史资料,这些历史资料便是先验知识,有了这些先验知识,便在决定对一个产品是否需要每天质检时便有了依据,如果以往的历史资料显示,某产品的不合格率只有0.01%,便可视为信得过产品或免检产品,只每月抽检一两次,从而省去大量的人力物力。
-
-而**后验分布**π(θ|X)一般也认为是在给定样本X的情况下的θ条件分布,而使π(θ|X)达到最大的值θMD称为**最大后验估计**,类似于经典统计学中的**极大似然估计**。
-
-综合起来看,则好比是人类刚开始时对大自然只有少得可怜的先验知识,但随着不断观察、实验获得更多的样本、结果,使得人们对自然界的规律摸得越来越透彻。所以,贝叶斯方法既符合人们日常生活的思考方式,也符合人们认识自然的规律,经过不断的发展,最终占据统计学领域的半壁江山,与经典统计学分庭抗礼。
-
-### 2.3 贝叶斯定理
-
-**条件概率**(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
-
-
-
-比如上图,在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率:
-
-=\frac{P(A\cap_{.}B)}{P(B)})
-
-联合概率: 或者P(A,B))
-
-边缘概率(先验概率):P(A)或者P(B)
-
-### 2.4 贝叶斯网络
-
-贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model),是一种概率图模型,于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓朴结构是一个有向无环图(DAG)。
-
-
-
-贝叶斯网络的有向无环图中的节点表示随机变量 
-
-它们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。
-
-例如,假设节点E直接影响到节点H,即E→H,则用从E指向H的箭头建立结点E到结点H的有向弧(E,H),权值(即连接强度)用条件概率P(H|E)来表示,如下图所示:
-
-
-
-简言之,把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖,用圈表示随机变量(random variables),用箭头表示条件依赖(conditional dependencies)。
-
-此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
-
-=P(x_k|x_1,...,x_{k-1})...P(x_2|x_1)P(x_1))
-
-#### 2.4.1 贝叶斯网络的结构形式
-
-**1. head-to-head**
-
-
-
-依上图,所以有:P(a,b,c) = P(a)*P(b)*P(c|a,b)成立,即在c未知的条件下,a、b被阻断(blocked),是独立的,称之为head-to-head条件独立。
-
-**2. tail-to-tail**
-
-
-
-考虑c未知,跟c已知这两种情况:
-
-1. 在c未知的时候,有:P(a,b,c)=P(c)*P(a|c)*P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-2. 在c已知的时候,有:P(a,b|c)=P(a,b,c)/P(c),然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中,得到:P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c),即c已知时,a、b独立。
-
-**3. head-to-tail**
-
-
-
-还是分c未知跟c已知这两种情况:
-
-1. c未知时,有:P(a,b,c)=P(a)*P(c|a)*P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-
-2. c已知时,有:P(a,b|c)=P(a,b,c)/P(c),且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c),可化简得到:
-
- 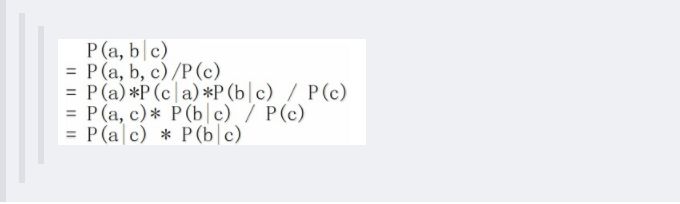
-
- 所以,在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
-
- 这个head-to-tail其实就是一个链式网络,如下图所示:
-
- 
-
- 根据之前对head-to-tail的讲解,我们已经知道,在xi给定的条件下,xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢?意味着:xi+1的分布状态只和xi有关,和其他变量条件独立。通俗点说,当前状态只跟上一状态有关,跟上上或上上之前的状态无关。这种顺次演变的随机过程,就叫做**马尔科夫链**(Markov chain)。对于马尔科夫链我们下一节再细讲。
-
-#### 2.4.2 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔科夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-### 2.5 朴素贝叶斯
-
-朴素贝叶斯(Naive Bayesian)是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯原理简单,也很容易实现,多用于文本分类,比如垃圾邮件过滤。**朴素贝叶斯可以看做是贝叶斯网络的特殊情况:即该网络中无边,各个节点都是独立的。 **
-
-朴素贝叶斯朴素在哪里呢? —— **两个假设**:
-
-- 一个特征出现的概率与其他特征(条件)独立;
-- 每个特征同等重要。
-
-贝叶斯公式如下:
-
-
-
-下面以一个例子来解释朴素贝叶斯,给定数据如下:
-
-
-
-现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
-
-这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!这里我们联系到朴素贝叶斯公式:
-
-
-
-我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,这三个变量都能通过统计的方法求得。
-
-等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
-
-**但是为什么需要假设特征之间相互独立呢?**
-
-1. 我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
-
- 36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
-
-2. 假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
-
-根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
-
-**朴素贝叶斯优点**:
-
-- 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
-- 分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
-
-**朴素贝叶斯缺点**:
-
-理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
-
-朴素贝叶斯模型(Naive Bayesian Model)的**朴素(Naive)的含义是"很简单很天真"**地假设样本特征彼此独立. 这个假设现实中基本上不存在, 但特征相关性很小的实际情况还是很多的, 所以这个模型仍然能够工作得很好。
-
-## 3. 基于贝叶斯的一些问题
-
-1. 解释朴素贝叶斯算法里面的先验概率、似然估计和边际似然估计?
- - **先验概率:**就是因变量(二分法)在数据集中的比例。这是在你没有任何进一步的信息的时候,是对分类能做出的最接近的猜测。
- - **似然估计:**似然估计是在其他一些变量的给定的情况下,一个观测值被分类为1的概率。例如,“FREE”这个词在以前的垃圾邮件使用的概率就是似然估计。
- - **边际似然估计:**边际似然估计就是,“FREE”这个词在任何消息中使用的概率。
-
-## 4. 生成式模型和判别式模型的区别
-
-- **判别模型**(discriminative model)通过求解条件概率分布P(y|x)或者直接计算y的值来预测y。
-
- 线性回归(Linear Regression),逻辑回归(Logistic Regression),支持向量机(SVM), 传统神经网络(Traditional Neural Networks),线性判别分析(Linear Discriminative Analysis),条件随机场(Conditional Random Field)
-
-- **生成模型**(generative model)通过对观测值和标注数据计算联合概率分布P(x,y)来达到判定估算y的目的。
-
- 朴素贝叶斯(Naive Bayes), 隐马尔科夫模型(HMM),贝叶斯网络(Bayesian Networks)和隐含狄利克雷分布(Latent Dirichlet Allocation)、混合高斯模型
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-
-## 6. 参考文献
-
-[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 diff --git a/Machine Learning/5.2 Markov/5.2 Markov.md b/Machine Learning/5.2 Markov/5.2 Markov.md
deleted file mode 100644
index 1ac1a38..0000000
--- a/Machine Learning/5.2 Markov/5.2 Markov.md
+++ /dev/null
@@ -1,284 +0,0 @@
-## 目录
-
-- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
-- [2. 马尔可夫模型](#2-马尔可夫模型)
- - [2.1 马尔可夫过程](#21-马尔可夫过程)
-- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- - [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
-- [4. 马尔可夫网络](#4-马尔可夫网络)
- - [4.1 因子图](#41-因子图)
- - [4.2 马尔可夫网络](#42-马尔可夫网络)
-- [5. 条件随机场(CRF)](#5-条件随机场crf)
-- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
-- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
-
-相信大家都看过上一节我讲得贝叶斯网络,都明白了概率图模型是怎样构造的,如果现在还没明白,请看我上一节的总结:[贝叶斯网络](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md)
-
-这一节我们重点来讲一下马尔可夫,正如题目所示,看了会一脸蒙蔽,好在我们会一点一点的来解释上面的概念,请大家按照顺序往下看就会完全弄明白了,这里我给一个通俗易懂的定义,后面我们再来一个个详解。
-
-以下共分六点说明这些概念,分成条目只是方便边阅读边思考,这6点是依次递进的,不要跳跃着看。
-
-1. 将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个**网络**。
-2. 如果该网络是有向无环图,则这个网络称为**贝叶斯网络。**
-3. 如果这个图退化成线性链的方式,则得到**马尔可夫模型**;因为每个结点都是随机变量,将其看成各个时刻(或空间)的相关变化,以随机过程的视角,则可以看成是**马尔可夫过程**。
-4. 若上述网络是无向的,则是无向图模型,又称**马尔可夫随机场或者马尔可夫网络**。
-5. 如果在给定某些条件的前提下,研究这个马尔可夫随机场,则得到**条件随机场**。
-6. 如果使用条件随机场解决标注问题,并且进一步将条件随机场中的网络拓扑变成线性的,则得到**线性链条件随机场**。
-
-## 2. 马尔可夫模型
-
-### 2.1 马尔可夫过程
-
-马尔可夫过程(Markov process)是一类随机过程。它的原始模型马尔可夫链,由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性:在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变 (过去 )。例如森林中动物头数的变化构成——马尔可夫过程。在现实世界中,有很多过程都是马尔可夫过程,如液体中微粒所作的布朗运动、传染病受感染的人数、车站的候车人数等,都可视为马尔可夫过程。
-
-每个状态的转移只依赖于之前的n个状态,这个过程被称为1个n阶的模型,其中n是影响转移状态的数目。最简单的马尔可夫过程就是一阶过程,**每一个状态的转移只依赖于其之前的那一个状态**,这个也叫作**马尔可夫性质**。用数学表达式表示就是下面的样子:
-
-假设这个模型的每个状态都只依赖于之前的状态,这个假设被称为**马尔科夫假设**,这个假设可以大大的简化这个问题。显然,这个假设可能是一个非常糟糕的假设,导致很多重要的信息都丢失了。
-
-=P(X_{n+1}=x|X_n=x_n))
-
-假设天气服从**马尔可夫链**:
-
-
-
-从上面这幅图可以看出:
-
-- 假如今天是晴天,明天变成阴天的概率是0.1
-- 假如今天是晴天,明天任然是晴天的概率是0.9,和上一条概率之和为1,这也符合真实生活的情况。
-
-| | 晴 | 阴 |
-| ------ | ---- | ---- |
-| **晴** | 0.9 | 0,1 |
-| **阴** | 0.5 | 0.5 |
-
-由上表我们可以得到马尔可夫链的**状态转移矩阵**:
-
-
-
-因此,一阶马尔可夫过程定义了以下三个部分:
-
-- **状态**:晴天和阴天
-- **初始向量**:定义系统在时间为0的时候的状态的概率
-- **状态转移矩阵**:每种天气转换的概率
-
-马尔可夫模型(Markov Model)是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法。
-
-## 3. 隐马尔可夫模型(HMM)
-
-在某些情况下马尔科夫过程不足以描述我们希望发现的模式。回到之前那个天气的例子,一个隐居的人可能不能直观的观察到天气的情况,但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合,一个可以观察到的状态集合(海藻的状态)和一个隐藏的状态(天气的状况)。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。
-
-而这个算法就叫做**隐马尔可夫模型(HMM)**。
-
-
-
-隐马尔可夫模型 (Hidden Markov Model) 是一种统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。**它是结构最简单的动态贝叶斯网,这是一种著名的有向图模型**,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
-
-### 3.1 隐马尔可夫三大问题
-
-1. 给定模型,如何有效计算产生观测序列的概率?换言之,如何评估模型与观测序列之间的匹配程度?
-2. 给定模型和观测序列,如何找到与此观测序列最匹配的状态序列?换言之,如何根据观测序列推断出隐藏的模型状态?
-3. 给定观测序列,如何调整模型参数使得该序列出现的概率最大?换言之,如何训练模型使其能最好地描述观测数据?
-
-前两个问题是模式识别的问题:1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(**评价**);2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(**解码**)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型(**学习**)。
-
-对应的三大问题解法:
-
-1. 向前算法(Forward Algorithm)、向后算法(Backward Algorithm)
-2. 维特比算法(Viterbi Algorithm)
-3. 鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)
-
-下面我们以一个场景来说明这些问题的解法到底是什么?
-
-小明现在有三天的假期,他为了打发时间,可以在每一天中选择三件事情来做,这三件事情分别是散步、购物、打扫卫生(**对应着可观测序列**),可是在生活中我们所做的决定一般都受到天气的影响,可能晴天的时候想要去购物或者散步,可能下雨天的时候不想出门,留在家里打扫卫生。而天气(晴天、下雨天)就属于隐藏状态,用一幅概率图来表示这一马尔可夫过程:
-
-
-
-那么,我们提出三个问题,分别对应马尔可夫的三大问题:
-
-1. 已知整个模型,我观测到连续三天做的事情是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
-2. 同样知晓这个模型,同样是这三件事,我想猜,这三天的天气是怎么样的。
-3. 最复杂的,我只知道这三天做了这三件事儿,而其他什么信息都没有。我得建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况选择做某事的概率分布。
-
-下面我们就依据这个场景来一一解答这些问题。
-
-#### 3.1.1 第一个问题解法
-
-**遍历算法**:
-
-这个是最简单的算法了,假设第一天(T=1 时刻)是晴天,想要购物,那么就把图上的对应概率相乘就能够得到了。
-
-第二天(T=2 时刻)要做的事情,在第一天的概率基础上乘上第二天的概率,依次类推,最终得到这三天(T=3 时刻)所要做的事情的概率值,这就是遍历算法,简单而又粗暴。但问题是用遍历算法的复杂度会随着观测序列和隐藏状态的增加而成指数级增长。
-
-复杂度为: 
-
-于是就有了第二种算法
-
-**前向算法**:
-
-1. 假设第一天要购物,那么就计算出第一天购物的概率(包括晴天和雨天);假设第一天要散步,那么也计算出来,依次枚举。
-2. 假设前两天是购物和散步,也同样计算出这一种的概率;假设前两天是散步和打扫卫生,同样计算,枚举出前两天行为的概率。
-3. 第三步就是计算出前三天行为的概率。
-
-细心的读者已经发现了,第二步中要求的概率可以在第一步的基础上进行,同样的,第三步也会依赖于第二步的计算结果。那么这样做就能够**节省很多计算环节,类似于动态规划**。
-
-这种算法的复杂度为: 
-
-**后向算法**
-
-跟前向算法相反,我们知道总的概率肯定是1,那么B_t=1,也就是最后一个时刻的概率合为1,先计算前三天的各种可能的概率,在计算前两天、前一天的数据,跟前向算法相反的计算路径。
-
-#### 3.1.2 第二个问题解法
-
-**维特比算法(Viterbi)**
-
-> 说起安德鲁·维特比(Andrew Viterbi),通信行业之外的人可能知道他的并不多,不过通信行业的从业者大多知道以他的名字命名的维特比算法(ViterbiAlgorithm)。维特比算法是现代数字通信中最常用的算法,同时也是很多自然语言处理采用的解码算法。可以毫不夸张地讲,维特比是对我们今天的生活影响力最大的科学家之一,因为基于CDMA的3G移动通信标准主要就是他和厄文·雅各布(Irwin Mark Jacobs)创办的高通公司(Qualcomm)制定的,并且高通公司在4G时代依然引领移动通信的发展。
-
-维特比算法是一个特殊但应用最广的**动态规划算法**。利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图—篱笆网络(Lattice)的有向图最短路径问题而提出的。它之所以重要,是因为凡是使用隐含马尔可夫模型描述的问题都可以用它来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
-
-维特比算法一般用于模式识别,通过观测数据来反推出隐藏状态,下面一步步讲解这个算法。
-
-
-
-因为是要根据观测数据来反推,所以这里要进行一个假设,**假设这三天所做的行为分别是:散步、购物、打扫卫生,**那么我们要求的是这三天的天气(路径)分别是什么。
-
-1. 初始计算第一天下雨和第一天晴天去散步的概率值:
-
- )表示第一天下雨的概率
-
- 表示中间的状态(下雨)s概率
-
- )表示下雨并且散步的概率
-
- 表示下雨天到下雨天的概率
-
-=\pi_R*b_R(O_1=w)=0.6*0.1=0.06)
-
-=\pi_S*b_S(O_1=w)=0.4*0.6=0.24)
-
- 初始路径为:
-
- =Rainy)
-
- =Sunny)
-
-2. 计算第二天下雨和第二天晴天去购物的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-3. 计算第三天下雨和第三天晴天去打扫卫生的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-4. 比较每一步中 $\bigtriangleup$ 的概率大小,选取**最大值**并找到对应的路径,依次类推就能找到最有可能的**隐藏状态路径**。
-
- 第一天的概率最大值为 ,对应路径为Sunny,
-
- 第二天的概率最大值为 ,对应路径为Sunny,
-
- 第三天的概率最大值为 ,对应路径为Rainy。
-
-5. 合起来的路径就是Sunny->Sunny->Rainy,这就是我们所求。
-
-以上是比较通俗易懂的维特比算法,如果需要严谨表述,可以查看《数学之美》这本书的第26章,讲的就是维特比算法,很详细。附:《数学之美》下载地址,[点击下载](https://www.lanzous.com/i3ousch)
-
-#### 3.1.3 第三个问题解法
-
-鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法),详细讲解请见:[监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-
-## 4. 马尔可夫网络
-
-### 4.1 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-### 4.2 马尔可夫网络
-
-我们已经知道,有向图模型,又称作贝叶斯网络,但在有些情况下,强制对某些结点之间的边增加方向是不合适的。**使用没有方向的无向边,形成了无向图模型**(Undirected Graphical Model,UGM), 又被称为**马尔可夫随机场或者马尔可夫网络**(Markov Random Field, MRF or Markov network)。
-
-
-
-设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量,若随机变量Y构成一个无向图 G=(V,E)表示的马尔可夫随机场(MRF),则条件概率分布P(Y|X)称为**条件随机场**(Conditional Random Field, 简称CRF,后续新的博客中可能会阐述CRF)。如下图所示,便是一个线性链条件随机场的无向图模型:
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔可夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 5. 条件随机场(CRF)
-
-**一个通俗的例子**
-
-假设你有许多小明同学一天内不同时段的照片,从小明提裤子起床到脱裤子睡觉各个时间段都有(小明是照片控!)。现在的任务是对这些照片进行分类。比如有的照片是吃饭,那就给它打上吃饭的标签;有的照片是跑步时拍的,那就打上跑步的标签;有的照片是开会时拍的,那就打上开会的标签。问题来了,你准备怎么干?
-
-一个简单直观的办法就是,不管这些照片之间的时间顺序,想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据,训练出一个模型,直接根据照片的特征来分类。例如,如果照片是早上6:00拍的,且画面是黑暗的,那就给它打上睡觉的标签;如果照片上有车,那就给它打上开车的标签。
-
-乍一看可以!但实际上,由于我们忽略了这些照片之间的时间顺序这一重要信息,我们的分类器会有缺陷的。举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。
-
-所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它**相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!**这就有点类似于词性标注了,只不过把照片换成了句子而已,本质上是一样的。
-
-如同马尔可夫随机场,条件随机场为具有无向的[图模型](https://baike.baidu.com/item/图模型),图中的顶点代表随机变量,顶点间的连线代表随机变量间的相依关系,在条件随机场中,[随机变量](https://baike.baidu.com/item/随机变量)Y 的分布为条件机率,给定的观察值则为随机变量 X。下图就是一个线性连条件随机场。
-
-
-
-条件概率分布P(Y|X)称为**条件随机场**。
-
-## 6. EM算法、HMM、CRF的比较
-
-1. **EM算法**是用于含有隐变量模型的极大似然估计或者极大后验估计,有两步组成:E步,求期望(expectation);M步,求极大(maxmization)。本质上EM算法还是一个迭代算法,通过不断用上一代参数对隐变量的估计来对当前变量进行计算,直到收敛。注意:EM算法是对初值敏感的,而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法,也就是说**EM算法不能保证找到全局最优值**。对于EM的导出方法也应该掌握。
-
-2. **隐马尔可夫模型**是用于标注问题的生成模型。有几个参数(π,A,B):初始状态概率向量π,状态转移矩阵A,观测概率矩阵B。称为马尔科夫模型的三要素。马尔科夫三个基本问题:
-
- 概率计算问题:给定模型和观测序列,计算模型下观测序列输出的概率。–》前向后向算法
-
- 学习问题:已知观测序列,估计模型参数,即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。
-
- 预测问题:已知模型和观测序列,求解对应的状态序列。–》近似算法(贪心算法)和维比特算法(动态规划求最优路径)
-
-3. **条件随机场CRF**,给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场,而我们平时看到的大多是线性链条随机场,也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
-
-4. 之所以总把HMM和CRF进行比较,主要是因为CRF和HMM都利用了图的知识,但是CRF利用的是马尔科夫随机场(无向图),而HMM的基础是贝叶斯网络(有向图)。而且CRF也有:概率计算问题、学习问题和预测问题。大致计算方法和HMM类似,只不过不需要EM算法进行学习问题。
-
-5. **HMM和CRF对比:**其根本还是在于基本的理念不同,一个是生成模型,一个是判别模型,这也就导致了求解方式的不同。
-
-## 7. 参考文献
-
-1. [条件随机场的简单理解](https://blog.csdn.net/weixin_41911765/article/details/82465697)
-2. [如何轻松愉快地理解条件随机场(CRF)](https://blog.csdn.net/dcx_abc/article/details/78319246)
-3. [《数学之美》](https://www.lanzous.com/i3ousch)
-4. [监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-5. [从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 8. 词性标注代码实现
-
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
diff --git a/Machine Learning/5.2 Markov/5.2 Markov.md b/Machine Learning/5.2 Markov/5.2 Markov.md
deleted file mode 100644
index 1ac1a38..0000000
--- a/Machine Learning/5.2 Markov/5.2 Markov.md
+++ /dev/null
@@ -1,284 +0,0 @@
-## 目录
-
-- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
-- [2. 马尔可夫模型](#2-马尔可夫模型)
- - [2.1 马尔可夫过程](#21-马尔可夫过程)
-- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- - [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
-- [4. 马尔可夫网络](#4-马尔可夫网络)
- - [4.1 因子图](#41-因子图)
- - [4.2 马尔可夫网络](#42-马尔可夫网络)
-- [5. 条件随机场(CRF)](#5-条件随机场crf)
-- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
-- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
-
-相信大家都看过上一节我讲得贝叶斯网络,都明白了概率图模型是怎样构造的,如果现在还没明白,请看我上一节的总结:[贝叶斯网络](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md)
-
-这一节我们重点来讲一下马尔可夫,正如题目所示,看了会一脸蒙蔽,好在我们会一点一点的来解释上面的概念,请大家按照顺序往下看就会完全弄明白了,这里我给一个通俗易懂的定义,后面我们再来一个个详解。
-
-以下共分六点说明这些概念,分成条目只是方便边阅读边思考,这6点是依次递进的,不要跳跃着看。
-
-1. 将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个**网络**。
-2. 如果该网络是有向无环图,则这个网络称为**贝叶斯网络。**
-3. 如果这个图退化成线性链的方式,则得到**马尔可夫模型**;因为每个结点都是随机变量,将其看成各个时刻(或空间)的相关变化,以随机过程的视角,则可以看成是**马尔可夫过程**。
-4. 若上述网络是无向的,则是无向图模型,又称**马尔可夫随机场或者马尔可夫网络**。
-5. 如果在给定某些条件的前提下,研究这个马尔可夫随机场,则得到**条件随机场**。
-6. 如果使用条件随机场解决标注问题,并且进一步将条件随机场中的网络拓扑变成线性的,则得到**线性链条件随机场**。
-
-## 2. 马尔可夫模型
-
-### 2.1 马尔可夫过程
-
-马尔可夫过程(Markov process)是一类随机过程。它的原始模型马尔可夫链,由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性:在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变 (过去 )。例如森林中动物头数的变化构成——马尔可夫过程。在现实世界中,有很多过程都是马尔可夫过程,如液体中微粒所作的布朗运动、传染病受感染的人数、车站的候车人数等,都可视为马尔可夫过程。
-
-每个状态的转移只依赖于之前的n个状态,这个过程被称为1个n阶的模型,其中n是影响转移状态的数目。最简单的马尔可夫过程就是一阶过程,**每一个状态的转移只依赖于其之前的那一个状态**,这个也叫作**马尔可夫性质**。用数学表达式表示就是下面的样子:
-
-假设这个模型的每个状态都只依赖于之前的状态,这个假设被称为**马尔科夫假设**,这个假设可以大大的简化这个问题。显然,这个假设可能是一个非常糟糕的假设,导致很多重要的信息都丢失了。
-
-=P(X_{n+1}=x|X_n=x_n))
-
-假设天气服从**马尔可夫链**:
-
-
-
-从上面这幅图可以看出:
-
-- 假如今天是晴天,明天变成阴天的概率是0.1
-- 假如今天是晴天,明天任然是晴天的概率是0.9,和上一条概率之和为1,这也符合真实生活的情况。
-
-| | 晴 | 阴 |
-| ------ | ---- | ---- |
-| **晴** | 0.9 | 0,1 |
-| **阴** | 0.5 | 0.5 |
-
-由上表我们可以得到马尔可夫链的**状态转移矩阵**:
-
-
-
-因此,一阶马尔可夫过程定义了以下三个部分:
-
-- **状态**:晴天和阴天
-- **初始向量**:定义系统在时间为0的时候的状态的概率
-- **状态转移矩阵**:每种天气转换的概率
-
-马尔可夫模型(Markov Model)是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法。
-
-## 3. 隐马尔可夫模型(HMM)
-
-在某些情况下马尔科夫过程不足以描述我们希望发现的模式。回到之前那个天气的例子,一个隐居的人可能不能直观的观察到天气的情况,但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合,一个可以观察到的状态集合(海藻的状态)和一个隐藏的状态(天气的状况)。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。
-
-而这个算法就叫做**隐马尔可夫模型(HMM)**。
-
-
-
-隐马尔可夫模型 (Hidden Markov Model) 是一种统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。**它是结构最简单的动态贝叶斯网,这是一种著名的有向图模型**,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
-
-### 3.1 隐马尔可夫三大问题
-
-1. 给定模型,如何有效计算产生观测序列的概率?换言之,如何评估模型与观测序列之间的匹配程度?
-2. 给定模型和观测序列,如何找到与此观测序列最匹配的状态序列?换言之,如何根据观测序列推断出隐藏的模型状态?
-3. 给定观测序列,如何调整模型参数使得该序列出现的概率最大?换言之,如何训练模型使其能最好地描述观测数据?
-
-前两个问题是模式识别的问题:1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(**评价**);2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(**解码**)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型(**学习**)。
-
-对应的三大问题解法:
-
-1. 向前算法(Forward Algorithm)、向后算法(Backward Algorithm)
-2. 维特比算法(Viterbi Algorithm)
-3. 鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)
-
-下面我们以一个场景来说明这些问题的解法到底是什么?
-
-小明现在有三天的假期,他为了打发时间,可以在每一天中选择三件事情来做,这三件事情分别是散步、购物、打扫卫生(**对应着可观测序列**),可是在生活中我们所做的决定一般都受到天气的影响,可能晴天的时候想要去购物或者散步,可能下雨天的时候不想出门,留在家里打扫卫生。而天气(晴天、下雨天)就属于隐藏状态,用一幅概率图来表示这一马尔可夫过程:
-
-
-
-那么,我们提出三个问题,分别对应马尔可夫的三大问题:
-
-1. 已知整个模型,我观测到连续三天做的事情是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
-2. 同样知晓这个模型,同样是这三件事,我想猜,这三天的天气是怎么样的。
-3. 最复杂的,我只知道这三天做了这三件事儿,而其他什么信息都没有。我得建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况选择做某事的概率分布。
-
-下面我们就依据这个场景来一一解答这些问题。
-
-#### 3.1.1 第一个问题解法
-
-**遍历算法**:
-
-这个是最简单的算法了,假设第一天(T=1 时刻)是晴天,想要购物,那么就把图上的对应概率相乘就能够得到了。
-
-第二天(T=2 时刻)要做的事情,在第一天的概率基础上乘上第二天的概率,依次类推,最终得到这三天(T=3 时刻)所要做的事情的概率值,这就是遍历算法,简单而又粗暴。但问题是用遍历算法的复杂度会随着观测序列和隐藏状态的增加而成指数级增长。
-
-复杂度为: 
-
-于是就有了第二种算法
-
-**前向算法**:
-
-1. 假设第一天要购物,那么就计算出第一天购物的概率(包括晴天和雨天);假设第一天要散步,那么也计算出来,依次枚举。
-2. 假设前两天是购物和散步,也同样计算出这一种的概率;假设前两天是散步和打扫卫生,同样计算,枚举出前两天行为的概率。
-3. 第三步就是计算出前三天行为的概率。
-
-细心的读者已经发现了,第二步中要求的概率可以在第一步的基础上进行,同样的,第三步也会依赖于第二步的计算结果。那么这样做就能够**节省很多计算环节,类似于动态规划**。
-
-这种算法的复杂度为: 
-
-**后向算法**
-
-跟前向算法相反,我们知道总的概率肯定是1,那么B_t=1,也就是最后一个时刻的概率合为1,先计算前三天的各种可能的概率,在计算前两天、前一天的数据,跟前向算法相反的计算路径。
-
-#### 3.1.2 第二个问题解法
-
-**维特比算法(Viterbi)**
-
-> 说起安德鲁·维特比(Andrew Viterbi),通信行业之外的人可能知道他的并不多,不过通信行业的从业者大多知道以他的名字命名的维特比算法(ViterbiAlgorithm)。维特比算法是现代数字通信中最常用的算法,同时也是很多自然语言处理采用的解码算法。可以毫不夸张地讲,维特比是对我们今天的生活影响力最大的科学家之一,因为基于CDMA的3G移动通信标准主要就是他和厄文·雅各布(Irwin Mark Jacobs)创办的高通公司(Qualcomm)制定的,并且高通公司在4G时代依然引领移动通信的发展。
-
-维特比算法是一个特殊但应用最广的**动态规划算法**。利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图—篱笆网络(Lattice)的有向图最短路径问题而提出的。它之所以重要,是因为凡是使用隐含马尔可夫模型描述的问题都可以用它来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
-
-维特比算法一般用于模式识别,通过观测数据来反推出隐藏状态,下面一步步讲解这个算法。
-
-
-
-因为是要根据观测数据来反推,所以这里要进行一个假设,**假设这三天所做的行为分别是:散步、购物、打扫卫生,**那么我们要求的是这三天的天气(路径)分别是什么。
-
-1. 初始计算第一天下雨和第一天晴天去散步的概率值:
-
- )表示第一天下雨的概率
-
- 表示中间的状态(下雨)s概率
-
- )表示下雨并且散步的概率
-
- 表示下雨天到下雨天的概率
-
-=\pi_R*b_R(O_1=w)=0.6*0.1=0.06)
-
-=\pi_S*b_S(O_1=w)=0.4*0.6=0.24)
-
- 初始路径为:
-
- =Rainy)
-
- =Sunny)
-
-2. 计算第二天下雨和第二天晴天去购物的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-3. 计算第三天下雨和第三天晴天去打扫卫生的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-4. 比较每一步中 $\bigtriangleup$ 的概率大小,选取**最大值**并找到对应的路径,依次类推就能找到最有可能的**隐藏状态路径**。
-
- 第一天的概率最大值为 ,对应路径为Sunny,
-
- 第二天的概率最大值为 ,对应路径为Sunny,
-
- 第三天的概率最大值为 ,对应路径为Rainy。
-
-5. 合起来的路径就是Sunny->Sunny->Rainy,这就是我们所求。
-
-以上是比较通俗易懂的维特比算法,如果需要严谨表述,可以查看《数学之美》这本书的第26章,讲的就是维特比算法,很详细。附:《数学之美》下载地址,[点击下载](https://www.lanzous.com/i3ousch)
-
-#### 3.1.3 第三个问题解法
-
-鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法),详细讲解请见:[监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-
-## 4. 马尔可夫网络
-
-### 4.1 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-### 4.2 马尔可夫网络
-
-我们已经知道,有向图模型,又称作贝叶斯网络,但在有些情况下,强制对某些结点之间的边增加方向是不合适的。**使用没有方向的无向边,形成了无向图模型**(Undirected Graphical Model,UGM), 又被称为**马尔可夫随机场或者马尔可夫网络**(Markov Random Field, MRF or Markov network)。
-
-
-
-设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量,若随机变量Y构成一个无向图 G=(V,E)表示的马尔可夫随机场(MRF),则条件概率分布P(Y|X)称为**条件随机场**(Conditional Random Field, 简称CRF,后续新的博客中可能会阐述CRF)。如下图所示,便是一个线性链条件随机场的无向图模型:
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔可夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 5. 条件随机场(CRF)
-
-**一个通俗的例子**
-
-假设你有许多小明同学一天内不同时段的照片,从小明提裤子起床到脱裤子睡觉各个时间段都有(小明是照片控!)。现在的任务是对这些照片进行分类。比如有的照片是吃饭,那就给它打上吃饭的标签;有的照片是跑步时拍的,那就打上跑步的标签;有的照片是开会时拍的,那就打上开会的标签。问题来了,你准备怎么干?
-
-一个简单直观的办法就是,不管这些照片之间的时间顺序,想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据,训练出一个模型,直接根据照片的特征来分类。例如,如果照片是早上6:00拍的,且画面是黑暗的,那就给它打上睡觉的标签;如果照片上有车,那就给它打上开车的标签。
-
-乍一看可以!但实际上,由于我们忽略了这些照片之间的时间顺序这一重要信息,我们的分类器会有缺陷的。举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。
-
-所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它**相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!**这就有点类似于词性标注了,只不过把照片换成了句子而已,本质上是一样的。
-
-如同马尔可夫随机场,条件随机场为具有无向的[图模型](https://baike.baidu.com/item/图模型),图中的顶点代表随机变量,顶点间的连线代表随机变量间的相依关系,在条件随机场中,[随机变量](https://baike.baidu.com/item/随机变量)Y 的分布为条件机率,给定的观察值则为随机变量 X。下图就是一个线性连条件随机场。
-
-
-
-条件概率分布P(Y|X)称为**条件随机场**。
-
-## 6. EM算法、HMM、CRF的比较
-
-1. **EM算法**是用于含有隐变量模型的极大似然估计或者极大后验估计,有两步组成:E步,求期望(expectation);M步,求极大(maxmization)。本质上EM算法还是一个迭代算法,通过不断用上一代参数对隐变量的估计来对当前变量进行计算,直到收敛。注意:EM算法是对初值敏感的,而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法,也就是说**EM算法不能保证找到全局最优值**。对于EM的导出方法也应该掌握。
-
-2. **隐马尔可夫模型**是用于标注问题的生成模型。有几个参数(π,A,B):初始状态概率向量π,状态转移矩阵A,观测概率矩阵B。称为马尔科夫模型的三要素。马尔科夫三个基本问题:
-
- 概率计算问题:给定模型和观测序列,计算模型下观测序列输出的概率。–》前向后向算法
-
- 学习问题:已知观测序列,估计模型参数,即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。
-
- 预测问题:已知模型和观测序列,求解对应的状态序列。–》近似算法(贪心算法)和维比特算法(动态规划求最优路径)
-
-3. **条件随机场CRF**,给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场,而我们平时看到的大多是线性链条随机场,也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
-
-4. 之所以总把HMM和CRF进行比较,主要是因为CRF和HMM都利用了图的知识,但是CRF利用的是马尔科夫随机场(无向图),而HMM的基础是贝叶斯网络(有向图)。而且CRF也有:概率计算问题、学习问题和预测问题。大致计算方法和HMM类似,只不过不需要EM算法进行学习问题。
-
-5. **HMM和CRF对比:**其根本还是在于基本的理念不同,一个是生成模型,一个是判别模型,这也就导致了求解方式的不同。
-
-## 7. 参考文献
-
-1. [条件随机场的简单理解](https://blog.csdn.net/weixin_41911765/article/details/82465697)
-2. [如何轻松愉快地理解条件随机场(CRF)](https://blog.csdn.net/dcx_abc/article/details/78319246)
-3. [《数学之美》](https://www.lanzous.com/i3ousch)
-4. [监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-5. [从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 8. 词性标注代码实现
-
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 -
diff --git a/Machine Learning/5.2 Markov/5.2 HMM.ipynb b/Machine Learning/5.2 Markov/HMM.ipynb
similarity index 100%
rename from Machine Learning/5.2 Markov/5.2 HMM.ipynb
rename to Machine Learning/5.2 Markov/HMM.ipynb
diff --git a/Machine Learning/5.2 Markov/README.md b/Machine Learning/5.2 Markov/README.md
index 1ac1a38..294f27b 100644
--- a/Machine Learning/5.2 Markov/README.md
+++ b/Machine Learning/5.2 Markov/README.md
@@ -1,17 +1,21 @@
## 目录
+- [目录](#目录)
- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
- [2. 马尔可夫模型](#2-马尔可夫模型)
- [2.1 马尔可夫过程](#21-马尔可夫过程)
- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
+ - [3.1.1 第一个问题解法](#311-第一个问题解法)
+ - [3.1.2 第二个问题解法](#312-第二个问题解法)
+ - [3.1.3 第三个问题解法](#313-第三个问题解法)
- [4. 马尔可夫网络](#4-马尔可夫网络)
- [4.1 因子图](#41-因子图)
- [4.2 马尔可夫网络](#42-马尔可夫网络)
- [5. 条件随机场(CRF)](#5-条件随机场crf)
- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+- [8. 词性标注代码实现](#8-词性标注代码实现)
## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
@@ -274,7 +278,7 @@ wikipedia上是这样定义因子图的:将一个具有多变量的全局函
## 8. 词性标注代码实现
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/HMM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/Liner Regression/1.Liner Regression.md b/Machine Learning/Liner Regression/1.Liner Regression.md
deleted file mode 100644
index 90ab3a7..0000000
--- a/Machine Learning/Liner Regression/1.Liner Regression.md
+++ /dev/null
@@ -1,111 +0,0 @@
-## 目录
-- [1.什么是线性回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#1什么是线性回归)
-- [2. 能够解决什么样的问题](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#2-能够解决什么样的问题)
-- [3. 一般表达式是什么](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#3-一般表达式是什么)
-- [4. 如何计算](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#4-如何计算)
-- [5. 过拟合、欠拟合如何解决](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#5-过拟合欠拟合如何解决)
- - [5.1 什么是L2正则化(岭回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#51-什么是l2正则化岭回归)
- - [5.2 什么场景下用L2正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#52-什么场景下用l2正则化)
- - [5.3 什么是L1正则化(Lasso回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#53-什么是l1正则化lasso回归)
- - [5.4 什么场景下使用L1正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#54-什么场景下使用l1正则化)
- - [5.5 什么是ElasticNet回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#55-什么是elasticnet回归)
- - [5.6 ElasticNet回归的使用场景](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#56--elasticnet回归的使用场景)
-- [6. 线性回归要求因变量服从正态分布?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#6-线性回归要求因变量服从正态分布)
-- [7. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-## 1.什么是线性回归
-
-- 线性:两个变量之间的关系**是**一次函数关系的——图象**是直线**,叫做线性。
-- 非线性:两个变量之间的关系**不是**一次函数关系的——图象**不是直线**,叫做非线性。
-- 回归:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算**回归到真实值**,这就是回归的由来。
-
-## 2. 能够解决什么样的问题
-
-对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如:对房价的预测、判断信用评价、电影票房预估等。
-
-## 3. 一般表达式是什么
-
-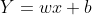
-
-w叫做x的系数,b叫做偏置项。
-
-## 4. 如何计算
-
-### 4.1 Loss Function--MSE
-
-^2)
-
-利用**梯度下降法**找到最小值点,也就是最小误差,最后把 w 和 b 给求出来。
-
-## 5. 过拟合、欠拟合如何解决
-
-使用正则化项,也就是给loss function加上一个参数项,正则化项有**L1正则化、L2正则化、ElasticNet**。加入这个正则化项好处:
-
-- 控制参数幅度,不让模型“无法无天”。
-- 限制参数搜索空间
-- 解决欠拟合与过拟合的问题。
-
-### 5.1 什么是L2正则化(岭回归)
-
-方程:
-
-
-
-表示上面的 loss function ,在loss function的基础上加入w参数的平方和乘以 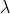 ,假设:
-
-)
-
-回忆以前学过的单位元的方程:
-
-
-
-正和L2正则化项一样,此时我们的任务变成在L约束下求出J取最小值的解。求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-L表示为图中的黑色圆形,随着梯度下降法的不断逼近,与圆第一次产生交点,而这个交点很难出现在坐标轴上。这就说明了L2正则化不容易得到稀疏矩阵,同时为了求出损失函数的最小值,使得w1和w2无限接近于0,达到防止过拟合的问题。
-
-### 5.2 什么场景下用L2正则化
-
-只要数据线性相关,用LinearRegression拟合的不是很好,**需要正则化**,可以考虑使用岭回归(L2), 如何输入特征的维度很高,而且是稀疏线性关系的话, 岭回归就不太合适,考虑使用Lasso回归。
-
-### 5.3 什么是L1正则化(Lasso回归)
-
-L1正则化与L2正则化的区别在于惩罚项的不同:
-
-)
-
-求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-惩罚项表示为图中的黑色棱形,随着梯度下降法的不断逼近,与棱形第一次产生交点,而这个交点很容易出现在坐标轴上。**这就说明了L1正则化容易得到稀疏矩阵。**
-
-### 5.4 什么场景下使用L1正则化
-
-**L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0**,从而增强模型的泛化能力 。对于高的特征数据,尤其是线性关系是稀疏的,就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征,那么L1正则化(Lasso回归)更是首选了。
-
-### 5.5 什么是ElasticNet回归
-
-**ElasticNet综合了L1正则化项和L2正则化项**,以下是它的公式:
-
-^2+\lambda\sum_{j=1}^{n}\theta_j^2]+\lambda\sum_{j=1}^{n}|\theta|))
-
-### 5.6 ElasticNet回归的使用场景
-
-ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候,可以考虑使用ElasticNet回归来综合,得到比较好的结果。
-
-## 6. 线性回归要求因变量服从正态分布?
-
-我们假设线性回归的噪声服从均值为0的正态分布。 当噪声符合正态分布N(0,delta^2)时,因变量则符合正态分布N(ax(i)+b,delta^2),其中预测函数y=ax(i)+b。这个结论可以由正态分布的概率密度函数得到。也就是说当噪声符合正态分布时,其因变量必然也符合正态分布。
-
-在用线性回归模型拟合数据之前,首先要求数据应符合或近似符合正态分布,否则得到的拟合函数不正确。
-
-## 7. [代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-------
-
-> 作者:[@mantchs](https://github.com/mantchs)
->
-> 欢迎大家加入讨论!共同完善此项目!
-
diff --git a/Machine Learning/5.2 Markov/5.2 HMM.ipynb b/Machine Learning/5.2 Markov/HMM.ipynb
similarity index 100%
rename from Machine Learning/5.2 Markov/5.2 HMM.ipynb
rename to Machine Learning/5.2 Markov/HMM.ipynb
diff --git a/Machine Learning/5.2 Markov/README.md b/Machine Learning/5.2 Markov/README.md
index 1ac1a38..294f27b 100644
--- a/Machine Learning/5.2 Markov/README.md
+++ b/Machine Learning/5.2 Markov/README.md
@@ -1,17 +1,21 @@
## 目录
+- [目录](#目录)
- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
- [2. 马尔可夫模型](#2-马尔可夫模型)
- [2.1 马尔可夫过程](#21-马尔可夫过程)
- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
+ - [3.1.1 第一个问题解法](#311-第一个问题解法)
+ - [3.1.2 第二个问题解法](#312-第二个问题解法)
+ - [3.1.3 第三个问题解法](#313-第三个问题解法)
- [4. 马尔可夫网络](#4-马尔可夫网络)
- [4.1 因子图](#41-因子图)
- [4.2 马尔可夫网络](#42-马尔可夫网络)
- [5. 条件随机场(CRF)](#5-条件随机场crf)
- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+- [8. 词性标注代码实现](#8-词性标注代码实现)
## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
@@ -274,7 +278,7 @@ wikipedia上是这样定义因子图的:将一个具有多变量的全局函
## 8. 词性标注代码实现
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/HMM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/Liner Regression/1.Liner Regression.md b/Machine Learning/Liner Regression/1.Liner Regression.md
deleted file mode 100644
index 90ab3a7..0000000
--- a/Machine Learning/Liner Regression/1.Liner Regression.md
+++ /dev/null
@@ -1,111 +0,0 @@
-## 目录
-- [1.什么是线性回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#1什么是线性回归)
-- [2. 能够解决什么样的问题](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#2-能够解决什么样的问题)
-- [3. 一般表达式是什么](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#3-一般表达式是什么)
-- [4. 如何计算](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#4-如何计算)
-- [5. 过拟合、欠拟合如何解决](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#5-过拟合欠拟合如何解决)
- - [5.1 什么是L2正则化(岭回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#51-什么是l2正则化岭回归)
- - [5.2 什么场景下用L2正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#52-什么场景下用l2正则化)
- - [5.3 什么是L1正则化(Lasso回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#53-什么是l1正则化lasso回归)
- - [5.4 什么场景下使用L1正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#54-什么场景下使用l1正则化)
- - [5.5 什么是ElasticNet回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#55-什么是elasticnet回归)
- - [5.6 ElasticNet回归的使用场景](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#56--elasticnet回归的使用场景)
-- [6. 线性回归要求因变量服从正态分布?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#6-线性回归要求因变量服从正态分布)
-- [7. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-## 1.什么是线性回归
-
-- 线性:两个变量之间的关系**是**一次函数关系的——图象**是直线**,叫做线性。
-- 非线性:两个变量之间的关系**不是**一次函数关系的——图象**不是直线**,叫做非线性。
-- 回归:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算**回归到真实值**,这就是回归的由来。
-
-## 2. 能够解决什么样的问题
-
-对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如:对房价的预测、判断信用评价、电影票房预估等。
-
-## 3. 一般表达式是什么
-
-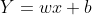
-
-w叫做x的系数,b叫做偏置项。
-
-## 4. 如何计算
-
-### 4.1 Loss Function--MSE
-
-^2)
-
-利用**梯度下降法**找到最小值点,也就是最小误差,最后把 w 和 b 给求出来。
-
-## 5. 过拟合、欠拟合如何解决
-
-使用正则化项,也就是给loss function加上一个参数项,正则化项有**L1正则化、L2正则化、ElasticNet**。加入这个正则化项好处:
-
-- 控制参数幅度,不让模型“无法无天”。
-- 限制参数搜索空间
-- 解决欠拟合与过拟合的问题。
-
-### 5.1 什么是L2正则化(岭回归)
-
-方程:
-
-
-
-表示上面的 loss function ,在loss function的基础上加入w参数的平方和乘以  ,假设:
-
-)
-
-回忆以前学过的单位元的方程:
-
-
-
-正和L2正则化项一样,此时我们的任务变成在L约束下求出J取最小值的解。求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-L表示为图中的黑色圆形,随着梯度下降法的不断逼近,与圆第一次产生交点,而这个交点很难出现在坐标轴上。这就说明了L2正则化不容易得到稀疏矩阵,同时为了求出损失函数的最小值,使得w1和w2无限接近于0,达到防止过拟合的问题。
-
-### 5.2 什么场景下用L2正则化
-
-只要数据线性相关,用LinearRegression拟合的不是很好,**需要正则化**,可以考虑使用岭回归(L2), 如何输入特征的维度很高,而且是稀疏线性关系的话, 岭回归就不太合适,考虑使用Lasso回归。
-
-### 5.3 什么是L1正则化(Lasso回归)
-
-L1正则化与L2正则化的区别在于惩罚项的不同:
-
-)
-
-求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-惩罚项表示为图中的黑色棱形,随着梯度下降法的不断逼近,与棱形第一次产生交点,而这个交点很容易出现在坐标轴上。**这就说明了L1正则化容易得到稀疏矩阵。**
-
-### 5.4 什么场景下使用L1正则化
-
-**L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0**,从而增强模型的泛化能力 。对于高的特征数据,尤其是线性关系是稀疏的,就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征,那么L1正则化(Lasso回归)更是首选了。
-
-### 5.5 什么是ElasticNet回归
-
-**ElasticNet综合了L1正则化项和L2正则化项**,以下是它的公式:
-
-^2+\lambda\sum_{j=1}^{n}\theta_j^2]+\lambda\sum_{j=1}^{n}|\theta|))
-
-### 5.6 ElasticNet回归的使用场景
-
-ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候,可以考虑使用ElasticNet回归来综合,得到比较好的结果。
-
-## 6. 线性回归要求因变量服从正态分布?
-
-我们假设线性回归的噪声服从均值为0的正态分布。 当噪声符合正态分布N(0,delta^2)时,因变量则符合正态分布N(ax(i)+b,delta^2),其中预测函数y=ax(i)+b。这个结论可以由正态分布的概率密度函数得到。也就是说当噪声符合正态分布时,其因变量必然也符合正态分布。
-
-在用线性回归模型拟合数据之前,首先要求数据应符合或近似符合正态分布,否则得到的拟合函数不正确。
-
-## 7. [代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-------
-
-> 作者:[@mantchs](https://github.com/mantchs)
->
-> 欢迎大家加入讨论!共同完善此项目! -
diff --git a/README.md b/README.md
index a3e6afb..6ab3dcc 100644
--- a/README.md
+++ b/README.md
@@ -19,17 +19,17 @@
| 模块 | 章节 | 负责人(GitHub) | 联系QQ |
| -------- | ------------------------------------------------------------ | --------------------------------------- | --------- |
-| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression/1.Liner%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree/Desition%20Tree.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest/3.1%20Random%20Forest.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/4.%20SVM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | 5. 概率图模型(Probabilistic Graphical Model) | | |
-| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20Markov.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [5.3 主题模型(Topic Model)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/5.3%20Topic%20Model) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [6.最大期望算法(EM)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/6.%20EM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [7.聚类(Clustering)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/7.%20Clustering) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-
diff --git a/README.md b/README.md
index a3e6afb..6ab3dcc 100644
--- a/README.md
+++ b/README.md
@@ -19,17 +19,17 @@
| 模块 | 章节 | 负责人(GitHub) | 联系QQ |
| -------- | ------------------------------------------------------------ | --------------------------------------- | --------- |
-| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression/1.Liner%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree/Desition%20Tree.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest/3.1%20Random%20Forest.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/4.%20SVM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | 5. 概率图模型(Probabilistic Graphical Model) | | |
-| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20Markov.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [5.3 主题模型(Topic Model)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/5.3%20Topic%20Model) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [6.最大期望算法(EM)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/6.%20EM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [7.聚类(Clustering)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/7.%20Clustering) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
 diff --git a/Machine Learning/3.2 GBDT/3.2 GBDT.md b/Machine Learning/3.2 GBDT/3.2 GBDT.md
deleted file mode 100644
index 41d75f5..0000000
--- a/Machine Learning/3.2 GBDT/3.2 GBDT.md
+++ /dev/null
@@ -1,118 +0,0 @@
-## 目录
-- [1. 解释一下GBDT算法的过程](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#1-解释一下gbdt算法的过程)
- - [1.1 Boosting思想](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#11-boosting思想)
- - [1.2 GBDT原来是这么回事](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#12-gbdt原来是这么回事)
-- [2. 梯度提升和梯度下降的区别和联系是什么?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#2-梯度提升和梯度下降的区别和联系是什么)
-- [3. GBDT的优点和局限性有哪些?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#3-gbdt的优点和局限性有哪些)
- - [3.1 优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#31-优点)
- - [3.2 局限性](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#32-局限性)
-- [4. RF(随机森林)与GBDT之间的区别与联系](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#4-rf随机森林与gbdt之间的区别与联系)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-## 1. 解释一下GBDT算法的过程
-
-GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,使用的是**Boosting**的思想。
-
-### 1.1 Boosting思想
-
-Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
-
-Bagging与Boosting的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
-
-### 1.2 GBDT原来是这么回事
-
-GBDT的原理很简单,就是所有弱分类器的结果相加等于预测值,然后下一个弱分类器去拟合误差函数对预测值的残差(这个残差就是预测值与真实值之间的误差)。当然了,它里面的弱分类器的表现形式就是各棵树。
-
-举一个非常简单的例子,比如我今年30岁了,但计算机或者模型GBDT并不知道我今年多少岁,那GBDT咋办呢?
-
-- 它会在第一个弱分类器(或第一棵树中)随便用一个年龄比如20岁来拟合,然后发现误差有10岁;
-- 接下来在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
-- 接着在第三棵树中用3岁拟合剩下的差距,发现差距只有1岁了;
-- 最后在第四课树中用1岁拟合剩下的残差,完美。
-- 最终,四棵树的结论加起来,就是真实年龄30岁(实际工程中,gbdt是计算负梯度,用负梯度近似残差)。
-
-**为何gbdt可以用用负梯度近似残差呢?**
-
-回归任务下,GBDT 在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数,
-
-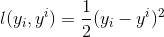
-
-那此时的负梯度是这样计算的
-
-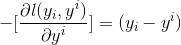
-
-所以,当损失函数选用均方损失函数是时,每一次拟合的值就是(真实值 - 当前模型预测的值),即残差。此时的变量是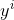,即“当前预测模型的值”,也就是对它求负梯度。
-
-**训练过程**
-
-简单起见,假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练,会得到如下图所示结果:
-
-
-
-现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点做多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图所示结果:
-
-
-
-在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两拨,每拨用平均年龄作为预测值。
-
-- 此时计算残差(残差的意思就是:A的实际值 - A的预测值 = A的残差),所以A的残差就是实际值14 - 预测值15 = 残差值-1。
-- 注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值。
-
-然后拿它们的残差-1、1、-1、1代替A B C D的原值,到第二棵树去学习,第二棵树只有两个值1和-1,直接分成两个节点,即A和C分在左边,B和D分在右边,经过计算(比如A,实际值-1 - 预测值-1 = 残差0,比如C,实际值-1 - 预测值-1 = 0),此时所有人的残差都是0。残差值都为0,相当于第二棵树的预测值和它们的实际值相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了,即每个人都得到了真实的预测值。
-
-换句话说,现在A,B,C,D的预测值都和真实年龄一致了。Perfect!
-
-- A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
-- B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
-- C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
-- D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
-
-所以,GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
-
-## 2. 梯度提升和梯度下降的区别和联系是什么?
-
-下表是梯度提升算法和梯度下降算法的对比情况。可以发现,两者都是在每 一轮迭代中,利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更 新,只不过在梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参 数的更新。而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函 数空间中,从而大大扩展了可以使用的模型种类。
-
-
-
-## 3. **GBDT**的优点和局限性有哪些?
-
-### 3.1 优点
-
-1. 预测阶段的计算速度快,树与树之间可并行化计算。
-2. 在分布稠密的数据集上,泛化能力和表达能力都很好,这使得GBDT在Kaggle的众多竞赛中,经常名列榜首。
-3. 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性,能够自动发现特征间的高阶关系。
-
-### 3.2 局限性
-
-1. GBDT在高维稀疏的数据集上,表现不如支持向量机或者神经网络。
-2. GBDT在处理文本分类特征问题上,相对其他模型的优势不如它在处理数值特征时明显。
-3. 训练过程需要串行训练,只能在决策树内部采用一些局部并行的手段提高训练速度。
-
-## 4. RF(随机森林)与GBDT之间的区别与联系
-
-**相同点**:
-
-- 都是由多棵树组成,最终的结果都是由多棵树一起决定。
-- RF和GBDT在使用CART树时,可以是分类树或者回归树。
-
-**不同点**:
-
-- 组成随机森林的树可以并行生成,而GBDT是串行生成
-- 随机森林的结果是多数表决表决的,而GBDT则是多棵树累加之和
-- 随机森林对异常值不敏感,而GBDT对异常值比较敏感
-- 随机森林是减少模型的方差,而GBDT是减少模型的偏差
-- 随机森林不需要进行特征归一化。而GBDT则需要进行特征归一化
-
-## 5. 代码实现
-
-GitHub:[https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!qq群号:【541954936】
diff --git a/Machine Learning/3.2 GBDT/3.2 GBDT.md b/Machine Learning/3.2 GBDT/3.2 GBDT.md
deleted file mode 100644
index 41d75f5..0000000
--- a/Machine Learning/3.2 GBDT/3.2 GBDT.md
+++ /dev/null
@@ -1,118 +0,0 @@
-## 目录
-- [1. 解释一下GBDT算法的过程](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#1-解释一下gbdt算法的过程)
- - [1.1 Boosting思想](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#11-boosting思想)
- - [1.2 GBDT原来是这么回事](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#12-gbdt原来是这么回事)
-- [2. 梯度提升和梯度下降的区别和联系是什么?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#2-梯度提升和梯度下降的区别和联系是什么)
-- [3. GBDT的优点和局限性有哪些?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#3-gbdt的优点和局限性有哪些)
- - [3.1 优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#31-优点)
- - [3.2 局限性](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#32-局限性)
-- [4. RF(随机森林)与GBDT之间的区别与联系](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.2%20GBDT#4-rf随机森林与gbdt之间的区别与联系)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-## 1. 解释一下GBDT算法的过程
-
-GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,使用的是**Boosting**的思想。
-
-### 1.1 Boosting思想
-
-Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
-
-Bagging与Boosting的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
-
-### 1.2 GBDT原来是这么回事
-
-GBDT的原理很简单,就是所有弱分类器的结果相加等于预测值,然后下一个弱分类器去拟合误差函数对预测值的残差(这个残差就是预测值与真实值之间的误差)。当然了,它里面的弱分类器的表现形式就是各棵树。
-
-举一个非常简单的例子,比如我今年30岁了,但计算机或者模型GBDT并不知道我今年多少岁,那GBDT咋办呢?
-
-- 它会在第一个弱分类器(或第一棵树中)随便用一个年龄比如20岁来拟合,然后发现误差有10岁;
-- 接下来在第二棵树中,用6岁去拟合剩下的损失,发现差距还有4岁;
-- 接着在第三棵树中用3岁拟合剩下的差距,发现差距只有1岁了;
-- 最后在第四课树中用1岁拟合剩下的残差,完美。
-- 最终,四棵树的结论加起来,就是真实年龄30岁(实际工程中,gbdt是计算负梯度,用负梯度近似残差)。
-
-**为何gbdt可以用用负梯度近似残差呢?**
-
-回归任务下,GBDT 在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数,
-
-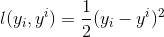
-
-那此时的负梯度是这样计算的
-
-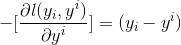
-
-所以,当损失函数选用均方损失函数是时,每一次拟合的值就是(真实值 - 当前模型预测的值),即残差。此时的变量是,即“当前预测模型的值”,也就是对它求负梯度。
-
-**训练过程**
-
-简单起见,假定训练集只有4个人:A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练,会得到如下图所示结果:
-
-
-
-现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点做多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图所示结果:
-
-
-
-在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为左右两拨,每拨用平均年龄作为预测值。
-
-- 此时计算残差(残差的意思就是:A的实际值 - A的预测值 = A的残差),所以A的残差就是实际值14 - 预测值15 = 残差值-1。
-- 注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值。
-
-然后拿它们的残差-1、1、-1、1代替A B C D的原值,到第二棵树去学习,第二棵树只有两个值1和-1,直接分成两个节点,即A和C分在左边,B和D分在右边,经过计算(比如A,实际值-1 - 预测值-1 = 残差0,比如C,实际值-1 - 预测值-1 = 0),此时所有人的残差都是0。残差值都为0,相当于第二棵树的预测值和它们的实际值相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了,即每个人都得到了真实的预测值。
-
-换句话说,现在A,B,C,D的预测值都和真实年龄一致了。Perfect!
-
-- A: 14岁高一学生,购物较少,经常问学长问题,预测年龄A = 15 – 1 = 14
-- B: 16岁高三学生,购物较少,经常被学弟问问题,预测年龄B = 15 + 1 = 16
-- C: 24岁应届毕业生,购物较多,经常问师兄问题,预测年龄C = 25 – 1 = 24
-- D: 26岁工作两年员工,购物较多,经常被师弟问问题,预测年龄D = 25 + 1 = 26
-
-所以,GBDT需要将多棵树的得分累加得到最终的预测得分,且每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差。
-
-## 2. 梯度提升和梯度下降的区别和联系是什么?
-
-下表是梯度提升算法和梯度下降算法的对比情况。可以发现,两者都是在每 一轮迭代中,利用损失函数相对于模型的负梯度方向的信息来对当前模型进行更 新,只不过在梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参 数的更新。而在梯度提升中,模型并不需要进行参数化表示,而是直接定义在函 数空间中,从而大大扩展了可以使用的模型种类。
-
-
-
-## 3. **GBDT**的优点和局限性有哪些?
-
-### 3.1 优点
-
-1. 预测阶段的计算速度快,树与树之间可并行化计算。
-2. 在分布稠密的数据集上,泛化能力和表达能力都很好,这使得GBDT在Kaggle的众多竞赛中,经常名列榜首。
-3. 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性,能够自动发现特征间的高阶关系。
-
-### 3.2 局限性
-
-1. GBDT在高维稀疏的数据集上,表现不如支持向量机或者神经网络。
-2. GBDT在处理文本分类特征问题上,相对其他模型的优势不如它在处理数值特征时明显。
-3. 训练过程需要串行训练,只能在决策树内部采用一些局部并行的手段提高训练速度。
-
-## 4. RF(随机森林)与GBDT之间的区别与联系
-
-**相同点**:
-
-- 都是由多棵树组成,最终的结果都是由多棵树一起决定。
-- RF和GBDT在使用CART树时,可以是分类树或者回归树。
-
-**不同点**:
-
-- 组成随机森林的树可以并行生成,而GBDT是串行生成
-- 随机森林的结果是多数表决表决的,而GBDT则是多棵树累加之和
-- 随机森林对异常值不敏感,而GBDT对异常值比较敏感
-- 随机森林是减少模型的方差,而GBDT是减少模型的偏差
-- 随机森林不需要进行特征归一化。而GBDT则需要进行特征归一化
-
-## 5. 代码实现
-
-GitHub:[https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/GBDT_demo.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!qq群号:【541954936】 -
-
-
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md b/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
deleted file mode 100644
index 99cc3fb..0000000
--- a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
+++ /dev/null
@@ -1,119 +0,0 @@
-## 目录
-- [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
- - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
- - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
- - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
- - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
-- [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
-- [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
-- [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-- [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
-
-## 1. 什么是XGBoost
-
-XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
-
-说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
-
-关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
-
-### 1.1 XGBoost树的定义
-
-先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
-
-
-
-就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
-
-
-
-恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
-
-事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
-
-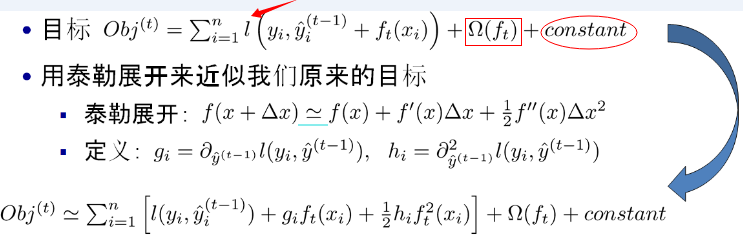
-
-其中:
-
-- 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
-- 红色方框所框起来的是正则项(包括L1正则、L2正则)
-- 红色圆圈所圈起来的为常数项
-- 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
-
-看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-XGBoost的**核心算法思想**不难,基本就是:
-
-1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
-2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
-3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
-
-显然,我们的目标是要使得树群的预测值尽量接近真实值,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
-
-
-
-那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
-
-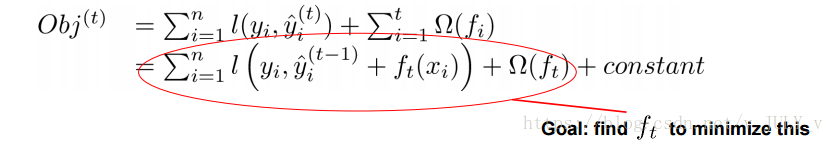
-
-实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
-
-### 1.2 正则项:树的复杂度
-
-XGBoost对树的复杂度包含了两个部分:
-
-- 一个是树里面叶子节点的个数T
-- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
-
-
-
-我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
-
-=\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
-
-正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
-
-### 1.3 树该怎么长
-
-很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
-
-不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
-
-总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
-
-### 1.4 如何停止树的循环生成
-
-凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
-
-1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
-2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
-3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
-
-## 2. XGBoost与GBDT有什么不同
-
-除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
-
-1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
-2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
-3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
-4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
-5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
-6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
-
-## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
-
-XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
-
-## 4. 代码实现
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-
-## 5. 参考文献
-
-[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
-
-
-
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md b/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
deleted file mode 100644
index 99cc3fb..0000000
--- a/Machine Learning/3.3 XGBoost/3.3 XGBoost.md
+++ /dev/null
@@ -1,119 +0,0 @@
-## 目录
-- [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
- - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
- - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
- - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
- - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
-- [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
-- [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
-- [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-- [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
-
-## 1. 什么是XGBoost
-
-XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
-
-说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
-
-关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
-
-### 1.1 XGBoost树的定义
-
-先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
-
-
-
-就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
-
-
-
-恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
-
-事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
-
-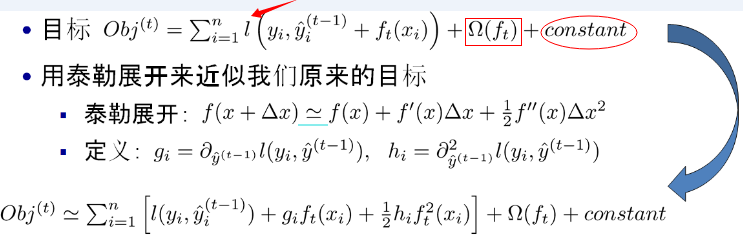
-
-其中:
-
-- 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
-- 红色方框所框起来的是正则项(包括L1正则、L2正则)
-- 红色圆圈所圈起来的为常数项
-- 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
-
-看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-XGBoost的**核心算法思想**不难,基本就是:
-
-1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
-2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
-3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
-
-显然,我们的目标是要使得树群的预测值尽量接近真实值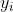,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
-
-
-
-那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
-
-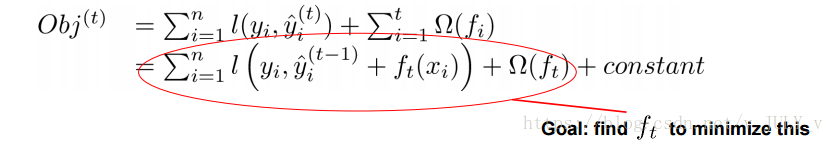
-
-实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
-
-### 1.2 正则项:树的复杂度
-
-XGBoost对树的复杂度包含了两个部分:
-
-- 一个是树里面叶子节点的个数T
-- 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
-
-
-
-我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
-
-=\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
-
-正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
-
-### 1.3 树该怎么长
-
-很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
-
-不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
-
-总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
-
-### 1.4 如何停止树的循环生成
-
-凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
-
-1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
-2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
-3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
-
-## 2. XGBoost与GBDT有什么不同
-
-除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
-
-1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
-2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
-3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
-4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
-5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
-6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
-
-## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
-
-XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
-
-## 4. 代码实现
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
-
-## 5. 参考文献
-
-[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 diff --git a/Machine Learning/3.3 XGBoost/README.md b/Machine Learning/3.3 XGBoost/README.md
index 99cc3fb..045129f 100644
--- a/Machine Learning/3.3 XGBoost/README.md
+++ b/Machine Learning/3.3 XGBoost/README.md
@@ -106,7 +106,7 @@ XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更
## 4. 代码实现
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/XGBoost.ipynb)
## 5. 参考文献
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb b/Machine Learning/3.3 XGBoost/XGBoost.ipynb
similarity index 100%
rename from Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb
rename to Machine Learning/3.3 XGBoost/XGBoost.ipynb
diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md b/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
deleted file mode 100644
index 2413005..0000000
--- a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
+++ /dev/null
@@ -1,86 +0,0 @@
-## 目录
-- [1. LightGBM是什么东东](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#1-lightgbm是什么东东)
- - [1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#11-lightgbm在哪些地方进行了优化----区别xgboost)
- - [1.2 Histogram算法](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#12-histogram算法)
- - [1.3 带深度限制的Leaf-wise的叶子生长策略](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#13-带深度限制的leaf-wise的叶子生长策略)
- - [1.4 直方图差加速](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#14-直方图差加速)
- - [1.5 直接支持类别特征](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#15-直接支持类别特征)
-- [2. LightGBM优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#2-lightgbm优点)
-- [3. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-## 1. LightGBM是什么东东
-
-不久前微软DMTK(分布式机器学习工具包)团队在GitHub上开源了性能超越其他boosting工具的LightGBM,在三天之内GitHub上被star了1000次,fork了200次。知乎上有近千人关注“如何看待微软开源的LightGBM?”问题,被评价为“速度惊人”,“非常有启发”,“支持分布式”,“代码清晰易懂”,“占用内存小”等。
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练。
-
-LightGBM在Higgs数据集上LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6,并且准确率也有提升。GBDT在每一次迭代的时候,都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据,普通的GBDT算法是不能满足其需求的。
-
-LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。
-
-### 1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?
-
-- 基于Histogram的决策树算法
-- 带深度限制的Leaf-wise的叶子生长策略
-- 直方图做差加速直接
-- 支持类别特征(Categorical Feature)
-- Cache命中率优化
-- 基于直方图的稀疏特征优化多线程优化。
-
-
-
-### 1.2 Histogram算法
-
-直方图算法的基本思想是先把连续的浮点特征值离散化成k个整数(其实又是分桶的思想,而这些桶称为bin,比如[0,0.1)→0, [0.1,0.3)→1),同时构造一个宽度为k的直方图。
-
-在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
-
-
-
-使用直方图算法有很多优点。首先,最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果,而且可以只保存特征离散化后的值,而这个值一般用8位整型存储就足够了,内存消耗可以降低为原来的1/8。然后在计算上的代价也大幅降低,预排序算法每遍历一个特征值就需要计算一次分裂的增益,而直方图算法只需要计算k次(k可以认为是常数),时间复杂度从O(#data*#feature)优化到O(k*#features)。
-
-### 1.3 带深度限制的Leaf-wise的叶子生长策略
-
-在XGBoost中,树是按层生长的,称为Level-wise tree growth,同一层的所有节点都做分裂,最后剪枝,如下图所示:
-
-
-
-Level-wise过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
-
-在Histogram算法之上,LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise)
-的决策树生长策略,而使用了带有深度限制的按叶子生长 (leaf-wise)算法。
-
-
-
-Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
-
-### 1.4 直方图差加速
-
-LightGBM另一个优化是Histogram(直方图)做差加速。一个容易观察到的现象:一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
-
-利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
-
-### 1.5 直接支持类别特征
-
-实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。据我们所知,LightGBM是第一个直接支持类别特征的GBDT工具。
-
-## 2. LightGBM优点
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有以下优点:
-
-- 更快的训练速度
-- 更低的内存消耗
-- 更好的准确率
-- 分布式支持,可以快速处理海量数据
-
-## 3. 代码实现
-
-为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
diff --git a/Machine Learning/3.3 XGBoost/README.md b/Machine Learning/3.3 XGBoost/README.md
index 99cc3fb..045129f 100644
--- a/Machine Learning/3.3 XGBoost/README.md
+++ b/Machine Learning/3.3 XGBoost/README.md
@@ -106,7 +106,7 @@ XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更
## 4. 代码实现
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/XGBoost.ipynb)
## 5. 参考文献
diff --git a/Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb b/Machine Learning/3.3 XGBoost/XGBoost.ipynb
similarity index 100%
rename from Machine Learning/3.3 XGBoost/3.3 XGBoost.ipynb
rename to Machine Learning/3.3 XGBoost/XGBoost.ipynb
diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md b/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
deleted file mode 100644
index 2413005..0000000
--- a/Machine Learning/3.4 LightGBM/3.4 LightGBM.md
+++ /dev/null
@@ -1,86 +0,0 @@
-## 目录
-- [1. LightGBM是什么东东](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#1-lightgbm是什么东东)
- - [1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#11-lightgbm在哪些地方进行了优化----区别xgboost)
- - [1.2 Histogram算法](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#12-histogram算法)
- - [1.3 带深度限制的Leaf-wise的叶子生长策略](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#13-带深度限制的leaf-wise的叶子生长策略)
- - [1.4 直方图差加速](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#14-直方图差加速)
- - [1.5 直接支持类别特征](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#15-直接支持类别特征)
-- [2. LightGBM优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#2-lightgbm优点)
-- [3. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-## 1. LightGBM是什么东东
-
-不久前微软DMTK(分布式机器学习工具包)团队在GitHub上开源了性能超越其他boosting工具的LightGBM,在三天之内GitHub上被star了1000次,fork了200次。知乎上有近千人关注“如何看待微软开源的LightGBM?”问题,被评价为“速度惊人”,“非常有启发”,“支持分布式”,“代码清晰易懂”,“占用内存小”等。
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练。
-
-LightGBM在Higgs数据集上LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6,并且准确率也有提升。GBDT在每一次迭代的时候,都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据,普通的GBDT算法是不能满足其需求的。
-
-LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。
-
-### 1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?
-
-- 基于Histogram的决策树算法
-- 带深度限制的Leaf-wise的叶子生长策略
-- 直方图做差加速直接
-- 支持类别特征(Categorical Feature)
-- Cache命中率优化
-- 基于直方图的稀疏特征优化多线程优化。
-
-
-
-### 1.2 Histogram算法
-
-直方图算法的基本思想是先把连续的浮点特征值离散化成k个整数(其实又是分桶的思想,而这些桶称为bin,比如[0,0.1)→0, [0.1,0.3)→1),同时构造一个宽度为k的直方图。
-
-在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
-
-
-
-使用直方图算法有很多优点。首先,最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果,而且可以只保存特征离散化后的值,而这个值一般用8位整型存储就足够了,内存消耗可以降低为原来的1/8。然后在计算上的代价也大幅降低,预排序算法每遍历一个特征值就需要计算一次分裂的增益,而直方图算法只需要计算k次(k可以认为是常数),时间复杂度从O(#data*#feature)优化到O(k*#features)。
-
-### 1.3 带深度限制的Leaf-wise的叶子生长策略
-
-在XGBoost中,树是按层生长的,称为Level-wise tree growth,同一层的所有节点都做分裂,最后剪枝,如下图所示:
-
-
-
-Level-wise过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
-
-在Histogram算法之上,LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise)
-的决策树生长策略,而使用了带有深度限制的按叶子生长 (leaf-wise)算法。
-
-
-
-Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
-
-### 1.4 直方图差加速
-
-LightGBM另一个优化是Histogram(直方图)做差加速。一个容易观察到的现象:一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
-
-利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
-
-### 1.5 直接支持类别特征
-
-实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。据我们所知,LightGBM是第一个直接支持类别特征的GBDT工具。
-
-## 2. LightGBM优点
-
-LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有以下优点:
-
-- 更快的训练速度
-- 更低的内存消耗
-- 更好的准确率
-- 分布式支持,可以快速处理海量数据
-
-## 3. 代码实现
-
-为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb b/Machine Learning/3.4 LightGBM/LightGBM.ipynb
similarity index 100%
rename from Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb
rename to Machine Learning/3.4 LightGBM/LightGBM.ipynb
diff --git a/Machine Learning/3.4 LightGBM/README.md b/Machine Learning/3.4 LightGBM/README.md
index 2413005..f468a5e 100644
--- a/Machine Learning/3.4 LightGBM/README.md
+++ b/Machine Learning/3.4 LightGBM/README.md
@@ -77,7 +77,7 @@ LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Micr
为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/LightGBM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/4. SVM/4. SVM.md b/Machine Learning/4. SVM/4. SVM.md
deleted file mode 100644
index 3b4faae..0000000
--- a/Machine Learning/4. SVM/4. SVM.md
+++ /dev/null
@@ -1,225 +0,0 @@
-## 目录
-- [1. 讲讲SVM](#1-讲讲svm)
- - [1.1 一个关于SVM的童话故事](#11-一个关于svm的童话故事)
- - [1.2 理解SVM:第一层](#12-理解svm第一层)
- - [1.3 深入SVM:第二层](#13-深入svm第二层)
- - [1.4 SVM的应用](#14-svm的应用)
-- [2. SVM的一些问题](#2-svm的一些问题)
-- [3. LR和SVM的联系与区别](#3-lr和svm的联系与区别)
-- [4. 线性分类器与非线性分类器的区别以及优劣](#4-线性分类器与非线性分类器的区别以及优劣)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 讲讲SVM
-
-### 1.1 一个关于SVM的童话故事
-
-支持向量机(Support Vector Machine,SVM)是众多监督学习方法中十分出色的一种,几乎所有讲述经典机器学习方法的教材都会介绍。关于SVM,流传着一个关于天使与魔鬼的故事。
-
-传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务。魔鬼又加入了更多的球。随着球的增多,似乎有的球不能再被原来的木棍正确分开,如下图所示。
-
-
-
-SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开。
-
-看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使一个新的挑战,如下图所示。
-
-
-
-
-
-按照这种球的摆法,世界上貌似没有一根木棒可以将它们 完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借 念力抓起一张纸片,插在了两类球的中间。从魔鬼的角度看这些 球,则像是被一条曲线完美的切开了。
-
-
-
-后来,“无聊”的科学家们把这些球称为“数据”,把木棍称为“分类面”,找到最 大间隔的木棒位置的过程称为“优化”,拍桌子让球飞到空中的念力叫“核映射”,在 空中分隔球的纸片称为“分类超平面”。这便是SVM的童话故事。
-
-### 1.2 理解SVM:第一层
-
-支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
-
-**线性分类器:**给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者0,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( wT中的T代表转置):
-
-
-
-这里可以查看我之前的逻辑回归章节回顾:[点击打开](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md)
-
-这个超平面可以用分类函数 =w^Tx+b)表示,当f(x) 等于0的时候,x便是位于超平面上的点,而f(x)大于0的点对应 y=1 的数据点,f(x)小于0的点对应y=-1的点,如下图所示:
-
-
-
-#### 1.2.1 函数间隔与几何间隔
-
-在超平面w*x+b=0确定的情况下,|w*x+b|能够表示点x到距离超平面的远近,而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了**函数间隔**(functional margin)的概念。
-
-函数间隔公式: =yf(x))
-
-而超平面(w,b)关于数据集T中所有样本点(xi,yi)的函数间隔最小值(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
-
-)
-
-但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),所以只有函数间隔还远远不够。
-
-**几何间隔**
-
-事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔(geometrical margin)的概念。假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x0 ,w 是垂直于超平面的一个向量,$\gamma$为样本x到超平面的距离,如下图所示:
-
-
-
-这里我直接给出几何间隔的公式,详细推到请查看博文:[点击进入](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-几何间隔: 
-
-从上述函数间隔和几何间隔的定义可以看出:几何间隔就是**函数间隔除以||w||**,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
-
-#### 1.2.2 最大间隔分类器的定义
-
-对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
-
-
-
-通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 =w^Tx+b)的值任意大,亦即函数间隔可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上了,使得在缩放w和b的时候几何间隔的值是不会改变的,它只随着超平面的变动而变动,因此,这是更加合适的一个间隔。换言之,这里要找的最大间隔分类超平面中的**“间隔”指的是几何间隔。**
-
-如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔,两条虚线间隔边界之间的距离等于2倍几何间隔,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足 =1),对于所有不是支持向量的点,则显然有 >1)。
-
-
-
-OK,到此为止,算是了解到了SVM的第一层,对于那些只关心怎么用SVM的朋友便已足够,不必再更进一层深究其更深的原理。
-
-#### 1.2.3 最大间隔损失函数Hinge loss
-
-SVM 求解使通过建立二次规划原始问题,引入拉格朗日乘子法,然后转换成对偶的形式去求解,这是一种理论非常充实的解法。这里换一种角度来思考,在机器学习领域,一般的做法是经验风险最小化 (empirical risk minimization,ERM),即构建假设函数(Hypothesis)为输入输出间的映射,然后采用损失函数来衡量模型的优劣。求得使损失最小化的模型即为最优的假设函数,采用不同的损失函数也会得到不同的机器学习算法。SVM采用的就是Hinge Loss,用于“最大间隔(max-margin)”分类。
-
-_j-(f(x_i,W)_{y_i}-\bigtriangleup)))
-
-- 对于训练集中的第i个数据xi
-- 在W下会有一个得分结果向量f(xi,W)
-- 第j类的得分为我们记作f(xi,W)j
-
-要理解这个公式,首先先看下面这张图片:
-
-
-
-1. 在生活中我们都会认为没有威胁的才是最好的,比如拿成绩来说,自己考了第一名99分,而第二名紧随其后98分,那么就会有不安全的感觉,就会认为那家伙随时都有可能超过我。如果第二名是85分,那就会感觉安全多了,第二名需要花费很大的力气才能赶上自己。拿这个例子套到上面这幅图也是一样的。
-2. 上面这幅图delta左边的红点是一个**安全警戒线**,什么意思呢?也就是说**预测错误得分**超过这个安全警戒线就会得到一个惩罚权重,让这个预测错误值退回到安全警戒线以外,这样才能够保证预测正确的结果具有唯一性。
-3. 对应到公式中, _j)就是错误分类的得分。后面一项就是 **正确得分 - delta = 安全警戒线值**,两项的差代表的就是惩罚权重,越接近正确得分,权重越大。当错误得分在警戒线以外时,两项相减得到负数,那么损失函数的最大值是0,也就是没有损失。
-4. 一直往复循环训练数据,直到最小化损失函数为止,也就找到了分类超平面。
-
-### 1.3 深入SVM:第二层
-
-#### 1.3.1 从线性可分到线性不可分
-
-接着考虑之前得到的目标函数(令函数间隔=1):
-
-\ge1,i=1,...,n)
-
-**转换为对偶问题**,解释一下什么是对偶问题,对偶问题是实质相同但从不同角度提出不同提法的一对问题。
-
-由于求 的最大值相当于求 的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,很明显,两者问题等价):
-
-\ge1,i=1,...,n)
-
-因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
-
-此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:**一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。**
-
-详细过程请参考文章末尾给出的参考链接。
-
-#### 1.3.2 核函数Kernel
-
-事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
-
-具体来说,**在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。**如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
-
-
-
-
-
-通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:**多项式核、高斯核、线性核。**
-
-读者可能还是没明白核函数到底是个什么东西?我再简要概括下,即以下三点:
-
-1. 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
-2. 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的。那咋办呢?
-3. 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,避免了直接在高维空间中的复杂计算。
-
-**如果数据中出现了离群点outliers,那么就可以使用松弛变量来解决。**
-
-#### 1.3.3 总结
-
-不准确的说,SVM它本质上即是一个分类方法,用 w^T+b 定义分类函数,于是求w、b,为寻最大间隔,引出1/2||w||^2,继而引入拉格朗日因子,化为对拉格朗日乘子a的求解(求解过程中会涉及到一系列最优化或凸二次规划等问题),如此,求w.b与求a等价,而a的求解可以用一种快速学习算法SMO,至于核函数,是为处理非线性情况,若直接映射到高维计算恐维度爆炸,故在低维计算,等效高维表现。
-
-OK,理解到这第二层,已经能满足绝大部分人一窥SVM原理的好奇心,针对于面试来说已经足够了。
-
-### 1.4 SVM的应用
-
-SVM在很多诸如**文本分类,图像分类,生物序列分析和生物数据挖掘,手写字符识别等领域有很多的应用**,但或许你并没强烈的意识到,SVM可以成功应用的领域远远超出现在已经在开发应用了的领域。
-
-## 2. SVM的一些问题
-
-1. 是否存在一组参数使SVM训练误差为0?
-
- 答:存在
-
-2. 训练误差为0的SVM分类器一定存在吗?
-
- 答:一定存在
-
-3. 加入松弛变量的SVM的训练误差可以为0吗?
-
- 答:使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由 于我们的优化目标改变了,并不再是使训练误差最小。
-
-4. **带核的SVM为什么能分类非线性问题?**
-
- 答:核函数的本质是两个函数的內积,通过核函数将其隐射到高维空间,在高维空间非线性问题转化为线性问题, SVM得到超平面是高维空间的线性分类平面。其分类结果也视为低维空间的非线性分类结果, 因而带核的SVM就能分类非线性问题。
-
-5. **如何选择核函数?**
-
- - 如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
- - 如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
- - 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。
-
-## 3. LR和SVM的联系与区别
-
-### 3.1 相同点
-
-- 都是线性分类器。本质上都是求一个最佳分类超平面。
-- 都是监督学习算法。
-- 都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有:KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
-
-### 3.2 不同点
-
-- LR是参数模型,svm是非参数模型,linear和rbf则是针对数据线性可分和不可分的区别;
-- 从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
-- SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
-- 逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
-- logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
-
-## 4. 线性分类器与非线性分类器的区别以及优劣
-
-线性和非线性是针对模型参数和输入特征来讲的;比如输入x,模型y=ax+ax^2 那么就是非线性模型,如果输入是x和X^2则模型是线性的。
-
-- 线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
-
- LR,贝叶斯分类,单层感知机、线性回归
-
-- 非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
-
- 决策树、RF、GBDT、多层感知机
-
-**SVM两种都有(看线性核还是高斯核)**
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-
-## 6. 参考文献
-
-[支持向量机通俗导论(理解SVM的三层境界)](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
diff --git a/Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb b/Machine Learning/3.4 LightGBM/LightGBM.ipynb
similarity index 100%
rename from Machine Learning/3.4 LightGBM/3.4 LightGBM.ipynb
rename to Machine Learning/3.4 LightGBM/LightGBM.ipynb
diff --git a/Machine Learning/3.4 LightGBM/README.md b/Machine Learning/3.4 LightGBM/README.md
index 2413005..f468a5e 100644
--- a/Machine Learning/3.4 LightGBM/README.md
+++ b/Machine Learning/3.4 LightGBM/README.md
@@ -77,7 +77,7 @@ LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Micr
为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
-GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
+GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/LightGBM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/4. SVM/4. SVM.md b/Machine Learning/4. SVM/4. SVM.md
deleted file mode 100644
index 3b4faae..0000000
--- a/Machine Learning/4. SVM/4. SVM.md
+++ /dev/null
@@ -1,225 +0,0 @@
-## 目录
-- [1. 讲讲SVM](#1-讲讲svm)
- - [1.1 一个关于SVM的童话故事](#11-一个关于svm的童话故事)
- - [1.2 理解SVM:第一层](#12-理解svm第一层)
- - [1.3 深入SVM:第二层](#13-深入svm第二层)
- - [1.4 SVM的应用](#14-svm的应用)
-- [2. SVM的一些问题](#2-svm的一些问题)
-- [3. LR和SVM的联系与区别](#3-lr和svm的联系与区别)
-- [4. 线性分类器与非线性分类器的区别以及优劣](#4-线性分类器与非线性分类器的区别以及优劣)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 讲讲SVM
-
-### 1.1 一个关于SVM的童话故事
-
-支持向量机(Support Vector Machine,SVM)是众多监督学习方法中十分出色的一种,几乎所有讲述经典机器学习方法的教材都会介绍。关于SVM,流传着一个关于天使与魔鬼的故事。
-
-传说魔鬼和天使玩了一个游戏,魔鬼在桌上放了两种颜色的球。魔鬼让天使用一根木棍将它们分开。这对天使来说,似乎太容易了。天使不假思索地一摆,便完成了任务。魔鬼又加入了更多的球。随着球的增多,似乎有的球不能再被原来的木棍正确分开,如下图所示。
-
-
-
-SVM实际上是在为天使找到木棒的最佳放置位置,使得两边的球都离分隔它们的木棒足够远。依照SVM为天使选择的木棒位置,魔鬼即使按刚才的方式继续加入新球,木棒也能很好地将两类不同的球分开。
-
-看到天使已经很好地解决了用木棒线性分球的问题,魔鬼又给了天使一个新的挑战,如下图所示。
-
-
-
-
-
-按照这种球的摆法,世界上貌似没有一根木棒可以将它们 完美分开。但天使毕竟有法力,他一拍桌子,便让这些球飞到了空中,然后凭借 念力抓起一张纸片,插在了两类球的中间。从魔鬼的角度看这些 球,则像是被一条曲线完美的切开了。
-
-
-
-后来,“无聊”的科学家们把这些球称为“数据”,把木棍称为“分类面”,找到最 大间隔的木棒位置的过程称为“优化”,拍桌子让球飞到空中的念力叫“核映射”,在 空中分隔球的纸片称为“分类超平面”。这便是SVM的童话故事。
-
-### 1.2 理解SVM:第一层
-
-支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
-
-**线性分类器:**给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者0,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( wT中的T代表转置):
-
-
-
-这里可以查看我之前的逻辑回归章节回顾:[点击打开](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md)
-
-这个超平面可以用分类函数 =w^Tx+b)表示,当f(x) 等于0的时候,x便是位于超平面上的点,而f(x)大于0的点对应 y=1 的数据点,f(x)小于0的点对应y=-1的点,如下图所示:
-
-
-
-#### 1.2.1 函数间隔与几何间隔
-
-在超平面w*x+b=0确定的情况下,|w*x+b|能够表示点x到距离超平面的远近,而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了**函数间隔**(functional margin)的概念。
-
-函数间隔公式: =yf(x))
-
-而超平面(w,b)关于数据集T中所有样本点(xi,yi)的函数间隔最小值(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
-
-)
-
-但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),所以只有函数间隔还远远不够。
-
-**几何间隔**
-
-事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离--几何间隔(geometrical margin)的概念。假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x0 ,w 是垂直于超平面的一个向量,$\gamma$为样本x到超平面的距离,如下图所示:
-
-
-
-这里我直接给出几何间隔的公式,详细推到请查看博文:[点击进入](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-几何间隔: 
-
-从上述函数间隔和几何间隔的定义可以看出:几何间隔就是**函数间隔除以||w||**,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
-
-#### 1.2.2 最大间隔分类器的定义
-
-对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
-
-
-
-通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 =w^Tx+b)的值任意大,亦即函数间隔可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上了,使得在缩放w和b的时候几何间隔的值是不会改变的,它只随着超平面的变动而变动,因此,这是更加合适的一个间隔。换言之,这里要找的最大间隔分类超平面中的**“间隔”指的是几何间隔。**
-
-如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔,两条虚线间隔边界之间的距离等于2倍几何间隔,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足 =1),对于所有不是支持向量的点,则显然有 >1)。
-
-
-
-OK,到此为止,算是了解到了SVM的第一层,对于那些只关心怎么用SVM的朋友便已足够,不必再更进一层深究其更深的原理。
-
-#### 1.2.3 最大间隔损失函数Hinge loss
-
-SVM 求解使通过建立二次规划原始问题,引入拉格朗日乘子法,然后转换成对偶的形式去求解,这是一种理论非常充实的解法。这里换一种角度来思考,在机器学习领域,一般的做法是经验风险最小化 (empirical risk minimization,ERM),即构建假设函数(Hypothesis)为输入输出间的映射,然后采用损失函数来衡量模型的优劣。求得使损失最小化的模型即为最优的假设函数,采用不同的损失函数也会得到不同的机器学习算法。SVM采用的就是Hinge Loss,用于“最大间隔(max-margin)”分类。
-
-_j-(f(x_i,W)_{y_i}-\bigtriangleup)))
-
-- 对于训练集中的第i个数据xi
-- 在W下会有一个得分结果向量f(xi,W)
-- 第j类的得分为我们记作f(xi,W)j
-
-要理解这个公式,首先先看下面这张图片:
-
-
-
-1. 在生活中我们都会认为没有威胁的才是最好的,比如拿成绩来说,自己考了第一名99分,而第二名紧随其后98分,那么就会有不安全的感觉,就会认为那家伙随时都有可能超过我。如果第二名是85分,那就会感觉安全多了,第二名需要花费很大的力气才能赶上自己。拿这个例子套到上面这幅图也是一样的。
-2. 上面这幅图delta左边的红点是一个**安全警戒线**,什么意思呢?也就是说**预测错误得分**超过这个安全警戒线就会得到一个惩罚权重,让这个预测错误值退回到安全警戒线以外,这样才能够保证预测正确的结果具有唯一性。
-3. 对应到公式中, _j)就是错误分类的得分。后面一项就是 **正确得分 - delta = 安全警戒线值**,两项的差代表的就是惩罚权重,越接近正确得分,权重越大。当错误得分在警戒线以外时,两项相减得到负数,那么损失函数的最大值是0,也就是没有损失。
-4. 一直往复循环训练数据,直到最小化损失函数为止,也就找到了分类超平面。
-
-### 1.3 深入SVM:第二层
-
-#### 1.3.1 从线性可分到线性不可分
-
-接着考虑之前得到的目标函数(令函数间隔=1):
-
-\ge1,i=1,...,n)
-
-**转换为对偶问题**,解释一下什么是对偶问题,对偶问题是实质相同但从不同角度提出不同提法的一对问题。
-
-由于求 的最大值相当于求 的最小值,所以上述目标函数等价于(w由分母变成分子,从而也有原来的max问题变为min问题,很明显,两者问题等价):
-
-\ge1,i=1,...,n)
-
-因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
-
-此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:**一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。**
-
-详细过程请参考文章末尾给出的参考链接。
-
-#### 1.3.2 核函数Kernel
-
-事实上,大部分时候数据并不是线性可分的,这个时候满足这样条件的超平面就根本不存在。在上文中,我们已经了解到了SVM处理线性可分的情况,那对于非线性的数据SVM咋处理呢?对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
-
-具体来说,**在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。**如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
-
-
-
-
-
-通常人们会从一些常用的核函数中选择(根据问题和数据的不同,选择不同的参数,实际上就是得到了不同的核函数),例如:**多项式核、高斯核、线性核。**
-
-读者可能还是没明白核函数到底是个什么东西?我再简要概括下,即以下三点:
-
-1. 实际中,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(映射到高维空间后,相关特征便被分开了,也就达到了分类的目的);
-2. 但进一步,如果凡是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到可怕的。那咋办呢?
-3. 此时,核函数就隆重登场了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,避免了直接在高维空间中的复杂计算。
-
-**如果数据中出现了离群点outliers,那么就可以使用松弛变量来解决。**
-
-#### 1.3.3 总结
-
-不准确的说,SVM它本质上即是一个分类方法,用 w^T+b 定义分类函数,于是求w、b,为寻最大间隔,引出1/2||w||^2,继而引入拉格朗日因子,化为对拉格朗日乘子a的求解(求解过程中会涉及到一系列最优化或凸二次规划等问题),如此,求w.b与求a等价,而a的求解可以用一种快速学习算法SMO,至于核函数,是为处理非线性情况,若直接映射到高维计算恐维度爆炸,故在低维计算,等效高维表现。
-
-OK,理解到这第二层,已经能满足绝大部分人一窥SVM原理的好奇心,针对于面试来说已经足够了。
-
-### 1.4 SVM的应用
-
-SVM在很多诸如**文本分类,图像分类,生物序列分析和生物数据挖掘,手写字符识别等领域有很多的应用**,但或许你并没强烈的意识到,SVM可以成功应用的领域远远超出现在已经在开发应用了的领域。
-
-## 2. SVM的一些问题
-
-1. 是否存在一组参数使SVM训练误差为0?
-
- 答:存在
-
-2. 训练误差为0的SVM分类器一定存在吗?
-
- 答:一定存在
-
-3. 加入松弛变量的SVM的训练误差可以为0吗?
-
- 答:使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由 于我们的优化目标改变了,并不再是使训练误差最小。
-
-4. **带核的SVM为什么能分类非线性问题?**
-
- 答:核函数的本质是两个函数的內积,通过核函数将其隐射到高维空间,在高维空间非线性问题转化为线性问题, SVM得到超平面是高维空间的线性分类平面。其分类结果也视为低维空间的非线性分类结果, 因而带核的SVM就能分类非线性问题。
-
-5. **如何选择核函数?**
-
- - 如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
- - 如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
- - 如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。
-
-## 3. LR和SVM的联系与区别
-
-### 3.1 相同点
-
-- 都是线性分类器。本质上都是求一个最佳分类超平面。
-- 都是监督学习算法。
-- 都是判别模型。判别模型不关心数据是怎么生成的,它只关心信号之间的差别,然后用差别来简单对给定的一个信号进行分类。常见的判别模型有:KNN、SVM、LR,常见的生成模型有:朴素贝叶斯,隐马尔可夫模型。
-
-### 3.2 不同点
-
-- LR是参数模型,svm是非参数模型,linear和rbf则是针对数据线性可分和不可分的区别;
-- 从目标函数来看,区别在于逻辑回归采用的是logistical loss,SVM采用的是hinge loss,这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
-- SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。
-- 逻辑回归相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些,SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。
-- logic 能做的 svm能做,但可能在准确率上有问题,svm能做的logic有的做不了。
-
-## 4. 线性分类器与非线性分类器的区别以及优劣
-
-线性和非线性是针对模型参数和输入特征来讲的;比如输入x,模型y=ax+ax^2 那么就是非线性模型,如果输入是x和X^2则模型是线性的。
-
-- 线性分类器可解释性好,计算复杂度较低,不足之处是模型的拟合效果相对弱些。
-
- LR,贝叶斯分类,单层感知机、线性回归
-
-- 非线性分类器效果拟合能力较强,不足之处是数据量不足容易过拟合、计算复杂度高、可解释性不好。
-
- 决策树、RF、GBDT、多层感知机
-
-**SVM两种都有(看线性核还是高斯核)**
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/4.%20SVM/news%20classification)
-
-## 6. 参考文献
-
-[支持向量机通俗导论(理解SVM的三层境界)](https://blog.csdn.net/v_july_v/article/details/7624837)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 -
diff --git a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md b/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
deleted file mode 100644
index 8d97b78..0000000
--- a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
+++ /dev/null
@@ -1,223 +0,0 @@
-## 目录
-- [1. 对概率图模型的理解](#1-对概率图模型的理解)
-- [2. 细数贝叶斯网络](#2-细数贝叶斯网络)
- - [2.1 频率派观点](#21-频率派观点)
- - [2.2 贝叶斯学派](#22-贝叶斯学派)
- - [2.3 贝叶斯定理](#23-贝叶斯定理)
- - [2.4 贝叶斯网络](#24-贝叶斯网络)
- - [2.5 朴素贝叶斯](#25-朴素贝叶斯)
-- [3. 基于贝叶斯的一些问题](#3-基于贝叶斯的一些问题)
-- [4. 生成式模型和判别式模型的区别](#4-生成式模型和判别式模型的区别)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 对概率图模型的理解
-
-概率图模型是用图来表示变量概率依赖关系的理论,结合概率论与图论的知识,利用图来表示与模型有关的变量的联合概率分布。由图灵奖获得者Pearl开发出来。
-
-如果用一个词来形容概率图模型(Probabilistic Graphical Model)的话,那就是“优雅”。对于一个实际问题,我们希望能够挖掘隐含在数据中的知识。概率图模型构建了这样一幅图,用观测结点表示观测到的数据,用隐含结点表示潜在的知识,用边来描述知识与数据的相互关系,**最后基于这样的关系图获得一个概率分布**,非常“优雅”地解决了问题。
-
-概率图中的节点分为隐含节点和观测节点,边分为有向边和无向边。从概率论的角度,节点对应于随机变量,边对应于随机变量的依赖或相关关系,其中**有向边表示单向的依赖,无向边表示相互依赖关系**。
-
-概率图模型分为**贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)**两大类。贝叶斯网络可以用一个有向图结构表示,马尔可夫网络可以表 示成一个无向图的网络结构。更详细地说,概率图模型包括了朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等,在机器学习的诸多场景中都有着广泛的应用。
-
-## 2. 细数贝叶斯网络
-
-### 2.1 频率派观点
-
-长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。而且概率虽然未知,但最起码是一个确定的值。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,而且不论你取了多少次,取得白球的**概率θ始终都是1/2**,即不随观察结果X 的变化而变化。
-
-这种**频率派**的观点长期统治着人们的观念,直到后来一个名叫Thomas Bayes的人物出现。
-
-### 2.2 贝叶斯学派
-
-托马斯·贝叶斯Thomas Bayes(1702-1763)在世时,并不为当时的人们所熟知,很少发表论文或出版著作,与当时学术界的人沟通交流也很少,用现在的话来说,贝叶斯就是活生生一民间学术“屌丝”,可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”,翻译过来则是:机遇理论中一个问题的解。你可能觉得我要说:这篇论文的发表随机产生轰动效应,从而奠定贝叶斯在学术史上的地位。
-
-
-
-这篇论文可以用上面的例子来说明,“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率θ是多少?”贝叶斯认为取得白球的概率是个不确定的值,因为其中含有机遇的成分。比如,一个朋友创业,你明明知道创业的结果就两种,即要么成功要么失败,但你依然会忍不住去估计他创业成功的几率有多大?你如果对他为人比较了解,而且有方法、思路清晰、有毅力、且能团结周围的人,你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式,便是**贝叶斯式的思考方式。**
-
-**先简单总结下频率派与贝叶斯派各自不同的思考方式:**
-
-- 频率派把需要推断的参数θ看做是固定的未知常数,即概率虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
-- 而贝叶斯派的观点则截然相反,他们认为参数是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数的分布。
-
-贝叶斯派既然把看做是一个随机变量,所以要计算的分布,便得事先知道的无条件分布,即在有样本之前(或观察到X之前),有着怎样的分布呢?
-
-比如往台球桌上扔一个球,这个球落会落在何处呢?如果是不偏不倚的把球抛出去,那么此球落在台球桌上的任一位置都有着相同的机会,即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为**先验分布,或着无条件分布**。
-
-其中,先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决,解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如,某工厂每天都要对产品进行质检,以评估产品的不合格率θ,经过一段时间后便会积累大量的历史资料,这些历史资料便是先验知识,有了这些先验知识,便在决定对一个产品是否需要每天质检时便有了依据,如果以往的历史资料显示,某产品的不合格率只有0.01%,便可视为信得过产品或免检产品,只每月抽检一两次,从而省去大量的人力物力。
-
-而**后验分布**π(θ|X)一般也认为是在给定样本X的情况下的θ条件分布,而使π(θ|X)达到最大的值θMD称为**最大后验估计**,类似于经典统计学中的**极大似然估计**。
-
-综合起来看,则好比是人类刚开始时对大自然只有少得可怜的先验知识,但随着不断观察、实验获得更多的样本、结果,使得人们对自然界的规律摸得越来越透彻。所以,贝叶斯方法既符合人们日常生活的思考方式,也符合人们认识自然的规律,经过不断的发展,最终占据统计学领域的半壁江山,与经典统计学分庭抗礼。
-
-### 2.3 贝叶斯定理
-
-**条件概率**(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
-
-
-
-比如上图,在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率:
-
-=\frac{P(A\cap_{.}B)}{P(B)})
-
-联合概率: 或者P(A,B))
-
-边缘概率(先验概率):P(A)或者P(B)
-
-### 2.4 贝叶斯网络
-
-贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model),是一种概率图模型,于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓朴结构是一个有向无环图(DAG)。
-
-
-
-贝叶斯网络的有向无环图中的节点表示随机变量 
-
-它们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。
-
-例如,假设节点E直接影响到节点H,即E→H,则用从E指向H的箭头建立结点E到结点H的有向弧(E,H),权值(即连接强度)用条件概率P(H|E)来表示,如下图所示:
-
-
-
-简言之,把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖,用圈表示随机变量(random variables),用箭头表示条件依赖(conditional dependencies)。
-
-此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
-
-=P(x_k|x_1,...,x_{k-1})...P(x_2|x_1)P(x_1))
-
-#### 2.4.1 贝叶斯网络的结构形式
-
-**1. head-to-head**
-
-
-
-依上图,所以有:P(a,b,c) = P(a)*P(b)*P(c|a,b)成立,即在c未知的条件下,a、b被阻断(blocked),是独立的,称之为head-to-head条件独立。
-
-**2. tail-to-tail**
-
-
-
-考虑c未知,跟c已知这两种情况:
-
-1. 在c未知的时候,有:P(a,b,c)=P(c)*P(a|c)*P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-2. 在c已知的时候,有:P(a,b|c)=P(a,b,c)/P(c),然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中,得到:P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c),即c已知时,a、b独立。
-
-**3. head-to-tail**
-
-
-
-还是分c未知跟c已知这两种情况:
-
-1. c未知时,有:P(a,b,c)=P(a)*P(c|a)*P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-
-2. c已知时,有:P(a,b|c)=P(a,b,c)/P(c),且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c),可化简得到:
-
- 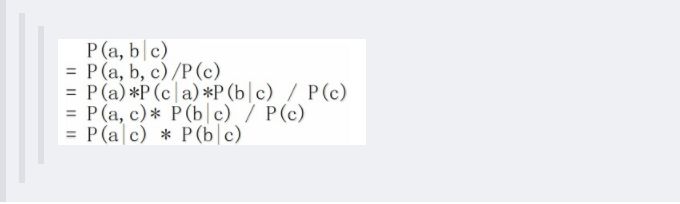
-
- 所以,在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
-
- 这个head-to-tail其实就是一个链式网络,如下图所示:
-
- 
-
- 根据之前对head-to-tail的讲解,我们已经知道,在xi给定的条件下,xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢?意味着:xi+1的分布状态只和xi有关,和其他变量条件独立。通俗点说,当前状态只跟上一状态有关,跟上上或上上之前的状态无关。这种顺次演变的随机过程,就叫做**马尔科夫链**(Markov chain)。对于马尔科夫链我们下一节再细讲。
-
-#### 2.4.2 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔科夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-### 2.5 朴素贝叶斯
-
-朴素贝叶斯(Naive Bayesian)是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯原理简单,也很容易实现,多用于文本分类,比如垃圾邮件过滤。**朴素贝叶斯可以看做是贝叶斯网络的特殊情况:即该网络中无边,各个节点都是独立的。 **
-
-朴素贝叶斯朴素在哪里呢? —— **两个假设**:
-
-- 一个特征出现的概率与其他特征(条件)独立;
-- 每个特征同等重要。
-
-贝叶斯公式如下:
-
-
-
-下面以一个例子来解释朴素贝叶斯,给定数据如下:
-
-
-
-现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
-
-这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!这里我们联系到朴素贝叶斯公式:
-
-
-
-我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,这三个变量都能通过统计的方法求得。
-
-等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
-
-**但是为什么需要假设特征之间相互独立呢?**
-
-1. 我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
-
- 36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
-
-2. 假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
-
-根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
-
-**朴素贝叶斯优点**:
-
-- 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
-- 分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
-
-**朴素贝叶斯缺点**:
-
-理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
-
-朴素贝叶斯模型(Naive Bayesian Model)的**朴素(Naive)的含义是"很简单很天真"**地假设样本特征彼此独立. 这个假设现实中基本上不存在, 但特征相关性很小的实际情况还是很多的, 所以这个模型仍然能够工作得很好。
-
-## 3. 基于贝叶斯的一些问题
-
-1. 解释朴素贝叶斯算法里面的先验概率、似然估计和边际似然估计?
- - **先验概率:**就是因变量(二分法)在数据集中的比例。这是在你没有任何进一步的信息的时候,是对分类能做出的最接近的猜测。
- - **似然估计:**似然估计是在其他一些变量的给定的情况下,一个观测值被分类为1的概率。例如,“FREE”这个词在以前的垃圾邮件使用的概率就是似然估计。
- - **边际似然估计:**边际似然估计就是,“FREE”这个词在任何消息中使用的概率。
-
-## 4. 生成式模型和判别式模型的区别
-
-- **判别模型**(discriminative model)通过求解条件概率分布P(y|x)或者直接计算y的值来预测y。
-
- 线性回归(Linear Regression),逻辑回归(Logistic Regression),支持向量机(SVM), 传统神经网络(Traditional Neural Networks),线性判别分析(Linear Discriminative Analysis),条件随机场(Conditional Random Field)
-
-- **生成模型**(generative model)通过对观测值和标注数据计算联合概率分布P(x,y)来达到判定估算y的目的。
-
- 朴素贝叶斯(Naive Bayes), 隐马尔科夫模型(HMM),贝叶斯网络(Bayesian Networks)和隐含狄利克雷分布(Latent Dirichlet Allocation)、混合高斯模型
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-
-## 6. 参考文献
-
-[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
-
diff --git a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md b/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
deleted file mode 100644
index 8d97b78..0000000
--- a/Machine Learning/5.1 Bayes Network/5.1 Bayes Network.md
+++ /dev/null
@@ -1,223 +0,0 @@
-## 目录
-- [1. 对概率图模型的理解](#1-对概率图模型的理解)
-- [2. 细数贝叶斯网络](#2-细数贝叶斯网络)
- - [2.1 频率派观点](#21-频率派观点)
- - [2.2 贝叶斯学派](#22-贝叶斯学派)
- - [2.3 贝叶斯定理](#23-贝叶斯定理)
- - [2.4 贝叶斯网络](#24-贝叶斯网络)
- - [2.5 朴素贝叶斯](#25-朴素贝叶斯)
-- [3. 基于贝叶斯的一些问题](#3-基于贝叶斯的一些问题)
-- [4. 生成式模型和判别式模型的区别](#4-生成式模型和判别式模型的区别)
-- [5. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-- [6. 参考文献](#6-参考文献)
-
-## 1. 对概率图模型的理解
-
-概率图模型是用图来表示变量概率依赖关系的理论,结合概率论与图论的知识,利用图来表示与模型有关的变量的联合概率分布。由图灵奖获得者Pearl开发出来。
-
-如果用一个词来形容概率图模型(Probabilistic Graphical Model)的话,那就是“优雅”。对于一个实际问题,我们希望能够挖掘隐含在数据中的知识。概率图模型构建了这样一幅图,用观测结点表示观测到的数据,用隐含结点表示潜在的知识,用边来描述知识与数据的相互关系,**最后基于这样的关系图获得一个概率分布**,非常“优雅”地解决了问题。
-
-概率图中的节点分为隐含节点和观测节点,边分为有向边和无向边。从概率论的角度,节点对应于随机变量,边对应于随机变量的依赖或相关关系,其中**有向边表示单向的依赖,无向边表示相互依赖关系**。
-
-概率图模型分为**贝叶斯网络(Bayesian Network)和马尔可夫网络(Markov Network)**两大类。贝叶斯网络可以用一个有向图结构表示,马尔可夫网络可以表 示成一个无向图的网络结构。更详细地说,概率图模型包括了朴素贝叶斯模型、最大熵模型、隐马尔可夫模型、条件随机场、主题模型等,在机器学习的诸多场景中都有着广泛的应用。
-
-## 2. 细数贝叶斯网络
-
-### 2.1 频率派观点
-
-长久以来,人们对一件事情发生或不发生的概率,只有固定的0和1,即要么发生,要么不发生,从来不会去考虑某件事情发生的概率有多大,不发生的概率又是多大。而且概率虽然未知,但最起码是一个确定的值。比如如果问那时的人们一个问题:“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率是多少?”他们会想都不用想,会立马告诉你,取出白球的概率就是1/2,要么取到白球,要么取不到白球,即θ只能有一个值,而且不论你取了多少次,取得白球的**概率θ始终都是1/2**,即不随观察结果X 的变化而变化。
-
-这种**频率派**的观点长期统治着人们的观念,直到后来一个名叫Thomas Bayes的人物出现。
-
-### 2.2 贝叶斯学派
-
-托马斯·贝叶斯Thomas Bayes(1702-1763)在世时,并不为当时的人们所熟知,很少发表论文或出版著作,与当时学术界的人沟通交流也很少,用现在的话来说,贝叶斯就是活生生一民间学术“屌丝”,可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”,翻译过来则是:机遇理论中一个问题的解。你可能觉得我要说:这篇论文的发表随机产生轰动效应,从而奠定贝叶斯在学术史上的地位。
-
-
-
-这篇论文可以用上面的例子来说明,“有一个袋子,里面装着若干个白球和黑球,请问从袋子中取得白球的概率θ是多少?”贝叶斯认为取得白球的概率是个不确定的值,因为其中含有机遇的成分。比如,一个朋友创业,你明明知道创业的结果就两种,即要么成功要么失败,但你依然会忍不住去估计他创业成功的几率有多大?你如果对他为人比较了解,而且有方法、思路清晰、有毅力、且能团结周围的人,你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式,便是**贝叶斯式的思考方式。**
-
-**先简单总结下频率派与贝叶斯派各自不同的思考方式:**
-
-- 频率派把需要推断的参数θ看做是固定的未知常数,即概率虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
-- 而贝叶斯派的观点则截然相反,他们认为参数是随机变量,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数的分布。
-
-贝叶斯派既然把看做是一个随机变量,所以要计算的分布,便得事先知道的无条件分布,即在有样本之前(或观察到X之前),有着怎样的分布呢?
-
-比如往台球桌上扔一个球,这个球落会落在何处呢?如果是不偏不倚的把球抛出去,那么此球落在台球桌上的任一位置都有着相同的机会,即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为**先验分布,或着无条件分布**。
-
-其中,先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决,解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如,某工厂每天都要对产品进行质检,以评估产品的不合格率θ,经过一段时间后便会积累大量的历史资料,这些历史资料便是先验知识,有了这些先验知识,便在决定对一个产品是否需要每天质检时便有了依据,如果以往的历史资料显示,某产品的不合格率只有0.01%,便可视为信得过产品或免检产品,只每月抽检一两次,从而省去大量的人力物力。
-
-而**后验分布**π(θ|X)一般也认为是在给定样本X的情况下的θ条件分布,而使π(θ|X)达到最大的值θMD称为**最大后验估计**,类似于经典统计学中的**极大似然估计**。
-
-综合起来看,则好比是人类刚开始时对大自然只有少得可怜的先验知识,但随着不断观察、实验获得更多的样本、结果,使得人们对自然界的规律摸得越来越透彻。所以,贝叶斯方法既符合人们日常生活的思考方式,也符合人们认识自然的规律,经过不断的发展,最终占据统计学领域的半壁江山,与经典统计学分庭抗礼。
-
-### 2.3 贝叶斯定理
-
-**条件概率**(又称后验概率)就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
-
-
-
-比如上图,在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于B,那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率:
-
-=\frac{P(A\cap_{.}B)}{P(B)})
-
-联合概率: 或者P(A,B))
-
-边缘概率(先验概率):P(A)或者P(B)
-
-### 2.4 贝叶斯网络
-
-贝叶斯网络(Bayesian network),又称信念网络(Belief Network),或有向无环图模型(directed acyclic graphical model),是一种概率图模型,于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型,其网络拓朴结构是一个有向无环图(DAG)。
-
-
-
-贝叶斯网络的有向无环图中的节点表示随机变量 
-
-它们可以是可观察到的变量,或隐变量、未知参数等。认为有因果关系(或非条件独立)的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(children)”,两节点就会产生一个条件概率值。
-
-例如,假设节点E直接影响到节点H,即E→H,则用从E指向H的箭头建立结点E到结点H的有向弧(E,H),权值(即连接强度)用条件概率P(H|E)来表示,如下图所示:
-
-
-
-简言之,把某个研究系统中涉及的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖,用圈表示随机变量(random variables),用箭头表示条件依赖(conditional dependencies)。
-
-此外,对于任意的随机变量,其联合概率可由各自的局部条件概率分布相乘而得出:
-
-=P(x_k|x_1,...,x_{k-1})...P(x_2|x_1)P(x_1))
-
-#### 2.4.1 贝叶斯网络的结构形式
-
-**1. head-to-head**
-
-
-
-依上图,所以有:P(a,b,c) = P(a)*P(b)*P(c|a,b)成立,即在c未知的条件下,a、b被阻断(blocked),是独立的,称之为head-to-head条件独立。
-
-**2. tail-to-tail**
-
-
-
-考虑c未知,跟c已知这两种情况:
-
-1. 在c未知的时候,有:P(a,b,c)=P(c)*P(a|c)*P(b|c),此时,没法得出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-2. 在c已知的时候,有:P(a,b|c)=P(a,b,c)/P(c),然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中,得到:P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c),即c已知时,a、b独立。
-
-**3. head-to-tail**
-
-
-
-还是分c未知跟c已知这两种情况:
-
-1. c未知时,有:P(a,b,c)=P(a)*P(c|a)*P(b|c),但无法推出P(a,b) = P(a)P(b),即c未知时,a、b不独立。
-
-2. c已知时,有:P(a,b|c)=P(a,b,c)/P(c),且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c),可化简得到:
-
- 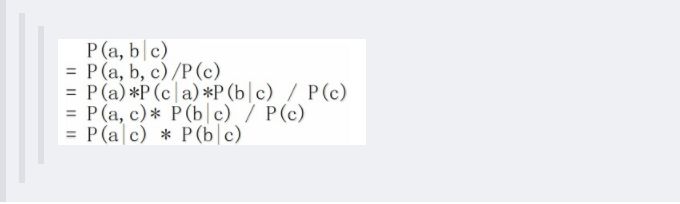
-
- 所以,在c给定的条件下,a,b被阻断(blocked),是独立的,称之为head-to-tail条件独立。
-
- 这个head-to-tail其实就是一个链式网络,如下图所示:
-
- 
-
- 根据之前对head-to-tail的讲解,我们已经知道,在xi给定的条件下,xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢?意味着:xi+1的分布状态只和xi有关,和其他变量条件独立。通俗点说,当前状态只跟上一状态有关,跟上上或上上之前的状态无关。这种顺次演变的随机过程,就叫做**马尔科夫链**(Markov chain)。对于马尔科夫链我们下一节再细讲。
-
-#### 2.4.2 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔科夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-### 2.5 朴素贝叶斯
-
-朴素贝叶斯(Naive Bayesian)是经典的机器学习算法之一,也是为数不多的基于概率论的分类算法。朴素贝叶斯原理简单,也很容易实现,多用于文本分类,比如垃圾邮件过滤。**朴素贝叶斯可以看做是贝叶斯网络的特殊情况:即该网络中无边,各个节点都是独立的。 **
-
-朴素贝叶斯朴素在哪里呢? —— **两个假设**:
-
-- 一个特征出现的概率与其他特征(条件)独立;
-- 每个特征同等重要。
-
-贝叶斯公式如下:
-
-
-
-下面以一个例子来解释朴素贝叶斯,给定数据如下:
-
-
-
-现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
-
-这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!这里我们联系到朴素贝叶斯公式:
-
-
-
-我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,这三个变量都能通过统计的方法求得。
-
-等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
-
-**但是为什么需要假设特征之间相互独立呢?**
-
-1. 我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
-
- 36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
-
-2. 假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
-
-根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
-
-**朴素贝叶斯优点**:
-
-- 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
-- 分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
-
-**朴素贝叶斯缺点**:
-
-理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
-
-朴素贝叶斯模型(Naive Bayesian Model)的**朴素(Naive)的含义是"很简单很天真"**地假设样本特征彼此独立. 这个假设现实中基本上不存在, 但特征相关性很小的实际情况还是很多的, 所以这个模型仍然能够工作得很好。
-
-## 3. 基于贝叶斯的一些问题
-
-1. 解释朴素贝叶斯算法里面的先验概率、似然估计和边际似然估计?
- - **先验概率:**就是因变量(二分法)在数据集中的比例。这是在你没有任何进一步的信息的时候,是对分类能做出的最接近的猜测。
- - **似然估计:**似然估计是在其他一些变量的给定的情况下,一个观测值被分类为1的概率。例如,“FREE”这个词在以前的垃圾邮件使用的概率就是似然估计。
- - **边际似然估计:**边际似然估计就是,“FREE”这个词在任何消息中使用的概率。
-
-## 4. 生成式模型和判别式模型的区别
-
-- **判别模型**(discriminative model)通过求解条件概率分布P(y|x)或者直接计算y的值来预测y。
-
- 线性回归(Linear Regression),逻辑回归(Logistic Regression),支持向量机(SVM), 传统神经网络(Traditional Neural Networks),线性判别分析(Linear Discriminative Analysis),条件随机场(Conditional Random Field)
-
-- **生成模型**(generative model)通过对观测值和标注数据计算联合概率分布P(x,y)来达到判定估算y的目的。
-
- 朴素贝叶斯(Naive Bayes), 隐马尔科夫模型(HMM),贝叶斯网络(Bayesian Networks)和隐含狄利克雷分布(Latent Dirichlet Allocation)、混合高斯模型
-
-## 5. 代码实现
-
-新闻分类 GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/Naive%20Bayes%20Classifier.ipynb)
-
-## 6. 参考文献
-
-[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 diff --git a/Machine Learning/5.2 Markov/5.2 Markov.md b/Machine Learning/5.2 Markov/5.2 Markov.md
deleted file mode 100644
index 1ac1a38..0000000
--- a/Machine Learning/5.2 Markov/5.2 Markov.md
+++ /dev/null
@@ -1,284 +0,0 @@
-## 目录
-
-- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
-- [2. 马尔可夫模型](#2-马尔可夫模型)
- - [2.1 马尔可夫过程](#21-马尔可夫过程)
-- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- - [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
-- [4. 马尔可夫网络](#4-马尔可夫网络)
- - [4.1 因子图](#41-因子图)
- - [4.2 马尔可夫网络](#42-马尔可夫网络)
-- [5. 条件随机场(CRF)](#5-条件随机场crf)
-- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
-- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
-
-相信大家都看过上一节我讲得贝叶斯网络,都明白了概率图模型是怎样构造的,如果现在还没明白,请看我上一节的总结:[贝叶斯网络](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md)
-
-这一节我们重点来讲一下马尔可夫,正如题目所示,看了会一脸蒙蔽,好在我们会一点一点的来解释上面的概念,请大家按照顺序往下看就会完全弄明白了,这里我给一个通俗易懂的定义,后面我们再来一个个详解。
-
-以下共分六点说明这些概念,分成条目只是方便边阅读边思考,这6点是依次递进的,不要跳跃着看。
-
-1. 将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个**网络**。
-2. 如果该网络是有向无环图,则这个网络称为**贝叶斯网络。**
-3. 如果这个图退化成线性链的方式,则得到**马尔可夫模型**;因为每个结点都是随机变量,将其看成各个时刻(或空间)的相关变化,以随机过程的视角,则可以看成是**马尔可夫过程**。
-4. 若上述网络是无向的,则是无向图模型,又称**马尔可夫随机场或者马尔可夫网络**。
-5. 如果在给定某些条件的前提下,研究这个马尔可夫随机场,则得到**条件随机场**。
-6. 如果使用条件随机场解决标注问题,并且进一步将条件随机场中的网络拓扑变成线性的,则得到**线性链条件随机场**。
-
-## 2. 马尔可夫模型
-
-### 2.1 马尔可夫过程
-
-马尔可夫过程(Markov process)是一类随机过程。它的原始模型马尔可夫链,由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性:在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变 (过去 )。例如森林中动物头数的变化构成——马尔可夫过程。在现实世界中,有很多过程都是马尔可夫过程,如液体中微粒所作的布朗运动、传染病受感染的人数、车站的候车人数等,都可视为马尔可夫过程。
-
-每个状态的转移只依赖于之前的n个状态,这个过程被称为1个n阶的模型,其中n是影响转移状态的数目。最简单的马尔可夫过程就是一阶过程,**每一个状态的转移只依赖于其之前的那一个状态**,这个也叫作**马尔可夫性质**。用数学表达式表示就是下面的样子:
-
-假设这个模型的每个状态都只依赖于之前的状态,这个假设被称为**马尔科夫假设**,这个假设可以大大的简化这个问题。显然,这个假设可能是一个非常糟糕的假设,导致很多重要的信息都丢失了。
-
-=P(X_{n+1}=x|X_n=x_n))
-
-假设天气服从**马尔可夫链**:
-
-
-
-从上面这幅图可以看出:
-
-- 假如今天是晴天,明天变成阴天的概率是0.1
-- 假如今天是晴天,明天任然是晴天的概率是0.9,和上一条概率之和为1,这也符合真实生活的情况。
-
-| | 晴 | 阴 |
-| ------ | ---- | ---- |
-| **晴** | 0.9 | 0,1 |
-| **阴** | 0.5 | 0.5 |
-
-由上表我们可以得到马尔可夫链的**状态转移矩阵**:
-
-
-
-因此,一阶马尔可夫过程定义了以下三个部分:
-
-- **状态**:晴天和阴天
-- **初始向量**:定义系统在时间为0的时候的状态的概率
-- **状态转移矩阵**:每种天气转换的概率
-
-马尔可夫模型(Markov Model)是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法。
-
-## 3. 隐马尔可夫模型(HMM)
-
-在某些情况下马尔科夫过程不足以描述我们希望发现的模式。回到之前那个天气的例子,一个隐居的人可能不能直观的观察到天气的情况,但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合,一个可以观察到的状态集合(海藻的状态)和一个隐藏的状态(天气的状况)。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。
-
-而这个算法就叫做**隐马尔可夫模型(HMM)**。
-
-
-
-隐马尔可夫模型 (Hidden Markov Model) 是一种统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。**它是结构最简单的动态贝叶斯网,这是一种著名的有向图模型**,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
-
-### 3.1 隐马尔可夫三大问题
-
-1. 给定模型,如何有效计算产生观测序列的概率?换言之,如何评估模型与观测序列之间的匹配程度?
-2. 给定模型和观测序列,如何找到与此观测序列最匹配的状态序列?换言之,如何根据观测序列推断出隐藏的模型状态?
-3. 给定观测序列,如何调整模型参数使得该序列出现的概率最大?换言之,如何训练模型使其能最好地描述观测数据?
-
-前两个问题是模式识别的问题:1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(**评价**);2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(**解码**)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型(**学习**)。
-
-对应的三大问题解法:
-
-1. 向前算法(Forward Algorithm)、向后算法(Backward Algorithm)
-2. 维特比算法(Viterbi Algorithm)
-3. 鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)
-
-下面我们以一个场景来说明这些问题的解法到底是什么?
-
-小明现在有三天的假期,他为了打发时间,可以在每一天中选择三件事情来做,这三件事情分别是散步、购物、打扫卫生(**对应着可观测序列**),可是在生活中我们所做的决定一般都受到天气的影响,可能晴天的时候想要去购物或者散步,可能下雨天的时候不想出门,留在家里打扫卫生。而天气(晴天、下雨天)就属于隐藏状态,用一幅概率图来表示这一马尔可夫过程:
-
-
-
-那么,我们提出三个问题,分别对应马尔可夫的三大问题:
-
-1. 已知整个模型,我观测到连续三天做的事情是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
-2. 同样知晓这个模型,同样是这三件事,我想猜,这三天的天气是怎么样的。
-3. 最复杂的,我只知道这三天做了这三件事儿,而其他什么信息都没有。我得建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况选择做某事的概率分布。
-
-下面我们就依据这个场景来一一解答这些问题。
-
-#### 3.1.1 第一个问题解法
-
-**遍历算法**:
-
-这个是最简单的算法了,假设第一天(T=1 时刻)是晴天,想要购物,那么就把图上的对应概率相乘就能够得到了。
-
-第二天(T=2 时刻)要做的事情,在第一天的概率基础上乘上第二天的概率,依次类推,最终得到这三天(T=3 时刻)所要做的事情的概率值,这就是遍历算法,简单而又粗暴。但问题是用遍历算法的复杂度会随着观测序列和隐藏状态的增加而成指数级增长。
-
-复杂度为: 
-
-于是就有了第二种算法
-
-**前向算法**:
-
-1. 假设第一天要购物,那么就计算出第一天购物的概率(包括晴天和雨天);假设第一天要散步,那么也计算出来,依次枚举。
-2. 假设前两天是购物和散步,也同样计算出这一种的概率;假设前两天是散步和打扫卫生,同样计算,枚举出前两天行为的概率。
-3. 第三步就是计算出前三天行为的概率。
-
-细心的读者已经发现了,第二步中要求的概率可以在第一步的基础上进行,同样的,第三步也会依赖于第二步的计算结果。那么这样做就能够**节省很多计算环节,类似于动态规划**。
-
-这种算法的复杂度为: 
-
-**后向算法**
-
-跟前向算法相反,我们知道总的概率肯定是1,那么B_t=1,也就是最后一个时刻的概率合为1,先计算前三天的各种可能的概率,在计算前两天、前一天的数据,跟前向算法相反的计算路径。
-
-#### 3.1.2 第二个问题解法
-
-**维特比算法(Viterbi)**
-
-> 说起安德鲁·维特比(Andrew Viterbi),通信行业之外的人可能知道他的并不多,不过通信行业的从业者大多知道以他的名字命名的维特比算法(ViterbiAlgorithm)。维特比算法是现代数字通信中最常用的算法,同时也是很多自然语言处理采用的解码算法。可以毫不夸张地讲,维特比是对我们今天的生活影响力最大的科学家之一,因为基于CDMA的3G移动通信标准主要就是他和厄文·雅各布(Irwin Mark Jacobs)创办的高通公司(Qualcomm)制定的,并且高通公司在4G时代依然引领移动通信的发展。
-
-维特比算法是一个特殊但应用最广的**动态规划算法**。利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图—篱笆网络(Lattice)的有向图最短路径问题而提出的。它之所以重要,是因为凡是使用隐含马尔可夫模型描述的问题都可以用它来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
-
-维特比算法一般用于模式识别,通过观测数据来反推出隐藏状态,下面一步步讲解这个算法。
-
-
-
-因为是要根据观测数据来反推,所以这里要进行一个假设,**假设这三天所做的行为分别是:散步、购物、打扫卫生,**那么我们要求的是这三天的天气(路径)分别是什么。
-
-1. 初始计算第一天下雨和第一天晴天去散步的概率值:
-
- )表示第一天下雨的概率
-
- 表示中间的状态(下雨)s概率
-
- )表示下雨并且散步的概率
-
- 表示下雨天到下雨天的概率
-
-=\pi_R*b_R(O_1=w)=0.6*0.1=0.06)
-
-=\pi_S*b_S(O_1=w)=0.4*0.6=0.24)
-
- 初始路径为:
-
- =Rainy)
-
- =Sunny)
-
-2. 计算第二天下雨和第二天晴天去购物的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-3. 计算第三天下雨和第三天晴天去打扫卫生的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-4. 比较每一步中 $\bigtriangleup$ 的概率大小,选取**最大值**并找到对应的路径,依次类推就能找到最有可能的**隐藏状态路径**。
-
- 第一天的概率最大值为 ,对应路径为Sunny,
-
- 第二天的概率最大值为 ,对应路径为Sunny,
-
- 第三天的概率最大值为 ,对应路径为Rainy。
-
-5. 合起来的路径就是Sunny->Sunny->Rainy,这就是我们所求。
-
-以上是比较通俗易懂的维特比算法,如果需要严谨表述,可以查看《数学之美》这本书的第26章,讲的就是维特比算法,很详细。附:《数学之美》下载地址,[点击下载](https://www.lanzous.com/i3ousch)
-
-#### 3.1.3 第三个问题解法
-
-鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法),详细讲解请见:[监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-
-## 4. 马尔可夫网络
-
-### 4.1 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-### 4.2 马尔可夫网络
-
-我们已经知道,有向图模型,又称作贝叶斯网络,但在有些情况下,强制对某些结点之间的边增加方向是不合适的。**使用没有方向的无向边,形成了无向图模型**(Undirected Graphical Model,UGM), 又被称为**马尔可夫随机场或者马尔可夫网络**(Markov Random Field, MRF or Markov network)。
-
-
-
-设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量,若随机变量Y构成一个无向图 G=(V,E)表示的马尔可夫随机场(MRF),则条件概率分布P(Y|X)称为**条件随机场**(Conditional Random Field, 简称CRF,后续新的博客中可能会阐述CRF)。如下图所示,便是一个线性链条件随机场的无向图模型:
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔可夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 5. 条件随机场(CRF)
-
-**一个通俗的例子**
-
-假设你有许多小明同学一天内不同时段的照片,从小明提裤子起床到脱裤子睡觉各个时间段都有(小明是照片控!)。现在的任务是对这些照片进行分类。比如有的照片是吃饭,那就给它打上吃饭的标签;有的照片是跑步时拍的,那就打上跑步的标签;有的照片是开会时拍的,那就打上开会的标签。问题来了,你准备怎么干?
-
-一个简单直观的办法就是,不管这些照片之间的时间顺序,想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据,训练出一个模型,直接根据照片的特征来分类。例如,如果照片是早上6:00拍的,且画面是黑暗的,那就给它打上睡觉的标签;如果照片上有车,那就给它打上开车的标签。
-
-乍一看可以!但实际上,由于我们忽略了这些照片之间的时间顺序这一重要信息,我们的分类器会有缺陷的。举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。
-
-所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它**相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!**这就有点类似于词性标注了,只不过把照片换成了句子而已,本质上是一样的。
-
-如同马尔可夫随机场,条件随机场为具有无向的[图模型](https://baike.baidu.com/item/图模型),图中的顶点代表随机变量,顶点间的连线代表随机变量间的相依关系,在条件随机场中,[随机变量](https://baike.baidu.com/item/随机变量)Y 的分布为条件机率,给定的观察值则为随机变量 X。下图就是一个线性连条件随机场。
-
-
-
-条件概率分布P(Y|X)称为**条件随机场**。
-
-## 6. EM算法、HMM、CRF的比较
-
-1. **EM算法**是用于含有隐变量模型的极大似然估计或者极大后验估计,有两步组成:E步,求期望(expectation);M步,求极大(maxmization)。本质上EM算法还是一个迭代算法,通过不断用上一代参数对隐变量的估计来对当前变量进行计算,直到收敛。注意:EM算法是对初值敏感的,而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法,也就是说**EM算法不能保证找到全局最优值**。对于EM的导出方法也应该掌握。
-
-2. **隐马尔可夫模型**是用于标注问题的生成模型。有几个参数(π,A,B):初始状态概率向量π,状态转移矩阵A,观测概率矩阵B。称为马尔科夫模型的三要素。马尔科夫三个基本问题:
-
- 概率计算问题:给定模型和观测序列,计算模型下观测序列输出的概率。–》前向后向算法
-
- 学习问题:已知观测序列,估计模型参数,即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。
-
- 预测问题:已知模型和观测序列,求解对应的状态序列。–》近似算法(贪心算法)和维比特算法(动态规划求最优路径)
-
-3. **条件随机场CRF**,给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场,而我们平时看到的大多是线性链条随机场,也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
-
-4. 之所以总把HMM和CRF进行比较,主要是因为CRF和HMM都利用了图的知识,但是CRF利用的是马尔科夫随机场(无向图),而HMM的基础是贝叶斯网络(有向图)。而且CRF也有:概率计算问题、学习问题和预测问题。大致计算方法和HMM类似,只不过不需要EM算法进行学习问题。
-
-5. **HMM和CRF对比:**其根本还是在于基本的理念不同,一个是生成模型,一个是判别模型,这也就导致了求解方式的不同。
-
-## 7. 参考文献
-
-1. [条件随机场的简单理解](https://blog.csdn.net/weixin_41911765/article/details/82465697)
-2. [如何轻松愉快地理解条件随机场(CRF)](https://blog.csdn.net/dcx_abc/article/details/78319246)
-3. [《数学之美》](https://www.lanzous.com/i3ousch)
-4. [监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-5. [从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 8. 词性标注代码实现
-
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】
diff --git a/Machine Learning/5.2 Markov/5.2 Markov.md b/Machine Learning/5.2 Markov/5.2 Markov.md
deleted file mode 100644
index 1ac1a38..0000000
--- a/Machine Learning/5.2 Markov/5.2 Markov.md
+++ /dev/null
@@ -1,284 +0,0 @@
-## 目录
-
-- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
-- [2. 马尔可夫模型](#2-马尔可夫模型)
- - [2.1 马尔可夫过程](#21-马尔可夫过程)
-- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- - [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
-- [4. 马尔可夫网络](#4-马尔可夫网络)
- - [4.1 因子图](#41-因子图)
- - [4.2 马尔可夫网络](#42-马尔可夫网络)
-- [5. 条件随机场(CRF)](#5-条件随机场crf)
-- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
-- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
-
-相信大家都看过上一节我讲得贝叶斯网络,都明白了概率图模型是怎样构造的,如果现在还没明白,请看我上一节的总结:[贝叶斯网络](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md)
-
-这一节我们重点来讲一下马尔可夫,正如题目所示,看了会一脸蒙蔽,好在我们会一点一点的来解释上面的概念,请大家按照顺序往下看就会完全弄明白了,这里我给一个通俗易懂的定义,后面我们再来一个个详解。
-
-以下共分六点说明这些概念,分成条目只是方便边阅读边思考,这6点是依次递进的,不要跳跃着看。
-
-1. 将随机变量作为结点,若两个随机变量相关或者不独立,则将二者连接一条边;若给定若干随机变量,则形成一个有向图,即构成一个**网络**。
-2. 如果该网络是有向无环图,则这个网络称为**贝叶斯网络。**
-3. 如果这个图退化成线性链的方式,则得到**马尔可夫模型**;因为每个结点都是随机变量,将其看成各个时刻(或空间)的相关变化,以随机过程的视角,则可以看成是**马尔可夫过程**。
-4. 若上述网络是无向的,则是无向图模型,又称**马尔可夫随机场或者马尔可夫网络**。
-5. 如果在给定某些条件的前提下,研究这个马尔可夫随机场,则得到**条件随机场**。
-6. 如果使用条件随机场解决标注问题,并且进一步将条件随机场中的网络拓扑变成线性的,则得到**线性链条件随机场**。
-
-## 2. 马尔可夫模型
-
-### 2.1 马尔可夫过程
-
-马尔可夫过程(Markov process)是一类随机过程。它的原始模型马尔可夫链,由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性:在已知目前状态(现在)的条件下,它未来的演变(将来)不依赖于它以往的演变 (过去 )。例如森林中动物头数的变化构成——马尔可夫过程。在现实世界中,有很多过程都是马尔可夫过程,如液体中微粒所作的布朗运动、传染病受感染的人数、车站的候车人数等,都可视为马尔可夫过程。
-
-每个状态的转移只依赖于之前的n个状态,这个过程被称为1个n阶的模型,其中n是影响转移状态的数目。最简单的马尔可夫过程就是一阶过程,**每一个状态的转移只依赖于其之前的那一个状态**,这个也叫作**马尔可夫性质**。用数学表达式表示就是下面的样子:
-
-假设这个模型的每个状态都只依赖于之前的状态,这个假设被称为**马尔科夫假设**,这个假设可以大大的简化这个问题。显然,这个假设可能是一个非常糟糕的假设,导致很多重要的信息都丢失了。
-
-=P(X_{n+1}=x|X_n=x_n))
-
-假设天气服从**马尔可夫链**:
-
-
-
-从上面这幅图可以看出:
-
-- 假如今天是晴天,明天变成阴天的概率是0.1
-- 假如今天是晴天,明天任然是晴天的概率是0.9,和上一条概率之和为1,这也符合真实生活的情况。
-
-| | 晴 | 阴 |
-| ------ | ---- | ---- |
-| **晴** | 0.9 | 0,1 |
-| **阴** | 0.5 | 0.5 |
-
-由上表我们可以得到马尔可夫链的**状态转移矩阵**:
-
-
-
-因此,一阶马尔可夫过程定义了以下三个部分:
-
-- **状态**:晴天和阴天
-- **初始向量**:定义系统在时间为0的时候的状态的概率
-- **状态转移矩阵**:每种天气转换的概率
-
-马尔可夫模型(Markov Model)是一种统计模型,广泛应用在语音识别,词性自动标注,音字转换,概率文法等各个自然语言处理等应用领域。经过长期发展,尤其是在语音识别中的成功应用,使它成为一种通用的统计工具。到目前为止,它一直被认为是实现快速精确的语音识别系统的最成功的方法。
-
-## 3. 隐马尔可夫模型(HMM)
-
-在某些情况下马尔科夫过程不足以描述我们希望发现的模式。回到之前那个天气的例子,一个隐居的人可能不能直观的观察到天气的情况,但是有一些海藻。民间的传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合,一个可以观察到的状态集合(海藻的状态)和一个隐藏的状态(天气的状况)。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。
-
-而这个算法就叫做**隐马尔可夫模型(HMM)**。
-
-
-
-隐马尔可夫模型 (Hidden Markov Model) 是一种统计模型,用来描述一个含有隐含未知参数的马尔可夫过程。**它是结构最简单的动态贝叶斯网,这是一种著名的有向图模型**,主要用于时序数据建模,在语音识别、自然语言处理等领域有广泛应用。
-
-### 3.1 隐马尔可夫三大问题
-
-1. 给定模型,如何有效计算产生观测序列的概率?换言之,如何评估模型与观测序列之间的匹配程度?
-2. 给定模型和观测序列,如何找到与此观测序列最匹配的状态序列?换言之,如何根据观测序列推断出隐藏的模型状态?
-3. 给定观测序列,如何调整模型参数使得该序列出现的概率最大?换言之,如何训练模型使其能最好地描述观测数据?
-
-前两个问题是模式识别的问题:1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(**评价**);2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(**解码**)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型(**学习**)。
-
-对应的三大问题解法:
-
-1. 向前算法(Forward Algorithm)、向后算法(Backward Algorithm)
-2. 维特比算法(Viterbi Algorithm)
-3. 鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)
-
-下面我们以一个场景来说明这些问题的解法到底是什么?
-
-小明现在有三天的假期,他为了打发时间,可以在每一天中选择三件事情来做,这三件事情分别是散步、购物、打扫卫生(**对应着可观测序列**),可是在生活中我们所做的决定一般都受到天气的影响,可能晴天的时候想要去购物或者散步,可能下雨天的时候不想出门,留在家里打扫卫生。而天气(晴天、下雨天)就属于隐藏状态,用一幅概率图来表示这一马尔可夫过程:
-
-
-
-那么,我们提出三个问题,分别对应马尔可夫的三大问题:
-
-1. 已知整个模型,我观测到连续三天做的事情是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
-2. 同样知晓这个模型,同样是这三件事,我想猜,这三天的天气是怎么样的。
-3. 最复杂的,我只知道这三天做了这三件事儿,而其他什么信息都没有。我得建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况选择做某事的概率分布。
-
-下面我们就依据这个场景来一一解答这些问题。
-
-#### 3.1.1 第一个问题解法
-
-**遍历算法**:
-
-这个是最简单的算法了,假设第一天(T=1 时刻)是晴天,想要购物,那么就把图上的对应概率相乘就能够得到了。
-
-第二天(T=2 时刻)要做的事情,在第一天的概率基础上乘上第二天的概率,依次类推,最终得到这三天(T=3 时刻)所要做的事情的概率值,这就是遍历算法,简单而又粗暴。但问题是用遍历算法的复杂度会随着观测序列和隐藏状态的增加而成指数级增长。
-
-复杂度为: 
-
-于是就有了第二种算法
-
-**前向算法**:
-
-1. 假设第一天要购物,那么就计算出第一天购物的概率(包括晴天和雨天);假设第一天要散步,那么也计算出来,依次枚举。
-2. 假设前两天是购物和散步,也同样计算出这一种的概率;假设前两天是散步和打扫卫生,同样计算,枚举出前两天行为的概率。
-3. 第三步就是计算出前三天行为的概率。
-
-细心的读者已经发现了,第二步中要求的概率可以在第一步的基础上进行,同样的,第三步也会依赖于第二步的计算结果。那么这样做就能够**节省很多计算环节,类似于动态规划**。
-
-这种算法的复杂度为: 
-
-**后向算法**
-
-跟前向算法相反,我们知道总的概率肯定是1,那么B_t=1,也就是最后一个时刻的概率合为1,先计算前三天的各种可能的概率,在计算前两天、前一天的数据,跟前向算法相反的计算路径。
-
-#### 3.1.2 第二个问题解法
-
-**维特比算法(Viterbi)**
-
-> 说起安德鲁·维特比(Andrew Viterbi),通信行业之外的人可能知道他的并不多,不过通信行业的从业者大多知道以他的名字命名的维特比算法(ViterbiAlgorithm)。维特比算法是现代数字通信中最常用的算法,同时也是很多自然语言处理采用的解码算法。可以毫不夸张地讲,维特比是对我们今天的生活影响力最大的科学家之一,因为基于CDMA的3G移动通信标准主要就是他和厄文·雅各布(Irwin Mark Jacobs)创办的高通公司(Qualcomm)制定的,并且高通公司在4G时代依然引领移动通信的发展。
-
-维特比算法是一个特殊但应用最广的**动态规划算法**。利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图—篱笆网络(Lattice)的有向图最短路径问题而提出的。它之所以重要,是因为凡是使用隐含马尔可夫模型描述的问题都可以用它来解码,包括今天的数字通信、语音识别、机器翻译、拼音转汉字、分词等。
-
-维特比算法一般用于模式识别,通过观测数据来反推出隐藏状态,下面一步步讲解这个算法。
-
-
-
-因为是要根据观测数据来反推,所以这里要进行一个假设,**假设这三天所做的行为分别是:散步、购物、打扫卫生,**那么我们要求的是这三天的天气(路径)分别是什么。
-
-1. 初始计算第一天下雨和第一天晴天去散步的概率值:
-
- )表示第一天下雨的概率
-
- 表示中间的状态(下雨)s概率
-
- )表示下雨并且散步的概率
-
- 表示下雨天到下雨天的概率
-
-=\pi_R*b_R(O_1=w)=0.6*0.1=0.06)
-
-=\pi_S*b_S(O_1=w)=0.4*0.6=0.24)
-
- 初始路径为:
-
- =Rainy)
-
- =Sunny)
-
-2. 计算第二天下雨和第二天晴天去购物的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-3. 计算第三天下雨和第三天晴天去打扫卫生的概率值:
-
- 
-
- 对应路径为:
-
- 
-
-4. 比较每一步中 $\bigtriangleup$ 的概率大小,选取**最大值**并找到对应的路径,依次类推就能找到最有可能的**隐藏状态路径**。
-
- 第一天的概率最大值为 ,对应路径为Sunny,
-
- 第二天的概率最大值为 ,对应路径为Sunny,
-
- 第三天的概率最大值为 ,对应路径为Rainy。
-
-5. 合起来的路径就是Sunny->Sunny->Rainy,这就是我们所求。
-
-以上是比较通俗易懂的维特比算法,如果需要严谨表述,可以查看《数学之美》这本书的第26章,讲的就是维特比算法,很详细。附:《数学之美》下载地址,[点击下载](https://www.lanzous.com/i3ousch)
-
-#### 3.1.3 第三个问题解法
-
-鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法),详细讲解请见:[监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-
-## 4. 马尔可夫网络
-
-### 4.1 因子图
-
-wikipedia上是这样定义因子图的:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)。
-
-通俗来讲,所谓因子图就是对函数进行因子分解得到的**一种概率图**。一般内含两种节点:变量节点和函数节点。我们知道,一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
-
-举个例子,现在有一个全局函数,其因式分解方程为:
-
-=f_A(x_1)f_B(x_2)f_C(x1,x2,x3)f_D(x_3,x_4)f_E(x_3,x_5))
-
-其中fA,fB,fC,fD,fE为各函数,表示变量之间的关系,可以是条件概率也可以是其他关系。其对应的因子图为:
-
-
-
-
-
-### 4.2 马尔可夫网络
-
-我们已经知道,有向图模型,又称作贝叶斯网络,但在有些情况下,强制对某些结点之间的边增加方向是不合适的。**使用没有方向的无向边,形成了无向图模型**(Undirected Graphical Model,UGM), 又被称为**马尔可夫随机场或者马尔可夫网络**(Markov Random Field, MRF or Markov network)。
-
-
-
-设X=(X1,X2…Xn)和Y=(Y1,Y2…Ym)都是联合随机变量,若随机变量Y构成一个无向图 G=(V,E)表示的马尔可夫随机场(MRF),则条件概率分布P(Y|X)称为**条件随机场**(Conditional Random Field, 简称CRF,后续新的博客中可能会阐述CRF)。如下图所示,便是一个线性链条件随机场的无向图模型:
-
-
-
-在概率图中,求某个变量的边缘分布是常见的问题。这问题有很多求解方法,其中之一就是把贝叶斯网络或马尔可夫随机场转换成因子图,然后用sum-product算法求解。换言之,基于因子图可以用**sum-product 算法**高效的求各个变量的边缘分布。
-
-详细的sum-product算法过程,请查看博文:[从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 5. 条件随机场(CRF)
-
-**一个通俗的例子**
-
-假设你有许多小明同学一天内不同时段的照片,从小明提裤子起床到脱裤子睡觉各个时间段都有(小明是照片控!)。现在的任务是对这些照片进行分类。比如有的照片是吃饭,那就给它打上吃饭的标签;有的照片是跑步时拍的,那就打上跑步的标签;有的照片是开会时拍的,那就打上开会的标签。问题来了,你准备怎么干?
-
-一个简单直观的办法就是,不管这些照片之间的时间顺序,想办法训练出一个多元分类器。就是用一些打好标签的照片作为训练数据,训练出一个模型,直接根据照片的特征来分类。例如,如果照片是早上6:00拍的,且画面是黑暗的,那就给它打上睡觉的标签;如果照片上有车,那就给它打上开车的标签。
-
-乍一看可以!但实际上,由于我们忽略了这些照片之间的时间顺序这一重要信息,我们的分类器会有缺陷的。举个例子,假如有一张小明闭着嘴的照片,怎么分类?显然难以直接判断,需要参考闭嘴之前的照片,如果之前的照片显示小明在吃饭,那这个闭嘴的照片很可能是小明在咀嚼食物准备下咽,可以给它打上吃饭的标签;如果之前的照片显示小明在唱歌,那这个闭嘴的照片很可能是小明唱歌瞬间的抓拍,可以给它打上唱歌的标签。
-
-所以,为了让我们的分类器能够有更好的表现,在为一张照片分类时,我们必须将与它**相邻的照片的标签信息考虑进来。这——就是条件随机场(CRF)大显身手的地方!**这就有点类似于词性标注了,只不过把照片换成了句子而已,本质上是一样的。
-
-如同马尔可夫随机场,条件随机场为具有无向的[图模型](https://baike.baidu.com/item/图模型),图中的顶点代表随机变量,顶点间的连线代表随机变量间的相依关系,在条件随机场中,[随机变量](https://baike.baidu.com/item/随机变量)Y 的分布为条件机率,给定的观察值则为随机变量 X。下图就是一个线性连条件随机场。
-
-
-
-条件概率分布P(Y|X)称为**条件随机场**。
-
-## 6. EM算法、HMM、CRF的比较
-
-1. **EM算法**是用于含有隐变量模型的极大似然估计或者极大后验估计,有两步组成:E步,求期望(expectation);M步,求极大(maxmization)。本质上EM算法还是一个迭代算法,通过不断用上一代参数对隐变量的估计来对当前变量进行计算,直到收敛。注意:EM算法是对初值敏感的,而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法,也就是说**EM算法不能保证找到全局最优值**。对于EM的导出方法也应该掌握。
-
-2. **隐马尔可夫模型**是用于标注问题的生成模型。有几个参数(π,A,B):初始状态概率向量π,状态转移矩阵A,观测概率矩阵B。称为马尔科夫模型的三要素。马尔科夫三个基本问题:
-
- 概率计算问题:给定模型和观测序列,计算模型下观测序列输出的概率。–》前向后向算法
-
- 学习问题:已知观测序列,估计模型参数,即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。
-
- 预测问题:已知模型和观测序列,求解对应的状态序列。–》近似算法(贪心算法)和维比特算法(动态规划求最优路径)
-
-3. **条件随机场CRF**,给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场,而我们平时看到的大多是线性链条随机场,也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。
-
-4. 之所以总把HMM和CRF进行比较,主要是因为CRF和HMM都利用了图的知识,但是CRF利用的是马尔科夫随机场(无向图),而HMM的基础是贝叶斯网络(有向图)。而且CRF也有:概率计算问题、学习问题和预测问题。大致计算方法和HMM类似,只不过不需要EM算法进行学习问题。
-
-5. **HMM和CRF对比:**其根本还是在于基本的理念不同,一个是生成模型,一个是判别模型,这也就导致了求解方式的不同。
-
-## 7. 参考文献
-
-1. [条件随机场的简单理解](https://blog.csdn.net/weixin_41911765/article/details/82465697)
-2. [如何轻松愉快地理解条件随机场(CRF)](https://blog.csdn.net/dcx_abc/article/details/78319246)
-3. [《数学之美》](https://www.lanzous.com/i3ousch)
-4. [监督学习方法与Baum-Welch算法](https://blog.csdn.net/qq_37334135/article/details/86302735)
-5. [从贝叶斯方法谈到贝叶斯网络](https://blog.csdn.net/v_july_v/article/details/40984699)
-
-## 8. 词性标注代码实现
-
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
-
-> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
->
-> GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
->
-> 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 -
diff --git a/Machine Learning/5.2 Markov/5.2 HMM.ipynb b/Machine Learning/5.2 Markov/HMM.ipynb
similarity index 100%
rename from Machine Learning/5.2 Markov/5.2 HMM.ipynb
rename to Machine Learning/5.2 Markov/HMM.ipynb
diff --git a/Machine Learning/5.2 Markov/README.md b/Machine Learning/5.2 Markov/README.md
index 1ac1a38..294f27b 100644
--- a/Machine Learning/5.2 Markov/README.md
+++ b/Machine Learning/5.2 Markov/README.md
@@ -1,17 +1,21 @@
## 目录
+- [目录](#目录)
- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
- [2. 马尔可夫模型](#2-马尔可夫模型)
- [2.1 马尔可夫过程](#21-马尔可夫过程)
- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
+ - [3.1.1 第一个问题解法](#311-第一个问题解法)
+ - [3.1.2 第二个问题解法](#312-第二个问题解法)
+ - [3.1.3 第三个问题解法](#313-第三个问题解法)
- [4. 马尔可夫网络](#4-马尔可夫网络)
- [4.1 因子图](#41-因子图)
- [4.2 马尔可夫网络](#42-马尔可夫网络)
- [5. 条件随机场(CRF)](#5-条件随机场crf)
- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+- [8. 词性标注代码实现](#8-词性标注代码实现)
## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
@@ -274,7 +278,7 @@ wikipedia上是这样定义因子图的:将一个具有多变量的全局函
## 8. 词性标注代码实现
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/HMM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/Liner Regression/1.Liner Regression.md b/Machine Learning/Liner Regression/1.Liner Regression.md
deleted file mode 100644
index 90ab3a7..0000000
--- a/Machine Learning/Liner Regression/1.Liner Regression.md
+++ /dev/null
@@ -1,111 +0,0 @@
-## 目录
-- [1.什么是线性回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#1什么是线性回归)
-- [2. 能够解决什么样的问题](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#2-能够解决什么样的问题)
-- [3. 一般表达式是什么](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#3-一般表达式是什么)
-- [4. 如何计算](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#4-如何计算)
-- [5. 过拟合、欠拟合如何解决](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#5-过拟合欠拟合如何解决)
- - [5.1 什么是L2正则化(岭回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#51-什么是l2正则化岭回归)
- - [5.2 什么场景下用L2正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#52-什么场景下用l2正则化)
- - [5.3 什么是L1正则化(Lasso回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#53-什么是l1正则化lasso回归)
- - [5.4 什么场景下使用L1正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#54-什么场景下使用l1正则化)
- - [5.5 什么是ElasticNet回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#55-什么是elasticnet回归)
- - [5.6 ElasticNet回归的使用场景](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#56--elasticnet回归的使用场景)
-- [6. 线性回归要求因变量服从正态分布?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#6-线性回归要求因变量服从正态分布)
-- [7. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-## 1.什么是线性回归
-
-- 线性:两个变量之间的关系**是**一次函数关系的——图象**是直线**,叫做线性。
-- 非线性:两个变量之间的关系**不是**一次函数关系的——图象**不是直线**,叫做非线性。
-- 回归:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算**回归到真实值**,这就是回归的由来。
-
-## 2. 能够解决什么样的问题
-
-对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如:对房价的预测、判断信用评价、电影票房预估等。
-
-## 3. 一般表达式是什么
-
-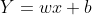
-
-w叫做x的系数,b叫做偏置项。
-
-## 4. 如何计算
-
-### 4.1 Loss Function--MSE
-
-^2)
-
-利用**梯度下降法**找到最小值点,也就是最小误差,最后把 w 和 b 给求出来。
-
-## 5. 过拟合、欠拟合如何解决
-
-使用正则化项,也就是给loss function加上一个参数项,正则化项有**L1正则化、L2正则化、ElasticNet**。加入这个正则化项好处:
-
-- 控制参数幅度,不让模型“无法无天”。
-- 限制参数搜索空间
-- 解决欠拟合与过拟合的问题。
-
-### 5.1 什么是L2正则化(岭回归)
-
-方程:
-
-
-
-表示上面的 loss function ,在loss function的基础上加入w参数的平方和乘以  ,假设:
-
-)
-
-回忆以前学过的单位元的方程:
-
-
-
-正和L2正则化项一样,此时我们的任务变成在L约束下求出J取最小值的解。求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-L表示为图中的黑色圆形,随着梯度下降法的不断逼近,与圆第一次产生交点,而这个交点很难出现在坐标轴上。这就说明了L2正则化不容易得到稀疏矩阵,同时为了求出损失函数的最小值,使得w1和w2无限接近于0,达到防止过拟合的问题。
-
-### 5.2 什么场景下用L2正则化
-
-只要数据线性相关,用LinearRegression拟合的不是很好,**需要正则化**,可以考虑使用岭回归(L2), 如何输入特征的维度很高,而且是稀疏线性关系的话, 岭回归就不太合适,考虑使用Lasso回归。
-
-### 5.3 什么是L1正则化(Lasso回归)
-
-L1正则化与L2正则化的区别在于惩罚项的不同:
-
-)
-
-求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-惩罚项表示为图中的黑色棱形,随着梯度下降法的不断逼近,与棱形第一次产生交点,而这个交点很容易出现在坐标轴上。**这就说明了L1正则化容易得到稀疏矩阵。**
-
-### 5.4 什么场景下使用L1正则化
-
-**L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0**,从而增强模型的泛化能力 。对于高的特征数据,尤其是线性关系是稀疏的,就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征,那么L1正则化(Lasso回归)更是首选了。
-
-### 5.5 什么是ElasticNet回归
-
-**ElasticNet综合了L1正则化项和L2正则化项**,以下是它的公式:
-
-^2+\lambda\sum_{j=1}^{n}\theta_j^2]+\lambda\sum_{j=1}^{n}|\theta|))
-
-### 5.6 ElasticNet回归的使用场景
-
-ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候,可以考虑使用ElasticNet回归来综合,得到比较好的结果。
-
-## 6. 线性回归要求因变量服从正态分布?
-
-我们假设线性回归的噪声服从均值为0的正态分布。 当噪声符合正态分布N(0,delta^2)时,因变量则符合正态分布N(ax(i)+b,delta^2),其中预测函数y=ax(i)+b。这个结论可以由正态分布的概率密度函数得到。也就是说当噪声符合正态分布时,其因变量必然也符合正态分布。
-
-在用线性回归模型拟合数据之前,首先要求数据应符合或近似符合正态分布,否则得到的拟合函数不正确。
-
-## 7. [代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-------
-
-> 作者:[@mantchs](https://github.com/mantchs)
->
-> 欢迎大家加入讨论!共同完善此项目!
-
diff --git a/Machine Learning/5.2 Markov/5.2 HMM.ipynb b/Machine Learning/5.2 Markov/HMM.ipynb
similarity index 100%
rename from Machine Learning/5.2 Markov/5.2 HMM.ipynb
rename to Machine Learning/5.2 Markov/HMM.ipynb
diff --git a/Machine Learning/5.2 Markov/README.md b/Machine Learning/5.2 Markov/README.md
index 1ac1a38..294f27b 100644
--- a/Machine Learning/5.2 Markov/README.md
+++ b/Machine Learning/5.2 Markov/README.md
@@ -1,17 +1,21 @@
## 目录
+- [目录](#目录)
- [1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别](#1-马尔可夫网络马尔可夫模型马尔可夫过程贝叶斯网络的区别)
- [2. 马尔可夫模型](#2-马尔可夫模型)
- [2.1 马尔可夫过程](#21-马尔可夫过程)
- [3. 隐马尔可夫模型(HMM)](#3-隐马尔可夫模型hmm)
- [3.1 隐马尔可夫三大问题](#31-隐马尔可夫三大问题)
+ - [3.1.1 第一个问题解法](#311-第一个问题解法)
+ - [3.1.2 第二个问题解法](#312-第二个问题解法)
+ - [3.1.3 第三个问题解法](#313-第三个问题解法)
- [4. 马尔可夫网络](#4-马尔可夫网络)
- [4.1 因子图](#41-因子图)
- [4.2 马尔可夫网络](#42-马尔可夫网络)
- [5. 条件随机场(CRF)](#5-条件随机场crf)
- [6. EM算法、HMM、CRF的比较](#6-em算法hmmcrf的比较)
- [7. 参考文献](#7-参考文献)
-- [8. 词性标注代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+- [8. 词性标注代码实现](#8-词性标注代码实现)
## 1. 马尔可夫网络、马尔可夫模型、马尔可夫过程、贝叶斯网络的区别
@@ -274,7 +278,7 @@ wikipedia上是这样定义因子图的:将一个具有多变量的全局函
## 8. 词性标注代码实现
-HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20HMM.ipynb)
+HMM词性标注,GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/HMM.ipynb)
> 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
>
diff --git a/Machine Learning/Liner Regression/1.Liner Regression.md b/Machine Learning/Liner Regression/1.Liner Regression.md
deleted file mode 100644
index 90ab3a7..0000000
--- a/Machine Learning/Liner Regression/1.Liner Regression.md
+++ /dev/null
@@ -1,111 +0,0 @@
-## 目录
-- [1.什么是线性回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#1什么是线性回归)
-- [2. 能够解决什么样的问题](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#2-能够解决什么样的问题)
-- [3. 一般表达式是什么](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#3-一般表达式是什么)
-- [4. 如何计算](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#4-如何计算)
-- [5. 过拟合、欠拟合如何解决](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#5-过拟合欠拟合如何解决)
- - [5.1 什么是L2正则化(岭回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#51-什么是l2正则化岭回归)
- - [5.2 什么场景下用L2正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#52-什么场景下用l2正则化)
- - [5.3 什么是L1正则化(Lasso回归)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#53-什么是l1正则化lasso回归)
- - [5.4 什么场景下使用L1正则化](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#54-什么场景下使用l1正则化)
- - [5.5 什么是ElasticNet回归](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#55-什么是elasticnet回归)
- - [5.6 ElasticNet回归的使用场景](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#56--elasticnet回归的使用场景)
-- [6. 线性回归要求因变量服从正态分布?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression#6-线性回归要求因变量服从正态分布)
-- [7. 代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-## 1.什么是线性回归
-
-- 线性:两个变量之间的关系**是**一次函数关系的——图象**是直线**,叫做线性。
-- 非线性:两个变量之间的关系**不是**一次函数关系的——图象**不是直线**,叫做非线性。
-- 回归:人们在测量事物的时候因为客观条件所限,求得的都是测量值,而不是事物真实的值,为了能够得到真实值,无限次的进行测量,最后通过这些测量数据计算**回归到真实值**,这就是回归的由来。
-
-## 2. 能够解决什么样的问题
-
-对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如:对房价的预测、判断信用评价、电影票房预估等。
-
-## 3. 一般表达式是什么
-
-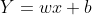
-
-w叫做x的系数,b叫做偏置项。
-
-## 4. 如何计算
-
-### 4.1 Loss Function--MSE
-
-^2)
-
-利用**梯度下降法**找到最小值点,也就是最小误差,最后把 w 和 b 给求出来。
-
-## 5. 过拟合、欠拟合如何解决
-
-使用正则化项,也就是给loss function加上一个参数项,正则化项有**L1正则化、L2正则化、ElasticNet**。加入这个正则化项好处:
-
-- 控制参数幅度,不让模型“无法无天”。
-- 限制参数搜索空间
-- 解决欠拟合与过拟合的问题。
-
-### 5.1 什么是L2正则化(岭回归)
-
-方程:
-
-
-
-表示上面的 loss function ,在loss function的基础上加入w参数的平方和乘以  ,假设:
-
-)
-
-回忆以前学过的单位元的方程:
-
-
-
-正和L2正则化项一样,此时我们的任务变成在L约束下求出J取最小值的解。求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-L表示为图中的黑色圆形,随着梯度下降法的不断逼近,与圆第一次产生交点,而这个交点很难出现在坐标轴上。这就说明了L2正则化不容易得到稀疏矩阵,同时为了求出损失函数的最小值,使得w1和w2无限接近于0,达到防止过拟合的问题。
-
-### 5.2 什么场景下用L2正则化
-
-只要数据线性相关,用LinearRegression拟合的不是很好,**需要正则化**,可以考虑使用岭回归(L2), 如何输入特征的维度很高,而且是稀疏线性关系的话, 岭回归就不太合适,考虑使用Lasso回归。
-
-### 5.3 什么是L1正则化(Lasso回归)
-
-L1正则化与L2正则化的区别在于惩罚项的不同:
-
-)
-
-求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图:
-
-
-
-惩罚项表示为图中的黑色棱形,随着梯度下降法的不断逼近,与棱形第一次产生交点,而这个交点很容易出现在坐标轴上。**这就说明了L1正则化容易得到稀疏矩阵。**
-
-### 5.4 什么场景下使用L1正则化
-
-**L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0**,从而增强模型的泛化能力 。对于高的特征数据,尤其是线性关系是稀疏的,就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征,那么L1正则化(Lasso回归)更是首选了。
-
-### 5.5 什么是ElasticNet回归
-
-**ElasticNet综合了L1正则化项和L2正则化项**,以下是它的公式:
-
-^2+\lambda\sum_{j=1}^{n}\theta_j^2]+\lambda\sum_{j=1}^{n}|\theta|))
-
-### 5.6 ElasticNet回归的使用场景
-
-ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候,可以考虑使用ElasticNet回归来综合,得到比较好的结果。
-
-## 6. 线性回归要求因变量服从正态分布?
-
-我们假设线性回归的噪声服从均值为0的正态分布。 当噪声符合正态分布N(0,delta^2)时,因变量则符合正态分布N(ax(i)+b,delta^2),其中预测函数y=ax(i)+b。这个结论可以由正态分布的概率密度函数得到。也就是说当噪声符合正态分布时,其因变量必然也符合正态分布。
-
-在用线性回归模型拟合数据之前,首先要求数据应符合或近似符合正态分布,否则得到的拟合函数不正确。
-
-## 7. [代码实现](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/Liner%20Regression/demo)
-
-------
-
-> 作者:[@mantchs](https://github.com/mantchs)
->
-> 欢迎大家加入讨论!共同完善此项目! -
diff --git a/README.md b/README.md
index a3e6afb..6ab3dcc 100644
--- a/README.md
+++ b/README.md
@@ -19,17 +19,17 @@
| 模块 | 章节 | 负责人(GitHub) | 联系QQ |
| -------- | ------------------------------------------------------------ | --------------------------------------- | --------- |
-| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression/1.Liner%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree/Desition%20Tree.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest/3.1%20Random%20Forest.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/4.%20SVM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | 5. 概率图模型(Probabilistic Graphical Model) | | |
-| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20Markov.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [5.3 主题模型(Topic Model)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/5.3%20Topic%20Model) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [6.最大期望算法(EM)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/6.%20EM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [7.聚类(Clustering)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/7.%20Clustering) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-
diff --git a/README.md b/README.md
index a3e6afb..6ab3dcc 100644
--- a/README.md
+++ b/README.md
@@ -19,17 +19,17 @@
| 模块 | 章节 | 负责人(GitHub) | 联系QQ |
| -------- | ------------------------------------------------------------ | --------------------------------------- | --------- |
-| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression/1.Liner%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression/2.Logistics%20Regression.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree/Desition%20Tree.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest/3.1%20Random%20Forest.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/4.%20SVM.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [1. 线性回归(Liner Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/Liner%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [2. 逻辑回归(Logistics Regression)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/2.Logistics%20Regression) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3. 决策树(Desision Tree)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.Desition%20Tree) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.1 随机森林(Random Forest)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.1%20Random%20Forest) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.2 梯度提升决策树(GBDT)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.3 XGBoost](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [3.4 LightGBM](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [4. 支持向量机(SVM)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/4.%20SVM/) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | 5. 概率图模型(Probabilistic Graphical Model) | | |
-| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network/5.1%20Bayes%20Network.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
-| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov/5.2%20Markov.md) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.1 贝叶斯网络(Bayesian Network)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.1%20Bayes%20Network) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
+| 机器学习 | [5.2 马尔科夫(Markov)](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/5.2%20Markov) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [5.3 主题模型(Topic Model)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/5.3%20Topic%20Model) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [6.最大期望算法(EM)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/6.%20EM) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |
| 机器学习 | [7.聚类(Clustering)](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/7.%20Clustering) | [@mantchs](https://github.com/NLP-LOVE) | 448966528 |