图形学 - 关于透视矫正插值那些事 - 知乎 (zhihu.com)
矫正透视投影插值及属性插值详解 - 知乎 (zhihu.com)
屏幕空间的插值不一定与原三维空间的插值保持线性关系。但是两者之间存在某种联系。事实上，屏幕空间上的“属性”和原空间z 分量的商是线性的：
$$\frac{attr_0}{z_0}=\alpha\frac{attr_1}{z_1}+\beta\frac{attr_2}{z_2}+\gamma\frac{attr_3}{z_3}$$
可以这么简单理解：3 维点在右乘透视投影变换矩阵时整个系统仍然是线性的，而让整个系统失去线性性质的操作是透视除法——通过除以 w 分量找到齐次坐标系下对应的 3 维点。
因此可以这么说：在原空间保持线性性质的属性，除以 z，才能在屏幕空间上保持线性性质；相反的，在屏幕空间上保持线性性质的属性，乘以 z，才能在原空间上保持线性性质。
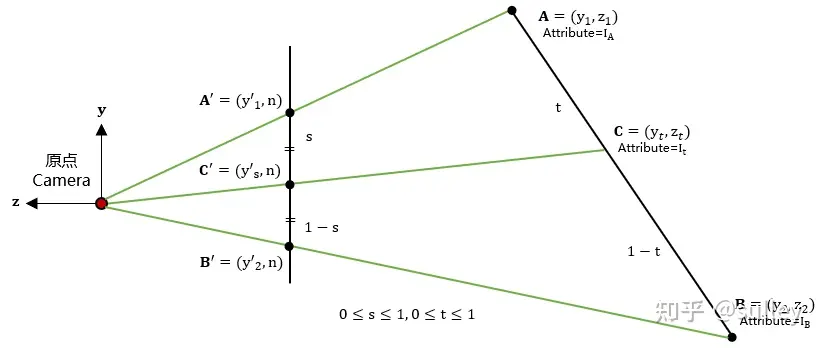我们的目标是找到原空间和屏幕空间插值权重的关系，先在 2 维空间中推导，然后推广到 3 维空间。
那么假设原空间中的两个点 A 和 B，它们使用插值权重 t 得到的新点称为 C，显然 C 位于 AB 线段上：
$$A=[x_1,y_1,z_1]^T\quad B=[x_2,y_2,z_2]^T$$
$$C=(1-t)*A+(t)*B=\begin{bmatrix} (1 - t) x_1 + t x_2\(1 - t) y_1 + t y_2\(1 - t) z_1 + t z_2 \end{bmatrix}$$
它们对应的齐次坐标为：
$$A=[x_1,y_1,z_1,1]^T\quad B=[x_2,y_2,z_2,1]^T$$
$$C=(1-t)*A+(t)*B=\begin{bmatrix} (1 - t) x_1 + t x_2\(1 - t) y_1 + t y_2\(1 - t) z_1 + t z_2\1 \end{bmatrix}$$
透视变换矩阵为，这里的 n 和 f 分别是近平面距离和远平面距离：
$$M=\begin{bmatrix} n&0&0&0\0&n&0&0\0&0&n+f&-nf\0&0&1&0 \end{bmatrix}$$
接下来对 ABC 点做透视投影变换，称变换后的新点为 A‘B’C‘：
$$A'=M\cdot A=\begin{bmatrix} n x_1\ n y_1\ -nf + (f + n) z_1\ z_1 \end{bmatrix}$$
$$B'=M\cdot B=\begin{bmatrix} n x_2\ n y_2\ -nf + (f + n) z_2\ z_2 \end{bmatrix}$$
$$
C'=M\cdot C=\begin{bmatrix} n ((1 - t) x_1 + t x_2)\ n ((1 - t) y_1 +
t y_2)\ -nf + (f + n) ((1 - t) z_1 + t z_2)\ (1 - t) z_1 + t z_2 \end{bmatrix}
$$
接下来使用透视除法找到它们对应的笛卡尔坐标下的点：
$$A'=\begin{bmatrix} (n x_1)/z_1\ (n y_1)/z_1\ (-nf + (f + n) z_1)/z_1\ 1 \end{bmatrix}$$
$$B'=\begin{bmatrix} (n x_2)/z_2\ (n y_2)/z_2\ (-nf + (f + n) z_2)/z_2\ 1 \end{bmatrix}$$
$$
C'=\begin{bmatrix} (n ((1 - t) x_1 + t x_2))/((1 - t) z_1 +
t z_2)\ (n ((1 - t) y_1 + t y_2))/((1 - t) z_1 +
t z_2)\ n+f-\frac{nf}{(1 - t) z_1 + t z_2} \ 1 \end{bmatrix}
$$
在屏幕空间上 A’B‘C’应当仍然保持着线性的关系，只不过比例应该和原空间中不一样了。这里假设插值的权为 s。另外，顶点满足线性关系的同时的，它的分量也应当满足线性关系，这里取坐标的第 3 维度：
$$C'=(1-s)A'+(s)B'$$
$$n+f-\frac{nf}{(1 - t) z_1 + t z_2}=(1-s)\left( \frac{-nf + (f + n) z_1}{z_1} \right)+(s)\left( \frac{-nf + (f + n) z_2}{z_2} \right)$$
这里我使用 Mathematica 软件帮我求解这个方程：
解得 t：
$$t(s)=\frac{sz_1}{z_2+a(z_1-z_2)}\tag{1}$$
得到原空间上的插值比例后，首先试试求出插值在原空间中的真实 z 轴坐标吧（z 轴分量也是 C 点的属性之一，事实上 C 点的坐标、光照强度、纹理 uv 都可以成为被插值的属性）。思路上很简单，使用原空间的两点 A 和 B，利用 t 为权值插值：
$$z_3=(1-t)z_1+(t)z_2\quad and \quad t(s)=\frac{sz_1}{z_2+a(z_1-z_2)}$$
解得：
$$z_3=\frac{z_1z_2}{(1-s)z_2+sz_1}=\frac{1}{\frac{1-s}{z_1}+\frac{s}{z_2}}$$
接下来考虑一些真正的属性，比如光照强度 I（同样的我们将(1)式带入）：
$$I_3=(1-t)I_1+(t)I_2=z_3\left( (1-s) \frac{I_1}{z_1}+(s) \frac{I_2}{z_2} \right)$$
有没有发现什么规律？
$$\frac{I_3}{z_3}=(1-s) \frac{I_1}{z_1}+(s) \frac{I_2}{z_2}$$
这说明”属性与原空间 z 分量的商呈线性关系“。有了这个公式之后，我们就可以随心所欲的根据插值原理求出自己想要的属性了。
这样的插值在 3 维空间中则是：
$$\frac{attr_0}{z_0}=\alpha\frac{attr_1}{z_1}+\beta\frac{attr_2}{z_2}+\gamma\frac{attr_3}{z_3}\quad and \quad \alpha+\beta+\gamma=1$$
另外，插值点在原空间的 z 分量我们也是可以求的：
$$z_0=\frac{1}{\frac{\alpha}{z_1}+ \frac{\beta}{z_2}+ \frac{\gamma}{z_3}}\quad and \quad \alpha+\beta+\gamma=1$$
事实上，在经过透视投影变换和透视除法之后 z 分量被映射到一个反比例函数的空间：
$$z\to (n+f)- \frac{nf}{z}$$
在这个空间中，z 不再是线性的，而$\frac{1}{z}$才是线性的，因此，插值点在原空间的 z 分量我们也可以这么写：
$$\frac{1}{z_0}=\alpha\frac{1}{z_1}+\beta\frac{1}{z_2}+\gamma\frac{1}{z_3} \quad and \quad \alpha+\beta+\gamma=1$$
解得 t：