Hermes (Electro-Magnetically Rapidly Exploring Trees)
Introduction:
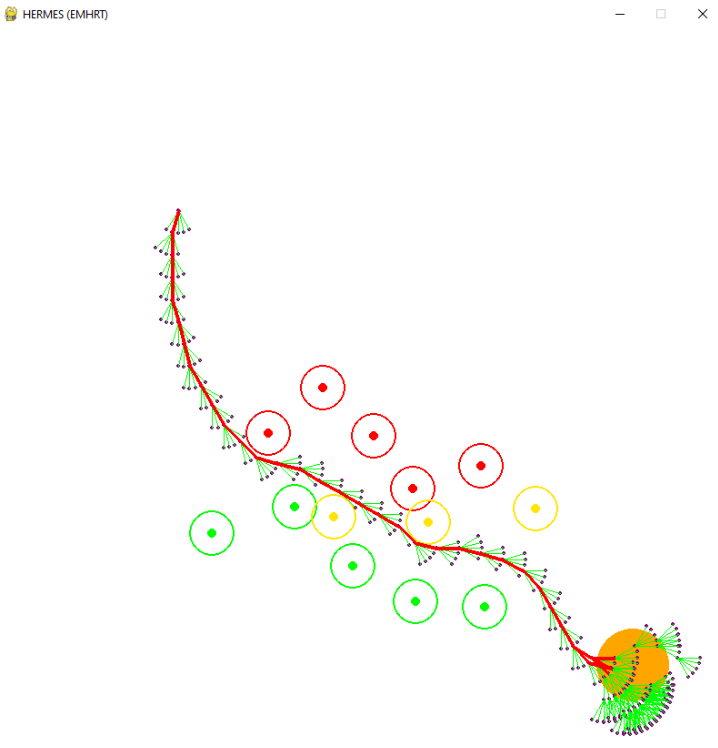
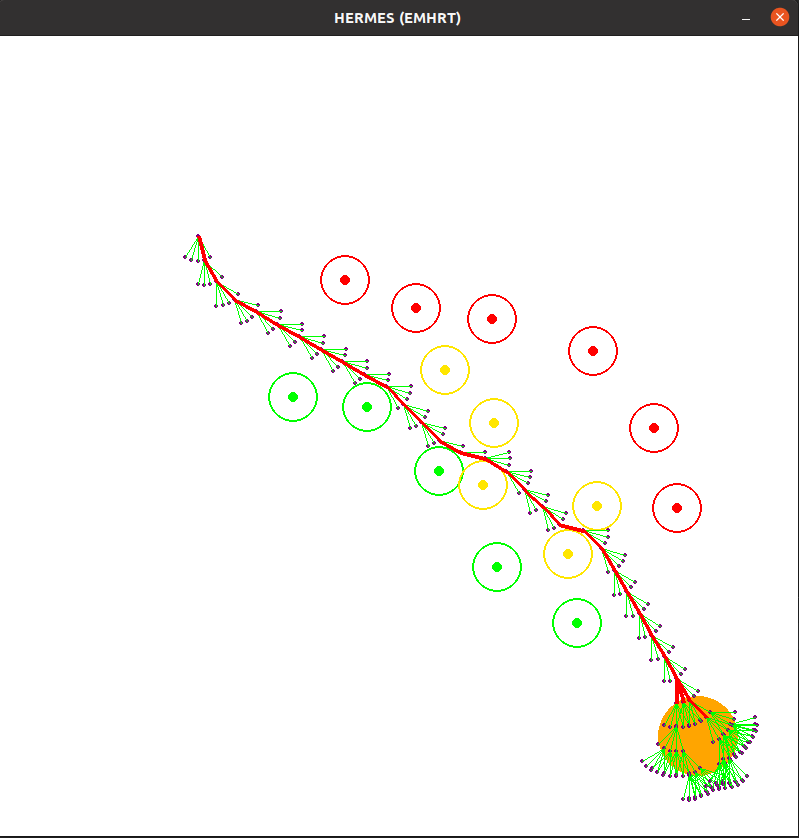
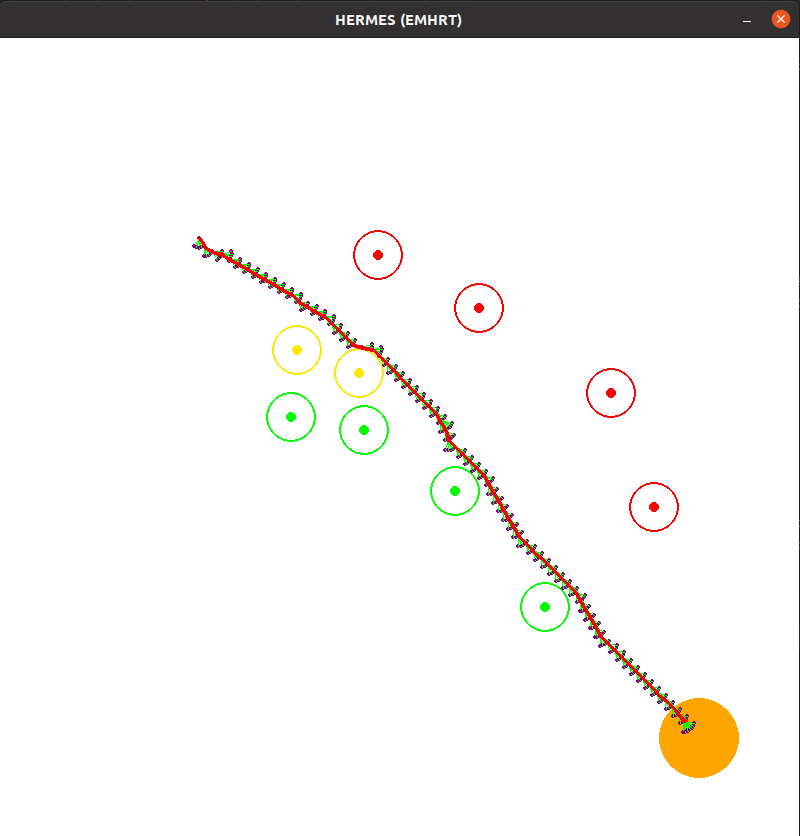
The goal of this path planning method is to provide an optimal path and fast execution time. Since will not be considering an omni-directional robot, the possible movement of the vehicle needs to be included in the expansion of the tree. To constraint the path planning, we will be trying to go in- between sets of red markers on the left side of the vehicle and green markers on the right side. The video below shows the working scenario and an example of the desired behavior.
https://www.youtube.com/watch?v=kjssdifs0DQ
Solution:
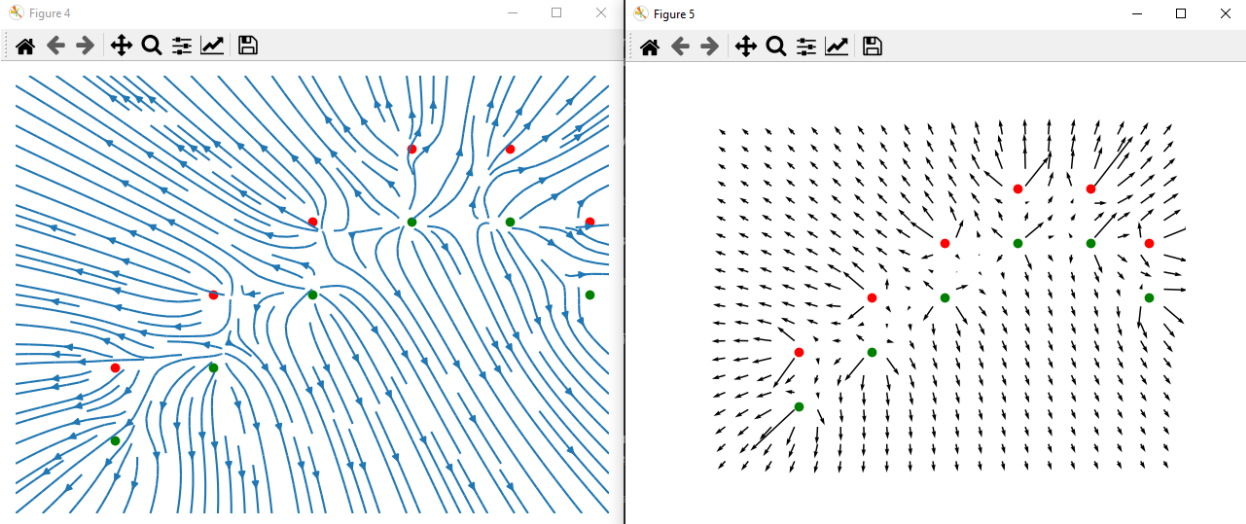
To achieve the predetermined goal with the path planning constraints, it was necessary to combine concepts from both A* and RRT*. Both have drawbacks and positives but if we incorporate the best of both the drawbacks become insignificant. The main drawback of A* is that it works with an already existing network/graph. RRT makes its own nodes, so it’s not bound by a discrete graph. RRT normally takes a slightly longer time since the expansion of the tree is random so it may expand in the opposite direction of the goal. If we use the heuristic cost function to sort the order of expanding the trees, we can quickly select the node with the highest chance of reaching the goal with the least error. To avoid objects, we can treat every obstacle as having the same polarity as the agent. This diverging vector field can be used to repel the agent from the obstacles and make sure the selected path has good clearance. Since there is a requirement of keeping the markers in the right orientation, this can and should be included in the cost function and expansion decision. To do so we can treat red markers as having north polarity and green markers as south polarity. The resulting vector field along with the divergence field can be used as a guide. Now we can simply prioritize the nodes that are more aligned with the combined EM field and are also closer to the path-goal. After the node with the least heuristic cost has been found we can spawn N number of Nodes from it in a specific cone. This cone parametrizes the possible movement of the vehicle with L length and 𝜃 angle of possible turn. By incorporating the movement in the path planning we can arrive at a path that needs no post-processing/smoothing to follow.
Formulas:
EM field with 100% Curl Gain and 10% Divergence Gain.
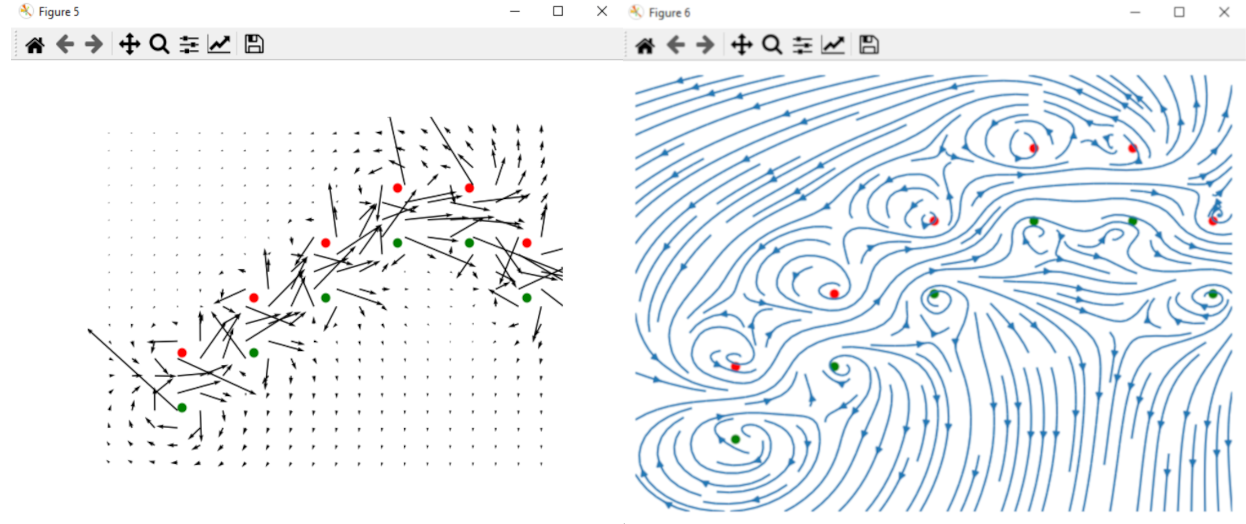
EM field with 10% Curl Gain and 100% Divergence Gain.
 Conclusion:
This work is a showcase of how making compromises between different methods can give optimal
results by removing each other’s drawbacks and concentrating on their pros. This path planning
algorithm is as direct as it gets because it’s based on the principle of least resistance path to imitating the
natural movement of electrons in an Electromagnetic field.
Conclusion:
This work is a showcase of how making compromises between different methods can give optimal
results by removing each other’s drawbacks and concentrating on their pros. This path planning
algorithm is as direct as it gets because it’s based on the principle of least resistance path to imitating the
natural movement of electrons in an Electromagnetic field.
Path Planning Results:
HERMES Cluttered Results:
HERMES Cluttered Results 2:
HERMES Small Step Size:
TODO:
-Exploring Distance as a Function of Cost Gradient
-Velocity as a function of Curvature
-Hermes + LP-DLL