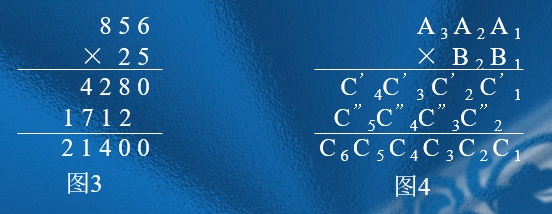利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。
本节介绍常用的几种高精度计算的方法。
数据的接收和存贮:当输入的数很长时:
- 可采用字符串方式输入,这样可输入数字很长的数,利用字符串函数和操作运算,将每一位数取出,存入数组中。
void init(int a[]) //传入一个数组
{
string s;
cin>>s; //读入字符串s
a[0]=s.length(); //用a[0]计算字符串s的位数
for(i=1;i<=a[0];i++)
a[i]=s[a[0]-i]-'0'; //将数串s转换为数组a,并倒序存储
}- 另一种方法是直接用循环加数组方法输入数据。
位数的确定:接收时往往是用字符串的,所以它的位数就等于字符串的长度。
加法进位:
c[i]=a[i]+b[i];
if (c[i]>=10) {
c[i]%=10; ++c[i+1];
}减法借位:
if (a[i]<b[i]) {
--a[i+1];
a[i]+=10;
}
c[i]=a[i]-b[i];乘法进位:
c[i+j-1]= a[i]*b[j] + x + c[i+j-1];
x = c[i+j-1]/10;
c[i+j-1] %= 10;商和余数处理:视被除数和除数的位数情况进行处理。
输入两个数到两个变量中,然后用赋值语句求它们的和,输出。但是,我们知道,在C++语言中任何数据类型都有一定的表示范围。而当两个被加数很大时,上述算法显然不能求出精确解,因此我们需要寻求另外一种方法。
在读小学时,我们做加法都采用竖式方法,如图1。
这样,我们方便写出两个整数相加的算法。
如果我们用数组A、B分别存储加数和被加数,用数组C存储结果。
则上例有A[1]=6,A[2]=5, A[3]=8,B[1]=5,B[2]=5,B[3]=2,C[4]=1,C[3]=1,C[2]=1,C[1]=1,两数相加如图2所示。
int c[100];
void add(int a[],int b[]) //a,b,c都为数组,分别存储被加数、加数、结果
{
int i=1,x=0; //x是进位
while ((i<=a数组长度)||(i<=b数组的长度))
{
c[i]=a[i]+b[i]+x; //第i位相加并加上次的进位
x=c[i]/10; //向高位进位
c[i]%=10; //存储第i位的值
i++; //位置下标变量
}
}
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int main()
{
char a1[100],b1[100];
int a[100],b[100],c[100],lena,lenb,lenc,i,x;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
gets(a1);
gets(b1); //输入加数与被加数
lena=strlen(a1);
lenb=strlen(b1);
for (i=0;i<=lena-1;i++) a[lena-i]=a1[i]-48; //加数放入a数组
for (i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-48; //加数放入b数组
lenc =1;
x=0;
while (lenc <=lena||lenc <=lenb)
{
c[lenc]=a[lenc]+b[lenc]+x; //两数相加
x=c[lenc]/10;
c[lenc]%=10;
lenc++;
}
c[lenc]=x;
if (c[lenc]==0)
lenc--; //处理最高进位
for (i=lenc;i>=1;i--)
cout<<c[i]; //输出结果
cout<<endl;
return 0;
}
类似加法,可以用竖式求减法。在做减法运算时,需要注意的是:被减数必须比减数大,同时需要处理借位。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int main()
{
int a[256],b[256],c[256],lena,lenb,lenc,i;
char n[256],n1[256],n2[256];
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
printf("Input minuend:"); gets(n1); //输入被减数
printf("Input subtrahend:"); gets(n2); //输入减数
if (strlen(n1)<strlen(n2)||(strlen(n1)==strlen(n2)&&strcmp(n1,n2)<0))
//strcmp()为字符串比较函数,当n1==n2, 返回0;
//n1>n2时,返回正整数;n1<n2时,返回负整数
{ //处理被减数和减数,交换被减数和减数
strcpy(n,n1); //将n1数组的值完全赋值给n数组
strcpy(n1,n2);
strcpy(n2,n);
cout<<"-"; //交换了减数和被减数,结果为负数
}
lena=strlen(n1); lenb=strlen(n2);
for (i=0;i<=lena-1;i++) a[lena-i]=int(n1[i]-'0'); //被减数放入a数组
for (i=0;i<=lenb-1;i++) b[lenb-i]=int(n2[i]-'0'); //减数放入b数组
i=1;
while (i<=lena||i<=lenb)
{
if (a[i]<b[i])
{
a[i]+=10; //不够减,那么向高位借1当10
a[i+1]--;
}
c[i]=a[i]-b[i]; //对应位相减
i++;
}
lenc=i;
while ((c[lenc]==0)&&(lenc>1)) lenc--; //最高位的0不输出
for (i=lenc;i>=1;i--) cout<<c[i]; //输出结果
cout<<endl;
return 0;
}
类似加法,可以用竖式求乘法。在做乘法运算时,同样也有进位,同时对每一位进行乘法运算时,必须进行错位相加,如图3、图4。
分析c数组下标的变化规律,可以写出如下关系式:ci = c’i +c”i +…由此可见,c i跟a[i]*b[j]乘积有关,跟上次的进位有关,还跟原c i的值有关,分析下标规律,有
c[i+j-1]= a[i]*b[j]+ x + c[i+j-1];
x=c[i+j-1]/10 ;
c[i+j-1]%=10;#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int main()
{
char a1[100],b1[100];
int a[100],b[100],c[100],lena,lenb,lenc,i,j,x;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
gets(a1);gets(b1);
lena=strlen(a1);lenb=strlen(b1);
for (i=0;i<=lena-1;i++) a[lena-i]=a1[i]-48;
for (i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-48;
for (i=1;i<=lena;i++)
{
x=0; //用于存放进位
for (j=1;j<=lenb;j++) //对乘数的每一位进行处理
{
c[i+j-1]=a[i]*b[j]+x+c[i+j-1]; //当前乘积+上次乘积进位+原数 x=c[i+j-1]/10;
c[i+j-1] %= 10;
}
c[i+lenb]=x; //进位
}
lenc=lena+lenb;
while (c[lenc]==0&&lenc>1) //删除前导0
lenc--;
for (i=lenc;i>=1;i--)
cout<<c[i];
cout<<endl;
return 0;
}
做除法时,每一次上商的值都在0~9,每次求得的余数连接以后的若干位得到新的被除数,继续做除法。
因此,在做高精度除法时,要涉及到乘法运算和减法运算,还有移位处理。
当然,为了程序简洁,可以避免高精度除法,用0~9次循环减法取代得到商的值。这里,我们讨论一下高精度数除以单精度数的结果,采取的方法是按位相除法。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int main()
{
char a1[100],c1[100];
int a[100],c[100],lena,i,x=0,lenc,b;
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
gets(a1);
cin>>b;
lena=strlen(a1);
for (i=0;i<=lena-1;i++)
a[i+1]=a1[i]-48;
for (i=1;i<=lena;i++) //按位相除
{
c[i]=(x*10+a[i])/b;
x=(x*10+a[i])%b;
}
lenc=1;
while (c[lenc]==0&&lenc<lena)
lenc++; //删除前导0
for (i=lenc;i<=lena;i++)
cout<<c[i];
cout<<endl;
return 0;
}
实质上,在做两个高精度数运算时候,存储高精度数的数组元素可以不仅仅只保留一个数字,而采取保留多位数(例如一个整型或长整型数据等),这样,在做运算(特别是乘法运算)时,可以减少很多操作次数。
例如图5就是采用4位保存的除法运算,其他运算也类似。具体程序可以修改上述例题予以解决,程序请读者完成。
高精除以低精是对被除数的每一位(这里的“一位”包含前面的余数,以下都是如此)都除以除数,而高精除以高精则是用减法模拟除法,对被除数的每一位都减去除数,一直减到当前位置的数字(包含前面的余数)小于除数(由于每一位的数字小于10,所以对于每一位最多进行10次计算)
#include<iostream>
#include<cstring>
using namespace std;
int a[101],b[101],c[101],d,i;
void init(int a[])
{ string s;
cin>>s; //读入字符串s
a[0]=s.length(); //用a[0]计算字符串 s的位数
for(i=1;i<=a[0];i++)
a[i]=s[a[0]-i]-'0'; //将数串s转换为数组a,并倒序存储.
}
void print(int a[]) //打印输出
{
if (a[0]==0){cout<<0<<endl;return;}
for(int i=a[0];i>0;i--) cout<<a[i];
cout<<endl;
return ;
}
int compare (int a[],int b[])
//比较a和b的大小关系,若a>b则为1,a<b则为-1,a=b则为0
{
if(a[0]>b[0]) return 1; //a的位数大于b则a比b大
if(a[0]<b[0]) return -1; //a的位数小于b则a比b小
for(i=a[0];i>0;i--) //从高位到低位比较
{
if (a[i]>b[i]) return 1;
if (a[i]<b[i]) return -1;
}
return 0; //各位都相等则两数相等。
}
void numcpy(int p[],int q[],int det) //复制p数组到q数组从det开始的地方
{
for (int i=1;i<=p[0];i++) q[i+det-1]=p[i];
q[0]=p[0]+det-1;
}
void jian(int a[],int b[]) //计算a=a-b
{
int flag,i;
flag=compare(a,b); //调用比较函数判断大小
if (flag==0) {a[0]=0;return;} //相等
if(flag==1) //大于
{
for(i=1;i<=a[0];i++)
{
if(a[i]<b[i]){ a[i+1]--;a[i]+=10;} //若不够减则向上借一位
a[i]-=b[i];
}
while(a[0]>0&&a[a[0]]==0) a[0]--; //修正a的位数
return;
}
}
void chugao(int a[],int b[],int c[])
{
int tmp[101];
c[0]=a[0]-b[0]+1;
for (int i=c[0];i>0;i--)
{
memset(tmp,0,sizeof(tmp)); //数组清零
numcpy(b,tmp,i);
while(compare(a,tmp)>=0){c[i]++;jian(a,tmp);} //用减法来模拟
}
while(c[0]>0&&c[c[0]]==0)c[0]--;
return ;
}
int main()
{
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
memset(c,0,sizeof(c));
init(a);init(b);
chugao(a,b,c);
print(c);
print(a);
return 0;
}