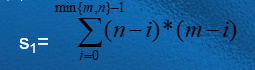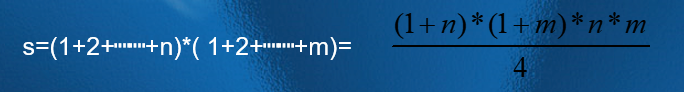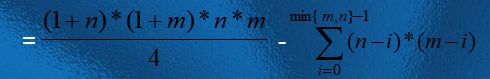递推法是一种重要的数学方法,在数学的各个领域中都有广泛的运用,也是计算机用于数值计算的一个重要算法。
这种算法特点是:一个问题的求解需一系列的计算,在已知条件和所求问题之间总存在着某种相互联系的关系,在计算时,如果可以找到前后过程之间的数量关系(即递推式),那么,从问题出发逐步推到已知条件,此种方法叫逆推。
无论顺推还是逆推,其关键是要找到递推式。
这种处理问题的方法能使复杂运算化为若干步重复的简单运算,充分发挥出计算机擅长于重复处理的特点。
递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公式的麻烦,把一个复杂的问题的求解,分解成了连续的若干步简单运算。一般说来,可以将递推算法看成是一种特殊的迭代算法。
在所有的递推关系中,Fibonacci数列应该是最为大家所熟悉的。在最基础的程序设计语言Logo语言中,就有很多这类的题目。而在较为复杂的Basic、Pascal、C语言中,Fibonacci数列类的题目因为解法相对容易一些,逐渐退出了竞赛的舞台。可是这不等于说Fibonacci数列没有研究价值,恰恰相反,一些此类的题目还是能给我们一定的启发的。
Fibonacci数列的代表问题是由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题”(又称“Fibonacci问题”)。
问题的提出:有雌雄一对兔子,假定过两个月便可繁殖雌雄各一的一对小兔子。问过n个月后共有多少对兔子?
设满x个月共有兔子Fx对,其中当月新生的兔子数目为Nx对。第x-1个月留下的兔子数目设为Fx-1对。则:
Fx=Nx+ Fx-1,Nx=Fx-2
(即第x-2个月的所有兔子到第x个月都有繁殖能力了)
∴ Fx=Fx-1+Fx-2 边界条件:F0=0,F1=1
由上面的递推关系可依次得到
F2=F1+F0=1,F3=F2+F1=2,F4=F3+F2=3,F5=F4+F3=5,……。
Fabonacci数列常出现在比较简单的组合计数问题中,例如以前的竞赛中出现的“骨牌覆盖”问题。在优选法中,Fibonacci数列的用处也得到了较好的体现。
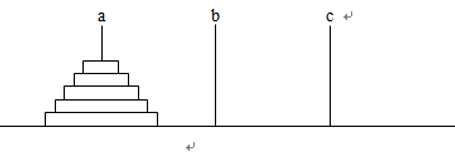
问题的提出:Hanoi塔由n个大小不同的圆盘和三根木柱a,b,c组成。开始时,这n个圆盘由大到小依次套在a柱上,如图3-11所示。
要求把a柱上n个圆盘按下述规则移到c柱上:
(1)一次只能移一个圆盘;
(2)圆盘只能在三个柱上存放;
(3)在移动过程中,不允许大盘压小盘。
问将这n个盘子从a柱移动到c柱上,总计需要移动多少个盘次?
设hn为n个盘子从a柱移到c柱所需移动的盘次。
显然,当n=1时,只需把a 柱上的盘子直接移动到c柱就可以了,故h1=1。
当n=2时,先将a柱上面的小盘子移动到b柱上去;然后将大盘子从a柱移到c 柱;最后,将b柱上的小盘子移到c柱上,共记3个盘次,故h2=3。
以此类推,当a柱上有n(n2)个盘子时,总是先借助c柱把上面的n-1个盘子移动到b柱上,然后把a柱最下面的盘子移动到c柱上;
再借助a柱把b柱上的n-1个盘子移动到c柱上;总共移动hn-1+1+hn-1个盘次。
∴hn=2hn-1+1 边界条件:h1=1
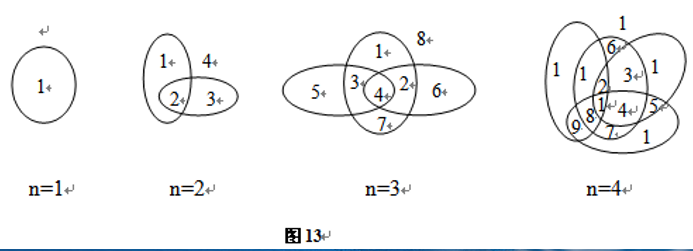
问题的提出:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
设an为n条封闭曲线把平面分割成的区域个数。 由图3-13可以看出:a2-a1=2;a3-a2=4;a4-a3=6。
从这些式子中可以看出an-an-1=2(n-1)。当然,上面的式子只是我们通过观察4幅图后得出的结论,它的正确性尚不能保证。
下面不妨让我们来试着证明一下。当平面上已有n-1条曲线将平面分割成an-1�个区域后,第n-1条曲线每与曲线相交一次,就会增加一个区域,因为平面上已有了n-1条封闭曲线,且第n条曲线与已有的每一条闭曲线恰好相交于两点,且不会与任两条曲线交于同一点,故平面上一共增加2(n-1)个区域,加上已有的an-1个区域,一共有an-1+2(n-1)个区域。所以本题的递推关系是an=an-1+2(n-1),边界条件是a1=1。
平面分割问题是竞赛中经常触及到的一类问题,由于其灵活多变,常常感到棘手
Catalan数首先是由Euler在精确计算对凸n边形的不同的对角三角形剖分的个数问题时得到的,它经常出现在组合计数问题中。
问题的提出:在一个凸n边形中,通过不相交于n边形内部的对角线,把n边形拆分成若干三角形,不同的拆分数目用hn表示,hn即为Catalan数。例如五边形有如下五种拆分方案(图3-14),故h5=5。求对于一个任意的凸n边形相应的hn。

在五类典型的递推关系中,第二类Stirling是最不为大家所熟悉的。也正因为如此,我们有必要先解释一下什么是第二类Strling数。
**【定义2】**n个有区别的球放到m个相同的盒子中,要求无一空盒,其不同的方案数用S(n,m)表示,称为第二类Stirling数。
下面就让我们根据定义来推导带两个参数的递推关系——第二类Stirling数。
解:设有n个不同的球,分别用b1,b2,……bn表示。从中取出一个球bn,bn的放法有以下两种:
①bn独自占一个盒子;那么剩下的球只能放在m-1个盒子中,方案数为S2(n-1,m-1);
②bn与别的球共占一个盒子;那么可以事先将b1,b2,……bn-1这n-1个球放入m个盒子中,然后再将球bn可以放入其中一个盒子中,方案数为mS2(n-1,m)。
综合以上两种情况,可以得出第二类Stirling数定理:
**【定理】**S2(n,m)=mS2(n-1,m)+S2(n-1,m-1) (n>1,m1)
边界条件可以由定义2推导出:
S2(n,0)=0;S2(n,1)=1;S2(n,n)=1;S2(n,k)=0(k>n)。
第二类Stirling数在竞赛中较少出现,但在竞赛中也有一些题目与其类似,甚至更为复杂。读者不妨自己来试着建立其中的递推关系。
小结:通过上面对五种典型的递推关系建立过程的探讨,可知对待递推类的题目,要具体情况具体分析,通过找到某状态与其前面状态的联系,建立相应的递推关系。
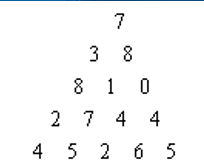
**【例1】**数字三角形。如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
1、 一步可沿左斜线向下或右斜线向下走;
2、 三角形行数小于等于100;
3、 三角形中的数字为0,1,…,99;
测试数据通过键盘逐行输入,如上例数据应以如下所示格式输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
【算法分析】
此题解法有多种,从递推的思想出发,设想,当从顶层沿某条路径走到第i层向第i+1层前进时,我们的选择一定是沿其下两条可行路径中最大数字的方向前进,为此,我们可以采用倒推的手法,设a[i][j]存放从i,j 出发到达n层的最大值,则a[i][j]=max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]},a[1][1] 即为所求的数字总和的最大值。
【参考程序】
#include<iostream>
using namespace std;
int main()
{
int n,i,j,a[101][101];
cin>>n;
for (i=1;i<=n;i++)
for (j=1;j<=i;j++)
cin>>a[i][j]; //输入数字三角形的值
for (i=n-1;i>=1;i--)
for (j=1;j<=i;j++)
{
if (a[i+1][j]>=a[i+1][j+1]) a[i][j]+=a[i+1][j]; //路径选择
else a[i][j]+=a[i+1][j+1];
}
cout<<a[1][1]<<endl;
}
【例2】 有 2χn的一个长方形方格,用一个1*2的骨牌铺满方格。
编写一个程序,试对给出的任意一个****n(n>0), 输出铺法总数。
【算法分析】
(1)面对上述问题,如果思考方法不恰当,要想获得问题的解答是相当困难的。可以用递推方法归纳出问题解的一般规律。
(2)当n=1时,只能是一种铺法,铺法总数有示x1=1。
(3)当n=2时:骨牌可以两个并列竖排,也可以并列横排,再无其他方法,如下左图所示,因此,铺法总数表示为x2=2;
(4)当n=3时:骨牌可以全部竖排,也可以认为在方格中已经有一个竖排骨牌,则需要在方格中排列两个横排骨牌(无重复方法),若已经在方格中排列两个横排骨牌,则必须在方格中排列一个竖排骨牌。如上右图,再无其他排列方法,因此铺法总数表示为x3=3。
由此可以看出,当n=3时的排列骨牌的方法数是n=1和n=2排列方法数的和。
(5)推出一般规律:对一般的n,要求xn可以这样来考虑,若第一个骨牌是竖排列放置,剩下有n-1个骨牌需要排列,这时排列方法数为xn-1;若第一个骨牌是横排列,整个方格至少有2个骨牌是横排列(1*2骨牌),因此剩下n-2个骨牌需要排列,这是骨牌排列方法数为xn-2。从第一骨牌排列方法考虑,只有这两种可能,所以有:
xn=xn-1+xn-2 (n>2)
x1=1
x2=2
xn=xn-1+xn-2就是问题求解的递推公式。任给n都可以从中获得解答。例如n=5,
x3=x2+x1=3
x4=x3+x2=5
x5=x4+x3=8
下面是输入n,输出x1~xn的c++程序:
#include<iostream>
using namespace std;
int main()
{
int n,i,j,a[101];
cout<<"input n:"; //输入骨牌数
cin>>n;
a[1]=1;a[2]=2;
cout<<"x[1]="<<a[1]<<endl;
cout<<"x[2]="<<a[2]<<endl;
for (i=3;i<=n;i++) //递推过程
{
a[i]=a[i-1]+a[i-2];
cout<<"x["<<i<<"]="<<a[i]<<endl;
}
}
下面是运行程序输入 n=30,输出的结果:
input n: 30
x[1]=1
x[2]=2
x[3]=3
........
x[29]=832040
x[30]=1346269
问题的结果就是有名的斐波那契数。
【例3】棋盘格数
设有一个N*M方格的棋盘( l≤ N≤100,1≤M≤100)。求出该棋盘中包含有多少个正方形、多少个长方形(不包括正方形)。
例如:当 N=2, M=3时:
正方形的个数有8个:即边长为1的正方形有6个;边长为2的正方形有2个。
长方形的个数有10个:即21的长方形有4个:12的长方形有3个:31的长方形有2个:32的长方形有1个:
程序要求:输入:N,M
输出:正方形的个数与长方形的个数
如上例:输入:2 3
输出:8 10
【算法分析】
1.计算正方形的个数s1
边长为1的正方形个数为n*m
边长为2的正方形个数为(n-1)*(m-1)
边长为3的正方形个数为(n-2)*(m-2)
…………
边长为min{n,m}的正方形个数为(m-min{n,m}+1)*(n-min{n,m}+1)
根据加法原理得出:
2.长方形和正方形的个数之和s
宽为1的长方形和正方形有m个,宽为2的长方形和正方形有m-1个,┉┉,宽为m的长方形和正方形有1个;
长为1的长方形和正方形有n个,长为2的长方形和正方形有n-1个,┉┉,长为n的长方形和正方形有1个;
根据乘法原理
3.长宽不等的长方形个数s2
显然,s2=s-s1=
由此得出算法:
#include<iostream>
using namespace std;
int main()
{
int n,m;
cin>>m>>n;
int m1=m,n1=n,s1=m*n; //计算正方形的个数s1
while (m1!=0&&n1!=0)
{
m1--;n1--;
s1+=m1*n1;
}
int s2=((m+1)*(n+1)*m*n)/4-s1; // 计算长方形的个数s2
cout<<s1<<" "<<s2<<endl;
}
**【例4】**昆虫繁殖
【问题描述】
科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过X个月产卵),问过Z个月以后,共有成虫多少对?0=<X<=20,1<=Y<=20,X=<Z<=50
【输入格式】
x,y,z的数值
【输出格式】
过Z个月以后,共有成虫对数
【输入样例】
1 2 8
【输出样例】
37
【参考程序】
#include<iostream>
using namespace std;
int main()
{
long long a[101]={0},b[101]={0},i,j,x,y,z;
cin>>x>>y>>z;
for(i=1;i<=x;i++){a[i]=1;b[i]=0;}
for(i=x+1;i<=z+1;i++) //因为要统计到第z个月后,所以要for到z+1
{
b[i]=y*a[i-x];
a[i]=a[i-1]+b[i-2];
}
cout<<a[z+1]<<endl;
return 0;
}
**【例5】**位数问题
【问题描述】
在所有的N位数中,有多少个数中有偶数个数字3?由于结果可能很大,你只需要输出这个答案对12345取余的值。
【输入格式】
读入一个数N
【输出格式】
输出有多少个数中有偶数个数字3。
【输入样例】
2
【输出样例】
73
【数据规模】
1<=N<=1000
【样例说明】
在所有的2位数字,包含0个3的数有72个,包含2个3的数有1个,共73个
可以列出公式,在n个格子中放x个3(其中x为偶数,包括0).。
c(n,x)*9^(n-x)-c(n-1,x)*9^(n-x-1) 含义为在n个格子中取x个3,且不考虑第一位的特殊情况为c(n,x)*9^(n-x)。
而第一位为0的情况,为c(n-1,x)*9^(n-x-1),两者减下,就为答案。
考虑这种题目,一般来说都是从第i-1位推导第i位,且当前位是取偶数还是取奇数的。
恍然大悟.可以用f[i][0]表示前i位取偶数个3有几种情况,f[i][1]表示前i位取奇数个3有几种情况。
则状态转移方程可以表示为:
f[i][0]=f[i-1][0]*9+f[i-1][1];f[i][1]=f[i-1][0]+f[i-1][1]*9;
边界条件:f[1][1]=1;f[1][0]=9;
【参考程序】
#include<iostream>
using namespace std;
int main()
{
int f[1001][2],n,i,x;
cin>>n;
f[1][1]=1;f[1][0]=9;
for(i=2;i<=n;i++)
{
x=f[1][0];
if(i==n)x--;
f[i][0]=(f[i-1][0]*x+f[i-1][1])%12345;
f[i][1]=(f[i-1][1]*x+f[i-1][0])%12345;
}
cout<<f[n][0];
return 0;
}【例6】过河卒(Noip2002)
【问题描述】
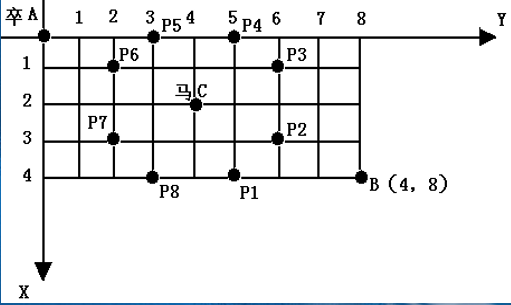
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点,如图3-1中的C点和P1,……,P8,卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。
跳马是一道老得不能再老的题目,我想每位编程初学者都学过,可能是在学回溯或搜索等算法的时候,很多书上也有类似的题目,一些比赛中也出现过这一问题的变形(如NOIP1997初中组的第三题)。有些同学一看到这条题目就去搜索,即使你编程调试全通过了,运行时你也会发现:当n,m=15就会超时。
其实,本题稍加分析就能发现,要到达棋盘上的一个点,只能从左边过来(我们称之为左点)或是从上面过来(我们称之为上点),所以根据加法原理,到达某一点的路径数目,就等于到达其相邻的上点和左点的路径数目之和,因此我们可以使用逐列(或逐行)递推的方法来求出从起点到终点的路径数目。障碍点(马的控制点)也完全适用,只要将到达该点的路径数目设置为0即可。
用F[i][j]表示到达点(i,j)的路径数目,g[i][j]表示点(i, j)有无障碍,g[i][j]=0表示无障碍,g[i][j]=1表示有障碍。
则,递推关系式如下:
F[i][j] = F[i-1][j] + F[i][j-1] //i>0且j>0且g[i][j]= 0
递推边界有4个:
F[i][j] = 0 //g[i][j] = 1
F[i][0] = F[i-1][0] //i > 0且g[i][j] = 0
F[0][j] = F[0][j-1] //j > 0且g[i][j] = 0
F[0][0] = 1
考虑到最大情况下:n=20,m=20,路径条数可能会超过231-1,所以要用高精度。
**【例7】**邮票问题
【问题描述】
设有已知面额的邮票m种,每种有n张,用总数不超过n张的邮票,能从面额1开始,最多连续组成多少面额。(1≤m≤100,1≤n≤100,1≤邮票面额≤255)
【输入格式】
第一行:m,n的值,中间用一空格隔开。
第二行:A[1..m](面额),每个数中间用一空格隔开。
【输出格式】
连续面额数的最大值
【输入样例】stamp.in
3 4
1 2 4
【输出样例】samp.out
14
一看到这个题目,给人的第一感觉是用回溯算法,从面额1开始,每种面额都用回溯进行判断,算法复杂度并不高,但是当m,n取到极限值100时,程序明显超时,因此,回溯算法在这里并不可取。 能否用递推完成呢?我们有一个思路:从面额1开始,建立递推关系方程,就用范例来说吧,面额1,2,4只用1张邮票行了,面额3可以表示为面额1,2的邮票和1+1=2,面额5有两种表示方式min(面额1+面额4,面额2+面额3),照此类推,递推关系方程不难建立,就拿邮票问题来说,以下是递推的一种方法:
#include<iostream>
using namespace std;
int n,m,i,j,k;
int c[256]; //面额
int a[31001]; //递推数组
bool b1;
void readfile() //读入数据
{
cin >> m >> n;
b1 = true;
for (i = 1; i <= m; i++)
{
cin >> c[i];
if (c[i] == 1) b1 = false;
}
}
void work()
{
if (b1 == true) cout << "MAX=0"; //不存在面额1时输出无解
else
{
i = 1; a[i] = 1;
do
{
i++;
for (j = 1; j <= m; j++)
if (((i % c[j] == 0) && ((i / c[j]) < a[i])) || (a[i] == 0))
a[i] = i / c[j]; //判断它能否被题目给定面额整除
for (j = 1; j <= i/2; j++)
if (a[j] + a[i-j] < a[i])
a[i] = a[j] + a[i-j]; //寻找(1<=j<=i),使a[j]+a[i-j]值最小
}
while ((a[i] <= n) && (a[i] != 0));
cout << i-1; //输出
}
}
int main ( )
{
readfile() ;
work();
return 0;
}
这种递推方法虽然简单,由于1<=邮票面额<=255,1<=n<=100,因此MAX值最多可达到25500,25500次循环里必定还有嵌套循环,因此算法不加优化,很难在规定时间内得出最优值。这就需要递推的算法优化。 一味递推不寻求算法优化,速度较之搜索提高不少,但一旦数据规模过大,很难在规定时间内得出最优值。 这种递推方法原理是:对于某种要求得到的面额,判断它能否被题目给定面额整除,再寻找(1<=j<=i),使A[j]+A[i-j]值最小,求出凑成某种面额最少邮票数,算法虽然简单,但还可以进一步优化。何不将用m种面额邮票作循环,建立递推关系式:A[i]=MAX(A[I-C[j]]+1),于是当取到极限值时,程序减少了约1.6*10^8次循环,递推优化作用不言而喻。
#include<iostream>
#include<cstring>
using namespace std;
int x[256];
int pieces[30001];
int m,n,i,j;
int main()
{
cin >> m >> n;
for (i = 1; i <= m; i++)
cin >> x[i];
memset(pieces,0,sizeof(pieces));
int maxx = 0;
do //递推循环
{
maxx++;
for (i = 1; i <= m; i++)
if (maxx - x[i] >= 0)
{ //循环,建立递推关系式PIECES[i]=MAX(PIECES[I-X[j]]+1)
if (pieces[maxx] == 0) pieces[maxx] = pieces[maxx-x[i]] + 1;
if (pieces[maxx]>pieces[maxx-x[i]]+1) pieces[maxx] = pieces[maxx-x[i]]+1;
}
if ((pieces[maxx] == 0) || (pieces[maxx] > n))
{
cout << maxx - 1;
break;
}
}
while (true);
return 0;
}