According to Wikipedia:
In computer science, a binomial heap is a heap similar to a binary heap but also supports quick merging of two heaps. This is achieved by using a special tree structure. It is important as an implementation of the mergeable heap abstract data type (also called meldable heap), which is a priority queue supporting merge operation. Binomial heaps were invented in 1978 by J. Vuillemin
A binomial heap is a specific implementation of the heap data structure. Binomial heaps are collections of binomial trees that are linked together where each tree is an ordered heap. In a binomial heap, there are either one or zero binomial trees of order k, where k helps describe the number of elements a given tree can have: 2k. Binomial heaps are similar to binary heaps but binomial heaps have a more specific structure and allow for efficient merging of heaps. Heaps are often used to implement priority queues which are in turn used in implementations of many types of algorithms such as shortest-path finding algorithms—these fast operations help make these algorithms more efficient.
Shown below are Binomial trees of order 0 to 3: Each tree has a root node with subtrees of all lower ordered binomial trees, which have been highlighted. For example, the order 3 binomial tree is connected to an order 2, 1, and 0 (highlighted as blue, green and red respectively) binomial tree.
Binomial heaps are made up of binomial trees.
A binomial tree Bk is made up of two binomial trees Bk-1 that are linked together such that the root of one is the leftmost child of the root of the other.
Binomial trees are defined recursively as follows:
- A binomial tree of order 0 is a single node.
- A binomial tree of order k has a root node whose children are roots of binomial trees of orders k−1, k−2, ..., 2, 1, 0 (in this order).
The image below is a collection of binomial trees with orders 0, 1, 2, and 3 (from left to right). The order represents how many children the root node is able to have. For example, there are three children coming out of the order 3 node and no children coming out of the order 0 node.
An order k binomial tree Bk has the following properties:
- The height of the tree is k. For example, in the image above, if the tree only contained the 0th order node, the height would be 0. Since the entire tree is order 3, the height is 3.
- There are a total of 2k nodes in the tree.
- The tree has
nodes at depth i
- The degree of the root is k
- Deleting the root yields k binomial trees: Bk-1,...,B0
Binomial heaps can be implemented by using doubly linked lists to store the root nodes. Each node stores information about the parent pointer, left and right sibling pointers, left most child pointer, the number of children it has, and its key. Since the list is doubly linked, the parent nodes have pointers to the children and the children have pointers to the parent. Using the doubly linked list allows for constant time inserts and deletes from the root list, constant time to merge for two root lists together, and more.
The structure of a binomial heap is similar to the binary number system. For example, a binomial heap containing elements will contain binomial trees of order 1, 2, 3, 4, 5 and 6 since it takes six digits to write the decimal number 63 in binary. 63 in binary is 111111.
For a binomial heap with n nodes,
- the node containing the minimum element is a root of either
or
- in total, the heap has
binomial trees;
- the height of the heap is
A binomial heap must satisfy the binomial heap property. The property is as follows:
Binomial Heap Property
- Every binomial tree in a binomial min heap obeys the min-heap property (that the key of a node
is greater than or equal to the key of its parent) and every binomial tree in a binomial
max heap obeys the max-heap property (that the key of a node is less than or equal to the
key of its parent).
- There can only be either one or zero binomial trees for each order. In other words, for
every k, there is at most one binomial tree of order k in the heap.
The first property ensures that the min/max-heap properties hold throughout the heap.
The second property implies that a binomial heap with n nodes consists of at most log n + 1 binomial trees, which is a property of binomial heaps. In order to maintain this property, the heaps may need to be consolidated after an operation. For example, if an operation results in two heaps of order two, steps must be taken to correct this so that the binomial heap property holds.
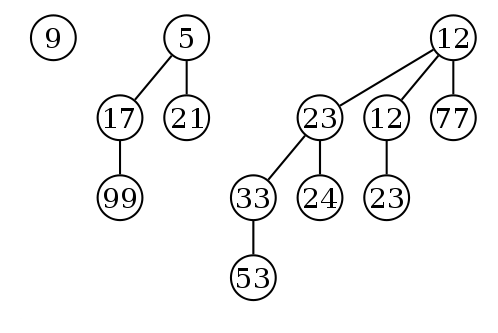
The diagram above is an example of a binomial heap containing 13 nodes with distinct keys. The heap consists of three binomial trees with orders 0, 2, and 3.
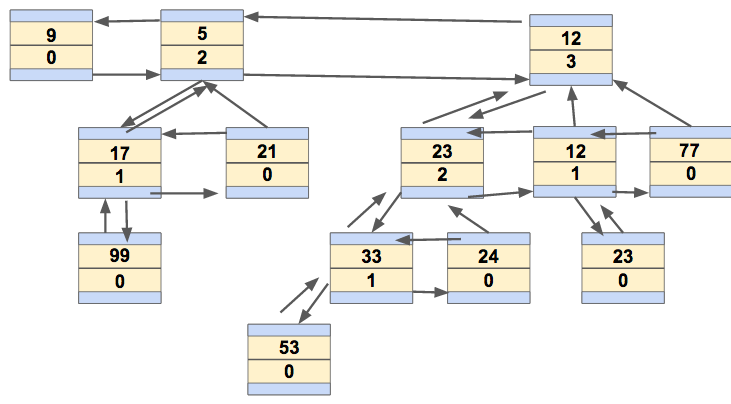
The children of a node are linked together in a doubly linked list. Each child has a pointer to its parent, and the parent has a pointer to one of the children. Here is what the above binomial heap looks like as a linked list of the roots:
| Operation | Complexity |
|---|---|
| Insertion | O(1) |
| Deletion | O(log n) |
| Find Min | O(1) |
| Extract Min | O(log n) |
| Decrease Key | O(log n) |
| Merge | O(log n) |
Here is how binomial heaps implement the basic functionalities of heaps and the time complexity of each operation. These operations are decribed in terms of min binomial heaps, but could easily be adapted to max binomial heaps.
Decrease key reduces the specified node’s key and then bubbles it up through its ancestors until the tree meets the conditions of a heap.
Delete is performed by calling decrease key to reducing the node to negative infinity which pulls the node to the top of the tree.
The tree is then detached from the rest of the heap and the node removed. The fragments of the old tree are reversed and linked together to form a new heap.
The two heaps can then be combined using the union operation.
Extract minimum iterates through the roots of each binomial tree in the heap to find the smallest node which is removed. The tree fragments are then reversed to form another heap.
The two heaps can then be combined using the union operation.
Find minimum iterates through the roots of each binomial tree in the heap.
Insert creates a new heap with the inserted element which are then combined using the union operation.
The union operation merges the two heaps together by continually linking trees of the same order until no two trees of the same order exist.