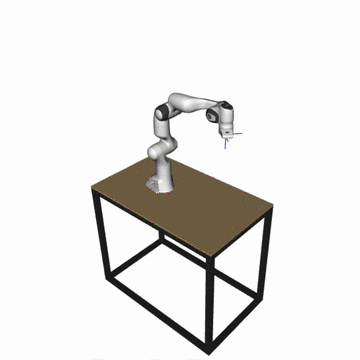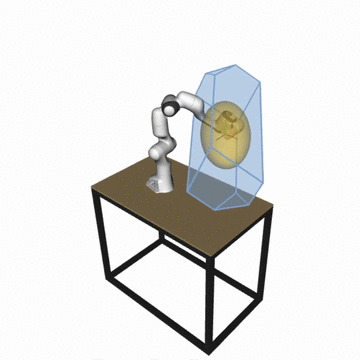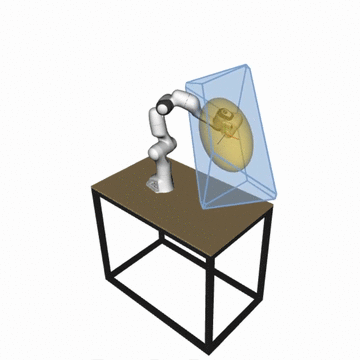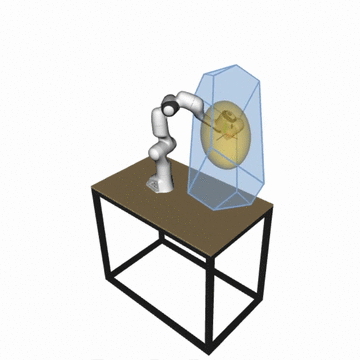
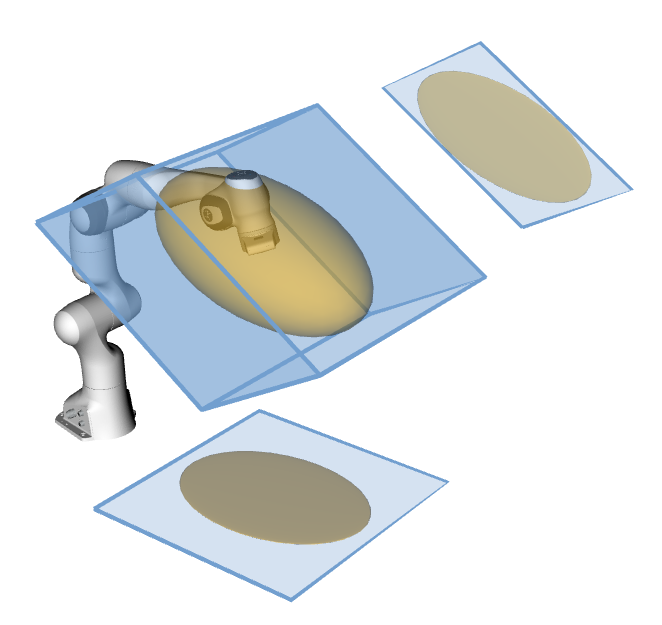
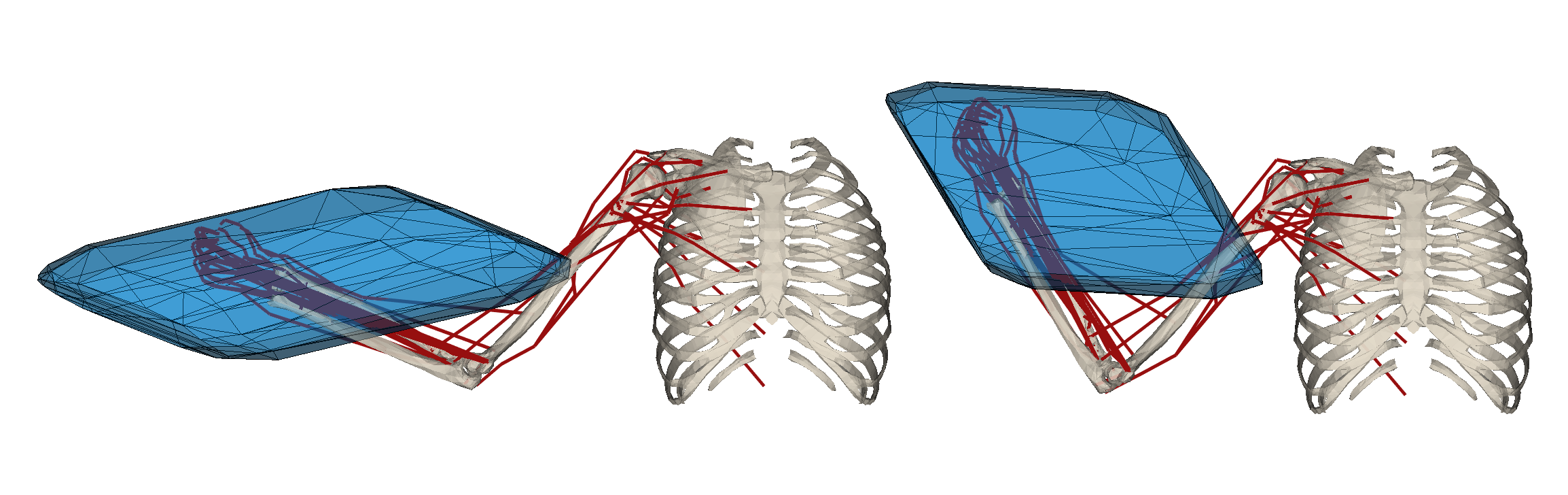
📢 New version of the pycapacity package is out - version v2.1.7! - see full changelog
Python package pycapacity provides a set of tools for evaluating task space physical ability metrics for humans and robots, based on polytopes and ellipsoids.
The aim of pycapacity is to provide a set of efficient tools for their evaluation in an easy to use framework that can be easily integrated with standard robotics
and biomechanics libraries. The package implements several state of the art algorithms for polytope evaluation that bring many of the
polytope metrics to the few milliseconds evaluation time, making it possible to use them in online and interactive applications.
The package can be easily interfaced with standard libraries for robotic manipulator rigid body simulation such as robotic-toolbox, pinocchio and mujoco, as well as human musculoskeletal model biomechanics
softwares opensim and biorbd. The package can also be used with the Robot Operating System (ROS).
The package additionally implements a set of visualization tools for polytopes and ellipsoids based on the
Python package matplotlib intended for fast prototyping and quick and interactive visualization.
| Library | Example |
|---|---|
| OpenSim | Tutorial |
| pyomeca biorbd | Tutorial |
| pinocchio | Tutorial |
| Robotics toolbox | Tutorial |
| Robot Operating System (ROS) | Tutorial |
| Mujoco | Tutorial |
See full API documentation and docs.
For the robotic manipulators the package integrates several velocity, force and acceleration capacity calculation functions based on ellipsoids:
- Velocity (manipulability) ellipsoid
E_vel = {dx | dx = J.dq, ||dq||<1 } - Acceleration (dynamic manipulability) ellipsoid
E_acc = {ddx | ddx = J.M^(-1).t, ||t||<1 } - Force ellipsoid
E_for = {f | J^T.f = t, ||t||<1 }
And polytopes:
- Velocity polytope
P_vel = {dx | dx = J.dq, dq_min < dq < dq_max} - Acceleration polytope
P_acc = {ddx | ddx = J.M^(-1).t, t_min < t < t_max} - Force polytope
P_for = {f | J^T.f = t, t_min < t < t_max} - Reachable space of the robot with a horizon
T
P_x = {x | x = JM(-1)tT^2/2, t_min < t < t_max, dq_min < M^(-1)tT < dq_max, q_min < M^(-1)tT^2/2 < q_max} - Force polytopes Minkowski sum and intersection
- NEW 📢: Sampling-based reachable space approximation with a horizon
T
C_x = {x | x = f(q0 + dq*T), q_min < q0 + dq*T < q_max, dq_min < dq < dq_max}
Where J is the robot jacobian matrix, f is the vector of cartesian forces,dx and ddx are vectors fo cartesian velocities and accretions, dq is the vector of the joint velocities and t is the vector of joint torques.
Reachable space polytope approximation is based on this paper:
Approximating robot reachable space using convex polytopes
by Skuric, Antun, Vincent Padois, and David Daney.
In: Human-Friendly Robotics 2022: HFR: 15th International Workshop on Human-Friendly Robotics. Cham: Springer International Publishing, 2023.
The force polytope functions have been implemented according to the paper:
On-line force capability evaluation based on efficient polytope vertex search
by A.Skuric, V.Padois and D.Daney
Published on ICRA2021
The force polytope functions have been implemented according to the paper:
On-line force capability evaluation based on efficient polytope vertex search
by A.Skuric, V.Padois and D.Daney
Published on ICRA2021
And the velocity and acceleration polytopes are resolved using the Hyper-plane shifting method:
Characterization of Parallel Manipulator Available Wrench Set Facets
by Gouttefarde M., Krut S.
In: Lenarcic J., Stanisic M. (eds) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010)
For the human musculoskeletal models this package implements the ellipsoid and polytope evaluation functions. The implemented ellipsoids are:
- Velocity (manipulability) ellipsoid
E_vel = {dx | dx = J.dq, dl = L.dq, ||dl||<1 } - Acceleration (dynamic manipulability) ellipsoid
E_acc = {ddx | ddx = J.M^(-1).N.F, ||F||<1 } - Force ellipsoid
E_for = {f | J^T.f = N.F, ||F||<1 }
And polytopes:
- Velocity polytope
P_vel = {dx | dx = J.dq, dl = L.dq dl_min < dl < dl_max} - Acceleration polytope
P_acc = {ddx | ddx = J.M^(-1).N.F, F_min < F < F_max} - Force polytope
P_for = {f | J^T.f = N.F, F_min < F < F_max}
Where J is the model's jacobian matrix, L si the muscle length jacobian matrix, N= -L^T is the moment arm matrix, f is the vector of cartesian forces,dx and ddx are vectors fo cartesian velocities and accretions, dq is the vector of the joint velocities, t is the vector of joint torques, dl is the vector of the muscle stretching velocities and F is the vector of muscular forces.
The force and velocity polytope functions have been implemented according to the paper:
On-line feasible wrench polytope evaluation based on human musculoskeletal models: an iterative convex hull method
by A.Skuric, V.Padois, N.Rezzoug and D.Daney
Submitted to RAL & ICRA2022
And the acceleration polytopes are resolved using the Hyper-plane shifting method:
Characterization of Parallel Manipulator Available Wrench Set Facets
by Gouttefarde M., Krut S.
In: Lenarcic J., Stanisic M. (eds) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010)
There are three methods implemented in this paper to resolve all the polytope calculations:
- Hyper-plane shifting method (HPSM)
- Iterative convex hull method (ICHM)
- Vertex enumeration algorithm (VEPOLI2)
All of the methods are implemented in the module pycapacity.algorithms and can be used as standalone functions. See in docs for more info.
Characterization of Parallel Manipulator Available Wrench Set Facets
by Gouttefarde M., Krut S.
In: Lenarcic J., Stanisic M. (eds) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010)
This method finds the half-space representation of the polytope of a class:
P = {x | x = By, y_min <= y <= y_max }
To find the vertices of the polytope after finding the half-space representation Hx <= d an convex-hull algorithm is used.
The method is a part of the pycapacity.algorithms module hyper_plane_shift_method, See in docs for more info.
On-line feasible wrench polytope evaluation based on human musculoskeletal models: an iterative convex hull method
by A.Skuric, V.Padois, N.Rezzoug and D.Daney
Submitted to RAL & ICRA2022
This method finds both vertex and half-space representation of the class of polytopes:
P = {x | Ax = By, y_min <= y <= y_max }
And it can be additionally extended to the case where there is an additional projection matrix P making a class of problems:
P = {x | x= Pz, Az = By, y_min <= y <= y_max }
The method is a part of the pycapacity.algorithms module iterative_convex_hull_method. See the docs for more info
On-line force capability evaluation based on efficient polytope vertex search
by A.Skuric, V.Padois and D.Daney
Published on ICRA2021
This method finds vertex representation of the class of polytopes:
P = {x | Ax = y, y_min <= y <= y_max }
To find the half-space representation (faces) of the polytope after finding the vertex representation an convex-hull algorithm is used.
The method is a part of the pycapacity.algorithms module vertex_enumeration_vepoli2. See the docs for more info
All you need to do to install it is:
pip install pycapacity
And include it to your python project
import pycapacity.robot
# and/or
import pycapacity.human
#and/or
import pycapacity.algorithms
#and/or
import pycapacity.visual
#and/or
import pycapacity.objects Other way to install the code is by installing it directly from the git repo:
pip install git+https://github.com/auctus-team/pycapacity.git
See full docs at the link
For all the questions regarding the potential implementation, applications, supported hardware and similar please don't hesitate to leave an issue or start a discussion
It is always helpful to hear the stories/problems/suggestions of people implementing the code!
Please do not hesitate to leave an issue if you have problems/advices/suggestions regarding the code!
If you'd like to contribute to this project but you are not very familiar with github, don't worry, let us know either by starting the discussion or posting a github issue.
We are very happy that pycapacity has been used as a component of several research project and has made its way to several scientific papers. We are hoping that this trend is going to continue as the project matures and becomes more robust!
A short resume paper about pycapacity has been published in the Journal of Open Source Software:
pycapacity: a real-time task-space capacity calculation package for robotics and biomechanics
A. Skuric, V. Padois and D. Daney
Journal of Open Source Software, 8(89), 5670, https://doi.org/10.21105/joss.05670
If you are interested in citing pycapacity in your research, we suggest you to cite our paper:
@article{Skuric2023pycapacity,
author = {Skuric, Antun and Padois, Vincent and Daney, David},
doi = {10.21105/joss.05670},
journal = {Journal of Open Source Software},
month = sep,
number = {89},
pages = {5670},
title = {{Pycapacity: a real-time task-space capacity calculation package for robotics and biomechanics}},
url = {https://joss.theoj.org/papers/10.21105/joss.05670},
volume = {8},
year = {2023}
}See more examples in the tutorials
This code snippet shows how to calculate the force polytope of the Franka Emika Panda robot and visualise it in the Swift visualisation tool.
Click to see the code
import roboticstoolbox as rp
import numpy as np
panda = rp.models.DH.Panda()
# random initial pose
q_min = np.array([-2.7437, -1.7837, -2.9007, -3.0421, -2.8065, 0.5445, -3.0159])
q_max = np.array([2.7437, 1.7837, 2.9007, -0.1518, 2.8065, 4.5169, 3.0159])
q= np.random.uniform(q_min,q_max)
panda.q = q
# joint torque limits
t_max = np.array([87, 87, 87, 87, 20, 20, 20])
t_min = -t_max
# polytope python module
import pycapacity.robot as pyc
# robot matrices
Jac = panda.jacob0(q)[:3,:]
# gravity torque
gravity = panda.gravload(q).reshape((-1,1))
# calculate for the polytope
f_poly = pyc.force_polytope(Jac, t_max, t_min, gravity)
# calculate the face representation of the polytope
f_poly.find_faces()
# visualise panda
panda = rp.models.Panda()
import swift.Swift as Swift
panda.q = q
env = Swift()
env.launch()
env.add(panda)
# polytope visualisation
import trimesh
# save polytope as mesh file
scaling = 500
# create the mesh
mesh = trimesh.Trimesh(vertices=(f_poly.vertices.T/scaling + panda.fkine(q).t),
faces=f_poly.face_indices, use_embree=True, validate=True)
# absolute path to the temporary polytope file saved
# in the stl format
import os
file_path = os.path.join(os.getcwd(),'tmp_polytope_file.stl')
f = open(file_path, "wb")
f.write(trimesh.exchange.stl.export_stl(mesh))
f.close()
# robot visualisation
from spatialgeometry import Mesh
poly_mesh = Mesh(file_path)
poly_mesh.color = (0.9,0.6,0.0,0.5)
env.add(poly_mesh)See more examples in the tutorials
This example shows how to calculate the velocity polytope and ellipsoid of the Franka Emika Panda robot and visualise it in the Meshcat visualisation tool.
Click to see the code
import pinocchio as pin
import numpy as np
import time
from example_robot_data import load
# import pycapacity
import pycapacity as pycap
# get panda robot usinf example_robot_data
robot = load('panda')
# get joint position ranges
q_max = robot.model.upperPositionLimit.T
q_min = robot.model.lowerPositionLimit.T
# get max velocity
dq_max = robot.model.velocityLimit
dq_min = -dq_max
# Use robot configuration.
# q0 = np.random.uniform(q_min,q_max)
q0 = (q_min+q_max)/2
# calculate the jacobian
data = robot.model.createData()
pin.framesForwardKinematics(robot.model,data,q0)
pin.computeJointJacobians(robot.model,data, q0)
J = pin.getFrameJacobian(robot.model, data, robot.model.getFrameId(robot.model.frames[-1].name), pin.LOCAL_WORLD_ALIGNED)
# use only position jacobian
J = J[:3,:]
# end-effector pose
Xee = data.oMf[robot.model.getFrameId(robot.model.frames[-1].name)]
## visualise the robot
from pinocchio.visualize import MeshcatVisualizer
viz = MeshcatVisualizer(robot.model, robot.collision_model, robot.visual_model)
# Start a new MeshCat server and client.
viz.initViewer(open=True)
# Load the robot in the viewer.
viz.loadViewerModel()
viz.display(q0)
# small time window for loading the model
# if meshcat does not visualise the robot properly, augment the time
# it can be removed in most cases
time.sleep(0.2)
## visualise the polytope and the ellipsoid
import meshcat.geometry as g
# calculate the polytope
opt = {'calculate_faces':True}
# calculate the polytope
vel_poly = pycap.robot.velocity_polytope(J, dq_min, dq_max,options=opt)
# meshcat triangulated mesh
poly = g.TriangularMeshGeometry(vertices=vel_poly.vertices.T/10 + Xee.translation, faces=vel_poly.face_indices)
viz.viewer['poly'].set_object(poly, g.MeshBasicMaterial(color=0x0022ff, wireframe=True, linewidth=3, opacity=0.2))
# calculate the ellipsoid
vel_ellipsoid = pycap.robot.velocity_ellipsoid(J, dq_max)
# meshcat ellipsoid
ellipsoid = g.Ellipsoid(radii=vel_ellipsoid.radii/10)
viz.viewer['ellipse'].set_object(ellipsoid, g.MeshBasicMaterial(color=0xff5500, transparent=True, opacity=0.2))
viz.viewer['ellipse'].set_transform(pin.SE3(vel_ellipsoid.rotation, Xee.translation).homogeneous)See more examples in the tutorials
This example shows how to calculate the force polytope of the MoBL-ARMS Upper Extremity Model and visualise it in the OpenSim visualisation tool.
Click to see the code
# include the pyosim module
from utils import getStationJacobian, getMomentArmMatrix, getQIndicesOfClampedCoord, getMuscleTensions, getBodyPosition, setCoordinateValues
# include opensim package
import opensim as osim
# pycappacity for polytope calculationreate
from pycapacity.human import force_polytope
# some utils
import numpy as np
import time
## Constructor of the OsimModel class.
model = osim.Model("opensim_models/upper_body/unimanual/MoBL-ARMS Upper Extremity Model/MOBL_ARMS_fixed_41.osim")
endEffectorBody = 'hand'
state = model.initSystem()
joint_pos = [0,0.5,0,1.3,0,1.0,0]
setCoordinateValues(model,state,joint_pos)
start = time.time()
coordNames, coordIds = getQIndicesOfClampedCoord(model, state)
model.equilibrateMuscles(state)
J = getStationJacobian(model, state, endEffectorBody, osim.Vec3(0), coordIds)
N = getMomentArmMatrix(model, state, coordNames=coordNames)
F_min, F_max = getMuscleTensions(model, state)
print("time", time.time() - start)
# polytope calculation
start = time.time()
f_poly = force_polytope(J, N, F_min, F_max, 0.01)
print("time", time.time() - start)
# create the polytope
import trimesh
# find hand position
hand_orientation, hand_position = getBodyPosition(model,state, endEffectorBody)
# save the mesh to disk
mesh = trimesh.Trimesh(vertices=(f_poly.vertices.T/2000 + hand_position.reshape((3,))) ,
faces=f_poly.face_indices, use_embree=True, validate=True)
# save polytope as stl file
f = open("polytope.stl", "wb")
f.write(trimesh.exchange.stl.export_stl(mesh))
f.close()
# adding polytope faces
mesh = osim.Mesh("./polytope.stl")
model.get_ground().attachGeometry(mesh)
mesh.setColor(osim.Vec3(0.1,0.1,1))
mesh.setOpacity(0.3)
# adding polytope vireframe
mesh = osim.Mesh("./polytope.stl")
model.get_ground().attachGeometry(mesh)
mesh.setColor(osim.Vec3(0.1,0.1,1))
mesh.setRepresentation(2)
# visualise the model and polytope
model.setUseVisualizer(True)
state = model.initSystem()
mviz = model.getVisualizer()
setCoordinateValues(model,state,joint_pos)
mviz.show(state)See more examples in the tutorials
This is an interactive example that shows how to calculate the force polytope of the different robots in the Mujoco simulator and visualise it in the Mujoco visualisation tool.
Click to see the code
import mujoco
import mujoco.viewer
import numpy as np
from robot_descriptions.loaders.mujoco import load_robot_description
# Loading a variant of the model, e.g. panda without a gripper.
# model = load_robot_description("xarm7_mj_description", variant="xarm7_nohand"); frame_name = "link7"
# model = load_robot_description("iiwa14_mj_description"); frame_name = "link7"
# model = load_robot_description("gen3_mj_description"); frame_name = "forearm_link"
model = load_robot_description("panda_mj_description", variant="panda_nohand"); frame_name = "link7"
# model = load_robot_description("ur10e_mj_description"); frame_name = "wrist_3_link"
# model = load_robot_description("ur5e_mj_description"); frame_name = "wrist_3_link"
# model = load_robot_description("fr3_mj_description"); frame_name = "fr3_link6"
# Create a data structure to hold the state of the robot
data = mujoco.MjData(model)
# force polytope calculation function
from pycapacity.robot import force_polytope
# visualisation utils from pycapacity package
import pycapacity.visual as pyviz
# get max and min joint torques
tau_max = model.actuator_forcerange[:,1]
if np.any(tau_max <= 0):
print("Warning: Negative or zero torque limits detected, using default value of 10 Nm")
tau_max = np.ones_like(tau_max)*10
tau_min = -tau_max
# Launch viewer
with mujoco.viewer.launch_passive(model, data) as viewer:
while viewer.is_running():
mujoco.mj_step(model, data)
viewer.opt.flags[mujoco.mjtVisFlag.mjVIS_TEXTURE] = 0 # Disable textures
# Compute the Jacobian of the end-effector
J_pos = np.zeros((3, model.nv)) # Linear Jacobian (3xnq)
J_rot = np.zeros((3, model.nv)) # Rotational Jacobian (3xnq)
mujoco.mj_jacBodyCom(model, data, J_pos, J_rot, model.body(frame_name).id)
J = J_pos # Use only the linear Jacobian
# Compute the force polytope
poly = force_polytope(J, tau_min, tau_max)
# Shift polytope to the current end-effector position
# and scale it for easier visualization
poly.vertices = poly.vertices / 500 + data.site_xpos[0][:,None]
# Draw force polytope
pyviz.mj_draw_polytope(viewer, poly, edges=True, faces=True)
# Update the viewer
viewer.sync()See more examples in the tutorials