Skip to content

Latest commit

 

History

History
134 lines (67 loc) · 5.8 KB

README.md

File metadata and controls

134 lines (67 loc) · 5.8 KB
Raw

libmusic_m

View libmusic_m on File Exchange

This is a MATLAB implementation of spectral methods based on signal space decomposition. The idea behind those methods is to decompose noisy signal into pure signal and noise. Methods provided here are:

  • MUSIC (and special case of Pisarenko)
  • EV
  • Minimum Norm

ev_mn

You will find examples in examples folder and tests in tests folder. There is also specific support for DTMF (dual tone signals), including a toy testing framework for them. Just ignore them or reuse that for your own purposes.

Using in MATLAB

  1. Add the whole folder and subfolders to MATLAB's path (or core folder and sounds at minimum, if you don't plan to run tests)

  2. Create a method handle

     method = lm_spectral_method(kind, M, 2*P);

where kind is one of pisarenko/music/ev/mn, M is autocorrelation order and P is number of real signal sources.

  1. Process input samples and optionally capture the intermediate results (all eigenvectors, signal eigenvectors, noise eigenvectors, eigenvalues, autocorrelation matrix)

     [Vy,Vx,Ve,A,Ry] = method.process(y);

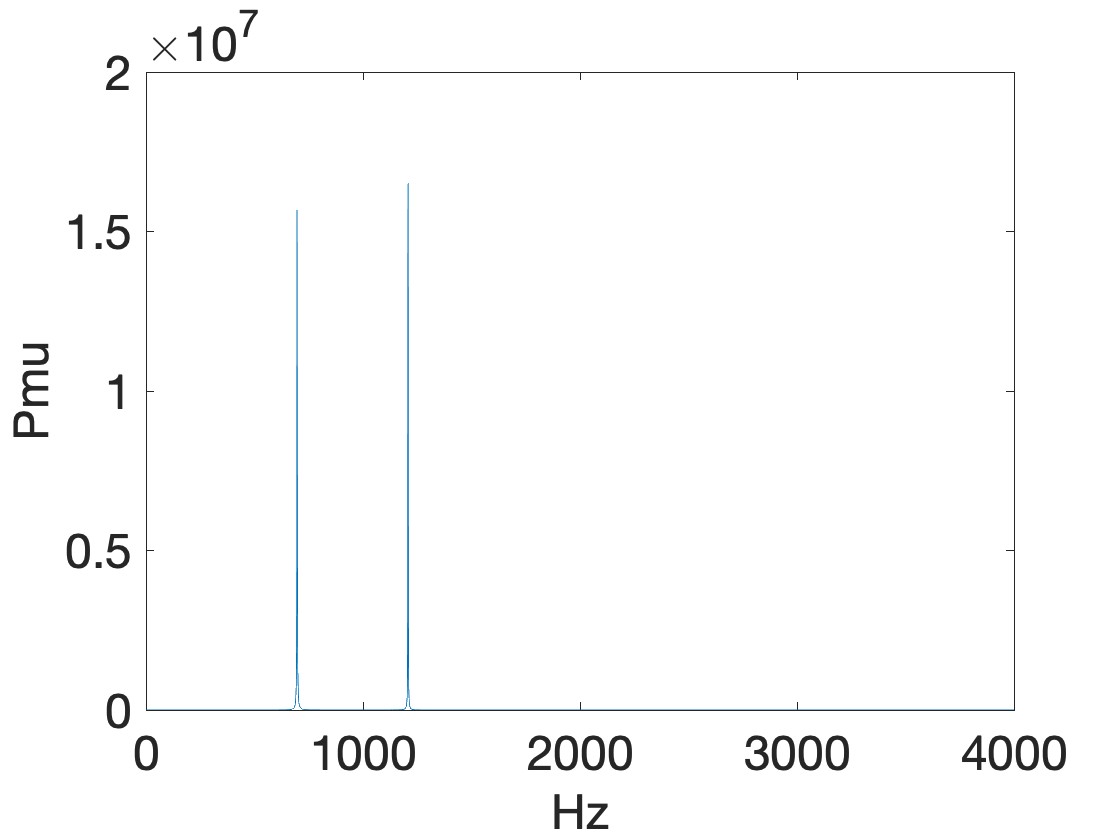
  2. Compute full PSD for frequencies 1 - 4000 Hz (sampling rate is 8 kHz)

     [X2,d2] = method.psd(method, 1:1:4000, 8000);
 plot(1:1:4000,X2)

2tone_psd

  1. Get frequency components by eigenrooting (roots of the Z-transforms of noise eigenvectors)

     [fs] = method.eigenrooting(Fs, 0, 0)

  2. Get detected frequencies by peak searching (considering only these frequencies that are passed in fs). peakWidth is a width of a peak, use 0 for default

     [peaks, pmu] = method.peaks(fs, Fs, peakWidth)

  3. In case of 1 or 2 sinusoids, get amplitudes by correlation method

     A = method.single_tone_amplitude()
 A = method.dual_tone_amplitude(f1, f2, Fs)

  4. In case of any number of sinusoids, get all amplitudes (for each frequency component given in fs)

     A = method.solve_for_amplitudes([fs], Fs);

This is MATLAB sandbox for libmusic

Copyright (C) 2022, Piotr Gregor piotr@dataandsignal.com

lm5

Performance in noise

In a noisy environment, MUSIC performs well as long as SNR is above 66.53 dB.

Applications

In telephony, DTMF symbols must be removed from stream, due too sensitive data protection. Often though, fractions of those DTMFs are left in a stream and must be removed. This cannot be done with Goertzel algorithm as it needs more than 110 samples to achieve right frequency resolution, to be able to detect DTMF frequencies. An example of such DTMF fraction is shown on the picture. This one is 14 samples in length (1.75 ms at a sampling rate of 8000 Hz).

dtmf_test_vector_valid

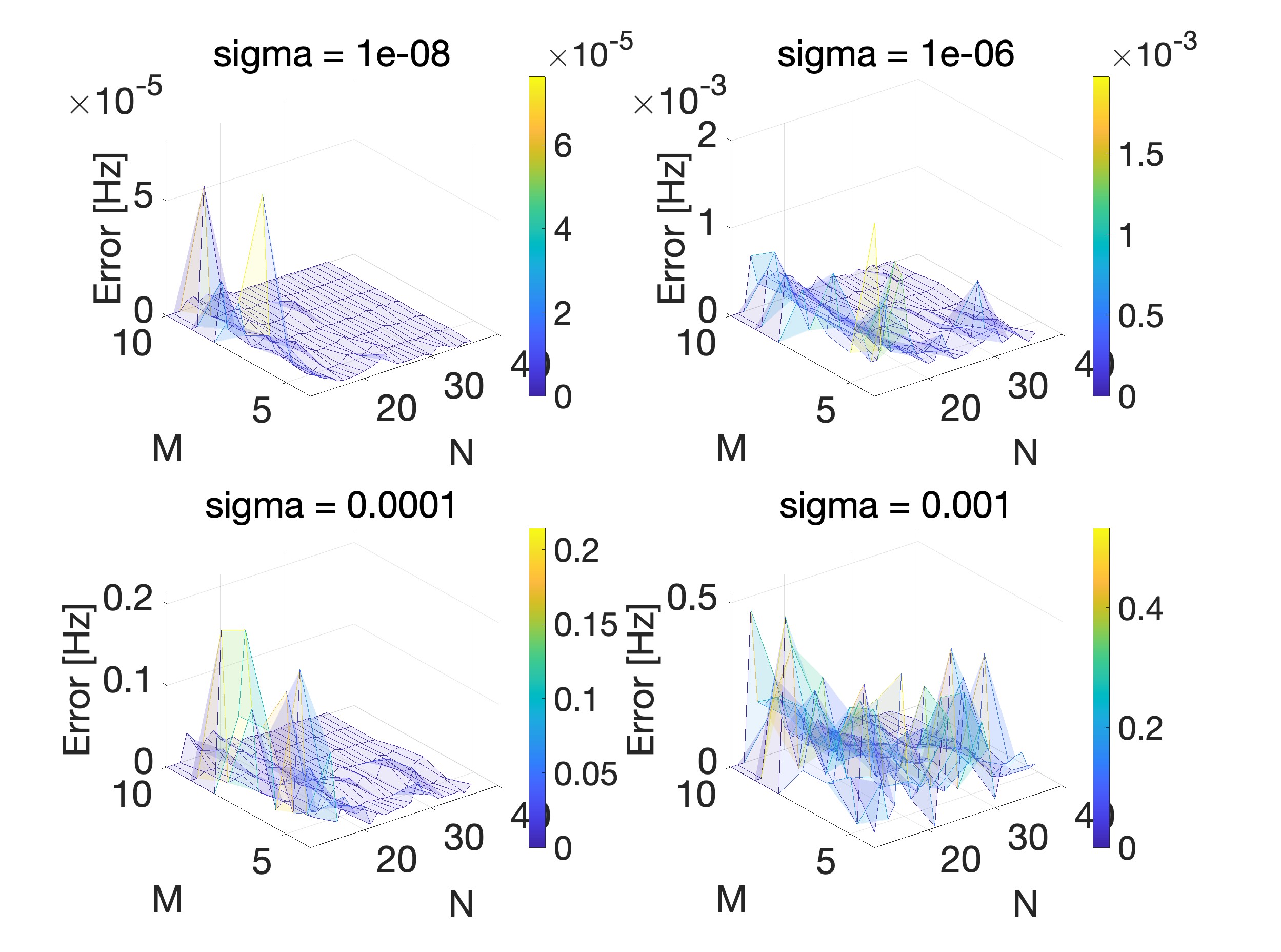
With MUSIC, samples requirement is reduced from 110 to 8 and frequency resolution (accuracy) increased from 72.73 Hz to 10^-2 Hz in the same time. This picture presents correctness as a percentage of detected fractions of dual tone signals (DTMFs), by input vector length N (8,9,10,11,12,14), autocorrelation order M (4-8) and fraction length L (8-28 samples).

dtmf_test_valid_freq_2

For example, using a block of N=12 samples, all fractions of length L=10 and above can be detected (with autocorrelation order M={6,7}). N=8 detects all fractions longer than 8 samples (1 ms) with M=4.

Discussion

If you have any questions, or would like to share your thoughts, request new features, etc. - please post them to Discussions.

Issues

If you would like to report an issue, please do it on issues page.

C library

A C library built on these results is libmusic

Repository

URL: https://github.com/dataandsignal/libmusic_m

MATLAB File Exchange

You can download this directly from View libmusic_m on File Exchange

Further reading, references

A good references about spectral analysis and space decomposition methods are:

  • Hayes M. H., Statistical Digital Signal Processing And Modeling, Georgia Institute of Technology, Wiley, 2008
  • Lawrence Marple S. Jr., Digital Spectral Analysis, Dover Publications, 2019
  • Schmidt R. O., Multiple Emitter Location and Signal Parameter Estimation, IEEE Transactions on Antennas and Propagation, Vol. AP-34, No. 3, 1986

These references are missing though (or skipping intentionally) a crucial result about autocorrelation and sinusoids embedded in a vector space whose elements are shifted samples of that same sinusoid (with all the phases). This is a fundamental finding space decomposition methods are built on.

This is explained in more detail in:

  • Penny W. D., Signal Processing Course, University College London, 2000

  • and also in my engineering thesis (written in polish, probably will be translated to english)

Copyright

LIBMUSIC

Copyright (C) 2018-2022, Piotr Gregor piotr@dataandsignal.com

August 2022