| comments | difficulty | edit_url | tags | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
true |
中等 |
|
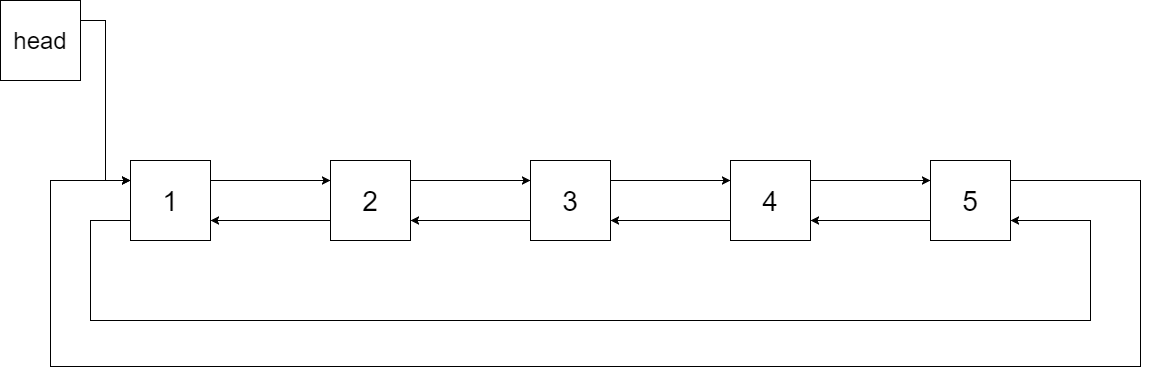
将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表 。
对于双向循环列表,你可以将左右孩子指针作为双向循环链表的前驱和后继指针,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
特别地,我们希望可以 原地 完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针。
示例 1:
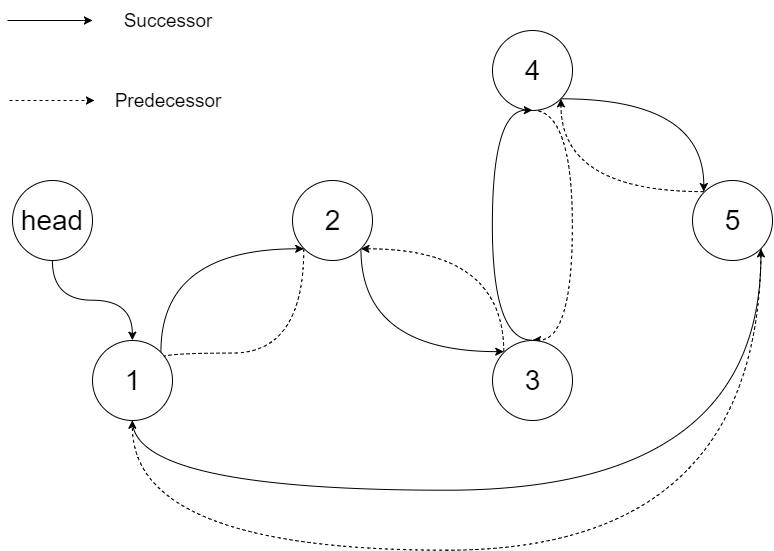
输入:root = [4,2,5,1,3]输出:[1,2,3,4,5] 解释:下图显示了转化后的二叉搜索树,实线表示后继关系,虚线表示前驱关系。
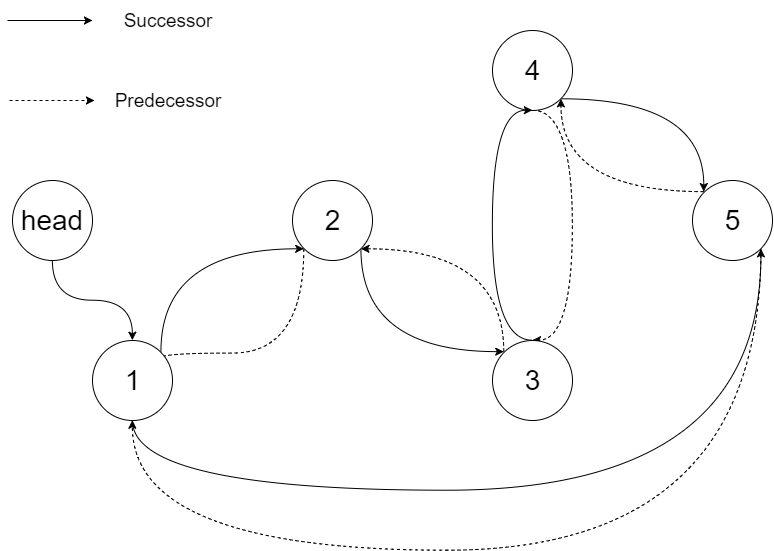
示例 2:
输入:root = [2,1,3] 输出:[1,2,3]
提示:
- 树中节点的数量在范围
[0, 2000]中 -1000 <= Node.val <= 1000- 树中的所有值都是 独一无二 的
"""
# Definition for a Node.
class Node:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
"""
class Solution:
def treeToDoublyList(self, root: 'Optional[Node]') -> 'Optional[Node]':
def dfs(root):
if root is None:
return
nonlocal prev, head
dfs(root.left)
if prev:
prev.right = root
root.left = prev
else:
head = root
prev = root
dfs(root.right)
if root is None:
return None
head = prev = None
dfs(root)
prev.right = head
head.left = prev
return head/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
private Node prev;
private Node head;
public Node treeToDoublyList(Node root) {
if (root == null) {
return null;
}
prev = null;
head = null;
dfs(root);
prev.right = head;
head.left = prev;
return head;
}
private void dfs(Node root) {
if (root == null) {
return;
}
dfs(root.left);
if (prev != null) {
prev.right = root;
root.left = prev;
} else {
head = root;
}
prev = root;
dfs(root.right);
}
}/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node() {}
Node(int _val) {
val = _val;
left = NULL;
right = NULL;
}
Node(int _val, Node* _left, Node* _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
public:
Node* prev;
Node* head;
Node* treeToDoublyList(Node* root) {
if (!root) return nullptr;
prev = nullptr;
head = nullptr;
dfs(root);
prev->right = head;
head->left = prev;
return head;
}
void dfs(Node* root) {
if (!root) return;
dfs(root->left);
if (prev) {
prev->right = root;
root->left = prev;
} else
head = root;
prev = root;
dfs(root->right);
}
};/**
* Definition for a Node.
* type Node struct {
* Val int
* Left *Node
* Right *Node
* }
*/
func treeToDoublyList(root *Node) *Node {
if root == nil {
return root
}
var prev, head *Node
var dfs func(root *Node)
dfs = func(root *Node) {
if root == nil {
return
}
dfs(root.Left)
if prev != nil {
prev.Right = root
root.Left = prev
} else {
head = root
}
prev = root
dfs(root.Right)
}
dfs(root)
prev.Right = head
head.Left = prev
return head
}/**
* // Definition for a Node.
* function Node(val, left, right) {
* this.val = val;
* this.left = left;
* this.right = right;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var treeToDoublyList = function (root) {
if (!root) return root;
let prev = null;
let head = null;
function dfs(root) {
if (!root) return;
dfs(root.left);
if (prev) {
prev.right = root;
root.left = prev;
} else {
head = root;
}
prev = root;
dfs(root.right);
}
dfs(root);
prev.right = head;
head.left = prev;
return head;
};