README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0700-0799/0742.Closest%20Leaf%20in%20a%20Binary%20Tree/README.md	树 深度优先搜索 广度优先搜索 二叉树

742. 二叉树最近的叶节点 🔒

English Version

题目描述

给定一个 每个结点的值互不相同 的二叉树，和一个目标整数值 k，返回 树中与目标值 k  最近的叶结点 。 

与叶结点最近 表示在二叉树中到达该叶节点需要行进的边数与到达其它叶结点相比最少。而且，当一个结点没有孩子结点时称其为叶结点。

 

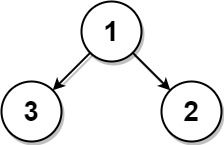
示例 1：

输入：root = [1, 3, 2], k = 1
输出： 2
解释： 2 和 3 都是距离目标 1 最近的叶节点。

示例 2：

输入：root = [1], k = 1
输出：1
解释：最近的叶节点是根结点自身。

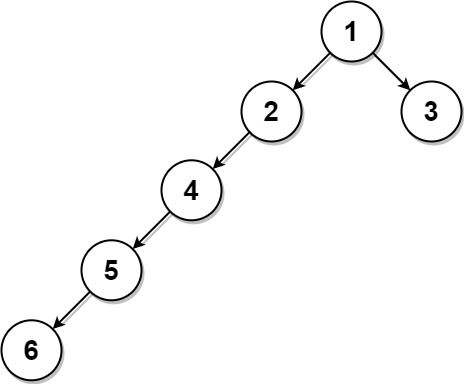
示例 3：

输入：root = [1,2,3,4,null,null,null,5,null,6], k = 2
输出：3
解释：值为 3（而不是值为 6）的叶节点是距离结点 2 的最近结点。

 

提示：

• 二叉树节点数在 [1, 1000] 范围内
• 1 <= Node.val <= 1000
• 每个节点值都 不同
• 给定的二叉树中有某个结点使得 node.val == k

解法

方法一：DFS + BFS

我们首先使用深度优先搜索构建一个无向图 $g$，其中 $g[node]$ 表示与节点 $node$ 相邻的节点集合。然后我们从节点 $k$ 开始进行广度优先搜索，直到找到一个叶节点为止，即为答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为二叉树节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findClosestLeaf(self, root: Optional[TreeNode], k: int) -> int:
        def dfs(root: Optional[TreeNode], fa: Optional[TreeNode]):
            if root:
                g[root].append(fa)
                g[fa].append(root)
                dfs(root.left, root)
                dfs(root.right, root)

        g = defaultdict(list)
        dfs(root, None)
        q = deque(node for node in g if node and node.val == k)
        vis = set(q)
        while 1:
            node = q.popleft()
            if node:
                if node.left == node.right:
                    return node.val
                for nxt in g[node]:
                    if nxt not in vis:
                        vis.add(nxt)
                        q.append(nxt)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<TreeNode, List<TreeNode>> g = new HashMap<>();

    public int findClosestLeaf(TreeNode root, int k) {
        dfs(root, null);
        Deque<TreeNode> q = new LinkedList<>();
        Set<TreeNode> vis = new HashSet<>(q.size());
        for (TreeNode node : g.keySet()) {
            if (node != null && node.val == k) {
                vis.add(node);
                q.offer(node);
                break;
            }
        }
        while (true) {
            TreeNode node = q.poll();
            if (node != null) {
                if (node.left == node.right) {
                    return node.val;
                }
                for (TreeNode nxt : g.get(node)) {
                    if (vis.add(nxt)) {
                        q.offer(nxt);
                    }
                }
            }
        }
    }

    private void dfs(TreeNode root, TreeNode fa) {
        if (root != null) {
            g.computeIfAbsent(root, k -> new ArrayList<>()).add(fa);
            g.computeIfAbsent(fa, k -> new ArrayList<>()).add(root);
            dfs(root.left, root);
            dfs(root.right, root);
        }
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findClosestLeaf(TreeNode* root, int k) {
        unordered_map<TreeNode*, vector<TreeNode*>> g;
        function<void(TreeNode*, TreeNode*)> dfs = [&](TreeNode* root, TreeNode* fa) {
            if (root) {
                g[root].push_back(fa);
                g[fa].push_back(root);
                dfs(root->left, root);
                dfs(root->right, root);
            }
        };
        dfs(root, nullptr);
        queue<TreeNode*> q;
        unordered_set<TreeNode*> vis;
        for (auto& [node, _] : g) {
            if (node && node->val == k) {
                q.push(node);
                vis.insert(node);
            }
        }
        while (1) {
            auto node = q.front();
            q.pop();
            if (node) {
                if (node->left == node->right) {
                    return node->val;
                }
                for (auto& nxt : g[node]) {
                    if (vis.count(nxt)) {
                        continue;
                    }
                    q.push(nxt);
                    vis.insert(nxt);
                }
            }
        }
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func findClosestLeaf(root *TreeNode, k int) int {
	g := map[*TreeNode][]*TreeNode{}
	var dfs func(*TreeNode, *TreeNode)
	dfs = func(root, fa *TreeNode) {
		if root != nil {
			g[root] = append(g[root], fa)
			g[fa] = append(g[fa], root)
			dfs(root.Left, root)
			dfs(root.Right, root)
		}
	}
	dfs(root, nil)
	q := []*TreeNode{}
	vis := map[*TreeNode]bool{}
	for node := range g {
		if node != nil && node.Val == k {
			q = append(q, node)
			vis[node] = true
			break
		}
	}
	for {
		node := q[0]
		q = q[1:]
		if node != nil {
			if node.Left == node.Right {
				return node.Val
			}
			for _, nxt := range g[node] {
				if !vis[nxt] {
					vis[nxt] = true
					q = append(q, nxt)
				}
			}
		}
	}
}