| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
中等 |
|
你正在把积木堆成金字塔。每个块都有一个颜色,用一个字母表示。每一行的块比它下面的行 少一个块 ,并且居中。
为了使金字塔美观,只有特定的 三角形图案 是允许的。一个三角形的图案由 两个块 和叠在上面的 单个块 组成。模式是以三个字母字符串的列表形式 allowed 给出的,其中模式的前两个字符分别表示左右底部块,第三个字符表示顶部块。
- 例如,
"ABC"表示一个三角形图案,其中一个“C”块堆叠在一个'A'块(左)和一个'B'块(右)之上。请注意,这与"BAC"不同,"B"在左下角,"A"在右下角。
你从作为单个字符串给出的底部的一排积木 bottom 开始,必须 将其作为金字塔的底部。
在给定 bottom 和 allowed 的情况下,如果你能一直构建到金字塔顶部,使金字塔中的 每个三角形图案 都是在 allowed 中的,则返回 true ,否则返回 false 。
示例 1:
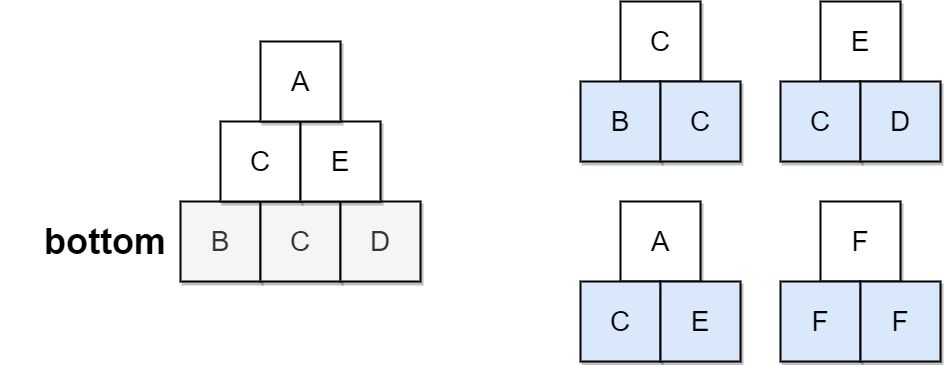
输入:bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"] 输出:true 解释:允许的三角形图案显示在右边。 从最底层(第 3 层)开始,我们可以在第 2 层构建“CE”,然后在第 1 层构建“E”。 金字塔中有三种三角形图案,分别是 “BCC”、“CDE” 和 “CEA”。都是允许的。
示例 2:
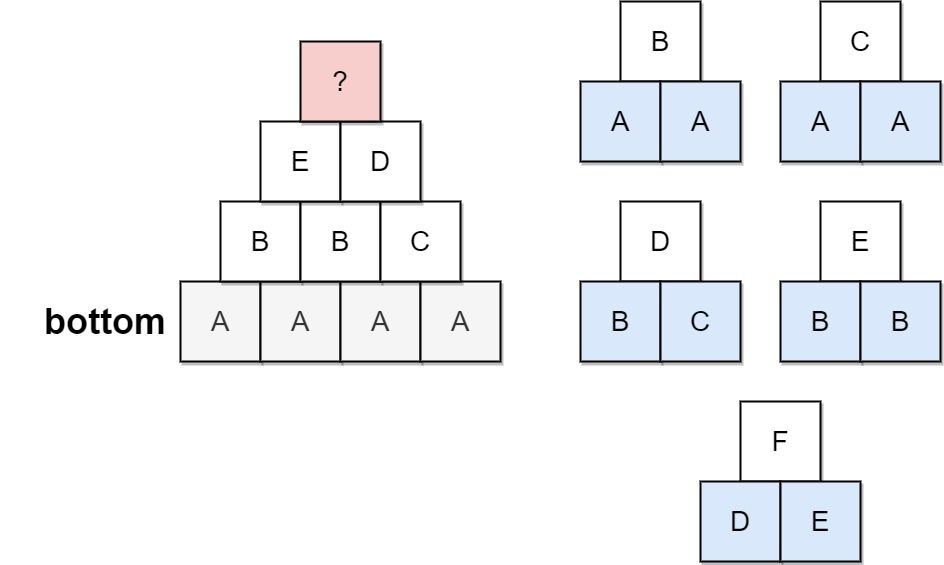
输入:bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"] 输出:false 解释:允许的三角形图案显示在右边。 从最底层(即第 4 层)开始,创造第 3 层有多种方法,但如果尝试所有可能性,你便会在创造第 1 层前陷入困境。
提示:
2 <= bottom.length <= 60 <= allowed.length <= 216allowed[i].length == 3- 所有输入字符串中的字母来自集合
{'A', 'B', 'C', 'D', 'E', 'F'}。 -
allowed中所有值都是 唯一的
定义哈希表
从最底层开始,对于每一层的每两个相邻的字符,如果它们可以组成一个三角形图案,那么就将三角形图案的顶部字符加入到下一层的对应位置的字符列表中,然后对下一层进行递归处理。
时间复杂度 bottom 字符串的长度。
class Solution:
def pyramidTransition(self, bottom: str, allowed: List[str]) -> bool:
@cache
def dfs(s):
if len(s) == 1:
return True
t = []
for a, b in pairwise(s):
cs = d[a, b]
if not cs:
return False
t.append(cs)
return any(dfs(''.join(nxt)) for nxt in product(*t))
d = defaultdict(list)
for a, b, c in allowed:
d[a, b].append(c)
return dfs(bottom)class Solution {
private int[][] f = new int[7][7];
private Map<String, Boolean> dp = new HashMap<>();
public boolean pyramidTransition(String bottom, List<String> allowed) {
for (String s : allowed) {
int a = s.charAt(0) - 'A', b = s.charAt(1) - 'A';
f[a][b] |= 1 << (s.charAt(2) - 'A');
}
return dfs(bottom, new StringBuilder());
}
boolean dfs(String s, StringBuilder t) {
if (s.length() == 1) {
return true;
}
if (t.length() + 1 == s.length()) {
return dfs(t.toString(), new StringBuilder());
}
String k = s + "." + t.toString();
if (dp.containsKey(k)) {
return dp.get(k);
}
int a = s.charAt(t.length()) - 'A', b = s.charAt(t.length() + 1) - 'A';
int cs = f[a][b];
for (int i = 0; i < 7; ++i) {
if (((cs >> i) & 1) == 1) {
t.append((char) ('A' + i));
if (dfs(s, t)) {
dp.put(k, true);
return true;
}
t.deleteCharAt(t.length() - 1);
}
}
dp.put(k, false);
return false;
}
}class Solution {
public:
int f[7][7];
unordered_map<string, bool> dp;
bool pyramidTransition(string bottom, vector<string>& allowed) {
memset(f, 0, sizeof f);
for (auto& s : allowed) {
int a = s[0] - 'A', b = s[1] - 'A';
f[a][b] |= 1 << (s[2] - 'A');
}
return dfs(bottom, "");
}
bool dfs(string& s, string t) {
if (s.size() == 1) {
return true;
}
if (t.size() + 1 == s.size()) {
return dfs(t, "");
}
string k = s + "." + t;
if (dp.count(k)) {
return dp[k];
}
int a = s[t.size()] - 'A', b = s[t.size() + 1] - 'A';
int cs = f[a][b];
for (int i = 0; i < 7; ++i) {
if ((cs >> i) & 1) {
if (dfs(s, t + (char) (i + 'A'))) {
dp[k] = true;
return true;
}
}
}
dp[k] = false;
return false;
}
};func pyramidTransition(bottom string, allowed []string) bool {
f := make([][]int, 7)
for i := range f {
f[i] = make([]int, 7)
}
for _, s := range allowed {
a, b := s[0]-'A', s[1]-'A'
f[a][b] |= 1 << (s[2] - 'A')
}
dp := map[string]bool{}
var dfs func(s string, t []byte) bool
dfs = func(s string, t []byte) bool {
if len(s) == 1 {
return true
}
if len(t)+1 == len(s) {
return dfs(string(t), []byte{})
}
k := s + "." + string(t)
if v, ok := dp[k]; ok {
return v
}
a, b := s[len(t)]-'A', s[len(t)+1]-'A'
cs := f[a][b]
for i := 0; i < 7; i++ {
if ((cs >> i) & 1) == 1 {
t = append(t, byte('A'+i))
if dfs(s, t) {
dp[k] = true
return true
}
t = t[:len(t)-1]
}
}
dp[k] = false
return false
}
return dfs(bottom, []byte{})
}