| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
2189 |
第 139 场周赛 Q4 |
|
给出矩阵 matrix 和目标值 target,返回元素总和等于目标值的非空子矩阵的数量。
子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。
如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同(如:x1 != x1'),那么这两个子矩阵也不同。
示例 1:
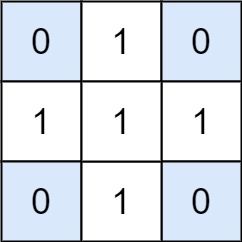
输入:matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0 输出:4 解释:四个只含 0 的 1x1 子矩阵。
示例 2:
输入:matrix = [[1,-1],[-1,1]], target = 0 输出:5 解释:两个 1x2 子矩阵,加上两个 2x1 子矩阵,再加上一个 2x2 子矩阵。
示例 3:
输入:matrix = [[904]], target = 0 输出:0
提示:
1 <= matrix.length <= 1001 <= matrix[0].length <= 100-1000 <= matrix[i][j] <= 1000-10^8 <= target <= 10^8
我们可以枚举矩阵的上下边界
那么题目就变成了:给定一个数组
函数
- 定义一个哈希表
$d$ ,用来记录出现过的前缀和以及其出现次数,初始时$d[0] = 1$ ; - 初始化变量
$s = 0, cnt = 0$ ,其中$s$ 表示前缀和,而$cnt$ 表示和为$target$ 的子数组个数; - 从左到右遍历数组
$nums$ ,对于当前遍历到的元素$x$ ,更新前缀和$s = s + x$ ,如果$d[s - target]$ 的值存在,那么更新$cnt = cnt + d[s - target]$ ,即子数组个数增加$d[s - target]$ 。然后更新哈希表中元素$d[s]$ 的值,即$d[s] = d[s] + 1$ ;继续遍历下一个元素; - 遍历结束之后,返回子数组个数
$cnt$ 。
时间复杂度
class Solution:
def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
def f(nums: List[int]) -> int:
d = defaultdict(int)
d[0] = 1
cnt = s = 0
for x in nums:
s += x
cnt += d[s - target]
d[s] += 1
return cnt
m, n = len(matrix), len(matrix[0])
ans = 0
for i in range(m):
col = [0] * n
for j in range(i, m):
for k in range(n):
col[k] += matrix[j][k]
ans += f(col)
return ansclass Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
int ans = 0;
for (int i = 0; i < m; ++i) {
int[] col = new int[n];
for (int j = i; j < m; ++j) {
for (int k = 0; k < n; ++k) {
col[k] += matrix[j][k];
}
ans += f(col, target);
}
}
return ans;
}
private int f(int[] nums, int target) {
Map<Integer, Integer> d = new HashMap<>();
d.put(0, 1);
int s = 0, cnt = 0;
for (int x : nums) {
s += x;
cnt += d.getOrDefault(s - target, 0);
d.merge(s, 1, Integer::sum);
}
return cnt;
}
}class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int ans = 0;
for (int i = 0; i < m; ++i) {
vector<int> col(n);
for (int j = i; j < m; ++j) {
for (int k = 0; k < n; ++k) {
col[k] += matrix[j][k];
}
ans += f(col, target);
}
}
return ans;
}
int f(vector<int>& nums, int target) {
unordered_map<int, int> d{{0, 1}};
int cnt = 0, s = 0;
for (int& x : nums) {
s += x;
if (d.count(s - target)) {
cnt += d[s - target];
}
++d[s];
}
return cnt;
}
};func numSubmatrixSumTarget(matrix [][]int, target int) (ans int) {
m, n := len(matrix), len(matrix[0])
for i := 0; i < m; i++ {
col := make([]int, n)
for j := i; j < m; j++ {
for k := 0; k < n; k++ {
col[k] += matrix[j][k]
}
ans += f(col, target)
}
}
return
}
func f(nums []int, target int) (cnt int) {
d := map[int]int{0: 1}
s := 0
for _, x := range nums {
s += x
if v, ok := d[s-target]; ok {
cnt += v
}
d[s]++
}
return
}function numSubmatrixSumTarget(matrix: number[][], target: number): number {
const m = matrix.length;
const n = matrix[0].length;
let ans = 0;
for (let i = 0; i < m; ++i) {
const col: number[] = new Array(n).fill(0);
for (let j = i; j < m; ++j) {
for (let k = 0; k < n; ++k) {
col[k] += matrix[j][k];
}
ans += f(col, target);
}
}
return ans;
}
function f(nums: number[], target: number): number {
const d: Map<number, number> = new Map();
d.set(0, 1);
let cnt = 0;
let s = 0;
for (const x of nums) {
s += x;
if (d.has(s - target)) {
cnt += d.get(s - target)!;
}
d.set(s, (d.get(s) || 0) + 1);
}
return cnt;
}