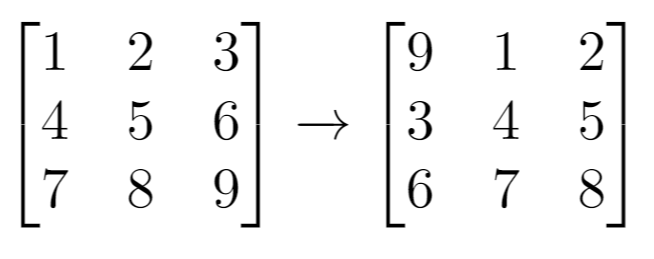| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
简单 |
1337 |
第 163 场周赛 Q1 |
|
给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。
每次「迁移」操作将会引发下述活动:
- 位于
grid[i][j](j < n - 1)的元素将会移动到grid[i][j + 1]。 - 位于
grid[i][n - 1]的元素将会移动到grid[i + 1][0]。 - 位于
grid[m - 1][n - 1]的元素将会移动到grid[0][0]。
请你返回 k 次迁移操作后最终得到的 二维网格。
示例 1:
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[9,1,2],[3,4,5],[6,7,8]]
示例 2:
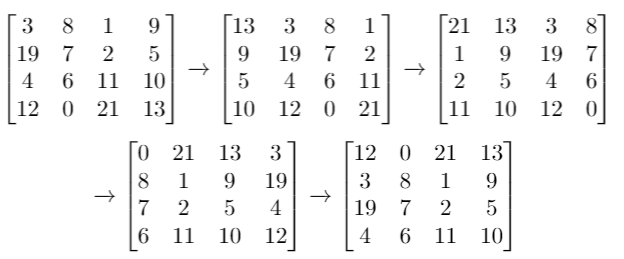
输入:grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
输出:[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]
示例 3:
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
输出:[[1,2,3],[4,5,6],[7,8,9]]
提示:
m == grid.lengthn == grid[i].length1 <= m <= 501 <= n <= 50-1000 <= grid[i][j] <= 10000 <= k <= 100
根据题目描述,如果我们将二维数组展开成一维数组,那么每次迁移操作就是将数组中的元素向右移动一个位置,最后一个元素移动到数组的首位。
因此,我们可以将二维数组展开成一维数组,然后计算每个元素在最后的位置 ans[x][y] = grid[i][j] 即可。
时间复杂度 grid 的行数和列数。需要遍历二维数组 grid 一次,计算每个元素在最后的位置。忽略答案数组的空间消耗,空间复杂度
class Solution:
def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
m, n = len(grid), len(grid[0])
ans = [[0] * n for _ in range(m)]
for i, row in enumerate(grid):
for j, v in enumerate(row):
x, y = divmod((i * n + j + k) % (m * n), n)
ans[x][y] = v
return ansclass Solution {
public List<List<Integer>> shiftGrid(int[][] grid, int k) {
int m = grid.length, n = grid[0].length;
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; ++i) {
List<Integer> row = new ArrayList<>();
for (int j = 0; j < n; ++j) {
row.add(0);
}
ans.add(row);
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int idx = (i * n + j + k) % (m * n);
int x = idx / n, y = idx % n;
ans.get(x).set(y, grid[i][j]);
}
}
return ans;
}
}class Solution {
public:
vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>> ans(m, vector<int>(n));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int idx = (i * n + j + k) % (m * n);
int x = idx / n, y = idx % n;
ans[x][y] = grid[i][j];
}
}
return ans;
}
};func shiftGrid(grid [][]int, k int) [][]int {
m, n := len(grid), len(grid[0])
ans := make([][]int, m)
for i := range ans {
ans[i] = make([]int, n)
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
idx := (i*n + j + k) % (m * n)
x, y := idx/n, idx%n
ans[x][y] = grid[i][j]
}
}
return ans
}function shiftGrid(grid: number[][], k: number): number[][] {
const [m, n] = [grid.length, grid[0].length];
const ans: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => 0));
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
const idx = (i * n + j + k) % (m * n);
const [x, y] = [Math.floor(idx / n), idx % n];
ans[x][y] = grid[i][j];
}
}
return ans;
}