| comments | difficulty | edit_url | rating | source | tags | |||||
|---|---|---|---|---|---|---|---|---|---|---|
true |
Medium |
1845 |
Weekly Contest 196 Q3 |
|
Given an m x n binary matrix mat, return the number of submatrices that have all ones.
Example 1:
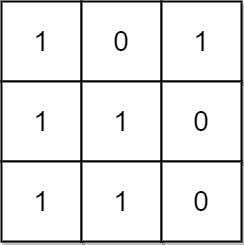
Input: mat = [[1,0,1],[1,1,0],[1,1,0]] Output: 13 Explanation: There are 6 rectangles of side 1x1. There are 2 rectangles of side 1x2. There are 3 rectangles of side 2x1. There is 1 rectangle of side 2x2. There is 1 rectangle of side 3x1. Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
Example 2:
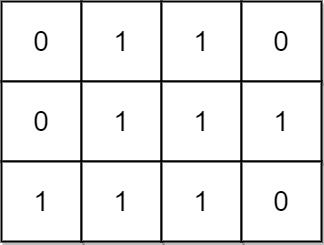
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] Output: 24 Explanation: There are 8 rectangles of side 1x1. There are 5 rectangles of side 1x2. There are 2 rectangles of side 1x3. There are 4 rectangles of side 2x1. There are 2 rectangles of side 2x2. There are 2 rectangles of side 3x1. There is 1 rectangle of side 3x2. Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
Constraints:
1 <= m, n <= 150mat[i][j]is either0or1.
We can enumerate the bottom-right corner
Therefore, we can preprocess a 2D array
The time complexity is
class Solution:
def numSubmat(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
g = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
if mat[i][j]:
g[i][j] = 1 if j == 0 else 1 + g[i][j - 1]
ans = 0
for i in range(m):
for j in range(n):
col = inf
for k in range(i, -1, -1):
col = min(col, g[k][j])
ans += col
return ansclass Solution {
public int numSubmat(int[][] mat) {
int m = mat.length, n = mat[0].length;
int[][] g = new int[m][n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] == 1) {
g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
}
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int col = 1 << 30;
for (int k = i; k >= 0 && col > 0; --k) {
col = Math.min(col, g[k][j]);
ans += col;
}
}
}
return ans;
}
}class Solution {
public:
int numSubmat(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> g(m, vector<int>(n));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] == 1) {
g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
}
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int col = 1 << 30;
for (int k = i; k >= 0 && col > 0; --k) {
col = min(col, g[k][j]);
ans += col;
}
}
}
return ans;
}
};func numSubmat(mat [][]int) (ans int) {
m, n := len(mat), len(mat[0])
g := make([][]int, m)
for i := range g {
g[i] = make([]int, n)
for j := range g[i] {
if mat[i][j] == 1 {
if j == 0 {
g[i][j] = 1
} else {
g[i][j] = 1 + g[i][j-1]
}
}
}
}
for i := range g {
for j := range g[i] {
col := 1 << 30
for k := i; k >= 0 && col > 0; k-- {
col = min(col, g[k][j])
ans += col
}
}
}
return
}function numSubmat(mat: number[][]): number {
const m = mat.length;
const n = mat[0].length;
const g: number[][] = Array.from({ length: m }, () => Array(n).fill(0));
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (mat[i][j]) {
g[i][j] = j === 0 ? 1 : 1 + g[i][j - 1];
}
}
}
let ans = 0;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
let col = Infinity;
for (let k = i; k >= 0; k--) {
col = Math.min(col, g[k][j]);
ans += col;
}
}
}
return ans;
}