| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
困难 |
2116 |
第 201 场周赛 Q4 |
|
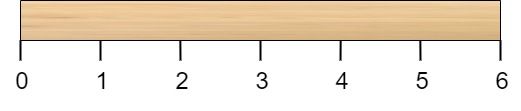
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
示例 1:
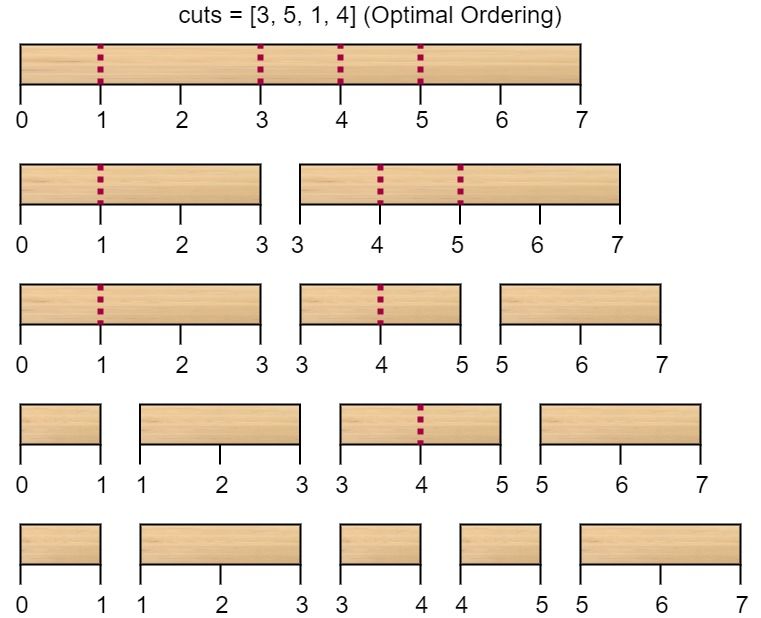
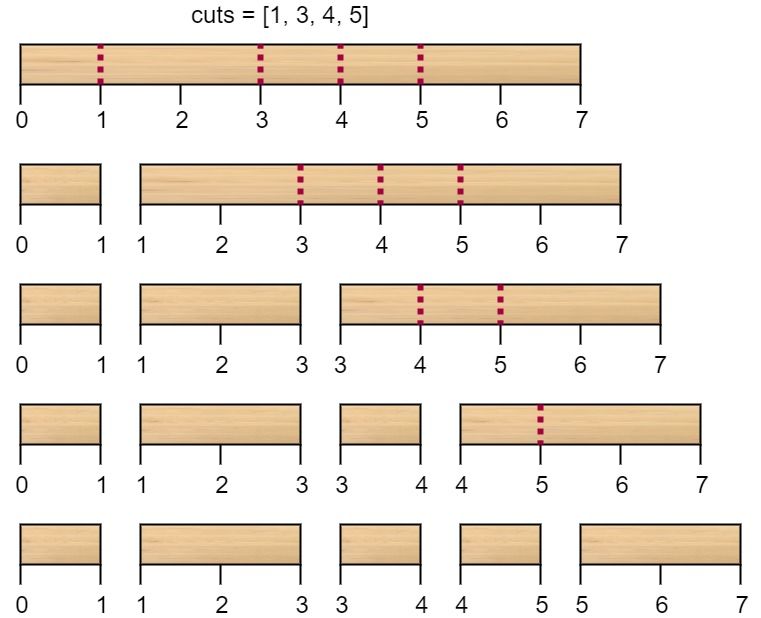
输入:n = 7, cuts = [1,3,4,5] 输出:16 解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示:第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。 而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
示例 2:
输入:n = 9, cuts = [5,6,1,4,2] 输出:22 解释:如果按给定的顺序切割,则总成本为 25 。总成本 <= 25 的切割顺序很多,例如,[4, 6, 5, 2, 1] 的总成本 = 22,是所有可能方案中成本最小的。
提示:
2 <= n <= 10^61 <= cuts.length <= min(n - 1, 100)1 <= cuts[i] <= n - 1cuts数组中的所有整数都 互不相同
我们可以往切割点数组
接下来,我们定义
如果一个区间只有两个切割点,也就是说,我们无需切割这个区间,那么
否则,我们枚举区间的长度
最后,我们返回
时间复杂度
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
cuts.extend([0, n])
cuts.sort()
m = len(cuts)
f = [[0] * m for _ in range(m)]
for l in range(2, m):
for i in range(m - l):
j = i + l
f[i][j] = inf
for k in range(i + 1, j):
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i])
return f[0][-1]class Solution {
public int minCost(int n, int[] cuts) {
List<Integer> nums = new ArrayList<>();
for (int x : cuts) {
nums.add(x);
}
nums.add(0);
nums.add(n);
Collections.sort(nums);
int m = nums.size();
int[][] f = new int[m][m];
for (int l = 2; l < m; ++l) {
for (int i = 0; i + l < m; ++i) {
int j = i + l;
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + nums.get(j) - nums.get(i));
}
}
}
return f[0][m - 1];
}
}class Solution {
public:
int minCost(int n, vector<int>& cuts) {
cuts.push_back(0);
cuts.push_back(n);
sort(cuts.begin(), cuts.end());
int m = cuts.size();
int f[110][110]{};
for (int l = 2; l < m; ++l) {
for (int i = 0; i + l < m; ++i) {
int j = i + l;
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
}
}
}
return f[0][m - 1];
}
};func minCost(n int, cuts []int) int {
cuts = append(cuts, []int{0, n}...)
sort.Ints(cuts)
m := len(cuts)
f := make([][]int, m)
for i := range f {
f[i] = make([]int, m)
}
for l := 2; l < m; l++ {
for i := 0; i+l < m; i++ {
j := i + l
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]+cuts[j]-cuts[i])
}
}
}
return f[0][m-1]
}function minCost(n: number, cuts: number[]): number {
cuts.push(0, n);
cuts.sort((a, b) => a - b);
const m = cuts.length;
const f: number[][] = Array.from({ length: m }, () => Array(m).fill(0));
for (let l = 2; l < m; l++) {
for (let i = 0; i < m - l; i++) {
const j = i + l;
f[i][j] = Infinity;
for (let k = i + 1; k < j; k++) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
}
}
}
return f[0][m - 1];
}我们也可以从大到小枚举
时间复杂度
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
cuts.extend([0, n])
cuts.sort()
m = len(cuts)
f = [[0] * m for _ in range(m)]
for i in range(m - 1, -1, -1):
for j in range(i + 2, m):
f[i][j] = inf
for k in range(i + 1, j):
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i])
return f[0][-1]class Solution {
public int minCost(int n, int[] cuts) {
List<Integer> nums = new ArrayList<>();
for (int x : cuts) {
nums.add(x);
}
nums.add(0);
nums.add(n);
Collections.sort(nums);
int m = nums.size();
int[][] f = new int[m][m];
for (int i = m - 1; i >= 0; --i) {
for (int j = i + 2; j < m; ++j) {
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + nums.get(j) - nums.get(i));
}
}
}
return f[0][m - 1];
}
}class Solution {
public:
int minCost(int n, vector<int>& cuts) {
cuts.push_back(0);
cuts.push_back(n);
sort(cuts.begin(), cuts.end());
int m = cuts.size();
int f[110][110]{};
for (int i = m - 1; ~i; --i) {
for (int j = i + 2; j < m; ++j) {
f[i][j] = 1 << 30;
for (int k = i + 1; k < j; ++k) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
}
}
}
return f[0][m - 1];
}
};func minCost(n int, cuts []int) int {
cuts = append(cuts, []int{0, n}...)
sort.Ints(cuts)
m := len(cuts)
f := make([][]int, m)
for i := range f {
f[i] = make([]int, m)
}
for i := m - 1; i >= 0; i-- {
for j := i + 2; j < m; j++ {
f[i][j] = 1 << 30
for k := i + 1; k < j; k++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]+cuts[j]-cuts[i])
}
}
}
return f[0][m-1]
}function minCost(n: number, cuts: number[]): number {
cuts.push(0);
cuts.push(n);
cuts.sort((a, b) => a - b);
const m = cuts.length;
const f: number[][] = Array.from({ length: m }, () => Array(m).fill(0));
for (let i = m - 2; i >= 0; --i) {
for (let j = i + 2; j < m; ++j) {
f[i][j] = 1 << 30;
for (let k = i + 1; k < j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j] + cuts[j] - cuts[i]);
}
}
}
return f[0][m - 1];
}