| comments | difficulty | edit_url | rating | source | tags | ||
|---|---|---|---|---|---|---|---|
true |
简单 |
1443 |
第 203 场周赛 Q1 |
|
给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成,扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛,该马拉松全程由 m 个阶段组成。其中,第 i 个阶段将会从扇区 rounds[i - 1] 开始,到扇区 rounds[i] 结束。举例来说,第 1 阶段从 rounds[0] 开始,到 rounds[1] 结束。
请你以数组形式返回经过次数最多的那几个扇区,按扇区编号 升序 排列。
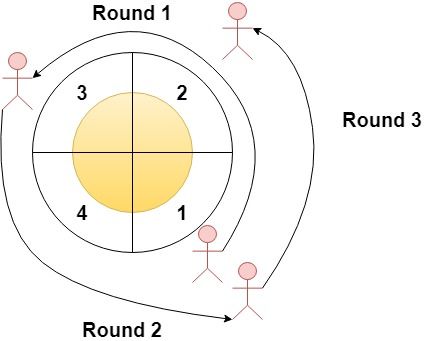
注意,赛道按扇区编号升序逆时针形成一个圆(请参见第一个示例)。
示例 1:
输入:n = 4, rounds = [1,3,1,2] 输出:[1,2] 解释:本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示: 1 --> 2 --> 3(阶段 1 结束)--> 4 --> 1(阶段 2 结束)--> 2(阶段 3 结束,即本场马拉松结束) 其中,扇区 1 和 2 都经过了两次,它们是经过次数最多的两个扇区。扇区 3 和 4 都只经过了一次。
示例 2:
输入:n = 2, rounds = [2,1,2,1,2,1,2,1,2] 输出:[2]
示例 3:
输入:n = 7, rounds = [1,3,5,7] 输出:[1,2,3,4,5,6,7]
提示:
2 <= n <= 1001 <= m <= 100rounds.length == m + 11 <= rounds[i] <= nrounds[i] != rounds[i + 1],其中0 <= i < m
由于每个阶段的结束位置是下一个阶段的开始位置,并且每个阶段都是逆时针方向的,所以我们可以根据开始和结束的位置关系来确定每个扇区的经过次数。
如果
否则,从
时间复杂度
class Solution:
def mostVisited(self, n: int, rounds: List[int]) -> List[int]:
if rounds[0] <= rounds[-1]:
return list(range(rounds[0], rounds[-1] + 1))
return list(range(1, rounds[-1] + 1)) + list(range(rounds[0], n + 1))class Solution {
public List<Integer> mostVisited(int n, int[] rounds) {
int m = rounds.length - 1;
List<Integer> ans = new ArrayList<>();
if (rounds[0] <= rounds[m]) {
for (int i = rounds[0]; i <= rounds[m]; ++i) {
ans.add(i);
}
} else {
for (int i = 1; i <= rounds[m]; ++i) {
ans.add(i);
}
for (int i = rounds[0]; i <= n; ++i) {
ans.add(i);
}
}
return ans;
}
}class Solution {
public:
vector<int> mostVisited(int n, vector<int>& rounds) {
int m = rounds.size() - 1;
vector<int> ans;
if (rounds[0] <= rounds[m]) {
for (int i = rounds[0]; i <= rounds[m]; ++i) {
ans.push_back(i);
}
} else {
for (int i = 1; i <= rounds[m]; ++i) {
ans.push_back(i);
}
for (int i = rounds[0]; i <= n; ++i) {
ans.push_back(i);
}
}
return ans;
}
};func mostVisited(n int, rounds []int) []int {
m := len(rounds) - 1
var ans []int
if rounds[0] <= rounds[m] {
for i := rounds[0]; i <= rounds[m]; i++ {
ans = append(ans, i)
}
} else {
for i := 1; i <= rounds[m]; i++ {
ans = append(ans, i)
}
for i := rounds[0]; i <= n; i++ {
ans = append(ans, i)
}
}
return ans
}function mostVisited(n: number, rounds: number[]): number[] {
const ans: number[] = [];
const m = rounds.length - 1;
if (rounds[0] <= rounds[m]) {
for (let i = rounds[0]; i <= rounds[m]; ++i) {
ans.push(i);
}
} else {
for (let i = 1; i <= rounds[m]; ++i) {
ans.push(i);
}
for (let i = rounds[0]; i <= n; ++i) {
ans.push(i);
}
}
return ans;
}