| comments | difficulty | edit_url | rating | source | tags | |||||
|---|---|---|---|---|---|---|---|---|---|---|
true |
Hard |
2077 |
Biweekly Contest 119 Q4 |
|
There is a company with n branches across the country, some of which are connected by roads. Initially, all branches are reachable from each other by traveling some roads.
The company has realized that they are spending an excessive amount of time traveling between their branches. As a result, they have decided to close down some of these branches (possibly none). However, they want to ensure that the remaining branches have a distance of at most maxDistance from each other.
The distance between two branches is the minimum total traveled length needed to reach one branch from another.
You are given integers n, maxDistance, and a 0-indexed 2D array roads, where roads[i] = [ui, vi, wi] represents the undirected road between branches ui and vi with length wi.
Return the number of possible sets of closing branches, so that any branch has a distance of at most maxDistance from any other.
Note that, after closing a branch, the company will no longer have access to any roads connected to it.
Note that, multiple roads are allowed.
Example 1:
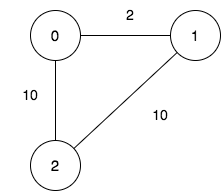
Input: n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]] Output: 5 Explanation: The possible sets of closing branches are: - The set [2], after closing, active branches are [0,1] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 5 possible sets of closing branches.
Example 2:
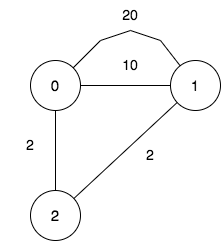
Input: n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]] Output: 7 Explanation: The possible sets of closing branches are: - The set [], after closing, active branches are [0,1,2] and they are reachable to each other within distance 4. - The set [0], after closing, active branches are [1,2] and they are reachable to each other within distance 2. - The set [1], after closing, active branches are [0,2] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 7 possible sets of closing branches.
Example 3:
Input: n = 1, maxDistance = 10, roads = [] Output: 2 Explanation: The possible sets of closing branches are: - The set [], after closing, the active branch is [0]. - The set [0], after closing, there are no active branches. It can be proven, that there are only 2 possible sets of closing branches.
Constraints:
1 <= n <= 101 <= maxDistance <= 1050 <= roads.length <= 1000roads[i].length == 30 <= ui, vi <= n - 1ui != vi1 <= wi <= 1000- All branches are reachable from each other by traveling some roads.
We notice that
For each subset of departments, we can use the Floyd algorithm to calculate the shortest distance between the remaining departments, and then judge whether it meets the requirements of the problem. Specifically, we first enumerate the middle point
The time complexity is
class Solution:
def numberOfSets(self, n: int, maxDistance: int, roads: List[List[int]]) -> int:
ans = 0
for mask in range(1 << n):
g = [[inf] * n for _ in range(n)]
for u, v, w in roads:
if mask >> u & 1 and mask >> v & 1:
g[u][v] = min(g[u][v], w)
g[v][u] = min(g[v][u], w)
for k in range(n):
if mask >> k & 1:
g[k][k] = 0
for i in range(n):
for j in range(n):
# g[i][j] = min(g[i][j], g[i][k] + g[k][j])
if g[i][k] + g[k][j] < g[i][j]:
g[i][j] = g[i][k] + g[k][j]
if all(
g[i][j] <= maxDistance
for i in range(n)
for j in range(n)
if mask >> i & 1 and mask >> j & 1
):
ans += 1
return ansclass Solution {
public int numberOfSets(int n, int maxDistance, int[][] roads) {
int ans = 0;
for (int mask = 0; mask < 1 << n; ++mask) {
int[][] g = new int[n][n];
for (var e : g) {
Arrays.fill(e, 1 << 29);
}
for (var e : roads) {
int u = e[0], v = e[1], w = e[2];
if ((mask >> u & 1) == 1 && (mask >> v & 1) == 1) {
g[u][v] = Math.min(g[u][v], w);
g[v][u] = Math.min(g[v][u], w);
}
}
for (int k = 0; k < n; ++k) {
if ((mask >> k & 1) == 1) {
g[k][k] = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
}
}
}
}
int ok = 1;
for (int i = 0; i < n && ok == 1; ++i) {
for (int j = 0; j < n && ok == 1; ++j) {
if ((mask >> i & 1) == 1 && (mask >> j & 1) == 1) {
if (g[i][j] > maxDistance) {
ok = 0;
}
}
}
}
ans += ok;
}
return ans;
}
}class Solution {
public:
int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
int ans = 0;
for (int mask = 0; mask < 1 << n; ++mask) {
int g[n][n];
memset(g, 0x3f, sizeof(g));
for (auto& e : roads) {
int u = e[0], v = e[1], w = e[2];
if ((mask >> u & 1) & (mask >> v & 1)) {
g[u][v] = min(g[u][v], w);
g[v][u] = min(g[v][u], w);
}
}
for (int k = 0; k < n; ++k) {
if (mask >> k & 1) {
g[k][k] = 0;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}
}
}
}
int ok = 1;
for (int i = 0; i < n && ok == 1; ++i) {
for (int j = 0; j < n && ok == 1; ++j) {
if ((mask >> i & 1) & (mask >> j & 1) && g[i][j] > maxDistance) {
ok = 0;
}
}
}
ans += ok;
}
return ans;
}
};func numberOfSets(n int, maxDistance int, roads [][]int) (ans int) {
for mask := 0; mask < 1<<n; mask++ {
g := make([][]int, n)
for i := range g {
g[i] = make([]int, n)
for j := range g[i] {
g[i][j] = 1 << 29
}
}
for _, e := range roads {
u, v, w := e[0], e[1], e[2]
if mask>>u&1 == 1 && mask>>v&1 == 1 {
g[u][v] = min(g[u][v], w)
g[v][u] = min(g[v][u], w)
}
}
for k := 0; k < n; k++ {
if mask>>k&1 == 1 {
g[k][k] = 0
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
g[i][j] = min(g[i][j], g[i][k]+g[k][j])
}
}
}
}
ok := 1
for i := 0; i < n && ok == 1; i++ {
for j := 0; j < n && ok == 1; j++ {
if mask>>i&1 == 1 && mask>>j&1 == 1 && g[i][j] > maxDistance {
ok = 0
}
}
}
ans += ok
}
return
}function numberOfSets(n: number, maxDistance: number, roads: number[][]): number {
let ans = 0;
for (let mask = 0; mask < 1 << n; ++mask) {
const g: number[][] = Array.from({ length: n }, () => Array(n).fill(Infinity));
for (const [u, v, w] of roads) {
if ((mask >> u) & 1 && (mask >> v) & 1) {
g[u][v] = Math.min(g[u][v], w);
g[v][u] = Math.min(g[v][u], w);
}
}
for (let k = 0; k < n; ++k) {
if ((mask >> k) & 1) {
g[k][k] = 0;
for (let i = 0; i < n; ++i) {
for (let j = 0; j < n; ++j) {
g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
}
}
}
}
let ok = 1;
for (let i = 0; i < n && ok; ++i) {
for (let j = 0; j < n && ok; ++j) {
if ((mask >> i) & 1 && (mask >> j) & 1 && g[i][j] > maxDistance) {
ok = 0;
}
}
}
ans += ok;
}
return ans;
}