-
Notifications
You must be signed in to change notification settings - Fork 50
Calibration
At first thought, calibration might seem like a simple thing; just measure how much off the sensor is, using a trusted reference - e.g. the sensor might show 20 degrees while the real temperature is 25 - and then always add the difference to the measured temperature.
However, this is not always good enough, as the sensor might be off by different amunts depending on the actual temperature, e.g. it might show 0 degrees when the real temperature is 5, yet show 100 degrees when it is really 95, with a straight line between those points.
And sometimes it's not even linear, but a curve - e.g. showing correct temperatures at 0 and 100, but showing 50 degrees when it's really 60, with a smooth curve between those points.
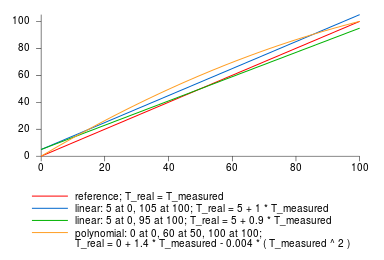
To the right is a graph giving a visual representation of these examples.
In this graph, the X-axis (horizontal) is the measured temperature, while the Y axis (vertical) is the real (corrected or reference) temperature.
Now, I believe that most of these cases can be represented by a fairly simple polynomial, of the form y = a + b*x + c*x^2 + d*x^3 + ... , where x is the measured temperature and y is the real temperature, and a, b, c etc are the factors for each power of x.
So, this is the type of calibration that is implemented in tempered (well, technically mostly in libtempered-util), with some shortcuts that should make it fairly easy to use in the simpler cases, and hopefully not much harder in the more complex ones.
The only thing you need to provide is the values of the factors (a, b, c etc.), and the rest will be taken care of.
The way this is done with tempered is the --calibrate-temp option (short option -c), which takes one parameter, which is a colon-separated list of these factors (a:b:c:...).
Only the ones you need have to be specified, so if you have a constant offset (e.g. 5 degrees as above), you only need to provide that single number: -c 5
If it's a linear relationship (e.g. y = 5 + 0.9*x as above), provide the two numbers: -c 5:0.9
If it's a polynomial of higher order, provide as many factors as needed (e.g. three for the above second-order one): -c 0:1.4:-0.004
(If you want to know how I derived these three numbers, see here.)
You may want to note that empty strings are treated like 0, so -c 5: would give you a constant 5 degree output regardless of the measured temperature, since it would correspond to the equation y = 5 + 0*x.