0895

895. 最长上升子序列

题目

给定一个长度为 $N$ 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式

第一行包含整数 $N$。

第二行包含 $N$ 个整数，表示完整序列。

输出格式

输出一个整数，表示最大长度。

数据范围

$1 \le N \le 1000$，

$-10^9 \le 数列中的数 \le 10^9$

输入样例：

7
3 1 2 1 8 5 6

输出样例：

4

题解

前置题目：0898

前置知识：无

本题知识：动态规划-线性DP

题目分析

子序列是可以不连续的，可以从中抽取，且性质是严格单调递增

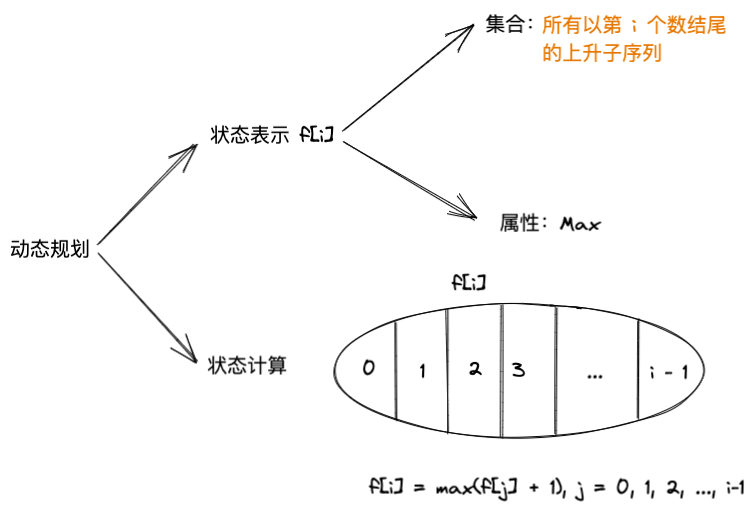
动态规划的解题思路，难点在状态的分解

集合的分解方法：所有以第 i 个数结尾的上升子序列，倒数第二个数是什么

• 不存在，整个长度为 1
• 是第 1 个数
• 是第 2 个数
• ...
• 是第 n-1 个数

这些分解的情况不一定都存在，要满足 f[j] < f[i]

最大值就是 f[i], i = 1, 2, ..., n 中的最大值

复杂度

时间复杂度 = 状态数量 x 转移计算量 = O(n) * O(n) = O(n^2)