参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
在 本周小结!(回溯算法系列三) 中一位录友对 整棵树的本层和同一节点的本层有疑问,也让我重新思考了一下,发现这里确实有问题,所以专门写一篇来纠正,感谢录友们的积极交流哈!
接下来我再把这块再讲一下。
在回溯算法:求子集问题(二)中的去重和 回溯算法:递增子序列中的去重 都是 同一父节点下本层的去重。
回溯算法:求子集问题(二)也可以使用set针对同一父节点本层去重,但子集问题一定要排序,为什么呢?
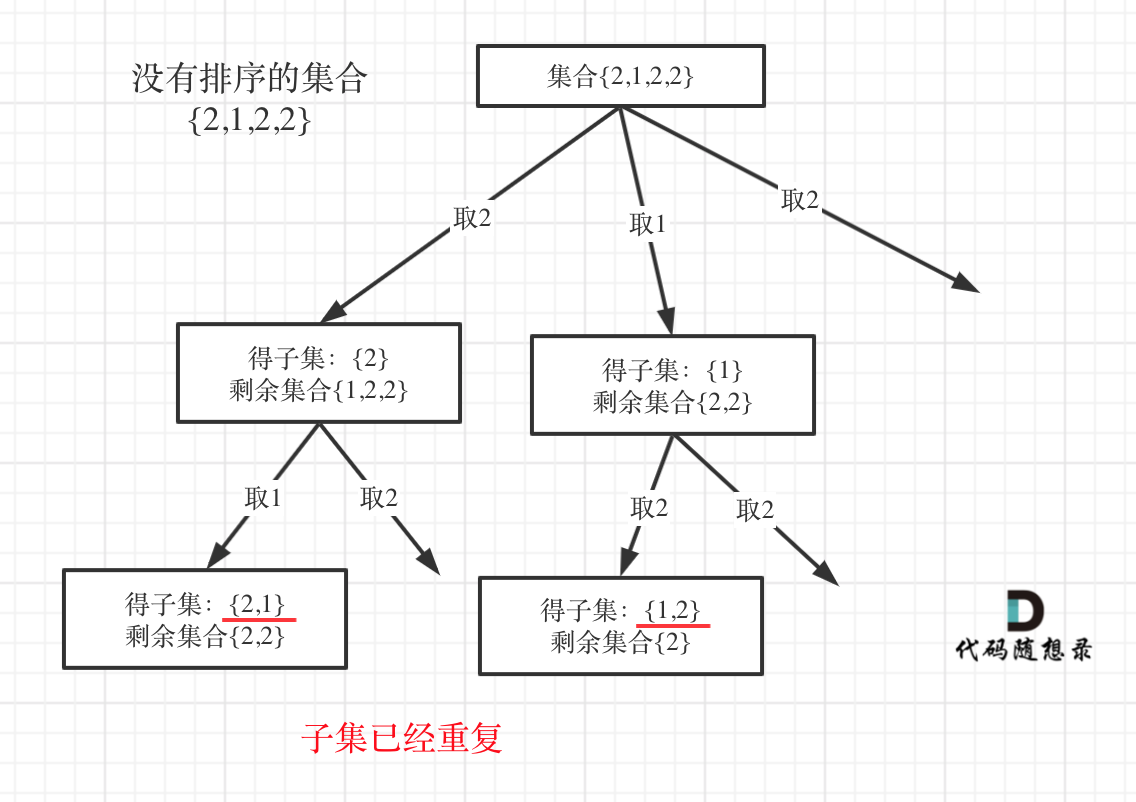
我用没有排序的集合{2,1,2,2}来举例子画一个图,如图:
图中,大家就很明显的看到,子集重复了。
那么下面我针对回溯算法:求子集问题(二) 给出使用set来对本层去重的代码实现。
used数组去重版本: 回溯算法:求子集问题(二)
使用set去重的版本如下:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
unordered_set<int> uset; // 定义set对同一节点下的本层去重
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) { // 如果发现出现过就pass
continue;
}
uset.insert(nums[i]); // set跟新元素
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end()); // 去重需要排序
backtracking(nums, 0, used);
return result;
}
};
针对留言区录友们的疑问,我再补充一些常见的错误写法,
把uset定义放到类成员位置,然后模拟回溯的样子 insert一次,erase一次。
例如:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
unordered_set<int> uset; // 把uset定义放到类成员位置
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // 递归之前insert
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
uset.erase(nums[i]); // 回溯再erase
}
}
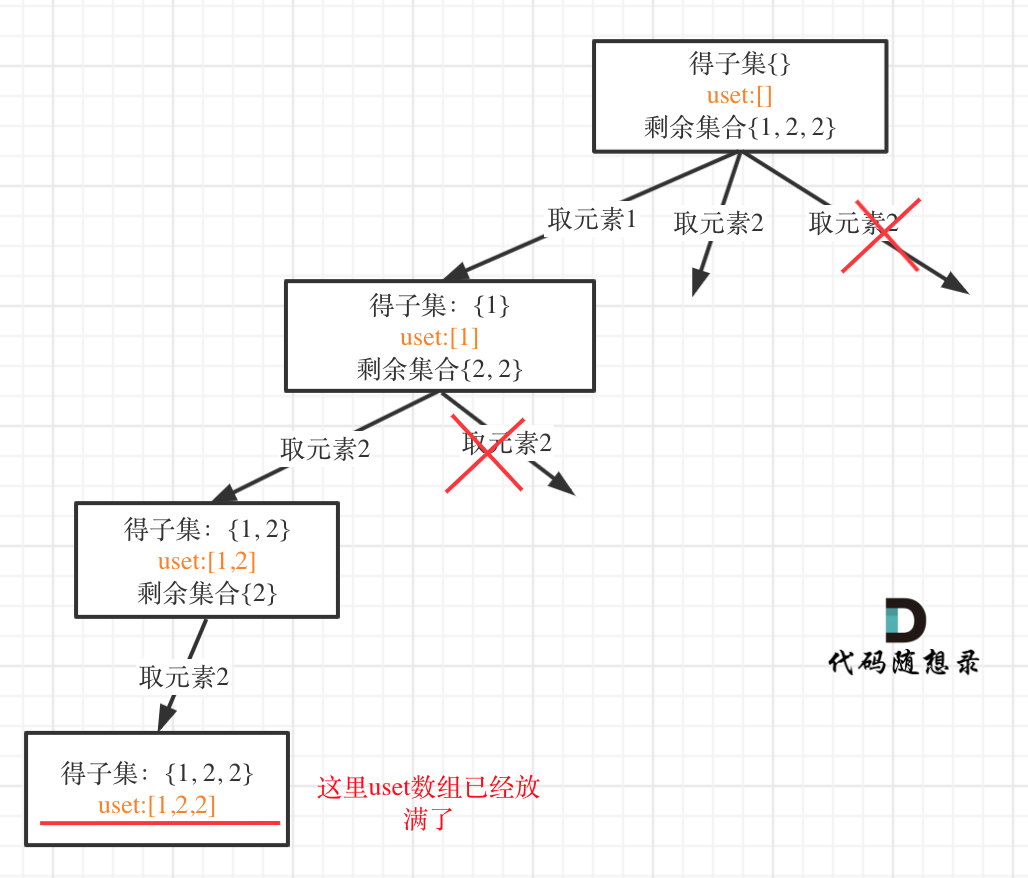
在树形结构中,如果把unordered_set uset放在类成员的位置(相当于全局变量),就把树枝的情况都记录了,不是单纯的控制某一节点下的同一层了。
如图:
可以看出一旦把unordered_set uset放在类成员位置,它控制的就是整棵树,包括树枝。
所以这么写不行!
有同学把 unordered_set uset; 放到类成员位置,然后每次进入单层的时候用uset.clear()。
代码如下:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
unordered_set<int> uset; // 把uset定义放到类成员位置
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
uset.clear(); // 到每一层的时候,清空uset
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // set记录元素
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
}
}uset已经是全局变量,本层的uset记录了一个元素,然后进入下一层之后这个uset(和上一层是同一个uset)就被清空了,也就是说,层与层之间的uset是同一个,那么就会相互影响。
所以这么写依然不行!
组合问题和排列问题,其实也可以使用set来对同一节点下本层去重,下面我都分别给出实现代码。
使用used数组去重版本:回溯算法:求组合总和(三)
使用set去重的版本如下:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
return;
}
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
if (uset.find(candidates[i]) != uset.end()) {
continue;
}
uset.insert(candidates[i]); // 记录元素
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i + 1);
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
path.clear();
result.clear();
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0);
return result;
}
};使用used数组去重版本:回溯算法:排列问题(二)
使用set去重的版本如下:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
for (int i = 0; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
if (used[i] == false) {
uset.insert(nums[i]); // 记录元素
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 排序
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};需要注意的是:使用set去重的版本相对于used数组的版本效率都要低很多,大家在leetcode上提交,能明显发现。
原因在回溯算法:递增子序列中也分析过,主要是因为程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且insert的时候其底层的符号表也要做相应的扩充,也是费时的。
而使用used数组在时间复杂度上几乎没有额外负担!
使用set去重,不仅时间复杂度高了,空间复杂度也高了,在本周小结!(回溯算法系列三)中分析过,组合,子集,排列问题的空间复杂度都是$O(n)$,但如果使用set去重,空间复杂度就变成了$O(n^2)$,因为每一层递归都有一个set集合,系统栈空间是n,每一个空间都有set集合。
那有同学可能疑惑 用used数组也是占用$O(n)$的空间啊?
used数组可是全局变量,每层与每层之间公用一个used数组,所以空间复杂度是$O(n + n)$,最终空间复杂度还是$O(n)$。
本篇本打算是对本周小结!(回溯算法系列三)的一个点做一下纠正,没想到又写出来这么多!
这个点都源于一位录友的疑问,然后我思考总结了一下,就写着这一篇,所以还是得多交流啊!
如果大家对「代码随想录」文章有什么疑问,尽管打卡留言的时候提出来哈,或者在交流群里提问。
其实这就是相互学习的过程,交流一波之后都对题目理解的更深刻了,我如果发现文中有问题,都会在评论区或者下一篇文章中即时修正,保证不会给大家带跑偏!
Java: 47.全排列II
class Solution {
private List<List<Integer>> res = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
private boolean[] used = null;
public List<List<Integer>> permuteUnique(int[] nums) {
used = new boolean[nums.length];
Arrays.sort(nums);
backtracking(nums);
return res;
}
public void backtracking(int[] nums) {
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
HashSet<Integer> hashSet = new HashSet<>();//层去重
for (int i = 0; i < nums.length; i++) {
if (hashSet.contains(nums[i]))
continue;
if (used[i] == true)//枝去重
continue;
hashSet.add(nums[i]);//记录元素
used[i] = true;
path.add(nums[i]);
backtracking(nums);
path.remove(path.size() - 1);
used[i] = false;
}
}
}Python:
90.子集II
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
nums.sort()
def backtracking(start, path):
res.append(path)
uset = set()
for i in range(start, len(nums)):
if nums[i] not in uset:
backtracking(i + 1, path + [nums[i]])
uset.add(nums[i])
backtracking(0, [])
return res40. 组合总和 II
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
candidates.sort()
def backtracking(start, path):
if sum(path) == target:
res.append(path)
elif sum(path) < target:
used = set()
for i in range(start, len(candidates)):
if candidates[i] in used:
continue
else:
used.add(candidates[i])
backtracking(i + 1, path + [candidates[i]])
backtracking(0, [])
return res47. 全排列 II
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
path = []
res = []
used = [False]*len(nums)
def backtracking():
if len(path) == len(nums):
res.append(path.copy())
deduplicate = set()
for i, num in enumerate(nums):
if used[i] == True:
continue
if num in deduplicate:
continue
used[i] = True
path.append(nums[i])
backtracking()
used[i] = False
path.pop()
deduplicate.add(num)
backtracking()
return resGo: