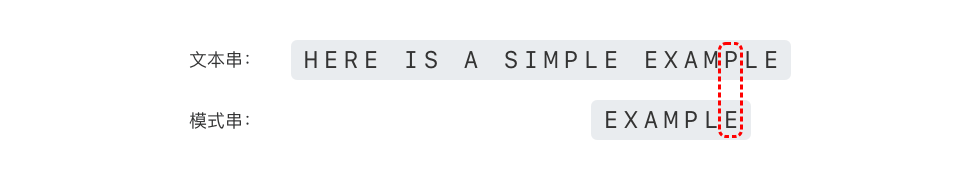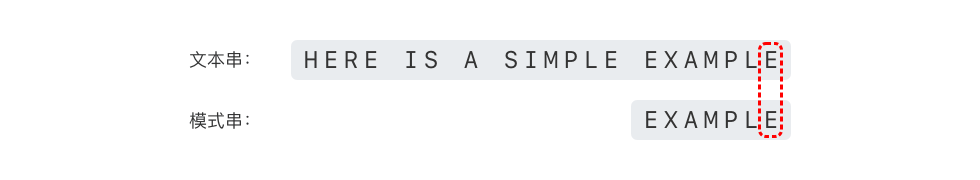1. Boyer Moore 算法介绍

Boyer Moore 算法：简称为 BM 算法，是由它的两位发明者 Robert S. Boyer 和 J Strother Moore 的名字来命名的。BM 算法是他们在 1977 年提出的高效字符串搜索算法。在实际应用中，比 KMP 算法要快 3~5 倍。

BM 算法思想：对于给定文本串 $T$ 与模式串 $p$，先对模式串 $p$ 进行预处理。然后在匹配的过程中，当发现文本串 $T$ 的某个字符与模式串 $p$ 不匹配的时候，根据启发策略，能够直接尽可能地跳过一些无法匹配的情况，将模式串多向后滑动几位。

BM 算法的精髓在于使用了两种不同的启发策略来计算后移位数：「坏字符规则（The Bad Character Rule）」 和 「好后缀规则（The Good Suffix Shift Rule）」。

这两种启发策略的计算过程只与模式串 $p$ 相关，而与文本串 $T$ 无关。因此在对模式串 $p$ 进行预处理时，可以预先生成「坏字符规则后移表」和「好后缀规则后移表」，然后在匹配的过程中，只需要比较一下两种策略下最大的后移位数进行后移即可。

同时，还需要注意一点。BM 算法在移动模式串的时候和常规匹配算法一样是从左到右进行，但是在进行比较的时候是从右到左，即基于后缀进行比较。

下面我们来讲解一下 BF 算法中的两种不同启发策略：「坏字符规则」和「好后缀规则」。

2. Boyer Moore 算法启发策略

2.1 坏字符规则

坏字符规则（The Bad Character Rule）：当文本串 $T$ 中某个字符跟模式串 $p$ 的某个字符不匹配时，则称文本串 $T$ 中这个失配字符为 「坏字符」，此时模式串 $p$ 可以快速向右移动。

「坏字符规则」的移动位数分为两种情况：

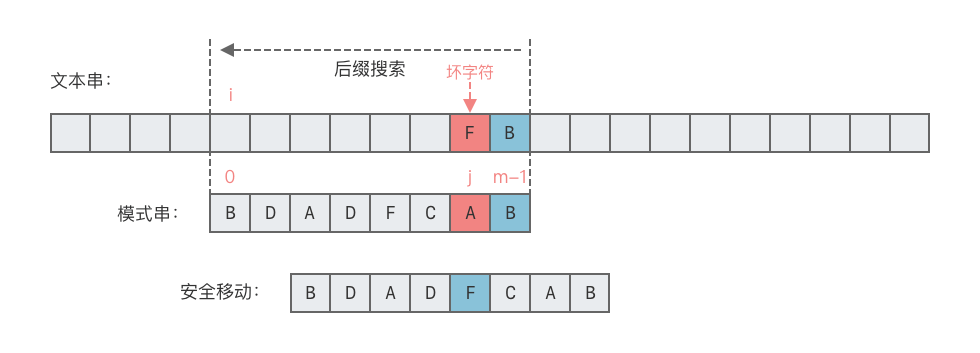
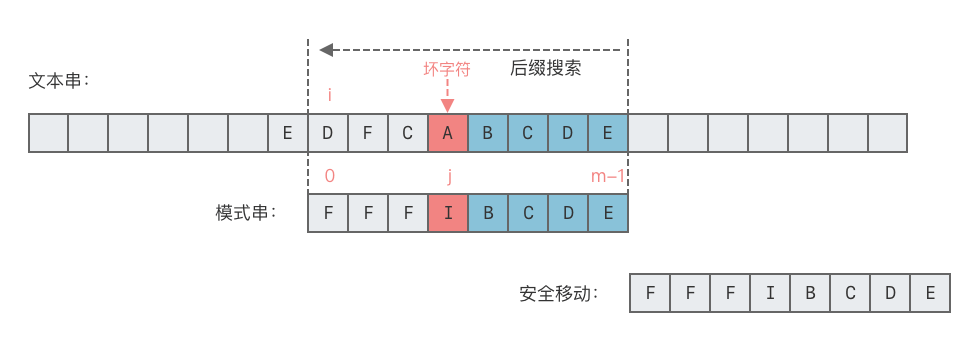
情况 1：坏字符出现在模式串 $p$ 中。
- 这种情况下，可将模式串中最后一次出现的坏字符与文本串中的坏字符对齐，如下图所示。
- 向右移动位数 = 坏字符在模式串中的失配位置 - 坏字符在模式串中最后一次出现的位置。

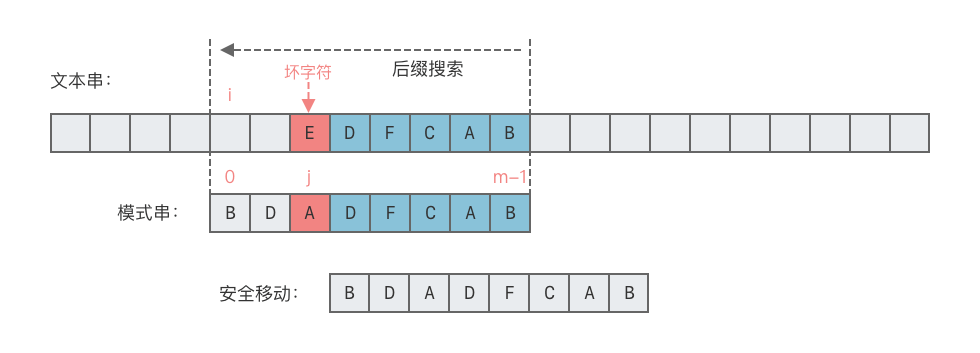
情况 2：坏字符没有出现在模式串 $p$ 中。
- 这种情况下，可将模式串向右移动一位，如下图所示。
- 向右移动位数 = 坏字符在模式串中的失配位置 + 1。

2.2 好后缀规则

好后缀规则（The Good Suffix Shift Rule）：当文本串 $T$ 中某个字符跟模式串 $p$ 的某个字符不匹配时，则称文本串 $T$ 中已经匹配好的字符串为 「好后缀」，此时模式串 $p$ 可以快速向右移动。

「好后缀规则」的移动方式分为三种情况：

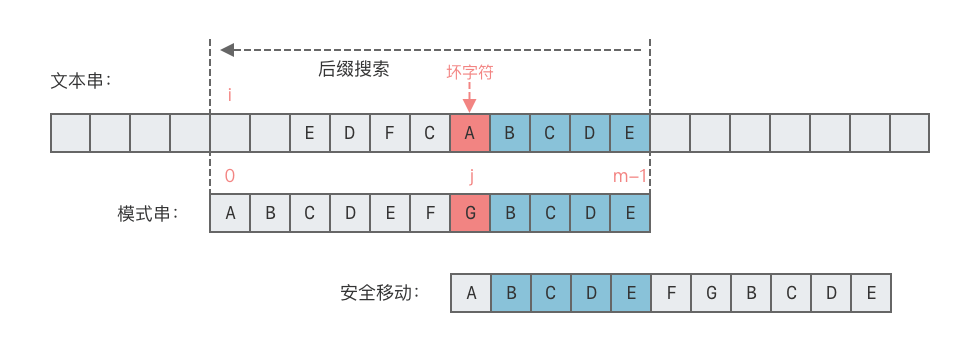
情况 1：模式串中有子串匹配上好后缀。
- 这种情况下，移动模式串，让该子串和好后缀对齐即可。如果超过一个子串匹配上好后缀，则选择最右侧的子串对齐，如下图所示。
- 向右移动位数 = 好后缀的最后一个字符在模式串中的位置 - 匹配的子串最后一个字符出现的位置。

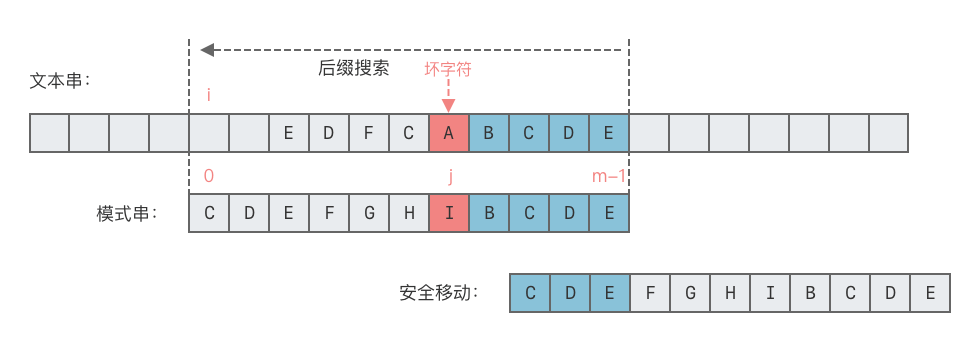
情况 2：模式串中无子串匹配上好后缀，但有最长前缀匹配好后缀的后缀。
- 这种情况下，我们需要在模式串的前缀中寻找一个最长前缀，该前缀等于好后缀的后缀。找到该前缀后，让该前缀和好后缀的后缀对齐。
- 向右移动位数 = 好后缀的后缀的最后一个字符在模式串中的位置 - 最长前缀的最后一个字符出现的位置。

情况 3：模式串中无子串匹配上好后缀，也找不到前缀匹配。
- 可将模式串整个右移。
- 向右移动位数 = 模式串的长度。

3. Boyer Moore 算法匹配过程示例

下面我们根据 J Strother Moore 教授给出的例子，先来介绍一下 BF 算法的匹配过程，顺便加深对 「坏字符规则」 和 「好后缀规则」 的理解。

::: tabs#Boyer-Moore

@tab <1>

假设文本串为 "HERE IS A SIMPLE EXAMPLE"，模式串为 "EXAMPLE"，如下图所示。

@tab <2>

首先，令模式串与文本串的头部对齐，然后从模式串的尾部开始逐位比较，如下图所示。

可以看出来，'S' 与 'E' 不匹配。这时候，不匹配的字符 'S' 就被称为「坏字符（Bad Character）」，对应着模式串的第 $6$ 位。并且 'S' 并不包含在模式串 "EXAMPLE" 中（相当于'S' 在模式串中最后一次出现的位置是 $-1$）。根据「坏字符规则」，可以把模式串直接向右移动 $6 - (-1) = 7$ 位，即将文本串中 'S' 的后一位上。

@tab <3>

将模式串向右移动 $7$ 位。然后依然从模式串尾部开始比较，发现 'P' 和 'E' 不匹配，则 'P' 是坏字符，如下图所示。

但是 'P' 包含在模式串 "EXAMPLE" 中，'P' 这个坏字符在模式串中的失配位置是第 $6$ 位，并且在模式串中最后一次出现的位置是 $4$（编号从 $0$ 开始）。

@tab <4>

根据「坏字符规则」，可以将模式串直接向右移动 $6 - 4 = 2$ 位，将文本串的 'P' 和模式串中的 'P' 对齐，如下图所示。

@tab <5>

我们继续从尾部开始逐位比较。先比较文本串的 'E' 和模式串的 'E'，如下图所示。可以看出文本串的 'E' 和模式串的 'E' 匹配，则 "E" 为好后缀，"E" 在模式串中的位置为 $6$（编号从 $0$ 开始）。

@tab <6>

继续比较前面一位，即文本串的 'L' 和模式串的 'L'，如下图所示。可以看出文本串的 'L' 和模式串的 'L' 匹配。则 "LE" 为好后缀，"LE" 在模式串中的位置为 $6$（编号从 $0$ 开始）。

@tab <7>

继续比较前面一位，即文本串中的 'P' 和模式串中的 'P'，如下图所示。可以看出文本串中的 'P' 和模式串中的 'P' 匹配，则 "PLE" 为好后缀，"PLE" 在模式串中的位置为 $6$（编号从 $0$ 开始）。

@tab <8>

继续比较前面一位，即文本串中的 'M' 和模式串中的 'M'，如下图所示。可以看出文本串中的 'M' 和模式串中的 'M' 匹配，则 "MPLE" 为好后缀。"MPLE" 在模式串中的位置为 $6$（编号从 $0$ 开始）。

@tab <9>

继续比较前面一位，即文本串中的 'I' 和模式串中的 'A'，如下图所示。可以看出文本串中的 'I' 和模式串中的 'A' 不匹配。

此时，如果按照「坏字符规则」，模式串应该向右移动 $2 - (-1) = 3$ 位。但是根据「好后缀规则」，我们还有更好的移动方法。

在好后缀 "MPLE" 和好后缀的后缀 "PLE"、"LE"、"E" 中，只有好后缀的后缀 "E" 和模式串中的前缀 "E" 相匹配，符合好规则的第二种情况。好后缀的后缀 "E" 的最后一个字符在模式串中的位置为 $6$，最长前缀 "E"的最后一个字符出现的位置为 $0$，则根据「好后缀规则」，可以将模式串直接向右移动 $6 - 0 = 6$ 位。如下图所示。

@tab <10>

继续从模式串的尾部开始逐位比较，如下图所示。

可以看出，'P' 与'E' 不匹配，'P' 是坏字符。根据「坏字符规则」，可以将模式串直接向右移动 $6 - 4 = 2$ 位，如下图所示。

@tab <11>

继续从模式串的尾部开始逐位比较，发现模式串全部匹配，于是搜索结束，返回模式串在文本串中的位置。

:::

4. Boyer Moore 算法步骤

整个 BM 算法步骤描述如下：

计算出文本串 $T$ 的长度为 $n$，模式串 $p$ 的长度为 $m$。
先对模式串 $p$ 进行预处理，生成坏字符位置表 $bc\underline{\hspace{0.5em}}table$ 和好后缀规则后移位数表 $gs\underline{\hspace{0.5em}}talbe$。
将模式串 $p$ 的头部与文本串 $T$ 对齐，将 $i$ 指向文本串开始位置，即 $i = 0$。$j$ 指向模式串末尾位置，即 $j = m - 1$，然后从模式串末尾位置开始进行逐位比较。
1. 如果文本串对应位置 $T[i + j]$ 上的字符与 $p[j]$ 相同，则继续比较前一位字符。
  1. 如果模式串全部匹配完毕，则返回模式串 $p$ 在文本串中的开始位置 $i$。
2. 如果文本串对应位置 $T[i + j]$ 上的字符与 $p[j]$ 不相同，则：
  1. 根据坏字符位置表计算出在「坏字符规则」下的移动距离 $bad\underline{\hspace{0.5em}}move$。
  2. 根据好后缀规则后移位数表计算出在「好后缀规则」下的移动距离 $good\underline{\hspace{0.5em}}mode$。
  3. 取两种移动距离的最大值，然后对模式串进行移动，即 $i += max(bad\underline{\hspace{0.5em}}move, good\underline{\hspace{0.5em}}move)$。
如果移动到末尾也没有找到匹配情况，则返回 $-1$。

5. Boyer Moore 算法代码实现

BM 算法的匹配过程实现起来并不是很难，而整个算法实现的难点在于预处理阶段的「生成坏字符位置表」和「生成好后缀规则后移位数表」这两步上。尤其是「生成好后缀规则后移位数表」，实现起来十分复杂。下面我们一一进行讲解。

5.1 生成坏字符位置表代码实现

生成坏字符位置表的代码实现比较简单。具体步骤如下：

使用一个哈希表 $bc\underline{\hspace{0.5em}}table$， $bc\underline{\hspace{0.5em}}table[bad\underline{\hspace{0.5em}}char]$ 表示坏字符 $bad\underline{\hspace{0.5em}}char$ 在模式串中出现的最右位置。
遍历模式串，以当前字符 $p[i]$ 为键，所在位置下标为值存入字典中。如果出现重复字符，则新的位置下标值会将之前存放的值覆盖掉。这样哈希表中存放的就是该字符在模式串中出现的最右侧位置。

这样如果在 BM 算法的匹配过程中，如果 $bad\underline{\hspace{0.5em}}char$ 不在 $bc\underline{\hspace{0.5em}}table$ 中时，可令 $bad\underline{\hspace{0.5em}}char$ 在模式串中出现的最右侧位置为 $-1$。如果 $bad\underline{\hspace{0.5em}}char$ 在 $bc\underline{\hspace{0.5em}}table$ 中时，$bad\underline{\hspace{0.5em}}char$ 在模式串中出现的最右侧位置就是 $bc\underline{\hspace{0.5em}}table[bad\underline{\hspace{0.5em}}char]$。这样就可以根据公式计算出可以向右移动的位数了。

生成坏字符位置表的代码如下：

# 生成坏字符位置表
# bc_table[bad_char] 表示坏字符在模式串中最后一次出现的位置
def generateBadCharTable(p: str):
    bc_table = dict()
    
    for i in range(len(p)):
        bc_table[p[i]] = i                          # 更新坏字符在模式串中最后一次出现的位置
    return bc_table

5.2 生成好后缀规则后移位数表代码实现

为了生成好后缀规则后移位数表，我们需要先定义一个后缀数组 $suffix$，其中 $suffix[i] = s$ 表示为以下标 $i$ 为结尾的子串与模式串后缀匹配的最大长度为 $s$。即满足 $p[i-s...i] == p[m-1-s, m-1]$ 的最大长度为 $s$。

构建 $suffix$ 数组的代码如下：

# 生成 suffix 数组
# suffix[i] 表示为以下标 i 为结尾的子串与模式串后缀匹配的最大长度
def generageSuffixArray(p: str):
    m = len(p)
    suffix = [m for _ in range(m)]                  # 初始化时假设匹配的最大长度为 m
    for i in range(m - 2, -1, -1):                  # 子串末尾从 m - 2 开始
        start = i                                   # start 为子串开始位置
        while start >= 0 and p[start] == p[m - 1 - i + start]:
            start -= 1                              # 进行后缀匹配，start 为匹配到的子串开始位置
        suffix[i] = i - start                       # 更新以下标 i 为结尾的子串与模式串后缀匹配的最大长度
    return suffix

有了 $suffix$ 数组，我们就可以在此基础上定义好后缀规则后移位数表 $gs\underline{\hspace{0.5em}}list$。我们使用一个数组来表示好后缀规则后移位数表。其中 $gs\underline{\hspace{0.5em}}list[j]$ 表示在 $j$ 下标处遇到坏字符时，可根据好规则向右移动的距离。

由「2.2 好后缀规则」中可知，好后缀规则的移动方式可以分为三种情况。

情况 1：模式串中有子串匹配上好后缀。
情况 2：模式串中无子串匹配上好后缀，但有最长前缀匹配好后缀的后缀。
情况 3：模式串中无子串匹配上好后缀，也找不到前缀匹配。

这 3 种情况中，情况 2 和情况 3 可以合并，因为情况 3 可以看做是匹配到的最长前缀长度为 $0$。而如果遇到一个坏字符同时满足多种情况，则我们应该选择满足情况中最小的移动距离才不会漏掉可能匹配的情况，比如说当模式串中既有子串可以匹配上好后缀，又有前缀可以匹配上好后缀的后缀，则应该按照前者的方式移动模式串。

为了得到精确的 $gs\underline{\hspace{0.5em}}list[j]$，我们可以先假定所有情况都为情况 3，即 $gs\underline{\hspace{0.5em}}list[i] = m$。
然后通过后缀和前缀匹配的方法，更新情况 2 下 $gs\underline{\hspace{0.5em}}list$ 中坏字符位置处的值，即 $gs\underline{\hspace{0.5em}}list[j] = m - 1 - i$，其中 $j$ 是好后缀前的坏字符位置，$i$ 是最长前缀的末尾位置，$m - 1 - i$ 是可向右移动的距离。
最后再计算情况 1 下 $gs\underline{\hspace{0.5em}}list$ 中坏字符位置处的值，更新在好后缀的左端点处（$m - 1 - suffix[i]$ 处）遇到坏字符可向后移动位数，即 $gs\underline{\hspace{0.5em}}list[m - 1 - suffix[i]] = m - 1 - i$。

生成好后缀规则后移位数表 $gs\underline{\hspace{0.5em}}list$ 代码如下：

# 生成好后缀规则后移位数表
# gs_list[j] 表示在 j 下标处遇到坏字符时，可根据好规则向右移动的距离
def generageGoodSuffixList(p: str):
    # 好后缀规则后移位数表
    # 情况 1: 模式串中有子串匹配上好后缀
    # 情况 2: 模式串中无子串匹配上好后缀，但有最长前缀匹配好后缀的后缀
    # 情况 3: 模式串中无子串匹配上好后缀，也找不到前缀匹配
    
    m = len(p)
    gs_list = [m for _ in range(m)]                 # 情况 3：初始化时假设全部为情况 3
    suffix = generageSuffixArray(p)                 # 生成 suffix 数组
    
    j = 0                                           # j 为好后缀前的坏字符位置
    for i in range(m - 1, -1, -1):                  # 情况 2：从最长的前缀开始检索
        if suffix[i] == i + 1:                      # 匹配到前缀，即 p[0...i] == p[m-1-i...m-1]
            while j < m - 1 - i:
                if gs_list[j] == m:
                    gs_list[j] = m - 1 - i          # 更新在 j 处遇到坏字符可向后移动位数
                j += 1
        
    for i in range(m - 1):                          # 情况 1：匹配到子串， p[i-s...i] == p[m-1-s, m-1]
        gs_list[m - 1 - suffix[i]] = m - 1 - i      # 更新在好后缀的左端点处遇到坏字符可向后移动位数
    return gs_list

5.3 Boyer Moore 算法整体代码实现

# BM 匹配算法
def boyerMoore(T: str, p: str) -> int:
    n, m = len(T), len(p)
    
    bc_table = generateBadCharTable(p)              # 生成坏字符位置表
    gs_list = generageGoodSuffixList(p)             # 生成好后缀规则后移位数表
    
    i = 0
    while i <= n - m:
        j = m - 1
        while j > -1 and T[i + j] == p[j]:          # 进行后缀匹配，跳出循环说明出现坏字符
            j -= 1
        if j < 0:
            return i                                # 匹配完成，返回模式串 p 在文本串 T 中的位置
        bad_move = j - bc_table.get(T[i + j], -1)   # 坏字符规则下的后移位数
        good_move = gs_list[j]                      # 好后缀规则下的后移位数
        i += max(bad_move, good_move)               # 取两种规则下后移位数的最大值进行移动
    return -1
            
    
# 生成坏字符位置表
# bc_table[bad_char] 表示坏字符在模式串中最后一次出现的位置
def generateBadCharTable(p: str):
    bc_table = dict()
    
    for i in range(len(p)):
        bc_table[p[i]] = i                          # 更新坏字符在模式串中最后一次出现的位置
    return bc_table

# 生成好后缀规则后移位数表
# gs_list[j] 表示在 j 下标处遇到坏字符时，可根据好规则向右移动的距离
def generageGoodSuffixList(p: str):
    # 好后缀规则后移位数表
    # 情况 1: 模式串中有子串匹配上好后缀
    # 情况 2: 模式串中无子串匹配上好后缀，但有最长前缀匹配好后缀的后缀
    # 情况 3: 模式串中无子串匹配上好后缀，也找不到前缀匹配
    
    m = len(p)
    gs_list = [m for _ in range(m)]                 # 情况 3：初始化时假设全部为情况 3
    suffix = generageSuffixArray(p)                 # 生成 suffix 数组
    
    j = 0                                           # j 为好后缀前的坏字符位置
    for i in range(m - 1, -1, -1):                  # 情况 2：从最长的前缀开始检索
        if suffix[i] == i + 1:                      # 匹配到前缀，即 p[0...i] == p[m-1-i...m-1]
            while j < m - 1 - i:
                if gs_list[j] == m:
                    gs_list[j] = m - 1 - i          # 更新在 j 处遇到坏字符可向后移动位数
                j += 1
        
    for i in range(m - 1):                          # 情况 1：匹配到子串 p[i-s...i] == p[m-1-s, m-1]
        gs_list[m - 1 - suffix[i]] = m - 1 - i      # 更新在好后缀的左端点处遇到坏字符可向后移动位数
    return gs_list

# 生成 suffix 数组
# suffix[i] 表示为以下标 i 为结尾的子串与模式串后缀匹配的最大长度
def generageSuffixArray(p: str):
    m = len(p)
    suffix = [m for _ in range(m)]                  # 初始化时假设匹配的最大长度为 m
    for i in range(m - 2, -1, -1):                  # 子串末尾从 m - 2 开始
        start = i                                   # start 为子串开始位置
        while start >= 0 and p[start] == p[m - 1 - i + start]:
            start -= 1                              # 进行后缀匹配，start 为匹配到的子串开始位置
        suffix[i] = i - start                       # 更新以下标 i 为结尾的子串与模式串后缀匹配的最大长度
    return suffix

print(boyerMoore("abbcfdddbddcaddebc", "aaaaa"))
print(boyerMoore("", ""))

6. Boyer Moore 算法分析

BM 算法在预处理阶段的时间复杂度为 $O(n + \sigma)$，其中 $\sigma$ 是字符集的大小。
BM 算法在搜索阶段最好情况是每次匹配时，模式串 $p$ 中不存在与文本串 $T$ 中第一个匹配的字符。这时的时间复杂度为 $O(n / m)$。
BM 算法在搜索阶段最差情况是文本串 $T$ 中有多个重复的字符，并且模式串 $p$ 中有 $m - 1$ 个相同字符前加一个不同的字符组成。这时的时间复杂度为 $O(m * n)$。
当模式串 $p$ 是非周期性的，在最坏情况下，BM 算法最多需要进行 $3 * n$ 次字符比较操作。

参考资料

【书籍】柔性字符串匹配 - 中科院计算所网络信息安全研究组译
【文章】不用找了，学习 BM 算法，这篇就够了（思路+详注代码）- BoCong-Deng 的博客
【文章】字符串匹配的 Boyer-Moore 算法 - 阮一峰的网络日志
【文章】 bm 算法好后缀 java 实现 - 长笛小号的博客 - CSDN博客
【文章】BM算法详解 - 简单爱_wxg - 博客园
【文章】grep 之字符串搜索算法 Boyer-Moore 由浅入深 - Alexia(minmin) - 博客园
【文章】字符串匹配基础（中）- 数据结构与算法之美 - 极客时间
【代码】BM算法附有解释 - 实现 strStr() - 力扣

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

04.String-Boyer-Moore.md

04.String-Boyer-Moore.md

1. Boyer Moore 算法介绍

2. Boyer Moore 算法启发策略

2.1 坏字符规则

2.2 好后缀规则

3. Boyer Moore 算法匹配过程示例

4. Boyer Moore 算法步骤

5. Boyer Moore 算法代码实现

5.1 生成坏字符位置表代码实现

5.2 生成好后缀规则后移位数表代码实现

5.3 Boyer Moore 算法整体代码实现

6. Boyer Moore 算法分析

参考资料

Files

04.String-Boyer-Moore.md

Latest commit

History

04.String-Boyer-Moore.md

File metadata and controls

1. Boyer Moore 算法介绍

2. Boyer Moore 算法启发策略

2.1 坏字符规则

2.2 好后缀规则

3. Boyer Moore 算法匹配过程示例

4. Boyer Moore 算法步骤

5. Boyer Moore 算法代码实现

5.1 生成坏字符位置表代码实现

5.2 生成好后缀规则后移位数表代码实现

5.3 Boyer Moore 算法整体代码实现

6. Boyer Moore 算法分析

参考资料