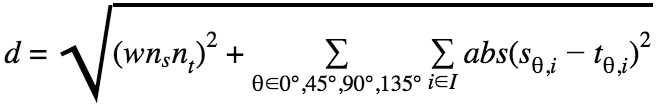Levi developed a novel algorithm for real-time gesture recognition from ink data. This was extended from work done in a UCR course on Pen-Based Computing algorithms and techniques.
- The Algorithm
- Strengths
- Weaknesses
- Improvements
- Performance
- Additional Features
The general idea of the algorithm is to first create four template bitmaps to represent the ink directional probability of a given shape class, then an unknown shape instance is classified as the class whose directional templates it most closely matches.
First, angle values are computed for all points in all strokes in a given shape instance. These angles are based off zero degrees along the horizontal axis. The angle value for a point is calculated as the average of the angles of the line segments connecting that point to its previous and next neighbors. These angles are then convoluted with a Gaussian smoothing kernel.
Next, the given shape instance is uniformly scaled and translated so that its x and y coordinate values range from 0 to 1. It is also translated so that it is centered in this hypothetical, square, 1x1 canvas.
Directional pixel values are then computed for the given shape instance. There are four directional components associated with each pixel—the lines along 0°, 45°, 90°, and 135°. The value of a point for each of these four directions is 1 if the angle is different by 0°, 0 if the angle is different by 45° degrees or more, and linearly interpolated between 0 and 1 for angles differing by 0°-45°. Note that these directions also match with their opposites; i.e., if a point has an angle of 215°, then it has a difference of 0° with the 45° line, and its value for its 45° directional pixel is 1.
The entire bitmap region is not stored for each shape instance; in order to save space and time, a mapping from pixel indices to directional intensity values is created, and this mapping contains a key for a given pixel if and only if the shape instance contains a point in that pixel. There are actually four such mappings for each shape instance— one for each of the four directions. These mappings are created by looping over each of the points, determining in which pixel a point lies, and storing the four directional values of this point at this pixel index within the four mappings. If multiple points in a shape instance have values for the same direction in the same pixel, then the largest value is saved.
The discretization of ink means that we have two special cases to consider: when a single pixel contains multiple consecutive points, and when the line segment between two consecutive points intersects a pixel in which neither point actually lies. The former case is actually handled well with the aforementioned policy of saving a pixel's maximal intensity value for each direction. An alternative approach for this could have been to use the average angle values for consecutive points lying within the same pixel, but this causes a good deal of information to be lost within pixels containing high curvature—i.e., corners. The latter case could be handled robustly by calculating the intermediate pixels via the Bresenham line algorithm, but the lost pixels become less significant with more training examples. Also, a 3x3 Gaussian smoothing kernel is used to smooth the final values of the templates. However, these two points do not address the lost pixels from an unknown shape instance being recognized, and further research could be performed to determine whether the application of the Bresenham line algorithm would increase recognition accuracy.
After each shape instance has been preprocessed, actually creating the templates is a simple process. For each shape class, four complete bitmaps are created—one for each direction—and then all of the pixel intensity values for each of the training shape instances are added together into the appropriate bitmaps. Each pixel in each bitmap is then normalized by the number of training instances for the given shape class template. Finally, a 3x3 Gaussian smoothing kernel is used to smooth the final values of each of the directional bitmaps for each template.
To recognize a given unknown shape instance, a simple distance metric is used, and the shape is classified as whichever class yields the smallest distance. This distance between a shape instance and a class template is computed as
where I is the list of the pixel indices—i.e., keys—in the pixel indices to directional intensity values mappings, sθi is the directional intensity value from the θ directional mapping of the pixel at index i for the unknown shape instance, tθi is the directional intensity value from the θ directional bitmap of the pixel at index i for the shape class template, ns is the number of pixels containing ink for the unknown shape instance, nt is the average number of pixels containing ink for the shape class template, and w is a weight parameter.
The term relating to the number of pixels containing ink is important, because this distance metric only considers pixels which are covered by the unknown shape instance. To understand why this is a problem, consider the example of the unknown shape instance being the letter P, and there are templates both for the letter P and the letter R. Because the distance only considers the pixels from the shape instance P, the P and R templates will be found to have roughly the same distance. This term for the number of pixels containing ink allows the distance metric to match the P shape instance more closely to the P template than the R template.
It may seem that rather than using this term for the number of pixels containing ink, that the distance metric could simply sum over all of the pixels in the template bitmap rather than only over the pixels covered by the shape instance, but this leads to its own problem. This would mean that whichever class template contains the least ink—in our case '-'—would nearly always be found to have the lowest distance.
w = 0.09 template side length (they are square) = 14 number of smoothing iterations for the templates = 3 number of smoothing iterations for the point angle values = 1
These values have been selected by hand.
In order to test this algorithm, a shape collection was compiled from 18 people each drawing 15 shapes 5 times with a few instances being lost due to collection error.
Then an 18-fold cross-validation was performed with single-user hold outs. The averages from this test are presented in this confusion matrix.
*NOTE: this screen shot should instead say "18-fold"
The largest strength of this recognition algorithm is that it is extremely fast both to train and to recognize. It took, on average, 0.36 to perform the 18-fold cross-validation, 0.02 seconds to train, and 0.00006 seconds to recognize a shape instance.
This algorithm is scale invariant.
This algorithm is rotationally variant, so it would not perform well with a system in which rotation mattered.
This algorithm does not fully take into account the conditional probabilities of the ink. The templates naturally represent a form of Gaussian probability for ink around a segment of the shape class—i.e., there is a higher probability of the ink in an instance of the shape class lying in the center of the segment of the template than off to either side of the segment. However, given that a point in an instance of the shape class does lie off to one side of a segment of the shape class template, it is much more likely that the next point also will lie off to that side, and much less likely that the next point will lie off to the other side. This algorithm does not take advantage of this conditional probability.
This algorithm could be extended to become rotationally invariant. This could possibly be done by rotating each shape instance according to an indicative angle from the centroid to the furthest point from the centroid.
The conditional ink probability—addressed in the weaknesses section—could be taken advantage of with a "super pixel" scheme. In this scheme, each pixel in each directional bitmap could contain four additional mxm sub-bitmaps of pixel values. These sub-bitmaps would represent the conditional directional ink probabilities of the neighbors of the given center pixel. Adapting the training of the templates for these bitmaps of super pixels and the distance metric would be a fairly straightforward extension of their current versions. However, this super-pixel scheme would have a much higher time and space complexity.
This shows the directional bitmaps for the sigma shape class template. More intense coloration represents higher probabilities.
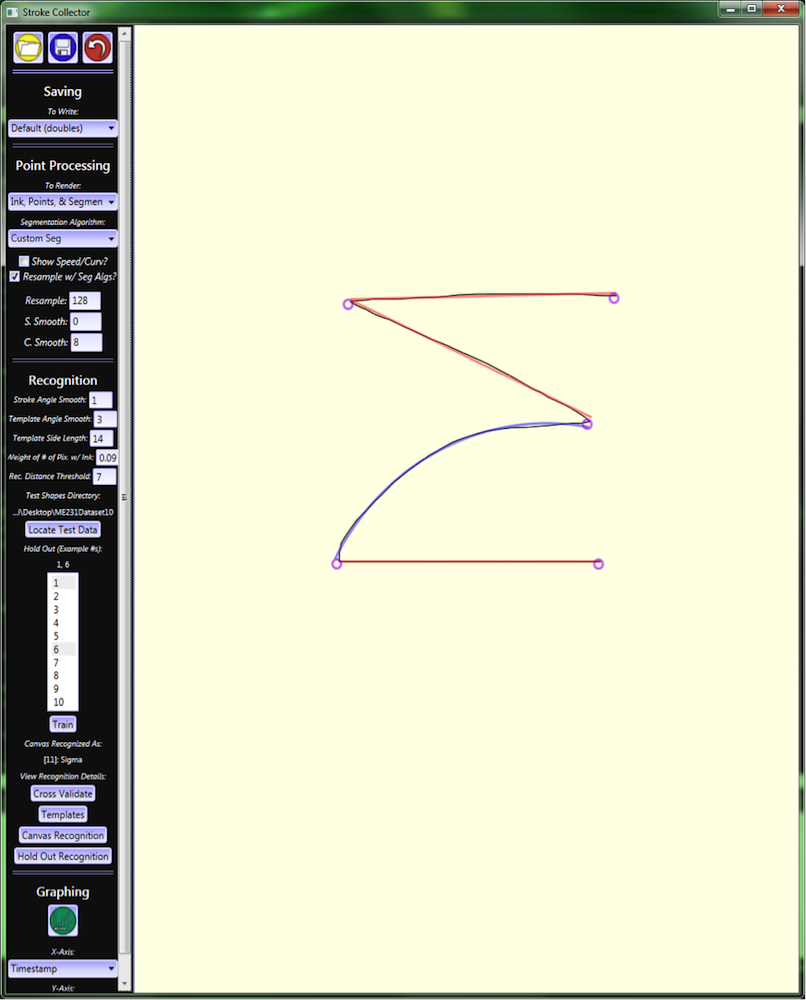
This shows the program with a sigma shape drawn by the user. The system parameters can be seen on the right. The recognizer in this case has been trained on the sample student data with a hold out of first and sixth instances of each shape from each user. The system recognizes the current canvas ink as a sigma shape.
This shows the directional pixel values for the ink shown in the previous image.
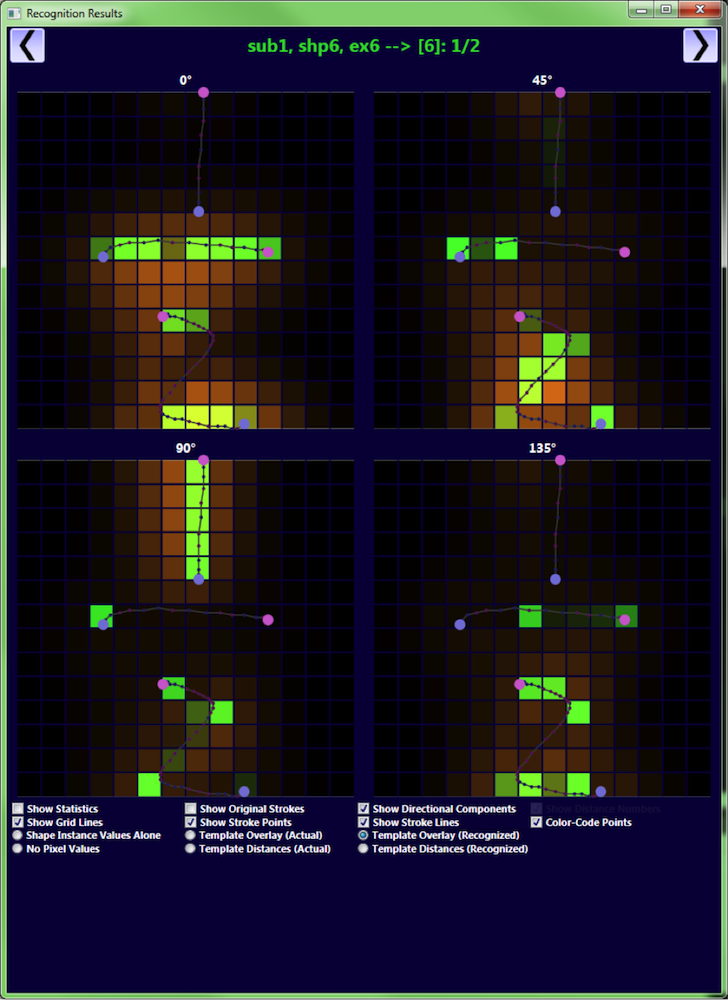
This shows the directional pixel values for a holdout shape overlaid on top of the directional bitmaps for the shape class template to which it was matched.
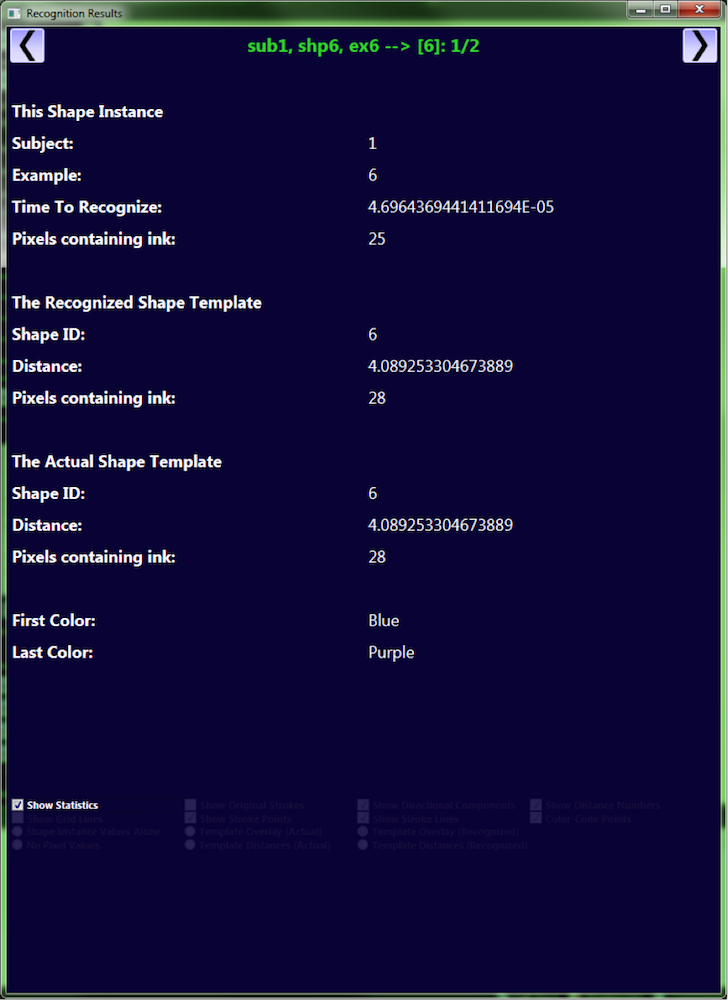
This shows the recognition details for the shape instance shown in the previous image.
======