Skip to content

Latest commit

 

History

History
292 lines (240 loc) · 8.1 KB

README.md

File metadata and controls

292 lines (240 loc) · 8.1 KB

305. 岛屿数量 II

English Version

题目描述

给你一个大小为 m x n 的二进制网格 grid 。网格表示一个地图，其中，0 表示水，1 表示陆地。最初，grid 中的所有单元格都是水单元格（即，所有单元格都是 0）。

可以通过执行 addLand 操作，将某个位置的水转换成陆地。给你一个数组 positions ，其中 positions[i] = [ri, ci] 是要执行第 i 次操作的位置 (ri, ci) 。

返回一个整数数组 answer ，其中 answer[i] 是将单元格 (ri, ci) 转换为陆地后，地图中岛屿的数量。

岛屿 的定义是被「水」包围的「陆地」，通过水平方向或者垂直方向上相邻的陆地连接而成。你可以假设地图网格的四边均被无边无际的「水」所包围。

 

示例 1：

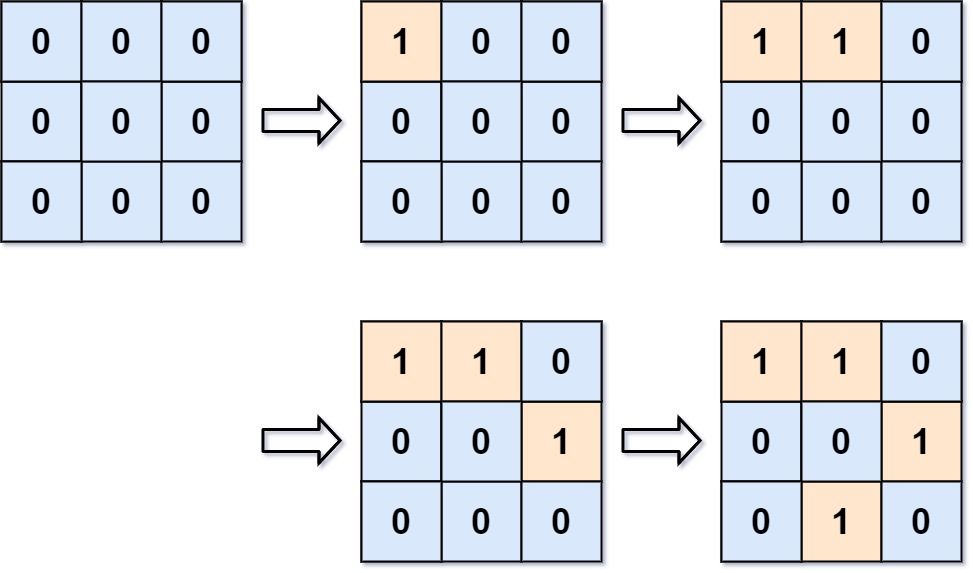
输入：m = 3, n = 3, positions = [[0,0],[0,1],[1,2],[2,1]]
输出：[1,1,2,3]
解释：
起初，二维网格 grid 被全部注入「水」。（0 代表「水」，1 代表「陆地」）
- 操作 #1：addLand(0, 0) 将 grid[0][0] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #2：addLand(0, 1) 将 grid[0][1] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #3：addLand(1, 2) 将 grid[1][2] 的水变为陆地。此时存在 2 个岛屿。
- 操作 #4：addLand(2, 1) 将 grid[2][1] 的水变为陆地。此时存在 3 个岛屿。

示例 2：

输入：m = 1, n = 1, positions = [[0,0]]
输出：[1]

 

提示：

  • 1 <= m, n, positions.length <= 104
  • 1 <= m * n <= 104
  • positions[i].length == 2
  • 0 <= ri < m
  • 0 <= ci < n

 

进阶：你可以设计一个时间复杂度 O(k log(mn)) 的算法解决此问题吗？（其中 k == positions.length）

解法

并查集。

并查集模板：

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]


# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

Python3

class Solution:
    def numIslands2(self, m: int, n: int, positions: List[List[int]]) -> List[int]:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        grid = [[0] * n for _ in range(m)]
        cnt = 0
        p = list(range(m * n))
        ans = []
        for i, j in positions:
            if grid[i][j] == 1:
                ans.append(cnt)
                continue
            grid[i][j] = 1
            cnt += 1
            for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y] == 1 and find(i * n + j) != find(x * n + y):
                    p[find(i * n + j)] = find(x * n + y)
                    cnt -= 1
            ans.append(cnt)
        return ans

Java

class Solution {
    private int[] p;

    public List<Integer> numIslands2(int m, int n, int[][] positions) {
        p = new int[m * n];
        for (int i = 0; i < p.length; ++i) {
            p[i] = i;
        }
        int[][] grid = new int[m][n];
        int cnt = 0;
        List<Integer> ans = new ArrayList<>();
        int[] dirs = {-1, 0, 1, 0, -1};
        for (int[] pos : positions) {
            int i = pos[0];
            int j = pos[1];
            if (grid[i][j] == 1) {
                ans.add(cnt);
                continue;
            }
            grid[i][j] = 1;
            ++cnt;
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k];
                int y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1
                    && find(x * n + y) != find(i * n + j)) {
                    p[find(x * n + y)] = find(i * n + j);
                    --cnt;
                }
            }
            ans.add(cnt);
        }
        return ans;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    vector<int> p;

    vector<int> numIslands2(int m, int n, vector<vector<int>>& positions) {
        p.resize(m * n);
        for (int i = 0; i < p.size(); ++i) p[i] = i;
        vector<vector<int>> grid(m, vector<int>(n));
        vector<int> ans;
        int cnt = 0;
        vector<int> dirs = {-1, 0, 1, 0, -1};
        for (auto& pos : positions) {
            int i = pos[0], j = pos[1];
            if (grid[i][j] == 1) {
                ans.push_back(cnt);
                continue;
            }
            grid[i][j] = 1;
            ++cnt;
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && find(x * n + y) != find(i * n + j)) {
                    p[find(x * n + y)] = find(i * n + j);
                    --cnt;
                }
            }
            ans.push_back(cnt);
        }
        return ans;
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

Go

func numIslands2(m int, n int, positions [][]int) []int {
	p := make([]int, m*n)
	for i := 0; i < len(p); i++ {
		p[i] = i
	}
	grid := make([][]int, m)
	for i := 0; i < m; i++ {
		grid[i] = make([]int, n)
	}
	var find func(x int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	var ans []int
	cnt := 0
	dirs := []int{-1, 0, 1, 0, -1}
	for _, pos := range positions {
		i, j := pos[0], pos[1]
		if grid[i][j] == 1 {
			ans = append(ans, cnt)
			continue
		}
		grid[i][j] = 1
		cnt++
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && find(x*n+y) != find(i*n+j) {
				p[find(x*n+y)] = find(i*n + j)
				cnt--
			}
		}
		ans = append(ans, cnt)
	}
	return ans
}

...