Skip to content

Latest commit

 

History

History
379 lines (312 loc) · 9.89 KB

README.md

File metadata and controls

379 lines (312 loc) · 9.89 KB

1971. 寻找图中是否存在路径

English Version

题目描述

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

 

示例 1：

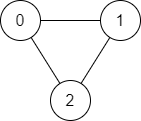
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

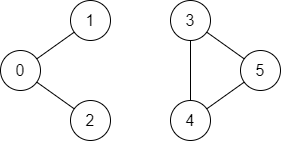
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

 

提示：

  • 1 <= n <= 2 * 105
  • 0 <= edges.length <= 2 * 105
  • edges[i].length == 2
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 0 <= source, destination <= n - 1
  • 不存在重复边
  • 不存在指向顶点自身的边

解法

方法一：DFS

我们先将 edges 转换成邻接表 $g$，然后使用 DFS，判断是否存在从 source 到 destination 的路径。

过程中，我们用数组 vis 记录已经访问过的顶点，避免重复访问。

时间复杂度 $O(n + m)$，其中 $n$ 和 $m$ 分别是节点数和边数。

方法二：并查集

判断图中两个节点是否连通，一种比较简单直接的方法是使用并查集。

先构建并查集，然后将每条边的两个节点合并。

最后查询 source 和 destination 的祖宗节点是否相同，相同则说明两个节点连通。

时间复杂度 $O(n + m \times \alpha(m))$，空间复杂度 $O(n)$。其中 $n$ 和 $m$ 分别是节点数和边数。

附并查集相关介绍以及常用模板：

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的合并及查询问题。 它支持两种操作：

  1. 查找（Find）：确定某个元素处于哪个子集，单次操作时间复杂度 $O(\alpha(n))$
  2. 合并（Union）：将两个子集合并成一个集合，单次操作时间复杂度 $O(\alpha(n))$

其中 $\alpha$ 为阿克曼函数的反函数，其增长极其缓慢，也就是说其单次操作的平均运行时间可以认为是一个很小的常数。

以下是并查集的常用模板，需要熟练掌握。其中：

  • n 表示节点数
  • p 存储每个点的父节点，初始时每个点的父节点都是自己
  • size 只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
  • find(x) 函数用于查找 $x$ 所在集合的祖宗节点
  • union(a, b) 函数用于合并 $a$ 和 $b$ 所在的集合
p = list(range(n))
size = [1] * n

def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]


def union(a, b):
    pa, pb = find(a), find(b)
    if pa == pb:
        return
    p[pa] = pb
    size[pb] += size[pa]
int[] p = new int[n];
int[] size = new int[n];
for (int i = 0; i < n; ++i) {
    p[i] = i;
    size[i] = 1;
}

int find(int x) {
    if (p[x] != x) {
        // 路径压缩
        p[x] = find(p[x]);
    }
    return p[x];
}

void union(int a, int b) {
    int pa = find(a), pb = find(b);
    if (pa == pb) {
        return;
    }
    p[pa] = pb;
    size[pb] += size[pa];
}
vector<int> p(n);
iota(p.begin(), p.end(), 0);
vector<int> size(n, 1);

int find(int x) {
    if (p[x] != x) {
        // 路径压缩
        p[x] = find(p[x]);
    }
    return p[x];
}

void unite(int a, int b) {
    int pa = find(a), pb = find(b);
    if (pa == pb) return;
    p[pa] = pb;
    size[pb] += size[pa];
}
p := make([]int, n)
size := make([]int, n)
for i := range p {
    p[i] = i
    size[i] = 1
}

func find(x int) int {
    if p[x] != x {
        // 路径压缩
        p[x] = find(p[x])
    }
    return p[x]
}

func union(a, b int) {
    pa, pb := find(a), find(b)
    if pa == pb {
        return
    }
    p[pa] = pb
    size[pb] += size[pa]
}

Python3

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        def dfs(i):
            if i == destination:
                return True
            vis.add(i)
            for j in g[i]:
                if j not in vis and dfs(j):
                    return True
            return False

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = set()
        return dfs(source)
class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        for u, v in edges:
            p[find(u)] = find(v)
        return find(source) == find(destination)

Java

class Solution {
    private boolean[] vis;
    private List<Integer>[] g;

    public boolean validPath(int n, int[][] edges, int source, int destination) {
        vis = new boolean[n];
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        return dfs(source, destination);
    }

    private boolean dfs(int source, int destination) {
        if (source == destination) {
            return true;
        }
        vis[source] = true;
        for (int nxt : g[source]) {
            if (!vis[nxt] && dfs(nxt, destination)) {
                return true;
            }
        }
        return false;
    }
}
class Solution {
    private int[] p;

    public boolean validPath(int n, int[][] edges, int source, int destination) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        for (int[] e : edges) {
            p[find(e[0])] = find(e[1]);
        }
        return find(source) == find(destination);
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<bool> vis(n);
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        function<bool(int)> dfs = [&](int i) -> bool {
            if (i == destination) return true;
            vis[i] = true;
            for (int& j : g[i]) {
                if (!vis[j] && dfs(j)) {
                    return true;
                }
            }
            return false;
        };
        return dfs(source);
    }
};
class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        function<int(int)> find = [&](int x) -> int {
            if (p[x] != x) p[x] = find(p[x]);
            return p[x];
        };
        for (auto& e : edges) p[find(e[0])] = find(e[1]);
        return find(source) == find(destination);
    }
};

Go

func validPath(n int, edges [][]int, source int, destination int) bool {
	vis := make([]bool, n)
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int) bool
	dfs = func(i int) bool {
		if i == destination {
			return true
		}
		vis[i] = true
		for _, j := range g[i] {
			if !vis[j] && dfs(j) {
				return true
			}
		}
		return false
	}
	return dfs(source)
}
func validPath(n int, edges [][]int, source int, destination int) bool {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	var find func(x int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	for _, e := range edges {
		p[find(e[0])] = find(e[1])
	}
	return find(source) == find(destination)
}

...