Fell free to use this repository for anything you want. The code is free as in beer, and I require no attribution. I highly appreciate suggestions and you can contact me via the issues page.
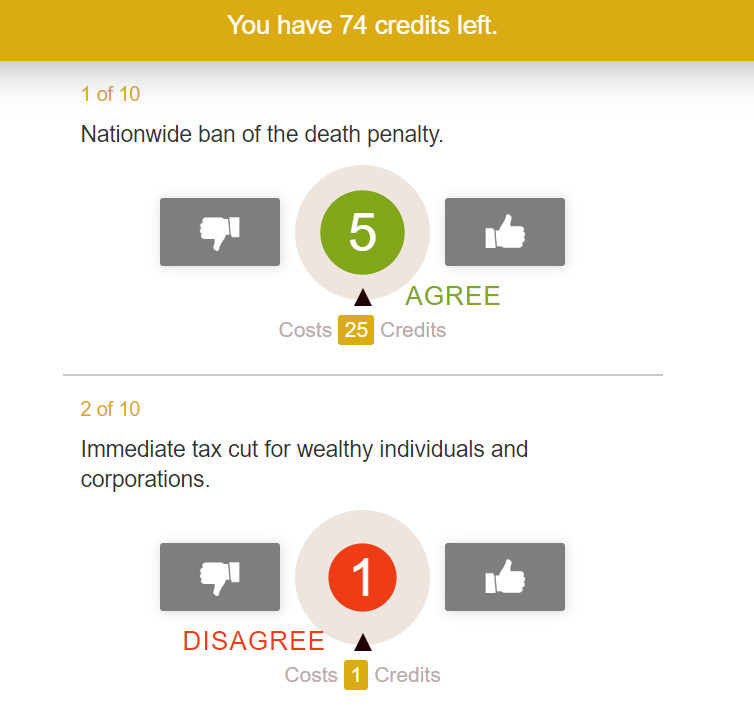
Notice in the picture below that to cast 5 votes you have to spend 25 Credits.
from Radical Markets: Uprooting Capitalism and Democracy for a Just Society!
So 1 credit gives you 1 vote, 4 credits gives you 2 votes, 9 credits - 3 votes and so on. Why is this important ? Checkout the explanation section
Usually a KYC (or by using some electronic SSN, employees id etc), each person is give PERIODICALLY a number of tokens. They can keep it, or spend it to vote for the issues they care about. Everything is tracked at blockchain level (usually a private one).
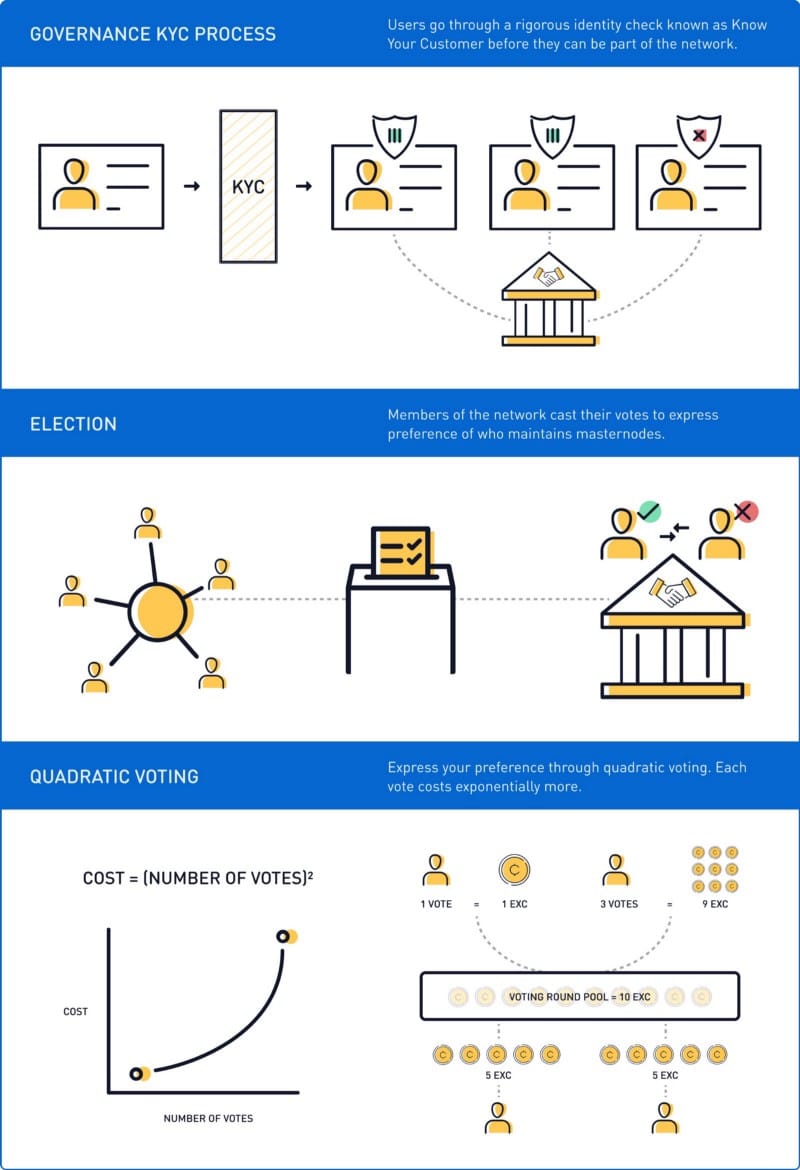 Picture by https://twitter.com/eximchainexc?lang=en
Picture by https://twitter.com/eximchainexc?lang=en
Collective decision making using a majority rule of 50+1 is a standard procedure used by many firms and countries to decide whether a policy should be implemented. However, this mechanism is subject to the “tiranny of the majority” and therefore may give rise to situations that deviate the collective decision-making process from optimality (Posner and Weyl, 2014). Consider for instance a minority that care much more intensely about getting a public good (e.g. a road or a anti-discrimination law) than the majority does for the opposite outcome. With the use of a simple majoritarian rule it might be the case that the losses caused to the majority are greater than the benefits provided to the majority, an inefficient outcome from an utilitarian point of view. More generally, take a binary collective decision with a distribution of preferences such that preferring one of the choices is represented by a positive valuation whereas preferring the complementary choice is represented by a negative valuation. A majority voting system will lead to an inefficient outcome when the expected value and the median value are on opposite sides of the valuation space.
The Quadratic Voting mechanism (henceforth QV) proposed by Weyl (2013) is a novel electoral design which can yield more efficient outcomes than a majority voting system in these situations. Under the QV mechanism individuals buy votes at a quadratic unit cost and receive a reimbursement equal to the average of the others’ expenditures in votes. Hence, the marginal cost of an additional vote is proportional to the votes already purchased, and the marginal benefit of an additional vote is proportional to the cardinal value of changing the policy. Furthermore, because individuals receive a reimbursement equal to the average of others’ payment, the mechanism is budget balanced. In addition, QV tries to resolve other problems of mechanism design such as the collusion problem of the Vickrey-Clarke-Groves (VCG) mechanism, and the information problems of the Expected Externality mechanism, where a social planner needs to know the distribution of the valuations that agents have.
you can read more here: https://pdfs.semanticscholar.org/974c/ee1137b4a56372af58772a88361b3ff4b9d6.pdf
According to its authors Steven P. Lalley and E. Glen Weyl, Quadratic voting is claimed to achieve the greatest possible good for the greatest number of group members, although other proponents of Quadratic Voting state that this is only true approximately. It addresses issues of voting paradox and majority-rule.
Based on market principles, each voter is endowed with a budget of “voice credits” that they may spend influencing the outcome of a range of decisions. If a participant has a strong preference for or against a particular decision, additional votes can be allocated. A vote pricing rule determines the cost of additional votes, whereby each vote increasingly becomes more expensive.
The quadratic nature of the voting means that a voter can use his or her votes more efficiently spread across many issues. For example, a voter with a budget of 16 vote credits can apply 1 vote credit to each of 16 issues. However, if they feel strongly about a single issue, they can apply 4 votes at the cost of 16 credits to a single issue. This will use their entire budget. This also means there is a large incentive to buy and sell votes, although using a strictly secret ballot gives some protection against vote buying as the purchase cannot be verified.
Please read CONTRIBUTING.md for details on our code of conduct, and the process for submitting pull requests to us.
This project is licensed under the MIT License - see the LICENSE.md file for details