%load_ext itikz

from matplotlib import pyplot
import numpy
import pandas

Künstliche Intelligenz und Evolution

Rent-a-Scientist 2021

von Carsten Fortmann-Grote, Max-Planck-Institut für Evolutionsbiologie, 24306 Plön

Begrüßung

Wer bin ich?

Abitur 1998 in Eutin (OH)
Physikstudium, Promotion 2008
Postdoc USA
Scientific Software Developer, QuantumWise (Kopenhagen, DK)
Wissenschaftler am Europäischen Röntgen-Freie Elektronenlaser (XFEL), Schenefeld bei Hamburg
Seit 2019 am MPI Evolutionsbiologie in Plön (Wissenschaftliches Rechnen)

Woran forsche ich?

Simulation von Evolutionsprozessen (stochastische Prozesse)
Anwendung von Hochleistungsrechnern und Hochdurchsatzrechnern in der biologischen Datenverarbeitung
“Deep Learning” im Bereich der Lebenswissenschaften

Gliederung

Was ist Künstliche Intelligenz
Maschinelles Lernen mit Neuronalen Netzen: Deep Learning
Das Neuron als Grundbaustein von Neuronalen Netzen
Gewichte und Aktivierungsfunktionen
1. Beispiel: Berechnung einer Ausgleichsgeraden mit einem Neuron
Tiefe Neuronale Netze (“Deep Neural Networks”)
Parameter und Hyperparameter
Training Neuronaler Netze
Overfitting und Dropout
Genetischer Algorithmus
Anwendungsbeispiel: Optimierung eines Neuronalen Netzes mit verteiltem Genetischen Algorithmus
Zusammenfassung
Ausblick

Einleitung

Künstliche Intelligenz und Turing Test

Eine Maschine (Computer) hat den Turing Test bestanden, wenn sie sich in einem Chat nicht von einem menschlichen Gesprächspartner unterscheiden lässt.

Eine Arbeitsdefinition für KI

KI umfasst Forschungs- und Technologiebereiche an den Schnittstellen von Computerwissenschaften, Informatik, Kybernetik, Neurowissenschaften, Didaktik und anderen. Im weitesten Sinne bezeichnet KI, die Möglichkeit programmierbaren (Turing) Maschinen, die Rezeption (Erkennung) und anschliessende Verarbeitung von Information mit dem Ziel eines mehr oder minder spezifischen Erkenntnisgewinns im weitesten Sinne beizubringen. Phänologisch ähnelt die Response künstlich intelligenter Systeme intelligentem (menschlichen) Verhalten in Anbetracht derselben oder analoger Daten oder Situationen.

Maschinelles Lernen (ML) ist ein Teilbereich der KI und Deep Learning (DL) widerum ein Teilbereich von ML.

Quelle:

Traditionelle KI: Deterministisches Modell, das alle Möglichen Situationen und die “richtigen” Antworten darauf beinhaltet.
Moderne KI: Algorithmus trainiert sich selbst anhand verfügbarer Daten. Ermöglicht durch Big Data.

Deep Learning = Maschinelles Lernen mit künstlichen Neuronalen

Netzen

Beispiele

Bildverbeitung: Klassifizierung (2 fach)
\ Den Eingangdaten (Pixelwerten RGB) werden Label zugeordnet: Hund oder Katze
Bildverarbeitung (Erkennung 10-fach)

Den Eingangsdaten (Pixelwerte Schwarz-Weiss) werden Label zugeordnet (0,1,2,3,4,5,6,7,8,9)

Bildverbeitung: Objekterkennung (oder Segmentierung) Bildbereichen werden Label (Ja/Nein) zugeordnet.
Empfehlungen in Internetsuche, Sozialen Medien

Komplexen Daten (Interpreten, Tonsequenzen, Likes) werden andere komplexe Daten zugeordnet.

F. Chollet (Deep Learning with Python 2018):

Beaufsichtigtes Lernen mit Neuronalen Netzen (supervised Deep

Learning)

Im Gegensatz zu unbeaufsichtigtem DL (Datenrepräsentationen, Verschlüsselung, Kompression)
Daten bestehen aus Eingangswerten ($X$) und Ausgangswerten ($Y$), sowie der Zuordnung $X→ Y$
Z.B. Bild -> Hund oder Katze, Bild -> Zahl 0-9, Lied -> Lied
Das Neuronale Netz soll diese Zuordnungen lernen um dann zu gegebenen neuen Eingangsdaten $X_\mathrm{neu}$ die richtigen aber bisher unbekannten Label $Y_\mathrm{neu}$ zu finden.

Hund-Katze Beispiel:

(Kuenstliche) Neuronale Netze

Neuronale Netze als Analogon zu biologischen Neuronalen Netzen

Das Neuron (Nervenzelle)

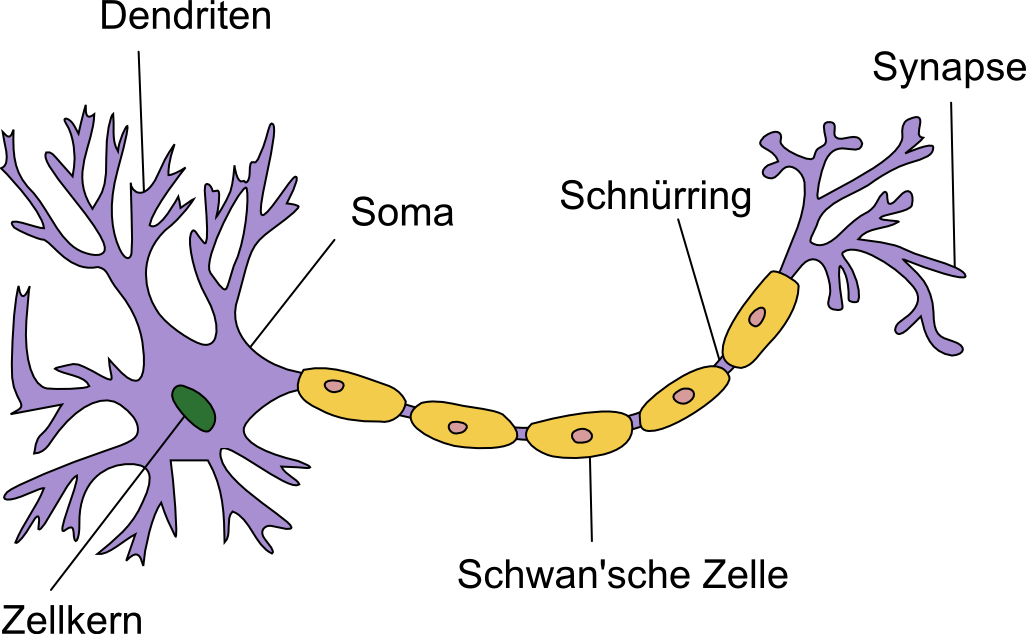
Elektronenmikroskopische Aufnahme einer Nervenzelle

Quelle: https://www.canadiannaturephotographer.com/rberdan_scanning_electron_microscopy2017.html

Quelle:

Das Künstliche Neuron (Perzeptron)

%%itikz --file-prefix neuron --implicit-pic --scale 2
\node[circle,draw,fill=red] (neuron) at (2,0) {$\mathcal{N}$};
\node[circle,draw] (I1) at (0,1) {$I_1$};

\node[circle,draw] (O)  at (4,0) {$O$};
\draw[-](I1) -- (neuron) ;

\draw[->](neuron) -- (O);

$I_1$: Erstes Eingangssignal (Input)
$\mathcal{N}$: Neuron
$O$: Ausgang (Output)

%%itikz --file-prefix neuron --implicit-pic --scale 2
\node[circle,draw,fill=red] (neuron) at (2,0) {$\mathcal{N}$};
\node[circle,draw] (I1) at (0,1) {$I_1$};
\node[circle,draw] (I2) at (0,0.5) {$I_2$};

\node[circle,draw] (O)  at (4,0) {$O$};
\draw[-](I1) -- (neuron) ;
\draw(I2) -- (neuron);

\draw[->](neuron) -- (O);

$I_1$: Erstes Eingangssignal (Input)
$I_2$: Erstes Eingangssignal (Input)
$\mathcal{N}$: Neuron
$O$: Ausgang (Output)

%%itikz --file-prefix neuron --implicit-pic --scale 2
\node[circle,draw,fill=red] (neuron) at (2,0) {$\mathcal{N}$};
\node[circle,draw] (I1) at (0,1) {$I_1$};
\node[circle,draw] (I2) at (0,0.5) {$I_2$};
\node[circle,draw] (I3) at (0,0.0) {$I_3$};

\node(dots1) at (0, -0.5) {$\ldots$};

\node[circle,draw] (IN) at (0,-1) {$I_N$};
\node[circle,draw] (O)  at (4,0) {$O$};
\draw[-](I1) -- (neuron) ;
\draw(I2) -- (neuron);
\draw(I3) -- (neuron);
\draw(IN) -- (neuron);
\draw[->](neuron) -- (O);

$I_1$: Erstes Eingangssignal (Input)
$I_2$: Erstes Eingangssignal (Input)
$I_3$: Drittes Eingangssignal
$\ldots$
$I_N$: Ntes Eingangssignal
$\mathcal{N}$: Neuron
$O$: Ausgang (Output)

Das Aktionspotenzial

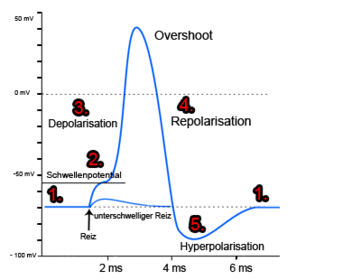
Die Nervenzelle leitet die Erregung erst ab Überschreiten des Schwellenpotentials ab.
Die Hyperpolarisation sorgt dafür, dass keine Reize “zurück fliessen”.

Das Ausgangssignal ist eine Funktion der gewichteten Summe der

Eingangssignale

Einzelnes Neuron

# %%itikz --file-prefix neuron --implicit-pic --scale 2
# \node[circle,draw,fill=red] (neuron) at (2,0) {$\mathcal{N}$};
# \node[circle,draw] (I1) at (0,1) {$I_1$};
# \node(w1) at (0.8,0.6) {$w_1$};

# \node[circle,draw] (O)  at (4,0) {$O$};
# \draw[-](I1) -- (w1) ;
# \draw[->](w1) -- (neuron) ;

# \draw[->](neuron) -- (O);

$ O = \mathcal{N}(I_1⋅ w_1)$

Neuron mit zwei Eingängen

# %%itikz --file-prefix neuron --implicit-pic --scale 2
# \node[circle,draw,fill=red] (neuron) at (2,0) {$\mathcal{N}$};
# \node[circle,draw] (I1) at (0,1) {$I_1$};
# \node(w1) at (0.8,0.6) {$w_1$};
# \node[circle,draw] (I2) at (0,0.5) {$I_2$};
# \node(w2) at (0.8,0.3) {$w_2$};

# \node[circle,draw] (O)  at (4,0) {$O$};
# \draw[-](I1) -- (w1) ;
# \draw[->](w1) -- (neuron) ;
# \draw(I2) -- (w2);
# \draw[->](w2) -- (neuron);

# \draw[->](neuron) -- (O);

$O = \mathcal{N}(I_1⋅ w_1 + I_2⋅ w_2)$

Neuron mit N Eingängen

# %%itikz --file-prefix neuron --implicit-pic --scale 2
# \node[circle,draw,fill=red] (neuron) at (2,0) {$\mathcal{N}$};
# \node[circle,draw] (I1) at (0,1) {$I_1$};
# \node(w1) at (0.8,0.6) {$w_1$};
# \node[circle,draw] (I2) at (0,0.5) {$I_2$};
# \node(w2) at (0.8,0.3) {$w_2$};

# \node[circle,draw] (I3) at (0,0.0) {$I_3$};
# \node(w3) at (0.8,0.0) {$w_3$};

# \node(dots1) at (0, -0.5) {$\ldots$};
# \node(dots2) at (0.8, -0.3) {$\ldots$};

# \node[circle,draw] (IN) at (0,-1) {$I_N$};
# \node(wN) at (0.8,-0.6) {$w_N$};
# \node[circle,draw] (O)  at (4,0) {$O$};
# \draw[-](I1) -- (w1) ;
# \draw[->](w1) -- (neuron) ;
# \draw(I2) -- (w2);
# \draw[->](w2) -- (neuron);
# \draw(I3) -- (w3);
# \draw[->](w3) -- (neuron);
# \draw(IN) -- (wN);
# \draw[->](wN) -- (neuron);
# \draw[->](neuron) -- (O);

$O = \mathcal{N}(I_1⋅ w_1 + I_2⋅ w_2 + … I_N⋅ w_N)$

$w_1, w_2, \ldots w_N$ sind die Gewichtsfaktoren.

Wir schreiben kurz
$O = \mathcal{N}(∑_i=1^N I_i ⋅ w_i)$

Oder noch kürzer als Skalarprodukt (Inneres Produkt) zweier Vektoren:
$O = \mathcal{N}(\vec{I}⋅ \vec w)$

$\vec{I}$ ist der Signalvektor, $\vec{w}$ ist der Gewichtsvektor.

Maschinelles Lernen mit Neuronalen Netzen = Optimierung der

Gewichtsfaktoren

Die Aktivierungsfunktion $\mathcal{N}$

Für die Aktivierungsfunktion haben sich eine Handvoll verschiedener Formen etabliert, hier einige Beispiele:

Sprungfunktion

x = numpy.linspace(-1,1,1024)
def sprungfunktion(x):
    y = numpy.zeros_like(x)
    y[x>0] = 1.0
    return y

y = sprungfunktion(x)
pyplot.plot(x, y, label='Sprungfunktion')
pyplot.legend()

<matplotlib.legend.Legend at 0x7ffa1edf8b50>

Tanh

x = numpy.linspace(-1,1,1024)
y = numpy.tanh(10*x)

pyplot.plot(x, y, label="tanh")
pyplot.legend()

<matplotlib.legend.Legend at 0x7ffa48a01a00>

Relu Funktion

def relu(x):
    y = numpy.zeros_like(x)
    y[x>0] = x[x>0]
    return y

x = numpy.linspace(-1,1,1024)
y = relu(x)

pyplot.plot(x, y,label="Relu")
pyplot.legend()

<matplotlib.legend.Legend at 0x7ffa1e52c730>

Beispiel: “Lernen” einer Ausgleichsgeraden (oder lineare Regression)

Ein Team von Biolog*Innen untersucht wie gut sich Bakterien in Abhängigkeit von der Temperatur vermehren.

Dazu erhöhen sie die Temperatur im Labor von 20 auf 30 Grad in 1 Grad Schritten. Nach jeder Einstellung messen Sie die Bakterienzahlen die sich nach 3 Stunden ergibt bei jeweils der gleichen Anfangspopulation. Daraus ergibt sich der Wachstumsfaktor $F$.

Sie messen die folgenden Daten

T = numpy.arange(20,31)

F = 2.*T + numpy.random.normal(0.0, 1,size=T.shape)

data = pandas.DataFrame(data={"Temperatur":T, "Wachstum":F})

data.index = range(1,12); data

    Temperatur   Wachstum
1           20  39.218535
2           21  41.522353
3           22  42.705500
4           23  46.655774
5           24  47.209419
6           25  49.266511
7           26  50.161706
8           27  53.784164
9           28  55.277513
10          29  56.467867
11          30  59.607640

data.plot(x="Temperatur", y="Wachstum", style="o")

<AxesSubplot:xlabel='Temperatur'>

Aufgabe: Entwickle eine Modell, dass das Bakterienwachstum als

Funktion der Temperatur angibt.

Wir nutzen hierzu das einfachste Netzwerk, das man sich vorstellen kann: Es besteht aus einem Neuron mit genau einem Eingang und einem Ausgang. Die Aktivierungsfunktion ist die lineare Funktion $F = \mathcal{N}(w⋅ T) = w⋅ T$.

# %%itikz --file-prefix implicit-demo- --implicit-pic --scale 3
# \node[circle,draw,fill=red] (neuron) at (2,0) {$F = w\cdot T$};
# \node[circle,draw] (T) at (0,0) {Temperatur $T$};
# \node(w) at (0.8,0.0) {$w$};

# \node[circle,draw] (O)  at (4,0) {Wachstum $F$};
# \draw[-](T) -- (w) ;
# \draw[->](w) -- (neuron) ;

# \draw[->](neuron) -- (O);

Im Training werden wir den Gewichtsparameter $w$ so einstellen, dass die Vorhersage $\hat N_i = w⋅ T_i$ möglichst gut an den tatsächlich gemessenen Wachstumsfaktoren liegt.

Was bedeutet möglichst gut? Im Idealfall sollte die Differenz $\hat N_i - N_i$ für alle i verschwinden, dann wäre das Modell perfekt.

Andererseits wissen wir, dass Messdaten immer mit einer Unsicherheit versehen sind. Hätten wir ein Modell, das perfekt unsere Daten wiedergibt, so würde dasselbe Modell bei einer wiederholten Messung aller Wahrscheinlichkeit nach sehr schlecht abschneiden. Wir brauchen also ein Modell, das im Mittel die Daten gut annähert. Und wir benötigen ein Mass für die statistische Abweichung zwischen unserem Modell und den Daten. Dieses Mass der Abweichung gilt es dann zu minimieren.

Ein gebräuchliches Mass für die Abweichung zwischen einem Modell und Daten ist die mittlere quadratische Abweichung. Sie lautet $V = ∑_i=1^N (\hat F_i - F_i)^2$.

In unserem Fall (11 Messwerte, also $N=11$) bedeuted dies: $V =(\hat F_1 - F_1)^2 + (\hat F_2 - F_2)^2 + (\hat F_3 - F_3)^2 + \ldots

(\hat F₁₁ - F₁₁)^2 $

$\ \ \ = (w⋅ T_1 - F_1)^2 + (w⋅ T_2 - F_2)^2 + (w⋅ T_3 - F_3)^2 + \ldots + (w⋅ T₁₁ - F₁₁)^2$ $\ \ \ = ∑_i=1¹¹ (w⋅ T_i - F_i)^2$

Diesen Ausdruck wollen wir nun minimieren.

Das Extremum einer Funktion ist durch das Nullwerden der ersten Ableitung gegeben:

$ \frac{dV}{dw} = V’ = 0 $
$ = \left[ ∑_i=1¹¹ (w⋅ T_i - F_i)^2\right]’$\ $ = ∑_i=1¹¹ 2⋅(w⋅ T_i - F_i)⋅ T_i $\ $ = 2⋅ w⋅\sum_i=1¹¹ T_i^2 - 2⋅\sum_i=1¹¹ T_i⋅ F_i = 0$\ $ 2⋅ w⋅\sum_i=1¹¹ T_i^2 = 2⋅\sum_i=1¹¹ T_i⋅ F_i $\ $ w⋅\sum_i=1¹¹ T_i^2 = ∑_i=1¹¹ T_i⋅ F_i $\ $ w = \frac{∑_i=1¹¹ T_i⋅ F_i}{∑_i=1¹¹ T_i^2}$

Daraus ergibt sich das optimale Gewicht $w$. Wir können es nun direkt aus den Daten bestimmen:

wopt = (data["Temperatur"]*data["Wachstum"]).sum() / (data["Temperatur"]**2).sum(); wopt

1.97044770719104

Nun können wir zu den vermessenen Temperaturen die Vorhersagen unseres Modells berechnen und mit den tatsächlich gemessenen Werten vergleichen:

model = wopt*data["Temperatur"]; model

1     39.408954
2     41.379402
3     43.349850
4     45.320297
5     47.290745
6     49.261193
7     51.231640
8     53.202088
9     55.172536
10    57.142984
11    59.113431
Name: Temperatur, dtype: float64

data.plot(x="Temperatur", y="Wachstum", style="o")
pyplot.plot(data["Temperatur"], model, "--s", label="Model")
pyplot.legend()

<matplotlib.legend.Legend at 0x7ffa1e3567f0>

Wir sehen, dass unser Modell eine Gerade ergibt, die im Mittel durch die Messwerte hindurchgeht. Dieses Modell wird auch Lineare Regression genannt und ist ein wichtiges Werkzeug der Datenanalyse.

Wir haben gesehen, dass wir Lineare Regression auch als einfache Anwendung von Maschinellem Lernen verstehen können. Dabei lernt das Modell einen einzigen Gewichtsfaktor, $w$. In diesem einfachen Fall können wir $w$ analytisch (also ohne Computerrechnung) bestimmen. Dies ist aber die Ausnahme. In den allermeisten Anwendungsfällen für maschinelles Lernen müssen die Gewichtfaktoren in einem numerischen Algorithmus optimiert werden. Dieser Algorithmus besteht aus den folgenden Elementen:

Initialisierung aller Gewichte $w_i^0$ mit Zufallszahlen
Berechnung der Modellvorhersage
Wie nah oder fern ist die Modellvorhersage von den Trainingsdaten?
Korrektur der Gewichte $w_i^0 → w_i^1$
Berechnung der Modellvorhersage …

Der Trainingsalgorithmus

# %%itikz --file-prefix ML_flow --implicit-pic --scale 3

# \draw[-](0,0) -- (2,0) -- (2,1) -- (0,1) -- (0,0);
# \node(eingangsdaten)  at (1.0,0.5) {Eingangsdaten (z.B. Temperatur)};
# \draw[-](3,1) -- (5,1) -- (5,0) -- (3,0) -- (3,1);
# \node(eingangsdaten)  at (4.0,0.5) {Zielwerte (z.B. Wachstum)};
# \draw[->, very thick](1,0) -- (1,-0.5);
# \draw[-](0,-.5) -- (2,-.5) -- (2,-1.5) -- (0,-1.5) -- (0, -.5);
# \node(ml)  at (1.0,-1.0) {ML $\mathcal{N}(\vec w\cdot \vec I)$};
# \draw[->, very thick](2,-1) -- (3,-1.0);
# \draw[-](3,-.5) -- (5,-.5) -- (5,-1.5) -- (3,-1.5) -- (3, -.5);
# \node(ml)  at (4.0,-1.0) {Ausgabe  $O = \mathcal{N}(\vec w\cdot \vec I)$};
# \draw[->, very thick](4,-1.5) -- (4,-2.0);
# \draw[-](3,-2) -- (5,-2) -- (5,-3) -- (3,-3) -- (3, -2);
# \node(ml)  at (4.0,-2.5) {Abweichung  $D(\vec w) = |$Ziel - Ausgabe$| $};
# \draw[->, very thick](5,0.5) -- (6,0.5) -- (6,-2.5) -- (5, -2.5);
# \draw[->, very thick](3,-2.5) -- (2,-2.5);
# \draw[-](0,-2) -- (2,-2) -- (2,-3) -- (0,-3) -- (0, -2);
# \node(ml)  at (1.0,-2.5) {Aktualisiere  $\vec w \leftarrow \vec w-\frac{\delta D(\vec w)}{\delta \vec w}\cdot \Delta w$};
# \draw[->, very thick](1,-2) -- (1,-1.5);

Wie finde ich das Minimum der Funktion $D(\vec w)$?

In einer Dimension

Auf der Tafel

In zwei Dimensionen (z.B. ein Neuron mit zwei Eingängen oder zwei

Neuronen mit jeweils einem Eingang.)

In zwei Dimensionen können wir die Funktion $D(\vec w) = D(w_x, w_y)$ als Höhenkarte interpretieren.

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
np = numpy

fig = plt.figure(figsize=(15,10))
ax = fig.add_subplot(111, projection="3d")
X, Y = np.mgrid[-1:1:60j, -1:1:60j]
Z = 1.-0.9*np.exp(-(X-0.5)**2/0.05-(Y-0.5)**2/0.05)-np.exp(-(X-0.5)**2/0.2-(Y+0.5)**2/0.1)+0.6*np.exp(-(X)**2/0.1-(Y)**2/0.1)+np.exp(-(X+0.5)**2/0.05-(Y-0.5)**2/0.1)+np.sin(np.pi*(X**2/2+Y/3)/2)
ax.plot_surface(X, Y, Z, cmap="coolwarm", rstride=1, cstride=1)
ax.set_xlabel(r"$w_x$")
ax.set_ylabel(r"$w_y$")
ax.set_zlabel(r"$D(w_x,w_y)$")
plt.show()

fig = plt.figure(figsize=(15,10))
ax = fig.add_subplot(111,)
ax.contourf(X, Y, Z, cmap="coolwarm", levels=32)
ax.set_xlabel(r"$w_x$")
ax.set_ylabel(r"$w_y$")
plt.show()

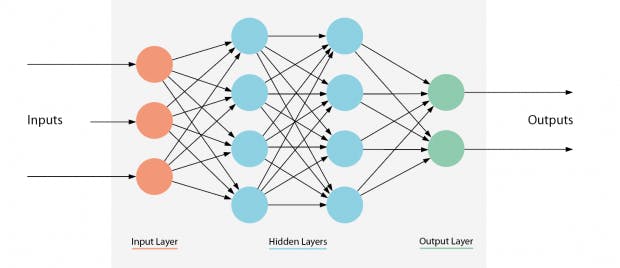
Ein Beispiel für ein künstliches Neuronales Netz mit 2 versteckten

Schichten

Credits: https://t3n.de/magazin/frameworks-fuer-machine-learning-gelingt-einstieg-247180/

In höheren Dimensionen?

In produktiv genutzten NNen ist die Anzahl der Gewichtsparamer und damit die Dimension der Landschaft sehr gross. Hier kann man das Problem nicht mehr so einfach veranschaulichen, aber die Mathematik ist die gleiche: Das Minimum von $D(\vec w)$ wird gesucht, in dem man ausgehend von einem zufällig gewählten Anfangspunkt immer dem steilsten Anstieg in umgekehrter Richtung folgt. Dabei ist das Problem der lokalen Senken zu beachten. Dies kann dadurch abgemildert werden, dass man Sprünge in Richtung der positiven Steigung von Zeit zu Zeit zulässt.

Die Steigung der “Landschaft” lässt sich bei sehr vielen Dimensionen nicht mehr effektiv berechnen. Man geht daher zu einer Methode über, die sich Methode des “stochastische Gradientenabstiegs” (stochastic gradient descent, sgd) nennt. Dabei werden widerum zufällig einige Gewichte ausgesucht und die Steigung nur mit diesen berechnet. Ausserdem werden die Trainingsdaten in sog. Batches unterteilt und die Steigung mit jeweils einem Batch berechnet. Eine vollständige Iteration, also Berechnung des Ausgangssignals, Vergleich mit den Trainingslabeln, Abstandsmetrik, Steigung, Korrektur der Gewichte für alle Batches nennt man eine Trainingsepoche.

Training, Validierung, Testen

Wie bereits angedeutet, ist es wichtig beim eine Maschine nicht zu genau zu trainieren, da sie sonst zwar die trainierten Daten sehr genau kennt und richtig widergibt, aber bei der Anwendung auf neue Daten eher schlecht abschneidet. Diese Tatsache wird Overfitting genannt und ist das zentrale Problem der KI.

Um das Problem des Overfitting wenn nicht zu lösen, dann doch zumindest zu erkennen, hat sich folgender Arbeitsablauf beim Training eines KI Algorithmus etabliert. Dabei trennt man von den zur Verfügung stehenden Daten zunächst in einen Testdatensatz ab. Den Testdatensatz lässt man während der gesamten Trainingsphase unangetastet und benutzt ihn erst als allerletztes um zu evaluieren, wie gut (oder schlecht) der trainierte Algorithmus abschneidet, wenn er auf Daten angewendet wird, die er zuvor noch nie gesehen hat.

Die übrigen Daten werden in einen Trainings- und einen Validierungsdatensatz aufgeteilt. Mit den Trainingsdaten wird das Netzwerk trainiert, also iterativ die Gewichte $w$ eingestellt bis der Unterschied zwischen Ausgang und den Labeln des Testdatensatzes minimiert ist. Mit den Validierungdaten wird nach jeder Trainingsepoche (=eine Iteration über alle Trainingsdaten) validiert wie gut das Netzwerk auf neuen Daten abschneidet.

Als Kriterium wie gut das Netzwerk auf neuen Daten arbeitet, kann man z.B. die Verlustfunktion, also den Abstand zwischen Netzwerkausgang und Trainingslabeln gegen die Anzahl der Trainingsdurchläufe grafisch darstellen:

Wie erwartet sinkt der Abstand zwischen Ausgang und Trainingslabeln mit jeder Iteration. Angewendet auf die Validierungsdaten zeigt sich aber bereits nach 5 Epochen, dass das Netzwerk zu gut an die Trainingsdaten angepasst ist und neue Daten nicht versteht.

In diesem Beispiel würde man das Netzwerk nur maximal 5 Epochen lang trainieren, um Overfitting zu vermeiden.

Hier haben wir das erste Beispiel dafür, dass neben den Gewichten des Netzwerks noch andere Eigenschaften angepasst oder optimiert werden müssen, hier nämlich die Anzahl der Trainingsepochen. Zur Abgrenzung zu den Netzwerkparametern (bisher Gewichte genannt), werden diese anderen Eigenschaften Hyperparameter genannt. Die Optimierung der Hyperparameter ist ein eigenes Forschungsgebiet mit verschiedenen Ansätzen und Methoden. Im zweiten Teil der Unterrichtseinheit werden wir eine Methode, den Genetischen Algorithmus kennenlernen und selbst anwenden.

Dropout als Strategie zur Vermeidung von Overfitting

Eine Dropout Schicht im Netzwerk sortiert zufällig ausgewählte Daten aus. Dadurch sieht der Trainingsalgorithmus bei jeder Iteration einen anderen Teil der Trainingsdaten. Der Algorithmus hat weniger Möglichkeit, sich an die Trainingsdaten zu gewöhnen. Der relative Anteil aussortierter Daten ist die sog. Dropout Rate.

data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAYUAAAEKCAYAAAD9xUlFAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VPW9//HXh4CmIgIqWipLgIJsgQhh8eKGe0VAtLVw%0AuVb0qqWVSm3rT1t6S6jtvdZa/V3FDa2gLXUBK/Lr1aqtgsWlBbxxAZU10bhGFBCRGsjn98c5GYYw%0ASSaZPfN+Ph7nMXPOnJn5ZBjOZ767uTsiIiIAbTIdgIiIZA8lBRERiVBSEBGRCCUFERGJUFIQEZEI%0AJQUREYlQUhARkQglBRERiVBSEBGRiLaZDqC5Dj/8cC8qKsp0GCIiOWX16tUfuXuXps7LuaRQVFTE%0AqlWrMh2GiEhOMbPKeM5T9ZGIiEQoKYiISISSgoiIRORcm0IsNTU1VFVVsWvXrkyHItKgwsJCunXr%0ARrt27TIdikiDWkVSqKqqokOHDhQVFWFmmQ5HZD/uzpYtW6iqqqJXr16ZDkekQa2i+mjXrl0cdthh%0ASgiStcyMww47TKXZPFdWltnnx6NVJAVACUGynr6jMmdOZp8fj1aTFEREJHFKCklSVVXFxIkT6du3%0AL3369GHmzJl88cUXMc999913+frXv97ka5511lls3bq1RfGUlZVxww03tOi58VqwYAEzZsxI+ByR%0A1qysDMyCDfbej7cqKNHnN1deJ4Vkfajuzrnnnss555zD+vXrWbduHTt27GDWrFn7nbt7926+8pWv%0AsHjx4iZf97HHHqNTp07JCVJEMqKsDNyDDfbeb05SSOT5zZXXSSFZ9XNPP/00hYWFXHTRRQAUFBRw%0A0003cc8997Bz504WLFjAhAkTOPnkkznllFOoqKhg8ODBAOzcuZPzzz+fgQMHMmnSJEaNGhWZxqOo%0AqIiPPvqIiooKBgwYwKWXXsqgQYM4/fTT+fzzzwG46667GDFiBEOHDuW8885j586djcY6bdo0vvOd%0A7zB69Gh69+7NsmXLuPjiixkwYADTpk2LnHf//fdTXFzM4MGDufrqqyPH58+fT79+/Rg5ciTPPfdc%0A5Hh1dTXnnXceI0aMYMSIEfs8JiK5I6+TQrKsWbOG4cOH73PskEMOoUePHmzYsAGAl156icWLF7N8%0A+fJ9zrvtttvo3Lkza9eu5dprr2X16tUx32P9+vVcfvnlrFmzhk6dOvHwww8DcO6557Jy5Upefvll%0ABgwYwG9/+9sm4/3kk0944YUXuOmmm5gwYQJXXnkla9as4dVXX6W8vJx3332Xq6++mqeffpry8nJW%0ArlzJkiVLeO+995g9ezbPPfccK1asYO3atZHXnDlzJldeeSUrV67k4Ycf5pJLLmnWZyiSD2bPzuzz%0A49Eqxik0R1nZviWEunq62bNT293rtNNO49BDD93v+IoVK5g5cyYAgwcPZsiQITGf36tXL0pKSgAY%0APnw4FRUVALz22mv89Kc/ZevWrezYsYMzzjijyVjGjx+PmVFcXMyRRx5JcXExAIMGDaKiooLKykpO%0AOukkunQJJlScOnUqzz77LMA+x7/5zW+ybt06AP7yl7/skyS2b9/Ojh07moxFJJ/kQpfUvEwKdR+s%0A2d56ukQMHDhwvzaC7du389Zbb/HVr36Vl156ifbt2yf0HgceeGDkfkFBQaT6aNq0aSxZsoShQ4ey%0AYMECli1bFvdrtWnTZp/XbdOmDbt3727RiNva2lpefPFFCgsLm/1cEckeqj5KglNOOYWdO3dy3333%0AAbBnzx5++MMfMm3aNA466KBGnztmzBgeeughANauXcurr77arPf+9NNP6dq1KzU1NSxcuLBlf0A9%0AI0eOZPny5Xz00Ufs2bOH+++/nxNPPJFRo0axfPlytmzZQk1NDYsWLYo85/TTT+eWW26J7JeXlycl%0AFhFJr7xOCsmqnzMzHnnkERYtWkTfvn3p168fhYWF/Od//meTz/3ud79LdXU1AwcO5Kc//SmDBg2i%0AY8eOcb/3tddey6hRoxgzZgz9+/dP5M+I6Nq1K9dddx1jx45l6NChDB8+nIkTJ9K1a1fKyso49thj%0AGTNmDAMGDIg85+abb2bVqlUMGTKEgQMHcscddyQlFhFJL/Nk1J+kUWlpqddfZOf111/f5wKVS/bs%0A2UNNTQ2FhYVs3LiRU089lTfffJMDDjgg06FJCuTyd1Vym5mtdvfSps7LuzaFbLNz507Gjh1LTU0N%0A7s5tt92mhCAiGaOkkGEdOnTQ8qIikjXyuk1BRET2paQgIiIRSgoiIhKhpCAieSMdI4JznZJCkhQU%0AFFBSUsKgQYMYOnQov/nNb6itrc1YPEuWLNln2ol0Ovjgg5v9nESmCa+zbNkyzj777IReoynRkxkm%0Aco5kRjoWqcl1eZkUFi6EoiJo0ya4TcZA4C996UuUl5ezZs0annrqKR5//HHmxPgG7t69O/E3i0O8%0AScHdM5q86t5f04SLZIe8SwoLF8Jll0FlZTDvUWVlsJ+kGSIAOOKII5g3bx5z587F3febOtvdueqq%0Aqxg8eDDFxcU8+OCDQPBL94QTTmDcuHEcffTRTJ8+PXLBbmgq6+hf5YsXL2batGk8//zzLF26lKuu%0AuoqSkhI2bty4T3wVFRUcffTRfOtb32Lw4MG8/fbbPPnkkxx77LEMGzaMb3zjG5HJ7B577DH69+/P%0A8OHDueKKKyK/xOsv4jN48ODIJH11duzYwSmnnMKwYcMoLi7m0UcfbfD966YJv+OOOygpKaGkpIRe%0AvXoxduxYgAbj+/Of/0z//v0ZNmwYf/zjH2P+eyxYsIBzzjmH0047jaKiIubOncuNN97IMcccw+jR%0Ao/n444+BYGqO0aNHM2TIECZNmsQnn3wCwOrVqxk6dChDhw7l1ltvjbzunj17uOqqqxgxYgRDhgzh%0AzjvvbPK7IemX7kVqcp6759Q2fPhwr2/t2rX7HWtIz551S1Tsu/XsGfdLxNS+ffv9jnXs2NHff/99%0Anz9/vh911FG+ZcsWd3dfvHixn3rqqb57925///33vXv37v7uu+/6M8884wceeKBv3LjRd+/e7aee%0AeqovWrTI33nnHe/evbt/+OGHXlNT42PHjvVHHnlkv/ddtGiRX3jhhe7ufuGFF/qiRYtixrp582Y3%0AM3/hhRfc3b26utqPP/5437Fjh7u7X3fddT5nzhz//PPPvVu3br5p0yZ3d588ebKPGzfO3d1nz57t%0Av/71ryOvOWjQIN+8efM+MdXU1Pi2bdsi79GnTx+vra3d7/3d3Xv27OnV1dWR/S+++MKPO+44X7p0%0AaZPxrVu3zmtra/0b3/hGJL5o8+fP9z59+vj27dv9ww8/9EMOOcRvv/12d3f//ve/7zfddJO7uxcX%0AF/uyZcvc3f0//uM/fObMmZHjy5cvd3f3H/3oRz5o0CB3d7/zzjv92muvdXf3Xbt2+fDhw33Tpk2+%0AefPmyDn1Nee7KskHmY4gc4BVHsc1Nu9KCm+91bzjyRI9dfaKFSuYMmUKBQUFHHnkkZx44omsXLkS%0ACCaj6927NwUFBUyZMoUVK1awcuXKyJTVbdu23Wcq65bq2bMno0ePBuDFF19k7dq1jBkzhpKSEu69%0A914qKyt544036N27N7169QJgypQpzXoPd+cnP/kJQ4YM4dRTT+Wdd97hgw8+2O/9Y5k5cyYnn3wy%0A48ePbzS+Xr160bdvX8yMf/u3f2vw9caOHUuHDh3o0qULHTt2ZPz48QAUFxdTUVHBtm3b2Lp1Kyee%0AeCIAF154Ic8++yxbt25l69atnHDCCQBccMEFkdd88sknue+++ygpKWHUqFFs2bKF9evXN+szEsk2%0AeTeiuUePoMoo1vFk2rRpEwUFBRxxxBEAcU+dbXVl3Ab2Gzt/165dMc95++23IxfB6dOnc+aZZ+4T%0Aj7tz2mmncf/99+/zvMZmOm3btu0+bRGx3nvhwoVUV1ezevVq2rVrR1FRUeS8xj6PBQsWUFlZydy5%0Ac1scX331pwiPnj68pe087s4tt9yy3xoW9avRJHukY5GaXJd3JYVf/hLqz2Z90EHB8WSprq5m+vTp%0AzJgxI+ZF/fjjj+fBBx9kz549VFdX8+yzzzJy5EgA/vGPf7B582Zqa2t58MEHOe644xqcyhrgyCOP%0A5PXXX6e2tpZHHnkk8h4dOnTg008/BaB79+6Ul5dTXl7O9OnT94tn9OjRPPfcc5FV4j777DPWrVvH%0A0UcfzaZNmyIXubq2DwiWCn3ppZeAYFW5zZs37/e627Zt44gjjqBdu3Y888wzVMbKxvWsXr2aG264%0Agd///ve0adOm0fj69+9PRUVFpM2kftJojo4dO9K5c2f+9re/AfC73/2OE088kU6dOtGpUydWrFgB%0AsM/05GeccQa33347NTU1AKxbt47PPvusxTFI6qkdoWl5V1KYOjW4nTUrqDLq0SNICHXHW+rzzz+n%0ApKSEmpoa2rZtywUXXMAPfvCDmOdOmjSJF154gaFDh2JmXH/99Xz5y1/mjTfeYMSIEcyYMYMNGzYw%0AduxYJk2aRJs2bSJTWbs748aNY+LEiQBcd911nH322XTp0oXS0tJIA+zkyZO59NJLufnmm1m8eDF9%0A+vRpMPYuXbqwYMECpkyZwj//+U8AfvGLX9CvXz9uu+22SMlixIgRkeecd9553HfffQwaNIhRo0bR%0Ar1+//V536tSpjB8/nuLiYkpLS+Oa2nvu3Ll8/PHHkQbm0tJS7r777gbjmzdvHuPGjeOggw7i+OOP%0AjyTClrj33nuZPn06O3fupHfv3syfPx8I1qW++OKLMTNOP/30yPmXXHIJFRUVDBs2DHenS5cuLFmy%0ApMXvL5INNHV2Flm2bBk33HADf/rTnzIdSsSOHTs4+OCDcXcuv/xy+vbty5VXXpnpsHJWa/muSu6J%0Ad+rslFYfmdmZZvammW0ws2tiPH6TmZWH2zozS2z0kiTdXXfdFRmUt23bNr797W9nOiQRSaGUlRTM%0ArABYB5wGVAErgSnuHnNElZl9DzjG3S9u7HVbc0lBWj99VyVTsqGkMBLY4O6b3P0L4AFgYiPnTwFa%0A3FKYa9Vgkn/0HZVckMqkcBTwdtR+VXhsP2bWE+gFPN2SNyosLGTLli36TydZy93ZsmULhYWFmQ5F%0ApFHZ0vtoMrDY3ffEetDMLgMuA+gRY0BBt27dqKqqorq6OqVBiiSisLCQbt26ZToMSUBZWevv1prK%0ANoVjgTJ3PyPc/zGAu/9XjHP/F7jc3Z9v6nVjtSmIiKSDWTAxTi7KhjaFlUBfM+tlZgcQlAaW1j/J%0AzPoDnYEXUhiLiIjEIWVJwd13AzOAJ4DXgYfcfY2Z/dzMJkSdOhl4wNUgICJZKN9mWW0Vg9dERNJB%0A1UciIpJXlBREROKUD7OsKimIiMSptbYjRFNSEBGRCCUFERGJUFIQEZEIJQUREYlQUhARkQglBRER%0AiVBSEBGRCCUFERGJUFIQEZEIJQUREYlQUhARkQglBRERiVBSEBGRCCUFERGJUFIQkZyRD1NXZ5qS%0AgojkjDlzMh1B66ekICIiEUoKIpLVysrALNhg731VJaWGuXumY2iW0tJSX7VqVabDEJEMMIMcu2Rl%0ADTNb7e6lTZ2nkoKIiEQoKYhIzpg9O9MRtH5KCiKSM9SOkHpKCiIiEqGkICIiEUoKIiISoaQgIiIR%0ASgoiIhKhpCAiIhFNJgUza29mbcL7/cxsgpm1S31oIiKSbvGUFJ4FCs3sKOBJ4AJgQTwvbmZnmtmb%0AZrbBzK5p4JzzzWytma0xsz/EG7iIiCRf2zjOMXffaWb/Dtzm7tebWXmTTzIrAG4FTgOqgJVmttTd%0A10ad0xf4MTDG3T8xsyNa9meIiEgyxFNSMDM7FpgK/E94rCCO540ENrj7Jnf/AngAmFjvnEuBW939%0AEwB3/zC+sEVEJBXiSQrfJ/g1/4i7rzGz3sAzcTzvKODtqP2q8Fi0fkA/M3vOzF40szNjvZCZXWZm%0Aq8xsVXV1dRxvLSIiLdFk9ZG7LweWA4QNzh+5+xVJfP++wElAN+BZMyt29631YpgHzINg6uwkvbeI%0AiNQTT++jP5jZIWbWHngNWGtmV8Xx2u8A3aP2u4XHolUBS929xt03A+sIkoSIiGRAPNVHA919O3AO%0A8DjQi6AHUlNWAn3NrJeZHQBMBpbWO2cJQSkBMzucoDppU3yhi4hIssWTFNqF4xLOIfxVDzRZhePu%0Au4EZwBPA68BDYZvEz81sQnjaE8AWM1tL0E5xlbtvackfIiIiiYunS+qdQAXwMkGdf09gezwv7u6P%0AAY/VO/azqPsO/CDcREQkw5osKbj7ze5+lLuf5YFKYGwaYhORVkaL5GS/eBqaO5rZjXVdQs3sN0D7%0ANMQmIq3MnDmZjkCaEk+bwj3Ap8D54bYdmJ/KoEREJDPiSQp93H12ODJ5k7vPAXqnOjARaR3KysAs%0A2GDvfVUlZad4ksLnZnZc3Y6ZjQE+T11IItKalJWBe7DB3vtKCtkpnt5H3wHuNbOOgAEfA9NSGZSI%0AiGRGPNNclANDzeyQcD+u7qgiIvXNnp3pCKQpDSYFM4s5dsDCikF3vzFFMYlIK6Uqo+zXWEmhQ9qi%0AEBGRrNBgUgh7GYmISB6Jp/eRiIjkCSUFERGJUFIQEZGIeOY+OtDM/tXMfmJmP6vb0hGciEhrsHAh%0AFBVBmzbB7cKFmY6oYfGUFB4FJgK7gc+iNhHJM+pS2nwLF8Jll0FlZTCSu7Iy2M/WxGDuja+XY2av%0AufvgNMXTpNLSUl+1alWmwxDJS2Z7p6uQ+BQVBYmgvp49oaIifXGY2Wp3L23qvHhKCs+bWXESYhIR%0AyTtvvdW845kWT1I4DlhtZm+a2Stm9qqZvZLqwEQkO2iW08T06NG847Gks00inuqjnrGOhyuwpZ2q%0Aj0QyR9VHzVfXprBz595jBx0E8+bB1Kmpf36dpFUfhRf/TsD4cOuUqYQgIpJrpk4NLuA9ewZJtWfP%0A5l3QZ83aNyFAsD9rVvJjhfi6pM4EFgJHhNvvzex7qQlHRFIp0SofzXLaMlOnBo3KtbXBbXN+4ae7%0ATSKe6qNXgGPd/bNwvz3wgrsPSU1IjVP1kUjLqfon9ySr91Iyex8ZsCdqf094TEREUuyXvwzaEKId%0AdFBwPBXiSQrzgb+bWZmZlQEvAr9NTTgikmzqPZTbEm2TaK4mq48AzGwYQddUgL+5+/+mJpymqfpI%0ApOVUfZS/4q0+amzltUPcfbuZHQpUhFvdY4e6+8fJCFRERLJHYyuv/QE4G1gNRP+2sHC/dwrjEpEU%0AUO8haUqDbQrufnZ428vde0dtvdxdCUEkAxJtB1A7gjQlnnEKf43nmIik3hwtkisp1mBSMLPCsD3h%0AcDPrbGaHhlsRcFS6AhQRybRcWg8hUY2VFL5N0J7QP7yt2x4F5qY+NBEBdSnNtFxbDyFR8Yxo/p67%0A39KiFzc7E/hvoAC4292vq/f4NODXwDvhobnufndjr6kuqZLP1KU0/bJlPYREJdwltY6732Jmg4GB%0AQGHU8fuaCKAAuBU4DagCVprZUndfW+/UB919RlNxiIhkQq6th5CoeBqaZwO3hNtY4HpgQhyvPRLY%0A4O6b3P0L4AGCZT1FpIXUpTT9krEeQi6JZ5qLrwOnAO+7+0XAUKBjHM87Cng7ar+K2A3U54WL9yw2%0As+6xXsjMLjOzVWa2qrq6Oo63Fmmd1I6QfumeeyjT4kkKn7t7LbDbzA4BPgRiXrxb4P8BReGMq08B%0A98Y6yd3nuXupu5d26dIlSW8tItK0dM89lGlNtikAq8ysE3AXQe+jHcALcTzvHfZNHt3Y26AMgLtv%0Aidq9m6BqSkQkq0yd2nqTQH3xNDR/N7x7h5n9GTjE3eNZo3kl0NfMehEkg8nAv0afYGZd3f29cHcC%0A8HrckYuISNI1NnhtWP0NOBRoG95vlLvvBmYATxBc7B9y9zVm9nMzq2uovsLM1pjZy8AVwLRE/yAR%0AaX3yafBYpjU4TsHMngnvFgKlwMsEk+ENAVa5+7FpibAejVMQyS/JWrg+3yW88pq7j3X3scB7wLCw%0AoXc4cAz12gZERFIlGQvXq6QRv3gamo9291frdtz9NTMbkMKYREQiEh08Vr+kUTdNBaikEUs8XVJf%0AMbO7zeykcLsLiKehWUQkYYkOHktGSSOfxJMULgLWADPDbW14LGeo6CiSuxIdPJZv01QkKp4uqbuA%0Am8It56joKJLb6v6fzpoVXMh79AgSQrz/f3v0iD2hXWudpiJRjfU+esjdzzezV9l3OU4AwlHIadfc%0A3ketZYZDEWkZ9V4KJGOW1Jnh7dnJCSkzVHQUyW+JljTyTYNJoW6ksbvH+J2dO1R0FJF8mqYiUY2N%0AaP7UzLbH2D41s+3pDDIR+TbDoUg2UmeP3NFYSaFDOgNJFRUdRTJLnT1ySzxdUgEwsyPMrEfdlsqg%0Akm3q1KBRubY2uNUXUaR5Evmlr3ECuSWeldcmmNl6YDOwHKgAHk9xXCKtTq4ukJPowvXq7JFb4ikp%0AXAuMBta5ey+CVdheTGlUIq3QnDmZjqBlEv2ln2/LWea6eJJCTbgYThsza+PuzxDMmioieSDRX/rq%0A7JFb4kkKW83sYOBZYKGZ/TfwWWrDEmkdysqCJRzNgv26+7lUlZToL/18W84y1zU4ojlygll7YBfB%0AWgpTgY7AwnpLaaaN1lOQXGUW1MnnGo0Ibh0SXk/BzG41szHu/pm773H33e5+r7vfnKmEICLpp1/6%0A+aWxaS7WATeYWVfgIeB+d//f9IQl0vrMnp3pCFpOI4LzR2Mrr/13uOTmicAW4B4ze8PMZptZv7RF%0AKNJK5FI7guSvJhua3b3S3X/l7scAU4BzgNdTHpmIiKRdPIPX2prZeDNbSDBo7U3g3JRHJiIiaddY%0AQ/NpZnYPUAVcCvwP0MfdJ7v7o+kKUCRbqPpH8kFjJYUfA88DA9x9grv/wd01PkFyVqIX9VwdkSzS%0AHE2OU8g2GqcgLZXoOIFcHWcgAkkYpyAirWNEskhzKClIq5boRb2sLCgd1JUQ6u4rKUhrpeojyRuq%0APpJ8puojkSTL5IjkRJez1HKYEq/GprkQaVUSvahnqsoo0eUstRymNIeqj0SyXFFRcCGvr2fPYHnZ%0AVD9fWgdVH4m0EokucqPlMKU5UpoUzOxMM3vTzDaY2TWNnHeembmZaUU3kXoSXeRGy2FKc6QsKZhZ%0AAXAr8DVgIDDFzAbGOK8DMBP4e6pikeygbpwtk+hylloOU5ojlSWFkcAGd9/k7l8ADwATY5x3LfAr%0AgtXdpBXTNBEtk+giN1okR5ojlb2PjgLejtqvAkZFn2Bmw4Du7v4/ZnZVCmMRyWmJLnKjRXIkXhlr%0AaDazNsCNwA/jOPcyM1tlZquqq6tTH5wkjaaJEMktKeuSambHAmXufka4/2MAd/+vcL8jsBHYET7l%0Ay8DHwAR3b7DPqbqk5i6NCBbJnGzokroS6GtmvczsAGAysLTuQXff5u6Hu3uRuxcBL9JEQhARkdRK%0AWVJw993ADOAJguU7H3L3NWb2czObkKr3leyVywvXi+QLjWgWEckD2VB9JJJUapwWST0lBckZGucg%0AknpKCiIiEqGkIFlN4xxE0ktJQbJaa1gOUwvcSC7RIjsiKaQFbiTXqKQgOSMXxznMmrU3IdTZuTM4%0ALpKNlBTioOJ/dsilKqM6WuBGco2SQhPqiv+VlUFddl3xX4lB4qEFbiTXKCk0QcV/SYQWuJFco6TQ%0ABBX/JZHqQy1wI7lGvY+a0KNHUGUU67i0fsnoPaQFbiSXqKTQBBX/85uqDyXfKCk0QcX//KbqQ8k3%0Aqj6Kg4r/+UvVh5Jv8qqkkIv93CWzVH0o+SavkoKmXpbmUvWh5BtVH4k0QdWHkk9afUlBUy8njz4z%0AkdYvL5JCrk+9nC1ytfpNc1eJxE/VR9KqaepqkeZp9SWFaLk49XKm5Xr1mwafiTSPeV29So4oLS31%0AVatWZTqMvGS2txouV7RpEztmM6itTX88IpliZqvdvbSp8/KqpCD5R1NXizSPkoLELRer3zT4TKR5%0AlBQkbrnSjhBNg89Emke9j6TV0+AzkfippCAiIhFKCnkkF6t/QIPPRNJJSSGP5OKI5LrBZ5WVQdfS%0AusFnSgwiqaGkIFlNg89E0iulScHMzjSzN81sg5ldE+Px6Wb2qpmVm9kKMxuYynjyUa6PSNbKZyLp%0AlbKkYGYFwK3A14CBwJQYF/0/uHuxu5cA1wM3piqefJUNEwIm0iagwWci6ZXKksJIYIO7b3L3L4AH%0AgInRJ7j79qjd9kCOTaIQn3xuKE20TUCDz0TSK5VJ4Sjg7aj9qvDYPszscjPbSFBSuCKF8WRENjWU%0AZmJEcqJtAhp8JpJeKZsQz8y+Dpzp7peE+xcAo9x9RgPn/ytwhrtfGOOxy4DLAHr06DG8MtZK6lmq%0AqCj2wu89e0JFRfNeq6wsd9oC6mhCOpHskA0T4r0DdI/a7xYea8gDwDmxHnD3ee5e6u6lXbp0SWKI%0AqZfMhtJc7FKqNgGR3JLKpLAS6GtmvczsAGAysDT6BDPrG7U7DlifwngS1pJf6fl+UVSbgEhuSVlS%0AcPfdwAzgCeB14CF3X2NmPzezCeFpM8xsjZmVAz8A9qs6yiYt+aWe6EUx17uUqk1AJLdokZ1maOki%0AMwsXBg2rlZXBRfGXv2zZRTFTi9zUxf/WW0EJp6Xxi0jmZEObQquQjF/qU6fubVSuqEj/BTWRLrHZ%0A1HtKRFJPSaEJ2TT4C9J/Udc0EyL5RUkhxRItaURf1CH9F3VNMyGSX9Sm0AyJjhNoSZtAouMcEh0n%0AkMxxFiKSOWpTSIFM9PhJ9Jd6ol1i1aVUJL8oKaRRS6aZyPRFXV1KRfKLkkIataSkkQ0X9breU7W1%0Amek9JSLp0zbTAUjj6i7AiYwT0ML1IhIvJYUcoIu6iKSLqo9ERCRCSUFERCKUFEREJEJJQUREIpQU%0AREQkIuemuTCzaiBb1+M8HPgo00E0QvElJtvjg+yPUfElJpH4erp7k0tX5lxSyGZmtiqeuUUyRfEl%0AJtvjg+yPUfElJh3xqfpIREQilBRERCRCSSG55mU6gCYovsRke3yQ/TEqvsSkPD61KYiISIRKCiIi%0AEqGk0Eyz/KDqAAAGF0lEQVRm1t3MnjGztWa2xsxmxjjnJDPbZmbl4fazNMdYYWavhu+93zJ1FrjZ%0AzDaY2StmNiyNsR0d9bmUm9l2M/t+vXPS/vmZ2T1m9qGZvRZ17FAze8rM1oe3nRt47oXhOevN7MI0%0AxfZrM3sj/Pd7xMw6NfDcRr8LKY6xzMzeifp3PKuB555pZm+G38dr0hjfg1GxVZhZeQPPTeln2NA1%0AJWPfP3fX1owN6AoMC+93ANYBA+udcxLwpwzGWAEc3sjjZwGPAwaMBv6eoTgLgPcJ+k9n9PMDTgCG%0AAa9FHbseuCa8fw3wqxjPOxTYFN52Du93TkNspwNtw/u/ihVbPN+FFMdYBvwoju/ARqA3cADwcv3/%0AT6mKr97jvwF+lonPsKFrSqa+fyopNJO7v+fuL4X3PwVeB47KbFTNNhG4zwMvAp3MrGsG4jgF2Oju%0AGR+M6O7PAh/XOzwRuDe8fy9wToynngE85e4fu/snwFPAmamOzd2fdPfd4e6LQLdkvmdzNfD5xWMk%0AsMHdN7n7F8ADBJ97UjUWn5kZcD5wf7LfNx6NXFMy8v1TUkiAmRUBxwB/j/HwsWb2spk9bmaD0hoY%0AOPCkma02s8tiPH4U8HbUfhWZSWyTafg/YiY/vzpHuvt74f33gSNjnJMNn+XFBCW/WJr6LqTajLCK%0A654Gqj+y4fM7HvjA3dc38HjaPsN615SMfP+UFFrIzA4GHga+7+7b6z38EkGVyFDgFmBJmsM7zt2H%0AAV8DLjezE9L8/k0yswOACcCiGA9n+vPbjwdl9azrqmdms4DdwMIGTsnkd+F2oA9QArxHUEWTjabQ%0AeCkhLZ9hY9eUdH7/lBRawMzaEfzjLXT3P9Z/3N23u/uO8P5jQDszOzxd8bn7O+Hth8AjBEX0aO8A%0A3aP2u4XH0ulrwEvu/kH9BzL9+UX5oK5aLbz9MMY5GfsszWwacDYwNbxo7CeO70LKuPsH7r7H3WuB%0Auxp474x+F82sLXAu8GBD56TjM2zgmpKR75+SQjOF9Y+/BV539xsbOOfL4XmY2UiCz3lLmuJrb2Yd%0A6u4TNEi+Vu+0pcC3wl5Io4FtUcXUdGnw11kmP796lgJ1vTkuBB6Ncc4TwOlm1jmsHjk9PJZSZnYm%0A8H+ACe6+s4Fz4vkupDLG6HaqSQ2890qgr5n1CkuPkwk+93Q5FXjD3atiPZiOz7CRa0pmvn+palFv%0ArRtwHEEx7hWgPNzOAqYD08NzZgBrCHpSvAj8Sxrj6x2+78thDLPC49HxGXArQa+PV4HSNH+G7Qku%0A8h2jjmX08yNIUO8BNQT1sv8OHAb8FVgP/AU4NDy3FLg76rkXAxvC7aI0xbaBoC657jt4R3juV4DH%0AGvsupPHz+134/XqF4ALXtX6M4f5ZBD1uNqYqxljxhccX1H3vos5N62fYyDUlI98/jWgWEZEIVR+J%0AiEiEkoKIiEQoKYiISISSgoiIRCgpiIhIhJKCSMjM9ti+M7gmbcZOMyuKnqFTJFu1zXQAIlnkc3cv%0AyXQQIpmkkoJIE8L59K8P59T/h5l9NTxeZGZPhxO+/dXMeoTHj7RgjYOXw+1fwpcqMLO7wjnznzSz%0AL4XnXxHOpf+KmT2QoT9TBFBSEIn2pXrVR9+MemybuxcDc4H/Gx67BbjX3YcQTEh3c3j8ZmC5BxP6%0ADSMYCQvQF7jV3QcBW4HzwuPXAMeErzM9VX+cSDw0olkkZGY73P3gGMcrgJPdfVM4cdn77n6YmX1E%0AMHVDTXj8PXc/3MyqgW7u/s+o1ygimPe+b7h/NdDO3X9hZn8GdhDMBrvEw8kARTJBJQWR+HgD95vj%0An1H397C3TW8cwVxUw4CV4cydIhmhpCASn29G3b4Q3n+eYFZPgKnA38L7fwW+A2BmBWbWsaEXNbM2%0AQHd3fwa4GugI7FdaEUkX/SIR2etLtu/i7X9297puqZ3N7BWCX/tTwmPfA+ab2VVANXBReHwmMM/M%0A/p2gRPAdghk6YykAfh8mDgNudvetSfuLRJpJbQoiTQjbFErd/aNMxyKSaqo+EhGRCJUUREQkQiUF%0AERGJUFIQEZEIJQUREYlQUhARkQglBRERiVBSEBGRiP8PEnLZyMua1xUAAAAASUVORK5CYII=%0A

Credits: F. Chollet, Deep Learning with Python, 2018)

Anwendungsbeispiel: Automatisches Erkennen handgeschriebener Zahlen:

Der MNIST Datensatz

Eingangsdaten: Bilder von 28x28 Pixeln, Schwarz-Weiss Ausgangsschicht: 10 Kanäle

Genetischer Algorithmus

Genotyp und Phänotyp

Der Genotyp (das Genom) bestimmt die Bandbreite, innerhalb derer sich der Phänotyp ausbilden kann.
Keine Eins-zu-Eins Beziehung sondern komplexes Netzwerk aus kodierenden und regulativen Sequenzen. Ausserdem Umwelteinflüsse, Prägung während der Entwicklung, Epigenetische Faktoren.
Aktives Forschungsgebiet
In neuerer Zeit vermehrt Anwendungen von Neuronalen Netzen zur Auflösung der Genotyp-Phänotyp Beziehung

Genetischer Algorithmus

Quelle: Dissertation Andreas Teckentrup 2000 (Uni Erlangen). Online https://www2.chemie.uni-erlangen.de/services/dissonline/data/dissertation/Andreas_Teckentrup/html/ (Besucht am 24.11.2020)

Uebertragung auf Neuronale Netze

Ein NN Chromosom hat folgende Gene:
- Anzahl der Netzschichten
- Typ der Schicht (Dense, Dropout)
- Anzahl der Neuronen
- Batchgröße
- Dropout Rate
- …
Während der Lernphase bildet das NN einen Phänotyp heraus (Optimieren der Gewichte bei vorgegebener Netzwerktopologie)
Die Validierung des trainierten NNs ordnet dem Phänotyp und damit dem Chromosom einen Score zu

Die NNe mit den besten Scores und ein paar schlechtere werden als Eltern der nächsten Generation ausgewählt.
Durch Crossover und Mutation wird die nächste Generation gebildet.
Die neue Generation wird trainiert und gescort.

1. Generation

Selektion (nach Performance Score)

Selektion nach Zufall

Ausgangspunkt der nächsten Generation

Kopie

Kreuzung (engl. Crossover)

Mutation

Konstruktion der nächsten Generation

Konstruktion der neuen NNe, Training, Validierung, …

Genetischer Algorithmus im Ueberblick

Zusammenfassung

Maschinelles Lernen mit neuronalen Netzen macht aus grossen Datenmengen (Big Data) aussagekräftige Modelle.
Ein neuronales Netz extrahiert aus den Daten die zugrundeliegenden Strukturen und Zusammenhänge.
Das Training einen neuronalen Netzes ist ein hochdimensionales Optimierungsproblem.
- Netzparameter (Gewichte)
- Hyperparameter:
  - Topologie
  - Aktivierungsfunktion
  - Optimierungsalgorithmus
  - Batch Size
  - Dropout rate
  - Loss Funktion
Training der Netzparameter: Gradientenmethode, Backpropagation
- Problem: Overfitting
- Dropout als Gegenmittel
Hyperparameter/training/: Aktives Forschungsgebiet, bisher kein Goldstandard gefunden.
Hier: Optimierung der Hyperparameter mit Genetischem Algorithmus

Ausblick

Chancen und Risiken der KI
- Wer mitreden will sollte wissen worum es geht und wie es funktioniert
Interessantes (weil interdisziplinäres) Forschungsfeld
Generelle KI ist (noch) weit weg.
Paradigmenwechsel:
- Optimierung, gestelltes Problem soll möglichst gut gelöst werden (Konvergenz)
- <-> Evolution: Artenvielfalt, Divergenz. Wen oder was optimiert die Evolution?
- Erkundung neuer Möglichkeiten (Divergenz)
- Belohne Neuigkeit, nicht Nähe zum althergebrachten -> Vermeidung lokaler Minima
- Suche nach einem immer weiter divergierenden Algorithmus, der immer wieder neue aber gute Lösungen findet.
- PicBreeder: http://picbreeder.org

Files

Evolution_und_KI.org

Latest commit

History

Evolution_und_KI.org

File metadata and controls

Künstliche Intelligenz und Evolution

Rent-a-Scientist 2021

Begrüßung

Wer bin ich?

Woran forsche ich?

Gliederung

Einleitung

Künstliche Intelligenz und Turing Test

Eine Arbeitsdefinition für KI

Deep Learning = Maschinelles Lernen mit künstlichen Neuronalen

Beispiele

Beaufsichtigtes Lernen mit Neuronalen Netzen (supervised Deep

Hund-Katze Beispiel:

(Kuenstliche) Neuronale Netze

Neuronale Netze als Analogon zu biologischen Neuronalen Netzen

Das Neuron (Nervenzelle)

Das Künstliche Neuron (Perzeptron)

Das Aktionspotenzial

Das Ausgangssignal ist eine Funktion der gewichteten Summe der

Einzelnes Neuron

Neuron mit zwei Eingängen

Neuron mit N Eingängen

Maschinelles Lernen mit Neuronalen Netzen = Optimierung der

Die Aktivierungsfunktion \(\mathcal{N}\)

Sprungfunktion

Tanh

Relu Funktion

Beispiel: “Lernen” einer Ausgleichsgeraden (oder lineare Regression)

Aufgabe: Entwickle eine Modell, dass das Bakterienwachstum als

Der Trainingsalgorithmus

Wie finde ich das Minimum der Funktion \(D(\vec w)\)?

In einer Dimension

In zwei Dimensionen (z.B. ein Neuron mit zwei Eingängen oder zwei

Ein Beispiel für ein künstliches Neuronales Netz mit 2 versteckten

In höheren Dimensionen?

Training, Validierung, Testen

Dropout als Strategie zur Vermeidung von Overfitting

Anwendungsbeispiel: Automatisches Erkennen handgeschriebener Zahlen:

Genetischer Algorithmus

Genotyp und Phänotyp

Genetischer Algorithmus

Uebertragung auf Neuronale Netze

1. Generation

Selektion (nach Performance Score)

Selektion nach Zufall

Ausgangspunkt der nächsten Generation

Kopie

Kreuzung (engl. Crossover)

Mutation

Konstruktion der nächsten Generation

Konstruktion der neuen NNe, Training, Validierung, …

Genetischer Algorithmus im Ueberblick

Zusammenfassung

Ausblick

Herzlichen Dank!