Beautiful mathematics at your fingertips.
Saphyra /səˈfaɪ.ɹə/ is a proof assistant under active development, a personal project created and maintained entirely by @pennzht.
Saphyra aims to be simple and user-friendly. As of October 25, 2024, the proof repository has 67 tautologies and 17 natural number theorems verified. Tactics exist for each axiom, and also for rewriting equations based on proven statements.
Visit Saphyra Web to explore the current proof repository. Loading may take a few seconds.
Currently Saphyra is built on a foundation of higher-order logic and Peano arithmetic, but it can be adjusted to use other rulesets, such as set theory. The axioms can be found in axioms.js.
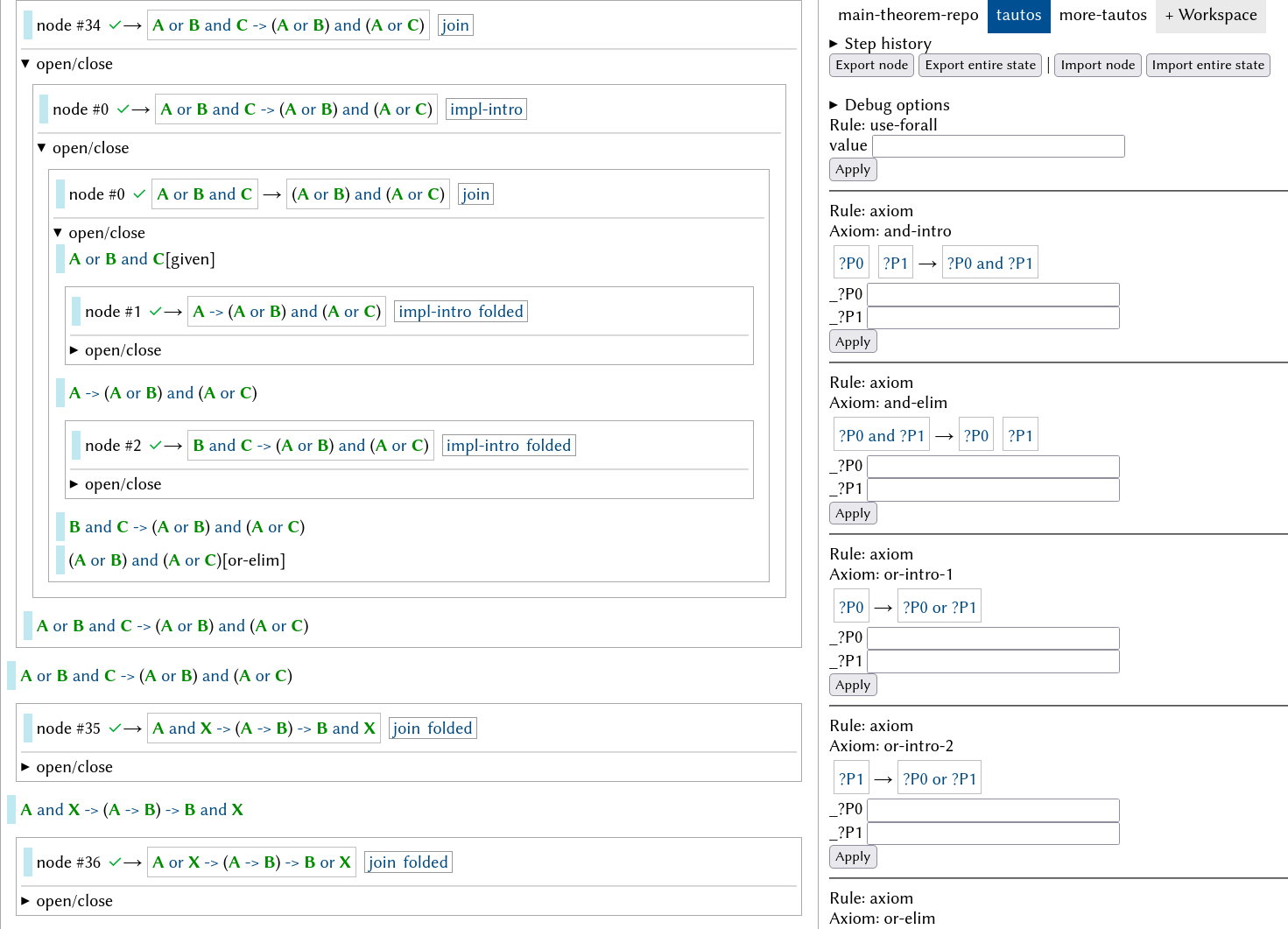
Each proof or collection of proofs is a node. A node may have inputs, outputs, and subnodes, representing a conditional truth that if all inputs hold, and if all subnodes are valid, then all outputs hold. In a sense, a node is similar to a sequent, and subnodes are other sequents which the parent node depends on. Unlike a sequent, a node's outputs are conjunctive instead of disjunctive.
The verification process is defined in proof_module_2.js.
Saphyra uses a Web interface. Using the buttons “Export entire state” and “Import entire state”, one can import a proof repository, work on it, and save it. Clicking on goals (statements not yet proven) will show usable tactics on the right, where the user can provide parameters and apply them.
The menu “Step history” provides basic undo/redo support.
Nodes may be folded to unclutter the view.
Prof. Freek Wiedijk maintains a list of 100 theorems and their formalizations. This is a good measure of both the maturity of a proof assistant and the maturity of formal methods as a field.
By December 15, 2024, I aim to prove the following in Saphyra (2 of 100 theorems):
- Irrationality of √2
- Infinitude of primes
By March 31, 2025, I aim to prove the following (15 of 100 theorems, accumulated):
- Divisibility by 3 rule
- The Fundamental Theorem of Arithmetic
- The Number of Subsets of a Set
- Wilson’s Theorem
- Euler’s Generalization of Fermat’s Little Theorem
- The Denumerability of the Rational Numbers
- The Binomial Theorem
- Konigsberg Bridges Problem
- Sum of a Geometric Series
- The Cauchy-Schwarz Inequality
- The Intermediate Value Theorem
- Principle of Inclusion/Exclusion
- Schroeder-Bernstein Theorem