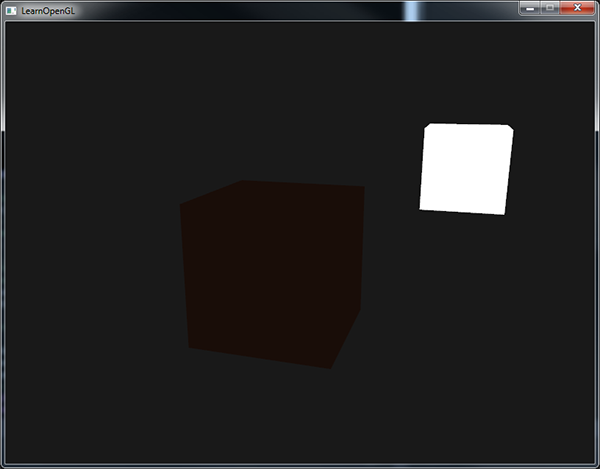
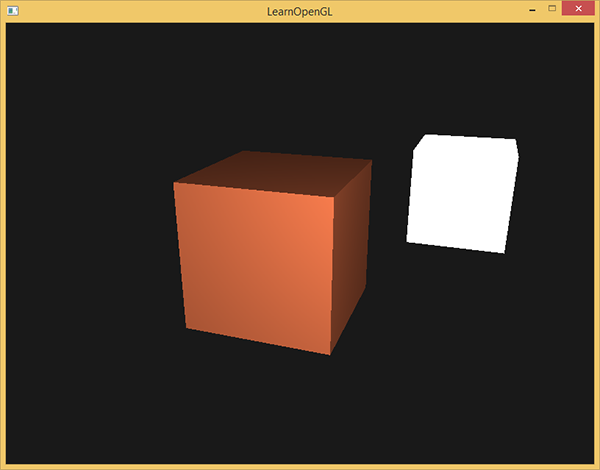
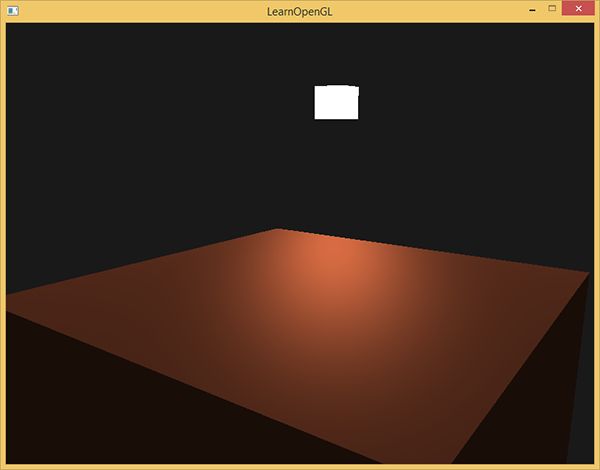
- 环境光照(Ambient Lighting):即使在黑暗的情况下,世界上通常也仍然有一些光亮(月亮、远处的光),所以物体几乎永远不会是完全黑暗的。为了模拟这个,我们会使用一个环境光照常量,它永远会给物体一些颜色。
- 漫反射光照(Diffuse Lighting):模拟光源对物体的方向性影响(Directional Impact)。它是冯氏光照模型中视觉上最显著的分量。物体的某一部分越是正对着光源,它就会越亮。
- 镜面光照(Specular Lighting):模拟有光泽物体上面出现的亮点。镜面光照的颜色相比于物体的颜色会更倾向于光的颜色。
GI(Global Illumination),全局照明。开销大、复杂。可以前期烘焙Lightmap
环境光照:
void main()
{
float ambientStrength = 0.1;
vec3 ambient = ambientStrength * lightColor;
vec3 result = ambient * objectColor;
FragColor = vec4(result, 1.0);
}法向量是一个垂直于顶点表面的(单位)向量。
传入fs中。
对norm和lightDir向量进行点乘。
两个向量之间的角度越大,漫反射分量就会越小。
模型矩阵左上角的逆矩阵的转置矩阵
它使用了一些线性代数的操作来移除对法向量错误缩放的影响。如果你想知道这个矩阵是如何计算出来的,建议去阅读这个文章。
Normal = mat3(transpose(inverse(model))) * aNormal;注意我们还要把被处理过的矩阵强制转换为3×3矩阵,来保证它失去了位移属性以及能够乘以vec3的法向量。
即使是对于着色器来说,逆矩阵也是一个开销比较大的运算,因此,只要可能就应该避免在着色器中进行逆矩阵运算,它们必须为你场景中的每个顶点都进行这样的处理。用作学习目这样做是可以的,但是对于一个对效率有要求的应用来说,在绘制之前你最好用CPU计算出法线矩阵,然后通过uniform把值传递给着色器(像模型矩阵一样)。
证明:
对每一个FragPos进行视角方向计算,再同光源反射先点乘,得出反光强度。
float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);此处32是Shininess(反射因子),越大则镜面反射效果越强,即表现得更光滑,反之更粗糙。
| 函数 | 描述 |
|---|---|
| float length(vec2/vec3/vec4 x) | 返回x向量的长度 |
| float distance(vec p0,vec p1) | 返回p0和p1之间的距离 |
| float dot(vec x,vec y) | 返回x和y的点乘结果 |
| vec3 cross(vec3 x,vec3 y) | 返回x和y的叉乘结果 |
| vec normalize(vec x) | 返回和x方向相同的单位长度向量 |
| vec faceforward(vec N,vec I,vec nRef) | 如果dot(Nref,l)<0则返回N,否则返回-N |
| vec reflect(vec l,vec N) | 返回入射向量l的反射方向和表面法线方向N |
| vec refract(vec vec N,float eta) | 返回入射向量l的反射方向、表面法线方向N和折射指数比eta |
reflect(-A,B) == - reflect(A,B) //true