在 X-Y 平面上表示的校园中,有 n 名工人和 m 辆自行车,其中 n <= m。
给定一个长度为 n 的数组 workers ,其中 worker [i] = [xi, yi] 表示第 i 个工人的位置。你也得到一个长度为 m 的自行车数组 bikers ,其中 bikes[j] = [xj, yj] 是第 j 辆自行车的位置。所有给定的位置都是 唯一 的。
我们需要为每位工人分配一辆自行车。在所有可用的自行车和工人中,我们选取彼此之间 曼哈顿距离 最短的工人自行车对 (workeri, bikej) ,并将其中的自行车分配給工人。
如果有多个 (workeri, bikej) 对之间的 曼哈顿距离 相同,那么我们选择 工人索引最小 的那对。类似地,如果有多种不同的分配方法,则选择 自行车索引最小 的一对。不断重复这一过程,直到所有工人都分配到自行车为止。
返回长度为 n 的向量 answer,其中 answer[i] 是第 i 位工人分配到的自行车的索引(从 0 开始)。
给定两点 p1 和 p2 之间的 曼哈顿距离 为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。
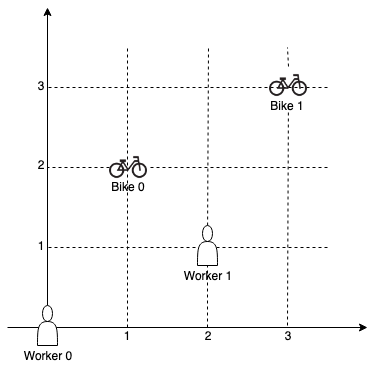
示例 1:
输入:workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]] 输出:[1,0] 解释:工人 1 分配到自行车 0,因为他们最接近且不存在冲突,工人 0 分配到自行车 1 。所以输出是 [1,0]。
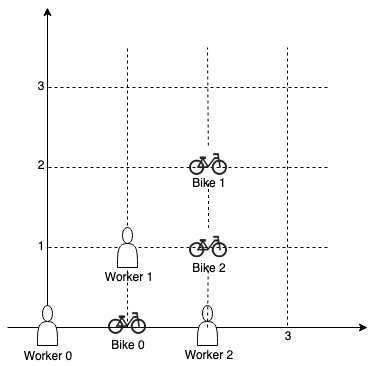
示例 2:
输入:workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]] 输出:[0,2,1] 解释:工人 0 首先分配到自行车 0 。工人 1 和工人 2 与自行车 2 距离相同,因此工人 1 分配到自行车 2,工人 2 将分配到自行车 1 。因此输出为 [0,2,1]。
提示:
n == workers.lengthm == bikes.length1 <= n <= m <= 1000workers[i].length == bikes[j].length == 20 <= xi, yi < 10000 <= xj, yj < 1000- 所有工人和自行车的位置都不相同