README_EN.md

1368. Minimum Cost to Make at Least One Valid Path in a Grid

中文文档

Description

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

 

Example 1:

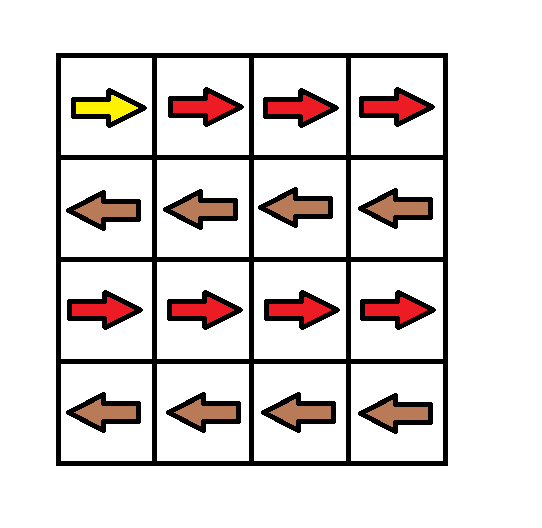
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

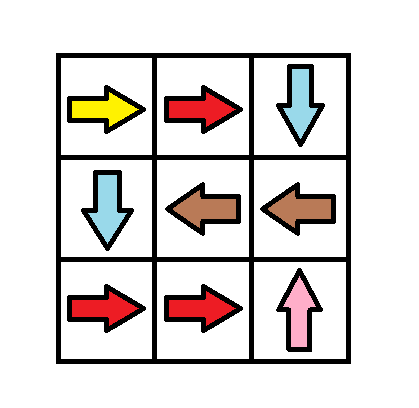
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

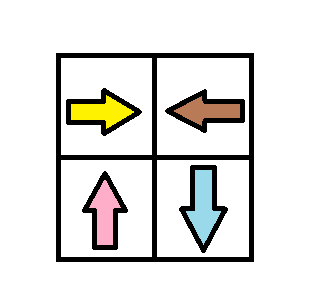
Input: grid = [[1,2],[4,3]]
Output: 1

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• 1 <= grid[i][j] <= 4

Solutions

BFS using deque.

Python3

class Solution:
    def minCost(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dirs = [[0, 0], [0, 1], [0, -1], [1, 0], [-1, 0]]
        q = deque([(0, 0, 0)])
        vis = set()
        while q:
            i, j, d = q.popleft()
            if (i, j) in vis:
                continue
            vis.add((i, j))
            if i == m - 1 and j == n - 1:
                return d
            for k in range(1, 5):
                x, y = i + dirs[k][0], j + dirs[k][1]
                if 0 <= x < m and 0 <= y < n:
                    if grid[i][j] == k:
                        q.appendleft((x, y, d))
                    else:
                        q.append((x, y, d + 1))
        return -1

Java

class Solution {
    public int minCost(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        boolean[][] vis = new boolean[m][n];
        Deque<int[]> q = new ArrayDeque<>();
        q.offer(new int[]{0, 0, 0});
        int[][] dirs = {{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1], d = p[2];
            if (i == m - 1 && j == n - 1) {
                return d;
            }
            if (vis[i][j]) {
                continue;
            }
            vis[i][j] = true;
            for (int k = 1; k <= 4; ++k) {
                int x = i + dirs[k][0], y = j + dirs[k][1];
                if (x >= 0 && x < m && y >= 0 && y < n) {
                    if (grid[i][j] == k) {
                        q.offerFirst(new int[]{x, y, d});
                    } else {
                        q.offer(new int[]{x, y, d + 1});
                    }
                }
            }
        }
        return -1;
    }
}

C++

class Solution {
public:
    int minCost(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<bool>> vis(m, vector<bool>(n));
        vector<vector<int>> dirs = {{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        deque<pair<int, int>> q;
        q.push_back({0, 0});
        while (!q.empty())
        {
            auto p = q.front();
            q.pop_front();
            int i = p.first / n, j = p.first % n, d = p.second;
            if (i == m - 1 && j == n - 1) return d;
            if (vis[i][j]) continue;
            vis[i][j] = true;
            for (int k = 1; k <= 4; ++k)
            {
                int x = i + dirs[k][0], y = j + dirs[k][1];
                if (x >= 0 && x < m && y >= 0 && y < n)
                {
                    if (grid[i][j] == k) q.push_front({x * n + y, d});
                    else q.push_back({x * n + y, d + 1});
                }
            }
        }
        return -1;
    }
};

Go

func minCost(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	q := doublylinkedlist.New()
	q.Add([]int{0, 0, 0})
	dirs := [][]int{{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}}
	vis := make([][]bool, m)
	for i := range vis {
		vis[i] = make([]bool, n)
	}
	for !q.Empty() {
		v, _ := q.Get(0)
		p := v.([]int)
		q.Remove(0)
		i, j, d := p[0], p[1], p[2]
		if i == m-1 && j == n-1 {
			return d
		}
		if vis[i][j] {
			continue
		}
		vis[i][j] = true
		for k := 1; k <= 4; k++ {
			x, y := i+dirs[k][0], j+dirs[k][1]
			if x >= 0 && x < m && y >= 0 && y < n {
				if grid[i][j] == k {
					q.Insert(0, []int{x, y, d})
				} else {
					q.Add([]int{x, y, d + 1})
				}
			}
		}
	}
	return -1
}

...