给定一个数字 N,当它满足以下条件的时候返回 true:
原数字旋转 180° 以后可以得到新的数字。
如 0, 1, 6, 8, 9 旋转 180° 以后,得到了新的数字 0, 1, 9, 8, 6 。
2, 3, 4, 5, 7 旋转 180° 后,得到的不是数字。
易混淆数 (confusing number) 在旋转180°以后,可以得到和原来不同的数,且新数字的每一位都是有效的。
示例 1:
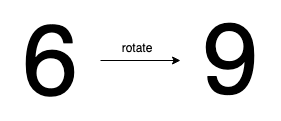
输入:6 输出:true 解释: 把 6 旋转 180° 以后得到 9,9 是有效数字且 9!=6 。
示例 2:
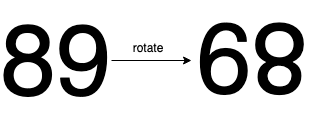
输入:89
输出:true
解释:
把 89 旋转 180° 以后得到 68,86 是有效数字且 86!=89 。
示例 3:
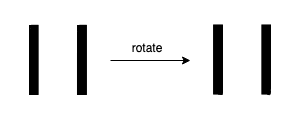
输入:11 输出:false 解释: 把 11 旋转 180° 以后得到 11,11 是有效数字但是值保持不变,所以 11 不是易混淆数字。
示例 4:
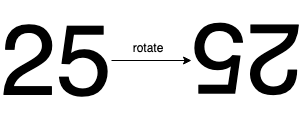
输入:25 输出:false 解释: 把 25 旋转 180° 以后得到的不是数字。
提示:
0 <= N <= 10^9- 可以忽略掉旋转后得到的前导零,例如,如果我们旋转后得到
0008那么该数字就是8。
我们先用一个长度为
将 false。否则,我们将数字 true。
时间复杂度
相似题目:788. 旋转数字
class Solution:
def confusingNumber(self, n: int) -> bool:
x, y = n, 0
d = [0, 1, -1, -1, -1, -1, 9, -1, 8, 6]
while x:
x, v = divmod(x, 10)
if d[v] < 0:
return False
y = y * 10 + d[v]
return y != nclass Solution {
public boolean confusingNumber(int n) {
int[] d = new int[] {0, 1, -1, -1, -1, -1, 9, -1, 8, 6};
int x = n, y = 0;
while (x > 0) {
int v = x % 10;
if (d[v] < 0) {
return false;
}
y = y * 10 + d[v];
x /= 10;
}
return y != n;
}
}class Solution {
public:
bool confusingNumber(int n) {
vector<int> d = {0, 1, -1, -1, -1, -1, 9, -1, 8, 6};
int x = n, y = 0;
while (x) {
int v = x % 10;
if (d[v] < 0) {
return false;
}
y = y * 10 + d[v];
x /= 10;
}
return y != n;
}
};func confusingNumber(n int) bool {
d := []int{0, 1, -1, -1, -1, -1, 9, -1, 8, 6}
x, y := n, 0
for x > 0 {
v := x % 10
if d[v] < 0 {
return false
}
y = y*10 + d[v]
x /= 10
}
return y != n
}