你还记得那条风靡全球的贪吃蛇吗?
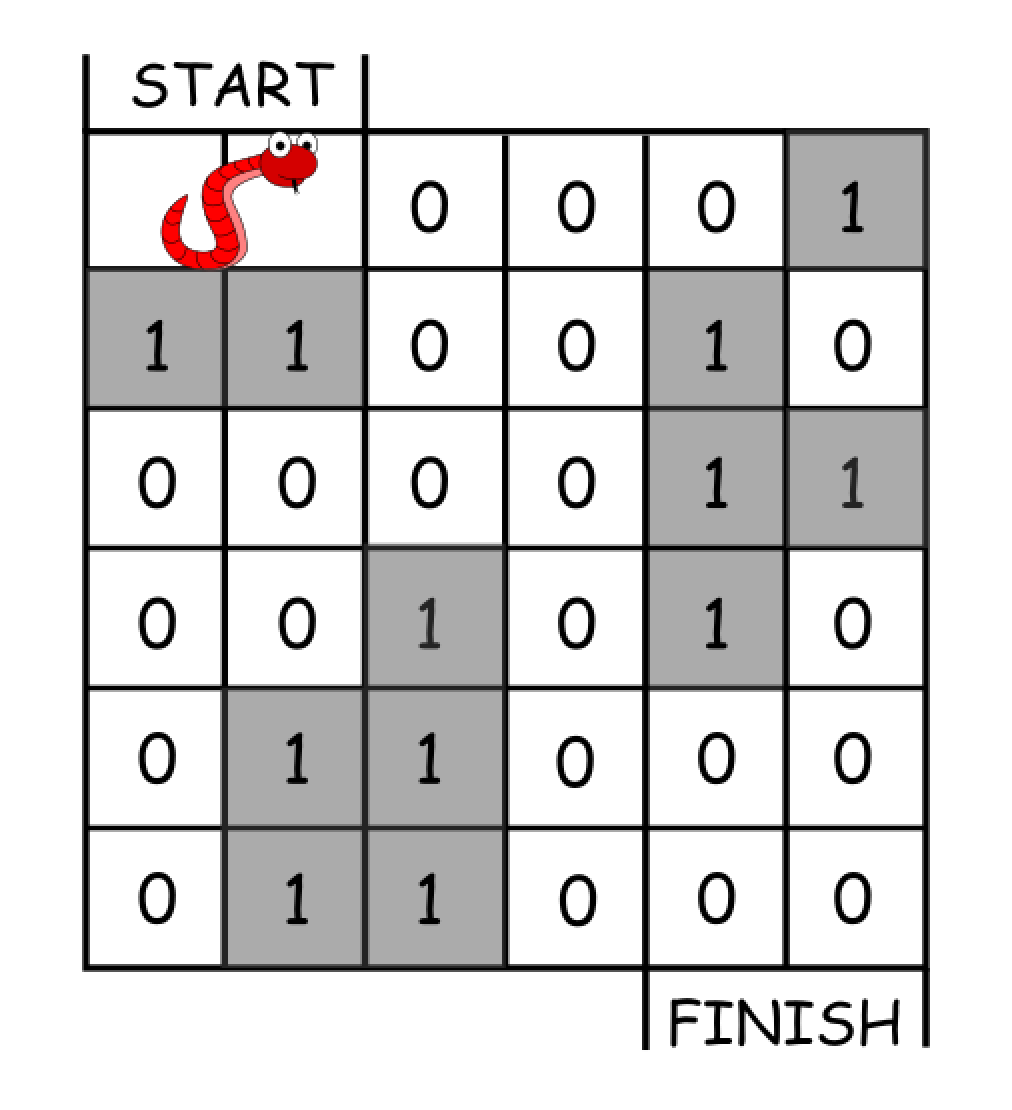
我们在一个 n*n 的网格上构建了新的迷宫地图,蛇的长度为 2,也就是说它会占去两个单元格。蛇会从左上角((0, 0) 和 (0, 1))开始移动。我们用 0 表示空单元格,用 1 表示障碍物。蛇需要移动到迷宫的右下角((n-1, n-2) 和 (n-1, n-1))。
每次移动,蛇可以这样走:
- 如果没有障碍,则向右移动一个单元格。并仍然保持身体的水平/竖直状态。
- 如果没有障碍,则向下移动一个单元格。并仍然保持身体的水平/竖直状态。
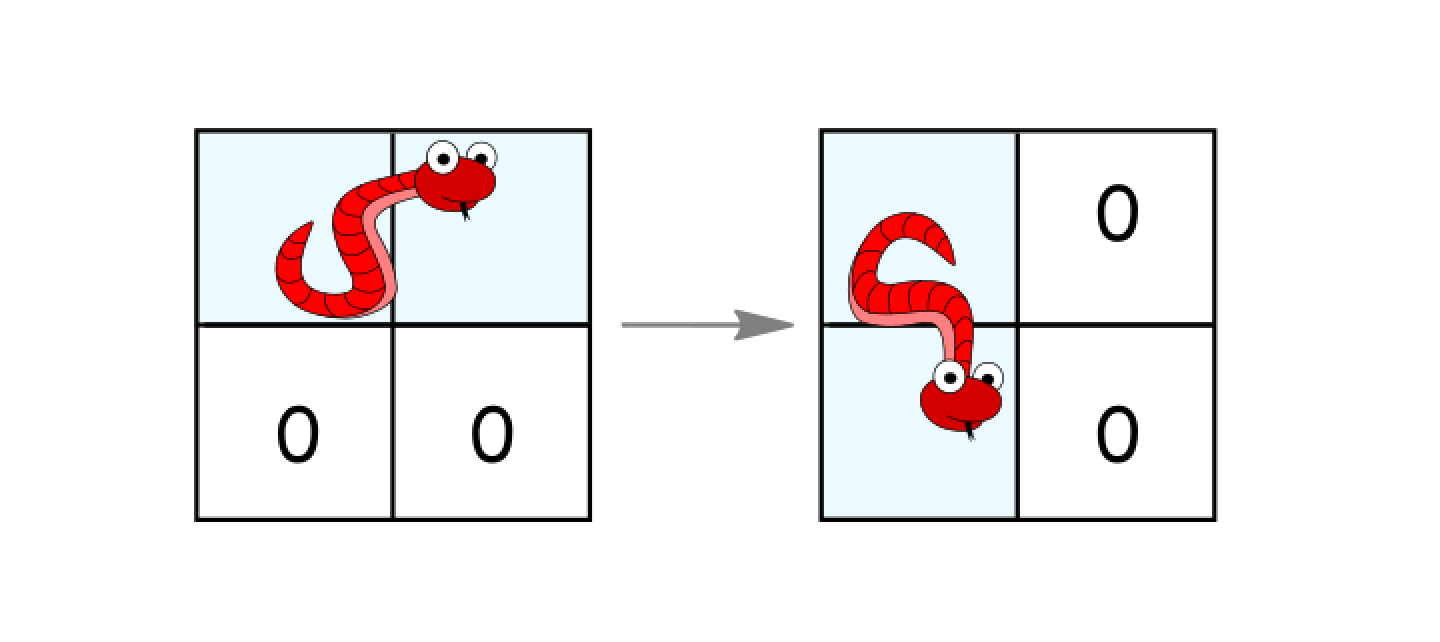
- 如果它处于水平状态并且其下面的两个单元都是空的,就顺时针旋转 90 度。蛇从(
(r, c)、(r, c+1))移动到 ((r, c)、(r+1, c))。
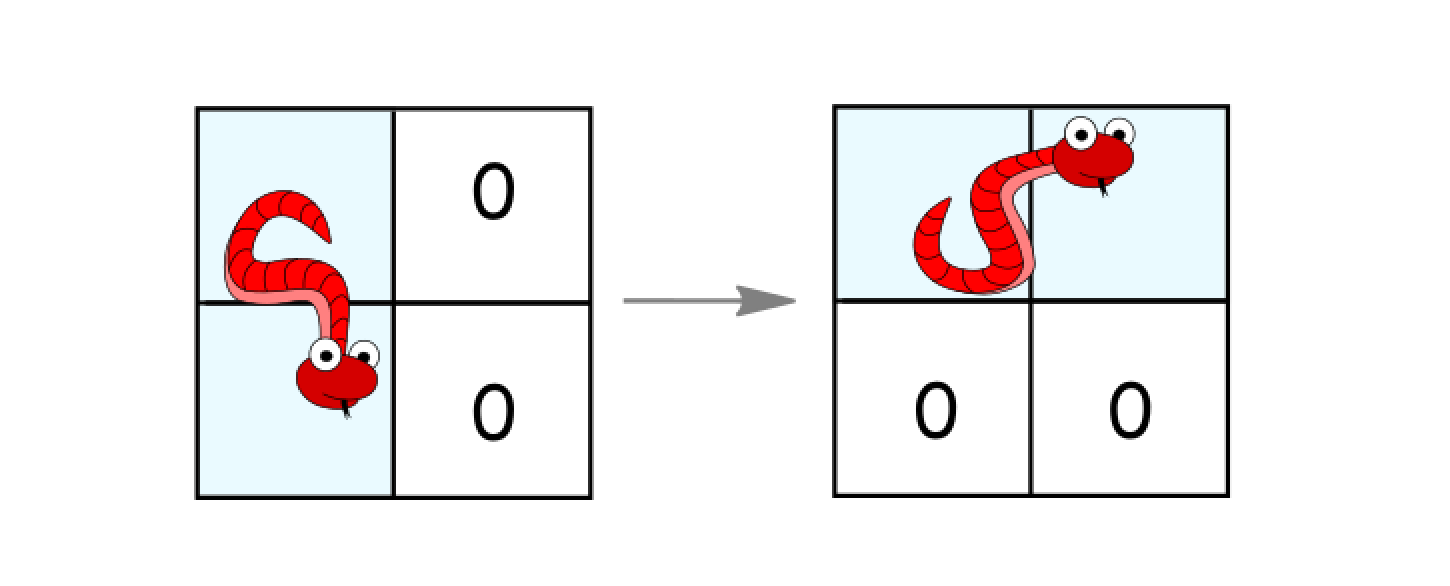
- 如果它处于竖直状态并且其右面的两个单元都是空的,就逆时针旋转 90 度。蛇从(
(r, c)、(r+1, c))移动到((r, c)、(r, c+1))。
返回蛇抵达目的地所需的最少移动次数。
如果无法到达目的地,请返回 -1。
示例 1:
输入:grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
输出:11
解释:
一种可能的解决方案是 [右, 右, 顺时针旋转, 右, 下, 下, 下, 下, 逆时针旋转, 右, 下]。
示例 2:
输入:grid = [[0,0,1,1,1,1], [0,0,0,0,1,1], [1,1,0,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,0]] 输出:9
提示:
2 <= n <= 1000 <= grid[i][j] <= 1- 蛇保证从空单元格开始出发。
方法一:BFS
class Solution:
def minimumMoves(self, grid: List[List[int]]) -> int:
def check(a, b):
if (a, b) not in vis:
vis.add((a, b))
q.append((a, b))
n = len(grid)
target = (n * n - 2, n * n - 1)
q = deque([(0, 1)])
vis = {(0, 1)}
ans = 0
while q:
for _ in range(len(q)):
a, b = q.popleft()
if (a, b) == target:
return ans
i1, j1 = a // n, a % n
i2, j2 = b // n, b % n
if (
j1 + 1 < n
and j2 + 1 < n
and grid[i1][j1 + 1] == 0
and grid[i2][j2 + 1] == 0
):
check(i1 * n + j1 + 1, i2 * n + j2 + 1)
if j1 == j2:
check(a, i1 * n + j2 + 1)
if (
i1 + 1 < n
and i2 + 1 < n
and grid[i1 + 1][j1] == 0
and grid[i2 + 1][j2] == 0
):
check((i1 + 1) * n + j1, (i2 + 1) * n + j2)
if i1 == i2:
check(a, (i2 + 1) * n + j1)
ans += 1
return -1class Solution {
public int minimumMoves(int[][] grid) {
int n = grid.length;
int[] target = new int[] {n * n - 2, n * n - 1};
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {0, 1});
boolean[][] vis = new boolean[n * n][n * n];
int ans = 0;
vis[0][1] = true;
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
int[] p = q.poll();
if (p[0] == target[0] && p[1] == target[1]) {
return ans;
}
int a = p[0], b = p[1];
int i1 = a / n, j1 = a % n;
int i2 = b / n, j2 = b % n;
if (j1 + 1 < n && j2 + 1 < n && grid[i1][j1 + 1] == 0 && grid[i2][j2 + 1] == 0) {
check(i1 * n + j1 + 1, i2 * n + j2 + 1, q, vis);
if (j1 == j2) {
check(a, i1 * n + j2 + 1, q, vis);
}
}
if (i1 + 1 < n && i2 + 1 < n && grid[i1 + 1][j1] == 0 && grid[i2 + 1][j2] == 0) {
check((i1 + 1) * n + j1, (i2 + 1) * n + j2, q, vis);
if (i1 == i2) {
check(a, (i2 + 1) * n + j1, q, vis);
}
}
}
++ans;
}
return -1;
}
private void check(int a, int b, Deque<int[]> q, boolean[][] vis) {
if (!vis[a][b]) {
vis[a][b] = true;
q.offer(new int[] {a, b});
}
}
}class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
int n = grid.size();
vector<int> target = {n * n - 2, n * n - 1};
queue<vector<int>> q;
q.push({0, 1});
vector<vector<bool>> vis(n * n, vector<bool>(n * n));
int ans = 0;
vis[0][1] = true;
while (!q.empty()) {
for (int k = q.size(); k; --k) {
auto p = q.front();
if (p == target) return ans;
q.pop();
int a = p[0], b = p[1];
int i1 = a / n, j1 = a % n;
int i2 = b / n, j2 = b % n;
if (j1 + 1 < n && j2 + 1 < n && grid[i1][j1 + 1] == 0 && grid[i2][j2 + 1] == 0) {
check(i1 * n + j1 + 1, i2 * n + j2 + 1, q, vis);
if (j1 == j2) check(a, i1 * n + j2 + 1, q, vis);
}
if (i1 + 1 < n && i2 + 1 < n && grid[i1 + 1][j1] == 0 && grid[i2 + 1][j2] == 0) {
check((i1 + 1) * n + j1, (i2 + 1) * n + j2, q, vis);
if (i1 == i2) check(a, (i2 + 1) * n + j1, q, vis);
}
}
++ans;
}
return -1;
}
void check(int a, int b, queue<vector<int>>& q, vector<vector<bool>>& vis) {
if (!vis[a][b]) {
vis[a][b] = true;
q.push({a, b});
}
}
};func minimumMoves(grid [][]int) int {
n := len(grid)
target := []int{n*n - 2, n*n - 1}
q := [][]int{{0, 1}}
vis := make([][]bool, n*n)
for i := range vis {
vis[i] = make([]bool, n*n)
}
vis[0][1] = true
ans := 0
check := func(a, b int) {
if !vis[a][b] {
vis[a][b] = true
q = append(q, []int{a, b})
}
}
for len(q) > 0 {
for k := len(q); k > 0; k-- {
p := q[0]
q = q[1:]
if p[0] == target[0] && p[1] == target[1] {
return ans
}
a, b := p[0], p[1]
i1, j1 := a/n, a%n
i2, j2 := b/n, b%n
if j1+1 < n && j2+1 < n && grid[i1][j1+1] == 0 && grid[i2][j2+1] == 0 {
check(i1*n+j1+1, i2*n+j2+1)
if j1 == j2 {
check(a, i1*n+j2+1)
}
}
if i1+1 < n && i2+1 < n && grid[i1+1][j1] == 0 && grid[i2+1][j2] == 0 {
check((i1+1)*n+j1, (i2+1)*n+j2)
if i1 == i2 {
check(a, (i2+1)*n+j1)
}
}
}
ans++
}
return -1
}